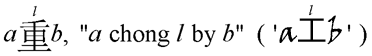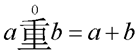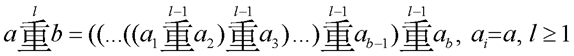M. Vincent van MechelenTHE CHONG-3 SQUARES OF SQUARES
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
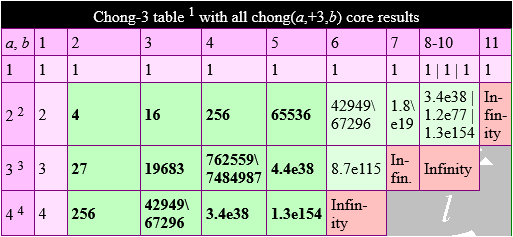
screenshot
of the top of the original table
|
|||||||||
|
In this display, notes and note numbers are not the same as in the
original.
1 A chong-l table shows the result of a重lb for a particular value of a and of b by means of a 重(a,l,b) or chong(a,l,b) function. The core results are those for which both a≥2 and b≥2. The term Infinity should not be taken literally, but it is a program result for when the system cannot cope anymore with a number of the size concerned. (See the table below for some more information on the use of this term.) 2 Every row displays a chong-3-generated sequence, in this case, with a=2, the 2重3b sequence for which each term xs = (xs-1)^2. This is the chong-3-generated head-2 power-2 sequence of the squares of squares, which plays a paramount role in a universal integrated linguistic-mathematical numeral supersystem. (Of course, 9^2=81, 81^2=6561, 6561^2=43046721, etc. are also squares of squares, but they are not members of a complete chong sequence of which the sequential head and power numbers are the same, nor of a substring of such a sequence.) 3 The row at a=3 contains the chong-3-generated head-3 power-3 sequence of (3, 27 and) the cubes of cubes, represented by 3重3b, for which each term xs = (xs-1)^3. The initial value 3 is followed by 3^3=27, followed by 27^3=19683, that is, (3^3)^3. 4 The row at a=4 contains the chong sequence represented by 4重3b for which each term xs = (xs-1)^4. Note that this sequence covers only half of the squares of squares generated under head 2: it does not contain the results 16, 65536, 1.8e19 and 1.2e77. 5 The complete table continues until a=144, where 'Infinity' is the only quantity left. It is the provisional practical value of chong(144,3,2) on the basis of a JavaScript calculation in the source code of the original page. Altho a scientific calculator can already show that 144^144 = 6.3708717381247861841182616291357e+310, also such a calculator will be coming to an end. |
|||||||||
|
screenshot of the bottom of the
original table
 |
DEFINITION AND CALCULATION FORMULAS
Defining versus calculating
Like any sequence, a chong-generated sequence has a definition formula and a calculation formula, as there is an essential difference between defining a sequence of numbers and calculating its terms or 'members'. While defining a sequence of numbers, size or other properties of the individual terms do not play a role. It is the relation between the terms which count. (See the paragraph on definition and calculation in my article A Substantive Terminology for Sequences and Cycles.)
The definition formula
The definition formula tells you how a new term xn+1 follows after and from (usually) one or more previous terms. Its general form is xn+1= fd(xn, xn-1, xn-2, ... x1, x0) in which d stands for definition. The definition formula may be considered an 'indirect access' formula, since it does not give the value of a term in a direct way, but only via the previous term or one or more other terms preceding it. A chong-generated sequence on the lth level of iteration, that is, a chong-l-generated sequence has a definition formula of which the operator is of level l-1. In the first chong-3 sequence (after the trivial 1重3b one) the definition formula is xn+1= xn重22, with n≥0 and x0=2. Note that the value 2 occurs in the chong-3 table as the value for a=2 and b=1. This initial value is the source of the sequence generated and cannot be left out of the formula, even if we are interested in squares, and especially squares of squares, only. Note also that the index s which will be used for the squares of squares, starting with 0 for the number 4 and 1 for the number 16, is not the same as the index n in the definition formula, starting with 0 for the number 2, 1 for the number 4 and 2 for the number 16! Since the definition formula uses merely a chong-2 operator, which is a pre-universalization operator, we can express the definition formula simply as xn+1=xn2.
The calculation formula
The general form of a calculation formula is xn= fc(n) in which c stands for calculation. This may be considered a 'direct access' formula as it enables one to calculate the value of a term without making use of the value of any other term in the sequence, with the exception of the initial value. The other values may be and remain completely unknown. To find the calculation formula itself, however, we must first mount the index ladder until we have a clear enough view of what happens in the process. It starts with x0=2=2重31. For n=1, x1=4=2重32. For n=2, x2=16=2重33. For n=3, x3=256=2重34. For n=4, x4=65536=2重35. At this stage we should have sufficient information to conclude that the calculation formula is xn=2重3(n+1). Because the chong-3 operator is a universal one the question arises of how to use this operator in traditional calculations, if possible at all. One method is to forget about those traditional calculations and use or write a computer program with a left-associative recursive function which can do the job for any level of iteration. I have done this myself in the preparation for the chong tables, of which the chong-3 table above is only a lower- or intermediate-level one. Another method, however, is to reduce the expression with the chong-3 operator to an expression in which only chong-2 and/or lower-level operators occur. Let's pursue that path here. We know that the chong-3 level is the level of reiterative, that is, systematically repeated, exponentiation, and therefore one of the (eight) exponent rules will probably be very helpful: the Power-raised-to-power Rule or 'the Power-of-power Law'. According to this rule (am)n= am×n, (am×n)p= a(m×n)×p, (am×n×p)q= a(m×n×p)×q, and so on. The a is the same as in the chong-3 formula: a=2. All we have to do now is to keep track of the number of as. The calculation formula tells us that xn=2重3(n+1). We need an index and substitute a for 2: a重3(n+1)= ((((a1^a2) ^a3) ... ) ^an) ^an+1= a1^ (a2×a3× ... ×an×an+1)= a^(a^n)= 2^(2^n). This is precisely the kind of formula one would expect, a formula with exponentiation within the exponent. Keep in mind tho that n is the index of the whole sequence originally generated, from 2 on.
The only chong-generated sequence of squares of squares
We have discovered that while there may be an infinite number of sequences of squares, even of squares of squares, there is only one 'chong-generated sequence', that is, a sequence generated by a single chong operator, which contains the and all consecutive squares of squares. The complete sequence generated starts with 2, 4 and 16, but 2 itself is not a square of integers, to which we have confined ourselves here. The term 4 is a square of integers but not a square of a square, like 16, the first term that is. Hence, if we want to justify our speaking of 'the sequence of squares of squares', 16 should be the first member of that sequence, the one with index 1, while 4 may be considered a member with index 0. The head-16 power-2 'sequence' is a subsequence of the head-2 power- or 'chong-2 functor'-2 sequence —on the definitory chong-2 level power is the functor— with its own index for which i will use the letter symbol s. Hence, s=x-1, and to obtain specifically the value of a square of squares the formula xs=2^(2^(s+1)) must be used. For example, the value of 'square 4', the fourth square (of squares), is 2^(2^(4+1))= 2^(2^5)= 2^32= 4,294,967,296.
Two types of chong-generated subsequence
One should take care not to confuse the head-16 power-2 subsequence of squares of squares with the head-16 power-16 sequence which is a standard chong-3-generated sequence like the head-2 power-2 sequence. The former is generated by 2重3b, whereas the latter is generated by 16重3b! The head-16 power-16 sequence starts with the value 16 (the initial number) and continues with 16^16, (16^16)^16, ((16^16)^16)^16, and so on, ad infinitum. It can be proved that the calculation formula for this sequence is 16重3n= 2^(2^(2+4×(n-1)), which means that 16重3n= 2^(2^(4n-2)). When we compare this with the 2重3b-generated sequence, the difference of 2 in the second exponent accounts for the fact that 16 occurs at b=3 in the head-2 power-2 sequence and at b=1 in the head-16 power-16 sequence. Compared with the calculation formula 2^(2^n) the index is also multiplied by 4, which proves that the head-16 power-16 sequence is also a subsequence of the head-2 power-2 sequence (just like the head-4 power-4 sequence with the calculation formula 4重3n=2^(2^(2n-1))). Nonetheless, the head-16 chong-generated sequence (and the head-4 chong-generated sequence) is a very different type of subsequence: it skips three of the elements of the head-2 chong-generated sequence at evey step (but without changing the order of the elements). The head-16 subsequence of the squares of squares, however, skips only the first two elements of the head-2 chong-generated sequence and then includes all its elements until infinity consecutively. Such a subsequence is called a "substring". The head-16 substring is almost the same as the complete sequence itself; no more than a slight adjustment of it at the beginning.
RECAPITULATION
the head-2 power-2 sequence
(those generated by 4重3b and 16重3b constitute subsequences of it which are not substrings)
the definition formula
i.e., xn+1=xn2
the calculation formula
i.e., xn=2^(2^n)
the squares of squares
IN THE WAY OF THE RUT
Anything special about the squares of squares?
The fact that the 4-16-256 sequence is single-chong-level-generated may be a unique feature of that sequence among sequences of squares, it does not mean, as we have seen, that there is not an infinite number of other single-chong-level generated sequences, even an infinite number of other chong-3-generated ones, such as the 27-19,683-7,625,597,484,987 sequence of cubes of cubes. Is there, perhaps, something that makes the sequence of squares of squares even stand out among (almost) all chong-generated sequences as well? To tackle this issue we should analyze a part of the squares of squares individually, because a JavaScript program which takes us from 4 to a number with the approximate value of 1.3e154 (or 1.3E+154) is not likely to be the final means to a definite answer, if at all possible.
Approximations are not exact numbers
Let's first take the way of the rut. In a literal sense this 'rut' is the deep narrow track worn by the many wheels which have followed the same course thru a field for many months or years, perhaps, since time immemorial. In a figurative sense applied to arithmetic it is the impress left on the human mind by the use of a particular age-old, time-honored numeral system in calculations and the languages of speech communities. The rut which we will follow here is that of the established radix or 'base' 10 numeral system, presently the one most frequently employed in human intercourse. Even with a simple JavaScript program it should be no big deal to get the notation of the fifth square of squares in denary figures: it is 18,446,744,073,709,551,616. This is the exact number satisfying the present standard notation of numbers: the real fifth square does not even deviate from it by 1 or 0.0000000000000000054%, if only because its last digit must be 6! From the sixth square, or so, on exact numbers may not be given anymore, but a so-called 'standard (index) form' or 'scientific form/notation' is used — a misnomer, because the only standard/scientific form is the exact number to the last digit. Of course, towards the infinitely large and the infinitesimally small the standard notation of numbers is just becoming too long to write it out in full. So, what we get instead of the really standard and scientific form (the exact number) is a (scientific) approximation in the shape of 3.402823669209384634633746e+38 meaning 3.402823669209384634633746×(10^(+38)). (The small e may also be a capital E, and the + sign may be left out where no confusion is possible.) In tables i may abbreviate this to 3.4e38, provided that this much shorter approximation (which is something like 10^23 times less accurate) does not eradicate the difference with any other number in the same table.
When even the exponents become approximations
For the time being you may be lucky that you get to the ninth square, for that is about where a JavaScript program may confront you with 'Infinity'. When you continue with a scientific calculator 'Infinity' turns out to be approximately of the size 1.797693134862315907729305e+308 or, less accurately, 1.8e308. If you are lucky again your calculator or general-purpose computer may spew out the approximation 1.415461031044954789001553e+9864, say 1.4e9864, for the fourteenth square, just before the fifteenth where it cannot handle it anymore. Now it is not 'Infinity' but 'Overflow' which stops you. However, even without the shelter of a well-funded exact sciences organization with a supercomputer at its disposal, you need not despair (yet). There are websites on the internet which will let you go on to at least the 21st square of squares as far as exact numbers are concerned, and to at least the 1101st square of squares as far as approximations are concerned. But in the latter case even the powers of 10 in the approximations, which were always exact numbers in the beginning, have turned into approximations themselves.
Beyond one googol, but not yet one googolplex
The table below lists 101 squares of squares and gives the exact numbers of the first five (squares 1 to 5) and of the twenty-first (square 21, in the Appendix). Of squares 6 to 21, square 65, square 81 and square 101 the approximations are given. Of all other squares neither an exact number nor an approximation is known (by me), and they have not been calculated (yet) because, supposedly, they will only show more of the same of a size between a smaller and a larger square of which the exact number or approximation is already given. Those interested in, familiar with, or obsessed by googols and googolplexes ought to understand that radix-10 numbers or values like those cannot be found under the squares of squares, but they may be pleased to know that the number googol (1.0e100 and actually 1e100) is located somewhere between square 7, of which the approximation is 1.2e77, and square 8, of which the approximation is 1.3e154. None of the squares in this table has a value anywhere near the value of googolplex: the googolplex value is exactly 10^(10^100), whereas the value of square 101 is approximately 10^(10^30.2), as i will show later. Why, then, a table of 101 squares: why not many less, or many more? This choice is, indeed, nothing to do with the sizes of the squares. It is everything to do with the final-digit cycles in their radix-10 notations. More about that after the presentation of this table.
THE SQUARES OF SQUARES IN RADIX-10 NOTATION
| s | exact numbers (bold) and approximations |
last 1 d. |
last 2 d. |
last 3 d. |
last 4 dig. |
last 5 digits |
|---|---|---|---|---|---|---|
| 0 | 4 | 4 | 04 | 004 | 0004 | 00004 |
| 1 1 | 16 | 6 | 16 | 016 | 0016 | 00016 |
| 2 | 256 | 6 | 56 | 256 | 0256 | 00256 |
| 3 | 65,536 | 6 | 36 | 536 | 5536 | 65536 |
| 4 | 4,294,967,296 | 6 | 96 | 296 | 7296 | 67296 |
| 5 | 18,446,744,073,709,551,616 | 6 | 16 | 616 | 1616 | 51616 |
| 6 | 3.402823669209384634633746e+38 2 | 6 | 56 | 456 | 1456 | 11456 |
| 7 | 1.157920892373161954235710e+77 | 6 | 36 | 936 | 9936 | 39936 |
| 8 | 1.340780792994259709957403e+154 | 6 | 96 | 096 | 4096 | 84096 |
| 9 | Infinity (in a JavaScript program) 3 1.797693134862315907729305e+308 |
6 | 16 | 216 | 7216 | 37216 |
| 10 | 3.231700607131100730071488e+616 | 6 | 56 | 656 | 0656 | 30656 |
| 11 | 1.044388881413152506691753e+1233 | 6 | 36 | 336 | 0336 | 90336 |
| 12 | 1.090748135619415929462984e+2466 | 6 | 96 | 896 | 2896 | 92896 |
| 13 | 1.189731495357231765085759e+4932 | 6 | 16 | 816 | 6816 | 66816 |
| 14 | 1.415461031044954789001553e+9864 | 6 | 56 | 856 | 7856 | 77856 |
| 15 | Overflow (in a scientific calculator) 2.003529930406846464979072e+19728 |
6 | 36 | 736 | 6736 | 56736 |
| 16 | 4.014132182036063039166060e+39456 | 6 | 96 | 696 | 3696 | 73696 |
| 17 | 1.611325717485760473619572e+78913 | 6 | 16 | 416 | 0416 | 00416 |
| 18 | 2.59637056783100077612660e+157826 | 6 | 56 | 056 | 3056 | 73056 |
| 19 | 6.74114012549907340226907e+315652 | 6 | 36 | 136 | 9136 | 79136 |
| 20 | 4.54429701916136630999616e+631305 | 6 | 96 | 496 | 6496 | 06496 |
| 21 | 2.0650635398358879243991e+1262611 For exact number see Appendix |
6 | 16 | 016 | 8016 | 98016 |
| 22 | [2^(2^23)=?] | 6 | 56 | 256 | 6256 | 36256 |
| 23 | [2^(2^24)=?] | 6 | 36 | 536 | 7536 | 97536 |
| 24 | [2^(2^25)=?] | 6 | 96 | 296 | 1296 | 71296 |
| 25 | [2^(2^26)=?] | 6 | 16 | 616 | 9616 | 19616 |
| 26 | [2^(2^27)=?] | 6 | 56 | 456 | 7456 | 87456 |
| 27 | [2^(2^28)=?] | 6 | 36 | 936 | 1936 | 51936 |
| 28 | [2^(2^29)=?] | 6 | 96 | 096 | 8096 | 48096 |
| 29 | [2^(2^30)=?] | 6 | 16 | 216 | 5216 | 25216 |
| 30 | [2^(2^31)=?] | 6 | 56 | 656 | 6656 | 46656 |
| 31 | [2^(2^32)=?] | 6 | 36 | 336 | 2336 | 82336 |
| 32 | [2^(2^33)=?] | 6 | 96 | 896 | 6896 | 16896 |
| 33 | [2^(2^34)=?] | 6 | 16 | 816 | 4816 | 74816 |
| 34 | [2^(2^35)=?] | 6 | 56 | 856 | 3856 | 33856 |
| 35 | [2^(2^36)=?] | 6 | 36 | 736 | 8736 | 28736 |
| 36 | [2^(2^37)=?] | 6 | 96 | 696 | 7696 | 57696 |
| 37 | [2^(2^38)=?] | 6 | 16 | 416 | 8416 | 28416 |
| 38 | [2^(2^39)=?] | 6 | 56 | 056 | 9056 | 69056 |
| 39 | [2^(2^40)=?] | 6 | 36 | 136 | 1136 | 31136 |
| 40 | [2^(2^41)=?] | 6 | 96 | 496 | 0496 | 50496 |
| 41 | ? | 6 | 16 | 016 | 6016 | 46016 |
| 42 | ? | 6 | 56 | 256 | 2256 | 72256 |
| 43 | ? | 6 | 36 | 536 | 9536 | 29536 |
| 44 | ? | 6 | 96 | 296 | 5296 | 75296 |
| 45 | ? | 6 | 16 | 616 | 7616 | 87616 |
| 46 | ? | 6 | 56 | 456 | 3456 | 63456 |
| 47 | ? | 6 | 36 | 936 | 3936 | 63936 |
| 48 | ? | 6 | 96 | 096 | 2096 | 12096 |
| 49 | ? | 6 | 16 | 216 | 3216 | 13216 |
| 50 | ? | 6 | 56 | 656 | 2656 | 62656 |
| 51 | ? | 6 | 36 | 336 | 4336 | 74336 |
| 52 | ? | 6 | 96 | 896 | 0896 | 40896 |
| 53 | ? | 6 | 16 | 816 | 2816 | 82816 |
| 54 | ? | 6 | 56 | 856 | 9856 | 89856 |
| 55 | ? | 6 | 36 | 736 | 0736 | 00736 |
| 56 | ? | 6 | 96 | 696 | 1696 | 41696 |
| 57 | ? | 6 | 16 | 416 | 6416 | 56416 |
| 58 | ? | 6 | 56 | 056 | 5056 | 65056 |
| 59 | ? | 6 | 36 | 136 | 3136 | 83136 |
| 60 | ? | 6 | 96 | 496 | 4496 | 94496 |
| 61 | ? | 6 | 16 | 016 | 4016 | 94016 |
| 62 | ? | 6 | 56 | 256 | 8256 | 08256 |
| 63 | ? | 6 | 36 | 536 | 1536 | 61536 |
| 64 | ? | 6 | 96 | 296 | 9296 | 79296 |
| 65 | See radix-16 notation for more details | 6 | 16 | 616 | 5616 | 55616 |
| 66 | ? | 6 | 56 | 456 | 9456 | 39456 |
| 67 | ? | 6 | 36 | 936 | 5936 | 75936 |
| 68 | ? | 6 | 96 | 096 | 6096 | 76096 |
| 69 | ? | 6 | 16 | 216 | 1216 | 01216 |
| 70 | ? | 6 | 56 | 656 | 8656 | 78656 |
| 71 | ? | 6 | 36 | 336 | 6336 | 66336 |
| 72 | ? | 6 | 96 | 896 | 4896 | 64896 |
| 73 | ? | 6 | 16 | 816 | 0816 | 90816 |
| 74 | ? | 6 | 56 | 856 | 5856 | 45856 |
| 75 | ? | 6 | 36 | 736 | 2736 | 72736 |
| 76 | ? | 6 | 96 | 696 | 5696 | 25696 |
| 77 | ? | 6 | 16 | 416 | 4416 | 84416 |
| 78 | ? | 6 | 56 | 056 | 1056 | 61056 |
| 79 | ? | 6 | 36 | 136 | 5136 | 35136 |
| 80 | ? | 6 | 96 | 496 | 8496 | 38496 |
| 81 | See radix-16 notation for more details | 6 | 16 | 016 | 2016 | 42016 |
| 82 | ? | 6 | 56 | 256 | 4256 | 44256 |
| 83 | ? | 6 | 36 | 536 | 3536 | 93536 |
| 84 | ? | 6 | 96 | 296 | 3296 | 83296 |
| 85 | ? | 6 | 16 | 616 | 3616 | 23616 |
| 86 | ? | 6 | 56 | 456 | 5456 | 15456 |
| 87 | ? | 6 | 36 | 936 | 7936 | 87936 |
| 88 | ? | 6 | 96 | 096 | 0096 | 40096 |
| 89 | ? | 6 | 16 | 216 | 9216 | 89216 |
| 90 | ? | 6 | 56 | 656 | 4656 | 94656 |
| 91 | ? | 6 | 36 | 336 | 8336 | 58336 |
| 92 | ? | 6 | 96 | 896 | 8896 | 88896 |
| 93 | ? | 6 | 16 | 816 | 8816 | 98816 |
| 94 | ? | 6 | 56 | 856 | 1856 | 01856 |
| 95 | ? | 6 | 36 | 736 | 4736 | 44736 |
| 96 | ? | 6 | 96 | 696 | 9696 | 09696 |
| 97 | ? | 6 | 16 | 416 | 2416 | 12416 |
| 98 | ? | 6 | 56 | 056 | 7056 | 57056 |
| 99 | ? | 6 | 36 | 136 | 7136 | 87136 |
| 100 | ? | 6 | 96 | 496 | 2496 | 82496 |
| 101 | See radix-16 notation for more details | 6 | 16 | 016 | 0016 | 90016 |
|
1 Squares 1, 5, 9, 13, etc. (with white backgrounds)
are squares 1, 2, 3, 4, etc. of the head-16 power-16 sequence, a
contiguous sequence of squares of squares which is itself a
subsequence of the head-2 power-2 sequence, where it is not a
contiguous string.
2 From the sixth square of squares (3.4e+38) the 1, 2, 3, 4 or 5 last digits are calculated by squaring the integer with the same number of last digits in the previous square of squares, and by taking the same number of last digits from that square. The last (1) digit of the fifth square of squares is 6, 6^2=36, of which the last digit is 6 again. The last 2 digits of the fifth square of squares are 1 (and) 6, 16^2=256, of which the last 2 digits are 56. The last 3 digits of the fifth square of squares are 616, 616^2=379456, of which the last 3 digits are 456; the last 4 digits of the fifth square of squares are 1616, 1616^2=2611456, of which the last 4 digits are 1456; and the last 5 digits of the fifth square of squares are 51616, 51616^2=2664211456, of which the last 5 digits are 11456. (Of course, if you know beforehand how many final digits you want or need to show or have, the last step will just suffice.) As soon as 6, 16, 016, 0016 or 00016 returns at the end of a larger square of squares this is the beginning of a new final-digit cycle. The number of terms in the one-digit cycle is 1; in the two-digit cycle 4; in the three-digit cycle 20, and in the four-digit cycle 100. The number of one hundred and one squares is far too small to establish a five-digit cycle. 3 Infinity is the result given by a Javascript program which uses the 重(a,l,b) or 'chong(a,l,b)' function for calculating the values of a重lb, among which the squares of squares in 2重3b. In the system used it means that the calculated value exceeds a number close to, but smaller than, 144^144 = 6.4e+310, which is 6.4×(10^210×10^100) or 6.4×10^210 times 'one googol'. |
||||||
FINAL DIGIT CYCLES
Getting the last ten digits of squares 1 to 7
The above table with its one hundred and one squares of squares shows the last one, two, three, four and five digits of each square, regardless of its complete radix-10 notation being known or being shown anywhere. This may seem intriguing, but it is only possible if the same number of last digits of the previous square is known. It is explained for the last five digits in the second note of the table above, but i will demonstrate it here for the seven squares of squares in the table below, in which even the last ten digits have been calculated separately. The calculation starts with 0000000004, that is, the number 4 with nine leading zeros, so that we have a ten-digit notation. When 0000000004 is squared we get 16 preceded by eighteen 0s, of which we only use the ten last digits, that is, 0000000016, which is the 10-digit radix-10 notation for (the) square (of squares) 1. The ten last digits of square 2 are obtained by squaring 0000000016, which is 256 preceded by seventeen 0s, of which the abbreviation is 0000000256. The number 0000000256 squared is 65536 preceded by fifteen 0s, but abbreviated to 000006553, the 10-digit radix-10 notation for square 3. Square 4 is the first square without leading zeros in its 10-digit tail, because 256^2=4,294,967,296, which is exactly ten digits long. Squaring 4294967296 yields 18,446,744,073,709,551,616 in a scientific calculator, which is the whole notation for square 5, of which the last ten digits are 3709551616. From now on the last ten digits will form only the end part of the number in radix-10 notation. At the same time, calculating the whole number by just squaring the previous square may not be possible anymore. Just try 18446744073709551616^2 and what you (may) get is 3.4028236692093846346337460743177e+38, which is an approximation, not the exact number! However, in this case we can combine this approximation with our precise knowledge of the last ten digits and so contruct the exact number. (See note 2 in the table below.) Squaring 3709551616 yields 13,760,773,191,768,211,456, of which the last ten digits are 1768211456, the 10-digit end of the notation for square 6. Squaring 1768211456 results in 3,126,571,753,129,639,936, of which the last ten digits are 3129639936, the end of square 7.
The 1- and 4-term one- and two-digit cycles
The long table above starts with the same eight squares, but it shows the final digit cycles as well. Since 6^2=36, which ends in 6 too, the first cycle is a one-term one-digit cycle, shown alternately in light yellow and light aqua or 'cyan'. The second set of vertically arranged numbers is {16,56,36,96}, which, apart from the sixes of the first cycle does not tell us anything. But once the first number reappears in the same column, we know that the whole set {16,56,36,96} must reappear, and that this set represents a four-term final two-digit cycle. It is shown alternately in light green or 'lime' and light purple.
A 20-term three-digit cycle
Four terms is a short cycle, but what do we do with the final 3-digit set {016,256,536,296,616,456,936} in the first seven squares of squares? So far, there is no return of 016 te be seen, but there is an occurrence of 616, precisely at the place where the previous, two-digit cycle restarts. Hence, as long as 016 does not show up, there is a good reason for paying special attention to the numbers where the previous cycle restarts. And, indeed, all numbers in those places end in 16: square 5 has 616 as we knew already, square 9 has 216, square 13 has 816 and square 17 has 416. Is there just a chance of 1 in 10 that 016 will turn up among 116, 216, 316, 416, and so on? The succession of numbers in {016,616,216,816,416} looks wholly arbitrary, and yet, on closer inspection there is a regularity, given that it is actually only the last three digits we are seeing. The difference 616-016=600 and 216-616=-400, which is of no help. However, if we take the 600 as a common difference in an arithmetic sequence, then what follows after 616 is 1216 without the first 1; and then 1816 without the first 1; and then 2416 without the first 2. If this is correct, what follows should be 3016 without the first 3, which is indeed the case, and the beginning of the second occurrence of the same 20-term final three-digit cycle, shown in light yellow and light aqua again. We are lucky that the three-digit cycle is only 20 terms long, because, all other things being equal, we had a 1 in 10 chance that the first digit was 0 and, in view of the two-digit cycle, a 1 in 4 chance that the second digit was 1, altogether a 1 in 40 chance that 01 followed by 6 would reappear.
A 100-term four-digit cycle
There is no regularity in the lengths of the first three cycles: they are, in the number of terms, 1, 4 and 20 (instead of, say, 16). Since 20=1.25*16, the fourth cycle threatens to be about 1.25*5*20=125 terms long; and what is the size of that square 125, or its neighbor, going to be, given that square 15 cannot even be approximated anymore by a scientific calculator because of overflow? Moreover, the arithmetic sequence found in {016,616,216,816,416} by allowing these terms to stand for numbers with an extra digit in front, is nowhere to be found in the set {16,56,36,96}, where 36 does not fit into any similar scheme. The column with the final four-digit numbers may be as unpredictable as the one with the final two-digit numbers and keep us waiting for more than 125 squares before 0016 occurs again. There is a 1 in 10 chance of 0 returning at the place of the first digit. After that, there is a 1 in 20 chance of 016 returning in the place of the second, third and fourth digits, in view of the three-digit cycle. Hence, the chance of 0016 returning is 1 in 200. Fortunately, the numbers at the beginning of each three-digit cycle tell us more: 0016 for square 1, 8016 for square 21, 6016 for square 41. Given that each quartet of digits may have a hidden digit in front, the set {0016,8016,6016} may be read as {0016,8016,16016}, which is the three-term beginning of the arithmetic sequence {0016,8016,16016,24016,32016,40016} with 8000 as the common difference. When we reduce the six-term beginning to six quartets again there emerges the set {0016,8016,6016,4016,2016,0016} which shows the return of 0016 after five 3-digit cycles of 20 terms, that is, one 4-digit cycle of 100 terms. The figures in the four-digit column of the table do indeed confirm this.
A 5-term five-digit (sub?)cycle starting from square 101
Is it possible to discern a five-digit cycle with the information in the table above? Let's assume that the regular pattern we have found in the three- and four-digit cycles persists, what data do we need then? We need at least the final five digits of square 101, because now it will be the squares 101, 201, 301, 401, and so on, which determine where to look for the return of 00016 in this five-digit cycle. The difference between square 1 and square 101 should become the addend or 'common difference' of an arithmetic sequence then, a sequence which can tell us in advance how long the five-digit cycle is going to be. In my table the last five digits of square 101 have been derived from the last five of square 100, and WolframAlpha at www.wolframalpha.com/, giving the last ten digits of the output for 2^(2^102), confirms that the last five are indeed 90016. This means that the addend might be 90,000 and the beginning of the sequence {00016, 90016, 80016, 70016, 60016} for the squares 1, 101, 201, 301 and 401 respectively. However, consulting WolframAlpha for the squares 201 to 401 i found the final-digit strings 30016 for square 201 and 10016 for square 401; only square 301 was 'predicted' correctly. Nonetheless, the crucial question which remained was still, Does the string 00016 return somewhere among the squares with order number 201, 301, 401, 501, and so on? I checked this until square 1101, a number as large as 10^(10^331.2), only to find out that 00016 does not return (within this range). And yet, my search was not fruitless, because i did find a 5-term 5-digit cycle (or subcycle?), but it does not begin at square 1; it begins at square 101! The final 5-digit strings for squares 101 to 1101 are: 90016, 30016, 70016, 10016, 50016, 90016, 30016, 70016, 10016 and 50016. Looking at them as numbers in there own right, we see the head-90016 addend-40000 sequence {90016, 130016, 170016, 210016, 250016, 290016, 330016, 370016, 410016, 450016}. Looking at them as strings again, and confining ourselves to the last five digits, we discover the consecutively recurring strings 90016, 30016, 70016, 10016 and 50016. For now, this leaves the squares 1 to 100 without any five-digit cycle, putting an end to my attempt to find the length of the final five-digit cycle in the radix-10 notation of the squares of squares. It does give a good impression, however, of what order of magnitude is involved here. (While the value of square 1101 is 10^(10^331.2), one googolplex is 'only' 10^(10^100)!)
| s | numbers (bold) and approximations |
last 7 digits |
last 8 digits |
last 9 digits |
last 10 digits |
|
|---|---|---|---|---|---|---|
| 0 | 4 | 0000004 | 00000004 | 000000004 | 0000000004 | |
| 1 | 16 | 0000016 | 00000016 | 000000016 | 0000000016 | |
| 2 | 256 | 0000256 | 00000256 | 000000256 | 0000000256 | |
| 3 | 65,536 | 0065536 | 00065536 | 000065536 | 0000065536 | |
| 4 | 4,294,967,296 | 4967296 | 94967296 | 294967296 | 4294967296 | |
| 5 | 18,446,744,073,709,\ 551,616 |
9551616 | 09551616 | 709551616 | 3709551616 | |
| 6 | 3.40282366920938\ 463463374607e+38 1 |
8211456 | 68211456 | 768211456 | 1768211456 | |
| 340,282,366,920,938,\ 463,463,374,607,431,\ 768,211,456 |
exact number obtained by adding the last 8 digits manually to the machine calculation 2 | |||||
| 7 | 1.15792089237316\ 195423570985e+77 |
9639936 | 29639936 | 129639936 | 3129639936 | 115,792,089,237,316,\ 195,423,570,985,008,\ 687,907,853,269,984,\ 665,640,564,039,457,\ 584,007,913,129,639,\ 936 |
exact number obtained by calculating the exponent 2^(b-1) in the formula 重(2,+3,b) = 2^(2^(b-1)), which is 256 here (b=s+2) 3 |
|
1 From the sixth square of squares (3.4e+38) also
the 7, 8, 9 or 10 last digits are calculated by squaring the integer
with the same number of last digits in the previous square of
squares, and by taking the same number of last digits from that
square.
The last 10 digits of the fifth square of squares are 3(,)
7(,) 0(,) 9(,) 5(,) 5(,) 1(,)
6(,) 1 (and) 6.
Looking at these digits as a number in itself, its square is
3709551616^2=13760773191768211456, of which the last 10 digits are
1768211456.
2 When the approximate number 3.4028236692093846346337460743177e+38 is given, we know that 34028236692093846346337460743177 counts 32 digits, and that, as far as the length of the notation is concerned, 38+1-32=7 digits are still missing. (For 1.0e+1=10 you need two digits, for 1.5e+2=150 three digits.) However, it would be mistaken to add simply 8211456 after 177, because 3.4...177e+38 may stand for any number in the range between 3.4...1765e+38 and 3.4...1775e+38; so, what follows after 17 in the exact number may be a 6 instead of another 7! Not until we have the last eight digits can we decide that it is not 8211456 which follows 177, but 68211456 which follows 17. The last nine and last ten digits are further proofs of that. 3 Consider the values of the first eight members of the sequence: for s=0, 2^2=4; for s=1, (2^2)^2=2^4=16; for s=2, (2^4)^2=2^8=256; for s=3, (2^8)^2=2^16=65536; for s=4, (2^16)^2=2^32= 4294967296; for s=5, (2^32)^2=2^64= 18 446 744 073 709 551 616 (with a space as segment separator); for s=6, (2^64)^2=2^128= 340 282 366 920 938 463 463 374 607 431 768 211 456; and for s=7, (2^128)^2=2^256= 115 792 089 237 316 195 423 570 985 008 687 907 853 269 984 665 640 564 039 457 584 007 913 129 639 936. A power of 2 such as 2^256 can be found, e.g., at www.wolframalpha.com or defuse.ca/big-number-calculator.htm |
||||||
THE DISTRIBUTION OF SQUARES OF SQUARES
The universalization of operators may be a big, perhaps, revolutionary contemporary step forward in arithmetic, an even bigger step was the introduction of multiplication in ancient times, because it was in this stage that a formalized operation of iteration was first introduced. (Doubtless, numerical repetition existed long before that stage already, but it was a revolution to treat it as a systematic process in itself.) With multiplication arithmetic moved from a noniterative chong-0 stage to an iterative chong-1 stage. It was also in this stage that a distinction was discovered between integers which can be created by means of multiplication and integers which cannot; or, conversely, larger composite numbers which are the product of two smaller integers, and those which are not. The latter ones were called "prime numbers" by ancient Greek mathematicians. They are in present terms positive integers which cannot be generated with a chong-1 operator other than on or by 1. These 'prime' numbers have fascinated number players and number theorists ever since. However little the prime numbers which cannot be generated on the first level of iteration and the squares of squares which can be generated on the third level of iteration have in common, there is one interesting feature which they share: they occur less and less frequently as they become larger, without disappearing entirely.
In the table below i show the distribution of the members of the chong-3 sequence of squares of squares by counting the number of integers left out between them from square 0 to square 7. It starts with a mere 11 integers between 4 (square 0) and 16 (square 1); it ends, that is, 'pauses', with approximately 1.1 times 10^77 integers between 340 282 366 920 938 463 463 374 607 431 768 211 456 (square 6) and 115 792 089 237 316 195 423 570 985 008 687 907 853 269 984 665 640 564 039 457 584 007 913 129 639 936 (square 7). In prime number theory there is a prime number theorem describing the asymptotic distribution of the prime numbers among the positive integers. There is already an analog for this theorem describing the 'distribution' of irreducible polynomials over a finite field. (See, e.g., en.wikipedia.org/[ ]wiki/Prime_number_theorem.) I do not know whether there will, similarly, ever be an analog for the sequence of squares of squares.
| s | Number of integers between square s and s+1 1 |
|---|---|
| 0 | 11 = 16 - (4+1) until the first square of squares 2 |
| 1 | 239 = 256 - (16+1) until the next square of squares |
| 2 | 65,279 = 65,536 - (256+1) |
| 3 | 4,294,901,759 = 4,294,967,296 - (65,536+1) |
| 4 | 18,446,744,069,414,584,319 |
| 5 | 340,282,366,920,938,463,444,927,863,358,058,659,839 |
| 6 | 115,792,089,237,316,195,423,570,985,008,687,907,852,\ 929,702,298,719,625,575,994,209,400,481,361,428,479 |
|
1 The number does not include the two squares
themselves, altho it may include squares, and even squares of squares,
which do not belong to the 2重3b sequence.
2 For the first four squares (and rows) not only the number of integers itself, but also the way it is calculated are shown. |
|
IN THE WAY OF THE SQUARES
Two-to-one and many-to-one correspondences
It is part of the way of the rut to think of a numeral system as a distinct system with one radix isolated from other numbers for being the most suitable or least unsuitable base or 'radix' there is. People who have thought about alternatives to the common base-10 numeral system, may swear by a new radix such as 12 or 16 —2 and 8 are for the computer— as 'the true one', as one radix of one system without any connection to other numeral systems. Now, 12 may be quite a distance from 144, and 256 an even greater distance from 16 when considering one's choice of radix, this type of relatively remote connection is not at all characteristic of what we encounter when we start at the beginning. At the very beginning there is 2, followed by 4 (2^2), 8 (2^3), 16 (itself 2^4), 32 (2^5), 64 (2^6) and 128 (2^7) before we get close to 144. And at the beginning there is 3, followed by 9 (3^2), 27 (3^3) and 81 (3^4). These numbers may seem of little interest, until it turns out that they represent fixed correspondences between number notations for varying radixes: two-to-one correspondences in which each couple of figures in the notations of the one numeral system can be directly replaced, that is, without any need for (further) calculation, with one figure in the other numeral system; three-to-one correspondences in which each triplet in the one system can be directly replaced with one figure in the other; four-to-one correspondences, and so on and so forth. Therefore, those who think they are choosing a radix and a single numeral system are actually choosing a numeral supersystem, for the right or for the wrong reason (or a mixture of the two).
Numeral supersystems
The concept of a numeral supersystem must play a central role in any adequate integrated linguistic-mathematical treatment of numbers, and i cannot fully discuss it in this article. May it suffice here to describe it in outline, while confining myself to positive integers. To start with, instead of just having a radix the supersystem has one superradix and an infinite number of subradixes which can be mathematically derived from it, the sole criterion being that a larger subradix will yield a shorter notation in a fixed two- or many-to-one correspondence between the figures in these notations. If the superradix is 2, the square of 2 and all squares of squares of 2 will be quadratic subradixes. Consider, for example, the number 14, of which the notation is 1110 with radix 2: it will be 32 with radix 2^2=4 after replacing the 11 pair with 3 (the notation for 3 in the radix-4 subsystem) and 10 with 2 (the notation for 2). Note that such a correspondence also applies to the subradix 16, where two two-to-one correspondences amount to one four-to-one correspondence between the radix-2 and -16 subsystems. It does not apply, however, to 8 as a subradix: the notation for the number 15, for instance, is 1111 with radix 2, 33 with radix 4, and 17 (1*8+7) with radix 8, which cannot be directly derived. Yet, 8 is a subradix too, as 8=2^3; and the subradix a cubic one. For cubic subradixes there is a three-to-one correspondence between their notation and the one with the superradix or previous subradix. Starting from 1111 for 15, we should first read this as 001111 with two triplets, 001, which is 1, and 111, which is 7 with radix 2; together 17 for 15 again. The following table shows the number of quadratic, cubic and other subradixes between 4 and 128 inclusive for the first eleven numeral supersystems. (The eleventh, the system with superradix 12, does not even have one subradix in this range!)
| super- radix |
quad- ratic |
cubic | 5th- pow. |
6th- pow. |
7th- pow. |
|---|---|---|---|---|---|
| 2 | 4 & 16 | 8 | 32 | 64 | 128 |
| 3 | 9 & 81 | 27 | - | ||
| 4 | 16 | 64 | - | ||
| 5 | 25 | 125 | - | ||
| 6 | 36 | - | |||
| 7 | 49 | - | |||
| 8 | 64 | - | |||
| 9 | 81 | - | |||
| 10 | 100 | - | |||
| 11 | 121 | - | |||
| 12 | - | ||||
|
The column for the 4th power of the superradix is not shown, as all 4th-power subradixes are also 2nd-power or 'quadratic' subradixes. A 6th-power subradix is not such a quadratic or cubic one, for it is not a square of a square, nor a cube of a cube. |
|||||
The (micro)macrobinary supersystem
There are at least three good reasons to opt for a superradix 2, with the radixes 4, 8 and 16 in its wake:
- the number 2 is the elementary integer radix for a place-value system, which can even be used to deal with the true and the false
- the radix-2 supersystem is the supersystem with by far the most subradixes of all of them, thus providing within its system the most two-to-one and many-to-one correspondences with other radixes
- the radix-2, -4 and -16 supersystems are the only ones which cover all squares of squares as subradixes, altho they also cover squares which are subradixes for other reasons (such as 64=2^6=4^3=8^2)
Of course, the divisibility of a radix also plays a role: 6=2*3, 10=2*5, 15=3*5 and 30=2*3*5 all have something a radix derived from the superradix 2 does not have. In a final choice this too will have to be taken into account, but the answer is not as simplistic as tradionalists may expect, for the systematic selection of a radix must not depend on facts and feelings which are generated or engendered by the use of one or more different radixes in the past or at the same time. Take the subdivision of the naturally given whole day, for instance, which has, like the subdivision of the logically given full circle, grown into a radical hotchpotch. For an integrated linguistic-mathematical system there is also the indispensable criterion that a radix must not require more morphemes than are (made) available for the naming of numbers. Moreover, it should not be forgotten that one has to be able to more or less easily remember all these morphemes (and the tables of addition and multiplication which come with them)! Because of the high density of subradixes in the superradix-2 system especially these latter criterions can be satisfied better than in any other numeral supersystem. In this article i shall use a traditional 'scientific' terminology for its name and call it "the micromacrobinary supersystem" or, since i have only discussed integer radixes here, just "the macrobinary supersystem". It should come as no surprise now, that the squares of squares in particular are waiting for a macrobinary approach.
THE SQUARES OF SQUARES IN TWO OTHER NOTATIONS
| s | exact numbers in radix-4 notation |
exp. in rad.-10 | exact numbers in radix-16 notation |
exp. in rad.-10 |
|---|---|---|---|---|
| 0 | 10 = 1E+1 | 1 | 4 1 | — |
| 1 | 100 = 1E+2 | 2 | 10 = 1E+1 | 1 |
| 2 | 1,0000 = 1E+10 2 | 4 | 100 = 1E+2 | 2 |
| 3 | 1,0000,0000 = 1E+20 | 8 | 1,0000 = 1E+4 | 4 |
| 4 | 1,0000,0000,0000,0000 =1E+100 3 |
16 | 1,0000,0000 =1E+8 4 |
8 |
| 5 | 1E+200 | 32 | 1E+10 | 16 |
| 6 | 1E+1000 | 64 | 1E+20 | 32 |
| 7 | 1E+2000 | 128 | 1E+40 | 64 |
| 8 | 1E+1,0000 | 256 | 1E+80 | 128 |
| 9 | 1E+2,0000 | 512 | 1E+100 | 256 |
| 10 | 1E+10,0000 | 1024 | 1E+200 | 512 |
| 11 | 1E+20,0000 | 2048 | 1E+400 | 1024 |
| 12 | 1E+100,0000 | 4096 | 1E+800 | 2048 |
| 13 | 1E+200,0000 | 8192 | 1E+1000 | 4096 |
| 14 | 1E+1000,0000 | 16384 | 1E+2000 | 8192 |
| 15 | 1E+2000,0000 | 32768 | 1E+4000 | 16384 |
| 16 | 1E+1,0000,0000 | 65536 | 1E+8000 | 32768 |
| 17 | 1E+2,0000,0000 | 131072 | 1E+1,0000 | 65536 |
| 18 | 1E+10,0000,0000 | 262144 | 1E+2,0000 | 131072 |
| 19 | 1E+20,0000,0000 | 524288 | 1E+4,0000 | 262144 |
| 20 | 1E+100,0000,0000 | 1048576 | 1E+8,0000 | 524288 |
| 21 | 1E+200,0000,0000 | 2097152 | 1E+10,0000 5 | 1048576 |
|
1 In these notations the (Hindu-Arabic) figures
themselves are not different from those traditionally used
in the radix-ten or decimal-denary system.
2 The division of the micro-macro-binary number notations into parts is, naturally, based on segments of four digits. 3 The radix-4 expression 1E+100 stands for 1*(10^100), which is in radix-10 terms 1*(4^16)=4,294,967,296. The 1 is definitely 1, and not 1.0, for the number is the exact number rather than an approximation. (In denary terms: 1.0 may refer to 1, but at the same time it refers to any number between 0.95 and 1.05.) 4 The radix-16 expression 1E+8 stands for 1*(10^8), which is in radix-10 terms 1*(16^8)=4,294,967,296. This equals, as it is supposed to, its radix-4 counterpart. 5 The radix-16 expression 1E+10,0000 stands for 1*(10^10,0000), which is in radix-10 terms 1*(16^1048576)= (2^4)^1048576= 2^4194304. Upon entering this expression the Online Big Number Calculator at defuse.ca/big-number-calculator.htm gives the exact number at once, while the WolframAlpha calculator at www.wolframalpha.com gives useful information about the number, among which its beginning and end. Thus, its decimal-denary length is 1,262,612 digits of which the last 10 digits are 8394198016. (The last four of these correspond with my calculation in the table of the first 22 squares above.) Its decimal approximation is 2.06506353983588792439911949458165\ 01695274360493029670347841664176... × 10^1262611 to start with, while its power-of-10 representation is 10^(10^6.101269676953261). |
||||
IN RADIX-16 NOTATION
A conversion which needs hardly any calculating
When converting a number from a radix-R to a radix-R2 numeral system, each pair of digits in the radix-R system is being replaced, in the same order, with one in the radix-R2 system. (If the number of digits is odd, you will have to add 0 in front.) Hence, 111001 [2] (111001 in the radix-2 system) will be 321 [4] (321 in the radix-4 system), with binary 11 read as "3", binary 10 as "2", and (every) 01 as "1". And, in turn, 321 [4], the same as 0321 [4], will be 39 [16], with 03 read as "3", and 21 as "9". (While this number may be 3*16+9*1=48+9=57 in denary terms, such a calculation is not by any manner of means part of the conversions.) Thus, when we see in the above table that Square Three is 1 0000 0000 0000 0000 in radix-4 notation (with a space between the segments instead of a comma for typographical reasons), we may conclude immediately that this will be 1 0000 0000 in radix-16 notation, because every couple 00 in the former notation corresponds with one 0 in the latter, and 1 or 01 refers to 1 in both numeral systems. However, in the scientific notation the exponent cannot be converted in the same direct way. It needs a little calculation, because, for x>0, 4x has a value which differs from 16x! Nonetheless, if x is the exponent in the radix-4 system and y the one in the radix-16 system, 4x=16y implies that 4x=(42)y, from which it follows that x=2*y and y=x/2. Given that Square Three equals 1E+20 in radix-4 notation, it is therefore not 20 which must be converted, but a pair with half its value, that is, 10; and this 10 refers to 4 in the radix-4 system, while 4 refers to 4 in the radix-16 system. It follows that 1E+20 [4]=1E+4 [16]. In the case of Square Twenty-one it is the 200 which must first be reduced to 100 or 0100; the number of zeros following will also have to be reduced from 8 (two four-digit segments) to 4 (one four-digit segment). Since 0100 [4]=10 [16], the radix-16 equivalent of 1E+200 0000 0000 [4] will be 1E+10 0000 [16]. In other words, there is no need anymore to show radix 4 side by side with radix 16. Radix 16 suffices.
An unchanging head and ever-elongating tail
With the changeover from the radix-10 to the radix-16 notations for squares of squares their intriguing final-digit cycles disappear like snow in summer. From Square One on all squares of squares simply end in a zero, albeit in an increasing number of them: one zero in Square One (10=1E+1) to more than a million zeros in Square Twenty-one (1E+10,0000), as shown by the table above; and, for short- and long-scale base-10 'illionaires', to more than 340 uncillion or 'sextillion' zeros in Square One-hundred-and-twenty-nine (1E+1;0000,0000,0000,0000;0000,0000,0000,0000), as shown by the table below. Some will, perhaps, argue that there is a one-term final one-digit cycle not unlike the one in the radix-10 notation of the squares of squares, except that this one digit is 0 instead of 6. But if this is accepted as correct, it only is so in a very trivial sense, because, in the radix-10 notation, the squares never end in (6(6...6)6)66 —they end in 16, 56, 36 or 96— whereas, in the radix-16 notation, they all end in (0(0...0)0)0. Is there perhaps a nontrivial cycle at the beginning instead? Looking at the two macrobinary tables, there seems to be a four-term initial one-digit cycle in which the terms start with 1, 2, 4 and 8, after which the 1 returns in 10 (2*8=16 [10]=10 [16]). This, however, is a miserable illusion, for it may be a real cycle in the exponents of the shorthand representation of the numbers, it is not at all a cycle in the numbers themselves. At each step the string of zeros in a square becomes twice as long in the next square. (Compare, for example, 10,0002 = 10,000*10,000 = (10^4)*(10^4) = 10^(2*4) = 10^8 =100,000,000.) While the notation of the squares of squares starts with 1, there follows first only 1 zero (in 10), then 2 zeros (in 100), 4 zeros (in 1,0000), 8 zeros (in 1,0000,0000, the number 1E+8 [16] refers to), 16 zeros (in the number 1E+10 [16] refers to), and so on and so forth. It is with a head remaining 1 forever, an ever-elongating tail of no more than zeros, and no body in between, that the broad or 'long' jumper in track-and-field mathematics attempts to reach the infinitely large, jump by jump.
| s | exact numbers in radix-16 notation |
exponent in radix-10 |
|---|---|---|
| 21 | 1E+10,0000 for full number see Appendix |
1048576 |
| 22 | 1E+20,0000 | 2097152 |
| 23 | 1E+40,0000 | 4194304 |
| 24 | 1E+80,0000 | 8388608 |
| 25 | 1E+100,0000 | 16777216 |
| 26 | 1E+200,0000 | 33554432 |
| 27 | 1E+400,0000 | 67108864 |
| 28 | 1E+800,0000 | 134217728 |
| 29 | 1E+1000,0000 | 268435456 |
| 30 | 1E+2000,0000 | 536870912 |
| 31 | 1E+4000,0000 | 1073741824 |
| 32 | 1E+8000,0000 | 2147483648 |
| 33 | 1E+1,0000,0000 | 4294967296 |
| 34 | 1E+2,0000,0000 | 8589934592 |
| 35 | 1E+4,0000,0000 | 17179869184 |
| 36 | 1E+8,0000,0000 | 34359738368 |
| 37 | 1E+10,0000,0000 | 68719476736 |
| 38 | 1E+20,0000,0000 | 137438953472 |
| 39 | 1E+40,0000,0000 | 274877906944 |
| 40 | 1E+80,0000,0000 | 549755813888 |
| 41 | 1E+100,0000,0000 | 1099511627776 |
| 42 | 1E+200,0000,0000 | 2199023255552 |
| 43 | 1E+400,0000,0000 | 4398046511104 |
| 44 | 1E+800,0000,0000 | 8796093022208 |
| 45 | 1E+1000,0000,0000 | 17592186044416 |
| 46 | 1E+2000,0000,0000 | 35184372088832 |
| 47 | 1E+4000,0000,0000 | 70368744177664 |
| 48 | 1E+8000,0000,0000 | 140737488355328 |
| 49 | 1E+1,0000,0000,0000 | 281474976710656 |
| 50 | 1E+2,0000,0000,0000 | [2x] |
| 51 | 1E+4,0000,0000,0000 | [4x] |
| 52 | 1E+8,0000,0000,0000 | [8x] |
| 53 | 1E+10,0000,0000,0000 | 45035996273704\ 96 |
| 54 | 1E+20,0000,0000,0000 | [2x] |
| 55 | 1E+40,0000,0000,0000 | [4x] |
| 56 | 1E+80,0000,0000,0000 | [8x] |
| 57 | 1E+100,0000,0000,0000 | 72057594037927\ 936 |
| 58 | 1E+200,0000,0000,0000 | [2x] |
| 59 | 1E+400,0000,0000,0000 | [4x] |
| 60 | 1E+800,0000,0000,0000 | [8x] |
| 61 | 1E+1000,0000,0000,0000 | 11529215046068\ 46976 |
| 62 | 1E+2000,0000,0000,0000 | [2x] |
| 63 | 1E+4000,0000,0000,0000 | [4x] |
| 64 | 1E+8000,0000,0000,0000 | [8x] |
| 65 | 1E+1;0000,0000,0000,0000 1 2 | 18446744073709\ 551616 |
| 66 | 1E+2;0000,0000,0000,0000 | |
| 67 | 1E+4;0000,0000,0000,0000 | |
| 68 | 1E+8;0000,0000,0000,0000 | |
| 69 | 1E+10;0000,0000,0000,0000 | |
| 70 | 1E+20;0000,0000,0000,0000 | |
| 71 | 1E+40;0000,0000,0000,0000 | |
| 72 | 1E+80;0000,0000,0000,0000 | |
| 73 | 1E+100;0000,0000,0000,0000 | |
| 74 | 1E+200;0000,0000,0000,0000 | |
| 75 | 1E+400;0000,0000,0000,0000 | |
| 76 | 1E+800;0000,0000,0000,0000 | |
| 77 | 1E+1000;0000,0000,0000,0000 | |
| 78 | 1E+2000;0000,0000,0000,0000 | |
| 79 | 1E+4000;0000,0000,0000,0000 | |
| 80 | 1E+8000;0000,0000,0000,0000 | |
| 81 | 1E+1,0000;0000,0000,0000,0000 3 | 12089258196146\ 29174706176 |
| 82 | 1E+2,0000;0000,0000,0000,0000 | |
| 83 | 1E+4,0000;0000,0000,0000,0000 | |
| 84 | 1E+8,0000;0000,0000,0000,0000 | |
| 85 | 1E+10,0000;0000,0000,0000,0000 | |
| 86 | 1E+20,0000;0000,0000,0000,0000 | |
| 87 | 1E+40,0000;0000,0000,0000,0000 | |
| 88 | 1E+80,0000;0000,0000,0000,0000 | |
| 89 | 1E+100,0000;0000,0000,0000,0000 | |
| 90 | 1E+200,0000;0000,0000,0000,0000 | |
| 91 | 1E+400,0000;0000,0000,0000,0000 | |
| 92 | 1E+800,0000;0000,0000,0000,0000 | |
| 93 | 1E+1000,0000;0000,0000,0000,0000 | |
| 94 | 1E+2000,0000;0000,0000,0000,0000 | |
| 95 | 1E+4000,0000;0000,0000,0000,0000 | |
| 96 | 1E+8000,0000;0000,0000,0000,0000 | |
| 97 | 1E+1,0000,0000;0000,0000,0000,0000 | |
| 98 | 1E+2,0000,0000;0000,0000,0000,0000 | |
| 99 | 1E+4,0000,0000;0000,0000,0000,0000 | |
| 100 | 1E+8,0000,0000;0000,0000,0000,0000 | |
| 101 | 1E+10,0000,0000;0000,0000,0000,0000 4 | 12676506002282\ 29401496703205\ 376 |
| 102 | 1E+20,0000,0000;0000,0000,0000,0000 | |
| 103 | 1E+40,0000,0000;0000,0000,0000,0000 | |
| 104 | 1E+80,0000,0000;0000,0000,0000,0000 | |
| 105 | 1E+100,0000,0000;0000,0000,0000,0000 | |
| 106 | 1E+200,0000,0000;0000,0000,0000,0000 | |
| 107 | 1E+400,0000,0000;0000,0000,0000,0000 | |
| 108 | 1E+800,0000,0000;0000,0000,0000,0000 | |
| 109 | 1E+1000,0000,0000;0000,0000,0000,0000 | |
| 110 | 1E+2000,0000,0000;0000,0000,0000,0000 | |
| 111 | 1E+4000,0000,0000;0000,0000,0000,0000 | |
| 112 | 1E+8000,0000,0000;0000,0000,0000,0000 | |
| 113 | 1E+1,0000,0000,0000;0000,0000,0000,0000 | |
| 114 | 1E+2,0000,0000,0000;0000,0000,0000,0000 | |
| 115 | 1E+4,0000,0000,0000;0000,0000,0000,0000 | |
| 116 | 1E+8,0000,0000,0000;0000,0000,0000,0000 | |
| 117 | 1E+10,0000,0000,0000;0000,0000,0000,0000 | |
| 118 | 1E+20,0000,0000,0000;0000,0000,0000,0000 | |
| 119 | 1E+40,0000,0000,0000;0000,0000,0000,0000 | |
| 120 | 1E+80,0000,0000,0000;0000,0000,0000,0000 | |
| 121 | 1E+100,0000,0000,0000;0000,0000,0000,0000 | |
| 122 | 1E+200,0000,0000,0000;0000,0000,0000,0000 | |
| 123 | 1E+400,0000,0000,0000;0000,0000,0000,0000 | |
| 124 | 1E+800,0000,0000,0000;0000,0000,0000,0000 | |
| 125 | 1E+1000,0000,0000,0000;0000,0000,0000,0000 | |
| 126 | 1E+2000,0000,0000,0000;0000,0000,0000,0000 | |
| 127 | 1E+4000,0000,0000,0000;0000,0000,0000,0000 | |
| 128 | 1E+8000,0000,0000,0000;0000,0000,0000,0000 | |
| 129 | 1E+1;0000,0000,0000,0000;0000,0000,0000,0000 5 6 |
34028236692093\ 84634633746074\ 31768211456 |
|
1 While in the radix-16 system a comma is used to
separate 4-digit segments from one another, a semicolon is used
to separate 16-digit supersegments consisting of four
4-digit subsegments from one another.
2 The 65th square of squares is written as 1E+1;0000,0000,0000,0000, but as even the exponent is getting larger and larger with more and more zeros, we could also abbreviate the exponent, because it has the value of the fifth square, namely 1;0000,0000,0000,0000 = 1E+10. In this way, the notation becomes triple-layered, for 1E+1;0000,0000,0000,0000 is the same, then, as 1E+(1E+10). In radix-16 terms this stands for 10^(10^10); in radix-10 terms for 16^(16^16). In this expression 16^16=18446744073709551616. Hence, the value of the square is (2^4)^18446744073709551616 = 2^73,786,976,294,838,206,464. Some radix-10 data about this expression are, according to WolframAlpha at https://www.wolframalpha.com/.:
Power of 10 representation: 10^(10^19.34658948616843)
The last four digits are the same as those calculated by me
for the 65th square in the radix-10 table.
Number length: 22212093154093428530 ≈ 2.22121×10^19 decimal digits Last [ten] decimal digits: 2070255616 3 The value of the 81st square of squares is 16^(2^80) = (2^4)^(2^80) = 2^(4*(2^80)) = 2^(4*1208925819614629174706176) = 2^4835703278458516698824704. Some radix-10 data about this expression are, according to WolframAlpha:
Power of 10 representation: 10^(10^24.16306941679213)
The last four digits are the same as those calculated by me
for the 81st square in the radix-10 table.
Number length: 1455691736946666932084499 ≈ 1.45569×10^24 decimal digits Last [ten] decimal digits: 3309142016 4 The value of the 101st square of squares is 16^(2^100) = (2^4)^(2^100) = 2^(4*(2^100)) = 2^(4*1267650600228229401496703205376) = 2^5070602400912917605986812821504. Some radix-10 data about this expression are, according to WolframAlpha:
Power of 10 representation: 10^(10^30.18366933007175)
The last four digits are the same as those calculated by me
for the 101st square in the radix-10 table.
Number length: 1526403418760588224977435309442 ≈ 1.5264×10^30 decimal digits Last [ten] decimal digits: 3851990016 5 The 129th square of squares has been chosen as the last one here on the basis of a typically radix-16 criterion: in its notation this number consists of a 1 followed by exactly two supersegments of 0s. (The reason not to stop at a 1 followed by one supersegment of 0s was that stopping at the 65th square with this radix-16 notation would not enable us to establish the 100-term final 4-digit cycle in the radix-10 notation.) 6 The value of the 129th square of squares is 16^(2^128) = (2^4)^(2^128) = 2^(4*(2^128)). The value of 2^128 = 340282366920938463463374607431768211456. The value of 4*(2^128) = 1361129467683753853853498429727072845824. (The values of 2^128 and 4*(2^128) calculated with the Online Big Number Calculator at https://defuse.ca/big-number-calculator.htm, but the last step, the value of 2^(4*(2^128)) was too big a step.) Some radix-10 data about 2^1361129467683753853853498429727072845824 are, according to WolframAlpha:
Power of 10 representation: 10^(10^38.61250920866323)
The last four digits are the same as those calculated and
predicted by me for the squares 29, 129, 229, 329, 429 and so on.
Number length: 409740797754957455000048437000412930801 ≈ 4.09741×10^38 decimal digits Last [ten] decimal digits: 6873865216 |
||
The connection between the squares and morphemic economy
In the special paragraph about the micromacrobinary supersystem i have already touched upon the fact that in an integrated linguistic-mathematical system a radix must not require too many morphemes, a reason why a superradix larger than, say, twenty stands no, or little, chance of ever becoming the superradix of an integrated numeral system. Furthermore, it would be totally out of place to select, for exampple, a radix 16 and to continue to call numbers such as 13 [10]=D [16] and 31 [10]=1F [16] "thirteen" and "thirty-one", because their names of two and three morphemes could only acquire their meaning in a denary morphemic arithmetic. Another point is —and this depends, of course, on the natural or synthetic language used— that morphemes have to be assigned more carefully and more sparingly as fewer of them are or can be made available. Thus, in English there is a special morpheme for 1,000 (thousand), whereas there is no common morpheme (anymore) for 10,000. (Myriad is antiquated, while Chinese, for instance, has always had traditional 萬 or simplified 万, wàn.) From the perspective of morphemic economy you would call 1,000 "ten hundred", unless you have plenty of morphemes left; and you would use a new morpheme for 10,000, because a duplication of the same numerical morpheme on the same level, as in hundredhundred is undefined on morphemic-arithmetic grounds. (For the same reason 100 itself is not named "tenten".) In English there is a special morpheme for 1,000,000 too (million), but in a radix-16 system the special morpheme should go to 1,0000,0000, a 'hundred million' as far as the number of zeros is concerned. (In Chinese, the character and morpheme for this number is 億 or 亿, yì.) In general, you need either a new morpheme when you reach the next square of squares or you must have some type of formula which tells you which combination of at least one formulaic morpheme and one or more morphemes for smaller numbers refers to the larger number. In any event, keeping track of the sequence of squares of squares will be indispensable.
CONCLUSION
Universalization, a penetratingly far-reaching form of innovation, opens up new vistas, by putting an end to outdated preconceptions and old prejudices; and also by defying certain conventions. One such convention is right-associativity in mathematics. In the universalization of arithmetic operations the exponents of right-associativity never seriously analysed the pros and cons of the two mutually exclusive universalizations possible: they stuck to their convention and were probably pleased that it led to the biggest numbers in the fastest way. In this article i have discussed one of the most impressive features of the left-associative chong operators: the chong-3 sequence of squares of squares. Initially i used radix 10 to show how extraordinary this sequence is, before changing over to radix 16, not as a paragon in itself, but as a subradix in a supersystem with the first radix of all. My radix-10 presentation led to numerous interesting observations; my radix-16 presentation proved how futile they were, even tho similar observations may be quite useful in other cases. As far as i know, no-one before has shown any serious interest in an integrated linguistic-mathematical numeral system, if only because linguistics and mathematics do their work on branches of the tree of science very remote from each other. Yet, these two branches need to meet where it concerns the vocabulary of arithmetic, especially the words for numbers. I have not denied, let alone disproved, that right-associativity in arithmetic universalization serves the BIC best. Ironically, however, it is the entirely systematic approach of the squares of squares which discloses a numerical world in which googols and googolplexes (of size 10^(10^100) [10]) are mere peanuts in comparison with a number such as Square Four-hundred-and-one (of size 10^(10^120.49) [10]) and its successors. Nevertheless, no approach in arithmetic and in the history of counting is systematic that implicitly and unquestioningly takes the primacy of integers over portions (denigratingly called "fractions") for granted. I have confined myself to integers only temporarily in order to make it easier to read for a contemporary audience of whom most may suffer from an (adult) integer bias; and of whom all lack the terminological apparatus to deal with portions on an equal footing. This may be an incitement rather than part of a conclusion: that the systematic number traveler goes up to the infinite and down to the infinitessimal in one move, without fear or favor.
APPENDIX:
The 21st Square of Squares Written in Full
Showing the exact radix-16 notation for Square Twenty-one
Since the value of the twenty-first member of the elementary sequence of
the squares of squares is 1E+10,0000 in radix-16 notation, and since
100000[16] = 1048576[10], the number written in
full in radix-16 notation will consist of one 1 followed by
1,048,576 zeros, a total length of 1,048,577 digits.
Below it will be explained that the total length of the same number in
radix-10 notation is 1,262,612 digits, which is 214,035 digits longer.
Nonetheless, the length of the radix-16 notation is still 83.0% of the
length of the radix-10 notation.
Of course, more impressive is that the former notation uses only one digit
(0) after the very first 1, whereas the latter notation uses
all ten digits almost endlessly.
You may have a look at the radix-10 notation now and content yourself with
the idea that the radix-16 notation is one-fifth shorter, and that after
a 1 every figure you see there will be a simple 0.
Should you like to see the radix-16 notation on its own, then you can have
it generated here by a JavaScript program (which only takes care of
the presentation).
There are 65,536 16-zero supersegments of which the four-zero subsegments
are separated by a space, so that the appearance of the number will not
adversely affect the general layout of this page.
Push the following button if you want to see the whole 1,048,577-digit
number in five steps, starting from the first 1/16th part (6.25%).
Finding and showing the exact radix-10 notation for Square Twenty-one
Since the value of the sth square of squares, for s≥1, is
2^(2^(s+1)), the value of the 21st square of squares is 2^(2^(21+1))=
2^(2^22)= 2^4194304. But how much is this?
2^4194304=? [according to WolframAlpha (at www.wolframalpha.com/), which
gives the following information about the number]
Number length: 1262612 decimal digits
Last few decimal digits: ...8394198016
Power of 10 representation: 10^(10^6.101269676953261)
Decimal approximation:
2.06506353983588792439911949458165\ 01695274360493029670347841664176...
× 10^1262611
The ten last digits shown by WolframAlpha correspond with the outcome of
the Online Big Number Calculator at
defuse.ca/big-number-calculator.htm.
Push the following button if you want to see the whole 1,262,612-digit
number in seven steps, starting from the first 1/64th part (1.56%).
2^4194304 = [according to the Online Big Number Calculator,
which offers the exact number itself; first 10 digits of each part
shown in red by author]
020 650 635 398 358 879 243 991 194 945 816 501 695 274 360 493 029 670 347 841 664 176 800 041 553 335 652 936 057 509 677 535 527 151 427 868 237 064 574 934 824 549 293 767 546 359 077 920 008 818 501 313 826 426 823 106 013 346 012 778 095 984 519 801 219 909 531 075 504 287 833 161 324 840 811 684 971 720 284 491 337 186 421 302 100 076 509 403 419 310 287 743 147 286 205 798 438 391 891 910 433 320 816 354 801 660 161 002 935 402 954 568 571 003 081 410 242 475 346 704 885 642 194 132 346 012 204 417 456 032 430 353 391 417 591 466 278 673 352 755 565 006 094 263 750 177 280 726 036 253 113 510 694 507 482 207 519 754 056 595 315 720 092 484 784 103 391 134 845 232 251 829 862 635 063 872 880 713 703 849 779 393 812 835 168 305 411 518 046 989 472 329 311 728 260 530 608 777 421 831 520 043 254 548 404 201 827 005 795 137 367 646 261 052 061 654 579 029 323 493 859 679 786 690 498 837 065 698 423 477 573 821 529 014 844 741 574 575 824 006 613 498 018 575 107 042 468 295 045 569 151 710 203 003 120 728 243 352 497 582 775 250 167 786 050 106 244 195 250 645 288 190 283 533 077 837 288 052 527 533 280 640 970 024 559 638 002 882 824 665 824 080 142 766 202 780 625 376 961 666 657 630 997 398 134 787 448 681 657 178 837 727 788 110 375 597 422 716 407 295 985 335 777 454 833 638 174 398 931 969 736 624 526 255 124 137 734 328 090 369 360 079 548 102 682 566 791 774 231 733 756 652 407 037 854 427 276 867 019 479 574 350 087 127 958 512 940 606 349 448 808 415 959 634 200 733 958 014 722 918 126 641 150 929 877 229 980 036 015 090 690 098 587 383 449 290 065 840 861 968 628 403 770 557 600 824 569 449 945 692 977 916 986 590 020 768 596 954 800 079 495 642 370 966 170 563 205 713 536 877 346 406 241 525 149 141 116 970 415 522 548 423 511 903 060 423 476 474 847 692 579 492 769 123 210 954 116 060 977 251 929 029 210 342 331 182 360 039 483 549 136 142 916 608 606 499 103 817 079 107 742 457 998 684 662 157 493 889 313 988 894 597 363 001 812 651 584 278 186 406 925 881 730 528 942 785 280 131 523 440 821 730 492 965 282 487 708 607 263 815 347 784 811 920 503 948 625 758 271 307 978 475 205 236 865 735 463 269 055 211 276 546 773 127 188 134 656 800 409 245 768 696 999 421 318 531 125 153 875 652 239 426 896 347 836 006 026 320 000 184 637 588 791 399 752 269 884 683 503 838 813 236 714 126 333 082 989 272 225 916 087 656 005 897 978 857 199 846 731 321 966 234 455 392 121 391 915 037 833 159 860 368 421 798 697 269 175 900 770 018 931 838 227 462 014 232 109 387 847 386 567 268 693 173 238 346 235 322 127 079 245 049 553 734 232 383 970 467 240 074 957 944 865 882 899 051 332 716 801 084 258 149 770 826 613 065 495 480 552 699 057 769 518 536 892 521 846 116 133 533 014 561 662 729 512 945 896 476 307 398 786 979 826 357 295 347 152 554 932 272 533 137 280 672 882 879 566 787 294 438 514 332 078 468 679 434 614 654 455 414 223 736 886 718 601 041 377 747 112 959 418 317 897 096 193 695 285 020 099 917 349 565 807 341 290 865 319 208 917 776 939 056 435 583 080 174 798 668 704 937 874 107 890 539 301 087 799 439 060 649 208 756 713 343 345 920 295 993 038 851 826 640 651 736 711 179 583 262 742 825 990 137 162 655 502 415 662 387 396 190 012 487 317 543 943 038 289 911 667 314 878 343 049 671 714 498 524 392 745 324 890 536 000 714 221 872 491 963 265 925 930 748 323 545 213 793 085 571 688 669 929 063 564 591 181 905 347 504 338 195 872 119 998 034 393 299 900 105 043 249 185 728 873 004 515 222 998 351 704 120 003 427 062 153 831 029 987 186 632 866 557 403 710 504 931 151 452 370 510 371 310 488 053 624 305 567 887 975 421 711 504 626 290 010 603 881 022 042 968 965 801 070 532 536 042 546 027 060 284 280 239 098 199 347 908 822 473 940 947 878 906 932 383 071 214 806 666 605 954 816 142 041 392 169 855 659 621 832 058 047 830 264 596 461 995 647 593 266 405 239 340 499 260 027 131 689 397 307 163 200 891 396 366 156 979 820 547 112 846 633 003 032 530 135 488 885 041 572 341 648 542 585 979 281 808 377 793 012 395 796 823 585 146 880 424 785 199 826 982 441 261 717 325 752 549 609 594 921 867 319 114 551 333 450 031 087 774 456 261 388 644 452 605 031 263 456 148 748 673 482 266 297 390 128 683 919 661 551 784 915 124 105 233 290 721 060 981 043 506 782 088 004 823 123 907 487 907 546 693 884 671 089 672 679 435 044 235 297 522 645 441 202 601 236 964 016 714 741 143 744 480 127 212 175 637 744 963 834 790 996 817 802 860 195 224 687 955 779 537 406 743 247 473 877 286 766 577 466 649 669 557 890 452 775 498 169 023 704 281 951 356 850 580 508 561 392 323 131 359 353 172 690 876 397 105 282 422 982 427 823 436 037 859 729 567 152 594 308 102 166 508 047 400 305 960 332 163 398 756 867 823 541 438 385 602 592 826 978 278 118 036 696 636 178 416 096 298 071 111 466 258 904 766 181 440 411 950 702 504 321 148 740 948 092 964 102 382 939 980 657 232 430 440 521 122 181 578 045 304 611 287 694 120 710 729 336 901 919 040 887 079 059 001 648 504 838 468 420 464 974 971 555 301 339 931 223 306 392 065 431 365 458 031 336 553 661 839 895 653 505 959 791 047 544 622 260 200 718 488 676 184 837 391 256 404 380 945 687 003 054 983 452 101 251 177 505 592 053 304 029 469 457 097 983 954 909 343 339 866 014 560 495 095 267 414 146 189 826 994 283 231 524 234 579 442 033 445 546 274 769 337 027 687 828 931 248 824 610 231 942 673 019 854 143 430 425 465 870 988 850 676 419 133 336 491 042 936 654 291 108 533 601 345 065 567 112 197 709 555 834 237 742 245 563 496 262 722 573 617 656 504 688 008 122 360 733 037 334 140 276 525 554 175 744 901 500 452 916 654 036 288 303 764 177 277 240 479 274 733 104 500 528 750 056 226 300 738 307 928 341 896 015 280 273 071 885 701 369 712 902 355 989 104 882 343 398 988 261 335 127 259 052 391 286 734 863 747 975 389 457 407 643 241 182 579 665 653 843 711 945 595 182 020 127 490 041 273 829 967 378 655 152 217 825 923 491 569 042 837 417 485 053 120 210 620 092 997 556 075 066 458 879 141 398 131 610 852 031 585 698 813 739 008 570 137 926 286 131 150 626 143 383 314 729 504 322 597 350 110 367 495 518 532 659 239 341 345 774 918 156 040 345 476 886 194 146 649 452 447 175 531 320 933 532 968 322 704 481 641 893 969 072 400 161 939 473 610 421 016 579 314 314 095 312 856 324 535 155 391 671 182 783 053 601 375 887 923 847 038 632 123 175 648 473 255 191 717 088 266 706 512 989 096 258 110 450 820 596 151 435 828 471 891 531 575 470 729 052 257 459 405 670 631 186 212 588 579 432 698 739 574 012 453 270 979 815 981 244 403 193 890 542 179 869 130 396 214 762 373 656 748 806 709 450 726 194 908 004 458 928 658 129 204 999 395 766 301 665 503 644 256 629 120 811 148 140 989 493 916 977 075 019 398 432 710 345 886 717 400 741 355 400 023 621 244 106 192 004 463 601 110 417 319 440 515 164 956 446 683 451 768 014 929 112 768 126 407 594 782 178 275 046 269 875 869 612 643 537 982 517 781 501 858 654 714 912 617 431 784 957 742 447 376 213 323 572 635 907 152 741 406 279 169 889 716 420 833 071 810 540 404 029 890 919 931 409 437 331 573 916 082 434 934 548 180 349 310 770 738 158 788 421 800 721 887 241 350 481 398 709 077 577 825 060 906 056 931 060 497 788 672 190 869 162 508 205 557 178 092 426 560 291 996 114 409 748 774 656 794 109 369 020 546 522 966 979 575 773 145 099 418 857 648 274 003 295 160 270 544 500 672 534 647 640 382 622 949 023 728 752 295 948 780 150 182 626 197 603 301 850 881 483 780 069 510 482 699 393 168 123 629 558 945 350 262 969 707 623 776 623 381 471 011 750 852 075 978 118 678 776 449 052 152 538 903 595 998 610 745 458 855 152 208 313 359 717 224 768 653 069 237 100 103 738 769 668 923 078 595 712 601 822 693 034 817 955 926 388 557 018 532 220 268 957 350 228 325 878 197 759 238 822 723 584 374 978 179 686 982 593 046 376 952 592 546 105 956 821 123 752 555 132 165 979 998 955 164 754 692 556 815 449 972 651 146 829 770 708 919 250 303 635 825 904 394 300 620 334 156 697 222 470 022 010 629 757 218 655 623 627 464 565 119 331 723 671 988 812 041 845 850 186 055 057 733 724 836 481 419 759 756 400 692 496 801 504 632 764 993 080 954 137 383 595 537 140 624 797 489 601 657 367 868 485 657 207 528 857 112 787 421 425 100 838 867 117 894 788 218 273 408 342 526 241 270 888 971 645 274 987 257 105 687 819 248 384 800 893 542 954 242 362 765 592 197 716 158 765 640 179 989 361 646 276 679 455 402 990 999 089 631 849 925 443 032 740 340 379 987 891 233 157 360 093 559 979 624 726 681 499 120 530 145 236 797 084 548 672 756 839 217 196 674 468 069 949 571 672 954 839 434 654 003 414 970 523 995 617 728 788 552 230 402 869 734 490 532 822 788 407 871 198 063 785 048 332 837 977 151 323 449 464 512 367 983 598 207 785 734 323 999 287 719 537 841 943 615 665 311 500 604 331 289 652 260 286 891 427 419 260 280 027 524 058 637 974 118 307 821 154 332 252 640 260 779 834 621 594 110 498 324 047 249 047 497 547 033 792 372 111 711 230 892 734 949 494 010 868 975 811 964 767 643 503 791 512 931 864 578 789 050 895 800 030 077 738 941 188 949 300 953 214 659 039 665 268 743 350 203 136 185 026 418 419 591 895 035 559 831 191 683 895 962 965 783 470 343 187 936 077 039 299 597 329 246 834 409 674 637 556 076 241 449 974 996 856 576 487 764 677 556 288 806 620 426 922 502 283 490 196 554 566 826 768 001 997 524 354 712 302 398 539 755 738 547 912 841 321 384 401 729 014 503 960 826 577 324 827 519 416 538 186 800 243 236 377 930 458 084 996 779 004 869 552 464 450 349 375 148 417 519 222 475 350 780 810 088 161 886 034 436 171 172 286 206 342 162 257 597 353 388 032 599 996 303 717 983 494 453 859 928 128 775 422 993 468 375 266 909 004 095 337 540 232 379 729 271 066 972 760 435 636 288 009 065 801 095 971 202 175 578 071 369 429 661 119 388 744 381 129 314 380 199 071 628 883 213 998 649 632 403 916 173 512 131 199 710 807 837 309 834 766 122 054 157 258 331 187 030 595 136 287 194 491 042 800 597 663 061 932 769 615 278 044 705 770 683 635 726 107 438 211 523 740 564 555 926 097 971 137 205 545 320 645 249 886 632 248 498 275 582 382 476 146 190 949 315 534 766 570 617 404 567 919 776 548 286 424 591 312 725 575 037 945 759 207 114 660 819 219 715 011 357 909 770 853 154 974 164 856 263 021 316 814 632 576 380 367 153 886 042 708 594 609 822 282 788 993 459 117 322 945 336 408 337 484 177 952 041 111 562 232 980 795 961 453 274 024 105 261 203 168 703 087 710 115 030 110 902 709 991 642 553 958 449 375 297 526 602 530 935 282 604 851 882 885 174 380 724 180 074 225 255 016 029 152 878 329 699 844 002 871 198 187 690 649 701 499 640 835 267 184 152 498 306 149 096 992 057 368 312 048 087 545 866 770 173 376 552 311 492 230 560 905 434 968 196 266 717 819 643 677 109 139 368 710 195 879 666 504 921 688 142 561 962 465 665 907 329 754 111 753 217 855 182 711 377 523 730 147 753 285 837 561 920 226 484 025 962 711 199 994 066 741 608 004 297 795 699 497 057 274 962 181 859 668 314 198 859 119 925 062 195 117 792 398 389 248 498 414 918 762 220 304 433 468 630 698 460 263 844 479 224 652 823 967 793 434 845 091 540 382 199 009 379 451 811 068 458 853 304 967 061 287 071 238 751 973 692 480 044 486 616 462 935 460 336 597 407 953 227 630 348 680 973 183 621 556 366 075 886 365 785 945 551 656 356 720 196 514 070 212 475 887 816 497 524 798 708 785 602 190 189 127 417 000 501 042 440 747 659 860 851 599 246 847 801 032 770 494 657 933 337 097 447 010 357 381 629 494 063 402 968 982 060 313 838 296 819 479 148 319 143 289 890 818 863 671 506 065 071 840 646 765 061 933 197 362 272 497 857 502 075 421 433 484 037 780 125 188 475 230 460 408 237 161 661 125 100 706 928 487 243 173 654 295 768 253 788 613 704 914 158 505 055 694 095 625 419 687 889 052 939 683 128 198 430 163 533 605 430 243 790 274 072 039 022 338 501 378 779 863 405 246 899 165 533 572 192 297 822 281 515 635 416 707 282 792 431 350 114 336 153 062 636 067 699 736 129 265 752 302 953 459 529 644 289 925 198 580 557 477 050 808 172 195 748 913 482 830 324 319 103 867 744 112 555 293 108 965 999 381 228 242 392 363 301 780 407 886 096 277 936 491 129 019 956 009 656 840 482 182 933 251 658 701 208 116 547 389 397 399 876 883 055 849 358 212 140 572 132 502 446 087 697 724 827 226 015 391 791 503 657 507 854 632 606 913 701 780 977 223 528 518 058 205 148 371 680 773 906 757 810 945 903 520 833 884 487 774 047 929 130 603 845 959 297 939 473 349 201 458 718 268 802 533 824 436 803 160 415 480 319 414 698 821 525 498 984 639 378 268 794 296 327 306 508 125 065 606 224 857 179 491 892 084 118 491 051 053 520 022 336 570 852 794 281 323 292 350 597 633 731 075 828 100 157 260 905 867 971 085 139 595 367 348 654 105 767 071 987 458 622 629 382 092 301 052 323 181 397 200 464 366 752 955 126 858 384 557 847 101 449 511 076 976 913 946 331 782 357 354 979 034 545 470 451 231 313 234 934 091 724 942 731 776 607 266 210 301 092 397 803 623 330 696 519 967 236 319 085 334 207 699 417 691 044 016 714 923 659 321 059 091 707 472 917 327 391 767 576 766 850 310 717 308 792 481 678 222 121 936 384 216 765 274 078 143 273 728 143 338 695 025 976 133 791 987 721 778 066 989 120 462 117 204 821 189 532 232 342 431 820 004 859 482 593 049 482 317 144 913 799 322 320 714 886 221 411 708 309 741 091 130 449 991 430 207 087 905 693 360 655 695 167 890 071 223 158 733 507 354 484 875 507 331 328 611 016 811 916 752 842 856 426 016 513 525 076 074 332 514 712 960 653 075 189 998 883 148 385 901 467 821 152 899 600 353 653 984 173 855 336 990 604 926 373 803 231 990 796 818 782 350 594 045 481 548 104 324 994 520 491 323 454 730 526 671 751 837 752 192 092 956 583 461 623 263 250 750 884 205 006 767 322 302 580 137 780 194 060 682 524 287 407 335 488 288 532 230 980 466 524 275 143 056 122 473 627 029 906 701 557 403 981 747 064 731 049 972 870 521 030 785 797 751 298 346 520 052 111 691 568 822 304 544 370 475 599 635 274 175 014 447 407 545 060 003 573 196 916 383 359 138 307 133 064 746 292 635 841 430 171 316 571 426 552 487 988 029 080 462 530 776 925 812 324 728 907 392 670 391 727 000 549 384 617 701 184 158 797 656 188 978 027 233 245 512 956 743 447 193 026 962 424 712 592 900 669 351 816 064 897 858 762 691 112 131 703 819 223 778 075 120 938 382 675 484 197 499 364 703 524 272 697 256 309 034 181 656 946 988 069 823 941 070 251 924 132 108 774 593 462 295 056 653 879 183 322 743 301 456 686 612 302 898 315 931 798 724 088 529 441 266 109 428 994 886 257 744 635 868 358 301 852 863 761 789 619 993 481 563 874 552 136 733 108 481 694 171 596 141 830 658 522 420 343 583 558 381 041 872 387 585 119 743 558 889 509 514 900 576 730 016 883 693 743 408 837 433 645 498 579 079 164 244 965 725 608 069 119 039 919 404 167 285 204 494 330 825 676 335 610 197 313 356 396 180 306 421 227 870 200 327 774 748 278 957 848 830 148 239 902 684 752 601 141 177 256 187 545 582 557 120 867 205 543 730 458 874 530 682 279 149 470 202 439 897 517 977 442 359 147 940 835 896 004 364 192 250 184 562 416 071 751 671 783 425 980 805 791 718 804 686 379 930 884 935 004 392 416 409 651 718 388 877 505 893 408 964 954 535 474 538 498 896 892 639 029 544 366 987 066 679 490 146 506 679 031 040 033 383 704 980 874 880 726 107 019 567 293 865 317 694 832 828 768 307 226 425 979 942 685 070 108 287 501 356 848 471 648 007 532 709 024 497 904 800 180 784 897 443 422 506 191 171 846 468 767 504 563 551 631 522 660 699 270 569 213 123 442 715 785 687 344 896 041 149 410 372 491 361 601 021 048 696 850 798 554 328 542 126 284 808 689 321 150 546 294 590 107 500 322 235 541 014 799 126 119 397 265 916 865 298 630 846 389 055 355 577 652 953 846 309 546 357 094 040 753 805 856 668 818 136 778 129 861 453 448 641 974 116 829 562 782 197 214 075 723 491 978 602 109 332 068 945 249 474 861 042 695 592 598 690 747 017 504 910 485 833 577 872 592 376 803 166 584 385 288 551 890 943 703 663 665 823 714 744 950 984 654 589 510 192 152 816 675 850 051 388 691 336 811 673 381 735 101 807 196 316 982 332 771 540 890 154 621 443 030 815 541 076 705 814 576 216 568 069 715 328 495 090 311 426 636 597 952 902 971 663 617 554 941 411 569 454 946 585 011 139 622 210 186 933 296 189 616 638 582 043 995 176 366 483 017 540 495 906 501 968 550 639 804 798 991 623 736 482 840 528 511 839 125 461 658 757 605 829 419 643 492 752 516 763 353 243 255 928 100 449 660 930 819 725 804 816 743 350 966 227 367 592 912 394 437 781 296 531 765 112 207 566 601 841 775 749 544 645 702 570 064 127 039 513 066 186 159 934 663 574 923 379 399 899 628 614 190 153 002 159 823 497 929 689 462 781 567 758 383 238 566 266 487 846 940 896 762 265 737 692 303 220 779 047 986 864 618 620 103 985 131 133 609 707 034 027 782 220 848 606 406 413 063 619 289 532 900 716 164 022 484 475 772 711 751 928 080 154 241 743 425 347 787 929 012 624 757 057 405 444 848 450 240 141 229 857 051 710 324 430 067 356 158 904 058 706 513 154 405 902 430 784 356 714 561 954 386 118 523 313 343 255 334 329 112 697 052 804 394 054 918 078 677 517 704 263 419 856 358 905 400 357 672 692 586 499 833 422 708 857 844 599 594 415 914 485 017 882 582 603 527 274 101 264 695 508 467 506 764 462 351 903 817 015 848 597 229 260 081 369 977 636 318 552 966 463 060 325 934 056 472 475 578 670 671 372 874 244 229 213 656 818 311 062 823 508 255 616 425 100 345 384 013 449 447 094 014 880 774 860 917 750 230 774 650 505 702 698 742 824 319 751 906 366 402 566 153 870 581 044 256 481 055 063 807 059 470 327 829 390 265 783 446 474 469 098 530 357 197 333 393 093 194 325 951 646 349 209 017 920 350 963 725 666 874 776 401 120 556 958 755 751 524 082 625 236 845 326 319 956 469 922 983 587 861 939 114 754 056 020 076 155 561 053 698 120 101 727 672 975 078 600 515 917 438 835 586 748 331 850 236 964 486 807 515 975 205 604 819 688 444 887 029 329 736 338 604 338 551 643 840 722 695 207 432 061 402 060 528 759 882 296 909 621 308 088 877 946 771 257 409 203 437 456 599 739 361 656 612 933 808 472 975 386 885 099 515 785 793 608 664 587 857 753 047 146 719 539 072 493 225 381 150 695 521 224 376 686 551 545 809 765 115 112 184 941 189 286 646 996 221 393 455 113 837 110 851 470 634 462 183 702 421 078 555 986 349 311 314 962 590 516 233 900 630 344 943 732 975 833 726 195 366 725 907 323 073 044 463 718 009 496 572 788 486 321 720 122 195 118 855 727 680 808 441 529 109 078 722 422 824 638 136 494 639 946 043 869 056 262 471 710 085 234 458 485 057 037 980 895 974 324 162 909 631 994 352 753 227 620 847 733 679 413 391 680 973 938 964 368 061 105 799 540 444 361 958 162 840 798 653 109 030 574 686 292 591 342 308 008 669 697 045 774 151 308 523 397 026 648 925 750 341 279 120 225 752 066 679 551 732 149 916 252 072 673 775 539 409 176 253 344 882 718 979 975 185 618 708 048 520 096 872 137 778 948 628 051 191 414 005 340 951 507 031 222 264 384 318 251 026 224 376 810 354 902 985 959 923 713 117 681 387 953 435 956 074 329 558 442 918 705 245 051 737 677 245 451 469 165 966 131 808 658 044 057 876 605 048 841 182 127 140 613 312 356 831 193 260 016 788 134 255 448 874 251 492 867 414 928 735 431 024 066 431 703 476 382 784 775 799 933 167 163 027 240 595 340 114 234 972 754 105 673 552 742 349 142 882 347 624 627 666 593 622 728 354 499 659 494 332 882 928 275 408 681 948 601 190 440 761 793 852 958 064 067 144 583 616 756 579 236 433 267 286 222 090 752 698 571 900 295 766 927 649 349 341 254 306 826 858 382 487 465 564 764 380 853 003 407 320 633 144 153 967 116 779 953 732 932 956 113 311 521 175 732 503 260 373 296 853 615 452 198 217 826 554 016 186 963 121 041 409 031 289 804 639 872 303 194 965 030 038 605 666 880 885 970 350 519 800 814 606 911 024 501 547 683 194 855 288 396 055 360 890 571 638 369 923 113 821 286 338 891 913 747 959 952 285 090 915 753 403 685 897 104 514 686 243 362 153 165 925 346 093 938 982 781 299 937 032 603 553 235 261 393 021 815 968 371 281 374 173 009 795 339 720 714 507 855 244 323 810 236 036 205 842 431 673 789 356 322 570 947 128 092 996 913 403 931 764 451 534 244 115 771 501 389 519 124 787 599 658 189 755 504 173 050 043 987 737 779 384 520 366 815 784 696 925 791 467 613 770 081 541 038 265 741 682 149 196 762 131 160 484 108 802 336 517 294 132 854 436 075 540 400 086 204 163 827 113 182 619 285 113 481 697 150 217 424 397 457 221 561 534 075 223 084 955 830 074 373 903 592 177 624 122 211 683 968 024 022 155 166 469 632 142 873 203 832 902 576 981 749 774 356 165 860 924 936 321 267 260 904 546 409 443 930 863 639 545 642 453 123 121 096 576 631 133 747 686 293 230 922 693 688 016 792 378 310 818 317 715 748 854 503 150 473 455 375 739 396 974 229 127 173 224 480 018 043 277 454 222 642 510 619 072 174 968 062 133 792 681 675 766 315 548 039 549 452 930 116 567 583 034 806 345 731 893 399 187 678 946 936 493 871 043 469 425 046 909 364 454 836 231 525 172 295 520 232 569 715 910 026 064 104 996 196 478 064 309 823 263 555 000 755 785 132 093 490 247 994 520 331 525 902 735 978 904 619 966 369 639 607 293 072 621 713 250 977 880 478 704 393 760 266 619 163 028 992 607 112 657 757 590 412 227 365 249 528 719 691 413 613 429 473 797 809 130 514 012 094 619 033 828 540 009 000 734 730 967 348 631 010 772 426 029 220 206 829 634 732 773 622 474 181 351 103 908 779 589 018 407 052 551 914 202 073 406 383 390 449 130 360 096 746 040 733 938 630 718 085 767 226 287 074 618 899 430 175 600 726 543 035 340 415 189 607 185 510 548 721 534 905 045 957 554 140 048 416 964 262 700 574 729 586 451 247 562 839 414 680 608 923 101 991 921 161 194 467 831 030 757 572 236 997 545 643 355 164 505 248 541 706 109 410 807 170 979 585 865 888 265 292 532 870 737 345 616 955 058 680 978 117 598 093 624 946 014 903 312 660 758 594 170 157 895 122 161 054 830 616 733 742 737 107 255 414 684 097 918 013 783 920 065 273 806 561 553 603 440 279 799 887 562 119 183 521 261 073 251 263 206 289 871 237 866 230 522 688 251 456 686 525 168 768 426 171 391 039 646 384 792 522 368 574 938 300 637 643 115 437 128 045 109 775 528 314 632 751 274 710 316 880 214 011 158 255 077 774 516 630 394 054 510 693 768 452 597 166 805 535 160 201 234 530 154 016 315 019 537 919 208 166 365 503 173 654 013 119 626 569 262 151 842 719 892 937 075 484 302 846 791 646 298 641 751 359 237 670 433 815 243 228 202 139 823 439 022 606 226 153 068 437 822 256 929 746 203 715 714 762 725 461 726 082 212 031 169 117 941 781 406 826 092 467 027 860 458 785 933 694 680 362 650 637 939 775 498 674 293 227 845 844 824 393 361 512 986 288 375 667 969 105 358 495 263 029 460 504 104 262 405 145 658 955 034 291 332 433 909 129 034 870 394 847 224 936 716 388 961 276 632 083 026 501 266 663 919 872 259 805 582 258 761 911 262 327 969 192 398 204 600 786 568 898 116 531 224 707 484 821 915 583 373 415 498 628 796 235 941 506 367 406 659 234 827 012 164 288 548 482 419 929 362 945 528 083 264 423 464 762 204 023 728 076 982 331 310 840 529 738 369 573 703 395 739 010 997 325 720 205 052 935 681 785 571 577 612 172 827 132 940 868 033 283 947 409 702 018 826 072 460 968 250 820 388 959 547 570 845 655 886 653 113 067 119 516 591 579 585 311 302 314 126 637 480 583 778 391 657 752 919 950 829 035 450 754 630 128 088 646 346 233 864 452 510 448 978 123 847 229 112 138 355 178 504 242 358 511 534 098 733 008 348 735 867 647 455 343 483 510 689 082 308 148 910 140 528 901 698 965 290 700 577 696 094 142 139 568 801 805 228 684 878 192 258 452 819 393 161 558 794 230 569 479 013 362 253 745 645 760 513 026 343 711 561 323 716 584 647 797 617 413 217 224 934 224 835 460 899 444 643 471 133 529 431 694 864 520 256 629 649 313 307 428 771 397 447 858 086 989 798 790 561 950 117 708 414 100 911 728 185 846 995 719 866 782 070 294 185 420 283 915 964 070 952 757 467 769 059 943 595 248 849 222 424 781 588 412 765 790 721 329 448 299 326 129 586 693 597 092 566 036 124 232 939 607 871 239 581 917 015 903 953 958 549 809 774 890 324 831 897 285 817 725 080 667 553 152 322 965 147 937 992 429 948 945 416 790 246 974 393 261 860 031 292 954 485 088 965 296 921 619 590 923 349 059 320 881 636 083 707 587 491 127 840 881 671 252 307 010 452 999 752 006 133 720 706 611 042 243 183 426 974 468 740 981 099 400 559 906 974 998 813 958 331 782 249 988 714 180 628 491 083 599 331 872 049 634 545 434 771 079 895 770 658 723 142 523 678 433 798 659 529 688 310 206 542 129 394 911 288 664 157 268 694 908 252 985 186 335 995 035 583 475 392 616 873 040 873 902 980 570 237 874 424 498 548 540 610 680 799 524 403 056 862 673 361 035 715 241 619 541 862 600 385 117 984 487 591 824 906 933 065 543 185 080 764 709 976 532 774 089 748 631 449 797 427 193 033 781 177 117 368 567 775 086 706 680 001 541 946 912 946 205 947 171 192 515 852 074 477 581 310 445 301 119 847 960 992 280 278 336 025 488 997 047 197 730 482 577 785 184 504 822 615 801 871 957 722 963 758 066 015 399 621 400 589 307 890 185 909 236 398 952 923 553 595 491 693 818 148 018 926 316 039 356 133 572 048 780 192 575 964 818 721 388 835 057 481 770 733 553 499 611 627 785 801 070 101 830 995 519 543 521 384 714 470 007 902 637 843 213 563 597 078 774 428 419 086 667 052 503 379 883 671 018 788 012 497 164 688 220 259 978 847 301 735 269 409 405 388 428 155 722 190 830 305 420 853 112 386 595 689 020 778 087 126 706 498 271 284 248 366 369 540 577 054 359 525 785 787 383 966 525 854 603 077 699 312 111 395 845 247 114 980 563 274 900 969 350 341 340 914 445 733 292 606 684 171 100 652 582 278 976 291 406 499 574 511 728 304 706 849 115 095 124 691 830 292 867 111 886 905 532 893 268 845 041 912 356 090 406 807 960 337 664 072 113 435 482 768 891 237 135 528 025 099 438 571 348 423 388 327 781 641 120 998 394 309 975 631 286 775 566 736 279 551 918 163 154 219 493 555 757 890 041 536 726 286 475 580 773 175 539 186 431 377 686 774 663 822 547 356 522 129 613 832 719 224 667 921 350 892 728 724 232 923 867 567 310 252 301 380 029 099 584 069 182 241 427 723 557 238 768 469 165 456 585 612 356 473 880 025 066 899 593 915 962 197 642 430 352 209 777 925 013 561 280 817 258 275 618 901 624 634 784 526 388 862 432 285 676 839 915 085 707 647 047 996 718 082 622 755 610 034 670 929 118 521 910 826 019 360 505 982 532 536 486 616 928 516 439 975 355 240 300 752 491 508 516 119 645 108 258 900 117 280 597 695 508 530 414 899 097 992 393 785 198 571 113 157 505 465 152 247 273 295 943 431 345 982 438 570 021 093 499 992 091 752 783 259 328 261 077 221 114 373 988 426 805 055 533 768 329 925 168 482 163 808 696 346 398 011 923 896
636 283 990 026 657 915 429 471 580 037 609 446 157 177 215 138 420 654 396 556 286 027 321 427 341 048 767 840 909 687 684 831 483 067 756 772 633 038 652 882 301 989 551 039 066 623 164 682 363 230 436 386 796 765 540 522 938 334 458 671 934 575 191 041 600 177 183 646 426 051 781 098 799 400 040 533 712 911 983 016 373 749 064 284 114 341 205 090 395 409 049 942 611 286 833 803 971 790 903 757 528 495 401 188 781 684 235 347 927 306 258 227 800 218 389 831 981 596 801 023 754 304 364 498 237 888 491 808 901 631 754 080 418 622 813 484 068 418 285 831 198 098 215 670 269 973 901 605 149 554 321 126 410 814 957 604 023 246 484 503 444 583 413 087 644 995 428 135 732 143 922 533 722 627 772 075 646 449 099 438 609 259 136 364 923 279 801 919 527 918 498 612 013 443 915 197 990 277 926 060 446 264 649 806 035 405 602 320 789 372 063 959 792 473 436 096 577 672 700 240 601 576 541 686 077 605 571 166 469 013 731 082 548 646 724 624 971 277 397 757 672 309 915 528 863 056 522 332 460 281 596 850 495 723 923 121 649 676 261 661 294 940 621 890 150 041 745 223 927 746 647 785 267 137 596 777 777 690 241 061 795 606 295 833 030 240 952 730 768 332 693 744 298 710 689 437 819 292 526 080 065 938 338 190 832 661 743 146 972 057 617 833 452 899 267 207 376 795 882 887 728 185 914 919 274 154 392 970 370 302 738 310 080 408 256 094 187 593 568 435 140 470 781 210 550 270 565 015 817 905 588 806 793 516 145 865 639 344 953 058 604 196 408 173 395 403 083 751 439 003 488 364 593 188 778 703 292 334 650 154 670 862 696 868 307 741 081 277 467 474 293 886 445 323 262 365 060 291 620 469 983 846 328 039 563 429 398 853 844 363 733 358 884 933 045 774 676 042 568 604 936 875 246 324 305 557 631 136 506 450 581 151 077 635 172 441 237 353 008 140 005 029 718 059 760 572 933 728 184 838 469 272 905 588 428 396 206 462 368 624 186 341 990 224 188 272 415 153 981 431 375 030 968 728 368 712 370 422 375 338 406 849 142 283 597 827 858 545 572 823 378 750 843 502 001 921 204 831 386 172 343 830 648 675 268 150 165 681 043 641 855 339 886 966 239 756 814 377 179 371 755 541 894 541 500 083 435 781 213 080 627 052 138 877 545 580 225 898 702 267 118 177 464 254 048 076 261 736 594 780 735 114 544 170 201 403 547 941 957 893 844 989 284 532 242 500 308 384 987 838 357 815 862 430 626 852 759 390 194 819 807 686 054 288 537 584 031 757 702 071 135 538 403 944 831 454 478 600 251 647 266 457 667 925 953 813 202 277 820 057 131 517 226 626 004 389 455 718 678 597 980 120 398 685 564 276 262 908 411 551 437 736 374 408 217 245 548 016 046 655 358 944 007 457 083 215 307 782 160 608 164 743 471 919 112 432 105 386 745 788 057 753 310 304 789 309 210 933 028 949 571 945 338 413 502 557 221 767 816 629 327 711 435 154 401 779 639 620 105 044 601 861 220 662 107 996 699 634 913 544 060 307 228 131 622 448 267 081 626 384 575 042 247 357 171 666 051 843 925 725 853 737 210 175 327 938 048 266 380 333 532 093 955 193 520 188 347 998 191 581 887 611 661 507 625 708 503 700 105 393 544 341 099 006 998 289 307 645 633 400 539 719 808 051 513 402 025 320 441 934 801 437 563 618 418 247 462 334 383 515 394 981 341 121 563 707 613 073 832 767 979 661 476 324 741 998 039 054 188 861 426 860 097 833 220 391 961 695 122 245 227 015 700 786 252 817 587 105 436 616 337 280 133 377 672 190 341 142 425 645 280 529 735 688 336 495 577 752 172 484 547 509 762 869 602 946 397 235 282 171 975 127 898 950 427 594 564 569 448 177 190 423 935 368 223 260 614 122 038 010 607 713 735 649 469 686 334 195 021 209 010 509 662 496 332 726 358 175 766 770 740 981 469 144 222 085 405 902 261 557 732 042 279 480 643 073 414 116 792 394 962 009 985 954 253 972 945 429 293 219 299 850 723 083 716 130 111 811 920 919 808 312 926 973 638 986 527 362 076 405 475 435 968 102 824 733 483 352 549 297 927 532 180 874 987 466 200 994 756 549 523 017 142 576 899 750 057 938 419 216 880 542 022 185 881 987 779 625 084 786 812 312 974 965 477 473 212 570 575 410 081 794 664 292 152 473 756 634 215 997 805 014 367 450 078 999 080 478 228 064 981 168 339 819 384 701 678 163 333 776 538 636 408 838 183 476 091 934 916 466 873 463 374 975 096 564 418 826 567 718 623 061 162 111 139 280 490 562 677 659 435 044 674 233 214 588 513 178 548 193 711 632 518 660 093 390 489 193 396 687 049 568 401 911 080 612 260 139 692 105 497 036 122 300 158 714 747 801 134 136 386 266 138 720 939 890 549 253 602 840 669 869 774 289 494 715 549 780 333 837 984 064 588 662 570 255 306 104 362 536 312 365 214 156 129 823 803 507 024 145 513 553 448 637 714 406 599 249 588 236 891 962 835 005 257 254 206 032 159 851 142 925 561 441 550 837 662 101 035 488 983 854 581 042 593 543 994 175 849 816 169 736 433 657 151 615 054 409 701 296 862 497 451 129 760 964 732 424 352 207 739 385 884 834 703 624 003 829 951 541 063 169 775 208 463 634 442 298 896 253 057 506 841 886 167 346 895 497 093 163 032 772 620 274 518 960 757 534 138 162 397 283 429 383 336 770 554 413 083 130 638 169 746 775 213 454 790 572 397 629 713 583 167 892 532 300 760 277 744 066 061 767 148 397 811 401 957 749 008 327 591 152 229 887 535 046 509 470 950 439 075 335 425 730 185 147 808 133 453 552 301 524 388 267 629 178 319 461 292 187 519 495 987 046 425 718 617 819 332 104 399 818 736 444 858 362 993 639 947 077 771 810 701 904 800 063 267 760 694 875 431 044 673 328 139 371 689 906 587 343 349 354 782 797 657 972 464 299 063 598 348 617 982 706 180 915 221 284 062 954 917 126 078 871 752 335 595 971 186 685 775 282 063 550 881 863 631 437 327 286 885 581 810 398 430 134 091 104 435 237 742 824 689 308 755 062 813 880 101 562 229 123 804 960 613 389 287 517 865 409 770 512 930 023 722 636 086 353 976 858 633 703 050 565 918 942 301 746 751 176 866 043 161 089 744 306 710 639 480 531 927 390 506 801 692 532 227 174 589 473 830 011 926 943 648 139 372 286 552 122 022 602 559 952 939 677 210 206 862 438 245 475 821 883 484 826 544 569 153 433 865 031 397 719 008 229 109 880 481 912 230 733 053 019 186 040 399 703 481 436 489 875 202 107 425 487 989 484 540 152 591 088 815 808 367 261 426 322 823 219 505 339 809 194 124 356 775 007 982 734 267 416 089 565 955 563 937 032 570 083 577 802 902 137 167 148 710 992 519 714 440 618 767 616 527 156 556 847 541 033 327 139 724 997 126 048 509 994 627 697 239 639 899 332 420 440 371 499 321 446 958 365 696 468 081 604 254 938 296 236 783 258 744 642 336 334 868 186 657 759 466 965 982 029 460 203 627 787 369 968 139 886 053 596 020 048 115 774 787 811 500 630 815 977 185 178 704 712 855 322 441 747 389 521 183 822 956 036 854 886 113 649 595 850 490 556 535 050 359 001 754 730 621 876 645 621 952 431 539 639 159 415 198 816 132 477 561 707 068 490 279 655 809 098 407 603 629 251 967 390 037 809 958 700 766 814 709 623 833 404 405 100 500 966 353 215 585 869 581 434 099 537 254 382 954 857 332 595 278 367 123 647 946 302 536 614 464 554 117 957 333 641 449 107 523 665 940 027 471 801 930 054 254 081 099 047 521 495 279 140 161 237 868 051 394 722 668 806 047 634 505 722 508 569 417 609 631 111 817 356 870 507 909 149 700 548 481 345 460 721 269 441 912 637 786 251 936 270 458 039 999 567 965 824 579 571 200 830 478 976 088 191 294 292 518 350 625 268 745 643 900 105 449 531 311 491 506 477 440 008 684 364 634 448 927 627 401 491 153 410 275 012 720 336 628 976 112 270 341 961 373 460 653 542 861 177 040 237 757 993 124 464 066 243 190 619 021 514 312 748 467 278 345 017 334 337 307 203 851 436 836 218 176 396 290 011 735 725 810 197 906 611 278 381 919 960 169 706 119 828 026 860 643 773 929 304 130 637 436 071 716 790 286 006 128 154 602 920 984 871 634 787 179 702 973 606 899 483 563 851 314 196 182 978 824 246 422 457 364 199 240 261 810 811 657 403 255 989 287 076 343 365 001 329 015 802 587 645 689 292 926 909 005 036 498 903 192 091 909 706 514 497 624 868 908 232 873 042 531 445 271 055 185 153 515 459 569 491 690 828 618 894 783 481 090 739 172 401 655 850 960 858 403 337 512 913 975 221 340 329 549 833 777 661 869 337 603 414 437 377 821 914 136 216 531 926 042 904 980 381 622 229 838 443 296 231 323 644 932 293 099 112 663 013 687 296 783 668 842 786 565 031 549 080 898 765 172 324 983 736 875 534 944 102 138 458 016 070 241 172 213 619 834 361 406 476 289 566 107 091 312 365 676 674 191 034 649 491 727 592 848 653 890 665 534 877 884 863 036 776 484 682 831 304 506 352 198 109 148 145 477 962 082 003 929 766 807 509 187 083 730 335 661 028 207 056 674 275 424 545 232 953 477 363 227 699 453 264 346 391 556 984 941 747 509 088 972 457 383 955 848 786 208 673 239 126 643 517 354 542 721 820 773 524 360 199 942 688 936 046 676 102 644 408 388 654 054 916 879 311 910 410 397 125 564 169 545 503 442 824 077 189 937 065 900 310 548 971 609 460 116 030 611 991 420 124 053 731 632 076 805 339 477 038 416 379 641 004 414 081 938 893 058 279 591 286 709 986 668 579 968 913 851 948 535 107 751 106 634 885 913 032 806 756 822 444 685 851 279 308 413 161 488 290 370 039 098 683 879 091 675 070 254 079 609 411 529 069 802 085 991 511 223 049 819 522 118 459 134 441 168 668 637 029 189 606 613 420 670 100 964 895 474 483 384 804 207 972 070 306 059 288 143 016 067 163 061 174 577 412 709 228 319 315 470 090 629 094 487 282 022 194 501 544 651 360 279 681 882 089 898 297 820 081 725 761 791 534 726 207 876 065 337 776 960 950 687 744 977 516 460 455 085 993 474 402 069 042 900 528 924 511 909 106 759 921 440 927 694 289 442 511 043 924 172 486 242 594 459 828 332 007 885 256 003 145 725 821 514 287 767 155 088 166 604 463 847 898 681 008 099 759 064 458 214 521 679 326 033 128 990 450 583 030 963 906 981 126 313 225 635 918 206 138 769 776 617 250 145 049 653 618 976 648 158 899 134 524 207 777 930 098 788 280 335 083 545 427 628 410 230 555 200 804 573 350 328 314 651 897 294 667 624 827 119 252 850 842 691 939 371 078 232 897 122 358 317 738 224 706 270 519 607 010 701 948 631 314 449 512 874 884 325 028 293 281 774 488 766 365 544 395 004 087 812 539 510 715 826 501 014 604 509 714 132 944 616 743 760 625 119 949 802 663 134 610 900 287 292 929 148 811 446 389 273 417 757 728 445 681 300 340 234 203 897 326 242 599 466 458 624 293 454 767 104 007 362 160 919 845 072 809 001 894 411 959 374 763 179 611 417 141 411 154 572 465 762 950 860 565 136 302 055 277 376 245 385 135 059 922 090 448 464 585 961 447 334 383 580 074 298 198 761 423 127 103 073 383 733 558 374 679 910 636 583 980 808 010 774 028 187 842 367 042 976 268 550 970 734 624 461 576 736 489 055 858 144 958 949 794 117 783 548 121 688 079 189 347 083 585 030 988 522 700 205 700 777 704 079 238 940 282 291 708 300 792 963 239 140 602 586 206 327 023 593 557 104 361 501 783 798 413 444 055 116 906 910 203 983 955 048 141 016 099 261 768 849 862 216 748 666 156 113 955 648 680 692 168 256 623 337 445 718 158 295 182 091 068 501 627 884 973 837 820 061 452 082 323 402 611 380 755 884 656 576 966 478 758 406 945 937 151 341 795 041 225 997 911 456 882 281 534 248 656 225 517 080 933 974 304 526 862 227 541 668 731 644 548 459 489 538 124 772 655 525 704 315 218 831 212 704 041 330 094 358 549 216 982 487 602 029 822 532 891 746 439 650 309 020 114 478 287 734 716 951 509 748 884 847 261 774 428 252 759 059 467 288 615 464 869 457 919 881 833 338 336 206 699 448 076 883 960 511 956 855 496 455 273 873 306 887 095 648 151 392 136 896 738 651 299 399 124 858 504 146 642 019 379 413 266 549 425 690 684 009 255 794 304 922 618 674 255 606 504 744 340 445 706 100 845 305 873 146 602 170 181 415 068 909 008 598 259 208 719 013 380 311 670 806 867 737 037 399 387 651 318 566 402 628 122 323 479 452 976 143 589 225 996 775 268 130 851 804 382 954 003 930 305 917 563 235 747 656 697 626 845 180 907 918 673 756 535 926 046 597 485 346 138 690 315 253 953 740 906 623 638 268 946 760 504 760 436 150 893 830 090 453 708 864 901 926 700 354 247 036 785 984 082 471 390 791 384 605 045 894 829 825 567 154 063 194 766 559 603 668 623 999 860 445 333 684 203 073 687 343 813 920 284 735 854 482 168 314 541 309 803 152 323 160 544 848 603 489 163 163 034 405 320 864 435 440 397 963 609 774 747 341 409 478 155 057 987 165 144 340 065 912 649 625 886 415 791 884 191 423 250 715 449 686 292 747 186 758 232 124 423 037 854 590 777 885 256 442 040 862 274 341 036 405 605 295 674 402 310 067 477 880 677 825 679 070 864 645 927 422 560 484 270 221 559 073 660 419 277 974 143 006 158 202 463 666 185 588 505 054 483 147 208 740 292 452 323 469 284 439 505 821 422 648 616 905 852 815 104 739 843 886 180 400 934 197 987 486 547 875 472 970 516 210 230 449 220 539 247 302 481 237 285 764 452 838 286 038 518 145 754 512 625 109 318 102 446 609 756 123 915 875 480 446 204 898 896 692 234 066 768 353 930 833 227 442 130 368 476 512 498 008 277 895 009 271 655 751 940 166 652 410 342 338 892 940 895 596 888 093 676 306 913 255 150 466 396 939 825 315 071 349 774 622 288 330 758 808 458 486 293 083 382 120 372 832 050 862 599 233 151 748 773 452 827 216 315 416 180 193 594 786 553 823 464 501 206 011 455 990 717 779 000 664 140 149 218 783 854 792 624 633 178 613 763 423 128 140 596 373 159 088 311 242 324 093 430 400 961 613 318 981 546 642 180 482 640 509 292 198 867 589 169 535 244 824 368 182 590 125 568 821 456 414 056 499 359 982 730 844 426 009 641 761 232 641 625 201 484 988 377 908 240 362 713 217 467 963 648 374 417 468 765 624 199 319 605 525 825 981 572 768 289 785 815 989 110 529 267 357 166 313 811 351 812 881 442 197 438 908 790 448 470 609 999 626 946 332 398 149 193 654 682 406 021 927 729 880 684 616 597 595 181 782 038 767 997 105 892 540 337 024 915 134 195 115 862 339 651 154 507 958 662 604 140 449 640 037 815 281 313 516 797 972 992 376 036 289 779 770 848 218 350 638 052 766 977 676 060 735 288 717 126 643 195 761 451 705 014 394 331 091 557 278 927 560 404 992 689 723 905 868 488 394 981 349 486 878 659 350 684 823 152 594 269 287 140 880 723 722 618 044 166 520 663 516 263 302 056 451 867 396 864 686 578 881 781 719 920 283 731 983 966 808 709 634 524 945 694 442 641 972 876 776 326 870 463 484 194 559 478 032 505 605 899 564 384 750 792 360 151 477 254 536 221 297 362 961 870 974 147 721 771 221 459 962 892 949 051 037 685 483 121 877 245 778 539 563 644 720 571 650 885 092 112 511 430 386 846 825 141 628 307 833 568 733 493 897 506 078 453 420 368 546 695 714 571 579 677 596 935 689 988 632 557 441 754 912 450 208 513 472 506 975 515 788 319 147 306 114 222 630 206 299 583 278 990 656 304 210 344 888 743 353 490 722 147 781 816 014 120 143 334 409 226 575 122 085 547 323 829 540 763 845 528 007 360 159 954 359 365 118 740 586 352 200 095 280 477 652 913 697 581 960 726 779 349 663 391 634 211 366 405 984 450 119 574 300 556 372 870 614 807 546 445 902 382 630 187 080 669 013 443 692 514 771 531 202 829 967 876 244 104 936 655 799 235 098 651 415 411 080 988 751 981 529 145 037 786 355 350 346 311 786 271 657 480 571 694 348 218 490 954 095 880 984 503 034 303 003 031 837 924 670 078 873 213 328 748 068 662 541 576 517 690 402 681 354 262 759 933 486 327 299 528 065 900 582 855 629 458 231 180 832 489 323 872 295 350 290 478 016 739 908 585 115 651 626 370 933 280 693 012 308 058 009 042 441 126 591 869 000 268 967 408 460 654 796 245 600 995 150 200 790 222 205 303 710 551 490 100 681 917 421 037 661 693 113 813 654 971 202 338 632 696 081 779 561 607 480 548 364 727 599 295 198 323 039 137 356 624 626 017 050 846 502 181 173 967 924 704 796 069 356 861 566 620 169 785 925 751 735 660 839 832 048 970 217 467 799 477 904 030 213 723 554 383 565 117 378 535 684 881 622 976 438 605 683 484 572 288 291 023 097 511 714 679 528 976 747 132 889 350 686 343 122 213 989 672 217 240 792 092 540 408 176 265 113 970 933 645 675 819 212 233 511 170 057 992 502 714 511 937 058 979 188 206 482 011 778 048 408 708 454 508 027 700 693 942 602 155 825 716 117 109 566 091 283 103 698 971 344 252 363 040 448 366 822 973 182 025 330 751 736 633 967 449 253 641 637 046 670 686 301 746 666 031 659 025 233 126 865 997 594 824 493 666 005 891 505 022 145 133 795 142 099 056 531 421 828 933 831 054 131 801 627 631 246 708 233 724 019 403 145 181 601 299 645 451 514 070 802 497 480 551 020 770 556 677 015 002 208 062 410 264 570 255 098 159 090 437 043 125 661 981 598 628 134 754 301 278 046 533 620 296 654 228 395 413 993 860 760 828 955 953 321 919 400 242 361 617 690 178 744 608 389 236 560 647 906 629 047 648 258 392 157 725 204 366 483 908 155 384 655 898 867 872 643 969 810 697 594 843 736 567 358 243 151 186 465 958 487 040 891 364 929 374 777 808 878 580 486 646 406 327 278 708 931 044 671 584 127 633 349 984 250 542 284 084 871 717 186 265 392 500 685 581 444 842 870 010 672 498 020 140 151 651 172 527 101 180 189 231 384 898 117 686 259 219 487 079 193 109 868 931 353 162 390 873 550 009 772 873 457 342 365 689 401 402 072 014 595 143 294 660 786 920 608 027 801 647 968 967 206 119 556 893 148 471 096 120 496 350 708 567 756 821 169 424 993 745 262 137 388 224 189 744 851 856 640 738 151 053 257 526 475 701 012 725 808 458 345 809 458 931 077 242 351 812 810 302 615 704 464 635 183 152 180 682 301 540 289 501 322 042 977 584 878 090 216 550 836 493 670 412 359 810 900 662 884 902 116 028 563 072 192 249 587 240 287 554 649 371 592 125 545 925 532 949 771 148 676 499 066 310 197 821 805 785 202 959 651 016 790 367 939 989 266 254 235 812 580 247 727 011 523 096 886 970 627 094 915 068 633 931 271 985 732 691 704 726 297 518 120 157 887 063 002 850 452 508 881 409 893 120 314 829 035 935 149 581 326 831 641 286 621 285 627 721 479 856 886 944 415 864 521 243 655 178 885 007 723 321 896 403 038 452 724 708 294 004 304 855 679 074 263 073 431 343 714 709 309 405 750 457 835 854 129 427 662 707 294 750 310 375 640 435 319 064 741 401 680 175 012 796 174 905 911 285 634 165 460 012 835 933 020 430 825 553 354 258 056 693 756 542 840 704 218 862 570 168 946 320 622 004 088 533 756 476 021 895 178 885 873 711 405 288 143 945 104 368 595 198 326 776 946 110 350 865 708 454 655 690 370 259 764 235 255 474 347 001 358 951 200 338 710 123 555 754 118 583 408 330 285 322 660 991 133 250 081 101 498 682 885 154 362 768 631 116 458 676 893 971 673 599 700 163 403 668 083 358 103 720 036 198 232 882 659 427 534 092 644 774 294 267 250 390 011 469 138 515 116 036 501 603 927 199 401 246 879 185 780 216 804 849 484 397 711 768 394 495 571 031 221 049 848 168 524 210 730 893 524 708 478 317 930 150 062 911 347 658 082 555 209 796 942 243 225 237 684 012 960 570 153 935 020 933 777 051 186 828 548 144 644 179 727 031 580 590 019 967 909 890 204 677 302 466 443 087 964 791 584 971 719 450 560 311 362 244 871 143 235 003 431 562 683 810 761 114 575 385 410 812 855 258 144 084 366 587 161 503 533 138 487 360 019 551 321 176 110 774 904 605 663 884 683 081 430 515 428 939 721 771 705 205 525 438 918 075 702 998 330 694 272 872 636 126 446 402 155 097 807 385 236 768 216 216 902 761 544 086 521 141 353 089 567 757 309 992 754 880 927 884 549 302 691 350 901 504 397 389 912 418 036 546 985 066 887 566 687 368 463 271 679 843 385 022 018 884 069 237 741 163 179 145 158 252 731 597 516 444 696 114 395 375 963 702 326 236 903 395 715 009 991 688 661 473 404 863 770 138 594 835 705 950 223 784 004 079 457 026 392 710 747 580 386 255 891 203 546 145 272 430 479 142 242 140 366 332 785 857 573 682 471 297 178 091 209 633 124 312 780 893 049 385 607 301 181 575 295 245 860 004 282 024 614 220 488 600 787 961 245 355 254 582 931 851 454 341 930 630 840 626 882 533 819 679 032 303 890 219 183 605 229 555 721 128 091 599 039 446 002 193 959 203 786 863 002 474 000 751 518 202 599 471 856 011 761 388 038 049 566 343 074 969 633 308 810 014 899 452 491 412 469 971 012 296 716 290 643 884 917 633 942 199 178 327 630 988 509 465 284 427 168 021 366 063 074 687 438 597 681 304 398 006 223 415 717 111 587 004 331 696 869 288 168 843 229 841 154 639 780 289 441 408 861 597 821 862 568 209 898 711 430 527 955 495 328 425 857 289 740 738 522 237 569 337 123 724 762 537 519 094 954 216 092 778 175 800 130 005 061 909 901 355 080 380 331 913 101 543 256 238 688 710 098 197 447 477 496 145 791 549 602 796 375 295 709 610 336 492 531 738 215 765 162 259 731 005 042 643 471 861 984 704 856 772 628 163 405 267 121 722 379 550 462 009 431 459 244 867 291 064 618 857 437 663 044 396 336 606 131 279 487 083 512 184 940 482 468 538 203 385 449 093 670 432 471 721 552 671 655 971 567 052 663 919 146 282 592 038 685 849 783 840 875 011 845 295 514 403 341 806 074 896 740 901 051 793 079 360 246 390 319 718 737 898 213 131 394 034 030 363 253 981 616 631 221 769 497 483 566 291 389 353 662 859 120 676 549 078 681 959 462 024 209 951 129 246 904 702 619 237 429 432 943 999 321 639 805 123 436 910 470 738 734 821 891 644 054 725 713 392 171 239 385 725 490 156 129 431 024 459 590 425 200 908 928 895 876 537 646 210 608 522 590 275 231 559 937 709 270 227 185 451 938 954 127 061 099 654 165 353 159 004 335 020 081 841 996 211 547 383 937 662 896 579 715 390 060 010 367 991 397 009 854 735 032 286 910 614 647 634 348 519 847 883 374 564 564 588 717 777 009 509 259 792 698 528 871 771 428 013 050 387 893 323 371 700 634 717 426 206 107 020 212 202 587 703 653 596 139 448 776 559 031 278 963 233 763 195 679 028 816 561 257 494 508 745 226 513 444 917 191 217 925 361 975 902 267 469 012 015 020 169 356 533 877 598 289 444 729 725 452 018 013 724 498 513 274 967 533 548 931 379 250 687 966 820 120 236 547 632 165 150 741 981 047 732 122 627 864 351 327 361 106 178 861 764 187 831 335 167 759 355 775 989 586 844 597 640 002 814 392 718 365 843 588 601 940 311 056 870 596 683 004 448 304 671 170 790 995 824 016 930 071 630 640 557 359 002 066 979 637 061 769 513 839 531 686 934 670 371 386 862 689 536 658 850 879 117 364 857 610 351 316 444 473 246 009 868 533 199 315 394 124 360 388 239 817 092 148 636 685 904 107 970 733 071 200 458 226 283 936 089 471 818 199 714 360 639 057 595 761 974 763 784 582 717 253 226 662 160 395 458 446 396 952 830 412 342 216 875 350 765 454 737 633 609 046 500 095 792 266 762 390 117 879 599 955 421 045 326 756 051 586 151 378 410 281 594 813 983 217 843 357 865 100 264 171 209 066 499 121 689 687 204 376 742 379 692 638 391 513 820 626 940 057 163 032 690 015 225 680 943 406 097 891 496 803 905 394 628 828 092 657 243 095 250 403 405 454 106 565 251 123 144 401 970 689 923 596 036 433 869 357 056 349 844 030 739 003 578 284 416 970 887 675 704 912 998 132 345 490 552 392 309 662 129 816 265 821 497 296 043 053 672 323 099 428 993 826 929 839 137 680 076 132 950 110 325 727 772 199 389 849 906 101 560 307 021 540 392 834 427 886 061 509 435 391 073 789 140 233 367 973 425 416 308 811 014 654 141 010 684 094 402 237 653 062 019 701 556 589 319 052 664 948 201 878 732 158 395 287 800 599 740 308 149 083 447 402 723 907 042 591 122 378 958 929 198 235 493 172 689 449 121 666 301 734 958 315 366 075 200 570 383 895 613 486 832 776 869 335 312 269 742 811 315 701 762 508 410 087 267 560 017 353 184 247 271 113 065 383 561 804 527 138 276 581 389 556 749 034 210 641 675 315 830 915 801 889 746 098 455 605 820 332 041 539 685 532 844 720 327 413 508 598 109 249 449 208 282 194 602 739 592 718 501 600 940 807 622 666 379 253 517 694 870 736 285 199 461 108 705 991 846 911 225 926 988 282 273 448 300 214 497 517 854 381 816 947 232 808 269 845 571 826 535 760 297 734 370 702 038 501 234 691 816 723 102 145 435 394 237 055 213 468 762 068 796 815 465 592 935 911 939 754 775 158 861 756 767 398 971 059 723 383 622 521 059 706 598 105 479 843 275 644 170 752 543 637 205 562 947 851 051 308 934 430 140 196 227 852 071 267 096 232 295 237 271 766 190 784 324 086 126 309 026 578 575 245 148 606 286 049 289 753 814 656 490 997 300 569 390 733 532 152 260 059 264 368 383 707 359 175 347 554 967 882 435 383 741 314 592 440 402 264 249 305 922 670 245 281 962 875 566 265 707 029 281 803 355 071 092 048 310 608 522 514 820 198 680 521 288 736 794 716 621 951 944 820 300 129 178 333 504 259 344 537 488 179 930 917 189 617 056 945 418 381 088 815 599 759 321 246 793 031 576 100 543 183 716 142 838 655 760 801 224 261 469 451 985 465 779 895 805 239 868 444 186 351 213 117 854 949 022 115 333 859 914 703 307 658 236 573 215 888 224 895 434 074 245 862 331 293 101 766 460 353 775 493 433 715 626 911 860 365 170 314 844 633 318 942 171 277 084 355 181 882 098 157 777 462 837 010 570 467 406 586 964 188 224 382 348 467 592 268 380 471 399 662 335 990 907 387 567 317 107 106 005 177 174 525 095 400 696 317 445 842 070 828 805 683 129 601 229 688 223 884 547 012 516 266 289 529 901 517 909 317 718 379 931 264 926 968 536 467 008 851 482 210 151 973 907 001 393 256 337 821 651 815 314 687 938 765 416 627 133 810 745 612 182 126 641 002 802 142 946 210 726 337 405 218 265 847 484 017 855 437 803 541 630 995 772 270 151 177 830 114 160 348 860 005 269 164 990 326 889 373 240 139 892 758 499 605 021 956 079 542 789 091 245 972 438 235 362 302 206 400 222 791 983 183 648 156 268 361 440 244 090 890 322 753 383 348 835 666 288 361 319 450 807 421 532 646 971 721 061 821 125 551 230 319 813 867 761 622 606 605 348 395 341 073 237 901 749 128 724 878 821 464 789 315 165 279 914 677 598 313 564 151 872 502 856 204 243 965 399 538 342 938 161 605 253 787 936 337 059 318 404 862 259 658 878 901 670 247 969 046 409 195 018 146 559 891 486 195 745 398 235 924 620 000 729 420 771 460 369 193 608 730 341 883 355 132 731 925 353 318 000 394 829 988 635 684 749 349 342 610 386 165 730 662 827 978 483 298 486 341 965 470 168 898 689 831 827 907 099 014 327 893 886 713 118 085 454 491 164 152 558 599 160 227 879 312 561 971 279 084 817 222 727 513 643 493 412 015 046 509 017 488 951 784 752 950 002 801 774 919 612 381 577 990 531 993 811 382 936 998 144 891 117 555 415 037 597 496 294 210 563 079 962 791 319 743 727 073 190 883 308 766 157 784 984 516 890 269 179 302 322 830 149 356 412 147 022 636 940 231 807 444 021 796 353 529 569 792 866 428 089 632 225 793 801 658 582 423 214 586 605 665 672 458 362 175 075 055 845 843 805 077 581 758 452 765 924 481 411 934 939 848 624 786 813 057 143 338 910 588 661 165 097 235 103 048 627 094 993 121 853 495 011 712 761 263 380 088 781 817 553 908 851 239 631 404 762 108 032 834 655 775 794 102 571 974 128 284 931 662 351 217 460 032 019 633 349 521 299 675 830 098 298 386 449 059 918 102 405 083 447
050 317 985 002 689 330 636 769 157 588 763 778 242 034 687 308 878 436 663 367 871 953 782 287 435 376 478 198 830 481 577 076 397 186 185 685 097 041 017 740 743 617 584 368 872 822 613 046 404 764 215 778 171 882 291 209 555 659 852 332 994 474 295 414 258 972 605 234 770 342 157 902 710 691 379 111 671 640 587 776 508 818 933 800 302 871 476 034 493 861 390 406 020 280 777 550 071 619 002 974 491 993 882 507 655 059 298 266 961 378 819 879 150 533 908 819 432 514 883 750 346 042 207 379 919 130 046 268 852 368 531 247 401 281 900 398 259 403 150 823 967 318 444 411 852 098 470 652 229 342 821 113 868 245 813 530 362 593 582 013 934 860 551 726 237 039 563 437 134 675 993 025 483 970 459 182 564 050 644 472 554 345 534 823 557 301 909 774 397 690 653 940 035 227 621 276 230 052 176 145 069 115 122 050 392 053 195 448 273 937 501 965 194 879 482 407 659 581 613 014 439 742 520 135 389 931 688 895 527 608 049 262 658 336 465 321 733 897 121 404 234 001 303 431 114 002 343 051 338 810 492 328 301 713 340 117 371 277 903 180 537 007 805 918 834 817 486 922 636 927 204 569 670 639 829 897 842 431 880 885 013 968 306 511 559 315 795 780 111 411 363 220 668 989 223 206 640 202 280 603 657 991 693 605 876 763 975 638 966 554 314 262 382 232 163 036 949 747 671 116 486 889 381 857 547 641 638 639 726 205 808 049 808 574 598 009 733 124 087 438 098 395 178 515 193 938 470 299 156 368 527 631 062 183 977 078 001 858 299 271 441 693 719 622 934 917 110 454 940 851 499 690 352 969 020 368 668 699 330 982 449 006 791 266 952 184 206 761 670 123 476 363 721 976 098 763 890 954 964 602 870 633 577 468 533 870 737 649 540 560 320 854 266 170 216 202 725 921 014 524 477 147 095 689 410 419 336 441 054 438 026 043 686 990 306 561 765 338 720 984 565 686 693 966 113 533 552 242 207 295 202 521 404 835 285 964 018 380 773 558 332 034 606 909 947 680 717 397 268 991 242 376 252 500 652 594 299 967 004 243 733 968 453 257 317 902 809 130 338 809 898 560 765 708 024 721 784 776 270 335 031 111 314 025 835 295 054 581 191 434 706 737 759 603 079 457 333 591 423 068 759 767 334 997 819 249 697 582 727 356 068 904 904 767 272 327 790 287 829 510 585 970 997 470 367 013 024 970 302 683 589 950 676 910 832 575 998 684 626 691 568 966 727 360 135 054 391 975 366 881 350 193 142 756 390 279 058 540 869 759 280 608 724 121 844 934 359 085 229 142 056 073 515 394 199 529 488 485 298 161 430 264 076 160 940 854 659 980 463 086 049 447 643 790 022 832 007 767 326 879 590 956 276 485 617 311 511 356 489 424 428 666 987 403 594 735 412 846 940 618 109 863 902 693 127 012 791 351 161 060 849 141 919 758 479 127 119 755 611 977 120 207 940 462 230 432 328 968 967 804 115 118 755 471 568 015 674 464 477 554 221 013 142 792 477 017 271 475 418 467 348 386 922 763 899 788 807 271 043 944 209 573 049 545 903 625 488 765 606 118 431 380 622 362 340 996 365 813 500 784 759 653 906 058 378 738 610 444 650 029 147 113 864 676 063 455 007 635 767 953 100 324 493 588 858 924 544 684 758 646 735 737 962 318 208 004 743 786 386 020 014 596 940 319 145 592 250 839 379 279 937 235 747 898 829 074 931 556 154 304 037 805 792 720 243 381 099 656 047 990 614 253 407 133 423 232 879 506 863 286 619 118 287 256 938 003 795 003 253 016 106 522 855 963 193 581 433 976 964 225 666 282 805 092 001 197 874 829 412 220 822 299 663 522 803 476 624 212 074 793 019 348 078 952 998 869 834 334 935 334 264 777 630 564 530 053 701 346 359 807 228 683 252 132 454 731 923 099 291 146 469 059 798 008 181 458 899 215 034 959 275 228 743 839 389 679 474 606 746 496 460 375 001 855 420 672 734 354 726 496 983 588 688 953 869 791 461 936 124 709 563 263 206 442 950 690 977 277 282 671 622 863 105 691 776 603 476 297 651 583 043 035 046 213 125 882 842 673 748 112 968 869 034 739 165 141 493 014 148 024 555 554 649 570 286 400 961 848 205 766 165 437 120 475 059 138 921 689 337 996 103 347 666 356 963 077 131 604 924 709 713 118 413 733 536 715 420 068 746 032 356 114 345 541 503 592 540 591 591 730 301 993 003 601 962 525 925 211 122 574 129 296 210 376 872 506 364 514 308 396 782 752 040 721 544 834 745 543 051 342 804 033 944 811 879 881 705 644 320 425 303 041 076 316 338 292 513 630 252 024 176 922 116 747 227 577 494 902 848 744 991 979 697 004 384 106 903 771 317 126 271 467 822 355 615 514 941 800 710 056 755 261 979 941 053 607 746 106 071 084 955 173 509 169 818 345 053 414 529 995 540 742 223 797 003 929 160 834 636 666 646 725 308 038 992 909 366 148 471 971 434 928 484 391 305 680 778 445 731 269 982 616 938 180 650 300 544 190 414 351 093 547 612 036 250 606 203 724 339 771 655 412 429 804 071 890 124 612 726 073 049 216 880 062 809 830 776 371 516 053 673 166 937 029 909 774 071 216 931 638 441 941 393 429 762 031 898 296 407 108 542 481 709 455 564 979 089 869 821 604 029 674 347 501 274 825 496 353 520 157 036 283 977 737 257 524 999 583 040 415 611 464 926 648 025 741 054 483 318 214 246 200 577 073 874 929 719 980 850 068 387 122 011 403 183 214 340 454 209 697 811 677 985 066 477 698 156 926 935 568 997 960 132 784 011 003 521 843 872 824 580 217 737 633 602 137 023 658 989 959 034 182 660 618 311 806 415 016 846 244 428 076 681 320 898 373 012 576 821 957 261 230 206 706 075 705 572 013 002 178 074 952 459 971 787 032 809 175 053 189 599 547 849 225 059 824 009 143 893 471 546 357 725 733 637 040 329 218 883 320 681 016 223 082 075 842 092 066 572 540 803 935 384 274 876 549 124 182 221 367 478 821 327 888 047 511 089 843 477 170 730 176 059 087 308 396 576 116 887 248 559 737 073 816 197 505 546 571 270 947 780 106 084 454 580 195 211 000 595 831 009 412 706 418 244 286 679 289 398 639 635 246 120 149 179 817 628 938 994 210 378 156 443 705 962 614 162 113 815 464 546 967 381 966 414 871 096 281 098 754 421 352 698 861 796 378 646 297 813 099 106 522 670 903 161 234 374 806 885 433 320 170 682 538 640 906 123 933 898 861 919 536 106 978 097 102 747 252 057 946 444 390 399 850 493 165 613 038 217 443 816 286 958 350 437 432 395 449 261 796 230 766 309 840 519 063 495 161 670 146 725 395 441 943 825 329 149 777 829 304 635 785 471 964 837 090 144 012 669 640 428 486 045 380 908 753 168 795 246 063 719 204 139 680 409 524 347 772 187 268 449 719 165 101 386 526 361 650 693 035 463 659 156 609 859 297 137 941 642 911 765 477 704 348 390 427 854 541 794 388 242 264 968 534 424 878 871 231 342 210 751 337 227 616 266 115 786 255 020 868 305 987 445 798 495 870 375 670 075 346 878 442 570 104 382 638 755 985 981 361 274 212 346 530 619 002 386 283 658 824 817 127 663 492 254 055 298 034 481 001 998 226 584 313 174 880 613 956 786 981 624 364 005 712 910 761 698 062 923 874 355 799 615 879 685 560 516 499 938 770 762 221 218 905 486 967 131 012 319 342 511 732 114 896 881 542 549 406 746 310 269 898 225 245 960 896 114 971 486 894 948 662 913 899 025 157 711 347 569 453 262 081 494 457 448 798 960 205 890 544 244 680 772 716 121 346 879 733 409 260 385 414 645 300 522 747 998 138 870 480 512 005 972 311 483 071 880 954 783 843 110 800 096 561 996 598 721 998 631 993 901 237 018 887 173 567 034 618 328 583 093 314 204 908 796 477 421 547 945 362 573 533 480 780 611 415 700 578 039 060 441 492 810 531 558 783 788 524 315 205 655 388 387 533 551 711 280 508 269 126 246 182 925 451 017 460 068 880 379 885 075 768 151 674 091 428 451 103 690 504 135 280 449 255 199 605 601 378 889 023 076 140 785 419 422 292 479 350 181 128 740 348 666 497 729 615 544 882 676 076 719 840 104 801 534 386 887 704 462 429 236 259 358 264 894 726 867 962 869 916 953 722 569 117 710 365 593 764 097 984 374 406 226 404 009 254 711 234 804 190 141 262 917 713 717 627 916 285 638 262 771 669 837 910 083 739 657 697 160 478 133 568 551 915 110 520 105 771 737 613 343 408 569 938 152 967 089 847 141 880 175 636 099 276 413 713 365 277 914 230 021 162 670 542 676 387 524 436 648 784 925 469 593 212 419 892 681 382 862 189 152 946 643 769 999 959 414 939 597 093 094 886 011 754 126 540 550 766 532 618 384 260 139 525 344 633 755 091 684 019 899 800 710 266 933 823 145 990 576 779 306 294 205 497 423 004 796 723 816 299 736 786 802 277 274 764 503 935 706 911 923 189 644 709 254 133 016 811 915 725 509 564 179 906 993 133 504 041 107 428 258 642 072 138 535 754 278 922 312 046 352 202 811 959 183 290 769 437 704 612 028 015 884 465 874 688 533 402 976 209 115 138 546 416 586 000 104 108 873 375 573 553 737 436 529 699 080 993 119 974 534 087 051 538 988 890 563 476 484 942 611 370 247 714 730 382 621 709 793 333 896 493 533 261 508 248 341 851 287 371 605 000 679 709 621 035 189 791 623 414 409 696 688 107 481 283 506 259 091 282 605 406 009 236 280 349 237 256 507 270 705 413 200 547 313 368 234 100 038 797 913 492 913 593 644 086 518 954 224 874 796 752 999 735 255 595 912 300 808 843 428 470 769 299 735 524 120 743 768 117 955 809 115 950 951 990 570 145 698 722 098 159 779 147 115 063 421 122 520 185 712 423 900 399 817 093 685 793 441 332 048 862 599 207 431 690 118 569 099 454 556 968 098 982 937 012 081 726 027 968 353 801 287 359 118 895 872 348 196 186 866 866 222 032 900 362 296 376 427 666 365 310 668 655 867 304 628 021 730 879 747 347 444 696 251 448 853 788 171 664 985 298 636 826 553 007 562 539 931 378 946 428 050 720 518 661 609 257 217 626 169 055 452 563 876 001 057 329 902 568 679 195 757 477 832 616 733 233 239 490 987 193 931 645 004 437 653 968 907 327 327 917 683 379 732 046 726 980 024 887 532 929 042 280 985 549 963 618 019 184 639 167 443 070 015 794 104 570 156 334 262 421 044 600 456 634 922 617 343 627 435 959 664 937 057 777 272 596 285 304 965 166 687 807 718 692 635 430 847 891 161 841 051 670 431 966 086 336 345 365 198 283 490 624 268 253 354 792 198 787 318 856 582 649 297 718 728 551 083 460 874 052 676 872 143 299 885 606 200 414 753 520 207 738 624 835 322 067 766 475 044 031 746 066 377 193 628 898 151 458 966 578 381 859 343 456 425 872 228 527 837 171 110 761 941 327 137 902 346 712 005 127 418 062 043 097 397 969 677 847 650 036 183 981 540 500 614 469 514 945 519 685 328 763 756 149 865 770 373 298 876 127 819 097 068 487 933 783 858 761 270 839 484 002 359 587 617 688 116 530 551 449 828 750 766 083 898 161 392 250 350 112 248 544 065 560 352 144 875 635 045 928 919 343 098 909 257 024 369 488 392 501 883 472 516 958 005 935 148 870 196 106 085 433 483 365 296 016 045 871 868 390 318 494 618 084 908 341 575 367 759 550 256 804 680 934 698 664 687 687 318 300 986 326 004 398 418 207 548 943 577 782 243 493 955 346 240 536 037 999 493 195 582 358 762 281 329 302 912 735 102 440 500 643 440 349 894 662 247 855 312 768 324 291 996 370 921 522 950 066 276 802 312 791 504 331 230 757 370 556 640 139 627 994 497 145 810 738 454 099 153 634 985 490 976 887 617 933 195 480 935 757 383 252 915 994 722 658 440 672 833 086 993 843 337 715 211 041 717 082 376 152 241 296 346 728 930 258 935 921 469 061 943 711 440 513 543 392 995 815 685 711 764 180 791 416 388 604 085 819 685 301 571 391 324 382 046 017 909 603 745 548 223 868 831 550 634 040 742 621 369 946 394 525 302 697 520 860 295 799 753 750 528 220 557 402 607 778 598 833 190 246 654 258 062 991 957 750 287 819 755 405 057 710 073 010 805 054 240 765 459 139 185 693 211 738 988 500 022 735 034 353 770 623 124 263 571 161 872 858 798 094 547 244 206 147 184 456 211 874 688 888 964 832 938 313 090 609 112 693 547 805 130 112 716 973 421 803 363 333 169 517 265 321 074 596 232 622 553 802 215 640 570 736 275 936 837 136 174 388 225 935 088 834 747 254 792 541 453 704 930 855 244 530 997 252 338 679 703 272 568 692 742 903 407 492 426 585 928 572 593 062 959 663 486 314 348 404 080 891 914 131 517 033 093 502 191 631 738 888 346 186 170 140 915 873 234 319 274 641 469 931 113 706 415 594 951 047 279 227 624 117 124 440 003 018 832 020 653 365 159 833 499 762 735 770 152 646 911 927 142 855 746 561 906 311 930 070 046 256 676 637 490 574 466 190 253 651 340 381 034 238 178 143 747 741 793 884 291 743 221 366 375 401 034 029 526 142 703 271 489 207 151 788 285 655 111 832 125 039 873 581 564 683 977 765 160 601 211 791 219 583 183 934 173 441 325 204 871 982 787 751 438 190 929 966 907 488 462 006 290 020 999 631 155 712 975 112 314 301 144 670 155 780 388 521 620 473 117 872 936 450 377 400 161 845 107 263 938 731 926 521 814 677 729 325 451 301 758 145 284 031 515 096 962 021 811 601 708 488 903 276 969 420 374 537 169 635 648 674 205 838 206 200 532 739 612 458 773 198 848 932 107 591 405 913 899 945 525 184 350 515 666 041 486 361 430 513 362 043 249 577 974 312 197 887 525 853 062 194 485 162 843 466 226 010 920 927 395 600 228 658 294 079 388 858 316 451 691 406 343 316 387 574 561 148 893 391 461 781 485 228 728 115 879 119 991 150 123 396 467 901 298 237 154 812 549 795 028 742 416 021 854 413 610 313 722 943 665 337 707 399 911 274 227 952 060 801 758 625 249 259 862 531 227 708 625 631 621 663 432 795 056 530 890 531 478 976 556 835 959 949 631 782 759 268 667 221 617 353 549 898 645 974 267 727 715 364 753 096 710 807 966 076 858 843 351 005 866 172 890 266 996 584 190 232 413 883 299 305 290 496 743 263 625 686 693 639 460 636 718 466 905 433 119 336 825 768 553 872 817 384 361 495 718 334 713 785 956 454 715 316 993 438 317 554 337 396 460 338 127 146 181 462 558 159 563 551 254 944 833 236 617 240 773 676 188 837 591 013 724 914 285 746 841 527 329 126 896 144 621 081 490 071 837 918 172 076 362 744 352 172 452 453 634 799 784 404 666 999 444 059 947 534 824 281 439 702 626 096 667 232 698 636 238 409 596 642 427 876 792 831 718 326 586 208 412 405 437 267 431 749 845 215 588 763 684 392 778 049 589 738 517 466 706 856 063 741 455 872 863 588 716 168 443 230 196 796 510 745 248 359 149 618 469 327 601 360 599 568 379 662 302 611 667 453 620 305 743 628 191 293 586 954 354 947 620 015 951 236 123 551 085 191 263 713 712 976 466 581 253 592 013 620 718 941 453 203 461 661 033 736 203 607 611 174 505 133 473 703 999 336 794 332 163 757 857 415 379 920 665 861 817 956 081 401 896 373 562 828 663 713 024 846 089 220 013 447 962 986 248 826 324 163 372 023 558 254 452 652 409 446 640 932 840 039 770 127 824 922 947 613 769 527 079 522 428 063 297 883 167 296 272 795 016 336 428 796 262 996 911 362 790 509 470 562 891 845 604 096 099 515 572 111 221 771 873 574 633 667 476 612 751 077 419 348 947 310 862 766 265 961 359 971 277 925 936 982 169 470 812 238 395 510 491 959 287 189 042 322 057 593 166 645 027 811 440 801 688 736 716 104 129 112 251 210 253 860 147 627 315 385 632 911 447 164 442 301 731 458 160 028 724 367 326 847 745 220 040 711 299 619 216 541 019 689 651 611 776 147 429 483 760 512 130 830 606 909 748 313 140 840 835 359 280 255 187 166 983 981 728 489 722 157 002 460 870 010 955 865 862 340 423 905 204 203 753 081 101 989 102 696 920 879 809 174 469 730 399 263 749 111 237 942 487 446 369 248 460 906 287 825 704 280 812 447 572 066 818 131 899 726 041 771 978 796 662 743 471 488 634 906 278 048 612 141 504 680 714 004 116 694 809 939 673 429 642 861 176 820 051 806 774 116 045 038 760 858 777 689 093 468 520 036 420 507 891 310 643 335 185 447 928 049 027 543 926 239 098 176 163 707 014 020 281 753 071 972 595 873 088 265 536 587 614 447 382 768 044 664 520 528 233 348 464 654 657 445 376 697 012 295 499 157 802 712 791 410 470 192 004 060 260 655 581 056 725 515 770 484 389 053 069 886 143 267 880 497 737 758 747 462 675 734 445 468 336 330 212 065 233 590 427 827 309 097 068 221 162 124 885 748 780 700 899 760 937 517 232 895 057 358 702 071 060 750 372 131 212 051 828 840 957 414 934 696 050 726 767 319 161 701 534 194 734 387 361 995 740 582 599 903 048 602 467 537 852 218 984 087 557 682 050 191 257 400 049 030 795 973 060 578 924 898 524 362 066 991 668 144 337 931 708 152 422 974 977 340 978 130 261 597 834 072 256 196 659 431 790 041 013 007 522 820 886 220 345 073 200 342 096 410 272 163 596 356 791 086 280 931 882 860 090 447 210 258 843 673 984 577 199 351 985 486 940 854 333 590 925 805 826 768 612 198 858 750 729 268 459 653 609 614 125 852 202 422 983 692 249 448 222 527 369 190 486 589 097 428 889 443 012 723 372 036 726 620 270 860 141 454 748 568 389 929 404 833 954 886 461 535 879 331 954 868 765 245 410 713 320 206 533 276 276 595 925 953 971 680 829 881 349 651 661 784 428 654 380 347 699 039 778 576 559 459 925 096 296 625 344 376 614 071 342 722 876 842 682 374 978 995 867 728 878 048 254 878 054 171 680 057 092 721 894 600 958 619 464 934 432 307 006 397 537 719 606 925 974 667 271 447 644 282 219 048 535 479 126 519 331 712 413 107 686 812 845 639 886 665 904 642 502 367 968 182 840 362 179 308 651 358 666 348 415 430 977 574 210 958 799 045 121 177 379 848 906 936 138 648 336 983 639 800 959 929 939 346 655 297 261 111 070 209 622 934 562 126 162 958 712 544 787 812 035 752 776 686 700 970 367 755 832 818 796 688 222 801 710 796 406 295 989 384 708 476 304 038 035 756 969 972 146 736 900 295 591 961 833 848 688 266 777 752 438 021 099 575 133 845 982 379 081 398 666 009 570 814 994 220 463 868 864 156 686 533 088 257 120 584 706 503 506 022 022 150 654 586 885 336 902 772 378 721 090 088 909 414 498 074 120 925 584 140 340 148 381 541 129 798 617 892 010 952 546 886 573 174 883 423 865 293 976 293 485 677 632 356 905 661 565 796 967 949 887 327 392 558 356 207 831 387 975 889 029 729 231 784 409 217 322 486 283 362 102 295 533 213 324 928 619 876 441 375 236 996 803 833 474 041 875 240 330 295 302 982 714 878 393 958 677 918 482 381 500 151 386 181 191 726 495 837 419 310 894 948 398 850 962 138 436 996 163 180 891 575 830 444 464 304 990 869 135 700 824 725 334 463 778 713 690 464 916 472 735 178 724 166 333 500 835 870 846 642 853 098 856 726 968 071 894 074 880 012 907 893 621 698 086 647 058 036 930 900 560 906 040 841 076 576 879 917 634 105 545 615 735 488 146 453 118 395 633 295 706 622 850 195 169 326 558 007 318 708 383 017 528 862 595 380 388 380 122 305 237 680 315 061 741 668 126 596 394 571 275 182 004 933 232 901 075 190 377 486 016 190 580 062 980 537 072 657 037 151 951 454 466 884 206 879 741 676 713 724 111 985 997 394 600 776 120 785 899 984 572 948 011 639 575 476 690 458 959 271 478 664 619 109 623 698 371 016 720 927 864 617 311 722 582 806 739 119 571 146 922 671 058 848 193 219 095 422 770 080 818 245 888 725 357 227 827 071 350 445 696 438 921 345 584 904 224 662 991 401 287 030 376 647 035 595 937 389 602 831 624 968 406 956 255 294 475 611 920 321 066 038 592 516 246 091 601 784 937 873 886 916 642 774 922 408 384 694 027 327 583 531 057 781 492 031 575 078 257 133 774 591 963 059 908 160 324 282 358 104 816 175 887 669 630 069 950 463 472 702 735 577 837 875 309 987 981 871 917 122 191 216 486 328 973 722 244 684 482 259 359 754 020 087 343 376 618 705 058 023 582 136 307 896 537 833 823 879 876 307 276 772 133 348 874 259 376 245 436 522 984 578 898 935 034 225 018 532 031 757 431 676 973 382 739 632 865 061 038 173 897 467 573 410 138 056 933 090 182 582 837 182 571 051 534 601 171 831 927 611 991 415 796 795 645 973 890 596 094 626 106 075 906 534 834 108 519 492 821 349 020 575 899 227 227 591 765 459 218 488 319 388 691 176 638 745 375 916 148 675 980 389 414 060 279 013 380 605 537 959 191 561 697 456 189 033 773 935 955 902 858 566 250 780 983 584 406 952 959 368 205 590 389 147 636 782 534 030 436 026 646 870 556 235 558 024 271 247 893 147 374 693 050 942 896 227 814 030 430 734 885 538 503 078 934 771 379 769 311 541 906 284 098 416 706 878 214 329 836 254 050 676 647 051 389 256 393 472 563 097 727 015 069 871 001 375 113 484 525 736 088 931 300 876 992 643 129 463 471 402 946 327 292 034 002 173 882 607 588 439 273 023 402 939 578 616 605 851 877 165 293 837 140 779 631 935 821 832 454 321 695 393 788 448 570 547 806 364 789 349 464 333 612 097 145 779 714 287 992 865 922 292 932 768 304 522 297 594 471 820 965 639 249 755 215 906 250 577 187 962 875 738 096 593 926 308 068 118 359 759 293 805 095 235 389 876 041 847 028 370 932 850 536 034 717 010 543 490 381 124 558 152 365 278 141 551 519 455 688 345 052 778 532 482 716 488 832 844 127 252 401 310 814 587 737 450 228 804 453 096 443 035 963 467 552 230 378 584 025 162 437 569 584 777 801 173 350 668 711 451 902 576 691 368 783 319 061 815 786 010 827 461 288 467 708 771 958 887 026 882 536 643 251 837 419 474 972 957 949 457 575 074 076 187 345 455 287 875 963 441 225 034 878 052 482 491 882 357 369 352 259 670 056 277 666 180 999 227 983 750 147 940 589 338 577 358 815 126 431 279 398 520 731 818 811 649 392 231 156 048 505 852 724 229 556 100 686 861 433 411 533 308 126 571 718 212 344 192 958 564 384 036 915 300 043 555 401 989 366 444 150 966 736 428 099 608 674 636 628 823 268 532 574 757 650 173 026 974 960 183 023 712 296 940 454 452 299 576 810 665 711 716 622 834 406 670 282 219 508 464 823 489 631 679 855 853 798 300 130 471 008 338 146 930 671 844 068 746 695 094 490 503 583 323 913 382 838 769 322 230 478 137 313 703 266 564 441 084 891 875 661 563 036 077 204 561 323 675 139 265 318 302 815 018 801 646 387 881 471 040 736 560 886 904 510 560 688 484 126 466 611 143 046 110 930 854 810 564 968 735 164 669 684 573 647 554 692 749 072 113 923 783 897 406 294 036 128 569 595 204 576 309 267 860 920 143 513 765 896 948 476 208 171 327 717 613 084 464 074 887 656 616 808 831 212 089 506 025 026 024 849 395 667 743 057 847 570 092 393 193 785 487 785 170 735 975 793 758 989 344 277 465 103 567 946 730 746 014 731 441 591 437 616 864 524 439 306 597 920 776 338 585 529 389 194 711 265 998 858 915 564 109 700 579 862 435 531 164 419 054 360 064 463 378 587 788 749 265 520 929 519 174 138 389 072 793 680 071 125 939 464 686 452 724 940 262 117 003 341 361 430 939 507 028 506 452 747 066 554 404 564 795 659 699 990 175 941 824 778 627 742 978 959 615 500 391 691 312 350 952 770 683 984 369 640 547 177 017 412 940 493 336 437 623 073 642 112 932 894 910 579 709 606 448 642 054 722 131 400 005 317 277 665 160 591 047 269 955 080 891 219 035 686 294 171 298 676 485 165 385 385 926 729 566 526 143 856 073 826 672 484 066 183 175 357 477 980 959 526 517 652 251 343 877 641 226 680 666 279 607 816 490 261 517 182 119 371 952 303 257 214 219 388 223 316 773 370 968 440 101 235 558 183 182 491 235 767 106 591 853 055 456 375 290 496 533 015 713 390 610 915 027 414 482 564 151 984 490 721 663 876 630 491 871 528 363 644 450 422 848 206 131 514 541 709 048 162 111 919 639 604 452 370 509 461 692 449 514 640 540 532 019 108 068 634 605 231 995 725 745 315 049 810 442 337 578 372 576 820 825 795 335 528 947 960 808 273 733 661 783 197 257 527 438 996 181 302 507 489 505 738 713 358 320 193 111 503 471 164 767 245 223 138 693 053 981 020 999 951 257 313 665 348 204 617 570 603 008 238 686 335 075 927 373 626 881 668 707 507 399 224 715 015 711 187 078 206 310 323 261 176 885 243 195 723 381 819 712 524 268 866 562 288 518 491 058 986 456 962 040 113 741 657 354 482 965 289 063 730 376 902 329 126 998 685 329 794 987 523 854 391 384 952 171 575 336 755 702 612 635 535 017 927 852 382 876 127 047 233 154 967 204 570 801 584 359 719 678 476 351 991 984 459 263 173 468 881 766 095 263 655 880 958 908 690 807 557 049 935 110 554 946 136 799 166 449 351 845 083 713 337 303 911 087 361 029 466 647 890 928 992 446 961 875 503 988 667 714 609 161 623 637 881 576 207 829 693 625 485 324 713 184 594 281 018 999 519 227 665 678 397 387 408 522 489 842 406 615 393 168 214 331 997 010 391 629 333 515 069 422 683 407 343 499 227 911 214 942 869 353 319 950 259 141 401 680 396 956 241 544 400 984 745 206 654 882 616 103 795 382 231 802 150 022 126 363 428 041 637 031 752 022 087 352 609 938 953 213 939 166 872 900 904 658 422 231 318 650 266 068 083 760 252 830 280 107 724 716 418 531 770 416 170 075 123 979 620 010 040 724 703 573 768 494 937 279 071 783 430 224 639 632 672 816 701 416 327 416 765 762 697 215 376 934 731 500 677 041 116 518 333 676 859 378 679 158 121 951 079 782 445 219 278 483 304 147 826 105 409 896 796 505 233 721 825 697 298 463 961 353 952 356 239 238 897 626 360 643 091 109 116 869 794 952 175 671 234 190 116 866 005 910 855 509 989 658 930 716 614 198 822 726 010 647 523 726 648 335 427 740 663 759 402 840 465 683 053 628 170 119 211 131 188 070 960 326 543 842 757 649 450 948 640 956 724 051 520 573 100 818 837 173 098 838 335 141 739 406 099 407 156 622 814 228 242 006 542 128 110 284 211 392 137 199 453 265 311 863 290 842 096 665 968 450 867 290 347 509 724 363 758 319 837 455 655 446 409 932 010 418 796 721 645 111 366 013 348 567 325 608 222 995 470 104 354 493 710 735 319 358 961 791 763 214 872 602 334 893 806 363 800 727 775 045 106 303 073 948 274 141 358 155 057 069 863 823 888 193 653 819 070 562 340 312 206 048 327 959 422 313 706 095 464 384 535 584 027 447 924 009 729 271 167 787 371 285 225 948 866 976 222 964 031 654 320 778 999 244 837 332 789 736 351 201 619 099 878 607 728 187 031 423 882 744 324 567 393 879 692 437 238 113 953 277 005 720 759 073 361 465 035 795 918 862 121 843 298 107 243 297 702 686 207 849 016 665 863 675 819 735 484 813 388 449 505 287 342 116 416 984 467 993 964 293 379 332 429 712 793 862 910 732 862 328 541 769 009 191 136 179 915 113 560 405 986 521 209 176 727 606 989 385 796 791 320 465 907 761 168 034 218 723 466 266 317 475 592 139 670 340 940 055 111 401 387 497 737 350 275 540 137 983 712 891 136 540 929 656 360 020 372 720 282 013 440 997 786 756 703 029 725 494 504 334 965 980 559 522 971 487 972 379 649 561 491 045 045 741 984 132 537 422 953 769 278 487 332 505 965 653 776 315 786 676 841 969 707 372 710 633 987 689 900 707 241 930 795 760 036 099 258 259 171 679 700 702 759 302 964 730 829 803 982 166 365 157 806 199 751 135 811 043 263 626 756 341 973 125 198 900 217 086 864 650 807 939 128 785 089 615 465 255 751 399 457 475 175 375 499 710 891 373 227 439 929 828 637 675 878 956 099 222 557 732 113 625 365 909 952 113 336 696 429 982 309 695 192 798 819 126 365 698 956 271 609 377 507 363 725 143 414 858 029 563 668 381 747 906 346 827 274 998 459 420 128 837 579 477 914 883 725 656 594 611 622 885 460 885 756 160 618 671 416 654 428 566 377 912 410 094 559 499 206 977 020 908 923 339 102 322 563 326 216 044 222 102 686 603 630 911 641 370 514 858 229 893 096 975 444 563 132 305 631 007 220 448 193 982 370 180 917 540 924 949 467 135 097 327 160 551 414 527 977 316 620 749 658 998 902 647 569 232 731 870 504 501 058 589 278 757 112 692 803 877 943 888 915 690 069 925 478 066 699 043 889 241 260 119 482 236 903 095 259 373 187 349 456 434 371 210 382 478 545 584 487 926 211 720 837 952 477 650 255 471 252 382 038 723 520 230 751 060 599 668 094 037 050 813 656 824 138 157 051 078 959 631 317 655 094 622 187 363 616 387 091 484 193 404 911 914 657 909 229 540 119 637 765 576 294 508 420 098 689 146 770 617 900 569 000 705 549 312 296 257 541 494 865 766 274 160 712 996 395 728 553 691 116 917 587 576 352 515 648 386 997 900 333 324 359 983 921 801 203 562 804 215 964 858 726 722 874 164 706 815 534 499 440 841 228 171 555 234 895 839 569 271 477 681 959 538 912 077 312 658 784 495 838 313 913 652 242 343 891 245 586 134 655 306 325 683 844 226 662 941 219 336 382 120 904 021 950 580 035 616 956 161 780 193 122 005 593 376 006 627 019 687 944 133 715 962 668 009 089 877 868 868 027 625 745 333 959 655 537 286 759 222 360 764 493 573 898 318 405 819 807 374 214 414 185 185 670 425 180 155 987 380 549 320 053 043 270 848 333 374 501 513 433 592 529 006 155 685 025 293 180 080 318 700 726 855 707 754 333 839 966 259 291 426 098 032 529 906 784 255 715 857 990 260 126 293 030 813 722 642 541 957 748 650 812 061 798 322 385 950 473 622 566 154 879 784 945 892 488 853 444 221 162 300 958 522 741 548 338 632 330 602 023 115 880 272 266 030 472 931 939 801 062 583 102 643 244 049 603 171 171 861 595 621 195 080 569 435 854 820 922 839 758 119 904 254 088 119 905 045 665 099 545 514 002 324 727 278 009 216 912 972 447 082 165 597 927 486 373 341 337 468 576 902 709 159 203 982 369 381 817 375 234 658 066 850 307 190 379 828 637 786 519 271 134 956 908 195 465 530 152 560 576 163 009 302 595 099 294 495 808 545 988 173 222 616 543 083 365 598 615 862 342 267 245 213 315 073 483 120 851 162 149 390 212 399 511 871 376 088 796 482 068 244 783 693 036 686 393 356 943 575 087 679 945 512 712 033 508 369 668 229 262 684 573 132 537 204 881 507 442 066 471 431 388 255 670 039 514 106 020 309 015 970 714 002 385 642 474 560 183 524 778 307 121 623 460 488 517 644 346 059 680 466 907 874 310 290 016 138 278 154 834 989 871 009 652 702 938 112 578 454 516 882 244 445 751 507 750 350 546 738 032 563 197 425 651 406 844 838 130 547 439 768 758 790 049 761 637 645 023 995 327 099 882 690 311 281 541 412 499 311 763 235 090 197 191 617 393 196 604 578 032 285 866 714 371 111 423 475 191 774 265 421 585 908 903 140 662 011 097 331 535 786 667 557 884 142 559 878 970 691 921 680 508 582 865 019 370 559 256 294 395 679 836 700 360 579 732 324 665 470 840 684 741 603 477 393 647 226 646 381 686 989 012 982 308 735 416 771 575 497 214 756 268 956 642 548 932 295 763 394 381 431 431 298 715 167 517 981 951 404 465 857 741 318 266 108 972 948 076 681 447 240 534 330 642 366 927 272 879 076 075 844 201 386 983 774 445 538 408 309 370 348 046 119 726 095 440 868 352 403 465 448 393 242 124 075 772 472 100 510 163 182 052 500 532 290 397 663 004 445 111 286 452 835 892 170 669 605 840 841 714 712 024 097 682 285 609 787 134 960 883 006 447 060 725 488 390 834 758 280 686 611 552 432 759 447 035 810 298 277 272 668 007 179 246 565 174 643 321 027 987 636 633 786 598 841 227 845 840 280 642 158 002 435 735 544 355 101 996 490 827 374 307 575 156 729 029 014 043 650 335 700 956 211 692 732 564 218 173 050 417 240 826 335 732 062 112 030 098 568 146 897 658 746 236 617 293 900 499 689 098 040 665 851 709 925 315 776 387 643 825 661 628 196 269 049 732 714 970 617 820 443 813 899 413 973 476 921 376 795 030 782 993 345 650 495 153 012 611 373 047 425 199 033 990 894 939 133 475 821 808 297 178 245 266 189 562 323 238 166 035 723 088 724 650 014 652 811 184 909 972 720 012 050 317 157 280 196 873 143 634 486 661 760 054 714 059 882 323 776 748 300 722 386 230 102 048 622 650 784 010 614 251 530 033 101 566 344 420 726 091 166 125 428 223 550 721 969 579 382 637 178 469 325 841 475 620 549 633 914 097 080 355 358 902 128 948 149 098 980 936 675 864 691 735 202 534 450 549 758 959 160 882 339 473 326 638 274 867 997 831 068 665 270 521 193 029 622 230 558 866 700 515 451 760 984 956 861 330 306 200 081 040 844 734 880 479 993 065 086 097 086 770 717 405 076 181 452 070 381 240 420 973 828 506 422 930 084 169 767 594 391 858 261 071 119 347 965 880 917 745 787 266 391 063 303 799 738 584 775 093 073 390 189 382 305 987 753 415 339 136 837 656 149 875 176 021 059 898 138 098 297 427 192 418 214 813 827 958 892 510 565 013 704 456 278 938 280 236 585 976 571 917 670 500 296 536 249 812 185 943 393 083 622 060 648 020 150 143 665 249 830 397 778 412 093 400 592 857 068 943 198 486 761 565 976 157 509 881 332 981 662 764 135 258 069 103 150 368 011 152 616 585 204 605 545 540 538 849 285 667 161 758 703 012 354 256 749 928 914 383 907 347 301 448 453 300 378 900 685 657 816 168 057 980 540 189 198 557 835 662 710 230 526 064 661 251 435 054 569 149 646 732 387 942 417 415 845 160 919 357 213 077 255 246 668 096 719 781 833 519 255 809 163 890 641 516 300 394 114 778 985 788 579 271 203 249 962 171 391 584 993 210 407 839 150 320 002 638 713 642 577 064 390 812 741 295 089 509 420 907 607 959 342 654 365 766 287 765 121 348 467 277 821 156 904 240 479 497 629 376 188 626 172 098 952 953 880 000 219 492 586 384 353 492 921 310 820 219 271 076 304 300 055 409 014 357 552 626 823 787 208 134 136 422 369 186 166 682 500 520 971 187 034 678 525 360 870 962 443 552 061 172 059 922 414 730 690 529 693 464 170 524 769 237 313 364 825 626 459 503 233 075 395 315 082 799 077 355 504 029 022 645 867 132 446 715 205 751 658 845 758 795 091 141 310 278 933 645 987 300 418 221 037 022 628 467 771 295 466 618 548 887 841 426 659 539 936 227 342 504 166 680 797 683 254 562 743 237 259 046 145 050 168 754 039 142 724 664 398 619 430 452 066 912 092 412 577 632 867 966 663 126 366 712 436 031 814 647 050 992 676 850 596 111 799 085 169 593 228 370 689 219 540 854 496 930 661 297 197 693 278 542 757 174 762 720 469 271 899 828 658 337 386 915 889 771 386 612 925 846 778 220 909 298 188 546 190 812 360 271 201 041 187 678 638 485 636 518 970 056 248 598 932 625 625 233 655 286 855 190 186 163 962 776 614 710 135 025 692 013 312 164 291 128 623 186 823 869 210 076 983 384 756 627 130 536 373 726 374 925 995 880 933 192 071 495 108 491 675 410 775 427 416 525 951 501 556 342 867 201 329 114 998 192 548 519 032 787 226 397 756 754 853 845 769 879 995 201 899 697 942 624 794 011 480 373 077 415 651 195 526 024 160 952 872 154 136 137 583 315 111 491 769 349 028 716 620 166 862 681 883 993 319 037 147 971 776 457 685 982 557 326 808 135 190 900 138 295 277 329 502 400 015 115 557 642 711 397 909 266 474 186 579 513 352 163 474 134 033 483 131 118 214 243 855 356 772 270 135 544 947 572 323 671 167 772 023 764 444 867 398 988 283 558 976 672 464 925 680 362 126 163 839 719 552 446 120 079 336 803 346 048 470 283 524 538 745 207 036 371 343 235 832 390 795 300 318 028 685 527 688 032 070 333 466 125 009 271 525 803 241 478 016 288 527 614 187 137 142 978 020 769 460 838 245 788 892 159 658 980 041 306 407 696 000 246 976 617 614 379 150 531 782 791 592 739 545 676 865 687 472 513 835 730 918 133 972 264 451 717 506 594 870 124 510 835 229 634 304 507 143 138 844 105 023 898 700 131 256 875 679 681 585 631 254 495 075 341 275 081 798 077 453 519 666 738 933 683 270 451 728 014 845 614 584 349 866 539 552 722 662 287 986 005 899 267 346 523 156 860 773 633 438 775 017 129 236 360 961 435 154 657 595 726 871 540 903 825 080 581 038 583 412 110 681 051 317 953 466 133 506 463 525 056 772 430 441 409 123 646 672 425 166 258 347 373 207 007 537 051 655 979 685 680 420 855 569 192 869 769 835 929 461 011 426 547 710 253 999 378 260 030 862 850 316 892 973 734 135 110 316 457 610 384 387 410 279 475 210 316 114 992 677 550 144 373 313 641 691 923 262 185 972 386 837 276 870 433 963 236 732 636 064 508 667 266 846 000 844 448 678 510 621 784 463 916 053 686 878 459 018 591 308 104 433 919 576 541 273 310 156 241 245 512 164 253 101 847 316 906 321 024 819 248 749 402 256 832 873 750 481 233 128 863 386 565 254 661 175 533 701 526 030 554 292 920 040 916 215 745 394 104 880 272 790 783 387 163 371 707 455 325 770 434 107 241 936 977 430 745 573 384 760 234 491 499 379 493 980 395 587 640 040 550 805 272 129 070 661 115 973 986 837 432 918 212 450 667 449 758 532 047 514 925 715 374 721 524 865 832 068 902 338 947 651 571 184 589 509 426 830 520 350 876 030 612 428 240 818 561 275 744 948 100 821 080 131 020 339 048 694 287 312 662 188 704 399 255 001 641 345 934 805 237 792 562 988 681 427 203 985 734 497 274 943 450 895 210 855 727 118 413 157 345 352 096 279 895 788 524 894 784 120 218 648 830 009 428 212 806 651 520 364 245 297 939 973 887 009 347 331 152 408 898 398 497 578 944 253 913 219 576 666 206 054 344 710 954 503 556 860 512 980 308 456 618 277 076 542 945 478 468 867 797 983 832 551 038 837 233 929 407 882 166 038 828 532 094 726 753 869 311 299 647 016 948 328 494 716 132 816 580 513 625 273 389 398 214 307 045 493 823 244 394 470 136 696 288 897 550 614 878 071 161 486 612 332 787 829 705 171 093 775 335 832 398 087 627 494 690 774 766 853 114 504 126 101 953 178 071 337 160 687 504 295 953 008 341 627 987 116 346 899 236 075 956 693 490 155 718 909 476 848 103 797 411 855 370 552 704 859 208 146 086 615 855 816 848 550 031 837 533 308 937 084 738 785 015 849 643 105 307 609 254 768 144 284 744 146 206 518 310 320 894 300 770 443 172 462 514 282 772 885 182 297 544 735 539 942 739 073 631 281 841 593 937 064 660 020 979 307 286 371 367 428 771 926 667 946 721 319 578 257 192 893 819 585 038 965 410 816 468 939 006 678 159 261 793 112 979 011 132 167 845 121 027 812 000 770 009 823 389 862 222 691 382 825 063 970 781 442 733 753 248 202 108 988 316 076 543 785 862 049 430 435 619 260 518 230 994 966 269 286 404 681 584 770 408 948 578 157 148 757 922 679 990 379 284 699 730 705 905 764 031 178 643 772 568 850 799 092 878 063 554 014 736 368 983 285 403 292 763 380 759 620 947 642 852 466 116 421 022 076 070 897 107 366 988 915 339 253 235 547 595 169 765 613 042 790 941 564 206 232 596 866 588 622 443 630 261 268 555 233 908 615 977 689 178 792 336 457 025 446 552 144 633 420 070 150 207 461 570 079 284 934 525 197 015 484 673 021 277 815 394 665 219 467 768 859 497 848 076 142 887 194 976 193 735 823 664 667 293 966 563 232 883 718 212 266 896 261 827 091 958 194 719 212 953 404 008 750 476 844 163 818 395 297 136 366 425 141 340 515 482 670 590 082 314 257 869 741 174 531 938 455 468 546 658 262 091 387 281 681 479 694 466 288 094 757 596 603 112 238 046 481 128 346 970 528 916 310 883 148 279 167 006 708 228 853 880 028 713 920 013 764 848 261 031 744 887 535 166 913 146 776 913 693 764 024 500 023 935 368 823 339 111 453 619 551 933 988 973 348 685 042 259 944 166 331 379 134 791 834 068 128 902 868 662 913 871 886 566 340 870 750 675 020 435 252 774 553 614 645 337 458 774 657 809 364 658 018 784 071 996 242 436 799 322 029 032 156 852 417 644 542 510 866 481 448 462 850 077 866 274 432 106 729 627 312 816 966 744 302 813 856 774 937 559 208 440 120 713 173 942 421 787 081 683 801 136 589 953 485 099 998 773 979 427 688 507 974 218 123 382 508 950 971 679 463 243 086 761 125 197 508 275 772 513 263 263 449 066 710 321 984 190 011 410 539 266 450 883 052 346 545 813 559 349 339 122 113 274 133 659 370 290 146 989 433 705 842 372 363 078 601 894 044 372 165 742 807 785 688 243 354 204 487 865 798 172 464 477 564 436 490 165 326 835 007 450 846 689 227 527 087 781 370 829 400 507 847 665 350 894 389 325 292 964 097 385 983 875 851 095 143 833 727 321 938 108 312 036 075 966 462 881 437 120 530 420 588 914 766 820 250 682 429 234 788 081 363 547 040 469 932 242 405 357 966 954 356 786 037 300 246 556 346 651 806 744 387 250 820 517 355 419 148 876 652 450 692 784 995 778 545 845 400 341 583 549 879 742 674 110 575 157 760 320 985 013 467 943 855 113 491 803 181 339 807 403 481 992 398 883 475 493 567 189 745 922 719 080 523 545 170 160 585 508 025 230 056 248 091 232 544 623 663 144 467 908 011 795 787 433 734 105 343 625 239 867 021 789 827 301 414 248 857 644 675 223 291 852 411 462 710 106 703 057 098 267 386 015 735 402 110 356 772 267 710 930 188 427 905 689 672 290 971 303 132 662 606 018 685 043 872 649 965 954 865 039 146 730 445 377 991 247 654 868 002 010 838 887 737 480 714 493 296 850 306 762 913 003 024 420 716 641 415 116 335 546 531 246 012 912 587 630 438 248 016 651 463 209 145 361 200 911 702 193 610 096 747 776 590 211 374 114 267 983 652 973 356 988 681 122 838 239 092 333 138 204 444 596 727 099 154 533 437 554 625 291 251 945 418 216 669 823 412 902 112 006 399 150 825 271 301 924 059 307 118 672 860 115 009 758 268 305 287 746 520 247 101 626 528 796 013 789 167 676 875 876 789 929 388 541 028 763 040 715 856 083 118 661 286 822 868 993 753 534 872 584 909 282 949 361 159 017 654 454 887 363 764 748 589 998 956 325 871 337 691 462 481 273 936 391 905 096 769 411 448 574 761 575 060 360 029 391 427 384 737 477 117 764 110 618 016 114 003 113 567 943 602 577 739 264 908 196 430 619 515 287 316 231 458 407 648 882 794 569 481 000 701 233 527 642 243 898 868 500 599 185 523 048 252 706 125 712 300 432 074 210 066 475 669 223 121 122 760 309 648 751 450 046 168 390 923 964 683 573 113 932 413 821 335 111 804 327 618 203 082 660 786 154 231 528 622 620 892 634 754 629 267 936 700 900 460 430 170 961 836 371 465 063 451 376 047 511 804 770 620 026 975 755 522 515 483 407 388 860 941 771 866 345 154 823 217 658 402 839 229 367 339 095 725 743 472 520 985 360 330 793 490 145 689 521 057 617 996 813 539 245 560 388 595 144 814 190 356 871 048 634 157 855 824 621 255 117 796 976 611 624 407 203 753 239 138 847 874 630 648 679 669 268 905 956 262 937 667 583 370 000 456 590 657 697 125 578 439 187 893 953 884 526 074 624 454 901 617 765 465 204 564 832 208 854 914 317 463 182 639 101 320 822 097 115 362 153 755 979 861 179 828 666 542 042 245 895 856 429 751 659 497 706 780 592 037 572 538 219 973 193 146 636 269 649 853 080 360 271 383 325 314 775 470 478 467 428 008 198 855 237 658 226 830 570 066 576 918 619 073 107 430 200 163 445 658 200 407 662 872 179 164 457 299 343 361 302 225 385 939 608 742 984 473 143 426 619 878 462 127 305 105 523 045 448 116 123 206 835 375 550 830 998 196 477 471 785 144 042 478 190 538 602 822 734 298 952 413 570 395 554 774 772 516 714 872 362 438 541 392 248 629 214 932 326 702 646 740 216 959 642 142 356 239 611 193 259 521 815 369 209 796 223 729 112 624 259 806 799 680 301 272 347 193 759 742 508 364 105 646 465 999 350 348 123 427 730 427 563 582 807 574 385 895 725 494 047 199 402 485 151 918 856 188 916 506 875 501 258 865 140 786 506 815 987 412 588 309 555 846 524 574 751 902 773 017 355 356 265 476 029 098 023 110 913 519 356 420 751 179 278 476 315 226 815 280 025 647 311 268 947 590 078 207 021 474 763 067 676 052 722 764 584 362 735 242 610 247 330 529 485 413 939 530 606 095 366 116 663 574 995 454 329 653 066 841 162 384 232 304 800 632 025 143 159 892 209 928 923 186 991 020 790 511 786 384 198 154 868 700 767 800 183 337 767 427 527 033 285 119 250 192 551 931 328 727 219 517 229 464 428 481 121 274 274 219 960 301 671 989 013 087 524 248 026 894 972 278 359 253 115 254 761 407 431 664 216 544 821 094 313 599 862 727 612 084 557 617 274 084 770 400 143 005 342 001 110 289 104 865 976 929 037 095 766 460 405 196 759 125 276 684 268 468 427 946 987 074 442 381 847 805 475 309 317 458 615 008 743 181 859 404 308 926 460 091 539 256 971 077 605 070 362 130 548 787 025 555 065 865 390 674 771 392 763 922 737 416 421 457 294 580 356 919 698 746 155 160 549 641 147 957 377 510 259 243 565 335 000 259 710 394 415 860 734 043 997 439 795 018 964 178 250 566 316 745 299 886 678 034 310 402 246 664 862 296 702 907 290 197 545 714 539 688 941 738 953 703 480 147 449 776 895 049 008 135 716 166 534 963 459 034 820 004 913 724 013 985 679 274 707 624 312 226 282 642 957 720 562 068 415 265 269 595 044 247 311 915 562 536 039 742 687 266 863 019 636 313 571 759 716 673 763 422 402 256 142 868 929 383 469 746 499 344 620 559 814 281 181 673 080 236 655 657 460 807 908 441 078 579 789 392 541 750 380 065 974 618 394 389 622 310 864 257 066 706 309 335 490 909 552 646 912 491 659 661 243 596 603 943 022 980 931 557 147 024 277 600 611 482 196 942 572 512 445 344 729 828 621 983 281 286 189 243 271 287 220 448 373 280 509 867 031 357 456 755 679 771 281 301 078 866 486 896 247 564 855 444 601 052 882 518 405 193 329 951 700 235 563 164 823 949 810 404 006 490 579 857 227 126 349 284 575 296 368 693 435 591 720 959 598 111 606 749 495 955 725 226 641 353 918 764 866 315 046 370 646 248 307 100 980 004 320 574 730 761 638 091 431 739 834 873 728 406 931 894 728 839 507 217 571 153 349 800 240 639 317 447 909 098 009 414 245 800 151 535 100 395 882 744 085 138 982 362 519 291 609 882 457 008 553 783 662 788 124 239 576 860 112 601 138 865 804 309 370 318 555 115 351 909 456 165 025 715 340 720 139 140 205 117 193 382 834 695 767 929 834 837 497 344 768 588 394 287 606 032 051 142 227 242 036 578 390 232 010 906 482 448 121 875 958 142 618 309 444 959 437 152 066 784 204 016 845 855 455 034 813 232 685 360 200 398 115 577 923 331 840 826 907 161 206 678 965 755 208 463 045 489 231 832 873 538 907 230 550 861 484 970 699 229 968 369 502 833 326 946 607 509 056 931 710 492 979 625 461 457 922 118 512 687 964 675 704 685 588 241 286 866 741 837 976 220 627 677 803 385 185 171 183 895 554 478 058 856 985 356 540 487 023 637 106 881 396 568 842 118 031 883 835 333 237 179 002 317 113 026 457 623 834 758 477 392 467 122 419 591 207 649 301 786 925 412 273 734 014 881 420 711 964 276 368 749 154 245 859 566 365 285 050 201 356 482 129 959 862 132 290 505 490 457 205 476 981 244 381 072 102 486 362 519 112 583 732 659 264 442 672 562 897 416 138 248 155 023 634 789 990 622 633 997 009 646 125 648 745 379 691 468 932 796 383 375 100 454 829 177 980 529 027 628 613 134 902 692 943 324 838 705 193 267 571 396 536 850 887 149 456 538 927 542 664 157 490 226 565 376 238 986 179 073 550 544 104 907 310 685 421 384 602 823 334 247 922 549 882 490 829 006 816 862 513 824 161 714 293 978 796 036 717 414 891 262 629 370 270 237 618 817 573 088 427 389 013 936 052 539 277 979 497 770 288 160 560 330 220 757 173 615 696 700 628 626 257 780 744 936 464 596 483 884 219 502 874 845 662 980 992 841 002 538 128 847 018 114 366 925 416 293 662 272 289 151 944 680 388 011 145 507 093 243 861 492 285 704 376 350 949 745 885 334 032 567 626 890 608 610 910 992 063 423 175 206 687 755 426 212 654 170 737 274 374 448 807 438 678 100 610 526 438 937 376 692 689 700 731 049 737 636 892 810 293 132 410 397 287 228 301 755 476 949 687 289 701 784 573 924 362 194 923 162 485 926 616 275 488 563 752 270 841 585 690 006 624 391 370 552 503 774 318 869 598 107 413 667 500 177 225 697 706 324 197 706 764 072 712 748 516 533 411 886 355 471 615 104 367 786 519 584 401 447 315 807 555 522 468 916 392 857 883 805 008 111 301 294 600 787 152 140 315 102 085 130 976 156 972 108 221 529 670 605 169 016 822 517 720 449 061 843 436 034 235 978 089 069 442 698 791 345 529 095 534 959 259 572 729 745 597 956 460 746 388 504 080 624 044 068 780 510 558 693 478 815 401 238 925 113 634 133 028 354 587 589 042 086 962 295 890 139 106 754 772 210 947 203 656 244 419 513 002 341 718 462 973 817 199 973 206 218 206 937 541 123 793 054 523 537 625 024 052 894 741 207 580 689 946 801 463 391 497 534 866 810 375 917 571 921 524 182 400 021 397 773 201 970 054 717 712 757 574 759 235 989 253 383 805 067 538 381 894 079 810 835 898 897 215 566 458 984 460 842 502 827 722 515 892 756 328 220 292 421 541 501 660 025 853 026 619 974 843 295 441 221 755 692 166 610 249 673 026 374 127 342 834 726 086 019 713 582 428 030 090 992 898 018 006 317 876 028 692 480 870 516 339 160 418 028 208 548 140 053 087 368 495 179 470 774 928 932 981 516 552 092 914 222 269 910 837 706 898 546 611 564 758 928 218 679 269 332 103 305 989 187 615 733 619 668 269 089 821 919 526 328 216 877 939 065 880 482 145 010 523 607 334 591 095 590 421 897 780 165 021 202 094 777 631 967 951 882 895 714 034 537 769 497 827 900 276 041 062 160 808 151 310 329 025 063 851 291 008 943 247 824 331 812 048 115 289 465 052 715 044 793 500 639 398 310 253 536 814 199 749 779 375 781 903 375 480 520 222 966 136 737 223 795 698 666 842 096 865 433 068 781 755 532 826 617 109 393 724 821 600 148 702 194 410 847 287 860 249 777 699 158 984 087 725 376 748 959 533 274 519 799 507 465 020 000 371 748 210 862 491 815 321 389 044 750 133 064 775 389 474 624 369 758 163 044 397 378 895 694 366 906 902 835 627 797 416 580 513 996 245 253 220 661 189 604 868 620 219 595 459 814 845 317 377 816 639 458 421 922 179 687 566 026 168 555 424 069 049 777 478 461 102 057 642 922 439 982 891 489 206 720 222 173 447 242 502 772 483 692 368 616 359 763 560 794 598 845 948 162 900 122 730 676 778 340 281 528 488 580 564 630 816 859 267 287 534 283 710 533 652 667 725 303 272 427 035 276 840 144 142 615 922 151 602 556 301 675 288 901 560 978 993 547 731 132 844 359 052 701 596 470 765 417 199 723 175 624 240 137 988 392 170 318 277 719 467 504 062 523 593 595 113 202 780 865 841 374 352 701 979 502 289 407 787 781 351 023 129 252 285 440 027 361 262 112 807 997 120 090 372 238 660 278 221 553 951 514 593 278 710 094 931 121 146 360 464 528 068 383 280 591 419 750 840 390 919 788 794 823 192 398 789 647 354 253 895 195 281 635 026 545 759 766 409 261 043 788 066 488 164 915 250 543 523 796 699 138 643 954 847 878 253 407 194 757 504 097 224 008 273 222 852 003 909 611 134 248 158 572 438 481 261 081 211 460 185 325 085 829 530 593 962 125 167 983 409 984 339 986 959 984 907 376 276 247 261 917 071 925 881 006 620 855 333 800 890 112 232 028 017 917 058 960 818 004 674 649 209 072 755 415 077 583 825 376 663 809 866 582 578 700 279 803 804 340 755 743 280 124 590 249 942 184 562 006 820 813 907 674 523 489 533 859 726 871 099 276 454 907 093 704 889 247 715 515 973 585 126 814 034 013 470 111 828 503 282 339 475 567 436 610 964 535 438 301 900 872 500 474 586 834 315 933 627 669 295 391 347 900 910 427 976 895 710 221 514 303 016 478 266 641 790 447 777 990 765 918 894 599 171 079 092 907 919 764 271 218 904 358 636 842 681 095 767 457 136 879 145 339 887 752 343 171 084 893 964 915 059 125 589 912 414 556 130 382 841 415 582 831 587 277 243 404 359 330 563 953 400 633 417 458 054 480 427 117 419 142 121 384 253 428 397 459 014 197 807 613 746 745 446 095 977 333 895 705 763 032 702 149 331 797 371 605 827 085 673 159 747 596 098 881 552 392 777 510 556 267 996 199 515 435 899 370 929 237 085 435 131 097 429 481 656 361 831 486 655 703 903 211 211 360 327 546 580 099 326 730 678 957 273 433 792 064 818 655 097 635 766 485 611 704 388 891 877 405 186 082 869 821 791 489 660 826 737 592 593 045 859 124 503 761 258 910 946 291 957 535 939 538 380 168 400 911 100 388 035 388 573 447 739 212 016 004 754 614 894 479 453 390 446 096 370 044 243 752 582 835 925 164 372 901 630 784 871 379 910 429 253 069 892 288 775 149 100 535 753 109 141 344 438 658 517 572 987 676 883 098 107 050 706 463 033 918 422 558 381 042 938 632 892 559 105 008 633 006 767 570 022 589 883 590 940 793 183 516 146 874 855 245 173 357 215 399 078 106 498 104 719 611 421 944 862 001 050 739 474 528 669 812 714 379 021 152 222 418 484 015 381 663 898 040 319 329 071 171 814 823 441 477 983 990 816 585 314 288 834 637 770 602 222 794 206 522 552 629 458 279 268 128 450 417 083 372 288 235 553 261 295 789 671 798 554 504 438 920 891 554 229 124 258 759 966 698 841 349 330 501 159 465 462 818 189 490 388 476 974 169 544 856 677 971 477 486 482 238 745 171 033 926 527 074 912 042 088 271 167 592 027 566 891 635 358 276 199 757 463 112 711 954 657 621 368 556 770 475 751 958 473 815 888 945 625 956 959 544 794 675 024 380 251 333 270 680 120 726 619 475 204 154 343 805 797 329 685 263 050 315 530 644 780 180 768 739 203 647 273 875 827 703 297 332 584 161 675 305 484 223 048 161 861 820 846 518 103 925 336 746 479 137 661 993 935 176 007 979 020 658 675 718 149 655 901 820 798 785 362 886 441 493 837 689 419 275 187 743 752 195 715 963 023 140 712 508 902 129 075 576 322 458 246 620 255 570 578 040 533 110 344 766 462 655 237 340 571 309 451 176 612 246 960 224 552 576 843 354 287 529 137 382 034 020 740 895 252 299 668 472 630 260 001 472 126 140 214 649 029 346 223 095 269 628 809 533 329 192 566 963 568 077 908 405 645 713 939 263 463 381 974 368 889 839 655 004 328 054 563 335 571 943 698 322 177 665 837 578 693 720 214 026 533 899 473 004 776 643 897 042 386 801 590 890 330 885 160 809 080 757 745 853 777 339 679 384 926 814 886 607 659 231 946 867 843 972 401 876 076 163 594 466 507 738 044 244 232 972 032 485 642 407 915 570 422 734 642 708 822 939 169 640 153 675 918 564 821 129 546 252 346 986 907 166 422 637 978 585 858 538 964 299 834 551 837 135 484 228 587 696 386 037 892 028 668 436 295 142 519 882 161 293 089 771 345 105 949 040 494 128 242 820 848 931 783 918 970 930 884 706 928 683 189 298 695 260 520 106 874 129 183 366 051 662 993 588 760 569 901 518 172 587 927 928 875 870 467 761 795 966 808 169 515 361 308 652 473 704 837 480 059 501 172 122 553 768 519 412 355 125 453 270 571 519 255 358 922 776 495 346 375 209 200 459 084 412 333 012 256 711 581 914 636 218 973 081 610 891 169 848 706 584 571 472 885 375 479 017 633 400 818 701 285 652 976 536 564 411 884 073 155 569 440 995 767 345 565 987 618 883 563 631 807 966 504 580 386 306 051 395 139 703 575 975 458 867 720 198 637 465 482 607 598 145 943 787 228 390 263 472 852 464 648 619 325 044 955 662 909 205 304 837 182 404 780 794 229 183 855 343 222 500 688 928 231 429 154 295 332 039 656 800 270 956 116 555 806 110 435 725 905 741 789 708 213 987 366 346 000 156 510 112 854 317 717 766 197 489 933 318 910 505 314 383 563 486 775 036 548 754 566 766 593 115 674 275 423 776 336 000 679 793 905 366 819 518 375 126 874 157 516 968 719 330 974 953 449 854 182 568 869 458 921 729 799 900 304 795 296 138 576 973 472 708 364 482 312 682 281 352 269 461 978 280 373 042 160 234 893 626 409 331 137 924 336 739 810 083 563 708 325 404 384 705 489 261 099 589 184 660 515 279 486 576 303 558 904 773 035 398 508 279 789 129 987 880
575 819 389 468 734 908 260 398 666 545 800 205 678 345 430 708 808 043 750 654 556 482 755 077 854 460 796 549 536 980 547 414 396 188 433 039 686 601 442 104 485 744 325 476 150 963 009 080 788 271 150 008 880 749 565 752 291 578 121 028 407 531 622 925 213 733 136 215 533 841 740 232 322 897 067 505 758 867 754 233 086 282 437 718 526 285 994 601 262 606 129 926 675 074 969 334 495 718 195 396 828 072 238 376 580 010 227 511 454 350 232 225 969 678 000 951 648 434 709 504 370 927 326 890 559 743 031 148 240 039 295 251 254 832 237 235 184 809 471 017 395 643 721 257 904 783 162 291 488 513 896 716 625 694 848 947 855 103 431 484 539 906 474 351 253 346 995 303 205 280 323 701 343 065 321 835 859 704 329 410 651 792 257 330 033 812 971 926 706 405 637 807 596 306 947 715 363 297 759 668 822 529 507 980 197 663 941 303 537 427 354 126 161 170 505 790 396 969 059 350 393 622 580 962 223 396 189 248 542 478 968 842 856 504 831 531 436 046 087 599 283 680 469 713 273 787 246 491 719 454 956 148 493 837 420 982 688 624 271 368 522 922 392 096 463 403 648 121 440 048 876 174 100 942 632 594 339 264 733 866 332 910 196 076 873 606 058 948 034 998 931 287 952 018 341 440 891 029 080 731 947 071 263 691 456 692 420 028 352 800 639 251 727 646 951 216 937 304 868 728 659 572 550 638 827 941 481 623 531 276 012 946 444 079 362 346 413 211 374 443 731 799 757 841 153 995 465 860 822 898 083 708 770 809 837 898 061 696 555 760 954 471 799 857 117 225 604 142 298 409 861 318 638 011 937 787 139 191 617 163 784 796 537 926 722 976 168 919 526 411 026 030 906 918 744 582 564 635 486 394 290 169 122 947 597 175 248 872 554 271 190 540 296 823 134 023 463 628 491 966 714 377 198 640 133 983 551 643 942 258 861 386 561 512 013 885 679 767 299 754 830 446 499 362 875 286 083 148 168 129 848 653 026 674 615 423 401 602 403 414 033 718 071 061 321 399 242 323 017 501 994 266 335 634 355 289 000 214 241 076 015 462 586 972 149 135 111 575 359 640 220 809 858 243 430 065 787 813 490 166 764 386 037 951 977 440 537 380 344 576 950 757 106 333 511 136 799 477 553 367 075 641 940 780 555 402 230 214 046 713 489 406 141 311 703 714 394 921 300 709 857 060 723 864 143 114 263 494 153 038 999 080 963 059 925 866 376 289 636 708 677 762 083 198 346 528 487 535 524 418 451 220 886 200 551 530 122 860 922 252 301 822 404 227 687 727 038 338 315 846 311 806 361 939 856 790 401 978 155 465 764 992 047 166 084 102 932 037 093 770 819 999 102 199 615 969 642 809 196 442 139 713 821 467 367 766 842 772 729 003 221 192 363 234 826 288 699 873 798 226 294 449 517 760 806 141 453 892 972 778 011 580 389 361 971 817 877 660 312 905 609 320 316 321 522 922 865 696 549 726 655 108 715 914 062 897 912 160 384 669 399 090 837 525 853 176 767 673 183 392 113 789 067 232 919 981 933 054 567 954 056 888 458 055 086 462 639 638 742 938 241 243 110 358 190 263 557 873 564 802 616 317 045 828 579 806 956 652 933 483 183 115 771 448 969 947 174 519 474 792 790 454 526 256 167 281 796 333 714 883 087 776 991 628 785 103 542 023 156 904 640 092 730 206 574 125 877 749 674 656 233 488 823 742 324 970 392 120 950 493 635 156 903 715 088 012 653 095 195 474 965 522 399 166 360 779 680 281 160 866 832 446 276 284 789 108 387 983 991 723 442 781 758 143 595 875 604 050 575 490 949 501 967 622 127 802 970 437 360 211 295 612 308 951 695 265 455 949 267 381 595 785 804 392 549 449 698 061 047 238 894 736 994 826 898 253 280 307 287 730 894 993 667 242 144 188 313 275 871 545 869 775 549 221 552 696 391 309 924 351 695 129 855 102 631 574 651 539 920 568 663 540 056 947 325 532 349 937 712 968 935 883 330 861 379 750 272 256 409 455 255 331 835 536 538 308 326 406 104 607 192 239 152 883 572 960 678 077 749 084 466 320 537 317 131 166 603 998 546 308 224 539 989 359 747 089 316 740 583 141 718 051 010 170 041 419 845 758 704 597 273 301 673 588 446 423 408 753 130 232 478 779 470 062 017 829 672 606 574 991 662 243 228 649 755 084 442 899 337 060 752 509 038 633 132 517 810 541 000 534 141 952 650 996 752 826 482 811 665 086 448 750 292 668 883 234 539 971 048 704 171 628 011 284 885 197 635 041 610 957 280 218 460 842 739 737 867 563 466 330 628 424 579 779 045 850 471 383 489 402 962 556 884 693 727 615 166 040 533 066 886 686 879 728 315 970 914 621 128 648 098 993 919 474 603 312 190 907 154 215 026 611 650 898 679 206 152 778 429 193 866 272 477 767 367 056 552 047 798 238 920 318 291 603 616 758 408 244 200 726 587 670 160 210 040 178 690 207 710 830 668 388 062 194 940 894 424 367 433 443 386 693 603 293 149 391 812 008 783 744 241 663 996 758 802 819 188 004 017 570 884 780 830 973 897 418 303 741 972 441 623 341 714 190 980 822 408 074 965 440 986 194 372 848 740 548 272 121 191 072 429 641 664 314 953 806 885 485 810 430 414 658 688 238 141 420 795 673 579 109 881 254 268 461 730 840 970 918 851 057 927 510 456 192 634 528 234 596 745 372 970 229 277 957 671 842 985 962 962 440 924 844 333 400 935 059 977 411 142 580 592 886 489 358 710 727 355 730 196 964 621 070 357 692 280 776 727 026 788 418 071 119 103 387 781 781 831 106 511 891 486 155 960 293 529 793 814 034 610 972 305 833 366 844 567 254 147 122 145 410 483 330 600 986 543 809 364 058 976 318 329 326 568 277 062 741 320 993 957 147 873 654 665 614 685 412 749 591 003 264 076 948 859 309 436 241 153 833 780 662 186 136 800 173 100 125 013 559 619 547 524 771 249 239 977 011 564 566 746 294 693 439 196 101 946 895 025 559 479 143 697 300 073 000 540 130 835 773 452 518 957 378 167 180 432 874 775 511 800 719 592 250 639 860 303 393 406 069 463 042 500 692 267 850 719 272 322 426 033 979 242 508 820 157 759 126 504 889 657 548 521 001 320 831 272 427 187 801 737 584 612 666 173 355 291 248 679 721 920 214 500 251 425 988 443 390 934 463 115 297 107 943 714 762 015 377 949 694 126 309 647 665 425 037 348 166 597 555 420 320 640 715 197 119 567 859 023 037 073 890 859 124 768 354 485 943 053 670 379 874 981 344 932 106 900 391 737 349 730 965 576 593 211 410 366 864 061 195 201 909 151 469 847 072 423 845 866 212 799 450 003 683 877 412 572 509 258 884 987 181 475 087 005 599 029 364 043 811 064 981 303 356 991 974 358 210 617 006 932 779 318 257 505 936 623 459 906 964 198 080 006 825 366 126 703 313 050 928 737 079 835 247 595 489 563 089 240 951 604 248 754 352 996 634 505 052 383 351 272 211 738 708 640 305 297 925 194 128 178 326 814 636 964 384 371 551 838 198 425 853 566 531 115 148 636 547 254 164 871 796 768 675 997 922 259 962 896 055 275 220 356 887 629 121 495 658 228 864 448 638 319 519 005 323 421 890 518 697 264 420 721 102 442 854 985 317 843 916 513 135 899 398 935 289 556 735 880 264 465 464 291 395 578 599 859 134 352 310 320 748 429 175 835 166 605 718 208 448 265 081 001 892 169 029 246 401 237 931 829 413 452 069 949 918 104 725 847 607 089 781 878 293 490 254 540 792 576 762 934 653 870 179 849 017 117 299 960 457 281 377 646 526 996 568 511 198 675 454 628 048 158 453 608 132 581 232 268 507 969 224 334 063 486 051 648 578 910 462 093 487 980 189 063 626 724 913 290 565 125 321 975 314 490 654 324 201 681 928 486 567 516 653 908 059 445 324 052 297 348 302 449 025 784 292 420 310 929 223 981 477 683 713 768 699 093 269 873 383 931 117 246 435 387 398 798 773 634 368 273 565 635 366 319 588 739 650 433 725 206 783 360 102 093 882 399 087 820 668 516 339 034 266 713 393 357 720 471 109 860 114 568 600 995 060 136 271 059 572 416 681 991 287 393 089 333 665 924 275 965 868 862 847 844 369 417 261 195 586 680 498 081 267 587 077 494 438 594 880 294 822 589 720 869 944 564 853 737 300 667 348 946 255 344 105 671 012 221 020 333 204 303 323 971 453 430 785 251 418 300 557 772 761 504 502 913 965 864 593 575 940 738 194 434 634 234 848 420 298 599 273 720 112 023 481 708 462 202 885 021 159 175 970 080 554 204 910 608 249 514 849 551 641 341 360 676 856 864 919 412 486 264 993 566 518 607 939 171 917 249 642 826 286 151 547 766 691 706 417 642 783 045 027 628 029 209 542 259 192 158 173 861 192 102 247 990 327 140 117 371 821 771 620 098 205 999 791 725 127 078 787 151 180 309 054 757 335 948 560 587 297 213 605 794 322 895 391 164 077 274 298 656 256 668 870 784 655 527 148 954 885 612 816 683 976 601 884 884 005 533 000 520 533 822 298 088 986 142 828 784 933 844 984 244 556 877 276 932 403 355 931 011 022 234 320 403 395 099 284 104 954 223 138 398 781 453 555 477 501 548 456 488 513 577 862 969 986 768 669 473 797 216 493 018 600 475 497 978 351 934 361 763 686 331 598 903 761 163 686 202 101 949 563 745 930 116 027 727 298 903 110 394 210 488 270 536 078 286 172 071 534 532 017 432 420 069 619 879 672 138 435 972 483 714 697 439 210 199 491 274 123 678 689 939 698 546 067 290 987 815 595 899 981 326 008 012 109 050 896 800 703 625 980 397 631 698 562 025 607 851 869 985 636 492 848 582 288 579 128 067 602 073 192 764 433 247 576 720 854 731 003 680 965 222 506 912 359 033 633 306 146 940 520 204 928 412 026 004 848 630 631 236 015 580 961 764 546 363 877 545 885 944 263 207 128 802 420 133 914 263 833 280 856 903 774 208 931 786 938 340 913 093 552 917 856 730 864 976 520 534 459 422 522 752 958 148 876 320 663 855 005 200 384 598 172 853 701 331 506 643 511 087 223 980 039 059 222 596 654 146 844 656 838 824 126 002 643 198 734 978 646 560 163 891 086 244 078 094 926 476 048 465 201 160 603 414 758 603 019 544 052 958 103 639 192 279 743 988 560 651 941 482 194 447 521 350 317 916 686 045 030 045 269 142 150 631 559 835 355 632 757 186 105 800 604 171 360 334 744 427 954 680 414 105 338 738 715 574 068 599 313 281 246 444 101 907 502 086 740 076 120 547 709 643 659 533 145 610 508 655 400 207 663 499 005 449 868 110 481 299 011 625 599 683 933 895 843 107 896 611 033 685 720 441 543 836 193 153 170 166 076 645 036 537 565 188 770 810 782 451 292 473 861 114 547 311 785 411 822 550 050 257 485 571 207 699 682 449 488 606 326 400 020 787 428 164 246 855 094 316 184 755 262 409 862 310 495 944 131 725 360 837 421 339 331 845 128 971 963 511 723 863 991 230 023 341 665 018 045 826 439 670 321 696 923 270 427 119 756 296 973 099 696 631 039 091 612 223 974 533 670 957 319 148 220 885 109 800 992 869 437 153 368 403 198 865 241 003 823 745 072 634 311 295 102 759 676 292 681 331 893 136 243 799 916 079 732 015 356 672 625 762 194 420 783 275 611 541 736 743 126 614 806 449 383 329 729 151 716 996 208 573 113 816 972 598 723 647 917 274 434 813 412 092 349 213 355 050 427 907 331 213 067 096 104 864 519 975 932 362 835 454 606 336 603 771 663 845 403 237 621 701 280 606 711 954 164 883 804 872 574 367 029 969 059 820 779 362 293 281 281 181 502 272 746 805 895 531 983 348 025 107 482 797 207 929 711 999 892 254 827 946 274 085 621 696 033 036 662 195 814 218 221 943 350 248 992 147 668 650 816 210 372 245 880 034 295 257 067 464 348 935 881 010 683 784 022 614 961 540 814 529 349 766 282 220 210 889 656 285 961 822 189 726 849 429 607 975 830 128 169 531 781 962 764 527 877 151 001 559 257 559 747 270 076 850 771 550 528 876 027 156 988 309 884 688 962 004 103 234 089 871 341 739 863 084 647 292 152 339 817 938 727 560 043 099 602 226 979 101 942 045 834 953 120 766 545 152 119 784 568 248 325 127 430 381 748 294 478 665 225 551 975 550 889 580 342 193 491 592 136 659 814 735 164 916 768 373 029 861 799 864 624 289 750 116 132 959 020 675 264 448 057 889 364 766 220 556 601 574 318 979 002 582 927 812 727 372 160 435 020 646 299 843 525 659 910 854 708 608 527 558 395 989 509 796 579 548 867 792 606 770 488 641 907 535 631 960 811 448 158 723 749 618 105 772 369 552 578 941 839 404 168 924 113 532 016 165 421 914 083 964 059 934 880 534 899 995 339 109 921 402 178 036 283 460 104 296 939 665 877 127 273 837 501 083 900 834 066 322 851 944 824 023 446 953 705 766 191 030 341 684 937 964 283 582 177 852 940 531 676 630 010 104 779 050 922 843 226 454 736 425 910 156 723 142 059 659 508 308 498 131 898 685 917 857 104 722 331 362 747 681 425 891 777 604 178 502 671 194 442 965 011 544 116 167 081 756 926 354 262 593 125 828 888 754 787 454 243 369 527 866 374 341 817 156 057 553 702 984 297 291 376 399 324 614 755 190 293 369 942 379 671 467 427 392 282 901 099 017 668 599 874 229 745 323 932 543 425 479 017 253 947 370 741 002 678 152 528 012 787 099 310 279 004 713 018 888 338 002 413 812 638 407 860 313 469 343 128 343 335 454 045 362 058 219 060 454 380 091 333 821 246 805 551 317 656 120 707 429 474 264 736 550 954 474 795 234 079 156 605 814 180 385 482 035 416 805 349 764 454 590 521 572 140 164 718 370 821 028 510 599 594 692 600 974 580 730 212 983 433 668 955 176 744 273 283 960 367 575 369 111 878 240 147 248 361 796 510 591 524 786 981 908 206 463 124 120 697 502 120 072 848 759 723 259 175 707 447 207 446 759 336 633 939 908 911 955 919 995 916 908 343 043 986 681 637 564 591 413 412 093 648 294 433 817 360 723 892 017 927 954 964 003 835 431 254 186 827 001 130 263 011 580 143 639 906 690 759 306 179 299 416 490 575 221 273 819 809 126 242 006 407 359 245 594 847 414 065 820 332 253 110 040 927 929 445 592 363 064 623 232 055 724 889 865 595 777 884 483 592 265 188 499 266 881 104 783 323 676 045 220 001 353 642 918 638 787 676 506 004 778 152 223 613 484 790 476 534 525 753 696 472 693 610 882 284 769 769 594 687 442 935 534 058 616 500 905 205 302 911 128 596 952 704 968 633 134 417 206 111 440 734 009 790 939 105 108 497 100 855 204 577 428 370 452 433 930 076 455 202 053 970 851 127 885 202 328 081 809 154 536 916 003 586 211 423 744 790 207 988 899 317 408 665 918 111 766 602 527 570 788 771 406 379 464 750 670 682 391 684 726 088 254 615 679 037 252 141 246 282 613 967 025 074 288 901 850 593 284 184 503 657 053 828 621 895 070 665 003 895 867 067 007 598 978 368 477 131 183 530 333 399 094 391 920 027 365 509 434 988 315 034 962 442 833 787 705 782 136 813 928 775 241 986 167 414 459 137 331 054 518 243 811 789 003 486 265 406 709 797 672 487 583 132 953 477 488 274 614 425 710 312 241 974 189 023 260 230 657 417 015 968 905 489 147 867 494 750 164 237 306 861 862 635 305 108 859 337 746 517 863 524 089 910 164 605 846 144 437 908 632 455 462 841 316 004 914 798 676 952 091 111 381 356 328 448 881 152 287 453 319 084 677 794 976 982 643 320 795 685 636 893 346 105 238 007 324 597 364 840 703 411 398 953 727 366 458 068 678 932 248 189 768 607 251 624 359 770 001 955 731 520 232 719 621 594 110 093 204 904 590 821 580 516 719 012 781 044 566 239 231 264 730 377 941 987 580 623 160 533 193 092 873 455 433 294 082 642 679 084 114 456 005 953 589 448 424 371 701 094 528 010 769 031 120 076 918 243 787 781 888 154 375 272 717 862 446 159 715 170 454 221 763 290 737 112 990 551 117 964 199 140 441 165 786 626 004 027 181 211 925 936 793 131 388 301 391 664 650 230 419 069 518 025 055 324 894 384 282 466 485 465 735 723 909 447 291 532 342 684 520 750 542 042 715 551 552 844 154 950 215 858 791 480 458 134 856 911 863 743 431 938 872 843 737 876 134 957 647 908 892 794 227 795 567 676 531 211 676 922 220 256 301 255 232 706 043 997 974 933 994 161 350 151 222 414 536 659 654 497 866 941 411 616 073 948 238 184 061 362 676 272 155 384 764 805 977 055 244 234 702 890 429 413 350 456 455 226 878 244 160 701 540 673 987 538 583 655 390 833 170 646 854 445 366 862 112 454 214 810 417 341 033 452 764 237 627 640 718 772 365 103 051 823 296 851 336 180 020 677 380 896 303 480 699 706 915 822 070 497 234 109 958 819 755 824 297 132 615 815 342 836 870 492 266 038 336 999 768 928 022 296 523 609 919 920 182 412 981 950 056 912 559 022 855 822 288 180 950 166 488 490 945 189 902 560 646 847 461 421 771 228 595 182 158 629 675 751 883 982 887 319 134 820 539 393 607 650 088 255 118 576 093 305 273 546 359 502 434 839 557 868 099 906 610 120 269 896 533 715 695 598 926 050 168 733 622 481 085 392 243 101 199 590 172 018 265 727 777 949 044 033 098 801 290 453 364 018 755 846 366 432 520 993 789 751 462 429 256 575 118 661 830 798 479 020 897 014 472 476 508 050 382 785 868 136 232 690 147 923 021 753 101 598 789 573 254 300 532 233 457 142 447 381 186 339 961 483 056 067 299 533 629 474 963 815 434 560 635 871 791 148 925 952 712 146 716 936 116 443 265 676 623 920 895 782 738 169 298 889 343 624 673 169 647 548 592 753 044 020 603 624 955 918 272 095 316 638 338 578 474 576 796 999 751 399 101 974 342 619 705 694 919 535 785 343 587 121 229 170 906 159 541 983 746 043 033 753 745 032 180 599 913 529 725 507 538 336 108 780 714 731 510 728 576 191 515 279 856 445 328 421 115 575 082 791 900 041 797 601 792 421 458 064 441 877 834 790 397 637 423 725 595 142 226 682 980 783 465 935 437 303 999 533 705 615 012 815 590 365 724 428 874 521 701 900 975 036 248 762 250 614 307 073 250 099 012 726 628 312 680 574 755 907 631 168 056 181 628 937 737 136 962 765 936 894 949 320 997 447 383 310 640 267 619 276 456 951 449 314 276 854 170 448 887 624 576 480 470 246 467 035 992 819 833 780 502 669 720 803 453 981 097 557 326 468 950 787 383 955 207 464 079 254 252 634 914 024 009 085 899 579 554 303 743 768 050 209 209 074 061 630 804 520 896 659 526 431 502 778 493 028 059 483 542 650 011 805 884 326 545 083 835 491 239 155 337 189 587 393 785 298 944 329 989 381 680 473 464 616 356 638 566 281 891 164 478 616 350 411 237 932 284 592 034 945 673 280 633 450 356 472 283 970 253 266 880 921 395 775 983 189 288 541 096 834 880 602 575 869 918 980 364 403 101 547 607 853 322 952 897 468 452 550 461 399 735 112 063 304 511 652 237 390 975 639 751 746 655 854 816 005 968 458 621 757 220 891 031 057 220 288 322 931 649 900 316 758 946 100 345 674 372 941 601 456 227 586 736 187 752 676 977 872 540 000 876 393 503 488 799 701 185 337 253 281 203 267 343 395 233 874 882 083 920 910 585 502 881 632 664 327 812 843 565 417 443 612 524 655 816 720 769 325 036 051 862 991 039 384 249 857 543 392 844 645 210 910 982 176 194 576 562 980 239 730 592 399 205 182 624 500 743 837 456 861 088 660 500 136 519 335 848 140 986 326 652 499 763 601 809 881 161 989 691 402 885 450 883 223 466 109 519 198 893 349 791 354 026 436 246 532 637 554 345 006 201 946 955 663 245 502 004 298 230 280 357 584 121 841 356 545 377 329 954 427 067 301 115 603 974 199 443 453 846 100 260 567 157 901 689 392 512 871 585 180 493 325 300 568 333 569 381 373 141 655 414 772 267 356 935 055 744 020 768 129 096 847 034 475 000 867 318 488 278 317 423 777 594 894 115 451 609 526 982 297 697 565 778 292 413 761 447 320 667 215 385 686 614 985 252 581 445 062 177 396 183 879 571 001 638 313 523 361 636 844 494 036 855 433 687 110 870 417 670 225 760 660 279 457 502 572 871 339 612 289 220 948 874 069 779 867 839 716 587 646 069 712 428 080 730 992 824 257 860 163 937 942 569 618 545 481 540 945 589 917 192 577 379 070 602 622 284 260 844 615 421 006 054 122 260 365 425 069 748 164 018 976 300 385 200 309 230 939 550 759 095 283 415 525 587 978 784 035 263 298 969 023 972 209 972 776 738 994 352 827 746 393 786 359 328 895 539 070 149 847 210 478 194 895 535 610 302 075 353 299 195 787 559 091 119 014 420 720 679 554 229 727 363 353 890 635 428 879 539 753 857 303 561 289 560 424 441 683 680 295 632 391 821 315 281 642 412 480 127 812 920 075 286 497 559 815 073 648 838 464 528 655 565 010 198 811 974 955 592 562 939 856 799 095 763 669 208 586 180 055 376 204 579 872 209 209 767 695 083 247 287 311 317 810 015 556 134 753 753 588 852 987 311 613 286 714 401 404 188 545 326 335 809 766 518 503 284 187 492 476 599 779 656 526 959 797 112 519 902 765 464 152 447 591 383 685 706 364 706 036 110 956 628 320 779 706 156 199 065 569 758 895 591 885 733 086 210 895 105 650 442 433 311 926 549 770 019 798 425 171 624 813 844 031 694 304 155 090 462 988 097 472 852 142 849 492 826 983 345 714 952 434 406 650 395 367 916 661 884 336 420 614 365 324 770 998 136 088 227 655 354 969 373 282 395 073 340 775 626 089 947 221 345 666 407 923 158 329 434 904 784 328 945 451 365 009 209 235 675 544 530 888 974 025 458 703 496 751 666 884 960 470 540 728 087 102 421 391 276 932 090 959 721 741 420 620 820 561 190 539 685 295 020 036 802 741 559 693 254 943 825 195 115 745 826 686 909 838 309 499 071 881 609 921 652 448 960 515 185 781 226 945 257 344 963 381 731 306 723 801 734 900 081 664 580 546 246 753 371 948 698 202 739 769 696 787 373 995 940 561 349 170 634 423 268 753 778 340 344 043 751 543 547 252 494 443 052 612 649 234 964 552 501 871 426 950 778 082 454 066 346 639 555 270 604 720 314 122 175 566 893 575 235 312 302 831 533 032 894 867 936 665 993 118 455 360 614 952 381 333 213 545 898 684 775 257 969 931 160 774 627 830 803 054 629 896 589 119 912 965 083 980 253 843 214 971 205 332 160 801 767 139 007 095 287 666 358 370 887 642 754 397 474 490 289 901 235 292 073 357 780 617 411 677 313 113 119 166 344 836 886 339 322 918 977 284 234 340 821 177 415 650 629 726 413 083 841 413 213 293 065 958 570 948 850 593 169 779 406 648 650 593 233 368 349 483 235 974 367 714 783 875 299 496 783 581 219 664 346 318 385 402 468 681 788 073 105 548 429 702 805 165 529 669 259 423 927 944 023 923 102 909 201 434 487 306 276 847 701 801 941 333 522 651 779 063 651 177 431 245 219 844 352 969 180 014 121 737 760 504 238 198 179 450 242 680 718 734 231 959 601 285 390 969 315 841 071 448 290 349 270 139 015 613 896 650 406 555 101 517 802 872 501 484 483 942 568 797 062 307 060 173 803 010 403 857 708 132 667 910 573 630 663 735 653 819 357 657 759 968 222 151 976 134 408 953 896 442 971 179 786 830 860 303 477 763 261 566 378 279 513 792 992 946 654 058 283 715 225 504 322 963 097 330 751 994 587 008 759 077 248 712 796 127 797 389 547 349 747 020 648 901 953 452 856 503 989 335 241 871 809 509 860 695 066 937 568 532 044 594 885 638 664 841 052 419 061 860 171 325 076 071 048 092 243 052 097 798 304 031 040 602 962 494 472 242 491 304 939 967 335 907 531 309 343 070 582 784 975 193 976 613 802 576 160 821 988 078 400 550 023 503 037 637 489 411 857 746 144 985 952 820 106 664 225 956 855 649 115 032 750 935 337 639 521 632 444 430 381 522 406 177 979 392 499 697 159 990 123 015 197 020 814 791 817 405 882 470 965 348 304 159 259 820 719 496 885 748 668 484 240 727 214 390 205 696 533 669 710 992 755 980 326 217 777 558 631 128 718 072 006 864 868 918 160 049 915 841 459 520 563 694 303 339 201 499 791 156 618 150 911 393 176 415 425 969 855 840 013 541 226 010 800 794 082 173 791 495 283 907 711 258 149 300 235 505 597 400 109 325 045 519 401 190 894 992 706 981 875 379 557 342 055 444 731 454 557 963 952 621 388 807 224 581 511 266 505 158 675 289 140 794 496 736 875 496 827 061 183 539 977 727 421 729 020 893 819 208 844 302 053 221 101 747 658 141 308 665 835 575 001 745 766 416 959 753 785 274 047 192 278 856 595 199 457 013 488 325 688 212 657 342 262 013 246 573 808 468 938 921 694 637 666 662 393 306 267 077 889 979 219 101 450 316 603 981 209 490 708 340 321 229 221 135 280 623 279 942 295 139 125 254 121 981 149 387 227 861 898 479 804 408 818 656 740 749 522 203 111 861 721 442 784 422 135 869 396 097 422 348 096 619 803 126 667 767 253 554 523 061 573 644 722 887 210 576 642 843 964 131 848 654 591 192 630 740 573 373 728 311 602 184 887 053 591 490 717 811 213 584 306 861 734 641 947 929 092 126 302 739 156 382 340 476 789 684 694 845 795 757 564 934 728 642 919 253 329 146 062 975 634 441 497 737 539 413 973 380 950 617 677 921 745 226 982 225 240 624 148 543 589 567 157 787 931 637 740 804 073 234 024 476 572 167 831 445 769 351 522 689 073 477 122 601 437 323 551 919 412 960 337 183 231 432 109 993 113 803 666 849 381 272 078 267 348 635 808 579 390 359 812 626 894 891 607 912 206 387 210 781 148 524 570 776 366 128 006 039 813 810 640 155 448 534 700 687 773 114 711 890 989 160 972 279 609 586 586 344 909 694 836 717 144 184 398 625 469 300 326 128 312 487 412 331 872 448 525 345 122 229 878 832 555 672 035 534 156 990 609 598 472 756 466 483 258 371 495 879 462 031 225 509 854 236 809 562 519 833 787 883 300 040 195 721 044 447 611 840 908 385 012 472 188 816 846 566 348 564 348 326 619 710 541 225 529 328 415 934 298 476 448 778 442 905 619 191 724 563 888 108 035 467 175 590 646 809 348 284 610 590 305 748 512 932 970 284 444 204 672 185 579 534 279 045 164 588 073 622 829 575 182 901 758 651 484 258 892 673 958 200 483 505 051 237 497 120 007 170 571 347 078 216 099 908 258 576 312 617 474 105 127 970 105 789 971 578 839 689 977 823 208 359 284 807 342 436 379 523 203 634 097 514 510 754 661 246 656 886 673 908 377 895 283 597 716 040 018 711 491 779 989 895 789 104 958 595 828 476 075 407 461 302 681 004 841 112 790 526 050 499 143 701 365 065 157 774 940 457 427 253 082 056 679 934 903 550 425 828 467 439 820 653 769 572 753 353 961 132 824 431 244 923 986 406 528 637 452 744 254 081 837 626 155 295 597 294 303 532 027 702 283 878 623 498 035 240 980 388 185 863 578 576 227 904 314 310 187 765 109 991 290 676 314 685 612 042 038 549 192 935 132 973 561 301 412 220 100 398 463 052 233 386 588 560 468 335 778 118 147 687 307 634 074 465 490 209 148 741 045 213 037 283 654 189 073 009 312 719 858 731 888 005 192 579 683 284 516 984 186 141 949 802 310 439 663 532 620 011 360 547 156 155 105 334 375 096 633 405 162 988 409 238 548 749 756 509 472 760 005 910 733 950 791 704 948 599 929 983 682 939 145 318 118 626 329 414 142 276 624 640 174 079 388 847 844 328 168 674 874 016 869 865 415 484 841 836 310 615 916 046 220 222 105 857 890 561 687 568 999 833 076 918 608 135 256 294 182 291 431 922 209 405 341 791 081 184 190 577 262 911 556 832 931 239 508 001 815 863 976 181 907 574 844 611 602 944 560 418 922 320 379 790 252 957 914 821 021 973 401 229 837 820 404 299 619 677 036 659 437 082 963 884 587 810 649 099 520 093 021 449 710 745 179 515 931 688 743 947 019 651 561 546 988 741 597 528 816 555 051 506 169 934 745 643 460 216 582 739 418 853 846 619 804 710 651 304 739 438 018 135 262 673 666 469 684 857 774 544 005 724 426 633 658 279 244 360 645 494 890 085 971 374 606 014 107 158 514 132 897 341 094 309 500 722 279 810 383 070 467 770 109 289 250 188 033 291 459 662 625 524 979 573 951 479 303 607 585 995 059 369 066 977 743 009 153 181 241 166 749 278 264 664 089 569 043 258 048 770 672 497 611 278 417 986 565 204 682 636 868 358 197 173 245 417 165 832 953 056 847 755 061 922 411 788 980 120 551 912 574 578 978 256 388 539 889 863 911 530 722 675 646 562 141 632 658 086 767 312 706 685 889 872 701 113 681 992 119 808 560 998 133 946 604 704 538 443 587 399 279 563 548 747 206 859 378 689 945 252 789 936 423 782 472 166 533 725 045 955 789 363 570 125 425 419 339 996 110 125 066 008 609 931 786 448 792 614 888 323 297 053 421 826 233 038 113 083 021 543 614 077 555 994 337 211 261 513 622 696 236 238 020 137 825 998 440 157 478 168 186 568 398 717 558 543 703 790 713 934 642 149 386 947 439 885 534 264 857 404 249 883 539 207 763 037 014 712 800 348 289 484 728 625 588 146 481 556 438 034 145 289 380 418 779 419 492 136 605 143 005 359 653 859 499 406 245 877 319 506 221 109 709 496 277 835 499 820 434 184 365 977 846 331 345 261 384 382 240 426 076 846 244 845 708 127 402 975 602 852 523 988 666 669 182 741 036 160 241 089 770 908 614 232 027 154 899 381 939 725 064 984 263 543 803 475 204 075 774 254 396 808 469 948 941 327 625 061 209 501 946 517 611 387 644 067 550 678 361 845 167 767 134 748 567 493 832 083 998 064 616 083 885 968 098 697 719 064 866 030 282 430 398 450 046 180 787 113 392 228 946 211 889 799 022 086 960 140 654 728 936 752 556 226 938 506 870 900 817 626 820 423 813 389 642 024 917 912 260 228 444 160 623 925 997 047 038 652 977 341 578 038 304 000 230 595 715 740 868 690 629 708 252 634 367 706 069 820 001 398 754 938 473 458 530 910 306 703 539 847 532 731 325 751 052 984 832 049 154 760 744 432 350 847 032 594 038 642 612 380 694 090 623 021 052 638 137 128 194 489 325 031 297 339 254 569 841 520 741 099 806 123 427 719 993 330 303 702 853 698 827 163 721 081 861 250 042 228 560 007 121 411 752 899 460 270 334 182 953 166 045 940 158 116 551 107 197 638 962 816 081 829 927 730 481 370 766 175 529 762 281 824 478 196 069 038 461 163 220 741 300 133 828 768 541 123 070 104 841 570 852 541 834 852 082 558 986 802 266 025 105 875 012 783 390 345 070 771 904 246 635 530 815 635 041 790 341 158 936 583 472 334 707 107 203 818 571 092 283 455 088 335 558 564 358 290 929 575 071 609 294 018 587 069 173 722 476 729 184 603 790 792 015 305 624 534 164 534 573 513 654 415 105 383 959 304 349 961 361 287 784 551 541 469 512 703 320 490 159 737 789 057 173 663 241 997 086 678 869 795 835 280 996 726 360 074 986 847 917 193 757 701 783 010 888 306 519 167 262 558 774 201 815 111 220 230 549 042 970 891 812 110 797 700 331 930 228 807 716 372 438 132 364 800 408 521 960 393 922 258 849 038 336 006 417 254 259 962 203 272 308 813 513 144 156 637 812 843 499 824 421 872 526 144 683 102 485 417 720 422 884 972 336 083 855 988 788 666 092 043 117 562 451 405 668 200 387 793 082 387 619 130 583 880 976 348 639 830 987 253 610 068 297 483 325 949 764 838 910 632 260 001 223 263 443 823 767 033 299 575 665 241 514 518 070 871 648 349 894 272 939 172 685 318 169 249 216 556 430 649 206 536 999 877 046 977 473 463 373 082 051 682 964 680 880 731 720 919 035 977 182 497 536 923 933 405 187 174 108 846 562 432 209 667 161 080 239 495 917 541 154 038 442 132 593 341 319 065 710 128 404 024 235 433 975 719 947 343 488 208 491 643 723 770 401 139 825 029 427 283 567 824 760 363 478 909 803 185 478 465 693 792 905 609 330 308 373 788 475 370 826 321 200 277 239 850 039 836 979 796 717 680 047 196 335 819 135 486 492 231 363 618 137 416 022 055 267 688 604 346 679 858 488 700 115 779 998 515 645 402 435 782 973 146 832 408 229 793 851 679 818 158 940 851 035 514 952 615 777 294 400 331 018 843 557 455 976 384 942 886 690 153 208 907 670 733 158 309 599 162 802 415 149 480 419 404 698 817 144 422 640 247 252 976 876 734 846 712 064 060 321 000 862 706 257 166 429 137 138 726 618 897 943 135 411 977 580 737 990 833 339 977 380 679 050 596 954 776 725 517 523 364 850 385 118 795 261 844 435 764 310 533 470 165 093 615 021 323 540 158 095 369 121 556 923 752 302 851 077 592 729 466 943 325 417 825 854 360 666 602 731 857 160 080 749 719 654 956 929 903 349 750 597 640 566 908 470 942 696 913 993 039 835 142 100 387 857 964 272 285 525 324 700 304 025 527 388 402 017 048 118 085 758 698 219 282 015 984 030 254 809 212 844 350 385 845 805 111 522 615 708 847 535 541 043 427 566 238 724 746 395 977 068 669 952 405 088 683 664 148 113 148 024 868 997 220 600 429 992 425 597 316 360 424 660 595 277 504 340 040 362 604 610 934 408 845 610 680 512 674 629 713 876 380 752 748 107 831 791 227 885 613 600 375 985 982 915 425 160 978 891 410 039 289 413 794 276 378 921 859 004 329 183 666 030 757 919 381 331 876 267 400 661 454 501 853 589 967 102 098 304 479 266 316 746 352 390 401 171 161 251 476 645 680 932 563 412 491 785 547 246 475 530 340 409 051 567 638 012 848 435 743 285 199 865 931 872 709 970 655 756 359 388 930 318 005 171 932 011 953 623 554 404 753 862 305 539 775 106 323 138 458 176 736 888 728 999 342 713 201 565 674 273 196 075 760 562 498 106 489 400 079 519 117 910 305 015 360 409 343 461 686 995 311 092 635 154 976 329 948 507 295 572 654 641 742 206 197 141 115 792 767 945 911 913 151 171 590 711 154 729 430 253 324 709 661 769 069 573 054 193 938 107 367 877 710 221 946 288 864 498 923 743 582 232 752 842 792 743 487 519 675 343 666 103 692 099 720 156 617 857 692 849 647 760 762 733 999 103 219 868 976 372 359 107 815 764 157 382 401 340 290 168 451 995 217 178 978 928 610 619 411 056 355 041 361 132 381 188 930 128 263 882 107 025 771 396 352 805 575 364 488 027 806 081 082 136 907 440 310 032 583 287 079 135 536 297 391 832 846 163 570 388 488 136 136 150 027 277 516 283 870 998 099 085 983 257 207 847 767 166 828 676 079 389 432 843 418 828 680 860 105 883 163 504 537 920 180 259 627 280 390 969 396 619 918 302 702 131 081 193 432 456 369 295 295 394 914 355 559 856 863 818 683 291 962 467 304 352 746 380 041 224 790 630 264 116 485 613 547 900 042 328 610 853 343 930 334 765 516 952 035 721 180 931 694 076 830 232 951 176 504 301 807 095 806 592 551 365 740 591 274 647 048 435 178 821 047 349 127 683 411 709 789 197 641 924 773 361 863 241 948 346 503 397 004 800 865 221 518 946 532 796 459 670 112 899 946 927 374 058 897 102 787 043 837 761 241 296 409 735 646 841 506 273 944 590 901 006 516 279 633 512 043 309 982 905 998 183 032 846 757 051 922 399 252 019 115 730 678 611 360 728 388 358 127 468 605 607 995 259 309 717 608 878 266 226 268 436 662 926 812 342 101 875 945 120 513 250 683 372 174 371 514 146 085 077 353 876 898 665 428 556 725 113 342 787 780 181 153 916 122 024 955 404 348 172 798 169 087 062 969 754 142 220 522 444 844 086 740 452 099 888 390 597 923 672 894 149 762 847 487 656 895 538 048 279 033 148 229 127 300 900 825 496 886 244 978 854 675 566 084 828 666 776 069 453 619 309 989 578 865 342 929 815 241 739 442 929 083 671 084 274 865 746 613 865 435 707 247 662 725 007 024 383 695 732 443 377 904 685 921 947 674 898 464 343 592 466 072 832 500 715 397 927 219 296 139 189 694 514 229 638 985 363 188 391 608 426 576 091 159 378 203 769 342 269 118 059 817 112 879 846 241 709 322 132 561 135 943 832 078 947 974 666 604 569 256 308 006 317 490 298 001 129 896 757 467 702 769 666 379 404 906 455 655 227 224 640 345 917 341 061 956 982 621 021 791 393 505 195 194 127 673 969 563 730 987 621 625 182 856 888 751 880 555 939 953 065 999 759 712 138 502 893 723 243 711 038 753 750 713 233 328 566 850 541 534 890 454 170 061 804 330 284 717 913 544 759 615 938 384 491 208 980 847 144 900 554 811 682 903 535 876 177 436 760 324 347 590 718 612 908 864 949 058 640 871 315 643 809 531 504 895 990 249 888 319 179 650 079 806 879 536 557 176 817 780 248 792 055 147 628 388 179 565 342 498 781 427 550 392 429 158 705 922 345 449 976 433 105 624 011 015 739 185 371 841 292 590 000 238 974 597 679 753 221 971 359 400 185 608 466 970 224 902 853 919 887 293 242 999 730 903 368 257 434 930 910 280 446 577 126 173 453 270 911 301 411 490 699 178 391 133 100 948 427 257 258 887 535 861 059 080 747 771 356 049 602 298 016 424 915 773 157 329 883 028 902 489 803 872 033 566 973 843 460 613 425 504 752 688 385 395 043 164 000 254 331 784 625 607 692 293 731 477 177 345 835 533 066 716 893 046 079 289 118 257 220 740 829 453 769 512 873 204 749 935 839 021 896 877 247 791 231 810 152 608 626 314 187 613 544 728 748 394 669 118 199 308 852 928 176 564 044 357 151 857 796 758 895 866 534 087 994 745 347 463 201 145 625 741 492 838 439 071 615 682 222 916 750 235 628 897 440 870 489 759 356 440 961 185 924 026 726 490 492 620 313 006 559 977 221 388 369 491 046 605 130 848 445 666 119 954 025 789 994 110 953 959 340 917 141 442 768 858 827 487 634 256 421 174 472 666 163 777 244 209 407 635 575 446 916 334 409 864 387 430 788 191 041 826 010 474 332 395 478 111 912 994 520 569 991 038 725 104 367 064 281 912 285 636 976 917 919 455 556 499 489 510 295 751 695 852 807 166 488 421 647 431 238 142 007 906 208 758 181 887 918 062 136 370 029 545 031 881 431 445 444 214 960 001 160 673 994 519 393 118 525 698 962 863 447 002 551 083 096 825 968 456 047 842 942 851 044 345 548 851 352 646 036 369 227 103 529 000 100 643 548 141 369 139 369 507 955 872 384 856 664 584 097 427 484 534 991 437 210 031 753 252 012 702 628 538 940 437 976 681 295 331 646 274 794 721 290 618 633 952 056 931 205 791 898 190 544 409 841 891 087 356 177 559 433 894 468 983 789 304 671 596 603 606 313 510 253 167 056 205 534 519 678 090 140 970 228 237 786 369 100 146 788 439 455 747 458 065 176 107 249 797 561 950 470 426 339 816 671 245 218 256 199 741 353 649 356 230 509 843 003 447 704 685 110 838 990 726 103 461 126 240 762 601 448 831 699 843 239 275 834 036 687 926 277 635 961 616 120 225 674 301 193 935 299 157 719 833 899 681 260 258 447 449 480 249 096 050 079 356 563 465 805 227 442 598 763 549 477 645 757 625 711 066 771 248 436 757 947 308 959 685 110 805 738 913 680 106 203 134 400 597 894 372 976 219 881 318 015 070 015 847 768 512 375 433 995 970 152 822 028 609 602 807 974 882 978 840 571 560 491 557 205 610 925 271 239 180 156 418 472 188 848 342 884 367 018 210 560 357 664 981 685 715 554 411 507 601 454 957 053 049 929 184 991 906 197 202 893 037 309 606 724 683 998 990 659 985 114 972 651 351 665 410 288 280 593 979 124 431 517 449 891 138 338 067 081 871 320 215 423 197 924 561 618 612 578 176 726 819 077 787 463 421 677 129 325 818 343 367 176 319 394 265 878 025 738 996 036 662 647 912 662 310 086 183 689 136 422 076 784 521 365 786 830 846 032 847 191 213 937 314 628 618 063 882 888 764 013 829 155 086 255 884 075 760 095 043 103 480 015 199 967 352 455 946 770 705 013 807 029 423 680 520 594 604 986 728 516 188 694 216 384 500 805 501 450 310 840 438 448 679 126 075 310 542 329 549 581 256 954 612 126 126 185 488 559 483 937 125 349 311 686 582 130 401 189 688 803 717 277 924 876 943 845 536 076 799 932 267 451 822 333 718 734 943 247 677 868 978 184 901 579 708 805 637 880 747 350 850 249 779 006 632 491 724 075 889 024 384 259 287 548 675 545 528 149 130 888 409 781 833 664 884 977 670 894 484 272 347 764 713 255 368 455 219 571 208 887 909 934 728 309 188 698 214 718 747 674 455 467 841 393 301 830 976 962 307 458 152 742 368 200 283 266 601 060 430 690 421 306 653 305 245 296 365 237 199 652 713 664 031 552 134 171 172 343 732 059 307 099 905 870 700 988 323 511 148 648 851 384 438 725 377 610 873 265 285 794 076 136 184 840 705 579 693 335 199 627 999 451 386 447 906 290 183 448 363 724 612 779 616 081 121 548 049 049 019 631 061 660 238 401 702 995 829 428 809 073 504 734 948 336 241 489 598 103 790 367 108 691 799 786 029 580 735 267 189 020 681 033 537 783 388 148 832 861 484 418 740 703 686 699 427 242 415 135 982 789 535 899 937 152 833 576 722 119 331 170 014 820 057 661 723 106 927 323 475 240 139 155 889 789 761 313 235 020 667 071 776 904 015 004 612 667 810 365 019 532 969 348 440 700 462 127 670 570 531 621 886 765 930 627 051 886 627 382 077 365 470 440 912 186 814 574 675 871 550 263 290 843 632 541 820 022 262 962 310 292 439 560 482 649 340 954 943 505 991 499 699 360 490 960 723 028 578 449 477 244 720 180 078 660 282 421 543 925 099 891 752 452 848 347 801 619 626 166 818 339 401 446 884 262 015 314 562 400 875 409 942 767 685 728 345 889 054 669 268 977 824 468 775 687 394 186 659 980 610 754 923 596 828 395 313 008 357 784 677 484 572 939 723 206 608 560 343 148 816 887 390 701 878 385 577 047 408 236 061 419 423 696 530 124 800 865 992 742 557 926 983 404 165 606 437 880 676 504 014 658 705 693 785 678 329 513 955 227 023 165 182 893 426 318 461 392 600 271 597 841 172 583 362 763 334 083 637 688 989 294 458 628 702 311 851 449 089 968 193 726 784 994 382 474 110 247 605 641 964 351 022 692 859 014 639 814 003 810 091 353 954 210 459 042 725 976 950 516 603 201 440 441 835 169 437 578 062 430 266 194 778 599 631 727 887 175 331 310 563 481 115 143 206 972 537 547 589 335 693 384 170 284 897 535 296 505 347 512 019 620 403 379 138 338 427 115 701 394 326 736 381 263 240 472 528 486 391 576 950 790 445 848 785 724 085 368 143 204 775 745 904 471 780 734 512 316 740 353 930 693 350 531 569 325 507 848 704 644 433 793 935 320 778 659 737 922 453 385 818 807 795 487 204 235 252 761 681 866 897 832 501 743 575 155 247 895 172 612 563 122 462 143 780 219 029 861 651 056 867 793 838 537 542 677 357 826 696 951 945 899 101 424 319 130 557 378 541 976 518 700 477 237 948 333 683 016 041 276 864 498 214 413 124 415 475 074 816 596 476 893 305 305 305 708 730 732 257 797 374 707 745 267 915 760 978 274 180 911 586 940 449 063 413 866 616 874 060 471 314 729 701 839 573 798 141 947 970 242 479 992 204 549 586 107 821 793 294 538 084 708 227 751 301 005 482 757 293 333 414 172 418 751 657 027 251 171 911 979 711 631 447 696 313 575 117 125 358 601 511 805 510 107 976 064 649 416 803 032 174 218 162 319 679 054 232 037 793 444 051 801 846 240 135 285 592 464 021 052 028 683 895 441 081 965 529 818 121 157 466 466 647 053 663 438 480 092 849 400 217 262 148 304 798 049 683 928 601 942 637 423 471 956 366 226 117 019 967 750 231 337 445 499 082 093 496 062 505 714 891 903 722 436 973 241 338 057 891 772 257 945 387 691 226 898 650 507 891 566 223 383 872 397 521 505 709 522 913 977 725 906 532 087 581 863 349 091 888 340 142 993 487 387 833 108 803 794 876 946 881 294 366 816 008 012 422 688 295 312 821 095 442 129 337 617 694 427 914 456 796 485 876 155 507 840 641 564 021 587 892 509 947 048 920 389 753 058 015 867 727 134 645 960 707 968 667 575 269 507 030 411 446 743 893 320 497 582 765 052 048 387 866 210 665 418 203 306 850 929 732 196 025 877 690 982 964 547 671 029 404 498 400 310 911 403 892 993 652 944 739 246 552 246 180 646 422 753 630 674 758 871 885 311 131 394 584 157 499 541 278 988 334 537 135 893 905 987 700 006 680 254 223 052 131 757 797 956 011 154 763 255 735 505 541 849 428 497 008 841 712 789 909 250 944 244 802 494 840 920 521 457 464 008 339 635 991 808 807 907 819 709 604 497 275 454 556 609 802 627 759 719 778 651 838 691 480 629 550 916 402 911 841 665 115 500 807 035 480 540 776 698 659 313 654 884 548 133 034 875 457 172 373 461 608 983 243 457 031 970 011 256 463 815 343 470 236 173 236 489 095 234 690 609 130 905 144 375 349 002 446 042 198 923 399 204 872 609 318 400 393 975 315 470 508 342 430 422 365 230 141 945 814 881 865 835 810 851 903 413 009 218 710 991 391 122 909 592 026 559 500 051 507 658 444 891 214 522 284 178 254 286 936 728 467 683 839 536 493 392 589 405 767 959 551 085 247 137 185 053 311 551 517 332 033 859 444 093 537 591 969 577 291 167 566 496 734 248 096 047 526 550 470 828 954 761 036 384 565 310 590 911 737 809 036 327 187 484 745 045 599 165 599 172 411 661 401 777 768 226 675 187 842 810 529 820 003 521 078 784 885 948 677 980 347 982 599 993 810 214 059 890 061 771 671 094 299 522 275 787 219 875 492 215 263 561 135 576 423 978 695 833 075 990 349 348 833 903 907 582 494 363 956 042 008 890 240 159 721 173 352 284 655 216 964 073 734 061 446 650 365 721 361 204 692 957 937 643 755 986 473 595 962 325 800 398 851 012 007 200 563 499 920 719 858 987 560 292 738 780 735 693 057 735 186 429 933 707 287 089 654 735 024 321 631 203 492 213 940 984 898 868 429 464 537 226 668 363 457 584 862 422 163 602 064 432 199 449 194 257 260 114 043 684 502 331 931 113 140 003 699 182 893 372 111 753 427 123 536 725 869 845 932 613 198 670 117 293 209 409 911 095 096 218 050 479 235 432 615 029 089 956 866 413 985 880 473 307 453 292 389 552 417 306 292 660 421 021 371 142 943 510 550 540 212 175 451 649 613 283 567 288 866 756 498 022 898 525 637 606 800 813 384 547 933 446 994 548 467 805 021 785 619 710 581 460 953 445 550 909 543 938 229 433 884 795 103 150 018 792 733 216 423 243 725 851 043 684 852 364 070 741 596 215 148 852 443 478 521 479 048 237 646 417 807 776 070 784 643 569 035 362 403 465 662 762 156 943 825 661 656 986 902 772 254 333 813 778 329 789 273 863 933 436 980 175 860 593 917 288 617 395 444 890 501 149 200 566 843 716 695 459 610 694 966 367 913 540 456 787 031 819 057 162 472 644 031 728 235 894 122 429 017 320 482 105 318 608 800 040 810 949 520 014 096 094 725 418 030 556 456 812 509 321 890 957 827 646 583 074 142 985 412 341 638 972 769 664 734 785 872 966 362 506 169 038 481 470 842 513 421 394 198 510 502 466 038 881 003 588 899 879 818 905 475 963 238 797 063 786 243 957 978 673 533 205 886 493 445 010 190 542 060 534 541 748 489 839 736 813 703 110 596 961 349 146 621 760 131 538 810 243 396 140 013 490 186 768 956 973 947 681 664 972 097 249 126 673 333 680 572 604 985 967 846 574 374 202 159 001 327 975 967 801 386 056 052 919 884 506 209 490 999 491 672 758 070 657 688 141 699 855 826 351 550 691 867 083 225 807 288 447 180 603 952 448 652 993 556 498 966 332 735 821 319 844 438 360 269 074 296 657 033 631 404 115 795 356 817 814 291 755 628 724 117 565 220 459 806 995 656 278 366 909 432 830 397 425 993 863 901 146 129 896 598 348 392 390 391 837 860 206 711 250 789 592 169 501 699 074 429 322 518 525 968 795 790 454 635 697 075 116 199 854 594 080 879 510 269 870 950 767 450 342 986 578 668 909 578 192 141 198 669 042 403 680 988 605 589 038 033 680 319 523 602 135 064 829 337 154 348 871 659 896 712 015 984 421 709 911 409 930 796 436 387 004 028 490 945 789 841 542 996 105 796 000 698 737 940 353 044 386 002 276 738 913 297 713 913 273 482 337 685 296 708 142 744 061 722 817 888 745 777 639 432 508 428 914 969 940 778 191 834 903 405 227 491 106 885 356 141 081 781 960 168 462 112 048 932 508 221 766 487 610 288 809 092 336 811 582 892 469 083 169 100 861 823 259 336 099 687 278 991 908 555 599 844 237 884 998 876 994 106 406 075 612 661 058 036 039 362 483 907 448 523 204 508 610 145 217 316 453 554 776 507 880 272 782 607 640 393 909 420 100 571 569 003 029 011 422 456 930 030 068 400 036 999 013 478 805 105 135 644 826 640 212 919 223 549 135 602 667 226 319 049 019 961 005 923 655 511 312 288 908 661 664 117 479 228 331 647 521 213 486 700 618 766 707 306 165 985 487 569 034 991 675 678 673 453 481 347 705 498 706 942 186 585 732 037 368 209 078 745 590 967 037 548 465 982 486 256 812 798 834 063 541 929 942 415 808 323 351 063 048 516 940 516 045 330 937 919 135 010 387 611 687 050 426 498 478 784 064 977 153 437 429 211 641 245 371 190 712 683 316 831 100 485 952 814 918 415 961 558 888 972 307 382 938 758 634 528 886 691 428 736 467 584 075 783 983 048 558 586 768 567 771 622 342 217 760 360 266 316 956 268 686 628 401 995 115 621 039 123 910 174 321 636 062 031 754 355 684 119 710 984 259 252 565 653 756 184 505 190 076 125 093 703 596 608 913 284 089 235 025 908 294 643 696 140 819 217 425 571 173 212 329 337 531 964 931 171 850 679 363 804 389 581 009 447 511 919 343 100 669 092 253 439 809 217 840 382 464 131 933 308 803 100 979 353 176 700 334 323 469 298 174 707 854 151 686 345 028 586 625 335 344 557 448 866 237 133 439 270 283 919 008 440 750 468 907 866 060 314 212 181 534 130 302 726 599 052 908 293 827 174 766 778 024 242 870 105 610 305 086 822 309 468 073 538 123 409 489 844 141 870 134 085 166 395 350 016 431 214 854 401 682 521 247 539 585 905 433 096 971 653 131 216 174 343 560 031 789 086 449 843 663 051 593 345 164 774 134 523 329 016 563 867 429 124 342 914 456 726 634 997 836 987 580 917 744 671 478 485 465 336 016 634 572 305 035 302 413 406 016 933 127 603 608 392 584 446 996 684 011 367 551 889 117 031 622 581 143 113 852 069 476 041 683 410 036 230 329 219 033 953 429 171 310 791 429 378 224 364 695 291 487 016 813 197 272 487 107 140 433 376 923 591 888 594 075 234 366 293 089 808 655 386 113 601 596 465 426 688 945 683 677 010 537 927 822 680 617 496 077 553 674 307 845 544 717 268 570 793 939 919 152 842 783 185 241 397 240 147 468 747 753 568 619 752 419 388 126 607 491 730 802 343 985 043 973 443 357 695 294 052 256 398 188 150 675 584 831 640 108 275 564 417 634 592 509 723 874 959 374 361 094 734 373 881 279 573 434 581 287 041 497 186 422 356 446 016 326 828 501 767 220 665 005 974 425 389 551 391 743 914 782 239 237 566 814 773 126 082 242 321 614 450 603 007 358 222 252 374 385 169 423 452 190 073 860 498 817 727 687 107 461 017 700 255 424 880 593 479 285 058 306 579 999 874 962 779 681 149 258 778 764 432 323 991 439 599 616 301 506 707 217 277 611 596 158 574 274 505 340 870 913 776 463 360 995 195 463 294 018 171 067 530 187 786 855 975 324 508 326 636 607 877 678 961 955 166 151 231 903 747 536 021 610 989 801 538 204 560 973 192 910 414 836 203 382 413 686 436 880 372 122 082 956 922 145 019 247 594 653 533 911 126 097 781 876 330 161 311 775 644 352 544 760 178 847 659 701 572 502 341 290 704 488 557 249 226 841 675 049 398 439 358 271 479 502 640 361 201 300 069 689 060 912 307 151 980 288 207 128 225 538 377 546 370 443 155 040 086 351 880 046 921 677 571 807 522 566 398 173 106 400 898 054 286 345 764 596 093 529 961 523 804 514 786 337 978 558 729 261 339 193 345 878 561 170 438 331 369 276 086 139 837 521 672 367 364 963 893 251 176 955 221 403 882 829 865 808 409 692 633 856 306 537 583 031 406 107 656 574 872 715 043 237 297 269 011 135 564 260 376 766 089 022 653 274 057 032 205 857 313 567 104 771 586 467 563 677 545 363 950 200 844 837 131 044 373 756 150 199 564 160 063 912 287 601 887 666 343 205 516 098 916 840 138 107 471 470 580 838 510 945 787 775 741 677 923 121 386 911 059 280 332 411 106 644 860 434 345 424 151 616 466 800 614 741 526 751 542 360 246 174 731 100 997 813 912 715 329 838 360 220 400 360 758 991 256 980 493 748 435 180 088 241 722 004 106 894 414 467 491 382 355 472 292 112 943 483 269 793 910 438 239 585 905 722 994 240 158 535 875 106 240 806 193 997 957 445 375 922 804 371 062 511 773 340 018 065 844 008 651 069 658 678 662 889 344 032 995 165 432 720 242 197 177 881 138 053 994 000 114 128 697 689 200 063 019 309 311 076 756 928 141 744 698 947 862 143 000 043 132 109 677 264 997 023 280 339 486 259 170 971 535 053 062 628 737 205 067 048 752 268 643 421 422 007 133 403 033 940 266 390 823 565 566 152 930 763 425 311 727 093 357 980 134 945 977 872 437 398 944 113 274 729 167 742 172 364 555 546 422 932 592 807 696 105 894 383 441 695 387 191 614 891 126 582 865 454 629 418 919 353 112 266 678 803 480 946 773 018 570 894 260 785 506 645 823 345 988 718 202 729 636 182 058 875 667 950 580 249 276 596 020 299 980 632 500 817 899 048 151 205 068 082 185 793 724 809 636 786 800 124 455 083 085 058 682 607 311 548 770 603 333 554 466 675 386 794 431 143 942 659 196 188 391 629 588 248 057 860 933 365 901 229 260 560 833 766 513 215 533 684 803 877 724 449 593 703 631 510 676 455 793 826 653 218 649 353 665 370 943 924 567 069 899 039 184 368 312 041 362 818 375 054 768 678 514 954 641 598 962 598 844 560 779 624 933 939 972 522 644 405 907 449 850 005 977 152 194 327 932 844 300 278 381 916 685 970 405 359 650 961 952 936 352 008 354 246 021 007 292 510 086 407 952 765 513 465 018 613 233 333 187 281 538 965 347 541 250 818 343 467 387 872 495 965 864 254 652 765 565 056 282 633 559 992 811 503 818 021 505 820 104 829 017 132 974 995 469 882 885 038 740 993 017 473 986 838 224 391 337 004 187 617 127 303 222 589 976 265 408 438 489 437 265 374 964 491 163 448 129 645 642 387 784 802 788 248 249 961 934 849 377 814 613 351 514 664 210 282 110 954 268 830 523 260 705 568 379 174 202 353 109 996 674 567 158 842 346 996 668 134 144 006 788 606 038 005 805 983 315 237 091 648 720 881 915 010 318 888 222 341 467 972 960 693 865 058 001 943 138 171 267 643 289 297 907 683 197 180 185 525 102 037 355 433 126 471 452 049 869 176 077 861 800 845 185 661 823 797 164 758 285 781 348 611 389 640 269 781 123 837 929 674 790 095 498 797 993 144 952 381 113 467 459 059 173 663 885 466 468 576 438 680 219 212 956 409 161 173 317 777 882 394 257 655 623 902 593 696 454 136 828 612 890 378 255 920 233 831 370 166 270 189 599 453 507 200 353 746 864 750 348 094 574 254 723 228 679 335 982 221 023 674 062 169 470 060 549 016 135 659 005 130 238 501 503 034 851 678 069 919 438 455 966 206 253 350 922 813 630 652 409 322 341 822 749 935 041 029 695 039 176 213 505 229 024 125 659 867 328 614 464 261 515 637 685 738 459 998 087 106 591 639 793 640 270 462 190 160 360 774 469 098 105 973 820 681 006 562 816 928 381 297 711 518 378 050 106 154 422 600 160 358 923 383 118 058 503 621 670 398 499 753 165 373 825 900 657 834 687 944 132 983 670 709 205 660 371 185 866 906 551 669 534 511 375 400 581 076 063 663 653 667 722 610 092 021 367 066 633 951 841 692 677 493 305 812 920 335 365 371 768 132 536 656 413 009 522 186 966 967 183 223 654 007 564 488 569 983 866 613 327 083 994 055 528 960 443 616 186 022 704 922 618 679 358 748 321 623 169 716 469 088 080 476 317 142 207 993 606 200 268 726 868 845 114 069 722 715 371 487 763 165 505 602 967 049 773 645 047 096 504 275 682 662 644 000 388 852 174 607 124 766 218 553 033 764 799 457 236 920 503 804 754 244 748 112 126 733 493 713 602 605 212 563 548 926 063 793 273 035 932 685 079 026 771 537 334 722 605 330 604 196 975 838 439 650 323 888 492 759 154 774 543 426 822 144 268 087 324 786 363 913 774 049 994 495 767 681 887 784 821 537 411 027 201 146 501 326 007 206 399 463 576 526 525 571 260 944 110 255 158 859 770 737 610 824 225 748 315 178 129 473 903 736 234 241 151 410 460 514 137 412 229 392 274 820 668 787 544 610 257 609 440 528 152 919 597 688 277 993 911 251 702 203 650 013 383 001 902 103 867 271 041 261 258 577 124 940 359 183 600 242 377 412 942 506 153 353 119 705 291 759 358 536 711 183 131 192 875 207 666 655 803 640 472 382 726 698 193 811 781 925 997 979 100 279 475 329 707 317 060 570 826 534 780 810 199 898 926 733 910 131 278 318 899 863 127 408 260 812 200 687 239 526 646 663 556 073 763 650 359 995 474 407 167 042 149 224 315 249 087 564 400 265 100 395 941 182 870 192 419 332 702 187 009 914 537 652 378 703 967 569 530 508 104 088 534 844 725 717 838 598 272 525 543 799 321 217 491 156 705 641 344 345 178 864 244 016 400 020 250 371 285 041 457 377 792 257 197 608 133 114 538 786 320 032 987 991 555 706 330 828 265 559 963 626 295 271 393 387 054 013 520 919 859 564 334 627 507 673 135 229 735 889 825 428 597 069 366 649 521 478 590 552 674 251 798 716 324 770 754 015 932 170 960 930 042 133 124 104 628 640 928 065 999 577 043 570 453 249 775 484 864 952 942 740 384 222 144 373 492 026 177 109 903 220 954 523 976 371 396 963 241 790 619 737 043 687 955 232 225 575 772 476 078 013 202 912 323 546 728 326 657 444 908 151 347 347 641 613 957 693 066 228 714 914 540 617 203 539 576 456 251 432 905 493 858 637 639 691 171 420 248 208 929 220 164 712 769 499 392 824 430 485 005 667 322 140 383 476 923 310 377 304 344 622 640 871 661 073 653 305 124 836 283 190 307 878 348 340 471 862 625 497 269 532 027 511 147 766 931 714 022 811 115 361 612 440 101 859 563 474 568 917 981 906 628 998 175 488 380 805 936 921 015 169 138 948 093 220 441 108 548 397 543 769 366 732 694 390 252 391 561 804 069 996 454 697 407 726 885 514 109 554 602 967 891 104 739 291 302 553 893 698 612 836 998 377 256 521 207 705 131 062 959 497 305 241 247 473 893 617 576 544 393 013 012 658 417 839 650 377 209 980 891 405 224 842 447 360 062 155 691 302 721 834 511 341 387 053 349 044 832 007 861 897 622 096 707 022 163 171 710 474 043 657 929 591 135 483 588 507 381 389 398 970 415 465 362 883 384 399 376 539 874 041 333 168 560 040 462 657 068 652 094 363 858 772 107 796 603 152 367 264 425 078 684 506 364 557 645 787 531 335 584 816 879 034 253 591 618 269 985 089 459 300 014 926 150 788 861 882 136 922 063 787 785 151 079 367 605 928 408 592 540 261 399 559 656 071 076 238 323 924 259 833 940 278 426 672 180 395 088 599 747 668 529 327 508 534 329 224 009 685 067 536 226 028 937 240 137 516 196 852 247 375 621 323 851 426 365 087 532 032 850 194 465 010 557 918 661 438 819 191 022 455 442 875 826 300 206 995 984 630 525 428 603 381 780 677 024 744 238 434 031 510 976 343 665 123 424 547 461 099 542 112 299 232 440 898 121 179 163 503 177 375 731 671 543 989 458 636 287 961 772 007 578 908 640 498 284 968 670 355 624 104 775 928 896 079 550 640 948 422 994 206 315 805 035 189 258 424 062 615 431 509 736 725 057 316 389 162 655 476 274 118 863 250 341 325 340 881 779 346 561 581 129 519 325 385 376 889 086 883 995 813 796 852 354 602 695 907 101 774 194 940 394 658 752 179 922 916 272 894 594 494 380 124 576 204 966 864 573 024 746 121 574 786 546 557 215 424 939 758 674 634 786 463 160 113 523 871 600 424 496 731 945 065 079 796 503 063 253 926 236 610 209 118 243 367 530 475 769 819 463 467 543 420 872 094 503 441 672 998 468 703 007 264 871 999 114 796 313 834 600 345 541 559 409 687 344 923 978 236 092 107 927 821 916 264 124 467 134 803 336 833 186 305 543 445 834 428 919 988 678 112 654 431 880 040 321 062 957 026 684 506 984 271 085 558 270 320 787 065 454 457 756 211 660 947 225 919 174 833 771 883 491 631 495 453 679 428 611 448 352 787 555 392 458 525 554 038 151 153 962 955 323 642 864 597 194 568 089 460 468 750 470 068 159 714 930 856 921 024 478 909 156 821 034 218 576 574 898 242 503 088 065 824 824 188 144 429 208 414 197 566 670 715 580 018 589 516 550 887 191 636 301 140 130 701 985 421 435 165 679 707 833 000 826 344 445 538 035 113 822 162 293 951 574 302 256 728 820 872 642 730 933 143 455 327 239 389 753 302 692 364 139 892 348 070 711 405 571 339 767 689 310 598 577 320 542 000 989 153 609 386 890 504 106 493 913 518 351 850 100 816 951 336 234 484 716 963 215 768 955 074 606 892 245 093 139 069 857 097 979 255 713 196 700 936 030 809 420 961 018 399 853 958 499 550 526 969 871 628 980 598 196 475 271 145 768 575 011 472 521 711 060 908 727 182 938 474 966 564 597 766 415 549 056 250 621 872 864 373 359 300 758 562 515 522 953 260 746 968 720 446 546 378 941 668 979 867 116 426 507 387 456 696 808 143 125 444 094 010 252 927 236 353 022 718 442 861 507 906 874 734 757 015 584 264 920 799 584 921 868 057 958 186 636 595 682 319 907 200 577 201 085 450 307 544 696 012 584 754 032 610 076 814 789 336 642 451 011 753 579 845 701 261 874 659 166 555 425 599 767 445 983 013 317 097 374 623 162 079 606 661 273 050 796 693 705 284 790 131 799 696 349 895 921 190 126 527 410 278 828 495 410 544 285 855 023 827 891 371 552 385 134 380 315 865 240 402 476 694 102 084 766 463 712 774 993 153 982 974 952 140 938 847 999 384 393 731 785 516 904 650 854 261 053 249 326 204 773 062 505 508 011 502 048 858 715 078 049 450 557 926 819 302 110 435 547 091 233 161 976 447 084 298 554 738 398 447 399 157 648 027 205 620 190 847 457 526 346 880 198 550 160 612 688 782 998 138 197 034 119 002 693 173 612 314 155 349 276 737 264 558 838 116 801 862 399 096 832 880 907 465 172 910 702 878 948 129 094 241 564 670 973 121 228 230 256 435 526 157 935 511 443 140 391 936 055 749 942 361 713 609 340 728 621 101 260 566 162 070 627 035 327 663 750 967 560 282 496 872 238 990 541 063 229 061 940 116 049 153 122 201 147 297 576 064 279 700 287 948 946 797 509 831 597 364 617 784 280 781 592 099 405 664 852 700 056 391 993 930 488 549 164 836 953 174 173 034 616 601 986 514 711 682 988 481 019 945 322 457 021 677 006 422 697 178 869 212 674 361 770 424 566 607 748 593 015 793 781 573 738 961 382 588 214 212 554 300 541 445 896 074 167 231 212 503 670 308 457 189 868 820 790 254 064 397 734 156 058 993 432 360 824 863 591 799 967 894 897 166 336 343 291 067 680 490 879 683 211 179 220 676 027 884 549 373 590 759 150 556 196 624 585 423 121 003 805 711 128 422 997 901 720 185 738 504 971 409 854 187 188 868 633 418 193 564 053 023 256 401 863 901 892 218 806 271 815 932 709 099 494 069 526 229 015 872 640 002 812 685 306 793 133 369 712 474 222 180 523 392 963 858 056 718 359 911 934 289 355 749 983 630 630 838 872 818 526 942 087 458 320 167 827 504 204 900 388 951 493 189 923 100 120 683 942 004 065 880 354 938 598 878 061 723 347 845 578 645 362 007 430 414 158 132 916 005 198 634 744 917 647 601 346 822 621 198 031 102 553 263 927 787 674 292 699 110 759 184 921 108 170 290 157 175 834 531 777 873 036 734 623 763 946 581 506 277 039 439 985 634 630 844 422 236 864 153 874 522 378 231 915 569 371 550 046 767 999 620 972 517 312 688 766 697 858 705 302 108 527 716 920 481 163 983 031 837 072 992 944 509 495 596 023 526 078 546 869 396 823 445 578 729 879 465 576 374 269 219 947 428 076 751 817 866 776 375 550 628 435 665 915 633 479 593 325 696 111 102 289 106 510 544 499 879 751 459 750 464 947 062 843 046 675 033 793 496 108 383 572 227 828 627 487 952 581 134 413 698 399 223 720 231 623 677 752 589 778 334 793 328 039 181 238 296 086 491 300 455 813 943 584 270 090 971 331 604 209 953 847 358 743 454 442 929 626 857 509 894 151 472 342 122 208 874 169 395 659 235 089 866 058 249 076 697 799 872 174 105 632 553 231 726 503 907 399 664 158 196 048 774 223 205 994 850 095 295 985 030 414 503 888 031 397 273 937 307 392 133 894 693 417 464 424 934 548 387 414 388 043 457 647 449 852 973 361 887 142 835 024 598 319 530 897 094 222 459 018 652 585 049 237 949 089 876 249 510 189 951 667 768 675 348 027 187 920 607 044 552 039 025 519 937 597 531 580 538 376 478 139 502 525 705 855 818 126 066 279 565 604 047 260 957 680 527 095 457 658 358 462 423 525 281 556 589 239 286 633 463 891 276 288 026 999 384 306 351 441 357 750 047 979 625 644 122 384 967 158 502 881 947 133 431 311 824 286 446 988 157 842 602 968 259 973 923 045 098 230 292 743 362 089 309 132 519 907 459 505 931 761 652 177 819 001 756 080 201 570 504 536 802 444 976 460 022 975 194 900 240 537 760 756 238 321 772 957 923 734 136 571 799 485 128 611 407 839 948 809 445 001 235 533 832 645 388 801 852 146 354 416 284 018 207 006 863 188 036 652 094 429 558 945 980 095 648 976 190 030 591 512 664 596 070 544 625 960 880 515 988 681 695 567 758 979 794 804 248 647 480 697 592 676 575 801 629 058 919 135 593 706 472 560 456 956 192 942 331 197 404 113 678 321 540 779 058 625 516 438 738 337 230 682 172 229 888 858 146 160 863 237 708 605 556 531 587 255 452 792 190 706 335 816 863 428 430 399 855 980 278 253 286 068 675 238 817 988 460 779 083 199 385 297 335 402 623 337 945 362 475 559 581 195 936 348 361 690 482 409 652 114 921 579 064 325 476 268 911 989 870 600 109 813 769 182 556 357 257 036 048 902 499 441 170 850 471 793 158 483 801 315 592 290 742 735 000 951 264 659 627 428 252 271 120 399 089 521 673 472 545 871 440 512 675 758 366 281 028 483 046 374 763 401 136 543 972 434 917 503 480 521 800 388 879 690 746 361 568 068 968 518 905 780 419 078 573 920 264 232 798 513 261 673 981 524 947 823 861 763 052 170 964 321 695 832 915 962 374 511 853 930 790 787 020 405 138 263 485 826 544 914 753 618 056 907 331 953 149 495 435 716 136 631 109 316 926 861 977 074 408 673 007 664 647 538 833 988 918 256 809 504 055 096 539 675 578 652 858 999 546 542 561 283 605 093 944 019 396 738 896 736 761 689 566 171 032 425 482 705 267 631 158 275 800 812 667 730 731 445 831 864 314 118 355 815 155 832 883 692 434 243 969 797 898 681 957 398 731 615 010 575 055 316 473 726 518 086 843 616 220 445 930 401 887 437 593 010 254 085 027 087 849 160 433 768 107 198 379 696 946 074 040 365 075 756 353 270 921 166 436 409 193 120 767 269 915 448 671 772 568 998 192 955 938 387 858 456 169 157 585 753 372 428 795 132 820 916 880 390 963 110 058 071 615 574 813 589 272 125 094 611 395 102 352 284 436 714 412 740 668 383 642 403 267 162 836 672 488 665 527 661 911 358 864 126 632 400 782 042 847 507 567 054 444 505 809 704 046 066 115 111 290 415 617 203 612 677 754 691 948 119 944 464 788 719 584 983 980 153 515 589 987 115 196 656 080 110 440 311 393 422 638 315 003 630 165 132 876 864 604 825 382 972 372 680 626 412 264 939 739 049 663 893 510 341 481 486 504 213 742 833 871 954 601 864 704 783 757 267 014 830 544 419 055 647 120 479 758 294 972 163 683 246 355 561 582 024 072 064 251 659 113 230 848 007 072 370 763 716 785 476 434 175 546 528 476 299 863 707 769 368 831 167 360 681 754 031 804 079 575 501 102 892 594 985 398 615 945 975 215 851 903 793 580 008 411 757 288 365 347 101 542 667 051 220 318 857 629 439 444 044 277 068 548 236 033 397 846 474 885 615 410 722 108 736 300 994 129 118 204 500 130 559 267 145 907 854 479 048 054 232 070 277 186 003 852 684 610 688 846 490 013 531 138 870 885 933 114 095 096 206 695 186 837 825 861 482 427 423 491 791 467 345 969 129 648 005 019 881 308 434 844 660 489 174 736 967 702 106 646 392 096 745 039 147 258 141 161 276 404 418 689 582 139 536 757 938 844 414 287 824 666 037 996 442 567 642 553 056 411 283 031 055 019 779 180 943 243 669 428 986 680 571 699 536 209 320 124 232 529 633 515 126 577 795 240 391 996 545 689 678 496 124 915 224 628 072 156 676 993 144 980 873 890 423 063 488 813 506 821 699 295 673 571 030 353 506 960 330 830 311 067 666 313 330 990 674 934 612 748 077 958 153 924 824 945 314 322 165 638 225 480 728 872 057 582 904 905 883 246 822 129 782 787 924 305 727 671 558 143 458 141 438 151 888 548 868 659 108 115 968 243 265 843 991 377 869 469 391 274 975 783 123 620 920 286 457 679 943 197 811 772 928 266 232 318 233 757 466 990 930 730 760 294 379 134 733 532 742 888 614 501 764 159 606 950 495 598 927 101 722 914 495 937 716 829 272 512 888 946 924 535 405 430 667 536 247 084 171 203 275 654 402 552 012 176 363 534 485 611 553 481 129 361 688 717 494 766 403 063 827 870 798 440 692 669 257 500 595 471 151 147 558 620 929 324 001 265 471 773 258 069 362 704 237 829 277 173 751 102 027 165 984 363 562 303 591 536 788 792 723 463 579 433 053 680 026 914 590 832 233 985 681 104 698 602 486 803 209 438 245 107 234 498 412 307 013 266 217 828 001 465 138 775 173 533 828 465 483 834 526 509 381 447 502 812 491 991 888 185 840 294 836 373 355 712 253 296 063 631 258 215 735 849 449 870 643 398 255 005 565 867 734 183 700 860 953 348 280 843 958 252 425 376 598 161 250 897 710 330 799 612 058 836 129 648 561 189 286 696 843 528 751 863 353 150 559 102 032 628 171 971 833 073 626 242 272 776 565 790 191 975 211 309 699 032 732 313 198 391 867 629 955 921 079 970 134 998 755 010 133 606 990 738 398 645 898 062 806 878 977 723 743 325 105 639 357 570 812 473 499 790 442 233 843 177 418 971 486 462 285 811 024 762 909 038 889 285 508 484 318 005 172 365 308 281 266 291 852 730 116 424 929 285 894 473 273 608 047 072 245 312 809 853 023 680 987 470 587 963 038 855 196 167 572 739 608 457 578 978 042 215 604 495 644 385 367 022 698 213 311 116 076 335 469 476 202 211 558 276 090 572 739 276 855 176 656 480 339 104 886 343 616 830 020 915 462 918 439 607 217 788 807 597 166 345 462 266 680 507 152 399 801 611 406 039 861 524 260 615 638 347 925 943 483 275 809 569 513 576 854 190 922 123 077 873 223 642 814 610 958 622 266 164 872 860 134 716 907 299 564 224 693 596 312 505 312 506 964 680 675 219 865 332 055 234 024 209 355 530 266 283 947 673 124 378 628 369 331 737 826 471 847 549 720 400 391 051 348 819 490 583 606 059 063 789 115 637 568 046 739 785 442 602 167 757 334 989 236 260 409 810 034 974 232 165 645 938 679 678 302 403 914 788 264 962 221 126 432 884 363 051 754 915 555 271 443 042 188 481 110 798 039 565 266 000 733 345 129 505 156 615 954 158 160 608 835 914 998 127 063 882 267 337 406 341 805 684 689 359 813 750 351 829 820 447 557 453 003 339 459 468 616 748 909 312 373 394 821 713 345 425 196 961 728 515 127 869 493 250 156 859 118 607 939 536 997 645 996 580 299 981 495 980 589 510 121 218 878 084 102 731 935 005 787 726 695 245 152 693 846 520 398 515 056 778 955 267 813 834 454 897 477 600 221 286 744 317 890 635 033 747 966 431 466 633 555 699 445 814 414 777 255 820 470 812 383 747 136 246 975 431 560 785 392 748 204 569 755 148 156 913 857 123 897 852 502 826 148 882 353 996 627 112 918 605 076 007 611 326 324 587 317 559 756 780 393 414 571 644 461 358 043 102 420 221 529 901 207 104 459 517 414 983 796 277 450 879 202 527 826 688 700 462 581 175 969 038 688 448 306 759 059 553 692 619 712 655 888 797 434 950 721 479 034 948 424 094 570 177 222 525 259 879 090 682 718 289 222 073 960 787 959 203 781 058 374 940 316 748 679 911 588 131 955 864 552 495 354 162 871 512 375 687 182 285 166 518 175 905 393 990 016 933 548 604 078 038 323 725 435 658 012 170 908 979 818 297 739 069 212 456 788 814 708 917 714 464 113 450 248 957 131 934 429 545 588 233 002 270 589 245 180 450 943 204 295 866 016 229 697 600 778 751 852 634 673 771 651 546 417 129 392 895 073 195 501 118 724 962 049 500 245 912 022 305 218 610 839 622 927 483 860 995 136 039 496 516 839 362 136 533 818 572 159 300 591 926 710 494 899 880 600 489 802 004 974 403 953 462 008 648 679 722 695 701 381 120 192 613 836 642 994 001 329 208 926 962 342 589 555 909 642 965 738 203 226 675 970 209 788 993 780 222 913 580 560 416 577 185 019 459 530 816 786 752 704 463 225 452 897 935 759 236 868 882 186 837 746 811 559 947 796 731 155 232 996 513 489 194 991 658 315 759 993 470 144 364 569 975 723 781 599 107 248 441 183 615 259 310 109 544 855 452 292 566 218 984 200 793 544 306 921 494 084 119 491 328 881 680 623 067 064 655 159 837 912 697 581 915 740 267 858 644 978 915 207 597 142 689 983 205 874 126 141 182 137 792 336 219 106 765 931 493 085 787 140 599 124 165 451 262 726 469 516 456 761 118 159 281 744 709 536 333 264 880 533 397 876 163 996 589 929 075 508 851 993 162 014 278 886 904 630 551 799 265 322 313 333 217 660 623 348 563 666 846 625 947 148 699 652 867 761 488 562 676 235 514 182 609 807 951 563 951 138 509 703 439 144 713 115 187 611 094 629 822 732 469 171 757 074 122 420 966 416 048 241 582 325 650 030 269 900 269 867 088 570 007 150 117 772 776 303 689 477 234 464 262 807 802 781 965 790 861 341 953 901 772 795 771 004 649 433 497 761 982 738 254 439 022 146 092 971 296 142 324 906 060 525 465 551 904 697 540 118 301 333 396 976 892 740 382 043 882 992 242 743 154 651 671 301 945 303 303 769 055 070 424 850 867 619 857 640 019 841 491 316 673 444 058 212 326 849 970 160 447 318 197 322 787 049 445 730 126 984 609 582 331 557 006 809 162 759 382 648 799 708 867 932 067 034 878 901 002 446 120 078 863 232 952 795 371 847 521 300 238 453 735 417 542 096 733 422 678 936 406 489 205 456 962 422 306 345 703 240 909 117 678 517 707 853 890 306 926 167 762 847 166 180 351 588 130 467 199 789 576 119 161 942 256 068 620 266 329 853 524 454 387 735 656 543 836 205 657 277 308 710 444 668 282 429 504 609 707 188 186 890 426 802 155 984 267 757 485 855 438 232 874 353 782 635 618 802 778 291 369 255 830 298 287 619 026 469 946 828 763 235 034 132 490 991 045 438 214 823 930 652 278 600 923 734 119 082 390 226 922 745 065 285 678 152 319 949 971 358 949 493 390 844 456 731 561 702 647 201 878 301 238 698 167 071 118 032 491 363 570 733 092 587 694 595 651 101 696 087 793 542 363 562 619 696 391 283 757 000 587 566 270 151 762 908 136 079 864 798 852 610 169 429 515 268 426 834 588 297 028 927 194 491 527 177 538 034 956 578 222 991 344 568 421 393 420 566 560 843 599 402 120 969 255 248 931 645 513 653 440 821 006 183 836 751 747 640 851 776 036 187 824 088 495 468 708 916 687 281 650 474 585 429 902 957 690 342 485 836 360 971 212 688 659 493 179 140 522 665 360 291 556 106 891 220 262 617 347 427 003 029 860 182 110 079 868 914 414 307 089 218 269 377 537 151 513 277 453 232 780 585 676 634 124 685 881 829 105 831 849 683 566 035 348 830 446 055 999 987 620 328 307 359 314 746 287 001 798 381 281 154 831 628 953 992 205 025 911 341 355 262 185 966 085 170 089 035 400 843 699 553 028 015 169 631 998 483 323 621 038 230 496 702 694 545 051 816 524 494 554 100 331 284 620 392 989 279 127 213 565 008 415 814 125 631 699 029 424 193 467 937 408 346 626 358 485 308 013 599 466 970 738 351 187 393 013 218 317 073 613 684 272 312 661 741 803 870 913 560 989 249 379 938 728 143 239 767 956 113 466 179 211 790 941 339 580 302 941 218 732 099 865 706 826 833 932 402 927 964 953 562 250 800 736 662 445 199 438 507 560 309 910 200 310 996 469 589 496 299 779 784 482 562 716 205 929 692 919 498 706 798 258 000 252 490 946 176 549 325 615 703 963 645 277 746 053 825 735 884 546 197 943 182 203 951 471 413 874 184 445 466 505 056 162 817 637 294 708 355 569 848 613 663 368 635 162 407 411 523 288 555 433 709 379 138 734 250 760 167 753 865 565 017 447 545 667 072 839 870 858 997 665 034 717 892 076 672 859 846 001 076 791 032 538 192 832 058 475 843 454 072 943 873 879 346 120 332 973 718 248 223 581 840 610 659 498 186 849 332 950 106 652 649 831 022 492 714 444 381 593 569 530 671 557 867 768 227 916 669 600 762 940 348 610 232 413 749 685 615 692 614 070 507 979 431 243 935 157 645 796 487 759 862 799 139 680 710 679 185 618 124 947 662 286 969 001 027 374 657 437 428 652 651 400 983 431 608 556 950 621 803 271 677 296 199 714 653 846 220 993 404 050 831 205 445 535 758 091 853 352 603 418 771 568 855 697 754 920 265 926 362 946 233 613 246 296 851 306 553 673 734 368 716 710 702 467 359 782 549 338 230 775 608 468 528 878 584 439 770 153 334 289 418 935 956 414 187 633 439 533 291 670 039 879 432 047 897 204 961 849 429 760 556 371 715 604 009 249 110 224 083 161 325 499 356 411 647 124 582 218 114 938 784 326 700 328 406 107 875 361 573 239 347 848 719 826 122 719 556 913 301 821 346 401 285 291 544 325 260 947 592 787 531 350 395 587 226 947 898 500 803 475 337 788 112 466 800 656 373 001 185 272 654 096 786 183 763 557 595 431 978 139 350 080 172 949 141 805 630 336 005 434 234 990 190 794 263 774 335 505 454 943 964 218 036 915 655 507 457 396 054 652 535 872 666 315 090 820 883 832 231 677 664 439 963 839 141 064 420 251 399 296 371 547 099 585 694 136 419 773 554 397 130 574 109 388 034 082 463 215 027 024 066 640 598 596 751 628 533 792 936 368 717 339 558 519 689 434 687 893 895 691 608 344 275 849 275 758 067 155 049 266 291 694 803 685 676 907 478 619 248 599 621 404 521 945 725 842 905 625 647 909 632 102 857 639 307 635 986 038 138 943 996 018 933 069 621 154 278 122 941 363 510 234 073 627 668 470 141 140 304 388 465 422 297 268 345 236 254 971 956 440 455 427 037 581 983 157 108 465 381 541 569 181 539 768 021 256 336 885 658 092 084 696 597 156 872 683 592 610 406 163 813 913 730 899 214 527 045 256 453 573 583 237 848 288 702 933 850 837 271 468 221 575 830 267 256 734 276 835 596 774 004 210 521 757 457 249 578 782 417 663 897 579 978 402 320 020 914 469 382 891 932 594 801 686 156 888 936 121 346 732 389 195 867 901 243 637 544 542 146 681 904 354 444 335 566 298 222 600 418 039 264 922 174 533 920 579 865 617 478 357 199 865 925 662 860 089 764 479 796 786 640 601 361 870 009 249 628 093 273 847 999 334 785 087 424 523 351 356 224 836 050 233 379 704 563 106 360 575 476 678 187 520 066 726 042 520 116 073 644 240 332 680 638 851 570 503 218 056 148 017 635 523 945 949 712 957 312 983 886 062 709 244 935 303 440 583 280 100 536 870 159 879 426 501 298 258 944 798 509 090 092 148 721 841 336 531 990 980 610 334 601 140 751 446 630 330 897 675 469 281 944 422 955 942 694 364 278 769 987 832 978 107 674 217 670 441 643 652 720 568 802 072 075 542 100 591 780 155 790 839 088 128 777 904 639 710 463 258 348 502 866 725 520 446 314 077 606 206 731 679 570 971 817 897 650 646 923 547 842 978 857 264 728 095 342 664 148 643 077 081 792 942 738 619 711 069 785 986 750 011 246 442 681 841 313 233 761 494 489 733 064 465 408 264 747 338 289 209 838 391 541 177 177 459 971 301 933 729 948 218 722 676 684 462 099 888 198 815 309 181 302 197 155 888 699 461 502 721 142 197 505 778 900 372 026 254 928 168 514 020 843 153 502 355 761 416 713 571 915 222 437 548 424 452 566 964 890 547 040 787 567 789 834 828 983 938 363 045 460 446 154 229 943 391 103 889 383 907 643 922 282 879 994 258 542 547 044 740 286 238 474 470 777 299 608 229 867 743 673 556 730 952 798 536 852 652 677 028 863 040 699 878 169 959 428 375 593 489 543 446 685 650 960 195 633 871 206 523 570 071 955 638 352 434 995 817 176 738 645 817 984 542 896 221 022 296 072 506 515 058 147 271 100 753 995 052 084 483 813 473 125 424 831 004 393 297 488 013 342 041 011 850 250 919 676 209 534 995 154 364 125 151 227 565 531 411 847 124 979 786 558 729 314 645 116 322 474 824 758 313 037 596 668 787 262 243 760 138 442 735 038 523 116 796 572 876 059 720 544 326 789 408 215 614 826 406 909 694 395 452 817 541 548 876 663 588 491 517 536 969 544 203 901 950 512 502 070 098 505 271 209 079 895 862 918 568 123 686 012 119 171 769 577 808 204 769 961 853 646 525 758 105 328 080 089 223 442 683 607 071 608 006 496 212 756 125 586 032 603 461 808 426 381 308 129 667 691 306 254 876 128 283 811 346 532 933 854 100 086 316 830 382 573 603 452 632 729 918 786 230 955 638 286 167 569 792 514 681 448 373 478 140 405 755 082 775 185 259 010 748 362 797 723 291 956 047 889 535 531 963 735 136 939 209 561 033 253 031 539 312 663 426 492 516 176 388 274 673 437 239 204 527 393 488 485 759 947 701 508 965 304 301 090 234 209 981 352 186 325 825 883 008 432 268 976 581 096 102 712 184 642 906 955 707 371 443 321 241 327 593 452 114 974 782 827 731 847 949 531 432 660 776 830 996 173 948 222 099 799 363 783 524 780 243 099 601 746 844 188 871 002 205 391 292 872 399 376 312 239 002 558 694 601 466 396 410 232 431 292 839 993 296 780 944 869 973 268 987 087 707 182 837 866 958 175 351 532 843 664 662 319 438 164 518 216 633 448 333 991 149 994 001 188 722 436 172 247 197 115 025 321 047 363 774 250 801 946 090 859 699 388 788 660 607 419 688 241 121 584 792 221 503 652 030 052 570 890 942 421 251 108 333 222 647 069 785 934 762 552 489 603 920 687 560 821 087 937 364 255 404 067 801 358 919 287 943 228 873 928 017 446 228 066 254 977 651 104 008 387 873 169 468 363 771 842 928 090 294 467 899 948 368 277 642 407 675 778 580 277 890 750 618 616 617 982 066 611 764 831 968 881 998 432 329 080 356 243 245 131 719 474 397 276 114 373 402 571 479 343 339 732 449 267 034 858 252 246 617 058 040 549 913 183 318 755 258 492 410 080 496 663 941 672 102 852 025 449 175 930 696 020 407 068 589 441 194 563 048 187 357 092 775 547 244 761 788 427 878 821 234 737 473 291 473 083 394 785 982 755 319 685 300 997 874 823 086 987 015 771 012 214 262 502 983 127 086 908 653 883 646 122 122 280 188 032 296 395 457 699 293 684 126 258 459 438 103 353 307 615 205 457 842 720 464 634 595 487 048 336 261 601 242 619 761 509 672 887 536 017 701 245 529 486 812 598 448 836 474 777 892 731 711 487 317 588 889 571 823 525 908 357 876 127 295 822 193 761 390 317 415 846 517 105 842 080 265 930 370 164 849 678 536 005 618 384 559 830 074 715 712 046 994 282 310 536 574 731 268 507 098 237 982 454 208 027 005 871 326 672 340 884 988 286 092 598 044 802 483 797 031 327 033 082 823 644 278 737 144 781 938 631 790 844 535 878 195 424 818 507 745 374 614 943 752 863 345 994 654 516 789 706 966 116 822 967 663 989 201 591 520 234 765 525 636 764 363 198 002 319 590 104 764 703 854 518 112 747 699 432 624 748 371 999 735 344 669 343 315 200 849 179 469 149 849 221 747 153 160 479 328 620 915 123 436 787 935 453 431 597 451 953 462 384 225 809 170 821 398 102 645 670 977 408 965 433 778 136 599 615 112 078 541 819 652 060 006 177 734 911 722 385 193 065 667 376 224 846 106 190 250 538 491 705 893 860 315 934 716 494 528 250 003 938 021 897 282 772 164 828 447 062 722 294 632 872 574 676 589 662 299 456 618 721 741 354 451 807 837 167 773 042 658 149 697 153 193 981 285 425 353 148 133 643 222 822 290 974 746 322 404 109 891 259 664 187 825 273 064 866 668 534 669 698 106 273 339 215 726 975 511 164 212 098 254 022 990 844 393 613 156 177 254 620 355 997 786 168 820 582 485 306 482 784 920 770 125 167 702 131 696 220 657 343 352 190 671 190 683 252 797 339 673 788 818 974 091 645 551 154 664 281 788 509 272 547 778 771 948 569 925 772 995 218 461 852 713 882 748 793 386 090 078 034 471 446 804 535 690 694 406 196 142 252 517 819 134 390 315 242 438 594 737 734 132 494 691 202 373 180 079 178 305 714 516 475 794 330 936 480 795 874 759 076 042 779 684 169 397 080 025 833 701 240 436 498 132 943 415 485 683 994 944 449 283 798 617 168 839 267 820 165 659 482 047 759 653 753 146 634 144 834 231 023 980 237 575 760 206 646 659 075 728 096 875 030 558 662 849 137 343 263 594 046 616 660 350 814 359 536 161 662 225 624 880 570 504 792 935 591 825 877 543 185 693 686 223 053 367 479 185 155 263 166 489 731 136 339 808 016 912 075 311 444 292 006 910 718 987 263 148 913 082 504 211 294 808 216 496 673 018 080 408 486 208 855 704 193 923 155 038 753 139 842 270 463 488 391 083 552 911 856 365 686 750 944 011 469 464 925 478 111 944 728 822 210 183 760 327 350 992 664 275 760 197 069 457 941 630 954 703 285 745 499 450 698 610 498 719 800 244 908 380 062 863 456 221 821 014 176 510 313 331 399 273 485 250 186 107 527 523 659 360 359 806 748 987 570 910 446 609 624 861 023 567 405 580 688 757 857 909 348 069 864 387 871 699 710 580 985 054 143 663 642 354 532 098 027 324 297 062 105 567 132 503 214 187 306 583 287 188 441 681 825 479 969 590 334 114 382 454 748 678 596 070 550 087 073 644 259 835 156 653 245 291 728 947 823 835 416 093 296 981 402 579 247 398 944 264 434 853 736 668 653 042 862 312 160 962 068 451 938 445 808 209 758 762 357 957 486 210 898 244 367 384 402 518 278 150 947 678 339 570 880 389 687 650 871 096 471 657 311 096 752 561 956 387 582 804 140 927 531 017 959 964 793 215 725 752 016 871 025 219 501 476 010 529 247 121 465 718 078 284 570 507 715 568 698 903 888 075 707 968 225 323 926 572 549 162 844 503 599 509 211 550 465 588 774 575 604 865 459 084 944 517 889 844 989 458 495 560 638 615 488 482 040 200 247 193 095 278 355 394 699 945 300 866 835 886 466 929 662 297 368 148 302 951 163 595 301 036 019 934 705 853 532 518 906 127 833 337 974 471 816 324 705 955 156 728 369 535 371 658 203 528 297 584 503 038 498 711 271 890 293 794 534 391 171 909 191 734 456 164 436 754 507 383 799 455 957 451 426 808 402 444 680 985 458 149 191 740 438 844 538 152 423 996 236 217 051 724 472 606 232 387 632 580 293 161 101 480 480 380 523 331 285 742 317 432 848 601 806 778 017 414 657 879 504 381 574 383 889 775 745 482 501 661 205 852 794 345 963 566 755 383 335 951 381 123 035 281 107 682 315 607 335 185 533 110 195 440 968 562 245 898 719 617 234 215 299 175 459 093 585 827 977 603 887 613 138 428 042 417 164 880 964 168 774 353 346 710 512 368 770 840 265 216 701 012 574 144 305 981 918 386 235 899 029 167 357 911 039 592 789 605 804 572 906 995 220 870 973 674 919 060 491 495 729 888 972 691 855 203 870 489 418 912 949 656 931 190 544 494 480 676 748 041 108 912 358 930 528 707 399 702 908 535 066 985 548 650 766 739 238 376 768 954 696 384 764 986 566 953 937 698 572 476 346 825 682 679 738 804 590 158 662 674 625 479 268 170 876 265 405 029 473 316 667 898 692 034 632 797 978 578 269 344 423 242 126 843 057 169 567 287 434 624 786 585 501 716 140 220 493 432 871 042 681 189 640 517 804 737 150 018 014 681 424 046 091 211 814 920 503 572 829 133 832 759 200 365 136 231 637 442 343 754 077 921 869 988 913 199 791 238 928 394 323 894 348 687 232 573 258 126 366 030 321 738 575 881 221 203 161 204 106 522 066 007 114 773 801 326 734 894 798 679 372 330 748 379 259 438 916 845 997 846 700 434 010 077 627 562 069 368 979 185 252 429 116 500 142 554 214 600 509 336 855 625 339 296 645 162 828 696 672 004 935 284 667 874 639 662 499 371 787 723 647 885 572 631 953 497 408 884 447 346 148 563 382 353 006 708 971 298 181 097 528 713 165 228 318 224 736 188 826 120 639 275 525 351 206 583 682 515 892 261 111 167 147 640 654 547 235 459 694 830 973 091 499 468 228 706 894 897 389 234 045 998 842 519 427 050 919 715 862 313 071 179 549 233 177 039 637 656 268 641 807 014 388 210 776 793 515 850 185 581 967 337 805 035 984 882 675 509 851 676 811 491 830 338 304 397 759 020 623 224 700 721 285 049 827 352 236 294 896 756 626 104 260 010 152 689 507 110 356 927 415 482 852 228 298 212 614 131 141 895 899 324 755 219 435 425 582 113 968 321 904 334 356 108 477 458 973 379 944 617 917 640 463 081 844 963 258 008 048 188 511 557 976 535 728 545 045 958 648 290 918 756 574 670 887 576 046 771 483 062 828 829 405 479 152 716 150 913 008 355 379 994 346 631 025 820 479 956 413 730 841 369 792 660 955 039 542 245 004 215 720 727 110 630 923 896 009 763 087 969 615 863 493 364 950 528 801 199 440 000 300 434 140 819 558 238 978 368 882 317 671 943 183 648 974 929 918 625 949 956 514 091 004 551 686 544 467 891 486 453 319 786 844 049 495 045 694 206 059 972 663 422 700 824 650 021 260 179 446 065 425 555 682 044 453 373 266 797 614 606 190 705 081 268 202 869 666 576 971 701 230 170 017 709 519 773 687 952 677 438 112 899 350 626 270 807 735 988 203 955 990 534 656 414 427 156 909 422 109 592 632 297 430 408 162 125 356 354 822 305 846 207 743 597 791 458 413 689 711 891 266 160 503 280 823 823 668 438 727 174 166 139 610 571 790 612 267 315 887 941 412 595 320 620 936 731 544 294 833 083 458 410 695 675 234 264 270 274 161 419 400 405 645 646 288 178 132 967 984 458 886 834 622 050 366 113 852 191 815 582 429 604 900 609 796 258 502 411 463 960 877 716 161 779 280 212 315 350 326 509 925 183 351 556 260 687 516 050 299 486 244 535 343 027 617 220 761 635 237 765 139 533 574 146 152 384 574 034 206 787 699 022 098 313 620 542 116 924 520 794 184 183 455 114 919 541 278 089 385 898 587 880 179 617 732 989 187 889 049 604 008 603 162 352 564 367 579 389 985 904 222 064 966 842 324 659 561 472 508 577 942 197 157 175 454 784 021 515 484 606 128 661 955 572 502 928 234 332 931 702 340 336 519 758 719 315 964 876 045 085 229 652 868 375 832 983 845 425 989 501 576 981 820 278 486 605 988 928 869 095 497 111 802 877 142 842 890 235 551 245 926 923 025 635 510 101 341 252 296 015 974 081 620 487 460 520 749 280 774 057 801 290 971 247 962 091 864 941 157 201 112 159 454 522 146 051 592 400 309 944 657 604 297 071 782 476 016 881 599 965 091 640 314 726 701 702 802 509 051 212 629 205 260 095 356 252 242 790 922 011 222 185 245 632 085 199 931 840 257 067 913 188 379 420 621 213 523 421 728 801 708 343 800 404 391 871 666 670 408 873 162 091 255 605 030 533 464 998 710 968 805 936 749 504 688 292 470 367 670 196 864 082 009 181 537 253 045 721 154 369 176 225 033 415 526 602 367 862 259 312 350 272 773 155 634 653 609 424 690 622 854 966 017 442 502 705 370 800 331 563 357 408 595 692 006 060 859 430 079 978 747 937 347 357 020 801 467 796 443 906 380 553 163 166 132 386 748 572 877 048 531 968 311 812 005 403 310 666 588 601 974 658 501 387 377 627 305 406 921 599 798 868 398 222 124 072 266 725 567 552 479 726 374 707 632 730 451 955 693 998 660 592 201 830 132 548 701 464 829 014 815 334 150 964 404 471 009 160 683 035 901 572 584 596 938 383 480 776 445 362 354 294 074 345 460 165 869 098 410 875 466 343 054 499 761 986 064 314 111 803 332 708 958 070 918 867 852 173 094 092 863 793 123 465 712 729 287 657 842 538 513 072 533 209 541 850 438 780 650 309 930 030 509 873 279 403 789 842 183 886 677 561 007 174 810 163 203 348 203 299 331 103 846 069 183 485 949 898 990 976 415 228 990 413 577 987 174 577 210 212 440 515 843 611 609 770 068 318 100 419 211 230 497 333 666 499 391 271 711 917 545 044 507 765 015 601 386 647 107 908 390 271 462 960 424 627 237 390 847 767 405 085 448 790 726 113 183 672 518 376 248 455 965 882 670 766 957 328 716 527 983 511 229 682 513 895 159 896 895 835 913 053 238 766 697 727 768 917 695 578 059 862 325 415 607 320 439 855 943 299 981 172 253 613 307 768 131 307 022 814 132 650 334 921 227 105 776 558 710 177 681 689 835 660 807 612 985 217 727 217 215 701 563 660 681 516 888 720 486 300 947 325 040 209 441 902 620 884 679 233 759 870 602 755 062 686 352 447 230 595 033 146 945 296 969 786 634 701 606 278 566 710 149 080 529 522 732 332 468 525 218 741 087 781 397 001 057 972 487 185 153 979 738 632 359 120 121 313 598 430 424 690 338 923 012 690 176 260 665 565 985 235 679 658 946 836 326 807 587 043 310 202 383 964 346 560 330 470 596 495 238 219 943 498 467 011 259 934 323 950 466 245 165 591 574 553 378 420 740 320 071 046 765 685 014 704 830 659 752 815 417 104 903 295 422 207 324 965 491 139 492 143 729 966 142 811 166 759 182 590 023 184 805 372 400 150 673 982 247 956 993 869 296 975 465 893 366 819 743 322 929 542 728 800 560 461 295 146 053 319 511 802 080 473 335 271 359 870 149 885 322 107 294 113 661 701 083 580 393 901 677 364 934 130 612 156 318 042 403 468 258 707 418 021 375 694 069 523 114 806 776 250 011 021 930 132 727 570 016 300 032 242 558 462 715 163 716 394 021 738 270 414 275 333 052 832 478 365 979 667 111 236 498 535 807 265 111 860 046 307 659 182 093 641 494 776 582 207 658 731 089 231 707 586 721 873 163 434 775 873 201 875 356 827 371 058 673 533 791 162 382 586 910 928 814 854 935 126 292 266 271 523 277 301 909 438 258 277 392 652 951 900 400 304 261 525 205 363 088 650 773 323 705 708 126 593 563 400 836 207 793 919 619 725 899 082 870 341 302 803 491 670 082 418 170 779 330 031 605 824 490 128 801 110 527 530 102 689 340 288 075 682 108 982 016 280 467 844 068 897 429 619 620 261 843 638 557 282 602 381 357 931 638 526 326 573 904 642 756 126 583 825 529 204 712 011 876 806 209 340 609 869 421 236 761 676 553 044 220 258 935 261 376 190 591 088 475 011 596 384 830 500 345 086 905 030 031 389 076 139 962 329 575 920 607 837 973 519 016 410 244 700 577 944 323 842 091 632 952 896 466 991 774 435 574 489 987 315 842 122 155 439 360 559 309 839 336 480 870 471 480 548 563 804 076 700 589 722 211 913 848 026 866 294 599 462 622 087 249 277 683 705 065 725 581 389 240 882 518 125 891 553 080 475 916 048 435 869 138 411 011 620 890 504 289 505 645 219 400 578 702 275 107 127 504 337 123 655 517 770 778 170 972 720 351 562 458 550 319 822 753 225 113 290 467 329 944 119 613 306 878 370 529 025 009 438 261 521 091 351 630 935 039 127 199 352 488 440 531 240 855 394 754 114 508 645 163 286 794 279 577 345 229 771 049 207 687 503 877 095 098 018 383 518 676 313 470 871 655 022 985 811 112 788 026 711 121 986 894 881 849 529 740 461 418 066 058 097 509 047 018 670 019 918 348 187 533 073 256 116 862 038 601 043 204 426 053 915 088 102 594 126 604 035 387 960 380 904 300 928 445 697 921 711 017 074 950 495 561 664 360 637 361 050 014 345 851 599 091 792 788 105 451 646 111 512 245 507 330 732 099 353 351 419 556 581 984 888 762 732 932 718 463 517 365 837 504 803 754 284 928 059 447 250 012 216 872 974 558 475 367 691 152 915 584 468 295 665 798 129 818 141 772 684 666 378 092 340 753 172 398 818 002 439 445 470 228 772 846 217 731 675 510 096 564 540 477 767 221 339 286 714 049 531 518 210 221 242 506 382 547 733 611 798 643 007 077 083 019 153 550 082 952 230 824 203 613 698 383 161 023 503 039 435 733 520 630 356 133 109 541 292 527 896 318 688 668 216 120 505 669 761 136 256 517 019 194 343 558 608 454 650 317 034 245 881 114 323 029 885 035 898 346 882 919 584 121 230 229 014 308 319 669 762 526 759 224 117 773 095 742 564 606 771 074 614 572 447 824 841 316 819 557 692 899 860 143 097 666 332 753 843 187 653 911 152 187 178 144 958 582 789 452 209 631 936 120 778 322 440 490 376 609 793 829 656 783 427 473 863 264 264 247 198 366 773 507 296 552 919 861 302 687 310 626 549 194 038 465 422 299 079 777 037 584 986 944 902 922 096 467 425 374 553 950 105 087 306 162 944 007 145 004 143 003 460 091 001 102 887 938 216 039 694 998 865 266 319 023 137 215 677 798 178 219 646 011 263 176 845 284 529 664 265 622 103 004 834 369 216 199 120 229 456 935 108 901 791 178 487 550 179 539 251 605 176 610 890 829 033 121 869 447 610 386 285 046 595 193 170 558 003 294 384 809 878 283 102 531 464 298 660 928 418 480 187 069 779 555 285 082 664 414 672 385 737 405 872 278 552 314 934 946 898 554 469 078 685 884 228 785 691 933 430 257 584 145 500 772 780 695 032 206 224 761 902 912 425 356 359 484 717 118 186 866 261 645 634 843 641 569 281 116 109 061 356 217 665 412 899 673 160 628 789 314 250 084 804 429 988 063 871 422 584 088 089 145 716 104 169 733 254 390 748 130 840 609 525 078 057 244 151 296 034 478 366 867 846 445 538 817 393 536 158 051 335 650 171 177 615 097 982 574 536 658 117 220 544 186 008 686 731 838 253 290 356 844 254 439 139 753 087 382 323 328 494 793 656 344 199 440 371 284 353 060 085 021 114 303 900 760 094 452 229 149 517 955 112 159 702 314 855 798 381 448 412 485 336 065 714 821 499 927 549 164 783 899 212 698 985 688 474 185 038 656 218 113 871 083 252 991 070 457 390 713 651 241 947 211 960 448 052 085 289 651 365 342 856 317 337 738 229 574 481 835 207 811 047 443 640 634 891 822 099 984 529 535 055 365 274 817 796 347 805 119 374 176 490 229 000 733 479 813 592 428 342 754 365 122 784 855 643 069 049 699 530 190 617 576 341 228 523 137 361 500 163 416 978 839 336 408 245 015 284 738 668 894 308 889 786 001 844 509 211 586 625 394 516 817 223 960 359 966 215 705 897 339 934 732 650 762 250 460 339 831 915 441 342 986 357 009 236 422 728 240 372 592 422 814 313 222 460 561 033 853 837 719 940 266 338 840 346 267 476 231 274 206 189 747 470 025 728 785 726 990 724 030 954 434 547 587 008 965 184 501 595 882 803 421 352 344 160 747 965 079 054 364 454 818 058 373 619 529 870 050 711 552 551 653 223 336 971 767 925 723 975 644 397 981 932 587 706 893 668 164 257 431 387 856 721 419 823 288 794 932 411 361 929 316 087 491 505 436 350 008 196 708 648 578 296 140 389 025 591 130 258 251 290 230 398 268 211 720 281 093 586 543 065 353 996 156 230 185 408 599 997 787 234 535 392 585 361 199 562 047 126 082 100 696 978 226 078 540 449 276 179 772 260 171 279 424 431 376 447 976 120 840 760 046 714 688 979 463 084 769 297 047 099 886 955 633 337 459 801 495 376 523 511 887 914 916 638 369 580 448 728 223 129 149 181 941 129 265 652 643 797 669 683 705 122 983 017 189 891 552 084 577 686 082 183 605 214 286 410 525 160 151 883 115 048 467 967 743 955 532 439 100 923 061 293 774 967 765 617 293 617 954 533 068 914 383 446 399 907 258 654 113 963 839 511 195 954 552 762 655 112 140 990 600 741 171 829 000 347 955 882 739 327 804 757 226 712 425 686 718 582 678 987 530 603 373 141 170 072 328 348 534 890 443 866 468 271 243 873 843 493 877 961 930 033 614 875 911 786 179 921 691 085 064 178 464 257 466 131 423 207 518 611 889 143 967 634 876 484 384 672 384 504 361 161 423 380 945 133 068 337 661 336 960 133 917 354 136 783 184 215 923 253 430 511 445 827 014 856 985 437 485 273 280 484 649 143 231 965 740 608 604 988 041 876 794 694 209 199 737 904 763 386 279 713 763 687 843 435 075 942 092 661 166 562 824 284 283 215 448 272 129 584 286 435 957 322 662 040 619 943 119 879 022 137 943 225 390 964 813 440 429 184 663 020 067 314 027 779 986 499 963 876 575 708 016 849 808 922 689 489 506 910 116 119 325 141 990 263 501 427 658 996 304 490 476 890 743 426 289 346 416 086 930 461 441 291 957 858 844 184 637 687 514 477 768 739 918 572 916 436 814 221 308 760 185 731 583 873 339 365 775 688 398 496 411 645 951 140 587 628 301 689 993 125 920 118 218 030 080 381 640 901 501 483 399 562 263 598 855 957 194 127 081 202 162 751 941 877 596 490 557 365 378 882 837 561 566 231 000 833 170 637 622 502 382 419 671 316 355 009 853 080 888 196 808 697 156 365 067 634 241 929 274 059 821 398 385 724 195 113 557 299 080 052 811 574 919 142 512 043 154 782 890 079 409 293 766 692 866 416 325 416 792 216 237 851 383 716 318 209 610 368 832 010 635 512 962 063 917 713 921 275 892 418 805 780 613 310 519 169 041 283 611 777 534 376 696 632 517 999 701 670 086 346 576 731 370 518 422 994 218 572 260 824 913 824 725 417 773 463 232 523 934 301 108 590 698 721 684 153 675 870 529 963 338 180 507 805 442 928 523 732 068 899 067 204 856 777 527 181 108 726 433 694 777 531 746 327 196 829 832 326 918 210 249 512 634 141 463 701 243 958 537 347 721 784 683 227 354 925 963 463 199 766 295 921 184 792 825 760 133 908 454 465 320 227 750 318 246 653 160 095 278 183 977 311 221 967 183 951 639 621 646 979 825 300 437 122 755 655 156 468 607 440 504 633 443 267 195 817 096 374 284 791 826 605 527 364 264 902 590 932 923 564 313 895 011 427 094 360 333 533 058 635 920 114 949 001 735 860 081 246 500 145 831 599 890 910 117 799 177 323 914 426 525 689 788 426 858 490 002 037 472 540 696 078 881 060 255 771 375 402 879 146 108 029 017 679 533 150 376 825 664 571 951 447 860 680 840 701 906 343 592 826 686 570 645 692 656 258 018 490 982 484 070 288 157 618 101 514 553 880 511 514 605 613 529 310 418 867 687 510 002 140 351 526 905 369 345 226 020 478 902 788 616 945 363 346 265 269 272 669 144 683 768 215 576 917 520 897 731 260 485 609 353 763 749 571 419 100 155 570 558 247 085 915 533 807 544 293 554 250 527 038 474 249 469 579 118 972 063 742 828 226 192 375 767 339 509 536 306 327 832 420 161 133 560 868 879 133 345 401 339 117 973 092 153 363 669 218 084 392 930 087 560 041 324 989 979 671 636 846 957 729 475 330 980 552 414 260 253 717 420 762 776 175 694 918 781 561 294 698 234 007 099 498 759 759 819 930 586 312 618 622 864 787 599 635 883 872 114 786 702 670 670 750 593 799 834 296 337 422 715 830 836 279 991 317 327 270 809 880 922 296 019 412 513 836 088 561 886 920 781 319 909 056 966 285 382 184 628 386 850 423 715 618 760 733 063 197 487 361 421 364 481 527 605 864 017 999 529 000 212 822 367 445 151 932 544 587 798 503 219 193 752 694 230 294 168 199 667 841 361 563 401 475 442 536 044 181 347 448 370 574 760 268 438 077 650 635 598 148 204 905 047 472 541 557 588 251 070 580 794 583 451 681 810 839 096 749 769 580 855 981 812 593 851 933 215 094 164 051 003 277 487 873 173 747 775 013 609 730 556 279 199 053 888 816 535 102 647 415 851 928 194 740 948 825 401 129 384 311 837 351 578 689 594 326 827 140 738 121 135 371 877 438 973 956 518 712 402 474 930 509 863 463 320 569 169 525 688 778 752 266 599 551 023 800 182 680 185 040 270 912 839 211 331 863 077 550 541 740 098 662 519 841 100 169 284 751 111 027 885 184 406 737 019 992 192 678 356 969 170 085 755 181 772 060 091 418 497 720 582 735 947 118 898 987 841 851 976 278 482 598 198 591 294 813 649 313 416 701 548 166 132 533 326 013 361 601 833 222 301 841 733 183 248 156 069 221 295 621 171 405 475 007 674 636 608 015 353 224 258 338 926 515 685 866 908 307 228 877 766 250 210 293 930 772 023 844 095 319 716 236 180 107 469 504 782 596 586 852 608 009 515 326 820 731 986 070 887 711 672 218 307 963 856 214 427 952 071 615 272 153 005 625 923 515 365 812 806 716 982 620 331 908 037 238 591 375 718 107 098 760 080 841 945 537 264 317 203 140 004 820 770 145 919 151 815 538 410 398 530 906 701 590 690 007 982 283 819 992 489 877 638 091 602 900 563 339 197 938 567 939 942 108 266 233 594 508 715 779 609 761 749 010 029 492 810 637 624 965 446 483 054 384 938 892 848 599 663 743 036 648 969 681 858 060 283 914 956 687 192 634 377 280 094 765 271 017 520 103 440 216 243 433 535 130 624 366 559 789 372 162 325 142 743 464 054 011 541 958 517 516 948 327 705 516 901 824 102 008 123 550 266 986 699 300 121 588 059 809 946 675 268 127 942 031 567 056 906 897 754 057 708 393 915 182 703 394 415 297 596 776 850 103 831 490 423 228 998 506 155 182 171 161 494 305 851 541 095 956 545 774 387 474 998 887 079 907 489 844 539 003 480 715 673 119 808 744 706 494 280 724 887 697 520 498 629 540 777 387 601 374 302 823 457 366 389 104 401 950 804 164 112 708 718 791 587 815 398 257 857 511 969 868 172 725 230 853 724 043 835 600 237 680 726 047 951 972 200 860 504 750 728 605 242 680 268 409 811 228 711 916 019 861 457 659 483 665 351 856 272 088 633 250 891 336 500 538 600 730 520 451 259 715 245 340 364 818 285 682 226 396 336 897 519 295 699 695 068 937 295 841 352 535 474 775 621 428 866 121 239 809 826 992 573 967 362 753 561 209 671 814 596 003 273 384 841 479 995 502 616 592 365 163 339 354 603 790 476 719 301 923 575 438 796 682 710 166 532 477 261 946 077 258 040 236 885 216 701 953 473 499 327 361 166 770 241 825 109 286 647 277 216 287 191 604 238 685 586 855 767 197 401 243 013 097 994 892 251 762 526 764 110 206 195 784 479 921 802 516 478 856 038 253 393 647 404 425 901 766 360 261 261 911 076 597 894 263 704 011 046 214 424 386 183 495 329 398 035 259 285 927 675 404 394 414 500 928 203 272 836 479 627 029 204 547 995 999 379 521 242 169 088 827 897 303 038 148 082 129 201 995 250 175 720 113 093 041 751 770 369 402 758 197 160 649 056 264 284 159 222 069 649 440 733 645 779 709 672 876 720 905 985 569 229 886 936 596 864 176 501 432 423 085 103 087 149 154 956 841 987 191 192 066 679 139 255 626 248 689 404 610 641 916 066 435 632 489 698 180 848 250 149 006 193 127 027 176 684 502 478 972 599 024 782 438 112 974 497 161 689 884 330 892 790 964 985 222 672 589 431 336 419 778 345 698 852 916 315 848 202 781 818 254 213 298 365 995 066 835 163 306 993 513 083 809 085 131 965 728 182 874 853 284 038 105 832 345 515 792 726 480 746 475 731 359 268 601 018 944 720 944 282 060 106 004 108 141 133 917 935 814 969 459 152 983 491 757 512 183 809 765 903 835 315 124 954 378 577 844 086 990 751 711 645 293 273 656 579 743 443 724 948 495 323 609 919 277 780 585 485 589 984 376 261 144 021 703 340 796 634 390 739 183 335 166 143 273 380 564 941 852 327 838 025 109 449 568 460 842 620 403 661 290 798 450 102 604 365 635 479 505 136 072 975 044 914 299 239 611 990 687 448 291 134 913 383 168 900 789 948 919 763 201 191 799 364 953 355 348 339 826 569 113 438 540 581 811 324 755 925 497 251 726 588 440 294 917 432 906 858 546 151 627 246 760 040 975 671 511 126 677 149 919 727 319 472 539 014 797 326 548 653 046 161 004 390 163 509 700 071 377 467 788 650 209 344 222 861 584 602 496 042 961 430 222 122 653 205 758 746 023 708 521 426 505 103 416 926 552 643 178 815 637 659 177 317 937 792 035 375 476 969 823 745 464 286 152 095 594 772 922 921 432 511 426 216 640 419 240 344 304 382 219 409 405 872 059 483 424 158 323 277 009 169 892 794 833 775 574 170 308 069 774 128 336 389 564 640 823 963 403 276 170 593 311 274 572 454 304 652 374 825 108 313 921 566 942 761 565 822 746 668 975 232 327 418 049 684 320 151 725 504 183 974 467 539 310 780 508 036 805 789 539 118 109 643 547 257 242 605 554 963 632 209 625 533 084 042 068 761 489 636 012 235 045 487 726 238 147 827 911 259 427 169 539 356 764 177 085 468 402 329 489 781 443 789 067 941 600 023 091 905 650 354 361 167 379 730 827 074 683 335 662 057 005 893 910 028 780 298 065 234 378 139 795 174 907 330 092 533 987 650 853 155 996 849 617 949 155 453 205 522 116 943 108 880 935 167 262 547 819 778 706 595 235 351 281 925 235 651 874 797 617 126 605 090 831 326 749 636 472 836 671 838 983 246 541 749 001 566 816 311 631 681 038 547 708 524 400 278 001 092 065 554 863 799 182 199 613 453 424 270 136 792 256 450 710 330 975 990 711 415 364 973 551 440 246 174 419 101 772 826 955 593 686 471 001 962 880 332 594 076 309 183 565 047 811 574 146 262 190 640 700 346 765 841 226 317 003 413 537 806 509 894 744 066 792 435 332 640 191 431 383 836 829 280 967 971 995 629 475 046 913 513 236 740 603 887 404 059 403 047 416 381 932 104 927 814 771 671 651 376 583 119 924 937 485 260 984 858 190 554 590 083 270 711 132 944 868 774 840 952 594 281 717 178 821 542 393 125 050 530 479 748 582 378 100 511 363 977 314 815 041 820 061 125 191 561 845 414 787 878 526 223 666 933 912 256 341 301 197 530 357 288 971 430 074 290 986 418 730 129 473 560 028 519 633 874 252 962 105 767 165 989 163 279 660 893 921 720 849 179 224 016 817 635 690 842 831 171 059 130 612 857 261 869 186 109 913 396 329 009 859 204 038 063 886 296 690 570 975 733 005 467 919 291 636 402 646 730 932 227 774 067 551 379 098 576 503 171 436 963 514 583 896 938 849 149 016 565 973 027 431 194 925 719 611 023 966 327 570 987 137 667 909 804 333 673 323 420 835 685 884 131 434 061 827 052 081 431 095 047 429 439 046 807 170 927 859 277 432 663 351 583 835 868 932 122 667 942 267 873 525 993 688 383 769 505 067 351 439 596 287 225 069 868 881 016 739 845 334 241 410 028 817 567 203 494 364 643 271 612 160 322 474 959 609 092 051 412 244 814 158 297 783 377 464 804 940 420 929 971 238 194 273 310 431 487 783 851 894 218 950 229 033 360 551 926 607 109 739 161 109 526 623 070 322 337 507 284 294 131 141 433 392 704 472 990 455 598 899 478 304 946 322 116 347 664 595 473 994 742 945 479 922 497 471 655 861 402 708 006 853 208 783 224 941 017 051 442 348 276 555 924 703 767 630 436 887 264 077 633 644 912 464 863 406 815 842 039 444 503 977 092 593 565 019 850 174 902 184 131 134 489 323 733 722 513 593 875 733 283 886 626 147 074 771 460 926 656 046 942 808 105 511 472 742 585 203 522 777 907 077 541 934 739 186 991 633 845 583 965 555 943 421 072 069 718 303 130 106 041 610 047 903 867 100 050 546 975 241 905 728 497 339 883 350 006 657 825 686 313 866 680 432 288 006 698 221 099 486 214 008 654 971 690 629 115 201 129 715 655 831 868 941 090 055 939 308 340 674 222 757 454 243 563 679 028 329 060 957 209 329 967 945 036 083 945 507 221 173 487 763 682 397 237 212 171 925 533 951 522 024 288 518 860 791 319 141 737 443 095 581 226 574 336 575 320 832 131 936 693 267 507 423 122 070 097 373 368 632 231 087 644 545 147 577 564 259 431 171 898 731 960 774 017 128 875 998 802 389 351 533 231 111 544 940 654 406 764 945 203 467 809 724 769 984 653 564 183 137 986 310 884 549 353 220 517 080 404 832 672 734 732 815 949 414 137 435 283 320 306 188 873 131 283 812 929 681 231 805 834 395 062 532 619 770 126 070 988 984 942 403 911 970 424 162 491 174 096 849 862 465 155 583 983 270 337 976 427 541 025 363 196 237 582 559 963 066 122 188 920 682 948 592 598 649 414 672 244 654 125 505 407 077 705 675 492 963 423 101 980 627 720 266 136 914 056 743 700 441 354 901 331 836 762 642 294 897 700 334 206 647 192 407 234 351 075 472 909 509 175 465 521 348 382 699 502 044 748 484 348 790 112 058 285 829 085 214 039 960 243 776 000 664 322 674 805 799 308 987 236 378 334 945 589 685 718 685 833 362 959 129 956 336 566 533 038 146 489 620 967 861 162 200 962 373 536 063 434 170 453 585 179 056 435 758 325 139 458 887 042 937 816 331 574 018 045 808 902 451 318 668 211 169 149 724 512 558 468 151 604 591 659 318 660 117 910 183 281 550 366 934 171 837 590 157 548 832 200 459 985 262 161 840 146 906 610 672 238 606 544 575 493 580 344 804 561 934 799 268 678 024 556 793 529 844 108 521 593 789 421 088 185 698 749 979 913 572 389 266 880 629 254 678 958 330 971 244 079 831 314 310 404 333 460 178 700 342 976 854 835 799 789 087 800 707 743 974 723 090 336 133 184 754 354 154 730 606 026 502 370 171 316
392 575 443 245 422 586 321 735 990 442 327 427 119 062 153 312 034 687 597 434 775 623 388 120 947 734 220 061 923 645 005 390 830 823 412 521 591 576 726 076 683 073 651 313 206 248 102 668 235 758 497 312 539 860 804 334 913 514 412 193 419 431 327 375 743 065 284 514 943 403 694 545 325 277 493 081 759 959 487 180 607 181 876 381 919 828 919 022 055 752 221 817 549 562 645 094 470 235 179 885 829 171 653 953 564 315 389 074 862 901 092 787 604 369 800 915 185 324 640 834 701 859 219 879 165 026 116 182 617 246 155 895 385 541 798 475 896 131 764 250 394 055 517 421 449 749 754 161 996 165 552 197 018 372 456 580 468 842 777 486 922 933 602 257 852 045 782 441 308 689 024 219 813 450 534 031 092 763 656 024 391 033 124 277 086 949 699 098 686 136 057 212 067 692 897 433 201 066 653 393 284 352 269 196 499 028 616 445 442 744 409 312 103 136 941 638 130 045 601 233 298 725 400 327 665 076 767 331 400 017 581 996 585 327 928 757 920 573 001 874 204 625 648 486 473 696 449 652 028 183 801 112 816 320 999 705 408 151 656 065 934 934 460 721 836 618 782 944 450 545 819 942 328 289 515 176 024 117 437 404 818 292 706 203 981 255 443 378 059 189 973 392 036 598 133 102 002 748 241 021 078 671 038 668 274 772 061 210 582 816 853 990 433 102 287 714 490 797 802 920 107 957 334 484 298 632 805 022 836 375 356 661 759 927 513 401 553 698 355 460 285 343 397 756 122 470 015 158 355 941 085 275 425 112 143 541 909 394 017 618 502 865 676 163 975 590 819 587 689 939 281 112 194 637 092 646 648 900 185 472 463 678 843 523 241 991 604 652 228 761 469 415 632 033 782 677 653 462 939 571 866 134 552 007 358 313 370 025 529 044 931 488 907 160 196 068 449 761 964 857 458 363 321 764 902 180 947 887 295 064 523 885 981 423 017 611 765 314 238 091 387 537 436 814 434 857 538 627 634 279 806 446 021 654 782 800 729 502 848 207 811 331 906 758 359 136 898 215 322 512 970 559 061 053 617 784 339 255 862 042 851 700 089 240 249 260 077 105 152 505 100 167 619 970 223 429 638 994 021 296 262 047 738 198 483 636 146 898 166 634 895 337 158 500 022 237 199 731 883 615 333 017 496 606 712 694 218 044 344 131 932 940 468 319 116 492 330 112 986 273 285 118 732 064 270 966 941 897 077 976 401 273 811 325 089 139 608 217 161 046 443 090 636 025 470 156 475 958 692 664 780 840 122 121 964 741 099 663 472 429 786 787 338 095 916 208 065 779 426 432 619 819 977 109 269 299 957 305 980 509 963 104 682 214 850 682 787 581 946 965 386 327 859 649 990 999 117 178 035 926 179 655 479 681 487 078 155 258 964 072 447 324 709 385 492 182 580 757 029 045 949 546 893 429 766 049 561 166 161 940 129 407 719 462 882 967 541 651 073 113 860 139 857 035 291 099 530 566 364 586 250 585 848 673 409 338 091 111 098 993 152 539 077 634 737 104 735 926 470 665 535 542 365 618 927 827 025 268 302 642 223 081 726 745 946 570 439 539 329 286 089 263 107 890 580 662 185 415 092 395 438 262 080 741 747 567 539 224 117 947 407 509 640 227 570 072 644 162 312 725 505 712 665 568 218 415 817 526 312 170 026 534 850 348 562 569 364 438 501 021 287 234 617 985 487 800 577 619 636 166 609 992 229 600 077 735 832 542 087 198 820 609 437 753 821 573 130 407 219 480 541 152 195 810 133 834 190 689 216 326 580 314 953 423 369 286 408 467 468 091 652 114 711 220 404 688 149 786 973 492 488 607 374 845 251 951 115 117 211 658 044 230 866 747 141 935 152 609 560 812 012 632 241 229 233 232 587 007 376 379 680 315 695 842 820 514 705 415 689 096 327 188 649 974 115 922 326 326 533 134 664 172 773 400 959 057 814 374 482 929 564 221 794 741 742 822 041 868 631 741 974 269 073 314 149 333 183 647 864 882 655 226 156 604 699 851 758 163 193 579 375 170 600 842 905 791 052 459 513 293 706 438 704 953 053 207 471 365 952 621 279 261 933 058 641 466 259 563 888 305 716 918 146 145 984 111 486 598 889 324 941 019 368 815 612 548 549 761 107 140 641 448 835 476 718 095 284 227 588 364 146 448 786 776 438 199 623 275 625 323 463 165 498 328 880 754 142 304 060 457 166 939 066 569 303 542 527 794 147 381 256 256 728 266 995 567 128 893 681 053 959 228 177 118 461 970 347 814 044 918 604 521 957 831 937 913 807 513 760 966 652 625 839 418 942 778 942 026 451 370 921 465 551 901 292 607 269 927 475 557 778 910 002 612 464 560 121 008 322 173 522 828 587 003 526 195 878 722 307 898 534 714 334 885 719 538 606 697 364 290 004 599 997 764 113 441 002 900 503 506 121 016 963 776 082 383 998 305 006 994 890 749 173 681 457 354 651 359 515 659 014 784 570 442 694 702 548 278 927 120 518 893 821 222 267 409 412 799 151 530 053 546 679 911 944 768 078 577 539 500 543 744 482 346 882 438 183 347 473 596 843 260 132 325 077 466 201 207 252 276 713 179 605 208 470 724 179 678 834 428 769 427 106 377 705 249 278 130 316 789 744 657 749 295 712 096 875 593 340 692 575 606 317 240 603 249 517 824 073 567 967 082 808 816 354 912 540 110 932 043 866 452 377 015 917 672 694 929 633 470 691 223 364 287 525 066 483 860 202 813 226 947 914 447 799 767 616 310 365 116 023 032 252 152 138 521 327 668 011 891 363 769 077 752 539 280 207 023 081 471 670 037 623 619 080 791 369 736 907 784 047 112 901 852 142 428 235 565 706 334 466 281 814 690 327 136 310 621 294 434 324 971 684 127 407 031 131 689 524 599 069 104 731 083 758 197 182 368 715 214 756 427 518 222 822 636 155 582 839 855 490 211 763 651 962 667 206 110 896 197 069 269 745 382 646 684 682 627 523 085 455 028 954 490 939 102 021 169 913 197 984 249 756 262 571 758 800 015 592 586 176 913 538 194 480 818 763 442 938 641 116 696 513 271 820 652 227 476 985 972 433 581 382 011 063 401 019 982 370 565 266 194 983 744 223 395 115 648 332 559 752 446 654 212 764 050 808 110 608 263 134 672 914 920 483 455 286 240 823 702 549 855 973 107 452 584 603 157 939 331 507 074 479 284 453 969 434 832 510 479 641 614 702 072 156 687 080 506 460 557 901 929 726 708 079 902 346 968 823 980 486 244 818 791 222 976 057 919 100 760 596 137 900 164 997 750 689 516 815 162 214 841 617 686 424 335 130 695 804 521 977 622 614 749 735 476 766 040 064 410 710 074 345 767 529 820 318 896 793 311 025 978 503 944 004 887 379 666 250 318 001 923 187 251 066 124 375 918 730 516 464 413 903 189 136 405 979 503 901 203 532 882 184 509 869 770 468 797 438 589 997 008 854 425 765 160 620 857 415 107 071 243 386 787 572 304 402 922 461 551 018 378 634 953 692 674 421 160 871 966 740 722 120 839 215 076 960 059 682 272 475 829 249 576 092 323 662 050 018 125 498 754 515 397 578 151 883 033 166 921 591 099 890 350 614 752 550 489 090 586 470 772 405 079 493 149 164 794 644 763 983 661 951 690 444 913 470 327 756 672 662 272 091 335 475 737 132 161 813 912 187 718 010 770 910 873 575 395 090 436 847 727 866 551 215 983 438 020 366 643 966 263 956 302 053 746 464 334 121 691 879 412 542 339 130 827 645 368 774 548 746 384 755 261 920 215 100 230 551 901 571 828 147 609 366 326 379 024 089 725 716 212 066 444 555 970 260 975 235 187 632 083 818 318 782 914 571 804 454 812 831 551 648 304 788 352 761 211 020 827 667 692 534 506 111 550 448 646 756 144 181 622 099 217 660 568 464 499 294 113 098 351 226 237 765 501 853 367 090 183 096 919 631 083 927 590 096 471 886 622 317 282 534 043 766 522 700 640 399 845 778 026 563 413 790 750 511 401 667 896 653 570 718 094 190 564 942 154 721 284 813 339 480 512 327 763 281 382 225 816 019 662 098 052 385 764 867 508 386 670 421 620 196 766 134 039 268 262 970 534 369 683 166 907 976 929 138 337 292 186 316 116 907 253 320 144 067 954 887 966 858 088 218 624 212 751 009 807 954 861 349 548 841 765 577 784 622 162 290 365 738 443 370 121 230 841 672 795 298 837 957 179 602 454 942 210 910 893 492 087 202 784 463 323 221 386 335 107 922 226 622 047 305 782 219 866 313 099 266 887 101 432 647 519 688 842 947 986 343 874 052 790 121 609 219 086 031 941 267 144 591 974 753 461 389 002 354 346 670 023 659 941 238 676 329 188 015 129 547 015 412 569 344 172 987 506 163 440 826 313 843 004 052 904 092 387 723 262 842 320 860 983 971 795 676 487 731 745 456 107 714 009 699 898 917 902 885 112 029 420 847 213 768 020 821 756 720 040 899 687 367 519 960 830 599 160 726 158 251 951 178 153 956 871 193 991 566 834 931 057 711 098 053 757 058 950 074 712 923 076 520 931 895 608 594 662 783 868 440 911 161 434 992 226 023 340 066 420 446 058 647 884 513 228 729 981 475 575 993 184 552 825 041 896 235 800 107 926 433 655 907 672 351 666 468 051 665 216 066 442 828 833 209 396 104 653 104 330 640 240 414 431 624 868 485 613 122 584 767 365 918 863 330 911 809 922 791 939 376 736 614 675 125 832 402 968 443 392 992 304 833 462 749 427 188 558 839 805 042 343 872 828 646 757 614 404 943 329 018 541 245 879 303 354 594 522 205 394 929 410 517 554 077 057 595 311 828 650 694 146 798 783 939 443 973 854 248 064 447 534 561 405 954 634 570 313 168 965 528 046 163 883 904 984 613 993 618 304 314 218 375 194 689 014 533 273 841 839 707 757 030 889 555 318 300 718 138 009 810 026 690 162 050 203 516 934 149 175 097 297 661 827 954 877 298 268 823 080 702 685 805 486 990 201 332 773 433 078 539 027 562 416 451 591 054 864 867 233 138 164 545 329 082 330 981 952 737 108 485 402 964 499 893 375 781 266 730 385 523 509 660 771 746 387 724 134 814 698 839 899 808 393 147 760 328 311 882 222 906 498 084 097 217 406 978 006 943 585 129 958 547 375 877 528 880 319 694 748 764 123 955 843 540 363 281 402 366 357 093 715 471 795 424 385 566 769 635 869 735 673 638 115 154 388 876 638 544 379 594 033 658 141 035 231 722 367 235 017 774 239 981 457 632 499 879 640 834 316 123 245 723 628 458 464 752 247 945 858 254 914 300 574 462 006 394 924 170 845 208 896 552 687 535 347 640 685 840 371 833 898 528 898 087 398 589 620 394 308 534 534 426 625 837 975 398 345 360 420 143 239 706 022 902 366 582 745 191 604 889 179 152 679 612 706 224 186 963 271 610 388 845 753 001 429 006 881 961 445 565 183 529 769 543 535 967 995 801 592 963 309 768 175 760 097 643 750 925 226 129 760 798 947 638 643 089 838 812 017 047 901 086 414 187 683 622 375 186 208 845 834 409 546 778 232 604 300 582 143 015 750 197 627 907 281 802 984 695 871 610 565 346 192 523 621 664 974 662 530 421 409 549 846 098 651 645 268 671 741 856 328 751 065 294 839 191 300 384 743 096 755 483 403 188 488 444 587 701 176 588 843 935 082 973 606 308 145 282 450 093 412 829 458 080 018 043 651 790 836 642 937 283 372 775 100 560 944 809 218 249 973 289 061 498 956 362 106 212 047 936 561 344 448 314 456 305 295 839 236 345 431 443 231 556 616 309 879 946 862 036 561 203 349 722 285 457 768 508 890 897 160 302 444 052 696 406 452 077 341 059 683 316 828 748 033 777 600 176 960 014 746 158 503 016 532 390 241 658 383 678 075 201 808 852 505 073 470 483 443 957 334 757 544 806 772 382 005 477 962 759 034 289 779 035 534 459 093 233 031 874 176 300 334 950 199 649 233 509 756 534 472 512 171 493 218 408 507 785 684 565 869 928 571 953 598 144 563 870 063 055 032 547 794 269 774 917 803 834 414 827 883 861 982 772 038 581 298 274 818 781 696 968 507 119 763 541 074 743 155 574 428 447 979 862 519 652 982 724 810 158 776 720 142 077 220 946 914 098 686 451 355 295 439 622 618 547 594 773 806 341 809 720 196 505 855 283 820 530 058 871 826 693 690 386 305 201 377 632 712 125 072 510 528 757 155 887 162 018 052 921 999 001 133 350 199 369 962 829 501 956 412 401 855 835 175 807 549 076 383 318 791 661 105 601 610 707 054 126 060 982 343 602 207 435 692 616 978 653 196 690 979 686 594 144 781 405 453 042 293 876 808 557 731 049 004 656 450 758 448 180 125 078 277 816 856 926 705 932 258 919 332 194 437 899 088 524 601 249 644 811 340 339 203 956 318 543 179 917 485 946 326 592 960 248 329 015 087 950 210 120 689 502 568 644 518 788 417 150 056 855 804 372 231 855 254 500 863 715 229 221 250 304 284 501 639 966 706 236 453 479 419 166 567 627 209 055 961 212 263 955 946 672 022 272 107 120 151 213 988 455 320 408 478 028 719 594 795 377 469 282 867 778 410 267 881 726 917 189 394 697 737 279 237 933 624 507 073 648 264 087 830 863 833 402 734 697 471 380 816 707 700 901 366 993 355 930 303 550 609 769 595 339 672 807 570 936 121 702 592 860 062 742 437 614 742 048 435 474 035 669 343 003 769 151 496 277 382 839 444 711 538 949 981 680 094 818 473 930 689 294 860 812 576 876 053 221 440 568 703 010 848 843 488 217 439 884 258 915 159 343 041 053 169 787 257 954 662 883 845 820 568 089 811 088 691 097 099 720 722 293 486 744 112 882 509 388 205 117 101 251 294 369 803 087 089 920 205 210 859 779 950 644 634 067 910 946 784 440 354 308 627 784 162 196 883 311 369 273 568 071 747 754 922 005 202 742 941 266 957 272 559 576 951 969 821 502 679 689 600 440 460 269 847 235 101 783 725 113 937 073 248 422 071 132 121 325 285 217 821 427 423 748 507 654 463 425 726 188 628 401 668 854 669 500 741 216 463 522 495 090 442 627 649 181 369 948 283 535 604 955 567 814 151 359 673 724 910 081 907 116 989 430 505 839 141 414 487 286 462 452 173 209 324 543 294 090 281 575 766 675 409 384 842 974 560 501 709 010 407 952 691 999 426 405 841 489 434 287 988 304 328 237 085 838 226 686 284 071 315 375 152 707 390 139 580 359 784 116 973 847 739 824 916 651 300 229 128 013 477 155 536 725 657 003 047 234 520 948 929 839 903 899 319 145 492 866 028 648 890 124 925 633 108 922 022 186 927 871 910 079 212 806 859 903 418 598 418 816 929 434 781 687 007 219 255 389 049 962 435 581 900 681 440 877 523 239 044 245 440 393 053 553 246 076 988 907 011 876 967 075 916 990 767 496 693 885 798 448 698 832 634 490 330 434 599 131 585 461 653 538 520 661 689 357 105 050 674 486 985 961 517 624 493 787 428 209 930 771 252 252 075 453 786 868 663 037 235 847 017 896 439 234 428 675 393 239 577 148 532 822 993 042 402 894 204 819 663 680 595 943 161 171 837 966 119 922 701 361 248 960 076 335 316 159 936 910 453 701 697 972 261 763 241 782 712 118 176 582 347 205 830 319 608 273 717 757 672 055 311 848 800 004 046 441 433 033 020 840 951 369 274 930 895 092 196 474 939 669 832 929 529 358 519 422 393 681 064 912 657 553 761 452 257 911 902 134 522 658 109 173 172 487 995 419 341 879 673 378 406 860 711 747 145 115 401 463 048 882 222 600 624 035 972 586 480 613 470 541 913 005 549 789 246 168 966 261 077 947 528 720 122 792 251 596 574 817 421 150 064 461 722 923 997 947 958 471 696 742 460 202 911 312 240 982 283 875 761 790 771 819 644 958 153 719 953 129 321 010 078 463 127 961 569 710 467 291 822 723 896 906 739 826 580 317 864 687 156 295 878 515 884 423 276 254 362 076 225 415 260 448 724 582 607 987 006 298 402 334 380 522 134 576 955 589 210 171 086 217 012 745 942 126 777 689 973 573 472 050 944 091 041 567 405 245 322 549 417 607 103 993 516 112 983 432 602 528 592 904 852 890 285 079 161 531 213 889 381 264 101 172 762 474 020 270 387 366 751 127 777 668 771 907 789 294 722 992 274 380 128 109 399 980 886 568 379 525 863 598 115 755 063 358 424 840 267 529 006 811 617 432 971 669 369 238 454 685 301 710 163 691 305 442 637 808 515 217 547 990 167 868 526 913 801 293 562 927 227 344 667 837 781 578 786 825 099 187 013 268 841 105 627 247 335 008 542 150 319 629 643 015 195 382 818 775 028 613 218 423 412 462 800 798 009 759 544 929 966 039 558 223 795 843 062 698 577 182 834 664 281 232 154 188 128 064 294 083 109 224 346 217 122 512 475 864 093 351 516 146 934 245 211 527 063 544 402 852 910 116 732 123 314 676 493 101 277 638 120 120 186 272 079 695 190 411 899 809 133 235 888 996 684 510 529 895 961 808 882 676 404 320 985 964 123 831 050 502 959 337 216 393 051 677 152 815 624 626 126 088 010 084 181 489 071 885 235 014 815 008 086 166 387 594 529 361 622 423 465 407 246 226 436 227 287 017 980 424 080 068 634 818 154 504 735 549 130 510 696 920 520 850 533 209 623 873 430 128 454 707 380 758 582 239 906 976 575 768 270 756 129 735 849 923 453 527 460 538 628 190 941 059 981 846 570 337 650 444 756 500 092 483 787 913 370 682 751 276 158 748 325 279 813 082 986 772 128 068 512 785 945 855 714 641 759 703 411 061 061 191 654 723 799 032 135 691 781 187 099 051 667 514 678 150 168 027 143 240 231 082 740 554 084 823 557 392 555 646 046 289 895 647 978 546 257 726 064 413 671 395 544 697 211 033 375 398 384 135 860 748 702 713 002 661 045 639 292 085 744 260 765 074 168 596 578 300 780 421 360 825 468 286 884 855 426 581 706 008 258 559 626 760 473 187 371 983 169 318 526 478 149 942 000 669 807 776 129 141 425 227 638 261 873 432 362 147 972 303 500 749 296 425 540 170 251 979 601 492 630 020 154 091 862 405 744 933 239 563 637 993 332 849 910 153 341 677 870 781 257 578 435 845 611 806 955 941 729 617 321 737 784 417 886 047 985 702 943 923 158 180 210 370 570 051 663 887 740 620 195 088 321 564 918 807 728 631 903 621 063 703 211 669 076 291 706 675 001 345 875 174 915 477 597 267 636 329 072 599 706 760 506 485 133 810 015 453 480 339 531 023 016 166 458 916 819 646 080 355 916 964 747 185 009 787 839 567 291 017 688 646 871 978 914 524 929 197 584 110 199 134 346 247 670 349 680 670 266 858 468 307 481 559 745 861 698 758 837 488 085 281 844 401 610 920 912 629 861 366 096 289 786 959 743 664 535 814 145 304 328 092 809 438 242 473 591 057 338 341 919 921 246 126 438 764 870 819 605 942 900 688 149 880 679 056 328 663 275 684 135 005 642 057 882 484 654 710 328 946 849 643 215 170 993 804 099 368 496 582 357 346 757 294 687 429 235 557 873 569 385 707 576 158 983 289 167 270 651 700 168 923 921 438 406 229 341 148 350 560 512 280 081 147 931 805 280 333 518 197 345 268 560 728 109 359 775 038 931 437 770 749 077 685 210 320 380 110 088 868 104 314 353 431 793 430 398 817 333 209 995 564 659 225 706 380 574 392 611 989 073 232 080 513 986 312 903 818 681 099 070 425 190 740 315 271 421 592 413 821 484 560 834 706 938 590 826 917 705 961 679 775 308 784 503 922 943 729 752 050 357 926 191 910 384 938 053 071 626 267 454 233 703 653 198 172 805 972 591 825 499 307 991 070 436 317 765 220 155 620 408 489 441 354 660 624 937 173 377 985 989 503 923 966 763 272 570 704 654 442 195 384 177 571 305 406 869 783 510 648 807 210 324 369 679 816 986 897 731 315 101 261 594 548 273 811 057 827 322 299 505 465 717 954 744 816 922 918 188 550 962 731 416 479 327 588 707 365 662 263 736 268 988 432 980 406 418 971 946 610 814 315 943 139 139 684 140 144 342 455 148 808 715 126 024 359 259 230 255 778 894 612 325 681 083 915 209 929 002 300 211 947 513 350 690 952 902 522 032 221 584 193 906 122 043 500 279 906 151 641 908 748 913 129 681 803 511 798 944 450 765 789 940 321 065 163 393 468 808 720 812 632 052 338 095 394 317 416 750 407 911 750 236 004 435 408 805 496 525 139 424 110 427 135 188 999 339 228 544 861 369 780 230 217 183 778 830 433 349 255 716 553 543 262 644 818 536 183 539 447 528 880 940 270 000 894 060 742 827 075 289 965 927 302 578 114 904 436 281 393 668 237 206 273 689 049 694 626 774 201 908 343 659 604 813 399 345 038 545 312 959 874 825 333 232 586 413 954 580 901 437 433 755 435 345 700 539 996 676 315 384 162 207 303 304 259 129 083 718 187 665 932 630 115 345 139 118 032 443 696 259 539 730 431 529 360 385 591 672 709 727 009 543 782 539 807 530 977 052 027 773 815 095 272 459 405 018 915 475 098 370 105 149 513 913 886 876 687 177 226 469 218 562 196 801 639 356 540 465 734 877 006 455 049 957 372 910 153 679 430 106 180 949 308 899 383 558 388 530 549 623 201 654 625 479 585 120 716 061 255 603 670 180 559 499 752 925 961 845 339 347 810 618 102 625 833 799 481 471 128 895 268 463 871 904 900 751 867 421 007 665 626 193 924 122 250 036 480 186 899 428 123 048 018 312 308 347 379 502 861 242 769 518 091 872 016 675 919 568 483 548 446 376 414 561 338 710 426 129 853 516 414 776 625 170 517 797 004 324 496 617 945 941 350 062 419 277 196 462 366 652 164 667 873 766 385 205 160 496 991 785 634 725 453 479 486 025 549 599 257 144 475 931 668 173 495 365 091 267 252 186 153 121 792 814 524 628 687 117 291 367 600 317 199 268 678 731 104 849 474 660 009 171 916 948 482 819 640 366 387 501 237 879 598 688 757 311 649 542 836 812 143 273 611 189 395 846 546 599 812 873 676 654 216 443 205 375 145 559 909 191 452 226 481 687 349 399 399 791 984 771 333 272 248 954 117 910 063 598 032 536 160 394 003 763 189 871 863 071 199 407 948 316 189 652 428 032 866 667 392 544 800 148 859 820 804 730 451 161 231 427 901 445 724 871 704 801 664 406 571 740 538 166 104 706 537 720 678 226 068 051 061 310 222 451 962 488 693 621 926 263 005 160 921 042 759 198 953 220 067 921 863 719 867 808 502 665 746 153 474 645 927 482 387 819 970 631 627 514 877 882 775 006 077 406 178 527 100 083 542 975 497 668 094 723 692 875 781 539 018 261 722 894 775 801 545 129 607 855 479 490 906 770 370 522 694 548 642 205 976 598 498 907 081 693 655 929 683 468 517 960 892 371 730 232 396 544 375 642 775 687 558 121 104 109 532 508 481 699 671 656 841 302 862 838 853 231 112 090 627 760 137 481 000 810 430 335 714 737 064 064 448 009 961 256 165 820 851 469 631 296 889 585 441 144 985 931 556 260 174 480 307 820 012 197 442 671 155 562 923 588 287 189 397 139 833 041 902 874 790 148 824 976 058 861 134 458 912 398 941 489 918 048 731 346 488 520 451 748 083 496 968 119 280 104 627 161 411 469 080 801 049 206 221 135 305 221 126 847 660 368 414 135 046 404 320 659 596 007 610 251 460 053 674 801 007 527 047 157 078 561 882 338 457 541 554 366 931 650 967 720 843 923 608 807 726 145 370 566 910 544 420 923 710 111 869 273 282 364 613 453 543 949 119 788 619 950 218 025 406 251 342 449 566 717 026 429 561 710 631 993 900 191 455 311 702 474 411 564 203 169 349 777 699 409 317 890 283 410 757 764 044 508 583 436 383 343 034 342 459 156 317 434 258 099 239 895 459 867 604 928 797 886 987 612 378 899 779 694 042 322 405 524 389 768 746 396 899 241 512 576 295 807 650 434 343 796 369 370 557 252 976 707 806 412 241 139 935 188 014 547 757 903 755 615 048 459 030 001 370 166 637 288 479 178 743 691 632 121 716 691 934 827 072 372 600 663 303 865 685 640 814 531 265 604 277 085 680 998 188 801 338 228 921 128 745 163 750 871 059 670 357 127 554 391 087 861 575 369 092 892 580 517 331 586 993 218 991 437 158 625 227 629 611 557 907 321 838 444 708 535 456 381 506 815 582 888 058 401 268 209 937 660 029 275 328 372 650 756 875 570 140 863 706 865 364 154 492 711 760 123 886 552 309 954 238 493 652 521 387 300 521 769 230 859 241 605 791 707 360 767 508 380 234 170 733 362 639 261 632 485 848 683 074 843 488 101 622 579 148 780 647 118 313 769 448 220 039 251 463 154 074 509 865 382 712 304 024 732 431 389 204 475 237 586 234 306 808 699 992 183 504 489 455 459 186 261 396 234 110 629 806 577 178 112 152 085 365 474 207 731 959 157 201 112 774 147 004 848 035 212 824 118 442 190 561 984 162 596 394 186 199 032 774 463 463 654 587 537 989 568 995 545 762 553 339 855 198 349 383 281 620 390 623 166 660 488 027 272 479 111 931 599 270 627 756 732 994 834 408 366 000 732 902 156 986 218 637 453 633 852 731 640 184 347 756 324 241 116 278 812 156 003 426 293 520 326 353 107 135 467 345 853 560 957 007 155 462 385 618 598 456 843 479 566 297 176 954 826 984 581 687 847 851 334 284 548 073 587 399 579 692 383 795 905 282 984 049 757 655 056 231 473 676 508 645 034 441 326 020 440 968 762 556 259 318 542 029 450 419 513 672 760 524 122 709 965 403 034 838 092 685 825 359 154 120 662 062 257 857 816 590 786 735 831 603 946 270 038 001 939 972 588 202 338 589 680 747 754 447 803 538 473 451 910 133 569 435 123 538 395 403 430 957 412 114 710 960 511 718 128 915 408 873 978 060 306 096 088 004 286 175 300 311 122 134 611 416 043 831 429 263 784 695 219 320 099 137 029 694 011 433 521 419 259 336 919 192 213 067 683 700 787 788 271 170 194 172 828 627 532 728 024 136 915 787 952 040 525 606 919 150 969 148 971 171 035 286 924 052 204 795 705 759 168 332 744 698 671 771 295 047 168 669 064 540 660 376 507 246 014 313 093 344 001 306 718 242 269 686 949 706 731 096 223 912 243 700 936 828 931 342 715 634 926 029 153 286 614 260 199 401 389 437 703 077 014 509 722 817 068 035 095 300 294 109 171 766 702 554 400 475 696 252 105 217 066 244 570 266 293 559 624 077 427 535 983 759 001 912 037 143 355 480 323 126 843 420 282 384 255 274 997 971 641 116 048 089 173 248 394 065 009 296 926 575 777 766 824 105 586 286 347 818 748 916 111 547 857 043 280 244 645 140 200 942 954 490 942 106 345 681 951 264 030 270 264 428 018 106 563 409 594 896 305 936 688 562 544 222 120 794 976 501 807 393 630 427 416 205 991 152 531 050 260 307 766 905 555 242 125 579 041 919 858 991 466 773 859 384 281 416 483 466 461 172 718 478 634 868 669 317 816 419 018 672 688 010 947 707 791 006 906 650 916 964 846 236 237 789 398 851 788 110 111 323 682 542 256 074 412 709 353 570 440 800 670 702 840 078 304 465 121 475 261 997 962 597 040 651 480 939 231 958 705 570 572 573 493 086 858 444 838 678 008 134 367 876 303 113 043 586 882 339 704 938 031 472 222 457 770 212 476 555 318 083 567 479 050 320 739 630 531 248 697 193 354 683 226 411 355 510 569 572 886 615 936 484 021 681 139 659 341 188 881 924 357 303 630 423 736 013 201 799 366 662 333 388 086 336 498 719 678 426 660 397 122 401 478 565 891 288 037 940 219 585 491 809 150 147 709 460 380 173 321 659 706 603 947 952 668 016 856 340 195 427 942 302 381 298 325 964 131 962 132 842 653 191 888 352 102 792 852 410 828 039 930 890 828 697 796 864 066 698 571 438 277 825 960 009 214 618 415 918 173 948 748 126 535 733 146 669 008 669 060 967 477 017 301 914 149 730 772 992 117 917 885 357 658 285 980 770 741 409 409 086 492 273 862 053 112 480 531 050 844 764 402 985 577 203 914 600 118 742 356 775 549 884 874 424 172 680 750 343 085 335 888 571 825 676 134 542 196 088 266 847 492 284 083 077 387 092 450 755 037 566 156 374 213 496 948 401 105 696 639 364 093 429 615 088 881 941 575 487 664 217 475 239 412 433 452 930 136 282 646 997 923 752 225 922 256 998 929 373 523 431 213 801 291 645 130 420 610 782 096 645 132 584 999 634 537 829 100 987 949 698 619 539 161 905 341 406 812 478 229 913 386 221 244 912 664 612 317 637 224 769 155 776 932 724 964 472 844 497 848 058 423 397 388 418 629 364 418 869 031 854 462 260 329 333 488 299 387 277 151 824 159 981 553 268 400 329 154 993 278 326 740 928 510 096 487 621 924 400 816 974 452 946 196 322 111 192 470 256 610 172 008 893 988 581 045 454 159 646 178 376 101 849 037 590 543 167 154 897 476 880 582 211 945 818 008 194 457 734 351 863 963 481 936 495 976 748 634 970 789 741 301 810 843 255 671 540 517 090 771 806 533 994 012 570 142 691 570 158 673 101 895 556 426 497 142 949 598 452 484 275 642 395 276 192 438 209 651 114 221 057 901 549 558 195 785 568 584 593 075 926 466 899 771 156 209 239 372 533 110 753 863 633 785 581 842 658 739 741 829 024 672 759 849 799 951 975 061 508 746 298 688 404 694 749 800 497 158 156 718 187 240 298 886 073 389 835 892 288 249 103 442 932 844 072 266 362 415 376 092 469 590 828 331 744 718 594 123 405 893 863 834 832 996 085 320 619 572 460 313 758 454 681 004 558 118 062 207 070 590 962 845 238 175 737 279 223 058 303 658 876 510 535 529 596 685 778 855 321 921 958 352 907 905 140 702 521 006 267 967 070 537 359 301 896 906 752 132 313 397 635 557 849 163 625 056 863 754 873 267 783 210 478 891 442 249 998 914 560 993 271 131 116 987 602 180 125 650 210 807 422 713 945 203 658 518 282 430 922 512 356 885 612 826 442 001 665 878 257 352 549 683 124 677 021 411 912 366 544 477 090 135 917 170 538 430 905 711 600 486 136 293 102 125 157 905 182 923 733 457 315 127 207 280 876 094 348 780 620 208 263 444 268 847 592 562 815 743 943 579 662 088 073 897 421 328 786 201 362 206 516 200 440 752 281 354 069 544 350 608 171 893 608 698 144 251 656 997 232 246 758 744 661 531 848 737 420 631 441 683 696 788 525 168 149 212 705 754 881 797 116 436 256 134 960 126 550 412 658 914 947 344 787 172 407 296 472 807 981 269 983 178 380 925 778 514 933 964 241 481 622 399 289 433 928 209 360 353 248 251 209 176 654 117 315 675 014 686 134 075 853 088 777 535 599 162 958 399 214 153 031 729 867 541 423 120 182 778 490 645 532 523 523 160 492 655 884 548 211 183 891 321 631 424 791 096 361 290 659 662 442 228 852 608 807 482 344 955 126 141 063 767 581 805 827 023 692 362 178 287 812 758 910 341 096 638 056 150 965 241 633 813 114 220 067 476 216 436 428 250 716 467 117 191 398 134 589 984 798 745 487 197 523 559 985 231 414 323 230 908 815 396 676 091 362 933 545 940 276 283 097 959 192 335 860 382 506 931 019 732 619 354 613 642 228 452 488 399 436 995 023 915 517 682 144 549 287 218 827 802 889 281 906 739 294 109 078 414 649 321 936 366 639 955 657 204 907 429 522 778 081 434 178 672 281 358 476 277 991 831 658 676 978 491 958 290 394 597 362 012 610 049 049 289 137 298 168 760 468 776 987 267 447 536 185 396 402 118 095 548 070 265 164 113 288 754 046 483 825 407 542 157 230 908 550 810 535 371 548 262 905 961 175 747 061 073 777 982 583 223 003 103 685 167 300 217 310 122 101 676 262 428 111 003 729 503 535 011 691 481 325 536 417 882 785 569 077 999 179 423 786 710 834 747 485 614 659 769 813 770 496 313 912 458 759 847 272 337 036 896 231 551 296 054 316 899 792 132 406 740 932 678 829 318 105 290 536 644 719 643 861 501 541 426 814 902 893 270 493 490 036 618 211 115 325 063 288 356 089 011 008 104 393 781 549 831 426 103 746 425 005 681 872 297 484 398 284 031 547 747 986 796 237 048 013 055 414 633 282 612 802 441 722 405 869 842 326 655 824 818 673 332 498 406 612 187 850 150 413 799 813 099 060 713 870 758 594 724 398 099 007 322 241 487 729 134 460 239 983 152 225 968 498 102 668 118 355 915 605 379 130 306 424 944 547 650 005 229 044 281 283 038 093 250 176 450 237 354 314 067 034 843 352 057 789 274 184 071 051 242 341 164 400 923 397 577 374 520 710 243 423 775 461 667 465 553 971 486 605 001 615 749 435 479 248 396 067 758 331 567 580 921 699 666 756 034 407 684 973 825 458 248 613 191 411 525 728 944 685 530 820 273 919 135 028 708 720 455 951 551 123 003 586 230 589 007 292 084 420 782 868 794 359 772 182 845 115 967 656 561 611 090 919 658 946 319 317 063 762 150 370 664 472 073 288 480 669 079 975 569 096 305 661 006 246 380 360 418 591 883 331 844 183 085 162 181 631 328 112 899 729 161 783 305 697 265 414 424 997 179 482 434 517 720 597 756 031 999 234 675 136 330 323 342 423 877 224 213 008 909 267 290 689 453 040 274 539 920 461 811 727 569 510 729 340 837 254 720 677 593 045 838 558 355 338 803 615 571 688 070 824 194 611 402 962 671 158 041 993 545 031 758 047 939 978 998 725 864 442 754 819 911 886 932 853 868 816 971 753 957 966 997 580 972 164 503 526 023 027 357 608 683 279 649 928 308 778 099 816 105 644 159 483 768 289 712 659 038 125 222 631 519 163 861 397 877 618 564 163 241 309 518 833 033 155 830 956 347 940 422 348 339 306 778 468 771 134 334 940 010 942 586 649 373 168 114 967 622 182 485 548 000 053 502 391 392 351 730 024 848 614 957 189 218 806 064 270 445 900 722 452 417 998 752 364 281 230 698 729 264 811 127 049 527 031 652 245 403 429 903 155 440 795 094 467 601 398 461 144 472 773 143 598 251 549 002 860 104 213 621 028 484 482 122 279 863 486 627 412 346 311 370 154 337 427 583 674 175 160 633 835 969 666 239 738 240 906 954 130 651 300 630 516 094 106 144 723 901 086 494 395 902 742 221 700 978 208 048 332 960 179 157 373 031 597 811 057 902 246 519 117 996 888 702 134 849 377 039 913 264 910 967 757 165 630 043 517 377 882 383 777 952 805 993 398 826 496 739 388 723 345 725 650 734 779 550 755 430 555 368 386 650 644 945 421 013 583 934 054 079 885 658 396 926 687 571 178 863 820 870 754 827 405 754 904 025 450 658 860 424 628 564 342 953 024 403 666 156 066 833 105 150 465 193 292 744 678 875 402 900 064 461 355 463 574 889 300 230 200 066 087 138 612 679 651 258 071 785 445 126 711 699 140 733 173 749 895 930 698 124 790 852 133 114 377 674 087 201 060 071 331 596 385 142 505 122 904 565 621 930 394 614 893 750 302 262 413 230 750 189 997 169 523 396 895 598 176 277 576 703 599 697 165 437 316 621 481 927 661 003 006 402 106 290 149 745 230 676 136 407 241 260 649 688 064 660 286 054 160 161 557 479 411 762 786 081 387 164 299 324 668 649 311 279 224 039 766 451 493 141 210 689 146 503 129 349 275 915 459 024 135 472 610 795 843 839 373 397 869 796 024 860 760 899 643 538 053 037 370 473 639 467 160 289 112 111 360 133 592 316 660 213 185 629 046 550 485 966 047 867 353 053 694 335 297 558 064 917 380 414 736 236 105 595 059 964 726 849 889 072 721 033 792 511 093 536 378 053 868 253 222 808 704 408 589 907 703 875 332 017 656 334 454 142 668 356 627 106 430 464 376 587 268 408 180 710 799 990 546 221 093 777 132 055 191 295 816 556 745 981 675 380 079 425 651 216 803 809 584 391 948 512 524 889 237 588 481 160 027 595 745 676 634 824 477 430 604 690 881 172 974 240 817 160 053 241 473 388 323 482 392 665 799 333 695 213 373 890 470 210 769 308 944 218 193 210 053 414 648 568 255 279 022 557 649 038 047 682 384 225 921 116 614 336 045 476 521 550 858 663 801 369 113 626 780 058 894 234 628 459 095 917 656 515 219 719 439 562 347 091 281 452 674 127 540 150 153 309 219 852 775 249 725 409 352 508 765 354 861 925 818 298 340 798 557 639 727 053 423 176 068 869 079 813 324 448 179 587 306 892 356 892 977 675 159 579 597 290 933 231 589 777 097 317 355 595 367 680 488 465 305 915 713 903 876 753 604 681 881 293 960 179 739 353 728 313 186 199 129 001 013 444 886 644 466 174 522 302 823 892 349 314 011 353 973 536 673 258 990 139 949 858 873 679 060 827 039 069 054 798 624 737 752 669 965 825 866 197 386 507 256 499 302 354 676 762 402 309 454 054 167 652 213 059 273 064 477 550 284 879 780 426 050 677 814 320 337 374 799 691 471 915 161 103 293 386 984 507 674 906 783 338 010 901 202 805 956 393 109 530 872 117 484 115 158 680 989 817 097 685 976 738 647 718 666 562 042 485 396 702 961 973 730 648 898 871 761 153 062 280 587 280 806 432 581 670 879 497 066 144 715 660 374 586 506 003 768 975 131 148 129 723 427 914 795 822 316 236 001 416 421 524 780 656 110 199 677 587 283 522 251 630 551 547 749 648 544 534 061 464 769 748 674 420 411 400 941 772 747 717 207 441 464 847 709 368 100 626 429 042 517 094 793 243 117 555 404 676 408 451 089 997 331 983 724 737 990 162 381 889 374 258 755 021 413 352 301 415 039 770 249 110 524 897 611 323 609 314 330 086 930 499 120 121 467 247 488 690 732 340 259 614 692 108 851 371 716 176 037 668 295 530 080 512 097 713 358 669 958 085 880 974 971 670 560 412 812 873 774 452 465 551 505 377 653 689 530 951 255 913 696 501 322 726 568 816 563 092 314 832 556 600 889 330 815 293 799 379 236 649 090 634 568 050 669 660 192 269 730 984 158 926 252 051 347 631 721 574 237 138 898 154 415 760 360 368 831 359 616 918 233 527 273 053 370 174 716 975 538 909 743 771 077 647 308 067 555 226 346 077 237 233 311 526 886 000 119 271 176 681 376 517 426 452 674 697 677 678 721 957 270 505 137 917 475 121 452 575 577 511 532 184 482 400 756 278 685 648 418 226 860 787 023 906 822 270 327 879 916 440 839 064 244 369 668 860 152 715 636 103 400 404 302 091 556 887 880 491 854 285 289 294 254 137 684 304 482 736 928 025 136 974 553 062 239 958 731 388 556 451 161 127 712 033 533 465 101 045 705 809 655 231 858 230 577 503 776 143 925 487 421 033 795 446 402 885 805 208 618 125 284 708 841 795 661 111 630 465 493 757 711 931 895 899 256 504 644 423 367 784 033 467 674 255 814 435 998 732 530 674 078 581 943 285 418 210 022 428 983 777 468 174 106 181 411 051 879 376 132 466 465 417 394 029 098 762 388 866 233 763 011 949 414 435 753 723 326 611 839 178 043 812 329 104 837 861 835 470 537 510 815 346 153 298 244 371 466 965 597 469 141 391 735 732 947 266 218 103 113 240 645 743 637 114 739 547 021 874 604 444 559 543 630 036 800 280 970 686 865 858 813 707 382 548 241 721 546 106 075 585 145 779 089 797 647 812 642 682 458 095 668 008 279 603 592 778 954 327 136 741 143 119 313 964 727 357 804 433 683 869 289 195 141 199 368 699 139 662 763 548 330 046 719 213 018 125 339 014 885 670 221 528 454 611 489 921 606 804 904 257 711 415 947 702 951 734 398 367 055 595 332 563 160 801 917 735 186 041 762 122 496 720 597 189 221 146 569 363 659 144 513 938 822 597 560 832 238 544 282 136 204 217 503 178 829 791 514 869 782 800 682 543 800 351 255 438 536 869 832 278 607 665 953 199 502 631 602 799 176 788 857 747 481 264 740 043 867 328 226 696 632 035 624 136 645 491 392 635 196 508 311 727 997 010 162 070 285 873 552 908 950 497 228 660 794 606 480 321 973 655 826 612 908 728 185 745 138 973 666 168 529 675 262 879 952 704 583 812 279 086 936 857 175 802 788 236 174 846 971 401 424 451 318 904 434 108 586 691 203 817 506 912 628 547 070 523 889 654 444 913 132 281 213 838 931 491 765 072 499 192 268 444 755 077 447 469 800 231 336 122 174 243 870 404 672 942 902 725 096 283 537 953 476 017 644 403 134 897 062 723 250 163 229 864 417 424 982 342 662 168 955 929 723 911 597 796 226 209 635 950 118 375 204 975 538 298 812 521 351 252 598 119 430 198 610 965 711 574 864 533 107 804 997 905 208 570 143 302 670 486 892 644 270 665 933 117 508 887 546 118 178 332 473 163 887 969 205 530 007 018 345 791 353 983 584 641 750 404 170 623 358 379 561 358 152 258 300 390 863 863 075 542 225 354 175 614 866 258 342 658 648 768 536 425 311 356 258 430 640 648 957 474 371 226 884 443 787 148 368 794 119 170 428 068 948 619 816 609 029 874 078 813 718 713 087 809 775 118 348 448 773 366 876 755 634 567 429 754 948 138 053 666 410 839 443 788 913 460 596 301 352 053 392 301 139 326 944 896 856 945 783 928 009 563 640 376 159 657 331 203 827 328 941 463 270 259 340 000 027 496 795 227 327 509 098 231 731 424 223 299 189 197 708 354 484 099 083 088 045 095 198 863 291 536 375 526 478 958 759 683 134 141 521 195 465 556 985 859 198 132 289 977 169 908 041 277 353 016 751 779 700 363 481 340 804 695 759 938 232 273 128 518 320 713 881 791 784 095 084 760 421 605 651 138 014 387 231 349 770 932 030 169 304 128 897 592 651 224 288 883 236 399 114 097 693 261 107 208 973 432 620 660 438 169 022 952 654 248 308 954 908 996 241 573 901 469 323 383 941 794 534 018 437 027 784 445 144 829 289 829 670 216 221 918 445 981 974 376 282 651 222 460 275 476 063 142 016 613 787 877 268 734 860 107 710 171 610 732 385 456 903 896 415 773 561 648 842 418 392 901 834 276 910 723 913 976 969 857 909 192 302 949 278 647 990 831 994 728 894 525 370 660 639 244 227 121 910 913 419 817 311 561 842 387 796 909 700 683 980 157 473 724 935 601 960 023 328 429 596 732 613 315 594 030 924 959 546 826 702 733 689 282 077 163 487 002 086 222 364 919 716 038 801 738 744 180 497 723 283 212 779 789 282 956 406 674 818 764 779 827 313 970 844 228 599 242 276 171 874 859 763 956 045 370 938 616 761 404 690 737 352 869 877 779 709 581 046 158 818 653 364 612 587 114 177 670 040 239 853 612 217 793 153 343 103 884 722 024 395 065 583 423 171 286 629 469 574 094 969 060 635 123 391 708 362 474 464 151 862 666 061 994 438 026 998 767 252 103 692 458 963 580 736 963 663 363 467 370 205 773 841 556 642 290 769 289 986 555 372 455 127 819 100 130 976 237 734 233 228 511 337 957 865 902 473 494 764 376 658 777 987 199 213 033 131 885 617 111 265 242 842 304 201 338 828 361 760 437 683 848 163 311 917 102 052 989 529 325 186 515 802 768 902 423 052 730 921 213 749 717 077 977 508 697 258 648 460 317 541 610 924 306 440 913 561 573 599 579 304 049 374 768 626 689 065 126 486 302 126 573 541 169 615 122 355 105 342 682 531 192 591 110 537 484 040 006 917 785 614 832 465 886 607 750 646 031 408 587 656 940 239 810 552 585 314 097 067 977 131 799 674 443 848 760 938 730 694 217 866 370 714 152 571 311 122 432 292 715 389 215 068 665 114 690 338 991 397 975 071 262 442 537 794 740 843 364 663 296 295 242 938 663 626 806 729 703 650 339 361 631 745 494 735 229 925 732 489 185 936 862 604 151 241 848 494 769 001 874 198 551 222 394 727 638 467 948 509 774 464 923 895 164 875 038 238 171 719 989 100 735 003 362 004 111 205 145 821 914 097 772 356 622 341 926 429 365 681 336 703 997 949 170 838 382 785 630 139 815 060 975 806 274 661 320 264 847 234 696 371 279 277 695 024 999 978 517 405 641 022 112 122 068 570 840 501 926 112 990 585 876 333 163 634 774 448 250 748 192 374 589 488 225 283 447 738 608 122 641 525 598 358 790 260 368 015 932 720 038 211 622 502 694 760 901 749 023 635 934 285 917 833 118 089 094 216 660 855 488 476 087 368 797 894 376 140 469 147 256 825 765 441 095 598 415 063 708 841 040 876 469 910 554 451 098 947 301 906 338 232 061 007 381 563 004 543 548 272 240 370 546 008 293 641 001 466 912 874 937 407 368 183 097 093 248 899 505 966 762 733 591 367 680 032 532 800 030 518 717 276 299 801 010 269 098 324 643 459 216 901 982 110 114 758 994 252 023 565 084 941 826 633 134 022 858 815 071 804 509 767 883 293 062 853 699 376 607 819 310 872 642 322 850 243 020 853 333 776 880 481 726 036 102 692 566 524 329 686 262 897 224 955 684 838 499 318 237 532 716 720 820 683 319 425 567 338 298 718 070 700 159 281 981 820 250 393 148 329 844 080 939 862 847 296 691 713 808 611 931 178 583 716 924 600 717 948 160 683 273 365 202 045 358 761 788 841 975 302 235 951 012 730 503 362 617 408 214 036 215 535 436 236 946 833 778 779 626 797 214 825 127 359 159 033 982 104 690 904 094 848 357 553 210 176 150 009 442 925 267 060 632 305 384 359 920 092 360 417 632 720 139 137 645 791 238 711 589 693 260 977 156 356 178 896 542 270 278 686 058 785 081 865 461 145 724 129 189 999 149 926 116 875 317 463 813 021 656 505 531 681 746 564 039 689 670 409 265 945 924 207 012 641 225 372 155 236 417 555 778 842 879 449 428 997 816 459 322 404 259 211 817 542 642 033 772 670 394 058 916 129 504 871 432 304 991 783 203 761 619 292 646 647 228 574 124 631 715 287 873 008 926 101 789 643 220 316 855 267 158 980 737 969 211 374 566 315 507 422 215 239 206 671 420 854 072 609 816 390 802 354 295 074 224 955 042 297 521 120 114 203 968 483 691 159 512 448 517 549 635 338 459 109 699 808 093 197 114 371 822 329 648 175 422 087 096 732 638 011 247 805 116 020 311 393 552 637 691 617 641 898 328 218 498 840 322 856 963 128 359 609 559 946 895 490 195 076 761 218 808 105 705 449 323 876 313 710 384 665 642 417 724 150 630 421 525 381 720 067 062 322 830 503 678 737 128 435 458 657 426 103 872 889 944 275 268 678 486 779 464 209 840 273 454 665 480 345 802 948 722 351 264 204 751 504 789 874 396 602 151 803 077 193 927 617 469 491 618 569 517 712 189 398 290 784 717 315 449 102 956 175 318 344 924 399 363 377 158 274 843 432 836 616 534 179 821 214 858 770 926 241 088 043 660 394 603 616 510 953 009 439 057 713 710 252 888 143 672 993 221 139 036 069 588 901 442 188 783 780 713 344 066 635 071 183 072 375 027 990 744 177 369 779 438 003 236 646 385 970 801 389 908 747 051 073 505 561 935 421 883 603 294 364 662 339 205 907 858 454 486 891 053 923 006 828 216 174 856 677 727 292 516 669 450 595 443 841 851 435 145 067 957 065 119 566 727 007 907 736 769 557 963 407 453 425 252 669 642 666 558 223 642 233 086 701 993 827 457 497 966 538 285 048 483 802 536 805 439 703 842 659 738 442 937 072 955 388 476 930 390 628 999 662 225 535 174 370 958 078 635 145 756 357 502 089 601 562 879 252 334 727 471 521 923 295 491 296 758 457 325 692 366 234 469 329 953 831 915 132 442 497 538 879 080 134 121 370 137 222 632 645 684 946 772 339 612 719 736 628 398 307 501 585 953 190 345 918 319 722 283 713 215 948 997 789 814 606 610 671 872 638 848 161 328 002 245 745 580 181 202 661 374 899 826 343 010 907 021 933 847 086 686 785 555 365 731 542 538 587 403 459 474 827 109 072 996 897 447 915 118 372 835 717 320 221 875 516 349 045 053 149 405 800 363 066 883 456 314 611 514 419 836 799 384 881 911 925 430 659 621 670 438 549 987 420 820 789 214 376 618 458 792 587 528 815 133 024 390 727 608 260 289 043 914 083 974 381 768 243 561 129 445 696 756 884 942 607 862 105 744 257 290 387 326 827 074 678 880 993 513 948 732 866 033 105 043 756 527 767 143 030 647 936 755 498 149 636 680 921 303 909 362 148 307 249 911 526 048 986 810 852 706 645 984 917 128 650 412 272 795 736 177 453 663 159 904 754 292 989 477 992 397 429 173 377 090 241 463 390 209 470 911 714 081 576 375 939 738 386 067 797 050 096 874 715 760 896 575 001 505 893 448 118 055 248 112 790 832 809 314 376 053 518 788 108 212 101 489 728 146 216 439 761 279 095 977 714 982 760 323 595 919 072 712 258 741 354 319 470 898 709 276 671 566 924 100 360 870 042 858 461 744 031 221 636 507 165 718 099 679 401 706 943 919 087 947 618 265 690 148 258 111 232 074 558 322 182 241 852 546 535 004 375 597 378 908 274 805 591 829 224 342 886 502 310 007 150 782 509 103 953 486 702 912 725 315 456 793 787 172 803 102 569 610 801 493 774 185 252 347 788 491 261 047 393 827 185 308 065 672 580 994 863 344 942 841 326 352 252 004 740 123 065 288 208 406 859 659 759 739 902 126 573 350 154 098 141 024 973 666 632 632 959 888 924 494 343 245 409 687 235 482 850 595 381 025 468 213 795 850 327 659 210 278 792 911 784 931 339 920 246 619 807 458 454 696 861 127 415 639 761 451 298 572 056 238 130 604 341 600 376 262 758 688 362 516 939 951 356 183 670 353 931 756 984 746 242 941 877 454 061 118 004 375 122 366 936 189 297 439 788 145 519 226 376 728 945 026 229 445 861 322 837 636 921 359 908 997 170 054 667 505 870 315 250 931 538 752 703 588 341 373 292 309 042 692 248 045 192 374 551 530 674 850 823 659 390 802 747 987 183 622 841 183 315 033 701 605 362 692 309 617 789 874 135 291 276 027 119 662 752 867 933 358 617 243 452 403 374 110 108 024 175 899 162 988 181 852 868 231 215 052 230 701 315 817 819 761 998 602 552 150 111 590 947 829 542 362 443 642 917 254 146 493 774 589 515 061 150 951 763 822 380 650 813 775 734 192 961 819 688 763 483 206 821 118 229 290 536 058 390 814 814 111 439 544 307 308 588 728 321 081 721 219 939 056 561 773 028 208 703 302 895 497 401 048 782 846 033 210 383 752 149 808 999 604 002 850 985 136 662 442 513 361 346 322 099 456 073 193 494 429 181 537 924 499 797 447 037 717 680 688 527 802 261 197 614 695 317 642 927 704 699 217 051 792 958 320 669 976 500 430 447 830 068 173 135 600 479 745 472 531 667 055 595 246 176 073 464 313 309 770 741 543 423 789 315 831 723 644 944 564 203 249 800 288 704 912 521 203 381 307 835 405 497 025 078 974 318 835 927 304 239 449 993 935 168 985 286 867 511 026 803 256 661 634 699 436 869 960 119 837 640 999 197 752 921 248 176 225 642 378 862 651 121 877 203 063 148 361 195 138 558 963 489 505 378 913 859 838 860 750 636 734 420 342 673 962 021 583 371 277 842 164 178 658 505 458 772 535 637 006 255 899 527 856 668 473 314 979 668 560 228 120 519 053 802 618 058 625 978 824 050 606 778 883 942 060 487 492 162 984 294 310 618 550 031 728 972 466 930 930 363 612 153 483 695 837 490 704 024 866 497 695 637 757 004 775 244 260 582 217 815 094 466 305 084 392 012 877 434 942 670 350 728 109 027 830 347 921 951 186 992 719 309 810 285 766 770 392 003 634 507 535 947 178 657 665 231 010 338 946 127 567 188 933 841 963 398 112 560 803 988 426 888 749 702 790 134 402 308 470 629 014 273 500 251 112 146 983 630 735 910 226 310 844 784 272 848 989 293 508 554 449 582 196 055 915 759 403 698 630 526 925 509 528 130 945 704 618 331 231 367 814 947 582 426 936 391 789 362 342 234 329 481 029 769 571 936 525 333 994 767 540 415 228 264 610 045 087 760 822 527 446 904 594 209 171 423 811 742 812 851 190 189 177 366 560 660 713 749 605 115 324 145 466 079 468 492 250 130 853 450 683 218 348 479 444 029 052 108 709 722 443 206 600 191 205 764 361 346 922 985 684 581 732 383 315 461 383 003 837 573 486 191 499 613 605 467 554 133 230 318 386 190 501 404 049 305 469 883 014 714 090 145 744 995 842 610 530 357 805 137 170 475 602 729 735 365 589 434 862 813 227 869 730 615 475 546 898 210 226 546 301 823 283 814 729 160 837 359 894 638 433 405 856 524 712 705 431 511 198 974 720 572 755 064 601 965 807 710 421 440 735 186 764 506 937 977 803 657 990 979 142 566 513 636 383 431 229 853 716 581 787 632 672 295 586 591 403 956 259 421 416 191 060 892 413 576 304 377 073 428 188 099 510 704 323 248 147 003 823 822 912 817 316 834 515 569 921 624 214 227 183 516 186 028 972 164 244 348 861 232 565 003 558 740 303 720 693 682 064 321 300 882 683 698 604 414 132 424 144 241 037 503 810 094 442 200 104 955 576 587 234 253 518 120 133 729 728 660 738 078 725 816 766 155 389 550 775 042 806 168 423 098 895 937 027 405 478 742 166 953 032 694 306 157 992 533 214 420 789 914 156 754 783 584 017 184 754 700 463 096 263 982 397 511 372 556 250 042 280 819 491 961 295 392 961 289 883 949 444 371 402 544 119 270 792 102 988 886 168 006 807 712 225 119 151 695 303 497 153 503 111 546 203 447 255 666 628 857 780 987 031 178 335 362 974 231 044 594 887 590 244 313 097 753 179 103 620 833 275 362 347 567 893 657 598 411 588 640 320 316 308 711 546 391 915 210 039 375 035 300 946 827 217 724 980 294 428 908 123 307 090 723 170 545 823 156 789 505 305 815 195 578 139 243 158 215 413 989 400 529 597 150 241 492 925 075 893 997 533 038 144 543 683 876 422 473 181 119 330 939 603 109 489 946 770 170 093 438 290 734 871 419 869 211 847 449 505 556 786 801 712 887 397 250 558 738 435 142 358 049 389 729 621 131 092 099 141 690 970 368 829 256 814 646 878 971 757 732 587 279 839 310 754 009 933 968 008 280 174 925 697 773 305 226 877 613 294 197 985 689 314 000 269 555 090 651 396 439 855 440 757 348 925 210 175 373 760 684 412 500 843 277 716 279 666 339 781 405 986 696 073 125 995 042 529 876 029 184 910 276 174 893 866 118 136 802 577 593 988 094 722 115 429 486 826 077 369 881 386 310 372 350 438 370 258 461 201 156 393 855 598 471 305 162 582 403 632 880 298 587 056 253 619 419 989 026 423 758 772 029 663 050 020 109 359 099 818 088 453 261 009 943 259 733 579 333 870 747 650 917 125 630 736 637 204 669 189 181 943 760 019 753 359 595 178 825 771 542 252 142 881 676 947 772 498 200 709 317 845 241 620 375 050 860 554 981 409 884 142 226 756 175 380 854 720 813 820 763 442 272 670 298 505 134 685 245 885 496 462 732 459 680 535 535 546 766 785 971 546 923 769 589 643 630 222 571 108 954 831 786 653 049 091 536 359 551 786 705 955 344 351 289 696 342 879 427 209 928 826 773 456 513 676 368 737 896 528 676 499 742 349 454 264 266 174 160 067 932 422 592 787 836 340 488 443 163 452 446 084 391 237 679 128 454 861 049 634 579 084 713 894 970 671 142 576 515 116 781 880 386 181 978 885 356 731 616 866 171 783 903 583 677 124 098 322 264 922 058 231 133 094 663 276 296 717 224 699 520 634 393 936 195 955 888 089 017 461 263 995 954 880 491 707 741 467 487 907 091 684 679 143 655 979 907 503 651 050 829 780 042 165 709 673 856 182 610 051 186 488 325 463 963 576 922 003 790 115 114 084 702 935 608 666 033 586 158 610 295 269 061 308 584 717 979 265 616 424 644 262 773 481 908 427 978 333 941 652 365 908 610 680 777 138 180 222 498 238 808 722 286 886 699 699 779 724 297 123 818 642 755 161 396 337 456 443 412 842 707 992 988 106 223 026 441 757 516 345 881 086 564 497 049 618 979 144 775 781 115 655 888 551 471 408 868 528 310 520 483 777 926 992 599 160 223 396 176 153 174 333 371 222 544 151 107 863 046 395 595 498 033 231 635 954 804 354 563 359 586 391 034 325 039 542 169 521 239 781 948 515 395 365 708 078 191 794 604 935 520 651 325 898 531 664 375 171 266 291 539 050 838 130 434 410 726 547 126 343 207 992 577 900 633 148 613 859 837 436 531 563 018 397 122 445 366 180 991 436 934 689 770 622 467 592 689 085 873 300 110 324 177 012 992 232 480 578 201 236 297 394 811 830 970 000 779 104 500 713 323 713 576 270 529 740 823 102 848 180 445 011 822 992 681 383 728 764 028 590 904 831 491 421 247 483 400 650 249 701 958 509 647 853 926 327 590 556 470 940 787 015 420 504 332 662 815 301 990 319 271 872 618 427 105 968 064 001 978 181 712 035 150 009 769 266 798 384 538 276 208 158 034 397 284 379 526 103 058 253 336 669 163 179 221 023 087 211 220 300 592 764 295 742 735 609 856 450 982 436 638 224 067 990 987 378 272 114 909 919 717 965 337 940 354 278 483 239 430 537 575 759 091 510 867 687 662 458 081 892 292 859 230 927 397 129 089 745 302 083 802 732 770 169 046 503 695 786 319 922 171 442 419 530 993 748 956 439 378 281 579 613 682 683 784 797 557 662 651 259 422 213 934 442 512 023 361 497 826 658 355 765 943 856 488 296 365 795 238 373 342 287 081 329 028 678 043 696 038 857 905 531 313 875 722 259 362 177 574 189 132 350 768 907 939 847 444 735 112 023 038 233 883 675 259 820 017 203 779 524 568 605 256 670 198 027 670 612 404 197 253 185 809 636 694 842 326 046 506 524 658 382 976 401 960 248 050 173 385 155 888 274 244 911 597 339 164 757 341 868 115 673 840 149 249 173 770 301 445 899 063 332 574 527 322 656 468 919 993 737 904 987 336 536 871 070 323 282 697 635 369 192 223 317 724 660 274 511 339 869 214 781 147 983 948 668 058 431 832 406 896 363 155 704 127 628 204 623 696 493 309 213 659 134 437 459 726 442 570 473 976 914 419 330 987 689 794 565 336 111 520 650 219 748 784 831 486 272 366 228 164 335 864 883 835 813 786 780 587 824 088 585 119 830 230 116 453 357 058 884 560 067 076 172 779 872 768 442 826 664 392 261 937 132 404 734 904 552 925 155 724 561 031 601 971 437 217 210 961 383 701 013 638 035 351 592 828 481 363 076 717 782 117 679 169 313 686 044 550 146 227 857 415 212 315 204 722 351 476 108 582 874 399 133 449 092 200 709 410 680 693 031 972 046 565 802 372 214 904 196 028 693 573 893 013 372 610 307 377 036 570 482 088 131 271 178 037 564 885 993 022 412 392 798 941 691 435 841 991 265 815 475 228 638 998 636 529 466 109 670 719 936 825 334 921 598 259 705 821 884 082 488 340 543 289 908 467 678 425 991 089 417 275 902 924 636 023 309 124 756 012 625 438 467 501 949 553 658 307 687 256 373 269 886 738 554 339 314 789 597 298 030 158 056 606 492 523 484 883 681 053 754 009 942 091 120 592 841 991 374 062 871 467 768 052 461 861 304 009 877 474 650 390 505 903 648 993 991 306 398 924 665 934 605 505 557 156 230 751 311 059 183 712 932 983 042 604 887 121 497 510 263 798 025 047 356 031 663 093 098 882 829 948 274 775 509 742 529 904 156 596 001 176 366 592 875 198 027 640 336 168 589 235 169 270 362 426 943 324 374 025 281 867 914 907 379 603 478 827 191 860 170 295 469 073 303 026 023 744 965 644 185 619 024 102 060 085 786 098 299 865 359 482 936 328 425 929 871 737 834 487 655 328 735 089 969 253 144 431 866 916 666 455 021 967 270 291 154 725 108 704 428 633 178 366 271 863 549 881 641 414 002 764 820 064 189 318 255 870 899 462 421 369 733 842 321 570 957 489 393 114 846 069 721 213 073 857 614 736 993 777 616 306 199 400 673 122 679 207 142 824 647 478 510 251 576 722 111 940 181 301 509 122 170 854 102 712 204 385 487 563 795 557 090 961 817 602 177 355 600 611 880 906 715 103 493 693 675 490 266 503 196 184 126 351 843 501 726 143 831 142 082 821 483 242 169 413 552 230 755 945 091 478 523 190 337 931 186 697 407 803 777 439 739 238 779 419 448 586 045 683 900 655 554 227 255 448 099 232 452 314 421 062 514 336 684 090 460 337 741 613 445 305 891 808 236 523 855 217 822 910 185 379 325 173 181 641 626 833 117 990 097 315 785 807 016 135 376 223 440 260 334 206 756 230 790 839 784 786 782 546 902 958 167 049 574 820 780 638 235 205 087 913 558 661 938 124 706 808 501 204 631 636 976 099 403 743 552 716 873 739 342 035 505 532 273 667 637 905 601 165 277 307 351 733 169 609 566 714 553 251 258 558 895 293 334 160 782 207 848 368 298 418 174 779 546 622 799 284 324 791 580 016 949 808 659 890 809 410 690 431 104 209 566 865 268 768 455 021 737 960 001 156 716 535 809 822 470 322 177 568 844 628 063 651 885 657 306 673 507 959 972 192 517 899 962 538 173 830 105 261 017 149 513 738 949 037 401 940 508 733 302 298 096 097 857 531 438 278 108 493 505 423 378 261 205 730 699 629 279 798 440 743 708 975 515 901 635 700 367 621 787 674 787 099 007 418 773 417 583 549 516 477 712 942 861 073 401 232 624 378 340 595 599 384 060 011 888 729 109 693 815 244 772 680 501 227 305 127 019 660 390 380 011 294 495 591 053 151 345 292 091 305 163 226 541 021 115 062 254 712 506 986 715 997 878 410 957 638 474 365 276 670 555 964 923 916 905 333 045 849 689 192 123 349 611 570 900 546 366 630 087 599 929 410 758 247 436 623 841 501 390 534 035 065 477 129 299 765 330 880 280 995 126 258 534 528 538 272 482 877 130 751 520 375 650 979 466 512 926 659 157 934 031 721 835 542 591 494 733 589 320 947 288 514 983 067 328 029 670 548 697 059 283 610 792 140 160 328 572 694 568 877 853 093 021 469 029 996 454 493 132 996 185 340 219 774 821 677 268 026 872 129 750 533 529 791 710 313 938 668 925 205 267 952 091 399 614 326 662 572 348 855 885 354 033 160 918 249 769 835 249 090 639 406 353 258 985 433 946 298 993 190 700 872 405 812 790 872 432 687 688 711 936 176 469 030 708 859 867 145 685 736 912 712 874 003 795 880 355 688 467 847 290 025 651 185 474 519 323 700 641 585 875 686 642 732 840 550 057 131 551 652 593 986 784 718 627 140 330 994 162 332 219 061 101 697 983 425 716 544 470 090 130 554 180 178 864 004 730 726 265 175 117 482 587 741 106 379 715 152 384 384 784 562 389 038 143 660 417 163 131 988 394 294 933 355 007 677 731 545 302 882 478 862 903 700 275 148 310 321 640 899 570 783 812 451 979 542 751 438 783 164 247 728 473 397 545 462 737 888 843 241 923 369 630 948 810 944 943 849 767 706 609 269 871 449 821 447 394 888 264 244 756 231 351 428 261 401 267 965 757 896 030 718 308 280 656 953 732 097 216 740 751 508 244 417 509 272 481 840 684 822 491 702 456 542 509 741 884 213 411 671 453 099 068 609 172 517 765 255 635 680 754 464 519 337 832 734 591 292 663 629 773 055 494 076 992 269 402 238 600 055 905 023 727 996 547 976 645 692 738 214 677 721 323 834 479 721 156 721 671 259 906 094 659 563 651 445 744 956 649 052 839 269 069 261 918 244 117 829 414 567 861 662 013 072 193 435 584 715 818 611 221 330 154 468 521 840 885 824 891 415 209 766 069 337 948 999 485 862 401 516 952 181 223 867 960 563 474 706 343 875 106 169 530 896 836 250 748 711 732 745 376 354 281 269 596 064 828 568 183 314 728 384 365 859 169 293 080 679 311 805 387 338 364 987 348 737 841 507 480 010 235 453 267 087 143 461 781 380 549 608 815 042 353 367 162 649 108 849 723 266 330 644 514 241 415 406 748 301 864 604 302 590 547 702 502 519 057 373 084 019 289 957 114 358 520 228 717 904 120 921 333 385 494 547 579 870 029 665 602 173 108 486 456 538 371 473 639 352 887 947 638 097 691 336 475 660 097 980 119 212 071 642 314 735 328 608 184 918 598 966 857 550 879 829 308 320 221 132 291 468 829 413 954 091 019 689 428 503 249 551 211 591 245 911 079 813 488 568 510 167 549 998 388 345 941 765 661 377 144 798 741 512 455 777 208 673 101 211 548 306 618 453 955 420 356 934 385 624 234 469 707 933 964 177 590 210 420 906 491 681 610 791 850 549 036 643 219 584 014 848 316 780 781 397 659 624 097 183 920 667 667 525 312 016 766 118 304 456 695 848 068 497 310 020 187 104 288 315 276 907 300 376 061 141 113 704 992 083 126 297 136 633 641 183 350 267 406 626 621 807 487 674 898 381 787 121 548 807 691 131 466 010 542 827 627 110 605 418 183 326 105 237 653 911 426 297 165 445 758 022 577 249 511 405 491 751 659 464 985 258 610 993 423 206 122 670 421 596 059 498 156 485 909 993 083 698 744 233 082 802 454 385 653 931 675 207 165 439 844 375 714 684 398 210 469 123 382 051 472 683 663 505 356 572 627 709 970 168 002 794 729 703 824 112 346 265 064 934 356 786 580 486 047 424 604 765 019 113 942 420 300 137 287 548 850 617 911 422 341 251 179 064 354 598 567 135 039 267 169 749 659 388 611 148 635 070 991 953 729 910 323 033 795 708 444 211 942 521 108 997 329 283 427 853 373 555 468 039 888 823 077 223 899 149 466 595 617 298 007 567 444 649 996 375 306 857 617 336 381 099 663 707 990 047 981 332 630 568 958 152 992 966 060 718 906 709 637 973 991 147 311 588 831 194 764 627 856 013 406 323 963 184 823 500 331 066 362 844 132 285 138 689 198 661 644 553 469 761 560 635 687 296 976 050 924 682 011 668 749 109 346 593 673 221 608 355 802 031 870 424 942 046 469 545 992 543 814 938 969 691 428 256 035 573 375 516 884 940 185 928 668 561 577 374 309 655 687 351 093 769 827 995 131 779 612 714 818 810 933 468 900 897 744 454 376 987 414 507 614 410 662 450 669 571 129 760 668 451 970 185 648 781 690 274 014 119 790 042 618 153 671 121 879 069 153 643 372 566 350 859 165 106 808 582 552 232 613 015 617 765 489 346 864 245 839 287 992 559 909 168 499 984 302 147 108 009 950 503 654 775 314 421 872 485 532 487 754 271 852 089 942 593 417 187 712 548 635 378 021 581 912 782 491 243 741 390 185 109 303 298 513 211 325 372 069 694 319 828 947 569 821 667 241 607 684 982 722 682 582 492 845 743 793 920 575 925 528 624 209 719 748 613 863 167 509 012 047 742 596 832 901 536 665 415 490 457 090 822 480 409 912 557 338 480 352 755 496 126 138 990 313 134 075 721 627 826 830 300 157 015 769 155 665 891 454 418 751 877 601 123 300 866 846 751 580 956 187 398 841 001 346 477 928 100 856 285 944 796 813 305 595 423 017 226 993 527 612 490 973 039 500 338 408 090 897 960 799 120 872 206 462 531 816 930 120 224 742 708 417 766 955 223 147 442 256 398 890 334 423 806 079 709 527 391 071 400 612 151 913 945 450 352 486 705 722 444 075 546 255 476 579 792 386 367 811 175 632 451 831 976 114 555 583 010 299 611 005 176 401 803 845 461 355 188 664 010 347 564 440 256 824 525 974 067 081 781 410 242 412 597 380 329 519 605 254 676 432 724 338 927 966 720 506 075 510 466 002 676 922 481 568 091 420 165 531 579 795 868 037 018 141 083 891 362 471 074 863 493 236 068 108 885 186 180 326 320 993 630 089 425 177 068 477 326 569 054 670 034 056 350 481 092 820 332 624 210 028 244 675 519 271 099 005 202 972 607 005 585 886 724 693 512 897 210 851 399 719 368 079 015 557 290 329 599 641 582 354 777 033 602 159 086 744 936 402 862 417 434 916 418 212 425 986 649 429 956 934 312 495 463 580 704 213 237 640 258 332 583 744 447 227 855 217 310 417 013 129 646 799 604 018 091 707 374 647 801 352 293 859 165 236 064 786 461 365 259 611 475 294 374 547 888 584 387 480 996 223 994 261 609 928 875 975 520 281 628 984 572 940 774 817 586 949 935 691 666 779 341 791 080 574 110 098 733 805 682 316 238 387 924 339 581 339 350 085 865 017 250 204 248 570 250 633 072 339 488 353 913 180 270 383 908 270 075 662 995 033 315 587 013 908 385 178 021 731 404 747 992 286 269 965 663 877 424 090 155 800 426 244 415 354 691 320 687 433 069 071 458 880 527 497 026 831 403 054 418 827 360 528 279 529 572 524 814 130 138 569 328 927 642 041 783 182 678 225 838 530 495 369 445 716 262 880 187 327 172 566 535 232 693 863 658 228 667 860 543 591 892 837 171 687 436 565 554 949 730 695 165 678 266 629 209 077 498 191 061 345 204 146 102 544 601 124 403 885 042 432 905 303 957 315 816 487 208 987 725 783 781 227 777 496 448 566 550 259 436 988 751 752 669 548 235 705 101 294 102 015 977 617 150 376 910 270 136 001 823 943 520 780 754 626 318 491 975 439 103 386 435 442 151 172 430 954 709 156 170 988 114 179 424 850 828 396 183 184 257 226 797 426 741 089 651 375 774 792 057 339 244 116 473 239 432 052 838 686 251 880 616 252 238 703 043 593 349 499 000 550 491 596 782 053 553 028 232 759 901 763 522 966 021 175 032 936 415 678 425 841 424 449 345 870 478 773 576 503 949 155 316 545 944 312 163 039 315 639 087 087 374 513 920 512 782 280 852 929 479 225 118 398 419 490 781 398 867 961 164 938 931 166 723 608 310 494 107 576 716 304 260 890 291 806 468 611 423 804 521 296 181 991 745 764 982 130 306 211 910 650 568 378 575 240 184 838 278 916 469 607 193 833 897 380 343 175 251 843 474 324 442 979 774 760 037 054 600 889 543 896 143 595 313 227 935 149 067 494 904 085 911 811 131 546 737 974 115 407 558 829 810 512 696 223 587 742 883 650 770 680 119 986 946 427 191 715 435 122 255 076 327 191 761 582 711 574 631 804 749 888 177 720 448 134 446 132 269 971 824 252 848 170 418 789 930 226 794 752 869 983 952 225 180 278 656 328 790 316 946 362 633 828 151 558 092 859 372 346 847 804 992 460 385 561 563 790 655 703 675 510 097 596 679 287 532 977 930 082 752 451 999 660 644 712 506 427 186 548 196 946 438 238 942 621 064 995 218 468 680 256 625 036 423 106 302 654 737 817 416 989 037 100 157 419 909 232 117 876 840 763 563 671 668 295 164 129 626 600 086 617 031 505 820 359 658 139 721 177 487 035 059 704 040 540 085 703 088 411 140 005 631 928 010 372 913 276 755 507 431 535 598 666 894 778 555 114 344 703 151 788 288 028 076 248 449 436 640 815 042 286 569 293 827 499 657 454 006 406 749 156 016 489 711 540 814 255 331 770 548 953 666 832 536 060 249 070 584 202 459 708 959 310 855 790 167 781 637 491 111 292 585 246 833 335 378 924 713 955 124 707 735 424 603 850 635 986 292 069 231 431 952 474 864 900 509 179 961 303 926 893 901 797 122 138 586 928 086 171 654 884 592 980 058 456 167 840 874 428 584 907 259 233 624 340 536 529 891 902 082 983 934 538 742 405 488 690 071 974 415 078 613 402 352 013 302 565 188 111 082 925 515 084 954 258 219 027 020 533 972 345 697 680 078 022 042 257 632 004 325 804 302 936 784 717 725 945 508 866 312 887 460 709 504 619 797 855 452 484 440 586 209 246 280 311 237 720 366 023 918 297 355 488 529 908 756 299 044 001 799 419 083 440 081 313 213 862 935 933 242 267 024 295 896 778 926 561 378 165 491 221 989 956 473 282 120 259 724 029 652 345 243 101 169 189 084 311 368 136 783 169 721 641 528 558 252 597 622 954 257 125 159 022 998 104 786 924 858 847 418 095 539 099 446 292 185 959 648 009 704 375 601 477 734 356 561 657 844 939 076 875 943 055 169 937 891 684 192 218 640 188 548 355 591 338 140 571 229 993 386 235 506 220 660 995 295 399 378 900 562 406 169 170 354 616 093 194 723 717 819 515 192 114 002 693 626 959 597 975 202 323 302 321 064 390 431 117 727 818 290 048 440 814 274 310 985 416 743 220 891 603 880 519 425 764 721 975 660 364 100 913 575 574 413 754 275 706 483 950 527 254 732 799 109 719 289 123 032 861 652 044 102 337 873 435 306 831 471 430 647 136 344 120 435 663 086 078 283 344 526 272 452 388 671 230 871 630 825 612 907 958 809 209 728 698 742 268 059 125 709 435 740 679 554 797 271 354 511 360 341 712 558 601 178 321 684 440 239 341 726 367 657 369 816 635 230 593 831 079 189 409 329 542 069 837 439 546 818 482 353 445 077 832 697 131 954 620 284 556 562 279 436 684 653 204 346 365 545 374 993 995 893 997 903 290 882 895 531 388 169 749 221 611 624 832 506 487 017 908 114 793 631 568 108 775 422 348 157 753 198 280 122 172 888 655 421 590 356 738 474 042 783 017 066 480 775 304 032 188 999 154 140 686 329 824 094 944 794 061 823 515 690 688 634 008 252 125 653 051 721 045 295 415 469 295 030 403 215 378 680 922 763 954 039 469 928 814 185 456 079 185 521 291 817 979 265 674 593 152 999 662 587 448 956 603 674 909 328 255 057 042 410 523 037 385 204 663 468 105 040 824 963 609 092 427 245 548 535 260 118 382 851 017 548 062 186 217 634 285 929 646 475 250 691 718 879 113 090 457 887 935 434 437 266 335 530 033 272 683 907 657 630 022 025 968 660 940 221 377 272 690 748 954 313 473 964 593 571 705 017 170 488 333 358 987 606 473 677 589 070 442 692 551 689 594 915 876 453 061 697 870 308 561 487 562 240 120 148 927 912 073 430 076 219 216 412 489 165 865 926 056 833 108 789 796 694 480 193 723 107 584 946 775 479 260 285 876 727 844 766 344 306 752 395 027 634 804 240 381 895 013 908 932 419 350 915 006 770 796 576 146 314 183 502 611 727 601 938 644 242 690 655 643 144 898 795 581 270 799 187 395 869 089 191 860 603 129 873 844 053 510 264 007 227 742 179 233 969 322 382 794 370 989 458 123 763 571 344 983 207 272 236 256 044 272 679 579 668 305 548 595 285 823 589 465 869 812 925 056 555 175 973 694 518 470 655 652 990 253 180 297 190 087 107 556 295 945 897 538 744 272 357 344 899 864 730 496 414 034 763 476 798 899 836 223 918 038 079 480 144 207 138 062 230 608 977 362 010 188 299 582 516 492 463 660 687 542 735 181 088 911 823 135 456 366 964 739 595 798 539 564 450 419 574 974 182 320 708 825 026 743 824 916 442 767 803 473 172 936 708 696 784 524 858 113 769 562 555 124 354 096 637 571 967 539 360 250 059 828 438 682 487 691 867 823 215 400 050 879 267 706 512 623 783 596 897 050 329 629 221 540 232 474 061 414 950 434 148 419 606 460 468 235 280 926 462 465 585 566 885 688 834 100 901 362 152 742 773 342 029 515 430 327 760 476 242 433 319 463 017 811 208 821 175 549 099 463 082 896 613 560 864 725 678 052 310 599 989 020 183 025 807 109 261 860 803 813 604 943 802 310 049 128 376 789 789 733 488 695 970 406 730 921 626 469 508 340 634 190 221 888 057 064 193 632 801 443 349 265 092 455 843 398 386 799 546 557 864 821 457 903 373 514 487 592 565 726 599 224 142 048 146 956 009 932 819 963 089 916 752 285 131 042 602 936 484 810 541 863 985 912 402 942 860 173 351 560 204 977 001 597 989 122 859 360 240 123 042 841 452 996 606 591 484 754 519 423 642 389 984 106 235 796 143 135 907 601 745 510 564 588 719 345 103 695 545 554 279 223 901 349 581 487 556 142 929 315 372 345 607 459 164 936 711 067 985 145 268 547 346 974 793 377 561 642 782 712 221 137 475 061 111 076 390 931 920 687 420 980 195 133 167 217 719 758 673 915 340 241 047 157 588 557 394 697 051 732 478 586 065 826 369 366 839 670 963 906 174 974 874 342 314 969 232 823 462 338 866 249 702 057 025 369 904 367 961 790 664 230 312 055 875 859 806 627 070 811 356 358 325 070 403 663 399 216 465 813 750 110 802 916 768 514 567 452 245 880 901 739 034 642 987 084 806 523 872 436 106 949 042 768 651 896 250 472 009 415 042 116 019 781 386 077 512 074 540 343 105 566 183 336 544 808 005 361 659 992 789 528 541 230 765 148 705 429 790 988 443 991 013 015 105 840 170 572 733 401 732 832 903 365 141 786 320 061 901 782 149 844 420 560 336 035 698 367 820 977 684 492 179 149 370 307 087 626 386 224 646 439 211 154 733 005 586 799 128 591 292 487 658 123 433 247 440 432 607 123 121 498 353 568 946 692 408 412 270 853 190 034 077 635 345 129 390 134 249 400 467 550 692 263 384 141 776 420 133 407 957 625 560 896 100 836 403 009 317 623 320 298 393 481 559 199 636 812 875 501 998 012 937 926 026 184 786 835 259 238 814 839 130 700 226 713 786 469 557 272 015 455 750 737 796 852 724 890 770 923 137 717 819 324 665 305 659 434 856 269 021 838 368 188 962 308 987 706 568 961 511 604 221 010 547 385 440 421 198 349 256 134 127 559 602 222 094 647 043 937 789 043 935 938 507 619 407 229 276 137 261 371 212 566 640 007 841 663 191 811 102 775 891 909 252 886 064 769 530 682 239 045 059 062 265 425 938 237 250 998 540 958 880 517 015 295 679 371 653 071 496 771 223 059 136 885 988 434 898 330 787 404 285 667 080 210 625 555 954 083 246 615 580 172 694 306 703 857 220 607 179 205 546 380 664 731 421 678 775 845 225 849 822 930 849 686 118 919 736 239 369 638 569 195 071 285 746 945 965 574 418 798 376 936 664 606 293 588 188 249 197 285 909 049 475 558 014 728 060 015 615 247 488 623 183 935 091 086 333 784 718 632 294 352 138 526 681 125 714 625 180 799 223 525 793 473 071 691 317 522 282 993 706 745 562 488 359 021 117 734 426 723 602 710 388 134 984 554 438 072 424 582 943 109 713 565 106 065 266 905 604 517 131 683 646 193 681 753 983 905 929 857 518 697 843 249 595 269 935 241 859 821 622 717 006 086 459 885 524 264 641 521 247 468 687 147 564 739 808 678 492 382 512 722 205 195 593 160 638 528 665 223 563 283 702 677 847 153 486 706 453 335 459 849 957 271 542 712 376 903 075 107 635 116 287 508 261 294 032 933 520 590 960 402 993 835 931 311 244 952 855 450 000 657 079 208 503 726 633 312 486 403 849 916 158 718 162 174 435 219 633 952 596 132 359 978 249 391 458 711 067 365 760 028 669 856 192 618 575 629 105 934 148 799 714 838 886 617 049 213 644 543 896 349 036 067 418 436 821 841 043 934 779 817 850 502 093 331 493 114 910 619 229 952 907 441 654 984 552 217 717 930 245 421 517 939 751 224 089 641 911 272 453 391 869 601 596 295 817 072 910 166 240 196 814 320 638 325 639 860 902 285 005 346 907 382 601 122 775 400 517 477 132 016 469 159 615 846 188 577 561 027 185 177 038 023 097 919 461 551 947 485 814 266 849 583 170 073 364 355 559 340 013 826 785 063 069 926 174 074 312 041 887 221 098 086 905 313 937 595 821 121 722 166 162 022 167 096 330 673 975 968 352 119 023 101 956 171 435 413 469 251 824 972 726 776 685 991 171 361 933 633 569 669 961 241 829 068 179 477 776 727 107 916 924 809 033 464 104 011 905 246 208 931 902 121 355 928 209 607 825 928 356 686 070 559 748 893 002 540 611 963 375 402 987 190 451 378 694 439 038 028 476 831 022 388 146 428 802 532 917 327 484 732 097 332 475 563 483 795 076 878 556 916 363 652 240 105 286 337 010 875 900 652 799 287 524 221 389 980 310 666 838 379 619 507 993 722 879 356 350 305 749 883 924 108 775 016 925 532 824 272 026 915 634 180 174 867 400 112 321 468 810 791 558 803 672 612 422 794 183 911 276 412 574 965 367 079 359 385 529 607 601 735 517 482 406 895 535 205 611 441 239 790 786 539 862 587 720 941 080 973 173 496 169 725 415 315 654 746 087 303 671 265 438 059 840 755 270 828 947 986 086 491 618 255 888 868 768 002 955 260 490 784 526 441 645 202 466 698 118 325 406 468 354 956 705 916 596 738 308 694 096 055 902 751 135 062 222 128 444 189 233 677 129 370 392 241 836 812 425 345 298 761 737 268 915 399 814 061 019 710 463 715 776 709 566 464 414 163 349 828 652 127 601 436 564 657 594 046 296 923 290 338 943 552 803 882 721 272 141 536 550 770 444 700 265 137 491 992 687 994 733 560 941 155 462 743 137 437 914 208 692 180 361 300 300 271 078 738 482 446 214 362 075 294 787 317 583 987 360 065 985 747 697 409 252 995 575 153 669 916 660 355 645 173 771 330 257 237 578 758 808 361 067 264 583 441 070 102 234 145 533 858 812 562 275 924 347 551 020 012 643 060 147 652 089 470 612 206 624 820 426 475 217 949 662 332 463 361 263 163 018 000 436 535 357 664 097 495 827 932 450 267 009 000 599 960 814 501 762 831 803 117 787 256 667 377 871 825 662 795 090 838 501 872 251 625 071 131 263 070 321 141 318 317 664 284 342 630 803 184 833 500 290 973 944 633 655 605 174 183 027 446 562 672 271 215 033 918 642 291 142 698 774 475 411 789 125 331 235 351 962 292 608 332 902 989 208 551 395 726 635 119 871 558 936 125 832 625 600 416 853 023 986 261 839 852 384 085 565 422 584 927 794 517 604 262 630 414 591 735 916 626 791 276 771 311 849 156 591 127 950 318 482 641 706 785 771 392 065 555 336 044 792 848 141 748 281 730 896 249 631 212 040 211 509 638 491 717 688 022 860 682 969 588 742 023 437 845 007 277 078 034 374 616 163 338 064 093 370 663 489 922 719 002 965 371 542 799 764 113 826 570 507 765 278 991 808 671 848 409 979 824 635 766 897 139 584 664 291 674 817 240 140 049 731 256 036 096 732 078 097 254 885 392 727 567 964 539 223 056 890 411 623 440 964 780 325 654 960 605 625 470 041 979 390 190 869 534 168 665 734 009 354 431 595 793 397 464 615 737 476 205 379 545 100 709 467 979 323 397 451 434 364 328 325 390 403 876 962 374 713 230 877 048 183 191 961 124 158 290 572 754 711 255 016 167 685 747 047 652 302 101 346 744 586 374 228 899 285 515 075 197 715 176 894 572 348 989 610 147 589 510 652 715 094 831 572 025 373 612 075 573 787 824 128 793 919 931 141 937 944 664 338 302 013 641 351 890 596 231 353 338 613 783 880 278 348 709 255 815 982 641 294 638 770 786 081 708 671 649 152 395 656 436 242 044 275 735 237 571 017 958 567 923 977 085 391 120 668 439 848 707 416 358 222 138 124 179 781 819 472 932 562 096 982 663 363 010 442 409 999 823 599 022 435 858 972 834 622 554 987 722 217 170 811 935 799 909 501 277 198 083 848 063 286 905 088 122 676 709 384 940 936 600 531 222 641 719 296 561 489 020 485 691 440 584 454 542 264 922 702 775 767 815 324 928 483 772 816 579 297 373 275 455 825 336 739 296 076 135 622 161 369 699 234 491 715 219 688 498 734 194 813 226 291 908 881 335 609 754 475 636 857 384 903 803 952 481 599 613 090 017 491 149 771 788 286 556 303 184 701 316 812 328 500 110 725 580 712 806 390 519 733 237 063 398 739 467 631 116 961 578 740 745 134 764 248 248 940 334 162 698 502 437 266 202 528 036 022 045 345 776 276 962 175 289 241 665 697 913 673 683 853 459 610 027 778 203 101 779 744 054 777 138 953 539 400 738 897 864 711 882 229 054 734 884 355 570 397 387 841 686 230 026 162 873 957 586 392 761 917 158 885 810 548 818 388 439 112 591 246 813 446 947 272 666 563 190 747 189 081 814 816 981 730 680 888 472 650 639 480 935 220 467 121 069 639 363 631 165 719 071 508 559 122 518 563 659 839 090 126 175 482 554 490 714 521 769 086 704 222 977 069 891 113 603 202 620 168 851 066 762 445 338 190 342 054 448 919 108 321 406 258 115 578 672 886 449 150 008 338 172 189 733 606 871 594 794 107 041 916 585 976 184 865 625 379 289 906 235 536 253 498 803 409 264 955 145 526 873 189 503 945 466 744 789 600 686 198 918 232 096 224 471 577 722 376 265 008 461 606 577 980 289 149 320 911 141 250 899 119 989 572 159 960 229 473 591 928 449 308 585 533 240 451 020 600 533 420 919 929 977 075 851 913 321 126 808 956 260 542 908 135 378 018 198 711 987 820 345 975 665 817 761 053 345 279 467 253 832 596 091 832 461 496 147 836 887 191 535 490 815 355 927 205 202 598 796 834 965 113 142 763 792 943 236 897 473 843 220 926 957 494 542 805 924 937 381 730 797 324 246 436 071 677 719 405 100 378 104 401 087 501 229 589 441 498 326 105 577 314 579 906 437 991 521 154 262 859 298 106 608 267 047 877 262 358 821 580 026 059 386 012 726 464 690 484 111 119 627 320 112 377 469 558 251 244 976 395 774 470 107 965 205 337 279 330 515 271 951 332 419 107 966 257 204 397 674 744 853 010 135 047 637 224 844 799 357 272 617 304 672 346 529 800 728 142 379 331 453 786 863 345 388 822 373 494 488 271 548 170 171 292 872 989 098 657 733 780 370 196 184 026 097 502 828 477 705 519 660 256 568 301 707 627 675 559 005 890 482 796 502 362 715 688 055 070 798 366 541 851 328 372 675 825 518 752 254 593 702 212 168 529 533 920 677 078 913 353 982 201 521 996 054 063 506 447 187 367 750 021 887 187 196 933 857 190 915 100 248 145 977 617 236 922 815 104 606 127 724 742 915 101 840 904 720 433 823 613 452 791 529 717 838 013 633 423 641 032 419 179 324 618 373 415 075 685 083 802 751 000 710 969 672 633 269 710 834 837 413 622 268 900 497 581 531 318 440 896 668 628 522 491 496 220 376 686 957 494 581 038 802 804 059 037 590 839 974 428 450 129 353 673 812 527 506 622 687 696 411 966 453 763 267 807 532 110 168 450 465 845 768 854 455 006 682 517 804 223 874 352 682 348 023 319 870 951 595 440 554 156 260 161 593 259 242 373 018 560 967 771 509 644 440 944 593 853 570 395 053 412 167 528 696 502 303 923 113 802 282 093 465 668 061 755 856 071 036 348 170 635 056 172 592 265 727 616 762 871 070 519 333 274 741 458 004 692 028 867 926 845 624 025 592 567 504 232 374 966 440 011 683 655 573 699 033 318 731 012 304 081 075 290 051 481 763 839 778 213 997 884 827 252 740 487 059 351 086 078 994 274 440 440 715 694 890 331 975 547 390 407 922 262 969 459 539 895 897 809 269 838 266 078 128 988 548 742 744 577 045 610 059 990 835 893 621 697 073 201 524 814 367 354 582 834 959 487 142 624 341 074 927 080 339 216 156 481 156 315 319 971 913 288 582 909 295 139 333 819 123 505 056 804 201 140 067 099 601 724 761 300 916 017 869 398 495 489 728 635 575 045 752 203 465 135 138 678 185 636 783 910 510 046 652 349 969 507 582 956 031 169 625 864 299 088 131 678 551 599 326 724 792 042 090 975 778 635 331 856 351 254 827 687 778 518 625 146 958 964 549 501 484 233 293 528 749 256 823 113 083 851 971 631 020 742 841 093 789 472 639 918 576 882 162 169 359 416 907 831 870 557 252 288 380 268 171 705 985 103 505 450 630 258 657 735 562 329 984 894 734 325 235 055 130 583 060 797 011 142 643 842 052 695 362 638 063 392 955 175 038 605 011 674 153 290 277 910 476 855 842 421 087 029 763 708 065 557 834 695 642 009 106 278 879 087 713 764 399 133 640 830 403 265 101 324 701 832 345 481 833 696 810 290 845 958 087 788 384 869 469 418 454 369 357 854 865 778 338 826 816 326 913 991 748 546 735 929 423 000 371 602 130 485 419 173 270 443 128 393 483 647 737 135 228 465 686 617 463 892 007 520 923 839 385 036 655 785 116 798 712 026 441 011 485 863 197 449 152 231 487 319 245 102 665 223 080 101 490 427 277 115 506 231 769 204 624 423 190 454 844 821 102 684 916 324 330 097 518 763 883 861 130 994 278 024 128 514 282 550 802 934 018 412 410 943 690 214 639 207 845 613 111 618 777 660 456 915 237 993 606 483 936 070 330 318 169 728 772 890 737 567 909 831 322 153 180 716 616 396 694 463 400 846 407 206 154 610 875 659 827 470 303 100 370 035 727 983 655 757 202 589 648 824 511 893 036 640 170 157 822 695 330 490 608 298 174 460 682 934 139 935 959 858 066 416 707 463 575 839 293 578 241 583 714 375 689 815 203 015 085 452 564 204 716 112 473 580 409 343 542 450 700 043 611 024 420 870 397 823 211 223 364 835 255 120 016 692 758 630 645 876 856 800 015 235 552 945 684 875 273 580 025 975 916 506 890 423 402 197 729 870 489 782 564 338 472 851 792 900 252 673 285 751 673 143 108 530 329 564 149 937 994 268 518 286 283 825 979 624 763 650 376 631 118 945 012 077 718 735 776 434 338 036 061 314 329 226 061 342 557 570 799 453 724 023 586 283 448 870 373 517 990 325 873 837 609 006 605 101 289 909 449 413 773 192 889 314 331 735 931 202 998 923 950 135 395 922 289 901 124 773 452 913 594 770 639 086 085 614 968 829 531 590 684 365 063 053 616 827 434 463 727 294 876 658 321 235 683 749 404 854 113 075 282 851 593 618 485 815 859 907 161 327 761 738 985 876 177 575 686 993 283 624 301 346 999 442 130 474 118 073 723 703 573 042 710 145 234 035 252 359 625 568 715 923 435 753 008 530 746 095 782 062 158 175 178 767 467 721 785 135 614 433 151 984 620 933 611 968 152 150 681 424 761 374 477 479 021 084 405 382 381 561 733 970 150 368 713 993 170 898 747 754 347 591 469 729 356 789 356 604 019 676 351 749 083 144 017 640 051 608 622 874 940 684 572 024 498 366 365 129 961 917 433 878 665 836 288 354 479 836 338 222 828 436 134 305 045 190 118 822 216 212 016 035 718 913 189 010 262 674 094 163 502 332 615 589 401 629 760 281 647 263 748 476 333 949 075 759 771 344 375 878 563 235 706 945 218 069 011 344 805 575 493 425 232 350 125 245 273 942 503 319 563 878 222 237 623 348 435 001 364 022 516 481 883 319 243 567 616 130 133 760 482 842 086 013 444 512 786 522 245 595 629 704 836 882 794 987 270 222 544 883 149 494 264 429 087 445 607 888 985 991 073 171 124 896 656 830 412 383 359 875 220 282 052 670 958 386 210 789 816 928 825 835 866 734 743 073 369 104 199 788 486 362 039 042 033 523 962 452 463 043 492 127 917 122 416 084 535 524 640 256 717 942 424 314 266 198 998 309 043 321 793 135 577 582 113 821 776 712 721 077 746 922 992 013 603 498 127 562 051 146 393 625 105 140 992 302 573 070 540 728 523 939 879 017 599 577 935 195 473 439 537 850 082 782 448 077 390 517 690 952 708 650 358 646 400 930 857 453 202 930 089 618 367 263 199 664 204 971 291 146 104 855 023 826 241 292 158 592 940 818 869 540 925 809 396 472 828 792 267 637 332 251 259 554 515 304 169 039 366 551 215 923 589 037 398 175 176 160 061 060 342 487 879 932 399 465 894 985 485 520 066 351 104 797 386 877 536 181 830 538 194 262 304 681 096 551 174 742 271 064 677 174 555 101 585 463 318 281 441 797 583 215 974 196 505 505 005 987 915 512 429 358 432 852 408 332 152 716 956 630 364 533 237 846 388 874 374 959 237 716 228 218 504 759 937 677 666 948 628 160 965 071 721 373 330 729 085 731 266 326 084 480 538 025 193 456 971 647 432 868 398 118 349 552 020 222 961 592 555 634 583 591 076 682 455 262 951 886 622 545 886 209 202 847 060 718 427 556 870 890 359 022 107 536 720 105 595 329 831 142 100 759 611 880 307 008 225 366 404 995 530 277 696 953 996 762 695 849 644 911 284 573 044 246 685 659 147 929 189 804 506 406 097 089 897 306 119 240 723 852 720 350 097 295 726 481 716 089 879 743 586 262 679 480 017 465 980 468 354 769 682 878 948 035 977 794 318 082 919 261 420 063 832 191 599 747 455 888 221 462 699 164 857 211 768 632 345 314 383 931 107 296 620 218 728 223 388 887 056 336 845 943 965 012 652 170 886 385 324 340 621 990 043 506 052 128 291 654 835 536 099 722 974 205 874 335 372 984 693 338 490 081 267 750 510 301 355 280 094 416 444 275 016 109 469 259 501 395 249 158 700 161 443 458 994 319 442 515 925 209 025 085 505 813 961 256 956 879 202 509 177 234 320 935 305 144 534 869 620 418 372 158 583 393 328 740 635 899 469 239 540 502 385 443 582 398 274 956 311 179 011 215 091 739 364 455 609 937 277 310 451 119 730 795 516 820 720 842 142 959 674 593 830 099 826 674 478 020 873 835 207 683 646 509 488 455 807 728 387 436 792 016 232 489 344 039 470 983 958 035 152 344 786 405 758 385 574 980 021 258 977 103 016 072 115 659 423 759 620 102 364 209 025 982 347 918 222 849 000 837 005 073 263 069 676 470 589 517 814 088 630 119 477 650 372 148 858 678 661 197 336 418 509 509 062 211 753 674 364 931 848 825 725 282 598 994 338 562 810 879 760 625 210 069 990 601 599 288 510 990 341 300 276 136 025 859 363 414 121 815 996 725 573 126 834 397 167 304 062 583 596 142 311 516 235 645 983 890 579 388 909 875 023 854 873 420 480 515 922 510 096 471 081 126 074 392 502 771 985 027 849 621 401 865 877 154 664 741 270 856 141 368 852 198 056 470 181 024 813 844 413 249 738 891 477 171 867 427 827 503 600 440 966 470 309 714 427 256 037 742 825 550 101 986 699 190 498 141 723 083 847 787 063 950 726 944 435 869 421 294 144 327 778 572 053 785 193 015 576 597 788 169 385 456 369 140 383 611 450 678 965 171 472 521 532 149 278 776 323 790 887 767 614 622 340 174 363 276 154 924 119 859 375 081 800 426 806 651 537 272 450 553 275 271 511 787 219 585 392 856 120 894 031 959 211 567 995 223 980 076 840 289 349 454 829 303 876 796 506 968 070 108 780 793 396 018 988 045 137 135 878 219 708 893 036 903 376 798 510 241 617 815 290 659 840 485 516 132 401 418 502 956 307 927 110 571 598 226 602 477 349 127 663 189 013 173 448 840 610 430 833 730 797 185 071 185 362 495 840 466 844 732 820 796 716 056 908 987 162 251 348 814 350 116 502 801 174 240 256 168 702 115 922 913 727 636 625 987 621 131 903 171 600 218 551 757 574 192 001 093 659 962 397 613 105 792 866 122 520 978 012 813 542 810 359 154 799 632 550 437 067 151 184 127 839 073 367 531 302 627 133 479 379 083 218 267 252 933 554 772 096 249 038 577 040 436 602 253 208 969 162 097 900 745 990 878 607 733 786 945 163 548 333 083 685 503 693 409 404 969 525 547 854 692 249 151 320 529 684 508 224 714 863 022 899 087 423 948 659 561 490 619 598 061 830 325 745 082 999 745 103 869 679 274 028 971 474 813 915 119 560 713 170 658 975 445 227 133 943 305 281 030 818 082 542 826 038 722 169 919 166 311 113 472 746 125 283 786 736 015 764 016 583 034 432 709 460 918 161 497 435 948 407 123 471 641 778 644 725 230 693 085 917 607 478 870 913 431 099 414 351 249 545 604 702 970 585 045 815 413 002 052 819 203 098 880 183 385 255 461 549 486 761 187 136 806 110 327 967 172 440 363 966 335 861 446 431 224 128 570 054 216 100 682 623 461 666 714 870 927 865 613 274 315 786 821 088 098 488 309 454 773 517 284 202 357 184 454 917 664 274 912 592 001 352 485 052 337 228 158 473 761 235 202 107 180 000 230 716 944 352 222 920 889 356 934 959 022 281 629 576 413 077 981 474 951 986 542 826 435 651 999 844 860 399 205 069 797 683 780 714 006 873 821 139 724 236 539 884 503 173 072 472 629 604 994 512 012 864 439 512 446 997 729 449 763 402 218 412 821 884 490 219 322 558 062 810 791 650 528 746 695 508 929 981 368 212 634 091 540 823 216 567 149 645 610 070 435 692 230 605 015 926 219 514 801 547 381 651 395 819 034 617 059 195 824 822 785 797 257 316 397 742 974 666 730 101 640 866 327 494 697 759 830 148 476 064 347 601 233 375 017 980 407 960 522 583 311 661 620 824 918 972 591 612 409 065 277 897 616 792 817 568 925 898 583 167 913 516 814 422 419 424 159 293 449 526 127 075 550 060 778 752 406 876 915 356 312 587 696 549 792 444 072 014 158 811 352 737 647 366 616 438 624 551 314 483 379 679 347 822 719 344 865 902 091 835 976 931 773 838 921 801 918 888 644 876 296 725 825 778 328 745 033 316 787 790 430 892 024 007 608 038 110 572 949 009 456 892 035 433 117 138 827 178 907 163 236 312 766 097 342 006 165 142 690 554 714 366 238 732 238 191 418 475 833 905 202 282 890 461 076 259 868 638 824 879 128 658 432 332 901 140 118 782 924 464 454 000 691 886 335 994 492 708 648 165 167 057 073 085 014 427 574 689 420 469 540 601 017 644 420 009 083 250 459 311 470 593 077 951 424 589 317 598 105 290 921 189 679 969 259 604 209 346 497 069 789 035 003 898 971 942 825 038 788 493 131 934 336 401 786 954 895 690 199 179 874 965 845 866 205 629 534 216 660 794 077 352 633 167 127 093 812 006 231 643 422 186 939 400 165 411 099 122 603 067 829 878 910 141 985 298 772 368 119 277 811 791 070 287 385 934 848 487 854 984 131 532 021 424 626 519 445 123 136 020 250 733 730 800 410 767 335 544 223 595 487 354 113 160 936 588 446 272 694 999 099 722 590 194 771 481 579 102 490 920 790 537 207 120 669 474 323 356 932 374 711 628 524 095 142 151 414 164 144 262 198 271 800 050 908 717 504 547 358 091 251 546 523 188 640 757 577 547 911 529 907 134 061 336 721 713 639 678 187 823 595 038 290 578 263 248 049 444 352 950 824 443 854 883 520 904 650 500 788 738 967 084 000 642 294 877 449 012 071 456 045 356 789 504 408 315 403 094 433 119 905 924 391 177 456 688 169 999 149 244 945 910 732 572 866 785 830 181 146 044 697 164 185 139 909 105 082 632 965 038 906 065 607 558 434 456 017 494 889 731 655 775 097 903 920 045 602 775 577 192 468 042 369 106 027 851 490 468 290 992 201 506 780 092 570 046 699 888 195 801 832 682 526 019 559 213 149 603 011 756 072 251 820 493 736 922 777 822 739 197 298 317 454 316 595 020 361 045 159 415 017 245 268 561 022 101 740 527 611 432 714 736 025 985 200 376 912 630 005 226 378 269 165 763 411 954 527 459 930 358 373 562 195 093 792 177 302 258 143 029 246 344 968 943 362 801 553 559 477 912 231 522 220 785 564 440 434 060 347 170 700 908 688 767 541 211 879 164 471 732 786 639 934 728 924 457 440 633 506 876 937 690 115 203 983 446 416 454 355 257 155 575 117 417 806 402 560 553 283 557 422 673 896 388 891 414 070 951 600 047 675 570 110 113 757 613 788 907 996 981 718 872 447 618 404 773 686 442 516 372 850 910 182 439 226 575 213 188 346 900 246 916 174 594 186 949 242 709 052 503 017 722 062 286 125 361 889 917 743 901 928 506 340 361 722 221 936 562 842 652 556 878 882 148 826 788 553 932 137 157 989 317 861 170 368 539 944 393 941 813 809 589 583 367 095 537 826 786 088 342 062 206 263 087 241 537 511 810 931 605 416 125 515 477 724 385 482 855 239 652 656 824 108 815 219 344 088 427 775 022 635 474 784 895 030 139 331 051 357 223 427 699 766 195 387 949 007 171 433 153 173 442 336 913 017 860 015 292 728 933 890 746 922 320 683 151 480 812 758 473 854 640 374 374 778 266 018 139 024 931 020 047 298 432 007 724 650 313 279 651 593 758 529 926 460 342 233 724 827 782 466 068 075 220 004 859 081 006 574 671 796 495 885 785 012 215 142 357 111 919 985 873 849 977 442 810 321 089 294 319 847 249 904 046 579 522 436 922 690 611 962 057 636 579 345 235 985 259 314 695 579 439 116 353 758 816 081 299 686 457 137 347 142 862 676 229 373 551 214 640 058 633 038 961 591 591 952 953 742 007 223 770 490 016 942 922 503 476 682 663 994 254 405 548 981 625 421 600 105 056 019 069 450 508 060 960 224 325 033 975 529 192 560 920 208 086 494 913 733 941 076 703 604 946 384 605 974 029 205 220 537 927 251 292 283 076 374 445 277 453 798 663 688 540 500 819 138 638 439 363 407 021 412 565 665 206 901 553 855 177 349 673 454 618 576 075 401 471 265 607 374 561 144 862 353 410 703 513 850 647 682 872 844 943 452 830 232 113 809 227 566 142 324 788 904 090 149 370 837 511 955 955 446 313 372 571 073 096 017 223 029 801 632 188 924 983 372 234 025 036 192 996 438 304 841 500 178 922 725 307 623 710 207 384 958 225 666 587 786 807 826 825 008 873 125 563 166 963 235 702 556 854 869 485 800 794 360 969 440 724 733 439 383 392 500 845 231 126 372 399 078 721 423 877 402 474 441 404 781 107 455 713 109 559 562 284 936 114 939 701 198 300 156 328 321 900 456 394 142 421 330 790 505 433 358 366 298 057 562 709 462 840 697 172 088 840 016 003 040 650 821 703 034 876 764 108 298 427 392 536 306 532 262 811 032 948 291 421 523 642 939 657 042 100 944 556 008 659 470 879 154 524 100 921 516 623 501 159 418 384 802 257 954 907 842 289 404 423 293 358 116 078 663 860 250 368 188 482 539 866 577 481 939 444 504 417 241 497 467 677 954 333 887 221 650 183 360 671 357 296 295 716 495 326 935 317 611 623 149 306 458 940 333 580 546 179 114 427 851 738 391 036 325 840 883 808 431 769 330 491 578 065 914 164 466 740 174 658 482 443 683 907 256 368 951 920 029 279 755 456 725 940 914 095 172 886 493 214 107 180 085 631 312 465 779 775 805 250 523 884 789 706 072 231 738 692 519 218 816 030 909 679 082 951 556 543 574 842 919 125 058 468 767 534 343 438 381 591 995 085 529 513 705 265 744 370 792 966 552 262 489 973 735 827 379 931 654 575 529 905 635 899 776 102 974 384 660 628 515 206 284 211 002 610 538 044 002 316 739 768 785 323 244 430 801 158 744 890 722 810 347 002 324 427 422 177 042 891 588 513 161 937 981 781 981 120 361 068 617 074 507 146 969 873 961 776 709 414 801 099 789 758 669 815 147 250 839 644 565 139 157 008 903 158 421 697 554 037 195 820 773 785 570 872 605 092 010 961 658 903 097 239 103 084 943 360 687 608 061 948 575 200 021 998 824 106 571 169 170 057 935 930 659 605 896 900 807 268 386 712 891 500 560 334 068 845 842 386 486 661 929 970 838 889 966 947 302 159 783 253 378 130 256 725 737 916 008 340 209 188 997 741 820 353 192 236 112 451 012 065 295 049 710 930 820 185 764 608 743 674 698 042 855 352 671 550 348 334 028 600 356 749 468 416 384 405 126 369 493 200 702 775 908 806 528 920 570 625 681 085 118 501 597 559 635 128 568 054 692 272 254 039 576 668 033 965 457 728 367 387 093 717 535 700 228 305 395 019 228 446 059 944 504 224 344 500 289 229 070 267 850 248 535 383 258 594 571 298 124 075 113 989 424 324 794 283 554 235 907 120 388 490 019 402 746 486 837 578 293 867 387 566 202 714 466 264 841 793 473 729 453 976 994 571 207 568 497 933 587 995 913 426 341 335 933 489 829 020 252 518 253 903 016 296 305 383 295 361 319 892 495 942 818 627 408 871 058 119 334 637 128 941 376 124 580 805 806 088 034 575 248 322 919 050 981 936 294 300 358 821 629 017 266 554 587 174 973 596 231 489 882 525 602 261 459 251 863 311 101 488 806 143 088 231 593 186 523 906 825 290 024 466 724 154 370 225 009 002 508 689 410 548 773 973 422 311 614 444 737 813 780 314 410 148 639 983 698 599 007 576 856 648 664 485 507 814 099 472 899 198 188 087 037 986 220 590 068 632 912 849 193 938 622 472 264 502 109 985 346 053 831 987 797 317 447 894 436 406 630 661 526 364 317 132 452 753 848 048 846 839 068 795 709 128 835 569 579 408 749 110 308 161 448 929 201 653 771 431 495 279 455 062 262 423 517 958 109 016 279 056 995 233 410 820 645 194 089 984 747 203 747 116 468 499 507 662 000 367 173 809 942 135 995 490 431 932 795 959 700 125 181 523 325 815 142 403 786 848 540 175 410 059 713 674 893 309 454 731 503 256 169 009 796 787 037 221 281 914 640 481 833 984 678 340 217 768 707 853 513 138 369 049 991 204 869 306 395 420 553 918 897 728 040 987 938 682 746 476 110 226 136 784 773 625 037 994 484 309 787 096 910 945 720 592 835 304 256 693 024 358 176 723 063 527 811 994 151 046 863 880 992 509 756 140 903 949 838 184 425 034 784 739 507 439 199 777 723 727 530 217 989 607 715 287 865 181 931 724 093 218 279 369 175 447 653 914 166 037 545 200 452 680 970 358 251 139 193 658 095 201 352 382 277 188 554 050 202 165 491 455 319 661 289 149 405 531 824 196 662 825 967 831 301 718 568 136 861 465 000 165 171 729 958 954 737 300 786 656 218 273 689 590 337 641 009 696 784 545 095 430 366 696 537 142 845 592 959 950 347 486 929 038 724 813 727 589 680 190 425 754 402 755 975 469 194 987 316 565 361 820 265 694 683 415 571 265 885 485 679 483 196 939 902 462 962 404 984 253 923 656 110 679 133 471 018 690 797 447 927 213 171 227 634 883 186 699 248 087 913 621 188 304 279 370 435 803 478 465 661 066 783 228 387 849 092 972 338 522 132 111 851 206 272 665 277 728 896 033 149 433 762 308 570 329 278 215 614 713 275 739 200 095 387 687 596 529 780 998 306 538 281 702 252 261 547 773 540 324 916 884 096 461 728 098 969 324 515 303 338 113 192 354 215 052 445 582 738 743 506 786 842 459 706 687 992 376 701 365 039 275 092 685 673 016 611 240 652 252 717 291 863 898 454 505 299 243 543 864 499 052 736 250 348 657 415 425 939 733 852 064 195 112 679 465 867 231 873 220 697 292 752 308 370 058 945 109 466 959 877 696 158 711 818 070 898 639 665 310 747 234 596 741 185 259 272 603 706 227 477 515 303 916 516 605 266 258 566 227 100 733 943 964 046 419 796 837 891 557 723 946 955 797 756 813 080 564 065 549 468 133 421 731 136 758 267 081 528 305 171 792 280 552 833 594 000 952 482 138 567 465 624 520 492 185 440 668 500 302 859 198 250 592 944 268 387 156 265 422 385 372 335 115 693 257 101 030 357 236 403 692 245 710 213 373 392 759 433 852 266 348 151 600 608 942 858 756 514 853 276 144 226 952 768 770 324 560 970 334 274 069 237 869 432 972 230 441 091 249 237 834 667 468 786 055 185 041 907 033 472 761 703 289 800 792 024 720 759 916 136 072 993 951 873 606 116 477 733 674 511 598 031 746 067 188 003 970 120 772 555 397 219 977 937 600 340 897 956 169 288 465 992 243 415 918 923 942 241 096 375 941 348 953 807 846 212 166 013 153 507 181 904 614 770 495 225 141 727 079 626 923 656 767 589 850 382 223 274 621 355 762 150 984 118 394 974 273 520 789 560 088 019 985 674 221 263 473 352 988 223 132 672 648 608 945 203 257 233 200 351 913 993 186 783 344 453 031 409 062 912 027 980 232 401 771 210 772 923 438 086 875 740 004 090 976 920 478 061 724 177 860 391 425 612 224 281 928 174 846 036 827 110 155 605 496 404 993 174 293 067 229 146 515 657 610 790 105 214 321 260 327 679 302 761 004 037 758 521 428 696 830 662 825 559 847 294 185 339 482 339 904 253 744 017 998 296 909 245 009 751 753 485 578 806 209 025 183 257 583 537 412 828 959 916 128 492 614 724 784 563 568 478 934 558 652 057 373 563 361 716 252 769 192 043 494 564 798 250 185 353 989 793 470 832 330 814 511 252 433 218 874 593 548 399 562 637 360 630 867 432 524 223 276 021 701 162 027 285 330 376 339 030 766 297 112 485 625 337 146 893 680 155 202 982 267 858 768 424 390 753 355 696 900 499 515 820 981 670 478 964 737 782 435 820 739 706 645 223 061 569 138 126 585 716 231 001 933 881 327 890 434 877 376 216 058 382 597 148 072 808 452 653 963 047 947 780 909 457 288 757 675 981 195 545 218 979 896 569 945 710 622 399 455 414 681 405 422 763 758 164 433 230 937 238 595 027 916 567 706 132 922 599 416 169 440 403 556 067 502 113 763 390 908 267 987 990 499 639 238 844 535 312 431 333 076 408 480 065 137 695 978 580 178 768 208 363 143 610 641 301 803 923 583 925 816 845 396 627 161 208 671 381 945 181 234 473 324 794 329 026 935 077 131 451 276 646 050 433 344 992 468 243 379 337 450 985 663 549 269 232 047 571 256 072 430 787 435 085 085 992 115 060 633 492 831 209 642 906 049 024 144 848 828 826 762 940 739 878 766 868 118 458 805 181 285 209 261 125 764 641 392 422 616 197 332 000 598 953 718 247 623 656 683 331 941 388 428 563 665 705 911 382 132 688 581 529 551 100 476 249 433 262 834 853 738 618 066 141 658 618 855 903 510 776 382 412 087 761 854 628 493 505 725 192 246 010 462 470 441 156 037 226 390 880 778 096 271 758 589 886 052 226 592 910 090 646 636 314 011 203 566 834 547 032 166 170 777 031 567 288 894 071 545 878 435 893 721 632 350 885 180 363 814 851 647 172 483 762 040 348 065 996 316 452 010 990 921 398 275 517 593 300 135 462 204 151 773 475 870 385 334 650 741 412 182 275 553 954 511 762 476 745 399 651 839 167 069 989 132 098 734 140 432 102 344 485 966 813 220 620 757 483 262 976 983 991 758 264 112 116 502 343 705 289 582 248 688 201 232 763 931 768 250 326 655 624 183 600 138 359 786 858 591 268 361 282 788 600 868 021 853 070 355 637 839 036 755 372 863 829 554 504 945 825 795 814 111 472 345 654 146 190 018 579 545 488 101 053 341 823 540 670 574 731 366 466 905 020 160 743 953 459 513 969 938 929 847 486 244 733 367 386 776 799 404 043 259 062 168 643 110 488 783 444 860 766 027 243 277 243 093 636 840 454 154 222 378 584 698 846 726 983 486 134 699 812 842 908 672 970 275 458 502 715 574 349 351 768 781 682 351 459 390 130 624 980 313 808 047 664 460 965 331 709 648 118 919 036 658 757 668 544 366 409 455 516 044 558 469 800 886 162 674 856 660 138 365 026 704 996 914 022 495 985 454 063 416 405 098 472 174 597 592 576 130 726 676 219 697 437 085 710 479 787 072 077 813 648 574 253 671 608 831 727 278 965 366 412 724 756 366 438 233 655 185 046 632 647 186 761 310 793 141 335 861 373 103 416 507 120 253 091 533 553 980 687 772 023 585 832 713 473 763 001 445 118 516 433 368 419 813 538 932 000 582 659 559 687 077 890 623 850 254 451 171 040 656 282 726 353 874 496 163 115 863 082 973 059 844 270 766 575 200 119 522 093 434 662 953 112 376 257 343 477 806 728 050 105 678 357 178 808 414 383 029 627 006 925 298 562 939 523 951 660 918 600 920 217 229 648 040 390 206 245 919 791 502 329 382 382 961 182 744 177 853 472 281 521 974 554 036 117 785 917 414 427 983 315 612 953 904 775 980 133 344 510 870 963 439 695 490 686 344 321 726 620 418 343 144 917 095 687 147 014 010 427 456 729 328 545 763 444 995 596 487 518 414 989 737 836 661 234 641 241 696 940 420 743 258 288 157 636 357 121 051 563 865 891 619 647 838 304 543 109 046 071 845 484 817 937 034 613 434 509 152 921 105 139 943 626 355 778 680 117 793 663 400 100 282 055 644 491 765 140 346 108 924 142 887 497 235 411 684 077 748 200 474 770 640 235 145 846 896 512 918 921 800 096 895 973 417 886 165 894 063 983 737 360 171 553 692 794 465 351 575 745 516 807 046 281 308 166 742 194 485 131 049 559 541 637 352 671 379 692 060 469 472 518 800 337 104 533 695 549 397 500 007 024 702 177 381 384 954 925 574 927 574 308 176 732 657 623 666 506 181 427 504 756 294 224 561 509 774 247 810 230 758 323 336 631 325 950 536 694 969 896 219 628 343 048 133 532 993 545 533 531 146 202 944 861 998 063 298 729 334 571 686 763 160 757 962 037 619 379 738 818 904 527 517 111 115 473 723 110 484 690 449 283 679 583 079 229 918 753 165 429 187 282 908 361 551 853 925 578 013 549 160 169 526 836 996 515 398 468 301 762 040 888 619 584 888 718 159 038 178 316 514 777 385 607 520 551 326 854 314 040 905 897 646 592 347 243 518 411 493 965 327 179 132 411 482 748 900 402 746 167 232 657 337 966 323 953 657 950 921 921 529 355 296 023 231 094 500 592 542 791 951 977 449 714 952 214 660 054 299 091 018 348 088 972 521 299 631 190 484 223 420 282 663 654 561 331 940 070 417 200 018 975 679 491 174 688 816 382 439 043 135 647 143 056 714 225 941 780 648 698 829 351 731 029 548 534 400 236 934 933 108 678 008 504 804 645 730 397 241 986 566 446 862 915 600 751 296 766 414 573 610 193 317 839 446 973 219 805 686 800 766 058 392 702 395 841 653 631 688 775 055 406 680 629 351 308 227 899 133 299 038 844 800 850 148 370 031 412 635 803 153 555 416 959 641 273 269 706 454 530 716 834 603 793 682 299 094 424 613 798 229 319 216 460 216 737 398 964 358 175 676 417 023 147 606 226 307 301 979 389 165 922 423 345 233 938 874 038 664 219 560 861 220 596 862 976 212 733 482 107 520 364 651 462 382 041 227 661 625 070 576 138 620 412 889 588 516 776 959 943 878 638 702 169 773 302 428 633 110 001 564 407 104 369 215 303 303 205 119 220 988 983 389 957 737 913 976 226 611 212 097 379 386 274 126 252 846 286 510 318 655 681 138 369 139 035 701 788 439 568 972 865 422 315 593 873 773 591 336 169 701 895 849 963 846 661 438 600 951 606 116 867 405 909 710 387 189 655 515 485 039 877 294 908 279 261 064 412 105 792 203 002 066 776 204 045 518 393 867 436 286 480 892 069 495 238 851 112 028 364 555 787 559 354 446 438 526 881 834 270 630 195 274 854 116 098 390 616 635 626 409 071 970 958 794 668 312 253 371 210 848 677 426 633 918 788 142 671 110 352 933 519 348 403 527 476 253 641 076 266 490 498 525 259 383 879 023 520 093 735 115 774 784 994 125 921 670 280 774 009 934 110 588 437 404 711 892 291 565 388 523 846 458 901 629 274 080 624 449 082 016 986 160 927 807 234 632 292 206 654 496 995 421 416 249 383 528 368 825 123 387 931 680 855 445 155 797 583 715 928 133 843 608 058 523 416 352 128 959 327 286 977 066 049 184 302 433 524 363 853 882 271 857 559 018 020 618 553 027 710 069 680 656 748 685 604 514 016 119 085 804 110 703 480 265 576 611 384 260 426 182 199 507 464 484 348 346 247 806 509 387 371 006 359 002 241 992 697 484 692 177 922 906 753 634 274 556 480 607 804 079 273 198 224 169 666 855 396 175 115 171 140 436 256 286 829 213 566 973 108 600 246 811 633 980 883 494 107 500 865 586 400 126 850 116 445 259 260 335 412 446 700 543 528 196 190 641 418 923 462 534 475 214 672 314 574 769 091 307 046 297 587 953 337 446 655 096 012 892 638 692 538 788 669 291 569 137 940 398 299 113 312 105 590 175 053 545 434 120 980 024 604 960 556 253 899 207 665 157 499 341 588 067 469 399 038 813 761 913 372 589 506 320 849 015 775 212 073 992 127 191 267 847 889 451 305 935 875 153 569 492 128 157 821 746 390 503 319 302 388 468 876 096 388 326 563 818 353 577 437 211 470 867 879 687 946 278 758 802 154 944 379 095 021 955 947 081 878 013 905 988 630 757 922 606 352 916 171 524 236 376 390 605 589 015 460 258 356 224 255 797 211 753 414 236 519 472 503 482 393 832 580 640 350 497 262 283 400 840 011 109 201 151 328 132 538 275 897 215 483 085 971 531 710 201 230 630 913 125 725 244 459 791 979 212 796 357 851 351 127 323 166 980 991 925 482 832 199 530 861 773 801 095 251 522 868 606 499 843 335 612 981 855 621 107 677 618 657 504 282 897 493 001 856 901 499 184 132 134 598 585 351 200 519 090 635 357 917 550 538 482 163 793 877 310 603 859 182 831 042 542 286 937 560 643 450 641 196 600 567 193 380 207 378 450 485 882 843 416 111 265 353 282 203 517 816 737 229 345 031 188 766 848 284 152 276 738 376 894 095 892 689 697 630 053 279 919 456 734 582 172 109 706 479 872 790 092 126 612 612 492 304 992 126 327 507 050 779 137 072 902 593 633 524 492 147 572 452 044 155 063 550 130 303 639 591 563 062 532 732 623 510 834 974 627 377 948 257 318 212 311 728 487 674 347 766 337 628 743 374 950 153 238 463 210 862 921 047 300 831 434 629 845 254 614 004 507 061 784 393 049 560 859 744 444 460 389 367 297 660 930 468 088 751 968 062 458 517 521 206 359 623 936 335 647 419 751 659 569 146 827 926 098 533 390 766 131 615 100 064 925 360 467 025 750 350 213 876 302 093 748 445 867 494 412 114 580 716 337 998 283 000 644 864 214 775 410 726 294 114 498 523 015 014 629 982 463 460 208 041 074 383 936 172 421 981 330 635 917 735 892 485 646 104 142 162 466 288 691 188 957 172 837 781 827 190 912 197 498 378 502 689 890 806 040 447 962 178 686 203 855 610 415 361 564 030 691 237 154 770 528 231 370 771 348 209 155 336 813 606 021 792 399 177 282 178 032 064 757 281 359 628 360 866 269 866 062 759 544 891 050 468 248 244 697 049 496 888 830 620 897 670 396 314 727 723 528 774 763 218 710 825 050 603 795 490 631 836 949 736 528 650 884 633 398 564 695 454 804 885 719 791 823 133 213 725 974 058 134 487 361 258 623 683 500 796 910 449 090 265 485 349 721 171 546 374 352 070 522 172 271 480 885 315 446 260 947 447 786 669 595 149 072 068 848 817 118 486 656 618 816 527 077 811 517 069 427 789 222 261 564 878 167 053 735 171 221 577 065 148 160 637 764 445 601 639 420 768 903 683 883 657 427 342 292 370 703 670 414 235 167 450 133 510 940 573 962 922 658 478 844 504 371 867 479 834 376 325 172 064 825 248 793 609 760 197 832 073 970 050 406 775 539 071 197 927 849 676 650 678 078 611 088 960 139 598 054 787 972 871 688 712 878 319 604 145 107 392 256 685 910 499 544 720 821 729 703 549 454 886 517 113 295 869 453 602 025 826 704 540 533 972 594 950 373 286 945 499 569 552 543 819 112 532 484 275 270 379 133 604 199 644 491 712 720 993 809 223 990 261 460 439 692 922 392 319 661 783 698 440 120 242 055 915 741 331 665 452 544 284 262 252 779 813 885 896 120 705 263 463 052 021 078 355 288 857 768 417 786 464 295 056 626 731 031 613 913 735 683 183 779 773 838 814 517 254 143 661 486 011 175 547 998 626 190 382 040 602 524 222 609 680 974 884 298 264 141 581 496 541 811 007 134 414 724 674 314 331 537 317 476 363 967 590 143 238 018 457 204 302 179 210 082 740 440 014 096 777 420 962 357 713 655 355 260 584 246 846 369 584 183 886 083 620 232 697 550 807 758 304 205 707 012 085 006 963 980 220 293 992 015 126 729 642 412 922 756 340 125 277 662 458 855 744 762 377 877 268 865 541 088 824 049 900 122 896 355 425 903 666 857 018 862 731 260 263 907 199 705 169 355 229 153 214 829 527 979 168 527 109 587 171 652 354 238 268 768 236 459 042 292 588 387 398 020 005 586 742 877 586 515 617 764 844 172 807 663 818 654 073 547 308 054 231 948 334 846 906 851 949 758 267 382 012 525 100 893 569 755 850 877 838 407 506 654 107 152 628 068 317 149 631 598 305 735 290 257 568 823 496 043 902 036 762 791 794 126 527 441 424 461 838 695 304 821 233 679 659 815 805 302 869 288 948 385 043 124 573 874 868 088 999 176 621 185 583 972 262 905 722 498 148 898 169 674 060 491 762 352 120 282 540 456 996 943 257 325 559 904 080 014 565 584 871 300 590 217 967 887 994 131 510 468 457 348 885 146 331 457 330 277 510 531 228 282 586 349 148 866 627 714 001 965 826 518 682 970 410 740 983 917 381 659 496 356 194 321 161 513 083 030 777 677 765 653 980 923 144 116 585 048 130 623 950 233 079 341 262 981 329 992 395 801 193 581 962 350 060 936 674 259 438 041 088 223 290 748 015 430 758 271 762 465 493 463 086 010 433 608 629 189 973 256 193 941 437 340 618 001 356 235 058 903 095 755 845 483 292 000 866 592 232 550 545 833 368 370 367 528 133 152 400 008 012 185 285 024 682 128 785 151 099 702 885 372 435 325 308 450 632 719 595 934 261 213 794 690 802 026 518 774 419 994 867 279 020 782 989 313 684 215 734 487 669 705 226 967 478 560 606 058 336 479 808 441 621 461 515 185 767 922 580 480 966 949 754 729 999 883 882 118 286 595 991 690 041 267 349 968 569 347 497 363 375 228 567 576 102 503 135 130 927 630 155 936 959 568 284 452 045 070 920 208 566 978 209 296 730 866 758 143 620 211 164 484 072 485 447 192 129 881 133 925 555 542 290 498 268 305 326 908 756 495 651 984 731 690 705 961 499 286 830 666 127 999 376 835 124 082 934 641 786 762 440 183 926 727 877 441 418 882 311 724 988 882 603 399 430 612 210 893 811 385 907 613 871 104 216 977 672 795 708 400 721 948 592 746 950 298 492 282 535 597 735 116 191 598 777 874 438 912 680 086 898 438 136 984 598 233 530 321 763 390 778 580 324 446 129 271 188 081 401 758 927 021 866 461 961 588 298 727 425 574 189 767 818 947 173 258 240 036 048 037 905 268 114 841 103 778 770 805 734 590 603 904 526 280 519 072 731 875 361 506 699 237 718 539 803 916 281 114 568 558 473 732 809 871 609 914 318 924 988 863 974 592 851 799 831 925 828 358 866 126 056 121 372 315 982 968 940 500 444 797 976 362 551 143 442 933 266 045 832 765 653 648 517 599 186 745 546 214 678 153 376 032 334 582 389 002 983 317 599 868 370 033 995 888 792 399 849 092 382 170 047 644 558 080 881 794 548 157 893 866 579 096 084 051 734 352 365 320 118 044 014 292 039 305 316 135 448 778 032 729 942 071 716 935 003 850 583 972 449 331 393 023 850 809 492 944 135 028 527 387 770 602 785 845 353 102 561 673 767 853 533 630 665 770 299 164 617 546 457 042 067 901 984 659 624 219 926 019 234 915 041 605 503 733 688 770 179 639 015 017 060 171 948 658 878 701 140 558 322 026 595 573 660 025 691 149 650 148 120 248 552 500 188 310 838 056 286 665 125 098 710 308 206 743 333 822 148 167 163 899 526 225 924 635 760 447 847 400 197 174 863 036 409 364 459 213 059 246 625 645 249 673 339 960 510 132 713 399 782 335 301 590 347 344 069 160 263 712 002 681 009 876 394 907 629 306 543 716 378 831 662 561 578 552 948 468 508 893 954 882 017 932 841 856 712 023 384 988 913 350 867 936 446 243 987 607 631 491 987 852 893 954 263 175 950 459 485 949 315 704 681 076 632 449 004 333 023 562 924 755 386 333 440 369 019 451 950 391 437 234 012 826 674 699 344 264 688 410 285 760 432 707 320 267 268 731 015 255 367 619 471 961 861 921 543 682 613 081 968 596 156 584 482 198 568 770 751 247 311 453 278 110 897 237 240 978 393 313 021 744 503 283 416 135 413 708 419 134 357 581 590 865 060 894 952 457 116 021 809 621 061 996 390 027 551 048 258 432 200 582 246 009 906 004 704 980 360 569 032 783 652 394 947 661 198 414 338 789 266 074 051 961 205 921 245 047 528 303 165 298 053 776 722 296 930 157 935 039 574 533 790 640 693 572 509 959 353 632 831 731 709 651 179 206 142 632 528 121 178 405 396 620 655 518 955 051 918 650 041 243 910 514 100 912 277 008 486 884 138 773 857 905 669 558 869 419 786 275 837 650 754 381 040 501 130 898 247 727 008 866 876 848 679 356 625 308 316 783 467 300 377 043 199 936 661 462 673 212 464 436 644 901 533 149 061 365 058 735 388 341 793 432 912 299 800 318 317 417 292 066 024 366 444 287 244 896 528 390 705 061 874 803 042 880 062 871 298 682 939 935 003 613 875 599 351 869 517 540 078 243 057 033 871 483 070 954 575 337 813 498 555 967 927 520 942 101 303 162 127 893 771 237 127 141 661 263 599 219 537 655 577 706 565 795 240 754 787 175 184 653 622 798 197 215 273 802 513 829 936 277 674 839 834 003 726 734 333 201 064 702 643 183 310 592 165 790 246 314 378 834 279 490 585 102 788 762 740 551 552 510 190 897 566 788 767 380 532 235 039 670 691 368 635 714 095 294 710 628 479 065 410 902 602 745 268 013 938 696 873 666 395 298 593 683 575 095 012 842 987 986 563 559 515 764 813 264 396 272 406 886 178 255 556 144 864 029 742 827 774 867 121 828 904 938 182 545 011 834 285 577 390 121 586 431 252 987 546 455 220 621 145 086 159 724 048 232 260 149 375 760 645 914 758 332 099 878 769 536 375 874 565 939 629 853 680 928 461 723 396 933 956 950 402 112 326 164 109 793 148 967 308 192 463 660 441 986 573 923 369 030 140 434 043 201 463 067 653 629 548 264 562 676 856 030 353 409 721 377 803 983 147 508 233 756 112 254 078 490 106 957 801 640 638 130 849 728 663 228 158 485 363 876 804 627 075 601 290 357 699 416 166 800 713 191 947 835 578 776 730 605 276 672 696 961 749 445 317 342 652 754 331 934 872 555 512 748 382 007 952 839 980 261 351 399 362 878 668 631 986 878 615 539 090 563 042 013 165 450 553 722 845 226 204 636 726 505 095 685 923 733 813 474 469 846 559 263 515 389 149 546 825 525 965 777 715 315 361 175 523 635 449 832 175 185 060 466 775 194 669 968 253 331 808 059 376 563 229 189 711 079 890 776 856 444 313 570 145 985 679 356 881 551 606 552 888 214 047 544 545 393 918 735 705 111 723 713 470 202 453 734 603 954 620 328 181 077 623 175 736 638 560 638 828 554 683 552 905 820 389 927 390 746 983 304 216 753 364 085 163 547 318 726 309 357 479 135 254 203 262 134 442 920 172 137 693 619 951 061 771 955 369 612 156 063 318 537 254 958 619 774 101 588 401 802 271 867 017 152 203 417 620 590 188 011 937 965 506 461 148 896 802 010 696 600 581 873 761 024 323 210 140 317 705 704 694 334 593 220 926 701 765 870 052 003 417 663 294 826 266 768 640 214 103 679 859 795 852 170 564 214 927 771 444 891 650 252 383 279 916 395 211 983 635 069 786 700 184 560 853 243 670 003 443 285 362 048 894 991 560 807 851 340 038 044 623 370 458 617 537 222 998 067 453 558 260 003 935 857 508 819 303 643 494 883 868 249 327 158 184 525 724 429 980 230 575 340 845 233 271 751 912 755 953 133 566 138 265 269 114 710 847 232 579 316 240 486 918 531 051 852 897 845 545 956 129 660 396 959 311 867 737 387 328 654 564 756 556 644 715 944 216 254 051 787 239 517 682 293 414 747 289 456 137 050 473 474 722 879 502 642 604 492 337 730 894 661 495 169 745 289 348 487 511 926 197 867 126 410 177 826 206 693 529 716 432 133 973 805 256 307 506 025 669 144 878 369 352 488 118 479 103 371 386 418 825 833 839 794 435 074 563 818 680 185 953 692 139 218 974 777 355 003 961 383 665 080 545 276 983 677 722 259 706 339 461 381 117 174 156 110 212 392 066 216 499 612 365 614 225 381 092 811 251 884 828 825 573 057 870 837 089 423 533 221 174 769 639 327 668 180 248 693 201 838 023 765 544 487 678 189 378 213 605 771 018 702 528 360 989 089 389 558 390 901 045 387 124 297 113 752 842 512 806 447 084 271 385 440 762 132 588 941 512 797 644 855 420 172 887 397 241 381 840 194 809 025 805 364 531 356 952 415 250 270 494 809 912 469 950 221 550 732 738 753 328 881 578 326 767 453 698 178 265 027 340 712 162 217 757 510 818 356 776 135 445 094 077 454 033 243 727 970 964 345 417 825 279 075 606 749 390 009 635 298 036 057 160 072 614 010 987 989 431 800 421 893 719 500 228 740 358 737 303 938 306 608 060 880 063 679 572 499 304 281 565 727 965 988 384 307 958 169 930 536 641 491 360 213 048 323 702 854 712 228 924 009 355 721 460 564 763 355 099 087 299 005 528 675 125 600 888 419 224 317 531 766 930 295 926 567 151 282 380 923 505 876 345 617 073 825 545 209 890 104 366 529 287 049 962 367 319 797 929 714 217 155 108 187 600 651 135 950 729 891 299 626 964 781 680 580 839 240 170 101 104 934 743 866 825 540 130 122 895 004 387 727 464 464 347 706 092 875 802 662 184 095 454 505 302 999 722 174 608 405 266 395 427 752 972 570 492 715 370 646 582 901 204 863 253 358 437 035 007 186 325 067 406 066 173 423 538 398 820 951 182 532 526 947 851 932 383 602 288 475 490 849 005 737 280 867 407 895 974 265 067 088 107 161 948 071 924 017 710 633 481 084 693 754 565 787 973 395 313 915 655 314 607 975 397 151 336 358 621 561 492 232 038 832 449 636 177 139 280 105 542 722 819 702 974 468 420 935 802 477 287 127 414 413 913 016 309 333 145 469 527 081 942 262 554 265 078 515 631 358 143 144 856 878 215 816 376 587 011 518 511 115 335 722 987 109 791 545 163 034 743 533 382 701 696 443 298 805 877 351 988 168 311 196 156 506 249 498 373 522 772 566 309 564 843 366 157 630 073 648 513 980 070 426 060 965 449 703 918 374 618 522 724 796 641 515 425 380 623 971 265 279 608 300 535 351 783 967 139 528 367 565 384 493 444 059 877 033 731 699 196 204 087 708 620 409 046 431 207 021 651 125 642 623 777 530 713 953 554 427 114 975 980 975 464 226 476 090 226 514 749 758 267 742 170 764 846 836 682 855 087 477 461 868 419 701 698 493 999 526 553 371 398 794 938 398 431 297 511 963 407 396 841 479 720 187 281 147 233 180 489 319 058 714 637 397 376 867 372 650 423 034 639 284 453 515 588 603 423 044 286 435 311 394 457 969 160 012 319 217 180 418 492 762 284 288 627 345 604 141 146 634 795 887 888 098 181 636 060 149 004 414 772 658 662 493 550 320 725 638 829 018 368 895 014 299 417 795 659 315 923 793 651 257 369 048 199 746 442 012 409 095 851 109 186 416 295 142 833 586 367 374 232 947 238 601 365 346 160 780 725 120 354 072 990 888 763 810 749 314 652 487 045 406 862 707 273 044 190 081 961 512 534 090 937 633 036 334 674 395 925 792 519 379 530 384 976 076 728 471 300 772 675 890 555 903 698 947 232 348 069 191 695 125 717 219 729 481 967 255 961 209 989 779 661 100 788 831 762 680 972 776 736 530 986 940 122 768 314 920 534 775 938 618 531 989 964 827 360 916 582 555 714 247 864 996 543 476 006 706 590 586 291 733 391 291 655 418 369 965 296 838 034 615 085 391 949 764 262 467 298 823 286 944 074 420 748 109 390 590 258 384 318 051 975 321 278 139 568 678 067 614 714 309 865 694 073 188 279 253 053 513 895 312 833 247 336 837 966 488 340 785 590 638 512 579 061 073 790 123 812 541 055 208 053 865 601 167 215 812 175 409 745 667 129 516 274 132 766 766 907 882 590 908 250 668 015 037 953 227 285 027 689 374 413 956 850 485 883 666 808 950 481 546 413 721 664 478 021 760 213 267 051 272 135 959 401 514 591 881 682 264 253 848 041 661 302 872 268 387 633 266 833 360 950 725 011 128 572 292 346 189 959 778 486 771 770 879 216 204 165 639 423 668 684 990 557 681 349 148 200 365 637 691 767 499 936 960 267 925 451 873 536 036 185 927 465 485 589 400 596 480 884 635 278 862 801 829 549 751 064 580 168 531 574 892 167 702 953 892 103 133 920 554 194 173 077 601 492 982 350 775 034 364 683 853 330 633 752 379 436 140 731 138 080 874 596 262 909 664 114 991 127 073 270 491 175 633 463 488 490 315 207 080 298 854 124 773 047 515 979 282 652 509 135 140 831 902 463 146 860 637 325 393 063 013 366 963 555 219 433 597 331 694 557 959 903 770 210 602 102 328 915 821 445 377 880 383 332 175 281 957 947 050 050 211 194 827 210 602 101 332 341 988 642 948 174 936 298 279 612 329 593 060 407 472 790 368 952 414 989 530 931 732 863 803 781 449 796 568 262 076 528 176 235 606 073 850 250 442 681 156 691 746 336 832 259 657 941 895 175 048 501 363 206 688 951 401 535 480 268 786 746 047 055 825 544 724 656 188 966 842 276 926 429 643 338 143 006 854 216 595 554 380 272 962 404 575 382 999 365 644 422 431 865 851 588 185 249 761 687 074 865 564 052 998 504 790 727 370 064 875 667 838 937 426 517 673 670 706 287 593 457 405 534 269 061 412 285 071 722 318 716 788 928 893 190 361 807 604 525 544 743 924 038 167 893 801 360 012 691 448 898 742 827 015 150 420 630 704 921 108 447 423 604 931 416 333 503 831 049 424 888 589 458 986 637 081 100 996 198 080 127 063 731 318 225 061 031 363 084 281 482 400 628 031 827 408 753 015 711 841 789 295 110 701 607 000 912 750 766 007 708 743 722 770 541 929 408 170 503 147 403 901 962 918 779 782 245 343 470 401 246 860 147 342 026 499 489 456 994 100 176 871 836 866 485 175 623 248 864 384 931 554 892 853 912 131 012 294 676 673 985 453 133 678 882 049 144 410 899 589 568 171 140 551 036 185 506 442 401 140 435 944 991 763 985 056 772 902 249 714 605 991 166 915 489 032 885 536 874 333 497 632 372 650 104 065 739 580 313 834 494 072 303 701 404 334 466 479 960 522 786 755 777 280 961 723 745 183 298 576 404 024 506 039 376 799 974 471 830 825 954 546 388 213 230 049 388 227 420 095 498 456 559 183 099 640 035 990 930 411 776 694 943 954 599 654 795 994 587 802 200 816 993 788 056 222 095 008 537 690 970 129 618 326 475 092 333 248 528 324 477 896 214 981 668 317 299 176 726 991 709 202 080 273 043 947 083 660 325 540 849 654 596 603 308 519 749 756 018 936 410 920 800 185 981 262 010 001 347 302 217 188 645 084 514 095 444 674 684 654 793 922 734 083 727 139 176 268 117 195 879 149 335 492 417 610 174 717 373 268 006 907 179 277 409 914 322 163 034 567 344 997 430 485 021 810 336 005 624 100 053 315 756 611 166 172 552 468 958 669 872 956 101 800 156 310 958 003 421 074 040 753 171 230 026 391 761 669 054 280 364 406 212 117 529 320 094 216 712 972 343 900 777 350 313 153 208 603 002 457 725 727 269 063 890 501 353 048 969 140 968 412 714 610 158 097 148 378 517 800 545 791 541 518 607 364 206 573 832 053 005 284 209 730 792 486 600 643 419 274 998 179 569 306 753 780 387 286 014 724 753 869 700 174 348 716 805 874 708 209 842 025 129 223 956 457 246 112 528 294 819 972 938 949 176 536 780 530 756 313 561 297 654 901 372 873 821 299 794 112 424 084 614 201 077 859 507 165 217 762 930 521 550 197 526 960 539 899 654 667 457 600 547 313 832 493 979 312 011 416 124 858 964 943 767 326 529 503 781 272 045 438 872 410 493 337 298 967 813 446 646 174 806 412 243 612 619 992 177 545 851 746 068 198 841 589 841 600 654 377 580 736 911 497 032 646 113 711 416 025 522 739 093 200 881 459 655 049 026 404 930 042 654 435 032 404 046 892 301 902 765 537 680 382 762 270 552 584 441 366 641 043 832 005 032 011 894 944 850 077 752 905 976 977 913 823 226 057 887 804 364 786 235 193 277 416 512 440 345 767 857 439 875 030 182 055 990 169 205 944 267 615 725 487 636 474 888 615 418 931 054 259 613 836 892 539 145 348 245 145 121 997 709 880 529 551 937 258 019 002 323 057 903 462 819 351 216 729 978 813 082 505 606 061 247 318 947 078 038 385 376 698 501 794 573 402 801 532 005 514 725 501 222 039 789 289 150 142 702 215 139 917 331 480 750 130 658 105 735 059 738 830 493 084 044 263 225 127 190 807 436 012 765 645 526 251 992 903 925 432 111 849 509 894 959 457 090 292 102 308 057 082 379 322 887 190 556 740 872 931 174 126 496 754 628 389 966 520 781 379 739 350 593 990 843 973 274 308 156 952 383 462 261 896 633 725 491 581 455 587 441 649 801 499 909 349 537 202 604 763 403 501 587 447 584 836 215 197 351 435 558 920 110 282 669 353 825 951 980 089 138 657 447 422 271 467 164 332 648 070 248 247 223 648 874 012 273 785 264 473 726 686 674 704 067 118 875 835 790 313 991 216 309 629 139 994 130 043 320 954 658 239 552 817 427 804 147 639 772 279 757 984 777 655 175 141 617 078 426 887 648 929 978 589 558 885 462 209 442 993 911 721 985 885 285 147 177 192 373 085 320 314 627 194 030 463 079 253 041 191 836 981 136 021 239 410 912 356 869 709 145 817 475 312 438 633 989 581 726 636 002 644 634 974 491 701 229 949 615 322 759 435 554 865 501 391 672 070 617 629 826 731 680 808 391 962 605 041 953 425 522 181 393 203 785 933 914 637 486 470 197 381 214 739 944 950 249 912 120 832 891 830 780 031 889 231 291 196 643 223 573 020 996 647 938 346 302 408 368 161 906 425 673 347 588 185 937 030 978 002 967 750 838 267 688 724 401 001 910 162 687 477 131 078 574 043 496 776 155 448 379 727 875 852 903 576 452 157 885 808 257 654 969 848 868 435 942 923 120 244 118 848 282 875 511 057 598 289 799 313 253 100 267 004 096 710 786 200 591 985 964 923 069 093 699 688 117 959 130 023 528 597 625 121 111 966 578 919 292 550 386 851 370 116 347 192 139 624 508 937 742 774 681 369 609 081 418 082 959 676 998 675 525 329 826 224 795 738 954 048 129 030 755 472 481 651 682 967 465 871 397 543 585 111 060 214 635 658 354 497 812 698 469 858 945 204 813 525 954 900 113 670 871 389 312 285 292 201 847 602 389 545 577 214 696 254 326 556 441 942 578 654 500 261 457 126 108 354 530 688 314 070 557 996 006 364 147 949 217 490 742 058 415 303 776 175 733 712 232 977 818 223 773 585 036 294 108 819 096 544 941 167 976 623 679 062 657 824 292 082 521 279 458 648 936 267 685 253 432 664 698 896 608 418 588 409 154 837 996 955 963 238 148 941 151 840 834 609 198 456 389 952 955 562 705 259 470 374 643 263 807 561 606 400 519 034 637 585 110 185 926 394 440 395 225 454 860 095 868 205 665 932 932 432 663 403 333 793 684 137 197 168 223 855 122 964 299 339 712 747 078 469 127 952 006 402 530 231 455 288 117 106 298 273 881 171 875 119 078 681 546 434 731 616 489 460 625 542 029 908 183 033 853 407 033 921 823 959 599 053 438 691 209 010 255 480 064 796 919 205 205 150 604 545 391 597 498 405 820 479 254 790 366 903 182 083 690 134 936 354 280 900 940 879 946 793 009 138 763 709 424 161 663 019 314 318 313 627 699 168 293 643 932 007 306 708 111 129 589 310 868 906 394 293 713 684 455 998 474 705 427 274 736 628 394 763 772 272 527 466 644 912 199 674 102 669 090 627 781 084 745 433 475 153 994 527 524 110 926 544 671 593 220 704 189 924 984 274 078 739 242 123 720 579 298 505 437 672 791 061 183 911 436 775 740 861 822 567 310 382 875 410 408 235 019 621 967 775 080 327 736 707 781 246 937 999 226 840 974 514 015 683 367 758 699 120 018 788 537 012 341 168 049 602 623 125 118 262 664 750 427 330 780 331 327 410 976 202 771 231 876 795 064 382 302 374 143 650 578 457 364 095 316 755 871 901 501 307 771 712 404 034 018 092 860 615 832 488 897 647 665 206 427 199 195 908 825 654 129 971 708 151 955 210 917 389 842 188 091 202 319 041 282 742 969 600 506 905 870 818 999 419 368 356 160 733 816 752 965 495 794 576 577 276 880 493 745 752 372 839 110 644 489 297 002 169 657 222 693 911 961 561 417 562 343 705 292 789 099 591 919 931 650 084 138 189 755 092 625 450 534 051 912 311 830 389 816 698 538 417 859 967 905 288 057 584 622 899 247 319 361 589 100 522 783 190 223 353 441 225 634 132 924 140 230 970 071 433 323 781 312 340 921 850 133 770 586 809 841 805 915 378 463 268 807 220 770 424 933 141 776 410 408 035 302 441 142 643 927 798 287 330 960 233 297 308 605 703 146 421 438 148 227 764 538 859 382 580 239 434 847 703 971 447 008 530 341 648 466 579 632 023 089 610 701 792 962 435 291 295 119 430 426 670 783 539 241 026 518 700 084 364 761 069 494 415 667 099 510 315 653 780 417 401 231 197 184 989 626 118 787 155 734 151 121 945 714 350 637 287 554 037 488 694 439 848 087 676 197 086 227 855 602 964 484 923 387 415 375 362 325 356 997 873 973 386 552 528 921 589 508 436 338 250 351 134 707 107 220 417 191 306 452 369 399 964 839 386 378 247 081 233 019 661 710 401 346 047 480 797 539 399 245 878 692 290 002 124 201 790 933 773 880 973 251 190 833 368 790 184 510 881 807 437 319 265 694 991 437 689 260 036 974 182 205 455 213 203 948 720 696 079 640 143 331 760 790 240 601 897 724 805 694 722 455 619 621 761 321 653 470 253 442 934 209 731 463 716 940 396 946 966 521 741 956 898 212 698 906 941 052 661 072 835 343 906 074 324 615 341 192 266 243 833 153 208 839 905 003 259 268 159 364 605 180 574 066 560 956 139 920 692 818 832 511 368 645 576 071 840 656 169 219 226 734 468 465 423 892 549 293 990 088 047 247 000 284 340 488 603 096 813 125 259 012 866 231 714 092 752 479 299 201 108 706 283 525 081 702 443 594 406 054 895 200 840 256 336 036 409 729 784 562 500 180 681 768 506 907 974 604 622 945 173 589 915 365 286 333 624 426 057 742 349 831 262 137 784 030 898 988 370 901 107 796 917 077 508 637 007 695 147 715 992 499 783 163 299 210 676 563 221 468 606 931 838 469 693 712 387 091 411 376 388 124 627 051 124 055 115 224 857 667 093 900 033 112 491 079 958 386 254 828 646 620 960 512 973 876 073 752 326 828 811 520 195 950 813 446 967 548 409 277 139 311 173 709 676 799 184 573 920 479 050 161 833 590 641 217 061 565 956 883 310 590 137 858 221 490 922 524 750 893 729 245 684 287 169 306 158 333 040 655 308 685 673 205 069 354 269 115 036 854 329 550 910 687 144 865 947 807 406 276 262 787 620 587 705 512 847 160 415 205 268 684 992 340 053 048 774 858 745 269 697 143 099 949 559 460 679 053 868 469 939 712 780 504 623 330 603 199 366 550 923 588 076 923 074 256 245 388 773 997 263 975 061 561 480 054 863 126 108 469 992 544 470 311 792 372 041 267 423 155 434 189 184 946 121 356 669 597 549 229 959 045 749 366 155 348 637 178 711 006 752 213 290 552 642 908 527 139 630 898 160 003 983 142 150 920 547 369 400 624 501 778 711 301 318 903 957 851 077 095 070 444 988 237 885 843 895 088 004 018 112 296 728 591 218 132 586 516 541 133 162 653 493 134 393 809 446 566 055 034 337 340 176 926 347 308 825 867 176 603 989 668 725 362 719 868 428 051 718 138 635 243 896 082 135 769 416 428 998 463 445 747 307 367 593 089 439 951 889 976 850 021 849 698 221 892 544 955 088 135 513 872 379 791 686 609 526 671 008 808 712 882 551 239 748 323 870 736 404 393 412 535 590 180 618 678 869 221 764 127 236 335 065 555 131 287 984 707 293 424 761 091 838 298 617 899 326 913 596 673 276 161 477 476 555 612 049 827 571 627 406 270 370 650 265 517 130 742 817 178 266 532 422 438 345 102 792 027 639 716 371 665 045 858 971 127 154 563 975 328 842 969 754 489 238 586 287 367 293 164 775 837 063 144 668 961 745 425 846 211 137 068 500 117 325 290 603 934 269 781 528 964 039 725 911 920 382 633 895 962 179 527 889 022 481 342 245 388 713 474 276 796 970 129 390 130 844 691 170 380 864 428 534 573 664 289 447 942 668 848 280 047 099 590 834 247 724 540 247 357 624 372 209 178 571 878 561 288 680 743 560 333 542 464 899 715 188 137 722 660 438 201 605 529 439 878 968 695 113 676 193 626 758 484 243 345 721 914 561 860 313 888 632 196 064 746 636 490 277 451 796 874 036 982 754 508 870 192 137 967 548 071 148 330 513 190 372 837 752 196 500 992 687 189 289 410 606 807 297 146 359 138 560 814 620 475 065 444 339 501 737 971 338 572 405 576 414 301 577 358 059 251 346 387 222 467 479 307 890 976 518 587 473 448 615 094 322 998 301 310 663 352 047 195 055 734 680 745 296 251 329 474 717 265 904 715 576 365 145 762 568 509 312 762 855 973 306 089 962 365 035 419 020 597 841 937 664 458 362 981 702 912 213 569 939 742 899 529 047 355 155 018 191 013 094 112 432 193 657 644 081 168 565 239 891 128 353 515 037 992 777 843 154 570 773 206 501 514 586 750 797 735 495 967 849 572 003 434 738 730 831 918 424 336 532 273 496 109 940 081 195 825 443 586 022 788 490 800 474 616 419 648 321 439 914 673 693 749 127 308 413 262 601 292 119 579 305 564 056 799 185 467 640 706 299 006 434 149 913 653 947 580 013 670 404 088 514 414 221 258 559 833 249 195 583 175 355 211 975 941 887 451 712 860 539 627 076 185 890 837 643 819 875 228 874 690 581 641 643 640 037 907 401 366 331 583 920 508 750 544 113 292 712 700 732 286 705 353 615 063 051 378 880 311 765 195 443 676 087 916 104 760 547 723 695 095 340 841 740 648 938 015 736 072 103 916 616 141 547 538 819 673 952 107 856 197 203 754 438 090 178 756 041 646 132 782 087 068 749 226 579 100 916 808 394 077 691 339 456 269 114 417 686 215 297 353 346 447 656 171 702 775 813 214 978 719 552 287 764 154 598 410 418 503 777 736 461 876 520 226 313 575 164 740 913 589 506 434 942 738 299 612 931 571 985 039 320 093 695 979 325 072 053 426 165 975 967 480 744 552 402 593 091 219 062 927 892 306 105 185 947 484 204 582 833 473 553 167 912 875 057 379 092 587 839 201 885 376 222 761 631 540 356 638 181 235 855 707 979 021 450 535 792 399 485 726 578 805 229 174 736 650 373 754 174 319 063 901 051 971 387 403 372 618 726 786 392 071 677 919 920 237 775 100 827 612 621 033 980 875 716 828 542 132 101 248 224 769 365 708 059 942 196 827 202 374 699 906 522 474 355 061 460 721 213 207 416 481 846 030 371 045 741 679 987 783 082 069 367 833 766 570 856 499 567 381 149 598 826 213 300 216 360 023 726 706 648 465 871 096 924 617 111 281 537 227 210 530 923 520 739 917 385 634 211 565 841 422 233 364 449 906 096 816 656 089 340 046 428 395 676 117 333 631 308 908 766 480 881 104 708 947 772 340 436 201 176 433 660 114 356 966 520 178 612 950 462 834 627 192 463 303 995 116 764 884 648 094 598 603 113 334 909 379 529 241 892 442 589 452 817 202 320 659 048 439 566 414 215 837 509 267 938 259 547 942 789 104 966 946 242 179 278 189 752 500 416 753 930 222 169 356 303 087 430 430 644 413 234 664 133 227 020 969 531 747 389 699 290 447 210 744 927 163 315 458 512 754 647 995 705 774 729 197 996 933 973 060 565 271 541 197 490 793 435 795 858 421 717 670 492 128 099 329 184 932 223 499 757 475 809 647 419 025 295 868 958 439 194 545 490 619 181 151 583 285 358 861 400 721 397 857 609 781 661 120 159 174 269 802 898 248 982 916 066 093 792 805 112 454 756 642 253 117 770 949 814 998 594 916 837 051 325 737 158 844 478 600 345 386 780 814 834 544 456 079 024 603 135 535 385 324 999 551 927 224 149 650 047 091 109 822 775 760 702 237 706 367 846 017 993 587 806 612 336 161 188 118 767 057 803 187 697 019 304 133 618 699 797 536 010 676 746 918 789 294 839 840 231 072 578 807 572 280 671 125 115 775 250 718 711 405 483 602 978 457 937 795 955 878 952 890 689 596 444 518 652 613 497 243 833 276 849 171 976 813 176 254 767 594 423 116 092 789 398 386 313 480 871 932 582 579 321 082 724 268 500 989 515 224 389 985 382 812 251 130 048 926 982 953 512 810 419 744 228 962 293 960 009 942 834 649 988 847 398 867 643 977 979 267 276 148 764 434 485 405 432 267 507 323 966 165 333 891 567 211 787 881 769 953 717 509 193 578 114 943 496 617 259 074 004 194 455 072 510 276 080 348 180 452 193 909 197 742 640 053 999 311 756 932 263 893 392 492 823 657 333 873 162 501 960 954 460 848 158 061 279 241 741 408 138 129 975 173 597 345 219 950 699 927 367 082 825 825 149 313 528 838 920 935 923 872 501 854 265 894 534 942 172 211 409 112 308 965 738 020 359 232 302 232 753 065 748 696 310 619 783 202 485 054 397 560 344 213 940 054 548 216 369 552 143 922 568 521 487 026 724 903 797 221 904 140 678 678 943 529 301 157 205 561 300 085 970 660 114 132 358 008 501 902 795 430 075 774 820 423 344 792 976 766 800 452 138 587 261 476 368 140 116 064 592 194 149 151 284 408 631 747 640 712 662 036 543 359 269 698 849 511 084 362 663 346 255 684 179 016 326 492 872 688 707 962 704 557 986 761 354 428 098 246 799 715 775 875 284 596 917 559 151 440 255 953 532 001 098 277 381 814 625 191 611 708 831 734 742 358 217 207 996 871 845 306 330 247 918 327 368 318 813 427 936 057 214 237 617 515 782 403 960 342 611 376 802 571 546 872 902 210 548 808 259 054 109 844 822 354 523 269 963 900 337 357 805 492 612 600 429 429 777 511 342 829 833 794 131 026 160 746 145 564 829 555 348 847 089 666 304 894 923 264 725 051 477 551 872 805 037 831 902 949 079 497 691 029 705 398 156 685 710 179 759 954 967 275 792 084 879 920 732 303 345 473 610 004 357 026 469 971 565 345 509 859 937 683 525 276 172 329 019 216 005 301 645 494 266 686 286 624 460 398 605 776 342 901 162 610 328 893 341 936 195 459 311 348 053 628 617 329 487 272 772 686 338 654 157 890 325 765 966 815 754 037 257 217 193 460 150 110 780 880 860 271 160 685 741 876 755 049 009 648 604 211 750 470 553 896 700 420 106 034 582 275 308 133 768 962 119 628 907 666 598 103 527 600 161 593 336 275 867 339 758 301 036 311 664 481 266 858 079 352 222 622 672 763 876 417 247 420 737 295 804 793 013 678 065 342 077 564 305 004 663 331 249 576 289 599 506 913 247 543 090 721 243 941 903 580 403 335 615 243 004 536 679 635 404 502 466 414 445 196 647 547 809 928 976 019 511 239 566 788 990 344 392 083 032 077 254 851 333 372 494 398 627 973 789 806 930 155 998 703 982 881 307 563 616 459 534 722 866 175 390 319 254 052 277 732 133 841 864 740 103 876 044 430 614 186 081 603 604 333 803 043 334 544 818 759 279 021 689 499 227 328 374 447 526 002 974 358 812 447 341 487 300 805 512 109 137 248 616 938 495 180 955 462 677 560 481 948 627 877 062 960 791 650 859 717 612 266 605 021 472 175 852 301 788 650 249 270 763 720 641 974 855 960 285 425 011 273 387 448 852 671 693 509 204 131 278 241 638 186 153 094 492 584 343 654 029 602 547 262 598 025 560 678 010 706 503 516 498 042 257 961 067 410 075 742 565 003 144 920 661 310 361 328 225 889 689 905 892 350 237 456 576 650 752 908 490 765 024 735 672 446 312 493 481 349 033 980 446 954 356 327 193 497 904 557 655 597 498 161 779 158 040 446 726 253 444 117 311 555 354 293 890 786 108 889 146 583 818 471 392 798 234 102 623 162 014 271 063 596 202 061 934 001 049 025 486 073 655 487 580 155 835 043 913 125 588 952 668 053 977 569 915 709 133 336 704 316 852 000 605 415 804 995 503 948 825 302 739 638 131 213 905 546 583 968 077 572 325 105 587 862 877 925 844 189 585 762 708 930 542 373 859 255 634 494 312 953 274 912 884 471 112 203 664 584 696 204 550 995 580 546 708 686 853 974 705 827 582 984 659 961 423 511 065 238 996 121 506 959 228 953 104 651 110 050 940 951 173 978 563 846 421 789 811 665 040 347 951 960 561 420 425 487 267 307 134 812 983 740 023 138 496 876 737 139 610 803 422 527 618 437 746 269 988 587 076 473 011 000 492 592 258 588 281 518 206 574 949 385 300 820 854 436 100 168 250 411 055 892 262 389 797 349 442 353 263 134 719 723 073 714 595 372 936 422 638 657 182 204 426 015 522 314 769 381 746 769 883 170 104 285 351 033 279 786 663 412 230 374 345 088 735 839 560 681 195 488 152 172 282 075 807 412 122 647 341 411 185 273 630 430 999 179 143 795 402 840 425 888 480 061 095 278 841 042 320 312 285 117 425 925 313 044 935 126 211 363 512 370 656 707 190 932 151 552 285 367 391 520 785 314 336 314 906 194 906 346 366 988 495 910 705 940 214 835 759 249 648 952 402 018 801 653 878 149 811 604 754 955 539 092 517 964 619 294 381 938 484 931 296 785 346 378 202 536 368 083 267 591 303 835 251 994 488 786 965 367 660 499 309 552 914 129 892 637 217 528 138 253 964 450 391 232 713 726 406 254 714 713 302 803 470 220 911 440 221 706 417 318 036 989 571 778 531 881 037 498 340 121 124 867 099 667 010 220 810 628 304 035 202 684 069 098 281 467 684 263 039 682 949 141 353 447 683 312 776 647 692 888 812 248 971 423 936 325 343 908 586 738 438 413 041 137 088 313 781 583 234 087 255 183 711 851 557 682 083 789 922 546 149 130 452 023 759 854 353 633 073 955 342 533 197 414 812 923 527 879 209 529 021 072 346 938 327 128 749 084 748 864 681 130 127 882 953 119 029 510 969 223 304 406 022 032 631 590 828 682 025 796 314 966 425 641 054 706 194 749 342 606 165 149 276 418 450 077 548 639 650 544 901 624 949 296 638 999 813 197 010 437 936 350 354 478 081 315 869 876 032 248 334 250 737 935 281 316 764 703 511 372 580 556 741 013 250 024 495 480 891 423 265 998 495 382 969 803 611 310 315 262 429 379 170 341 787 610 298 915 845 546 493 853 550 311 474 535 555 699 792 577 555 618 511 784 078 555 175 954 571 143 637 552 247 694 144 786 092 230 810 118 653 937 751 476 256 192 715 572 559 092 607 885 136 851 255 790 104 483 822 142 313 039 428 973 935 498 100 097 753 729 257 901 861 480 125 583 112 712 673 378 616 530 894 740 561 702 730 681 887 573 679 141 062 004 595 553 824 402 927 143 012 540 799 280 343 074 105 906 787 580 845 036 164 759 644 433 148 871 675 662 380 835 725 409 397 422 969 671 180 112 472 609 112 345 641 985 859 229 605 226 445 939 051 194 643 104 904 766 834 965 010 777 554 827 580 636 689 747 433 974 688 526 850 381 505 245 591 039 226 224 164 759 017 021 788 042 813 603 130 431 704 789 031 268 410 074 647 680 447 437 826 461 246 052 400 778 224 875 265 556 136 669 584 648 447 969 333 412 528 797 674 407 233 256 572 304 585 481 066 126 329 067 031 926 542 422 949 976 579 089 907 365 776 824 421 034 605 164 491 027 474 825 966 117 225 811 653 274 160 464 121 852 434 931 963 705 457 406 066 925 319 349 901 467 081 281 018 959 395 771 976 829 328 717 119 440 582 678 118 158 508 127 273 213 864 821 192 590 673 561 593 115 815 882 499 659 933 055 550 374 077 187 839 513 430 731 476 191 434 055 271 154 673 467 394 488 646 192 377 531 540 034 038 143 729 605 282 521 786 715 156 304 869 377 185 914 906 342 022 093 040 150 099 874 284 970 697 851 561 417 029 726 217 894 537 822 184 751 403 479 934 451 174 071 214 565 552 954 016 817 145 568 822 790 530 768 345 583 789 278 794 034 016 116 694 680 449 358 177 937 170 486 792 261 878 297 351 230 127 557 779 692 137 301 030 599 704 545 697 234 541 169 601 111 481 010 809 270 552 388 688 666 053 708 444 715 456 324 218 048 750 388 349 292 342 985 983 436 683 038 860 026 702 884 539 969 492 450 848 427 165 698 026 137 434 822 370 018 345 508 322 640 019 613 713 011 052 319 761 329 000 565 247 588 732 406 445 686 249 630 293 153 957 937 435 326 965 292 989 301 137 982 144 614 215 745 229 245 885 229 602 518 465 689 590 608 464 480 008 065 509 076 447 219 002 258 434 306 755 738 292 747 573 655 495 042 590 509 955 522 065 227 989 687 882 152 773 031 497 602 668 588 921 340 773 281 495 544 167 019 184 913 190 609 797 053 940 617 006 079 382 740 455 826 895 287 085 406 286 617 624 062 529 072 509 065 653 216 571 697 998 461 590 558 690 885 622 226 696 374 920 494 535 348 497 780 036 304 127 723 755 667 016 078 695 061 304 111 815 786 217 691 841 994 986 068 040 174 660 508 592 794 933 636 132 918 688 628 185 177 997 383 413 471 716 033 127 561 358 311 322 901 653 756 186 241 671 196 370 614 873 260 327 442 768 320 334 804 816 153 814 347 543 541 832 642 246 276 918 855 301 349 299 592 719 564 472 345 954 007 435 930 956 978 709 436 193 430 055 365 507 973 874 411 640 003 362 959 613 956 981 566 219 317 009 110 419 743 160 522 258 961 152 857 420 744 265 912 061 727 769 561 408 531 858 027 969 907 561 058 443 246 771 167 792 642 740 681 512 677 704 774 117 738 770 523 027 853 164 434 061 994 062 696 207 070 431 803 521 404 919 150 510 987 963 814 975 934 673 757 608 094 110 736 666 625 987 184 964 303 233 482 561 701 473 602 098 204 617 127 488 469 382 917 484 771 520 707 286 879 585 952 136 061 472 447 977 343 903 051 926 946 696 668 215 077 627 962 498 424 689 514 764 279 208 930 603 982 589 207 880 009 669 655 423 796 193 675 660 257 703 800 411 374 262 532 109 390 676 508 300 614 804 613 106 741 107 838 290 174 232 409 441 892 957 025 297 051 262 270 670 767 027 161 450 678 785 465 405 506 845 465 402 152 648 456 906 177 112 910 998 732 933 379 401 558 105 799 634 959 624 293 274 797 738 345 250 801 507 081 251 253 263 845 118 855 718 147 152 072 330 143 956 039 070 718 855 063 135 531 754 624 679 789 308 746 820 986 762 973 763 578 463 319 987 689 466 895 296 382 752 969 953 890 152 581 995 213 239 232 143 543 926 419 347 993 371 150 294 038 340 626 152 978 488 930 137 094 150 636 043 063 453 581 380 531 786 515 531 488 355 870 428 909 690 846 557 166 780 492 508 936 698 915 185 439 469 139 732 179 018 696 851 761 771 092 558 515 611 768 972 879 833 290 489 000 446 312 079 810 504 840 250 576 937 214 725 478 608 823 110 508 830 709 693 253 147 485 404 887 455 166 114 331 325 587 455 063 028 624 783 732 277 200 318 817 054 488 850 248 146 422 868 725 973 474 862 397 767 171 343 029 720 756 151 354 150 555 662 575 597 068 463 834 766 906 382 587 294 924 895 376 286 199 869 777 971 920 182 902 840 494 695 363 358 808 099 890 051 699 603 632 109 956 366 120 035 108 354 254 082 582 495 312 082 794 706 733 991 521 402 621 451 726 564 069 668 751 852 739 747 371 124 670 100 841 409 082 206 974 122 217 000 620 538 725 781 934 859 970 886 090 179 565 453 679 923 500 092 239 009 661 666 598 092 705 702 821 309 637 955 479 298 111 894 794 917 602 017 555 439 786 198 218 161 267 321 515 064 615 107 907 838 352 114 066 461 714 140 356 733 829 959 501 577 402 994 719 581 695 780 453 090 545 510 599 314 200 833 448 709 900 225 417 877 234 524 618 518 286 747 675 429 607 028 620 987 609 743 108 866 453 528 775 533 534 971 354 588 700 258 351 095 950 422 091 567 435 189 701 096 276 003 285 677 956 946 453 657 632 236 827 735 684 984 182 367 907 670 604 040 167 498 799 024 655 653 998 886 148 804 522 717 515 552 891 156 742 612 904 981 832 116 253 234 208 690 839 773 230 922 117 883 040 015 125 464 844 536 796 775 419 316 676 704 079 845 187 844 085 786 271 811 165 648 087 814 123 284 216 350 967 759 810 037 143 717 588 651 458 782 040 980 126 055 352 784 288 596 215 566 967 468 986 477 577 196 151 132 941 385 810 245 943 121 958 115 016 989 945 977 831 815 004 500 549 634 591 466 165 873 801 024 359 414 877 718 231 789 034 964 123 231 766 310 382 470 331 722 776 911 150 255 247 760 375 694 967 448 997 363 694 969 512 567 940 878 003 924 813 107 855 734 897 352 960 640 409 334 407 488 629 152 457 145 364 661 904 562 136 363 110 593 975 487 047 034 110 776 467 868 978 346 284 406 771 957 852 150 441 694 937 600 326 125 641 621 715 476 965 438 126 079 259 206 244 418 717 190 218 530 313 514 090 586 498 537 212 939 799 906 060 799 189 519 085 111 275 849 032 480 840 480 818 087 418 462 720 484 324 457 311 988 086 115 477 337 122 901 291 347 875 041 586 099 146 985 693 051 332 887 807 877 553 297 414 327 321 703 543 426 159 309 620 291 625 840 948 015 673 238 309 416 840 036 974 184 259 596 945 445 734 922 222 475 543 820 594 878 816 819 337 929 058 450 580 501 774 718 657 088 990 713 560 578 652 739 555 094 767 739 328 095 902 930 028 992 664 174 367 239 601 583 562 359 101 603 779 608 642 266 872 516 031 726 390 823 830 570 292 325 384 893 939 125 762 830 996 484 830 055 487 892 158 748 239 361 111 312 114 030 128 315 103 808 913 416 044 770 665 562 155 855 323 006 103 728 525 042 039 843 327 729 023 858 814 020 040 125 655 648 742 986 755 691 442 569 308 993 253 364 451 724 272 176 465 167 647 846 604 547 202 308 675 676 621 650 344 560 295 866 051 952 145 742 014 815 870 241 913 993 069 242 616 300 954 531 054 498 191 369 811 617 700 798 903 201 553 943 930 272 482 606 462 373 286 320 213 171 249 047 256 578 482 842 691 098 804 215 479 872 613 334 103 277 248 314 179 645 335 869 715 083 108 213 234 758 600 962 254 621 334 281 592 087 327 315 653 716 103 750 093 328 135 764 838 065 485 363 719 055 415 735 923 626 843 029 226 143 757 777 240 684 294 600 693 021 727 883 403 455 833 665 002 408 438 026 486 520 138 438 641 479 503 177 403 039 791 765 999 973 720 238 043 457 980 689 892 896 831 134 816 595 120 945 969 689 928 623 304 269 667 506 417 637 879 776 419 054 801 534 337 240 899 059 685 044 883 662 485 668 009 426 964 361 498 068 990 681 703 569 587 128 823 259 263 218 202 439 025 693 894 483 107 094 098 184 129 604 312 105 880 001 352 296 919 477 630 781 499 419 147 029 938 885 082 829 695 181 940 296 197 534 031 067 972 044 582 894 519 708 734 372 098 122 243 507 485 612 962 269 137 214 396 368 899 299 446 969 557 305 293 663 258 805 375 593 536 298 378 414 584 005 782 216 065 172 427 268 263 716 759 974 169 367 625 431 127 694 204 729 131 406 306 012 766 805 636 415 491 777 932 026 354 028 851 379 789 265 107 769 927 417 102 008 424 031 460 978 787 907 637 937 415 715 944 708 318 648 867 766 412 137 908 943 893 778 390 017 918 046 252 962 908 408 582 984 918 453 293 779 696 819 094 072 834 851 720 781 400 646 780 441 481 133 774 948 193 833 657 164 582 232 504 037 379 653 608 377 830 858 746 247 350 562 299 846 521 126 163 317 679 571 487 172 133 095 450 645 386 981 998 196 163 257 652 802 371 361 637 315 289 201 257 526 474 333 144 145 097 033 424 023 359 469 933 542 975 250 012 484 431 987 821 322 215 342 462 887 849 988 755 184 673 171 123 630 722 997 925 207 007 057 472 100 564 655 465 730 173 266 082 663 409 219 913 578 034 911 143 182 514 035 280 204 587 673 381 275 704 836 290 150 587 721 116 193 712 737 843 864 475 183 622 130 151 599 801 221 834 510 735 220 330 951 670 493 162 813 519 698 699 044 125 887 356 479 231 315 257 856 580 243 256 249 425 109 417 505 404 263 201 726 288 629 121 656 395 648 708 114 552 014 798 865 064 551 817 341 179 640 269 500 060 203 688 587 904 323 451 067 451 784 057 239 071 579 583 954 235 722 661 469 715 177 249 411 441 671 205 788 134 807 683 691 855 056 642 099 662 575 023 240 455 895 929 088 810 480 940 414 524 372 044 059 756 099 948 814 238 272 711 825 272 556 394 721 979 568 092 075 378 999 986 656 198 098 366 389 203 394 217 820 837 238 128 114 180 851 967 852 397 274 002 082 184 415 009 763 458 341 065 041 007 955 422 910 806 180 177 856 429 875 693 208 827 851 803 962 928 526 129 560 695 939 514 868 162 553 401 909 170 429 677 824 850 282 530 081 250 628 727 909 274 292 888 821 494 648 461 521 068 225 086 167 842 134 132 552 786 393 650 350 711 891 683 623 493 014 000 037 116 291 830 540 484 520 939 853 451 914 216 028 618 919 977 418 361 361 056 611 696 475 910 668 812 737 373 933 785 791 849 172 970 916 853 787 317 490 026 752 384 189 228 226 967 390 528 275 392 664 556 216 764 416 327 995 705 306 585 408 236 117 996 880 976 316 250 330 875 869 699 665 984 321 414 782 990 040 837 749 563 565 647 641 081 422 146 304 572 195 984 557 482 269 588 713 548 210 871 892 364 922 211 359 206 098 718 186 098 438 369 326 670 740 678 957 938 191 481 773 859 542 623 942 319 839 698 697 904 335 154 110 924 933 691 772 842 540 827 855 542 604 285 356 137 650 675 380 293 280 587 953 563 173 235 424 467 763 383 746 932 581 458 031 462 414 120 718 770 810 211 375 628 870 909 068 624 520 079 067 443 994 140 407 480 077 739 790 975 810 860 756 751 022 336 836 447 152 117 690 446 753 256 167 829 971 057 337 145 667 630 781 917 753 606 505 216 123 768 536 841 008 785 198 447 908 746 246 849 623 818 384 361 445 509 850 658 629 495 066 346 768 580 169 002 956 445 993 333 197 295 188 950 140 243 819 597 667 657 195 155 894 062 406 086 585 711 638 502 911 074 567 517 559 397 429 742 790 304 543 974 863 582 921 756 912 941 830 037 359 800 436 574 037 048 506 635 415 585 452 359 704 535 256 876 568 182 346 026 545 860 686 011 290 661 361 098 795 165 756 889 030 624 387 282 397 696 099 437 775 379 376 730 972 737 455 485 408 927 237 776 559 870 713 879 079 575 719 763 505 287 702 538 067 066 330 155 648 166 813 560 409 437 116 983 899 239 706 389 826 891 663 389 820 197 981 352 103 910 523 656 077 906 304 269 423 269 150 070 438 969 158 684 981 897 354 298 548 754 374 911 987 201 696 584 968 670 904 586 856 070 632 771 713 566 849 092 735 481 396 046 512 313 249 212 061 390 662 530 115 325 287 251 544 076 446 319 345 890 005 434 368 103 434 570 296 104 263 566 177 052 401 608 741 262 307 385 667 322 846 753 306 049 021 396 318 010 323 562 674 438 548 694 382 650 426 829 122 108 492 757 076 875 185 750 017 960 360 905 697 030 465 183 624 545 033 697 871 337 669 097 015 331 955 115 686 368 707 867 545 679 258 929 075 881 105 145 825 659 842 468 440 213 884 862 228 502 592 920 053 075 105 737 103 400 389 739 118 903 463 932 169 265 363 492 817 581 719 408 150 881 300 173 272 713 784 796 376 567 226 045 111 449 382 835 740 313 355 969 426 717 070 744 043 292 935 976 175 569 784 333 103 872 323 600 000 802 864 942 380 837 630 405 463 530 939 912 633 535 457 341 745 913 382 348 661 292 487 278 918 450 598 697 338 679 154 114 977 244 319 540 722 190 535 808 631 879 978 304 172 037 250 682 032 153 696 700 174 594 409 223 127 498 250 079 478 614 397 042 645 077 429 281 790 488 781 873 460 232 563 048 589 930 041 316 338 866 359 512 817 604 106 330 904 127 964 021 138 980 620 826 574 967 516 348 956 079 031 346 129 851 855 423 910 313 319 546 376 650 754 621 939 127 154 365 968 823 009 388 656 720 445 196 089 214 690 982 733 624 039 025 984 064 781 205 452 528 163 608 673 200 196 310 495 484 475 387 468 726 315 467 434 444 756 855 275 756 548 601 301 484 109 687 875 445 618 324 030 016 912 658 774 314 977 106 673 171 744 331 088 952 961 440 231 630 870 152 466 501 260 587 261 915 942 219 280 865 238 345 795 726 293 538 006 149 072 024 737 390 813 481 552 183 933 819 710 304 089 728 284 917 828 891 400 576 098 460 004 326 993 001 097 076 758 677 619 980 361 941 688 541 492 730 964 153 154 381 381 319 303 443 007 290 693 751 513 731 422 222 503 352 255 805 068 929 531 885 238 233 553 986 170 837 531 197 328 476 347 611 901 238 135 506 642 157 345 674 889 387 123 556 353 704 812 424 230 842 518 146 945 493 955 489 462 252 001 910 119 727 358 643 603 586 475 502 986 612 545 308 336 729 473 540 283 329 009 558 142 861 910 618 109 313 740 938 477 817 648 876 729 826 615 657 291 888 810 803 667 038 521 202 980 385 412 656 452 817 231 190 286 066 551 788 843 874 845 333 924 385 155 521 417 709 265 840 681 569 927 236 862 268 763 876 487 330 006 505 686 382 280 479 433 179 549 090 168 216 950 855 028 048 885 120 543 444 072 780 302 736 336 208 358 192 559 105 853 554 739 654 254 370 756 927 061 879 265 814 891 243 781 971 691 760 791 161 397 438 399 554 382 936 336 444 440 197 327 625 174 142 756 286 414 937 580 844 637 799 496 855 936 567 384 649 462 992 113 953 056 486 690 589 792 568 342 573 772 320 943 975 461 406 453 079 435 580 038 819 452 511 153 455 941 083 776 871 910 571 574 740 568 473 476 536 895 090 036 102 810 554 959 593 733 547 412 033 738 155 355 173 050 684 560 324 233 974 002 969 123 247 192 653 183 047 182 435 241 344 602 404 503 120 940 435 988 241 585 569 683 777 027 078 745 815 728 042 766 300 180 721 946 759 138 875 741 109 728 425 265 902 033 605 614 379 054 591 864 509 528 089 712 891 206 797 017 485 580 301 158 748 229 436 187 302 431 430 093 235 787 937 636 044 544 062 940 328 601 565 433 302 899 876 337 322 030 332 441 309 627 749 463 609 399 156 944 089 595 527 329 237 401 889 322 884 487 110 024 538 573 007 294 601 712 946 855 083 450 147 561 194 735 196 540 338 348 192 309 796 295 243 210 612 023 253 975 996 774 432 565 086 336 501 702 844 698 579 649 281 268 484 484 401 150 676 912 304 764 781 557 149 217 567 318 373 114 124 060 608 055 191 122 989 607 342 116 142 104 510 445 513 375 667 884 058 823 008 380 405 684 637 210 285 444 453 108 237 771 246 161 069 732 754 779 493 702 240 540 845 789 932 511 954 209 322 734 386 632 655 349 422 186 026 337 130 093 298 028 807 053 097 696 367 035 274 232 414 219 882 496 370 058 108 263 034 628 733 541 140 663 398 983 054 855 828 042 945 061 304 966 247 618 623 820 372 537 201 845 751 499 160 664 837 266 745 448 877 692 059 231 783 952 855 536 013 762 362 981 216 406 516 064 152 973 881 403 487 093 213 533 472 485 670 896 782 939 960 381 857 581 802 569 546 321 406 954 407 679 040 235 779 060 540 134 692 976 062 811 959 910 047 579 566 941 550 920 765 839 769 731 294 815 344 472 046 032 332 648 615 052 208 234 751 965 605 824 208 447 890 572 597 705 301 849 890 566 610 922 627 839 856 690 099 537 787 193 316 801 003 710 306 638 992 771 137 218 450 074 537 527 295 552 914 268 947 694 278 871 903 260 189 728 796 280 010 669 699 306 947 514 329 080 119 515 046 291 134 824 976 136 709 700 189 190 525 980 779 779 190 351 629 011 749 806 111 584 198 025 826 064 833 189 017 515 782 290 559 658 731 756 619 059 792 941 734 707 009 776 826 711 572 757 996 637 049 688 903 741 611 770 540 413 366 970 242 072 189 378 972 232 844 663 484 815 105 320 760 378 239 042 717 488 444 630 480 830 643 802 891 639 553 561 458 136 082 457 736 781 314 594 956 222 038 199 187 151 525 389 101 588 002 666 391 677 271 129 668 528 971 401 054 314 284 218 866 471 522 434 221 262 820 690 716 216 242 997 862 119 493 694 879 493 737 290 431 607 453 135 467 243 475 905 573 245 380 010 119 488 072 499 392 894 648 906 977 786 933 681 375 107 926 229 340 216 625 215 390 265 363 013 056 003 416 737 057 486 863 876 354 961 486 673 656 283 345 213 609 169 372 024 652 701 057 155 745 907 547 222 330 920 972 089 090 747 425 382 013 807 244 998 548 563 907 863 690 680 978 433 257 359 242 339 982 323 488 643 816 721 201 143 535 003 784 525 732 596 308 208 912 462 813 263 296 946 672 241 105 897 464 939 702 128 040 557 683 192 613 927 212 413 405 689 769 621 525 044 997 470 863 052 637 231 357 874 345 326 884 489 263 936 673 408 604 945 147 773 892 992 738 370 791 259 054 703 461 513 718 160 496 175 625 820 021 204 379 481 231 051 040 686 074 478 199 181 236 442 637 484 960 317 210 660 252 269 190 262 627 068 973 451 778 211 137 971 561 946 774 429 315 921 531 020 913 804 264 414 350 209 800 782 940 589 315 485 329 220 971 637 591 785 721 309 044 292 431 042 689 208 802 689 064 854 003 484 378 789 595 200 022 120 282 880 590 202 177 191 474 018 456 599 449 190 466 985 162 339 824 993 234 340 705 326 318 445 744 707 858 232 642 006 701 445 012 781 044 842 100 486 393 853 642 063 394 304 235 162 019 371 573 681 093 591 623 308 107 293 754 900 118 561 666 125 788 122 438 297 724 176 043 148 543 735 939 921 945 909 626 409 883 411 050 951 244 291 842 596 958 564 065 559 949 783 455 043 345 569 117 704 328 011 554 812 108 924 142 182 091 674 386 998 292 465 062 595 007 761 607 665 366 395 515 412 586 967 569 590 605 050 881 388 362 769 850 018 807 632 514 013 379 909 386 072 755 443 224 775 308 285 836 674 914 195 904 965 481 070 292 900 592 121 160 713 665 441 211 857 404 953 247 319 646 098 421 793 597 754 960 774 832 435 645 692 960 439 575 197 771 100 633 113 930 195 473 164 485 333 584 273 028 649 165 330 109 618 004 556 403 835 556 950 879 383 425 007 314 016 580 648 869 776 315 521 863 146 520 411 987 492 893 767 592 154 870 237 809 177 957 718 294 837 966 613 757 926 056 917 427 848 168 587 479 951 923 147 778 211 170 672 155 435 867 559 678 922 198 726 238 484 205 284 793 942 816 629 050 803 063 951 797 979 914 787 150 594 169 769 711 226 809 442 112 748 531 461 596 076 989 265 230 210 816 221 979 353 342 248 034 957 976 212 905 264 240 524 797 209 018 348 794 514 686 732 248 812 052 591 134 607 612 693 244 717 813 953 732 055 426 883 454 635 843 498 156 452 395 971 449 648 630 212 523 392 695 020 548 493 249 110 099 269 155 506 385 026 306 233 581 660 237 382 020 409 422 821 804 498 319 799 568 254 463 260 898 180 560 742 884 864 101 004 367 999 133 705 342 951 662 094 790 838 698 523 000 007 194 649 319 282 821 497 063 668 967 566 912 552 853 171 848 891 748 149 044 900 310 610 208 539 952 537 385 073 226 203 395 146 466 419 402 455 959 814 338 433 829 728 245 769 992 948 807 733 354 979 608 448 549 890 766 998 710 275 361 288 091 301 884 858 589 176 725 099 977 732 203 780 947 932 880 496 747 405 379 589 022 648 626 489 949 272 434 542 331 226 758 959 784 410 519 324 067 570 266 195 773 483 730 116 715 193 759 223 335 204 464 112 571 446 376 319 272 076 945 748 976 286 088 907 240 878 055 968 178 982 838 086 525 299 134 113 489 628 804 085 482 315 634 398 824 622 344 184 300 684 163 021 031 759 636 068 734 334 603 942 399 089 497 905 630 117 923 442 633 921 293 093 588 253 325 711 613 388 498 690 531 744 190 858 997 927 361 854 802 536 756 246 720 677 923 923 818 613 628 802 355 745 530 423 184 878 648 370 699 600 296 028 906 409 910 541 398 290 176 581 772 508 104 548 827 817 968 523 624 364 706 705 816 943 077 185 934 991 290 023 033 258 803 281 312 049 326 713 865 203 535 015 085 168 562 787 796 353 231 510 680 105 365 664 227 879 837 128 818 444 156 042 209 525 001 804 260 894 902 508 652 684 514 448 163 469 431 329 423 050 365 173 311 744 182 008 783 787 556 833 904 770 055 875 793 274 477 830 450 602 361 166 442 924 900 035 916 360 953 517 330 013 361 422 194 355 090 781 673 003 890 276 161 309 778 493 789 384 689 303 848 569 272 105 146 920 256 290 270 906 071 727 744 847 548 996 674 647 718 500 492 819 699 546 706 470 068 950 897 565 580 553 489 058 650 583 723 081 310 983 240 422 147 012 916 321 531 615 024 482 592 645 127 285 355 198 138 110 871 656 573 968 651 842 703 477 930 380 567 238 641 466 412 843 406 214 145 955 136 736 562 167 169 326 375 916 855 947 900 820 577 395 614 481 357 837 448 635 219 938 340 639 677 643 180 244 461 534 069 737 060 159 356 031 146 040 759 883 926 910 810 940 743 445 216 439 394 118 646 918 690 715 880 226 613 993 740 822 262 060 691 032 070 852 748 058 777 535 156 603 741 395 740 455 019 288 399 052 721 576 154 840 446 500 669 562 192 182 864 212 628 514 874 632 449 619 838 059 374 911 858 908 549 641 695 706 390 368 112 824 576 822 236 234 841 405 120 623 609 563 366 426 634 931 168 906 556 410 157 565 530 790 190 626 195 377 609 846 508 214 250 072 888 349 281 885 394 632 380 367 223 956 389 760 658 859 245 393 855 326 982 432 604 171 865 027 072 470 807 071 497 051 170 776 216 990 956 290 089 602 109 204 431 687 085 348 038 651 626 558 865 344 868 038 398 708 771 279 751 176 052 913 003 151 170 760 971 041 176 982 058 636 907 633 856 415 465 914 557 048 825 488 308 791 687 618 271 180 557 241 202 981 735 373 439 702 260 386 362 097 004 616 711 761 793 808 339 837 939 266 439 703 624 959 404 938 398 014 274 903 874 561 004 589 007 966 369 823 591 540 181 088 761 433 508 986 812 361 752 639 625 522 933 107 263 153 984 644 293 934 199 933 565 469 976 012 675 723 519 124 781 855 581 456 609 262 641 172 012 320 748 296 825 738 445 297 882 208 140 911 861 679 897 309 976 467 656 463 496 329 822 511 404 207 874 635 745 612 358 147 294 730 163 050 545 958 315 984 725 195 978 104 715 148 156 142 131 836 028 370 397 217 659 998 383 302 196 954 104 640 386 346 500 654 498 891 355 749 230 262 601 852 915 909 656 395 973 769 771 389 132 365 564 969 373 126 439 083 029 777 235 607 179 709 419 785 578 715 308 731 865 369 386 389 405 502 610 570 417 572 796 752 257 330 031 914 242 705 190 360 103 099 642 628 685 405 076 481 858 945 274 522 979 063 501 387 506 391 566 077 132 667 840 060 846 602 271 221 874 421 295 809 931 911 407 746 107 473 221 450 563 463 931 742 488 156 225 874 247 213 023 817 679 151 390 068 368 451 346 684 563 001 874 907 126 548 045 939 211 616 999 233 060 061 558 877 464 138 819 901 262 536 551 583 770 606 676 726 144 210 439 124 035 383 999 876 137 639 801 275 196 592 799 858 030 955 944 559 053 482 756 367 149 646 148 016 684 953 688 669 342 134 824 973 116 474 675 639 844 353 643 287 529 425 356 778 890 116 677 055 553 531 117 056 283 596 275 098 313 010 130 779 692 912 616 493 443 991 225 212 316 133 083 499 666 884 677 246 504 920 146 110 879 348 938 391 518 689 694 217 376 082 776 645 224 661 681 432 176 811 366 485 089 839 528 742 525 488 262 507 205 653 360 838 133 099 965 791 394 118 340 228 540 039 375 866 511 845 148 285 145 300 124 850 028 919 142 376 009 248 186 976 828 954 102 144 940 916 440 770 448 841 975 531 563 319 265 872 951 529 616 499 668 903 088 639 442 999 079 504 339 362 008 314 724 403 430 896 529 374 027 105 572 067 298 712 269 436 492 373 098 828 882 592 784 821 201 670 168 218 736 324 445 251 989 514 280 167 734 096 833 199 074 929 635 790 780 318 124 564 799 479 763 055 042 259 082 137 664 099 244 532 297 784 438 785 372 147 745 117 044 832 966 502 653 077 664 268 067 822 865 586 011 266 262 288 330 151 374 087 039 066 009 884 356 159 912 714 311 640 615 073 555 790 656 276 198 958 394 590 056 877 375 618 192 791 241 205 385 814 704 213 259 082 017 966 321 245 952 356 075 474 531 163 748 798 624 852 530 821 820 445 748 562 494 300 088 508 958 600 342 694 524 461 915 865 160 920 158 077 047 039 830 206 449 409 008 270 059 357 963 354 328 420 331 224 919 835 699 721 115 117 327 197 661 481 006 616 104 651 881 771 194 330 026 510 034 066 826 300 062 054 832 473 030 923 813 984 019 791 709 454 974 999 498 207 613 766 957 455 448 694 161 096 364 637 888 353 497 360 263 309 166 635 197 272 122 631 237 975 724 112 160 879 750 084 097 927 417 087 739 848 574 076 646 509 420 753 774 649 255 880 045 779 204 807 277 023 377 455 454 379 082 113 804 432 411 406 505 965 148 606 362 172 744 650 920 852 622 060 927 479 169 492 673 359 165 221 482 199 469 162 712 002 856 419 472 171 758 273 671 546 110 705 583 025 277 580 988 195 560 161 156 391 585 955 176 902 479 763 736 630 480 169 421 883 369 692 626 047 008 445 092 695 793 556 721 308 014 528 836 379 148 527 469 740 184 098 574 268 433 241 006 021 073 187 952 867 951 874 123 714 967 014 879 862 901 590 356 747 172 841 099 108 621 718 997 738 127 985 702 401 978 526 285 427 525 680 991 029 270 242 073 704 204 887 841 924 512 379 974 253 910 121 813 823 374 040 967 879 426 519 141 131 128 221 560 625 499 124 844 965 585 648 927 161 485 721 600 725 816 473 001 979 495 210 606 760 216 131 383 097 962 567 654 841 452 168 590 320 073 708 524 327 109 900 865 759 761 810 047 228 490 762 726 833 976 236 429 732 163 563 261 997 291 487 646 255 060 724 261 456 384 201 143 482 565 042 958 616 604 231 061 703 199 728 140 971 341 564 134 911 854 119 509 826 316 268 413 022 310 825 721 136 710 141 542 386 830 150 487 542 957 220 078 126 967 488 355 737 504 700 847 637 232 381 971 531 720 393 815 772 489 014 938 239 137 372 557 901 459 894 983 980 863 778 332 134 550 738 105 680 795 639 814 670 269 537 833 191 440 937 879 890 829 219 736 879 154 737 320 716 230 495 008 128 468 078 679 531 329 412 457 819 800 226 080 062 262 510 443 243 847 040 951 697 349 666 216 613 312 933 335 164 400 174 687 553 199 303 409 250 351 105 768 972 679 584 605 419 009 236 101 945 321 694 124 075 190 616 404 182 676 287 282 445 215 049 453 206 112 057 344 255 145 787 482 045 447 377 496 743 308 773 593 917 001 993 288 129 457 120 034 940 408 321 767 224 607 665 388 199 332 315 351 412 456 666 534 582 386 952 365 738 174 769 443 762 601 794 444 786 095 869 848 655 914 006 137 890 187 321 053 139 658 103 477 855 296 197 885 287 334 958 218 837 348 695 664 527 322 738 230 022 169 702 537 746 179 557 070 344 241 191 010 830 684 022 802 215 888 436 033 502 593 236 832 873 383 600 666 499 580 977 845 318 713 572 447 319 142 566 419 569 794 006 890 400 358 383 128 712 051 780 020 593 798 917 858 732 765 370 670 038 525 630 826 764 835 315 697 331 057 875 191 548 637 329 885 928 053 777 229 616 961 834 642 493 747 373 225 323 932 343 079 264 781 990 569 331 330 216 474 142 542 511 446 336 875 668 400 979 922 054 844 362 864 746 546 930 546 773 633 750 680 431 680 226 336 975 867 394 098 895 331 682 399 326 548 541 389 509 082 386 080 217 099 950 912 845 171 696 516 262 948 909 172 091 639 933 926 177 441 587 276 326 892 829 423 874 188 262 398 764 766 000 138 183 920 807 337 007 519 589 884 524 285 075 864 876 316 015 601 348 829 166 680 413 710 546 185 192 957 658 854 764 404 774 894 724 128 839 324 281 797 294 438 184 640 138 561 285 535 844 434 217 549 795 303 451 597 520 879 988 957 233 564 224 569 902 418 878 974 259 749 467 377 900 784 371 473 355 766 594 463 980 782 637 041 511 670 527 320 486 676 111 481 166 256 658 408 683 015 358 755 779 483 222 239 470 973 009 554 138 060 278 771 308 969 280 856 580 862 584 735 726 545 768 138 272 092 915 522 796 971 674 879 919 164 366 646 295 348 088 677 572 299 673 371 566 053 357 434 407 965 597 629 299 568 301 908 443 394 098 558 593 604 477 172 631 531 536 557 813 140 645 413 474 749 284 366 471 945 454 840 779 508 735 807 733 028 155 711 474 090 584 931 545 077 092 116 627 211 255 479 000 930 390 920 598 767 949 834 103 012 783 315 992 203 303 000 507 863 273 845 605 122 152 732 015 635 140 583 786 484 739 050 702 573 372 167 527 262 562 717 641 124 207 422 577 219 997 702 517 258 995 892 850 200 678 338 253 036 539 501 225 771 881 575 559 786 838 624 129 964 661 428 578 493 616 351 361 378 500 045 191 423 521 888 012 941 951 189 289 694 514 757 279 784 798 873 731 023 332 014 274 212 914 677 121 969 648 644 670 425 553 403 324 296 556 493 975 236 782 343 241 426 901 508 745 677 491 770 063 248 469 954 356 298 798 911 209 210 498 206 661 306 514 314 756 524 284 574 618 632 072 218 210 540 595 653 063 238 654 187 138 431 286 285 905 965 466 048 953 924 507 079 957 473 905 794 792 788 069 762 484 631 484 527 094 559 547 897 353 849 434 098 419 457 623 937 495 973 760 186 968 029 983 750 027 923 547 992 187 257 489 369 725 948 970 463 891 217 658 907 973 343 523 373 655 791 857 486 419 298 062 147 998 191 508 464 223 136 883 071 007 239 111 603 876 952 989 100 666 532 814 398 420 222 020 186 709 117 984 600 124 764 224 892 348 199 014 505 635 064 957 011 301 191 454 976 414 705 004 957 627 389 969 583 169 131 566 275 861 192 772 580 276 161 444 423 068 048 737 140 698 291 433 602 712 758 363 488 917 606 207 703 105 150 880 439 988 116 549 327 602 512 064 693 433 016 986 679 581 849 668 147 038 834 190 000 271 920 757 517 814 756 535 176 679 026 699 933 138 275 228 813 200 744 334 150 643 567 458 969 250 993 385 243 867 017 175 284 152 044 150 223 269 858 281 482 591 586 288 170 742 137 044 422 329 570 057 115 207 709 609 521 613 520 137 055 337 323 148 425 595 673 626 270 013 914 808 486 722 722 202 039 610 588 207 602 360 031 524 312 712 741 499 275 715 750 731 829 176 476 918 349 587 633 121 323 408 135 139 904 669 125 032 511 941 635 165 869 854 714 862 381 825 677 897 247 219 997 902 202 478 814 262 819 284 362 803 393 919 063 169 464 996 736 291 353 941 710 803 742 748 242 521 436 896 765 358 783 631 768 855 743 295 671 326 428 484 009 951 164 202 531 839 535 239 180 618 265 275 712 961 806 743 230 543 899 752 691 320 352 871 956 286 073 005 311 803 103 192 509 111 394 022 969 909 822 224 391 845 760 682 627 777 573 302 076 533 925 553 366 696 199 604 973 676 774 128 692 181 721 771 195 416 465 414 418 163 153 409 201 164 173 897 172 836 553 439 804 854 916 206 358 478 197 291 412 917 241 302 534 993 273 746 097 474 511 806 213 190 497 639 474 511 914 143 155 648 135 631 974 440 450 424 826 536 910 133 391 389 769 403 747 985 361 990 299 103 494 280 086 799 045 359 274 657 207 772 788 102 740 389 814 144 473 693 654 948 378 484 389 462 360 818 348 885 336 273 990 510 387 434 350 320 572 145 586 017 039 434 779 606 405 602 572 420 762 562 021 829 916 733 995 269 267 626 349 249 835 096 355 374 842 133 058 724 489 652 909 305 394 131 698 907 238 646 486 701 716 125 208 139 807 210 269 057 879 872 312 516 428 153 206 086 364 755 108 100 176 459 093 257 234 188 556 450 272 067 041 234 537 551 505 444 797 255 763 794 868 097 352 820 907 964 023 547 359 947 418 970 408 656 243 080 059 607 155 457 261 788 219 340 765 405 178 443 352 890 700 516 192 637 084 305 264 265 851 316 567 105 507 864 548 110 167 176 611 802 037 887 242 394 172 353 173 974 205 666 740 860 070 906 694 233 073 531 530 315 429 126 564 090 530 811 334 554 865 681 176 455 992 906 383 776 430 590 879 539 559 304 194 961 498 513 918 704 692 989 217 045 178 905 636 116 082 861 650 388 141 216 870 204 309 444 921 432 886 716 690 809 086 202 468 729 900 034 206 535 819 064 385 444 458 684 724 616 088 007 427 948 713 564 832 901 013 493 481 582 713 750 485 744 168 937 910 249 683 291 617 486 401 850 015 090 742 543 677 505 935 018 188 800 607 477 168 533 070 072 321 424 873 401 251 509 973 246 393 759 855 875 259 168 748 917 090 686 724 715 144 931 181 110 558 918 607 351 423 793 091 942 151 140 723 568 070 349 880 551 019 449 232 249 923 102 412 982 909 269 346 131 228 845 918 954 526 790 685 443 254 651 943 420 629 541 307 218 671 262 507 661 050 824 215 655 683 517 081 320 793 741 900 599 292 460 854 137 548 175 419 033 555 857 226 483 696 105 384 343 097 273 541 048 612 735 332 441 265 655 019 948 956 014 621 323 744 073 402 808 326 326 176 592 114 182 421 708 193 299 464 089 276 821 389 276 086 497 653 058 583 574 566 320 468 366 621 332 632 743 470 057 349 308 343 153 664 143 500 134 948 311 544 529 648 537 622 753 414 719 210 418 588 708 840 049 930 469 826 463 004 252 995 404 106 726 933 300 507 987 343 804 543 644 553 361 543 010 172 046 968 629 921 006 136 034 691 691 649 811 641 523 715 384 591 894 670 123 347 410 015 766 758 049 781 978 974 173 489 205 923 975 405 435 604 083 546 360 438 032 006 678 014 095 394 081 920 501 407 931 980 732 360 218 295 821 954 950 375 568 688 784 401 544 585 075 505 283 627 932 046 905 158 406 889 306 313 513 408 622 974 833 772 385 836 993 317 051 048 904 221 778 260 565 848 152 443 404 176 403 708 199 456 153 447 120 331 644 507 517 043 160 682 970 945 140 511 996 634 238 499 966 678 964 338 355 045 776 104 473 452 692 974 396 167 026 716 305 484 854 726 353 569 148 477 267 774 540 025 056 633 297 466 197 886 539 143 703 958 233 626 501 598 931 624 894 121 793 707 781 683 537 630 058 996 376 020 714 368 400 950 987 262 590 456 764 383 371 011 866 198 701 225 635 447 370 724 381 005 121 151 549 222 810 108 939 514 516 166 468 287 501 487 464 053 786 621 848 788 745 072 806 061 275 093 109 755 860 773 232 967 194 659 675 447 900 989 730 168 805 133 197 703 561 798 346 357 001 651 611 099 910 457 550 556 672 087 444 588 357 344 721 920 126 206 107 686 930 963 364 602 560 695 350 357 016 225 707 693 616 996 404 410 330 591 904 929 466 525 497 678 510 187 017 516 202 092 440 569 609 885 523 428 602 797 509 158 664 659 387 609 537 914 595 110 326 441 875 715 119 412 761 431 242 129 257 291 458 127 042 357 244 344 731 043 054 011 147 113 833 624 526 543 785 925 738 211 345 925 623 864 852 032 397 407 796 599 468 646 081 966 654 019 853 700 871 543 139 624 603 897 081 846 656 304 761 617 425 663 769 693 679 608 355 461 070 888 200 450 425 409 389 255 018 243 857 990 391 566 057 101 247 536 782 314 908 836 627 256 687 792 399 001 473 492 964 693 090 505 636 822 609 563 942 013 706 088 422 664 165 555 159 606 534 808 316 748 181 352 591 410 841 169 473 838 815 583 524 367 234 158 254 736 247 634 712 427 873 917 121 961 783 540 021 773 520 805 177 263 668 679 982 408 982 744 816 696 730 812 664 821 781 260 074 591 674 217 345 968 450 431 605 061 696 294 393 224 355 271 460 609 279 401 756 919 519 015 234 029 208 010 820 035 575 411 723 163 559 286 176 823 192 200 917 201 753 410 104 605 707 537 694 551 635 092 313 480 264 938 026 292 024 465 108 928 672 258 986 210 788 216 521 437 441 537 421 103 307 708 856 400 087 914 897 714 453 577 013 059 958 609 968 063 218 377 525 499 378 812 720 837 056 248 155 098 880 573 903 559 781 031 515 151 715 269 692 671 576 851 823 917 872 724 907 894 669 721 313 159 820 316 058 200 098 976 314 318 913 958 665 759 485 820 565 570 031 263 405 854 012 899 301 504 656 637 590 558 991 824 431 535 524 817 344 494 738 571 741 301 431 795 851 161 754 284 587 248 298 455 329 465 473 013 528 340 314 727 418 160 519 495 295 941 859 700 065 561 459 358 640 101 917 885 722 013 316 964 869 428 240 851 636 914 809 992 104 605 421 492 601 453 033 853 515 751 401 857 952 740 112 170 167 222 523 821 537 882 315 123 151 492 846 709 113 492 102 091 508 913 143 686 373 029 765 787 020 686 588 053 792 619 491 375 211 539 645 230 768 570 770 263 491 292 777 767 774 282 045 776 370 921 874 683 586 823 045 095 011 509 252 560 929 111 174 164 310 326 925 699 008 124 156 908 634 507 531 278 152 350 914 133 766 505 772 754 988 037 274 356 396 574 207 642 600 146 825 359 156 829 266 833 632 157 113 834 209 189 397 568 890 991 206 181 978 831 897 547 435 582 361 991 249 680 001 246 604 741 303 925 004 242 378 108 056 677 909 690 614 813 812 391 623 794 871 950 343 757 452 561 119 431 751 097 570 088 852 386 335 845 404 692 972 617 299 280 108 946 959 519 064 481 929 889 959 081 006 997 561 147 107 113 868 862 937 259 500 306 063 505 431 090 042 656 001 942 478 675 289 020 581 361 422 408 180 860 690 351 616 379 775 992 091 637 445 283 927 086 421 737 767 593 345 327 312 175 073 084 589 621 320 006 741 561 337 735 652 268 949 765 926 593 902 927 094 996 682 751 746 420 831 679 046 611 218 903 669 737 354 634 304 548 659 053 470 549 732 970 888 549 348 294 041 934 639 128 055 737 735 506 189 310 040 738 085 687 884 769 707 314 506 802 085 205 238 818 773 188 781 164 875 559 483 247 402 698 534 742 966 117 963 723 501 865 650 126 184 082 729 589 782 919 584 114 176 366 625 423 623 547 644 270 924 604 448 591 374 047 560 914 529 236 227 409 085 457 373 750 091 240 492 380 019 532 464 718 696 282 322 793 388 610 877 304 213 669 154 450 651 807 715 076 430 017 408 478 616 511 484 801 387 002 008 868 235 787 706 708 087 746 397 214 746 574 039 200 180 127 610 177 653 176 326 911 409 709 094 128 083 286 130 458 614 511 615 671 880 751 076 765 515 221 162 319 137 096 413 600 166 379 812 453 251 524 452 642 150 710 576 728 070 548 190 104 066 922 753 392 603 434 848 975 487 018 863 508 766 210 477 127 143 465 291 527 935 602 351 914 757 291 180 151 321 063 684 381 401 691 930 948 711 677 774 183 565 199 446 551 322 832 557 175 032 608 840 374 254 142 449 461 684 813 249 986 227 823 700 975 939 802 993 259 669 885 279 112 063 657 503 081 550 898 050 802 139 827 610 718 986 359 579 709 540 336 775 867 932 696 518 885 755 114 763 567 870 637 037 645 453 414 332 085 425 481 193 629 411 229 555 356 194 298 587 005 205 372 181 712 898 983 391 770 377 581 410 175 853 159 055 907 970 702 213 486 427 065 322 314 182 787 923 216 660 645 687 195 125 328 714 442 629 258 083 145 731 460 333 202 338 457 295 800 935 121 320 150 087 490 451 697 438 411 262 969 915 818 564 498 850 583 258 312 829 163 971 132 353 464 700 531 963 153 826 602 687 494 068 607 417 525 812 472 680 669 827 997 443 972 200 520 440 977 321 531 252 890 084 461 051 461 485 978 193 614 306 018 362 658 530 075 856 544 448 254 635 908 590 497 391 049 967 465 257 895 180 764 601 850 299 735 770 306 873 818 275 959 695 377 410 992 006 992 839 874 134 766 312 560 647 546 060 246 976 285 844 001 174 193 818 393 250 751 866 927 304 360 057 694 841 374 091 893 749 838 813 451 056 782 663 902 268 312 987 911 609 809 882 526 473 083 619 797 414 854 213 550 663 722 713 398 908 902 785 930 188 659 226 663 837 223 825 869 737 781 222 328 767 597 807 021 677 241 097 250 959 871 456 490 014 186 236 510 852 577 550 881 606 276 287 334 089 325 833 157 809 164 280 572 865 457 448 557 016 640 578 978 776 251 145 067 165 246 626 369 772 450 389 385 646 192 101 043 989 870 845 599 866 706 565 422 070 325 270 828 568 815 028 278 415 155 854 746 159 223 630 356 946 616 177 771 821 834 950 009 091 049 117 276 566 486 291 770 956 790 377 567 695 253 065 046 671 996 846 569 466 908 727 370 967 741 298 317 183 148 972 603 554 349 891 934 905 768 972 778 837 338 007 735 507 669 319 314 913 581 901 155 245 126 305 973 862 900 161 413 638 692 453 254 714 436 483 467 713 573 227 058 079 561 016 854 188 749 632 371 152 461 509 377 869 447 836 560 067 890 244 897 060 517 908 300 902 430 739 082 454 938 082 098 681 104 204 678 524 589 590 075 428 913 406 477 170 135 445 589 861 211 488 938 870 568 001 109 610 880 660 487 540 165 565 003 875 882 895 593 106 135 987 151 719 521 326 954 578 408 849 740 391 345 301 719 142 951 462 320 362 770 338 848 929 682 238 673 185 600 641 140 695 704 349 654 493 746 587 706 773 818 317 707 512 570 945 240 618 772 253 489 973 538 815 615 421 360 477 644 127 759 467 363 305 040 951 433 479 288 191 189 156 439 529 649 129 871 899 661 865 348 265 519 521 366 821 160 882 738 111 216 818 100 978 021 791 844 590 617 666 937 890 837 851 158 466 805 286 698 242 096 425 557 546 513 983 297 239 135 572 425 522 875 894 503 848 592 817 038 504 693 606 473 374 130 018 523 937 991 944 700 420 283 447 208 605 534 363 180 559 277 261 221 107 297 479 140 805 100 177 147 912 357 167 757 062 990 611 475 148 010 323 931 116 688 849 488 084 880 321 273 411 078 987 818 548 810 770 481 763 881 593 631 740 396 170 883 288 622 027 904 562 223 354 869 628 169 957 300 497 580 934 564 577 591 588 534 967 454 139 554 525 075 274 103 531 973 904 929 571 685 057 996 674 513 526 896 270 100 732 770 901 322 671 273 867 978 546 433 152 328 498 039 702 980 138 365 578 238 147 894 306 173 586 347 660 058 119 386 059 805 433 078 588 738 442 794 091 835 735 724 018 130 236 437 053 411 473 024 475 606 026 500 947 388 270 301 461 312 986 929 038 132 934 871 825 395 316 935 368 224 952 782 081 702 435 254 713 783 687 512 137 828 231 190 438 465 424 173 093 721 488 770 157 218 151 912 495 407 643 128 271 826 551 910 753 220 056 910 202 543 049 235 530 923 899 554 859 037 966 052 039 402 711 589 329 356 948 398 320 875 609 496 334 071 645 683 821 317 669 201 199 430 278 748 158 173 839 357 276 444 535 401 978 543 810 088 780 154 140 061 739 864 587 813 052 787 265 924 756 430 094 549 925 847 226 625 665 788 407 639 935 904 285 899 117 117 838 377 640 282 050 399 617 765 366 655 872 829 670 924 486 772 572 590 522 714 031 937 025 995 047 241 089 823 204 424 942 517 431 325 291 651 288 274 097 547 483 062 212 082 723 160 654 121 319 248 949 927 100 326 965 275 272 254 481 810 896 321 519 907 766 851 443 126 257 817 362 601 224 707 224 315 150 314 632 634 158 170 140 251 560 556 984 180 410 812 000 500 406 958 989 651 604 492 760 449 614 128 071 300 934 709 857 128 729 862 510 927 742 217 814 670 148 102 584 780 103 149 570 969 991 632 860 671 464 903 343 941 518 410 669 412 179 667 560 677 805 146 438 310 109 806 511 981 370 923 993 434 440 843 211 643 431 180 586 531 747 741 754 711 514 230 770 440 888 058 042 464 297 691 955 127 204 096 120 612 442 141 800 483 648 746 716 316 473 084 223 220 555 418 669 977 618 533 747 642 720 437 026 570 368 449 497 886 522 928 279 739 449 091 433 753 107 428 556 640 419 699 330 055 437 405 170 181 371 394 331 550 410 951 725 863 482 428 747 548 212 482 197 606 137 102 421 249 295 480 481 980 725 304 801 726 402 746 963 977 024 878 509 307 543 677 190 194 016 565 530 803 790 784 268 893 449 893 163 837 171 940 734 579 099 358 597 834 768 132 809 743 412 394 301 804 490 221 426 285 468 361 792 856 343 282 267 609 325 818 749 708 590 028 975 453 399 310 985 384 397 346 016 784 770 984 608 281 369 609 538 159 184 457 477 686 266 374 777 920 680 684 538 716 847 369 632 062 738 756 383 454 532 143 792 811 914 908 719 063 269 367 849 893 617 741 742 477 782 821 868 096 703 728 398 823 152 785 528 794 112 652 660 468 439 402 652 765 613 980 517 706 140 884 207 431 277 841 087 322 509 450 553 653 277 406 528 897 059 978 395 986 505 220 828 748 083 812 612 871 330 785 525 477 953 294 860 997 881 989 670 291 349 355 131 187 897 186 349 130 784 121 373 372 705 834 849 254 125 304 357 004 516 519 284 053 337 366 938 950 799 756 603 040 245 635 028 048 640 668 378 936 882 742 907 714 081 936 852 803 760 909 298 206 854 473 534 371 140 188 322 168 113 880 091 684 033 265 075 457 825 776 584 958 714 691 298 598 136 519 569 601 512 836 254 388 523 318 183 268 161 485 299 968 254 624 323 834 125 423 964 313 044 182 640 658 551 941 003 509 590 276 616 531 197 480 721 817 404 920 619 488 247 359 785 718 819 100 239 152 578 711 531 689 442 693 706 114 717 857 383 250 975 532 564 838 836 663 751 515 088 336 603 559 041 886 152 458 502 037 964 643 909 679 630 149 306 049 400 667 475 085 069 641 729 392 912 981 732 404 226 873 480 816 565 192 133 521 567 683 354 742 578 992 632 567 336 844 854 733 934 976 608 864 818 987 733 335 895 328 928 841 923 842 015 176 476 139 413 214 240 451 255 474 861 072 737 167 011 012 753 549 736 924 480 134 339 584 652 062 364 366 675 073 961 698 617 557 835 618 245 170 896 053 614 768 546 617 780 469 842 498 153 158 985 333 909 086 923 848 112 092 328 725 881 491 210 592 278 956 141 211 802 879 503 606 717 504 469 121 345 453 518 851 277 868 728 240 526 070 645 720 279 504 001 900 480 357 577 178 575 781 929 554 883 479 674 961 704 862 208 684 759 307 842 961 297 829 055 213 062 919 503 124 493 634 267 536 469 504 508 840 533 966 142 331 839 338 868 286 603 751 913 191 238 829 977 348 064 654 291 091 771 472 751 699 359 349 550 212 336 001 997 532 464 496 699 746 801 130 317 255 247 970 688 543 713 792 227 953 713 615 962 109 537 479 141 848 616 105 988 493 438 547 530 502 752 270 171 369 264 064 917 337 165 986 044 353 775 162 044 209 553 624 368 369 464 361 829 888 005 397 224 357 692 821 838 694 488 428 103 363 969 666 782 679 081 188 728 284 663 805 946 524 101 325 996 878 235 486 855 483 130 967 709 205 250 529 209 848 123 922 799 083 557 138 624 861 372 165 354 714 185 858 128 839 010 925 073 780 690 345 330 019 809 765 372 950 062 696 584 798 625 692 611 399 613 834 330 268 557 773 491 341 822 251 704 182 457 527 241 816 740 356 454 867 703 631 769 648 112 058 805 066 080 599 898 739 435 839 024 496 170 544 261 023 882 089 245 399 901 535 497 264 196 989 127 071 085 794 718 683 074 626 987 005 079 478 092 341 775 746 692 284 257 670 269 506 001 460 147 566 023 145 670 521 506 335 785 833 739 963 583 222 353 686 153 563 798 435 626 928 754 689 611 144 130 481 877 871 962 033 984 187 165 725 870 999 835 062 907 151 150 517 604 798 811 554 395 608 645 102 204 084 610 365 658 092 184 500 023 771 389 391 900 527 229 176 295 715 191 527 116 829 194 891 434 106 061 518 857 145 800 867 511 006 966 277 339 731 259 281 154 748 140 962 104 604 585 681 583 749 920 250 276 520 378 472 685 778 108 980 480 694 398 446 221 472 173 871 706 935 641 086 664 545 483 108 162 093 105 477 190 962 856 396 078 557 111 980 846 267 285 187 894 474 581 710 471 823 361 623 431 516 354 783 553 649 646 872 361 045 589 534 688 042 042 248 951 099 627 337 467 525 449 440 964 975 312 556 710 366 792 967 290 422 079 065 647 204 027 595 392 117 452 963 327 654 742 452 617 287 476 689 739 207 120 622 092 083 544 932 007 492 818 727 779 288 237 260 087 664 787 951 893 114 228 082 872 707 395 817 400 625 339 379 659 853 740 913 098 737 049 464 232 505 742 937 815 411 982 261 026 641 456 761 937 005 196 392 572 009 460 605 290 207 208 098 374 988 860 665 907 105 079 155 644 056 082 239 484 237 831 204 245 556 070 261 193 961 616 575 692 841 595 480 480 274 779 750 059 458 537 942 094 394 397 859 429 617 671 825 980 562 292 231 633 448 725 294 199 636 913 674 956 209 160 039 086 305 855 748 728 480 712 084 658 014 940 965 659 561 509 478 560 750 156 909 419 975 869 384 187 590 666 524 598 571 640 413 650 306 189 557 008 454 469 431 979 015 910 096 357 399 000 409 301 218 682 192 365 829 569 559 286 740 274 021 079 579 289 059 105 313 828 380 472 720 613 249 591 124 697 331 372 857 600 562 861 099 118 271 979 551 001 051 954 582 802 151 022 338 330 320 242 132 051 808 748 504 817 342 642 497 583 590 509 388 265 615 737 896 249 009 680 478 307 305 151 913 450 239 130 315 711 071 914 237 199 111 615 493 591 498 488 193 276 323 587 095 279 524 561 200 702 332 627 346 053 350 227 539 427 255 887 004 195 774 109 792 482 645 996 385 654 698 332 408 184 448 326 681 388 087 534 493 295 444 266 805 078 973 415 724 687 551 875 340 958 983 707 286 372 394 273 793 729 315 004 467 444 797 243 928 616 082 440 079 757 515 896 912 607 570 140 535 062 391 498 352 188 174 235 801 697 846 340 937 371 109 403 064 030 937 251 092 590 812 946 309 385 549 286 451 154 070 464 258 288 729 322 105 312 786 708 609 470 106 258 388 654 832 523 800 382 425 637 158 352 755 573 568 529 095 705 503 660 398 844 823 656 312 602 936 059 980 697 018 924 903 777 198 714 704 938 610 787 635 082 417 863 292 068 013 136 598 116 541 101 653 345 247 297 702 466 017 786 386 398 072 965 101 677 506 305 714 355 664 647 465 448 511 275 077 475 384 089 625 290 642 661 258 861 847 212 067 935 976 101 783 296 506 168 244 174 601 036 783 478 087 274 943 053 214 140 696 574 952 058 787 467 973 064 132 994 717 701 624 055 304 726 871 566 317 280 184 056 044 552 500 832 043 408 928 508 379 455 502 034 416 691 957 426 050 283 533 500 843 466 094 610 698 431 368 674 850 529 814 946 854 476 365 743 648 975 540 118 460 044 272 695 535 498 213 630 853 473 554 096 476 401 237 289 749 679 699 922 419 476 993 455 253 283 732 357 338 345 710 358 499 806 378 708 055 744 842 277 364 673 904 332 770 019 847 556 119 605 847 435 898 381 489 097 667 178 546 486 092 333 633 603 409 913 462 351 233 473 830 829 986 465 510 332 055 864 064 739 412 413 873 983 145 097 178 507 164 142 627 251 414 004 019 274 474 692 793 637 326 055 846 288 713 035 459 186 118 567 891 217 349 740 894 895 050 512 464 222 178 379 147 594 780 565 693 797 553 011 322 646 242 679 254 665 749 556 812 640 670 897 436 543 353 053 689 034 615 749 224 699 434 702 522 858 224 159 775 002 957 370 842 267 768 741 605 434 403 903 647 351 125 960 975 176 115 902 667 730 853 207 669 117 511 657 531 962 826 028 020 534 642 666 507 333 192 960 972 261 507 301 720 735 492 161 493 477 446 808 563 585 322 012 080 768 152 786 711 336 224 843 735 602 253 925 908 278 533 907 701 155 552 776 536 728 136 039 636 756 593 842 879 831 816 808 313 756 237 991 780 681 717 960 413 150 920 335 137 128 451 183 158 949 419 199 129 789 187 955 232 295 413 094 141 481 060 173 516 298 058 599 563 250 553 921 033 815 744 577 374 993 404 908 598 559 802 310 631 583 349 861 877 631 165 555 994 516 501 991 654 033 553 720 906 357 019 845 022 134 181 334 714 861 470 100 613 186 654 649 469 023 445 086 289 801 013 889 434 448 785 893 886 092 360 005 705 429 019 061 911 802 291 967 067 427 495 920 603 970 281 520 283 979 239 079 810 026 656 848 530 827 767 676 015 175 026 460 174 907 962 181 358 783 886 528 533 111 371 294 197 968 904 443 944 787 164 769 446 884 181 637 254 614 059 474 554 970 042 619 194 882 730 723 925 674 566 162 488 135 423 285 771 097 234 662 983 271 568 173 083 729 646 500 728 428 917 507 503 420 926 305 900 680 812 023 125 005 624 262 646 038 994 021 475 971 644 249 682 971 554 327 734 589 729 800 520 152 381 597 366 949 535 529 913 063 883 507 104 930 774 979 299 971 868 068 804 267 975 404 699 382 943 823 898 539 480 855 383 935 156 789 191 698 762 519 868 504 699 661 329 375 361 089 431 186 547 312 266 816 238 209 097 423 879 644 553 831 032 770 147 571 620 169 015 476 117 359 880 701 187 322 429 003 712 258 244 322 930 121 731 948 311 909 529 954 304 564 001 990 619 203 658 854 356 627 141 022 202 499 184 581 569 766 744 377 242 941 087 721 734 124 079 823 037 036 836 787 394 619 473 038 222 712 682 988 918 664 250 404 881 401 192 069 454 966 044 498 523 611 823 578 614 472 707 037 531 310 729 888 614 400 282 060 363 809 626 704 974 122 866 224 472 424 097 236 762 889 582 447 067 763 597 225 521 063 710 353 929 061 449 559 688 765 262 800 217 860 695 050 664 958 543 480 983 786 706 963 187 613 504 694 870 098 811 380 568 359 814 073 372 038 174 364 941 362 969 560 001 643 715 034 733 758 341 857 759 928 984 856 742 881 403 706 888 251 600 688 483 695 334 278 247 767 947 277 173 526 309 588 251 161 675 454 210 176 386 971 617 354 467 875 882 056 104 682 115 749 925 202 754 110 099 581 853 989 057 022 555 156 692 509 995 917 495 860 563 088 368 670 088 951 366 243 064 713 301 420 096 879 815 370 057 069 198 606 897 464 946 826 566 149 737 993 613 005 371 587 356 581 863 579 819 649 459 038 756 649 730 155 295 982 270 903 386 684 051 899 329 829 738 293 571 092 019 215 549 071 705 348 206 615 091 479 202 052 990 673 433 446 615 771 216 918 703 332 059 282 305 142 681 408 403 982 138 974 907 928 068 967 166 494 842 074 099 258 544 837 309 431 146 209 499 693 895 616 902 334 718 749 813 491 722 410 624 791 849 217 836 038 026 029 619 508 381 849 052 002 148 776 280 124 314 540 362 642 589 652 349 617 963 374 167 751 149 148 169 881 643 068 554 511 808 061 733 529 118 820 971 200 646 913 661 444 973 074 784 461 772 089 339 486 163 360 159 583 602 266 854 868 710 050 828 776 501 919 081 830 165 729 187 476 678 638 841 571 836 069 911 039 529 124 092 094 723 382 666 296 415 198 451 673 303 888 244 431 733 705 139 626 607 287 771 113 925 758 718 872 961 008 164 937 021 854 562 225 406 729 760 587 753 480 144 889 475 637 263 920 711 830 081 872 333 333 564 371 416 439 704 386 714 119 724 682 370 793 216 560 662 097 493 325 355 704 575 900 133 044 537 356 988 939 705 449 946 154 640 131 117 325 064 904 895 808 190 335 086 424 425 903 546 213 580 956 238 908 328 174 717 924 582 589 061 515 172 352 084 934 843 888 647 758 056 788 341 339 470 793 482 519 305 951 373 714 097 889 500 640 152 279 823 004 521 778 398 856 583 890 189 186 832 820 185 692 699 013 109 119 082 372 391 475 400 115 530 925 008 876 337 597 643 154 571 636 294 880 716 489 804 764 924 948 550 072 825 948 021 764 105 061 436 928 158 144 097 874 557 610 316 534 280 049 803 355 555 586 957 424 769 975 732 065 010 935 216 639 146 614 427 926 505 114 321 033 358 921 990 202 383 198 679 935 439 473 820 108 754 611 872 142 888 385 672 795 395 915 179 682 851 558 522 010 262 069 877 413 026 031 893 019 401 996 767 287 941 161 702 148 217 188 783 834 598 056 129 544 592 934 170 533 416 963 089 407 218 259 375 357 665 054 819 882 664 231 266 985 797 789 545 488 930 691 971 266 195 761 447 463 439 104 050 574 503 307 058 874 381 469 769 072 729 917 189 399 823 730 757 125 125 624 807 833 861 156 886 480 578 370 377 731 329 479 332 402 236 644 216 090 058 283 655 001 509 810 644 275 755 497 953 511 121 580 489 336 243 181 258 069 665 946 852 106 406 552 152 036 063 888 409 606 995 251 560 608 922 390 089 616 677 072 419 797 060 157 143 207 981 718 504 566 673 806 775 832 263 716 581 305 885 758 422 254 760 856 755 707 996 309 271 082 121 824 028 575 799 156 434 461 965 965 493 777 566 212 362 889 551 297 899 925 903 487 094 656 669 395 620 753 910 379 130 490 183 182 432 140 002 872 424 222 906 946 963 689 859 551 672 625 604 228 465 189 586 524 017 161 843 201 118 328 363 565 514 964 002 381 237 770 770 548 715 711 477 666 415 111 770 174 526 107 641 696 122 932 626 840 740 302 005 374 306 279 903 147 870 684 235 190 680 714 638 329 996 640 070 582 989 737 229 998 657 496 963 469 955 463 751 185 965 456 403 621 238 741 499 914 044 293 424 176 541 937 658 014 284 094 748 699 179 897 782 310 849 903 634 082 842 605 219 734 303 150 314 739 308 571 633 382 503 012 314 239 396 860 583 083 381 495 123 764 627 061 407 511 007 190 220 075 110 844 260 559 017 297 238 391 204 073 886 000 071 361 067 968 826 000 082 010 671 045 237 531 396 860 173 695 114 743 875 313 868 857 694 671 787 484 541 187 345 543 628 853 348 249 675 925 686 455 577 339 754 622 826 221 106 378 077 987 968 593 534 408 467 044 398 950 171 518 631 194 315 527 912 162 448 905 047 176 004 457 766 351 034 453 859 093 507 478 294 193 038 865 939 174 488 912 644 204 981 313 187 708 700 532 849 786 076 962 148 072 897 230 904 949 036 377 073 951 488 807 565 872 243 475 999 949 977 184 962 565 821 369 594 680 063 724 418 482 957 813 795 604 989 799 139 948 361 332 838 527 922 940 688 448 585 173 650 899 625 681 175 026 653 045 985 377 495 226 838 631 889 082 414 809 280 253 509 787 892 609 934 272 822 626 596 190 922 514 245 889 898 949 894 981 153 932 860 725 958 822 659 313 413 047 192 553 780 264 851 835 883 775 057 258 617 793 470 781 174 429 287 951 812 101 585 942 124 418 581 501 409 888 465 064 088 444 949 961 433 346 416 520 585 889 231 636 233 024 468 949 598 777 241 459 746 733 180 875 501 149 140 027 972 058 035 973 948 657 583 354 755 709 103 461 866 766 055 971 746 654 842 895 310 620 544 544 129 478 762 558 358 972 020 406 065 233 511 312 659 948 190 243 564 535 852 682 475 184 656 878 227 520 530 640 116 722 533 409 957 960 934 393 134 231 469 198 495 236 886 478 297 011 489 807 302 718 289 675 311 732 974 943 380 399 136 513 909 480 468 118 995 401 376 473 038 236 229 861 826 651 867 036 749 902 591 130 613 434 674 748 475 147 167 572 352 177 094 339 385 348 762 235 560 609 405 349 828 199 572 109 332 357 379 382 917 985 742 059 029 700 171 914 899 401 447 916 742 708 109 402 172 980 497 291 801 229 877 244 802 652 821 676 686 966 188 781 665 587 980 799 317 667 919 014 032 245 076 820 291 405 646 412 802 414 423 547 103 151 814 779 689 403 104 817 956 495 003 694 226 996 643 292 690 775 514 112 080 208 981 562 492 181 152 783 048 197 216 336 713 208 691 415 678 505 979 728 892 206 129 316 512 902 832 326 962 652 569 489 975 911 827 651 085 934 675 683 937 460 705 398 773 671 557 082 397 393 932 569 959 906 550 921 846 076 176 273 392 421 670 199 281 375 112 091 286 658 731 407 280 447 287 909 766 090 153 979 863 100 889 666 432 249 518 881 894 748 644 993 670 407 208 433 692 064 828 652 688 249 007 977 792 232 436 575 606 498 658 262 747 156 068 398 849 977 103 613 663 245 053 554 049 146 755 267 614 964 794 586 621 096 730 005 263 661 391 969 404 692 389 136 628 608 490 077 612 420 545 719 315 712 226 655 996 807 676 059 775 949 313 348 652 104 427 677 201 936 004 486 687 894 625 648 260 745 066 083 257 460 521 565 282 884 762 522 513 852 455 748 798 065 500 489 082 524 575 145 770 159 479 933 131 550 341 810 049 108 455 864 963 275 498 093 492 876 738 077 505 592 828 639 380 813 355 926 814 721 276 177 349 453 420 895 326 139 144 806 089 964 051 511 889 532 222 613 841 845 701 494 282 246 347 137 687 241 749 585 183 045 579 891 327 255 841 225 834 032 204 825 213 761 839 537 519 629 028 931 121 255 105 087 593 244 107 135 045 789 974 626 194 483 499 756 003 558 494 458 120 018 928 703 803 189 653 925 777 184 993 853 918 575 099 010 180 338 264 432 972 003 876 139 979 417 424 182 787 890 508 979 836 505 028 535 489 599 210 291 560 800 537 577 475 999 254 162 468 044 460 105 055 013 162 252 421 089 575 583 626 552 487 213 544 720 354 813 694 306 629 957 506 257 018 552 057 450 957 173 287 112 970 023 798 660 361 374 464 937 535 346 623 878 307 901 164 460 010 378 609 962 297 831 091 542 664 616 633 837 997 366 950 998 455 342 594 355 088 685 114 112 347 407 475 419 975 895 631 108 208 490 230 130 157 118 008 696 337 762 020 175 111 865 849 332 210 102 000 896 755 296 948 216 761 229 459 527 749 308 895 481 865 469 753 790 151 478 334 774 003 939 736 630 183 347 451 578 646 981 832 874 126 803 760 885 549 964 814 610 094 350 975 908 999 032 515 065 715 541 166 747 357 806 126 915 594 968 184 487 842 021 420 397 780 863 177 584 885 819 741 190 546 875 099 082 467 195 312 133 638 032 221 694 112 126 380 444 834 250 949 920 742 261 282 273 756 407 873 435 395 455 098 859 708 883 444 738 397 602 881 366 390 985 418 311 192 811 169 623 596 191 886 688 938 780 182 282 760 670 634 846 670 863 983 678 634 970 122 735 199 914 504 371 613 071 542 122 739 596 693 859 668 253 799 544 540 836 661 660 651 664 172 741 211 128 461 385 725 770 846 009 561 421 918 507 535 240 070 752 025 685 747 535 330 360 291 627 181 622 940 752 265 946 706 947 969 031 148 840 384 904 062 993 636 253 561 364 493 384 943 641 526 713 629 391 859 461 993 803 507 915 173 889 380 952 548 448 192 221 680 774 979 756 934 928 181 087 210 920 628 804 894 922 578 445 340 957 620 503 416 174 577 313 613 970 870 813 456 786 635 199 291 156 699 234 856 734 433 208 628 627 128 456 184 887 586 859 377 968 759 014 765 021 345 311 328 334 897 414 722 936 404 475 776 200 704 257 360 104 245 696 372 067 369 411 013 007 521 871 785 861 594 972 876 134 083 719 721 432 218 535 054 366 736 964 336 396 184 833 403 958 342 131 548 201 054 696 255 815 502 057 212 221 630 885 649 080 978 874 074 476 155 358 261 819 942 525 956 367 841 377 337 653 791 226 361 582 776 129 604 339 192 177 161 288 483 169 533 267 666 770 234 981 084 604 819 130 093 693 265 751 470 819 060 205 290 275 465 999 650 319 084 565 652 507 464 494 577 974 890 486 643 062 594 717 268 959 092 377 140 320 952 848 269 564 164 405 911 099 640 752 531 578 867 399 465 197 292 807 241 760 554 877 718 603 127 316 520 213 276 618 907 083 101 316 597 571 423 934 429 991 852 951 473 288 258 908 332 864 904 624 355 604 662 709 856 478 031 749 542 013 590 820 756 196 260 096 989 569 729 818 844 827 521 731 401 501 611 981 461 004 554 571 882 599 512 931 864 613 855 853 452 164 508 185 625 675 387 837 941 717 557 427 238 616 978 008 307 220 834 658 475 496 551 581 019 436 424 434 703 514 165 274 819 609 689 239 830 780 597 814 022 676 908 590 840 988 180 055 233 074 824 733 226 909 730 871 732 326 661 150 428 097 124 513 333 430 103 041 910 702 242 716 217 446 057 571 729 941 342 403 101 553 236 910 561 768 163 053 606 224 374 594 199 286 469 926 029 493 523 256 703 570 282 522 658 852 461 235 799 468 490 630 131 101 488 453 032 511 935 296 108 289 641 002 310 706 588 711 406 606 441 926 261 629 032 830 517 052 172 238 981 181 779 111 596 807 098 512 197 838 874 145 164 115 193 190 602 534 819 718 723 438 707 724 129 785 777 602 742 539 494 934 225 204 130 751 789 451 085 505 278 778 361 038 821 016 809 074 888 533 007 671 801 384 282 075 029 313 405 051 896 525 368 492 061 623 769 243 938 786 061 520 266 289 233 298 758 044 981 854 507 220 425 946 475 996 988 454 425 784 111 138 037 962 822 978 026 817 120 688 064 723 761 381 188 346 277 271 426 414 114 827 358 940 766 830 179 584 347 826 182 056 046 770 619 452 590 487 879 591 067 848 341 164 314 376 996 463 818 993 755 626 461 790 898 618 966 561 393 263 607 238 374 995 722 640 386 032 293 343 542 708 675 758 295 075 340 835 540 384 135 054 913 685 234 950 186 874 289 180 445 287 055 058 584 681 181 881 837 354 315 759 243 471 955 917 169 304 903 183 103 666 766 671 983 764 214 229 488 152 200 335 072 822 458 988 919 406 186 868 163 144 541 332 026 410 256 264 268 969 190 313 800 655 105 496 549 185 774 344 102 188 171 022 202 254 141 865 923 016 014 907 372 607 546 274 863 688 276 430 625 026 934 876 961 592 932 613 702 584 628 678 989 495 966 819 388 410 472 629 771 540 215 566 842 314 262 084 638 143 126 309 298 642 521 879 793 365 365 532 271 221 860 520 885 973 821 661 179 559 852 913 403 707 354 077 245 496 783 812 372 179 246 351 811 620 921 769 767 583 824 464 911 139 393 015 152 099 120 901 323 513 906 308 138 496 335 191 172 923 086 328 004 260 037 038 934 383 396 330 966 366 213 296 915 619 156 948 727 225 118 034 528 223 809 464 303 489 529 326 729 633 141 405 619 194 323 225 072 750 280 548 987 997 363 021 956 460 624 208 609 361 749 383 263 662 592 698 360 983 021 452 680 330 449 243 685 667 631 401 996 933 615 044 537 777 536 284 626 234 805 501 682 508 461 150 635 672 774 329 598 089 507 078 012 325 869 931 023 845 196 322 759 665 378 168 280 026 853 464 426 779 645 192 349 306 664 253 757 928 716 903 535 822 131 337 359 867 738 582 958 592 028 825 236 429 374 174 667 071 714 504 488 506 325 316 277 557 804 194 173 961 579 897 518 731 254 284 756 463 788 549 806 749 220 222 090 270 834 061 636 063 515 114 883 690 757 041 546 294 955 608 479 316 122 388 831 563 044 515 573 799 637 835 968 714 451 365 201 710 363 338 778 287 047 426 624 105 400 749 413 504 313 876 989 340 408 150 654 337 495 245 069 864 804 262 659 680 606 853 752 530 383 256 692 238 604 630 692 070 507 176 684 625 169 473 380 839 337 374 074 323 811 452 673 164 269 424 328 317 198 889 399 328 686 564 990 918 623 161 911 888 424 113 307 238 435 073 827 235 439 056 021 914 615 223 067 143 483 678 816 891 814 051 453 809 823 819 685 101 525 404 712 322 003 648 129 375 309 711 474 860 897 862 289 530 201 308 600 745 875 907 383 946 039 504 898 017 088 004 096 757 244 405 504 172 193 459 610 551 230 735 355 104 672 864 281 358 386 089 742 879 921 504 064 380 438 725 114 115 161 650 983 186 342 415 142 872 186 563 864 432 946 130 129 594 704 732 215 075 780 753 868 099 039 901 916 241 900 233 290 836 739 028 115 397 436 194 364 601 406 575 503 348 866 661 106 999 239 129 714 778 900 970 244 028 316 136 238 885 272 678 654 723 648 689 692 648 498 295 637 090 843 407 604 182 956 742 702 737 042 186 493 481 189 866 240 711 237 951 583 406 041 770 529 569 114 277 749 498 576 242 099 069 084 801 233 373 439 900 990 418 707 705 759 664 743 245 452 824 593 507 621 581 846 276 374 081 183 371 981 840 179 767 461 923 795 937 454 175 651 064 415 102 099 475 459 189 823 409 728 719 535 853 946 250 106 921 381 725 774 436 704 527 185 878 812 023 671 372 056 046 335 436 356 453 102 629 524 108 157 990 924 993 527 670 769 064 942 105 851 259 890 814 733 469 589 525 440 958 562 772 220 450 047 913 851 981 913 286 033 873 478 329 647 446 513 326 107 051 382 936 356 405 018 250 408 192 055 443 709 744 048 929 196 771 712 988 774 232 248 037 251 978 145 367 702 520 173 809 219 177 335 313 425 767 775 520 889 737 752 865 329 333 837 275 293 990 117 962 429 235 651 943 000 578 146 330 439 288 341 331 245 778 105 420 076 062 264 318 414 167 255 806 448 276 983 294 049 650 799 117 607 430 122 423 148 244 759 550 723 395 816 541 816 558 463 850 778 135 926 652 840 876 509 867 985 255 975 045 052 248 185 469 578 163 945 150 675 089 805 937 414 420 207 478 955 273 627 377 059 161 913 061 164 002 220 679 521 979 647 561 326 910 356 772 651 587 114 925 887 455 845 584 897 013 500 165 801 206 689 627 148 230 254 607 026 272 305 113 482 817 621 546 278 195 502 115 021 882 294 864 699 269 613 633 807 007 596 336 451 549 655 401 383 970 349 305 458 481 198 978 541 990 894 748 428 639 418 382 456 373 242 089 854 893 114 884 936 753 081 423 399 183 544 624 094 287 939 393 333 436 596 705 696 476 451 354 763 368 321 159 245 588 019 213 646 546 027 037 232 809 719 740 506 968 865 704 369 450 269 825 600 639 925 221 338 289 758 213 771 173 864 591 654 854 826 992 025 334 780 001 670 438 779 179 244 498 843 994 106 704 607 020 532 408 240 886 173 399 026 669 348 841 678 371 963 356 153 470 820 849 884 752 790 257 607 550 858 645 658 216 137 584 656 357 985 882 830 806 525 570 046 743 728 243 698 007 970 565 262 911 812 611 678 105 891 097 279 348 740 883 355 528 029 296 513 060 724 155 180 441 269 457 471 175 329 127 911 125 243 759 023 288 045 429 882 344 101 981 999 721 056 955 991 362 076 307 603 071 164 709 137 236 672 593 657 775 150 989 542 904 009 937 057 254 665 732 837 738 158 420 576 869 784 616 078 361 913 792 510 240 636 971 847 331 105 733 573 687 516 472 237 228 950 291 534 506 172 253 126 200 336 294 056 049 344 877 533 213 945 084 677 290 722 930 637 975 840 100 144 525 558 261 223 358 879 008 290 510 036 816 397 323 616 200 161 052 419 537 119 640 667 586 879 290 334 942 725 074 033 525 073 828 187 571 485 150 335 962 905 089 465 563 946 234 936 293 526 635 510 336 372 730 007 057 667 320 933 688 226 028 133 748 250 628 760 042 276 670 339 073 593 075 195 096 208 499 520 901 729 636 587 492 831 780 054 692 189 199 091 503 147 215 983 925 508 879 527 777 472 206 755 099 035 225 147 678 286 693 709 139 445 024 449 147 110 141 733 151 098 696 995 666 976 211 784 165 092 172 269 895 099 688 888 497 261 140 660 376 862 628 186 294 878 355 538 133 857 866 279 930 062 552 374 991 916 422 278 319 622 958 222 897 924 209 518 543 949 223 503 411 413 671 518 041 647 969 799 859 500 034 848 395 731 902 500 748 622 753 937 167 273 024 798 485 133 473 791 192 536 807 685 705 027 645 252 970 815 029 293 552 305 094 458 285 032 669 944 898 950 650 790 373 989 873 579 055 207 944 041 745 365 469 862 958 431 613 885 150 004 080 364 181 916 207 604 017 409 900 341 977 674 343 714 455 949 637 015 834 179 107 065 533 984 390 034 450 870 877 666 141 265 875 662 009 618 962 881 488 719 043 443 540 550 784 664 256 396 198 136 918 607 608 348 881 551 704 534 347 745 066 223 938 267 296 837 489 713 158 596 630 856 025 859 328 556 274 042 797 182 987 264 012 710 251 386 268 156 108 885 031 754 725 925 744 538 889 418 773 169 056 269 805 464 838 368 154 542 810 204 655 648 811 326 211 581 406 690 429 222 552 683 692 697 018 464 226 892 239 939 529 999 321 524 933 968 057 256 249 492 900 765 106 931 678 808 424 935 806 015 005 413 087 418 137 397 873 168 212 316 973 867 761 301 775 428 348 008 451 856 756 344 361 636 385 064 341 617 899 626 067 226 356 219 474 497 292 575 089 979 545 029 998 833 754 493 634 618 476 829 905 129 430 913 086 145 534 819 848 957 865 838 244 309 982 095 458 552 270 617 184 003 849 521 152 886 654 775 979 357 089 910 161 931 528 932 035 104 503 861 985 944 368 221 165 279 378 546 468 360 286 852 452 100 591 105 973 211 625 645 761 665 369 383 423 995 914 325 475 557 219 215 735 078 840 983 282 476 403 893 678 876 819 048 078 707 094 099 788 964 612 120 187 965 700 441 685 738 463 438 057 687 892 974 376 458 351 790 812 147 308 848 633 626 094 092 299 529 543 655 691 391 927 992 666 639 737 439 333 634 194 101 371 255 954 792 917 305 162 257 154 293 682 996 863 662 638 896 430 072 592 610 396 399 969 824 539 243 243 452 579 276 853 998 948 319 495 095 159 881 556 199 651 923 783 476 492 180 720 129 169 271 794 512 495 492 106 408 228 449 334 228 345 040 993 883 503 284 572 802 301 461 428 439 631 949 592 266 825 066 794 320 844 071 915 309 242 200 177 943 491 544 731 931 697 279 534 552 180 115 245 050 018 001 399 253 629 143 268 193 936 557 203 445 304 835 871 854 533 636 991 629 114 034 296 575 891 323 219 135 412 097 253 449 259 438 686 896 779 241 119 666 406 356 419 343 645 763 781 372 653 287 278 443 100 879 913 911 934 823 689 520 986 842 619 525 907 577 965 424 529 186 687 402 592 780 852 927 607 855 663 478 994 231 382 475 415 690 535 778 451 779 356 857 882 469 704 620 411 261 568 295 373 979 652 412 640 047 477 068 509 802 093 145 651 068 460 693 362 687 347 239 707 064 612 835 631 735 413 133 079 863 578 137 417 725 436 523 941 269 827 343 756 602 005 665 391 518 554 348 982 688 835 039 904 622 763 095 847 863 195 808 580 525 626 584 704 750 111 922 066 626 505 780 693 646 672 464 975 968 666 822 126 395 374 298 390 935 238 619 095 192 464 276 780 310 135 902 203 414 213 414 535 151 253 228 143 276 276 815 258 697 374 173 084 431 151 373 515 971 275 820 079 381 722 096 372 899 738 464 738 402 820 166 308 681 175 834 544 790 421 343 067 822 162 258 375 824 998 399 118 379 619 282 797 220 456 519 844 333 306 455 186 390 319 507 607 382 162 426 118 950 158 312 552 861 059 642 876 374 153 827 520 773 409 662 153 365 517 009 304 068 582 710 164 276 711 931 225 536 771 883 854 610 672 220 850 327 194 630 640 224 953 097 978 175 268 526 283 664 927 577 014 841 696 183 181 796 805 276 225 598 860 844 173 394 277 483 736 098 582 048 469 984 026 975 329 745 293 197 873 828 641 348 065 323 160 099 912 597 390 387 782 389 365 739 681 664 999 103 433 772 438 127 454 568 258 491 750 342 902 663 725 191 749 198 792 435 468 127 567 789 996 847 172 206 786 604 548 102 843 406 784 779 516 103 053 098 858 069 036 310 745 349 120 861 629 306 604 691 529 432 084 239 071 015 214 196 138 121 565 932 530 853 226 830 861 338 699 019 778 889 713 496 861 400 830 680 225 412 929 045 963 250 798 001 756 403 787 269 588 124 165 913 501 700 527 204 716 379 888 787 963 921 807 775 385 451 681 272 019 254 345 837 717 064 038 511 140 711 472 517 537 897 140 207 199 277 802 716 278 940 430 268 138 119 720 101 013 315 340 723 040 420
217 513 526 428 771 514 450 386 146 158 626 827 098 151 375 891 999 508 452 733 360 117 335 101 994 158 075 798 447 423 743 725 190 443 060 483 329 514 711 222 009 443 265 223 933 444 468 659 116 326 492 068 956 845 964 096 960 344 236 198 401 882 174 729 130 010 372 426 626 231 307 378 762 526 177 842 659 590 657 316 244 235 710 244 599 644 510 453 933 802 950 946 012 149 888 351 531 462 393 694 260 505 246 377 923 883 522 825 891 328 491 814 591 895 967 585 266 579 378 616 384 944 603 123 440 816 028 785 165 336 422 065 426 736 439 247 899 482 536 494 989 995 780 610 767 041 243 568 638 541 886 220 433 137 206 280 916 316 433 490 004 697 075 039 019 847 944 113 292 904 389 599 944 929 934 106 378 227 512 516 726 340 211 532 634 716 821 647 970 193 612 077 035 572 442 693 762 850 128 089 021 562 376 588 229 746 921 910 294 039 600 530 158 266 092 312 763 635 443 557 222 554 430 601 372 705 824 218 432 090 544 759 177 694 303 342 871 342 161 357 896 918 616 306 055 239 749 026 175 917 902 268 436 164 011 241 821 769 792 622 139 939 513 353 545 604 496 052 113 313 166 889 776 929 782 222 811 376 377 454 675 427 440 660 975 569 610 983 690 483 081 626 930 721 647 703 449 227 774 616 719 498 678 784 507 288 213 242 590 548 622 120 180 570 954 204 475 863 634 319 920 134 958 757 084 547 287 161 103 722 024 398 459 066 406 238 837 828 121 536 444 108 113 236 262 855 057 513 261 666 753 906 075 357 737 731 357 540 748 259 634 098 285 217 896 134 297 340 996 205 627 640 897 282 738 206 551 768 521 224 835 943 395 773 073 744 931 055 849 742 212 644 718 236 935 747 346 794 230 182 647 300 944 176 904 308 585 685 685 617 798 908 749 956 403 813 824 024 900 863 317 906 485 382 032 303 454 660 840 296 724 130 974 587 688 781 202 626 711 684 901 914 099 321 263 135 186 129 079 958 839 365 742 100 539 131 886 898 160 070 085 275 559 739 655 639 577 855 571 978 925 847 021 249 840 533 531 209 064 547 312 477 093 461 250 744 975 424 932 273 740 053 343 818 173 315 594 061 702 832 349 048 344 005 122 582 573 299 067 242 289 543 546 448 495 584 403 196 028 177 433 229 392 796 867 527 041 511 783 483 378 645 513 574 852 349 691 274 035 856 058 392 432 836 887 468 605 737 044 828 296 974 840 486 728 014 413 222 503 046 961 429 125 509 561 927 572 942 729 963 549 112 622 761 362 895 689 172 081 523 773 309 867 230 716 728 854 882 569 986 911 612 073 466 203 741 874 226 290 380 378 124 379 050 489 913 540 600 853 302 667 818 109 065 951 851 681 158 139 880 050 028 541 247 461 705 849 320 948 076 871 117 848 332 770 514 047 614 761 585 297 357 457 388 782 496 911 490 486 075 458 063 580 318 203 965 626 276 210 587 152 992 736 346 242 800 748 285 948 497 627 468 497 378 114 945 566 984 135 179 258 294 153 727 298 249 724 063 606 824 043 139 285 993 141 165 545 976 802 197 182 408 845 006 121 840 145 837 522 294 333 158 346 139 264 912 077 248 889 168 077 115 906 798 618 825 608 898 136 903 831 110 065 538 369 399 405 200 738 890 583 636 351 937 503 955 663 042 840 582 072 921 533 200 305 472 478 394 131 261 813 900 990 085 695 099 020 189 303 325 642 503 139 607 936 891 057 143 376 789 549 861 663 884 923 061 605 694 690 259 623 416 662 147 622 915 089 609 107 808 896 700 537 213 796 495 844 393 066 334 768 791 283 625 778 097 446 708 927 728 818 968 050 123 980 182 187 549 957 270 991 023 903 304 498 153 274 396 664 408 107 400 820 783 664 908 997 362 167 394 751 599 543 753 490 017 763 748 585 794 225 335 502 901 650 849 322 239 450 553 044 201 538 494 565 331 235 179 626 151 457 843 845 717 387 821 559 079 275 625 590 341 146 088 782 075 301 557 143 234 496 323 204 055 073 694 727 023 097 473 315 057 455 809 076 925 484 824 199 483 939 960 673 440 103 976 484 153 068 224 756 365 492 039 197 650 064 169 393 481 653 199 387 130 355 427 914 940 294 916 626 058 706 753 476 784 722 749 332 051 052 751 810 807 312 912 629 305 947 299 699 503 092 530 517 982 354 781 780 338 386 644 825 839 471 046 141 901 427 535 055 448 987 166 968 289 435 901 579 876 233 639 366 251 026 553 228 721 727 938 118 726 420 436 622 864 539 594 083 369 830 072 902 309 727 060 345 074 153 920 679 764 018 417 397 625 554 907 148 102 095 617 854 923 121 332 665 021 126 609 039 201 778 247 376 794 293 193 181 007 759 961 492 335 472 911 659 586 892 716 799 054 729 640 029 937 062 423 850 958 228 742 077 252 767 135 715 940 898 131 923 469 341 893 547 534 025 810 707 226 946 704 177 489 699 315 567 446 133 271 309 873 968 208 321 699 053 893 942 483 239 861 441 145 689 164 577 829 911 950 516 465 266 336 388 503 861 679 712 410 299 318 005 806 776 903 858 336 582 238 679 126 069 161 117 720 883 779 792 825 009 000 755 808 168 333 669 919 590 324 844 402 169 351 533 743 138 382 510 617 702 831 111 978 465 812 182 495 375 110 633 594 714 817 870 195 204 693 656 304 586 506 659 074 735 078 625 148 057 002 603 318 549 727 533 565 688 519 301 871 370 910 911 147 956 194 753 655 796 382 186 240 208 255 980 354 910 627 382 540 802 471 038 822 141 290 133 906 984 712 555 255 432 136 381 047 940 971 689 220 853 172 665 107 107 853 916 902 141 841 531 600 250 332 281 220 525 651 325 814 353 413 714 925 002 703 394 389 714 427 684 482 318 210 615 408 316 972 815 013 602 154 971 945 033 514 546 088 518 128 668 846 941 294 901 237 803 426 747 486 136 940 322 722 567 401 181 249 982 230 989 089 693 875 626 185 530 386 722 566 029 194 151 937 623 115 300 266 742 714 106 711 778 134 050 206 478 923 568 385 315 178 475 522 564 610 675 467 022 003 285 016 295 896 138 356 803 089 264 481 675 854 981 467 437 130 836 593 041 100 897 469 414 323 625 938 569 198 029 024 923 899 283 335 388 303 737 741 073 441 386 432 622 950 218 541 570 757 319 079 179 256 420 041 947 065 511 227 659 818 745 182 881 495 381 449 602 471 386 620 160 809 240 799 651 700 815 895 151 462 627 760 779 621 802 265 500 608 261 818 336 920 202 040 460 917 694 208 176 343 747 144 427 487 975 764 043 944 983 979 247 217 177 562 642 833 073 538 294 182 009 969 896 238 329 028 583 083 271 736 331 000 577 983 710 703 713 634 209 778 705 458 158 573 704 157 097 596 033 651 763 150 841 395 513 001 020 755 468 042 668 040 648 458 655 021 593 999 271 941 649 783 572 293 759 046 501 337 892 971 555 024 450 354 139 810 612 448 014 523 842 160 594 118 015 239 313 941 610 851 423 337 526 470 897 043 489 448 486 022 068 290 148 091 029 095 701 193 903 810 776 964 027 459 931 921 696 871 106 230 583 151 381 865 213 649 149 139 658 600 992 462 714 376 332 214 828 713 174 489 032 061 912 245 637 844 776 098 324 978 867 072 920 332 833 376 154 053 724 854 024 096 530 243 692 971 252 995 878 815 191 203 312 071 840 403 195 788 590 170 862 107 538 812 467 516 988 755 331 556 697 228 066 718 729 248 624 438 828 386 855 234 767 281 451 868 896 669 194 413 241 584 252 611 485 437 341 292 406 633 122 861 266 781 870 076 955 592 218 699 715 242 752 564 957 950 468 557 945 716 542 532 321 722 915 106 220 267 843 356 087 699 803 177 496 199 628 685 057 477 409 201 293 774 417 169 869 535 761 841 494 595 153 583 551 808 513 505 559 233 733 713 112 610 307 826 284 440 740 323 211 038 555 135 705 994 669 619 608 108 171 064 343 536 745 615 418 105 105 466 532 619 238 857 955 020 989 785 114 166 572 604 632 641 331 560 033 127 478 521 468 985 767 246 480 979 858 482 658 090 831 309 844 614 809 845 445 136 119 642 928 659 558 498 169 227 519 754 706 510 087 925 281 793 357 252 745 611 695 341 332 847 482 389 588 348 730 833 866 682 868 640 557 255 792 192 057 470 528 395 825 273 934 065 686 215 890 626 557 490 654 142 466 863 568 436 812 125 943 238 381 031 981 485 511 007 977 679 451 796 087 178 713 007 168 897 405 682 732 530 216 760 776 012 449 313 707 611 415 032 739 656 623 169 793 765 532 999 206 991 281 864 378 126 021 557 724 887 877 192 356 746 445 591 813 667 091 819 593 901 104 507 500 294 946 970 201 198 269 935 370 096 393 922 218 016 187 135 737 057 265 711 655 976 317 179 506 164 610 819 723 873 382 736 012 098 911 500 857 898 285 509 008 195 605 910 193 777 742 588 560 994 920 484 322 642 618 739 443 287 760 319 781 456 045 656 436 031 828 595 431 180 094 205 956 796 424 834 204 400 348 199 452 764 595 229 185 466 171 432 436 573 012 708 549 448 302 462 976 435 511 136 969 475 139 384 355 151 178 950 477 812 229 017 745 706 918 579 981 842 739 993 670 124 148 534 193 007 822 102 283 913 492 872 407 445 318 427 688 362 602 301 803 407 180 571 620 237 646 256 799 264 271 105 926 927 856 484 308 110 030 030 453 921 176 167 422 477 041 963 934 114 638 859 847 235 452 193 450 495 783 945 540 889 767 709 899 158 870 942 623 558 468 717 142 764 048 183 987 992 334 568 229 381 093 891 968 179 495 405 927 664 232 372 898 073 064 101 903 916 542 487 261 996 569 262 149 333 007 736 975 876 804 025 954 309 129 059 443 098 310 131 049 081 307 966 412 280 019 774 116 064 901 049 247 490 242 644 229 521 133 271 025 050 779 117 662 400 636 421 556 254 244 358 016 122 907 806 455 493 348 098 306 141 132 766 543 153 570 611 064 298 694 939 995 792 663 164 522 659 397 092 210 472 565 646 193 699 783 823 100 839 923 681 983 487 217 911 933 184 940 567 154 487 234 713 971 109 183 921 359 452 625 275 902 042 428 251 841 084 434 404 179 765 110 893 018 118 468 289 567 483 299 702 737 932 119 604 662 943 059 269 607 053 510 051 321 845 107 139 895 317 260 111 249 818 567 090 293 159 574 386 110 335 425 864 724 955 387 910 763 975 630 269 001 064 744 087 611 325 175 541 388 821 802 879 524 965 469 038 063 349 960 860 575 603 787 254 605 068 358 397 749 296 094 772 051 483 086 829 391 310 878 124 039 129 498 634 386 653 668 284 554 286 388 720 575 425 860 717 728 566 064 421 591 019 309 290 238 244 575 581 011 539 606 572 311 111 344 307 508 450 339 581 847 386 572 188 095 826 966 385 857 850 107 608 055 881 023 646 358 683 402 943 357 556 124 613 072 735 493 497 736 919 489 985 799 233 593 466 580 588 466 047 690 617 654 178 629 785 763 621 651 148 329 315 632 453 766 405 461 965 328 654 089 743 959 405 261 793 540 831 191 872 374 386 451 591 834 108 101 236 508 754 975 645 258 363 394 140 317 325 572 774 206 785 299 012 997 052 392 043 115 646 709 412 358 207 728 479 131 705 882 593 851 912 213 914 110 487 395 309 313 779 558 485 169 747 603 642 820 425 463 109 442 027 746 579 133 051 091 124 962 546 213 931 202 941 660 310 498 443 709 865 487 666 504 222 241 997 278 918 330 524 972 379 045 721 479 376 736 251 930 340 390 759 320 501 610 865 181 113 821 264 030 399 127 731 901 159 067 361 318 297 889 207 794 889 935 973 065 688 523 017 544 220 160 675 543 693 473 515 952 480 366 502 581 092 688 280 352 626 451 164 297 019 799 319 407 128 530 930 066 433 706 041 011 187 949 100 817 047 329 859 277 465 332 758 474 329 124 302 974 967 334 320 152 529 506 370 983 847 848 698 175 888 946 013 332 538 569 451 930 141 785 459 485 094 770 252 420 493 399 333 609 867 996 996 730 347 099 372 746 470 475 322 796 738 632 678 343 757 790 830 388 131 772 703 193 318 920 987 308 770 620 300 479 212 881 872 181 253 033 634 447 510 669 482 985 680 901 544 291 250 285 206 146 720 462 007 237 617 550 566 329 830 252 261 895 409 139 942 189 350 653 292 976 616 903 396 150 260 288 383 136 145 159 115 516 302 334 580 759 169 359 291 367 263 148 779 469 254 797 593 129 833 739 108 609 098 162 959 008 746 794 163 977 967 212 628 557 128 930 016 987 565 481 348 919 698 324 519 234 985 726 069 069 164 107 672 898 232 394 444 096 529 887 127 025 997 098 728 358 002 107 717 399 408 154 265 531 472 224 073 315 625 175 634 300 297 848 186 423 190 902 900 715 112 416 777 177 766 288 620 992 519 958 776 390 520 570 619 224 354 655 014 175 389 531 253 593 248 800 945 305 592 267 194 212 424 465 183 003 713 068 354 181 587 462 179 806 542 911 792 583 615 026 831 812 718 833 547 179 527 119 534 841 710 532 567 215 238 418 414 141 863 125 756 176 604 420 306 508 725 153 866 720 614 194 689 891 646 387 164 969 121 754 726 068 705 322 801 905 922 337 974 583 369 454 215 780 522 901 837 937 843 409 267 834 420 576 134 684 390 026 002 842 267 326 505 982 727 825 783 387 831 553 409 163 475 356 094 331 742 010 506 321 010 600 935 393 014 104 421 473 012 713 288 399 253 573 734 009 221 538 027 446 140 158 342 604 666 827 418 401 517 592 323 631 173 245 693 924 247 332 869 848 310 766 874 690 245 155 185 420 006 475 743 459 813 316 212 106 586 510 817 078 847 950 961 984 771 442 789 516 910 802 727 074 368 426 831 885 287 616 906 172 587 872 624 321 552 238 759 101 185 402 021 219 998 937 713 366 907 377 544 341 088 690 904 593 863 795 193 542 472 794 595 148 274 512 946 550 733 332 165 826 446 970 957 432 617 056 998 019 775 870 231 470 716 009 579 752 751 923 022 556 465 329 387 425 099 339 043 686 766 821 100 200 831 330 720 569 837 676 929 988 622 432 673 764 654 037 117 167 818 868 625 878 975 179 418 562 529 516 067 236 683 859 610 812 117 229 902 002 065 788 475 026 347 066 121 422 239 890 731 023 416 405 755 652 709 030 404 851 882 229 346 163 360 190 379 097 953 566 791 607 916 189 243 791 851 445 604 168 904 277 366 146 989 881 082 385 255 621 501 346 329 965 682 292 559 133 496 812 412 407 478 235 466 365 643 643 341 433 530 129 329 020 879 445 778 805 724 347 737 546 577 122 635 995 054 850 872 125 563 890 772 938 939 999 898 863 423 591 579 516 648 848 787 692 445 611 594 112 721 390 598 539 401 146 905 996 493 110 994 900 660 027 206 873 440 276 053 136 619 469 099 715 360 649 701 682 944 062 252 126 876 457 080 081 751 924 624 433 169 073 008 803 016 875 997 699 145 120 410 931 331 431 889 151 851 237 220 569 260 334 327 599 530 201 553 025 106 182 200 537 068 076 473 051 390 703 643 915 974 310 427 117 554 925 806 061 681 577 971 122 308 417 823 899 964 677 731 513 223 745 933 971 180 041 928 718 597 216 394 602 275 800 898 202 272 137 546 333 870 656 456 152 884 439 804 805 622 132 360 287 868 219 889 432 021 473 108 987 719 205 108 826 098 708 968 554 898 010 764 700 551 407 343 242 703 746 807 366 957 903 805 421 158 143 957 196 999 830 786 515 723 318 233 405 770 941 532 982 256 356 501 965 667 820 753 022 418 552 616 109 723 684 804 448 989 709 700 697 119 254 610 104 843 795 478 540 862 931 822 702 942 110 003 381 614 712 044 692 018 554 377 217 094 009 490 093 152 602 674 567 465 243 653 451 754 472 895 605 053 410 564 249 604 569 845 947 062 567 755 198 262 014 079 043 006 620 763 083 876 881 496 228 703 360 722 497 867 433 172 342 480 135 906 148 358 098 928 518 864 730 329 192 304 396 838 421 143 560 979 097 574 683 673 313 718 035 033 260 472 439 319 841 443 330 033 844 629 081 133 013 876 832 674 260 644 964 723 143 849 565 238 600 860 934 958 014 555 303 288 668 208 173 494 410 356 226 381 065 160 056 248 744 795 264 602 673 427 065 488 642 737 464 632 712 730 318 167 703 745 418 207 012 092 104 620 103 972 483 711 917 520 470 616 591 686 729 015 567 653 596 268 728 818 594 189 416 568 488 586 577 921 579 067 717 972 227 678 740 518 690 464 940 593 700 513 207 952 363 312 015 721 989 184 759 228 584 850 260 800 418 817 744 265 356 625 817 567 771 196 550 121 029 326 726 826 897 153 218 063 117 519 612 811 499 580 032 099 912 388 662 050 755 851 087 602 094 601 564 201 124 065 651 486 291 016 607 634 388 752 973 381 158 162 536 517 072 868 795 684 148 882 054 399 602 272 885 573 024 586 201 575 580 351 477 242 334 449 113 696 903 601 066 225 391 777 052 730 628 112 403 994 439 950 481 002 829 586 990 542 686 817 558 570 546 604 011 743 997 920 362 517 653 059 008 349 648 025 686 179 124 284 699 091 851 976 121 654 194 186 236 411 576 693 136 026 327 237 234 094 960 937 873 201 025 086 112 895 072 910 463 986 241 007 067 293 098 411 144 775 934 250 478 268 091 106 284 077 405 852 796 663 457 821 527 438 404 017 170 988 774 360 739 387 630 830 608 542 632 597 434 348 293 674 132 421 687 980 060 734 521 696 974 050 783 953 422 988 717 750 709 251 842 780 646 236 335 831 053 758 369 535 522 459 970 431 469 453 321 290 511 712 546 359 875 687 611 563 934 704 196 133 011 854 124 411 584 000 078 840 181 439 959 741 837 086 750 456 497 108 221 736 471 660 577 452 333 636 526 338 162 582 783 031 188 337 166 748 829 683 865 282 463 464 193 739 733 850 594 650 969 251 942 299 489 747 764 644 759 169 604 443 695 954 396 690 305 913 034 007 506 669 449 038 697 010 483 206 927 444 086 363 559 145 421 573 651 675 061 391 855 894 367 231 256 816 703 599 439 302 294 715 668 868 717 757 222 492 341 558 556 897 608 895 657 891 208 063 000 135 950 975 508 930 500 362 508 683 232 536 781 270 464 929 746 380 352 132 455 567 241 685 596 432 555 748 278 323 936 102 179 769 288 460 490 307 399 767 536 129 263 519 085 215 703 095 328 753 741 946 688 312 652 306 724 850 367 402 738 271 898 906 884 344 241 179 066 759 786 538 199 751 691 667 167 830 324 474 604 869 301 133 263 603 516 780 439 693 950 635 264 028 546 454 540 285 044 165 055 271 860 663 843 880 770 820 816 207 830 905 770 180 563 259 294 471 916 044 926 829 905 200 447 338 755 236 475 993 345 712 435 807 626 876 525 967 664 080 018 830 221 339 542 486 720 852 879 456 977 630 029 690 010 323 797 707 523 175 266 201 170 526 447 174 935 276 270 344 351 603 329 094 883 389 052 611 370 836 627 568 851 088 868 402 108 242 959 599 535 714 158 376 298 941 013 759 222 434 729 512 474 000 228 775 239 232 660 815 877 643 068 531 844 086 292 728 813 754 996 155 017 808 850 751 099 599 141 988 475 314 182 403 291 371 691 239 394 013 764 064 649 938 130 614 645 546 333 232 954 409 035 188 908 239 228 218 403 786 206 048 812 760 353 605 467 657 136 137 379 888 276 457 721 943 853 444 675 495 838 399 536 872 174 609 023 541 408 550 589 626 149 494 142 914 198 914 079 923 281 959 212 194 660 846 390 129 722 169 299 158 707 660 518 799 451 860 939 530 910 380 429 265 336 040 073 151 353 417 280 195 652 216 011 051 106 925 365 375 476 846 894 416 022 359 877 506 180 118 368 566 612 600 772 991 474 211 319 428 804 633 939 810 265 789 523 269 668 386 312 001 728 192 894 615 026 043 899 263 662 975 320 260 556 285 135 734 463 462 749 942 882 161 957 219 634 427 287 834 030 415 372 407 453 513 518 429 491 112 377 025 820 854 908 526 427 935 021 270 422 112 084 293 284 853 107 050 702 677 918 150 425 729 457 377 362 061 594 822 762 949 873 570 310 481 971 026 043 342 828 635 879 682 668 250 950 411 666 524 007 888 075 753 358 109 260 334 171 254 009 560 924 597 546 994 369 756 398 736 063 884 169 989 266 459 537 474 542 370 315 082 695 767 270 466 304 255 126 729 656 383 303 082 087 878 833 703 287 424 115 825 070 950 090 768 000 064 685 144 120 930 013 598 507 300 652 278 206 965 977 318 059 863 464 173 711 092 750 817 249 228 908 823 479 591 326 968 412 801 111 642 385 014 751 552 797 693 839 139 261 432 578 914 238 111 228 348 542 779 923 008 690 099 106 755 990 873 745 596 493 884 457 450 824 041 986 140 368 570 463 414 189 230 986 580 797 371 127 247 843 367 257 860 722 527 798 281 673 960 977 304 137 863 626 585 003 938 850 303 463 187 622 787 231 282 499 747 371 834 492 678 786 202 603 894 741 283 776 340 632 857 165 734 383 720 808 470 143 078 184 748 136 013 686 268 447 671 561 240 956 299 990 602 964 151 227 183 214 742 745 057 973 454 037 856 227 344 653 548 798 449 977 562 828 016 561 092 302 093 889 236 874 937 768 323 370 824 784 760 010 714 026 102 034 305 292 119 832 652 078 669 282 096 243 422 075 781 090 122 610 671 940 498 325 202 593 256 446 214 508 279 699 589 314 487 608 344 529 644 232 680 761 016 633 482 054 771 118 799 826 962 095 486 152 665 197 304 919 388 883 307 661 615 518 792 310 368 116 244 941 577 279 404 215 168 345 290 231 222 797 649 605 183 760 713 044 327 333 475 479 942 824 220 979 516 172 672 969 182 414 249 124 821 520 398 479 659 174 578 201 440 593 539 451 316 710 813 739 580 234 754 020 692 266 433 260 166 326 073 577 915 886 328 363 104 908 355 686 498 056 113 744 010 272 424 598 173 332 826 276 752 093 614 197 422 051 003 641 259 685 722 938 069 761 583 618 068 287 964 954 185 244 824 547 571 257 687 901 003 037 842 880 234 962 724 792 917 760 212 711 350 621 055 947 893 142 610 230 700 090 304 449 023 244 195 454 767 736 475 846 120 309 292 516 119 671 372 401 449 947 188 376 528 831 792 912 829 522 627 796 632 976 285 159 992 118 280 205 088 533 112 668 354 397 461 259 071 554 341 379 153 370 767 134 597 004 473 609 215 156 206 604 771 499 753 272 975 133 391 237 428 572 644 042 472 068 267 329 532 236 218 998 404 561 001 902 241 452 229 671 377 028 973 870 821 472 572 155 392 388 120 477 098 010 295 247 315 297 805 467 707 218 395 634 993 771 466 700 690 955 368 847 697 369 942 893 600 232 693 456 227 772 409 843 890 478 553 789 936 808 999 768 244 741 398 856 697 926 852 029 921 638 451 654 073 853 044 628 366 932 225 846 781 786 577 435 108 471 208 299 418 727 779 680 337 455 900 769 811 240 996 068 243 330 145 025 690 323 418 554 250 983 227 039 713 544 974 702 620 838 492 194 480 228 168 426 509 803 968 552 245 142 349 596 113 690 790 630 379 109 957 839 257 872 069 683 443 957 956 295 902 113 942 466 967 230 732 903 412 696 309 428 555 939 547 828 337 701 205 396 661 042 776 658 573 671 442 059 798 099 939 361 817 924 993 231 889 224 000 757 597 146 947 136 078 714 065 742 630 369 130 231 590 844 485 965 090 426 051 694 245 218 925 897 106 986 288 288 996 152 826 830 276 242 213 975 920 398 096 497 627 220 138 272 238 557 071 239 429 889 971 945 929 149 665 127 241 931 581 999 584 424 126 152 897 898 844 098 315 234 123 855 647 252 764 283 690 967 900 713 205 773 688 673 452 533 066 077 045 189 699 053 622 719 836 670 095 702 310 826 555 733 371 261 197 863 888 583 295 855 096 895 329 029 446 221 876 517 057 913 237 886 015 632 542 969 203 546 336 040 863 064 566 109 437 744 320 371 164 277 173 711 636 221 878 998 771 239 700 026 736 783 540 275 564 567 446 133 340 191 925 316 638 208 210 140 095 497 008 579 279 880 566 696 662 679 156 313 524 804 078 010 702 840 468 060 001 921 584 100 659 796 690 304 337 746 999 261 308 247 183 175 514 594 515 333 604 650 153 632 395 921 141 561 834 772 510 230 118 909 568 653 553 881 599 035 825 688 779 802 368 274 141 595 547 683 464 278 386 330 105 430 280 968 483 753 669 789 044 474 774 902 391 530 614 964 678 723 073 019 203 492 486 824 185 494 900 827 025 082 557 411 633 211 386 310 235 798 448 438 733 325 818 936 528 546 871 365 674 242 671 818 495 394 602 791 819 519 673 425 006 121 973 386 248 628 812 595 388 195 828 476 846 808 069 084 027 647 395 015 065 908 537 681 016 649 548 551 284 143 908 197 179 240 295 900 069 330 303 412 440 060 680 072 743 666 738 271 908 919 660 922 059 462 916 189 397 046 875 964 161 517 664 253 010 816 979 426 025 412 517 206 580 931 399 306 191 463 356 102 198 901 799 762 238 016 675 880 814 429 063 678 348 270 145 345 864 698 622 086 293 145 231 254 323 108 189 654 829 249 304 157 045 412 428 113 810 839 592 631 336 809 473 520 527 122 943 319 541 017 769 852 156 626 386 759 729 415 050 368 262 362 871 436 223 944 862 321 017 645 385 450 831 209 039 954 914 771 574 032 597 804 206 912 016 116 790 451 207 405 478 106 169 672 391 573 973 881 664 141 350 011 832 280 653 937 830 384 832 529 636 718 513 643 104 588 224 882 426 735 261 292 144 520 075 392 907 797 199 814 386 362 398 156 868 255 468 243 239 869 859 794 075 754 711 434 256 612 919 833 176 871 055 075 269 802 195 588 554 020 646 791 999 408 289 136 539 211 201 415 065 143 042 959 824 566 987 736 481 879 094 917 976 961 826 142 382 396 492 140 176 879 252 220 187 408 620 427 881 491 947 103 460 597 706 255 040 515 718 038 376 647 436 461 207 891 383 797 286 001 922 207 079 143 790 338 232 250 669 221 780 524 575 311 449 300 567 876 719 473 446 101 325 763 626 369 185 802 899 987 202 662 515 005 324 345 433 937 373 266 638 714 532 793 754 661 374 286 120 848 942 162 870 349 077 580 777 576 431 311 516 576 172 032 117 074 294 482 928 758 562 690 038 536 900 512 084 457 424 699 421 588 148 287 348 121 168 587 147 164 273 352 633 279 811 269 525 906 242 713 229 435 938 485 415 074 573 804 705 414 220 404 312 126 636 773 697 908 166 121 809 659 846 939 207 075 419 738 975 372 576 949 976 408 458 973 612 615 223 422 223 801 406 785 577 477 154 389 684 147 486 075 777 717 318 618 305 935 147 434 185 855 542 369 231 586 464 958 973 449 955 948 300 205 938 793 048 383 583 395 941 517 098 907 275 732 607 715 698 848 916 274 886 918 772 530 346 958 557 400 216 002 876 131 626 083 559 166 265 409 332 775 080 543 779 004 545 663 337 821 328 804 804 007 631 915 617 977 557 053 658 502 758 369 798 125 697 804 680 710 038 233 699 003 571 730 496 649 156 045 126 689 604 177 962 347 224 449 807 239 351 935 633 005 326 632 337 366 553 107 281 824 253 113 021 518 684 864 369 455 064 785 877 526 523 106 442 868 466 451 351 499 842 543 802 770 016 211 587 722 390 818 045 966 781 412 049 272 596 650 777 555 311 685 644 994 999 543 255 452 948 769 092 336 238 995 437 502 537 528 619 879 469 536 089 671 966 413 593 346 590 018 031 360 686 201 746 385 929 486 024 990 357 464 635 302 833 833 883 037 040 436 108 622 620 869 117 018 903 334 975 287 866 050 205 094 360 847 248 050 093 043 080 289 343 164 168 260 665 748 640 874 203 607 857 684 708 228 269 666 862 595 347 570 340 961 349 302 937 797 746 294 304 769 745 836 804 410 333 389 044 960 988 176 568 760 532 450 012 209 760 830 794 427 688 398 230 609 120 405 436 589 165 240 135 792 817 900 771 152 325 997 781 527 279 748 877 403 725 278 354 100 949 091 018 744 263 476 955 151 208 037 374 540 481 647 912 173 251 194 383 873 862 667 558 963 987 205 760 600 408 473 700 343 642 808 658 090 109 916 290 024 580 671 589 683 304 051 004 987 562 195 985 793 419 134 083 246 906 507 505 430 007 328 601 818 921 788 536 531 817 746 834 401 620 522 251 513 214 310 952 567 254 057 618 404 991 422 894 441 449 457 298 385 534 475 374 263 044 738 832 362 174 535 098 408 090 892 603 946 756 226 099 087 753 457 393 056 016 319 967 708 676 601 140 164 601 467 578 337 932 225 498 281 808 474 493 425 134 246 729 892 955 271 560 579 001 480 838 427 563 704 321 047 003 673 754 721 184 836 778 850 215 066 077 687 428 243 884 048 137 020 189 645 261 513 485 439 043 730 793 623 868 130 761 186 004 913 421 073 296 446 031 697 000 866 785 216 782 260 968 230 738 619 741 982 482 614 397 513 881 671 723 417 660 517 584 241 959 651 011 556 609 303 753 935 027 459 918 787 061 374 197 564 194 474 155 159 026 297 921 089 281 205 893 693 304 341 483 311 533 058 986 937 819 546 104 814 121 828 224 891 372 216 737 490 080 252 206 650 401 644 080 125 984 693 678 196 255 328 918 161 734 585 906 117 222 597 141 459 931 033 135 444 729 280 253 427 948 184 140 724 097 719 883 172 001 758 414 802 775 602 352 561 893 229 502 065 570 180 788 406 978 703 904 899 998 683 832 979 217 227 975 192 983 933 656 467 746 086 708 599 865 416 628 887 215 021 763 881 184 673 356 668 743 755 968 297 144 957 490 958 787 519 800 824 405 289 018 579 568 431 098 858 594 175 953 131 669 075 033 502 610 580 230 845 183 296 737 954 483 455 866 877 676 040 500 548 563 037 107 123 542 193 586 860 490 617 156 240 938 039 854 713 028 533 682 880 261 975 105 602 091 138 604 046 949 473 717 473 347 544 012 179 280 195 991 134 912 800 110 633 034 989 987 743 146 360 987 370 448 051 827 975 278 888 075 203 925 287 856 347 041 991 049 224 001 023 663 146 964 058 641 228 101 009 463 499 139 729 629 054 583 751 865 845 912 182 229 721 743 624 032 029 404 265 674 060 180 919 639 123 653 950 744 039 208 737 834 861 134 437 460 115 002 703 072 145 735 193 998 047 706 348 585 746 328 126 690 194 888 727 671 884 324 157 601 121 926 201 208 608 900 591 542 029 535 413 409 495 683 338 893 997 542 425 138 659 752 203 367 243 635 770 371 889 360 157 462 595 258 725 408 869 856 851 875 112 414 428 070 537 681 098 580 342 843 921 034 171 174 029 018 541 154 184 011 870 653 287 279 575 562 245 719 347 943 753 345 739 873 450 638 352 684 844 126 122 040 874 208 617 250 389 349 542 286 039 342 688 602 049 909 492 428 902 916 372 962 444 649 602 366 406 377 877 815 470 209 959 992 639 991 709 980 409 615 232 660 758 113 832 143 327 849 574 388 555 244 483 955 330 265 018 944 737 896 571 597 281 780 813 824 501 406 088 353 251 203 732 220 414 326 527 267 396 303 772 167 595 494 002 777 215 494 768 353 098 214 187 167 853 129 218 055 755 720 088 044 161 577 250 961 891 010 356 490 818 776 823 148 985 395 361 853 217 032 203 623 192 116 345 162 737 366 325 331 753 822 605 687 087 779 717 388 368 046 245 461 556 423 411 006 615 246 065 900 943 476 456 817 760 629 261 034 539 253 716 813 072 491 292 356 761 496 712 469 943 195 214 382 711 748 201 382 132 469 868 425 494 881 896 007 172 021 461 412 238 112 867 866 146 604 343 883 048 455 730 482 168 745 723 827 294 938 537 286 740 312 238 392 766 242 156 691 805 582 872 535 921 089 655 563 678 131 301 401 048 947 508 847 720 806 460 834 316 799 601 942 377 352 727 425 106 771 459 873 646 778 320 326 580 871 398 439 058 003 025 716 617 242 163 507 847 702 703 306 858 954 749 645 781 250 474 977 668 574 455 124 403 504 061 179 392 768 649 260 018 821 037 158 283 574 119 312 616 318 246 067 041 197 388 191 727 295 700 051 684 971 984 347 479 186 169 797 754 919 564 910 044 859 935 305 404 760 782 437 896 717 163 437 136 273 761 028 327 839 891 566 500 513 969 455 212 825 339 711 629 759 462 057 823 233 134 153 124 192 877 564 516 140 653 649 089 317 701 956 190 379 666 097 888 986 662 349 265 732 850 660 119 988 350 891 474 952 992 811 993 441 796 207 473 601 811 219 727 647 713 135 899 719 936 256 132 420 967 459 878 704 639 239 357 978 526 325 988 925 106 788 205 595 209 036 280 507 371 568 538 443 250 406 223 894 777 159 165 413 816 110 284 471 974 210 482 528 064 376 500 535 577 208 760 485 360 055 581 486 472 552 370 155 136 624 554 380 081 260 282 109 860 916 526 748 074 623 229 817 219 263 465 025 692 318 111 567 033 907 863 214 472 753 543 905 313 248 377 958 604 259 682 373 550 300 584 772 823 563 493 824 661 598 326 819 848 935 802 939 559 524 307 491 405 626 288 844 934 141 666 978 389 037 718 468 706 964 414 633 552 427 596 027 045 719 447 802 719 306 962 530 840 325 770 733 869 591 992 713 607 345 093 665 614 528 624 760 266 606 234 852 120 124 117 231 495 177 895 789 729 839 649 373 236 080 054 315 769 679 410 387 528 188 589 015 924 173 907 599 609 513 328 041 065 442 877 138 648 864 679 671 547 510 924 234 772 714 670 383 949 783 370 201 093 105 429 042 143 784 788 005 120 336 178 226 316 391 177 136 838 163 588 012 670 126 820 505 451 300 945 439 652 063 018 369 893 082 965 227 142 926 047 677 540 051 891 965 271 868 788 793 338 214 394 274 199 410 413 952 327 108 927 081 726 284 582 288 874 737 245 117 834 433 769 973 950 596 736 801 393 852 380 907 228 196 360 202 898 133 498 213 624 392 442 068 067 888 327 076 300 485 321 222 648 267 517 586 388 730 611 696 652 150 846 542 061 544 335 427 442 432 506 898 609 178 788 660 534 916 153 198 224 015 147 070 619 740 607 237 247 135 284 270 110 201 617 024 943 738 110 110 305 484 122 561 433 700 417 047 066 353 003 834 097 136 042 692 869 572 231 900 883 158 562 829 323 363 113 737 337 076 755 534 648 592 205 965 334 428 337 758 489 564 017 782 846 095 434 745 637 261 911 272 709 082 810 445 239 582 510 792 452 798 929 580 379 290 542 122 151 857 460 538 548 457 042 252 451 900 620 796 550 350 201 257 184 537 396 228 050 539 143 456 967 194 422 931 274 248 828 870 519 082 172 410 355 560 796 991 558 332 039 928 115 187 009 131 961 167 229 593 091 812 820 902 226 126 222 778 957 500 879 576 280 704 362 967 060 974 909 434 517 423 746 700 336 763 351 280 699 701 263 185 900 073 492 331 854 328 650 086 224 267 888 401 602 782 577 972 769 653 977 975 895 970 578 849 125 925 755 051 256 076 262 086 960 020 412 787 213 689 649 378 333 661 980 697 482 323 571 608 122 101 383 646 338 145 514 408 206 391 459 262 961 483 119 775 002 792 995 974 257 864 131 921 281 543 939 698 591 435 897 098 765 229 208 591 580 606 599 123 834 215 662 368 688 826 526 721 000 677 127 433 671 291 776 741 694 285 041 792 330 289 346 566 978 314 974 292 028 282 536 160 509 258 914 304 081 010 749 796 103 449 422 628 796 534 523 419 240 304 477 466 792 698 590 712 631 576 137 192 260 665 923 432 718 949 492 795 917 108 917 371 041 836 934 832 432 284 063 365 882 831 454 133 761 618 184 357 597 568 255 620 684 797 813 324 035 474 158 619 475 753 558 019 194 171 986 918 993 286 264 062 656 329 664 327 034 170 713 179 312 494 529 125 894 540 133 289 516 458 918 373 692 048 081 178 782 083 665 359 130 441 585 530 587 648 091 301 684 061 023 158 607 865 188 597 565 759 977 304 500 092 146 382 653 325 095 266 845 221 075 876 992 367 576 184 517 023 769 351 893 294 514 146 156 543 598 956 227 142 416 353 087 988 577 076 733 785 410 567 950 079 210 260 274 876 882 985 027 442 084 482 462 363 723 881 143 977 564 224 831 567 636 016 350 353 778 950 310 757 102 127 465 052 199 856 192 952 636 574 940 217 060 707 778 865 715 414 404 125 137 431 852 443 263 669 582 324 541 939 158 683 513 592 375 471 607 524 864 360 158 987 365 339 386 372 551 694 267 179 383 452 387 133 106 621 736 016 505 433 573 669 345 771 953 954 133 676 959 976 447 844 679 141 713 647 942 947 720 925 338 679 259 638 246 916 947 589 173 011 823 461 744 522 590 291 126 828 763 030 147 753 871 696 467 370 907 258 952 861 228 391 515 359 809 376 247 655 945 074 685 060 238 472 704 737 767 259 515 608 480 685 815 432 384 544 047 510 531 777 897 593 609 155 439 068 640 772 831 191 744 478 710 006 768 561 173 241 219 849 860 413 495 880 063 282 948 783 078 292 413 415 951 594 318 126 327 043 473 614 955 082 522 963 445 012 816 405 921 242 019 473 552 403 377 159 801 079 382 851 666 795 922 260 472 117 102 703 266 549 610 672 585 693 306 569 382 627 968 556 008 850 868 145 119 730 108 092 850 259 442 122 874 967 784 030 882 793 338 592 691 717 969 951 667 142 462 359 620 300 718 827 586 078 840 533 534 418 469 275 785 665 672 076 504 526 805 071 728 626 298 388 387 173 469 258 359 065 847 354 654 969 145 786 217 119 039 435 588 726 293 260 035 101 951 607 173 327 448 773 100 553 184 875 471 285 052 713 586 036 445 836 272 665 989 796 148 926 467 661 945 309 161 719 198 443 842 031 653 412 947 740 382 585 661 551 121 045 006 830 704 039 486 903 096 047 900 224 531 996 100 718 028 695 414 061 331 114 459 218 247 822 661 086 212 587 352 426 087 902 913 620 061 611 522 711 168 285 711 704 971 689 460 380 190 779 463 010 625 978 033 401 402 686 593 569 500 793 462 932 875 432 058 956 204 445 608 506 473 144 539 343 093 425 074 891 668 019 508 868 998 244 832 772 719 361 546 423 099 384 278 843 199 819 428 387 979 349 107 007 321 243 842 950 571 587 456 217 889 199 852 293 940 779 305 739 596 309 924 004 589 406 888 370 951 405 400 057 821 453 038 253 594 880 998 255 677 994 463 084 893 634 811 525 033 417 131 666 500 467 898 551 677 792 462 464 828 570 478 598 812 086 668 432 360 521 759 129 529 903 954 200 814 360 848 653 598 544 544 023 994 860 567 943 706 986 573 960 154 089 016 278 709 899 468 801 559 430 958 928 827 227 649 028 066 942 752 755 295 780 078 814 475 542 330 749 498 610 383 789 975 230 470 143 339 018 494 136 947 368 819 026 147 283 493 636 624 445 356 429 794 150 310 965 535 855 080 402 346 600 190 154 114 944 411 114 426 803 010 094 482 591 257 831 891 131 974 838 359 431 044 085 685 904 885 092 970 169 419 101 456 313 344 283 738 919 168 552 974 839 772 812 906 430 952 726 066 905 440 879 383 264 620 688 403 700 903 104 091 476 150 754 397 106 854 172 043 322 626 350 580 779 304 002 551 424 401 269 764 165 675 583 731 106 565 710 504 278 726 138 895 732 764 657 910 389 382 549 992 736 262 322 416 611 024 906 071 530 273 204 541 222 298 561 911 000 228 839 405 479 088 012 838 668 093 861 810 525 654 541 434 131 474 530 402 673 003 681 272 264 930 728 567 084 069 637 273 710 683 109 910 622 360 548 393 540 280 924 865 523 205 432 162 100 462 171 954 439 363 435 060 531 037 134 055 086 164 705 827 255 293 380 257 827 513 247 846 750 617 579 188 589 698 078 639 190 951 721 288 640 041 340 442 336 390 251 748 401 009 552 708 884 169 336 770 233 974 845 421 403 163 947 990 684 747 245 949 388 793 369 180 977 356 913 064 953 633 756 899 483 364 464 657 392 830 377 220 815 801 005 929 493 080 547 690 671 553 396 062 769 506 792 247 854 176 045 280 270 177 025 138 721 207 228 169 824 433 120 975 832 672 035 312 712 152 748 544 644 566 943 058 966 739 419 506 363 554 974 626 355 268 988 456 614 702 285 999 542 719 868 363 634 818 220 032 740 170 483 824 183 217 963 909 262 449 929 594 037 201 893 655 130 761 667 989 266 527 825 509 255 526 478 038 502 255 948 514 032 724 800 299 008 722 845 044 198 348 658 740 282 671 394 749 215 468 508 880 366 865 068 471 378 792 630 460 433 105 574 134 471 206 087 178 107 275 341 121 526 120 149 157 328 261 309 335 233 601 408 431 137 383 032 856 804 791 561 370 972 951 977 543 536 416 142 151 079 780 147 347 888 654 714 555 187 127 474 222 616 953 251 104 573 547 343 841 220 819 970 294 564 167 178 300 182 224 738 762 351 122 598 968 856 554 659 543 131 889 260 696 879 421 369 797 010 958 611 722 770 142 521 813 294 358 771 350 881 107 266 345 227 969 318 034 822 282 479 202 666 291 268 850 093 989 337 161 759 502 625 388 592 875 928 929 864 605 179 897 085 248 681 598 239 429 926 161 262 376 325 410 472 428 041 458 949 488 208 744 204 139 652 100 348 669 318 174 926 245 449 105 891 748 004 227 056 832 714 376 160 950 828 790 535 226 081 581 234 775 986 697 560 716 128 065 617 415 049 198 906 210 947 926 198 373 566 196 198 866 987 511 415 152 955 695 804 020 838 076 325 128 041 424 484 235 503 761 305 260 007 461 236 542 215 413 535 055 204 581 059 842 412 987 554 298 144 410 180 648 081 248 589 646 866 983 323 415 861 884 341 053 741 650 478 837 139 447 967 124 408 407 574 260 228 822 750 163 401 184 749 987 218 628 550 360 771 930 621 195 546 265 784 744 300 435 355 197 167 842 637 304 747 339 783 747 366 578 838 665 498 812 563 446 209 884 952 610 611 978 902 782 825 968 219 243 557 107 909 765 169 632 135 727 327 812 903 387 762 370 794 929 737 305 076 679 057 342 105 711 904 395 308 854 647 614 661 014 725 590 966 735 904 163 495 379 036 761 721 772 007 858 110 873 613 990 950 902 181 952 435 197 375 103 937 200 062 183 326 498 580 806 532 714 484 701 056 082 148 660 354 297 387 335 534 299 834 032 135 268 636 837 760 956 893 312 105 662 864 539 793 037 202 331 408 649 227 873 012 045 381 185 478 827 881 179 213 673 211 213 706 537 015 814 691 394 847 377 434 575 896 646 250 481 631 322 954 693 359 754 509 979 074 174 544 543 161 939 752 612 016 866 759 541 673 699 549 397 136 785 998 934 798 689 080 724 286 799 072 650 566 064 568 327 520 108 890 148 880 998 837 955 008 285 976 947 933 848 036 226 597 813 525 145 510 443 669 983 496 528 796 686 612 821 575 037 203 408 033 426 269 067 006 304 746 610 345 145 138 284 625 151 842 053 245 473 961 453 108 949 417 456 265 558 573 806 467 250 558 138 451 906 380 117 726 792 175 179 293 798 415 798 379 578 864 874 049 897 534 168 877 577 866 853 782 203 430 111 845 229 789 248 154 583 784 776 810 074 671 082 556 109 963 194 505 309 374 022 182 659 305 979 167 397 375 513 213 733 456 241 650 413 714 115 859 932 208 871 261 371 883 397 670 133 816 306 784 690 406 815 326 196 723 130 051 946 793 827 495 353 080 327 512 045 208 647 696 221 814 610 263 490 753 234 428 030 315 994 032 943 765 293 969 547 577 300 636 568 831 818 250 034 300 175 585 069 505 718 155 735 052 852 574 822 185 916 943 232 527 874 236 832 205 019 970 051 323 631 415 342 521 073 517 261 523 865 814 060 871 756 011 012 000 022 894 072 151 671 763 338 933 338 076 842 535 370 004 130 264 889 364 284 293 708 077 451 112 167 952 732 112 662 414 682 050 107 419 038 294 597 980 633 980 175 462 449 392 516 613 305 064 543 338 946 544 455 123 216 699 637 964 419 976 073 358 904 350 755 528 895 643 277 455 989 723 532 881 299 677 108 629 325 003 323 906 787 099 448 018 970 173 745 903 700 886 941 794 631 446 545 470 425 973 765 142 734 063 247 306 081 873 093 631 775 288 434 475 289 488 852 679 958 718 675 343 224 545 977 798 059 946 617 225 282 660 723 532 071 939 739 065 376 063 491 116 844 430 202 769 930 380 844 978 793 092 252 020 688 653 476 732 244 442 319 640 090 036 202 894 637 533 536 417 516 254 389 958 296 107 402 487 108 595 707 569 780 265 524 189 236 121 555 741 188 004 685 690 828 046 534 174 851 188 378 180 659 809 356 517 278 126 632 008 157 459 906 209 510 561 389 002 685 768 507 800 642 343 096 972 105 348 673 405 098 746 306 087 043 589 256 724 098 467 271 712 818 049 009 091 963 582 373 516 078 526 182 424 635 307 985 755 242 741 125 519 434 402 931 774 211 666 703 836 906 183 337 591 487 399 891 617 356 905 437 660 627 790 858 475 346 441 686 878 362 620 312 994 688 850 828 287 021 069 257 918 865 359 060 019 568 022 888 242 521 750 686 819 677 736 623 295 481 216 055 933 120 555 062 327 200 814 730 738 388 606 139 063 972 814 759 615 417 905 755 748 490 726 064 340 696 906 165 239 087 956 007 227 248 011 088 798 155 200 292 790 956 657 491 798 359 543 721 106 168 757 499 209 680 396 336 312 945 940 055 307 442 868 411 996 688 529 085 085 442 698 710 038 716 534 055 627 485 466 958 617 114 162 934 922 234 350 864 196 880 384 129 340 857 597 582 327 847 449 312 610 373 642 130 786 494 065 965 216 844 071 724 801 508 934 395 903 625 704 630 261 574 387 184 910 643 187 252 519 419 385 358 847 922 493 083 942 575 079 382 594 432 081 834 729 067 498 341 033 699 631 072 439 096 991 131 003 905 179 270 422 072 781 115 493 203 049 288 491 741 960 202 921 649 049 020 116 787 698 094 820 397 414 249 043 587 862 795 533 538 796 753 981 407 854 214 091 610 297 643 269 470 296 397 590 614 380 787 127 213 619 865 741 920 217 493 868 294 826 421 565 275 296 522 203 646 253 572 566 282 337 166 584 772 084 875 910 682 840 287 506 107 635 239 398 212 334 110 667 540 959 501 356 660 798 960 084 091 743 234 587 061 773 725 247 500 743 144 652 223 667 408 009 683 492 687 046 185 531 195 989 889 496 856 610 997 909 930 545 380 863 657 561 815 980 364 651 197 525 087 790 954 673 253 418 707 522 681 419 482 274 089 173 587 116 958 225 431 293 681 633 728 227 610 907 271 015 286 227 710 231 175 502 795 182 677 393 467 916 641 486 153 168 685 359 093 310 139 008 208 891 032 201 845 541 688 334 786 735 035 313 478 745 638 715 187 121 672 372 481 706 800 018 335 676 491 147 071 994 829 507 395 320 328 591 702 780 062 427 820 803 191 133 942 755 502 449 052 896 498 167 392 625 993 008 883 746 461 734 208 214 458 802 005 707 227 112 795 587 705 758 063 982 558 855 692 997 460 412 991 599 794 412 120 087 419 758 698 364 628 560 922 857 503 239 788 072 492 131 798 479 702 126 140 650 129 058 164 159 597 817 516 263 003 867 203 034 913 470 065 174 515 181 937 262 973 685 054 295 531 828 342 064 202 502 769 930 808 185 369 746 198 435 629 340 440 231 342 124 711 053 308 836 226 383 290 432 231 405 934 887 941 623 356 010 724 712 131 322 462 324 869 159 692 851 978 458 630 226 052 885 008 364 408 602 566 951 561 261 221 296 403 508 455 944 455 411 504 854 017 508 870 257 951 991 394 837 383 786 849 207 920 691 956 199 834 445 666 517 377 459 287 243 545 323 576 877 701 230 121 855 076 325 489 337 483 983 613 854 501 935 694 212 032 363 277 838 730 973 751 953 540 557 316 928 505 496 761 350 842 033 955 737 973 219 234 410 615 865 902 770 920 509 576 246 112 479 286 359 643 157 730 307 739 751 923 100 138 814 680 587 446 214 526 660 126 826 044 325 914 903 689 055 110 572 391 784 354 440 340 246 223 914 329 452 816 245 893 807 727 516 779 429 649 565 521 603 274 216 597 173 497 500 144 571 427 166 846 699 459 870 007 070 418 239 120 613 080 884 494 324 829 881 671 004 528 610 392 685 924 629 715 707 274 473 337 337 008 384 348 750 810 331 983 032 339 103 299 760 874 413 912 715 160 759 954 655 350 879 130 638 224 697 562 041 359 424 150 225 020 370 974 553 147 277 003 251 951 580 652 430 771 423 345 588 526 578 815 834 893 110 469 763 633 300 371 912 926 713 972 505 465 846 739 888 911 273 680 921 418 796 995 649 114 889 035 272 683 756 353 587 920 181 533 289 721 769 207 674 391 437 963 069 014 507 654 919 638 187 027 746 869 205 880 027 091 174 682 303 989 405 247 961 980 414 679 594 603 467 366 405 300 375 011 003 705 456 630 458 680 993 863 906 613 558 060 299 555 426 252 383 440 260 464 617 658 619 792 218 740 742 686 947 983 598 973 484 616 256 771 030 983 734 832 214 330 744 841 841 989 450 414 637 792 713 479 872 224 303 813 236 819 386 641 344 039 670 990 419 550 424 181 053 393 950 909 468 216 687 104 357 185 798 060 954 240 110 497 444 060 729 585 709 827 597 090 124 415 892 402 816 100 705 472 159 510 706 285 311 123 866 757 867 156 306 011 508 471 445 770 274 249 298 614 938 105 440 807 969 424 617 230 624 417 765 648 341 801 248 659 628 212 206 735 913 733 923 006 169 125 352 423 937 465 161 099 769 143 977 528 038 303 256 125 618 358 458 513 279 551 728 688 730 541 386 451 680 036 034 336 536 389 356 067 126 354 383 022 319 171 191 270 104 887 248 884 156 269 275 491 922 299 617 235 300 067 220 105 023 227 091 785 884 160 749 133 430 546 097 423 966 286 838 687 782 656 945 391 223 122 282 857 963 369 490 290 185 229 409 986 348 657 366 141 475 024 421 169 813 477 495 176 203 977 814 198 985 031 978 839 037 284 574 496 938 552 657 985 797 225 191 030 510 577 995 688 129 269 965 311 414 485 006 838 369 873 298 144 037 848 667 193 254 539 977 251 853 469 387 541 440 134 687 808 652 181 687 163 700 041 676 313 405 108 905 707 486 532 550 783 203 113 881 836 496 560 182 216 739 083 616 947 509 962 721 890 217 833 981 039 800 223 891 431 273 478 313 963 724 225 343 873 514 079 589 575 188 033 735 149 616 856 965 201 986 717 853 244 857 212 228 891 325 747 233 663 174 262 115 023 759 093 625 336 172 247 396 920 708 344 656 402 725 377 922 257 771 418 293 350 519 957 695 968 415 058 061 040 022 477 380 327 596 152 047 265 095 341 278 341 466 261 757 319 225 692 248 557 050 673 676 889 901 092 886 961 832 272 310 642 389 390 945 310 262 798 990 135 761 890 864 060 004 081 333 743 910 087 040 813 117 580 196 395 574 076 934 370 005 525 903 722 757 175 107 874 967 451 189 559 711 986 083 183 019 841 268 544 718 329 685 408 346 753 659 718 854 662 679 118 611 150 766 427 375 734 384 169 008 256 334 043 859 021 991 046 864 399 984 838 249 351 060 581 573 642 187 579 189 604 835 563 379 760 844 287 507 314 734 565 620 106 595 275 192 362 105 378 487 963 153 944 212 687 845 710 270 203 624 712 264 341 015 044 349 223 387 903 296 696 294 673 751 518 950 258 782 376 174 195 661 272 793 572 695 330 655 927 353 447 549 110 983 030 260 454 868 367 233 368 452 590 409 206 633 190 030 963 713 830 853 746 856 115 413 603 663 266 554 855 029 149 979 913 873 935 185 645 519 611 539 947 625 193 796 617 591 859 325 447 874 160 687 932 449 414 540 767 451 575 909 712 073 357 142 695 530 272 725 935 953 523 954 690 581 060 332 615 690 269 113 665 162 594 685 682 014 595 697 409 925 033 723 811 351 906 448 680 158 975 723 319 358 628 915 298 782 628 883 237 169 509 170 570 281 327 891 926 125 848 282 360 905 748 912 849 156 483 253 886 328 693 708 269 019 825 465 702 744 696 565 973 276 860 834 759 710 790 737 295 672 791 256 993 156 779 983 095 313 600 496 285 383 718 122 511 772 493 932 693 795 580 140 275 238 217 848 943 608 742 465 545 889 532 923 714 719 868 664 888 031 620 988 558 635 664 121 648 407 151 900 657 220 321 947 769 618 304 649 005 994 367 178 661 804 503 946 403 698 059 207 721 275 747 148 742 132 102 088 547 742 596 141 609 570 651 987 023 058 414 100 789 976 726 267 078 492 360 504 131 543 639 148 938 984 093 527 407 278 616 089 844 259 735 506 319 278 070 884 325 372 279 423 807 720 570 999 541 752 734 320 216 011 675 554 954 814 740 132 598 654 925 800 295 073 694 751 780 977 632 503 473 717 471 381 410 632 288 021 935 323 975 621 316 100 535 366 179 875 462 158 551 775 280 304 702 122 698 126 120 319 980 314 059 924 018 590 845 751 241 755 509 575 503 026 468 230 122 739 804 925 267 222 894 388 118 687 138 430 939 506 262 796 412 161 876 078 479 246 093 733 558 385 830 108 361 693 898 159 247 885 524 656 177 412 484 795 704 840 276 854 457 430 736 167 176 074 810 263 946 434 281 227 411 697 665 192 224 877 416 150 932 122 674 397 029 701 982 505 970 570 255 252 042 546 218 528 515 445 140 447 444 050 360 863 883 008 853 326 907 511 332 639 304 097 884 273 202 633 932 054 841 212 809 906 543 443 121 043 672 649 191 920 494 965 118 923 640 312 851 109 472 096 726 572 164 924 548 469 246 174 522 285 444 229 474 910 935 773 501 076 755 463 222 148 877 182 037 762 941 173 052 966 769 691 344 123 362 213 273 960 071 365 149 636 910 180 203 610 698 891 262 104 071 213 792 101 881 827 749 582 806 602 689 890 334 084 397 790 773 981 514 797 119 489 458 050 252 488 066 763 617 612 796 537 571 820 327 777 011 468 898 404 116 190 967 350 675 189 746 585 967 837 706 834 212 981 025 114 455 875 821 538 123 621 309 410 880 871 203 829 137 462 414 294 573 007 010 443 074 496 816 331 462 087 897 736 329 578 323 916 950 491 722 984 453 672 532 184 390 994 987 607 080 696 372 447 992 471 981 629 671 250 294 131 026 475 977 587 523 257 099 311 921 306 867 359 166 888 067 510 115 352 002 795 902 193 880 427 980 445 811 393 481 406 382 071 128 572 250 281 603 142 706 914 614 623 695 015 083 150 618 089 958 663 777 226 990 216 181 598 936 425 037 451 100 553 745 722 962 854 178 900 032 330 714 081 098 651 850 320 419 808 568 827 662 387 551 143 803 736 693 093 953 311 274 086 292 121 532 880 415 034 134 765 100 638 964 121 638 452 112 623 191 969 968 369 588 680 117 546 130 569 490 288 800 418 303 192 864 907 163 797 118 763 251 446 295 751 927 947 334 614 993 389 589 332 599 656 722 913 258 302 403 030 342 905 557 291 892 908 302 050 545 086 307 627 819 004 401 632 140 465 453 729 248 205 259 758 627 254 408 979 562 365 211 041 640 990 683 166 816 534 339 115 815 994 962 322 536 066 036 832 117 143 040 948 526 119 428 642 539 341 746 997 513 515 048 198 767 291 934 025 238 667 948 507 457 835 559 418 253 912 705 282 436 215 932 059 999 584 316 996 161 159 886 952 513 823 004 554 079 246 415 463 881 561 713 819 048 068 734 300 670 379 497 701 495 188 188 559 690 655 654 981 633 716 334 983 613 665 460 939 590 868 538 684 139 818 380 838 178 776 865 267 499 749 293 692 448 573 558 065 192 487 511 867 082 461 224 556 109 701 898 789 067 092 506 239 487 495 353 479 539 097 775 993 616 189 730 193 214 270 069 132 806 713 777 504 123 848 383 478 746 865 235 262 517 886 251 682 616 446 721 366 299 820 081 018 338 551 600 323 381 842 689 950 662 083 018 909 324 067 646 760 854 976 122 808 442 925 830 400 132 543 177 025 713 934 243 012 378 227 725 872 781 824 597 541 685 382 978 656 630 297 096 410 035 426 482 027 552 344 664 184 951 092 183 497 394 295 076 202 334 550 160 353 944 471 344 625 016 231 580 461 518 408 221 577 068 648 556 360 374 737 635 850 980 231 037 326 880 364 632 480 212 572 687 354 653 086 677 078 498 084 819 606 498 439 480 353 993 516 421 953 467 346 279 800 844 355 600 936 584 599 606 220 962 598 544 619 502 574 625 823 291 535 646 595 775 697 042 341 005 955 268 411 866 412 717 290 223 619 632 929 881 250 439 270 046 591 300 561 614 011 554 466 156 952 973 944 545 388 684 992 134 570 717 054 870 628 000 806 283 882 600 578 831 630 191 977 903 449 259 494 466 674 839 144 162 202 576 148 312 813 113 512 919 965 895 461 231 570 234 281 657 007 435 534 449 996 503 150 776 424 605 355 424 881 335 545 338 370 325 542 629 979 632 830 463 775 432 607 942 895 038 928 298 008 692 220 604 883 084 410 627 725 405 653 890 398 476 505 097 172 903 944 627 766 292 426 116 969 638 341 971 779 633 901 587 894 686 167 502 365 845 005 516 953 623 072 214 419 489 698 886 132 093 230 508 548 069 780 857 198 769 886 833 272 821 002 238 921 000 509 848 812 338 831 169 379 992 519 782 628 952 145 774 932 566 612 533 367 371 724 653 234 941 882 090 892 753 904 403 121 287 034 088 703 570 361 751 040 823 228 642 528 091 643 129 311 933 333 742 700 262 354 272 880 242 708 075 679 667 017 309 300 453 994 948 874 222 218 785 091 121 538 088 559 131 818 472 705 548 634 992 209 629 619 473 749 490 550 967 997 634 957 796 135 880 370 652 729 300 343 290 766 604 359 512 347 174 169 064 045 568 549 160 774 046 044 598 578 906 426 866 852 003 505 634 911 038 725 462 026 055 598 569 518 268 423 236 561 076 734 134 983 200 813 367 871 366 791 298 491 790 718 597 400 524 218 951 132 517 938 988 906 423 115 663 705 101 044 144 642 442 119 337 801 327 684 104 235 192 191 741 086 759 778 767 978 674 806 938 696 777 071 053 039 486 662 607 774 906 460 457 720 086 721 608 722 025 213 897 075 399 557 514 881 405 750 419 615 224 354 736 868 504 121 002 513 367 550 563 280 245 312 709 147 483 015 738 361 569 883 271 741 195 267 735 863 239 574 235 308 527 557 206 436 076 143 554 651 888 609 756 726 723 796 640 812 659 538 279 205 978 551 139 649 519 965 210 916 252 281 954 773 240 416 892 747 957 807 158 075 000 432 969 575 262 658 331 846 070 954 358 009 063 027 279 181 043 744 898 194 717 055 057 536 133 771 510 676 311 877 841 500 103 114 501 928 279 773 699 738 507 886 853 679 111 935 645 613 260 362 859 823 430 432 926 718 860 590 128 382 810 035 920 966 508 481 557 487 285 289 815 941 631 888 531 001 150 091 601 727 842 451 403 152 718 322 951 505 279 042 482 108 021 785 167 243 673 608 596 256 026 215 466 094 794 843 278 091 300 098 612 513 832 706 919 083 540 757 354 772 774 470 589 907 108 397 242 586 969 664 024 003 504 765 380 941 833 720 126 752 199 455 417 722 632 311 274 145 172 852 804 011 342 635 170 788 339 924 398 254 039 671 567 249 304 493 013 241 769 047 280 062 888 953 073 095 506 441 111 295 990 531 635 097 034 036 548 841 597 128 819 523 082 221 688 858 745 592 207 419 264 402 084 947 435 042 265 986 462 514 624 218 640 236 031 828 331 522 983 325 110 971 950 542 592 106 809 879 204 817 202 367 661 727 759 106 462 111 892 495 579 898 100 097 016 696 980 233 141 608 516 381 991 421 806 176 352 671 781 059 587 710 700 661 084 659 199 364 244 125 779 930 833 783 632 334 738 629 728 614 607 759 455 398 949 993 944 711 569 496 531 599 239 459 468 028 685 453 532 707 771 240 383 535 659 515 227 773 671 093 102 554 894 840 676 747 093 616 938 150 004 961 339 353 151 775 516 403 914 582 397 111 337 657 611 168 847 067 108 202 284 735 668 586 697 421 692 495 025 050 840 197 821 143 566 685 069 634 514 265 606 111 168 046 223 382 860 178 752 086 175 200 202 545 839 257 637 532 897 085 439 576 885 440 557 381 097 332 154 436 619 632 639 477 273 014 595 381 499 577 256 980 511 865 292 396 315 554 821 774 986 942 732 539 171 940 702 577 879 133 479 836 102 964 656 259 428 726 278 415 817 206 363 255 503 166 475 236 662 509 428 382 181 221 693 017 509 999 456 127 117 137 769 765 746 472 345 783 383 790 174 583 868 041 678 422 230 019 307 156 450 194 452 220 312 042 983 492 257 308 759 676 062 777 117 038 100 730 398 704 682 361 291 353 913 041 154 195 768 535 459 674 626 827 601 470 805 700 804 792 693 912 850 529 559 815 428 611 191 965 860 845 203 540 076 329 283 167 121 667 545 562 328 165 925 737 749 526 253 761 637 979 072 612 014 284 062 448 031 249 882 486 686 350 358 643 123 814 656 780 609 974 645 866 820 305 822 729 326 804 287 803 547 246 085 623 643 861 928 189 325 974 940 214 020 762 548 451 934 451 809 085 462 275 468 182 654 391 666 026 392 698 822 737 549 709 878 949 742 915 083 379 610 260 003 668 292 452 482 182 913 615 804 607 439 206 217 444 471 947 582 741 777 945 322 583 681 323 260 371 499 045 179 508 467 064 188 528 239 915 953 321 355 408 408 129 622 297 425 209 878 119 555 997 930 099 305 404 653 950 634 442 900 349 838 011 888 592 456 886 246 644 469 077 183 492 021 279 166 784 004 985 439 974 040 066 067 117 474 243 490 695 164 083 810 506 229 301 257 446 542 190 130 082 508 935 909 315 385 651 439 099 657 849 245 360 387 630 521 180 452 872 569 005 216 833 241 706 621 473 309 057 660 029 034 240 270 860 686 192 922 533 980 839 576 752 599 741 386 715 669 862 395 938 276 288 202 339 855 376 008 815 082 330 576 891 130 004 764 875 387 920 519 031 604 780 523 240 993 784 542 927 305 207 042 481 938 389 093 635 551 164 480 846 377 973 370 448 450 478 327 124 016 991 833 044 544 040 750 465 164 157 039 835 526 947 839 579 021 044 208 623 849 353 756 320 593 046 696 376 665 190 515 322 562 631 952 059 776 931 789 353 173 883 094 159 694 504 821 934 282 192 585 445 977 429 620 252 607 142 482 130 266 797 034 784 592 296 306 650 701 567 583 312 258 686 423 437 880 496 362 188 405 063 832 779 630 234 382 181 685 720 427 463 422 954 309 398 682 868 057 382 592 872 911 567 276 947 205 377 816 515 935 948 426 761 283 748 833 050 402 639 778 631 950 634 339 537 242 781 385 257 411 550 070 509 153 874 589 489 960 428 716 994 524 441 025 530 448 792 449 681 227 490 483 206 346 437 374 533 419 442 331 963 668 837 356 796 928 644 591 522 740 281 958 354 722 766 867 287 373 814 373 977 252 318 393 534 325 053 377 113 921 626 650 518 913 999 053 912 530 613 949 074 286 037 861 970 382 241 162 078 208 136 713 003 549 132 180 858 609 202 588 611 368 608 153 272 915 154 619 566 568 984 613 671 011 836 795 843 207 660 913 089 268 711 821 061 533 797 664 649 667 432 008 938 310 769 638 548 281 726 993 671 573 422 444 138 044 081 614 562 484 895 789 130 908 473 740 635 522 309 563 645 227 077 699 966 650 999 976 803 238 803 205 421 030 229 934 742 120 086 765 598 793 658 793 483 118 185 991 147 455 342 711 847 582 666 753 289 444 032 315 921 935 427 958 657 771 674 723 668 866 445 671 978 071 366 472 787 846 925 834 327 490 280 858 370 790 050 469 854 352 268 465 143 319 112 573 882 686 779 076 421 780 757 512 594 184 710 531 495 752 309 193 366 044 158 922 112 956 561 156 254 206 592 565 233 589 319 699 868 439 714 629 441 764 017 597 548 158 188 046 815 097 130 027 429 766 884 929 333 974 322 031 002 161 895 629 081 866 884 902 703 010 915 925 147 440 397 101 781 012 630 223 676 975 709 400 910 322 538 126 249 886 909 554 520 108 938 156 414 431 692 989 566 480 104 332 112 217 667 011 708 265 009 195 306 726 765 058 343 019 166 231 254 046 831 754 005 818 005 124 170 045 210 252 676 651 164 151 803 252 326 367 193 508 486 232 880 965 725 069 679 035 371 241 073 727 377 120 777 514 142 125 452 110 757 755 236 620 927 922 569 388 673 529 686 517 170 659 014 521 576 993 467 942 984 551 759 437 073 386 095 851 559 408 915 113 870 660 047 746 180 056 687 132 565 634 921 938 773 390 255 916 144 150 522 339 648 280 336 171 858 392 399 226 043 577 907 313 197 802 791 289 087 262 266 731 552 212 283 053 586 194 237 981 458 675 968 691 231 394 138 546 432 778 670 654 532 922 797 313 964 186 277 998 407 032 941 214 090 123 076 322 011 748 607 909 101 369 519 670 832 989 455 908 665 094 108 873 359 170 027 761 743 816 995 631 996 774 210 660 350 855 656 338 088 988 454 923 559 699 076 646 485 337 337 185 218 421 788 128 577 739 161 620 652 148 247 102 052 696 889 293 485 253 497 284 760 891 453 202 297 947 295 821 755 580 698 794 211 137 641 471 468 963 613 321 313 827 342 978 510 244 944 863 051 426 567 088 652 282 201 664 946 835 667 688 871 336 410 705 986 149 514 384 347 398 845 830 215 204 542 522 142 090 214 100 014 002 726 428 303 233 981 436 539 330 821 525 229 171 955 610 234 288 644 811 749 904 645 001 359 076 641 280 541 384 423 187 925 644 261 087 740 746 291 465 070 069 413 800 613 564 560 241 336 637 840 458 661 340 463 100 958 468 970 191 181 607 198 630 103 349 297 557 963 585 114 877 163 815 406 765 647 979 629 601 267 070 378 129 323 288 545 241 955 734 774 682 173 501 098 388 064 925 422 036 631 543 175 576 903 231 228 328 498 813 931 313 418 694 832 614 469 361 153 023 078 505 306 899 711 649 064 186 146 138 304 735 410 630 087 934 608 873 560 546 516 838 964 628 384 546 478 377 977 350 996 320 293 649 955 238 010 264 951 271 709 073 890 946 381 727 851 147 241 635 300 867 441 120 636 104 858 375 247 711 900 151 720 704 685 958 859 474 938 837 730 922 146 297 073 332 590 773 839 649 805 126 284 091 020 461 179 550 727 431 041 758 052 997 083 274 324 337 270 827 853 068 952 586 045 458 046 455 823 300 649 109 429 225 781 600 975 579 104 728 175 031 995 275 952 907 994 443 552 576 539 317 314 261 231 376 351 601 461 863 533 286 319 503 562 503 961 368 818 452 609 982 652 831 322 577 694 702 800 950 427 493 941 147 018 847 590 236 020 240 072 595 478 636 191 670 480 882 362 076 084 987 648 032 003 175 241 446 777 999 437 255 721 916 494 442 501 610 989 567 461 894 695 836 945 580 375 418 948 664 507 572 583 247 021 763 060 616 875 469 230 846 121 062 154 956 574 107 065 464 079 276 544 374 453 991 805 910 359 669 623 738 444 103 632 458 367 138 999 373 839 100 009 422 720 161 769 171 868 827 421 004 401 194 461 366 991 448 564 861 323 707 811 987 571 842 743 123 147 037 558 407 081 412 164 101 691 034 299 262 733 502 552 223 180 199 060 199 188 019 224 209 969 461 892 315 693 614 587 914 737 542 768 574 319 635 274 911 275 037 129 944 384 568 013 815 308 482 619 923 635 377 125 032 553 285 514 419 920 852 907 354 352 391 124 502 913 124 952 324 348 440 841 887 577 505 639 228 295 080 697 148 298 166 268 695 964 807 632 539 799 477 909 786 559 818 765 432 666 385 310 993 598 395 760 283 946 086 552 036 971 186 875 181 520 140 105 440 858 873 804 526 640 215 075 122 319 926 465 500 301 944 545 857 622 545 646 282 339 477 857 531 543 632 028 941 823 560 285 507 278 775 638 567 429 947 277 460 321 724 990 561 007 145 828 312 158 107 344 600 024 083 306 511 112 785 561 246 764 560 676 342 752 209 227 553 650 476 257 736 201 145 347 573 816 963 542 063 621 082 914 527 883 241 935 909 975 251 497 013 833 396 739 467 532 005 161 499 349 371 678 529 862 466 153 112 431 917 244 013 912 824 966 792 247 950 809 976 359 863 577 880 246 130 320 381 906 828 964 784 427 510 627 180 219 349 771 688 733 661 111 334 805 201 615 696 983 839 347 275 736 192 496 565 889 880 538 866 424 576 698 330 918 474 704 686 620 003 300 960 817 213 559 664 038 492 591 829 372 665 564 186 337 389 896 509 681 806 902 356 154 652 126 417 567 481 603 108 081 187 903 567 024 511 879 669 845 012 190 067 563 877 897 310 340 559 209 664 493 301 529 314 608 147 914 839 795 596 174 549 176 523 796 285 215 583 274 188 629 544 763 573 607 979 891 273 688 997 888 407 214 355 026 405 800 783 466 410 846 921 738 560 064 942 736 670 914 853 446 650 429 486 045 593 867 091 871 585 316 844 141 978 453 713 648 135 802 436 745 261 188 579 687 468 612 629 241 563 371 944 992 647 993 033 166 599 676 986 076 109 645 527 175 371 706 566 405 177 474 868 650 758 815 386 518 470 866 502 115 671 826 215 303 279 785 618 243 885 454 912 359 492 085 586 312 706 529 142 646 251 011 757 245 348 031 257 813 344 960 359 407 036 404 261 911 887 175 579 988 742 151 460 873 022 921 639 713 960 466 695 250 961 445 735 818 958 960 198 795 606 560 039 837 149 346 271 073 959 194 217 540 211 832 526 336 372 535 352 753 727 336 659 823 727 855 934 840 137 965 418 385 072 316 787 069 431 934 119 831 329 426 971 261 319 002 470 140 430 598 541 655 711 039 254 004 275 229 767 480 002 639 856 126 509 831 118 372 783 536 995 628 978 979 474 110 028 310 941 451 667 930 452 120 285 209 964 894 152 624 655 606 990 314 041 291 067 799 992 734 835 696 670 554 291 456 013 314 628 745 650 982 255 334 719 107 131 359 021 971 749 263 126 335 351 776 657 951 952 856 292 672 809 681 988 993 177 973 127 881 316 620 371 912 053 290 333 997 799 336 202 030 955 451 703 340 648 155 448 434 043 940 353 919 118 389 834 768 526 615 927 698 991 353 939 862 072 997 391 100 744 813 112 643 494 962 132 603 024 154 754 296 099 223 426 717 113 163 588 415 607 093 534 216 114 711 114 757 146 154 203 275 031 844 287 284 343 575 419 835 841 542 400 324 308 889 857 855 307 275 644 994 528 984 685 784 328 733 523 110 825 686 787 965 092 748 865 838 780 794 089 176 564 184 256 357 803 320 680 687 737 762 664 246 275 812 536 039 314 081 769 070 001 032 062 272 760 097 298 250 258 106 696 663 617 299 680 948 369 967 261 766 783 474 420 603 055 400 554 249 619 865 728 070 743 106 832 820 690 584 666 084 763 999 104 212 659 658 935 941 358 113 748 636 804 212 453 937 570 009 296 710 804 925 521 221 711 172 580 130 918 421 380 731 434 768 709 089 442 766 406 385 894 095 781 503 372 323 467 118 571 780 872 199 487 756 374 809 768 488 035 467 862 558 878 529 252 009 965 744 556 413 034 902 635 504 144 261 544 442 872 104 897 897 374 004 758 756 006 969 206 326 756 691 326 535 355 248 398 429 298 219 818 143 249 361 697 356 800 937 338 648 903 429 855 526 926 331 512 161 070 563 157 148 371 470 614 624 011 070 834 638 810 485 169 041 879 268 287 592 406 646 704 320 158 694 501 349 172 363 428 835 912 807 571 546 576 339 381 534 687 446 377 706 416 891 175 987 856 692 212 219 558 589 861 810 110 421 569 752 335 332 345 101 547 825 402 057 544 160 839 415 133 239 949 591 247 310 464 755 908 248 565 711 307 043 615 006 823 342 644 941 516 004 171 228 417 341 082 475 130 002 247 596 332 055 823 165 185 270 393 896 116 462 791 366 689 912 097 832 974 397 235 327 323 195 472 560 333 211 249 044 050 803 058 486 935 692 866 751 495 221 160 344 428 045 989 283 448 552 830 349 817 832 488 868 849 462 184 515 310 654 373 505 181 782 195 078 581 160 471 222 408 082 771 459 381 990 474 607 503 873 440 284 728 163 486 743 657 316 506 418 510 176 143 156 377 085 045 195 728 718 934 338 298 977 584 121 817 797 143 919 700 479 973 996 227 755 716 861 689 189 511 467 388 151 637 375 734 388 710 099 852 222 665 592 906 995 969 294 631 287 612 916 631 640 038 688 503 448 194 855 639 351 211 679 888 824 014 837 218 468 926 388 534 594 707 248 518 054 359 124 679 609 938 305 228 923 861 800 637 208 172 685 907 008 527 582 507 730 047 687 990 400 231 819 204 488 838 347 372 630 629 859 855 844 339 778 966 742 782 496 942 869 304 610 493 080 516 064 864 016 295 614 386 579 751 035 517 693 320 200 385 623 608 362 398 289 868 680 960 205 821 767 582 079 588 537 175 997 659 660 645 455 845 781 605 809 316 870 956 167 419 724 723 598 968 014 372 836 536 939 032 026 593 484 183 152 232 994 757 673 775 313 525 124 973 925 151 305 091 981 755 186 347 025 305 164 117 752 357 953 381 361 012 642 738 243 505 511 374 854 931 434 612 725 374 709 555 488 128 692 543 228 055 444 100 542 852 511 702 617 630 422 213 231 266 768 342 152 465 935 989 882 677 159 494 955 074 831 450 445 204 023 224 610 340 179 569 109 059 176 790 044 813 690 081 592 678 746 405 747 385 352 112 381 887 841 491 505 174 840 922 125 618 549 670 658 190 733 115 441 186 316 072 244 703 764 141 943 335 499 138 012 713 292 608 947 055 665 929 106 615 090 628 526 695 573 389 798 214 648 973 038 888 449 185 927 373 602 523 851 363 230 863 695 787 488 100 645 223 769 944 860 854 712 945 734 636 305 176 394 814 878 674 025 915 386 622 660 703 880 228 938 051 613 088 727 165 519 692 473 222 846 518 752 006 336 003 197 692 275 966 578 136 564 058 688 189 587 967 656 764 620 272 891 413 934 872 765 520 358 019 452 839 760 843 911 634 774 957 118 939 848 331 394 412 974 194 552 461 511 307 564 036 401 648 713 071 986 630 121 023 106 745 198 349 375 984 668 137 486 535 906 862 518 427 073 589 923 099 179 827 584 548 372 696 505 412 597 037 615 096 233 073 620 852 572 040 069 932 301 411 570 614 788 714 005 792 977 948 819 314 879 947 963 735 379 210 166 966 469 100 769 969 805 111 204 859 524 262 307 481 797 081 394 935 106 008 232 555 913 240 606 344 175 291 754 876 857 675 005 261 556 274 075 206 907 316 980 201 352 779 736 654 478 950 004 712 239 800 232 342 168 273 450 382 388 501 698 672 920 647 227 531 460 465 515 012 420 109 336 262 044 784 588 883 863 199 071 954 214 977 296 636 417 136 796 796 100 242 903 568 889 733 891 734 928 243 613 388 134 134 384 682 115 140 015 924 838 056 878 478 230 190 191 651 005 678 574 649 578 397 129 477 688 166 724 446 590 655 219 718 129 012 757 521 308 932 107 857 408 882 767 573 953 124 305 843 761 577 456 723 259 757 931 861 050 185 551 855 024 931 745 031 176 598 518 441 474 885 428 351 066 823 729 753 674 781 020 619 518 640 922 818 571 628 322 554 180 890 761 172 001 960 424 209 203 092 686 960 325 844 131 196 636 110 690 242 782 765 705 090 787 013 870 931 957 228 685 761 473 523 728 232 856 336 409 061 003 897 955 506 459 165 210 351 891 596 858 040 315 819 774 891 234 081 984 265 242 430 096 601 867 297 166 714 762 497 782 557 647 000 380 607 204 372 554 468 030 598 594 532 260 906 293 281 884 955 327 890 797 781 492 651 543 667 510 490 953 594 590 465 014 889 591 209 080 304 486 352 702 077 568 348 464 845 413 844 933 820 018 833 259 981 372 699 136 203 007 334 025 366 552 808 155 805 022 442 080 718 171 104 384 482 780 443 776 829 128 638 523 318 893 973 471 892 290 424 997 042 269 590 714 606 572 272 518 123 270 200 592 030 462 086 046 837 854 909 853 415 011 827 225 118 940 071 586 056 568 284 568 993 564 132 286 395 957 975 797 372 094 197 195 046 714 213 224 770 333 319 602 840 769 531 873 533 290 194 852 243 836 509 836 595 981 561 464 773 197 798 944 108 354 684 101 253 323 394 930 627 002 864 025 721 410 738 438 033 794 603 376 649 646 451 674 693 413 815 518 860 552 264 392 071 927 122 686 140 259 663 047 456 727 787 448 551 341 798 876 977 772 631 629 585 564 605 809 914 993 195 490 897 537 341 710 634 209 055 872 652 706 069 618 730 011 530 895 633 568 049 795 229 343 299 326 248 332 916 371 216 000 007 409 418 549 101 829 166 221 106 593 624 870 716 032 169 465 480 815 657 117 403 231 415 575 021 902 316 576 272 069 675 299 473 013 442 924 852 488 193 228 714 720 977 357 675 633 271 633 691 639 617 479 627 401 580 970 150 440 422 919 290 822 062 051 672 248 549 127 087 478 317 943 591 918 366 506 091 866 902 444 605 484 321 949 207 131 867 694 261 767 556 449 601 531 588 992 648 789 713 732 539 102 723 757 421 430 490 838 096 550 799 671 546 522 954 901 928 124 151 515 393 074 217 223 706 534 837 853 043 489 844 085 771 238 653 929 304 074 448 064 110 110 516 755 737 322 668 656 238 878 556 554 756 337 195 606 590 504 380 326 164 918 237 682 369 523 694 193 848 173 432 431 917 694 219 830 126 118 967 264 437 646 256 064 771 028 915 872 042 588 394 737 161 872 319 613 851 944 750 568 860 127 415 036 743 779 282 737 355 771 472 415 967 656 328 036 599 990 501 986 183 242 009 894 766 190 743 788 836 764 165 928 622 413 243 703 330 434 340 767 116 636 665 107 927 936 869 173 132 631 189 904 574 088 243 535 707 440 642 562 261 342 278 465 755 669 220 452 268 963 934 999 974 433 973 847 733 147 194 580 935 759 104 991 378 273 975 351 173 445 852 909 795 927 182 983 676 038 112 553 457 657 548 488 097 778 816 079 452 877 851 972 955 901 807 542 796 569 617 933 956 237 711 664 510 301 477 584 669 547 805 510 405 803 462 263 023 100 987 348 262 988 490 443 866 249 680 080 789 624 013 158 429 110 422 007 818 451 490 738 256 758 632 320 966 901 335 951 637 073 871 171 762 656 061 011 777 375 245 323 516 497 376 363 836 978 060 213 958 799 876 900 422 467 748 937 983 643 002 670 176 104 447 194 898 001 251 130 465 219 559 281 794 565 026 149 125 913 961 656 836 321 312 600 047 890 786 797 267 186 114 802 956 843 182 725 614 457 981 618 464 050 481 453 132 730 775 108 497 977 531 335 848 150 873 488 694 936 333 962 623 796 062 006 079 907 974 617 946 394 457 004 400 634 303 968 383 404 091 422 351 036 409 833 602 041 693 854 131 555 541 113 669 025 843 242 836 184 090 561 540 463 999 724 272 959 897 471 392 544 045 806 512 272 711 929 980 777 727 913 853 709 772 675 869 891 171 351 415 630 126 951 964 718 513 356 775 423 702 978 526 963 401 869 945 368 534 245 352 248 452 547 480 790 458 018 612 352 444 742 644 960 834 559 422 647 246 693 424 556 467 196 486 888 771 349 412 436 601 645 714 860 738 589 964 851 977 161 544 857 901 196 876 951 591 366 612 567 843 353 623 662 749 166 663 143 456 956 277 951 947 796 719 834 128 817 711 206 202 022 567 455 467 317 663 397 123 371 175 797 826 568 971 042 743 838 204 952 697 180 294 794 907 734 315 982 756 480 329 408 846 840 940 210 518 822 001 949 364 497 925 980 826 491 745 844 374 878 573 822 452 230 812 185 724 809 052 345 097 360 558 314 767 320 289 323 297 909 242 458 628 167 553 884 909 964 442 859 680 929 714 054 905 422 728 812 810 903 201 470 967 206 209 299 378 441 499 668 547 551 296 834 600 957 617 158 587 960 095 971 983 410 432 352 221 614 507 386 483 648 699 635 509 652 027 925 007 545 088 355 681 947 287 586 132 517 068 633 193 949 701 396 871 606 253 511 201 955 037 342 038 810 608 972 989 914 136 734 301 834 147 412 578 716 506 176 765 055 330 525 462 843 603 831 856 008 199 263 385 928 694 513 945 040 206 377 836 157 366 777 327 272 405 458 858 031 270 739 494 225 427 992 790 737 931 040 545 780 195 090 095 135 073 553 971 107 523 440 140 981 955 050 658 053 728 639 704 531 519 335 611 285 576 613 260 993 812 851 551 303 115 707 420 934 470 565 954 107 089 901 446 453 765 782 878 603 770 200 664 370 916 881 593 008 218 752 635 030 497 635 261 378 240 345 978 715 669 084 199 095 031 523 615 053 511 815 247 957 042 703 717 228 587 080 564 614 953 290 964 570 918 536 616 803 047 068 723 751 922 371 941 752 850 026 160 869 560 614 925 275 301 366 672 948 633 087 859 703 300 514 327 092 058 095 638 323 368 185 367 895 437 304 195 699 506 553 590 973 787 289 462 565 397 526 563 660 389 683 255 631 074 924 303 445 424 268 775 771 078 410 107 647 266 140 764 470 979 461 509 057 024 840 458 102 041 429 462 673 283 544 130 439 003 067 850 506 281 181 969 847 819 395 555 370 810 952 719 414 652 499 056 170 702 708 118 343 019 947 721 221 722 164 279 685 533 516 753 471 728 228 808 719 420 841 649 821 365 738 215 102 543 315 209 134 194 140 539 503 507 277 104 068 006 508 671 187 313 521 794 614 747 774 317 012 049 403 665 218 677 981 758 582 357 011 209 478 442 916 074 013 143 998 377 020 454 669 018 250 441 362 723 379 881 792 585 241 319 851 712 313 013 808 412 239 702 761 579 638 636 274 123 246 220 896 319 391 683 232 202 074 425 953 667 734 859 797 836 056 050 105 650 040 625 279 257 455 757 655 136 238 255 491 712 217 915 063 235 867 302 112 185 852 376 940 262 720 936 702 330 597 372 066 303 856 518 941 351 130 415 302 209 888 933 575 821 630 353 093 172 598 918 373 930 836 724 611 474 968 029 006 768 556 363 311 114 369 526 304 164 710 734 945 930 234 879 475 648 199 956 312 065 648 238 753 536 247 181 112 789 476 011 884 230 961 010 663 891 744 671 567 086 315 763 477 545 120 492 130 505 153 399 013 361 551 745 010 601 984 600 791 065 287 602 391 520 659 062 941 761 463 292 993 647 828 450 416 025 678 311 416 248 404 188 917 463 545 096 504 530 212 373 619 722 947 733 964 598 456 322 783 216 452 854 397 675 120 344 063 420 782 338 003 041 010 277 942 832 018 454 729 563 756 793 744 295 221 341 401 225 185 425 936 577 324 522 162 908 126 513 860 070 987 934 906 000 909 694 339 141 017 516 165 356 574 671 396 319 291 798 614 375 117 945 995 997 354 984 512 829 551 518 343 861 575 587 720 486 274 153 120 349 933 220 651 697 102 629 774 260 347 537 762 730 423 989 031 761 400 069 560 367 489 526 588 303 430 346 136 823 366 625 439 595 738 565 245 980 384 330 141 371 233 540 563 083 844 849 826 413 202 065 050 702 109 680 097 206 957 429 437 810 565 927 217 458 260 757 326 988 583 930 837 369 164 337 951 484 183 076 168 427 176 481 082 073 871 246 635 785 409 199 293 196 037 101 503 225 194 353 512 856 208 078 599 856 091 686 003 747 176 369 348 356 242 328 228 198 160 319 829 742 241 290 226 315 261 787 819 249 044 028 194 859 733 447 698 320 263 739 680 532 793 799 191 265 092 070 650 343 053 911 906 111 408 195 866 215 482 081 374 948 291 803 467 169 287 761 108 808 231 119 268 818 466 926 518 308 641 449 861 578 531 001 377 714 551 899 611 357 450 244 627 852 566 013 084 465 104 900 170 029 004 546 489 754 161 735 760 548 593 386 866 020 083 645 776 901 168 796 891 490 817 095 525 496 531 377 713 401 260 107 131 712 480 959 525 523 204 614 615 463 745 781 596 221 804 635 440 884 063 146 203 053 449 394 330 834 049 963 747 163 232 278 337 828 496 362 030 387 538 132 832 200 622 625 835 577 056 107 581 934 288 378 109 870 099 635 287 684 212 613 605 877 030 134 675 215 293 097 297 618 084 848 875 887 644 265 004 718 294 449 598 624 977 625 722 393 057 014 464 324 171 362 899 224 045 180 447 364 942 549 751 408 982 880 506 875 944 031 238 207 329 807 142 906 592 619 042 391 531 954 332 887 984 901 074 661 923 874 305 767 278 695 538 372 047 141 902 364 336 699 812 515 975 694 800 327 393 496 443 220 868 398 581 791 712 001 616 477 732 523 528 486 223 571 401 792 107 578 105 504 913 820 968 324 467 343 565 141 163 457 336 356 202 183 043 444 489 665 782 353 511 188 045 810 658 779 166 331 471 762 086 735 925 477 746 710 136 655 465 768 805 558 300 433 151 831 911 997 944 735 628 847 551 636 417 151 331 550 930 959 284 608 616 539 369 590 082 141 174 572 088 801 274 572 564 971 993 119 248 670 748 675 066 743 673 749 426 629 495 179 535 264 846 220 398 008 804 195 622 826 544 763 516 680 426 327 115 579 556 939 051 046 669 665 893 185 265 587 683 456 986 019 212 260 305 353 997 142 466 047 786 172 870 776 689 421 693 527 478 902 690 498 531 399 982 381 159 055 457 601 572 103 491 924 330 355 349 392 549 545 983 721 386 850 408 982 533 385 929 803 470 728 071 060 302 984 189 864 324 015 852 362 988 770 288 535 039 701 021 846 317 652 077 115 776 708 584 049 027 690 975 123 643 509 570 018 288 135 485 901 868 483 632 646 308 618 676 773 059 673 889 529 595 696 104 087 263 564 906 493 914 969 333 029 180 031 658 076 670 183 410 064 754 973 041 993 194 989 212 695 778 345 391 749 925 926 454 794 209 555 955 300 188 751 062 206 125 417 468 510 049 447 510 012 163 945 718 008 223 612 292 559 748 892 561 111 472 676 313 778 715 644 317 679 514 107 572 404 506 215 356 870 290 098 563 572 934 691 469 209 711 191 322 614 570 002 288 240 059 035 079 311 826 614 867 013 381 411 893 871 121 948 505 747 834 727 857 720 649 441 996 694 653 014 467 818 706 489 082 855 904 083 231 858 179 099 396 359 912 739 263 321 461 956 230 036 416 008 621 783 553 290 087 103 745 868 400 293 504 563 045 993 838 341 758 889 890 814 133 162 180 162 315 537 386 376 446 767 625 853 246 029 668 140 421 162 109 859 904 539 033 391 988 736 289 905 292 616 370 969 406 452 906 019 874 792 802 374 239 780 701 735 207 667 212 628 325 731 748 112 721 986 583 685 265 549 427 094 693 233 046 090 529 432 919 049 401 334 973 613 165 262 312 413 490 611 543 019 274 633 225 781 575 294 300 323 220 393 918 727 981 279 367 705 382 776 643 358 252 551 445 541 174 005 709 527 596 956 032 055 993 126 993 740 936 232 135 821 992 286 088 664 880 476 757 023 380 753 048 506 136 493 623 539 269 450 371 000 151 918 932 120 494 965 635 598 163 342 703 161 841 180 941 098 883 684 655 793 465 138 348 780 921 801 315 742 800 848 602 299 535 622 292 210 558 516 206 626 794 305 129 290 647 565 606 290 364 958 533 365 460 975 486 099 999 707 279 135 618 926 101 828 081 418 459 054 557 113 460 525 039 441 062 285 979 357 535 821 526 836 918 570 475 620 092 375 917 682 420 185 426 582 894 441 322 874 725 125 700 768 353 263 863 322 394 800 758 652 771 330 972 551 362 005 281 371 771 606 212 801 443 267 330 317 740 067 869 764 871 390 055 316 186 821 732 986 978 818 990 088 575 113 013 355 868 685 331 779 882 346 436 555 933 837 068 094 710 951 809 108 131 502 892 562 381 208 059 992 833 582 678 148 204 211 090 374 898 420 288 195 317 029 423 830 980 077 866 983 811 048 624 784 752 069 181 738 003 846 889 080 828 534 205 780 982 586 748 512 687 708 413 151 756 591 175 645 242 522 551 384 896 416 059 026 046 579 691 885 946 649 353 865 763 396 064 906 033 255 759 308 646 306 763 242 806 709 360 029 988 839 755 112 221 690 763 467 270 162 989 492 333 004 214 001 519 710 142 784 449 970 343 137 909 181 910 720 888 982 892 001 806 037 779 270 622 742 648 627 767 082 474 102 036 034 848 234 122 385 295 203 758 020 746 924 855 666 723 737 358 639 656 730 230 595 934 371 828 820 427 307 136 080 277 450 296 430 970 024 606 201 037 008 001 760 877 436 629 912 898 061 338 581 702 421 008 783 551 550 193 631 947 352 778 623 038 291 875 514 957 352 504 143 206 546 865 100 444 089 815 455 628 544 700 554 832 064 447 071 978 166 615 473 583 441 790 716 398 020 492 850 084 372 726 673 283 015 707 333 842 489 585 209 103 193 837 052 464 659 351 655 215 700 112 785 868 058 310 663 168 498 790 672 994 206 929 775 697 860 412 959 411 490 315 674 728 296 336 813 838 410 785 762 602 871 328 352 163 895 699 706 422 077 762 148 391 437 083 271 658 872 658 667 776 019 343 617 153 388 610 906 360 570 023 554 253 853 006 854 797 171 408 605 161 738 169 904 540 993 868 808 892 863 215 820 859 747 505 717 700 157 442 287 220 857 789 393 083 098 118 284 521 342 689 501 542 551 159 811 507 101 190 947 274 587 978 787 662 411 676 075 219 764 141 201 978 286 699 453 479 378 480 748 029 161 963 889 593 572 715 200 120 671 768 331 595 309 891 579 579 071 020 529 398 081 448 581 735 386 984 894 796 012 068 285 693 058 819 592 101 066 096 407 959 100 714 333 819 943 257 361 232 393 070 700 682 129 880 623 350 773 597 520 381 056 998 045 598 829 409 704 832 145 776 243 447 525 378 719 834 944 226 700 041 538 053 743 063 991 394 631 147 825 211 935 225 391 471 298 353 054 294 512 722 816 347 054 939 598 252 800 785 026 554 332 582 108 006 787 543 812 098 750 381 587 783 056 956 902 530 527 645 062 004 414 779 994 400 207 141 459 439 881 518 167 358 145 297 662 789 073 655 820 692 808 431 236 842 123 810 667 317 012 450 854 224 403 518 119 185 615 354 574 918 300 886 006 972 957 683 780 716 656 979 740 375 816 959 713 670 140 365 921 308 722 330 784 516 127 759 919 771 321 993 974 171 155 377 495 347 100 706 770 449 361 859 090 842 318 726 622 170 729 041 079 309 675 068 443 135 869 604 950 449 127 267 031 971 808 483 237 562 236 347 678 949 896 765 998 419 498 903 772 539 880 332 650 968 743 103 796 738 025 397 473 906 296 920 749 019 959 161 478 253 140 516 154 167 547 324 073 483 069 248 235 714 725 211 150 320 873 606 885 247 333 173 250 917 744 750 172 070 701 398 564 509 431 515 695 539 370 464 678 632 052 240 006 889 750 027 295 572 769 581 645 124 019 658 674 138 248 120 828 693 891 080 032 950 875 129 531 149 212 239 175 889 744 700 468 601 924 007 471 105 851 944 010 876 389 220 083 654 168 231 370 375 243 575 907 170 592 846 913 518 585 789 482 891 536 073 685 474 446 779 727 794 478 970 645 737 150 413 141 426 524 895 732 239 438 674 400 634 098 397 213 385 566 302 407 985 722 167 555 197 366 185 389 270 004 917 980 494 103 997 664 694 245 399 751 576 528 050 741 155 126 465 960 805 994 057 928 661 754 737 079 109 412 114 710 014 205 187 527 750 964 229 531 600 163 853 279 099 918 450 065 147 468 400 167 385 728 837 404 004 035 357 355 050 510 788 087 032 657 208 923 798 900 842 689 977 123 965 526 349 007 280 947 440 656 519 017 742 264 347 283 211 015 621 058 504 764 399 678 033 827 640 437 334 414 973 182 251 039 629 045 528 639 688 513 764 894 634 670 100 515 464 754 669 134 979 233 939 183 097 694 460 666 090 402 405 790 175 951 819 266 893 197 534 572 856 381 478 077 599 298 862 214 926 776 647 997 080 072 605 239 197 514 634 706 286 857 516 429 151 818 712 016 392 736 471 663 610 479 344 518 438 391 552 990 532 420 556 090 290 153 760 940 914 223 513 906 488 640 863 347 012 079 352 473 153 621 093 919 402 106 571 151 223 468 277 107 460 112 071 783 467 352 537 880 765 647 418 286 679 286 739 330 812 926 711 654 590 669 236 717 216 749 459 736 183 604 630 199 970 870 697 620 842 547 649 643 918 555 768 197 397 023 941 079 844 902 112 265 589 875 370 587 235 328 163 106 431 796 361 697 456 077 554 396 295 550 769 420 233 437 163 509 434 244 880 289 277 324 168 322 516 689 166 785 812 742 198 002 734 116 237 684 484 386 467 448 835 125 791 430 345 035 677 021 288 579 035 812 905 691 205 759 355 178 581 101 466 127 406 227 154 523 088 897 031 275 793 851 662 937 550 025 323 962 821 629 695 877 962 566 908 460 507 744 709 413 350 918 111 368 306 967 457 779 741 200 675 692 157 062 380 029 717 355 468 192 132 387 293 584 605 160 020 445 505 141 844 237 163 715 551 841 933 334 858 200 164 974 191 338 056 922 689 323 412 414 085 823 306 076 804 577 043 626 066 375 460 760 855 421 278 756 797 651 004 351 488 499 750 418 259 923 402 378 522 548 989 156 622 688 210 181 868 351 760 648 395 270 275 523 032 572 827 390 144 566 000 182 325 473 365 363 144 409 327 872 931 825 612 152 848 161 907 905 184 763 042 182 992 154 584 762 990 277 434 977 912 716 378 337 682 787 946 067 862 315 987 885 181 542 788 936 792 567 911 656 268 183 323 464 199 818 627 673 648 120 931 158 428 865 562 532 280 302 823 670 310 559 287 369 024 244 113 337 789 503 666 368 206 150 261 423 701 061 867 604 584 927 862 782 508 210 378 899 692 856 266 080 109 091 493 825 075 332 174 185 541 922 177 804 395 083 161 982 784 479 458 684 341 617 192 899 092 543 888 414 959 152 906 204 328 832 808 667 362 527 308 455 025 198 409 942 404 195 812 328 592 521 458 907 070 958 046 534 788 526 044 204 018 883 430 038 055 271 571 155 224 948 165 839 034 342 663 659 742 753 333 892 328 143 079 800 260 105 232 479 202 019 047 107 305 224 058 385 014 932 043 876 515 891 451 221 570 862 381 136 358 981 698 908 731 699 321 507 245 944 375 548 872 806 387 233 350 472 136 308 861 823 433 931 980 953 516 835 398 044 747 831 575 547 937 301 095 426 150 299 307 925 896 376 287 453 382 564 872 762 084 118 949 314 858 488 792 435 204 000 985 257 896 392 579 186 883 515 488 426 259 108 381 192 520 981 785 975 951 587 057 050 979 496 889 763 656 254 460 099 420 492 629 809 707 797 645 906 278 754 930 528 298 483 569 795 877 383 913 611 150 250 930 767 875 651 644 346 146 303 677 342 027 757 475 086 739 534 525 326 919 652 428 585 156 145 670 725 878 361 644 807 333 643 715 631 440 073 673 897 587 740 178 108 025 872 684 504 526 883 282 153 793 287 646 872 392 882 197 486 008 109 739 688 511 647 805 683 090 638 289 268 079 777 436 038 483 703 254 087 468 418 826 910 962 655 990 407 234 325 913 397 670 254 813 288 756 597 020 407 452 091 650 858 674 913 784 515 256 227 385 320 071 265 530 356 388 912 903 253 822 673 834 334 007 156 549 439 038 071 158 372 532 191 972 256 790 458 980 413 712 956 155 581 382 920 576 399 080 752 750 474 303 866 623 758 195 285 833 104 139 817 395 944 479 337 964 857 351 748 802 344 589 867 662 542 468 293 349 727 306 449 482 731 194 581 562 770 998 675 028 215 304 947 096 993 920 988 065 335 884 886 734 278 763 931 996 469 620 880 504 834 082 762 222 687 992 969 235 419 847 862 945 630 079 276 988 967 773 056 472 993 892 902 965 474 027 841 288 102 841 165 209 950 521 839 591 980 404 972 566 144 219 404 527 102 778 973 693 621 966 871 266 659 771 190 923 943 492 455 264 295 041 797 980 859 746 145 759 663 619 653 368 061 446 949 384 673 589 324 494 022 088 414 574 617 457 560 514 949 890 735 633 078 552 839 550 872 816 107 796 892 873 477 086 304 663 128 678 520 283 419 594 219 836 973 864 936 206 659 070 477 781 941 359 027 620 756 380 241 043 734 257 588 931 118 467 264 064 305 662 056 197 881 931 991 603 310 342 251 770 284 917 865 215 151 552 228 179 193 478 934 578 261 749 403 761 868 928 522 341 364 041 057 331 711 313 523 601 883 315 959 966 689 358 720 429 765 452 619 289 542 088 920 135 910 520 960 421 762 381 272 938 423 411 605 162 124 897 997 130 685 100 008 685 588 180 230 570 991 150 845 183 981 671 340 433 166 283 518 136 805 129 761 645 799 544 506 572 842 300 963 043 196 960 201 464 475 123 658 668 170 296 151 792 861 509 173 731 256 602 481 532 751 878 590 510 935 369 335 662 507 834 651 065 937 931 055 501 815 749 261 652 631 573 294 783 933 590 454 933 605 047 500 126 590 999 958 249 336 253 684 366 962 886 360 659 055 285 422 947 982 229 867 329 839 926 442 295 433 867 294 005 254 032 481 704 912 835 068 284 926 325 645 693 292 284 315 073 544 002 837 290 423 620 957 389 641 503 253 954 513 543 713 987 155 950 051 079 424 635 150 912 021 614 362 308 261 300 844 119 087 575 435 127 797 005 441 883 651 957 325 285 414 996 209 515 399 335 912 073 996 192 368 137 350 646 324 326 615 078 688 496 746 707 136 830 774 517 393 572 526 753 734 988 981 929 453 775 546 502 004 909 568 215 155 950 344 445 915 034 998 399 566 777 132 978 108 788 259 919 185 438 273 241 166 916 515 326 028 875 078 288 370 728 312 225 447 540 599 328 113 606 595 456 396 506 057 233 780 424 537 747 462 168 959 146 253 354 441 013 809 989 704 372 807 238 621 776 002 096 503 757 262 005 475 531 022 129 806 643 989 870 760 850 341 266 369 708 258 459 640 629 005 312 126 456 574 751 209 772 970 135 077 071 863 271 671 063 345 157 320 887 136 626 902 936 011 296 176 207 346 647 644 316 307 532 414 740 676 111 768 081 788 382 583 169 432 341 716 542 792 367 274 195 947 032 753 815 316 673 080 335 672 734 706 907 242 942 651 071 795 161 868 293 579 098 888 134 293 607 998 680 721 109 999 190 245 904 178 078 899 837 908 091 483 604 322 480 513 548 135 843 433 791 653 758 927 813 508 413 361 781 644 122 319 328 373 729 651 462 548 033 483 759 473 609 602 749 681 699 514 567 027 681 479 963 610 149 759 177 349 448 529 307 474 848 629 958 074 013 235 447 578 595 863 245 586 556 149 902 898 104 166 705 073 541 626 737 052 198 758 910 648 943 320 450 456 653 010 760 329 747 497 101 010 632 080 311 718 033 995 869 401 960 641 721 431 739 048 024 495 365 218 035 297 755 066 636 166 352 918 363 463 092 703 045 486 832 019 651 951 795 009 953 206 778 699 954 265 059 804 458 709 875 407 625 248 572 080 619 236 357 540 595 116 638 611 564 218 330 467 125 218 626 114 572 784 034 017 384 533 157 707 429 055 500 181 783 386 077 428 388 728 519 373 118 344 798 823 623 466 114 800 712 556 935 696 386 614 560 209 522 841 854 591 550 342 091 296 524 720 032 513 034 107 669 449 856 878 305 499 703 848 231 085 146 421 027 019 789 573 312 458 418 850 467 325 062 967 551 712 939 165 423 919 282 452 796 418 914 780 200 761 815 001 753 934 204 748 353 173 583 741 481 043 645 280 409 798 925 643 661 070 581 377 298 984 474 351 637 855 657 923 560 114 754 089 511 766 184 538 834 833 183 424 099 153 680 317 324 947 103 890 995 358 186 107 128 249 168 451 504 299 461 725 086 806 528 703 953 049 460 153 082 064 068 333 369 789 622 856 962 299 732 498 440 071 695 432 467 645 536 063 521 540 386 995 038 975 367 613 927 692 258 662 596 682 192 135 162 158 992 218 800 081 775 786 875 195 597 040 702 867 151 525 187 116 244 439 490 616 758 989 622 978 268 339 541 053 180 333 590 160 092 218 662 641 885 563 566 161 237 039 495 276 712 475 659 330 122 874 872 697 438 843 881 223 689 351 292 177 931 831 057 994 712 245 875 124 293 274 120 191 732 672 842 657 685 545 738 081 842 862 549 962 477 099 568 567 675 995 331 826 469 656 727 686 810 088 202 988 335 102 669 620 240 326 329 366 246 935 041 360 209 024 074 720 559 310 753 571 805 508 743 150 088 896 014 817 813 235 321 564 315 760 278 830 068 133 910 730 094 256 931 586 411 714 282 103 051 851 040 278 182 359 736 955 289 252 239 687 915 529 715 917 274 920 830 366 904 261 416 157 759 025 719 786 202 153 012 309 504 680 528 025 333 043 878 164 058 490 564 836 759 108 867 433 649 566 153 515 570 292 006 968 258 545 171 369 499 692 032 298 682 899 374 449 663 321 622 396 357 948 253 652 886 869 066 976 458 273 539 746 207 111 887 736 987 624 150 997 923 711 852 238 015 736 579 162 273 814 802 837 296 892 650 295 256 892 936 241 492 146 652 552 234 563 054 955 302 653 119 804 966 724 755 527 120 121 429 365 493 840 362 727 307 842 047 433 376 920 582 700 503 295 563 043 558 454 443 246 019 068 938 992 846 380 157 721 192 193 006 901 600 882 470 057 830 057 316 086 433 821 049 121 542 137 182 362 241 736 016 200 959 042 454 246 424 603 623 731 271 818 714 857 136 552 647 945 934 215 420 690 035 473 321 640 799 953 624 916 792 577 273 701 100 522 866 241 587 803 218 493 929 785 920 818 643 966 566 213 351 121 033 195 688 583 168 597 065 894 043 165 063 279 509 809 482 354 414 251 282 656 031 247 321 387 555 391 190 369 038 071 363 653 062 842 929 226 494 213 042 558 689 132 297 111 182 969 531 706 255 334 285 436 145 330 850 152 372 848 949 214 746 476 353 747 202 285 664 697 147 803 894 545 882 820 555 496 753 380 476 714 210 622 991 725 363 062 761 637 873 483 356 717 479 058 280 373 441 975 284 415 656 070 998 653 764 975 466 441 207 524 922 850 536 274 863 684 110 305 563 512 148 575 831 858 268 405 317 669 035 114 358 686 278 503 821 624 374 340 924 246 950 325 616 983 352 234 821 350 454 834 749 244 189 482 495 124 106 161 144 129 756 953 017 783 017 669 750 326 985 422 171 172 595 230 150 194 052 796 627 955 546 558 358 940 799 635 460 956 424 927 675 697 959 722 126 033 060 783 800 631 888 219 129 025 554 671 596 446 796 371 071 622 976 794 422 993 259 888 306 780 240 333 211 989 485 955 021 555 726 871 050 648 605 334 553 310 612 936 997 614 081 070 632 597 624 013 877 639 691 119 576 534 407 617 773 251 697 141 819 115 609 101 373 937 008 586 745 235 367 663 236 832 989 767 042 678 358 511 768 931 754 249 381 454 709 299 361 642 946 767 995 820 212 183 196 349 071 434 935 127 147 404 040 234 234 232 676 882 453 706 131 057 749 301 704 640 500 521 125 219 427 676 712 192 779 830 321 573 420 732 778 071 030 682 619 702 212 579 848 238 112 019 324 825 662 773 565 649 145 659 204 839 261 078 147 523 469 200 553 499 897 856 153 631 569 449 469 580 748 978 981 268 207 739 188 225 752 059 301 212 650 537 352 217 040 845 427 716 431 871 063 623 564 215 651 337 493 474 470 239 914 623 005 193 963 732 758 607 166 392 778 845 958 412 586 759 219 570 010 463 615 479 260 628 219 107 147 504 072 953 686 024 959 403 981 916 822 044 125 739 964 936 840 154 645 343 968 538 183 872 892 623 254 729 488 711 674 230 586 261 218 822 882 719 675 904 043 118 626 119 406 920 779 509 749 546 182 270 062 628 894 937 521 396 911 201 132 331 988 968 410 125 088 036 211 244 381 482 512 974 105 864 246 443 122 282 214 804 468 491 726 532 966 348 502 838 247 522 228 604 075 421 006 620 501 883 840 572 948 076 354 298 556 456 838 440 276 942 959 097 461 556 014 224 649 262 212 159 570 246 763 568 866 941 378 955 433 716 281 293 481 470 294 279 256 842 187 634 405 286 051 011 281 027 879 910 278 219 516 012 495 989 907 749 750 292 029 514 246 664 201 655 063 891 247 429 460 548 533 378 637 161 012 959 014 727 744 215 838 385 789 853 713 396 433 569 454 250 825 258 557 742 450 447 113 316 393 304 140 787 604 967 524 744 474 061 368 702 575 608 175 236 212 090 678 269 994 228 331 916 748 034 065 365 748 231 582 780 750 994 929 356 934 978 034 474 349 297 475 029 864 888 788 455 310 817 871 290 346 494 192 013 236 555 672 960 224 239 604 144 216 807 700 261 245 387 230 586 262 664 669 545 466 760 278 350 046 859 601 543 295 992 373 451 192 773 108 705 069 568 349 288 465 195 060 119 123 171 921 661 964 424 389 248 916 468 318 792 986 517 038 269 604 928 466 404 803 486 939 731 223 458 012 022 131 575 616 732 756 157 268 822 313 628 950 782 555 391 707 078 624 218 155 597 333 309 099 789 359 044 180 670 260 319 454 717 819 335 907 333 970 596 392 984 421 531 834 164 022 467 038 860 840 323 756 087 530 731 365 480 220 954 290 278 810 718 065 667 317 058 427 664 448 624 664 587 891 609 153 046 054 791 885 229 018 780 123 151 722 125 848 807 873 141 103 368 053 503 706 570 474 764 844 308 027 954 907 913 331 046 123 871 794 070 395 315 305 508 912 275 050 517 461 654 287 461 287 336 530 263 257 284 742 856 018 543 051 606 197 751 711 034 852 126 754 546 721 483 163 033 853 264 062 828 725 504 879 058 122 868 800 459 376 519 774 813 282 843 041 960 141 912 918 144 184 165 756 759 254 132 653 214 252 248 213 125 094 814 203 878 770 345 114 283 726 236 348 009 640 526 885 026 554 854 418 298 452 387 060 496 005 394 882 796 721 541 675 112 469 761 254 286 506 214 313 596 138 763 218 922 235 762 012 667 111 642 651 951 115 873 489 587 391 354 092 846 935 574 301 070 832 966 109 275 068 032 946 205 746 517 048 068 491 179 744 522 409 417 724 706 629 593 562 900 984 040 141 734 452 182 727 330 534 092 460 078 120 221 322 835 470 431 902 897 225 721 071 228 304 389 369 649 056 825 264 814 873 319 319 875 482 114 987 430 359 183 526 604 349 626 486 968 754 449 358 612 724 108 011 420 785 480 891 623 300 296 953 426 076 150 686 082 928 178 981 669 743 267 981 573 171 797 980 391 629 720 674 933 336 103 895 302 945 021 928 737 064 251 453 137 960 342 325 473 447 965 708 242 631 783 894 797 559 077 678 939 245 932 016 036 995 498 919 568 074 062 519 974 163 096 524 749 493 082 385 869 875 704 692 325 744 594 423 320 104 985 507 405 425 797 751 610 383 287 964 428 715 775 038 123 471 332 638 030 493 674 378 766 348 366 951 851 688 206 876 294 803 585 282 745 017 378 216 144 690 036 108 782 484 548 756 647 381 067 493 369 267 017 495 964 873 346 434 812 742 841 879 071 694 595 425 525 443 412 329 856 738 056 709 349 179 363 977 533 186 538 065 780 900 853 831 927 268 286 768 165 215 568 177 398 226 995 695 865 874 494 280 645 795 815 813 624 591 836 002 727 814 535 959 659 234 486 250 918 934 522 102 866 695 074 399 595 720 155 720 518 198 538 750 916 198 398 793 303 015 561 224 610 735 846 362 680 051 613 885 297 683 188 513 637 578 945 747 120 192 219 330 296 580 607 770 847 062 001 511 507 553 760 369 010 123 211 222 902 259 234 013 509 403 951 035 858 545 656 239 643 721 928 425 827 991 640 000 098 264 607 958 154 350 475 886 418 604 083 488 497 639 316 949 176 909 201 466 406 688 948 321 525 783 376 457 913 212 885 156 253 096 185 518 753 798 274 722 081 215 623 869 714 149 092 702 168 870 520 244 586 624 941 418 621 610 388 681 803 036 612 565 775 470 512 309 235 422 823 551 285 889 862 247 535 366 431 168 819 603 980 232 679 770 747 699 188 646 384 379 788 400 000 899 390 309 127 740 569 499 010 911 895 127 124 661 180 420 030 783 311 437 166 558 936 166 850 008 963 661 952 724 391 389 979 037 835 163 564 295 638 460 141 822 255 590 219 805 177 936 314 668 368 658 104 054 559 914 865 429 399 892 924 098 409 181 077 390 384 116 080 933 722 555 335 909 079 043 950 908 014 844 147 293 260 240 936 246 634 438 271 861 415 159 001 107 369 925 940 751 146 931 932 536 435 548 273 800 248 569 293 629 262 312 902 382 540 295 368 984 809 180 274 425 734 657 309 894 169 576 974 367 432 238 811 735 722 867 678 588 286 019 681 759 324 688 365 825 159 389 826 743 158 186 579 074 776 124 023 408 664 119 343 034 607 517 265 337 219 176 697 846 896 666 150 547 761 386 057 836 251 894 958 948 053 386 145 807 009 352 550 376 445 326 738 798 734 597 974 132 909 161 972 980 282 961 204 279 437 038 960 663 662 349 874 902 260 606 637 702 538 022 987 503 352 855 479 100 567 352 459 567 000 702 483 658 536 197 669 255 330 890 455 767 631 346 350 691 155 948 769 030 286 697 595 455 996 454 206 688 839 674 835 030 740 775 680 852 720 014 405 511 906 993 729 817 340 981 950 495 627 470 096 779 487 012 673 457 311 243 806 724 273 404 650 983 385 974 678 127 335 005 639 843 809 090 948 815 679 540 247 515 275 655 318 620 473 639 612 415 736 069 906 260 808 653 120 388 850 931 249 877 263 507 670 999 323 350 261 585 272 211 235 819 352 129 278 132 720 693 314 789 054 398 954 223 944 527 836 550 720 142 712 622 841 645 059 531 386 424 630 606 758 167 118 384 614 854 366 630 286 178 657 716 472 388 178 323 503 991 973 236 691 533 874 825 228 150 970 655 436 631 874 151 160 689 495 612 866 550 303 980 128 490 701 032 404 886 565 298 770 608 626 538 072 693 210 510 760 122 286 798 974 785 823 694 055 844 662 221 428 076 737 348 841 604 681 075 554 879 907 602 613 678 962 980 539 467 650 852 629 195 791 365 631 914 348 728 545 431 690 946 330 280 928 330 029 599 960 770 904 789 551 704 779 213 544 739 383 510 262 778 960 550 123 641 488 935 063 014 636 720 714 507 520 754 063 283 041 745 036 497 144 474 280 216 267 175 729 778 897 988 168 368 775 745 412 916 161 896 098 131 895 701 305 199 980 600 415 955 917 919 266 402 600 375 891 547 559 661 111 534 137 911 850 170 206 020 182 637 902 079 512 700 814 889 986 567 792 938 069 789 345 079 514 203 627 967 684 477 114 402 467 119 588 204 182 872 331 826 088 126 503 476 949 348 723 987 817 876 011 482 430 229 631 884 181 146 966 369 504 560 276 479 265 474 272 157 070 152 244 836 645 051 364 128 151 139 559 586 120 084 725 545 507 156 678 590 487 017 331 855 893 338 446 955 833 375 516 982 054 168 237 363 093 631 765 987 579 861 152 507 377 889 936 853 041 219 282 780 186 511 445 587 943 153 875 684 994 010 083 153 622 643 945 721 259 728 147 719 424 945 876 299 545 993 599 177 030 449 235 787 526 470 328 162 226 054 454 843 735 072 514 381 124 958 787 915 657 278 653 742 537 810 322 893 138 914 176 017 935 163 094 745 958 678 931 380 600 265 246 152 104 429 170 197 191 611 996 001 386 948 105 635 801 357 605 100 528 340 420 242 273 809 890 012 435 220 289 388 749 207 619 985 496 263 403 119 619 431 539 941 016 265 322 486 121 248 785 478 481 423 538 935 672 767 776 516 140 591 923 284 387 405 671 793 509 015 530 212 014 968 026 512 659 175 971 510 698 581 369 191 269 764 044 572 672 866 506 990 032 302 074 531 561 180 763 962 585 561 314 004 250 283 264 530 008 721 876 253 812 589 027 129 946 123 251 171 758 350 532 492 472 152 131 708 648 854 874 899 183 242 653 598 522 342 375 823 368 975 876 027 642 532 507 238 356 058 317 242 088 209 206 383 924 948 292 504 650 804 117 363 217 143 850 181 539 467 856 807 956 028 729 382 467 461 895 124 003 670 309 714 052 476 174 053 646 742 769 252 515 139 250 284 729 118 584 610 898 894 958 563 297 293 518 629 170 982 434 015 982 473 162 695 992 860 650 389 282 549 217 328 871 178 653 911 771 703 185 315 359 305 702 772 483 094 675 969 733 499 239 372 771 611 858 797 180 694 667 794 634 237 481 955 031 479 445 021 138 373 811 734 193 636 114 289 872 898 560 387 606 243 278 959 134 580 354 540 403 516 178 241 167 172 740 328 730 951 652 802 414 849 581 921 873 514 957 179 286 133 568 921 264 637 006 991 036 829 113 056 114 112 108 005 816 089 064 576 502 706 855 668 507 338 845 025 883 060 966 116 638 892 475 712 654 675 706 323 646 710 382 022 941 852 114 114 324 841 613 330 465 331 818 777 933 860 474 761 419 642 020 090 953 685 726 304 672 549 484 994 727 709 849 565 640 413 718 627 105 400 753 428 019 895 340 153 352 126 580 339 217 026 748 674 439 576 485 658 331 264 286 021 186 133 176 726 684 287 792 871 790 242 334 071 823 111 407 780 968 893 626 131 576 216 999 747 272 325 748 495 882 287 690 420 971 727 178 750 599 821 636 685 548 170 191 714 756 319 960 735 463 690 743 756 096 300 180 938 210 159 017 669 744 600 463 926 066 424 349 795 850 951 134 462 606 804 277 475 013 661 333 489 616 395 893 365 263 771 410 341 123 110 033 458 308 072 080 397 851 536 119 588 517 929 546 181 422 605 279 093 027 338 682 579 656 567 009 470 707 490 575 224 590 097 627 443 384 656 457 800 039 271 552 664 101 086 978 007 602 327 436 126 862 085 386 157 170 809 678 146 326 002 355 482 161 199 146 488 945 997 801 251 581 063 891 719 667 563 355 832 038 234 332 366 542 899 468 156 640 144 296 272 060 073 130 897 115 793 523 059 099 950 099 892 315 364 795 361 877 787 451 256 582 689 879 397 669 352 604 103 333 267 076 614 411 922 679 757 845 631 411 883 155 823 969 746 858 360 579 988 111 492 967 100 632 353 926 865 621 979 089 385 637 262 016 778 311 352 218 635 925 794 206 415 264 665 543 315 079 126 926 347 956 512 611 663 879 513 625 096 933 093 164 107 849 557 059 277 058 389 698 376 561 868 911 400 355 529 444 907 792 242 438 540 061 213 186 540 808 421 075 125 073 769 875 664 614 952 090 856 076 148 876 218 030 415 971 096 371 236 865 637 310 066 216 445 568 314 012 532 004 229 852 152 159 934 151 898 159 991 967 582 328 729 146 504 272 343 129 659 166 789 855 129 036 770 954 433 894 475 918 481 753 590 407 372 726 199 627 843 273 185 696 798 762 347 632 993 961 262 574 043 343 008 507 028 820 991 199 308 304 690 258 595 953 047 687 177 214 310 609 950 908 449 036 019 110 027 445 551 905 320 276 706 490 937 784 882 411 846 483 682 488 374 552 023 835 055 494 635 052 760 072 608 548 386 714 288 614 933 671 241 641 138 725 892 179 964 425 375 166 081 592 980 459 355 981 011 942 703 584 539 405 677 234 990 968 575 959 342 049 353 996 648 878 725 489 446 571 942 490 034 220 325 759 131 407 700 365 070 236 956 171 546 045 063 813 221 601 429 976 641 025 400 510 608 883 849 925 904 958 493 422 223 729 398 854 074 138 752 937 841 640 579 540 626 256 087 282 089 980 510 917 677 504 807 959 352 412 511 439 943 805 943 157 529 610 772 432 571 359 749 428 419 397 103 076 208 525 053 622 347 075 858 109 831 195 610 901 211 241 103 862 697 904 580 164 022 336 847 540 251 360 527 920 502 577 256 087 730 037 973 750 507 863 424 834 173 775 915 872 692 293 710 152 529 951 532 636 807 173 262 328 075 565 199 358 269 208 047 519 628 271 458 481 731 626 522 882 876 387 498 378 072 950 378 510 682 457 076 601 731 005 086 965 234 225 718 314 610 775 402 304 564 877 500 228 435 963 004 509 966 570 724 259 679 213 423 246 750 669 151 689 189 256 085 664 772 060 982 955 964 791 368 882 199 778 699 119 905 709 011 907 495 323 524 268 305 912 745 826 145 576 894 936 525 616 221 540 869 836 640 485 392 174 527 869 526 677 866 189 962 983 648 043 638 262 289 889 548 643 442 470 784 374 416 075 962 721 657 327 359 976 108 745 033 495 313 618 289 803 574 324 936 947 816 300 546 920 623 409 141 795 684 514 842 991 710 179 291 488 695 086 296 961 587 095 909 431 043 725 706 290 824 202 150 167 901 332 221 314 553 366 261 230 456 833 791 466 100 288 241 629 625 924 606 295 047 512 507 487 645 995 752 735 874 990 934 838 682 982 107 373 811 582 403 819 784 974 003 527 751 462 687 056 079 746 633 237 475 087 576 868 001 873 694 952 146 529 174 543 389 143 139 282 248 893 660 193 444 191 962 676 511 976 943 935 935 250 690 707 623 520 491 842 707 671 125 140 763 171 287 976 046 296 129 719 159 166 023 991 177 255 274 153 897 591 734 200 499 082 115 874 855 452 194 760 120 914 737 863 995 157 350 857 223 588 864 815 498 975 526 367 641 664 555 690 378 688 916 977 681 565 152 403 697 413 120 378 924 248 229 586 501 164 147 311 542 791 831 714 516 516 964 232 774 264 434 899 468 345 032 649 313 350 155 994 913 388 625 708 244 736 448 618 658 121 140 411 803 117 514 762 502 370 949 228 622 221 445 016 774 820 271 739 816 564 270 591 286 871 445 640 655 518 951 959 717 473 236 928 487 888 157 516 998 389 460 214 381 366 547 260 496 435 446 096 684 567 755 879 351 626 742 178 104 211 920 420 248 689 646 950 186 306 606 806 898 851 940 452 742 760 290 220 839 925 203 069 869 913 660 412 780 453 986 326 740 331 620 144 019 265 653 766 439 300 713 278 760 496 050 779 942 294 583 852 592 210 173 928 318 296 572 595 936 935 710 550 631 421 594 540 919 151 054 160 267 431 575 779 790 891 840 831 549 165 856 657 819 447 233 511 063 546 609 481 070 661 484 746 827 801 607 597 420 806 508 925 604 913 679 795 242 363 294 029 217 804 589 446 012 151 688 675 254 108 528 065 139 299 783 642 022 187 019 027 051 867 882 485 124 468 888 348 283 576 158 179 081 995 562 487 045 503 675 716 245 785 309 205 664 645 694 399 092 898 096 875 644 451 994 064 156 520 693 271 096 060 892 251 398 592 731 164 153 591 194 391 713 410 582 556 553 709 534 212 330 086 407 799 254 630 932 864 664 654 917 666 298 646 284 476 478 579 117 089 304 605 146 174 696 468 142 244 036 692 777 815 739 096 222 743 510 184 041 858 435 057 771 876 027 139 842 333 233 790 849 396 391 504 901 721 026 441 424 296 682 187 693 251 011 026 411 328 823 410 725 343 529 071 710 063 487 542 835 809 526 767 002 516 988 868 255 324 076 694 867 956 443 773 636 196 694 607 092 399 751 989 730 460 727 853 574 218 256 473 645 884 043 793 615 743 072 093 921 587 981 158 762 638 695 173 718 648 527 470 949 287 006 776 462 839 927 478 374 515 814 733 435 355 960 393 906 832 317 489 099 473 716 344 183 244 107 854 117 770 991 122 637 421 792 426 653 528 686 549 038 010 994 168 134 850 502 271 418 139 460 871 676 778 780 758 423 588 297 527 608 107 635 386 333 441 158 268 206 674 985 472 493 153 156 606 710 397 848 126 338 117 311 744 479 871 912 205 563 609 814 321 678 018 418 316 513 317 489 120 411 157 148 968 053 003 599 924 919 564 863 835 302 679 211 798 773 240 738 983 561 168 669 077 280 416 984 754 868 434 603 544 913 116 596 961 464 686 747 633 411 797 908 734 033 304 830 755 677 081 185 902 323 551 864 051 513 595 009 270 136 536 975 047 766 445 637 961 628 105 309 144 070 539 744 245 050 544 422 681 082 352 888 159 823 682 490 812 543 793 634 291 998 561 766 904 472 342 565 284 751 471 991 301 024 401 764 938 615 488 019 567 485 882 012 302 835 010 084 680 843 917 252 789 502 890 234 179 720 879 708 880 598 520 907 479 620 895 612 677 953 264 965 849 243 360 393 209 318 459 245 324 289 745 529 661 999 987 272 870 995 582 391 236 146 096 903 900 879 133 348 772 074 564 466 878 056 990 023 805 314 938 154 630 938 716 370 577 290 645 931 826 202 859 999 786 717 065 234 003 990 732 554 799 360 928 145 744 709 543 488 352 662 877 108 630 131 378 317 630 029 899 166 925 435 621 897 414 856 547 692 324 624 328 249 492 415 184 668 309 497 605 504 393 852 576 907 811 641 056 589 653 762 194 591 814 444 035 733 652 617 176 348 622 270 375 799 418 745 925 716 290 348 905 440 549 517 901 173 761 490 241 479 256 801 042 571 852 721 354 908 063 441 624 291 434 201 611 447 106 325 258 843 102 861 931 169 399 541 354 649 076 084 605 650 764 228 469 110 567 613 438 830 410 330 662 881 344 811 227 929 383 655 674 865 489 508 728 889 639 001 352 424 004 181 897 168 394 579 048 759 526 746 151 614 565 154 873 623 112 800 186 967 775 009 048 278 392 611 515 125 212 967 273 295 065 837 081 844 323 634 234 904 347 146 984 703 944 362 560 861 283 141 866 075 411 016 012 744 057 930 055 984 604 356 493 786 239 696 997 074 347 081 661 196 490 154 928 424 990 040 446 108 130 456 046 851 611 838 588 018 241 480 345 183 940 866 790 482 298 112 624 715 865 052 240 045 067 412 804 078 902 587 293 678 129 172 828 093 819 850 891 244 024 921 398 860 400 661 334 898 931 938 553 487 964 081 831 106 046 038 359 324 202 349 766 171 659 391 385 658 946 983 709 287 693 480 409 187 308 637 852 625 608 155 546 721 190 853 854 272 392 153 386 798 646 774 044 981 838 705 385 088 661 151 665 085 817 500 108 379 515 153 120 362 538 950 494 590 531 724 065 934 446 563 147 248 144 756 009 300 582 502 977 318 920 256 056 457 386 799 878 247 267 191 544 699 981 263 907 160 120 951 823 903 766 162 230 383 468 978 558 241 886 078 429 922 138 296 995 462 013 836 266 011 831 470 885 203 319 658 021 602 955 430 160 494 985 913 652 239 878 142 483 997 192 158 830 293 290 156 999 192 910 996 625 314 835 917 825 016 598 938 666 427 879 121 457 287 276 769 661 032 384 728 743 648 511 604 466 809 690 225 650 447 240 280 684 363 526 499 451 680 888 244 609 978 847 154 710 081 919 694 075 386 986 198 363 572 065 851 536 943 087 051 267 139 853 823 340 818 264 734 746 599 771 596 602 965 478 500 349 110 271 118 388 737 300 072 985 323 338 683 646 802 567 988 123 566 310 284 219 135 305 091 544 336 471 654 322 703 572 054 357 117 353 668 083 219 506 517 109 043 128 887 432 747 974 359 245 119 902 447 465 320 156 708 905 052 796 746 680 103 748 735 549 709 218 813 477 047 538 652 516 327 518 559 261 806 034 321 922 105 261 402 711 560 750 442 312 240 124 585 783 009 203 541 022 944 083 883 891 921 869 745 784 396 914 552 562 698 434 429 659 835 193 679 102 925 473 589 843 369 831 302 962 503 912 376 887 086 236 011 155 010 811 501 493 743 741 447 916 155 625 842 789 221 901 059 428 965 519 472 228 868 549 024 885 083 826 502 552 424 236 295 090 756 384 923 434 471 191 561 488 887 910 628 680 632 207 241 666 399 991 677 286 440 013 610 019 010 318 470 216 833 316 053 338 551 624 036 303 479 871 871 625 516 530 745 065 460 850 587 541 683 431 773 951 856 998 004 855 415 757 907 556 290 724 855 771 914 455 290 823 378 033 689 251 614 410 834 310 478 309 970 521 061 195 960 698 812 168 849 725 097 219 522 346 330 331 437 303 378 191 872 151 177 257 643 284 914 341 505 430 205 537 098 628 549 631 981 128 559 014 211 851 222 735 509 189 010 879 375 815 375 059 294 423 050 905 329 139 569 443 201 527 243 074 133 414 598 097 176 580 848 881 851 845 185 713 741 633 006 739 356 484 935 610 100 578 698 020 282 761 884 835 384 062 078 874 944 819 005 012 098 523 028 425 709 192 797 609 091 787 800 070 179 012 496 631 631 487 599 635 926 993 021 047 694 469 367 025 048 612 671 952 434 200 689 057 038 344 463 284 160 692 292 858 745 078 684 813 944 892 173 406 292 181 806 672 707 408 176 231 261 813 997 981 500 196 851 569 740 202 616 759 946 321 331 747 903 641 771 439 215 485 414 635 985 178 838 318 603 734 159 631 107 529 048 234 581 377 361 537 147 612 683 123 290 773 607 741 024 756 981 896 962 595 546 290 163 880 356 146 439 809 116 386 397 309 086 149 264 175 329 488 054 559 307 918 400 685 752 074 404 509 503 594 092 339 665 395 675 973 576 175 909 681 721 587 406 976 196 676 606 959 866 744 522 425 256 880 949 622 558 453 536 254 169 397 582 282 944 825 328 486 037 722 415 880 082 056 993 397 453 032 885 822 347 457 501 270 499 180 437 042 576 667 393 197 013 996 021 657 889 106 308 523 848 289 312 221 602 339 027 389 031 425 031 606 533 032 610 068 398 967 177 927 837 715 129 575 169 215 578 628 071 025 055 142 959 567 923 755 933 373 732 802 496 267 664 874 543 009 349 954 178 587 306 675 965 030 971 629 759 770 346 551 494 171 266 374 305 789 151 868 678 092 502 162 482 720 302 067 871 280 371 278 283 061 933 748 232 880 546 060 916 112 231 256 502 550 707 143 858 116 771 105 084 678 383 566 118 517 291 497 062 121 642 386 530 943 119 440 534 818 244 072 359 593 594 594 577 146 785 177 650 518 196 062 397 254 874 143 595 310 350 131 769 988 907 004 035 380 251 878 845 390 236 278 241 334 796 857 327 007 420 776 909 176 098 675 994 906 545 630 850 036 659 772 373 573 931 304 922 048 676 443 745 013 818 620 688 427 638 501 110 312 690 888 485 808 342 444 614 350 353 547 568 886 899 263 106 819 076 903 997 851 525 154 143 987 130 452 900 531 097 031 460 213 271 010 283 276 105 516 220 876 208 226 236 648 777 642 887 419 017 065 896 344 634 055 165 317 246 474 746 893 377 518 791 774 573 624 883 963 695 815 415 827 378 016 993 636 215 202 484 397 404 633 156 471 502 491 141 707 600 433 286 840 753 706 212 527 158 446 839 317 979 588 812 279 763 639 889 992 156 243 954 873 167 803 727 046 802 810 889 169 213 572 148 256 266 426 087 474 682 432 907 780 816 751 415 345 760 700 055 004 126 132 359 789 119 028 183 269 675 537 212 719 276 659 570 814 261 070 171 142 289 483 188 327 382 168 771 425 244 141 104 274 174 536 759 475 508 367 292 957 399 354 158 244 046 747 661 382 851 542 140 263 543 339 644 487 605 133 624 842 230 844 965 586 201 825 331 790 693 910 605 307 493 918 433 448 682 768 103 577 759 784 174 317 048 773 966 576 982 451 876 211 289 318 038 508 286 273 503 283 506 889 443 219 163 277 632 314 251 548 059 135 960 894 543 658 230 693 774 665 526 592 190 858 683 217 071 976 374 659 689 685 208 828 211 146 773 137 659 203 745 504 957 827 775 639 440 254 221 284 137 086 033 253 821 795 054 492 428 109 605 730 464 997 889 797 620 018 914 002 991 266 705 515 627 633 812 013 631 030 107 396 269 120 827 980 989 719 531 610 764 923 145 018 793 480 462 199 098 276 913 195 177 031 972 510 283 316 231 858 582 647 846 698 145 648 333 616 038 466 541 837 318 167 689 443 082 740 396 930 596 759 576 284 102 597 129 500 710 968 900 940 752 192 794 691 341 127 881 928 579 937 298 817 679 046 610 807 708 777 481 029 772 686 131 859 312 936 006 794 981 593 058 180 995 590 319 319 139 464 938 640 374 722 529 328 290 887 447 488 994 285 804 109 811 094 965 926 988 913 503 480 570 588 669 976 851 383 863 687 429 637 516 457 624 083 681 303 842 948 986 107 029 798 306 478 306 952 088 570 989 588 097 288 266 227 131 098 925 290 729 205 867 991 025 867 686 269 603 762 671 237 511 938 602 700 823 568 677 918 457 971 671 302 109 745 263 061 770 321 511 317 163 039 873 865 987 851 031 049 939 614 095 983 969 619 913 870 834 927 461 182 801 141 403 693 600 250 067 173 599 416 369 494 011 174 424 713 698 956 668 231 781 047 618 817 312 483 875 247 786 342 321 523 826 613 546 559 064 678 397 159 080 450 748 321 769 037 868 974 990 621 895 730 910 817 198 944 530 945 274 324 105 713 678 736 075 971 846 044 923 256 286 213 590 256 195 898 302 600 398 491 634 411 579 861 715 258 580 504 353 282 927 319 031 023 755 785 275 209 807 554 266 616 340 457 896 986 950 212 576 662 308 999 626 981 987 939 997 569 401 802 173 354 767 548 579 469 711 440 068 700 921 725 885 587 071 244 708 059 564 392 794 445 354 276 458 244 593 273 921 119 880 183 388 972 319 619 729 606 607 714 139 916 592 298 906 439 600 716 266 243 077 886 325 530 969 917 229 844 170 104 613 908 284 190 327 817 975 559 144 824 791 322 865 918 577 974 659 011 999 240 721 788 788 447 011 659 463 135 304 707 129 674 171 372 409 428 958 457 938 870 497 524 101 271 090 913 429 816 241 083 041 473 529 572 318 954 812 549 481 924 534 938 239 993 628 178 828 528 130 789 486 447 766 894 622 493 410 963 102 433 018 805 717 167 907 749 636 445 549 686 074 372 332 794 118 262 274 057 733 738 197 565 361 355 280 253 460 930 272 026 255 543 595 599 869 016 954 174 890 578 287 555 590 887 892 046 177 093 746 438 208 836 579 490 179 178 851 688 089 684 928 426 018 274 412 980 134 470 169 275 926 699 560 901 831 092 766 639 884 637 376 217 074 574 920 482 267 781 804 688 719 335 082 132 200 007 782 626 027 453 665 362 504 436 198 811 350 051 015 453 670 978 990 386 444 157 141 424 876 264 326 881 482 729 987 648 619 019 927 348 769 634 597 604 890 969 547 949 928 951 562 683 674 178 705 125 163 500 889 569 731 702 579 742 371 284 912 233 242 043 098 421 396 967 498 901 603 503 573 047 004 067 660 749 385 361 745 547 726 570 668 283 317 020 945 852 692 811 428 674 953 476 908 452 305 897 391 956 374 041 291 455 154 134 690 093 237 335 993 301 001 001 375 173 378 181 857 813 122 913 490 159 653 903 090 813 825 097 962 629 758 100 635 934 012 560 920 943 454 666 778 811 550 423 409 050 013 249 429 721 692 245 885 336 689 782 015 338 287 673 045 080 907 304 167 243 177 976 149 845 216 082 565 878 725 544 015 276 609 240 783 011 779 330 246 999 443 585 268 847 963 126 454 975 364 175 144 207 902 620 596 840 790 187 035 751 698 865 012 311 269 962 811 156 605 042 918 935 655 539 678 802 885 022 847 190 165 902 830 012 028 692 068 437 152 666 483 160 978 134 399 703 654 319 719 944 495 585 719 186 925 475 747 489 670 835 880 827 377 640 648 783 759 321 068 152 919 349 696 802 268 820 525 736 820 848 601 990 115 697 966 929 836 623 840 722 290 350 657 944 688 930 725 261 971 499 013 026 127 574 247 612 519 047 601 033 048 681 987 678 904 036 759 349 942 143 732 279 971 557 043 562 078 397 971 166 638 783 344 661 743 736 871 726 890 890 577 289 485 207 781 156 011 624 815 163 936 305 347 800 494 944 388 168 363 524 907 007 225 445 210 195 359 489 096 562 549 585 267 367 368 423 956 080 449 012 795 853 985 708 989 966 750 273 491 760 339 960 296 955 557 700 772 280 782 339 399 150 314 745 094 630 102 496 693 608 837 515 562 855 382 996 257 960 307 099 147 824 334 464 926 360 333 506 685 209 215 465 471 209 546 431 128 511 368 161 288 921 310 651 896 984 807 228 291 605 490 432 058 505 851 210 325 806 869 350 294 994 542 920 032 728 216 114 080 957 733 151 999 604 977 117 042 764 603 706 117 978 739 284 635 058 967 399 841 752 114 762 454 405 621 524 061 655 458 574 488 164 174 743 731 018 849 424 968 886 105 523 675 074 091 996 685 913 227 676 212 986 077 120 690 622 340 907 798 023 604 496 294 880 892 944 648 512 766 766 193 393 934 124 370 907 486 716 607 488 371 883 919 111 224 578 116 724 747 901 168 658 059 489 718 238 290 577 506 352 540 617 727 702 031 824 790 542 060 283 230 002 168 668 137 213 282 521 999 298 121 396 118 342 406 917 247 116 319 708 101 557 521 212 703 115 674 463 093 741 509 553 887 600 725 499 877 522 429 180 814 975 925 749 266 820 664 083 857 072 721 125 324 108 358 260 085 397 204 613 208 623 082 993 317 734 807 874 939 145 682 203 241 425 666 841 191 172 111 343 363 324 706 904 461 904 098 600 324 120 601 835 380 123 728 842 830 652 929 814 375 507 648 875 984 056 222 096 957 516 311 542 250 220 501 533 469 803 018 805 273 799 371 324 523 082 031 225 140 502 487 661 157 834 110 698 280 962 359 125 037 438 192 337 396 331 244 216 395 810 088 410 107 562 459 241 652 821 960 993 624 796 039 279 881 257 241 855 108 072 762 923 800 345 989 589 498 982 976 588 355 232 924 347 716 361 786 886 377 223 860 467 189 701 090 210 350 882 208 091 118 938 222 013 423 203 900 365 390 913 855 469 465 302 586 245 258 676 571 198 535 587 854 738 218 001 129 571 404 406 137 502 681 195 662 794 513 879 390 313 069 051 924 120 621 446 981 461 458 593 459 235 751 239 582 891 209 549 851 732 081 337 442 973 656 195 364 150 778 706 495 059 730 735 795 411 912 768 753 412 874 946 164 686 968 223 680 256 076 400 465 277 704 692 746 829 011 910 096 872 331 988 445 806 441 824 568 031 611 506 528 922 215 461 398 374 053 057 709 498 529 013 135 839 443 131 066 329 402 404 140 355 970 492 774 425 976 909 567 210 871 969 556 627 564 878 490 839 297 247 315 820 343 791 755 002 856 041 338 276 239 361 415 322 027 999 869 182 575 447 982 490 912 556 714 161 466 611 647 564 743 877 110 943 774 999 644 612 290 267 026 762 928 281 863 806 831 060 117 008 922 042 460 156 469 028 114 887 078 207 969 258 803 917 447 608 886 583 585 698 143 827 962 919 579 761 928 472 130 414 524 536 915 370 287 894 090 285 470 467 878 146 047 433 404 473 341 056 225 697 968 266 542 805 491 582 911 376 731 116 375 661 504 882 050 821 615 636 970 238 358 139 266 895 420 579 760 119 333 322 757 921 671 890 922 949 712 015 568 937 533 337 807 958 411 975 721 883 433 463 180 933 149 811 133 461 950 000 735 527 303 167 843 239 483 953 477 082 651 233 283 679 793 240 119 653 229 712 634 099 436 087 796 788 543 161 685 301 428 518 116 699 361 384 267 599 894 421 170 067 294 677 471 807 045 110 282 720 166 237 289 432 375 679 123 220 965 047 316 215 110 446 020 338 972 256 098 018 016 179 543 488 167 521 477 721 251 699 396 234 524 786 735 769 686 123 386 744 656 605 382 718 495 934 947 215 222 283 377 940 234 879 789 724 696 301 839 102 837 895 583 165 148 671 009 287 820 502 750 612 951 691 802 044 844 005 697 160 672 200 350 124 638 890 810 989 686 874 220 724 323 024 463 011 738 294 178 226 849 318 072 460 745 770 077 695 134 322 530 633 581 826 819 893 492 157 841 549 184 092 552 135 668 062 616 824 252 739 551 187 974 721 398 104 785 391 808 397 121 745 395 302 571 136 016 067 575 770 414 305 036 958 136 801 977 336 863 892 187 671 781 541 605 200 398 476 046 774 066 533 628 401 284 205 671 173 574 906 878 370 267 546 021 631 812 781 369 002 792 272 658 545 472 726 555 703 783 709 323 954 810 627 695 398 680 967 713 509 509 158 684 029 146 412 153 637 871 648 200 155 900 479 136 614 609 208 032 388 109 641 562 314 612 099 446 644 719 525 173 624 462 929 450 593 392 812 232 786 954 472 851 826 404 867 212 834 540 145 441 028 457 972 429 657 709 664 929 471 713 988 601 804 327 676 321 739 037 409 245 582 434 109 380 477 949 129 798 829 231 688 426 428 313 901 035 096 331 402 079 434 791 677 903 908 271 935 499 800 440 162 771 099 599 234 454 500 753 420 358 290 646 617 333 495 373 180 466 420 497 968 920 262 138 430 027 232 934 307 964 227 697 924 966 279 574 757 923 674 959 512 737 086 581 225 298 168 061 604 449 273 307 882 948 651 548 862 629 195 892 268 428 341 142 163 966 423 736 003 486 282 058 985 924 483 135 168 145 944 962 795 540 018 399 895 819 928 631 411 000 264 187 553 065 291 130 422 895 805 359 097 204 855 941 483 592 817 678 903 072 562 991 053 253 392 705 984 772 565 096 366 726 258 989 486 944 452 153 073 047 490 217 162 382 448 347 517 379 742 404 994 857 145 350 035 706 269 074 656 528 192 341 435 384 020 759 845 097 443 188 969 893 812 161 732 086 859 265 327 280 980 352 155 271 824 866 235 747 574 218 981 319 919 611 006 586 644 323 186 379 723 545 979 685 748 641 742 770 950 016 212 411 056 347 669 197 468 559 933 940 707 532 388 832 236 307 086 504 474 262 948 175 957 284 694 499 136 864 562 591 415 577 338 206 939 571 753 511 605 472 159 544 809 305 915 933 222 627 899 979 025 707 014 000 302 085 087 463 244 358 063 305 114 923 305 381 896 858 687 803 342 992 734 744 531 302 455 558 884 365 584 869 958 124 807 759 145 206 189 213 607 104 039 624 548 627 573 708 798 455 407 253 697 886 539 138 929 999 200 292 132 552 045 816 552 902 275 088 284 555 320 612 672 731 017 412 195 241 891 447 050 182 467 502 848 660 756 997 500 843 343 805 375 522 079 241 376 321 746 150 061 747 119 881 200 741 760 035 227 791 860 324 354 950 312 507 870 655 079 905 323 833 365 231 339 607 668 070 281 830 683 373 420 967 836 892 956 378 975 503 427 614 181 952 800 636 831 727 266 567 083 795 991 605 262 096 799 329 356 008 253 119 298 806 895 512 630 250 013 781 303 084 739 309 618 055 883 209 607 305 866 459 214 667 853 172 151 634 021 922 227 558 273 526 940 095 572 169 804 269 027 080 833 370 669 843 002 828 325 195 728 219 286 438 296 111 085 187 939 100 098 193 611 479 130 742 554 151 485 910 356 772 829 927 387 248 106 035 036 264 748 696 375 827 660 225 923 353 762 570 147 282 325 332 148 823 087 029 713 090 574 272 160 626 517 585 649 423 447 466 692 162 816 522 965 051 012 284 599 329 606 666 815 019 434 772 000 745 786 659 103 400 763 012 470 287 251 190 775 883 184 589 709 953 355 092 248 128 678 526 352 428 314 045 005 808 477 354 829 229 373 804 326 760 104 394 135 308 433 974 609 233 453 404 093 889 577 629 000 878 061 355 802 153 422 435 140 537 784 772 594 825 988 292 578 088 486 506 352 564 062 290 518 249 908 523 082 632 886 486 889 654 597 241 836 551 365 709 107 022 482 957 915 807 234 582 561 082 932 938 652 397 763 768 736 659 402 794 153 068 822 241 422 203 380 307 086 865 432 438 817 050 715 671 091 762 490 380 089 170 899 408 155 288 121 971 059 916 225 880 187 042 288 156 604 831 933 116 379 933 932 902 277 263 833 241 559 989 387 008 266 934 999 141 758 045 683 890 556 073 094 132 882 102 120 524 520 896 467 143 208 271 742 303 206 348 849 699 724 884 883 811 539 717 049 919 434 627 346 483 195 265 112 895 037 848 499 614 826 231 686 583 142 072 994 692 394 086 663 846 003 246 174 206 021 098 415 936 367 078 186 773 441 461 767 233 728 979 912 328 359 654 185 514 911 917 220 010 523 861 149 383 274 333 496 449 756 364 797 552 002 931 842 770 670 280 063 016 635 039 735 777 380 272 857 264 782 753 003 430 780 791 479 003 498 126 196 243 210 647 645 810 314 007 966 298 542 184 036 518 697 992 985 311 039 186 566 195 773 825 092 664 043 493 918 223 614 672 593 881 248 965 497 228 870 064 594 968 531 853 957 084 924 322 108 326 518 354 316 808 792 870 270 058 316 122 451 273 405 930 070 383 174 248 347 437 167 692 891 309 867 827 507 223 317 660 171 042 262 938 951 375 236 510 445 066 108 067 749 826 713 086 014 259 945 625 370 523 551 583 459 132 828 381 912 956 213 259 635 705 418 366 549 600 429 769 809 482 339 562 287 937 156 765 324 120 675 251 740 668 525 374 567 878 774 574 604 591 020 817 914 965 358 490 177 724 969 187 045 020 641 400 010 757 634 416 157 193 167 831 013 676 596 646 320 864 454 810 287 135 612 361 730 614 358 804 320 514 627 221 478 267 605 540 139 590 587 305 655 829 367 673 583 162 625 841 105 182 428 361 837 090 684 248 353 308 366 347 720 578 544 741 563 312 233 033 963 970 197 346 421 433 236 392 706 417 748 163 794 248 831 121 168 435 334 225 285 433 530 533 625 001 976 786 651 003 924 927 926 039 625 840 886 883 332 012 272 131 983 918 386 945 192 944 870 858 191 506 907 048 528 070 563 287 055 859 916 622 980 457 531 448 383 685 596 328 352 581 703 041 569 069 344 106 707 602 455 372 692 772 788 039 108 315 534 143 754 072 470 494 723 573 152 519 120 828 012 755 112 769 797 178 236 381 867 977 797 969 328 186 382 630 961 603 663 278 718 070 718 577 394 176 192 167 688 999 366 654 821 298 932 105 172 554 008 800 660 669 942 802 204 114 624 588 389 217 303 029 355 451 393 586 812 543 180 036 267 232 477 769 487 292 019 478 581 973 131 908 893 960 665 698 328 300 505 322 302 855 102 076 247 121 823 490 811 982 065 468 702 964 072 308 162 345 702 165 834 804 468 000 183 965 544 891 808 978 303 563 280 194 864 748 292 075 275 064 159 306 539 502 706 241 945 303 273 020 303 010 310 029 791 647 250 337 790 768 138 333 021 986 038 105 623 405 101 796 777 462 255 608 040 837 301 290 355 817 402 171 645 691 555 952 734 330 586 490 947 655 425 081 639 514 427 275 720 606 054 612 160 655 564 263 871 002 453 470 289 166 756 564 931 408 746 341 629 987 728 270 352 556 682 471 186 532 684 609 549 636 907 061 376 857 415 167 882 500 295 121 846 039 135 181 484 625 756 300 002 108 551 666 111 353 261 690 661 850 524 998 922 334 595 570 127 196 450 991 093 906 852 902 807 275 541 912 194 424 276 431 170 674 056 934 204 182 454 259 102 007 258 687 071 274 429 322 337 718 195 668 039 654 812 989 826 318 306 273 558 169 041 248 878 167 959 518 421 803 290 961 614 601 478 383 844 886 758 087 672 050 634 028 837 764 833 312 128 341 882 600 010 413 120 218 538 825 992 695 373 284 340 669 868 968 244 908 021 368 040 311 731 452 922 504 457 305 298 566 991 285 289 487 583 068 303 312 966 230 441 465 003 170 349 181 475 481 534 882 990 656 563 755 296 994 582 981 048 886 563 466 800 289 447 401 530 488 931 886 312 523 926 032 955 851 623 376 820 361 115 566 612 159 100 659 123 513 858 836 241 296 363 253 241 099 456 234 786 383 295 897 257 542 671 169 003 754 329 565 461 875 146 612 859 064 217 977 064 029 313 817 954 964 584 112 009 609 309 838 764 744 208 386 561 415 913 832 383 491 142 730 168 159 142 303 109 048 584 873 281 957 329 655 231 536 297 108 536 257 804 335 656 997 629 948 589 809 176 200 673 228 644 623 808 622 172 668 413 738 650 528 986 850 753 820 648 510 634 514 442 306 482 563 330 623 740 256 713 354 418 030 147 189 465 278 122 207 356 533 937 462 242 113 061 127 462 235 421 308 964 778 485 825 284 059 932 697 121 798 873 998 726 622 725 863 800 895 875 274 108 286 285 768 873 280 363 044 018 385 191 851 606 718 408 986 685 577 530 864 160 456 499 173 754 082 128 718 967 112 863 394 271 748 923 445 024 276 619 256 814 168 000 794 761 637 993 884 668 780 469 746 167 287 798 992 047 810 246 799 244 606 891 870 225 793 894 157 585 899 516 697 232 813 106 549 203 093 211 870 053 282 742 681 579 924 588 557 369 959 366 370 017 465 151 390 603 656 198 864 223 814 334 333 339 527 343 591 705 014 599 928 601 967 510 360 371 630 663 194 539 225 752 444 792 392 537 979 726 357 439 005 537 179 543 757 286 861 521 265 988 390 062 832 021 998 056 428 985 225 710 361 595 783 593 116 877 477 943 300 978 301 254 740 871 655 468 087 732 813 557 843 237 217 591 983 325 074 060 820 419 169 282 088 966 682 768 901 892 895 845 627 183 667 771 050 220 667 510 146 498 630 270 549 596 339 386 500 939 740 129 246 977 846 282 232 868 865 510 990 653 525 407 764 922 104 242 911 894 503 756 562 947 300 177 565 377 609 913 362 734 219 366 833 575 345 286 383 174 899 146 843 608 764 478 234 134 954 794 111 133 626 897 171 552 396 151 763 508 570 363 738 159 899 357 915 451 785 442 473 747 142 535 722 681 422 100 554 688 721 722 501 817 228 311 750 896 364 856 919 968 401 029 001 780 110 666 833 242 069 020 709 966 330 422 585 831 963 424 825 870 029 256 389 897 100 518 050 690 127 751 054 586 579 984 630 051 464 106 465 585 644 979 027 974 179 202 863 419 841 920 575 806 865 261 183 890 230 795 328 383 019 862 276 645 047 302 634 534 341 081 115 726 268 425 528 971 538 906 154 846 437 479 851 439 337 231 169 598 086 612 869 173 099 386 011 071 177 143 044 387 556 082 078 517 550 824 722 756 084 703 838 541 551 428 932 761 292 063 339 381 692 816 138 553 127 656 177 330 346 924 046 401 466 994 719 375 735 018 558 930 909 196 489 170 053 333 941 797 208 148 457 272 000 860 305 966 423 144 216 808 746 900 638 143 069 854 580 689 733 571 835 362 261 971 835 354 537 972 678 789 739 449 508 659 623 493 246 083 654 506 806 751 144 489 523 435 917 393 142 733 323 909 199 544 917 038 986 396 254 163 625 028 931 228 708 713 212 049 464 725 494 994 610 007 295 729 311 602 535 745 041 325 892 269 537 825 295 195 291 418 887 541 257 056 006 255 934 608 500 073 698 575 026 255 140 348 687 622 983 390 104 679 427 454 241 106 650 662 323 894 805 750 164 894 149 913 532 333 456 417 239 436 664 431 420 312 724 353 775 018 775 834 739 200 082 095 435 571 437 777 485 356 015 231 501 965 823 375 312 638 547 284 845 149 491 926 313 290 272 489 384 360 984 821 110 258 460 650 541 145 714 515 722 558 831 443 976 746 366 237 359 280 368 736 490 733 265 902 961 518 139 424 576 123 248 525 129 438 998 843 052 483 456 819 030 856 675 187 317 844 968 639 652 886 693 738 566 317 280 207 403 313 887 286 613 784 559 423 463 045 361 948 122 562 722 135 955 961 292 427 739 175 238 293 144 818 166 986 008 128 972 590 003 893 958 507 394 912 674 637 454 021 869 225 000 321 202 478 320 291 492 193 800 688 738 148 960 497 360 645 520 300 511 798 730 661 778 274 078 018 264 532 707 008 912 736 488 781 706 082 752 835 745 944 456 036 823 327 359 228 458 293 821 338 356 975 274 915 107 638 605 125 487 701 251 843 557 299 297 386 149 523 973 076 337 671 003 849 256 820 506 156 758 847 040 992 998 977 428 790 026 763 077 456 348 970 173 961 504 691 246 285 768 764 310 348 345 637 800 999 362 125 523 456 112 266 988 246 107 781 060 569 230 947 187 269 375 307 022 700 302 187 876 465 436 922 937 966 040 796 328 269 545 959 932 661 721 791 835 404 662 975 451 377 075 937 931 702 121 919 575 025 838 380 020 221 250 049 705 814 252 276 968 590 227 246 994 661 315 083 438 754 411 720 546 446 569 870 599 223 982 996 084 932 735 874 689 564 495 129 501 620 623 053 155 244 026 384 723 777 935 566 818 907 353 300 094 925 117 967 156 725 312 232 617 603 376 727 271 911 748 155 121 138 229 460 750 990 294 049 724 571 410 185 983 880 291 021 875 423 216 906 649 726 362 878 282 089 414 854 075 281 794 048 335 733 930 718 261 751 940 906 312 656 953 806 805 059 972 758 960 200 040 326 822 133 751 265 955 381 360 920 661 781 968 127 081 626 912 273 681 996 268 877 947 739 150 422 326 432 229 687 353 735 078 243 549 441 256 770 467 545 160 964 470 642 092 302 484 260 898 604 314 283 415 162 055 057 433 708 323 211 887 754 444 996 607 780 770 362 193 925 540 082 800 687 508 422 972 022 397 023 977 020 405 150 974 159 034 992 072 108 177 290 343 284 482 294 903 391 096 072 153 883 295 484 436 344 382 156 459 792 476 936 456 922 301 203 659 235 375 564 971 416 567 386 792 628 076 529 523 888 215 675 030 316 110 188 867 651 591 140 809 219 489 352 948 976 735 177 170 885 505 698 363 595 227 772 065 858 458 991 685 530 696 925 241 702 461 825 987 623 422 402 234 469 757 134 938 062 839 142 787 713 840 875 664 045 283 095 067 872 782 492 879 627 855 026 153 919 620 068 289 542 423 808 336 757 074 479 189 005 614 775 987 284 016 850 762 104 687 087 185 788 185 050 879 582 944 410 685 203 620 917 592 535 120 678 105 844 255 420 106 168 464 184 900 959 095 358 235 461 046 660 623 266 042 208 565 893 504 239 546 322 254 987 499 493 549 364 862 235 142 508 401 596 046 947 054 839 763 684 670 798 677 563 076 607 275 595 585 044 426 550 825 276 408 991 698 206 922 459 791 694 282 752 152 909 830 800 618 775 497 420 162 016 536 145 857 512 290 063 973 061 978 699 820 218 250 620 895 941 927 809 795 063 470 879 114 079 044 153 097 444 951 399 981 840 993 294 999 806 339 511 885 870 480 607 884 038 901 084 379 883 035 865 290 956 042 788 516 005 130 046 964 813 538 228 043 735 390 222 542 121 431 365 717 760 743 453 549 728 566 934 498 553 079 290 118 580 426 871 992 880 805 607 835 962 833 975 067 044 830 363 751 126 747 671 554 471 795 761 909 887 252 302 685 249 517 678 464 295 884 137 063 424 117 088 047 034 046 275 385 065 984 521 925 613 102 328 221 947 993 642 929 348 417 404 939 048 031 651 519 537 523 364 919 360 544 851 675 389 733 202 516 682 114 582 832 147 160 308 791 454 508 873 359 379 334 257 648 933 494 295 181 544 111 771 008 989 571 544 409 271 598 531 444 532 944 276 508 556 025 736 423 480 242 571 975 845 511 205 429 739 306 668 448 706 025 175 990 392 913 233 238 226 769 686 641 046 432 511 931 269 996 766 919 376 309 847 040 032 015 737 380 863 667 321 216 520 446 829 855 755 865 412 208 318 640 926 981 336 611 713 678 311 068 383 174 102 556 987 271 994 093 591 561 003 208 583 280 346 113 721 097 170 069 692 199 876 069 447 989 182 292 599 102 629 703 521 785 959 961 238 402 592 186 563 562 019 962 807 142 954 664 898 467 723 837 326 389 144 526 668 504 105 140 527 359 509 866 220 078 060 247 399 041 563 230 494 744 111 888 325 348 739 253 260 760 999 356 352 692 446 949 423 015 857 178 487 883 801 182 052 763 202 282 828 838 723 412 882 075 050 645 067 047 150 979 716 973 025 064 486 513 544 247 236 895 240 922 415 311 199 363 167 118 181 078 619 667 263 230 628 886 632 326 210 712 493 544 379 353 375 696 251 370 669 635 604 673 671 477 996 384 515 836 613 617 692 259 905 245 580 317 699 111 256 312 151 660 887 931 118 711 947 798 669 547 902 867 935 098 925 070 363 230 284 682 114 080 124 850 403 177 075 451 195 701 763 990 845 656 625 445 360 392 711 083 907 013 387 764 377 050 455 016 790 128 528 860 063 739 127 314 560 845 184 790 178 151 640 862 390 966 367 718 711 627 311 838 287 472 055 256 161 380 531 109 153 752 826 850 585 583 843 205 645 109 680 995 818 041 034 435 236 973 361 629 786 440 289 225 692 737 550 974 159 283 145 881 215 303 691 334 503 955 944 197 985 920 557 845 739 177 685 483 026 379 472 365 959 727 364 088 381 645 411 835 950 008 049 967 557 306 062 394 546 697 584 399 947 490 535 321 461 631 664 373 516 614 088 484 077 679 750 496 224 132 675 724 613 548 216 466 332 766 131 591 943 926 267 453 332 855 869 329 609 819 968 575 074 500 036 578 261 774 767 178 471 626 304 416 626 185 299 394 177 505 158 488 337 184 544 178 780 704 578 116 028 370 536 858 237 769 824 954 400 771 449 999 196 150 052 290 072 522 322 701 557 164 726 223 954 751 918 875 441 768 385 468 939 163 272 169 598 223 330 427 120 752 670 794 607 272 595 290 618 083 761 572 034 909 181 742 333 487 903 089 328 855 937 002 042 469 714 147 336 165 936 647 499 232 170 176 020 296 902 473 750 507 012 544 727 382 539 072 112 825 930 546 722 635 083 225 630 301 225 967 854 495 323 038 870 543 660 986 366 122 427 571 493 681 044 031 567 235 709 955 301 536 428 579 792 881 360 228 605 722 086 472 437 364 604 189 705 762 376 155 261 213 362 242 078 584 932 293 131 628 131 542 429 354 036 709 423 844 352 957 872 234 305 181 604 225 783 519 293 564 774 214 020 178 086 779 282 135 538 709 819 472 715 141 388 850 684 210 699 552 689 011 768 711 855 729 005 091 981 971 016 216 537 415 067 041 470 518 934 350 639 544 111 229 402 366 268 226 041 353 517 182 181 726 020 289 945 419 571 671 439 622 606 665 562 643 785 994 001 060 679 506 624 669 913 209 865 366 952 800 044 653 620 464 529 807 038 194 229 386 747 237 993 126 143 664 422 158 941 002 681 977 685 711 654 438 344 193 705 983 798 855 554 454 763 473 365 889 926 949 741 256 666 725 405 583 279 162 229 881 343 919 809 447 159 251 333 609 637 324 575 751 087 881 519 235 095 270 306 430 226 034 246 277 827 066 584 191 840 501 763 552 411 059 737 599 449 057 697 593 037 558 307 904 188 716 416 337 331 015 751 025 502 402 074 190 917 632 450 277 674 762 826 583 377 592 985 380 559 841 495 535 988 184 775 199 778 129 764 033 836 999 742 144 783 885 496 431 263 512 623 375 469 117 331 272 535 809 440 471 825 966 421 358 971 683 046 652 960 757 679 657 012 997 430 237 030 737 939 897 562 355 454 536 832 795 096 936 700 239 674 459 854 796 211 857 403 963 901 085 171 748 754 368 737 606 315 703 637 141 775 566 226 006 568 163 339 224 964 825 687 443 404 369 142 746 287 083 160 300 265 474 949 967 922 637 676 261 079 567 996 089 998 253 172 196 476 500 925 311 431 623 780 305 094 256 240 851 419 150 168 356 375 174 477 470 972 792 960 405 760 896 184 606 787 373 077 379 811 135 779 600 006 495 143 091 523 845 505 200 298 711 778 812 822 737 594 636 122 446 870 059 038 801 134 202 400 734 479 638 494 293 608 995 759 430 142 807 027 374 099 368 674 757 532 483 798 599 913 515 756 447 276 745 594 674 767 460 549 063 269 543 414 568 283 352 903 416 553 688 164 688 797 213 594 431 877 282 586 666 174 737 900 605 384 225 187 201 226 080 954 786 536 872 681 854 967 650 986 314 739 935 878 333 401 535 758 830 652 891 174 776 711 328 265 504 533 544 455 946 299 304 058 032 906 000 176 103 238 888 517 036 911 191 363 988 915 302 522 166 347 079 505 293 997 232 787 114 963 903 483 922 793 893 481 385 780 066 324 775 815 152 983 265 912 152 427 678 933 625 077 537 291 789 330 237 670 185 104 260 611 125 332 508 473 831 724 703 976 673 181 111 218 784 471 647 898 456 896 485 116 177 712 991 368 812 971 067 722 831 929 939 787 762 393 544 564 229 858 656 011 854 805 425 798 771 574 453 811 393 040 981 700 834 637 081 391 276 788 521 795 223 443 824 484 784 375 596 620 274 508 584 952 295 550 721 774 001 166 082 294 677 566 242 592 654 917 963 584 534 534 464 287 160 190 002 344 079 607 232 971 837 240 357 741 556 876 859 637 916 832 637 533 564 040 109 489 341 395 399 386 044 231 582 858 950 955 864 913 996 850 626 552 703 666 994 905 295 718 924 150 722 131 860 695 507 941 952 437 529 813 156 522 736 982 735 480 274 458 518 619 361 096 633 890 984 563 673 963 372 234 305 905 264 272 110 168 742 911 427 757 350 834 099 165 459 892 559 204 623 697 619 475 438 286 185 150 256 773 359 793 963 593 937 419 958 789 525 376 935 506 269 807 281 432 587 696 258 226 887 111 953 992 763 729 141 387 967 049 780 597 934 337 356 833 235 426 172 297 423 868 173 428 827 382 654 023 341 576 127 692 328 388 700 797 388 563 774 247 578 631 040 143 073 947 292 048 810 594 202 149 703 057 751 684 921 439 096 019 186 886 724 251 994 785 044 466 422 046 677 624 802 488 026 368 523 487 446 230 348 263 470 629 742 351 316 933 251 821 276 845 959 857 360 785 790 213 635 640 162 055 266 471 277 770 861 928 735 877 241 064 465 811 528 714 687 679 875 851 885 619 077 271 767 817 639 347 985 897 507 880 706 561 269 967 851 566 134 268 797 347 831 419 448 096 504 327 742 765 445 014 615 040 644 014 161 415 846 005 916 735 820 411 943 393 908 584 842 913 308 328 807 064 283 720 283 754 164 232 607 753 336 038 216 471 989 523 176 050 155 711 865 545 196 526 646 816 750 418 090 783 346 769 064 332 669 810 874 705 462 517 032 925 442 131 235 631 457 782 755 699 014 494 217 152 742 342 397 557 253 098 969 852 485 471 658 639 162 936 434 511 162 432 488 427 186 652 445 717 528 422 551 229 960 908 836 915 539 843 888 717 995 408 230 934 917 004 023 214 948 807 582 572 638 789 209 757 463 269 500 707 028 523 746 882 761 278 037 403 084 093 630 639 846 422 280 329 601 970 644 474 840 468 308 572 060 050 753 098 502 200 160 764 162 152 882 376 365 143 193 683 926 562 167 391 485 957 448 645 062 591 957 762 098 227 947 709 055 430 760 580 754 210 996 903 093 394 181 289 764 521 223 313 639 332 336 126 142 184 980 287 552 451 732 724 543 594 708 670 409 666 178 012 684 529 075 881 993 267 359 832 879 152 626 367 790 255 073 827 879 736 812 914 398 276 130 428 666 292 614 953 810 840 422 083 736 744 480 996 857 593 473 867 566 901 670 629 419 061 871 017 835 316 844 676 241 942 797 623 920 601 748 443 164 941 196 646 139 732 316 006 975 493 698 866 850 077 456 459 515 322 019 522 713 481 940 970 599 377 103 880 456 088 282 158 408 171 044 306 086 145 685 985 733 229 436 574 162 337 321 118 284 516 613 696 913 362 218 728 557 099 224 265 950 013 158 451 354 891 324 717 461 313 593 857 218 206 828 041 204 348 266 715 787 272 578 857 747 425 442 116 651 200 052 705 115 713 672 552 268 837 593 164 585 115 283 026 351 074 563 826 238 264 226 147 082 655 611 478 688 351 987 408 217 530 259 749 460 626 271 832 045 798 389 997 847 302 107 993 477 171 835 455 346 305 600 695 596 075 612 684 989 366 606 613 018 336 337 497 454 748 579 293 267 199 331 869 032 095 787 370 713 316 708 744 385 960 372 190 071 365 714 991 862 797 902 446 138 710 539 211 915 537 389 874 537 330 309 968 090 686 321 812 124 550 113 985 571 707 427 670 377 686 738 251 877 683 081 910 712 801 473 270 317 452 084 919 798 365 521 825 953 837 378 184 123 859 585 489 303 481 360 217 969 172 583 172 721 980 893 855 363 207 559 963 750 776 199 571 981 830 957 898 638 590 271 709 835 114 163 309 790 432 126 814 674 511 626 743 398 341 363 865 322 690 673 940 363 340 473 886 247 743 236 842 452 276 748 621 131 139 224 722 217 290 597 415 906 696 780 615 253 913 414 762 006 121 814 549 749 437 757 901 038 196 689 673 209 291 131 576 344 166 870 905 465 076 518 610 371 848 643 493 311 327 891 037 742 414 377 429 983 956 042 862 130 141 862 497 652 142 336 753 444 882 115 740 225 727 338 570 430 412 750 985 600 776 270 562 905 495 912 028 325 271 032 097 009 040 415 306 028 373 531 436 649 551 351 354 371 208 258 998 932 507 981 365 091 689 974 659 576 898 409 179 686 435 644 811 163 329 978 581 819 641 374 879 663 178 633 687 023 027 333 238 251 196 472 683 941 129 382 271 812 520 590 321 449 614 444 315 219 896 593 699 223 079 957 048 361 083 556 739 878 242 626 433 258 960 610 560 072 900 584 793 995 698 574 944 257 408 810 655 286 026 360 424 243 361 265 247 604 038 505 866 867 934 233 647 501 618 502 871 925 052 831 950 657 019 232 322 554 539 716 776 930 379 981 409 406 846 067 738 479 473 622 446 586 293 028 092 583 379 889 799 648 553 170 418 676 013 070 193 708 679 411 756 167 845 033 613 924 231 432 358 274 450 489 137 099 031 109 092 722 332 201 189 515 625 644 288 930 898 821 558 441 511 854 642 276 108 399 715 452 341 427 559 810 722 626 981 678 552 458 953 297 296 753 497 939 821 942 098 636 895 696 560 185 338 679 162 694 729 545 707 701 343 822 173 961 495 844 762 587 513 849 877 124 331 131 218 134 641 641 578 873 871 182 494 375 567 390 910 779 111 176 364 711 913 607 245 957 612 058 526 290 357 931 689 773 355 621 419 856 847 247 486 136 960 485 544 621 164 397 590 855 175 905 050 529 252 719 297 047 315 700 770 204 527 787 380 557 579 650 141 042 201 724 651 193 754 804 798 457 368 769 983 504 548 950 666 683 252 314 359 804 370 542 345 198 717 145 043 051 082 050 109 535 309 613 104 869 520 056 030 623 536 213 470 894 891 106 713 686 827 924 908 358 077 079 336 605 343 712 796 459 703 372 712 852 882 299 680 622 071 010 636 325 016 518 434 303 656 153 486 029 594 160 904 140 143 858 561 172 761 862 623 856 383 521 365 147 553 890 743 196 478 092 189 060 404 190 699 814 404 089 365 695 060 831 688 788 806 015 689 627 378 685 422 221 775 493 441 361 988 985 650 510 994 103 938 866 312 196 060 065 874 380 332 857 462 712 763 393 936 069 287 284 721 579 583 061 902 699 282 343 988 135 768 041 455 315 446 539 910 709 748 303 843 823 009 684 123 124 811 771 818 423 449 210 625 958 289 791 702 446 946 814 400 760 852 710 409 434 831 942 167 222 676 662 863 304 438 652 006 392 352 860 538 824 336 921 631 322 245 298 142 139 391 143 144 834 366 157 616 376 005 467 021 509 424 218 591 606 939 950 500 793 922 647 959 035 882 678 691 651 311 944 621 562 059 720 097 753 873 688 508 507 340 060 192 044 801 709 346 363 887 436 688 842 724 626 389 442 116 809 826 498 612 908 159 901 521 536 483 560 391 692 216 732 261 325 493 350 452 629 047 771 473 229 355 386 853 374 020 737 900 069 529 815 109 431 890 316 817 547 769 280 722 804 296 517 110 817 378 921 738 667 069 279 797 083 685 508 367 530 363 464 041 748 561 999 526 876 222 240 006 108 580 465 963 824 281 383 082 503 299 755 173 059 782 855 027 279 037 620 638 359 231 044 331 110 613 503 289 252 418 640 231 390 154 201 317 346 315 059 543 034 237 535 463 466 780 570 153 502 914 655 658 958 388 158 205 913 808 585 346 150 051 456 289 866 519 194 043 787 605 045 271 378 920 855 772 715 270 634 983 981 220 638 203 790 844 586 636 243 320 864 125 191 772 058 302 534 148 032 296 482 120 147 499 566 718 270 779 061 689 951 954 205 749 296 917 341 503 978 636 721 726 371 620 594 260 618 584 726 755 836 252 072 961 669 779 136 122 130 400 506 561 255 684 389 710 559 076 291 118 542 875 448 523 362 435 115 572 118 462 655 429 051 049 060 286 599 541 787 842 348 591 219 359 146 178 479 992 583 123 537 786 788 375 998 439 456 616 437 337 396 444 413 098 863 815 130 164 799 826 980 565 242 654 488 503 732 300 860 119 616 774 892 787 508 863 901 729 672 636 019 344 000 576 445 636 751 104 554 494 238 507 934 854 979 150 145 040 097 426 059 083 267 035 713 383 032 619 979 664 394 819 413 404 583 841 156 735 743 329 483 133 531 491 910 018 856 780 081 177 450 123 913 322 497 450 294 744 799 013 913 579 419 590 872 678 254 343 040 387 865 921 837 506 121 056 527 888 452 776 293 015 671 398 840 615 875 950 417 896 931 384 450 162 999 758 574 659 616 119 631 476 420 068 170 179 813 587 649 056 476 076 322 400 259 403 679 633 399 542 170 278 515 759 611 884 947 830 435 231 128 881 460 632 853 814 400 352 582 869 491 615 002 754 361 862 043 944 522 084 025 791 896 449 775 795 153 368 534 078 017 190 469 987 791 041 237 967 784 974 283 808 354 327 022 798 793 384 700 293 675 458 033 286 795 963 288 610 576 095 953 167 402 752 873 470 347 050 619 948 339 552 974 590 880 638 269 001 914 350 145 284 316 745 283 778 846 929 963 246 687 617 107 564 206 863 805 023 625 106 669 546 406 202 818 177 941 890 323 208 269 088 151 786 570 837 974 285 579 930 746 353 966 597 853 696 573 913 795 932 535 969 569 422 665 601 845 929 101 854 128 709 970 897 726 020 351 246 411 198 729 838 940 360 461 650 751 432 315 875 375 445 363 023 908 138 914 683 892 618 036 843 286 512 762 319 125 705 527 297 622 802 339 610 324 332 603 145 484 207 767 172 985 284 797 537 726 501 681 842 858 482 371 116 469 077 610 405 337 807 842 997 053 872 428 006 213 853 464 208 032 683 541 205 199 861 298 191 838 703 206 315 339 241 560 211 242 585 603 780 123 303 103 487 890 505 399 895 924 589 519 441 178 831 672 640 758 395 789 144 407 917 727 093 223 574 526 923 433 210 487 351 565 575 431 643 186 304 905 929 470 639 578 505 947 619 692 156 115 870 513 716 813 936 137 317 619 488 288 475 603 386 820 843 603 833 662 016 220 342 043 498 286 955 608 567 985 283 755 503 831 206 153 028 477 548 885 418 472 199 008 765 100 614 822 482 821 314 035 859 107 012 929 644 345 877 055 194 375 944 251 290 116 083 268 020 439 021 168 040 690 467 523 430 260 790 234 255 065 490 108 559 815 305 284 722 957 697 899 074 055 193 076 223 933 517 862 856 703 538 082 893 167 221 883 438 250 251 963 493 070 317 557 585 855 396 618 258 163 696 314 075 024 694 583 627 778 855 987 520 785 891 169 760 977 140 822 699 361 131 788 247 064 898 447 884 663 434 407 881 677 858 493 600 053 841 860 439 804 400 780 459 132 672 881 222 045 616 355 209 130 257 535 436 199 567 158 768 270 665 196 786 704 730 080 110 775 101 697 599 948 708 055 060 781 442 358 963 088 873 821 163 992 987 890 959 075 666 369 441 566 761 247 876 123 083 046 180 941 308 147 343 270 106 973 550 746 657 537 600 629 301 738 948 091 175 884 399 902 548 450 176 099 894 252 423 210 640 274 390 590 888 754 728 442 800 381 268 172 301 551 752 318 322 390 430 909 903 161 625 073 873 575 090 216 551 364 829 501 754 498 346 648 095 142 157 420 252 290 449 445 951 909 605 712 987 096 555 406 149 712 752 533 211 232 955 322 653 386 637 754 774 123 439 588 382 403 109 360 093 400 159 553 039 902 748 824 859 550 110 145 231 181 237 592 727 989 887 782 200 875 896 556 919 085 140 799 226 009 077 773 914 906 391 374 026 286 036 042 505 294 086 509 662 325 979 768 287 485 377 432 583 732 231 525 642 011 651 594 462 099 610 083 449 082 921 974 524 404 524 167 950 430 523 792 212 111 388 330 153 669 399 113 671 041 055 372 549 561 415 692 522 904 116 053 526 017 314 551 178 627 071 071 632 860 792 988 943 318 723 772 071 290 574 534 468 051 357 447 747 395 835 260 388 820 943 711 698 487 481 866 346 216 419 909 147 854 096 932 513 478 101 293 898 548 100 276 270 579 547 213 958 319 338 990 055 485 460 638 606 755 989 923 829 664 906 173 167 462 837 970 224 847 165 156 757 664 823 612 434 820 767 880 116 878 536 273 011 849 960 720 477 014 159 595 896 224 032 863 973 620 283 768 164 655 115 187 851 128 598 350 315 824 864 766 410 708 328 842 955 178 951 816 434 611 828 630 878 930 960 482 395 902 615 047 310 158 782 773 267 086 268 870 978 527 735 388 467 105 759 712 682 129 161 699 417 995 614 833 627 295 336 889 015 160 057 001 807 114 215 046 249 499 224 664 587 656 371 632 080 611 225 376 293 603 746 962 034 621 678 116 112 630 284 555 414 972 124 598 992 865 650 129 513 356 877 636 204 771 759 430 240 438 805 769 884 932 652 263 318 778 557 705 670 676 658 167 065 360 647 758 200 767 875 067 636 929 602 549 183 118 051 110 604 356 369 388 455 016 912 747 485 208 463 883 935 315 237 781 006 612 559 323 916 764 571 937 529 270 996 076 359 349 959 870 844 118 348 502 671 716 600 663 417 760 273 473 193 583 329 371 641 502 502 332 261 727 071 982 225 235 366 658 040 713 248 410 015 091 441 651 395 189 921 539 355 259 847 741 975 517 740 095 249 627 297 990 160 752 695 266 584 297 290 765 356 015 272 929 462 437 571 454 088 320 186 550 369 851 031 240 040 985 983 277 489 530 253 545 544 028 918 697 096 013 916 765 399 612 847 035 977 673 009 138 904 604 715 639 961 705 160 745 068 946 459 044 260 981 930 073 997 593 709 109 630 481 301 338 061 808 628 918 867 558 662 737 718 327 441 270 911 246 033 741 505 560 710 484 113 945 866 165 361 601 351 826 072 926 385 450 268 870 888 269 141 934 229 553 547 144 856 390 306 611 367 755 742 469 738 145 760 721 096 738 843 153 003 751 549 552 467 454 148 033 614 025 259 087 968 202 210 288 661 524 098 172 307 691 020 722 883 422 855 977 125 627 057 264 638 429 664 060 837 402 791 529 792 650 726 424 883 312 321 458 795 393 967 886 936 763 881 105 832 174 612 211 807 447 285 171 448 800 000 582 777 624 131 961 816 107 643 610 328 961 208 061 333 838 233 533 864 348 254 195 037 427 924 942 581 119 278 199 461 353 277 974 748 828 704 319 862 658 069 505 639 402 741 224 328 434 912 047 627 202 947 044 837 862 381 395 859 751 255 856 656 863 185 403 991 532 516 729 848 487 263 987 936 665 529 668 520 376 122 272 277 880 933 845 080 860 371 953 863 597 815 946 549 057 717 862 534 602 430 179 202 708 081 422 039 510 791 245 925 583 574 160 832 429 690 805 048 516 646 819 161 691 104 748 259 465 788 655 178 326 571 936 639 856 225 185 327 856 093 620 454 633 918 055 154 168 435 368 891 661 412 505 647 818 543 012 808 286 759 946 660 188 925 275 756 238 416 582 546 903 053 310 209 581 095 963 053 249 623 754 374 946 689 829 218 431 770 758 443 281 510 353 809 744 218 620 354 039 646 000 469 548 204 214 963 301 516 221 964 109 597 429 202 162 402 350 551 741 641 327 426 776 599 975 683 781 954 351 983 074 608 791 814 881 625 978 254 496 404 864 069 141 351 506 382 149 528 385 628 778 473 212 178 573 805 953 717 573 473 607 363 297 498 234 967 225 864 323 594 818 782 871 000 653 932 394 339 607 069 349 297 142 457 421 847 545 602 459 585 420 211 313 822 607 894 188 632 207 321 713 449 162 066 763 943 446 201 592 679 226 084 581 217 322 947 541 303 202 883 322 503 883 369 553 737 337 752 029 977 234 682 644 842 200 160 362 063 653 074 575 476 189 798 110 264 243 844 678 983 076 193 598 514 915 546 054 587 824 463 591 580 726 915 889 967 969 625 974 673 381 304 357 386 627 117 521 670 346 066 486 824 845 076 777 120 106 356 312 711 759 681 135 619 345 941 256 763 117 724 147 986 074 422 000 429 991 419 393 019 274 421 223 511 379 634 764 493 314 234 215 241 785 728 425 072 184 672 948 731 264 845 672 403 122 496 683 756 575 738 820 491 467 675 204 652 884 917 708 804 834 172 320 098 573 614 854 531 292 601 795 062 364 932 384 602 977 619 923 892 784 195 588 964 658 550 624 207 731 147 748 111 724 130 604 254 917 358 585 300 285 232 786 527 489 772 542 951 680 173 088 757 573 587 233 700 862 868 465 953 040 669 071 820 500 990 968 798 031 902 798 851 051 160 911 865 136 447 285 100 457 979 723 893 283 017 448 607 961 785 634 091 782 704 918 370 591 383 575 432 621 981 160 560 687 014 534 321 533 522 013 465 262 847 987 484 886 079 775 774 202 123 042 917 810 693 700 391 321 244 909 436 906 207 238 688 484 351 368 078 627 098 998 485 171 281 529 112 954 450 556 802 974 361 255 442 307 495 826 633 704 714 477 809 664 926 305 366 789 860 597 394 754 982 290 595 844 536 993 262 610 014 921 849 679 121 505 103 357 757 052 588 757 759 151 988 269 939 206 962 126 799 955 221 050 529 612 871 882 086 614 311 018 074 302 083 461 582 758 950 416 048 232 737 623 379 305 513 362 996 703 417 400 273 376 914 021 904 974 095 559 404 929 363 595 812 271 507 205 352 883 726 942 439 643 553 983 296 103 340 031 750 950 913 957 199 182 480 416 698 552 258 207 824 395 063 246 407 638 383 623 040 513 811 267 666 423 683 082 978 311 797 993 067 395 063 645 321 675 490 872 434 316 301 984 395 552 836 865 606 505 571 508 693 148 658 954 069 436 716 981 782 286 183 200 204 165 428 708 752 042 867 223 361 705 525 279 877 947 856 149 279 853 995 611 979 315 151 093 428 956 136 580 402 085 001 156 199 926 636 391 316 841 083 434 401 493 571 534 671 435 730 183 544 692 573 736 887 961 478 459 810 550 403 359 778 287 283 921 086 274 633 061 522 400 973 853 740 047 037 378 132 401 656 479 646 617 438 863 833 680 013 336 053 229 222 633 438 726 970 173 691 579 292 547 035 505 676 436 288 524 704 439 455 883 832 829 384 049 029 982 434 307 177 803 381 152 561 384 656 428 806 267 230 681 258 812 820 559 334 586 997 935 713 365 328 546 118 509 234 012 701 682 213 515 351 350 030 486 969 067 608 077 820 153 519 578 467 688 979 433 250 376 527 236 461 696 880 345 350 655 812 519 454 913 503 460 091 010 391 944 512 375 394 161 056 737 531 583 777 015 931 619 862 772 861 249 826 320 118 377 826 511 265 997 583 054 796 361 282 615 155 538 733 045 087 529 765 820 020 397 371 906 858 849 418 805 801 138 672 941 855 168 484 161 165 966 028 434 351 364 298 207 937 251 020 694 446 091 438 383 384 965 691 845 800 710 481 200 175 113 828 510 100 995 197 233 596 231 618 511 020 754 087 654 749 958 783 466 180 258 984 762 101 430 920 910 891 528 888 169 562 399 767 189 890 697 532 144 602 502 504 336 132 133 447 322 523 259 743 581 080 795 032 961 533 029 771 831 015 931 842 461 163 011 049 674 502 927 430 622 434 306 682 976 452 587 366 336 319 333 155 903 945 074 108 541 095 795 258 946 171 833 221 299 325 874 347 262 619 516 223 460 144 734 119 513 217 821 890 592 305 022 239 391 207 637 170 569 162 863 857 705 050 919 410 589 287 431 845 446 086 463 200 980 576 461 527 013 034 891 878 998 863 081 241 224 109 571 967 726 252 387 219 602 464 764 499 476 380 745 390 637 049 215 067 172 669 921 871 154 239 273 041 152 311 546 145 754 793 659 664 643 702 327 530 337 716 443 666 804 172 138 560 556 085 063 568 453 418 021 533 198 430 827 234 004 147 408 397 865 925 870 781 923 368 789 450 834 355 171 541 563 849 801 625 439 095 090 582 291 561 244 746 319 009 432 611 128 089 465 761 006 084 956 509 660 059 883 951 257 791 687 754 587 628 297 142 299 039 210 825 832 048 308 706 789 272 093 299 494 378 547 720 476 263 749 553 191 430 356 598 472 320 726 924 315 437 058 300 617 388 830 151 770 836 224 986 751 684 324 278 963 556 714 323 883 019 276 284 106 533 751 825 142 048 046 373 549 735 414 264 903 197 431 130 453 897 673 894 124 642 348 370 053 535 174 437 705 511 758 104 831 725 008 950 676 256 940 729 200 547 219 303 950 695 830 164 101 283 707 440 359 729 739 787 281 157 427 801 627 967 609 010 187 718 271 575 950 486 270 041 623 075 052 932 633 520 400 470 058 388 222 111 470 144 045 731 917 022 559 523 015 210 360 520 254 643 727 314 824 070 279 881 144 505 318 122 998 990 303 587 155 450 168 646 368 599 442 248 317 608 730 935 724 429 583 529 347 834 062 549 636 541 542 549 575 359 186 061 927 135 354 134 973 813 265 032 728 269 128 927 083 891 858 156 522 468 301 878 804 059 646 832 048 922 642 944 253 099 358 154 386 237 804 060 399 676 178 305 306 746 592 227 497 160 881 674 167 779 563 003 643 303 310 561 825 870 872 620 488 726 957 185 944 252 525 698 145 816 319 395 865 943 392 466 141 257 961 162 353 983 802 290 997 280 079 067 395 192 158 046 782 367 727 979 079 119 348 581 044 859 875 159 237 646 011 175 253 776 143 750 424 006 620 483 810 171 419 443 074 709 029 274 736 730 664 629 153 726 053 131 008 914 375 282 706 589 272 053 500 852 086 976 580 339 464 146 054 319 942 405 425 412 098 887 458 106 106 187 832 911 536 172 308 498 144 223 899 826 069 706 603 229 190 822 871 292 913 509 987 202 202 775 308 546 282 949 448 682 482 636 178 954 082 779 772 223 680 465 796 265 471 682 027 045 430 509 896 028 932 693 556 945 451 636 724 039 194 300 723 102 863 828 811 427 689 923 646 557 581 733 142 531 308 149 629 436 189 270 011 784 954 656 856 379 691 247 555 742 806 028 552 382 081 597 513 846 472 451 225 805 691 097 463 535 403 694 500 037 204 749 015 401 771 065 885 896 149 419 808 838 172 239 805 638 264 419 199 388 893 343 753 997 473 060 381 236 045 979 708 736 237 606 584 627 274 992 461 427 951 506 054 394 977 470 486 075 019 342 963 695 801 580 820 531 228 973 560 902 000 260 350 029 608 293 156 105 037 097 507 898 736 088 575 263 415 051 156 498 109 750 851 152 884 412 401 482 461 827 731 640 011 028 590 801 677 461 427 705 400 823 860 953 146 202 349 669 530 468 674 192 083 610 430 123 252 572 647 298 790 048 125 604 876 403 789 829 692 454 664 524 085 760 374 565 229 021 878 264 437 181 098 244 562 569 042 638 371 176 931 977 697 867 027 297 317 665 360 760 340 491 409 335 663 313 825 480 512 857 657 600 195 486 530 690 352 504 613 078 865 441 709 615 914 117 912 811 028 437 283 377 532 026 641 727 170 622 203 514 902 410 484 526 343 811 483 137 747 275 884 003 012 963 360 674 033 859 648 347 251 563 684 844 865 059 838 659 910 848 101 260 020 461 220 429 290 921 816 208 747 731 276 026 422 640 767 635 171 124 471 131 908 810 042 701 657 016 379 966 793 436 375 899 150 594 327 398 960 202 348 315 824 986 810 774 281 667 461 120 549 856 987 125 295 669 760 804 936 304 326 802 028 142 478 433 148 828 265 250 508 189 003 963 926 291 477 414 309 509 893 271 796 174 882 227 057 013 425 492 480 918 762 462 207 358 270 939 912 635 487 623 516 198 534 136 178 832 329 839 057 866 622 056 794 685 265 828 451 376 485 099 846 516 596 070 119 404 523 334 560 060 507 734 608 856 766 987 224 023 456 669 234 680 306 393 061 497 959 790 917 236 404 575 530 858 830 774 578 532 161 257 484 312 192 199 989 423 285 681 240 787 162 579 097 397 147 885 244 489 299 078 133 434 332 228 632 198 616 768 816 383 907 340 126 928 865 915 453 548 796 565 186 473 101 326 245 409 375 130 109 774 798 253 015 443 526 422 509 641 572 972 269 909 725 374 911 317 724 919 023 293 819 620 012 957 112 436 070 133 452 309 095 098 504 200 546 439 748 852 891 951 388 844 102 468 346 898 201 752 178 396 583 899 572 670 071 825 998 824 072 840 831 053 452 365 581 095 277 054 111 583 740 534 957 155 146 433 525 605 101 439 682 334 234 996 991 705 927 753 069 409 660 792 203 789 589 006 699 115 963 348 387 236 976 440 666 501 522 888 570 374 847 702 222 987 786 239 843 319 965 792 224 288 155 240 088 970 750 199 786 376 544 800 115 333 789 671 673 608 972 803 275 378 098 155 942 678 699 563 269 553 298 088 092 087 559 236 741 662 746 591 651 425 551 635 204 634 686 519 666 309 445 779 924 890 415 745 009 680 715 402 215 959 826 919 961 549 193 110 261 932 479 196 699 349 520 415 446 789 885 589 372 970 664 553 046 631 221 129 720 360 068 056 730 939 053 178 782 716 501 152 946 804 513 895 654 032 305 394 192 086 056 710 509 587 408 083 904 231 421 562 236 682 406 667 482 157 081 976 827 099 223 954 890 034 238 708 873 995 392 165 294 123 526 555 784 631 932 248 113 396 357 803 206 814 479 221 132 969 716 591 628 822 241 415 210 045 231 760 964 299 505 164 886 111 302 561 800 345 155 372 385 539 794 902 309 566 590 359 392 701 513 644 986 739 388 151 880 926 963 109 668 528 441 163 471 770 467 066 786 887 729 042 012 296 785 633 066 291 273 609 050 609 147 129 124 172 158 906 794 419 416 044 389 581 191 396 635 893 480 274 645 611 917 597 544 643 004 604 632 200 725 476 334 131 645 686 944 657 714 566 078 564 895 820 224 277 470 015 691 826 566 789 349 603 368 494 947 351 778 596 953 955 665 074 893 259 734 998 763 957 970 584 811 224 932 088 425 587 254 203 725 397 627 916 228 671 317 438 093 486 441 854 853 101 131 863 674 851 000 432 968 435 251 049 767 742 781 916 842 558 102 786 635 022 428 510 557 835 428 007 850 599 053 415 449 007 465 960 821 183 143 165 745 462 326 033 978 361 234 247 193 982 468 739 319 540 902 817 076 174 106 542 645 317 106 324 744 645 715 617 058 962 065 352 503 427 800 493 349 663 323 249 849 903 575 018 388 238 248 693 116 326 538 434 405 955 654 060 099 336 756 109 040 688 028 662 695 362 163 336 810 559 105 795 022 787 814 783 473 856 180 526 083 502 634 968 872 438 674 228 035 900 333 740 737 405 312 448 887 036 807 995 963 718 947 728 112 152 587 502 462 848 617 181 683 786 310 368 740 551 882 476 106 767 495 521 137 016 669 811 778 540 003 696 900 642 712 409 795 079 870 180 062 497 590 439 497 691 705 066 337 846 942 980 878 844 249 300 534 796 891 208 192 002 520 515 651 546 815 788 789 313 289 324 590 886 222 322 361 602 993 688 863 310 088 977 235 636 617 650 100 310 731 878 883 983 018 995 338 538 421 458 215 845 160 794 939 226 674 894 618 744 977 356 824 432 541 650 740 843 441 577 716 055 277 918 312 241 555 722 855 487 622 762 631 019 262 805 203 409 534 890 153 752 723 086 300 477 432 438 133 225 430 130 731 818 863 501 257 409 346 502 351 023 804 251 410 457 292 175 782 164 514 637 721 503 679 555 579 070 852 262 871 057 832 268 079 555 257 738 523 642 559 393 050 709 179 197 495 802 889 695 311 778 728 419 828 380 318 528 140 208 269 162 708 151 197 295 819 903 389 552 786 830 584 248 783 715 346 930 201 226 607 409 934 681 447 928 156 575 585 352 944 265 891 555 501 807 552 079 157 818 327 894 632 800 555 321 991 692 262 448 568 129 204 918 650 178 911 403 992 006 214 126 950 465 532 961 095 212 844 815 190 509 563 411 813 148 168 253 796 475 451 496 418 939 627 919 995 094 067 153 915 228 032 688 899 721 442 680 174 977 593 712 090 412 108 592 935 327 596 814 665 151 575 236 388 432 365 992 504 273 004 356 425 920 631 629 635 544 820 669 714 474 567 065 855 642 721 592 149 146 824 254 693 792 969 781 638 927 964 165 067 075 196 251 152 476 687 209 810 841 310 035 134 174 445 229 101 256 444 881 536 208 617 523 470 208 205 624 743 478 631 153 252 904 193 131 525 051 654 407 244 995 005 578 181 141 331 798 336 617 812 498 015 474 467 478 912 298 181 263 525 333 400 030 087 842 176 821 004 605 045 318 771 792 816 914 586 181 008 710 437 293 604 697 988 086 087 630 055 279 896 485 788 778 560 863 435 107 724 330 537 923 361 765 541 928 763 115 080 642 816 370 405 029 652 825 526 844 188 111 654 879 820 974 640 972 961 709 730 679 754 796 650 950 752 001 699 549 367 485 848 660 040 285 914 338 897 965 405 633 298 723 410 694 469 828 497 356 242 809 617 089 928 022 708 329 701 102 689 851 588 414 036 654 499 542 159 615 818 477 633 018 247 144 963 555 442 928 632 276 252 192 514 120 526 598 044 221 745 775 706 147 274 416 309 656 848 547 179 739 189 569 157 826 335 096 919 234 523 915 912 562 059 408 725 859 580 994 018 288 082 058 025 272 919 237 944 926 489 562 544 835 415 293 162 239 908 911 476 721 448 965 287 236 688 591 492 212 538 077 193 494 555 849 178 750 945 646 639 963 743 312 329 450 015 899 684 297 943 328 986 294 663 765 743 502 741 470 249 792 825 499 421 281 604 520 711 345 817 277 857 671 590 316 509 122 981 687 269 411 500 916 602 157 841 854 538 424 703 564 896 593 222 864 619 877 290 360 753 580 499 763 892 493 815 239 874 584 206 881 271 305 464 241 952 742 088 944 718 564 979 556 753 485 361 623 520 941 961 910 914 918 164 019 274 439 447 160 246 047 745 916 498 710 010 440 808 536 645 161 784 514 312 867 639 470 890 129 449 890 832 972 698 841 153 222 870 195 501 593 301 445 362 967 790 992 651 161 322 386 549 916 076 567 074 782 999 191 406 045 415 336 085 682 561 309 035 629 168 865 946 356 225 009 170 684 274 492 323 473 325 392 423 880 241 112 549 477 949 145 049 196 030 889 128 543 815 850 053 654 614 464 459 767 263 581 060 548 039 394 598 707 233 190 473 351 920 070 441 520 671 485 300 087 073 471 408 660 285 006 107 205 804 476 411 427 570 298 611 246 964 537 113 513 905 428 812 761 204 492 560 098 192 073 929 541 711 345 128 403 316 883 698 170 654 359 663 743 851 636 920 487 320 586 510 815 648 848 755 713 843 831 021 306 259 415 132 217 943 449 365 210 648 024 000 189 036 622 319 277 440 291 904 804 287 556 539 358 099 319 310 988 171 861 234 095 409 858 167 490 838 197 120 718 981 482 456 619 504 671 817 607 340 436 303 924 752 989 235 552 971 461 530 509 931 145 362 361 058 880 942 060 850 926 506 130 243 127 220 960 164 240 152 542 540 693 215 205 744 436 465 086 739 638 560 638 245 898 551 990 147 533 790 533 167 654 901 392 502 309 878 619 969 570 283 648 334 477 502 069 231 986 655 804 944 229 028 486 442 384 540 135 558 818 712 258 866 278 579 994 773 857 312 545 353 966 525 637 604 196 779 208 670 192 581 767 584 142 072 031 896 311 954 369 061 110 381 684 126 724 896 590 587 417 237 989 491 630 264 445 410 837 306 847 368 469 473 380 385 238 788 437 842 164 624 997 794 283 555 751 495 614 702 525 431 269 691 447 467 023 373 074 908 717 416 384 561 825 338 847 525 140 198 202 664 755 373 703 835 217 572 838 779 918 043 176 558 088 207 326 650 134 701 421 914 823 394 651 567 552 948 129 002 420 494 329 057 840 442 222 020 472 872 393 807 804 067 386 584 477 980 179 159 678 363 270 348 893 440 127 478 386 898 160 424 331 729 607 379 107 712 975 507 889 858 096 985 235 866 517 861 430 306 488 732 602 678 271 953 691 831 310 274 517 457 200 317 547 909 776 818 118 641 248 387 658 707 588 686 026 186 671 932 378 758 878 167 639 093 815 338 259 157 005 055 192 097 585 183 078 524 942 381 445 504 011 649 188 480 863 784 655 767 263 902 903 394 420 868 538 778 439 750 092 769 686 588 223 542 002 154 360 506 957 182 685 197 322 070 303 555 784 711 459 122 643 679 858 764 057 879 179 636 786 228 305 457 059 412 566 706 164 732 755 472 889 737 127 434 697 108 972 850 441 086 324 342 903 553 979 351 227 008 468 620 237 856 639 037 116 231 362 729 511 707 324 337 220 017 938 388 847 012 710 514 748 807 018 545 388 063 150 213 057 907 560 904 456 175 198 270 845 979 303 822 220 385 320 973 667 779 194 949 351 515 260 621 220 886 877 346 314 273 877 319 055 742 919 765 804 180 998 849 787 949 990 006 861 680 269 896 307 237 925 250 249 799 091 334 156 249 985 354 913 365 685 216 267 002 002 257 726 054 650 863 474 261 307 932 925 628 833 616 448 011 742 321 122 620 972 905 311 159 402 036 781 983 320 624 130 406 182 814 418 152 554 758 435 464 315 471 943 543 882 581 211 673 570 314 575 168 079 422 945 946 094 524 796 075 583 147 840 121 149 543 835 074 325 438 174 472 992 813 654 850 160 988 864 363 039 456 898 121 317 532 162 431 043 433 088 672 869 883 266 913 287 707 334 649 779 810 771 641 476 576 020 169 852 589 326 009 992 971 770 912 767 408 103 922 217 030 348 947 382 791 982 234 824 027 801 493 644 299 305 905 789 369 614 854 141 224 828 387 960 655 516 629 925 913 341 401 113 814 708 855 799 243 061 351 795 267 872 079 566 715 043 214 096 090 840 766 926 807 674 628 248 056 936 160 353 937 662 582 154 459 250 431 857 363 751 014 737 624 289 677 256 426 789 644 066 387 063 705 031 801 804 784 633 857 356 457 477 359 127 744 249 236 462 358 397 663 018 016 217 263 030 509 484 844 554 140 800 771 040 553 925 165 755 536 864 016 720 081 531 272 433 261 272 792 549 946 101 376 731 223 907 069 180 400 983 789 768 244 943 215 048 607 114 413 277 397 504 924 386 851 389 999 094 192 169 392 408 333 773 561 845 233 493 715 302 852 703 756 236 162 772 960 193 723 957 695 841 385 229 368 536 627 437 289 704 861 123 999 379 576 752 516 718 099 346 402 415 858 774 286 698 588 143 807 279 996 004 649 586 843 459 527 315 616 341 854 924 118 930 021 114 657 547 023 175 305 411 712 015 701 461 385 159 096 078 694 768 560 463 754 807 725 205 235 433 594 325 269 897 884 318 419 774 154 969 925 440 489 609 738 226 713 589 153 594 979 729 957 187 001 982 695 231 718 119 233 254 047 583 599 264 324 471 395 419 164 419 840 768 255 919 393 045 083 335 526 182 344 173 797 158 614 832 443 135 584 652 336 901 665 685 297 922 780 248 218 625 088 417 173 700 894 547 925 812 462 912 060 481 273 352 583 667 248 436 289 465 384 088 948 468 171 051 500 242 797 453 675 041 730 118 155 930 488 908 929 785 503 718 314 412 051 926 066 383 371 600 916 198 050 676 554 098 892 794 139 632 652 642 667 269 679 641 123 317 587 460 931 011 361 438 432 954 972 296 850 996 694 181 600 193 782 998 003 727 412 382 005 420 577 859 599 628 476 328 934 372 575 256 201 789 615 441 697 318 038 220 454 900 037 628 781 697 835 004 922 799 130 628 162 920 513 042 945 566 335 045 081 734 813 917 691 421 648 855 860 156 612 979 887 741 792 054 920 155 881 880 499 601 938 704 257 542 423 969 703 897 544 791 898 839 447 552 759 952 256 172 768 629 161 989 587 353 775 843 839 492 213 335 903 180 733 823 564 157 030 922 851 842 403 783 390 400 650 621 410 435 679 441 094 852 933 509 902 968 678 859 658 167 508 268 793 192 779 455 527 989 604 305 091 898 523 303 670 183 059 266 205 648 925 826 773 702 883 816 304 396 255 197 588 610 022 306 043 893 810 908 279 260 927 262 270 575 268 689 042 695 085 207 365 851 746 160 812 299 443 860 798 717 159 951 021 991 070 854 900 368 287 122 213 116 771 850 096 023 485 774 524 618 686 537 360 596 252 235 322 648 610 606 830 411 195 916 232 976 382 119 368 944 289 237 272 396 550 638 817 934 393 062 620 017 447 631 911 905 814 119 691 517 645 454 342 160 282 897 275 809 515 903 763 807 642 888 617 722 850 983 106 950 083 083 882 034 537 971 678 944 656 913 198 398 543 567 343 979 814 598 335 305 430 852 396 229 256 449 590 055 020 513 864 692 282 295 698 432 260 603 918 558 213 081 764 156 946 131 855 297 051 410 382 885 392 834 315 477 873 999 618 959 005 628 209 264 275 583 016 917 823 930 981 670 955 392 691 688 077 994 919 881 851 812 229 771 296 527 361 277 952 171 853 447 661 078 397 617 968 016 152 555 013 243 602 085 576 894 277 537 867 264 586 885 777 934 586 404 883 505 050 587 467 806 951 762 912 195 194 660 192 100 026 547 478 021 966 263 554 282 387 220 578 791 620 187 573 013 734 386 690 638 450 651 602 660 353 936 054 283 862 217 878 493 080 157 551 358 696 362 342 527 871 758 261 320 701 153 599 813 636 499 646 472 136 632 306 198 899 196 615 343 741 439 589 733 506 341 508 120 142 850 062 539 689 204 916 446 651 234 533 747 472 400 890 456 644 207 621 016 479 675 583 039 970 987 995 439 865 660 891 638 905 431 365 975 832 181 618 329 333 348 678 115 920 221 118 256 237 680 152 269 595 454 217 084 402 105 325 491 501 201 429 809 947 190 689 043 140 288 932 455 037 987 990 800 831 945 916 414 260 368 630 569 880 138 282 922 183 121 028 013 849 748 722 055 131 066 984 811 484 264 856 494 454 154 271 110 635 082 519 199 364 764 880 925 250 595 009 018 836 869 530 531 606 596 486 936 754 854 796 672 236 106 895 187 245 007 058 954 042 381 921 263 120 607 493 617 026 000 320 942 947 705 412 843 560 285 850 181 925 183 568 006 260 786 519 033 999 210 385 995 865 132 473 391 139 122 453 865 535 090 207 140 524 012 150 061 075 133 732 624 395 373 362 236 273 595 909 341 433 581 691 564 591 044 855 639 746 133 140 248 522 617 544 320 846 047 976 707 866 653 140 323 500 322 573 308 834 729 076 627 377 650 803 250 121 003 671 965 040 987 728 265 362 017 649 536 384 460 519 663 919 432 200 301 386 044 210 552 787 564 300 852 026 452 801 566 748 509 629 966 184 865 991 765 415 938 199 619 648 580 692 014 690 020 462 416 518 445 377 513 782 691 489 303 098 865 096 222 174 072 811 915 885 754 796 428 695 978 325 087 693 229 426 229 709 661 668 498 365 250 024 611 412 332 161 276 342 116 078 030 205 610 563 463 831 539 680 630 736 349 157 709 501 333 657 187 250 086 905 001 472 323 730 995 137 288 705 193 173 726 203 132 602 807 464 874 666 734 594 026 154 704 049 739 289 153 879 525 940 614 067 990 069 207 703 155 997 611 193 812 531 211 900 170 056 704 045 311 431 012 807 763 095 055 326 210 313 596 391 643 834 236 645 313 331 235 775 922 076 598 659 416 600 426 771 508 242 084 880 926 771 788 637 367 258 208 518 559 678 689 742 047 609 143 654 296 825 880 337 076 788 499 546 303 395 229 749 782 797 836 541 719 325 329 408 769 336 825 007 828 562 141 829 419 067 718 986 451 076 231 336 815 116 564 000 888 872 056 446 451 309 853 613 470 836 368 583 245 939 246 682 878 085 148 478 647 694 214 031 737 603 920 066 262 338 794 742 343 522 765 207 402 024 614 935 012 534 807 535 387 304 500 095 365 619 364 275 637 858 200 266 758 480 560 436 758 889 460 072 961 941 773 692 564 472 817 084 946 456 788 089 220 349 362 744 197 665 169 819 182 534 372 092 073 755 581 697 100 219 311 673 949 481 170 537 737 604 239 782 120 875 611 341 970 835 086 511 525 329 368 660 321 496 450 567 964 632 873 664 307 547 065 666 484 164 525 123 535 190 858 493 118 451 924 574 861 295 772 202 481 971 756 154 426 323 181 149 076 679 265 863 233 262 842 743 368 802 694 778 816 645 763 141 093 518 349 461 454 400 984 502 635 987 373 765 820 410 062 235 933 764 974 531 189 907 594 214 303 353 615 781 811 153 558 549 951 754 652 331 311 121 790 803 278 500 107 411 710 221 166 768 125 781 577 120 787 846 303 589 849 673 918 484 060 793 218 555 522 526 148 464 748 255 135 632 548 650 547 163 389 289 337 451 828 678 999 198 906 612 539 072 547 415 284 512 107 114 415 243 038 936 650 846 570 189 654 702 659 632 241 280 125 189 158 168 008 076 629 671 461 548 144 088 791 136 084 707 225 273 044 258 819 177 741 568 208 772 520 854 923 920 545 803 341 456 959 708 876 771 190 863 856 504 960 449 333 067 935 220 722 745 668 519 401 379 635 360 866 628 868 338 513 677 143 924 388 962 015 932 835 679 775 220 144 614 062 567 719 830 890 901 345 560 427 484 992 210 405 791 602 527 297 713 945 888 375 665 859 752 124 510 406 762 950 561 509 320 285 190 086 331 561 867 409 162 377 065 948 790 699 133 723 663 373 809 759 431 169 498 568 791 570 962 968 773 509 225 313 577 317 007 532 689 916 016 039 076 959 632 870 297 432 803 235 846 474 383 784 393 114 560 184 729 222 681 074 260 998 578 794 085 922 083 817 319 109 903 543 266 970 803 469 668 974 475 192 988 854 127 058 342 487 602 897 821 111 817 950 646 531 654 645 552 414 122 003 403 443 946 941 255 479 588 479 444 872 162 158 296 826 256 340 703 364 445 323 677 464 879 600 305 594 384 092 126 267 048 778 654 648 387 074 652 891 161 494 170 074 985 998 611 015 321 827 801 942 166 308 682 844 295 187 347 563 014 540 999 288 876 314 440 531 180 933 320 946 741 429 435 676 023 296 068 773 417 371 119 475 786 529 030 512 400 024 211 016 292 284 371 313 782 860 151 416 422 326 035 396 224 366 708 062 704 596 293 496 659 141 538 703 024 901 300 819 572 403 837 418 894 927 554 094 907 645 070 021 257 306 840 518 332 222 139 195 591 703 080 134 454 582 961 878 847 940 165 237 623 211 084 973 253 716 659 005 431 740 004 646 710 497 094 783 212 547 813 708 005 789 061 773 137 988 707 862 374 174 310 957 153 581 692 164 537 103 325 281 814 446 358 124 344 627 990 137 685 791 053 712 729 636 834 810 971 916 361 504 178 765 596 382 917 343 769 894 065 912 808 965 349 631 654 590 139 505 228 623 312 397 725 899 373 441 770 395 552 970 133 122 584 508 330 486 923 794 400 050 781 797 769 779 752 638 586 745 132 151 575 503 886 616 076 517 562 621 795 143 727 416 427 868 979 493 603 637 348 970 957 144 857 956 197 962 144 035 704 742 280 862 128 223 878 590 258 871 169 667 704 594 450 129 822 545 980 443 540 719 082 580 474 668 532 589 661 701 591 998 219 253 629 947 266 444 632 663 606 745 554 243 772 380 208 372 058 031 874 695 160 800 406 430 370 516 591 397 447 533 527 236 202 231 002 696 290 776 270 642 409 528 452 262 716 777 497 889 540 823 148 242 615 747 142 199 144 332 934 210 755 920 960 454 165 265 685 433 470 512 322 788 494 325 598 235 930 747 432 623 647 007 242 602 949 821 594 663 300 996 155 606 301 264 114 623 512 284 702 330 622 203 743 278 576 476 625 243 486 563 012 135 050 235 216 967 543 499 661 342 381 493 429 665 278 816 814 643 656 254 799 429 837 847 609 031 599 620 034 019 221 029 245 164 236 818 574 948 227 381 836 473 984 549 802 801 030 641 652 963 856 355 429 178 818 093 058 150 880 304 133 899 797 813 232 532 213 743 847 256 944 605 335 953 564 333 261 177 546 681 496 358 801 545 574 675 287 985 072 830 622 086 566 924 335 958 949 531 160 094 935 823 725 878 553 222 589 596 136 162 566 421 425 271 915 975 726 702 533 592 479 004 196 884 434 852 989 748 452 989 392 303 158 931 176 901 035 932 065 216 087 758 583 874 347 855 226 040 517 896 621 479 900 820 471 091 872 309 434 064 989 905 058 809 606 644 393 071 757 513 974 888 468 393 124 634 500 477 242 809 665 536 941 874 173 368 641 427 899 625 172 687 537 381 076 970 901 099 089 492 247 080 885 983 830 580 882 778 970 118 096 594 080 767 966 323 475 694 825 735 606 129 233 913 169 626 530 981 681 539 317 463 270 497 553 989 338 678 685 677 192 463 662 354 377 823 662 627 992 535 584 075 189 318 718 429 614 422 284 168 574 480 192 980 238 304 179 955 319 499 128 075 597 572 661 903 457 961 899 064 972 036 336 603 244 171 379 037 818 189 259 260 945 462 403 464 478 848 725 304 996 269 546 953 208 924 739 312 362 465 288 750 106 448 241 660 182 716 000 485 235 046 579 796 128 145 364 334 542 461 617 607 953 031 753 870 691 968 724 734 294 793 466 607 872 210 567 722 789 507 813 466 702 690 987 424 599 801 659 916 268 429 660 745 422 296 237 382 706 283 134 291 014 646 786 277 064 686 069 579 684 032 756 783 161 190 448 708 857 423 312 689 900 360 225 993 413 861 538 661 815 377 904 351 833 235 201 126 414 358 041 931 029 521 161 301 117 846 551 379 083 810 416 790 594 589 781 398 324 878 441 335 475 518 722 574 186 022 223 021 384 757 254 005 859 043 797 607 337 608 547 381 644 200 791 890 679 684 271 526 992 510 865 950 601 837 287 340 762 099 405 419 077 243 677 853 748 869 384 130 442 541 199 354 657 926 308 465 889 115 167 510 455 872 203 014 378 758 342 515 547 553 847 535 579 638 972 859 844 573 735 278 174 684 452 682 899 970 789 835 908 987 386 897 860 902 331 729 010 997 528 235 035 087 112 797 708 754 321 309 235 649 641 458 448 546 202 641 325 025 116 529 145 343 826 780 698 137 010 715 232 827 563 397 955 177 301 092 036 512 212 709 652 397 330 557 492 552 129 447 411 869 632 662 989 208 666 495 442 357 711 773 977 566 312 805 249 817 883 278 819 946 729 876 844 013 783 351 782 749 069 920 143 344 155 368 367 625 612 491 223 818 404 962 295 912 779 558 490 993 156 692 671 425 246 967 693 304 231 384 385 773 277 986 283 469 810 079 781 594 032 037 751 593 029 354 267 741 095 767 081 143 665 737 347 849 962 423 926 131 022 101 091 671 792 120 706 817 865 007 550 634 607 140 598 439 940 720 065 114 756 277 584 724 354 011 628 612 180 602 577 117 920 088 447 284 785 760 100 413 986 052 461 886 215 528 090 417 485 583 968 753 855 450 299 468 141 301 249 702 016 757 092 334 687 521 643 384 879 075 545 369 924 714 308 550 713 253 445 288 866 223 788 695 405 119 975 537 214 992 242 633 937 270 315 788 296 455 894 443 131 676 675 205 216 799 682 435 550 689 996 496 002 253 059 457 595 257 213 042 679 204 372 267 650 853 901 845 672 104 028 923 598 294 857 536 949 068 286 193 303 315 518 718 439 339 981 816 139 051 432 543 498 242 753 281 030 861 749 881 565 283 654 882 332 000 917 611 123 309 844 311 666 539 011 375 735 302 802 131 884 527 368 794 006 740 457 695 360 475 721 273 835 998 507 145 267 964 203 969 679 281 373 379 964 636 313 410 566 483 081 963 276 057 599 096 219 837 136 057 715 311 511 958 149 593 024 993 820 297 075 241 024 775 361 700 116 599 475 316 519 178 972 871 118 577 073 348 450 982 184 461 590 713 792 141 611 432 169 361 991 266 545 328 806 672 658 394 297 151 043 118 840 035 876 260 035 644 899 603 077 685 339 697 041 481 555 491 097 414 009 427 725 169 939 978 550 293 678 298 669 493 686 618 246 939 625 960 079 040 674 791 105 868 290 723 365 373 685 658 617 310 630 968 590 694 808 722 580 215 247 582 367 735 299 319 378 033 911 188 962 343 028 529 707 366 521 884 490 482 428 568 608 513 134 485 882 842 518 789 824 490 737 313 485 572 431 944 089 163 261 910 461 734 663 504 347 754 866 105 100 326 903 945 455 639 743 346 160 316 585 162 590 894 703 698 620 340 307 139 668 420 198 332 237 436 152 351 635 589 389 692 752 049 789 292 669 722 110 188 723 009 077 349 885 317 177 893 339 938 077 103 623 045 823 831 033 585 103 484 890 523 734 935 628 405 136 305 780 936 414 915 604 979 900 833 937 102 832 614 099 617 492 003 605 184 816 522 309 093 856 799 606 356 658 834 902 137 768 653 539 917 835 272 720 426 011 405 155 494 446 332 904 653 674 149 466 718 016 253 117 916 558 896 782 449 101 338 580 338 060 155 844 906 537 231 027 735 226 553 034 394 409 687 983 139 270 286 437 440 391 738 943 910 949 044 855 021 917 801 008 723 425 223 832 894 238 616 054 465 768 498 019 202 946 287 729 262 455 809 344 625 120 255 070 361 130 061 047 290 694 689 426 404 242 813 461 480 104 427 080 648 411 794 021 599 958 691 443 518 628 321 198 904 228 197 313 421 067 179 559 563 926 697 389 947 254 479 226 121 482 935 128 320 816 994 762 057 284 009 533 789 682 882 057 213 953 631 780 867 173 426 170 944 029 250 417 814 748 328 198 442 954 426 394 526 239 516 426 010 539 893 191 773 850 070 232 709 961 213 487 182 149 136 208 423 456 350 779 170 861 767 890 006 771 013 676 276 827 379 626 545 321 204 147 399 247 798 989 114 163 840 581 716 138 567 260 583 959 609 478 786 022 952 513 015 761 343 739 996 047 713 294 839 316 030 292 063 129 596 908 175 397 636 638 267 222 138 373 118 061 101 697 189 157 727 853 069 671 735 866 013 492 016 888 458 271 801 430 127 286 270 433 351 750 514 832 273 768 551 692 690 129 409 090 122 514 549 894 596 608 474 252 584 917 066 571 836 103 623 496 884 667 353 727 560 066 724 916 885 718 966 255 622 601 079 993 592 476 990 461 759 931 438 953 801 415 765 985 923 608 630 362 089 151 710 235 947 081 238 403 262 902 159 793 249 592 704 579 568 279 861 290 958 371 904 680 614 511 661 643 727 195 748 861 311 933 415 186 155 998 004 202 991 275 020 354 024 027 644 410 899 576 962 277 653 705 108 717 515 670 322 009 682 856 439 131 106 600 803 124 841 739 030 982 341 671 264 062 415 618 690 830 641 357 830 993 094 222 508 543 476 741 954 920 935 720 934 973 738 948 833 775 451 280 748 344 339 545 323 550 714 515 918 450 882 204 901 268 622 480 399 120 126 293 816 053 324 066 634 319 045 058 236 996 277 545 947 430 915 629 682 625 630 130 606 702 294 330 839 662 730 325 546 053 500 861 333 986 040 093 393 344 140 681 702 180 124 103 255 033 551 726 380 579 126 885 579 373 300 433 737 106 490 674 936 203 887 358 658 191 668 184 427 242 206 816 683 989 838 632 174 854 704 366 054 936 594 299 427 687 556 462 515 011 276 741 417 205 502 479 598 320 995 858 791 647 236 592 672 153 031 105 722 230 328 084 731 588 172 092 623 852 028 644 916 817 015 568 820 107 189 039 373 828 300 370 540 967 036 773 275 923 781 457 231 838 332 823 353 250 126 909 216 218 051 203 889 871 793 361 708 462 248 524 940 542 515 212 547 670 159 795 460 493 926 440 827 534 362 348 127 259 710 475 338 115 850 175 291 087 743 250 569 390 754 140 068 571 455 537 529 013 954 839 343 321 513 527 925 511 301 509 623 786 363 989 927 881 347 614 930 093 226 680 458 488 594 354 764 351 884 753 938 012 409 679 462 225 396 358 689 780 721 134 413 281 041 572 609 119 024 684 006 283 463 331 860 521 114 749 139 388 462 673 468 394 588 536 555 400 925 319 856 022 264 710 905 830 696 471 665 088 238 713 285 748 783 368 041 626 773 294 486 543 959 285 382 569 817 407 340 431 414 108 384 401 494 036 799 503 755 292 972 032 998 020 225 086 874 085 890 535 359 542 122 912 793 007 215 723 768 031 508 194 061 180 916 895 197 589 831 335 442 601 173 699 108 967 886 240 003 324 542 818 679 855 430 793 022 301 497 447 932 297 397 305 133 052 702 452 366 862 016 623 994 883 586 870 208 906 969 138 087 247 724 997 507 314 366 606 374 851 694 657 780 758 385 563 268 929 703 192 959 471 046 994 281 970 556 292 968 560 762 483 795 415 977 077 161 131 221 278 083 649 174 096 590 990 546 110 250 818 375 129 907 466 450 812 552 155 851 977 673 168 161 599 532 750 506 138 429 308 890 348 681 789 861 579 915 528 236 682 193 808 296 773 835 030 948 658 992 718 135 151 741 600 089 214 718 427 952 655 701 849 088 891 343 409 714 689 893 454 443 749 446 056 865 447 835 031 911 270 969 195 478 716 221 143 222 675 450 775 500 418 567 804 635 240 831 696 300 549 376 295 418 141 071 780 472 776 784 634 694 741 827 858 976 472 066 772 554 589 162 391 330 557 584 449 125 548 150 451 255 289 312 532 326 241 332 631 025 404 866 526 870 142 929 718 736 803 314 243 924 775 616 225 702 959 890 860 319 301 169 550 960 993 237 850 076 223 069 757 015 761 312 984 296 825 449 051 192 108 026 923 070 120 439 012 230 687 645 183 304 456 417 697 485 510 334 804 676 984 081 411 401 836 599 411 389 678 885 260 626 059 956 154 624 447 803 271 873 240 116 265 980 003 966 923 595 607 850 690 436 809 132 666 623 700 084 620 678 116 523 402 124 968 865 179 327 458 265 354 776 342 081 384 238 245 090 190 254 049 495 692 266 031 872 898 286 097 753 663 497 536 485 571 199 763 496 898 356 201 681 370 292 815 609 591 644 314 902 200 657 841 021 252 388 353 368 942 560 608 686 952 778 499 091 274 277 530 455 349 056 836 620 442 584 656 546 123 473 303 098 953 006 044 615 521 241 946 929 255 611 623 654 953 001 414 407 981 790 119 512 425 709 290 643 798 474 505 295 206 821 999 299 729 186 109 414 797 914 803 465 699 255 523 841 949 402 181 220 808 313 766 103 669 110 314 915 161 114 721 721 545 376 391 853 704 405 365 293 713 475 569 819 172 071 286 069 175 403 603 421 515 977 286 448 891 739 270 044 438 728 457 418 182 058 249 838 903 618 715 743 707 944 883 293 343 149 503 525 178 449 669 561 508 846 709 149 908 829 572 561 389 696 743 264 058 714 058 933 329 620 144 782 214 318 007 753 237 251 583 673 599 580 861 753 835 124 589 964 457 411 498 865 619 452 297 698 029 329 778 774 267 871 154 205 398 865 917 768 118 317 597 345 570 909 894 052 115 509 814 772 787 945 739 568 606 089 073 022 955 597 154 452 449 577 037 474 868 061 949 421 234 062 052 890 173 014 662 672 898 608 416 288 025 352 138 167 230 590 756 423 107 426 112 617 498 948 007 441 919 933 503 135 858 725 569 452 784 019 919 152 278 916 269 733 462 901 747 668 162 818 277 935 542 593 785 714 456 335 073 159 170 555 343 599 524 594 982 635 756 276 122 650 849 237 413 409 490 896 098 044 441 716 002 744 276 136 691 356 746 836 251 338 444 990 888 126 355 488 184 773 388 126 639 094 775 205 873 304 683 095 071 036 228 427 981 459 640 013 438 694 834 115 593 679 026 836 341 765 441 976 265 621 176 762 062 601 505 869 460 584 570 590 328 110 648 287 887 857 183 816 829 412 471 673 586 489 665 504 762 927 494 971 106 234 543 759 303 577 782 208 896 592 327 530 227 534 752 133 746 654 325 464 205 862 516 019 421 278 860 543 090 456 829 550 001 434 554 709 334 241 413 644 217 550 256 455 702 434 811 995 327 781 092 831 500 467 988 705 107 767 303 400 828 068 229 664 688 764 224 044 823 455 916 014 278 351 456 985 596 392 557 070 572 572 685 744 245 179 074 671 569 813 689 480 528 581 782 846 198 623 897 884 359 624 368 710 572 035 450 203 742 273 963 066 322 493 187 868 334 117 033 747 599 491 014 526 786 163 959 664 340 323 232 477 143 298 560 449 776 458 731 338 486 168 061 551 109 546 834 524 260 404 483 253 555 242 183 143 087 772 381 474 742 691 867 933 749 483 296 825 646 462 610 136 699 798 023 613 685 276 180 219 851 544 271 856 088 860 635 966 103 944 090 679 640 702 591 419 119 804 637 068 057 746 322 775 529 741 457 654 090 705 067 403 566 129 560 382 880 722 812 000 807 199 639 677 358 318 605 876 281 068 090 686 342 705 210 877 805 004 084 268 940 878 756 135 711 045 511 817 746 071 022 651 266 861 859 819 616 177 297 041 891 962 952 498 443 152 521 159 184 293 057 024 454 827 906 073 945 670 941 892 072 507 015 915 116 321 898 912 687 187 386 410 783 477 242 544 363 653 329 106 182 341 278 464 644 284 989 992 199 220 167 193 238 159 327 441 178 363 870 350 366 993 142 115 198 567 171 893 119 570 540 208 236 456 624 375 018 587 593 960 297 804 933 146 054 422 065 699 352 145 167 080 236 383 365 945 208 764 614 705 003 179 064 491 515 639 950 936 945 717 440 489 981 060 587 158 259 058 727 290 366 991 670 856 514 900 088 757 816 432 938 673 274 712 726 203 774 304 935 434 096 307 756 907 039 437 430 294 409 069 266 424 972 088 520 484 971 358 888 996 403 439 807 138 504 671 667 203 392 169 009 888 243 338 253 246 019 991 917 013 170 227 982 152 612 963 233 478 043 925 963 526 718 266 074 296 694 494 235 681 059 752 750 951 468 559 672 328 549 392 804 968 438 875 269 260 349 017 127 006 599 360 803 123 971 020 871 215 460 728 462 453 518 279 593 025 162 271 656 301 767 595 214 497 318 373 199 395 845 683 713 241 112 652 482 451 878 032 986 677 977 688 475 081 420 866 125 474 729 737 238 002 658 519 850 993 645 102 947 189 779 562 181 984 813 531 022 586 570 024 391 926 352 047 307 880 655 092 143 200 076 546 970 180 219 400 304 738 176 269 142 336 537 420 539 820 828 678 945 277 856 735 621 975 271 787 777 219 119 179 636 528 179 888 000 358 304 389 933 358 838 169 839 661 969 829 326 474 889 117 468 939 560 108 387 132 110 838 414 879 959 944 923 984 836 641 997 971 935 127 182 946 730 454 115 178 469 077 227 906 223 475 324 493 934 090 782 130 989 900 268 322 611 540 320 626 324 244 958 296 955 909 079 243 868 630 181 004 874 242 573 478 427 809 511 354 704 142 733 678 298 259 572 260 352 612 503 295 611 562 612 745 251 161 345 100 802 452 590 954 842 515 865 082 545 951 734 317 776 870 424 064 887 909 813 578 472 554 376 999 841 013 675 771 247 677 287 233 487 155 748 018 772 544 271 238 114 044 095 425 588 350 504 007 160 537 622 717 277 325 163 877 027 188 858 392 890 154 418 158 360 677 596 331 295 820 939 266 991 710 579 427 597 309 721 055 692 542 100 738 333 866 561 215 192 751 595 131 586 959 165 606 805 674 651 529 426 526 641 136 190 601 001 477 567 441 222 586 231 850 630 457 427 158 780 233 995 546 844 550 073 994 341 030 784 534 211 267 454 401 990 085 470 353 367 140 995 703 149 266 358 294 346 603 834 615 105 166 628 668 873 145 763 138 526 816 514 834 589 842 352 003 313 968 822 201 595 658 557 903 152 921 808 964 957 549 699 985 115 478 912 447 810 682 262 392 794 363 204 136 959 197 252 735 596 335 456 868 774 589 815 985 451 173 282 354 625 354 227 178 150 687 533 240 543 500 975 755 878 175 922 094 124 415 786 426 433 887 405 777 381 829 172 931 654 708 766 967 460 152 115 783 118 508 593 525 015 781 657 474 973 289 468 857 325 164 108 826 398 561 558 366 596 611 061 089 433 195 311 308 534 955 097 061 142 901 847 385 579 052 098 899 590 618 539 472 669 169 192 201 290 789 970 773 497 362 728 037 626 954 852 438 616 063 579 610 840 119 716 934 057 889 604 249 916 013 672 233 006 213 304 851 630 651 802 990 118 852 794 053 970 899 332 072 772 429 869 038 162 161 020 854 906 837 507 369 950 729 367 668 938 849 486 061 332 314 572 078 646 158 421 193 664 840 308 873 526 075 749 967 499 857 832 536 306 477 091 478 989 350 178 203 248 220 922 057 419 828 399 125 414 812 372 637 471 684 586 783 555 900 694 624 811 791 838 186 223 719 834 164 662 070 468 414 200 946 312 146 099 474 731 167 936 963 244 013 310 484 976 333 614 794 608 432 108 257 170 239 033 194 406 244 663 214 506 869 432 998 909 078 754 939 025 976 835 522 319 847 601 988 765 582 713 493 816 051 398 524 341 532 019 564 214 952 337 085 615 144 303 605 011 242 771 046 698 431 542 566 322 725 208 916 233 791 379 408 190 363 104 859 757 908 301 383 393 650 832 284 864 852 684 716 567 246 476 088 282 840 651 999 712 708 018 482 845 223 266 822 452 874 534 207 094 998 985 777 699 069 889 198 177 025 520 197 441 836 635 564 327 307 448 682 951 204 954 122 357 752 942 378 669 312 158 273 753 541 177 019 350 091 238 886 025 319 144 559 840 094 286 656 756 866 272 779 377 235 052 689 781 853 683 639 226 526 308 861 900 642 604 282 830 022 121 690 916 589 869 269 707 921 544 272 609 046 091 964 164 078 215 646 956 731 722 940 777 284 278 948 988 135 224 010 964 586 537 917 803 159 057 905 897 971 092 120 139 645 364 601 653 119 787 109 545 959 398 516 188 418 452 700 281 626 522 692 917 827 195 671 035 325 044 550 698 301 874 971 508 686 695 896 319 985 101 078 349 108 459 308 472 314 561 483 284 750 121 615 147 366 921 144 607 639 349 766 041 684 157 541 982 429 247 943 030 156 014 677 732 657 436 050 792 206 661 985 896 110 167 372 113 129 409 178 949 902 781 919 482 174 296 489 063 819 569 768 441 562 470 822 135 759 266 192 791 214 930 586 555 289 724 266 604 175 407 842 833 407 397 794 609 730 524 665 754 413 523 029 110 607 214 364 302 631 610 362 214 887 557 896 404 303 395 962 748 775 247 334 489 488 804 469 282 219 852 679 810 172 764 074 748 270 730 077 460 556 317 106 371 027 287 755 558 565 990 697 274 711 107 946 211 318 665 187 554 538 731 061 786 323 852 383 540 494 733 539 215 438 320 176 918 877 519 107 187 667 958 240 096 656 550 253 209 845 309 704 522 570 464 576 163 218 897 031 710 677 940 072 133 039 679 756 737 775 068 169 357 645 671 933 711 376 272 009 021 451 335 600 041 605 705 236 923 245 079 051 502 317 004 825 982 548 359 919 076 795 878 371 936 525 225 078 625 179 455 509 939 764 173 716 776 199 408 923 950 618 904 672 480 027 743 651 294 666 022 916 761 259 970 092 638 512 039 405 656 333 436 027 742 045 653 334 934 593 121 811 519 122 704 718 082 771 255 865 245 540 560 461 654 733 071 735 247 272 654 889 385 643 837 470 857 454 813 334 958 540 162 877 432 615 426 994 632 123 836 344 067 133 331 040 148 820 363 672 850 423 814 467 238 029 545 316 431 391 618 670 446 576 225 280 261 060 128 405 228 428 305 665 049 665 221 540 458 767 317 046 506 558 153 379 157 663 924 214 632 060 479 248 852 866 969 187 971 885 373 740 004 599 313 882 433 234 559 992 681 976 729 447 879 210 535 771 836 051 665 218 246 337 925 064 262 646 378 201 807 934 550 466 243 298 036 838 360 040 038 639 281 539 839 901 484 456 778 642 426 640 545 102 612 538 212 603 561 517 830 082 422 820 971 507 574 510 437 592 565 927 171 054 533 772 490 297 727 974 314 879 788 762 440 192 162 947 817 798 674 191 199 247 715 560 111 075 224 294 114 949 595 137 733 545 131 078 612 032 766 209 598 817 000 897 346 608 827 951 670 007 358 670 109 200 403 764 004 773 679 798 577 959 787 581 894 050 273 577 361 698 108 744 601 810 199 631 915 447 801 659 699 544 009 590 664 997 043 217 762 776 718 371 708 917 378 677 351 272 490 503 238 847 534 910 872 463 166 559 093 714 078 438 629 860 504 623 453 080 746 880 912 760 833 008 968 371 328 429 768 386 420 562 990 011 510 047 271 237 942 326 985 482 869 394 407 152 822 967 097 101 369 261 030 949 579 096 434 985 284 870 680 058 659 353 418 182 233 917 112 122 517 440 301 719 415 351 703 340 531 814 383 046 404 268 844 469 733 515 045 307 746 800 602 487 881 427 976 350 341 131 270 566 639 669 225 828 529 514 330 414 902 602 471 579 571 410 422 144 078 416 563 607 889 639 175 203 263 324 012 234 775 977 143 346 710 460 507 759 513 191 731 975 332 318 931 993 404 724 759 478 531 566 154 230 954 838 180 989 028 320 151 422 137 648 618 383 632 371 849 681 054 079 567 776 280 906 728 628 946 932 652 673 847 116 153 392 092 666 050 514 939 087 060 517 951 577 677 940 275 346 261 679 552 551 407 212 809 889 789 862 747 456 613 864 027 440 845 682 640 924 748 938 591 989 894 847 088 026 779 956 784 147 531 831 650 006 534 045 617 794 519 359 015 016 618 607 245 035 219 666 640 613 963 260 203 639 908 219 789 351 803 821 793 802 608 341 876 905 083 882 305 097 888 681 899 610 031 190 878 787 406 456 921 958 488 715 805 460 740 642 314 882 344 614 233 298 305 761 750 926 356 739 821 135 759 306 515 500 654 874 900 080 749 767 976 340 343 040 838 763 411 135 140 626 690 198 554 904 838 429 977 016 355 409 516 243 691 429 162 242 381 823 383 979 332 584 100 768 578 836 093 043 332 511 023 808 043 541 244 736 449 136 550 158 520 126 672 372 197 726 304 765 640 719 545 582 507 670 997 186 350 787 572 333 721 829 022 996 627 852 529 316 314 116 367 131 427 371 763 281 535 461 043 844 034 881 940 233 339 058 773 862 937 403 192 689 117 100 021 270 684 767 303 657 816 562 469 183 048 892 059 171 311 332 051 436 261 050 320 818 112 176 115 942 060 104 551 952 695 525 270 478 856 656 057 897 998 870 414 587 975 217 337 937 745 096 539 223 619 370 157 315 699 985 560 155 541 026 675 436 192 493 462 357 131 760 458 701 551 474 398 147 212 270 434 183 353 032 546 430 152 654 102 648 817 129 100 588 351 582 454 844 639 892 956 194 181 713 853 192 921 210 723 470 979 582 524 898 215 574 847 295 406 608 511 209 882 881 749 807 797 292 639 408 255 685 709 474 162 049 586 409 279 567 129 932 114 831 719 383 590 339 724 982 868 304 751 851 467 321 985 846 446 859 543 834 262 957 951 232 907 832 565 088 107 094 310 069 439 763 005 990 700 472 743 978 364 929 881 952 691 383 958 402 132 988 011 153 212 699 750 857 764 490 803 944 478 469 700 502 189 783 727 131 512 042 616 695 913 269 144 779 236 517 600 767 301 801 090 481 887 812 883 240 039 666 611 838 278 570 978 558 864 508 020 450 132 000 869 081 879 897 187 204 879 297 857 262 694 251 839 072 218 771 080 229 898 238 124 854 041 932 057 064 545 221 647 620 238 129 484 907 276 043 275 903 285 094 882 509 016 323 551 541 528 256 134 286 917 714 386 560 624 623 557 937 627 127 288 218 002 959 162 219 536 724 979 962 868 944 649 186 905 229 214 460 980 216 418 970 715 014 620 092 504 601 366 890 499 751 144 402 806 325 451 032 067 219 551 686 013 566 267 469 443 822 453 976 486 150 639 797 675 562 093 060 163 308 836 334 701 744 401 283 320 419 543 335 626 273 483 366 034 028 529 809 715 243 999 335 247 832 170 271 615 441 328 437 499 695 749 435 018 946 767 683 316 329 067 123 225 736 898 287 766 432 898 183 304 940 230 239 609 020 086 499 043 569 187 755 182 789 701 783 350 059 093 737 416 752 074 457 409 239 273 871 060 596 668 555 614 562 632 764 638 618 051 042 790 743 727 349 389 662 865 127 255 611 392 109 368 394 515 644 781 185 355 372 660 000 180 845 005 714 716 652 207 786 147 394 554 613 112 682 872 590 016 165 466 183 218 488 720 552 174 026 619 882 656 473 942 157 017 524 945 657 276 296 317 631 669 780 521 577 936 926 733 650 840 208 704 143 240 414 213 105 979 117 137 183 055 569 650 847 523 943 364 086 703 859 480 223 613 231 691 389 713 260 847 927 313 346 099 650 941 531 754 956 872 362 992 791 339 552 788 073 983 259 394 009 674 870 485 449 585 545 767 947 155 135 184 099 207 657 419 628 369 028 668 556 248 051 002 081 958 044 680 234 315 068 661 918 696 026 025 089 389 524 983 307 261 668 692 670 857 639 758 952 408 436 706 415 079 742 391 969 823 922 183 405 143 109 264 115 020 313 993 796 565 457 706 633 350 661 806 857 598 768 250 756 762 983 966 988 135 251 893 000 537 778 572 597 477 838 837 935 615 254 081 490 326 727 149 137 025 117 199 933 065 900 955 198 320 607 953 903 606 038 695 815 858 394 152 884 655 833 519 752 589 643 567 206 570 948 607 632 742 316 804 685 823 818 757 753 259 206 975 858 609 364 890 003 708 364 578 054 874 636 903 049 443 764 204 343 541 475 913 614 608 258 236 190 401 122 335 209 304 137 899 383 643 958 201 703 755 596 269 371 595 455 167 374 985 144 956 294 873 864 692 761 467 987 852 415 812 113 466 235 719 452 692 481 777 212 243 302 493 309 169 056 910 419 043 479 868 778 267 346 941 336 655 140 728 264 781 168 950 778 903 596 905 423 991 723 350 102 772 995 355 683 557 053 012 892 895 276 434 870 787 003 253 266 477 863 053 726 201 373 080 882 718 476 154 950 153 754 228 749 612 561 661 226 952 824 996 732 357 630 630 396 106 957 191 999 593 111 949 138 912 207 977 397 042 743 950 609 609 764 112 239 103 529 941 845 990 938 567 175 100 180 783 860 729 533 211 796 658 555 050 066 284 860 836 285 126 297 601 515 810 571 673 879 326 560 003 566 389 516 890 287 550 148 097 058 912 041 622 693 043 495 761 713 120 701 069 283 791 541 159 041 987 625 062 708 848 262 325 512 550 688 080 427 064 642 444 104 979 010 223 920 261 472 946 642 631 092 266 171 170 988 230 424 969 842 916 823 730 538 377 567 350 472 319 619 326 043 384 987 334 844 206 900 043 281 293 529 666 553 190 336 307 601 312 068 754 833 747 688 440 509 552 780 832 991 924 511 609 507 924 186 537 158 474 068 798 873 174 163 006 959 990 748 515 968 218 562 085 016 246 824 918 770 205 436 086 300 104 111 820 347 173 459 171 335 262 589 042 029 627 787 900 391 789 019 193 685 920 594 580 185 870 124 649 718 074 326 791 601 390 481 104 830 876 241 678 111 776 800 392 346 692 935 507 983 290 163 461 756 477 455 864 563 223 267 190 735 351 231 114 625 505 439 735 169 232 245 592 267 480 331 617 154 014 433 245 760 086 186 858 878 565 226 631 384 120 860 519 313 333 879 665 322 260 488 706 906 174 868 291 865 447 108 745 587 163 257 791 015 954 547 831 148 690 057 506 008 148 552 014 238 318 229 004 795 186 462 330 168 445 234 210 923 205 113 941 044 532 710 964 984 441 050 767 967 462 799 143 420 878 576 391 030 442 775 596 571 380 434 808 800 732 112 370 755 343 673 443 360 779 920 332 034 589 169 159 853 787 822 289 196 064 071 219 000 975 758 748 443 442 261 262 588 502 898 065 602 208 106 114 818 628 691 493 518 711 546 583 122 473 129 206 700 961 152 270 648 910 182 009 533 386 473 527 984 477 425 222 540 475 131 492 864 776 231 004 809 455 150 327 629 716 256 004 768 486 270 071 083 984 927 933 916 793 391 616 484 318 377 486 432 184 919 696 683 625 966 691 642 389 162 559 217 317 951 381 225 324 975 322 303 197 740 707 922 547 595 991 263 749 716 236 967 871 929 866 603 679 989 285 756 477 819 596 653 161 434 562 415 341 669 478 641 560 545 621 453 496 902 757 683 529 445 982 046 199 372 457 455 092 165 376 431 927 950 614 947 996 954 800 311 005 183 373 356 970 843 657 816 414 357 188 724 374 507 806 960 699 649 194 695 178 428 888 848 719 398 775 914 431 614 087 139 234 231 596 414 604 228 047 638 596 415 389 385 853 732 934 395 196 322 103 018 457 964 335 883 781 458 255 750 563 946 070 196 888 290 747 756 244 257 269 584 953 986 259 084 021 192 675 478 732 127 851 794 268 984 729 945 755 863 705 914 624 593 932 307 630 403 257 251 859 239 646 681 048 376 381 183 783 608 890 712 780 380 569 525 465 925 661 598 081 192 309 134 501 973 522 234 858 063 453 453 682 615 846 284 160 102 709 242 918 945 866 904 937 868 654 170 517 621 650 680 239 404 570 533 229 882 006 587 827 165 418 787 058 636 855 416 991 899 722 968 437 693 596 933 542 370 945 329 736 275 881 785 734 533 300 655 608 213 267 633 422 471 428 508 113 919 328 934 529 826 400 284 699 374 396 757 713 406 978 909 816 059 188 997 581 770 936 394 579 043 397 184 171 792 094 147 378 254 459 952 693 000 755 294 428 574 645 909 416 548 435 013 512 815 740 544 475 903 407 865 425 092 136 248 626 226 186 403 110 313 279 601 620 632 211 054 371 582 632 034 464 045 795 294 814 860 638 828 012 721 779 593 472 578 209 298 595 736 893 842 073 350 144 862 520 223 803 157 106 748 585 659 402 132 730 851 129 208 572 052 998 387 720 116 693 399 669 924 618 972 092 788 882 539 707 285 684 828 377 502 655 036 495 716 740 702 358 525 375 982 724 384 669 137 996 791 041 935 388 109 742 643 894 315 955 127 025 839 982 585 515 378 968 182 655 311 117 830 442 208 462 121 510 650 605 625 377 630 663 367 137 904 414 243 657 899 908 091 638 023 189 573 602 029 799 460 974 427 880 332 300 567 245 256 073 038 324 032 103 678 655 184 209 746 085 637 906 340 424 642 857 843 619 072 923 160 439 300 635 739 741 433 334 075 075 379 089 568 812 567 399 640 901 878 133 347 139 685 631 407 077 948 101 987 918 498 473 702 594 330 283 163 096 319 313 674 144 017 293 671 989 200 865 696 198 137 930 051 169 100 912 668 050 776 581 009 450 990 780 130 093 815 861 901 249 817 137 547 465 986 820 761 583 354 270 828 757 086 908 218 221 490 416 150 568 088 509 444 531 984 430 442 737 741 985 562 290 887 737 275 406 822 600 010 660 091 978 305 793 517 616 118 465 628 825 476 689 530 477 828 789 507 134 753 250 593 255 038 401 052 328 237 510 158 215 934 286 163 419 333 872 110 451 037 593 069 644 304 455 803 666 714 524 449 257 009 965 991 465 773 721 666 541 113 008 941 650 621 222 645 773 380 872 921 696 303 006 919 670 136 029 459 731 522 804 811 460 515 759 744 289 491 459 083 757 081 867 278 136 661 037 108 609 729 182 357 874 577 294 893 611 557 069 478 950 700 634 995 417 096 418 824 313 727 290 664 387 806 800 924 036 603 584 118 426 837 377 896 468 194 924 466 705 086 311 512 548 082 825 691 767 762 817 755 405 149 540 395 597 409 503 137 618 218 687 757 497 555 218 240 893 928 054 160 766 630 925 491 166 453 990 164 463 431 052 930 844 803 729 944 437 244 964 474 660 120 703 179 184 459 500 588 485 267 196 698 595 639 027 792 311 004 712 568 147 531 583 643 354 079 129 734 779 735 503 042 882 845 450 380 195 074 713 982 107 308 670 779 512 461 387 532 292 139 418 579 642 808 212 887 199 890 585 931 426 948 835 577 719 035 808 159 091 282 682 383 269 512 765 379 754 312 927 404 812 770 033 678 048 880 449 022 012 460 426 242 111 019 448 748 792 850 201 446 517 789 516 937 007 553 379 353 586 198 782 343 575 182 620 311 302 798 400 924 581 265 283 443 848 166 169 658 759 992 456 188 494 541 304 347 877 616 035 621 079 407 919 133 319 329 494 794 258 542 497 315 008 888 680 234 234 713 082 477 915 830 934 098 613 690 245 993 855 826 438 014 702 511 220 252 351 125 029 173 248 048 396 376 832 578 719 327 262 785 416 356 062 309 647 955 013 804 607 958 973 871 957 407 264 034 418 383 053 232 723 617 892 082 629 380 166 444 889 774 191 085 383 173 999 645 803 369 212 829 615 262 194 543 745 459 459 257 203 344 058 274 467 795 194 018 062 085 723 370 780 942 896 433 653 146 673 477 352 593 757 100 938 058 544 140 155 040 713 882 933 540 106 744 566 703 356 765 425 359 904 610 883 692 962 374 188 565 553 146 344 099 092 726 386 985 088 846 985 458 020 958 595 607 050 670 029 606 289 143 684 320 773 997 331 355 883 681 697 884 136 921 683 541 706 085 417 287 399 338 838 404 750 967 662 065 094 271 526 637 902 996 326 444 599 758 041 961 377 682 762 512 815 256 485 095 572 685 002 187 480 295 222 520 901 526 688 602 116 989 687 937 984 983 948 184 901 417 980 398 218 203 197 050 439 721 881 420 618 850 426 133 940 015 058 881 040 238 955 299 774 228 407 610 647 187 115 969 476 377 649 734 237 070 955 502 221 764 198 029 763 171 029 190 345 142 670 402 749 179 640 124 931 010 016 166 942 616 559 421 866 508 280 450 040 521 755 101 392 045 218 244 277 664 154 615 146 768 721 771 237 306 591 947 277 692 686 222 981 952 251 224 431 263 562 095 258 557 514 358 200 712 782 493 392 276 951 753 365 044 981 060 187 159 798 816 640 785 413 860 341 244 336 082 653 212 770 400 326 720 077 404 097 679 888 515 214 631 190 254 633 352 772 277 150 728 878 863 463 121 371 528 412 982 487 344 657 834 914 885 558 011 846 542 135 170 129 987 332 493 683 322 102 079 874 302 455 688 839 278 586 073 431 033 291 773 359 006 614 281 193 890 133 558 991 097 188 894 573 791 078 841 193 143 536 704 386 604 867 523 606 219 466 752 465 500 941 789 045 930 866 069 988 332 072 729 147 079 763 300 963 982 635 250 298 335 659 047 641 034 820 944 693 808 404 718 654 228 366 001 926 600 942 724 624 354 794 647 261 405 649 161 896 124 223 889 068 352 927 754 600 987 220 433 484 481 166 537 949 600 126 674 131 252 319 125 369 982 845 726 134 711 609 537 481 191 543 213 409 021 186 544 584 472 470 157 805 748 794 146 118 448 868 633 061 435 883 789 296 098 064 862 505 932 396 155 131 504 313 270 163 147 201 060 146 067 193 871 523 694 809 915 336 145 110 406 386 868 552 710 275 129 640 546 000 581 432 822 584 939 249 422 144 175 765 628 633 404 718 659 214 502 950 489 687 978 882 754 648 491 688 381 774 139 615 045 395 941 749 058 389 418 013 454 381 774 851 421 894 725 135 959 083 944 434 285 813 617 370 220 488 154 174 692 479 288 890 361 679 516 456 318 320 423 607 233 754 734 728 101 977 681 447 450 444 416 151 032 132 773 037 423 786 319 670 262 412 400 460 714 966 555 223 356 003 697 994 284 188 276 118 662 027 025 605 639 828 773 323 245 963 223 904 849 366 987 658 693 602 690 591 577 367 458 741 352 715 036 091 443 414 932 895 473 675 378 469 725 788 320 637 435 974 985 087 732 245 835 737 811 459 732 181 819 158 296 263 712 826 599 868 471 936 856 410 016 466 733 249 292 201 517 614 032 503 304 067 495 559 893 008 386 577 091 059 845 766 250 608 873 999 836 723 178 173 052 460 453 085 231 975 199 334 941 030 904 744 287 592 330 684 732 850 040 928 396 125 641 393 188 892 248 377 767 975 464 932 644 012 273 423 006 147 469 285 565 502 855 214 644 638 838 674 519 487 797 574 502 045 501 946 548 672 457 391 515 591 509 633 746 000 100 102 936 533 848 204 799 012 975 625 651 867 880 929 824 628 855 486 946 941 962 935 556 944 001 215 480 005 703 336 207 431 830 148 712 339 659 550 858 253 605 776 254 879 548 516 404 446 664 548 867 348 302 070 786 836 455 133 748 577 288 020 122 178 038 340 568 398 120 938 622 613 695 063 631 731 814 518 626 693 880 621 777 295 195 522 834 274 396 537 508 828 337 868 569 403 489 028 181 359 230 281 419 769 881 581 171 515 110 039 110 696 981 143 343 408 324 126 160 191 292 638 152 858 453 999 870 948 783 824 987 463 353 804 123 587 168 551 934 564 382 444 544 405 220 427 952 356 128 151 292 570 792 792 663 284 043 300 419 227 790 548 287 205 917 068 321 722 165 834 592 868 256 137 530 736 820 098 805 023 756 535 907 476 647 369 741 103 447 488 769 112 479 435 386 231 480 802 006 578 801 824 351 747 703 832 150 687 411 642 690 566 346 918 121 545 386 272 684 802 454 712 368 665 137 826 447 293 578 158 167 047 217 037 898 267 827 616 936 496 448 486 543 360 149 272 475 389 916 595 721 981 666 992 982 548 850 735 363 993 731 249 978 203 112 997 029 562 425 103 416 798 585 004 192 631 063 983 649 481 991 412 874 597 881 693 419 328 050 709 534 462 734 820 544 372 564 587 618 961 865 159 518 796 924 802 398 901 595 321 402 172 849 023 999 061 350 142 566 704 819 372 680 498 374 243 808 411 926 289 655 130 860 803 215 745 420 206 179 533 636 876 374 671 518 159 981 459 677 320 430 350 704 519 246 032 850 270 729 483 508 627 485 304 765 582 543 707 220 106 298 048 853 540 002 385 712 099 807 264 811 466 852 623 187 704 581 590 467 068 981 824 038 754 939 689 561 292 100 618 383 231 098 789 870 764 352 340 615 247 185 686 094 084 620 294 048 299 451 976 745 120 222 634 068 810 742 221 831 419 050 594 692 665 354 613 009 345 913 832 947 965 904 946 221 622 549 506 138 250 850 126 524 700 673 266 938 288 949 935 072 676 583 615 802 454 185 517 724 467 480 546 605 818 659 978 590 316 886 078 172 201 351 281 127 951 755 394 235 326 352 463 062 692 895 535 739 725 626 355 399 244 992 630 327 301 462 439 210 212 351 079 488 229 761 851 865 285 478 511 598 773 552 369 679 039 526 304 096 703 597 166 008 258 506 881 525 616 525 399 946 709 480 619 237 734 492 004 539 363 687 962 258 620 129 333 618 225 188 853 895 211 874 880 361 508 928 836 939 313 538 651 637 393 038 477 016 764 635 025 069 021 113 906 354 248 524 937 695 848 223 442 483 164 712 393 192 552 248 450 029 914 995 744 188 242 882 966 967 350 550 533 880 117 657 252 416 220 318 589 988 503 007 272 332 917 616 478 048 245 578 111 846 215 286 760 312 234 885 752 873 273 158 897 951 242 641 884 571 034 889 750 206 632 703 909 622 589 692 036 514 967 304 161 553 284 982 076 241 785 056 449 785 990 903 969 020 344 542 230 458 061 191 167 178 187 968 501 685 858 700 137 588 262 963 060 824 391 634 034 910 570 036 904 761 448 416 494 099 844 227 032 191 308 134 979 919 844 214 730 845 367 309 718 110 286 066 666 837 337 932 847 894 457 694 848 248 774 785 027 569 553 363 195 007 206 277 949 841 636 410 782 298 740 964 575 493 616 718 013 517 651 361 019 561 131 027 908 334 357 080 762 280 570 860 842 576 885 242 470 726 606 015 128 584 034 402 491 072 602 074 273 685 155 150 977 483 014 858 964 378 512 154 539 043 323 095 591 198 511 211 268 532 400 567 146 493 520 304 076 856 097 056 369 198 742 756 704 750 362 092 372 089 430 893 198 567 554 633 123 596 715 909 273 662 268 598 088 461 150 829 036 522 165 776 938 132 234 403 283 433 312 671 810 873 275 887 605 938 921 110 652 817 934 392 716 170 634 625 995 630 970 386 140 111 925 906 279 363 571 455 380 212 125 777 770 153 762 583 201 538 641 582 912 191 509 447 199 328 896 825 345 048 347 951 223 817 253 985 689 176 982 271 268 875 889 402 459 205 033 539 078 569 052 163 813 816 029 373 302 443 010 051 986 735 468 985 349 905 092 136 352 875 686 665 173 762 372 034 280 689 849 471 488 361 070 826 418 530 152 843 721 371 625 781 466 932 011 812 143 586 823 490 425 843 832 267 827 148 836 368 188 063 263 241 598 690 423 393 132 714 785 201 699 951 241 939 568 470 428 744 480 205 204 248 006 284 550 664 421 267 643 869 794 743 797 194 908 597 048 605 595 943 632 271 617 430 469 872 055 882 357 208 838 622 939 653 886 242 850 615 872 146 223 340 732 063 855 854 305 129 244 366 624 174 284 084 995 906 153 510 236 460 992 817 146 665 573 085 329 045 747 035 290 037 704 519 633 099 856 346 780 142 175 886 427 190 733 973 814 081 356 833 273 102 731 880 233 132 088 971 992 343 431 262 501 274 980 613 223 817 794 308 012 842 797 114 183 588 157 849 081 771 238 458 318 661 724 706 261 083 481 370 838 551 424 851 597 991 813 335 296 931 259 137 183 328 487 655 002 524 226 532 614 451 309 662 574 739 378 427 748 624 277 783 105 544 322 866 454 683 872 998 361 465 907 774 956 817 502 003 509 918 750 536 304 993 628 017 890 826 391 365 041 694 779 897 392 352 372 083 827 187 412 273 027 685 887 136 367 005 266 480 182 057 868 321 394 538 469 873 151 150 548 536 301 652 842 299 628 500 321 162 836 060 393 227 548 852 329 814 328 171 218 859 009 744 768 421 206 217 624 053 103 797 873 509 604 592 257 569 281 361 286 593 151 102 791 536 963 273 892 543 694 858 387 914 823 318 098 370 024 141 082 558 428 944 758 633 985 413 607 817 366 656 825 475 106 376 806 899 182 866 699 756 971 394 700 623 697 832 376 321 667 682 927 280 461 746 819 022 956 320 781 397 239 901 288 340 332 577 589 067 759 749 335 254 725 353 450 594 398 475 964 463 888 515 391 068 791 169 452 072 201 972 906 091 485 304 418 753 093 132 010 726 654 711 266 574 480 025 633 538 465 263 616 927 045 362 550 585 486 242 435 092 890 380 055 716 257 635 250 211 356 910 970 298 228 739 022 227 200 802 619 277 631 942 918 956 060 864 216 284 556 911 525 838 957 225 607 989 117 191 637 062 184 652 250 495 134 312 285 693 907 005 712 164 664 089 167 033 199 156 024 761 695 391 039 572 682 440 651 290 143 033 893 904 860 503 608 432 382 516 675 837 305 230 004 356 339 496 905 692 276 590 778 344 678 829 884 986 678 123 468 306 168 962 758 341 551 382 831 229 313 424 130 838 868 632 509 227 163 748 121 533 581 871 651 327 464 326 942 528 352 712 345 006 931 778 763 910 713 016 415 167 866 600 966 860 222 685 703 785 069 967 150 103 554 423 072 810 002 370 180 270 276 064 918 389 663 799 496 644 381 825 553 783 467 313 298 815 546 159 256 027 784 751 533 013 903 777 518 323 561 719 822 333 854 379 599 094 282 180 131 864 302 090 632 398 909 199 773 704 041 432 292 219 536 656 315 555 440 246 456 290 092 136 894 779 387 989 976 697 987 407 080 040 775 901 122 905 587 957 127 459 159 975 635 094 453 941 021 718 143 962 130 923 389 151 241 141 672 582 891 178 885 167 041 997 818 170 529 567 360 851 790 518 236 596 286 562 676 734 707 653 778 152 979 268 958 182 342 762 500 680 222 360 799 930 028 340 423 344 779 718 850 654 967 328 382 804 029 995 676 526 934 592 856 537 904 044 106 806 284 592 007 395 917 145 130 164 377 659 947 515 946 664 796 480 724 630 505 660 171 303 999 261 188 056 214 434 421 229 134 913 077 984 557 066 657 034 697 889 499 350 138 621 883 106 134 962 498 982 116 016 260 171 099 314 006 193 239 555 002 352 001 769 902 783 727 241 908 535 960 026 375 980 732 675 239 432 234 728 357 014 493 109 639 235 798 263 270 379 679 613 624 594 356 391 839 386 520 802 315 498 715 350 536 527 773 621 876 047 353 885 234 604 950 947 419 482 905 571 657 330 775 907 626 501 362 515 203 050 249 723 921 540 042 161 317 927 416 726 660 483 660 316 658 273 616 764 358 070 931 557 958 353 084 145 324 327 491 261 044 679 769 647 358 507 861 642 829 846 953 364 118 850 038 120 285 475 685 395 401 304 613 646 441 409 929 858 935 960 104 873 184 732 295 284 167 969 999 465 620 099 321 115 449 001 678 569 070 873 017 441 633 126 596 270 653 870 948 002 219 937 848 236 578 405 090 932 999 066 917 406 703 831 052 262 432 530 790 011 927 632 348 599 438 639 521 328 664 965 240 058 565 889 557 632 763 126 349 222 914 310 698 347 260 495 395 668 438 403 794 515 885 031 457 573 362 770 675 527 768 263 589 623 845 235 154 755 302 003 689 790 018 330 331 986 238 721 904 002 994 306 471 202 043 496 071 234 848 945 690 157 393 465 949 252 243 516 419 052 037 478 945 715 598 145 611 619 408 343 356 914 481 212 323 105 420 426 800 315 326 878 043 288 301 216 027 427 696 898 103 664 136 308 330 390 090 504 320 251 985 659 351 251 725 464 720 886 582 628 780 031 970 025 291 654 803 688 233 976 031 166 688 261 274 929 141 316 208 814 985 077 461 047 997 836 754 631 317 681 929 871 486 573 281 657 719 156 927 517 413 011 395 554 399 316 671 002 136 034 200 673 947 869 191 844 211 555 688 841 662 854 943 882 129 194 066 441 341 238 274 773 028 470 278 042 512 295 496 456 696 443 900 456 489 580 814 347 572 535 331 157 225 396 860 244 921 557 544 405 358 951 887 957 557 041 368 627 867 914 536 967 606 608 001 219 725 171 461 565 021 844 204 049 561 160 929 346 216 504 533 267 060 632 130 883 076 913 164 466 350 278 500 524 802 028 837 494 531 498 953 970 830 849 919 858 709 638 809 115 215 761 804 010 468 571 510 627 441 042 545 061 073 272 845 115 387 124 103 095 336 025 834 261 053 474 946 109 582 696 112 241 763 041 234 862 306 180 940 641 489 317 344 946 683 234 027 701 121 282 874 799 431 693 275 726 012 546 011 991 209 693 980 977 189 084 594 249 563 368 339 260 453 117 532 810 194 101 730 233 391 151 654 787 290 768 184 217 327 254 697 004 589 179 460 053 833 880 407 018 323 712 377 443 317 384 340 969 417 903 811 405 589 904 192 931 166 424 319 811 026 303 216 605 024 942 422 322 844 213 386 531 402 651 156 876 523 270 962 634 296 362 240 355 633 374 045 120 183 806 036 337 568 475 929 387 349 093 211 059 268 069 645 926 129 882 845 273 712 647 580 077 851 111 441 350 100 662 686 654 870 713 703 842 142 702 830 917 256 262 794 798 678 766 206 098 957 058 197 579 620 853 314 009 679 948 649 285 084 772 534 707 354 126 252 592 934 932 055 263 496 959 725 858 756 503 455 368 015 382 589 013 992 405 156 060 746 381 040 061 303 724 113 172 089 712 704 018 994 325 287 825 855 983 488 090 943 856 297 268 310 014 226 920 299 229 386 235 259 884 326 916 083 063 354 661 310 244 965 862 859 333 690 915 762 032 472 777 404 356 027 905 495 591 141 585 399 154 372 582 600 093 938 579 493 180 694 180 648 314 485 954 157 611 806 190 748 967 575 875 113 304 957 230 916 072 346 354 627 309 703 443 510 604 602 194 766 211 747 922 745 971 224 561 502 913 493 646 816 036 253 486 971 141 541 711 458 669 948 095 400 197 263 540 211 636 538 190 519 200 358 529 636 429 377 996 786 808 009 350 134 531 814 634 943 979 529 805 501 832 609 863 910 206 820 272 442 218 592 214 621 058 446 672 263 567 283 011 169 396 709 117 883 288 897 918 172 034 803 063 085 711 585 190 856 925 273 738 099 336 113 624 550 295 579 698 437 204 666 507 217 451 549 293 403 597 974 838 429 203 305 747 120 720 258 803 380 691 153 794 704 882 650 603 144 003 541 428 177 627 878 707 032 334 380 026 986 409 151 855 096 403 426 167 929 795 595 396 040 196 165 928 397 050 078 787 839 903 999 876 098 331 353 889 507 334 230 010 693 779 062 452 309 443 407 908 336 511 114 485 947 862 214 370 323 902 816 474 070 041 524 312 794 714 065 113 583 977 888 357 139 697 140 596 958 929 245 514 729 740 651 619 580 505 744 843 407 112 742 432 699 584 685 528 799 641 766 723 226 964 485 971 337 664 870 369 758 766 296 006 096 851 272 207 976 248 710 515 437 324 997 406 336 196 079 348 831 208 567 358 288 368 628 245 305 570 759 001 174 807 636 203 586 635 216 255 590 613 429 377 097 217 093 359 946 272 676 946 123 417 696 221 840 465 884 458 275 526 765 348 214 937 125 513 259 972 201 737 828 106 158 629 696 113 342 089 845 314 049 174 132 702 863 588 823 813 582 171 574 060 682 110 587 779 930 101 158 634 050 937 034 325 135 280 799 038 192 398 187 724 268 623 138 231 965 911 947 250 279 829 613 516 854 198 961 439 939 163 740 458 296 989 413 921 309 737 848 339 691 613 786 215 514 755 349 609 422 938 469 651 147 414 966 129 996 861 259 206 271 035 598 779 341 800 725 989 433 710 709 623 691 742 836 365 907 125 588 123 606 146 419 499 322 319 687 352 048 556 683 669 754 155 812 060 285 546 712 744 466 979 273 833 418 908 749 892 821 657 106 804 213 088 706 478 016 431 040 191 065 535 580 628 126 017 478 779 201 035 917 850 020 170 562 775 556 077 852 980 093 702 400 144 850 707 032 470 978 199 699 969 583 607 570 190 251 443 213 018 123 507 019 126 416 575 720 322 062 108 686 647 409 188 792 396 146 420 117 652 245 489 920 542 933 050 030 173 403 707 948 996 405 297 581 712 037 047 208 750 198 635 160 452 025 413 429 947 259 179 643 168 213 249 853 284 623 276 229 202 735 897 083 392 916 330 513 463 441 900 295 083 335 054 076 824 855 082 890 356 553 288 921 174 750 000 344 752 757 486 286 924 996 144 757 570 249 742 433 242 623 336 230 123 342 573 030 786 611 963 605 893 657 438 095 869 386 973 154 128 220 167 369 941 685 663 625 677 199 637 546 906 776 361 805 244 229 608 499 113 104 218 948 512 952 638 461 239 787 538 040 576 448 616 081 172 475 914 711 817 434 429 301 181 435 530 713 538 893 190 373 746 682 833 857 649 863 224 026 813 501 647 529 525 614 033 369 314 283 575 920 537 078 586 885 209 526 352 985 828 340 823 420 932 911 753 289 585 070 240 010 369 302 965 197 196 807 630 986 315 342 625 409 847 689 001 849 384 408 080 673 566 031 999 453 007 210 962 069 365 547 899 000 330 340 224 790 432 299 859 116 241 079 225 457 884 939 694 854 696 824 070 665 132 587 126 919 634 847 617 231 356 092 539 735 211 951 619 353 707 025 072 793 411 122 973 410 266 833 532 215 050 446 044 376 844 506 365 497 273 741 419 131 417 061 481 401 088 257 317 922 171 433 594 669 507 801 119 998 979 581 014 250 107 479 633 738 159 022 088 922 358 706 223 043 129 158 619 376 494 013 558 726 268 812 459 481 651 782 753 135 324 026 133 417 296 681 525 061 204 661 054 396 027 344 955 508 757 979 421 044 714 458 803 539 692 690 958 630 675 282 682 207 456 487 466 834 579 186 456 873 864 195 892 004 039 206 050 575 805 585 139 641 931 924 218 222 610 829 667 811 406 988 280 263 460 980 328 068 111 838 690 802 302 827 614 781 281 794 203 729 040 456 242 831 382 656 090 035 103 295 719 233 453 415 530 455 726 192 263 153 164 521 906 378 917 896 801 096 671 868 566 703 329 878 166 935 918 092 714 085 540 536 206 127 066 098 220 345 089 809 731 971 695 875 967 561 929 379 552 715 529 083 248 786 349 512 212 341 502 232 964 052 577 015 311 573 965 192 639 536 034 826 116 767 987 696 964 386 164 192 858 121 988 921 728 173 553 449 058 878 852 749 480 021 692 658 866 105 767 292 028 243 521 116 822 260 949 707 689 866 644 757 465 083 111 833 855 868 245 538 880 156 526 991 226 222 566 444 538 133 248 622 592 193 124 477 812 333 800 855 350 149 005 979 550 251 334 977 041 158 051 369 216 202 286 263 689 690 341 255 463 510 257 282 087 733 539 103 410 133 789 136 109 303 801 346 914 567 565 194 010 189 708 242 528 335 101 323 482 053 631 472 738 020 782 816 049 481 590 900 511 381 864 295 229 641 747 742 331 632 867 149 357 234 825 258 868 275 237 593 488 100 721 563 739 615 892 123 514 449 599 336 139 492 095 898 708 328 495 772 851 922 178 939 254 238 619 778 973 243 401 823 483 060 928 315 931 550 793 106 791 750 565 042 478 594 105 278 628 495 792 472 504 195 373 831 769 481 108 848 966 546 711 332 948 363 342 163 505 467 654 939 571 363 129 469 080 962 213 899 934 251 140 311 895 860 215 772 120 182 007 867 603 204 228 440 254 637 157 149 953 104 916 970 334 072 448 128 809 842 790 500 519 446 157 472 375 917 785 871 613 130 385 696 893 122 165 810 830 283 527 392 403 647 058 127 260 318 599 289 113 310 346 268 249 427 431 903 388 966 463 996 111 164 206 445 368 241 468 165 774 282 169 002 238 342 624 632 157 971 603 460 294 602 889 183 143 896 803 215 337 271 813 404 974 764 773 843 253 854 138 596 250 819 590 973 087 676 044 217 566 828 019 950 111 038 009 015 849 999 310 170 552 948 006 086 933 163 418 665 918 079 456 117 092 605 664 478 842 853 073 897 694 668 878 895 025 003 912 865 028 199 952 107 675 181 143 218 536 136 718 826 724 419 303 200 318 546 620 596 186 583 921 491 199 143 444 786 554 638 714 371 715 222 779 498 413 100 761 879 994 811 498 818 712 359 255 003 985 261 016 002 774 647 779 159 376 034 999 459 262 480 517 811 296 166 796 028 838 232 066 191 116 504 656 126 620 553 165 598 918 064 747 303 278 948 459 326 351 749 003 553 111 655 610 160 336 054 418 652 243 248 619 840 163 443 658 752 434 724 902 235 671 642 312 561 446 972 100 397 682 941 008 328 978 135 594 236 296 968 283 654 453 795 867 850 174 861 731 035 292 814 104 117 686 898 902 782 031 885 736 518 769 432 299 035 448 220 440 557 582 556 387 253 847 387 738 877 124 712 185 186 077 458 154 803 717 327 160 924 216 862 571 985 678 267 614 820 576 685 954 227 773 089 548 261 275 727 480 654 132 905 038 348 586 160 975 410 459 856 313 723 053 644 399 085 669 813 373 070 895 790 771 665 380 487 850 311 632 687 719 272 091 326 153 933 197 199 916 160 117 103 713 263 147 641 351 866 373 165 551 007 682 984 000 655 205 499 683 456 224 210 135 109 806 292 035 612 085 706 506 009 238 109 738 103 128 639 296 525 972 666 735 102 545 867 298 459 874 475 990 513 357 249 536 649 234 685 392 834 225 987 180 273 939 250 021 074 862 459 631 594 985 334 197 150 195 413 492 525 676 386 059 500 912 620 707 426 315 876 555 055 713 175 759 472 089 983 118 353 089 614 399 139 574 353 196 028 515 835 852 605 506 683 158 491 711 670 998 563 849 068 695 965 524 464 745 399 794 886 008 276 217 913 172 581 167 046 230 908 117 021 754 407 876 034 160 752 693 238 850 247 346 642 272 036 544 363 843 326 237 730 724 644 331 101 296 210 431 569 337 007 109 750 847 662 028 440 925 318 036 631 110 713 611 798 105 507 385 250 997 194 794 481 057 778 129 631 144 617 299 405 395 483 616 078 646 667 146 214 037 797 570 217 024 312 022 012 467 429 662 951 380 129 434 381 485 257 667 409 525 202 732 506 149 310 103 794 979 872 493 526 225 669 777 622 839 301 291 481 911 455 371 992 854 638 838 126 055 249 877 770 961 760 574 884 529 115 366 888 643 289 495 567 336 826 940 844 244 590 221 651 516 130 453 312 810 809 200 603 593 232 111 702 895 092 935 750 069 207 630 510 485 737 925 404 335 569 114 863 601 477 647 699 984 816 919 466 091 271 318 167 340 547 262 469 536 654 191 498 871 935 588 436 135 694 750 534 322 952 313 470 329 163 791 209 019 879 107 827 661 576 434 536 409 910 729 166 302 567 353 571 247 208 969 517 937 961 113 016 786 890 400 658 259 259 921 561 512 005 352 250 040 709 118 331 152 137 118 798 165 600 766 835 408 538 215 047 105 566 252 541 689 325 727 141 214 358 309 342 929 589 425 933 722 870 004 773 067 487 716 559 611 066 253 986 972 883 581 194 271 991 526 497 117 050 579 214 766 409 003 374 507 412 287 183 244 414 190 119 210 740 903 184 125 219 785 829 626 212 760 819 092 875 308 889 064 545 360 318 408 288 259 958 139 311 746 919 120 877 682 543 665 327 376 515 229 501 839 199 240 425 426 538 503 453 213 835 728 740 998 192 032 761 485 517 922 905 080 003 878 333 843 155 202 794 438 253 122 974 581 902 985 207 632 387 377 021 880 969 165 714 318 413 758 524 867 074 705 941 821 619 037 037 435 388 023 227 238 516 138 820 335 258 918 594 999 324 218 649 279 013 660 818 790 087 391 853 562 339 919 148 883 991 855 157 556 001 665 170 194 973 410 364 422 044 233 709 512 261 454 597 864 143 303 786 932 072 899 455 019 179 133 524 654 136 477 328 784 421 269 296 971 700 514 631 057 076 591 085 921 558 856 896 965 895 468 327 328 552 209 411 287 792 679 200 056 321 774 364 068 941 801 099 656 137 446 585 903 104 658 473 588 578 479 434 912 575 962 322 260 173 021 161 974 041 027 613 219 833 342 347 034 390 980 825 512 882 475 973 030 697 396 233 857 015 795 920 365 916 886 843 820 141 685 309 785 420 915 546 712 675 734 917 040 238 625 897 285 138 366 269 984 168 248 315 711 926 678 578 798 978 211 330 086 009 718 126 375 360 253 605 180 982 009 183 911 499 856 272 269 935 391 753 196 165 822 378 657 686 186 390 956 079 777 586 100 166 873 093 952 661 400 861 225 505 070 481 145 977 207 019 296 889 776 750 223 856 237 070 742 424 977 668 072 471 423 874 898 163 621 553 544 712 614 330 876 379 107 278 913 715 113 646 566 228 104 347 264 962 619 951 946 306 849 846 713 538 110 744 096 189 660 572 647 998 230 667 601 048 916 139 807 469 859 894 712 105 050 582 423 807 644 481 033 706 570 681 492 718 373 175 615 249 031 497 567 141 738 887 912 895 043 523 151 502 845 809 659 365 577 484 059 328 123 367 009 876 311 134 371 252 988 308 838 417 294 226 542 990 499 996 159 636 094 192 468 843 760 396 920 610 244 149 057 227 707 759 584 826 620 439 111 293 143 908 107 706 415 991 962 032 647 356 296 403 789 467 673 775 097 417 347 690 864 050 363 515 905 541 250 281 144 683 559 225 350 606 634 816 785 525 944 340 498 000 811 018 163 918 339 977 349 850 500 992 228 398 339 221 502 172 951 971 474 829 679 177 426 215 489 325 967 658 071 949 695 550 759 049 834 619 856 865 066 398 780 081 318 817 845 329 588 599 071 594 996 056 974 282 996 035 788 772 409 222 201 557 533 783 096 069 060 722 560 214 731 282 640 269 958 353 996 691 504 301 072 437 977 733 372 260 933 422 202 236 947 762 461 292 995 977 570 926 640 049 961 498 913 375 023 697 364 326 278 304 166 043 914 409 865 687 133 107 655 482 210 571 140 207 995 209 831 806 244 562 695 029 832 522 306 534 831 692 883 681 910 808 351 865 234 629 679 039 264 784 237 232 154 269 614 250 022 374 981 556 376 262 378 095 596 918 272 685 505 703 187 254 390 674 595 686 559 190 524 520 538 974 976 443 578 542 688 850 097 526 903 660 625 985 726 335 071 154 332 967 005 282 909 785 093 491 341 309 714 084 888 923 387 112 673 139 210 090 960 402 955 711 570 113 882 884 216 485 793 833 162 409 938 314 562 935 822 525 595 874 264 855 094 903 111 121 629 654 392 035 385 464 566 837 865 557 707 945 155 216 512 077 322 879 174 878 021 655 568 351 413 510 031 913 409 363 439 633 935 541 150 203 307 968 403 307 916 305 103 449 438 617 626 687 613 822 888 852 462 787 428 642 000 279 759 543 206 423 575 254 933 507 446 600 057 366 542 695 805 054 982 207 208 366 975 359 659 771 946 684 292 254 370 957 264 206 571 901 389 748 023 191 294 881 781 720 794 938 007 133 654 307 619 225 313 425 141 608 646 057 887 107 151 007 239 612 178 992 331 394 959 407 200 541 447 441 787 843 479 080 492 606 591 936 282 565 318 962 113 290 127 219 128 760 261 676 197 088 016 180 309 874 313 309 570 406 667 252 231 870 140 379 979 581 711 244 580 175 218 186 079 673 907 027 208 204 288 300 618 152 928 551 925 717 535 643 312 614 920 895 504 771 485 656 963 451 896 781 925 227 145 207 380 613 898 795 099 541 979 516 386 619 037 712 691 979 083 175 932 500 048 258 232 261 334 275 579 242 005 900 067 592 399 560 694 064 734 959 209 905 007 134 412 692 949 737 593 324 139 249 579 860 654 909 607 511 947 773 617 811 603 696 299 649 637 499 117 032 227 310 715 818 419 313 739 805 895 600 393 017 078 306 768 223 581 947 454 917 398 699 264 302 266 652 493 551 445 056 292 439 184 157 920 207 906 284 731 778 279 363 014 381 115 996 073 544 923 450 187 063 757 170 734 362 963 343 736 130 204 642 373 798 643 390 490 946 696 603 126 979 921 661 288 816 852 205 561 400 867 004 958 273 874 530 905 823 087 323 206 576 060 888 681 773 545 367 827 422 289 129 029 075 608 931 655 406 157 576 471 655 611 296 143 825 201 861 236 751 312 854 160 561 048 371 055 113 982 046 415 561 607 992 344 975 647 648 104 131 267 111 810 051 131 631 492 086 220 751 061 372 156 717 753 667 658 274 907 037 309 329 430 180 998 119 710 926 481 208 568 802 611 697 285 358 552 499 193 171 662 439 707 356 824 829 031 317 049 514 116 280 706 857 219 375 331 081 753 496 678 691 359 044 146 633 930 775 918 268 240 648 704 136 301 820 200 951 282 686 053 237 213 652 876 688 623 745 363 481 199 352 192 374 399 644 589 052 598 595 497 078 611 376 819 320 131 982 098 145 469 832 728 044 202 863 133 167 363 725 460 190 403 195 270 626 939 985 218 270 108 736 836 961 924 562 057 549 566 674 906 322 065 200 042 749 741 244 584 612 027 841 889 677 994 356 395 214 032 599 159 691 265 122 923 197 633 779 921 350 258 554 134 959 252 251 307 425 769 474 798 356 412 010 364 641 541 821 534 411 342 766 126 341 690 634 990 414 689 966 558 521 756 018 205 541 064 087 118 011 308 787 517 058 169 195 514 453 460 340 125 435 450 829 493 086 336 826 922 986 926 380 250 973 185 903 074 441 127 249 393 429 829 363 111 398 837 920 848 422 445 225 838 625 956 551 676 473 349 790 683 096 982 362 411 147 323 583 464 074 929 247 182 743 579 688 110 226 327 938 764 724 449 522 698 752 234 814 762 090 729 125 045 232 801 171 519 491 288 766 779 294 136 990 400 541 590 075 547 890 386 447 005 381 948 569 515 845 300 495 903 159 229 256 673 190 119 544 383 706 648 582 845 908 701 840 551 799 723 549 633 297 971 041 584 433 661 747 280 611 512 854 900 330 553 901 697 239 554 928 560 400 689 714 573 208 504 224 030 184 194 389 903 449 340 366 631 531 562 430 833 701 603 376 452 510 395 047 412 182 117 860 118 989 202 978 974 598 198 630 557 454 654 887 533 535 102 099 334 601 244 573 889 959 532 104 048 568 170 270 810 871 118 469 207 377 185 726 886 925 300 552 375 687 432 701 311 497 351 085 490 843 205 281 245 914 444 069 870 965 277 653 613 804 702 919 895 292 440 259 439 383 136 022 756 790 339 288 929 346 550 646 105 345 047 419 054 191 374 572 380 245 258 477 266 882 974 478 955 561 906 130 941 982 231 803 332 289 761 779 176 389 577 883 126 107 237 295 385 689 747 017 618 876 365 267 369 542 057 846 050 600 417 491 917 142 038 667 517 666 658 340 485 139 795 586 182 715 277 863 046 250 105 347 032 257 887 834 102 400 977 811 284 129 196 006 927 765 830 778 476 932 045 383 137 941 018 124 865 643 294 136 890 881 832 685 104 774 914 866 067 264 624 810 567 319 061 963 453 446 908 986 221 163 626 016 443 783 463 948 655 547 258 871 603 686 326 266 894 814 583 484 291 366 619 243 485 317 410 886 945 625 688 132 780 999 803 105 622 141 978 920 497 165 691 528 847 769 578 870 484 410 470 392 761 108 782 896 198 578 725 292 389 026 322 745 965 556 285 694 375 355 090 540 455 649 678 647 964 841 954 227 250 690 661 613 162 520 337 483 865 826 712 900 729 809 939 337 688 091 023 475 924 653 582 031 636 316 912 507 940 970 849 514 375 983 350 231 534 573 238 204 202 689 857 430 617 930 053 735 136 420 131 315 036 396 777 522 247 562 931 661 123 231 890 091 044 852 639 296 784 542 444 621 514 000 887 544 911 714 052 876 685 812 726 119 320 443 279 417 804 861 822 870 880 437 144 219 689 593 819 007 568 721 014 299 455 597 280 842 762 994 292 086 047 488 682 322 054 103 328 096 195 697 168 193 754 114 363 023 068 520 287 516 199 892 756 832 020 307 161 692 826 998 743 391 661 460 487 013 416 232 857 706 088 150 579 123 117 533 550 831 235 609 378 826 728 490 165 977 274 649 177 020 113 926 584 588 800 854 462 098 432 193 383 079 605 492 914 290 160 083 670 458 711 392 481 881 151 244 849 531 116 307 556 871 785 299 662 313 811 085 555 439 262 101 771 100 895 964 716 364 053 499 200 606 334 118 415 182 869 398 369 133 267 481 020 626 809 348 939 706 222 541 677 583 978 820 463 826 637 612 098 085 985 089 802 639 855 601 370 526 980 443 296 278 340 056 348 110 508 616 583 170 629 045 237 038 308 814 272 649 242 112 481 598 643 540 623 819 361 689 220 804 618 680 437 527 778 808 637 716 847 550 356 851 995 262 586 433 796 107 957 333 220 496 604 414 332 118 389 178 426 110 547 517 156 010 927 734 778 105 324 177 134 690 782 375 372 865 480 982 515 219 384 153 717 621 576 450 667 706 756 648 972 494 829 946 416 368 309 873 331 137 096 684 405 003 947 261 800 624 602 096 362 866 344 518 034 595 053 127 865 360 045 685 854 769 704 627 234 534 249 446 778 958 192 676 154 246 788 217 685 132 082 153 263 242 167 628 046 067 756 714 122 988 135 607 304 552 615 367 014 284 470 828 421 285 172 600 123 090 239 676 665 440 575 998 013 130 007 328 144 335 611 638 051 131 028 467 641 253 048 668 658 638 273 781 455 063 278 522 603 552 349 078 532 219 584 850 567 748 390 122 220 078 725 635 174 535 315 650 252 614 658 475 308 589 069 609 463 106 713 380 112 776 226 069 893 536 688 542 181 643 253 241 835 299 866 078 903 687 506 779 988 180 419 071 659 705 451 688 082 755 418 712 578 643 095 534 119 384 000 671 080 297 506 554 867 877 156 777 069 263 008 177 915 655 056 848 440 322 649 353 895 247 096 889 966 089 382 252 708 154 221 320 828 150 190 284 916 309 539 067 004 876 068 678 900 939 097 668 447 385 978 179 698 183 146 313 289 762 173 193 764 267 080 262 527 381 766 304 746 244 291 668 042 526 813 758 836 877 673 615 181 114 624 890 674 301 445 217 823 596 038 477 247 472 184 128 137 880 291 651 081 255 774 617 623 858 699 472 444 989 826 194 487 141 963 740 333 578 416 637 112 474 320 454 509 778 730 985 521 624 585 637 414 669 328 239 636 326 601 483 200 445 745 948 132 424 810 556 408 257 445 378 027 835 338 198 676 124 492 931 670 132 514 945 892 611 880 848 805 779 609 952 819 459 566 676 811 773 840 126 103 760 406 685 186 763 100 551 791 321 972 572 697 614 430 581 975 940 204 950 605 332 570 004 489 574 865 523 304 729 078 159 458 377 913 028 818 938 744 166 808 118 392 429 765 142 383 998 655 458 404 342 971 995 678 126 451 311 498 413 075 222 452 929 862 958 389 768 799 552 113 151 917 398 282 397 535 490 477 763 436 474 377 603 987 146 615 336 761 093 016 482 652 162 125 303 035 665 756 662 687 258 710 754 050 649 775 490 000 259 589 553 121 515 091 052 001 113 855 301 482 752 917 927 089 455 035 507 613 574 606 920 890 745 396 423 858 499 396 124 356 776 899 852 770 318 166 997 704 533 586 909 762 177 252 745 451 140 551 811 878 755 106 269 496 818 124 771 934 202 838 184 990 069 339 756 992 038 087 773 375 178 136 540 916 857 658 759 858 819 062 010 399 097 967 564 213 340 217 853 332 600 026 855 011 151 163 479 169 034 857 007 481 276 510 690 166 066 522 060 672 669 207 392 745 549 195 916 622 901 150 175 296 424 007 537 235 716 996 031 851 203 251 963 468 701 524 222 937 598 570 083 858 230 709 917 770 484 525 095 344 336 385 708 950 666 147 897 666 827 114 883 566 087 250 778 777 395 050 470 546 954 826 901 935 518 520 362 554 872 146 446 159 924 333 766 702 379 291 336 769 671 833 925 332 789 293 352 734 943 256 288 482 608 357 279 517 366 545 110 058 709 682 905 119 235 217 687 867 938 316 902 149 344 637 817 647 302 688 609 376 688 823 355 779 916 711 815 847 198 778 085 145 078 247 435 071 238 952 760 061 093 346 427 763 952 374 679 420 678 891 443 767 148 322 201 931 452 565 971 444 182 090 185 345 083 943 278 529 626 847 902 995 928 976 273 357 111 556 769 954 868 608 781 589 778 746 804 648 326 177 294 607 518 374 170 922 632 906 028 663 301 184 239 125 652 482 486 234 192 801 246 939 703 814 258 346 483 380 185 045 437 590 758 483 770 370 843 925 240 999 669 467 431 356 913 502 859 791 087 249 376 949 505 116 488 001 824 390 510 211 295 513 456 229 653 607 056 321 997 509 961 272 264 635 790 414 994 673 332 531 060 077 218 850 174 385 869 375 940 354 576 920 446 098 668 550 734 219 195 484 877 718 705 402 791 291 580 925 208 784 938 065 627 353 325 387 355 170 664 711 370 486 333 795 137 515 757 731 946 094 541 822 804 732 687 938 638 055 284 975 026 235 966 326 419 941 826 574 078 596 899 255 672 349 980 884 249 239 363 359 228 456 540 648 347 454 093 470 327 348 704 760 318 539 645 990 533 007 129 642 461 621 536 652 807 958 872 827 551 495 491 860 731 647 511 138 370 170 847 999 853 695 318 748 901 421 324 118 577 517 567 005 603 361 654 077 399 026 592 984 320 118 475 900 079 757 755 587 346 178 985 105 954 175 508 782 971 615 996 781 387 165 382 882 489 089 755 497 624 614 076 649 282 379 777 524 127 170 571 546 103 145 752 501 549 256 750 214 456 335 686 718 079 472 288 010 631 948 388 041 224 567 284 281 511 400 206 572 210 136 271 335 603 668 064 322 762 134 782 414 994 204 044 441 048 325 951 838 566 588 890 815 336 578 351 937 729 886 214 231 746 159 913 886 941 142 978 105 672 724 462 465 509 712 709 265 907 342 015 429 421 636 107 421 509 303 111 208 170 863 085 632 588 926 605 904 724 914 396 790 014 370 173 035 539 302 462 329 466 653 971 554 709 542 429 007 011 968 906 318 250 534 361 337 464 571 171 456 395 620 887 041 580 045 756 264 946 049 381 813 651 869 755 435 805 437 006 961 338 231 787 835 518 010 614 456 849 055 125 085 478 373 065 615 345 101 381 441 435 199 227 230 595 039 224 672 969 567 891 251 243 637 256 944 009 502 295 362 498 245 775 784 255 703 113 272 776 782 009 002 965 022 555 624 793 297 776 821 479 784 732 797 211 568 739 994 513 173 380 695 077 100 347 086 961 978 694 411 301 494 196 217 923 069 356 044 357 195 584 192 951 172 110 777 297 341 870 847 913 953 261 523 258 985 775 312 129 737 136 917 119 727 916 602 307 242 732 849 501 817 869 131 855 524 344 835 381 096 278 571 399 146 346 933 891 587 719 502 589 640 612 978 963 907 928 193 810 862 647 027 559 402 371 987 128 031 134 530 624 133 434 008 726 537 454 958 141 585 719 233 852 736 514 412 822 594 422 701 833 627 154 346 970 512 842 851 654 908 545 635 559 704 473 005 249 011 294 506 791 138 586 319 457 953 042 118 904 520 775 257 977 269 940 438 047 967 827 650 342 381 517 408 906 609 955 381 762 274 255 065 166 590 655 705 979 151 942 820 884 664 418 427 709 500 963 607 299 603 599 808 186 090 123 120 174 413 829 597 984 769 714 864 505 879 011 185 968 822 994 626 397 780 174 129 206 653 763 499 992 147 383 609 256 223 229 118 104 791 288 084 334 449 199 484 866 041 265 010 287 730 808 823 060 811 312 850 296 493 067 542 060 874 671 531 373 835 928 085 599 010 945 402 310 721 765 522 372 750 865 271 118 639 305 797 163 987 975 796 246 677 267 006 142 511 315 568 889 417 941 665 004 234 935 129 663 602 081 432 712 973 808 585 129 220 495 030 332 458 061 973 916 625 379 837 618 058 813 680 244 698 730 111 190 983 520 166 002 694 360 749 651 344 695 281 334 482 220 782 988 233 426 257 142 953 102 719 199 888 445 405 890 861 445 593 351 368 276 943 228 057 146 457 293 999 898 085 810 306 163 219 375 599 375 505 208 240 146 764 638 178 224 680 295 846 149 514 852 629 089 609 242 988 113 744 357 881 896 356 599 491 055 553 107 394 694 596 275 018 936 560 866 168 614 920 562 740 915 340 880 823 716 382 278 843 759 659 004 416 851 646 679 057 043 151 644 481 106 801 172 360 059 021 118 183 225 080 461 658 624 087 429 407 604 033 744 179 437 623 653 468 614 783 268 827 164 115 323 598 585 769 729 912 596 460 764 881 636 430 360 561 895 241 047 142 522 284 597 076 491 862 886 094 220 904 194 903 885 448 479 701 578 751 399 162 295 453 145 356 379 863 240 970 139 269 098 049 672 983 410 873 250 224 481 610 547 961 714 783 046 072 679 822 394 966 615 899 296 056 793 357 378 571 107 334 536 610 550 337 745 629 001 861 367 873 629 010 488 817 121 214 998 648 229 109 835 092 598 287 078 751 226 301 615 534 085 346 612 456 768 638 884 725 413 970 317 070 830 918 859 429 767 784 569 246 148 675 465 214 781 396 227 701 656 817 502 360 573 219 712 108 472 775 396 086 476 265 887 655 398 616 259 401 402 901 136 311 194 477 272 649 259 650 340 413 405 917 399 713 918 478 748 404 845 414 529 102 785 339 048 094 715 034 899 294 298 991 082 315 039 393 821 153 984 956 954 088 442 411 076 002 335 249 475 473 272 167 148 334 286 239 087 761 699 307 725 098 043 324 519 868 123 344 421 442 802 616 038 052 466 508 638 262 760 143 774 225 622 425 392 551 594 295 329 402 849 711 839 988 383 943 872 100 492 677 170 392 970 321 072 840 432 102 131 372 279 170 766 400 249 598 682 757 740 816 951 115 719 130 457 191 455 265 729 862 577 164 290 329 475 238 942 937 605 596 038 589 656 220 044 298 765 334 381 971 420 697 310 820 711 978 599 957 695 990 955 864 589 588 464 619 668 397 251 661 182 285 070 256 621 541 072 229 923 595 642 033 768 881 683 400 682 524 909 445 641 952 210 498 038 847 466 342 668 103 779 259 621 817 132 567 809 431 698 404 548 289 597 415 353 348 250 804 739 029 636 019 085 089 893 216 797 013 873 021 325 777 635 228 880 095 831 559 834 136 075 883 559 040 205 455 224 714 892 067 965 578 464 925 968 730 228 942 041 308 462 883 496 664 180 771 686 172 812 472 465 432 189 587 347 558 673 440 607 441 124 007 629 082 998 868 399 410 377 950 623 247 814 565 955 805 281 924 255 785 770 898 369 443 876 872 117 504 672 120 856 344 341 489 717 049 049 709 243 370 867 203 775 824 170 257 506 542 129 819 949 039 919 572 041 135 055 626 232 471 487 116 945 632 652 130 572 845 860 875 732 853 777 384 331 016 488 576 818 811 473 531 521 886 638 858 072 018 695 684 650 658 619 112 779 692 554 052 663 622 490 581 931 707 860 792 997 004 524 840 219 976 460 522 178 226 608 292 146 324 350 014 734 710 921 346 769 866 006 735 556 834 281 162 959 156 286 651 925 200 890 699 431 954 257 696 834 640 895 993 445 077 926 227 514 255 156 830 742 447 439 424 693 711 065 098 405 567 863 794 104 253 110 094 690 183 760 774 871 821 244 468 203 886 956 800 404 566 067 415 436 769 077 148 296 084 077 411 504 203 988 499 557 857 965 632 375 193 488 829 146 580 846 252 551 359 887 759 279 761 495 162 474 979 567 355 763 495 318 930 436 797 507 572 324 768 699 399 199 714 682 645 984 475 487 755 170 788 369 974 307 842 721 674 678 607 123 024 296 754 298 925 761 070 407 263 065 555 445 613 401 122 449 956 704 994 328 683 369 078 290 338 691 361 003 865 041 717 828 943 431 018 256 612 832 512 684 702 529 133 139 537 765 209 307 073 025 961 096 955 472 993 778 077 894 076 474 659 991 125 320 773 464 221 894 758 467 915 084 981 015 313 330 134 858 168 458 207 901 352 458 650 026 842 416 859 211 391 265 604 224 873 443 949 940 540 644 877 367 886 875 372 655 749 877 744 928 625 268 860 557 223 173 884 630 425 297 204 713 756 418 159 538 643 536 864 914 953 234 843 746 950 329 496 229 435 819 204 126 629 173 021 362 240 383 911 597 213 326 649 163 946 871 601 396 430 738 741 617 211 420 762 776 138 797 235 201 272 878 475 943 464 645 252 002 513 140 827 712 385 658 189 067 540 613 359 182 805 024 204 169 210 545 758 122 487 738 943 937 973 674 908 781 140 494 426 648 312 769 713 569 173 179 652 793 958 973 726 263 344 931 669 646 907 317 168 688 291 224 518 209 395 987 870 338 424 440 655 845 915 217 090 532 553 925 781 904 063 588 930 448 997 010 042 743 355 818 427 160 024 108 938 496 771 729 319 186 883 726 427 447 842 291 301 753 803 728 218 503 080 124 988 766 563 573 024 171 398 472 784 225 470 402 157 463 369 040 940 256 405 882 053 698 389 214 430 900 483 043 258 330 089 975 773 464 697 151 697 761 661 443 919 391 627 518 474 552 302 996 353 370 644 675 916 895 147 797 332 870 362 929 216 002 113 870 304 695 724 843 063 182 327 322 533 788 924 494 510 574 670 578 704 204 151 090 273 415 743 804 067 891 408 863 235 762 830 870 061 581 731 337 632 126 187 403 567 697 543 614 844 376 155 658 875 475 684 677 187 839 320 237 645 428 600 854 033 109 051 260 804 981 639 850 379 620 055 985 483 751 574 436 341 334 114 916 377 406 696 002 987 272 054 496 175 174 451 862 635 222 730 303 635 272 893 535 907 374 281 624 177 463 284 972 617 491 293 965 008 569 821 350 769 809 353 090 398 588 388 405 188 988 738 173 301 817 893 020 732 782 883 243 222 750 466 991 955 028 102 944 153 015 236 489 121 646 759 297 152 286 243 281 421 162 983 019 536 662 057 392 311 962 954 170 235 088 891 296 276 963 823 031 030 983 425 692 275 367 992 281 580 557 083 181 555 096 696 103 417 498 902 431 962 605 482 270 529 028 220 534 912 429 174 199 684 706 353 452 603 306 865 408 882 815 924 857 940 009 463 043 540 949 097 430 083 266 658 832 761 639 034 062 676 858 872 497 274 165 668 810 772 713 475 288 009 683 694 267 479 369 878 128 188 265 365 250 344 479 837 205 577 361 721 045 417 926 226 009 322 238 196 704 085 175 755 274 177 927 328 035 264 509 075 320 971 847 633 730 943 853 733 470 784 834 482 454 897 899 313 656 938 329 205 496 635 763 107 990 038 618 983 529 147 244 935 252 771 744 338 290 787 889 818 818 186 501 962 764 283 875 417 804 523 106 401 603 956 686 770 820 412 863 489 983 393 576 323 146 867 515 979 895 368 879 852 386 138 313 256 755 634 006 856 674 907 951 583 153 359 030 239 327 886 953 103 257 656 924 518 361 026 619 291 469 331 552 013 476 369 972 541 557 276 161 136 964 441 562 717 940 055 883 831 844 752 965 549 844 261 278 612 472 316 332 122 592 406 355 689 677 528 238 516 160 271 341 333 043 419 931 999 496 029 218 337 562 429 278 982 132 149 987 672 733 369 769 300 252 362 507 771 953 507 017 107 825 359 405 314 511 807 498 158 866 946 970 979 491 258 463 002 021 856 293 902 974 342 179 833 856 241 930 130 923 290 024 489 259 627 690 400 611 496 885 752 642 249 769 613 865 582 160 152 931 966 811 369 581 996 551 032 193 039 685 396 250 314 654 203 580 784 299 372 494 055 803 433 895 105 173 968 584 755 821 249 187 046 980 403 223 528 086 902 152 531 544 817 337 311 709 134 986 702 473 500 009 522 263 653 030 371 547 271 343 136 271 973 542 248 838 149 654 159 106 993 996 528 419 981 872 306 080 177 421 439 304 805 988 625 012 454 927 519 183 736 825 105 557 661 482 972 692 334 158 490 845 558 552 155 438 541 606 037 649 780 226 323 083 530 222 478 647 387 760 651 441 229 198 069 514 287 313 053 866 628 048 921 117 002 852 328 014 320 785 793 203 101 484 703 201 983 853 273 971 508 046 114 377 440 717 713 337 815 869 289 422 537 339 975 477 697 412 864 975 092 126 119 577 118 578 194 936 057 089 895 296 991 838 766 108 470 206 495 326 547 202 880 160 868 138 861 159 825 382 195 660 787 795 355 166 244 997 618 217 060 971 357 850 922 831 700 796 290 057 407 284 102 746 381 852 631 073 081 768 723 837 417 497 323 646 461 952 895 711 736 045 815 912 938 086 442 570 702 905 674 559 199 495 605 209 228 617 160 141 686 344 917 434 720 456 656 054 560 660 871 937 076 340 219 709 612 389 786 494 141 171 854 734 990 837 280 289 078 165 030 422 019 493 357 414 994 753 855 036 299 049 315 256 492 034 682 681 376 876 442 755 652 394 759 783 417 319 260 636 761 948 426 588 445 932 845 122 281 675 359 769 595 617 427 180 401 262 618 235 981 163 699 993 002 080 972 044 055 342 321 643 023 500 911 492 314 439 162 564 082 708 247 807 875 309 839 386 435 069 824 460 856 757 818 932 176 338 315 771 457 767 192 006 566 411 485 186 274 763 821 002 470 927 640 850 605 546 615 050 522 336 703 353 378 688 283 997 459 023 387 840 079 875 738 847 105 357 178 601 772 774 418 628 074 310 583 309 704 464 077 938 818 023 926 859 268 753 180 872 332 991 065 441 841 758 504 471 679 345 013 858 139 898 035 266 597 281 873 547 756 840 551 674 829 968 308 443 132 897 679 704 592 870 838 529 698 292 704 103 839 564 061 262 653 714 248 628 103 550 617 470 806 859 797 944 249 709 261 879 441 498 769 905 879 438 944 376 761 222 020 007 785 500 036 268 769 063 012 148 247 905 569 943 394 297 360 399 527 690 354 144 134 217 723 909 367 999 489 268 897 418 452 613 058 922 044 747 420 251 044 431 327 561 648 197 132 754 364 199 705 031 185 473 217 144 981 284 989 720 239 489 871 136 622 259 743 588 774 369 372 500 583 222 032 137 672 944 785 186 745 914 464 880 948 789 130 309 441 061 438 653 431 677 461 768 687 998 634 832 126 850 803 487 382 075 836 023 633 285 701 534 264 156 646 008 652 130 431 668 577 259 117 511 516 831 548 531 847 156 284 085 549 776 870 418 457 799 977 413 315 182 101 914 526 442 401 809 185 620 733 112 914 712 511 957 438 347 744 242 348 962 438 686 387 624 453 583 823 772 177 748 150 032 117 896 605 624 355 376 448 429 389 774 092 066 232 630 150 769 870 081 620 720 268 811 142 871 258 626 824 300 286 897 837 078 596 118 510 279 077 918 874 583 117 118 078 369 169 300 855 593 913 807 711 007 229 829 158 121 688 216 675 675 842 367 775 418 998 646 456 313 262 670 577 470 295 404 900 085 314 619 441 575 838 213 578 631 929 069 326 955 581 055 322 280 100 577 730 785 243 916 759 659 801 522 184 055 275 370 379 993 712 767 832 546 776 932 158 987 623 649 174 045 662 061 964 196 859 028 810 454 111 501 287 870 776 437 514 074 397 040 121 610 728 905 517 512 484 256 780 003 960 799 077 475 521 592 393 500 795 576 266 663 824 400 132 599 409 591 635 383 671 636 353 122 807 537 758 825 293 503 605 246 889 343 504 538 800 440 713 758 651 048 875 709 992 226 157 860 505 595 389 067 386 559 832 237 554 005 311 475 762 052 861 897 554 582 355 172 849 064 984 484 579 027 114 061 407 832 242 020 994 975 330 891 847 247 343 808 580 610 784 427 196 051 889 083 988 140 268 794 404 744 490 277 475 052 982 556 812 392 711 331 083 234 969 345 436 391 704 771 500 733 423 010 607 151 943 567 779 748 053 266 522 722 643 316 311 788 791 370 468 448 182 001 477 213 891 764 736 925 898 455 135 531 959 980 912 131 201 486 133 061 058 528 201 940 580 602 664 339 292 694 483 089 921 956 188 793 849 061 216 893 705 511 320 756 535 392 928 353 192 909 413 136 260 454 769 678 248 605 270 500 570 838 869 765 664 243 350 133 671 439 542 519 319 062 581 284 154 103 897 751 669 998 429 159 089 130 775 276 782 904 653 612 506 232 867 288 395 232 524 297 784 485 349 410 242 405 677 473 044 576 733 019 126 789 729 281 820 711 980 050 899 299 952 009 247 182 137 051 712 551 074 307 989 392 721 030 608 102 059 290 108 886 791 613 380 959 144 501 113 261 673 776 285 308 279 552 025 812 658 125 887 391 332 109 710 236 873 896 742 234 076 249 892 333 518 784 907 189 934 758 485 864 864 922 471 734 210 200 180 716 474 013 554 864 939 116 436 863 421 032 181 315 096 030 318 516 325 362 274 427 891 597 288 524 391 664 039 595 616 233 848 658 426 128 739 951 739 493 238 497 621 712 999 715 414 971 414 730 262 591 069 753 216 850 437 669 769 059 240 917 802 215 027 760 185 462 972 022 431 653 314 503 632 706 236 479 943 958 907 945 727 580 000 066 902 208 394 026 308 790 598 587 833 221 966 865 811 458 936 646 931 865 613 559 412 400 312 221 675 175 508 245 558 684 285 023 296 979 401 293 438 947 694 476 558 225 746 995 048 230 599 277 670 484 425 888 538 742 506 093 919 937 366 307 181 861 561 762 186 862 675 833 988 255 342 989 340 839 236 180 978 380 205 288 374 714 376 219 590 707 196 170 738 049 266 468 525 705 727 560 322 753 467 795 085 642 634 327 297 167 356 014 162 328 029 026 955 083 215 905 707 647 179 641 258 178 938 003 564 685 362 184 044 465 051 868 065 527 569 128 848 610 844 421 241 355 603 057 074 979 663 756 686 291 340 989 145 420 214 919 347 128 962 461 158 648 093 935 950 050 637 553 150 976 441 940 391 329 282 809 206 750 176 565 004 684 416 958 717 692 871 248 314 145 139 594 868 994 255 017 431 703 818 315 591 811 506 932 940 236 698 922 688 203 507 100 604 972 756 206 724 248 679 858 872 632 156 996 670 650 352 533 109 663 997 431 384 064 911 652 531 235 048 425 115 335 143 334 357 114 123 291 479 167 591 038 215 752 917 203 933 569 650 371 713 810 987 317 028 910 982 252 661 510 531 799 000 708 025 626 922 475 656 760 345 284 565 641 180 031 999 062 085 310 290 034 065 367 749 067 395 514 840 562 703 329 862 464 219 874 049 713 557 809 538 806 671 231 235 053 249 750 623 956 538 072 148 832 017 373 477 914 637 418 804 011 327 470 892 054 962 222 385 019 391 977 183 904 401 953 346 415 934 782 260 005 135 782 130 524 569 478 903 673 841 771 256 489 139 782 599 062 830 323 775 317 723 500 332 491 329 718 727 130 883 141 769 779 791 915 054 537 300 422 937 901 839 234 273 694 904 443 367 499 574 422 937 202 982 586 007 535 015 329 521 330 034 245 110 723 430 369 959 787 766 056 889 292 726 141 250 684 617 390 318 780 620 710 576 532 957 379 999 848 232 032 298 578 560 673 536 283 949 506 885 197 223 457 352 675 651 790 001 050 804 195 702 788 266 762 647 601 875 814 790 526 371 425 001 436 396 739 652 024 960 384 726 372 555 476 904 528 875 308 457 535 580 786 471 263 139 744 069 126 078 018 724 888 596 505 645 286 561 562 113 485 073 869 320 156 609 477 050 818 423 545 007 041 954 096 695 171 805 961 248 462 396 574 053 260 346 710 130 160 613 636 821 015 069 393 206 920 448 585 561 130 705 650 125 057 267 119 113 251 428 215 637 788 942 714 266 984 862 689 163 689 063 450 189 491 018 439 226 111 451 587 020 738 975 792 830 617 443 083 266 293 888 185 994 647 756 542 714 700 218 266 246 828 887 889 387 530 188 000 525 222 141 336 413 543 887 322 960 990 489 091 319 093 888 676 319 899 417 195 227 544 087 635 819 359 369 514 136 725 006 837 951 704 747 723 118 008 132 742 544 931 506 912 131 684 280 324 242 668 031 100 979 355 767 840 316 648 630 929 702 384 468 988 384 981 653 772 795 098 722 983 500 029 905 347 839 481 268 254 176 364 634 365 876 629 664 837 345 864 264 389 122 627 156 554 492 604 732 230 989 536 841 421 376 417 795 684 798 395 612 193 434 544 969 521 166 227 927 060 584 167 321 643 798 702 610 086 006 682 271 486 805 304 469 958 278 651 595 984 627 836 864 896 826 253 550 293 457 168 474 294 253 951 215 150 504 415 488 066 984 025 214 709 180 869 626 408 542 345 945 911 781 111 220 893 216 592 051 949 399 446 375 521 415 289 335 985 878 341 707 574 953 020 850 851 281 866 294 137 310 333 561 284 623 092 790 230 776 677 931 831 294 842 573 167 027 646 753 053 091 850 682 427 994 151 684 159 420 703 083 636 732 097 468 284 070 065 048 980 090 774 042 953 619 942 065 779 220 284 335 943 017 412 713 583 807 979 558 832 993 394 818 701 779 473 807 593 476 922 168 323 984 587 988 661 235 807 073 201 762 918 300 632 753 798 179 280 970 733 035 882 108 262 396 562 361 184 782 799 376 708 024 075 637 059 393 992 870 825 207 419 460 922 509 091 323 860 249 472 019 519 384 648 759 914 960 785 813 356 125 458 612 352 733 436 397 294 595 287 140 420 119 931 826 768 518 767 261 103 544 803 805 738 642 045 410 910 523 865 220 784 877 764 861 097 327 479 385 278 636 857 970 867 104 038 557 829 788 071 799 981 566 227 287 401 530 095 559 923 541 456 566 773 359 383 855 632 234 402 151 555 810 389 227 880 009 932 674 593 726 234 360 252 992 363 137 345 023 194 843 042 437 141 556 872 125 954 755 565 901 863 302 342 381 999 340 078 169 520 038 352 779 111 352 888 614 117 904 970 027 218 049 530 778 156 006 679 670 557 657 406 219 526 623 250 341 531 606 379 340 125 720 365 313 189 894 829 041 503 482 049 372 046 824 540 047 602 422 531 100 152 719 501 465 065 700 793 971 733 579 472 643 253 555 543 714 319 553 572 416 146 674 397 607 927 950 756 600 587 172 681 385 424 078 985 870 523 010 580 885 719 407 579 074 886 247 613 307 279 977 273 234 631 953 912 186 346 907 914 343 155 462 625 736 393 218 421 708 719 343 258 616 877 016 956 648 147 684 869 070 740 355 456 255 484 364 276 918 718 723 266 212 171 868 169 482 792 610 715 664 483 125 178 836 797 325 856 843 563 696 078 966 790 934 328 831 650 869 290 308 448 602 954 437 030 650 038 356 349 676 226 978 530 758 100 126 903 116 809 546 773 251 110 190 804 368 357 777 817 365 860 819 639 746 029 396 217 047 800 978 705 957 719 926 089 247 969 129 636 302 524 326 658 685 701 736 018 488 477 563 669 213 306 566 346 075 796 212 030 975 202 857 951 565 128 636 772 608 018 344 585 638 466 152 855 114 746 211 220 665 461 405 927 136 486 128 196 794 741 384 097 063 071 431 129 888 304 723 690 052 034 006 073 692 933 710 920 282 998 647 130 785 192 416 319 508 206 012 892 349 803 677 859 544 414 778 329 590 313 386 445 820 988 279 731 129 141 745 675 596 107 792 866 695 310 497 836 945 528 446 895 743 825 781 743 426 664 704 228 099 203 920 417 253 559 316 886 294 575 325 662 452 830 175 007 456 776 812 222 609 439 348 741 972 110 987 754 856 594 144 221 880 728 004 600 889 488 492 921 000 180 059 529 233 250 767 044 277 245 868 015 109 291 263 765 851 010 942 771 988 458 592 110 527 300 963 019 192 744 617 458 825 588 945 323 660 124 271 955 403 175 132 350 688 778 944 005 708 507 161 039 503 035 030 706 946 489 527 916 053 522 794 755 847 860 552 769 161 138 705 970 884 758 086 537 994 980 565 940 462 496 551 739 480 634 831 850 544 028 592 468 378 788 895 570 724 084 766 903 194 023 879 980 891 654 639 241 503 434 372 011 269 226 037 989 831 567 541 956 565 981 357 770 869 484 509 373 576 976 276 350 019 439 901 283 072 385 769 556 212 195 719 611 691 566 194 573 315 800 218 270 816 658 152 343 029 337 542 605 967 171 599 739 136 445 915 379 720 273 052 477 235 127 223 302 689 123 957 890 509 346 865 162 279 544 884 467 165 219 698 127 354 508 666 333 972 370 394 057 389 827 740 036 695 350 959 983 421 233 199 839 904 475 803 637 136 840 901 903 458 344 487 281 949 595 303 418 652 434 071 215 123 771 794 793 157 201 552 992 203 822 080 363 516 726 465 794 285 538 152 997 788 040 844 859 124 843 449 859 471 013 961 436 323 889 881 833 124 559 583 524 304 027 456 855 736 434 116 603 502 126 229 107 784 187 022 287 404 272 170 088 733 703 121 058 275 477 383 521 861 037 755 421 488 950 469 358 127 149 387 300 403 286 325 281 513 224 159 662 795 635 925 432 924 020 674 354 819 311 033 841 963 563 176 196 856 032 689 813 809 457 217 709 944 406 450 095 869 259 030 021 008 099 250 349 376 196 617 639 371 778 915 775 013 020 520 737 389 970 969 705 143 207 392 536 990 389 736 966 485 302 959 079 283 149 962 488 918 372 247 676 561 395 990 789 430 060 329 955 715 477 658 512 645 496 657 390 506 800 654 520 480 687 965 923 019 820 948 099 293 154 205 459 269 936 321 590 932 131 994 681 820 193 027 436 669 478 220 357 152 780 454 045 353 330 642 429 453 736 319 577 089 979 578 193 223 408 993 792 640 262 373 762 950 437 577 109 798 890 148 910 762 140 630 260 676 579 386 190 401 209 912 775 075 581 148 132 569 793 026 002 964 348 682 549 482 679 226 119 218 438 376 241 441 114 573 486 109 327 050 079 819 455 922 466 620 101 099 734 947 893 573 150 263 074 662 528 266 120 599 019 770 550 267 852 829 568 450 734 480 970 360 921 075 421 471 912 917 863 822 561 442 081 061 868 619 735 225 558 046 144 481 559 697 736 590 560 745 990 746 148 758 258 549 808 258 217 354 600 960 526 599 999 121 923 626 450 668 040 960 741 995 836 044 430 573 475 151 193 811 966 942 593 793 601 334 700 654 536 515 927 719 456 564 868 093 577 154 348 702 838 947 796 832 936 847 105 500 845 862 942 505 530 075 625 379 138 014 838 581 456 683 963 846 000 779 704 080 618 123 947 854 195 202 392 713 222 563 646 881 467 517 068 992 557 667 120 120 746 018 124 720 589 686 841 576 061 823 933 266 841 082 454 421 207 088 163 475 438 887 521 755 994 937 031 271 847 210 459 594 309 433 763 420 847 464 434 188 602 212 590 799 477 930 629 997 021 497 125 600 836 968 454 160 130 438 958 787 579 340 915 338 905 090 969 872 417 326 456 708 461 104 748 296 618 206 047 006 142 716 279 604 248 283 674 685 617 532 615 696 932 401 786 802 511 937 163 046 347 444 914 831 430 441 858 737 736 739 016 529 619 731 200 784 561 041 178 401 462 134 801 274 289 851 385 102 794 386 830 912 218 955 220 998 731 791 036 079 742 136 454 660 107 609 063 483 198 310 544 588 920 178 241 990 763 268 765 546 015 525 721 272 537 643 018 660 409 387 694 091 874 407 065 877 398 370 220 238 723 027 910 434 061 567 290 255 470 217 562 022 353 400 539 680 724 330 596 701 122 047 443 078 082 268 653 475 712 366 928 019 517 703 024 569 633 837 926 454 518 271 709 089 004 802 378 509 211 253 013 298 270 390 732 636 158 242 041 538 436 539 376 942 711 986 546 397 865 462 997 164 622 161 085 257 972 534 720 130 678 423 012 010 578 373 387 699 098 244 435 336 451 856 909 432 152 677 859 637 142 449 244 054 817 316 686 361 582 174 310 897 461 393 564 502 336 007 455 669 887 546 429 979 206 902 073 026 655 782 419 800 881 289 335 900 476 277 260 746 540 223 452 277 081 162 584 842 949 080 720 639 659 629 786 754 250 199 548 728 544 903 689 759 994 336 415 362 731 113 323 057 774 631 898 458 434 094 158 376 121 127 791 404 129 038 408 878 090 063 001 199 436 713 732 049 275 954 399 582 288 064 109 378 915 252 052 074 648 653 360 597 302 603 783 058 305 489 989 993 372 324 926 075 233 000 428 357 786 060 835 131 513 800 494 249 947 023 533 905 472 617 115 516 706 574 868 873 574 172 977 359 520 666 639 322 057 454 167 850 581 432 507 674 446 849 707 342 395 533 953 237 498 418 036 926 748 883 031 572 993 499 995 787 060 805 057 500 974 341 761 460 457 007 747 397 048 849 733 543 646 353 579 938 450 284 070 606 937 812 301 299 524 487 569 979 526 359 705 241 121 877 332 163 960 274 378 881 074 859 058 453 496 257 284 158 703 526 049 332 470 162 312 160 837 639 955 611 464 766 401 866 382 940 215 129 880 130 887 262 784 193 131 620 437 039 538 471 371 679 522 648 291 520 566 191 989 011 622 915 616 243 758 581 824 221 098 427 078 067 498 722 907 397 003 376 683 184 053 101 875 546 137 699 830 238 216 545 585 884 871 063 376 031 188 740 789 873 897 751 390 945 252 829 449 930 775 980 106 755 699 072 668 088 194 669 824 424 664 186 544 819 092 726 607 522 370 840 358 968 986 322 989 299 465 408 702 149 165 544 798 097 316 182 517 615 299 877 888 847 489 409 335 887 113 284 948 308 018 075 744 490 122 341 960 722 104 156 255 575 864 322 832 852 096 952 144 920 845 370 706 384 399 336 869 081 225 385 188 333 220 877 990 486 636 512 417 069 928 458 788 548 711 575 816 560 462 395 554 947 698 857 203 322 093 376 334 281 002 251 592 826 254 625 357 776 684 761 449 082 917 766 707 289 461 999 826 330 883 935 194 810 253 042 221 839 420 245 060 246 028 891 260 198 155 484 746 751 836 161 596 784 592 626 857 303 984 667 571 492 296 480 559 776 253 683 771 756 538 089 579 229 058 336 637 448 756 031 239 302 652 855 897 099 938 803 662 807 033 755 639 455 311 779 135 291 139 078 832 096 771 991 956 849 560 858 156 375 057 012 175 441 769 687 448 731 316 944 801 588 800 653 863 892 351 224 066 725 793 913 380 576 463 406 566 700 703 781 134 803 019 339 396 713 175 427 738 011 135 003 649 544 326 871 879 010 654 185 658 694 730 004 930 119 589 410 677 841 400 689 574 134 272 362 393 529 919 662 817 790 130 039 984 367 793 185 310 480 427 147 072 691 952 187 790 055 617 099 342 430 974 485 400 945 877 637 948 549 612 998 159 003 442 473 396 981 155 432 267 790 026 078 832 497 801 561 214 810 585 001 245 867 010 243 764 078 833 415 641 732 385 996 435 922 193 018 943 568 809 968 359 842 312 772 464 451 559 287 011 196 992 331 747 620 011 007 205 942 176 106 803 752 302 962 242 173 902 271 716 644 014 109 865 350 142 429 901 415 187 309 811 987 874 354 530 388 564 666 794 105 704 416 875 230 290 831 902 260 885 149 154 379 790 340 079 642 423 597 884 675 606 947 593 189 033 799 888 360 576 008 034 338 887 850 676 106 142 064 523 807 017 159 622 548 601 085 274 087 694 872 615 760 425 847 504 139 445 156 007 555 004 363 864 386 121 210 004 883 744 591 499 217 811 052 171 197 119 848 712 496 947 915 969 762 746 731 672 403 287 303 655 544 916 436 922 615 927 122 336 747 701 921 062 372 485 202 642 633 477 633 448 437 320 791 517 497 775 501 881 950 602 936 531 734 864 291 290 539 755 993 532 827 318 823 218 867 629 382 014 969 094 728 340 728 802 583 204 061 915 983 807 569 446 111 999 488 625 634 585 057 938 343 830 424 740 172 073 175 262 047 046 163 854 595 953 325 428 170 812 977 868 273 668 598 133 771 464 966 258 179 990 060 169 012 897 721 415 942 997 145 426 363 673 459 784 547 132 527 658 204 035 059 437 022 734 553 366 599 575 787 800 471 593 588 176 327 387 778 667 262 595 722 147 547 825 618 661 945 487 090 916 226 598 352 343 538 119 557 331 817 249 014 259 658 159 755 073 299 695 232 698 263 150 528 685 939 713 769 664 749 844 477 992 379 236 895 258 976 859 456 696 536 969 205 948 028 056 144 417 536 283 420 919 116 652 207 563 339 780 281 193 859 293 442 047 467 736 737 650 979 701 304 883 878 336 492 836 424 208 620 025 588 501 193 500 825 987 187 159 162 274 020 621 592 631 388 607 341 962 524 000 136 959 730 926 436 118 541 592 810 588 432 582 508 434 192 948 012 548 624 316 378 486 574 132 954 734 077 073 537 610 640 340 383 300 602 007 740 319 335 249 145 678 383 514 391 009 792 269 314 962 557 691 087 466 713 284 795 333 742 771 009 207 217 368 764 830 176 174 897 096 529 891 394 890 639 301 010 602 834 920 910 346 337 296 151 545 524 475 537 535 588 799 338 654 397 323 553 001 018 073 767 218 006 772 011 029 452 782 288 782 257 037 650 984 273 111 371 371 736 749 012 480 742 084 771 205 769 554 399 415 747 109 971 398 800 208 134 566 163 241 784 394 249 013 334 590 212 323 737 423 992 533 773 766 138 061 889 705 001 906 874 491 629 564 112 499 261 528 893 393 745 066 072 506 994 224 137 765 195 676 295 692 047 254 767 284 344 515 371 067 655 986 712 704 566 969 541 488 240 982 625 186 580 214 884 632 458 115 748 037 391 874 025 849 079 689 857 064 911 472 828 982 578 093 633 337 824 019 418 121 520 565 620 023 540 127 471 817 565 585 905 237 735 459 572 075 463 271 536 561 087 424 027 257 963 613 332 337 382 669 589 079 776 295 144 221 889 905 483 777 286 285 036 115 061 436 579 917 113 716 673 983 148 332 712 021 707 137 252 814 691 461 948 543 701 010 882 833 755 123 252 719 948 748 973 933 418 420 614 744 780 151 319 992 620 454 329 250 028 524 993 068 383 508 750 559 679 075 045 386 360 555 702 129 065 486 947 609 164 478 814 897 979 993 592 687 338 862 432 845 606 893 672 220 452 962 598 299 494 313 198 340 199 527 405 138 980 629 347 524 173 074 753 882 988 192 589 013 811 218 418 652 888 589 405 932 494 403 727 813 449 784 322 572 159 978 592 235 038 278 899 921 125 122 485 397 018 529 820 824 695 956 335 360 728 219 282 457 405 296 206 534 852 685 532 625 924 673 497 000 981 976 972 258 859 224 462 172 541 831 350 606 934 059 026 552 385 395 917 548 022 049 041 356 117 155 895 174 260 826 657 222 222 721 309 811 291 804 121 971 754 729 917 044 199 309 394 996 614 540 887 097 222 539 522 215 558 329 657 216 075 953 732 385 615 398 652 957 890 655 381 745 941 402 924 344 531 600 754 648 281 108 930 551 069 513 835 300 622 642 788 750 926 974 704 305 957 386 639 904 491 804 373 715 622 641 585 417 637 532 401 951 174 553 915 185 660 116 020 249 419 100 866 513 717 071 263 031 500 593 295 100 951 050 303 976 993 502 531 777 423 914 679 428 450 629 514 440 344 791 963 882 799 118 813 618 256 857 301 485 662 627 418 294 755 835 868 529 181 416 554 205 623 923 417 170 066 172 989 131 969 030 596 436 920 191 392 458 112 842 719 142 761 568 791 990 958 795 064 882 627 548 724 033 253 453 693 973 074 213 314 141 766 270 680 593 804 530 996 992 871 576 702 136 313 196 600 358 596 021 132 281 124 468 383 453 975 053 522 341 484 389 807 332 255 444 930 351 268 788 251 100 389 480 562 387 210 852 304 745 030 679 444 576 620 714 391 494 589 100 695 713 105 477 938 407 309 261 871 983 130 897 218 787 561 941 856 724 676 550 592 508 972 569 152 748 626 224 099 642 468 799 409 995 819 340 240 331 687 165 513 370 288 373 219 648 514 630 959 792 065 131 106 703 200 289 653 523 605 087 889 524 286 595 895 778 034 773 453 773 467 660 476 313 933 913 387 521 778 130 876 613 312 565 077 573 565 992 131 236 327 025 144 514 067 626 084 760 201 459 725 639 026 154 616 348 958 984 675 131 794 742 721 724 613 364 728 204 273 784 332 827 581 713 629 799 545 211 462 888 872 379 756 826 014 076 439 401 950 876 428 768 879 472 118 445 253 659 343 392 397 056 213 852 050 387 354 906 730 900 237 612 015 063 076 257 354 238 752 436 496 053 569 274 551 585 620 815 188 098 686 401 234 477 787 868 943 577 175 011 867 637 736 778 927 876 725 636 798 075 716 987 065 026 944 195 914 835 144 392 888 750 354 116 850 075 376 640 326 682 508 477 693 645 435 864 916 436 577 942 983 848 079 983 247 515 232 594 859 569 811 052 445 348 375 943 618 326 543 789 410 983 972 064 045 915 894 749 561 043 309 583 706 950 170 638 662 371 594 868 654 028 295 074 882 199 463 205 090 144 690 220 780 188 537 301 218 583 955 474 987 301 305 806 224 621 711 355 430 411 988 840 837 324 332 137 391 266 780 288 976 729 625 083 395 516 514 935 694 468 167 918 959 938 351 819 459 391 413 954 046 067 858 389 243 288 248 471 769 778 581 748 078 195 715 892 510 243 691 616 933 380 265 341 061 051 287 705 041 216 658 752 325 735 144 823 632 658 701 392 537 237 164 998 452 344 594 442 167 596 301 437 616 167 562 126 028 008 460 077 362 081 592 006 778 552 714 883 474 155 363 744 600 510 314 656 836 428 803 778 180 383 500 206 552 060 570 467 371 111 594 066 315 771 207 010 560 072 917 163 427 881 429 538 669 629 519 086 090 422 922 450 641 199 952 717 348 316 966 959 167 275 876 408 114 920 115 536 534 259 596 292 373 516 674 421 740 149 687 901 101 695 268 127 969 244 250 682 076 716 289 027 898 820 146 024 319 588 677 044 944 224 663 715 822 978 089 380 583 017 637 819 268 414 187 537 167 683 141 374 034 495 430 614 394 703 527 614 869 539 812 159 238 012 938 949 733 290 138 761 781 555 832 652 790 371 928 938 090 899 044 073 472 043 497 208 740 802 237 549 751 982 510 995 389 209 711 856 562 683 306 545 641 264 867 619 274 488 693 699 202 125 235 237 544 385 678 067 766 730 998 737 897 137 213 622 679 416 412 741 992 825 251 929 135 650 447 256 556 654 868 773 798 199 623 991 549 642 660 074 259 428 256 149 658 793 144 023 780 329 316 732 847 641 344 232 008 016 513 263 323 209 692 158 347 478 129 883 356 674 930 913 084 559 981 851 327 528 945 475 270 425 933 619 224 712 239 401 583 751 551 291 327 951 587 294 216 602 271 384 369 855 643 527 629 114 310 481 495 378 950 689 819 096 109 465 314 783 500 204 182 783 248 969 606 793 014 734 423 225 611 819 837 845 083 469 175 769 656 147 761 515 572 954 430 391 722 991 605 725 516 771 146 114 497 259 591 296 145 702 070 889 645 372 059 798 095 962 523 713 092 042 072 103 521 776 596 196 113 453 289 246 617 878 552 295 598 308 933 221 954 662 081 658 309 243 482 618 771 908 108 258 847 363 590 041 705 874 800 408 144 058 710 938 410 973 895 265 825 783 110 899 656 338 451 966 489 001 381 114 111 554 555 065 710 523 483 887 927 000 974 689 062 422 035 302 752 331 939 601 935 416 422 879 655 461 370 632 739 277 221 623 379 708 351 300 551 048 878 420 218 021 305 809 261 658 304 537 066 914 246 603 619 843 724 191 450 338 096 199 752 990 821 166 708 654 965 333 867 529 986 224 744 171 241 590 113 013 647 679 162 793 465 221 319 167 609 717 846 266 324 078 746 757 900 482 694 359 410 649 664 944 765 595 952 818 649 793 640 306 446 931 648 755 566 150 905 305 662 126 572 209 245 055 589 852 089 394 081 606 588 755 445 290 997 423 287 735 846 958 535 908 371 096 550 828 130 485 302 112 930 848 174 875 201 586 011 933 778 594 383 444 192 707 191 694 024 760 064 742 725 492 859 130 543 160 081 688 511 722 526 362 416 868 855 883 793 196 109 594 358 025 774 914 782 761 132 696 466 102 754 584 190 012 135 318 018 349 608 028 272 210 404 807 540 229 330 777 333 844 457 156 382 911 279 283 407 949 135 669 776 297 802 945 664 393 147 929 688 248 738 484 902 851 071 576 311 636 955 942 836 164 427 629 293 835 133 771 733 041 104 420 185 640 230 104 040 446 972 918 278 828 973 996 991 566 454 032 322 664 083 389 940 176 551 530 003 855 595 618 998 817 972 230 498 528 715 217 851 333 940 751 203 709 278 406 930 613 864 397 419 491 117 764 468 455 498 411 281 686 841 902 928 834 797 935 232 937 479 724 462 879 387 105 992 413 061 432 253 917 345 536 482 600 354 308 630 211 748 499 657 036 691 360 191 150 567 898 198 968 186 206 536 699 323 482 064 930 348 343 660 002 226 572 259 429 295 510 398 632 204 390 141 958 179 514 755 190 923 623 212 297 799 553 287 317 793 172 916 395 814 764 877 471 720 774 337 950 804 406 636 811 377 767 202 396 000 049 108 233 787 249 542 641 156 374 606 664 033 655 371 604 979 022 590 267 104 107 577 255 918 795 914 806 243 774 965 085 579 871 092 105 661 087 720 571 787 720 575 496 330 281 254 189 169 884 263 117 854 420 048 572 471 173 032 571 286 222 058 023 122 620 822 112 981 719 799 471 946 863 255 377 247 625 454 824 946 209 412 932 121 474 368 042 884 714 554 041 337 746 035 308 104 251 636 239 739 291 133 257 753 347 646 091 501 594 960 774 031 778 326 664 669 919 991 207 691 967 663 193 875 488 704 175 539 206 492 992 711 312 168 634 335 706 803 200 273 991 963 544 302 747 031 198 288 842 001 731 802 715 643 429 329 593 185 078 143 419 738 381 717 784 991 261 825 911 274 046 486 632 288 187 748 431 630 108 322 042 562 534 214 550 382 958 870 761 696 037 169 801 601 365 459 939 455 836 888 423 238 660 598 613 676 113 938 983 400 584 800 043 422 533 204 489 112 827 323 558 900 580 084 043 630 383 357 899 747 923 101 309 028 145 234 065 153 462 850 154 934 112 323 576 019 581 313 448 673 374 479 526 140 891 369 681 032 421 786 768 789 248 420 867 928 517 425 048 329 800 472 198 559 436 799 755 747 427 500 126 034 673 265 447 981 639 954 473 187 373 104 887 549 368 664 193 309 071 680 971 606 435 025 716 340 721 020 453 161 237 159 197 606 138 986 981 674 385 079 857 849 378 742 833 826 453 593 233 930 269 777 169 960 668 004 668 132 516 612 315 153 617 484 727 865 900 131 801 963 476 209 453 347 400 054 989 359 918 463 125 857 765 666 952 774 699 673 657 485 815 189 039 375 031 106 647 759 664 328 757 853 343 640 499 588 025 286 559 626 326 371 330 761 155 959 484 620 344 045 684 487 146 620 259 991 733 867 479 430 654 900 500 670 382 393 616 150 009 111 696 498 384 977 307 862 974 360 791 845 495 162 375 739 393 862 320 654 962 479 405 588 756 683 276 273 727 008 146 175 997 859 637 973 115 019 004 247 694 205 681 649 842 722 574 225 245 288 969 982 904 174 911 082 137 756 804 380 017 764 114 600 677 855 684 013 813 817 028 520 561 352 332 246 289 411 511 012 394 861 144 411 971 230 746 251 244 571 135 178 077 013 882 128 992 697 322 258 169 182 555 082 823 622 035 083 243 973 665 014 552 228 807 610 168 501 953 989 879 417 611 283 202 580 605 831 672 938 198 586 380 656 715 284 366 117 591 532 732 317 281 375 506 099 246 191 522 350 395 324 304 187 467 785 859 523 205 013 809 816 332 585 481 669 523 826 153 034 486 424 711 338 244 001 016 268 219 299 456 055 553 323 735 146 431 960 455 869 649 867 402 063 737 984 595 614 449 271 764 715 376 436 765 676 284 847 305 474 558 950 438 230 444 185 577 749 933 267 577 231 793 312 189 382 142 265 389 099 543 436 580 020 016 230 029 829 563 356 719 166 159 163 901 719 722 359 040 545 004 455 713 325 757 417 316 770 436 862 237 174 335 778 095 827 304 332 594 568 215 702 241 939 164 761 556 181 210 157 586 332 689 883 850 032 374 042 283 684 064 184 542 417 966 962 986 111 643 353 878 604 346 773 667 840 143 204 185 672 121 382 449 153 505 704 563 135 103 325 790 461 034 782 942 949 090 764 632 571 042 194 577 795 347 504 757 264 136 704 441 814 058 237 795 792 602 438 780 840 297 952 631 332 336 674 121 956 856 594 499 228 485 424 619 081 315 565 856 949 958 865 312 760 420 343 896 921 674 324 936 465 414 034 411 075 197 588 596 445 027 847 557 119 453 344 799 700 668 540 160 005 413 251 197 512 467 436 472 558 693 436 187 613 934 888 546 362 056 083 716 560 425 802 884 815 523 313 793 292 475 766 007 309 440 201 268 092 424 500 034 761 019 804 352 898 511 430 026 662 706 953 100 623 132 151 980 090 759 229 748 979 109 377 423 140 558 776 609 347 127 370 772 999 965 041 869 788 143 960 748 493 502 842 648 867 467 439 044 461 032 336 499 900 909 385 275 718 661 551 586 599 488 793 305 374 185 820 152 748 739 418 973 742 932 914 234 909 302 491 782 760 301 752 023 760 578 091 790 717 757 490 268 778 277 590 791 569 723 494 018 497 107 568 358 592 736 687 252 726 109 183 956 618 830 251 978 090 093 891 807 299 868 690 200 254 694 674 816 097 956 825 177 825 340 066 081 054 325 607 089 159 511 098 989 535 026 204 229 719 401 832 052 847 756 343 392 041 765 732 153 087 227 343 910 632 494 042 605 341 332 439 931 298 258 813 627 235 387 928 971 911 229 298 788 575 338 171 839 346 691 824 460 904 169 622 402 789 498 319 799 007 482 886 266 555 316 895 647 629 103 604 680 785 221 160 218 151 352 753 829 929 929 569 668 953 257 907 570 139 107 844 196 608 330 257 563 780 223 854 248 362 880 517 433 902 659 519 789 706 959 347 924 365 207 710 826 682 276 837 963 168 230 757 173 628 321 077 862 910 777 583 802 653 328 210 551 982 417 527 947 174 188 995 249 805 553 033 608 108 871 710 121 619 279 953 283 555 823 379 251 087 868 553 286 035 949 677 744 448 195 546 731 276 536 024 701 175 697 398 529 570 680 469 507 058 633 078 880 166 170 080 754 876 130 055 137 004 051 408 060 214 501 514 187 295 575 619 549 813 841 696 162 250 597 189 619 204 911 282 899 424 942 049 310 458 961 713 868 881 724 263 351 020 030 728 279 329 184 595 886 045 431 340 201 987 951 575 873 929 546 451 946 198 326 871 488 043 945 529 269 340 721 087 725 120 970 005 706 887 760 571 862 960 870 321 384 446 803 819 821 156 573 946 688 048 463 920 117 815 065 614 349 576 738 499 146 881 341 312 612 885 654 378 722 608 499 730 742 795 107 349 895 339 161 708 569 926 938 985 512 824 089 711 040 135 868 386 872 021 036 813 774 882 522 774 974 960 542 703 149 671 727 848 937 091 021 404 760 402 753 994 281 567 769 084 369 028 983 045 601 861 753 233 239 805 783 009 161 301 341 087 371 143 674 448 427 228 922 274 470 525 923 035 142 832 186 933 020 098 289 308 645 388 724 472 552 381 202 607 544 544 073 713 276 530 506 109 497 300 099 691 603 305 707 171 858 561 410 604 215 246 223 112 306 651 311 977 420 933 441 948 400 025 637 616 001 512 767 453 354 301 157 176 563 693 046 472 906 326 413 021 673 216 732 206 838 644 038 743 520 423 938 196 656 829 796 479 947 551 437 097 892 703 630 317 802 776 873 708 783 335 869 343 015 520 731 501 876 128 239 565 429 492 517 797 765 443 338 614 237 394 772 914 778 743 654 830 769 873 541 573 509 121 289 306 484 852 399 321 568 456 152 465 682 488 872 743 478 382 480 033 831 420 601 979 051 784 712 309 290 348 297 597 500 286 481 176 335 373 617 154 843 519 748 101 601 848 248 467 423 680 443 915 331 275 767 464 857 720 122 509 418 880 996 996 527 314 529 520 447 546 047 995 829 510 765 343 375 151 596 721 084 904 183 506 622 574 567 995 802 922 016 996 701 246 685 770 912 550 957 610 838 733 067 392 011 928 024 114 996 292 552 072 120 579 934 872 977 517 005 606 351 091 734 174 157 215 945 224 413 325 579 098 032 361 384 043 646 615 223 622 928 586 492 020 413 080 654 255 034 636 003 078 976 980 408 117 891 146 920 799 493 315 107 360 978 795 324 474 368 495 351 425 707 437 699 570 757 459 649 772 443 776 879 464 751 694 494 233 982 865 468 790 282 607 391 750 014 366 274 027 547 105 287 195 837 434 111 646 870 060 138 861 926 398 740 093 912 533 755 190 233 097 845 360 008 198 977 482 223 699 970 136 085 676 437 009 012 124 787 022 050 912 185 060 958 547 072 233 475 817 186 922 909 123 732 801 985 892 294 539 214 967 952 532 384 097 046 293 844 692 004 909 205 923 806 603 582 211 230 177 191 682 416 430 239 180 835 720 138 709 772 270 016 027 746 056 666 286 405 057 332 587 645 430 622 406 714 403 436 336 632 259 970 996 516 665 280 629 212 492 436 694 275 660 042 169 733 823 729 870 237 750 637 097 172 629 375 109 135 179 179 537 031 078 387 101 832 870 863 998 700 337 012 695 186 647 464 440 692 957 837 528 267 042 775 797 094 757 466 830 983 649 464 109 316 220 810 066 171 660 408 892 195 934 349 736 971 739 377 571 305 512 430 849 796 235 698 802 688 862 157 732 373 949 108 252 378 525 672 122 286 723 798 102 921 513 897 492 439 432 180 922 426 947 973 492 187 024 156 940 874 742 431 018 311 317 935 664 825 184 717 176 989 961 229 608 282 363 472 739 359 816 329 545 437 587 239 025 601 773 765 556 958 958 155 710 633 147 443 289 897 502 259 448 105 374 890 724 238 188 211 467 136 820 146 865 146 660 071 018 914 705 760 218 806 601 073 198 620 126 897 752 019 965 172 014 027 507 143 457 520 387 170 202 670 066 373 577 769 551 504 767 393 398 673 092 042 280 214 232 657 586 264 807 668 247 758 765 169 116 790 372 036 040 090 254 950 848 181 152 362 731 567 032 266 463 890 282 311 224 986 629 742 033 599 974 801 112 325 390 456 923 747 203 619 681 381 844 618 930 879 877 702 744 955 301 988 596 896 765 932 451 959 774 310 377 886 386 760 750 260 083 158 496 347 209 521 278 802 665 313 942 723 891 155 075 663 325 870 227 882 247 979 986 851 660 185 500 447 250 272 206 932 848 041 990 386 902 073 001 099 445 714 553 823 540 866 999 386 143 984 499 929 563 318 845 520 936 833 904 284 043 112 662 703 667 974 643 178 237 124 123 139 399 731 199 983 740 736 081 339 045 403 607 414 955 132 950 797 557 515 172 106 887 246 797 271 714 591 203 974 240 960 260 833 203 459 792 806 667 160 211 901 112 786 079 065 749 500 106 211 883 913 832 973 740 445 937 186 830 055 361 899 827 310 939 651 199 154 530 116 113 804 444 338 759 439 584 213 298 146 055 783 832 846 151 017 344 952 852 842 504 947 417 449 939 899 608 524 354 741 339 019 994 961 651 914 278 377 023 712 231 938 155 840 387 959 304 433 247 952 316 801 086 587 450 821 318 246 874 851 101 869 500 973 928 609 976 972 871 434 636 923 750 769 840 532 068 390 217 194 044 536 834 386 912 407 795 797 877 944 306 453 686 127 908 449 984 304 849 266 156 901 026 142 467 427 928 815 891 034 321 276 220 618 832 977 124 837 436 675 533 882 278 631 146 062 522 006 410 657 785 461 839 461 091 475 593 959 990 519 509 481 786 457 029 132 444 311 787 829 817 914 331 740 123 838 600 365 104 694 594 314 311 386 340 459 860 811 538 836 564 229 290 280 801 376 407 601 273 884 051 777 427 372 203 709 607 974 786 434 393 450 343 228 438 226 784 603 911 347 493 526 624 398 364 347 404 150 806 376 196 554 526 020 993 664 311 984 832 798 031 524 986 567 799 124 044 479 448 628 999 343 207 895 795 223 979 885 121 644 323 941 050 889 912 723 441 015 073 827 123 376 993 490 433 206 427 645 474 388 334 659 727 046 233 054 901 955 015 640 119 351 136 678 043 155 543 009 148 417 989 652 526 480 858 924 086 504 728 299 182 938 910 582 431 619 298 921 053 462 291 354 617 067 070 244 150 016 612 714 447 113 063 178 259 005 020 430 431 918 268 053 979 337 845 647 056 545 616 044 526 096 405 306 957 382 234 092 229 027 358 295 925 284 666 323 748 719 635 516 930 776 559 829 109 268 595 353 657 005 949 992 709 973 461 671 540 183 231 286 192 404 044 100 506 145 794 969 380 371 859 673 471 331 159 406 882 558 562 629 509 353 389 139 024 959 986 733 900 802 800 058 137 145 083 971 502 305 355 973 356 384 535 901 845 336 697 111 495 627 908 365 839 495 799 166 394 233 197 329 502 364 195 297 351 782 413 813 261 205 521 547 344 803 081 352 472 464 604 877 578 104 650 356 380 994 058 943 941 627 208 812 022 865 581 546 004 622 549 826 275 484 958 305 951 584 621 204 635 235 457 148 804 028 353 293 410 843 293 247 699 921 221 908 878 955 780 775 254 855 326 958 351 139 468 236 156 645 995 347 688 959 099 942 976 987 406 030 491 004 427 047 392 960 148 475 783 626 609 763 118 584 105 329 166 498 967 417 803 853 308 663 297 435 002 556 166 036 792 027 899 693 671 145 751 339 479 388 997 775 820 715 858 905 202 278 656 838 844 770 681 225 523 072 988 388 008 236 400 104 783 536 808 827 160 050 295 236 930 135 061 937 009 333 835 903 248 952 100 439 372 469 558 225 935 684 249 773 728 928 983 076 621 614 073 689 727 641 715 353 680 283 657 916 991 993 179 050 107 997 895 199 215 788 236 492 077 435 143 905 690 921 563 664 833 833 823 633 441 317 983 807 677 779 874 467 309 390 340 779 020 856 322 068 461 499 845 645 585 991 572 345 973 120 223 477 499 931 814 803 714 885 703 540 778 293 999 162 501 227 844 693 340 961 326 593 637 192 895 069 878 572 149 334 781 901 865 716 206 241 500 646 852 354 079 558 610 880 283 253 365 389 980 094 407 158 873 804 184 810 560 466 992 719 027 088 157 091 259 354 731 652 595 273 592 233 732 075 428 680 083 966 652 165 135 797 888 182 560 424 932 709 548 688 474 858 189 160 776 846 193 859 806 587 845 135 760 502 215 621 194 363 108 744 067 170 286 752 110 658 102 811 924 729 797 059 167 956 584 762 933 933 296 405 174 436 550 869 195 721 361 958 531 247 693 293 559 811 573 036 251 237 584 878 008 117 282 872 450 826 123 126 658 280 972 437 781 799 499 206 911 971 409 512 090 957 418 602 987 185 072 415 007 207 088 777 187 057 539 553 370 219 864 313 499 306 151 622 708 879 652 247 786 123 302 472 563 533 390 683 011 238 967 164 128 356 144 358 627 641 170 090 184 438 637 337 560 759 985 150 387 542 987 610 320 475 397 731 787 201 873 059 054 440 254 765 212 259 345 635 971 216 619 287 693 680 849 780 893 354 024 059 613 483 002 235 375 383 018 162 488 834 007 361 973 278 876 886 189 109 898 102 063 435 542 074 658 534 881 825 807 446 317 625 111 674 210 372 460 224 052 143 619 930 320 051 975 536 229 199 418 895 326 813 150 571 655 697 149 992 263 212 550 912 504 344 682 263 319 913 278 731 918 815 105 549 674 390 964 918 354 774 596 119 370 370 041 428 831 071 406 123 722 784 491 224 082 177 743 667 694 878 332 211 147 628 340 914 294 713 670 228 575 736 470 883 407 036 656 786 068 807 430 921 442 692 075 324 347 977 819 646 009 034 688 569 891 132 135 753 355 232 380 830 309 973 631 736 558 846 617 429 582 435 650 955 940 087 468 286 399 982 084 735 560 046 708 707 552 199 518 218 092 028 317 238 781 601 525 849 272 876 001 497 755 120 346 998 431 028 486 655 529 769 204 780 962 040 853 436 646 939 069 770 209 197 514 912 848 358 893 974 730 502 866 196 623 120 880 410 807 363 086 261 566 985 657 047 172 515 021 931 596 155 945 555 769 700 988 039 589 287 358 872 942 396 293 501 401 935 337 927 119 517 229 177 420 459 211 615 453 270 946 623 498 332 829 874 844 231 572 235 709 897 245 240 327 278 624 624 484 253 507 020 606 662 785 860 047 230 424 789 188 858 010 662 374 928 447 568 967 228 190 065 710 932 774 375 798 886 290 829 350 083 087 301 297 900 993 379 141 986 515 215 918 100 277 597 388 531 121 957 346 289 427 627 208 682 798 238 316 471 038 314 597 307 858 131 652 167 490 499 773 677 514 729 579 504 466 561 436 151 673 925 793 720 120 180 327 768 238 117 521 211 692 607 153 527 818 468 484 177 776 529 950 098 045 702 516 286 272 330 181 786 578 849 444 069 542 857 563 755 906 941 501 974 227 263 849 717 956 277 195 304 542 290 930 976 301 205 285 807 608 366 898 842 711 325 259 312 177 469 993 058 290 471 252 501 069 988 572 146 868 150 535 524 773 730 337 076 557 925 179 952 854 104 387 604 727 661 453 864 017 157 211 218 269 308 943 998 549 459 200 488 774 090 709 116 307 172 428 981 084 598 138 183 022 081 713 236 104 753 700 168 747 390 494 757 950 919 033 736 349 771 151 770 271 660 268 728 754 970 173 053 563 006 892 491 508 989 325 407 320 539 559 286 844 990 840 101 227 506 529 503 816 032 069 916 828 600 925 222 058 874 136 332 973 203 146 345 296 705 714 095 209 335 191 336 374 017 044 783 357 368 778 652 270 622 219 400 257 054 975 228 190 947 285 346 386 258 137 608 782 075 774 179 946 108 972 067 879 175 805 096 580 189 726 388 348 068 333 030 733 539 872 123 562 596 503 777 128 548 697 187 953 770 532 833 926 926 269 028 446 140 174 771 360 160 434 693 322 934 075 770 879 554 184 033 532 963 317 743 886 223 136 639 820 765 331 722 074 274 523 877 922 522 439 681 483 789 780 226 184 315 923 502 055 064 285 672 272 399 027 781 559 805 206 600 796 709 686 171 095 719 873 575 886 111 254 690 202 086 621 758 288 967 729 559 340 734 552 632 029 770 095 613 497 621 331 644 248 117 242 942 730 587 370 866 075 792 532 041 817 583 341 861 260 755 015 093 045 781 069 029 296 167 997 634 851 275 622 957 552 391 186 808 315 529 369 131 215 935 793 598 304 611 471 333 827 342 597 269 995 644 848 007 750 788 114 575 988 641 668 860 999 318 210 490 552 610 214 530 657 986 910 382 516 004 070 224 639 130 429 970 494 330 325 580 485 022 082 706 468 819 906 356 564 874 592 788 697 175 739 454 983 252 502 799 650 779 805 914 714 163 922 983 612 276 135 870 483 143 615 877 236 588 051 208 881 732 084 342 494 043 547 551 339 432 980 272 183 308 455 848 011 939 105 551 867 342 998 865 787 126 823 326 840 744 913 082 688 281 976 928 186 094 523 018 216 672 978 518 909 055 384 543 911 292 994 869 060 010 395 456 751 077 308 150 272 479 844 060 870 735 811 949 352 056 316 902 443 373 035 412 601 047 919 556 793 247 429 497 125 978 439 644 135 348 454 481 693 166 988 675 898 260 779 677 281 522 506 972 766 396 924 528 358 662 009 638 771 136 142 939 348 081 070 669 254 050 797 587 309 550 320 730 977 870 725 973 883 335 984 067 726 337 088 217 938 657 269 566 993 289 532 853 538 754 078 323 509 485 862 002 977 531 861 974 130 841 913 863 387 343 258 499 235 419 029 757 099 519 595 588 631 702 121 079 397 477 041 212 042 864 112 418 130 637 209 301 878 709 829 291 480 288 328 999 946 771 192 937 943 743 022 348 426 558 085 581 712 896 790 060 130 388 445 942 313 378 381 742 291 603 858 752 849 735 442 738 717 081 867 033 991 750 542 933 639 912 203 219 235 826 872 817 733 326 631 812 634 740 600 975 517 159 940 689 529 965 369 968 253 935 827 559 257 903 893 960 305 322 703 223 111 074 615 989 093 753 951 935 342 975 949 482 782 486 768 068 682 029 084 313 290 443 179 373 363 207 600 616 153 006 790 890 216 758 588 777 460 807 090 686 386 256 819 648 497 825 244 850 656 928 203 509 455 689 573 125 857 352 072 747 809 504 600 456 231 713 995 467 075 463 056 656 850 915 413 428 125 802 796 734 745 280 257 795 854 441 160 218 903 671 562 229 379 175 204 649 014 343 172 835 500 518 284 568 848 682 666 785 457 912 198 342 195 319 947 752 099 657 382 196 453 318 011 830 615 569 154 444 394 274 722 222 878 986 075 003 008 841 131 119 320 447 128 667 718 349 667 845 805 531 484 714 900 394 985 046 381 270 727 274 587 879 585 992 692 057 901 057 942 754 059 167 755 111 427 416 078 906 211 395 103 351 071 368 040 364 156 109 005 310 870 449 654 873 595 976 452 038 555 387 195 362 690 028 380 408 041 031 922 877 651 854 895 151 010 836 500 574 295 388 673 887 520 463 325 534 615 777 148 412 129 649 729 865 429 717 713 658 505 672 770 831 131 443 442 078 493 673 910 457 815 276 026 107 162 507 879 415 481 173 346 893 455 957 422 989 425 260 447 461 914 543 013 420 215 851 599 323 936 362 552 390 972 722 532 673 690 263 796 101 193 157 790 327 110 893 965 092 910 309 962 100 204 879 795 665 192 579 077 036 284 924 325 646 269 454 698 679 418 464 597 758 656 770 500 176 243 447 651 851 095 206 040 015 665 543 306 868 735 234 631 892 910 371 364 130 889 728 788 794 729 300 044 476 671 706 035 417 613 228 472 600 371 777 384 101 312 116 260 388 412 581 280 038 639 222 081 971 149 142 015 513 498 321 504 822 689 152 592 710 424 290 101 410 381 071 946 926 068 945 510 811 438 443 270 740 823 320 575 628 776 237 959 543 210 523 043 072 601 672 082 152 821 291 610 597 577 418 297 530 348 674 961 750 178 644 970 240 450 008 809 991 008 633 952 442 250 177 370 885 937 329 254 558 245 012 081 896 243 863 074 880 622 047 926 495 844 042 788 990 171 010 212 512 642 735 513 344 988 304 402 536 614 852 881 153 006 065 932 190 129 662 739 411 694 600 606 404 535 887 157 294 962 068 586 526 496 346 723 869 005 751 426 007 561 534 682 038 918 962 312 161 109 796 874 498 653 859 015 720 742 419 475 088 513 370 503 955 037 573 177 582 516 684 859 507 664 177 557 101 728 062 220 019 176 854 954 473 129 510 363 138 072 640 220 248 027 196 189 755 043 640 086 068 914 361 020 173 779 342 236 122 342 238 961 338 377 109 701 971 829 111 976 627 877 873 536 324 027 220 748 083 978 948 238 097 536 137 293 016 560 597 539 686 278 499 444 420 456 545 153 810 265 202 190 914 838 979 517 032 329 447 991 829 999 611 895 684 937 064 481 679 186 512 015 775 751 572 277 586 593 697 808 568 314 503 791 477 615 324 023 816 296 983 000 164 681 233 852 950 032 921 257 561 429 121 363 912 700 493 580 344 015 771 394 675 111 941 947 481 095 304 384 907 642 345 282 562 582 797 965 743 807 654 668 113 048 137 775 023 675 380 186 552 408 067 096 455 842 593 698 317 126 472 143 600 428 384 788 960 867 379 691 976 667 443 405 822 441 512 994 385 201 099 998 096 216 712 994 388 113 366 335 853 227 519 095 559 007 470 602 734 163 067 331 803 195 448 127 419 415 775 637 315 277 835 834 250 391 424 830 150 788 183 601 389 497 821 699 338 553 329 137 849 653 003 819 977 175 151 637 965 260 079 063 375 597 621 666 339 489 392 857 819 103 246 963 178 603 427 719 555 780 896 399 652 683 603 495 663 778 524 956 114 145 128 801 367 896 759 283 676 424 825 593 399 521 670 803 849 433 157 698 412 995 740 900 234 082 267 760 504 482 350 940 925 851 908 131 108 284 078 398 236 771 138 435 094 199 095 244 508 484 890 323 509 684 794 505 709 996 344 378 419 480 733 860 938 174 100 201 603 691 901 054 803 014 898 790 070 895 649 457 786 688 641 975 346 108 723 713 981 752 255 851 785 335 529 973 370 047 033 601 673 593 634 226 316 842 470 431 848 124 607 921 776 806 923 596 530 234 358 242 884 747 938 689 815 134 161 352 086 114 198 651 235 422 963 108 667 046 128 276 137 144 777 553 121 437 464 124 131 714 601 141 989 178 987 793 424 531 477 556 575 880 360 979 113 341 762 159 841 587 963 402 448 089 214 267 979 872 722 181 215 712 134 227 630 546 589 155 342 345 518 016 807 561 866 359 629 746 378 083 701 358 259 157 076 291 752 575 164 314 209 524 258 049 998 313 357 298 754 481 254 690 105 420 875 454 935 045 909 544 897 351 220 386 409 356 858 974 615 148 327 881 918 568 881 011 234 036 517 617 671 862 851 195 259 627 670 307 303 581 291 844 409 599 055 993 332 842 846 222 494 391 011 628 279 174 236 819 597 733 824 253 332 824 288 843 302 247 436 084 186 602 101 412 664 119 055 331 732 688 565 777 793 857 879 648 625 197 737 300 691 926 980 548 371 979 901 156 768 560 082 893 393 574 246 152 342 909 506 317 497 282 908 896 721 725 371 118 394 206 128 047 950 706 082 051 750 552 816 858 123 031 198 863 215 769 722 602 085 065 287 159 569 941 705 034 958 624 201 300 013 209 185 083 005 399 506 633 100 710 195 375 161 311 334 392 272 314 814 931 547 856 933 513 433 190 417 407 398 874 762 757 848 186 215 893 005 289 055 845 585 728 897 503 192 498 652 798 573 557 442 615 616 292 170 440 511 189 492 503 249 952 700 138 226 751 348 785 656 705 893 383 335 463 965 426 446 642 574 651 348 394 146 804 000 853 100 620 490 191 235 236 445 756 052 386 510 728 813 417 408 778 210 963 318 117 471 515 249 889 829 000 343 791 729 755 755 330 036 564 499 661 528 313 993 306 079 496 735 429 253 034 098 553 690 944 899 791 909 824 342 949 583 341 780 170 691 827 652 980 601 829 815 457 144 373 284 310 067 185 728 055 030 880 052 591 551 321 950 888 922 421 429 473 061 176 282 107 015 321 583 616 168 170 454 610 972 916 068 682 443 876 517 508 705 786 086 645 971 113 520 963 053 748 348 030 850 268 588 485 367 530 673 777 051 731 794 371 204 413 028 807 281 833 442 494 389 182 815 444 714 783 783 689 144 636 071 977 412 278 817 859 777 820 473 409 189 477 281 855 499 016 725 459 631 683 055 835 274 885 257 500 715 838 654 751 269 445 982 284 495 031 554 195 879 027 565 346 215 598 669 522 635 195 586 844 100 689 106 980 390 700 153 624 586 171 818 006 539 664 565 148 436 122 815 900 630 010 962 542 710 102 655 191 124 725 671 654 060 874 113 736 327 071 335 706 672 275 148 543 576 191 905 093 870 996 500 085 638 800 933 479 249 150 415 199 010 483 630 928 254 896 563 330 058 248 783 202 823 827 380 367 250 526 367 054 489 847 365 019 981 910 359 151 583 059 794 861 335 301 145 751 244 287 418 964 269 906 182 970 516 803 327 819 358 481 201 569 628 257 343 533 306 462 426 259 790 531 312 874 617 140 808 943 404 213 507 175 864 216 097 832 034 045 271 695 798 923 846 181 876 324 383 404 015 933 623 280 431 489 546 417 779 963 476 219 436 486 594 525 422 188 556 258 198 231 961 185 604 551 761 469 880 230 550 514 864 789 004 595 281 577 000 969 977 728 836 063 551 486 038 336 103 269 628 106 355 335 955 435 775 781 780 384 202 839 639 894 950 568 336 361 738 411 337 886 552 080 712 521 244 374 784 890 199 752 428 687 961 786 864 558 920 989 445 274 617 865 176 872 190 985 632 153 631 339 496 477 087 750 348 395 286 083 835 775 651 777 731 692 702 622 048 966 415 990 598 599 183 733 178 211 317 159 121 934 091 355 960 268 119 266 307 367 876 722 619 717 221 057 763 928 815 829 282 670 075 693 565 059 232 754 720 178 148 849 600 267 538 209 023 025 934 137 727 798 356 455 105 517 966 776 610 512 555 852 160 786 626 232 902 596 807 196 011 700 833 825 471 768 042 697 219 388 520 858 020 819 082 322 076 359 956 754 352 538 752 956 080 525 348 134 911 042 158 612 605 311 759 190 282 860 476 227 525 662 252 484 912 398 901 037 695 238 319 990 543 656 925 752 792 694 448 921 804 415 631 114 351 779 468 311 044 791 126 620 545 636 400 639 969 856 306 893 394 158 822 464 823 878 378 500 166 558 722 037 498 995 691 302 445 563 425 430 389 284 917 900 978 312 002 024 448 932 150 781 984 038 632 856 678 677 660 502 491 925 014 391 167 256 873 117 414 941 836 851 524 646 595 122 289 338 444 119 987 501 223 999 404 279 101 574 612 285 231 869 565 300 478 066 145 924 052 387 024 645 701 491 735 619 770 883 334 697 112 756 639 362 629 522 773 403 146 184 066 858 350 183 542 617 695 238 269 161 631 094 847 669 690 385 665 173 977 369 686 561 181 202 128 247 083 168 746 632 410 783 280 083 567 555 849 229 092 869 180 175 112 128 880 691 224 001 924 300 380 528 262 554 328 233 267 993 829 790 668 071 027 287 006 478 267 457 235 889 190 382 254 694 590 385 699 391 191 395 584 570 407 460 022 167 650 545 735 729 939 616 645 345 406 915 630 145 928 354 958 862 251 359 913 599 350 977 750 828 497 796 803 692 800 267 257 633 373 811 428 869 207 417 065 439 196 720 526 406 686 781 227 000 903 364 418 919 958 028 136 956 052 709 253 134 993 015 121 402 781 757 530 625 740 861 909 222 648 423 523 003 272 413 088 877 368 291 720 815 431 720 296 454 469 372 416 764 696 289 495 019 840 777 888 208 963 531 160 209 054 911 903 622 120 099 665 015 787 031 012 560 945 722 871 227 248 236 296 655 546 006 811 653 393 212 911 750 568 649 958 690 109 955 878 888 301 668 058 645 105 191 287 951 854 627 422 458 780 572 648 232 102 510 445 067 448 977 607 824 987 176 773 530 149 811 348 493 595 513 015 010 953 221 884 277 267 173 388 443 560 025 139 235 706 831 859 318 185 863 082 542 406 604 228 171 021 809 441 861 891 581 867 838 244 446 755 538 834 858 408 967 388 048 894 317 576 443 512 000 997 436 001 184 229 396 894 639 811 380 781 719 554 633 386 151 846 333 878 704 039 188 365 726 989 062 088 133 611 931 028 155 258 143 584 148 471 260 587 299 963 039 038 614 112 519 408 812 966 226 012 011 328 082 402 489 246 115 814 323 055 126 825 936 933 767 409 185 655 163 636 857 805 567 324 550 719 371 208 696 585 051 470 631 508 873 029 016 894 180 203 710 975 642 857 545 601 149 271 263 948 590 282 297 091 570 699 995 420 486 693 656 575 370 247 462 546 143 922 914 630 882 290 267 980 237 202 916 442 368 653 944 832 593 185 762 878 563 834 382 722 582 947 390 273 784 025 320 059 656 978 547 789 128 770 207 412 086 544 757 043 648 493 316 128 997 874 560 680 965 879 400 546 133 506 322 816 046 275 038 248 950 557 395 981 435 221 322 259 288 123 779 143 363 885 846 456 430 710 150 683 256 232 903 701 483 862 459 729 684 250 262 986 699 975 035 108 604 778 224 856 504 267 074 565 644 109 219 850 447 542 165 241 867 083 777 574 696 330 953 378 218 637 114 903 385 427 474 613 260 084 746 696 980 825 989 217 707 585 444 261 213 228 948 124 147 975 872 519 684 782 591 230 401 706 064 642 273 957 613 661 927 378 726 498 811 373 030 846 453 679 694 626 618 067 052 250 111 875 366 766 656 729 521 208 725 028 669 484 017 414 649 359 188 629 226 255 737 322 444 147 399 058 983 331 992 200 167 149 480 189 603 261 776 642 542 171 418 898 002 986 980 815 603 187 482 410 182 419 074 750 541 075 833 229 878 338 753 693 189 215 799 725 658 563 523 518 302 477 964 621 859 104 100 481 900 990 083 983 881 137 682 794 503 737 378 112 714 920 215 814 125 902 157 740 118 855 974 974 332 202 240 577 031 758 664 333 065 248 510 203 462 591 317 906 935 501 424 259 063 869 339 474 818 188 027 500 641 684 085 427 532 407 232 006 778 379 555 657 982 867 659 998 306 231 646 785 474 055 117 854 188 116 341 633 224 288 251 696 367 841 284 540 857 151 195 867 137 883 410 759 254 407 252 685 840 594 765 080 257 999 967 979 852 307 413 893 441 506 348 955 368 450 655 022 703 183 069 981 002 310 949 990 878 084 091 245 792 289 831 437 170 070 785 950 690 361 444 837 743 954 938 552 771 732 225 614 011 322 867 461 963 078 151 981 943 917 757 211 426 023 684 984 128 505 081 648 921 129 972 935 457 991 021 507 395 491 189 821 685 470 465 561 743 966 907 680 743 333 787 929 350 648 450 342 900 537 228 853 885 536 001 358 991 686 291 287 109 308 162 567 632 577 135 191 332 177 800 975 681 187 207 429 762 584 519 399 022 509 957 605 826 283 968 831 344 841 252 916 228 994 873 315 225 833 903 447 888 969 335 469 956 364 328 921 976 081 645 089 552 676 807 474 219 984 404 873 880 908 713 807 510 938 823 378 908 039 314 609 133 333 236 440 445 184 864 533 689 910 864 375 120 369 105 111 163 564 978 969 593 146 891 657 645 179 434 320 912 867 445 122 427 028 494 985 173 567 356 060 239 055 437 097 673 362 089 452 991 034 510 996 925 861 198 013 428 961 062 279 260 730 000 916 297 186 259 887 549 289 454 492 315 246 580 747 100 362 278 784 825 648 792 234 903 123 949 523 518 946 723 952 718 374 856 349 211 579 564 965 886 586 507 439 844 559 906 147 283 142 711 168 845 569 063 097 251 757 209 550 991 122 244 710 927 103 560 588 980 630 052 810 676 011 062 638 999 378 050 514 567 688 878 717 370 734 173 669 301 824 720 025 798 318 419 707 016 268 312 848 894 448 351 079 402 804 938 806 966 830 875 937 868 896 868 195 605 343 908 859 784 877 436 461 531 342 038 657 861 548 879 799 903 420 214 283 853 244 038 776 815 216 473 532 387 965 306 722 778 518 275 071 473 614 996 018 719 751 361 048 409 368 661 964 455 463 271 168 862 390 098 423 268 446 008 501 348 036 988 624 386 522 160 162 136 747 366 598 508 967 982 558 371 733 177 297 443 294 680 759 261 545 915 064 113 162 292 314 817 301 601 008 121 406 610 699 255 035 360 868 389 817 668 914 294 508 431 597 896 165 023 370 175 971 116 191 012 725 960 064 016 298 681 496 453 670 410 830 704 218 388 141 917 057 997 996 837 428 654 701 201 060 515 464 637 426 174 759 114 553 790 985 780 936 896 672 965 101 420 436 391 088 869 751 815 346 892 245 990 662 018 740 218 747 051 724 520 213 656 076 881 170 858 286 329 689 208 042 246 709 952 336 827 459 149 426 929 156 475 800 075 806 389 079 411 238 918 497 272 713 840 978 730 602 719 386 792 216 487 536 312 142 738 496 252 758 941 060 981 655 444 565 938 070 780 556 760 991 373 891 184 316 577 175 714 228 248 818 245 500 661 830 360 016 721 676 773 947 237 548 287 715 351 494 638 005 564 613 207 340 291 710 523 235 714 228 751 095 142 011 069 062 644 318 900 283 712 711 775 112 394 878 315 004 028 101 384 090 003 846 597 327 240 589 374 458 372 239 228 069 263 599 463 282 691 003 380 499 011 135 500 551 731 043 459 075 744 461 123 939 410 807 305 675 840 064 750 451 835 019 211 469 644 183 731 852 237 389 202 577 113 446 674 847 250 252 643 882 468 564 187 466 571 024 885 439 824 121 789 785 783 918 470 749 743 368 561 972 132 587 436 265 778 111 751 247 327 097 099 584 816 009 973 060 348 542 131 322 820 869 867 132 397 580 173 312 262 790 333 080 033 757 188 568 061 356 291 688 418 497 582 954 509 418 850 914 321 325 459 249 098 553 854 469 909 503 276 904 944 518 244 328 750 298 937 523 295 906 709 816 926 661 022 117 245 828 820 747 498 228 655 131 348 990 415 093 274 383 294 969 250 751 273 260 857 389 238 645 851 907 622 894 667 255 974 378 015 828 405 048 465 581 650 261 640 443 871 645 867 220 854 400 601 050 402 841 352 119 352 450 661 460 966 271 603 871 411 027 600 179 581 602 912 276 709 849 479 910 715 925 829 424 468 464 848 400 126 719 778 215 647 370 731 885 428 684 980 810 728 676 871 046 471 269 822 160 407 661 453 701 115 482 921 224 257 931 430 179 526 234 228 663 554 735 338 381 929 018 999 268 349 865 056 167 290 215 083 365 467 916 485 933 453 524 294 507 499 002 239 151 304 652 657 889 173 832 469 758 102 179 896 322 624 924 231 961 576 541 923 260 302 498 958 347 424 230 689 286 780 969 619 552 921 429 964 753 545 485 883 503 477 520 634 592 938 274 130 247 485 906 709 836 647 174 134 906 663 343 117 000 444 708 605 385 872 226 871 274 573 127 154 461 971 177 499 043 899 386 648 848 730 904 817 245 224 404 379 677 284 517 298 160 417 505 237 894 642 157 734 129 527 782 965 832 957 783 061 357 308 553 502 719 650 109 617 378 522 388 997 484 750 697 767 100 484 414 532 654 155 506 013 699 586 419 476 620 971 354 152 090 081 276 255 089 207 747 299 212 361 997 528 633 288 669 855 581 386 789 812 561 070 169 108 989 298 569 930 749 914 523 814 319 323 374 924 760 124 728 967 573 518 775 529 041 064 228 464 204 440 461 024 937 665 900 817 840 312 357 997 709 299 708 939 896 836 666 665 786 251 431 361 008 048 788 000 057 184 269 829 187 057 233 306 710 696 673 955 799 706 758 228 692 132 916 218 827 668 168 049 561 966 247 212 101 504 494 496 829 549 246 441 381 420 360 721 238 423 204 390 004 759 828 839 207 985 336 630 535 342 798 805 318 484 517 457 578 498 386 440 829 332 111 617 801 651 634 389 599 783 966 149 647 824 773 276 244 488 553 471 307 399 690 155 758 179 435 716 213 283 464 756 691 332 975 145 756 563 748 233 090 886 970 819 843 221 958 675 243 981 204 204 120 277 634 029 564 447 145 678 381 880 895 305 250 516 358 697 257 249 550 604 657 472 470 789 902 213 593 305 356 042 097 288 210 386 541 213 778 355 623 747 793 229 486 730 574 035 028 058 859 698 699 951 802 178 740 462 789 460 372 361 485 144 973 182 644 699 178 876 234 318 263 794 638 278 500 738 489 619 456 255 631 543 625 878 235 453 590 232 249 468 557 515 518 502 775 732 540 934 139 240 664 130 807 579 175 397 084 001 735 968 490 468 299 233 358 480 249 162 805 965 270 021 455 252 622 437 763 684 838 721 483 559 838 650 081 046 728 592 759 853 070 522 052 856 501 073 213 025 345 750 689 805 490 344 941 006 614 516 758 242 340 105 324 164 522 988 055 083 309 919 534 601 712 980 291 247 729 964 975 244 687 019 784 944 466 014 811 882 896 199 738 532 622 853 205 758 870 503 952 048 245 413 222 817 090 627 625 948 897 956 257 951 830 346 642 946 889 397 240 440 703 851 152 494 724 551 753 591 889 260 140 388 824 305 666 471 155 458 079 280 918 444 694 440 479 869 307 296 743 160 077 929 269 265 265 018 399 187 931 652 150 592 749 824 050 124 464 506 976 434 686 101 276 042 469 017 197 908 249 560 259 670 593 841 538 274 996 547 352 260 331 420 146 921 722 272 163 565 107 636 606 376 549 391 220 808 292 244 896 125 631 984 741 137 512 443 021 618 179 556 498 829 805 460 301 035 789 757 360 627 573 464 483 634 068 883 769 904 458 144 580 454 671 368 676 343 931 175 958 931 847 440 419 190 597 336 394 694 831 076 886 993 797 091 816 389 274 992 467 154 696 946 819 560 831 525 850 031 104 979 601 109 569 492 903 944 902 779 406 562 884 893 601 879 664 127 301 999 215 386 197 671 398 000 502 953 348 770 133 704 873 009 009 331 455 877 115 323 168 524 876 245 788 553 046 536 408 058 135 837 205 956 511 578 723 529 461 056 088 871 507 298 495 872 805 445 269 754 002 161 030 816 294 397 080 990 957 802 593 749 061 135 646 377 767 845 007 043 009 268 330 102 066 179 144 612 840 843 484 181 911 882 283 517 235 461 044 787 678 408 420 989 978 152 473 284 202 070 052 150 859 149 085 468 152 839 293 485 198 354 635 988 643 327 154 837 412 093 231 912 793 901 171 093 182 629 270 610 638 123 646 843 926 292 110 166 912 818 822 073 523 736 312 560 329 232 878 064 007 734 257 580 490 500 025 518 604 731 286 760 411 861 739 632 027 407 708 435 877 522 956 764 555 003 112 591 876 944 582 464 170 748 431 947 815 348 243 995 504 464 631 232 501 525 209 438 019 362 890 510 159 192 315 279 465 462 144 007 329 788 979 842 630 798 178 267 026 077 632 292 344 199 681 538 024 351 348 047 467 491 231 199 355 777 304 283 485 808 376 898 282 625 274 240 649 818 123 809 494 463 789 107 585 765 606 134 157 550 585 051 889 235 137 718 757 623 883 745 115 598 041 863 539 045 060 237 214 834 279 281 201 439 551 220 733 301 912 009 472 359 143 604 895 935 517 188 479 284 270 740 812 228 779 558 269 713 249 166 027 444 974 731 717 600 051 945 213 413 014 282 715 433 715 998 471 329 096 219 659 355 510 718 712 607 615 956 199 054 972 844 550 364 051 192 391 026 056 114 991 606 454 977 293 886 083 289 480 154 858 467 122 167 900 911 431 898 171 461 896 803 199 545 976 009 926 001 495 450 721 287 895 500 583 731 301 839 624 696 886 855 130 861 855 988 458 776 382 007 368 290 113 568 290 514 354 405 530 783 616 058 974 779 450 686 117 794 382 049 648 254 564 087 752 791 220 489 761 345 400 483 709 035 474 460 197 197 702 342 703 155 171 793 682 351 330 106 279 371 772 565 993 632 351 009 479 587 576 433 097 868 248 313 626 491 068 303 774 428 229 376 522 343 673 611 266 789 844 358 969 767 350 332 830 249 210 898 182 739 235 738 541 289 441 025 585 795 279 957 808 322 257 420 995 016 597 730 546 766 248 654 254 622 040 133 274 459 302 034 244 106 600 765 001 313 513 768 410 807 480 596 883 598 154 708 111 544 489 957 950 091 714 744 539 670 546 884 467 585 367 994 845 620 306 635 455 110 422 910 328 801 617 978 066 468 350 499 057 456 008 058 272 367 851 093 017 702 709 069 871 632 242 578 828 570 661 424 455 937 479 404 362 441 927 792 080 673 240 652 796 001 152 291 061 211 909 290 179 622 992 376 366 065 883 753 619 828 692 553 497 047 577 933 824 094 294 631 277 490 516 919 284 682 531 553 996 985 581 029 914 386 749 262 277 958 238 803 717 602 828 923 328 014 383 769 752 024 871 451 406 049 908 638 150 884 692 251 353 365 246 768 494 914 792 241 822 524 426 569 768 953 472 087 292 508 176 735 520 768 152 200 911 470 689 208 145 245 041 812 980 011 923 002 315 368 630 789 999 256 989 042 436 759 153 133 890 266 771 886 126 013 964 244 044 328 987 783 636 154 675 007 143 663 377 243 703 309 584 694 148 874 064 070 907 367 508 905 498 594 068 210 544 649 917 673 765 718 369 371 615 615 816 904 063 969 108 044 699 943 091 290 551 412 965 484 574 225 590 104 164 411 138 511 663 262 104 120 969 075 537 487 283 865 689 498 906 238 549 401 326 129 339 380 046 442 376 038 432 304 418 300 982 062 479 746 697 375 876 308 945 507 527 291 309 821 177 549 325 565 591 058 731 814 188 535 823 533 976 261 277 285 312 302 361 997 798 762 620 484 179 766 207 425 184 460 983 599 349 126 903 755 946 708 876 504 153 151 420 695 439 499 799 869 257 054 628 795 343 861 623 413 113 307 764 825 889 673 222 829 912 118 820 098 057 871 707 295 651 581 779 481 064 479 562 822 524 780 550 241 766 097 734 803 027 975 726 529 420 427 348 419 196 376 433 908 814 607 564 144 944 648 585 977 072 270 396 846 051 272 629 024 894 444 215 086 208 645 130 090 107 830 310 853 403 060 424 204 017 320 546 193 747 467 310 452 180 883 932 324 336 543 485 103 366 269 457 570 656 778 259 147 048 501 870 178 699 955 306 467 880 085 589 740 482 837 122 024 656 995 375 770 240 057 561 090 620 977 521 382 962 398 821 598 333 140 933 524 859 649 880 273 803 778 806 202 877 362 457 833 563 374 920 682 799 126 399 067 308 703 883 026 353 812 770 914 809 006 659 527 157 219 527 167 070 379 628 528 542 203 941 796 295 274 308 015 410 950 355 770 855 995 866 458 812 326 770 401 724 494 634 450 142 312 990 834 980 344 157 221 140 634 332 600 071 382 814 710 886 024 007 211 568 934 524 536 985 648 902 756 998 644 614 783 706 999 164 998 401 764 274 351 539 427 450 165 900 555 038 793 044 111 986 343 369 551 121 906 714 594 230 135 216 909 278 430 234 080 055 976 815 136 080 742 571 519 751 414 544 395 046 359 779 949 439 064 178 003 196 949 721 917 814 511 421 274 720 931 828 236 339 836 924 327 714 890 093 277 174 329 841 479 792 774 872 776 515 859 104 765 251 795 350 955 662 511 167 717 156 006 385 088 636 959 283 114 575 323 822 825 344 607 094 108 985 094 633 133 606 377 983 086 094 017 344 526 587 973 785 053 174 011 093 397 340 580 222 205 628 635 799 277 920 501 639 829 853 483 664 071 000 271 491 240 341 815 539 215 248 732 836 874 359 821 400 540 195 839 714 684 356 108 211 650 427 228 225 819 455 008 587 053 812 354 542 543 719 859 138 920 046 684 614 176 275 476 409 338 226 843 578 165 239 445 387 124 694 803 385 551 224 981 125 976 801 897 423 576 407 371 826 381 275 680 395 778 745 987 643 453 391 107 792 495 569 089 998 128 838 054 842 967 820 456 140 675 873 116 644 198 144 835 833 945 985 275 921 802 544 032 861 061 988 940 794 280 153 653 046 246 546 307 378 031 200 876 961 953 345 884 456 944 797 543 138 479 918 726 332 978 205 729 688 521 750 196 188 472 895 289 727 844 017 887 986 774 050 966 579 859 864 446 109 584 691 322 923 187 931 884 728 985 839 987 275 875 002 513 362 095 262 360 363 873 568 844 351 610 258 002 329 443 495 827 610 953 793 640 956 683 790 319 176 036 303 325 278 068 640 976 151 253 810 920 525 672 269 900 292 158 585 139 069 690 251 166 339 421 977 524 645 000 275 014 413 639 414 930 066 958 689 060 342 560 882 459 176 942 668 981 937 909 265 091 057 030 410 370 432 173 354 965 520 176 336 802 735 651 851 358 704 922 626 045 585 573 172 145 366 175 938 926 223 030 897 999 297 775 859 362 561 438 482 649 800 839 484 402 750 497 026 826 938 029 852 177 861 639 513 385 854 511 766 980 208 292 475 141 409 314 467 526 897 007 012 080 919 131 473 118 156 597 774 846 517 768 270 251 518 710 994 326 909 046 621 505 812 182 714 114 552 486 766 287 723 265 105 742 055 980 707 257 376 141 737 223 878 010 575 080 024 715 008 156 298 803 798 287 537 277 602 783 236 824 898 686 595 006 939 672 604 997 590 090 127 992 983 637 547 323 866 676 117 978 307 034 295 329 115 539 627 325 892 217 852 620 595 290 810 032 912 059 701 865 367 655 209 459 903 574 325 559 967 790 412 328 357 720 960 328 268 306 396 383 348 919 704 671 936 901 840 468 935 530 924 881 554 144 210 139 171 085 132 389 193 740 381 637 634 574 000 330 846 186 430 395 793 285 504 565 077 466 038 651 983 436 943 140 756 814 420 818 099 984 571 881 913 391 482 393 465 245 283 483 273 656 923 102 350 436 061 778 881 963 194 530 883 854 325 757 393 025 164 285 605 161 142 670 918 873 771 420 860 510 198 449 258 495 729 154 860 632 663 074 492 409 087 901 568 350 749 066 719 807 642 740 480 344 639 530 134 272 748 527 715 208 360 498 513 777 754 507 975 063 203 283 366 268 621 677 022 856 769 348 185 356 421 650 211 157 251 991 728 668 706 252 428 293 257 673 702 724 126 399 717 378 114 406 261 003 683 645 970 123 230 038 776 961 449 378 281 951 049 313 961 433 961 075 785 922 141 121 452 662 943 732 200 253 419 830 225 446 134 507 819 119 715 832 855 128 166 222 985 458 027 140 510 478 896 860 861 380 820 225 908 974 988 715 773 070 322 684 914 585 494 587 587 611 451 583 864 998 700 210 637 930 963 688 635 347 088 002 387 873 222 029 947 471 590 718 035 445 997 666 805 135 333 070 550 567 677 273 862 546 236 971 490 201 692 592 660 654 545 949 662 370 766 081 252 665 036 220 407 861 880 040 764 146 628 221 012 299 635 495 072 332 421 810 193 926 996 658 461 855 741 551 756 600 271 908 089 299 800 268 812 104 041 385 911 030 479 166 734 317 677 127 526 188 660 039 368 773 167 817 225 921 105 338 147 485 495 173 401 092 955 575 178 561 404 067 915 154 267 332 506 974 631 887 961 647 949 620 894 047 133 702 155 956 582 990 531 790 906 671 917 957 912 862 369 770 210 915 687 560 689 306 038 230 571 117 512 078 702 519 354 544 555 419 471 580 709 022 053 246 818 189 295 842 516 522 809 198 546 725 096 237 109 882 378 410 151 426 742 940 608 401 810 105 365 272 376 650 384 516 111 009 359 601 075 822 194 781 005 016 665 140 125 698 605 194 438 669 624 867 908 867 812 923 382 121 217 579 318 892 708 773 610 277 257 530 087 001 681 242 006 059 869 942 067 837 442 591 698 538 806 434 136 029 533 645 848 291 160 138 809 144 510 867 112 627 755 200 118 943 695 369 618 366 336 806 854 789 425 449 262 214 243 264 900 287 906 072 620 700 524 614 455 282 174 706 441 562 702 450 509 239 268 634 891 457 414 656 154 289 095 249 954 814 549 639 746 518 722 433 819 905 120 886 837 094 326 896 348 533 420 222 701 116 786 661 741 903 922 284 090 015 432 896 799 681 550 594 484 582 794 850 666 782 578 886 987 759 966 665 250 680 242 347 182 340 214 846 094 640 965 105 233 247 013 179 886 835 979 712 037 807 909 241 889 306 976 551 269 058 645 665 703 858 978 362 553 920 700 036 156 087 432 826 513 523 534 683 752 914 947 607 672 392 663 870 615 075 744 571 741 213 451 330 617 805 670 660 298 173 147 562 055 194 175 898 073 719 881 076 304 023 178 196 107 511 083 155 691 984 190 009 081 030 742 751 666 992 259 056 917 153 873 995 847 698 104 380 871 017 258 997 230 698 252 077 450 344 541 698 719 600 047 508 733 414 008 333 057 062 150 225 020 822 306 187 672 222 767 323 481 738 234 065 057 102 497 889 518 759 589 073 097 854 041 497 144 545 225 612 389 197 671 257 275 386 489 890 992 294 866 868 519 041 681 865 260 347 960 697 897 553 524 445 330 712 953 250 916 868 548 458 603 082 567 241 542 416 855 240 937 593 980 167 218 521 291 824 572 741 021 601 165 357 408 474 631 104 341 290 147 418 887 780 028 847 164 630 394 281 043 386 539 092 283 644 879 158 020 943 149 674 447 040 804 664 604 736 734 236 605 770 248 183 055 407 638 348 861 086 826 466 620 837 183 997 416 502 921 575 626 291 744 868 790 495 164 101 207 230 184 158 071 383 812 133 503 682 692 651 833 484 330 763 652 377 675 296 058 088 451 899 700 074 003 976 829 479 946 206 596 169 797 906 127 459 498 706 953 492 451 787 451 706 482 391 756 124 945 671 590 806 714 320 579 780 885 474 739 779 625 530 300 262 789 804 720 806 456 628 083 871 739 882 618 884 411 280 728 668 984 090 178 005 117 371 728 965 336 237 170 170 630 861 496 702 595 520 077 866 002 981 103 465 689 846 029 539 212 138 449 706 448 385 096 477 280 028 451 541 551 691 554 604 154 034 798 398 771 093 358 983 295 612 973 252 680 102 805 739 759 464 200 556 004 601 478 948 699 438 047 094 083 365 159 808 123 273 127 406 831 047 783 665 334 471 531 763 759 285 657 738 671 304 617 985 275 799 448 776 472 242 843 929 720 148 074 395 670 194 431 110 291 953 095 140 344 946 345 134 997 467 720 069 303 149 066 998 486 246 550 431 201 896 109 250 441 531 087 336 139 463 142 589 454 206 276 351 445 571 446 053 197 144 622 291 693 051 332 742 828 055 887 113 689 675 629 961 433 189 874 354 477 679 845 773 207 797 936 379 323 188 941 659 783 971 576 541 210 236 381 106 150 874 331 327 128 016 528 799 058 484 480 563 943 557 697 497 115 288 347 597 949 017 472 247 065 876 971 988 061 550 386 394 256 079 651 046 509 687 359 695 995 950 635 285 807 748 141 296 181 290 987 672 933 703 263 594 960 486 204 249 554 514 149 826 881 577 151 247 163 214 441 189 937 592 664 210 606 318 610 838 083 853 778 509 782 483 064 642 253 076 006 667 148 158 249 880 535 664 788 623 636 994 935 382 049 088 487 590 214 733 845 085 823 383 335 171 808 890 090 820 835 420 495 461 012 594 903 296 888 219 545 388 712 591 691 123 728 788 287 189 028 155 481 407 412 195 176 090 020 844 971 353 353 267 111 885 379 161 887 387 681 076 003 933 768 529 508 195 190 297 981 381 164 069 803 646 114 300 647 393 073 278 213 593 056 393 639 431 368 108 695 629 136 746 576 172 129 652 694 389 904 611 789 959 377 078 484 717 763 579 392 180 932 133 695 743 928 583 135 217 192 489 836 616 182 925 425 636 059 263 886 292 298 467 042 958 050 652 357 084 245 321 480 030 184 016 509 512 691 337 531 783 453 865 994 889 133 681 148 197 792 927 418 597 330 088 844 065 064 606 795 620 534 814 635 473 613 162 775 272 343 233 218 210 313 861 530 989 076 093 731 973 028 989 220 195 818 039 867 872 430 195 089 874 970 762 182 632 078 281 633 229 918 477 304 898 539 632 559 853 763 157 979 546 488 700 922 516 061 041 685 178 148 697 845 479 873 606 548 867 594 667 920 442 377 202 585 776 103 859 912 594 355 447 328 845 488 270 958 916 729 133 076 682 831 047 639 212 058 620 309 862 001 074 449 415 560 429 076 956 494 621 661 644 012 955 750 381 157 144 652 146 004 066 954 190 890 893 338 586 833 881 114 477 598 587 296 227 575 629 358 764 250 486 464 688 026 699 593 828 575 129 279 396 185 775 466 538 052 933 218 665 112 505 657 183 343 157 417 322 093 129 290 295 192 528 848 631 368 703 536 577 913 761 202 788 211 799 132 755 097 099 652 309 521 979 020 048 232 974 700 134 471 108 381 337 898 139 416 698 599 118 400 777 929 265 759 384 779 326 163 659 184 694 180 298 504 310 160 937 505 791 833 046 530 378 961 570 291 864 265 626 863 224 539 095 127 813 826 668 318 685 736 406 361 434 360 940 211 783 937 030 509 529 742 862 265 219 305 520 196 693 030 455 086 510 561 316 893 665 659 480 258 466 229 485 171 634 874 776 430 617 853 651 508 278 625 791 663 883 508 925 178 093 891 362 112 626 432 838 191 062 271 666 929 061 145 777 213 111 381 138 169 141 954 968 900 000 870 770 598 176 667 783 313 234 806 674 975 856 899 213 151 279 902 581 601 793 237 477 064 614 918 155 030 703 498 973 974 915 940 131 397 934 414 645 580 310 880 934 777 843 689 665 230 140 324 392 565 150 578 253 899 990 340 109 470 825 645 204 189 863 613 264 963 844 818 249 404 802 214 396 136 579 914 157 691 341 974 502 639 384 111 720 888 023 412 042 063 339 504 789 577 482 120 894 285 142 418 453 389 147 067 008 898 174 395 853 327 085 514 116 244 670 656 401 870 162 177 848 209 919 107 837 524 782 781 493 632 483 161 345 457 322 537 900 758 568 048 129 854 463 493 315 288 074 769 953 712 920 201 466 414 207 206 225 053 720 590 314 846 577 654 582 127 052 588 825 038 436 175 677 318 093 776 770 805 453 799 218 965 005 840 786 352 963 054 636 041 013 632 155 068 120 212 224 375 190 640 068 739 839 656 392 513 771 566 057 265 081 620 431 255 098 200 543 148 500 842 788 841 643 224 712 048 749 063 340 574 201 431 437 345 118 841 736 057 865 927 907 179 365 879 222 276 018 944 135 899 453 676 442 568 787 587 653 004 398 743 453 728 207 796 016 535 273 874 370 379 644 232 080 607 374 314 524 778 122 532 489 468 491 218 033 870 708 009 744 029 637 853 659 185 372 998 070 672 995 607 386 379 636 002 291 927 433 452 236 442 895 949 767 082 151 196 812 133 174 181 724 612 549 205 094 545 138 560 336 130 397 043 704 348 747 263 401 934 347 339 151 352 899 316 192 178 682 517 012 640 421 574 826 951 938 245 758 880 208 062 218 883 103 740 431 642 372 586 757 484 755 344 467 156 624 433 919 885 207 102 592 817 329 274 159 219 903 826 796 449 777 020 838 934 969 038 093 062 123 121 827 159 404 701 652 129 703 609 220 419 972 535 156 911 298 759 449 626 353 990 485 117 437 791 307 318 983 299 905 106 658 507 318 811 377 218 948 517 300 765 955 920 634 234 856 827 583 692 818 401 167 515 786 436 600 632 753 681 021 705 836 145 535 369 880 678 576 534 941 259 380 000 140 158 516 568 017 940 042 879 935 919 670 744 142 337 221 462 082 454 151 704 135 447 665 293 737 693 489 600 196 870 745 761 053 532 594 220 978 780 651 298 305 044 309 991 917 584 204 697 829 149 903 410 547 021 421 655 659 846 488 679 770 314 234 304 329 553 648 650 294 839 040 884 905 482 148 825 064 463 030 756 436 115 167 890 806 237 776 791 970 800 734 931 670 862 330 612 498 875 762 338 495 709 330 241 951 671 557 993 302 083 455 010 082 509 167 200 339 208 292 458 851 790 056 815 568 422 704 811 236 035 361 866 983 541 533 230 198 106 697 996 664 609 708 812 678 138 518 171 948 802 724 424 846 581 649 995 132 821 121 071 747 133 591 409 791 112 061 789 770 887 047 264 611 313 310 872 332 061 949 764 152 570 503 322 068 253 068 214 211 771 321 286 427 929 345 236 429 033 527 767 833 955 564 187 709 029 689 055 490 092 769 166 417 749 985 788 238 678 245 284 624 689 232 971 281 816 418 401 483 101 894 665 659 423 838 395 916 212 186 873 033 605 657 037 549 660 221 559 602 956 115 539 903 543 860 762 690 915 316 465 309 679 251 083 579 110 560 025 457 660 633 805 099 783 762 153 223 006 917 562 660 751 733 575 796 691 663 086 927 335 678 186 800 532 105 469 473 578 920 128 565 870 952 850 437 589 653 403 720 066 329 444 399 132 324 273 085 325 076 706 670 975 230 158 478 186 726 899 790 675 442 727 701 015 062 267 143 976 803 334 095 303 600 932 674 518 555 357 428 887 407 992 799 513 101 236 612 396 577 396 440 891 095 378 978 796 798 334 849 685 671 517 947 061 813 741 687 523 951 878 242 314 665 085 591 868 872 457 478 969 466 353 706 460 204 314 705 533 448 443 423 500 681 128 819 640 179 642 995 685 856 496 774 767 396 730 804 498 933 085 510 781 080 752 826 927 279 307 506 097 384 236 153 667 865 416 677 835 269 344 659 703 015 078 211 463 656 703 404 480 536 102 527 897 581 089 575 123 507 142 621 176 245 880 835 224 158 555 325 907 534 277 575 940 567 130 946 746 870 246 301 102 191 880 879 207 369 520 642 027 274 250 427 762 057 605 624 114 948 660 934 213 380 202 229 163 263 604 297 955 830 715 622 107 367 377 630 387 919 270 861 116 170 753 660 283 047 673 849 295 467 482 011 076 074 911 552 383 508 216 815 225 338 304 757 501 695 271 029 298 809 530 512 750 869 058 997 543 360 140 196 869 853 516 188 891 108 426 939 751 328 568 005 127 949 993 031 831 867 078 989 460 776 536 524 350 286 391 270 816 352 386 212 405 593 034 493 724 758 106 514 796 147 281 723 294 474 051 103 838 493 699 594 262 469 284 974 339 757 941 840 139 262 831 314 889 444 330 215 988 539 153 620 255 079 265 531 698 865 729 397 474 403 934 471 550 582 823 553 391 767 249 704 015 547 508 550 964 985 230 754 025 132 377 156 509 823 198 085 874 281 980 496 716 534 372 402 111 905 593 965 727 594 944 899 440 362 999 328 799 029 986 806 862 642 150 020 195 271 109 938 759 028 147 100 064 194 745 745 790 417 684 433 009 938 176 087 017 556 449 283 388 212 796 906 234 399 755 111 806 412 728 665 565 108 268 504 187 826 940 361 068 101 933 422 254 699 744 291 793 325 156 163 110 036 453 574 695 141 049 867 091 288 214 145 635 253 730 971 812 359 377 543 240 186 008 388 958 637 520 898 998 456 006 592 421 201 895 295 225 792 501 097 857 843 278 468 578 904 679 016 884 118 925 538 840 097 854 548 847 882 572 168 852 748 002 155 915 395 010 244 293 149 592 174 723 767 137 907 237 082 700 883 092 921 719 823 171 375 083 163 389 815 791 204 841 438 489 174 273 866 420 238 416 697 205 932 311 149 285 231 894 764 960 075 047 317 644 058 605 244 166 611 701 066 024 167 627 253 306 988 912 392 105 371 161 314 118 092 054 506 972 564 499 095 559 712 064 208 845 582 090 204 149 992 155 167 466 903 376 554 406 256 196 290 577 961 164 768 064 218 461 239 815 973 116 991 948 696 704 522 875 618 803 570 826 182 224 828 412 985 355 313 341 826 041 116 711 405 743 144 728 954 569 193 689 853 266 354 442 160 035 469 382 128 847 226 968 222 378 764 652 229 307 542 053 789 547 233 182 733 185 154 301 551 928 756 743 661 000 418 153 306 480 062 674 828 304 116 482 608 546 109 939 058 549 354 865 547 219 704 655 647 335 050 413 639 776 224 458 966 523 484 242 152 399 244 046 981 754 272 195 182 283 630 606 161 509 172 848 680 204 834 773 328 294 525 188 745 041 279 581 198 327 293 925 825 579 821 107 454 175 377 715 482 343 128 617 416 004 304 867 592 720 216 970 304 395 750 911 140 481 714 337 838 993 962 455 423 546 554 545 631 909 969 860 922 403 974 189 824 288 678 517 607 101 679 527 532 766 348 482 163 237 495 911 288 497 585 827 632 244 668 585 427 044 535 578 839 416 259 577 645 346 586 891 756 973 475 174 703 223 246 149 322 011 448 771 854 580 597 101 761 636 951 059 783 670 028 259 566 739 308 000 625 567 930 926 854 492 198 972 631 975 287 495 262 400 345 856 459 064 496 082 457 356 909 115 966 978 462 798 019 978 692 260 432 742 793 872 896 176 969 040 489 782 405 085 122 758 885 413 426 593 054 867 328 380 377 137 375 805 237 119 781 143 171 777 520 020 299 012 857 259 939 961 730 346 715 950 193 456 178 720 108 054 014 974 107 743 394 464 387 104 053 839 679 339 794 940 728 960 619 323 339 551 101 343 062 120 819 375 075 756 550 881 831 042 208 476 023 260 229 874 850 839 330 190 541 710 533 840 321 311 925 602 488 710 190 398 901 443 216 694 231 762 581 281 546 989 745 540 858 124 586 041 142 543 151 554 254 030 106 250 261 401 055 525 200 283 783 346 572 227 782 877 309 137 283 934 303 694 978 267 082 955 413 542 627 782 901 727 849 568 120 268 200 390 854 958 042 844 778 490 985 100 720 228 268 199 552 023 414 960 005 791 905 367 327 763 375 227 406 007 620 453 196 122 931 571 731 329 067 253 000 610 627 052 403 214 803 401 995 735 503 538 433 517 848 632 947 961 481 312 271 215 776 951 375 321 878 237 424 009 689 901 356 272 998 089 828 240 146 950 032 680 157 487 403 693 661 543 795 529 616 052 406 915 645 884 129 436 259 989 472 645 221 480 532 121 295 172 150 271 577 644 333 535 093 639 589 105 709 937 331 753 901 200 734 318 845 992 178 856 734 714 411 495 176 236 970 337 357 691 724 879 726 876 140 425 438 614 887 340 918 302 414 758 259 636 971 155 534 044 144 780 221 046 176 085 508 691 527 705 823 637 973 863 470 427 651 087 348 778 498 369 934 371 853 053 653 348 783 401 693 477 108 042 507 771 626 171 916 805 457 838 241 450 801 855 401 586 159 855 430 051 203 971 644 558 620 901 772 165 289 543 831 867 647 590 777 029 902 012 176 272 260 881 948 421 851 973 522 457 220 686 225 937 361 386 455 392 991 628 402 593 106 942 466 340 588 008 248 930 057 341 191 883 888 551 236 726 433 996 697 718 078 716 245 516 695 470 030 268 575 771 937 465 747 045 912 500 025 058 578 603 956 923 641 891 642 567 557 005 618 250 959 053 035 033 356 244 252 387 346 530 586 519 470 649 381 253 724 844 229 393 634 659 292 996 646 319 422 499 268 328 910 354 482 930 653 528 078 950 974 511 787 887 906 355 498 797 528 061 994 131 209 937 775 966 411 247 082 400 170 755 046 409 991 354 079 386 148 219 620 904 012 897 555 632 531 828 458 484 765 989 448 913 536 971 525 612 696 935 097 726 763 529 106 420 977 334 258 496 360 831 018 056 359 826 186 912 951 530 609 578 354 887 724 721 433 451 117 249 331 751 248 970 385 484 069 211 584 059 086 940 750 713 456 232 792 246 817 183 652 595 815 838 561 216 917 091 088 562 483 193 148 566 068 108 557 439 027 958 728 498 113 136 198 036 197 685 305 288 861 874 612 057 836 490 156 179 740 949 515 687 558 171 620 927 281 667 791 574 721 018 034 857 199 850 392 560 548 836 906 565 404 591 817 971 404 604 046 003 735 310 243 811 988 437 200 463 808 687 883 430 646 735 850 092 960 665 040 896 974 010 336 032 733 552 583 764 989 586 265 213 704 493 051 753 784 097 986 041 451 892 376 886 364 645 009 844 602 782 569 211 043 916 998 430 389 044 685 111 097 218 839 650 707 307 898 673 599 497 548 421 118 258 751 680 689 365 262 503 643 513 125 701 832 572 585 881 265 866 050 786 426 525 517 393 577 003 561 013 985 327 109 188 764 456 800 290 254 253 719 200 051 014 832 665 817 596 709 264 743 043 595 648 137 542 563 020 874 356 876 187 686 758 726 553 939 256 447 601 411 875 527 805 167 525 702 583 853 970 528 469 345 048 260 547 957 683 259 220 299 382 324 507 575 972 174 344 452 435 854 169 238 065 676 361 709 511 209 220 259 859 929 603 986 844 077 470 635 986 762 643 201 970 614 055 822 185 653 281 705 481 466 859 064 105 401 017 747 624 495 169 563 010 913 465 179 738 743 103 690 521 615 843 083 952 865 750 186 752 558 994 231 259 724 634 525 951 765 626 164 893 048 430 242 755 289 451 738 480 967 121 577 877 771 081 723 141 222 580 262 717 526 365 345 022 895 837 034 627 448 757 581 748 300 973 485 115 951 157 881 988 738 314 751 461 676 422 124 876 551 843 699 897 021 728 807 349 763 702 290 389 416 933 077 955 786 810 249 186 509 305 340 928 999 486 442 924 911 514 015 488 601 563 816 340 722 785 925 223 057 177 129 463 382 870 856 319 680 557 486 717 610 194 214 270 968 324 208 806 446 319 587 876 252 265 957 558 832 362 312 141 050 273 025 625 758 773 314 355 100 833 196 876 430 520 023 218 092 799 549 899 836 656 457 644 477 579 024 077 863 939 510 139 143 035 982 101 244 710 074 819 420 409 612 404 736 033 078 460 754 259 049 874 134 404 466 800 828 083 289 369 913 176 059 292 161 685 592 435 478 691 370 394 763 852 317 601 636 782 094 743 501 682 817 049 373 714 788 938 465 740 106 338 997 383 849 181 413 475 030 752 207 116 528 277 411 833 893 898 751 571 288 310 143 016 377 324 713 817 485 821 624 732 102 534 295 505 236 013 990 655 613 045 177 945 682 217 034 960 276 146 535 995 782 559 316 541 788 422 566 394 463 962 254 729 341 214 625 270 488 071 458 695 536 818 526 300 494 093 750 467 935 399 558 079 062 903 244 073 501 793 232 163 083 861 525 080 749 883 701 745 992 281 035 344 699 036 970 169 512 400 944 828 848 505 974 922 454 808 220 017 220 510 788 388 998 797 475 035 263 802 856 190 635 343 653 402 102 506 850 502 650 782 996 489 022 093 876 953 942 481 696 466 900 024 177 549 765 812 203 704 344 838 883 674 340 241 073 184 688 634 598 654 381 999 941 527 325 900 901 493 808 902 199 054 169 711 601 171 300 316 965 057 136 529 944 044 201 398 772 463 673 897 230 934 024 223 775 428 595 377 395 836 991 047 113 854 216 124 943 881 485 237 728 918 203 865 852 187 005 953 634 754 340 752 844 015 960 562 075 595 277 271 534 014 421 323 849 326 761 045 672 605 414 563 588 211 904 577 221 885 354 984 187 179 869 286 459 103 789 899 047 793 654 448 293 746 513 658 720 912 447 985 512 483 577 758 026 066 319 467 808 899 816 646 494 998 420 210 310 177 749 968 234 235 502 209 374 465 255 414 619 940 386 325 487 961 218 783 782 606 037 868 130 348 448 071 629 194 132 638 017 477 122 242 715 299 985 466 373 035 995 883 070 705 362 859 081 082 862 086 617 785 813 567 167 698 341 812 480 968 980 111 548 861 271 621 813 052 289 116 233 871 954 098 813 785 852 907 655 854 133 361 769 253 099 797 479 382 589 790 696 577 422 503 419 377 761 086 733 432 601 923 951 966 427 260 047 374 425 572 199 007 126 743 231 115 862 949 215 901 923 121 318 366 682 822 442 863 554 841 493 929 699 970 481 160 075 961 163 273 105 919 909 555 275 327 737 595 217 179 107 675 070 509 913 318 666 568 094 440 513 881 757 762 498 967 234 382 786 323 737 767 413 874 838 978 307 814 472 467 290 219 422 758 553 385 621 400 327 984 995 479 095 081 934 248 352 433 142 759 410 708 531 844 558 690 937 836 069 176 401 996 651 899 502 786 122 499 891 137 905 371 586 243 898 983 443 898 885 072 085 204 451 879 329 004 191 082 456 883 102 014 404 762 326 667 128 421 220 399 311 043 818 199 178 933 291 077 490 821 865 814 121 806 166 675 533 101 030 470 387 388 027 463 544 458 576 903 410 170 476 533 398 088 047 721 935 076 419 849 805 607 774 757 728 837 997 408 437 027 281 057 409 948 114 367 388 932 546 001 578 293 039 627 175 749 037 495 206 294 271 732 793 010 393 591 471 063 870 818 010 017 056 832 259 876 341 773 559 213 125 853 409 860 225 172 926 449 452 121 234 530 575 655 413 347 682 985 200 869 525 896 412 371 638 338 123 876 474 928 209 621 565 145 013 559 593 227 099 584 534 575 221 338 429 212 373 985 983 508 582 993 000 440 570 803 091 817 650 958 203 550 436 261 084 261 505 874 914 129 819 534 928 076 333 942 717 472 495 476 797 744 295 018 675 032 905 098 290 251 180 816 584 896 434 035 842 054 271 140 669 992 431 394 045 249 908 853 275 379 136 435 556 457 180 821 743 060 386 357 883 686 780 968 531 567 719 678 570 633 501 227 118 307 552 019 252 355 428 164 412 684 888 634 668 004 349 488 133 765 585 697 083 135 738 381 119 746 110 322 756 166 879 509 162 630 157 689 899 902 158 188 920 783 787 606 994 056 940 436 253 191 644 826 357 144 185 886 537 089 224 929 498 434 628 303 161 661 809 379 336 346 246 508 231 511 558 672 328 763 073 905 503 839 774 161 093 958 078 989 797 232 368 431 978 644 235 692 547 346 805 691 367 302 218 165 123 125 812 252 679 797 988 802 043 662 353 292 624 396 606 147 377 323 371 658 993 365 905 311 073 052 232 367 308 062 897 413 878 085 814 076 776 733 481 532 714 499 090 201 946 178 316 068 356 105 234 898 118 360 274 212 904 172 378 723 170 781 185 644 698 234 588 650 683 011 175 132 800 207 837 953 707 823 665 404 101 273 603 965 181 087 757 320 127 190 462 131 998 854 538 450 190 962 334 521 981 115 316 001 676 130 646 524 438 159 268 754 732 481 613 498 242 701 726 867 746 515 191 344 379 598 186 786 678 122 415 789 343 949 513 986 718 564 802 821 263 746 656 414 266 340 322 459 578 061 143 053 911 380 180 452 853 537 623 213 279 245 297 532 015 334 049 289 520 506 681 310 523 127 603 854 472 042 498 394 803 756 689 554 085 237 656 279 043 229 309 363 360 591 909 630 920 891 325 045 706 369 113 544 139 672 097 978 190 503 670 047 382 315 764 936 592 351 670 759 573 454 548 529 876 717 416 669 527 016 943 502 060 529 126 605 988 024 223 601 007 527 108 113 576 373 228 077 327 314 701 854 141 989 915 987 840 622 048 494 576 464 652 856 144 318 687 146 393 534 184 994 359 215 260 491 323 312 777 847 367 697 679 548 706 850 901 353 273 164 492 980 041 158 055 762 004 473 830 805 094 784 720 165 607 976 808 660 932 701 571 120 041 326 787 053 981 790 673 324 135 965 785 374 687 513 401 062 288 065 533 087 194 371 093 364 625 318 304 008 175 333 179 781 788 297 935 139 941 520 165 508 613 302 665 549 528 108 661 044 461 111 644 076 560 147 755 784 667 037 257 912 782 671 584 274 383 423 088 593 200 544 837 768 659 034 826 966 075 493 007 642 885 613 800 357 350 011 760 174 232 172 987 579 939 429 084 421 172 328 127 173 087 296 654 955 187 094 566 055 736 810 637 143 098 742 183 313 486 874 094 054 962 973 952 055 370 883 273 586 816 375 704 606 414 034 941 850 092 686 538 886 481 601 781 443 465 053 985 451 849 966 197 326 638 465 762 169 316 338 664 397 844 042 834 344 374 356 338 964 098 425 623 277 843 661 180 658 252 861 897 126 400 638 642 086 211 656 286 763 471 774 121 654 027 216 587 128 346 923 082 854 268 993 939 399 845 220 216 459 197 408 074 265 665 676 004 301 577 865 439 484 243 718 356 251 301 347 984 026 802 681 709 825 105 747 643 705 135 278 470 340 347 986 112 813 108 145 271 852 632 811 094 739 576 308 030 073 358 953 858 991 370 780 623 560 589 039 131 235 116 539 225 030 571 004 110 872 318 315 002 089 307 329 914 376 377 754 107 535 092 623 879 801 638 810 567 198 141 834 337 914 439 658 293 658 852 438 592 476 469 463 915 762 979 709 503 367 051 406 872 740 998 738 236 288 665 073 981 830 713 536 955 154 525 212 874 590 534 340 274 016 501 938 559 230 294 332 702 752 178 915 407 979 579 206 223 378 921 723 553 584 609 760 666 769 467 666 753 012 743 357 025 243 337 949 520 231 247 226 225 702 197 594 941 802 149 699 896 303 115 383 271 038 242 361 072 073 596 559 599 948 624 131 899 945 958 568 132 373 029 308 429 158 258 097 481 610 959 053 121 494 863 420 245 801 737 683 730 117 538 638 716 025 025 497 782 130 497 855 083 833 725 696 199 491 074 378 047 982 538 750 227 773 816 805 378 515 290 353 607 346 529 088 950 081 782 806 480 030 663 777 430 104 333 248 093 556 039 845 926 009 468 775 177 857 305 586 658 304 329 048 848 143 700 230 265 296 438 647 452 015 973 005 205 829 912 436 166 431 305 368 685 723 300 979 882 853 997 855 837 402 337 772 465 695 687 992 228 961 507 623 266 996 466 464 979 239 926 667 306 634 849 251 099 183 270 987 345 659 829 150 360 196 763 495 686 794 946 659 615 978 884 084 593 088 188 752 835 353 463 650 897 551 948 512 267 339 414 322 063 740 523 976 017 636 505 203 781 435 370 660 140 948 268 220 087 405 013 382 540 996 348 572 453 874 718 632 644 843 258 119 165 422 689 682 812 369 839 411 484 253 735 361 749 723 019 434 985 631 619 625 917 358 469 639 673 365 127 002 022 526 005 101 685 828 724 743 278 710 825 728 670 136 728 378 198 503 523 845 478 335 735 023 782 952 096 547 206 424 674 625 587 630 815 152 990 137 759 023 025 830 166 976 539 590 254 689 830 088 184 043 395 220 362 575 386 094 770 025 979 324 579 758 928 364 310 650 991 568 420 254 623 709 031 326 644 193 513 086 058 838 761 987 783 415 244 883 213 219 505 561 362 852 787 948 488 659 531 604 000 373 136 307 655 837 725 577 653 727 573 213 003 176 807 867 802 175 381 300 268 851 945 130 835 443 744 100 249 767 822 033 443 870 884 152 402 533 650 780 216 517 681 984 334 685 342 061 396 870 544 589 852 828 620 211 074 151 985 046 657 940 788 695 034 999 838 732 808 695 332 192 004 346 927 965 730 715 000 253 164 812 461 622 798 118 908 800 761 709 100 969 182 750 228 337 921 846 786 151 141 610 737 233 503 346 271 035 652 681 538 722 613 617 418 934 977 058 320 573 101 747 945 205 782 966 958 863 026 263 279 218 590 709 223 825 947 821 708 492 335 856 244 540 903 612 051 565 973 030 703 160 670 084 062 349 698 036 170 041 944 695 273 819 574 603 555 757 210 418 777 293 374 462 033 816 651 915 071 137 363 957 934 207 756 596 051 290 817 111 037 592 631 615 593 031 341 967 150 942 670 299 909 995 743 964 577 344 025 123 767 207 508 864 595 091 081 755 665 894 538 531 754 661 947 562 296 953 204 965 546 433 578 786 024 865 635 735 638 999 475 661 308 748 482 689 258 692 965 496 496 029 931 500 727 572 085 967 487 248 564 884 697 546 472 134 556 963 853 275 669 440 894 717 879 883 077 228 994 796 609 374 367 004 071 235 249 394 912 534 249 309 099 089 437 703 895 603 778 779 108 383 929 825 640 595 059 742 996 015 151 281 290 199 523 273 989 395 697 173 634 904 236 413 119 563 801 560 297 530 644 635 052 458 091 022 991 799 443 358 599 235 471 150 332 624 689 605 578 944 455 599 374 524 628 275 047 984 122 424 304 359 099 685 572 108 451 948 180 540 006 520 708 421 500 877 550 590 907 605 884 968 561 550 526 867 635 506 481 311 771 983 777 398 060 219 131 046 761 526 543 910 701 331 108 033 909 704 996 303 784 653 823 984 558 801 765 120 907 459 080 903 184 958 610 273 400 574 392 927 408 785 790 758 936 200 318 766 331 847 108 990 132 251 097 303 476 451 566 822 661 792 193 187 586 875 401 868 206 768 809 180 576 063 038 758 843 100 675 837 865 263 264 573 728 894 585 011 452 076 325 759 929 880 971 119 955 157 845 024 384 531 817 654 456 208 060 891 981 051 252 588 097 653 842 731 265 597 785 070 193 502 103 379 642 361 154 697 726 452 519 879 162 432 645 678 395 353 766 245 747 042 074 917 663 605 477 091 747 728 346 289 892 993 781 578 841 015 999 160 901 262 241 738 264 441 087 573 316 702 633 704 241 192 032 656 183 366 260 288 432 144 678 412 499 987 438 546 785 480 147 284 878 714 648 236 234 956 107 724 186 651 738 968 904 140 922 519 642 563 061 284 850 716 125 560 764 703 865 278 136 053 541 654 203 352 466 132 315 332 634 792 216 412 411 930 504 327 732 084 833 851 194 568 706 053 172 551 771 126 584 933 118 520 130 791 304 027 925 596 109 456 128 560 265 561 172 825 572 230 759 866 941 450 984 747 086 845 809 850 888 296 274 684 415 410 353 832 707 852 668 513 325 750 818 141 948 366 219 090 622 577 773 359 288 242 493 103 873 907 136 208 462 657 079 861 147 864 383 553 429 477 397 074 458 611 239 902 281 869 407 588 629 097 654 266 773 636 226 838 490 062 460 914 461 994 584 308 956 577 350 317 306 849 989 198 027 386 072 907 783 589 359 505 121 530 735 473 821 691 619 472 219 492 703 687 424 508 860 318 554 026 928 861 616 019 351 409 562 950 150 507 733 102 501 041 316 205 013 961 590 696 088 408 921 975 524 909 946 501 756 894 277 874 131 816 098 861 258 979 135 628 443 424 999 438 604 315 252 145 194 038 571 688 586 571 211 702 223 829 893 235 339 362 492 431 840 583 267 700 423 253 204 543 075 933 688 915 460 816 830 466 753 289 529 504 245 559 890 628 095 715 019 748 138 318 848 885 927 824 301 529 858 558 097 256 247 800 670 256 132 420 094 302 488 194 379 204 360 584 360 171 339 876 576 034 468 006 220 513 964 119 628 969 447 612 771 724 324 829 164 959 862 887 412 668 614 510 507 699 492 261 467 222 313 008 783 802 943 368 545 789 505 249 561 872 643 610 485 886 789 334 171 357 658 830 502 386 247 665 049 171 238 473 078 342 329 610 897 363 259 729 030 708 691 050 607 724 125 370 882 380 178 072 834 704 476 456 681 100 636 218 340 155 435 453 612 757 297 237 262 243 400 393 343 724 479 500 180 092 780 589 215 638 909 481 217 375 103 367 037 211 212 311 562 342 025 848 409 410 039 851 663 483 520 506 879 591 508 614 849 804 791 125 929 484 860 210 187 499 764 761 279 286 770 612 722 485 851 882 800 331 790 597 206 398 053 887 332 014 672 059 155 760 562 063 915 784 815 122 764 247 755 559 266 835 803 787 121 534 851 770 356 119 401 163 432 421 466 810 325 493 930 525 976 077 258 797 421 975 559 026 881 431 650 732 653 708 603 280 375 477 731 957 364 081 480 629 701 314 707 539 696 209 556 711 699 756 587 723 918 243 979 016 512 443 532 207 914 312 592 083 623 067 530 422 187 480 823 037 027 841 557 445 421 361 186 961 858 558 283 011 651 369 149 819 493 330 569 329 825 824 578 018 357 714 027 801 565 290 918 843 409 929 090 823 371 139 685 417 313 284 541 850 124 262 815 397 316 973 592 924 234 139 586 802 274 921 694 432 596 375 781 926 771 761 765 501 943 514 882 641 244 397 287 525 406 541 904 275 685 336 628 037 016 553 351 477 112 170 902 316 804 430 204 533 896 844 305 764 108 915 046 451 093 307 104 447 367 686 849 474 182 339 991 293 077 089 318 153 010 708 374 763 239 659 993 109 987 361 659 396 297 675 744 579 287 698 834 763 240 381 693 287 208 376 833 522 492 614 795 505 612 352 102 932 134 064 653 196 132 045 909 414 351 424 447 031 498 845 029 181 721 427 603 587 156 047 991 829 187 432 139 829 484 844 435 673 668 877 066 100 758 799 537 956 711 108 151 649 926 240 401 255 312 932 029 576 203 210 891 221 057 096 059 224 880 799 569 956 948 002 774 386 047 603 211 392 495 395 230 540 850 774 696 426 498 722 559 999 868 847 108 434 694 013 854 209 983 464 544 627 275 867 339 556 550 662 742 746 748 672 426 105 991 453 810 118 787 532 007 459 813 536 303 049 661 031 319 032 777 296 250 589 497 340 183 607 180 123 746 751 829 979 832 624 648 318 219 611 307 546 577 496 868 052 167 161 050 843 761 181 581 207 921 485 991 513 075 487 761 368 425 956 385 057 141 416 400 464 853 299 834 067 982 755 251 583 257 122 159 768 443 896 559 507 170 756 534 608 999 576 193 991 701 525 891 628 886 632 531 186 810 444 669 224 306 882 979 592 428 340 052 068 404 707 283 789 567 819 559 453 750 573 866 976 572 246 428 761 515 122 172 678 286 913 901 457 686 818 558 274 702 499 014 242 517 456 676 904 699 732 690 686 217 047 097 569 370 170 274 711 290 383 019 877 516 327 562 789 461 486 121 597 807 844 999 958 148 072 532 483 836 649 702 990 562 826 565 601 921 919 110 248 243 186 032 742 762 392 999 682 764 730 359 182 496 426 718 844 727 829 909 731 396 201 313 871 917 557 655 890 639 771 111 819 108 832 234 866 833 275 811 842 324 454 042 310 831 351 062 203 868 187 655 346 021 443 478 124 241 840 199 229 355 390 383 374 869 759 208 690 994 530 014 623 837 512 709 443 216 816 483 172 116 194 227 730 698 946 281 719 135 154 595 855 098 909 112 220 313 761 184 359 221 624 682 897 322 926 346 656 437 291 548 281 938 584 310 099 969 979 544 817 869 760 664 425 458 271 773 751 754 914 055 985 353 253 722 372 372 254 796 765 201 667 935 532 554 484 230 840 522 939 121 716 259 526 287 516 665 021 035 704 963 347 548 540 251 219 352 245 224 782 312 266 248 995 360 130 126 036 286 947 255 880 990 890 017 991 018 766 965 476 735 900 639 530 612 635 775 460 080 554 949 689 153 926 341 281 252 006 809 300 629 647 733 610 768 237 962 815 807 126 927 323 659 175 860 368 599 880 724 875 299 809 090 966 584 164 422 613 648 351 757 736 869 192 117 532 725 999 737 527 782 433 605 454 944 220 451 007 613 440 322 668 987 699 013 901 920 356 785 430 441 182 426 122 880 291 684 856 334 033 163 163 848 972 790 096 152 600 241 051 295 011 938 017 442 638 806 624 559 441 388 997 255 933 985 544 423 035 933 477 561 226 161 534 913 107 073 830 159 501 900 889 936 176 625 572 789 396 756 050 891 301 279 841 534 364 061 363 639 901 928 599 078 606 489 130 470 727 723 296 340 525 144 096 713 487 202 456 005 860 115 254 688 164 301 347 022 080 735 341 499 288 913 872 555 943 311 875 364 647 665 578 470 058 002 232 245 214 826 596 532 535 204 007 733 316 932 021 357 156 331 860 645 960 320 015 223 627 230 877 827 182 071 672 520 569 781 959 325 921 094 520 854 972 710 061 243 939 367 408 654 491 702 603 588 174 704 452 793 707 759 550 062 853 600 982 554 275 376 199 424 216 241 636 177 210 617 151 841 506 925 124 099 087 178 759 276 079 418 260 131 849 202 401 282 121 615 512 244 103 019 430 350 699 734 865 831 333 242 044 929 261 830 937 148 968 763 771 859 249 621 591 414 829 977 473 409 741 204 495 599 417 997 126 875 804 792 364 477 363 721 616 365 249 691 224 871 509 425 600 906 062 333 118 967 175 279 646 374 429 423 046 473 506 967 626 203 629 656 443 793 643 381 492 595 786 101 739 085 616 618 685 969 289 823 700 088 370 109 882 340 674 544 228 273 178 360 955 357 642 405 608 364 003 193 495 091 268 893 873 752 475 180 768 501 079 700 846 237 886 879 605 812 851 434 360 331 845 471 867 003 765 174 203 130 594 924 059 692 010 230 742 101 601 715 589 216 263 051 057 618 211 561 247 670 359 488 938 950 453 291 388 231 039 718 388 255 678 116 689 158 283 019 911 212 556 078 231 323 702 660 958 394 514 953 407 773 848 744 110 420 396 328 235 832 804 030 709 505 800 463 624 696 830 902 320 056 649 405 776 976 687 459 281 967 315 829 350 463 360 586 043 953 956 402 546 288 071 634 483 235 638 112 813 655 799 731 792 682 994 145 240 470 419 966 228 535 338 874 833 991 307 782 321 668 691 397 239 899 920 687 839 261 104 423 362 111 243 325 496 837 536 325 287 767 066 104 638 990 552 229 692 585 752 930 671 052 610 781 436 527 496 111 686 741 326 325 819 114 232 891 335 141 583 358 880 487 833 600 223 968 131 183 803 025 969 197 581 316 647 747 627 932 336 354 358 778 911 432 379 800 210 892 844 219 567 929 856 319 595 876 425 774 233 947 712 313 649 991 800 406 134 631 596 430 664 097 931 670 877 055 866 923 327 738 900 486 888 955 298 617 519 286 959 372 056 994 769 466 313 231 010 517 870 559 379 023 554 661 624 286 059 835 767 465 448 850 387 563 933 021 780 487 172 570 667 806 030 293 576 733 677 250 711 200 891 507 293 624 445 131 781 791 542 242 722 925 043 451 348 944 640 206 914 931 389 334 068 332 920 758 566 299 742 554 131 979 227 515 132 680 040 319 770 095 836 687 800 536 098 844 580 718 964 194 265 934 174 533 010 450 922 838 842 298 897 182 528 622 806 084 294 108 342 347 300 152 235 906 800 458 664 716 777 421 361 783 414 470 134 181 049 564 428 434 505 154 613 902 072 230 742 945 318 566 147 211 042 487 056 928 136 138 240 816 744 526 434 212 400 437 877 786 566 157 784 308 078 367 023 570 656 189 703 019 103 055 476 466 886 544 443 928 443 313 722 262 769 985 493 282 064 062 365 141 491 244 650 220 121 790 301 226 335 846 851 505 846 885 136 959 015 622 060 782 253 812 971 155 483 770 823 762 570 761 295 307 291 983 279 818 735 321 470 436 318 005 641 452 025 658 433 014 354 323 996 714 274 641 557 257 116 179 477 678 926 351 412 045 982 983 920 967 122 779 622 204 947 699 469 916 882 215 437 891 245 648 327 541 501 484 534 127 206 833 812 574 632 247 030 959 122 623 336 937 437 005 867 536 951 836 032 746 586 877 783 788 349 127 747 437 292 764 663 435 715 999 964 531 936 028 338 365 470 872 695 134 777 546 328 578 498 138 725 744 516 177 905 656 894 017 243 452 132 870 045 728 177 462 652 320 163 089 728 717 922 441 334 517 821 945 942 241 528 167 714 923 554 383 700 149 764 292 413 227 906 797 979 334 706 176 411 066 369 690 077 257 610 874 321 173 737 180 570 786 991 741 329 959 807 510 244 709 224 195 798 538 479 041 770 757 066 036 932 162 299 476 407 911 150 417 429 569 973 193 544 742 924 181 013 735 395 209 730 904 550 728 467 951 131 200 436 308 420 525 618 397 793 669 615 062 210 013 114 401 925 810 344 332 373 942 610 734 412 704 300 122 780 856 797 214 884 344 009 747 774 341 260 682 298 238 500 213 522 638 069 505 341 806 860 895 990 384 622 364 164 153 913 967 034 344 803 201 366 414 579 618 892 507 772 200 169 090 760 940 335 165 695 830 352 467 580 694 637 560 559 125 617 478 058 571 289 436 940 941 122 836 275 189 841 501 064 210 462 043 294 182 805 932 509 861 522 011 451 833 144 401 910 609 978 751 363 565 069 673 150 671 503 857 871 662 469 015 458 142 804 995 471 162 380 175 137 090 927 096 099 280 008 041 036 009 073 722 859 725 262 257 544 753 578 245 575 259 243 737 356 968 081 998 816 717 703 607 239 912 586 376 336 307 054 722 038 596 035 123 771 762 496 268 796 393 783 778 253 960 446 554 761 646 614 859 417 701 387 771 977 662 079 489 733 671 795 997 671 677 545 114 932 277 702 353 920 341 605 197 580 666 576 589 367 095 762 702 601 143 610 727 074 976 196 232 799 717 984 014 475 836 001 992 675 617 568 545 135 319 246 043 974 393 516 263 900 455 542 836 004 523 071 165 891 096 112 222 868 822 762 556 800 347 888 221 625 237 110 848 687 024 983 442 155 753 346 749 942 966 839 203 698 913 896 905 887 959 134 649 235 269 659 709 666 945 792 487 432 491 641 004 851 224 052 531 550 127 737 779 203 895 313 850 091 072 816 227 351 325 662 224 261 977 250 808 651 182 150 601 879 646 816 113 437 859 543 042 506 568 141 710 799 184 146 640 382 510 278 820 849 548 858 013 365 031 515 789 986 987 247 907 990 092 179 149 494 577 500 750 835 704 747 536 716 523 805 626 444 242 324 539 086 865 133 176 268 162 725 418 971 143 006 562 301 695 534 893 069 152 360 787 167 045 856 368 239 554 312 585 713 081 995 766 353 502 831 671 821 534 141 540 346 708 967 521 485 765 766 588 498 703 502 367 769 092 028 111 580 853 504 788 278 526 858 207 142 737 918 516 202 945 787 806 753 546 450 071 199 458 138 470 325 466 004 961 691 266 381 539 635 653 054 741 334 506 867 415 835 135 830 410 221 027 960 216 420 462 788 447 998 427 051 454 063 455 030 884 949 290 436 844 656 340 208 023 922 542 645 685 500 542 352 128 124 028 723 721 567 631 648 802 327 132 810 780 833 970 795 536 705 467 883 981 869 281 834 967 667 768 790 515 788 081 762 769 410 553 171 365 579 220 070 788 350 617 506 257 379 477 570 173 037 433 675 894 317 063 993 084 828 872 823 799 286 411 559 136 973 858 417 990 340 298 876 835 636 698 641 218 211 385 827 938 843 176 543 745 779 862 924 552 768 649 241 186 758 529 760 350 054 574 520 105 086 158 121 369 293 251 358 238 087 308 547 480 016 285 675 308 304 362 768 888 320 112 215 354 639 036 576 705 046 948 963 724 201 086 728 232 644 711 336 866 203 000 780 772 612 768 289 857 032 668 861 522 900 981 188 232 268 526 331 312 588 846 227 403 624 654 714 410 460 959 610 257 350 217 603 524 034 322 408 627 629 332 469 569 832 214 538 919 266 037 112 594 251 071 842 429 378 994 850 064 296 361 789 148 534 195 310 976 306 605 205 371 903 460 724 563 280 279 740 004 115 572 199 438 033 012 396 027 241 183 505 714 510 180 876 138 983 334 821 820 464 556 128 433 922 815 107 649 030 508 504 304 440 533 056 075 072 326 456 475 496 903 456 992 824 912 780 977 584 374 801 061 389 085 446 765 934 113 167 537 962 146 104 981 892 441 390 041 165 409 710 715 907 773 695 627 477 032 257 955 218 017 945 385 002 191 540 735 157 356 070 057 554 523 497 449 903 162 718 218 653 482 171 311 018 375 834 087 364 804 237 728 493 097 088 171 420 368 609 789 998 150 604 428 659 366 870 613 189 647 399 846 775 972 516 105 683 056 223 521 428 949 672 150 624 580 191 133 349 959 542 963 303 905 209 488 885 239 967 004 493 862 574 540 786 005 708 606 777 367 528 581 727 381 727 009 052 967 389 951 334 097 879 735 351 008 370 110 505 395 774 346 174 786 458 333 696 798 218 288 782 043 294 471 271 378 812 413 065 696 876 782 263 275 863 809 400 899 620 022 096 977 517 226 996 642 121 472 531 261 312 816 131 252 709 114 439 479 229 623 980 191 297 512 034 959 512 741 927 537 198 663 024 218 219 300 627 230 943 408 723 819 925 332 734 588 872 880 906 145 328 772 880 806 721 705 256 662 581 780 094 046 257 922 300 518 311 007 244 846 157 225 027 283 835 020 452 848 611 431 414 048 652 321 368 398 858 391 348 589 569 732 051 831 289 614 953 282 759 796 706 437 981 181 319 381 883 815 899 787 088 670 048 423 591 303 959 554 993 529 546 402 474 738 986 484 721 570 251 830 387 621 080 533 211 563 061 897 457 610 073 840 016 843 551 440 517 834 277 365 163 097 794 986 377 142 967 544 632 638 103 656 961 729 113 894 381 205 061 923 815 719 983 457 623 744 829 187 158 707 343 892 225 211 165 827 168 504 837 794 762 987 015 567 763 466 489 312 230 727 343 373 838 550 797 181 247 919 791 257 504 989 655 718 525 421 491 081 911 945 516 778 610 658 409 446 716 863 453 597 356 500 149 212 117 203 194 534 364 038 613 065 224 506 861 310 701 466 702 571 549 513 621 361 157 235 675 097 498 595 946 551 453 520 485 180 873 425 390 257 278 596 971 465 726 609 215 640 220 092 466 142 858 556 671 530 857 272 980 654 323 034 382 106 020 711 001 317 638 010 195 770 783 013 535 810 240 159 699 355 193 410 256 514 773 482 927 317 572 279 016 691 284 517 390 744 158 575 617 885 861 578 516 556 066 683 157 193 553 743 357 771 212 565 145 986 787 015 126 035 371 687 853 260 035 212 824 797 811 759 155 383 560 217 268 173 231 192 847 625 921 693 775 974 588 796 173 296 316 070 850 548 940 634 659 796 516 139 409 581 409 061 099 051 784 353 296 271 604 076 114 966 732 259 008 823 210 239 508 441 911 302 435 338 284 782 602 098 342 238 480 886 843 367 833 559 489 889 953 041 500 650 091 478 109 838 112 157 921 645 711 442 526 760 125 007 562 886 923 078 421 864 391 974 273 220 946 878 698 474 663 503 409 217 009 538 124 858 038 771 606 563 016 498 735 022 774 452 271 645 560 221 587 442 750 375 175 784 394 176 629 179 818 905 264 039 764 873 252 003 378 513 779 540 027 152 420 277 745 285 442 577 405 851 246 683 142 085 363 187 251 097 772 725 261 485 333 476 701 340 921 377 821 496 494 992 325 069 226 680 654 002 178 186 771 019 738 591 384 155 177 633 857 435 868 699 682 243 625 201 556 847 664 659 076 227 646 610 837 090 986 460 453 769 598 909 866 905 071 244 248 740 587 313 025 702 901 882 103 360 823 977 031 766 750 022 482 633 747 975 289 782 003 478 211 113 810 110 314 626 352 659 264 843 321 812 566 201 005 045 444 223 639 878 727 640 545 136 982 898 476 940 014 906 127 706 987 401 054 059 355 700 384 724 828 795 441 540 607 300 535 846 682 940 353 129 299 256 011 114 856 342 328 029 818 142 616 714 077 210 776 596 911 270 398 992 085 153 558 955 793 084 879 038 169 004 244 072 925 193 134 038 400 192 766 154 803 762 109 479 365 310 231 974 622 542 521 972 891 915 120 759 280 153 531 103 422 134 233 249 993 119 923 642 811 779 158 138 001 036 187 931 006 280 489 170 472 446 465 052 102 354 146 411 938 234 641 574 767 716 815 087 417 724 012 994 400 669 328 767 636 330 422 805 910 557 734 826 378 352 817 367 914 069 678 346 805 875 437 864 755 123 190 193 587 688 620 669 403 574 980 976 576 916 187 963 251 400 717 004 866 478 801 638 920 113 797 843 582 549 258 510 803 732 221 504 015 661 400 037 710 416 373 186 269 518 383 712 764 159 381 520 017 743 344 402 262 425 218 419 986 005 052 665 163 513 977 613 612 662 367 425 670 349 125 415 903 880 737 799 725 224 574 795 514 185 408 950 908 607 116 819 221 979 427 993 768 332 727 215 628 518 441 116 493 049 411 311 161 400 749 530 744 998 217 275 799 251 959 326 132 737 167 006 004 797 639 273 221 074 161 891 447 658 409 927 590 693 620 597 364 091 813 953 138 651 887 494 281 477 385 208 663 752 096 708 196 084 385 194 202 223 136 231 242 766 761 430 224 964 722 863 568 213 392 189 255 755 317 838 820 226 997 914 443 731 710 597 425 823 483 247 959 966 718 167 313 002 401 066 015 827 914 566 502 941 839 122 115 636 195 828 104 251 398 383 899 725 777 484 940 257 535 379 245 806 876 530 122 746 327 426 585 010 125 551 103 680 874 805 140 282 465 045 202 068 909 805 024 477 197 238 754 479 267 805 461 744 745 930 650 583 083 018 717 114 430 701 236 178 554 441 685 791 845 041 980 031 944 461 032 736 175 920 245 179 330 803 960 071 835 881 746 922 625 282 321 538 230 394 065 417 392 169 264 865 441 214 394 452 739 383 026 875 002 553 123 205 792 759 930 261 220 189 329 885 694 987 813 438 274 213 308 243 538 148 147 667 735 108 960 197 033 040 688 424 243 402 844 764 300 169 149 848 884 514 296 543 459 626 952 101 190 378 153 684 244 105 951 055 760 433 139 710 268 216 788 318 456 646 641 104 683 679 696 642 137 040 525 170 991 993 488 241 789 953 791 719 567 999 002 312 832 913 007 827 390 921 928 735 731 861 655 186 102 840 684 855 788 440 259 930 956 325 478 423 872 051 786 017 442 190 769 689 036 302 397 822 107 303 443 004 090 508 385 691 136 785 330 284 583 274 266 378 139 727 536 266 141 703 216 969 442 170 689 668 304 406 581 914 666 372 739 801 165 713 322 924 884 448 793 005 032 237 916 014 815 620 829 024 925 208 200 800 914 570 520 949 834 251 725 140 820 498 105 241 357 462 038 377 925 488 910 911 371 711 265 154 395 468 913 472 532 401 121 429 586 797 528 689 312 435 506 738 741 821 924 997 820 361 016 184 632 725 573 945 615 363 917 076 543 431 174 088 374 152 256 042 630 559 399 017 851 186 989 376 257 228 654 108 412 883 794 842 300 095 788 591 145 999 578 544 630 326 085 753 265 960 062 566 015 218 320 503 512 148 818 675 153 519 171 932 709 698 438 515 779 283 695 164 683 531 611 830 269 233 030 832 449 354 936 678 043 058 921 261 775 144 963 049 131 588 244 804 660 312 380 913 644 682 500 393 415 861 865 599 485 069 270 886 818 290 761 366 061 875 587 884 372 530 575 298 432 223 574 482 907 741 389 513 456 228 961 968 483 668 371 053 337 124 263 702 304 372 005 307 708 489 093 106 176 223 892 736 308 741 928 285 927 093 302 717 565 665 054 027 111 530 270 841 067 021 262 300 627 633 499 375 954 048 921 691 481 151 706 645 568 575 595 467 548 317 882 014 969 393 626 743 429 476 770 615 066 014 334 641 930 065 845 102 570 970 425 067 210 110 452 292 722 560 474 665 855 539 273 532 110 640 209 904 581 011 551 861 660 122 639 999 567 781 264 744 008 758 645 115 859 006 908 332 520 444 751 556 555 489 333 572 188 903 806 519 823 797 944 825 001 951 947 930 198 218 170 753 775 347 498 293 261 839 768 646 581 993 290 977 235 939 798 974 260 827 540 297 471 418 849 507 084 068 478 366 369 805 843 716 559 681 132 441 537 879 461 987 340 081 442 295 410 016 752 984 987 494 462 351 422 919 846 444 689 990 750 094 353 539 121 079 691 468 959 303 089 579 358 231 949 012 643 418 628 160 467 229 025 922 619 282 780 452 938 533 507 344 697 987 725 722 863 638 562 295 567 150 040 208 520 264 545 756 767 947 311 028 313 772 126 531 250 567 046 302 771 521 580 239 520 413 806 699 780 481 746 882 895 678 667 587 549 422 781 913 600 221 658 292 352 520 302 768 468 904 921 231 107 549 016 756 797 178 594 616 559 119 129 706 569 500 182 158 956 840 272 054 688 821 086 479 921 739 662 620 968 926 596 312 266 752 871 379 267 125 327 956 015 279 998 928 196 979 731 221 981 335 571 765 718 807 601 181 254 737 862 579 589 994 158 173 261 792 569 794 532 332 118 925 359 000 022 688 997 662 620 040 589 866 823 701 575 356 387 739 978 773 205 852 498 978 035 033 163 546 982 192 427 694 101 414 409 899 905 977 607 118 594 034 872 459 971 068 178 166 471 068 460 566 098 923 323 870 593 085 221 833 548 313 258 704 921 867 967 772 496 003 960 790 115 591 624 032 159 635 081 282 967 037 487 843 761 916 757 297 807 039 855 748 018 916 701 184 590 331 252 340 718 298 963 999 223 476 757 346 968 763 548 510 099 054 483 372 485 369 130 884 903 524 004 101 249 808 606 960 264 792 196 858 165 545 070 190 973 079 576 513 592 978 849 173 738 524 307 327 164 779 339 881 738 930 906 353 773 277 290 230 053 320 632 982 491 697 737 282 389 569 636 670 291 746 157 281 975 550 178 181 128 190 216 831 786 682 222 054 566 909 450 511 510 754 718 752 610 627 156 794 283 953 790 200 603 129 898 798 317 675 375 603 389 879 807 770 840 271 459 433 083 033 056 982 967 935 191 653 018 524 175 277 305 240 529 137 585 601 595 130 120 856 071 200 853 931 265 195 132 203 065 803 535 944 145 162 964 064 284 699 306 685 372 582 655 279 591 022 642 988 596 721 977 026 980 425 514 895 454 201 021 417 376 048 036 759 731 362 731 973 892 913 158 808 085 645 927 736 240 830 792 306 522 389 940 937 119 075 816 536 032 669 701 613 494 894 441 397 108 455 516 023 942 278 079 712 667 537 270 336 581 488 551 975 161 793 553 099 452 894 884 852 363 693 809 348 343 626 516 869 548 569 691 847 578 943 420 101 095 985 523 425 628 700 057 260 197 065 637 022 013 377 180 915 858 718 651 966 868 023 325 905 412 854 936 511 886 057 980 874 153 852 461 100 324 343 412 710 503 863 538 203 258 868 566 001 901 369 350 963 505 821 713 633 996 577 319 239 754 764 110 771 287 031 190 715 164 551 485 977 661 718 148 374 556 512 685 775 855 684 392 085 663 896 310 414 825 338 628 086 970 062 756 840 867 836 642 991 103 126 084 499 892 374 246 233 917 850 188 900 931 216 367 869 917 368 008 295 639 850 290 853 721 591 544 373 197 766 044 012 851 534 861 716 128 123 353 295 882 902 202 535 996 135 836 459 540 874 003 193 692 520 920 335 467 560 529 646 108 306 177 294 412 454 843 535 731 011 592 848 085 754 909 625 315 242 471 429 733 080 381 432 398 941 374 787 512 914 121 234 777 063 329 559 722 982 676 388 434 374 157 855 723 985 480 432 336 193 311 029 449 111 048 992 284 809 073 813 683 681 147 667 240 577 469 667 987 540 558 181 590 613 454 016 696 205 976 247 704 217 006 624 260 198 062 924 101 785 804 344 046 478 184 767 619 850 047 717 017 234 318 637 534 596 975 008 623 852 088 121 979 620 321 855 106 136 199 237 936 504 298 074 979 442 701 283 902 698 927 371 134 144 286 148 877 803 204 672 509 221 158 400 095 254 213 349 512 686 848 447 787 374 942 132 045 889 819 006 712 279 107 754 989 303 254 412 188 711 161 630 120 719 028 149 755 085 417 140 157 094 147 124 145 051 215 162 794 486 868 520 717 306 195 704 271 106 240 039 969 085 424 891 488 603 216 405 614 054 276 910 849 550 803 338 045 034 877 754 078 088 354 781 871 169 874 234 738 805 137 995 887 002 893 884 477 587 893 862 031 855 319 231 554 510 688 095 593 760 090 890 520 313 924 181 243 317 504 361 896 535 536 362 866 384 563 048 062 359 781 761 100 275 789 852 780 082 544 775 906 791 749 049 725 705 147 279 905 339 001 157 953 837 306 157 227 529 116 673 508 360 836 632 098 572 824 652 552 814 002 198 629 343 224 181 523 071 381 681 682 854 426 315 132 968 182 633 161 489 865 314 533 727 826 898 849 825 643 024 696 241 672 444 145 260 984 587 250 203 732 965 999 240 540 656 466 500 106 237 446 898 107 501 428 132 960 282 062 001 255 276 264 540 488 442 754 428 146 476 163 514 725 811 040 045 425 208 302 253 497 337 140 797 014 291 287 312 901 387 608 151 575 195 121 664 990 222 299 737 442 552 224 782 110 279 550 114 376 921 854 713 555 228 287 598 209 217 444 829 698 004 259 451 716 723 084 626 606 538 412 213 268 456 134 421 319 406 106 058 990 467 216 654 782 354 548 487 756 692 707 111 104 293 174 736 728 740 342 936 496 265 611 530 985 723 128 095 435 212 604 179 689 151 529 567 965 682 745 324 039 769 078 908 104 388 936 681 299 653 959 317 051 317 974 360 418 532 834 814 760 478 330 894 062 981 118 649 032 815 239 602 294 624 121 705 130 472 526 331 672 261 763 715 997 673 186 591 722 320 681 285 454 399 339 798 336 645 273 423 962 517 337 973 427 998 134 697 866 282 834 773 196 295 198 052 646 605 732 869 732 675 327 694 129 339 336 098 421 196 894 925 881 712 378 129 926 425 383 658 401 188 634 670 126 555 872 445 738 888 227 230 911 465 490 400 494 349 351 446 690 158 972 346 864 971 117 593 037 834 109 257 603 826 170 507 886 541 155 144 427 384 032 914 855 706 188 785 041 986 120 817 853 017 517 545 421 378 735 719 934 043 741 015 961 429 966 717 504 723 643 182 123 944 870 558 029 004 047 728 642 866 608 481 053 392 134 815 722 018 316 129 403 473 504 959 846 955 877 007 708 540 046 968 138 980 151 438 007 642 802 361 016 510 924 787 351 744 759 458 436 498 041 387 818 565 409 841 687 294 879 163 817 734 031 111 540 414 463 379 382 754 722 616 897 800 149 510 341 431 678 196 274 516 379 252 478 950 022 092 073 110 935 794 954 694 720 031 288 342 518 363 813 249 649 135 248 877 494 131 507 590 206 718 469 136 967 672 190 555 353 491 918 139 721 721 007 000 623 034 263 768 893 569 735 385 878 425 433 556 809 561 488 904 066 771 511 757 324 988 632 095 600 151 480 343 511 678 357 524 514 867 680 125 838 989 937 326 339 585 556 463 786 188 399 414 942 012 245 635 791 580 229 198 022 922 186 685 788 517 543 342 371 661 519 725 721 866 828 851 825 592 318 178 473 815 727 693 624 740 059 471 206 199 724 762 244 658 721 840 629 128 619 606 911 212 822 086 240 446 266 047 932 026 411 191 919 478 431 884 711 195 356 053 014 472 343 297 367 703 452 097 369 634 880 721 507 171 863 116 327 841 903 936 447 124 383 021 962 457 784 913 044 285 150 728 972 406 451 784 524 235 484 962 093 839 497 854 907 843 319 352 373 857 935 309 146 662 159 102 489 851 366 100 543 616 789 664 912 023 290 885 751 920 853 292 513 651 468 351 714 574 539 613 285 037 183 764 203 924 719 947 020 765 048 232 016 723 303 541 689 289 357 427 959 100 395 723 135 753 018 120 515 967 999 810 436 869 554 154 752 063 074 451 284 187 872 925 572 449 489 580 445 553 235 117 178 410 885 833 815 229 328 539 431 380 389 036 949 243 974 837 009 612 800 748 017 801 770 780 484 159 963 238 113 716 265 408 881 323 481 673 720 690 436 290 365 888 272 040 537 146 528 427 464 565 530 784 316 871 216 076 641 366 131 375 585 113 657 904 246 299 715 521 748 886 899 750 489 864 144 154 551 801 160 752 305 612 854 915 241 407 813 903 149 027 364 750 811 785 423 166 068 447 538 550 866 094 610 288 432 957 936 714 761 320 744 657 736 634 221 937 514 113 229 049 641 570 239 137 249 495 868 245 071 501 043 535 230 948 536 546 285 914 248 069 993 431 854 777 101 822 249 511 837 985 635 680 331 754 966 427 414 889 806 903 387 975 423 406 801 846 249 612 492 129 579 429 325 476 067 100 583 616 282 975 246 821 821 187 491 741 894 220 352 086 314 996 496 251 375 625 396 971 970 781 423 470 163 580 502 068 666 615 818 185 637 118 256 125 007 388 124 830 878 417 713 357 291 397 878 291 448 195 125 621 538 446 833 560 372 281 222 551 021 601 307 985 594 336 461 657 320 657 974 904 763 162 209 582 813 671 276 515 550 676 113 152 247 843 343 280 258 767 781 436 763 306 296 471 733 997 005 595 120 404 620 880 436 700 290 581 930 865 120 737 334 160 093 688 449 563 017 075 579 458 509 944 712 678 188 225 066 322 669 395 281 784 909 756 629 294 912 732 160 539 698 708 930 031 207 686 437 210 952 366 824 591 052 081 696 823 844 767 297 762 391 526 858 919 269 426 101 483 479 980 397 965 352 788 484 858 465 602 236 292 886 257 010 935 107 591 865 870 858 972 130 109 816 231 421 101 722 570 918 420 657 767 441 834 283 789 613 925 002 848 620 047 232 246 118 892 138 587 961 582 959 281 720 046 064 793 413 079 373 088 374 334 253 411 101 344 310 642 744 706 675 671 162 660 971 703 667 872 369 379 412 056 079 413 919 555 613 411 342 561 695 932 102 597 321 221 934 110 760 277 589 440 063 932 117 482 587 411 132 335 979 402 031 830 506 598 649 747 658 772 254 773 707 061 080 388 424 495 952 129 593 308 984 153 813 633 180 681 301 042 986 729 746 748 710 139 207 263 823 087 904 412 211 726 982 811 295 783 289 557 644 121 673 790 232 766 330 065 777 133 532 128 552 753 707 109 429 746 835 092 964 638 827 760 360 734 614 738 786 553 847 090 266 916 436 283 869 564 121 181 269 754 047 126 110 201 735 032 566 815 453 701 011 828 555 572 694 332 968 151 584 423 487 268 763 035 813 145 095 941 521 265 641 624 335 936 810 677 787 025 203 537 195 921 559 689 684 657 451 420 666 182 941 528 034 328 136 575 210 032 771 835 683 758 154 711 417 585 158 395 899 573 574 661 140 351 569 288 235 339 425 409 341 809 756 106 804 483 886 283 009 840 802 396 069 811 740 132 343 205 684 833 265 846 092 835 837 367 638 789 943 101 360 856 512 893 751 329 734 975 170 288 680 910 413 435 402 411 484 659 922 431 195 603 603 705 938 321 210 419 377 038 824 567 616 650 386 867 569 983 599 242 320 719 087 866 653 971 430 558 645 203 968 155 823 430 082 649 562 470 422 983 851 071 236 790 913 634 797 721 355 807 287 726 328 609 329 987 583 422 927 536 038 480 049 449 437 050 370 747 179 660 827 854 802 440 284 593 103 360 980 254 899 289 189 843 380 882 758 366 001 448 457 914 886 426 957 718 747 479 687 032 688 262 152 516 942 057 733 502 580 287 714 137 088 310 759 834 906 813 881 213 376 759 272 973 269 258 805 969 785 097 069 560 817 817 255 931 887 511 795 674 798 914 912 965 594 836 060 518 811 117 008 344 157 330 495 437 491 307 554 994 088 496 953 620 786 198 889 535 429 627 263 839 296 687 390 112 536 583 339 548 002 230 132 735 847 854 757 952 605 887 471 542 747 427 507 452 013 025 116 607 111 392 637 713 913 598 539 645 709 999 310 705 346 110 727 295 702 403 830 327 054 933 076 207 506 936 003 282 384 004 099 505 284 283 174 816 434 807 140 806 161 740 209 490 379 889 928 688 542 266 129 439 634 638 914 433 744 408 075 796 657 275 826 890 198 254 364 597 620 670 759 072 714 773 467 326 525 971 942 142 403 439 947 413 570 733 543 045 470 759 404 711 266 647 437 521 099 017 671 660 224 065 120 920 267 263 120 983 882 128 769 899 920 789 946 219 377 795 200 512 263 428 218 506 946 081 960 071 970 102 252 050 578 629 944 236 589 310 767 741 730 604 030 464 686 004 278 235 048 583 180 668 352 632 756 256 001 218 133 842 144 212 321 855 824 359 770 079 409 935 646 775 670 221 195 134 660 010 755 984 414 572 015 483 659 686 392 674 849 537 052 440 574 867 983 037 096 154 290 767 491 286 984 525 061 197 065 234 569 044 235 395 049 248 366 885 248 234 592 615 042 913 401 563 174 465 984 222 350 428 791 420 612 627 794 029 079 265 588 593 000 673 753 428 027 884 611 936 410 398 692 367 491 779 397 393 994 551 583 856 725 239 513 715 459 379 993 271 750 285 389 844 147 200 338 117 165 480 874 932 918 127 562 192 918 395 656 048 249 699 436 239 238 658 869 773 718 225 101 472 650 869 200 640 167 910 534 514 363 651 672 176 564 736 183 593 139 869 012 475 293 701 158 038 985 703 516 418 825 207 215 090 456 565 591 808 761 017 129 386 690 536 482 110 459 820 313 992 180 806 757 990 996 253 143 344 231 446 363 801 405 382 120 706 003 364 626 525 807 125 333 651 787 715 810 841 284 464 893 905 736 022 616 058 656 095 573 888 481 123 757 176 692 017 830 078 802 022 698 878 996 438 297 838 595 884 860 407 041 396 545 643 032 021 439 239 463 501 595 061 888 204 578 095 814 699 889 512 814 255 236 126 238 640 265 942 684 335 760 429 282 911 063 067 313 624 501 555 614 964 945 161 516 592 444 157 507 756 656 788 418 192 295 997 258 265 999 793 180 680 086 978 303 191 120 151 890 544 445 335 644 718 407 364 151 938 238 282 290 210 411 396 330 323 352 030 807 590 167 458 635 364 413 758 879 274 434 991 086 418 450 412 640 130 760 675 662 587 598 068 361 462 737 042 779 743 132 774 242 643 116 069 598 413 077 166 445 483 402 999 542 707 094 791 509 792 966 244 783 051 930 639 653 907 515 387 339 742 800 348 974 634 925 793 175 830 607 595 611 614 752 974 458 586 278 673 789 559 281 527 544 399 792 990 520 865 611 387 452 077 967 635 934 939 237 898 442 623 381 947 677 187 450 153 528 085 156 494 218 305 148 185 865 689 099 220 604 190 569 867 733 605 361 824 788 698 882 347 986 135 442 113 131 302 115 830 678 763 115 902 752 039 119 946 158 342 571 130 957 133 192 504 533 975 793 041 545 452 937 758 977 134 119 357 030 164 091 025 378 673 331 432 047 245 479 566 728 445 087 952 887 047 861 516 985 721 115 528 167 878 173 128 218 227 403 527 874 130 942 740 002 787 555 874 244 384 934 597 301 856 467 451 363 944 587 271 271 958 274 984 592 972 327 414 855 801 637 264 259 851 982 796 640 312 808 480 568 643 404 463 301 303 530 783 367 916 318 859 771 469 607 375 917 652 172 961 733 516 656 727 357 464 140 917 694 299 145 666 993 712 785 837 218 200 237 616 599 714 697 149 988 375 328 043 886 196 341 723 936 671 955 751 954 269 105 316 381 934 372 485 487 257 696 110 940 219 801 864 770 612 067 595 082 333 231 163 028 701 706 220 829 563 488 886 241 916 828 389 168 654 146 575 923 157 755 310 338 727 765 737 222 028 513 019 109 791 648 875 590 094 459 269 018 912 838 291 195 559 574 653 803 567 556 322 269 067 142 920 737 833 440 927 842 119 889 502 348 338 303 221 640 747 518 551 121 377 615 186 222 577 139 995 433 150 839 415 983 147 116 417 606 422 475 504 444 410 874 248 610 813 776 266 698 222 681 617 871 766 694 464 911 420 269 431 388 844 980 295 675 928 201 529 947 209 065 677 392 334 160 590 494 781 493 292 029 370 441 823 673 624 712 248 713 290 451 573 025 280 221 944 386 629 632 433 345 157 391 227 380 884 276 246 714 481 156 785 320 345 754 308 865 650 147 296 152 956 461 295 494 968 443 824 540 442 787 649 913 647 191 574 729 246 478 458 285 953 421 166 284 870 208 533 374 423 434 019 864 688 674 075 896 017 788 195 525 994 231 164 717 120 699 165 670 411 027 602 330 840 877 118 941 192 469 119 037 833 835 605 672 102 555 843 901 506 101 279 565 597 288 760 868 779 162 272 996 813 903 006 793 329 300 455 674 977 277 697 578 334 249 556 950 705 340 316 075 199 910 653 450 494 002 823 853 372 095 454 611 854 652 645 423 818 980 780 815 104 280 703 718 368 898 816 404 364 129 427 790 342 305 422 804 376 818 212 629 080 719 654 278 512 304 846 500 352 982 835 159 783 470 204 510 202 835 744 693 437 572 296 111 381 750 807 495 403 541 069 938 360 971 686 671 374 871 276 860 032 191 252 825 759 073 778 547 375 033 905 908 701 823 109 272 229 757 959 960 603 807 755 803 482 678 304 929 876 857 212 432 184 013 519 286 231 764 442 404 060 502 666 655 423 099 981 247 373 181 477 226 677 785 482 112 538 108 484 674 324 977 955 743 987 101 067 610 913 216 940 051 443 839 822 513 407 486 789 686 776 580 661 620 196 729 671 067 009 321 684 203 294 894 333 162 602 742 280 439 416 980 668 929 003 885 188 971 111 036 425 486 328 802 602 163 743 688 107 626 347 393 061 872 338 087 642 744 673 690 655 803 761 405 462 574 136 141 007 779 887 955 406 275 901 964 651 777 495 368 779 456 248 578 481 445 046 658 791 913 854 962 173 116 691 031 353 198 095 691 928 739 403 722 938 126 953 188 952 459 006 248 651 861 981 283 596 779 517 493 741 187 365 850 857 444 342 015 568 521 480 583 709 862 727 634 614 545 964 457 288 613 812 742 730 485 400 136 533 577 801 908 492 811 747 478 220 996 015 579 947 962 064 510 346 536 291 141 033 685 934 501 386 303 111 671 773 598 471 263 497 245 184 797 657 072 598 379 944 277 490 913 813 273 843 886 279 414 574 112 487 356 127 520 087 850 357 658 205 441 219 233 530 427 210 739 234 334 654 794 192 858 158 824 936 041 598 394 382 428 528 120 847 020 223 263 434 412 424 048 670 431 150 043 256 825 171 332 297 662 858 309 149 520 695 095 019 202 559 128 763 272 926 665 037 947 723 451 281 568 874 307 516 899 053 680 670 471 046 340 208 116 406 154 875 621 791 043 567 867 931 252 913 095 229 745 409 411 367 701 605 481 111 656 196 080 641 965 578 216 899 815 044 751 542 070 592 204 447 429 172 042 058 183 608 171 726 028 712 848 105 654 087 398 666 138 858 132 606 131 149 553 324 815 085 794 977 084 585 059 793 139 694 064 351 118 040 100 224 955 055 453 028 144 918 929 374 442 170 781 313 305 084 682 195 135 783 378 200 001 683 108 081 052 219 444 829 174 628 147 808 590 708 782 672 695 359 508 522 292 103 818 510 306 916 087 814 079 471 398 873 934 697 933 628 379 707 820 856 406 706 569 489 501 102 796 505 716 472 329 799 400 140 099 124 125 301 816 980 270 049 088 572 576 525 463 785 102 013 639 159 571 294 729 089 971 532 096 735 038 228 008 867 120 836 188 306 144 232 406 275 676 415 833 846 555 810 958 616 386 142 928 361 248 156 937 665 630 781 612 837 160 945 242 469 147 622 612 674 604 466 396 653 460 666 579 818 682 343 163 518 587 306 628 903 256 004 497 050 348 154 885 902 951 924 630 831 420 001 162 505 568 883 039 368 801 852 097 631 850 636 289 937 027 585 492 432 714 364 191 613 564 030 310 528 879 239 671 192 161 817 323 447 384 319 367 913 652 632 323 781 884 883 854 378 470 300 237 257 563 854 965 507 223 118 766 498 570 094 845 668 432 237 291 475 408 289 967 501 823 468 683 180 716 377 306 765 413 745 840 742 930 941 792 130 574 870 975 460 629 563 521 478 562 837 314 589 077 556 901 407 147 718 565 006 860 054 974 713 053 513 011 832 545 117 942 914 407 313 196 477 654 117 282 611 421 056 453 159 525 221 181 827 691 628 654 282 551 661 912 421 819 137 899 668 940 902 076 156 494 773 824 695 032 226 699 763 083 522 866 862 269 988 166 726 109 060 752 265 350 614 058 357 954 204 372 558 428 072 631 945 867 111 681 684 161 171 185 508 341 673 532 147 274 120 241 426 431 376 250 981 617 524 760 853 214 182 555 397 918 842 432 546 289 352 203 077 523 351 680 154 758 067 560 299 173 422 091 038 746 164 510 870 387 984 359 324 148 700 999 701 176 837 279 461 392 728 308 371 537 825 278 646 937 430 323 379 200 100 240 923 432 907 291 721 430 716 369 775 554 112 917 331 307 772 610 566 737 957 522 989 604 455 832 127 841 803 706 285 348 500 586 827 179 996 474 751 455 416 343 403 008 941 515 294 814 600 837 488 436 266 262 415 468 236 683 578 296 736 906 113 129 583 500 247 825 135 566 484 186 597 235 546 658 494 503 260 972 371 824 632 486 987 575 338 349 385 405 516 056 383 397 959 674 871 643 169 974 890 363 538 618 823 893 587 192 876 555 021 655 183 522 346 100 808 921 404 204 662 481 614 463 116 482 158 478 024 610 142 734 129 383 523 331 636 775 148 826 758 839 645 106 514 132 598 136 841 039 775 024 476 435 059 945 680 677 875 733 776 669 359 045 692 211 867 292 592 777 312 999 000 561 480 475 278 998 881 458 233 794 209 055 728 209 252 733 621 063 857 766 793 603 259 556 574 321 117 514 149 665 883 819 466 663 036 396 277 364 127 317 758 893 099 082 180 273 229 438 381 791 675 492 426 643 649 504 017 941 008 215 813 227 176 141 837 446 103 183 752 182 195 931 687 628 418 677 982 892 345 325 743 329 708 388 225 921 522 072 302 550 264 970 352 365 081 511 124 072 899 755 125 952 067 085 530 170 845 207 778 609 999 563 759 593 991 647 555 712 067 131 735 179 626 129 852 864 461 783 078 992 366 387 631 107 158 078 026 924 035 678 930 499 483 353 781 830 322 410 530 232 246 132 275 267 228 066 898 631 656 167 950 471 629 684 807 946 260 195 118 443 284 413 495 081 136 078 937 313 216 565 853 471 378 032 310 916 766 976 881 008 965 914 154 803 716 691 748 773 552 188 504 019 634 560 964 874 409 011 531 638 900 894 840 626 306 605 842 394 070 448 840 507 718 260 665 096 258 561 946 871 198 966 117 566 243 951 214 444 657 567 511 977 676 412 230 138 748 864 325 799 049 192 794 021 753 772 596 662 116 346 698 666 249 356 145 923 710 539 397 107 354 772 234 104 045 255 669 367 953 047 250 126 297 422 263 181 246 700 805 842 537 680 404 259 491 698 933 221 757 913 316 179 327 508 205 020 140 061 928 824 596 274 070 978 470 537 782 605 156 733 003 093 012 904 666 886 940 843 696 038 425 570 916 253 916 292 027 976 581 375 026 904 490 589 689 699 410 447 733 497 689 273 130 376 705 780 977 496 737 483 162 097 943 632 839 192 360 628 810 889 965 797 646 548 052 695 535 947 504 425 354 822 628 661 060 757 570 522 896 169 112 798 765 542 785 243 425 324 505 927 505 671 059 994 833 644 626 248 725 282 515 635 190 241 338 144 264 953 743 295 803 421 901 323 498 959 060 459 864 637 004 317 394 266 053 640 825 999 861 601 549 413 413 917 234 177 310 273 020 198 411 088 114 148 358 327 934 439 839 026 574 948 543 456 677 301 874 848 544 755 195 626 230 028 988 875 860 512 992 799 300 283 698 351 083 490 036 170 964 031 332 184 800 291 885 028 657 335 913 211 352 874 074 432 048 680 475 225 716 166 819 409 262 997 146 735 881 218 799 671 656 604 975 470 188 860 360 283 610 985 226 732 438 375 867 274 044 970 502 945 817 633 146 524 441 712 179 238 670 356 461 545 860 556 997 817 827 098 010 963 548 680 677 147 121 413 555 105 273 848 787 053 473 920 110 350 604 501 164 567 881 964 829 976 943 294 113 956 491 162 938 914 545 868 920 499 470 641 762 280 782 705 506 587 893 201 329 179 314 000 235 068 780 133 294 419 747 562 974 518 175 852 718 554 023 391 390 341 177 411 045 938 175 166 538 695 059 941 165 229 934 973 462 546 269 044 385 659 183 366 524 665 943 311 545 161 664 552 688 416 885 506 553 039 030 842 757 287 736 842 160 867 139 888 822 049 477 447 786 548 520 626 730 145 778 471 209 822 546 978 871 609 334 251 729 553 405 674 838 373 812 098 176 122 912 349 994 060 898 797 447 710 674 155 137 735 203 516 914 644 119 688 793 462 120 100 493 300 595 399 055 718 408 759 687 074 596 191 530 369 104 074 475 496 820 957 106 348 500 613 921 639 906 132 690 065 388 247 637 093 586 325 555 585 685 921 419 577 586 172 793 693 819 153 644 709 102 468 623 835 935 414 514 667 410 353 350 821 903 511 392 193 385 657 513 392 179 193 296 431 143 264 761 102 643 225 777 167 094 109 172 916 239 686 045 070 939 582 208 102 444 724 708 705 074 057 564 350 446 315 148 325 868 159 882 186 962 342 403 781 058 818 189 597 677 156 139 714 386 580 678 247 878 615 317 392 050 792 421 863 771 999 578 310 406 285 466 075 479 055 891 549 237 784 248 001 051 844 375 620 634 227 498 389 621 976 609 638 118 301 706 055 544 462 935 377 390 868 571 538 845 399 237 972 515 536 853 359 046 647 523 827 313 496 579 003 042 720 022 344 881 258 441 701 174 449 557 107 446 787 809 097 991 259 509 529 308 374 058 596 384 600 180 942 005 750 197 035 634 554 801 560 010 826 136 142 446 192 540 003 968 000 041 781 725 606 273 989 667 853 042 713 726 518 845 684 069 778 289 232 452 197 974 853 448 135 994 603 687 162 566 622 161 126 635 017 383 155 375 000 179 691 464 612 333 312 198 898 086 732 903 284 853 303 367 243 727 280 087 388 435 104 483 283 772 633 880 529 912 767 997 602 026 044 964 111 725 939 400 851 819 026 302 752 913 324 591 337 956 188 344 909 139 755 009 489 797 139 017 211 668 741 262 072 783 024 924 212 936 618 631 609 622 995 759 342 411 190 191 933 670 931 694 931 211 014 482 912 992 699 904 534 864 478 476 209 627 905 171 253 711 013 940 602 072 965 859 682 717 989 456 389 801 522 742 886 354 487 407 364 371 282 779 824 450 161 711 224 316 155 121 769 567 332 609 767 259 506 675 242 219 896 213 787 881 399 193 085 686 977 951 011 013 018 610 559 983 882 593 483 280 203 219 169 378 485 589 496 065 900 296 685 788 438 072 577 913 967 156 008 031 800 452 733 910 268 778 399 909 989 923 584 589 780 245 996 932 533 624 644 937 464 766 179 688 063 996 136 989 252 202 938 298 120 919 007 923 619 291 937 845 819 389 791 693 300 798 462 434 732 602 058 614 292 764 822 617 885 010 599 613 503 382 187 615 449 836 865 003 720 954 962 655 003 949 276 592 340 184 105 688 205 670 639 290 033 844 355 138 556 975 041 294 031 243 014 043 477 435 664 918 358 388 200 420 256 874 886 390 080 642 734 184 921 110 458 424 154 900 543 154 729 823 644 554 631 223 642 357 846 404 461 662 258 732 494 719 949 332 373 987 687 599 014 803 187 851 739 688 187 893 092 979 077 942 399 360 872 642 150 498 964 087 266 009 428 758 971 190 426 944 139 978 188 988 403 550 201 908 032 014 410 643 529 985 550 283 177 294 539 255 793 693 308 630 561 438 526 753 762 861 554 973 082 879 336 084 075 262 637 046 453 706 191 864 654 699 976 913 510 632 339 548 979 126 412 662 030 834 286 001 490 001 383 785 708 933 180 850 235 937 772 779 696 251 256 436 783 953 843 337 644 979 799 532 727 430 666 195 270 920 168 494 084 710 183 254 388 452 683 984 872 712 811 212 593 753 287 535 994 650 009 615 681 334 775 754 377 828 485 088 426 652 326 430 323 340 181 190 254 220 860 685 157 448 508 199 780 867 577 492 235 773 875 523 149 915 595 529 152 613 679 557 246 111 649 912 348 185 032 472 386 220 954 076 757 966 355 928 855 491 479 952 322 713 115 961 060 288 676 092 196 553 676 862 075 844 271 358 463 640 057 522 349 798 375 771 845 864 133 085 119 345 687 907 807 087 320 726 263 559 320 661 295 119 614 605 253 790 938 502 951 910 018 950 048 988 127 382 095 110 556 104 021 648 651 029 594 530 209 036 759 926 413 401 697 494 103 370 520 568 337 581 449 457 871 062 285 403 808 005 004 519 037 878 175 900 581 662 369 984 670 631 979 712 460 265 638 117 066 242 950 415 441 773 720 128 574 553 292 093 443 522 062 851 172 834 278 830 947 446 047 489 660 548 093 534 445 919 945 170 559 368 046 973 424 988 728 539 162 345 135 503 727 885 824 404 380 844 954 495 190 995 670 466 810 288 512 608 506 017 232 873 909 000 089 980 700 467 404 204 913 488 224 259 558 652 914 331 055 230 077 845 061 509 878 073 768 953 628 810 600 830 904 287 688 573 127 022 059 265 622 906 530 100 133 833 293 857 896 125 992 117 230 712 896 697 859 335 124 716 513 251 543 825 060 705 840 815 217 124 607 167 381 835 490 319 790 423 929 231 060 524 618 830 068 949 626 930 572 024 040 831 638 182 646 190 382 146 824 773 298 861 478 280 956 227 490 071 375 865 533 659 913 307 776 023 692 010 405 491 461 431 839 250 330 153 668 610 222 392 292 633 915 752 912 159 421 446 589 952 735 930 340 857 840 144 371 370 227 839 570 252 291 091 069 736 923 747 898 192 499 516 672 298 990 741 411 007 130 850 462 053 836 818 123 631 104 591 711 065 413 878 897 374 509 538 723 050 646 673 713 502 927 591 477 625 300 874 535 613 099 429 968 657 410 202 493 477 106 058 446 890 010 837 343 699 366 887 590 008 924 923 364 019 922 317 454 384 792 860 822 976 986 230 481 761 217 467 940 259 352 383 962 495 541 458 840 012 902 366 919 608 722 960 702 424 785 802 898 515 147 376 077 293 865 580 968 669 134 254 169 513 702 896 622 035 812 869 840 036 843 304 752 025 598 038 005 968 728 073 031 480 137 001 416 112 597 080 957 394 639 626 743 361 275 801 885 672 388 367 563 660 069 172 307 453 245 372 072 720 198 940 289 073 081 094 937 899 209 976 123 907 746 757 814 595 159 745 389 119 606 584 672 584 458 039 402 573 963 829 493 930 504 800 435 308 095 755 563 248 208 718 898 268 149 647 839 038 104 868 578 232 563 808 484 891 048 614 046 743 474 641 568 890 457 872 835 517 548 056 949 374 747 829 993 377 857 061 498 394 588 305 019 065 044 711 174 235 272 531 458 005 111 730 638 292 265 356 934 411 019 718 258 628 038 174 567 907 034 009 825 876 922 881 154 612 636 128 173 877 812 103 813 258 183 893 490 042 713 939 634 617 200 009 368 931 585 702 053 621 359 608 562 173 167 516 823 710 732 379 458 496 090 504 781 924 176 551 988 264 539 629 923 330 277 136 636 761 003 879 265 425 331 270 144 794 924 031 166 800 963 605 036 071 842 598 266 097 736 180 562 515 795 079 490 321 077 349 546 887 219 751 529 914 970 454 326 078 235 204 142 140 333 079 786 923 345 255 119 598 186 039 216 348 144 332 254 729 318 830 274 135 141 498 622 172 127 006 106 396 557 783 686 146 598 200 097 097 056 205 683 992 328 444 034 709 599 147 450 630 483 495 425 962 311 274 817 524 126 115 513 629 275 963 925 012 449 859 232 801 414 108 075 662 221 070 951 044 232 580 439 441 902 231 355 687 897 608 916 977 740 889 080 128 468 254 513 918 638 602 811 927 341 886 278 791 233 339 089 186 823 120 112 880 776 047 837 760 209 731 282 537 467 773 281 619 693 772 752 961 804 059 691 986 930 615 126 819 468 373 665 002 913 668 905 143 446 977 929 892 499 017 321 337 089 304 864 818 822 124 526 830 328 879 673 325 330 672 617 708 664 247 528 913 787 376 161 847 172 598 639 260 223 596 175 302 523 273 920 374 179 301 985 882 961 712 507 123 393 964 292 946 246 818 478 958 334 563 250 457 120 229 720 687 298 137 893 391 325 435 024 966 023 189 375 638 292 992 825 242 611 657 100 802 323 812 953 758 398 737 461 299 881 588 319 124 079 317 225 635 761 556 697 912 263 439 633 644 195 507 839 254 867 966 993 923 248 897 431 722 344 879 514 128 476 061 116 674 361 425 877 069 538 289 116 230 436 772 863 214 364 669 188 537 754 575 607 098 470 089 104 550 258 588 562 696 646 891 269 717 431 580 375 246 568 606 812 324 886 477 422 999 776 665 711 705 445 296 453 018 427 164 096 575 079 047 698 475 776 383 597 291 692 993 737 946 724 940 995 216 195 564 462 014 119 697 966 830 861 151 965 641 741 293 894 394 170 167 586 950 897 036 312 765 718 597 243 716 416 298 529 143 481 330 126 713 493 236 882 776 336 532 717 549 080 648 102 102 512 524 801 459 779 928 748 202 181 905 873 504 196 377 609 100 591 826 370 996 173 711 001 077 734 195 154 599 434 994 748 316 199 789 122 473 183 810 227 159 177 869 097 116 063 639 490 983 113 922 678 150 768 051 272 608 777 110 856 525 637 397 241 226 398 712 239 111 957 076 791 730 962 616 798 941 791 033 539 288 200 198 469 592 879 423 808 785 739 339 545 271 443 197 536 374 170 646 557 708 364 146 911 569 647 985 481 365 801 178 355 017 056 177 627 546 557 982 882 041 021 703 429 766 621 760 725 850 929 843 425 499 316 475 769 221 247 821 924 888 967 917 839 064 463 838 635 588 990 165 526 215 830 840 834 164 421 910 746 125 895 329 055 988 355 738 857 504 179 976 870 763 709 856 050 485 123 077 587 089 414 850 043 262 739 294 137 575 890 438 839 035 468 081 632 371 511 545 172 003 677 083 467 368 759 986 970 303 250 005 728 616 740 925 355 909 897 649 892 579 553 628 114 216 840 000 921 761 098 120 849 429 708 120 986 097 011 595 423 968 669 126 948 251 624 320 028 393 215 097 026 302 599 182 043 748 407 633 472 420 531 464 411 258 620 285 087 986 343 447 200 201 571 355 895 067 323 177 914 574 595 384 038 205 669 996 954 227 644 286 483 883 318 925 753 492 416 357 064 930 694 014 291 261 587 610 060 426 787 654 608 589 383 656 643 146 824 850 339 786 154 447 565 210 343 832 998 255 059 747 525 645 211 495 564 793 235 205 626 091 743 241 230 840 059 804 511 124 974 898 898 234 209 479 007 122 671 089 393 862 948 746 415 610 785 247 396 059 626 066 175 756 610 982 932 793 932 901 454 021 408 640 746 927 980 897 701 305 282 821 600 828 257 504 849 482 617 526 643 262 050 153 172 838 791 484 474 783 100 871 195 928 554 437 915 534 866 075 963 214 639 512 440 336 418 734 553 061 755 437 777 373 006 005 582 639 489 551 172 346 373 166 581 946 530 038 648 212 311 614 929 568 430 524 592 033 297 614 081 820 770 268 443 557 207 907 071 457 618 909 261 135 053 926 198 779 488 204 716 400 401 439 376 578 392 889 582 668 743 050 458 023 325 404 054 211 766 605 802 899 892 551 671 835 024 312 851 326 324 159 089 765 472 738 378 520 616 884 205 469 402 835 215 612 575 465 310 096 742 420 988 718 095 053 629 799 421 077 900 601 461 355 131 738 041 272 162 661 450 713 371 402 758 315 013 574 927 347 822 968 336 300 614 005 325 861 352 808 626 237 439 898 850 544 124 083 814 449 221 820 190 921 608 600 783 689 675 970 078 511 633 056 238 360 973 089 033 460 932 708 478 662 642 908 436 789 850 437 611 319 176 437 237 122 641 094 176 776 875 756 479 820 287 653 336 035 994 329 943 233 219 651 938 410 030 632 634 196 289 398 802 214 863 913 716 567 517 910 274 389 997 000 465 529 455 077 380 102 520 193 719 691 269 159 701 824 377 298 519 405 498 129 658 607 260 749 648 142 176 015 330 172 402 665 099 440 186 432 381 183 433 388 051 378 509 844 668 926 394 096 526 338 183 495 532 191 440 782 100 728 580 917 220 215 482 121 935 890 317 990 906 154 170 716 081 296 424 308 797 065 708 412 682 650 954 652 108 237 128 233 791 219 694 193 280 901 391 946 646 642 704 909 535 091 874 691 457 904 744 400 242 234 893 992 966 037 989 311 331 554 016 255 934 965 579 672 182 569 798 925 984 469 390 491 069 202 730 434 985 057 215 638 030 063 248 616 870 884 065 570 067 391 878 964 162 097 349 536 003 556 201 746 591 814 304 194 258 836 872 682 605 005 497 010 775 674 536 782 422 027 679 147 759 165 709 500 813 571 254 278 896 356 371 790 092 178 725 343 212 617 547 165 448 654 917 966 696 349 643 615 574 483 719 303 845 367 722 461 607 340 531 759 151 134 182 621 769 128 355 520 684 790 639 322 298 061 263 736 947 089 184 230 619 970 948 558 538 739 907 382 023 493 537 300 116 838 409 609 153 014 217 229 958 516 760 352 900 319 986 880 301 364 458 080 786 036 067 410 608 203 944 551 270 989 329 685 908 545 693 962 092 252 263 021 590 418 179 220 460 629 072 003 713 175 734 379 249 783 311 761 648 910 476 340 974 048 217 162 092 360 464 276 349 815 073 349 078 009 583 894 386 581 409 555 181 555 387 028 252 797 868 647 910 049 175 984 272 591 091 311 705 503 091 053 592 338 835 398 035 557 085 742 989 684 839 209 833 566 396 983 773 593 515 686 488 780 530 059 853 086 738 305 257 423 687 222 206 553 154 953 870 006 391 714 201 037 074 328 066 269 478 406 005 892 865 057 157 795 070 516 017 496 946 624 061 764 509 223 518 652 942 373 046 372 708 366 643 274 012 168 981 493 004 345 236 910 357 370 039 275 543 473 405 954 476 959 148 367 650 398 658 640 719 813 088 450 797 047 313 752 771 205 655 425 304 271 889 199 557 462 447 985 157 077 568 968 696 656 284 670 671 354 759 698 310 510 598 879 742 084 514 572 175 599 128 950 645 684 018 080 809 362 458 271 924 782 277 599 312 690 434 253 491 856 604 908 288 367 150 106 520 766 284 399 004 795 369 524 574 651 469 648 763 986 147 199 449 267 131 801 836 566 652 951 595 982 550 605 949 201 813 867 174 536 785 206 229 699 907 353 429 723 776 398 585 311 764 697 355 326 771 021 043 479 046 998 587 311 663 905 100 830 461 517 716 474 436 555 333 580 761 733 546 553 001 057 364 281 984 645 580 010 123 399 314 173 203 807 605 123 190 064 941 499 258 606 013 534 730 168 929 602 636 782 886 431 044 606 443 609 873 316 854 414 235 296 909 713 486 233 183 901 531 227 745 146 255 367 669 429 972 679 336 708 011 428 017 097 286 178 457 774 120 770 378 733 603 789 880 905 913 791 288 937 465 129 405 722 119 423 549 727 620 344 018 976 450 323 671 871 445 403 541 312 848 635 236 380 750 048 702 404 428 094 822 563 550 746 220 752 538 535 175 127 583 158 147 519 805 183 141 828 341 246 011 704 810 484 764 426 545 969 852 253 136 276 757 805 446 646 612 927 426 092 795 427 429 014 811 983 472 715 998 395 601 323 205 477 117 625 242 980 904 467 172 212 375 118 650 091 624 337 255 535 786 242 349 180 390 900 315 265 833 117 940 894 503 181 527 691 084 659 336 805 394 326 566 547 555 020 203 350 795 368 014 734 629 772 886 372 534 999 473 809 729 401 119 952 059 412 883 720 735 555 070 610 089 256 190 888 734 141 666 653 483 182 723 609 450 279 935 709 076 429 927 012 437 497 969 400 919 381 812 388 838 916 937 070 344 281 734 889 586 791 476 496 454 677 661 933 510 429 780 915 412 337 771 051 802 712 177 090 401 279 808 580 471 144 492 539 132 395 208 836 364 672 644 299 629 900 563 465 364 704 835 897 212 794 834 095 732 984 105 559 041 666 158 532 458 486 629 081 941 917 374 520 883 155 830 499 366 522 170 938 562 234 816 140 865 716 394 395 247 171 871 406 810 303 895 520 565 485 826 312 181 053 051 518 043 491 991 164 129 350 623 417 762 393 755 038 053 125 509 198 293 461 883 277 879 560 206 962 393 938 369 299 463 336 479 742 029 377 370 051 434 133 109 008 119 493 106 198 210 417 945 292 265 653 185 918 601 845 812 018 984 620 449 021 111 595 596 324 708 306 401 994 978 856 504 396 711 250 017 011 981 373 634 352 065 154 161 426 930 237 736 688 378 427 213 396 906 436 792 937 980 108 184 395 394 168 296 484 086 701 694 903 947 457 518 486 389 317 098 439 988 282 423 385 228 809 164 723 190 711 791 531 827 949 912 828 517 332 308 160 848 846 812 520 740 137 768 423 417 590 811 375 924 477 285 789 501 327 806 134 576 580 250 722 686 061 987 186 211 895 228 446 637 793 487 826 419 280 235 220 003 421 916 526 319 195 009 859 238 750 126 809 837 319 651 227 969 605 226 595 050 802 584 300 455 568 993 133 867 860 905 816 535 903 193 106 722 762 629 221 008 117 654 265 970 910 449 737 338 606 378 760 952 040 208 928 470 739 543 432 643 048 920 182 736 340 327 107 550 026 910 392 452 699 498 700 185 052 778 825 540 861 052 572 243 870 417 630 361 812 230 462 387 566 989 605 994 990 966 937 821 931 227 021 160 305 279 325 755 794 117 385 622 103 208 046 922 340 869 319 052 771 147 675 710 110 987 529 640 904 179 296 209 698 770 659 577 572 289 445 126 315 636 355 061 821 995 071 435 261 288 320 423 218 674 554 667 173 159 209 453 642 860 060 709 554 890 599 644 851 985 948 409 245 749 327 516 452 230 114 925 470 293 266 942 601 601 602 108 579 645 202 823 543 677 000 917 595 807 220 558 286 801 980 396 874 428 083 043 787 418 158 177 168 533 592 461 743 685 061 692 212 036 474 179 101 795 553 942 018 670 901 919 774 016 188 653 403 230 792 220 046 490 867 459 717 068 942 655 815 414 503 358 073 990 683 407 835 039 438 622 807 897 001 048 709 464 549 368 072 198 706 181 076 518 271 411 443 980 821 124 827 853 135 756 809 406 816 336 614 729 128 610 743 015 209 701 661 882 345 696 864 895 145 540 157 283 460 997 421 628 677 061 406 299 731 801 195 727 610 015 861 315 569 162 220 495 123 394 536 258 840 862 671 559 674 250 571 231 010 876 363 451 197 880 785 827 567 206 044 584 470 245 238 004 149 829 555 420 229 049 391 205 214 096 189 624 337 544 411 111 071 537 006 836 465 288 178 034 992 897 980 813 830 896 665 477 369 668 069 168 723 837 358 366 635 220 695 389 578 491 908 705 720 147 591 866 919 512 437 589 545 617 388 481 114 887 392 404 039 765 204 380 695 676 111 747 164 840 439 759 404 434 890 059 081 078 698 105 903 297 074 747 352 737 107 338 506 287 213 298 599 105 983 753 557 582 827 162 697 464 654 614 831 109 704 985 753 181 656 145 661 443 960 257 549 936 854 811 785 650 371 184 697 834 974 528 220 678 973 361 609 011 405 949 469 882 353 227 007 528 931 749 286 419 055 117 076 720 182 594 930 817 688 941 256 040 811 683 614 251 305 076 388 045 241 513 307 285 346 358 760 233 125 338 944 238 582 863 938 473 731 763 738 115 015 099 386 346 299 314 265 475 295 224 477 305 568 695 420 194 300 287 578 892 550 145 582 526 222 947 744 714 049 925 547 404 296 626 580 885 883 311 538 652 584 213 945 031 593 236 668 305 788 685 076 845 035 979 612 621 709 211 904 318 660 169 136 229 240 723 913 125 372 459 605 958 351 383 576 162 501 688 996 956 211 842 537 411 170 227 667 311 615 357 872 633 934 458 441 652 376 440 707 505 578 966 031 099 692 332 080 642 511 386 773 623 153 507 935 921 334 346 604 366 427 853 503 118 337 950 250 183 170 596 751 816 680 127 829 824 710 712 105 741 545 036 967 205 548 396 697 663 276 585 693 761 433 396 168 681 785 025 062 514 696 057 503 146 385 358 070 964 603 430 525 835 076 519 554 311 758 501 035 036 386 638 994 506 893 801 957 592 127 560 897 995 085 361 767 100 339 216 530 372 686 473 460 710 615 253 550 177 613 372 644 652 930 353 820 364 866 549 054 421 089 055 857 436 134 006 296 558 279 123 294 078 505 886 869 504 812 649 024 001 850 409 101 548 837 655 191 331 881 590 650 819 500 023 541 909 368 596 603 972 033 843 676 925 442 097 841 831 623 430 051 675 099 942 098 275 959 742 016 863 733 904 632 666 773 430 251 014 369 374 805 363 358 276 448 772 423 725 688 118 622 299 428 444 893 267 186 452 884 997 663 465 560 284 476 163 831 324 602 680 347 613 996 179 236 920 594 664 624 059 739 397 417 435 663 377 226 805 986 353 620 647 053 246 850 722 083 712 674 932 041 242 725 287 174 630 251 585 546 747 363 211 596 792 535 810 181 487 219 429 098 098 620 577 251 448 724 088 019 337 506 608 528 145 396 671 427 625 362 325 888 169 344 318 573 981 996 697 331 677 919 561 649 307 899 768 522 410 973 692 207 495 212 981 195 381 128 557 216 597 847 536 779 766 085 755 437 010 879 465 716 738 058 587 336 427 000 750 190 891 634 793 233 564 805 513 867 507 742 509 734 742 561 511 287 943 748 241 232 513 124 873 053 698 179 051 617 664 433 441 441 709 827 566 592 789 360 697 045 973 315 594 361 693 317 402 967 254 864 571 376 217 814 354 683 506 161 298 603 580 746 892 288 425 325 412 698 233 998 953 015 908 492 725 528 417 022 388 367 738 323 546 871 983 975 867 738 778 047 989 644 669 702 852 172 931 838 711 370 859 069 799 400 825 233 601 500 149 124 622 242 242 962 731 797 641 412 167 662 790 916 963 852 094 728 182 534 453 906 556 986 825 725 585 118 665 516 822 212 790 568 380 490 761 994 629 668 896 083 304 023 946 832 049 815 602 066 731 137 283 756 752 968 566 915 978 118 015 776 799 156 303 118 525 461 629 826 811 457 348 874 336 338 484 179 601 866 846 299 062 702 621 377 883 919 424 467 403 184 194 214 584 336 278 901 059 655 700 540 019 376 669 918 820 266 909 437 182 272 101 054 813 723 599 866 298 499 267 850 765 499 965 592 335 097 730 891 469 811 080 896 760 337 762 204 037 741 009 644 302 538 997 451 303 065 520 500 571 454 569 423 062 178 076 318 439 753 390 226 013 475 298 761 876 173 071 701 323 455 052 445 185 462 272 110 497 925 191 352 089 629 728 409 753 184 810 422 264 974 197 904 584 863 003 972 569 277 479 068 304 418 520 504 745 216 930 787 798 433 725 111 574 192 528 550 365 730 252 956 758 899 541 169 763 986 073 226 808 402 981 473 899 990 164 422 491 401 063 424 046 637 360 159 029 799 830 984 357 570 595 443 818 120 623 479 688 624 274 438 074 837 971 840 448 368 230 928 063 770 951 039 487 168 772 544 952 129 864 654 624 319 634 519 446 681 084 978 309 946 308 920 883 466 323 651 946 040 601 499 718 317 247 565 457 346 135 012 653 997 810 210 158 257 713 342 047 721 494 796 668 594 157 021 173 708 250 972 560 046 608 046 131 989 936 647 839 071 986 271 958 009 852 190 950 405 922 054 752 948 434 729 724 874 046 265 285 970 274 524 231 868 673 939 816 496 579 699 353 283 025 717 829 327 832 952 668 018 948 135 177 864 982 886 986 868 098 286 656 139 723 991 312 315 556 589 567 192 235 715 962 222 436 087 749 875 935 983 063 741 098 236 407 033 957 772 407 501 583 485 854 421 418 288 619 733 485 108 480 196 456 028 550 653 922 380 041 896 176 179 622 226 968 410 676 434 088 702 782 554 529 296 194 891 688 355 127 577 501 376 221 891 001 677 714 369 459 280 926 275 028 740 491 298 911 441 683 430 961 678 611 854 759 370 159 153 081 943 350 239 031 254 069 939 743 329 035 977 864 437 398 560 757 075 930 087 563 308 611 111 670 556 272 040 966 430 031 781 117 786 895 573 293 485 972 140 554 231 718 719 844 421 782 452 864 539 647 390 545 998 322 707 183 407 101 559 091 485 312 832 734 358 534 485 715 398 635 206 569 552 780 506 905 801 664 291 848 140 556 699 164 156 941 673 203 349 726 253 618 046 466 651 013 405 442 199 275 358 963 807 570 254 599 425 310 048 536 076 209 937 602 642 300 851 888 135 168 505 582 509 208 307 493 959 643 940 447 911 297 562 668 427 939 568 321 305 789 873 661 111 553 895 877 871 024 069 561 940 419 704 106 460 825 547 364 587 555 933 187 186 872 840 922 718 952 679 438 182 117 110 104 408 076 156 318 759 095 818 648 438 688 187 666 821 483 907 428 225 373 048 241 807 426 834 605 788 846 353 996 692 657 309 167 744 450 948 082 446 479 479 864 740 998 489 011 277 110 417 011 664 327 818 603 684 086 094 730 332 836 612 506 513 431 877 056 672 940 956 527 964 997 029 601 965 196 220 475 426 969 343 452 799 138 254 279 100 643 045 115 134 531 921 840 134 335 444 137 396 142 076 029 494 510 038 518 443 524 138 236 600 255 208 786 446 461 323 684 559 956 949 302 956 694 882 802 186 904 218 630 614 750 850 177 837 290 027 205 145 059 739 984 719 569 274 005 293 118 404 528 942 675 888 216 326 664 983 387 431 181 161 823 129 314 482 738 298 959 155 053 704 215 364 317 603 178 106 827 783 940 039 315 528 042 006 759 890 007 263 961 356 898 176 500 974 663 956 195 389 855 044 009 493 130 806 384 424 172 614 084 245 469 238 622 537 252 893 772 948 444 387 558 204 231 907 919 671 034 420 700 739 682 940 526 860 280 831 260 768 340 407 698 977 808 047 474 507 835 189 773 286 719 434 061 466 649 314 048 879 275 351 547 391 008 310 183 535 768 893 818 509 404 153 123 750 341 360 740 597 988 396 237 460 167 588 215 057 017 760 424 520 613 619 959 301 459 207 713 593 787 798 072 149 734 853 782 340 957 979 715 369 428 230 727 281 129 776 135 813 997 573 821 553 716 400 136 997 483 377 598 084 042 050 492 536 811 225 949 538 313 154 313 201 077 435 950 228 380 194 444 638 052 609 848 083 417 528 204 008 495 577 775 324 189 728 604 564 895 783 524 293 868 777 250 227 567 428 397 642 634 469 967 945 426 797 805 839 622 013 491 539 788 548 662 166 562 459 742 363 176 707 838 496 595 156 741 299 964 389 252 151 292 842 070 497 082 300 075 654 749 595 237 297 135 217 272 031 279 664 574 021 319 416 772 227 774 625 780 061 219 057 633 846 744 328 105 859 821 580 061 149 144 326 647 258 550 352 323 329 241 008 671 734 511 141 349 085 920 116 145 859 391 700 949 545 445 374 375 041 723 084 882 741 686 325 767 338 824 064 210 142 133 711 275 682 680 111 078 556 246 272 531 837 841 230 377 439 897 490 881 605 944 552 939 194 592 491 079 218 961 711 429 476 936 571 845 947 899 509 894 151 317 434 207 988 765 536 790 719 962 857 602 987 601 003 173 586 904 027 670 285 276 203 102 423 608 401 927 481 874 142 646 410 378 220 837 582 030 846 009 186 543 960 439 247 829 225 591 985 610 524 793 109 683 237 270 398 979 037 594 838 457 045 944 572 968 343 796 586 322 622 469 062 671 155 110 477 737 702 498 907 486 052 240 056 591 817 396 827 358 851 879 172 610 748 777 145 024 453 038 264 229 204 854 322 282 816 071 987 313 646 617 721 524 635 593 881 125 969 975 876 827 665 079 926 897 919 604 759 183 043 242 864 924 193 034 346 726 294 620 165 882 666 738 001 014 337 555 382 662 843 099 078 702 199 798 310 954 134 325 879 508 729 921 413 037 765 505 187 374 677 463 858 942 106 001 200 774 104 688 116 210 361 437 714 929 226 270 684 331 851 815 065 966 590 180 624 795 914 489 453 835 650 823 096 429 875 010 534 719 545 438 376 073 324 088 179 686 141 615 476 180 133 860 140 358 517 512 890 174 947 460 227 151 712 711 877 210 589 933 979 272 179 737 014 559 205 056 885 250 121 350 940 814 133 911 582 407 501 339 694 301 767 411 921 100 767 043 268 827 904 172 620 921 615 056 332 810 927 708 429 448 612 234 729 723 500 118 501 754 002 066 685 820 857 248 081 532 359 216 427 124 374 672 103 672 299 445 847 900 259 877 904 484 741 609 085 328 038 646 939 128 518 086 876 958 388 974 222 392 375 449 568 576 206 837 629 032 709 126 224 786 684 336 272 612 916 282 063 076 714 049 783 864 904 761 352 841 091 359 521 620 539 210 681 676 972 061 356 665 276 694 906 538 402 133 389 324 376 599 747 321 960 863 311 281 067 739 494 404 251 210 804 958 145 284 906 600 925 744 724 296 839 280 600 268 886 764 746 109 195 707 335 688 559 677 707 322 432 146 053 558 830 828 576 945 986 060 129 410 190 019 513 719 766 861 158 809 183 353 016 437 023 087 712 634 613 681 991 578 911 638 466 035 841 302 294 847 202 269 930 404 727 506 043 817 215 090 852 690 601 644 392 212 323 975 162 848 918 001 096 296 642 073 928 682 446 984 030 273 029 949 972 962 383 747 702 063 223 863 454 037 884 688 674 569 817 132 098 600 614 135 644 227 743 300 399 717 070 641 220 393 437 564 109 592 278 715 453 458 206 831 634 169 956 502 901 940 839 966 445 732 430 568 845 974 845 154 877 968 646 638 024 855 816 831 690 640 950 114 799 010 186 129 781 646 472 211 117 429 054 060 594 281 700 605 317 374 167 208 406 436 759 148 111 863 806 230 535 794 208 517 141 589 678 559 012 488 264 430 377 780 172 639 192 127 290 424 446 213 994 124 627 101 424 423 571 534 407 859 036 937 792 005 118 142 991 167 137 716 514 079 424 286 624 811 744 535 305 450 401 855 489 630 579 930 650 600 592 537 910 879 577 574 081 449 946 128 680 636 112 429 447 309 028 188 185 264 144 743 413 397 189 036 804 940 544 446 538 396 603 594 388 298 581 460 568 613 023 988 040 408 345 398 606 014 344 772 491 160 226 188 493 882 824 276 318 763 072 972 646 720 976 512 284 325 564 254 139 539 775 167 450 218 722 563 136 045 977 027 233 339 836 224 041 203 209 895 931 282 165 314 160 297 478 461 234 163 123 142 266 804 951 434 489 122 015 081 851 243 317 099 460 382 580 717 079 675 080 129 112 174 728 970 833 239 157 788 122 715 546 731 033 015 612 358 916 549 463 068 637 050 809 938 609 490 923 902 248 198 171 226 837 626 470 025 511 960 395 331 709 226 969 732 512 700 190 463 502 500 120 605 970 617 460 332 334 146 441 868 459 038 429 015 571 827 260 741 576 897 793 673 160 951 989 441 125 057 539 283 316 350 098 291 939 402 598 671 542 234 355 981 890 526 228 558 143 773 362 103 836 339 533 499 588 205 734 081 826 291 236 628 623 522 367 445 576 920 221 639 802 294 029 369 916 710 785 680 048 313 033 653 108 801 631 745 390 089 317 992 596 398 729 417 458 990 673 326 036 008 888 004 449 479 698 923 154 814 931 047 851 851 797 304 696 894 348 597 600 201 571 959 494 074 031 066 241 977 157 590 031 439 502 214 369 352 433 027 830 378 525 290 306 920 738 554 524 294 796 722 824 349 231 638 967 571 214 445 173 967 735 256 497 427 045 281 470 034 110 156 166 111 136 823 762 662 157 981 968 070 884 180 418 424 994 339 843 111 541 393 043 641 045 982 279 409 965 332 709 914 445 499 968 834 820 132 098 136 276 605 829 930 087 236 795 533 216 942 915 057 701 503 076 222 896 555 165 191 903 911 763 704 456 140 312 617 048 021 231 273 383 349 726 227 081 144 540 522 841 800 250 947 152 551 789 860 269 065 395 632 849 990 130 705 815 334 200 158 729 632 342 780 158 584 932 774 090 770 175 859 597 945 000 598 345 706 161 456 602 481 841 288 336 925 758 844 395 135 639 478 331 361 277 348 698 214 328 701 189 049 188 439 795 529 377 037 970 376 099 936 183 963 259 322 458 201 466 073 116 010 401 095 900 747 059 226 010 394 439 438 663 190 407 247 157 827 931 593 584 971 362 290 735 721 266 779 989 395 581 825 650 997 402 612 049 749 490 804 090 300 539 903 599 038 363 843 318 010 229 031 479 173 499 521 836 243 244 329 203 941 090 208 790 273 863 179 892 913 744 834 849 850 934 906 934 289 291 654 401 835 433 587 206 793 798 849 146 890 777 557 010 776 301 728 672 863 132 628 023 081 264 811 111 564 010 673 543 469 327 082 987 379 028 671 985 352 788 474 999 375 124 778 997 548 496 592 895 782 823 391 170 330 583 410 916 913 552 423 958 242 139 560 993 244 967 172 835 716 687 421 559 245 775 964 710 881 468 214 874 804 396 209 207 018 888 729 498 867 126 097 650 321 347 248 237 517 456 403 017 939 313 849 963 416 692 352 276 750 323 886 737 554 231 865 437 729 059 915 693 111 909 781
542 951 859 451 808 511 331 327 397 448 666 104 090 660 074 092 614 954 052 214 919 140 825 300 309 577 258 555 479 506 842 186 905 075 661 228 909 703 245 560 194 477 879 017 369 310 407 780 286 114 984 972 740 147 836 608 429 943 575 318 654 667 648 019 642 145 725 835 167 549 544 286 952 342 893 892 069 835 999 441 950 610 829 309 861 391 032 089 698 711 748 047 629 470 391 694 647 249 290 928 024 095 374 986 638 355 436 827 141 428 266 418 133 051 017 125 131 139 272 722 282 751 602 598 419 676 810 525 265 824 582 783 200 231 753 541 776 619 543 664 591 538 530 911 770 460 600 563 617 366 471 375 547 700 803 759 091 581 332 643 618 083 305 376 814 804 142 054 070 819 749 574 170 947 799 848 305 137 978 377 108 483 995 029 354 424 006 478 853 833 617 985 265 716 355 630 335 152 406 567 121 831 476 774 191 458 856 061 846 268 533 711 223 531 468 275 957 449 474 563 070 132 371 356 287 083 522 204 422 580 885 239 209 163 792 425 595 824 483 951 666 576 777 834 878 200 015 497 028 986 786 045 446 966 772 973 007 060 836 655 801 162 163 930 901 737 003 730 588 046 048 885 551 044 384 273 695 007 439 290 355 878 404 367 008 153 931 500 950 519 377 356 096 592 483 372 924 933 792 821 611 179 085 120 142 154 644 664 167 147 948 824 525 014 994 312 232 322 047 646 588 988 163 495 039 448 619 256 138 545 682 333 598 078 225 932 080 147 165 033 221 953 671 789 785 435 236 595 931 892 081 177 124 207 519 182 023 673 804 680 576 201 718 483 527 472 769 458 693 483 635 605 386 124 835 286 562 744 278 878 222 992 370 393 627 858 555 430 895 880 411 133 495 459 353 701 323 137 166 701 145 886 281 943 995 848 764 177 858 814 287 463 652 956 285 693 036 941 285 966 817 033 309 230 734 768 604 545 935 886 399 413 371 579 224 877 464 036 378 652 158 688 604 040 851 566 347 798 782 574 001 235 581 177 258 841 524 183 219 572 327 021 257 044 254 844 564 097 531 249 858 115 392 461 038 705 879 872 097 886 926 326 973 845 387 438 057 909 635 201 873 847 613 601 884 599 218 693 805 846 534 746 952 920 006 332 905 931 633 664 911 242 580 095 647 362 844 703 421 098 228 504 510 746 512 148 431 459 164 699 954 059 899 144 741 579 720 970 159 946 217 166 464 899 593 781 122 418 742 905 051 119 301 932 940 756 315 501 248 596 351 107 392 774 819 304 308 296 127 339 773 816 907 422 121 822 920 303 391 244 576 137 175 312 268 943 540 810 530 257 151 147 136 747 269 829 838 150 029 473 801 238 644 713 791 898 217 181 011 799 636 356 971 175 697 588 577 022 734 229 923 142 823 320 933 332 751 191 039 609 097 313 496 928 425 957 245 633 703 350 448 227 442 826 862 209 651 723 234 116 041 357 704 420 489 642 541 559 222 158 435 422 113 401 596 874 474 501 013 826 016 899 593 962 073 655 588 000 399 241 482 273 860 295 485 053 898 979 593 390 418 365 421 895 906 637 153 124 602 159 853 323 745 799 433 351 182 647 171 191 936 100 433 758 062 825 793 630 785 213 956 528 546 737 742 091 787 295 980 923 335 850 728 030 714 483 225 421 398 304 320 994 650 918 403 117 071 235 471 232 990 060 413 117 205 541 340 572 039 220 494 153 961 107 115 884 836 076 026 794 383 314 938 116 523 589 934 461 236 490 107 946 986 006 787 444 304 679 341 946 785 376 089 148 280 420 384 470 674 788 892 891 804 863 252 341 730 700 484 842 137 908 095 089 134 396 189 019 723 130 810 754 739 822 146 572 502 543 257 630 237 235 100 913 980 590 662 974 603 402 983 416 277 690 399 355 802 368 452 031 780 918 527 689 125 936 615 470 812 737 567 928 773 890 903 973 918 160 053 487 552 451 505 906 550 829 635 861 600 237 478 084 493 600 103 542 193 737 154 825 037 647 738 149 915 149 076 938 678 946 295 956 115 767 169 322 817 381 736 166 549 970 382 534 713 734 348 127 641 789 207 302 386 107 770 054 090 276 485 701 530 163 638 628 642 963 462 974 371 160 633 083 427 765 084 909 100 011 647 395 853 279 353 761 651 805 788 183 123 403 859 077 023 832 463 515 790 049 491 789 751 736 412 162 368 856 203 612 468 874 321 132 373 381 549 237 450 629 954 568 198 339 200 761 050 428 272 205 088 148 883 108 704 122 909 117 382 204 257 301 691 273 066 319 632 600 876 518 691 588 922 826 577 439 562 532 953 497 723 718 270 366 584 502 825 267 387 707 386 917 043 929 326 609 533 279 307 760 781 279 372 358 719 680 105 711 370 595 897 865 305 043 607 842 310 905 837 318 738 154 059 198 843 847 670 315 768 111 392 361 622 505 905 224 668 369 162 285 995 073 831 942 067 308 436 070 944 959 943 342 913 052 485 859 743 785 765 473 086 857 975 262 500 957 501 587 589 825 946 960 289 326 755 139 644 428 040 912 649 951 942 296 671 490 695 248 642 306 909 274 701 169 662 498 645 649 213 435 581 284 949 700 596 683 101 041 276 963 682 517 696 980 358 464 389 072 378 876 233 177 002 962 386 190 950 512 588 123 719 177 683 030 460 569 436 382 871 339 373 453 452 446 794 647 442 487 980 251 751 684 319 734 915 571 740 539 173 569 330 191 857 131 786 420 041 505 634 901 244 247 352 558 917 876 652 558 240 004 268 106 906 106 926 917 502 994 437 138 702 457 937 906 258 965 859 781 269 686 828 188 428 296 542 673 025 343 299 917 104 375 640 780 737 565 552 406 289 535 708 679 418 224 315 090 909 422 123 571 036 401 924 565 719 970 424 355 753 262 637 525 119 605 111 675 969 116 577 954 285 110 714 002 664 083 272 531 233 993 509 469 338 045 626 992 648 616 836 001 372 092 813 140 212 573 763 514 477 813 315 640 550 031 924 222 691 309 420 095 831 018 321 775 798 756 450 439 412 773 188 846 928 993 267 936 174 234 924 833 620 180 751 040 143 820 651 401 917 444 861 333 556 785 111 012 046 640 777 995 810 031 955 138 791 349 945 034 767 799 675 527 131 541 839 274 236 581 679 023 178 353 469 970 676 233 352 648 219 939 796 385 741 752 569 635 810 594 847 913 663 353 645 427 670 043 371 422 335 695 618 111 921 967 737 156 592 657 970 872 439 300 743 618 778 931 502 720 753 473 441 409 887 858 381 493 281 635 431 916 678 114 523 446 852 507 126 405 941 803 327 566 967 698 045 761 348 327 607 342 705 219 520 628 770 999 588 523 624 831 882 560 369 225 383 692 528 681 060 389 512 790 246 105 481 739 852 118 551 989 424 161 314 209 437 074 268 932 647 774 321 295 253 521 384 897 253 524 071 826 601 245 706 996 838 772 753 913 140 860 214 534 847 767 722 472 360 661 454 830 578 359 342 247 625 610 595 345 688 114 394 145 274 032 244 998 428 176 959 798 957 963 010 029 543 476 888 253 093 666 851 425 313 517 064 118 043 829 089 033 481 466 825 346 521 674 890 007 170 728 675 173 655 380 262 499 160 771 736 956 629 780 501 300 958 132 198 511 809 513 152 150 274 838 542 289 462 772 521 848 926 669 220 924 071 455 636 618 681 637 623 091 886 012 091 978 351 237 013 213 776 569 900 423 350 602 525 276 233 415 075 669 467 794 895 494 214 840 797 520 260 035 661 237 082 816 934 464 312 910 725 319 840 387 911 911 428 957 450 657 070 630 640 494 685 893 294 291 817 571 491 952 904 439 469 367 988 923 685 911 638 382 840 435 081 866 867 239 176 246 830 197 897 258 333 285 132 829 314 628 503 085 144 431 641 736 806 550 019 356 141 347 503 589 721 748 341 956 698 636 450 336 681 228 510 783 739 955 966 392 570 637 293 447 382 888 805 832 178 595 668 396 617 521 835 650 938 124 143 817 634 370 145 730 754 153 189 485 062 054 093 077 785 579 623 663 788 822 900 434 141 930 998 158 421 365 203 265 585 918 455 280 431 228 132 279 081 826 686 857 649 388 261 131 220 582 432 389 305 356 055 014 102 895 183 911 529 696 112 483 446 989 505 967 780 189 637 971 134 384 359 718 532 160 728 532 670 811 571 023 412 948 233 970 590 719 336 971 728 376 882 178 014 598 807 571 686 066 889 915 778 453 217 375 711 659 148 769 723 587 916 003 749 910 527 768 526 601 789 301 930 282 700 522 629 583 269 857 639 784 172 173 196 799 822 552 085 296 551 137 717 515 166 900 469 127 736 036 120 666 645 824 863 036 457 080 766 487 331 927 169 196 971 461 767 435 883 004 843 401 458 294 080 324 818 863 626 662 761 657 240 358 433 297 544 988 244 394 946 016 008 048 534 637 475 506 682 510 760 474 550 768 465 424 466 942 082 711 948 455 039 672 840 154 949 219 891 670 430 099 020 195 686 538 714 292 805 830 670 572 588 807 388 417 088 645 192 507 380 127 837 597 887 801 922 484 239 039 583 833 596 197 925 554 340 561 749 991 015 065 860 751 014 901 094 173 680 462 314 607 883 729 408 695 254 899 815 392 874 801 223 493 581 595 982 619 107 974 006 400 667 266 785 571 222 747 014 121 973 575 806 807 954 023 501 966 859 879 830 891 064 052 029 025 930 042 121 735 591 214 701 113 643 600 177 664 962 253 408 706 841 371 827 418 005 275 192 513 257 797 005 731 087 519 389 358 698 474 085 617 873 249 505 999 088 411 321 429 243 112 176 772 065 002 502 279 587 415 700 762 181 853 346 991 163 561 890 441 792 989 366 661 521 673 592 384 745 239 999 130 672 914 631 827 283 998 709 864 731 952 428 904 358 142 202 493 864 595 104 810 306 093 824 523 967 125 281 456 761 939 427 310 767 200 284 057 550 563 280 306 682 578 955 124 336 422 971 039 856 343 038 129 438 592 300 333 689 828 048 061 301 044 805 791 490 969 653 994 058 612 554 834 071 164 461 447 663 368 165 254 660 473 398 677 545 147 909 914 978 822 252 101 230 634 729 261 564 058 236 528 742 481 158 359 312 237 005 502 282 724 567 383 861 524 265 344 302 095 676 486 139 303 674 935 341 541 682 161 580 619 061 021 811 205 938 153 268 659 991 160 619 885 879 160 519 996 350 903 525 648 302 183 376 053 456 645 456 440 864 762 335 037 854 446 467 830 407 420 098 884 528 356 449 646 214 477 448 026 673 362 332 345 640 369 524 991 956 665 273 310 826 122 016 394 514 801 283 567 413 287 302 914 088 784 865 505 126 398 272 818 396 528 775 202 224 665 209 035 454 045 160 037 967 584 571 669 143 997 088 400 575 573 834 382 776 599 011 066 654 361 196 002 496 415 560 608 499 803 527 025 134 539 424 288 703 059 395 786 147 917 330 464 064 538 013 091 204 026 074 243 175 594 220 341 342 067 098 049 777 107 424 764 565 382 841 018 076 704 567 571 423 291 741 730 878 341 034 098 443 942 211 288 969 950 228 971 681 562 346 105 444 297 849 222 248 146 191 824 913 189 076 452 976 045 681 254 521 145 357 290 519 089 002 778 665 413 812 385 853 159 406 927 387 600 583 821 942 944 103 551 586 965 556 213 915 777 064 530 999 456 823 391 091 094 114 203 006 754 253 703 348 182 201 781 282 024 330 692 520 972 867 651 370 692 464 673 139 356 759 606 824 912 056 169 077 707 054 895 608 648 856 586 113 722 321 797 865 748 592 134 856 482 586 406 693 074 667 624 530 097 605 489 510 682 200 687 645 748 536 916 258 164 316 163 006 798 227 453 525 819 474 492 169 345 054 185 536 271 314 198 782 669 700 795 947 573 883 906 132 851 485 196 308 941 288 268 889 546 035 561 030 115 725 514 341 497 689 222 289 799 193 927 166 369 539 619 981 645 281 498 840 510 556 220 204 542 415 351 724 002 849 340 522 683 246 313 755 147 239 263 924 778 231 942 181 593 001 152 685 835 925 829 243 020 628 988 323 140 824 944 038 802 718 640 428 991 425 386 287 479 458 630 005 511 746 296 802 961 350 197 372 510 431 139 126 111 817 679 638 266 656 014 717 305 759 689 688 335 293 106 494 759 400 385 672 833 166 999 153 501 187 988 513 773 219 752 113 047 872 662 792 258 562 627 654 051 182 691 528 073 063 582 065 100 020 207 389 462 343 900 343 827 259 912 757 485 595 014 385 223 154 000 507 214 000 021 309 131 461 411 781 010 987 708 303 695 604 194 061 293 015 931 108 059 797 843 342 700 748 027 639 134 512 674 371 510 184 189 230 769 027 893 535 196 404 776 794 911 359 842 810 924 227 635 111 974 442 118 883 005 042 892 108 495 185 269 098 151 662 677 153 025 886 607 080 280 710 115 791 601 037 940 654 330 515 028 076 856 423 570 622 501 346 117 864 202 149 041 847 749 391 843 378 664 926 387 450 698 129 397 369 359 921 061 237 068 388 892 002 449 869 389 287 134 277 337 641 618 904 470 853 429 605 550 311 911 974 190 462 204 099 411 815 407 114 537 777 124 157 273 169 877 399 260 874 351 429 487 858 997 932 973 472 073 671 529 289 485 509 070 105 852 397 254 311 557 997 001 740 369 730 541 827 544 671 981 230 326 465 395 742 528 523 269 562 256 408 655 122 940 327 582 421 321 470 774 788 787 807 421 279 988 064 764 319 279 916 178 946 395 402 778 039 388 207 687 383 149 048 527 824 200 770 881 276 821 602 268 104 809 597 723 462 891 473 732 885 486 169 791 351 671 896 359 337 122 417 103 076 680 057 311 592 256 466 566 445 485 953 629 348 926 791 360 263 737 595 319 363 481 069 224 398 508 930 857 855 332 470 519 157 592 517 570 168 680 945 553 176 695 408 449 125 212 535 238 685 350 896 070 326 501 040 425 674 989 153 776 503 307 451 219 548 623 169 619 895 334 632 063 246 771 627 789 375 345 978 232 159 136 967 448 136 226 900 299 620 985 674 637 234 667 201 782 332 890 147 178 297 162 013 668 232 978 012 964 830 731 897 579 282 802 831 603 671 012 338 693 296 449 623 091 162 557 801 682 235 563 843 696 380 268 188 551 060 389 797 170 975 266 027 428 889 312 599 645 815 550 517 061 173 221 495 194 175 483 494 495 449 655 496 154 220 338 121 331 850 985 043 655 238 116 657 375 600 699 586 477 400 846 391 921 494 682 025 100 359 435 827 659 510 952 406 786 712 511 244 493 337 372 551 151 704 288 364 046 245 295 610 880 693 641 189 288 129 372 634 927 845 529 351 310 021 325 791 916 083 418 991 709 012 241 907 959 373 959 201 693 857 704 890 498 545 038 036 096 138 591 147 317 599 480 197 024 520 791 417 188 679 927 735 214 661 215 031 519 195 288 609 359 022 594 046 983 409 522 489 380 508 071 529 859 736 660 605 600 980 081 633 235 783 590 145 167 126 441 569 639 639 585 766 940 217 733 858 825 900 677 033 033 027 578 577 903 260 109 633 609 009 960 092 791 730 159 048 245 231 317 478 429 191 160 869 416 364 518 694 617 361 153 646 694 777 874 958 913 694 317 350 744 784 688 837 372 231 969 799 990 158 568 120 544 875 947 391 907 139 875 425 360 480 262 200 456 434 935 014 275 938 292 499 263 546 938 171 409 736 756 051 098 537 499 886 898 700 339 923 203 600 212 012 958 073 080 805 804 989 221 275 672 442 253 497 537 268 007 486 608 670 841 776 561 770 219 311 516 581 953 165 093 247 270 638 478 473 402 224 733 225 597 929 955 541 660 894 648 153 334 354 186 048 951 119 997 879 961 672 000 488 732 263 023 521 621 059 666 923 702 793 747 406 030 039 583 440 220 336 428 289 667 865 104 252 760 269 590 597 135 438 074 512 541 345 251 666 127 786 614 567 651 275 960 234 699 017 771 108 609 688 046 252 328 309 554 833 142 074 647 788 929 191 645 964 885 967 025 057 058 714 781 066 645 255 641 124 008 887 555 075 351 160 365 366 418 045 366 214 939 633 016 847 988 818 783 023 289 783 389 396 593 690 215 000 474 209 247 544 880 880 187 120 523 232 829 115 913 643 378 973 398 301 608 129 097 004 584 068 755 118 479 813 119 787 110 772 649 697 624 428 689 076 862 175 502 199 711 523 171 021 989 585 422 225 009 197 525 488 037 233 366 550 473 447 517 530 192 739 887 644 081 210 512 440 471 946 552 592 657 921 473 481 899 378 659 433 397 063 562 804 009 054 672 343 330 800 665 459 325 018 784 103 976 109 286 908 653 081 723 967 637 254 340 397 908 713 723 446 187 071 669 856 094 834 957 938 824 639 239 663 442 015 942 004 108 664 168 972 418 030 797 671 940 900 280 351 265 795 810 741 749 859 587 116 983 291 444 886 467 225 236 966 571 015 895 868 491 386 002 657 761 835 675 838 176 671 628 381 011 291 681 214 933 993 358 017 836 618 715 933 223 801 782 430 321 559 951 596 895 818 981 448 619 805 122 732 130 454 337 723 243 595 300 404 766 050 806 752 988 526 083 616 628 144 015 618 374 458 279 442 313 887 874 332 867 515 595 092 738 842 900 919 009 081 206 660 227 850 830 281 343 491 103 405 709 373 468 733 918 906 494 241 025 416 518 348 747 702 645 661 898 216 551 523 487 345 791 693 266 873 475 639 247 242 523 417 057 016 338 013 471 545 774 639 762 993 216 950 794 884 341 397 614 324 247 564 680 919 589 353 175 076 755 384 823 012 008 433 977 798 408 401 822 500 898 097 876 017 128 457 275 478 162 525 407 904 197 777 426 188 222 608 979 827 204 585 036 197 026 620 359 512 832 402 005 168 855 989 356 394 225 240 725 944 557 176 069 625 292 386 841 258 779 721 519 473 589 297 571 746 529 416 407 746 426 399 039 830 223 495 872 093 717 543 566 396 500 040 357 970 297 907 959 759 215 785 625 760 251 503 297 106 790 944 558 208 080 851 263 054 145 956 737 384 829 881 290 781 291 832 568 666 792 675 327 730 836 982 717 495 364 454 134 315 268 457 209 552 272 526 214 742 787 348 370 833 965 975 374 317 007 784 010 290 710 603 529 473 838 662 410 859 469 714 493 408 157 662 995 907 685 324 451 699 485 804 837 603 906 856 818 376 890 338 003 208 506 016 282 021 750 268 488 086 573 944 425 641 802 606 936 707 849 350 494 895 335 628 627 344 114 978 425 921 736 817 853 317 785 777 341 630 762 297 132 598 400 738 055 006 638 900 101 502 656 154 877 922 344 757 344 352 028 217 227 041 051 600 864 447 713 085 222 955 906 389 059 626 992 022 168 653 217 746 052 618 227 347 970 285 941 836 456 565 273 614 850 639 815 747 910 272 721 088 568 807 346 417 465 818 199 664 451 754 354 536 612 650 046 652 499 067 132 911 639 332 447 444 124 904 747 906 574 590 063 188 252 927 820 154 690 868 560 569 360 037 204 060 398 750 232 721 331 584 216 453 544 216 351 824 079 674 979 972 747 506 355 389 950 359 017 857 930 630 533 590 172 576 971 018 357 527 129 778 206 527 097 745 021 730 226 945 155 942 746 976 574 105 382 835 925 973 092 238 598 135 668 402 096 587 663 799 471 005 598 726 307 021 456 075 313 947 973 030 312 696 638 679 845 189 041 240 827 266 346 807 301 635 147 184 559 400 552 879 450 746 630 536 197 921 032 493 531 663 836 284 118 835 382 575 188 902 643 310 073 225 291 754 304 180 983 572 177 008 863 208 143 052 648 406 682 470 598 202 590 939 821 786 620 460 490 415 866 081 092 524 474 456 275 869 603 793 601 515 529 157 606 994 304 420 304 529 580 280 650 172 388 344 192 982 455 631 845 088 326 980 923 342 014 342 187 825 798 493 599 123 727 222 121 581 234 752 996 013 820 691 620 008 455 953 632 070 118 668 864 113 778 651 535 169 115 254 966 690 855 979 615 587 492 087 853 553 827 216 952 476 789 644 561 395 379 039 760 538 248 386 316 787 957 033 724 128 974 781 932 587 614 298 781 708 658 012 482 344 927 750 889 429 370 297 651 308 150 923 170 438 340 255 602 446 354 060 637 674 821 489 478 417 583 024 819 345 119 905 936 937 423 798 352 524 707 353 253 028 600 254 952 927 772 228 877 363 974 597 540 293 851 842 914 832 989 237 395 464 082 156 622 597 788 496 567 023 770 519 339 592 858 285 407 667 703 746 480 873 160 407 774 791 293 603 408 992 349 782 543 416 660 576 024 447 094 537 565 114 467 587 119 796 298 316 351 176 084 866 948 369 136 947 155 888 090 609 146 793 033 317 517 887 661 567 170 646 805 827 186 557 308 545 954 020 163 414 484 886 833 401 601 058 439 712 157 510 362 513 560 682 127 749 744 683 442 187 900 079 561 797 115 924 824 677 762 653 042 409 390 586 148 322 964 195 633 676 146 130 096 020 242 304 856 059 154 758 078 713 576 910 826 157 891 901 243 794 005 667 080 357 336 960 784 182 967 484 989 332 801 133 709 244 398 643 143 799 351 342 414 342 822 411 414 861 242 425 534 631 786 916 315 201 843 539 393 157 128 027 590 307 036 994 821 640 199 644 037 371 852 782 520 223 383 859 398 991 860 132 993 196 523 166 253 583 990 682 523 103 565 314 542 867 046 709 402 240 186 620 782 880 189 796 059 165 666 902 906 175 776 829 688 353 329 773 546 925 347 872 276 131 573 270 429 619 767 720 184 577 892 676 696 070 601 283 910 253 163 840 116 323 163 426 422 765 938 557 093 027 891 481 699 561 539 582 530 948 119 611 936 294 690 008 131 113 408 984 035 947 776 759 991 544 870 243 208 000 096 067 867 799 082 644 908 174 047 769 655 717 700 881 073 845 280 373 510 403 269 333 173 381 968 860 569 528 205 978 004 779 062 942 233 809 536 335 340 710 120 651 171 089 828 102 855 432 674 392 527 242 495 344 347 792 710 283 254 411 771 533 312 135 366 634 099 832 190 765 685 122 391 156 388 116 376 527 029 871 201 225 671 688 588 940 027 931 775 211 360 553 416 509 312 499 379 523 004 056 337 613 583 955 127 220 188 757 456 573 405 903 404 385 536 273 831 631 543 210 139 922 809 472 523 719 674 878 696 893 204 935 449 879 570 309 505 196 505 397 490 143 738 941 412 445 891 433 190 575 659 349 701 161 035 473 314 856 054 900 196 219 040 817 196 583 628 932 886 631 407 524 527 315 250 831 789 355 311 319 344 471 086 603 146 570 767 534 887 617 206 384 834 568 247 788 649 605 936 766 321 180 145 188 964 787 306 620 673 534 968 908 752 400 515 885 048 643 603 267 766 726 014 531 265 272 350 941 534 145 465 304 833 828 879 412 070 379 085 799 436 585 474 618 191 709 911 796 281 507 836 478 540 417 510 865 859 085 780 727 935 614 077 157 463 895 537 792 997 297 274 158 444 373 556 633 872 924 596 406 694 751 671 527 670 135 930 090 758 791 626 514 704 016 801 193 253 404 808 171 342 755 707 180 016 952 768 202 927 981 723 883 214 213 342 346 754 692 159 239 691 714 195 612 067 704 744 082 071 425 716 230 550 605 905 495 928 348 260 957 792 792 477 293 023 214 278 378 857 154 221 612 404 327 664 629 808 921 362 056 293 014 944 903 882 662 783 202 057 375 108 171 339 407 202 936 471 937 740 469 748 134 259 873 483 962 411 800 478 651 699 865 728 672 471 879 245 763 569 117 081 863 355 190 629 652 255 980 384 997 089 730 509 146 466 797 128 935 538 369 828 147 087 471 004 178 547 936 856 536 881 054 325 939 258 342 939 414 686 438 164 072 308 693 557 885 820 457 635 094 042 143 422 348 026 716 098 879 970 379 232 914 996 912 599 939 918 027 809 161 921 630 113 431 829 114 148 335 480 536 446 544 938 215 029 300 573 544 203 965 072 129 310 028 740 243 422 407 823 349 283 173 757 630 745 550 380 831 266 998 940 999 508 843 220 064 228 228 349 779 688 385 581 489 701 005 741 974 007 715 928 144 242 119 842 395 351 946 435 612 723 415 868 832 666 739 111 273 987 462 328 874 892 034 498 634 148 854 946 069 299 516 465 639 506 021 247 361 228 519 977 314 560 003 564 578 543 416 401 944 900 783 249 907 889 895 119 631 152 241 669 803 458 117 897 559 822 883 030 413 044 941 952 581 089 655 395 199 862 864 296 456 111 016 219 165 745 300 056 991 062 140 607 765 764 272 149 121 190 852 965 906 131 534 271 731 289 626 577 444 304 447 393 074 304 861 729 136 041 759 789 569 550 335 787 102 745 497 761 116 635 117 837 395 391 948 624 153 980 940 076 623 427 706 370 643 327 903 439 041 138 376 106 402 676 740 100 657 262 053 262 213 633 907 361 316 013 917 816 044 614 241 508 851 007 522 307 501 761 270 145 406 111 374 998 825 112 680 501 852 603 068 591 306 637 722 461 824 007 630 992 375 389 186 458 835 066 131 751 449 223 883 649 365 774 208 594 481 963 275 329 853 964 857 807 181 774 090 475 371 973 511 377 898 824 146 075 894 344 622 342 628 655 236 057 296 459 487 015 311 831 046 215 279 356 338 173 747 786 801 762 076 739 256 551 015 151 749 620 518 994 161 862 340 409 769 439 292 187 660 908 003 461 450 072 755 317 733 199 190 615 044 058 883 419 620 331 108 579 789 007 235 241 445 671 937 162 374 508 430 629 319 210 217 750 778 497 559 566 129 518 680 784 417 208 457 904 023 251 589 259 246 613 154 918 482 139 582 153 046 760 723 967 619 290 090 876 130 662 732 116 452 735 446 874 035 269 082 643 937 856 491 550 857 979 638 490 349 679 239 017 200 406 387 893 964 435 821 481 258 951 098 009 897 659 182 311 054 028 546 261 305 513 289 577 317 127 027 689 192 630 980 995 118 140 471 159 147 035 419 916 868 748 385 468 876 510 180 583 686 563 714 226 795 153 847 618 609 094 456 849 025 742 478 931 660 964 894 095 224 318 803 050 370 957 925 838 312 946 185 102 796 129 711 610 536 921 428 731 113 747 660 687 435 752 400 975 563 378 565 025 786 675 519 185 542 511 042 972 424 460 090 384 228 133 774 724 710 446 860 483 295 613 812 723 680 093 182 861 200 295 888 930 153 099 902 957 182 870 822 286 310 814 238 056 350 483 495 263 820 093 743 749 113 191 250 966 238 692 943 484 306 713 137 845 931 083 139 137 982 761 417 777 097 582 305 588 124 214 886 807 109 933 634 322 882 447 157 864 803 612 289 456 507 566 356 470 728 857 166 138 957 328 724 579 800 253 103 525 735 250 175 597 204 141 643 627 487 753 771 915 266 021 010 560 043 447 896 814 664 269 559 773 735 406 665 544 037 713 383 429 054 640 945 874 990 214 253 002 454 042 699 715 604 852 826 797 999 363 455 268 102 729 873 875 770 169 301 018 961 995 760 373 296 841 466 490 157 474 663 196 436 724 116 468 544 094 083 112 234 293 942 738 849 409 656 430 266 462 739 655 733 151 806 254 090 005 122 454 197 146 692 988 534 728 863 010 794 926 960 523 289 993 115 524 676 265 869 452 026 591 045 153 266 531 342 506 708 515 773 850 012 003 736 458 113 722 505 286 746 624 663 894 203 152 155 071 183 254 226 451 219 772 220 603 733 361 329 930 224 824 059 969 880 135 962 692 012 673 610 381 130 244 458 155 999 562 003 001 599 230 382 639 400 193 622 221 499 053 626 326 631 202 096 139 425 923 890 606 927 083 877 434 625 396 113 734 841 493 559 487 362 145 201 673 502 515 334 068 777 959 028 082 945 752 145 102 975 537 920 458 600 730 912 531 470 977 496 425 598 343 225 439 551 908 427 410 382 363 072 902 804 498 733 689 420 657 138 389 280 824 171 184 964 441 850 795 891 806 201 219 766 626 561 253 971 150 448 965 174 556 132 170 847 080 516 704 039 127 248 915 611 768 901 843 969 386 100 167 331 599 514 482 274 581 970 488 459 247 796 258 891 266 309 311 929 065 406 897 734 546 537 373 391 433 351 785 084 456 558 635 048 661 353 605 491 890 330 064 931 515 156 384 757 340 662 023 667 735 498 936 700 332 678 554 155 820 011 817 086 476 720 164 800 377 080 534 250 678 322 288 174 464 578 360 056 121 862 217 385 908 863 200 554 446 264 623 724 728 695 277 330 045 569 650 629 750 678 719 889 328 253 579 948 977 453 657 743 725 847 580 536 249 582 872 628 965 376 196 067 381 751 940 846 176 925 454 747 755 476 996 159 054 443 412 686 703 976 050 431 824 072 750 648 084 432 409 474 221 780 796 906 517 891 524 369 959 470 653 211 252 955 274 077 516 012 783 371 045 158 822 282 338 652 964 991 102 372 458 847 116 618 626 744 827 873 596 838 156 677 776 720 230 190 060 917 452 381 389 531 030 136 728 540 306 728 869 849 815 099 240 330 669 981 444 935 718 576 059 087 526 761 983 842 438 023 172 050 908 536 814 717 715 988 697 375 599 473 793 733 248 297 015 485 659 061 220 406 141 883 303 758 229 574 074 994 635 802 837 544 937 156 501 312 732 534 093 418 043 397 420 132 469 136 163 978 741 997 029 699 652 954 416 759 645 386 939 993 918 207 079 326 939 105 497 900 513 242 597 544 909 985 059 206 310 989 777 683 770 606 454 364 994 178 120 713 278 706 576 854 689 377 561 856 950 629 812 907 909 007 861 779 131 617 109 664 243 052 748 994 164 129 835 950 473 735 703 520 812 874 283 625 150 885 483 728 776 652 615 422 881 283 303 740 099 937 435 965 659 294 946 605 424 243 908 791 039 161 395 999 873 914 149 231 321 292 962 923 042 769 721 575 600 202 581 893 345 224 176 238 162 790 493 675 903 935 618 822 722 622 182 599 608 005 316 878 500 146 824 922 832 285 397 575 272 424 525 990 254 629 439 727 646 372 545 909 451 534 569 623 919 836 663 928 165 217 000 641 491 247 932 211 988 704 848 998 028 967 123 134 413 043 288 297 882 068 707 014 098 699 500 790 628 839 820 456 555 118 680 808 565 599 152 498 788 240 151 371 024 099 501 803 615 488 479 426 565 873 027 001 167 849 413 180 853 435 033 690 400 683 926 577 795 306 420 417 427 222 925 017 940 895 979 286 532 393 821 293 962 570 196 746 189 857 610 792 294 832 003 555 219 628 816 044 458 802 027 786 354 863 982 922 575 356 843 472 478 214 335 877 799 224 723 313 652 514 248 355 569 686 205 530 135 897 505 058 037 601 548 531 086 003 772 276 377 223 383 578 574 445 794 472 335 917 589 450 506 268 466 248 757 857 440 211 413 110 862 030 483 475 303 000 492 958 564 897 880 613 662 932 338 305 958 829 325 314 950 463 910 459 450 750 539 827 939 138 760 602 967 771 016 133 056 001 166 715 365 560 347 353 120 218 442 914 117 175 775 676 275 612 384 269 808 690 547 712 514 389 852 267 348 062 966 112 952 869 258 065 740 127 199 047 122 158 481 552 487 382 395 875 684 771 399 410 771 988 130 430 760 007 081 285 724 309 864 826 752 755 522 709 595 467 520 460 068 646 514 336 916 723 313 741 865 515 867 137 650 003 636 685 179 852 491 392 696 392 514 315 874 536 720 653 752 076 849 758 059 063 629 570 128 915 036 624 128 332 475 018 895 112 165 473 109 793 969 259 472 737 136 512 770 917 604 329 008 164 530 000 636 459 583 517 582 816 435 588 796 820 576 373 360 312 443 482 820 586 212 930 797 188 209 152 220 905 648 845 334 128 306 865 677 911 111 673 817 640 075 899 635 032 589 579 932 921 248 559 904 443 968 427 299 089 685 182 293 243 659 732 902 945 320 900 601 560 083 635 570 850 161 821 513 242 015 642 919 374 242 063 855 828 886 923 425 582 952 064 464 824 500 327 530 959 753 644 704 331 491 736 948 871 829 426 858 805 560 715 881 871 447 358 742 849 581 457 527 739 141 729 416 347 543 033 248 536 841 764 628 493 600 860 159 376 241 707 252 590 467 707 815 996 810 088 443 815 411 372 991 498 724 878 259 581 177 032 207 892 880 575 992 473 292 864 822 946 802 348 740 538 854 718 545 916 933 707 015 980 123 481 129 118 004 835 192 208 335 514 514 450 642 142 428 200 377 921 140 058 193 524 763 734 910 012 329 489 894 106 827 474 690 773 666 019 984 418 931 345 247 988 785 933 420 935 195 433 149 017 384 411 682 775 915 712 297 977 147 936 668 103 679 673 600 743 185 667 358 270 107 674 316 826 868 081 286 991 269 390 487 349 057 585 558 130 605 086 137 286 976 588 055 705 538 520 998 625 480 112 602 327 832 775 303 722 902 173 044 052 962 213 519 214 491 031 942 812 708 899 563 041 300 951 086 226 399 864 384 485 183 405 920 939 565 248 501 886 687 683 715 587 969 075 236 055 746 396 877 724 211 344 089 850 992 174 588 400 025 756 538 179 479 710 798 117 710 927 408 022 218 431 940 890 763 772 905 024 567 275 013 332 489 008 387 690 158 838 971 634 715 534 504 895 960 330 135 007 578 629 778 264 420 848 724 935 489 361 491 361 860 482 246 025 685 839 849 134 755 929 550 472 708 480 408 505 629 515 609 755 212 679 704 549 493 244 710 250 306 227 945 794 596 874 804 873 073 281 700 988 456 673 803 447 685 588 617 137 178 963 632 966 086 464 371 138 239 581 519 881 267 689 212 350 784 552 306 701 466 465 293 194 755 907 392 886 690 532 251 771 386 612 525 196 935 525 685 640 953 699 011 104 244 259 089 277 194 893 220 016 897 944 724 517 293 009 798 683 733 028 136 575 967 234 614 435 313 796 174 391 283 603 413 785 280 372 140 015 339 007 350 102 633 710 857 366 575 866 973 131 208 056 515 582 729 127 849 780 711 222 316 856 997 041 637 809 690 885 731 858 561 844 890 477 006 678 833 747 056 637 311 614 508 814 048 566 213 771 390 265 873 143 379 272 851 012 978 936 595 576 689 772 740 717 581 142 720 698 296 024 509 727 007 194 107 960 168 548 679 003 307 314 557 471 329 797 180 006 963 641 101 576 737 678 512 363 976 766 235 923 544 500 205 053 597 237 615 391 823 387 933 555 078 054 078 760 827 458 401 169 648 438 441 021 791 420 365 952 437 304 228 019 762 726 914 477 030 402 105 801 717 902 988 121 708 540 869 439 946 380 945 701 536 553 182 659 843 663 234 487 177 591 520 038 894 133 146 841 527 141 613 596 602 020 906 959 918 988 015 732 229 900 290 239 383 622 173 111 300 685 136 910 731 019 204 145 556 840 213 901 414 787 488 897 474 573 646 659 298 120 672 890 004 725 584 881 540 190 584 580 411 768 228 274 604 325 468 665 537 959 071 183 804 394 884 489 359 977 479 340 661 745 204 487 505 813 908 110 283 624 796 457 048 566 955 224 751 430 355 503 993 683 612 487 365 759 802 258 899 071 640 646 659 770 980 445 091 971 867 793 431 420 335 305 618 924 365 810 372 762 298 331 213 499 913 332 474 226 993 781 467 669 538 907 665 258 439 292 833 065 941 114 244 958 231 460 158 349 532 928 273 507 189 397 225 555 370 109 619 336 765 325 836 361 792 392 980 701 726 412 171 894 193 779 819 475 459 047 435 184 866 512 322 742 849 331 038 714 509 136 562 236 896 893 963 067 550 819 212 705 089 472 017 665 036 418 795 464 282 574 204 869 548 072 470 263 011 408 907 723 391 596 455 555 467 046 763 489 994 583 516 285 130 411 360 398 818 388 749 267 767 242 560 921 790 639 311 534 705 079 190 163 761 661 952 462 493 156 361 695 256 334 928 796 259 047 994 758 811 389 494 590 009 880 445 371 174 736 644 960 672 705 082 894 351 430 085 754 554 306 962 961 626 668 122 230 977 978 292 611 806 252 990 350 656 300 532 072 889 491 666 479 702 428 681 635 273 550 357 865 768 000 498 000 438 127 482 412 180 545 748 198 903 533 151 271 916 778 367 183 047 483 294 808 169 456 604 345 120 883 631 276 565 003 935 045 421 400 472 572 578 499 666 936 066 568 011 513 713 138 238 781 641 011 189 097 822 777 980 579 010 485 393 513 990 427 967 116 469 109 693 318 162 233 204 684 891 609 502 784 679 036 934 844 690 346 248 354 314 849 102 373 985 894 483 831 409 928 000 454 433 510 599 469 651 764 140 973 193 276 694 566 495 096 490 495 215 692 611 060 682 056 400 312 552 630 576 641 854 728 720 361 271 425 375 455 892 076 302 412 899 866 211 077 429 191 770 091 260 974 671 436 738 657 148 843 696 965 435 840 532 155 962 258 242 436 366 833 032 913 382 726 001 710 671 592 534 684 854 428 326 077 377 227 369 314 592 823 422 418 592 853 028 924 700 839 919 704 990 196 722 056 341 041 873 675 968 079 948 225 699 725 247 273 164 878 632 383 176 437 904 856 967 029 890 139 820 145 348 167 498 775 071 710 650 943 169 984 017 962 501 852 385 218 520 431 357 667 476 436 799 423 150 596 183 786 587 872 689 824 104 488 486 954 758 211 008 742 991 433 713 128 377 616 987 594 482 558 868 768 383 997 417 293 832 363 155 917 223 049 287 804 788 174 055 032 654 124 904 500 241 106 704 271 798 255 064 163 620 558 848 161 571 363 024 040 195 498 056 126 021 790 468 672 873 790 191 349 398 858 803 370 716 686 451 403 025 203 419 882 912 271 411 300 136 207 520 080 078 448 492 367 759 839 755 270 904 925 556 630 995 784 761 105 535 738 193 357 726 877 768 033 501 217 838 487 737 997 107 294 022 262 476 564 495 905 597 409 638 826 448 027 174 908 222 127 011 104 008 141 589 741 411 396 637 141 255 755 608 966 531 424 600 237 569 033 383 746 864 253 161 316 233 666 007 628 629 695 020 097 875 191 243 365 987 598 204 537 581 910 392 762 662 670 997 897 979 612 966 155 747 775 840 412 020 312 908 764 045 636 452 750 954 753 319 394 000 190 433 458 817 858 934 711 408 911 310 445 842 883 969 382 236 589 078 535 829 337 337 942 593 688 497 632 039 149 126 357 302 156 541 805 853 140 206 612 327 856 140 705 052 571 859 291 501 356 956 966 136 452 107 300 543 156 713 591 045 630 268 503 637 977 029 994 230 455 244 556 001 699 028 930 061 443 192 681 641 231 778 516 369 400 019 223 296 170 553 888 370 071 745 439 520 798 253 023 778 986 409 939 006 420 369 404 895 205 507 260 705 660 772 973 137 792 864 703 188 029 818 714 603 258 167 196 088 473 312 468 006 500 244 708 646 734 239 478 175 660 240 662 075 916 560 454 937 121 858 366 048 181 499 238 302 836 448 851 634 875 494 904 648 483 634 795 109 194 685 770 976 891 229 974 552 694 799 711 757 246 955 175 614 992 431 243 522 370 851 026 975 870 430 670 023 526 571 944 001 886 426 569 575 952 296 809 565 176 644 315 401 274 005 919 875 714 559 463 090 613 529 595 503 065 085 873 814 579 255 162 610 171 135 535 384 123 750 860 874 469 754 604 111 567 171 026 222 929 724 790 979 726 542 636 742 130 441 447 383 786 323 799 240 699 431 737 165 722 899 984 238 311 196 009 681 239 751 405 705 253 139 765 029 746 305 583 386 696 678 759 166 420 775 708 450 118 629 204 724 653 499 518 561 682 362 720 220 731 675 979 550 547 647 503 833 854 816 568 863 372 055 972 641 027 662 259 770 751 912 615 654 187 005 432 453 081 368 655 283 602 406 795 953 625 522 025 734 807 990 450 080 362 933 471 461 488 351 440 769 480 369 672 911 619 932 937 809 048 307 886 131 567 385 374 199 620 178 947 914 987 086 645 696 502 324 571 949 064 686 612 020 844 434 873 170 445 471 419 350 803 155 214 303 646 023 021 411 131 520 076 511 091 755 467 680 993 918 478 918 648 822 262 196 857 461 003 591 713 747 538 867 642 499 752 070 927 772 122 836 535 773 494 562 152 834 464 710 773 177 740 504 589 549 367 245 781 939 306 550 463 016 810 906 454 724 419 280 228 045 973 699 329 111 408 022 779 582 825 307 471 366 070 311 970 078 380 597 302 077 013 644 826 472 196 103 240 095 021 045 496 340 014 423 597 620 931 169 038 098 681 452 188 662 342 773 356 080 734 563 587 512 289 594 619 153 564 698 564 831 517 677 782 357 403 519 554 545 739 421 669 519 334 208 313 535 744 591 863 767 675 121 526 798 422 013 704 974 889 172 120 530 062 399 919 265 478 147 797 371 958 028 547 448 437 850 497 075 499 910 678 458 210 269 347 298 940 065 766 917 957 516 193 669 134 814 047 908 362 483 883 582 970 270 928 630 775 157 481 772 308 414 321 178 586 236 468 139 482 396 172 511 137 765 241 190 634 198 786 021 916 626 417 890 333 672 356 515 568 390 590 137 021 738 149 626 863 146 907 707 870 836 017 174 931 913 893 682 182 673 258 041 183 182 470 839 635 501 417 814 060 047 980 266 708 299 350 955 072 605 538 769 205 018 467 934 583 730 509 921 694 851 153 043 893 141 006 202 349 250 818 878 971 216 223 816 872 127 773 176 309 619 322 570 407 546 841 629 833 977 246 020 127 855 935 580 747 971 248 506 379 081 919 206 664 570 421 265 217 599 448 815 311 672 792 326 163 664 094 791 254 670 784 521 139 324 100 316 950 600 037 316 630 885 314 035 022 810 676 063 197 530 199 446 770 514 039 970 057 859 544 167 550 186 188 437 193 534 218 340 644 785 052 917 947 950 496 640 462 263 901 463 502 553 468 089 192 629 421 942 021 894 364 639 918 738 618 001 781 256 657 224 915 471 529 474 054 907 012 950 735 149 917 629 185 346 038 839 726 020 657 616 881 864 040 206 730 693 929 909 798 376 901 027 678 743 803 053 435 080 060 222 960 765 209 016 719 495 465 065 880 817 655 105 587 550 627 371 133 580 007 208 685 503 634 553 734 555 939 535 468 690 132 711 953 093 269 085 560 448 519 824 703 548 816 254 495 542 234 918 747 693 224 057 340 297 973 408 296 573 130 695 625 972 254 940 682 575 216 056 709 121 263 199 490 521 367 169 264 713 422 916 421 017 644 290 436 559 873 936 249 860 264 423 571 159 538 394 918 795 026 627 955 964 532 970 434 700 250 299 028 069 757 500 453 999 535 563 357 008 681 577 786 535 912 697 445 001 143 214 516 343 520 287 616 322 924 564 365 628 394 764 983 771 382 802 920 963 793 584 908 296 776 861 312 578 465 711 021 427 603 257 833 820 453 341 878 019 639 003 521 898 791 872 222 616 627 702 164 965 098 779 359 597 283 020 199 203 367 836 847 092 866 516 690 535 741 369 258 400 633 853 238 389 755 869 387 807 380 683 615 026 239 838 055 604 372 309 542 368 477 078 338 199 835 246 669 636 925 259 801 877 861 640 266 119 912 783 623 071 782 436 656 260 680 576 849 795 658 541 650 053 808 396 210 321 576 065 378 709 711 790 584 589 601 240 449 182 905 257 933 332 395 402 005 308 196 314 657 393 632 538 438 609 535 509 098 353 209 167 854 360 476 505 746 650 266 219 079 667 731 789 271 317 432 472 639 183 801 982 463 227 601 408 613 049 077 115 960 477 601 767 292 598 994 569 889 925 667 429 371 631 384 316 368 780 839 476 237 667 772 616 929 279 637 252 848 955 166 184 191 305 528 091 650 346 381 617 773 254 000 915 243 848 713 071 822 301 751 349 663 917 103 713 366 879 759 210 327 241 286 160 085 616 701 845 372 863 361 485 043 111 311 469 904 852 310 180 153 545 116 098 922 450 983 861 870 190 558 172 679 276 305 703 767 713 165 150 873 698 867 779 239 455 752 050 816 836 290 384 538 674 521 955 119 936 502 355 036 195 420 940 218 180 829 380 621 281 217 772 299 508 056 426 740 443 639 508 422 341 549 451 568 456 350 822 617 276 268 937 676 624 752 697 497 104 899 713 589 926 803 198 579 783 848 231 953 340 881 303 308 305 240 437 975 805 641 716 873 338 148 439 664 826 830 379 516 054 899 354 655 833 361 138 282 114 520 358 241 260 995 915 717 115 266 740 807 312 492 725 532 596 328 848 812 538 140 026 967 585 166 997 885 517 285 805 292 827 994 964 449 482 722 796 003 350 138 081 422 903 565 816 955 034 806 232 277 243 657 983 605 983 904 587 166 699 503 490 299 189 321 499 809 353 861 234 792 911 176 116 632 008 089 702 844 829 909 291 217 342 600 726 809 624 607 751 831 938 670 969 246 954 518 407 416 644 536 237 234 746 483 226 285 674 067 349 642 538 033 901 949 291 813 804 400 651 192 174 426 060 553 126 754 741 038 015 695 883 733 411 365 736 943 991 925 423 726 242 422 760 447 071 361 545 793 824 978 540 541 536 228 025 449 309 595 344 986 005 756 307 727 643 484 201 979 244 019 616 899 709 655 517 281 703 752 231 641 964 313 323 014 079 459 499 729 988 697 089 503 143 578 493 123 944 105 878 328 701 073 752 167 660 355 866 628 007 937 263 002 104 311 412 771 980 713 272 169 063 859 062 174 044 007 059 875 403 706 308 830 143 906 318 340 573 818 183 892 769 811 491 171 615 033 880 792 507 092 886 290 509 073 392 316 145 764 833 130 405 134 936 737 688 572 242 087 926 801 943 075 683 655 397 931 174 885 219 547 373 832 475 728 053 361 055 601 516 459 489 244 153 338 132 129 904 919 816 796 228 542 211 884 847 976 623 290 879 408 308 126 910 762 159 353 820 993 331 056 752 191 535 007 788 063 902 487 347 303 115 505 857 193 451 247 022 473 315 708 512 042 463 885 354 745 600 440 512 807 254 450 116 370 653 467 583 975 807 320 247 214 741 209 762 340 296 029 809 430 742 788 878 357 541 739 268 581 600 993 371 606 805 425 679 876 681 564 576 987 958 095 116 149 352 612 141 691 976 101 596 294 577 462 264 207 987 840 868 650 021 726 917 371 189 557 855 218 060 912 042 317 829 723 285 261 723 645 819 334 311 165 721 167 023 214 782 558 609 019 879 545 944 087 913 154 115 145 890 031 210 833 524 016 333 305 782 628 057 536 024 662 047 120 960 405 301 640 421 474 703 517 579 719 878 331 377 451 794 947 526 658 016 334 589 166 887 222 552 344 566 348 795 930 081 298 513 140 948 418 941 442 298 827 389 880 688 168 446 932 965 178 431 151 246 766 393 286 852 122 314 101 445 602 066 959 131 887 550 664 519 398 176 995 665 627 411 131 955 385 438 170 471 949 990 679 214 203 128 148 890 604 035 571 692 958 659 090 059 301 437 684 556 759 491 235 252 958 500 445 432 691 812 707 811 948 457 104 744 315 987 807 073 487 634 073 058 654 638 898 876 047 884 278 783 961 673 568 846 083 441 365 500 340 508 683 318 648 711 428 830 488 291 943 876 273 096 975 895 233 392 754 544 422 773 261 512 620 828 169 959 395 251 632 703 561 202 890 520 677 093 259 106 501 932 657 628 497 811 811 592 433 840 449 320 910 620 445 759 858 650 321 252 744 610 650 544 965 287 015 909 534 974 842 993 235 666 349 372 519 320 481 148 062 448 218 008 988 348 556 734 598 209 611 912 090 484 177 751 655 604 749 296 319 919 411 983 877 640 812 562 395 794 286 381 146 175 126 977 980 463 823 539 135 861 031 191 763 040 786 295 720 856 792 083 155 799 908 101 123 698 230 525 096 202 006 870 888 858 188 590 203 389 866 536 640 645 077 265 111 371 632 173 105 952 898 730 068 188 613 300 937 203 876 388 959 044 801 586 095 419 208 153 901 738 851 264 602 631 679 829 540 870 209 309 176 482 670 566 912 870 126 922 243 488 636 032 711 302 355 858 358 513 947 662 008 769 940 543 914 959 986 113 809 926 584 785 251 321 050 679 101 206 708 769 502 765 974 335 278 090 420 525 183 019 763 841 799 430 995 243 730 599 446 961 046 232 222 801 953 200 848 906 118 614 351 839 039 150 062 678 812 077 065 391 076 689 029 608 270 799 880 622 072 466 841 684 343 701 763 176 799 251 719 782 454 277 372 688 747 133 325 535 849 723 273 906 986 157 274 800 582 715 364 007 535 953 976 881 203 429 556 169 021 445 561 216 280 770 935 728 913 865 636 405 016 837 567 770 054 100 560 449 294 790 645 216 957 418 148 158 210 413 781 315 758 517 233 880 921 677 219 469 749 608 349 768 036 483 026 561 705 056 487 203 206 000 446 755 552 269 523 126 762 380 773 407 114 294 607 220 555 585 648 751 329 691 260 369 272 769 713 938 885 662 723 535 814 673 246 476 241 366 927 232 260 475 220 431 638 638 401 713 016 595 015 259 452 399 747 492 717 108 705 853 020 185 282 185 307 434 430 402 189 844 292 385 928 399 018 719 722 782 910 417 256 529 166 643 110 486 334 183 808 352 124 233 918 887 922 210 692 261 114 529 833 016 861 086 560 254 593 256 143 553 917 733 998 976 542 919 184 025 210 478 079 805 824 928 121 179 086 636 370 880 386 108 529 514 675 129 254 442 671 474 409 827 514 184 389 855 492 859 446 378 690 485 915 652 471 107 591 030 525 855 434 529 821 593 863 574 853 070 198 687 031 145 429 852 887 288 434 374 551 179 800 354 393 288 270 579 477 450 664 784 362 768 932 566 568 356 112 264 624 824 943 088 612 688 350 468 523 336 265 224 824 312 504 299 769 290 180 621 111 405 642 598 800 938 386 881 932 163 393 431 934 044 768 388 417 788 134 078 162 938 785 545 843 421 547 104 330 565 526 145 645 444 899 634 818 795 466 500 435 421 877 549 820 221 185 538 025 301 544 849 396 564 527 945 700 061 027 509 024 900 040 769 398 113 342 910 372 099 859 236 446 006 258 127 472 372 678 912 149 955 764 698 096 726 006 630 336 581 042 765 690 640 879 182 192 553 426 351 716 242 199 345 617 137 951 192 659 725 632 113 216 082 464 738 512 089 330 868 452 327 626 239 314 281 335 092 536 549 694 004 048 466 653 020 473 353 536 693 700 086 025 039 142 502 822 324 518 788 426 389 626 349 518 967 093 540 187 485 134 999 635 630 287 778 124 077 906 356 710 984 885 669 660 554 790 533 520 830 983 918 029 266 775 886 142 927 520 200 777 166 176 765 299 353 068 477 620 883 506 176 637 959 248 492 542 359 834 730 522 886 668 049 834 918 118 707 523 249 570 565 049 824 878 592 331 644 119 486 359 363 467 105 671 794 739 966 417 277 229 837 373 892 404 869 805 605 826 289 497 266 863 568 089 807 748 209 465 977 007 675 309 803 442 761 152 011 407 516 965 416 811 727 637 078 832 036 966 317 187 785 870 031 821 466 905 034 015 433 505 740 843 689 826 015 839 837 400 581 884 142 543 332 984 880 115 431 364 255 443 310 435 030 411 078 228 423 837 479 499 135 377 730 072 779 322 817 562 843 548 000 694 882 718 382 448 229 225 025 734 631 773 299 276 288 981 222 017 261 159 690 238 387 492 697 317 391 587 055 125 451 109 297 945 626 311 223 058 413 589 740 908 928 361 039 996 942 372 075 264 673 635 853 634 637 053 867 164 435 898 164 030 776 002 684 169 721 420 125 590 024 361 641 060 103 922 102 904 200 999 329 790 010 645 981 021 956 885 539 875 780 975 662 924 049 898 279 298 305 262 352 813 500 829 206 146 700 015 101 830 605 865 523 285 553 650 234 133 164 021 480 914 100 178 429 710 657 115 164 424 587 961 217 436 842 732 365 457 875 272 838 624 211 031 375 001 543 870 671 383 854 651 286 564 247 517 274 871 198 283 114 767 474 463 809 660 935 099 727 511 703 850 039 264 959 188 122 301 691 582 367 173 736 980 991 881 001 001 987 063 836 533 227 561 079 658 489 056 357 750 700 637 674 226 352 790 745 775 379 599 062 035 724 110 397 942 028 921 410 278 190 100 516 717 065 616 999 672 752 267 993 560 241 494 517 073 341 677 196 564 736 534 151 634 810 918 915 354 754 365 936 023 365 657 521 131 058 001 340 226 254 073 441 040 018 362 271 213 691 682 726 400 079 890 470 303 976 119 509 476 104 673 161 082 170 539 536 995 061 624 056 617 205 497 436 651 175 444 096 311 401 688 551 319 934 197 784 611 523 696 868 446 313 056 713 364 773 150 970 246 968 107 578 443 881 670 456 355 542 130 429 165 185 017 758 242 315 715 274 982 871 115 764 186 604 719 677 502 832 545 327 934 611 575 893 753 948 898 394 789 645 169 912 183 324 224 029 616 355 427 884 370 234 129 992 885 007 066 095 881 355 312 744 474 870 076 307 053 773 537 486 635 830 712 424 825 828 974 468 043 652 180 299 994 187 856 781 490 123 409 055 812 621 772 087 937 387 051 708 137 372 702 804 223 342 804 751 809 905 761 585 426 773 894 938 684 447 658 284 040 546 405 465 718 676 006 771 559 424 823 128 330 200 024 235 836 167 480 728 284 404 630 945 999 984 757 822 994 581 567 862 157 919 885 952 912 700 144 239 055 971 096 878 358 974 256 724 550 545 795 136 897 587 630 924 416 823 326 603 229 904 449 982 877 109 016 653 921 476 832 743 972 084 832 697 301 263 108 878 390 333 002 316 397 549 245 992 473 405 441 996 326 893 039 384 604 567 873 807 612 632 312 842 322 040 942 213 624 156 410 494 545 485 120 957 043 959 564 610 727 205 236 776 224 598 016 035 036 560 441 820 922 454 637 545 317 702 061 490 417 050 313 901 171 418 752 133 397 666 582 289 978 508 552 807 076 821 667 822 704 178 558 560 468 053 291 060 035 231 414 534 393 593 424 336 147 334 521 866 811 454 618 406 007 903 974 458 263 121 374 293 497 827 020 138 375 301 529 883 923 826 909 163 584 766 761 017 335 367 048 948 553 285 272 576 700 283 294 062 622 099 662 032 041 233 709 292 865 392 795 555 451 702 399 157 346 835 910 811 084 301 185 908 412 798 689 164 932 292 115 476 132 364 707 258 022 322 076 123 356 582 725 715 202 832 438 760 935 905 236 096 648 360 981 366 589 593 802 546 169 297 014 590 543 770 329 364 708 853 181 666 651 406 697 115 170 451 093 234 544 595 356 710 868 934 742 060 114 591 442 096 945 989 548 380 559 854 021 284 164 963 837 247 965 248 169 161 489 679 133 166 085 959 771 473 750 072 014 589 273 231 220 367 458 077 982 786 852 820 463 654 487 682 666 767 937 732 339 131 888 853 695 441 693 502 328 466 586 257 262 473 757 584 300 983 635 276 696 100 202 975 327 605 858 076 344 491 149 506 042 580 213 119 093 341 926 087 908 112 057 078 254 296 231 450 932 018 893 486 585 335 762 734 586 578 340 556 008 767 366 489 387 345 434 812 564 730 569 145 830 458 795 603 618 560 187 874 591 158 742 385 012 575 834 619 685 439 041 467 037 871 126 583 499 892 434 106 557 630 736 536 857 494 238 775 267 459 636 306 627 370 346 249 535 185 525 778 361 573 170 449 236 516 288 384 790 571 306 958 469 584 789 653 443 596 760 824 380 863 907 955 792 211 475 113 997 598 681 349 705 255 605 067 954 694 876 319 955 384 668 176 800 769 631 165 026 053 047 439 431 678 135 697 683 592 833 358 918 820 218 701 315 144 856 985 439 260 797 522 727 814 982 969 239 956 441 999 725 538 125 177 943 397 213 096 185 762 640 601 584 838 651 446 612 788 140 905 058 995 472 624 268 427 473 833 463 804 056 741 674 534 364 567 457 460 582 062 700 192 614 099 726 668 883 401 933 757 157 997 917 422 804 461 676 904 230 537 703 574 401 114 699 619 958 921 052 416 111 452 412 360 288 476 662 442 415 026 043 972 265 615 001 774 475 196 951 032 245 499 033 714 813 942 710 226 828 239 160 075 648 405 798 336 901 718 802 774 019 353 208 606 914 094 320 082 011 601 356 451 940 271 579 165 615 316 821 756 283 770 563 637 649 938 947 349 179 977 346 334 530 585 277 562 752 327 011 254 228 470 289 888 893 218 536 108 585 921 623 126 616 619 877 410 865 906 604 378 762 739 647 502 834 797 004 220 620 353 587 587 527 236 000 180 722 311 190 782 543 844 155 696 847 933 062 871 120 915 382 329 512 388 798 674 244 532 036 413 996 468 271 413 043 748 265 047 293 773 365 034 773 846 681 584 237 034 702 829 335 473 954 935 034 668 569 929 595 595 515 016 039 350 086 703 262 785 852 942 830 647 943 336 961 116 805 381 488 601 644 313 468 231 496 403 347 014 967 144 155 233 082 381 393 260 070 039 937 613 308 090 881 746 454 952 953 965 569 738 063 042 273 426 416 711 196 180 589 673 202 681 123 231 181 746 344 596 917 105 814 818 415 771 228 239 824 998 181 192 272 441 530 645 168 985 954 358 461 712 452 875 275 400 647 982 765 009 453 390 907 353 574 101 596 002 977 965 433 088 617 770 855 648 353 766 579 633 477 126 457 092 548 187 087 852 288 090 252 857 523 502 873 493 035 044 356 570 695 397 974 556 752 186 968 105 475 784 919 280 374 436 090 954 406 315 185 585 452 401 606 573 309 484 813 635 216 188 148 920 191 847 298 959 495 076 109 521 451 593 864 911 301 661 253 519 666 115 016 861 826 034 853 445 000 375 554 514 529 877 188 645 082 273 780 046 723 732 960 814 626 923 145 344 797 624 144 216 546 817 806 320 979 443 463 280 534 574 181 896 193 329 705 267 225 020 226 844 852 165 335 268 323 270 883 994 882 544 753 042 505 399 144 560 458 510 768 391 418 271 251 517 552 659 182 167 477 153 264 048 600 069 764 362 654 073 214 317 480 690 340 988 836 693 310 546 671 643 421 649 192 085 388 276 488 849 745 085 994 909 675 968 913 245 089 055 068 706 080 036 008 153 692 242 240 123 276 252 308 496 971 072 990 989 199 467 734 851 901 315 211 686 084 244 345 380 745 160 283 077 780 395 698 674 856 513 355 017 298 268 961 092 167 249 379 563 979 929 939 310 361 707 244 281 935 428 006 231 092 672 668 908 977 786 210 410 452 878 656 040 455 577 773 930 891 417 719 045 636 436 596 232 087 283 168 999 804 281 385 788 909 741 192 260 187 309 644 305 035 602 227 130 048 165 616 854 459 363 627 766 228 882 097 673 216 118 655 841 469 607 621 466 006 988 417 649 610 866 102 707 954 734 211 854 990 693 868 882 953 677 182 869 157 230 576 821 038 441 375 382 908 755 699 108 013 519 765 951 371 504 133 566 371 491 349 210 557 166 277 110 123 707 930 577 647 307 773 565 891 063 879 009 382 666 614 786 417 159 186 211 398 093 894 297 567 677 923 653 722 284 518 252 359 710 856 858 820 831 170 651 870 163 930 456 780 420 898 951 196 395 669 631 659 531 107 670 866 981 179 682 296 947 288 913 439 510 758 902 498 572 727 012 272 989 123 118 844 578 422 774 285 680 017 518 040 708 597 063 119 372 771 313 709 023 936 264 835 593 455 632 741 694 946 664 444 937 602 868 051 853 534 485 224 647 093 578 557 327 348 347 365 624 718 444 796 573 785 604 969 010 601 014 095 795 215 664 042 727 340 909 193 423 925 103 004 060 336 182 372 160 999 418 039 405 927 411 575 250 755 994 880 337 718 487 942 025 885 360 379 057 622 138 134 745 165 900 483 273 095 735 351 693 757 948 251 819 149 998 636 331 401 166 768 936 785 212 656 607 511 771 517 573 359 131 171 610 252 116 074 671 358 265 633 251 053 696 638 971 372 278 306 690 385 672 696 879 258 277 526 098 996 693 552 165 384 508 365 580 730 806 664 962 895 135 777 214 644 353 641 969 816 651 292 953 325 260 188 333 510 480 979 221 011 121 516 028 630 393 811 088 975 250 100 115 496 038 451 388 691 756 940 026 316 376 352 471 656 703 108 155 735 884 719 331 805 381 676 927 999 052 699 441 908 598 758 596 836 599 505 906 201 654 593 180 883 428 634 605 136 811 161 319 813 849 726 695 315 400 655 656 842 896 402 827 809 409 254 137 152 259 220 229 465 687 513 216 955 037 810 188 727 851 585 256 913 135 386 053 884 280 849 784 161 447 352 254 553 924 528 695 473 247 579 788 000 399 683 937 810 086 018 009 250 830 262 929 323 964 194 860 582 312 562 807 016 984 895 888 352 650 622 863 279 169 536 553 783 977 436 008 368 967 902 985 849 185 372 501 538 996 059 820 340 648 445 863 983 715 999 663 391 559 704 324 528 432 837 792 010 550 825 862 494 882 976 550 297 328 950 742 824 501 633 628 944 544 083 745 124 387 663 154 882 053 141 213 375 171 044 662 779 796 850 270 150 973 774 622 482 154 039 944 849 246 666 073 416 467 827 778 577 590 845 360 972 382 081 028 714 771 354 107 392 118 334 080 963 708 930 669 007 009 440 340 551 634 738 913 409 903 965 418 052 386 665 588 663 382 557 187 640 839 969 031 138 331 568 059 186 770 900 250 000 583 586 294 495 811 611 242 476 133 685 753 924 285 041 146 815 855 137 368 077 653 213 199 215 910 334 007 996 167 415 239 069 586 109 219 608 015 765 488 081 634 707 279 451 453 960 786 472 603 145 668 193 789 339 345 818 581 516 284 983 302 151 928 776 461 422 877 743 900 559 013 934 191 604 758 785 809 023 748 187 083 702 472 082 199 020 969 411 962 035 418 950 038 320 449 994 325 527 901 657 511 458 530 338 180 170 317 472 712 344 644 137 710 915 104 371 612 852 945 246 278 567 635 030 537 699 772 671 673 934 285 120 860 647 740 039 134 681 814 395 831 471 980 233 313 856 269 224 116 937 608 122 797 328 913 426 259 111 043 171 795 928 924 598 548 305 819 897 487 721 936 215 482 922 204 334 778 301 544 052 721 333 936 050 006 452 532 325 496 727 490 493 490 559 807 039 217 104 082 959 744 240 597 683 504 627 797 152 059 944 596 203 480 214 782 805 171 323 381 680 796 096 867 840 428 901 405 919 831 282 651 538 264 757 649 384 201 266 021 921 395 339 242 926 788 061 521 055 576 011 992 751 064 215 835 520 704 610 782 907 958 568 703 531 849 297 173 377 816 292 336 706 602 583 476 448 460 753 242 233 604 079 340 339 502 298 104 459 485 273 927 200 623 399 326 662 670 610 939 184 987 782 405 929 886 528 809 088 459 002 165 761 599 700 660 573 660 385 121 718 708 953 553 756 309 159 415 696 458 715 619 502 536 121 573 166 661 633 778 519 504 042 161 133 623 482 776 187 812 904 788 293 404 647 449 864 432 489 189 958 928 280 176 688 499 674 742 729 574 004 389 619 179 345 092 362 139 310 398 090 131 565 610 677 504 793 635 348 186 648 964 132 818 790 939 050 800 099 437 397 419 212 075 776 781 221 800 842 504 755 457 752 244 751 994 315 732 172 201 490 048 312 286 124 919 404 725 688 259 103 943 275 260 622 453 102 500 612 950 287 824 485 858 132 994 306 830 217 995 099 316 739 110 137 324 636 481 725 553 625 616 796 531 269 861 293 215 506 556 380 500 866 334 115 788 136 662 527 585 044 218 276 457 771 654 134 692 453 637 561 126 528 702 206 126 441 876 084 416 930 068 940 674 453 528 609 260 835 266 004 867 356 315 201 641 866 621 029 007 192 610 988 099 687 550 210 200 561 082 206 177 348 292 262 166 834 902 258 183 294 668 130 484 605 288 750 752 251 005 135 532 655 917 932 963 086 883 462 980 009 079 196 332 807 526 348 243 547 763 433 236 179 169 197 218 742 813 586 306 141 277 381 303 057 210 055 929 704 173 345 223 382 270 731 177 818 090 756 840 810 077 166 527 191 869 412 642 583 881 553 331 752 029 458 997 135 130 971 916 831 421 089 815 357 260 636 662 167 214 029 660 260 454 567 949 844 579 069 822 341 057 746 981 237 483 988 648 119 992 143 372 307 442 180 156 403 573 404 253 269 657 152 574 339 459 410 424 352 243 179 293 090 317 650 511 061 631 329 551 517 939 391 981 785 281 830 127 932 322 909 627 660 415 075 956 610 563 082 263 840 070 269 265 447 576 160 542 144 945 638 334 055 995 007 437 845 519 683 693 212 006 717 911 739 284 638 436 913 036 658 867 268 960 758 890 217 920 113 705 451 515 765 423 939 386 589 955 041 757 191 796 588 373 954 872 141 574 804 089 638 922 001 102 479 571 355 096 485 960 984 883 338 595 958 571 060 014 021 714 485 217 536 110 562 123 858 973 768 988 528 320 957 982 164 516 142 301 716 963 774 651 289 765 282 183 456 678 761 417 427 338 551 357 928 598 295 140 040 472 510 918 376 429 756 225 769 023 807 168 774 998 107 549 585 050 029 890 205 735 144 029 223 177 616 006 353 876 138 841 776 103 984 264 414 454 535 939 560 065 093 415 315 356 330 086 763 342 400 410 336 747 532 492 860 421 128 551 142 795 648 099 000 804 121 014 461 070 443 764 161 642 830 612 229 914 469 451 768 583 085 918 275 239 761 806 132 650 249 463 179 391 419 380 425 041 743 410 946 918 174 464 668 876 702 779 478 664 954 317 105 575 395 731 214 132 828 120 020 633 143 957 123 899 821 737 604 242 926 094 989 197 190 040 837 821 834 809 776 325 785 623 435 617 638 977 462 197 171 039 244 010 318 233 980 085 671 788 968 523 634 629 677 052 214 384 517 007 282 557 143 167 667 669 564 567 584 989 337 690 913 436 411 982 566 373 874 633 761 784 415 900 000 267 462 337 781 291 993 989 479 255 129 173 777 713 462 096 408 086 764 005 206 116 683 504 670 957 099 485 573 809 672 907 090 331 596 664 424 964 144 812 382 047 267 052 694 774 091 073 357 059 769 694 463 053 015 781 721 245 530 017 265 974 656 469 170 870 389 612 648 920 139 565 262 968 110 894 875 681 482 755 500 431 011 763 401 048 294 472 888 820 391 959 219 441 001 839 821 079 058 401 921 966 342 312 798 585 447 366 456 788 760 844 456 732 148 351 381 524 706 553 665 242 739 538 725 838 749 173 394 334 055 562 413 343 539 542 773 678 125 676 057 979 733 140 468 047 027 524 306 748 776 846 967 927 198 786 739 318 249 930 538 964 790 550 847 803 234 416 409 975 035 733 137 841 978 797 882 520 617 695 637 740 727 263 606 786 298 453 502 713 379 963 846 916 723 129 400 401 457 951 914 111 323 174 914 735 688 101 843 178 332 979 283 396 182 979 704 780 820 671 679 585 345 412 048 442 999 471 681 683 121 912 695 270 966 794 819 693 207 712 602 765 204 401 932 337 485 188 744 848 267 717 791 165 785 658 323 634 017 307 956 412 370 693 655 445 792 237 110 525 867 279 798 085 057 902 935 434 590 908 562 543 533 268 144 981 994 911 741 057 679 022 454 100 438 143 752 416 710 976 776 211 435 856 285 868 733 352 956 872 143 420 654 608 697 526 711 130 027 226 054 963 852 103 950 437 378 828 195 789 478 318 962 206 714 807 852 196 773 081 325 126 174 164 765 276 185 572 122 019 468 709 764 466 892 631 154 072 882 945 797 483 377 597 605 503 151 616 814 939 761 772 109 292 188 227 800 577 180 365 405 640 059 760 005 898 230 607 096 885 384 680 147 626 732 429 361 307 924 936 853 459 154 629 335 712 872 927 047 741 258 604 417 118 607 666 990 803 032 197 955 834 812 804 484 064 393 160 879 339 603 196 569 267 970 245 184 603 846 611 109 732 651 409 526 381 551 478 929 169 396 893 743 978 308 051 436 561 344 464 552 610 804 153 505 702 329 916 614 881 256 764 776 350 576 198 617 872 539 031 067 821 513 964 873 647 643 799 308 403 596 567 718 967 088 884 159 299 882 208 262 144 878 642 465 881 117 826 899 501 978 260 017 703 090 938 554 250 710 719 666 079 411 386 867 256 828 765 972 605 293 724 440 746 983 518 502 050 018 070 789 489 853 037 363 311 710 166 424 411 078 486 039 839 061 651 053 612 763 175 813 842 075 192 540 939 673 082 937 239 487 407 646 459 712 966 442 405 341 988 216 157 125 344 480 616 866 185 602 809 836 856 376 556 522 168 504 184 810 431 566 923 781 046 362 801 298 959 420 846 881 426 871 439 852 000 648 697 960 287 939 444 500 087 661 228 014 302 562 777 993 133 524 294 255 669 490 992 034 636 650 018 463 735 230 399 909 420 888 623 662 367 099 780 765 475 289 171 475 174 614 420 098 110 926 166 493 634 011 145 664 222 724 561 234 647 371 420 482 577 604 550 236 802 769 375 719 237 103 057 776 689 364 765 413 605 009 489 451 823 842 148 296 177 421 828 411 171 531 443 934 238 993 974 928 873 045 253 097 268 166 287 847 913 328 785 388 191 947 578 991 100 489 815 720 158 805 086 359 592 649 830 673 732 501 522 440 978 371 278 965 705 742 965 869 800 447 812 237 640 158 011 362 234 574 992 205 583 837 329 395 739 622 988 931 056 914 319 568 287 603 091 636 428 467 795 124 529 081 235 438 712 755 512 259 493 247 896 034 061 388 084 190 706 511 894 414 202 706 949 858 265 929 188 365 585 895 052 528 406 577 538 850 762 985 606 434 082 532 451 040 546 798 169 592 684 863 000 793 651 540 291 541 324 265 616 800 394 889 790 292 285 137 730 710 744 031 021 925 455 684 689 560 268 824 035 516 196 103 113 008 453 056 912 320 682 806 463 692 258 707 556 930 472 956 225 713 632 236 334 475 068 504 044 305 876 947 571 350 774 340 858 714 150 149 380 312 006 693 281 528 970 487 172 732 533 137 669 946 826 353 734 578 420 977 294 328 474 872 944 519 863 912 171 760 467 217 259 015 596 854 635 613 266 190 472 840 064 910 924 310 786 220 308 813 233 845 964 751 121 388 946 300 236 505 568 254 988 512 223 378 445 950 923 171 743 179 330 913 879 598 898 522 750 202 388 840 394 302 792 136 988 736 340 603 176 081 941 636 008 348 270 023 765 926 754 407 962 357 759 596 028 865 145 239 513 526 987 370 734 108 573 730 351 929 957 712 424 226 428 372 457 034 328 377 087 126 819 488 088 145 749 439 932 749 987 293 309 760 826 272 951 562 947 363 646 560 080 930 813 121 181 592 153 881 861 545 229 077 016 493 124 126 774 359 157 294 864 062 728 917 503 889 958 201 782 800 178 501 277 745 438 956 693 631 930 805 843 862 467 842 805 460 116 027 992 089 518 068 057 017 080 081 475 240 751 940 324 404 045 210 469 722 502 760 671 414 231 251 222 136 515 526 990 112 102 795 684 903 787 072 157 892 276 532 803 893 274 789 849 624 815 494 589 909 250 528 655 992 091 310 738 912 955 072 922 723 125 695 350 649 800 357 661 707 790 291 760 653 476 173 993 211 136 959 750 253 076 833 888 653 758 615 544 845 610 203 938 205 314 467 831 058 190 475 709 526 378 973 748 258 270 276 116 984 374 271 801 454 930 096 697 658 130 673 739 273 307 311 162 177 692 918 582 167 274 206 072 150 143 381 914 329 089 241 110 522 614 137 894 837 724 908 598 051 772 610 787 081 044 537 526 081 171 874 008 348 140 970 623 663 252 368 936 662 974 410 390 270 452 214 110 296 036 783 026 969 328 910 973 019 939 287 336 545 621 878 584 227 034 604 144 927 910 027 304 350 686 002 348 823 376 334 064 301 742 689 162 530 506 594 694 539 760 955 145 054 710 765 995 936 514 122 510 046 181 013 962 698 465 105 456 484 445 550 733 648 859 694 063 146 276 527 624 823 632 359 792 524 028 998 342 890 008 039 195 859 833 713 756 642 413 895 945 024 683 494 223 386 503 903 719 855 586 730 049 278 205 808 121 107 472 959 254 702 932 490 275 411 043 619 234 908 529 169 377 351 658 851 793 268 420 321 351 990 276 819 307 941 043 924 975 934 298 322 663 345 685 706 626 998 401 260 786 009 609 352 607 608 905 316 695 741 020 101 408 936 077 840 394 636 050 670 914 179 713 163 291 533 624 120 995 352 923 387 498 421 399 858 312 125 097 997 822 246 160 842 154 920 766 945 048 867 938 667 334 360 185 877 374 314 281 736 659 872 536 571 203 325 564 686 163 389 552 615 270 567 628 271 709 387 841 411 048 748 540 284 051 381 182 414 286 681 072 561 817 407 478 342 630 713 819 130 727 396 648 467 159 015 881 099 022 930 679 005 456 418 461 630 466 737 361 562 618 933 450 085 051 784 945 997 566 096 509 690 866 458 525 111 353 018 764 944 414 843 843 220 411 220 713 518 387 592 513 000 117 753 606 424 146 987 209 835 437 147 742 978 040 717 777 639 259 381 136 415 789 340 670 096 395 073 728 600 443 548 929 876 750 432 656 456 651 522 517 038 567 400 799 359 093 044 986 025 814 767 891 358 761 204 336 003 883 239 792 086 433 799 198 501 254 482 846 933 243 529 125 440 598 442 062 704 808 479 539 232 086 348 075 809 668 414 659 476 740 874 680 146 618 655 697 977 040 038 979 948 793 815 355 436 188 661 656 178 172 007 431 834 117 831 814 207 718 480 592 366 290 392 736 238 229 514 362 337 942 471 609 505 944 097 874 031 220 590 071 949 706 085 066 881 519 259 245 404 986 933 110 648 452 879 438 032 349 249 960 313 448 119 986 775 990 706 455 677 219 924 430 027 606 409 917 951 785 375 695 729 378 561 458 373 376 327 208 551 386 999 708 295 106 710 404 800 990 206 343 561 964 919 268 844 270 255 424 169 778 554 371 835 415 274 530 775 608 321 585 353 173 724 353 959 752 176 759 445 163 418 926 095 921 265 741 299 201 619 523 971 680 885 209 000 976 835 358 760 774 954 355 502 435 879 600 701 100 936 375 469 394 458 888 291 758 901 871 547 229 773 989 162 042 363 454 823 204 223 628 292 066 871 948 258 925 387 810 120 000 821 583 775 961 804 861 828 900 849 932 676 968 537 293 699 185 058 958 058 464 511 536 301 828 303 573 991 372 412 138 970 357 646 872 017 992 614 459 341 195 251 950 878 698 691 891 961 335 322 020 025 004 179 002 710 170 394 384 827 077 781 448 084 933 598 535 096 889 866 463 490 889 184 758 611 804 103 309 883 976 250 280 402 873 424 792 479 880 012 550 743 297 503 569 511 479 071 947 606 931 645 437 328 171 738 320 921 428 424 165 219 466 165 211 263 809 747 613 539 001 232 404 427 288 679 224 397 924 876 281 375 657 688 549 963 535 704 023 983 436 238 277 583 083 379 729 036 294 428 270 997 886 702 177 961 832 540 484 512 683 702 221 778 396 911 004 982 055 572 694 423 327 531 131 890 945 915 081 613 676 972 230 298 504 222 843 810 592 417 294 403 862 756 998 196 423 076 319 076 909 407 662 060 960 896 823 034 019 531 508 958 820 460 049 312 483 268 757 685 862 928 361 571 766 420 379 040 709 979 996 766 619 223 822 459 520 835 190 318 406 057 714 426 322 173 223 216 949 991 534 148 295 017 547 033 774 819 165 909 186 134 671 434 093 296 193 260 528 848 907 863 576 003 066 290 779 696 970 321 400 320 441 140 499 675 141 900 449 531 975 642 450 223 561 508 983 370 713 271 061 167 314 083 411 321 589 020 535 915 858 878 341 963 213 708 254 464 278 534 270 307 178 645 004 372 482 919 586 567 132 549 019 388 967 573 482 132 285 854 838 945 552 079 729 963 527 921 269 221 454 331 472 301 781 216 776 116 788 518 919 183 966 947 282 470 615 992 691 648 058 124 375 976 652 545 668 518 901 897 764 619 908 999 537 949 815 295 243 172 502 566 769 711 235 262 648 101 947 909 694 664 580 369 886 294 769 808 547 770 275 641 572 788 089 865 840 871 989 656 976 290 354 442 050 108 347 785 766 341 161 167 219 179 183 008 983 459 335 959 299 372 809 546 177 408 658 085 561 017 084 186 546 762 017 127 894 773 320 232 446 355 009 819 321 171 956 052 473 484 279 762 020 831 133 859 372 296 250 779 993 860 658 546 508 996 733 904 038 688 390 112 728 564 750 958 864 987 763 283 340 868 532 354 855 226 388 711 546 783 470 978 360 224 308 251 727 743 012 214 958 586 535 579 456 931 641 881 852 070 021 740 231 052 362 851 606 678 371 958 766 305 917 533 796 668 977 543 312 538 140 653 176 932 300 685 512 333 312 337 801 496 856 702 955 286 537 501 033 639 039 795 167 826 405 168 847 753 019 902 121 770 853 281 743 720 981 180 516 473 417 512 944 176 905 456 658 935 715 332 589 808 231 182 472 167 110 801 908 911 884 677 257 494 669 493 196 673 948 294 329 023 704 075 252 878 150 244 148 374 939 950 931 368 349 412 103 368 863 172 864 679 383 987 390 876 747 724 736 360 685 052 157 760 597 648 697 125 846 153 914 933 447 690 845 590 052 926 513 617 421 961 444 171 967 106 335 236 904 166 768 405 087 414 213 493 391 330 788 276 122 934 844 905 708 410 944 446 857 170 605 645 893 043 015 655 366 231 880 562 294 872 751 290 659 554 993 599 504 138 713 718 068 016 793 813 142 105 754 381 856 542 630 142 686 004 703 643 695 810 515 994 357 050 384 040 775 867 774 316 406 437 599 699 221 732 518 603 847 317 163 205 409 111 348 691 251 937 369 067 760 472 866 476 148 644 675 974 508 735 688 332 473 040 401 071 661 112 809 968 258 610 506 575 861 488 803 543 609 999 300 915 251 103 809 612 820 081 715 809 524 432 012 014 168 317 809 745 840 289 617 374 643 884 805 786 597 264 562 781 463 713 457 585 365 818 141 071 522 013 102 970 124 544 408 076 057 147 584 724 424 444 082 645 911 056 221 395 863 365 659 754 756 861 497 727 927 785 703 954 560 959 065 496 228 815 180 906 644 437 203 212 775 790 943 818 375 241 529 196 120 150 699 590 640 301 321 352 347 889 188 300 652 699 108 025 690 378 025 495 006 253 128 363 123 252 271 710 692 089 511 988 338 748 563 411 136 253 379 374 630 234 688 564 087 151 594 227 554 569 420 376 805 164 365 363 929 745 357 108 508 606 699 839 871 455 703 549 094 447 903 399 672 795 147 012 108 303 296 748 990 906 421 579 645 729 595 198 978 079 665 267 803 457 637 823 494 900 079 959 181 180 618 076 964 294 855 097 228 228 318 721 003 023 668 625 838 157 851 710 956 243 808 253 667 811 117 825 574 270 515 760 525 473 615 521 214 462 379 303 340 572 760 393 631 333 846 266 223 532 187 002 478 802 842 344 781 475 337 801 321 881 583 922 543 622 891 172 329 729 703 038 491 774 743 872 947 165 628 820 052 202 927 645 631 699 275 876 353 226 024 720 017 670 935 124 020 997 348 704 417 537 178 717 634 784 621 252 422 447 509 898 076 394 919 484 797 797 567 985 526 530 777 651 694 204 352 231 638 912 636 784 616 553 166 871 521 025 052 223 483 348 818 235 804 604 996 063 004 490 680 236 506 762 820 905 009 463 781 491 820 731 823 032 271 161 359 402 281 046 075 312 999 074 935 742 704 196 052 988 790 472 087 541 955 023 557 635 409 900 275 771 069 946 413 775 599 173 182 384 454 001 048 706 337 526 113 619 653 136 594 002 014 910 078 582 654 695 029 871 735 741 353 611 793 424 119 006 516 146 135 140 269 858 439 490 763 217 927 342 882 651 073 452 378 049 049 574 908 979 183 091 440 267 758 698 112 808 568 714 297 219 853 419 918 009 510 937 459 665 331 361 995 658 457 952 205 052 591 336 995 435 099 114 173 418 849 140 771 532 665 497 694 051 812 385 274 173 750 349 138 427 285 030 583 419 530 274 197 365 625 424 644 860 347 881 297 468 889 192 433 872 108 771 107 373 771 786 808 431 163 822 943 194 539 822 423 000 743 664 695 391 533 111 315 983 150 325 649 763 356 760 131 130 550 434 373 103 071 309 629 861 895 291 257 547 860 747 298 021 975 059 556 704 124 614 977 599 296 360 527 101 421 775 306 737 005 373 935 782 377 153 624 959 089 855 911 195 571 054 024 094 228 110 823 344 871 083 080 421 049 893 073 694 614 108 163 896 588 221 540 572 565 013 355 214 058 427 242 543 283 209 819 250 395 304 085 058 393 810 767 941 079 935 641 607 941 279 149 670 084 361 102 096 919 826 907 548 604 414 078 711 269 125 069 043 529 300 879 400 742 531 168 971 203 616 522 574 814 647 185 746 487 377 800 940 612 592 830 557 845 571 869 156 597 519 390 298 918 372 542 405 092 690 715 175 191 739 479 598 804 043 435 756 163 319 154 778 179 768 262 345 582 257 668 069 767 738 177 349 215 068 393 297 123 645 301 507 520 607 403 990 850 938 566 955 645 665 658 420 603 093 020 634 088 889 860 449 962 584 045 300 864 291 115 110 345 977 311 064 998 323 872 603 798 431 353 463 967 315 338 055 472 536 053 819 825 766 337 896 821 121 415 809 498 281 703 457 641 361 147 032 806 314 351 883 459 073 738 922 088 636 199 947 696 174 281 918 160 205 672 985 301 320 346 102 873 089 024 205 002 183 280 272 703 739 707 820 832 533 217 018 213 988 427 831 227 002 319 622 160 615 849 628 265 445 052 535 259 929 107 606 577 423 260 732 081 600 301 986 495 017 433 224 363 905 817 242 648 647 695 373 583 998 621 766 167 459 842 891 112 613 790 552 048 757 464 947 728 970 861 425 207 896 401 550 937 991 912 060 609 269 168 009 936 590 341 991 825 167 900 031 746 114 350 390 225 216 478 781 601 285 276 159 983 377 448 186 772 775 857 797 795 851 302 219 414 367 928 491 943 364 312 915 292 133 024 010 394 642 820 292 399 645 122 462 173 141 077 245 839 550 010 633 032 982 283 653 436 990 813 155 604 774 080 656 295 949 853 143 731 145 624 499 699 515 630 715 744 684 663 312 541 338 707 998 236 236 641 637 413 049 883 107 244 756 565 657 679 078 029 137 963 924 307 739 521 688 495 534 573 697 712 032 067 728 985 159 946 075 257 125 548 639 456 346 898 745 553 846 069 834 475 733 693 538 317 644 322 381 372 646 487 029 326 060 730 557 466 608 675 616 689 128 807 888 711 824 902 293 049 571 912 977 127 629 905 071 132 964 804 454 157 396 583 004 407 413 124 585 483 043 830 960 149 327 521 184 845 116 856 695 680 764 611 734 652 213 082 829 887 536 254 413 000 997 019 477 004 035 350 930 105 092 248 611 983 657 531 666 665 828 013 691 846 058 957 186 183 063 269 681 567 365 163 140 247 020 969 304 480 895 809 705 172 965 009 100 531 364 258 676 094 088 628 141 185 123 838 176 461 417 667 806 906 855 686 529 301 965 809 325 546 518 085 699 159 314 576 773 897 931 255 791 761 680 525 382 292 795 546 144 422 680 995 354 758 438 342 599 579 949 012 329 483 032 255 161 904 805 327 596 982 877 136 706 740 494 738 721 294 175 068 890 467 482 233 272 371 369 078 082 946 950 342 901 108 860 373 721 237 945 776 671 860 656 644 284 294 973 144 657 808 267 502 126 259 803 079 362 908 910 021 187 894 289 767 929 123 723 394 559 149 923 888 817 761 235 156 168 317 214 864 472 212 624 026 478 218 701 776 671 427 098 269 524 533 848 049 308 098 785 734 657 023 564 117 329 263 517 949 756 697 648 490 992 149 703 669 987 308 665 609 399 605 306 112 932 247 551 763 943 080 263 111 186 488 663 180 331 199 500 684 627 527 864 597 723 574 748 663 600 155 623 680 520 681 692 109 895 710 672 539 026 356 071 413 969 390 183 067 845 881 164 595 178 321 092 811 765 053 535 855 236 014 764 908 119 569 786 224 954 302 650 200 313 668 178 261 011 736 787 617 525 222 825 916 135 231 948 402 022 494 935 369 913 725 715 634 442 383 803 010 269 861 430 908 176 399 761 716 003 687 346 879 267 774 885 349 747 749 638 736 257 342 541 974 559 700 243 098 044 285 075 429 092 401 047 790 390 175 243 472 310 643 854 771 410 668 421 931 389 352 409 578 840 456 972 724 234 720 121 795 959 362 744 172 541 118 738 595 547 556 683 352 641 993 331 348 760 425 220 522 098 348 150 392 048 038 182 532 266 378 497 698 157 941 322 381 753 351 698 910 855 568 313 941 097 747 977 959 583 570 359 898 048 369 633 972 958 930 870 745 340 191 229 440 152 499 861 632 499 000 220 699 389 577 570 750 990 618 535 141 044 520 720 253 435 962 214 755 124 776 548 537 931 796 698 384 749 274 562 629 413 128 441 790 509 087 832 564 604 145 161 196 575 801 674 968 046 474 625 632 677 992 600 684 160 293 207 438 480 266 723 528 300 661 851 758 489 363 773 247 007 066 302 926 313 133 412 957 556 583 496 592 377 461 147 018 596 569 816 796 055 776 365 109 505 745 934 640 154 176 653 582 655 558 587 472 181 877 453 942 265 860 570 225 467 799 406 519 156 872 265 824 137 335 575 321 217 241 735 072 334 289 342 670 076 964 629 549 741 830 267 936 747 844 564 087 088 637 134 583 305 850 885 030 691 123 570 873 351 588 916 355 092 491 358 824 687 027 642 641 314 509 112 813 988 724 512 965 473 042 338 966 363 405 547 134 508 063 498 717 586 460 107 407 418 076 736 555 922 413 502 146 438 568 354 573 939 283 979 624 368 176 206 889 558 080 388 450 175 975 062 971 260 023 046 650 892 889 843 060 125 877 454 344 532 971 030 246 999 950 856 698 066 513 847 813 575 270 697 183 122 059 439 078 916 914 461 592 216 122 628 865 298 956 713 268 255 213 518 607 609 781 569 021 831 828 447 219 450 529 140 298 771 592 408 260 189 283 620 069 371 586 609 177 935 982 057 367 617 754 302 138 119 872 732 033 742 661 204 146 564 949 002 796 744 926 558 548 411 637 906 751 431 256 822 032 780 842 911 263 082 765 440 240 764 101 512 109 605 468 721 019 974 844 107 928 237 419 997 689 732 363 041 802 917 779 163 392 486 331 561 725 746 882 871 658 237 289 861 306 385 021 337 727 975 392 494 232 404 076 160 784 565 197 697 393 794 789 207 110 879 695 809 906 570 005 731 952 102 166 552 762 997 902 813 268 979 592 789 585 061 321 188 971 665 278 035 993 659 815 626 619 724 647 518 472 574 077 182 413 323 343 664 206 120 111 119 304 895 976 835 330 765 298 434 180 320 030 155 785 398 795 982 657 921 018 926 809 757 996 308 528 123 233 790 442 629 755 831 514 390 977 169 694 167 138 755 179 544 998 901 660 806 045 218 949 054 751 943 864 863 927 840 813 869 642 702 684 735 206 806 498 415 687 824 290 076 250 535 701 047 743 929 679 590 877 634 666 538 145 243 752 721 386 578 395 877 502 001 984 013 459 615 700 044 716 778 816 716 557 903 406 872 573 071 030 389 803 260 553 522 322 940 263 917 990 635 291 434 080 554 081 942 460 661 053 281 525 105 566 551 715 099 111 432 944 217 059 998 595 741 119 649 332 703 034 705 796 909 080 776 104 049 146 567 228 536 924 628 577 381 244 710 708 947 115 989 367 778 740 957 457 263 546 409 232 506 973 238 683 356 200 409 340 782 716 402 439 907 734 226 088 451 517 296 400 168 464 511 656 575 128 566 815 202 306 961 073 906 499 238 772 629 015 816 598 433 366 313 031 158 989 032 723 524 108 602 589 851 059 940 856 226 436 075 871 142 789 045 502 044 677 288 391 841 733 716 119 246 198 246 412 913 453 968 880 820 835 841 521 421 959 056 045 753 366 879 917 468 863 441 862 895 301 318 181 164 265 536 422 127 600 599 840 274 761 991 479 107 530 184 347 774 834 247 129 973 842 827 972 463 450 510 904 249 628 543 370 785 182 090 126 460 434 270 017 152 083 853 040 085 077 556 038 681 025 391 995 091 842 948 075 707 636 788 518 795 214 318 864 118 650 750 147 330 583 760 434 777 439 955 867 517 889 404 440 973 519 016 221 089 833 736 799 361 172 432 724 164 071 042 554 080 200 084 273 538 108 767 837 221 855 302 870 240 924 887 204 538 338 020 660 547 961 641 864 314 020 976 530 087 688 340 135 568 473 678 701 379 240 151 156 620 904 158 765 206 842 706 458 742 019 600 891 563 348 789 893 105 268 935 481 417 900 433 095 806 329 980 132 939 692 778 023 521 687 102 283 172 154 382 526 203 197 338 365 918 455 773 787 279 136 325 206 102 079 631 703 556 187 758 475 510 425 856 897 153 912 141 211 087 680 915 841 580 501 389 091 573 179 433 709 976 972 129 376 081 388 453 079 683 564 339 309 443 125 425 516 559 896 608 411 505 896 548 499 676 092 305 933 467 968 648 807 816 593 412 011 654 128 515 668 611 982 916 967 975 253 249 695 138 286 576 400 249 432 174 916 548 448 311 466 629 820 577 146 487 840 983 420 000 705 655 704 327 738 459 547 657 763 907 781 633 913 216 705 848 382 161 216 532 058 885 425 564 955 131 005 958 802 413 264 675 146 221 077 445 749 027 114 664 594 628 188 194 622 386 483 248 300 083 535 765 803 571 593 602 309 757 024 177 576 747 395 888 724 941 194 245 991 453 695 548 764 091 713 204 548 340 067 102 253 991 969 432 452 089 049 974 338 417 816 422 700 626 719 897 220 985 261 373 000 043 818 579 657 624 468 374 501 996 980 054 317 942 556 883 342 597 072 578 802 000 041 612 654 711 919 414 615 522 252 093 913 395 274 019 381 059 577 430 967 376 496 118 672 988 414 849 051 176 674 658 738 931 494 783 416 815 472 495 035 354 177 109 176 304 707 963 247 534 749 954 799 905 286 993 345 695 564 201 458 020 801 013 230 938 777 020 013 496 495 600 807 317 463 071 473 791 688 979 866 284 765 959 804 739 774 772 262 359 554 500 455 123 709 136 792 399 028 346 899 986 090 191 571 895 023 959 404 554 624 029 972 380 524 055 566 248 063 939 025 589 107 690 003 433 469 531 919 575 441 199 929 213 457 692 624 231 327 585 627 776 693 359 398 405 299 531 003 727 995 657 623 077 572 094 791 524 064 584 824 575 650 683 536 292 791 901 852 987 768 615 365 558 305 405 609 855 104 878 235 208 734 072 904 067 176 346 681 052 956 312 244 780 954 830 905 544 354 530 410 486 845 204 584 154 042 332 452 263 877 728 130 209 272 580 245 274 153 564 288 624 541 117 074 504 116 952 661 168 339 648 866 808 052 254 535 411 259 308 246 653 830 991 825 728 148 142 702 234 495 380 515 181 020 255 861 483 994 386 369 305 205 381 904 320 761 563 106 398 522 672 833 889 612 109 271 820 196 654 786 482 877 331 288 366 871 131 036 674 009 259 709 654 723 586 358 538 706 660 213 172 064 845 254 076 959 747 142 640 737 515 143 801 872 145 889 523 165 921 047 352 668 368 871 977 024 097 896 078 554 119 705 884 705 443 853 896 438 801 558 466 540 605 047 410 462 003 334 620 915 041 927 496 192 596 116 664 781 306 291 444 135 140 158 093 334 180 178 018 610 569 240 198 324 801 348 686 304 003 119 204 391 851 091 841 807 578 646 656 969 921 011 355 554 364 059 089 978 133 214 952 288 505 933 279 071 982 561 091 661 776 622 656 952 481 252 800 347 908 365 885 101 111 773 800 232 786 772 746 828 279 798 141 609 067 429 199 656 985 567 684 964 031 771 647 632 957 051 430 242 276 588 184 836 298 646 976 353 003 959 964 794 736 907 100 034 505 814 512 652 462 274 756 202 003 817 703 491 423 887 272 471 368 262 646 572 708 796 475 554 258 747 960 364 547 783 953 143 947 278 703 414 795 670 346 816 077 566 189 828 263 141 045 598 232 481 319 931 851 105 595 977 696 606 335 439 277 713 972 174 249 847 524 448 170 762 998 609 487 721 370 899 350 212 029 232 484 571 577 043 484 877 852 433 521 257 872 252 395 407 686 573 595 480 584 681 474 835 671 922 178 034 888 600 382 197 642 828 623 707 159 520 137 166 423 361 114 071 846 358 974 152 469 521 726 671 872 056 063 470 710 548 958 073 257 128 748 084 101 210 310 963 736 893 243 091 188 840 718 354 876 982 413 105 066 389 302 517 278 071 356 615 943 451 775 965 941 772 488 537 710 012 864 466 631 109 223 220 334 627 786 187 945 960 565 315 848 839 378 067 814 143 076 443 330 783 466 784 874 657 790 242 587 412 891 168 806 538 460 095 258 119 254 899 497 586 604 817 901 804 472 307 723 744 116 654 279 307 782 075 351 188 058 077 694 700 392 700 330 802 707 846 049 186 347 328 947 006 226 803 919 541 600 057 889 217 914 253 626 368 385 991 699 520 037 720 960 642 481 005 884 812 276 761 837 061 288 313 985 268 464 545 377 546 793 657 803 088 291 621 286 466 237 216 088 136 584 965 383 688 269 954 178 583 676 861 024 299 222 659 644 798 726 382 692 657 701 753 725 524 070 322 667 570 518 209 804 622 373 958 229 423 228 099 368 011 801 905 117 348 069 823 325 154 470 187 115 526 240 722 534 221 428 215 150 795 500 963 485 596 025 853 547 176 489 439 060 149 999 529 984 834 137 472 947 975 965 457 936 501 196 913 294 623 529 581 068 083 774 692 565 881 282 653 173 039 150 674 781 376 412 156 384 030 946 728 177 032 607 888 805 408 139 662 649 263 168 523 006 614 104 300 389 682 227 666 849 449 447 971 418 831 284 199 146 719 309 646 416 045 356 629 375 835 072 931 069 124 188 598 001 534 810 550 465 294 429 510 624 412 964 421 581 310 056 881 228 457 337 133 495 675 495 232 536 972 181 077 207 935 848 337 925 315 132 155 269 794 770 235 209 758 746 458 455 373 704 282 902 738 139 096 841 974 208 043 081 955 372 093 773 203 225 356 329 703 946 664 744 456 829 266 159 779 414 977 381 170 872 872 353 469 440 575 353 901 889 635 996 963 156 647 725 537 429 090 645 590 783 157 908 271 739 774 909 541 807 666 730 646 315 870 456 062 894 439 676 160 645 390 487 736 133 316 331 924 982 604 729 268 579 635 973 504 747 436 275 777 325 147 365 398 259 304 149 154 336 433 369 149 702 288 379 299 239 258 834 981 685 353 968 056 542 483 207 503 152 350 819 967 192 146 545 445 365 501 815 716 908 149 039 951 506 514 028 542 799 384 761 451 352 032 548 012 320 134 162 064 507 343 130 895 220 424 551 117 926 179 950 667 983 383 718 922 831 070 419 663 992 836 915 496 112 098 413 567 468 812 391 996 268 679 873 426 479 419 895 238 617 854 254 637 098 948 508 756 324 616 222 852 450 957 901 336 988 444 365 927 648 757 796 272 557 855 914 888 599 959 708 165 974 700 400 883 951 703 917 170 026 691 510 762 030 575 695 334 062 474 395 877 290 384 324 204 777 809 405 909 338 925 054 769 383 576 134 062 824 307 053 695 876 087 952 156 341 537 728 241 790 307 206 856 369 991 234 700 768 124 734 734 431 089 528 068 785 067 398 432 922 631 192 836 584 284 848 443 975 653 919 220 990 529 569 034 602 926 103 693 546 649 201 645 542 424 969 454 236 818 837 098 259 018 928 096 150 634 906 226 199 556 851 921 782 199 644 968 351 135 156 292 337 605 139 145 920 505 013 013 766 338 280 565 462 075 471 617 661 596 288 349 705 794 969 824 366 939 346 496 978 831 931 817 428 443 616 000 500 858 793 373 599 301 533 334 871 705 027 327 536 481 304 657 825 310 653 631 520 469 078 418 586 004 803 665 249 803 046 264 726 747 106 373 140 651 957 316 795 467 399 113 656 183 688 884 223 506 738 484 743 193 681 627 485 593 403 859 663 737 795 648 218 922 489 013 443 168 771 477 667 548 571 482 494 527 768 695 005 347 055 901 634 025 472 004 586 906 639 292 952 471 888 425 257 215 738 695 106 434 655 073 191 070 722 544 590 776 277 243 081 661 994 882 038 951 427 921 760 939 634 734 478 719 307 179 160 473 908 332 346 320 357 233 262 645 105 408 718 777 105 515 978 392 422 249 987 855 642 988 188 575 154 267 289 839 523 233 715 847 117 250 656 346 190 322 999 454 878 900 300 553 861 664 641 029 417 685 889 163 433 905 165 806 060 388 892 046 156 445 683 937 740 295 276 717 429 510 972 243 157 415 833 803 714 520 429 878 788 306 879 755 087 321 619 820 415 346 698 667 299 358 222 373 515 191 462 993 118 708 617 827 068 930 153 457 748 291 998 865 821 151 239 549 683 902 250 538 254 535 633 014 688 335 672 705 931 382 620 865 652 038 184 292 747 323 592 750 562 558 453 991 403 201 524 032 737 081 025 030 911 142 573 106 048 404 216 009 140 998 221 235 073 650 962 502 075 646 155 554 399 823 972 561 180 348 056 156 758 667 997 654 654 005 850 499 825 066 897 852 261 058 789 644 455 056 356 046 701 497 036 530 664 632 716 618 685 390 843 257 084 445 015 644 724 853 756 345 029 745 394 617 168 759 897 414 263 757 720 657 435 152 758 793 603 500 148 156 808 840 112 648 713 118 308 105 090 746 041 937 089 353 601 712 731 671 823 539 771 878 236 206 548 374 653 249 363 105 189 009 603 991 555 272 627 880 064 735 038 683 472 005 667 296 349 388 664 799 988 206 562 324 648 329 520 581 404 917 861 748 569 248 334 576 559 082 824 243 053 873 986 254 769 658 635 655 081 562 905 773 806 142 843 398 649 430 778 227 331 742 481 068 713 352 544 165 248 584 587 356 367 212 239 299 376 728 342 099 941 778 509 829 229 034 901 697 561 854 274 902 937 024 240 254 536 625 330 868 684 118 828 827 451 322 797 530 472 808 765 131 999 226 598 519 012 255 015 538 594 021 151 198 375 192 388 386 683 230 339 758 895 253 378 764 756 658 115 728 845 852 726 748 622 274 777 920 950 391 320 163 052 756 511 778 820 577 761 920 852 138 518 436 296 548 032 956 317 510 452 386 245 145 943 041 407 651 717 935 443 012 237 194 625 844 865 594 886 172 822 152 034 682 672 952 265 252 271 553 494 007 470 795 669 201 850 383 155 049 251 178 133 641 777 698 512 529 780 819 275 250 947 377 177 887 547 654 388 596 128 305 986 921 214 010 276 233 671 579 713 232 812 197 103 817 933 556 455 842 669 584 910 229 729 903 567 746 512 100 623 992 608 046 742 128 303 617 641 564 315 699 773 833 868 000 250 717 505 681 682 197 288 779 981 101 082 088 976 109 979 010 679 067 616 480 985 771 726 580 436 921 497 463 544 324 598 001 825 098 223 043 868 387 704 007 101 526 858 283 397 382 706 833 183 838 016 866 283 609 399 265 299 526 026 127 806 931 666 482 122 220 974 316 501 872 088 512 170 544 834 590 072 251 285 694 813 318 400 066 364 033 129 683 642 518 809 122 389 504 503 439 712 797 224 494 687 181 404 392 765 232 981 282 803 118 502 207 635 310 110 480 386 713 824 808 668 198 631 100 116 624 434 254 186 924 953 707 924 784 135 801 366 930 915 454 507 172 265 132 682 585 869 769 469 444 087 403 990 349 582 637 935 431 537 777 267 850 676 399 870 092 578 731 355 251 565 503 400 682 048 410 173 517 494 539 004 094 861 744 709 092 949 938 464 847 549 237 648 212 507 233 951 661 679 583 071 564 177 944 055 607 035 195 477 835 126 053 904 717 206 754 308 493 352 646 663 821 290 233 400 668 763 019 180 635 655 204 817 249 072 142 610 608 484 029 506 602 836 824 760 828 356 886 874 811 651 812 919 574 000 294 865 336 645 871 242 140 622 668 753 901 668 097 866 279 839 108 554 019 356 287 540 786 085 401 480 760 496 751 725 230 213 038 539 214 836 567 022 679 612 557 067 501 485 046 537 923 784 465 317 825 023 583 703 902 778 492 004 534 903 053 471 842 900 161 060 201 492 056 945 059 783 131 950 290 493 444 953 976 907 400 095 938 551 761 550 519 026 665 179 496 446 248 230 253 909 671 647 789 768 979 898 216 771 734 921 158 804 278 905 395 804 644 381 626 783 852 583 646 132 314 616 958 589 081 323 073 341 058 560 131 588 825 407 259 626 772 544 239 449 296 714 637 175 948 524 870 114 470 443 831 309 508 819 728 330 684 097 612 059 162 453 669 983 247 488 295 327 706 041 829 829 300 029 156 399 102 804 428 085 272 229 413 568 436 370 409 969 871 027 460 900 359 937 512 331 294 131 305 471 343 540 818 588 184 004 921 207 057 031 093 228 658 742 912 457 859 704 198 319 734 805 085 512 093 200 349 580 369 755 433 579 033 103 193 093 535 346 909 281 219 613 812 375 202 044 723 804 128 237 731 882 586 732 845 436 677 731 808 166 969 640 180 484 597 977 357 560 927 008 610 643 389 930 149 504 842 985 885 448 726 574 460 464 252 079 810 058 735 109 646 931 209 394 610 941 954 446 307 480 715 193 632 668 670 045 751 334 271 926 542 414 108 003 426 365 563 228 793 987 167 840 825 826 677 502 915 938 592 117 801 838 436 790 206 141 785 915 460 237 208 942 871 667 118 203 008 651 633 810 597 992 692 823 302 899 789 289 940 038 444 282 330 565 053 862 983 932 727 610 848 840 331 393 062 033 845 720 347 343 320 492 760 792 410 934 537 119 147 596 861 736 038 606 489 818 606 924 977 677 733 185 602 390 132 105 296 192 902 538 962 178 054 455 158 333 754 166 534 861 247 425 012 158 580 852 330 025 418 990 831 915 029 927 519 124 160 068 216 916 824 659 787 358 382 822 217 418 593 424 149 791 766 444 836 370 123 974 680 441 435 324 928 658 984 076 795 095 060 536 865 243 394 744 422 566 555 414 008 622 379 043 328 318 040 476 828 296 084 154 192 690 878 890 915 139 437 567 835 384 723 019 694 648 734 163 778 378 462 757 018 631 657 339 444 844 872 281 221 513 821 548 693 863 024 912 579 594 170 276 390 870 246 059 499 229 382 530 575 861 660 738 442 916 898 321 758 595 517 976 407 231 979 563 649 580 968 081 634 449 855 838 936 127 172 509 616 372 865 051 235 813 021 427 307 250 874 675 147 077 917 662 566 181 769 569 401 521 294 114 861 755 734 296 496 305 403 331 875 790 849 577 689 736 429 197 811 290 108 366 645 533 984 620 958 616 080 503 744 709 040 471 679 312 027 930 415 726 302 861 800 116 359 985 376 526 080 525 491 211 583 020 406 451 376 772 688 325 047 446 454 092 393 964 049 996 433 591 904 309 203 324 820 950 669 991 667 101 836 545 317 560 010 198 537 380 155 663 474 266 768 173 766 838 124 339 227 649 456 113 183 364 527 442 946 903 577 383 246 320 599 901 455 878 159 458 148 527 897 090 827 692 182 555 094 253 232 587 918 177 014 663 147 414 643 295 206 065 558 796 237 546 552 642 093 390 322 223 440 035 567 353 552 429 597 869 151 711 545 238 198 977 359 606 285 001 071 923 507 539 887 867 047 296 541 824 347 030 731 414 811 707 755 341 285 869 685 031 023 363 722 926 980 860 754 223 403 764 640 187 031 147 293 033 576 494 257 470 757 675 620 775 084 993 876 177 955 226 044 788 164 137 503 746 886 184 818 442 929 726 864 823 152 552 852 122 735 658 005 069 215 026 842 632 581 897 121 663 542 471 861 450 183 301 682 015 941 353 780 888 337 655 526 289 314 913 958 683 277 260 951 977 251 343 620 181 239 198 361 139 637 255 851 261 425 839 316 495 935 444 188 172 523 248 044 650 868 897 953 670 654 418 196 267 534 939 389 471 965 510 641 161 810 489 352 774 188 784 030 463 665 237 173 602 412 237 875 322 588 904 138 287 212 059 441 595 722 839 618 880 948 245 575 768 048 651 661 567 143 432 454 476 604 802 258 197 451 339 839 218 445 334 340 467 841 413 468 134 206 015 541 085 573 523 893 323 121 861 826 983 280 075 896 791 141 759 884 061 441 755 092 159 365 329 307 412 990 158 513 369 107 129 918 508 558 398 096 171 803 132 984 955 040 909 943 253 878 441 175 533 233 041 270 625 173 974 414 936 583 037 249 083 048 177 065 306 925 897 600 888 679 466 884 231 771 819 251 476 755 771 260 665 645 842 412 928 133 131 128 659 516 901 239 539 898 869 488 486 933 466 760 567 706 388 905 650 729 329 879 835 536 714 363 076 305 746 686 625 624 990 898 669 007 963 436 703 409 534 366 640 440 245 188 412 454 028 242 739 141 801 050 954 759 533 083 432 984 571 788 247 699 783 632 629 244 095 783 219 362 493 857 505 213 887 974 134 803 634 067 990 805 398 636 518 519 789 687 782 439 018 022 143 710 706 290 895 181 064 892 457 797 921 788 185 876 105 994 861 072 417 271 940 721 865 711 556 586 163 740 603 733 231 927 055 643 994 204 754 054 184 932 613 379 534 951 833 695 656 221 273 241 616 767 864 227 292 119 970 262 428 473 862 735 994 590 200 448 762 757 249 275 207 208 724 221 550 846 662 141 024 064 960 502 014 436 151 978 174 953 718 251 609 840 859 849 997 592 522 844 438 062 982 018 927 173 702 587 877 213 079 588 352 249 856 923 801 524 032 043 228 037 819 067 003 407 038 942 381 472 824 663 191 500 833 707 340 871 281 162 375 071 639 911 565 130 602 581 642 048 165 747 764 669 426 838 643 593 085 883 512 547 560 297 324 740 448 270 616 490 903 118 928 625 313 011 275 686 418 627 899 455 224 157 428 336 997 651 957 311 377 791 881 623 905 069 061 636 937 248 184 980 968 010 762 169 026 686 440 921 463 529 315 196 586 583 069 146 436 879 008 823 547 334 259 543 063 999 446 612 803 744 438 333 487 857 980 138 888 710 088 207 717 466 608 425 835 359 066 889 789 164 025 249 739 888 909 114 976 214 810 180 801 512 168 359 158 385 872 414 416 296 219 560 057 222 026 672 597 573 534 491 287 020 397 271 423 855 982 068 066 832 004 791 070 105 603 033 723 192 959 154 330 895 232 321 057 480 743 073 540 281 900 243 648 786 569 848 207 509 219 528 595 872 554 876 342 670 818 087 979 690 533 219 679 506 454 839 089 025 329 363 104 879 226 539 927 335 777 345 284 477 274 939 987 510 969 232 509 923 036 172 544 574 298 191 637 396 677 500 258 106 255 617 127 195 323 556 839 732 951 309 311 608 870 147 653 395 431 176 050 208 063 486 073 490 588 532 425 434 121 974 466 025 281 966 761 067 834 247 567 837 646 700 471 303 959 424 369 690 715 826 553 870 686 497 664 368 756 845 848 563 847 547 476 967 232 663 670 849 943 255 281 217 049 283 616 851 003 165 560 075 928 388 372 316 021 407 499 477 262 190 880 166 282 714 958 499 230 586 612 085 032 979 264 570 741 867 616 478 293 579 735 965 220 464 214 879 190 653 955 136 454 366 233 770 328 575 521 175 759 412 845 002 051 225 493 547 095 001 733 055 804 514 056 081 178 865 388 388 601 765 943 128 551 553 992 386 119 750 651 967 254 170 704 739 083 352 654 359 930 181 570 670 081 964 130 577 618 253 902 523 956 823 123 459 469 049 422 347 012 695 501 622 662 991 518 698 326 377 262 121 731 732 854 533 421 945 943 248 133 338 463 961 971 883 222 992 005 438 429 369 217 993 053 310 495 844 206 986 429 509 673 935 068 392 173 449 952 934 577 360 988 940 073 174 683 096 888 386 541 615 131 638 713 761 422 250 842 645 745 212 603 333 756 748 674 649 199 923 166 205 356 509 896 464 542 624 816 057 332 868 114 171 755 483 996 997 738 521 689 964 866 709 181 808 533 036 888 560 880 004 903 043 827 559 434 636 574 888 301 638 220 416 657 014 726 750 128 245 293 421 020 695 331 066 954 576 731 639 180 553 257 302 284 548 175 829 779 148 036 342 105 519 482 879 994 581 450 765 216 464 308 546 836 029 169 752 514 177 345 024 745 629 353 386 618 200 833 342 964 825 482 287 445 770 564 075 598 622 624 140 488 610 025 357 210 735 507 821 465 930 677 434 998 663 977 133 895 708 733 360 621 610 261 741 839 601 253 932 500 949 811 543 965 154 925 873 270 348 504 399 026 181 774 623 551 186 357 259 139 937 513 638 450 853 464 150 661 102 242 379 802 013 875 680 972 256 218 284 623 231 967 040 143 996 901 278 146 363 580 687 235 880 940 079 391 710 192 754 539 649 738 558 651 188 950 839 492 648 669 377 955 953 380 886 552 996 657 062 361 796 768 387 195 309 481 337 058 986 195 578 323 020 234 515 882 579 454 466 299 714 402 781 424 349 784 455 265 269 678 303 188 698 603 893 545 062 904 285 214 448 190 500 117 180 453 024 183 014 897 501 768 611 481 080 450 092 603 994 099 507 528 822 009 304 214 806 487 290 683 578 029 294 949 328 954 887 482 870 909 863 248 301 505 087 530 547 931 807 036 672 240 641 800 190 237 381 417 850 815 656 074 714 267 571 864 096 515 004 591 498 962 819 272 772 643 939 845 609 562 234 984 901 848 795 561 059 587 610 374 062 581 081 332 866 759 598 935 675 116 781 878 396 462 382 035 333 238 062 179 602 040 324 953 644 828 929 068 911 535 297 294 254 686 021 115 793 360 795 359 028 519 722 812 469 647 867 658 304 304 810 068 514 920 109 517 483 842 148 516 645 079 323 678 546 590 860 668 673 631 612 991 676 547 108 036 957 523 816 756 055 916 803 463 066 094 055 086 283 238 096 498 005 570 590 637 361 630 277 257 805 093 257 897 593 741 950 618 514 793 137 646 645 888 871 216 782 081 703 336 563 375 228 987 610 253 309 769 535 627 087 897 676 459 735 825 526 779 816 103 098 457 290 879 077 929 412 450 363 129 557 871 172 695 135 709 389 266 828 899 690 959 096 742 054 351 839 458 415 724 265 757 982 217 323 069 357 709 262 399 086 834 423 110 681 272 367 344 547 264 928 704 177 035 124 661 131 104 059 429 564 341 199 546 541 216 371 179 950 345 842 917 224 714 674 557 812 190 955 496 615 001 618 630 966 845 622 186 947 515 595 752 126 537 293 269 797 030 693 549 297 246 811 125 426 710 550 512 986 071 874 134 807 030 382 876 501 922 875 125 589 085 673 949 377 798 438 275 525 862 325 748 461 430 420 346 585 167 993 300 742 319 404 909 207 219 378 729 754 651 595 200 384 415 140 668 839 980 809 445 010 988 384 747 186 358 533 030 798 896 175 154 269 048 203 582 577 219 031 530 478 889 091 675 142 772 851 217 529 754 244 690 037 702 326 378 297 348 338 391 267 324 769 989 237 602 593 179 732 161 979 129 355 741 831 515 122 029 073 313 590 682 273 280 086 677 617 385 269 835 545 140 008 085 385 030 511 513 462 038 586 976 028 106 823 411 834 948 798 798 200 633 243 461 923 495 616 339 916 785 402 946 234 787 001 679 271 195 555 164 079 521 097 261 899 239 769 385 785 406 290 434 245 315 877 547 079 052 485 107 056 727 620 731 782 263 435 821 585 014 168 894 161 870 493 749 642 559 438 296 888 620 576 549 698 666 801 293 143 521 931 638 541 645 810 025 004 947 353 475 038 398 523 380 462 885 239 039 326 185 142 376 842 294 122 297 740 191 822 393 115 583 831 899 473 831 229 331 911 776 076 895 700 372 900 722 527 367 587 973 242 235 722 315 616 140 086 386 990 014 124 902 909 060 702 385 948 560 016 373 912 556 424 648 872 814 212 972 051 476 217 256 944 984 225 926 609 940 484 694 143 057 515 929 849 135 593 439 526 124 315 212 836 874 068 994 769 470 345 567 399 225 354 133 053 485 122 633 773 284 296 282 742 816 515 555 289 006 320 864 251 905 206 596 661 977 840 879 541 837 839 135 382 939 312 153 771 361 106 995 219 744 545 049 769 301 388 848 944 231 402 405 230 494 386 080 850 180 763 479 997 056 637 473 300 449 796 634 966 896 469 568 003 164 449 856 462 965 910 889 887 067 169 121 992 633 144 744 038 481 580 845 661 345 892 230 122 549 063 048 141 932 923 290 879 941 079 618 889 024 747 996 481 109 900 894 255 399 098 448 420 888 505 227 081 159 545 030 935 845 004 806 347 397 325 390 261 375 102 833 851 953 867 684 331 893 585 378 288 273 635 209 662 286 800 182 994 877 225 800 048 482 765 034 115 460 464 373 977 714 226 790 482 647 980 033 555 247 827 640 180 607 157 142 605 129 213 247 207 716 611 797 788 342 487 734 438 320 651 384 032 371 321 447 286 868 897 583 692 281 508 366 055 321 368 532 576 591 885 260 517 665 707 596 379 392 764 113 425 729 957 188 496 871 762 555 445 574 580 082 494 703 583 581 056 405 795 741 879 468 929 983 340 109 372 898 380 988 932 035 102 029 188 431 895 596 926 252 183 593 659 953 200 249 166 854 732 959 862 305 958 010 578 114 649 034 741 145 209 485 087 062 387 817 387 675 136 626 954 650 004 801 555 340 949 415 317 793 170 011 372 097 163 158 682 771 556 334 361 097 071 452 384 285 200 987 194 514 182 792 740 165 856 704 720 913 236 378 382 005 271 521 561 399 017 642 821 875 730 434 203 481 084 239 205 572 397 499 085 478 900 044 453 489 025 725 342 455 152 811 281 292 461 412 866 353 708 496 113 143 412 198 507 042 355 169 095 086 605 913 395 205 037 829 566 551 896 262 871 855 448 658 998 794 692 023 829 107 778 130 165 700 853 982 672 287 481 872 814 951 110 529 934 586 535 657 711 645 474 657 006 941 427 727 612 232 929 129 700 620 043 900 656 752 066 740 729 270 633 709 000 959 221 414 234 753 299 208 882 685 621 442 964 345 725 968 618 471 434 347 008 280 659 458 134 689 630 069 151 936 753 736 187 220 263 358 228 432 097 186 031 139 242 666 918 416 601 786 384 041 314 272 536 805 174 808 770 511 743 262 411 141 387 557 617 871 133 221 782 566 416 458 337 821 763 938 815 885 544 045 950 046 464 648 032 849 227 899 764 953 780 292 180 419 646 743 747 283 599 138 123 406 610 369 089 244 410 578 230 568 665 947 101 596 114 013 309 558 016 289 062 711 562 777 338 573 339 945 594 990 516 682 056 759 285 146 677 305 489 102 603 328 306 834 024 817 582 305 072 792 104 533 223 526 694 904 528 533 783 059 115 726 941 889 225 210 911 093 151 194 254 315 632 002 227 429 268 585 004 026 688 998 338 944 556 575 395 250 921 224 146 438 366 712 987 051 832 460 292 482 183 413 239 726 259 604 387 739 882 410 421 237 955 888 037 296 689 577 619 244 683 897 463 065 023 675 734 601 111 800 209 970 338 309 981 595 783 359 546 676 642 998 765 128 609 700 463 830 406 219 104 474 498 133 086 630 926 121 954 098 563 458 538 301 361 605 842 498 397 169 815 050 570 934 308 757 503 215 330 407 008 788 410 248 214 973 342 986 410 591 742 158 673 033 623 536 004 600 125 722 524 648 745 845 352 515 408 870 962 093 595 663 805 457 067 714 773 961 720 338 199 934 637 920 305 863 992 083 626 220 476 586 650 432 877 116 789 866 061 982 769 759 101 639 201 098 485 531 018 256 201 880 465 341 823 804 124 896 496 939 693 912 481 131 116 087 351 458 869 153 659 225 257 913 170 253 114 788 756 584 381 617 651 113 379 711 310 762 308 623 604 491 335 304 929 039 735 642 606 476 525 034 850 054 571 705 855 409 037 325 644 668 646 533 426 946 148 017 892 495 872 932 250 693 305 392 149 475 752 974 703 447 704 933 488 208 202 819 735 302 906 280 342 045 020 211 632 341 282 949 897 686 592 473 888 462 962 969 890 165 350 350 492 308 717 855 281 505 775 348 741 269 300 427 123 253 106 895 794 557 749 599 525 560 282 875 999 579 584 363 563 329 003 362 735 891 794 239 489 244 157 520 409 869 566 379 123 433 590 813 922 161 464 516 177 966 813 492 621 380 880 325 029 820 668 687 820 689 792 513 553 247 440 137 805 895 420 975 219 606 255 300 824 207 996 676 868 788 588 138 858 426 385 641 697 003 298 509 051 160 758 824 543 760 024 268 789 216 667 519 906 509 248 289 697 217 453 247 453 944 193 068 824 214 545 084 985 829 241 809 697 092 718 719 920 678 683 382 315 060 088 652 625 672 138 827 379 212 510 178 522 437 050 540 689 453 327 589 791 732 521 470 814 168 088 071 429 707 802 148 091 475 501 875 369 687 241 009 076 991 303 643 705 374 742 188 062 006 513 028 611 527 841 000 252 255 040 283 323 357 062 906 274 906 805 390 076 084 218 902 186 929 816 798 125 716 232 867 613 851 801 515 863 408 081 579 044 445 347 861 202 546 906 573 709 819 064 642 954 104 503 542 549 423 951 416 169 988 270 361 904 919 112 367 681 883 300 854 443 381 961 796 235 525 594 511 184 818 512 263 878 718 505 778 880 684 806 246 330 122 847 975 694 472 900 548 620 373 140 079 672 283 854 964 717 457 220 118 414 476 407 161 385 025 010 764 897 617 467 158 132 088 480 404 546 953 049 464 612 868 368 191 370 069 305 508 639 430 907 511 428 230 719 525 621 910 142 681 031 680 269 554 643 689 288 893 996 928 144 925 436 666 911 657 527 213 749 680 133 682 690 942 107 871 388 691 882 652 711 785 966 658 634 801 264 288 974 383 442 569 978 727 209 914 074 097 494 254 637 505 746 104 773 431 646 444 906 943 490 850 386 198 228 938 179 428 948 252 297 111 244 735 132 570 361 867 351 025 183 500 732 342 229 229 298 706 479 140 849 680 708 384 362 088 509 807 102 711 000 549 599 182 527 644 278 892 610 292 668 727 656 876 685 112 419 436 517 400 138 032 635 927 827 426 455 633 331 097 793 375 328 671 469 037 286 253 646 065 885 310 610 213 803 902 163 034 295 833 577 706 561 873 065 948 249 139 680 979 399 309 711 575 098 168 452 466 691 206 681 952 492 973 025 057 654 840 102 135 325 194 096 506 638 586 373 058 167 130 982 941 960 343 487 132 993 286 403 818 628 493 094 194 848 608 420 480 949 281 504 305 093 449 817 732 506 384 833 128 364 114 554 235 729 002 723 745 367 676 100 932 160 522 660 490 964 009 185 032 704 733 334 801 821 283 676 228 731 224 191 431 967 975 764 753 857 864 775 443 398 000 788 478 570 355 342 393 883 280 942 779 484 817 773 614 726 930 673 443 810 547 237 421 345 406 163 617 610 052 893 220 381 078 042 926 180 918 647 705 435 335 923 305 049 852 288 388 354 186 212 220 709 245 529 474 373 371 971 643 573 204 221 870 279 041 075 191 913 587 460 201 002 547 396 897 821 050 962 140 485 702 919 871 276 633 825 921 994 401 930 539 748 029 584 551 390 442 616 502 546 292 290 994 947 936 711 029 098 876 849 815 852 377 013 852 973 556 797 052 172 842 255 557 994 841 571 850 530 392 496 977 946 036 771 359 596 603 630 917 953 071 390 624 813 805 819 202 215 720 136 996 017 717 351 759 272 763 139 367 386 153 434 802 029 634 553 997 847 103 888 065 011 489 861 985 767 660 114 998 053 063 431 889 025 655 129 607 313 617 824 591 557 780 521 691 644 942 518 975 844 031 576 511 534 215 397 682 331 250 266 679 910 932 036 522 838 686 288 315 388 504 827 682 463 758 681 953 613 917 523 952 682 920 837 796 451 877 163 285 006 701 037 473 412 973 208 981 472 159 387 626 292 811 114 087 303 271 281 545 697 467 866 601 106 582 911 121 704 842 502 211 192 593 842 437 174 702 671 263 353 057 578 159 176 657 157 931 341 519 191 871 473 210 091 441 636 628 435 384 859 497 186 448 202 743 795 211 712 733 305 767 496 143 233 178 795 680 916 735 505 228 452 676 233 224 279 817 905 022 724 238 345 618 274 318 732 824 993 107 261 349 308 715 338 517 844 763 793 522 043 113 741 118 040 119 242 193 649 121 390 314 326 434 459 062 323 711 225 235 793 360 388 422 738 080 689 587 131 356 293 174 436 334 552 128 669 157 903 332 134 103 021 996 281 551 169 978 871 428 505 032 857 515 490 677 330 084 019 954 298 621 580 973 539 334 454 407 280 930 714 892 256 458 713 148 282 449 090 164 469 149 351 348 886 070 493 725 117 587 908 665 864 397 282 502 929 819 121 941 348 610 636 859 310 219 748 841 013 345 437 695 177 608 444 519 274 433 749 729 672 935 611 545 227 905 604 686 810 674 446 703 255 072 691 239 668 666 632 247 283 128 309 950 226 018 966 329 611 552 291 452 388 327 600 544 721 649 761 531 630 987 683 549 730 245 834 249 845 880 674 382 989 444 417 762 269 668 404 019 238 071 078 225 162 473 674 270 535 171 690 503 811 454 106 344 637 047 082 764 814 339 560 477 563 576 448 395 679 930 211 747 167 734 078 533 451 147 122 672 398 922 306 664 727 867 962 454 399 093 742 032 626 020 503 103 507 949 042 600 426 767 091 819 909 132 690 497 212 233 444 146 510 126 881 226 927 193 293 246 732 774 100 721 549 040 494 711 452 548 605 226 470 169 134 207 736 862 731 566 365 998 658 275 092 075 678 739 824 463 962 510 031 778 244 285 063 671 320 003 173 110 836 448 153 654 822 564 316 219 206 547 664 336 352 505 252 381 656 982 274 042 504 079 351 658 299 272 274 398 418 172 063 057 075 415 562 387 420 472 145 232 244 468 427 373 847 480 082 942 729 093 299 875 607 605 881 732 877 204 837 862 281 641 760 829 524 827 225 081 298 219 031 721 778 381 040 285 984 722 008 693 087 991 863 622 140 545 673 190 022 419 852 225 378 310 623 293 627 338 615 971 914 622 263 914 578 704 547 572 341 230 041 156 279 258 485 076 828 488 998 048 594 145 223 594 190 303 061 934 291 476 145 658 275 601 172 546 103 358 367 519 457 316 003 445 453 106 171 497 537 454 296 309 120 972 499 863 048 735 978 509 978 433 834 001 352 892 975 039 525 031 434 042 987 572 774 060 179 807 193 777 352 689 570 857 324 276 298 984 228 096 369 122 094 301 439 843 475 967 225 024 665 888 196 444 156 337 077 571 217 555 168 219 211 642 873 851 810 503 085 936 550 426 824 408 122 415 843 351 209 213 252 143 012 454 367 493 186 867 720 896 829 347 203 937 637 529 367 231 575 261 451 732 659 139 250 169 871 945 562 393 994 661 167 186 167 574 790 045 417 365 343 092 811 763 361 986 398 584 537 521 752 767 165 146 751 795 886 101 798 478 428 123 247 121 163 171 075 474 572 852 310 835 591 511 880 805 102 615 260 234 390 027 953 127 607 333 051 375 446 489 831 355 967 734 750 650 189 001 376 325 732 870 569 124 697 809 737 837 544 701 558 844 713 789 799 627 790 606 310 855 388 079 115 489 788 140 386 080 911 077 993 238 191 167 918 236 715 357 671 803 745 655 234 508 905 756 032 608 247 097 513 155 320 199 918 611 217 587 851 226 452 892 013 936 420 618 798 074 944 343 998 345 852 728 517 082 218 313 415 198 729 212 020 666 884 039 411 046 209 444 918 439 424 009 273 286 870 116 833 228 713 044 167 229 176 967 672 261 220 814 624 392 233 011 012 599 596 455 644 955 864 694 006 817 029 892 431 216 165 918 359 917 530 483 141 533 839 428 311 801 074 372 775 409 723 583 221 778 355 974 347 450 053 937 900 721 690 266 689 141 859 449 135 239 789 327 432 254 540 198 454 268 790 439 848 193 422 731 752 451 122 037 419 096 597 464 467 131 102 645 342 093 461 365 329 226 990 975 972 051 670 093 958 121 945 555 622 289 041 459 714 901 311 220 354 979 874 205 085 657 811 312 522 389 991 404 051 395 947 677 419 645 421 513 497 814 404 324 601 355 115 997 969 350 954 685 939 094 463 353 035 187 616 485 771 498 159 564 318 823 834 402 674 578 697 736 351 364 998 963 462 718 806 549 763 599 599 278 432 573 472 280 568 574 701 065 218 419 943 732 203 296 943 591 472 084 737 089 376 739 479 656 376 704 174 486 696 805 964 302 718 148 109 000 959 925 446 096 711 664 281 331 128 745 904 796 278 704 443 049 057 893 989 892 950 310 190 034 782 575 022 255 229 677 388 910 155 954 106 644 811 758 094 631 080 968 373 288 400 204 669 200 971 672 794 217 735 973 821 550 376 396 915 093 834 201 321 822 099 766 282 379 522 111 607 795 364 389 837 048 388 003 849 319 848 874 524 967 581 811 295 673 599 628 442 423 293 712 460 544 412 828 383 686 371 884 088 234 550 986 101 551 636 269 908 532 437 655 392 608 664 195 262 620 714 849 660 562 296 599 587 587 265 253 683 741 875 449 677 449 171 549 079 727 413 213 611 237 531 930 839 776 200 732 219 958 812 356 490 832 358 151 567 234 307 381 066 894 564 897 717 960 971 576 756 271 989 230 160 375 610 152 383 452 787 880 289 260 559 214 963 521 587 203 812 836 461 380 566 291 089 890 948 999 529 429 627 453 640 025 387 478 605 163 817 168 886 051 662 908 702 269 227 749 365 689 357 173 459 449 108 672 626 628 417 744 161 061 597 270 320 968 706 455 970 556 958 505 029 142 658 028 754 925 543 141 395 608 859 423 376 741 776 926 590 221 580 227 523 103 666 330 377 916 258 061 552 882 368 018 632 275 177 526 194 908 774 288 334 544 239 737 207 434 740 176 951 935 123 971 931 602 633 719 307 025 761 158 863 240 357 635 008 504 360 693 771 443 876 423 686 944 928 286 278 418 314 370 493 280 552 156 337 254 132 883 855 348 908 653 465 146 838 000 733 672 705 094 249 668 797 319 876 817 644 695 943 515 072 003 572 770 391 795 675 340 040 649 428 215 301 609 882 866 245 165 751 836 699 985 225 425 590 340 013 964 717 092 792 188 186 327 373 311 695 879 475 187 245 655 374 867 144 569 860 037 424 408 025 924 768 443 262 370 561 662 985 069 763 268 226 024 917 007 728 366 608 622 183 773 014 707 251 937 586 548 155 102 331 829 388 442 923 841 262 684 248 193 610 645 840 687 251 194 678 302 837 793 933 893 507 366 785 545 799 288 285 854 982 300 250 129 781 695 824 005 143 217 333 594 127 570 353 489 783 739 802 685 316 688 527 875 906 584 721 991 057 638 989 265 702 452 339 052 327 230 427 162 412 170 241 969 875 454 990 984 365 384 376 574 746 725 346 962 189 142 166 625 509 069 356 200 320 506 023 271 617 003 491 454 357 721 413 729 815 434 938 234 863 554 459 065 415 645 109 815 648 400 216 671 761 994 369 251 208 919 180 581 848 049 189 396 300 039 792 704 517 986 579 092 584 515 848 186 732 339 802 204 461 793 578 676 571 016 708 301 554 831 399 931 505 060 269 810 550 255 452 618 703 841 630 416 558 873 793 554 286 810 326 171 401 846 676 646 055 501 783 796 267 469 551 782 606 150 091 997 175 793 051 193 116 400 376 738 734 489 335 043 377 094 134 723 350 685 702 264 559 715 084 245 719 111 483 474 352 042 049 201 920 069 588 497 264 839 900 273 407 827 136 235 987 562 458 925 718 933 409 832 693 197 650 481 734 026 265 134 369 467 301 756 195 730 651 103 616 104 176 770 942 927 329 387 503 720 441 562 676 909 304 006 739 101 259 844 520 422 777 170 266 943 530 483 924 044 920 636 570 733 391 072 284 847 443 565 598 705 719 248 020 722 378 646 842 763 935 762 144 554 375 186 577 425 449 067 223 608 095 689 550 264 680 328 886 983 007 219 768 058 409 522 257 125 606 449 278 058 510 846 909 681 082 536 529 289 687 521 854 189 559 224 645 199 862 123 677 817 795 784 469 213 496 181 755 637 713 827 812 315 398 436 811 373 587 187 911 486 679 950 404 955 921 768 664 319 924 895 145 966 129 973 595 990 019 403 432 688 646 225 653 951 177 330 370 869 928 894 298 595 937 032 599 672 069 098 054 604 553 480 565 728 705 103 729 832 277 341 174 394 940 583 868 036 062 097 245 619 550 347 975 270 553 438 693 277 323 363 858 605 710 835 622 749 318 429 341 870 125 030 694 786 717 031 874 667 479 317 473 466 253 696 397 007 843 261 153 130 577 103 798 107 353 742 242 560 306 571 556 591 700 851 923 443 802 504 653 729 841 561 473 929 663 397 421 854 829 327 709 333 557 295 094 781 757 127 739 278 161 125 270 333 523 320 173 381 440 340 794 667 090 828 453 139 727 053 111 515 930 219 491 461 364 204 165 338 247 645 672 620 181 149 745 616 288 754 014 027 603 041 345 065 032 499 217 186 554 787 752 110 298 232 684 700 830 811 104 467 219 515 759 995 943 364 609 665 737 943 558 882 817 176 153 056 696 362 804 602 400 318 304 886 845 154 418 729 224 582 848 924 962 697 898 230 151 348 559 117 080 546 303 791 483 265 970 434 804 320 948 256 745 359 120 558 477 651 572 583 159 287 464 899 469 518 209 193 736 392 558 143 185 292 130 318 843 127 017 187 857 367 405 314 589 901 661 071 858 959 418 872 933 745 904 978 613 691 377 368 412 187 794 772 037 045 958 755 516 658 381 402 298 888 119 685 864 619 248 810 306 179 188 924 016 758 212 312 207 311 440 171 893 291 661 029 673 443 515 860 919 279 258 746 500 295 792 120 430 642 417 035 723 920 397 931 507 437 501 802 457 981 001 813 701 117 217 574 312 428 837 388 698 383 493 524 806 688 986 906 530 642 909 031 489 470 115 571 809 184 972 104 232 239 784 301 365 202 071 992 676 566 965 369 963 351 394 605 645 013 272 814 883 368 278 747 287 787 014 164 046 284 506 713 021 107 159 892 470 198 927 332 141 138 954 502 239 123 084 620 030 286 970 491 187 519 835 262 171 397 006 081 058 546 286 811 386 445 271 228 577 805 806 655 624 577 289 496 811 575 607 608 856 124 558 185 461 475 802 230 218 324 349 539 842 124 760 582 975 900 994 996 677 685 833 473 546 406 147 617 612 915 463 055 137 145 639 562 882 037 912 181 881 818 404 145 636 982 110 196 527 594 209 932 105 395 742 267 289 981 501 445 477 537 011 641 531 708 843 473 467 716 816 173 660 108 870 620 028 297 762 427 891 355 857 677 950 956 702 691 183 559 812 924 775 483 604 677 222 110 020 504 407 065 321 564 844 010 001 557 493 688 155 117 589 135 859 468 244 135 817 029 676 967 002 046 798 911 339 818 119 518 771 484 269 062 235 290 390 251 730 736 793 599 139 853 747 011 070 741 710 078 821 709 762 293 172 278 816 694 773 652 866 779 115 073 847 274 666 665 728 745 128 172 621 945 826 421 178 677 398 556 664 934 326 314 459 646 972 913 623 524 663 337 837 842 858 415 289 994 992 041 132 046 344 550 106 081 445 356 760 524 281 973 128 704 492 928 337 235 826 907 560 282 864 458 920 512 885 059 959 380 854 722 875 656 655 485 833 168 668 515 055 018 583 672 290 308 793 493 967 944 294 308 657 020 161 214 326 426 518 656 325 166 666 242 167 671 664 954 235 658 919 104 508 854 187 231 886 040 028 202 116 074 081 555 824 237 048 715 278 436 287 217 285 100 648 266 636 281 400 685 942 858 551 079 228 958 749 031 193 332 501 389 259 203 666 599 486 021 865 239 040 455 043 993 066 606 496 654 729 457 173 451 012 046 410 734 821 318 443 376 829 201 135 956 667 665 203 043 894 928 904 927 360 981 303 152 682 360 082 397 845 320 916 398 293 882 277 912 972 119 610 038 977 393 381 270 160 248 618 628 869 626 317 072 133 582 129 370 614 568 735 985 596 476 319 939 538 701 229 055 733 789 928 854 471 456 315 594 002 913 188 629 082 845 450 986 731 250 249 586 003 148 512 624 732 804 692 221 649 468 867 815 008 381 636 950 944 729 446 229 281 541 648 390 203 036 801 669 827 684 653 049 073 203 664 320 319 271 181 911 588 791 055 118 461 311 911 598 335 096 473 929 798 268 025 070 615 858 145 871 068 018 222 709 256 160 899 711 123 919 623 730 062 136 259 805 433 097 645 265 671 308 786 778 605 308 813 277 039 152 491 760 017 626 282 993 970 598 416 816 220 220 398 753 166 370 065 438 281 869 427 041 394 560 369 658 332 039 569 062 755 719 580 385 590 832 015 406 606 220 239 513 546 673 737 676 898 924 018 720 463 662 068 976 693 837 527 988 245 778 559 037 086 401 541 113 314 548 503 418 578 878 776 180 436 865 700 566 293 546 556 682 797 074 438 704 783 589 302 425 924 965 736 057 271 630 927 497 523 198 551 570 752 041 769 298 420 405 567 114 207 609 197 850 461 718 519 781 295 571 440 657 560 605 634 234 415 599 123 092 685 091 740 459 788 050 178 891 434 934 149 759 407 464 824 433 481 459 813 632 582 641 726 104 677 001 992 032 241 762 613 638 878 874 708 452 262 123 147 354 310 450 266 352 473 099 587 459 825 725 328 590 612 016 642 700 194 183 189 373 320 068 297 007 115 401 181 713 562 567 400 832 229 428 854 160 895 412 894 061 355 383 311 402 216 879 096 812 207 827 457 351 601 999 794 109 214 184 581 574 743 668 830 694 628 739 811 719 993 725 947 751 086 869 037 862 826 612 134 702 363 233 347 280 770 435 826 906 639 472 476 032 011 314 858 800 707 315 403 018 682 174 029 044 219 590 755 883 121 164 718 562 965 476 599 357 729 170 591 989 936 778 799 312 371 096 230 556 513 691 790 642 942 768 796 361 637 288 820 451 840 773 028 131 205 290 611 395 251 080 287 971 621 364 635 705 894 446 920 573 482 574 123 666 867 930 608 601 132 913 341 842 189 245 299 813 387 595 986 396 269 938 931 314 874 206 153 043 552 171 948 769 830 469 757 147 718 913 065 465 946 723 997 280 268 375 377 237 090 290 767 161 341 848 007 646 648 881 777 219 839 389 244 276 788 977 907 409 206 415 732 269 121 833 846 064 484 330 293 692 165 381 820 277 602 588 886 796 869 784 571 563 887 696 166 983 011 794 065 666 933 988 314 383 563 662 654 735 586 226 709 727 118 343 668 573 737 501 905 758 973 603 598 147 043 956 158 677 211 037 014 363 638 301 125 085 135 740 930 464 317 929 649 337 959 303 945 247 159 062 747 434 450 838 984 104 496 761 032 740 597 271 259 433 470 220 158 514 394 775 600 565 796 002 678 217 441 132 432 518 931 388 909 292 946 278 146 403 167 402 544 695 983 318 742 641 609 890 413 270 202 431 722 006 925 816 896 555 925 990 091 551 504 732 932 495 297 084 101 351 167 196 743 327 220 823 128 567 609 985 938 942 364 573 795 264 827 093 339 575 420 013 743 013 430 825 273 684 409 000 105 445 747 706 086 917 183 263 675 651 611 850 274 751 746 701 754 889 423 169 866 332 515 668 356 425 838 364 038 908 137 280 153 275 352 978 111 836 175 196 610 377 343 630 669 640 908 470 956 978 848 595 860 269 895 967 160 001 244 333 838 109 700 515 409 438 809 014 308 015 860 544 624 646 783 785 521 123 427 350 114 010 958 952 744 362 445 579 602 747 371 773 664 570 927 491 348 492 572 443 576 471 334 008 191 429 479 458 584 581 057 687 434 726 909 442 384 787 791 204 507 396 136 413 514 164 911 686 873 441 088 372 778 033 884 963 520 334 570 069 936 236 738 369 849 787 447 061 796 492 335 827 929 309 962 066 513 564 808 768 515 154 319 509 726 396 250 993 507 135 633 093 925 089 378 823 358 296 736 986 783 438 483 288 389 156 725 809 086 256 635 922 029 739 907 738 246 013 956 077 111 807 516 537 498 239 256 401 167 238 362 696 807 189 177 663 374 120 155 345 040 791 669 648 162 456 553 150 918 880 482 828 689 866 994 741 393 595 146 677 156 245 726 729 525 426 651 119 675 981 276 142 724 070 436 991 754 615 508 758 401 297 644 317 168 427 419 281 529 463 361 261 241 202 250 673 539 322 285 778 205 644 894 657 013 606 246 589 982 569 612 126 165 269 672 270 055 316 956 911 750 254 623 777 425 458 297 893 594 274 214 181 917 019 850 932 509 709 380 066 535 613 486 621 517 161 936 697 912 003 370 137 289 396 172 503 888 205 076 771 078 357 955 545 575 044 788 117 283 529 350 841 135 039 471 325 297 382 522 374 948 196 623 679 067 629 117 877 078 386 687 208 064 363 698 799 317 616 432 767 342 126 669 826 279 684 875 178 519 356 392 881 104 344 150 787 316 706 010 096 320 219 568 212 968 282 885 789 909 445 020 371 351 560 216 877 877 286 875 870 547 946 609 554 848 758 113 657 860 574 971 865 564 339 543 285 488 435 586 269 465 702 280 105 484 270 373 039 712 130 504 413 896 002 660 517 610 284 467 990 492 792 915 229 015 412 863 847 623 476 267 015 224 241 377 682 677 918 854 144 705 594 721 610 042 175 251 850 578 569 378 601 936 216 093 860 794 171 825 739 102 058 104 118 308 309 390 313 832 555 993 549 744 988 146 163 255 609 212 019 178 049 466 676 902 697 094 649 815 352 965 657 787 553 515 545 055 245 077 099 114 415 620 191 582 060 830 392 627 314 907 362 330 899 665 555 971 330 545 560 974 258 952 322 712 699 558 704 635 508 265 179 118 494 505 606 562 159 823 459 670 966 666 116 125 983 498 007 190 106 717 392 284 243 286 597 671 838 400 085 760 973 975 916 000 601 395 642 067 847 260 769 112 215 378 402 953 772 846 412 714 949 265 025 237 520 686 335 089 106 853 338 284 823 437 015 784 945 169 528 422 484 392 314 127 752 599 252 552 202 520 256 173 061 798 543 797 523 882 154 856 869 346 682 690 868 268 904 437 661 848 114 841 984 878 301 556 599 668 314 107 198 362 105 820 283 357 101 402 383 417 359 683 638 009 681 073 855 778 838 444 154 154 454 722 198 292 117 778 260 248 418 752 641 513 269 877 169 691 215 354 500 785 810 832 059 344 995 179 392 047 898 389 634 929 492 560 863 176 955 762 423 596 928 326 249 594 254 164 623 347 963 268 076 533 806 538 613 621 360 184 446 901 675 461 753 036 655 435 507 662 996 124 449 586 496 600 065 789 430 658 843 173 155 684 976 535 794 923 475 944 461 310 855 760 074 922 922 528 574 679 867 938 477 450 048 056 805 573 060 554 054 255 476 878 930 887 690 282 259 775 423 327 635 285 884 278 246 785 602 770 629 848 995 621 486 036 930 726 732 906 313 494 018 557 810 219 234 014 539 914 947 170 034 087 549 984 648 359 942 703 298 643 420 017 984 150 595 239 080 251 612 684 203 696 864 142 601 082 197 839 108 956 811 815 332 040 474 803 824 585 110 254 460 950 885 047 788 954 042 469 258 052 125 263 397 288 787 079 907 846 076 920 193 532 491 338 530 418 241 058 480 338 768 448 172 627 775 762 569 207 211 852 199 068 352 028 341 990 227 248 102 472 558 990 799 450 824 507 993 942 287 587 126 367 360 421 070 908 072 775 986 559 280 781 201 460 668 968 283 608 458 770 337 636 463 078 538 304 232 893 049 954 704 992 228 909 807 659 133 253 060 171 953 191 427 070 118 409 006 502 322 613 059 892 318 029 890 031 655 947 839 544 039 676 820 156 239 693 726 702 606 389 693 475 546 243 275 939 168 589 159 630 587 948 710 099 806 654 827 266 765 074 064 378 697 570 900 025 416 775 571 139 939 113 341 003 132 438 359 886 251 687 771 736 861 165 702 494 002 146 105 973 647 930 643 713 045 682 260 465 596 606 967 696 226 016 573 011 175 188 220 491 968 582 376 969 073 270 740 265 283 228 553 909 861 261 196 237 244 314 213 137 762 678 631 262 664 075 518 517 163 398 315 506 857 872 703 519 945 050 333 509 526 207 998 156 812 229 872 474 667 591 775 970 409 625 962 519 765 670 321 963 000 679 579 261 544 790 028 941 455 672 460 658 151 975 609 824 469 607 115 615 336 485 510 736 223 476 860 716 841 070 575 790 779 777 946 080 533 953 726 300 626 985 622 528 774 529 816 727 312 824 444 035 154 899 684 603 395 536 244 858 409 675 190 659 074 140 176 439 011 929 373 822 345 843 640 584 470 275 022 935 487 365 546 290 058 017 787 840 071 802 505 418 416 572 114 453 540 427 664 883 263 069 388 416 981 055 915 463 652 001 310 198 203 433 659 364 173 958 786 692 285 762 709 646 133 831 032 429 640 129 264 029 120 912 931 138 810 751 197 352 981 469 887 450 469 458 339 529 609 891 342 058 126 688 903 634 450 636 007 029 904 419 777 941 476 601 444 935 718 801 363 450 123 733 052 402 333 044 140 886 358 546 492 971 579 020 587 981 073 812 153 214 469 295 152 865 282 447 965 185 082 358 836 780 454 345 455 367 079 340 597 024 206 471 757 393 443 473 179 021 802 725 159 771 102 364 076 511 075 475 729 661 070 395 094 329 544 385 064 279 488 685 951 605 727 301 898 639 042 342 526 515 301 536 161 972 939 069 412 341 466 279 783 873 819 153 453 115 550 959 255 823 368 950 630 205 838 978 083 472 439 039 332 076 075 851 140 569 272 707 878 685 704 054 789 212 851 951 419 337 662 727 655 990 323 800 156 560 777 720 950 973 874 711 668 516 035 668 077 114 835 596 612 392 844 148 615 185 566 753 214 017 052 210 356 395 015 149 504 103 557 350 293 760 981 816 509 337 838 759 475 844 450 150 929 323 381 985 165 851 146 683 299 359 004 205 711 012 717 005 169 850 815 730 295 461 968 750 835 297 341 650 015 857 390 238 054 074 023 043 456 368 887 259 556 624 074 268 174 364 228 820 156 266 309 185 883 064 319 467 513 034 249 932 925 275 250 169 526 621 709 206 702 767 447 992 801 133 478 575 863 193 992 369 124 970 556 066 275 915 025 710 186 145 786 090 308 910 115 230 751 738 054 506 472 565 346 147 035 983 433 149 147 853 828 778 433 601 159 326 073 992 924 965 436 715 881 981 000 349 510 293 117 976 375 181 114 373 133 625 344 370 066 302 424 677 669 874 328 374 181 509 428 552 595 616 580 969 241 147 253 373 376 477 077 489 805 728 258 461 624 758 635 044 818 940 680 515 553 550 893 076 401 654 773 169 987 626 383 022 015 035 113 163 075 865 415 090 694 438 572 476 442 452 046 939 710 109 348 539 127 995 844 618 867 616 295 811 178 153 282 397 147 519 576 518 120 031 688 963 691 023 591 660 589 510 577 877 860 277 325 044 549 866 468 399 559 477 692 642 851 378 606 674 431 934 708 602 337 425 331 147 785 590 139 638 117 443 658 644 617 716 588 496 167 741 880 203 496 590 547 320 704 812 537 774 305 036 763 196 753 818 391 303 894 647 399 749 138 478 581 748 122 273 306 220 532 914 908 332 664 227 461 814 741 140 185 633 256 791 235 413 324 143 760 463 239 748 482 483 013 018 496 039 343 085 968 960 805 224 223 596 970 788 655 245 934 340 995 214 951 507 152 796 396 954 295 837 129 098 553 947 994 120 444 420 075 219 447 182 760 535 073 688 357 264 068 153 236 641 580 454 571 314 939 692 581 691 926 460 673 188 612 436 826 669 314 814 298 711 239 140 892 507 229 451 590 494 188 862 462 432 963 574 193 617 512 182 663 573 419 771 938 019 911 962 860 066 173 049 635 323 259 491 370 352 903 933 155 451 740 125 945 977 914 174 025 593 552 869 155 056 217 690 240 176 154 835 413 292 711 845 069 162 943 785 474 733 851 898 291 929 658 063 843 710 276 497 127 666 123 086 426 929 876 601 940 028 595 328 555 951 237 875 757 714 212 658 468 031 307 277 477 261 443 216 820 490 507 684 561 863 107 462 225 866 383 314 638 029 552 061 750 032 644 537 878 502 179 379 135 493 099 003 563 711 916 003 155 110 222 347 346 285 663 663 923 293 912 165 668 431 529 305 920 099 216 183 676 095 373 276 098 818 606 479 724 643 923 734 825 399 581 483 144 643 343 309 794 038 498 322 944 810 829 585 673 969 787 588 751 559 671 283 132 821 225 358 851 476 240 447 543 799 497 967 463 281 748 569 556 712 182 300 188 260 895 001 540 428 007 706 888 800 051 365 098 978 744 103 296 427 558 717 434 569 489 741 467 476 689 057 080 276 864 706 207 046 463 379 205 559 964 160 823 030 141 682 392 804 006 385 967 650 812 614 892 972 897 563 308 266 787 885 530 660 772 929 233 499 767 565 476 543 393 471 165 166 577 134 589 197 664 642 716 645 071 872 438 562 685 327 493 363 378 637 941 980 948 534 486 197 041 968 127 393 140 227 625 596 213 821 912 328 986 484 784 230 786 658 474 589 075 838 635 418 600 435 019 556 830 706 658 760 795 220 595 331 154 211 309 057 918 665 852 206 537 783 674 959 204 048 836 218 639 228 391 426 770 081 093 637 225 278 980 422 990 792 473 557 251 636 585 008 939 273 870 681 702 577 709 053 909 813 924 392 026 189 499 496 857 670 565 432 093 145 763 642 226 420 098 077 012 844 037 585 688 699 467 223 767 778 061 177 296 552 407 096 066 658 740 760 408 351 719 308 926 145 922 881 217 876 873 590 834 860 736 329 012 827 452 946 183 567 433 604 131 181 344 542 706 876 613 243 022 861 652 858 127 123 694 210 599 358 951 864 811 700 666 862 028 303 841 591 162 294 109 817 416 105 922 415 458 630 022 454 673 481 748 553 708 048 045 771 519 113 541 138 962 221 209 640 355 272 691 740 216 924 791 879 278 566 202 319 250 731 388 132 070 773 067 264 935 035 441 128 271 353 234 078 160 034 798 211 264 981 542 640 359 605 098 520 376 292 992 367 770 837 138 616 219 178 106 704 534 684 183 395 306 658 908 319 239 918 840 320 963 382 884 886 967 552 019 359 683 332 299 512 194 568 585 436 050 622 479 617 936 524 655 765 717 511 640 470 316 424 463 882 807 624 170 789 298 339 128 066 820 939 337 164 369 566 679 135 555 142 031 595 197 192 399 437 404 586 896 507 216 406 270 314 889 389 693 973 748 858 971 762 916 131 229 954 808 476 849 920 869 226 228 610 443 352 418 347 020 157 999 239 161 524 722 833 405 026 686 945 428 114 575 926 387 665 440 271 774 316 704 388 037 975 555 955 917 180 852 564 757 860 049 073 068 299 350 692 001 513 750 712 862 463 009 103 055 561 119 830 355 254 179 625 876 329 411 787 674 369 804 028 179 744 498 070 423 522 953 409 866 597 136 221 260 127 985 573 770 519 414 927 118 729 734 342 539 143 742 409 665 106 846 338 716 118 951 705 955 933 250 218 094 423 190 254 489 230 298 111 913 164 772 405 956 873 884 173 349 437 089 728 363 378 945 474 187 214 232 692 826 860 329 722 802 632 622 257 074 368 702 243 340 368 458 685 539 498 690 912 799 663 967 434 434 894 840 054 430 857 369 624 849 989 809 690 097 005 606 387 692 065 467 033 322 433 919 786 377 417 239 495 053 535 895 700 707 028 765 355 444 544 357 970 921 555 406 325 239 986 296 631 348 221 049 335 107 515 015 953 258 966 489 259 995 459 692 946 767 458 453 995 811 483 436 090 123 410 706 253 453 659 410 347 276 796 397 969 947 207 468 616 498 159 803 949 155 784 862 265 765 887 451 039 038 871 876 935 571 658 178 790 177 198 628 548 885 139 262 605 342 896 674 974 862 615 471 006 842 816 399 266 610 898 524 500 035 113 611 781 825 011 444 454 118 055 570 178 494 530 308 044 452 572 958 902 478 184 858 303 513 963 547 891 566 626 656 871 849 817 177 413 269 318 128 724 955 678 362 149 409 898 083 909 845 139 497 754 697 779 628 666 701 371 063 163 098 363 258 224 449 085 190 999 010 851 921 148 385 043 615 895 336 005 525 231 546 355 296 945 598 092 447 114 866 961 206 447 535 871 083 146 052 675 490 783 473 282 580 287 908 087 092 034 895 633 462 998 857 570 336 159 336 342 356 929 116 443 981 383 045 477 648 831 590 583 520 861 126 499 170 962 680 892 200 604 978 086 424 112 156 290 773 000 262 788 146 855 448 707 488 882 575 460 803 567 381 932 880 754 948 981 355 140 619 098 898 789 000 080 100 337 791 347 902 003 672 089 813 274 842 563 438 717 734 005 456 300 248 729 018 180 153 094 063 628 581 178 371 121 022 914 953 755 333 451 045 947 935 177 674 261 220 692 145 472 346 541 700 525 100 021 501 804 113 624 110 905 747 412 193 184 264 473 960 100 687 685 165 441 491 862 377 971 545 852 522 092 472 049 715 062 532 070 779 717 796 719 770 917 938 535 232 151 588 898 674 736 260 740 081 847 653 382 746 135 761 888 551 532 245 573 067 851 803 604 983 587 289 176 276 755 883 356 237 866 191 270 372 412 005 734 694 955 781 879 459 752 172 412 596 144 580 739 399 644 553 141 969 187 858 619 630 611 707 384 910 799 351 300 534 851 754 227 526 938 736 175 131 111 822 301 110 201 152 988 348 395 981 732 465 475 498 129 176 539 092 616 043 452 747 128 119 415 954 086 224 622 426 193 683 035 580 570 285 451 559 844 883 099 842 083 392 483 154 899 863 188 747 941 124 681 639 202 177 659 160 837 513 056 800 874 712 074 662 124 393 541 358 823 731 320 462 916 652 233 520 894 224 857 352 939 207 232 602 502 216 638 038 146 549 939 926 704 780 344 717 789 662 510 905 087 089 516 201 182 031 221 870 669 312 703 739 630 288 031 998 055 753 502 672 012 164 347 839 403 305 049 846 113 412 425 187 619 685 376 557 067 998 305 439 011 620 417 245 680 043 277 219 684 651 535 089 929 560 683 570 087 043 282 880 383 208 174 382 066 776 324 507 053 587 484 919 424 817 970 485 127 633 861 905 612 918 160 708 355 871 149 215 032 591 851 361 471 473 226 576 372 964 319 655 015 475 198 652 842 119 188 565 821 199 506 347 666 326 137 754 757 548 422 125 257 848 567 810 167 508 844 816 506 026 273 304 536 867 871 063 189 449 208 770 623 253 874 474 004 058 538 007 731 179 891 883 201 755 817 245 296 597 527 174 594 814 571 913 852 345 530 888 050 580 997 012 932 799 335 020 296 880 434 537 601 726 734 177 964 781 221 478 210 221 069 186 210 907 806 996 107 400 732 703 234 567 242 165 275 287 941 679 444 442 532 452 387 842 070 838 278 082 521 987 115 346 287 517 376 301 928 007 876 173 962 728 341 530 324 598 768 385 187 000 387 847 228 748 036 815 382 651 965 004 102 825 764 114 038 176 767 466 329 371 573 908 744 815 800 591 654 873 927 209 471 912 334 372 616 380 083 107 206 130 519 154 317 904 293 499 680 942 869 269 632 963 836 324 790 580 557 555 823 516 310 799 223 273 218 317 510 354 178 757 910 093 164 066 231 749 044 506 695 134 711 364 873 649 445 068 949 317 461 273 695 834 314 516 324 479 294 964 958 569 252 403 393 598 414 899 130 546 603 335 981 934 735 946 126 320 266 765 412 827 553 730 819 456 974 145 328 028 186 544 682 946 791 461 682 455 302 015 626 769 515 027 610 584 847 534 894 326 420 840 606 659 279 164 082 426 656 516 766 815 949 524 097 088 212 460 885 326 067 464 233 507 326 391 521 932 875 703 678 788 909 364 746 155 596 721 068 991 261 349 226 172 864 728 805 827 452 198 231 810 485 957 118 058 046 142 469 776 154 572 151 351 531 117 380 963 373 514 639 726 258 572 479 516 858 113 924 949 990 312 372 066 954 894 253 448 713 054 753 623 685 399 041 338 570 128 145 644 236 518 803 639 986 065 618 781 188 214 258 145 244 001 898 615 621 314 921 582 246 167 001 313 267 899 090 699 406 150 126 006 025 978 346 680 207 378 753 939 929 601 513 451 540 087 325 198 740 947 234 601 958 462 692 665 897 843 863 993 563 832 520 837 785 808 972 261 198 298 744 711 249 843 872 994 619 794 509 572 296 114 159 818 503 493 263 378 192 514 290 052 254 924 503 278 243 290 282 312 383 786 202 656 048 587 547 053 598 535 021 004 482 006 464 464 259 867 265 490 032 784 057 577 074 913 435 447 300 124 058 660 673 773 041 801 591 642 403 541 153 081 663 979 288 908 937 718 918 328 856 735 803 057 667 473 976 816 517 733 805 208 968 997 572 343 546 125 597 865 268 613 682 261 648 099 258 488 378 164 531 265 938 841 850 137 542 799 849 993 058 020 852 254 929 531 160 451 981 455 489 377 644 703 006 456 534 262 058 269 261 337 738 997 661 094 466 793 744 897 668 669 848 261 801 307 880 228 085 386 121 975 680 448 341 661 998 411 397 261 730 623 796 179 955 085 559 454 788 601 501 158 155 645 611 635 672 661 189 851 972 998 073 834 909 763 982 089 094 540 956 567 276 773 412 581 671 398 873 141 017 929 419 015 515 176 778 538 191 694 622 355 856 919 224 682 207 678 612 516 615 349 946 693 036 311 387 124 490 214 319 129 672 010 892 088 821 892 858 549 543 207 139 833 370 662 172 964 905 175 450 936 340 896 081 893 952 258 795 970 204 780 055 888 823 422 979 696 205 660 167 658 484 985 872 104 403 588 340 091 701 224 073 289 337 669 807 163 342 487 661 165 148 090 772 886 577 891 200 865 234 035 604 229 018 239 015 585 925 972 610 712 408 386 911 330 789 415 255 585 857 591 419 577 707 679 440 565 791 199 571 909 471 046 241 392 222 660 189 680 550 778 520 572 119 057 124 096 422 445 217 938 980 694 668 237 920 562 770 886 173 278 519 745 287 478 243 762 384 546 386 793 167 065 410 125 814 881 008 365 269 356 447 937 828 261 510 372 373 092 715 157 730 675 456 151 950 259 507 377 444 852 978 207 965 174 788 728 639 257 858 862 362 458 316 445 652 955 564 629 901 670 986 385 925 209 981 142 334 983 218 984 614 323 933 606 250 713 462 730 537 905 317 140 709 699 897 330 481 788 309 581 761 086 062 697 426 884 045 169 609 733 407 363 888 258 201 054 214 703 700 303 512 759 828 406 898 073 534 754 800 199 187 006 395 208 626 262 375 601 208 742 345 353 510 371 000 625 188 828 636 081 079 738 647 730 395 687 637 727 305 352 950 921 570 003 108 668 979 068 450 589 200 926 420 979 879 202 020 014 209 625 676 532 193 576 479 741 513 043 778 964 354 220 834 091 502 578 109 180 699 966 804 330 262 163 977 237 249 715 384 381 875 907 551 141 746 975 120 326 970 717 873 656 034 727 145 891 698 419 762 242 277 815 724 891 307 056 479 595 692 085 474 992 289 097 618 787 105 063 059 964 127 543 762 900 565 307 827 660 428 941 108 633 794 603 435 257 988 693 774 405 610 967 328 914 777 495 301 310 911 818 434 408 001 642 754 970 818 464 538 806 435 631 737 606 102 697 623 796 125 761 204 476 360 375 273 356 133 860 244 746 062 911 697 483 187 773 041 175 157 516 059 879 373 184 320 502 707 356 913 202 020 481 627 599 072 282 152 216 398 685 531 338 550 159 725 919 648 249 079 900 950 353 854 598 576 096 005 335 013 717 470 526 172 093 477 176 127 155 466 214 900 213 254 390 877 356 649 954 690 776 944 761 758 885 557 161 200 311 690 153 274 774 032 978 124 893 712 387 163 690 617 906 473 842 480 886 020 628 739 980 115 359 237 953 544 191 544 687 674 431 405 915 592 270 411 655 120 285 234 498 585 228 856 767 727 172 348 240 574 992 914 805 192 497 117 573 883 348 789 821 983 938 501 310 688 402 646 561 608 064 208 999 592 047 290 038 317 285 426 217 199 540 937 324 665 157 193 298 982 873 659 654 665 811 366 835 661 126 227 243 021 344 728 997 332 798 969 096 092 676 154 529 357 463 731 349 500 701 830 506 479 677 715 400 384 523 638 984 789 666 200 776 100 369 179 604 094 764 466 136 046 947 195 257 031 011 036 267 882 804 223 256 397 455 491 769 901 791 820 304 681 207 453 336 537 390 698 322 915 404 973 703 519 439 181 250 746 463 443 017 695 381 626 154 724 372 095 204 095 873 538 849 771 357 462 359 766 489 864 257 619 850 450 587 158 530 679 501 017 683 182 637 659 227 617 096 123 893 204 356 146 526 788 777 303 622 788 020 984 047 693 184 144 715 805 886 327 141 170 374 293 107 611 778 090 826 999 293 536 280 948 531 681 340 220 206 830 820 267 047 249 672 527 005 228 186 419 193 185 806 587 891 061 185 351 138 040 899 784 819 600 378 719 070 118 553 652 849 040 531 135 300 937 272 851 985 586 611 949 642 199 021 857 573 631 428 083 958 115 055 490 695 562 781 555 002 731 109 115 302 169 315 598 528 393 892 474 085 727 402 729 013 100 135 536 413 485 216 943 582 949 077 341 312 048 183 061 910 149 671 885 104 055 894 853 756 780 277 166 631 812 456 093 963 223 938 616 093 451 328 062 883 565 237 429 386 179 679 983 563 613 898 692 471 234 513 548 743 526 267 785 624 870 173 882 284 945 544 668 012 956 317 441 451 304 538 119 180 085 955 833 572 853 099 252 948 780 600 041 629 598 774 100 085 622 855 022 616 184 999 310 966 495 355 025 638 851 837 997 844 371 353 171 883 455 530 310 585 432 102 374 164 553 414 780 827 710 465 837 878 408 207 324 253 552 176 912 458 424 914 848 532 347 121 142 523 724 267 920 258 447 670 234 725 678 656 929 698 090 595 147 485 512 939 759 783 925 882 976 576 436 015 086 176 064 487 237 056 741 273 106 122 299 631 117 484 656 188 400 695 585 329 993 664 814 294 410 786 815 524 489 773 156 839 322 755 346 999 988 751 817 781 162 421 904 983 439 943 836 172 189 273 578 999 308 639 186 806 430 841 597 890 706 007 770 534 414 362 760 942 967 803 670 133 819 530 969 542 331 960 696 907 458 942 004 029 413 058 080 078 129 766 355 020 029 499 249 672 465 085 086 689 226 910 481 243 027 663 912 984 494 660 905 829 804 172 882 671 029 755 039 309 321 168 112 023 051 529 616 904 974 490 469 170 550 265 615 797 306 184 949 430 865 952 424 206 408 545 541 036 164 188 994 535 621 574 668 945 465 858 648 316 753 387 832 448 494 846 952 471 876 586 037 976 298 825 787 565 861 363 347 112 292 832 644 545 977 785 436 755 525 278 560 418 253 876 557 972 121 215 751 736 025 133 554 143 497 527 188 431 201 868 916 179 192 189 218 844 869 713 217 488 432 947 719 723 178 370 363 021 103 253 256 953 677 844 582 715 177 669 655 111 941 758 052 007 563 187 411 613 226 616 365 768 464 614 561 468 072 474 409 973 206 556 676 197 667 381 579 279 065 471 412 231 636 427 462 456 367 563 247 381 314 485 354 534 736 168 732 118 729 414 684 389 554 680 980 440 003 855 234 460 872 566 591 119 045 006 665 281 821 287 001 334 607 951 492 917 067 732 196 850 329 464 361 106 578 478 172 665 345 646 654 885 695 011 881 737 898 654 635 984 804 525 441 191 282 387 886 448 820 050 371 342 493 867 241 226 831 823 270 024 588 559 037 014 063 316 450 168 715 705 586 971 517 120 209 367 729 199 806 180 458 765 944 315 185 924 567 550 304 091 620 601 867 464 391 982 959 484 758 235 558 583 887 420 108 200 613 881 267 823 951 456 473 810 193 062 929 779 943 210 671 954 762 832 931 560 172 140 194 969 785 827 508 753 668 494 740 639 152 133 622 079 558 263 648 934 164 525 524 462 204 026 392 363 928 014 515 236 963 620 881 156 368 365 503 210 571 055 879 718 177 964 705 274 309 964 739 383 094 841 809 580 156 470 998 966 677 077 643 888 393 886 735 213 952 739 159 518 155 837 434 535 116 907 533 273 118 293 557 696 518 832 587 961 530 350 307 135 553 692 007 028 000 739 221 930 846 523 076 935 062 831 213 227 289 736 150 101 372 339 912 331 354 263 546 335 265 578 345 082 903 644 714 048 322 879 443 065 102 688 051 632 615 738 700 004 601 853 819 272 603 585 213 536 770 103 000 340 870 676 406 580 515 522 552 292 313 692 048 029 637 665 753 380 098 972 883 543 647 699 887 886 599 629 657 229 886 464 965 129 088 356 399 431 756 762 795 969 358 705 589 232 363 389 647 593 943 975 982 175 426 135 211 340 200 480 206 413 741 002 397 611 575 050 082 143 773 596 410 866 872 151 883 509 374 773 284 813 945 077 766 784 647 211 135 536 610 747 521 371 683 816 721 790 358 289 401 991 959 511 555 510 958 821 280 918 858 008 538 104 656 349 155 238 632 994 148 275 730 102 118 356 059 338 136 504 436 758 716 176 318 700 622 050 896 101 823 313 096 744 288 915 392 709 184 158 259 543 981 295 373 902 165 818 893 252 636 179 776 087 611 973 198 185 309 287 057 649 145 757 643 842 370 152 976 447 938 145 963 647 273 432 816 511 744 074 557 406 263 586 055 249 453 502 278 833 780 791 870 325 145 553 308 985 076 902 932 755 219 021 463 467 341 966 981 692 370 993 651 108 542 294 629 588 675 868 181 620 811 960 103 750 187 623 321 200 452 178 353 810 264 520 085 598 592 303 715 801 745 623 112 593 801 140 394 626 135 002 216 399 270 830 749 894 113 418 972 972 790 920 231 290 523 747 401 518 429 500 572 597 001 967 220 464 937 579 827 273 335 926 583 844 428 217 320 990 856 960 415 489 745 538 810 366 086 840 693 289 622 998 202 169 388 769 728 969 403 903 504 770 808 013 019 496 601 387 705 757 211 296 577 936 604 719 842 958 054 714 801 534 706 013 801 314 521 385 798 193 226 012 088 773 217 252 823 998 641 830 548 455 985 400 235 601 537 350 942 187 066 815 465 720 301 208 719 080 397 051 442 242 157 128 849 394 448 132 428 087 979 584 614 305 081 042 078 746 106 423 358 943 118 769 811 314 710 404 282 581 262 637 198 902 365 779 982 999 660 050 185 875 205 906 113 840 652 264 843 758 789 098 193 339 984 360 691 008 898 462 957 644 185 428 814 440 624 941 141 252 295 548 354 992 327 424 503 304 055 089 927 633 708 949 457 798 238 861 352 915 053 825 892 661 208 744 144 074 221 375 816 748 856 762 275 183 098 376 617 320 210 037 773 040 030 886 235 872 979 584 344 464 021 815 492 788 375 849 855 258 101 536 890 652 733 190 558 342 465 614 920 518 225 815 689 418 262 275 927 541 100 161 544 462 078 602 334 931 662 069 591 690 637 839 255 091 016 464 849 589 431 390 770 654 177 401 992 940 180 382 693 839 076 706 026 209 578 287 059 195 225 888 827 468 419 837 383 876 718 213 808 078 027 610 052 554 987 351 807 902 773 657 053 440 984 917 857 124 717 870 044 293 205 452 240 038 843 566 809 933 352 784 891 269 409 862 989 918 111 782 438 494 327 544 812 675 159 453 099 293 885 060 382 146 210 636 430 391 938 229 297 327 153 456 189 784 732 345 362 384 983 464 307 861 829 085 517 166 025 622 094 217 516 198 653 907 134 982 811 400 343 676 447 586 495 587 020 857 400 731 454 826 333 563 931 958 877 366 103 275 501 312 595 760 574 265 212 820 308 058 932 909 793 904 284 661 414 188 480 650 495 265 893 662 736 557 781 685 284 521 342 824 051 050 987 326 347 221 675 806 054 013 167 674 897 658 679 118 992 476 552 371 094 764 255 748 626 440 942 998 392 915 063 775 995 023 174 259 865 614 608 312 608 396 564 099 894 963 693 946 219 281 892 829 013 110 587 880 956 659 420 810 538 241 968 745 117 176 689 657 589 808 572 896 090 884 527 968 782 816 977 558 142 806 066 646 325 850 427 957 405 449 722 094 449 366 774 659 839 603 231 858 141 793 482 572 222 923 125 476 966 793 692 145 574 101 749 452 721 695 760 879 727 877 821 470 610 644 190 326 625 593 406 994 294 201 884 956 376 345 843 055 760 249 015 344 030 243 485 329 420 212 127 166 074 842 841 621 702 831 277 360 959 909 488 723 937 582 863 740 250 379 191 364 644 822 722 268 971 529 538 377 211 902 869 407 470 464 559 391 512 443 597 279 844 929 231 456 581 796 267 973 275 158 819 704 273 289 394 316 103 611 263 187 292 070 728 427 931 579 691 980 241 818 183 478 797 641 714 036 676 768 618 567 343 945 992 670 665 974 955 409 349 620 031 469 909 619 250 481 586 024 623 681 088 376 935 550 754 592 581 472 341 743 681 011 426 572 441 336 097 741 519 584 593 673 176 388 752 522 997 487 869 571 178 211 986 958 138 222 306 813 498 429 529 428 294 220 435 394 335 588 128 921 897 923 976 016 152 621 520 606 388 355 505 592 279 633 288 569 276 108 192 081 538 336 745 958 982 753 485 691 843 434 216 769 665 019 673 936 107 961 765 857 505 049 812 634 868 180 096 179 563 780 431 257 720 422 779 887 070 025 012 452 688 070 679 015 128 713 383 913 109 060 842 230 557 183 177 572 447 562 957 477 978 338 139 379 250 292 289 148 005 881 767 089 672 029 929 950 206 310 616 064 958 078 599 020 220 408 650 145 210 756 519 398 475 878 063 897 264 761 530 885 716 922 040 448 989 548 739 394 517 948 887 529 244 663 573 141 600 668 539 971 846 291 525 418 390 907 663 756 573 199 223 054 721 745 434 627 026 649 452 872 946 982 804 137 562 833 765 122 810 424 101 445 274 917 387 225 566 818 506 412 428 480 252 617 630 298 300 742 984 508 157 974 860 230 841 979 412 178 776 584 632 013 513 444 461 433 187 609 317 742 878 768 467 696 445 494 628 766 206 704 882 763 083 354 692 336 665 761 544 581 227 703 348 521 547 981 276 073 527 971 238 477 914 730 366 605 343 134 016 905 181 096 229 338 147 613 376 260 439 709 325 458 476 774 041 141 610 681 675 455 237 333 432 986 960 844 290 845 400 608 589 372 243 940 423 008 460 616 522 698 997 526 421 624 975 718 495 216 878 530 540 413 584 212 993 398 865 563 082 080 327 052 339 378 381 399 112 458 737 211 903 004 859 610 700 995 146 370 073 682 247 334 819 295 873 720 932 801 467 537 170 506 989 435 827 731 269 684 698 154 955 271 131 139 746 469 618 425 260 449 511 329 641 248 324 540 221 311 195 768 063 342 572 472 223 688 915 117 564 949 543 821 567 121 229 968 880 241 325 688 066 125 418 710 631 190 453 016 727 738 974 363 027 693 701 977 785 231 104 486 144 106 836 461 978 503 256 730 320 194 433 328 555 850 573 455 669 450 594 216 591 096 354 232 748 059 663 660 869 525 762 822 596 066 793 883 969 055 895 626 588 410 561 429 387 702 125 119 562 369 135 917 276 446 192 378 039 704 347 083 392 964 918 483 738 970 097 650 245 028 120 914 994 217 317 062 676 432 221 553 445 267 987 393 126 255 947 463 500 169 358 065 737 701 948 284 026 331 713 782 936 773 199 113 554 375 406 444 703 990 671 433 241 726 742 138 897 117 384 904 579 462 468 832 945 808 680 430 300 905 820 851 563 755 461 751 117 412 701 160 989 115 592 287 635 842 624 218 019 623 769 254 598 036 086 817 841 404 801 346 367 265 673 412 374 657 874 903 157 526 125 309 521 174 845 540 228 939 731 307 054 368 667 169 477 509 136 323 829 263 498 630 154 951 686 134 283 490 859 300 275 118 544 974 112 612 475 759 257 752 229 323 328 426 989 610 948 243 378 936 608 027 083 833 182 274 240 052 646 083 051 151 115 472 082 909 457 894 645 129 731 224 837 092 021 874 592 593 232 358 863 361 432 155 634 233 901 724 618 674 508 531 119 830 952 674 030 945 120 546 579 710 020 730 206 248 669 355 469 833 142 424 682 665 633 739 692 543 182 477 200 864 278 541 104 127 449 869 391 032 850 394 530 242 184 343 854 034 543 188 115 896 730 234 154 769 864 648 188 239 523 646 986 154 134 213 568 684 408 903 350 587 010 645 124 289 505 499 940 844 427 984 945 058 545 698 231 016 309 819 748 186 980 160 275 809 018 905 446 189 439 754 438 263 196 466 277 761 935 711 932 313 939 668 295 961 041 893 948 978 463 634 158 419 996 798 509 143 979 821 062 777 805 037 363 768 735 433 195 743 437 899 231 168 441 654 150 834 732 464 132 544 852 075 227 738 746 045 202 367 277 238 652 110 054 446 326 518 268 918 711 343 017 015 147 803 828 955 017 706 241 157 168 169 183 266 463 097 599 980 660 754 791 151 892 263 389 752 798 403 936 929 051 393 824 501 933 105 271 597 110 153 429 501 554 995 873 179 237 506 062 584 677 941 204 779 155 545 442 348 479 085 415 960 096 313 188 959 980 797 052 647 551 184 672 734 540 309 386 685 624 273 866 864 435 102 450 537 193 484 707 552 013 400 575 793 352 408 807 632 817 643 741 853 917 970 793 016 099 866 335 974 728 478 968 337 439 681 089 297 488 362 519 318 328 804 765 070 025 510 439 492 803 862 137 943 153 945 826 307 629 849 129 580 166 679 010 429 732 275 858 133 187 809 796 787 037 912 134 681 831 401 920 523 052 866 850 417 327 122 901 514 635 516 985 343 840 216 153 543 751 860 305 131 819 980 198 748 989 684 470 481 566 228 475 648 893 753 977 879 278 927 828 288 421 524 795 430 032 085 069 634 272 821 042 425 390 852 509 895 713 631 087 510 529 067 860 022 258 541 085 274 927 300 922 760 440 689 414 794 987 616 354 380 792 846 411 090 784 760 490 042 371 823 249 107 400 001 267 103 158 076 210 744 836 569 320 594 141 177 543 989 348 753 156 563 027 532 658 338 079 097 381 374 218 935 492 953 631 683 702 783 296 783 294 621 661 024 247 330 040 159 026 037 948 253 547 220 520 145 213 039 086 921 060 351 575 255 122 756 134 277 862 151 683 392 308 710 132 802 474 551 694 930 031 833 322 589 812 193 288 417 198 466 941 647 054 244 284 824 449 754 196 075 274 698 415 431 843 839 023 384 970 890 669 299 620 911 405 921 470 637 403 304 189 969 980 999 478 114 909 535 332 996 286 657 387 937 735 000 445 448 298 639 215 966 926 681 109 812 137 313 006 902 929 082 909 224 108 556 041 788 889 808 739 776 418 121 048 930 735 433 043 934 628 502 091 785 403 827 515 063 137 745 497 837 861 829 465 593 934 878 922 280 844 464 883 033 685 639 943 308 154 459 492 439 505 038 419 390 715 682 429 693 341 250 981 242 774 345 588 428 796 523 795 132 548 514 944 680 263 913 927 107 660 529 244 493 570 197 289 406 995 808 822 527 553 845 837 107 944 408 289 009 999 178 395 269 149 509 188 349 367 180 062 654 327 661 178 756 373 977 185 298 481 368 753 838 093 047 530 812 988 689 865 882 343 286 534 151 993 725 313 327 647 199 277 493 660 632 260 266 835 915 275 687 544 475 797 746 129 633 562 631 136 722 717 028 411 949 262 144 756 537 750 590 377 038 115 630 684 065 127 515 143 941 778 205 437 680 591 113 690 894 456 891 480 834 164 840 267 550 360 843 224 632 252 605 029 978 038 369 432 853 341 855 953 287 587 727 166 056 952 149 855 152 706 024 920 685 150 852 310 332 530 809 891 868 014 560 895 787 240 862 444 794 869 612 233 189 018 107 267 056 904 851 618 383 781 375 101 254 690 016 010 511 742 597 509 002 472 678 120 369 398 792 316 991 117 914 156 221 131 188 680 451 161 328 379 270 179 577 296 797 514 127 675 205 522 529 858 271 013 742 102 107 121 383 431 362 264 365 845 580 698 712 615 285 559 972 649 819 534 541 941 242 240 506 301 491 177 743 593 073 822 482 517 557 851 743 966 682 719 933 133 218 163 512 649 815 434 938 088 096 854 514 969 268 458 845 453 730 335 199 340 649 271 478 437 353 850 119 461 182 661 393 550 603 578 127 384 512 189 521 342 742 691 889 170 615 943 779 221 963 713 488 999 764 297 195 504 786 070 576 393 683 477 990 252 719 269 052 977 264 049 143 052 774 387 289 280 023 095 427 926 177 839 686 617 981 469 643 125 682 204 011 656 308 370 154 528 031 914 092 936 798 373 985 540 944 797 938 295 510 093 864 624 206 196 039 701 449 369 583 952 585 757 358 550 136 628 522 844 280 138 289 884 039 214 082 587 424 181 464 628 308 963 254 393 591 055 448 699 038 389 200 525 105 293 948 845 405 533 578 639 859 242 807 491 419 452 969 267 550 138 144 736 733 481 701 385 450 670 083 767 649 469 574 545 210 578 049 161 817 018 769 118 107 219 035 733 700 410 817 027 183 842 483 078 953 825 347 922 216 435 988 570 563 806 219 510 426 291 433 616 362 205 849 355 874 628 476 312 335 437 818 828 374 264 246 930 652 791 186 811 025 384 928 783 683 326 052 746 620 637 150 060 661 320 302 281 846 296 026 423 695 806 934 846 928 211 702 091 815 619 350 043 182 589 197 348 602 964 621 651 894 526 917 501 871 102 650 007 931 876 715 404 802 176 120 668 693 711 514 846 531 302 082 730 423 320 566 602 132 606 024 551 980 569 997 780 250 617 906 220 957 729 943 827 976 390 249 014 921 759 509 091 421 990 592 166 387 320 554 326 369 548 706 253 056 281 434 123 310 569 036 450 028 917 976 056 188 200 596 691 034 655 472 302 858 587 766 478 605 754 219 683 856 750 830 426 889 633 933 432 617 174 755 045 064 716 238 978 344 043 448 104 688 197 224 442 271 993 528 244 148 401 738 816 951 901 161 206 405 429 278 578 132 971 229 677 813 283 077 723 500 946 830 622 336 073 338 971 862 759 375 993 131 379 992 476 517 439 798 726 709 331 595 440 787 885 217 820 552 024 259 594 404 466 832 753 699 005 997 862 187 817 699 384 535 194 657 708 636 192 368 483 906 390 269 792 308 687 940 363 402 337 818 163 471 605 307 029 404 563 855 275 717 605 205 665 829 322 087 941 143 145 930 743 123 366 339 081 070 839 525 094 330 325 441 609 630 984 572 992 604 237 593 012 546 761 755 685 555 336 041 471 892 779 576 486 496 912 882 470 557 501 306 122 505 567 130 236 372 434 991 489 097 757 821 250 278 940 323 994 562 625 486 964 081 678 997 606 463 537 042 363 788 546 168 304 768 486 308 587 352 171 392 170 908 313 273 324 393 073 146 326 295 981 831 979 436 980 544 500 690 660 041 753 716 577 870 377 288 532 004 977 189 800 885 591 794 635 088 846 926 037 754 726 836 864 919 537 114 668 036 908 495 046 753 749 897 732 202 626 107 706 177 079 239 503 042 235 052 820 637 122 040 662 268 523 742 583 461 220 574 462 281 547 915 331 929 108 669 009 795 656 942 154 629 778 575 868 918 992 651 793 845 284 092 491 979 248 006 693 063 664 258 902 110 621 760 817 097 503 078 473 591 652 708 110 138 500 270 546 261 637 322 835 328 795 745 911 978 422 944 866 486 630 651 909 443 059 495 686 590 522 560 191 873 203 303 519 827 189 239 583 001 363 702 288 720 506 649 823 637 218 552 514 788 710 530 765 503 575 544 299 834 411 379 398 931 516 407 604 218 285 437 050 370 551 364 338 491 690 211 279 082 257 442 615 349 017 782 286 546 205 149 552 753 073 595 058 715 111 336 159 249 482 196 919 344 318 055 074 405 706 470 535 304 084 204 724 729 607 784 207 280 117 181 868 893 117 475 017 345 742 246 641 475 841 510 304 984 905 516 186 972 312 970 908 072 128 952 129 145 666 704 669 757 977 724 223 793 886 246 601 495 019 251 980 160 053 297 715 669 787 359 300 030 422 386 847 821 591 111 507 747 227 342 895 717 007 917 524 871 339 093 973 859 011 082 888 371 187 771 519 678 556 718 323 114 918 151 446 226 394 633 621 270 695 168 566 603 985 201 884 203 369 946 397 311 410 223 693 513 085 369 359 271 076 879 508 892 748 010 760 353 388 428 918 744 229 504 445 128 153 019 720 888 895 711 100 525 167 888 185 384 160 792 142 779 092 778 316 677 819 531 173 264 175 174 142 851 183 817 349 018 288 622 171 367 551 001 197 686 568 156 664 811 653 495 358 299 135 910 433 914 335 144 997 146 192 355 979 664 015 875 579 840 718 284 839 685 109 708 262 564 226 609 646 865 136 897 840 608 463 880 520 030 652 100 200 017 234 629 178 279 606 053 585 356 652 229 611 384 351 738 451 409 975 895 150 875 393 324 958 532 194 023 536 543 220 329 952 484 867 860 034 549 560 036 586 659 688 453 365 701 973 379 762 579 499 061 575 098 095 154 031 205 102 443 686 761 992 171 589 911 179 645 768 196 805 281 616 654 553 175 828 558 981 727 642 899 206 323 656 044 752 377 368 495 075 429 929 887 879 822 168 332 480 935 801 051 297 218 834 922 707 934 936 093 436 473 095 938 911 893 527 488 111 619 135 805 596 957 614 458 479 179 385 366 720 212 422 103 592 563 060 378 933 577 537 092 983 731 624 133 790 954 268 503 815 520 717 415 395 271 229 409 861 872 664 363 523 984 272 988 085 730 519 126 684 900 294 920 991 897 042 213 250 770 376 757 330 023 212 509 971 140 575 208 922 831 466 443 359 156 687 873 629 980 601 542 867 433 529 637 337 815 607 833 388 686 298 893 514 488 166 328 584 849 071 031 703 039 262 039 228 395 862 040 851 908 787 085 533 693 981 651 979 030 044 330 170 712 307 723 610 958 739 452 473 339 001 572 198 946 207 166 804 142 028 490 796 281 831 546 919 626 333 410 922 801 368 818 997 901 908 336 188 315 077 205 278 506 775 534 882 047 338 530 244 838 982 576 317 574 463 535 304 033 893 845 514 102 469 511 683 023 800 569 756 415 618 055 753 937 036 755 474 815 630 828 451 642 151 354 381 339 976 917 182 517 547 018 368 397 816 588 107 145 419 148 323 799 188 564 646 980 850 521 730 083 846 293 818 557 090 356 464 520 489 889 808 141 865 348 567 662 998 401 526 016 199 639 581 602 981 583 765 300 345 291 951 124 375 965 388 018 699 851 606 878 671 622 198 614 012 370 071 796 347 933 744 856 708 757 320 325 865 398 895 708 120 412 550 633 558 153 291 261 630 071 024 324 461 170 117 332 150 741 985 894 155 390 145 699 639 204 033 873 445 907 412 366 292 410 533 620 713 862 126 454 296 476 721 836 491 014 457 663 207 698 879 620 397 904 102 856 022 450 533 819 360 728 426 888 823 043 702 747 122 121 504 146 121 382 373 881 324 203 739 012 057 449 937 456 292 340 621 666 729 839 733 355 308 042 104 988 024 513 085 646 831 845 489 708 970 762 626 276 964 448 371 846 918 069 173 404 909 958 385 080 610 213 194 475 738 617 854 038 280 690 613 271 669 728 724 087 093 946 874 356 461 802 303 616 077 994 438 074 416 088 515 205 404 884 192 879 492 477 590 774 363 037 231 230 573 913 996 737 131 004 523 763 448 439 953 120 929 791 352 517 170 129 638 805 262 226 524 579 708 637 049 351 413 973 472 272 594 614 362 537 337 195 191 486 846 895 967 062 828 247 946 430 263 512 173 911 934 608 707 150 149 586 085 135 115 776 586 660 775 829 218 509 550 658 551 886 526 174 759 165 715 812 982 845 070 706 909 159 464 120 417 741 840 096 760 527 442 450 878 218 696 201 875 061 935 362 729 666 447 237 082 314 919 280 679 607 283 567 345 078 537 748 931 381 795 167 405 709 006 033 173 991 329 500 072 003 742 901 477 566 794 560 181 567 084 575 929 767 090 092 599 005 029 799 802 581 890 615 196 890 964 292 486 304 573 366 596 736 785 841 304 833 331 096 786 145 425 509 138 235 313 513 854 820 986 709 312 115 196 092 096 032 518 689 531 667 306 041 311 807 068 170 235 714 264 681 197 440 903 799 378 233 043 307 417 118 603 239 751 286 411 702 590 560 858 366 898 952 022 049 855 685 623 840 065 175 176 628 598 292 172 420 404 736 739 097 835 993 790 400 944 778 700 665 527 017 678 483 898 031 416 094 107 562 364 608 332 634 792 079 218 280 906 724 229 910 804 311 666 503 118 456 199 909 615 415 330 802 694 491 275 301 910 122 997 685 839 633 900 105 167 030 282 941 589 573 076 982 701 870 393 734 074 010 969 820 429 201 650 144 929 855 745 316 773 021 379 950 785 125 307 503 770 387 529 810 639 123 499 445 802 370 246 410 928 953 778 356 087 327 280 533 825 066 746 651 446 786 100 172 475 622 321 568 695 046 051 320 583 483 173 328 468 311 902 539 878 943 053 672 767 019 314 496 619 414 829 249 109 890 934 301 181 773 586 177 672 400 389 128 458 501 826 183 618 620 918 375 558 364 196 501 504 627 403 123 308 413 001 410 737 088 245 652 083 690 776 241 135 384 629 662 521 667 914 835 849 441 345 876 643 496 777 291 049 210 162 415 301 260 127 812 938 905 088 010 858 313 925 758 668 514 671 005 306 436 368 991 485 134 878 556 223 354 275 426 807 388 409 657 181 997 586 845 934 102 761 329 784 286 898 214 756 145 014 673 099 217 650 401 597 942 715 660 291 627 959 573 339 977 845 041 517 074 326 335 888 411 292 194 475 500 994 093 847 024 226 904 796 646 343 845 955 008 907 015 950 849 116 160 349 603 024 089 613 634 848 870 832 921 315 652 536 881 486 098 781 499 949 848 592 734 374 385 614 608 422 578 845 166 054 588 051 927 590 386 067 577 041 509 602 870 943 006 327 490 784 714 416 446 395 395 038 457 837 393 744 139 056 939 529 632 426 775 921 161 075 192 236 022 916 687 432 943 832 117 787 743 143 015 546 852 641 697 112 895 180 241 218 525 900 344 897 089 487 501 906 771 929 644 515 946 987 151 424 153 630 242 987 490 771 872 274 719 107 630 604 429 444 030 606 704 480 310 211 959 624 898 263 679 511 794 702 876 476 755 339 979 055 004 729 837 965 094 985 016 126 358 120 685 597 880 559 786 747 651 775 595 934 283 542 498 965 333 706 315 205 397 839 694 788 001 374 142 134 653 133 403 754 625 744 064 893 823 699 782 842 275 071 817 828 448 462 681 514 210 840 327 552 724 845 296 484 707 443 423 431 618 837 232 807 693 898 517 259 586 071 243 328 424 400 061 049 492 982 354 109 983 796 547 317 145 343 260 537 235 435 122 062 506 509 805 379 946 184 233 304 118 181 204 118 453 226 551 833 386 802 623 672 865 252 216 966 179 703 963 525 343 528 284 856 530 607 635 672 167 415 021 784 293 536 509 009 011 206 670 039 134 569 047 254 155 794 062 211 118 707 746 542 473 010 152 106 711 504 830 792 093 055 446 607 678 024 591 717 002 881 589 515 005 930 681 896 998 097 290 168 344 387 870 232 952 650 247 228 322 001 993 235 001 479 898 338 507 297 566 432 789 318 877 232 496 725 715 824 277 464 680 797 128 457 966 731 362 743 317 446 712 865 949 334 318 873 788 611 589 852 225 875 022 684 366 209 968 562 477 721 881 441 839 927 500 030 839 115 751 672 905 474 372 319 713 356 254 575 709 762 125 519 473 121 458 514 552 095 983 860 338 529 194 314 819 272 530 395 728 473 528 204 011 993 987 030 639 371 456 343 367 227 686 778 353 180 148 626 511 293 063 519 212 548 751 547 090 878 731 539 438 630 810 259 697 029 942 082 643 123 038 292 201 395 312 163 670 810 914 627 170 711 508 553 528 290 763 998 999 808 677 764 115 600 090 726 298 092 382 338 396 286 671 044 731 365 970 162 796 507 742 911 792 712 742 035 066 813 309 352 330 583 448 176 448 481 195 774 610 653 611 756 556 176 620 243 344 108 314 784 551 657 305 046 963 315 509 569 497 461 701 148 215 877 145 153 299 067 952 731 541 011 040 624 680 201 139 419 181 477 242 839 135 841 982 323 177 246 639 541 131 456 778 814 257 528 169 207 073 662 188 409 889 192 155 206 544 439 657 502 461 924 900 507 486 955 553 629 585 943 322 429 363 165 688 555 292 471 703 368 939 721 412 831 613 270 205 074 953 473 523 192 973 679 542 108 876 357 477 988 190 192 130 792 837 931 352 598 837 724 636 615 791 165 393 531 149 635 461 297 152 864 247 830 061 974 207 824 490 701 808 525 554 060 104 910 491 695 023 433 685 252 021 869 685 682 153 523 869 501 137 144 773 963 521 938 179 817 313 674 973 274 103 381 779 954 825 549 666 325 522 005 042 142 690 636 514 735 434 943 400 931 841 708 593 695 402 231 971 550 969 766 536 323 196 934 440 305 893 329 438 243 042 140 005 695 207 299 788 019 374 130 082 033 212 951 716 618 023 926 404 238 810 060 634 694 928 149 336 803 325 880 029 670 643 470 333 925 666 434 768 706 233 918 742 905 240 750 938 203 008 188 380 976 899 704 177 468 046 549 172 665 260 930 411 176 869 645 180 566 341 025 211 177 439 615 570 593 178 838 905 959 523 653 817 776 837 163 082 334 257 962 357 607 873 581 075 301 276 499 777 569 230 009 274 105 810 632 771 082 567 952 560 318 255 592 231 656 615 475 796 289 823 885 396 694 988 957 637 293 360 980 506 399 996 328 137 489 892 899 509 074 681 736 294 843 999 035 247 376 956 759 608 466 547 589 286 999 854 710 548 710 973 889 979 007 136 168 792 704 554 813 471 433 107 368 592 501 233 453 063 094 256 536 759 602 454 717 482 887 557 704 743 605 566 973 612 801 705 321 733 544 662 991 869 269 791 917 466 874 862 421 243 349 416 591 791 235 955 858 419 107 669 080 117 419 761 829 531 736 528 842 243 174 745 714 373 967 347 818 767 174 109 910 012 153 270 201 134 652 892 938 512 728 693 968 550 650 887 301 068 275 144 615 250 031 717 648 790 492 682 140 513 833 631 660 052 890 342 490 709 825 310 357 186 256 116 280 496 176 598 168 996 864 935 378 100 851 390 274 822 483 564 258 500 676 316 698 388 636 418 180 641 608 174 325 030 956 357 018 909 736 221 851 043 068 093 330 578 895 079 853 843 963 386 257 834 205 996 018 590 439 568 569 146 215 753 402 663 120 750 024 680 090 480 095 508 973 114 538 770 710 176 655 567 949 962 868 451 854 481 581 343 230 549 851 735 467 471 826 582 205 331 112 374 962 417 955 125 176 282 794 749 480 508 960 376 206 765 879 569 975 694 037 720 164 756 902 147 209 402 398 300 543 914 222 088 492 474 767 526 553 094 291 177 282 079 933 385 987 414 751 497 746 507 781 959 672 282 030 109 175 803 215 903 354 919 639 168 261 224 333 435 646 598 160 941 305 656 335 784 510 053 802 481 675 269 372 929 722 781 558 620 696 430 363 199 859 734 225 059 672 249 450 250 719 988 642 077 205 523 511 416 635 491 197 964 239 934 151 882 366 552 592 989 165 072 318 056 161 858 763 890 963 634 003 705 016 170 415 470 530 292 301 524 641 220 168 642 450 953 807 455 095 376 191 156 418 941 908 264 881 803 707 394 291 740 628 870 274 411 537 253 954 549 049 086 598 723 822 709 641 040 529 461 963 778 175 853 622 800 530 053 377 844 908 126 171 687 981 157 854 640 696 847 396 343 254 647 800 746 758 518 341 571 363 344 958 421 751 245 998 589 319 748 955 614 556 444 555 033 602 784 147 463 613 993 278 373 519 726 685 690 581 183 859 402 399 252 669 236 090 151 302 065 742 855 451 422 332 396 517 862 457 019 521 253 923 869 157 530 852 368 814 428 435 310 211 458 752 377 792 613 773 673 938 566 379 596 920 964 598 353 398 932 146 736 886 116 498 906 557 373 344 895 089 634 744 383 752 011 011 109 481 055 616 743 572 766 060 289 458 259 954 367 519 738 024 108 166 351 724 447 317 596 731 116 031 699 197 108 707 337 476 007 995 575 872 391 917 720 144 347 294 314 267 949 349 538 450 022 202 561 117 463 177 764 518 976 333 550 322 188 729 993 197 320 585 171 364 438 563 065 638 576 227 757 664 171 498 440 331 773 461 432 506 738 947 148 396 370 155 150 855 154 865 043 996 988 842 710 945 902 250 579 799 314 186 737 215 379 317 430 347 687 838 089 152 012 414 491 752 803 448 332 054 799 365 127 251 223 581 895 712 388 333 294 377 444 479 117 514 462 550 281 602 371 430 780 442 439 805 669 950 641 579 175 818 264 258 144 326 220 122 289 654 526 237 141 304 452 985 147 793 088 378 139 270 248 961 597 934 550 501 867 752 689 385 867 489 472 195 424 072 479 764 085 286 862 506 497 197 479 177 954 752 550 355 250 186 043 935 595 046 740 938 492 587 384 763 663 418 813 900 056 565 335 826 555 236 029 203 457 605 176 294 933 354 388 227 240 432 428 966 513 733 071 127 752 449 701 636 545 738 259 521 300 643 888 735 935 990 223 477 585 437 977 121 488 386 833 653 615 124 588 205 512 259 804 597 830 537 155 163 010 709 716 239 586 192 855 194 044 378 392 841 395 482 767 076 843 988 426 191 744 902 649 349 262 170 360 826 191 695 684 680 048 735 080 189 718 400 750 054 594 658 081 561 379 080 992 555 573 855 821 398 999 467 858 571 567 179 274 633 015 263 801 274 799 773 204 713 451 089 189 752 708 965 665 294 846 224 183 447 201 221 203 178 470 545 382 243 153 386 324 121 807 880 881 364 023 760 894 132 188 283 926 803 218 583 194 494 942 205 917 549 971 003 336 416 246 458 427 997 309 700 033 521 558 455 294 919 563 756 046 947 333 175 594 062 127 318 773 804 463 463 023 590 468 109 866 940 230 555 505 610 541 392 694 659 202 295 971 043 911 280 379 208 026 944 673 325 110 577 228 264 205 636 711 407 454 147 835 308 148 266 441 550 038 199 075 247 459 944 042 066 027 583 166 473 442 796 144 946 734 956 756 965 425 907 003 595 133 201 694 496 418 080 602 136 336 800 705 629 579 938 850 785 802 429 772 755 037 361 075 254 136 903 389 057 262 123 716 729 167 479 288 576 469 104 509 094 244 994 594 405 499 603 539 124 580 068 516 063 230 319 046 676 402 213 097 289 854 296 333 224 647 533 460 404 329 170 703 804 048 471 381 683 919 630 235 373 265 939 869 346 138 203 505 849 387 717 358 236 689 241 341 039 546 792 039 308 468 361 536 862 300 032 753 678 866 728 099 545 785 175 071 761 184 308 537 244 363 119 320 744 095 777 257 987 001 826 990 778 132 097 757 121 754 235 367 537 769 786 477 610 238 003 895 157 574 614 394 959 773 295 615 988 944 119 586 182 656 689 850 753 668 205 096 756 148 460 143 492 754 031 708 466 966 249 988 098 878 633 888 247 826 897 228 793 631 579 536 771 127 771 290 549 460 517 371 890 868 430 379 728 419 925 799 896 455 734 118 454 215 106 491 205 790 395 031 356 055 908 898 100 909 268 407 121 074 029 184 725 459 356 996 999 108 339 961 676 537 271 365 118 183 466 774 582 445 814 549 156 311 492 436 038 464 627 677 966 292 018 480 480 495 632 891 274 526 152 071 467 110 646 301 276 115 176 160 412 721 140 698 849 272 477 129 039 941 738 115 516 819 136 441 799 813 453 516 716 057 162 197 363 303 131 348 141 850 373 283 218 998 914 500 374 714 321 540 748 170 156 247 444 479 630 465 932 027 751 209 279 459 807 238 681 556 075 813 167 641 554 216 056 161 591 235 298 561 125 342 161 048 438 324 357 602 401 058 216 191 563 173 052 190 935 197 615 199 537 413 686 342 747 200 027 992 414 801 298 738 389 782 922 802 445 474 832 299 119 512 275 378 249 441 819 454 006 610 163 291 147 851 308 413 245 580 059 512 953 726 469 507 369 432 191 554 856 554 543 568 803 297 477 351 418 576 973 528 759 527 574 727 863 598 397 975 479 278 908 759 891 613 616 063 524 123 190 549 302 988 674 335 876 169 074 166 846 680 381 936 569 709 530 108 291 227 509 238 836 668 983 455 870 835 979 646 850 932 518 938 114 980 119 608 270 941 605 875 537 645 305 704 664 007 594 374 812 671 934 574 595 538 958 411 474 538 386 226 367 444 790 201 751 549 917 967 249 937 429 798 899 811 565 939 458 121 561 752 799 917 183 645 966 849 920 610 366 781 162 209 002 929 436 305 420 263 198 167 086 141 248 351 237 286 852 736 442 238 123 634 413 269 647 797 229 859 753 589 768 061 929 367 916 333 905 891 292 050 484 945 587 499 152 964 614 291 444 361 298 911 713 150 791 353 500 043 103 606 964 893 415 077 810 037 664 676 430 153 150 390 261 847 964 462 206 722 425 613 977 591 604 900 426 086 466 280 438 702 104 488 257 603 036 026 757 488 311 976 779 983 807 213 929 416 591 619 157 521 305 140 973 764 971 151 880 525 737 256 837 305 939 599 729 837 627 361 794 041 852 538 973 168 278 597 746 478 240 266 472 746 066 229 556 164 316 396 461 201 728 552 719 217 858 495 882 870 474 670 664 871 556 896 270 738 259 174 434 643 269 738 438 913 630 994 355 482 032 025 762 949 859 662 173 785 401 236 062 592 954 467 882 785 820 558 887 285 362 006 884 730 832 727 354 625 690 214 503 330 881 810 830 691 492 952 907 288 027 068 731 448 728 155 247 849 796 489 596 457 417 130 501 980 747 966 911 722 467 549 629 968 482 048 266 497 461 769 359 202 125 146 173 905 948 554 008 530 259 768 656 708 782 380 996 757 979 969 542 268 218 706 502 551 535 711 067 701 837 817 994 357 468 762 332 788 628 034 808 154 389 131 864 263 039 473 592 712 849 655 408 615 960 970 227 965 888 827 356 659 145 398 598 820 441 303 459 062 755 911 005 845 335 050 009 581 130 240 322 500 245 315 700 460 340 219 777 569 867 264 000 705 784 878 194 326 581 379 514 366 936 622 166 468 604 997 769 729 153 900 090 887 659 121 590 713 022 571 598 283 994 425 704 049 124 739 892 066 920 889 616 884 335 451 422 584 716 461 698 317 435 407 335 508 578 740 902 823 985 941 149 095 916 332 396 818 523 909 072 912 153 688 677 583 266 303 376 705 150 976 356 450 751 824 336 592 807 581 927 885 364 034 030 289 457 792 018 379 210 994 557 959 653 999 011 433 199 266 125 333 996 562 110 247 674 877 661 938 611 248 193 078 023 549 002 029 768 973 474 047 820 363 738 227 205 001 859 408 108 112 761 839 741 716 274 494 284 098 473 713 146 034 024 399 851 406 587 917 212 189 006 414 531 177 786 644 325 571 445 857 856 036 076 904 172 238 238 721 390 485 634 936 762 654 524 965 483 103 139 057 002 858 254 212 755 284 742 161 575 261 977 203 272 208 521 555 843 780 555 399 232 960 733 804 206 299 770 360 068 200 207 883 094 104 269 868 350 160 265 515 492 867 355 014 590 684 432 449 564 067 908 445 448 764 028 288 396 176 477 736 288 410 931 609 233 975 410 884 263 599 849 903 066 736 645 696 061 002 856 456 690 743 422 562 004 958 197 195 554 240 524 996 183 192 600 263 244 335 177 481 636 795 858 767 855 557 429 877 072 387 773 357 205 789 616 147 349 897 853 960 466 806 316 295 122 828 456 483 865 539 238 835 683 473 730 413 726 054 401 237 238 449 922 752 260 876 275 520 306 761 907 811 924 150 456 981 737 699 070 736 179 984 273 254 847 383 230 585 392 332 271 776 617 897 780 645 976 264 648 313 727 050 407 669 069 654 983 826 637 199 645 272 482 255 757 013 558 405 263 658 083 555 190 254 656 022 436 552 109 770 572 710 633 846 681 497 218 336 413 114 484 465 375 758 941 054 404 677 288 360 934 860 141 789 443 740 997 665 869 197 010 671 170 226 253 979 912 699 687 351 725 512 995 032 148 670 729 356 373 524 111 119 535 415 563 558 642 694 575 754 199 400 602 848 932 445 325 953 310 268 413 520 692 717 671 351 200 561 693 321 237 538 496 185 743 092 453 057 843 810 156 647 456 230 022 391 896 069 022 294 367 020 556 399 832 215 306 585 173 348 742 124 518 611 837 357 725 652 662 499 500 357 379 722 832 631 273 119 295 078 741 964 257 805 113 515 202 899 984 059 967 715 650 379 308 117 384 128 363 040 892 934 306 749 273 175 477 666 032 962 626 175 649 491 450 904 826 600 138 624 465 646 532 578 361 007 664 642 904 097 324 480 982 959 236 348 226 065 779 703 076 532 968 822 127 338 617 148 206 376 135 168 081 571 159 029 851 712 666 444 903 306 818 439 837 023 214 613 850 314 998 587 531 718 185 177 778 985 570 702 770 316 713 275 823 837 074 374 123 384 868 099 596 982 050 485 977 136 425 363 293 860 923 895 384 896 437 656 696 633 056 538 948 331 522 684 109 604 292 791 213 767 997 395 930 183 390 670 905 817 644 655 033 482 583 752 525 401 826 261 104 977 534 855 354 335 986 158 267 048 753 957 719 142 082 551 164 938 180 254 407 138 035 217 377 587 033 959 817 387 381 770 235 961 236 617 489 907 072 640 551 707 670 052 130 680 836 046 976 870 716 391 966 557 346 632 142 939 729 725 356 185 396 913 247 502 303 249 343 198 186 986 249 918 061 525 534 629 376 306 803 630 355 444 214 442 359 169 590 393 791 359 291 641 960 840 816 661 263 495 306 829 846 601 699 627 970 140 435 656 238 352 864 753 175 795 246 861 841 704 428 316 776 980 746 570 398 263 647 770 086 193 446 110 172 864 651 343 950 521 510 217 897 439 782 101 126 541 877 320 773 761 239 190 671 705 710 253 902 653 416 589 638 461 700 668 785 388 299 166 148 799 071 339 984 614 605 726 614 237 973 119 014 528 799 984 941 131 101 406 111 879 883 920 599 832 402 973 474 049 111 628 717 127 088 683 384 423 532 629 131 219 131 314 203 534 790 989 030 347 179 661 608 132 286 478 332 327 300 485 111 732 807 069 266 422 370 895 748 187 767 139 055 224 305 730 919 572 469 924 028 430 263 938 042 385 075 213 859 504 725 880 890 815 283 677 955 583 131 107 523 589 307 447 522 493 885 934 594 625 032 202 889 774 400 820 119 559 990 629 997 449 454 702 890 698 925 661 494 692 762 927 406 321 070 094 650 656 891 729 996 420 087 546 310 769 346 469 091 349 192 650 226 839 401 609 203 486 424 176 198 978 097 958 944 097 648 190 669 816 201 565 054 971 880 531 611 843 779 872 759 473 033 663 461 002 014 715 430 013 354 282 598 947 050 640 735 487 905 422 025 032 831 126 425 378 887 575 933 568 001 879 830 425 563 433 109 101 244 871 528 377 355 232 650 592 640 356 160 766 540 323 619 510 800 463 442 271 305 096 345 687 199 663 435 030 881 731 628 953 890 961 504 608 196 889 313 963 490 711 822 189 777 816 199 793 261 075 373 170 409 406 207 556 774 736 389 526 828 593 703 946 959 145 270 994 427 436 814 749 892 962 899 685 540 068 694 681 979 024 535 301 942 966 559 882 678 657 492 517 099 732 219 386 508 871 062 828 460 217 489 306 383 792 915 322 585 298 111 082 524 630 474 473 704 488 670 975 925 295 974 885 167 831 069 312 536 656 367 894 159 168 524 199 491 816 988 704 786 311 005 348 295 249 184 055 564 533 390 389 456 670 600 909 494 583 271 173 088 190 309 375 771 274 083 146 423 764 533 349 509 065 036 847 828 793 195 331 628 325 391 755 703 761 629 136 720 159 590 695 771 480 994 810 615 284 118 745 843 762 855 428 380 366 172 281 382 344 957 923 687 249 143 989 455 943 751 514 954 510 817 852 054 576 436 786 020 655 094 201 943 979 325 781 685 177 052 957 048 978 834 031 899 367 361 803 573 901 833 690 550 148 530 594 522 795 289 485 978 335 571 755 247 994 366 167 883 303 181 176 768 571 197 956 129 291 549 900 180 809 993 551 390 207 413 900 723 405 823 499 489 297 245 790 739 603 549 519 193 968 131 694 707 121 735 624 403 743 085 812 536 822 249 907 382 983 598 252 221 172 020 562 823 144 989 680 589 833 391 878 542 621 530 437 238 471 225 002 228 208 897 721 342 047 654 632 021 695 702 114 663 756 032 980 410 682 787 194 207 025 090 603 581 760 205 961 703 347 063 499 780 738 838 147 541 649 833 836 464 879 784 856 893 809 940 896 883 544 994 383 463 047 924 614 742 030 212 223 274 062 385 299 993 226 303 138 038 855 824 411 760 436 049 814 416 953 837 226 003 312 762 156 282 553 893 818 022 054 956 892 920 754 867 824 179 502 790 248 007 337 175 059 207 206 421 213 140 480 763 598 440 778 282 369 933 705 609 497 324 358 752 275 875 369 900 793 776 873 620 921 774 427 902 375 699 372 782 919 810 443 524 390 607 688 139 987 507 386 451 407 227 692 097 140 466 384 359 304 554 118 824 805 257 964 676 433 107 969 574 943 021 350 051 873 020 622 423 138 027 561 777 377 286 442 172 457 398 592 236 400 544 933 680 312 813 425 509 880 721 005 046 584 222 673 812 389 934 965 439 127 439 680 789 333 433 414 659 332 753 487 157 557 293 802 157 098 564 968 647 554 889 337 706 239 673 262 525 505 357 627 321 065 809 534 533 346 089 548 262 868 704 934 154 423 886 910 503 616 294 967 721 443 252 994 157 374 369 561 328 538 999 644 481 100 764 144 922 295 608 231 408 295 754 015 617 274 582 046 744 324 157 753 425 017 611 429 156 704 500 675 207 051 304 212 170 091 342 691 980 622 674 825 593 038 879 358 957 898 682 366 803 276 714 485 030 563 018 416 603 206 822 780 331 276 780 986 535 575 954 663 371 096 477 915 395 569 637 608 311 331 678 827 628 460 026 019 232 021 822 701 091 115 439 971 427 539 321 195 172 958 092 077 231 209 401 815 829 270 900 324 531 043 083 329 173 832 836 738 479 437 559 029 242 748 466 229 790 263 531 671 803 195 504 652 158 467 975 471 000 809 170 811 113 468 935 762 375 164 194 775 935 020 490 305 242 780 380 860 236 424 770 163 905 841 114 862 719 997 038 047 906 501 140 803 678 862 084 700 277 273 134 523 164 395 108 207 534 438 135 109 739 986 858 856 926 583 548 312 210 995 245 289 932 267 667 718 026 686 432 029 247 012 720 321 986 431 321 349 905 407 907 687 651 493 432 929 251 611 099 226 572 134 776 811 757 202 168 895 524 681 418 794 248 402 590 138 712 196 202 626 300 484 677 040 739 447 931 136 469 048 324 698 874 021 673 975 434 038 973 272 956 450 153 951 975 848 520 437 063 736 726 015 081 443 373 712 519 383 631 521 914 369 776 269 090 466 884 220 592 666 463 714 731 677 797 602 133 416 485 338 084 284 925 775 578 496 190 841 251 231 884 789 700 580 480 310 305 095 806 342 048 722 879 448 068 001 299 477 563 383 677 406 000 926 101 478 505 309 100 561 398 591 901 641 004 851 877 899 312 815 097 382 055 683 808 752 050 893 751 955 501 413 217 376 076 967 343 805 976 740 125 215 917 828 223 965 333 135 327 316 902 062 354 751 899 832 625 831 673 528 417 633 635 511 022 979 694 895 588 214 378 755 676 651 041 476 234 432 990 953 600 282 013 602 067 878 266 321 631 016 259 331 579 136 393 726 760 350 448 516 546 003 329 210 477 433 074 862 935 291 475 323 371 537 619 629 603 546 191 656 189 512 986 878 582 376 886 991 525 959 932 478 244 690 075 960 877 693 610 544 908 002 510 392 790 124 304 520 820 637 420 468 150 262 892 983 436 418 576 174 080 629 169 293 005 927 715 735 563 518 992 399 129 877 710 514 432 801 663 516 403 219 243 346 880 628 583 321 448 099 668 917 525 433 355 611 448 809 813 448 234 378 403 304 723 623 734 125 174 188 332 755 975 103 239 307 608 526 552 288 590 192 842 702 517 365 839 651 972 043 658 621 775 425 211 931 861 256 342 689 948 896 226 263 318 529 547 766 877 582 641 796 225 591 615 324 572 292 191 875 352 979 804 592 546 347 523 612 575 682 294 567 971 308 217 423 651 651 028 427 161 874 209 941 740 524 207 106 081 254 337 679 067 786 552 698 047 502 601 457 508 420 091 442 882 081 537 850 958 054 307 960 750 310 033 043 874 446 072 534 158 790 440 360 580 970 778 446 658 300 625 334 046 063 045 400 602 075 996 487 317 270 418 119 379 591 932 081 485 374 201 878 463 936 972 705 238 502 104 887 791 106 211 395 135 076 766 959 925 684 901 666 687 494 097 064 135 270 505 504 185 947 828 201 508 657 639 141 642 520 039 148 671 135 831 282 872 865 474 342 391 399 207 948 059 204 566 860 574 269 891 834 845 592 492 408 976 180 448 166 754 521 658 206 098 675 263 665 278 992 448 412 702 073 483 660 879 225 187 488 583 869 018 977 569 525 545 795 948 035 126 732 121 867 805 222 419 184 578 057 966 670 567 176 553 211 293 455 681 146 522 890 072 056 466 987 461 736 916 748 499 709 283 042 172 243 236 919 397 050 770 584 115 310 118 673 788 324 723 474 415 537 892 010 915 464 015 496 564 381 849 916 528 134 116 398 049 382 821 635 526 993 318 353 293 275 988 563 173 753 268 845 488 425 630 241 462 593 886 392 358 603 489 743 959 027 335 310 505 371 381 983 492 134 386 383 172 077 469 915 371 794 091 034 251 799 696 669 313 875 142 976 618 338 665 585 785 981 585 684 496 290 584 634 829 315 633 921 342 703 777 363 947 149 903 915 691 614 768 687 066 766 044 580 313 838 850 177 601 185 800 020 874 304 479 849 709 438 217 257 121 117 338 599 130 972 938 662 133 583 292 409 866 453 280 527 342 162 055 544 615 770 621 163 483 931 365 308 383 379 392 895 825 438 963 380 493 385 130 757 982 006 956 591 233 413 596 679 064 979 711 458 138 869 251 876 006 179 067 723 174 635 489 634 974 717 018 877 342 928 137 913 185 063 547 392 918 141 653 643 441 402 580 026 005 849 988 245 675 399 702 501 350 209 140 161 157 401 290 326 407 935 119 964 222 584 136 164 178 926 215 178 360 292 806 003 435 422 860 740 447 558 057 655 491 855 868 360 604 400 694 124 713 206 692 455 766 173 806 939 112 170 450 378 966 514 989 901 349 986 357 325 065 294 408 902 171 211 296 231 659 571 364 192 701 698 542 414 962 798 481 226 346 894 263 654 770 275 042 189 137 561 718 903 322 888 738 464 203 411 948 565 867 833 029 520 175 282 057 513 972 494 865 620 221 447 056 470 211 193 976 215 968 585 276 837 922 156 485 843 945 509 603 286 566 118 555 070 965 058 224 780 810 908 443 089 986 668 398 023 300 431 718 257 671 138 094 884 199 091 224 667 675 224 200 521 902 786 424 755 187 005 845 166 401 134 571 723 995 426 865 168 717 028 878 652 376 102 409 394 245 774 394 975 898 681 604 373 204 749 831 453 359 730 230 323 608 136 464 586 834 808 972 564 423 059 019 756 522 455 324 504 665 007 266 933 532 354 213 382 890 132 250 058 016 577 990 749 101 253 618 054 424 757 970 779 321 629 998 684 764 569 386 436 365 729 830 577 439 332 994 071 090 863 293 463 121 520 754 175 878 213 350 825 218 681 987 801 566 451 333 019 777 547 917 205 925 700 122 284 805 344 363 102 533 950 898 963 220 367 475 210 399 557 674 131 227 877 616 621 464 881 995 711 975 541 267 004 522 118 490 315 394 785 819 144 229 789 364 942 251 610 090 089 095 059 107 310 211 744 716 732 541 035 411 208 181 354 439 270 494 300 583 266 970 218 932 722 774 516 918 262 493 444 511 208 899 434 822 074 561 256 904 295 451 268 417 654 164 779 100 765 002 429 633 535 606 998 661 412 441 915 863 041 545 807 808 515 814 693 334 183 492 272 874 451 834 614 821 287 888 590 018 882 415 718 302 581 975 214 245 577 747 934 913 051 774 602 773 648 663 228 081 876 280 648 009 301 600 853 457 885 641 604 870 585 851 460 213 393 745 645 143 411 832 436 687 537 632 442 470 286 325 165 246 014 914 945 161 705 603 710 950 076 730 112 191 407 424 319 620 804 782 703 623 177 915 173 137 344 910 982 185 428 938 720 944 311 481 993 577 823 193 799 998 997 137 282 527 516 058 665 603 089 661 746 423 165 334 024 393 372 201 529 781 642 248 273 269 855 051 073 528 231 785 091 320 719 320 815 374 507 793 783 976 671 068 475 559 698 143 341 725 475 225 833 413 764 982 944 874 997 139 102 203 107 599 212 042 996 416 479 950 042 584 168 585 988 495 543 750 974 478 525 306 923 197 115 555 250 874 283 055 560 473 228 533 462 868 284 652 187 252 345 191 292 165 575 809 649 295 829 982 439 080 615 245 246 727 506 315 650 454 302 216 833 417 377 940 827 011 642 753 361 790 172 943 109 682 249 329 624 888 325 646 475 557 103 624 628 313 662 026 883 718 886 918 768 387 405 746 586 519 096 601 050 780 382 868 419 667 349 113 566 170 792 273 808 756 069 588 219 249 123 668 668 892 193 018 977 937 552 960 389 099 568 733 179 547 061 602 525 832 196 325 935 552 943 038 013 656 646 855 290 748 823 401 640 974 297 958 425 188 521 282 094 172 805 618 468 595 197 146 801 464 250 666 751 605 064 790 883 455 515 140 360 889 112 182 284 217 932 693 534 914 731 762 470 909 192 781 237 829 458 469 707 686 033 635 109 076 453 427 795 908 267 031 935 910 021 600 437 381 857 813 158 235 439 545 767 546 735 311 468 451 568 487 884 988 542 374 070 618 141 550 191 668 060 166 573 121 286 181 589 370 438 546 570 023 741 163 437 366 304 791 546 620 130 214 884 418 784 490 748 363 894 222 098 445 896 082 037 198 710 545 966 371 237 766 482 734 378 727 147 125 105 073 863 207 177 066 054 142 630 167 482 526 185 660 618 236 905 490 637 864 421 706 303 793 026 271 688 047 977 373 427 847 166 942 442 358 676 888 982 438 248 829 458 840 504 862 040 539 203 186 447 202 550 695 787 359 464 436 605 800 107 911 988 492 994 862 601 164 797 824 489 234 267 071 799 025 482 728 652 952 777 234 445 459 699 933 289 897 260 582 065 926 786 643 596 932 222 053 572 253 236 667 084 430 725 236 555 588 848 041 019 511 005 817 317 335 205 858 034 325 088 516 591 925 099 680 624 729 550 713 378 275 034 732 964 907 538 512 894 520 478 295 932 155 197 770 662 029 960 316 128 373 673 253 494 140 395 126 732 723 679 562 575 171 089 939 397 021 663 395 273 738 592 742 266 905 421 132 374 217 163 831 881 119 985 097 100 890 671 007 710 983 915 002 070 279 727 821 050 675 169 057 635 355 410 249 587 071 878 291 582 923 484 730 822 896 470 526 745 009 580 382 694 662 042 561 895 513 502 704 612 944 226 821 739 473 448 908 223 681 553 734 752 463 592 564 663 068 433 035 059 715 615 210 276 560 331 192 130 314 030 523 719 500 456 155 937 444 955 405 969 817 289 873 498 089 466 866 713 652 472 162 541 002 752 011 354 839 335 991 815 924 106 240 180 477 396 039 311 814 539 577 207 064 274 585 381 387 959 929 121 224 726 822 406 775 250 981 770 149 767 440 911 123 597 910 206 270 881 628 408 064 950 319 064 496 961 903 248 766 664 660 845 974 748 204 686 161 083 268 006 898 743 757 997 517 032 472 370 313 677 911 120 601 571 990 444 934 896 640 153 007 098 818 859 385 930 129 074 013 417 687 404 735 739 130 662 088 603 911 089 249 132 669 173 516 836 103 970 296 317 885 822 698 394 463 121 247 081 420 440 229 811 027 910 633 125 888 322 140 289 453 154 133 652 567 316 687 904 397 242 018 380 024 745 970 655 089 560 993 874 863 748 148 858 969 189 458 111 398 186 341 091 061 398 565 611 151 754 214 609 856 514 262 693 033 840 350 124 924 922 847 608 097 098 820 181 546 245 009 200 953 340 223 413 927 563 798 730 232 702 387 899 487 109 338 247 426 637 963 987 995 515 194 186 578 239 156 979 196 984 582 243 921 259 114 689 134 852 224 617 477 748 585 223 880 072 879 918 829 865 908 042 663 224 653 582 443 055 602 786 271 576 982 889 493 947 884 480 384 169 367 399 770 112 689 168 244 821 380 743 964 363 413 675 919 724 269 036 852 395 482 782 658 744 553 159 685 063 379 251 222 316 175 826 390 824 830 410 086 953 488 415 280 820 673 344 653 728 136 997 679 917 136 331 775 131 865 426 919 955 002 955 559 232 115 216 617 034 465 668 058 024 052 647 708 938 146 952 929 147 201 133 491 486 096 805 848 390 586 234 254 972 339 217 435 165 223 033 598 268 467 109 740 300 921 952 878 073 000 972 501 997 345 920 379 694 094 309 619 641 570 238 615 829 124 184 532 669 958 343 374 664 165 627 718 714 268 877 305 486 028 127 326 820 870 800 213 022 486 492 092 730 003 396 556 977 683 559 353 099 542 078 437 046 068 909 575 515 905 481 824 655 507 563 627 722 949 464 218 419 224 337 585 625 001 108 887 684 693 751 962 194 562 775 776 465 782 065 557 789 467 168 052 970 501 368 483 873 750 956 428 850 639 658 061 380 561 024 947 016 816 835 584 641 194 816 226 040 357 203 101 025 668 649 529 700 160 164 766 323 403 890 684 630 518 529 644 783 631 095 707 627 732 126 563 609 307 756 383 719 257 990 160 211 137 391 347 908 750 944 985 263 857 921 929 039 198 384 426 335 985 926 373 173 045 311 181 311 269 183 974 691 173 480 376 790 446 603 443 238 797 073 354 998 906 759 723 063 905 525 704 472 082 532 877 714 158 423 422 290 368 532 155 096 940 408 556 809 144 114 499 224 980 863 640 291 194 201 260 239 533 509 823 469 515 062 852 810 136 009 670 891 476 884 681 792 161 138 525 877 085 128 973 653 496 091 344 890 125 272 940 371 921 767 040 898 128 550 251 334 727 613 466 793 840 871 796 890 804 156 551 575 790 491 407 863 879 637 514 470 615 699 516 210 239 490 585 538 234 869 875 888 606 231 712 404 808 949 097 968 757 270 437 545 124 038 951 851 664 582 880 632 387 081 987 302 684 858 869 845 594 797 346 087 760 187 439 935 511 619 302 040 728 723 851 153 363 386 368 611 177 123 110 944 779 317 573 645 558 049 442 283 906 184 976 608 191 995 402 446 704 841 466 976 472 441 933 425 054 576 588 722 008 876 055 664 466 591 968 846 789 641 732 682 127 517 602 429 485 288 323 624 479 700 785 885 346 349 468 831 140 761 576 707 727 084 880 374 957 147 111 039 167 295 175 544 227 079 797 082 538 965 799 792 713 322 439 369 978 476 317 517 072 190 299 993 300 423 654 420 509 201 653 795 547 524 910 523 960 140 383 451 777 287 719 760 047 521 836 728 972 511 880 187 504 658 701 556 904 041 787 045 267 594 562 190 465 223 109 746 804 052 659 403 827 744 499 538 220 083 739 502 363 517 074 790 191 926 586 238 188 010 519 067 298 420 841 378 530 265 092 530 884 995 596 791 001 165 651 346 688 133 780 421 305 588 386 797 626 890 561 409 065 758 725 546 479 297 087 206 401 437 424 254 152 181 232 609 178 196 247 113 226 416 793 349 540 124 707 889 528 023 335 135 017 875 601 248 478 885 827 975 525 730 977 498 101 741 331 668 506 598 004 970 220 928 697 812 376 784 855 109 299 179 799 069 627 203 983 873 923 862 080 756 813 181 027 567 767 435 777 496 088 160 176 640 531 925 718 719 398 942 412 938 444 595 712 594 846 715 330 515 178 601 744 141 967 693 136 219 653 777 968 956 585 717 762 365 140 571 663 806 979 097 627 531 784 540 159 261 166 172 259 292 166 673 208 041 729 935 024 432 655 084 840 330 146 002 599 387 093 092 804 241 759 926 837 222 666 108 191 904 726 713 295 160 588 118 487 280 423 438 989 981 344 361 870 370 335 619 940 918 831 214 701 763 038 682 015 235 862 187 132 137 551 082 601 626 288 450 518 033 703 535 301 463 939 185 732 616 900 267 254 823 564 337 303 923 370 681 245 638 042 195 764 394 865 363 569 899 448 148 077 323 562 035 990 513 253 442 581 650 141 068 502 882 975 853 609 694 844 571 437 327 709 106 070 646 548 876 439 520 388 245 388 164 829 165 220 594 726 387 527 652 799 504 426 774 387 536 483 138 681 244 272 131 886 433 116 221 043 398 785 099 691 840 815 421 989 329 201 366 734 374 438 430 292 550 904 457 207 647 409 542 798 830 879 550 618 345 657 068 820 964 494 867 350 622 911 606 055 873 447 227 596 143 308 626 718 946 778 490 137 974 212 329 558 024 754 273 008 259 618 661 456 157 130 690 217 310 824 144 396 077 856 676 313 562 510 943 286 459 671 605 111 344 975 855 230 264 511 838 530 506 486 932 635 151 054 219 253 928 202 386 021 275 732 131 867 190 305 337 076 563 239 127 939 340 306 552 173 880 171 646 230 397 843 841 486 491 805 017 469 301 364 281 557 361 587 809 648 324 061 618 280 005 758 885 372 912 630 336 289 298 035 698 941 936 393 533 766 855 373 023 815 137 136 139 886 542 876 169 526 730 684 708 700 562 292 996 606 557 927 181 952 628 941 451 765 356 004 596 823 990 961 210 618 954 816 920 804 706 265 422 611 786 384 417 840 018 475 407 602 304 775 460 326 296 692 312 883 378 762 217 969 993 182 639 161 406 007 405 367 453 167 316 040 481 853 131 179 275 981 415 833 828 668 022 385 642 667 517 661 028 865 234 530 345 389 706 383 342 205 799 293 635 837 579 011 560 998 096 825 959 210 914 291 390 982 254 645 232 436 035 036 470 236 054 516 185 086 597 049 193 326 925 815 704 811 858 988 855 552 984 877 362 054 542 037 795 879 863 328 883 765 833 029 067 155 646 931 904 826 647 688 920 896 449 984 522 648 552 457 170 194 770 193 625 727 684 801 537 992 435 849 211 270 902 831 917 497 031 326 582 961 997 401 076 394 913 176 710 409 606 332 362 198 392 008 155 564 141 472 713 330 383 999 436 458 379 361 084 636 816 711 589 213 764 144 817 269 091 316 678 288 300 859 432 407 335 335 928 736 659 352 557 895 857 318 541 033 318 898 517 616 383 566 848 210 939 424 720 858 132 459 442 283 746 126 823 374 371 881 302 425 982 095 251 532 413 104 102 520 559 630 842 175 228 986 625 871 415 039 101 768 837 410 242 743 041 311 532 093 410 878 897 642 752 726 453 559 030 656 927 407 163 992 007 026 271 112 260 712 150 688 940 859 991 938 999 861 358 745 229 565 964 884 316 531 961 479 087 055 013 250 554 942 928 136 499 146 729 366 902 579 710 148 444 892 423 563 892 353 656 115 094 025 847 225 504 683 761 552 269 970 329 247 882 057 132 875 867 208 623 730 502 086 703 719 006 119 617 294 752 372 869 791 883 157 500 286 603 238 676 391 094 468 047 835 585 919 318 667 893 531 547 953 485 199 551 963 389 433 842 121 478 626 552 259 175 072 385 063 914 107 396 174 320 035 383 029 918 621 434 516 358 507 190 132 916 121 601 452 183 229 714 296 413 310 681 723 353 450 693 014 135 566 767 248 879 433 746 690 150 318 440 936 454 622 331 379 314 340 854 575 848 449 411 906 634 709 359 998 372 072 117 069 308 454 070 951 262 494 213 552 243 224 164 635 931 765 716 075 537 583 225 795 569 608 772 089 559 063 213 091 461 223 711 463 319 270 264 841 373 278 593 676 663 177 324 987 916 980 417 892 287 948 135 829 742 996 233 712 223 141 970 366 022 051 031 426 257 579 001 271 826 726 751 793 649 624 137 401 474 991 298 096 390 527 409 846 211 662 030 158 194 730 598 605 135 530 650 604 449 660 471 125 923 255 272 144 862 707 492 795 356 316 727 068 474 141 236 881 102 592 076 639 035 242 856 750 295 163 576 078 561 846 168 939 715 379 206 299 676 770 132 093 070 786 555 781 579 923 418 884 236 801 860 055 970 894 619 175 276 910 164 173 339 538 955 790 225 213 208 527 781 880 903 829 353 089 475 568 864 366 691 288 985 403 345 437 471 925 890 595 399 718 802 446 135 588 631 049 370 233 168 140 796 365 704 137 592 949 627 575 617 307 113 938 976 819 218 881 125 330 032 845 762 402 629 540 834 043 880 629 659 363 519 398 158 144 681 269 385 148 269 191 867 793 227 848 750 362 178 767 576 558 738 928 136 079 916 827 212 816 831 450 172 161 232 715 956 340 147 015 781 999 873 782 101 835 392 467 199 575 020 161 924 544 540 452 478 792 171 823 094 904 746 392 052 185 349 127 302 639 845 415 696 215 218 531 636 857 982 952 511 932 835 094 254 252 743 694 049 587 697 124 858 585 232 956 514 288 335 756 624 830 579 518 690 918 902 481 900 982 551 500 609 614 774 054 007 527 699 937 091 427 983 328 150 187 753 853 902 629 607 754 040 695 311 618 962 320 249 813 390 341 347 311 034 042 300 894 474 163 013 742 884 841 307 301 547 457 096 918 042 661 102 089 687 689 698 060 681 960 100 422 059 038 839 074 599 494 198 834 397 456 786 158 883 759 352 093 774 458 032 084 956 674 757 465 511 166 859 096 357 042 309 886 801 198 935 412 217 125 788 383 935 607 956 079 227 084 110 769 366 053 485 735 482 487 172 088 939 785 275 032 196 026 584 735 903 583 397 216 519 591 084 874 394 409 753 400 465 889 413 318 530 816 838 344 198 388 291 028 043 022 320 767 081 833 948 123 756 059 188 450 092 330 855 843 951 202 670 388 985 402 934 252 765 692 760 190 068 282 843 212 324 457 070 703 370 886 428 479 431 724 906 653 531 279 353 375 444 493 805 202 802 367 146 317 671 699 068 607 765 731 187 348 425 692 687 751 603 214 118 698 376 729 612 823 181 843 784 517 118 805 630 766 399 048 206 028 526 340 237 609 218 962 433 758 499 167 248 653 558 274 325 046 206 488 047 500 398 480 958 616 486 821 983 209 431 722 972 919 396 840 643 808 244 583 474 181 500 776 519 719 195 557 852 324 632 508 119 416 045 294 460 172 578 107 800 252 002 523 496 649 984 401 118 570 610 366 680 423 102 224 885 577 220 840 429 221 735 809 588 030 567 343 661 116 854 056 877 168 331 948 304 520 474 755 309 261 335 154 620 083 072 411 386 278 361 909 561 420 034 509 606 566 492 261 448 187 963 497 831 213 531 684 258 062 761 106 934 122 530 802 512 995 023 638 754 619 231 289 085 511 614 386 862 001 826 708 778 253 827 611 312 910 900 263 289 828 876 754 086 619 964 767 287 402 386 403 457 528 497 244 337 625 388 823 553 777 076 487 534 469 694 300 073 695 435 253 339 273 959 742 115 839 910 477 983 568 636 118 270 291 833 534 811 324 754 529 346 781 434 489 003 960 517 263 118 519 696 022 335 714 425 296 879 197 123 897 586 777 318 018 949 124 353 585 657 937 657 453 727 691 777 006 538 221 631 462 993 317 598 567 274 338 583 171 271 477 825 468 578 042 356 225 725 819 952 821 230 448 584 497 240 440 349 505 493 558 013 286 875 555 143 145 505 831 818 644 094 159 420 388 408 938 348 460 135 102 371 909 776 840 313 446 003 090 414 692 742 973 284 970 004 427 001 664 396 720 171 423 489 991 974 063 811 998 854 913 362 961 347 312 765 842 555 090 318 469 339 094 530 893 766 873 027 030 996 587 463 919 906 096 438 661 389 008 652 342 939 825 620 960 222 043 366 493 814 845 787 964 492 927 875 448 234 224 266 091 384 810 087 568 476 632 142 650 342 423 045 953 143 886 050 488 556 911 895 223 683 135 682 690 200 050 422 228 360 173 432 536 239 745 691 687 329 783 105 356 556 911 801 573 375 860 429 943 130 131 016 512 214 323 829 614 295 605 820 410 852 939 786 896 161 992 569 896 552 384 264 345 504 026 302 719 388 708 835 028 618 718 605 963 179 804 758 312 941 708 317 607 697 761 790 831 070 304 211 931 918 040 282 270 590 088 181 031 727 039 949 138 845 251 823 304 095 117 164 569 180 488 346 627 591 048 502 135 972 339 554 209 739 808 449 615 000 633 574 229 744 379 478 203 133 830 409 785 202 837 969 822 059 144 218 628 182 451 885 201 401 259 428 588 679 529 123 564 654 308 128 062 886 524 939 483 688 861 815 902 105 118 830 441 260 262 610 080 540 007 208 122 293 890 761 280 924 068 703 163 669 175 917 684 517 759 247 001 949 534 243 278 693 522 663 091 092 008 197 539 703 596 476 386 536 585 839 248 269 579 016 665 935 572 875 328 570 895 288 957 118 835 998 204 115 461 301 209 667 794 818 261 672 443 310 795 002 992 245 534 480 239 355 925 236 886 715 690 560 392 588 423 883 610 764 273 495 856 146 924 391 416 121 621 390 470 380 007 709 171 058 763 738 738 494 216 849 345 771 568 393 768 726 193 837 950 078 357 774 877 485 683 019 463 718 684 290 363 091 128 148 719 574 002 882 326 014 990 192 977 999 905 555 594 676 738 931 935 949 711 735 894 838 564 697 638 646 924 379 559 577 593 960 315 462 308 672 970 134 752 639 782 011 988 093 260 057 270 936 330 075 168 042 895 730 493 365 927 165 854 953 907 619 346 670 983 618 995 771 116 334 262 375 327 698 135 910 731 371 572 671 725 253 211 639 893 188 389 734 633 869 865 629 049 991 406 125 783 567 984 873 956 255 993 429 851 822 324 056 825 136 582 129 885 350 853 477 154 173 808 669 918 872 987 953 621 508 728 719 913 442 620 188 889 375 026 938 011 729 358 256 696 138 247 491 980 180 894 064 388 676 861 997 654 453 280 706 145 109 265 637 703 742 849 944 582 230 345 363 720 810 432 538 541 558 467 829 556 445 954 130 368 809 738 472 211 546 838 045 164 749 611 649 916 412 486 574 316 753 520 827 881 821 123 867 327 347 760 221 797 875 590 225 099 006 345 863 833 782 008 495 934 174 386 796 516 790 204 343 368 320 708 770 521 606 284 579 047 197 695 847 411 642 392 026 720 797 370 155 033 851 715 504 724 593 099 583 459 412 804 168 949 315 015 147 510 713 292 888 647 079 504 125 096 876 819 369 565 314 988 506 793 401 139 919 066 427 863 100 334 727 448 998 086 334 309 663 662 681 062 184 020 852 211 337 892 841 586 629 970 482 377 557 843 875 699 556 002 460 584 375 383 271 246 982 178 121 441 530 988 236 275 132 130 552 835 201 908 313 018 781 505 608 217 522 879 560 565 599 749 418 559 092 915 883 973 455 349 194 513 924 858 874 151 453 345 297 245 672 427 999 426 958 220 113 939 519 009 795 465 651 396 724 037 214 149 080 804 334 550 042 389 453 333 773 427 079 258 753 045 187 498 552 070 975 412 000 699 317 926 530 772 442 890 259 954 527 712 024 530 768 295 415 170 015 320 582 824 164 521 438 681 646 590 556 114 255 065 108 116 834 663 870 517 004 173 692 675 038 993 660 744 014 290 566 959 282 616 036 173 947 289 238 861 614 793 985 654 731 009 810 554 339 604 326 020 760 569 997 679 294 836 068 828 942 586 053 016 340 301 110 826 303 698 942 239 803 614 521 318 188 441 850 064 629 662 989 715 827 274 781 377 285 893 379 252 646 348 510 310 922 766 086 921 709 290 920 751 196 713 057 881 287 966 641 719 084 706 441 168 636 636 513 363 250 324 934 181 136 403 910 710 390 141 823 435 660 027 715 009 424 148 560 859 443 265 504 694 526 800 652 579 109 928 451 910 248 910 677 251 223 294 893 824 784 845 833 206 253 438 987 162 058 004 798 562 231 356 652 384 423 907 122 026 352 567 188 357 498 625 006 208 074 149 104 183 311 515 600 053 926 027 114 440 162 817 056 231 052 302 378 028 059 945 549 006 130 503 856 350 987 521 852 452 589 641 370 751 522 728 001 179 259 597 605 673 284 076 078 205 301 984 666 426 573 132 239 318 106 909 199 685 964 640 822 298 610 652 586 897 484 499 405 299 334 865 865 267 483 315 830 768 607 046 025 834 142 006 653 847 147 695 686 270 441 547 527 124 634 673 794 954 040 018 123 346 237 711 475 031 998 249 944 751 068 310 012 814 175 695 463 471 421 250 525 880 804 269 973 264 436 925 024 390 289 977 403 952 254 885 781 867 704 147 593 897 339 750 937 073 377 562 965 225 699 247 685 011 280 342 320 144 542 504 261 311 119 964 074 454 815 308 847 261 416 985 444 632 858 235 338 726 189 392 391 705 804 552 008 840 962 182 616 723 687 063 928 685 636 639 556 995 893 708 471 179 980 973 826 368 705 229 150 051 147 142 508 159 825 408 868 980 850 292 147 717 866 945 060 179 674 372 634 151 752 441 771 249 746 255 432 789 513 055 387 417 485 876 424 285 602 456 241 949 384 345 310 386 068 873 316 962 946 902 427 023 413 558 022 291 248 269 475 686 468 611 351 835 222 549 310 360 677 740 747 038 212 630 997 899 904 339 406 738 701 006 506 235 280 861 017 270 537 506 371 007 683 542 574 971 945 545 856 230 931 388 135 034 212 890 606 271 811 240 171 352 195 365 290 867 113 025 580 757 960 918 298 480 299 407 252 722 444 707 039 055 488 292 466 909 771 869 717 687 389 233 987 153 437 701 118 847 267 207 065 775 351 430 583 165 034 248 594 570 250 126 374 882 930 625 085 415 803 605 235 826 607 447 130 482 961 048 093 853 405 012 233 448 873 193 399 081 958 784 624 758 796 703 855 811 384 598 085 582 105 746 624 515 586 118 116 165 288 720 220 013 650 152 426 263 034 177 978 289 752 517 253 500 722 102 621 593 202 039 225 047 782 860 606 715 532 250 486 872 867 721 215 873 496 471 510 032 438 462 380 125 711 833 406 226 771 496 329 809 729 882 594 272 898 828 993 877 384 552 284 867 899 277 490 977 828 524 914 497 932 446 403 166 460 955 624 497 565 890 530 371 104 333 829 182 833 681 186 925 011 441 894 343 988 369 226 644 142 551 121 213 958 853 583 530 989 954 073 795 284 336 244 233 742 419 710 099 941 814 652 996 601 393 796 200 242 441 064 778 786 205 011 274 845 429 704 545 192 575 981 567 673 151 153 802 144 452 013 392 508 205 022 868 499 907 044 673 867 112 903 851 064 351 651 830 410 170 182 607 779 936 904 984 017 867 931 101 905 398 184 889 083 298 800 795 694 173 425 413 313 671 001 106 617 363 730 495 557 382 552 848 584 466 164 086 329 946 897 898 502 876 803 689 274 668 129 889 186 765 763 889 303 605 444 770 336 720 569 633 516 694 485 847 744 869 710 082 404 670 606 752 372 810 644 713 785 055 991 645 479 086 305 325 350 840 849 394 200 729 352 623 618 033 872 280 917 441 719 549 930 338 365 810 008 270 653 936 969 060 990 798 153 673 034 548 564 278 005 388 722 037 110 468 113 135 980 431 145 796 237 119 323 885 133 806 382 431 614 260 219 459 574 780 426 877 500 261 166 668 108 741 716 431 268 024 219 496 910 992 653 084 277 020 511 628 852 149 124 613 342 072 912 036 662 332 728 787 475 082 302 631 861 722 276 514 334 792 299 527 375 232 628 754 527 384 078 701 711 990 984 456 546 970 510 774 574 442 587 717 612 622 863 265 216 012 912 844 786 246 892 452 060 734 122 478 560 649 170 866 611 594 573 643 956 342 605 661 155 664 635 340 651 950 024 196 793 848 731 570 598 415 662 216 416 992 777 324 910 813 713 056 457 728 835 193 292 276 273 494 689 718 868 112 785 177 293 591 202 290 059 969 123 326 898 935 408 203 476 856 943 051 183 327 815 640 079 373 486 232 375 912 958 837 946 707 990 582 183 152 694 003 933 711 483 378 169 374 824 644 564 128 192 263 694 427 175 939 912 371 086 618 353 906 242 015 554 281 674 960 239 262 370 586 167 924 863 495 597 909 747 826 273 259 603 967 605 899 404 119 793 825 612 706 629 516 568 930 608 374 096 914 597 757 360 482 359 009 254 112 639 387 522 128 231 343 582 178 114 877 468 918 491 882 158 207 847 048 536 313 585 262 018 430 198 129 242 239 438 224 313 523 445 302 071 091 791 196 249 139 982 532 014 251 141 380 143 039 050 951 309 131 046 521 304 990 030 914 377 639 060 556 949 606 989 322 597 193 836 418 533 867 895 093 125 423 887 723 674 925 239 622 496 316 352 742 316 629 363 851 698 755 621 980 001 180 958 461 711 631 037 431 818 952 695 985 870 251 689 062 101 199 762 503 483 812 257 495 363 529 366 539 419 325 962 020 604 250 745 404 903 322 972 692 563 074 740 692 958 760 763 143 316 475 990 184 728 012 928 776 534 188 247 748 140 289 245 064 333 841 873 952 922 957 611 370 719 812 058 165 238 938 513 424 006 509 705 835 858 627 470 693 571 064 163 515 000 291 481 647 823 883 108 130 012 022 603 954 041 319 837 682 949 455 029 710 010 528 379 535 813 284 913 003 049 984 652 748 061 636 257 755 574 209 560 202 361 217 689 860 020 655 490 238 331 069 959 759 865 474 464 469 100 563 516 610 070 832 756 932 805 251 181 781 201 567 256 866 033 674 065 166 485 798 229 294 992 471 247 980 025 755 301 607 786 278 680 009 688 637 108 226 673 646 182 050 065 159 073 192 060 070 139 478 137 602 455 554 456 572 338 793 921 262 732 797 215 083 962 315 834 276 281 069 079 909 300 078 981 701 802 822 808 048 439 001 428 929 847 887 962 204 558 173 692 298 208 267 520 366 848 998 706 487 703 938 785 509 257 263 591 791 843 497 906 942 332 106 913 115 355 965 990 228 750 622 954 214 862 401 253 726 127 858 531 723 317 310 317 835 985 056 720 935 804 355 027 121 524 671 300 274 476 919 608 471 735 871 617 456 414 828 647 492 855 878 124 172 621 180 085 516 233 757 832 729 956 040 494 174 930 225 827 281 223 395 842 520 030 499 640 401 677 038 141 380 340 023 363 210 104 830 122 589 417 463 809 193 955 472 765 782 914 622 130 802 740 687 787 477 293 257 433 020 227 363 351 245 859 405 436 582 560 484 093 310 194 254 506 755 139 358 548 950 671 349 477 693 006 181 514 709 561 857 243 637 433 557 696 023 817 328 478 569 439 139 169 351 431 330 659 226 631 866 144 449 544 365 619 341 173 123 714 101 856 353 337 749 379 291 525 399 589 136 759 084 951 134 888 281 323 516 411 141 683 194 593 987 222 400 316 570 650 146 715 995 178 328 569 650 899 210 657 863 184 865 222 694 443 133 414 719 590 901 151 778 202 980 051 713 330 694 109 706 767 558 911 483 231 742 160 130 759 011 775 919 552 330 003 302 522 325 109 228 278 614 444 131 130 810 423 082 170 453 632 302 678 109 117 319 439 313 680 998 186 220 856 651 777 747 080 478 577 532 875 590 646 132 251 858 329 919 230 465 560 900 918 061 286 053 931 639 473 318 234 144 353 082 613 407 317 228 148 560 095 032 060 222 065 852 111 082 791 327 753 824 476 904 016 028 367 540 481 958 118 867 336 430 598 925 861 933 385 126 307 028 848 623 051 115 611 071 371 997 280 777 833 285 612 153 253 867 952 282 752 629 341 272 798 392 389 298 782 800 817 376 991 229 065 539 932 258 720 617 408 140 864 895 615 940 720 067 935 830 225 888 356 230 525 831 965 869 008 189 964 522 345 366 918 308 237 086 480 912 984 352 278 746 920 220 227 984 545 652 367 569 564 705 804 859 456 062 746 079 852 508 156 410 665 905 089 805 779 447 440 234 434 675 297 429 313 375 543 502 500 668 272 386 662 374 866 894 477 307 968 393 998 295 910 458 555 552 955 926 660 814 018 334 751 069 844 492 887 917 909 065 412 348 339 262 615 249 263 723 154 999 546 097 339 923 292 919 057 290 311 851 314 405 851 196 792 609 384 200 111 897 204 258 092 558 026 362 171 291 280 284 635 070 624 390 136 205 730 362 854 086 558 067 267 859 116 838 722 698 673 780 891 512 858 615 727 315 533 669 206 702 000 003 652 209 041 356 862 397 738 573 116 523 409 972 911 308 040 710 725 781 961 118 809 761 832 488 174 703 253 033 435 155 906 881 008 198 227 767 595 815 455 064 194 583 990 097 506 038 337 656 191 054 422 234 246 222 515 190 034 269 001 124 796 734 894 803 146 516 721 896 575 939 266 330 208 798 022 842 322 234 555 868 539 395 156 433 050 456 340 165 945 616 801 029 237 532 236 334 536 451 507 711 252 839 095 824 500 256 595 817 333 290 960 777 127 513 965 916 260 989 707 554 304 233 652 028 008 490 767 103 025 535 036 886 572 685 647 634 374 260 641 711 296 119 584 180 127 131 187 738 360 897 525 052 279 350 318 902 208 200 312 022 065 431 020 591 608 114 411 956 228 492 774 149 053 049 949 911 153 252 850 715 400 777 246 781 874 571 843 499 589 952 987 575 694 393 557 603 245 487 094 067 026 035 609 903 868 040 353 957 781 293 058 880 991 233 124 304 381 966 667 429 757 013 320 893 822 169 639 902 495 216 121 865 223 384 476 783 367 100 421 770 752 674 430 099 986 578 684 526 734 826 136 563 358 755 172 767 329 558 391 923 780 191 421 998 797 335 751 076 037 010 082 210 807 725 295 724 853 245 515 755 766 662 861 187 235 906 191 560 761 187 552 534 903 660 327 808 237 435 813 231 016 756 231 003 892 155 321 849 668 037 641 944 739 624 774 962 237 229 746 640 799 426 999 415 794 717 485 251 161 971 281 953 335 459 037 271 906 879 624 680 920 332 104 637 567 015 761 177 352 702 665 628 426 921 872 372 296 760 718 993 105 206 157 740 970 793 610 215 674 509 005 231 054 298 819 594 681 431 329 177 458 224 426 452 920 949 571 246 828 064 938 067 947 887 354 595 482 706 755 218 229 459 663 970 853 096 256 772 550 246 312 426 142 576 066 371 416 145 682 289 411 311 684 921 041 755 075 673 823 645 436 164 742 516 747 146 311 656 216 003 737 915 309 057 870 505 045 449 221 586 158 209 793 188 927 143 351 253 004 718 161 986 428 460 218 581 988 059 702 745 504 741 342 622 815 258 792 915 038 195 482 703 137 731 915 282 429 267 269 005 566 586 117 470 879 911 285 737 879 892 391 600 136 319 980 555 502 279 225 275 397 927 966 666 919 597 749 166 189 204 734 707 774 909 241 658 478 884 933 729 222 280 364 953 720 245 644 654 414 803 014 934 589 894 370 118 722 259 260 546 621 255 888 760 888 509 897 127 590 811 781 858 241 969 367 023 371 016 472 915 123 909 883 667 616 354 954 439 762 365 752 905 432 809 212 255 359 665 331 483 032 039 725 688 146 869 465 532 034 727 956 876 473 826 623 583 848 447 525 401 207 917 230 386 654 378 672 992 799 621 839 838 983 113 678 707 446 020 476 201 121 584 266 077 270 854 721 950 601 015 891 839 936 822 743 085 131 406 470 196 784 202 746 888 335 273 026 244 644 745 423 317 979 446 248 392 643 462 167 076 847 007 190 159 636 380 334 931 735 666 813 674 011 948 636 033 682 752 168 118 058 487 733 557 047 703 423 994 914 894 865 878 928 761 106 895 446 361 902 919 774 931 237 486 975 571 931 100 688 656 731 629 738 254 325 213 860 931 274 931 170 681 120 790 622 168 109 499 654 144 594 106 582 212 195 429 698 193 144 991 299 601 347 246 587 941 139 392 639 322 900 724 549 480 758 773 393 955 757 054 405 693 046 335 236 404 201 131 856 321 917 817 029 034 687 443 248 270 157 347 212 028 137 069 336 109 660 728 512 084 989 034 193 851 115 199 100 089 914 172 100 173 007 921 439 164 927 175 976 728 567 721 540 454 845 494 069 335 313 559 222 046 379 382 769 956 392 344 024 947 693 304 480 307 107 652 588 765 898 420 833 776 765 486 784 550 488 180 086 611 437 721 292 342 511 713 480 503 136 898 917 729 713 591 467 450 630 411 811 798 771 184 425 718 196 210 503 338 690 547 971 360 816 589 340 227 531 628 182 046 173 854 978 324 385 293 085 377 928 320 209 626 888 324 121 814 496 394 793 769 364 081 295 923 268 338 277 490 192 015 131 207 913 463 377 139 366 446 360 612 785 701 527 993 001 907 706 664 951 063 793 714 039 966 614 916 837 718 550 533 153 911 933 449 854 328 681 567 366 024 298 963 857 609 824 769 274 784 862 525 610 166 403 536 894 733 983 243 320 461 655 048 993 594 024 471 860 091 788 027 672 169 258 046 411 714 582 696 214 473 936 984 100 453 605 203 249 844 211 950 334 114 158 705 232 406 464 950 418 864 425 043 648 770 546 370 241 017 797 312 195 293 097 388 474 354 164 170 339 921 561 019 367 640 531 055 499 962 277 822 860 507 853 960 063 137 906 823 969 038 731 026 599 983 612 508 785 482 525 000 300 974 787 032 790 359 860 509 478 994 224 739 126 509 283 217 506 472 273 237 967 772 578 390 212 366 077 525 125 204 310 429 234 745 466 299 940 471 295 808 533 295 336 895 763 124 056 957 759 034 663 722 517 740 184 627 584 763 891 131 692 629 145 806 713 128 772 193 294 662 629 001 314 111 326 777 912 807 928 956 092 237 068 876 711 331 940 476 948 934 910 422 908 539 443 268 986 448 265 439 982 968 931 016 843 697 504 535 568 192 320 906 682 761 293 613 129 087 414 326 149 285 797 505 660 810 225 103 257 386 999 829 626 184 369 316 335 445 155 066 469 201 689 219 456 915 221 633 751 799 988 461 678 480 756 578 070 206 416 077 527 522 083 308 059 501 585 426 648 597 922 783 495 041 811 386 522 754 405 395 909 217 271 086 912 371 256 554 327 096 654 315 161 969 693 804 365 845 827 912 679 499 917 464 838 566 310 262 668 207 690 975 485 709 046 222 179 559 619 846 415 405 427 134 149 132 770 301 698 496 274 961 097 716 741 965 499 039 634 265 995 955 680 499 657 293 668 440 062 328 232 434 644 491 210 287 076 728 197 775 561 664 517 626 052 327 855 010 815 147 290 353 527 807 443 626 593 670 087 156 694 062 808 433 858 521 586 021 249 564 754 595 029 254 842 559 028 089 329 147 089 305 648 917 916 989 466 095 449 090 592 531 078 930 485 859 711 174 435 856 132 237 547 373 117 373 018 122 888 200 283 698 882 753 366 757 708 685 332 559 808 643 252 970 355 543 885 970 614 991 081 901 215 595 990 459 312 005 646 287 180 002 452 355 495 876 242 921 958 840 245 820 209 019 898 434 843 990 571 179 910 414 115 463 660 726 456 880 907 076 776 630 079 523 063 953 436 226 386 854 883 455 237 415 020 366 815 203 092 731 453 753 826 240 570 001 500 077 402 847 582 263 970 761 850 590 773 622 925 594 428 254 314 131 709 279 747 318 458 245 499 881 914 741 247 830 092 720 074 426 858 510 024 768 979 905 572 113 318 367 205 331 360 567 858 423 616 793 768 856 561 119 789 029 272 810 255 506 105 443 078 862 324 053 757 703 512 937 619 644 776 352 952 373 124 553 006 634 749 722 613 433 204 107 185 134 902 799 954 515 553 406 647 849 168 750 372 035 753 217 886 906 049 847 369 800 369 059 772 142 635 093 015 818 198 973 946 599 463 103 756 835 363 868 119 038 934 427 062 854 173 737 303 864 982 873 320 749 873 543 662 338 187 379 866 550 728 668 865 470 616 704 182 303 321 053 047 014 840 112 108 447 577 912 225 334 514 600 394 272 312 721 501 352 348 401 931 905 678 493 763 493 004 153 308 245 306 442 761 037 382 682 569 356 355 580 644 015 084 754 167 678 708 670 300 666 215 834 736 958 162 389 505 807 598 682 242 485 576 659 507 855 370 820 893 076 859 801 470 466 560 616 633 196 216 992 317 589 869 652 468 228 913 375 198 114 176 184 990 113 286 884 193 535 621 740 104 517 734 473 134 588 410 298 567 753 503 331 918 915 979 563 491 275 759 422 369 773 360 544 529 565 452 974 420 759 041 535 357 485 270 097 905 562 131 876 292 752 115 892 237 873 521 227 533 601 737 252 098 329 633 546 791 467 071 144 217 727 179 989 740 389 280 178 309 975 868 057 150 711 469 221 939 848 122 200 680 829 665 374 398 942 361 368 121 623 120 377 044 811 253 908 189 587 560 596 955 631 613 363 030 166 997 856 035 260 016 602 467 439 032 792 417 833 259 506 439 082 217 633 629 155 225 623 710 521 435 528 690 532 106 588 101 789 580 271 674 098 024 500 218 228 808 179 860 746 926 215 849 878 478 998 381 854 517 050 543 336 281 312 539 126 832 538 607 899 742 899 899 089 707 919 204 559 239 196 243 596 090 357 869 665 698 751 536 700 887 641 806 334 676 087 292 764 840 213 511 332 970 828 199 189 228 358 180 724 891 397 000 230 924 589 634 612 078 519 555 686 940 215 952 324 426 426 932 113 525 111 708 171 986 978 317 778 778 144 569 982 058 232 295 230 002 776 589 963 724 946 574 250 342 388 524 786 829 021 200 125 512 109 547 491 543 144 880 339 203 802 171 489 509 798 995 932 014 346 285 392 257 430 416 629 243 713 485 746 251 927 088 247 903 995 014 040 195 859 473 924 110 920 866 364 011 341 191 232 572 157 584 172 949 349 773 441 137 575 890 676 003 087 859 207 933 248 620 410 645 064 655 406 115 038 356 737 187 227 580 153 415 389 668 345 458 836 441 742 362 862 041 244 260 169 582 910 583 906 933 820 531 626 654 500 517 851 593 373 041 697 234 796 092 713 716 576 787 273 172 810 898 190 239 119 255 035 430 173 691 288 193 841 188 036 575 509 441 937 254 433 685 854 067 439 719 674 258 243 602 698 503 739 327 945 272 953 314 809 988 437 876 551 829 925 056 791 960 577 117 724 758 446 289 698 803 185 087 201 449 492 189 001 439 562 319 164 221 520 752 460 075 663 554 078 540 099 929 809 165 053 957 317 784 880 014 480 689 744 936 991 966 845 603 979 244 375 034 044 394 835 202 961 304 889 198 060 932 973 020 823 401 381 759 981 254 251 280 820 767 676 559 334 722 989 112 519 530 866 893 454 183 229 244 097 040 506 710 079 021 404 160 167 022 959 881 683 285 156 654 977 266 868 174 942 761 889 879 323 462 227 415 905 184 524 968 380 179 525 977 254 787 883 187 453 633 437 665 641 977 700 801 350 336 793 765 223 726 106 976 279 636 170 209 239 689 561 380 820 423 353 994 299 088 693 844 071 344 540 202 855 685 861 668 751 467 533 962 046 514 874 165 184 409 326 040 392 948 778 801 196 273 362 392 062 522 582 308 735 749 586 994 057 796 495 069 906 003 024 414 732 119 114 118 665 899 408 640 689 750 336 052 829 212 931 978 581 905 838 379 335 892 197 055 468 423 962 819 740 895 759 077 132 332 892 702 148 824 448 517 945 332 781 303 417 592 370 821 998 074 425 355 692 235 819 482 968 898 606 536 406 624 580 784 765 401 446 065 383 951 105 162 369 792 866 154 413 044 382 232 004 447 777 092 383 175 327 807 687 218 491 803 825 461 107 651 250 401 744 749 853 299 049 754 231 213 614 611 942 656 583 129 192 995 079 743 071 457 296 491 053 041 873 871 126 858 425 809 210 969 534 164 337 290 756 938 165 135 248 691 520 229 770 017 989 226 779 906 407 290 551 744 579 939 754 239 092 659 474 918 665 294 267 028 042 423 770 188 221 378 738 312 987 594 302 854 844 747 407 052 990 011 180 504 256 873 145 872 942 862 111 709 482 023 373 255 905 806 786 078 903 334 855 535 671 491 982 414 229 406 116 887 319 029 861 593 544 806 569 217 091 095 162 440 919 963 595 064 625 643 417 224 802 930 342 728 261 203 893 468 682 290 176 368 467 921 795 078 587 237 308 197 583 880 933 821 187 994 395 546 719 949 523 144 091 578 519 091 773 542 431 966 661 486 379 976 825 803 521 751 163 253 136 817 244 998 444 944 506 218 332 859 896 467 055 642 110 210 896 291 315 038 454 279 851 627 119 064 678 618 309 404 016 878 518 173 626 113 586 340 068 322 948 411 534 767 460 991 544 802 124 675 659 073 718 921 293 151 999 253 057 957 583 868 788 021 122 713 339 201 181 435 531 070 232 186 339 606 432 089 746 872 074 803 601 602 945 294 435 446 495 151 282 983 710 637 948 324 893 832 820 405 181 589 161 381 636 157 658 082 952 190 485 163 277 660 456 841 513 083 842 454 396 026 742 708 096 026 314 824 322 463 668 865 083 747 646 767 687 072 596 029 264 912 919 287 399 555 730 879 879 552 389 505 173 065 311 152 006 753 067 088 632 553 623 791 979 657 700 324 214 608 480 203 859 350 379 726 311 187 298 699 021 219 225 025 094 023 493 090 994 166 166 495 140 067 201 792 383 809 906 350 499 164 255 520 880 384 772 103 063 849 455 627 931 475 684 881 180 242 353 343 859 815 302 694 215 734 543 969 508 264 141 257 540 745 662 942 726 365 614 138 920 929 716 156 085 613 389 813 397 058 432 878 503 072 029 218 361 652 297 704 687 770 090 782 437 702 019 262 050 559 425 175 597 865 773 387 533 259 086 353 245 324 930 527 065 506 445 978 658 411 107 056 378 926 408 131 730 634 391 957 639 550 134 948 343 224 191 936 394 031 088 804 157 479 004 106 647 436 076 592 731 907 492 961 188 931 046 100 171 457 618 413 294 504 365 804 197 582 845 374 244 636 750 140 454 265 814 389 082 892 528 918 500 200 225 301 152 007 946 259 056 648 134 688 230 557 260 451 721 526 289 870 480 297 714 137 586 976 262 714 136 413 910 198 489 574 417 734 604 838 088 900 217 118 623 450 605 802 143 385 837 602 601 052 161 203 992 736 670 159 037 439 161 708 698 522 505 259 754 212 331 828 897 312 981 148 184 352 558 306 189 107 576 699 512 729 087 220 378 550 024 657 798 034 813 547 084 633 330 242 464 498 996 632 716 512 208 690 999 287 703 229 273 307 905 766 269 444 065 333 604 208 052 711 351 912 270 866 542 894 986 446 557 342 861 824 603 922 164 147 722 951 084 709 599 310 020 307 208 861 283 030 715 058 154 660 430 897 473 231 313 514 997 398 894 981 813 586 982 231 833 954 708 462 868 859 819 146 457 420 741 832 238 526 748 332 565 364 636 950 002 590 634 753 546 601 385 318 319 729 699 280 311 033 841 316 073 075 042 495 309 641 523 862 844 735 364 220 595 122 021 819 526 414 518 608 517 410 722 204 825 362 904 227 004 459 110 389 604 022 278 837 239 152 976 293 726 777 727 588 602 201 849 557 720 893 268 741 395 843 569 860 301 245 602 088 185 524 069 109 726 967 667 034 793 680 252 723 562 402 215 192 488 624 136 615 962 081 375 868 999 529 128 958 334 324 210 718 678 057 861 291 132 625 176 042 342 781 111 486 358 295 089 974 532 380 095 666 341 092 953 375 717 729 085 062 230 033 722 056 985 982 835 658 362 609 577 158 363 691 369 637 329 894 162 061 464 456 452 247 888 668 273 057 936 989 242 280 467 160 006 085 144 151 149 998 510 426 670 695 897 279 612 162 577 064 999 978 704 440 288 327 575 252 936 572 747 459 816 014 201 298 293 488 846 200 822 212 163 186 065 145 461 521 104 258 744 265 910 353 068 361 719 079 614 582 844 755 091 337 829 668 911 553 496 090 520 789 098 400 580 749 710 902 306 328 199 140 134 285 722 355 207 675 390 406 472 215 477 012 107 089 297 743 055 956 814 962 772 872 150 815 272 614 201 172 936 857 974 336 716 320 790 670 953 582 401 491 254 142 580 235 485 561 397 145 060 293 496 392 801 014 059 423 024 923 541 429 935 496 804 296 588 159 608 209 500 058 949 575 309 119 716 483 463 970 552 374 107 960 590 770 158 985 096 351 047 335 013 107 173 028 639 707 406 317 750 882 389 658 419 537 601 725 994 996 167 881 063 539 628 871 244 728 443 771 647 525 209 328 524 654 962 226 671 994 976 309 433 265 370 726 900 604 615 605 513 340 493 287 075 966 070 708 383 117 165 942 556 578 402 652 986 688 048 522 685 415 285 680 160 544 696 512 958 226 586 273 325 999 656 352 433 229 114 921 047 478 515 158 688 405 332 193 126 612 206 749 514 137 403 951 063 405 263 643 015 160 856 350 980 585 900 488 060 164 382 980 456 854 393 868 698 841 703 544 626 676 438 996 768 318 293 119 640 403 820 230 580 507 222 320 517 068 211 849 542 713 077 824 108 891 680 372 653 196 635 597 072 575 621 515 874 333 945 406 601 873 932 396 897 868 083 188 282 458 924 191 607 773 111 347 735 845 597 162 128 396 186 578 144 304 012 725 396 026 640 784 890 803 254 006 115 907 657 181 163 633 724 989 898 846 790 115 719 317 944 405 651 704 611 265 497 300 512 990 867 720 916 998 776 919 108 256 012 032 990 160 581 926 009 784 739 954 073 341 295 843 107 025 546 409 008 997 694 537 298 170 771 869 662 398 570 734 945 933 372 248 766 248 464 903 490 418 194 347 795 159 705 334 864 028 748 215 030 400 334 841 237 288 420 351 102 151 095 975 337 593 689 974 494 861 768 556 252 885 780 073 355 378 527 535 328 918 118 909 543 369 213 485 875 518 525 365 165 210 704 967 015 982 422 445 330 961 109 197 614 345 341 747 068 765 709 009 016 044 770 604 451 343 339 774 472 269 293 066 025 056 708 013 606 713 715 948 679 066 065 884 335 693 950 907 582 138 422 418 691 651 369 899 979 539 347 071 430 659 965 106 469 959 261 599 964 686 344 665 867 535 996 587 369 811 023 431 524 699 405 051 628 559 311 685 566 309 448 755 861 040 655 992 117 049 527 582 868 564 963 471 686 541 660 766 465 327 156 628 536 225 214 939 573 171 902 766 081 043 778 673 245 305 247 734 652 485 990 459 393 929 205 395 127 812 512 027 814 275 505 072 805 869 972 729 171 816 127 301 866 900 260 204 296 740 049 295 667 455 215 005 109 117 927 938 560 257 167 586 017 335 936 954 471 869 239 852 636 876 512 456 660 640 256 523 908 036 942 317 438 677 255 314 529 107 131 524 875 226 335 231 864 058 470 118 042 311 446 169 902 845 987 468 834 388 015 859 183 859 031 572 537 978 935 306 607 654 900 647 252 297 118 290 781 727 429 354 772 254 834 236 309 241 580 437 501 048 275 835 125 773 229 313 276 269 481 344 947 370 722 115 509 345 207 529 096 432 973 726 914 817 971 377 276 796 847 066 709 428 083 636 650 449 410 761 578 123 711 024 597 920 391 542 772 643 410 604 849 038 201 397 841 044 419 940 018 265 554 893 986 550 479 282 938 815 724 908 931 674 025 771 183 918 527 149 363 000 532 480 814 298 704 703 498 502 827 253 536 180 300 949 251 609 359 666 307 494 800 398 463 411 519 127 681 868 481 584 554 019 976 749 869 404 238 081 965 774 577 460 682 433 783 204 681 142 643 789 726 722 404 974 274 601 385 088 290 910 882 511 815 084 653 164 957 989 799 513 481 091 148 616 456 553 268 650 198 484 944 881 788 421 769 538 747 847 374 436 584 605 380 355 738 853 516 349 964 490 401 940 312 673 804 305 749 815 011 788 392 948 791 734 776 973 644 349 137 722 630 543 313 466 721 102 024 602 422 906 190 308 500 966 975 981 704 306 106 274 049 044 778 185 159 064 515 555 635 293 384 221 587 554 032 126 000 373 756 950 734 471 498 784 972 189 502 589 395 946 726 444 842 097 853 978 210 199 213 843 706 928 919 664 568 122 903 279 964 502 601 306 832 317 055 836 865 981 572 859 155 235 343 784 945 361 692 962 866 458 992 400 035 186 391 564 086 301 702 231 108 477 698 768 399 506 035 400 725 483 400 761 842 488 640 021 141 900 517 721 073 179 845 646 151 307 928 766 641 402 764 680 150 478 575 493 837 911 088 933 295 827 775 596 133 575 066 137 103 621 170 536 964 043 188 907 345 331 591 943 960 307 984 416 287 468 451 226 176 516 402 420 744 357 611 917 996 789 860 130 530 784 031 781 079 370 980 937 788 660 670 007 831 852 328 617 414 797 492 470 311 834 490 370 251 836 795 823 057 938 996 688 028 109 015 401 649 193 821 680 967 475 403 064 753 478 665 591 479 695 665 652 698 706 349 129 518 578 166 967 509 388 830 900 728 368 477 717 514 092 853 377 973 037 497 072 337 116 732 311 978 224 154 784 288 906 907 901 916 840 175 600 208 428 746 751 291 393 622 013 580 461 139 580 966 381 324 440 936 538 074 255 083 327 884 933 494 949 773 429 168 087 618 587 579 210 824 882 665 210 143 005 461 731 936 433 004 821 793 997 918 698 525 192 550 511 730 783 263 781 955 255 493 712 345 530 598 888 467 054 955 792 007 797 729 913 354 383 812 302 459 168 400 025 442 844 278 795 690 438 007 675 405 524 996 283 325 581 895 029 220 196 119 172 846 674 570 714 533 011 925 810 791 937 180 695 858 487 332 784 730 532 262 584 740 165 950 590 502 065 900 240 437 895 933 066 676 018 494 229 510 885 011 683 498 261 696 385 253 582 730 319 111 849 100 762 336 616 722 716 119 267 443 942 656 965 323 212 077 881 575 014 502 288 385 134 974 105 254 313 761 689 656 210 333 424 656 765 043 980 417 032 164 145 588 408 166 144 137 559 761 168 323 854 545 283 484 283 298 352 702 916 138 312 133 830 211 462 928 734 436 593 425 514 345 197 225 299 592 434 853 432 368 046 080 198 743 624 755 938 220 582 944 660 146 059 460 444 986 044 349 115 184 290 427 040 056 684 011 205 465 952 180 729 820 188 960 476 500 128 924 538 984 044 795 142 904 622 258 507 325 034 767 998 071 778 970 796 759 164 770 157 892 427 842 279 359 247 076 902 897 197 886 715 631 037 418 997 179 108 239 486 903 052 733 657 950 849 771 509 768 263 522 263 113 872 141 883 891 680 870 733 650 871 712 203 898 559 391 583 300 706 578 157 841 291 897 788 068 562 978 376 659 071 598 301 555 422 208 695 470 277 290 187 744 423 988 544 098 598 462 016 816 646 233 692 729 272 138 626 955 705 242 672 224 035 049 593 382 397 323 749 966 057 483 449 421 215 444 212 855 863 278 603 641 671 246 044 746 249 653 579 841 152 429 407 968 938 195 687 251 075 213 714 825 233 287 217 583 392 844 531 971 524 862 383 449 486 767 822 216 387 353 962 609 375 754 903 973 196 360 234 021 648 059 896 541 228 197 210 011 926 870 804 554 974 805 489 964 561 610 280 196 032 929 389 691 656 254 812 713 738 512 785 310 838 351 735 794 214 395 570 586 747 218 338 321 219 149 757 548 064 476 218 637 820 439 175 208 655 595 807 371 879 512 701 932 472 803 973 591 033 809 549 031 013 535 394 298 621 991 216 750 802 391 307 051 461 996 341 863 732 877 609 570 777 596 080 490 334 109 685 889 868 465 948 294 539 290 464 441 203 970 068 928 362 366 117 614 366 853 224 270 235 697 456 861 620 797 654 133 429 332 657 170 978 844 859 721 009 527 034 028 036 430 199 215 829 230 575 724 240 298 552 572 125 573 851 060 603 471 855 828 883 732 093 475 132 550 930 140 006 843 939 047 572 257 023 697 104 794 572 794 894 639 757 812 959 144 219 189 743 402 195 202 707 488 310 822 991 809 654 617 369 578 342 698 476 736 805 328 495 972 580 945 374 368 089 462 346 408 416 216 345 374 029 052 512 718 143 223 846 134 992 522 434 262 720 637 601 183 614 870 758 214 093 351 820 842 281 705 526 973 912 437 992 553 387 745 177 842 962 544 288 858 965 102 630 164 535 816 070 560 825 252 465 344 443 530 077 149 418 440 798 337 742 816 027 274 072 908 985 622 342 961 045 783 714 599 142 385 549 106 013 043 134 937 059 619 863 063 534 714 491 363 193 682 996 577 930 832 597 925 549 551 850 070 722 420 658 306 736 773 873 711 335 649 824 494 180 725 869 112 594 619 461 130 674 139 573 066 739 265 316 837 575 008 555 469 525 579 951 771 341 557 379 151 831 730 394 586 862 841 684 734 024 936 592 364 373 463 318 340 592 479 285 309 615 545 931 946 367 128 811 526 783 303 019 518 489 455 015 569 311 762 896 507 971 507 764 376 671 025 361 121 794 069 163 465 069 663 475 923 095 670 934 904 212 668 131 116 307 657 080 036 565 862 783 047 580 281 880 204 771 154 463 758 140 452 462 068 337 438 956 877 002 574 378 595 111 604 930 644 175 937 439 196 644 750 385 381 652 417 872 324 020 034 430 898 717 605 553 082 884 349 035 765 364 280 340 326 713 412 282 707 576 109 583 202 983 235 186 784 566 164 100 392 705 094 323 667 807 858 193 814 568 309 892 569 701 018 767 999 942 648 203 971 736 530 678 378 247 647 164 974 103 796 648 586 516 381 001 195 601 669 467 440 647 686 033 327 287 540 406 005 383 290 249 982 608 227 922 494 001 700 544 228 501 864 907 350 412 280 774 780 238 347 120 057 382 076 617 487 008 633 683 842 016 879 590 759 245 238 789 347 694 272 018 559 582 048 369 722 161 393 218 401 360 551 976 471 946 512 036 136 406 712 318 913 118 450 857 916 185 957 848 416 129 944 310 981 898 279 287 693 151 648 690 934 405 533 913 177 404 750 342 412 714 593 052 141 709 588 624 893 190 146 140 008 258 638 138 135 317 686 329 834 721 685 656 089 970 052 842 930 714 148 424 741 307 370 195 108 400 156 471 553 483 952 505 932 497 841 755 755 891 540 922 331 644 143 677 246 511 914 997 272 933 816 035 265 359 849 464 445 667 347 675 769 679 063 711 065 116 443 978 092 641 720 198 766 578 009 315 286 221 559 010 904 271 274 876 188 113 229 486 649 419 462 107 478 892 220 124 529 969 816 011 106 380 344 545 375 950 841 097 433 705 655 772 363 230 055 372 863 550 397 122 477 888 971 045 742 197 880 718 939 603 660 767 704 868 423 795 818 672 921 214 955 577 458 860 512 680 895 476 350 729 025 421 959 247 591 524 492 264 547 747 569 859 786 649 927 716 207 193 138 100 604 770 685 100 607 267 133 516 418 653 429 351 924 870 598 026 354 097 336 538 801 692 569 284 916 676 890 240 699 557 096 311 626 915 446 005 802 096 292 780 928 503 382 748 446 821 739 457 726 682 135 875 563 915 269 033 396 294 625 829 925 220 621 382 460 047 489 865 732 114 221 132 834 541 186 676 740 957 462 515 463 175 155 800 402 213 919 598 853 735 166 742 358 134 577 960 258 227 165 626 796 434 363 050 948 710 113 393 132 886 254 397 358 074 600 431 206 146 683 314 069 920 334 964 287 418 149 609 435 176 344 777 622 180 426 169 054 228 397 837 963 473 560 101 341 263 386 239 313 505 346 970 805 733 728 873 742 204 530 026 697 697 379 408 863 006 012 348 993 063 110 136 449 486 551 666 835 925 250 456 081 691 558 655 185 004 753 547 250 775 654 501 628 185 783 330 831 071 886 283 760 351 605 634 792 637 608 702 146 571 378 956 571 637 536 582 386 123 297 988 819 089 511 782 539 266 455 555 323 228 892 237 531 590 787 030 819 204 813 121 210 843 589 343 966 297 515 712 720 385 217 144 463 259 075 049 688 182 608 249 947 252 095 992 326 351 255 022 861 682 580 298 395 707 791 984 766 752 681 863 570 395 630 531 647 697 544 451 516 429 392 262 940 448 806 084 304 593 046 523 488 283 765 370 624 684 252 051 834 260 330 728 120 626 341 603 008 378 890 459 100 696 505 243 823 058 955 438 632 167 448 974 166 873 869 138 802 553 555 773 450 943 820 986 402 902 900 563 505 198 540 780 517 904 045 303 559 780 217 272 522 832 031 569 484 316 830 485 767 533 143 048 757 441 941 970 494 329 293 213 869 701 011 793 402 136 336 015 490 180 518 397 906 171 407 512 405 246 073 177 548 317 335 042 679 817 401 247 816 604 459 951 878 927 230 629 139 814 082 688 951 856 813 553 969 185 820 420 203 513 624 283 247 382 571 397 921 774 466 011 578 452 265 926 151 162 139 558 401 342 872 532 254 411 465 091 762 002 127 713 247 246 289 314 682 630 815 827 824 815 689 736 559 287 721 036 107 612 691 595 694 124 198 095 022 842 400 721 039 135 174 599 878 841 858 909 403 734 638 518 394 089 939 862 887 112 802 164 829 301 083 046 775 468 507 358 045 577 256 083 070 869 551 934 602 886 467 418 926 319 947 685 450 972 386 550 276 075 779 850 927 278 649 923 653 867 778 662 218 957 125 934 398 648 261 577 829 719 472 077 952 922 073 697 918 305 543 326 674 361 113 314 207 603 436 456 332 824 907 908 098 203 483 991 325 621 253 083 528 517 136 970 157 736 685 960 117 428 594 829 131 941 495 699 041 633 220 598 727 807 870 532 242 200 293 407 729 437 503 495 905 125 724 293 236 433 285 172 620 103 953 173 188 085 089 085 278 540 696 095 036 504 580 056 391 661 270 027 380 494 091 328 174 854 388 888 602 372 028 739 087 401 585 595 564 105 399 036 592 154 342 373 080 146 941 332 563 583 953 572 241 542 285 450 441 323 939 034 240 360 584 756 197 428 122 576 586 920 926 138 161 745 511 006 509 968 591 773 305 635 453 160 413 351 552 264 609 312 803 160 165 253 107 169 825 832 372 772 547 956 204 458 926 699 927 145 677 383 225 872 829 557 425 916 182 866 886 199 934 073 775 604 078 637 918 611 961 513 502 395 673 984 750 958 689 741 767 369 426 757 042 811 534 913 790 840 994 388 797 994 656 063 372 318 944 160 346 639 824 261 138 326 609 328 166 547 995 240 051 510 023 162 164 983 617 392 242 262 347 660 041 001 784 928 962 291 851 274 819 957 787 321 489 359 483 961 078 180 525 476 423 333 085 948 486 477 304 848 313 659 756 576 162 248 480 929 011 679 164 995 853 537 207 928 298 216 550 283 027 204 301 065 924 434 777 872 666 128 135 413 515 783 406 494 686 637 980 735 302 849 043 866 008 015 163 104 010 433 186 141 745 274 535 696 486 958 123 004 711 774 775 275 634 395 243 059 883 985 020 086 077 255 685 413 403 897 504 228 877 376 660 184 468 941 127 776 339 747 454 568 832 377 491 655 626 945 385 570 054 956 191 239 350 911 476 582 896 373 440 542 857 923 716 977 688 428 940 011 268 817 853 858 424 715 820 256 907 036 106 552 738 255 926 248 644 626 916 779 799 792 042 825 701 383 976 638 782 710 823 687 960 049 379 444 753 072 663 169 575 506 601 522 275 372 368 994 985 647 356 696 971 044 355 261 801 871 185 401 828 092 014 541 115 364 241 923 286 013 185 268 959 448 023 309 906 033 141 416 974 894 675 434 174 950 735 719 834 117 077 008 907 871 137 348 761 098 777 341 277 825 409 388 264 931 143 109 086 182 954 704 300 374 433 066 892 640 755 170 345 602 410 428 660 835 701 283 336 798 913 849 266 611 810 471 185 844 615 226 429 328 752 159 714 901 462 878 981 345 363 054 931 936 744 394 175 748 423 107 381 548 684 149 249 424 084 108 392 450 487 771 821 816 134 434 998 392 804 210 986 340 290 519 349 242 106 359 013 707 821 613 385 669 394 451 715 611 697 276 483 889 158 347 516 590 843 157 933 877 997 577 559 743 992 621 138 003 252 916 700 746 115 722 565 280 759 074 988 902 574 166 636 311 451 923 243 180 173 216 177 262 616 580 183 478 743 501 783 816 085 671 512 616 593 514 075 939 323 657 346 413 771 640 357 394 312 883 274 999 723 369 345 035 570 491 228 129 823 963 124 669 177 636 578 597 520 009 656 621 400 454 493 470 650 383 249 942 816 551 085 121 785 326 493 711 940 126 769 615 913 524 677 187 243 794 804 694 295 143 509 747 321 931 853 937 297 214 029 655 026 544 742 138 089 020 374 644 611 529 602 074 379 371 540 783 249 353 925 815 654 953 638 931 257 294 394 090 952 859 210 511 666 656 174 635 784 046 003 637 588 179 779 449 293 856 057 928 037 867 346 010 322 846 259 159 900 590 499 771 231 944 976 587 872 331 818 231 007 811 133 492 789 414 261 412 164 243 612 582 444 685 828 337 300 018 459 957 902 735 747 178 637 654 689 549 932 733 283 506 701 097 381 205 752 604 378 497 661 266 996 493 559 521 935 503 359 275 209 960 019 315 093 041 164 580 316 858 715 166 142 907 923 765 377 188 372 429 130 677 358 707 863 227 201 122 726 520 382 717 012 505 059 534 142 453 790 320 380 473 116 799 795 100 012 714 756 124 679 136 586 807 356 161 107 553 318 547 204 659 620 691 608 199 736 461 480 778 732 154 221 810 512 138 223 713 816 520 386 171 534 151 582 182 253 803 195 582 781 800 894 458 852 068 962 040 217 859 050 575 073 221 200 490 581 305 679 862 298 111 478 492 152 793 128 218 275 664 584 827 572 720 616 091 122 448 289 036 713 984 472 663 280 036 775 471 141 686 548 406 302 409 677 046 383 639 871 675 988 564 947 744 458 257 164 678 032 465 663 333 881 169 843 304 891 111 503 753 973 272 600 471 216 182 502 910 803 770 676 076 231 391 901 281 936 963 182 884 248 794 471 133 961 478 964 591 373 165 588 356 304 942 696 778 182 246 316 502 124 165 120 268 180 262 414 452 163 240 467 529 165 401 404 503 069 403 832 258 375 363 711 970 909 293 859 941 547 173 535 996 849 501 047 593 619 459 244 732 014 315 330 214 990 573 418 671 410 312 592 717 729 965 069 243 097 459 228 987 000 007 719 063 244 682 615 289 895 650 500 307 324 689 968 635 759 749 300 861 094 774 068 483 767 058 538 482 789 920 977 494 194 427 235 339 601 627 624 780 449 260 370 540 253 969 817 088 721 680 849 901 260 463 866 278 978 200 383 939 785 030 252 948 288 736 317 500 430 534 416 730 899 235 077 986 074 163 527 724 055 047 850 632 751 636 082 162 743 823 433 659 862 242 296 009 120 865 337 784 419 769 160 265 410 663 484 643 578 687 734 019 563 633 293 360 864 236 955 665 539 493 836 502 422 337 696 171 501 815 952 397 150 777 711 988 510 778 233 621 706 376 746 426 204 980 131 401 476 776 350 314 537 622 198 704 423 689 708 995 665 306 173 256 932 334 767 176 152 369 742 418 683 450 271 849 399 625 220 789 194 247 992 784 844 889 801 958 980 950 488 936 059 462 068 734 041 202 433 056 236 252 922 954 397 636 996 300 529 289 379 947 783 687 926 313 441 646 876 187 999 621 994 711 400 517 291 765 254 609 133 785 643 348 207 089 479 106 188 139 502 950 533 922 930 878 291 238 559 600 055 640 412 447 221 803 984 349 690 616 813 811 564 550 853 465 178 615 030 544 245 413 013 694 725 295 888 542 710 288 290 470 200 082 729 852 265 526 325 124 148 445 396 479 409 693 699 502 867 743 386 262 298 569 344 744 605 198 738 485 195 930 361 994 676 927 286 053 043 803 220 106 861 864 511 714 539 738 522 236 663 378 581 300 020 270 575 402 075 751 801 919 114 128 497 118 352 539 277 026 594 207 832 013 937 727 066 551 434 945 573 938 877 860 507 509 018 659 589 879 480 168 250 820 482 206 326 470 337 999 325 783 450 347 519 280 617 777 435 403 613 125 744 980 173 982 794 365 311 171 366 818 724 090 501 611 109 011 477 023 360 587 009 259 969 851 154 706 407 326 490 095 858 126 210 287 921 691 806 856 763 436 590 048 829 728 278 146 140 195 921 505 503 976 380 190 239 100 326 055 227 715 061 204 068 914 826 549 836 025 694 701 342 035 920 978 797 195 549 522 029 480 801 216 521 300 790 040 122 524 054 769 288 418 496 468 646 751 147 491 808 069 253 073 830 399 480 756 028 670 657 301 822 264 057 484 221 115 777 932 254 088 617 871 217 615 825 335 610 020 395 478 153 110 969 256 335 765 421 971 245 938 191 774 690 304 435 366 991 066 027 068 887 613 669 177 104 341 315 503 043 038 681 974 044 963 386 809 164 621 559 364 044 065 868 355 474 976 199 560 124 447 418 019 150 887 100 156 543 532 340 129 275 214 115 132 954 898 399 688 283 302 431 712 971 819 322 811 740 766 632 223 261 725 167 084 572 935 684 804 531 413 161 541 536 860 377 785 463 845 806 924 565 303 439 071 406 780 987 641 911 367 299 464 632 399 080 769 692 699 929 648 083 694 038 384 516 359 344 866 563 734 180 902 377 799 640 279 081 724 959 840 929 683 863 667 598 899 216 659 244 193 393 072 760 504 824 971 143 859 336 570 165 707 629 951 490 470 755 584 764 010 914 443 943 543 665 623 515 256 833 978 413 484 443 852 526 886 922 519 362 497 632 088 747 860 333 050 142 485 005 625 603 406 901 074 532 004 560 349 772 808 830 511 613 857 145 942 326 773 671 052 462 530 369 994 252 937 673 096 808 363 303 883 028 719 868 312 629 462 859 967 980 464 842 886 942 624 747 480 662 773 549 457 574 306 748 855 123 877 300 232 480 465 688 897 826 694 352 487 200 732 265 740 280 030 703 734 737 147 852 643 983 613 062 447 802 284 163 133 472 861 277 778 469 707 245 854 687 193 022 393 634 382 850 320 881 006 813 163 254 857 735 304 053 967 179 443 857 281 451 463 990 291 991 152 879 958 637 057 058 642 840 980 264 684 497 295 491 170 528 673 854 564 137 588 027 737 354 024 972 934 910 390 174 452 651 974 455 951 408 921 135 186 557 581 011 038 706 906 864 283 337 636 436 491 257 648 634 773 120 096 666 248 362 941 549 591 198 996 261 881 832 439 234 655 223 533 600 991 808 597 468 786 247 907 915 415 808 935 979 115 162 718 343 613 006 377 712 602 815 911 147 458 655 711 350 012 601 420 890 381 787 135 457 252 374 778 836 975 817 126 527 215 166 470 807 316 098 639 507 958 342 816 360 424 139 633 124 396 337 916 734 960 804 833 156 277 225 744 115 404 947 789 475 636 923 721 457 648 616 935 050 724 352 905 672 113 802 540 258 397 951 051 210 017 905 873 346 492 335 796 597 335 379 298 428 048 547 764 035 028 711 863 624 354 133 653 112 096 149 148 159 312 572 430 467 491 099 007 192 078 048 778 462 743 143 508 369 166 204 219 720 455 800 798 330 202 233 856 191 052 426 594 743 667 281 123 630 454 598 365 993 463 319 081 801 835 801 614 118 875 239 564 334 323 087 646 041 319 388 585 456 304 236 013 463 987 061 434 101 438 115 890 075 222 285 739 301 555 482 177 304 326 865 353 529 889 892 277 814 037 646 814 070 593 847 265 797 287 278 050 736 956 525 281 013 761 988 096 946 293 031 925 658 541 195 999 095 442 761 452 575 946 922 918 136 006 385 180 800 028 166 627 761 449 453 360 466 297 784 983 484 616 727 347 068 234 057 419 285 392 876 417 889 280 774 650 317 063 354 245 373 817 167 014 401 385 640 130 657 370 198 426 125 465 768 692 791 129 052 285 270 387 377 667 298 193 564 095 556 682 862 814 739 370 169 370 594 698 495 624 806 628 473 814 504 818 491 527 441 116 036 395 257 816 108 016 528 040 373 831 113 383 322 303 673 373 801 262 821 337 204 630 991 796 722 398 316 533 203 159 033 456 637 384 768 135 077 234 485 634 671 525 896 602 323 127 707 174 044 585 100 110 416 719 584 099 280 545 300 792 604 098 582 158 547 367 685 906 034 305 787 966 145 356 785 110 384 172 996 127 113 207 323 567 551 280 673 450 251 374 640 848 245 044 845 189 624 935 797 578 330 060 220 501 626 119 460 416 663 884 519 420 778 392 136 833 902 475 467 347 482 610 533 954 301 776 963 949 849 079 598 060 216 745 530 833 982 233 862 980 095 108 992 119 986 106 305 138 942 073 326 941 659 387 270 163 717 076 721 591 616 975 894 921 409 708 509 121 804 189 291 718 336 493 309 166 784 415 170 426 686 560 911 266 727 652 815 365 260 550 610 319 333 591 820 132 226 540 780 484 624 730 574 055 262 977 496 139 978 342 561 499 387 555 455 806 846 476 254 850 054 950 026 850 666 736 736 400 909 143 759 989 068 713 572 353 859 570 628 231 847 343 731 455 785 144 799 035 629 785 156 908 301 469 651 032 639 159 243 331 858 693 070 012 907 594 863 459 148 566 434 550 679 841 395 624 890 257 940 679 954 327 912 658 230 320 991 394 619 511 416 398 925 448 393 977 503 743 143 597 928 019 445 098 064 767 185 589 668 974 517 177 033 812 302 084 793 815 049 451 691 445 247 453 542 317 145 360 693 217 728 615 444 504 195 325 736 025 032 493 333 768 429 046 408 591 546 027 091 656 949 277 588 864 017 641 184 234 744 832 817 086 435 982 542 302 778 410 992 164 366 605 520 077 443 482 229 870 557 446 569 070 546 246 862 884 934 582 006 606 226 059 689 668 233 936 371 932 404 106 594 036 485 040 460 979 372 732 104 868 160 334 809 606 381 781 804 612 839 916 877 249 858 933 941 138 750 451 143 946 117 614 647 947 169 641 747 980 868 543 027 652 246 044 049 210 899 992 733 085 343 216 164 829 788 261 564 452 083 093 808 568 517 839 062 435 218 841 351 090 362 043 938 221 560 942 992 336 692 926 449 408 305 623 102 390 670 752 749 470 672 561 478 779 376 046 716 840 029 683 677 335 843 063 101 435 982 888 664 870 741 318 354 307 769 058 744 260 385 741 953 296 482 366 124 346 615 067 138 333 243 543 458 833 615 519 625 219 947 643 060 898 973 490 252 974 631 170 525 750 177 200 594 062 077 552 792 442 646 836 312 456 223 629 772 756 383 149 367 563 460 624 187 733 027 032 374 547 313 478 226 494 949 574 767 081 639 738 842 059 949 561 485 346 226 127 603 479 112 992 906 643 283 425 105 552 754 323 011 706 110 179 712 504 265 420 266 920 353 083 927 020 713 709 443 069 038 763 191 422 489 027 478 708 440 249 268 515 796 065 037 378 537 225 626 180 160 269 836 500 068 387 019 210 722 069 907 474 777 270 179 992 377 913 204 078 026 322 102 045 597 668 417 734 808 422 034 693 784 127 129 130 508 485 748 396 877 196 957 121 830 002 704 664 304 945 485 115 200 550 146 071 108 622 288 608 966 870 613 902 269 121 361 913 251 256 249 848 025 756 606 933 718 987 445 794 718 819 250 559 641 956 528 118 089 594 062 299 596 289 824 754 321 664 331 322 316 425 075 019 400 700 652 924 297 978 312 877 450 227 502 387 095 593 952 029 148 312 030 194 410 474 933 389 537 978 175 419 991 990 925 468 377 862 006 695 572 732 141 847 725 496 361 735 139 918 310 078 271 949 695 088 632 008 358 804 420 553 685 843 914 131 914 199 950 670 058 751 542 045 330 955 091 912 073 963 990 166 103 265 007 974 066 985 701 075 454 374 574 197 371 369 130 847 904 678 000 156 508 041 392 433 020 546 511 139 049 401 761 124 784 708 463 463 536 500 333 050 302 796 437 462 845 895 437 076 397 012 323 649 933 391 057 958 664 818 770 822 512 556 300 219 403 131 850 571 578 242 307 350 992 002 551 203 786 368 328 451 254 253 653 766 203 942 266 672 149 644 100 888 518 735 315 791 989 836 271 646 707 303 257 801 064 860 568 426 009 740 940 282 575 821 575 915 009 319 631 861 969 231 360 363 681 248 505 270 117 816 962 515 186 211 557 766 539 537 381 626 544 165 706 086 180 010 697 065 199 902 852 780 947 186 830 744 163 697 918 658 468 732 098 038 641 993 458 932 132 452 864 237 712 899 918 495 061 097 801 346 258 335 807 641 394 700 093 390 291 200 365 043 221 532 248 439 305 170 181 533 460 451 258 379 593 729 667 354 029 187 218 858 529 916 048 393 249 113 723 053 086 487 778 048 315 016 101 430 125 299 920 438 112 345 102 879 469 434 231 559 577 045 423 114 150 082 374 362 331 284 574 330 190 978 991 259 396 270 992 527 351 846 498 600 144 186 331 869 457 332 158 515 082 586 989 754 609 780 255 210 202 256 010 541 896 860 113 051 351 758 897 189 361 119 847 002 035 137 714 596 485 214 325 146 973 204 642 894 667 940 334 985 448 805 004 202 496 378 904 729 537 505 852 285 988 881 237 371 734 377 264 320 828 450 372 037 443 453 885 792 709 552 146 337 656 690 067 146 209 014 472 602 046 166 123 103 088 048 066 816 092 355 134 495 695 303 998 148 866 859 612 895 296 782 631 733 141 294 096 071 029 066 450 042 690 834 433 395 677 166 000 839 971 534 107 769 443 055 495 593 045 932 435 454 894 683 187 141 886 994 094 189 171 447 059 734 512 320 274 269 153 330 507 789 294 284 888 576 694 604 415 580 756 294 355 139 074 938 197 423 586 348 678 496 958 887 145 842 534 109 153 000 419 961 956 552 928 872 301 425 977 336 722 400 444 068 202 433 464 852 851 546 162 812 183 611 246 498 829 173 072 274 659 995 751 877 174 727 499 130 544 484 213 260 962 912 606 842 697 464 260 810 718 908 574 476 093 849 453 074 951 945 438 123 180 936 713 518 500 576 712 260 115 305 569 808 358 144 335 471 947 192 148 497 582 538 199 185 854 075 769 236 229 395 663 183 594 354 066 169 492 068 311 056 444 723 513 976 607 913 356 373 409 854 058 495 490 381 734 035 252 235 825 381 024 230 664 915 985 168 576 315 376 699 574 813 539 289 169 246 175 064 948 544 460 724 102 719 263 952 906 680 116 687 633 119 525 527 053 287 921 992 891 588 137 206 396 686 356 423 036 201 575 453 195 708 695 630 906 066 476 215 474 684 695 635 615 535 598 587 070 726 188 338 032 768 342 109 840 066 082 808 180 851 265 934 312 802 640 897 930 439 077 916 394 059 845 300 512 060 583 291 415 639 801 870 241 080 231 326 374 509 507 527 537 409 305 686 267 360 698 134 304 756 246 569 667 321 821 432 377 358 046 732 633 414 194 210 977 801 035 044 192 797 410 751 838 156 273 961 072 460 063 206 918 109 761 177 003 216 901 888 174 758 195 878 463 510 718 256 065 975 690 376 360 036 212 698 061 465 846 579 878 672 549 217 249 306 091 521 174 130 083 399 448 425 241 035 794 451 909 127 522 780 121 959 239 313 890 045 962 323 183 957 529 430 991 943 152 688 418 411 308 703 513 374 958 223 222 917 261 464 870 736 437 979 986 797 536 708 360 643 588 281 450 012 164 321 532 048 836 093 943 336 643 005 280 877 545 516 578 037 332 126 904 545 088 905 371 347 153 328 495 443 090 810 699 088 207 749 137 726 727 197 573 011 227 723 962 363 228 067 060 015 753 478 821 343 051 941 802 595 283 527 321 656 235 614 695 430 372 554 316 904 614 087 543 169 552 566 258 648 413 205 186 963 161 895 935 851 539 969 146 141 830 193 094 132 395 011 458 404 342 208 686 110 243 266 298 469 622 699 489 242 733 699 701 858 954 998 593 618 226 586 008 090 590 259 189 744 766 832 229 505 511 833 809 205 937 242 713 688 514 786 996 549 557 970 675 377 102 878 799 879 370 743 258 578 781 982 451 675 987 435 020 366 423 685 092 828 639 583 598 175 445 679 135 544 549 966 924 460 754 988 937 899 814 454 106 236 778 528 319 031 840 545 060 711 729 647 665 690 158 116 614 712 858 163 894 158 971 951 351 519 705 126 112 898 700 331 264 962 011 772 498 911 629 659 880 089 299 909 151 059 825 285 767 629 536 115 934 884 847 806 756 222 802 113 304 995 332 435 118 904 970 797 022 345 433 877 687 584 301 233 598 958 466 975 427 164 476 872 336 319 866 485 981 268 748 756 185 860 886 637 767 762 541 738 743 192 638 882 091 614 326 752 549 986 524 866 092 875 220 408 731 952 353 542 633 264 094 764 951 990 891 680 621 694 670 441 946 492 136 769 445 143 279 833 655 443 032 709 136 073 312 148 443 335 084 907 573 861 621 679 556 708 894 284 450 860 241 498 601 742 381 121 782 020 500 249 047 027 882 361 269 981 198 358 079 525 054 392 031 552 791 615 987 991 016 412 796 125 646 532 075 980 579 534 073 775 079 706 150 888 735 754 636 554 510 957 957 482 480 698 880 971 079 432 958 198 348 323 598 319 783 981 862 210 418 447 320 423 131 969 344 709 814 599 288 385 460 277 447 050 685 491 579 434 611 012 481 657 478 126 025 913 010 163 504 821 937 887 335 775 206 692 545 737 536 018 640 149 768 792 937 364 347 512 791 682 512 872 336 528 466 765 989 308 563 029 681 789 941 285 019 870 752 963 167 836 942 123 853 521 094 448 480 585 294 367 239 252 754 526 683 079 814 583 610 244 743 400 504 452 236 016 288 683 148 119 310 520 132 846 173 148 079 212 401 570 889 821 412 808 468 923 610 876 334 674 419 373 789 639 098 248 758 219 158 270 375 769 417 186 551 190 258 534 139 873 422 295 144 005 441 410 923 872 182 173 818 830 800 651 581 286 734 335 159 145 711 150 247 633 113 665 593 183 337 140 235 235 124 808 415 190 564 707 018 700 455 401 563 246 980 474 519 621 044 258 078 450 537 342 685 700 164 939 542 712 179 919 783 561 883 447 264 582 480 687 496 060 166 951 634 766 860 335 953 562 729 541 792 541 157 419 060 495 195 223 996 847 359 280 960 011 085 316 474 238 802 447 964 889 139 592 339 407 581 074 487 175 663 986 343 593 612 974 862 314 942 779 538 251 031 984 252 493 894 836 827 959 766 654 168 406 553 477 845 888 431 276 245 263 542 104 744 890 587 111 713 405 618 298 215 935 894 280 264 335 635 121 018 489 750 362 446 387 417 347 554 821 026 049 066 738 755 199 249 726 332 555 585 732 013 371 454 689 003 542 248 545 824 263 256 462 908 724 988 037 453 528 044 717 242 352 737 359 292 498 323 981 061 624 783 067 146 105 536 147 619 447 599 317 805 449 191 953 977 526 262 589 604 340 481 581 928 815 834 241 504 674 511 283 824 057 024 995 704 786 999 459 568 841 272 239 587 016 835 161 787 408 877 256 023 370 729 459 572 486 824 423 439 809 865 590 720 443 736 697 676 664 799 834 013 846 415 829 235 590 713 781 323 464 587 705 107 919 677 410 094 868 460 822 842 217 372 209 155 702 214 617 264 682 743 653 788 390 374 348 769 324 827 382 191 793 558 557 370 036 066 619 925 171 662 856 033 463 303 201 705 056 868 604 920 944 152 189 725 670 550 427 315 154 132 030 925 669 196 507 412 954 882 930 327 752 438 305 764 515 806 403 471 533 474 017 862 880 904 491 867 561 255 035 411 991 676 252 713 168 679 417 521 551 941 955 757 796 178 474 524 074 894 786 725 675 237 785 683 864 209 715 245 981 194 219 190 443 425 793 995 714 576 967 665 507 751 605 767 020 129 371 881 820 743 911 281 138 862 035 366 285 200 318 002 666 832 472 460 688 430 905 153 629 779 135 201 502 760 763 061 542 398 698 509 595 262 601 427 901 003 298 086 689 145 959 110 745 979 004 447 171 541 473 878 647 255 159 293 008 805 115 441 383 231 091 469 176 258 603 057 482 528 528 033 954 285 033 432 043 191 585 446 016 905 185 472 108 968 745 401 973 293 886 209 268 955 117 284 573 681 023 964 740 936 963 065 647 849 438 348 651 691 302 944 153 674 756 157 233 181 718 658 931 942 212 999 488 171 018 543 769 342 294 867 041 898 699 149 201 890 076 601 646 429 235 161 755 919 573 479 176 251 170 788 733 946 045 515 905 800 593 021 910 964 786 454 438 885 176 474 974 954 974 221 071 653 420 191 357 250 042 529 379 186 567 451 625 723 624 235 914 674 926 169 752 502 094 179 965 394 726 043 802 802 651 649 575 223 597 980 746 463 512 298 494 489 129 613 385 192 068 909 873 826 147 785 892 324 754 889 575 710 424 748 965 595 632 193 168 007 229 405 798 840 028 517 870 208 436 770 358 419 421 762 756 028 800 960 474 826 064 336 048 501 768 576 935 949 979 592 385 933 114 072 160 236 726 091 555 347 923 838 909 859 331 585 997 981 042 646 173 215 485 669 271 941 169 526 658 515 772 407 018 169 933 840 279 709 571 096 943 066 182 866 995 952 999 571 469 664 007 392 941 936 360 075 385 562 144 330 843 120 358 543 107 202 104 481 807 020 765 186 295 347 277 508 799 958 601 933 852 472 882 796 282 408 352 939 162 574 683 236 932 425 271 838 494 789 397 564 918 797 701 459 988 444 228 420 921 209 270 302 999 723 339 080 879 376 120 479 009 712 896 120 313 288 925 520 220 671 104 697 216 807 475 759 109 931 316 538 665 579 932 183 888 869 470 225 709 004 627 517 884 968 180 059 116 229 839 377 517 375 175 499 342 887 345 594 924 702 073 406 707 291 559 968 810 162 695 372 862 566 793 057 831 287 698 845 216 185 081 560 401 010 990 687 497 963 940 033 951 589 232 539 105 812 694 300 098 766 532 779 950 403 541 348 115 255 020 687 582 967 813 442 323 124 463 991 269 732 282 027 058 290 329 410 697 216 768 357 071 850 158 923 060 766 369 101 759 660 573 092 625 310 045 410 976 607 898 437 278 565 577 460 360 921 018 729 414 004 978 298 215 039 445 713 089 497 932 615 459 944 048 855 329 346 986 723 160 216 382 580 920 352 218 644 139 590 277 520 643 844 823 890 015 796 481 835 923 839 035 407 588 755 506 914 691 333 277 833 968 817 958 420 914 560 320 727 313 006 188 215 965 513 415 598 548 551 613 243 718 375 859 042 145 690 517 945 232 155 922 845 517 832 315 594 650 027 863 307 058 534 067 309 493 817 449 360 121 465 249 910 220 688 855 236 935 568 646 779 685 160 235 874 491 533 159 353 885 894 194 606 677 935 784 636 702 516 020 869 424 230 145 721 690 661 424 598 734 876 425 680 334 353 693 208 005 601 238 841 453 543 821 359 417 737 899 419 550 762 310 128 249 327 755 725 353 377 064 933 920 780 676 888 553 231 217 847 930 231 888 587 107 219 806 677 059 947 544 052 437 904 144 808 730 365 471 852 963 810 579 285 127 563 965 102 787 779 614 521 557 827 243 320 215 724 665 526 513 002 259 665 986 482 957 216 086 156 440 546 951 743 922 114 002 476 848 962 157 658 417 123 638 620 634 481 957 953 133 302 325 287 097 731 483 689 189 563 839 406 232 848 637 491 899 037 416 108 778 119 016 433 217 853 349 953 245 553 515 948 224 110 995 322 517 690 560 247 479 350 736 651 832 942 959 391 897 010 077 557 876 437 033 744 593 795 145 550 437 134 038 872 948 452 553 272 830 189 106 438 490 945 799 488 766 646 523 097 950 522 690 894 238 253 657 004 319 064 531 091 311 783 592 340 567 527 477 129 839 385 924 569 824 405 294 064 304 848 156 223 484 271 786 739 571 457 064 593 054 744 943 367 155 600 448 700 580 350 290 225 412 650 153 564 999 302 551 088 665 981 434 557 408 491 777 478 685 959 318 239 107 238 579 752 745 843 959 309 304 357 280 770 000 619 320 072 030 456 140 085 949 788 329 295 220 623 356 711 261 494 872 288 387 830 199 276 635 732 025 556 695 531 507 868 693 400 703 501 459 030 270 934 052 736 315 566 632 142 294 613 677 268 717 479 095 536 968 684 266 113 082 705 791 797 211 613 279 820 556 407 979 009 102 597 674 729 585 147 787 293 629 493 185 071 411 773 656 606 254 573 715 742 564 989 210 746 426 728 049 921 267 085 247 692 319 893 162 146 498 821 801 125 801 171 214 193 819 175 108 338 011 620 997 976 322 452 954 348 678 207 753 925 479 969 278 634 748 293 213 701 452 388 422 183 906 291 501 714 888 798 393 118 759 405 693 966 885 439 977 129 839 949 633 186 417 007 535 061 439 063 292 962 951 897 582 319 421 238 562 121 453 441 808 207 193 651 445 129 240 681 528 184 393 946 854 943 120 014 290 970 815 516 690 799 939 527 456 628 673 586 643 343 838 141 808 452 935 620 364 115 727 747 115 635 396 165 743 198 642 930 647 612 307 111 115 777 788 856 320 162 123 324 763 390 078 615 768 750 959 768 746 046 392 620 134 852 941 766 184 055 673 502 303 360 662 745 798 475 881 942 298 158 584 129 486 757 366 231 497 395 861 171 330 070 081 243 112 767 857 451 248 290 188 244 298 771 252 447 107 106 792 512 177 046 808 026 663 210 956 524 550 625 582 435 867 587 972 599 723 025 053 844 542 284 600 242 955 094 757 734 656 670 492 443 767 385 533 551 255 009 798 138 809 525 931 600 996 718 830 131 556 077 657 252 095 558 235 920 687 714 504 298 254 653 568 329 497 821 958 786 199 812 917 482 691 030 975 463 093 547 542 130 896 743 025 516 947 230 863 924 631 570 706 709 685 422 376 100 378 428 154 403 173 086 722 415 532 437 146 345 899 927 810 773 987 382 657 786 182 893 630 955 719 709 204 519 577 463 101 228 664 519 274 564 066 119 610 709 838 363 900 818 802 776 819 234 963 769 219 612 134 976 999 013 612 427 439 068 854 612 834 103 539 206 846 090 988 719 813 671 679 744 526 963 474 526 835 781 731 194 361 765 892 528 711 763 763 912 202 214 892 450 833 878 363 294 263 064 505 239 393 393 928 295 644 679 637 093 932 614 882 915 264 123 547 256 184 124 562 393 656 073 783 129 955 139 194 760 620 619 246 624 461 772 619 226 613 641 380 223 060 313 074 610 649 616 964 158 900 111 390 480 759 753 391 107 685 557 608 329 788 376 615 228 305 407 490 847 844 649 014 559 631 510 576 574 451 608 400 753 706 778 673 603 127 236 135 753 589 256 602 087 636 970 061 810 301 585 283 472 248 046 734 927 095 628 560 456 152 837 899 177 566 195 241 905 984 899 097 152 988 801 303 969 149 899 250 909 185 400 850 336 043 719 754 560 095 844 931 608 429 799 404 955 910 710 436 408 012 617 752 581 833 276 393 573 036 073 561 759 332 779 392 701 762 926 512 396 763 521 090 320 118 845 046 882 116 799 245 823 004 485 978 845 060 851 125 899 333 646 672 058 545 449 476 734 885 760 504 025 765 257 403 688 227 446 565 614 873 089 184 745 621 192 312 208 034 506 595 285 133 960 977 393 482 880 409 021 893 758 412 007 397 531 267 854 296 222 810 771 975 834 653 245 793 019 247 623 704 077 089 421 861 122 967 658 792 941 843 509 403 852 408 777 557 778 909 728 947 806 189 266 016 156 194 743 370 109 846 753 112 601 412 733 829 404 993 706 893 720 318 924 988 760 032 713 313 146 464 969 098 279 471 285 915 953 072 606 070 236 760 138 337 533 233 111 907 530 220 290 776 897 536 260 541 866 131 255 940 649 665 073 042 202 683 959 547 446 246 301 546 150 627 692 765 766 805 742 161 122 407 990 799 113 652 626 022 984 526 411 935 206 451 002 332 858 357 670 612 986 583 411 435 893 065 392 804 093 389 108 139 809 693 544 494 826 223 111 295 690 654 199 622 164 335 056 601 998 626 577 589 761 370 852 915 630 295 162 554 799 645 904 839 251 668 863 625 659 667 305 066 323 269 951 591 309 932 041 685 289 069 150 338 385 338 429 823 388 725 821 906 314 357 330 612 307 675 951 698 644 159 834 327 313 863 579 080 170 517 691 905 460 131 168 187 168 524 819 304 717 380 175 389 008 326 399 913 752 899 603 273 478 388 917 292 878 495 515 930 795 142 502 895 365 368 735 194 798 147 716 608 108 662 167 548 778 277 837 382 307 895 452 440 003 519 120 214 734 098 960 291 034 406 340 310 559 718 088 811 974 265 241 948 413 919 979 900 602 725 131 295 962 462 915 831 419 555 826 976 224 206 488 111 800 939 423 723 715 250 138 788 813 110 442 297 202 944 165 394 958 911 226 146 361 944 397 474 409 567 270 961 492 709 302 289 937 056 831 820 262 735 139 415 536 235 853 423 238 041 216 718 204 390 028 814 054 754 072 534 127 649 989 737 340 185 923 905 140 261 790 156 910 860 501 228 428 351 105 862 007 547 362 706 307 829 866 405 338 009 002 406 951 825 344 500 432 890 638 811 636 235 890 221 159 222 383 620 335 293 494 729 143 296 167 972 921 941 867 173 781 965 089 571 327 693 458 306 309 030 943 768 166 536 146 294 027 884 592 121 593 011 216 334 948 155 251 359 717 985 919 445 520 402 709 326 452 271 242 818 308 039 269 548 787 344 643 297 637 656 437 020 964 659 531 518 125 419 704 987 648 712 885 763 798 010 420 097 762 263 179 977 632 202 340 432 595 982 170 924 325 932 522 299 954 357 541 019 881 912 993 438 124 751 849 078 618 245 845 178 157 998 339 378 979 776 815 858 309 517 801 833 244 805 409 805 489 838 702 525 731 062 502 426 264 628 673 718 495 295 900 253 671 370 959 064 045 678 064 397 311 293 665 022 351 048 881 325 424 321 284 262 909 592 993 610 858 020 506 755 701 795 759 825 473 995 829 037 105 064 290 600 268 685 387 205 967 171 751 223 605 548 892 359 853 178 368 561 373 776 316 632 726 983 461 721 664 051 776 477 637 875 544 448 666 300 579 556 457 003 059 416 446 382 309 037 415 049 516 182 612 746 785 145 468 798 451 515 646 303 490 055 413 665 635 749 762 369 798 606 641 729 195 657 796 346 354 462 270 163 906 161 926 559 794 409 680 558 984 200 485 660 229 081 965 649 350 115 910 848 211 095 296 442 588 642 815 440 365 161 874 344 882 231 845 030 878 360 475 620 241 417 099 390 904 473 983 994 758 237 985 104 091 947 313 692 978 363 422 224 136 810 818 500 384 919 849 854 552 043 018 813 477 818 935 799 426 972 454 138 957 101 403 448 497 506 202 212 977 616 140 511 475 502 059 599 012 175 919 093 649 265 070 137 180 832 010 177 301 139 664 142 703 453 628 930 255 543 482 402 563 269 113 639 747 760 041 377 764 354 396 841 314 620 110 564 806 533 613 739 367 738 466 022 697 713 418 311 540 753 945 401 496 349 704 575 586 372 556 808 550 212 189 716 721 258 977 093 379 960 535 755 423 949 714 300 331 063 285 335 609 637 646 465 381 146 725 618 997 480 361 142 294 923 775 982 620 544 401 955 467 962 627 471 449 379 914 356 585 468 780 660 529 630 190 447 863 995 315 023 048 987 498 885 417 327 224 964 825 168 422 613 708 337 434 993 348 196 788 611 272 942 252 767 367 324 885 550 070 343 287 267 096 990 539 266 836 081 447 426 250 214 022 520 639 936 739 312 410 347 873 904 541 904 897 614 345 487 725 736 283 950 462 923 270 254 475 993 090 872 880 880 873 720 574 899 266 419 356 474 057 855 884 031 794 696 573 245 768 820 986 313 325 185 864 601 069 198 843 360 568 170 448 920 048 038 586 931 854 136 748 488 856 427 613 338 343 618 450 113 431 736 923 670 939 911 129 545 457 180 810 041 320 194 073 129 583 480 048 384 022 681 110 292 253 846 710 659 975 883 633 057 816 734 976 509 234 520 157 994 601 294 696 291 876 276 987 228 619 779 921 544 707 425 884 427 032 505 478 258 455 091 183 216 805 031 710 534 397 561 925 596 364 421 972 057 361 328 917 975 950 596 021 632 397 757 359 007 778 175 968 384 508 926 137 608 870 408 423 165 392 660 498 383 442 590 823 223 473 501 294 559 121 137 592 239 092 444 313 056 649 404 604 824 333 759 836 478 917 487 851 927 982 430 719 576 282 696 800 604 352 800 153 168 195 970 662 327 860 457 814 975 131 809 378 830 296 544 114 401 265 420 435 102 847 511 797 525 955 717 779 120 834 507 919 181 954 415 938 592 242 224 960 324 559 923 107 179 968 732 387 906 857 113 624 964 483 005 546 979 998 025 647 174 610 509 582 343 478 748 035 307 897 991 213 685 312 592 538 177 496 172 643 480 478 038 804 456 170 613 933 127 062 155 602 194 005 251 660 729 711 467 778 794 119 513 531 288 715 824 475 527 113 608 155 999 282 101 404 865 711 751 300 937 096 981 206 644 102 708 530 379 809 197 100 652 650 979 639 632 959 852 207 932 146 451 164 652 111 485 048 640 674 352 859 536 828 594 987 784 718 280 434 188 681 284 616 465 680 242 986 436 397 505 263 993 122 365 341 735 692 960 449 018 922 540 846 411 049 829 146 827 822 206 042 929 322 177 421 361 566 819 171 179 753 226 957 998 929 599 247 928 065 590 532 721 734 510 083 851 128 480 542 901 193 144 134 178 755 752 722 266 008 070 542 666 680 654 988 169 929 112 396 153 082 580 454 144 470 670 747 045 118 727 098 820 633 772 191 281 595 094 430 086 053 967 052 567 321 663 750 811 326 972 272 165 030 271 404 885 106 111 985 153 243 186 817 005 212 035 367 641 829 594 864 871 422 114 941 126 631 221 675 708 177 771 201 930 450 989 450 730 819 701 153 707 424 890 859 868 955 716 159 473 250 055 804 616 131 999 414 548 083 978 237 257 215 911 166 007 555 418 690 309 550 471 315 400 498 558 256 092 776 550 452 685 357 723 177 806 808 406 884 681 136 204 320 898 277 983 535 261 897 828 559 306 107 385 056 659 920 691 798 419 977 020 675 526 023 031 114 492 708 583 719 704 018 507 252 994 897 062 001 965 681 164 469 764 218 134 721 271 908 814 475 275 538 486 032 205 502 493 939 547 253 262 596 470 424 907 155 728 130 330 359 428 243 244 452 975 200 022 916 098 112 808 796 923 971 805 458 356 925 181 304 920 849 586 438 448 012 998 111 694 393 704 744 799 935 178 582 785 261 744 533 151 724 134 180 890 557 809 166 711 914 067 134 322 588 328 711 597 396 642 735 676 334 719 877 996 435 027 423 850 502 285 315 630 653 340 592 791 648 553 019 672 110 826 221 703 216 060 389 364 854 142 526 945 114 367 039 642 547 853 478 517 609 720 973 006 402 513 962 106 948 472 390 571 104 156 219 300 919 995 084 597 944 826 473 879 103 404 720 648 766 398 935 318 208 129 079 688 175 797 514 062 170 334 370 674 196 850 900 773 037 243 652 127 344 032 766 402 328 679 980 558 818 653 770 414 121 433 626 402 429 724 425 363 666 642 166 822 504 601 967 444 641 165 232 445 694 484 350 018 241 825 353 865 545 928 646 964 514 764 287 785 118 234 227 024 695 886 067 203 906 713 477 771 853 145 541 081 580 726 094 977 088 568 159 850 544 650 025 963 972 656 257 574 954 818 139 662 097 141 817 281 867 613 863 610 552 769 936 349 274 657 727 964 352 683 497 291 628 013 002 056 983 008 387 340 839 289 802 538 570 424 067 641 983 255 324 538 021 751 106 406 098 136 946 018 435 813 898 434 650 364 647 853 110 012 957 917 783 960 186 652 788 448 838 370 033 568 263 089 114 047 265 335 952 983 690 829 472 069 812 729 982 889 427 096 197 646 401 730 721 750 657 510 115 440 975 198 451 499 469 501 194 859 681 409 455 260 791 447 101 860 302 450 542 720 647 051 177 177 021 910 225 032 069 440 696 419 539 671 189 611 118 706 657 171 684 636 305 498 673 780 609 908 028 749 161 405 178 718 905 748 774 523 232 638 594 675 269 116 230 840 206 931 045 960 852 477 766 459 725 620 307 004 508 290 727 110 652 437 103 566 473 137 655 438 254 472 170 430 463 812 779 968 136 132 849 638 861 467 360 569 148 719 190 476 739 544 657 179 924 011 923 679 148 930 802 516 985 040 881 941 068 686 214 183 600 592 271 035 979 855 959 215 744 867 828 528 397 083 683 814 990 758 640 976 148 279 921 166 868 754 111 256 354 175 933 326 452 801 424 990 037 718 589 428 172 126 505 560 154 448 900 792 255 691 629 723 349 933 251 514 598 836 120 450 578 063 938 318 163 506 417 027 001 560 987 455 987 854 487 360 100 898 455 436 045 075 099 045 702 307 636 839 359 229 010 435 860 555 722 350 767 488 346 465 289 923 237 463 922 866 244 991 898 150 088 248 314 645 093 546 944 422 018 663 443 579 765 485 890 845 288 060 465 806 515 790 616 711 944 910 380 047 277 262 809 280 468 077 941 081 933 476 640 473 145 019 739 508 176 699 869 747 147 843 329 128 283 832 893 749 832 202 524 484 654 789 859 735 953 705 432 289 862 227 850 815 447 957 852 765 298 689 448 954 539 377 421 167 301 257 349 496 122 407 301 169 845 615 402 916 757 607 546 062 459 942 598 283 984 283 089 743 920 409 411 505 914 002 106 553 358 910 310 014 597 407 342 434 026 741 926 511 446 465 863 678 361 239 986 973 832 144 383 361 116 382 441 867 955 494 337 798 511 887 392 653 393 050 131 595 002 243 653 186 179 810 017 712 815 739 864 121 031 786 605 516 055 358 241 977 063 173 682 972 588 963 540 536 803 193 740 963 783 528 303 193 283 355 968 810 935 875 329 015 644 762 476 841 550 443 622 612 656 741 150 585 922 504 082 569 320 439 508 994 187 060 901 695 042 066 164 023 621 893 973 346 630 678 334 694 941 622 906 254 395 152 857 355 763 015 935 173 017 835 160 182 756 321 670 006 660 866 472 330 822 548 625 046 446 807 501 005 040 437 950 242 847 893 086 616 446 467 846 188 003 961 424 613 017 570 038 785 930 289 398 841 205 582 803 447 951 925 038 539 005 170 201 607 659 731 520 374 274 255 212 170 068 583 221 199 185 480 927 928 823 047 058 802 001 469 313 291 572 156 959 603 877 527 336 752 587 653 166 867 806 446 609 027 170 535 118 777 581 258 037 890 853 447 974 010 074 353 542 043 022 505 947 064 303 298 500 778 859 206 256 980 296 657 526 943 076 455 039 389 222 108 734 501 880 712 769 982 081 649 706 836 927 170 240 711 976 023 998 583 759 341 087 977 350 612 101 394 957 534 753 525 509 292 907 232 032 141 336 948 481 674 248 091 381 409 222 631 526 036 727 903 907 119 830 845 509 138 580 194 416 594 831 940 099 365 700 681 197 252 131 865 442 851 522 565 898 110 598 937 342 316 826 200 265 325 530 575 944 900 306 444 576 468 585 483 920 387 632 081 986 240 627 781 587 872 522 290 626 968 814 320 515 782 440 385 364 054 458 141 730 765 416 663 005 154 366 356 290 797 145 598 385 027 561 617 560 310 361 656 476 581 091 415 804 162 074 241 371 254 272 158 817 050 579 357 664 139 369 551 010 038 482 369 328 499 855 811 394 234 228 718 640 150 333 896 054 579 481 518 390 834 818 990 458 855 355 809 876 220 619 782 891 590 524 235 257 437 968 009 840 092 913 893 244 951 880 226 380 901 941 150 149 195 135 375 211 726 723 764 818 530 583 688 688 772 423 285 865 807 304 482 583 768 163 315 158 943 559 339 523 482 815 494 781 048 073 441 706 758 249 585 392 290 208 048 024 638 924 834 936 071 058 086 486 310 178 953 420 677 948 532 986 389 702 956 650 694 927 416 275 011 477 902 151 682 800 903 447 524 801 062 236 199 398 458 674 918 433 288 723 308 619 802 158 611 944 065 125 795 844 546 746 802 166 350 033 495 774 479 999 256 984 090 766 973 754 414 318 765 755 580 634 384 513 565 413 783 518 682 660 717 330 985 258 545 022 880 218 605 965 707 699 265 379 385 372 383 036 268 937 444 788 011 884 568 468 689 908 015 995 239 054 805 008 138 903 653 238 294 891 567 335 862 566 550 468 267 505 684 886 667 050 586 635 464 193 639 769 352 342 416 557 428 879 824 781 202 472 827 118 098 483 329 956 509 672 613 575 748 207 837 212 185 239 299 362 867 721 609 424 243 616 202 398 072 216 261 065 712 807 915 548 061 793 440 468 020 226 395 475 163 848 633 980 069 504 112 302 565 759 503 596 329 908 530 644 810 992 150 990 123 179 876 484 001 061 651 751 683 839 694 913 659 248 632 909 780 073 278 351 722 018 523 527 068 948 142 232 690 682 131 938 738 109 998 885 420 710 922 464 131 119 210 737 022 152 675 089 442 155 550 518 407 768 270 265 356 097 284 075 979 267 496 020 159 941 752 997 988 208 640 184 926 967 531 420 090 957 096 991 805 315 178 623 970 257 919 616 284 162 504 469 453 756 414 187 355 042 313 060 640 409 048 652 333 989 249 778 587 211 184 228 955 065 693 832 433 434 050 030 950 805 002 887 926 513 352 334 737 233 314 462 071 235 947 437 976 505 693 726 366 126 151 055 321 898 132 076 610 962 970 086 635 509 624 737 563 520 152 233 175 129 267 644 338 346 693 049 964 264 101 745 418 052 967 031 161 051 901 443 544 118 211 645 679 688 042 495 762 482 646 158 352 731 034 279 040 437 441 376 680 644 030 601 784 865 866 762 984 419 488 914 723 919 116 525 061 856 402 284 853 745 774 381 193 968 268 828 260 208 181 490 112 813 155 238 078 022 702 506 068 411 397 026 768 183 074 660 778 043 566 437 396 750 239 338 080 001 903 241 078 036 962 237 471 560 028 714 698 625 764 656 204 371 552 308 692 577 114 866 712 005 801 159 076 522 485 866 245 505 087 140 962 481 480 473 944 711 058 903 329 177 917 856 086 518 404 125 091 591 874 075 458 788 019 479 205 053 807 474 919 529 656 745 460 163 531 425 927 822 713 843 623 154 955 361 165 497 339 404 265 661 842 293 509 838 792 834 922 803 685 554 936 452 844 881 722 197 954 061 902 060 198 845 398 123 120 607 376 194 638 903 310 329 597 853 863 397 931 226 558 644 403 865 846 009 512 502 830 389 854 561 548 662 932 922 741 907 469 953 573 468 600 369 581 685 949 171 527 656 825 365 627 484 759 206 395 211 930 800 428 360 986 776 935 434 740 496 697 033 663 493 985 012 612 629 884 551 251 316 425 666 907 781 430 109 132 906 810 522 474 622 941 130 844 304 823 349 443 144 481 685 882 320 407 249 498 897 476 787 169 683 288 644 644 082 776 449 625 232 185 353 833 126 007 683 414 320 084 411 187 819 144 252 669 414 919 102 993 796 174 110 222 212 090 917 112 257 167 708 608 623 620 881 729 774 987 307 200 504 043 031 526 772 753 673 469 630 378 833 892 969 841 126 758 716 498 713 001 804 427 989 246 347 526 054 307 608 637 968 308 480 111 020 537 530 755 083 368 102 585 037 217 380 995 080 483 234 126 796 560 277 445 662 840 258 887 643 841 377 869 608 360 637 496 071 976 695 604 540 740 682 901 613 768 452 353 679 274 864 366 356 836 309 686 283 983 221 286 375 664 962 511 671 195 805 168 586 708 648 883 245 602 881 034 257 742 354 972 195 523 031 894 587 619 732 910 586 834 818 774 673 486 808 694 441 138 389 752 714 262 217 929 494 855 709 196 462 192 863 788 544 327 486 557 574 198 469 453 022 825 258 007 446 926 025 370 824 290 734 120 445 713 151 922 342 521 450 292 339 565 091 203 715 811 561 084 357 464 935 501 699 543 860 139 864 931 327 285 356 316 820 176 996 384 681 714 365 341 500 459 277 753 055 062 158 511 127 632 581 977 005 605 152 619 598 593 892 132 838 520 190 319 297 546 835 039 385 190 617 769 193 706 349 412 862 923 389 236 802 158 907 613 417 092 655 496 536 220 642 138 193 366 375 420 621 461 139 932 743 803 833 022 626 306 725 125 059 749 115 240 980 094 632 163 318 918 643 736 769 939 152 326 991 100 076 780 016 843 086 118 820 831 205 315 427 414 098 005 823 753 852 879 492 476 662 349 235 839 568 700 573 805 826 008 518 808 503 038 193 226 164 174 896 183 997 608 444 715 714 157 944 471 793 156 526 877 712 648 389 271 953 824 164 127 315 035 226 858 225 937 467 849 117 316 998 387 509 795 767 917 017 421 752 173 434 729 324 925 518 446 776 033 332 045 631 284 327 115 657 191 399 587 851 630 318 134 651 125 471 440 769 990 930 460 367 332 411 843 084 298 555 337 354 644 369 315 121 510 723 680 207 858 392 479 366 229 843 438 126 535 757 962 770 548 716 535 287 374 955 350 832 557 562 577 283 951 889 055 997 661 303 416 583 876 137 663 502 999 896 873 323 350 121 586 752 916 707 465 756 985 811 685 295 367 482 303 032 654 346 662 457 937 830 567 201 342 312 447 712 693 779 271 883 906 633 965 808 652 832 931 335 756 286 943 100 076 732 078 778 979 597 623 136 301 402 656 184 925 034 982 251 006 032 431 888 604 789 247 667 332 711 099 180 506 067 925 255 843 027 692 879 971 537 269 351 065 574 352 032 030 382 395 552 466 606 408 166 416 945 237 400 053 280 246 860 187 135 582 662 475 105 980 885 215 195 636 203 135 170 187 448 150 026 681 899 171 007 754 183 344 985 520 712 904 080 366 220 974 523 257 407 896 341 146 731 259 538 447 301 312 066 725 944 113 652 646 787 096 066 220 796 173 184 230 677 159 951 948 198 417 468 027 578 867 022 744 871 657 551 335 758 210 005 682 935 412 483 232 512 763 645 520 298 027 422 780 608 325 385 662 860 011 631 611 009 765 095 186 518 774 845 774 815 653 896 821 601 135 448 517 424 535 238 788 633 433 242 130 515 881 981 056 074 341 474 033 873 053 961 283 582 882 338 612 433 649 604 434 079 832 666 531 615 252 389 119 029 458 137 760 350 874 914 249 026 367 865 317 815 180 260 602 207 179 182 342 346 476 345 569 341 839 510 062 471 169 844 976 835 268 840 517 280 123 918 704 442 754 130 586 727 490 367 536 083 338 538 265 835 366 166 906 934 815 819 060 945 109 208 926 924 836 363 069 626 266 995 408 868 566 066 059 580 293 460 497 579 651 265 518 334 422 673 386 060 301 057 307 974 327 733 614 959 312 015 010 417 329 780 023 050 671 951 638 528 304 352 064 768 517 992 077 175 038 322 567 416 780 420 508 703 743 872 582 354 503 796 081 964 037 010 131 414 305 107 301 040 332 872 103 329 868 848 824 141 739 214 884 116 626 044 867 149 281 368 753 635 107 852 181 192 657 142 249 063 468 265 923 316 987 559 444 173 186 231 560 390 758 600 397 308 997 059 769 531 152 361 023 648 515 974 884 856 448 239 132 366 566 304 285 177 024 443 318 429 476 685 326 116 627 265 207 873 563 669 208 056 642 855 787 166 120 285 187 229 194 983 612 551 013 484 626 867 083 134 748 064 478 474 983 297 261 889 097 266 850 073 128 674 905 720 464 070 541 203 630 626 952 518 073 979 870 504 407 772 592 045 629 018 601 292 058 132 022 408 053 477 083 312 301 599 700 895 641 480 040 353 643 258 395 483 574 556 724 969 480 914 030 615 520 920 707 457 820 590 041 437 392 715 281 194 129 464 571 758 824 864 023 369 088 202 085 929 568 939 384 167 067 651 184 491 579 842 516 336 980 250 662 008 412 153 043 088 472 218 078 719 777 719 560 568 306 167 062 336 258 104 697 956 345 695 845 676 710 391 912 512 893 943 553 745 057 360 876 028 227 721 935 813 941 015 924 873 230 704 752 650 939 949 365 960 276 577 794 848 234 539 432 520 699 014 316 764 478 252 713 551 478 055 481 637 258 371 646 824 003 210 825 026 923 737 400 377 063 903 644 826 718 346 833 330 001 719 578 143 513 154 111 861 765 607 025 805 245 128 051 333 276 377 952 085 171 046 711 927 488 622 692 022 915 675 041 450 444 914 104 833 069 158 987 748 458 581 350 238 660 151 225 323 042 722 930 039 258 089 259 171 664 724 431 529 381 478 425 055 532 288 855 802 114 057 057 563 750 349 431 947 033 675 642 943 564 656 234 660 334 169 754 655 002 605 938 576 475 875 259 266 420 551 655 501 887 301 055 755 020 717 321 504 021 894 386 648 900 973 040 674 919 614 333 080 921 867 940 265 023 410 685 400 716 093 169 532 545 799 623 230 788 588 307 937 392 469 971 325 008 708 087 138 866 232 132 220 524 483 842 073 217 168 271 149 976 744 161 576 071 470 539 867 225 617 985 217 138 432 536 107 013 397 783 375 659 452 304 860 135 372 048 378 576 508 101 196 676 738 957 156 584 293 673 442 292 335 327 340 476 054 919 805 701 704 018 326 339 666 151 604 508 856 748 032 386 610 651 584 839 824 892 434 254 212 856 576 861 556 881 931 088 796 754 713 394 153 863 702 241 425 128 976 776 291 110 184 401 668 358 138 259 448 429 479 193 209 712 750 333 436 948 992 571 758 504 485 087 361 414 337 215 746 377 755 158 774 639 583 724 519 708 520 370 954 504 073 223 060 073 119 879 112 884 264 792 528 841 732 468 277 315 411 677 047 557 637 836 006 301 229 336 742 465 964 011 266 189 316 573 555 685 084 426 644 716 403 400 430 360 715 855 042 201 190 482 809 396 060 437 247 535 989 862 892 347 515 103 954 131 233 727 675 040 120 416 595 609 007 417 475 943 700 974 666 414 448 477 364 307 963 786 005 081 881 102 464 384 382 957 687 260 707 875 937 051 564 360 600 179 315 895 114 846 521 425 751 663 740 432 434 351 665 177 838 547 724 491 051 747 083 584 225 806 802 436 237 574 035 467 373 217 820 491 363 374 435 047 452 981 713 930 900 653 711 347 306 668 980 160 675 056 225 568 495 047 120 734 590 458 326 143 373 624 093 571 931 246 371 949 812 217 800 726 674 878 098 776 796 037 123 320 235 333 641 324 549 569 419 390 526 036 137 866 952 157 120 494 070 613 722 169 222 420 826 132 368 890 446 091 613 776 912 780 689 725 321 137 814 239 390 630 947 804 168 743 844 437 407 975 088 799 250 242 484 898 401 003 206 327 858 009 550 128 614 859 090 589 682 888 464 515 911 691 830 583 926 445 168 196 063 115 218 776 445 924 798 235 023 480 737 424 962 198 064 606 711 794 365 816 494 908 873 579 323 359 071 987 619 185 521 113 060 329 984 472 250 943 192 721 550 646 504 427 179 731 615 722 115 989 405 111 846 582 063 210 522 776 298 427 269 707 215 560 813 825 787 459 032 348 370 022 629 463 267 490 876 100 430 807 269 254 012 349 184 412 589 077 656 890 954 135 753 725 094 486 596 335 841 368 694 315 732 070 632 081 939 624 663 466 947 683 317 732 771 687 761 842 210 065 829 079 025 511 091 448 481 341 329 391 509 435 149 564 256 184 981 221 618 438 772 564 105 244 636 904 853 251 445 870 150 999 573 640 148 070 655 944 383 137 321 979 875 186 576 657 051 932 292 339 133 438 060 006 850 844 216 767 280 028 062 065 805 104 990 057 182 618 634 425 816 971 719 469 197 925 161 749 962 532 238 674 403 181 319 727 309 653 588 996 955 514 326 555 264 694 709 390 473 400 400 422 291 937 758 383 093 486 038 542 921 093 352 733 400 596 895 562 153 733 699 170 660 873 089 607 672 552 296 582 198 734 125 097 667 814 217 354 530 208 196 401 137 822 276 105 561 875 946 547 525 751 727 838 375 001 196 027 748 384 397 303 652 403 836 926 296 155 736 812 761 349 931 160 828 411 229 291 418 968 506 247 711 442 918 449 538 374 671 887 160 853 561 592 433 644 519 332 834 720 809 906 855 252 160 003 387 768 023 088 740 213 450 032 605 760 486 741 117 660 911 280 197 697 648 181 223 492 455 578 153 005 666 128 084 650 908 786 610 833 057 595 592 972 966 680 542 620 887 295 845 054 134 106 372 875 247 026 009 789 159 215 516 339 821 771 400 410 206 459 622 900 691 066 412 379 910 261 127 190 552 402 467 649 860 228 179 319 300 902 198 816 157 207 547 900 266 770 439 752 647 343 980 041 705 835 814 600 911 623 759 518 573 871 007 189 193 363 098 203 142 816 326 736 130 674 236 562 458 314 578 179 965 184 995 712 914 797 683 848 441 477 817 348 021 275 692 911 347 027 481 970 191 072 194 340 830 424 872 429 807 460 087 575 431 697 311 856 418 682 954 170 738 114 065 780 415 081 553 215 666 945 971 039 830 938 301 074 366 495 812 158 344 858 563 172 442 056 858 480 987 612 857 295 098 584 400 219 654 487 963 405 309 787 907 890 458 275 205 724 603 387 858 451 912 112 945 729 810 135 342 858 578 076 593 172 523 125 236 461 401 169 875 273 404 320 182 414 477 335 479 734 594 839 708 567 934 752 056 273 372 424 227 153 581 632 089 850 148 752 952 849 430 688 297 829 588 825 453 261 614 129 312 595 901 001 790 745 912 640 287 514 581 482 411 960 550 926 230 488 340 255 249 842 937 745 371 287 157 965 604 927 429 932 950 351 882 989 981 946 531 558 315 150 703 809 825 532 007 486 170 418 351 201 988 329 753 207 313 520 745 201 833 928 367 107 359 558 133 266 907 416 025 342 257 244 946 286 235 120 862 508 699 201 550 187 704 357 516 899 368 329 235 067 793 822 957 451 621 743 615 979 296 743 913 808 126 632 224 356 892 019 055 242 042 562 888 594 205 643 223 800 353 435 922 709 732 292 662 931 203 080 324 714 774 472 537 623 467 081 686 240 579 667 247 529 987 984 088 599 527 327 121 408 316 857 988 813 233 692 855 171 209 002 223 614 649 105 028 868 657 438 188 508 970 530 547 207 074 519 995 481 271 831 133 139 039 281 723 620 120 126 102 512 215 430 079 316 964 469 184 372 467 086 234 362 704 378 065 705 238 765 534 285 584 935 610 453 516 209 956 022 201 915 240 048 615 769 391 855 769 440 182 768 385 325 310 708 650 902 257 251 228 976 780 022 382 342 218 202 311 464 174 270 362 011 012 580 137 646 679 472 798 424 105 110 678 787 989 492 268 697 458 458 981 563 762 495 604 329 006 777 374 472 386 014 469 638 026 815 473 742 154 380 831 061 215 218 981 056 668 542 535 866 900 912 810 360 647 962 462 883 007 848 261 747 702 626 697 604 575 009 214 562 401 495 459 598 874 914 545 274 488 736 287 357 853 033 166 004 618 215 784 875 381 016 689 767 532 650 333 669 403 697 338 331 378 818 491 906 220 710 748 119 085 526 223 944 116 679 833 112 353 505 006 558 346 599 827 977 115 474 594 817 237 018 198 974 463 742 237 578 642 633 964 520 514 497 907 880 577 074 759 923 795 066 876 472 798 358 207 875 592 836 601 428 775 252 688 943 134 190 487 657 789 692 761 754 696 592 419 427 020 903 632 176 772 936 935 719 659 424 816 122 936 900 589 779 103 502 024 515 316 178 583 459 407 267 131 929 306 751 879 802 910 863 097 992 883 696 997 279 586 937 100 239 865 317 388 135 365 459 292 436 597 375 941 655 781 228 301 215 869 227 646 279 070 297 337 686 798 946 151 475 424 431 536 434 284 211 999 332 925 314 428 045 876 432 041 214 222 285 095 878 797 904 204 972 892 627 271 391 457 633 104 005 108 579 563 178 747 011 713 059 555 036 861 514 237 715 991 370 006 200 445 468 281 930 762 265 926 915 050 236 636 941 071 109 633 205 639 052 656 059 330 302 085 650 305 989 195 584 648 043 494 540 243 085 794 018 407 020 457 350 731 159 749 062 992 299 705 086 178 184 698 681 877 974 366 472 838 933 108 074 592 252 677 508 734 507 989 800 069 696 314 047 613 840 790 550 454 641 530 001 730 623 007 839 609 347 956 904 468 466 581 895 763 259 968 744 045 417 594 197 653 931 213 080 385 566 879 760 146 658 149 876 608 744 310 872 149 962 955 597 446 382 785 436 094 558 826 913 954 469 658 856 269 462 751 211 624 518 804 765 122 129 447 328 304 089 798 470 501 148 310 818 558 894 097 381 761 384 689 398 245 930 581 211 781 615 315 193 639 556 892 313 299 990 224 744 510 370 174 327 927 178 553 599 779 975 601 984 022 819 007 953 210 459 189 828 989 964 365 788 723 990 749 473 000 354 743 116 968 415 219 849 178 360 606 981 061 729 148 530 066 217 062 036 326 678 297 786 341 252 221 354 033 631 293 581 789 692 706 567 407 760 974 090 586 790 333 582 212 860 217 252 793 167 696 506 151 990 615 472 101 590 219 973 215 456 112 404 465 080 401 632 724 506 213 964 943 464 906 171 013 741 873 452 862 519 790 265 949 443 946 794 815 894 506 633 317 962 094 732 856 402 840 633 111 015 049 741 162 343 272 039 925 633 664 110 150 364 591 009 959 148 889 039 477 618 663 796 171 701 971 814 289 124 734 549 062 621 674 221 544 469 314 927 599 779 760 375 044 845 225 062 230 844 023 383 987 133 709 812 628 825 218 385 392 674 227 599 255 455 674 790 592 291 244 344 457 678 264 829 733 593 409 069 075 413 353 978 360 364 188 208 425 823 213 521 145 178 186 966 319 083 437 336 405 995 395 415 330 484 516 686 152 830 569 518 212 495 579 971 790 825 805 519 692 625 403 792 283 855 934 405 372 224 210 064 142 531 971 790 674 242 124 257 943 190 425 339 814 566 551 131 723 380 498 957 723 624 113 071 520 507 792 470 349 345 728 830 926 403 699 759 956 110 470 945 804 214 363 772 012 952 816 802 132 157 510 118 470 830 032 814 598 344 336 346 590 034 428 009 427 865 896 601 649 269 092 069 099 232 215 440 440 688 561 540 784 971 425 985 002 410 427 254 531 476 272 299 913 369 538 732 356 140 618 345 913 222 864 296 426 285 629 413 984 128 051 966 328 866 829 899 836 969 093 317 886 234 716 774 609 361 096 809 041 198 935 574 499 537 626 653 314 682 895 570 755 180 959 644 075 400 636 448 827 399 290 281 375 860 915 546 535 752 754 828 832 720 086 332 352 327 729 901 566 363 136 170 046 600 584 837 106 674 936 095 684 058 766 719 083 015 966 414 682 304 221 254 402 088 141 222 018 550 824 799 948 396 155 828 181 616 141 236 116 285 746 719 858 704 680 378 823 063 423 635 671 198 600 108 910 130 393 938 708 391 885 626 710 521 341 879 546 395 520 248 401 510 599 712 175 780 699 762 815 487 534 179 593 273 918 100 095 994 642 224 815 348 311 762 499 079 973 551 982 233 549 546 070 897 105 402 696 942 012 160 211 881 540 428 364 303 966 662 965 594 063 945 330 682 915 654 341 092 593 152 938 610 725 181 380 027 376 226 521 988 915 221 738 725 790 805 460 635 474 659 721 011 664 676 277 905 702 214 378 782 473 710 810 122 914 839 020 302 756 020 389 628 243 749 230 138 253 588 998 673 153 561 824 985 705 497 977 430 077 820 207 778 812 864 224 871 083 557 907 503 966 175 381 282 354 912 697 368 199 809 626 030 132 822 856 357 192 917 243 418 970 733 224 214 880 465 668 139 938 493 866 060 335 548 001 295 299 651 591 185 449 163 020 152 284 520 227 864 119 642 304 832 125 266 305 238 484 284 943 860 282 326 513 542 784 596 604 988 370 886 234 033 738 552 641 000 967 826 121 826 524 254 614 931 945 772 114 512 802 993 097 573 809 527 283 664 161 880 502 440 726 550 120 223 209 207 216 585 447 397 066 616 000 644 243 956 429 027 076 868 693 250 222 076 298 308 887 874 433 033 620 028 358 119 139 840 655 356 777 133 040 932 226 132 344 914 623 914 694 041 669 284 111 537 871 121 221 717 688 865 451 397 181 755 262 137 385 865 589 437 903 546 573 303 410 021 492 875 893 192 371 818 669 231 209 268 610 590 804 931 472 894 535 652 600 664 425 174 487 901 952 914 853 793 978 659 954 822 811 649 846 414 613 991 933 212 841 945 087 235 776 652 511 481 556 454 347 922 696 753 903 004 957 025 401 516 631 472 344 556 415 903 119 347 254 760 124 248 958 570 833 590 561 010 230 141 777 869 750 670 471 420 551 893 394 363 944 378 664 894 026 849 030 701 005 739 836 976 506 787 481 784 302 930 916 748 010 385 281 809 388 688 358 482 333 178 847 340 274 346 429 219 621 755 830 516 323 373 013 514 736 986 149 763 817 795 978 650 833 572 255 774 473 761 951 961 527 063 754 291 090 572 258 990 493 897 195 165 720 463 042 398 342 784 809 047 705 933 770 540 861 776 687 007 189 899 420 874 197 334 423 146 973 599 050 234 789 180 863 394 087 599 752 522 178 911 191 050 280 678 249 719 839 006 466 591 633 367 589 456 174 939 763 502 585 924 003 698 775 504 792 940 777 856 271 108 620 693 184 242 318 623 331 163 746 446 034 943 044 181 179 866 071 098 424 771 558 276 352 839 760 767 592 679 630 067 726 412 365 136 240 026 843 829 861 814 719 959 375 376 439 155 819 620 516 907 615 454 193 028 853 086 162 994 555 502 584 624 865 729 319 401 167 015 031 312 041 556 060 235 272 823 448 363 749 700 756 910 310 620 872 685 758 120 382 522 609 374 316 552 879 608 155 412 039 918 843 438 618 960 515 121 013 202 250 229 968 886 192 950 380 352 588 540 199 227 204 876 496 490 515 969 885 698 600 859 707 593 454 367 344 551 494 157 304 396 488 855 210 178 910 172 140 988 488 005 891 397 347 261 092 694 635 809 380 521 159 804 680 156 675 620 752 090 560 569 408 375 606 823 266 920 150 303 396 749 960 936 784 371 725 272 787 146 961 324 989 355 451 655 630 723 279 945 182 789 530 294 091 466 045 888 509 264 223 876 707 185 216 784 521 201 142 483 979 339 147 010 285 712 089 823 168 061 415 601 996 137 964 037 626 956 223 832 482 624 369 340 201 477 033 614 246 192 647 351 546 237 115 541 730 084 964 801 196 166 310 668 815 469 627 501 527 313 448 756 923 626 509 695 645 689 586 796 716 862 038 688 801 996 411 724 804 724 995 999 277 721 848 096 259 832 893 908 216 628 325 721 493 140 367 019 618 022 875 063 671 611 754 719 447 638 049 059 344 886 438 881 160 121 859 252 793 671 288 649 782 849 250 518 909 290 897 714 092 043 309 334 230 649 080 633 878 824 635 434 241 313 902 754 238 204 986 707 045 966 468 773 129 351 701 420 011 358 202 352 540 924 603 846 711 138 134 312 542 549 949 957 241 779 406 631 476 042 255 785 983 972 908 702 763 882 450 734 965 381 620 121 560 275 664 273 054 923 363 995 505 432 800 514 883 728 168 153 567 790 327 038 478 334 518 673 224 109 198 103 678 426 474 844 978 539 472 450 498 114 459 358 960 442 458 190 846 722 222 603 499 265 961 507 112 124 876 534 524 809 496 028 109 698 745 313 995 169 775 250 375 948 787 773 991 757 276 853 452 302 919 228 287 160 642 583 208 308 343 032 572 548 432 892 610 200 772 187 736 829 609 028 494 846 511 836 324 010 471 510 934 864 398 004 365 370 780 939 728 112 680 709 616 474 192 110 245 064 378 270 858 472 186 699 274 136 644 366 711 363 278 010 156 963 325 666 721 105 266 919 014 599 385 339 857 258 339 182 744 007 680 959 130 579 207 153 143 695 162 321 165 863 738 108 848 706 176 201 805 655 571 117 092 249 612 592 527 817 286 718 044 440 038 160 659 257 180 041 274 348 433 937 765 741 418 974 007 920 685 510 638 591 723 615 363 841 650 667 401 117 533 347 895 393 361 628 509 398 954 500 948 323 471 690 013 909 566 542 083 463 925 865 222 205 681 214 254 262 006 557 634 905 833 018 536 798 047 901 761 734 073 814 021 754 901 900 169 652 173 911 211 537 198 514 848 513 638 077 100 884 221 467 801 221 529 441 538 452 187 541 484 989 524 450 613 855 422 726 024 011 349 024 417 149 699 816 320 870 304 045 690 332 862 316 312 799 904 829 108 320 923 134 467 202 693 968 120 934 561 184 617 381 498 326 732 836 993 606 357 193 699 974 443 013 832 984 012 235 644 038 724 835 119 739 343 179 297 189 062 762 369 514 136 036 897 069 799 090 831 682 253 982 543 565 611 206 518 989 780 458 970 711 505 221 221 351 999 200 601 005 796 226 799 545 620 496 171 319 822 629 159 912 396 353 147 459 615 113 425 359 951 469 125 952 596 447 644 093 783 275 339 183 068 841 171 221 474 614 002 043 602 426 070 206 595 374 297 944 496 626 385 392 691 179 763 316 012 338 985 504 807 355 002 946 229 703 398 158 645 789 108 811 885 152 206 255 551 629 324 341 638 591 535 556 260 818 147 282 220 802 349 122 839 873 648 634 590 031 600 648 062 487 488 580 961 171 464 753 099 843 292 844 058 788 650 309 997 957 262 168 908 408 453 902 883 949 154 316 550 187 298 777 335 607 709 524 661 330 441 149 327 175 262 884 652 810 154 805 214 687 780 043 718 641 373 168 294 901 468 293 006 983 582 802 868 668 833 125 241 189 835 851 343 469 317 420 416 345 062 979 537 798 151 580 499 971 004 070 548 418 173 156 356 117 358 591 907 568 897 552 124 298 463 123 564 762 540 303 930 834 663 162 354 773 589 674 370 689 605 264 532 528 187 320 197 098 283 023 977 222 587 430 043 470 111 703 186 474 545 907 361 751 875 745 876 212 723 084 655 863 658 556 997 794 131 820 151 525 783 622 259 853 011 420 534 362 458 209 051 412 277 291 536 839 008 963 408 385 109 719 392 969 667 997 698 743 539 990 611 402 527 747 934 342 844 232 129 797 376 890 119 789 439 185 367 597 285 240 306 249 605 284 596 439 241 142 246 777 506 247 808 556 776 007 740 053 559 189 372 377 513 848 722 150 400 947 414 664 447 383 337 672 908 067 634 232 276 495 493 336 398 128 120 619 230 209 288 747 355 064 882 518 536 226 022 319 497 763 402 952 114 017 132 461 709 555 491 590 965 412 821 600 012 342 294 765 707 019 002 040 199 324 356 859 576 174 908 356 563 592 210 010 784 064 140 302 966 787 534 515 950 251 854 359 615 758 440 136 266 478 553 264 962 429 328 288 562 120 543 186 859 604 324 207 302 599 955 327 970 246 405 589 334 252 361 617 071 403 136 907 504 105 856 654 545 874 425 443 153 641 675 312 812 510 784 841 348 892 474 945 325 595 335 572 508 412 556 222 290 753 788 242 239 550 955 562 617 538 688 749 517 161 154 137 422 093 056 626 764 293 721 349 607 275 277 909 542 275 199 785 148 590 862 583 986 030 372 493 531 208 941 835 563 396 193 498 824 590 761 711 572 261 284 344 713 025 808 173 743 319 490 693 352 385 729 504 407 553 822 412 432 425 502 183 301 888 057 984 068 055 704 945 502 617 409 352 553 161 298 852 213 691 341 665 390 331 955 666 558 654 870 071 148 881 461 260 265 043 563 419 266 349 519 006 943 301 495 387 088 200 146 765 471 762 836 394 928 921 252 150 393 906 370 757 410 790 598 587 114 504 641 159 974 236 505 086 993 551 920 919 625 091 532 842 356 672 512 416 649 067 652 862 937 937 359 841 897 945 308 013 348 638 547 089 123 569 698 412 830 037 465 242 728 280 314 193 573 747 707 731 740 043 513 153 002 838 105 493 192 800 881 843 139 765 686 583 895 244 504 739 720 716 452 392 699 868 544 059 613 833 762 480 085 431 247 446 901 632 627 157 153 340 733 691 052 205 543 588 192 992 783 169 050 393 650 301 774 677 809 271 338 815 939 088 509 460 048 931 389 362 204 492 081 278 733 899 210 792 100 835 232 352 322 146 384 761 168 094 971 638 599 594 557 059 536 280 206 993 959 530 235 774 537 566 111 179 993 348 569 932 155 425 313 337 274 234 416 805 199 385 893 912 625 480 867 694 493 108 561 736 155 007 680 639 102 975 523 910 052 856 942 631 389 228 671 277 224 265 169 656 312 927 289 395 535 100 468 348 708 222 967 231 726 886 619 501 107 260 462 456 148 486 740 241 443 636 116 069 924 878 325 664 065 324 798 599 647 279 751 814 547 684 536 808 076 335 920 629 734 636 543 927 780 883 378 951 012 627 286 392 815 063 668 038 292 614 573 470 289 657 758 865 878 825 628 675 218 612 388 211 489 934 911 451 813 291 621 238 144 091 200 292 794 187 756 911 011 198 590 884 744 716 434 658 340 745 858 635 400 265 645 273 418 040 902 010 282 535 855 455 113 422 340 604 865 437 526 327 065 053 007 129 969 240 575 937 522 207 646 746 326 177 492 997 031 381 193 303 057 925 371 941 525 018 368 409 951 489 988 659 533 033 904 031 587 289 674 582 366 844 878 870 208 727 543 217 022 808 018 728 910 489 655 334 660 641 385 979 059 501 044 527 101 181 589 562 480 342 370 071 519 835 443 369 598 890 444 167 790 611 528 757 692 924 132 784 707 151 487 315 538 901 394 135 442 315 478 305 971 750 956 591 031 081 825 777 319 673 273 547 670 576 486 750 228 943 446 363 776 909 649 173 700 056 100 537 666 036 715 221 899 201 642 509 673 893 490 779 508 479 112 876 073 504 973 362 967 326 459 612 599 081 150 041 984 153 623 099 061 136 032 388 014 473 032 682 220 441 267 124 971 651 001 267 498 539 713 243 395 153 343 055 685 903 313 095 893 960 743 040 463 429 920 389 579 620 385 692 512 859 252 845 891 708 708 588 010 511 230 430 454 398 028 730 950 981 045 367 911 704 384 862 373 051 114 270 761 553 844 723 814 654 846 200 529 979 101 404 775 329 492 070 261 158 289 177 219 113 004 342 360 135 387 956 416 502 245 641 785 699 053 329 005 002 200 653 299 369 479 299 780 564 811 726 546 462 992 867 293 061 921 960 886 982 994 686 125 788 698 565 896 571 654 188 480 677 614 637 990 948 834 530 480 158 681 274 837 452 596 492 473 080 724 113 723 165 783 567 549 893 427 870 066 689 640 533 036 580 013 703 392 638 586 305 483 992 407 955 991 161 943 758 859 072 156 050 502 997 676 446 446 391 006 754 841 743 226 318 034 375 915 902 466 408 793 654 302 553 285 617 661 505 784 255 991 247 229 111 292 855 656 581 466 096 068 710 742 515 418 613 675 732 497 840 937 890 513 904 567 827 425 131 685 220 769 441 194 938 197 507 142 040 673 783 144 848 727 246 523 672 152 637 563 715 949 683 507 195 892 515 022 103 983 639 373 052 750 871 410 866 112 237 222 397 897 360 527 072 209 103 865 767 552 262 745 273 854 951 482 858 920 117 816 224 496 945 691 115 988 593 318 213 448 060 706 188 849 398 368 238 642 322 627 139 355 467 813 867 934 702 066 793 681 323 599 294 744 107 838 091 972 246 403 983 561 137 929 623 242 697 704 657 860 016 613 225 605 549 361 837 500 097 791 969 049 411 390 782 618 806 903 537 935 024 070 451 717 775 603 620 407 527 668 360 187 807 802 453 348 402 407 540 906 052 748 256 279 885 184 380 769 436 951 420 413 629 257 641 741 347 707 974 815 462 720 219 895 855 784 539 681 899 425 173 420 826 914 808 946 131 221 818 518 507 549 676 135 876 763 367 127 805 983 282 820 815 774 322 241 127 671 866 942 455 975 649 924 560 632 295 442 184 990 835 483 644 374 863 629 158 045 683 196 903 482 421 881 402 762 548 107 187 855 879 219 929 953 689 622 709 501 435 330 260 227 799 099 008 725 958 967 632 175 441 714 749 479 832 742 411 243 449 018 643 207 471 827 837 768 773 289 507 942 852 246 199 888 720 788 713 910 084 038 011 897 270 217 791 506 804 679 310 836 942 402 427 320 117 280 116 344 895 012 879 299 869 990 701 458 306 701 564 162 824 310 323 751 640 785 965 976 324 158 891 505 345 018 986 772 765 150 011 340 352 854 048 721 870 197 618 027 275 584 106 182 039 105 201 458 482 568 855 786 394 357 833 166 666 069 010 796 800 964 764 067 684 167 906 877 025 433 406 625 197 804 343 960 262 834 291 361 805 887 287 957 230 459 138 983 108 168 128 754 680 834 895 410 284 940 989 417 364 448 432 799 049 785 653 557 329 967 893 647 480 108 428 825 725 368 155 079 014 769 470 526 362 639 852 508 534 595 706 490 282 831 463 979 281 080 853 720 928 041 235 438 237 420 812 733 129 512 679 440 234 309 031 325 388 689 842 269 540 496 590 112 942 314 336 099 552 466 069 301 002 937 910 426 133 205 621 509 825 451 516 866 505 805 063 094 640 720 394 373 101 338 550 331 085 460 594 768 537 787 619 748 259 680 665 014 046 304 481 622 462 997 783 876 818 141 590 039 413 302 585 167 204 345 852 366 434 700 021 419 538 300 326 979 541 064 642 707 329 617 167 847 980 950 290 202 695 220 838 502 452 515 551 764 489 266 379 373 033 862 769 492 293 496 927 388 519 690 605 966 674 299 145 024 977 449 029 574 330 443 516 681 688 502 104 687 549 976 016 251 290 712 245 695 052 661 780 303 712 529 954 623 563 776 626 159 593 988 139 274 797 947 852 868 425 559 084 266 581 208 631 118 714 181 116 187 263 052 650 979 474 112 007 889 759 745 840 557 148 611 991 872 023 806 339 921 542 882 083 906 547 332 933 704 698 033 165 843 496 192 697 714 525 067 008 817 174 801 406 562 801 242 909 109 400 408 001 828 358 704 811 392 262 583 631 569 734 698 020 684 081 262 986 532 416 430 907 569 520 917 430 786 467 513 690 019 834 183 833 182 270 673 142 186 844 120 544 196 871 063 464 293 866 512 578 322 381 138 136 959 567 160 349 647 440 093 290 634 168 213 350 328 950 257 328 661 586 031 286 572 547 520 362 550 925 350 220 668 614 406 829 297 956 264 393 209 096 946 516 594 931 598 676 609 276 796 380 036 503 552 508 517 314 524 486 042 776 890 769 204 353 513 051 159 157 237 538 273 735 568 460 681 779 880 804 138 344 715 924 094 747 573 110 460 845 392 375 687 403 474 867 890 980 740 239 273 236 186 081 705 509 614 474 171 225 729 749 301 146 512 677 514 614 735 432 475 169 355 726 383 527 168 457 493 036 257 313 195 772 076 216 642 339 728 098 810 234 847 352 212 783 148 427 524 785 612 512 731 059 258 630 705 428 854 639 563 286 511 137 501 271 843 230 970 190 528 731 155 871 644 936 553 738 693 222 240 204 186 974 423 734 112 413 354 005 174 532 866 164 990 992 802 203 218 178 338 976 880 491 954 809 724 733 356 167 616 437 452 230 380 566 434 477 426 228 774 028 630 293 552 436 635 252 779 861 301 040 923 830 333 448 487 188 869 639 255 003 221 443 875 876 974 779 956 609 791 705 072 896 426 024 569 248 704 414 795 954 545 942 429 918 462 521 829 388 331 182 195 118 133 536 990 834 680 042 678 046 144 633 081 895 204 579 727 204 752 183 193 583 551 698 159 078 186 369 384 673 420 618 026 794 107 110 737 649 049 552 668 983 695 276 440 993 798 794 915 776 269 781 829 372 450 172 548 406 662 436 909 940 387 914 431 076 638 132 136 671 131 574 859 458 203 875 612 887 433 742 786 208 650 742 907 119 853 054 222 633 252 653 059 157 259 532 738 520 955 638 734 371 057 674 754 800 403 300 476 066 481 763 127 728 597 873 439 768 019 138 006 398 750 378 463 422 681 913 129 900 462 500 933 696 520 562 173 289 286 253 645 726 444 174 619 343 902 117 495 699 270 875 735 407 914 397 422 361 339 846 510 388 692 147 304 247 595 436 019 167 600 942 061 326 572 628 423 972 725 649 610 626 321 753 189 107 300 905 847 410 123 451 614 671 833 469 793 877 677 470 033 162 716 372 706 638 047 679 160 222 857 555 947 428 395 805 927 310 512 959 337 957 131 197 418 318 075 437 893 946 237 942 988 699 295 462 041 431 453 931 701 160 886 071 735 006 551 711 931 188 062 478 742 590 676 349 931 415 484 373 763 308 704 949 146 811 423 362 824 403 492 812 883 858 870 351 148 177 931 677 558 633 245 015 646 407 680 697 557 731 384 650 181 052 879 609 799 184 503 341 391 185 109 161 811 603 726 417 547 934 758 045 891 123 525 617 952 210 558 909 174 661 470 633 794 261 248 316 521 064 584 554 492 877 415 470 708 069 722 061 428 088 685 528 057 667 143 189 539 581 713 586 547 060 030 087 364 080 015 307 702 007 288 987 958 229 954 375 855 320 467 056 612 459 751 214 468 212 230 297 635 675 423 968 701 251 336 116 780 417 279 761 048 680 477 471 070 693 926 168 264 587 805 048 917 810 539 103 286 556 261 309 720 687 722 157 802 808 762 792 477 393 186 618 386 740 457 800 435 304 425 251 747 165 726 624 120 166 755 496 012 862 335 227 054 699 878 057 856 839 300 189 294 639 924 088 297 754 486 918 387 564 247 602 044 374 971 082 341 080 580 844 527 505 820 454 421 707 900 468 066 821 387 767 825 654 220 392 557 563 035 032 598 679 185 491 345 059 452 637 689 713 431 395 642 533 775 571 836 911 969 768 948 842 542 608 470 346 821 431 736 733 511 361 905 742 610 350 227 141 109 657 987 641 986 337 455 356 965 652 555 996 978 377 827 081 202 776 154 182 086 492 791 224 402 186 257 465 355 027 074 514 053 724 347 759 132 807 540 634 342 476 872 563 467 396 357 214 210 243 394 100 268 430 926 345 071 366 726 045 298 780 468 659 889 145 111 773 289 402 667 663 321 324 500 187 903 296 283 662 834 999 319 321 920 464 722 260 074 361 790 098 560 937 984 995 637 881 019 241 254 842 835 958 401 202 516 070 330 731 502 645 007 014 935 001 494 123 218 122 574 133 949 169 191 337 792 869 390 499 456 967 085 662 830 425 413 683 093 328 299 001 016 315 195 370 364 690 528 659 334 004 297 447 751 853 921 057 936 319 598 062 677 837 338 576 493 571 306 560 249 406 824 822 188 649 446 820 830 213 344 772 777 401 700 451 221 579 424 908 742 072 939 468 397 103 094 033 040 766 169 374 636 698 041 609 712 939 526 287 914 128 335 861 395 696 117 829 656 958 712 721 322 669 888 821 977 128 603 258 851 974 409 918 700 210 554 537 369 351 308 740 738 092 237 533 003 663 423 521 744 553 208 544 537 283 235 831 419 354 750 490 647 997 080 480 420 037 310 296 760 259 995 539 771 669 744 263 403 566 370 709 542 436 582 801 427 012 775 748 217 090 573 622 651 043 255 309 266 115 359 156 568 492 990 795 811 606 630 132 464 518 686 897 632 021 768 879 554 540 895 394 574 668 468 840 100 983 849 063 875 619 360 774 464 850 471 684 747 300 349 772 117 172 423 408 476 241 340 703 875 616 375 885 789 238 104 106 378 050 832 401 960 526 823 020 779 732 212 797 943 699 628 850 715 520 672 646 566 312 043 799 472 447 112 678 265 887 433 691 402 920 260 901 278 983 023 943 510 710 303 732 570 006 832 032 906 849 438 208 026 176 091 174 216 113 986 783 469 204 796 908 809 749 020 039 457 177 151 068 559 497 350 345 639 145 282 001 585 046 344 311 852 969 470 572 433 530 466 720 385 959 177 264 932 134 283 931 290 831 011 806 217 427 309 787 471 087 152 935 124 874 021 477 089 902 516 674 766 577 248 204 847 966 982 324 762 228 086 406 494 019 418 329 020 880 966 808 779 563 996 503 263 579 888 061 146 892 698 164 993 431 572 028 495 909 961 524 736 165 349 917 340 482 734 549 794 510 685 211 357 527 118 039 311 363 661 297 853 051 189 255 298 505 284 526 512 640 900 090 113 812 904 763 315 168 787 445 580 983 924 974 952 372 490 277 418 076 915 292 718 784 360 212 603 785 312 022 177 461 457 358 721 977 197 040 098 464 747 782 069 306 876 839 052 104 877 399 135 024 976 427 952 642 354 310 879 170 146 113 084 965 194 243 043 666 345 221 164 849 189 134 742 361 933 043 244 324 693 083 115 460 914 520 274 354 832 204 154 432 623 444 050 889 318 890 289 028 296 801 060 506 859 054 845 894 500 545 579 302 437 384 734 562 154 611 437 840 805 405 511 082 570 467 531 454 368 591 543 004 973 552 554 455 202 596 935 433 046 619 875 266 655 826 691 250 863 349 455 251 639 783 379 525 841 793 883 558 873 483 563 979 867 738 024 997 998 481 330 052 505 066 243 410 034 852 430 057 194 137 573 080 553 934 792 166 063 438 338 409 204 063 980 884 678 848 327 356 508 458 640 433 808 521 538 032 306 431 283 824 195 219 123 334 607 486 490 619 727 199 720 019 793 154 458 801 685 908 151 146 736 849 370 687 214 894 713 367 676 398 626 350 671 099 376 694 136 433 955 341 687 654 801 918 541 594 347 588 314 973 287 654 131 180 886 173 858 467 507 561 560 531 063 739 078 575 244 765 954 446 454 617 565 548 945 582 908 460 816 597 107 051 867 836 305 780 829 534 953 719 115 562 319 151 616 502 551 996 517 794 160 680 975 017 374 985 411 972 199 912 627 253 294 872 836 491 721 191 098 870 998 561 587 336 822 270 837 756 557 326 330 182 032 296 035 962 486 073 149 721 510 296 922 379 879 220 231 405 319 142 687 276 205 195 426 695 562 670 309 828 168 443 413 989 671 168 060 756 118 595 444 807 960 182 933 773 659 038 373 252 320 521 490 569 463 578 492 040 577 424 433 833 501 350 791 484 095 772 244 072 851 055 330 013 164 471 981 707 974 805 281 663 546 782 125 527 795 500 036 987 177 027 636 298 975 757 462 009 015 118 469 460 833 093 980 515 644 542 073 380 283 794 971 007 136 535 712 089 628 025 248 197 109 302 390 380 127 654 701 085 143 880 814 768 661 069 347 371 980 439 678 008 051 207 299 748 349 907 684 294 596 046 297 381 597 129 729 930 550 102 541 883 138 422 758 532 142 206 876 694 996 485 149 121 177 968 648 139 391 793 716 767 421 015 059 758 302 098 812 462 505 390 827 412 946 612 650 739 072 422 371 745 549 867 743 014 077 418 884 207 657 344 163 158 096 458 773 363 783 057 016 535 056 124 770 479 586 556 871 415 953 142 961 564 184 682 218 793 069 619 908 665 081 084 951 499 459 760 242 859 994 586 804 645 793 129 227 157 321 887 175 395 844 496 896 317 837 341 109 172 997 433 263 402 737 821 807 204 369 045 548 653 353 253 647 147 083 245 628 466 781 025 623 787 222 820 198 651 006 764 425 020 735 282 198 551 301 747 662 180 978 897 450 081 068 647 882 285 023 403 107 779 134 491 570 206 217 655 069 091 640 118 217 964 271 893 698 460 512 480 254 375 315 939 212 245 127 461 602 714 286 521 066 739 120 354 341 510 879 098 364 779 989 855 750 911 142 653 176 794 849 158 964 702 768 019 321 072 632 014 367 969 771 862 147 334 354 221 378 484 128 638 194 335 875 663 964 561 314 555 097 295 501 913 118 128 570 212 641 422 099 778 086 457 463 806 497 434 917 809 369 591 023 202 575 241 955 313 820 875 315 662 097 866 195 555 566 668 796 147 700 641 005 814 334 505 608 465 013 637 491 451 716 356 752 706 045 474 513 901 632 004 550 836 413 050 436 344 440 363 782 081 552 932 998 745 611 243 354 316 838 029 417 601 820 332 564 983 050 159 776 187 604 226 133 448 571 417 803 187 366 241 008 133 010 523 592 326 117 777 835 879 318 587 413 849 740 087 214 232 042 783 198 203 267 518 068 174 121 223 601 080 216 683 058 209 804 588 175 231 888 827 006 097 167 157 791 399 674 572 812 613 159 490 179 326 244 160 530 698 191 326 221 500 296 955 537 716 714 277 805 787 227 808 543 013 739 438 149 470 641 807 418 496 050 001 610 764 726 026 869 749 933 058 269 236 110 190 633 615 219 249 733 814 116 891 162 454 538 321 624 422 422 757 685 198 414 107 219 454 391 526 644 365 660 253 838 558 055 245 761 886 809 648 469 757 622 493 413 721 430 575 243 977 477 227 384 200 833 442 060 041 024 484 236 690 331 971 513 693 415 336 326 948 081 720 883 280 199 015 430 381 043 418 872 951 003 438 766 596 485 336 632 288 195 718 847 668 109 359 195 096 068 886 218 740 044 609 986 061 976 201 321 725 966 873 287 250 905 107 933 530 646 579 313 066 661 401 116 060 302 103 528 706 922 068 795 668 504 954 190 018 040 912 490 780 906 545 913 796 899 196 059 106 388 832 085 383 797 299 420 841 093 414 337 906 640 012 330 606 003 831 466 308 739 335 634 152 135 504 028 920 201 124 679 063 048 308 787 976 013 888 883 151 004 325 100 675 474 341 773 727 310 760 635 184 698 299 684 002 108 725 910 451 085 281 268 277 860 545 866 877 271 052 793 038 822 962 106 456 640 694 017 866 580 114 009 652 937 457 942 127 091 424 533 933 892 320 762 776 546 146 082 083 004 828 893 434 760 702 304 061 411 642 325 114 391 167 225 024 855 229 601 120 233 773 277 877 627 801 112 187 012 137 192 547 937 416 700 598 309 649 899 329 561 136 980 479 767 396 617 071 501 372 947 388 260 160 146 854 389 124 607 168 835 379 309 712 286 811 365 332 867 404 333 436 346 179 651 377 239 856 367 504 309 795 280 463 283 936 300 853 154 520 592 154 250 896 555 710 635 529 036 985 381 369 363 354 839 866 219 106 511 645 190 293 783 245 331 009 479 905 584 860 452 633 989 720 463 447 088 602 003 353 124 734 853 024 073 394 010 296 476 649 030 956 762 322 501 161 514 597 018 048 643 995 103 955 374 482 050 307 212 532 592 068 084 857 075 086 292 844 448 226 848 291 989 017 853 687 641 789 476 503 303 463 438 568 719 231 354 409 473 988 952 648 463 485 781 274 203 386 836 727 854 172 910 609 829 650 060 998 095 994 103 665 796 699 866 503 523 548 788 154 639 418 265 056 736 547 090 379 159 288 269 682 037 569 078 135 693 882 995 259 528 601 606 738 207 403 659 003 687 163 392 283 946 988 745 381 442 294 924 557 282 214 609 831 290 690 665 326 387 282 616 446 902 874 528 212 813 026 705 624 770 528 728 654 022 298 844 105 679 334 589 115 824 205 185 453 635 746 672 530 159 324 710 162 586 947 462 958 601 264 892 528 317 778 181 564 551 484 754 488 671 826 153 086 703 077 865 667 048 933 899 241 486 149 517 629 989 695 228 913 525 371 076 015 924 362 427 492 213 053 526 015 353 460 870 914 583 597 255 755 809 237 888 581 508 029 288 294 366 096 300 934 193 372 473 355 337 676 444 909 054 108 050 888 097 615 309 757 009 322 505 515 766 140 481 317 398 077 002 625 164 853 994 369 608 315 710 332 936 305 682 066 575 395 788 473 002 835 702 147 787 637 089 453 930 961 525 988 666 025 406 110 230 995 766 203 989 857 208 943 464 447 644 759 980 511 919 905 511 925 333 420 400 557 408 000 676 571 669 405 401 352 339 735 274 279 187 933 183 918 432 116 766 898 250 271 136 053 680 670 639 313 253 668 792 965 900 264 512 491 858 783 402 797 146 411 676 232 577 433 213 592 788 453 682 590 014 159 181 781 724 514 537 535 629 340 960 786 218 647 463 548 477 091 692 311 330 980 226 614 615 938 280 237 413 083 163 383 959 746 703 969 301 616 220 617 458 514 178 685 169 257 633 680 487 424 371 917 779 826 842 538 941 940 907 659 738 193 739 676 130 157 872 142 546 735 906 552 326 184 291 966 579 530 299 461 377 367 755 614 859 688 679 330 478 877 920 015 068 889 232 773 931 127 954 602 499 576 329 389 149 431 767 141 135 073 522 110 620 003 304 140 628 451 855 090 948 082 942 118 208 054 945 725 604 821 906 653 344 596 468 534 384 430 450 515 952 010 028 272 688 791 894 536 575 346 478 313 936 563 048 474 873 010 330 666 915 222 874 179 644 898 118 140 204 699 688 108 470 101 574 234 637 528 223 705 312 731 976 316 991 452 797 904 726 052 040 336 279 974 890 854 548 889 298 526 928 692 312 650 670 913 699 509 686 862 832 712 422 668 966 581 626 233 107 431 494 746 927 913 612 362 589 331 820 720 323 462 782 210 299 602 045 927 105 526 848 273 820 886 606 112 970 705 103 438 806 557 756 943 915 136 580 324 672 038 609 109 538 362 535 950 423 479 783 275 992 022 984 227 656 035 792 736 772 664 002 475 531 434 648 540 773 746 150 780 432 322 774 496 220 469 534 037 889 201 631 341 983 567 610 257 575 524 654 948 759 168 631 309 607 217 688 201 166 460 466 767 944 454 302 255 187 239 409 592 125 580 872 369 124 330 107 321 327 590 301 242 193 781 503 276 192 949 583 229 655 957 139 195 513 722 466 321 898 422 173 923 474 152 160 094 342 047 755 789 417 742 344 142 518 003 097 498 479 960 390 939 076 509 480 202 940 510 665 683 532 949 047 363 932 420 760 061 736 107 014 783 104 408 575 955 769 283 867 445 688 936 227 169 205 961 563 771 753 896 020 399 426 147 787 057 522 117 312 592 375 985 025 562 684 898 388 656 520 442 110 090 205 971 192 543 155 755 161 549 347 207 773 088 383 399 606 106 188 763 548 745 183 960 650 733 694 431 997 228 008 642 303 972 258 139 273 391 248 217 698 440 358 759 674 332 319 322 732 950 464 286 584 190 421 541 568 890 161 252 168 974 658 522 963 050 010 928 207 350 669 653 153 206 986 962 307 805 234 433 303 390 841 942 445 000 338 129 483 963 210 344 394 569 914 662 634 762 008 872 178 016 512 993 295 411 603 695 641 084 572 767 419 480 251 207 178 446 479 999 937 675 876 284 780 869 090 713 231 860 633 843 979 665 781 143 948 955 845 111 220 924 746 002 130 794 219 432 208 072 372 675 346 460 789 684 474 983 475 157 805 396 241 959 517 280 049 623 742 530 804 341 260 244 275 792 119 703 654 320 310 638 345 313 798 557 792 964 660 040 936 231 149 009 813 851 113 675 367 877 472 792 799 958 198 034 597 014 292 056 886 157 379 264 422 852 521 039 966 759 073 073 295 429 654 574 086 788 850 632 921 285 620 812 431 049 291 431 821 097 713 395 744 695 638 133 154 524 077 058 085 611 190 052 534 032 118 367 345 360 160 277 108 103 323 337 831 546 131 321 505 907 575 523 281 385 306 135 228 700 939 188 451 846 462 492 394 392 166 557 430 615 834 940 199 644 993 274 829 835 031 374 408 139 927 732 267 743 394 886 380 324 331 545 724 842 623 229 027 854 351 709 755 514 162 379 085 121 781 439 380 092 719 542 481 772 834 937 120 318 316 673 794 699 719 122 568 029 722 445 519 160 476 639 841 758 838 598 851 315 639 336 770 566 526 840 858 911 010 997 923 730 132 540 866 452 381 949 908 230 396 060 861 175 152 774 829 038 697 791 769 393 212 289 377 071 817 565 681 958 779 518 946 825 991 606 906 319 196 345 392 191 402 454 897 079 628 304 725 874 312 608 985 283 188 439 804 580 897 283 605 862 218 055 117 914 162 971 209 829 407 783 695 113 975 260 052 410 719 353 471 884 449 947 783 844 772 811 247 216 715 835 606 616 432 758 358 428 374 881 178 369 546 368 803 566 091 425 801 671 307 263 477 964 311 980 543 239 434 376 030 076 330 696 388 057 450 438 960 834 729 170 044 390 842 212 784 564 286 485 419 960 005 280 103 689 609 316 919 261 586 362 550 743 784 695 308 009 416 181 301 682 671 015 444 624 528 084 232 849 946 444 640 775 618 233 105 816 751 664 562 118 361 574 845 185 665 455 376 250 650 453 643 657 750 902 286 482 896 586 181 465 386 083 840 464 515 121 662 889 868 110 869 772 200 968 244 592 713 446 136 844 943 455 901 214 687 104 199 519 726 302 130 369 406 081 107 718 057 034 084 843 819 756 883 799 717 661 340 117 834 466 796 040 757 107 508 822 431 938 174 314 818 775 790 411 729 710 082 736 659 572 720 316 584 613 918 455 318 683 113 106 897 167 948 165 669 248 135 773 039 879 515 098 908 848 558 705 952 660 165 826 901 967 554 870 936 766 314 782 123 309 457 530 900 088 797 187 635 294 841 526 808 675 942 930 249 616 430 648 983 042 304 304 557 408 261 857 944 701 390 214 821 995 947 092 047 413 383 447 391 266 967 471 632 958 314 151 551 903 080 185 470 955 668 333 186 944 427 499 854 886 861 444 323 164 197 565 242 388 110 023 482 973 826 874 065 818 206 295 490 347 887 286 880 890 424 842 353 698 704 852 550 880 630 918 116 203 503 896 803 144 658 876 601 505 689 064 681 855 988 209 999 427 349 500 837 643 839 816 067 513 176 307 664 432 969 423 031 370 670 334 775 041 892 749 831 628 335 392 630 130 464 951 602 897 288 239 415 065 611 994 879 117 835 632 230 588 803 799 891 194 063 533 140 906 197 161 031 195 999 237 854 511 910 388 679 467 313 396 029 150 036 004 608 963 801 467 654 220 873 753 244 985 961 620 724 877 233 948 803 222 770 096 159 850 117 034 879 951 669 765 604 589 553 745 589 000 699 441 002 947 626 446 171 023 202 951 705 505 952 175 340 037 034 216 317 867 018 743 299 781 481 478 863 038 504 013 697 441 937 258 310 484 439 534 860 325 598 741 926 953 199 693 837 192 224 200 181 396 736 196 485 207 460 754 854 681 807 364 739 840 168 231 933 704 998 565 993 569 444 596 162 499 052 006 063 070 738 519 182 653 406 165 519 736 512 862 039 008 233 522 367 218 626 032 231 706 622 869 856 441 297 893 090 252 656 338 687 058 022 708 985 296 803 275 404 309 341 224 012 883 672 773 223 637 415 732 204 990 139 425 920 328 743 508 654 104 369 237 676 760 735 259 870 854 349 241 325 281 980 656 957 067 476 474 715 117 993 522 209 817 835 633 306 416 594 543 305 570 454 623 869 446 088 653 559 326 265 564 345 113 052 679 539 801 082 519 315 661 632 984 029 090 871 096 642 153 550 086 169 244 094 388 275 278 577 466 565 821 903 398 559 259 535 101 439 142 159 327 997 431 218 020 522 445 492 717 113 539 059 339 885 999 678 732 284 121 237 380 836 940 247 027 891 136 606 251 345 412 776 556 036 072 787 467 230 611 169 411 444 574 068 676 037 868 179 988 571 910 442 090 441 139 502 618 624 376 223 870 819 970 463 278 925 529 869 906 142 301 752 266 487 865 479 436 782 926 873 941 992 769 791 748 862 613 547 515 896 331 214 997 223 096 458 934 473 389 046 466 064 456 155 795 368 753 858 323 268 272 649 115 518 526 266 321 718 180 952 630 146 787 470 331 721 155 374 159 108 412 036 160 813 957 456 966 486 292 486 769 164 370 408 976 285 046 428 832 701 514 002 492 862 151 012 051 340 556 728 135 485 736 976 759 556 081 270 687 987 658 948 965 950 846 777 169 230 745 285 759 182 360 263 704 082 909 455 255 046 272 872 187 250 622 798 261 845 026 841 771 151 562 103 417 782 944 143 639 550 414 290 707 500 612 669 993 790 713 749 720 388 175 007 486 069 791 347 676 164 671 104 502 356 994 757 979 832 841 425 004 765 900 750 971 705 517 091 559 891 764 005 901 817 799 175 171 582 746 376 843 714 204 294 414 569 134 233 555 977 288 789 362 601 664 405 901 413 065 717 458 625 601 072 841 735 265 242 162 042 197 984 785 532 798 159 871 695 383 862 662 227 999 761 605 138 655 087 704 446 070 961 627 564 751 255 522 570 483 228 304 878 024 667 858 903 967 511 932 142 537 574 806 416 018 180 837 270 095 258 003 005 738 488 680 525 952 775 983 381 732 411 030 942 982 566 998 016 513 107 865 026 407 874 918 627 620 852 769 059 195 497 581 139 653 213 361 870 839 490 091 289 359 147 866 251 703 151 757 257 687 835 761 892 644 166 328 382 737 318 569 186 297 945 652 982 736 305 690 450 081 085 707 365 425 259 877 904 370 734 362 054 952 728 746 522 467 758 082 008 082 953 979 777 364 834 647 781 003 519 752 737 259 864 962 272 215 176 202 376 779 121 604 242 030 706 632 593 948 786 628 858 232 684 982 529 960 549 982 357 164 256 259 715 002 679 907 745 781 678 756 102 451 140 243 995 249 352 509 091 856 512 149 207 494 773 347 963 618 760 053 313 519 470 215 998 410 224 186 573 403 642 276 976 101 457 536 019 033 085 741 535 904 578 048 465 519 615 683 075 020 395 190 503 773 503 991 900 899 142 315 433 923 565 868 696 652 255 169 255 600 610 488 608 838 263 355 587 853 639 892 201 578 895 679 988 452 215 296 871 595 404 981 524 590 057 190 787 033 158 492 644 806 475 785 098 817 637 642 961 927 474 382 126 824 284 765 530 096 205 317 544 561 665 096 746 507 895 296 690 814 258 886 504 278 362 492 078 710 006 919 197 883 890 520 105 212 298 826 648 859 842 080 800 652 109 859 599 516 759 852 681 219 949 669 176 041 581 555 440 895 683 364 228 262 391 471 042 817 955 242 410 260 458 622 676 671 293 518 527 085 002 140 747 079 118 615 065 494 899 538 730 901 111 013 114 248 328 576 745 159 886 358 940 069 842 673 260 120 889 777 840 241 057 401 902 827 184 816 332 625 818 473 743 794 274 778 373 658 634 929 908 814 621 882 047 349 751 584 855 501 258 138 282 793 694 007 848 379 765 309 691 707 751 433 687 320 549 160 569 458 776 018 172 801 968 441 650 718 629 605 634 594 687 793 803 054 136 756 662 295 959 794 383 607 188 139 416 944 697 673 993 836 285 290 273 729 104 524 191 066 244 551 552 314 878 858 676 884 737 357 535 176 164 291 425 263 226 977 129 281 075 289 689 834 240 035 700 103 569 077 190 004 365 989 300 301 412 442 960 079 572 498 625 834 102 567 100 024 826 670 090 029 121 901 403 255 551 855 896 892 835 175 809 403 048 579 097 080 866 145 877 064 994 657 780 732 112 258 397 905 740 527 212 841 946 455 685 870 472 937 215 070 101 839 618 158 948 379 899 455 822 650 060 389 776 951 730 559 702 377 988 195 709 400 233 246 577 561 988 794 657 405 201 263 146 298 264 245 737 030 339 662 625 644 214 470 283 922 312 066 272 856 175 581 741 755 028 488 856 606 438 368 165 874 267 356 836 345 400 476 315 616 050 717 374 037 696 313 612 401 686 834 705 388 264 567 551 362 301 030 322 918 635 574 499 303 295 077 726 521 079 982 271 947 675 522 382 279 139 740 011 073 265 230 103 409 362 494 579 133 607 599 034 139 792 356 094 649 375 735 755 575 515 162 571 754 698 386 600 866 209 738 192 649 232 900 160 991 837 155 379 887 602 938 913 345 118 846 627 495 370 746 320 913 636 927 585 559 464 905 988 112 499 696 138 314 620 347 449 338 745 644 404 962 248 845 791 436 903 570 619 428 997 925 987 567 437 593 221 235 085 911 769 940 186 112 125 670 936 095 830 577 816 322 458 763 137 568 439 370 326 724 148 800 711 260 908 837 189 444 631 956 005 667 064 805 970 508 112 097 096 483 724 985 819 174 573 971 938 471 505 104 645 425 685 514 217 457 359 549 741 776 068 337 316 112 014 030 803 985 739 651 194 239 244 910 418 935 685 965 121 558 916 623 176 304 922 629 241 017 246 212 978 934 096 552 525 159 357 457 849 855 267 241 551 366 282 791 096 654 376 779 074 638 469 266 574 536 071 177 969 737 370 478 040 941 641 089 225 607 798 707 005 882 124 421 461 930 997 595 943 927 499 071 700 567 416 821 927 383 615 807 049 625 231 653 574 936 131 501 261 716 209 612 899 624 047 736 521 955 722 681 983 763 017 769 388 158 323 553 344 959 921 510 815 948 601 913 046 575 989 140 992 982 888 321 655 587 623 662 507 991 734 682 690 927 541 696 336 679 743 483 428 679 239 531 561 599 120 775 511 041 117 825 882 284 154 107 194 691 795 172 136 388 233 482 498 158 749 354 124 764 599 323 508 829 005 255 718 128 709 572 696 253 131 963 337 901 016 118 690 711 657 939 993 913 250 270 720 505 297 958 845 603 414 579 984 325 095 146 682 157 242 202 770 581 861 278 223 507 009 357 403 343 685 144 150 991 521 412 222 741 389 659 156 765 956 765 833 030 218 478 510 437 134 087 939 443 642 766 257 450 790 239 183 834 135 095 304 444 788 050 921 172 414 853 306 709 052 861 789 325 580 049 348 884 113 043 617 605 761 003 906 713 748 487 475 307 749 103 629 983 460 055 634 894 154 244 856 393 177 551 835 736 383 128 088 930 283 742 320 443 678 124 977 353 991 601 510 684 379 898 224 007 464 843 831 849 220 431 825 067 724 367 017 257 514 809 207 165 979 594 119 377 244 587 997 533 005 962 150 269 787 478 136 830 239 602 117 206 180 023 411 035 019 344 366 591 151 032 915 909 029 835 137 643 670 956 693 693 289 440 626 898 796 741 233 899 703 973 604 917 087 543 409 671 874 781 574 432 086 775 476 495 003 654 969 141 970 030 136 161 120 976 958 844 120 859 455 388 852 951 687 040 926 378 071 029 287 289 269 353 417 594 009 699 735 167 600 781 476 041 665 198 978 880 411 533 149 355 323 004 853 267 892 277 770 903 269 407 486 752 809 869 512 827 147 561 802 949 683 636 174 014 012 741 451 551 991 493 987 823 592 828 160 561 009 687 976 068 734 347 791 339 160 176 039 382 708 813 486 217 037 861 349 417 117 718 737 656 878 160 261 225 029 870 322 947 772 051 824 146 501 759 907 087 314 887 540 239 698 116 411 564 489 984 628 305 755 252 831 506 589 928 889 716 040 026 915 059 951 330 485 422 156 499 684 165 869 468 102 594 420 472 885 304 632 772 014 338 299 921 387 804 940 849 041 658 059 845 271 544 998 683 018 970 918 485 862 384 074 785 330 101 190 226 165 053 539 231 362 362 535 217 013 220 364 538 257 254 051 207 620 417 973 326 494 227 008 985 702 299 689 437 334 226 978 524 060 721 809 544 665 155 062 469 891 260 442 066 429 440 092 261 951 962 566 669 699 994 043 415 581 834 231 439 208 873 253 041 563 659 650 596 340 065 562 134 563 386 256 305 682 706 318 944 692 446 110 138 370 189 709 667 095 997 303 610 095 324 627 650 510 291 571 038 694 497 215 287 106 377 500 942 491 325 598 830 549 563 323 856 773 654 966 880 723 026 780 924 658 103 069 360 448 978 537 961 769 597 296 215 749 508 743 360 751 255 929 739 765 702 218 120 588 620 039 182 278 851 652 344 606 361 071 630 038 240 570 025 571 970 586 663 923 993 507 437 185 391 800 662 370 480 294 379 688 663 343 405 566 590 917 542 491 968 022 584 020 385 382 794 865 444 627 461 447 742 134 563 309 554 578 391 660 754 273 600 690 016 372 945 284 158 600 757 754 711 985 224 072 042 006 309 829 587 286 209 852 455 943 325 648 555 018 277 879 196 031 407 197 150 333 430 528 770 297 085 307 119 730 468 835 749 406 340 933 051 597 622 141 326 734 706 684 151 347 772 024 908 607 285 072 555 003 573 320 791 042 292 580 514 223 040 666 983 023 354 594 908 689 231 585 633 913 645 166 242 428 630 413 551 024 078 871 655 532 326 507 225 467 951 453 634 011 718 312 208 171 823 746 858 630 625 428 659 052 472 151 872 808 059 611 493 557 623 021 670 123 540 395 727 417 134 716 816 335 991 229 629 358 042 167 449 653 521 454 617 339 058 857 417 801 673 987 811 533 793 981 291 542 169 281 393 273 466 549 950 472 643 420 273 316 694 373 042 495 805 864 955 791 860 219 187 328 204 010 653 087 842 614 925 341 663 181 400 764 591 595 014 063 540 610 993 156 971 884 398 423 428 449 602 781 721 641 222 683 486 147 748 090 918 489 855 571 359 643 713 036 703 695 418 919 039 078 543 643 214 959 053 589 079 341 459 760 455 497 556 809 060 266 288 544 990 724 790 184 207 430 384 456 715 050 030 240 657 323 523 570 307 139 370 987 803 890 539 716 908 074 104 328 716 027 423 869 234 956 382 338 086 325 610 849 068 155 933 255 439 749 694 873 311 279 058 773 594 912 147 300 822 495 235 053 600 349 778 377 830 385 464 394 516 929 324 547 155 312 720 292 927 715 735 737 914 316 744 761 611 411 815 727 403 332 276 771 603 424 458 061 650 830 387 270 945 306 166 421 033 257 425 500 609 686 531 957 814 975 123 305 081 247 137 072 761 123 304 607 381 018 306 103 469 545 317 971 637 272 856 359 485 798 074 253 141 676 194 963 702 391 609 452 266 055 671 210 877 644 237 568 021 342 350 914 133 778 816 280 120 575 078 307 937 903 032 870 075 349 519 751 295 271 807 731 619 177 899 756 876 466 927 403 144 398 817 990 838 274 184 420 534 472 024 931 744 905 150 459 816 927 196 528 941 646 745 588 248 234 512 088 384 319 172 494 378 687 218 266 393 647 849 814 030 230 299 421 364 254 618 747 417 860 483 838 276 550 837 763 809 920 158 226 238 801 082 108 730 595 725 482 927 431 344 262 004 260 815 639 781 927 426 312 904 388 967 607 107 344 117 826 753 418 115 184 561 471 823 343 692 496 637 747 617 354 536 041 431 401 462 333 592 420 523 685 231 655 901 436 629 767 224 082 950 535 803 065 804 782 275 491 951 903 910 589 855 054 563 695 958 817 074 780 048 275 886 366 106 818 161 014 008 976 279 129 962 027 711 572 204 329 303 753 721 980 723 158 815 076 123 035 534 440 550 932 655 774 141 225 416 752 488 912 333 956 744 386 465 338 893 494 011 162 208 354 729 244 265 274 810 400 354 075 692 028 502 207 550 240 817 401 057 704 738 294 247 968 975 898 201 263 429 073 022 799 087 322 603 352 995 334 491 486 091 244 437 434 093 644 277 586 638 737 994 860 034 570 087 007 527 541 305 852 210 363 582 989 465 523 416 483 402 132 171 421 873 760 692 213 926 898 252 283 691 003 462 437 173 713 636 780 421 966 620 378 714 997 993 377 189 073 957 594 564 638 228 421 543 805 128 398 090 240 587 040 247 476 775 859 382 262 838 437 321 053 087 228 191 059 125 441 085 090 746 915 788 679 225 853 950 018 391 820 022 757 132 675 484 563 406 286 541 670 757 265 328 759 230 036 580 129 974 505 377 323 729 276 285 641 666 137 011 505 321 019 619 415 726 694 030 386 704 599 441 087 254 035 572 858 499 352 690 143 933 843 482 490 056 101 155 773 254 816 870 684 557 273 801 755 816 970 915 993 975 458 747 617 782 450 681 626 721 510 199 477 139 217 341 915 308 980 949 028 600 448 000 275 328 111 895 854 428 490 321 545 560 935 547 911 770 752 868 406 349 077 986 063 116 138 260 489 255 295 416 853 330 773 598 321 967 360 072 889 183 406 914 142 180 598 622 240 660 688 651 650 290 619 016 966 792 701 248 969 817 077 040 357 890 830 478 376 006 590 420 893 250 432 371 946 671 693 180 226 537 262 919 226 613 210 665 268 657 920 013 574 600 891 835 312 104 782 252 282 219 430 427 983 259 317 355 235 622 255 546 994 940 012 021 763 693 071 279 032 186 095 937 684 471 486 406 094 291 571 348 358 054 883 144 331 476 590 962 126 985 680 427 355 834 200 415 535 190 722 894 249 198 372 841 433 014 245 182 364 849 939 755 134 404 543 243 450 121 666 484 104 682 495 945 732 512 197 287 415 948 148 896 604 906 556 052 767 505 806 498 674 329 801 851 603 832 080 843 473 554 656 172 575 066 960 303 115 536 445 260 862 908 617 523 204 762 682 214 343 314 548 349 196 612 948 708 725 518 769 437 167 939 399 457 474 685 915 009 620 889 699 404 809 481 674 634 975 433 313 948 715 912 738 075 603 011 330 352 414 285 515 037 583 464 924 325 489 993 639 209 377 429 395 785 625 861 262 662 426 122 820 712 373 193 837 519 724 373 871 127 604 785 518 035 408 396 213 290 954 356 176 647 687 197 255 904 291 378 569 605 177 182 455 116 699 706 316 661 605 597 215 493 588 250 437 353 036 254 613 831 744 258 802 303 337 857 371 806 512 087 785 131 211 679 213 070 214 673 047 360 090 249 258 036 194 391 140 631 118 599 434 241 318 017 622 146 467 700 523 200 824 556 780 308 757 166 310 274 573 304 336 983 552 359 727 584 313 351 986 676 386 474 319 161 468 931 553 857 745 260 029 002 241 415 609 925 826 738 629 866 308 811 301 892 684 246 648 821 324 401 532 221 052 270 434 394 094 999 811 817 416 684 024 334 821 859 105 950 295 144 931 450 802 553 014 124 487 210 976 568 392 075 933 686 032 499 973 997 627 406 149 855 520 536 379 350 156 708 588 787 684 880 972 948 169 772 881 336 880 423 845 700 893 220 234 647 511 342 101 597 763 726 669 070 837 344 395 210 498 356 623 412 842 317 604 442 454 116 725 701 593 456 956 433 038 582 562 137 858 638 312 202 193 105 261 416 717 339 965 287 594 672 822 286 500 699 702 334 957 304 852 042 839 968 476 913 002 564 173 444 721 454 009 705 917 927 284 867 034 026 128 109 995 676 507 125 369 186 052 147 754 677 780 532 410 327 516 866 823 728 333 819 738 411 801 261 027 156 395 226 939 438 584 636 420 573 483 825 371 319 774 761 521 942 353 337 246 619 611 302 437 242 820 211 588 359 038 763 462 730 632 164 439 754 114 116 415 785 235 943 407 514 243 892 151 193 042 683 347 294 633 195 684 500 893 501 293 174 062 434 319 418 560 632 824 806 986 041 808 357 378 855 455 990 290 312 543 489 581 751 029 652 472 823 674 280 638 585 154 558 165 295 141 208 958 697 597 042 003 824 940 533 017 576 454 653 181 652 311 868 723 928 837 760 405 670 384 770 591 737 853 954 708 780 419 719 403 616 860 550 042 733 565 633 726 612 656 966 055 336 103 558 929 682 022 185 584 219 398 930 450 948 527 816 232 336 837 620 880 954 168 235 008 238 210 569 496 247 083 140 233 001 931 525 128 394 826 838 900 931 979 348 811 267 863 283 682 852 707 344 550 483 884 152 239 029 060 991 583 756 044 809 029 694 959 431 094 997 679 549 321 334 852 381 977 722 759 305 092 037 656 344 362 794 971 130 466 587 910 771 749 027 507 198 589 151 112 812 161 449 100 884 452 803 527 333 170 077 698 582 580 212 340 874 155 572 517 257 323 022 228 389 240 501 665 800 710 873 111 902 586 295 215 342 304 131 181 823 150 899 367 758 460 708 768 967 415 951 154 619 550 847 734 305 055 127 231 637 334 719 410 603 868 535 354 392 832 691 442 179 903 565 002 969 706 445 906 594 069 748 305 409 311 707 028 873 065 148 863 189 348 140 856 371 722 021 405 572 250 786 037 048 307 369 320 814 012 362 581 966 913 034 693 838 208 688 824 922 832 326 019 893 136 917 148 988 765 940 274 849 891 403 090 246 453 410 601 144 714 707 020 902 092 168 204 267 128 730 852 565 549 252 984 229 287 750 911 532 729 612 525 017 190 764 148 482 392 790 042 879 464 706 315 716 381 051 897 144 479 629 191 098 319 024 506 480 313 965 366 657 324 866 020 493 382 054 695 622 836 860 990 437 385 529 224 466 406 318 201 947 746 484 636 429 235 247 565 780 295 722 329 830 637 453 768 124 466 123 809 315 725 639 545 170 745 266 546 022 288 206 324 106 696 111 054 171 857 621 478 070 082 818 025 699 254 379 936 143 813 611 923 300 496 666 877 648 096 926 237 075 541 255 452 114 183 567 296 792 128 341 011 827 911 345 504 646 780 563 648 566 757 482 976 101 409 075 199 572 421 508 510 224 467 622 854 535 839 639 889 439 255 705 297 431 609 992 137 596 265 096 302 105 033 684 385 961 263 418 522 817 908 212 014 744 809 635 083 185 213 748 466 288 773 259 473 186 713 584 290 774 459 732 463 971 608 333 414 691 107 470 656 908 848 978 255 443 954 884 864 162 022 930 877 862 025 818 251 852 928 452 370 100 032 786 083 264 368 033 271 675 564 583 692 411 590 898 331 712 776 639 288 784 767 088 215 799 357 515 966 437 097 786 687 350 369 589 532 369 806 604 823 673 311 257 170 138 711 852 057 381 098 788 437 059 969 938 368 105 422 478 841 192 697 648 847 302 498 769 746 957 851 084 594 387 482 801 066 923 964 922 252 774 402 299 339 501 202 460 016 912 143 100 410 128 788 377 309 525 581 188 674 815 685 346 608 831 499 068 302 998 072 161 634 933 826 097 265 209 521 238 045 939 038 275 087 371 517 193 364 045 637 832 993 315 015 408 462 085 768 943 655 392 030 459 198 076 979 049 971 933 279 902 582 241 721 926 644 859 737 631 414 844 439 961 597 569 515 566 584 959 853 617 528 592 443 906 430 882 008 066 384 166 646 460 816 811 578 589 220 382 912 785 595 330 304 398 396 730 596 930 876 035 123 446 682 119 897 624 850 596 576 608 189 706 038 324 220 162 611 685 997 254 767 675 399 814 771 893 836 625 603 523 861 736 620 617 010 761 810 982 147 371 052 618 953 758 284 508 178 659 405 417 451 378 900 116 075 532 629 912 447 028 429 155 755 552 963 560 630 350 128 596 868 958 562 169 863 411 411 648 210 373 159 442 165 372 548 637 864 780 867 332 719 681 409 062 681 485 117 373 169 817 954 013 408 507 729 855 312 514 557 651 262 772 012 558 584 330 346 748 228 054 895 110 681 645 537 140 787 023 633 036 840 685 474 586 157 207 755 594 104 071 299 254 761 430 874 287 838 351 229 596 397 839 289 772 801 680 176 994 408 093 298 695 909 340 263 737 963 682 261 139 567 138 247 577 921 742 185 659 723 769 277 801 692 710 524 730 185 356 981 562 733 968 765 796 806 680 997 522 918 669 987 529 804 072 920 428 442 693 212 859 811 499 618 497 801 492 459 793 718 449 209 101 177 461 424 285 872 203 820 796 905 370 992 510 845 735 174 054 013 923 994 755 571 079 873 538 061 110 359 360 749 068 891 271 925 301 963 110 675 619 805 952 945 111 932 196 320 932 020 952 818 922 715 793 061 560 431 946 785 199 381 273 286 259 988 497 251 386 140 453 562 863 281 848 883 342 206 931 984 310 010 162 403 055 408 986 719 677 130 525 171 023 768 767 918 884 171 381 117 063 152 379 789 324 362 795 735 688 237 977 843 985 241 954 636 995 040 117 927 019 239 470 519 973 553 825 565 924 858 552 955 843 775 569 234 948 389 204 219 132 888 915 064 195 156 138 914 674 083 300 969 099 607 581 263 414 540 732 498 153 139 466 499 725 589 952 816 005 633 086 723 767 601 940 785 670 923 623 069 468 148 720 691 198 090 166 626 156 180 904 888 304 375 351 539 205 542 186 409 249 120 414 994 937 360 929 854 303 515 141 027 680 092 648 033 725 874 771 042 231 300 134 561 257 289 646 381 551 582 847 479 379 460 364 270 746 289 270 403 753 725 676 614 293 846 420 244 314 668 171 218 360 552 128 450 073 219 417 686 265 368 490 852 378 663 476 259 208 214 940 808 125 080 518 064 256 019 314 626 280 982 780 160 383 757 689 339 879 285 485 956 877 855 256 380 579 069 266 605 550 422 460 463 404 312 328 717 559 302 387 655 728 871 327 958 965 441 486 310 884 797 472 602 234 136 083 979 890 034 724 800 790 608 996 902 200 995 409 487 290 032 032 441 461 019 946 328 402 516 201 799 758 830 169 707 735 199 261 044 257 688 691 397 190 796 799 220 937 354 504 680 886 465 681 847 714 774 468 049 902 234 200 225 083 201 589 831 318 441 206 844 559 136 208 751 099 047 265 441 171 158 344 955 947 509 844 295 076 315 462 777 069 047 228 422 283 119 229 294 397 749 666 047 272 783 333 446 889 683 228 945 980 815 900 028 965 718 989 797 952 175 173 989 426 245 699 191 601 896 807 126 257 687 962 139 704 800 761 946 980 133 894 011 058 697 942 772 297 508 898 746 809 130 728 385 882 093 866 688 945 968 490 783 558 856 332 112 758 365 562 591 956 151 619 616 302 509 783 561 120 372 383 079 473 578 651 296 035 247 099 099 146 864 580 118 335 717 300 761 961 308 810 999 774 987 702 434 052 252 058 019 789 562 908 023 753 408 726 568 156 916 863 671 476 337 593 371 155 996 864 731 262 589 796 518 525 684 516 535 487 836 410 825 511 119 171 536 012 359 709 643 477 849 317 381 707 198 261 088 842 527 115 430 089 772 884 636 193 994 532 294 262 580 158 631 655 700 208 058 993 240 851 251 796 462 693 739 926 821 037 676 502 232 339 767 831 683 831 962 839 676 242 258 430 155 168 467 559 728 892 493 394 781 428 420 981 839 023 464 259 179 458 277 028 594 640 077 126 984 008 926 076 459 862 330 600 918 533 817 062 950 612 813 299 292 964 335 572 530 799 574 285 461 616 378 820 477 065 580 243 057 746 301 783 463 847 061 256 940 425 233 214 989 805 069 517 889 418 526 926 584 201 608 632 983 592 562 183 933 710 095 884 967 197 753 788 081 143 424 515 085 761 070 071 183 523 591 203 324 810 800 653 485 883 351 059 937 323 176 531 241 245 742 985 620 626 605 117 531 412 950 382 862 929 712 463 599 251 046 286 387 931 063 315 491 061 549 481 616 705 714 308 782 596 782 292 270 577 557 923 621 935 433 806 148 371 160 737 948 672 766 060 784 310 863 272 785 116 163 698 448 942 950 340 075 690 054 444 264 771 653 646 635 322 518 433 921 844 420 261 337 859 997 590 893 310 588 871 153 808 162 956 872 949 962 367 353 693 104 957 143 099 327 186 583 776 122 934 557 510 916 004 459 619 624 803 772 477 995 087 821 752 736 747 339 723 696 612 284 282 104 376 872 633 028 924 593 063 690 579 429 340 662 150 280 477 825 400 512 610 040 663 801 641 241 949 821 498 375 409 900 143 247 479 047 889 835 438 307 413 377 088 630 874 319 302 945 404 258 503 891 393 060 400 841 060 299 674 489 693 125 352 647 207 062 309 462 959 807 819 940 040 503 207 861 810 712 929 401 541 166 683 545 159 159 729 561 020 003 770 734 659 885 115 801 884 626 525 703 594 669 946 514 939 254 651 801 564 227 247 465 321 245 404 541 025 612 090 842 452 091 478 681 586 142 054 202 845 452 061 223 817 014 330 477 080 251 425 120 589 417 378 080 742 090 556 765 096 345 943 442 077 341 053 277 624 880 690 719 370 633 831 250 482 436 764 776 530 462 275 899 436 491 761 450 177 144 421 772 763 800 290 700 491 137 798 303 192 837 808 828 934 342 535 882 199 524 296 489 382 713 518 099 509 090 355 356 299 759 111 100 819 750 363 349 125 346 395 627 261 815 724 573 837 089 837 456 089 241 329 416 789 664 082 576 244 213 353 166 410 228 051 585 245 307 927 997 644 970 729 944 667 022 512 369 367 439 871 071 547 226 761 387 716 439 241 667 219 921 603 914 942 247 482 497 077 164 527 897 626 239 367 346 816 127 337 378 483 038 048 695 886 725 662 606 024 334 437 210 447 931 449 814 838 120 252 469 946 165 192 708 248 560 096 333 766 792 079 996 497 614 386 317 541 489 773 068 892 754 387 261 685 464 189 883 838 056 791 776 000 725 125 727 545 455 238 232 902 389 248 274 571 085 072 600 422 125 188 118 375 329 022 989 164 433 227 922 382 768 269 681 559 772 199 779 923 000 188 299 192 311 209 394 959 372 567 776 847 684 913 300 307 707 068 002 253 908 754 762 721 591 743 934 437 891 043 977 000 417 765 453 610 875 566 536 010 295 870 005 181 147 921 273 593 930 938 119 600 973 524 922 269 917 802 500 526 661 945 097 248 889 339 363 713 461 800 694 551 764 426 013 492 337 004 751 723 670 253 228 827 991 261 204 381 531 326 254 193 112 545 591 349 214 946 774 312 430 565 697 783 353 810 240 546 991 731 827 035 910 636 016 809 249 128 206 133 353 138 797 362 106 890 830 268 682 196 686 891 318 255 860 701 896 283 986 445 010 550 702 284 763 103 304 581 781 280 188 384 183 843 058 793 076 461 329 793 272 070 650 703 806 606 123 036 337 350 844 278 922 857 023 322 890 845 146 226 223 540 499 049 238 773 644 803 504 770 300 090 699 088 726 568 285 717 260 279 207 638 119 183 339 657 641 214 983 062 378 591 525 021 216 222 020 404 118 679 503 702 947 999 349 863 529 290 641 021 551 061 104 922 308 714 364 518 950 558 339 440 035 261 305 254 923 495 076 288 728 337 750 770 551 042 543 675 089 723 446 209 803 881 602 781 914 319 324 618 593 977 574 361 496 409 121 448 260 156 181 422 447 910 993 666 132 635 824 823 153 106 284 045 670 730 923 190 160 383 451 626 158 028 778 886 783 687 640 563 218 653 175 822 921 147 810 690 788 436 521 252 157 118 872 466 343 597 095 996 175 245 594 968 600 994 927 759 200 514 174 786 361 705 935 080 647 675 547 841 853 392 371 638 083 091 638 528 674 562 914 618 241 448 763 818 781 764 382 234 016 179 246 768 344 220 355 428 891 184 051 755 151 473 840 468 224 864 833 399 265 848 201 797 111 413 001 401 336 374 924 653 109 493 410 535 504 709 923 468 566 231 770 208 488 857 224 849 139 654 895 422 430 360 721 493 813 431 851 976 558 037 014 133 628 566 017 303 415 092 704 677 146 836 648 828 535 809 586 502 738 990 214 395 631 275 285 395 302 453 224 882 273 248 383 039 517 084 299 316 600 380 087 290 297 794 422 344 888 596 817 973 576 178 861 751 802 383 667 326 739 152 896 319 850 026 245 221 816 106 134 760 656 127 808 051 712 969 793 714 952 091 105 652 170 520 322 891 780 179 579 561 662 464 852 763 752 042 472 356 462 705 419 740 382 331 165 229 240 942 425 099 432 906 600 857 145 130 641 017 957 942 354 688 031 579 482 545 229 523 005 350 987 148 970 567 839 728 157 175 574 679 553 952 786 426 980 332 372 815 146 976 733 694 651 412 154 744 510 090 742 703 584 864 729 645 274 711 182 007 013 244 005 981 280 731 345 026 259 133 218 066 215 764 880 132 562 443 103 525 712 162 279 584 185 911 217 075 120 120 268 290 799 881 506 430 638 255 066 587 419 911 942 038 797 241 565 565 035 066 844 392 845 915 107 344 629 228 488 958 316 057 335 702 712 245 612 016 005 802 956 858 973 639 069 469 514 063 419 219 481 010 589 613 378 199 565 808 742 359 478 075 946 038 829 602 374 568 660 229 371 535 194 972 909 221 506 895 483 158 312 005 443 177 035 413 377 792 037 387 937 586 992 523 699 709 351 266 866 906 782 633 288 208 572 653 067 338 924 026 769 370 776 208 716 402 512 682 972 058 372 032 860 464 545 233 564 453 379 357 409 308 803 573 757 869 956 663 668 471 144 829 852 548 939 559 654 090 966 286 406 833 182 652 598 086 405 417 052 616 242 630 946 623 199 276 573 305 165 952 599 984 571 481 811 709 275 653 783 558 662 900 275 147 698 602 330 711 304 500 248 976 659 122 047 412 997 491 938 065 409 836 725 389 920 223 185 202 505 617 225 939 823 590 144 601 334 387 871 594 208 661 664 627 183 050 804 650 545 900 795 861 505 884 472 280 209 023 070 067 046 798 692 077 126 809 968 224 855 658 074 868 829 555 718 735 571 827 005 110 790 865 662 133 770 550 142 052 428 663 679 292 196 013 657 250 792 402 191 596 793 631 487 076 114 954 775 123 972 923 696 153 035 635 253 227 035 060 078 661 268 232 237 566 827 076 839 678 211 054 161 575 961 567 492 430 724 719 402 800 776 593 024 199 171 616 648 351 131 521 151 405 211 744 141 798 469 006 947 736 341 578 005 035 231 421 735 987 781 416 081 552 299 356 279 539 153 444 856 013 296 735 931 740 787 242 210 091 727 008 425 181 831 740 685 710 255 337 598 766 249 842 789 338 769 134 610 385 297 604 863 107 173 439 473 570 287 258 501 804 090 237 790 097 202 688 403 375 838 021 500 834 206 366 087 556 015 669 412 603 666 089 524 988 550 263 482 887 884 533 596 665 796 391 080 440 016 060 127 536 025 746 626 901 322 045 159 420 284 892 872 701 827 969 383 207 741 589 802 380 327 580 399 144 525 790 691 358 724 554 754 395 863 307 758 502 623 528 482 822 461 030 127 526 916 358 016 423 233 196 309 120 226 223 971 434 876 231 829 278 425 243 211 649 308 789 074 051 920 262 235 689 140 779 006 297 340 796 207 470 575 881 851 340 247 268 785 573 531 963 362 135 824 512 834 277 625 866 331 410 506 918 070 002 578 775 921 568 463 001 849 165 301 124 082 144 514 188 885 583 410 534 146 957 129 395 550 140 536 872 990 165 081 405 002 215 809 384 912 922 948 330 096 891 729 766 579 659 124 135 656 372 061 290 745 810 707 781 456 327 052 620 747 396 753 739 713 644 633 749 631 656 098 152 369 336 784 951 204 420 163 871 373 855 029 032 159 839 963 250 538 154 058 024 441 610 613 719 552 152 691 644 917 777 822 346 579 843 153 041 586 002 426 271 243 168 098 144 961 192 352 011 092 214 776 032 535 185 977 221 901 266 776 688 965 213 415 817 926 432 066 978 051 041 032 795 779 051 374 952 059 213 806 732 259 820 578 767 205 434 204 757 713 442 430 273 942 756 289 047 731 525 391 650 696 597 814 968 357 970 208 688 270 298 527 863 696 958 845 908 047 930 522 204 864 907 745 118 405 812 891 597 107 804 188 403 234 687 847 226 712 850 755 422 268 524 161 203 277 931 329 742 418 116 389 927 814 514 371 697 615 086 763 563 470 437 072 354 209 270 852 144 286 498 600 521 761 021 478 970 818 202 414 599 530 284 586 228 486 851 846 792 875 015 778 582 849 429 986 049 814 732 273 017 099 320 774 529 516 757 321 768 716 062 566 422 304 345 671 893 870 210 781 093 273 333 629 181 139 606 343 208 297 602 147 185 337 843 365 678 754 591 332 141 792 653 274 125 813 625 532 342 762 453 083 518 175 923 047 542 147 283 625 015 172 494 208 490 987 059 041 192 988 087 406 198 529 909 291 751 428 679 265 531 917 596 319 351 357 296 210 836 859 645 996 453 952 780 207 413 906 039 708 336 145 729 119 045 268 628 693 245 359 582 846 794 588 040 188 021 944 301 800 273 921 608 101 370 817 503 100 715 950 591 432 379 650 655 851 944 665 824 678 744 617 631 724 604 104 775 014 773 701 047 454 170 219 885 968 103 296 317 173 884 861 672 473 688 040 680 777 779 776 819 377 560 408 883 864 106 957 105 754 829 046 107 695 089 652 171 025 859 539 392 903 340 869 799 142 829 424 040 509 565 575 549 721 959 531 684 638 836 372 705 488 788 434 744 075 776 599 521 671 100 761 361 369 746 190 095 228 615 716 433 349 325 311 422 496 019 835 435 051 096 703 855 764 974 049 760 578 037 681 981 130 035 170 819 828 252 639 875 910 607 949 169 308 920 340 997 066 208 923 746 427 977 456 034 081 160 368 313 648 228 065 109 561 410 366 607 459 820 858 874 241 760 689 933 898 947 438 865 205 354 682 000 028 582 295 123 854 999 133 066 274 678 322 873 889 853 096 516 362 995 240 762 682 782 064 840 681 478 753 821 716 627 907 875 595 311 923 392 807 435 027 925 529 038 511 873 985 268 106 602 545 210 261 925 625 886 284 536 555 564 145 007 449 229 185 629 649 848 716 856 974 733 978 061 335 313 639 995 936 071 407 966 937 818 280 834 992 520 659 539 302 319 970 404 022 714 384 771 697 517 793 960 740 147 323 920 204 772 502 731 496 405 584 251 480 653 683 601 390 464 712 697 407 310 833 296 024 236 955 667 983 113 665 093 281 133 940 751 055 407 910 117 335 320 481 863 843 213 880 126 454 181 925 039 086 755 797 723 313 744 417 413 040 401 867 274 761 743 775 640 282 189 060 814 589 301 331 252 139 745 824 242 481 296 970 298 985 871 276 190 099 796 037 256 550 724 133 863 651 504 609 136 832 344 789 795 990 737 898 958 320 738 476 615 075 497 864 728 951 727 177 565 321 656 430 496 740 909 819 687 643 713 493 113 068 812 131 190 846 906 366 292 236 038 426 592 327 274 925 738 858 352 543 825 131 268 135 597 416 577 506 571 060 411 495 937 760 432 482 936 554 594 840 288 681 722 242 841 997 589 498 388 759 817 313 328 928 601 185 267 664 508 873 182 924 019 939 284 834 732 298 449 561 504 779 954 421 619 216 773 825 147 983 688 263 620 631 007 458 259 858 034 501 194 590 736 457 780 093 176 794 288 214 488 943 971 051 496 960 585 616 186 160 799 860 648 868 264 669 416 258 892 094 176 820 959 161 878 006 204 905 003 696 335 680 016 451 047 523 491 056 976 288 770 657 311 402 361 594 055 741 308 413 364 533 116 546 924 199 640 098 565 519 451 576 880 319 752 413 050 007 466 820 943 250 752 097 408 055 606 617 654 969 021 256 815 148 098 749 799 680 057 041 837 574 753 268 241 753 357 064 163 766 466 618 783 675 744 049 743 523 037 913 328 442 832 044 562 928 493 900 567 375 272 480 865 382 457 236 901 003 945 517 482 663 113 844 895 080 303 964 891 144 952 421 972 419 215 925 752 845 106 168 682 473 262 109 193 348 911 336 394 603 418 356 499 711 296 090 887 464 596 931 874 844 927 247 157 536 143 940 428 786 196 815 179 562 222 438 793 766 275 960 694 798 825 353 596 934 598 958 194 870 891 442 611 731 220 151 265 843 759 014 634 179 196 933 726 464 544 369 959 795 610 700 376 934 514 863 291 245 642 301 720 156 013 613 990 988 091 062 273 789 291 589 391 936 128 170 584 947 615 841 932 112 797 623 868 784 428 661 991 936 722 386 339 574 133 376 335 082 731 528 904 456 285 242 541 425 036 527 413 331 860 775 571 433 000 480 034 573 357 711 205 806 974 761 146 127 853 223 511 102 612 545 281 498 244 693 481 492 150 500 779 503 443 732 687 823 530 094 073 743 236 268 606 993 279 126 217 784 725 318 983 523 199 009 903 286 090 577 618 936 805 792 954 461 859 428 501 422 495 423 166 715 427 582 503 036 737 708 621 059 121 999 878 130 029 247 802 720 482 128 485 428 428 562 496 668 322 686 865 210 950 983 530 308 890 011 952 879 966 130 971 942 283 049 374 600 490 917 936 067 569 049 725 156 794 163 617 688 157 588 322 973 591 082 786 287 441 086 170 117 064 652 373 053 098 190 826 464 725 511 315 473 103 377 312 878 638 543 758 536 807 115 163 064 700 550 230 864 748 863 932 170 281 308 493 315 699 233 717 246 474 308 189 190 225 257 587 631 892 182 901 053 319 907 754 938 605 450 212 259 031 674 984 672 778 884 845 230 161 286 653 766 165 474 604 073 575 687 775 332 547 625 082 470 576 540 164 994 317 437 006 454 803 738 163 333 092 626 428 537 280 338 377 525 461 325 459 961 001 264 910 599 000 595 391 384 808 658 632 520 640 867 597 933 091 035 536 127 131 319 077 122 089 714 488 602 388 837 453 058 400 448 265 984 070 122 369 795 594 054 647 930 971 956 424 041 943 124 199 433 986 635 889 438 923 926 403 726 026 336 009 723 976 771 162 058 497 973 027 650 146 766 579 073 114 093 145 127 226 846 335 671 934 737 690 393 779 739 663 779 137 790 028 522 224 701 623 696 001 637 134 014 651 819 480 112 524 869 379 122 094 973 693 232 241 866 631 054 967 298 893 097 461 818 880 293 883 741 707 412 044 008 585 946 139 270 575 660 521 393 739 415 244 599 909 717 539 166 396 389 398 026 255 021 024 269 611 969 880 901 799 601 503 781 338 639 202 192 053 748 898 705 235 613 071 720 928 289 997 941 678 368 528 206 849 360 189 060 409 449 344 935 882 618 720 528 257 545 447 900 435 043 122 649 465 846 751 834 776 376 166 314 476 548 627 366 253 417 821 205 638 186 032 785 117 332 001 676 341 392 812 961 860 451 276 712 649 527 904 948 884 002 386 393 298 429 067 371 519 357 220 577 759 198 800 793 952 649 608 354 953 478 368 960 361 654 288 503 352 445 591 319 209 133 145 505 948 889 610 429 405 539 521 154 858 748 490 976 128 660 635 699 890 371 633 746 051 137 536 880 038 265 471 232 424 270 795 251 231 010 741 991 273 726 703 788 741 024 741 822 115 656 424 361 652 310 059 383 203 326 990 823 582 746 363 413 633 503 608 513 333 775 995 736 793 635 793 421 672 265 923 475 240 718 897 141 295 463 880 979 826 770 514 643 195 619 169 338 413 009 292 054 066 056 860 249 690 862 154 882 699 555 950 080 883 609 955 161 817 572 297 671 258 606 795 044 119 734 269 486 906 677 574 441 011 053 334 348 988 376 238 701 527 870 688 157 002 346 576 050 413 096 682 176 025 344 750 789 501 907 256 253 702 846 874 668 342 920 091 520 678 418 045 705 321 193 216 257 572 292 595 383 389 862 917 848 773 024 162 022 774 339 575 504 334 734 261 383 935 024 373 365 310 345 860 516 242 804 900 784 600 982 091 143 458 638 363 094 357 160 141 267 674 234 266 422 193 652 875 123 254 637 589 532 176 506 635 265 895 731 295 425 772 269 427 019 769 212 022 029 977 300 720 237 408 464 042 109 861 894 441 390 241 847 907 658 673 315 166 690 813 938 519 463 658 692 166 263 624 482 097 007 282 594 908 883 700 386 223 191 159 441 769 292 867 039 791 071 052 845 713 500 511 716 766 390 060 756 472 586 489 011 089 489 732 397 472 250 222 295 239 527 637 075 656 714 034 674 914 597 518 894 717 091 977 256 871 517 479 856 889 342 413 892 566 979 895 755 082 721 069 409 250 143 864 741 692 445 702 809 736 127 660 347 635 061 706 745 294 359 062 986 977 569 220 571 757 870 041 769 458 187 565 461 458 211 646 421 089 785 428 454 983 781 899 324 126 449 604 839 341 925 784 777 768 738 542 052 239 123 483 958 710 603 992 030 861 327 760 986 372 350 053 022 937 543 840 774 619 479 122 030 337 747 858 906 777 546 658 150 650 455 480 246 232 685 947 166 886 479 335 737 798 977 253 457 745 396 547 443 328 865 188 735 021 688 008 115 266 203 184 093 328 348 330 152 605 862 387 713 748 530 604 679 544 868 175 058 434 255 854 013 974 657 330 525 679 219 547 612 406 812 280 295 740 241 924 071 174 686 041 096 263 672 440 264 497 706 037 506 433 727 514 604 582 811 892 496 439 989 441 159 215 698 451 143 939 922 513 355 659 142 714 566 918 074 066 066 021 740 899 054 479 416 651 718 690 776 474 147 736 752 664 783 906 148 670 470 877 503 869 691 858 227 383 912 304 837 313 749 576 135 838 056 536 239 058 808 164 619 341 448 549 467 238 505 336 697 958 515 878 834 148 994 967 194 201 896 239 843 799 911 810 609 491 669 845 093 636 948 033 991 727 946 721 671 992 623 326 054 392 709 566 505 144 321 965 773 152 965 336 209 654 882 115 989 166 954 187 438 661 622 876 352 664 076 738 573 699 653 949 490 218 149 118 623 042 982 913 373 383 907 065 654 029 798 797 762 423 851 040 744 578 647 249 369 193 699 255 421 658 583 646 976 984 464 870 348 304 638 914 352 764 868 087 505 548 432 828 849 172 978 778 153 787 914 284 695 440 902 136 277 652 695 479 401 724 276 900 224 544 638 473 486 473 624 976 284 833 179 261 718 369 908 460 081 276 068 609 715 890 314 776 741 943 157 392 022 948 315 205 002 680 896 306 336 286 919 119 832 079 326 768 201 571 672 684 132 690 462 020 323 421 682 712 161 479 458 052 701 455 957 316 898 287 339 539 230 223 052 381 088 530 241 737 145 225 285 024 190 833 769 842 578 475 827 923 902 543 563 546 611 406 122 965 882 863 108 003 380 653 459 734 961 812 968 417 671 830 596 582 137 679 625 693 995 904 685 458 581 178 053 970 935 034 096 880 331 869 277 206 718 004 900 483 736 875 490 311 067 216 214 333 718 313 403 281 752 293 240 529 887 726 809 445 782 818 807 677 335 537 553 906 811 450 001 356 282 585 679 320 183 162 981 682 867 672 709 894 485 930 768 309 380 623 252 273 013 115 688 223 981 763 505 054 510 495 638 752 781 879 934 894 067 861 310 263 056 320 786 193 976 663 163 077 525 741 443 814 039 983 314 926 095 306 526 922 615 370 657 803 956 486 282 328 723 184 612 912 517 978 093 245 772 733 321 634 815 679 147 557 544 407 939 661 578 876 993 194 390 357 369 623 545 636 242 148 181 145 169 687 300 597 321 484 481 658 889 563 083 746 594 137 260 184 165 979 596 578 800 372 430 534 658 799 255 957 232 310 506 845 156 534 213 851 024 642 362 025 511 201 024 572 812 759 573 520 707 637 017 551 262 593 852 542 488 181 181 898 132 752 030 032 908 832 444 845 845 296 972 077 958 680 350 171 382 029 322 749 478 255 562 784 349 723 325 496 740 201 765 092 991 361 098 094 459 497 595 264 271 881 686 387 922 504 500 773 566 723 249 884 249 823 334 792 727 695 239 887 398 159 393 722 876 437 827 097 438 100 139 342 374 862 497 183 598 720 859 821 533 295 443 640 432 539 701 057 923 405 128 745 308 952 271 001 606 556 476 607 215 210 515 569 715 126 275 825 120 478 018 453 413 488 316 125 707 020 646 737 544 273 987 405 445 130 187 275 948 678 572 799 532 458 686 343 235 635 565 562 762 628 961 430 589 049 249 245 985 477 878 099 185 260 880 616 395 461 178 318 372 235 247 789 774 364 549 928 615 085 213 243 921 459 449 585 661 851 326 773 135 706 951 848 282 073 639 527 714 403 361 796 587 785 087 538 748 908 331 306 862 341 092 181 707 951 240 337 606 386 501 351 745 182 278 224 684 475 536 206 666 045 444 670 009 135 842 635 903 951 629 281 498 130 181 574 749 555 232 951 930 900 801 197 337 479 546 617 477 000 073 310 737 244 071 012 608 063 671 648 725 790 592 169 843 253 535 729 201 456 224 124 082 646 931 397 713 014 719 907 080 410 555 532 151 346 558 323 792 135 278 417 869 952 487 868 276 040 266 570 415 161 611 850 697 017 061 027 533 219 796 924 907 933 154 506 143 772 856 679 560 067 142 671 339 768 030 138 758 908 013 727 262 002 325 924 870 861 758 824 924 255 500 149 677 669 823 826 599 017 481 051 627 217 464 132 830 693 491 825 240 947 996 329 838 970 906 687 467 902 224 840 969 567 108 153 735 251 898 104 309 788 210 486 561 297 572 281 920 087 214 478 929 004 994 952 718 972 514 811 035 912 433 118 491 282 783 712 163 289 607 266 148 531 951 946 057 955 490 938 476 150 355 316 943 579 122 489 884 198 123 571 866 562 118 019 338 013 604 263 836 132 454 850 733 804 074 248 876 946 325 622 896 507 915 218 212 220 222 179 211 246 318 254 337 986 514 705 800 043 203 216 266 231 694 288 586 802 649 019 372 597 736 754 404 007 354 447 795 662 492 076 055 578 262 931 827 582 245 705 676 083 655 713 900 102 916 690 867 910 955 286 994 446 482 753 282 934 707 610 000 268 395 404 264 039 492 109 242 479 088 734 559 183 538 171 948 205 119 577 381 641 691 602 016 840 908 137 706 675 613 581 849 602 423 310 300 903 590 671 931 577 651 087 166 694 702 653 868 978 337 924 189 460 625 211 140 030 146 606 430 607 128 963 544 722 589 970 559 095 638 790 734 664 015 418 749 035 118 721 988 344 905 469 001 019 112 262 009 240 717 784 415 940 101 231 327 907 114 011 979 081 190 157 311 630 957 655 391 579 175 332 703 754 934 008 324 545 609 017 437 602 451 504 412 039 338 496 074 815 609 000 362 853 403 713 849 388 897 792 253 234 820 074 551 943 024 669 923 680 336 485 018 378 120 217 305 553 812 566 357 030 736 798 717 112 060 504 442 978 082 218 217 307 768 140 127 449 639 548 556 150 468 858 682 176 613 185 995 192 225 558 779 308 407 669 090 166 049 176 516 842 253 928 112 070 315 424 086 584 848 671 276 603 019 206 405 239 570 609 494 607 244 177 515 792 385 264 929 855 221 316 935 929 933 054 420 742 103 150 195 665 179 573 508 751 736 767 824 278 494 186 623 643 132 253 905 599 614 027 963 044 583 917 779 803 898 819 825 009 343 338 134 613 516 441 971 648 389 374 077 871 901 267 536 226 159 370 838 806 835 165 387 337 429 251 063 703 022 707 528 661 646 241 393 724 100 768 519 106 323 756 341 647 678 276 839 899 711 971 789 897 789 043 599 343 760 064 981 686 978 244 599 496 133 055 124 273 516 956 661 319 984 804 225 860 605 038 247 279 123 340 176 219 890 388 299 589 824 439 012 273 317 220 823 148 133 903 233 973 111 891 480 889 696 123 531 322 960 147 173 450 959 045 291 824 052 457 682 336 402 386 577 668 279 682 231 085 458 464 981 194 998 191 838 415 410 788 169 877 236 903 052 355 151 753 939 949 517 577 620 672 217 402 583 536 028 903 255 973 851 069 188 321 067 842 907 834 998 100 093 060 367 784 887 753 660 644 586 798 304 828 241 822 085 679 959 324 245 993 463 179 864 823 370 495 672 830 060 547 467 145 024 476 233 036 542 823 972 425 501 448 815 295 492 184 480 812 829 299 763 009 194 363 423 820 134 827 776 535 486 540 859 850 313 507 692 492 562 027 590 145 061 324 427 989 246 633 662 408 347 463 111 633 504 977 000 081 387 623 099 283 705 180 247 346 361 321 859 744 317 281 970 725 138 884 587 708 502 303 228 030 350 816 197 603 819 603 421 572 710 699 646 540 090 979 563 700 889 821 869 541 676 575 474 954 036 177 834 489 261 892 020 629 680 991 052 013 225 785 832 405 766 705 320 787 377 018 739 886 847 062 214 840 597 230 699 963 491 833 267 125 434 450 868 788 007 495 725 784 990 336 179 866 185 534 064 880 840 848 602 681 879 721 296 314 655 294 043 281 414 814 258 020 111 960 425 918 401 611 032 660 220 353 087 760 223 708 534 949 285 339 347 485 435 871 620 660 267 652 686 128 865 982 930 613 058 808 958 101 096 738 990 730 376 339 280 147 282 202 794 534 584 800 438 301 116 422 047 066 974 095 058 887 783 995 899 939 185 892 708 253 542 157 456 720 055 785 772 782 141 669 574 932 160 970 544 078 528 689 103 417 391 456 871 134 495 819 203 617 368 295 160 761 246 394 089 173 826 284 762 635 014 968 823 518 408 403 538 005 905 309 830 988 772 900 057 961 423 375 129 316 661 723 550 420 923 767 383 715 354 102 978 182 268 144 704 299 084 920 169 478 396 835 573 100 175 176 127 449 585 947 963 151 169 567 051 244 602 031 151 902 614 389 277 140 483 232 535 879 043 947 204 442 462 816 219 610 902 814 569 471 507 024 561 890 378 982 210 385 487 682 212 604 505 492 162 541 704 189 757 084 637 528 493 974 075 671 838 694 798 880 965 289 513 788 504 934 295 856 501 425 756 244 938 317 631 492 824 227 769 251 379 422 195 887 125 047 116 509 254 424 728 863 656 579 844 125 458 284 998 703 836 291 348 518 596 847 239 083 720 233 620 168 733 395 248 354 148 445 844 532 604 867 047 399 049 559 626 863 127 326 482 715 677 548 424 816 999 510 108 402 314 366 066 390 007 765 161 997 110 553 408 993 711 770 672 836 205 328 994 721 076 536 292 672 997 756 838 150 443 797 264 308 273 430 929 775 702 921 665 124 270 167 245 969 838 527 787 639 221 627 392 298 313 995 843 650 928 884 193 545 164 516 547 636 010 671 563 674 940 764 924 581 317 036 314 124 734 830 012 539 382 937 884 617 467 583 686 348 184 924 541 604 458 657 580 569 572 052 828 040 779 329 556 331 758 370 740 533 963 086 284 281 016 457 361 553 222 194 458 676 057 044 013 107 805 541 366 441 960 346 218 878 603 194 925 215 215 677 981 543 584 990 992 900 504 116 360 023 356 854 843 506 036 404 773 157 481 798 040 458 266 579 268 972 970 216 477 944 196 864 558 412 428 884 834 431 211 021 233 572 083 266 155 405 458 851 522 580 603 336 512 661 496 049 723 448 830 363 552 788 347 216 206 317 331 873 834 748 454 978 068 231 262 736 492 703 261 882 193 406 374 094 389 633 967 602 552 533 243 635 585 616 004 627 426 545 465 070 173 917 879 929 641 913 905 209 242 369 314 970 472 134 510 612 628 389 331 829 874 380 713 247 139 839 630 156 095 620 716 087 536 490 177 331 228 190 959 569 729 375 321 864 199 507 974 372 087 576 596 808 016 020 449 971 938 648 081 288 604 128 176 250 092 963 462 337 986 981 342 885 075 678 433 876 683 277 321 017 936 141 206 301 272 413 414 215 029 879 741 915 212 833 330 752 673 164 187 250 222 486 626 039 197 634 039 613 873 282 784 681 963 390 175 037 630 080 566 235 535 223 195 932 309 533 513 865 821 283 787 499 937 514 419 180 205 339 876 457 767 867 665 877 925 638 587 875 705 495 657 227 315 971 502 286 618 144 167 999 698 854 868 604 946 408 754 851 879 513 193 107 829 342 951 676 282 089 406 312 354 250 285 215 265 302 313 959 906 591 298 242 052 334 079 531 390 906 491 382 904 734 717 132 165 937 752 803 979 454 652 787 518 764 723 072 527 325 030 384 395 280 566 852 323 911 557 545 953 594 007 828 807 441 387 746 442 709 294 457 149 538 620 512 144 268 195 248 319 110 255 735 497 189 023 022 827 676 828 538 177 303 619 500 375 038 129 293 676 540 392 677 181 720 815 271 779 551 961 288 154 672 423 425 761 116 540 861 096 329 225 412 481 497 968 817 607 575 242 095 077 631 929 655 333 263 255 735 117 323 658 465 444 937 444 806 855 984 176 772 571 133 270 643 920 171 305 100 679 514 266 204 054 092 445 293 928 333 104 670 067 724 857 772 829 766 246 575 666 367 849 526 986 766 328 150 743 946 342 885 647 448 356 891 532 994 678 516 556 472 707 120 472 053 447 741 137 251 827 162 609 484 992 370 753 197 933 494 763 786 666 064 473 669 125 228 146 942 260 371 339 829 765 625 469 805 016 654 678 117 153 371 198 759 426 036 503 365 459 257 757 236 961 033 619 953 237 677 800 965 371 722 182 920 516 342 830 447 441 674 927 370 980 257 454 273 640 339 944 228 670 603 383 251 959 499 358 488 949 442 133 039 992 126 638 132 343 651 135 242 416 451 893 134 714 016 697 582 334 824 617 854 268 588 857 084 415 579 584 423 052 399 662 287 185 070 136 616 614 670 151 508 347 840 827 408 861 703 751 327 564 166 119 717 102 713 125 774 966 381 444 459 116 340 312 910 067 546 089 431 449 552 469 294 262 632 716 391 038 204 272 432 611 180 604 933 742 352 949 097 224 528 157 280 229 065 881 846 899 280 463 066 219 923 826 818 298 893 574 058 426 830 597 714 243 965 708 521 979 922 653 124 069 286 136 417 272 134 019 273 042 540 749 072 903 592 038 418 209 629 107 614 145 448 515 334 883 610 272 505 605 077 620 611 014 696 888 427 521 991 713 275 028 390 985 325 828 565 612 966 619 501 924 880 590 888 019 066 444 890 720 692 001 862 835 058 235 775 683 020 080 903 307 614 710 162 129 853 535 918 114 623 663 783 347 800 042 059 083 159 644 848 925 027 837 683 917 789 539 308 732 347 188 425 499 989 496 487 537 805 437 918 204 995 503 087 757 615 455 908 628 056 804 101 518 900 130 026 592 111 076 365 305 805 665 657 924 370 990 946 814 310 798 850 234 527 940 133 451 333 562 732 561 563 881 208 735 714 597 523 858 828 216 240 673 962 978 088 660 717 260 238 574 903 180 396 052 195 325 051 248 643 279 145 715 143 476 671 011 502 971 572 732 250 646 111 687 679 373 115 188 518 250 149 398 139 706 166 983 583 916 242 788 089 794 015 268 229 953 947 389 298 891 025 043 685 235 945 110 797 515 445 093 530 766 136 968 152 073 453 800 030 835 194 977 165 586 317 926 430 494 803 001 454 640 417 033 387 467 483 856 866 515 541 575 873 600 647 995 732 331 680 719 520 428 222 092 060 095 482 271 536 611 742 486 333 675 441 974 301 722 244 937 191 886 539 071 229 949 359 753 079 385 910 663 513 870 604 627 736 595 280 789 864 441 517 643 992 890 266 039 132 256 821 589 433 812 700 680 444 110 607 645 730 961 040 414 572 301 463 950 232 669 032 996 603 937 861 497 176 943 303 018 185 339 251 406 195 552 649 302 994 521 712 696 559 096 654 316 924 693 899 191 774 290 175 891 617 897 360 227 119 003 333 046 661 670 626 400 085 240 418 885 929 414 927 109 738 634 357 438 984 662 897 210 047 442 064 761 923 916 277 205 258 376 053 816 721 320 502 160 737 569 675 519 222 789 384 473 322 160 205 844 554 034 645 095 965 783 906 723 796 496 190 660 390 685 539 719 841 995 520 442 365 012 729 213 632 441 509 975 047 090 935 753 639 481 806 000 100 091 919 384 006 897 446 248 471 319 678 437 629 111 499 986 442 038 766 075 030 408 326 984 060 771 245 735 330 348 097 465 591 048 728 653 726 655 749 330 017 571 131 313 298 424 209 059 735 939 535 511 017 438 457 532 233 198 836 342 398 201 159 548 878 522 158 701 822 378 498 038 512 611 376 261 975 510 200 863 043 123 778 411 593 383 528 737 745 187 073 472 161 804 995 948 379 984 689 860 271 194 548 686 105 743 902 440 196 215 857 627 150 240 325 386 711 403 918 627 408 818 347 410 793 776 189 792 171 666 819 563 434 173 106 417 985 691 591 094 733 247 858 814 087 113 552 388 636 183 404 456 989 379 646 283 092 388 170 024 256 634 890 535 871 715 957 728 246 411 342 896 370 485 394 482 720 418 909 720 593 701 658 769 236 067 743 482 242 983 952 912 357 265 959 085 634 552 654 034 527 396 723 738 119 715 906 941 180 130 222 723 258 035 661 880 153 617 119 455 219 287 801 565 140 745 927 507 735 865 126 693 160 117 072 879 581 133 605 865 143 141 364 644 303 315 661 362 750 134 431 305 466 532 437 516 387 061 016 038 040 027 405 524 442 136 514 932 015 824 259 036 355 309 674 159 528 159 008 633 028 999 774 273 831 419 540 132 768 538 370 087 718 719 829 402 099 427 814 425 334 715 390 020 031 840 094 819 062 442 775 504 585 898 130 746 459 775 403 008 774 215 559 815 142 795 550 322 307 161 761 708 583 745 230 464 565 471 444 630 144 704 229 397 504 715 854 724 227 750 825 851 413 677 504 664 791 516 617 365 012 004 932 040 622 768 994 775 612 642 199 205 370 924 376 635 541 434 250 093 982 680 834 986 025 808 724 897 829 472 976 634 525 973 265 617 214 278 305 044 143 890 104 128 707 425 561 304 984 779 217 168 192 197 940 455 143 846 192 035 066 085 541 419 755 703 409 926 333 528 455 189 502 345 319 053 696 375 996 391 631 513 344 617 875 259 265 560 233 204 934 869 911 401 375 199 989 269 521 713 707 804 927 893 173 416 629 275 950 288 455 029 967 014 292 255 916 323 397 940 399 301 236 700 163 520 299 193 644 470 420 988 544 853 275 382 818 533 535 281 016 003 690 186 889 181 382 379 555 462 768 151 971 843 555 681 312 153 296 990 431 428 942 288 246 611 663 536 091 109 409 543 541 504 196 137 662 168 694 849 148 446 345 227 109 078 010 876 861 904 803 225 611 267 334 745 915 121 785 531 005 275 738 724 874 900 004 307 321 905 392 745 981 371 796 219 528 257 695 295 110 029 268 289 826 798 526 508 078 887 195 254 567 821 510 515 060 048 210 867 900 780 790 361 218 668 069 753 830 850 302 422 930 222 830 201 800 797 468 633 037 337 710 062 278 498 110 582 361 455 613 326 494 357 097 437 137 441 058 781 574 608 402 095 073 546 175 376 720 823 030 453 322 566 847 358 723 366 388 065 623 506 149 709 765 800 703 887 950 910 039 842 348 938 479 258 144 225 587 784 679 970 290 690 465 756 144 014 889 380 009 566 487 130 559 290 813 179 584 245 819 111 269 668 880 868 599 653 721 777 827 362 865 778 198 647 471 336 227 560 324 249 335 923 715 618 240 838 131 986 022 767 587 363 386 436 194 668 696 503 773 174 865 910 451 932 909 141 434 917 494 732 876 442 973 519 703 340 736 456 985 862 795 926 242 436 656 473 020 002 136 790 287 429 673 740 869 995 204 084 615 564 519 596 854 024 493 440 795 669 208 592 693 412 730 938 113 553 478 184 424 273 384 725 723 275 467 162 562 176 510 425 344 477 131 982 564 107 802 265 198 763 346 525 190 583 546 709 915 761 783 763 932 219 561 211 009 436 311 278 469 543 528 467 779 283 435 759 981 107 593 018 310 706 861 577 060 655 385 869 592 147 361 327 989 620 797 465 722 427 232 702 329 189 069 131 318 041 084 062 858 441 438 601 963 711 307 967 927 021 914 089 999 678 852 280 437 359 295 054 321 209 776 655 568 265 190 184 412 248 713 321 523 959 539 513 963 423 486 325 548 065 540 488 979 935 354 594 868 097 845 609 866 889 212 915 519 641 801 080 572 492 493 297 532 286 654 943 836 547 957 945 029 692 058 320 551 440 436 892 423 159 671 246 570 179 526 751 639 485 156 808 981 070 588 899 017 652 153 746 119 631 849 721 955 693 205 682 282 404 146 001 155 120 586 831 327 412 097 491 201 528 541 682 980 597 280 303 151 614 826 021 123 385 966 951 501 474 571 308 766 901 243 895 306 756 848 336 176 383 480 556 392 702 754 951 306 774 906 709 288 776 401 908 855 087 719 033 230 754 989 613 505 018 807 061 826 507 885 756 154 141 680 258 779 595 875 403 202 425 047 285 982 499 939 325 877 147 443 589 731 707 340 671 580 800 519 307 280 899 800 269 116 583 629 472 608 181 125 939 178 423 088 210 952 130 037 227 187 784 855 883 953 965 578 025 177 670 210 076 946 450 897 206 709 965 740 627 174 498 198 920 399 500 932 827 490 661 708 596 350 891 174 939 189 542 531 746 719 160 547 016 022 462 800 447 941 722 900 074 179 845 374 972 836 766 043 028 789 395 967 649 476 960 339 684 635 664 965 332 827 395 125 636 893 738 139 823 820 388 752 658 169 367 927 454 994 429 381 252 819 144 429 152 774 081 548 489 310 630 761 462 350 271 299 423 698 479 138 497 149 736 515 143 301 783 925 412 880 374 423 725 743 600 511 668 362 324 309 994 054 280 475 107 869 205 659 947 689 143 312 833 203 943 878 126 848 288 095 424 858 521 955 218 901 808 074 531 425 039 053 297 356 762 807 934 894 559 283 314 127 007 186 647 476 845 070 759 525 594 799 406 792 101 165 223 793 993 498 442 573 183 796 049 002 655 177 777 381 329 600 954 986 616 473 664 085 415 045 390 742 831 888 311 691 757 686 460 278 147 584 801 643 927 974 417 456 388 208 463 074 674 193 896 740 094 770 505 663 195 162 799 278 310 779 289 021 359 682 780 290 189 994 919 404 916 222 582 062 760 040 937 293 532 975 508 723 530 993 760 453 294 423 614 698 218 643 736 413 466 889 748 430 419 406 816 554 804 411 219 654 782 553 518 720 351 588 169 954 053 625 506 017 297 291 644 125 826 031 664 168 048 462 551 023 895 291 105 018 725 804 790 056 159 231 640 836 688 441 193 660 449 220 866 256 507 239 219 957 063 780 890 465 815 246 207 299 487 179 844 395 351 708 848 405 964 362 723 232 053 235 545 907 474 235 005 317 066 163 540 256 593 287 016 887 929 372 072 215 467 287 130 553 306 361 336 299 925 466 419 791 120 222 114 998 012 148 995 366 454 449 324 813 561 698 892 159 613 910 317 738 626 548 620 996 858 494 720 981 575 227 755 887 358 982 114 990 709 370 204 886 108 990 732 215 158 591 450 032 414 760 369 096 706 518 897 235 884 377 599 088 733 996 630 812 416 708 365 989 492 126 547 464 327 378 619 701 158 986 894 953 100 454 947 859 785 456 521 015 969 406 251 578 509 471 016 622 740 138 480 978 716 228 590 070 838 592 115 033 041 431 994 661 307 748 607 652 911 919 073 745 828 498 646 007 874 923 845 100 079 355 413 627 180 145 074 490 485 739 789 008 100 128 577 510 017 511 324 636 090 203 123 421 982 835 049 245 354 961 025 916 868 768 386 340 570 718 021 560 122 697 827 651 813 812 346 118 279 457 904 727 139 050 052 622 001 394 835 396 526 659 651 631 446 202 501 192 867 663 565 023 172 071 663 279 482 038 256 398 646 356 304 614 354 295 574 285 036 505 175 326 667 579 602 868 683 535 035 062 383 416 520 522 876 357 148 295 349 637 746 088 135 010 397 960 754 481 453 842 391 758 412 802 702 287 176 948 715 434 225 257 522 982 227 185 725 555 741 197 664 413 496 761 428 861 483 188 240 487 587 153 840 786 932 131 006 608 120 232 811 178 952 559 434 382 260 068 369 024 089 331 847 108 110 791 389 028 607 707 134 753 263 544 360 370 019 460 022 420 507 559 361 795 992 065 972 632 707 089 837 866 711 419 852 313 101 957 836 628 298 026 721 966 535 607 991 397 517 180 678 154 709 019 305 201 800 998 347 793 440 081 467 057 998 208 648 085 752 064 727 490 104 509 619 753 559 784 257 042 226 437 889 718 304 859 511 169 652 342 456 835 859 143 195 504 998 497 573 384 647 791 499 203 392 135 333 441 472 434 195 711 592 997 434 433 376 078 660 445 537 839 222 061 633 830 892 996 166 508 335 159 855 339 614 493 127 487 673 033 548 545 559 347 296 513 666 745 624 398 449 472 874 784 868 247 521 484 837 003 011 117 661 258 628 771 552 471 460 139 328 751 776 893 915 500 065 832 492 037 173 967 934 975 404 611 500 901 356 358 366 176 227 281 814 059 345 005 745 708 938 870 791 363 297 950 026 871 559 416 023 489 407 648 262 296 811 279 581 123 484 830 715 105 306 545 852 397 419 994 946 037 441 551 017 228 829 672 542 898 681 383 045 730 669 911 762 196 998 210 440 742 286 831 282 430 830 337 298 087 851 521 236 497 306 726 442 594 062 601 128 900 001 726 961 063 189 271 049 798 988 700 378 881 096 225 258 325 998 735 273 114 980 823 952 424 878 203 777 188 812 438 043 188 435 784 321 708 563 157 785 683 283 556 344 602 627 043 635 209 814 096 103 341 705 501 718 690 045 178 021 317 831 647 631 283 860 791 315 152 024 611 237 593 254 427 056 598 946 414 555 462 414 443 245 662 829 707 614 601 016 800 814 058 934 236 743 290 931 005 068 985 702 907 449 888 419 484 037 834 900 155 118 536 651 463 490 088 049 445 815 532 472 925 283 138 366 218 379 720 706 329 298 329 154 535 532 291 757 501 966 082 288 893 980 879 095 478 972 145 286 845 774 945 428 807 459 378 624 384 190 513 832 611 475 906 880 209 168 512 230 087 816 026 693 542 340 420 388 486 849 180 400 605 146 291 721 694 884 624 848 394 850 142 207 563 262 482 250 909 692 704 713 637 697 829 004 019 538 583 484 800 196 293 076 174 405 292 608 668 537 047 832 450 979 676 899 902 580 538 110 661 558 510 428 612 257 296 624 632 060 463 708 634 897 526 826 262 690 898 140 256 914 372 824 944 431 233 651 921 459 969 221 422 027 794 883 860 257 045 556 711 863 517 020 036 070 039 230 153 074 773 095 354 322 201 480 727 980 797 224 257 664 054 878 001 936 703 026 922 285 927 300 134 212 428 975 892 671 161 351 546 839 841 215 194 308 014 214 768 768 498 077 037 063 752 708 798 565 939 883 674 469 195 196 027 935 634 506 193 532 512 760 412 374 757 134 593 902 271 152 987 420 850 000 758 370 160 171 642 828 397 560 418 809 317 788 229 733 156 837 996 928 112 776 948 239 845 178 512 955 100 261 203 348 816 792 148 631 405 193 776 315 417 784 850 618 385 932 977 052 238 661 222 347 786 541 611 614 910 881 687 565 973 147 720 863 078 502 925 784 029 311 012 164 030 464 106 465 435 613 635 161 289 808 922 851 181 967 911 540 707 662 507 873 929 945 780 939 305 638 396 934 546 335 681 979 117 587 662 411 044 379 622 407 073 430 672 891 795 773 830 966 856 940 129 584 365 355 831 163 197 495 019 264 947 920 103 736 258 972 545 878 447 201 473 921 900 540 869 765 919 829 166 349 664 106 934 565 357 457 127 632 251 815 442 045 230 948 863 457 016 906 934 543 402 865 363 507 709 186 962 720 107 412 669 781 981 289 805 619 892 635 163 643 398 114 201 058 697 209 447 806 770 963 180 158 614 689 518 927 517 448 482 441 685 251 763 637 103 264 469 917 023 110 921 966 858 871 389 437 158 524 132 876 800 001 801 470 687 332 783 012 949 180 056 936 620 208 272 714 959 867 226 642 242 262 942 165 470 663 556 549 915 693 134 223 795 667 304 128 531 357 396 862 283 277 307 728 742 746 192 523 216 094 456 935 342 728 436 384 917 957 048 665 272 289 361 884 989 739 031 831 249 076 568 423 779 623 188 446 760 557 815 841 036 707 985 383 941 158 896 578 621 518 955 476 301 142 414 626 482 646 958 632 417 384 794 486 594 341 767 172 656 628 337 372 004 792 467 098 666 223 399 795 963 951 033 869 656 519 361 691 042 248 467 824 059 291 259 074 828 854 425 246 138 097 190 868 113 689 859 543 915 337 322 089 961 615 845 844 701 530 172 140 680 254 748 304 128 090 453 252 074 199 830 207 790 501 215 958 092 112 927 408 212 000 562 957 844 783 577 847 043 909 795 912 231 558 635 413 786 697 736 697 128 388 785 120 972 549 825 858 310 779 113 687 583 589 330 691 272 512 362 488 675 365 799 857 977 816 832 079 782 275 916 931 815 255 195 658 133 629 032 089 351 047 286 130 873 965 732 138 205 237 435 179 528 701 091 673 056 718 244 019 645 770 127 469 335 818 185 839 333 702 367 178 813 426 965 057 391 982 688 421 381 940 264 894 407 479 855 197 920 689 282 748 491 869 404 335 001 393 984 078 106 169 186 197 657 162 537 537 892 206 389 515 122 578 580 900 462 277 256 136 106 456 667 947 814 216 200 232 700 891 768 820 448 588 189 054 036 891 175 924 692 791 685 662 783 183 896 724 002 411 633 539 355 560 881 048 544 056 894 231 870 946 768 604 393 233 043 175 968 346 778 442 355 011 580 806 440 700 717 467 333 138 954 121 012 250 255 684 741 413 300 116 299 536 714 886 242 009 204 585 893 760 544 318 211 822 120 897 747 253 616 754 343 652 461 965 588 744 578 518 705 576 118 888 976 158 004 152 912 213 066 720 036 952 616 117 129 786 953 352 395 884 042 274 434 800 228 539 679 417 846 289 815 862 762 579 797 099 722 007 382 402 108 516 475 568 396 068 437 809 626 721 841 843 116 681 741 135 335 874 029 754 521 221 261 360 766 363 902 742 144 193 066 849 411 529 270 796 819 287 724 762 888 415 558 734 228 731 958 108 039 281 397 022 378 256 579 608 760 058 553 362 308 878 063 714 268 600 122 285 069 734 100 383 932 267 720 815 545 661 497 833 116 355 333 872 941 159 940 705 698 324 220 037 844 275 233 433 977 658 298 298 861 130 015 520 636 459 624 446 252 933 933 915 032 905 121 868 229 825 557 017 738 673 436 444 507 560 924 676 389 656 141 853 086 064 532 924 145 397 587 469 369 792 910 561 450 484 265 408 653 720 711 443 403 921 877 155 909 007 106 334 640 131 708 620 768 840 604 487 930 294 577 445 899 440 006 441 648 357 884 790 576 210 673 657 847 474 536 066 227 452 054 498 831 543 996 938 161 884 976 039 436 752 476 471 905 555 708 185 182 726 049 054 805 751 921 155 621 993 382 353 644 373 174 958 956 373 819 310 489 368 156 741 373 745 324 681 001 768 463 158 569 338 777 961 946 721 755 676 391 884 875 273 826 207 998 903 712 315 161 266 607 874 621 157 687 340 956 028 987 120 954 404 330 024 795 115 920 460 186 908 695 788 267 011 217 436 882 622 503 600 280 863 726 051 110 662 229 908 174 161 152 124 526 138 776 951 289 745 758 300 003 290 058 431 204 156 883 281 388 187 287 784 989 538 949 384 350 141 489 062 658 287 693 534 475 479 027 620 850 372 056 834 986 685 373 128 647 946 678 645 244 995 186 248 985 072 099 568 986 567 169 032 868 797 924 142 616 304 001 910 065 217 409 712 951 524 721 239 554 623 920 490 826 414 487 439 738 329 404 401 671 948 577 477 558 681 039 878 118 210 515 084 039 376 371 307 788 822 601 867 402 802 410 361 624 240 593 284 854 262 617 211 355 383 267 650 130 479 640 934 011 965 021 521 282 559 776 955 399 117 626 899 645 679 186 999 337 619 115 329 006 180 642 718 759 698 854 262 343 759 364 972 334 063 219 610 872 716 265 795 507 007 207 609 528 516 977 861 324 457 299 086 787 924 278 197 363 067 236 860 791 778 515 824 391 672 871 859 032 357 062 054 142 329 278 582 446 268 265 682 400 384 365 030 240 979 231 381 116 720 848 479 199 682 808 117 901 042 722 507 636 829 259 165 396 915 619 977 635 868 924 746 666 332 621 354 518 917 883 436 279 007 048 900 617 609 712 665 548 866 045 855 713 250 104 221 317 463 873 757 595 231 719 313 804 293 518 057 378 975 275 583 775 963 679 476 097 954 398 239 225 938 918 473 819 739 763 183 282 776 600 414 083 972 688 462 110 710 804 160 604 394 137 478 333 045 929 047 377 486 646 980 289 098 942 345 206 366 074 650 041 865 546 228 443 268 225 462 983 967 965 303 502 119 867 491 389 858 212 449 527 544 013 449 024 557 742 506 796 296 028 869 712 263 040 434 548 310 447 374 514 149 817 290 552 126 071 099 936 777 562 451 384 109 220 035 031 478 399 259 872 880 912 010 209 171 098 987 531 458 331 381 100 422 107 060 665 381 195 542 597 419 738 594 989 542 891 806 183 777 324 470 944 808 989 984 492 196 027 899 444 146 862 399 546 354 223 817 654 574 508 687 351 531 880 374 691 196 373 678 717 214 740 999 877 504 793 207 406 644 948 411 750 436 019 367 494 268 531 909 120 778 466 808 553 457 020 899 667 099 868 456 401 238 811 963 565 435 101 804 648 328 193 227 992 840 246 827 492 058 316 548 364 061 527 620 528 575 191 532 910 491 276 659 532 993 417 470 472 526 490 027 930 714 340 646 600 475 380 748 821 704 516 524 364 703 202 838 492 357 498 267 032 339 384 412 430 193 480 807 166 315 834 641 293 961 972 209 419 872 396 127 670 533 276 247 833 844 294 140 792 706 746 124 728 503 978 227 803 105 826 245 401 486 923 588 986 620 533 511 150 610 142 901 534 970 127 356 969 825 402 015 639 240 376 297 515 197 684 054 401 222 328 088 721 472 263 125 386 343 859 228 529 267 688 413 486 650 637 241 286 394 526 739 870 842 774 090 204 928 426 958 117 314 392 833 016 377 483 844 352 268 330 480 725 401 850 103 086 752 560 913 862 060 262 980 912 790 256 006 214 283 409 370 530 837 662 062 422 184 806 266 263 086 354 995 472 249 292 992 563 699 132 584 910 731 991 441 325 496 892 044 919 443 709 104 917 036 293 117 930 025 661 115 427 148 790 688 757 319 909 898 012 280 037 181 410 922 182 259 745 782 887 799 914 270 635 234 460 592 732 149 638 578 661 985 326 972 382 987 715 420 620 979 519 167 464 142 821 609 791 639 077 308 304 365 197 733 519 775 930 190 381 759 959 769 895 363 509 471 521 201 118 520 474 469 364 206 967 232 863 192 889 034 588 889 169 071 677 183 795 480 361 707 968 295 786 897 741 276 629 104 329 660 056 369 017 939 288 508 915 217 933 545 761 947 154 214 155 073 729 122 943 127 566 784 888 042 842 614 342 996 596 406 318 662 043 438 054 887 481 017 368 664 388 031 681 207 604 847 810 036 910 650 968 286 131 035 969 345 507 201 577 791 514 463 500 448 628 811 691 961 355 929 813 577 507 254 950 583 028 960 278 764 085 241 316 723 395 026 693 537 687 497 297 808 380 653 510 185 681 254 421 923 891 888 297 970 742 168 165 643 019 087 597 424 480 934 409 481 330 693 851 621 888 523 656 560 378 180 298 388 770 918 161 185 091 022 293 284 957 739 811 026 729 706 403 777 644 281 275 295 638 002 810 054 260 124 478 787 011 557 426 917 461 058 416 643 930 667 566 006 262 936 270 393 952 748 149 918 057 882 907 164 826 156 595 025 220 278 306 126 400 180 018 221 170 772 853 159 958 552 444 720 839 245 952 515 097 985 021 313 437 595 197 366 514 788 774 617 021 218 161 680 144 062 900 588 153 051 023 236 236 088 461 133 081 958 857 232 841 840 023 529 465 958 184 806 255 274 726 580 947 180 731 080 853 738 322 302 736 676 572 162 279 872 272 806 804 959 403 550 485 767 637 332 483 708 588 682 414 604 505 711 674 541 596 331 588 247 963 590 617 762 077 044 747 003 543 334 071 991 796 644 115 120 417 427 728 286 806 866 750 656 519 907 367 166 567 200 321 358 348 717 048 586 485 670 282 896 778 380 090 338 751 203 958 611 606 216 746 951 828 805 491 808 569 687 193 894 613 242 340 050 317 126 111 156 277 929 494 025 319 492 458 592 502 012 838 616 381 132 821 868 135 766 076 722 044 178 155 454 767 261 980 411 547 196 414 632 806 221 750 141 265 116 926 110 997 690 310 934 310 776 790 194 337 372 448 654 894 717 426 233 930 151 782 452 791 614 381 975 194 326 072 363 526 465 463 050 411 926 067 270 154 504 303 336 649 134 619 802 510 498 259 750 955 569 054 058 400 776 032 147 182 781 309 478 339 867 939 923 635 696 777 543 505 820 578 217 900 130 252 623 464 673 579 182 660 693 432 013 274 337 356 705 063 882 054 003 230 104 647 075 437 725 227 889 410 196 888 400 945 325 000 484 318 973 341 239 311 911 019 598 731 569 611 665 459 674 016 359 324 653 974 354 084 087 823 476 659 675 079 592 547 834 711 050 691 243 862 605 251 023 350 474 807 745 796 027 713 960 393 496 940 007 366 209 752 672 036 609 344 246 516 137 734 978 682 573 437 337 175 312 625 465 774 260 681 542 223 204 388 094 505 567 532 079 210 912 518 578 124 824 354 832 433 254 810 054 549 471 819 998 200 198 198 002 903 923 365 387 395 662 341 798 854 858 765 003 781 212 968 231 216 635 689 960 550 841 458 813 414 862 843 584 869 158 200 406 246 515 766 423 551 044 398 053 304 332 272 821 179 852 041 961 016 467 737 814 058 333 528 515 079 521 397 750 150 389 700 935 183 813 742 793 840 363 893 993 490 603 103 125 770 711 746 098 767 722 474 294 788 626 492 884 600 383 008 936 109 207 554 660 388 989 315 285 793 444 450 434 250 767 705 721 177 260 917 134 089 819 817 687 886 068 152 592 202 492 881 881 776 092 153 591 191 609 442 674 226 372 665 830 746 583 286 342 365 252 920 038 339 890 030 601 014 934 586 250 058 361 771 534 845 567 098 606 579 184 861 358 735 476 663 626 219 965 987 694 140 466 811 545 337 209 981 263 398 435 683 068 283 207 987 605 754 505 165 441 691 286 558 750 958 569 252 986 687 014 230 203 627 892 944 405 999 928 138 840 880 212 080 715 873 031 638 010 527 576 326 538 248 177 501 736 642 031 158 527 419 080 026 366 857 731 029 574 030 652 468 864 059 078 930 791 739 629 651 982 782 578 223 981 079 581 085 823 467 643 094 683 062 514 647 279 108 518 140 942 117 611 311 117 315 117 681 067 447 834 870 729 184 145 286 426 613 789 174 638 911 935 961 405 469 116 809 243 313 841 601 680 113 309 328 387 490 114 650 137 411 982 608 964 321 537 815 344 266 730 342 691 819 463 060 190 538 604 819 465 931 922 188 159 570 210 987 426 659 899 612 739 118 107 222 944 379 159 653 826 547 895 274 172 526 768 820 871 362 314 216 504 638 665 771 940 756 520 166 901 715 175 132 743 283 132 604 758 330 957 452 192 685 762 345 995 951 385 045 446 184 052 116 038 924 221 062 365 372 830 650 302 982 382 918 367 915 361 533 073 470 009 394 672 081 101 938 333 791 860 867 107 439 828 534 834 455 737 313 619 940 498 257 336 001 536 395 436 251 929 529 277 513 714 633 010 857 572 586 228 790 392 149 731 978 138 695 497 285 085 445 833 139 681 005 932 445 793 516 276 670 164 107 660 080 161 520 735 126 943 698 858 716 153 981 361 018 808 945 926 407 200 036 344 616 946 150 887 595 980 124 136 072 897 449 842 560 136 343 681 705 116 312 097 664 697 952 706 192 641 082 559 385 332 051 491 019 147 435 251 921 438 368 378 528 095 956 721 479 327 289 013 340 966 590 143 930 369 104 620 501 339 350 359 526 301 938 001 697 798 967 596 470 674 631 023 140 944 839 292 732 286 755 423 324 553 764 623 960 102 062 818 837 447 961 562 735 430 210 384 288 665 309 392 880 204 246 915 091 809 847 829 483 894 601 076 015 380 998 100 897 618 208 369 264 394 040 423 160 511 811 004 285 920 930 343 041 357 276 450 346 233 899 137 421 143 771 215 990 878 476 201 875 839 303 266 714 394 390 501 252 136 882 381 631 708 741 127 224 071 070 578 758 440 236 455 442 825 774 326 878 107 580 896 791 668 560 032 116 714 157 796 716 426 435 649 651 967 018 520 629 446 204 279 469 368 957 798 406 393 723 043 117 845 838 194 963 085 865 985 130 238 405 301 667 932 773 487 818 047 341 199 803 177 639 628 013 451 283 494 522 380 365 933 656 107 391 664 394 065 780 683 407 973 955 903 848 898 086 916 194 780 558 329 161 244 940 636 676 422 829 342 548 047 764 870 094 826 434 462 829 227 330 154 359 806 965 438 519 868 374 407 729 870 903 000 540 433 853 717 825 093 817 463 779 396 064 715 015 674 393 118 329 577 591 809 565 175 745 593 828 723 294 997 006 836 815 998 361 973 232 294 991 701 478 785 015 004 041 761 625 006 515 489 445 390 183 751 837 518 471 015 246 536 255 902 773 408 203 744 263 316 205 908 605 761 059 701 957 535 916 013 723 588 052 573 320 386 601 460 597 752 940 851 901 087 560 337 877 498 652 264 889 643 755 804 824 100 833 629 634 614 514 713 764 396 905 513 690 340 636 328 536 315 981 786 784 392 365 769 867 361 394 563 717 169 950 553 762 910 218 816 340 247 119 884 677 541 425 532 939 058 907 995 004 435 321 255 483 649 862 817 706 624 296 766 341 028 721 939 220 727 730 654 426 831 306 193 790 709 531 751 394 554 576 177 771 138 201 360 392 568 056 726 037 204 215 423 517 989 954 637 543 922 452 340 039 689 808 396 948 500 800 546 370 927 901 091 043 733 797 238 506 324 355 798 256 643 520 680 246 386 331 544 096 907 309 018 697 249 529 578 238 019 016 461 002 371 749 670 131 297 024 297 839 512 911 178 825 813 638 008 163 035 453 470 503 287 747 178 275 789 238 887 285 842 120 445 302 539 601 540 090 263 086 457 457 115 942 023 042 893 886 984 126 882 811 585 626 532 403 324 452 311 249 862 378 308 032 037 127 024 608 992 791 635 817 598 888 521 931 615 822 063 203 633 520 060 906 776 995 731 730 718 779 385 125 351 414 875 819 799 946 987 552 542 782 609 363 182 426 228 564 351 480 194 024 043 674 983 117 751 588 371 156 462 900 706 078 614 684 871 537 059 295 308 454 164 864 131 651 672 570 278 274 664 683 128 827 466 454 031 865 023 083 583 169 094 147 025 537 014 300 526 681 163 781 203 811 673 331 062 486 997 332 525 645 753 900 083 901 822 364 614 264 695 187 068 665 665 651 121 201 791 905 753 327 966 287 761 986 053 573 646 315 668 306 885 147 120 526 341 025 290 351 247 089 884 523 389 888 599 509 429 809 520 009 560 533 118 879 996 649 468 591 234 395 501 649 384 614 222 710 830 791 809 412 555 084 728 845 861 540 279 982 737 141 797 481 101 937 977 195 928 742 138 831 590 135 097 517 234 847 834 139 185 918 979 699 141 171 220 608 862 955 367 389 809 596 970 393 656 673 176 219 254 260 911 142 232 310 434 480 164 546 363 748 280 657 647 186 409 154 146 450 350 483 774 031 663 291 226 257 983 223 579 130 563 998 559 613 810 900 023 270 917 980 436 706 714 134 384 053 525 810 151 430 640 516 076 859 381 738 561 553 079 563 641 153 480 343 005 090 042 756 032 376 758 801 701 356 294 600 141 848 674 412 094 056 082 409 641 221 840 099 387 162 444 394 015 576 209 739 454 000 884 199 322 031 630 814 863 115 473 266 796 247 703 678 205 272 232 987 996 002 020 718 935 820 646 499 645 270 005 838 531 064 338 228 377 617 828 357 351 782 775 013 866 157 570 794 426 413 934 105 376 264 807 429 336 676 889 307 825 563 163 658 867 715 311 434 640 907 335 276 291 539 526 532 789 264 607 921 859 521 794 968 128 732 761 327 538 542 386 196 240 278 329 453 684 898 054 335 057 519 885 738 511 466 925 056 727 592 600 211 510 986 988 067 247 561 738 372 573 473 591 563 739 843 818 340 936 457 835 958 208 921 279 664 841 338 635 671 622 579 634 570 010 165 130 081 026 747 223 391 680 468 303 019 832 824 342 463 783 336 222 719 851 695 363 263 018 378 592 091 867 618 272 693 424 284 449 729 137 074 502 933 194 888 590 213 567 224 644 018 189 561 006 286 891 508 265 497 869 562 129 485 169 587 196 561 995 032 633 041 579 521 038 961 781 612 016 083 012 934 417 992 440 763 500 468 528 161 429 042 448 779 436 638 533 271 450 549 006 496 847 945 027 381 992 772 035 689 807 983 769 005 498 682 911 940 130 539 599 223 624 075 583 017 419 028 296 027 288 113 759 282 906 747 931 805 445 117 033 962 970 328 187 300 690 940 580 904 754 277 472 540 072 647 642 483 124 136 971 708 455 144 918 760 689 974 292 996 603 024 601 905 740 244 761 961 191 867 601 709 575 955 202 631 112 059 347 937 575 333 280 934 732 778 227 064 419 073 270 159 084 268 613 750 875 798 675 505 853 541 654 883 198 009 070 483 500 478 683 192 007 538 667 491 309 291 121 517 152 137 324 456 269 358 456 458 557 016 007 170 501 702 732 817 563 472 279 176 370 171 448 952 765 843 600 408 313 913 603 534 030 444 377 120 420 533 240 520 433 158 246 458 380 455 081 681 379 476 540 063 533 712 542 333 459 490 258 719 637 570 932 155 390 524 746 386 572 593 333 670 135 726 235 063 478 547 110 375 178 120 401 212 694 749 257 878 145 394 806 332 440 634 092 454 103 892 890 383 673 553 221 816 904 720 218 677 218 035 517 166 110 138 457 096 509 772 552 993 664 246 016 386 170 627 414 833 846 747 820 845 645 288 474 187 888 437 157 335 901 702 434 989 369 254 149 983 399 353 486 466 109 738 331 129 759 624 461 564 859 233 523 306 614 604 708 603 736 296 456 354 317 161 938 834 921 572 560 278 818 911 349 937 019 538 703 751 783 931 910 023 250 130 311 972 950 658 861 886 800 920 942 641 243 381 520 927 956 228 915 998 515 399 998 742 059 348 327 914 177 097 177 229 235 393 610 953 725 694 906 840 284 693 312 087 598 233 804 655 014 297 553 597 437 706 180 793 668 262 470 322 083 795 327 350 033 204 430 945 083 209 168 956 630 510 054 516 214 030 288 665 857 503 526 999 252 018 362 948 737 968 645 625 234 143 399 500 903 750 748 255 924 386 927 495 958 708 031 910 648 946 998 114 299 273 139 346 794 375 943 916 762 034 432 689 133 225 145 412 837 015 815 147 518 266 097 711 698 287 863 365 278 881 294 345 350 367 950 360 620 930 784 830 921 238 633 007 693 536 668 420 951 384 647 322 800 428 157 155 549 364 433 821 458 529 510 372 437 488 190 603 517 475 477 087 830 010 386 650 717 566 172 118 554 880 138 427 652 092 509 839 834 413 307 991 647 470 157 572 711 145 443 544 891 809 465 542 518 066 228 804 858 596 117 088 050 232 691 583 241 370 394 567 860 642 800 499 588 249 981 021 740 821 117 700 585 262 682 234 825 335 066 099 634 215 957 873 286 001 280 480 257 100 284 967 597 679 902 808 445 122 563 092 251 654 022 388 336 944 666 547 153 442 295 589 402 516 723 241 466 881 812 064 861 157 493 243 782 265 416 334 488 290 727 450 773 456 714 352 672 757 080 367 134 414 873 734 588 344 399 512 681 786 892 567 229 940 426 401 080 421 185 368 975 776 259 238 419 190 196 734 534 176 349 867 839 472 127 426 080 686 501 175 106 224 885 395 874 195 897 397 025 988 205 379 837 512 333 146 806 847 915 912 892 909 380 026 727 618 250 238 512 750 571 715 102 077 590 078 290 687 852 223 374 049 211 050 336 367 327 944 251 089 299 211 169 159 171 727 034 117 417 533 783 770 858 213 852 060 268 111 997 793 071 957 109 313 453 209 747 903 156 440 755 208 227 194 600 209 561 634 525 062 151 980 946 856 094 891 689 327 562 337 195 202 984 314 602 745 076 045 434 026 796 057 463 732 400 809 109 970 943 053 271 866 567 211 838 087 210 077 615 182 214 385 439 846 744 054 417 170 407 338 075 295 131 660 756 470 377 181 376 866 140 249 644 105 486 115 146 703 129 827 348 011 474 809 001 535 441 477 221 556 953 899 207 166 755 328 422 834 150 721 737 445 788 094 241 503 152 185 772 102 026 886 994 433 245 036 920 680 120 195 261 471 590 619 144 159 191 358 607 682 099 616 088 723 928 502 155 124 691 169 465 685 715 684 486 914 720 613 663 578 675 159 301 412 225 193 613 596 831 951 606 800 348 098 091 653 345 527 438 333 110 994 569 339 761 514 600 819 176 945 262 760 524 655 746 007 884 580 688 557 943 614 144 001 181 792 278 935 923 089 500 029 855 937 579 811 891 597 185 339 172 388 813 752 555 409 849 467 269 008 793 292 104 105 923 332 498 749 646 486 188 279 484 865 357 176 910 925 253 278 150 433 335 904 528 117 935 847 151 159 497 206 535 323 303 129 933 916 119 625 663 614 295 260 310 564 281 252 644 367 652 437 939 490 851 232 376 937 806 040 790 843 505 355 889 548 300 132 828 177 394 941 295 107 686 048 355 676 699 976 210 099 310 855 369 931 452 752 978 521 063 768 342 708 679 730 172 464 806 502 899 808 074 713 141 552 683 564 110 088 115 598 990 833 865 447 123 619 276 336 155 543 818 504 376 555 798 792 843 059 766 531 541 620 158 600 072 532 332 234 292 018 824 144 674 529 149 524 657 038 293 391 599 082 635 255 443 147 853 081 883 264 564 671 999 170 928 321 879 483 263 659 276 454 037 384 901 611 345 853 580 838 897 101 572 143 617 052 977 511 779 468 253 081 718 998 135 412 568 110 171 867 781 891 344 495 917 970 922 522 029 004 701 268 777 462 939 005 421 863 247 389 740 388 717 215 684 283 597 215 852 198 579 941 450 501 542 715 295 227 240 217 178 083 347 820 173 286 327 991 722 540 998 592 437 120 626 304 951 614 930 873 568 416 941 951 589 793 128 328 048 388 098 608 507 780 257 286 671 984 572 019 708 404 953 003 936 234 717 243 678 908 155 707 165 492 476 967 203 095 497 952 067 489 839 583 814 530 694 640 303 002 669 485 016 951 256 100 699 659 459 499 961 512 351 108 378 022 783 224 457 819 925 111 166 639 101 113 904 490 180 542 652 700 671 029 330 965 150 296 932 488 906 616 218 012 864 664 775 041 740 680 573 415 272 498 000 861 270 739 414 700 363 247 562 663 493 026 041 611 367 834 018 216 968 814 390 898 072 920 179 200 394 148 525 004 096 980 609 737 297 538 181 900 764 392 199 644 084 836 937 263 312 231 201 692 626 759 188 064 505 911 659 564 027 783 574 684 264 575 708 091 843 078 709 477 401 349 873 949 959 556 318 049 057 935 940 281 131 979 227 958 583 568 707 196 106 364 678 485 271 049 053 770 921 639 257 277 591 617 116 718 623 963 195 778 015 285 102 121 415 119 784 045 737 543 893 073 086 797 825 672 911 233 943 638 328 098 724 907 852 859 484 945 716 671 079 877 273 354 538 425 130 726 132 203 335 785 685 768 263 878 150 383 805 771 503 727 743 033 552 420 236 033 670 866 812 485 725 449 117 405 010 359 218 936 869 349 303 590 677 612 049 471 849 492 461 060 889 095 352 378 952 674 375 249 563 362 221 549 845 752 212 331 047 416 319 849 656 137 198 829 712 818 475 525 970 190 721 297 002 406 283 433 046 990 087 049 473 500 927 615 163 068 651 082 426 992 969 670 796 757 713 346 224 048 694 759 064 837 053 372 503 797 176 127 002 105 804 895 451 597 195 133 793 352 103 612 763 110 266 172 342 986 940 994 468 257 050 240 232 353 134 617 251 346 152 894 415 575 571 170 988 085 915 867 310 829 509 422 514 504 374 992 521 873 383 509 608 171 970 127 516 066 024 339 697 027 862 824 745 312 794 169 782 581 206 992 644 818 897 589 323 943 567 552 282 538 158 016 967 886 103 941 259 240 673 869 916 637 879 740 056 676 448 008 018 471 956 484 692 567 445 860 559 167 252 339 265 528 417 918 595 979 608 097 470 930 857 037 597 831 841 802 235 022 450 346 759 732 706 928 680 944 184 794 205 983 098 162 467 963 514 506 851 034 684 806 036 307 062 231 234 883 112 772 252 014 108 321 105 864 408 616 832 120 910 672 398 738 817 861 534 681 835 384 328 217 909 038 553 210 614 603 459 890 240 304 620 353 881 172 026 140 544 383 073 720 971 958 341 167 178 501 795 680 848 544 106 433 300 512 426 460 764 901 184 206 539 207 143 001 002 559 077 252 659 686 303 481 697 738 799 825 112 396 992 617 585 724 783 034 971 022 024 742 774 453 868 825 683 563 884 067 887 546 916 678 031 278 525 185 403 718 440 407 535 429 243 201 478 719 292 556 003 592 543 614 116 108 052 147 484 956 201 646 395 151 312 578 940 051 032 561 124 813 726 570 027 730 060 501 276 869 656 974 867 976 049 908 047 906 692 535 027 358 732 361 779 148 325 931 287 665 443 158 874 148 336 633 925 003 318 609 197 786 320 701 196 621 124 905 688 378 263 953 729 126 916 793 350 286 414 548 244 414 426 394 004 324 203 414 317 611 882 823 361 223 936 731 820 788 527 535 818 172 854 195 190 074 005 313 144 101 345 680 668 184 716 462 719 557 324 496 388 884 774 631 567 533 114 659 997 471 956 439 832 068 352 933 791 010 642 343 216 381 920 814 975 875 106 440 242 919 331 154 897 118 914 284 684 918 434 171 455 825 528 767 112 066 509 394 413 600 998 665 265 475 484 824 856 330 602 963 993 547 546 995 905 585 275 698 649 867 190 962 090 553 442 862 774 380 011 552 359 543 265 424 802 999 524 545 091 605 122 050 265 703 134 142 875 678 650 909 409 486 951 045 936 252 837 589 563 244 566 762 890 729 862 242 589 361 495 462 860 342 931 879 739 930 656 550 208 970 028 725 172 223 882 738 322 276 130 777 570 681 892 505 082 730 848 745 299 663 187 975 297 402 315 295 025 987 431 171 815 722 902 092 677 139 124 368 575 189 006 697 150 272 736 900 856 205 521 913 050 027 870 122 941 210 911 736 131 797 309 988 474 289 412 546 749 129 288 174 488 753 955 423 303 369 560 848 304 596 295 963 098 617 774 597 422 388 696 163 845 824 974 594 913 510 704 916 850 971 192 294 909 296 769 104 230 827 076 391 366 434 319 680 282 682 845 684 501 678 936 847 464 108 034 473 369 441 279 987 358 852 613 975 580 522 314 098 616 933 619 893 179 297 762 588 227 291 479 531 883 043 023 831 772 845 495 982 485 023 725 000 982 816 211 819 109 402 654 190 878 071 785 244 153 458 773 203 554 111 893 196 847 521 275 997 935 771 184 516 446 599 699 023 940 292 957 054 734 797 422 915 010 015 313 744 566 036 152 381 330 810 230 391 140 671 607 376 229 091 448 430 675 382 522 915 021 683 688 005 900 805 531 581 865 923 165 675 974 615 563 962 688 859 408 340 572 440 783 777 555 710 297 976 264 510 948 644 190 937 395 672 406 921 571 941 944 698 733 646 839 925 228 220 060 053 540 274 642 369 663 423 980 624 642 076 537 055 745 114 493 770 214 173 905 565 884 266 967 097 254 749 553 898 910 447 644 159 761 322 771 318 308 758 171 999 204 288 598 956 945 387 705 661 741 945 389 066 525 941 652 131 247 805 917 179 767 424 229 997 701 584 735 344 951 116 777 004 313 303 310 933 674 425 518 364 579 851 302 706 678 849 412 058 876 819 344 738 474 814 905 080 256 797 613 233 964 081 935 202 191 269 756 499 960 075 922 564 997 268 520 638 947 430 422 044 667 170 485 546 588 560 064 618 617 341 851 945 968 142 805 842 185 756 828 219 781 889 069 985 187 820 648 170 322 835 518 105 771 505 265 564 191 658 542 237 411 109 191 101 271 601 619 402 866 306 494 248 653 945 246 854 346 260 639 325 985 881 833 571 714 360 510 594 565 227 367 487 294 938 018 484 332 412 100 598 823 502 847 046 961 446 080 904 995 059 584 272 764 176 225 002 385 702 847 860 831 044 747 961 818 043 200 782 835 593 057 991 127 519 227 576 465 758 064 670 005 563 540 903 794 791 467 100 748 085 055 670 477 369 983 344 079 188 005 983 262 561 803 912 537 175 763 601 854 850 682 111 378 340 234 095 025 353 328 662 110 140 419 597 790 506 949 675 654 090 812 443 004 973 739 295 025 029 648 572 578 422 047 901 191 438 152 671 788 831 162 861 610 949 312 910 438 019 620 729 920 039 383 869 589 663 257 518 984 131 457 124 245 044 264 697 265 098 219 416 866 404 231 558 607 094 340 238 420 392 368 093 574 334 967 075 694 324 062 426 503 084 603 764 375 323 400 452 549 149 277 391 188 636 460 562 490 623 159 568 536 587 492 768 685 866 858 535 571 914 439 306 350 439 773 643 078 155 132 615 868 774 057 149 319 464 087 874 253 079 372 991 178 254 188 266 266 657 320 621 392 461 128 785 569 506 094 443 958 621 570 258 973 898 907 290 468 387 205 683 615 070 134 324 671 822 737 563 672 897 581 435 722 399 024 377 240 032 743 949 825 328 414 404 334 117 843 031 702 549 624 055 374 433 489 818 875 479 984 954 453 068 110 251 999 035 116 609 230 773 872 051 050 012 627 254 328 470 386 194 091 306 205 875 038 696 194 738 392 979 503 167 291 573 164 669 654 009 403 893 914 505 785 034 046 887 018 512 916 694 640 744 615 598 018 717 399 975 708 277 758 768 702 704 676 340 496 756 716 270 143 312 683 110 445 771 618 490 942 242 203 709 408 673 711 862 624 001 738 153 738 818 812 212 202 628 496 476 795 695 663 359 514 169 936 803 661 136 545 677 732 987 524 690 344 293 634 966 400 268 393 503 276 511 747 271 918 465 869 102 832 696 112 118 718 023 342 931 293 528 024 499 642 283 285 681 029 711 330 736 904 686 053 861 932 519 461 787 724 931 773 976 579 131 700 946 234 020 458 190 522 753 664 922 023 480 159 012 195 777 395 563 763 165 169 999 366 672 128 353 648 485 096 423 175 295 228 893 911 239 865 582 994 672 402 975 382 814 630 773 096 492 413 604 676 110 324 729 308 510 940 400 001 196 098 012 367 063 707 254 444 715 704 800 884 332 249 838 488 854 821 035 972 395 652 308 751 208 064 512 855 348 746 242 234 654 068 515 565 846 357 614 037 834 717 851 735 351 874 164 089 959 022 105 521 038 755 121 533 758 744 414 212 161 487 418 070 142 359 845 261 431 370 355 803 991 614 284 110 542 254 129 862 973 772 791 430 851 994 479 210 352 598 210 400 234 464 635 624 105 909 869 374 063 188 267 440 483 492 859 239 855 800 577 704 925 512 580 889 717 078 344 405 832 958 433 143 084 155 758 174 498 047 134 366 414 813 152 836 822 762 902 116 107 707 380 159 379 291 942 961 585 046 635 224 523 210 831 352 645 801 685 528 724 762 119 261 244 517 914 182 540 108 464 925 924 892 858 852 071 725 481 391 200 645 908 810 266 122 849 429 892 040 988 650 327 027 498 825 265 382 698 376 126 971 680 236 799 806 553 618 373 404 909 217 492 860 636 608 776 162 854 412 109 470 388 032 940 964 387 649 889 838 235 188 718 206 400 557 047 797 497 931 851 404 844 042 259 585 665 895 560 438 143 762 124 334 926 296 818 984 986 972 274 674 152 898 117 658 497 047 861 175 459 518 083 243 906 734 332 985 407 871 282 145 649 314 663 863 265 045 315 709 167 056 169 083 214 912 660 044 671 931 148 826 481 117 197 449 859 192 223 482 864 386 246 918 538 570 602 257 656 500 602 352 433 374 727 445 707 336 705 599 648 339 434 925 959 456 823 368 157 453 566 672 379 539 584 717 630 490 585 243 052 544 075 962 047 544 479 738 257 357 695 156 608 525 932 131 097 170 371 544 322 921 963 651 957 049 476 561 075 151 434 579 336 144 466 988 865 355 971 911 526 575 792 449 464 616 403 718 275 453 630 616 339 360 333 499 969 827 462 744 316 595 526 762 834 699 380 391 233 040 520 780 874 573 646 555 469 921 322 543 956 096 858 656 948 148 174 885 810 995 087 254 101 415 605 523 933 817 936 299 856 110 198 748 256 086 975 342 527 755 981 207 121 680 119 794 544 930 292 766 185 151 289 361 207 595 321 196 713 168 375 753 395 252 139 025 143 486 536 905 995 817 697 421 744 599 418 920 257 889 464 984 679 908 084 528 699 070 588 740 953 571 647 205 087 312 178 510 234 745 591 848 019 273 469 973 369 709 572 098 443 718 656 902 878 816 036 968 711 009 722 213 449 764 226 768 160 639 066 293 349 435 777 627 742 723 129 775 201 538 198 779 506 954 088 746 681 852 210 843 206 090 515 724 695 749 030 132 321 202 584 451 324 830 758 826 410 425 619 845 081 240 969 088 578 803 536 023 821 583 379 284 320 104 749 866 790 028 019 494 296 809 844 357 670 995 911 273 242 438 951 625 166 494 700 171 099 049 386 697 436 151 298 145 264 010 716 215 584 371 198 336 915 694 161 610 132 113 572 441 005 832 771 022 830 774 889 579 645 210 613 031 108 333 785 346 135 195 963 760 150 648 586 690 193 017 149 658 830 506 531 532 267 033 749 630 018 491 312 509 872 347 434 708 113 753 343 660 740 603 415 002 313 689 843 267 622 881 636 730 920 653 982 282 122 726 594 262 183 219 219 770 344 656 941 654 829 099 017 265 929 040 615 581 277 720 081 121 156 937 455 755 954 740 753 326 219 705 207 455 843 330 841 702 935 019 745 071 965 938 503 941 277 225 202 365 131 416 960 468 881 878 147 175 824 650 159 617 929 820 001 749 315 435 629 811 852 814 070 542 545 297 644 601 035 717 094 866 022 627 700 477 287 353 044 213 102 668 123 977 418 311 639 466 724 997 673 941 901 035 087 749 567 905 994 632 337 638 544 745 173 355 638 393 801 551 923 095 331 596 313 964 116 113 374 311 666 768 984 279 699 988 463 153 460 962 854 861 967 680 681 992 758 350 688 081 921 775 362 018 961 731 768 976 186 250 888 129 289 358 452 169 942 994 695 151 935 976 100 760 386 648 240 467 547 807 205 998 027 190 967 265 212 106 447 686 007 299 354 180 022 029 768 951 932 304 119 702 754 225 767 535 111 529 404 701 215 760 972 448 137 450 263 594 093 890 155 416 481 434 567 292 476 306 688 889 642 975 010 368 715 949 223 213 700 998 768 213 403 370 849 763 172 585 725 368 854 491 477 019 741 456 712 210 591 464 520 491 904 823 562 958 029 162 167 405 133 649 488 764 407 432 859 711 978 393 962 288 611 882 986 941 259 243 863 870 190 175 857 289 861 071 054 918 920 478 029 327 521 973 405 147 048 441 274 652 329 876 414 974 730 164 558 294 661 740 783 571 596 595 545 564 138 181 974 443 687 452 293 935 956 388 414 125 468 234 363 808 656 197 006 928 624 002 740 560 731 053 440 846 340 238 510 993 109 933 119 831 632 408 244 956 775 971 559 961 663 608 854 800 883 545 594 889 417 896 970 587 356 130 992 877 259 329 121 763 720 739 132 240 152 376 077 107 543 452 151 820 786 982 745 515 077 213 168 028 253 296 248 298 661 582 511 985 343 388 382 673 497 671 340 379 482 769 649 170 976 296 674 636 208 299 533 111 838 246 423 419 203 304 355 726 927 988 235 320 267 453 999 106 475 939 167 342 191 111 440 284 054 009 859 218 585 087 068 349 659 870 526 663 425 257 898 600 192 825 025 141 934 273 506 512 813 244 019 888 511 624 328 054 555 386 956 502 347 751 952 919 060 007 340 141 627 133 472 176 772 790 136 860 244 536 087 265 232 838 088 513 012 998 800 612 624 929 941 441 342 096 144 473 022 549 723 923 180 956 960 661 609 244 153 757 155 843 122 028 072 998 794 775 000 823 965 314 991 274 963 359 987 921 007 394 809 882 543 790 715 177 622 273 775 960 557 952 505 228 572 653 110 267 072 040 525 572 846 475 601 288 480 487 274 487 278 825 325 839 332 443 515 969 958 311 971 634 927 008 541 570 250 339 130 409 673 573 840 401 200 384 380 199 129 406 333 404 348 630 720 541 782 409 992 938 659 658 395 922 313 578 439 934 861 768 555 902 758 032 700 949 137 433 271 815 099 829 976 758 560 807 593 786 488 954 727 601 339 065 374 122 394 600 082 288 763 167 660 666 475 802 117 074 546 399 577 708 778 443 425 124 725 146 723 563 615 767 197 675 827 195 501 508 150 423 461 018 819 406 538 166 719 525 940 961 985 362 229 168 735 587 545 217 714 918 542 336 344 435 309 924 038 928 526 126 875 897 254 578 904 660 291 363 761 945 001 043 922 551 612 081 029 569 948 169 792 559 513 438 935 567 508 558 055 321 930 662 473 039 581 216 581 559 636 454 710 239 110 455 902 358 862 359 288 194 851 029 093 577 564 896 832 407 403 579 952 437 486 891 625 619 421 560 162 494 315 297 946 392 169 248 797 331 277 489 062 488 018 412 202 423 134 535 387 201 043 145 129 165 619 723 724 591 380 775 324 307 400 608 106 897 932 929 956 860 642 410 010 434 092 941 983 609 989 857 007 011 513 484 817 596 353 386 223 178 929 371 342 067 452 420 612 307 747 404 783 358 321 261 322 995 492 386 872 337 840 725 310 245 110 001 636 431 939 772 365 860 897 617 383 027 838 363 374 043 459 005 776 367 378 986 363 734 149 580 168 631 981 857 565 718 930 382 559 575 085 829 947 544 333 525 930 668 055 258 762 957 179 282 171 436 157 225 295 155 329 219 513 017 373 955 671 437 712 117 269 641 080 687 505 458 762 360 502 109 477 610 422 392 375 247 642 260 586 791 286 826 801 157 892 657 630 911 062 614 865 983 532 635 176 928 874 363 881 049 332 805 731 093 917 879 797 395 444 677 422 668 763 916 593 337 773 187 317 586 396 488 203 277 392 906 823 736 634 029 541 510 041 173 758 585 450 575 782 915 549 614 752 593 003 972 466 336 305 961 189 299 225 573 200 408 590 892 084 122 100 351 999 565 991 434 890 970 570 852 392 243 821 742 516 317 104 374 228 851 868 318 267 448 104 830 576 962 887 855 554 497 655 910 550 211 105 211 092 382 414 116 352 602 306 373 504 068 962 515 709 200 951 792 425 014 882 385 545 653 743 123 272 773 201 762 138 129 838 613 035 044 834 174 447 537 198 288 577 063 708 975 334 751 347 941 321 557 189 638 211 691 433 541 870 450 718 003 341 013 721 020 890 005 935 682 744 365 792 882 643 785 528 524 309 821 970 564 039 456 463 671 670 436 284 813 848 875 473 643 377 639 518 647 269 853 099 343 392 073 120 818 105 301 282 294 335 357 061 009 829 349 309 374 488 887 726 603 216 871 951 208 337 378 844 998 550 119 335 972 587 654 353 593 319 221 203 607 713 843 728 335 934 583 180 302 850 257 996 253 122 379 893 193 355 844 075 571 541 101 961 139 495 577 648 538 471 799 699 658 810 319 822 200 489 738 049 189 322 907 671 327 523 878 869 892 522 596 285 645 296 291 360 844 833 539 385 534 616 211 733 493 774 149 294 633 673 936 315 231 646 013 695 358 150 893 019 212 449 944 073 900 563 796 152 280 216 946 732 010 190 929 401 472 360 685 809 739 155 959 693 531 474 816 059 716 201 408 333 396 961 460 839 120 655 699 398 945 325 215 448 857 185 868 022 274 234 897 369 738 113 733 045 946 837 961 885 458 085 569 165 792 239 753 023 284 891 103 729 226 592 072 182 564 868 587 406 891 389 121 058 423 416 146 870 800 980 716 902 556 953 329 607 332 735 365 522 017 796 834 722 586 249 786 925 304 179 524 451 491 435 151 002 227 126 402 995 934 782 184 423 221 276 407 104 299 287 045 234 290 761 263 221 392 182 264 262 761 056 243 272 191 354 308 868 650 367 531 885 942 239 452 607 688 584 547 860 274 965 737 333 867 410 425 156 441 385 974 432 440 427 628 504 292 556 770 929 673 900 530 997 142 100 406 027 027 831 655 438 475 380 389 965 889 615 490 605 800 744 531 124 464 350 512 743 673 163 145 481 478 049 350 641 630 187 042 425 701 852 707 420 067 823 019 013 457 649 326 893 682 221 385 430 346 181 104 169 220 053 147 282 827 674 933 550 826 215 344 214 407 859 304 940 647 202 583 067 249 063 014 452 731 553 758 349 978 411 928 507 870 473 724 721 658 614 287 512 874 371 478 092 037 674 388 055 731 867 050 187 846 402 662 125 656 388 313 505 826 762 201 455 014 979 665 225 614 792 451 351 105 615 304 224 180 989 022 409 720 495 092 104 464 562 772 313 967 558 038 317 587 774 663 875 778 441 031 815 131 475 488 814 262 061 074 636 003 900 924 852 881 678 626 741 956 221 080 408 780 873 187 627 022 047 054 081 048 163 872 583 237 931 762 225 081 421 943 674 740 976 106 985 872 367 194 762 225 781 761 604 008 977 400 440 430 562 389 883 070 684 548 723 857 046 704 408 831 135 454 322 346 813 880 933 078 274 570 316 456 356 182 762 758 456 222 107 274 438 670 736 515 307 619 499 824 059 159 125 173 641 153 993 266 776 022 470 644 233 026 867 524 090 568 104 098 286 056 956 382 802 577 748 139 400 517 472 650 572 223 236 266 222 933 222 562 626 482 234 507 925 510 836 024 676 394 956 974 365 900 820 780 628 569 366 990 085 947 837 756 261 123 103 614 832 812 075 373 843 517 148 488 484 462 755 868 290 016 269 819 040 997 729 277 810 897 690 552 782 565 307 307 244 067 857 567 119 193 643 502 705 846 171 325 259 501 091 727 410 985 109 030 311 259 221 154 861 658 926 842 840 555 901 795 446 975 861 295 817 683 225 833 877 792 600 101 828 729 871 635 021 948 135 316 103 889 163 946 639 769 686 365 522 733 881 294 543 708 522 728 710 779 237 687 479 893 663 457 864 421 930 619 741 191 950 116 729 130 228 650 940 593 624 912 680 184 033 001 996 917 037 528 712 385 885 908 663 895 864 735 120 867 099 795 282 652 671 693 648 755 548 311 545 648 395 097 440 841 075 064 962 334 398 450 096 078 877 578 153 666 044 948 604 950 258 966 923 380 430 136 322 682 640 731 439 527 387 735 070 104 772 320 770 065 460 275 780 599 573 660 794 395 354 363 806 453 510 881 908 843 748 200 258 399 796 978 796 031 810 455 839 638 365 978 637 624 772 696 647 136 608 784 955 621 952 150 648 657 478 338 162 103 982 745 353 033 961 182 350 912 810 194 743 514 971 919 183 263 538 236 795 431 303 888 000 472 416 494 199 040 006 782 965 882 380 907 986 295 059 630 914 294 450 708 786 747 835 982 523 973 426 104 423 464 977 161 426 157 349 647 515 695 028 409 938 669 550 137 393 504 888 384 676 025 345 037 632 255 827 241 179 617 409 687 834 375 206 466 652 504 892 254 408 191 214 220 073 353 283 048 352 785 758 659 514 602 982 695 073 114 564 138 619 543 566 677 546 899 191 718 068 626 499 311 148 025 264 863 737 328 526 542 554 704 824 324 134 390 548 629 058 409 094 337 669 202 823 443 022 679 229 366 337 454 778 773 263 427 423 905 472 403 267 234 391 939 271 359 296 279 808 459 906 379 911 007 694 757 278 999 815 701 347 525 538 862 146 823 909 341 989 399 134 876 399 570 961 366 594 038 679 108 405 489 528 859 777 700 463 815 042 586 185 567 674 178 180 959 106 704 132 225 726 511 948 452 571 889 946 122 788 736 276 842 042 084 392 339 849 737 576 012 189 731 474 846 331 386 260 002 775 317 484 252 410 531 882 489 703 672 049 325 058 611 366 892 210 361 127 332 208 464 630 793 978 188 884 705 657 543 186 277 755 111 937 865 682 509 910 137 760 100 449 134 416 587 894 330 351 674 503 192 019 788 505 440 558 258 220 539 757 960 674 909 405 644 609 097 688 627 367 628 968 676 684 270 998 230 436 563 070 071 536 825 156 670 684 356 058 308 548 680 387 396 064 656 190 897 203 591 235 480 224 556 337 840 832 172 105 226 450 926 204 704 544 946 443 806 242 828 218 795 958 363 299 159 559 485 484 434 176 184 342 173 834 189 192 004 918 180 772 324 477 775 608 603 047 065 842 314 974 907 001 957 037 308 209 251 887 053 156 851 744 676 330 486 875 604 635 142 653 941 365 062 082 526 342 342 449 611 784 446 181 540 816 572 115 349 882 821 204 322 202 964 271 822 998 710 577 633 061 173 820 194 944 550 452 275 488 184 942 661 846 163 386 787 343 339 953 903 245 302 069 248 425 123 934 398 255 463 964 858 161 786 979 293 132 229 228 017 580 286 962 149 311 935 483 643 886 457 200 524 191 463 951 330 878 310 642 740 980 891 176 914 500 251 186 925 963 273 121 958 537 395 438 985 752 943 075 827 755 511 917 710 019 262 650 174 146 815 426 697 741 661 517 024 246 664 807 392 030 793 936 097 722 816 688 760 264 696 516 399 061 317 438 358 943 364 289 327 940 530 155 022 554 957 787 316 574 915 385 925 072 549 765 856 329 830 137 385 352 833 444 911 026 427 162 975 506 549 973 908 557 675 910 044 016 005 552 736 731 762 493 895 124 810 204 126 248 435 885 623 729 633 605 673 710 796 473 610 777 571 185 731 255 588 744 668 668 391 655 359 881 904 723 757 954 485 404 150 005 135 342 409 393 468 906 105 537 228 649 776 387 810 018 517 475 313 615 669 729 102 344 963 060 304 723 148 565 588 991 314 681 688 798 377 311 684 257 123 908 581 352 981 768 193 790 123 813 936 573 112 892 420 254 244 719 284 669 470 638 698 273 316 721 623 357 896 550 049 914 708 869 863 715 751 593 979 263 221 868 035 060 511 416 041 683 614 528 880 714 073 131 561 213 942 003 231 301 309 419 236 704 134 322 738 510 359 280 510 886 680 965 252 432 615 777 659 220 297 256 327 046 339 665 594 586 230 684 331 882 097 514 683 735 969 120 763 914 013 653 015 157 864 589 824 663 381 561 332 575 528 304 409 424 664 536 389 219 635 137 781 225 576 166 487 162 710 527 006 820 238 458 818 685 533 638 055 420 208 886 297 535 497 925 514 851 440 331 692 172 376 621 477 965 535 028 726 348 879 587 064 676 505 022 268 633 208 770 114 401 795 250 612 652 104 287 602 909 091 524 423 953 917 427 847 668 487 376 360 266 835 852 334 746 741 230 149 713 029 070 989 662 582 126 083 173 989 087 493 635 146 903 969 121 774 108 665 057 801 872 009 397 537 613 124 525 702 338 116 906 013 514 540 640 041 857 354 982 829 637 777 788 029 522 205 778 381 888 588 326 673 162 631 232 718 307 872 924 955 762 677 975 099 134 775 773 349 275 273 728 565 592 144 889 957 227 028 933 479 875 534 684 853 814 012 572 717 186 769 069 139 403 632 924 760 409 164 149 192 880 542 691 214 172 049 105 639 647 755 305 700 157 399 267 909 882 271 157 886 581 559 124 202 896 893 096 839 396 622 402 462 034 752 844 126 656 143 557 418 491 989 448 154 908 269 578 251 190 957 163 782 973 560 935 834 242 805 244 825 783 470 092 070 506 492 821 246 327 100 262 528 948 570 016 947 075 055 065 292 212 413 744 264 138 074 647 114 930 262 941 447 672 950 685 548 414 536 671 182 672 316 284 513 177 679 016 900 820 618 943 724 673 221 911 096 929 855 160 942 734 438 506 677 266 877 429 540 086 019 921 321 217 390 106 300 774 438 514 998 580 485 519 264 793 537 480 950 493 034 128 701 807 397 927 909 489 809 907 924 857 924 906 862 253 237 324 181 363 001 278 352 833 748 059 367 308 069 311 313 711 120 129 973 891 018 037 232 502 090 479 596 709 026 571 283 227 819 909 756 960 585 825 251 228 192 797 256 914 195 214 027 221 849 996 944 769 731 397 838 452 740 190 810 429 096 876 979 293 168 933 739 960 956 075 423 482 912 378 671 456 535 695 893 005 084 622 071 642 460 478 614 648 304 728 477 678 619 646 302 805 756 939 920 821 785 406 128 185 987 345 152 906 976 709 040 194 531 773 200 577 153 667 297 260 495 241 418 256 746 735 304 595 554 326 313 099 697 231 730 261 718 731 949 133 076 251 393 364 764 405 157 494 856 668 548 957 618 679 205 033 267 100 420 863 604 306 174 371 905 293 924 340 022 973 300 147 171 535 774 752 601 303 123 140 904 837 459 776 252 479 365 392 214 085 709 699 301 982 414 304 877 212 237 557 920 498 755 596 282 123 244 364 229 608 269 703 256 434 796 314 994 261 392 620 471 756 107 535 288 664 226 336 820 894 676 736 888 701 421 452 162 191 199 671 257 084 351 365 915 138 187 569 489 961 207 423 174 877 798 172 496 913 947 087 638 941 591 536 465 842 954 009 396 152 910 276 001 146 683 152 070 114 932 405 570 435 300 826 600 610 460 041 973 380 061 321 884 657 322 089 666 910 952 275 929 736 630 478 596 134 254 167 443 980 190 593 727 753 197 031 014 939 913 727 032 764 904 073 903 655 579 030 573 966 255 762 211 214 574 777 086 442 928 653 789 570 596 136 983 396 542 185 502 578 562 702 126 770 376 519 897 435 655 592 507 553 681 619 856 813 520 217 438 615 141 099 009 812 306 767 115 316 929 242 588 017 780 728 640 447 333 698 346 197 198 799 485 283 738 438 454 428 611 862 419 728 942 354 139 078 499 213 978 451 381 020 634 293 701 945 413 210 253 805 943 148 868 487 821 873 878 218 649 127 594 655 227 076 193 851 118 287 346 159 583 093 174 189 827 625 628 587 356 966 397 343 724 976 715 342 972 103 261 213 620 843 734 569 750 706 186 483 433 802 546 695 161 542 379 150 951 851 516 568 482 280 754 969 274 549 504 383 783 495 736 572 961 100 249 668 130 856 738 225 123 578 685 912 919 620 739 312 097 364 682 813 503 676 267 431 207 914 190 805 381 867 297 691 736 213 705 404 516 453 204 102 986 235 934 330 223 714 940 565 245 115 804 920 428 312 710 363 561 342 973 694 517 917 169 037 344 593 063 366 122 154 849 232 240 806 934 754 024 226 778 061 855 795 522 930 448 229 897 021 465 070 482 921 172 639 573 445 264 452 859 380 469 617 732 377 022 046 203 985 877 217 904 766 300 136 007 716 016 950 861 854 726 534 210 313 377 927 167 109 671 535 528 016 615 159 933 659 009 289 037 009 889 214 385 325 920 379 104 514 420 784 376 375 035 674 497 530 354 841 782 068 525 002 877 826 553 019 023 770 205 686 064 915 262 711 392 642 240 761 301 557 279 661 789 829 973 666 076 759 980 616 165 713 505 667 412 993 379 384 157 410 670 948 367 222 174 942 036 176 837 144 054 618 174 794 132 317 905 246 958 201 058 945 803 537 447 371 444 246 570 123 673 270 544 162 374 853 867 963 351 600 640 357 405 815 436 679 223 229 192 579 280 988 091 683 994 403 677 779 662 398 101 781 986 634 062 432 019 695 398 260 240 616 430 272 831 775 051 214 480 011 319 114 452 065 750 589 903 295 267 715 500 691 612 455 094 767 223 191 842 979 313 513 284 767 854 794 584 443 731 533 122 664 955 849 296 547 330 843 769 917 814 112 915 500 602 545 348 830 907 884 914 844 645 618 195 363 196 659 283 054 461 428 645 946 457 194 250 026 660 691 512 139 255 047 721 617 279 019 842 225 776 324 576 475 171 195 592 448 537 113 738 830 995 403 016 946 071 681 985 962 657 371 902 833 347 245 351 825 545 908 525 431 278 497 335 973 523 382 693 048 904 962 392 310 171 258 896 598 623 196 239 513 387 889 467 878 437 325 287 634 362 457 406 415 513 338 632 263 304 414 536 504 303 404 469 420 328 360 453 232 474 946 986 751 305 558 139 785 622 751 315 386 474 403 185 841 875 587 734 891 183 349 799 466 898 252 795 730 844 818 224 036 269 688 406 935 161 347 127 772 695 398 081 682 256 554 700 019 828 283 590 098 824 561 249 631 011 543 546 136 918 874 959 668 190 019 502 519 828 806 765 033 761 659 828 319 828 537 818 994 712 742 814 313 310 685 934 030 966 339 383 782 859 587 929 553 265 166 911 278 510 387 113 957 678 065 895 914 082 512 122 626 449 005 018 037 502 560 616 648 813 993 490 600 429 600 466 282 899 271 745 226 442 233 112 295 279 876 759 535 105 682 989 079 203 066 221 261 677 204 107 624 167 443 688 927 888 390 727 363 721 238 209 440 149 164 424 880 355 330 869 735 458 014 340 157 222 931 413 279 912 081 131 025 814 858 890 431 246 289 812 885 665 741 343 184 904 537 964 868 037 070 147 696 962 747 655 940 009 944 885 265 714 624 381 360 989 841 682 591 327 507 667 868 908 646 307 228 216 170 247 584 896 715 297 848 978 983 192 033 813 274 800 646 675 087 941 110 407 184 794 861 518 312 863 574 515 425 898 612 703 965 881 777 536 563 076 628 510 195 920 977 946 878 332 931 064 107 854 828 838 787 907 004 590 198 511 284 914 626 041 376 346 065 747 647 204 023 875 937 168 310 027 805 645 867 038 409 975 022 154 411 276 293 292 982 070 977 315 881 439 359 159 009 066 582 081 629 328 525 980 130 088 908 933 423 451 463 510 145 783 739 271 080 276 010 192 282 439 780 603 383 632 194 671 228 606 930 371 416 984 279 991 024 587 700 620 943 928 460 152 071 287 887 285 182 074 399 988 818 524 548 628 802 857 902 042 274 171 724 633 961 447 683 601 381 454 132 861 636 937 849 768 076 528 927 182 413 610 476 049 076 651 265 234 425 244 808 082 612 592 643 708 643 797 643 927 600 432 090 595 558 140 340 663 559 645 622 568 662 283 300 592 334 371 448 508 571 570 037 429 855 661 477 651 494 176 348 884 703 255 584 378 913 138 658 572 548 660 996 887 707 142 897 074 626 917 854 387 864 696 063 449 084 044 885 552 487 184 832 503 799 500 464 407 702 833 252 731 646 991 485 043 431 843 934 458 513 349 282 028 604 172 136 865 723 137 352 209 391 145 450 560 514 393 229 369 850 896 311 415 120 266 215 239 237 441 751 849 992 314 554 517 881 694 291 063 277 401 517 617 152 247 767 090 323 415 949 719 136 940 181 287 623 589 598 973 552 787 386 554 645 295 498 840 460 089 985 413 158 908 899 557 379 878 818 864 901 308 360 869 538 604 069 739 933 304 755 512 756 035 701 191 270 431 592 923 625 425 263 537 256 389 757 354 795 848 136 875 146 896 236 138 400 435 465 917 735 285 648 958 959 291 273 720 428 293 934 643 034 768 984 891 991 729 600 863 477 062 396 794 668 756 210 908 489 413 560 430 215 105 624 245 131 966 432 550 316 516 847 161 092 871 391 941 730 909 713 759 833 708 321 720 573 680 657 415 361 843 801 155 009 607 203 130 681 680 832 127 562 451 768 061 696 606 513 749 553 532 940 003 392 647 982 255 616 331 779 743 385 117 853 240 296 674 587 645 466 712 858 846 742 235 770 263 350 343 920 181 950 288 150 617 006 790 821 959 626 774 409 326 191 726 024 611 590 279 244 469 893 120 496 230 521 110 959 593 837 081 105 687 199 513 259 037 098 721 396 032 300 822 646 908 166 448 010 425 606 171 770 417 757 565 862 458 086 376 158 004 020 572 438 165 176 793 947 407 867 856 019 349 511 021 840 900 389 815 231 258 979 555 909 558 532 605 835 814 437 660 210 838 900 035 644 580 944 298 566 923 949 421 535 624 205 897 956 750 261 235 728 078 173 525 128 135 665 521 698 520 238 433 817 829 783 080 977 886 659 408 209 324 074 408 669 829 367 135 571 900 728 157 996 635 402 260 147 928 252 160 335 504 860 473 346 619 605 468 764 669 536 336 177 481 453 945 353 663 122 541 746 174 910 621 652 838 846 277 299 067 098 043 971 610 400 330 477 592 317 320 438 007 868 367 810 880 979 281 616 891 495 399 791 400 198 550 149 123 742 357 733 488 983 883 717 748 411 113 524 363 297 695 486 463 262 784 422 450 658 542 402 644 879 918 857 549 942 204 874 602 795 077 785 607 720 984 941 507 092 232 716 305 813 359 893 775 295 056 852 378 670 650 054 828 110 853 174 072 284 408 381 164 038 397 567 960 327 224 025 793 963 993 294 564 351 303 190 747 062 900 269 968 829 818 544 391 933 680 385 734 812 787 581 007 916 879 435 246 226 766 599 223 090 639 233 675 071 206 142 194 940 406 986 028 496 439 087 981 789 391 931 434 831 493 123 649 644 669 192 397 983 324 137 587 743 255 739 109 665 584 352 754 932 966 133 236 055 800 538 233 069 543 301 306 677 830 710 373 143 102 849 626 799 025 470 728 356 701 221 120 856 457 738 114 970 659 653 509 787 325 702 742 112 717 835 467 059 573 032 078 878 823 476 118 358 629 712 715 831 154 257 695 950 807 818 380 600 044 132 054 780 571 199 466 493 809 991 218 016 874 302 229 308 908 559 233 425 526 384 771 161 761 706 119 128 772 736 857 329 005 485 822 739 236 782 177 144 342 858 631 755 208 339 687 152 465 986 853 539 151 206 577 047 849 738 290 021 865 108 809 717 673 296 791 229 307 080 325 771 422 914 320 678 878 385 474 033 753 787 381 822 085 597 090 758 412 062 412 481 691 126 815 290 808 063 966 155 146 801 699 297 065 315 173 050 361 459 831 720 106 566 494 733 026 130 192 104 439 546 859 093 319 347 102 646 290 838 997 475 442 164 081 245 611 928 359 528 440 659 280 829 419 202 181 397 413 678 231 746 424 867 417 051 202 405 883 081 503 717 923 204 998 594 038 169 073 777 112 291 244 740 993 724 611 633 055 649 837 127 693 564 982 133 445 023 740 560 523 591 379 074 776 471 917 671 413 081 670 556 026 649 142 259 477 711 802 687 264 872 193 187 234 106 242 952 250 096 194 244 468 812 289 751 467 212 589 422 717 808 482 602 864 988 613 685 341 603 648 424 865 902 348 919 221 305 472 657 746 910 959 621 661 816 320 634 651 416 558 644 128 908 312 982 094 979 861 950 425 123 049 790 370 803 395 835 584 681 185 522 321 809 528 398 252 941 043 200 464 707 374 826 720 743 246 663 828 833 679 906 433 209 673 906 876 779 454 569 012 903 216 608 722 369 840 676 461 083 163 237 291 506 666 044 663 817 672 192 242 898 113 880 069 631 846 272 285 530 945 988 074 145 270 294 163 743 796 425 868 964 557 994 880 970 055 156 646 477 149 668 011 426 236 598 184 206 695 384 240 664 832 548 126 376 866 489 101 790 433 952 501 903 807 129 366 702 418 181 668 011 108 874 322 249 583 352 811 767 037 596 028 338 741 366 045 577 698 660 093 824 038 011 509 138 437 215 270 400 463 752 412 666 412 583 266 535 120 294 528 467 948 789 746 059 926 416 424 070 841 995 453 270 736 361 604 303 919 897 512 135 395 990 014 049 301 875 911 352 017 153 632 038 870 509 637 694 715 249 316 139 538 221 193 935 866 000 468 724 331 068 822 076 780 041 675 902 292 311 971 833 793 702 669 866 501 943 611 658 234 462 174 121 534 458 370 312 650 443 577 148 622 443 669 649 285 895 853 580 926 096 163 223 842 741 854 792 996 106 417 177 639 238 054 293 079 650 594 913 727 736 061 534 727 751 039 451 623 599 746 563 524 425 982 659 432 179 225 084 343 384 035 371 890 965 899 409 721 246 240 069 041 191 082 780 601 512 850 404 554 474 960 252 714 306 441 997 370 664 232 848 177 149 761 141 291 691 717 900 461 997 380 072 150 998 359 086 439 020 680 029 018 628 308 380 613 815 392 853 552 745 078 657 834 662 876 928 991 814 378 116 749 272 258 622 851 629 079 771 572 321 217 099 379 330 701 086 970 202 663 287 366 109 510 387 468 626 317 136 958 967 511 936 282 193 125 477 293 835 998 572 014 701 324 130 750 250 778 161 377 785 163 063 802 673 057 176 607 571 343 342 969 202 829 956 467 645 885 840 271 695 907 971 117 676 597 389 021 640 227 028 460 650 783 581 412 486 538 258 428 916 905 201 531 682 233 927 072 058 039 993 616 270 765 681 405 281 745 685 833 169 251 114 936 594 039 165 364 167 344 313 593 914 027 812 658 032 954 120 202 918 874 147 892 712 538 755 238 016 051 230 198 020 816 157 435 755 615 151 771 028 028 177 601 888 165 860 939 803 897 849 940 054 508 417 209 968 161 310 928 528 107 591 244 663 344 392 072 300 407 911 272 749 829 403 132 663 518 879 488 077 976 551 262 626 768 442 399 196 071 397 399 147 172 109 905 088 823 695 025 214 757 965 349 289 334 404 169 274 194 430 746 855 606 031 876 187 366 868 018 627 757 560 617 364 916 494 102 767 197 340 757 170 896 255 369 131 828 002 811 964 235 195 897 658 839 044 666 334 974 899 065 531 448 831 021 588 314 397 409 089 122 517 475 440 833 747 231 953 378 935 743 425 130 765 609 865 392 617 158 550 769 926 285 143 381 253 072 404 091 684 838 733 050 716 644 538 962 365 165 695 223 967 793 574 920 414 939 185 173 661 472 362 432 821 270 892 662 368 422 226 539 319 587 497 701 460 804 156 935 578 280 524 950 058 139 711 132 709 459 313 193 481 946 913 741 191 767 531 263 576 205 222 174 553 474 921 943 536 284 255 895 410 049 322 269 766 358 963 570 934 779 647 495 439 951 421 307 156 743 094 796 022 628 585 781 466 847 054 408 942 946 034 746 322 377 453 558 939 754 873 883 807 929 728 080 001 637 376 421 269 886 249 691 468 927 120 999 878 371 670 245 853 268 041 297 580 453 363 916 345 241 335 775 647 792 300 733 785 092 041 332 809 111 886 255 512 680 010 837 325 599 822 929 819 279 589 056 732 183 764 812 066 825 659 603 716 661 506 428 679 710 598 052 667 839 867 701 650 039 908 728 880 179 594 243 897 935 961 633 937 189 478 408 313 296 031 275 475 042 253 109 887 529 171 286 559 820 384 046 069 065 588 436 850 972 713 998 471 388 329 190 956 459 085 955 476 774 029 701 453 480 354 471 880 474 604 800 165 479 199 397 892 254 771 378 217 463 025 295 196 987 671 844 491 302 957 458 302 141 313 661 881 424 116 335 365 904 386 114 707 782 798 445 169 157 574 107 536 543 262 412 213 339 541 441 345 103 074 968 005 590 931 823 979 013 528 153 152 652 448 051 870 866 793 071 227 150 295 604 544 244 659 760 527 572 117 287 443 227 327 817 379 126 838 412 250 241 664 618 933 465 243 727 297 625 217 534 420 797 513 978 487 581 168 865 964 186 276 105 420 884 514 825 508 738 463 695 508 109 974 763 437 133 775 919 233 094 344 141 685 252 453 714 951 937 392 437 228 343 158 724 393 059 578 661 406 288 133 746 854 768 339 818 866 170 670 399 374 012 175 014 517 937 120 303 645 397 692 109 105 106 973 278 590 650 110 031 099 611 786 897 951 372 216 573 147 293 469 290 312 287 495 226 180 945 295 252 016 523 116 932 712 280 270 362 850 180 843 183 888 394 655 245 210 237 398 497 928 746 700 317 196 461 194 086 126 840 202 021 398 904 282 087 331 335 785 471 482 588 511 743 390 805 174 254 749 020 473 634 641 520 007 337 981 422 719 398 196 571 769 024 257 929 710 980 454 721 514 603 223 776 304 931 974 416 153 456 495 891 953 382 095 962 165 681 407 820 197 132 550 748 371 275 323 314 111 846 151 507 313 605 294 964 837 705 567 139 935 340 192 475 622 728 569 189 711 341 248 781 069 275 006 388 786 561 446 175 028 380 945 311 476 939 923 018 910 055 338 252 287 998 716 716 664 944 940 005 002 089 841 241 222 703 511 581 995 976 649 135 187 404 571 081 925 026 337 663 623 325 525 592 597 783 676 068 635 732 890 962 577 643 002 877 712 101 361 881 752 833 266 858 351 990 199 754 226 437 133 489 264 193 138 729 703 275 650 489 043 768 973 468 667 491 945 989 727 460 961 791 812 975 827 863 390 938 295 040 276 141 909 617 851 773 307 672 607 221 173 295 044 237 763 718 598 974 154 760 185 215 868 031 714 217 106 697 260 309 185 551 819 908 704 353 731 662 852 262 567 739 107 533 702 288 060 117 775 921 256 918 393 052 615 604 277 323 249 421 603 458 055 596 174 211 703 323 014 166 027 696 135 925 178 544 829 043 562 189 414 814 192 219 478 451 886 386 778 347 836 683 477 860 581 694 850 400 271 548 762 717 093 319 027 317 673 470 527 095 328 814 404 309 888 158 762 806 947 317 632 307 704 364 890 763 472 025 839 581 104 801 405 985 883 276 043 086 244 029 873 512 092 076 997 530 915 546 039 442 736 399 421 074 287 220 625 164 279 447 362 713 983 366 399 432 897 031 525 230 639 404 027 064 579 587 856 021 683 373 486 066 856 813 767 784 334 634 742 942 521 768 975 768 481 996 822 778 736 071 475 830 514 456 659 114 710 689 639 934 045 863 973 771 693 762 033 682 290 213 065 489 842 690 237 193 791 503 217 029 825 339 732 541 652 264 448 114 514 549 554 243 271 859 927 562 162 943 747 399 936 210 950 159 781 756 672 916 390 355 404 406 306 639 461 172 642 083 167 296 482 683 483 316 090 875 466 809 598 928 179 290 144 720 589 310 810 044 866 562 970 291 890 878 166 912 669 042 478 226 933 563 626 770 991 724 630 274 898 846 340 616 563 823 117 940 368 014 622 642 210 904 951 089 482 514 021 736 648 388 090 610 793 816 164 138 284 432 114 381 292 291 762 220 889 320 205 123 447 684 197 579 984 734 342 613 125 675 698 354 747 592 105 417 738 177 108 484 731 635 044 885 287 605 069 939 767 034 394 823 199 214 079 889 834 824 668 199 040 046 289 831 441 609 553 903 545 077 187 042 637 345 771 398 177 806 173 388 346 804 852 982 362 915 142 736 749 397 133 554 812 842 548 588 135 728 411 529 277 085 848 450 304 087 634 875 402 982 597 789 503 964 476 027 684 260 890 232 153 791 275 139 802 131 460 181 061 250 790 760 067 120 792 114 953 101 279 627 085 642 488 827 653 586 970 428 994 147 729 005 557 374 200 225 918 282 444 611 150 093 826 374 457 032 228 503 827 787 757 414 712 006 422 417 272 254 212 760 459 771 358 200 987 368 890 677 607 915 366 779 247 323 201 115 151 945 268 629 224 458 748 020 343 520 123 085 059 902 718 357 197 227 077 707 882 734 292 659 255 585 107 949 218 881 863 507 362 147 332 548 023 037 366 361 095 876 359 923 934 021 383 690 749 193 722 968 817 657 455 965 069 145 265 892 457 748 729 376 300 956 727 345 262 735 425 629 307 418 352 146 013 036 433 255 454 392 225 576 805 554 332 563 575 090 286 904 744 925 174 151 336 840 110 107 957 406 463 017 094 147 626 116 070 468 260 641 739 492 600 274 564 848 118 280 549 609 957 664 644 079 829 939 114 247 114 269 045 463 300 686 265 177 109 744 722 482 220 537 225 807 134 544 624 616 494 640 279 979 831 549 260 319 049 259 392 744 837 384 478 601 709 884 981 530 629 652 917 210 274 213 634 141 898 425 837 303 906 291 582 459 633 966 345 926 714 262 981 394 020 485 534 747 294 176 529 896 938 463 441 303 251 466 034 789 552 721 262 798 564 194 186 801 819 712 121 691 985 231 397 029 957 091 585 000 430 825 362 834 972 688 912 744 577 123 590 002 673 549 941 754 484 439 387 926 275 161 882 350 357 464 211 773 128 008 776 838 689 852 013 561 611 266 811 791 298 752 998 529 230 975 634 555 020 435 156 175 636 807 408 286 445 341 612 987 616 851 832 156 514 229 165 276 895 340 923 430 313 364 055 450 421 887 902 109 989 857 525 124 592 070 737 899 255 785 985 274 891 616 251 639 354 694 551 208 000 995 552 257 698 313 407 587 282 176 993 800 275 468 957 975 276 015 123 107 002 242 646 763 335 587 406 666 729 535 743 880 914 055 395 250 402 324 267 773 986 677 696 143 564 984 826 514 836 713 309 924 925 653 411 763 754 544 768 098 289 813 088 210 207 842 766 542 423 146 167 126 513 755 773 791 430 084 692 879 644 752 726 248 593 662 023 076 316 988 302 150 296 379 667 097 458 307 025 542 689 990 146 359 610 375 402 791 952 231 945 061 031 784 846 936 200 991 963 417 939 939 122 568 340 781 221 701 217 174 332 241 637 907 107 524 448 210 840 192 980 256 861 551 374 316 657 115 537 622 082 214 580 076 986 406 032 823 122 338 389 908 018 412 598 890 132 706 918 321 840 262 891 958 534 331 054 788 209 170 766 836 209 576 427 536 157 678 686 303 890 585 521 487 688 800 443 837 235 058 431 829 966 160 504 555 293 764 806 881 875 039 263 409 283 885 528 878 067 943 072 933 589 397 530 506 572 932 155 462 715 285 247 312 837 800 942 931 306 915 865 569 012 206 411 624 499 245 498 726 244 375 639 122 658 755 075 130 099 326 245 413 110 878 076 654 614 132 145 724 756 175 685 217 091 476 540 938 015 095 110 639 331 267 469 567 729 403 090 769 565 286 716 001 076 097 893 290 786 716 358 229 322 179 230 189 476 012 435 062 696 894 794 862 897 376 782 050 955 590 962 707 567 887 262 667 734 380 485 017 444 555 141 520 106 953 409 375 213 840 030 663 462 877 560 537 174 732 397 945 642 475 605 350 463 574 911 729 403 034 656 991 455 298 632 873 848 266 702 349 938 060 566 895 707 329 718 626 177 048 684 567 654 010 858 186 998 160 715 833 488 623 370 706 215 326 914 345 725 419 760 801 212 088 501 668 912 988 532 695 239 108 817 187 128 036 247 725 436 760 898 277 259 412 558 083 781 899 437 426 663 533 530 492 926 720 962 755 143 059 368 718 513 384 852 711 194 625 939 560 680 307 582 578 722 966 983 172 250 900 301 909 636 549 884 001 805 885 588 793 156 995 758 249 304 410 651 397 314 495 516 855 876 851 750 850 207 153 877 450 701 516 826 813 449 508 795 319 634 748 226 033 808 804 078 875 863 848 885 187 227 401 275 982 046 423 986 157 202 547 581 083 970 779 988 561 080 195 092 888 362 084 678 474 121 514 613 932 469 128 873 731 070 066 081 001 368 865 527 001 128 905 226 895 828 830 252 656 406 453 412 073 492 916 727 337 313 903 081 489 058 610 008 638 461 631 660 835 150 445 680 109 039 632 019 533 064 990 380 468 072 344 270 030 652 812 236 490 257 276 813 459 155 594 483 751 179 121 111 629 718 325 454 996 423 212 111 415 109 868 586 337 836 945 258 747 430 911 496 083 217 156 759 496 011 452 305 408 510 492 631 607 536 557 184 031 964 272 684 546 457 055 736 254 351 867 936 098 922 881 156 348 622 284 118 304 981 341 905 057 886 866 539 733 631 337 176 720 218 178 163 115 251 785 863 622 955 631 581 620 893 753 922 197 884 430 452 983 266 371 882 379 501 748 716 139 013 192 129 859 954 033 163 503 478 427 140 701 860 036 760 294 180 488 962 931 140 406 009 799 695 764 903 194 051 926 379 501 658 595 690 633 457 903 170 554 019 397 279 103 878 750 240 721 539 520 976 895 531 749 898 439 787 869 382 933 996 474 390 020 415 228 242 815 992 166 999 589 236 918 124 636 301 901 080 988 812 971 955 398 284 363 177 694 465 512 109 972 975 030 740 845 620 354 121 237 129 049 633 900 030 725 239 251 890 720 902 204 228 917 937 971 876 054 828 604 448 666 694 675 727 924 736 972 751 247 824 402 536 215 822 227 497 819 037 360 391 104 815 440 909 214 232 061 532 813 388 681 320 386 267 305 700 397 912 557 150 993 460 412 966 197 920 222 878 746 302 847 977 872 497 736 546 325 230 087 476 534 767 756 385 637 729 421 269 643 176 370 647 800 420 467 173 941 978 516 241 894 112 968 872 165 087 816 608 230 213 707 569 562 658 738 647 240 734 946 031 459 151 995 558 451 187 289 055 546 777 766 301 328 084 018 444 032 706 805 703 751 278 636 281 866 818 154 369 557 748 908 725 378 166 632 614 165 494 678 188 521 974 489 924 043 978 318 502 966 291 692 088 782 191 147 440 708 253 102 106 927 485 754 626 118 842 410 114 420 057 786 921 766 946 569 653 412 614 333 616 218 450 533 599 293 927 398 588 970 720 337 425 783 990 554 114 874 522 359 782 917 493 832 565 653 571 699 158 535 996 179 401 283 028 100 014 234 749 046 049 910 609 365 699 637 204 948 398 981 274 915 664 372 289 027 237 616 174 639 243 596 546 733 610 067 203 499 413 592 926 408 272 802 551 980 009 779 587 360 711 993 138 423 790 957 745 378 601 089 373 181 809 229 750 757 628 682 862 729 223 355 124 752 827 545 622 016 819 272 333 193 052 371 770 371 399 360 843 342 441 862 975 760 186 010 593 958 132 631 620 039 945 899 000 853 952 198 911 184 722 970 689 106 303 214 975 985 356 734 144 771 986 637 286 027 731 521 245 624 525 250 975 615 836 204 650 818 317 343 486 563 929 655 744 387 911 379 800 634 770 234 141 806 341 256 498 942 724 451 051 025 023 554 050 630 580 602 122 768 113 428 401 784 090 163 000 188 174 414 136 244 871 776 145 015 417 703 511 803 132 091 606 515 606 508 692 648 907 450 404 527 835 364 398 908 635 651 195 762 176 324 969 426 099 762 714 523 227 371 804 860 765 983 907 351 213 025 729 115 707 280 670 000 162 353 872 115 346 280 375 124 391 687 243 085 987 156 956 087 587 540 511 592 533 953 356 294 347 294 403 019 248 165 836 581 339 069 596 643 556 830 610 651 068 391 318 900 834 000 151 390 696 607 335 588 933 710 221 193 377 076 723 632 525 682 230 021 212 817 750 447 915 271 297 915 572 263 479 971 206 513 062 352 461 522 382 770 576 646 679 175 136 079 570 067 770 453 161 013 912 834 483 368 358 502 354 957 144 430 941 686 762 376 070 922 827 011 195 275 163 654 376 988 190 439 615 331 478 000 650 518 201 565 978 809 358 890 235 899 985 312 520 397 864 814 546 908 424 799 997 602 916 443 437 640 691 686 086 567 456 157 308 736 448 564 661 912 426 749 253 585 119 333 610 485 252 671 770 496 479 914 848 533 618 076 726 961 497 701 397 679 412 511 652 763 639 142 251 399 923 607 268 504 626 624 947 063 644 952 888 823 014 295 999 777 011 722 513 496 940 008 382 387 016 622 336 938 203 921 088 699 109 738 065 496 229 739 210 901 756 912 804 259 650 666 704 667 067 151 527 204 926 011 038 670 054 050 907 862 295 427 843 120 303 575 522 304 261 003 591 372 273 488 150 307 684 908 725 525 588 885 988 179 983 535 044 039 262 938 585 990 025 310 908 821 589 800 425 831 469 223 779 915 066 358 544 020 635 993 010 495 277 918 791 715 550 433 897 588 384 113 408 740 133 213 825 233 090 213 227 543 845 757 989 603 524 256 919 007 636 716 744 814 206 224 647 101 484 444 385 866 932 037 352 271 741 005 543 497 200 659 650 693 743 290 696 644 352 532 353 196 351 358 913 596 001 313 170 878 313 201 057 778 383 154 222 609 017 957 007 173 734 606 853 526 916 002 804 057 908 663 754 482 981 307 398 310 538 483 588 285 802 108 423 747 210 027 002 855 191 449 162 131 875 441 853 556 842 489 770 507 566 321 589 445 893 752 468 205 911 315 998 624 374 346 458 730 286 083 841 315 205 374 100 713 388 793 792 011 308 942 049 684 044 307 561 694 995 773 428 028 016 802 112 373 245 486 069 626 186 816 449 724 059 999 425 279 199 936 170 066 991 673 416 345 784 137 214 405 278 597 782 296 198 803 859 814 834 924 008 139 531 018 289 728 344 111 472 562 039 692 683 993 307 446 576 791 075 618 259 445 517 236 661 982 772 935 772 731 679 191 849 609 829 943 438 811 527 181 705 980 577 384 041 558 553 019 414 299 108 006 992 485 741 899 889 394 790 706 671 993 910 334 404 733 968 340 338 980 072 670 743 478 400 877 213 776 299 155 801 945 642 819 360 497 053 132 944 564 515 637 292 368 370 020 397 424 327 687 964 894 450 494 317 623 221 787 644 200 350 516 972 405 370 038 504 206 481 955 144 134 777 524 720 277 474 443 527 525 652 697 011 504 529 860 674 767 178 300 778 333 909 085 710 003 310 964 211 687 136 375 673 885 646 267 731 004 639 135 416 519 901 283 772 794 338 433 168 069 361 587 849 544 944 569 129 990 614 649 448 818 487 018 017 456 144 244 255 606 496 319 461 964 354 461 116 926 488 489 025 507 970 680 754 529 441 680 711 937 628 105 098 736 850 034 727 762 154 084 544 152 462 011 020 447 079 827 561 214 580 994 446 946 068 688 483 421 817 470 974 309 789 220 081 910 060 028 072 835 896 147 938 081 206 069 108 154 636 476 034 827 406 492 663 423 812 743 062 911 421 358 454 853 950 796 651 464 511 554 183 466 564 608 040 946 000 748 996 932 414 413 508 547 126 836 194 929 736 656 100 783 941 080 406 444 437 543 718 694 901 621 172 724 757 214 241 648 377 326 240 045 586 473 104 082 964 456 625 759 607 320 940 059 856 484 962 285 994 516 701 174 720 636 066 128 227 031 727 232 322 865 578 898 211 057 106 318 805 722 125 813 717 757 753 739 303 968 830 127 217 256 951 877 105 931 930 670 005 588 638 511 883 106 101 036 181 123 546 528 906 692 186 034 777 570 437 952 726 547 162 952 648 814 997 505 021 076 318 082 317 171 272 497 660 000 823 026 343 425 404 299 900 588 078 766 952 887 513 107 921 140 010 364 595 205 894 036 189 320 036 385 823 911 773 565 860 301 905 901 009 678 827 844 505 105 255 911 084 743 168 874 684 430 847 155 265 550 054 868 254 765 689 958 819 695 344 516 489 816 877 399 676 513 476 232 670 443 656 799 452 633 920 571 612 062 453 085 355 504 464 736 819 526 057 315 260 482 432 707 562 594 835 088 083 044 788 571 365 538 123 744 663 160 213 830 825 192 469 036 625 492 833 584 101 787 255 293 422 576 490 661 027 706 981 597 439 753 315 752 269 498 121 219 941 813 013 339 227 127 852 574 426 518 938 052 242 655 871 303 937 784 505 060 461 457 311 608 352 798 139 764 754 982 660 289 937 371 183 824 369 061 037 105 686 841 727 615 489 731 854 251 476 470 005 489 142 567 001 416 143 604 429 751 227 745 367 770 504 731 953 283 312 432 709 483 489 480 859 252 901 286 651 040 478 084 945 008 294 132 319 555 814 613 192 692 866 551 676 084 460 322 483 898 856 126 174 572 900 737 130 326 634 774 011 632 840 450 409 569 681 618 495 722 200 175 821 226 916 057 194 550 313 694 880 549 091 067 328 210 030 431 124 767 029 769 742 437 136 900 763 889 592 429 807 717 695 312 010 237 826 701 936 186 467 369 196 132 993 344 491 226 807 912 864 361 350 298 013 047 794 363 966 512 643 649 558 752 261 016 786 352 543 040 908 231 307 532 592 913 799 489 364 703 913 895 886 932 669 191 465 025 385 379 520 977 576 367 194 972 485 571 233 452 095 040 877 986 279 308 557 582 388 400 599 760 065 254 184 004 552 720 682 794 205 582 249 276 546 147 242 601 103 506 932 144 433 894 656 222 298 261 561 272 521 178 297 713 948 378 948 123 680 912 761 236 668 343 695 959 562 621 501 209 604 478 812 710 271 566 092 185 542 358 324 339 337 717 140 514 081 920 471 322 436 106 805 457 287 350 774 226 645 504 117 912 184 098 316 018 284 747 237 465 595 211 801 351 027 133 163 614 382 406 832 043 092 491 492 279 942 633 640 959 484 285 419 585 640 836 421 704 888 594 578 814 392 221 154 576 467 628 676 651 368 266 523 135 428 718 111 318 923 405 940 723 107 521 785 168 243 768 278 365 404 517 727 344 693 476 627 187 159 649 107 602 821 174 466 396 819 126 915 383 117 123 517 482 365 352 480 120 851 732 419 484 759 789 907 124 228 161 239 510 835 195 478 754 632 736 276 889 231 137 592 624 329 431 147 476 754 323 081 216 766 716 479 700 347 504 841 529 671 531 389 049 205 131 680 735 397 797 532 704 072 954 109 599 826 442 135 837 995 474 441 213 595 639 837 451 440 627 554 487 751 991 237 044 602 959 994 492 540 013 321 108 655 072 183 742 019 328 532 066 277 074 862 430 756 792 687 165 739 191 071 834 003 029 014 666 806 623 593 211 959 456 165 462 300 255 411 169 106 950 340 728 921 352 988 277 958 128 325 016 589 618 103 861 049 981 314 272 128 819 624 276 279 252 910 413 224 532 155 589 451 433 978 279 205 047 504 364 975 263 561 193 363 777 433 473 262 125 583 959 922 162 502 464 645 137 221 394 282 547 914 348 006 066 538 935 487 761 101 759 321 707 562 669 603 267 661 376 470 473 069 738 316 690 384 186 058 741 562 767 686 147 605 716 484 524 406 146 966 824 995 154 930 354 050 191 239 097 320 927 886 571 567 549 826 554 329 195 500 244 185 796 118 230 971 360 810 474 499 433 601 882 375 027 555 810 051 540 375 005 061 008 352 286 863 547 706 566 601 012 560 438 224 928 071 223 401 561 970 426 863 910 691 182 883 540 641 077 489 534 713 113 793 113 860 553 346 549 114 290 939 706 141 096 552 506 440 461 103 832 100 467 616 396 803 897 041 489 170 939 915 150 398 167 340 861 860 621 121 949 401 384 460 480 176 089 951 188 796 486 477 152 318 344 860 820 656 135 819 320 783 160 265 289 909 291 926 901 354 101 564 121 223 813 087 365 578 870 229 836 102 591 807 532 927 453 263 748 927 455 551 009 995 156 405 354 719 272 704 766 753 643 491 162 272 658 038 599 406 532 797 262 722 242 069 801 179 447 906 216 905 034 881 117 253 240 496 065 414 730 759 026 430 119 454 464 406 922 139 734 693 045 890 209 364 394 331 368 653 874 647 758 801 225 409 549 892 862 955 821 700 375 521 460 354 414 323 070 521 928 114 238 335 147 819 180 306 808 790 295 145 119 182 128 901 639 620 193 621 520 634 350 678 497 058 842 666 495 383 775 472 113 826 387 800 765 608 841 263 147 731 429 247 632 865 896 669 616 613 402 932 692 603 939 426 591 083 550 152 251 477 740 670 373 403 431 088 849 093 936 188 755 662 129 544 768 198 819 826 040 871 934 570 795 102 590 361 388 144 261 464 443 011 101 284 196 715 222 154 671 889 048 563 837 732 927 995 184 400 139 946 846 992 773 060 466 017 575 762 781 151 053 039 447 844 110 268 589 896 576 509 103 113 905 255 458 940 332 557 606 359 045 280 056 785 385 691 527 725 536 389 134 977 688 851 809 352 216 280 554 776 376 334 253 062 966 801 153 239 111 389 456 910 545 736 167 691 268 759 688 792 277 911 975 287 532 947 098 095 757 775 514 103 588 321 670 354 361 362 964 133 284 361 268 996 799 379 832 190 333 918 219 168 712 372 661 436 650 196 399 986 158 131 973 978 140 422 022 603 135 136 957 107 797 135 800 890 683 480 326 034 853 284 516 682 121 953 811 486 466 498 083 572 204 512 814 137 057 952 437 247 733 144 802 847 437 156 546 052 202 614 440 260 729 309 375 264 015 710 911 310 527 432 126 072 023 173 063 457 307 989 853 222 902 437 249 090 629 587 841 884 837 174 467 145 909 261 263 320 558 109 571 591 231 839 771 851 228 389 030 967 406 970 706 540 539 803 657 700 950 474 870 590 967 024 941 250 813 982 610 149 929 145 252 142 604 602 872 442 048 960 228 169 768 315 038 592 990 171 301 018 281 223 553 275 811 455 186 568 750 872 595 999 539 803 768 411 002 974 146 424 146 431 243 891 085 805 212 668 406 086 075 291 758 421 446 719 614 052 726 114 674 216 267 731 816 189 729 310 665 393 240 659 349 158 896 325 801 267 463 522 971 380 624 107 470 064 997 478 538 025 030 845 306 800 559 967 338 369 350 238 241 771 914 702 311 584 409 313 046 446 573 293 256 477 506 968 006 558 696 861 192 759 704 532 678 889 579 302 987 854 499 104 843 620 228 929 569 083 547 071 986 438 247 116 477 790 492 185 787 071 213 768 499 234 169 645 135 323 063 907 980 775 512 120 225 129 597 298 792 824 767 764 931 402 250 336 550 677 740 637 829 212 382 957 389 683 649 924 324 704 082 763 168 225 232 404 504 016 595 639 448 123 887 818 950 697 923 619 744 199 067 747 267 939 094 644 164 827 982 099 584 280 534 521 959 798 076 812 811 346 335 748 356 108 012 851 781 026 142 555 782 957 104 309 750 569 440 579 724 115 950 912 058 113 790 411 243 656 582 380 620 289 521 975 436 655 817 439 634 743 072 977 958 248 157 954 198 434 918 473 948 652 156 618 639 834 396 389 813 824 342 767 604 902 382 040 107 445 263 187 766 561 496 878 278 719 168 522 340 219 073 027 171 452 776 178 740 303 086 721 367 541 826 961 968 552 657 233 317 256 186 422 000 868 583 036 848 264 798 549 052 529 382 787 974 781 881 405 353 609 142 648 917 908 021 512 693 071 692 282 649 706 186 448 411 569 882 162 469 081 113 815 103 586 240 885 575 458 958 605 907 461 622 080 008 672 055 956 231 402 919 593 119 367 822 018 009 389 445 783 955 399 378 371 901 406 770 420 452 555 478 723 947 122 857 815 985 985 993 952 305 080 910 684 386 525 187 315 534 371 672 513 996 176 237 060 729 990 954 286 562 015 920 011 965 586 334 807 939 153 262 900 332 239 104 991 823 081 833 881 468 290 642 697 190 752 647 015 807 094 441 873 404 303 175 962 481 274 923 445 874 277 673 438 302 425 655 333 428 151 909 716 750 897 175 976 993 672 773 181 289 509 431 179 852 352 885 494 608 616 585 774 960 474 362 152 360 127 195 199 560 544 924 115 404 080 102 668 617 665 661 144 673 709 881 024 507 686 443 053 986 821 923 263 295 741 560 867 163 659 402 037 611 292 441 561 248 139 382 885 424 318 102 081 336 432 420 606 876 332 482 999 795 143 764 167 644 476 919 203 342 393 243 920 853 739 227 944 304 915 140 228 039 898 982 089 125 733 654 809 477 228 347 791 973 026 335 299 994 268 390 773 238 742 955 407 502 389 139 250 580 119 629 913 984 929 262 871 322 596 373 161 578 610 976 920 578 563 391 344 990 499 719 962 215 805 540 066 203 080 889 564 018 214 437 819 093 419 385 530 599 822 205 743 797 787 511 221 933 826 360 857 534 796 603 015 270 822 563 794 800 815 455 454 093 405 830 116 731 204 579 692 391 855 265 917 826 149 407 920 800 525 147 047 429 470 871 349 865 811 310 150 951 019 120 964 961 393 321 055 690 399 452 252 546 607 316 493 762 653 389 915 789 647 077 262 225 409 381 566 439 156 447 466 334 734 638 501 656 913 014 953 615 614 284 621 967 561 014 789 012 061 147 409 535 121 912 576 572 503 259 224 336 541 805 521 154 604 398 219 990 225 300 733 767 805 439 753 842 315 061 144 310 100 505 952 177 892 325 565 409 344 523 968 682 798 486 245 192 402 353 520 041 782 219 547 096 550 725 577 624 741 477 449 590 993 090 044 798 595 414 946 157 227 630 171 053 248 229 036 849 731 385 959 444 010 218 477 677 370 891 677 451 109 598 515 056 955 397 633 648 631 341 422 491 892 702 294 566 563 397 567 055 244 813 057 060 245 050 189 052 395 681 509 547 774 747 328 629 955 663 355 170 422 484 741 920 898 402 383 645 905 651 414 007 186 541 607 032 058 755 637 954 450 475 204 153 339 347 599 777 931 638 450 090 896 649 182 391 432 706 969 822 351 619 997 945 360 480 408 816 956 476 937 582 022 403 874 646 315 444 525 710 955 602 742 157 985 102 571 352 600 440 394 133 143 605 820 600 447 051 950 129 495 961 643 861 535 549 852 968 137 744 370 770 925 393 101 597 541 099 664 909 324 447 389 085 705 417 888 132 222 344 509 918 000 099 616 936 919 652 664 419 637 927 156 682 502 591 678 206 518 264 727 742 778 173 572 806 578 811 267 511 289 254 796 369 936 926 256 654 909 596 056 168 449 406 617 609 526 877 414 712 792 255 167 417 937 541 146 593 728 070 157 362 620 181 265 491 572 227 539 634 391 614 131 005 964 153 682 768 506 098 256 927 296 195 703 361 968 773 945 346 689 697 665 256 780 449 186 617 562 506 156 009 851 914 985 095 870 613 119 106 006 457 138 515 307 830 434 176 700 591 293 464 112 787 294 997 492 111 008 061 534 786 405 612 441 622 848 217 040 640 311 194 155 944 724 155 063 069 375 040 758 221 257 359 163 578 298 512 945 350 617 906 800 462 555 218 680 704 921 798 572 182 082 049 940 063 964 663 101 693 310 853 066 099 601 762 106 221 533 152 550 427 343 775 798 416 528 814 576 071 134 398 312 478 094 528 314 809 092 917 774 066 130 449 954 702 749 688 839 896 652 088 176 880 344 752 256 276 839 086 973 125 362 810 106 653 566 736 713 247 300 009 748 913 571 758 434 300 925 721 077 722 702 563 355 143 745 956 312 382 681 461 631 927 550 087 754 794 391 501 760 270 218 071 828 623 006 508 177 992 773 828 997 893 662 746 263 393 297 848 398 313 258 935 695 734 332 750 326 366 397 252 872 904 271 016 675 817 500 818 905 951 690 940 065 201 216 174 803 644 014 383 347 865 273 726 119 512 180 016 606 359 976 674 829 858 058 069 440 879 063 121 345 223 638 318 660 293 310 564 450 697 634 883 817 420 176 529 573 170 309 203 644 612 168 952 458 512 257 132 214 760 399 555 217 794 080 487 840 929 900 405 535 314 460 067 236 560 673 310 554 440 485 909 007 462 025 385 555 066 272 023 486 181 935 817 122 526 282 860 670 642 042 068 628 417 751 206 981 523 536 268 345 381 437 471 947 486 113 468 844 369 393 225 561 555 812 953 496 270 179 948 948 594 993 506 188 247 232 631 828 004 421 337 193 613 007 422 987 812 338 074 225 706 601 310 540 098 850 506 756 202 361 139 332 101 679 652 472 958 870 975 774 351 889 720 183 333 238 259 061 587 414 031 560 904 872 731 779 994 909 958 821 321 488 368 977 580 369 407 123 795 424 831 531 487 725 408 980 848 935 076 129 271 000 237 267 683 571 845 991 318 020 183 630 345 558 861 200 366 998 494 019 365 758 560 397 170 636 283 294 958 821 661 387 488 671 778 168 987 467 273 235 027 755 048 898 017 203 077 290 438 633 256 817 771 893 946 070 439 949 216 056 254 545 640 580 702 019 867 283 061 672 219 058 482 295 239 362 159 969 745 260 423 607 097 089 317 088 676 964 137 798 925 416 454 774 245 652 640 612 161 460 466 156 406 691 816 155 346 892 831 004 743 571 211 417 236 788 746 407 864 426 828 655 516 334 683 195 739 163 635 799 138 977 245 930 848 329 272 834 476 778 496 908 673 464 844 369 872 029 439 165 093 680 280 301 727 552 005 210 536 649 455 324 896 562 012 354 483 923 867 504 579 238 421 895 029 533 158 619 243 543 884 694 104 013 240 442 377 112 388 298 763 145 541 641 511 193 010 978 334 316 535 275 347 823 706 699 888 682 373 111 301 620 436 292 991 947 887 532 450 781 431 111 076 241 689 148 270 907 805 342 392 482 758 926 780 590 086 054 339 326 637 550 279 813 241 936 402 209 056 228 816 341 651 504 460 541 683 238 576 636 641 194 396 171 713 213 090 551 486 065 260 547 426 040 809 404 292 915 687 756 658 475 355 413 755 238 972 453 699 638 552 905 294 434 451 205 320 459 004 910 060 365 940 687 244 402 546 398 244 646 376 762 946 436 852 333 220 558 102 423 313 331 733 840 707 961 857 769 799 506 866 675 549 646 751 717 060 459 394 732 806 948 670 635 033 326 724 617 999 635 077 599 592 862 203 799 804 772 119 886 148 612 546 683 625 231 508 277 885 516 345 549 198 852 917 703 344 742 138 239 112 139 815 945 296 754 238 545 401 199 128 403 698 205 203 455 872 179 382 422 235 827 999 871 030 568 072 374 437 078 369 007 039 458 004 889 981 193 802 418 917 515 079 939 149 106 645 366 524 196 297 788 444 743 397 556 357 859 013 778 610 650 690 110 707 622 765 555 536 089 837 268 376 310 481 209 783 142 600 005 425 563 603 774 165 262 278 181 878 961 666 243 866 483 856 592 718 779 972 068 002 386 561 514 888 444 278 637 422 096 814 902 805 396 765 699 342 717 711 237 756 746 501 024 195 145 711 117 243 652 199 616 104 389 625 042 518 428 075 866 410 586 055 512 014 921 417 511 309 521 185 382 043 785 612 898 896 273 617 314 558 868 737 236 594 851 843 693 181 112 850 365 120 882 741 661 961 185 615 963 319 699 837 059 134 927 246 882 664 674 374 957 368 347 262 126 693 525 193 594 504 766 917 087 654 016 012 131 575 224 634 172 897 350 851 858 385 972 483 736 671 777 888 128 297 855 286 529 328 985 628 690 338 836 809 757 188 154 356 060 891 546 584 950 010 028 069 073 554 595 802 267 238 143 353 348 553 861 942 777 475 689 640 877 448 111 235 633 245 430 548 850 512 397 459 498 581 385 786 520 386 034 831 203 610 631 565 966 927 973 490 371 061 018 552 218 291 639 354 635 860 701 035 193 270 053 818 817 004 637 694 470 687 090 204 061 459 444 335 651 820 654 328 749 947 018 569 150 988 949 461 804 928 635 878 607 885 931 044 116 183 364 035 641 556 112 794 724 663 967 409 090 361 019 496 862 351 991 085 178 507 682 206 731 530 909 597 345 649 401 432 276 326 494 975 084 301 379 301 568 257 684 267 099 619 864 836 424 258 392 447 806 846 836 865 764 440 391 168 221 625 268 993 005 177 999 004 628 370 385 133 739 983 163 063 662 340 812 304 725 759 714 447 864 555 146 626 869 595 126 628 382 461 192 905 019 376 454 127 261 009 208 729 359 662 709 117 224 657 555 043 479 524 149 644 925 167 836 702 597 009 942 617 554 756 709 533 521 485 931 137 903 096 440 018 544 486 738 023 363 005 648 488 084 331 096 066 252 849 227 479 603 322 343 172 761 711 287 920 395 042 769 706 903 567 240 300 729 248 543 615 640 465 693 130 538 155 012 235 610 238 448 429 072 384 657 519 288 134 786 966 954 989 642 774 632 533 281 687 803 238 917 067 828 766 278 442 614 594 592 134 671 481 540 885 578 669 212 618 231 063 236 627 588 758 317 577 193 636 221 250 621 430 495 468 488 219 775 093 678 074 652 392 714 922 362 653 456 427 893 464 613 275 328 698 692 193 947 734 831 079 141 512 511 831 010 709 719 478 415 970 623 787 717 826 527 994 188 606 945 203 321 237 532 606 847 545 894 641 514 284 120 173 383 387 422 707 852 083 690 197 872 550 541 066 569 411 501 887 642 716 658 492 387 694 690 884 964 952 279 500 402 290 029 352 625 006 943 611 904 979 098 523 353 789 725 200 174 182 708 380 493 574 581 775 698 393 724 236 161 676 112 107 767 462 924 996 937 339 555 923 578 547 062 798 131 972 261 508 281 735 736 410 530 709 770 852 697 209 710 695 162 392 550 517 447 890 677 855 616 505 088 989 657 931 407 614 629 860 337 514 746 416 271 035 247 438 358 019 362 815 646 639 511 269 218 315 765 047 041 041 855 857 223 263 707 457 520 209 742 404 056 673 899 374 862 472 902 744 562 738 066 885 905 456 641 731 595 579 531 768 846 157 935 367 466 430 372 845 254 399 689 005 832 051 784 753 597 297 241 957 795 184 895 626 811 034 507 192 889 798 053 589 569 591 211 736 369 838 546 516 322 403 269 790 163 644 096 654 560 846 303 375 078 374 337 392 798 594 047 766 527 206 035 482 143 017 193 873 213 379 573 426 142 482 754 734 904 162 818 575 726 232 916 554 223 389 293 902 933 984 104 735 283 567 527 994 291 210 289 933 265 685 860 568 248 379 879 002 348 693 221 531 753 801 067 356 633 761 634 604 688 032 182 891 330 440 434 631 417 953 638 304 608 670 747 931 455 704 934 074 862 468 278 257 464 403 114 688 329 489 614 685 463 031 055 986 348 294 845 405 313 806 643 522 621 493 731 970 156 870 082 069 279 522 326 506 803 900 672 822 545 797 397 270 879 118 993 374 505 600 076 474 381 471 023 480 655 225 171 211 136 994 851 041 264 963 251 179 790 304 962 865 620 520 984 993 527 752 250 945 257 633 060 164 676 147 995 741 622 898 292 868 663 939 375 950 213 183 886 336 292 036 138 586 866 300 725 394 814 016 657 095 097 188 056 150 186 773 998 642 002 549 388 576 145 156 182 249 760 318 926 238 542 674 409 961 239 283 673 835 069 369 269 237 578 929 637 026 664 296 402 268 462 411 493 944 968 905 987 705 497 026 414 146 794 418 020 051 198 316 820 704 534 378 663 931 322 462 945 600 772 439 949 572 332 702 548 553 655 256 286 793 630 185 193 224 615 765 131 843 504 158 565 069 311 786 369 971 046 345 890 158 865 848 921 475 471 152 506 285 604 594 447 927 249 426 932 031 850 786 248 381 975 121 120 239 262 118 823 665 046 286 098 502 641 320 257 710 707 127 591 112 335 566 443 941 508 489 602 737 715 549 765 969 970 064 340 684 051 274 944 935 116 087 132 100 982 643 724 252 558 910 928 984 078 605 910 778 869 912 827 850 178 530 759 813 835 884 199 972 788 403 271 302 151 833 412 725 905 477 715 882 723 789 722 759 670 376 924 678 346 478 275 498 631 368 687 252 851 441 843 628 457 223 721 293 579 995 763 062 675 971 531 489 710 432 431 434 773 383 917 547 927 172 404 165 405 866 604 588 444 486 384 717 867 570 878 627 197 466 394 446 256 549 361 014 940 931 745 976 980 958 656 751 051 954 626 125 108 207 139 072 180 477 372 979 727 831 788 061 017 114 493 782 920 554 617 772 805 600 872 816 106 506 283 113 080 847 962 899 293 620 922 887 524 194 002 146 859 615 967 828 890 347 500 808 440 835 525 022 490 684 623 909 972 858 888 807 749 910 799 839 781 832 432 207 371 811 923 112 847 358 237 310 785 861 914 408 772 780 580 386 057 034 300 142 828 709 784 243 456 898 199 967 264 866 395 626 317 840 538 627 243 144 629 283 971 471 353 160 794 058 814 367 135 297 515 000 429 198 032 733 222 250 359 572 386 245 684 692 117 063 195 718 455 151 553 485 262 239 736 045 653 677 098 226 162 246 778 936 616 874 033 690 670 755 660 361 027 052 518 190 960 847 246 025 731 618 320 707 522 124 488 903 182 470 449 865 771 122 759 728 687 272 330 110 583 259 554 467 368 275 237 738 574 803 839 544 409 583 891 246 493 800 661 702 911 382 262 304 844 493 902 941 347 422 168 740 004 743 640 117 841 230 922 041 702 816 243 544 340 892 879 150 740 910 276 398 745 617 597 109 330 166 470 542 251 196 023 367 415 125 873 152 606 908 733 935 222 201 626 760 099 340 707 413 813 139 211 593 912 557 061 694 911 065 537 481 339 054 905 300 834 185 667 774 205 833 039 369 270 300 323 962 115 779 371 593 370 753 693 045 233 021 543 351 099 516 047 101 790 578 555 596 802 079 160 190 331 095 594 133 168 142 500 097 876 181 576 347 628 671 965 466 939 161 599 871 304 478 385 336 838 702 576 780 189 671 332 225 218 786 931 544 359 884 707 495 610 979 315 254 027 592 336 349 509 997 471 938 418 604 477 462 862 550 479 775 410 853 476 167 417 437 579 906 095 455 563 293 013 703 330 013 899 200 161 432 721 204 917 955 102 959 233 942 149 161 253 073 335 838 824 036 866 323 397 320 412 823 332 055 618 279 082 398 661 421 046 168 467 883 847 903 872 378 143 437 795 333 197 188 872 501 464 614 271 514 711 393 313 874 545 387 073 491 382 177 262 819 832 500 401 035 896 481 222 351 494 572 749 457 515 614 695 505 958 809 094 641 949 373 112 433 113 835 266 099 573 934 902 147 751 702 668 230 651 980 335 062 898 950 052 139 059 845 926 153 763 201 941 467 435 424 797 672 414 502 904 219 072 342 664 738 923 954 561 264 846 037 604 362 881 475 108 541 451 938 599 823 404 717 186 625 262 485 181 672 182 599 852 078 319 203 328 144 574 680 395 352 116 240 337 852 957 658 191 626 905 749 340 490 381 432 721 298 746 403 543 215 743 965 170 788 657 606 233 932 479 594 203 678 881 792 552 053 100 151 432 102 915 946 514 612 072 680 213 239 526 108 030 208 393 129 647 629 595 360 314 708 702 395 123 682 295 209 388 809 740 541 286 147 571 205 702 477 740 814 326 388 129 082 358 725 054 254 539 472 930 869 253 782 824 452 533 605 886 589 777 711 484 119 522 006 177 849 389 284 075 214 061 884 326 987 453 945 911 831 159 061 853 941 951 439 388 837 301 250 486 871 463 217 134 157 150 260 751 222 702 494 052 821 166 470 952 382 584 990 958 754 396 850 147 438 851 893 312 769 361 481 480 803 083 023 722 404 109 637 876 120 772 402 895 425 150 397 835 720 953 466 854 686 267 743 411 998 347 542 765 570 428 873 105 595 194 669 685 931 446 129 312 997 695 521 190 094 013 753 360 836 223 673 311 935 840 735 922 899 008 523 258 770 388 980 609 580 815 150 825 149 128 175 533 299 920 423 092 842 121 707 861 927 567 291 666 244 144 057 756 782 430 670 446 783 085 022 575 684 524 027 715 790 934 183 531 820 004 466 923 893 688 238 556 870 024 803 269 038 781 078 853 397 558 758 330 433 072 134 310 228 748 290 383 825 582 108 273 467 113 636 737 404 507 613 614 748 192 301 364 109 103 818 870 936 620 042 604 234 945 143 026 488 545 588 403 512 641 977 452 731 924 961 323 719 368 465 529 047 492 318 918 345 633 041 928 783 629 592 595 967 625 051 793 994 519 935 063 248 781 185 449 286 180 716 388 021 822 721 974 621 402 143 765 371 279 935 615 896 187 847 520 321 414 701 498 183 811 522 568 334 851 187 420 067 778 731 620 831 471 741 969 934 863 066 190 644 595 013 892 557 542 876 821 989 482 363 964 794 273 834 818 226 777 086 910 196 287 299 932 562 407 780 917 697 392 354 020 864 958 265 509 405 654 425 781 023 730 949 083 804 515 470 870 124 932 949 627 963 361 348 606 122 031 036 565 104 931 807 585 601 779 631 671 618 663 897 877 422 290 146 286 789 030 599 965 323 752 837 545 812 360 312 208 010 211 625 571 338 952 538 482 699 788 225 501 543 598 695 994 969 641 349 797 433 283 259 717 537 409 888 621 794 296 148 012 343 911 956 807 150 672 226 677 280 654 782 530 544 626 725 400 459 660 495 817 886 728 927 128 856 364 912 594 858 460 376 338 121 934 311 027 881 419 245 939 699 169 822 056 224 005 438 504 409 394 389 813 730 799 877 952 374 722 484 166 391 872 784 375 683 246 469 644 145 803 216 371 890 106 758 936 955 732 451 574 765 468 601 095 910 939 568 727 262 446 595 327 211 215 072 354 386 678 369 937 152 128 273 261 647 291 173 498 990 155 803 494 300 776 801 435 344 815 382 015 033 817 231 771 013 865 126 341 480 244 249 175 240 349 327 758 213 400 130 128 800 964 101 135 742 987 232 884 683 496 400 067 226 710 837 109 135 924 884 320 882 919 011 719 937 428 619 002 872 928 523 417 366 241 996 567 456 910 357 981 752 054 642 819 335 395 966 298 697 060 143 733 075 303 970 838 645 743 679 108 110 295 921 316 349 885 090 984 226 295 512 209 573 738 017 977 000 129 410 749 196 534 246 471 824 028 448 112 006 208 259 302 519 149 473 754 214 648 180 838 287 727 005 261 525 517 732 617 325 722 673 656 400 686 107 368 403 099 985 242 633 056 915 967 566 379 989 010 947 682 339 774 776 223 873 994 317 237 763 902 814 025 718 492 356 692 875 176 441 987 951 319 988 126 262 594 700 799 309 242 326 647 581 490 493 812 345 080 644 257 317 145 550 205 302 598 180 804 681 651 160 350 813 427 287 474 887 338 533 918 894 477 572 813 042 142 090 329 769 046 789 823 544 202 438 640 302 621 872 230 403 299 255 951 270 275 826 119 233 033 013 992 114 926 021 396 155 297 258 459 632 286 136 351 010 916 914 450 813 144 104 032 466 632 397 454 033 344 177 917 063 422 923 020 591 039 486 625 958 961 844 043 345 941 930 627 929 112 259 694 052 067 226 968 307 324 945 635 735 159 375 012 507 962 846 559 002 391 562 440 531 337 585 155 258 510 143 648 920 045 026 777 388 706 691 506 401 158 992 168 436 512 179 429 751 288 756 758 318 652 781 169 535 812 588 600 682 025 074 766 309 664 915 492 657 696 535 420 797 372 738 949 968 241 692 248 790 106 420 479 878 131 788 776 540 946 942 041 604 988 621 230 728 907 393 532 426 134 210 432 663 528 441 016 165 687 414 701 197 481 725 242 743 615 985 514 911 005 238 260 811 567 352 589 590 229 146 856 432 752 045 085 608 192 561 430 012 212 946 658 946 518 903 597 001 687 069 171 210 179 165 918 431 726 774 218 989 461 632 273 262 348 171 874 979 168 182 949 589 637 897 286 690 036 596 326 182 117 524 798 461 344 099 721 142 649 695 768 439 622 529 913 321 110 856 837 929 298 949 149 142 672 020 087 631 303 114 602 126 511 731 546 318 167 347 951 213 845 571 268 980 266 269 187 137 803 183 770 423 525 254 944 494 754 143 791 828 542 187 711 233 278 560 485 901 611 234 823 496 043 164 240 404 424 825 602 941 731 064 265 706 785 309 950 974 349 857 891 982 226 515 528 501 047 969 184 133 836 351 673 780 458 919 205 452 362 064 521 712 584 296 065 698 600 570 814 787 050 791 059 728 130 947 244 249 605 593 283 197 653 958 751 558 081 905 035 123 957 442 848 092 679 545 336 525 911 565 301 617 049 459 677 466 323 679 109 010 061 377 799 547 275 781 910 664 903 025 679 009 841 725 015 161 718 259 439 900 803 362 147 299 098 672 223 333 700 261 368 890 295 217 153 839 049 429 973 503 409 252 809 176 509 073 411 701 370 488 320 468 145 429 931 655 466 171 591 529 115 348 238 260 959 119 012 977 417 425 165 740 697 437 891 099 041 863 422 004 865 071 218 753 492 402 442 074 623 836 766 231 536 754 082 066 079 167 248 985 921 865 226 949 206 830 481 001 536 225 750 972 205 987 722 264 027 418 384 934 413 278 779 196 798 535 997 385 095 993 661 100 771 297 353 121 921 142 389 651 467 530 669 312 818 034 899 575 599 787 400 228 370 934 311 724 913 082 733 402 425 198 068 937 722 127 668 072 007 004 994 679 123 598 223 015 717 046 087 204 984 380 974 836 766 500 222 885 409 607 425 062 276 579 086 767 531 737 541 784 902 911 707 907 256 434 845 823 688 925 018 288 832 409 781 715 825 909 193 861 259 317 425 301 675 986 467 006 604 246 653 763 687 774 650 795 899 653 627 177 180 874 533 514 332 403 458 900 297 995 114 341 688 252 176 454 938 397 385 081 984 795 909 962 217 656 005 639 093 141 862 444 201 525 200 182 807 963 894 395 751 447 134 490 233 545 315 882 590 093 469 586 990 017 853 582 106 974 426 195 202 140 039 472 721 942 921 483 570 863 896 291 947 871 404 474 175 905 188 486 990 090 828 380 539 929 278 731 136 607 788 917 579 885 623 717 136 463 628 877 873 394 238 594 278 746 338 609 397 157 398 057 739 457 059 918 775 829 288 013 794 808 796 222 162 769 887 115 178 564 229 213 571 927 526 346 013 796 489 331 287 264 070 207 075 656 984 638 783 170 579 670 521 034 245 691 667 859 384 334 079 608 592 387 048 848 364 629 909 295 729 552 975 778 597 229 769 875 062 489 793 003 094 151 143 653 607 701 169 177 735 610 088 684 825 250 533 060 010 288 540 015 629 935 753 627 415 137 301 501 728 762 829 471 911 363 595 158 683 625 350 347 478 323 686 866 430 786 598 498 190 009 028 844 065 112 026 890 351 567 834 535 843 035 040 662 910 095 162 404 782 973 440 763 835 195 414 751 664 495 485 639 781 192 750 002 907 218 618 029 678 142 599 498 470 455 402 124 148 734 788 983 202 851 331 623 582 148 527 094 055 829 898 162 563 954 063 738 850 106 664 212 694 722 786 235 756 016 587 977 589 621 900 918 137 083 380 462 682 952 440 739 829 234 012 459 616 120 810 269 708 557 035 438 488 025 023 331 117 913 032 198 577 837 321 242 568 817 894 632 275 031 194 287 396 934 837 548 516 322 467 120 056 093 574 811 208 091 306 394 964 141 272 347 612 585 033 569 914 552 032 233 639 882 644 135 553 913 682 728 053 520 032 547 935 325 967 095 371 158 366 741 943 649 280 053 986 517 503 410 056 974 366 830 125 991 746 080 357 327 391 085 516 920 534 159 052 673 352 256 103 799 602 477 675 692 902 985 837 546 906 326 863 946 923 236 872 258 663 504 780 986 112 130 816 000 451 045 753 723 797 986 963 503 370 797 544 599 237 057 270 855 154 839 438 704 538 167 379 724 398 225 732 776 834 258 170 348 047 152 468 404 204 374 944 232 218 440 983 508 999 432 593 077 546 423 940 770 159 178 954 706 403 195 695 748 148 733 136 818 267 997 111 063 866 388 363 582 115 491 871 058 595 755 635 365 649 925 943 528 496 399 630 298 113 156 794 262 006 333 724 072 136 430 322 340 502 561 833 843 346 301 301 566 970 015 957 077 972 500 401 803 613 974 416 516 524 820 559 393 832 135 038 370 036 444 494 206 146 110 785 771 929 096 484 992 022 637 866 299 643 772 512 395 503 335 559 290 610 407 619 234 380 610 179 064 760 289 699 364 007 162 875 919 496 121 683 204 102 168 258 238 676 860 759 445 841 491 655 966 026 588 248 171 246 513 099 864 639 970 880 882 736 866 225 038 270 136 123 338 312 528 120 536 450 164 514 751 996 267 081 374 312 196 824 461 380 682 590 343 024 193 387 932 658 838 818 703 261 961 520 916 842 632 680 442 345 343 094 831 201 081 001 255 464 084 347 535 784 148 619 272 527 954 791 371 433 149 244 503 344 415 381 043 045 077 208 171 751 379 699 800 046 423 594 728 412 415 764 628 138 303 854 003 597 284 407 870 771 256 931 760 280 110 616 518 838 887 621 753 853 132 023 174 518 998 487 064 897 831 902 888 128 370 933 748 318 595 950 122 968 522 005 284 384 194 779 093 509 037 619 131 103 867 561 458 435 735 580 044 389 127 199 145 637 261 028 877 847 290 859 874 098 858 408 739 944 928 649 225 990 286 563 797 365 850 732 990 085 324 673 590 369 465 042 919 094 687 820 484 190 383 778 844 156 715 841 861 640 141 831 422 119 592 519 089 539 517 808 796 344 592 273 012 604 989 194 119 555 942 389 925 506 293 861 181 859 029 286 005 078 540 392 168 606 121 898 923 059 921 814 925 606 791 533 084 240 712 888 839 186 860 176 834 734 102 720 335 375 645 127 951 939 248 095 554 624 610 318 274 851 616 822 896 325 289 598 525 975 422 790 187 992 185 993 470 248 115 382 163 796 932 816 093 041 683 723 308 569 510 954 017 809 113 332 261 086 267 338 347 194 175 681 108 470 864 897 702 469 158 432 805 023 677 703 635 212 275 794 914 852 634 911 410 424 252 224 496 500 393 697 559 524 614 993 045 580 602 454 365 844 778 200 409 930 515 708 718 530 192 965 535 533 716 674 112 736 811 871 749 772 500 155 581 561 513 472 904 561 238 696 108 316 066 460 485 397 179 260 912 782 902 903 310 353 614 524 168 364 169 105 788 307 371 927 108 496 186 246 868 128 749 071 691 395 045 636 358 716 649 322 318 197 902 793 364 086 584 900 434 182 958 178 724 466 358 936 995 560 516 505 553 963 247 897 861 114 130 840 228 736 568 402 369 022 739 034 955 501 748 364 325 617 367 062 609 873 144 088 881 050 523 330 094 383 963 024 698 715 842 323 086 332 449 653 865 973 054 469 873 049 638 005 543 636 301 818 158 961 604 910 841 067 889 146 383 396 817 274 613 456 568 996 828 412 917 414 605 033 947 211 014 535 927 780 475 973 125 967 580 314 127 299 826 575 142 797 202 437 913 366 410 823 680 304 936 423 286 811 124 146 752 521 511 350 832 853 221 584 919 624 161 347 825 086 044 058 150 053 509 053 091 966 119 019 732 219 670 061 358 534 845 092 983 152 160 938 040 606 303 167 628 488 396 320 122 298 238 246 278 440 291 543 181 504 874 400 219 448 682 180 773 076 083 048 843 743 497 701 122 127 451 209 004 567 113 061 220 998 529 017 871 534 874 994 325 422 660 291 250 671 150 874 155 680 348 273 752 873 729 868 040 640 972 651 092 473 781 051 114 554 247 764 435 270 889 102 989 828 191 029 006 294 099 729 101 838 516 553 392 580 450 489 322 239 625 036 843 272 127 641 931 700 296 817 671 416 029 394 719 670 784 208 205 921 282 758 369 568 921 098 449 834 523 774 712 796 641 342 761 111 781 513 545 202 258 493 590 583 705 455 131 764 713 190 337 376 384 524 772 541 269 859 217 663 889 616 056 219 919 102 793 626 336 320 677 477 717 121 552 547 926 903 085 992 817 619 934 657 014 798 076 128 201 459 575 940 231 790 533 538 064 168 593 967 411 831 301 942 085 964 622 682 087 604 793 915 135 066 904 457 621 603 960 186 209 104 100 501 839 138 559 317 864 916 065 736 725 679 982 589 450 073 524 249 452 979 746 547 153 826 403 428 571 107 198 899 450 163 743 591 824 027 593 000 792 463 245 870 942 902 419 919 902 163 471 478 393 649 075 518 976 485 231 001 263 305 252 377 882 138 457 905 425 980 029 237 841 908 475 185 364 241 393 210 947 761 163 495 232 664 482 883 641 206 974 132 403 308 728 605 814 277 836 163 374 641 788 373 731 513 607 607 511 052 841 490 169 737 614 846 184 756 266 356 235 255 016 021 306 550 280 059 884 499 327 052 644 640 511 730 495 472 394 688 774 244 537 230 628 450 942 315 765 773 901 364 494 518 886 820 782 087 829 996 227 573 642 659 085 879 229 464 448 656 904 334 627 127 398 948 416 745 801 832 695 376 004 162 871 318 510 653 832 313 793 668 985 124 310 554 718 243 495 571 778 372 468 281 979 795 656 768 845 781 209 596 668 406 577 497 745 975 303 001 448 911 189 495 465 853 751 796 882 939 658 294 823 175 413 225 220 526 479 636 613 217 064 746 427 376 579 656 401 974 576 902 489 787 120 104 845 425 994 202 408 635 020 792 961 428 690 732 688 271 916 873 629 433 484 833 325 059 933 476 126 695 744 043 468 397 504 562 031 690 805 823 580 259 619 245 211 673 774 473 566 502 982 045 580 093 980 536 651 470 747 120 327 148 517 053 784 939 220 894 506 132 067 890 224 903 335 288 445 965 329 274 211 450 906 892 124 348 087 921 549 741 434 194 582 873 462 217 681 820 455 623 421 298 564 133 047 256 147 887 430 176 530 332 966 709 398 099 585 239 227 670 572 042 600 731 334 579 521 358 806 166 127 420 305 203 145 979 861 877 196 670 106 693 347 417 378 139 435 449 651 996 843 155 644 173 704 581 046 515 517 528 530 410 185 266 091 701 172 624 923 898 531 322 974 663 769 307 280 917 487 589 392 928 833 146 764 574 352 643 706 047 426 143 193 158 791 381 850 404 877 858 688 464 451 108 076 701 679 132 819 294 755 053 172 899 379 873 871 490 706 660 467 686 474 952 213 233 987 373 413 378 952 200 460 895 634 138 287 340 109 993 482 067 950 483 536 890 367 609 055 192 515 161 380 974 332 040 054 390 485 485 796 940 895 234 128 345 643 122 404 506 028 951 532 549 419 214 851 435 672 868 761 823 367 200 254 876 671 617 659 191 248 944 763 221 436 295 575 539 743 394 736 243 139 620 964 615 140 218 794 019 078 496 799 532 273 096 214 452 097 359 858 151 034 055 516 056 518 931 581 454 841 019 216 889 598 817 507 631 018 721 090 803 399 454 078 889 506 429 452 158 024 175 121 570 314 843 781 350 889 824 796 013 526 663 656 233 785 804 993 465 141 402 955 743 233 450 374 815 415 243 574 814 926 426 961 127 358 499 257 336 033 366 457 262 922 275 690 348 498 379 990 902 714 698 048 568 914 605 787 838 166 075 732 660 688 059 728 603 191 220 771 882 057 196 376 579 314 463 111 287 119 335 764 318 270 398 653 001 159 504 349 093 606 135 364 451 039 610 237 024 276 667 100 416 105 081 961 544 004 499 480 281 200 754 525 319 306 711 459 147 196 131 660 374 153 438 844 675 936 882 589 151 052 712 627 114 853 526 301 567 869 368 261 715 156 540 627 590 589 886 061 837 774 568 153 176 426 851 573 511 275 430 036 002 323 153 491 184 441 527 891 056 078 004 988 775 236 907 659 055 603 691 516 711 005 331 261 804 935 201 784 442 694 580 652 598 874 247 831 845 375 203 111 339 621 609 761 648 786 217 432 752 749 354 579 701 517 134 247 511 486 397 146 959 118 224 109 166 602 182 060 566 229 134 934 936 389 943 436 618 579 481 785 402 024 694 345 712 153 992 082 969 838 451 285 094 489 601 047 847 558 427 538 883 931 929 293 034 366 158 553 658 237 348 250 801 819 124 459 244 032 941 964 614 680 608 838 699 615 791 028 445 889 268 695 344 374 272 760 697 476 256 135 564 442 720 488 026 833 732 224 144 446 687 893 655 188 963 285 723 723 696 685 901 021 388 212 761 472 216 468 187 916 618 072 727 408 865 113 186 778 905 753 287 837 032 229 283 508 321 403 762 369 436 449 944 643 743 738 755 992 963 807 990 942 914 253 019 072 771 678 076 612 588 571 025 794 814 163 052 985 316 389 022 991 838 205 506 193 493 832 504 899 062 435 677 690 804 832 071 063 877 849 490 323 398 766 513 971 762 831 738 561 563 625 973 118 198 914 638 325 833 142 123 691 404 162 043 126 951 152 705 494 428 823 848 994 992 044 092 288 552 447 533 692 700 153 581 330 419 438 565 650 753 621 550 247 004 690 474 926 726 702 620 257 668 744 322 191 773 861 090 339 600 844 022 609 579 793 440 931 924 227 442 346 140 000 490 507 857 178 089 299 938 508 074 652 770 260 940 887 878 583 408 665 781 522 010 232 239 799 836 702 280 410 194 088 402 551 897 137 086 289 019 661 183 362 056 139 596 387 391 582 037 106 426 394 112 840 737 323 546 467 552 331 444 577 579 926 346 426 826 277 412 070 832 814 881 314 433 610 293 661 836 162 004 444 956 255 249 301 386 489 027 346 758 481 880 902 520 251 518 053 152 541 587 550 252 967 067 575 632 442 627 142 636 377 101 124 881 756 301 888 560 872 327 517 890 689 770 458 646 802 847 852 513 228 622 481 087 767 386 830 889 877 720 702 944 568 029 852 061 298 394 165 781 088 154 083 519 659 796 429 172 968 712 916 797 875 278 928 302 026 916 598 757 923 914 675 234 907 451 053 242 179 370 666 847 185 841 173 849 182 160 883 686 643 821 118 259 385 470 468 551 486 784 706 815 919 139 733 144 740 924 270 184 774 896 276 023 374 357 616 831 107 321 776 781 226 184 214 436 969 110 478 252 413 227 446 677 408 400 797 522 158 202 963 396 523 092 680 421 203 514 825 183 149 731 597 466 066 034 573 500 019 434 357 611 710 534 380 696 357 241 081 121 410 255 658 222 727 120 858 870 798 313 908 857 665 172 187 779 513 993 744 626 020 354 012 626 136 674 280 183 286 519 467 108 998 792 105 116 027 405 632 631 919 215 227 638 054 454 727 071 824 500 385 866 066 303 186 380 801 537 910 497 910 322 567 284 021 098 019 857 396 116 597 217 762 060 379 971 284 216 950 912 862 069 005 093 788 612 141 291 020 887 388 670 714 135 817 459 884 240 210 201 646 442 380 805 855 567 457 811 394 755 394 847 946 899 398 949 105 232 410 418 823 736 692 637 355 398 809 756 923 352 899 554 385 819 639 932 199 034 920 196 924 579 734 360 372 314 574 204 639 783 462 973 311 812 999 796 865 098 975 061 413 116 868 976 623 478 588 053 268 061 628 717 666 071 475 508 886 561 976 757 862 156 477 041 525 828 024 943 054 701 183 404 323 598 911 890 152 344 399 399 316 247 929 497 231 066 477 026 121 630 080 302 300 084 753 422 703 531 693 018 194 080 561 665 802 045 398 774 304 046 749 084 972 678 889 633 898 951 601 528 484 813 406 288 291 963 178 149 751 503 913 670 118 128 907 699 481 972 942 392 663 209 734 923 549 644 738 959 639 746 775 571 733 601 973 007 765 036 088 000 396 529 762 085 951 394 296 389 553 310 423 309 865 100 923 434 782 412 120 129 167 232 703 718 916 283 204 406 623 137 068 888 097 828 188 687 647 571 916 621 606 020 916 636 332 156 089 720 813 565 714 172 379 314 527 307 369 047 908 421 196 557 749 703 607 685 663 791 418 892 202 648 181 478 634 724 331 226 140 813 297 290 929 697 863 531 967 525 299 097 700 321 789 158 025 900 741 791 779 466 791 981 902 308 901 923 256 124 821 694 356 777 825 249 263 908 618 218 528 480 446 660 758 251 487 708 286 091 998 615 003 829 463 750 222 826 122 174 508 281 935 114 580 288 843 782 306 582 416 517 065 827 117 390 172 693 167 054 137 485 497 401 142 600 631 668 205 647 386 385 790 365 316 046 542 911 768 232 163 095 347 765 949 411 047 428 595 545 738 072 300 976 750 740 717 041 128 582 074 646 490 620 842 749 499 463 556 086 933 626 446 210 466 364 313 588 421 217 919 468 514 300 598 520 075 369 157 638 829 491 111 709 619 760 436 251 986 348 599 344 708 817 257 847 865 389 022 644 045 409 711 880 653 380 165 483 174 713 123 802 858 997 925 364 448 999 192 017 359 853 481 170 863 984 072 942 201 831 969 881 544 151 868 186 748 589 624 388 516 065 034 363 025 053 768 165 569 499 564 992 766 286 945 901 924 692 645 425 785 347 106 129 539 324 757 098 105 903 197 301 312 890 639 844 032 440 664 210 559 386 356 361 573 146 820 984 652 035 893 104 143 584 927 718 383 059 200 043 734 691 439 127 026 565 560 775 475 511 878 150 304 084 395 384 724 369 065 361 819 067 706 410 265 126 328 624 536 387 286 647 215 368 727 484 334 723 532 025 846 435 974 117 511 721 755 715 483 964 894 309 073 581 616 710 591 044 459 976 294 179 958 610 022 671 742 998 430 541 725 195 520 303 660 765 482 142 894 905 687 107 517 629 828 606 965 814 181 614 306 615 651 307 522 800 890 855 807 794 081 429 388 212 715 177 363 637 312 409 122 229 826 664 696 853 500 611 921 635 983 033 569 409 551 438 161 453 540 488 393 312 547 413 002 340 185 937 241 682 684 798 507 692 931 105 150 089 906 813 475 086 690 808 141 294 645 662 553 877 903 342 734 820 954 633 061 186 452 552 735 836 595 290 361 872 213 238 708 444 251 975 283 450 376 758 187 158 171 771 511 231 552 480 345 320 384 718 330 041 886 661 408 920 772 699 571 174 771 818 514 787 169 294 129 410 661 463 046 421 459 594 268 127 753 891 427 643 730 370 313 258 686 081 198 453 842 903 891 979 748 334 280 936 133 894 341 068 951 803 153 570 794 717 617 504 451 634 062 961 440 010 183 399 902 311 807 967 155 608 735 417 141 993 552 331 358 567 444 432 668 745 905 389 160 013 415 026 436 802 573 078 039 828 571 320 521 589 554 907 561 907 509 428 897 260 579 543 629 793 676 269 734 855 624 820 085 918 443 756 999 288 535 018 078 270 593 602 011 052 085 885 891 872 261 926 968 234 430 621 831 988 832 891 152 009 167 242 525 646 660 022 873 533 806 020 756 369 550 705 802 478 616 267 009 912 389 706 956 425 629 462 698 468 037 926 083 673 183 750 870 214 870 497 225 006 287 742 182 549 740 703 032 604 641 620 417 189 271 368 095 838 185 433 376 568 938 628 334 257 813 265 557 265 774 170 702 461 688 280 498 660 217 092 851 361 814 099 599 524 703 533 073 823 374 564 332 064 586 093 788 846 293 595 124 538 163 225 934 587 022 570 369 302 600 091 307 198 311 613 769 335 394 514 734 611 002 487 603 224 089 647 551 561 603 045 716 351 899 869 673 495 354 997 863 454 927 648 862 241 587 476 884 101 611 126 854 212 607 594 731 866 145 343 047 323 730 476 005 616 986 782 357 247 981 142 401 677 279 498 116 467 045 127 212 060 038 140 600 697 982 981 478 218 351 587 138 759 254 121 842 827 528 031 640 085 359 407 236 889 459 739 043 759 288 924 619 547 484 286 308 644 567 253 722 398 523 731 840 634 227 541 330 919 038 652 198 904 701 001 072 063 115 767 425 757 547 724 206 762 300 436 019 047 100 379 630 206 152 117 051 783 869 564 853 740 559 688 879 441 703 879 393 520 862 595 440 577 359 381 678 077 015 056 979 361 888 168 747 399 466 853 803 325 061 139 431 157 961 487 553 368 890 812 348 050 685 884 450 088 604 220 383 176 692 540 821 030 285 637 469 437 228 105 807 125 932 316 210 751 822 333 704 596 369 065 074 209 413 691 478 428 322 304 452 765 619 678 748 186 484 921 108 064 539 261 645 880 523 113 238 915 433 657 080 563 568 779 773 070 323 305 008 770 086 043 041 953 086 006 403 237 284 504 442 740 625 699 355 670 422 691 998 045 336 956 344 086 163 468 265 172 607 027 870 148 982 257 394 291 337 280 339 601 436 637 266 768 490 911 093 274 339 177 026 813 226 565 113 282 176 094 059 083 684 847 521 808 640 417 198 325 179 923 216 802 332 487 923 142 771 064 183 671 623 041 835 774 801 701 767 970 261 204 005 034 480 857 513 135 904 303 031 227 886 882 172 400 612 283 812 036 173 094 637 391 693 049 015 106 538 878 123 772 982 685 123 296 743 926 649 675 914 513 193 578 915 786 672 346 834 761 277 741 701 216 691 897 777 985 097 863 542 686 459 728 646 783 411 109 862 011 248 758 050 095 820 919 151 787 304 219 738 507 350 008 485 577 727 378 138 122 494 715 923 585 196 303 441 821 200 166 082 555 670 080 519 470 891 611 957 989 234 108 938 718 813 461 953 602 111 761 573 877 863 160 773 426 770 362 185 188 391 818 407 722 648 980 551 468 613 308 307 182 133 551 810 091 295 441 340 171 637 592 609 471 352 393 147 460 651 533 923 491 232 581 471 953 543 077 773 472 737 629 709 018 508 005 514 804 327 239 834 745 207 302 351 238 581 226 813 269 837 198 871 052 602 004 089 302 317 871 241 595 209 189 225 817 697 787 099 918 087 523 135 330 478 812 781 033 337 393 917 762 386 159 316 538 149 364 502 890 165 449 176 088 248 686 808 295 524 488 639 862 514 841 067 259 336 843 034 784 674 352 545 695 502 948 576 840 155 747 365 066 177 149 250 209 178 695 216 263 533 016 904 790 084 951 851 774 904 895 036 488 239 945 830 013 384 716 616 577 043 424 249 990 489 990 884 863 467 056 193 604 533 738 440 201 243 918 855 103 572 388 402 478 649 965 248 655 202 859 485 619 018 071 826 081 910 816 975 913 867 928 204 092 053 539 609 878 975 072 968 181 294 174 994 351 660 158 463 301 455 997 340 966 268 002 267 947 557 315 394 008 088 858 824 502 072 813 381 431 209 465 692 595 524 685 576 090 740 941 782 137 898 337 543 986 858 691 277 694 746 268 317 244 037 847 068 369 643 289 906 227 409 224 064 326 180 685 084 880 657 646 262 635 221 142 350 705 613 232 949 616 971 917 575 390 300 191 182 339 780 950 744 496 456 659 108 985 863 135 233 337 615 586 581 508 720 097 763 229 320 824 546 254 736 695 063 981 632 191 166 740 541 522 045 866 594 718 334 451 626 439 634 472 380 362 754 230 686 096 916 055 754 140 191 038 263 303 310 177 369 845 057 690 957 824 097 157 325 391 842 204 947 065 492 553 257 038 101 407 122 091 626 416 448 704 000 830 933 654 079 426 702 360 002 145 792 657 181 839 894 946 090 809 933 301 350 844 082 807 846 499 323 300 956 044 435 338 226 828 363 982 195 395 396 656 278 357 224 551 692 628 642 523 749 498 427 803 117 015 455 570 796 634 348 866 597 668 196 943 347 106 114 845 061 984 360 025 001 167 716 889 486 127 707 415 750 017 799 308 009 539 825 881 541 930 009 124 651 866 702 481 233 899 668 146 971 983 411 340 498 395 741 130 723 595 464 418 277 126 065 607 697 013 918 236 501 009 123 880 556 039 008 844 010 436 045 222 930 781 988 385 705 625 381 924 866 399 783 446 069 633 696 203 036 810 162 458 642 649 347 091 631 828 789 391 576 688 020 382 987 831 975 687 221 233 400 410 054 777 671 960 948 165 564 010 446 195 631 060 857 023 549 448 917 349 883 330 739 964 404 764 968 122 674 797 453 546 780 694 920 832 704 062 278 112 955 431 015 431 283 273 373 123 032 355 363 738 286 148 570 648 366 163 761 676 510 671 015 977 015 681 656 775 319 178 546 625 092 983 481 135 006 192 274 447 076 904 382 170 599 662 821 243 183 288 228 441 374 663 714 307 233 454 776 485 793 106 198 310 721 160 677 217 947 745 066 654 641 154 010 651 573 935 627 952 615 011 542 361 728 718 568 144 730 036 763 194 535 076 627 777 515 021 337 762 217 110 860 721 435 985 831 583 053 709 277 608 000 315 245 336 050 648 657 555 462 122 152 630 316 113 405 003 677 276 892 220 316 131 781 031 321 372 246 509 161 958 422 701 690 896 544 144 386 577 072 386 954 055 631 893 167 079 550 876 167 525 575 505 326 810 077 504 226 294 523 420 794 792 887 604 149 092 943 408 156 653 081 243 648 964 387 540 065 522 375 167 669 016 184 131 553 117 405 192 108 687 452 598 079 117 463 678 894 968 039 744 699 653 771 498 542 506 224 995 982 113 096 846 343 530 717 420 371 064 104 632 521 881 499 338 810 388 693 566 695 568 404 196 722 437 168 702 383 995 613 667 621 678 243 536 892 134 877 884 181 549 585 812 159 282 218 033 676 086 884 510 398 451 838 949 255 818 996 306 835 902 707 929 143 902 006 626 809 699 772 362 927 702 937 767 908 246 469 994 078 617 331 573 665 600 096 849 948 597 567 955 091 149 442 134 488 595 068 482 405 958 724 781 609 109 555 052 882 316 017 512 917 683 962 977 406 804 553 485 314 705 024 299 064 473 328 539 263 555 011 188 598 230 434 315 834 796 979 115 445 109 272 747 968 268 641 218 548 252 984 410 795 622 238 152 542 100 602 674 894 187 674 925 919 608 653 203 913 551 383 283 782 875 378 990 194 771 487 862 829 392 544 780 602 762 323 295 488 349 131 099 820 221 332 611 329 719 111 124 648 319 700 094 256 715 733 626 562 903 558 861 055 449 295 431 897 667 027 972 346 125 341 830 438 355 234 759 542 840 020 665 167 339 391 220 411 638 342 867 102 343 823 813 219 686 671 207 462 949 631 609 190 167 420 807 411 654 279 560 578 994 309 503 501 907 609 267 030 506 110 240 307 927 718 655 459 666 982 138 236 407 852 546 021 460 034 524 298 583 420 505 558 750 250 769 586 215 244 433 596 859 913 228 054 180 886 122 501 156 896 584 639 781 600 021 951 861 078 246 599 517 262 940 974 311 237 432 572 479 771 153 633 560 108 547 606 783 074 454 516 715 236 485 605 286 689 656 202 383 445 804 306 023 599 314 430 655 786 640 725 311 409 556 979 133 528 482 829 773 998 658 544 807 474 190 652 335 593 618 985 251 088 505 127 318 990 585 955 658 464 376 962 114 499 394 758 266 821 669 947 082 431 999 623 464 409 851 082 320 637 063 027 775 225 357 346 244 025 928 427 528 539 293 404 426 951 119 563 573 643 100 873 584 778 198 239 982 507 926 656 369 253 832 975 822 286 221 495 949 848 161 788 562 743 440 446 656 873 832 214 457 189 870 239 544 902 783 162 561 500 115 563 609 754 412 966 289 820 545 848 192 530 441 008 249 923 947 729 010 368 799 773 673 985 755 639 028 377 330 816 425 067 236 648 122 244 708 816 516 293 256 251 275 881 974 700 768 817 618 551 604 025 242 671 717 885 921 650 594 573 119 112 836 461 227 079 229 134 846 081 882 536 402 694 539 885 831 190 266 431 842 378 961 021 619 448 216 191 938 333 084 755 503 091 644 966 608 857 695 406 920 352 189 741 881 092 000 211 201 489 879 131 897 421 579 211 617 238 549 636 568 055 802 995 456 021 369 662 545 072 543 393 891 648 665 298 682 103 607 346 772 444 204 668 894 118 102 395 034 634 125 864 867 753 360 150 473 328 599 401 904 862 445 628 442 118 712 101 989 228 321 990 199 666 708 694 999 442 922 211 473 636 482 648 417 210 352 507 479 811 401 717 027 078 805 129 645 492 962 278 978 140 033 434 205 904 332 332 259 545 383 392 162 055 344 100 082 958 894 210 211 192 819 697 242 042 135 422 288 472 399 686 447 650 543 963 098 314 995 169 521 624 967 041 424 973 680 273 168 105 778 961 051 514 198 530 466 824 075 818 922 161 283 848 184 850 143 525 268 700 584 241 090 612 659 446 440 274 989 266 886 984 712 944 564 696 387 144 175 047 419 731 894 872 764 753 763 440 544 351 457 859 783 726 626 510 919 737 437 510 663 281 123 444 825 256 650 235 630 934 798 192 841 704 543 638 848 515 163 141 388 364 907 744 745 186 767 862 285 429 147 255 598 274 477 574 003 393 441 741 330 363 193 688 452 864 128 317 494 598 851 318 355 907 653 307 161 560 625 731 032 205 406 249 843 886 602 768 243 837 823 559 826 561 704 444 793 905 418 201 805 116 705 058 392 361 629 670 963 959 558 732 805 518 373 291 962 710 209 114 580 422 335 402 115 273 673 957 161 837 446 634 037 600 586 570 872 904 074 282 742 515 736 681 074 686 561 992 276 322 738 329 532 299 879 778 891 493 915 402 931 943 650 448 429 535 203 083 420 744 297 057 648 467 744 225 857 982 923 471 557 291 935 724 029 111 924 583 721 356 409 905 775 507 477 372 265 262 742 245 613 342 768 585 132 959 906 520 004 731 236 251 171 164 722 835 238 226 243 667 495 256 499 919 132 641 529 840 100 744 279 979 680 043 083 554 978 394 195 774 051 128 935 391 183 144 992 848 054 555 595 067 404 793 926 023 009 180 766 051 698 691 004 528 603 909 757 288 155 387 139 386 795 603 811 948 395 732 252 795 291 658 379 348 018 223 376 412 179 365 797 417 917 637 719 449 843 468 081 625 261 518 188 598 100 716 779 983 627 859 926 501 827 541 678 248 590 212 601 783 313 615 703 634 511 133 667 971 993 648 696 021 968 109 658 516 634 684 938 997 761 569 513 655 417 178 291 321 563 337 031 335 517 853 200 204 527 599 057 939 950 772 316 933 206 053 811 981 519 011 989 357 508 388 815 672 444 049 213 577 246 050 748 809 671 475 263 329 323 959 457 090 083 859 744 304 567 924 626 857 566 748 877 869 017 722 960 930 358 634 895 549 054 955 877 820 273 286 925 488 361 086 291 285 463 534 578 117 695 384 243 654 144 866 152 159 911 190 848 864 780 196 962 419 935 192 121 357 181 177 970 601 590 733 568 870 509 295 942 467 495 906 572 161 463 517 508 782 260 241 647 811 218 340 367 709 877 241 227 436 673 108 311 102 512 037 809 174 066 338 186 289 167 774 634 737 126 870 508 831 179 735 597 379 581 263 090 015 781 385 574 246 959 003 444 081 910 362 890 400 055 742 751 885 619 347 403 660 644 594 042 078 430 159 203 995 630 734 781 898 435 191 822 587 030 956 801 463 839 910 313 062 401 545 259 160 085 839 188 870 194 802 439 828 523 584 213 384 727 207 356 430 073 848 823 471 534 274 511 105 555 129 568 136 684 010 452 182 309 729 041 090 175 800 296 735 571 415 169 880 582 976 091 461 255 495 248 119 564 430 968 658 872 771 473 332 233 910 994 299 045 643 179 354 862 015 325 202 683 518 674 619 511 854 437 849 736 981 849 649 512 745 360 800 918 851 937 592 847 457 179 922 660 810 462 982 972 322 343 412 909 595 798 507 408 311 148 152 600 796 032 559 863 127 188 308 881 226 391 534 712 208 193 266 328 233 452 038 887 326 175 061 087 245 214 236 364 957 028 788 246 306 709 968 045 855 536 646 148 601 832 950 060 090 558 657 012 110 337 464 767 756 187 975 592 398 256 381 940 569 094 595 638 203 165 259 743 092 000 352 877 403 307 762 979 268 028 058 433 890 565 284 214 287 348 910 171 738 033 761 155 712 965 684 180 936 148 295 125 292 445 206 541 838 857 787 480 310 094 466 495 584 612 930 432 018 471 225 687 619 083 779 113 515 631 447 022 066 390 677 038 275 400 869 855 421 979 216 362 837 213 028 492 807 888 766 512 750 525 589 590 294 735 300 574 945 560 083 202 153 463 792 865 457 524 998 886 795 937 674 512 650 778 558 075 766 457 750 833 743 791 995 997 015 566 236 429 014 494 436 447 996 772 324 480 979 376 428 730 940 120 140 144 540 520 738 477 942 436 481 623 134 646 477 621 411 683 436 722 343 477 766 603 269 890 245 224 603 882 664 164 731 996 917 207 294 525 102 881 796 730 528 205 375 515 845 853 462 983 952 945 660 112 650 046 082 671 692 157 740 207 937 740 833 747 228 008 565 637 292 462 577 901 981 171 413 686 650 463 862 880 089 847 799 630 267 117 104 364 104 661 305 853 996 777 906 218 865 526 593 033 672 795 826 150 882 548 548 143 705 143 902 186 581 449 982 970 418 870 317 064 080 311 414 122 342 819 472 587 445 346 541 215 597 877 615 704 186 988 961 167 908 606 760 742 097 285 141 580 609 025 469 289 480 557 362 047 025 937 344 417 779 786 587 304 952 482 954 711 206 662 316 130 140 111 740 498 166 852 211 505 894 735 345 265 233 836 647 363 864 399 748 756 066 095 475 435 743 994 040 354 207 359 504 181 699 379 933 692 848 166 213 523 463 002 260 939 430 407 554 309 207 923 575 468 254 137 883 116 556 933 869 765 103 175 427 010 740 185 128 271 343 972 704 500 968 493 090 680 853 002 384 290 961 181 029 756 937 703 379 646 478 700 208 918 394 371 347 320 129 271 223 175 067 500 443 359 939 212 215 495 828 759 179 850 792 997 076 510 914 995 760 490 072 853 707 602 857 113 862 226 715 591 808 372 557 884 738 105 114 852 734 651 895 091 719 685 266 545 769 292 888 388 241 599 801 893 227 693 720 089 954 319 789 696 341 519 445 100 393 274 559 007 149 124 069 950 755 874 847 355 780 924 685 320 212 598 862 936 087 993 533 306 235 771 327 732 059 677 273 018 268 332 594 329 165 920 555 948 407 497 187 868 745 565 060 101 325 498 437 438 152 432 741 124 536 333 451 225 947 274 042 595 142 876 183 741 972 953 782 003 269 463 182 857 885 827 565 370 100 172 376 554 860 434 767 880 353 951 758 812 189 508 359 294 462 378 022 919 452 978 041 421 257 769 841 886 441 962 878 218 467 718 445 191 074 657 347 426 891 703 713 492 894 855 897 603 495 530 025 661 167 630 372 010 637 156 598 339 652 654 099 139 721 118 913 729 402 240 661 475 557 805 908 035 117 816 113 202 959 299 537 271 780 479 414 026 158 631 184 259 834 409 164 138 523 324 755 995 182 767 669 687 284 075 572 984 852 537 325 662 023 251 368 120 785 682 298 213 834 781 071 827 344 560 998 358 240 053 805 389 445 323 314 257 655 663 205 686 730 678 822 230 811 853 313 365 796 155 981 832 324 699 280 073 485 688 176 845 210 850 452 919 540 490 103 724 020 463 409 350 431 652 956 275 411 396 996 381 560 352 188 865 913 972 359 024 638 334 257 417 025 889 199 128 071 796 400 747 414 625 917 515 227 724 778 622 562 222 465 877 864 195 804 163 154 894 580 921 368 261 001 484 966 308 014 653 015 234 068 920 231 601 958 333 568 168 539 329 359 272 002 154 828 530 244 188 567 383 031 683 107 804 939 789 264 666 003 178 119 466 313 644 849 872 300 782 867 349 108 244 227 567 455 763 782 272 555 298 420 982 827 430 642 852 298 509 422 337 820 773 529 931 846 489 720 632 986 976 055 313 080 705 897 127 420 280 285 631 482 594 674 764 667 488 810 485 962 444 504 580 420 185 428 903 261 061 810 749 625 044 197 880 398 236 139 258 881 715 593 100 368 782 720 550 927 800 516 981 551 064 349 586 883 827 877 798 379 611 828 748 913 213 977 115 155 587 526 750 260 071 091 256 209 309 098 121 850 908 849 518 940 079 383 305 580 000 684 609 925 782 598 509 768 107 940 472 115 770 383 699 962 166 240 751 020 672 878 447 061 839 609 615 341 772 900 287 937 058 840 860 105 732 190 329 481 568 304 728 211 913 315 068 474 592 977 332 415 667 827 786 768 130 697 043 587 611 473 476 690 576 530 831 706 419 676 753 703 201 296 104 491 198 153 130 342 000 163 347 287 279 519 653 293 210 024 394 203 984 701 375 592 457 858 263 133 443 774 108 537 853 496 723 888 539 883 415 228 428 082 729 591 811 834 301 425 740 899 974 210 411 737 932 259 372 344 419 974 648 659 275 624 893 294 476 734 320 550 954 305 961 859 466 765 200 255 957 556 047 817 536 539 286 053 913 599 453 291 510 294 175 151 816 052 197 494 804 132 354 300 274 431 202 043 181 177 928 647 374 550 868 322 708 294 530 990 372 518 566 356 176 464 106 632 340 673 436 026 283 339 402 840 131 681 328 111 598 814 663 293 321 765 927 381 367 805 055 484 973 526 910 337 222 430 691 424 396 240 867 663 144 439 307 595 668 532 805 406 131 292 242 701 081 744 409 727 150 494 885 790 748 283 060 394 228 232 739 284 556 153 116 966 011 528 978 800 599 052 645 650 657 594 509 420 675 848 260 942 256 793 971 287 049 097 143 050 335 914 966 864 187 535 176 082 959 363 194 073 689 252 430 609 352 067 721 820 781 923 887 827 293 501 513 134 827 435 444 019 600 126 502 815 822 165 398 027 737 649 973 082 761 766 905 769 714 017 003 120 830 368 310 528 049 964 944 300 771 388 608 267 349 928 224 440 191 492 293 863 021 056 968 961 584 064 784 854 166 732 338 661 098 145 935 956 694 940 632 158 679 898 953 683 025 697 852 816 641 045 984 559 838 292 359 995 729 602 720 866 394 766 951 958 079 483 660 000 879 432 120 062 586 011 864 756 183 537 636 084 647 796 532 835 490 960 048 448 877 777 806 836 236 582 891 912 224 331 182 605 972 406 147 172 264 087 632 399 626 486 688 367 159 789 839 019 051 952 998 455 966 232 374 177 840 157 142 973 643 099 328 850 076 397 658 885 647 097 415 698 406 454 069 818 451 564 881 453 665 269 458 020 604 646 195 850 887 303 811 707 676 583 265 648 145 689 524 878 315 856 710 685 871 072 530 510 609 828 352 996 790 016 362 725 158 171 148 598 679 169 327 575 531 198 807 142 111 812 138 506 464 616 845 760 047 473 561 732 219 614 716 341 239 675 296 637 706 275 756 937 886 818 245 019 309 992 060 783 458 943 190 568 454 453 788 640 782 756 484 697 262 480 016 793 405 711 697 121 246 300 676 888 446 297 313 340 060 168 823 024 734 645 835 198 182 081 362 262 665 457 945 935 632 054 234 134 397 614 134 057 151 867 238 169 809 185 603 422 907 391 607 959 609 500 764 650 685 641 010 092 600 486 205 557 830 009 325 891 993 629 349 442 433 144 501 533 878 892 093 715 607 080 250 068 757 530 200 766 432 424 776 888 072 286 880 163 458 722 087 766 761 999 437 333 485 678 229 039 614 048 521 783 615 997 861 109 013 606 489 608 019 652 370 368 217 530 570 792 228 879 742 050 918 937 147 054 539 434 185 762 841 874 725 266 337 905 239 342 770 162 567 242 767 624 951 423 999 224 058 938 780 945 426 959 739 639 507 907 265 231 613 724 637 450 647 279 456 722 714 099 066 974 388 305 759 053 985 369 103 868 932 624 768 102 251 555 654 680 708 459 269 661 166 958 213 099 476 598 153 955 036 103 991 385 637 274 745 031 597 598 187 570 609 544 391 412 777 188 811 694 467 586 761 087 193 790 459 632 956 351 959 948 636 014 100 128 627 058 468 925 643 788 113 805 720 564 120 668 631 946 087 233 737 836 203 474 788 194 019 259 435 531 871 517 468 763 044 204 673 140 553 240 342 441 362 108 420 227 002 053 552 085 698 041 637 404 352 131 026 853 360 873 693 442 642 183 178 107 817 426 004 657 785 595 802 542 342 941 077 394 251 464 510 137 717 124 155 803 044 187 204 158 872 268 880 303 678 888 209 303 968 061 250 175 495 069 213 397 771 326 091 491 909 282 607 966 167 461 027 537 999 160 512 652 287 909 733 450 097 371 522 163 195 360 302 411 979 330 676 139 125 223 513 408 809 810 109 945 274 929 193 654 929 760 045 773 276 871 598 286 276 524 178 716 077 493 579 398 181 239 721 448 123 401 080 500 249 647 445 420 939 864 560 702 298 544 265 346 892 680 870 160 133 811 160 003 154 830 197 990 922 319 072 159 131 842 731 053 659 577 721 227 550 788 385 179 652 502 366 686 598 858 557 706 911 095 568 306 827 993 294 077 855 750 388 179 040 934 113 309 402 381 529 764 518 245 169 871 271 105 486 298 331 441 901 566 268 579 525 673 119 312 921 416 820 404 881 158 434 331 149 159 015 010 197 091 536 721 585 269 085 139 712 107 266 202 610 587 601 219 033 644 604 791 013 874 101 785 781 292 042 637 724 557 034 016 801 098 190 320 180 211 437 591 931 842 428 289 463 347 990 529 624 653 499 032 493 442 737 994 629 435 164 258 796 615 987 477 384 152 993 896 341 526 351 117 797 977 812 519 209 000 573 657 430 594 320 672 350 527 762 744 974 840 336 926 690 730 796 876 323 254 269 796 958 469 769 597 514 935 518 245 751 742 599 558 370 952 458 838 535 469 142 701 965 405 200 066 376 708 209 754 494 888 459 452 361 291 244 232 402 097 711 049 973 782 137 743 127 648 682 083 305 235 884 299 353 006 351 249 061 751 414 358 607 410 212 997 999 304 536 808 083 745 664 010 014 993 273 622 394 155 405 824 039 161 810 493 698 739 290 569 656 811 881 448 112 789 493 794 454 544 387 378 239 689 085 749 426 847 194 191 155 845 585 080 549 400 300 244 126 527 692 658 891 529 969 610 779 460 471 961 056 434 409 638 319 753 267 221 782 863 744 400 731 445 079 376 456 365 613 585 954 705 557 246 023 389 967 190 431 698 144 720 671 780 961 247 309 408 132 556 000 011 319 769 247 015 695 143 442 061 081 906 548 809 009 754 826 670 029 896 426 395 611 332 639 006 257 615 000 870 889 158 401 133 330 247 319 285 533 150 814 158 023 389 895 911 610 060 398 892 699 113 953 091 424 745 951 407 704 285 712 183 862 873 882 610 077 964 330 014 407 857 987 156 113 397 318 477 062 147 337 245 829 581 431 772 595 293 069 938 546 927 744 899 342 761 570 062 243 979 736 199 566 679 595 646 757 956 679 166 823 117 227 483 184 867 157 865 003 679 717 592 429 559 230 644 196 040 866 184 239 277 201 346 698 188 667 146 804 390 818 149 782 883 010 724 439 194 971 397 477 012 927 126 874 332 588 512 815 708 648 507 274 139 730 877 842 681 075 261 562 471 284 925 655 883 381 133 927 760 698 064 171 317 880 126 650 574 510 790 734 756 567 195 377 225 467 593 493 816 067 781 419 282 202 218 832 824 288 037 639 562 875 274 291 879 859 914 892 005 504 647 096 972 337 992 672 369 007 379 015 000 626 657 752 036 307 571 544 623 780 272 768 447 893 965 098 188 036 843 843 238 875 600 342 589 655 477 775 560 322 530 170 861 296 560 548 572 785 453 138 487 287 844 584 381 475 481 997 491 122 897 432 803 841 389 786 127 577 526 283 028 598 826 418 667 563 189 051 741 076 458 765 858 566 325 919 416 986 654 460 037 663 738 421 763 967 741 746 209 773 624 330 467 576 247 079 967 713 920 535 803 624 712 552 266 481 473 261 978 151 475 662 787 342 964 385 119 443 427 087 722 666 095 099 935 690 934 287 083 370 414 964 567 120 160 501 953 653 021 205 028 357 049 500 357 232 558 667 057 316 478 404 931 636 592 673 365 063 622 869 668 709 034 584 588 705 604 924 855 259 543 433 162 168 620 226 243 928 591 749 888 504 174 277 739 247 187 692 518 447 860 431 795 815 333 752 726 429 500 438 156 269 837 654 508 178 052 875 278 355 384 054 532 229 400 226 526 329 359 282 455 381 415 830 758 172 324 109 426 273 902 891 606 442 003 035 541 989 050 644 352 632 376 027 024 104 677 190 065 405 846 434 344 061 554 186 254 851 466 217 468 168 507 897 976 006 423 551 759 959 680 442 810 374 242 183 255 885 685 017 831 117 209 394 586 385 994 021 591 179 185 767 311 532 594 251 003 735 344 519 098 034 174 878 176 208 608 137 190 989 232 334 035 345 087 778 592 042 660 180 326 765 964 002 089 983 085 064 017 760 133 938 080 995 636 662 797 541 331 058 854 956 602 917 349 524 326 202 312 337 820 245 159 739 897 387 284 752 877 999 342 004 619 118 975 943 079 052 314 922 089 743 001 663 899 421 746 571 364 790 252 572 538 762 075 991 401 086 042 646 825 605 214 771 218 843 839 235 212 180 074 797 947 392 774 558 299 624 216 154 686 338 118 560 952 339 264 329 472 436 857 526 819 030 447 724 551 677 302 094 495 341 593 377 179 658 554 197 175 511 509 232 516 181 469 764 578 014 362 355 075 667 611 419 383 566 903 390 372 347 543 995 353 372 556 010 210 129 778 046 172 400 145 986 216 768 070 632 890 662 415 406 999 443 826 359 490 890 236 678 134 035 654 041 921 273 611 912 105 829 838 819 122 321 428 673 130 237 871 763 003 072 039 393 938 540 260 430 334 122 950 978 844 233 252 059 962 968 215 992 536 311 287 242 260 022 141 370 059 639 859 422 733 828 917 391 212 617 304 538 487 729 713 407 080 148 819 255 515 390 613 691 133 898 338 417 023 057 095 078 239 078 354 012 079 866 657 339 934 278 316 246 418 916 668 921 793 684 095 128 045 096 477 309 327 235 565 414 033 191 077 532 439 900 978 447 157 211 826 228 473 699 735 675 761 118 669 553 378 892 660 868 050 096 425 968 842 069 331 726 652 666 075 538 272 170 757 413 803 236 775 827 749 386 004 171 844 329 851 101 769 270 277 570 589 241 005 594 374 558 542 245 874 917 706 337 134 933 361 606 728 530 489 195 491 733 766 360 179 570 057 478 650 822 878 994 856 995 823 533 438 492 562 780 831 205 883 605 563 929 652 663 273 519 950 676 051 459 113 711 602 510 886 194 420 933 086 495 156 857 485 054 969 210 570 884 563 709 144 872 064 270 894 827 999 546 617 619 834 617 203 545 476 804 685 559 134 396 904 331 565 235 500 162 972 015 930 168 680 035 873 664 650 008 998 062 148 672 495 910 924 329 517 621 990 293 525 617 017 585 167 868 445 669 371 731 658 222 975 616 151 224 748 701 714 263 756 733 660 744 805 088 592 422 981 582 894 856 835 080 977 254 970 606 610 629 073 664 357 536 103 316 615 292 496 719 438 035 014 684 353 285 652 334 330 825 473 890 726 929 878 043 074 506 586 228 132 859 914 138 825 319 727 398 138 537 886 914 664 001 109 092 153 776 496 655 562 492 779 832 189 072 602 986 457 476 068 596 024 206 040 011 151 731 186 244 495 611 664 994 963 719 178 722 103 411 566 640 641 485 690 798 871 108 521 079 633 222 146 434 687 415 264 216 757 246 762 845 718 136 037 519 779 546 825 102 667 002 551 330 828 513 542 838 125 145 990 460 696 585 708 019 843 456 247 978 542 332 400 909 222 652 326 387 675 597 680 164 527 303 016 249 372 883 664 596 775 965 973 406 324 561 428 216 297 752 392 440 109 663 126 004 270 890 032 811 076 539 713 088 782 696 624 520 072 174 669 009 049 218 854 673 292 259 692 639 236 609 381 225 647 815 517 305 115 449 120 335 589 938 803 895 923 919 569 396 186 000 561 662 366 105 505 646 616 794 934 581 291 348 856 441 674 370 807 584 228 530 097 048 517 133 857 669 922 584 282 162 345 432 021 698 877 052 403 010 079 305 570 653 775 119 006 909 449 946 615 347 199 124 363 503 509 156 345 632 767 098 859 446 669 018 282 236 347 113 158 959 056 198 032 829 872 697 748 372 418 247 622 606 990 614 965 208 166 080 248 636 041 593 629 600 500 195 541 701 907 504 683 053 926 961 042 088 660 383 590 622 622 044 994 711 219 411 801 379 846 894 947 160 154 612 986 928 051 247 761 774 943 502 350 441 833 506 574 363 314 538 031 299 487 477 270 718 271 142 629 291 429 583 604 288 229 596 037 464 073 423 707 541 696 863 299 857 654 064 677 953 404 704 316 150 836 303 738 738 437 705 774 663 453 428 847 404 321 652 713 329 123 097 375 903 450 137 432 104 123 071 961 176 143 831 808 561 702 036 704 048 423 338 031 816 132 703 177 304 116 251 963 458 823 307 203 338 076 109 211 100 110 154 998 562 490 952 205 021 845 076 368 022 498 076 805 262 331 503 541 304 562 002 589 594 699 392 719 580 889 078 273 983 956 032 170 968 829 167 295 743 190 231 750 845 935 851 121 274 884 815 967 038 022 504 424 563 130 989 251 602 194 289 406 118 922 906 231 470 718 324 830 230 578 804 123 425 449 870 409 792 171 124 683 737 588 953 480 991 909 245 925 844 690 954 222 544 993 446 582 565 913 918 737 964 574 148 543 080 097 469 263 526 404 906 882 365 813 831 723 347 994 208 167 391 655 209 515 530 492 657 080 050 231 123 457 324 371 105 509 029 018 218 535 448 392 194 912 300 289 908 298 404 576 320 990 861 324 602 320 795 723 707 859 514 260 680 215 417 147 042 023 836 698 243 962 786 967 594 407 187 723 482 256 155 221 277 229 102 485 367 221 356 756 151 050 220 061 011 577 974 698 076 678 780 126 256 457 740 850 087 109 407 693 053 312 134 481 875 457 613 748 803 184 307 470 670 679 958 103 741 855 717 092 908 869 644 825 333 394 829 155 766 549 023 254 968 988 857 085 653 316 740 286 385 317 180 154 287 636 665 171 882 750 991 025 430 685 464 986 061 248 032 973 825 131 444 041 709 678 262 465 510 486 361 573 253 296 114 833 438 983 543 129 292 211 249 818 117 091 611 384 827 847 636 328 727 895 116 920 924 603 756 284 032 979 248 385 017 678 684 908 875 329 437 629 762 710 321 718 021 915 823 510 096 845 551 090 455 075 397 892 884 343 695 288 047 004 707 229 264 162 581 027 850 289 846 470 233 997 109 008 639 533 414 498 998 515 426 025 214 383 323 009 694 817 866 358 139 705 359 219 863 348 702 368 371 948 931 779 843 413 775 689 360 561 536 943 748 595 910 603 474 840 031 132 870 549 346 254 483 201 789 291 766 228 520 202 980 450 510 432 983 937 270 354 099 511 517 507 014 055 695 378 107 691 866 586 897 178 791 105 679 666 642 443 178 575 229 869 639 042 416 373 968 111 294 954 222 670 810 853 893 276 832 017 197 979 909 938 106 077 229 615 399 338 260 454 915 142 253 383 666 752 589 808 395 039 963 684 304 604 800 849 048 301 655 975 571 992 515 453 427 026 680 628 286 326 804 424 750 328 676 432 404 858 294 691 128 236 707 102 510 828 266 048 191 392 566 498 346 470 842 889 904 067 428 946 102 515 519 162 238 624 811 983 733 239 269 012 683 736 795 587 896 762 356 031 802 305 322 599 847 863 149 190 375 066 873 849 301 305 934 371 618 812 384 420 099 633 581 069 762 677 329 851 897 163 150 266 570 647 692 971 219 862 805 586 213 539 468 668 821 900 906 246 465 546 768 260 725 113 211 918 974 223 306 395 084 246 984 394 889 779 802 648 374 694 881 100 134 081 732 714 556 177 954 097 832 330 274 439 302 481 802 159 338 703 533 420 773 686 278 316 308 729 061 268 501 563 922 028 134 401 311 581 899 870 523 383 735 158 239 109 198 599 038 819 245 159 094 102 956 029 249 857 149 438 586 587 744 300 497 173 972 727 115 333 875 528 140 588 646 803 195 187 759 107 104 019 522 671 376 376 611 258 738 304 566 316 290 721 430 161 774 663 586 037 532 349 141 395 641 737 658 698 051 142 213 264 088 340 953 912 801 621 795 679 665 266 977 124 010 890 130 768 754 415 254 981 607 783 043 975 094 483 078 612 351 733 120 164 256 710 432 668 676 344 919 949 446 328 492 847 475 232 042 172 488 620 220 240 513 944 783 049 183 559 092 726 419 705 164 709 491 056 096 336 833 463 408 361 592 764 511 428 672 943 274 846 958 237 109 826 204 586 295 473 950 459 865 147 190 688 348 169 830 614 860 066 082 565 263 748 764 882 687 538 697 245 662 199 028 518 076 579 331 292 855 026 688 234 480 317 727 776 269 287 766 548 488 505 831 275 031 979 549 765 501 534 946 729 704 421 384 896 986 384 828 845 687 534 352 936 101 635 620 863 218 448 192 157 913 688 621 483 918 080 827 140 324 921 752 163 566 454 449 892 731 540 705 193 205 327 082 727 526 863 107 020 953 099 965 677 507 064 283 244 287 782 716 285 553 957 395 046 548 393 926 014 005 144 375 824 916 588 349 571 954 025 303 898 807 507 659 817 282 813 284 915 331 978 479 595 563 599 395 317 857 719 717 210 183 402 404 812 518 021 431 216 831 632 340 972 109 969 109 416 050 961 902 990 736 929 322 180 973 881 917 946 346 977 396 489 294 138 063 798 459 365 188 771 398 868 024 537 380 879 472 176 059 328 427 877 245 424 140 367 572 231 797 588 912 910 753 462 664 131 713 066 084 883 958 698 696 460 793 974 496 776 474 865 091 469 414 987 761 598 385 035 661 317 481 543 511 628 292 172 933 247 241 454 626 492 822 952 408 239 135 133 755 713 933 998 096 742 966 172 938 861 230 769 882 351 246 677 876 452 106 430 519 655 204 644 372 428 510 075 173 870 333 555 297 991 569 931 131 645 167 353 966 119 362 564 337 003 224 099 465 798 896 903 394 693 073 018 204 030 276 464 204 912 690 491 382 455 720 371 891 091 690 343 654 569 003 728 275 669 697 473 339 003 168 791 006 614 790 462 175 548 450 734 479 938 180 415 746 153 698 620 822 353 952 977 073 465 861 087 314 838 160 594 157 994 608 666 910 101 139 730 675 852 672 746 031 437 785 833 950 729 542 632 829 759 231 456 216 725 613 393 650 319 055 318 888 769 212 142 086 201 294 884 027 484 020 058 961 713 178 435 663 497 648 022 411 163 733 481 085 652 319 420 184 485 943 869 432 650 661 532 110 250 233 742 472 640 035 947 438 552 706 925 023 250 458 610 416 329 849 142 994 134 854 697 448 591 826 599 740 674 730 875 513 756 494 514 054 156 651 413 648 974 589 234 897 347 551 396 839 528 849 570 772 259 197 484 922 227 553 479 382 542 251 134 845 014 066 446 782 311 466 065 750 191 092 273 449 015 107 834 871 984 659 012 509 626 047 641 424 022 619 531 850 996 833 762 489 852 622 767 986 064 786 053 893 635 923 116 723 174 792 694 328 008 839 470 456 833 504 665 504 063 821 654 637 696 688 036 721 737 094 535 318 603 405 191 371 166 415 507 831 726 723 145 618 061 388 091 098 185 464 004 972 689 787 297 555 530 201 507 115 619 946 088 720 961 738 329 696 469 296 557 868 758 570 359 826 165 462 812 044 489 405 425 336 821 183 927 483 085 171 914 608 891 019 903 628 408 856 875 349 299 097 063 350 281 472 642 085 364 363 731 741 239 231 275 325 669 108 931 888 286 429 969 385 763 108 482 609 429 356 126 704 583 625 252 115 835 963 599 983 424 831 493 472 643 051 375 674 277 300 809 979 270 697 175 428 841 310 603 941 684 077 562 781 821 401 410 311 979 325 393 603 619 617 803 477 543 415 644 769 927 034 967 195 219 260 403 408 025 785 199 577 898 578 181 676 369 938 489 575 093 936 834 515 146 534 242 039 914 762 303 309 551 436 998 653 605 486 042 631 539 598 837 968 441 109 877 448 032 996 768 523 899 919 781 976 270 174 963 519 117 233 375 018 400 260 096 138 607 337 441 471 320 816 258 446 385 490 277 973 782 956 022 786 785 527 610 347 341 565 407 837 686 788 474 015 567 621 070 681 821 273 683 849 942 581 789 507 244 129 001 908 217 100 152 935 424 559 844 042 791 730 475 594 677 265 362 617 652 815 494 535 966 083 397 896 517 860 029 141 356 518 081 256 906 670 278 380 014 113 481 077 158 977 288 476 525 717 533 962 458 509 927 384 802 953 142 775 092 547 111 355 550 396 997 500 542 667 853 271 670 550 636 714 409 555 938 245 662 088 566 942 156 129 111 141 811 767 469 057 773 544 725 033 790 898 969 438 515 858 679 259 248 681 714 141 526 672 326 429 190 751 582 713 842 354 102 054 006 588 035 834 422 361 601 316 565 488 662 253 222 056 938 093 683 322 351 030 446 133 545 411 799 177 389 522 438 108 748 356 288 230 204 224 317 051 700 537 375 351 800 185 523 154 233 919 250 207 516 731 990 057 428 142 479 009 749 565 687 972 726 034 829 769 918 926 748 652 415 985 216 611 402 456 702 180 635 652 469 914 950 128 754 865 148 659 212 751 829 072 838 664 799 900 384 671 377 049 181 338 174 948 029 555 659 007 516 737 328 549 676 100 781 669 986 208 832 487 609 145 060 566 961 849 373 084 903 921 951 918 242 684 405 994 207 499 724 990 077 495 781 745 499 300 616 145 660 705 850 624 228 763 784 354 200 368 544 809 909 213 194 064 121 572 766 830 892 630 101 640 894 195 222 321 475 151 594 662 788 306 213 300 734 046 900 378 354 180 470 479 836 228 940 142 756 147 342 320 357 542 538 068 453 147 335 190 788 269 533 542 348 844 881 047 567 736 259 724 944 763 195 072 552 177 731 275 501 811 157 623 231 919 227 770 533 380 209 825 922 866 516 949 072 773 911 556 236 247 226 062 202 458 811 381 956 923 308 729 303 695 614 342 296 450 551 599 041 486 449 899 977 572 049 108 584 841 636 756 070 362 979 632 810 551 974 818 424 356 273 331 130 590 548 109 877 971 427 188 772 214 345 666 952 896 080 447 403 226 269 270 719 411 144 757 132 086 800 255 325 106 979 120 580 003 826 484 586 971 501 042 482 026 902 283 988 322 527 622 570 713 635 016 944 544 820 995 593 241 786 889 184 898 030 493 805 334 060 597 715 976 542 741 746 713 672 162 383 268 520 954 749 834 552 617 130 752 318 737 714 009 405 837 931 254 481 682 544 012 600 576 457 645 915 881 572 602 040 851 804 680 571 066 007 471 666 170 641 393 282 665 717 126 242 181 945 853 389 048 903 155 498 001 822 887 994 179 169 675 617 715 892 026 150 348 752 278 216 775 121 611 742 485 975 617 773 567 064 233 208 948 240 652 329 476 057 545 597 450 785 313 629 650 061 401 693 460 436 741 048 843 154 227 423 746 311 484 586 530 532 647 730 822 899 484 327 510 892 805 868 037 150 625 293 418 741 315 057 226 343 484 891 296 221 016 314 392 260 735 148 213 053 716 357 763 448 160 996 907 769 758 151 551 474 940 883 503 936 104 327 070 460 464 894 528 741 067 054 347 078 891 002 909 438 492 473 066 076 387 538 092 519 781 670 797 726 397 781 117 679 399 002 990 190 503 676 419 088 374 349 713 571 061 960 717 216 620 722 037 246 744 729 883 263 108 984 565 339 618 322 148 076 260 147 787 050 862 892 524 627 609 119 465 083 030 315 943 165 515 635 845 625 239 687 690 567 123 333 679 665 074 977 299 726 126 588 114 063 123 666 612 511 847 844 647 844 767 971 988 617 820 408 665 217 752 419 901 709 416 699 335 648 430 674 670 100 568 794 084 515 748 612 186 163 309 367 403 066 798 034 687 493 945 942 728 056 517 129 083 336 607 582 915 881 654 802 388 588 580 548 349 305 768 624 381 235 524 112 154 568 608 005 931 477 089 635 499 463 304 486 536 764 146 128 485 703 847 277 688 257 714 968 671 477 458 084 904 050 186 777 691 489 944 844 170 914 287 826 533 603 347 002 442 002 816 957 883 793 315 552 728 733 409 521 103 230 506 546 732 000 729 475 927 938 482 635 211 025 541 342 840 388 602 405 705 639 768 828 001 803 811 056 701 804 764 508 875 775 738 935 088 539 582 913 460 166 144 397 440 544 310 432 224 644 146 026 057 136 349 184 088 561 502 225 707 155 959 278 847 814 259 690 089 657 800 937 536 773 928 495 607 055 338 558 054 112 104 681 198 747 685 857 005 219 015 852 539 230 262 458 088 720 793 674 006 528 458 466 468 580 059 307 132 544 280 987 105 020 968 423 809 122 219 732 369 380 628 002 329 976 976 338 741 368 374 612 401 195 381 689 069 351 075 202 660 914 576 074 066 743 457 988 413 954 469 334 682 436 660 469 482 363 062 012 010 923 102 758 217 996 855 900 455 400 797 643 858 060 378 281 363 868 412 199 070 405 586 909 279 105 145 901 379 266 047 169 333 588 736 511 361 967 489 588 829 083 464 446 728 419 649 838 432 885 846 333 634 751 011 859 260 043 784 565 080 436 957 585 495 643 203 120 131 770 018 133 066 806 310 275 302 415 302 851 339 812 776 739 144 339 784 779 323 323 548 822 612 315 346 302 500 730 922 694 150 054 904 466 009 060 814 110 846 858 418 610 417 809 402 864 135 272 295 019 126 017 121 406 890 042 111 499 491 515 907 733 175 094 064 734 916 403 218 379 800 739 172 943 452 437 851 240 538 758 713 158 543 874 797 402 736 791 970 256 115 636 509 484 765 635 157 385 435 149 432 166 432 529 891 602 334 966 756 863 222 140 369 479 933 502 125 086 368 002 232 815 929 999 658 968 026 756 041 989 251 952 906 680 862 313 832 830 431 550 158 554 607 758 030 758 939 901 474 654 250 228 620 935 631 532 571 921 520 651 815 293 680 223 695 829 759 569 177 919 543 529 234 008 110 577 132 430 098 969 654 366 435 508 824 517 317 533 637 668 955 409 051 185 557 346 716 798 983 192 072 295 070 629 549 382 321 339 425 479 937 930 462 074 107 185 058 341 455 291 324 567 791 316 098 215 019 281 299 479 206 255 374 973 789 644 073 078 905 376 668 728 321 019 843 959 929 183 985 737 233 095 574 046 856 216 033 885 506 729 653 469 139 012 089 138 953 774 733 570 080 415 872 801 658 897 426 358 515 698 682 277 559 253 706 498 159 327 888 900 580 735 128 433 020 286 249 828 001 928 255 145 141 666 202 817 860 032 793 245 469 100 160 688 451 940 564 329 091 286 075 101 754 066 137 814 902 825 273 755 170 908 142 724 152 431 608 722 045 426 758 172 575 070 900 552 659 046 814 676 810 975 320 555 593 554 811 050 092 431 493 558 724 094 212 073 742 179 732 657 380 858 087 312 690 329 260 584 307 510 671 443 355 847 710 540 326 732 861 549 342 226 871 524 681 496 611 188 971 117 620 281 449 491 433 577 277 093 512 667 721 502 329 492 992 331 451 155 521 935 194 004 214 517 569 479 938 265 175 756 458 626 832 429 610 868 264 326 301 440 064 197 402 949 630 708 634 167 876 589 385 660 277 324 106 060 602 241 527 356 912 753 254 796 697 827 783 406 576 304 933 809 386 579 884 447 075 239 106 779 066 567 320 364 980 397 892 646 605 848 688 995 060 111 587 519 923 121 435 731 793 005 027 681 600 827 774 374 046 648 437 270 656 515 565 267 194 450 582 905 439 658 612 362 019 722 921 849 245 426 424 459 396 999 311 925 148 196 009 345 860 674 577 910 112 421 680 704 017 160 271 487 950 951 112 492 993 225 935 946 566 418 484 195 193 525 704 012 479 593 871 839 345 085 694 789 347 944 185 943 631 801 793 309 020 844 753 518 349 998 766 661 022 296 139 894 097 772 553 977 308 178 617 064 249 554 113 867 486 825 763 557 640 086 731 222 581 638 031 377 681 425 439 632 752 557 480 938 231 745 809 493 274 581 987 995 913 714 402 393 131 494 338 292 698 865 402 861 934 821 844 832 860 081 306 244 228 610 922 405 065 289 689 448 218 256 469 145 895 539 891 510 015 630 086 770 008 392 407 647 451 934 716 304 911 855 936 964 501 369 067 682 819 039 556 867 668 374 789 289 474 427 707 436 644 812 140 394 972 147 954 617 610 743 968 664 962 806 509 100 181 388 691 542 169 662 855 669 733 845 966 847 846 024 211 579 004 048 784 475 687 059 950 545 848 885 604 746 745 821 973 707 309 048 781 174 081 153 498 457 714 206 861 914 742 105 344 234 149 141 614 172 883 618 562 202 269 570 842 058 937 479 391 680 561 567 075 399 710 929 225 920 895 731 953 627 893 441 669 184 073 764 809 878 078 688 800 162 439 966 609 693 966 676 081 734 344 133 650 700 249 432 290 988 331 247 118 447 600 492 914 979 647 809 519 536 817 941 398 615 290 044 269 050 459 212 168 977 806 975 561 593 617 449 267 809 672 509 504 440 533 093 652 747 665 590 388 905 208 727 115 243 287 387 700 576 822 521 486 715 006 664 205 015 916 819 342 991 214 621 203 515 939 972 498 490 442 150 666 524 970 045 424 392 235 705 057 706 008 677 057 882 157 672 781 528 938 597 930 540 898 866 443 083 084 861 452 869 761 283 714 499 903 880 764 135 459 301 736 945 206 022 920 717 158 726 574 071 661 772 467 905 858 131 814 746 017 319 093 398 224 924 964 322 516 492 709 333 806 194 665 602 600 406 484 447 457 609 550 379 047 013 003 087 483 823 297 434 749 187 624 382 821 983 621 247 181 880 742 956 465 261 334 201 805 392 330 264 522 941 535 364 529 512 046 539 193 452 822 812 394 660 333 826 176 490 012 603 239 542 789 930 320 577 027 688 726 033 494 249 886 828 561 935 838 940 812 513 753 854 956 851 370 658 323 209 004 197 799 532 299 478 543 463 537 317 436 713 516 621 537 722 788 766 278 523 193 316 557 021 638 258 759 855 997 781 160 629 953 191 848 240 142 052 044 262 329 329 288 893 497 806 105 774 528 799 499 941 082 074 083 091 872 793 985 143 602 480 824 617 719 952 368 119 826 755 515 727 789 286 568 071 342 239 749 060 545 972 958 776 525 478 089 847 408 391 556 346 125 647 196 316 729 236 603 551 367 476 197 728 495 374 311 248 441 369 472 616 233 592 216 855 399 311 310 815 714 727 620 898 311 254 612 839 598 352 214 139 593 317 048 984 309 890 631 935 941 058 477 751 115 030 056 458 962 145 637 119 652 006 959 576 414 293 900 226 906 003 997 978 113 343 911 078 493 339 508 800 875 617 086 057 935 471 674 842 729 870 222 738 058 478 184 183 660 931 271 923 812 808 776 988 634 207 898 874 132 929 300 117 980 820 764 852 205 790 043 529 310 313 010 707 036 300 964 636 602 808 763 588 608 690 856 685 341 569 985 664 465 793 079 066 420 173 966 710 407 163 895 367 143 697 457 595 233 692 758 893 300 897 367 014 303 010 496 221 972 552 148 902 004 409 225 074 191 690 702 717 539 203 193 184 508 051 285 470 513 418 123 037 014 342 746 673 890 031 686 012 548 201 713 538 994 862 424 496 222 615 925 354 313 343 330 577 571 401 912 061 678 649 270 089 729 220 710 259 018 770 304 024 215 186 896 890 907 193 995 926 161 220 294 586 643 429 712 463 581 846 521 187 728 735 345 558 911 076 812 308 616 796 390 424 183 580 228 297 083 412 967 869 379 936 592 133 099 253 537 435 301 790 242 779 883 919 613 268 788 746 330 539 677 868 523 719 255 725 892 543 173 471 658 675 888 187 272 297 012 243 945 655 562 481 534 654 460 098 327 348 618 938 038 306 097 959 532 113 772 693 973 812 410 046 979 402 039 815 410 699 669 609 630 526 713 575 136 822 042 736 649 307 171 311 266 107 370 363 043 212 812 081 859 003 899 810 171 111 672 963 460 098 731 423 892 435 959 657 215 675 347 881 958 821 716 627 290 239 636 465 124 587 028 821 879 925 850 977 687 880 859 294 525 410 911 804 178 561 648 258 358 390 120 510 351 450 076 831 342 939 562 777 966 814 847 959 937 279 048 093 451 578 718 044 265 728 889 337 895 889 383 756 028 889 624 627 761 587 255 946 724 998 163 582 287 724 479 043 307 814 827 961 253 316 194 871 370 771 398 128 613 208 066 128 335 374 666 170 762 113 467 822 968 339 890 907 610 870 068 907 375 160 410 273 057 428 270 379 393 570 687 361 552 876 964 541 808 338 605 448 319 127 028 899 959 973 564 306 700 025 016 442 498 276 733 897 000 689 527 405 139 551 519 402 505 590 850 477 574 793 893 046 808 267 907 407 147 028 384 880 500 517 167 624 340 344 487 595 484 773 371 438 775 171 663 014 116 883 172 949 703 685 997 486 922 473 152 118 392 521 288 002 989 524 704 081 543 496 849 685 874 635 157 963 144 166 463 783 098 559 842 618 557 023 594 023 600 690 458 131 713 548 748 158 538 353 790 473 489 606 038 127 683 831 561 552 895 148 695 265 626 813 460 317 141 375 988 590 622 904 137 566 220 983 482 195 207 946 115 397 755 002 506 564 678 963 087 834 899 269 924 892 646 981 232 021 366 662 392 056 151 281 257 411 110 770 349 576 641 915 357 619 281 564 548 673 884 897 960 028 495 024 502 718 828 677 750 471 049 825 665 955 297 204 825 208 824 552 560 013 694 215 948 720 076 104 737 326 639 851 991 378 511 977 239 824 090 359 889 141 146 764 274 681 011 654 450 940 116 861 532 040 356 799 403 854 637 761 707 480 040 153 087 888 021 169 573 165 075 793 416 903 899 237 750 649 273 775 940 250 603 885 344 805 220 153 132 228 885 835 887 973 418 333 634 008 388 919 096 044 559 256 670 446 198 236 540 626 560 908 098 098 932 465 485 276 321 250 533 625 075 950 025 553 142 200 660 476 266 496 119 038 724 161 621 737 468 820 190 122 905 482 456 146 456 231 855 727 153 448 499 537 191 691 187 346 749 159 713 205 882 727 399 346 949 618 427 836 654 373 483 862 236 351 879 103 429 213 446 397 493 049 891 993 990 002 650 874 078 006 330 500 203 940 730 919 010 170 638 313 397 442 625 577 483 429 863 487 321 535 426 216 562 907 340 216 557 659 531 518 790 604 103 938 091 496 808 238 744 680 434 461 618 455 971 848 370 637 707 416 241 822 651 781 183 273 608 955 219 005 498 557 048 939 428 460 496 001 683 237 498 577 646 369 529 647 811 862 151 490 478 726 419 385 035 167 574 261 799 076 734 965 980 902 754 130 001 810 064 788 464 611 981 642 382 280 339 752 779 216 433 978 027 312 840 246 505 036 155 270 827 327 252 568 833 164 439 781 369 527 459 605 363 429 851 361 472 821 373 070 467 570 053 119 869 665 814 196 488 890 621 497 420 977 861 062 860 975 803 667 444 023 611 693 787 987 864 056 114 479 900 702 662 855 879 553 045 097 762 595 741 077 854 502 005 825 630 642 791 633 083 315 875 557 796 619 548 235 379 881 664 759 601 975 129 634 188 129 332 072 185 712 616 900 031 406 254 160 796 013 253 224 004 700 715 892 727 153 018 345 139 365 341 609 811 732 041 238 807 911 070 568 828 799 335 555 959 184 410 329 482 433 931 640 259 849 391 414 062 815 631 079 988 880 021 155 027 630 021 900 580 904 341 517 561 549 503 964 045 907 708 605 469 562 926 333 877 771 172 768 703 784 133 532 306 664 534 268 799 008 313 668 703 560 876 810 254 138 017 655 535 855 219 204 835 741 018 368 931 446 631 657 093 328 455 609 982 710 551 501 541 245 154 690 581 866 881 005 791 963 969 615 534 065 939 024 651 754 378 650 543 571 109 963 930 093 228 503 692 675 978 320 131 744 847 004 019 634 455 740 434 051 309 523 432 358 922 297 925 299 324 502 984 583 766 271 872 684 202 160 745 020 528 752 701 865 293 805 615 201 402 914 811 257 234 488 701 113 050 002 428 779 578 371 120 027 789 968 135 648 975 459 739 495 895 738 544 450 596 713 326 441 575 122 804 968 382 249 903 108 828 054 958 335 844 228 413 880 399 245 005 454 607 950 433 881 632 386 043 433 758 639 394 724 109 836 180 820 923 796 068 094 583 913 352 911 314 830 351 366 008 407 615 575 722 796 448 613 379 805 409 838 697 368 618 245 524 455 760 497 252 315 239 186 975 306 768 195 689 654 058 497 124 220 224 485 004 259 471 246 681 537 417 675 590 239 739 403 051 959 987 219 950 823 347 993 220 588 501 110 887 018 624 936 314 771 706 324 470 171 271 410 347 709 277 598 042 828 504 590 196 511 717 969 550 411 603 281 872 802 581 556 105 509 741 387 662 352 881 992 061 409 953 072 472 357 131 519 242 233 663 246 485 815 279 244 554 688 194 050 911 765 867 155 132 878 495 458 634 782 952 968 413 268 042 379 367 819 539 475 272 863 257 699 321 915 523 118 601 792 412 009 759 996 665 992 772 376 984 037 475 807 736 754 134 372 549 568 799 552 818 978 267 668 119 831 610 605 511 267 754 589 979 100 304 887 099 014 675 572 721 821 624 379 582 195 919 405 681 921 744 139 178 523 315 491 810 417 512 196 766 840 213 821 000 523 326 329 870 995 427 852 706 258 750 658 983 518 825 363 184 097 494 920 651 825 819 794 150 658 169 915 341 674 651 793 489 695 002 255 801 878 303 657 397 729 755 242 105 972 406 693 119 469 716 202 917 616 957 001 036 348 796 278 309 051 460 978 481 730 406 411 831 022 083 793 234 145 930 717 579 376 227 934 477 520 713 124 396 452 895 760 386 175 966 305 990 968 822 347 630 619 235 653 222 582 002 304 568 759 125 234 725 739 295 216 107 382 948 545 267 251 557 488 368 071 668 974 949 910 431 385 540 488 776 028 902 735 233 690 374 997 782 283 175 438 100 189 225 514 424 272 432 186 315 243 511 577 872 524 036 343 035 363 201 567 320 768 400 029 524 456 318 349 899 734 128 540 513 362 936 586 874 207 185 983 914 336 423 421 645 253 822 837 878 241 997 628 267 872 138 673 560 411 672 127 008 455 572 173 900 239 585 110 395 592 359 106 663 407 164 203 282 937 706 103 116 823 692 651 211 043 012 326 189 163 425 289 179 497 399 470 711 760 428 761 888 324 592 717 615 080 405 777 555 824 417 594 133 863 233 750 045 889 892 171 218 259 136 999 242 005 477 220 921 542 444 467 535 146 954 514 963 107 144 711 837 485 074 036 233 517 018 978 691 620 202 056 635 469 114 939 855 180 061 553 325 536 887 704 144 980 986 580 822 428 794 863 056 794 472 862 495 894 478 604 065 721 290 384 710 844 269 802 507 643 818 171 763 197 506 521 293 266 541 645 037 208 660 613 040 864 544 584 112 053 868 579 024 298 731 973 661 049 483 811 512 233 720 376 055 424 213 777 852 914 447 970 720 497 599 009 106 840 131 152 935 035 523 199 236 250 851 883 462 097 387 242 229 590 029 999 716 491 043 883 213 359 354 536 548 275 864 212 943 850 436 907 035 624 466 804 397 775 130 343 239 986 977 170 911 875 528 088 630 349 596 075 453 670 905 647 232 439 188 370 570 849 993 074 640 943 263 044 980 238 914 449 677 035 602 968 304 971 390 124 477 567 666 130 233 002 289 368 682 737 843 115 582 685 453 899 767 894 790 164 620 485 857 035 958 697 414 111 759 127 612 059 909 317 967 559 570 049 968 325 122 894 401 658 099 964 065 782 724 702 376 242 452 485 983 410 831 016 874 734 462 767 276 799 325 377 913 733 832 892 143 769 804 528 623 559 502 051 428 452 759 312 415 141 771 676 623 107 402 857 932 924 578 558 890 190 739 497 999 623 874 904 950 658 828 758 948 148 473 268 692 394 876 100 374 333 982 742 653 268 716 816 094 862 119 654 601 410 191 630 693 485 906 688 409 536 733 837 459 650 835 470 221 093 526 339 445 411 936 447 737 003 339 562 534 621 561 529 188 439 152 478 812 702 507 128 073 509 097 978 746 775 850 955 670 587 791 954 000 104 574 696 920 721 589 838 894 488 022 318 875 754 151 085 063 625 659 791 342 040 117 277 290 764 299 104 602 942 072 106 148 635 601 273 621 898 452 940 143 944 840 130 014 490 298 786 240 110 443 438 294 785 452 562 409 799 345 074 378 637 344 861 953 432 330 074 532 697 479 953 886 554 793 279 220 154 635 227 104 508 710 117 438 583 056 713 632 532 021 229 662 396 702 280 315 525 676 783 127 086 860 642 402 914 565 393 009 848 689 015 941 307 745 214 975 801 799 829 103 194 164 478 013 417 834 780 374 291 874 399 633 058 226 626 645 404 817 844 494 101 485 839 862 110 561 693 919 763 815 448 526 381 945 579 891 050 157 659 788 396 544 727 838 936 324 757 445 606 056 897 721 382 474 106 362 356 050 459 858 696 070 126 950 186 247 846 631 295 195 207 920 328 574 116 881 176 694 551 470 410 805 932 751 470 864 375 480 637 491 679 852 615 808 883 624 923 053 233 103 562 771 680 657 025 436 150 263 048 492 658 764 957 193 757 957 370 794 058 999 591 238 598 042 940 362 875 287 912 330 141 419 905 788 246 498 473 009 012 053 281 570 188 104 701 140 697 166 803 350 608 369 369 011 162 819 174 257 316 179 003 764 938 868 883 014 017 389 943 593 125 733 494 796 691 771 743 809 356 618 714 763 033 804 055 871 542 493 723 092 779 936 825 976 237 687 045 410 819 490 314 366 156 039 354 777 743 843 362 032 986 527 203 182 779 839 091 951 769 742 632 915 825 417 453 073 828 541 113 887 562 821 659 845 046 008 846 971 665 277 577 008 161 204 999 427 458 803 161 540 138 199 225 610 928 510 933 777 015 480 627 249 088 106 398 921 071 872 361 247 111 847 187 646 410 657 289 231 651 238 351 868 191 933 420 871 304 075 881 155 027 677 246 747 220 604 760 003 074 370 524 057 777 307 359 936 494 224 262 806 279 738 578 863 857 243 116 373 136 319 862 304 932 442 895 377 238 068 735 729 493 320 396 336 634 515 925 261 636 223 685 862 233 937 871 089 656 331 390 694 980 293 836 009 969 063 225 326 298 622 780 779 178 514 048 489 924 105 708 262 355 906 832 811 893 935 331 421 491 413 030 587 612 325 620 065 408 290 790 479 619 320 522 519 134 105 912 633 037 769 375 041 011 410 604 355 580 499 193 423 384 548 516 337 590 107 817 508 028 830 375 695 177 312 192 662 966 337 728 710 587 485 502 607 890 832 960 860 024 956 547 472 268 451 771 485 242 590 971 423 845 155 506 204 569 991 769 318 524 761 864 404 750 047 353 075 895 783 982 850 800 225 216 311 611 848 145 832 831 311 421 240 966 305 469 351 408 863 465 116 534 790 460 905 969 091 994 321 347 972 453 179 503 058 753 876 537 464 810 771 710 900 632 260 202 634 360 697 196 779 216 417 862 093 730 622 682 920 169 523 577 086 355 412 582 009 159 478 629 988 296 765 749 362 956 256 552 708 204 034 622 957 387 315 806 459 173 019 219 002 644 191 612 738 449 053 844 668 360 496 388 914 772 314 240 948 407 287 323 343 579 119 096 172 451 077 195 457 323 977 532 064 704 257 281 893 358 692 844 162 912 710 362 257 912 877 711 194 984 871 210 630 150 699 181 358 469 688 013 608 317 470 683 936 868 164 284 018 188 786 328 792 832 500 618 441 664 103 117 758 948 061 162 417 764 040 107 048 498 903 103 644 053 735 323 656 426 961 238 514 325 866 121 998 273 887 283 311 368 961 807 131 012 478 933 555 303 208 749 360 731 314 522 255 179 400 368 066 434 982 557 020 384 912 321 091 309 775 980 743 968 548 897 312 687 285 745 927 079 698 418 718 357 751 434 168 817 294 015 801 012 160 112 908 097 859 367 441 180 040 821 326 389 166 205 384 335 937 642 718 930 434 244 570 973 888 867 089 330 269 182 011 571 063 938 279 643 087 890 213 479 129 940 782 778 221 558 383 687 356 683 707 425 176 454 659 465 059 052 326 434 655 650 363 317 875 755 165 785 543 943 244 659 708 335 290 726 578 236 491 092 669 197 212 101 326 089 059 359 454 659 978 129 884 131 392 679 370 861 314 722 464 396 642 349 768 018 615 641 705 054 670 557 293 775 833 984 845 450 799 647 114 637 201 847 512 973 065 171 131 383 895 942 826 075 824 593 235 787 704 922 987 948 409 451 318 960 558 600 620 439 637 628 474 919 859 832 760 479 391 075 962 728 401 224 173 056 603 248 483 495 937 269 549 235 186 405 377 889 349 466 138 965 551 935 687 778 315 517 677 096 833 653 084 774 397 284 051 190 830 441 195 518 375 495 529 187 723 504 618 484 952 860 802 026 071 808 093 272 448 963 152 472 831 179 363 428 838 459 527 630 700 853 689 654 912 236 295 318 197 682 665 926 497 371 206 609 780 839 963 046 173 648 864 663 130 613 337 403 934 375 584 993 719 429 343 570 047 637 800 072 865 791 873 323 684 632 938 756 198 900 555 342 438 614 198 044 674 050 297 697 155 712 003 847 175 687 408 926 396 909 054 679 481 187 243 622 518 398 053 525 863 301 489 820 566 884 157 585 477 218 796 947 697 929 252 114 831 880 701 418 382 305 335 775 578 323 680 459 903 233 323 974 065 069 897 982 547 319 687 750 841 070 263 710 697 148 743 754 829 617 830 060 236 921 565 229 826 234 109 706 185 809 282 044 714 305 954 031 237 264 234 534 792 002 810 316 238 066 562 846 277 311 767 710 670 288 105 445 776 397 891 820 293 660 475 925 748 693 867 604 311 584 687 467 759 500 480 426 446 123 546 678 992 393 503 219 364 504 664 305 800 057 551 036 586 946 434 374 064 509 238 321 204 163 857 993 730 090 203 978 303 484 756 137 502 965 266 154 067 689 042 963 060 243 958 862 929 542 715 508 548 620 065 611 080 387 765 805 583 611 457 481 035 464 501 925 797 891 043 944 689 546 397 226 418 286 216 642 969 459 187 731 690 410 349 613 060 165 813 810 572 473 716 821 937 570 218 051 453 751 953 910 364 659 415 397 236 738 470 402 801 900 258 304 528 385 660 413 507 895 938 882 767 690 140 973 548 874 171 354 271 894 807 010 810 912 131 174 421 304 404 816 280 544 633 734 474 514 617 687 084 434 605 844 405 402 867 480 125 432 870 335 260 960 530 972 516 072 499 766 154 067 899 593 988 696 865 649 061 549 002 784 289 162 126 585 748 960 391 545 399 960 641 964 322 284 961 232 345 019 680 874 690 504 787 734 410 207 818 539 079 458 563 869 552 192 992 693 159 314 381 232 096 867 096 392 191 009 392 141 376 300 557 371 508 103 267 311 677 521 952 048 788 100 164 621 448 586 720 177 722 965 074 172 577 296 706 374 897 696 531 455 214 106 919 858 686 507 653 290 199 955 632 084 539 291 537 651 125 544 860 128 963 389 447 208 407 596 037 658 751 397 114 641 025 909 775 510 555 081 591 113 471 000 092 801 384 904 591 299 816 869 341 759 784 199 813 993 377 901 955 206 193 552 268 921 236 013 263 962 824 117 685 851 368 913 494 183 385 773 274 782 982 518 718 823 524 266 828 495 930 578 719 172 982 213 039 734 843 625 691 408 028 575 411 167 897 106 240 681 720 127 497 772 966 851 752 575 170 241 481 481 335 264 649 110 516 140 234 339 452 096 423 221 703 163 693 192 969 600 104 831 006 818 769 719 392 980 810 471 539 809 512 639 833 146 129 785 875 977 008 720 046 471 490 155 006 018 032 509 639 933 276 950 588 351 507 060 692 284 784 243 566 173 509 480 492 096 919 654 465 768 371 225 601 064 600 208 454 417 655 209 855 301 085 955 051 573 941 191 681 890 123 906 845 443 174 529 920 822 200 281 428 523 340 758 886 283 536 158 000 598 444 214 125 481 860 144 145 305 510 715 339 580 288 367 671 045 572 050 779 687 842 734 086 322 520 457 161 483 280 499 195 874 879 399 981 572 281 997 190 786 493 490 512 493 449 395 898 154 277 984 412 500 225 038 178 309 795 000 808 445 558 989 311 821 018 702 551 224 249 996 969 858 233 285 629 832 364 681 207 243 606 851 993 036 667 124 181 785 040 776 442 112 279 702 385 502 569 415 167 802 789 532 525 884 254 087 145 630 289 555 019 954 537 984 369 032 382 814 490 500 170 355 510 302 326 018 867 308 281 995 745 563 699 102 108 912 300 656 654 472 818 488 907 570 403 847 487 878 795 056 134 906 242 416 771 468 261 899 396 434 992 567 525 676 883 270 767 691 458 661 315 272 447 005 457 077 731 480 802 528 475 344 551 568 290 217 270 558 950 920 923 806 378 008 412 489 374 645 085 297 998 981 212 302 566 676 130 482 054 395 414 169 338 778 618 298 919 389 437 706 757 429 732 285 918 316 082 743 875 041 815 061 911 188 679 891 353 547 942 379 788 070 681 613 444 815 567 124 081 113 160 421 438 889 467 527 979 229 260 489 061 646 204 016 695 089 072 593 115 640 693 515 603 589 089 979 757 190 522 226 805 995 386 726 738 103 045 489 691 010 127 758 693 087 153 775 859 471 570 150 240 456 427 292 678 200 487 721 852 351 395 904 797 887 108 241 270 457 595 518 540 655 053 150 596 108 995 991 804 036 210 694 280 062 739 157 224 739 805 671 532 192 834 612 982 189 767 877 004 322 657 927 212 195 314 265 497 626 220 576 228 696 772 640 384 418 521 895 566 668 789 650 857 568 405 312 240 381 392 055 502 761 388 783 268 241 313 714 465 150 140 124 033 938 138 933 506 574 155 102 966 371 492 717 718 671 442 988 336 126 796 247 553 911 610 636 435 349 704 640 971 662 266 268 622 113 017 618 974 220 011 389 088 612 927 374 456 883 288 214 886 214 891 553 779 834 175 745 190 609 389 440 336 930 489 275 243 917 919 508 993 023 422 388 503 571 290 030 555 221 272 228 075 773 077 040 450 638 491 498 650 571 081 709 288 927 306 662 656 253 502 235 474 175 230 841 772 637 174 494 062 390 864 048 001 741 047 777 626 836 492 713 685 568 469 179 331 031 146 057 368 326 681 461 335 918 228 662 394 743 986 443 254 882 380 884 017 118 548 693 591 439 634 822 096 062 537 997 079 780 135 824 709 757 262 300 340 367 371 707 712 553 204 890 680 740 079 312 463 097 933 954 728 392 445 853 339 677 771 078 555 601 523 813 753 635 881 392 731 917 204 029 583 154 744 231 981 146 217 531 879 065 750 055 654 769 294 332 118 844 044 191 382 031 367 415 672 722 992 901 238 146 463 738 654 612 406 893 316 227 509 159 993 398 685 643 505 919 914 617 643 872 379 238 623 091 954 422 505 803 356 249 188 310 536 683 356 758 034 508 987 288 960 956 929 281 244 464 722 402 510 084 622 065 068 445 055 292 576 308 821 140 249 544 774 716 355 213 250 355 991 120 016 852 856 090 177 672 031 843 256 753 279 648 317 048 288 323 874 173 273 571 212 079 412 795 223 942 255 799 146 033 003 980 484 514 240 579 851 021 347 217 271 191 280 748 725 428 220 229 083 242 533 986 151 702 510 620 740 596 520 244 284 440 864 369 864 645 583 904 561 957 921 428 246 132 676 674 739 840 981 343 719 707 431 410 820 883 862 518 295 901 840 123 100 595 919 030 959 947 869 279 309 393 021 924 754 685 108 692 273 625 775 456 905 364 762 490 636 761 795 045 821 350 615 867 756 958 092 943 568 421 947 177 080 306 078 336 621 281 122 985 888 184 799 721 617 798 371 141 020 766 069 782 554 462 144 000 158 290 940 380 624 942 759 870 335 836 042 232 522 799 259 332 668 219 817 517 177 654 861 076 363 707 180 503 373 653 680 775 271 541 928 354 386 054 308 913 808 413 308 826 176 879 037 889 173 418 602 897 158 569 070 798 309 009 619 484 052 682 047 068 114 496 879 477 146 152 048 540 602 841 028 234 693 125 398 336 082 084 642 164 631 033 633 759 359 024 556 991 069 215 174 465 827 245 861 033 824 006 096 020 707 112 973 145 267 097 655 418 219 435 134 661 788 296 185 082 997 093 795 340 737 966 358 499 871 523 904 944 129 679 754 029 052 045 412 937 150 961 453 333 620 323 113 942 264 962 214 904 833 525 080 804 701 162 193 299 069 749 892 571 212 468 722 988 310 357 873 610 742 577 172 152 688 158 850 729 585 376 808 006 138 238 201 619 904 483 878 886 548 318 931 547 240 506 892 458 405 693 068 172 789 404 405 017 768 572 312 366 341 213 562 906 487 419 304 870 126 879 270 764 761 189 029 838 807 816 059 648 721 220 276 682 049 692 492 958 898 273 813 464 664 181 481 953 238 239 948 632 347 032 169 188 454 533 596 577 940 523 783 233 774 299 390 547 164 970 936 263 462 090 317 756 039 506 558 191 477 522 770 444 585 598 254 361 713 062 626 234 117 621 562 996 314 564 600 489 531 865 306 934 317 599 966 532 116 765 776 112 460 654 569 802 871 879 494 778 256 616 397 965 686 966 198 311 363 013 331 391 239 446 326 199 181 202 741 372 086 036 360 538 727 570 018 984 090 027 510 789 594 066 731 105 022 515 127 787 634 472 281 049 895 313 250 708 624 070 220 386 078 081 598 195 041 101 063 202 001 556 759 227 735 904 391 177 514 470 414 763 890 692 953 891 680 636 093 227 978 527 014 979 130 162 700 779 698 417 603 865 235 274 625 704 535 031 376 890 550 820 675 821 356 168 795 235 005 156 266 202 052 988 026 586 734 660 526 257 517 652 647 132 750 040 930 917 735 002 147 758 404 736 933 513 412 612 249 793 639 837 445 789 781 939 656 355 201 153 048 564 283 366 283 157 771 353 844 144 340 113 402 863 165 121 563 973 685 317 704 227 705 015 640 281 083 008 169 530 399 153 311 012 403 065 483 288 315 873 865 658 721 144 035 141 815 313 968 789 316 809 608 505 738 157 983 255 955 281 540 364 590 087 788 937 456 491 343 528 992 509 122 707 065 891 486 007 648 220 364 345 432 192 940 750 239 678 452 771 725 857 599 759 549 895 965 733 177 039 178 302 560 941 368 279 206 562 408 131 111 960 096 797 064 585 776 893 572 445 683 815 510 356 552 237 904 155 164 826 011 167 983 932 108 640 773 592 958 056 829 609 007 165 253 797 829 616 416 779 288 493 675 425 844 576 838 707 426 951 608 367 079 955 046 601 707 196 959 055 184 070 457 203 907 540 639 531 266 005 834 063 207 602 429 539 101 356 180 859 120 493 560 172 386 840 978 097 242 089 641 664 240 284 511 390 773 913 156 947 792 566 347 634 895 996 350 395 991 172 854 881 784 782 864 358 117 063 557 405 148 118 866 078 608 064 993 927 744 819 176 702 970 681 063 670 607 323 153 607 689 727 105 439 881 158 802 609 684 764 248 173 393 503 106 164 452 606 748 427 432 695 423 316 605 325 332 655 888 159 402 431 896 793 300 282 834 521 532 734 592 578 863 730 594 658 940 315 786 557 814 519 828 389 090 345 720 605 073 451 850 661 833 955 409 484 244 055 401 812 071 865 585 036 507 991 050 104 732 599 854 210 010 915 099 655 658 159 186 423 660 151 022 539 852 577 095 383 883 561 281 081 903 409 725 134 215 900 759 407 639 906 365 613 247 939 713 519 297 001 775 670 230 663 248 712 589 028 787 557 223 211 257 663 863 342 250 785 676 849 186 619 864 405 231 768 552 312 676 404 779 212 060 508 733 796 882 978 484 345 748 530 038 578 864 014 302 769 086 919 799 541 856 299 076 601 107 028 892 636 461 546 239 378 565 107 349 598 270 607 875 383 815 761 867 424 766 569 221 731 321 143 648 783 911 992 238 251 218 719 214 580 302 495 230 717 004 514 806 033 215 074 691 817 959 445 898 422 499 019 449 221 302 890 411 011 503 701 618 503 716 176 131 585 414 037 953 695 784 525 734 973 018 976 310 702 692 346 437 778 281 717 051 793 845 973 173 030 998 313 653 043 841 768 415 709 858 180 990 958 836 791 935 753 007 280 142 670 361 977 723 168 137 668 306 825 662 459 508 009 555 568 578 027 538 132 399 266 514 005 816 492 004 171 662 051 186 270 733 247 794 197 585 984 286 805 164 583 165 822 481 518 524 944 075 354 477 695 085 529 304 803 748 152 955 485 598 981 127 639 928 147 196 071 917 932 218 395 404 760 794 999 364 776 894 943 377 545 180 433 934 391 995 133 403 728 078 730 844 601 090 506 935 506 436 316 016 379 394 714 180 738 502 538 217 723 940 426 658 324 179 311 878 340 988 640 976 307 896 416 522 425 153 345 138 319 025 843 044 195 870 560 911 585 872 188 042 629 554 976 859 713 346 907 399 649 694 685 636 666 403 060 572 016 242 745 477 125 111 441 150 507 402 537 325 139 017 912 696 062 489 759 451 589 460 538 939 196 021 095 469 546 319 022 989 984 010 041 504 475 098 165 305 395 520 845 077 376 664 129 732 566 170 893 600 393 439 810 480 854 582 840 023 844 036 043 985 415 901 832 766 215 641 343 407 967 768 265 873 694 293 012 295 370 856 909 127 155 207 653 271 361 075 025 040 321 509 648 756 839 856 736 314 515 258 178 416 892 404 666 017 006 156 608 803 805 954 185 848 771 100 751 122 460 851 053 968 207 059 966 944 348 753 112 235 650 296 861 754 879 909 981 751 539 858 234 106 439 564 910 424 371 894 280 958 685 691 151 603 757 529 715 986 926 136 809 881 064 091 912 962 926 648 192 728 363 526 314 111 189 893 378 315 653 478 169 397 738 070 308 942 633 196 308 831 542 088 176 141 506 453 309 482 124 997 019 573 531 594 807 417 005 120 743 937 880 535 076 372 999 834 959 170 188 591 873 351 454 472 620 633 666 691 878 795 478 136 428 588 232 787 941 663 412 852 411 571 551 218 662 627 842 630 260 012 650 661 965 486 092 667 154 690 469 990 993 194 905 123 449 536 865 962 583 074 829 515 089 414 009 123 830 782 481 067 088 556 677 885 469 645 602 523 261 911 299 105 566 617 194 830 960 657 846 892 194 693 995 207 564 178 771 081 420 729 475 629 263 986 777 588 331 655 314 310 288 023 414 524 787 602 294 648 840 742 666 151 137 256 728 987 046 934 544 673 543 987 362 424 217 745 620 625 589 572 403 903 867 928 867 845 218 728 178 567 442 978 426 778 569 620 825 583 016 901 011 092 717 459 866 552 216 905 981 394 422 156 001 931 960 320 948 000 833 898 222 329 389 879 186 967 363 819 496 025 392 597 305 599 977 640 095 774 354 560 947 383 922 994 766 753 315 835 495 745 892 145 480 817 476 905 081 494 506 661 183 705 503 686 340 813 925 959 503 249 925 382 048 789 544 415 440 817 276 859 492 891 428 172 401 347 410 475 771 552 363 702 356 171 155 117 758 190 136 720 207 583 120 278 747 997 248 655 438 499 233 949 859 586 359 872 180 795 595 920 161 851 184 509 909 344 198 909 676 821 087 772 503 133 692 451 938 942 847 277 069 625 134 686 559 440 265 015 606 899 825 463 723 684 197 191 691 439 880 481 137 068 691 965 418 282 031 246 861 764 867 684 735 919 677 227 448 451 510 379 586 143 959 968 463 699 984 683 785 334 892 484 835 220 077 724 808 796 843 153 195 342 834 898 860 193 922 997 304 382 652 193 673 252 594 742 906 793 955 350 312 218 032 792 504 077 702 912 990 110 113 213 766 041 427 249 890 341 969 162 849 194 450 314 080 890 190 161 102 801 312 465 308 104 038 175 275 734 319 253 196 268 962 270 411 273 745 978 012 544 466 538 695 034 841 178 482 805 380 639 245 976 344 997 574 491 866 014 385 355 085 411 394 312 248 569 243 017 793 371 859 947 001 095 040 439 804 650 106 423 409 439 058 313 567 460 427 396 422 872 125 376 227 544 838 982 484 119 480 334 694 763 989 349 847 524 536 475 026 894 017 555 420 239 816 809 518 176 776 095 165 169 885 450 706 196 056 326 901 263 212 199 708 536 123 018 110 880 660 675 719 908 774 497 138 316 439 857 533 111 775 924 180 053 002 661 353 856 864 198 436 476 132 253 562 595 667 421 317 973 080 991 128 105 475 726 328 469 492 403 172 683 541 330 773 009 251 734 925 442 921 955 571 345 245 659 314 886 754 734 946 414 783 633 054 465 662 253 964 373 954 320 154 594 469 108 479 163 897 190 755 592 110 972 394 022 102 766 094 586 878 086 982 289 482 789 261 299 236 834 760 351 742 739 286 748 383 996 370 648 096 757 627 126 524 469 326 968 493 905 640 127 551 206 686 589 202 192 899 199 437 206 666 403 718 092 388 405 867 814 892 008 258 935 979 438 211 679 103 355 061 752 133 171 719 739 042 042 632 653 027 577 195 242 828 146 660 743 170 740 047 038 950 549 818 647 053 811 718 563 226 813 529 766 703 692 959 641 887 277 891 735 655 648 272 495 681 388 248 362 237 271 860 257 598 360 490 852 263 824 095 915 252 005 202 242 034 617 495 666 898 317 235 436 186 223 067 777 910 776 279 984 191 555 722 428 346 869 860 032 787 348 336 532 440 146 295 765 778 492 525 389 467 240 224 585 404 053 681 975 101 315 413 385 137 494 544 879 513 188 016 606 010 832 990 879 825 790 408 304 518 025 374 697 419 778 764 019 912 852 077 431 747 145 429 391 023 172 957 588 427 152 109 737 697 577 347 197 903 919 451 309 941 109 057 843 418 007 485 895 161 502 110 117 594 353 899 920 522 747 936 031 542 444 182 724 658 529 277 315 500 523 240 163 165 246 391 227 169 116 363 196 262 510 838 601 176 284 869 718 038 777 164 912 662 960 090 602 486 346 336 065 107 335 682 763 173 909 028 881 414 000 357 212 115 506 315 038 295 821 315 299 660 867 647 956 100 395 471 404 685 658 215 595 878 435 275 852 894 500 725 480 254 401 840 393 546 530 296 192 870 998 073 659 322 511 341 538 430 606 889 653 393 593 720 890 894 373 035 108 509 532 352 465 349 189 071 007 521 626 518 040 400 683 178 860 792 156 182 051 655 558 607 931 358 775 374 089 796 378 147 054 240 560 175 340 545 431 350 340 097 884 913 460 177 744 139 542 995 117 769 760 643 864 770 944 834 734 449 484 546 088 650 831 355 388 308 058 137 983 014 367 653 960 603 266 395 370 970 327 769 931 256 409 266 937 964 987 949 139 564 033 944 076 288 721 997 863 469 596 448 032 863 591 591 087 339 688 519 859 471 562 276 840 694 528 517 150 411 854 842 827 659 313 006 115 511 232 726 532 317 643 909 548 735 743 236 630 292 639 435 235 801 045 272 456 974 323 988 784 917 352 742 457 421 746 261 535 394 582 898 141 045 136 436 589 312 646 587 181 449 513 277 878 777 863 242 930 076 958 216 299 224 790 119 757 280 188 879 976 710 183 748 617 619 446 980 640 629 889 407 681 035 001 680 504 033 894 925 820 055 021 872 135 546 801 814 105 530 908 740 055 599 309 385 618 793 325 373 235 453 513 351 834 263 814 474 349 863 306 512 241 968 188 987 715 494 164 127 243 847 863 269 584 399 117 843 117 620 078 927 380 068 772 451 522 243 548 098 671 168 314 630 094 000 248 513 577 826 783 399 415 522 050 960 185 236 920 101 261 399 932 206 956 218 566 869 654 360 339 335 146 219 753 012 560 204 947 570 959 054 683 587 918 307 729 101 957 351 626 957 371 402 293 362 188 837 522 083 529 633 458 959 893 235 826 190 781 293 165 845 362 742 958 121 253 214 373 856 374 389 769 645 635 447 129 231 560 514 231 827 171 443 199 667 987 102 038 083 553 308 210 203 651 592 148 964 583 923 476 446 417 495 366 409 624 646 498 928 787 233 287 932 633 671 941 457 688 276 568 756 124 696 998 536 907 070 874 575 696 048 767 701 437 629 300 196 047 582 799 121 232 298 867 123 731 492 306 685 987 901 369 716 521 899 841 835 031 143 774 303 408 268 495 493 476 150 668 138 725 448 426 360 898 265 274 706 079 601 349 219 416 834 636 572 907 834 203 932 425 661 991 314 379 491 682 523 037 542 811 743 970 579 941 485 196 190 165 873 887 968 056 345 583 022 633 980 089 422 281 501 828 250 410 437 636 902 019 197 657 103 473 808 633 956 056 854 491 078 866 712 329 263 995 936 341 302 905 523 973 652 968 019 480 721 991 538 455 958 729 005 014 889 978 560 514 624 530 026 653 003 973 497 928 458 996 785 267 708 240 396 952 460 807 225 573 252 639 861 746 086 036 401 446 900 781 863 510 519 012 992 005 959 129 033 219 284 418 112 478 361 363 794 334 036 635 182 560 068 229 530 235 535 308 361 426 678 918 397 042 524 739 367 834 948 946 774 166 092 988 921 520 987 481 007 378 103 632 996 155 879 106 556 117 595 544 267 712 344 661 576 681 755 966 505 652 230 139 233 958 929 432 736 427 580 995 263 462 523 236 050 486 896 354 999 589 377 869 136 655 313 777 602 360 377 002 974 809 791 047 956 249 196 177 569 270 925 011 447 151 506 643 633 694 076 726 368 395 069 767 019 706 569 089 433 922 551 944 812 683 223 751 723 593 547 497 144 555 469 515 649 338 685 453 012 740 442 395 238 825 676 082 944 778 310 234 191 640 055 578 773 729 185 896 392 442 984 009 437 408 134 086 953 535 237 431 070 336 052 574 464 455 187 096 498 673 749 477 369 586 611 487 522 908 403 114 950 097 246 226 090 207 636 696 660 718 038 087 011 155 168 142 363 311 462 107 466 226 444 389 243 864 551 508 106 795 975 598 166 061 202 370 225 603 333 538 372 029 324 816 323 744 313 095 287 956 121 455 056 691 560 468 395 429 135 266 521 583 594 575 948 036 932 939 637 081 864 903 846 153 351 555 777 080 059 200 095 267 178 495 983 461 995 543 689 195 813 069 164 593 916 604 604 383 360 323 721 077 586 249 191 745 338 597 631 678 653 925 841 397 498 145 440 781 469 251 422 331 716 637 842 772 575 192 137 112 546 446 389 708 867 178 460 327 628 872 400 877 363 397 223 591 234 166 463 798 849 452 957 703 668 287 414 957 628 895 863 819 180 990 975 953 134 539 546 035 550 250 779 669 084 358 621 774 800 268 762 744 605 673 700 366 553 057 612 503 536 871 920 280 053 034 437 017 457 135 401 778 894 097 833 041 951 172 956 340 200 295 305 757 840 355 714 261 663 274 316 064 514 079 086 775 267 637 345 060 673 384 053 274 054 338 471 824 021 836 661 700 957 921 472 686 820 413 257 355 148 148 774 954 076 141 026 767 697 654 399 102 465 305 570 383 958 865 084 006 216 172 118 019 802 567 149 700 519 420 384 725 806 750 044 122 579 858 656 698 540 101 125 229 772 238 815 819 428 432 485 153 412 882 717 961 252 067 004 699 310 585 435 980 606 460 794 913 378 459 763 028 147 478 331 391 191 499 199 688 491 788 802 765 805 033 928 928 498 101 410 008 676 144 273 497 222 553 205 822 415 529 373 701 380 590 102 248 637 301 197 639 582 599 492 600 115 895 905 740 144 423 778 337 975 417 035 932 334 420 816 700 952 399 383 463 490 000 652 551 077 907 065 274 077 568 861 980 109 778 351 901 718 447 753 686 443 007 524 602 415 514 129 114 568 737 207 789 701 924 925 506 811 587 742 309 331 090 897 777 364 662 009 604 798 658 992 760 295 346 624 197 497 986 752 127 589 449 599 565 062 586 371 744 297 975 078 447 569 125 754 389 228 653 436 211 591 886 564 933 838 057 466 962 087 388 606 503 519 641 454 320 611 999 311 025 765 409 557 307 408 338 383 595 236 282 449 795 907 194 277 018 778 360 806 062 804 313 927 022 774 511 371 243 227 161 041 497 501 540 654 762 521 738 753 248 114 652 370 588 451 294 207 466 109 900 404 460 244 282 864 951 068 387 674 427 926 472 320 640 724 685 701 933 608 022 496 166 956 875 533 790 545 001 415 184 137 955 588 924 647 203 718 453 333 037 736 934 333 610 470 130 991 931 393 915 033 844 872 112 853 942 797 707 434 226 807 508 584 808 817 828 419 885 031 539 489 266 413 622 916 722 638 213 933 274 045 898 309 535 946 655 113 609 632 563 728 233 040 088 525 294 545 080 808 552 546 778 005 063 929 679 454 333 573 249 270 294 125 052 935 867 926 919 194 867 288 214 232 755 946 033 191 012 644 817 225 499 151 123 650 263 935 104 775 531 646 814 467 291 127 906 033 052 418 819 494 414 067 019 862 034 493 046 069 399 541 625 139 339 141 470 835 540 600 646 947 571 050 345 463 153 694 077 366 572 122 419 972 447 578 540 775 514 122 015 450 156 280 440 912 294 232 920 625 506 175 840 273 719 883 302 254 419 410 122 500 622 969 039 550 557 079 809 230 918 265 073 478 081 578 013 929 046 057 033 474 941 339 711 975 496 746 506 333 955 336 001 634 095 311 427 704 259 719 658 995 480 123 457 243 249 127 432 357 212 485 221 060 006 366 735 003 835 078 070 512 590 006 258 129 271 781 761 157 186 439 373 261 902 157 544 895 416 711 690 785 783 941 414 478 766 156 407 198 134 869 442 016 792 035 649 044 900 662 433 275 509 544 505 718 856 784 863 056 673 721 717 741 179 364 845 062 501 187 176 174 010 163 445 938 912 842 857 562 942 072 051 187 366 789 573 432 748 079 910 406 468 306 327 770 146 395 485 687 779 825 130 450 142 842 479 336 317 327 820 088 893 827 678 456 420 442 936 056 887 093 403 520 770 476 994 843 378 140 753 647 347 194 151 688 811 211 432 752 283 552 039 669 521 560 815 090 368 080 688 761 497 357 788 930 935 588 550 426 208 311 484 677 307 918 302 096 245 662 175 488 882 650 354 897 769 855 299 676 218 160 399 581 034 406 730 416 971 293 471 810 955 426 230 580 513 308 864 773 861 089 141 788 173 129 357 213 785 489 106 090 705 114 052 251 222 879 854 012 828 626 126 819 739 627 650 126 014 166 897 431 536 506 578 047 906 960 714 655 488 929 564 300 814 664 628 505 292 027 328 192 928 973 430 942 027 670 094 950 616 255 930 183 564 687 804 212 273 658 392 540 125 786 214 073 520 153 037 772 668 659 037 581 234 716 140 706 014 770 303 156 771 730 910 516 295 475 033 307 445 603 730 684 815 582 212 728 520 757 964 016 388 271 016 890 127 357 914 355 340 891 131 635 029 084 148 857 007 101 796 440 951 214 703 226 537 776 176 816 358 752 054 219 151 064 458 155 611 520 236 396 637 940 688 270 261 792 494 413 695 900 173 207 483 171 393 890 907 708 793 625 697 645 481 327 750 052 440 582 336 644 747 138 636 021 351 388 015 635 175 688 729 305 566 050 682 004 803 579 687 115 281 875 638 587 119 894 635 963 569 820 867 418 589 373 595 764 398 381 713 349 981 010 175 027 205 153 568 606 379 263 009 783 577 147 537 847 759 809 655 190 041 748 865 632 179 314 456 976 673 245 739 615 379 071 731 693 374 443 105 209 843 094 640 197 283 444 266 677 456 738 650 613 431 339 373 421 513 645 626 323 180 403 811 710 261 374 823 378 773 815 096 502 225 337 233 324 021 320 483 173 448 077 456 875 862 629 555 029 455 805 408 795 090 390 925 946 179 070 204 413 333 894 544 884 109 880 743 069 482 203 805 204 677 284 241 617 354 278 033 983 739 980 579 309 009 075 047 566 267 411 554 859 286 966 273 440 559 407 402 496 390 075 051 015 225 174 339 506 215 339 841 580 765 907 535 194 568 978 190 778 572 475 754 192 628 231 220 355 986 938 535 715 598 679 591 421 567 362 370 048 708 588 346 304 202 468 141 511 840 619 771 192 066 716 488 071 053 040 007 344 202 372 801 025 197 414 460 061 801 905 461 679 701 173 082 123 623 088 165 321 883 350 721 973 384 612 611 307 139 756 908 157 266 844 656 604 577 165 281 970 287 249 619 452 776 989 569 788 503 477 743 732 636 470 319 592 826 820 632 411 741 406 226 686 558 082 308 374 053 518 759 196 755 210 057 140 159 756 737 072 351 819 198 789 749 464 791 832 414 908 585 632 703 952 739 944 954 292 025 694 157 213 909 020 079 001 160 380 079 187 046 602 508 291 074 749 300 174 156 412 777 664 545 264 826 617 737 868 604 291 708 347 440 224 411 626 105 210 057 555 000 132 831 981 734 986 973 734 488 893 115 199 002 056 217 040 123 379 564 712 384 612 798 417 512 380 343 369 120 132 830 959 877 956 650 489 232 864 492 023 796 080 781 941 476 857 140 940 216 587 136 161 437 424 773 046 992 171 188 902 937 036 592 762 634 826 180 135 254 702 892 636 845 725 348 047 698 214 923 693 588 502 760 041 823 089 368 301 244 076 121 361 220 872 751 173 193 085 016 300 630 732 560 149 783 276 534 571 234 130 356 581 565 514 890 652 643 530 570 266 305 210 162 107 825 514 274 807 714 624 422 401 121 239 520 741 936 570 102 838 176 936 719 463 232 703 747 997 397 211 859 267 403 890 392 462 175 666 607 310 126 472 027 301 575 666 488 942 733 798 380 817 033 487 274 623 779 311 145 696 549 799 785 098 725 550 111 584 101 461 182 799 302 202 627 000 788 279 530 829 707 920 218 008 878 118 636 869 318 968 160 923 523 887 189 730 454 390 072 244 611 439 998 533 360 335 386 099 393 998 254 807 911 920 851 846 899 514 412 108 767 027 021 440 433 530 175 062 223 963 003 502 886 838 722 764 684 711 485 240 105 990 168 223 710 538 069 905 159 644 209 463 818 738 982 439 600 472 353 043 699 821 077 187 284 827 771 696 285 588 399 601 072 910 754 902 789 928 523 349 575 625 980 308 376 225 316 883 781 469 251 568 610 657 746 565 221 572 160 300 802 034 899 546 276 167 434 112 496 782 845 754 695 674 463 201 301 663 153 361 721 469 573 376 627 780 704 195 677 109 970 071 857 735 470 122 460 613 353 343 999 587 795 723 264 614 638 106 199 721 130 644 043 531 649 314 931 869 839 018 848 507 724 085 881 760 595 642 548 764 894 950 195 630 488 050 752 312 825 423 248 656 589 421 904 651 620 980 945 755 013 150 830 539 578 168 729 374 957 729 143 046 350 386 439 276 105 879 387 745 961 189 299 868 264 606 491 862 549 317 516 358 647 576 782 557 756 270 430 817 405 663 806 358 967 744 724 205 971 251 795 438 373 028 413 531 573 384 735 490 402 718 561 792 778 309 647 160 615 239 373 031 960 852 932 639 219 185 788 562 530 866 978 247 030 767 736 945 329 702 126 048 359 264 043 213 217 547 984 288 987 376 866 101 971 360 410 594 608 141 928 200 567 184 799 036 987 249 181 242 081 294 780 118 741 122 863 164 914 233 677 573 840 135 364 078 769 148 880 713 251 709 207 888 901 834 948 166 686 326 155 080 129 585 729 140 689 382 299 387 423 185 610 602 051 849 424 936 844 624 093 788 170 212 065 655 002 935 602 554 956 234 137 700 873 613 750 512 508 133 042 130 276 587 536 325 448 915 222 344 329 635 746 681 250 449 782 893 683 617 464 932 220 918 557 718 819 600 854 726 267 250 845 485 739 537 073 752 201 655 994 057 130 298 642 449 515 036 377 659 956 682 178 454 087 726 740 455 970 265 465 770 775 550 618 526 023 589 617 998 458 127 614 989 125 062 202 933 140 660 100 048 260 422 541 958 237 779 573 305 724 324 686 190 930 611 075 314 945 508 366 689 823 970 525 638 150 103 594 477 901 631 858 802 734 344 068 926 234 063 515 137 218 933 612 304 757 783 978 905 375 204 876 236 770 969 353 724 190 198 707 953 390 903 278 639 429 235 120 061 064 083 785 227 453 086 302 473 117 197 250 536 955 623 785 687 709 269 388 930 197 804 341 030 150 710 303 434 632 335 080 609 591 529 463 524 507 913 525 602 458 521 301 247 307 391 563 839 635 342 082 572 873 898 554 412 859 458 204 974 797 983 554 770 243 493 802 408 698 810 061 437 852 959 312 879 483 334 846 876 022 304 384 835 639 739 776 872 445 259 230 005 835 296 036 458 468 990 682 553 892 256 884 892 516 126 692 428 012 438 989 815 961 649 378 549 461 980 452 471 102 324 680 473 365 981 353 996 225 977 851 644 301 824 328 337 183 656 284 756 773 271 864 022 414 856 060 704 235 409 806 482 707 436 413 630 000 793 063 360 368 092 284 338 502 059 783 136 259 298 212 125 554 173 891 783 137 360 074 779 204 229 485 406 593 670 772 666 270 923 290 408 296 424 116 998 370 982 029 858 763 682 768 607 307 118 352 200 652 900 530 173 489 035 456 571 353 926 241 968 942 223 211 851 434 241 488 585 135 732 202 234 740 794 487 253 558 735 253 240 872 332 994 728 092 340 648 077 114 793 701 450 835 454 440 551 945 205 244 799 734 708 975 976 730 897 693 505 237 918 640 605 063 046 113 844 474 912 986 539 362 069 482 359 277 465 915 369 634 497 512 571 654 452 851 397 594 680 060 783 043 059 043 115 419 469 216 219 686 404 185 236 078 547 391 897 544 164 037 550 554 309 858 642 161 124 671 416 661 909 540 092 926 612 595 903 496 225 678 793 541 320 288 012 550 621 197 573 712 702 221 640 165 132 509 342 270 778 137 668 076 119 513 311 560 924 503 656 402 487 622 744 282 771 623 865 844 794 085 753 490 994 871 558 507 249 513 978 246 854 529 200 737 666 079 774 186 000 926 364 181 431 008 362 027 226 080 746 782 520 189 589 027 298 205 834 980 069 789 702 309 622 079 071 436 938 419 661 273 988 717 755 974 303 942 663 336 001 075 088 715 718 347 543 835 389 302 197 491 313 149 086 403 675 775 984 579 889 154 534 279 489 639 061 216 185 591 388 885 763 108 641 686 179 724 036 457 189 817 734 137 538 416 174 072 447 883 299 427 731 178 775 718 616 459 879 942 251 705 410 159 764 056 477 184 167 826 803 233 866 285 082 773 973 642 109 102 499 830 081 406 334 001 505 876 248 129 346 860 067 752 830 279 131 944 555 451 768 501 303 465 605 520 363 762 522 432 743 201 084 240 230 171 259 278 745 199 518 428 480 226 205 944 954 529 669 805 318 344 091 330 064 654 200 910 640 251 073 142 001 991 156 916 586 802 691 126 961 700 715 306 818 330 864 584 477 781 415 546 227 773 737 033 159 254 718 926 545 097 363 973 235 441 724 609 725 678 217 307 243 563 323 646 962 016 488 925 581 086 344 615 223 506 675 950 686 017 551 510 340 084 010 587 784 444 288 441 471 693 293 869 855 480 175 133 274 186 268 558 027 317 381 951 561 180 616 046 036 201 298 176 518 082 187 865 551 121 198 783 959 386 069 082 930 459 951 823 438 874 188 893 617 935 815 247 588 930 180 206 144 649 318 022 354 826 939 903 357 430 971 155 326 360 914 301 110 056 373 998 023 686 989 435 541 053 003 329 379 840 659 159 782 942 215 503 787 023 674 160 620 886 762 082 818 335 619 836 578 345 135 804 585 866 617 298 932 874 215 932 885 991 379 723 081 634 750 666 039 793 096 001 849 687 658 301 481 115 991 873 752 978 640 889 288 458 515 179 867 710 699 711 951 754 175 479 067 322 433 433 073 964 231 776 141 776 799 094 197 723 312 936 529 782 446 812 375 336 793 009 372 564 889 220 740 234 348 665 588 350 891 339 592 456 990 395 359 991 792 105 331 112 002 531 566 548 732 586 106 542 641 379 518 395 441 450 771 176 801 698 444 881 600 198 974 262 950 362 395 981 807 261 539 170 097 854 444 694 617 386 204 158 045 891 515 321 012 525 570 105 322 200 345 386 483 272 045 335 543 646 186 769 687 887 974 825 002 901 739 178 903 100 226 330 647 613 383 659 781 517 867 193 779 223 844 627 315 548 650 032 547 264 651 240 994 066 925 318 216 840 135 445 679 002 397 013 297 296 398 194 663 821 860 218 911 481 487 354 482 239 840 481 976 235 159 930 964 668 614 292 360 594 926 734 840 283 653 984 505 339 871 638 513 422 999 126 228 678 325 073 446 518 676 920 113 260 032 850 677 997 163 030 700 122 820 399 128 473 898 112 175 989 256 214 975 553 904 542 335 858 861 841 671 397 893 021 102 473 837 357 377 175 714 654 186 616 189 020 278 309 586 707 752 810 896 057 659 672 790 501 406 503 516 068 096 158 310 367 432 653 170 087 559 647 844 070 447 526 285 580 699 233 280 585 991 896 211 875 409 351 375 499 805 855 697 354 460 650 495 094 087 016 176 100 784 235 124 057 464 722 563 628 537 755 796 854 521 169 718 469 725 889 664 720 469 056 471 740 943 948 103 834 641 217 437 841 761 966 880 416 240 143 528 014 925 059 296 151 472 782 705 307 167 449 586 426 698 810 833 190 127 179 536 003 830 059 556 422 729 802 238 940 136 189 495 513 015 815 031 489 688 719 045 622 572 333 032 648 487 249 008 147 134 866 863 354 910 165 500 798 297 795 583 898 435 842 145 854 141 646 528 909 508 974 801 940 798 700 410 521 496 449 090 441 193 351 944 770 199 795 178 553 737 551 315 721 373 058 610 667 826 138 424 340 402 163 081 032 080 819 482 889 252 791 985 227 143 981 892 234 257 846 351 692 311 390 603 406 084 653 240 303 172 986 582 037 188 451 668 289 298 626 980 720 558 212 165 722 901 502 786 492 989 261 364 499 978 551 603 673 906 850 107 848 747 305 408 488 902 432 287 763 951 815 177 284 008 093 778 389 300 465 788 608 102 021 326 908 388 954 606 373 685 017 058 885 395 238 411 582 945 026 003 952 835 611 516 949 025 333 607 775 845 507 930 243 503 966 704 662 607 039 195 345 816 046 393 970 195 562 342 712 741 811 445 189 820 582 225 364 139 760 973 716 704 102 472 404 924 684 028 851 020 206 215 394 961 244 982 807 929 527 631 012 665 876 674 905 876 114 494 459 371 675 039 248 555 192 505 443 231 317 105 414 482 771 537 321 672 259 005 440 470 459 420 149 754 251 426 700 756 993 624 997 800 284 034 221 746 495 994 946 201 405 740 310 852 787 457 617 293 592 845 975 144 742 286 918 644 602 634 316 602 389 795 399 929 381 888 763 140 843 301 168 339 793 280 762 594 219 564 308 623 471 414 828 542 842 304 694 368 061 413 858 568 410 867 532 841 823 743 241 760 295 625 594 242 018 679 720 379 897 012 225 241 657 436 926 532 359 490 494 135 013 658 880 968 995 573 374 354 487 367 588 832 191 242 165 454 889 011 441 116 816 984 083 775 101 431 476 214 376 571 453 599 632 285 006 064 219 251 023 003 133 118 789 000 478 452 996 824 127 360 522 573 757 418 336 384 091 263 738 312 888 973 253 365 985 996 426 395 518 862 554 795 719 003 316 868 746 262 168 464 615 425 088 379 187 918 972 120 096 509 787 880 132 803 127 280 270 829 075 222 084 965 101 459 804 889 253 703 295 495 841 618 589 724 292 279 944 284 879 656 283 698 611 542 562 029 447 349 414 736 618 463 243 450 812 649 709 523 466 335 394 506 970 788 670 609 356 482 002 293 024 591 894 209 444 835 342 269 377 584 224 724 059 313 668 230 914 889 282 556 044 320 686 255 593 752 578 689 218 670 623 001 883 628 758 469 239 819 963 598 892 892 541 442 532 585 902 467 337 464 434 449 642 861 972 231 920 085 931 107 553 916 270 894 797 763 734 408 053 280 233 526 404 394 179 981 645 260 234 234 418 435 273 869 759 326 044 819 849 169 192 702 455 272 724 902 502 122 879 093 660 515 317 347 978 938 916 533 748 560 135 658 540 856 936 451 827 383 152 633 003 883 391 347 220 052 021 820 602 607 752 144 666 822 496 800 210 567 463 584 379 960 786 462 027 331 208 620 839 342 447 092 407 011 629 325 831 700 117 600 737 730 471 945 461 509 011 399 089 238 502 578 741 394 302 321 763 100 120 314 677 146 219 522 064 856 722 805 561 144 580 485 185 413 128 961 203 055 132 532 644 434 651 579 480 850 787 473 051 668 874 060 535 865 102 836 521 989 751 590 051 735 293 701 123 727 601 507 121 694 141 676 568 590 471 235 387 299 517 201 951 265 830 037 321 143 208 878 141 051 660 153 413 637 555 188 388 989 487 925 401 434 902 965 053 825 089 318 062 182 748 353 793 380 189 716 680 573 538 952 979 114 445 159 624 892 150 617 103 049 924 319 906 567 360 339 314 163 234 907 960 106 861 073 584 751 417 150 079 679 951 786 595 920 808 538 971 932 908 321 105 396 178 672 671 990 219 805 175 648 504 389 706 080 649 448 162 030 420 118 566 180 378 895 797 457 142 985 505 647 143 517 680 646 050 543 262 699 496 995 920 947 292 042 709 084 606 942 351 290 323 078 243 421 548 848 227 148 078 740 477 130 652 915 599 637 429 638 207 413 307 448 613 137 602 863 484 834 468 647 154 921 187 431 428 983 929 164 713 220 667 800 173 543 776 893 712 775 367 343 667 070 869 908 199 591 910 255 659 047 780 778 438 630 917 366 817 407 746 105 986 982 970 695 165 182 258 214 679 633 241 201 078 809 624 482 622 937 749 032 789 712 987 688 845 999 827 667 617 823 919 721 219 709 431 838 933 272 712 621 563 012 665 907 564 946 405 630 369 546 886 085 054 203 537 733 186 812 414 092 495 292 356 878 226 743 721 445 934 711 329 600 722 475 986 734 115 531 263 228 183 354 598 968 128 525 644 407 766 707 157 501 978 500 434 338 257 498 373 704 032 016 360 326 932 352 405 780 117 854 310 486 796 855 137 533 261 071 017 651 252 352 560 260 055 125 904 612 462 916 463 573 806 235 295 510 235 675 250 730 845 780 710 810 487 212 807 863 462 987 171 302 558 833 041 996 953 664 198 131 171 763 939 541 706 101 863 801 743 331 009 903 648 906 211 077 960 498 601 016 364 807 611 368 613 843 973 173 726 753 493 813 731 091 593 556 753 569 581 598 887 792 665 855 994 883 173 804 178 565 515 467 336 734 217 416 004 918 745 463 994 210 180 536 138 893 710 599 625 838 157 840 681 856 056 354 716 635 100 907 002 844 765 736 548 075 633 166 343 150 314 050 014 946 333 591 915 965 554 091 928 623 805 731 891 104 343 492 964 614 442 716 033 443 571 266 020 632 309 260 504 160 477 471 975 900 013 819 374 320 427 684 683 643 316 652 085 093 266 210 367 018 710 185 714 964 372 770 049 575 769 766 090 631 625 637 112 933 496 663 933 164 454 021 099 763 438 058 462 037 612 401 708 181 323 761 264 777 368 635 610 467 847 584 543 063 241 942 619 329 338 726 266 145 518 581 372 954 941 281 692 045 989 330 284 906 496 591 662 059 090 334 807 072 800 617 639 399 705 139 822 738 528 025 338 571 168 852 702 554 650 657 823 050 737 955 208 086 892 696 524 533 941 650 850 619 171 558 202 516 897 503 370 860 404 620 513 070 841 590 076 932 109 560 006 055 724 258 225 213 246 770 203 834 295 883 927 192 148 040 137 156 235 118 602 501 358 195 659 619 618 469 872 362 395 718 921 924 780 737 493 242 262 707 747 821 419 098 153 222 983 968 381 538 783 520 072 187 197 749 307 248 286 009 957 915 562 242 398 606 301 121 573 253 576 594 812 594 630 759 467 819 787 293 695 468 086 160 960 929 578 958 079 032 977 273 723 442 340 872 308 374 820 875 380 759 535 986 675 009 270 855 206 983 853 779 747 038 306 172 542 070 204 715 962 590 813 447 419 886 355 686 239 026 455 159 602 066 319 356 897 416 788 348 920 312 977 189 124 144 276 123 294 614 492 912 860 603 981 871 174 105 564 157 474 800 237 299 392 461 301 379 875 599 259 968 670 198 132 493 508 265 937 196 732 286 507 686 411 545 107 685 476 458 580 278 564 849 764 706 597 008 669 987 143 085 540 723 083 537 201 292 830 381 109 455 678 453 137 844 506 228 215 432 116 289 742 216 296 583 605 341 638 961 544 748 345 079 213 470 979 039 711 989 454 385 407 726 786 795 964 973 425 344 017 058 624 410 652 230 643 594 738 568 172 191 745 746 749 350 712 478 336 163 331 928 220 481 506 621 143 690 301 380 116 316 963 174 498 681 726 987 857 108 230 640 672 348 996 342 093 548 760 028 464 597 637 680 782 944 715 901 077 497 659 615 399 117 536 125 248 737 001 071 597 173 751 514 816 947 687 918 661 356 805 732 410 885 339 292 284 911 927 271 887 680 424 779 286 446 474 238 665 834 635 153 882 727 663 091 712 358 797 329 010 222 715 776 205 037 187 383 529 916 713 745 737 434 304 377 341 946 068 862 885 711 925 282 386 963 625 266 193 244 925 429 657 563 184 705 537 726 715 114 614 454 626 802 996 978 095 431 069 980 425 490 222 377 460 536 123 245 613 378 803 609 981 785 858 439 722 605 424 007 269 172 968 258 178 049 797 319 403 777 850 550 903 266 048 819 399 486 908 917 466 087 150 004 293 836 932 205 043 666 029 103 223 496 829 648 304 213 726 529 757 397 365 461 930 223 955 210 840 932 787 595 738 530 255 778 262 423 948 079 429 615 004 983 186 209 244 133 595 517 103 201 674 818 973 222 629 549 196 046 675 367 346 834 197 320 320 475 560 777 381 436 933 334 830 308 786 485 941 044 022 964 453 451 558 005 549 185 369 085 560 888 646 007 117 873 996 329 141 046 715 413 991 651 998 954 896 891 411 240 555 228 961 446 987 720 654 092 415 623 062 385 016 327 338 121 782 775 849 657 179 668 635 743 724 139 598 999 080 065 404 680 059 745 331 445 660 844 246 809 826 413 680 883 373 292 306 398 466 782 042 142 811 934 135 856 891 275 642 578 735 271 972 373 488 713 721 275 731 258 326 242 790 652 230 493 808 017 532 625 840 899 689 985 500 002 210 685 992 211 092 514 515 844 821 171 026 078 132 692 647 767 910 313 048 329 038 045 363 928 452 252 790 299 711 005 944 641 940 189 923 436 976 454 877 932 888 841 156 386 874 757 114 672 285 439 081 831 139 037 724 617 669 210 250 819 930 354 244 157 997 766 935 152 319 610 991 792 768 409 532 194 462 281 671 740 060 302 967 158 848 302 660 730 979 128 165 513 026 871 535 513 681 213 001 415 817 153 546 204 335 154 453 996 102 374 761 236 592 016 725 417 394 903 306 359 502 526 252 626 773 060 968 300 042 118 424 428 422 214 924 029 824 909 315 306 719 304 577 159 605 833 685 851 141 272 862 834 521 391 035 013 593 099 713 278 810 478 140 497 496 670 774 073 898 751 449 077 405 594 905 143 685 752 261 061 229 791 567 069 305 406 823 456 804 251 923 269 783 127 272 294 582 927 613 906 279 148 281 325 816 631 888 511 869 396 983 388 439 411 508 970 142 669 220 609 910 948 178 903 669 816 852 361 541 967 430 094 628 031 175 522 434 511 045 122 708 137 005 965 017 987 031 925 872 021 853 306 906 781 680 843 297 029 445 009 211 004 629 962 034 660 568 963 221 420 188 194 861 525 257 797 708 648 945 187 465 582 795 156 473 081 324 394 008 855 926 965 345 787 031 244 661 867 025 868 256 962 758 744 057 517 725 784 213 607 734 016 407 712 424 316 728 408 706 881 792 038 977 480 019 488 134 686 587 566 079 608 407 873 982 807 344 468 568 251 096 478 268 410 601 994 565 983 970 793 545 694 258 175 394 548 095 591 709 775 558 747 411 903 778 375 076 563 309 691 821 418 011 859 138 433 818 131 808 421 159 223 132 864 895 411 195 006 261 152 684 509 091 616 431 809 657 376 685 081 186 781 746 106 309 162 819 344 803 608 247 218 881 856 994 192 478 879 750 477 780 559 456 507 285 685 613 782 428 021 127 944 593 651 165 713 115 584 131 313 597 229 044 889 251 650 854 308 723 282 177 390 147 726 300 921 649 838 768 326 790 650 592 680 410 224 816 451 314 250 494 095 649 843 787 474 346 412 377 697 095 955 115 350 702 605 478 299 588 104 703 693 958 135 416 435 936 422 121 674 004 048 242 598 285 067 401 271 626 974 015 887 529 951 179 370 547 917 425 354 648 088 055 426 460 904 409 231 749 782 112 885 321 807 131 495 976 018 781 372 155 391 395 460 283 442 762 882 385 477 972 046 455 918 229 064 156 529 292 636 232 178 725 910 591 295 448 040 573 818 251 229 591 745 914 987 942 281 046 638 846 236 852 921 552 648 758 223 689 346 498 163 646 511 498 547 825 544 536 969 134 938 180 952 576 574 562 626 216 946 075 960 296 323 322 928 774 128 376 976 033 667 760 097 896 244 241 231 902 769 552 936 047 918 333 931 400 103 823 710 471 574 955 551 591 515 485 924 241 108 876 430 335 421 051 267 792 082 311 600 249 286 052 925 194 695 944 862 685 972 907 791 001 873 102 692 178 148 546 324 948 570 601 244 006 119 183 865 708 402 436 158 583 248 298 143 490 218 937 612 172 326 179 896 577 468 252 383 024 558 581 803 491 244 627 424 539 011 792 778 734 859 843 984 955 399 644 936 730 028 540 159 341 398 980 991 163 949 450 400 179 211 728 777 500 367 884 466 825 093 089 788 596 019 448 422 866 391 707 944 202 192 312 512 855 328 500 602 709 813 607 792 835 751 734 458 923 198 312 010 250 547 334 736 127 639 725 878 382 829 918 877 769 661 391 936 630 174 120 404 874 478 473 010 224 154 667 703 366 174 895 020 451 838 038 869 795 658 567 882 653 674 596 595 586 734 762 459 369 259 889 487 309 968 958 494 406 347 331 278 531 012 824 527 685 983 824 193 584 860 429 973 944 726 478 826 645 740 451 452 558 835 849 828 176 866 841 922 973 856 230 771 232 434 949 013 726 391 162 941 316 439 764 525 703 676 140 999 186 030 882 953 320 115 867 658 822 118 732 595 455 190 693 226 355 048 800 398 030 247 918 302 672 277 199 299 710 027 611 784 638 905 081 596 833 077 692 685 161 460 981 537 625 648 096 288 281 363 147 634 061 744 640 436 410 253 251 429 656 401 910 751 466 731 366 820 708 303 549 480 742 378 360 209 552 174 853 500 699 543 601 932 508 970 714 574 378 957 525 727 549 305 883 473 404 943 024 687 884 265 926 781 419 512 235 544 941 267 442 899 547 363 127 194 545 465 774 777 857 073 245 903 275 531 471 875 556 167 066 242 857 363 745 169 201 688 419 216 086 044 885 276 137 878 411 028 761 595 582 018 705 121 777 857 952 557 250 539 974 634 402 078 852 804 864 794 510 996 806 743 836 982 464 037 539 798 708 183 136 825 698 924 325 065 364 152 716 061 605 636 072 476 226 717 546 687 179 138 670 200 290 460 337 435 269 649 956 336 755 709 326 556 727 381 619 722 635 690 161 810 783 943 378 940 796 178 417 829 879 347 045 687 074 951 344 388 714 834 767 439 551 484 031 132 914 877 555 842 341 430 539 237 246 896 823 308 512 572 662 317 885 293 608 537 778 946 842 803 284 217 725 180 868 813 702 607 051 104 434 434 855 566 070 278 598 528 340 154 628 554 785 825 429 889 375 705 507 324 489 611 032 409 342 347 737 878 421 620 641 137 976 113 776 426 895 724 616 412 422 112 851 392 273 273 254 840 983 221 461 702 010 942 575 490 677 589 511 717 651 313 890 177 559 342 028 496 681 718 076 024 456 904 504 348 056 311 805 346 599 890 997 832 746 667 566 918 596 189 836 198 341 354 122 164 347 946 257 362 215 047 474 249 250 689 855 626 527 172 342 475 176 161 252 504 225 893 823 733 506 107 718 799 147 480 796 244 687 102 916 224 866 370 160 762 501 890 141 461 999 914 691 222 979 753 137 811 762 991 250 745 250 559 772 348 442 770 493 920 537 619 543 248 766 936 881 672 278 342 178 180 132 711 663 972 259 998 490 030 934 648 191 260 974 770 191 530 221 703 114 995 622 689 057 936 621 627 276 557 955 767 161 148 074 584 474 440 424 026 238 599 114 805 971 195 593 995 931 563 900 654 785 383 783 102 377 791 955 197 960 546 684 862 754 794 768 456 359 662 616 359 345 718 817 784 568 826 215 174 692 501 466 121 052 485 863 386 699 921 473 052 552 350 404 332 922 778 696 618 017 922 790 145 281 315 870 286 931 713 321 137 992 759 888 335 261 364 300 523 919 030 999 009 745 456 907 114 162 728 652 782 173 027 729 123 267 797 480 170 980 646 163 893 979 587 243 649 158 498 918 499 862 253 063 748 309 134 620 831 633 705 434 161 896 370 733 284 568 086 968 348 917 699 144 004 587 399 493 637 681 814 371 475 770 967 545 067 920 096 608 013 501 424 463 873 448 602 375 296 829 663 471 959 144 798 395 885 889 933 645 625 867 889 958 640 284 003 247 140 430 436 709 259 959 218 378 608 953 577 795 137 805 656 334 729 352 753 143 091 040 560 082 720 885 750 651 915 217 927 392 598 291 554 523 617 391 115 383 772 242 592 236 978 405 352 052 447 316 965 089 817 491 117 594 090 395 405 894 965 703 718 979 007 794 906 028 232 797 451 281 263 452 967 279 650 646 947 604 280 208 154 385 525 060 944 427 325 625 005 151 093 175 832 351 318 352 146 130 008 535 943 313 299 992 918 369 506 141 858 232 804 605 312 459 448 445 305 058 741 571 958 038 778 747 772 131 799 111 105 262 190 196 674 547 514 257 879 460 193 884 636 528 771 505 252 010 999 839 843 012 298 479 484 701 917 043 772 115 592 839 117 949 092 644 185 161 805 852 413 693 515 407 273 417 410 448 826 328 929 890 487 410 476 891 109 746 100 045 200 881 641 893 559 075 994 520 723 430 023 263 580 068 661 833 558 550 235 548 029 233 457 668 226 888 837 231 867 106 102 909 225 071 192 820 293 453 173 821 710 833 569 151 982 229 515 106 567 655 034 222 246 542 386 915 887 077 971 103 147 834 779 442 014 856 431 707 810 471 436 266 420 005 072 955 587 237 887 835 605 413 579 691 439 260 118 075 540 307 821 206 436 795 952 048 950 629 191 964 939 786 375 306 298 741 474 140 820 900 856 968 218 144 461 155 210 773 108 975 026 856 026 895 580 735 304 694 764 265 766 595 168 186 776 100 083 816 526 988 903 757 051 018 229 934 879 266 953 601 082 681 148 717 476 591 332 288 027 340 831 742 404 717 262 467 609 199 796 283 751 019 031 565 253 486 094 214 042 185 671 998 873 054 409 777 404 823 989 350 137 162 862 842 224 470 213 329 748 046 842 434 030 639 537 368 753 960 567 843 437 931 997 568 513 929 659 820 976 494 569 697 970 064 366 999 737 611 597 983 623 544 488 691 173 498 900 208 211 878 905 466 988 854 450 151 044 014 680 573 517 591 964 072 139 966 599 683 320 617 587 170 914 273 403 704 256 160 354 657 500 080 223 920 503 754 231 362 213 815 859 161 600 077 664 411 599 616 448 532 392 027 307 703 325 835 796 270 892 768 112 334 240 104 293 938 854 674 280 617 500 820 600 793 816 331 787 353 350 203 144 950 725 845 158 175 815 908 482 802 139 392 369 878 853 628 116 881 728 114 912 496 532 084 390 362 791 502 185 956 941 909 336 909 308 891 426 433 090 348 250 166 934 777 733 457 199 123 818 921 420 292 402 656 790 459 894 905 762 624 990 355 744 110 730 021 052 108 835 221 024 023 023 155 623 705 673 983 429 730 589 530 707 362 086 100 087 928 844 026 363 811 363 094 393 478 137 456 537 904 938 239 148 662 833 466 876 897 660 618 098 352 923 485 010 464 098 923 698 200 644 891 625 424 139 108 466 553 195 104 248 082 181 987 189 244 598 252 398 000 311 897 894 252 990 783 505 600 880 548 536 742 505 744 530 227 734 859 137 545 657 362 907 387 349 583 631 174 941 142 899 518 077 038 482 865 357 003 557 292 672 550 315 109 417 761 832 404 155 711 487 451 266 899 079 229 870 220 672 240 232 947 934 779 891 758 845 378 718 398 760 627 491 598 345 456 167 391 800 497 875 568 471 058 971 865 939 730 444 212 143 699 881 514 244 329 512 505 161 617 871 304 646 125 653 154 476 938 621 740 009 571 899 018 893 492 981 950 044 936 712 963 573 665 759 915 334 012 447 011 628 204 473 794 678 180 386 863 029 046 640 556 641 198 814 255 397 751 002 922 085 889 645 758 020 605 788 690 977 798 827 330 598 113 228 867 730 073 367 459 295 321 207 289 658 745 394 485 970 040 088 801 041 139 968 143 491 067 099 142 829 582 112 294 427 594 772 775 929 762 645 979 453 958 825 054 136 678 545 882 210 170 339 277 087 089 818 424 611 640 130 391 857 851 465 064 679 730 153 102 140 080 118 305 884 082 126 896 461 360 913 662 090 401 148 778 543 457 115 462 080 580 548 799 141 896 281 361 455 548 232 132 255 566 436 374 369 040 993 064 068 481 646 162 301 918 843 362 448 787 124 715 845 450 212 285 494 160 050 439 971 983 693 098 174 154 236 351 095 739 980 944 933 530 739 351 679 772 898 301 987 638 016 955 290 835 652 945 591 221 583 310 635 715 931 397 579 680 160 575 102 380 762 806 909 390 055 347 325 632 445 489 092 984 965 461 846 807 722 546 099 306 996 126 699 606 919 299 703 539 825 261 682 672 430 705 782 041 337 851 375 960 938 898 598 266 677 793 873 697 178 818 326 041 837 524 117 549 039 620 941 551 661 518 477 572 652 074 584 009 371 446 147 628 298 201 653 228 019 566 641 874 820 724 555 754 468 540 660 467 019 755 470 965 599 672 823 478 238 974 531 563 690 246 684 375 984 485 067 135 487 289 677 618 544 825 369 349 515 261 351 689 636 307 914 353 675 011 968 840 586 829 679 368 159 063 051 384 037 393 522 019 735 893 182 872 872 219 805 916 294 008 404 567 681 648 432 100 937 086 311 755 438 816 866 645 661 892 325 007 376 321 537 111 066 732 443 569 551 097 527 902 040 656 887 088 636 843 581 380 063 148 893 955 810 599 377 047 552 599 973 349 973 682 400 149 149 856 689 639 099 213 133 754 355 762 171 060 521 556 001 322 978 351 817 718 326 085 902 178 010 490 065 234 864 213 756 745 943 711 229 353 284 435 691 661 695 354 151 322 157 934 383 615 542 455 503 509 630 352 871 245 014 708 294 487 204 193 233 156 544 655 194 414 793 389 168 125 890 996 209 262 715 548 356 937 592 415 049 354 714 143 157 029 346 154 627 526 489 648 255 522 022 902 683 172 350 923 604 250 109 108 995 291 483 626 553 306 422 922 383 223 536 403 513 130 972 098 139 344 948 579 433 386 153 623 431 555 365 516 876 673 780 749 244 903 958 551 388 271 705 842 580 939 180 911 067 108 872 092 104 754 697 863 049 948 983 342 456 266 989 064 802 855 429 533 289 717 740 145 257 100 331 199 685 821 076 509 456 773 801 550 712 943 279 162 146 043 693 468 663 324 846 260 820 588 092 030 061 414 514 383 325 567 211 246 990 409 065 491 414 690 119 017 165 216 362 683 558 905 905 947 571 950 570 553 883 769 096 284 990 508 223 187 924 984 797 451 572 558 859 539 381 517 755 081 212 333 608 681 632 895 975 057 290 798 050 074 486 725 616 801 351 215 297 211 357 479 391 411 997 322 495 690 188 019 271 980 595 895 151 709 513 292 659 063 130 536 008 724 358 009 359 973 078 026 089 996 696 865 932 032 205 804 404 272 807 563 221 379 073 771 190 737 791 799 025 642 077 420 067 313 820 978 779 733 560 069 819 428 139 724 165 421 115 528 406 065 686 718 546 061 678 231 133 820 205 917 784 501 475 537 611 730 088 589 899 812 575 278 980 720 413 409 572 822 951 704 334 877 754 759 899 512 295 608 835 438 785 571 222 123 663 396 323 951 106 519 456 195 714 223 637 301 949 864 966 575 012 493 994 929 312 691 728 157 839 914 611 509 619 462 051 866 577 451 007 599 456 709 541 762 309 807 241 823 171 255 326 018 761 664 540 108 356 258 544 044 356 336 451 214 883 615 788 140 590 726 178 909 128 026 205 090 727 582 919 064 964 284 477 332 464 285 577 153 509 948 222 043 219 019 019 033 314 322 500 287 337 168 824 774 579 110 829 428 267 522 081 731 899 409 844 455 406 953 126 533 450 916 199 896 422 294 854 232 140 945 285 390 774 100 216 505 869 426 907 852 082 995 544 229 480 655 034 443 142 486 680 385 217 931 527 475 552 086 080 658 439 966 701 191 407 131 819 047 005 621 146 353 365 654 401 520 888 695 946 048 620 724 008 201 126 171 917 808 773 621 810 318 473 242 351 733 987 019 977 922 420 574 482 771 555 277 333 577 103 536 325 060 109 105 721 949 157 840 531 248 113 411 093 124 898 683 371 083 128 587 701 856 397 432 000 190 314 458 134 699 296 141 724 961 958 900 429 213 728 622 797 609 299 856 413 461 074 193 540 032 548 370 600 939 270 562 819 940 902 405 469 905 175 959 395 991 614 992 144 749 672 491 930 191 369 018 608 349 357 801 210 484 032 145 381 688 444 550 428 474 078 627 345 320 685 819 110 614 542 520 114 392 870 279 857 809 217 185 232 092 357 506 208 016 422 561 347 573 394 318 410 575 793 199 925 244 259 256 869 540 199 072 945 386 471 547 909 946 462 605 171 116 680 608 816 867 874 892 339 786 317 736 297 964 580 806 943 890 776 866 579 333 444 984 222 576 677 602 319 578 444 955 015 872 998 054 966 012 915 424 730 635 023 657 586 439 608 363 593 350 434 704 265 764 183 910 317 783 712 770 135 187 011 317 270 332 064 755 619 160 413 538 197 913 395 790 591 585 069 192 545 447 378 007 254 597 302 465 885 915 079 975 221 144 588 552 980 130 353 600 625 373 913 787 815 281 152 526 490 404 016 765 016 955 021 879 486 024 426 836 777 345 583 817 951 085 076 037 260 086 159 797 102 832 307 332 474 850 813 999 270 871 521 270 672 216 604 123 249 082 554 250 256 923 382 521 602 000 416 038 477 605 107 471 920 837 709 074 266 020 404 618 451 297 440 009 029 817 381 731 565 523 402 541 944 642 947 333 760 731 592 726 502 827 453 287 602 180 832 238 859 343 683 180 548 870 926 858 996 589 748 683 346 859 354 706 719 903 353 135 965 508 601 517 454 201 411 114 497 267 631 903 203 222 700 896 868 592 291 395 632 385 939 990 285 519 748 995 233 816 343 703 457 431 829 219 074 869 651 291 720 961 502 349 489 132 581 523 720 599 121 157 418 955 259 167 056 373 330 293 283 961 698 479 067 051 419 214 936 690 778 676 954 491 076 628 697 550 021 687 835 856 850 629 136 739 702 065 488 669 841 151 713 721 648 640 907 890 909 638 618 224 923 682 310 150 237 685 969 442 144 759 177 211 397 558 954 687 683 480 799 436 414 571 496 907 364 874 377 926 856 228 357 115 796 968 184 290 256 370 568 188 647 982 608 884 894 811 846 203 428 964 718 819 907 627 816 417 418 220 014 101 559 012 932 201 654 437 016 960 458 802 757 774 536 930 178 544 397 844 939 070 642 605 273 420 133 359 878 889 830 046 456 546 614 588 963 316 529 664 349 283 287 225 752 087 293 306 635 837 987 608 028 823 692 341 052 524 015 328 719 635 302 163 143 161 465 210 986 031 307 499 145 767 812 118 874 434 386 871 667 058 289 102 183 118 699 783 577 839 721 749 871 550 903 841 509 180 199 050 360 307 680 917 561 916 903 469 975 249 759 707 360 936 972 959 863 185 493 973 500 651 349 769 608 313 200 406 826 198 501 728 347 444 248 890 702 649 413 547 737 295 102 890 133 223 419 906 384 449 546 101 972 324 269 963 649 637 816 493 011 796 883 261 818 480 844 641 330 675 743 602 217 569 153 700 559 516 772 630 761 586 395 342 445 258 320 398 794 413 371 396 120 545 158 833 545 957 822 198 496 870 809 021 407 123 943 391 449 245 621 324 026 756 045 184 891 782 493 266 276 624 286 807 591 516 059 716 043 031 714 863 602 797 539 222 302 279 249 290 767 940 678 796 020 454 652 628 726 605 186 528 485 077 088 905 535 528 186 689 229 578 384 435 966 496 360 511 005 868 782 270 146 816 552 969 835 417 691 505 614 934 206 956 444 423 249 617 658 059 452 023 174 118 991 279 814 026 925 558 544 210 920 976 600 290 929 043 649 004 831 536 811 501 639 134 864 096 953 675 638 745 274 582 254 423 321 897 420 167 120 664 796 368 997 353 349 816 523 919 668 311 243 371 120 202 072 062 616 223 616 515 085 094 547 643 497 281 578 850 445 788 274 793 571 807 683 309 371 648 593 153 393 296 968 564 463 107 801 862 777 717 835 204 000 596 353 057 736 378 816 247 880 055 266 979 959 071 392 987 581 250 398 867 889 687 451 062 142 160 950 763 742 100 215 497 338 521 171 859 363 057 256 489 774 326 758 173 692 975 666 837 334 832 519 147 634 086 043 954 640 902 489 343 708 686 269 021 735 803 700 395 997 238 488 217 816 204 985 263 036 887 111 883 300 895 815 058 286 624 200 119 351 341 520 221 836 252 997 269 798 071 019 962 525 591 741 757 409 115 368 222 516 442 994 317 463 523 313 399 866 285 701 067 768 028 494 854 331 667 983 005 249 987 692 991 099 503 602 313 873 026 320 389 963 445 412 004 394 005 779 264 479 750 392 992 493 481 292 726 761 309 019 263 208 608 958 027 736 638 984 901 283 188 370 327 975 008 911 723 012 814 595 324 604 253 769 955 029 031 803 850 165 655 636 018 909 330 671 031 802 005 699 927 066 873 090 129 106 160 685 598 542 837 320 795 721 608 781 519 972 449 167 730 053 668 106 149 922 430 005 791 775 843 573 492 886 436 891 182 296 991 770 400 895 163 015 177 400 870 553 213 489 209 241 114 772 780 375 965 007 667 244 984 977 947 837 260 991 576 205 783 341 797 956 867 751 136 590 986 992 064 618 442 917 036 925 184 871 789 257 545 580 850 079 476 843 215 840 619 165 423 523 349 794 073 750 393 033 743 205 730 850 383 520 663 348 320 175 473 575 732 154 640 924 473 901 033 001 813 858 368 284 363 440 968 930 540 495 020 724 655 844 756 820 979 913 233 357 845 649 952 763 942 466 417 994 188 526 781 275 384 782 731 804 736 849 467 977 440 363 290 554 694 883 564 834 180 416 132 710 148 396 392 752 374 126 583 633 833 052 251 025 043 447 500 810 197 031 569 693 013 095 443 681 725 356 857 943 518 291 738 897 220 340 933 940 729 163 119 438 751 046 255 296 705 830 363 219 809 621 771 240 575 491 485 012 464 127 681 435 688 982 768 477 969 132 953 312 077 140 749 402 112 325 982 390 603 715 563 151 107 135 150 817 381 153 955 209 018 280 466 264 328 107 245 419 231 392 547 806 822 032 837 722 742 956 596 073 853 927 907 657 500 948 994 533 641 707 779 164 051 813 938 580 094 575 531 442 221 871 925 381 894 902 096 140 548 671 287 516 358 054 600 399 467 619 767 453 919 234 699 789 896 183 718 454 725 602 774 178 234 992 621 627 837 346 962 653 080 145 921 247 146 480 409 099 466 862 002 690 922 564 580 089 124 606 011 438 128 168 251 300 704 489 709 080 605 968 070 513 995 590 556 860 822 571 202 731 413 474 302 256 297 161 507 849 865 375 079 174 067 909 978 472 067 003 407 225 420 778 873 225 049 767 659 529 573 046 535 488 792 262 735 551 594 073 135 658 838 726 636 480 602 988 954 491 104 885 499 161 505 228 818 641 883 841 965 064 772 690 310 511 523 826 566 763 100 156 746 648 173 410 114 759 240 630 505 529 940 120 695 891 880 892 235 715 006 553 167 621 047 378 443 480 797 979 257 445 059 475 717 650 587 179 551 038 559 982 380 883 827 926 787 443 086 561 303 407 196 443 098 909 684 630 453 194 174 602 950 945 906 829 336 263 633 145 110 005 458 684 127 954 984 134 842 148 276 099 655 752 678 279 523 055 603 776 065 364 765 270 621 999 856 503 758 835 990 994 770 050 185 605 857 409 841 821 015 423 783 864 287 862 914 189 463 611 425 976 390 377 944 928 076 764 744 244 916 897 764 109 437 701 176 793 957 942 215 532 868 467 566 708 353 926 284 666 051 349 161 656 208 854 068 960 616 676 063 129 149 644 471 842 113 278 609 395 972 754 979 033 431 334 197 590 560 010 372 468 684 191 186 696 798 590 618 757 288 813 846 832 868 268 089 219 736 780 318 896 215 295 784 423 202 473 693 736 622 727 845 603 860 766 608 532 985 059 845 332 612 833 832 255 485 799 754 137 777 718 207 261 364 131 188 695 928 974 099 530 454 659 470 829 366 998 743 166 396 836 507 060 661 638 517 022 530 398 405 059 521 096 259 199 616 859 059 958 079 873 018 887 882 272 414 533 314 008 419 637 781 538 488 971 667 683 203 809 820 169 433 950 371 217 883 574 052 424 829 263 068 466 993 281 901 918 742 656 653 598 208 183 958 781 629 092 882 963 402 582 950 963 638 132 846 794 308 187 666 412 654 763 530 063 610 360 290 546 629 428 702 990 030 065 030 672 366 854 724 421 698 975 333 191 319 261 716 023 349 642 574 208 710 021 509 072 602 665 161 288 291 872 278 074 478 339 245 900 428 891 491 249 736 690 386 225 202 543 466 194 144 661 391 711 043 342 505 069 857 514 587 478 873 874 872 091 850 522 899 940 798 859 667 219 827 218 052 233 832 581 671 886 315 346 425 513 244 759 105 152 224 696 330 312 717 273 737 718 084 385 223 609 309 966 298 909 331 801 921 813 601 801 088 877 311 286 677 525 784 383 624 350 596 547 659 300 907 152 974 645 365 048 598 112 100 205 215 237 042 661 667 860 347 812 454 899 080 661 004 379 267 189 215 231 904 145 533 683 070 852 433 740 726 089 963 634 774 872 297 434 161 141 193 959 930 808 281 347 799 398 600 486 233 005 376 367 437 212 274 254 055 579 100 237 225 772 965 977 332 265 516 507 695 255 553 481 811 170 647 961 302 355 065 624 374 296 546 363 598 154 124 502 744 328 574 354 344 364 423 136 256 236 034 885 325 487 223 392 889 772 918 499 202 979 829 160 417 837 630 492 008 358 967 098 426 974 561 589 870 597 122 917 340 575 452 689 710 936 879 054 851 525 734 275 901 356 407 119 871 996 782 584 020 573 478 867 893 437 499 567 283 302 985 977 078 352 677 214 594 923 902 064 404 559 369 278 115 595 762 428 321 000 973 618 040 365 536 338 203 080 638 783 364 051 478 081 894 645 858 803 177 531 595 354 909 822 245 958 332 294 738 283 932 489 014 689 580 684 853 891 872 555 540 128 444 253 198 870 588 478 400 323 038 118 341 220 944 502 790 635 881 131 523 690 193 746 924 933 234 130 565 755 515 565 975 490 005 086 873 808 417 192 582 101 871 372 257 131 081 416 102 528 040 885 163 493 942 081 694 287 909 778 918 388 491 047 213 157 397 285 388 804 836 471 638 376 340 506 208 702 495 362 960 334 068 532 533 002 725 537 268 353 916 275 239 139 446 866 108 305 479 856 108 347 982 579 434 827 654 593 038 670 956 538 807 848 459 711 945 379 260 194 487 691 098 109 386 780 307 278 340 564 915 174 874 971 011 973 570 251 693 770 085 366 910 052 067 241 073 414 733 239 549 864 728 569 358 395 977 000 804 187 559 545 678 931 880 775 336 499 045 774 207 841 354 978 364 651 129 944 086 010 608 076 478 999 777 874 799 360 339 887 603 880 366 530 213 058 052 990 451 115 522 967 699 430 959 644 332 257 682 846 184 954 296 429 430 499 575 991 313 837 866 524 658 542 462 636 837 448 602 849 201 903 612 232 263 806 411 793 001 610 477 075 458 418 002 400 275 358 201 319 549 579 643 790 381 003 879 957 968 276 448 977 564 599 952 106 722 329 989 594 600 044 735 196 796 932 731 584 185 628 708 250 055 284 000 783 935 615 365 106 606 812 459 110 408 890 690 167 472 645 483 655 750 955 311 729 307 892 038 308 543 696 546 825 479 408 597 503 386 180 141 612 843 090 243 630 263 843 478 913 547 536 445 048 121 161 486 877 798 535 529 437 494 264 833 544 979 787 097 223 364 019 985 643 659 779 430 953 872 146 395 365 216 497 829 176 267 870 733 181 446 295 061 698 455 736 993 002 381 848 901 265 831 448 703 429 778 373 380 359 633 154 360 626 686 047 856 430 091 687 142 619 021 378 201 529 346 007 465 174 169 730 336 162 522 809 887 050 575 849 703 203 193 188 539 380 073 811 055 633 657 539 740 862 678 190 875 803 171 924 628 786 828 010 439 737 868 161 806 861 801 464 825 996 181 303 273 106 153 219 855 094 797 458 738 666 643 854 175 785 149 690 184 891 159 739 770 898 721 850 294 390 460 739 011 689 253 940 462 458 876 454 905 113 175 173 852 061 698 639 081 436 542 784 577 157 688 821 307 385 307 534 405 973 171 562 168 297 681 885 514 515 499 149 447 346 009 233 671 596 711 873 332 859 546 879 894 257 288 723 772 793 617 476 351 177 269 372 916 475 485 921 877 825 443 485 137 736 809 962 564 847 495 226 750 238 709 323 055 513 576 332 335 573 688 315 934 511 636 159 988 898 309 008 346 718 696 898 614 171 086 404 732 725 277 600 977 351 272 987 261 719 417 694 665 559 063 636 703 728 285 783 468 626 412 654 117 837 945 178 031 638 831 992 376 497 572 380 200 324 831 304 132 369 456 877 065 649 981 688 075 564 246 108 715 606 385 603 064 560 348 793 973 006 231 079 780 062 827 140 016 375 099 400 887 713 664 037 293 492 144 087 009 122 384 048 385 642 318 972 802 941 363 008 100 352 865 370 574 580 902 437 604 659 302 794 960 360 254 136 106 095 372 821 135 096 209 912 959 296 276 006 329 787 143 765 294 070 403 700 626 826 167 755 442 880 777 551 307 309 015 223 240 782 923 754 739 631 025 812 908 697 597 896 802 663 377 702 949 133 298 964 037 520 139 539 519 953 722 543 641 589 732 043 524 702 010 166 916 084 415 647 052 758 235 590 285 090 707 806 571 646 016 650 733 514 184 452 116 170 955 134 026 285 588 541 597 906 160 896 764 578 693 027 955 532 503 439 203 771 871 773 096 143 811 334 494 222 952 993 865 477 043 860 039 294 164 518 423 962 820 989 396 011 743 823 788 936 175 008 576 964 414 034 826 016 246 276 782 846 017 607 617 567 743 593 724 628 688 936 699 145 713 361 276 506 889 784 676 611 114 828 622 534 783 350 623 118 805 682 375 574 365 986 083 355 205 839 212 168 754 448 361 411 535 206 423 361 266 186 854 829 221 190 214 530 076 780 162 407 840 657 810 627 025 829 992 670 081 159 965 563 508 766 911 617 516 896 643 368 604 366 935 811 891 687 514 053 305 112 513 012 240 116 481 241 846 361 769 295 762 887 578 038 268 001 569 925 471 340 839 952 332 515 667 547 759 211 825 071 326 282 698 670 588 954 618 224 238 060 694 876 719 311 207 170 100 959 559 166 603 734 250 040 559 639 719 332 578 563 170 816 740 650 011 091 990 805 813 274 523 562 463 193 816 914 326 914 066 168 511 897 322 712 491 486 574 361 707 764 571 544 586 884 307 963 871 107 530 679 728 010 840 097 285 859 413 686 571 853 879 515 675 976 766 543 981 551 607 445 553 138 988 493 695 870 099 316 643 927 365 872 675 530 950 827 324 852 865 257 653 656 264 343 727 641 309 162 811 943 156 255 638 685 687 901 171 717 476 114 770 998 043 818 245 232 772 263 026 121 063 145 243 340 761 867 600 129 410 486 293 307 901 427 954 924 442 259 680 535 132 914 216 206 786 807 264 598 148 989 697 979 497 191 811 799 131 204 812 608 290 515 566 472 392 254 739 229 803 661 996 701 211 541 341 477 192 307 685 790 119 854 046 427 576 143 366 640 594 804 198 956 715 240 468 469 180 908 160 209 751 904 554 068 839 711 008 481 622 836 088 923 441 988 800 112 567 526 665 706 719 848 903 706 145 440 488 141 651 020 177 720 558 429 798 566 400 008 341 710 189 872 087 648 492 210 132 127 974 181 955 847 140 959 038 925 319 332 467 499 307 418 340 388 982 080 020 940 436 097 368 692 930 027 810 384 280 945 740 415 195 206 455 848 528 535 965 522 538 639 872 424 570 188 585 885 268 355 483 606 175 588 779 102 928 847 551 614 516 744 376 128 588 909 496 195 405 324 379 395 944 311 674 580 051 330 011 627 145 304 973 056 496 144 914 128 207 350 338 990 644 591 531 998 703 697 916 899 940 430 923 144 386 810 927 408 509 262 884 736 181 171 213 611 675 194 057 617 812 003 402 640 797 409 135 417 546 920 537 439 601 921 012 690 647 132 964 117 561 742 919 681 659 597 766 108 566 370 588 492 069 780 752 903 220 777 752 165 085 043 016 372 676 258 473 388 395 800 663 225 399 685 348 141 217 221 871 425 667 173 277 309 972 302 810 448 780 212 711 616 056 008 410 402 329 007 446 162 830 643 807 096 755 502 438 231 119 223 554 681 678 788 086 749 866 587 099 334 788 909 074 481 492 870 772 884 640 001 234 883 497 039 680 697 637 956 102 709 100 408 580 210 696 706 124 084 158 624 726 798 119 174 121 667 134 365 353 681 636 586 355 617 370 594 112 224 889 576 741 091 524 298 679 364 954 740 414 365 347 516 073 782 870 614 103 251 345 101 353 327 750 222 680 493 381 867 323 380 204 212 067 294 440 534 352 692 936 069 440 895 619 414 153 028 739 613 958 573 791 629 541 002 896 207 666 590 955 748 120 550 910 829 547 479 247 142 778 820 160 072 274 255 231 408 294 247 297 712 671 434 843 613 159 497 137 515 857 339 790 785 636 777 016 134 386 646 632 772 093 061 949 936 866 263 103 311 998 291 433 511 516 565 249 758 243 748 588 105 863 861 589 263 785 133 558 255 999 653 699 339 537 089 660 679 367 641 859 161 191 307 980 798 372 672 926 217 681 076 728 229 958 262 055 053 158 421 844 325 483 925 448 101 578 363 025 481 494 274 358 634 734 563 927 403 330 427 103 647 489 982 650 824 471 403 806 735 788 423 343 828 032 354 502 903 795 842 987 953 226 770 323 367 867 269 181 868 613 945 677 777 835 601 236 267 512 104 572 561 823 535 536 422 052 578 600 332 320 829 093 527 742 788 343 497 007 306 980 744 877 979 895 187 280 243 819 037 711 787 378 909 881 283 745 630 975 265 878 523 222 861 777 674 605 630 408 315 289 201 827 686 660 879 033 124 503 496 995 186 612 023 051 120 500 128 271 032 966 221 075 164 853 733 058 522 778 401 718 521 534 887 685 720 145 460 344 137 661 129 818 761 012 888 420 152 763 937 922 595 657 883 803 192 882 065 113 322 780 346 813 716 898 016 909 744 511 350 477 603 497 998 574 365 183 213 430 673 619 093 059 856 332 547 648 255 642 517 695 116 719 606 182 587 339 369 114 185 263 954 259 603 827 340 487 906 533 194 464 806 219 315 474 915 950 427 276 963 466 975 911 585 237 466 593 800 649 071 364 839 962 221 411 782 550 731 798 755 146 260 058 974 997 697 943 274 510 211 555 379 587 625 866 781 407 878 578 110 649 082 720 621 858 732 718 475 177 728 992 799 391 248 956 800 049 911 673 949 262 235 245 748 687 350 443 215 471 988 229 211 482 159 097 393 003 074 831 714 917 123 068 147 667 033 662 892 956 601 793 343 545 712 441 351 511 196 492 976 057 212 832 787 661 175 156 828 777 328 947 485 373 156 473 193 309 774 066 644 623 033 979 480 061 210 150 996 852 468 672 733 972 615 604 463 973 080 717 248 765 389 050 424 466 839 395 614 822 646 045 153 237 860 938 613 979 735 494 880 033 686 740 040 295 524 664 368 278 214 393 769 777 273 802 703 559 996 621 003 088 067 799 257 604 784 791 318 203 544 896 330 036 655 716 643 996 000 670 627 216 884 711 464 943 702 879 424 138 616 608 866 359 211 053 301 143 296 515 812 293 246 437 870 770 119 106 364 479 658 675 434 398 186 103 178 497 511 849 695 363 294 705 231 381 323 981 259 754 040 488 449 975 202 998 909 552 855 986 018 733 241 886 535 468 253 491 162 091 866 018 447 141 442 648 290 628 441 652 511 613 108 932 674 117 877 072 756 854 199 735 387 560 642 641 512 179 787 078 349 811 696 961 682 011 034 672 563 477 790 843 451 713 387 234 687 798 052 130 966 671 754 250 760 438 865 996 760 367 576 485 676 841 048 052 751 188 444 278 238 678 947 463 535 449 199 896 365 366 552 962 364 231 097 428 010 268 001 595 998 348 036 567 208 133 094 466 728 185 258 639 693 370 335 479 214 246 294 837 975 939 662 962 325 701 441 812 676 761 439 622 120 268 549 749 223 614 424 542 863 673 409 760 621 503 367 223 507 601 244 706 965 880 001 266 994 460 828 351 685 639 540 686 937 205 942 602 134 695 000 595 539 200 822 466 019 112 727 582 046 646 541 305 840 245 866 223 379 515 341 204 481 764 257 648 802 696 336 682 579 030 309 515 019 215 529 040 498 976 962 209 955 398 877 516 878 889 328 985 316 543 549 752 783 617 874 666 862 896 614 015 677 826 631 678 879 219 518 027 302 836 540 734 249 726 851 296 430 050 486 854 302 392 853 135 998 967 386 812 431 835 601 890 549 826 438 560 801 073 293 620 005 211 586 081 496 188 159 291 299 498 140 724 011 085 974 818 937 288 963 772 512 893 081 791 471 557 517 086 362 139 599 709 311 680 378 553 480 842 088 666 210 073 228 561 596 010 317 836 270 524 063 632 022 917 103 814 259 233 217 300 351 083 152 235 242 207 756 620 373 065 614 574 415 320 545 498 929 057 923 314 122 736 590 379 414 321 570 288 070 131 494 350 688 737 964 922 331 848 832 706 523 735 608 795 483 062 230 424 024 976 724 047 071 018 092 943 107 398 883 244 441 242 618 722 225 941 776 278 760 536 667 477 921 538 954 289 931 141 052 341 177 301 390 084 798 580 636 574 408 922 110 719 558 394 654 129 985 272 629 427 767 231 038 430 405 547 543 479 759 904 118 482 387 944 504 861 263 148 306 904 502 602 779 916 969 438 196 413 152 684 728 540 152 554 989 290 401 147 246 259 125 109 575 548 419 875 377 924 641 882 631 668 556 441 997 303 773 714 743 460 872 601 253 366 841 362 997 443 433 081 411 828 188 401 446 785 051 592 537 653 035 473 924 691 324 488 413 807 785 944 596 426 974 090 072 940 144 735 525 029 246 539 296 532 815 163 894 168 272 131 822 354 330 955 845 353 207 347 241 163 535 763 317 706 501 572 781 267 872 435 323 091 404 864 303 120 891 371 917 289 942 482 294 447 540 615 137 923 988 456 153 091 141 784 678 205 717 580 885 721 525 483 759 311 253 631 882 457 958 611 948 175 726 266 926 264 180 412 388 641 429 587 202 855 939 910 243 732 426 381 833 310 352 487 404 953 094 268 376 529 600 641 380 910 689 156 553 863 931 067 827 555 090 695 396 473 778 247 664 820 127 579 638 374 426 101 477 371 738 917 862 435 423 770 766 976 709 520 404 354 801 650 972 058 637 068 046 384 205 392 448 695 169 027 053 807 317 279 673 353 980 214 503 134 017 644 146 026 151 770 282 554 705 609 409 817 945 193 134 631 720 639 958 529 002 249 999 160 336 001 778 417 186 168 636 169 236 312 348 005 995 212 089 991 910 048 123 324 030 129 465 802 476 011 708 315 268 082 052 625 027 291 600 320 237 834 902 804 826 399 806 742 325 799 517 848 087 634 903 234 691 392 435 190 730 382 562 663 831 002 948 819 688 387 856 977 108 511 710 714 080 415 564 067 659 192 093 600 273 949 938 033 953 423 523 470 765 220 157 021 881 058 248 533 450 840 916 684 246 766 422 824 163 510 724 394 350 324 234 698 320 043 560 288 444 475 955 518 647 371 852 402 874 085 296 998 576 319 058 621 104 132 947 430 433 986 427 073 894 633 978 611 087 009 331 223 957 164 361 949 023 703 271 132 597 877 747 085 057 349 629 845 841 119 881 751 800 432 104 014 217 527 881 259 211 932 497 423 425 725 713 855 691 244 091 810 506 832 570 249 137 622 031 857 226 738 503 375 017 753 217 968 379 725 735 912 936 116 668 464 547 957 345 705 230 340 060 241 390 948 041 527 439 950 006 465 034 950 992 880 554 905 499 243 742 927 062 508 479 606 338 679 470 485 214 447 262 792 424 435 611 375 891 309 823 662 006 193 177 873 763 549 812 338 915 502 378 482 472 221 090 754 706 631 381 552 521 374 327 447 482 116 471 838 873 556 127 697 176 337 991 263 352 441 848 446 146 795 334 174 529 569 659 596 715 925 182 535 751 607 199 088 394 107 839 310 829 144 097 845 418 677 959 391 431 179 177 728 958 993 737 162 690 094 389 735 766 890 912 126 152 304 665 805 767 752 403 316 518 076 150 475 207 263 296 938 810 437 977 610 177 766 708 606 296 804 455 513 154 856 576 516 590 605 201 561 278 371 460 817 623 347 786 261 867 137 884 283 443 685 528 949 078 594 389 484 993 374 863 351 034 475 860 394 399 499 316 108 001 853 729 446 095 014 156 192 448 851 657 135 711 539 363 228 355 994 320 822 303 597 191 019 659 167 377 218 231 447 491 345 815 837 791 685 015 194 321 938 881 266 073 623 168 241 149 894 206 367 262 904 319 317 225 632 421 771 428 863 022 418 320 378 214 443 852 606 781 823 455 724 382 115 254 965 994 939 134 486 949 911 067 752 345 034 460 468 124 960 526 635 814 254 747 013 630 107 836 271 321 748 874 237 654 899 727 782 246 097 677 410 711 273 228 359 353 550 115 392 006 937 415 197 402 809 689 911 323 163 740 466 625 886 698 580 561 370 822 386 382 983 632 752 655 937 655 275 764 775 015 855 728 563 078 604 413 110 388 517 482 323 981 907 548 985 177 342 267 357 840 124 975 541 183 896 722 847 547 131 461 372 057 012 263 670 113 508 055 128 534 135 664 402 533 936 606 001 754 744 345 693 949 386 188 121 744 787 411 278 837 515 782 109 272 594 463 465 472 694 522 970 750 574 678 149 479 388 456 128 347 111 720 746 350 503 331 897 711 264 116 673 445 263 508 216 151 205 303 163 436 123 775 024 509 840 559 637 041 739 431 094 151 762 071 701 293 976 836 624 460 372 488 796 127 828 608 557 210 434 128 215 739 626 756 066 672 587 294 888 987 250 593 598 299 582 389 401 798 795 466 905 601 391 795 156 128 239 976 856 429 186 898 916 397 012 817 456 933 084 573 190 271 285 052 260 010 538 844 169 559 708 052 027 827 048 114 768 355 111 726 676 055 661 407 502 283 919 696 136 195 231 724 534 670 836 619 860 176 979 305 260 725 090 930 640 017 334 262 435 983 880 737 218 638 941 858 076 092 352 158 908 222 185 784 608 683 913 548 962 486 649 966 666 391 494 319 500 466 098 068 536 823 332 725 606 895 837 641 483 077 526 219 097 551 123 564 844 700 569 123 514 373 278 210 620 312 735 567 273 540 093 594 495 369 927 464 039 576 971 802 639 385 120 235 735 321 254 956 034 203 020 265 667 086 554 467 324 726 139 396 989 421 561 130 967 090 587 046 945 114 176 437 679 888 425 903 824 593 521 625 489 777 597 668 837 157 160 923 454 924 475 416 464 317 624 304 664 798 986 340 350 752 051 100 245 783 266 327 607 124 535 084 393 982 979 519 920 877 254 256 447 538 449 543 603 439 298 986 642 245 817 498 959 783 050 933 298 354 945 194 963 503 717 744 989 640 726 954 118 383 539 449 745 589 537 543 886 969 677 351 091 665 821 126 889 333 842 014 562 432 812 477 877 137 188 571 819 161 596 912 127 154 428 340 762 504 114 702 587 502 054 844 529 432 288 779 036 459 865 203 416 145 886 857 794 760 376 493 082 535 172 487 819 672 312 498 020 103 026 279 253 645 483 885 590 898 322 428 276 521 276 475 790 176 457 719 977 086 055 845 272 048 212 333 140 230 635 682 229 044 889 322 124 471 155 960 844 838 563 614 831 150 076 585 526 788 264 728 938 331 860 726 439 660 895 300 545 688 402 074 694 161 667 895 547 910 768 844 258 717 636 672 280 658 566 044 519 772 089 932 998 109 174 965 102 228 119 731 982 170 855 642 560 523 171 246 711 036 738 042 424 671 736 325 161 125 679 951 446 527 383 015 580 301 152 448 182 188 857 967 358 500 842 990 659 254 566 761 061 438 186 077 006 455 248 182 593 673 743 232 989 556 032 115 265 344 338 200 162 375 799 831 225 793 614 743 687 413 722 157 354 319 544 010 362 866 140 377 853 369 055 006 994 633 815 357 539 051 298 167 215 799 714 158 955 938 995 796 682 079 020 886 172 144 160 082 201 776 720 317 697 294 875 980 202 393 584 831 673 483 439 521 630 580 982 887 474 757 574 780 624 059 166 183 342 546 041 678 102 599 983 145 222 958 674 027 069 371 383 727 311 958 483 421 234 787 185 576 006 312 692 127 189 732 619 602 107 094 619 570 695 165 443 954 789 394 015 856 345 437 817 263 632 201 607 007 927 000 829 938 291 484 270 518 064 478 220 349 465 058 492 698 344 895 845 595 982 656 722 095 534 777 773 953 953 342 527 678 720 261 063 172 900 189 434 292 759 947 702 882 334 170 757 532 653 795 131 403 083 795 388 493 310 126 231 238 953 261 018 479 471 896 167 347 512 319 373 803 924 102 110 364 447 174 692 037 762 028 563 659 614 398 912 621 107 868 805 137 343 186 900 778 525 761 721 624 675 123 873 194 966 084 157 256 239 577 815 904 570 245 971 908 724 094 240 225 858 769 033 069 026 874 527 029 860 847 626 618 924 363 945 305 193 610 530 356 994 398 212 862 355 590 296 597 491 571 233 620 694 143 460 679 779 706 684 570 683 557 313 804 967 081 940 707 072 172 103 938 082 177 492 827 095 905 492 991 972 036 929 371 164 909 124 815 375 234 306 624 760 163 093 294 396 562 523 748 639 827 294 505 193 913 525 564 207 001 290 906 523 316 212 985 011 903 217 301 659 474 439 965 166 275 869 110 655 232 142 899 612 162 841 546 896 776 740 455 151 609 343 658 895 653 343 941 596 237 390 660 078 797 119 168 890 590 693 468 616 935 725 651 820 533 670 251 840 694 993 966 990 936 410 961 479 400 477 771 544 649 319 291 488 091 538 926 016 721 058 325 237 031 029 445 387 111 963 412 298 339 966 783 397 797 954 438 813 892 742 371 152 112 661 467 690 073 557 722 417 361 576 096 438 842 571 196 861 959 951 514 538 044 800 768 462 110 029 562 383 908 942 720 306 913 407 328 994 366 465 007 102 798 863 588 302 742 241 821 581 071 169 852 781 183 942 176 009 250 252 144 762 941 411 970 331 467 742 873 452 902 960 155 710 295 212 623 616 978 901 230 667 580 040 920 496 200 640 242 812 763 679 594 424 558 339 348 719 105 984 128 934 551 856 977 880 818 723 809 048 339 419 185 854 186 332 058 468 966 846 488 432 258 236 716 425 900 686 561 659 314 211 940 588 466 931 926 988 255 641 253 484 265 551 942 412 558 679 934 170 820 536 114 518 415 892 291 911 091 204 615 778 932 881 686 777 196 196 078 193 442 270 121 572 154 014 406 938 233 663 177 067 927 714 747 428 709 129 617 594 631 754 384 652 185 354 001 255 433 989 174 147 139 375 073 861 169 788 065 434 894 022 986 037 670 162 989 541 062 339 685 339 297 909 096 428 482 679 350 092 580 977 041 736 677 181 803 864 122 774 605 405 694 667 398 074 978 085 987 160 343 950 536 051 338 128 261 644 241 694 215 877 122 483 865 947 666 806 416 760 729 485 554 473 060 260 611 195 749 239 497 796 792 590 077 438 268 272 443 855 738 459 630 360 052 022 308 000 139 768 132 890 073 776 765 965 846 970 005 779 619 960 716 200 077 988 088 710 714 180 444 065 567 110 699 299 026 324 793 007 749 013 737 657 904 583 210 757 686 399 815 502 418 706 446 918 307 885 560 047 414 165 232 933 969 072 509 770 862 388 146 764 361 071 786 589 086 542 219 628 146 819 366 904 627 000 415 100 852 637 211 569 149 531 055 701 760 990 001 899 130 771 115 870 304 722 978 472 562 401 022 822 611 150 688 974 661 043 252 934 421 078 557 830 930 867 788 010 133 829 484 138 756 103 690 415 247 554 706 453 056 488 647 786 865 073 369 456 730 933 378 371 368 361 892 563 438 311 128 825 164 109 436 676 246 436 787 138 544 065 489 990 779 209 764 969 734 749 352 607 576 927 920 209 144 354 406 168 407 482 782 520 766 930 711 067 781 435 938 170 589 716 674 046 955 320 855 332 882 367 206 600 911 177 684 689 905 603 293 658 789 331 457 307 738 144 760 078 399 135 924 518 372 854 584 366 175 390 566 076 487 438 945 571 617 548 148 416 500 568 582 307 712 724 164 405 469 471 393 007 460 554 895 454 020 721 185 538 353 753 172 063 012 569 136 263 921 471 922 582 130 780 198 146 283 042 471 342 166 074 284 841 092 477 180 615 126 155 239 463 138 931 793 942 185 152 236 336 464 183 049 938 081 876 284 355 730 656 520 852 098 685 146 812 632 483 498 169 721 714 268 307 596 527 975 549 146 664 909 026 210 159 567 764 985 772 029 369 805 547 860 065 011 149 685 984 308 372 470 624 602 996 819 346 506 439 380 740 892 711 036 076 789 378 392 622 542 708 886 864 101 571 217 129 644 423 744 165 890 159 893 894 076 774 286 476 863 192 955 962 460 356 249 830 971 226 836 925 463 150 898 655 844 850 342 806 352 802 014 872 460 074 369 370 305 632 667 730 417 653 592 482 006 033 939 403 508 839 100 311 987 846 585 780 150 599 728 103 687 265 600 716 420 891 863 833 899 921 516 746 324 514 308 374 439 700 017 287 136 481 927 776 554 190 017 564 049 318 738 808 930 879 285 406 092 591 404 752 881 005 815 308 808 092 948 433 931 283 219 573 109 812 820 862 939 060 612 667 538 832 603 761 038 519 600 359 304 365 917 398 374 788 874 035 547 443 568 346 605 549 501 949 521 994 312 570 928 910 044 486 601 128 383 011 876 860 639 996 576 792 243 278 307 247 907 365 649 770 488 249 028 536 578 214 107 710 483 950 369 263 881 270 956 787 065 599 259 415 413 059 575 277 460 393 759 752 855 416 169 822 697 109 006 533 733 117 170 215 804 219 422 128 965 602 411 381 808 985 609 407 631 110 491 645 692 789 106 267 650 846 322 044 657 808 163 638 498 585 125 847 294 327 206 864 291 467 927 089 425 001 063 870 643 012 142 180 157 043 579 487 962 218 273 704 100 930 290 528 776 067 340 983 849 556 332 865 347 410 357 070 444 453 323 923 632 488 510 475 799 661 625 400 540 227 314 803 583 286 731 497 728 667 744 037 969 803 367 074 247 302 334 767 953 541 059 142 325 949 146 077 275 294 861 831 736 633 391 639 438 116 555 017 098 273 649 178 519 683 661 488 195 162 393 786 378 540 265 531 979 114 465 529 162 011 281 490 761 425 232 257 291 187 057 779 435 899 119 837 624 819 996 752 537 549 195 510 110 727 938 361 046 220 447 552 836 635 197 410 032 355 441 837 896 662 160 765 105 026 570 471 574 733 762 550 451 723 351 119 797 100 966 320 345 040 241 820 494 635 647 824 694 917 418 514 134 326 157 558 205 700 272 083 091 257 543 902 034 133 268 244 190 468 546 483 830 215 505 162 111 696 954 124 968 766 926 428 693 925 037 394 919 340 788 014 879 983 562 912 051 092 846 048 570 150 653 988 241 407 487 952 144 646 802 882 226 692 622 280 557 551 391 046 563 974 725 634 844 451 716 450 416 539 145 451 842 500 909 023 433 227 890 084 756 908 640 036 459 736 237 542 324 797 233 509 043 264 282 495 254 169 158 090 929 767 743 536 675 309 366 636 920 827 634 823 640 681 386 190 056 405 098 833 868 634 645 393 096 621 451 351 713 305 793 429 118 661 755 304 617 122 997 552 512 729 705 441 719 583 550 559 346 781 691 557 771 521 548 892 628 865 692 661 385 553 395 232 875 398 945 155 600 530 643 893 658 155 291 492 601 002 593 714 815 629 844 309 114 918 530 899 860 582 344 818 938 915 756 174 928 743 903 480 110 551 764 377 016 445 888 949 652 188 952 359 341 125 615 172 159 518 482 029 756 904 574 480 199 092 733 663 774 505 245 051 233 583 203 874 396 046 833 172 588 560 860 285 427 157 409 430 865 081 644 512 965 205 768 834 511 956 356 988 767 361 757 684 506 307 114 790 930 000 388 528 512 220 093 787 258 721 113 635 616 408 495 335 422 591 280 898 533 412 799 404 521 864 774 430 717 912 451 430 849 875 586 819 282 806 392 123 788 042 416 194 907 832 491 239 419 825 808 025 108 646 078 205 752 445 793 691 129 208 392 494 390 831 937 090 987 404 005 060 825 671 160 107 358 238 506 471 285 400 922 224 950 342 427 531 319 895 808 360 282 576 551 158 230 745 490 365 424 700 768 495 702 997 111 518 726 142 391 539 117 587 296 812 745 314 812 066 130 982 836 392 991 856 680 370 922 904 006 671 096 593 108 765 883 103 429 855 547 804 112 328 598 482 518 647 070 754 158 816 403 518 026 205 819 311 077 189 974 913 187 220 871 621 617 866 057 280 356 459 153 298 932 740 330 498 450 038 846 689 838 235 368 494 087 572 707 529 033 020 537 718 929 205 068 193 060 722 387 225 187 088 121 457 514 920 472 452 556 612 083 096 772 019 560 139 488 068 233 345 774 960 846 214 079 859 854 660 435 911 241 398 429 264 647 909 571 300 468 947 367 670 333 226 264 274 056 020 454 005 373 571 526 148 269 909 785 805 296 059 743 392 491 927 883 666 907 037 941 993 109 881 101 200 096 698 913 014 712 232 514 938 211 505 112 312 469 020 347 385 300 702 809 845 956 214 471 655 345 268 831 777 362 501 188 917 963 739 916 708 574 365 681 509 489 097 797 490 980 871 617 650 210 232 875 103 674 309 657 527 875 229 507 790 082 226 800 555 881 875 258 095 674 303 380 304 158 025 525 561 997 879 083 535 771 920 561 897 727 047 228 396 677 767 098 222 792 233 720 335 570 560 247 842 301 363 012 891 195 110 862 328 864 718 076 484 067 576 182 222 930 577 862 160 501 332 210 054 695 281 192 333 049 747 321 767 658 104 562 000 169 472 167 782 353 839 181 981 312 213 396 306 657 958 845 949 083 565 787 398 755 525 249 293 648 880 977 826 435 252 423 052 421 761 401 212 111 754 249 884 044 787 401 015 313 055 766 802 819 167 072 379 795 058 307 168 155 503 622 513 849 710 489 938 350 135 647 115 092 374 632 273 110 003 485 094 305 878 613 957 368 470 603 667 489 797 426 195 216 682 710 639 530 944 777 216 015 643 395 779 531 605 539 131 856 559 511 953 415 701 842 882 410 529 366 410 942 158 448 619 874 443 346 733 825 717 737 469 053 394 445 312 447 048 917 342 039 304 192 851 448 058 788 753 210 141 664 195 421 701 936 438 607 094 795 110 081 699 250 762 074 008 263 258 072 764 535 329 968 219 871 368 672 913 448 500 121 796 491 952 952 481 923 632 981 011 456 949 615 539 053 413 369 170 141 990 895 459 811 317 181 565 108 444 079 831 550 399 629 926 993 924 173 494 150 231 854 492 403 004 107 959 057 839 085 904 307 669 951 261 285 161 685 738 906 591 647 320 887 437 265 066 133 921 725 646 959 211 045 058 671 944 599 958 422 973 927 334 180 374 352 126 951 399 065 528 046 786 864 992 160 439 887 893 447 518 342 422 446 880 955 335 830 192 675 228 423 635 623 228 590 787 102 330 603 753 630 109 606 544 824 799 328 706 221 627 211 480 566 455 682 777 259 084 324 809 973 370 625 696 152 356 722 318 094 130 092 083 454 730 746 301 393 242 188 496 869 078 025 898 732 755 168 240 552 263 639 764 892 990 079 935 726 678 748 333 913 458 575 808 243 845 886 713 447 651 203 927 596 276 204 942 153 937 748 660 729 240 346 352 933 201 419 800 714 289 410 508 068 896 017 243 723 854 807 689 934 643 763 984 867 450 215 020 727 843 687 266 137 354 947 060 636 718 925 880 503 792 486 954 298 604 530 510 923 918 875 570 834 799 304 955 382 859 019 161 309 749 880 083 975 736 640 826 677 137 781 137 958 413 744 052 488 313 686 880 858 265 842 031 253 632 302 811 155 917 148 550 046 086 609 615 220 680 116 440 237 301 795 455 434 872 482 542 808 418 232 074 904 163 060 361 338 290 136 354 758 588 704 529 450 782 673 992 046 403 419 483 400 176 121 609 671 919 281 872 907 704 355 195 697 672 637 255 940 616 916 356 145 353 414 441 621 439 711 156 518 471 881 462 378 276 195 725 936 441 001 806 593 037 570 127 788 897 539 361 135 362 343 864 074 964 900 626 777 642 284 815 948 844 734 339 339 885 460 349 687 399 816 896 430 341 418 155 580 498 605 485 238 161 204 142 663 220 884 336 276 480 212 926 955 015 605 808 520 045 152 779 085 317 854 741 299 680 968 984 113 813 246 600 262 109 400 935 710 404 432 982 669 594 553 338 245 113 811 958 038 502 564 555 434 179 523 785 307 430 184 000 867 114 463 615 023 643 674 994 518 579 665 530 586 837 349 832 158 302 763 388 380 878 500 266 559 071 696 517 339 415 118 391 914 451 892 827 497 688 352 608 658 908 213 761 922 261 575 723 324 797 784 989 387 132 075 331 726 762 291 981 121 904 600 606 391 895 318 036 119 421 655 638 453 620 949 551 190 450 954 185 590 176 564 096 848 817 048 897 516 634 846 239 209 086 236 753 593 492 002 743 083 513 939 775 277 719 195 102 247 388 617 814 633 881 083 999 087 503 829 118 925 269 826 265 256 356 938 892 615 638 811 351 550 965 893 778 642 173 270 956 365 464 551 259 988 242 297 002 678 644 767 662 979 940 615 372 280 516 301 132 940 386 786 977 844 913 161 299 423 879 204 154 281 887 071 598 053 006 746 448 033 802 054 846 107 827 881 315 082 176 726 141 379 485 683 970 643 591 160 683 236 045 695 341 283 033 749 305 907 471 909 673 355 222 496 278 369 585 740 106 626 759 920 862 938 975 883 282 076 192 755 291 318 832 854 530 885 607 911 503 568 026 310 362 375 225 671 899 144 234 167 088 696 170 829 349 397 639 685 849 798 643 986 273 123 320 461 897 259 570 667 746 297 387 076 548 205 160 725 411 112 399 582 500 761 364 578 035 370 516 622 493 689 391 143 881 604 610 034 361 213 931 697 266 008 779 897 888 264 758 225 236 815 599 418 768 604 058 095 292 639 373 553 590 515 100 775 158 201 821 144 053 370 729 678 373 881 697 925 591 002 335 315 079 821 813 401 123 845 700 814 577 473 080 631 665 004 776 322 591 306 555 745 788 271 231 875 468 624 993 180 616 665 974 577 295 040 213 425 824 855 917 275 608 418 810 348 035 471 436 614 722 202 055 961 946 628 948 302 555 429 952 701 126 559 074 156 507 772 715 275 247 725 277 535 698 818 656 019 077 646 274 401 636 532 729 675 292 582 894 626 127 510 242 601 597 758 523 408 288 681 249 227 660 215 530 571 303 222 463 291 358 539 753 278 764 105 494 497 931 526 686 394 980 062 954 580 539 009 849 858 957 552 854 705 310 067 190 110 212 107 873 193 907 969 389 839 826 482 109 039 001 295 341 222 407 450 789 394 719 967 292 694 578 637 956 211 198 935 578 227 587 682 034 626 215 553 808 076 775 750 467 495 809 872 545 824 352 882 333 334 101 636 677 850 060 856 817 475 350 779 138 458 116 291 008 408 709 471 419 847 597 786 289 505 270 042 413 452 217 984 911 069 648 166 855 485 954 920 341 256 222 193 271 551 440 742 560 132 894 955 520 104 349 472 961 582 097 238 708 554 168 481 893 358 018 557 952 044 199 259 960 533 180 655 460 213 147 784 128 273 128 664 777 532 480 274 646 009 394 627 987 323 586 434 338 062 798 651 231 604 989 215 276 336 931 335 078 522 908 734 019 668 456 463 238 319 253 796 772 905 832 189 541 624 077 500 722 129 423 961 518 430 871 498 156 943 523 719 774 655 630 676 150 606 648 525 646 443 971 493 651 695 822 477 938 334 832 507 334 286 338 749 972 687 928 814 694 261 130 738 973 014 628 636 793 204 875 157 405 695 019 274 176 253 071 397 938 114 942 224 596 089 844 658 360 590 183 712 814 379 251 763 517 690 203 411 153 322 887 708 443 506 908 188 196 779 679 361 635 776 357 732 246 617 419 413 331 515 709 123 806 245 006 236 689 156 568 368 438 097 229 148 105 020 597 594 148 297 862 873 271 770 487 754 060 289 677 288 240 127 152 287 732 624 204 001 697 452 521 524 978 865 885 784 008 869 549 011 525 503 805 295 391 479 597 646 896 551 833 773 333 512 334 793 644 860 790 335 647 334 093 320 726 506 351 095 193 949 854 111 264 628 158 331 534 910 103 458 538 007 193 524 461 220 771 073 598 102 866 304 514 889 521 926 927 802 615 263 096 169 511 116 747 189 146 096 384 291 655 158 264 575 665 593 609 350 835 622 132 569 670 264 844 459 567 688 923 545 050 180 310 749 712 689 055 493 627 920 211 112 989 784 762 207 399 956 427 192 457 886 587 892 431 361 668 777 127 773 016 579 700 499 907 108 323 247 905 791 186 985 388 394 724 529 791 966 127 980 623 620 645 814 698 729 352 698 843 153 362 930 517 121 272 238 395 092 928 479 131 218 273 770 296 588 443 253 319 293 036 486 136 875 683 713 757 162 195 925 491 714 778 880 297 029 068 125 767 643 499 537 018 999 467 863 166 688 443 161 087 984 692 864 705 137 989 585 874 352 775 200 002 149 703 443 339 255 473 413 380 223 878 278 527 608 200 968 752 456 098 485 254 833 795 447 952 215 180 241 692 035 326 719 696 572 923 722 654 684 733 114 041 202 193 941 483 142 087 557 609 361 280 767 900 406 369 451 603 196 412 584 898 212 971 298 725 983 050 493 479 391 697 656 992 396 286 094 139 727 697 411 478 361 270 787 857 641 784 106 892 489 926 839 891 807 639 909 516 924 204 822 414 405 369 088 545 605 714 338 025 004 355 145 230 166 193 395 496 617 523 721 562 627 735 609 831 022 968 703 251 834 543 451 163 077 787 642 766 539 267 037 621 376 694 708 589 539 529 754 773 930 169 795 999 546 137 220 180 133 411 574 461 272 399 895 436 705 961 992 745 521 808 986 578 803 378 635 592 991 863 438 705 355 685 316 763 972 247 888 815 416 068 835 741 997 522 355 678 584 204 020 801 329 299 305 082 643 563 203 047 003 221 060 023 418 878 220 104 618 309 565 593 969 329 526 286 041 924 077 371 083 228 756 380 111 299 416 529 103 552 902 469 141 642 070 259 241 507 637 641 415 169 202 237 686 681 242 113 315 299 632 679 933 256 724 529 507 142 466 968 451 360 196 248 929 875 369 524 969 926 479 538 434 692 192 591 508 574 198 508 003 070 240 289 563 738 580 229 830 327 964 514 251 194 733 995 788 971 911 780 340 874 630 753 004 102 935 963 258 334 158 644 152 027 865 734 158 345 726 599 941 421 761 753 821 367 077 675 370 422 523 657 878 877 106 151 928 657 179 906 537 490 833 075 527 565 667 533 740 242 474 935 683 334 914 315 084 119 964 051 405 503 096 158 919 523 838 249 607 378 392 713 122 842 285 474 956 185 346 340 796 309 311 808 531 307 004 869 540 171 273 169 455 975 243 169 190 069 333 314 594 291 410 652 898 659 594 064 159 345 643 839 661 884 857 890 444 411 250 152 544 780 856 820 417 139 360 519 500 528 659 547 751 648 095 431 009 950 727 028 755 477 518 028 644 557 482 037 175 015 483 401 526 083 152 786 866 944 651 138 852 801 107 119 704 087 229 502 694 495 374 022 831 490 086 445 203 618 705 288 691 650 979 646 345 636 824 382 962 336 399 615 650 743 534 937 258 960 567 360 131 086 818 985 388 370 132 484 096 872 682 193 393 879 247 635 557 299 775 205 078 580 934 906 777 078 675 389 410 209 957 030 001 249 631 554 070 211 084 967 970 906 281 275 023 036 016 316 375 005 669 306 394 966 467 103 083 817 739 942 238 458 615 382 707 587 447 095 581 422 131 792 254 564 535 284 577 588 109 616 039 976 978 613 470 190 093 867 029 574 652 009 671 714 301 147 215 789 215 453 085 648 590 122 036 964 091 275 208 508 175 184 160 349 407 113 854 364 611 981 414 380 404 755 962 820 267 294 336 364 134 181 358 456 997 976 006 888 467 102 985 550 747 170 935 195 062 141 984 110 183 014 358 124 691 615 587 926 153 846 517 676 900 332 160 812 014 547 624 345 958 510 688 311 852 249 594 672 672 800 889 938 446 398 376 316 790 545 824 618 861 342 546 398 892 006 056 405 107 142 249 924 807 024 219 782 576 809 499 060 433 006 205 609 477 583 581 018 519 360 548 112 165 643 764 368 008 014 773 233 005 867 505 362 210 427 048 562 628 591 371 547 533 466 764 914 304 846 995 578 714 875 226 124 334 500 938 861 710 261 513 197 415 741 409 689 651 086 367 018 576 894 321 622 466 217 351 226 249 683 196 118 115 622 971 057 984 951 324 423 741 164 537 732 663 975 573 005 335 984 179 213 552 225 174 863 308 240 089 296 980 621 681 649 521 138 186 026 200 366 339 613 470 778 216 583 359 377 481 754 669 567 878 513 290 562 481 281 081 446 896 727 815 544 870 637 416 352 206 904 472 188 065 661 867 896 548 693 751 889 457 291 010 462 087 405 003 738 121 360 513 557 309 836 258 034 915 562 394 412 946 703 555 407 027 430 281 271 574 732 505 318 534 123 469 582 030 990 201 109 313 288 596 740 511 758 052 097 635 998 806 920 845 461 551 588 509 874 490 421 304 130 237 095 458 514 531 506 343 553 583 436 943 216 364 344 300 494 727 885 228 893 896 805 916 372 685 804 337 789 477 455 563 516 853 300 047 789 435 292 243 669 476 689 790 013 555 755 905 458 763 449 244 384 946 624 042 519 548 610 434 091 983 471 719 374 422 406 560 185 569 910 709 787 144 705 954 976 392 434 506 508 248 299 744 973 990 441 878 664 481 583 836 358 394 256 638 614 921 783 813 873 220 135 489 355 942 654 684 647 005 096 381 275 837 986 873 858 572 920 173 645 917 415 308 412 924 710 778 682 969 882 569 842 999 939 758 264 847 370 358 994 975 953 179 216 074 752 840 530 049 829 477 175 644 567 122 508 266 845 871 975 056 928 707 083 826 813 556 400 947 212 834 665 005 814 127 957 120 311 118 775 477 135 645 465 908 305 139 918 831 190 200 472 151 575 685 184 524 928 552 780 579 071 810 653 836 568 963 101 361 003 092 840 150 809 277 937 209 065 251 380 616 226 219 429 582 824 570 394 282 914 914 066 783 577 337 757 218 897 547 722 675 961 487 909 202 440 442 567 972 528 215 153 670 118 577 122 807 312 863 437 466 816 105 748 027 211 695 408 152 054 539 923 783 037 357 543 414 906 552 825 376 612 508 706 443 913 122 925 627 832 358 401 247 521 696 738 487 724 090 943 246 272 194 493 843 273 732 504 989 842 482 293 941 853 489 212 761 783 822 388 589 648 997 258 837 984 825 763 632 415 704 036 306 726 325 939 079 867 710 750 507 234 566 444 678 454 578 071 647 226 047 940 954 617 603 351 236 861 450 445 925 917 225 642 380 433 734 572 669 249 691 325 658 475 961 784 967 797 197 018 212 476 398 721 069 328 350 564 743 362 497 896 432 467 394 064 436 520 618 572 154 448 572 636 081 794 118 434 972 805 008 043 280 681 110 198 318 326 256 439 765 996 425 438 806 837 945 257 877 625 703 176 958 768 773 078 373 005 393 214 776 349 917 862 441 435 614 791 429 946 922 038 546 258 630 004 316 961 586 723 574 625 904 022 009 863 014 090 348 394 952 962 626 089 895 981 511 364 718 277 685 817 570 426 592 730 813 191 231 746 897 950 179 026 417 809 614 170 456 005 449 198 924 976 750 098 996 943 232 862 741 726 144 517 116 911 630 837 262 687 750 381 213 572 969 800 965 066 922 072 684 479 728 205 333 704 703 228 228 248 610 584 471 821 271 452 164 109 669 675 868 199 914 453 343 192 866 948 238 168 928 793 206 924 931 723 391 755 609 001 921 364 685 354 457 339 903 756 707 601 596 876 217 315 303 122 271 245 468 904 929 154 281 013 352 483 199 916 201 224 127 636 695 024 982 540 207 175 651 072 303 994 335 481 874 929 496 161 339 928 758 768 382 292 345 635 753 921 097 409 469 584 937 378 410 580 942 146 250 693 420 381 545 406 301 406 710 562 008 332 188 940 439 104 167 622 548 170 670 609 056 917 567 120 066 371 615 213 106 208 456 216 304 043 624 922 138 013 271 974 945 085 052 447 987 433 877 073 567 167 370 943 142 217 654 589 515 315 288 709 080 911 811 571 190 040 916 574 398 947 216 809 892 309 954 754 952 632 334 734 788 325 630 575 459 352 464 964 383 516 027 325 743 925 692 535 744 353 291 478 873 519 620 435 270 860 699 314 117 363 037 793 650 926 621 850 120 514 537 074 164 459 166 565 113 334 628 800 251 368 881 220 553 435 006 222 745 348 505 365 505 583 406 024 059 372 149 990 501 945 790 105 460 692 887 999 972 272 218 116 144 741 283 279 537 447 404 225 267 491 352 905 967 601 495 548 744 737 138 577 901 378 699 107 896 635 824 795 901 482 601 906 735 710 448 262 781 829 378 304 729 756 747 342 154 928 726 849 719 537 957 527 658 618 204 417 412 690 591 250 503 692 563 658 714 012 012 049 584 834 170 771 127 132 150 927 364 522 522 303 064 764 822 052 726 479 034 292 609 054 718 561 851 194 242 293 202 563 908 947 202 734 095 991 689 920 610 756 112 967 882 781 321 851 549 769 649 771 974 938 693 233 420 495 508 599 572 787 484 106 056 013 979 578 993 538 025 434 810 168 534 226 169 804 512 688 894 385 216 529 403 676 334 253 881 560 923 383 866 566 836 571 685 349 894 894 451 667 661 750 191 288 283 858 296 255 287 416 142 367 657 713 452 614 234 134 798 172 743 924 334 167 020 915 562 352 135 944 674 018 156 885 523 564 088 388 989 366 632 287 556 847 418 562 325 505 050 021 937 841 789 579 379 187 759 848 639 511 648 702 236 190 979 441 795 603 017 722 959 947 850 991 237 315 702 538 375 986 975 092 698 112 491 005 063 487 586 457 140 334 949 126 615 956 924 142 368 990 927 506 501 532 848 048 191 124 519 731 474 947 179 362 506 695 198 595 767 769 495 452 910 103 529 625 254 526 289 301 439 661 845 550 725 417 978 307 963 243 136 787 127 961 833 757 567 050 608 909 121 733 035 475 841 260 415 228 860 400 677 765 317 936 089 264 171 764 535 932 589 583 841 486 125 377 922 057 446 006 392 743 345 027 353 485 403 693 145 357 123 740 526 481 943 733 008 659 201 081 019 117 551 678 954 083 727 691 354 404 570 141 519 385 417 391 040 162 860 679 447 396 287 845 005 640 758 910 746 645 297 337 073 863 133 512 211 989 999 723 344 777 648 888 503 657 575 125 725 552 775 916 969 002 982 574 652 861 589 818 668 730 902 312 466 648 047 422 617 951 047 101 036 416 640 379 962 717 041 593 118 155 807 072 973 712 639 120 844 455 095 924 804 249 967 900 174 570 971 461 667 291 275 714 356 667 450 436 686 726 424 347 533 911 630 570 267 149 690 346 827 507 017 107 720 363 443 494 774 192 841 443 058 957 181 480 439 814 774 833 215 687 743 996 857 207 125 973 115 496 537 427 644 878 886 596 840 907 357 793 108 874 332 184 806 212 934 095 187 995 612 003 375 372 002 393 077 878 124 393 278 846 159 114 938 822 058 955 832 356 641 781 628 045 085 291 715 429 300 619 082 612 001 561 568 608 352 043 868 004 235 285 778 999 300 941 689 772 969 668 662 808 814 090 470 639 889 757 705 362 120 790 578 598 090 996 647 107 857 998 974 097 726 851 339 207 284 005 798 210 358 730 200 787 254 509 702 383 374 082 898 740 686 141 040 796 880 012 024 028 397 783 811 190 912 464 262 016 696 893 044 596 614 013 363 593 839 837 742 619 167 106 120 858 061 052 331 943 644 184 355 492 868 649 307 404 447 056 219 687 429 201 533 906 308 132 345 118 826 215 135 460 752 563 041 135 395 797 925 263 368 028 570 001 524 356 627 974 336 710 734 229 742 336 202 144 861 243 208 031 371 386 797 532 304 701 498 777 668 822 945 074 092 956 441 300 973 136 506 227 821 767 427 321 784 498 982 842 116 455 904 400 288 523 122 762 449 323 638 228 125 811 948 565 803 399 494 822 471 013 482 398 615 596 034 196 144 887 222 259 939 683 215 375 660 243 313 283 552 871 312 484 672 651 747 755 823 703 292 868 086 857 742 612 127 426 166 679 713 915 005 006 034 937 589 728 852 729 067 093 331 853 621 758 092 235 962 473 027 624 137 066 218 506 389 237 407 390 993 775 354 576 360 684 822 934 666 414 604 401 752 714 397 963 514 756 410 758 465 187 255 773 058 673 232 861 315 070 106 239 702 388 206 218 663 148 874 224 889 745 433 945 919 051 224 114 767 537 053 551 718 197 878 700 528 934 661 047 603 063 954 272 253 892 205 190 595 348 352 192 203 274 766 506 049 058 948 920 586 185 335 456 978 633 077 065 007 638 469 147 036 807 963 009 009 849 580 337 774 265 255 568 724 571 688 237 241 209 059 350 684 798 187 936 384 317 329 191 662 647 563 636 673 966 307 865 112 877 691 634 160 805 817 581 130 562 806 097 525 841 742 360 081 741 215 452 129 912 483 135 192 901 883 101 092 955 919 037 449 134 721 304 617 258 900 230 581 100 949 807 574 117 933 706 558 161 338 477 834 666 529 070 662 475 831 409 088 963 629 129 484 652 794 344 163 869 745 738 365 435 990 933 393 085 191 708 850 603 445 594 472 530 855 225 306 515 700 861 974 146 791 528 832 252 869 613 368 407 825 602 245 210 816 938 106 695 939 981 655 684 866 221 346 637 727 711 848 045 250 303 693 860 372 752 868 068 818 320 568 331 960 214 517 794 391 072 007 508 549 756 266 932 587 191 225 894 094 371 722 201 548 357 747 860 474 067 898 334 752 281 416 156 040 321 882 650 984 546 203 936 155 033 802 307 608 276 478 043 367 733 781 232 332 632 047 394 251 876 276 160 946 462 732 703 174 192 320 204 459 808 405 793 888 444 082 304 814 580 406 763 313 121 453 752 241 653 693 971 455 566 219 209 734 602 328 643 449 860 630 850 295 328 789 755 020 667 611 209 246 569 084 325 966 219 806 512 907 636 502 522 599 792 290 552 018 018 524 113 459 089 181 427 585 581 612 391 545 904 032 087 327 495 209 941 931 108 740 719 938 859 560 838 529 476 358 052 974 839 517 732 330 923 287 329 597 434 139 715 212 574 688 037 512 998 941 360 514 944 410 496 722 551 000 307 940 187 432 443 082 878 684 392 924 440 523 313 237 447 348 781 562 685 294 095 271 028 112 862 748 094 363 790 911 263 802 366 033 317 027 516 538 194 884 473 538 587 033 096 209 027 016 213 093 576 599 637 621 160 755 477 750 964 890 710 656 946 827 548 762 894 854 768 030 534 975 809 054 363 598 093 442 699 913 417 302 935 262 142 813 536 156 510 435 025 634 173 750 484 894 377 028 711 141 261 546 146 538 818 517 064 186 217 480 543 318 387 747 892 487 835 264 993 587 606 694 330 858 559 188 068 341 374 774 074 227 444 145 420 569 628 472 296 082 391 847 870 192 046 090 742 275 792 752 888 065 727 279 285 927 431 048 721 957 090 915 782 097 904 179 444 117 814 650 963 219 508 720 438 364 379 162 775 122 331 315 334 832 554 754 427 703 838 655 328 541 457 502 298 656 726 579 284 757 075 653 721 012 176 422 779 045 344 851 627 217 135 554 394 719 573 188 968 961 120 225 447 925 585 555 161 456 808 914 350 661 293 830 663 513 866 229 822 407 303 216 117 955 046 988 145 546 573 961 824 533 493 642 473 238 884 213 857 046 577 804 588 024 398 036 188 738 889 336 561 678 215 351 606 270 021 213 528 505 474 356 063 879 020 522 993 052 406 827 625 707 835 820 541 918 112 871 105 332 504 858 176 985 619 316 950 253 683 081 243 690 596 825 235 552 376 626 902 728 484 788 341 375 530 591 064 940 103 939 275 790 025 352 269 337 159 610 737 990 138 437 899 067 618 538 772 727 572 575 593 830 751 278 645 735 408 946 515 893 184 489 787 514 191 092 439 448 252 569 439 191 877 329 903 061 159 510 488 089 725 093 468 494 507 902 994 627 117 234 879 494 202 477 462 982 453 232 427 206 041 694 614 773 927 330 455 260 096 124 764 834 975 718 003 791 993 905 213 769 289 437 577 303 211 556 360 174 719 022 262 837 806 642 739 996 541 485 109 028 241 394 369 122 844 480 084 621 548 929 885 887 320 645 045 773 963 454 348 878 622 941 553 732 076 254 696 754 354 651 338 977 363 679 395 942 967 088 426 497 962 436 047 432 754 819 251 247 382 759 154 711 929 112 151 242 532 275 350 501 561 618 229 963 273 748 769 981 037 773 614 609 424 436 073 600 800 536 124 217 657 051 878 111 102 999 708 007 936 660 492 133 960 293 901 717 543 773 099 322 221 964 636 552 215 105 996 924 769 994 584 674 362 107 955 537 900 384 064 352 685 682 210 816 664 226 398 035 672 404 834 369 912 599 749 690 195 584 541 426 355 189 071 424 655 610 724 548 966 369 525 654 489 705 495 555 942 858 224 025 535 580 132 445 902 015 732 369 920 913 615 648 402 753 944 488 740 694 906 490 691 993 306 087 279 637 119 760 107 320 139 407 449 376 232 683 648 193 731 719 309 444 062 214 215 393 060 679 116 277 057 913 093 246 351 327 357 090 059 668 691 268 523 091 776 609 904 348 370 887 267 786 028 226 146 937 529 760 410 322 103 973 719 992 163 340 064 471 560 007 107 749 477 042 934 708 864 600 867 564 968 329 472 563 448 453 166 961 161 040 346 905 836 748 048 192 975 852 038 154 175 375 861 654 809 913 471 833 481 609 170 319 937 283 221 699 308 391 463 083 187 542 993 646 710 908 262 759 446 361 088 254 603 461 965 676 819 644 356 841 016 903 794 487 656 130 640 951 503 224 903 841 912 488 931 603 115 631 647 680 761 671 860 629 431 613 236 218 255 963 260 065 294 957 064 405 175 395 866 019 467 985 157 236 447 167 593 425 992 187 310 547 451 569 827 787 758 564 755 780 841 424 432 089 569 389 175 295 409 737 876 662 538 525 841 022 076 379 126 827 909 104 534 756 457 820 557 642 702 637 214 076 477 527 209 416 899 337 799 894 110 219 915 070 213 470 278 298 331 626 333 959 826 455 360 246 036 837 932 949 129 473 265 521 693 425 093 040 966 766 588 176 533 292 058 976 091 381 707 247 824 767 617 353 737 906 051 652 429 874 818 719 555 885 332 184 001 058 907 984 001 254 140 872 689 015 132 276 485 630 437 895 170 162 381 074 683 111 487 157 130 010 035 729 686 174 072 940 307 633 937 203 687 254 945 055 650 650 115 535 688 062 698 043 967 927 121 006 639 884 316 133 942 788 052 805 653 152 717 974 037 534 976 624 101 453 293 053 913 572 407 569 318 497 511 550 167 039 031 108 110 216 125 601 395 414 715 637 408 189 348 533 709 048 133 758 675 127 975 032 275 906 583 110 385 886 797 042 613 938 166 420 611 743 152 172 977 604 415 758 183 461 373 996 738 544 642 388 875 231 324 526 454 227 311 422 221 631 138 391 264 924 380 890 447 327 288 024 664 648 478 296 617 344 683 292 325 171 381 282 764 382 271 443 962 271 474 699 280 775 312 011 085 156 081 113 587 849 862 374 779 409 530 484 987 412 223 391 904 614 064 373 907 699 600 621 128 125 766 887 489 016 139 375 101 676 138 981 010 453 875 567 900 880 038 586 616 738 389 526 680 388 114 514 092 948 866 729 491 407 779 736 623 333 629 711 035 859 238 304 255 810 995 184 742 900 030 882 893 287 167 624 935 781 059 373 732 649 130 729 526 856 310 789 831 400 664 568 468 973 590 673 582 621 099 413 749 944 126 123 220 291 110 964 808 169 215 017 512 959 614 856 811 723 926 711 080 663 157 342 329 778 599 885 080 371 796 042 182 310 256 692 420 945 655 037 157 209 140 139 845 960 403 167 290 336 832 750 525 446 470 021 547 391 421 634 953 681 177 302 244 753 517 820 067 012 253 854 250 726 327 762 175 202 815 452 743 492 908 403 412 080 652 765 324 621 213 501 598 298 182 624 060 572 803 634 833 517 215 695 191 604 364 602 443 421 830 435 328 524 704 749 404 291 325 339 428 197 253 832 575 122 509 887 326 780 191 198 860 983 588 040 746 153 961 434 450 662 658 500 874 197 386 055 904 773 309 954 511 298 089 557 595 910 485 869 407 586 837 646 350 336 812 252 548 216 917 737 153 254 677 932 965 117 471 774 816 671 386 135 450 410 129 343 519 560 295 860 186 993 980 352 511 467 689 979 619 762 637 948 979 190 530 515 010 397 163 023 278 682 949 698 593 511 302 876 154 968 136 977 997 381 544 898 512 488 901 890 874 526 574 734 142 450 793 112 612 341 677 369 041 583 490 549 389 989 260 965 099 379 278 161 894 367 290 610 062 900 473 573 387 903 060 234 131 695 202 487 866 705 218 445 660 811 878 678 651 839 159 477 835 107 353 969 584 818 814 878 155 748 524 319 346 053 843 128 839 078 260 710 890 936 411 005 762 019 392 045 805 310 307 098 896 763 335 859 455 627 334 043 198 041 077 615 669 726 492 546 445 694 275 674 623 732 449 578 908 128 891 833 755 999 414 320 179 555 243 241 398 481 620 187 921 066 343 319 345 975 937 505 774 378 022 349 959 257 608 087 345 124 020 291 297 579 187 210 757 020 998 253 481 950 996 425 437 477 116 949 842 739 124 753 885 616 078 084 422 236 190 266 051 641 786 681 755 697 566 118 610 225 190 237 895 042 787 967 149 055 060 676 436 327 984 228 617 558 933 821 346 726 982 526 510 915 095 078 805 576 838 577 009 309 488 378 543 216 266 558 961 212 802 500 144 985 265 984 940 751 128 523 890 543 008 446 098 833 465 061 924 954 178 216 866 824 711 427 607 885 549 399 918 993 782 622 570 944 854 823 739 721 655 309 927 275 431 055 907 710 150 048 607 163 175 098 497 987 101 477 626 845 810 939 107 184 565 912 660 081 465 357 711 409 267 322 637 477 175 757 900 715 017 339 446 290 240 798 434 918 798 165 280 152 231 587 691 705 375 810 225 033 763 085 263 620 700 720 675 658 819 636 589 927 550 775 120 780 386 167 253 734 973 770 008 306 061 805 034 728 533 708 567 348 356 720 989 604 046 265 632 991 440 579 540 734 780 857 262 025 996 865 782 936 392 712 043 374 547 036 234 724 932 123 076 241 118 446 486 705 192 172 061 265 538 003 909 272 248 786 909 410 068 625 308 840 324 157 255 999 079 807 021 161 589 676 226 678 003 024 886 637 655 400 839 082 041 376 258 884 560 427 971 047 091 350 800 341 348 783 642 869 018 319 817 661 456 348 134 959 522 154 480 961 634 683 999 675 411 757 169 902 478 072 605 322 283 076 177 720 779 213 422 005 925 670 574 737 848 302 874 233 767 231 111 279 006 958 833 928 272 147 426 744 357 432 692 872 730 190 488 675 791 208 103 676 800 036 099 556 362 471 986 483 194 076 411 783 727 878 214 704 531 084 167 708 012 941 692 413 393 008 103 375 576 367 724 476 182 538 469 781 525 322 233 191 602 584 719 235 808 133 704 548 940 978 769 249 283 352 768 160 459 149 377 551 877 021 674 113 014 505 438 181 684 452 141 339 324 685 788 464 923 109 518 779 952 099 306 161 910 809 329 721 702 143 588 224 466 284 527 523 802 365 511 759 187 715 554 193 405 934 353 540 004 798 910 134 123 682 430 677 123 596 190 922 415 541 504 066 850 652 635 632 869 210 517 675 766 026 114 463 291 522 578 469 342 283 746 505 840 921 508 829 921 881 487 740 498 256 619 224 706 933 892 666 675 493 454 775 582 396 369 293 870 876 845 416 132 712 369 013 808 137 277 740 921 007 030 324 815 748 561 641 244 157 232 521 630 438 404 880 745 215 757 887 485 979 009 690 468 013 621 525 170 182 979 555 837 658 812 638 068 534 172 580 062 317 503 898 761 704 626 762 852 650 253 768 533 816 839 526 032 001 460 020 849 036 310 459 319 935 324 443 882 689 434 056 152 313 666 400 038 434 248 823 396 986 254 869 542 581 261 633 568 315 260 053 622 582 976 345 611 997 229 228 261 364 969 338 554 248 878 347 599 590 844 042 817 140 328 688 175 779 395 492 038 027 644 916 244 003 487 229 141 668 159 945 479 665 682 984 371 461 169 046 436 262 637 666 415 349 820 025 608 727 787 201 135 898 649 326 689 745 237 799 926 996 930 163 773 232 571 432 196 236 220 054 052 515 604 263 672 910 375 153 769 102 349 081 433 836 543 832 196 073 083 571 295 157 931 209 191 010 161 824 517 649 809 324 210 245 767 698 069 755 923 302 405 962 039 176 338 474 933 234 224 730 940 552 139 433 928 277 433 635 408 088 991 372 827 657 690 276 478 940 167 923 183 456 929 467 862 259 572 146 293 008 065 548 780 514 623 539 541 947 158 902 031 624 376 746 041 153 066 661 492 040 192 226 579 002 545 175 044 716 254 998 306 459 723 197 978 308 203 423 135 060 031 300 264 616 167 215 250 974 989 053 068 010 660 857 632 196 864 951 859 174 349 686 086 672 817 776 639 578 222 113 181 209 155 192 978 329 750 035 063 559 182 336 897 363 735 948 410 115 528 538 056 531 119 997 255 244 209 316 017 659 432 185 519 690 390 735 714 741 658 181 218 864 401 693 770 629 356 969 517 884 585 784 848 168 270 905 499 113 111 909 170 393 962 316 092 349 258 136 642 760 595 337 316 165 793 280 604 275 977 092 337 794 751 576 554 537 317 144 044 916 492 525 591 033 538 894 812 319 570 622 183 490 738 185 178 778 579 462 588 108 194 185 060 852 434 390 690 162 612 913 099 938 845 430 124 072 251 057 692 401 764 516 297 791 039 239 980 495 884 596 193 528 380 453 961 950 098 146 158 352 502 653 183 399 291 279 169 533 626 220 377 561 629 327 501 279 118 131 873 125 233 549 671 558 814 424 212 098 663 990 402 690 198 945 571 165 939 342 633 776 471 066 681 866 954 728 850 798 566 434 912 227 098 314 945 662 259 631 466 391 722 380 381 236 766 842 920 242 538 976 199 149 626 081 402 961 978 073 780 565 831 307 418 827 997 511 924 107 993 642 642 224 753 677 179 578 037 393 816 702 869 978 756 590 286 509 754 898 486 598 925 461 462 917 501 028 028 714 370 663 007 442 349 741 366 144 306 405 723 203 246 217 593 170 103 612 184 331 101 555 370 109 822 019 019 483 191 821 757 963 322 838 146 972 349 455 709 592 050 006 797 534 942 333 559 540 232 470 920 063 426 567 047 835 188 843 402 803 743 756 613 898 662 778 541 557 239 767 315 673 542 053 655 644 421 404 481 617 094 190 888 266 027 716 524 631 778 071 565 458 404 918 618 009 761 651 438 518 701 626 080 527 731 747 089 865 847 317 911 956 743 080 484 265 687 775 976 264 231 598 713 951 008 764 995 582 079 081 269 319 309 643 488 938 871 987 526 219 584 813 351 881 987 550 032 152 442 831 587 417 201 457 474 052 219 755 608 818 663 376 965 747 893 434 507 294 617 102 821 308 113 952 456 617 612 362 871 861 607 087 240 924 855 166 353 205 838 385 795 640 388 635 480 692 939 583 435 121 755 687 868 210 372 134 609 468 575 585 446 772 760 819 758 695 868 735 695 267 464 896 516 672 096 408 930 010 276 053 515 776 743 561 440 488 944 569 448 513 966 670 137 891 177 054 819 739 500 731 347 522 017 164 174 685 854 276 751 876 631 693 445 791 057 632 148 653 283 714 890 015 621 251 295 722 108 599 738 357 907 743 931 425 350 889 521 104 978 670 722 735 723 931 614 463 285 890 313 499 053 705 528 463 459 111 031 621 838 228 155 924 848 249 728 008 263 137 474 504 397 676 520 460 476 685 571 265 172 472 103 464 509 219 509 523 418 215 226 972 065 190 683 951 267 226 647 311 178 587 276 049 757 530 933 978 289 044 552 209 968 681 059 541 887 499 153 826 006 789 120 227 254 370 162 696 909 929 083 044 264 625 137 678 303 255 919 083 435 962 729 808 957 242 688 491 219 168 579 158 938 292 122 979 703 473 628 100 408 559 213 948 496 773 482 316 185 796 618 775 220 203 448 821 274 374 476 142 987 542 976 489 410 249 821 452 532 295 062 713 640 874 791 631 992 216 828 687 320 657 358 874 076 335 397 635 188 064 080 438 342 423 119 642 260 159 723 742 117 635 681 997 849 818 366 851 529 999 806 797 366 094 525 992 795 740 193 246 899 029 316 591 037 514 090 811 039 717 221 391 156 997 571 333 646 292 399 365 290 160 332 018 382 499 896 444 318 859 137 777 715 086 548 546 945 487 002 874 281 417 111 985 729 255 323 282 531 527 489 264 556 058 027 470 061 785 900 588 045 133 100 810 687 631 887 473 210 416 178 426 823 448 901 410 919 935 951 323 856 637 182 656 334 244 071 327 346 860 484 107 883 488 627 636 270 474 161 310 981 718 111 328 525 964 405 095 164 366 216 940 893 757 505 580 338 379 722 294 157 082 258 243 077 973 355 478 488 084 533 436 090 562 625 454 001 909 405 807 094 686 036 067 073 813 049 770 002 186 172 924 310 980 269 989 442 693 781 011 629 951 353 590 691 732 405 668 574 301 055 168 612 044 053 935 869 060 533 662 047 197 645 276 801 026 312 481 396 663 937 639 200 623 299 010 032 398 077 316 250 866 337 577 775 401 089 729 922 569 031 516 246 587 533 519 871 901 075 959 367 481 824 458 625 970 174 499 856 725 863 924 697 240 408 815 345 709 499 545 590 104 623 958 225 358 756 702 006 695 460 265 115 530 193 865 372 629 444 558 561 740 506 046 463 217 773 816 767 334 288 707 972 349 496 304 768 750 437 822 251 741 974 606 140 586 281 105 214 299 029 969 148 272 960 910 026 013 268 580 253 287 746 060 657 197 706 776 580 502 497 171 586 433 579 147 583 928 241 787 892 612 492 701 580 799 502 046 041 357 506 849 210 290 470 767 440 315 227 593 101 753 721 526 656 780 531 972 241 117 728 188 763 552 706 259 658 539 309 146 532 453 809 836 966 177 498 913 276 018 210 094 046 651 431 061 913 925 368 153 983 436 407 223 617 129 653 203 560 036 373 682 646 978 527 235 667 234 056 493 203 235 693 836 539 009 952 141 978 517 133 636 385 399 918 943 990 423 138 614 933 284 529 021 115 155 361 599 916 040 552 045 971 381 706 217 460 922 197 959 738 323 498 233 385 050 690 557 437 979 171 797 358 495 330 076 427 144 989 114 696 398 456 602 202 536 108 502 546 569 213 566 302 331 661 003 429 241 178 372 321 736 993 290 136 906 605 947 281 637 447 867 310 741 415 205 548 305 515 106 983 988 046 418 845 338 887 474 187 587 836 954 850 181 468 453 000 800 490 534 431 838 822 518 910 206 691 034 893 443 183 395 518 908 954 413 970 240 515 685 341 405 890 956 973 330 557 948 362 761 782 126 448 492 663 898 566 896 843 497 913 704 217 026 956 222 816 010 165 132 874 084 488 593 316 373 500 493 443 853 829 701 422 618 984 337 618 043 066 535 855 748 531 237 237 324 336 501 227 826 318 349 703 948 197 281 818 973 015 577 260 536 849 055 105 549 906 693 501 730 061 582 946 264 861 872 889 811 456 411 007 258 690 688 915 446 213 652 182 238 211 216 901 730 456 769 449 754 106 171 779 811 097 247 893 916 256 788 992 711 142 876 338 373 281 883 937 847 499 839 323 098 580 733 796 588 447 828 149 407 296 895 561 715 227 739 067 739 068 066 744 110 122 735 269 580 778 691 993 725 360 539 376 926 371 031 938 621 817 087 885 679 442 483 545 477 877 076 659 984 420 714 507 524 237 993 756 050 113 905 349 682 891 529 064 102 246 337 829 699 594 712 261 673 825 399 631 041 299 020 886 868 001 903 214 591 333 837 067 808 592 136 272 438 661 680 899 693 048 537 271 849 622 925 943 909 075 579 399 611 459 535 614 866 520 639 078 416 917 044 460 624 877 713 923 839 129 448 777 657 529 233 353 486 291 044 201 741 060 720 434 106 258 638 289 258 632 125 432 598 842 151 076 272 126 334 726 750 943 876 491 183 912 268 992 376 803 948 827 669 139 982 651 564 092 426 214 926 725 571 726 657 765 289 516 037 997 171 456 402 783 118 741 974 498 453 874 108 989 488 792 892 763 124 281 331 887 206 686 587 743 922 244 767 105 218 379 119 058 025 595 541 301 935 461 758 816 328 701 257 722 956 282 818 686 093 145 881 602 690 284 470 875 813 228 773 133 354 620 453 130 178 117 653 958 420 313 818 803 562 073 137 593 792 511 268 584 868 981 660 341 021 864 852 622 347 323 890 725 584 176 480 305 739 457 109 168 453 301 220 418 296 453 491 892 870 834 748 097 113 390 962 550 933 225 072 453 927 280 651 367 243 641 088 297 189 175 489 528 649 450 567 219 326 995 130 695 378 675 426 582 317 255 858 069 493 574 466 976 590 443 422 071 232 415 902 286 109 108 548 719 221 047 251 365 436 489 452 583 888 435 510 313 231 423 804 322 543 156 595 618 291 483 864 772 041 170 361 950 553 922 035 773 229 887 047 340 103 996 674 286 767 563 639 484 013 312 516 044 365 934 950 908 404 141 837 880 056 453 901 154 617 170 776 335 238 670 653 893 349 336 502 282 915 956 776 568 304 611 005 644 701 240 256 513 020 659 108 866 050 368 166 636 054 340 812 402 786 777 083 166 021 919 411 083 901 236 568 882 720 692 538 639 661 056 251 064 947 862 408 999 755 469 737 515 986 422 612 779 202 379 750 778 090 393 760 091 962 943 290 037 231 811 070 491 748 124 701 657 538 085 022 321 346 025 123 481 721 377 997 449 434 959 746 194 048 388 398 418 846 111 594 511 405 466 182 256 258 891 803 995 758 102 688 915 366 346 038 085 153 701 363 593 111 117 126 941 863 858 538 021 925 477 461 466 392 402 802 693 979 654 405 186 360 615 721 901 517 008 809 475 626 539 085 797 070 722 547 676 182 646 046 404 152 336 747 891 490 571 118 928 833 143 426 593 066 831 216 240 462 324 388 408 576 579 411 019 045 301 811 093 986 248 433 841 762 769 212 662 059 637 727 202 045 530 165 762 233 732 726 495 493 528 515 490 710 581 004 280 774 138 380 013 891 208 864 052 690 672 584 388 302 987 747 294 578 839 335 618 574 310 755 837 018 151 080 014 669 951 738 881 580 518 401 145 185 198 202 886 487 260 031 049 245 995 353 940 816 229 205 341 305 793 254 451 828 974 750 185 090 163 090 061 376 675 551 920 689 809 723 084 304 034 879 817 012 187 833 770 486 816 867 870 289 410 792 944 508 283 116 784 312 323 654 253 471 998 919 592 191 731 581 400 822 355 151 642 887 686 770 191 100 557 145 319 826 821 407 605 771 213 040 024 985 509 902 913 215 409 312 661 768 806 747 199 919 959 262 387 583 822 446 345 590 838 059 509 971 143 034 922 348 853 215 844 600 109 496 791 060 428 653 246 853 704 366 682 753 517 108 343 458 654 106 539 169 134 752 091 134 636 540 984 631 676 920 574 053 177 307 898 463 004 566 979 755 560 413 669 609 024 425 468 664 739 750 477 319 975 148 986 566 630 809 177 358 296 759 299 018 410 844 571 295 800 694 629 044 727 388 935 098 832 287 196 203 518 375 140 499 776 284 401 655 338 813 942 351 587 534 798 695 557 826 907 822 943 888 483 331 875 445 857 496 996 716 105 714 520 981 960 205 099 887 010 931 819 910 635 524 389 987 858 421 865 611 107 432 467 615 176 999 893 400 960 207 692 178 306 377 985 935 058 056 758 505 817 144 877 307 196 874 574 833 292 825 708 323 498 448 033 548 412 399 816 315 640 565 359 155 876 844 453 935 345 192 185 341 525 440 693 698 591 858 158 074 650 287 011 167 233 820 012 960 320 565 394 746 075 459 965 575 839 677 214 548 218 087 049 619 628 550 388 773 019 164 748 364 475 754 225 452 048 660 367 319 223 023 217 816 913 474 014 650 519 177 228 673 896 292 811 369 968 282 526 671 153 824 054 280 969 031 998 951 012 437 422 975 168 542 299 763 759 043 110 597 425 351 317 682 467 632 817 749 132 775 564 846 547 681 149 352 065 117 408 057 124 641 044 506 689 887 874 901 481 338 461 133 076 413 901 781 851 328 214 199 854 591 311 452 287 098 385 966 614 635 545 437 844 824 883 996 880 241 635 925 688 075 677 483 156 543 625 394 258 200 146 667 235 122 518 134 002 160 088 974 776 557 238 125 344 717 710 918 875 221 501 359 947 776 608 593 748 734 284 813 324 584 145 965 672 291 765 700 395 698 839 270 441 247 774 443 950 210 193 414 051 522 964 315 635 798 999 443 006 554 070 063 945 988 710 184 837 471 275 594 111 935 441 633 436 939 793 556 623 932 514 087 800 233 508 058 316 019 831 658 116 849 964 533 292 194 698 752 549 497 727 569 181 803 614 014 154 371 967 090 989 532 690 185 746 951 162 100 410 333 588 539 314 237 488 945 564 874 079 243 315 626 335 682 083 011 608 441 766 400 402 389 776 126 088 533 920 966 471 621 580 748 793 928 549 877 226 890 875 698 602 571 134 999 887 775 327 258 471 017 987 743 276 300 717 557 951 264 520 856 447 577 059 280 212 692 283 276 737 117 578 040 582 239 909 005 236 755 613 040 064 342 944 534 080 343 596 685 728 920 138 074 494 367 802 821 158 040 054 057 290 479 056 429 020 552 630 176 302 843 191 199 439 211 498 698 647 409 080 006 973 153 628 225 462 519 718 440 726 513 472 698 111 756 954 806 153 869 004 967 865 603 202 291 177 999 409 717 894 233 824 616 697 452 825 424 737 215 641 950 370 499 005 696 118 253 728 082 154 448 590 942 518 915 693 461 436 243 051 521 941 236 918 175 869 286 453 655 283 380 647 391 848 751 927 901 193 425 670 092 128 495 673 204 777 638 728 568 637 661 540 213 723 647 583 394 612 136 855 287 383 382 338 640 966 751 547 868 285 493 062 144 917 098 223 990 177 512 637 441 672 809 526 702 732 834 528 614 408 688 869 240 198 114 241 750 583 624 507 540 255 148 226 132 440 910 645 767 483 836 711 814 833 815 051 256 365 999 240 008 672 104 313 322 795 395 493 931 694 946 426 388 342 059 389 172 276 635 112 475 283 413 519 313 775 330 829 346 774 049 827 518 800 445 910 153 508 218 310 305 894 683 641 115 544 654 629 626 504 047 457 228 584 804 670 430 587 686 421 927 112 345 872 543 862 158 065 279 869 569 563 577 119 914 233 077 830 499 890 407 776 173 345 701 298 125 409 730 037 837 361 117 568 588 055 908 651 760 692 495 496 992 385 673 281 564 398 932 785 361 441 845 607 147 833 520 497 551 788 424 924 110 776 578 833 922 447 035 684 456 871 651 157 971 645 882 875 803 661 022 274 287 345 680 429 566 719 045 764 912 024 149 134 184 090 596 496 242 912 492 320 945 053 350 014 508 633 924 398 955 018 442 662 643 633 140 487 831 969 774 764 207 000 653 703 722 207 781 764 313 437 491 203 224 825 089 192 261 629 026 909 764 858 252 286 882 748 705 978 496 786 190 084 130 563 693 521 072 521 605 997 151 967 567 157 217 035 806 392 802 748 941 387 885 834 124 608 256 781 264 078 808 482 620 911 630 175 370 333 076 386 019 846 227 332 859 148 098 773 483 462 383 397 153 178 889 199 492 548 221 980 782 582 022 237 852 552 773 494 905 400 149 499 590 017 096 070 312 478 056 608 893 496 215 253 432 425 212 135 940 349 038 605 355 870 225 691 155 351 203 896 350 489 392 419 559 926 147 273 010 518 642 354 059 401 461 029 810 306 503 784 869 958 500 604 225 736 880 215 154 201 334 646 926 157 696 536 841 688 158 005 793 718 264 638 528 265 156 690 688 163 846 696 461 263 230 710 403 005 621 029 732 082 105 833 144 391 340 776 179 324 565 141 569 873 934 331 301 470 106 753 573 524 696 094 104 217 283 272 753 668 899 346 516 288 295 849 477 760 738 742 509 969 780 474 647 950 422 615 296 826 285 503 169 689 969 173 180 620 616 072 783 967 927 316 539 955 524 258 847 282 020 182 089 132 489 324 406 178 167 569 865 885 387 443 895 812 605 515 566 138 052 435 483 841 959 205 292 884 203 691 919 406 514 405 169 870 124 337 376 759 523 594 778 841 560 047 305 795 811 705 390 109 688 355 607 039 368 524 985 590 547 402 091 807 034 197 423 152 864 953 436 034 647 063 039 357 530 683 574 129 933 043 428 683 456 676 564 736 897 295 589 962 367 017 764 100 311 844 832 292 188 300 669 704 354 370 377 545 256 448 132 060 930 961 570 962 614 632 722 016 055 118 830 416 972 222 147 962 831 976 035 751 143 760 858 935 493 461 681 014 625 775 696 546 390 531 457 623 130 360 861 450 667 715 652 872 357 540 235 630 225 593 952 923 296 077 086 977 724 398 568 930 699 759 034 726 363 337 894 039 855 254 486 870 882 295 537 430 003 709 728 436 925 160 136 447 360 241 973 937 791 134 832 465 405 032 425 353 830 464 392 763 697 546 680 958 723 650 665 921 867 957 544 565 172 663 891 152 874 732 127 971 355 561 418 294 571 518 951 013 427 769 069 800 550 002 101 315 306 490 029 508 869 963 952 876 653 369 134 701 460 088 620 706 911 151 518 088 952 280 688 259 636 270 418 901 006 463 343 241 326 120 550 837 619 209 762 160 192 940 327 640 143 936 334 487 182 518 896 767 305 989 175 424 332 716 333 002 308 434 948 407 730 368 135 746 542 599 275 748 083 299 599 609 284 883 131 038 260 908 982 999 739 288 044 648 444 020 082 174 473 572 831 541 530 881 020 754 477 052 524 778 744 879 139 974 242 705 083 470 324 052 467 789 945 879 092 193 952 938 485 267 317 728 550 458 649 704 008 652 568 680 156 458 476 365 042 369 368 630 933 933 042 546 102 548 657 429 181 008 183 997 703 096 123 538 508 867 795 394 154 385 211 427 472 603 523 993 047 027 372 176 826 295 054 862 729 033 937 066 586 078 304 833 810 209 416 250 337 868 713 547 040 467 630 997 921 291 859 032 627 332 252 635 570 838 320 305 530 193 711 629 191 369 328 466 131 658 201 926 254 154 826 101 033 207 466 229 327 651 555 989 854 746 339 834 825 061 831 091 728 550 293 220 470 320 701 489 943 774 148 597 538 051 845 934 362 034 191 042 624 253 089 452 810 354 098 164 384 575 890 937 347 922 219 925 664 558 148 636 061 870 243 253 495 430 555 918 849 556 987 147 737 518 684 675 624 769 823 538 471 066 647 785 665 865 558 287 774 463 253 395 265 923 519 646 578 499 841 607 880 278 226 291 741 301 896 728 390 942 329 812 033 546 618 985 198 467 829 491 449 982 229 612 931 241 972 150 746 157 561 894 334 728 409 707 335 401 717 032 630 321 129 751 769 713 774 474 320 312 241 376 366 976 850 579 442 317 364 646 954 288 850 365 163 028 403 647 029 588 577 240 422 880 451 379 322 316 065 371 958 745 934 536 798 423 911 555 546 621 607 148 722 639 237 392 590 239 157 270 121 147 919 410 576 902 724 640 451 715 050 538 951 220 898 210 960 896 453 116 200 891 131 997 592 794 705 193 234 047 628 097 134 082 147 631 070 427 902 916 964 732 731 687 184 729 578 761 473 896 904 312 178 329 834 750 324 080 943 457 796 486 457 480 138 191 406 563 969 902 052 460 369 146 222 194 046 643 481 666 034 677 752 307 672 270 889 843 854 284 946 682 897 122 750 885 568 553 275 685 383 031 300 680 444 200 526 298 946 802 376 807 958 854 000 479 186 908 332 112 300 108 856 888 666 417 322 767 544 033 852 064 592 127 715 567 199 969 305 602 522 812 106 999 381 497 163 432 914 540 682 509 631 847 678 340 019 621 378 584 450 847 913 856 308 269 242 208 484 493 938 110 368 643 745 280 118 040 124 963 302 157 284 360 459 224 206 114 862 264 658 710 150 308 330 831 457 002 946 280 439 617 826 121 742 179 901 303 699 104 409 485 690 201 470 785 039 008 001 725 542 337 398 001 178 885 266 539 617 409 741 287 118 948 112 062 886 393 693 315 792 649 178 170 767 221 673 621 201 134 636 750 304 727 491 477 690 431 991 474 501 724 245 897 224 916 201 877 235 300 467 117 196 561 203 797 229 863 586 390 643 938 708 133 637 432 564 858 685 238 250 670 117 171 472 636 194 849 083 354 232 534 814 683 430 023 120 974 891 796 751 116 229 317 751 116 542 105 865 392 324 489 307 001 023 950 880 255 826 321 875 864 019 997 292 802 694 452 734 208 797 289 017 335 319 046 849 134 938 076 116 458 388 797 317 849 321 546 224 665 279 393 074 627 383 721 256 492 704 076 914 510 630 307 680 937 485 220 782 129 937 023 019 567 909 409 588 611 285 701 548 700 375 543 832 427 472 337 793 161 334 846 426 241 768 513 681 412 934 452 509 627 112 955 456 350 599 778 051 415 648 471 755 919 137 485 264 551 184 879 796 834 415 221 869 401 159 408 081 679 715 485 438 396 793 143 068 660 925 891 695 878 553 980 024 883 222 331 349 505 946 352 421 449 529 341 572 872 806 175 154 246 137 447 616 439 863 963 577 485 825 220 730 563 326 279 897 536 004 961 649 935 792 287 541 716 183 827 213 145 899 573 350 051 131 706 188 091 763 431 396 569 359 231 934 561 695 741 072 443 702 932 052 193 024 749 853 513 249 486 503 230 157 398 015 054 942 297 017 972 362 264 611 786 508 762 825 362 560 888 008 758 304 234 366 016 489 017 310 069 858 298 160 835 753 869 835 521 251 398 228 397 660 315 367 326 982 847 030 754 249 024 767 829 269 650 525 254 755 973 424 394 700 874 688 938 436 241 690 656 385 261 609 414 292 948 111 461 186 611 472 371 710 507 656 896 710 461 277 613 002 645 801 597 707 720 253 990 463 949 305 304 725 952 467 893 357 609 189 495 668 851 237 614 639 710 644 402 664 820 844 017 743 639 748 361 682 093 251 021 332 020 867 601 899 172 488 772 321 592 236 649 914 926 367 538 718 390 014 100 162 829 781 220 045 906 086 220 255 133 841 505 696 617 861 027 808 614 251 926 391 315 359 035 476 891 403 213 265 270 774 153 404 075 327 371 932 519 026 751 043 741 235 607 917 838 581 130 708 925 714 757 217 830 625 057 123 961 097 337 159 664 956 721 182 068 755 773 650 307 444 195 811 386 868 193 638 366 683 362 969 219 481 981 072 550 899 507 197 767 869 615 084 152 288 224 327 817 761 981 297 664 852 048 701 455 433 047 673 742 898 394 773 106 020 804 979 913 523 742 048 447 965 731 603 074 013 850 848 488 669 773 991 404 063 257 150 881 942 835 692 443 572 906 083 756 932 242 886 743 169 310 707 203 592 765 933 757 233 727 302 538 595 008 920 226 705 973 968 860 160 223 679 485 137 415 976 937 756 453 529 847 312 973 299 355 676 451 499 855 882 887 591 141 678 851 565 404 858 714 407 566 350 408 261 728 132 350 292 757 785 374 709 232 304 197 132 931 183 550 757 840 108 868 262 780 396 567 835 555 061 556 733 110 136 234 911 091 313 231 781 843 599 837 767 322 413 506 222 525 108 217 922 491 181 381 664 657 242 241 983 904 511 915 133 444 689 042 058 522 383 849 563 405 407 341 265 576 674 493 437 017 727 757 350 674 931 858 968 065 426 058 070 686 626 426 260 609 421 910 923 465 469 965 772 947 587 451 906 134 538 453 446 771 854 315 053 283 157 796 789 991 535 900 565 340 624 299 200 460 826 573 174 945 588 109 975 125 775 200 321 498 244 601 057 166 544 379 713 464 464 436 896 034 522 139 934 334 480 704 682 612 069 978 701 731 841 744 732 574 536 447 919 913 667 589 738 229 425 675 796 726 123 701 655 113 395 234 809 243 143 714 309 072 123 985 509 278 018 586 658 202 121 528 382 040 795 060 020 410 841 422 433 805 784 313 168 227 138 576 407 387 051 541 627 104 310 097 322 946 363 966 838 313 866 572 479 442 657 885 759 530 659 832 525 511 545 789 437 972 875 617 159 899 720 400 660 097 644 786 590 214 839 765 232 340 241 082 312 502 455 576 354 248 478 117 197 899 114 733 891 735 057 926 386 781 707 891 858 106 929 061 399 031 075 771 934 220 140 132 106 611 692 529 164 031 948 723 325 539 627 231 355 549 078 424 891 687 489 400 240 059 930 267 018 357 677 945 728 712 401 951 554 446 612 874 655 727 908 370 614 957 161 523 838 708 598 089 557 827 163 914 517 520 336 891 486 209 872 495 256 399 607 822 473 966 878 124 830 955 529 791 736 674 625 012 668 451 699 802 338 821 775 358 477 407 965 464 818 254 534 642 047 719 613 962 013 424 846 900 702 082 129 360 485 184 964 630 931 304 681 509 343 131 994 111 533 943 373 435 127 567 940 488 875 229 290 996 375 760 897 171 800 114 020 342 906 489 106 406 851 380 284 853 042 825 534 993 831 830 797 704 562 926 541 959 237 557 364 036 731 297 929 489 887 110 042 501 446 392 464 936 305 618 704 609 529 840 232 790 206 698 696 153 394 895 811 630 387 136 035 191 994 588 520 131 962 858 668 104 102 440 161 375 045 001 063 451 599 581 961 203 727 224 949 757 862 370 653 876 195 685 227 118 057 550 896 681 782 396 827 196 246 302 501 389 342 213 857 977 490 115 297 331 261 098 609 793 600 495 618 414 381 008 530 032 001 600 443 943 893 802 250 915 156 919 300 839 795 427 013 380 844 901 396 177 789 334 745 427 388 170 728 037 299 427 190 085 591 961 768 788 327 728 220 041 425 334 088 860 712 336 300 264 010 635 590 656 928 471 861 712 320 882 618 116 672 185 275 899 170 384 385 402 018 869 989 176 759 604 157 926 175 097 894 951 382 366 471 073 554 433 786 055 580 481 268 889 820 475 623 261 289 384 015 189 994 495 902 958 409 931 212 112 740 743 911 066 348 515 964 121 375 442 264 504 310 843 384 724 951 183 028 168 986 810 127 865 695 786 977 440 312 168 831 595 588 486 367 374 321 582 589 654 934 634 562 323 215 303 532 951 881 342 383 921 036 224 724 865 570 555 784 800 724 414 284 857 298 902 896 768 805 491 203 593 177 145 808 541 749 928 563 875 935 051 789 491 533 693 033 485 792 584 670 236 333 805 000 217 550 409 639 073 335 925 228 276 143 029 057 512 205 489 018 419 516 630 125 775 524 964 062 748 898 708 657 936 333 881 199 963 714 438 101 284 965 614 668 353 133 100 782 613 997 466 051 931 146 953 737 957 147 680 479 590 459 329 244 163 496 437 476 257 108 331 837 767 172 229 202 019 925 142 161 640 625 966 794 636 634 766 118 980 192 155 690 349 800 036 860 185 321 851 776 664 632 756 426 169 803 668 186 335 507 605 914 294 620 936 308 443 043 307 033 462 249 540 087 278 541 956 823 233 089 639 453 481 180 264 672 048 529 958 703 500 546 482 853 386 502 022 647 493 703 790 814 482 670 852 136 152 704 532 456 769 860 374 250 484 064 985 614 640 622 296 922 668 012 299 309 407 624 883 598 619 003 660 504 608 577 367 503 849 113 952 241 077 512 495 356 024 339 903 570 021 675 009 135 678 843 630 544 387 305 369 320 896 463 083 670 496 082 908 690 853 172 076 874 347 008 098 825 009 440 884 733 006 368 864 390 419 572 669 394 338 087 150 362 115 795 207 657 183 313 341 475 080 858 609 427 851 221 888 641 668 675 155 390 249 145 464 663 289 847 550 385 878 318 266 994 345 836 711 515 416 719 264 699 167 171 803 555 730 501 303 211 799 077 445 381 079 519 001 453 413 173 320 120 813 333 332 378 930 838 062 510 893 882 713 104 803 986 677 814 702 009 392 577 376 922 729 246 299 981 146 517 925 600 223 069 108 760 655 802 300 793 174 634 791 857 245 299 365 233 814 763 862 238 598 870 779 705 921 831 942 624 494 769 430 793 805 468 860 504 329 371 256 636 888 900 097 020 832 024 732 635 945 159 788 647 187 822 206 649 951 637 805 830 371 818 771 880 598 161 706 486 537 935 531 263 569 919 036 239 702 196 641 731 902 413 301 197 801 395 429 514 318 937 359 294 601 042 957 760 003 349 629 989 629 943 187 673 234 396 084 056 380 646 749 826 684 868 488 755 106 541 182 130 800 123 989 027 338 724 868 531 123 404 525 610 923 303 967 446 773 995 642 156 362 619 378 289 490 728 546 958 840 894 592 241 918 126 486 071 079 500 724 456 684 237 080 533 280 848 923 924 524 903 947 036 083 723 044 803 452 914 825 479 352 555 545 408 073 292 390 068 616 824 382 360 402 066 196 933 680 775 272 781 304 141 255 387 786 347 501 160 646 560 597 506 368 787 327 347 894 072 601 433 423 584 332 018 099 647 184 249 237 784 613 212 793 919 487 887 714 514 435 420 148 898 185 213 640 633 064 516 354 056 687 267 344 124 051 508 090 826 417 444 155 091 912 519 183 868 245 952 164 534 242 027 600 265 031 036 138 482 120 269 197 520 177 721 143 549 799 169 776 657 757 751 029 549 381 637 957 402 229 941 243 824 291 192 172 997 845 797 371 128 788 724 755 237 280 547 437 077 670 404 558 360 475 498 206 471 116 161 307 600 485 801 774 431 434 571 182 227 083 357 573 707 532 946 742 964 855 512 443 099 612 381 350 002 551 009 959 205 436 027 347 581 817 374 935 307 085 928 531 232 794 167 783 023 045 714 517 039 837 307 417 637 781 334 424 042 768 971 858 232 169 892 927 526 284 856 101 438 066 103 416 799 878 515 391 626 442 619 189 762 391 702 373 781 529 465 618 361 999 373 446 536 203 230 949 682 835 557 751 190 430 614 880 606 818 452 522 267 392 998 520 705 042 490 362 100 869 375 610 101 925 193 059 896 442 817 294 860 288 758 268 576 935 572 758 921 601 339 579 533 867 189 507 623 738 063 063 436 484 180 791 100 867 244 858 932 563 303 456 922 080 126 095 184 666 332 497 922 921 427 389 738 465 081 804 292 967 790 329 658 986 988 194 964 825 546 017 726 732 921 066 425 221 972 509 611 967 230 425 912 020 463 309 896 055 752 413 307 844 779 559 020 890 615 291 210 489 518 116 883 727 578 730 574 825 648 913 079 734 996 788 873 157 995 351 069 132 238 144 248 121 603 617 553 071 087 271 585 060 843 764 883 704 708 732 727 136 120 032 234 203 602 335 119 366 159 085 843 068 577 665 355 495 857 221 644 110 683 427 937 094 492 857 374 269 485 349 120 812 803 896 819 441 681 633 020 243 750 316 157 084 584 036 163 042 007 068 550 059 895 150 680 101 715 883 656 753 282 259 333 359 564 446 553 343 389 196 651 580 945 689 667 476 514 335 372 240 939 243 215 456 396 516 705 540 720 564 640 308 382 906 305 954 949 751 514 654 612 825 718 047 697 212 226 156 735 175 192 166 599 060 359 636 850 254 900 063 484 207 860 215 136 095 816 195 786 963 052 079 014 343 050 464 052 755 642 629 874 536 201 358 607 334 808 820 507 499 301 271 245 628 663 187 767 134 880 945 124 457 601 228 135 246 503 083 733 203 988 988 297 321 859 307 839 412 525 135 118 137 850 142 789 678 687 181 828 792 746 463 698 615 999 388 551 267 387 505 200 581 306 026 116 094 388 008 168 620 769 683 436 893 625 888 355 084 813 320 021 392 913 824 435 989 105 576 349 109 832 329 169 057 569 389 166 825 861 057 517 171 761 498 453 651 128 350 061 364 956 807 756 365 706 113 077 141 653 316 793 603 000 405 292 310 067 668 312 938 498 381 594 711 604 627 958 592 226 075 561 509 315 835 456 657 773 910 545 498 141 875 514 994 505 327 419 721 798 466 763 815 957 327 778 678 680 549 772 971 425 989 092 538 560 406 974 487 717 390 875 103 925 031 260 402 655 705 688 417 328 293 083 965 909 777 640 069 816 463 309 748 810 261 765 051 898 668 668 367 721 478 917 757 044 564 699 531 622 835 065 001 893 728 698 276 788 892 062 556 012 130 797 470 694 710 558 709 828 337 198 286 233 329 583 281 646 915 092 892 398 157 234 802 221 684 599 929 728 721 627 419 915 059 359 603 333 462 510 184 715 632 929 240 501 109 495 954 764 646 211 326 294 830 817 657 138 498 230 037 831 529 458 144 206 798 423 392 026 113 014 297 900 746 773 357 171 335 306 497 613 330 084 078 428 364 605 781 127 718 730 661 693 205 933 628 036 505 008 031 516 205 936 431 592 010 523 794 934 538 489 072 141 970 304 483 335 137 475 753 117 963 184 459 647 128 936 575 615 017 510 552 695 938 163 784 335 706 643 800 838 948 073 496 282 192 363 278 145 153 819 333 049 400 074 950 754 278 937 161 895 866 617 288 935 930 397 326 004 304 706 871 089 427 502 775 434 251 169 133 613 937 956 684 328 790 381 712 429 573 247 082 773 314 649 219 375 388 598 803 976 649 717 654 139 057 656 724 692 332 458 489 638 496 940 896 402 216 144 723 767 499 410 054 079 675 695 264 144 620 246 352 089 865 968 009 988 204 985 903 451 577 428 810 686 815 650 452 433 581 507 661 073 815 243 119 177 435 166 449 067 417 352 537 117 788 957 196 661 989 098 591 819 035 454 793 971 944 710 182 780 710 785 044 559 804 519 060 111 231 834 099 692 884 003 348 670 781 118 338 840 557 350 063 956 205 169 344 804 154 692 856 422 151 842 631 393 553 039 149 675 853 702 280 027 966 633 014 498 801 647 649 711 417 459 332 883 530 910 076 435 265 154 053 038 676 736 905 668 827 515 861 976 859 297 777 995 282 806 950 534 903 890 504 610 363 297 258 678 897 236 094 987 582 829 289 472 321 553 689 556 565 957 236 401 670 189 052 915 113 322 180 231 461 141 684 059 677 676 857 921 168 721 260 056 816 598 523 238 614 047 296 142 157 558 252 873 303 637 369 016 053 737 893 360 812 606 185 937 885 692 324 784 229 712 031 933 520 220 694 022 345 007 218 280 915 313 619 746 992 520 547 098 797 658 928 613 576 049 083 712 966 843 849 611 897 678 371 778 318 295 458 768 357 453 266 073 558 443 082 665 082 810 899 690 164 047 105 777 284 575 736 352 523 426 133 140 318 381 552 856 396 178 905 019 796 630 081 276 015 336 999 843 864 237 864 040 301 469 640 289 954 643 555 174 979 488 552 344 793 188 563 639 660 315 861 927 991 050 676 067 048 870 787 573 529 770 964 708 132 053 427 407 662 763 756 193 646 553 919 930 731 887 425 456 948 713 988 116 577 880 274 148 323 733 702 309 293 357 584 415 892 182 180 349 672 625 715 746 134 656 245 283 547 239 848 275 609 376 353 182 608 776 304 835 684 695 117 577 858 836 949 848 378 438 529 118 794 273 436 703 134 669 900 464 614 175 848 627 653 838 502 094 609 072 117 461 995 770 291 321 045 939 903 496 949 666 463 544 158 755 569 769 740 328 716 862 995 222 039 170 111 465 818 568 075 825 284 404 255 486 729 724 475 514 288 689 851 695 811 780 022 894 775 859 333 699 810 555 015 135 128 602 889 825 547 417 941 749 335 213 264 287 491 504 311 884 538 924 006 446 394 664 001 744 253 650 457 696 998 172 353 981 294 501 512 465 531 034 790 545 528 745 846 337 085 303 619 661 285 295 460 018 642 685 820 251 770 270 123 412 535 696 126 224 940 792 750 442 943 548 382 163 961 298 239 185 489 397 377 656 267 539 059 621 515 356 067 044 610 836 133 618 059 541 046 550 162 011 125 767 083 513 770 954 634 296 344 051 873 998 489 340 841 272 385 627 967 170 132 744 344 864 112 595 428 929 138 627 718 130 630 022 787 778 061 488 722 072 739 553 869 444 031 424 962 096 249 575 971 126 814 235 664 784 909 200 608 837 084 232 543 098 565 158 189 535 119 659 616 216 916 356 715 177 646 123 536 185 145 266 796 668 286 716 978 305 189 793 567 559 348 714 307 177 351 817 867 939 576 146 931 163 820 923 829 433 126 971 333 903 901 381 411 909 510 467 749 763 591 292 921 262 033 155 654 564 615 285 444 476 050 276 476 039 888 771 887 359 429 411 917 469 576 083 435 853 035 006 533 030 029 609 986 894 305 226 735 126 996 729 633 958 360 915 964 587 071 310 697 477 667 347 183 057 988 498 472 788 207 543 625 804 254 084 939 810 294 200 211 139 170 891 647 443 421 022 970 340 520 966 484 021 515 760 341 866 590 073 398 327 152 622 030 661 949 573 772 113 634 217 863 528 880 973 696 289 054 568 362 315 055 689 767 017 859 575 084 471 005 058 981 210 009 903 825 361 649 761 283 286 301 464 395 961 247 453 113 464 708 481 788 443 255 055 596 126 435 858 704 113 854 874 440 172 072 657 819 774 035 995 879 136 065 191 041 410 993 782 461 821 545 098 803 341 112 471 817 560 224 073 268 015 210 293 915 291 364 312 360 913 192 700 931 161 292 579 788 234 044 053 283 411 681 027 376 659 088 758 648 725 876 978 196 671 270 829 449 851 190 350 069 234 891 501 552 330 199 227 857 196 225 883 556 467 060 615 661 890 610 341 232 358 071 154 047 880 880 579 326 366 455 636 142 101 227 791 455 221 841 048 069 781 666 557 689 207 362 464 266 966 724 960 331 142 986 444 528 415 819 805 443 093 113 703 770 340 536 325 583 843 609 442 703 269 595 742 838 625 629 914 588 719 122 927 211 929 227 948 915 826 218 145 092 426 938 836 790 412 905 851 248 966 347 858 621 946 480 668 906 104 488 913 364 534 905 826 814 357 009 642 452 847 692 306 404 804 093 625 618 492 804 733 639 977 521 710 376 581 661 442 270 728 668 009 327 117 351 829 406 583 115 022 129 164 124 472 211 995 829 068 196 217 083 715 104 841 224 260 935 993 083 130 453 696 434 073 750 683 328 363 713 020 032 409 506 284 706 395 219 569 859 084 808 861 994 508 866 953 752 448 135 026 815 852 155 588 207 957 790 008 775 458 691 908 472 235 664 417 861 403 740 489 937 161 238 760 724 441 302 355 082 051 218 035 306 587 784 698 318 370 936 752 813 056 402 427 623 552 404 826 271 019 543 630 379 622 416 492 187 122 735 856 530 682 530 843 805 093 792 653 515 072 623 981 971 012 736 707 057 768 474 187 241 373 910 413 343 227 364 754 241 920 457 070 362 004 762 943 833 370 937 848 868 877 355 665 964 140 605 054 813 050 989 194 537 981 301 389 437 392 605 429 653 592 331 273 137 677 897 398 974 483 668 800 614 389 246 906 058 055 013 207 543 472 411 438 929 292 376 751 704 340 561 209 068 964 396 983 681 830 469 574 339 904 118 038 025 119 280 797 961 678 079 060 544 087 748 645 993 745 662 858 832 545 698 522 339 127 307 673 742 248 042 339 819 334 579 906 977 617 764 319 631 951 111 341 510 064 374 645 816 183 842 235 600 382 976 177 481 198 052 806 820 555 658 581 183 193 848 896 254 925 043 102 453 366 997 361 428 965 959 103 153 601 074 140 686 753 733 371 608 694 328 815 374 376 475 846 839 108 078 454 318 718 063 179 194 216 510 696 430 395 451 457 974 727 603 420 994 180 436 619 428 302 566 837 810 033 957 887 532 778 406 258 928 367 769 045 069 055 506 103 040 454 178 712 874 202 999 117 556 721 140 150 011 927 977 458 459 724 586 300 417 079 663 068 467 340 488 014 881 714 892 579 360 225 050 533 931 424 215 957 474 626 074 149 587 213 760 251 886 042 902 127 487 328 050 512 169 448 105 342 628 323 384 748 168 227 455 086 344 002 814 077 069 716 632 705 777 115 163 242 944 417 850 869 014 391 582 373 661 506 136 083 685 321 343 247 170 303 154 864 489 228 343 096 188 609 548 072 521 362 022 939 258 445 051 963 724 258 645 787 348 736 604 701 525 674 591 125 598 232 744 778 388 825 814 513 281 803 607 066 148 442 370 827 168 054 878 310 080 367 113 960 479 090 891 234 218 013 657 892 704 227 775 550 364 915 146 008 979 765 159 327 785 082 891 286 782 075 871 171 427 646 821 823 854 974 456 215 343 800 983 031 984 125 065 783 840 120 953 227 863 027 503 346 732 230 823 486 529 398 513 388 506 569 262 805 897 739 288 767 204 267 198 989 660 472 942 394 968 703 166 188 011 476 269 739 278 967 350 062 602 406 550 109 541 501 047 593 849 997 920 545 407 951 787 616 914 992 388 173 506 681 481 467 329 007 171 250 130 012 730 967 048 407 850 526 884 998 668 692 301 623 878 461 639 497 387 464 053 915 610 701 337 829 122 950 999 897 246 434 958 336 828 799 860 123 539 838 241 987 636 710 334 206 336 926 816 378 164 857 567 757 540 859 814 957 705 933 836 069 432 492 273 923 763 677 667 462 426 262 455 664 156 437 855 478 140 886 685 387 420 042 681 643 864 850 952 529 282 305 840 019 751 874 809 714 716 100 907 792 170 214 314 104 989 574 892 318 052 449 935 299 241 810 178 813 083 346 527 594 705 055 500 677 214 672 266 271 229 793 472 989 724 982 720 587 983 332 123 228 828 230 681 321 894 882 165 194 371 689 098 689 160 211 822 657 166 093 623 582 070 189 730 382 079 520 309 390 295 006 875 808 286 847 012 632 632 575 255 490 587 080 903 274 388 969 848 385 874 791 425 292 488 459 225 603 402 015 913 150 345 308 604 961 498 251 621 277 589 781 415 759 966 137 723 387 202 969 446 050 714 781 558 211 156 950 516 416 671 793 348 456 519 810 545 812 644 580 676 655 805 956 081 387 239 323 880 861 312 747 092 791 349 861 646 438 294 644 048 923 479 408 529 573 289 344 038 398 294 544 905 361 623 037 693 173 864 013 463 284 128 454 624 412 979 914 995 833 330 096 245 315 400 153 890 035 967 183 743 297 276 133 512 238 392 480 662 406 611 941 077 579 612 347 620 945 931 774 023 993 219 455 286 237 523 203 075 556 852 217 223 464 753 510 621 727 103 234 608 614 097 134 438 867 154 926 555 904 052 631 294 619 503 981 987 407 813 812 483 372 563 805 593 255 931 637 599 086 890 870 175 368 618 265 215 880 290 741 457 498 263 573 625 612 053 922 805 445 839 937 843 469 873 384 952 704 940 797 172 683 798 327 989 961 202 238 027 923 144 611 731 541 670 185 322 202 852 717 265 255 378 291 971 355 542 397 222 970 365 861 990 319 092 543 988 233 934 194 781 836 020 588 892 270 297 923 732 683 779 337 464 657 004 866 618 804 660 181 735 404 340 132 641 487 187 023 896 553 725 591 888 338 859 763 607 733 237 643 924 712 157 205 228 951 835 170 719 963 236 276 393 299 701 762 115 617 795 528 031 481 222 695 529 132 506 293 555 169 023 948 061 217 414 422 122 825 627 014 704 246 893 957 096 371 682 518 991 714 359 549 066 170 268 327 093 865 619 027 693 611 098 067 821 140 200 451 888 758 155 891 649 536 707 611 587 940 151 210 237 374 192 706 509 406 743 166 874 062 432 110 417 680 667 150 035 213 484 455 145 636 150 395 966 865 586 406 322 019 517 387 906 457 809 700 363 155 518 257 052 981 214 541 172 986 286 272 788 267 618 041 141 791 610 420 914 473 494 604 969 187 479 679 822 252 800 440 418 927 061 518 330 520 353 327 849 613 531 213 919 384 556 701 984 101 311 335 030 100 112 499 599 647 546 075 382 220 453 456 068 755 226 338 761 905 368 738 277 918 213 260 699 402 258 514 651 284 625 535 501 153 137 433 103 900 114 980 840 698 752 406 831 144 755 471 100 637 494 557 925 871 774 786 033 185 563 482 068 511 359 153 416 901 805 507 796 186 053 617 071 303 564 942 151 325 302 544 714 853 345 914 875 913 810 272 116 867 757 171 568 013 873 627 864 638 750 355 910 129 433 023 360 857 565 440 034 220 548 727 956 183 170 854 522 318 268 386 079 717 807 366 772 076 361 366 367 175 325 677 702 129 269 563 530 625 344 222 749 235 903 265 070 917 859 643 981 748 996 598 722 446 189 264 590 013 721 448 626 366 350 809 488 055 290 275 865 198 744 068 335 082 604 254 749 944 711 078 116 276 926 152 516 721 318 818 119 464 327 784 710 406 591 897 299 842 249 694 292 946 240 445 323 385 894 244 395 677 568 214 564 675 685 500 884 151 098 679 723 121 471 923 216 729 251 459 194 573 180 784 727 289 591 125 630 580 005 092 043 818 892 748 912 158 097 608 997 672 255 007 133 062 801 339 898 214 171 982 770 141 261 469 671 745 475 388 131 679 817 325 139 306 005 045 501 703 858 857 550 624 678 443 894 047 714 240 716 595 187 065 766 630 225 488 045 440 798 439 502 402 656 701 891 449 711 636 952 041 717 833 455 936 356 440 480 460 846 329 793 043 991 548 986 104 327 371 233 900 489 748 432 631 147 504 729 552 427 113 843 391 678 415 315 752 114 376 056 385 385 640 745 248 152 845 182 875 309 269 120 345 120 419 881 010 676 445 544 035 635 567 003 747 357 680 796 581 921 260 324 556 687 196 502 507 413 689 012 676 094 413 727 019 424 152 511 905 770 893 864 237 260 446 318 975 731 288 550 871 141 902 481 657 830 307 062 254 921 193 261 782 136 231 123 664 361 128 472 227 763 428 114 775 745 077 819 844 778 565 538 843 089 882 182 265 080 913 344 635 570 010 079 545 215 162 365 698 811 688 566 150 654 198 827 202 470 962 852 080 467 368 224 498 866 440 055 579 053 237 752 973 427 749 306 907 138 382 788 868 687 674 734 507 454 454 902 498 225 965 740 568 719 596 312 351 128 928 308 493 357 862 798 509 033 724 114 986 600 069 248 067 710 449 450 308 341 055 009 720 607 966 179 593 856 118 272 475 057 441 866 028 519 108 754 462 065 145 154 041 108 597 633 478 921 647 839 118 427 955 712 159 759 586 343 107 983 102 805 027 408 294 214 138 914 735 239 377 338 737 057 034 382 721 142 704 196 897 281 269 125 252 641 393 904 466 842 936 690 308 169 154 457 412 277 897 523 938 014 644 982 755 191 064 686 187 156 012 377 361 251 758 409 206 612 014 112 862 943 256 049 065 284 457 824 923 774 627 986 949 114 660 215 797 417 936 904 635 494 210 892 287 101 358 138 168 932 506 426 961 809 258 666 322 459 203 659 896 709 366 785 916 285 181 604 496 014 922 227 008 745 421 507 899 989 240 063 479 466 351 020 797 249 249 823 649 125 457 629 505 080 868 180 756 020 625 616 762 423 649 048 276 311 320 201 327 703 803 822 573 546 547 773 289 561 028 291 332 837 806 890 936 559 178 817 334 079 471 662 371 520 723 983 008 631 792 310 822 712 815 270 482 277 650 568 127 530 237 289 093 779 027 212 767 948 789 925 625 878 204 188 948 650 378 742 979 208 542 122 506 895 361 129 309 752 405 145 365 864 433 643 321 963 529 699 929 946 838 085 525 781 100 073 934 576 535 148 940 024 043 885 276 595 522 057 408 087 497 746 506 047 652 367 451 136 882 651 608 643 628 895 843 944 373 147 346 310 604 248 225 201 127 469 940 902 111 854 505 065 723 229 481 001 248 793 618 114 572 136 046 055 451 810 021 361 539 585 679 096 272 844 714 486 970 265 179 056 815 836 692 276 856 278 578 632 051 731 482 637 175 481 952 027 647 287 023 429 541 958 734 289 626 421 800 564 542 442 205 975 708 854 681 728 629 330 998 744 747 249 396 432 841 281 475 840 233 496 477 337 475 976 548 762 780 257 861 338 664 262 232 691 377 950 605 600 509 724 975 346 781 352 437 802 081 656 163 507 167 930 982 628 936 288 996 112 574 030 684 447 780 419 999 128 794 907 730 630 697 776 091 768 853 710 420 949 693 689 336 185 809 524 829 386 414 125 213 942 813 959 878 629 236 649 221 227 375 711 702 332 311 250 689 988 393 880 117 825 975 898 424 759 698 235 039 804 144 581 654 932 965 099 837 057 696 490 484 117 625 501 439 856 068 263 732 406 025 875 238 568 095 000 163 695 023 967 049 479 023 886 617 248 154 830 840 602 404 844 483 526 384 449 963 647 986 225 911 248 450 817 059 498 042 696 767 221 271 310 377 835 833 252 179 192 441 044 658 738 504 970 455 048 346 564 962 206 933 623 394 194 143 182 295 282 553 571 303 624 226 196 243 028 335 372 992 803 602 313 202 160 055 611 800 892 358 897 314 782 040 137 196 015 296 318 573 413 933 656 284 917 055 835 941 845 735 782 749 378 658 111 217 977 583 777 429 467 206 865 666 047 252 827 387 954 738 569 928 523 951 243 913 342 683 944 263 119 870 229 082 751 034 347 521 229 366 926 000 732 619 855 656 982 255 599 390 073 579 095 421 896 636 182 450 000 205 590 687 947 071 327 814 159 468 345 973 913 240 322 768 219 124 780 476 565 302 580 103 443 805 088 048 601 440 340 438 809 643 832 089 945 675 282 774 249 111 934 926 047 567 679 754 648 295 952 493 219 343 696 692 320 458 698 257 775 015 040 455 359 566 844 909 872 533 254 591 296 326 355 824 453 106 714 276 672 440 021 768 094 658 849 997 885 319 246 846 707 886 875 518 610 741 186 725 402 420 365 624 311 631 469 370 604 717 156 116 056 930 399 389 983 370 212 077 182 849 836 146 411 903 483 236 781 012 706 536 182 808 216 563 947 530 149 010 062 657 205 595 469 918 728 614 541 359 401 354 874 494 335 650 549 181 972 103 622 337 003 910 914 279 598 558 556 648 957 165 046 820 201 113 604 009 286 170 135 355 299 550 633 464 857 470 312 748 034 983 293 842 417 730 882 132 889 548 337 213 995 813 947 012 430 146 125 833 905 390 970 300 716 128 642 275 283 345 054 470 574 046 106 149 354 350 573 464 652 829 084 021 440 980 657 281 152 126 249 038 106 312 363 979 473 957 196 216 209 988 037 636 484 142 626 336 320 546 047 314 859 811 457 742 791 213 080 859 514 361 106 040 615 224 905 719 303 097 057 020 707 865 573 589 857 790 585 456 321 183 591 329 591 577 031 042 284 994 904 635 013 598 179 523 800 620 558 457 691 798 261 740 693 931 272 704 411 228 297 059 025 527 231 709 421 756 999 880 827 406 207 334 955 739 791 038 799 120 762 235 140 054 339 087 504 810 219 506 486 023 961 754 257 441 096 192 870 987 951 819 901 027 460 165 687 867 363 237 282 873 692 869 708 007 737 473 859 685 555 183 684 521 448 946 465 346 182 467 220 639 663 042 931 418 206 200 477 471 178 898 966 370 406 852 198 667 051 562 290 868 972 739 651 619 358 746 306 657 732 967 998 320 086 691 409 449 022 068 194 794 642 250 005 713 202 080 021 182 419 790 777 617 466 426 882 196 304 019 077 398 934 147 130 459 837 506 271 700 703 186 996 082 203 296 072 113 799 866 174 266 117 104 793 445 641 337 000 443 078 659 462 737 697 474 515 277 113 964 098 022 412 992 186 592 418 013 337 660 865 083 313 497 981 828 762 368 167 920 716 785 165 448 521 848 818 700 348 645 711 853 058 047 414 625 752 190 238 090 537 283 861 139 942 357 533 898 137 256 373 138 044 741 628 925 224 170 593 228 255 782 957 070 447 110 517 879 814 304 116 325 914 287 403 900 638 808 490 730 956 285 981 696 998 385 869 766 104 424 842 790 683 374 739 621 895 028 190 609 422 112 026 207 661 961 239 149 449 687 413 792 781 947 123 294 226 586 629 150 727 617 998 301 017 714 491 123 183 203 567 973 199 984 603 315 933 930 988 185 596 215 146 202 243 672 160 273 953 674 238 734 833 881 859 556 658 829 290 421 865 372 247 945 261 896 000 013 013 248 532 955 604 053 885 917 897 545 566 248 467 536 752 251 555 908 979 840 694 164 485 342 080 975 240 646 793 808 037 473 764 989 492 529 362 125 349 902 765 789 093 571 121 017 564 792 651 022 188 805 028 604 830 658 795 248 678 020 412 470 374 082 913 271 450 056 544 036 321 259 027 542 430 110 580 516 636 558 221 767 440 080 254 005 031 643 411 303 988 998 408 894 412 891 183 230 259 210 736 220 327 104 850 804 414 088 389 364 450 882 252 447 658 021 052 939 102 672 820 392 079 776 107 853 604 535 117 455 619 824 194 164 420 225 276 119 331 948 577 300 176 291 494 321 991 235 538 778 413 844 170 646 903 998 052 300 645 907 726 936 618 828 340 392 972 396 081 049 788 829 787 303 626 141 379 728 093 150 640 160 564 717 134 172 144 174 274 512 538 626 244 222 727 100 171 124 056 241 503 676 350 079 115 007 142 073 360 681 143 588 475 871 048 444 902 213 302 336 059 764 264 876 343 767 825 308 854 529 659 695 235 405 727 603 675 392 189 516 647 938 652 456 074 678 731 254 141 690 117 656 327 378 359 867 610 281 873 581 528 780 732 367 052 561 800 974 403 210 369 841 388 091 111 419 241 051 548 548 932 758 578 283 176 192 725 601 560 067 275 291 296 766 558 802 593 899 265 649 589 879 265 897 019 436 331 943 241 657 636 393 309 255 695 331 534 464 729 966 852 970 117 241 134 461 351 725 176 484 872 585 570 708 072 803 172 240 441 929 725 916 677 579 049 744 502 020 530 579 660 801 706 280 161 442 040 413 028 851 360 851 967 518 623 087 721 794 089 186 007 715 610 770 997 999 928 881 420 623 328 041 924 399 526 123 139 566 073 531 763 520 722 032 268 216 490 255 462 538 217 287 821 542 325 037 215 716 241 570 784 903 674 538 541 900 115 803 612 824 660 869 088 016 408 912 676 044 762 601 789 636 406 221 333 714 706 372 706 899 728 657 660 257 487 568 916 890 410 132 102 650 798 271 528 748 865 032 271 156 669 572 045 434 965 531 621 200 258 556 603 115 966 579 877 616 773 535 452 371 636 102 264 082 152 406 075 755 519 798 927 066 054 034 788 661 390 034 331 146 666 716 009 039 841 917 980 962 494 743 680 259 584 269 017 927 441 247 151 758 507 873 906 982 661 312 794 895 730 790 603 936 479 731 090 347 794 535 598 986 679 905 628 802 827 147 267 774 899 061 358 889 618 104 738 329 092 551 124 140 971 799 693 709 674 925 114 339 473 495 476 384 442 281 872 420 080 334 656 101 863 901 108 153 465 955 471 646 428 831 670 356 632 025 559 687 140 475 529 433 088 578 576 479 253 616 224 057 787 713 802 389 959 541 200 852 712 254 002 721 060 228 299 123 818 374 166 760 636 813 381 350 031 102 235 204 669 975 560 274 528 814 673 262 317 376 218 829 662 156 761 775 576 507 378 495 837 187 699 543 152 398 244 290 879 252 031 864 179 272 429 167 250 472 314 721 341 489 583 657 301 352 263 736 118 183 527 068 373 117 409 467 093 007 885 551 622 243 030 972 474 733 281 920 433 998 036 278 519 725 452 228 083 815 273 126 457 926 710 195 873 376 551 996 531 206 916 977 370 761 343 546 386 908 657 257 436 979 638 452 962 869 225 700 303 833 531 776 918 046 042 841 558 694 110 875 032 577 249 414 363 060 830 991 505 376 083 866 875 306 791 557 399 290 362 609 535 699 758 183 590 766 210 647 991 789 765 721 556 600 132 969 856 179 833 283 096 138 323 202 176 710 721 050 251 366 808 664 402 884 960 437 656 435 575 812 065 866 557 595 656 927 099 899 848 602 330 996 230 161 421 456 416 045 479 196 279 373 402 554 818 587 267 979 068 875 815 352 436 052 916 748 213 253 272 815 316 724 446 461 462 623 595 891 043 353 592 229 858 592 520 185 696 991 599 251 064 079 208 795 436 053 581 406 496 723 836 249 440 573 752 368 417 817 546 273 676 289 629 758 914 838 824 931 036 924 491 461 675 754 531 712 755 833 073 711 779 506 802 392 298 511 330 840 195 530 664 541 223 499 033 228 482 999 674 141 608 787 888 685 478 559 835 579 557 658 499 034 903 222 861 243 684 438 248 278 463 198 306 848 114 845 447 136 445 191 431 628 692 465 683 658 716 608 519 673 959 357 292 925 916 505 330 926 567 443 636 566 801 336 197 138 558 983 759 657 952 585 832 931 585 662 577 188 909 121 212 500 575 944 964 768 465 128 857 018 248 143 556 231 858 477 983 298 404 501 756 901 345 661 983 155 715 545 179 404 184 241 707 175 407 940 020 499 333 366 471 551 240 772 339 379 216 983 378 863 938 109 131 489 463 135 102 795 630 432 617 634 576 876 114 603 167 037 667 022 532 680 272 364 637 343 261 611 430 771 623 617 588 336 441 981 287 361 071 333 192 766 859 150 519 739 774 240 654 749 064 678 415 582 346 089 480 375 638 162 544 261 095 814 201 779 316 169 561 254 669 790 247 738 199 435 190 123 245 278 161 400 554 646 603 547 073 170 124 474 396 228 044 252 949 959 877 749 948 007 508 382 593 113 107 623 254 704 588 407 625 336 571 947 065 832 822 830 580 899 486 644 227 457 491 996 615 021 023 678 466 949 546 162 726 276 612 283 455 066 235 911 795 274 766 273 283 630 599 799 884 153 309 558 643 288 853 793 629 001 476 209 449 604 637 627 445 491 213 024 003 749 020 005 678 296 208 502 024 421 884 650 371 323 542 166 216 512 400 124 205 581 107 434 006 883 418 197 933 931 595 831 642 225 800 309 559 744 587 624 411 378 585 582 782 840 068 605 148 216 503 467 571 536 912 224 909 356 571 719 018 994 370 053 097 774 204 848 200 144 509 354 099 372 400 821 972 469 499 947 620 181 651 609 495 804 244 215 634 282 685 951 668 390 541 223 172 514 791 043 770 454 265 066 440 034 018 364 426 254 701 823 083 922 597 008 018 721 694 720 499 219 008 784 577 386 662 435 894 541 483 211 951 817 214 843 701 902 440 548 454 577 849 940 022 380 630 465 531 925 864 995 882 591 267 975 441 447 181 966 103 795 689 905 581 844 422 557 007 182 668 026 067 890 391 962 505 675 548 678 473 731 267 444 637 512 972 476 696 809 439 366 503 338 513 199 334 080 517 147 472 672 955 196 947 295 036 536 310 159 514 691 291 135 696 352 845 665 821 422 226 134 587 048 696 414 379 739 136 973 780 612 401 614 895 162 766 413 723 692 180 637 175 192 728 844 776 520 444 138 636 540 459 724 286 884 261 953 636 066 689 165 706 255 916 128 440 424 239 686 776 753 874 530 444 267 995 246 634 606 734 498 555 408 430 340 320 310 931 584 203 708 545 233 632 621 684 021 117 502 103 600 598 763 156 597 895 224 677 913 068 603 479 558 712 539 108 739 292 227 300 334 594 230 396 960 075 703 514 907 582 154 827 369 457 282 219 438 863 045 727 268 472 639 601 541 717 549 501 708 659 819 571 108 372 014 748 028 052 307 989 979 774 465 712 374 958 287 998 559 332 402 236 642 577 704 089 076 038 510 309 137 326 803 984 475 172 110 372 151 176 922 989 469 469 722 734 169 235 060 159 941 046 008 794 213 981 081 339 066 289 671 259 092 163 896 083 159 787 550 158 518 747 110 755 589 903 719 279 026 955 378 814 893 394 655 591 204 890 520 339 510 306 564 555 903 258 778 294 182 494 506 706 969 601 711 429 122 440 542 036 772 204 108 503 512 629 043 043 673 071 620 237 561 540 688 421 474 788 357 593 158 815 433 190 562 829 647 631 521 738 533 023 977 930 785 758 727 720 923 957 607 338 640 965 355 333 179 453 465 045 613 535 649 432 023 644 879 900 268 139 211 547 590 350 398 113 314 688 307 327 928 625 779 648 723 980 727 099 684 626 031 314 804 666 634 351 427 605 756 682 959 860 593 354 748 036 307 839 076 150 484 263 781 407 076 421 571 239 598 641 671 264 108 263 596 976 197 331 470 121 927 093 096 790 531 498 446 836 013 530 502 976 885 270 519 177 426 350 945 723 718 628 516 435 568 157 516 184 986 413 527 547 875 308 712 214 075 533 478 855 369 609 223 008 130 638 032 606 151 626 976 459 416 746 980 904 548 238 274 463 467 942 066 495 057 474 982 863 791 841 214 074 724 054 103 158 988 195 056 318 084 916 140 652 038 393 078 625 375 823 696 706 385 728 126 719 164 811 689 251 549 383 618 354 994 909 442 152 112 904 487 339 573 949 467 017 206 147 102 111 118 461 672 638 571 790 102 889 076 392 625 068 778 183 853 933 601 366 144 993 007 993 545 376 695 790 277 736 874 900 027 083 764 470 499 481 207 634 389 847 663 364 088 464 640 449 499 124 313 168 465 383 808 076 551 662 661 557 763 806 154 850 209 211 564 846 576 750 561 537 388 490 747 824 709 327 703 569 334 969 772 668 268 255 070 034 194 473 765 863 793 386 884 952 202 000 705 793 179 121 696 926 640 571 184 963 818 614 482 402 922 016 238 915 193 223 586 689 680 589 079 594 342 553 004 751 610 638 417 928 523 227 450 719 688 196 125 179 337 352 765 079 071 835 564 175 987 846 484 451 890 304 445 864 144 811 248 063 660 547 012 525 044 997 561 928 008 797 496 021 980 346 241 313 342 716 708 498 615 959 492 456 736 193 258 227 547 805 215 269 164 867 391 868 594 538 975 683 274 428 545 261 459 914 069 398 234 808 007 412 556 205 238 974 476 708 579 701 819 586 562 516 532 402 633 408 568 542 099 384 815 545 677 792 715 101 510 901 832 604 908 569 426 037 974 485 997 756 550 261 108 147 950 485 399 050 256 642 083 621 950 308 381 238 512 551 050 076 797 236 736 313 222 112 744 500 413 799 026 458 552 868 474 697 432 435 521 492 111 077 677 901 092 387 465 673 658 453 371 882 128 026 019 984 505 416 468 614 402 459 060 327 643 396 495 279 998 228 010 588 825 519 123 637 874 678 409 117 171 189 604 853 972 158 823 310 092 928 572 825 762 155 686 154 476 954 027 627 076 964 525 180 646 813 050 512 046 344 747 840 474 589 164 510 712 717 452 330 068 813 631 146 885 576 163 771 284 884 882 318 478 305 814 467 563 176 659 729 655 919 551 994 936 699 046 778 868 987 748 036 207 353 265 099 165 027 656 055 495 642 298 919 728 434 140 017 206 730 158 658 881 278 766 005 531 059 617 878 730 309 908 413 726 778 818 168 730 381 179 836 182 275 880 621 167 943 376 553 713 949 381 773 969 517 691 482 699 567 341 856 973 042 159 545 415 342 922 471 096 470 842 696 215 804 036 346 413 195 369 878 830 319 330 915 946 106 611 233 102 249 283 482 357 965 365 136 553 366 741 440 131 549 438 751 219 057 154 443 339 775 393 626 738 244 670 936 992 103 825 214 543 341 944 911 543 200 063 707 878 971 360 052 548 477 084 654 336 795 942 586 640 733 863 700 479 843 206 860 010 879 720 689 745 007 267 839 186 943 452 754 661 005 231 717 830 238 852 069 760 254 759 095 043 802 531 177 343 426 547 680 141 507 400 995 573 458 124 032 911 341 236 207 429 358 088 254 962 820 125 972 404 630 382 868 791 275 129 122 340 294 412 490 644 652 168 268 948 632 613 874 392 386 150 467 595 494 090 893 713 957 760 466 153 268 184 320 127 708 570 020 484 818 143 876 866 819 371 082 934 871 485 665 410 591 853 875 455 572 237 465 350 875 580 602 119 426 048 359 183 669 667 623 673 065 205 121 972 176 601 200 253 873 034 817 964 154 576 488 504 608 987 460 514 475 229 511 491 035 188 406 918 196 610 458 952 907 201 700 645 072 852 863 604 082 523 052 417 197 692 092 119 201 898 469 772 310 566 186 476 846 651 993 809 154 245 392 545 060 757 189 897 365 832 111 845 331 314 242 453 026 883 809 727 147 542 097 552 730 209 521 964 317 997 609 762 515 123 127 341 084 556 959 234 906 998 512 284 140 586 184 288 879 460 956 275 363 674 164 977 765 560 631 854 036 462 052 897 044 849 003 032 817 113 354 064 998 366 135 503 812 439 205 169 178 140 917 836 083 684 492 571 971 058 742 880 509 584 817 760 258 731 853 611 918 986 953 513 271 169 158 694 041 493 524 621 213 579 832 215 279 601 985 405 375 841 097 856 716 473 176 659 693 378 376 260 998 181 139 330 898 470 817 953 714 604 217 156 819 269 906 799 116 893 808 236 147 266 763 862 966 071 667 780 480 574 300 759 224 657 114 906 387 357 279 450 568 573 445 932 973 664 833 056 441 695 238 910 658 315 052 276 224 790 630 110 681 111 188 341 037 538 993 062 897 217 872 987 233 523 034 918 599 555 598 156 152 518 870 500 493 499 364 860 230 637 451 216 463 432 767 902 395 986 220 090 564 304 386 086 184 377 094 420 468 240 471 415 965 013 874 262 257 409 334 939 658 547 282 635 872 056 916 716 834 703 794 135 174 271 076 767 298 829 218 895 759 069 024 525 996 906 848 565 432 732 413 314 944 127 293 246 561 886 228 352 182 900 261 229 171 967 917 724 055 569 060 075 141 173 615 114 634 210 001 308 411 164 468 939 816 438 695 471 580 421 846 164 380 467 400 601 318 446 432 244 142 313 559 435 493 091 231 053 866 033 807 407 608 552 754 996 456 801 695 371 103 511 909 620 618 895 027 078 999 306 137 907 684 406 406 296 237 243 454 994 500 708 894 796 945 803 362 857 213 424 127 648 768 843 701 931 352 742 001 532 051 916 797 261 749 937 608 989 000 584 060 701 261 399 165 338 798 748 503 453 468 453 296 429 454 657 829 506 480 906 235 587 889 138 897 172 056 358 627 925 618 656 563 201 055 954 891 816 365 697 127 748 495 355 437 313 955 943 386 707 473 443 532 076 734 535 616 743 884 342 813 203 060 363 671 606 619 457 563 468 457 543 434 859 493 918 700 891 373 391 511 163 797 132 285 904 112 761 260 382 268 722 284 576 247 725 686 494 988 545 398 485 739 040 112 206 247 780 282 075 038 421 371 824 759 577 010 746 068 556 393 829 670 159 924 424 946 375 450 478 939 128 390 452 916 333 226 622 166 478 636 677 714 163 046 842 643 753 315 018 334 664 800 318 489 764 941 675 059 676 876 713 771 302 196 923 441 222 557 894 672 813 292 254 734 735 092 068 991 522 998 589 731 627 082 098 817 081 019 455 008 254 481 307 013 359 036 746 920 101 189 333 877 837 673 472 647 760 906 172 410 170 587 948 262 146 287 804 153 353 094 083 075 285 575 600 724 424 882 219 608 582 357 930 848 352 539 778 743 536 959 150 337 320 925 039 160 835 217 688 381 615 127 136 238 951 219 774 099 793 118 828 661 081 531 611 351 871 628 168 487 786 964 492 486 096 462 613 954 826 974 815 034 663 041 714 134 129 009 188 946 039 961 271 603 949 814 059 132 624 178 950 896 202 019 618 972 045 981 458 620 142 559 048 555 185 641 620 879 347 349 450 822 423 994 379 249 756 301 483 353 340 944 025 449 765 147 653 198 640 774 368 804 270 748 472 471 114 961 374 268 971 910 791 506 898 491 699 598 531 826 400 493 860 323 855 012 157 468 607 495 510 142 918 465 953 288 842 487 052 923 719 124 220 048 426 964 264 305 734 490 548 257 924 388 332 146 469 371 881 255 401 149 165 281 226 908 660 718 642 579 906 423 680 294 827 575 453 642 652 632 045 861 286 776 885 412 945 782 880 052 631 144 636 001 287 812 000 754 355 377 182 308 443 327 745 873 704 348 530 832 790 142 607 143 893 726 888 235 272 344 012 041 332 575 173 920 746 799 772 309 885 254 544 193 596 880 642 257 088 698 528 559 998 307 862 491 375 411 162 597 149 465 175 021 671 577 845 448 568 620 254 977 793 540 716 901 874 022 508 797 776 463 827 335 483 611 041 041 165 798 014 765 099 470 797 061 659 981 974 057 191 315 588 954 312 536 326 900 128 350 387 280 899 310 625 398 152 030 306 517 385 686 931 302 862 935 843 033 140 768 971 806 321 616 876 475 864 618 866 975 972 438 028 428 728 571 121 024 709 790 771 994 586 409 289 854 450 820 890 259 014 500 796 775 753 904 209 911 786 872 760 939 433 235 353 431 078 670 589 936 759 356 861 359 779 766 906 006 455 070 122 395 402 478 905 774 726 030 020 751 631 694 194 611 853 051 336 714 768 900 112 371 219 122 555 910 754 815 541 849 069 262 111 434 860 354 586 982 383 319 150 425 496 601 075 811 593 828 558 529 208 036 766 549 448 399 450 099 796 341 602 023 101 355 543 211 667 143 218 021 896 814 535 136 490 878 593 463 510 818 797 035 977 919 180 332 080 662 403 079 980 424 550 934 850 789 441 462 847 623 726 317 621 989 096 496 918 393 575 333 150 870 359 222 197 412 981 976 506 187 502 956 103 518 550 491 923 475 101 594 097 229 449 204 897 223 069 921 098 261 301 860 991 237 783 868 773 470 900 126 855 068 073 626 535 189 172 986 928 759 812 889 275 456 646 489 704 662 502 863 501 088 396 409 312 965 261 690 301 523 037 214 022 534 189 726 424 982 070 596 125 726 508 741 760 370 558 108 382 867 935 137 853 997 075 313 830 585 362 477 108 726 237 044 589 869 149 135 747 311 242 951 925 780 307 868 272 340 788 699 591 073 672 644 192 826 082 226 370 761 049 846 320 738 985 325 609 541 527 835 310 320 323 242 202 651 897 384 538 658 876 283 632 534 601 074 614 228 283 978 763 881 755 030 686 163 280 469 717 603 606 079 033 254 353 172 300 407 716 270 476 024 530 702 911 201 801 170 737 091 571 032 548 998 609 626 913 381 255 109 170 257 011 834 105 218 466 394 292 236 781 517 086 839 557 246 345 074 642 756 758 676 477 282 203 673 728 377 789 041 965 773 412 596 355 005 160 039 677 754 186 325 490 318 765 196 835 006 489 448 777 651 338 393 474 429 863 501 787 889 941 046 054 983 658 860 341 115 957 272 356 042 459 980 342 699 502 420 178 587 661 125 385 385 528 789 004 823 720 798 266 432 593 958 645 799 955 827 897 679 110 947 648 382 509 889 108 439 679 514 009 329 358 665 150 918 297 433 291 093 155 298 571 717 636 564 048 523 151 604 308 691 454 478 312 916 723 787 410 067 827 548 357 749 174 705 071 665 450 119 439 662 872 004 576 200 404 861 867 743 392 331 388 701 644 136 931 220 472 661 005 642 303 077 790 383 760 879 552 125 739 381 118 127 847 839 322 519 399 953 817 784 574 555 882 170 599 994 628 194 760 657 869 706 635 204 144 072 401 794 185 761 239 696 474 238 760 828 958 570 411 705 736 935 079 119 791 769 195 525 657 573 288 575 253 769 585 499 076 789 288 902 835 498 336 379 657 108 126 811 085 629 766 936 569 743 066 037 173 438 844 322 227 631 386 864 788 385 721 633 742 520 741 041 015 186 431 943 400 760 996 236 787 813 974 824 985 589 420 134 876 106 203 754 046 908 401 308 139 147 507 072 036 502 316 707 433 928 709 131 761 255 655 782 250 733 887 647 153 280 908 358 572 103 121 592 703 919 781 697 145 533 533 750 740 479 744 600 647 041 127 275 368 997 968 088 470 518 663 258 167 849 746 683 691 189 264 725 284 998 779 692 577 612 863 370 386 077 199 983 877 754 819 862 624 405 218 078 729 041 502 268 757 516 200 299 701 455 406 765 601 275 707 129 343 245 546 608 886 174 832 864 150 675 849 079 575 452 993 040 752 278 290 453 110 959 644 542 233 739 022 601 190 728 473 108 998 437 747 687 313 045 790 304 476 547 989 014 728 498 102 520 316 117 514 222 568 881 131 630 134 371 858 352 722 252 745 050 504 094 975 540 736 898 042 262 947 872 393 627 860 972 639 668 129 651 074 892 704 310 856 855 898 094 336 748 925 141 374 518 279 236 141 137 406 123 219 431 565 919 114 474 327 318 412 369 839 703 657 000 667 716 118 225 492 089 106 959 434 441 563 882 841 954 943 244 237 261 891 837 795 046 464 808 272 782 322 710 298 158 244 235 412 986 539 038 941 154 664 729 461 863 744 504 414 151 630 390 495 597 631 938 353 470 066 155 288 549 230 027 143 428 531 389 013 668 780 619 259 353 668 030 490 702 498 675 731 883 370 695 989 329 170 113 238 252 060 994 687 212 981 437 010 656 337 443 822 919 556 955 224 386 804 050 880 530 885 158 020 093 306 099 380 556 640 610 433 469 699 475 143 623 444 455 141 262 094 984 868 885 551 288 082 539 220 756 464 166 383 372 910 159 444 431 613 135 188 094 107 909 190 598 071 286 230 321 405 694 137 637 989 045 289 401 659 215 910 386 690 438 616 266 122 841 741 365 253 691 590 973 036 572 832 788 081 933 448 601 690 298 105 128 309 464 559 973 760 795 470 160 169 913 681 641 911 030 746 717 033 794 216 308 078 876 263 474 342 058 101 020 415 239 207 697 154 562 558 385 250 514 904 969 439 292 763 208 936 819 407 620 663 512 464 704 166 808 381 327 924 154 321 787 629 986 443 374 203 881 097 908 808 047 125 004 123 041 066 053 982 745 665 485 795 391 494 138 686 141 203 203 979 115 280 454 207 478 089 119 816 713 512 617 515 824 501 133 287 447 077 129 883 995 598 380 681 045 406 475 471 598 928 012 880 333 483 835 948 607 076 992 255 022 323 215 250 706 382 352 184 635 337 208 761 011 207 747 059 147 718 210 787 922 675 983 936 278 851 087 471 092 137 084 947 491 421 769 166 818 253 779 424 099 607 487 893 452 544 303 958 695 733 939 450 771 399 856 585 214 834 523 642 483 639 715 017 041 418 582 971 984 477 599 559 607 945 086 804 589 540 855 348 904 111 612 217 572 873 745 444 679 889 365 321 356 115 001 443 229 426 876 018 552 232 105 611 117 802 803 181 047 261 748 763 240 008 942 882 901 798 731 060 836 521 401 903 845 522 482 283 396 711 465 710 647 507 799 364 296 040 110 696 261 919 936 455 091 859 068 890 955 245 551 424 239 835 646 786 680 851 141 156 985 517 477 423 353 337 267 456 428 315 240 967 172 694 784 848 579 171 861 558 403 559 852 234 878 929 767 368 520 565 385 061 085 620 359 712 382 550 870 971 951 563 927 733 740 544 076 718 933 505 855 762 507 820 849 526 861 549 214 353 187 315 588 098 397 080 941 729 045 575 297 378 820 096 413 522 530 324 404 537 520 768 871 392 375 292 117 709 582 145 206 805 686 428 321 507 067 910 479 209 118 024 993 324 601 012 225 655 205 607 333 202 679 954 412 956 258 426 346 545 248 088 148 481 788 124 230 527 217 196 622 587 576 389 165 727 237 002 527 679 789 924 960 801 646 631 639 475 091 529 488 405 705 314 055 673 542 469 852 011 745 036 705 532 071 290 875 210 360 820 743 468 014 770 219 372 823 123 030 115 244 943 472 961 349 590 045 479 393 585 544 636 328 532 591 346 433 302 725 772 891 999 321 441 597 040 397 389 797 464 578 964 176 820 882 440 940 474 024 580 876 705 666 878 371 093 749 028 567 343 623 546 394 482 833 849 675 090 414 639 076 261 190 060 370 810 349 994 789 098 099 290 668 857 360 844 262 082 398 235 235 404 095 533 935 376 726 436 320 718 508 276 727 417 707 493 518 225 425 138 450 581 293 645 682 733 996 210 458 003 260 489 802 947 034 817 287 640 160 400 256 671 203 270 934 593 284 417 099 869 909 274 778 363 407 339 716 745 202 238 803 158 339 785 085 044 408 457 250 715 158 650 158 759 797 968 371 414 292 981 000 909 046 771 581 326 542 334 462 003 225 259 219 359 440 898 718 133 282 048 980 157 896 282 565 924 056 510 848 141 545 609 919 053 985 442 284 632 606 924 808 593 005 059 493 133 482 558 004 349 903 520 148 911 059 366 170 198 940 631 947 991 768 892 408 489 097 350 330 120 397 519 627 456 216 710 527 045 985 389 629 039 290 608 802 020 881 355 404 905 636 797 297 543 944 480 249 843 628 668 919 604 033 504 268 163 770 276 163 948 460 924 827 986 203 226 762 976 163 565 901 059 397 414 228 396 085 412 287 474 542 694 729 268 103 035 929 308 246 350 912 159 258 338 648 807 434 694 546 928 761 577 804 269 599 236 656 990 439 536 799 255 429 902 881 761 062 882 785 571 734 402 263 739 063 587 764 111 827 133 932 149 889 506 256 135 773 040 230 150 469 434 967 036 794 206 518 166 291 703 238 384 150 697 972 870 030 527 194 646 772 872 995 179 915 936 276 881 535 101 971 497 208 825 633 858 595 717 281 804 653 862 908 113 830 846 858 562 537 428 971 570 301 987 869 986 308 600 889 624 570 444 458 936 861 952 180 314 710 570 588 710 083 465 696 037 723 133 421 128 486 486 701 483 174 510 058 698 146 613 437 410 743 350 107 134 520 661 554 189 594 819 647 073 659 134 362 949 046 877 601 566 946 269 587 966 260 729 582 404 849 325 429 313 629 850 877 911 483 039 300 487 270 872 409 767 592 116 151 791 027 484 310 862 880 106 348 092 699 463 472 691 407 613 962 531 594 559 943 972 196 659 478 393 701 097 678 847 861 545 851 770 107 925 622 434 194 904 215 740 543 306 021 411 663 265 630 529 708 296 246 490 643 387 934 265 526 281 356 439 066 787 542 787 052 008 183 419 857 114 730 329 763 487 011 686 249 159 090 903 118 237 651 270 356 647 037 531 428 965 533 826 553 556 552 852 630 347 366 641 968 226 082 545 570 665 565 969 313 048 294 439 642 561 225 765 860 122 629 194 122 049 565 384 608 651 312 976 473 603 136 491 111 340 015 573 846 971 598 562 782 173 896 999 867 286 953 259 142 652 138 761 102 579 481 215 329 465 424 365 030 088 056 463 593 534 294 202 165 479 158 575 815 549 877 444 487 055 481 007 066 224 387 005 209 980 507 648 451 585 355 825 127 105 774 653 288 059 338 897 786 343 457 138 675 415 160 585 621 528 775 082 600 134 975 032 561 419 323 165 804 446 255 331 966 523 875 587 656 077 520 411 074 974 839 931 554 501 478 140 174 646 827 289 326 780 802 581 973 162 682 499 066 607 679 528 729 336 404 420 577 267 104 787 516 270 987 979 510 658 523 355 519 311 497 338 096 050 435 459 837 228 758 391 443 014 071 734 826 210 649 343 216 531 141 426 267 347 822 980 493 944 058 881 864 775 997 498 759 704 947 479 030 137 401 139 034 958 456 804 175 777 104 949 575 114 052 081 106 586 517 330 180 526 565 042 160 681 676 478 971 475 687 735 760 047 659 756 677 982 127 044 682 978 735 665 949 602 810 502 892 157 595 974 361 077 009 134 558 806 181 639 807 423 761 960 277 287 211 662 046 470 301 700 154 890 833 492 315 468 003 564 126 198 619 023 944 343 401 624 162 786 686 452 314 060 167 236 785 647 271 143 444 577 700 002 547 919 103 435 762 267 847 027 490 034 334 626 729 477 112 493 952 223 972 808 899 451 703 267 903 059 706 061 636 533 824 528 726 503 728 518 878 354 424 558 936 802 644 213 038 776 910 844 402 262 883 238 794 214 901 009 266 151 674 617 413 844 353 386 606 263 927 423 573 692 183 810 736 997 387 020 439 496 387 522 576 739 815 173 054 331 090 288 537 729 739 598 608 547 489 139 723 640 123 862 615 922 126 655 071 733 352 589 639 014 054 179 261 727 101 010 766 857 601 628 238 030 933 989 611 828 358 667 439 228 571 073 294 192 594 385 626 232 369 723 749 711 575 593 117 839 915 382 469 897 634 758 583 831 085 293 960 097 933 824 119 752 296 498 921 370 363 486 594 449 636 709 031 328 009 961 175 279 157 610 982 586 619 736 712 366 224 069 050 344 966 415 296 533 565 012 244 495 474 432 996 435 076 743 220 122 011 239 001 571 892 266 497 678 462 890 668 525 642 703 742 153 018 045 301 806 983 289 162 674 854 175 517 423 295 754 388 607 946 864 320 537 395 874 462 317 481 222 989 389 067 772 984 941 189 941 785 954 230 585 138 461 125 368 324 809 545 719 290 995 315 430 275 979 774 374 791 191 697 590 149 148 123 258 334 130 401 221 031 591 917 307 539 240 450 800 201 922 511 996 782 436 035 305 464 095 960 733 999 439 113 880 616 080 990 626 372 697 901 713 033 160 351 789 681 741 637 279 252 874 016 266 651 940 034 035 775 540 123 123 010 685 401 989 455 494 312 919 970 354 731 708 032 480 336 123 483 004 527 637 243 495 131 439 471 741 788 660 766 339 011 616 936 160 439 913 143 104 265 956 810 716 332 859 002 528 071 551 727 777 232 391 702 129 916 583 860 145 730 130 035 628 380 578 029 808 162 311 464 743 974 956 173 376 837 658 962 356 989 900 908 366 643 195 224 228 292 995 223 941 339 779 084 445 252 210 101 430 124 820 035 839 502 268 381 291 660 059 251 329 287 119 866 279 559 396 098 934 795 570 832 011 733 006 301 988 316 089 406 310 159 515 137 284 007 752 856 869 086 449 061 142 427 692 021 875 887 957 627 789 713 530 991 228 304 663 424 515 917 864 963 260 582 909 546 532 055 860 977 066 056 586 978 618 198 903 052 639 749 806 614 619 146 110 556 042 387 650 086 789 247 548 812 930 242 057 425 574 202 408 055 991 355 255 965 479 065 729 995 200 250 052 328 647 201 297 988 342 400 652 329 421 907 550 289 482 778 269 472 766 878 785 191 783 139 073 649 103 627 274 446 696 410 432 093 691 296 853 089 399 467 568 243 287 823 392 507 484 878 510 369 789 334 875 593 712 864 426 720 958 970 215 079 370 917 651 091 642 281 684 184 499 495 624 046 546 872 607 171 232 892 846 599 901 387 876 000 663 527 531 670 777 723 927 014 973 924 754 588 409 995 926 571 104 361 532 512 714 771 292 312 607 584 189 059 083 022 264 828 800 657 714 221 767 706 863 267 724 909 575 095 386 090 366 998 978 562 796 441 168 667 560 925 608 307 665 060 098 295 895 685 751 002 947 560 135 030 761 911 632 577 005 902 616 082 543 950 677 536 035 453 740 560 091 532 249 946 005 156 101 386 618 164 290 675 644 857 788 820 834 619 940 193 514 455 548 252 435 741 034 765 924 466 061 239 792 722 666 227 746 483 293 283 761 818 700 767 701 527 148 416 223 188 529 548 493 430 785 329 265 485 339 419 859 864 111 323 719 566 528 773 559 325 268 957 971 002 289 382 216 380 483 118 832 646 238 695 011 649 781 057 880 270 136 628 039 409 991 877 927 414 170 462 577 715 618 162 630 417 684 395 798 235 651 153 480 199 812 859 929 685 263 510 318 709 466 362 229 510 744 106 183 851 966 356 712 491 202 509 713 018 509 000 961 329 970 812 627 196 825 000 874 822 678 172 251 590 100 726 163 910 827 907 592 033 244 594 144 853 234 048 007 302 982 522 422 678 864 070 856 246 474 731 261 387 759 553 720 604 860 775 783 096 826 192 269 937 384 265 586 933 028 086 959 637 767 414 325 860 193 383 815 157 114 691 201 798 660 299 574 916 810 485 703 943 584 265 087 842 058 276 446 411 243 271 617 410 815 407 390 312 054 255 050 966 463 815 313 598 697 510 798 955 429 715 116 426 619 917 731 679 487 677 523 478 043 248 429 903 561 056 028 004 746 704 139 644 875 018 703 966 260 686 678 768 897 283 005 943 894 092 386 896 865 407 946 278 807 568 369 746 270 221 084 309 572 467 901 576 600 490 461 497 725 558 928 424 416 430 873 929 191 433 965 615 625 247 872 728 401 597 302 321 469 602 377 333 810 595 777 189 156 450 520 495 262 018 500 798 770 578 175 837 791 817 247 412 187 212 179 457 531 432 919 197 035 587 768 014 906 942 094 101 174 436 755 375 153 206 667 753 017 599 964 722 509 926 298 724 663 021 948 921 686 953 113 343 078 534 647 284 568 796 343 591 912 553 766 967 215 423 590 101 596 196 870 827 634 650 078 920 882 339 422 583 316 944 145 773 652 691 018 643 313 578 587 296 557 579 496 118 871 242 525 542 344 373 087 755 509 449 449 002 605 617 508 105 911 225 587 233 960 211 867 304 204 393 385 516 175 021 328 083 151 799 775 099 789 716 983 426 430 563 894 187 466 233 326 453 129 586 592 263 270 946 750 575 467 072 008 631 362 377 807 789 222 312 807 930 107 538 851 848 720 219 627 314 586 480 831 224 106 375 211 028 953 456 551 356 095 462 988 210 875 974 446 186 995 358 534 052 639 594 440 145 138 127 369 896 818 114 138 300 646 942 400 298 853 211 332 398 627 734 563 527 290 058 024 160 333 805 840 658 823 002 560 442 267 299 099 992 848 500 376 210 015 512 855 133 690 721 302 076 856 755 524 316 972 696 615 519 444 676 354 566 319 484 521 138 507 771 778 431 638 242 147 384 047 909 212 215 109 259 179 647 360 863 281 380 929 647 183 313 460 347 146 626 167 867 269 574 728 293 538 797 123 845 383 549 858 598 077 335 884 503 191 699 175 621 412 612 996 044 235 672 661 884 103 130 112 534 902 074 115 506 636 587 885 384 200 037 474 302 128 714 532 495 665 715 289 877 638 668 807 300 602 658 942 102 446 387 501 629 449 589 945 372 229 001 525 947 345 475 761 157 345 473 616 651 136 709 567 660 137 668 524 433 321 248 760 734 888 702 555 383 916 848 357 567 408 504 866 412 197 996 764 603 248 798 422 889 941 616 169 026 360 882 012 966 316 454 045 598 194 058 843 894 144 379 330 896 302 279 053 837 584 386 530 797 689 690 702 266 970 574 795 070 082 736 858 084 086 355 473 435 344 973 054 301 921 420 953 666 341 181 275 538 233 955 697 578 355 925 716 553 971 905 426 312 397 486 661 081 417 743 588 547 481 204 820 835 022 833 961 945 368 673 972 961 077 819 157 674 271 573 220 477 878 213 084 167 953 823 864 657 149 815 496 197 380 046 623 152 861 990 255 791 003 533 016 475 329 415 530 739 630 777 076 104 764 791 038 510 521 595 091 381 573 260 942 044 954 466 278 427 671 155 867 915 564 166 362 743 197 916 426 535 115 184 739 084 126 467 217 788 101 019 267 510 678 163 631 334 969 592 567 423 508 618 030 426 768 063 947 524 401 541 390 671 341 543 729 606 896 138 903 346 167 470 985 578 114 854 979 934 586 409 989 153 383 193 948 396 947 620 444 410 927 539 983 543 321 199 739 538 652 244 245 706 107 162 372 080 157 033 252 535 624 845 283 469 914 358 290 539 247 544 698 689 469 609 190 814 063 369 449 831 778 409 668 166 639 829 610 489 276 826 067 820 223 976 195 277 317 591 490 256 499 481 035 892 068 756 411 879 288 881 982 171 073 489 447 995 135 745 475 506 423 948 234 993 462 859 525 713 406 302 000 887 730 906 180 140 395 584 060 312 413 682 783 970 464 803 018 468 361 143 073 222 480 083 624 599 305 667 667 246 560 727 808 243 469 267 492 171 205 264 079 290 527 874 925 785 606 211 813 886 448 615 812 660 940 914 138 145 458 616 548 256 908 314 560 772 894 161 831 966 399 366 321 432 710 345 904 442 942 459 938 131 706 003 796 144 766 917 963 967 473 781 185 800 410 280 979 626 415 009 520 111 923 647 075 319 413 844 427 488 785 266 581 992 673 943 418 737 408 470 403 953 739 322 914 939 141 841 943 608 063 872 584 709 695 967 785 484 744 966 727 022 784 339 616 435 622 532 841 315 952 890 470 456 672 542 597 924 544 148 620 028 054 623 372 048 716 348 729 133 018 679 324 348 745 389 396 613 933 239 162 909 667 958 188 514 220 682 868 326 839 544 392 490 200 638 925 453 884 111 817 761 092 048 084 132 172 734 070 939 227 080 602 097 315 395 187 730 157 414 328 342 052 360 746 220 699 644 282 664 215 482 738 907 656 848 663 606 532 270 289 760 034 656 440 077 377 603 132 345 016 352 961 600 697 927 382 295 684 528 308 318 289 566 026 937 880 841 809 992 343 384 459 140 894 316 811 757 194 806 716 523 338 058 101 989 918 484 179 186 228 596 882 270 678 391 176 233 033 928 400 464 654 838 846 439 497 244 020 892 734 673 519 978 108 738 095 880 919 501 836 053 034 068 668 681 913 998 230 503 612 386 308 973 413 000 785 812 687 370 647 608 382 795 418 316 628 233 793 937 314 468 857 399 988 775 189 479 718 955 834 160 323 742 173 241 985 927 907 478 122 781 475 075 680 271 861 401 533 487 864 397 678 153 307 132 783 251 990 527 871 144 705 980 531 199 537 584 700 887 351 568 778 781 186 038 526 569 704 125 915 503 586 578 078 590 568 587 684 214 696 186 304 749 984 916 708 041 923 461 925 553 432 618 799 086 020 524 082 219 070 665 791 125 783 318 017 090 472 062 413 260 297 577 145 930 281 227 229 626 001 545 306 426 337 618 899 198 165 344 954 370 629 264 438 898 354 355 364 380 906 314 924 847 324 030 136 067 720 526 781 426 137 169 521 032 812 595 877 556 024 832 004 914 321 345 827 873 391 133 064 203 561 578 729 273 436 556 980 697 484 696 129 295 527 205 354 399 029 893 172 298 398 638 126 301 301 392 290 961 956 330 077 846 414 405 889 145 513 904 400 201 106 447 242 704 403 438 038 029 645 489 713 983 375 882 713 740 984 991 134 497 743 324 653 677 228 061 317 541 134 022 231 013 403 918 315 812 419 048 961 567 564 880 007 806 686 496 034 238 124 788 914 748 364 923 374 270 309 056 323 498 250 612 454 429 710 719 814 255 847 862 381 179 524 791 334 047 719 386 116 184 079 265 653 485 387 272 119 141 339 823 887 930 709 881 304 877 909 177 209 026 761 673 159 317 728 667 224 693 851 726 593 768 639 463 717 003 084 665 070 826 616 623 675 637 246 724 963 150 980 644 723 014 853 284 127 807 704 063 238 734 938 822 542 693 531 739 658 422 477 164 030 766 916 543 973 604 035 988 258 185 455 848 639 481 970 000 051 113 263 640 816 615 768 410 029 764 419 790 648 458 757 659 568 889 141 681 544 180 791 700 145 982 678 736 973 753 338 131 335 401 094 071 810 818 480 744 565 675 907 808 326 268 668 602 766 355 803 556 931 352 724 930 544 609 593 844 643 088 795 043 213 484 873 084 832 896 243 095 830 408 551 228 851 168 926 363 516 545 207 751 907 724 099 763 234 502 451 816 370 159 019 055 030 801 777 088 758 790 497 220 787 819 948 756 092 971 515 705 860 070 886 118 789 669 639 764 825 050 262 516 709 349 258 307 192 632 994 497 629 457 080 012 177 912 211 530 482 511 145 430 688 020 112 188 782 030 845 670 040 183 152 108 400 744 475 080 314 252 971 972 212 841 216 437 822 674 092 714 880 905 751 588 797 067 642 770 193 038 624 507 577 022 843 382 771 255 410 947 073 772 620 217 407 894 208 552 970 023 132 181 020 548 330 548 270 186 447 871 032 313 115 142 691 940 336 904 255 737 871 806 390 236 683 702 368 495 519 595 857 983 520 618 014 229 719 729 725 090 900 155 081 168 397 587 487 570 822 106 193 267 160 607 706 497 887 736 217 865 243 478 962 026 396 409 299 373 816 686 124 888 410 173 442 048 570 116 956 211 753 696 385 479 279 076 869 204 238 267 191 012 277 211 553 486 704 301 452 295 653 402 697 761 014 321 972 564 287 430 842 077 025 571 950 067 866 368 142 771 664 017 990 446 514 430 542 045 191 548 909 484 687 045 414 868 456 332 646 359 299 377 033 046 785 602 158 812 545 558 580 604 744 143 123 876 114 457 526 890 185 753 454 667 065 515 174 119 336 620 360 765 932 565 339 071 588 353 042 742 174 485 493 407 447 068 090 831 470 466 684 821 248 557 867 219 403 605 234 266 717 799 059 094 880 199 675 452 989 294 225 067 785 670 248 292 876 984 679 437 276 447 409 939 323 773 054 449 361 192 953 554 443 371 126 346 719 634 386 622 300 562 931 720 233 185 727 698 160 811 492 370 976 274 232 414 354 797 995 119 652 340 751 640 137 221 707 248 485 377 199 577 891 001 525 289 779 363 283 605 628 384 749 238 186 605 500 641 657 255 488 885 766 389 641 919 005 740 019 692 530 372 301 513 772 343 765 782 199 035 226 288 348 215 011 293 898 841 996 436 199 344 546 476 764 838 466 385 177 783 279 980 620 774 990 304 272 345 933 035 975 413 213 302 939 101 596 806 824 375 822 616 542 431 352 002 855 170 774 378 195 145 478 833 838 122 439 488 319 766 753 215 576 870 129 401 855 117 896 053 288 068 527 942 600 787 382 713 624 965 611 289 708 691 255 099 542 114 895 191 576 563 456 747 424 636 924 366 986 969 795 594 490 221 227 592 594 794 323 265 512 304 217 692 660 279 601 185 823 656 279 714 774 861 607 123 156 612 120 068 116 181 099 688 240 206 586 243 627 966 259 400 441 291 999 626 461 799 440 514 835 668 514 377 051 162 619 616 761 836 021 935 862 636 992 395 916 276 951 624 697 116 625 178 422 446 420 878 030 487 473 209 563 128 555 836 661 482 334 114 425 465 481 820 826 661 932 628 659 912 651 855 994 474 354 598 167 138 781 343 159 624 961 743 752 664 474 919 470 217 249 398 398 387 298 128 538 686 655 945 957 628 537 721 168 840 148 857 335 389 340 923 219 253 264 464 358 272 739 720 989 614 166 212 697 230 027 932 718 630 377 455 095 257 136 073 641 729 422 258 391 776 094 113 915 589 151 522 313 499 960 091 082 517 726 168 348 801 751 593 853 172 535 953 146 672 057 619 103 886 115 988 608 450 410 773 997 527 920 395 451 775 987 009 958 632 772 026 557 866 791 308 896 726 762 727 773 261 231 587 588 460 279 731 965 385 052 773 416 304 811 491 883 911 389 228 344 471 501 194 380 086 466 636 894 766 454 774 195 409 055 836 050 694 170 210 680 191 327 175 741 823 380 465 238 350 029 092 730 493 015 326 008 395 788 898 443 837 777 712 125 010 248 327 658 150 400 168 705 442 898 435 132 983 241 881 776 884 743 970 971 612 792 981 908 858 901 755 400 912 305 076 437 585 921 351 720 107 879 992 199 791 648 033 113 683 559 743 250 130 436 439 284 681 312 782 295 579 360 723 851 877 954 225 629 358 973 395 129 077 034 603 824 029 388 616 135 749 655 243 013 850 824 397 052 426 321 948 182 403 100 181 006 911 010 108 092 671 859 257 704 683 974 488 849 088 333 287 856 688 880 377 327 013 994 117 508 065 816 594 217 275 038 195 267 272 559 641 103 425 220 460 887 049 806 552 764 839 941 846 601 860 076 380 237 136 991 647 380 125 867 408 604 502 247 222 628 305 458 782 061 578 124 005 176 951 256 924 715 001 555 516 849 815 353 321 639 291 467 893 855 142 086 385 481 720 648 088 129 947 846 098 473 937 135 540 298 891 347 344 300 539 645 833 341 111 340 658 348 211 803 050 467 616 411 645 862 023 211 276 308 893 878 552 820 320 947 682 989 271 103 718 103 476 247 227 013 121 936 432 146 237 728 517 578 420 022 459 290 332 041 714 021 219 403 806 947 968 624 666 427 818 521 648 253 898 069 941 989 234 462 243 736 137 946 026 031 328 754 531 814 720 140 440 156 529 043 269 612 153 294 013 427 293 136 896 336 871 768 267 980 856 820 663 457 224 638 811 985 491 921 256 099 973 656 919 561 461 065 622 913 036 733 317 850 344 168 273 636 855 179 131 606 907 156 889 571 295 117 477 109 418 068 379 409 617 274 167 162 349 210 211 796 199 581 958 246 967 694 488 063 202 292 993 146 163 580 704 527 084 555 601 570 234 390 981 160 195 735 536 947 011 050 241 670 911 752 811 157 480 641 700 338 635 784 495 734 661 891 382 394 248 414 186 306 905 233 785 663 132 895 458 653 841 282 478 860 943 661 800 072 628 095 999 262 926 498 352 778 236 359 557 423 129 084 955 326 811 800 727 696 255 649 760 866 227 371 298 905 287 553 667 463 967 862 104 743 308 859 425 488 879 324 686 432 552 990 459 749 844 859 268 889 257 800 350 002 810 334 410 195 324 026 042 009 506 021 464 468 074 816 121 887 799 817 359 278 988 864 536 770 313 832 103 775 613 252 188 162 283 677 729 171 385 239 260 421 272 068 015 307 815 683 988 473 537 681 954 083 852 952 107 257 132 766 651 501 064 724 474 998 298 403 360 434 604 660 410 658 046 713 000 185 433 340 498 285 368 074 512 659 968 418 954 649 206 093 100 052 916 364 350 030 758 789 559 821 661 522 068 230 151 929 336 030 019 492 195 233 892 781 440 106 821 347 572 261 748 619 861 000 912 221 588 500 624 096 401 294 407 984 891 075 730 310 313 469 082 659 606 074 744 822 138 752 844 738 671 821 771 275 241 076 760 519 487 130 561 283 324 953 846 710 349 064 305 729 431 403 776 483 929 704 175 688 966 094 820 522 211 462 405 043 862 470 275 721 646 986 745 164 660 552 926 081 810 564 276 284 465 994 602 157 908 152 769 704 208 443 818 211 815 860 088 243 708 180 691 930 916 077 344 824 385 087 724 938 560 535 309 407 499 649 528 220 454 368 023 022 176 204 097 304 843 198 026 038 144 208 851 784 512 165 776 655 839 150 646 256 427 856 452 948 369 690 331 776 199 901 231 627 841 482 899 005 805 941 039 380 760 439 604 419 618 376 825 265 258 882 699 092 492 806 293 304 193 443 801 466 997 739 938 683 998 387 936 140 597 442 868 336 435 366 022 557 411 015 588 248 170 949 934 024 977 627 936 281 174 213 418 028 261 602 941 002 687 898 633 929 740 229 558 750 908 931 937 322 910 077 965 002 150 408 732 067 226 968 041 521 992 509 946 611 463 742 189 699 275 021 878 175 073 302 378 963 853 389 723 250 904 610 039 575 760 833 359 681 249 821 423 081 519 332 884 039 263 827 562 515 087 516 411 761 584 563 237 979 263 053 862 570 724 688 318 541 802 477 799 833 219 676 112 345 244 667 461 407 366 345 280 510 447 577 240 406 650 017 504 899 754 181 732 596 743 517 190 837 651 340 231 356 034 341 058 783 682 452 561 087 355 837 725 398 995 399 088 983 789 842 155 034 735 579 392 905 345 995 791 736 931 109 893 683 350 959 340 719 475 251 857 615 304 753 817 021 828 116 495 406 479 249 306 149 675 231 005 792 639 507 433 707 832 525 049 723 410 909 255 951 843 163 540 638 109 194 828 429 288 544 038 576 220 473 263 366 727 800 178 145 556 322 705 200 609 481 933 477 418 304 620 875 551 257 068 527 493 938 354 526 500 632 513 265 865 485 492 586 446 525 156 023 352 754 680 263 534 934 779 224 564 500 603 386 771 783 601 155 967 419 513 948 835 661 105 945 038 360 234 507 824 190 558 672 290 172 608 509 093 914 626 876 824 659 104 624 641 971 578 324 215 734 449 371 298 791 658 761 860 407 581 526 885 892 612 337 544 658 076 736 488 084 345 688 877 416 333 790 527 245 262 058 890 892 298 823 066 889 681 075 777 613 805 028 252 953 183 137 659 874 696 440 431 796 066 062 440 746 350 390 202 309 449 329 201 169 641 569 714 824 422 325 644 778 030 395 554 662 605 817 722 940 377 114 925 171 935 382 048 848 505 282 918 958 024 872 255 197 793 626 200 992 574 671 083 687 614 373 473 814 711 331 979 963 650 681 185 939 392 107 114 450 387 657 683 209 753 092 972 670 665 916 198 385 358 465 942 868 014 772 598 897 659 467 823 738 713 692 513 835 302 856 594 196 394 585 828 974 953 589 402 272 592 924 936 289 522 990 993 147 035 332 041 315 340 278 710 828 407 672 327 022 081 325 771 819 426 168 454 170 446 027 418 986 466 507 437 446 805 478 815 266 084 336 354 087 165 713 132 953 980 048 909 936 160 402 824 907 925 655 477 295 308 635 487 716 877 489 045 073 724 667 154 941 078 222 419 358 536 382 620 634 234 706 475 264 685 114 006 361 659 506 981 689 125 839 813 904 704 727 332 875 664 365 100 565 898 545 701 757 792 152 775 527 038 634 018 974 325 403 415 178 889 451 967 921 812 125 681 989 660 439 871 172 432 168 298 293 553 643 165 345 381 183 271 471 964 220 326 958 074 495 102 314 670 064 010 985 303 793 503 723 868 883 361 442 933 161 662 000 121 076 186 468 361 761 156 722 867 931 684 950 162 816 960 059 414 304 382 736 871 513 069 119 885 755 476 630 242 976 088 784 384 242 357 797 896 913 386 223 761 907 502 307 105 774 073 791 934 062 723 710 170 101 833 051 587 117 856 417 452 112 822 468 214 538 621 366 135 287 496 999 429 050 262 756 840 862 150 425 068 946 269 334 372 686 612 687 265 038 310 948 403 413 143 249 199 938 422 106 384 351 353 280 186 227 705 311 753 497 096 332 967 287 441 037 752 974 134 802 987 391 846 479 556 240 839 955 419 228 763 730 301 232 441 059 404 780 678 029 695 767 677 669 745 791 274 383 502 914 054 977 022 732 332 649 619 061 474 834 287 956 120 602 571 061 572 758 424 557 969 129 961 392 255 955 020 311 135 409 608 730 090 109 842 906 283 941 976 180 552 057 863 305 598 076 870 634 915 161 157 896 636 154 993 765 154 247 752 279 065 262 104 463 336 550 694 425 300 195 448 881 432 370 200 909 394 464 796 222 806 178 587 198 711 635 695 056 299 092 928 390 098 312 178 100 825 673 061 975 398 576 375 144 379 408 864 980 744 327 842 818 021 551 039 628 859 705 048 404 849 652 626 579 334 728 047 716 657 371 941 612 171 720 750 865 499 003 578 443 278 794 241 183 757 622 136 589 354 907 674 677 377 434 753 977 910 272 513 243 822 652 126 088 584 186 408 789 879 341 551 352 300 685 996 429 988 760 323 068 673 213 910 669 814 814 229 463 512 106 738 526 456 937 888 214 397 862 073 193 500 602 092 626 241 497 079 600 464 508 479 738 153 924 346 692 776 843 276 893 302 459 362 319 269 344 906 287 520 939 626 031 137 282 515 910 211 836 778 450 063 398 747 754 396 157 067 375 343 020 281 778 872 007 486 652 921 680 286 902 172 745 962 499 727 719 019 451 880 326 725 516 968 085 744 472 230 990 740 932 255 366 054 671 637 417 888 617 520 041 888 238 226 169 632 692 492 456 684 207 236 319 493 816 257 273 738 285 213 155 768 653 241 434 351 922 752 156 927 539 986 106 207 134 949 735 708 898 293 449 510 221 968 030 050 620 487 157 028 920 473 332 163 849 848 463 241 293 777 493 922 956 556 577 217 730 217 306 888 940 071 792 600 038 934 034 338 438 381 266 201 982 945 630 646 629 735 872 089 993 823 804 947 026 338 046 636 895 660 317 418 175 094 645 512 480 231 435 665 681 798 073 391 844 624 716 770 606 288 998 064 217 022 297 275 388 592 964 858 368 240 540 587 734 632 011 747 926 789 862 737 750 797 677 468 174 481 209 768 335 840 314 498 350 673 244 862 502 436 807 621 344 381 769 822 347 082 642 724 136 543 607 239 303 429 462 481 414 736 479 083 154 737 705 170 034 876 902 224 348 299 810 877 430 437 449 529 624 315 512 947 663 301 615 248 540 840 553 582 907 697 134 511 238 189 106 315 786 182 726 709 803 390 049 540 134 324 819 200 975 063 424 137 823 888 443 441 547 066 379 022 344 124 494 520 305 390 620 946 867 986 713 573 271 656 264 893 800 533 643 385 303 425 521 505 781 433 002 011 908 353 360 760 133 856 932 024 203 706 493 091 032 638 287 664 350 359 064 356 381 717 787 985 800 756 638 806 423 500 763 309 896 909 730 374 734 848 617 940 140 490 335 317 767 531 441 928 053 578 911 199 633 120 254 072 997 244 982 494 417 629 305 423 982 962 685 338 132 273 711 361 431 044 398 488 579 070 016 321 384 589 078 399 162 090 410 639 202 567 692 398 049 471 350 427 943 170 350 990 322 378 324 107 799 531 672 419 158 070 637 887 093 910 608 952 572 937 532 188 538 454 862 048 403 508 388 928 220 552 981 018 588 441 263 226 368 467 732 156 519 464 322 316 691 935 654 630 778 281 252 144 797 406 971 473 325 771 446 615 230 313 130 783 662 240 658 058 423 765 548 864 771 809 186 567 917 907 390 219 022 235 905 032 574 380 896 444 207 003 781 223 600 633 110 408 009 956 223 199 559 627 396 536 535 249 000 693 182 274 566 492 360 444 367 606 705 353 344 176 121 918 305 435 427 142 304 630 647 849 090 931 347 115 506 976 553 174 786 941 605 519 104 732 692 287 174 833 187 732 356 794 825 171 673 669 023 579 937 062 270 934 606 814 839 584 239 124 251 010 863 136 417 570 360 381 244 242 550 045 884 435 073 809 786 645 837 220 678 358 018 127 784 105 497 118 584 603 169 278 175 588 724 945 168 864 065 582 235 183 453 498 498 964 635 699 410 794 263 981 056 149 899 689 454 974 466 717 464 017 750 025 384 657 187 806 678 177 611 718 400 485 270 161 926 195 210 171 362 452 568 624 699 207 389 021 683 270 339 572 744 888 957 495 148 090 139 816 218 484 848 124 629 755 077 886 536 435 430 803 780 914 104 325 383 862 375 437 017 179 970 715 088 745 353 936 266 993 463 329 713 789 504 012 832 437 654 595 730 311 021 773 782 295 289 887 702 965 317 637 828 934 989 833 733 755 451 077 705 347 621 908 393 659 974 963 257 063 551 514 306 721 333 237 141 248 068 285 222 283 218 599 812 244 215 333 757 538 255 674 376 585 157 920 235 337 749 300 553 280 135 326 280 981 515 052 130 442 449 583 986 425 329 008 401 701 695 066 585 603 047 655 832 595 722 266 921 602 111 102 031 602 825 187 749 414 000 102 867 291 296 601 102 840 709 566 606 626 676 846 988 404 506 485 341 640 941 829 231 883 574 092 434 783 289 381 865 366 399 896 606 866 589 503 205 847 878 423 444 162 519 293 389 879 274 069 824 890 750 988 614 273 383 080 776 751 978 073 770 888 451 743 820 942 052 900 972 706 786 896 911 243 497 626 516 503 416 378 614 080 063 997 554 189 134 848 582 699 528 110 977 003 637 780 512 461 494 712 226 586 584 536 121 520 291 006 510 835 859 438 410 345 002 180 609 036 011 431 990 349 338 200 228 715 386 643 172 571 120 068 874 229 718 773 577 828 317 484 438 291 365 627 611 961 019 189 389 637 471 704 965 541 136 021 157 133 269 765 983 991 557 413 040 810 616 055 642 585 549 473 804 266 339 566 362 807 801 421 187 407 821 325 958 556 646 942 197 114 378 637 146 209 880 616 484 823 084 240 594 720 900 966 751 633 811 192 620 320 810 802 800 151 613 299 777 195 173 583 412 784 833 129 105 435 591 590 721 008 960 670 136 337 952 441 692 412 826 489 348 258 868 968 909 056 750 446 731 235 795 326 044 277 239 832 218 711 804 761 375 586 014 171 199 135 157 674 849 595 901 386 821 342 529 059 414 705 440 597 494 504 256 753 575 013 646 773 458 706 529 208 307 250 392 856 499 025 738 418 255 589 765 668 808 713 655 526 287 365 820 508 602 758 468 692 361 873 771 305 609 687 054 668 170 010 259 587 125 008 971 050 515 559 269 397 435 320 161 687 534 272 034 897 180 423 919 825 989 358 483 709 211 949 943 493 567 863 805 226 118 317 696 197 771 252 875 056 862 797 579 440 452 906 561 266 626 114 402 189 479 343 841 817 541 361 683 815 953 354 394 068 763 471 373 829 411 228 934 323 246 169 387 556 298 426 217 658 897 929 890 134 672 915 037 307 421 722 824 531 710 986 950 356 276 336 378 484 332 724 635 510 903 954 297 286 198 986 272 926 013 034 749 244 735 019 137 521 302 435 694 732 676 921 824 250 194 596 036 316 912 708 178 872 039 026 627 869 468 163 166 113 247 601 820 847 587 334 223 227 593 111 906 356 268 719 969 456 949 323 685 212 466 282 464 461 768 873 087 930 933 531 509 388 074 723 127 601 392 935 407 777 670 375 814 703 297 838 351 544 247 512 927 735 912 222 097 280 245 830 474 662 508 360 348 528 895 691 487 210 329 945 156 436 543 987 614 957 427 861 359 151 019 511 033 620 588 475 021 919 613 455 395 302 928 971 409 100 602 193 170 684 506 298 347 081 269 900 136 977 287 432 025 351 409 379 332 818 194 231 165 676 997 325 520 372 752 881 812 866 565 340 308 267 480 079 266 950 816 104 231 234 901 015 862 801 019 764 122 084 042 899 617 378 996 547 014 529 573 174 612 715 229 706 062 863 417 724 444 673 984 942 662 407 968 890 920 186 783 146 890 106 328 922 454 946 396 849 155 471 968 897 932 434 080 657 580 588 877 846 997 986 801 062 526 602 166 550 263 173 786 829 596 302 471 907 474 811 378 969 131 301 878 711 295 154 650 379 860 236 462 668 680 585 003 819 864 700 006 479 996 639 420 890 787 721 592 151 610 623 466 001 908 574 060 233 208 826 633 118 805 161 800 210 589 313 296 735 496 591 147 339 480 043 443 130 632 468 657 779 384 686 634 830 349 276 816 756 897 106 861 118 645 993 236 572 783 658 899 843 097 271 542 008 734 235 455 956 125 555 150 990 767 904 662 089 932 867 795 248 323 181 211 405 608 949 623 517 144 378 540 468 152 446 254 710 222 588 852 472 706 019 815 639 265 933 986 357 591 216 128 779 352 589 146 316 954 298 305 908 103 787 300 135 704 932 136 505 590 484 366 919 990 855 939 824 578 123 124 189 486 330 725 935 903 060 311 861 027 401 359 756 875 158 602 722 330 419 533 308 189 724 203 957 591 456 509 414 993 869 294 407 546 402 535 921 610 591 895 023 411 920 734 058 660 313 703 970 517 206 320 839 991 829 485 756 235 970 592 646 828 992 158 174 592 971 435 513 454 230 104 110 193 734 265 459 997 091 652 183 585 829 384 921 724 675 745 517 906 218 109 626 459 850 629 748 723 928 924 270 268 833 186 887 425 884 305 238 030 103 406 977 284 042 428 770 249 408 410 495 728 235 242 789 152 423 170 626 961 612 623 250 733 255 337 190 353 567 942 829 247 953 600 406 417 822 811 402 581 712 478 420 906 622 690 221 645 684 182 686 708 652 813 392 117 865 274 588 949 410 256 934 936 719 699 545 649 072 731 866 196 006 758 410 917 336 258 780 309 824 343 917 451 046 712 612 540 242 358 232 400 155 788 917 710 512 616 955 909 076 604 367 827 729 017 872 401 778 034 196 849 077 237 387 181 264 293 266 871 028 879 434 087 582 867 314 460 968 781 802 968 718 136 586 485 729 754 185 625 732 856 832 373 122 233 395 233 004 824 517 040 828 713 555 700 645 730 234 031 949 489 422 894 920 101 293 267 812 677 751 900 382 594 104 772 188 301 227 596 373 611 780 980 503 049 207 587 697 089 055 186 205 420 984 118 610 773 392 079 221 534 682 174 971 238 186 393 524 904 223 115 234 761 559 732 312 482 411 803 994 509 447 211 389 814 294 822 357 269 558 859 377 346 103 126 482 967 772 592 788 308 942 850 838 301 517 469 910 807 547 342 941 913 145 645 346 005 609 444 108 758 889 986 135 982 697 267 540 941 018 218 011 593 121 410 425 936 632 081 638 589 082 866 423 689 131 664 697 391 540 286 755 406 668 057 644 134 208 736 845 355 898 300 758 992 359 475 350 789 441 064 780 786 890 129 987 132 991 828 922 815 978 406 237 538 662 671 915 526 711 136 834 070 812 607 064 917 199 631 079 468 529 463 010 550 885 413 472 705 918 795 352 468 686 140 244 370 639 842 005 739 730 997 247 053 112 431 937 603 501 477 122 924 161 389 633 986 613 900 265 822 736 080 857 504 221 817 833 629 664 839 143 705 577 276 664 850 431 716 465 317 313 891 027 702 049 195 073 026 418 178 148 576 065 369 391 173 518 714 733 928 764 456 075 811 035 849 181 312 488 884 256 882 653 027 923 938 332 508 274 298 217 736 160 904 180 810 397 281 186 223 825 112 026 474 372 204 334 089 368 396 838 972 215 637 353 509 547 052 179 944 208 799 435 301 897 325 928 507 803 261 783 825 057 448 952 739 324 794 560 743 467 463 321 929 022 909 810 036 392 541 523 550 057 450 041 124 659 620 737 687 685 537 929 719 272 967 036 249 173 497 432 106 896 272 357 280 635 319 468 774 831 713 290 754 908 161 474 195 584 896 852 466 841 597 973 117 585 018 470 739 406 068 311 415 066 906 941 141 449 670 625 272 569 449 411 933 974 257 167 911 810 549 584 980 006 192 820 126 076 706 681 818 626 297 614 231 370 387 279 168 230 281 521 609 439 097 101 248 919 627 279 156 894 752 500 386 764 435 010 138 430 408 344 117 523 026 288 008 411 101 550 882 755 900 785 850 958 366 375 210 243 881 396 664 237 131 415 416 886 435 347 454 410 780 574 403 219 887 877 827 897 327 611 600 201 675 803 547 762 981 586 294 055 195 002 885 370 941 725 114 014 535 445 576 431 484 803 353 404 968 433 737 837 791 128 559 475 250 497 102 591 724 870 270 780 827 001 351 812 767 018 987 375 982 767 603 267 008 920 840 914 830 511 122 719 581 162 476 954 437 494 080 739 147 294 025 939 542 053 027 777 893 497 802 476 543 511 521 513 297 043 038 848 620 469 031 001 353 042 530 349 038 927 126 100 766 094 390 599 684 663 575 206 654 414 988 684 852 541 848 351 790 743 023 048 638 674 691 468 007 993 406 903 685 630 911 038 045 478 782 644 431 755 296 254 922 251 620 013 261 939 208 572 041 155 038 939 398 693 173 524 888 343 371 796 470 469 501 792 210 255 109 244 602 557 277 696 394 233 887 835 740 060 048 794 347 378 017 140 773 161 852 532 878 569 486 181 901 028 903 549 716 472 832 787 870 706 435 519 257 323 625 098 050 009 824 255 879 825 535 958 139 963 549 048 902 478 054 761 004 441 882 120 626 108 377 611 012 027 947 630 731 656 006 948 604 142 725 396 825 505 806 645 304 773 774 460 853 934 237 217 395 140 405 533 522 365 566 223 029 683 602 365 047 902 528 277 395 943 128 834 172 010 935 926 058 600 432 518 855 676 481 783 449 509 692 490 208 732 143 477 386 516 059 102 851 479 428 243 877 248 390 087 823 613 562 156 454 783 992 675 119 314 054 009 957 434 849 736 827 373 589 031 790 128 196 847 303 012 233 772 377 633 103 325 294 373 376 155 454 936 802 315 786 255 768 188 572 525 494 541 809 058 629 396 593 924 897 079 204 206 344 063 869 568 536 980 222 737 531 068 845 615 286 643 303 977 246 700 611 836 366 308 441 907 680 227 186 412 097 665 162 670 573 185 151 149 945 391 043 753 671 393 734 362 263 155 080 819 458 912 466 196 857 395 127 956 586 934 212 949 081 673 788 319 637 496 805 919 123 094 985 700 559 773 178 519 892 561 745 956 942 520 098 135 529 622 486 434 014 134 094 105 423 844 281 507 417 712 544 741 342 877 789 252 705 328 519 301 422 623 217 159 124 253 571 924 548 792 233 832 073 414 617 076 488 475 924 866 112 797 656 324 698 154 934 501 131 390 277 008 709 541 230 310 781 992 200 100 227 617 185 010 901 505 756 313 623 997 961 793 172 043 712 123 804 778 900 839 382 950 455 472 258 870 596 318 922 333 582 196 481 150 384 756 617 252 439 739 590 844 486 121 735 784 625 098 566 925 307 246 583 259 443 818 653 361 394 534 155 133 111 110 679 332 659 212 919 412 725 155 385 861 866 958 333 043 938 262 423 805 097 711 512 148 282 046 543 467 322 963 855 551 587 075 328 426 520 707 476 727 278 425 966 885 210 526 872 555 047 917 378 235 470 045 160 224 178 021 208 269 527 979 461 607 002 963 571 288 603 683 749 804 384 907 766 266 091 698 182 132 546 834 495 777 524 071 656 788 796 875 379 922 024 560 972 601 636 039 777 148 897 260 563 295 677 620 872 720 291 009 130 866 715 562 249 016 432 119 930 880 473 173 656 487 153 553 513 262 464 822 075 367 038 370 006 694 964 595 141 435 770 373 863 435 850 528 589 426 992 672 016 508 648 994 252 143 895 417 507 296 767 656 421 410 695 697 174 777 393 902 845 367 737 443 197 301 818 139 435 870 367 897 810 936 932 914 399 863 022 892 296 601 550 270 481 500 581 629 964 437 495 204 434 884 031 922 100 035 690 780 817 745 420 165 442 291 527 456 851 730 954 840 767 642 709 306 257 883 932 057 527 030 310 072 996 575 223 256 452 376 786 929 489 564 746 316 073 669 700 637 550 889 029 030 023 990 215 245 111 878 983 742 733 636 071 368 308 139 215 721 440 538 557 403 005 152 528 450 255 120 948 603 131 493 007 190 782 855 293 795 525 487 656 391 499 285 324 252 804 723 964 753 519 568 633 075 085 003 810 099 506 854 465 405 147 106 362 720 853 891 621 534 799 330 737 489 621 851 294 827 368 916 858 761 204 926 185 203 260 470 417 540 449 674 268 940 625 996 629 126 092 785 367 925 656 372 504 555 703 241 526 970 818 744 268 260 697 579 453 093 996 993 777 008 031 391 944 621 934 228 949 611 016 377 232 218 388 064 870 700 167 325 384 583 723 540 724 662 071 696 685 174 476 421 432 602 372 516 800 994 911 686 115 299 954 377 742 794 468 664 041 160 693 783 703 399 668 203 527 297 260 055 290 364 859 627 011 196 005 194 340 323 915 657 526 960 086 759 117 763 586 489 238 017 050 966 476 419 895 125 949 671 639 705 266 116 452 165 016 825 288 209 563 426 974 178 483 889 264 411 988 201 828 968 666 705 003 919 170 549 395 402 862 972 846 385 532 026 113 121 759 900 104 739 403 401 417 277 693 178 626 073 821 028 297 787 493 579 807 951 969 083 174 856 870 887 326 293 355 610 658 446 296 718 751 445 312 863 535 181 992 448 943 497 323 473 306 843 525 697 675 601 966 625 019 987 226 923 945 877 258 617 451 387 425 205 714 166 958 631 955 968 998 815 333 591 429 068 942 006 079 575 120 139 952 481 192 755 096 946 343 577 769 942 018 306 590 660 541 560 123 259 209 236 601 088 838 030 027 182 915 268 580 155 328 948 728 720 390 418 736 022 433 070 034 392 053 266 349 868 298 003 358 001 359 558 643 147 299 972 117 436 900 708 357 074 497 411 502 035 648 952 732 068 580 688 942 021 785 652 680 521 830 684 709 650 140 160 658 407 950 190 654 348 751 101 604 128 533 304 957 168 358 200 498 959 457 755 562 537 067 974 033 993 000 452 873 907 867 941 336 017 920 881 630 564 294 069 061 233 667 641 441 005 607 165 814 445 274 976 063 077 560 976 081 468 319 841 133 556 642 440 438 433 915 447 875 898 046 755 711 147 429 608 477 138 094 146 078 525 255 858 286 155 104 690 392 316 845 467 086 580 825 927 720 673 447 436 440 945 758 098 291 175 177 457 367 749 311 245 805 402 637 662 904 032 629 674 402 503 898 068 157 439 364 291 065 536 974 553 135 005 493 911 346 537 166 165 030 227 864 459 920 042 418 744 412 598 643 265 417 033 981 065 459 930 019 791 814 319 003 212 594 310 611 004 030 213 756 301 445 559 337 958 119 365 259 892 470 580 731 803 508 502 881 892 278 346 765 889 102 661 769 966 830 003 588 597 941 566 956 177 138 182 471 546 125 182 818 883 091 079 700 238 056 069 209 847 666 463 107 043 081 576 064 327 515 230 637 079 627 484 850 368 198 201 722 247 040 896 118 162 404 745 314 205 997 282 912 974 445 147 998 266 746 869 401 240 246 960 881 832 746 045 854 281 842 801 604 176 114 481 112 878 739 649 081 708 166 787 980 292 170 444 640 505 875 054 065 452 358 962 011 109 238 482 746 452 722 043 544 376 201 516 647 629 003 646 481 392 287 051 572 410 793 901 778 669 882 392 411 808 827 313 504 579 471 844 419 422 333 330 823 831 824 890 807 808 635 150 277 379 723 916 932 186 508 936 082 059 272 689 786 687 289 965 715 536 436 778 386 702 603 107 202 392 404 035 110 805 988 299 526 116 936 160 013 387 911 155 633 329 550 857 141 789 050 272 465 374 011 047 453 161 192 227 329 784 274 733 181 372 525 071 453 773 718 870 140 636 885 913 655 894 556 786 806 038 756 979 656 171 310 938 917 686 865 319 715 789 452 244 045 511 359 971 725 070 640 047 370 403 332 556 317 053 629 670 634 187 340 608 009 183 722 467 268 613 267 373 609 507 018 940 331 035 023 552 538 626 599 434 603 863 111 132 402 172 720 799 647 177 877 692 426 092 325 361 095 881 929 665 926 755 049 204 283 707 428 199 734 524 769 537 215 622 469 695 202 152 525 846 047 104 321 498 711 728 882 370 943 473 377 007 622 238 256 584 942 354 205 821 672 690 331 000 011 755 404 857 055 502 620 451 599 354 510 113 914 097 352 658 953 802 757 049 019 952 960 822 236 306 323 983 772 801 269 843 046 937 279 823 356 486 879 364 212 625 631 224 936 139 715 688 822 773 422 871 425 453 263 928 972 841 670 012 823 679 512 803 421 126 595 031 344 857 311 876 634 318 586 554 307 839 081 819 974 000 250 303 776 266 464 933 321 883 495 654 987 261 094 555 789 151 083 648 400 812 660 398 576 053 320 493 407 946 123 871 603 067 744 067 467 057 160 114 253 243 706 675 070 113 383 875 759 856 669 108 281 124 442 998 335 004 953 413 354 180 490 626 664 642 087 398 631 805 940 736 732 983 053 182 240 571 401 743 754 051 294 484 829 164 230 274 671 888 460 912 405 385 319 325 519 637 499 692 278 753 237 594 212 315 189 032 783 978 338 729 423 134 790 762 398 327 131 151 162 424 952 468 341 040 072 313 772 340 314 398 501 625 250 428 898 169 235 443 739 599 329 222 936 170 519 175 893 629 052 837 537 314 553 769 724 260 438 311 136 608 923 500 314 040 132 157 386 515 461 024 765 712 311 887 006 701 648 639 682 917 040 749 234 089 837 342 791 140 349 513 201 776 753 229 824 666 842 640 318 463 680 205 912 188 729 643 236 122 240 432 781 843 961 018 769 012 224 959 492 366 168 596 515 393 796 407 015 874 870 013 234 840 044 787 611 664 074 001 500 258 291 929 261 008 879 028 372 172 958 946 332 477 443 537 969 081 117 469 031 315 208 742 724 563 747 137 259 799 951 877 138 833 465 848 527 604 615 240 610 748 700 424 269 940 942 053 040 930 927 365 616 795 027 251 342 865 060 269 239 109 408 730 613 324 050 886 576 877 646 738 476 079 889 211 065 760 546 500 626 922 176 369 981 453 397 389 517 728 200 053 945 416 489 375 777 201 897 436 502 320 434 139 395 838 084 498 421 691 433 273 127 075 461 810 143 101 009 815 954 925 254 894 412 090 527 197 941 933 128 365 239 508 843 458 865 396 817 740 214 436 140 061 893 840 551 597 604 389 117 752 779 065 601 364 336 425 294 498 307 419 847 287 090 548 795 130 944 336 095 537 228 339 948 817 112 860 919 003 229 418 238 830 347 032 068 171 085 548 577 784 615 414 822 454 570 767 625 611 020 674 829 327 101 422 295 219 324 688 679 928 680 208 940 104 075 673 870 886 908 391 495 998 973 877 021 821 367 406 270 224 449 355 129 305 967 598 916 664 002 579 767 126 427 454 416 904 282 152 986 433 771 648 734 452 163 044 295 534 548 276 279 621 666 840 655 952 088 565 148 338 956 233 634 200 634 550 025 554 999 178 258 268 514 024 429 815 665 260 970 479 389 863 931 488 490 008 727 929 189 097 151 528 997 812 597 934 615 450 723 094 836 525 682 755 860 975 641 763 765 949 557 507 240 769 064 558 892 884 697 371 631 191 251 470 504 200 397 528 155 753 731 291 158 908 013 724 552 606 314 481 704 576 037 245 385 013 997 334 662 422 529 389 139 120 100 996 983 974 881 515 130 603 793 400 672 762 292 704 500 247 872 450 017 493 060 477 320 416 241 578 698 403 305 692 122 002 820 692 228 915 231 354 193 819 916 110 366 231 282 142 860 437 104 558 906 166 444 031 800 684 975 031 209 403 364 946 854 438 781 032 638 730 099 249 393 336 969 098 704 765 019 146 700 717 748 836 563 545 895 925 172 890 810 820 612 345 803 500 932 926 685 545 345 366 245 337 924 358 626 818 876 110 415 826 169 578 902 505 317 126 586 376 658 882 120 637 668 233 367 361 627 222 893 470 685 024 095 231 059 355 993 282 553 038 038 591 651 614 840 289 824 106 196 172 350 613 293 538 092 115 599 897 440 376 305 530 636 284 598 871 548 637 640 387 269 751 706 914 882 230 728 740 366 798 646 215 712 733 821 677 313 159 540 753 762 378 648 489 827 252 974 856 820 593 941 742 410 717 496 379 932 423 907 869 901 096 592 992 065 213 974 682 291 775 989 084 280 448 340 459 236 600 456 725 995 702 645 778 465 487 429 260 871 045 568 247 311 643 270 937 404 439 175 185 144 876 469 780 174 203 145 462 743 854 095 908 154 695 951 343 403 703 503 718 933 107 273 312 275 406 241 813 457 379 124 221 164 873 074 194 580 788 003 017 070 044 066 694 717 547 396 823 475 273 318 219 898 156 046 312 194 255 995 197 618 046 340 571 836 302 737 333 522 389 621 014 537 662 343 203 308 087 758 026 031 806 793 629 615 402 478 384 757 587 381 108 426 212 012 009 416 641 400 465 165 360 947 997 427 978 775 560 392 741 893 700 138 995 896 231 831 682 228 569 360 253 198 210 379 373 846 204 317 860 732 644 018 252 075 988 924 270 986 108 276 681 305 890 722 741 780 010 882 545 121 868 502 189 714 687 288 775 906 227 833 125 662 325 368 991 878 404 102 139 660 960 686 485 111 342 245 522 379 689 645 060 907 155 350 508 585 639 860 394 863 071 750 038 603 669 654 167 718 951 325 236 468 942 568 694 288 866 505 797 822 296 758 696 408 861 469 824 237 044 799 853 975 766 905 687 530 479 715 272 086 044 348 234 972 923 225 166 341 944 234 391 755 473 658 057 924 168 903 490 958 903 409 689 312 132 936 281 691 456 336 076 577 811 695 983 113 009 615 868 133 835 159 088 954 164 920 479 532 141 373 229 532 231 767 150 091 254 137 394 366 147 148 146 312 589 954 976 908 018 278 730 918 834 802 616 109 920 795 281 222 058 066 809 077 342 345 946 993 573 476 076 795 765 946 154 772 272 670 722 532 775 155 807 366 486 172 006 813 273 105 923 862 529 771 943 004 259 846 231 427 200 057 987 015 012 968 117 305 254 669 519 371 153 637 978 208 115 067 519 051 117 555 446 314 048 907 715 312 604 254 631 191 192 971 777 634 529 194 580 902 962 984 263 868 892 483 624 897 551 079 184 407 776 654 198 131 341 249 466 832 339 364 602 796 642 136 005 699 173 296 140 396 227 948 875 225 007 964 784 393 739 168 181 170 814 708 639 527 556 806 662 387 054 775 400 031 415 542 240 861 650 081 887 160 178 617 680 366 644 980 073 744 243 728 690 988 478 693 566 704 503 597 624 694 258 951 828 084 937 816 553 694 272 679 083 154 005 008 886 398 313 918 946 980 902 530 268 855 659 001 636 585 841 197 333 279 370 045 595 370 934 333 246 252 860 872 664 094 930 421 148 409 546 893 437 019 026 124 586 813 712 999 774 562 979 729 674 311 755 701 230 253 679 241 853 606 018 853 254 452 884 627 115 596 430 540 186 800 682 387 193 819 089 727 064 740 176 218 974 012 957 496 139 298 978 432 180 263 760 166 578 985 905 198 773 568 958 783 899 260 900 395 672 992 816 362 712 242 174 659 786 560 767 661 346 348 260 282 000 678 726 711 098 632 998 654 678 156 947 630 273 139 687 165 985 551 076 857 211 081 692 169 936 642 660 627 164 927 604 473 395 460 744 236 309 634 499 336 225 761 540 467 487 979 238 018 564 604 747 780 917 659 425 661 776 096 844 991 973 219 375 023 218 427 888 688 788 614 259 293 233 692 448 770 506 420 243 476 198 291 120 883 957 930 474 482 303 767 257 380 924 348 187 272 417 917 246 533 490 903 121 922 277 632 134 143 172 774 460 285 356 224 027 506 259 946 653 418 466 052 118 432 716 537 973 442 510 159 239 612 330 045 003 730 448 717 614 891 808 196 963 789 949 378 887 672 876 784 502 402 838 250 083 875 501 412 686 588 866 376 277 193 373 383 876 959 543 477 698 781 421 395 636 045 574 091 267 007 676 718 115 039 709 112 356 083 150 827 315 519 006 534 866 997 203 544 421 812 385 600 108 968 897 350 993 794 608 889 630 145 569 381 783 385 888 330 421 449 783 751 010 966 969 217 738 517 666 844 792 282 104 203 608 512 747 803 110 657 520 002 635 601 368 620 897 693 377 772 820 918 792 341 676 663 983 804 229 583 838 294 253 077 186 895 956 885 166 210 959 779 756 544 924 426 131 763 305 253 300 841 616 902 822 159 322 773 481 116 843 194 437 411 791 902 810 985 987 369 535 110 348 526 126 212 839 613 187 596 492 209 636 433 008 230 018 001 219 013 251 249 538 423 824 158 222 321 839 457 830 159 231 896 953 412 131 278 785 287 466 755 266 939 133 973 320 846 136 549 263 487 006 189 580 415 838 110 027 000 657 519 249 874 425 521 583 341 727 793 547 476 020 037 381 095 882 452 046 588 528 272 480 008 096 881 056 833 500 122 500 416 644 178 188 390 113 090 376 664 158 612 062 151 760 371 628 989 571 573 467 095 333 680 741 969 684 743 102 168 853 255 953 275 633 830 594 930 706 794 039 370 995 024 569 494 709 182 800 584 191 553 723 771 041 312 866 457 572 025 823 157 456 139 787 636 435 407 431 342 043 099 505 257 950 514 184 979 982 194 896 395 553 348 010 281 351 560 835 879 016 238 554 157 024 316 547 550 232 084 142 883 849 993 271 548 722 492 227 517 878 176 299 599 583 283 150 018 378 011 420 323 594 623 958 259 806 603 581 034 138 117 420 483 053 240 499 588 882 646 204 234 720 282 004 662 478 600 088 980 888 295 171 387 904 049 910 804 989 001 256 537 292 027 940 049 648 629 276 598 878 904 826 957 236 828 886 862 551 884 026 883 190 301 047 527 959 478 287 540 502 874 512 665 388 312 818 345 657 463 373 319 403 319 907 351 394 757 924 339 579 911 753 192 606 850 234 464 098 224 982 442 327 702 572 600 342 158 269 322 239 606 842 406 852 296 193 684 981 931 437 234 279 433 451 863 397 893 644 675 777 409 299 804 256 892 589 718 883 587 832 876 727 210 152 311 578 505 200 210 708 528 290 389 918 204 090 652 477 769 025 223 765 809 504 486 525 033 075 929 967 754 695 099 373 695 064 679 902 771 575 368 014 353 158 357 257 967 156 258 264 664 114 249 374 462 091 470 411 646 848 613 892 508 220 617 253 952 032 334 476 602 175 275 079 472 842 160 865 050 321 899 472 699 729 388 505 919 329 646 294 675 468 859 019 768 772 547 185 872 718 321 839 350 071 998 743 102 977 824 892 858 689 598 329 602 043 727 982 588 281 086 289 748 118 333 472 236 584 896 609 392 081 517 270 354 925 547 765 494 137 844 405 511 859 160 814 449 107 377 368 340 773 204 482 342 153 125 394 944 204 891 551 745 120 493 971 248 162 492 751 008 757 563 366 370 563 110 786 366 707 417 886 339 075 478 043 425 545 162 490 523 296 387 723 363 706 042 211 123 428 956 126 938 576 064 342 229 585 941 049 785 878 674 048 666 242 300 464 901 235 012 736 905 395 529 969 847 767 272 689 681 329 627 793 522 495 246 524 435 387 173 226 296 097 876 210 963 236 362 743 948 403 678 486 987 739 419 257 092 415 204 315 135 832 258 137 358 659 118 250 220 324 894 260 757 492 791 785 950 600 085 247 335 515 661 539 324 786 934 609 989 017 125 742 476 540 506 738 147 917 271 718 334 121 652 519 749 002 334 221 336 480 596 869 885 237 597 353 349 350 726 057 212 697 366 675 901 791 886 625 815 027 792 964 697 854 335 271 282 184 986 431 843 799 891 164 294 430 902 184 892 452 586 165 445 288 662 733 003 585 192 165 322 139 857 559 444 477 532 825 161 412 061 648 306 755 383 161 093 229 855 837 233 256 877 089 402 716 590 610 201 737 546 578 353 969 071 896 816 275 010 986 124 056 495 445 967 235 384 340 823 460 692 614 719 102 579 849 899 225 578 809 359 429 177 752 326 485 988 596 023 333 884 603 390 812 506 403 979 318 171 724 609 169 531 106 957 290 869 813 996 165 758 560 310 706 645 963 844 677 580 216 531 473 008 880 563 102 073 993 262 488 292 286 823 871 089 752 069 605 123 504 858 267 930 827 286 084 716 980 823 998 569 233 576 858 808 919 926 401 675 922 527 845 248 370 929 111 806 985 075 085 053 556 606 799 748 629 050 192 950 571 795 822 114 267 168 526 520 980 806 457 823 489 755 782 751 009 726 269 838 933 240 214 691 092 856 040 508 264 840 929 339 128 138 699 384 823 380 391 460 804 218 460 395 184 359 666 655 662 922 975 488 320 841 761 023 331 837 041 898 527 332 073 618 140 297 915 222 619 440 478 837 816 023 430 250 457 661 012 531 690 521 498 635 852 988 536 253 161 332 052 695 380 532 098 813 067 815 774 316 492 866 475 086 876 474 281 445 701 475 461 536 488 024 852 585 081 694 007 377 752 508 028 055 472 657 999 439 602 416 344 939 771 843 558 973 228 626 531 326 672 328 509 060 576 837 677 861 697 467 057 985 324 568 541 546 516 178 552 407 071 303 483 443 785 346 989 750 900 339 414 398 740 065 895 937 075 316 615 899 942 811 008 109 898 739 460 363 308 788 006 606 405 074 581 773 465 948 181 426 848 588 238 769 544 602 103 724 631 759 901 640 238 570 287 418 899 116 718 770 641 927 078 365 331 642 226 347 793 371 681 772 522 981 898 320 720 160 330 399 925 628 746 083 247 779 638 067 033 101 348 606 681 353 512 995 427 942 314 795 541 254 493 517 363 186 862 551 067 450 901 365 826 599 079 453 828 772 606 891 379 315 591 887 250 262 936 213 498 444 941 961 656 102 627 425 880 695 917 868 135 546 883 465 687 416 002 933 641 691 467 267 909 955 190 687 049 885 897 403 514 220 707 181 346 298 692 996 085 153 611 886 866 803 334 605 175 734 417 246 394 514 096 542 666 426 084 252 067 650 516 728 067 402 310 563 477 378 569 987 924 346 860 817 729 268 455 565 086 615 025 750 552 026 477 369 881 720 887 020 073 664 454 028 386 591 122 327 993 845 687 657 074 621 147 348 298 037 227 781 505 730 787 194 766 299 893 148 445 972 204 333 171 275 435 914 122 454 130 482 856 719 693 872 331 752 594 842 365 808 204 321 526 267 369 388 012 910 475 643 175 245 422 492 263 990 232 428 350 322 982 296 780 993 680 820 014 550 524 100 460 905 211 927 232 221 670 373 054 471 216 001 454 123 790 888 886 729 356 618 745 477 378 879 251 320 501 723 078 904 519 404 752 128 842 009 161 772 401 496 095 809 576 854 145 435 184 071 160 560 663 798 387 253 356 764 990 441 016 553 248 019 346 811 284 199 862 470 562 509 736 848 465 524 359 790 686 532 278 403 767 837 067 238 556 073 748 125 101 475 249 764 346 891 684 491 542 086 804 067 307 702 391 256 404 894 857 538 771 322 679 953 602 938 497 497 290 133 192 632 378 175 068 220 222 375 519 973 076 534 451 521 501 226 389 926 406 130 477 533 051 687 871 751 190 548 760 914 671 520 593 227 239 170 551 349 621 265 852 935 618 315 862 050 924 240 653 691 368 466 041 545 068 647 766 714 221 463 866 831 847 037 214 646 339 984 309 487 178 582 334 678 539 617 879 094 683 675 380 511 677 837 602 563 723 154 741 542 878 848 470 860 244 485 755 578 007 191 747 102 564 618 476 066 584 180 927 046 239 768 015 147 606 310 495 835 371 282 452 399 830 761 943 320 239 390 120 205 425 525 052 569 498 936 976 233 215 457 757 565 335 674 741 948 870 057 391 844 991 715 655 071 901 621 919 216 519 347 671 647 718 112 109 149 146 420 887 273 977 203 344 538 269 966 156 983 376 636 424 269 594 203 842 390 775 543 056 549 834 680 153 493 532 794 780 476 695 804 359 677 125 448 243 951 565 483 622 293 425 034 882 214 226 786 612 097 484 090 535 555 361 208 535 044 600 326 529 906 277 834 039 620 140 513 790 310 763 574 298 801 677 331 143 274 654 013 144 213 327 847 351 321 203 276 480 725 987 386 429 321 631 478 500 660 924 639 470 099 579 105 800 463 924 459 546 201 099 570 873 532 395 402 472 223 197 040 303 413 442 291 605 497 031 622 282 627 140 719 220 382 065 346 408 428 327 060 428 975 044 411 591 388 062 921 001 624 233 508 568 180 241 370 977 785 500 110 457 676 803 011 179 965 736 461 425 941 418 558 013 300 193 322 210 122 406 115 406 814 630 744 867 194 725 039 120 738 279 687 517 296 756 321 800 794 511 749 275 584 191 611 901 139 918 324 374 405 636 409 428 333 125 864 886 173 239 230 730 969 002 871 672 614 241 964 191 236 627 929 981 616 339 936 260 102 720 812 336 419 217 759 216 205 881 650 121 128 882 225 696 476 361 801 958 515 490 869 316 958 235 299 782 939 299 470 414 351 749 964 709 659 074 952 750 875 034 273 388 367 689 842 210 299 066 380 205 039 103 030 789 439 127 755 530 703 433 180 482 100 585 893 614 194 638 063 867 752 402 204 976 906 109 652 173 763 798 749 753 929 569 765 644 418 493 997 802 343 682 314 376 498 320 583 241 733 293 317 624 032 759 712 222 029 867 669 985 868 085 834 789 537 688 139 864 743 577 095 915 939 378 547 541 182 754 370 590 180 003 640 111 010 459 212 716 046 194 729 111 855 471 806 656 138 289 186 049 852 452 950 482 536 720 064 631 146 292 970 676 668 053 033 540 184 920 614 772 584 536 959 539 889 586 778 294 220 298 246 939 335 972 582 310 755 762 146 688 027 306 725 671 889 246 085 345 965 355 467 624 728 131 408 731 901 131 534 223 684 378 371 322 716 736 300 986 672 747 410 729 289 254 031 079 150 602 754 296 975 435 469 533 733 503 743 593 694 050 480 858 659 876 378 007 529 824 928 986 421 293 076 671 104 249 227 966 663 200 396 897 505 239 745 898 987 968 515 794 018 947 056 705 922 537 459 288 779 512 528 112 560 076 660 890 473 638 285 972 450 703 958 562 256 675 526 016 315 613 449 653 028 798 673 233 285 514 060 480 146 662 995 679 174 841 843 561 884 569 513 324 301 733 758 188 389 592 878 275 603 295 793 218 110 185 042 801 345 918 330 999 120 187 443 600 342 839 571 770 076 703 937 763 687 522 058 306 740 405 965 498 539 988 377 441 537 318 763 837 735 054 473 329 212 712 363 202 144 871 666 090 188 965 696 515 447 497 378 200 912 028 504 324 550 598 074 529 895 651 084 636 963 053 808 800 151 949 010 093 982 457 046 846 992 482 664 660 730 716 798 216 107 682 682 112 921 569 409 447 820 518 065 665 240 105 258 079 251 566 484 025 217 803 267 124 618 350 279 935 646 938 395 705 638 784 576 630 438 205 466 363 530 887 734 958 122 883 135 935 414 745 013 466 769 979 015 672 530 982 524 752 436 719 748 646 860 316 745 190 953 003 817 665 910 037 454 609 794 718 575 306 732 959 182 337 482 729 096 320 213 800 674 984 299 673 817 485 191 567 164 222 433 325 740 587 935 952 802 757 423 306 163 182 122 526 600 991 440 041 140 943 752 056 092 795 939 239 896 297 934 938 211 654 241 130 672 729 561 478 013 317 358 455 031 507 866 117 789 145 236 503 713 529 509 482 859 227 891 808 091 530 883 632 170 286 402 172 613 461 176 077 091 920 154 280 615 932 180 428 310 673 035 881 828 297 714 407 693 971 403 518 424 195 127 253 653 956 598 144 460 652 392 246 846 021 485 103 659 420 877 978 557 002 490 426 310 950 138 505 982 057 744 307 795 802 961 694 461 714 290 336 622 461 518 929 731 111 397 685 829 830 810 695 521 399 237 941 310 629 941 267 943 688 422 869 974 947 690 622 271 636 222 199 506 083 481 011 579 036 181 207 782 869 733 200 148 172 332 107 981 234 863 873 338 207 993 422 730 696 792 480 099 528 064 695 957 557 180 483 732 281 157 530 808 118 851 366 637 464 902 050 519 870 470 179 022 485 457 421 380 911 391 172 806 861 492 374 700 227 451 397 437 631 763 977 518 596 933 986 155 479 898 304 649 513 886 737 582 933 366 086 342 492 630 496 269 135 861 105 252 389 538 270 069 511 243 353 114 439 417 869 454 460 932 071 783 508 406 509 314 322 698 073 706 298 560 638 430 759 711 907 602 824 671 466 251 733 711 719 719 368 861 295 043 214 721 880 988 115 325 965 375 904 327 393 496 391 447 206 661 394 159 161 955 539 463 613 878 281 435 529 660 968 040 881 882 493 162 739 115 467 568 673 230 553 759 170 693 521 620 630 469 599 284 054 245 791 723 384 083 891 767 118 073 077 193 066 337 832 438 706 086 400 162 888 573 677 428 683 599 400 050 122 023 354 647 731 489 477 437 445 641 129 472 695 553 713 646 109 585 320 135 102 350 543 465 842 180 639 218 784 218 461 981 317 619 551 208 405 140 768 187 795 504 879 477 713 282 863 756 079 710 880 923 460 315 579 658 733 684 336 457 681 105 066 679 243 580 785 074 874 460 760 136 251 336 225 994 782 160 920 197 226 971 012 204 347 334 532 252 212 701 262 668 344 023 380 139 657 513 654 366 380 405 276 325 091 522 170 715 281 233 683 492 474 292 113 779 459 022 639 727 642 656 645 213 151 994 732 472 071 810 335 803 536 219 961 121 698 563 663 880 650 287 614 827 454 026 387 690 615 815 157 140 427 583 573 142 371 437 920 297 940 899 632 865 881 903 135 005 712 035 455 980 503 890 790 565 842 102 013 080 614 096 426 556 298 356 921 670 177 961 510 765 132 347 745 436 391 574 442 393 306 075 275 933 960 977 139 137 116 525 147 083 890 219 112 327 161 621 789 372 274 737 198 537 783 469 700 364 818 619 981 818 203 763 589 041 452 277 656 254 347 457 683 473 387 244 543 352 472 931 263 488 628 725 687 804 880 943 538 128 255 640 411 987 547 060 738 514 231 741 834 184 527 327 001 945 828 235 581 917 470 046 537 816 401 924 636 272 411 122 110 145 527 521 008 725 490 187 117 861 424 282 130 220 197 219 020 995 156 855 343 995 220 172 240 557 100 949 987 592 118 707 352 935 191 305 977 364 322 393 419 377 084 927 542 082 821 247 974 430 573 478 759 065 188 229 315 666 893 479 698 709 573 560 786 782 614 980 526 039 014 850 184 383 542 423 915 550 065 324 904 180 262 391 176 036 735 203 095 197 197 429 291 414 594 860 955 620 563 745 453 790 586 985 675 490 295 840 721 226 928 451 461 108 116 880 171 134 524 622 591 062 041 079 628 218 392 506 698 599 159 327 219 234 176 701 902 785 042 044 398 456 317 767 590 465 724 005 108 354 082 683 225 543 520 144 877 248 020 040 747 352 669 830 426 048 727 762 389 805 887 388 265 809 014 630 383 026 375 729 800 813 173 950 879 251 500 877 179 453 427 203 513 715 111 740 219 859 226 713 705 959 041 066 105 786 134 187 494 503 858 964 771 272 572 148 061 754 177 092 058 813 923 018 226 280 529 890 052 442 811 726 402 652 719 239 038 994 525 433 082 188 147 771 518 813 108 095 344 607 000 851 479 287 132 632 085 750 795 509 992 810 150 147 692 288 639 249 752 715 574 502 542 317 215 321 470 528 310 358 589 329 633 473 949 113 497 241 342 022 303 507 548 622 533 062 465 824 403 267 203 764 378 239 237 012 792 784 028 305 891 889 683 577 737 884 564 537 820 000 571 168 992 034 939 890 050 057 515 691 820 343 355 292 042 175 029 890 410 548 205 386 934 723 193 586 043 068 534 371 723 328 746 622 710 829 229 379 343 687 428 943 784 358 592 491 100 261 855 586 046 380 916 908 566 362 515 169 660 598 325 908 913 405 680 084 590 300 200 829 326 512 323 921 126 298 081 442 145 724 191 986 115 119 876 915 114 516 604 495 097 470 059 979 859 045 949 439 553 929 606 556 676 893 204 511 343 443 275 336 187 484 102 226 460 158 427 460 418 550 006 332 634 981 085 565 414 196 670 748 174 564 814 683 656 504 915 352 239 379 025 827 409 914 289 064 944 012 026 432 724 540 386 914 634 866 112 665 472 293 283 238 095 242 276 211 995 963 695 847 563 246 336 966 373 075 902 940 464 534 480 522 989 290 249 649 860 954 369 655 600 653 711 031 168 227 691 996 496 391 471 108 534 224 573 997 983 151 590 082 306 871 906 107 390 380 742 008 967 838 642 011 815 412 630 837 425 843 263 732 454 852 893 608 343 472 456 681 013 826 102 430 298 771 582 640 574 982 922 554 768 389 830 827 993 413 777 124 131 267 817 538 890 894 587 267 064 213 472 370 906 547 534 699 510 745 851 054 586 914 512 078 095 618 099 792 039 668 282 538 290 880 959 028 457 864 416 180 984 137 048 508 571 393 443 294 781 090 996 847 685 969 542 646 862 294 628 296 178 221 855 808 050 141 360 775 286 277 600 698 034 452 916 982 207 691 674 534 714 668 151 153 272 845 161 054 934 303 468 275 094 400 389 734 384 956 684 056 776 626 842 455 816 615 791 606 868 201 456 196 976 275 273 480 320 706 858 903 178 301 072 851 328 930 934 027 675 408 588 324 428 194 706 540 348 125 079 860 015 719 613 157 164 449 548 541 284 397 568 822 205 936 908 597 761 897 499 531 308 963 574 014 260 271 428 228 382 978 532 136 776 695 365 572 247 141 650 465 180 052 206 497 227 921 889 367 955 062 438 147 313 257 392 114 196 227 998 808 286 890 999 347 917 734 170 684 028 863 246 700 165 984 323 174 077 521 566 349 830 951 300 842 270 770 515 583 500 508 377 031 952 158 384 883 355 342 524 486 029 459 657 474 151 158 635 447 077 979 311 306 418 142 829 391 601 315 993 900 686 569 113 584 784 719 524 445 160 388 439 612 067 544 858 371 558 466 548 279 908 805 599 810 786 291 041 295 872 815 772 808 956 544 247 787 489 926 772 144 045 345 690 385 733 098 315 315 986 092 189 577 857 460 749 068 145 649 343 684 311 378 273 663 205 833 204 560 738 230 520 230 869 879 364 224 004 112 516 245 707 419 561 611 000 868 690 407 614 588 999 848 592 783 900 042 987 195 015 698 245 927 461 307 880 685 368 617 256 444 643 711 778 845 397 788 926 710 530 115 155 969 584 904 856 538 567 880 477 104 425 496 829 919 851 011 285 141 919 741 392 876 876 569 134 097 857 811 139 831 651 535 146 927 195 722 730 536 344 835 595 421 802 423 560 595 930 602 979 723 504 284 615 098 809 781 267 626 171 247 850 375 613 405 287 572 480 363 083 163 276 920 525 720 276 126 213 629 503 069 117 777 072 969 919 314 137 633 053 214 841 910 796 933 658 210 821 514 908 457 468 706 672 856 837 696 135 729 608 361 096 156 352 995 769 067 817 698 115 448 340 186 502 343 006 009 503 679 960 997 102 245 871 151 067 580 688 355 834 688 715 905 323 308 773 388 512 385 643 956 020 673 947 878 204 538 248 159 004 899 274 238 006 928 997 231 933 013 108 814 722 283 545 982 240 277 948 779 826 203 105 694 142 770 679 905 518 101 874 303 906 570 481 806 613 841 579 122 725 112 536 595 162 265 200 978 090 451 926 135 005 490 276 677 736 262 627 423 047 791 541 958 997 370 414 286 682 188 718 619 739 920 592 989 863 730 609 925 135 090 480 014 717 979 599 338 723 081 072 372 070 631 312 885 907 871 864 248 022 458 615 571 397 782 775 021 856 201 965 133 096 859 428 059 545 144 277 968 425 122 433 759 160 776 722 046 855 542 275 741 916 748 791 377 565 798 215 916 603 538 757 425 034 672 793 980 611 944 359 160 953 870 009 531 073 979 380 070 617 759 992 375 437 930 221 382 760 115 909 718 693 530 963 200 000 112 399 481 064 064 215 146 058 315 590 554 610 875 583 962 326 146 052 567 924 162 787 498 673 424 974 420 992 916 159 415 430 130 861 192 412 377 373 234 184 933 184 152 842 811 114 420 505 116 149 665 963 026 771 497 618 134 432 928 940 597 609 211 128 656 476 398 922 267 958 479 067 243 274 406 883 398 561 055 422 814 032 303 124 164 598 624 058 598 827 126 224 650 670 363 254 269 782 931 712 421 369 484 266 521 248 686 037 965 961 873 958 355 819 245 002 971 986 669 865 302 923 248 915 236 026 811 897 271 469 216 287 103 259 231 414 513 939 353 877 120 405 101 437 240 154 012 671 395 477 279 680 237 505 646 657 938 163 005 134 507 298 947 833 786 404 658 157 317 257 164 758 400 554 088 336 570 512 667 917 666 795 002 231 435 845 545 798 673 388 432 580 380 976 663 797 716 932 017 250 913 938 446 896 385 447 863 321 598 832 628 108 039 760 988 410 615 284 023 536 019 911 639 868 385 012 020 845 238 500 551 775 211 476 110 555 588 920 397 092 831 783 469 477 656 397 705 141 658 867 850 385 622 752 125 252 438 133 488 997 946 194 005 890 636 100 058 783 521 946 478 828 212 246 790 222 574 868 821 827 744 356 843 081 874 136 787 190 702 593 295 527 497 065 887 569 894 511 039 670 963 086 676 860 629 415 436 161 230 654 297 475 314 681 091 893 472 936 163 880 043 312 173 435 040 599 353 553 227 303 642 173 641 232 241 718 231 428 639 696 482 306 837 229 348 962 876 369 331 828 324 784 504 221 654 686 336 751 829 931 795 805 431 727 906 079 732 592 515 023 823 225 532 170 977 424 774 346 588 993 263 132 504 089 498 198 893 009 395 443 575 383 642 309 613 188 569 314 010 591 246 546 683 609 645 399 675 884 527 057 940 490 165 049 866 898 125 908 008 894 137 276 623 724 819 441 077 568 161 686 499 275 271 027 750 370 086 679 318 954 909 963 814 254 477 886 639 531 283 989 309 811 334 656 120 335 275 083 503 071 378 336 948 712 141 305 440 112 229 356 553 707 947 219 959 155 096 334 942 456 863 078 096 123 382 891 332 435 437 085 027 150 805 118 937 080 343 219 661 147 682 722 904 895 981 159 627 010 672 590 914 942 243 807 596 455 557 968 352 738 904 733 913 022 250 392 632 237 583 338 937 775 735 984 171 364 125 996 775 247 586 311 867 718 505 228 427 204 663 732 491 872 148 114 734 263 325 161 334 378 149 363 265 556 557 153 086 120 014 781 267 409 372 798 086 399 383 736 203 988 315 264 170 349 897 805 709 080 521 417 836 933 812 517 530 211 359 779 445 755 598 470 195 765 076 754 191 011 521 563 118 502 248 214 452 527 673 109 552 558 580 476 991 178 252 337 763 361 947 509 148 698 590 548 717 790 162 800 928 549 858 364 263 561 486 003 897 084 293 237 287 579 844 238 661 065 689 047 441 966 276 481 726 257 376 046 010 644 484 024 440 778 564 318 938 295 055 810 541 209 141 956 624 758 061 921 924 132 427 238 074 923 363 581 177 215 642 606 125 212 732 338 502 604 480 522 209 344 349 825 307 849 772 742 749 329 925 219 105 382 121 093 679 960 620 835 448 211 446 674 820 952 390 556 014 987 412 221 557 987 262 592 237 720 126 448 164 644 969 111 597 363 263 653 680 836 391 541 823 411 303 494 821 995 980 936 002 274 524 800 180 915 794 154 838 747 674 971 860 999 521 543 860 120 188 758 523 654 158 018 052 969 393 290 828 541 285 590 118 599 306 006 348 113 648 722 913 813 636 814 733 698 177 452 411 921 300 059 472 102 721 122 759 964 276 775 482 664 340 649 441 179 922 537 758 101 018 816 781 306 055 284 421 527 515 932 864 154 274 651 951 456 243 194 104 928 677 338 535 699 252 564 907 535 652 141 151 242 770 542 819 035 257 149 251 364 125 472 209 252 647 161 777 618 006 274 966 867 655 299 078 173 578 750 501 553 261 788 879 261 480 605 028 083 171 821 362 958 875 253 560 822 864 740 484 755 714 332 015 728 361 119 106 541 608 674 630 289 891 655 472 733 863 665 391 511 398 176 334 897 258 467 373 463 928 425 695 524 200 922 147 759 438 097 124 024 922 922 055 629 695 172 951 708 740 489 955 385 357 283 280 531 621 811 868 264 562 232 933 040 107 085 670 993 434 862 581 807 481 279 807 402 245 373 695 074 190 056 952 789 250 417 704 945 913 146 991 674 279 060 583 010 463 299 462 151 262 660 612 851 063 020 135 935 986 965 894 821 888 978 842 023 038 453 091 666 890 214 946 373 529 392 118 754 807 588 168 298 131 254 725 111 401 467 947 590 887 098 838 552 322 496 129 952 628 156 031 374 625 966 066 831 734 614 248 002 832 371 577 054 199 079 233 665 039 936 998 840 128 533 757 086 109 221 748 122 872 977 738 147 011 491 549 711 934 193 343 098 871 234 720 451 590 775 850 462 969 966 666 452 687 015 589 969 182 790 167 748 200 067 313 108 884 563 181 348 757 360 600 670 202 110 172 978 894 887 277 636 444 379 645 859 077 896 217 044 335 335 787 327 695 521 565 455 857 453 091 672 522 469 617 331 461 695 811 145 435 809 812 271 824 731 841 875 635 764 064 030 006 702 791 781 240 390 164 779 222 623 064 780 163 007 471 008 067 914 825 209 248 266 897 082 233 690 755 379 023 881 561 680 046 870 455 521 866 585 916 653 181 867 636 268 425 280 912 108 308 237 760 424 299 136 128 297 246 367 309 247 944 065 299 972 872 611 716 642 523 356 970 449 897 732 616 796 572 304 159 322 725 028 019 379 616 394 695 304 751 145 855 801 932 505 541 423 551 532 410 922 652 537 716 132 220 854 714 660 894 676 613 680 250 539 353 557 911 500 924 366 731 252 139 868 102 548 232 269 449 390 580 338 908 953 535 525 586 367 284 813 356 238 629 789 092 888 408 607 946 124 942 790 003 927 998 039 727 407 266 023 873 864 152 626 398 973 506 038 786 105 315 652 160 923 894 383 108 094 175 971 541 978 942 383 467 304 347 613 644 146 821 498 745 238 549 586 991 479 091 975 361 197 142 200 698 641 356 979 048 689 521 519 282 744 180 736 722 548 688 071 054 728 709 141 062 738 105 957 683 195 556 093 377 315 489 663 368 848 638 515 607 330 572 417 287 899 064 475 515 693 489 281 951 552 545 749 163 340 105 253 949 038 405 975 308 468 534 169 782 954 094 565 134 073 085 431 811 448 624 656 931 572 986 546 583 197 363 124 702 687 094 420 487 072 299 371 655 781 780 257 387 092 572 035 727 337 265 311 646 825 888 053 595 430 320 396 191 583 354 966 462 731 173 615 614 397 694 250 432 069 837 168 445 884 791 009 151 536 629 115 296 847 129 093 565 795 819 240 573 837 214 425 733 032 566 330 704 334 900 036 425 969 120 520 493 298 947 797 676 416 917 639 017 715 981 465 183 554 560 195 644 793 577 854 283 790 875 786 708 784 902 199 373 374 057 869 588 053 391 748 783 586 715 069 349 435 786 257 288 883 533 722 249 066 122 128 342 529 432 914 189 187 730 664 120 029 799 723 604 070 062 260 174 038 173 711 452 330 041 797 693 337 648 840 450 655 317 813 244 867 218 899 002 483 146 219 627 814 634 893 234 202 679 447 294 516 704 901 809 861 182 014 730 389 212 481 236 788 954 303 164 679 797 612 087 859 898 299 068 167 831 212 832 718 126 595 346 618 161 944 223 052 251 995 989 366 096 433 587 489 299 353 269 555 891 883 421 215 700 646 135 515 564 933 891 795 938 543 966 874 104 854 592 854 925 228 078 282 925 720 657 345 459 929 218 179 364 206 833 359 588 197 248 493 112 895 866 943 729 639 892 058 848 414 798 673 006 519 290 790 942 536 338 942 001 908 439 216 614 225 489 541 272 812 899 591 385 803 011 912 671 529 212 745 999 964 596 861 844 052 135 754 815 073 828 864 285 279 270 577 986 078 408 723 962 903 572 885 428 817 174 921 688 764 511 596 153 549 231 140 616 800 573 387 458 789 789 090 440 939 876 397 509 686 870 276 169 274 644 460 075 148 538 029 758 680 140 530 079 549 303 480 268 434 056 518 073 093 297 211 603 552 770 783 094 660 098 171 499 092 550 981 199 991 174 413 630 599 134 690 696 052 944 915 360 054 904 854 561 572 953 530 708 959 994 736 285 974 386 539 512 312 044 432 280 134 062 797 499 246 610 217 354 762 101 889 874 235 009 256 270 329 847 139 093 780 100 609 082 191 412 092 965 971 399 421 349 559 842 669 380 965 545 066 675 710 756 734 928 480 231 231 570 940 235 126 929 407 125 463 689 173 413 473 084 279 352 259 923 478 269 193 410 427 939 234 172 345 823 001 493 530 598 812 135 402 821 147 950 307 559 240 144 411 229 790 128 750 955 448 606 806 826 375 960 341 679 435 412 229 465 257 009 970 489 288 631 585 022 378 203 438 392 323 339 490 075 208 302 515 851 510 316 099 926 770 415 747 754 062 318 970 817 398 498 914 384 290 947 702 986 200 463 061 334 992 795 820 667 447 149 337 754 651 418 160 570 916 501 112 913 255 342 593 490 512 747 980 023 317 529 538 736 948 809 936 905 771 647 493 507 376 331 732 954 746 370 627 215 585 992 743 573 897 119 387 114 327 394 867 171 184 444 104 177 961 241 821 778 187 237 482 100 843 621 851 993 498 665 904 744 572 998 153 733 032 150 311 814 756 326 523 054 832 957 363 321 887 439 642 247 961 611 770 900 502 684 876 763 170 894 728 619 700 055 800 656 985 249 766 647 053 819 818 142 695 106 183 149 747 913 145 069 431 234 472 465 403 000 077 728 920 762 081 778 655 018 931 207 058 170 852 076 800 230 294 830 568 006 082 940 564 406 997 697 731 924 092 196 296 775 484 194 135 907 488 427 550 506 427 306 902 458 191 771 565 805 368 776 276 424 600 901 257 646 444 122 359 237 810 397 485 415 418 816 863 121 558 235 126 277 113 400 192 701 997 957 255 525 539 929 212 872 384 387 067 013 077 761 946 539 640 689 516 481 847 726 340 303 562 336 592 908 485 916 779 405 951 537 382 065 913 534 409 217 427 662 315 891 505 082 626 996 414 718 739 083 562 474 563 752 259 989 849 509 123 392 966 843 885 544 768 052 905 719 290 231 588 289 049 842 936 749 541 839 875 598 492 105 232 908 188 687 178 208 694 418 274 589 737 970 005 624 873 570 108 788 845 585 972 733 053 800 690 036 721 532 755 366 636 799 128 646 260 473 806 916 621 475 116 719 587 904 972 882 036 285 888 409 844 879 323 818 513 149 223 572 011 043 538 835 973 318 017 780 680 812 921 950 098 557 487 061 333 722 244 603 990 977 208 639 602 297 182 803 882 847 358 849 687 146 607 362 667 309 894 910 005 898 149 072 126 162 705 477 947 582 148 680 973 912 566 639 054 545 535 056 907 163 639 855 593 306 204 957 254 562 850 146 808 043 275 780 334 948 172 601 736 834 161 118 962 239 804 834 411 098 845 341 602 126 954 485 446 723 649 669 955 127 452 369 106 915 173 322 470 144 702 080 197 404 589 210 665 224 459 317 251 481 205 789 418 800 282 873 635 896 311 951 681 347 424 223 608 795 528 688 559 054 337 815 489 749 925 783 744 796 338 982 283 765 559 024 459 495 885 565 485 096 514 179 135 471 806 202 890 419 362 075 719 784 474 543 973 530 946 772 448 994 571 891 920 670 744 746 867 341 528 566 223 938 970 753 025 331 687 756 055 305 069 572 543 868 589 890 179 460 553 390 874 480 374 389 351 910 309 424 984 901 610 369 265 471 822 663 607 106 672 891 502 930 081 251 840 699 559 671 302 084 630 591 310 770 098 018 669 611 853 562 821 585 796 509 506 343 959 372 250 999 282 980 248 779 433 278 403 549 684 979 905 252 032 784 909 381 259 630 209 691 361 815 320 423 294 277 412 088 861 806 090 816 371 341 067 598 038 633 121 511 742 832 228 117 955 147 185 358 044 717 562 974 171 176 899 597 434 247 012 387 852 123 896 715 171 553 533 659 054 913 817 382 825 360 963 401 590 844 783 762 152 201 326 715 003 906 654 539 163 460 680 774 371 167 272 071 250 493 665 818 461 901 599 400 531 786 179 863 588 692 731 344 480 071 365 240 552 573 617 239 297 714 420 015 030 818 354 970 663 593 440 025 178 225 176 024 795 934 097 459 879 471 461 146 250 879 380 088 244 103 005 186 475 008 276 480 672 699 480 916 553 917 239 581 274 065 425 665 037 165 428 378 303 095 489 597 945 942 761 432 683 679 594 019 319 120 091 581 322 650 087 484 234 905 380 113 014 708 400 347 125 516 436 841 498 511 257 182 592 471 306 704 060 992 372 877 583 988 991 223 650 862 879 590 088 515 636 868 188 437 416 257 435 916 373 160 716 767 917 808 197 988 167 478 126 586 791 937 958 977 151 967 808 990 646 628 897 152 100 411 442 396 733 254 535 255 469 023 340 864 543 773 438 479 399 455 167 948 723 651 641 990 577 541 440 851 435 035 855 023 105 481 803 643 333 942 820 781 317 725 546 594 984 137 794 746 112 791 804 792 364 348 254 682 341 429 956 762 278 319 162 853 679 514 606 131 129 596 417 787 998 410 866 374 701 861 408 667 063 567 384 008 592 725 793 209 718 184 017 705 204 393 166 971 278 266 722 541 662 896 960 719 726 147 342 278 241 299 158 778 976 728 506 094 259 421 085 454 445 719 440 359 098 906 340 055 141 362 261 670 296 219 827 513 431 713 185 370 533 980 341 067 001 786 104 379 938 853 975 495 828 365 091 558 353 127 373 606 351 010 325 850 373 432 553 659 654 706 313 796 732 592 142 549 468 689 424 632 275 234 907 306 412 235 853 473 349 037 537 672 217 201 435 957 685 292 871 357 528 071 920 052 322 977 267 806 341 083 945 672 601 047 954 609 967 869 570 984 591 440 653 601 208 831 444 204 858 242 329 413 514 436 365 108 316 832 057 944 306 087 976 417 368 129 513 841 465 773 322 845 224 841 172 569 084 773 565 419 122 901 957 335 279 140 043 015 358 000 834 200 905 105 635 506 751 258 908 089 146 232 076 574 709 931 287 301 733 066 607 932 426 714 575 517 357 426 572 071 196 913 919 937 591 867 175 436 338 824 338 347 755 976 918 202 362 928 432 882 292 452 437 850 455 745 744 200 809 893 147 166 534 412 193 611 866 490 056 969 452 225 753 101 038 579 268 126 832 410 961 541 364 487 282 197 126 929 856 668 688 682 349 986 195 395 559 581 153 794 058 938 062 236 126 760 751 903 530 055 028 691 254 446 514 504 764 400 402 585 600 055 961 279 469 046 378 803 608 159 804 050 705 911 482 720 580 803 884 035 668 131 071 007 292 809 404 078 928 320 344 129 155 800 219 685 646 601 147 613 745 521 889 821 366 062 392 063 720 810 500 879 020 744 896 299 099 732 765 326 781 727 479 735 832 265 618 022 087 234 396 371 778 452 277 168 933 371 641 432 921 393 041 997 961 154 843 148 808 479 560 624 034 771 019 200 467 877 671 336 655 835 278 476 753 071 834 236 885 639 984 968 005 026 770 142 558 314 965 471 862 275 815 834 375 963 069 248 178 350 317 762 036 010 737 283 170 608 731 482 282 678 764 045 310 202 031 324 598 618 500 268 115 061 824 355 966 607 621 835 812 849 173 359 505 872 851 292 308 097 222 418 495 175 707 109 176 521 320 362 109 081 829 076 622 467 040 277 565 809 989 665 922 517 153 362 227 978 037 786 663 458 403 003 105 507 268 692 382 249 076 431 365 341 075 389 380 721 227 769 111 909 975 072 830 981 106 229 434 682 830 377 947 454 317 737 398 642 372 881 462 643 581 655 935 531 475 921 347 518 638 154 927 609 272 236 629 242 775 903 723 705 357 717 371 188 924 817 425 325 467 936 738 545 786 196 774 407 486 036 565 518 558 918 184 972 181 989 600 413 027 401 468 658 948 028 153 156 207 027 534 570 904 729 206 874 182 936 179 359 683 012 468 834 376 900 057 747 350 414 792 109 883 733 759 988 558 776 044 839 687 937 841 694 694 662 284 059 240 434 943 286 065 193 393 195 627 771 296 201 861 769 331 652 189 113 624 211 062 801 975 684 667 402 140 672 428 569 448 889 769 921 194 283 835 607 915 636 363 258 567 886 579 470 836 146 761 479 368 655 697 076 348 791 351 439 445 016 966 042 257 466 114 896 951 108 394 315 658 977 666 556 003 153 029 500 366 939 842 227 507 366 374 747 954 644 423 668 497 219 604 633 999 300 636 150 363 666 786 681 678 601 188 527 680 273 048 410 377 842 355 966 266 246 759 925 072 806 324 586 080 664 635 794 573 642 836 741 427 965 259 232 980 307 789 518 315 860 164 119 211 415 668 302 643 600 396 290 962 044 884 776 582 004 989 200 189 891 719 303 705 222 360 153 454 110 115 662 646 755 845 988 419 386 074 315 803 747 997 582 118 572 031 889 256 342 349 128 650 498 662 113 410 002 702 655 885 891 433 396 010 780 628 387 491 580 787 751 070 523 829 200 211 804 852 076 000 273 358 849 565 409 570 222 985 287 186 487 463 603 840 898 332 905 407 249 096 620 885 367 100 921 476 126 647 886 036 357 560 606 256 035 791 234 260 906 329 822 044 888 149 016 234 376 410 208 092 441 268 731 568 667 849 902 399 936 458 858 647 762 040 659 178 347 588 882 903 602 325 859 314 883 139 005 255 695 461 153 245 870 341 282 402 339 339 876 666 708 199 673 017 350 258 495 519 600 490 856 238 476 486 392 388 442 981 559 392 367 227 613 841 102 667 693 728 207 119 768 581 580 190 242 580 087 942 424 539 510 082 425 231 944 036 500 046 099 686 212 989 405 270 436 122 777 473 570 386 795 446 451 218 834 961 291 359 923 691 583 012 465 598 968 407 833 279 325 055 656 713 363 219 107 172 723 372 522 947 246 508 141 165 714 104 568 700 706 658 879 341 018 422 157 129 032 961 659 286 166 204 699 755 891 376 599 447 362 533 962 067 664 399 562 383 745 338 155 497 820 160 388 698 746 350 263 313 790 623 905 566 362 347 049 808 169 422 960 203 802 772 478 238 296 774 538 344 111 500 724 140 795 462 831 578 010 505 304 315 289 190 971 037 867 966 315 519 936 822 883 552 149 482 549 982 212 098 073 211 436 308 623 169 639 065 189 855 403 599 355 143 590 362 559 724 217 705 958 335 594 286 544 260 252 252 837 580 609 280 041 157 933 157 451 889 234 783 865 422 005 107 493 287 368 982 943 570 651 131 979 132 814 937 802 942 451 435 964 922 469 897 229 626 601 533 747 608 594 017 532 945 302 763 127 986 426 293 082 557 761 093 103 310 177 214 803 543 663 634 155 990 029 210 532 810 577 438 818 502 555 516 737 386 642 968 877 516 353 549 162 857 807 205 884 095 809 167 578 859 238 385 218 498 165 630 103 640 384 911 835 416 158 606 888 778 564 469 665 697 668 171 493 170 947 457 414 870 990 096 221 628 975 744 176 073 273 550 023 285 805 194 141 646 503 626 890 969 548 591 774 301 989 383 321 562 235 073 473 171 058 092 627 267 705 378 218 907 960 339 100 609 183 272 385 170 371 918 325 068 588 730 489 293 246 595 374 283 984 969 001 993 344 379 234 050 684 361 166 686 205 076 567 395 191 905 970 892 467 170 822 960 046 590 099 668 211 075 282 194 852 156 636 437 996 627 868 566 620 146 881 322 932 640 541 344 994 923 333 023 747 071 002 230 077 264 545 070 483 724 842 049 306 429 022 504 691 132 404 763 788 636 217 390 606 633 314 532 594 347 391 476 858 889 184 987 181 238 807 580 947 186 033 684 057 281 213 034 517 635 239 605 461 689 414 726 738 918 249 599 347 687 035 000 545 282 727 970 306 606 112 634 322 026 918 647 705 597 550 095 769 111 542 088 176 190 114 170 276 626 699 683 931 383 578 264 485 772 703 437 272 622 796 486 223 621 599 682 207 889 304 649 483 610 359 095 708 561 738 905 751 987 678 280 722 097 728 096 016 901 252 497 227 935 144 929 734 655 833 404 621 876 439 366 678 485 118 116 175 974 845 997 409 123 422 147 025 979 269 036 827 117 425 254 515 105 314 675 857 531 650 666 931 558 997 991 672 926 927 977 994 812 543 133 865 687 742 992 960 873 687 235 578 887 931 089 306 961 189 075 803 564 238 447 752 698 931 868 338 832 419 144 651 495 649 644 234 902 836 209 669 090 688 760 325 398 988 874 584 514 997 397 490 006 698 347 171 873 159 957 742 163 466 907 496 415 565 659 966 458 362 247 427 147 063 237 113 786 305 395 288 893 024 161 609 037 609 862 961 203 019 125 801 322 341 378 647 508 934 529 500 530 179 587 379 673 633 488 092 038 540 269 466 805 429 851 252 640 577 442 343 070 955 527 742 593 609 379 405 621 326 712 484 352 252 109 963 222 863 553 535 544 837 971 319 664 047 765 266 416 344 487 549 902 455 070 762 337 818 299 128 912 038 238 015 961 742 789 216 996 337 857 554 628 667 139 646 594 738 938 598 584 182 881 971 148 386 726 624 271 697 831 355 726 270 471 852 400 751 916 310 027 623 883 811 296 570 398 863 770 648 724 554 827 676 972 372 357 763 698 625 518 378 366 458 909 998 084 077 121 537 505 303 648 777 852 222 044 132 623 632 691 839 539 798 505 838 215 564 840 062 594 221 881 520 043 756 299 714 765 667 246 366 426 135 296 533 304 748 599 193 938 043 526 001 060 867 064 675 837 552 830 843 049 073 130 778 941 417 326 404 738 846 172 461 207 875 509 565 539 082 967 124 845 374 764 878 741 051 783 112 439 840 062 437 285 654 539 704 431 513 875 243 395 331 811 473 897 012 540 350 170 024 968 380 423 752 887 892 164 896 959 603 364 159 004 364 257 864 031 294 050 555 986 770 032 393 761 538 046 616 250 518 572 596 165 544 334 670 095 870 151 784 805 307 692 877 903 398 777 158 236 632 529 031 694 227 433 017 873 252 272 183 361 618 832 723 885 307 901 377 840 653 028 950 279 907 000 747 180 115 806 287 047 912 772 830 076 061 748 023 382 854 157 241 170 122 408 592 764 090 187 410 428 803 777 835 920 971 325 077 597 161 229 591 553 403 055 709 207 407 547 302 629 969 563 988 743 369 427 146 695 960 611 358 104 588 325 504 354 781 715 425 596 164 286 095 128 080 089 854 314 494 832 730 166 027 863 660 172 200 874 791 335 310 469 226 447 800 423 022 554 117 776 789 801 052 937 918 512 975 605 990 485 215 107 239 840 645 240 601 210 408 813 735 357 107 231 579 896 689 103 932 930 710 704 693 005 583 122 323 477 104 365 231 225 220 480 437 745 544 881 893 915 205 843 469 459 268 010 994 398 025 554 079 679 454 481 281 118 364 855 064 762 433 688 776 974 693 376 435 468 918 310 236 368 610 731 436 679 946 859 987 227 643 147 527 337 276 999 614 447 063 400 605 530 380 883 601 035 284 639 825 997 923 905 099 199 160 329 543 470 657 948 040 974 525 737 668 901 250 484 545 977 515 584 370 444 221 885 183 851 839 448 709 244 182 992 272 353 227 664 023 560 863 794 488 733 404 425 315 318 078 168 277 569 645 592 820 132 034 336 773 316 954 550 239 629 304 239 611 081 343 298 116 318 437 744 527 411 693 722 164 637 663 697 708 973 735 969 993 058 561 837 862 461 278 958 538 767 015 576 653 639 302 487 070 005 200 734 410 270 663 926 748 202 601 071 931 301 389 261 112 484 239 700 366 859 016 859 387 665 106 273 582 962 249 671 457 769 169 966 893 409 768 221 572 718 761 655 219 507 182 658 596 797 980 432 865 704 593 566 637 576 077 152 483 617 808 381 620 835 207 509 571 630 370 460 561 683 578 351 349 544 985 999 416 858 824 210 298 966 453 995 671 573 461 781 166 749 890 877 881 544 140 889 423 712 460 505 057 003 999 846 465 719 526 668 935 234 853 857 648 413 984 618 894 658 305 743 777 675 431 486 880 241 188 012 840 483 180 372 327 641 471 857 455 966 523 475 819 857 564 226 429 404 994 006 887 314 913 751 315 355 411 343 682 336 003 346 094 464 733 879 648 845 558 462 933 139 639 727 037 827 162 316 526 097 492 502 307 694 057 246 234 954 978 086 249 636 305 868 525 885 906 222 006 859 831 841 257 752 266 167 545 158 111 467 842 185 935 739 400 309 698 011 115 133 171 943 473 479 117 736 299 589 946 713 511 537 036 146 378 681 712 153 823 614 128 284 343 637 278 096 884 788 010 563 459 925 138 061 158 733 192 461 014 603 074 320 905 527 806 646 237 895 927 695 857 055 410 335 653 883 547 835 934 272 573 327 941 342 179 089 336 061 482 412 326 926 451 414 966 136 123 231 420 111 755 062 404 432 427 078 093 516 073 826 237 766 089 903 432 551 243 272 421 337 276 590 843 003 049 764 659 157 912 212 188 620 754 487 395 712 030 510 849 410 608 460 156 742 228 690 718 099 750 914 021 028 749 884 399 788 506 921 843 313 123 096 114 537 631 758 203 248 723 046 615 511 529 478 448 856 763 812 566 067 667 212 884 252 903 253 987 042 213 221 692 677 772 452 738 710 588 784 076 657 832 134 712 797 067 869 632 107 655 133 352 384 656 815 036 198 554 767 218 270 889 914 866 443 278 023 031 900 928 095 460 175 274 725 442 813 122 637 853 284 695 022 022 986 752 100 823 947 134 665 433 760 856 102 239 289 030 396 754 694 145 068 159 634 087 340 371 178 919 486 795 784 005 485 093 825 967 892 361 039 858 931 460 016 441 935 011 363 669 653 808 796 614 616 966 147 562 424 295 526 512 125 047 826 470 818 128 974 101 132 976 470 894 636 689 593 782 214 867 264 634 998 689 104 735 154 205 592 348 523 089 299 577 481 644 880 385 283 666 702 041 858 985 498 192 427 817 120 293 152 282 947 508 838 138 581 443 097 792 905 950 816 216 117 576 693 098 755 657 444 199 080 451 899 195 496 325 758 033 165 292 018 159 014 691 491 232 615 586 322 718 351 967 910 185 206 163 516 726 534 958 583 067 119 090 020 604 583 421 094 775 504 237 446 327 569 808 309 078 499 691 228 515 015 029 555 352 714 912 741 799 872 775 402 265 932 232 288 146 528 563 302 705 539 587 652 540 676 601 827 884 218 042 078 381 303 635 593 246 205 473 485 985 610 390 122 615 717 979 699 798 358 567 306 410 516 730 730 257 537 284 999 688 028 596 812 262 864 093 752 885 490 376 471 666 358 578 646 366 619 400 432 506 729 583 154 618 976 105 380 898 960 987 567 753 056 948 678 484 938 096 471 088 597 424 577 376 226 126 197 482 600 849 877 633 057 250 588 235 854 394 640 601 604 840 917 769 151 900 524 956 394 461 786 387 367 939 686 448 891 382 979 703 291 138 527 742 998 509 049 209 515 304 240 866 781 876 890 726 193 848 877 575 550 330 924 185 184 237 554 067 281 113 405 892 424 713 809 456 786 939 268 498 262 397 988 544 437 613 215 779 125 755 225 794 192 560 877 234 233 715 024 706 703 773 194 353 489 600 514 301 424 842 585 394 982 383 587 500 907 650 705 987 553 412 288 405 596 852 974 505 732 500 751 188 924 205 519 927 836 063 893 061 639 450 723 667 693 113 096 120 884 698 334 819 092 033 115 411 394 265 059 348 577 883 005 102 563 612 898 460 323 061 237 391 385 736 937 317 509 878 849 341 385 378 134 149 021 460 833 219 464 106 294 622 554 954 503 583 641 663 276 810 620 329 111 870 963 494 575 196 845 996 985 800 752 872 283 312 034 119 844 397 702 794 366 669 411 241 284 660 430 255 844 386 570 182 620 736 102 408 536 237 259 908 375 885 644 071 613 478 332 905 127 878 507 239 953 811 763 221 743 418 742 292 256 951 586 334 435 661 958 165 124 620 682 878 241 899 451 909 979 373 420 891 908 687 061 414 110 044 212 068 250 094 864 588 728 434 753 497 919 008 281 222 553 275 090 482 821 990 064 317 566 922 474 367 799 746 834 582 660 853 282 781 527 762 259 135 697 657 228 062 989 597 565 792 996 887 478 714 441 322 195 683 212 020 227 821 658 612 099 493 985 467 834 264 760 591 685 005 335 604 192 784 264 379 352 614 346 025 783 862 868 651 528 778 671 964 017 710 254 693 260 300 019 102 744 320 971 510 524 037 350 875 562 598 844 842 212 011 509 504 542 135 584 564 399 096 029 528 251 156 820 543 050 464 590 777 069 647 997 920 784 574 214 302 479 948 104 471 206 107 077 579 128 577 639 249 566 846 059 566 900 054 051 207 908 677 112 461 093 118 807 056 602 995 966 990 403 672 527 008 281 926 034 748 481 471 113 259 520 545 212 297 528 864 704 288 538 054 773 642 483 291 274 664 007 171 757 270 063 035 995 318 800 463 505 035 013 800 901 312 532 575 040 473 526 661 533 185 170 590 662 424 284 813 494 982 810 897 895 606 777 982 675 331 864 435 395 726 807 316 503 163 751 008 040 599 861 311 962 549 729 401 843 075 809 163 313 929 539 579 104 548 013 113 202 269 223 323 021 301 977 680 290 996 948 468 387 703 009 097 473 915 963 354 338 418 797 511 422 194 449 748 171 743 852 562 989 779 512 968 249 588 876 505 806 327 315 051 163 752 079 776 707 709 434 530 071 797 857 287 440 873 833 129 755 041 196 151 593 260 960 528 700 493 903 153 403 767 824 725 712 329 437 939 112 815 960 473 199 641 591 486 676 545 683 344 130 725 539 265 505 873 955 815 516 473 195 999 623 308 834 926 205 887 989 833 570 399 669 223 055 548 585 807 168 077 709 920 395 860 296 021 284 340 314 594 258 978 999 195 565 382 774 694 379 818 308 064 280 069 647 308 257 584 394 392 928 507 879 356 736 130 172 999 143 652 873 358 680 360 947 293 851 738 051 557 869 079 076 527 825 122 975 172 512 030 414 515 479 236 453 497 722 089 177 594 316 138 003 125 282 715 458 870 071 871 724 371 387 128 003 394 923 894 034 458 368 745 099 118 469 606 898 898 624 117 004 309 199 447 959 491 316 650 453 553 959 730 227 827 535 861 752 132 043 443 132 865 747 998 119 760 138 548 165 847 014 034 954 349 344 100 479 570 155 782 510 694 972 102 056 253 422 469 302 631 789 938 827 415 212 723 492 076 260 110 078 922 510 957 907 060 122 935 178 511 154 447 908 850 335 538 200 744 570 137 741 095 740 673 312 144 613 368 634 188 373 232 832 420 860 116 016 474 114 423 544 341 636 475 281 167 879 199 441 602 595 714 234 772 791 847 204 930 192 033 128 360 876 615 013 711 583 948 669 064 321 185 554 418 123 321 664 857 331 729 653 262 413 976 243 694 889 612 109 310 363 634 669 491 532 051 096 538 316 917 300 168 877 038 303 683 095 399 265 863 404 566 447 207 814 003 093 645 258 503 925 979 459 166 080 733 464 015 079 493 697 314 383 251 729 632 248 901 431 786 127 855 161 779 108 000 261 995 490 514 185 254 449 430 280 342 982 840 070 249 045 948 284 432 490 470 536 759 842 842 873 568 053 734 260 657 584 840 632 546 625 473 397 012 905 338 220 383 816 221 420 817 364 693 800 823 203 869 788 463 047 243 809 335 919 655 769 427 857 295 153 725 155 340 627 969 498 038 507 272 531 825 942 333 439 958 762 005 255 144 255 595 542 319 542 653 452 224 858 645 130 868 042 783 593 305 987 938 248 500 175 387 422 719 482 997 018 937 147 953 728 541 276 117 355 959 904 124 929 391 215 060 201 114 713 245 919 569 656 180 633 853 736 988 413 310 916 636 092 568 493 552 742 340 068 652 013 029 026 620 351 740 223 038 274 546 368 408 355 010 264 892 658 279 646 365 375 641 521 206 079 444 013 385 184 475 791 476 369 833 659 049 202 078 221 400 342 703 176 333 501 943 586 944 697 031 542 125 358 464 592 236 384 974 501 323 884 348 272 701 153 981 327 311 782 901 822 396 991 607 130 205 299 683 405 671 506 810 342 913 110 056 366 773 904 646 563 354 572 268 107 422 216 460 216 647 104 356 069 304 704 094 041 437 145 220 217 767 395 576 410 320 272 716 508 709 621 110 156 668 423 271 525 808 576 837 708 937 866 199 197 267 037 255 853 676 187 508 374 642 410 575 632 371 006 273 652 512 078 286 099 243 037 080 903 369 555 179 787 337 069 138 768 122 926 399 533 957 115 373 799 048 194 087 162 881 398 805 656 822 958 132 870 710 212 716 583 360 582 563 919 871 143 267 472 790 396 362 400 709 437 667 938 252 454 289 307 040 755 737 769 974 628 754 782 028 376 623 124 271 591 273 009 913 865 593 856 609 940 570 715 995 860 267 185 779 540 813 221 230 579 679 395 818 539 468 092 575 963 432 690 770 481 132 055 686 240 801 333 841 617 467 995 389 514 730 062 439 237 390 055 915 219 923 661 410 034 616 598 135 060 658 276 173 493 559 294 930 779 062 327 676 687 052 429 156 126 203 992 523 318 446 628 729 757 903 761 268 066 054 405 445 847 425 377 298 411 025 673 578 398 585 426 767 738 755 423 108 446 145 181 805 774 651 329 710 450 052 583 371 888 358 331 601 799 368 997 443 623 761 775 432 199 422 744 825 756 581 108 033 205 218 834 007 413 777 912 647 098 683 937 081 377 430 327 043 675 871 626 783 793 247 962 448 692 755 698 504 893 005 740 312 404 644 347 963 719 667 782 739 171 335 321 681 844 636 287 008 040 835 055 507 843 629 759 784 316 894 562 400 803 892 145 626 130 726 791 322 092 153 702 211 376 645 734 011 817 085 905 208 129 847 343 733 378 170 402 291 827 339 464 218 171 256 595 108 572 038 414 687 291 707 346 790 707 059 555 360 493 296 294 396 876 863 737 717 556 627 624 514 266 531 439 719 406 263 819 946 498 680 844 480 647 693 866 196 121 866 075 752 277 079 806 617 561 655 251 821 360 219 155 658 231 039 847 694 881 125 293 165 038 578 552 548 006 921 296 753 497 782 902 164 473 962 609 282 364 771 310 011 603 636 418 635 113 680 114 437 545 737 251 907 298 751 200 703 265 364 616 360 834 241 476 409 571 552 359 577 038 219 704 180 544 947 554 293 760 453 166 303 878 688 487 381 792 515 575 634 829 785 748 582 947 485 220 862 416 657 586 114 889 284 050 891 489 467 477 082 269 674 651 223 996 064 719 799 543 754 003 764 932 315 981 037 183 355 717 004 208 410 615 797 046 374 415 167 895 951 108 702 795 659 845 401 589 287 328 826 537 065 914 398 243 573 526 908 600 849 914 554 407 911 976 775 767 773 672 002 134 317 947 589 371 769 412 743 979 136 788 150 965 281 972 581 677 905 290 092 697 608 452 523 083 990 368 470 776 526 278 806 152 609 515 321 879 132 035 983 993 519 261 596 881 125 194 505 326 923 635 421 595 557 574 942 949 910 471 630 985 332 593 963 309 835 638 386 145 730 481 470 899 985 628 285 815 642 828 842 891 069 684 109 589 319 921 324 465 671 145 747 575 911 259 675 287 679 369 657 058 197 966 165 535 159 787 212 442 676 293 818 593 153 047 897 075 039 949 581 729 613 213 538 143 486 864 175 373 432 764 413 721 902 379 883 797 369 961 802 188 292 692 832 713 374 300 406 338 401 267 673 803 116 753 875 358 465 509 192 498 457 055 291 694 580 713 462 811 746 937 902 767 110 578 012 531 964 483 764 925 031 747 004 234 686 487 636 586 447 879 296 551 081 414 227 167 886 131 643 947 834 255 546 067 986 978 521 119 048 394 955 081 071 424 297 436 573 231 127 858 784 992 612 350 955 769 210 441 554 827 903 199 856 444 327 845 621 083 883 224 552 802 163 723 595 966 004 936 317 729 496 666 037 996 893 396 782 999 044 723 574 098 366 159 109 910 664 898 444 652 806 073 545 302 386 087 230 538 262 374 105 656 241 700 168 821 277 608 789 327 275 405 190 793 491 648 270 902 322 377 089 734 285 263 988 327 150 941 544 357 481 894 672 658 762 589 286 356 336 558 896 532 893 531 449 585 952 473 780 380 116 212 177 378 820 811 080 583 039 466 281 951 529 430 614 742 697 543 178 485 230 778 424 540 946 856 813 996 657 449 493 212 691 744 273 928 110 905 467 934 552 866 276 828 734 330 697 636 739 969 970 574 013 609 374 761 240 970 672 074 138 534 009 895 221 612 599 398 928 940 622 712 323 163 122 992 087 803 096 386 969 411 143 314 247 249 890 912 664 903 609 886 518 110 030 425 164 451 616 825 309 346 697 139 230 967 345 213 695 537 759 211 153 573 202 557 287 010 275 926 442 994 573 893 092 078 970 715 687 051 419 444 313 706 103 545 363 666 247 989 176 030 684 816 385 989 077 879 802 779 004 715 269 374 732 671 155 853 218 920 218 020 755 227 373 104 193 976 051 290 477 366 256 617 272 440 864 305 388 111 449 195 315 915 766 016 405 902 854 296 938 423 139 863 841 565 295 511 335 170 385 606 912 960 944 037 513 842 605 305 496 039 003 440 106 758 006 002 491 180 551 984 031 831 266 601 191 680 246 184 058 513 237 535 729 832 445 267 971 435 769 710 872 099 536 960 994 685 195 337 959 944 524 721 749 925 492 090 174 799 971 079 483 005 588 083 325 968 080 061 714 228 864 897 442 899 094 568 785 285 315 059 515 421 901 090 820 467 092 639 338 814 895 991 524 690 196 577 413 092 800 561 440 079 947 888 636 169 438 013 746 603 517 288 556 749 043 333 538 927 293 622 432 308 491 029 771 942 138 848 272 955 054 670 677 799 574 821 778 169 735 913 731 918 395 132 905 221 317 616 921 793 965 279 419 424 602 584 233 559 035 110 028 184 762 454 903 499 417 710 502 876 289 147 817 090 189 830 818 187 482 478 485 885 840 428 913 521 433 937 515 538 306 469 024 259 022 775 996 517 701 117 627 524 820 550 791 021 978 280 740 220 461 674 474 099 953 039 859 336 750 354 820 370 018 458 179 644 121 317 839 874 385 626 579 826 336 489 619 335 194 378 789 366 709 334 335 801 225 535 681 989 741 154 919 395 566 972 801 692 516 816 049 493 227 393 148 388 015 824 000 448 541 920 149 867 158 553 935 227 537 641 868 430 282 541 815 038 280 974 710 253 036 338 781 316 044 241 662 383 671 024 701 704 658 109 331 866 802 859 255 624 226 766 178 426 125 663 729 083 938 015 341 129 052 892 449 242 157 137 154 358 713 816 277 163 551 609 472 408 380 497 561 818 499 938 439 800 353 718 169 444 323 602 892 912 239 949 904 851 397 566 238 240 458 208 667 944 148 728 876 716 854 432 399 797 320 121 439 689 014 530 707 857 868 132 135 276 310 334 228 495 106 776 152 644 010 793 270 230 374 266 298 748 614 702 618 330 901 465 406 147 435 956 044 786 070 696 222 539 954 131 300 857 084 670 376 568 814 431 078 039 851 815 001 199 965 250 751 476 787 061 546 100 263 071 983 425 988 142 345 805 821 236 762 009 529 094 039 791 454 083 888 929 764 367 323 464 196 685 649 396 733 371 431 425 000 812 274 869 758 030 337 372 634 226 058 820 724 687 934 609 924 298 973 523 875 161 351 587 988 592 434 252 392 913 212 475 012 143 486 268 826 738 888 791 545 892 159 801 376 570 376 671 433 184 225 416 311 136 215 902 822 098 059 809 753 140 935 864 019 369 948 626 220 755 268 740 427 890 283 307 164 132 764 696 675 620 452 775 420 643 020 815 263 227 302 932 704 532 887 930 349 095 313 365 592 728 034 289 032 891 433 182 896 149 129 501 807 586 136 321 951 553 377 994 589 513 235 324 056 624 292 367 117 718 978 425 508 094 389 918 707 692 489 157 240 571 485 531 092 478 462 809 004 366 622 424 169 213 721 388 113 343 228 828 548 641 218 205 153 782 402 203 517 902 887 540 381 810 306 011 554 307 074 205 306 450 995 115 680 939 993 441 359 403 881 259 901 411 211 737 904 860 821 025 976 241 152 824 954 914 562 946 186 911 126 187 073 951 412 213 466 854 825 361 777 735 724 474 772 388 623 863 831 873 118 743 125 139 329 924 990 399 116 748 679 442 382 636 139 945 335 041 229 562 775 095 671 111 142 600 257 437 659 959 805 090 382 922 111 775 633 257 384 069 288 276 144 623 626 613 454 095 433 241 082 826 462 756 461 830 756 044 565 967 121 259 025 545 136 320 969 057 577 007 704 751 455 742 583 488 920 160 524 492 206 663 198 544 289 265 477 283 203 327 146 513 756 009 760 923 204 356 096 908 909 929 993 214 752 670 085 149 608 713 113 919 293 134 462 997 639 028 757 203 375 470 816 312 032 857 246 413 834 896 428 287 477 681 127 424 079 250 189 622 227 997 809 262 044 822 025 694 545 786 746 632 079 627 070 014 351 210 019 462 950 921 795 653 896 303 901 889 464 703 901 589 413 977 675 201 453 427 078 629 499 627 987 276 932 336 328 467 012 628 686 590 283 821 089 607 780 729 697 901 022 086 031 760 677 199 384 812 634 794 850 309 402 341 916 381 910 234 057 828 153 760 801 929 746 948 799 759 653 237 075 168 562 947 284 767 091 603 479 317 172 884 487 932 925 472 420 203 759 735 409 320 322 184 797 823 718 902 656 763 763 581 752 456 515 587 128 852 089 100 561 493 396 529 398 394 160 572 586 223 838 356 219 460 081 842 746 716 473 487 688 079 280 979 149 848 744 713 687 379 495 789 204 458 320 504 980 770 215 478 266 338 923 212 526 551 189 947 020 777 024 541 364 348 851 867 868 933 443 812 620 817 625 884 250 976 639 278 797 275 632 901 780 804 960 115 356 081 639 087 920 734 214 831 937 659 715 569 335 473 876 121 983 933 339 552 307 117 786 818 526 094 090 245 911 820 352 338 544 671 851 563 975 745 725 204 909 958 408 046 755 543 600 901 565 118 898 668 326 956 522 110 353 435 529 548 673 171 852 176 199 068 892 799 035 792 433 664 309 863 175 942 559 484 155 252 774 835 904 479 046 153 380 721 578 831 034 652 246 918 920 567 691 293 510 438 278 113 757 384 443 317 791 444 168 007 613 237 690 407 640 058 593 151 961 361 923 651 336 359 264 591 282 707 689 316 988 369 975 525 095 421 074 359 973 500 228 666 468 162 031 565 663 213 375 600 158 346 933 431 958 429 280 574 477 930 710 151 041 316 047 753 634 456 089 585 532 432 194 992 737 322 403 294 738 549 786 550 661 634 861 289 854 312 133 590 363 449 175 085 824 556 529 981 191 662 623 274 285 767 149 053 141 107 404 271 500 321 977 845 514 927 492 157 072 778 551 214 151 083 028 993 644 240 790 683 488 581 312 630 542 765 576 941 848 535 501 032 395 959 580 966 692 175 664 642 418 452 562 756 640 458 705 801 184 995 577 226 579 857 285 378 193 864 331 389 244 163 655 344 869 979 577 942 290 326 402 515 630 641 840 845 115 955 108 550 483 028 544 611 101 343 907 060 284 134 591 514 628 531 994 740 842 551 851 242 132 984 083 430 397 950 587 517 373 097 877 487 812 870 600 960 091 291 169 906 057 057 475 353 745 463 882 548 282 009 371 838 356 992 263 429 820 397 375 473 835 532 938 082 687 813 447 419 327 783 165 927 489 414 319 474 444 279 790 740 310 148 829 144 452 342 232 860 985 833 037 854 187 890 996 495 944 459 308 023 314 540 922 556 955 137 222 188 709 250 904 982 792 966 273 406 480 436 312 571 078 046 508 553 986 163 774 243 519 577 561 436 783 882 613 376 195 381 905 257 460 385 752 232 691 980 832 916 528 541 365 451 134 351 000 942 837 540 461 445 279 623 057 449 803 780 251 265 289 275 245 732 813 043 971 429 822 039 061 454 608 489 538 628 855 562 091 503 967 514 602 554 727 135 774 538 279 228 377 055 004 077 840 375 897 109 645 487 219 784 377 245 710 146 245 351 969 974 341 471 698 319 469 108 618 125 538 861 462 353 722 839 382 874 682 661 727 661 889 033 164 470 973 116 816 668 046 852 329 815 066 817 834 683 179 051 273 510 695 836 127 506 304 973 507 854 375 812 950 746 782 481 678 129 944 947 394 896 673 053 507 119 028 882 712 170 296 300 993 743 437 856 987 844 640 491 906 346 839 829 170 110 418 462 402 951 988 179 103 228 793 754 876 081 886 508 240 691 169 173 568 168 959 136 933 296 051 236 698 394 198 016
This is the first 1/64th part (1.6%) of Square 21.
Click
+1/64
if you want to see the first 1/32nd part.
This is the first 1/32nd part (3.1%) of Square 21.
Click
+1/32
if you want to see the first 1/16th part.
This is the first 1/16th part (6.3%) of Square 21.
Click
+1/16
if you want to see the first 1/8th part.
This is the first 1/8th part (12.5%) of Square 21.
Click
+1/8
if you want to see the first one quarter.
This is Square Twenty-one in seven steps,
based on a binary iterative partition.
Calculation of the number of digits
2^4194304 = [according to the Online Big Number Calculator, which offers the exact number itself; first 10 digits of each part shown in red by author]
020 650 635 398 358 879 243 991 194 945 816 501 695 274 360 493 029 670 347 841 664 176 800 041 553 335 652 936 057 509 677 535 527 151 427 868 237 064 574 934 824 549 293 767 546 359 077 920 008 818 501 313 826 426 823 106 013 346 012 778 095 984 519 801 219 909 531 075 504 287 833 161 324 840 811 684 971 720 284 491 337 186 421 302 100 076 509 403 419 310 287 743 147 286 205 798 438 391 891 910 433 320 816 354 801 660 161 002 935 402 954 568 571 003 081 410 242 475 346 704 885 642 194 132 346 012 204 417 456 032 430 353 391 417 591 466 278 673 352 755 565 006 094 263 750 177 280 726 036 253 113 510 694 507 482 207 519 754 056 595 315 720 092 484 784 103 391 134 845 232 251 829 862 635 063 872 880 713 703 849 779 393 812 835 168 305 411 518 046 989 472 329 311 728 260 530 608 777 421 831 520 043 254 548 404 201 827 005 795 137 367 646 261 052 061 654 579 029 323 493 859 679 786 690 498 837 065 698 423 477 573 821 529 014 844 741 574 575 824 006 613 498 018 575 107 042 468 295 045 569 151 710 203 003 120 728 243 352 497 582 775 250 167 786 050 106 244 195 250 645 288 190 283 533 077 837 288 052 527 533 280 640 970 024 559 638 002 882 824 665 824 080 142 766 202 780 625 376 961 666 657 630 997 398 134 787 448 681 657 178 837 727 788 110 375 597 422 716 407 295 985 335 777 454 833 638 174 398 931 969 736 624 526 255 124 137 734 328 090 369 360 079 548 102 682 566 791 774 231 733 756 652 407 037 854 427 276 867 019 479 574 350 087 127 958 512 940 606 349 448 808 415 959 634 200 733 958 014 722 918 126 641 150 929 877 229 980 036 015 090 690 098 587 383 449 290 065 840 861 968 628 403 770 557 600 824 569 449 945 692 977 916 986 590 020 768 596 954 800 079 495 642 370 966 170 563 205 713 536 877 346 406 241 525 149 141 116 970 415 522 548 423 511 903 060 423 476 474 847 692 579 492 769 123 210 954 116 060 977 251 929 029 210 342 331 182 360 039 483 549 136 142 916 608 606 499 103 817 079 107 742 457 998 684 662 157 493 889 313 988 894 597 363 001 812 651 584 278 186 406 925 881 730 528 942 785 280 131 523 440 821 730 492 965 282 487 708 607 263 815 347 784 811 920 503 948 625 758 271 307 978 475 205 236 865 735 463 269 055 211 276 546 773 127 188 134 656 800 409 245 768 696 999 421 318 531 125 153 875 652 239 426 896 347 836 006 026 320 000 184 637 588 791 399 752 269 884 683 503 838 813 236 714 126 333 082 989 272 225 916 087 656 005 897 978 857 199 846 731 321 966 234 455 392 121 391 915 037 833 159 860 368 421 798 697 269 175 900 770 018 931 838 227 462 014 232 109 387 847 386 567 268 693 173 238 346 235 322 127 079 245 049 553 734 232 383 970 467 240 074 957 944 865 882 899 051 332 716 801 084 258 149 770 826 613 065 495 480 552 699 057 769 518 536 892 521 846 116 133 533 014 561 662 729 512 945 896 476 307 398 786 979 826 357 295 347 152 554 932 272 533 137 280 672 882 879 566 787 294 438 514 332 078 468 679 434 614 654 455 414 223 736 886 718 601 041 377 747 112 959 418 317 897 096 193 695 285 020 099 917 349 565 807 341 290 865 319 208 917 776 939 056 435 583 080 174 798 668 704 937 874 107 890 539 301 087 799 439 060 649 208 756 713 343 345 920 295 993 038 851 826 640 651 736 711 179 583 262 742 825 990 137 162 655 502 415 662 387 396 190 012 487 317 543 943 038 289 911 667 314 878 343 049 671 714 498 524 392 745 324 890 536 000 714 221 872 491 963 265 925 930 748 323 545 213 793 085 571 688 669 929 063 564 591 181 905 347 504 338 195 872 119 998 034 393 299 900 105 043 249 185 728 873 004 515 222 998 351 704 120 003 427 062 153 831 029 987 186 632 866 557 403 710 504 931 151 452 370 510 371 310 488 053 624 305 567 887 975 421 711 504 626 290 010 603 881 022 042 968 965 801 070 532 536 042 546 027 060 284 280 239 098 199 347 908 822 473 940 947 878 906 932 383 071 214 806 666 605 954 816 142 041 392 169 855 659 621 832 058 047 830 264 596 461 995 647 593 266 405 239 340 499 260 027 131 689 397 307 163 200 891 396 366 156 979 820 547 112 846 633 003 032 530 135 488 885 041 572 341 648 542 585 979 281 808 377 793 012 395 796 823 585 146 880 424 785 199 826 982 441 261 717 325 752 549 609 594 921 867 319 114 551 333 450 031 087 774 456 261 388 644 452 605 031 263 456 148 748 673 482 266 297 390 128 683 919 661 551 784 915 124 105 233 290 721 060 981 043 506 782 088 004 823 123 907 487 907 546 693 884 671 089 672 679 435 044 235 297 522 645 441 202 601 236 964 016 714 741 143 744 480 127 212 175 637 744 963 834 790 996 817 802 860 195 224 687 955 779 537 406 743 247 473 877 286 766 577 466 649 669 557 890 452 775 498 169 023 704 281 951 356 850 580 508 561 392 323 131 359 353 172 690 876 397 105 282 422 982 427 823 436 037 859 729 567 152 594 308 102 166 508 047 400 305 960 332 163 398 756 867 823 541 438 385 602 592 826 978 278 118 036 696 636 178 416 096 298 071 111 466 258 904 766 181 440 411 950 702 504 321 148 740 948 092 964 102 382 939 980 657 232 430 440 521 122 181 578 045 304 611 287 694 120 710 729 336 901 919 040 887 079 059 001 648 504 838 468 420 464 974 971 555 301 339 931 223 306 392 065 431 365 458 031 336 553 661 839 895 653 505 959 791 047 544 622 260 200 718 488 676 184 837 391 256 404 380 945 687 003 054 983 452 101 251 177 505 592 053 304 029 469 457 097 983 954 909 343 339 866 014 560 495 095 267 414 146 189 826 994 283 231 524 234 579 442 033 445 546 274 769 337 027 687 828 931 248 824 610 231 942 673 019 854 143 430 425 465 870 988 850 676 419 133 336 491 042 936 654 291 108 533 601 345 065 567 112 197 709 555 834 237 742 245 563 496 262 722 573 617 656 504 688 008 122 360 733 037 334 140 276 525 554 175 744 901 500 452 916 654 036 288 303 764 177 277 240 479 274 733 104 500 528 750 056 226 300 738 307 928 341 896 015 280 273 071 885 701 369 712 902 355 989 104 882 343 398 988 261 335 127 259 052 391 286 734 863 747 975 389 457 407 643 241 182 579 665 653 843 711 945 595 182 020 127 490 041 273 829 967 378 655 152 217 825 923 491 569 042 837 417 485 053 120 210 620 092 997 556 075 066 458 879 141 398 131 610 852 031 585 698 813 739 008 570 137 926 286 131 150 626 143 383 314 729 504 322 597 350 110 367 495 518 532 659 239 341 345 774 918 156 040 345 476 886 194 146 649 452 447 175 531 320 933 532 968 322 704 481 641 893 969 072 400 161 939 473 610 421 016 579 314 314 095 312 856 324 535 155 391 671 182 783 053 601 375 887 923 847 038 632 123 175 648 473 255 191 717 088 266 706 512 989 096 258 110 450 820 596 151 435 828 471 891 531 575 470 729 052 257 459 405 670 631 186 212 588 579 432 698 739 574 012 453 270 979 815 981 244 403 193 890 542 179 869 130 396 214 762 373 656 748 806 709 450 726 194 908 004 458 928 658 129 204 999 395 766 301 665 503 644 256 629 120 811 148 140 989 493 916 977 075 019 398 432 710 345 886 717 400 741 355 400 023 621 244 106 192 004 463 601 110 417 319 440 515 164 956 446 683 451 768 014 929 112 768 126 407 594 782 178 275 046 269 875 869 612 643 537 982 517 781 501 858 654 714 912 617 431 784 957 742 447 376 213 323 572 635 907 152 741 406 279 169 889 716 420 833 071 810 540 404 029 890 919 931 409 437 331 573 916 082 434 934 548 180 349 310 770 738 158 788 421 800 721 887 241 350 481 398 709 077 577 825 060 906 056 931 060 497 788 672 190 869 162 508 205 557 178 092 426 560 291 996 114 409 748 774 656 794 109 369 020 546 522 966 979 575 773 145 099 418 857 648 274 003 295 160 270 544 500 672 534 647 640 382 622 949 023 728 752 295 948 780 150 182 626 197 603 301 850 881 483 780 069 510 482 699 393 168 123 629 558 945 350 262 969 707 623 776 623 381 471 011 750 852 075 978 118 678 776 449 052 152 538 903 595 998 610 745 458 855 152 208 313 359 717 224 768 653 069 237 100 103 738 769 668 923 078 595 712 601 822 693 034 817 955 926 388 557 018 532 220 268 957 350 228 325 878 197 759 238 822 723 584 374 978 179 686 982 593 046 376 952 592 546 105 956 821 123 752 555 132 165 979 998 955 164 754 692 556 815 449 972 651 146 829 770 708 919 250 303 635 825 904 394 300 620 334 156 697 222 470 022 010 629 757 218 655 623 627 464 565 119 331 723 671 988 812 041 845 850 186 055 057 733 724 836 481 419 759 756 400 692 496 801 504 632 764 993 080 954 137 383 595 537 140 624 797 489 601 657 367 868 485 657 207 528 857 112 787 421 425 100 838 867 117 894 788 218 273 408 342 526 241 270 888 971 645 274 987 257 105 687 819 248 384 800 893 542 954 242 362 765 592 197 716 158 765 640 179 989 361 646 276 679 455 402 990 999 089 631 849 925 443 032 740 340 379 987 891 233 157 360 093 559 979 624 726 681 499 120 530 145 236 797 084 548 672 756 839 217 196 674 468 069 949 571 672 954 839 434 654 003 414 970 523 995 617 728 788 552 230 402 869 734 490 532 822 788 407 871 198 063 785 048 332 837 977 151 323 449 464 512 367 983 598 207 785 734 323 999 287 719 537 841 943 615 665 311 500 604 331 289 652 260 286 891 427 419 260 280 027 524 058 637 974 118 307 821 154 332 252 640 260 779 834 621 594 110 498 324 047 249 047 497 547 033 792 372 111 711 230 892 734 949 494 010 868 975 811 964 767 643 503 791 512 931 864 578 789 050 895 800 030 077 738 941 188 949 300 953 214 659 039 665 268 743 350 203 136 185 026 418 419 591 895 035 559 831 191 683 895 962 965 783 470 343 187 936 077 039 299 597 329 246 834 409 674 637 556 076 241 449 974 996 856 576 487 764 677 556 288 806 620 426 922 502 283 490 196 554 566 826 768 001 997 524 354 712 302 398 539 755 738 547 912 841 321 384 401 729 014 503 960 826 577 324 827 519 416 538 186 800 243 236 377 930 458 084 996 779 004 869 552 464 450 349 375 148 417 519 222 475 350 780 810 088 161 886 034 436 171 172 286 206 342 162 257 597 353 388 032 599 996 303 717 983 494 453 859 928 128 775 422 993 468 375 266 909 004 095 337 540 232 379 729 271 066 972 760 435 636 288 009 065 801 095 971 202 175 578 071 369 429 661 119 388 744 381 129 314 380 199 071 628 883 213 998 649 632 403 916 173 512 131 199 710 807 837 309 834 766 122 054 157 258 331 187 030 595 136 287 194 491 042 800 597 663 061 932 769 615 278 044 705 770 683 635 726 107 438 211 523 740 564 555 926 097 971 137 205 545 320 645 249 886 632 248 498 275 582 382 476 146 190 949 315 534 766 570 617 404 567 919 776 548 286 424 591 312 725 575 037 945 759 207 114 660 819 219 715 011 357 909 770 853 154 974 164 856 263 021 316 814 632 576 380 367 153 886 042 708 594 609 822 282 788 993 459 117 322 945 336 408 337 484 177 952 041 111 562 232 980 795 961 453 274 024 105 261 203 168 703 087 710 115 030 110 902 709 991 642 553 958 449 375 297 526 602 530 935 282 604 851 882 885 174 380 724 180 074 225 255 016 029 152 878 329 699 844 002 871 198 187 690 649 701 499 640 835 267 184 152 498 306 149 096 992 057 368 312 048 087 545 866 770 173 376 552 311 492 230 560 905 434 968 196 266 717 819 643 677 109 139 368 710 195 879 666 504 921 688 142 561 962 465 665 907 329 754 111 753 217 855 182 711 377 523 730 147 753 285 837 561 920 226 484 025 962 711 199 994 066 741 608 004 297 795 699 497 057 274 962 181 859 668 314 198 859 119 925 062 195 117 792 398 389 248 498 414 918 762 220 304 433 468 630 698 460 263 844 479 224 652 823 967 793 434 845 091 540 382 199 009 379 451 811 068 458 853 304 967 061 287 071 238 751 973 692 480 044 486 616 462 935 460 336 597 407 953 227 630 348 680 973 183 621 556 366 075 886 365 785 945 551 656 356 720 196 514 070 212 475 887 816 497 524 798 708 785 602 190 189 127 417 000 501 042 440 747 659 860 851 599 246 847 801 032 770 494 657 933 337 097 447 010 357 381 629 494 063 402 968 982 060 313 838 296 819 479 148 319 143 289 890 818 863 671 506 065 071 840 646 765 061 933 197 362 272 497 857 502 075 421 433 484 037 780 125 188 475 230 460 408 237 161 661 125 100 706 928 487 243 173 654 295 768 253 788 613 704 914 158 505 055 694 095 625 419 687 889 052 939 683 128 198 430 163 533 605 430 243 790 274 072 039 022 338 501 378 779 863 405 246 899 165 533 572 192 297 822 281 515 635 416 707 282 792 431 350 114 336 153 062 636 067 699 736 129 265 752 302 953 459 529 644 289 925 198 580 557 477 050 808 172 195 748 913 482 830 324 319 103 867 744 112 555 293 108 965 999 381 228 242 392 363 301 780 407 886 096 277 936 491 129 019 956 009 656 840 482 182 933 251 658 701 208 116 547 389 397 399 876 883 055 849 358 212 140 572 132 502 446 087 697 724 827 226 015 391 791 503 657 507 854 632 606 913 701 780 977 223 528 518 058 205 148 371 680 773 906 757 810 945 903 520 833 884 487 774 047 929 130 603 845 959 297 939 473 349 201 458 718 268 802 533 824 436 803 160 415 480 319 414 698 821 525 498 984 639 378 268 794 296 327 306 508 125 065 606 224 857 179 491 892 084 118 491 051 053 520 022 336 570 852 794 281 323 292 350 597 633 731 075 828 100 157 260 905 867 971 085 139 595 367 348 654 105 767 071 987 458 622 629 382 092 301 052 323 181 397 200 464 366 752 955 126 858 384 557 847 101 449 511 076 976 913 946 331 782 357 354 979 034 545 470 451 231 313 234 934 091 724 942 731 776 607 266 210 301 092 397 803 623 330 696 519 967 236 319 085 334 207 699 417 691 044 016 714 923 659 321 059 091 707 472 917 327 391 767 576 766 850 310 717 308 792 481 678 222 121 936 384 216 765 274 078 143 273 728 143 338 695 025 976 133 791 987 721 778 066 989 120 462 117 204 821 189 532 232 342 431 820 004 859 482 593 049 482 317 144 913 799 322 320 714 886 221 411 708 309 741 091 130 449 991 430 207 087 905 693 360 655 695 167 890 071 223 158 733 507 354 484 875 507 331 328 611 016 811 916 752 842 856 426 016 513 525 076 074 332 514 712 960 653 075 189 998 883 148 385 901 467 821 152 899 600 353 653 984 173 855 336 990 604 926 373 803 231 990 796 818 782 350 594 045 481 548 104 324 994 520 491 323 454 730 526 671 751 837 752 192 092 956 583 461 623 263 250 750 884 205 006 767 322 302 580 137 780 194 060 682 524 287 407 335 488 288 532 230 980 466 524 275 143 056 122 473 627 029 906 701 557 403 981 747 064 731 049 972 870 521 030 785 797 751 298 346 520 052 111 691 568 822 304 544 370 475 599 635 274 175 014 447 407 545 060 003 573 196 916 383 359 138 307 133 064 746 292 635 841 430 171 316 571 426 552 487 988 029 080 462 530 776 925 812 324 728 907 392 670 391 727 000 549 384 617 701 184 158 797 656 188 978 027 233 245 512 956 743 447 193 026 962 424 712 592 900 669 351 816 064 897 858 762 691 112 131 703 819 223 778 075 120 938 382 675 484 197 499 364 703 524 272 697 256 309 034 181 656 946 988 069 823 941 070 251 924 132 108 774 593 462 295 056 653 879 183 322 743 301 456 686 612 302 898 315 931 798 724 088 529 441 266 109 428 994 886 257 744 635 868 358 301 852 863 761 789 619 993 481 563 874 552 136 733 108 481 694 171 596 141 830 658 522 420 343 583 558 381 041 872 387 585 119 743 558 889 509 514 900 576 730 016 883 693 743 408 837 433 645 498 579 079 164 244 965 725 608 069 119 039 919 404 167 285 204 494 330 825 676 335 610 197 313 356 396 180 306 421 227 870 200 327 774 748 278 957 848 830 148 239 902 684 752 601 141 177 256 187 545 582 557 120 867 205 543 730 458 874 530 682 279 149 470 202 439 897 517 977 442 359 147 940 835 896 004 364 192 250 184 562 416 071 751 671 783 425 980 805 791 718 804 686 379 930 884 935 004 392 416 409 651 718 388 877 505 893 408 964 954 535 474 538 498 896 892 639 029 544 366 987 066 679 490 146 506 679 031 040 033 383 704 980 874 880 726 107 019 567 293 865 317 694 832 828 768 307 226 425 979 942 685 070 108 287 501 356 848 471 648 007 532 709 024 497 904 800 180 784 897 443 422 506 191 171 846 468 767 504 563 551 631 522 660 699 270 569 213 123 442 715 785 687 344 896 041 149 410 372 491 361 601 021 048 696 850 798 554 328 542 126 284 808 689 321 150 546 294 590 107 500 322 235 541 014 799 126 119 397 265 916 865 298 630 846 389 055 355 577 652 953 846 309 546 357 094 040 753 805 856 668 818 136 778 129 861 453 448 641 974 116 829 562 782 197 214 075 723 491 978 602 109 332 068 945 249 474 861 042 695 592 598 690 747 017 504 910 485 833 577 872 592 376 803 166 584 385 288 551 890 943 703 663 665 823 714 744 950 984 654 589 510 192 152 816 675 850 051 388 691 336 811 673 381 735 101 807 196 316 982 332 771 540 890 154 621 443 030 815 541 076 705 814 576 216 568 069 715 328 495 090 311 426 636 597 952 902 971 663 617 554 941 411 569 454 946 585 011 139 622 210 186 933 296 189 616 638 582 043 995 176 366 483 017 540 495 906 501 968 550 639 804 798 991 623 736 482 840 528 511 839 125 461 658 757 605 829 419 643 492 752 516 763 353 243 255 928 100 449 660 930 819 725 804 816 743 350 966 227 367 592 912 394 437 781 296 531 765 112 207 566 601 841 775 749 544 645 702 570 064 127 039 513 066 186 159 934 663 574 923 379 399 899 628 614 190 153 002 159 823 497 929 689 462 781 567 758 383 238 566 266 487 846 940 896 762 265 737 692 303 220 779 047 986 864 618 620 103 985 131 133 609 707 034 027 782 220 848 606 406 413 063 619 289 532 900 716 164 022 484 475 772 711 751 928 080 154 241 743 425 347 787 929 012 624 757 057 405 444 848 450 240 141 229 857 051 710 324 430 067 356 158 904 058 706 513 154 405 902 430 784 356 714 561 954 386 118 523 313 343 255 334 329 112 697 052 804 394 054 918 078 677 517 704 263 419 856 358 905 400 357 672 692 586 499 833 422 708 857 844 599 594 415 914 485 017 882 582 603 527 274 101 264 695 508 467 506 764 462 351 903 817 015 848 597 229 260 081 369 977 636 318 552 966 463 060 325 934 056 472 475 578 670 671 372 874 244 229 213 656 818 311 062 823 508 255 616 425 100 345 384 013 449 447 094 014 880 774 860 917 750 230 774 650 505 702 698 742 824 319 751 906 366 402 566 153 870 581 044 256 481 055 063 807 059 470 327 829 390 265 783 446 474 469 098 530 357 197 333 393 093 194 325 951 646 349 209 017 920 350 963 725 666 874 776 401 120 556 958 755 751 524 082 625 236 845 326 319 956 469 922 983 587 861 939 114 754 056 020 076 155 561 053 698 120 101 727 672 975 078 600 515 917 438 835 586 748 331 850 236 964 486 807 515 975 205 604 819 688 444 887 029 329 736 338 604 338 551 643 840 722 695 207 432 061 402 060 528 759 882 296 909 621 308 088 877 946 771 257 409 203 437 456 599 739 361 656 612 933 808 472 975 386 885 099 515 785 793 608 664 587 857 753 047 146 719 539 072 493 225 381 150 695 521 224 376 686 551 545 809 765 115 112 184 941 189 286 646 996 221 393 455 113 837 110 851 470 634 462 183 702 421 078 555 986 349 311 314 962 590 516 233 900 630 344 943 732 975 833 726 195 366 725 907 323 073 044 463 718 009 496 572 788 486 321 720 122 195 118 855 727 680 808 441 529 109 078 722 422 824 638 136 494 639 946 043 869 056 262 471 710 085 234 458 485 057 037 980 895 974 324 162 909 631 994 352 753 227 620 847 733 679 413 391 680 973 938 964 368 061 105 799 540 444 361 958 162 840 798 653 109 030 574 686 292 591 342 308 008 669 697 045 774 151 308 523 397 026 648 925 750 341 279 120 225 752 066 679 551 732 149 916 252 072 673 775 539 409 176 253 344 882 718 979 975 185 618 708 048 520 096 872 137 778 948 628 051 191 414 005 340 951 507 031 222 264 384 318 251 026 224 376 810 354 902 985 959 923 713 117 681 387 953 435 956 074 329 558 442 918 705 245 051 737 677 245 451 469 165 966 131 808 658 044 057 876 605 048 841 182 127 140 613 312 356 831 193 260 016 788 134 255 448 874 251 492 867 414 928 735 431 024 066 431 703 476 382 784 775 799 933 167 163 027 240 595 340 114 234 972 754 105 673 552 742 349 142 882 347 624 627 666 593 622 728 354 499 659 494 332 882 928 275 408 681 948 601 190 440 761 793 852 958 064 067 144 583 616 756 579 236 433 267 286 222 090 752 698 571 900 295 766 927 649 349 341 254 306 826 858 382 487 465 564 764 380 853 003 407 320 633 144 153 967 116 779 953 732 932 956 113 311 521 175 732 503 260 373 296 853 615 452 198 217 826 554 016 186 963 121 041 409 031 289 804 639 872 303 194 965 030 038 605 666 880 885 970 350 519 800 814 606 911 024 501 547 683 194 855 288 396 055 360 890 571 638 369 923 113 821 286 338 891 913 747 959 952 285 090 915 753 403 685 897 104 514 686 243 362 153 165 925 346 093 938 982 781 299 937 032 603 553 235 261 393 021 815 968 371 281 374 173 009 795 339 720 714 507 855 244 323 810 236 036 205 842 431 673 789 356 322 570 947 128 092 996 913 403 931 764 451 534 244 115 771 501 389 519 124 787 599 658 189 755 504 173 050 043 987 737 779 384 520 366 815 784 696 925 791 467 613 770 081 541 038 265 741 682 149 196 762 131 160 484 108 802 336 517 294 132 854 436 075 540 400 086 204 163 827 113 182 619 285 113 481 697 150 217 424 397 457 221 561 534 075 223 084 955 830 074 373 903 592 177 624 122 211 683 968 024 022 155 166 469 632 142 873 203 832 902 576 981 749 774 356 165 860 924 936 321 267 260 904 546 409 443 930 863 639 545 642 453 123 121 096 576 631 133 747 686 293 230 922 693 688 016 792 378 310 818 317 715 748 854 503 150 473 455 375 739 396 974 229 127 173 224 480 018 043 277 454 222 642 510 619 072 174 968 062 133 792 681 675 766 315 548 039 549 452 930 116 567 583 034 806 345 731 893 399 187 678 946 936 493 871 043 469 425 046 909 364 454 836 231 525 172 295 520 232 569 715 910 026 064 104 996 196 478 064 309 823 263 555 000 755 785 132 093 490 247 994 520 331 525 902 735 978 904 619 966 369 639 607 293 072 621 713 250 977 880 478 704 393 760 266 619 163 028 992 607 112 657 757 590 412 227 365 249 528 719 691 413 613 429 473 797 809 130 514 012 094 619 033 828 540 009 000 734 730 967 348 631 010 772 426 029 220 206 829 634 732 773 622 474 181 351 103 908 779 589 018 407 052 551 914 202 073 406 383 390 449 130 360 096 746 040 733 938 630 718 085 767 226 287 074 618 899 430 175 600 726 543 035 340 415 189 607 185 510 548 721 534 905 045 957 554 140 048 416 964 262 700 574 729 586 451 247 562 839 414 680 608 923 101 991 921 161 194 467 831 030 757 572 236 997 545 643 355 164 505 248 541 706 109 410 807 170 979 585 865 888 265 292 532 870 737 345 616 955 058 680 978 117 598 093 624 946 014 903 312 660 758 594 170 157 895 122 161 054 830 616 733 742 737 107 255 414 684 097 918 013 783 920 065 273 806 561 553 603 440 279 799 887 562 119 183 521 261 073 251 263 206 289 871 237 866 230 522 688 251 456 686 525 168 768 426 171 391 039 646 384 792 522 368 574 938 300 637 643 115 437 128 045 109 775 528 314 632 751 274 710 316 880 214 011 158 255 077 774 516 630 394 054 510 693 768 452 597 166 805 535 160 201 234 530 154 016 315 019 537 919 208 166 365 503 173 654 013 119 626 569 262 151 842 719 892 937 075 484 302 846 791 646 298 641 751 359 237 670 433 815 243 228 202 139 823 439 022 606 226 153 068 437 822 256 929 746 203 715 714 762 725 461 726 082 212 031 169 117 941 781 406 826 092 467 027 860 458 785 933 694 680 362 650 637 939 775 498 674 293 227 845 844 824 393 361 512 986 288 375 667 969 105 358 495 263 029 460 504 104 262 405 145 658 955 034 291 332 433 909 129 034 870 394 847 224 936 716 388 961 276 632 083 026 501 266 663 919 872 259 805 582 258 761 911 262 327 969 192 398 204 600 786 568 898 116 531 224 707 484 821 915 583 373 415 498 628 796 235 941 506 367 406 659 234 827 012 164 288 548 482 419 929 362 945 528 083 264 423 464 762 204 023 728 076 982 331 310 840 529 738 369 573 703 395 739 010 997 325 720 205 052 935 681 785 571 577 612 172 827 132 940 868 033 283 947 409 702 018 826 072 460 968 250 820 388 959 547 570 845 655 886 653 113 067 119 516 591 579 585 311 302 314 126 637 480 583 778 391 657 752 919 950 829 035 450 754 630 128 088 646 346 233 864 452 510 448 978 123 847 229 112 138 355 178 504 242 358 511 534 098 733 008 348 735 867 647 455 343 483 510 689 082 308 148 910 140 528 901 698 965 290 700 577 696 094 142 139 568 801 805 228 684 878 192 258 452 819 393 161 558 794 230 569 479 013 362 253 745 645 760 513 026 343 711 561 323 716 584 647 797 617 413 217 224 934 224 835 460 899 444 643 471 133 529 431 694 864 520 256 629 649 313 307 428 771 397 447 858 086 989 798 790 561 950 117 708 414 100 911 728 185 846 995 719 866 782 070 294 185 420 283 915 964 070 952 757 467 769 059 943 595 248 849 222 424 781 588 412 765 790 721 329 448 299 326 129 586 693 597 092 566 036 124 232 939 607 871 239 581 917 015 903 953 958 549 809 774 890 324 831 897 285 817 725 080 667 553 152 322 965 147 937 992 429 948 945 416 790 246 974 393 261 860 031 292 954 485 088 965 296 921 619 590 923 349 059 320 881 636 083 707 587 491 127 840 881 671 252 307 010 452 999 752 006 133 720 706 611 042 243 183 426 974 468 740 981 099 400 559 906 974 998 813 958 331 782 249 988 714 180 628 491 083 599 331 872 049 634 545 434 771 079 895 770 658 723 142 523 678 433 798 659 529 688 310 206 542 129 394 911 288 664 157 268 694 908 252 985 186 335 995 035 583 475 392 616 873 040 873 902 980 570 237 874 424 498 548 540 610 680 799 524 403 056 862 673 361 035 715 241 619 541 862 600 385 117 984 487 591 824 906 933 065 543 185 080 764 709 976 532 774 089 748 631 449 797 427 193 033 781 177 117 368 567 775 086 706 680 001 541 946 912 946 205 947 171 192 515 852 074 477 581 310 445 301 119 847 960 992 280 278 336 025 488 997 047 197 730 482 577 785 184 504 822 615 801 871 957 722 963 758 066 015 399 621 400 589 307 890 185 909 236 398 952 923 553 595 491 693 818 148 018 926 316 039 356 133 572 048 780 192 575 964 818 721 388 835 057 481 770 733 553 499 611 627 785 801 070 101 830 995 519 543 521 384 714 470 007 902 637 843 213 563 597 078 774 428 419 086 667 052 503 379 883 671 018 788 012 497 164 688 220 259 978 847 301 735 269 409 405 388 428 155 722 190 830 305 420 853 112 386 595 689 020 778 087 126 706 498 271 284 248 366 369 540 577 054 359 525 785 787 383 966 525 854 603 077 699 312 111 395 845 247 114 980 563 274 900 969 350 341 340 914 445 733 292 606 684 171 100 652 582 278 976 291 406 499 574 511 728 304 706 849 115 095 124 691 830 292 867 111 886 905 532 893 268 845 041 912 356 090 406 807 960 337 664 072 113 435 482 768 891 237 135 528 025 099 438 571 348 423 388 327 781 641 120 998 394 309 975 631 286 775 566 736 279 551 918 163 154 219 493 555 757 890 041 536 726 286 475 580 773 175 539 186 431 377 686 774 663 822 547 356 522 129 613 832 719 224 667 921 350 892 728 724 232 923 867 567 310 252 301 380 029 099 584 069 182 241 427 723 557 238 768 469 165 456 585 612 356 473 880 025 066 899 593 915 962 197 642 430 352 209 777 925 013 561 280 817 258 275 618 901 624 634 784 526 388 862 432 285 676 839 915 085 707 647 047 996 718 082 622 755 610 034 670 929 118 521 910 826 019 360 505 982 532 536 486 616 928 516 439 975 355 240 300 752 491 508 516 119 645 108 258 900 117 280 597 695 508 530 414 899 097 992 393 785 198 571 113 157 505 465 152 247 273 295 943 431 345 982 438 570 021 093 499 992 091 752 783 259 328 261 077 221 114 373 988 426 805 055 533 768 329 925 168 482 163 808 696 346 398 011 923 896 636 283 990 026 657 915 429 471 580 037 609 446 157 177 215 138 420 654 396 556 286 027 321 427 341 048 767 840 909 687 684 831 483 067 756 772 633 038 652 882 301 989 551 039 066 623 164 682 363 230 436 386 796 765 540 522 938 334 458 671 934 575 191 041 600 177 183 646 426 051 781 098 799 400 040 533 712 911 983 016 373 749 064 284 114 341 205 090 395 409 049 942 611 286 833 803 971 790 903 757 528 495 401 188 781 684 235 347 927 306 258 227 800 218 389 831 981 596 801 023 754 304 364 498 237 888 491 808 901 631 754 080 418 622 813 484 068 418 285 831 198 098 215 670 269 973 901 605 149 554 321 126 410 814 957 604 023 246 484 503 444 583 413 087 644 995 428 135 732 143 922 533 722 627 772 075 646 449 099 438 609 259 136 364 923 279 801 919 527 918 498 612 013 443 915 197 990 277 926 060 446 264 649 806 035 405 602 320 789 372 063 959 792 473 436 096 577 672 700 240 601 576 541 686 077 605 571 166 469 013 731 082 548 646 724 624 971 277 397 757 672 309 915 528 863 056 522 332 460 281 596 850 495 723 923 121 649 676 261 661 294 940 621 890 150 041 745 223 927 746 647 785 267 137 596 777 777 690 241 061 795 606 295 833 030 240 952 730 768 332 693 744 298 710 689 437 819 292 526 080 065 938 338 190 832 661 743 146 972 057 617 833 452 899 267 207 376 795 882 887 728 185 914 919 274 154 392 970 370 302 738 310 080 408 256 094 187 593 568 435 140 470 781 210 550 270 565 015 817 905 588 806 793 516 145 865 639 344 953 058 604 196 408 173 395 403 083 751 439 003 488 364 593 188 778 703 292 334 650 154 670 862 696 868 307 741 081 277 467 474 293 886 445 323 262 365 060 291 620 469 983 846 328 039 563 429 398 853 844 363 733 358 884 933 045 774 676 042 568 604 936 875 246 324 305 557 631 136 506 450 581 151 077 635 172 441 237 353 008 140 005 029 718 059 760 572 933 728 184 838 469 272 905 588 428 396 206 462 368 624 186 341 990 224 188 272 415 153 981 431 375 030 968 728 368 712 370 422 375 338 406 849 142 283 597 827 858 545 572 823 378 750 843 502 001 921 204 831 386 172 343 830 648 675 268 150 165 681 043 641 855 339 886 966 239 756 814 377 179 371 755 541 894 541 500 083 435 781 213 080 627 052 138 877 545 580 225 898 702 267 118 177 464 254 048 076 261 736 594 780 735 114 544 170 201 403 547 941 957 893 844 989 284 532 242 500 308 384 987 838 357 815 862 430 626 852 759 390 194 819 807 686 054 288 537 584 031 757 702 071 135 538 403 944 831 454 478 600 251 647 266 457 667 925 953 813 202 277 820 057 131 517 226 626 004 389 455 718 678 597 980 120 398 685 564 276 262 908 411 551 437 736 374 408 217 245 548 016 046 655 358 944 007 457 083 215 307 782 160 608 164 743 471 919 112 432 105 386 745 788 057 753 310 304 789 309 210 933 028 949 571 945 338 413 502 557 221 767 816 629 327 711 435 154 401 779 639 620 105 044 601 861 220 662 107 996 699 634 913 544 060 307 228 131 622 448 267 081 626 384 575 042 247 357 171 666 051 843 925 725 853 737 210 175 327 938 048 266 380 333 532 093 955 193 520 188 347 998 191 581 887 611 661 507 625 708 503 700 105 393 544 341 099 006 998 289 307 645 633 400 539 719 808 051 513 402 025 320 441 934 801 437 563 618 418 247 462 334 383 515 394 981 341 121 563 707 613 073 832 767 979 661 476 324 741 998 039 054 188 861 426 860 097 833 220 391 961 695 122 245 227 015 700 786 252 817 587 105 436 616 337 280 133 377 672 190 341 142 425 645 280 529 735 688 336 495 577 752 172 484 547 509 762 869 602 946 397 235 282 171 975 127 898 950 427 594 564 569 448 177 190 423 935 368 223 260 614 122 038 010 607 713 735 649 469 686 334 195 021 209 010 509 662 496 332 726 358 175 766 770 740 981 469 144 222 085 405 902 261 557 732 042 279 480 643 073 414 116 792 394 962 009 985 954 253 972 945 429 293 219 299 850 723 083 716 130 111 811 920 919 808 312 926 973 638 986 527 362 076 405 475 435 968 102 824 733 483 352 549 297 927 532 180 874 987 466 200 994 756 549 523 017 142 576 899 750 057 938 419 216 880 542 022 185 881 987 779 625 084 786 812 312 974 965 477 473 212 570 575 410 081 794 664 292 152 473 756 634 215 997 805 014 367 450 078 999 080 478 228 064 981 168 339 819 384 701 678 163 333 776 538 636 408 838 183 476 091 934 916 466 873 463 374 975 096 564 418 826 567 718 623 061 162 111 139 280 490 562 677 659 435 044 674 233 214 588 513 178 548 193 711 632 518 660 093 390 489 193 396 687 049 568 401 911 080 612 260 139 692 105 497 036 122 300 158 714 747 801 134 136 386 266 138 720 939 890 549 253 602 840 669 869 774 289 494 715 549 780 333 837 984 064 588 662 570 255 306 104 362 536 312 365 214 156 129 823 803 507 024 145 513 553 448 637 714 406 599 249 588 236 891 962 835 005 257 254 206 032 159 851 142 925 561 441 550 837 662 101 035 488 983 854 581 042 593 543 994 175 849 816 169 736 433 657 151 615 054 409 701 296 862 497 451 129 760 964 732 424 352 207 739 385 884 834 703 624 003 829 951 541 063 169 775 208 463 634 442 298 896 253 057 506 841 886 167 346 895 497 093 163 032 772 620 274 518 960 757 534 138 162 397 283 429 383 336 770 554 413 083 130 638 169 746 775 213 454 790 572 397 629 713 583 167 892 532 300 760 277 744 066 061 767 148 397 811 401 957 749 008 327 591 152 229 887 535 046 509 470 950 439 075 335 425 730 185 147 808 133 453 552 301 524 388 267 629 178 319 461 292 187 519 495 987 046 425 718 617 819 332 104 399 818 736 444 858 362 993 639 947 077 771 810 701 904 800 063 267 760 694 875 431 044 673 328 139 371 689 906 587 343 349 354 782 797 657 972 464 299 063 598 348 617 982 706 180 915 221 284 062 954 917 126 078 871 752 335 595 971 186 685 775 282 063 550 881 863 631 437 327 286 885 581 810 398 430 134 091 104 435 237 742 824 689 308 755 062 813 880 101 562 229 123 804 960 613 389 287 517 865 409 770 512 930 023 722 636 086 353 976 858 633 703 050 565 918 942 301 746 751 176 866 043 161 089 744 306 710 639 480 531 927 390 506 801 692 532 227 174 589 473 830 011 926 943 648 139 372 286 552 122 022 602 559 952 939 677 210 206 862 438 245 475 821 883 484 826 544 569 153 433 865 031 397 719 008 229 109 880 481 912 230 733 053 019 186 040 399 703 481 436 489 875 202 107 425 487 989 484 540 152 591 088 815 808 367 261 426 322 823 219 505 339 809 194 124 356 775 007 982 734 267 416 089 565 955 563 937 032 570 083 577 802 902 137 167 148 710 992 519 714 440 618 767 616 527 156 556 847 541 033 327 139 724 997 126 048 509 994 627 697 239 639 899 332 420 440 371 499 321 446 958 365 696 468 081 604 254 938 296 236 783 258 744 642 336 334 868 186 657 759 466 965 982 029 460 203 627 787 369 968 139 886 053 596 020 048 115 774 787 811 500 630 815 977 185 178 704 712 855 322 441 747 389 521 183 822 956 036 854 886 113 649 595 850 490 556 535 050 359 001 754 730 621 876 645 621 952 431 539 639 159 415 198 816 132 477 561 707 068 490 279 655 809 098 407 603 629 251 967 390 037 809 958 700 766 814 709 623 833 404 405 100 500 966 353 215 585 869 581 434 099 537 254 382 954 857 332 595 278 367 123 647 946 302 536 614 464 554 117 957 333 641 449 107 523 665 940 027 471 801 930 054 254 081 099 047 521 495 279 140 161 237 868 051 394 722 668 806 047 634 505 722 508 569 417 609 631 111 817 356 870 507 909 149 700 548 481 345 460 721 269 441 912 637 786 251 936 270 458 039 999 567 965 824 579 571 200 830 478 976 088 191 294 292 518 350 625 268 745 643 900 105 449 531 311 491 506 477 440 008 684 364 634 448 927 627 401 491 153 410 275 012 720 336 628 976 112 270 341 961 373 460 653 542 861 177 040 237 757 993 124 464 066 243 190 619 021 514 312 748 467 278 345 017 334 337 307 203 851 436 836 218 176 396 290 011 735 725 810 197 906 611 278 381 919 960 169 706 119 828 026 860 643 773 929 304 130 637 436 071 716 790 286 006 128 154 602 920 984 871 634 787 179 702 973 606 899 483 563 851 314 196 182 978 824 246 422 457 364 199 240 261 810 811 657 403 255 989 287 076 343 365 001 329 015 802 587 645 689 292 926 909 005 036 498 903 192 091 909 706 514 497 624 868 908 232 873 042 531 445 271 055 185 153 515 459 569 491 690 828 618 894 783 481 090 739 172 401 655 850 960 858 403 337 512 913 975 221 340 329 549 833 777 661 869 337 603 414 437 377 821 914 136 216 531 926 042 904 980 381 622 229 838 443 296 231 323 644 932 293 099 112 663 013 687 296 783 668 842 786 565 031 549 080 898 765 172 324 983 736 875 534 944 102 138 458 016 070 241 172 213 619 834 361 406 476 289 566 107 091 312 365 676 674 191 034 649 491 727 592 848 653 890 665 534 877 884 863 036 776 484 682 831 304 506 352 198 109 148 145 477 962 082 003 929 766 807 509 187 083 730 335 661 028 207 056 674 275 424 545 232 953 477 363 227 699 453 264 346 391 556 984 941 747 509 088 972 457 383 955 848 786 208 673 239 126 643 517 354 542 721 820 773 524 360 199 942 688 936 046 676 102 644 408 388 654 054 916 879 311 910 410 397 125 564 169 545 503 442 824 077 189 937 065 900 310 548 971 609 460 116 030 611 991 420 124 053 731 632 076 805 339 477 038 416 379 641 004 414 081 938 893 058 279 591 286 709 986 668 579 968 913 851 948 535 107 751 106 634 885 913 032 806 756 822 444 685 851 279 308 413 161 488 290 370 039 098 683 879 091 675 070 254 079 609 411 529 069 802 085 991 511 223 049 819 522 118 459 134 441 168 668 637 029 189 606 613 420 670 100 964 895 474 483 384 804 207 972 070 306 059 288 143 016 067 163 061 174 577 412 709 228 319 315 470 090 629 094 487 282 022 194 501 544 651 360 279 681 882 089 898 297 820 081 725 761 791 534 726 207 876 065 337 776 960 950 687 744 977 516 460 455 085 993 474 402 069 042 900 528 924 511 909 106 759 921 440 927 694 289 442 511 043 924 172 486 242 594 459 828 332 007 885 256 003 145 725 821 514 287 767 155 088 166 604 463 847 898 681 008 099 759 064 458 214 521 679 326 033 128 990 450 583 030 963 906 981 126 313 225 635 918 206 138 769 776 617 250 145 049 653 618 976 648 158 899 134 524 207 777 930 098 788 280 335 083 545 427 628 410 230 555 200 804 573 350 328 314 651 897 294 667 624 827 119 252 850 842 691 939 371 078 232 897 122 358 317 738 224 706 270 519 607 010 701 948 631 314 449 512 874 884 325 028 293 281 774 488 766 365 544 395 004 087 812 539 510 715 826 501 014 604 509 714 132 944 616 743 760 625 119 949 802 663 134 610 900 287 292 929 148 811 446 389 273 417 757 728 445 681 300 340 234 203 897 326 242 599 466 458 624 293 454 767 104 007 362 160 919 845 072 809 001 894 411 959 374 763 179 611 417 141 411 154 572 465 762 950 860 565 136 302 055 277 376 245 385 135 059 922 090 448 464 585 961 447 334 383 580 074 298 198 761 423 127 103 073 383 733 558 374 679 910 636 583 980 808 010 774 028 187 842 367 042 976 268 550 970 734 624 461 576 736 489 055 858 144 958 949 794 117 783 548 121 688 079 189 347 083 585 030 988 522 700 205 700 777 704 079 238 940 282 291 708 300 792 963 239 140 602 586 206 327 023 593 557 104 361 501 783 798 413 444 055 116 906 910 203 983 955 048 141 016 099 261 768 849 862 216 748 666 156 113 955 648 680 692 168 256 623 337 445 718 158 295 182 091 068 501 627 884 973 837 820 061 452 082 323 402 611 380 755 884 656 576 966 478 758 406 945 937 151 341 795 041 225 997 911 456 882 281 534 248 656 225 517 080 933 974 304 526 862 227 541 668 731 644 548 459 489 538 124 772 655 525 704 315 218 831 212 704 041 330 094 358 549 216 982 487 602 029 822 532 891 746 439 650 309 020 114 478 287 734 716 951 509 748 884 847 261 774 428 252 759 059 467 288 615 464 869 457 919 881 833 338 336 206 699 448 076 883 960 511 956 855 496 455 273 873 306 887 095 648 151 392 136 896 738 651 299 399 124 858 504 146 642 019 379 413 266 549 425 690 684 009 255 794 304 922 618 674 255 606 504 744 340 445 706 100 845 305 873 146 602 170 181 415 068 909 008 598 259 208 719 013 380 311 670 806 867 737 037 399 387 651 318 566 402 628 122 323 479 452 976 143 589 225 996 775 268 130 851 804 382 954 003 930 305 917 563 235 747 656 697 626 845 180 907 918 673 756 535 926 046 597 485 346 138 690 315 253 953 740 906 623 638 268 946 760 504 760 436 150 893 830 090 453 708 864 901 926 700 354 247 036 785 984 082 471 390 791 384 605 045 894 829 825 567 154 063 194 766 559 603 668 623 999 860 445 333 684 203 073 687 343 813 920 284 735 854 482 168 314 541 309 803 152 323 160 544 848 603 489 163 163 034 405 320 864 435 440 397 963 609 774 747 341 409 478 155 057 987 165 144 340 065 912 649 625 886 415 791 884 191 423 250 715 449 686 292 747 186 758 232 124 423 037 854 590 777 885 256 442 040 862 274 341 036 405 605 295 674 402 310 067 477 880 677 825 679 070 864 645 927 422 560 484 270 221 559 073 660 419 277 974 143 006 158 202 463 666 185 588 505 054 483 147 208 740 292 452 323 469 284 439 505 821 422 648 616 905 852 815 104 739 843 886 180 400 934 197 987 486 547 875 472 970 516 210 230 449 220 539 247 302 481 237 285 764 452 838 286 038 518 145 754 512 625 109 318 102 446 609 756 123 915 875 480 446 204 898 896 692 234 066 768 353 930 833 227 442 130 368 476 512 498 008 277 895 009 271 655 751 940 166 652 410 342 338 892 940 895 596 888 093 676 306 913 255 150 466 396 939 825 315 071 349 774 622 288 330 758 808 458 486 293 083 382 120 372 832 050 862 599 233 151 748 773 452 827 216 315 416 180 193 594 786 553 823 464 501 206 011 455 990 717 779 000 664 140 149 218 783 854 792 624 633 178 613 763 423 128 140 596 373 159 088 311 242 324 093 430 400 961 613 318 981 546 642 180 482 640 509 292 198 867 589 169 535 244 824 368 182 590 125 568 821 456 414 056 499 359 982 730 844 426 009 641 761 232 641 625 201 484 988 377 908 240 362 713 217 467 963 648 374 417 468 765 624 199 319 605 525 825 981 572 768 289 785 815 989 110 529 267 357 166 313 811 351 812 881 442 197 438 908 790 448 470 609 999 626 946 332 398 149 193 654 682 406 021 927 729 880 684 616 597 595 181 782 038 767 997 105 892 540 337 024 915 134 195 115 862 339 651 154 507 958 662 604 140 449 640 037 815 281 313 516 797 972 992 376 036 289 779 770 848 218 350 638 052 766 977 676 060 735 288 717 126 643 195 761 451 705 014 394 331 091 557 278 927 560 404 992 689 723 905 868 488 394 981 349 486 878 659 350 684 823 152 594 269 287 140 880 723 722 618 044 166 520 663 516 263 302 056 451 867 396 864 686 578 881 781 719 920 283 731 983 966 808 709 634 524 945 694 442 641 972 876 776 326 870 463 484 194 559 478 032 505 605 899 564 384 750 792 360 151 477 254 536 221 297 362 961 870 974 147 721 771 221 459 962 892 949 051 037 685 483 121 877 245 778 539 563 644 720 571 650 885 092 112 511 430 386 846 825 141 628 307 833 568 733 493 897 506 078 453 420 368 546 695 714 571 579 677 596 935 689 988 632 557 441 754 912 450 208 513 472 506 975 515 788 319 147 306 114 222 630 206 299 583 278 990 656 304 210 344 888 743 353 490 722 147 781 816 014 120 143 334 409 226 575 122 085 547 323 829 540 763 845 528 007 360 159 954 359 365 118 740 586 352 200 095 280 477 652 913 697 581 960 726 779 349 663 391 634 211 366 405 984 450 119 574 300 556 372 870 614 807 546 445 902 382 630 187 080 669 013 443 692 514 771 531 202 829 967 876 244 104 936 655 799 235 098 651 415 411 080 988 751 981 529 145 037 786 355 350 346 311 786 271 657 480 571 694 348 218 490 954 095 880 984 503 034 303 003 031 837 924 670 078 873 213 328 748 068 662 541 576 517 690 402 681 354 262 759 933 486 327 299 528 065 900 582 855 629 458 231 180 832 489 323 872 295 350 290 478 016 739 908 585 115 651 626 370 933 280 693 012 308 058 009 042 441 126 591 869 000 268 967 408 460 654 796 245 600 995 150 200 790 222 205 303 710 551 490 100 681 917 421 037 661 693 113 813 654 971 202 338 632 696 081 779 561 607 480 548 364 727 599 295 198 323 039 137 356 624 626 017 050 846 502 181 173 967 924 704 796 069 356 861 566 620 169 785 925 751 735 660 839 832 048 970 217 467 799 477 904 030 213 723 554 383 565 117 378 535 684 881 622 976 438 605 683 484 572 288 291 023 097 511 714 679 528 976 747 132 889 350 686 343 122 213 989 672 217 240 792 092 540 408 176 265 113 970 933 645 675 819 212 233 511 170 057 992 502 714 511 937 058 979 188 206 482 011 778 048 408 708 454 508 027 700 693 942 602 155 825 716 117 109 566 091 283 103 698 971 344 252 363 040 448 366 822 973 182 025 330 751 736 633 967 449 253 641 637 046 670 686 301 746 666 031 659 025 233 126 865 997 594 824 493 666 005 891 505 022 145 133 795 142 099 056 531 421 828 933 831 054 131 801 627 631 246 708 233 724 019 403 145 181 601 299 645 451 514 070 802 497 480 551 020 770 556 677 015 002 208 062 410 264 570 255 098 159 090 437 043 125 661 981 598 628 134 754 301 278 046 533 620 296 654 228 395 413 993 860 760 828 955 953 321 919 400 242 361 617 690 178 744 608 389 236 560 647 906 629 047 648 258 392 157 725 204 366 483 908 155 384 655 898 867 872 643 969 810 697 594 843 736 567 358 243 151 186 465 958 487 040 891 364 929 374 777 808 878 580 486 646 406 327 278 708 931 044 671 584 127 633 349 984 250 542 284 084 871 717 186 265 392 500 685 581 444 842 870 010 672 498 020 140 151 651 172 527 101 180 189 231 384 898 117 686 259 219 487 079 193 109 868 931 353 162 390 873 550 009 772 873 457 342 365 689 401 402 072 014 595 143 294 660 786 920 608 027 801 647 968 967 206 119 556 893 148 471 096 120 496 350 708 567 756 821 169 424 993 745 262 137 388 224 189 744 851 856 640 738 151 053 257 526 475 701 012 725 808 458 345 809 458 931 077 242 351 812 810 302 615 704 464 635 183 152 180 682 301 540 289 501 322 042 977 584 878 090 216 550 836 493 670 412 359 810 900 662 884 902 116 028 563 072 192 249 587 240 287 554 649 371 592 125 545 925 532 949 771 148 676 499 066 310 197 821 805 785 202 959 651 016 790 367 939 989 266 254 235 812 580 247 727 011 523 096 886 970 627 094 915 068 633 931 271 985 732 691 704 726 297 518 120 157 887 063 002 850 452 508 881 409 893 120 314 829 035 935 149 581 326 831 641 286 621 285 627 721 479 856 886 944 415 864 521 243 655 178 885 007 723 321 896 403 038 452 724 708 294 004 304 855 679 074 263 073 431 343 714 709 309 405 750 457 835 854 129 427 662 707 294 750 310 375 640 435 319 064 741 401 680 175 012 796 174 905 911 285 634 165 460 012 835 933 020 430 825 553 354 258 056 693 756 542 840 704 218 862 570 168 946 320 622 004 088 533 756 476 021 895 178 885 873 711 405 288 143 945 104 368 595 198 326 776 946 110 350 865 708 454 655 690 370 259 764 235 255 474 347 001 358 951 200 338 710 123 555 754 118 583 408 330 285 322 660 991 133 250 081 101 498 682 885 154 362 768 631 116 458 676 893 971 673 599 700 163 403 668 083 358 103 720 036 198 232 882 659 427 534 092 644 774 294 267 250 390 011 469 138 515 116 036 501 603 927 199 401 246 879 185 780 216 804 849 484 397 711 768 394 495 571 031 221 049 848 168 524 210 730 893 524 708 478 317 930 150 062 911 347 658 082 555 209 796 942 243 225 237 684 012 960 570 153 935 020 933 777 051 186 828 548 144 644 179 727 031 580 590 019 967 909 890 204 677 302 466 443 087 964 791 584 971 719 450 560 311 362 244 871 143 235 003 431 562 683 810 761 114 575 385 410 812 855 258 144 084 366 587 161 503 533 138 487 360 019 551 321 176 110 774 904 605 663 884 683 081 430 515 428 939 721 771 705 205 525 438 918 075 702 998 330 694 272 872 636 126 446 402 155 097 807 385 236 768 216 216 902 761 544 086 521 141 353 089 567 757 309 992 754 880 927 884 549 302 691 350 901 504 397 389 912 418 036 546 985 066 887 566 687 368 463 271 679 843 385 022 018 884 069 237 741 163 179 145 158 252 731 597 516 444 696 114 395 375 963 702 326 236 903 395 715 009 991 688 661 473 404 863 770 138 594 835 705 950 223 784 004 079 457 026 392 710 747 580 386 255 891 203 546 145 272 430 479 142 242 140 366 332 785 857 573 682 471 297 178 091 209 633 124 312 780 893 049 385 607 301 181 575 295 245 860 004 282 024 614 220 488 600 787 961 245 355 254 582 931 851 454 341 930 630 840 626 882 533 819 679 032 303 890 219 183 605 229 555 721 128 091 599 039 446 002 193 959 203 786 863 002 474 000 751 518 202 599 471 856 011 761 388 038 049 566 343 074 969 633 308 810 014 899 452 491 412 469 971 012 296 716 290 643 884 917 633 942 199 178 327 630 988 509 465 284 427 168 021 366 063 074 687 438 597 681 304 398 006 223 415 717 111 587 004 331 696 869 288 168 843 229 841 154 639 780 289 441 408 861 597 821 862 568 209 898 711 430 527 955 495 328 425 857 289 740 738 522 237 569 337 123 724 762 537 519 094 954 216 092 778 175 800 130 005 061 909 901 355 080 380 331 913 101 543 256 238 688 710 098 197 447 477 496 145 791 549 602 796 375 295 709 610 336 492 531 738 215 765 162 259 731 005 042 643 471 861 984 704 856 772 628 163 405 267 121 722 379 550 462 009 431 459 244 867 291 064 618 857 437 663 044 396 336 606 131 279 487 083 512 184 940 482 468 538 203 385 449 093 670 432 471 721 552 671 655 971 567 052 663 919 146 282 592 038 685 849 783 840 875 011 845 295 514 403 341 806 074 896 740 901 051 793 079 360 246 390 319 718 737 898 213 131 394 034 030 363 253 981 616 631 221 769 497 483 566 291 389 353 662 859 120 676 549 078 681 959 462 024 209 951 129 246 904 702 619 237 429 432 943 999 321 639 805 123 436 910 470 738 734 821 891 644 054 725 713 392 171 239 385 725 490 156 129 431 024 459 590 425 200 908 928 895 876 537 646 210 608 522 590 275 231 559 937 709 270 227 185 451 938 954 127 061 099 654 165 353 159 004 335 020 081 841 996 211 547 383 937 662 896 579 715 390 060 010 367 991 397 009 854 735 032 286 910 614 647 634 348 519 847 883 374 564 564 588 717 777 009 509 259 792 698 528 871 771 428 013 050 387 893 323 371 700 634 717 426 206 107 020 212 202 587 703 653 596 139 448 776 559 031 278 963 233 763 195 679 028 816 561 257 494 508 745 226 513 444 917 191 217 925 361 975 902 267 469 012 015 020 169 356 533 877 598 289 444 729 725 452 018 013 724 498 513 274 967 533 548 931 379 250 687 966 820 120 236 547 632 165 150 741 981 047 732 122 627 864 351 327 361 106 178 861 764 187 831 335 167 759 355 775 989 586 844 597 640 002 814 392 718 365 843 588 601 940 311 056 870 596 683 004 448 304 671 170 790 995 824 016 930 071 630 640 557 359 002 066 979 637 061 769 513 839 531 686 934 670 371 386 862 689 536 658 850 879 117 364 857 610 351 316 444 473 246 009 868 533 199 315 394 124 360 388 239 817 092 148 636 685 904 107 970 733 071 200 458 226 283 936 089 471 818 199 714 360 639 057 595 761 974 763 784 582 717 253 226 662 160 395 458 446 396 952 830 412 342 216 875 350 765 454 737 633 609 046 500 095 792 266 762 390 117 879 599 955 421 045 326 756 051 586 151 378 410 281 594 813 983 217 843 357 865 100 264 171 209 066 499 121 689 687 204 376 742 379 692 638 391 513 820 626 940 057 163 032 690 015 225 680 943 406 097 891 496 803 905 394 628 828 092 657 243 095 250 403 405 454 106 565 251 123 144 401 970 689 923 596 036 433 869 357 056 349 844 030 739 003 578 284 416 970 887 675 704 912 998 132 345 490 552 392 309 662 129 816 265 821 497 296 043 053 672 323 099 428 993 826 929 839 137 680 076 132 950 110 325 727 772 199 389 849 906 101 560 307 021 540 392 834 427 886 061 509 435 391 073 789 140 233 367 973 425 416 308 811 014 654 141 010 684 094 402 237 653 062 019 701 556 589 319 052 664 948 201 878 732 158 395 287 800 599 740 308 149 083 447 402 723 907 042 591 122 378 958 929 198 235 493 172 689 449 121 666 301 734 958 315 366 075 200 570 383 895 613 486 832 776 869 335 312 269 742 811 315 701 762 508 410 087 267 560 017 353 184 247 271 113 065 383 561 804 527 138 276 581 389 556 749 034 210 641 675 315 830 915 801 889 746 098 455 605 820 332 041 539 685 532 844 720 327 413 508 598 109 249 449 208 282 194 602 739 592 718 501 600 940 807 622 666 379 253 517 694 870 736 285 199 461 108 705 991 846 911 225 926 988 282 273 448 300 214 497 517 854 381 816 947 232 808 269 845 571 826 535 760 297 734 370 702 038 501 234 691 816 723 102 145 435 394 237 055 213 468 762 068 796 815 465 592 935 911 939 754 775 158 861 756 767 398 971 059 723 383 622 521 059 706 598 105 479 843 275 644 170 752 543 637 205 562 947 851 051 308 934 430 140 196 227 852 071 267 096 232 295 237 271 766 190 784 324 086 126 309 026 578 575 245 148 606 286 049 289 753 814 656 490 997 300 569 390 733 532 152 260 059 264 368 383 707 359 175 347 554 967 882 435 383 741 314 592 440 402 264 249 305 922 670 245 281 962 875 566 265 707 029 281 803 355 071 092 048 310 608 522 514 820 198 680 521 288 736 794 716 621 951 944 820 300 129 178 333 504 259 344 537 488 179 930 917 189 617 056 945 418 381 088 815 599 759 321 246 793 031 576 100 543 183 716 142 838 655 760 801 224 261 469 451 985 465 779 895 805 239 868 444 186 351 213 117 854 949 022 115 333 859 914 703 307 658 236 573 215 888 224 895 434 074 245 862 331 293 101 766 460 353 775 493 433 715 626 911 860 365 170 314 844 633 318 942 171 277 084 355 181 882 098 157 777 462 837 010 570 467 406 586 964 188 224 382 348 467 592 268 380 471 399 662 335 990 907 387 567 317 107 106 005 177 174 525 095 400 696 317 445 842 070 828 805 683 129 601 229 688 223 884 547 012 516 266 289 529 901 517 909 317 718 379 931 264 926 968 536 467 008 851 482 210 151 973 907 001 393 256 337 821 651 815 314 687 938 765 416 627 133 810 745 612 182 126 641 002 802 142 946 210 726 337 405 218 265 847 484 017 855 437 803 541 630 995 772 270 151 177 830 114 160 348 860 005 269 164 990 326 889 373 240 139 892 758 499 605 021 956 079 542 789 091 245 972 438 235 362 302 206 400 222 791 983 183 648 156 268 361 440 244 090 890 322 753 383 348 835 666 288 361 319 450 807 421 532 646 971 721 061 821 125 551 230 319 813 867 761 622 606 605 348 395 341 073 237 901 749 128 724 878 821 464 789 315 165 279 914 677 598 313 564 151 872 502 856 204 243 965 399 538 342 938 161 605 253 787 936 337 059 318 404 862 259 658 878 901 670 247 969 046 409 195 018 146 559 891 486 195 745 398 235 924 620 000 729 420 771 460 369 193 608 730 341 883 355 132 731 925 353 318 000 394 829 988 635 684 749 349 342 610 386 165 730 662 827 978 483 298 486 341 965 470 168 898 689 831 827 907 099 014 327 893 886 713 118 085 454 491 164 152 558 599 160 227 879 312 561 971 279 084 817 222 727 513 643 493 412 015 046 509 017 488 951 784 752 950 002 801 774 919 612 381 577 990 531 993 811 382 936 998 144 891 117 555 415 037 597 496 294 210 563 079 962 791 319 743 727 073 190 883 308 766 157 784 984 516 890 269 179 302 322 830 149 356 412 147 022 636 940 231 807 444 021 796 353 529 569 792 866 428 089 632 225 793 801 658 582 423 214 586 605 665 672 458 362 175 075 055 845 843 805 077 581 758 452 765 924 481 411 934 939 848 624 786 813 057 143 338 910 588 661 165 097 235 103 048 627 094 993 121 853 495 011 712 761 263 380 088 781 817 553 908 851 239 631 404 762 108 032 834 655 775 794 102 571 974 128 284 931 662 351 217 460 032 019 633 349 521 299 675 830 098 298 386 449 059 918 102 405 083 447 050 317 985 002 689 330 636 769 157 588 763 778 242 034 687 308 878 436 663 367 871 953 782 287 435 376 478 198 830 481 577 076 397 186 185 685 097 041 017 740 743 617 584 368 872 822 613 046 404 764 215 778 171 882 291 209 555 659 852 332 994 474 295 414 258 972 605 234 770 342 157 902 710 691 379 111 671 640 587 776 508 818 933 800 302 871 476 034 493 861 390 406 020 280 777 550 071 619 002 974 491 993 882 507 655 059 298 266 961 378 819 879 150 533 908 819 432 514 883 750 346 042 207 379 919 130 046 268 852 368 531 247 401 281 900 398 259 403 150 823 967 318 444 411 852 098 470 652 229 342 821 113 868 245 813 530 362 593 582 013 934 860 551 726 237 039 563 437 134 675 993 025 483 970 459 182 564 050 644 472 554 345 534 823 557 301 909 774 397 690 653 940 035 227 621 276 230 052 176 145 069 115 122 050 392 053 195 448 273 937 501 965 194 879 482 407 659 581 613 014 439 742 520 135 389 931 688 895 527 608 049 262 658 336 465 321 733 897 121 404 234 001 303 431 114 002 343 051 338 810 492 328 301 713 340 117 371 277 903 180 537 007 805 918 834 817 486 922 636 927 204 569 670 639 829 897 842 431 880 885 013 968 306 511 559 315 795 780 111 411 363 220 668 989 223 206 640 202 280 603 657 991 693 605 876 763 975 638 966 554 314 262 382 232 163 036 949 747 671 116 486 889 381 857 547 641 638 639 726 205 808 049 808 574 598 009 733 124 087 438 098 395 178 515 193 938 470 299 156 368 527 631 062 183 977 078 001 858 299 271 441 693 719 622 934 917 110 454 940 851 499 690 352 969 020 368 668 699 330 982 449 006 791 266 952 184 206 761 670 123 476 363 721 976 098 763 890 954 964 602 870 633 577 468 533 870 737 649 540 560 320 854 266 170 216 202 725 921 014 524 477 147 095 689 410 419 336 441 054 438 026 043 686 990 306 561 765 338 720 984 565 686 693 966 113 533 552 242 207 295 202 521 404 835 285 964 018 380 773 558 332 034 606 909 947 680 717 397 268 991 242 376 252 500 652 594 299 967 004 243 733 968 453 257 317 902 809 130 338 809 898 560 765 708 024 721 784 776 270 335 031 111 314 025 835 295 054 581 191 434 706 737 759 603 079 457 333 591 423 068 759 767 334 997 819 249 697 582 727 356 068 904 904 767 272 327 790 287 829 510 585 970 997 470 367 013 024 970 302 683 589 950 676 910 832 575 998 684 626 691 568 966 727 360 135 054 391 975 366 881 350 193 142 756 390 279 058 540 869 759 280 608 724 121 844 934 359 085 229 142 056 073 515 394 199 529 488 485 298 161 430 264 076 160 940 854 659 980 463 086 049 447 643 790 022 832 007 767 326 879 590 956 276 485 617 311 511 356 489 424 428 666 987 403 594 735 412 846 940 618 109 863 902 693 127 012 791 351 161 060 849 141 919 758 479 127 119 755 611 977 120 207 940 462 230 432 328 968 967 804 115 118 755 471 568 015 674 464 477 554 221 013 142 792 477 017 271 475 418 467 348 386 922 763 899 788 807 271 043 944 209 573 049 545 903 625 488 765 606 118 431 380 622 362 340 996 365 813 500 784 759 653 906 058 378 738 610 444 650 029 147 113 864 676 063 455 007 635 767 953 100 324 493 588 858 924 544 684 758 646 735 737 962 318 208 004 743 786 386 020 014 596 940 319 145 592 250 839 379 279 937 235 747 898 829 074 931 556 154 304 037 805 792 720 243 381 099 656 047 990 614 253 407 133 423 232 879 506 863 286 619 118 287 256 938 003 795 003 253 016 106 522 855 963 193 581 433 976 964 225 666 282 805 092 001 197 874 829 412 220 822 299 663 522 803 476 624 212 074 793 019 348 078 952 998 869 834 334 935 334 264 777 630 564 530 053 701 346 359 807 228 683 252 132 454 731 923 099 291 146 469 059 798 008 181 458 899 215 034 959 275 228 743 839 389 679 474 606 746 496 460 375 001 855 420 672 734 354 726 496 983 588 688 953 869 791 461 936 124 709 563 263 206 442 950 690 977 277 282 671 622 863 105 691 776 603 476 297 651 583 043 035 046 213 125 882 842 673 748 112 968 869 034 739 165 141 493 014 148 024 555 554 649 570 286 400 961 848 205 766 165 437 120 475 059 138 921 689 337 996 103 347 666 356 963 077 131 604 924 709 713 118 413 733 536 715 420 068 746 032 356 114 345 541 503 592 540 591 591 730 301 993 003 601 962 525 925 211 122 574 129 296 210 376 872 506 364 514 308 396 782 752 040 721 544 834 745 543 051 342 804 033 944 811 879 881 705 644 320 425 303 041 076 316 338 292 513 630 252 024 176 922 116 747 227 577 494 902 848 744 991 979 697 004 384 106 903 771 317 126 271 467 822 355 615 514 941 800 710 056 755 261 979 941 053 607 746 106 071 084 955 173 509 169 818 345 053 414 529 995 540 742 223 797 003 929 160 834 636 666 646 725 308 038 992 909 366 148 471 971 434 928 484 391 305 680 778 445 731 269 982 616 938 180 650 300 544 190 414 351 093 547 612 036 250 606 203 724 339 771 655 412 429 804 071 890 124 612 726 073 049 216 880 062 809 830 776 371 516 053 673 166 937 029 909 774 071 216 931 638 441 941 393 429 762 031 898 296 407 108 542 481 709 455 564 979 089 869 821 604 029 674 347 501 274 825 496 353 520 157 036 283 977 737 257 524 999 583 040 415 611 464 926 648 025 741 054 483 318 214 246 200 577 073 874 929 719 980 850 068 387 122 011 403 183 214 340 454 209 697 811 677 985 066 477 698 156 926 935 568 997 960 132 784 011 003 521 843 872 824 580 217 737 633 602 137 023 658 989 959 034 182 660 618 311 806 415 016 846 244 428 076 681 320 898 373 012 576 821 957 261 230 206 706 075 705 572 013 002 178 074 952 459 971 787 032 809 175 053 189 599 547 849 225 059 824 009 143 893 471 546 357 725 733 637 040 329 218 883 320 681 016 223 082 075 842 092 066 572 540 803 935 384 274 876 549 124 182 221 367 478 821 327 888 047 511 089 843 477 170 730 176 059 087 308 396 576 116 887 248 559 737 073 816 197 505 546 571 270 947 780 106 084 454 580 195 211 000 595 831 009 412 706 418 244 286 679 289 398 639 635 246 120 149 179 817 628 938 994 210 378 156 443 705 962 614 162 113 815 464 546 967 381 966 414 871 096 281 098 754 421 352 698 861 796 378 646 297 813 099 106 522 670 903 161 234 374 806 885 433 320 170 682 538 640 906 123 933 898 861 919 536 106 978 097 102 747 252 057 946 444 390 399 850 493 165 613 038 217 443 816 286 958 350 437 432 395 449 261 796 230 766 309 840 519 063 495 161 670 146 725 395 441 943 825 329 149 777 829 304 635 785 471 964 837 090 144 012 669 640 428 486 045 380 908 753 168 795 246 063 719 204 139 680 409 524 347 772 187 268 449 719 165 101 386 526 361 650 693 035 463 659 156 609 859 297 137 941 642 911 765 477 704 348 390 427 854 541 794 388 242 264 968 534 424 878 871 231 342 210 751 337 227 616 266 115 786 255 020 868 305 987 445 798 495 870 375 670 075 346 878 442 570 104 382 638 755 985 981 361 274 212 346 530 619 002 386 283 658 824 817 127 663 492 254 055 298 034 481 001 998 226 584 313 174 880 613 956 786 981 624 364 005 712 910 761 698 062 923 874 355 799 615 879 685 560 516 499 938 770 762 221 218 905 486 967 131 012 319 342 511 732 114 896 881 542 549 406 746 310 269 898 225 245 960 896 114 971 486 894 948 662 913 899 025 157 711 347 569 453 262 081 494 457 448 798 960 205 890 544 244 680 772 716 121 346 879 733 409 260 385 414 645 300 522 747 998 138 870 480 512 005 972 311 483 071 880 954 783 843 110 800 096 561 996 598 721 998 631 993 901 237 018 887 173 567 034 618 328 583 093 314 204 908 796 477 421 547 945 362 573 533 480 780 611 415 700 578 039 060 441 492 810 531 558 783 788 524 315 205 655 388 387 533 551 711 280 508 269 126 246 182 925 451 017 460 068 880 379 885 075 768 151 674 091 428 451 103 690 504 135 280 449 255 199 605 601 378 889 023 076 140 785 419 422 292 479 350 181 128 740 348 666 497 729 615 544 882 676 076 719 840 104 801 534 386 887 704 462 429 236 259 358 264 894 726 867 962 869 916 953 722 569 117 710 365 593 764 097 984 374 406 226 404 009 254 711 234 804 190 141 262 917 713 717 627 916 285 638 262 771 669 837 910 083 739 657 697 160 478 133 568 551 915 110 520 105 771 737 613 343 408 569 938 152 967 089 847 141 880 175 636 099 276 413 713 365 277 914 230 021 162 670 542 676 387 524 436 648 784 925 469 593 212 419 892 681 382 862 189 152 946 643 769 999 959 414 939 597 093 094 886 011 754 126 540 550 766 532 618 384 260 139 525 344 633 755 091 684 019 899 800 710 266 933 823 145 990 576 779 306 294 205 497 423 004 796 723 816 299 736 786 802 277 274 764 503 935 706 911 923 189 644 709 254 133 016 811 915 725 509 564 179 906 993 133 504 041 107 428 258 642 072 138 535 754 278 922 312 046 352 202 811 959 183 290 769 437 704 612 028 015 884 465 874 688 533 402 976 209 115 138 546 416 586 000 104 108 873 375 573 553 737 436 529 699 080 993 119 974 534 087 051 538 988 890 563 476 484 942 611 370 247 714 730 382 621 709 793 333 896 493 533 261 508 248 341 851 287 371 605 000 679 709 621 035 189 791 623 414 409 696 688 107 481 283 506 259 091 282 605 406 009 236 280 349 237 256 507 270 705 413 200 547 313 368 234 100 038 797 913 492 913 593 644 086 518 954 224 874 796 752 999 735 255 595 912 300 808 843 428 470 769 299 735 524 120 743 768 117 955 809 115 950 951 990 570 145 698 722 098 159 779 147 115 063 421 122 520 185 712 423 900 399 817 093 685 793 441 332 048 862 599 207 431 690 118 569 099 454 556 968 098 982 937 012 081 726 027 968 353 801 287 359 118 895 872 348 196 186 866 866 222 032 900 362 296 376 427 666 365 310 668 655 867 304 628 021 730 879 747 347 444 696 251 448 853 788 171 664 985 298 636 826 553 007 562 539 931 378 946 428 050 720 518 661 609 257 217 626 169 055 452 563 876 001 057 329 902 568 679 195 757 477 832 616 733 233 239 490 987 193 931 645 004 437 653 968 907 327 327 917 683 379 732 046 726 980 024 887 532 929 042 280 985 549 963 618 019 184 639 167 443 070 015 794 104 570 156 334 262 421 044 600 456 634 922 617 343 627 435 959 664 937 057 777 272 596 285 304 965 166 687 807 718 692 635 430 847 891 161 841 051 670 431 966 086 336 345 365 198 283 490 624 268 253 354 792 198 787 318 856 582 649 297 718 728 551 083 460 874 052 676 872 143 299 885 606 200 414 753 520 207 738 624 835 322 067 766 475 044 031 746 066 377 193 628 898 151 458 966 578 381 859 343 456 425 872 228 527 837 171 110 761 941 327 137 902 346 712 005 127 418 062 043 097 397 969 677 847 650 036 183 981 540 500 614 469 514 945 519 685 328 763 756 149 865 770 373 298 876 127 819 097 068 487 933 783 858 761 270 839 484 002 359 587 617 688 116 530 551 449 828 750 766 083 898 161 392 250 350 112 248 544 065 560 352 144 875 635 045 928 919 343 098 909 257 024 369 488 392 501 883 472 516 958 005 935 148 870 196 106 085 433 483 365 296 016 045 871 868 390 318 494 618 084 908 341 575 367 759 550 256 804 680 934 698 664 687 687 318 300 986 326 004 398 418 207 548 943 577 782 243 493 955 346 240 536 037 999 493 195 582 358 762 281 329 302 912 735 102 440 500 643 440 349 894 662 247 855 312 768 324 291 996 370 921 522 950 066 276 802 312 791 504 331 230 757 370 556 640 139 627 994 497 145 810 738 454 099 153 634 985 490 976 887 617 933 195 480 935 757 383 252 915 994 722 658 440 672 833 086 993 843 337 715 211 041 717 082 376 152 241 296 346 728 930 258 935 921 469 061 943 711 440 513 543 392 995 815 685 711 764 180 791 416 388 604 085 819 685 301 571 391 324 382 046 017 909 603 745 548 223 868 831 550 634 040 742 621 369 946 394 525 302 697 520 860 295 799 753 750 528 220 557 402 607 778 598 833 190 246 654 258 062 991 957 750 287 819 755 405 057 710 073 010 805 054 240 765 459 139 185 693 211 738 988 500 022 735 034 353 770 623 124 263 571 161 872 858 798 094 547 244 206 147 184 456 211 874 688 888 964 832 938 313 090 609 112 693 547 805 130 112 716 973 421 803 363 333 169 517 265 321 074 596 232 622 553 802 215 640 570 736 275 936 837 136 174 388 225 935 088 834 747 254 792 541 453 704 930 855 244 530 997 252 338 679 703 272 568 692 742 903 407 492 426 585 928 572 593 062 959 663 486 314 348 404 080 891 914 131 517 033 093 502 191 631 738 888 346 186 170 140 915 873 234 319 274 641 469 931 113 706 415 594 951 047 279 227 624 117 124 440 003 018 832 020 653 365 159 833 499 762 735 770 152 646 911 927 142 855 746 561 906 311 930 070 046 256 676 637 490 574 466 190 253 651 340 381 034 238 178 143 747 741 793 884 291 743 221 366 375 401 034 029 526 142 703 271 489 207 151 788 285 655 111 832 125 039 873 581 564 683 977 765 160 601 211 791 219 583 183 934 173 441 325 204 871 982 787 751 438 190 929 966 907 488 462 006 290 020 999 631 155 712 975 112 314 301 144 670 155 780 388 521 620 473 117 872 936 450 377 400 161 845 107 263 938 731 926 521 814 677 729 325 451 301 758 145 284 031 515 096 962 021 811 601 708 488 903 276 969 420 374 537 169 635 648 674 205 838 206 200 532 739 612 458 773 198 848 932 107 591 405 913 899 945 525 184 350 515 666 041 486 361 430 513 362 043 249 577 974 312 197 887 525 853 062 194 485 162 843 466 226 010 920 927 395 600 228 658 294 079 388 858 316 451 691 406 343 316 387 574 561 148 893 391 461 781 485 228 728 115 879 119 991 150 123 396 467 901 298 237 154 812 549 795 028 742 416 021 854 413 610 313 722 943 665 337 707 399 911 274 227 952 060 801 758 625 249 259 862 531 227 708 625 631 621 663 432 795 056 530 890 531 478 976 556 835 959 949 631 782 759 268 667 221 617 353 549 898 645 974 267 727 715 364 753 096 710 807 966 076 858 843 351 005 866 172 890 266 996 584 190 232 413 883 299 305 290 496 743 263 625 686 693 639 460 636 718 466 905 433 119 336 825 768 553 872 817 384 361 495 718 334 713 785 956 454 715 316 993 438 317 554 337 396 460 338 127 146 181 462 558 159 563 551 254 944 833 236 617 240 773 676 188 837 591 013 724 914 285 746 841 527 329 126 896 144 621 081 490 071 837 918 172 076 362 744 352 172 452 453 634 799 784 404 666 999 444 059 947 534 824 281 439 702 626 096 667 232 698 636 238 409 596 642 427 876 792 831 718 326 586 208 412 405 437 267 431 749 845 215 588 763 684 392 778 049 589 738 517 466 706 856 063 741 455 872 863 588 716 168 443 230 196 796 510 745 248 359 149 618 469 327 601 360 599 568 379 662 302 611 667 453 620 305 743 628 191 293 586 954 354 947 620 015 951 236 123 551 085 191 263 713 712 976 466 581 253 592 013 620 718 941 453 203 461 661 033 736 203 607 611 174 505 133 473 703 999 336 794 332 163 757 857 415 379 920 665 861 817 956 081 401 896 373 562 828 663 713 024 846 089 220 013 447 962 986 248 826 324 163 372 023 558 254 452 652 409 446 640 932 840 039 770 127 824 922 947 613 769 527 079 522 428 063 297 883 167 296 272 795 016 336 428 796 262 996 911 362 790 509 470 562 891 845 604 096 099 515 572 111 221 771 873 574 633 667 476 612 751 077 419 348 947 310 862 766 265 961 359 971 277 925 936 982 169 470 812 238 395 510 491 959 287 189 042 322 057 593 166 645 027 811 440 801 688 736 716 104 129 112 251 210 253 860 147 627 315 385 632 911 447 164 442 301 731 458 160 028 724 367 326 847 745 220 040 711 299 619 216 541 019 689 651 611 776 147 429 483 760 512 130 830 606 909 748 313 140 840 835 359 280 255 187 166 983 981 728 489 722 157 002 460 870 010 955 865 862 340 423 905 204 203 753 081 101 989 102 696 920 879 809 174 469 730 399 263 749 111 237 942 487 446 369 248 460 906 287 825 704 280 812 447 572 066 818 131 899 726 041 771 978 796 662 743 471 488 634 906 278 048 612 141 504 680 714 004 116 694 809 939 673 429 642 861 176 820 051 806 774 116 045 038 760 858 777 689 093 468 520 036 420 507 891 310 643 335 185 447 928 049 027 543 926 239 098 176 163 707 014 020 281 753 071 972 595 873 088 265 536 587 614 447 382 768 044 664 520 528 233 348 464 654 657 445 376 697 012 295 499 157 802 712 791 410 470 192 004 060 260 655 581 056 725 515 770 484 389 053 069 886 143 267 880 497 737 758 747 462 675 734 445 468 336 330 212 065 233 590 427 827 309 097 068 221 162 124 885 748 780 700 899 760 937 517 232 895 057 358 702 071 060 750 372 131 212 051 828 840 957 414 934 696 050 726 767 319 161 701 534 194 734 387 361 995 740 582 599 903 048 602 467 537 852 218 984 087 557 682 050 191 257 400 049 030 795 973 060 578 924 898 524 362 066 991 668 144 337 931 708 152 422 974 977 340 978 130 261 597 834 072 256 196 659 431 790 041 013 007 522 820 886 220 345 073 200 342 096 410 272 163 596 356 791 086 280 931 882 860 090 447 210 258 843 673 984 577 199 351 985 486 940 854 333 590 925 805 826 768 612 198 858 750 729 268 459 653 609 614 125 852 202 422 983 692 249 448 222 527 369 190 486 589 097 428 889 443 012 723 372 036 726 620 270 860 141 454 748 568 389 929 404 833 954 886 461 535 879 331 954 868 765 245 410 713 320 206 533 276 276 595 925 953 971 680 829 881 349 651 661 784 428 654 380 347 699 039 778 576 559 459 925 096 296 625 344 376 614 071 342 722 876 842 682 374 978 995 867 728 878 048 254 878 054 171 680 057 092 721 894 600 958 619 464 934 432 307 006 397 537 719 606 925 974 667 271 447 644 282 219 048 535 479 126 519 331 712 413 107 686 812 845 639 886 665 904 642 502 367 968 182 840 362 179 308 651 358 666 348 415 430 977 574 210 958 799 045 121 177 379 848 906 936 138 648 336 983 639 800 959 929 939 346 655 297 261 111 070 209 622 934 562 126 162 958 712 544 787 812 035 752 776 686 700 970 367 755 832 818 796 688 222 801 710 796 406 295 989 384 708 476 304 038 035 756 969 972 146 736 900 295 591 961 833 848 688 266 777 752 438 021 099 575 133 845 982 379 081 398 666 009 570 814 994 220 463 868 864 156 686 533 088 257 120 584 706 503 506 022 022 150 654 586 885 336 902 772 378 721 090 088 909 414 498 074 120 925 584 140 340 148 381 541 129 798 617 892 010 952 546 886 573 174 883 423 865 293 976 293 485 677 632 356 905 661 565 796 967 949 887 327 392 558 356 207 831 387 975 889 029 729 231 784 409 217 322 486 283 362 102 295 533 213 324 928 619 876 441 375 236 996 803 833 474 041 875 240 330 295 302 982 714 878 393 958 677 918 482 381 500 151 386 181 191 726 495 837 419 310 894 948 398 850 962 138 436 996 163 180 891 575 830 444 464 304 990 869 135 700 824 725 334 463 778 713 690 464 916 472 735 178 724 166 333 500 835 870 846 642 853 098 856 726 968 071 894 074 880 012 907 893 621 698 086 647 058 036 930 900 560 906 040 841 076 576 879 917 634 105 545 615 735 488 146 453 118 395 633 295 706 622 850 195 169 326 558 007 318 708 383 017 528 862 595 380 388 380 122 305 237 680 315 061 741 668 126 596 394 571 275 182 004 933 232 901 075 190 377 486 016 190 580 062 980 537 072 657 037 151 951 454 466 884 206 879 741 676 713 724 111 985 997 394 600 776 120 785 899 984 572 948 011 639 575 476 690 458 959 271 478 664 619 109 623 698 371 016 720 927 864 617 311 722 582 806 739 119 571 146 922 671 058 848 193 219 095 422 770 080 818 245 888 725 357 227 827 071 350 445 696 438 921 345 584 904 224 662 991 401 287 030 376 647 035 595 937 389 602 831 624 968 406 956 255 294 475 611 920 321 066 038 592 516 246 091 601 784 937 873 886 916 642 774 922 408 384 694 027 327 583 531 057 781 492 031 575 078 257 133 774 591 963 059 908 160 324 282 358 104 816 175 887 669 630 069 950 463 472 702 735 577 837 875 309 987 981 871 917 122 191 216 486 328 973 722 244 684 482 259 359 754 020 087 343 376 618 705 058 023 582 136 307 896 537 833 823 879 876 307 276 772 133 348 874 259 376 245 436 522 984 578 898 935 034 225 018 532 031 757 431 676 973 382 739 632 865 061 038 173 897 467 573 410 138 056 933 090 182 582 837 182 571 051 534 601 171 831 927 611 991 415 796 795 645 973 890 596 094 626 106 075 906 534 834 108 519 492 821 349 020 575 899 227 227 591 765 459 218 488 319 388 691 176 638 745 375 916 148 675 980 389 414 060 279 013 380 605 537 959 191 561 697 456 189 033 773 935 955 902 858 566 250 780 983 584 406 952 959 368 205 590 389 147 636 782 534 030 436 026 646 870 556 235 558 024 271 247 893 147 374 693 050 942 896 227 814 030 430 734 885 538 503 078 934 771 379 769 311 541 906 284 098 416 706 878 214 329 836 254 050 676 647 051 389 256 393 472 563 097 727 015 069 871 001 375 113 484 525 736 088 931 300 876 992 643 129 463 471 402 946 327 292 034 002 173 882 607 588 439 273 023 402 939 578 616 605 851 877 165 293 837 140 779 631 935 821 832 454 321 695 393 788 448 570 547 806 364 789 349 464 333 612 097 145 779 714 287 992 865 922 292 932 768 304 522 297 594 471 820 965 639 249 755 215 906 250 577 187 962 875 738 096 593 926 308 068 118 359 759 293 805 095 235 389 876 041 847 028 370 932 850 536 034 717 010 543 490 381 124 558 152 365 278 141 551 519 455 688 345 052 778 532 482 716 488 832 844 127 252 401 310 814 587 737 450 228 804 453 096 443 035 963 467 552 230 378 584 025 162 437 569 584 777 801 173 350 668 711 451 902 576 691 368 783 319 061 815 786 010 827 461 288 467 708 771 958 887 026 882 536 643 251 837 419 474 972 957 949 457 575 074 076 187 345 455 287 875 963 441 225 034 878 052 482 491 882 357 369 352 259 670 056 277 666 180 999 227 983 750 147 940 589 338 577 358 815 126 431 279 398 520 731 818 811 649 392 231 156 048 505 852 724 229 556 100 686 861 433 411 533 308 126 571 718 212 344 192 958 564 384 036 915 300 043 555 401 989 366 444 150 966 736 428 099 608 674 636 628 823 268 532 574 757 650 173 026 974 960 183 023 712 296 940 454 452 299 576 810 665 711 716 622 834 406 670 282 219 508 464 823 489 631 679 855 853 798 300 130 471 008 338 146 930 671 844 068 746 695 094 490 503 583 323 913 382 838 769 322 230 478 137 313 703 266 564 441 084 891 875 661 563 036 077 204 561 323 675 139 265 318 302 815 018 801 646 387 881 471 040 736 560 886 904 510 560 688 484 126 466 611 143 046 110 930 854 810 564 968 735 164 669 684 573 647 554 692 749 072 113 923 783 897 406 294 036 128 569 595 204 576 309 267 860 920 143 513 765 896 948 476 208 171 327 717 613 084 464 074 887 656 616 808 831 212 089 506 025 026 024 849 395 667 743 057 847 570 092 393 193 785 487 785 170 735 975 793 758 989 344 277 465 103 567 946 730 746 014 731 441 591 437 616 864 524 439 306 597 920 776 338 585 529 389 194 711 265 998 858 915 564 109 700 579 862 435 531 164 419 054 360 064 463 378 587 788 749 265 520 929 519 174 138 389 072 793 680 071 125 939 464 686 452 724 940 262 117 003 341 361 430 939 507 028 506 452 747 066 554 404 564 795 659 699 990 175 941 824 778 627 742 978 959 615 500 391 691 312 350 952 770 683 984 369 640 547 177 017 412 940 493 336 437 623 073 642 112 932 894 910 579 709 606 448 642 054 722 131 400 005 317 277 665 160 591 047 269 955 080 891 219 035 686 294 171 298 676 485 165 385 385 926 729 566 526 143 856 073 826 672 484 066 183 175 357 477 980 959 526 517 652 251 343 877 641 226 680 666 279 607 816 490 261 517 182 119 371 952 303 257 214 219 388 223 316 773 370 968 440 101 235 558 183 182 491 235 767 106 591 853 055 456 375 290 496 533 015 713 390 610 915 027 414 482 564 151 984 490 721 663 876 630 491 871 528 363 644 450 422 848 206 131 514 541 709 048 162 111 919 639 604 452 370 509 461 692 449 514 640 540 532 019 108 068 634 605 231 995 725 745 315 049 810 442 337 578 372 576 820 825 795 335 528 947 960 808 273 733 661 783 197 257 527 438 996 181 302 507 489 505 738 713 358 320 193 111 503 471 164 767 245 223 138 693 053 981 020 999 951 257 313 665 348 204 617 570 603 008 238 686 335 075 927 373 626 881 668 707 507 399 224 715 015 711 187 078 206 310 323 261 176 885 243 195 723 381 819 712 524 268 866 562 288 518 491 058 986 456 962 040 113 741 657 354 482 965 289 063 730 376 902 329 126 998 685 329 794 987 523 854 391 384 952 171 575 336 755 702 612 635 535 017 927 852 382 876 127 047 233 154 967 204 570 801 584 359 719 678 476 351 991 984 459 263 173 468 881 766 095 263 655 880 958 908 690 807 557 049 935 110 554 946 136 799 166 449 351 845 083 713 337 303 911 087 361 029 466 647 890 928 992 446 961 875 503 988 667 714 609 161 623 637 881 576 207 829 693 625 485 324 713 184 594 281 018 999 519 227 665 678 397 387 408 522 489 842 406 615 393 168 214 331 997 010 391 629 333 515 069 422 683 407 343 499 227 911 214 942 869 353 319 950 259 141 401 680 396 956 241 544 400 984 745 206 654 882 616 103 795 382 231 802 150 022 126 363 428 041 637 031 752 022 087 352 609 938 953 213 939 166 872 900 904 658 422 231 318 650 266 068 083 760 252 830 280 107 724 716 418 531 770 416 170 075 123 979 620 010 040 724 703 573 768 494 937 279 071 783 430 224 639 632 672 816 701 416 327 416 765 762 697 215 376 934 731 500 677 041 116 518 333 676 859 378 679 158 121 951 079 782 445 219 278 483 304 147 826 105 409 896 796 505 233 721 825 697 298 463 961 353 952 356 239 238 897 626 360 643 091 109 116 869 794 952 175 671 234 190 116 866 005 910 855 509 989 658 930 716 614 198 822 726 010 647 523 726 648 335 427 740 663 759 402 840 465 683 053 628 170 119 211 131 188 070 960 326 543 842 757 649 450 948 640 956 724 051 520 573 100 818 837 173 098 838 335 141 739 406 099 407 156 622 814 228 242 006 542 128 110 284 211 392 137 199 453 265 311 863 290 842 096 665 968 450 867 290 347 509 724 363 758 319 837 455 655 446 409 932 010 418 796 721 645 111 366 013 348 567 325 608 222 995 470 104 354 493 710 735 319 358 961 791 763 214 872 602 334 893 806 363 800 727 775 045 106 303 073 948 274 141 358 155 057 069 863 823 888 193 653 819 070 562 340 312 206 048 327 959 422 313 706 095 464 384 535 584 027 447 924 009 729 271 167 787 371 285 225 948 866 976 222 964 031 654 320 778 999 244 837 332 789 736 351 201 619 099 878 607 728 187 031 423 882 744 324 567 393 879 692 437 238 113 953 277 005 720 759 073 361 465 035 795 918 862 121 843 298 107 243 297 702 686 207 849 016 665 863 675 819 735 484 813 388 449 505 287 342 116 416 984 467 993 964 293 379 332 429 712 793 862 910 732 862 328 541 769 009 191 136 179 915 113 560 405 986 521 209 176 727 606 989 385 796 791 320 465 907 761 168 034 218 723 466 266 317 475 592 139 670 340 940 055 111 401 387 497 737 350 275 540 137 983 712 891 136 540 929 656 360 020 372 720 282 013 440 997 786 756 703 029 725 494 504 334 965 980 559 522 971 487 972 379 649 561 491 045 045 741 984 132 537 422 953 769 278 487 332 505 965 653 776 315 786 676 841 969 707 372 710 633 987 689 900 707 241 930 795 760 036 099 258 259 171 679 700 702 759 302 964 730 829 803 982 166 365 157 806 199 751 135 811 043 263 626 756 341 973 125 198 900 217 086 864 650 807 939 128 785 089 615 465 255 751 399 457 475 175 375 499 710 891 373 227 439 929 828 637 675 878 956 099 222 557 732 113 625 365 909 952 113 336 696 429 982 309 695 192 798 819 126 365 698 956 271 609 377 507 363 725 143 414 858 029 563 668 381 747 906 346 827 274 998 459 420 128 837 579 477 914 883 725 656 594 611 622 885 460 885 756 160 618 671 416 654 428 566 377 912 410 094 559 499 206 977 020 908 923 339 102 322 563 326 216 044 222 102 686 603 630 911 641 370 514 858 229 893 096 975 444 563 132 305 631 007 220 448 193 982 370 180 917 540 924 949 467 135 097 327 160 551 414 527 977 316 620 749 658 998 902 647 569 232 731 870 504 501 058 589 278 757 112 692 803 877 943 888 915 690 069 925 478 066 699 043 889 241 260 119 482 236 903 095 259 373 187 349 456 434 371 210 382 478 545 584 487 926 211 720 837 952 477 650 255 471 252 382 038 723 520 230 751 060 599 668 094 037 050 813 656 824 138 157 051 078 959 631 317 655 094 622 187 363 616 387 091 484 193 404 911 914 657 909 229 540 119 637 765 576 294 508 420 098 689 146 770 617 900 569 000 705 549 312 296 257 541 494 865 766 274 160 712 996 395 728 553 691 116 917 587 576 352 515 648 386 997 900 333 324 359 983 921 801 203 562 804 215 964 858 726 722 874 164 706 815 534 499 440 841 228 171 555 234 895 839 569 271 477 681 959 538 912 077 312 658 784 495 838 313 913 652 242 343 891 245 586 134 655 306 325 683 844 226 662 941 219 336 382 120 904 021 950 580 035 616 956 161 780 193 122 005 593 376 006 627 019 687 944 133 715 962 668 009 089 877 868 868 027 625 745 333 959 655 537 286 759 222 360 764 493 573 898 318 405 819 807 374 214 414 185 185 670 425 180 155 987 380 549 320 053 043 270 848 333 374 501 513 433 592 529 006 155 685 025 293 180 080 318 700 726 855 707 754 333 839 966 259 291 426 098 032 529 906 784 255 715 857 990 260 126 293 030 813 722 642 541 957 748 650 812 061 798 322 385 950 473 622 566 154 879 784 945 892 488 853 444 221 162 300 958 522 741 548 338 632 330 602 023 115 880 272 266 030 472 931 939 801 062 583 102 643 244 049 603 171 171 861 595 621 195 080 569 435 854 820 922 839 758 119 904 254 088 119 905 045 665 099 545 514 002 324 727 278 009 216 912 972 447 082 165 597 927 486 373 341 337 468 576 902 709 159 203 982 369 381 817 375 234 658 066 850 307 190 379 828 637 786 519 271 134 956 908 195 465 530 152 560 576 163 009 302 595 099 294 495 808 545 988 173 222 616 543 083 365 598 615 862 342 267 245 213 315 073 483 120 851 162 149 390 212 399 511 871 376 088 796 482 068 244 783 693 036 686 393 356 943 575 087 679 945 512 712 033 508 369 668 229 262 684 573 132 537 204 881 507 442 066 471 431 388 255 670 039 514 106 020 309 015 970 714 002 385 642 474 560 183 524 778 307 121 623 460 488 517 644 346 059 680 466 907 874 310 290 016 138 278 154 834 989 871 009 652 702 938 112 578 454 516 882 244 445 751 507 750 350 546 738 032 563 197 425 651 406 844 838 130 547 439 768 758 790 049 761 637 645 023 995 327 099 882 690 311 281 541 412 499 311 763 235 090 197 191 617 393 196 604 578 032 285 866 714 371 111 423 475 191 774 265 421 585 908 903 140 662 011 097 331 535 786 667 557 884 142 559 878 970 691 921 680 508 582 865 019 370 559 256 294 395 679 836 700 360 579 732 324 665 470 840 684 741 603 477 393 647 226 646 381 686 989 012 982 308 735 416 771 575 497 214 756 268 956 642 548 932 295 763 394 381 431 431 298 715 167 517 981 951 404 465 857 741 318 266 108 972 948 076 681 447 240 534 330 642 366 927 272 879 076 075 844 201 386 983 774 445 538 408 309 370 348 046 119 726 095 440 868 352 403 465 448 393 242 124 075 772 472 100 510 163 182 052 500 532 290 397 663 004 445 111 286 452 835 892 170 669 605 840 841 714 712 024 097 682 285 609 787 134 960 883 006 447 060 725 488 390 834 758 280 686 611 552 432 759 447 035 810 298 277 272 668 007 179 246 565 174 643 321 027 987 636 633 786 598 841 227 845 840 280 642 158 002 435 735 544 355 101 996 490 827 374 307 575 156 729 029 014 043 650 335 700 956 211 692 732 564 218 173 050 417 240 826 335 732 062 112 030 098 568 146 897 658 746 236 617 293 900 499 689 098 040 665 851 709 925 315 776 387 643 825 661 628 196 269 049 732 714 970 617 820 443 813 899 413 973 476 921 376 795 030 782 993 345 650 495 153 012 611 373 047 425 199 033 990 894 939 133 475 821 808 297 178 245 266 189 562 323 238 166 035 723 088 724 650 014 652 811 184 909 972 720 012 050 317 157 280 196 873 143 634 486 661 760 054 714 059 882 323 776 748 300 722 386 230 102 048 622 650 784 010 614 251 530 033 101 566 344 420 726 091 166 125 428 223 550 721 969 579 382 637 178 469 325 841 475 620 549 633 914 097 080 355 358 902 128 948 149 098 980 936 675 864 691 735 202 534 450 549 758 959 160 882 339 473 326 638 274 867 997 831 068 665 270 521 193 029 622 230 558 866 700 515 451 760 984 956 861 330 306 200 081 040 844 734 880 479 993 065 086 097 086 770 717 405 076 181 452 070 381 240 420 973 828 506 422 930 084 169 767 594 391 858 261 071 119 347 965 880 917 745 787 266 391 063 303 799 738 584 775 093 073 390 189 382 305 987 753 415 339 136 837 656 149 875 176 021 059 898 138 098 297 427 192 418 214 813 827 958 892 510 565 013 704 456 278 938 280 236 585 976 571 917 670 500 296 536 249 812 185 943 393 083 622 060 648 020 150 143 665 249 830 397 778 412 093 400 592 857 068 943 198 486 761 565 976 157 509 881 332 981 662 764 135 258 069 103 150 368 011 152 616 585 204 605 545 540 538 849 285 667 161 758 703 012 354 256 749 928 914 383 907 347 301 448 453 300 378 900 685 657 816 168 057 980 540 189 198 557 835 662 710 230 526 064 661 251 435 054 569 149 646 732 387 942 417 415 845 160 919 357 213 077 255 246 668 096 719 781 833 519 255 809 163 890 641 516 300 394 114 778 985 788 579 271 203 249 962 171 391 584 993 210 407 839 150 320 002 638 713 642 577 064 390 812 741 295 089 509 420 907 607 959 342 654 365 766 287 765 121 348 467 277 821 156 904 240 479 497 629 376 188 626 172 098 952 953 880 000 219 492 586 384 353 492 921 310 820 219 271 076 304 300 055 409 014 357 552 626 823 787 208 134 136 422 369 186 166 682 500 520 971 187 034 678 525 360 870 962 443 552 061 172 059 922 414 730 690 529 693 464 170 524 769 237 313 364 825 626 459 503 233 075 395 315 082 799 077 355 504 029 022 645 867 132 446 715 205 751 658 845 758 795 091 141 310 278 933 645 987 300 418 221 037 022 628 467 771 295 466 618 548 887 841 426 659 539 936 227 342 504 166 680 797 683 254 562 743 237 259 046 145 050 168 754 039 142 724 664 398 619 430 452 066 912 092 412 577 632 867 966 663 126 366 712 436 031 814 647 050 992 676 850 596 111 799 085 169 593 228 370 689 219 540 854 496 930 661 297 197 693 278 542 757 174 762 720 469 271 899 828 658 337 386 915 889 771 386 612 925 846 778 220 909 298 188 546 190 812 360 271 201 041 187 678 638 485 636 518 970 056 248 598 932 625 625 233 655 286 855 190 186 163 962 776 614 710 135 025 692 013 312 164 291 128 623 186 823 869 210 076 983 384 756 627 130 536 373 726 374 925 995 880 933 192 071 495 108 491 675 410 775 427 416 525 951 501 556 342 867 201 329 114 998 192 548 519 032 787 226 397 756 754 853 845 769 879 995 201 899 697 942 624 794 011 480 373 077 415 651 195 526 024 160 952 872 154 136 137 583 315 111 491 769 349 028 716 620 166 862 681 883 993 319 037 147 971 776 457 685 982 557 326 808 135 190 900 138 295 277 329 502 400 015 115 557 642 711 397 909 266 474 186 579 513 352 163 474 134 033 483 131 118 214 243 855 356 772 270 135 544 947 572 323 671 167 772 023 764 444 867 398 988 283 558 976 672 464 925 680 362 126 163 839 719 552 446 120 079 336 803 346 048 470 283 524 538 745 207 036 371 343 235 832 390 795 300 318 028 685 527 688 032 070 333 466 125 009 271 525 803 241 478 016 288 527 614 187 137 142 978 020 769 460 838 245 788 892 159 658 980 041 306 407 696 000 246 976 617 614 379 150 531 782 791 592 739 545 676 865 687 472 513 835 730 918 133 972 264 451 717 506 594 870 124 510 835 229 634 304 507 143 138 844 105 023 898 700 131 256 875 679 681 585 631 254 495 075 341 275 081 798 077 453 519 666 738 933 683 270 451 728 014 845 614 584 349 866 539 552 722 662 287 986 005 899 267 346 523 156 860 773 633 438 775 017 129 236 360 961 435 154 657 595 726 871 540 903 825 080 581 038 583 412 110 681 051 317 953 466 133 506 463 525 056 772 430 441 409 123 646 672 425 166 258 347 373 207 007 537 051 655 979 685 680 420 855 569 192 869 769 835 929 461 011 426 547 710 253 999 378 260 030 862 850 316 892 973 734 135 110 316 457 610 384 387 410 279 475 210 316 114 992 677 550 144 373 313 641 691 923 262 185 972 386 837 276 870 433 963 236 732 636 064 508 667 266 846 000 844 448 678 510 621 784 463 916 053 686 878 459 018 591 308 104 433 919 576 541 273 310 156 241 245 512 164 253 101 847 316 906 321 024 819 248 749 402 256 832 873 750 481 233 128 863 386 565 254 661 175 533 701 526 030 554 292 920 040 916 215 745 394 104 880 272 790 783 387 163 371 707 455 325 770 434 107 241 936 977 430 745 573 384 760 234 491 499 379 493 980 395 587 640 040 550 805 272 129 070 661 115 973 986 837 432 918 212 450 667 449 758 532 047 514 925 715 374 721 524 865 832 068 902 338 947 651 571 184 589 509 426 830 520 350 876 030 612 428 240 818 561 275 744 948 100 821 080 131 020 339 048 694 287 312 662 188 704 399 255 001 641 345 934 805 237 792 562 988 681 427 203 985 734 497 274 943 450 895 210 855 727 118 413 157 345 352 096 279 895 788 524 894 784 120 218 648 830 009 428 212 806 651 520 364 245 297 939 973 887 009 347 331 152 408 898 398 497 578 944 253 913 219 576 666 206 054 344 710 954 503 556 860 512 980 308 456 618 277 076 542 945 478 468 867 797 983 832 551 038 837 233 929 407 882 166 038 828 532 094 726 753 869 311 299 647 016 948 328 494 716 132 816 580 513 625 273 389 398 214 307 045 493 823 244 394 470 136 696 288 897 550 614 878 071 161 486 612 332 787 829 705 171 093 775 335 832 398 087 627 494 690 774 766 853 114 504 126 101 953 178 071 337 160 687 504 295 953 008 341 627 987 116 346 899 236 075 956 693 490 155 718 909 476 848 103 797 411 855 370 552 704 859 208 146 086 615 855 816 848 550 031 837 533 308 937 084 738 785 015 849 643 105 307 609 254 768 144 284 744 146 206 518 310 320 894 300 770 443 172 462 514 282 772 885 182 297 544 735 539 942 739 073 631 281 841 593 937 064 660 020 979 307 286 371 367 428 771 926 667 946 721 319 578 257 192 893 819 585 038 965 410 816 468 939 006 678 159 261 793 112 979 011 132 167 845 121 027 812 000 770 009 823 389 862 222 691 382 825 063 970 781 442 733 753 248 202 108 988 316 076 543 785 862 049 430 435 619 260 518 230 994 966 269 286 404 681 584 770 408 948 578 157 148 757 922 679 990 379 284 699 730 705 905 764 031 178 643 772 568 850 799 092 878 063 554 014 736 368 983 285 403 292 763 380 759 620 947 642 852 466 116 421 022 076 070 897 107 366 988 915 339 253 235 547 595 169 765 613 042 790 941 564 206 232 596 866 588 622 443 630 261 268 555 233 908 615 977 689 178 792 336 457 025 446 552 144 633 420 070 150 207 461 570 079 284 934 525 197 015 484 673 021 277 815 394 665 219 467 768 859 497 848 076 142 887 194 976 193 735 823 664 667 293 966 563 232 883 718 212 266 896 261 827 091 958 194 719 212 953 404 008 750 476 844 163 818 395 297 136 366 425 141 340 515 482 670 590 082 314 257 869 741 174 531 938 455 468 546 658 262 091 387 281 681 479 694 466 288 094 757 596 603 112 238 046 481 128 346 970 528 916 310 883 148 279 167 006 708 228 853 880 028 713 920 013 764 848 261 031 744 887 535 166 913 146 776 913 693 764 024 500 023 935 368 823 339 111 453 619 551 933 988 973 348 685 042 259 944 166 331 379 134 791 834 068 128 902 868 662 913 871 886 566 340 870 750 675 020 435 252 774 553 614 645 337 458 774 657 809 364 658 018 784 071 996 242 436 799 322 029 032 156 852 417 644 542 510 866 481 448 462 850 077 866 274 432 106 729 627 312 816 966 744 302 813 856 774 937 559 208 440 120 713 173 942 421 787 081 683 801 136 589 953 485 099 998 773 979 427 688 507 974 218 123 382 508 950 971 679 463 243 086 761 125 197 508 275 772 513 263 263 449 066 710 321 984 190 011 410 539 266 450 883 052 346 545 813 559 349 339 122 113 274 133 659 370 290 146 989 433 705 842 372 363 078 601 894 044 372 165 742 807 785 688 243 354 204 487 865 798 172 464 477 564 436 490 165 326 835 007 450 846 689 227 527 087 781 370 829 400 507 847 665 350 894 389 325 292 964 097 385 983 875 851 095 143 833 727 321 938 108 312 036 075 966 462 881 437 120 530 420 588 914 766 820 250 682 429 234 788 081 363 547 040 469 932 242 405 357 966 954 356 786 037 300 246 556 346 651 806 744 387 250 820 517 355 419 148 876 652 450 692 784 995 778 545 845 400 341 583 549 879 742 674 110 575 157 760 320 985 013 467 943 855 113 491 803 181 339 807 403 481 992 398 883 475 493 567 189 745 922 719 080 523 545 170 160 585 508 025 230 056 248 091 232 544 623 663 144 467 908 011 795 787 433 734 105 343 625 239 867 021 789 827 301 414 248 857 644 675 223 291 852 411 462 710 106 703 057 098 267 386 015 735 402 110 356 772 267 710 930 188 427 905 689 672 290 971 303 132 662 606 018 685 043 872 649 965 954 865 039 146 730 445 377 991 247 654 868 002 010 838 887 737 480 714 493 296 850 306 762 913 003 024 420 716 641 415 116 335 546 531 246 012 912 587 630 438 248 016 651 463 209 145 361 200 911 702 193 610 096 747 776 590 211 374 114 267 983 652 973 356 988 681 122 838 239 092 333 138 204 444 596 727 099 154 533 437 554 625 291 251 945 418 216 669 823 412 902 112 006 399 150 825 271 301 924 059 307 118 672 860 115 009 758 268 305 287 746 520 247 101 626 528 796 013 789 167 676 875 876 789 929 388 541 028 763 040 715 856 083 118 661 286 822 868 993 753 534 872 584 909 282 949 361 159 017 654 454 887 363 764 748 589 998 956 325 871 337 691 462 481 273 936 391 905 096 769 411 448 574 761 575 060 360 029 391 427 384 737 477 117 764 110 618 016 114 003 113 567 943 602 577 739 264 908 196 430 619 515 287 316 231 458 407 648 882 794 569 481 000 701 233 527 642 243 898 868 500 599 185 523 048 252 706 125 712 300 432 074 210 066 475 669 223 121 122 760 309 648 751 450 046 168 390 923 964 683 573 113 932 413 821 335 111 804 327 618 203 082 660 786 154 231 528 622 620 892 634 754 629 267 936 700 900 460 430 170 961 836 371 465 063 451 376 047 511 804 770 620 026 975 755 522 515 483 407 388 860 941 771 866 345 154 823 217 658 402 839 229 367 339 095 725 743 472 520 985 360 330 793 490 145 689 521 057 617 996 813 539 245 560 388 595 144 814 190 356 871 048 634 157 855 824 621 255 117 796 976 611 624 407 203 753 239 138 847 874 630 648 679 669 268 905 956 262 937 667 583 370 000 456 590 657 697 125 578 439 187 893 953 884 526 074 624 454 901 617 765 465 204 564 832 208 854 914 317 463 182 639 101 320 822 097 115 362 153 755 979 861 179 828 666 542 042 245 895 856 429 751 659 497 706 780 592 037 572 538 219 973 193 146 636 269 649 853 080 360 271 383 325 314 775 470 478 467 428 008 198 855 237 658 226 830 570 066 576 918 619 073 107 430 200 163 445 658 200 407 662 872 179 164 457 299 343 361 302 225 385 939 608 742 984 473 143 426 619 878 462 127 305 105 523 045 448 116 123 206 835 375 550 830 998 196 477 471 785 144 042 478 190 538 602 822 734 298 952 413 570 395 554 774 772 516 714 872 362 438 541 392 248 629 214 932 326 702 646 740 216 959 642 142 356 239 611 193 259 521 815 369 209 796 223 729 112 624 259 806 799 680 301 272 347 193 759 742 508 364 105 646 465 999 350 348 123 427 730 427 563 582 807 574 385 895 725 494 047 199 402 485 151 918 856 188 916 506 875 501 258 865 140 786 506 815 987 412 588 309 555 846 524 574 751 902 773 017 355 356 265 476 029 098 023 110 913 519 356 420 751 179 278 476 315 226 815 280 025 647 311 268 947 590 078 207 021 474 763 067 676 052 722 764 584 362 735 242 610 247 330 529 485 413 939 530 606 095 366 116 663 574 995 454 329 653 066 841 162 384 232 304 800 632 025 143 159 892 209 928 923 186 991 020 790 511 786 384 198 154 868 700 767 800 183 337 767 427 527 033 285 119 250 192 551 931 328 727 219 517 229 464 428 481 121 274 274 219 960 301 671 989 013 087 524 248 026 894 972 278 359 253 115 254 761 407 431 664 216 544 821 094 313 599 862 727 612 084 557 617 274 084 770 400 143 005 342 001 110 289 104 865 976 929 037 095 766 460 405 196 759 125 276 684 268 468 427 946 987 074 442 381 847 805 475 309 317 458 615 008 743 181 859 404 308 926 460 091 539 256 971 077 605 070 362 130 548 787 025 555 065 865 390 674 771 392 763 922 737 416 421 457 294 580 356 919 698 746 155 160 549 641 147 957 377 510 259 243 565 335 000 259 710 394 415 860 734 043 997 439 795 018 964 178 250 566 316 745 299 886 678 034 310 402 246 664 862 296 702 907 290 197 545 714 539 688 941 738 953 703 480 147 449 776 895 049 008 135 716 166 534 963 459 034 820 004 913 724 013 985 679 274 707 624 312 226 282 642 957 720 562 068 415 265 269 595 044 247 311 915 562 536 039 742 687 266 863 019 636 313 571 759 716 673 763 422 402 256 142 868 929 383 469 746 499 344 620 559 814 281 181 673 080 236 655 657 460 807 908 441 078 579 789 392 541 750 380 065 974 618 394 389 622 310 864 257 066 706 309 335 490 909 552 646 912 491 659 661 243 596 603 943 022 980 931 557 147 024 277 600 611 482 196 942 572 512 445 344 729 828 621 983 281 286 189 243 271 287 220 448 373 280 509 867 031 357 456 755 679 771 281 301 078 866 486 896 247 564 855 444 601 052 882 518 405 193 329 951 700 235 563 164 823 949 810 404 006 490 579 857 227 126 349 284 575 296 368 693 435 591 720 959 598 111 606 749 495 955 725 226 641 353 918 764 866 315 046 370 646 248 307 100 980 004 320 574 730 761 638 091 431 739 834 873 728 406 931 894 728 839 507 217 571 153 349 800 240 639 317 447 909 098 009 414 245 800 151 535 100 395 882 744 085 138 982 362 519 291 609 882 457 008 553 783 662 788 124 239 576 860 112 601 138 865 804 309 370 318 555 115 351 909 456 165 025 715 340 720 139 140 205 117 193 382 834 695 767 929 834 837 497 344 768 588 394 287 606 032 051 142 227 242 036 578 390 232 010 906 482 448 121 875 958 142 618 309 444 959 437 152 066 784 204 016 845 855 455 034 813 232 685 360 200 398 115 577 923 331 840 826 907 161 206 678 965 755 208 463 045 489 231 832 873 538 907 230 550 861 484 970 699 229 968 369 502 833 326 946 607 509 056 931 710 492 979 625 461 457 922 118 512 687 964 675 704 685 588 241 286 866 741 837 976 220 627 677 803 385 185 171 183 895 554 478 058 856 985 356 540 487 023 637 106 881 396 568 842 118 031 883 835 333 237 179 002 317 113 026 457 623 834 758 477 392 467 122 419 591 207 649 301 786 925 412 273 734 014 881 420 711 964 276 368 749 154 245 859 566 365 285 050 201 356 482 129 959 862 132 290 505 490 457 205 476 981 244 381 072 102 486 362 519 112 583 732 659 264 442 672 562 897 416 138 248 155 023 634 789 990 622 633 997 009 646 125 648 745 379 691 468 932 796 383 375 100 454 829 177 980 529 027 628 613 134 902 692 943 324 838 705 193 267 571 396 536 850 887 149 456 538 927 542 664 157 490 226 565 376 238 986 179 073 550 544 104 907 310 685 421 384 602 823 334 247 922 549 882 490 829 006 816 862 513 824 161 714 293 978 796 036 717 414 891 262 629 370 270 237 618 817 573 088 427 389 013 936 052 539 277 979 497 770 288 160 560 330 220 757 173 615 696 700 628 626 257 780 744 936 464 596 483 884 219 502 874 845 662 980 992 841 002 538 128 847 018 114 366 925 416 293 662 272 289 151 944 680 388 011 145 507 093 243 861 492 285 704 376 350 949 745 885 334 032 567 626 890 608 610 910 992 063 423 175 206 687 755 426 212 654 170 737 274 374 448 807 438 678 100 610 526 438 937 376 692 689 700 731 049 737 636 892 810 293 132 410 397 287 228 301 755 476 949 687 289 701 784 573 924 362 194 923 162 485 926 616 275 488 563 752 270 841 585 690 006 624 391 370 552 503 774 318 869 598 107 413 667 500 177 225 697 706 324 197 706 764 072 712 748 516 533 411 886 355 471 615 104 367 786 519 584 401 447 315 807 555 522 468 916 392 857 883 805 008 111 301 294 600 787 152 140 315 102 085 130 976 156 972 108 221 529 670 605 169 016 822 517 720 449 061 843 436 034 235 978 089 069 442 698 791 345 529 095 534 959 259 572 729 745 597 956 460 746 388 504 080 624 044 068 780 510 558 693 478 815 401 238 925 113 634 133 028 354 587 589 042 086 962 295 890 139 106 754 772 210 947 203 656 244 419 513 002 341 718 462 973 817 199 973 206 218 206 937 541 123 793 054 523 537 625 024 052 894 741 207 580 689 946 801 463 391 497 534 866 810 375 917 571 921 524 182 400 021 397 773 201 970 054 717 712 757 574 759 235 989 253 383 805 067 538 381 894 079 810 835 898 897 215 566 458 984 460 842 502 827 722 515 892 756 328 220 292 421 541 501 660 025 853 026 619 974 843 295 441 221 755 692 166 610 249 673 026 374 127 342 834 726 086 019 713 582 428 030 090 992 898 018 006 317 876 028 692 480 870 516 339 160 418 028 208 548 140 053 087 368 495 179 470 774 928 932 981 516 552 092 914 222 269 910 837 706 898 546 611 564 758 928 218 679 269 332 103 305 989 187 615 733 619 668 269 089 821 919 526 328 216 877 939 065 880 482 145 010 523 607 334 591 095 590 421 897 780 165 021 202 094 777 631 967 951 882 895 714 034 537 769 497 827 900 276 041 062 160 808 151 310 329 025 063 851 291 008 943 247 824 331 812 048 115 289 465 052 715 044 793 500 639 398 310 253 536 814 199 749 779 375 781 903 375 480 520 222 966 136 737 223 795 698 666 842 096 865 433 068 781 755 532 826 617 109 393 724 821 600 148 702 194 410 847 287 860 249 777 699 158 984 087 725 376 748 959 533 274 519 799 507 465 020 000 371 748 210 862 491 815 321 389 044 750 133 064 775 389 474 624 369 758 163 044 397 378 895 694 366 906 902 835 627 797 416 580 513 996 245 253 220 661 189 604 868 620 219 595 459 814 845 317 377 816 639 458 421 922 179 687 566 026 168 555 424 069 049 777 478 461 102 057 642 922 439 982 891 489 206 720 222 173 447 242 502 772 483 692 368 616 359 763 560 794 598 845 948 162 900 122 730 676 778 340 281 528 488 580 564 630 816 859 267 287 534 283 710 533 652 667 725 303 272 427 035 276 840 144 142 615 922 151 602 556 301 675 288 901 560 978 993 547 731 132 844 359 052 701 596 470 765 417 199 723 175 624 240 137 988 392 170 318 277 719 467 504 062 523 593 595 113 202 780 865 841 374 352 701 979 502 289 407 787 781 351 023 129 252 285 440 027 361 262 112 807 997 120 090 372 238 660 278 221 553 951 514 593 278 710 094 931 121 146 360 464 528 068 383 280 591 419 750 840 390 919 788 794 823 192 398 789 647 354 253 895 195 281 635 026 545 759 766 409 261 043 788 066 488 164 915 250 543 523 796 699 138 643 954 847 878 253 407 194 757 504 097 224 008 273 222 852 003 909 611 134 248 158 572 438 481 261 081 211 460 185 325 085 829 530 593 962 125 167 983 409 984 339 986 959 984 907 376 276 247 261 917 071 925 881 006 620 855 333 800 890 112 232 028 017 917 058 960 818 004 674 649 209 072 755 415 077 583 825 376 663 809 866 582 578 700 279 803 804 340 755 743 280 124 590 249 942 184 562 006 820 813 907 674 523 489 533 859 726 871 099 276 454 907 093 704 889 247 715 515 973 585 126 814 034 013 470 111 828 503 282 339 475 567 436 610 964 535 438 301 900 872 500 474 586 834 315 933 627 669 295 391 347 900 910 427 976 895 710 221 514 303 016 478 266 641 790 447 777 990 765 918 894 599 171 079 092 907 919 764 271 218 904 358 636 842 681 095 767 457 136 879 145 339 887 752 343 171 084 893 964 915 059 125 589 912 414 556 130 382 841 415 582 831 587 277 243 404 359 330 563 953 400 633 417 458 054 480 427 117 419 142 121 384 253 428 397 459 014 197 807 613 746 745 446 095 977 333 895 705 763 032 702 149 331 797 371 605 827 085 673 159 747 596 098 881 552 392 777 510 556 267 996 199 515 435 899 370 929 237 085 435 131 097 429 481 656 361 831 486 655 703 903 211 211 360 327 546 580 099 326 730 678 957 273 433 792 064 818 655 097 635 766 485 611 704 388 891 877 405 186 082 869 821 791 489 660 826 737 592 593 045 859 124 503 761 258 910 946 291 957 535 939 538 380 168 400 911 100 388 035 388 573 447 739 212 016 004 754 614 894 479 453 390 446 096 370 044 243 752 582 835 925 164 372 901 630 784 871 379 910 429 253 069 892 288 775 149 100 535 753 109 141 344 438 658 517 572 987 676 883 098 107 050 706 463 033 918 422 558 381 042 938 632 892 559 105 008 633 006 767 570 022 589 883 590 940 793 183 516 146 874 855 245 173 357 215 399 078 106 498 104 719 611 421 944 862 001 050 739 474 528 669 812 714 379 021 152 222 418 484 015 381 663 898 040 319 329 071 171 814 823 441 477 983 990 816 585 314 288 834 637 770 602 222 794 206 522 552 629 458 279 268 128 450 417 083 372 288 235 553 261 295 789 671 798 554 504 438 920 891 554 229 124 258 759 966 698 841 349 330 501 159 465 462 818 189 490 388 476 974 169 544 856 677 971 477 486 482 238 745 171 033 926 527 074 912 042 088 271 167 592 027 566 891 635 358 276 199 757 463 112 711 954 657 621 368 556 770 475 751 958 473 815 888 945 625 956 959 544 794 675 024 380 251 333 270 680 120 726 619 475 204 154 343 805 797 329 685 263 050 315 530 644 780 180 768 739 203 647 273 875 827 703 297 332 584 161 675 305 484 223 048 161 861 820 846 518 103 925 336 746 479 137 661 993 935 176 007 979 020 658 675 718 149 655 901 820 798 785 362 886 441 493 837 689 419 275 187 743 752 195 715 963 023 140 712 508 902 129 075 576 322 458 246 620 255 570 578 040 533 110 344 766 462 655 237 340 571 309 451 176 612 246 960 224 552 576 843 354 287 529 137 382 034 020 740 895 252 299 668 472 630 260 001 472 126 140 214 649 029 346 223 095 269 628 809 533 329 192 566 963 568 077 908 405 645 713 939 263 463 381 974 368 889 839 655 004 328 054 563 335 571 943 698 322 177 665 837 578 693 720 214 026 533 899 473 004 776 643 897 042 386 801 590 890 330 885 160 809 080 757 745 853 777 339 679 384 926 814 886 607 659 231 946 867 843 972 401 876 076 163 594 466 507 738 044 244 232 972 032 485 642 407 915 570 422 734 642 708 822 939 169 640 153 675 918 564 821 129 546 252 346 986 907 166 422 637 978 585 858 538 964 299 834 551 837 135 484 228 587 696 386 037 892 028 668 436 295 142 519 882 161 293 089 771 345 105 949 040 494 128 242 820 848 931 783 918 970 930 884 706 928 683 189 298 695 260 520 106 874 129 183 366 051 662 993 588 760 569 901 518 172 587 927 928 875 870 467 761 795 966 808 169 515 361 308 652 473 704 837 480 059 501 172 122 553 768 519 412 355 125 453 270 571 519 255 358 922 776 495 346 375 209 200 459 084 412 333 012 256 711 581 914 636 218 973 081 610 891 169 848 706 584 571 472 885 375 479 017 633 400 818 701 285 652 976 536 564 411 884 073 155 569 440 995 767 345 565 987 618 883 563 631 807 966 504 580 386 306 051 395 139 703 575 975 458 867 720 198 637 465 482 607 598 145 943 787 228 390 263 472 852 464 648 619 325 044 955 662 909 205 304 837 182 404 780 794 229 183 855 343 222 500 688 928 231 429 154 295 332 039 656 800 270 956 116 555 806 110 435 725 905 741 789 708 213 987 366 346 000 156 510 112 854 317 717 766 197 489 933 318 910 505 314 383 563 486 775 036 548 754 566 766 593 115 674 275 423 776 336 000 679 793 905 366 819 518 375 126 874 157 516 968 719 330 974 953 449 854 182 568 869 458 921 729 799 900 304 795 296 138 576 973 472 708 364 482 312 682 281 352 269 461 978 280 373 042 160 234 893 626 409 331 137 924 336 739 810 083 563 708 325 404 384 705 489 261 099 589 184 660 515 279 486 576 303 558 904 773 035 398 508 279 789 129 987 880 575 819 389 468 734 908 260 398 666 545 800 205 678 345 430 708 808 043 750 654 556 482 755 077 854 460 796 549 536 980 547 414 396 188 433 039 686 601 442 104 485 744 325 476 150 963 009 080 788 271 150 008 880 749 565 752 291 578 121 028 407 531 622 925 213 733 136 215 533 841 740 232 322 897 067 505 758 867 754 233 086 282 437 718 526 285 994 601 262 606 129 926 675 074 969 334 495 718 195 396 828 072 238 376 580 010 227 511 454 350 232 225 969 678 000 951 648 434 709 504 370 927 326 890 559 743 031 148 240 039 295 251 254 832 237 235 184 809 471 017 395 643 721 257 904 783 162 291 488 513 896 716 625 694 848 947 855 103 431 484 539 906 474 351 253 346 995 303 205 280 323 701 343 065 321 835 859 704 329 410 651 792 257 330 033 812 971 926 706 405 637 807 596 306 947 715 363 297 759 668 822 529 507 980 197 663 941 303 537 427 354 126 161 170 505 790 396 969 059 350 393 622 580 962 223 396 189 248 542 478 968 842 856 504 831 531 436 046 087 599 283 680 469 713 273 787 246 491 719 454 956 148 493 837 420 982 688 624 271 368 522 922 392 096 463 403 648 121 440 048 876 174 100 942 632 594 339 264 733 866 332 910 196 076 873 606 058 948 034 998 931 287 952 018 341 440 891 029 080 731 947 071 263 691 456 692 420 028 352 800 639 251 727 646 951 216 937 304 868 728 659 572 550 638 827 941 481 623 531 276 012 946 444 079 362 346 413 211 374 443 731 799 757 841 153 995 465 860 822 898 083 708 770 809 837 898 061 696 555 760 954 471 799 857 117 225 604 142 298 409 861 318 638 011 937 787 139 191 617 163 784 796 537 926 722 976 168 919 526 411 026 030 906 918 744 582 564 635 486 394 290 169 122 947 597 175 248 872 554 271 190 540 296 823 134 023 463 628 491 966 714 377 198 640 133 983 551 643 942 258 861 386 561 512 013 885 679 767 299 754 830 446 499 362 875 286 083 148 168 129 848 653 026 674 615 423 401 602 403 414 033 718 071 061 321 399 242 323 017 501 994 266 335 634 355 289 000 214 241 076 015 462 586 972 149 135 111 575 359 640 220 809 858 243 430 065 787 813 490 166 764 386 037 951 977 440 537 380 344 576 950 757 106 333 511 136 799 477 553 367 075 641 940 780 555 402 230 214 046 713 489 406 141 311 703 714 394 921 300 709 857 060 723 864 143 114 263 494 153 038 999 080 963 059 925 866 376 289 636 708 677 762 083 198 346 528 487 535 524 418 451 220 886 200 551 530 122 860 922 252 301 822 404 227 687 727 038 338 315 846 311 806 361 939 856 790 401 978 155 465 764 992 047 166 084 102 932 037 093 770 819 999 102 199 615 969 642 809 196 442 139 713 821 467 367 766 842 772 729 003 221 192 363 234 826 288 699 873 798 226 294 449 517 760 806 141 453 892 972 778 011 580 389 361 971 817 877 660 312 905 609 320 316 321 522 922 865 696 549 726 655 108 715 914 062 897 912 160 384 669 399 090 837 525 853 176 767 673 183 392 113 789 067 232 919 981 933 054 567 954 056 888 458 055 086 462 639 638 742 938 241 243 110 358 190 263 557 873 564 802 616 317 045 828 579 806 956 652 933 483 183 115 771 448 969 947 174 519 474 792 790 454 526 256 167 281 796 333 714 883 087 776 991 628 785 103 542 023 156 904 640 092 730 206 574 125 877 749 674 656 233 488 823 742 324 970 392 120 950 493 635 156 903 715 088 012 653 095 195 474 965 522 399 166 360 779 680 281 160 866 832 446 276 284 789 108 387 983 991 723 442 781 758 143 595 875 604 050 575 490 949 501 967 622 127 802 970 437 360 211 295 612 308 951 695 265 455 949 267 381 595 785 804 392 549 449 698 061 047 238 894 736 994 826 898 253 280 307 287 730 894 993 667 242 144 188 313 275 871 545 869 775 549 221 552 696 391 309 924 351 695 129 855 102 631 574 651 539 920 568 663 540 056 947 325 532 349 937 712 968 935 883 330 861 379 750 272 256 409 455 255 331 835 536 538 308 326 406 104 607 192 239 152 883 572 960 678 077 749 084 466 320 537 317 131 166 603 998 546 308 224 539 989 359 747 089 316 740 583 141 718 051 010 170 041 419 845 758 704 597 273 301 673 588 446 423 408 753 130 232 478 779 470 062 017 829 672 606 574 991 662 243 228 649 755 084 442 899 337 060 752 509 038 633 132 517 810 541 000 534 141 952 650 996 752 826 482 811 665 086 448 750 292 668 883 234 539 971 048 704 171 628 011 284 885 197 635 041 610 957 280 218 460 842 739 737 867 563 466 330 628 424 579 779 045 850 471 383 489 402 962 556 884 693 727 615 166 040 533 066 886 686 879 728 315 970 914 621 128 648 098 993 919 474 603 312 190 907 154 215 026 611 650 898 679 206 152 778 429 193 866 272 477 767 367 056 552 047 798 238 920 318 291 603 616 758 408 244 200 726 587 670 160 210 040 178 690 207 710 830 668 388 062 194 940 894 424 367 433 443 386 693 603 293 149 391 812 008 783 744 241 663 996 758 802 819 188 004 017 570 884 780 830 973 897 418 303 741 972 441 623 341 714 190 980 822 408 074 965 440 986 194 372 848 740 548 272 121 191 072 429 641 664 314 953 806 885 485 810 430 414 658 688 238 141 420 795 673 579 109 881 254 268 461 730 840 970 918 851 057 927 510 456 192 634 528 234 596 745 372 970 229 277 957 671 842 985 962 962 440 924 844 333 400 935 059 977 411 142 580 592 886 489 358 710 727 355 730 196 964 621 070 357 692 280 776 727 026 788 418 071 119 103 387 781 781 831 106 511 891 486 155 960 293 529 793 814 034 610 972 305 833 366 844 567 254 147 122 145 410 483 330 600 986 543 809 364 058 976 318 329 326 568 277 062 741 320 993 957 147 873 654 665 614 685 412 749 591 003 264 076 948 859 309 436 241 153 833 780 662 186 136 800 173 100 125 013 559 619 547 524 771 249 239 977 011 564 566 746 294 693 439 196 101 946 895 025 559 479 143 697 300 073 000 540 130 835 773 452 518 957 378 167 180 432 874 775 511 800 719 592 250 639 860 303 393 406 069 463 042 500 692 267 850 719 272 322 426 033 979 242 508 820 157 759 126 504 889 657 548 521 001 320 831 272 427 187 801 737 584 612 666 173 355 291 248 679 721 920 214 500 251 425 988 443 390 934 463 115 297 107 943 714 762 015 377 949 694 126 309 647 665 425 037 348 166 597 555 420 320 640 715 197 119 567 859 023 037 073 890 859 124 768 354 485 943 053 670 379 874 981 344 932 106 900 391 737 349 730 965 576 593 211 410 366 864 061 195 201 909 151 469 847 072 423 845 866 212 799 450 003 683 877 412 572 509 258 884 987 181 475 087 005 599 029 364 043 811 064 981 303 356 991 974 358 210 617 006 932 779 318 257 505 936 623 459 906 964 198 080 006 825 366 126 703 313 050 928 737 079 835 247 595 489 563 089 240 951 604 248 754 352 996 634 505 052 383 351 272 211 738 708 640 305 297 925 194 128 178 326 814 636 964 384 371 551 838 198 425 853 566 531 115 148 636 547 254 164 871 796 768 675 997 922 259 962 896 055 275 220 356 887 629 121 495 658 228 864 448 638 319 519 005 323 421 890 518 697 264 420 721 102 442 854 985 317 843 916 513 135 899 398 935 289 556 735 880 264 465 464 291 395 578 599 859 134 352 310 320 748 429 175 835 166 605 718 208 448 265 081 001 892 169 029 246 401 237 931 829 413 452 069 949 918 104 725 847 607 089 781 878 293 490 254 540 792 576 762 934 653 870 179 849 017 117 299 960 457 281 377 646 526 996 568 511 198 675 454 628 048 158 453 608 132 581 232 268 507 969 224 334 063 486 051 648 578 910 462 093 487 980 189 063 626 724 913 290 565 125 321 975 314 490 654 324 201 681 928 486 567 516 653 908 059 445 324 052 297 348 302 449 025 784 292 420 310 929 223 981 477 683 713 768 699 093 269 873 383 931 117 246 435 387 398 798 773 634 368 273 565 635 366 319 588 739 650 433 725 206 783 360 102 093 882 399 087 820 668 516 339 034 266 713 393 357 720 471 109 860 114 568 600 995 060 136 271 059 572 416 681 991 287 393 089 333 665 924 275 965 868 862 847 844 369 417 261 195 586 680 498 081 267 587 077 494 438 594 880 294 822 589 720 869 944 564 853 737 300 667 348 946 255 344 105 671 012 221 020 333 204 303 323 971 453 430 785 251 418 300 557 772 761 504 502 913 965 864 593 575 940 738 194 434 634 234 848 420 298 599 273 720 112 023 481 708 462 202 885 021 159 175 970 080 554 204 910 608 249 514 849 551 641 341 360 676 856 864 919 412 486 264 993 566 518 607 939 171 917 249 642 826 286 151 547 766 691 706 417 642 783 045 027 628 029 209 542 259 192 158 173 861 192 102 247 990 327 140 117 371 821 771 620 098 205 999 791 725 127 078 787 151 180 309 054 757 335 948 560 587 297 213 605 794 322 895 391 164 077 274 298 656 256 668 870 784 655 527 148 954 885 612 816 683 976 601 884 884 005 533 000 520 533 822 298 088 986 142 828 784 933 844 984 244 556 877 276 932 403 355 931 011 022 234 320 403 395 099 284 104 954 223 138 398 781 453 555 477 501 548 456 488 513 577 862 969 986 768 669 473 797 216 493 018 600 475 497 978 351 934 361 763 686 331 598 903 761 163 686 202 101 949 563 745 930 116 027 727 298 903 110 394 210 488 270 536 078 286 172 071 534 532 017 432 420 069 619 879 672 138 435 972 483 714 697 439 210 199 491 274 123 678 689 939 698 546 067 290 987 815 595 899 981 326 008 012 109 050 896 800 703 625 980 397 631 698 562 025 607 851 869 985 636 492 848 582 288 579 128 067 602 073 192 764 433 247 576 720 854 731 003 680 965 222 506 912 359 033 633 306 146 940 520 204 928 412 026 004 848 630 631 236 015 580 961 764 546 363 877 545 885 944 263 207 128 802 420 133 914 263 833 280 856 903 774 208 931 786 938 340 913 093 552 917 856 730 864 976 520 534 459 422 522 752 958 148 876 320 663 855 005 200 384 598 172 853 701 331 506 643 511 087 223 980 039 059 222 596 654 146 844 656 838 824 126 002 643 198 734 978 646 560 163 891 086 244 078 094 926 476 048 465 201 160 603 414 758 603 019 544 052 958 103 639 192 279 743 988 560 651 941 482 194 447 521 350 317 916 686 045 030 045 269 142 150 631 559 835 355 632 757 186 105 800 604 171 360 334 744 427 954 680 414 105 338 738 715 574 068 599 313 281 246 444 101 907 502 086 740 076 120 547 709 643 659 533 145 610 508 655 400 207 663 499 005 449 868 110 481 299 011 625 599 683 933 895 843 107 896 611 033 685 720 441 543 836 193 153 170 166 076 645 036 537 565 188 770 810 782 451 292 473 861 114 547 311 785 411 822 550 050 257 485 571 207 699 682 449 488 606 326 400 020 787 428 164 246 855 094 316 184 755 262 409 862 310 495 944 131 725 360 837 421 339 331 845 128 971 963 511 723 863 991 230 023 341 665 018 045 826 439 670 321 696 923 270 427 119 756 296 973 099 696 631 039 091 612 223 974 533 670 957 319 148 220 885 109 800 992 869 437 153 368 403 198 865 241 003 823 745 072 634 311 295 102 759 676 292 681 331 893 136 243 799 916 079 732 015 356 672 625 762 194 420 783 275 611 541 736 743 126 614 806 449 383 329 729 151 716 996 208 573 113 816 972 598 723 647 917 274 434 813 412 092 349 213 355 050 427 907 331 213 067 096 104 864 519 975 932 362 835 454 606 336 603 771 663 845 403 237 621 701 280 606 711 954 164 883 804 872 574 367 029 969 059 820 779 362 293 281 281 181 502 272 746 805 895 531 983 348 025 107 482 797 207 929 711 999 892 254 827 946 274 085 621 696 033 036 662 195 814 218 221 943 350 248 992 147 668 650 816 210 372 245 880 034 295 257 067 464 348 935 881 010 683 784 022 614 961 540 814 529 349 766 282 220 210 889 656 285 961 822 189 726 849 429 607 975 830 128 169 531 781 962 764 527 877 151 001 559 257 559 747 270 076 850 771 550 528 876 027 156 988 309 884 688 962 004 103 234 089 871 341 739 863 084 647 292 152 339 817 938 727 560 043 099 602 226 979 101 942 045 834 953 120 766 545 152 119 784 568 248 325 127 430 381 748 294 478 665 225 551 975 550 889 580 342 193 491 592 136 659 814 735 164 916 768 373 029 861 799 864 624 289 750 116 132 959 020 675 264 448 057 889 364 766 220 556 601 574 318 979 002 582 927 812 727 372 160 435 020 646 299 843 525 659 910 854 708 608 527 558 395 989 509 796 579 548 867 792 606 770 488 641 907 535 631 960 811 448 158 723 749 618 105 772 369 552 578 941 839 404 168 924 113 532 016 165 421 914 083 964 059 934 880 534 899 995 339 109 921 402 178 036 283 460 104 296 939 665 877 127 273 837 501 083 900 834 066 322 851 944 824 023 446 953 705 766 191 030 341 684 937 964 283 582 177 852 940 531 676 630 010 104 779 050 922 843 226 454 736 425 910 156 723 142 059 659 508 308 498 131 898 685 917 857 104 722 331 362 747 681 425 891 777 604 178 502 671 194 442 965 011 544 116 167 081 756 926 354 262 593 125 828 888 754 787 454 243 369 527 866 374 341 817 156 057 553 702 984 297 291 376 399 324 614 755 190 293 369 942 379 671 467 427 392 282 901 099 017 668 599 874 229 745 323 932 543 425 479 017 253 947 370 741 002 678 152 528 012 787 099 310 279 004 713 018 888 338 002 413 812 638 407 860 313 469 343 128 343 335 454 045 362 058 219 060 454 380 091 333 821 246 805 551 317 656 120 707 429 474 264 736 550 954 474 795 234 079 156 605 814 180 385 482 035 416 805 349 764 454 590 521 572 140 164 718 370 821 028 510 599 594 692 600 974 580 730 212 983 433 668 955 176 744 273 283 960 367 575 369 111 878 240 147 248 361 796 510 591 524 786 981 908 206 463 124 120 697 502 120 072 848 759 723 259 175 707 447 207 446 759 336 633 939 908 911 955 919 995 916 908 343 043 986 681 637 564 591 413 412 093 648 294 433 817 360 723 892 017 927 954 964 003 835 431 254 186 827 001 130 263 011 580 143 639 906 690 759 306 179 299 416 490 575 221 273 819 809 126 242 006 407 359 245 594 847 414 065 820 332 253 110 040 927 929 445 592 363 064 623 232 055 724 889 865 595 777 884 483 592 265 188 499 266 881 104 783 323 676 045 220 001 353 642 918 638 787 676 506 004 778 152 223 613 484 790 476 534 525 753 696 472 693 610 882 284 769 769 594 687 442 935 534 058 616 500 905 205 302 911 128 596 952 704 968 633 134 417 206 111 440 734 009 790 939 105 108 497 100 855 204 577 428 370 452 433 930 076 455 202 053 970 851 127 885 202 328 081 809 154 536 916 003 586 211 423 744 790 207 988 899 317 408 665 918 111 766 602 527 570 788 771 406 379 464 750 670 682 391 684 726 088 254 615 679 037 252 141 246 282 613 967 025 074 288 901 850 593 284 184 503 657 053 828 621 895 070 665 003 895 867 067 007 598 978 368 477 131 183 530 333 399 094 391 920 027 365 509 434 988 315 034 962 442 833 787 705 782 136 813 928 775 241 986 167 414 459 137 331 054 518 243 811 789 003 486 265 406 709 797 672 487 583 132 953 477 488 274 614 425 710 312 241 974 189 023 260 230 657 417 015 968 905 489 147 867 494 750 164 237 306 861 862 635 305 108 859 337 746 517 863 524 089 910 164 605 846 144 437 908 632 455 462 841 316 004 914 798 676 952 091 111 381 356 328 448 881 152 287 453 319 084 677 794 976 982 643 320 795 685 636 893 346 105 238 007 324 597 364 840 703 411 398 953 727 366 458 068 678 932 248 189 768 607 251 624 359 770 001 955 731 520 232 719 621 594 110 093 204 904 590 821 580 516 719 012 781 044 566 239 231 264 730 377 941 987 580 623 160 533 193 092 873 455 433 294 082 642 679 084 114 456 005 953 589 448 424 371 701 094 528 010 769 031 120 076 918 243 787 781 888 154 375 272 717 862 446 159 715 170 454 221 763 290 737 112 990 551 117 964 199 140 441 165 786 626 004 027 181 211 925 936 793 131 388 301 391 664 650 230 419 069 518 025 055 324 894 384 282 466 485 465 735 723 909 447 291 532 342 684 520 750 542 042 715 551 552 844 154 950 215 858 791 480 458 134 856 911 863 743 431 938 872 843 737 876 134 957 647 908 892 794 227 795 567 676 531 211 676 922 220 256 301 255 232 706 043 997 974 933 994 161 350 151 222 414 536 659 654 497 866 941 411 616 073 948 238 184 061 362 676 272 155 384 764 805 977 055 244 234 702 890 429 413 350 456 455 226 878 244 160 701 540 673 987 538 583 655 390 833 170 646 854 445 366 862 112 454 214 810 417 341 033 452 764 237 627 640 718 772 365 103 051 823 296 851 336 180 020 677 380 896 303 480 699 706 915 822 070 497 234 109 958 819 755 824 297 132 615 815 342 836 870 492 266 038 336 999 768 928 022 296 523 609 919 920 182 412 981 950 056 912 559 022 855 822 288 180 950 166 488 490 945 189 902 560 646 847 461 421 771 228 595 182 158 629 675 751 883 982 887 319 134 820 539 393 607 650 088 255 118 576 093 305 273 546 359 502 434 839 557 868 099 906 610 120 269 896 533 715 695 598 926 050 168 733 622 481 085 392 243 101 199 590 172 018 265 727 777 949 044 033 098 801 290 453 364 018 755 846 366 432 520 993 789 751 462 429 256 575 118 661 830 798 479 020 897 014 472 476 508 050 382 785 868 136 232 690 147 923 021 753 101 598 789 573 254 300 532 233 457 142 447 381 186 339 961 483 056 067 299 533 629 474 963 815 434 560 635 871 791 148 925 952 712 146 716 936 116 443 265 676 623 920 895 782 738 169 298 889 343 624 673 169 647 548 592 753 044 020 603 624 955 918 272 095 316 638 338 578 474 576 796 999 751 399 101 974 342 619 705 694 919 535 785 343 587 121 229 170 906 159 541 983 746 043 033 753 745 032 180 599 913 529 725 507 538 336 108 780 714 731 510 728 576 191 515 279 856 445 328 421 115 575 082 791 900 041 797 601 792 421 458 064 441 877 834 790 397 637 423 725 595 142 226 682 980 783 465 935 437 303 999 533 705 615 012 815 590 365 724 428 874 521 701 900 975 036 248 762 250 614 307 073 250 099 012 726 628 312 680 574 755 907 631 168 056 181 628 937 737 136 962 765 936 894 949 320 997 447 383 310 640 267 619 276 456 951 449 314 276 854 170 448 887 624 576 480 470 246 467 035 992 819 833 780 502 669 720 803 453 981 097 557 326 468 950 787 383 955 207 464 079 254 252 634 914 024 009 085 899 579 554 303 743 768 050 209 209 074 061 630 804 520 896 659 526 431 502 778 493 028 059 483 542 650 011 805 884 326 545 083 835 491 239 155 337 189 587 393 785 298 944 329 989 381 680 473 464 616 356 638 566 281 891 164 478 616 350 411 237 932 284 592 034 945 673 280 633 450 356 472 283 970 253 266 880 921 395 775 983 189 288 541 096 834 880 602 575 869 918 980 364 403 101 547 607 853 322 952 897 468 452 550 461 399 735 112 063 304 511 652 237 390 975 639 751 746 655 854 816 005 968 458 621 757 220 891 031 057 220 288 322 931 649 900 316 758 946 100 345 674 372 941 601 456 227 586 736 187 752 676 977 872 540 000 876 393 503 488 799 701 185 337 253 281 203 267 343 395 233 874 882 083 920 910 585 502 881 632 664 327 812 843 565 417 443 612 524 655 816 720 769 325 036 051 862 991 039 384 249 857 543 392 844 645 210 910 982 176 194 576 562 980 239 730 592 399 205 182 624 500 743 837 456 861 088 660 500 136 519 335 848 140 986 326 652 499 763 601 809 881 161 989 691 402 885 450 883 223 466 109 519 198 893 349 791 354 026 436 246 532 637 554 345 006 201 946 955 663 245 502 004 298 230 280 357 584 121 841 356 545 377 329 954 427 067 301 115 603 974 199 443 453 846 100 260 567 157 901 689 392 512 871 585 180 493 325 300 568 333 569 381 373 141 655 414 772 267 356 935 055 744 020 768 129 096 847 034 475 000 867 318 488 278 317 423 777 594 894 115 451 609 526 982 297 697 565 778 292 413 761 447 320 667 215 385 686 614 985 252 581 445 062 177 396 183 879 571 001 638 313 523 361 636 844 494 036 855 433 687 110 870 417 670 225 760 660 279 457 502 572 871 339 612 289 220 948 874 069 779 867 839 716 587 646 069 712 428 080 730 992 824 257 860 163 937 942 569 618 545 481 540 945 589 917 192 577 379 070 602 622 284 260 844 615 421 006 054 122 260 365 425 069 748 164 018 976 300 385 200 309 230 939 550 759 095 283 415 525 587 978 784 035 263 298 969 023 972 209 972 776 738 994 352 827 746 393 786 359 328 895 539 070 149 847 210 478 194 895 535 610 302 075 353 299 195 787 559 091 119 014 420 720 679 554 229 727 363 353 890 635 428 879 539 753 857 303 561 289 560 424 441 683 680 295 632 391 821 315 281 642 412 480 127 812 920 075 286 497 559 815 073 648 838 464 528 655 565 010 198 811 974 955 592 562 939 856 799 095 763 669 208 586 180 055 376 204 579 872 209 209 767 695 083 247 287 311 317 810 015 556 134 753 753 588 852 987 311 613 286 714 401 404 188 545 326 335 809 766 518 503 284 187 492 476 599 779 656 526 959 797 112 519 902 765 464 152 447 591 383 685 706 364 706 036 110 956 628 320 779 706 156 199 065 569 758 895 591 885 733 086 210 895 105 650 442 433 311 926 549 770 019 798 425 171 624 813 844 031 694 304 155 090 462 988 097 472 852 142 849 492 826 983 345 714 952 434 406 650 395 367 916 661 884 336 420 614 365 324 770 998 136 088 227 655 354 969 373 282 395 073 340 775 626 089 947 221 345 666 407 923 158 329 434 904 784 328 945 451 365 009 209 235 675 544 530 888 974 025 458 703 496 751 666 884 960 470 540 728 087 102 421 391 276 932 090 959 721 741 420 620 820 561 190 539 685 295 020 036 802 741 559 693 254 943 825 195 115 745 826 686 909 838 309 499 071 881 609 921 652 448 960 515 185 781 226 945 257 344 963 381 731 306 723 801 734 900 081 664 580 546 246 753 371 948 698 202 739 769 696 787 373 995 940 561 349 170 634 423 268 753 778 340 344 043 751 543 547 252 494 443 052 612 649 234 964 552 501 871 426 950 778 082 454 066 346 639 555 270 604 720 314 122 175 566 893 575 235 312 302 831 533 032 894 867 936 665 993 118 455 360 614 952 381 333 213 545 898 684 775 257 969 931 160 774 627 830 803 054 629 896 589 119 912 965 083 980 253 843 214 971 205 332 160 801 767 139 007 095 287 666 358 370 887 642 754 397 474 490 289 901 235 292 073 357 780 617 411 677 313 113 119 166 344 836 886 339 322 918 977 284 234 340 821 177 415 650 629 726 413 083 841 413 213 293 065 958 570 948 850 593 169 779 406 648 650 593 233 368 349 483 235 974 367 714 783 875 299 496 783 581 219 664 346 318 385 402 468 681 788 073 105 548 429 702 805 165 529 669 259 423 927 944 023 923 102 909 201 434 487 306 276 847 701 801 941 333 522 651 779 063 651 177 431 245 219 844 352 969 180 014 121 737 760 504 238 198 179 450 242 680 718 734 231 959 601 285 390 969 315 841 071 448 290 349 270 139 015 613 896 650 406 555 101 517 802 872 501 484 483 942 568 797 062 307 060 173 803 010 403 857 708 132 667 910 573 630 663 735 653 819 357 657 759 968 222 151 976 134 408 953 896 442 971 179 786 830 860 303 477 763 261 566 378 279 513 792 992 946 654 058 283 715 225 504 322 963 097 330 751 994 587 008 759 077 248 712 796 127 797 389 547 349 747 020 648 901 953 452 856 503 989 335 241 871 809 509 860 695 066 937 568 532 044 594 885 638 664 841 052 419 061 860 171 325 076 071 048 092 243 052 097 798 304 031 040 602 962 494 472 242 491 304 939 967 335 907 531 309 343 070 582 784 975 193 976 613 802 576 160 821 988 078 400 550 023 503 037 637 489 411 857 746 144 985 952 820 106 664 225 956 855 649 115 032 750 935 337 639 521 632 444 430 381 522 406 177 979 392 499 697 159 990 123 015 197 020 814 791 817 405 882 470 965 348 304 159 259 820 719 496 885 748 668 484 240 727 214 390 205 696 533 669 710 992 755 980 326 217 777 558 631 128 718 072 006 864 868 918 160 049 915 841 459 520 563 694 303 339 201 499 791 156 618 150 911 393 176 415 425 969 855 840 013 541 226 010 800 794 082 173 791 495 283 907 711 258 149 300 235 505 597 400 109 325 045 519 401 190 894 992 706 981 875 379 557 342 055 444 731 454 557 963 952 621 388 807 224 581 511 266 505 158 675 289 140 794 496 736 875 496 827 061 183 539 977 727 421 729 020 893 819 208 844 302 053 221 101 747 658 141 308 665 835 575 001 745 766 416 959 753 785 274 047 192 278 856 595 199 457 013 488 325 688 212 657 342 262 013 246 573 808 468 938 921 694 637 666 662 393 306 267 077 889 979 219 101 450 316 603 981 209 490 708 340 321 229 221 135 280 623 279 942 295 139 125 254 121 981 149 387 227 861 898 479 804 408 818 656 740 749 522 203 111 861 721 442 784 422 135 869 396 097 422 348 096 619 803 126 667 767 253 554 523 061 573 644 722 887 210 576 642 843 964 131 848 654 591 192 630 740 573 373 728 311 602 184 887 053 591 490 717 811 213 584 306 861 734 641 947 929 092 126 302 739 156 382 340 476 789 684 694 845 795 757 564 934 728 642 919 253 329 146 062 975 634 441 497 737 539 413 973 380 950 617 677 921 745 226 982 225 240 624 148 543 589 567 157 787 931 637 740 804 073 234 024 476 572 167 831 445 769 351 522 689 073 477 122 601 437 323 551 919 412 960 337 183 231 432 109 993 113 803 666 849 381 272 078 267 348 635 808 579 390 359 812 626 894 891 607 912 206 387 210 781 148 524 570 776 366 128 006 039 813 810 640 155 448 534 700 687 773 114 711 890 989 160 972 279 609 586 586 344 909 694 836 717 144 184 398 625 469 300 326 128 312 487 412 331 872 448 525 345 122 229 878 832 555 672 035 534 156 990 609 598 472 756 466 483 258 371 495 879 462 031 225 509 854 236 809 562 519 833 787 883 300 040 195 721 044 447 611 840 908 385 012 472 188 816 846 566 348 564 348 326 619 710 541 225 529 328 415 934 298 476 448 778 442 905 619 191 724 563 888 108 035 467 175 590 646 809 348 284 610 590 305 748 512 932 970 284 444 204 672 185 579 534 279 045 164 588 073 622 829 575 182 901 758 651 484 258 892 673 958 200 483 505 051 237 497 120 007 170 571 347 078 216 099 908 258 576 312 617 474 105 127 970 105 789 971 578 839 689 977 823 208 359 284 807 342 436 379 523 203 634 097 514 510 754 661 246 656 886 673 908 377 895 283 597 716 040 018 711 491 779 989 895 789 104 958 595 828 476 075 407 461 302 681 004 841 112 790 526 050 499 143 701 365 065 157 774 940 457 427 253 082 056 679 934 903 550 425 828 467 439 820 653 769 572 753 353 961 132 824 431 244 923 986 406 528 637 452 744 254 081 837 626 155 295 597 294 303 532 027 702 283 878 623 498 035 240 980 388 185 863 578 576 227 904 314 310 187 765 109 991 290 676 314 685 612 042 038 549 192 935 132 973 561 301 412 220 100 398 463 052 233 386 588 560 468 335 778 118 147 687 307 634 074 465 490 209 148 741 045 213 037 283 654 189 073 009 312 719 858 731 888 005 192 579 683 284 516 984 186 141 949 802 310 439 663 532 620 011 360 547 156 155 105 334 375 096 633 405 162 988 409 238 548 749 756 509 472 760 005 910 733 950 791 704 948 599 929 983 682 939 145 318 118 626 329 414 142 276 624 640 174 079 388 847 844 328 168 674 874 016 869 865 415 484 841 836 310 615 916 046 220 222 105 857 890 561 687 568 999 833 076 918 608 135 256 294 182 291 431 922 209 405 341 791 081 184 190 577 262 911 556 832 931 239 508 001 815 863 976 181 907 574 844 611 602 944 560 418 922 320 379 790 252 957 914 821 021 973 401 229 837 820 404 299 619 677 036 659 437 082 963 884 587 810 649 099 520 093 021 449 710 745 179 515 931 688 743 947 019 651 561 546 988 741 597 528 816 555 051 506 169 934 745 643 460 216 582 739 418 853 846 619 804 710 651 304 739 438 018 135 262 673 666 469 684 857 774 544 005 724 426 633 658 279 244 360 645 494 890 085 971 374 606 014 107 158 514 132 897 341 094 309 500 722 279 810 383 070 467 770 109 289 250 188 033 291 459 662 625 524 979 573 951 479 303 607 585 995 059 369 066 977 743 009 153 181 241 166 749 278 264 664 089 569 043 258 048 770 672 497 611 278 417 986 565 204 682 636 868 358 197 173 245 417 165 832 953 056 847 755 061 922 411 788 980 120 551 912 574 578 978 256 388 539 889 863 911 530 722 675 646 562 141 632 658 086 767 312 706 685 889 872 701 113 681 992 119 808 560 998 133 946 604 704 538 443 587 399 279 563 548 747 206 859 378 689 945 252 789 936 423 782 472 166 533 725 045 955 789 363 570 125 425 419 339 996 110 125 066 008 609 931 786 448 792 614 888 323 297 053 421 826 233 038 113 083 021 543 614 077 555 994 337 211 261 513 622 696 236 238 020 137 825 998 440 157 478 168 186 568 398 717 558 543 703 790 713 934 642 149 386 947 439 885 534 264 857 404 249 883 539 207 763 037 014 712 800 348 289 484 728 625 588 146 481 556 438 034 145 289 380 418 779 419 492 136 605 143 005 359 653 859 499 406 245 877 319 506 221 109 709 496 277 835 499 820 434 184 365 977 846 331 345 261 384 382 240 426 076 846 244 845 708 127 402 975 602 852 523 988 666 669 182 741 036 160 241 089 770 908 614 232 027 154 899 381 939 725 064 984 263 543 803 475 204 075 774 254 396 808 469 948 941 327 625 061 209 501 946 517 611 387 644 067 550 678 361 845 167 767 134 748 567 493 832 083 998 064 616 083 885 968 098 697 719 064 866 030 282 430 398 450 046 180 787 113 392 228 946 211 889 799 022 086 960 140 654 728 936 752 556 226 938 506 870 900 817 626 820 423 813 389 642 024 917 912 260 228 444 160 623 925 997 047 038 652 977 341 578 038 304 000 230 595 715 740 868 690 629 708 252 634 367 706 069 820 001 398 754 938 473 458 530 910 306 703 539 847 532 731 325 751 052 984 832 049 154 760 744 432 350 847 032 594 038 642 612 380 694 090 623 021 052 638 137 128 194 489 325 031 297 339 254 569 841 520 741 099 806 123 427 719 993 330 303 702 853 698 827 163 721 081 861 250 042 228 560 007 121 411 752 899 460 270 334 182 953 166 045 940 158 116 551 107 197 638 962 816 081 829 927 730 481 370 766 175 529 762 281 824 478 196 069 038 461 163 220 741 300 133 828 768 541 123 070 104 841 570 852 541 834 852 082 558 986 802 266 025 105 875 012 783 390 345 070 771 904 246 635 530 815 635 041 790 341 158 936 583 472 334 707 107 203 818 571 092 283 455 088 335 558 564 358 290 929 575 071 609 294 018 587 069 173 722 476 729 184 603 790 792 015 305 624 534 164 534 573 513 654 415 105 383 959 304 349 961 361 287 784 551 541 469 512 703 320 490 159 737 789 057 173 663 241 997 086 678 869 795 835 280 996 726 360 074 986 847 917 193 757 701 783 010 888 306 519 167 262 558 774 201 815 111 220 230 549 042 970 891 812 110 797 700 331 930 228 807 716 372 438 132 364 800 408 521 960 393 922 258 849 038 336 006 417 254 259 962 203 272 308 813 513 144 156 637 812 843 499 824 421 872 526 144 683 102 485 417 720 422 884 972 336 083 855 988 788 666 092 043 117 562 451 405 668 200 387 793 082 387 619 130 583 880 976 348 639 830 987 253 610 068 297 483 325 949 764 838 910 632 260 001 223 263 443 823 767 033 299 575 665 241 514 518 070 871 648 349 894 272 939 172 685 318 169 249 216 556 430 649 206 536 999 877 046 977 473 463 373 082 051 682 964 680 880 731 720 919 035 977 182 497 536 923 933 405 187 174 108 846 562 432 209 667 161 080 239 495 917 541 154 038 442 132 593 341 319 065 710 128 404 024 235 433 975 719 947 343 488 208 491 643 723 770 401 139 825 029 427 283 567 824 760 363 478 909 803 185 478 465 693 792 905 609 330 308 373 788 475 370 826 321 200 277 239 850 039 836 979 796 717 680 047 196 335 819 135 486 492 231 363 618 137 416 022 055 267 688 604 346 679 858 488 700 115 779 998 515 645 402 435 782 973 146 832 408 229 793 851 679 818 158 940 851 035 514 952 615 777 294 400 331 018 843 557 455 976 384 942 886 690 153 208 907 670 733 158 309 599 162 802 415 149 480 419 404 698 817 144 422 640 247 252 976 876 734 846 712 064 060 321 000 862 706 257 166 429 137 138 726 618 897 943 135 411 977 580 737 990 833 339 977 380 679 050 596 954 776 725 517 523 364 850 385 118 795 261 844 435 764 310 533 470 165 093 615 021 323 540 158 095 369 121 556 923 752 302 851 077 592 729 466 943 325 417 825 854 360 666 602 731 857 160 080 749 719 654 956 929 903 349 750 597 640 566 908 470 942 696 913 993 039 835 142 100 387 857 964 272 285 525 324 700 304 025 527 388 402 017 048 118 085 758 698 219 282 015 984 030 254 809 212 844 350 385 845 805 111 522 615 708 847 535 541 043 427 566 238 724 746 395 977 068 669 952 405 088 683 664 148 113 148 024 868 997 220 600 429 992 425 597 316 360 424 660 595 277 504 340 040 362 604 610 934 408 845 610 680 512 674 629 713 876 380 752 748 107 831 791 227 885 613 600 375 985 982 915 425 160 978 891 410 039 289 413 794 276 378 921 859 004 329 183 666 030 757 919 381 331 876 267 400 661 454 501 853 589 967 102 098 304 479 266 316 746 352 390 401 171 161 251 476 645 680 932 563 412 491 785 547 246 475 530 340 409 051 567 638 012 848 435 743 285 199 865 931 872 709 970 655 756 359 388 930 318 005 171 932 011 953 623 554 404 753 862 305 539 775 106 323 138 458 176 736 888 728 999 342 713 201 565 674 273 196 075 760 562 498 106 489 400 079 519 117 910 305 015 360 409 343 461 686 995 311 092 635 154 976 329 948 507 295 572 654 641 742 206 197 141 115 792 767 945 911 913 151 171 590 711 154 729 430 253 324 709 661 769 069 573 054 193 938 107 367 877 710 221 946 288 864 498 923 743 582 232 752 842 792 743 487 519 675 343 666 103 692 099 720 156 617 857 692 849 647 760 762 733 999 103 219 868 976 372 359 107 815 764 157 382 401 340 290 168 451 995 217 178 978 928 610 619 411 056 355 041 361 132 381 188 930 128 263 882 107 025 771 396 352 805 575 364 488 027 806 081 082 136 907 440 310 032 583 287 079 135 536 297 391 832 846 163 570 388 488 136 136 150 027 277 516 283 870 998 099 085 983 257 207 847 767 166 828 676 079 389 432 843 418 828 680 860 105 883 163 504 537 920 180 259 627 280 390 969 396 619 918 302 702 131 081 193 432 456 369 295 295 394 914 355 559 856 863 818 683 291 962 467 304 352 746 380 041 224 790 630 264 116 485 613 547 900 042 328 610 853 343 930 334 765 516 952 035 721 180 931 694 076 830 232 951 176 504 301 807 095 806 592 551 365 740 591 274 647 048 435 178 821 047 349 127 683 411 709 789 197 641 924 773 361 863 241 948 346 503 397 004 800 865 221 518 946 532 796 459 670 112 899 946 927 374 058 897 102 787 043 837 761 241 296 409 735 646 841 506 273 944 590 901 006 516 279 633 512 043 309 982 905 998 183 032 846 757 051 922 399 252 019 115 730 678 611 360 728 388 358 127 468 605 607 995 259 309 717 608 878 266 226 268 436 662 926 812 342 101 875 945 120 513 250 683 372 174 371 514 146 085 077 353 876 898 665 428 556 725 113 342 787 780 181 153 916 122 024 955 404 348 172 798 169 087 062 969 754 142 220 522 444 844 086 740 452 099 888 390 597 923 672 894 149 762 847 487 656 895 538 048 279 033 148 229 127 300 900 825 496 886 244 978 854 675 566 084 828 666 776 069 453 619 309 989 578 865 342 929 815 241 739 442 929 083 671 084 274 865 746 613 865 435 707 247 662 725 007 024 383 695 732 443 377 904 685 921 947 674 898 464 343 592 466 072 832 500 715 397 927 219 296 139 189 694 514 229 638 985 363 188 391 608 426 576 091 159 378 203 769 342 269 118 059 817 112 879 846 241 709 322 132 561 135 943 832 078 947 974 666 604 569 256 308 006 317 490 298 001 129 896 757 467 702 769 666 379 404 906 455 655 227 224 640 345 917 341 061 956 982 621 021 791 393 505 195 194 127 673 969 563 730 987 621 625 182 856 888 751 880 555 939 953 065 999 759 712 138 502 893 723 243 711 038 753 750 713 233 328 566 850 541 534 890 454 170 061 804 330 284 717 913 544 759 615 938 384 491 208 980 847 144 900 554 811 682 903 535 876 177 436 760 324 347 590 718 612 908 864 949 058 640 871 315 643 809 531 504 895 990 249 888 319 179 650 079 806 879 536 557 176 817 780 248 792 055 147 628 388 179 565 342 498 781 427 550 392 429 158 705 922 345 449 976 433 105 624 011 015 739 185 371 841 292 590 000 238 974 597 679 753 221 971 359 400 185 608 466 970 224 902 853 919 887 293 242 999 730 903 368 257 434 930 910 280 446 577 126 173 453 270 911 301 411 490 699 178 391 133 100 948 427 257 258 887 535 861 059 080 747 771 356 049 602 298 016 424 915 773 157 329 883 028 902 489 803 872 033 566 973 843 460 613 425 504 752 688 385 395 043 164 000 254 331 784 625 607 692 293 731 477 177 345 835 533 066 716 893 046 079 289 118 257 220 740 829 453 769 512 873 204 749 935 839 021 896 877 247 791 231 810 152 608 626 314 187 613 544 728 748 394 669 118 199 308 852 928 176 564 044 357 151 857 796 758 895 866 534 087 994 745 347 463 201 145 625 741 492 838 439 071 615 682 222 916 750 235 628 897 440 870 489 759 356 440 961 185 924 026 726 490 492 620 313 006 559 977 221 388 369 491 046 605 130 848 445 666 119 954 025 789 994 110 953 959 340 917 141 442 768 858 827 487 634 256 421 174 472 666 163 777 244 209 407 635 575 446 916 334 409 864 387 430 788 191 041 826 010 474 332 395 478 111 912 994 520 569 991 038 725 104 367 064 281 912 285 636 976 917 919 455 556 499 489 510 295 751 695 852 807 166 488 421 647 431 238 142 007 906 208 758 181 887 918 062 136 370 029 545 031 881 431 445 444 214 960 001 160 673 994 519 393 118 525 698 962 863 447 002 551 083 096 825 968 456 047 842 942 851 044 345 548 851 352 646 036 369 227 103 529 000 100 643 548 141 369 139 369 507 955 872 384 856 664 584 097 427 484 534 991 437 210 031 753 252 012 702 628 538 940 437 976 681 295 331 646 274 794 721 290 618 633 952 056 931 205 791 898 190 544 409 841 891 087 356 177 559 433 894 468 983 789 304 671 596 603 606 313 510 253 167 056 205 534 519 678 090 140 970 228 237 786 369 100 146 788 439 455 747 458 065 176 107 249 797 561 950 470 426 339 816 671 245 218 256 199 741 353 649 356 230 509 843 003 447 704 685 110 838 990 726 103 461 126 240 762 601 448 831 699 843 239 275 834 036 687 926 277 635 961 616 120 225 674 301 193 935 299 157 719 833 899 681 260 258 447 449 480 249 096 050 079 356 563 465 805 227 442 598 763 549 477 645 757 625 711 066 771 248 436 757 947 308 959 685 110 805 738 913 680 106 203 134 400 597 894 372 976 219 881 318 015 070 015 847 768 512 375 433 995 970 152 822 028 609 602 807 974 882 978 840 571 560 491 557 205 610 925 271 239 180 156 418 472 188 848 342 884 367 018 210 560 357 664 981 685 715 554 411 507 601 454 957 053 049 929 184 991 906 197 202 893 037 309 606 724 683 998 990 659 985 114 972 651 351 665 410 288 280 593 979 124 431 517 449 891 138 338 067 081 871 320 215 423 197 924 561 618 612 578 176 726 819 077 787 463 421 677 129 325 818 343 367 176 319 394 265 878 025 738 996 036 662 647 912 662 310 086 183 689 136 422 076 784 521 365 786 830 846 032 847 191 213 937 314 628 618 063 882 888 764 013 829 155 086 255 884 075 760 095 043 103 480 015 199 967 352 455 946 770 705 013 807 029 423 680 520 594 604 986 728 516 188 694 216 384 500 805 501 450 310 840 438 448 679 126 075 310 542 329 549 581 256 954 612 126 126 185 488 559 483 937 125 349 311 686 582 130 401 189 688 803 717 277 924 876 943 845 536 076 799 932 267 451 822 333 718 734 943 247 677 868 978 184 901 579 708 805 637 880 747 350 850 249 779 006 632 491 724 075 889 024 384 259 287 548 675 545 528 149 130 888 409 781 833 664 884 977 670 894 484 272 347 764 713 255 368 455 219 571 208 887 909 934 728 309 188 698 214 718 747 674 455 467 841 393 301 830 976 962 307 458 152 742 368 200 283 266 601 060 430 690 421 306 653 305 245 296 365 237 199 652 713 664 031 552 134 171 172 343 732 059 307 099 905 870 700 988 323 511 148 648 851 384 438 725 377 610 873 265 285 794 076 136 184 840 705 579 693 335 199 627 999 451 386 447 906 290 183 448 363 724 612 779 616 081 121 548 049 049 019 631 061 660 238 401 702 995 829 428 809 073 504 734 948 336 241 489 598 103 790 367 108 691 799 786 029 580 735 267 189 020 681 033 537 783 388 148 832 861 484 418 740 703 686 699 427 242 415 135 982 789 535 899 937 152 833 576 722 119 331 170 014 820 057 661 723 106 927 323 475 240 139 155 889 789 761 313 235 020 667 071 776 904 015 004 612 667 810 365 019 532 969 348 440 700 462 127 670 570 531 621 886 765 930 627 051 886 627 382 077 365 470 440 912 186 814 574 675 871 550 263 290 843 632 541 820 022 262 962 310 292 439 560 482 649 340 954 943 505 991 499 699 360 490 960 723 028 578 449 477 244 720 180 078 660 282 421 543 925 099 891 752 452 848 347 801 619 626 166 818 339 401 446 884 262 015 314 562 400 875 409 942 767 685 728 345 889 054 669 268 977 824 468 775 687 394 186 659 980 610 754 923 596 828 395 313 008 357 784 677 484 572 939 723 206 608 560 343 148 816 887 390 701 878 385 577 047 408 236 061 419 423 696 530 124 800 865 992 742 557 926 983 404 165 606 437 880 676 504 014 658 705 693 785 678 329 513 955 227 023 165 182 893 426 318 461 392 600 271 597 841 172 583 362 763 334 083 637 688 989 294 458 628 702 311 851 449 089 968 193 726 784 994 382 474 110 247 605 641 964 351 022 692 859 014 639 814 003 810 091 353 954 210 459 042 725 976 950 516 603 201 440 441 835 169 437 578 062 430 266 194 778 599 631 727 887 175 331 310 563 481 115 143 206 972 537 547 589 335 693 384 170 284 897 535 296 505 347 512 019 620 403 379 138 338 427 115 701 394 326 736 381 263 240 472 528 486 391 576 950 790 445 848 785 724 085 368 143 204 775 745 904 471 780 734 512 316 740 353 930 693 350 531 569 325 507 848 704 644 433 793 935 320 778 659 737 922 453 385 818 807 795 487 204 235 252 761 681 866 897 832 501 743 575 155 247 895 172 612 563 122 462 143 780 219 029 861 651 056 867 793 838 537 542 677 357 826 696 951 945 899 101 424 319 130 557 378 541 976 518 700 477 237 948 333 683 016 041 276 864 498 214 413 124 415 475 074 816 596 476 893 305 305 305 708 730 732 257 797 374 707 745 267 915 760 978 274 180 911 586 940 449 063 413 866 616 874 060 471 314 729 701 839 573 798 141 947 970 242 479 992 204 549 586 107 821 793 294 538 084 708 227 751 301 005 482 757 293 333 414 172 418 751 657 027 251 171 911 979 711 631 447 696 313 575 117 125 358 601 511 805 510 107 976 064 649 416 803 032 174 218 162 319 679 054 232 037 793 444 051 801 846 240 135 285 592 464 021 052 028 683 895 441 081 965 529 818 121 157 466 466 647 053 663 438 480 092 849 400 217 262 148 304 798 049 683 928 601 942 637 423 471 956 366 226 117 019 967 750 231 337 445 499 082 093 496 062 505 714 891 903 722 436 973 241 338 057 891 772 257 945 387 691 226 898 650 507 891 566 223 383 872 397 521 505 709 522 913 977 725 906 532 087 581 863 349 091 888 340 142 993 487 387 833 108 803 794 876 946 881 294 366 816 008 012 422 688 295 312 821 095 442 129 337 617 694 427 914 456 796 485 876 155 507 840 641 564 021 587 892 509 947 048 920 389 753 058 015 867 727 134 645 960 707 968 667 575 269 507 030 411 446 743 893 320 497 582 765 052 048 387 866 210 665 418 203 306 850 929 732 196 025 877 690 982 964 547 671 029 404 498 400 310 911 403 892 993 652 944 739 246 552 246 180 646 422 753 630 674 758 871 885 311 131 394 584 157 499 541 278 988 334 537 135 893 905 987 700 006 680 254 223 052 131 757 797 956 011 154 763 255 735 505 541 849 428 497 008 841 712 789 909 250 944 244 802 494 840 920 521 457 464 008 339 635 991 808 807 907 819 709 604 497 275 454 556 609 802 627 759 719 778 651 838 691 480 629 550 916 402 911 841 665 115 500 807 035 480 540 776 698 659 313 654 884 548 133 034 875 457 172 373 461 608 983 243 457 031 970 011 256 463 815 343 470 236 173 236 489 095 234 690 609 130 905 144 375 349 002 446 042 198 923 399 204 872 609 318 400 393 975 315 470 508 342 430 422 365 230 141 945 814 881 865 835 810 851 903 413 009 218 710 991 391 122 909 592 026 559 500 051 507 658 444 891 214 522 284 178 254 286 936 728 467 683 839 536 493 392 589 405 767 959 551 085 247 137 185 053 311 551 517 332 033 859 444 093 537 591 969 577 291 167 566 496 734 248 096 047 526 550 470 828 954 761 036 384 565 310 590 911 737 809 036 327 187 484 745 045 599 165 599 172 411 661 401 777 768 226 675 187 842 810 529 820 003 521 078 784 885 948 677 980 347 982 599 993 810 214 059 890 061 771 671 094 299 522 275 787 219 875 492 215 263 561 135 576 423 978 695 833 075 990 349 348 833 903 907 582 494 363 956 042 008 890 240 159 721 173 352 284 655 216 964 073 734 061 446 650 365 721 361 204 692 957 937 643 755 986 473 595 962 325 800 398 851 012 007 200 563 499 920 719 858 987 560 292 738 780 735 693 057 735 186 429 933 707 287 089 654 735 024 321 631 203 492 213 940 984 898 868 429 464 537 226 668 363 457 584 862 422 163 602 064 432 199 449 194 257 260 114 043 684 502 331 931 113 140 003 699 182 893 372 111 753 427 123 536 725 869 845 932 613 198 670 117 293 209 409 911 095 096 218 050 479 235 432 615 029 089 956 866 413 985 880 473 307 453 292 389 552 417 306 292 660 421 021 371 142 943 510 550 540 212 175 451 649 613 283 567 288 866 756 498 022 898 525 637 606 800 813 384 547 933 446 994 548 467 805 021 785 619 710 581 460 953 445 550 909 543 938 229 433 884 795 103 150 018 792 733 216 423 243 725 851 043 684 852 364 070 741 596 215 148 852 443 478 521 479 048 237 646 417 807 776 070 784 643 569 035 362 403 465 662 762 156 943 825 661 656 986 902 772 254 333 813 778 329 789 273 863 933 436 980 175 860 593 917 288 617 395 444 890 501 149 200 566 843 716 695 459 610 694 966 367 913 540 456 787 031 819 057 162 472 644 031 728 235 894 122 429 017 320 482 105 318 608 800 040 810 949 520 014 096 094 725 418 030 556 456 812 509 321 890 957 827 646 583 074 142 985 412 341 638 972 769 664 734 785 872 966 362 506 169 038 481 470 842 513 421 394 198 510 502 466 038 881 003 588 899 879 818 905 475 963 238 797 063 786 243 957 978 673 533 205 886 493 445 010 190 542 060 534 541 748 489 839 736 813 703 110 596 961 349 146 621 760 131 538 810 243 396 140 013 490 186 768 956 973 947 681 664 972 097 249 126 673 333 680 572 604 985 967 846 574 374 202 159 001 327 975 967 801 386 056 052 919 884 506 209 490 999 491 672 758 070 657 688 141 699 855 826 351 550 691 867 083 225 807 288 447 180 603 952 448 652 993 556 498 966 332 735 821 319 844 438 360 269 074 296 657 033 631 404 115 795 356 817 814 291 755 628 724 117 565 220 459 806 995 656 278 366 909 432 830 397 425 993 863 901 146 129 896 598 348 392 390 391 837 860 206 711 250 789 592 169 501 699 074 429 322 518 525 968 795 790 454 635 697 075 116 199 854 594 080 879 510 269 870 950 767 450 342 986 578 668 909 578 192 141 198 669 042 403 680 988 605 589 038 033 680 319 523 602 135 064 829 337 154 348 871 659 896 712 015 984 421 709 911 409 930 796 436 387 004 028 490 945 789 841 542 996 105 796 000 698 737 940 353 044 386 002 276 738 913 297 713 913 273 482 337 685 296 708 142 744 061 722 817 888 745 777 639 432 508 428 914 969 940 778 191 834 903 405 227 491 106 885 356 141 081 781 960 168 462 112 048 932 508 221 766 487 610 288 809 092 336 811 582 892 469 083 169 100 861 823 259 336 099 687 278 991 908 555 599 844 237 884 998 876 994 106 406 075 612 661 058 036 039 362 483 907 448 523 204 508 610 145 217 316 453 554 776 507 880 272 782 607 640 393 909 420 100 571 569 003 029 011 422 456 930 030 068 400 036 999 013 478 805 105 135 644 826 640 212 919 223 549 135 602 667 226 319 049 019 961 005 923 655 511 312 288 908 661 664 117 479 228 331 647 521 213 486 700 618 766 707 306 165 985 487 569 034 991 675 678 673 453 481 347 705 498 706 942 186 585 732 037 368 209 078 745 590 967 037 548 465 982 486 256 812 798 834 063 541 929 942 415 808 323 351 063 048 516 940 516 045 330 937 919 135 010 387 611 687 050 426 498 478 784 064 977 153 437 429 211 641 245 371 190 712 683 316 831 100 485 952 814 918 415 961 558 888 972 307 382 938 758 634 528 886 691 428 736 467 584 075 783 983 048 558 586 768 567 771 622 342 217 760 360 266 316 956 268 686 628 401 995 115 621 039 123 910 174 321 636 062 031 754 355 684 119 710 984 259 252 565 653 756 184 505 190 076 125 093 703 596 608 913 284 089 235 025 908 294 643 696 140 819 217 425 571 173 212 329 337 531 964 931 171 850 679 363 804 389 581 009 447 511 919 343 100 669 092 253 439 809 217 840 382 464 131 933 308 803 100 979 353 176 700 334 323 469 298 174 707 854 151 686 345 028 586 625 335 344 557 448 866 237 133 439 270 283 919 008 440 750 468 907 866 060 314 212 181 534 130 302 726 599 052 908 293 827 174 766 778 024 242 870 105 610 305 086 822 309 468 073 538 123 409 489 844 141 870 134 085 166 395 350 016 431 214 854 401 682 521 247 539 585 905 433 096 971 653 131 216 174 343 560 031 789 086 449 843 663 051 593 345 164 774 134 523 329 016 563 867 429 124 342 914 456 726 634 997 836 987 580 917 744 671 478 485 465 336 016 634 572 305 035 302 413 406 016 933 127 603 608 392 584 446 996 684 011 367 551 889 117 031 622 581 143 113 852 069 476 041 683 410 036 230 329 219 033 953 429 171 310 791 429 378 224 364 695 291 487 016 813 197 272 487 107 140 433 376 923 591 888 594 075 234 366 293 089 808 655 386 113 601 596 465 426 688 945 683 677 010 537 927 822 680 617 496 077 553 674 307 845 544 717 268 570 793 939 919 152 842 783 185 241 397 240 147 468 747 753 568 619 752 419 388 126 607 491 730 802 343 985 043 973 443 357 695 294 052 256 398 188 150 675 584 831 640 108 275 564 417 634 592 509 723 874 959 374 361 094 734 373 881 279 573 434 581 287 041 497 186 422 356 446 016 326 828 501 767 220 665 005 974 425 389 551 391 743 914 782 239 237 566 814 773 126 082 242 321 614 450 603 007 358 222 252 374 385 169 423 452 190 073 860 498 817 727 687 107 461 017 700 255 424 880 593 479 285 058 306 579 999 874 962 779 681 149 258 778 764 432 323 991 439 599 616 301 506 707 217 277 611 596 158 574 274 505 340 870 913 776 463 360 995 195 463 294 018 171 067 530 187 786 855 975 324 508 326 636 607 877 678 961 955 166 151 231 903 747 536 021 610 989 801 538 204 560 973 192 910 414 836 203 382 413 686 436 880 372 122 082 956 922 145 019 247 594 653 533 911 126 097 781 876 330 161 311 775 644 352 544 760 178 847 659 701 572 502 341 290 704 488 557 249 226 841 675 049 398 439 358 271 479 502 640 361 201 300 069 689 060 912 307 151 980 288 207 128 225 538 377 546 370 443 155 040 086 351 880 046 921 677 571 807 522 566 398 173 106 400 898 054 286 345 764 596 093 529 961 523 804 514 786 337 978 558 729 261 339 193 345 878 561 170 438 331 369 276 086 139 837 521 672 367 364 963 893 251 176 955 221 403 882 829 865 808 409 692 633 856 306 537 583 031 406 107 656 574 872 715 043 237 297 269 011 135 564 260 376 766 089 022 653 274 057 032 205 857 313 567 104 771 586 467 563 677 545 363 950 200 844 837 131 044 373 756 150 199 564 160 063 912 287 601 887 666 343 205 516 098 916 840 138 107 471 470 580 838 510 945 787 775 741 677 923 121 386 911 059 280 332 411 106 644 860 434 345 424 151 616 466 800 614 741 526 751 542 360 246 174 731 100 997 813 912 715 329 838 360 220 400 360 758 991 256 980 493 748 435 180 088 241 722 004 106 894 414 467 491 382 355 472 292 112 943 483 269 793 910 438 239 585 905 722 994 240 158 535 875 106 240 806 193 997 957 445 375 922 804 371 062 511 773 340 018 065 844 008 651 069 658 678 662 889 344 032 995 165 432 720 242 197 177 881 138 053 994 000 114 128 697 689 200 063 019 309 311 076 756 928 141 744 698 947 862 143 000 043 132 109 677 264 997 023 280 339 486 259 170 971 535 053 062 628 737 205 067 048 752 268 643 421 422 007 133 403 033 940 266 390 823 565 566 152 930 763 425 311 727 093 357 980 134 945 977 872 437 398 944 113 274 729 167 742 172 364 555 546 422 932 592 807 696 105 894 383 441 695 387 191 614 891 126 582 865 454 629 418 919 353 112 266 678 803 480 946 773 018 570 894 260 785 506 645 823 345 988 718 202 729 636 182 058 875 667 950 580 249 276 596 020 299 980 632 500 817 899 048 151 205 068 082 185 793 724 809 636 786 800 124 455 083 085 058 682 607 311 548 770 603 333 554 466 675 386 794 431 143 942 659 196 188 391 629 588 248 057 860 933 365 901 229 260 560 833 766 513 215 533 684 803 877 724 449 593 703 631 510 676 455 793 826 653 218 649 353 665 370 943 924 567 069 899 039 184 368 312 041 362 818 375 054 768 678 514 954 641 598 962 598 844 560 779 624 933 939 972 522 644 405 907 449 850 005 977 152 194 327 932 844 300 278 381 916 685 970 405 359 650 961 952 936 352 008 354 246 021 007 292 510 086 407 952 765 513 465 018 613 233 333 187 281 538 965 347 541 250 818 343 467 387 872 495 965 864 254 652 765 565 056 282 633 559 992 811 503 818 021 505 820 104 829 017 132 974 995 469 882 885 038 740 993 017 473 986 838 224 391 337 004 187 617 127 303 222 589 976 265 408 438 489 437 265 374 964 491 163 448 129 645 642 387 784 802 788 248 249 961 934 849 377 814 613 351 514 664 210 282 110 954 268 830 523 260 705 568 379 174 202 353 109 996 674 567 158 842 346 996 668 134 144 006 788 606 038 005 805 983 315 237 091 648 720 881 915 010 318 888 222 341 467 972 960 693 865 058 001 943 138 171 267 643 289 297 907 683 197 180 185 525 102 037 355 433 126 471 452 049 869 176 077 861 800 845 185 661 823 797 164 758 285 781 348 611 389 640 269 781 123 837 929 674 790 095 498 797 993 144 952 381 113 467 459 059 173 663 885 466 468 576 438 680 219 212 956 409 161 173 317 777 882 394 257 655 623 902 593 696 454 136 828 612 890 378 255 920 233 831 370 166 270 189 599 453 507 200 353 746 864 750 348 094 574 254 723 228 679 335 982 221 023 674 062 169 470 060 549 016 135 659 005 130 238 501 503 034 851 678 069 919 438 455 966 206 253 350 922 813 630 652 409 322 341 822 749 935 041 029 695 039 176 213 505 229 024 125 659 867 328 614 464 261 515 637 685 738 459 998 087 106 591 639 793 640 270 462 190 160 360 774 469 098 105 973 820 681 006 562 816 928 381 297 711 518 378 050 106 154 422 600 160 358 923 383 118 058 503 621 670 398 499 753 165 373 825 900 657 834 687 944 132 983 670 709 205 660 371 185 866 906 551 669 534 511 375 400 581 076 063 663 653 667 722 610 092 021 367 066 633 951 841 692 677 493 305 812 920 335 365 371 768 132 536 656 413 009 522 186 966 967 183 223 654 007 564 488 569 983 866 613 327 083 994 055 528 960 443 616 186 022 704 922 618 679 358 748 321 623 169 716 469 088 080 476 317 142 207 993 606 200 268 726 868 845 114 069 722 715 371 487 763 165 505 602 967 049 773 645 047 096 504 275 682 662 644 000 388 852 174 607 124 766 218 553 033 764 799 457 236 920 503 804 754 244 748 112 126 733 493 713 602 605 212 563 548 926 063 793 273 035 932 685 079 026 771 537 334 722 605 330 604 196 975 838 439 650 323 888 492 759 154 774 543 426 822 144 268 087 324 786 363 913 774 049 994 495 767 681 887 784 821 537 411 027 201 146 501 326 007 206 399 463 576 526 525 571 260 944 110 255 158 859 770 737 610 824 225 748 315 178 129 473 903 736 234 241 151 410 460 514 137 412 229 392 274 820 668 787 544 610 257 609 440 528 152 919 597 688 277 993 911 251 702 203 650 013 383 001 902 103 867 271 041 261 258 577 124 940 359 183 600 242 377 412 942 506 153 353 119 705 291 759 358 536 711 183 131 192 875 207 666 655 803 640 472 382 726 698 193 811 781 925 997 979 100 279 475 329 707 317 060 570 826 534 780 810 199 898 926 733 910 131 278 318 899 863 127 408 260 812 200 687 239 526 646 663 556 073 763 650 359 995 474 407 167 042 149 224 315 249 087 564 400 265 100 395 941 182 870 192 419 332 702 187 009 914 537 652 378 703 967 569 530 508 104 088 534 844 725 717 838 598 272 525 543 799 321 217 491 156 705 641 344 345 178 864 244 016 400 020 250 371 285 041 457 377 792 257 197 608 133 114 538 786 320 032 987 991 555 706 330 828 265 559 963 626 295 271 393 387 054 013 520 919 859 564 334 627 507 673 135 229 735 889 825 428 597 069 366 649 521 478 590 552 674 251 798 716 324 770 754 015 932 170 960 930 042 133 124 104 628 640 928 065 999 577 043 570 453 249 775 484 864 952 942 740 384 222 144 373 492 026 177 109 903 220 954 523 976 371 396 963 241 790 619 737 043 687 955 232 225 575 772 476 078 013 202 912 323 546 728 326 657 444 908 151 347 347 641 613 957 693 066 228 714 914 540 617 203 539 576 456 251 432 905 493 858 637 639 691 171 420 248 208 929 220 164 712 769 499 392 824 430 485 005 667 322 140 383 476 923 310 377 304 344 622 640 871 661 073 653 305 124 836 283 190 307 878 348 340 471 862 625 497 269 532 027 511 147 766 931 714 022 811 115 361 612 440 101 859 563 474 568 917 981 906 628 998 175 488 380 805 936 921 015 169 138 948 093 220 441 108 548 397 543 769 366 732 694 390 252 391 561 804 069 996 454 697 407 726 885 514 109 554 602 967 891 104 739 291 302 553 893 698 612 836 998 377 256 521 207 705 131 062 959 497 305 241 247 473 893 617 576 544 393 013 012 658 417 839 650 377 209 980 891 405 224 842 447 360 062 155 691 302 721 834 511 341 387 053 349 044 832 007 861 897 622 096 707 022 163 171 710 474 043 657 929 591 135 483 588 507 381 389 398 970 415 465 362 883 384 399 376 539 874 041 333 168 560 040 462 657 068 652 094 363 858 772 107 796 603 152 367 264 425 078 684 506 364 557 645 787 531 335 584 816 879 034 253 591 618 269 985 089 459 300 014 926 150 788 861 882 136 922 063 787 785 151 079 367 605 928 408 592 540 261 399 559 656 071 076 238 323 924 259 833 940 278 426 672 180 395 088 599 747 668 529 327 508 534 329 224 009 685 067 536 226 028 937 240 137 516 196 852 247 375 621 323 851 426 365 087 532 032 850 194 465 010 557 918 661 438 819 191 022 455 442 875 826 300 206 995 984 630 525 428 603 381 780 677 024 744 238 434 031 510 976 343 665 123 424 547 461 099 542 112 299 232 440 898 121 179 163 503 177 375 731 671 543 989 458 636 287 961 772 007 578 908 640 498 284 968 670 355 624 104 775 928 896 079 550 640 948 422 994 206 315 805 035 189 258 424 062 615 431 509 736 725 057 316 389 162 655 476 274 118 863 250 341 325 340 881 779 346 561 581 129 519 325 385 376 889 086 883 995 813 796 852 354 602 695 907 101 774 194 940 394 658 752 179 922 916 272 894 594 494 380 124 576 204 966 864 573 024 746 121 574 786 546 557 215 424 939 758 674 634 786 463 160 113 523 871 600 424 496 731 945 065 079 796 503 063 253 926 236 610 209 118 243 367 530 475 769 819 463 467 543 420 872 094 503 441 672 998 468 703 007 264 871 999 114 796 313 834 600 345 541 559 409 687 344 923 978 236 092 107 927 821 916 264 124 467 134 803 336 833 186 305 543 445 834 428 919 988 678 112 654 431 880 040 321 062 957 026 684 506 984 271 085 558 270 320 787 065 454 457 756 211 660 947 225 919 174 833 771 883 491 631 495 453 679 428 611 448 352 787 555 392 458 525 554 038 151 153 962 955 323 642 864 597 194 568 089 460 468 750 470 068 159 714 930 856 921 024 478 909 156 821 034 218 576 574 898 242 503 088 065 824 824 188 144 429 208 414 197 566 670 715 580 018 589 516 550 887 191 636 301 140 130 701 985 421 435 165 679 707 833 000 826 344 445 538 035 113 822 162 293 951 574 302 256 728 820 872 642 730 933 143 455 327 239 389 753 302 692 364 139 892 348 070 711 405 571 339 767 689 310 598 577 320 542 000 989 153 609 386 890 504 106 493 913 518 351 850 100 816 951 336 234 484 716 963 215 768 955 074 606 892 245 093 139 069 857 097 979 255 713 196 700 936 030 809 420 961 018 399 853 958 499 550 526 969 871 628 980 598 196 475 271 145 768 575 011 472 521 711 060 908 727 182 938 474 966 564 597 766 415 549 056 250 621 872 864 373 359 300 758 562 515 522 953 260 746 968 720 446 546 378 941 668 979 867 116 426 507 387 456 696 808 143 125 444 094 010 252 927 236 353 022 718 442 861 507 906 874 734 757 015 584 264 920 799 584 921 868 057 958 186 636 595 682 319 907 200 577 201 085 450 307 544 696 012 584 754 032 610 076 814 789 336 642 451 011 753 579 845 701 261 874 659 166 555 425 599 767 445 983 013 317 097 374 623 162 079 606 661 273 050 796 693 705 284 790 131 799 696 349 895 921 190 126 527 410 278 828 495 410 544 285 855 023 827 891 371 552 385 134 380 315 865 240 402 476 694 102 084 766 463 712 774 993 153 982 974 952 140 938 847 999 384 393 731 785 516 904 650 854 261 053 249 326 204 773 062 505 508 011 502 048 858 715 078 049 450 557 926 819 302 110 435 547 091 233 161 976 447 084 298 554 738 398 447 399 157 648 027 205 620 190 847 457 526 346 880 198 550 160 612 688 782 998 138 197 034 119 002 693 173 612 314 155 349 276 737 264 558 838 116 801 862 399 096 832 880 907 465 172 910 702 878 948 129 094 241 564 670 973 121 228 230 256 435 526 157 935 511 443 140 391 936 055 749 942 361 713 609 340 728 621 101 260 566 162 070 627 035 327 663 750 967 560 282 496 872 238 990 541 063 229 061 940 116 049 153 122 201 147 297 576 064 279 700 287 948 946 797 509 831 597 364 617 784 280 781 592 099 405 664 852 700 056 391 993 930 488 549 164 836 953 174 173 034 616 601 986 514 711 682 988 481 019 945 322 457 021 677 006 422 697 178 869 212 674 361 770 424 566 607 748 593 015 793 781 573 738 961 382 588 214 212 554 300 541 445 896 074 167 231 212 503 670 308 457 189 868 820 790 254 064 397 734 156 058 993 432 360 824 863 591 799 967 894 897 166 336 343 291 067 680 490 879 683 211 179 220 676 027 884 549 373 590 759 150 556 196 624 585 423 121 003 805 711 128 422 997 901 720 185 738 504 971 409 854 187 188 868 633 418 193 564 053 023 256 401 863 901 892 218 806 271 815 932 709 099 494 069 526 229 015 872 640 002 812 685 306 793 133 369 712 474 222 180 523 392 963 858 056 718 359 911 934 289 355 749 983 630 630 838 872 818 526 942 087 458 320 167 827 504 204 900 388 951 493 189 923 100 120 683 942 004 065 880 354 938 598 878 061 723 347 845 578 645 362 007 430 414 158 132 916 005 198 634 744 917 647 601 346 822 621 198 031 102 553 263 927 787 674 292 699 110 759 184 921 108 170 290 157 175 834 531 777 873 036 734 623 763 946 581 506 277 039 439 985 634 630 844 422 236 864 153 874 522 378 231 915 569 371 550 046 767 999 620 972 517 312 688 766 697 858 705 302 108 527 716 920 481 163 983 031 837 072 992 944 509 495 596 023 526 078 546 869 396 823 445 578 729 879 465 576 374 269 219 947 428 076 751 817 866 776 375 550 628 435 665 915 633 479 593 325 696 111 102 289 106 510 544 499 879 751 459 750 464 947 062 843 046 675 033 793 496 108 383 572 227 828 627 487 952 581 134 413 698 399 223 720 231 623 677 752 589 778 334 793 328 039 181 238 296 086 491 300 455 813 943 584 270 090 971 331 604 209 953 847 358 743 454 442 929 626 857 509 894 151 472 342 122 208 874 169 395 659 235 089 866 058 249 076 697 799 872 174 105 632 553 231 726 503 907 399 664 158 196 048 774 223 205 994 850 095 295 985 030 414 503 888 031 397 273 937 307 392 133 894 693 417 464 424 934 548 387 414 388 043 457 647 449 852 973 361 887 142 835 024 598 319 530 897 094 222 459 018 652 585 049 237 949 089 876 249 510 189 951 667 768 675 348 027 187 920 607 044 552 039 025 519 937 597 531 580 538 376 478 139 502 525 705 855 818 126 066 279 565 604 047 260 957 680 527 095 457 658 358 462 423 525 281 556 589 239 286 633 463 891 276 288 026 999 384 306 351 441 357 750 047 979 625 644 122 384 967 158 502 881 947 133 431 311 824 286 446 988 157 842 602 968 259 973 923 045 098 230 292 743 362 089 309 132 519 907 459 505 931 761 652 177 819 001 756 080 201 570 504 536 802 444 976 460 022 975 194 900 240 537 760 756 238 321 772 957 923 734 136 571 799 485 128 611 407 839 948 809 445 001 235 533 832 645 388 801 852 146 354 416 284 018 207 006 863 188 036 652 094 429 558 945 980 095 648 976 190 030 591 512 664 596 070 544 625 960 880 515 988 681 695 567 758 979 794 804 248 647 480 697 592 676 575 801 629 058 919 135 593 706 472 560 456 956 192 942 331 197 404 113 678 321 540 779 058 625 516 438 738 337 230 682 172 229 888 858 146 160 863 237 708 605 556 531 587 255 452 792 190 706 335 816 863 428 430 399 855 980 278 253 286 068 675 238 817 988 460 779 083 199 385 297 335 402 623 337 945 362 475 559 581 195 936 348 361 690 482 409 652 114 921 579 064 325 476 268 911 989 870 600 109 813 769 182 556 357 257 036 048 902 499 441 170 850 471 793 158 483 801 315 592 290 742 735 000 951 264 659 627 428 252 271 120 399 089 521 673 472 545 871 440 512 675 758 366 281 028 483 046 374 763 401 136 543 972 434 917 503 480 521 800 388 879 690 746 361 568 068 968 518 905 780 419 078 573 920 264 232 798 513 261 673 981 524 947 823 861 763 052 170 964 321 695 832 915 962 374 511 853 930 790 787 020 405 138 263 485 826 544 914 753 618 056 907 331 953 149 495 435 716 136 631 109 316 926 861 977 074 408 673 007 664 647 538 833 988 918 256 809 504 055 096 539 675 578 652 858 999 546 542 561 283 605 093 944 019 396 738 896 736 761 689 566 171 032 425 482 705 267 631 158 275 800 812 667 730 731 445 831 864 314 118 355 815 155 832 883 692 434 243 969 797 898 681 957 398 731 615 010 575 055 316 473 726 518 086 843 616 220 445 930 401 887 437 593 010 254 085 027 087 849 160 433 768 107 198 379 696 946 074 040 365 075 756 353 270 921 166 436 409 193 120 767 269 915 448 671 772 568 998 192 955 938 387 858 456 169 157 585 753 372 428 795 132 820 916 880 390 963 110 058 071 615 574 813 589 272 125 094 611 395 102 352 284 436 714 412 740 668 383 642 403 267 162 836 672 488 665 527 661 911 358 864 126 632 400 782 042 847 507 567 054 444 505 809 704 046 066 115 111 290 415 617 203 612 677 754 691 948 119 944 464 788 719 584 983 980 153 515 589 987 115 196 656 080 110 440 311 393 422 638 315 003 630 165 132 876 864 604 825 382 972 372 680 626 412 264 939 739 049 663 893 510 341 481 486 504 213 742 833 871 954 601 864 704 783 757 267 014 830 544 419 055 647 120 479 758 294 972 163 683 246 355 561 582 024 072 064 251 659 113 230 848 007 072 370 763 716 785 476 434 175 546 528 476 299 863 707 769 368 831 167 360 681 754 031 804 079 575 501 102 892 594 985 398 615 945 975 215 851 903 793 580 008 411 757 288 365 347 101 542 667 051 220 318 857 629 439 444 044 277 068 548 236 033 397 846 474 885 615 410 722 108 736 300 994 129 118 204 500 130 559 267 145 907 854 479 048 054 232 070 277 186 003 852 684 610 688 846 490 013 531 138 870 885 933 114 095 096 206 695 186 837 825 861 482 427 423 491 791 467 345 969 129 648 005 019 881 308 434 844 660 489 174 736 967 702 106 646 392 096 745 039 147 258 141 161 276 404 418 689 582 139 536 757 938 844 414 287 824 666 037 996 442 567 642 553 056 411 283 031 055 019 779 180 943 243 669 428 986 680 571 699 536 209 320 124 232 529 633 515 126 577 795 240 391 996 545 689 678 496 124 915 224 628 072 156 676 993 144 980 873 890 423 063 488 813 506 821 699 295 673 571 030 353 506 960 330 830 311 067 666 313 330 990 674 934 612 748 077 958 153 924 824 945 314 322 165 638 225 480 728 872 057 582 904 905 883 246 822 129 782 787 924 305 727 671 558 143 458 141 438 151 888 548 868 659 108 115 968 243 265 843 991 377 869 469 391 274 975 783 123 620 920 286 457 679 943 197 811 772 928 266 232 318 233 757 466 990 930 730 760 294 379 134 733 532 742 888 614 501 764 159 606 950 495 598 927 101 722 914 495 937 716 829 272 512 888 946 924 535 405 430 667 536 247 084 171 203 275 654 402 552 012 176 363 534 485 611 553 481 129 361 688 717 494 766 403 063 827 870 798 440 692 669 257 500 595 471 151 147 558 620 929 324 001 265 471 773 258 069 362 704 237 829 277 173 751 102 027 165 984 363 562 303 591 536 788 792 723 463 579 433 053 680 026 914 590 832 233 985 681 104 698 602 486 803 209 438 245 107 234 498 412 307 013 266 217 828 001 465 138 775 173 533 828 465 483 834 526 509 381 447 502 812 491 991 888 185 840 294 836 373 355 712 253 296 063 631 258 215 735 849 449 870 643 398 255 005 565 867 734 183 700 860 953 348 280 843 958 252 425 376 598 161 250 897 710 330 799 612 058 836 129 648 561 189 286 696 843 528 751 863 353 150 559 102 032 628 171 971 833 073 626 242 272 776 565 790 191 975 211 309 699 032 732 313 198 391 867 629 955 921 079 970 134 998 755 010 133 606 990 738 398 645 898 062 806 878 977 723 743 325 105 639 357 570 812 473 499 790 442 233 843 177 418 971 486 462 285 811 024 762 909 038 889 285 508 484 318 005 172 365 308 281 266 291 852 730 116 424 929 285 894 473 273 608 047 072 245 312 809 853 023 680 987 470 587 963 038 855 196 167 572 739 608 457 578 978 042 215 604 495 644 385 367 022 698 213 311 116 076 335 469 476 202 211 558 276 090 572 739 276 855 176 656 480 339 104 886 343 616 830 020 915 462 918 439 607 217 788 807 597 166 345 462 266 680 507 152 399 801 611 406 039 861 524 260 615 638 347 925 943 483 275 809 569 513 576 854 190 922 123 077 873 223 642 814 610 958 622 266 164 872 860 134 716 907 299 564 224 693 596 312 505 312 506 964 680 675 219 865 332 055 234 024 209 355 530 266 283 947 673 124 378 628 369 331 737 826 471 847 549 720 400 391 051 348 819 490 583 606 059 063 789 115 637 568 046 739 785 442 602 167 757 334 989 236 260 409 810 034 974 232 165 645 938 679 678 302 403 914 788 264 962 221 126 432 884 363 051 754 915 555 271 443 042 188 481 110 798 039 565 266 000 733 345 129 505 156 615 954 158 160 608 835 914 998 127 063 882 267 337 406 341 805 684 689 359 813 750 351 829 820 447 557 453 003 339 459 468 616 748 909 312 373 394 821 713 345 425 196 961 728 515 127 869 493 250 156 859 118 607 939 536 997 645 996 580 299 981 495 980 589 510 121 218 878 084 102 731 935 005 787 726 695 245 152 693 846 520 398 515 056 778 955 267 813 834 454 897 477 600 221 286 744 317 890 635 033 747 966 431 466 633 555 699 445 814 414 777 255 820 470 812 383 747 136 246 975 431 560 785 392 748 204 569 755 148 156 913 857 123 897 852 502 826 148 882 353 996 627 112 918 605 076 007 611 326 324 587 317 559 756 780 393 414 571 644 461 358 043 102 420 221 529 901 207 104 459 517 414 983 796 277 450 879 202 527 826 688 700 462 581 175 969 038 688 448 306 759 059 553 692 619 712 655 888 797 434 950 721 479 034 948 424 094 570 177 222 525 259 879 090 682 718 289 222 073 960 787 959 203 781 058 374 940 316 748 679 911 588 131 955 864 552 495 354 162 871 512 375 687 182 285 166 518 175 905 393 990 016 933 548 604 078 038 323 725 435 658 012 170 908 979 818 297 739 069 212 456 788 814 708 917 714 464 113 450 248 957 131 934 429 545 588 233 002 270 589 245 180 450 943 204 295 866 016 229 697 600 778 751 852 634 673 771 651 546 417 129 392 895 073 195 501 118 724 962 049 500 245 912 022 305 218 610 839 622 927 483 860 995 136 039 496 516 839 362 136 533 818 572 159 300 591 926 710 494 899 880 600 489 802 004 974 403 953 462 008 648 679 722 695 701 381 120 192 613 836 642 994 001 329 208 926 962 342 589 555 909 642 965 738 203 226 675 970 209 788 993 780 222 913 580 560 416 577 185 019 459 530 816 786 752 704 463 225 452 897 935 759 236 868 882 186 837 746 811 559 947 796 731 155 232 996 513 489 194 991 658 315 759 993 470 144 364 569 975 723 781 599 107 248 441 183 615 259 310 109 544 855 452 292 566 218 984 200 793 544 306 921 494 084 119 491 328 881 680 623 067 064 655 159 837 912 697 581 915 740 267 858 644 978 915 207 597 142 689 983 205 874 126 141 182 137 792 336 219 106 765 931 493 085 787 140 599 124 165 451 262 726 469 516 456 761 118 159 281 744 709 536 333 264 880 533 397 876 163 996 589 929 075 508 851 993 162 014 278 886 904 630 551 799 265 322 313 333 217 660 623 348 563 666 846 625 947 148 699 652 867 761 488 562 676 235 514 182 609 807 951 563 951 138 509 703 439 144 713 115 187 611 094 629 822 732 469 171 757 074 122 420 966 416 048 241 582 325 650 030 269 900 269 867 088 570 007 150 117 772 776 303 689 477 234 464 262 807 802 781 965 790 861 341 953 901 772 795 771 004 649 433 497 761 982 738 254 439 022 146 092 971 296 142 324 906 060 525 465 551 904 697 540 118 301 333 396 976 892 740 382 043 882 992 242 743 154 651 671 301 945 303 303 769 055 070 424 850 867 619 857 640 019 841 491 316 673 444 058 212 326 849 970 160 447 318 197 322 787 049 445 730 126 984 609 582 331 557 006 809 162 759 382 648 799 708 867 932 067 034 878 901 002 446 120 078 863 232 952 795 371 847 521 300 238 453 735 417 542 096 733 422 678 936 406 489 205 456 962 422 306 345 703 240 909 117 678 517 707 853 890 306 926 167 762 847 166 180 351 588 130 467 199 789 576 119 161 942 256 068 620 266 329 853 524 454 387 735 656 543 836 205 657 277 308 710 444 668 282 429 504 609 707 188 186 890 426 802 155 984 267 757 485 855 438 232 874 353 782 635 618 802 778 291 369 255 830 298 287 619 026 469 946 828 763 235 034 132 490 991 045 438 214 823 930 652 278 600 923 734 119 082 390 226 922 745 065 285 678 152 319 949 971 358 949 493 390 844 456 731 561 702 647 201 878 301 238 698 167 071 118 032 491 363 570 733 092 587 694 595 651 101 696 087 793 542 363 562 619 696 391 283 757 000 587 566 270 151 762 908 136 079 864 798 852 610 169 429 515 268 426 834 588 297 028 927 194 491 527 177 538 034 956 578 222 991 344 568 421 393 420 566 560 843 599 402 120 969 255 248 931 645 513 653 440 821 006 183 836 751 747 640 851 776 036 187 824 088 495 468 708 916 687 281 650 474 585 429 902 957 690 342 485 836 360 971 212 688 659 493 179 140 522 665 360 291 556 106 891 220 262 617 347 427 003 029 860 182 110 079 868 914 414 307 089 218 269 377 537 151 513 277 453 232 780 585 676 634 124 685 881 829 105 831 849 683 566 035 348 830 446 055 999 987 620 328 307 359 314 746 287 001 798 381 281 154 831 628 953 992 205 025 911 341 355 262 185 966 085 170 089 035 400 843 699 553 028 015 169 631 998 483 323 621 038 230 496 702 694 545 051 816 524 494 554 100 331 284 620 392 989 279 127 213 565 008 415 814 125 631 699 029 424 193 467 937 408 346 626 358 485 308 013 599 466 970 738 351 187 393 013 218 317 073 613 684 272 312 661 741 803 870 913 560 989 249 379 938 728 143 239 767 956 113 466 179 211 790 941 339 580 302 941 218 732 099 865 706 826 833 932 402 927 964 953 562 250 800 736 662 445 199 438 507 560 309 910 200 310 996 469 589 496 299 779 784 482 562 716 205 929 692 919 498 706 798 258 000 252 490 946 176 549 325 615 703 963 645 277 746 053 825 735 884 546 197 943 182 203 951 471 413 874 184 445 466 505 056 162 817 637 294 708 355 569 848 613 663 368 635 162 407 411 523 288 555 433 709 379 138 734 250 760 167 753 865 565 017 447 545 667 072 839 870 858 997 665 034 717 892 076 672 859 846 001 076 791 032 538 192 832 058 475 843 454 072 943 873 879 346 120 332 973 718 248 223 581 840 610 659 498 186 849 332 950 106 652 649 831 022 492 714 444 381 593 569 530 671 557 867 768 227 916 669 600 762 940 348 610 232 413 749 685 615 692 614 070 507 979 431 243 935 157 645 796 487 759 862 799 139 680 710 679 185 618 124 947 662 286 969 001 027 374 657 437 428 652 651 400 983 431 608 556 950 621 803 271 677 296 199 714 653 846 220 993 404 050 831 205 445 535 758 091 853 352 603 418 771 568 855 697 754 920 265 926 362 946 233 613 246 296 851 306 553 673 734 368 716 710 702 467 359 782 549 338 230 775 608 468 528 878 584 439 770 153 334 289 418 935 956 414 187 633 439 533 291 670 039 879 432 047 897 204 961 849 429 760 556 371 715 604 009 249 110 224 083 161 325 499 356 411 647 124 582 218 114 938 784 326 700 328 406 107 875 361 573 239 347 848 719 826 122 719 556 913 301 821 346 401 285 291 544 325 260 947 592 787 531 350 395 587 226 947 898 500 803 475 337 788 112 466 800 656 373 001 185 272 654 096 786 183 763 557 595 431 978 139 350 080 172 949 141 805 630 336 005 434 234 990 190 794 263 774 335 505 454 943 964 218 036 915 655 507 457 396 054 652 535 872 666 315 090 820 883 832 231 677 664 439 963 839 141 064 420 251 399 296 371 547 099 585 694 136 419 773 554 397 130 574 109 388 034 082 463 215 027 024 066 640 598 596 751 628 533 792 936 368 717 339 558 519 689 434 687 893 895 691 608 344 275 849 275 758 067 155 049 266 291 694 803 685 676 907 478 619 248 599 621 404 521 945 725 842 905 625 647 909 632 102 857 639 307 635 986 038 138 943 996 018 933 069 621 154 278 122 941 363 510 234 073 627 668 470 141 140 304 388 465 422 297 268 345 236 254 971 956 440 455 427 037 581 983 157 108 465 381 541 569 181 539 768 021 256 336 885 658 092 084 696 597 156 872 683 592 610 406 163 813 913 730 899 214 527 045 256 453 573 583 237 848 288 702 933 850 837 271 468 221 575 830 267 256 734 276 835 596 774 004 210 521 757 457 249 578 782 417 663 897 579 978 402 320 020 914 469 382 891 932 594 801 686 156 888 936 121 346 732 389 195 867 901 243 637 544 542 146 681 904 354 444 335 566 298 222 600 418 039 264 922 174 533 920 579 865 617 478 357 199 865 925 662 860 089 764 479 796 786 640 601 361 870 009 249 628 093 273 847 999 334 785 087 424 523 351 356 224 836 050 233 379 704 563 106 360 575 476 678 187 520 066 726 042 520 116 073 644 240 332 680 638 851 570 503 218 056 148 017 635 523 945 949 712 957 312 983 886 062 709 244 935 303 440 583 280 100 536 870 159 879 426 501 298 258 944 798 509 090 092 148 721 841 336 531 990 980 610 334 601 140 751 446 630 330 897 675 469 281 944 422 955 942 694 364 278 769 987 832 978 107 674 217 670 441 643 652 720 568 802 072 075 542 100 591 780 155 790 839 088 128 777 904 639 710 463 258 348 502 866 725 520 446 314 077 606 206 731 679 570 971 817 897 650 646 923 547 842 978 857 264 728 095 342 664 148 643 077 081 792 942 738 619 711 069 785 986 750 011 246 442 681 841 313 233 761 494 489 733 064 465 408 264 747 338 289 209 838 391 541 177 177 459 971 301 933 729 948 218 722 676 684 462 099 888 198 815 309 181 302 197 155 888 699 461 502 721 142 197 505 778 900 372 026 254 928 168 514 020 843 153 502 355 761 416 713 571 915 222 437 548 424 452 566 964 890 547 040 787 567 789 834 828 983 938 363 045 460 446 154 229 943 391 103 889 383 907 643 922 282 879 994 258 542 547 044 740 286 238 474 470 777 299 608 229 867 743 673 556 730 952 798 536 852 652 677 028 863 040 699 878 169 959 428 375 593 489 543 446 685 650 960 195 633 871 206 523 570 071 955 638 352 434 995 817 176 738 645 817 984 542 896 221 022 296 072 506 515 058 147 271 100 753 995 052 084 483 813 473 125 424 831 004 393 297 488 013 342 041 011 850 250 919 676 209 534 995 154 364 125 151 227 565 531 411 847 124 979 786 558 729 314 645 116 322 474 824 758 313 037 596 668 787 262 243 760 138 442 735 038 523 116 796 572 876 059 720 544 326 789 408 215 614 826 406 909 694 395 452 817 541 548 876 663 588 491 517 536 969 544 203 901 950 512 502 070 098 505 271 209 079 895 862 918 568 123 686 012 119 171 769 577 808 204 769 961 853 646 525 758 105 328 080 089 223 442 683 607 071 608 006 496 212 756 125 586 032 603 461 808 426 381 308 129 667 691 306 254 876 128 283 811 346 532 933 854 100 086 316 830 382 573 603 452 632 729 918 786 230 955 638 286 167 569 792 514 681 448 373 478 140 405 755 082 775 185 259 010 748 362 797 723 291 956 047 889 535 531 963 735 136 939 209 561 033 253 031 539 312 663 426 492 516 176 388 274 673 437 239 204 527 393 488 485 759 947 701 508 965 304 301 090 234 209 981 352 186 325 825 883 008 432 268 976 581 096 102 712 184 642 906 955 707 371 443 321 241 327 593 452 114 974 782 827 731 847 949 531 432 660 776 830 996 173 948 222 099 799 363 783 524 780 243 099 601 746 844 188 871 002 205 391 292 872 399 376 312 239 002 558 694 601 466 396 410 232 431 292 839 993 296 780 944 869 973 268 987 087 707 182 837 866 958 175 351 532 843 664 662 319 438 164 518 216 633 448 333 991 149 994 001 188 722 436 172 247 197 115 025 321 047 363 774 250 801 946 090 859 699 388 788 660 607 419 688 241 121 584 792 221 503 652 030 052 570 890 942 421 251 108 333 222 647 069 785 934 762 552 489 603 920 687 560 821 087 937 364 255 404 067 801 358 919 287 943 228 873 928 017 446 228 066 254 977 651 104 008 387 873 169 468 363 771 842 928 090 294 467 899 948 368 277 642 407 675 778 580 277 890 750 618 616 617 982 066 611 764 831 968 881 998 432 329 080 356 243 245 131 719 474 397 276 114 373 402 571 479 343 339 732 449 267 034 858 252 246 617 058 040 549 913 183 318 755 258 492 410 080 496 663 941 672 102 852 025 449 175 930 696 020 407 068 589 441 194 563 048 187 357 092 775 547 244 761 788 427 878 821 234 737 473 291 473 083 394 785 982 755 319 685 300 997 874 823 086 987 015 771 012 214 262 502 983 127 086 908 653 883 646 122 122 280 188 032 296 395 457 699 293 684 126 258 459 438 103 353 307 615 205 457 842 720 464 634 595 487 048 336 261 601 242 619 761 509 672 887 536 017 701 245 529 486 812 598 448 836 474 777 892 731 711 487 317 588 889 571 823 525 908 357 876 127 295 822 193 761 390 317 415 846 517 105 842 080 265 930 370 164 849 678 536 005 618 384 559 830 074 715 712 046 994 282 310 536 574 731 268 507 098 237 982 454 208 027 005 871 326 672 340 884 988 286 092 598 044 802 483 797 031 327 033 082 823 644 278 737 144 781 938 631 790 844 535 878 195 424 818 507 745 374 614 943 752 863 345 994 654 516 789 706 966 116 822 967 663 989 201 591 520 234 765 525 636 764 363 198 002 319 590 104 764 703 854 518 112 747 699 432 624 748 371 999 735 344 669 343 315 200 849 179 469 149 849 221 747 153 160 479 328 620 915 123 436 787 935 453 431 597 451 953 462 384 225 809 170 821 398 102 645 670 977 408 965 433 778 136 599 615 112 078 541 819 652 060 006 177 734 911 722 385 193 065 667 376 224 846 106 190 250 538 491 705 893 860 315 934 716 494 528 250 003 938 021 897 282 772 164 828 447 062 722 294 632 872 574 676 589 662 299 456 618 721 741 354 451 807 837 167 773 042 658 149 697 153 193 981 285 425 353 148 133 643 222 822 290 974 746 322 404 109 891 259 664 187 825 273 064 866 668 534 669 698 106 273 339 215 726 975 511 164 212 098 254 022 990 844 393 613 156 177 254 620 355 997 786 168 820 582 485 306 482 784 920 770 125 167 702 131 696 220 657 343 352 190 671 190 683 252 797 339 673 788 818 974 091 645 551 154 664 281 788 509 272 547 778 771 948 569 925 772 995 218 461 852 713 882 748 793 386 090 078 034 471 446 804 535 690 694 406 196 142 252 517 819 134 390 315 242 438 594 737 734 132 494 691 202 373 180 079 178 305 714 516 475 794 330 936 480 795 874 759 076 042 779 684 169 397 080 025 833 701 240 436 498 132 943 415 485 683 994 944 449 283 798 617 168 839 267 820 165 659 482 047 759 653 753 146 634 144 834 231 023 980 237 575 760 206 646 659 075 728 096 875 030 558 662 849 137 343 263 594 046 616 660 350 814 359 536 161 662 225 624 880 570 504 792 935 591 825 877 543 185 693 686 223 053 367 479 185 155 263 166 489 731 136 339 808 016 912 075 311 444 292 006 910 718 987 263 148 913 082 504 211 294 808 216 496 673 018 080 408 486 208 855 704 193 923 155 038 753 139 842 270 463 488 391 083 552 911 856 365 686 750 944 011 469 464 925 478 111 944 728 822 210 183 760 327 350 992 664 275 760 197 069 457 941 630 954 703 285 745 499 450 698 610 498 719 800 244 908 380 062 863 456 221 821 014 176 510 313 331 399 273 485 250 186 107 527 523 659 360 359 806 748 987 570 910 446 609 624 861 023 567 405 580 688 757 857 909 348 069 864 387 871 699 710 580 985 054 143 663 642 354 532 098 027 324 297 062 105 567 132 503 214 187 306 583 287 188 441 681 825 479 969 590 334 114 382 454 748 678 596 070 550 087 073 644 259 835 156 653 245 291 728 947 823 835 416 093 296 981 402 579 247 398 944 264 434 853 736 668 653 042 862 312 160 962 068 451 938 445 808 209 758 762 357 957 486 210 898 244 367 384 402 518 278 150 947 678 339 570 880 389 687 650 871 096 471 657 311 096 752 561 956 387 582 804 140 927 531 017 959 964 793 215 725 752 016 871 025 219 501 476 010 529 247 121 465 718 078 284 570 507 715 568 698 903 888 075 707 968 225 323 926 572 549 162 844 503 599 509 211 550 465 588 774 575 604 865 459 084 944 517 889 844 989 458 495 560 638 615 488 482 040 200 247 193 095 278 355 394 699 945 300 866 835 886 466 929 662 297 368 148 302 951 163 595 301 036 019 934 705 853 532 518 906 127 833 337 974 471 816 324 705 955 156 728 369 535 371 658 203 528 297 584 503 038 498 711 271 890 293 794 534 391 171 909 191 734 456 164 436 754 507 383 799 455 957 451 426 808 402 444 680 985 458 149 191 740 438 844 538 152 423 996 236 217 051 724 472 606 232 387 632 580 293 161 101 480 480 380 523 331 285 742 317 432 848 601 806 778 017 414 657 879 504 381 574 383 889 775 745 482 501 661 205 852 794 345 963 566 755 383 335 951 381 123 035 281 107 682 315 607 335 185 533 110 195 440 968 562 245 898 719 617 234 215 299 175 459 093 585 827 977 603 887 613 138 428 042 417 164 880 964 168 774 353 346 710 512 368 770 840 265 216 701 012 574 144 305 981 918 386 235 899 029 167 357 911 039 592 789 605 804 572 906 995 220 870 973 674 919 060 491 495 729 888 972 691 855 203 870 489 418 912 949 656 931 190 544 494 480 676 748 041 108 912 358 930 528 707 399 702 908 535 066 985 548 650 766 739 238 376 768 954 696 384 764 986 566 953 937 698 572 476 346 825 682 679 738 804 590 158 662 674 625 479 268 170 876 265 405 029 473 316 667 898 692 034 632 797 978 578 269 344 423 242 126 843 057 169 567 287 434 624 786 585 501 716 140 220 493 432 871 042 681 189 640 517 804 737 150 018 014 681 424 046 091 211 814 920 503 572 829 133 832 759 200 365 136 231 637 442 343 754 077 921 869 988 913 199 791 238 928 394 323 894 348 687 232 573 258 126 366 030 321 738 575 881 221 203 161 204 106 522 066 007 114 773 801 326 734 894 798 679 372 330 748 379 259 438 916 845 997 846 700 434 010 077 627 562 069 368 979 185 252 429 116 500 142 554 214 600 509 336 855 625 339 296 645 162 828 696 672 004 935 284 667 874 639 662 499 371 787 723 647 885 572 631 953 497 408 884 447 346 148 563 382 353 006 708 971 298 181 097 528 713 165 228 318 224 736 188 826 120 639 275 525 351 206 583 682 515 892 261 111 167 147 640 654 547 235 459 694 830 973 091 499 468 228 706 894 897 389 234 045 998 842 519 427 050 919 715 862 313 071 179 549 233 177 039 637 656 268 641 807 014 388 210 776 793 515 850 185 581 967 337 805 035 984 882 675 509 851 676 811 491 830 338 304 397 759 020 623 224 700 721 285 049 827 352 236 294 896 756 626 104 260 010 152 689 507 110 356 927 415 482 852 228 298 212 614 131 141 895 899 324 755 219 435 425 582 113 968 321 904 334 356 108 477 458 973 379 944 617 917 640 463 081 844 963 258 008 048 188 511 557 976 535 728 545 045 958 648 290 918 756 574 670 887 576 046 771 483 062 828 829 405 479 152 716 150 913 008 355 379 994 346 631 025 820 479 956 413 730 841 369 792 660 955 039 542 245 004 215 720 727 110 630 923 896 009 763 087 969 615 863 493 364 950 528 801 199 440 000 300 434 140 819 558 238 978 368 882 317 671 943 183 648 974 929 918 625 949 956 514 091 004 551 686 544 467 891 486 453 319 786 844 049 495 045 694 206 059 972 663 422 700 824 650 021 260 179 446 065 425 555 682 044 453 373 266 797 614 606 190 705 081 268 202 869 666 576 971 701 230 170 017 709 519 773 687 952 677 438 112 899 350 626 270 807 735 988 203 955 990 534 656 414 427 156 909 422 109 592 632 297 430 408 162 125 356 354 822 305 846 207 743 597 791 458 413 689 711 891 266 160 503 280 823 823 668 438 727 174 166 139 610 571 790 612 267 315 887 941 412 595 320 620 936 731 544 294 833 083 458 410 695 675 234 264 270 274 161 419 400 405 645 646 288 178 132 967 984 458 886 834 622 050 366 113 852 191 815 582 429 604 900 609 796 258 502 411 463 960 877 716 161 779 280 212 315 350 326 509 925 183 351 556 260 687 516 050 299 486 244 535 343 027 617 220 761 635 237 765 139 533 574 146 152 384 574 034 206 787 699 022 098 313 620 542 116 924 520 794 184 183 455 114 919 541 278 089 385 898 587 880 179 617 732 989 187 889 049 604 008 603 162 352 564 367 579 389 985 904 222 064 966 842 324 659 561 472 508 577 942 197 157 175 454 784 021 515 484 606 128 661 955 572 502 928 234 332 931 702 340 336 519 758 719 315 964 876 045 085 229 652 868 375 832 983 845 425 989 501 576 981 820 278 486 605 988 928 869 095 497 111 802 877 142 842 890 235 551 245 926 923 025 635 510 101 341 252 296 015 974 081 620 487 460 520 749 280 774 057 801 290 971 247 962 091 864 941 157 201 112 159 454 522 146 051 592 400 309 944 657 604 297 071 782 476 016 881 599 965 091 640 314 726 701 702 802 509 051 212 629 205 260 095 356 252 242 790 922 011 222 185 245 632 085 199 931 840 257 067 913 188 379 420 621 213 523 421 728 801 708 343 800 404 391 871 666 670 408 873 162 091 255 605 030 533 464 998 710 968 805 936 749 504 688 292 470 367 670 196 864 082 009 181 537 253 045 721 154 369 176 225 033 415 526 602 367 862 259 312 350 272 773 155 634 653 609 424 690 622 854 966 017 442 502 705 370 800 331 563 357 408 595 692 006 060 859 430 079 978 747 937 347 357 020 801 467 796 443 906 380 553 163 166 132 386 748 572 877 048 531 968 311 812 005 403 310 666 588 601 974 658 501 387 377 627 305 406 921 599 798 868 398 222 124 072 266 725 567 552 479 726 374 707 632 730 451 955 693 998 660 592 201 830 132 548 701 464 829 014 815 334 150 964 404 471 009 160 683 035 901 572 584 596 938 383 480 776 445 362 354 294 074 345 460 165 869 098 410 875 466 343 054 499 761 986 064 314 111 803 332 708 958 070 918 867 852 173 094 092 863 793 123 465 712 729 287 657 842 538 513 072 533 209 541 850 438 780 650 309 930 030 509 873 279 403 789 842 183 886 677 561 007 174 810 163 203 348 203 299 331 103 846 069 183 485 949 898 990 976 415 228 990 413 577 987 174 577 210 212 440 515 843 611 609 770 068 318 100 419 211 230 497 333 666 499 391 271 711 917 545 044 507 765 015 601 386 647 107 908 390 271 462 960 424 627 237 390 847 767 405 085 448 790 726 113 183 672 518 376 248 455 965 882 670 766 957 328 716 527 983 511 229 682 513 895 159 896 895 835 913 053 238 766 697 727 768 917 695 578 059 862 325 415 607 320 439 855 943 299 981 172 253 613 307 768 131 307 022 814 132 650 334 921 227 105 776 558 710 177 681 689 835 660 807 612 985 217 727 217 215 701 563 660 681 516 888 720 486 300 947 325 040 209 441 902 620 884 679 233 759 870 602 755 062 686 352 447 230 595 033 146 945 296 969 786 634 701 606 278 566 710 149 080 529 522 732 332 468 525 218 741 087 781 397 001 057 972 487 185 153 979 738 632 359 120 121 313 598 430 424 690 338 923 012 690 176 260 665 565 985 235 679 658 946 836 326 807 587 043 310 202 383 964 346 560 330 470 596 495 238 219 943 498 467 011 259 934 323 950 466 245 165 591 574 553 378 420 740 320 071 046 765 685 014 704 830 659 752 815 417 104 903 295 422 207 324 965 491 139 492 143 729 966 142 811 166 759 182 590 023 184 805 372 400 150 673 982 247 956 993 869 296 975 465 893 366 819 743 322 929 542 728 800 560 461 295 146 053 319 511 802 080 473 335 271 359 870 149 885 322 107 294 113 661 701 083 580 393 901 677 364 934 130 612 156 318 042 403 468 258 707 418 021 375 694 069 523 114 806 776 250 011 021 930 132 727 570 016 300 032 242 558 462 715 163 716 394 021 738 270 414 275 333 052 832 478 365 979 667 111 236 498 535 807 265 111 860 046 307 659 182 093 641 494 776 582 207 658 731 089 231 707 586 721 873 163 434 775 873 201 875 356 827 371 058 673 533 791 162 382 586 910 928 814 854 935 126 292 266 271 523 277 301 909 438 258 277 392 652 951 900 400 304 261 525 205 363 088 650 773 323 705 708 126 593 563 400 836 207 793 919 619 725 899 082 870 341 302 803 491 670 082 418 170 779 330 031 605 824 490 128 801 110 527 530 102 689 340 288 075 682 108 982 016 280 467 844 068 897 429 619 620 261 843 638 557 282 602 381 357 931 638 526 326 573 904 642 756 126 583 825 529 204 712 011 876 806 209 340 609 869 421 236 761 676 553 044 220 258 935 261 376 190 591 088 475 011 596 384 830 500 345 086 905 030 031 389 076 139 962 329 575 920 607 837 973 519 016 410 244 700 577 944 323 842 091 632 952 896 466 991 774 435 574 489 987 315 842 122 155 439 360 559 309 839 336 480 870 471 480 548 563 804 076 700 589 722 211 913 848 026 866 294 599 462 622 087 249 277 683 705 065 725 581 389 240 882 518 125 891 553 080 475 916 048 435 869 138 411 011 620 890 504 289 505 645 219 400 578 702 275 107 127 504 337 123 655 517 770 778 170 972 720 351 562 458 550 319 822 753 225 113 290 467 329 944 119 613 306 878 370 529 025 009 438 261 521 091 351 630 935 039 127 199 352 488 440 531 240 855 394 754 114 508 645 163 286 794 279 577 345 229 771 049 207 687 503 877 095 098 018 383 518 676 313 470 871 655 022 985 811 112 788 026 711 121 986 894 881 849 529 740 461 418 066 058 097 509 047 018 670 019 918 348 187 533 073 256 116 862 038 601 043 204 426 053 915 088 102 594 126 604 035 387 960 380 904 300 928 445 697 921 711 017 074 950 495 561 664 360 637 361 050 014 345 851 599 091 792 788 105 451 646 111 512 245 507 330 732 099 353 351 419 556 581 984 888 762 732 932 718 463 517 365 837 504 803 754 284 928 059 447 250 012 216 872 974 558 475 367 691 152 915 584 468 295 665 798 129 818 141 772 684 666 378 092 340 753 172 398 818 002 439 445 470 228 772 846 217 731 675 510 096 564 540 477 767 221 339 286 714 049 531 518 210 221 242 506 382 547 733 611 798 643 007 077 083 019 153 550 082 952 230 824 203 613 698 383 161 023 503 039 435 733 520 630 356 133 109 541 292 527 896 318 688 668 216 120 505 669 761 136 256 517 019 194 343 558 608 454 650 317 034 245 881 114 323 029 885 035 898 346 882 919 584 121 230 229 014 308 319 669 762 526 759 224 117 773 095 742 564 606 771 074 614 572 447 824 841 316 819 557 692 899 860 143 097 666 332 753 843 187 653 911 152 187 178 144 958 582 789 452 209 631 936 120 778 322 440 490 376 609 793 829 656 783 427 473 863 264 264 247 198 366 773 507 296 552 919 861 302 687 310 626 549 194 038 465 422 299 079 777 037 584 986 944 902 922 096 467 425 374 553 950 105 087 306 162 944 007 145 004 143 003 460 091 001 102 887 938 216 039 694 998 865 266 319 023 137 215 677 798 178 219 646 011 263 176 845 284 529 664 265 622 103 004 834 369 216 199 120 229 456 935 108 901 791 178 487 550 179 539 251 605 176 610 890 829 033 121 869 447 610 386 285 046 595 193 170 558 003 294 384 809 878 283 102 531 464 298 660 928 418 480 187 069 779 555 285 082 664 414 672 385 737 405 872 278 552 314 934 946 898 554 469 078 685 884 228 785 691 933 430 257 584 145 500 772 780 695 032 206 224 761 902 912 425 356 359 484 717 118 186 866 261 645 634 843 641 569 281 116 109 061 356 217 665 412 899 673 160 628 789 314 250 084 804 429 988 063 871 422 584 088 089 145 716 104 169 733 254 390 748 130 840 609 525 078 057 244 151 296 034 478 366 867 846 445 538 817 393 536 158 051 335 650 171 177 615 097 982 574 536 658 117 220 544 186 008 686 731 838 253 290 356 844 254 439 139 753 087 382 323 328 494 793 656 344 199 440 371 284 353 060 085 021 114 303 900 760 094 452 229 149 517 955 112 159 702 314 855 798 381 448 412 485 336 065 714 821 499 927 549 164 783 899 212 698 985 688 474 185 038 656 218 113 871 083 252 991 070 457 390 713 651 241 947 211 960 448 052 085 289 651 365 342 856 317 337 738 229 574 481 835 207 811 047 443 640 634 891 822 099 984 529 535 055 365 274 817 796 347 805 119 374 176 490 229 000 733 479 813 592 428 342 754 365 122 784 855 643 069 049 699 530 190 617 576 341 228 523 137 361 500 163 416 978 839 336 408 245 015 284 738 668 894 308 889 786 001 844 509 211 586 625 394 516 817 223 960 359 966 215 705 897 339 934 732 650 762 250 460 339 831 915 441 342 986 357 009 236 422 728 240 372 592 422 814 313 222 460 561 033 853 837 719 940 266 338 840 346 267 476 231 274 206 189 747 470 025 728 785 726 990 724 030 954 434 547 587 008 965 184 501 595 882 803 421 352 344 160 747 965 079 054 364 454 818 058 373 619 529 870 050 711 552 551 653 223 336 971 767 925 723 975 644 397 981 932 587 706 893 668 164 257 431 387 856 721 419 823 288 794 932 411 361 929 316 087 491 505 436 350 008 196 708 648 578 296 140 389 025 591 130 258 251 290 230 398 268 211 720 281 093 586 543 065 353 996 156 230 185 408 599 997 787 234 535 392 585 361 199 562 047 126 082 100 696 978 226 078 540 449 276 179 772 260 171 279 424 431 376 447 976 120 840 760 046 714 688 979 463 084 769 297 047 099 886 955 633 337 459 801 495 376 523 511 887 914 916 638 369 580 448 728 223 129 149 181 941 129 265 652 643 797 669 683 705 122 983 017 189 891 552 084 577 686 082 183 605 214 286 410 525 160 151 883 115 048 467 967 743 955 532 439 100 923 061 293 774 967 765 617 293 617 954 533 068 914 383 446 399 907 258 654 113 963 839 511 195 954 552 762 655 112 140 990 600 741 171 829 000 347 955 882 739 327 804 757 226 712 425 686 718 582 678 987 530 603 373 141 170 072 328 348 534 890 443 866 468 271 243 873 843 493 877 961 930 033 614 875 911 786 179 921 691 085 064 178 464 257 466 131 423 207 518 611 889 143 967 634 876 484 384 672 384 504 361 161 423 380 945 133 068 337 661 336 960 133 917 354 136 783 184 215 923 253 430 511 445 827 014 856 985 437 485 273 280 484 649 143 231 965 740 608 604 988 041 876 794 694 209 199 737 904 763 386 279 713 763 687 843 435 075 942 092 661 166 562 824 284 283 215 448 272 129 584 286 435 957 322 662 040 619 943 119 879 022 137 943 225 390 964 813 440 429 184 663 020 067 314 027 779 986 499 963 876 575 708 016 849 808 922 689 489 506 910 116 119 325 141 990 263 501 427 658 996 304 490 476 890 743 426 289 346 416 086 930 461 441 291 957 858 844 184 637 687 514 477 768 739 918 572 916 436 814 221 308 760 185 731 583 873 339 365 775 688 398 496 411 645 951 140 587 628 301 689 993 125 920 118 218 030 080 381 640 901 501 483 399 562 263 598 855 957 194 127 081 202 162 751 941 877 596 490 557 365 378 882 837 561 566 231 000 833 170 637 622 502 382 419 671 316 355 009 853 080 888 196 808 697 156 365 067 634 241 929 274 059 821 398 385 724 195 113 557 299 080 052 811 574 919 142 512 043 154 782 890 079 409 293 766 692 866 416 325 416 792 216 237 851 383 716 318 209 610 368 832 010 635 512 962 063 917 713 921 275 892 418 805 780 613 310 519 169 041 283 611 777 534 376 696 632 517 999 701 670 086 346 576 731 370 518 422 994 218 572 260 824 913 824 725 417 773 463 232 523 934 301 108 590 698 721 684 153 675 870 529 963 338 180 507 805 442 928 523 732 068 899 067 204 856 777 527 181 108 726 433 694 777 531 746 327 196 829 832 326 918 210 249 512 634 141 463 701 243 958 537 347 721 784 683 227 354 925 963 463 199 766 295 921 184 792 825 760 133 908 454 465 320 227 750 318 246 653 160 095 278 183 977 311 221 967 183 951 639 621 646 979 825 300 437 122 755 655 156 468 607 440 504 633 443 267 195 817 096 374 284 791 826 605 527 364 264 902 590 932 923 564 313 895 011 427 094 360 333 533 058 635 920 114 949 001 735 860 081 246 500 145 831 599 890 910 117 799 177 323 914 426 525 689 788 426 858 490 002 037 472 540 696 078 881 060 255 771 375 402 879 146 108 029 017 679 533 150 376 825 664 571 951 447 860 680 840 701 906 343 592 826 686 570 645 692 656 258 018 490 982 484 070 288 157 618 101 514 553 880 511 514 605 613 529 310 418 867 687 510 002 140 351 526 905 369 345 226 020 478 902 788 616 945 363 346 265 269 272 669 144 683 768 215 576 917 520 897 731 260 485 609 353 763 749 571 419 100 155 570 558 247 085 915 533 807 544 293 554 250 527 038 474 249 469 579 118 972 063 742 828 226 192 375 767 339 509 536 306 327 832 420 161 133 560 868 879 133 345 401 339 117 973 092 153 363 669 218 084 392 930 087 560 041 324 989 979 671 636 846 957 729 475 330 980 552 414 260 253 717 420 762 776 175 694 918 781 561 294 698 234 007 099 498 759 759 819 930 586 312 618 622 864 787 599 635 883 872 114 786 702 670 670 750 593 799 834 296 337 422 715 830 836 279 991 317 327 270 809 880 922 296 019 412 513 836 088 561 886 920 781 319 909 056 966 285 382 184 628 386 850 423 715 618 760 733 063 197 487 361 421 364 481 527 605 864 017 999 529 000 212 822 367 445 151 932 544 587 798 503 219 193 752 694 230 294 168 199 667 841 361 563 401 475 442 536 044 181 347 448 370 574 760 268 438 077 650 635 598 148 204 905 047 472 541 557 588 251 070 580 794 583 451 681 810 839 096 749 769 580 855 981 812 593 851 933 215 094 164 051 003 277 487 873 173 747 775 013 609 730 556 279 199 053 888 816 535 102 647 415 851 928 194 740 948 825 401 129 384 311 837 351 578 689 594 326 827 140 738 121 135 371 877 438 973 956 518 712 402 474 930 509 863 463 320 569 169 525 688 778 752 266 599 551 023 800 182 680 185 040 270 912 839 211 331 863 077 550 541 740 098 662 519 841 100 169 284 751 111 027 885 184 406 737 019 992 192 678 356 969 170 085 755 181 772 060 091 418 497 720 582 735 947 118 898 987 841 851 976 278 482 598 198 591 294 813 649 313 416 701 548 166 132 533 326 013 361 601 833 222 301 841 733 183 248 156 069 221 295 621 171 405 475 007 674 636 608 015 353 224 258 338 926 515 685 866 908 307 228 877 766 250 210 293 930 772 023 844 095 319 716 236 180 107 469 504 782 596 586 852 608 009 515 326 820 731 986 070 887 711 672 218 307 963 856 214 427 952 071 615 272 153 005 625 923 515 365 812 806 716 982 620 331 908 037 238 591 375 718 107 098 760 080 841 945 537 264 317 203 140 004 820 770 145 919 151 815 538 410 398 530 906 701 590 690 007 982 283 819 992 489 877 638 091 602 900 563 339 197 938 567 939 942 108 266 233 594 508 715 779 609 761 749 010 029 492 810 637 624 965 446 483 054 384 938 892 848 599 663 743 036 648 969 681 858 060 283 914 956 687 192 634 377 280 094 765 271 017 520 103 440 216 243 433 535 130 624 366 559 789 372 162 325 142 743 464 054 011 541 958 517 516 948 327 705 516 901 824 102 008 123 550 266 986 699 300 121 588 059 809 946 675 268 127 942 031 567 056 906 897 754 057 708 393 915 182 703 394 415 297 596 776 850 103 831 490 423 228 998 506 155 182 171 161 494 305 851 541 095 956 545 774 387 474 998 887 079 907 489 844 539 003 480 715 673 119 808 744 706 494 280 724 887 697 520 498 629 540 777 387 601 374 302 823 457 366 389 104 401 950 804 164 112 708 718 791 587 815 398 257 857 511 969 868 172 725 230 853 724 043 835 600 237 680 726 047 951 972 200 860 504 750 728 605 242 680 268 409 811 228 711 916 019 861 457 659 483 665 351 856 272 088 633 250 891 336 500 538 600 730 520 451 259 715 245 340 364 818 285 682 226 396 336 897 519 295 699 695 068 937 295 841 352 535 474 775 621 428 866 121 239 809 826 992 573 967 362 753 561 209 671 814 596 003 273 384 841 479 995 502 616 592 365 163 339 354 603 790 476 719 301 923 575 438 796 682 710 166 532 477 261 946 077 258 040 236 885 216 701 953 473 499 327 361 166 770 241 825 109 286 647 277 216 287 191 604 238 685 586 855 767 197 401 243 013 097 994 892 251 762 526 764 110 206 195 784 479 921 802 516 478 856 038 253 393 647 404 425 901 766 360 261 261 911 076 597 894 263 704 011 046 214 424 386 183 495 329 398 035 259 285 927 675 404 394 414 500 928 203 272 836 479 627 029 204 547 995 999 379 521 242 169 088 827 897 303 038 148 082 129 201 995 250 175 720 113 093 041 751 770 369 402 758 197 160 649 056 264 284 159 222 069 649 440 733 645 779 709 672 876 720 905 985 569 229 886 936 596 864 176 501 432 423 085 103 087 149 154 956 841 987 191 192 066 679 139 255 626 248 689 404 610 641 916 066 435 632 489 698 180 848 250 149 006 193 127 027 176 684 502 478 972 599 024 782 438 112 974 497 161 689 884 330 892 790 964 985 222 672 589 431 336 419 778 345 698 852 916 315 848 202 781 818 254 213 298 365 995 066 835 163 306 993 513 083 809 085 131 965 728 182 874 853 284 038 105 832 345 515 792 726 480 746 475 731 359 268 601 018 944 720 944 282 060 106 004 108 141 133 917 935 814 969 459 152 983 491 757 512 183 809 765 903 835 315 124 954 378 577 844 086 990 751 711 645 293 273 656 579 743 443 724 948 495 323 609 919 277 780 585 485 589 984 376 261 144 021 703 340 796 634 390 739 183 335 166 143 273 380 564 941 852 327 838 025 109 449 568 460 842 620 403 661 290 798 450 102 604 365 635 479 505 136 072 975 044 914 299 239 611 990 687 448 291 134 913 383 168 900 789 948 919 763 201 191 799 364 953 355 348 339 826 569 113 438 540 581 811 324 755 925 497 251 726 588 440 294 917 432 906 858 546 151 627 246 760 040 975 671 511 126 677 149 919 727 319 472 539 014 797 326 548 653 046 161 004 390 163 509 700 071 377 467 788 650 209 344 222 861 584 602 496 042 961 430 222 122 653 205 758 746 023 708 521 426 505 103 416 926 552 643 178 815 637 659 177 317 937 792 035 375 476 969 823 745 464 286 152 095 594 772 922 921 432 511 426 216 640 419 240 344 304 382 219 409 405 872 059 483 424 158 323 277 009 169 892 794 833 775 574 170 308 069 774 128 336 389 564 640 823 963 403 276 170 593 311 274 572 454 304 652 374 825 108 313 921 566 942 761 565 822 746 668 975 232 327 418 049 684 320 151 725 504 183 974 467 539 310 780 508 036 805 789 539 118 109 643 547 257 242 605 554 963 632 209 625 533 084 042 068 761 489 636 012 235 045 487 726 238 147 827 911 259 427 169 539 356 764 177 085 468 402 329 489 781 443 789 067 941 600 023 091 905 650 354 361 167 379 730 827 074 683 335 662 057 005 893 910 028 780 298 065 234 378 139 795 174 907 330 092 533 987 650 853 155 996 849 617 949 155 453 205 522 116 943 108 880 935 167 262 547 819 778 706 595 235 351 281 925 235 651 874 797 617 126 605 090 831 326 749 636 472 836 671 838 983 246 541 749 001 566 816 311 631 681 038 547 708 524 400 278 001 092 065 554 863 799 182 199 613 453 424 270 136 792 256 450 710 330 975 990 711 415 364 973 551 440 246 174 419 101 772 826 955 593 686 471 001 962 880 332 594 076 309 183 565 047 811 574 146 262 190 640 700 346 765 841 226 317 003 413 537 806 509 894 744 066 792 435 332 640 191 431 383 836 829 280 967 971 995 629 475 046 913 513 236 740 603 887 404 059 403 047 416 381 932 104 927 814 771 671 651 376 583 119 924 937 485 260 984 858 190 554 590 083 270 711 132 944 868 774 840 952 594 281 717 178 821 542 393 125 050 530 479 748 582 378 100 511 363 977 314 815 041 820 061 125 191 561 845 414 787 878 526 223 666 933 912 256 341 301 197 530 357 288 971 430 074 290 986 418 730 129 473 560 028 519 633 874 252 962 105 767 165 989 163 279 660 893 921 720 849 179 224 016 817 635 690 842 831 171 059 130 612 857 261 869 186 109 913 396 329 009 859 204 038 063 886 296 690 570 975 733 005 467 919 291 636 402 646 730 932 227 774 067 551 379 098 576 503 171 436 963 514 583 896 938 849 149 016 565 973 027 431 194 925 719 611 023 966 327 570 987 137 667 909 804 333 673 323 420 835 685 884 131 434 061 827 052 081 431 095 047 429 439 046 807 170 927 859 277 432 663 351 583 835 868 932 122 667 942 267 873 525 993 688 383 769 505 067 351 439 596 287 225 069 868 881 016 739 845 334 241 410 028 817 567 203 494 364 643 271 612 160 322 474 959 609 092 051 412 244 814 158 297 783 377 464 804 940 420 929 971 238 194 273 310 431 487 783 851 894 218 950 229 033 360 551 926 607 109 739 161 109 526 623 070 322 337 507 284 294 131 141 433 392 704 472 990 455 598 899 478 304 946 322 116 347 664 595 473 994 742 945 479 922 497 471 655 861 402 708 006 853 208 783 224 941 017 051 442 348 276 555 924 703 767 630 436 887 264 077 633 644 912 464 863 406 815 842 039 444 503 977 092 593 565 019 850 174 902 184 131 134 489 323 733 722 513 593 875 733 283 886 626 147 074 771 460 926 656 046 942 808 105 511 472 742 585 203 522 777 907 077 541 934 739 186 991 633 845 583 965 555 943 421 072 069 718 303 130 106 041 610 047 903 867 100 050 546 975 241 905 728 497 339 883 350 006 657 825 686 313 866 680 432 288 006 698 221 099 486 214 008 654 971 690 629 115 201 129 715 655 831 868 941 090 055 939 308 340 674 222 757 454 243 563 679 028 329 060 957 209 329 967 945 036 083 945 507 221 173 487 763 682 397 237 212 171 925 533 951 522 024 288 518 860 791 319 141 737 443 095 581 226 574 336 575 320 832 131 936 693 267 507 423 122 070 097 373 368 632 231 087 644 545 147 577 564 259 431 171 898 731 960 774 017 128 875 998 802 389 351 533 231 111 544 940 654 406 764 945 203 467 809 724 769 984 653 564 183 137 986 310 884 549 353 220 517 080 404 832 672 734 732 815 949 414 137 435 283 320 306 188 873 131 283 812 929 681 231 805 834 395 062 532 619 770 126 070 988 984 942 403 911 970 424 162 491 174 096 849 862 465 155 583 983 270 337 976 427 541 025 363 196 237 582 559 963 066 122 188 920 682 948 592 598 649 414 672 244 654 125 505 407 077 705 675 492 963 423 101 980 627 720 266 136 914 056 743 700 441 354 901 331 836 762 642 294 897 700 334 206 647 192 407 234 351 075 472 909 509 175 465 521 348 382 699 502 044 748 484 348 790 112 058 285 829 085 214 039 960 243 776 000 664 322 674 805 799 308 987 236 378 334 945 589 685 718 685 833 362 959 129 956 336 566 533 038 146 489 620 967 861 162 200 962 373 536 063 434 170 453 585 179 056 435 758 325 139 458 887 042 937 816 331 574 018 045 808 902 451 318 668 211 169 149 724 512 558 468 151 604 591 659 318 660 117 910 183 281 550 366 934 171 837 590 157 548 832 200 459 985 262 161 840 146 906 610 672 238 606 544 575 493 580 344 804 561 934 799 268 678 024 556 793 529 844 108 521 593 789 421 088 185 698 749 979 913 572 389 266 880 629 254 678 958 330 971 244 079 831 314 310 404 333 460 178 700 342 976 854 835 799 789 087 800 707 743 974 723 090 336 133 184 754 354 154 730 606 026 502 370 171 316 392 575 443 245 422 586 321 735 990 442 327 427 119 062 153 312 034 687 597 434 775 623 388 120 947 734 220 061 923 645 005 390 830 823 412 521 591 576 726 076 683 073 651 313 206 248 102 668 235 758 497 312 539 860 804 334 913 514 412 193 419 431 327 375 743 065 284 514 943 403 694 545 325 277 493 081 759 959 487 180 607 181 876 381 919 828 919 022 055 752 221 817 549 562 645 094 470 235 179 885 829 171 653 953 564 315 389 074 862 901 092 787 604 369 800 915 185 324 640 834 701 859 219 879 165 026 116 182 617 246 155 895 385 541 798 475 896 131 764 250 394 055 517 421 449 749 754 161 996 165 552 197 018 372 456 580 468 842 777 486 922 933 602 257 852 045 782 441 308 689 024 219 813 450 534 031 092 763 656 024 391 033 124 277 086 949 699 098 686 136 057 212 067 692 897 433 201 066 653 393 284 352 269 196 499 028 616 445 442 744 409 312 103 136 941 638 130 045 601 233 298 725 400 327 665 076 767 331 400 017 581 996 585 327 928 757 920 573 001 874 204 625 648 486 473 696 449 652 028 183 801 112 816 320 999 705 408 151 656 065 934 934 460 721 836 618 782 944 450 545 819 942 328 289 515 176 024 117 437 404 818 292 706 203 981 255 443 378 059 189 973 392 036 598 133 102 002 748 241 021 078 671 038 668 274 772 061 210 582 816 853 990 433 102 287 714 490 797 802 920 107 957 334 484 298 632 805 022 836 375 356 661 759 927 513 401 553 698 355 460 285 343 397 756 122 470 015 158 355 941 085 275 425 112 143 541 909 394 017 618 502 865 676 163 975 590 819 587 689 939 281 112 194 637 092 646 648 900 185 472 463 678 843 523 241 991 604 652 228 761 469 415 632 033 782 677 653 462 939 571 866 134 552 007 358 313 370 025 529 044 931 488 907 160 196 068 449 761 964 857 458 363 321 764 902 180 947 887 295 064 523 885 981 423 017 611 765 314 238 091 387 537 436 814 434 857 538 627 634 279 806 446 021 654 782 800 729 502 848 207 811 331 906 758 359 136 898 215 322 512 970 559 061 053 617 784 339 255 862 042 851 700 089 240 249 260 077 105 152 505 100 167 619 970 223 429 638 994 021 296 262 047 738 198 483 636 146 898 166 634 895 337 158 500 022 237 199 731 883 615 333 017 496 606 712 694 218 044 344 131 932 940 468 319 116 492 330 112 986 273 285 118 732 064 270 966 941 897 077 976 401 273 811 325 089 139 608 217 161 046 443 090 636 025 470 156 475 958 692 664 780 840 122 121 964 741 099 663 472 429 786 787 338 095 916 208 065 779 426 432 619 819 977 109 269 299 957 305 980 509 963 104 682 214 850 682 787 581 946 965 386 327 859 649 990 999 117 178 035 926 179 655 479 681 487 078 155 258 964 072 447 324 709 385 492 182 580 757 029 045 949 546 893 429 766 049 561 166 161 940 129 407 719 462 882 967 541 651 073 113 860 139 857 035 291 099 530 566 364 586 250 585 848 673 409 338 091 111 098 993 152 539 077 634 737 104 735 926 470 665 535 542 365 618 927 827 025 268 302 642 223 081 726 745 946 570 439 539 329 286 089 263 107 890 580 662 185 415 092 395 438 262 080 741 747 567 539 224 117 947 407 509 640 227 570 072 644 162 312 725 505 712 665 568 218 415 817 526 312 170 026 534 850 348 562 569 364 438 501 021 287 234 617 985 487 800 577 619 636 166 609 992 229 600 077 735 832 542 087 198 820 609 437 753 821 573 130 407 219 480 541 152 195 810 133 834 190 689 216 326 580 314 953 423 369 286 408 467 468 091 652 114 711 220 404 688 149 786 973 492 488 607 374 845 251 951 115 117 211 658 044 230 866 747 141 935 152 609 560 812 012 632 241 229 233 232 587 007 376 379 680 315 695 842 820 514 705 415 689 096 327 188 649 974 115 922 326 326 533 134 664 172 773 400 959 057 814 374 482 929 564 221 794 741 742 822 041 868 631 741 974 269 073 314 149 333 183 647 864 882 655 226 156 604 699 851 758 163 193 579 375 170 600 842 905 791 052 459 513 293 706 438 704 953 053 207 471 365 952 621 279 261 933 058 641 466 259 563 888 305 716 918 146 145 984 111 486 598 889 324 941 019 368 815 612 548 549 761 107 140 641 448 835 476 718 095 284 227 588 364 146 448 786 776 438 199 623 275 625 323 463 165 498 328 880 754 142 304 060 457 166 939 066 569 303 542 527 794 147 381 256 256 728 266 995 567 128 893 681 053 959 228 177 118 461 970 347 814 044 918 604 521 957 831 937 913 807 513 760 966 652 625 839 418 942 778 942 026 451 370 921 465 551 901 292 607 269 927 475 557 778 910 002 612 464 560 121 008 322 173 522 828 587 003 526 195 878 722 307 898 534 714 334 885 719 538 606 697 364 290 004 599 997 764 113 441 002 900 503 506 121 016 963 776 082 383 998 305 006 994 890 749 173 681 457 354 651 359 515 659 014 784 570 442 694 702 548 278 927 120 518 893 821 222 267 409 412 799 151 530 053 546 679 911 944 768 078 577 539 500 543 744 482 346 882 438 183 347 473 596 843 260 132 325 077 466 201 207 252 276 713 179 605 208 470 724 179 678 834 428 769 427 106 377 705 249 278 130 316 789 744 657 749 295 712 096 875 593 340 692 575 606 317 240 603 249 517 824 073 567 967 082 808 816 354 912 540 110 932 043 866 452 377 015 917 672 694 929 633 470 691 223 364 287 525 066 483 860 202 813 226 947 914 447 799 767 616 310 365 116 023 032 252 152 138 521 327 668 011 891 363 769 077 752 539 280 207 023 081 471 670 037 623 619 080 791 369 736 907 784 047 112 901 852 142 428 235 565 706 334 466 281 814 690 327 136 310 621 294 434 324 971 684 127 407 031 131 689 524 599 069 104 731 083 758 197 182 368 715 214 756 427 518 222 822 636 155 582 839 855 490 211 763 651 962 667 206 110 896 197 069 269 745 382 646 684 682 627 523 085 455 028 954 490 939 102 021 169 913 197 984 249 756 262 571 758 800 015 592 586 176 913 538 194 480 818 763 442 938 641 116 696 513 271 820 652 227 476 985 972 433 581 382 011 063 401 019 982 370 565 266 194 983 744 223 395 115 648 332 559 752 446 654 212 764 050 808 110 608 263 134 672 914 920 483 455 286 240 823 702 549 855 973 107 452 584 603 157 939 331 507 074 479 284 453 969 434 832 510 479 641 614 702 072 156 687 080 506 460 557 901 929 726 708 079 902 346 968 823 980 486 244 818 791 222 976 057 919 100 760 596 137 900 164 997 750 689 516 815 162 214 841 617 686 424 335 130 695 804 521 977 622 614 749 735 476 766 040 064 410 710 074 345 767 529 820 318 896 793 311 025 978 503 944 004 887 379 666 250 318 001 923 187 251 066 124 375 918 730 516 464 413 903 189 136 405 979 503 901 203 532 882 184 509 869 770 468 797 438 589 997 008 854 425 765 160 620 857 415 107 071 243 386 787 572 304 402 922 461 551 018 378 634 953 692 674 421 160 871 966 740 722 120 839 215 076 960 059 682 272 475 829 249 576 092 323 662 050 018 125 498 754 515 397 578 151 883 033 166 921 591 099 890 350 614 752 550 489 090 586 470 772 405 079 493 149 164 794 644 763 983 661 951 690 444 913 470 327 756 672 662 272 091 335 475 737 132 161 813 912 187 718 010 770 910 873 575 395 090 436 847 727 866 551 215 983 438 020 366 643 966 263 956 302 053 746 464 334 121 691 879 412 542 339 130 827 645 368 774 548 746 384 755 261 920 215 100 230 551 901 571 828 147 609 366 326 379 024 089 725 716 212 066 444 555 970 260 975 235 187 632 083 818 318 782 914 571 804 454 812 831 551 648 304 788 352 761 211 020 827 667 692 534 506 111 550 448 646 756 144 181 622 099 217 660 568 464 499 294 113 098 351 226 237 765 501 853 367 090 183 096 919 631 083 927 590 096 471 886 622 317 282 534 043 766 522 700 640 399 845 778 026 563 413 790 750 511 401 667 896 653 570 718 094 190 564 942 154 721 284 813 339 480 512 327 763 281 382 225 816 019 662 098 052 385 764 867 508 386 670 421 620 196 766 134 039 268 262 970 534 369 683 166 907 976 929 138 337 292 186 316 116 907 253 320 144 067 954 887 966 858 088 218 624 212 751 009 807 954 861 349 548 841 765 577 784 622 162 290 365 738 443 370 121 230 841 672 795 298 837 957 179 602 454 942 210 910 893 492 087 202 784 463 323 221 386 335 107 922 226 622 047 305 782 219 866 313 099 266 887 101 432 647 519 688 842 947 986 343 874 052 790 121 609 219 086 031 941 267 144 591 974 753 461 389 002 354 346 670 023 659 941 238 676 329 188 015 129 547 015 412 569 344 172 987 506 163 440 826 313 843 004 052 904 092 387 723 262 842 320 860 983 971 795 676 487 731 745 456 107 714 009 699 898 917 902 885 112 029 420 847 213 768 020 821 756 720 040 899 687 367 519 960 830 599 160 726 158 251 951 178 153 956 871 193 991 566 834 931 057 711 098 053 757 058 950 074 712 923 076 520 931 895 608 594 662 783 868 440 911 161 434 992 226 023 340 066 420 446 058 647 884 513 228 729 981 475 575 993 184 552 825 041 896 235 800 107 926 433 655 907 672 351 666 468 051 665 216 066 442 828 833 209 396 104 653 104 330 640 240 414 431 624 868 485 613 122 584 767 365 918 863 330 911 809 922 791 939 376 736 614 675 125 832 402 968 443 392 992 304 833 462 749 427 188 558 839 805 042 343 872 828 646 757 614 404 943 329 018 541 245 879 303 354 594 522 205 394 929 410 517 554 077 057 595 311 828 650 694 146 798 783 939 443 973 854 248 064 447 534 561 405 954 634 570 313 168 965 528 046 163 883 904 984 613 993 618 304 314 218 375 194 689 014 533 273 841 839 707 757 030 889 555 318 300 718 138 009 810 026 690 162 050 203 516 934 149 175 097 297 661 827 954 877 298 268 823 080 702 685 805 486 990 201 332 773 433 078 539 027 562 416 451 591 054 864 867 233 138 164 545 329 082 330 981 952 737 108 485 402 964 499 893 375 781 266 730 385 523 509 660 771 746 387 724 134 814 698 839 899 808 393 147 760 328 311 882 222 906 498 084 097 217 406 978 006 943 585 129 958 547 375 877 528 880 319 694 748 764 123 955 843 540 363 281 402 366 357 093 715 471 795 424 385 566 769 635 869 735 673 638 115 154 388 876 638 544 379 594 033 658 141 035 231 722 367 235 017 774 239 981 457 632 499 879 640 834 316 123 245 723 628 458 464 752 247 945 858 254 914 300 574 462 006 394 924 170 845 208 896 552 687 535 347 640 685 840 371 833 898 528 898 087 398 589 620 394 308 534 534 426 625 837 975 398 345 360 420 143 239 706 022 902 366 582 745 191 604 889 179 152 679 612 706 224 186 963 271 610 388 845 753 001 429 006 881 961 445 565 183 529 769 543 535 967 995 801 592 963 309 768 175 760 097 643 750 925 226 129 760 798 947 638 643 089 838 812 017 047 901 086 414 187 683 622 375 186 208 845 834 409 546 778 232 604 300 582 143 015 750 197 627 907 281 802 984 695 871 610 565 346 192 523 621 664 974 662 530 421 409 549 846 098 651 645 268 671 741 856 328 751 065 294 839 191 300 384 743 096 755 483 403 188 488 444 587 701 176 588 843 935 082 973 606 308 145 282 450 093 412 829 458 080 018 043 651 790 836 642 937 283 372 775 100 560 944 809 218 249 973 289 061 498 956 362 106 212 047 936 561 344 448 314 456 305 295 839 236 345 431 443 231 556 616 309 879 946 862 036 561 203 349 722 285 457 768 508 890 897 160 302 444 052 696 406 452 077 341 059 683 316 828 748 033 777 600 176 960 014 746 158 503 016 532 390 241 658 383 678 075 201 808 852 505 073 470 483 443 957 334 757 544 806 772 382 005 477 962 759 034 289 779 035 534 459 093 233 031 874 176 300 334 950 199 649 233 509 756 534 472 512 171 493 218 408 507 785 684 565 869 928 571 953 598 144 563 870 063 055 032 547 794 269 774 917 803 834 414 827 883 861 982 772 038 581 298 274 818 781 696 968 507 119 763 541 074 743 155 574 428 447 979 862 519 652 982 724 810 158 776 720 142 077 220 946 914 098 686 451 355 295 439 622 618 547 594 773 806 341 809 720 196 505 855 283 820 530 058 871 826 693 690 386 305 201 377 632 712 125 072 510 528 757 155 887 162 018 052 921 999 001 133 350 199 369 962 829 501 956 412 401 855 835 175 807 549 076 383 318 791 661 105 601 610 707 054 126 060 982 343 602 207 435 692 616 978 653 196 690 979 686 594 144 781 405 453 042 293 876 808 557 731 049 004 656 450 758 448 180 125 078 277 816 856 926 705 932 258 919 332 194 437 899 088 524 601 249 644 811 340 339 203 956 318 543 179 917 485 946 326 592 960 248 329 015 087 950 210 120 689 502 568 644 518 788 417 150 056 855 804 372 231 855 254 500 863 715 229 221 250 304 284 501 639 966 706 236 453 479 419 166 567 627 209 055 961 212 263 955 946 672 022 272 107 120 151 213 988 455 320 408 478 028 719 594 795 377 469 282 867 778 410 267 881 726 917 189 394 697 737 279 237 933 624 507 073 648 264 087 830 863 833 402 734 697 471 380 816 707 700 901 366 993 355 930 303 550 609 769 595 339 672 807 570 936 121 702 592 860 062 742 437 614 742 048 435 474 035 669 343 003 769 151 496 277 382 839 444 711 538 949 981 680 094 818 473 930 689 294 860 812 576 876 053 221 440 568 703 010 848 843 488 217 439 884 258 915 159 343 041 053 169 787 257 954 662 883 845 820 568 089 811 088 691 097 099 720 722 293 486 744 112 882 509 388 205 117 101 251 294 369 803 087 089 920 205 210 859 779 950 644 634 067 910 946 784 440 354 308 627 784 162 196 883 311 369 273 568 071 747 754 922 005 202 742 941 266 957 272 559 576 951 969 821 502 679 689 600 440 460 269 847 235 101 783 725 113 937 073 248 422 071 132 121 325 285 217 821 427 423 748 507 654 463 425 726 188 628 401 668 854 669 500 741 216 463 522 495 090 442 627 649 181 369 948 283 535 604 955 567 814 151 359 673 724 910 081 907 116 989 430 505 839 141 414 487 286 462 452 173 209 324 543 294 090 281 575 766 675 409 384 842 974 560 501 709 010 407 952 691 999 426 405 841 489 434 287 988 304 328 237 085 838 226 686 284 071 315 375 152 707 390 139 580 359 784 116 973 847 739 824 916 651 300 229 128 013 477 155 536 725 657 003 047 234 520 948 929 839 903 899 319 145 492 866 028 648 890 124 925 633 108 922 022 186 927 871 910 079 212 806 859 903 418 598 418 816 929 434 781 687 007 219 255 389 049 962 435 581 900 681 440 877 523 239 044 245 440 393 053 553 246 076 988 907 011 876 967 075 916 990 767 496 693 885 798 448 698 832 634 490 330 434 599 131 585 461 653 538 520 661 689 357 105 050 674 486 985 961 517 624 493 787 428 209 930 771 252 252 075 453 786 868 663 037 235 847 017 896 439 234 428 675 393 239 577 148 532 822 993 042 402 894 204 819 663 680 595 943 161 171 837 966 119 922 701 361 248 960 076 335 316 159 936 910 453 701 697 972 261 763 241 782 712 118 176 582 347 205 830 319 608 273 717 757 672 055 311 848 800 004 046 441 433 033 020 840 951 369 274 930 895 092 196 474 939 669 832 929 529 358 519 422 393 681 064 912 657 553 761 452 257 911 902 134 522 658 109 173 172 487 995 419 341 879 673 378 406 860 711 747 145 115 401 463 048 882 222 600 624 035 972 586 480 613 470 541 913 005 549 789 246 168 966 261 077 947 528 720 122 792 251 596 574 817 421 150 064 461 722 923 997 947 958 471 696 742 460 202 911 312 240 982 283 875 761 790 771 819 644 958 153 719 953 129 321 010 078 463 127 961 569 710 467 291 822 723 896 906 739 826 580 317 864 687 156 295 878 515 884 423 276 254 362 076 225 415 260 448 724 582 607 987 006 298 402 334 380 522 134 576 955 589 210 171 086 217 012 745 942 126 777 689 973 573 472 050 944 091 041 567 405 245 322 549 417 607 103 993 516 112 983 432 602 528 592 904 852 890 285 079 161 531 213 889 381 264 101 172 762 474 020 270 387 366 751 127 777 668 771 907 789 294 722 992 274 380 128 109 399 980 886 568 379 525 863 598 115 755 063 358 424 840 267 529 006 811 617 432 971 669 369 238 454 685 301 710 163 691 305 442 637 808 515 217 547 990 167 868 526 913 801 293 562 927 227 344 667 837 781 578 786 825 099 187 013 268 841 105 627 247 335 008 542 150 319 629 643 015 195 382 818 775 028 613 218 423 412 462 800 798 009 759 544 929 966 039 558 223 795 843 062 698 577 182 834 664 281 232 154 188 128 064 294 083 109 224 346 217 122 512 475 864 093 351 516 146 934 245 211 527 063 544 402 852 910 116 732 123 314 676 493 101 277 638 120 120 186 272 079 695 190 411 899 809 133 235 888 996 684 510 529 895 961 808 882 676 404 320 985 964 123 831 050 502 959 337 216 393 051 677 152 815 624 626 126 088 010 084 181 489 071 885 235 014 815 008 086 166 387 594 529 361 622 423 465 407 246 226 436 227 287 017 980 424 080 068 634 818 154 504 735 549 130 510 696 920 520 850 533 209 623 873 430 128 454 707 380 758 582 239 906 976 575 768 270 756 129 735 849 923 453 527 460 538 628 190 941 059 981 846 570 337 650 444 756 500 092 483 787 913 370 682 751 276 158 748 325 279 813 082 986 772 128 068 512 785 945 855 714 641 759 703 411 061 061 191 654 723 799 032 135 691 781 187 099 051 667 514 678 150 168 027 143 240 231 082 740 554 084 823 557 392 555 646 046 289 895 647 978 546 257 726 064 413 671 395 544 697 211 033 375 398 384 135 860 748 702 713 002 661 045 639 292 085 744 260 765 074 168 596 578 300 780 421 360 825 468 286 884 855 426 581 706 008 258 559 626 760 473 187 371 983 169 318 526 478 149 942 000 669 807 776 129 141 425 227 638 261 873 432 362 147 972 303 500 749 296 425 540 170 251 979 601 492 630 020 154 091 862 405 744 933 239 563 637 993 332 849 910 153 341 677 870 781 257 578 435 845 611 806 955 941 729 617 321 737 784 417 886 047 985 702 943 923 158 180 210 370 570 051 663 887 740 620 195 088 321 564 918 807 728 631 903 621 063 703 211 669 076 291 706 675 001 345 875 174 915 477 597 267 636 329 072 599 706 760 506 485 133 810 015 453 480 339 531 023 016 166 458 916 819 646 080 355 916 964 747 185 009 787 839 567 291 017 688 646 871 978 914 524 929 197 584 110 199 134 346 247 670 349 680 670 266 858 468 307 481 559 745 861 698 758 837 488 085 281 844 401 610 920 912 629 861 366 096 289 786 959 743 664 535 814 145 304 328 092 809 438 242 473 591 057 338 341 919 921 246 126 438 764 870 819 605 942 900 688 149 880 679 056 328 663 275 684 135 005 642 057 882 484 654 710 328 946 849 643 215 170 993 804 099 368 496 582 357 346 757 294 687 429 235 557 873 569 385 707 576 158 983 289 167 270 651 700 168 923 921 438 406 229 341 148 350 560 512 280 081 147 931 805 280 333 518 197 345 268 560 728 109 359 775 038 931 437 770 749 077 685 210 320 380 110 088 868 104 314 353 431 793 430 398 817 333 209 995 564 659 225 706 380 574 392 611 989 073 232 080 513 986 312 903 818 681 099 070 425 190 740 315 271 421 592 413 821 484 560 834 706 938 590 826 917 705 961 679 775 308 784 503 922 943 729 752 050 357 926 191 910 384 938 053 071 626 267 454 233 703 653 198 172 805 972 591 825 499 307 991 070 436 317 765 220 155 620 408 489 441 354 660 624 937 173 377 985 989 503 923 966 763 272 570 704 654 442 195 384 177 571 305 406 869 783 510 648 807 210 324 369 679 816 986 897 731 315 101 261 594 548 273 811 057 827 322 299 505 465 717 954 744 816 922 918 188 550 962 731 416 479 327 588 707 365 662 263 736 268 988 432 980 406 418 971 946 610 814 315 943 139 139 684 140 144 342 455 148 808 715 126 024 359 259 230 255 778 894 612 325 681 083 915 209 929 002 300 211 947 513 350 690 952 902 522 032 221 584 193 906 122 043 500 279 906 151 641 908 748 913 129 681 803 511 798 944 450 765 789 940 321 065 163 393 468 808 720 812 632 052 338 095 394 317 416 750 407 911 750 236 004 435 408 805 496 525 139 424 110 427 135 188 999 339 228 544 861 369 780 230 217 183 778 830 433 349 255 716 553 543 262 644 818 536 183 539 447 528 880 940 270 000 894 060 742 827 075 289 965 927 302 578 114 904 436 281 393 668 237 206 273 689 049 694 626 774 201 908 343 659 604 813 399 345 038 545 312 959 874 825 333 232 586 413 954 580 901 437 433 755 435 345 700 539 996 676 315 384 162 207 303 304 259 129 083 718 187 665 932 630 115 345 139 118 032 443 696 259 539 730 431 529 360 385 591 672 709 727 009 543 782 539 807 530 977 052 027 773 815 095 272 459 405 018 915 475 098 370 105 149 513 913 886 876 687 177 226 469 218 562 196 801 639 356 540 465 734 877 006 455 049 957 372 910 153 679 430 106 180 949 308 899 383 558 388 530 549 623 201 654 625 479 585 120 716 061 255 603 670 180 559 499 752 925 961 845 339 347 810 618 102 625 833 799 481 471 128 895 268 463 871 904 900 751 867 421 007 665 626 193 924 122 250 036 480 186 899 428 123 048 018 312 308 347 379 502 861 242 769 518 091 872 016 675 919 568 483 548 446 376 414 561 338 710 426 129 853 516 414 776 625 170 517 797 004 324 496 617 945 941 350 062 419 277 196 462 366 652 164 667 873 766 385 205 160 496 991 785 634 725 453 479 486 025 549 599 257 144 475 931 668 173 495 365 091 267 252 186 153 121 792 814 524 628 687 117 291 367 600 317 199 268 678 731 104 849 474 660 009 171 916 948 482 819 640 366 387 501 237 879 598 688 757 311 649 542 836 812 143 273 611 189 395 846 546 599 812 873 676 654 216 443 205 375 145 559 909 191 452 226 481 687 349 399 399 791 984 771 333 272 248 954 117 910 063 598 032 536 160 394 003 763 189 871 863 071 199 407 948 316 189 652 428 032 866 667 392 544 800 148 859 820 804 730 451 161 231 427 901 445 724 871 704 801 664 406 571 740 538 166 104 706 537 720 678 226 068 051 061 310 222 451 962 488 693 621 926 263 005 160 921 042 759 198 953 220 067 921 863 719 867 808 502 665 746 153 474 645 927 482 387 819 970 631 627 514 877 882 775 006 077 406 178 527 100 083 542 975 497 668 094 723 692 875 781 539 018 261 722 894 775 801 545 129 607 855 479 490 906 770 370 522 694 548 642 205 976 598 498 907 081 693 655 929 683 468 517 960 892 371 730 232 396 544 375 642 775 687 558 121 104 109 532 508 481 699 671 656 841 302 862 838 853 231 112 090 627 760 137 481 000 810 430 335 714 737 064 064 448 009 961 256 165 820 851 469 631 296 889 585 441 144 985 931 556 260 174 480 307 820 012 197 442 671 155 562 923 588 287 189 397 139 833 041 902 874 790 148 824 976 058 861 134 458 912 398 941 489 918 048 731 346 488 520 451 748 083 496 968 119 280 104 627 161 411 469 080 801 049 206 221 135 305 221 126 847 660 368 414 135 046 404 320 659 596 007 610 251 460 053 674 801 007 527 047 157 078 561 882 338 457 541 554 366 931 650 967 720 843 923 608 807 726 145 370 566 910 544 420 923 710 111 869 273 282 364 613 453 543 949 119 788 619 950 218 025 406 251 342 449 566 717 026 429 561 710 631 993 900 191 455 311 702 474 411 564 203 169 349 777 699 409 317 890 283 410 757 764 044 508 583 436 383 343 034 342 459 156 317 434 258 099 239 895 459 867 604 928 797 886 987 612 378 899 779 694 042 322 405 524 389 768 746 396 899 241 512 576 295 807 650 434 343 796 369 370 557 252 976 707 806 412 241 139 935 188 014 547 757 903 755 615 048 459 030 001 370 166 637 288 479 178 743 691 632 121 716 691 934 827 072 372 600 663 303 865 685 640 814 531 265 604 277 085 680 998 188 801 338 228 921 128 745 163 750 871 059 670 357 127 554 391 087 861 575 369 092 892 580 517 331 586 993 218 991 437 158 625 227 629 611 557 907 321 838 444 708 535 456 381 506 815 582 888 058 401 268 209 937 660 029 275 328 372 650 756 875 570 140 863 706 865 364 154 492 711 760 123 886 552 309 954 238 493 652 521 387 300 521 769 230 859 241 605 791 707 360 767 508 380 234 170 733 362 639 261 632 485 848 683 074 843 488 101 622 579 148 780 647 118 313 769 448 220 039 251 463 154 074 509 865 382 712 304 024 732 431 389 204 475 237 586 234 306 808 699 992 183 504 489 455 459 186 261 396 234 110 629 806 577 178 112 152 085 365 474 207 731 959 157 201 112 774 147 004 848 035 212 824 118 442 190 561 984 162 596 394 186 199 032 774 463 463 654 587 537 989 568 995 545 762 553 339 855 198 349 383 281 620 390 623 166 660 488 027 272 479 111 931 599 270 627 756 732 994 834 408 366 000 732 902 156 986 218 637 453 633 852 731 640 184 347 756 324 241 116 278 812 156 003 426 293 520 326 353 107 135 467 345 853 560 957 007 155 462 385 618 598 456 843 479 566 297 176 954 826 984 581 687 847 851 334 284 548 073 587 399 579 692 383 795 905 282 984 049 757 655 056 231 473 676 508 645 034 441 326 020 440 968 762 556 259 318 542 029 450 419 513 672 760 524 122 709 965 403 034 838 092 685 825 359 154 120 662 062 257 857 816 590 786 735 831 603 946 270 038 001 939 972 588 202 338 589 680 747 754 447 803 538 473 451 910 133 569 435 123 538 395 403 430 957 412 114 710 960 511 718 128 915 408 873 978 060 306 096 088 004 286 175 300 311 122 134 611 416 043 831 429 263 784 695 219 320 099 137 029 694 011 433 521 419 259 336 919 192 213 067 683 700 787 788 271 170 194 172 828 627 532 728 024 136 915 787 952 040 525 606 919 150 969 148 971 171 035 286 924 052 204 795 705 759 168 332 744 698 671 771 295 047 168 669 064 540 660 376 507 246 014 313 093 344 001 306 718 242 269 686 949 706 731 096 223 912 243 700 936 828 931 342 715 634 926 029 153 286 614 260 199 401 389 437 703 077 014 509 722 817 068 035 095 300 294 109 171 766 702 554 400 475 696 252 105 217 066 244 570 266 293 559 624 077 427 535 983 759 001 912 037 143 355 480 323 126 843 420 282 384 255 274 997 971 641 116 048 089 173 248 394 065 009 296 926 575 777 766 824 105 586 286 347 818 748 916 111 547 857 043 280 244 645 140 200 942 954 490 942 106 345 681 951 264 030 270 264 428 018 106 563 409 594 896 305 936 688 562 544 222 120 794 976 501 807 393 630 427 416 205 991 152 531 050 260 307 766 905 555 242 125 579 041 919 858 991 466 773 859 384 281 416 483 466 461 172 718 478 634 868 669 317 816 419 018 672 688 010 947 707 791 006 906 650 916 964 846 236 237 789 398 851 788 110 111 323 682 542 256 074 412 709 353 570 440 800 670 702 840 078 304 465 121 475 261 997 962 597 040 651 480 939 231 958 705 570 572 573 493 086 858 444 838 678 008 134 367 876 303 113 043 586 882 339 704 938 031 472 222 457 770 212 476 555 318 083 567 479 050 320 739 630 531 248 697 193 354 683 226 411 355 510 569 572 886 615 936 484 021 681 139 659 341 188 881 924 357 303 630 423 736 013 201 799 366 662 333 388 086 336 498 719 678 426 660 397 122 401 478 565 891 288 037 940 219 585 491 809 150 147 709 460 380 173 321 659 706 603 947 952 668 016 856 340 195 427 942 302 381 298 325 964 131 962 132 842 653 191 888 352 102 792 852 410 828 039 930 890 828 697 796 864 066 698 571 438 277 825 960 009 214 618 415 918 173 948 748 126 535 733 146 669 008 669 060 967 477 017 301 914 149 730 772 992 117 917 885 357 658 285 980 770 741 409 409 086 492 273 862 053 112 480 531 050 844 764 402 985 577 203 914 600 118 742 356 775 549 884 874 424 172 680 750 343 085 335 888 571 825 676 134 542 196 088 266 847 492 284 083 077 387 092 450 755 037 566 156 374 213 496 948 401 105 696 639 364 093 429 615 088 881 941 575 487 664 217 475 239 412 433 452 930 136 282 646 997 923 752 225 922 256 998 929 373 523 431 213 801 291 645 130 420 610 782 096 645 132 584 999 634 537 829 100 987 949 698 619 539 161 905 341 406 812 478 229 913 386 221 244 912 664 612 317 637 224 769 155 776 932 724 964 472 844 497 848 058 423 397 388 418 629 364 418 869 031 854 462 260 329 333 488 299 387 277 151 824 159 981 553 268 400 329 154 993 278 326 740 928 510 096 487 621 924 400 816 974 452 946 196 322 111 192 470 256 610 172 008 893 988 581 045 454 159 646 178 376 101 849 037 590 543 167 154 897 476 880 582 211 945 818 008 194 457 734 351 863 963 481 936 495 976 748 634 970 789 741 301 810 843 255 671 540 517 090 771 806 533 994 012 570 142 691 570 158 673 101 895 556 426 497 142 949 598 452 484 275 642 395 276 192 438 209 651 114 221 057 901 549 558 195 785 568 584 593 075 926 466 899 771 156 209 239 372 533 110 753 863 633 785 581 842 658 739 741 829 024 672 759 849 799 951 975 061 508 746 298 688 404 694 749 800 497 158 156 718 187 240 298 886 073 389 835 892 288 249 103 442 932 844 072 266 362 415 376 092 469 590 828 331 744 718 594 123 405 893 863 834 832 996 085 320 619 572 460 313 758 454 681 004 558 118 062 207 070 590 962 845 238 175 737 279 223 058 303 658 876 510 535 529 596 685 778 855 321 921 958 352 907 905 140 702 521 006 267 967 070 537 359 301 896 906 752 132 313 397 635 557 849 163 625 056 863 754 873 267 783 210 478 891 442 249 998 914 560 993 271 131 116 987 602 180 125 650 210 807 422 713 945 203 658 518 282 430 922 512 356 885 612 826 442 001 665 878 257 352 549 683 124 677 021 411 912 366 544 477 090 135 917 170 538 430 905 711 600 486 136 293 102 125 157 905 182 923 733 457 315 127 207 280 876 094 348 780 620 208 263 444 268 847 592 562 815 743 943 579 662 088 073 897 421 328 786 201 362 206 516 200 440 752 281 354 069 544 350 608 171 893 608 698 144 251 656 997 232 246 758 744 661 531 848 737 420 631 441 683 696 788 525 168 149 212 705 754 881 797 116 436 256 134 960 126 550 412 658 914 947 344 787 172 407 296 472 807 981 269 983 178 380 925 778 514 933 964 241 481 622 399 289 433 928 209 360 353 248 251 209 176 654 117 315 675 014 686 134 075 853 088 777 535 599 162 958 399 214 153 031 729 867 541 423 120 182 778 490 645 532 523 523 160 492 655 884 548 211 183 891 321 631 424 791 096 361 290 659 662 442 228 852 608 807 482 344 955 126 141 063 767 581 805 827 023 692 362 178 287 812 758 910 341 096 638 056 150 965 241 633 813 114 220 067 476 216 436 428 250 716 467 117 191 398 134 589 984 798 745 487 197 523 559 985 231 414 323 230 908 815 396 676 091 362 933 545 940 276 283 097 959 192 335 860 382 506 931 019 732 619 354 613 642 228 452 488 399 436 995 023 915 517 682 144 549 287 218 827 802 889 281 906 739 294 109 078 414 649 321 936 366 639 955 657 204 907 429 522 778 081 434 178 672 281 358 476 277 991 831 658 676 978 491 958 290 394 597 362 012 610 049 049 289 137 298 168 760 468 776 987 267 447 536 185 396 402 118 095 548 070 265 164 113 288 754 046 483 825 407 542 157 230 908 550 810 535 371 548 262 905 961 175 747 061 073 777 982 583 223 003 103 685 167 300 217 310 122 101 676 262 428 111 003 729 503 535 011 691 481 325 536 417 882 785 569 077 999 179 423 786 710 834 747 485 614 659 769 813 770 496 313 912 458 759 847 272 337 036 896 231 551 296 054 316 899 792 132 406 740 932 678 829 318 105 290 536 644 719 643 861 501 541 426 814 902 893 270 493 490 036 618 211 115 325 063 288 356 089 011 008 104 393 781 549 831 426 103 746 425 005 681 872 297 484 398 284 031 547 747 986 796 237 048 013 055 414 633 282 612 802 441 722 405 869 842 326 655 824 818 673 332 498 406 612 187 850 150 413 799 813 099 060 713 870 758 594 724 398 099 007 322 241 487 729 134 460 239 983 152 225 968 498 102 668 118 355 915 605 379 130 306 424 944 547 650 005 229 044 281 283 038 093 250 176 450 237 354 314 067 034 843 352 057 789 274 184 071 051 242 341 164 400 923 397 577 374 520 710 243 423 775 461 667 465 553 971 486 605 001 615 749 435 479 248 396 067 758 331 567 580 921 699 666 756 034 407 684 973 825 458 248 613 191 411 525 728 944 685 530 820 273 919 135 028 708 720 455 951 551 123 003 586 230 589 007 292 084 420 782 868 794 359 772 182 845 115 967 656 561 611 090 919 658 946 319 317 063 762 150 370 664 472 073 288 480 669 079 975 569 096 305 661 006 246 380 360 418 591 883 331 844 183 085 162 181 631 328 112 899 729 161 783 305 697 265 414 424 997 179 482 434 517 720 597 756 031 999 234 675 136 330 323 342 423 877 224 213 008 909 267 290 689 453 040 274 539 920 461 811 727 569 510 729 340 837 254 720 677 593 045 838 558 355 338 803 615 571 688 070 824 194 611 402 962 671 158 041 993 545 031 758 047 939 978 998 725 864 442 754 819 911 886 932 853 868 816 971 753 957 966 997 580 972 164 503 526 023 027 357 608 683 279 649 928 308 778 099 816 105 644 159 483 768 289 712 659 038 125 222 631 519 163 861 397 877 618 564 163 241 309 518 833 033 155 830 956 347 940 422 348 339 306 778 468 771 134 334 940 010 942 586 649 373 168 114 967 622 182 485 548 000 053 502 391 392 351 730 024 848 614 957 189 218 806 064 270 445 900 722 452 417 998 752 364 281 230 698 729 264 811 127 049 527 031 652 245 403 429 903 155 440 795 094 467 601 398 461 144 472 773 143 598 251 549 002 860 104 213 621 028 484 482 122 279 863 486 627 412 346 311 370 154 337 427 583 674 175 160 633 835 969 666 239 738 240 906 954 130 651 300 630 516 094 106 144 723 901 086 494 395 902 742 221 700 978 208 048 332 960 179 157 373 031 597 811 057 902 246 519 117 996 888 702 134 849 377 039 913 264 910 967 757 165 630 043 517 377 882 383 777 952 805 993 398 826 496 739 388 723 345 725 650 734 779 550 755 430 555 368 386 650 644 945 421 013 583 934 054 079 885 658 396 926 687 571 178 863 820 870 754 827 405 754 904 025 450 658 860 424 628 564 342 953 024 403 666 156 066 833 105 150 465 193 292 744 678 875 402 900 064 461 355 463 574 889 300 230 200 066 087 138 612 679 651 258 071 785 445 126 711 699 140 733 173 749 895 930 698 124 790 852 133 114 377 674 087 201 060 071 331 596 385 142 505 122 904 565 621 930 394 614 893 750 302 262 413 230 750 189 997 169 523 396 895 598 176 277 576 703 599 697 165 437 316 621 481 927 661 003 006 402 106 290 149 745 230 676 136 407 241 260 649 688 064 660 286 054 160 161 557 479 411 762 786 081 387 164 299 324 668 649 311 279 224 039 766 451 493 141 210 689 146 503 129 349 275 915 459 024 135 472 610 795 843 839 373 397 869 796 024 860 760 899 643 538 053 037 370 473 639 467 160 289 112 111 360 133 592 316 660 213 185 629 046 550 485 966 047 867 353 053 694 335 297 558 064 917 380 414 736 236 105 595 059 964 726 849 889 072 721 033 792 511 093 536 378 053 868 253 222 808 704 408 589 907 703 875 332 017 656 334 454 142 668 356 627 106 430 464 376 587 268 408 180 710 799 990 546 221 093 777 132 055 191 295 816 556 745 981 675 380 079 425 651 216 803 809 584 391 948 512 524 889 237 588 481 160 027 595 745 676 634 824 477 430 604 690 881 172 974 240 817 160 053 241 473 388 323 482 392 665 799 333 695 213 373 890 470 210 769 308 944 218 193 210 053 414 648 568 255 279 022 557 649 038 047 682 384 225 921 116 614 336 045 476 521 550 858 663 801 369 113 626 780 058 894 234 628 459 095 917 656 515 219 719 439 562 347 091 281 452 674 127 540 150 153 309 219 852 775 249 725 409 352 508 765 354 861 925 818 298 340 798 557 639 727 053 423 176 068 869 079 813 324 448 179 587 306 892 356 892 977 675 159 579 597 290 933 231 589 777 097 317 355 595 367 680 488 465 305 915 713 903 876 753 604 681 881 293 960 179 739 353 728 313 186 199 129 001 013 444 886 644 466 174 522 302 823 892 349 314 011 353 973 536 673 258 990 139 949 858 873 679 060 827 039 069 054 798 624 737 752 669 965 825 866 197 386 507 256 499 302 354 676 762 402 309 454 054 167 652 213 059 273 064 477 550 284 879 780 426 050 677 814 320 337 374 799 691 471 915 161 103 293 386 984 507 674 906 783 338 010 901 202 805 956 393 109 530 872 117 484 115 158 680 989 817 097 685 976 738 647 718 666 562 042 485 396 702 961 973 730 648 898 871 761 153 062 280 587 280 806 432 581 670 879 497 066 144 715 660 374 586 506 003 768 975 131 148 129 723 427 914 795 822 316 236 001 416 421 524 780 656 110 199 677 587 283 522 251 630 551 547 749 648 544 534 061 464 769 748 674 420 411 400 941 772 747 717 207 441 464 847 709 368 100 626 429 042 517 094 793 243 117 555 404 676 408 451 089 997 331 983 724 737 990 162 381 889 374 258 755 021 413 352 301 415 039 770 249 110 524 897 611 323 609 314 330 086 930 499 120 121 467 247 488 690 732 340 259 614 692 108 851 371 716 176 037 668 295 530 080 512 097 713 358 669 958 085 880 974 971 670 560 412 812 873 774 452 465 551 505 377 653 689 530 951 255 913 696 501 322 726 568 816 563 092 314 832 556 600 889 330 815 293 799 379 236 649 090 634 568 050 669 660 192 269 730 984 158 926 252 051 347 631 721 574 237 138 898 154 415 760 360 368 831 359 616 918 233 527 273 053 370 174 716 975 538 909 743 771 077 647 308 067 555 226 346 077 237 233 311 526 886 000 119 271 176 681 376 517 426 452 674 697 677 678 721 957 270 505 137 917 475 121 452 575 577 511 532 184 482 400 756 278 685 648 418 226 860 787 023 906 822 270 327 879 916 440 839 064 244 369 668 860 152 715 636 103 400 404 302 091 556 887 880 491 854 285 289 294 254 137 684 304 482 736 928 025 136 974 553 062 239 958 731 388 556 451 161 127 712 033 533 465 101 045 705 809 655 231 858 230 577 503 776 143 925 487 421 033 795 446 402 885 805 208 618 125 284 708 841 795 661 111 630 465 493 757 711 931 895 899 256 504 644 423 367 784 033 467 674 255 814 435 998 732 530 674 078 581 943 285 418 210 022 428 983 777 468 174 106 181 411 051 879 376 132 466 465 417 394 029 098 762 388 866 233 763 011 949 414 435 753 723 326 611 839 178 043 812 329 104 837 861 835 470 537 510 815 346 153 298 244 371 466 965 597 469 141 391 735 732 947 266 218 103 113 240 645 743 637 114 739 547 021 874 604 444 559 543 630 036 800 280 970 686 865 858 813 707 382 548 241 721 546 106 075 585 145 779 089 797 647 812 642 682 458 095 668 008 279 603 592 778 954 327 136 741 143 119 313 964 727 357 804 433 683 869 289 195 141 199 368 699 139 662 763 548 330 046 719 213 018 125 339 014 885 670 221 528 454 611 489 921 606 804 904 257 711 415 947 702 951 734 398 367 055 595 332 563 160 801 917 735 186 041 762 122 496 720 597 189 221 146 569 363 659 144 513 938 822 597 560 832 238 544 282 136 204 217 503 178 829 791 514 869 782 800 682 543 800 351 255 438 536 869 832 278 607 665 953 199 502 631 602 799 176 788 857 747 481 264 740 043 867 328 226 696 632 035 624 136 645 491 392 635 196 508 311 727 997 010 162 070 285 873 552 908 950 497 228 660 794 606 480 321 973 655 826 612 908 728 185 745 138 973 666 168 529 675 262 879 952 704 583 812 279 086 936 857 175 802 788 236 174 846 971 401 424 451 318 904 434 108 586 691 203 817 506 912 628 547 070 523 889 654 444 913 132 281 213 838 931 491 765 072 499 192 268 444 755 077 447 469 800 231 336 122 174 243 870 404 672 942 902 725 096 283 537 953 476 017 644 403 134 897 062 723 250 163 229 864 417 424 982 342 662 168 955 929 723 911 597 796 226 209 635 950 118 375 204 975 538 298 812 521 351 252 598 119 430 198 610 965 711 574 864 533 107 804 997 905 208 570 143 302 670 486 892 644 270 665 933 117 508 887 546 118 178 332 473 163 887 969 205 530 007 018 345 791 353 983 584 641 750 404 170 623 358 379 561 358 152 258 300 390 863 863 075 542 225 354 175 614 866 258 342 658 648 768 536 425 311 356 258 430 640 648 957 474 371 226 884 443 787 148 368 794 119 170 428 068 948 619 816 609 029 874 078 813 718 713 087 809 775 118 348 448 773 366 876 755 634 567 429 754 948 138 053 666 410 839 443 788 913 460 596 301 352 053 392 301 139 326 944 896 856 945 783 928 009 563 640 376 159 657 331 203 827 328 941 463 270 259 340 000 027 496 795 227 327 509 098 231 731 424 223 299 189 197 708 354 484 099 083 088 045 095 198 863 291 536 375 526 478 958 759 683 134 141 521 195 465 556 985 859 198 132 289 977 169 908 041 277 353 016 751 779 700 363 481 340 804 695 759 938 232 273 128 518 320 713 881 791 784 095 084 760 421 605 651 138 014 387 231 349 770 932 030 169 304 128 897 592 651 224 288 883 236 399 114 097 693 261 107 208 973 432 620 660 438 169 022 952 654 248 308 954 908 996 241 573 901 469 323 383 941 794 534 018 437 027 784 445 144 829 289 829 670 216 221 918 445 981 974 376 282 651 222 460 275 476 063 142 016 613 787 877 268 734 860 107 710 171 610 732 385 456 903 896 415 773 561 648 842 418 392 901 834 276 910 723 913 976 969 857 909 192 302 949 278 647 990 831 994 728 894 525 370 660 639 244 227 121 910 913 419 817 311 561 842 387 796 909 700 683 980 157 473 724 935 601 960 023 328 429 596 732 613 315 594 030 924 959 546 826 702 733 689 282 077 163 487 002 086 222 364 919 716 038 801 738 744 180 497 723 283 212 779 789 282 956 406 674 818 764 779 827 313 970 844 228 599 242 276 171 874 859 763 956 045 370 938 616 761 404 690 737 352 869 877 779 709 581 046 158 818 653 364 612 587 114 177 670 040 239 853 612 217 793 153 343 103 884 722 024 395 065 583 423 171 286 629 469 574 094 969 060 635 123 391 708 362 474 464 151 862 666 061 994 438 026 998 767 252 103 692 458 963 580 736 963 663 363 467 370 205 773 841 556 642 290 769 289 986 555 372 455 127 819 100 130 976 237 734 233 228 511 337 957 865 902 473 494 764 376 658 777 987 199 213 033 131 885 617 111 265 242 842 304 201 338 828 361 760 437 683 848 163 311 917 102 052 989 529 325 186 515 802 768 902 423 052 730 921 213 749 717 077 977 508 697 258 648 460 317 541 610 924 306 440 913 561 573 599 579 304 049 374 768 626 689 065 126 486 302 126 573 541 169 615 122 355 105 342 682 531 192 591 110 537 484 040 006 917 785 614 832 465 886 607 750 646 031 408 587 656 940 239 810 552 585 314 097 067 977 131 799 674 443 848 760 938 730 694 217 866 370 714 152 571 311 122 432 292 715 389 215 068 665 114 690 338 991 397 975 071 262 442 537 794 740 843 364 663 296 295 242 938 663 626 806 729 703 650 339 361 631 745 494 735 229 925 732 489 185 936 862 604 151 241 848 494 769 001 874 198 551 222 394 727 638 467 948 509 774 464 923 895 164 875 038 238 171 719 989 100 735 003 362 004 111 205 145 821 914 097 772 356 622 341 926 429 365 681 336 703 997 949 170 838 382 785 630 139 815 060 975 806 274 661 320 264 847 234 696 371 279 277 695 024 999 978 517 405 641 022 112 122 068 570 840 501 926 112 990 585 876 333 163 634 774 448 250 748 192 374 589 488 225 283 447 738 608 122 641 525 598 358 790 260 368 015 932 720 038 211 622 502 694 760 901 749 023 635 934 285 917 833 118 089 094 216 660 855 488 476 087 368 797 894 376 140 469 147 256 825 765 441 095 598 415 063 708 841 040 876 469 910 554 451 098 947 301 906 338 232 061 007 381 563 004 543 548 272 240 370 546 008 293 641 001 466 912 874 937 407 368 183 097 093 248 899 505 966 762 733 591 367 680 032 532 800 030 518 717 276 299 801 010 269 098 324 643 459 216 901 982 110 114 758 994 252 023 565 084 941 826 633 134 022 858 815 071 804 509 767 883 293 062 853 699 376 607 819 310 872 642 322 850 243 020 853 333 776 880 481 726 036 102 692 566 524 329 686 262 897 224 955 684 838 499 318 237 532 716 720 820 683 319 425 567 338 298 718 070 700 159 281 981 820 250 393 148 329 844 080 939 862 847 296 691 713 808 611 931 178 583 716 924 600 717 948 160 683 273 365 202 045 358 761 788 841 975 302 235 951 012 730 503 362 617 408 214 036 215 535 436 236 946 833 778 779 626 797 214 825 127 359 159 033 982 104 690 904 094 848 357 553 210 176 150 009 442 925 267 060 632 305 384 359 920 092 360 417 632 720 139 137 645 791 238 711 589 693 260 977 156 356 178 896 542 270 278 686 058 785 081 865 461 145 724 129 189 999 149 926 116 875 317 463 813 021 656 505 531 681 746 564 039 689 670 409 265 945 924 207 012 641 225 372 155 236 417 555 778 842 879 449 428 997 816 459 322 404 259 211 817 542 642 033 772 670 394 058 916 129 504 871 432 304 991 783 203 761 619 292 646 647 228 574 124 631 715 287 873 008 926 101 789 643 220 316 855 267 158 980 737 969 211 374 566 315 507 422 215 239 206 671 420 854 072 609 816 390 802 354 295 074 224 955 042 297 521 120 114 203 968 483 691 159 512 448 517 549 635 338 459 109 699 808 093 197 114 371 822 329 648 175 422 087 096 732 638 011 247 805 116 020 311 393 552 637 691 617 641 898 328 218 498 840 322 856 963 128 359 609 559 946 895 490 195 076 761 218 808 105 705 449 323 876 313 710 384 665 642 417 724 150 630 421 525 381 720 067 062 322 830 503 678 737 128 435 458 657 426 103 872 889 944 275 268 678 486 779 464 209 840 273 454 665 480 345 802 948 722 351 264 204 751 504 789 874 396 602 151 803 077 193 927 617 469 491 618 569 517 712 189 398 290 784 717 315 449 102 956 175 318 344 924 399 363 377 158 274 843 432 836 616 534 179 821 214 858 770 926 241 088 043 660 394 603 616 510 953 009 439 057 713 710 252 888 143 672 993 221 139 036 069 588 901 442 188 783 780 713 344 066 635 071 183 072 375 027 990 744 177 369 779 438 003 236 646 385 970 801 389 908 747 051 073 505 561 935 421 883 603 294 364 662 339 205 907 858 454 486 891 053 923 006 828 216 174 856 677 727 292 516 669 450 595 443 841 851 435 145 067 957 065 119 566 727 007 907 736 769 557 963 407 453 425 252 669 642 666 558 223 642 233 086 701 993 827 457 497 966 538 285 048 483 802 536 805 439 703 842 659 738 442 937 072 955 388 476 930 390 628 999 662 225 535 174 370 958 078 635 145 756 357 502 089 601 562 879 252 334 727 471 521 923 295 491 296 758 457 325 692 366 234 469 329 953 831 915 132 442 497 538 879 080 134 121 370 137 222 632 645 684 946 772 339 612 719 736 628 398 307 501 585 953 190 345 918 319 722 283 713 215 948 997 789 814 606 610 671 872 638 848 161 328 002 245 745 580 181 202 661 374 899 826 343 010 907 021 933 847 086 686 785 555 365 731 542 538 587 403 459 474 827 109 072 996 897 447 915 118 372 835 717 320 221 875 516 349 045 053 149 405 800 363 066 883 456 314 611 514 419 836 799 384 881 911 925 430 659 621 670 438 549 987 420 820 789 214 376 618 458 792 587 528 815 133 024 390 727 608 260 289 043 914 083 974 381 768 243 561 129 445 696 756 884 942 607 862 105 744 257 290 387 326 827 074 678 880 993 513 948 732 866 033 105 043 756 527 767 143 030 647 936 755 498 149 636 680 921 303 909 362 148 307 249 911 526 048 986 810 852 706 645 984 917 128 650 412 272 795 736 177 453 663 159 904 754 292 989 477 992 397 429 173 377 090 241 463 390 209 470 911 714 081 576 375 939 738 386 067 797 050 096 874 715 760 896 575 001 505 893 448 118 055 248 112 790 832 809 314 376 053 518 788 108 212 101 489 728 146 216 439 761 279 095 977 714 982 760 323 595 919 072 712 258 741 354 319 470 898 709 276 671 566 924 100 360 870 042 858 461 744 031 221 636 507 165 718 099 679 401 706 943 919 087 947 618 265 690 148 258 111 232 074 558 322 182 241 852 546 535 004 375 597 378 908 274 805 591 829 224 342 886 502 310 007 150 782 509 103 953 486 702 912 725 315 456 793 787 172 803 102 569 610 801 493 774 185 252 347 788 491 261 047 393 827 185 308 065 672 580 994 863 344 942 841 326 352 252 004 740 123 065 288 208 406 859 659 759 739 902 126 573 350 154 098 141 024 973 666 632 632 959 888 924 494 343 245 409 687 235 482 850 595 381 025 468 213 795 850 327 659 210 278 792 911 784 931 339 920 246 619 807 458 454 696 861 127 415 639 761 451 298 572 056 238 130 604 341 600 376 262 758 688 362 516 939 951 356 183 670 353 931 756 984 746 242 941 877 454 061 118 004 375 122 366 936 189 297 439 788 145 519 226 376 728 945 026 229 445 861 322 837 636 921 359 908 997 170 054 667 505 870 315 250 931 538 752 703 588 341 373 292 309 042 692 248 045 192 374 551 530 674 850 823 659 390 802 747 987 183 622 841 183 315 033 701 605 362 692 309 617 789 874 135 291 276 027 119 662 752 867 933 358 617 243 452 403 374 110 108 024 175 899 162 988 181 852 868 231 215 052 230 701 315 817 819 761 998 602 552 150 111 590 947 829 542 362 443 642 917 254 146 493 774 589 515 061 150 951 763 822 380 650 813 775 734 192 961 819 688 763 483 206 821 118 229 290 536 058 390 814 814 111 439 544 307 308 588 728 321 081 721 219 939 056 561 773 028 208 703 302 895 497 401 048 782 846 033 210 383 752 149 808 999 604 002 850 985 136 662 442 513 361 346 322 099 456 073 193 494 429 181 537 924 499 797 447 037 717 680 688 527 802 261 197 614 695 317 642 927 704 699 217 051 792 958 320 669 976 500 430 447 830 068 173 135 600 479 745 472 531 667 055 595 246 176 073 464 313 309 770 741 543 423 789 315 831 723 644 944 564 203 249 800 288 704 912 521 203 381 307 835 405 497 025 078 974 318 835 927 304 239 449 993 935 168 985 286 867 511 026 803 256 661 634 699 436 869 960 119 837 640 999 197 752 921 248 176 225 642 378 862 651 121 877 203 063 148 361 195 138 558 963 489 505 378 913 859 838 860 750 636 734 420 342 673 962 021 583 371 277 842 164 178 658 505 458 772 535 637 006 255 899 527 856 668 473 314 979 668 560 228 120 519 053 802 618 058 625 978 824 050 606 778 883 942 060 487 492 162 984 294 310 618 550 031 728 972 466 930 930 363 612 153 483 695 837 490 704 024 866 497 695 637 757 004 775 244 260 582 217 815 094 466 305 084 392 012 877 434 942 670 350 728 109 027 830 347 921 951 186 992 719 309 810 285 766 770 392 003 634 507 535 947 178 657 665 231 010 338 946 127 567 188 933 841 963 398 112 560 803 988 426 888 749 702 790 134 402 308 470 629 014 273 500 251 112 146 983 630 735 910 226 310 844 784 272 848 989 293 508 554 449 582 196 055 915 759 403 698 630 526 925 509 528 130 945 704 618 331 231 367 814 947 582 426 936 391 789 362 342 234 329 481 029 769 571 936 525 333 994 767 540 415 228 264 610 045 087 760 822 527 446 904 594 209 171 423 811 742 812 851 190 189 177 366 560 660 713 749 605 115 324 145 466 079 468 492 250 130 853 450 683 218 348 479 444 029 052 108 709 722 443 206 600 191 205 764 361 346 922 985 684 581 732 383 315 461 383 003 837 573 486 191 499 613 605 467 554 133 230 318 386 190 501 404 049 305 469 883 014 714 090 145 744 995 842 610 530 357 805 137 170 475 602 729 735 365 589 434 862 813 227 869 730 615 475 546 898 210 226 546 301 823 283 814 729 160 837 359 894 638 433 405 856 524 712 705 431 511 198 974 720 572 755 064 601 965 807 710 421 440 735 186 764 506 937 977 803 657 990 979 142 566 513 636 383 431 229 853 716 581 787 632 672 295 586 591 403 956 259 421 416 191 060 892 413 576 304 377 073 428 188 099 510 704 323 248 147 003 823 822 912 817 316 834 515 569 921 624 214 227 183 516 186 028 972 164 244 348 861 232 565 003 558 740 303 720 693 682 064 321 300 882 683 698 604 414 132 424 144 241 037 503 810 094 442 200 104 955 576 587 234 253 518 120 133 729 728 660 738 078 725 816 766 155 389 550 775 042 806 168 423 098 895 937 027 405 478 742 166 953 032 694 306 157 992 533 214 420 789 914 156 754 783 584 017 184 754 700 463 096 263 982 397 511 372 556 250 042 280 819 491 961 295 392 961 289 883 949 444 371 402 544 119 270 792 102 988 886 168 006 807 712 225 119 151 695 303 497 153 503 111 546 203 447 255 666 628 857 780 987 031 178 335 362 974 231 044 594 887 590 244 313 097 753 179 103 620 833 275 362 347 567 893 657 598 411 588 640 320 316 308 711 546 391 915 210 039 375 035 300 946 827 217 724 980 294 428 908 123 307 090 723 170 545 823 156 789 505 305 815 195 578 139 243 158 215 413 989 400 529 597 150 241 492 925 075 893 997 533 038 144 543 683 876 422 473 181 119 330 939 603 109 489 946 770 170 093 438 290 734 871 419 869 211 847 449 505 556 786 801 712 887 397 250 558 738 435 142 358 049 389 729 621 131 092 099 141 690 970 368 829 256 814 646 878 971 757 732 587 279 839 310 754 009 933 968 008 280 174 925 697 773 305 226 877 613 294 197 985 689 314 000 269 555 090 651 396 439 855 440 757 348 925 210 175 373 760 684 412 500 843 277 716 279 666 339 781 405 986 696 073 125 995 042 529 876 029 184 910 276 174 893 866 118 136 802 577 593 988 094 722 115 429 486 826 077 369 881 386 310 372 350 438 370 258 461 201 156 393 855 598 471 305 162 582 403 632 880 298 587 056 253 619 419 989 026 423 758 772 029 663 050 020 109 359 099 818 088 453 261 009 943 259 733 579 333 870 747 650 917 125 630 736 637 204 669 189 181 943 760 019 753 359 595 178 825 771 542 252 142 881 676 947 772 498 200 709 317 845 241 620 375 050 860 554 981 409 884 142 226 756 175 380 854 720 813 820 763 442 272 670 298 505 134 685 245 885 496 462 732 459 680 535 535 546 766 785 971 546 923 769 589 643 630 222 571 108 954 831 786 653 049 091 536 359 551 786 705 955 344 351 289 696 342 879 427 209 928 826 773 456 513 676 368 737 896 528 676 499 742 349 454 264 266 174 160 067 932 422 592 787 836 340 488 443 163 452 446 084 391 237 679 128 454 861 049 634 579 084 713 894 970 671 142 576 515 116 781 880 386 181 978 885 356 731 616 866 171 783 903 583 677 124 098 322 264 922 058 231 133 094 663 276 296 717 224 699 520 634 393 936 195 955 888 089 017 461 263 995 954 880 491 707 741 467 487 907 091 684 679 143 655 979 907 503 651 050 829 780 042 165 709 673 856 182 610 051 186 488 325 463 963 576 922 003 790 115 114 084 702 935 608 666 033 586 158 610 295 269 061 308 584 717 979 265 616 424 644 262 773 481 908 427 978 333 941 652 365 908 610 680 777 138 180 222 498 238 808 722 286 886 699 699 779 724 297 123 818 642 755 161 396 337 456 443 412 842 707 992 988 106 223 026 441 757 516 345 881 086 564 497 049 618 979 144 775 781 115 655 888 551 471 408 868 528 310 520 483 777 926 992 599 160 223 396 176 153 174 333 371 222 544 151 107 863 046 395 595 498 033 231 635 954 804 354 563 359 586 391 034 325 039 542 169 521 239 781 948 515 395 365 708 078 191 794 604 935 520 651 325 898 531 664 375 171 266 291 539 050 838 130 434 410 726 547 126 343 207 992 577 900 633 148 613 859 837 436 531 563 018 397 122 445 366 180 991 436 934 689 770 622 467 592 689 085 873 300 110 324 177 012 992 232 480 578 201 236 297 394 811 830 970 000 779 104 500 713 323 713 576 270 529 740 823 102 848 180 445 011 822 992 681 383 728 764 028 590 904 831 491 421 247 483 400 650 249 701 958 509 647 853 926 327 590 556 470 940 787 015 420 504 332 662 815 301 990 319 271 872 618 427 105 968 064 001 978 181 712 035 150 009 769 266 798 384 538 276 208 158 034 397 284 379 526 103 058 253 336 669 163 179 221 023 087 211 220 300 592 764 295 742 735 609 856 450 982 436 638 224 067 990 987 378 272 114 909 919 717 965 337 940 354 278 483 239 430 537 575 759 091 510 867 687 662 458 081 892 292 859 230 927 397 129 089 745 302 083 802 732 770 169 046 503 695 786 319 922 171 442 419 530 993 748 956 439 378 281 579 613 682 683 784 797 557 662 651 259 422 213 934 442 512 023 361 497 826 658 355 765 943 856 488 296 365 795 238 373 342 287 081 329 028 678 043 696 038 857 905 531 313 875 722 259 362 177 574 189 132 350 768 907 939 847 444 735 112 023 038 233 883 675 259 820 017 203 779 524 568 605 256 670 198 027 670 612 404 197 253 185 809 636 694 842 326 046 506 524 658 382 976 401 960 248 050 173 385 155 888 274 244 911 597 339 164 757 341 868 115 673 840 149 249 173 770 301 445 899 063 332 574 527 322 656 468 919 993 737 904 987 336 536 871 070 323 282 697 635 369 192 223 317 724 660 274 511 339 869 214 781 147 983 948 668 058 431 832 406 896 363 155 704 127 628 204 623 696 493 309 213 659 134 437 459 726 442 570 473 976 914 419 330 987 689 794 565 336 111 520 650 219 748 784 831 486 272 366 228 164 335 864 883 835 813 786 780 587 824 088 585 119 830 230 116 453 357 058 884 560 067 076 172 779 872 768 442 826 664 392 261 937 132 404 734 904 552 925 155 724 561 031 601 971 437 217 210 961 383 701 013 638 035 351 592 828 481 363 076 717 782 117 679 169 313 686 044 550 146 227 857 415 212 315 204 722 351 476 108 582 874 399 133 449 092 200 709 410 680 693 031 972 046 565 802 372 214 904 196 028 693 573 893 013 372 610 307 377 036 570 482 088 131 271 178 037 564 885 993 022 412 392 798 941 691 435 841 991 265 815 475 228 638 998 636 529 466 109 670 719 936 825 334 921 598 259 705 821 884 082 488 340 543 289 908 467 678 425 991 089 417 275 902 924 636 023 309 124 756 012 625 438 467 501 949 553 658 307 687 256 373 269 886 738 554 339 314 789 597 298 030 158 056 606 492 523 484 883 681 053 754 009 942 091 120 592 841 991 374 062 871 467 768 052 461 861 304 009 877 474 650 390 505 903 648 993 991 306 398 924 665 934 605 505 557 156 230 751 311 059 183 712 932 983 042 604 887 121 497 510 263 798 025 047 356 031 663 093 098 882 829 948 274 775 509 742 529 904 156 596 001 176 366 592 875 198 027 640 336 168 589 235 169 270 362 426 943 324 374 025 281 867 914 907 379 603 478 827 191 860 170 295 469 073 303 026 023 744 965 644 185 619 024 102 060 085 786 098 299 865 359 482 936 328 425 929 871 737 834 487 655 328 735 089 969 253 144 431 866 916 666 455 021 967 270 291 154 725 108 704 428 633 178 366 271 863 549 881 641 414 002 764 820 064 189 318 255 870 899 462 421 369 733 842 321 570 957 489 393 114 846 069 721 213 073 857 614 736 993 777 616 306 199 400 673 122 679 207 142 824 647 478 510 251 576 722 111 940 181 301 509 122 170 854 102 712 204 385 487 563 795 557 090 961 817 602 177 355 600 611 880 906 715 103 493 693 675 490 266 503 196 184 126 351 843 501 726 143 831 142 082 821 483 242 169 413 552 230 755 945 091 478 523 190 337 931 186 697 407 803 777 439 739 238 779 419 448 586 045 683 900 655 554 227 255 448 099 232 452 314 421 062 514 336 684 090 460 337 741 613 445 305 891 808 236 523 855 217 822 910 185 379 325 173 181 641 626 833 117 990 097 315 785 807 016 135 376 223 440 260 334 206 756 230 790 839 784 786 782 546 902 958 167 049 574 820 780 638 235 205 087 913 558 661 938 124 706 808 501 204 631 636 976 099 403 743 552 716 873 739 342 035 505 532 273 667 637 905 601 165 277 307 351 733 169 609 566 714 553 251 258 558 895 293 334 160 782 207 848 368 298 418 174 779 546 622 799 284 324 791 580 016 949 808 659 890 809 410 690 431 104 209 566 865 268 768 455 021 737 960 001 156 716 535 809 822 470 322 177 568 844 628 063 651 885 657 306 673 507 959 972 192 517 899 962 538 173 830 105 261 017 149 513 738 949 037 401 940 508 733 302 298 096 097 857 531 438 278 108 493 505 423 378 261 205 730 699 629 279 798 440 743 708 975 515 901 635 700 367 621 787 674 787 099 007 418 773 417 583 549 516 477 712 942 861 073 401 232 624 378 340 595 599 384 060 011 888 729 109 693 815 244 772 680 501 227 305 127 019 660 390 380 011 294 495 591 053 151 345 292 091 305 163 226 541 021 115 062 254 712 506 986 715 997 878 410 957 638 474 365 276 670 555 964 923 916 905 333 045 849 689 192 123 349 611 570 900 546 366 630 087 599 929 410 758 247 436 623 841 501 390 534 035 065 477 129 299 765 330 880 280 995 126 258 534 528 538 272 482 877 130 751 520 375 650 979 466 512 926 659 157 934 031 721 835 542 591 494 733 589 320 947 288 514 983 067 328 029 670 548 697 059 283 610 792 140 160 328 572 694 568 877 853 093 021 469 029 996 454 493 132 996 185 340 219 774 821 677 268 026 872 129 750 533 529 791 710 313 938 668 925 205 267 952 091 399 614 326 662 572 348 855 885 354 033 160 918 249 769 835 249 090 639 406 353 258 985 433 946 298 993 190 700 872 405 812 790 872 432 687 688 711 936 176 469 030 708 859 867 145 685 736 912 712 874 003 795 880 355 688 467 847 290 025 651 185 474 519 323 700 641 585 875 686 642 732 840 550 057 131 551 652 593 986 784 718 627 140 330 994 162 332 219 061 101 697 983 425 716 544 470 090 130 554 180 178 864 004 730 726 265 175 117 482 587 741 106 379 715 152 384 384 784 562 389 038 143 660 417 163 131 988 394 294 933 355 007 677 731 545 302 882 478 862 903 700 275 148 310 321 640 899 570 783 812 451 979 542 751 438 783 164 247 728 473 397 545 462 737 888 843 241 923 369 630 948 810 944 943 849 767 706 609 269 871 449 821 447 394 888 264 244 756 231 351 428 261 401 267 965 757 896 030 718 308 280 656 953 732 097 216 740 751 508 244 417 509 272 481 840 684 822 491 702 456 542 509 741 884 213 411 671 453 099 068 609 172 517 765 255 635 680 754 464 519 337 832 734 591 292 663 629 773 055 494 076 992 269 402 238 600 055 905 023 727 996 547 976 645 692 738 214 677 721 323 834 479 721 156 721 671 259 906 094 659 563 651 445 744 956 649 052 839 269 069 261 918 244 117 829 414 567 861 662 013 072 193 435 584 715 818 611 221 330 154 468 521 840 885 824 891 415 209 766 069 337 948 999 485 862 401 516 952 181 223 867 960 563 474 706 343 875 106 169 530 896 836 250 748 711 732 745 376 354 281 269 596 064 828 568 183 314 728 384 365 859 169 293 080 679 311 805 387 338 364 987 348 737 841 507 480 010 235 453 267 087 143 461 781 380 549 608 815 042 353 367 162 649 108 849 723 266 330 644 514 241 415 406 748 301 864 604 302 590 547 702 502 519 057 373 084 019 289 957 114 358 520 228 717 904 120 921 333 385 494 547 579 870 029 665 602 173 108 486 456 538 371 473 639 352 887 947 638 097 691 336 475 660 097 980 119 212 071 642 314 735 328 608 184 918 598 966 857 550 879 829 308 320 221 132 291 468 829 413 954 091 019 689 428 503 249 551 211 591 245 911 079 813 488 568 510 167 549 998 388 345 941 765 661 377 144 798 741 512 455 777 208 673 101 211 548 306 618 453 955 420 356 934 385 624 234 469 707 933 964 177 590 210 420 906 491 681 610 791 850 549 036 643 219 584 014 848 316 780 781 397 659 624 097 183 920 667 667 525 312 016 766 118 304 456 695 848 068 497 310 020 187 104 288 315 276 907 300 376 061 141 113 704 992 083 126 297 136 633 641 183 350 267 406 626 621 807 487 674 898 381 787 121 548 807 691 131 466 010 542 827 627 110 605 418 183 326 105 237 653 911 426 297 165 445 758 022 577 249 511 405 491 751 659 464 985 258 610 993 423 206 122 670 421 596 059 498 156 485 909 993 083 698 744 233 082 802 454 385 653 931 675 207 165 439 844 375 714 684 398 210 469 123 382 051 472 683 663 505 356 572 627 709 970 168 002 794 729 703 824 112 346 265 064 934 356 786 580 486 047 424 604 765 019 113 942 420 300 137 287 548 850 617 911 422 341 251 179 064 354 598 567 135 039 267 169 749 659 388 611 148 635 070 991 953 729 910 323 033 795 708 444 211 942 521 108 997 329 283 427 853 373 555 468 039 888 823 077 223 899 149 466 595 617 298 007 567 444 649 996 375 306 857 617 336 381 099 663 707 990 047 981 332 630 568 958 152 992 966 060 718 906 709 637 973 991 147 311 588 831 194 764 627 856 013 406 323 963 184 823 500 331 066 362 844 132 285 138 689 198 661 644 553 469 761 560 635 687 296 976 050 924 682 011 668 749 109 346 593 673 221 608 355 802 031 870 424 942 046 469 545 992 543 814 938 969 691 428 256 035 573 375 516 884 940 185 928 668 561 577 374 309 655 687 351 093 769 827 995 131 779 612 714 818 810 933 468 900 897 744 454 376 987 414 507 614 410 662 450 669 571 129 760 668 451 970 185 648 781 690 274 014 119 790 042 618 153 671 121 879 069 153 643 372 566 350 859 165 106 808 582 552 232 613 015 617 765 489 346 864 245 839 287 992 559 909 168 499 984 302 147 108 009 950 503 654 775 314 421 872 485 532 487 754 271 852 089 942 593 417 187 712 548 635 378 021 581 912 782 491 243 741 390 185 109 303 298 513 211 325 372 069 694 319 828 947 569 821 667 241 607 684 982 722 682 582 492 845 743 793 920 575 925 528 624 209 719 748 613 863 167 509 012 047 742 596 832 901 536 665 415 490 457 090 822 480 409 912 557 338 480 352 755 496 126 138 990 313 134 075 721 627 826 830 300 157 015 769 155 665 891 454 418 751 877 601 123 300 866 846 751 580 956 187 398 841 001 346 477 928 100 856 285 944 796 813 305 595 423 017 226 993 527 612 490 973 039 500 338 408 090 897 960 799 120 872 206 462 531 816 930 120 224 742 708 417 766 955 223 147 442 256 398 890 334 423 806 079 709 527 391 071 400 612 151 913 945 450 352 486 705 722 444 075 546 255 476 579 792 386 367 811 175 632 451 831 976 114 555 583 010 299 611 005 176 401 803 845 461 355 188 664 010 347 564 440 256 824 525 974 067 081 781 410 242 412 597 380 329 519 605 254 676 432 724 338 927 966 720 506 075 510 466 002 676 922 481 568 091 420 165 531 579 795 868 037 018 141 083 891 362 471 074 863 493 236 068 108 885 186 180 326 320 993 630 089 425 177 068 477 326 569 054 670 034 056 350 481 092 820 332 624 210 028 244 675 519 271 099 005 202 972 607 005 585 886 724 693 512 897 210 851 399 719 368 079 015 557 290 329 599 641 582 354 777 033 602 159 086 744 936 402 862 417 434 916 418 212 425 986 649 429 956 934 312 495 463 580 704 213 237 640 258 332 583 744 447 227 855 217 310 417 013 129 646 799 604 018 091 707 374 647 801 352 293 859 165 236 064 786 461 365 259 611 475 294 374 547 888 584 387 480 996 223 994 261 609 928 875 975 520 281 628 984 572 940 774 817 586 949 935 691 666 779 341 791 080 574 110 098 733 805 682 316 238 387 924 339 581 339 350 085 865 017 250 204 248 570 250 633 072 339 488 353 913 180 270 383 908 270 075 662 995 033 315 587 013 908 385 178 021 731 404 747 992 286 269 965 663 877 424 090 155 800 426 244 415 354 691 320 687 433 069 071 458 880 527 497 026 831 403 054 418 827 360 528 279 529 572 524 814 130 138 569 328 927 642 041 783 182 678 225 838 530 495 369 445 716 262 880 187 327 172 566 535 232 693 863 658 228 667 860 543 591 892 837 171 687 436 565 554 949 730 695 165 678 266 629 209 077 498 191 061 345 204 146 102 544 601 124 403 885 042 432 905 303 957 315 816 487 208 987 725 783 781 227 777 496 448 566 550 259 436 988 751 752 669 548 235 705 101 294 102 015 977 617 150 376 910 270 136 001 823 943 520 780 754 626 318 491 975 439 103 386 435 442 151 172 430 954 709 156 170 988 114 179 424 850 828 396 183 184 257 226 797 426 741 089 651 375 774 792 057 339 244 116 473 239 432 052 838 686 251 880 616 252 238 703 043 593 349 499 000 550 491 596 782 053 553 028 232 759 901 763 522 966 021 175 032 936 415 678 425 841 424 449 345 870 478 773 576 503 949 155 316 545 944 312 163 039 315 639 087 087 374 513 920 512 782 280 852 929 479 225 118 398 419 490 781 398 867 961 164 938 931 166 723 608 310 494 107 576 716 304 260 890 291 806 468 611 423 804 521 296 181 991 745 764 982 130 306 211 910 650 568 378 575 240 184 838 278 916 469 607 193 833 897 380 343 175 251 843 474 324 442 979 774 760 037 054 600 889 543 896 143 595 313 227 935 149 067 494 904 085 911 811 131 546 737 974 115 407 558 829 810 512 696 223 587 742 883 650 770 680 119 986 946 427 191 715 435 122 255 076 327 191 761 582 711 574 631 804 749 888 177 720 448 134 446 132 269 971 824 252 848 170 418 789 930 226 794 752 869 983 952 225 180 278 656 328 790 316 946 362 633 828 151 558 092 859 372 346 847 804 992 460 385 561 563 790 655 703 675 510 097 596 679 287 532 977 930 082 752 451 999 660 644 712 506 427 186 548 196 946 438 238 942 621 064 995 218 468 680 256 625 036 423 106 302 654 737 817 416 989 037 100 157 419 909 232 117 876 840 763 563 671 668 295 164 129 626 600 086 617 031 505 820 359 658 139 721 177 487 035 059 704 040 540 085 703 088 411 140 005 631 928 010 372 913 276 755 507 431 535 598 666 894 778 555 114 344 703 151 788 288 028 076 248 449 436 640 815 042 286 569 293 827 499 657 454 006 406 749 156 016 489 711 540 814 255 331 770 548 953 666 832 536 060 249 070 584 202 459 708 959 310 855 790 167 781 637 491 111 292 585 246 833 335 378 924 713 955 124 707 735 424 603 850 635 986 292 069 231 431 952 474 864 900 509 179 961 303 926 893 901 797 122 138 586 928 086 171 654 884 592 980 058 456 167 840 874 428 584 907 259 233 624 340 536 529 891 902 082 983 934 538 742 405 488 690 071 974 415 078 613 402 352 013 302 565 188 111 082 925 515 084 954 258 219 027 020 533 972 345 697 680 078 022 042 257 632 004 325 804 302 936 784 717 725 945 508 866 312 887 460 709 504 619 797 855 452 484 440 586 209 246 280 311 237 720 366 023 918 297 355 488 529 908 756 299 044 001 799 419 083 440 081 313 213 862 935 933 242 267 024 295 896 778 926 561 378 165 491 221 989 956 473 282 120 259 724 029 652 345 243 101 169 189 084 311 368 136 783 169 721 641 528 558 252 597 622 954 257 125 159 022 998 104 786 924 858 847 418 095 539 099 446 292 185 959 648 009 704 375 601 477 734 356 561 657 844 939 076 875 943 055 169 937 891 684 192 218 640 188 548 355 591 338 140 571 229 993 386 235 506 220 660 995 295 399 378 900 562 406 169 170 354 616 093 194 723 717 819 515 192 114 002 693 626 959 597 975 202 323 302 321 064 390 431 117 727 818 290 048 440 814 274 310 985 416 743 220 891 603 880 519 425 764 721 975 660 364 100 913 575 574 413 754 275 706 483 950 527 254 732 799 109 719 289 123 032 861 652 044 102 337 873 435 306 831 471 430 647 136 344 120 435 663 086 078 283 344 526 272 452 388 671 230 871 630 825 612 907 958 809 209 728 698 742 268 059 125 709 435 740 679 554 797 271 354 511 360 341 712 558 601 178 321 684 440 239 341 726 367 657 369 816 635 230 593 831 079 189 409 329 542 069 837 439 546 818 482 353 445 077 832 697 131 954 620 284 556 562 279 436 684 653 204 346 365 545 374 993 995 893 997 903 290 882 895 531 388 169 749 221 611 624 832 506 487 017 908 114 793 631 568 108 775 422 348 157 753 198 280 122 172 888 655 421 590 356 738 474 042 783 017 066 480 775 304 032 188 999 154 140 686 329 824 094 944 794 061 823 515 690 688 634 008 252 125 653 051 721 045 295 415 469 295 030 403 215 378 680 922 763 954 039 469 928 814 185 456 079 185 521 291 817 979 265 674 593 152 999 662 587 448 956 603 674 909 328 255 057 042 410 523 037 385 204 663 468 105 040 824 963 609 092 427 245 548 535 260 118 382 851 017 548 062 186 217 634 285 929 646 475 250 691 718 879 113 090 457 887 935 434 437 266 335 530 033 272 683 907 657 630 022 025 968 660 940 221 377 272 690 748 954 313 473 964 593 571 705 017 170 488 333 358 987 606 473 677 589 070 442 692 551 689 594 915 876 453 061 697 870 308 561 487 562 240 120 148 927 912 073 430 076 219 216 412 489 165 865 926 056 833 108 789 796 694 480 193 723 107 584 946 775 479 260 285 876 727 844 766 344 306 752 395 027 634 804 240 381 895 013 908 932 419 350 915 006 770 796 576 146 314 183 502 611 727 601 938 644 242 690 655 643 144 898 795 581 270 799 187 395 869 089 191 860 603 129 873 844 053 510 264 007 227 742 179 233 969 322 382 794 370 989 458 123 763 571 344 983 207 272 236 256 044 272 679 579 668 305 548 595 285 823 589 465 869 812 925 056 555 175 973 694 518 470 655 652 990 253 180 297 190 087 107 556 295 945 897 538 744 272 357 344 899 864 730 496 414 034 763 476 798 899 836 223 918 038 079 480 144 207 138 062 230 608 977 362 010 188 299 582 516 492 463 660 687 542 735 181 088 911 823 135 456 366 964 739 595 798 539 564 450 419 574 974 182 320 708 825 026 743 824 916 442 767 803 473 172 936 708 696 784 524 858 113 769 562 555 124 354 096 637 571 967 539 360 250 059 828 438 682 487 691 867 823 215 400 050 879 267 706 512 623 783 596 897 050 329 629 221 540 232 474 061 414 950 434 148 419 606 460 468 235 280 926 462 465 585 566 885 688 834 100 901 362 152 742 773 342 029 515 430 327 760 476 242 433 319 463 017 811 208 821 175 549 099 463 082 896 613 560 864 725 678 052 310 599 989 020 183 025 807 109 261 860 803 813 604 943 802 310 049 128 376 789 789 733 488 695 970 406 730 921 626 469 508 340 634 190 221 888 057 064 193 632 801 443 349 265 092 455 843 398 386 799 546 557 864 821 457 903 373 514 487 592 565 726 599 224 142 048 146 956 009 932 819 963 089 916 752 285 131 042 602 936 484 810 541 863 985 912 402 942 860 173 351 560 204 977 001 597 989 122 859 360 240 123 042 841 452 996 606 591 484 754 519 423 642 389 984 106 235 796 143 135 907 601 745 510 564 588 719 345 103 695 545 554 279 223 901 349 581 487 556 142 929 315 372 345 607 459 164 936 711 067 985 145 268 547 346 974 793 377 561 642 782 712 221 137 475 061 111 076 390 931 920 687 420 980 195 133 167 217 719 758 673 915 340 241 047 157 588 557 394 697 051 732 478 586 065 826 369 366 839 670 963 906 174 974 874 342 314 969 232 823 462 338 866 249 702 057 025 369 904 367 961 790 664 230 312 055 875 859 806 627 070 811 356 358 325 070 403 663 399 216 465 813 750 110 802 916 768 514 567 452 245 880 901 739 034 642 987 084 806 523 872 436 106 949 042 768 651 896 250 472 009 415 042 116 019 781 386 077 512 074 540 343 105 566 183 336 544 808 005 361 659 992 789 528 541 230 765 148 705 429 790 988 443 991 013 015 105 840 170 572 733 401 732 832 903 365 141 786 320 061 901 782 149 844 420 560 336 035 698 367 820 977 684 492 179 149 370 307 087 626 386 224 646 439 211 154 733 005 586 799 128 591 292 487 658 123 433 247 440 432 607 123 121 498 353 568 946 692 408 412 270 853 190 034 077 635 345 129 390 134 249 400 467 550 692 263 384 141 776 420 133 407 957 625 560 896 100 836 403 009 317 623 320 298 393 481 559 199 636 812 875 501 998 012 937 926 026 184 786 835 259 238 814 839 130 700 226 713 786 469 557 272 015 455 750 737 796 852 724 890 770 923 137 717 819 324 665 305 659 434 856 269 021 838 368 188 962 308 987 706 568 961 511 604 221 010 547 385 440 421 198 349 256 134 127 559 602 222 094 647 043 937 789 043 935 938 507 619 407 229 276 137 261 371 212 566 640 007 841 663 191 811 102 775 891 909 252 886 064 769 530 682 239 045 059 062 265 425 938 237 250 998 540 958 880 517 015 295 679 371 653 071 496 771 223 059 136 885 988 434 898 330 787 404 285 667 080 210 625 555 954 083 246 615 580 172 694 306 703 857 220 607 179 205 546 380 664 731 421 678 775 845 225 849 822 930 849 686 118 919 736 239 369 638 569 195 071 285 746 945 965 574 418 798 376 936 664 606 293 588 188 249 197 285 909 049 475 558 014 728 060 015 615 247 488 623 183 935 091 086 333 784 718 632 294 352 138 526 681 125 714 625 180 799 223 525 793 473 071 691 317 522 282 993 706 745 562 488 359 021 117 734 426 723 602 710 388 134 984 554 438 072 424 582 943 109 713 565 106 065 266 905 604 517 131 683 646 193 681 753 983 905 929 857 518 697 843 249 595 269 935 241 859 821 622 717 006 086 459 885 524 264 641 521 247 468 687 147 564 739 808 678 492 382 512 722 205 195 593 160 638 528 665 223 563 283 702 677 847 153 486 706 453 335 459 849 957 271 542 712 376 903 075 107 635 116 287 508 261 294 032 933 520 590 960 402 993 835 931 311 244 952 855 450 000 657 079 208 503 726 633 312 486 403 849 916 158 718 162 174 435 219 633 952 596 132 359 978 249 391 458 711 067 365 760 028 669 856 192 618 575 629 105 934 148 799 714 838 886 617 049 213 644 543 896 349 036 067 418 436 821 841 043 934 779 817 850 502 093 331 493 114 910 619 229 952 907 441 654 984 552 217 717 930 245 421 517 939 751 224 089 641 911 272 453 391 869 601 596 295 817 072 910 166 240 196 814 320 638 325 639 860 902 285 005 346 907 382 601 122 775 400 517 477 132 016 469 159 615 846 188 577 561 027 185 177 038 023 097 919 461 551 947 485 814 266 849 583 170 073 364 355 559 340 013 826 785 063 069 926 174 074 312 041 887 221 098 086 905 313 937 595 821 121 722 166 162 022 167 096 330 673 975 968 352 119 023 101 956 171 435 413 469 251 824 972 726 776 685 991 171 361 933 633 569 669 961 241 829 068 179 477 776 727 107 916 924 809 033 464 104 011 905 246 208 931 902 121 355 928 209 607 825 928 356 686 070 559 748 893 002 540 611 963 375 402 987 190 451 378 694 439 038 028 476 831 022 388 146 428 802 532 917 327 484 732 097 332 475 563 483 795 076 878 556 916 363 652 240 105 286 337 010 875 900 652 799 287 524 221 389 980 310 666 838 379 619 507 993 722 879 356 350 305 749 883 924 108 775 016 925 532 824 272 026 915 634 180 174 867 400 112 321 468 810 791 558 803 672 612 422 794 183 911 276 412 574 965 367 079 359 385 529 607 601 735 517 482 406 895 535 205 611 441 239 790 786 539 862 587 720 941 080 973 173 496 169 725 415 315 654 746 087 303 671 265 438 059 840 755 270 828 947 986 086 491 618 255 888 868 768 002 955 260 490 784 526 441 645 202 466 698 118 325 406 468 354 956 705 916 596 738 308 694 096 055 902 751 135 062 222 128 444 189 233 677 129 370 392 241 836 812 425 345 298 761 737 268 915 399 814 061 019 710 463 715 776 709 566 464 414 163 349 828 652 127 601 436 564 657 594 046 296 923 290 338 943 552 803 882 721 272 141 536 550 770 444 700 265 137 491 992 687 994 733 560 941 155 462 743 137 437 914 208 692 180 361 300 300 271 078 738 482 446 214 362 075 294 787 317 583 987 360 065 985 747 697 409 252 995 575 153 669 916 660 355 645 173 771 330 257 237 578 758 808 361 067 264 583 441 070 102 234 145 533 858 812 562 275 924 347 551 020 012 643 060 147 652 089 470 612 206 624 820 426 475 217 949 662 332 463 361 263 163 018 000 436 535 357 664 097 495 827 932 450 267 009 000 599 960 814 501 762 831 803 117 787 256 667 377 871 825 662 795 090 838 501 872 251 625 071 131 263 070 321 141 318 317 664 284 342 630 803 184 833 500 290 973 944 633 655 605 174 183 027 446 562 672 271 215 033 918 642 291 142 698 774 475 411 789 125 331 235 351 962 292 608 332 902 989 208 551 395 726 635 119 871 558 936 125 832 625 600 416 853 023 986 261 839 852 384 085 565 422 584 927 794 517 604 262 630 414 591 735 916 626 791 276 771 311 849 156 591 127 950 318 482 641 706 785 771 392 065 555 336 044 792 848 141 748 281 730 896 249 631 212 040 211 509 638 491 717 688 022 860 682 969 588 742 023 437 845 007 277 078 034 374 616 163 338 064 093 370 663 489 922 719 002 965 371 542 799 764 113 826 570 507 765 278 991 808 671 848 409 979 824 635 766 897 139 584 664 291 674 817 240 140 049 731 256 036 096 732 078 097 254 885 392 727 567 964 539 223 056 890 411 623 440 964 780 325 654 960 605 625 470 041 979 390 190 869 534 168 665 734 009 354 431 595 793 397 464 615 737 476 205 379 545 100 709 467 979 323 397 451 434 364 328 325 390 403 876 962 374 713 230 877 048 183 191 961 124 158 290 572 754 711 255 016 167 685 747 047 652 302 101 346 744 586 374 228 899 285 515 075 197 715 176 894 572 348 989 610 147 589 510 652 715 094 831 572 025 373 612 075 573 787 824 128 793 919 931 141 937 944 664 338 302 013 641 351 890 596 231 353 338 613 783 880 278 348 709 255 815 982 641 294 638 770 786 081 708 671 649 152 395 656 436 242 044 275 735 237 571 017 958 567 923 977 085 391 120 668 439 848 707 416 358 222 138 124 179 781 819 472 932 562 096 982 663 363 010 442 409 999 823 599 022 435 858 972 834 622 554 987 722 217 170 811 935 799 909 501 277 198 083 848 063 286 905 088 122 676 709 384 940 936 600 531 222 641 719 296 561 489 020 485 691 440 584 454 542 264 922 702 775 767 815 324 928 483 772 816 579 297 373 275 455 825 336 739 296 076 135 622 161 369 699 234 491 715 219 688 498 734 194 813 226 291 908 881 335 609 754 475 636 857 384 903 803 952 481 599 613 090 017 491 149 771 788 286 556 303 184 701 316 812 328 500 110 725 580 712 806 390 519 733 237 063 398 739 467 631 116 961 578 740 745 134 764 248 248 940 334 162 698 502 437 266 202 528 036 022 045 345 776 276 962 175 289 241 665 697 913 673 683 853 459 610 027 778 203 101 779 744 054 777 138 953 539 400 738 897 864 711 882 229 054 734 884 355 570 397 387 841 686 230 026 162 873 957 586 392 761 917 158 885 810 548 818 388 439 112 591 246 813 446 947 272 666 563 190 747 189 081 814 816 981 730 680 888 472 650 639 480 935 220 467 121 069 639 363 631 165 719 071 508 559 122 518 563 659 839 090 126 175 482 554 490 714 521 769 086 704 222 977 069 891 113 603 202 620 168 851 066 762 445 338 190 342 054 448 919 108 321 406 258 115 578 672 886 449 150 008 338 172 189 733 606 871 594 794 107 041 916 585 976 184 865 625 379 289 906 235 536 253 498 803 409 264 955 145 526 873 189 503 945 466 744 789 600 686 198 918 232 096 224 471 577 722 376 265 008 461 606 577 980 289 149 320 911 141 250 899 119 989 572 159 960 229 473 591 928 449 308 585 533 240 451 020 600 533 420 919 929 977 075 851 913 321 126 808 956 260 542 908 135 378 018 198 711 987 820 345 975 665 817 761 053 345 279 467 253 832 596 091 832 461 496 147 836 887 191 535 490 815 355 927 205 202 598 796 834 965 113 142 763 792 943 236 897 473 843 220 926 957 494 542 805 924 937 381 730 797 324 246 436 071 677 719 405 100 378 104 401 087 501 229 589 441 498 326 105 577 314 579 906 437 991 521 154 262 859 298 106 608 267 047 877 262 358 821 580 026 059 386 012 726 464 690 484 111 119 627 320 112 377 469 558 251 244 976 395 774 470 107 965 205 337 279 330 515 271 951 332 419 107 966 257 204 397 674 744 853 010 135 047 637 224 844 799 357 272 617 304 672 346 529 800 728 142 379 331 453 786 863 345 388 822 373 494 488 271 548 170 171 292 872 989 098 657 733 780 370 196 184 026 097 502 828 477 705 519 660 256 568 301 707 627 675 559 005 890 482 796 502 362 715 688 055 070 798 366 541 851 328 372 675 825 518 752 254 593 702 212 168 529 533 920 677 078 913 353 982 201 521 996 054 063 506 447 187 367 750 021 887 187 196 933 857 190 915 100 248 145 977 617 236 922 815 104 606 127 724 742 915 101 840 904 720 433 823 613 452 791 529 717 838 013 633 423 641 032 419 179 324 618 373 415 075 685 083 802 751 000 710 969 672 633 269 710 834 837 413 622 268 900 497 581 531 318 440 896 668 628 522 491 496 220 376 686 957 494 581 038 802 804 059 037 590 839 974 428 450 129 353 673 812 527 506 622 687 696 411 966 453 763 267 807 532 110 168 450 465 845 768 854 455 006 682 517 804 223 874 352 682 348 023 319 870 951 595 440 554 156 260 161 593 259 242 373 018 560 967 771 509 644 440 944 593 853 570 395 053 412 167 528 696 502 303 923 113 802 282 093 465 668 061 755 856 071 036 348 170 635 056 172 592 265 727 616 762 871 070 519 333 274 741 458 004 692 028 867 926 845 624 025 592 567 504 232 374 966 440 011 683 655 573 699 033 318 731 012 304 081 075 290 051 481 763 839 778 213 997 884 827 252 740 487 059 351 086 078 994 274 440 440 715 694 890 331 975 547 390 407 922 262 969 459 539 895 897 809 269 838 266 078 128 988 548 742 744 577 045 610 059 990 835 893 621 697 073 201 524 814 367 354 582 834 959 487 142 624 341 074 927 080 339 216 156 481 156 315 319 971 913 288 582 909 295 139 333 819 123 505 056 804 201 140 067 099 601 724 761 300 916 017 869 398 495 489 728 635 575 045 752 203 465 135 138 678 185 636 783 910 510 046 652 349 969 507 582 956 031 169 625 864 299 088 131 678 551 599 326 724 792 042 090 975 778 635 331 856 351 254 827 687 778 518 625 146 958 964 549 501 484 233 293 528 749 256 823 113 083 851 971 631 020 742 841 093 789 472 639 918 576 882 162 169 359 416 907 831 870 557 252 288 380 268 171 705 985 103 505 450 630 258 657 735 562 329 984 894 734 325 235 055 130 583 060 797 011 142 643 842 052 695 362 638 063 392 955 175 038 605 011 674 153 290 277 910 476 855 842 421 087 029 763 708 065 557 834 695 642 009 106 278 879 087 713 764 399 133 640 830 403 265 101 324 701 832 345 481 833 696 810 290 845 958 087 788 384 869 469 418 454 369 357 854 865 778 338 826 816 326 913 991 748 546 735 929 423 000 371 602 130 485 419 173 270 443 128 393 483 647 737 135 228 465 686 617 463 892 007 520 923 839 385 036 655 785 116 798 712 026 441 011 485 863 197 449 152 231 487 319 245 102 665 223 080 101 490 427 277 115 506 231 769 204 624 423 190 454 844 821 102 684 916 324 330 097 518 763 883 861 130 994 278 024 128 514 282 550 802 934 018 412 410 943 690 214 639 207 845 613 111 618 777 660 456 915 237 993 606 483 936 070 330 318 169 728 772 890 737 567 909 831 322 153 180 716 616 396 694 463 400 846 407 206 154 610 875 659 827 470 303 100 370 035 727 983 655 757 202 589 648 824 511 893 036 640 170 157 822 695 330 490 608 298 174 460 682 934 139 935 959 858 066 416 707 463 575 839 293 578 241 583 714 375 689 815 203 015 085 452 564 204 716 112 473 580 409 343 542 450 700 043 611 024 420 870 397 823 211 223 364 835 255 120 016 692 758 630 645 876 856 800 015 235 552 945 684 875 273 580 025 975 916 506 890 423 402 197 729 870 489 782 564 338 472 851 792 900 252 673 285 751 673 143 108 530 329 564 149 937 994 268 518 286 283 825 979 624 763 650 376 631 118 945 012 077 718 735 776 434 338 036 061 314 329 226 061 342 557 570 799 453 724 023 586 283 448 870 373 517 990 325 873 837 609 006 605 101 289 909 449 413 773 192 889 314 331 735 931 202 998 923 950 135 395 922 289 901 124 773 452 913 594 770 639 086 085 614 968 829 531 590 684 365 063 053 616 827 434 463 727 294 876 658 321 235 683 749 404 854 113 075 282 851 593 618 485 815 859 907 161 327 761 738 985 876 177 575 686 993 283 624 301 346 999 442 130 474 118 073 723 703 573 042 710 145 234 035 252 359 625 568 715 923 435 753 008 530 746 095 782 062 158 175 178 767 467 721 785 135 614 433 151 984 620 933 611 968 152 150 681 424 761 374 477 479 021 084 405 382 381 561 733 970 150 368 713 993 170 898 747 754 347 591 469 729 356 789 356 604 019 676 351 749 083 144 017 640 051 608 622 874 940 684 572 024 498 366 365 129 961 917 433 878 665 836 288 354 479 836 338 222 828 436 134 305 045 190 118 822 216 212 016 035 718 913 189 010 262 674 094 163 502 332 615 589 401 629 760 281 647 263 748 476 333 949 075 759 771 344 375 878 563 235 706 945 218 069 011 344 805 575 493 425 232 350 125 245 273 942 503 319 563 878 222 237 623 348 435 001 364 022 516 481 883 319 243 567 616 130 133 760 482 842 086 013 444 512 786 522 245 595 629 704 836 882 794 987 270 222 544 883 149 494 264 429 087 445 607 888 985 991 073 171 124 896 656 830 412 383 359 875 220 282 052 670 958 386 210 789 816 928 825 835 866 734 743 073 369 104 199 788 486 362 039 042 033 523 962 452 463 043 492 127 917 122 416 084 535 524 640 256 717 942 424 314 266 198 998 309 043 321 793 135 577 582 113 821 776 712 721 077 746 922 992 013 603 498 127 562 051 146 393 625 105 140 992 302 573 070 540 728 523 939 879 017 599 577 935 195 473 439 537 850 082 782 448 077 390 517 690 952 708 650 358 646 400 930 857 453 202 930 089 618 367 263 199 664 204 971 291 146 104 855 023 826 241 292 158 592 940 818 869 540 925 809 396 472 828 792 267 637 332 251 259 554 515 304 169 039 366 551 215 923 589 037 398 175 176 160 061 060 342 487 879 932 399 465 894 985 485 520 066 351 104 797 386 877 536 181 830 538 194 262 304 681 096 551 174 742 271 064 677 174 555 101 585 463 318 281 441 797 583 215 974 196 505 505 005 987 915 512 429 358 432 852 408 332 152 716 956 630 364 533 237 846 388 874 374 959 237 716 228 218 504 759 937 677 666 948 628 160 965 071 721 373 330 729 085 731 266 326 084 480 538 025 193 456 971 647 432 868 398 118 349 552 020 222 961 592 555 634 583 591 076 682 455 262 951 886 622 545 886 209 202 847 060 718 427 556 870 890 359 022 107 536 720 105 595 329 831 142 100 759 611 880 307 008 225 366 404 995 530 277 696 953 996 762 695 849 644 911 284 573 044 246 685 659 147 929 189 804 506 406 097 089 897 306 119 240 723 852 720 350 097 295 726 481 716 089 879 743 586 262 679 480 017 465 980 468 354 769 682 878 948 035 977 794 318 082 919 261 420 063 832 191 599 747 455 888 221 462 699 164 857 211 768 632 345 314 383 931 107 296 620 218 728 223 388 887 056 336 845 943 965 012 652 170 886 385 324 340 621 990 043 506 052 128 291 654 835 536 099 722 974 205 874 335 372 984 693 338 490 081 267 750 510 301 355 280 094 416 444 275 016 109 469 259 501 395 249 158 700 161 443 458 994 319 442 515 925 209 025 085 505 813 961 256 956 879 202 509 177 234 320 935 305 144 534 869 620 418 372 158 583 393 328 740 635 899 469 239 540 502 385 443 582 398 274 956 311 179 011 215 091 739 364 455 609 937 277 310 451 119 730 795 516 820 720 842 142 959 674 593 830 099 826 674 478 020 873 835 207 683 646 509 488 455 807 728 387 436 792 016 232 489 344 039 470 983 958 035 152 344 786 405 758 385 574 980 021 258 977 103 016 072 115 659 423 759 620 102 364 209 025 982 347 918 222 849 000 837 005 073 263 069 676 470 589 517 814 088 630 119 477 650 372 148 858 678 661 197 336 418 509 509 062 211 753 674 364 931 848 825 725 282 598 994 338 562 810 879 760 625 210 069 990 601 599 288 510 990 341 300 276 136 025 859 363 414 121 815 996 725 573 126 834 397 167 304 062 583 596 142 311 516 235 645 983 890 579 388 909 875 023 854 873 420 480 515 922 510 096 471 081 126 074 392 502 771 985 027 849 621 401 865 877 154 664 741 270 856 141 368 852 198 056 470 181 024 813 844 413 249 738 891 477 171 867 427 827 503 600 440 966 470 309 714 427 256 037 742 825 550 101 986 699 190 498 141 723 083 847 787 063 950 726 944 435 869 421 294 144 327 778 572 053 785 193 015 576 597 788 169 385 456 369 140 383 611 450 678 965 171 472 521 532 149 278 776 323 790 887 767 614 622 340 174 363 276 154 924 119 859 375 081 800 426 806 651 537 272 450 553 275 271 511 787 219 585 392 856 120 894 031 959 211 567 995 223 980 076 840 289 349 454 829 303 876 796 506 968 070 108 780 793 396 018 988 045 137 135 878 219 708 893 036 903 376 798 510 241 617 815 290 659 840 485 516 132 401 418 502 956 307 927 110 571 598 226 602 477 349 127 663 189 013 173 448 840 610 430 833 730 797 185 071 185 362 495 840 466 844 732 820 796 716 056 908 987 162 251 348 814 350 116 502 801 174 240 256 168 702 115 922 913 727 636 625 987 621 131 903 171 600 218 551 757 574 192 001 093 659 962 397 613 105 792 866 122 520 978 012 813 542 810 359 154 799 632 550 437 067 151 184 127 839 073 367 531 302 627 133 479 379 083 218 267 252 933 554 772 096 249 038 577 040 436 602 253 208 969 162 097 900 745 990 878 607 733 786 945 163 548 333 083 685 503 693 409 404 969 525 547 854 692 249 151 320 529 684 508 224 714 863 022 899 087 423 948 659 561 490 619 598 061 830 325 745 082 999 745 103 869 679 274 028 971 474 813 915 119 560 713 170 658 975 445 227 133 943 305 281 030 818 082 542 826 038 722 169 919 166 311 113 472 746 125 283 786 736 015 764 016 583 034 432 709 460 918 161 497 435 948 407 123 471 641 778 644 725 230 693 085 917 607 478 870 913 431 099 414 351 249 545 604 702 970 585 045 815 413 002 052 819 203 098 880 183 385 255 461 549 486 761 187 136 806 110 327 967 172 440 363 966 335 861 446 431 224 128 570 054 216 100 682 623 461 666 714 870 927 865 613 274 315 786 821 088 098 488 309 454 773 517 284 202 357 184 454 917 664 274 912 592 001 352 485 052 337 228 158 473 761 235 202 107 180 000 230 716 944 352 222 920 889 356 934 959 022 281 629 576 413 077 981 474 951 986 542 826 435 651 999 844 860 399 205 069 797 683 780 714 006 873 821 139 724 236 539 884 503 173 072 472 629 604 994 512 012 864 439 512 446 997 729 449 763 402 218 412 821 884 490 219 322 558 062 810 791 650 528 746 695 508 929 981 368 212 634 091 540 823 216 567 149 645 610 070 435 692 230 605 015 926 219 514 801 547 381 651 395 819 034 617 059 195 824 822 785 797 257 316 397 742 974 666 730 101 640 866 327 494 697 759 830 148 476 064 347 601 233 375 017 980 407 960 522 583 311 661 620 824 918 972 591 612 409 065 277 897 616 792 817 568 925 898 583 167 913 516 814 422 419 424 159 293 449 526 127 075 550 060 778 752 406 876 915 356 312 587 696 549 792 444 072 014 158 811 352 737 647 366 616 438 624 551 314 483 379 679 347 822 719 344 865 902 091 835 976 931 773 838 921 801 918 888 644 876 296 725 825 778 328 745 033 316 787 790 430 892 024 007 608 038 110 572 949 009 456 892 035 433 117 138 827 178 907 163 236 312 766 097 342 006 165 142 690 554 714 366 238 732 238 191 418 475 833 905 202 282 890 461 076 259 868 638 824 879 128 658 432 332 901 140 118 782 924 464 454 000 691 886 335 994 492 708 648 165 167 057 073 085 014 427 574 689 420 469 540 601 017 644 420 009 083 250 459 311 470 593 077 951 424 589 317 598 105 290 921 189 679 969 259 604 209 346 497 069 789 035 003 898 971 942 825 038 788 493 131 934 336 401 786 954 895 690 199 179 874 965 845 866 205 629 534 216 660 794 077 352 633 167 127 093 812 006 231 643 422 186 939 400 165 411 099 122 603 067 829 878 910 141 985 298 772 368 119 277 811 791 070 287 385 934 848 487 854 984 131 532 021 424 626 519 445 123 136 020 250 733 730 800 410 767 335 544 223 595 487 354 113 160 936 588 446 272 694 999 099 722 590 194 771 481 579 102 490 920 790 537 207 120 669 474 323 356 932 374 711 628 524 095 142 151 414 164 144 262 198 271 800 050 908 717 504 547 358 091 251 546 523 188 640 757 577 547 911 529 907 134 061 336 721 713 639 678 187 823 595 038 290 578 263 248 049 444 352 950 824 443 854 883 520 904 650 500 788 738 967 084 000 642 294 877 449 012 071 456 045 356 789 504 408 315 403 094 433 119 905 924 391 177 456 688 169 999 149 244 945 910 732 572 866 785 830 181 146 044 697 164 185 139 909 105 082 632 965 038 906 065 607 558 434 456 017 494 889 731 655 775 097 903 920 045 602 775 577 192 468 042 369 106 027 851 490 468 290 992 201 506 780 092 570 046 699 888 195 801 832 682 526 019 559 213 149 603 011 756 072 251 820 493 736 922 777 822 739 197 298 317 454 316 595 020 361 045 159 415 017 245 268 561 022 101 740 527 611 432 714 736 025 985 200 376 912 630 005 226 378 269 165 763 411 954 527 459 930 358 373 562 195 093 792 177 302 258 143 029 246 344 968 943 362 801 553 559 477 912 231 522 220 785 564 440 434 060 347 170 700 908 688 767 541 211 879 164 471 732 786 639 934 728 924 457 440 633 506 876 937 690 115 203 983 446 416 454 355 257 155 575 117 417 806 402 560 553 283 557 422 673 896 388 891 414 070 951 600 047 675 570 110 113 757 613 788 907 996 981 718 872 447 618 404 773 686 442 516 372 850 910 182 439 226 575 213 188 346 900 246 916 174 594 186 949 242 709 052 503 017 722 062 286 125 361 889 917 743 901 928 506 340 361 722 221 936 562 842 652 556 878 882 148 826 788 553 932 137 157 989 317 861 170 368 539 944 393 941 813 809 589 583 367 095 537 826 786 088 342 062 206 263 087 241 537 511 810 931 605 416 125 515 477 724 385 482 855 239 652 656 824 108 815 219 344 088 427 775 022 635 474 784 895 030 139 331 051 357 223 427 699 766 195 387 949 007 171 433 153 173 442 336 913 017 860 015 292 728 933 890 746 922 320 683 151 480 812 758 473 854 640 374 374 778 266 018 139 024 931 020 047 298 432 007 724 650 313 279 651 593 758 529 926 460 342 233 724 827 782 466 068 075 220 004 859 081 006 574 671 796 495 885 785 012 215 142 357 111 919 985 873 849 977 442 810 321 089 294 319 847 249 904 046 579 522 436 922 690 611 962 057 636 579 345 235 985 259 314 695 579 439 116 353 758 816 081 299 686 457 137 347 142 862 676 229 373 551 214 640 058 633 038 961 591 591 952 953 742 007 223 770 490 016 942 922 503 476 682 663 994 254 405 548 981 625 421 600 105 056 019 069 450 508 060 960 224 325 033 975 529 192 560 920 208 086 494 913 733 941 076 703 604 946 384 605 974 029 205 220 537 927 251 292 283 076 374 445 277 453 798 663 688 540 500 819 138 638 439 363 407 021 412 565 665 206 901 553 855 177 349 673 454 618 576 075 401 471 265 607 374 561 144 862 353 410 703 513 850 647 682 872 844 943 452 830 232 113 809 227 566 142 324 788 904 090 149 370 837 511 955 955 446 313 372 571 073 096 017 223 029 801 632 188 924 983 372 234 025 036 192 996 438 304 841 500 178 922 725 307 623 710 207 384 958 225 666 587 786 807 826 825 008 873 125 563 166 963 235 702 556 854 869 485 800 794 360 969 440 724 733 439 383 392 500 845 231 126 372 399 078 721 423 877 402 474 441 404 781 107 455 713 109 559 562 284 936 114 939 701 198 300 156 328 321 900 456 394 142 421 330 790 505 433 358 366 298 057 562 709 462 840 697 172 088 840 016 003 040 650 821 703 034 876 764 108 298 427 392 536 306 532 262 811 032 948 291 421 523 642 939 657 042 100 944 556 008 659 470 879 154 524 100 921 516 623 501 159 418 384 802 257 954 907 842 289 404 423 293 358 116 078 663 860 250 368 188 482 539 866 577 481 939 444 504 417 241 497 467 677 954 333 887 221 650 183 360 671 357 296 295 716 495 326 935 317 611 623 149 306 458 940 333 580 546 179 114 427 851 738 391 036 325 840 883 808 431 769 330 491 578 065 914 164 466 740 174 658 482 443 683 907 256 368 951 920 029 279 755 456 725 940 914 095 172 886 493 214 107 180 085 631 312 465 779 775 805 250 523 884 789 706 072 231 738 692 519 218 816 030 909 679 082 951 556 543 574 842 919 125 058 468 767 534 343 438 381 591 995 085 529 513 705 265 744 370 792 966 552 262 489 973 735 827 379 931 654 575 529 905 635 899 776 102 974 384 660 628 515 206 284 211 002 610 538 044 002 316 739 768 785 323 244 430 801 158 744 890 722 810 347 002 324 427 422 177 042 891 588 513 161 937 981 781 981 120 361 068 617 074 507 146 969 873 961 776 709 414 801 099 789 758 669 815 147 250 839 644 565 139 157 008 903 158 421 697 554 037 195 820 773 785 570 872 605 092 010 961 658 903 097 239 103 084 943 360 687 608 061 948 575 200 021 998 824 106 571 169 170 057 935 930 659 605 896 900 807 268 386 712 891 500 560 334 068 845 842 386 486 661 929 970 838 889 966 947 302 159 783 253 378 130 256 725 737 916 008 340 209 188 997 741 820 353 192 236 112 451 012 065 295 049 710 930 820 185 764 608 743 674 698 042 855 352 671 550 348 334 028 600 356 749 468 416 384 405 126 369 493 200 702 775 908 806 528 920 570 625 681 085 118 501 597 559 635 128 568 054 692 272 254 039 576 668 033 965 457 728 367 387 093 717 535 700 228 305 395 019 228 446 059 944 504 224 344 500 289 229 070 267 850 248 535 383 258 594 571 298 124 075 113 989 424 324 794 283 554 235 907 120 388 490 019 402 746 486 837 578 293 867 387 566 202 714 466 264 841 793 473 729 453 976 994 571 207 568 497 933 587 995 913 426 341 335 933 489 829 020 252 518 253 903 016 296 305 383 295 361 319 892 495 942 818 627 408 871 058 119 334 637 128 941 376 124 580 805 806 088 034 575 248 322 919 050 981 936 294 300 358 821 629 017 266 554 587 174 973 596 231 489 882 525 602 261 459 251 863 311 101 488 806 143 088 231 593 186 523 906 825 290 024 466 724 154 370 225 009 002 508 689 410 548 773 973 422 311 614 444 737 813 780 314 410 148 639 983 698 599 007 576 856 648 664 485 507 814 099 472 899 198 188 087 037 986 220 590 068 632 912 849 193 938 622 472 264 502 109 985 346 053 831 987 797 317 447 894 436 406 630 661 526 364 317 132 452 753 848 048 846 839 068 795 709 128 835 569 579 408 749 110 308 161 448 929 201 653 771 431 495 279 455 062 262 423 517 958 109 016 279 056 995 233 410 820 645 194 089 984 747 203 747 116 468 499 507 662 000 367 173 809 942 135 995 490 431 932 795 959 700 125 181 523 325 815 142 403 786 848 540 175 410 059 713 674 893 309 454 731 503 256 169 009 796 787 037 221 281 914 640 481 833 984 678 340 217 768 707 853 513 138 369 049 991 204 869 306 395 420 553 918 897 728 040 987 938 682 746 476 110 226 136 784 773 625 037 994 484 309 787 096 910 945 720 592 835 304 256 693 024 358 176 723 063 527 811 994 151 046 863 880 992 509 756 140 903 949 838 184 425 034 784 739 507 439 199 777 723 727 530 217 989 607 715 287 865 181 931 724 093 218 279 369 175 447 653 914 166 037 545 200 452 680 970 358 251 139 193 658 095 201 352 382 277 188 554 050 202 165 491 455 319 661 289 149 405 531 824 196 662 825 967 831 301 718 568 136 861 465 000 165 171 729 958 954 737 300 786 656 218 273 689 590 337 641 009 696 784 545 095 430 366 696 537 142 845 592 959 950 347 486 929 038 724 813 727 589 680 190 425 754 402 755 975 469 194 987 316 565 361 820 265 694 683 415 571 265 885 485 679 483 196 939 902 462 962 404 984 253 923 656 110 679 133 471 018 690 797 447 927 213 171 227 634 883 186 699 248 087 913 621 188 304 279 370 435 803 478 465 661 066 783 228 387 849 092 972 338 522 132 111 851 206 272 665 277 728 896 033 149 433 762 308 570 329 278 215 614 713 275 739 200 095 387 687 596 529 780 998 306 538 281 702 252 261 547 773 540 324 916 884 096 461 728 098 969 324 515 303 338 113 192 354 215 052 445 582 738 743 506 786 842 459 706 687 992 376 701 365 039 275 092 685 673 016 611 240 652 252 717 291 863 898 454 505 299 243 543 864 499 052 736 250 348 657 415 425 939 733 852 064 195 112 679 465 867 231 873 220 697 292 752 308 370 058 945 109 466 959 877 696 158 711 818 070 898 639 665 310 747 234 596 741 185 259 272 603 706 227 477 515 303 916 516 605 266 258 566 227 100 733 943 964 046 419 796 837 891 557 723 946 955 797 756 813 080 564 065 549 468 133 421 731 136 758 267 081 528 305 171 792 280 552 833 594 000 952 482 138 567 465 624 520 492 185 440 668 500 302 859 198 250 592 944 268 387 156 265 422 385 372 335 115 693 257 101 030 357 236 403 692 245 710 213 373 392 759 433 852 266 348 151 600 608 942 858 756 514 853 276 144 226 952 768 770 324 560 970 334 274 069 237 869 432 972 230 441 091 249 237 834 667 468 786 055 185 041 907 033 472 761 703 289 800 792 024 720 759 916 136 072 993 951 873 606 116 477 733 674 511 598 031 746 067 188 003 970 120 772 555 397 219 977 937 600 340 897 956 169 288 465 992 243 415 918 923 942 241 096 375 941 348 953 807 846 212 166 013 153 507 181 904 614 770 495 225 141 727 079 626 923 656 767 589 850 382 223 274 621 355 762 150 984 118 394 974 273 520 789 560 088 019 985 674 221 263 473 352 988 223 132 672 648 608 945 203 257 233 200 351 913 993 186 783 344 453 031 409 062 912 027 980 232 401 771 210 772 923 438 086 875 740 004 090 976 920 478 061 724 177 860 391 425 612 224 281 928 174 846 036 827 110 155 605 496 404 993 174 293 067 229 146 515 657 610 790 105 214 321 260 327 679 302 761 004 037 758 521 428 696 830 662 825 559 847 294 185 339 482 339 904 253 744 017 998 296 909 245 009 751 753 485 578 806 209 025 183 257 583 537 412 828 959 916 128 492 614 724 784 563 568 478 934 558 652 057 373 563 361 716 252 769 192 043 494 564 798 250 185 353 989 793 470 832 330 814 511 252 433 218 874 593 548 399 562 637 360 630 867 432 524 223 276 021 701 162 027 285 330 376 339 030 766 297 112 485 625 337 146 893 680 155 202 982 267 858 768 424 390 753 355 696 900 499 515 820 981 670 478 964 737 782 435 820 739 706 645 223 061 569 138 126 585 716 231 001 933 881 327 890 434 877 376 216 058 382 597 148 072 808 452 653 963 047 947 780 909 457 288 757 675 981 195 545 218 979 896 569 945 710 622 399 455 414 681 405 422 763 758 164 433 230 937 238 595 027 916 567 706 132 922 599 416 169 440 403 556 067 502 113 763 390 908 267 987 990 499 639 238 844 535 312 431 333 076 408 480 065 137 695 978 580 178 768 208 363 143 610 641 301 803 923 583 925 816 845 396 627 161 208 671 381 945 181 234 473 324 794 329 026 935 077 131 451 276 646 050 433 344 992 468 243 379 337 450 985 663 549 269 232 047 571 256 072 430 787 435 085 085 992 115 060 633 492 831 209 642 906 049 024 144 848 828 826 762 940 739 878 766 868 118 458 805 181 285 209 261 125 764 641 392 422 616 197 332 000 598 953 718 247 623 656 683 331 941 388 428 563 665 705 911 382 132 688 581 529 551 100 476 249 433 262 834 853 738 618 066 141 658 618 855 903 510 776 382 412 087 761 854 628 493 505 725 192 246 010 462 470 441 156 037 226 390 880 778 096 271 758 589 886 052 226 592 910 090 646 636 314 011 203 566 834 547 032 166 170 777 031 567 288 894 071 545 878 435 893 721 632 350 885 180 363 814 851 647 172 483 762 040 348 065 996 316 452 010 990 921 398 275 517 593 300 135 462 204 151 773 475 870 385 334 650 741 412 182 275 553 954 511 762 476 745 399 651 839 167 069 989 132 098 734 140 432 102 344 485 966 813 220 620 757 483 262 976 983 991 758 264 112 116 502 343 705 289 582 248 688 201 232 763 931 768 250 326 655 624 183 600 138 359 786 858 591 268 361 282 788 600 868 021 853 070 355 637 839 036 755 372 863 829 554 504 945 825 795 814 111 472 345 654 146 190 018 579 545 488 101 053 341 823 540 670 574 731 366 466 905 020 160 743 953 459 513 969 938 929 847 486 244 733 367 386 776 799 404 043 259 062 168 643 110 488 783 444 860 766 027 243 277 243 093 636 840 454 154 222 378 584 698 846 726 983 486 134 699 812 842 908 672 970 275 458 502 715 574 349 351 768 781 682 351 459 390 130 624 980 313 808 047 664 460 965 331 709 648 118 919 036 658 757 668 544 366 409 455 516 044 558 469 800 886 162 674 856 660 138 365 026 704 996 914 022 495 985 454 063 416 405 098 472 174 597 592 576 130 726 676 219 697 437 085 710 479 787 072 077 813 648 574 253 671 608 831 727 278 965 366 412 724 756 366 438 233 655 185 046 632 647 186 761 310 793 141 335 861 373 103 416 507 120 253 091 533 553 980 687 772 023 585 832 713 473 763 001 445 118 516 433 368 419 813 538 932 000 582 659 559 687 077 890 623 850 254 451 171 040 656 282 726 353 874 496 163 115 863 082 973 059 844 270 766 575 200 119 522 093 434 662 953 112 376 257 343 477 806 728 050 105 678 357 178 808 414 383 029 627 006 925 298 562 939 523 951 660 918 600 920 217 229 648 040 390 206 245 919 791 502 329 382 382 961 182 744 177 853 472 281 521 974 554 036 117 785 917 414 427 983 315 612 953 904 775 980 133 344 510 870 963 439 695 490 686 344 321 726 620 418 343 144 917 095 687 147 014 010 427 456 729 328 545 763 444 995 596 487 518 414 989 737 836 661 234 641 241 696 940 420 743 258 288 157 636 357 121 051 563 865 891 619 647 838 304 543 109 046 071 845 484 817 937 034 613 434 509 152 921 105 139 943 626 355 778 680 117 793 663 400 100 282 055 644 491 765 140 346 108 924 142 887 497 235 411 684 077 748 200 474 770 640 235 145 846 896 512 918 921 800 096 895 973 417 886 165 894 063 983 737 360 171 553 692 794 465 351 575 745 516 807 046 281 308 166 742 194 485 131 049 559 541 637 352 671 379 692 060 469 472 518 800 337 104 533 695 549 397 500 007 024 702 177 381 384 954 925 574 927 574 308 176 732 657 623 666 506 181 427 504 756 294 224 561 509 774 247 810 230 758 323 336 631 325 950 536 694 969 896 219 628 343 048 133 532 993 545 533 531 146 202 944 861 998 063 298 729 334 571 686 763 160 757 962 037 619 379 738 818 904 527 517 111 115 473 723 110 484 690 449 283 679 583 079 229 918 753 165 429 187 282 908 361 551 853 925 578 013 549 160 169 526 836 996 515 398 468 301 762 040 888 619 584 888 718 159 038 178 316 514 777 385 607 520 551 326 854 314 040 905 897 646 592 347 243 518 411 493 965 327 179 132 411 482 748 900 402 746 167 232 657 337 966 323 953 657 950 921 921 529 355 296 023 231 094 500 592 542 791 951 977 449 714 952 214 660 054 299 091 018 348 088 972 521 299 631 190 484 223 420 282 663 654 561 331 940 070 417 200 018 975 679 491 174 688 816 382 439 043 135 647 143 056 714 225 941 780 648 698 829 351 731 029 548 534 400 236 934 933 108 678 008 504 804 645 730 397 241 986 566 446 862 915 600 751 296 766 414 573 610 193 317 839 446 973 219 805 686 800 766 058 392 702 395 841 653 631 688 775 055 406 680 629 351 308 227 899 133 299 038 844 800 850 148 370 031 412 635 803 153 555 416 959 641 273 269 706 454 530 716 834 603 793 682 299 094 424 613 798 229 319 216 460 216 737 398 964 358 175 676 417 023 147 606 226 307 301 979 389 165 922 423 345 233 938 874 038 664 219 560 861 220 596 862 976 212 733 482 107 520 364 651 462 382 041 227 661 625 070 576 138 620 412 889 588 516 776 959 943 878 638 702 169 773 302 428 633 110 001 564 407 104 369 215 303 303 205 119 220 988 983 389 957 737 913 976 226 611 212 097 379 386 274 126 252 846 286 510 318 655 681 138 369 139 035 701 788 439 568 972 865 422 315 593 873 773 591 336 169 701 895 849 963 846 661 438 600 951 606 116 867 405 909 710 387 189 655 515 485 039 877 294 908 279 261 064 412 105 792 203 002 066 776 204 045 518 393 867 436 286 480 892 069 495 238 851 112 028 364 555 787 559 354 446 438 526 881 834 270 630 195 274 854 116 098 390 616 635 626 409 071 970 958 794 668 312 253 371 210 848 677 426 633 918 788 142 671 110 352 933 519 348 403 527 476 253 641 076 266 490 498 525 259 383 879 023 520 093 735 115 774 784 994 125 921 670 280 774 009 934 110 588 437 404 711 892 291 565 388 523 846 458 901 629 274 080 624 449 082 016 986 160 927 807 234 632 292 206 654 496 995 421 416 249 383 528 368 825 123 387 931 680 855 445 155 797 583 715 928 133 843 608 058 523 416 352 128 959 327 286 977 066 049 184 302 433 524 363 853 882 271 857 559 018 020 618 553 027 710 069 680 656 748 685 604 514 016 119 085 804 110 703 480 265 576 611 384 260 426 182 199 507 464 484 348 346 247 806 509 387 371 006 359 002 241 992 697 484 692 177 922 906 753 634 274 556 480 607 804 079 273 198 224 169 666 855 396 175 115 171 140 436 256 286 829 213 566 973 108 600 246 811 633 980 883 494 107 500 865 586 400 126 850 116 445 259 260 335 412 446 700 543 528 196 190 641 418 923 462 534 475 214 672 314 574 769 091 307 046 297 587 953 337 446 655 096 012 892 638 692 538 788 669 291 569 137 940 398 299 113 312 105 590 175 053 545 434 120 980 024 604 960 556 253 899 207 665 157 499 341 588 067 469 399 038 813 761 913 372 589 506 320 849 015 775 212 073 992 127 191 267 847 889 451 305 935 875 153 569 492 128 157 821 746 390 503 319 302 388 468 876 096 388 326 563 818 353 577 437 211 470 867 879 687 946 278 758 802 154 944 379 095 021 955 947 081 878 013 905 988 630 757 922 606 352 916 171 524 236 376 390 605 589 015 460 258 356 224 255 797 211 753 414 236 519 472 503 482 393 832 580 640 350 497 262 283 400 840 011 109 201 151 328 132 538 275 897 215 483 085 971 531 710 201 230 630 913 125 725 244 459 791 979 212 796 357 851 351 127 323 166 980 991 925 482 832 199 530 861 773 801 095 251 522 868 606 499 843 335 612 981 855 621 107 677 618 657 504 282 897 493 001 856 901 499 184 132 134 598 585 351 200 519 090 635 357 917 550 538 482 163 793 877 310 603 859 182 831 042 542 286 937 560 643 450 641 196 600 567 193 380 207 378 450 485 882 843 416 111 265 353 282 203 517 816 737 229 345 031 188 766 848 284 152 276 738 376 894 095 892 689 697 630 053 279 919 456 734 582 172 109 706 479 872 790 092 126 612 612 492 304 992 126 327 507 050 779 137 072 902 593 633 524 492 147 572 452 044 155 063 550 130 303 639 591 563 062 532 732 623 510 834 974 627 377 948 257 318 212 311 728 487 674 347 766 337 628 743 374 950 153 238 463 210 862 921 047 300 831 434 629 845 254 614 004 507 061 784 393 049 560 859 744 444 460 389 367 297 660 930 468 088 751 968 062 458 517 521 206 359 623 936 335 647 419 751 659 569 146 827 926 098 533 390 766 131 615 100 064 925 360 467 025 750 350 213 876 302 093 748 445 867 494 412 114 580 716 337 998 283 000 644 864 214 775 410 726 294 114 498 523 015 014 629 982 463 460 208 041 074 383 936 172 421 981 330 635 917 735 892 485 646 104 142 162 466 288 691 188 957 172 837 781 827 190 912 197 498 378 502 689 890 806 040 447 962 178 686 203 855 610 415 361 564 030 691 237 154 770 528 231 370 771 348 209 155 336 813 606 021 792 399 177 282 178 032 064 757 281 359 628 360 866 269 866 062 759 544 891 050 468 248 244 697 049 496 888 830 620 897 670 396 314 727 723 528 774 763 218 710 825 050 603 795 490 631 836 949 736 528 650 884 633 398 564 695 454 804 885 719 791 823 133 213 725 974 058 134 487 361 258 623 683 500 796 910 449 090 265 485 349 721 171 546 374 352 070 522 172 271 480 885 315 446 260 947 447 786 669 595 149 072 068 848 817 118 486 656 618 816 527 077 811 517 069 427 789 222 261 564 878 167 053 735 171 221 577 065 148 160 637 764 445 601 639 420 768 903 683 883 657 427 342 292 370 703 670 414 235 167 450 133 510 940 573 962 922 658 478 844 504 371 867 479 834 376 325 172 064 825 248 793 609 760 197 832 073 970 050 406 775 539 071 197 927 849 676 650 678 078 611 088 960 139 598 054 787 972 871 688 712 878 319 604 145 107 392 256 685 910 499 544 720 821 729 703 549 454 886 517 113 295 869 453 602 025 826 704 540 533 972 594 950 373 286 945 499 569 552 543 819 112 532 484 275 270 379 133 604 199 644 491 712 720 993 809 223 990 261 460 439 692 922 392 319 661 783 698 440 120 242 055 915 741 331 665 452 544 284 262 252 779 813 885 896 120 705 263 463 052 021 078 355 288 857 768 417 786 464 295 056 626 731 031 613 913 735 683 183 779 773 838 814 517 254 143 661 486 011 175 547 998 626 190 382 040 602 524 222 609 680 974 884 298 264 141 581 496 541 811 007 134 414 724 674 314 331 537 317 476 363 967 590 143 238 018 457 204 302 179 210 082 740 440 014 096 777 420 962 357 713 655 355 260 584 246 846 369 584 183 886 083 620 232 697 550 807 758 304 205 707 012 085 006 963 980 220 293 992 015 126 729 642 412 922 756 340 125 277 662 458 855 744 762 377 877 268 865 541 088 824 049 900 122 896 355 425 903 666 857 018 862 731 260 263 907 199 705 169 355 229 153 214 829 527 979 168 527 109 587 171 652 354 238 268 768 236 459 042 292 588 387 398 020 005 586 742 877 586 515 617 764 844 172 807 663 818 654 073 547 308 054 231 948 334 846 906 851 949 758 267 382 012 525 100 893 569 755 850 877 838 407 506 654 107 152 628 068 317 149 631 598 305 735 290 257 568 823 496 043 902 036 762 791 794 126 527 441 424 461 838 695 304 821 233 679 659 815 805 302 869 288 948 385 043 124 573 874 868 088 999 176 621 185 583 972 262 905 722 498 148 898 169 674 060 491 762 352 120 282 540 456 996 943 257 325 559 904 080 014 565 584 871 300 590 217 967 887 994 131 510 468 457 348 885 146 331 457 330 277 510 531 228 282 586 349 148 866 627 714 001 965 826 518 682 970 410 740 983 917 381 659 496 356 194 321 161 513 083 030 777 677 765 653 980 923 144 116 585 048 130 623 950 233 079 341 262 981 329 992 395 801 193 581 962 350 060 936 674 259 438 041 088 223 290 748 015 430 758 271 762 465 493 463 086 010 433 608 629 189 973 256 193 941 437 340 618 001 356 235 058 903 095 755 845 483 292 000 866 592 232 550 545 833 368 370 367 528 133 152 400 008 012 185 285 024 682 128 785 151 099 702 885 372 435 325 308 450 632 719 595 934 261 213 794 690 802 026 518 774 419 994 867 279 020 782 989 313 684 215 734 487 669 705 226 967 478 560 606 058 336 479 808 441 621 461 515 185 767 922 580 480 966 949 754 729 999 883 882 118 286 595 991 690 041 267 349 968 569 347 497 363 375 228 567 576 102 503 135 130 927 630 155 936 959 568 284 452 045 070 920 208 566 978 209 296 730 866 758 143 620 211 164 484 072 485 447 192 129 881 133 925 555 542 290 498 268 305 326 908 756 495 651 984 731 690 705 961 499 286 830 666 127 999 376 835 124 082 934 641 786 762 440 183 926 727 877 441 418 882 311 724 988 882 603 399 430 612 210 893 811 385 907 613 871 104 216 977 672 795 708 400 721 948 592 746 950 298 492 282 535 597 735 116 191 598 777 874 438 912 680 086 898 438 136 984 598 233 530 321 763 390 778 580 324 446 129 271 188 081 401 758 927 021 866 461 961 588 298 727 425 574 189 767 818 947 173 258 240 036 048 037 905 268 114 841 103 778 770 805 734 590 603 904 526 280 519 072 731 875 361 506 699 237 718 539 803 916 281 114 568 558 473 732 809 871 609 914 318 924 988 863 974 592 851 799 831 925 828 358 866 126 056 121 372 315 982 968 940 500 444 797 976 362 551 143 442 933 266 045 832 765 653 648 517 599 186 745 546 214 678 153 376 032 334 582 389 002 983 317 599 868 370 033 995 888 792 399 849 092 382 170 047 644 558 080 881 794 548 157 893 866 579 096 084 051 734 352 365 320 118 044 014 292 039 305 316 135 448 778 032 729 942 071 716 935 003 850 583 972 449 331 393 023 850 809 492 944 135 028 527 387 770 602 785 845 353 102 561 673 767 853 533 630 665 770 299 164 617 546 457 042 067 901 984 659 624 219 926 019 234 915 041 605 503 733 688 770 179 639 015 017 060 171 948 658 878 701 140 558 322 026 595 573 660 025 691 149 650 148 120 248 552 500 188 310 838 056 286 665 125 098 710 308 206 743 333 822 148 167 163 899 526 225 924 635 760 447 847 400 197 174 863 036 409 364 459 213 059 246 625 645 249 673 339 960 510 132 713 399 782 335 301 590 347 344 069 160 263 712 002 681 009 876 394 907 629 306 543 716 378 831 662 561 578 552 948 468 508 893 954 882 017 932 841 856 712 023 384 988 913 350 867 936 446 243 987 607 631 491 987 852 893 954 263 175 950 459 485 949 315 704 681 076 632 449 004 333 023 562 924 755 386 333 440 369 019 451 950 391 437 234 012 826 674 699 344 264 688 410 285 760 432 707 320 267 268 731 015 255 367 619 471 961 861 921 543 682 613 081 968 596 156 584 482 198 568 770 751 247 311 453 278 110 897 237 240 978 393 313 021 744 503 283 416 135 413 708 419 134 357 581 590 865 060 894 952 457 116 021 809 621 061 996 390 027 551 048 258 432 200 582 246 009 906 004 704 980 360 569 032 783 652 394 947 661 198 414 338 789 266 074 051 961 205 921 245 047 528 303 165 298 053 776 722 296 930 157 935 039 574 533 790 640 693 572 509 959 353 632 831 731 709 651 179 206 142 632 528 121 178 405 396 620 655 518 955 051 918 650 041 243 910 514 100 912 277 008 486 884 138 773 857 905 669 558 869 419 786 275 837 650 754 381 040 501 130 898 247 727 008 866 876 848 679 356 625 308 316 783 467 300 377 043 199 936 661 462 673 212 464 436 644 901 533 149 061 365 058 735 388 341 793 432 912 299 800 318 317 417 292 066 024 366 444 287 244 896 528 390 705 061 874 803 042 880 062 871 298 682 939 935 003 613 875 599 351 869 517 540 078 243 057 033 871 483 070 954 575 337 813 498 555 967 927 520 942 101 303 162 127 893 771 237 127 141 661 263 599 219 537 655 577 706 565 795 240 754 787 175 184 653 622 798 197 215 273 802 513 829 936 277 674 839 834 003 726 734 333 201 064 702 643 183 310 592 165 790 246 314 378 834 279 490 585 102 788 762 740 551 552 510 190 897 566 788 767 380 532 235 039 670 691 368 635 714 095 294 710 628 479 065 410 902 602 745 268 013 938 696 873 666 395 298 593 683 575 095 012 842 987 986 563 559 515 764 813 264 396 272 406 886 178 255 556 144 864 029 742 827 774 867 121 828 904 938 182 545 011 834 285 577 390 121 586 431 252 987 546 455 220 621 145 086 159 724 048 232 260 149 375 760 645 914 758 332 099 878 769 536 375 874 565 939 629 853 680 928 461 723 396 933 956 950 402 112 326 164 109 793 148 967 308 192 463 660 441 986 573 923 369 030 140 434 043 201 463 067 653 629 548 264 562 676 856 030 353 409 721 377 803 983 147 508 233 756 112 254 078 490 106 957 801 640 638 130 849 728 663 228 158 485 363 876 804 627 075 601 290 357 699 416 166 800 713 191 947 835 578 776 730 605 276 672 696 961 749 445 317 342 652 754 331 934 872 555 512 748 382 007 952 839 980 261 351 399 362 878 668 631 986 878 615 539 090 563 042 013 165 450 553 722 845 226 204 636 726 505 095 685 923 733 813 474 469 846 559 263 515 389 149 546 825 525 965 777 715 315 361 175 523 635 449 832 175 185 060 466 775 194 669 968 253 331 808 059 376 563 229 189 711 079 890 776 856 444 313 570 145 985 679 356 881 551 606 552 888 214 047 544 545 393 918 735 705 111 723 713 470 202 453 734 603 954 620 328 181 077 623 175 736 638 560 638 828 554 683 552 905 820 389 927 390 746 983 304 216 753 364 085 163 547 318 726 309 357 479 135 254 203 262 134 442 920 172 137 693 619 951 061 771 955 369 612 156 063 318 537 254 958 619 774 101 588 401 802 271 867 017 152 203 417 620 590 188 011 937 965 506 461 148 896 802 010 696 600 581 873 761 024 323 210 140 317 705 704 694 334 593 220 926 701 765 870 052 003 417 663 294 826 266 768 640 214 103 679 859 795 852 170 564 214 927 771 444 891 650 252 383 279 916 395 211 983 635 069 786 700 184 560 853 243 670 003 443 285 362 048 894 991 560 807 851 340 038 044 623 370 458 617 537 222 998 067 453 558 260 003 935 857 508 819 303 643 494 883 868 249 327 158 184 525 724 429 980 230 575 340 845 233 271 751 912 755 953 133 566 138 265 269 114 710 847 232 579 316 240 486 918 531 051 852 897 845 545 956 129 660 396 959 311 867 737 387 328 654 564 756 556 644 715 944 216 254 051 787 239 517 682 293 414 747 289 456 137 050 473 474 722 879 502 642 604 492 337 730 894 661 495 169 745 289 348 487 511 926 197 867 126 410 177 826 206 693 529 716 432 133 973 805 256 307 506 025 669 144 878 369 352 488 118 479 103 371 386 418 825 833 839 794 435 074 563 818 680 185 953 692 139 218 974 777 355 003 961 383 665 080 545 276 983 677 722 259 706 339 461 381 117 174 156 110 212 392 066 216 499 612 365 614 225 381 092 811 251 884 828 825 573 057 870 837 089 423 533 221 174 769 639 327 668 180 248 693 201 838 023 765 544 487 678 189 378 213 605 771 018 702 528 360 989 089 389 558 390 901 045 387 124 297 113 752 842 512 806 447 084 271 385 440 762 132 588 941 512 797 644 855 420 172 887 397 241 381 840 194 809 025 805 364 531 356 952 415 250 270 494 809 912 469 950 221 550 732 738 753 328 881 578 326 767 453 698 178 265 027 340 712 162 217 757 510 818 356 776 135 445 094 077 454 033 243 727 970 964 345 417 825 279 075 606 749 390 009 635 298 036 057 160 072 614 010 987 989 431 800 421 893 719 500 228 740 358 737 303 938 306 608 060 880 063 679 572 499 304 281 565 727 965 988 384 307 958 169 930 536 641 491 360 213 048 323 702 854 712 228 924 009 355 721 460 564 763 355 099 087 299 005 528 675 125 600 888 419 224 317 531 766 930 295 926 567 151 282 380 923 505 876 345 617 073 825 545 209 890 104 366 529 287 049 962 367 319 797 929 714 217 155 108 187 600 651 135 950 729 891 299 626 964 781 680 580 839 240 170 101 104 934 743 866 825 540 130 122 895 004 387 727 464 464 347 706 092 875 802 662 184 095 454 505 302 999 722 174 608 405 266 395 427 752 972 570 492 715 370 646 582 901 204 863 253 358 437 035 007 186 325 067 406 066 173 423 538 398 820 951 182 532 526 947 851 932 383 602 288 475 490 849 005 737 280 867 407 895 974 265 067 088 107 161 948 071 924 017 710 633 481 084 693 754 565 787 973 395 313 915 655 314 607 975 397 151 336 358 621 561 492 232 038 832 449 636 177 139 280 105 542 722 819 702 974 468 420 935 802 477 287 127 414 413 913 016 309 333 145 469 527 081 942 262 554 265 078 515 631 358 143 144 856 878 215 816 376 587 011 518 511 115 335 722 987 109 791 545 163 034 743 533 382 701 696 443 298 805 877 351 988 168 311 196 156 506 249 498 373 522 772 566 309 564 843 366 157 630 073 648 513 980 070 426 060 965 449 703 918 374 618 522 724 796 641 515 425 380 623 971 265 279 608 300 535 351 783 967 139 528 367 565 384 493 444 059 877 033 731 699 196 204 087 708 620 409 046 431 207 021 651 125 642 623 777 530 713 953 554 427 114 975 980 975 464 226 476 090 226 514 749 758 267 742 170 764 846 836 682 855 087 477 461 868 419 701 698 493 999 526 553 371 398 794 938 398 431 297 511 963 407 396 841 479 720 187 281 147 233 180 489 319 058 714 637 397 376 867 372 650 423 034 639 284 453 515 588 603 423 044 286 435 311 394 457 969 160 012 319 217 180 418 492 762 284 288 627 345 604 141 146 634 795 887 888 098 181 636 060 149 004 414 772 658 662 493 550 320 725 638 829 018 368 895 014 299 417 795 659 315 923 793 651 257 369 048 199 746 442 012 409 095 851 109 186 416 295 142 833 586 367 374 232 947 238 601 365 346 160 780 725 120 354 072 990 888 763 810 749 314 652 487 045 406 862 707 273 044 190 081 961 512 534 090 937 633 036 334 674 395 925 792 519 379 530 384 976 076 728 471 300 772 675 890 555 903 698 947 232 348 069 191 695 125 717 219 729 481 967 255 961 209 989 779 661 100 788 831 762 680 972 776 736 530 986 940 122 768 314 920 534 775 938 618 531 989 964 827 360 916 582 555 714 247 864 996 543 476 006 706 590 586 291 733 391 291 655 418 369 965 296 838 034 615 085 391 949 764 262 467 298 823 286 944 074 420 748 109 390 590 258 384 318 051 975 321 278 139 568 678 067 614 714 309 865 694 073 188 279 253 053 513 895 312 833 247 336 837 966 488 340 785 590 638 512 579 061 073 790 123 812 541 055 208 053 865 601 167 215 812 175 409 745 667 129 516 274 132 766 766 907 882 590 908 250 668 015 037 953 227 285 027 689 374 413 956 850 485 883 666 808 950 481 546 413 721 664 478 021 760 213 267 051 272 135 959 401 514 591 881 682 264 253 848 041 661 302 872 268 387 633 266 833 360 950 725 011 128 572 292 346 189 959 778 486 771 770 879 216 204 165 639 423 668 684 990 557 681 349 148 200 365 637 691 767 499 936 960 267 925 451 873 536 036 185 927 465 485 589 400 596 480 884 635 278 862 801 829 549 751 064 580 168 531 574 892 167 702 953 892 103 133 920 554 194 173 077 601 492 982 350 775 034 364 683 853 330 633 752 379 436 140 731 138 080 874 596 262 909 664 114 991 127 073 270 491 175 633 463 488 490 315 207 080 298 854 124 773 047 515 979 282 652 509 135 140 831 902 463 146 860 637 325 393 063 013 366 963 555 219 433 597 331 694 557 959 903 770 210 602 102 328 915 821 445 377 880 383 332 175 281 957 947 050 050 211 194 827 210 602 101 332 341 988 642 948 174 936 298 279 612 329 593 060 407 472 790 368 952 414 989 530 931 732 863 803 781 449 796 568 262 076 528 176 235 606 073 850 250 442 681 156 691 746 336 832 259 657 941 895 175 048 501 363 206 688 951 401 535 480 268 786 746 047 055 825 544 724 656 188 966 842 276 926 429 643 338 143 006 854 216 595 554 380 272 962 404 575 382 999 365 644 422 431 865 851 588 185 249 761 687 074 865 564 052 998 504 790 727 370 064 875 667 838 937 426 517 673 670 706 287 593 457 405 534 269 061 412 285 071 722 318 716 788 928 893 190 361 807 604 525 544 743 924 038 167 893 801 360 012 691 448 898 742 827 015 150 420 630 704 921 108 447 423 604 931 416 333 503 831 049 424 888 589 458 986 637 081 100 996 198 080 127 063 731 318 225 061 031 363 084 281 482 400 628 031 827 408 753 015 711 841 789 295 110 701 607 000 912 750 766 007 708 743 722 770 541 929 408 170 503 147 403 901 962 918 779 782 245 343 470 401 246 860 147 342 026 499 489 456 994 100 176 871 836 866 485 175 623 248 864 384 931 554 892 853 912 131 012 294 676 673 985 453 133 678 882 049 144 410 899 589 568 171 140 551 036 185 506 442 401 140 435 944 991 763 985 056 772 902 249 714 605 991 166 915 489 032 885 536 874 333 497 632 372 650 104 065 739 580 313 834 494 072 303 701 404 334 466 479 960 522 786 755 777 280 961 723 745 183 298 576 404 024 506 039 376 799 974 471 830 825 954 546 388 213 230 049 388 227 420 095 498 456 559 183 099 640 035 990 930 411 776 694 943 954 599 654 795 994 587 802 200 816 993 788 056 222 095 008 537 690 970 129 618 326 475 092 333 248 528 324 477 896 214 981 668 317 299 176 726 991 709 202 080 273 043 947 083 660 325 540 849 654 596 603 308 519 749 756 018 936 410 920 800 185 981 262 010 001 347 302 217 188 645 084 514 095 444 674 684 654 793 922 734 083 727 139 176 268 117 195 879 149 335 492 417 610 174 717 373 268 006 907 179 277 409 914 322 163 034 567 344 997 430 485 021 810 336 005 624 100 053 315 756 611 166 172 552 468 958 669 872 956 101 800 156 310 958 003 421 074 040 753 171 230 026 391 761 669 054 280 364 406 212 117 529 320 094 216 712 972 343 900 777 350 313 153 208 603 002 457 725 727 269 063 890 501 353 048 969 140 968 412 714 610 158 097 148 378 517 800 545 791 541 518 607 364 206 573 832 053 005 284 209 730 792 486 600 643 419 274 998 179 569 306 753 780 387 286 014 724 753 869 700 174 348 716 805 874 708 209 842 025 129 223 956 457 246 112 528 294 819 972 938 949 176 536 780 530 756 313 561 297 654 901 372 873 821 299 794 112 424 084 614 201 077 859 507 165 217 762 930 521 550 197 526 960 539 899 654 667 457 600 547 313 832 493 979 312 011 416 124 858 964 943 767 326 529 503 781 272 045 438 872 410 493 337 298 967 813 446 646 174 806 412 243 612 619 992 177 545 851 746 068 198 841 589 841 600 654 377 580 736 911 497 032 646 113 711 416 025 522 739 093 200 881 459 655 049 026 404 930 042 654 435 032 404 046 892 301 902 765 537 680 382 762 270 552 584 441 366 641 043 832 005 032 011 894 944 850 077 752 905 976 977 913 823 226 057 887 804 364 786 235 193 277 416 512 440 345 767 857 439 875 030 182 055 990 169 205 944 267 615 725 487 636 474 888 615 418 931 054 259 613 836 892 539 145 348 245 145 121 997 709 880 529 551 937 258 019 002 323 057 903 462 819 351 216 729 978 813 082 505 606 061 247 318 947 078 038 385 376 698 501 794 573 402 801 532 005 514 725 501 222 039 789 289 150 142 702 215 139 917 331 480 750 130 658 105 735 059 738 830 493 084 044 263 225 127 190 807 436 012 765 645 526 251 992 903 925 432 111 849 509 894 959 457 090 292 102 308 057 082 379 322 887 190 556 740 872 931 174 126 496 754 628 389 966 520 781 379 739 350 593 990 843 973 274 308 156 952 383 462 261 896 633 725 491 581 455 587 441 649 801 499 909 349 537 202 604 763 403 501 587 447 584 836 215 197 351 435 558 920 110 282 669 353 825 951 980 089 138 657 447 422 271 467 164 332 648 070 248 247 223 648 874 012 273 785 264 473 726 686 674 704 067 118 875 835 790 313 991 216 309 629 139 994 130 043 320 954 658 239 552 817 427 804 147 639 772 279 757 984 777 655 175 141 617 078 426 887 648 929 978 589 558 885 462 209 442 993 911 721 985 885 285 147 177 192 373 085 320 314 627 194 030 463 079 253 041 191 836 981 136 021 239 410 912 356 869 709 145 817 475 312 438 633 989 581 726 636 002 644 634 974 491 701 229 949 615 322 759 435 554 865 501 391 672 070 617 629 826 731 680 808 391 962 605 041 953 425 522 181 393 203 785 933 914 637 486 470 197 381 214 739 944 950 249 912 120 832 891 830 780 031 889 231 291 196 643 223 573 020 996 647 938 346 302 408 368 161 906 425 673 347 588 185 937 030 978 002 967 750 838 267 688 724 401 001 910 162 687 477 131 078 574 043 496 776 155 448 379 727 875 852 903 576 452 157 885 808 257 654 969 848 868 435 942 923 120 244 118 848 282 875 511 057 598 289 799 313 253 100 267 004 096 710 786 200 591 985 964 923 069 093 699 688 117 959 130 023 528 597 625 121 111 966 578 919 292 550 386 851 370 116 347 192 139 624 508 937 742 774 681 369 609 081 418 082 959 676 998 675 525 329 826 224 795 738 954 048 129 030 755 472 481 651 682 967 465 871 397 543 585 111 060 214 635 658 354 497 812 698 469 858 945 204 813 525 954 900 113 670 871 389 312 285 292 201 847 602 389 545 577 214 696 254 326 556 441 942 578 654 500 261 457 126 108 354 530 688 314 070 557 996 006 364 147 949 217 490 742 058 415 303 776 175 733 712 232 977 818 223 773 585 036 294 108 819 096 544 941 167 976 623 679 062 657 824 292 082 521 279 458 648 936 267 685 253 432 664 698 896 608 418 588 409 154 837 996 955 963 238 148 941 151 840 834 609 198 456 389 952 955 562 705 259 470 374 643 263 807 561 606 400 519 034 637 585 110 185 926 394 440 395 225 454 860 095 868 205 665 932 932 432 663 403 333 793 684 137 197 168 223 855 122 964 299 339 712 747 078 469 127 952 006 402 530 231 455 288 117 106 298 273 881 171 875 119 078 681 546 434 731 616 489 460 625 542 029 908 183 033 853 407 033 921 823 959 599 053 438 691 209 010 255 480 064 796 919 205 205 150 604 545 391 597 498 405 820 479 254 790 366 903 182 083 690 134 936 354 280 900 940 879 946 793 009 138 763 709 424 161 663 019 314 318 313 627 699 168 293 643 932 007 306 708 111 129 589 310 868 906 394 293 713 684 455 998 474 705 427 274 736 628 394 763 772 272 527 466 644 912 199 674 102 669 090 627 781 084 745 433 475 153 994 527 524 110 926 544 671 593 220 704 189 924 984 274 078 739 242 123 720 579 298 505 437 672 791 061 183 911 436 775 740 861 822 567 310 382 875 410 408 235 019 621 967 775 080 327 736 707 781 246 937 999 226 840 974 514 015 683 367 758 699 120 018 788 537 012 341 168 049 602 623 125 118 262 664 750 427 330 780 331 327 410 976 202 771 231 876 795 064 382 302 374 143 650 578 457 364 095 316 755 871 901 501 307 771 712 404 034 018 092 860 615 832 488 897 647 665 206 427 199 195 908 825 654 129 971 708 151 955 210 917 389 842 188 091 202 319 041 282 742 969 600 506 905 870 818 999 419 368 356 160 733 816 752 965 495 794 576 577 276 880 493 745 752 372 839 110 644 489 297 002 169 657 222 693 911 961 561 417 562 343 705 292 789 099 591 919 931 650 084 138 189 755 092 625 450 534 051 912 311 830 389 816 698 538 417 859 967 905 288 057 584 622 899 247 319 361 589 100 522 783 190 223 353 441 225 634 132 924 140 230 970 071 433 323 781 312 340 921 850 133 770 586 809 841 805 915 378 463 268 807 220 770 424 933 141 776 410 408 035 302 441 142 643 927 798 287 330 960 233 297 308 605 703 146 421 438 148 227 764 538 859 382 580 239 434 847 703 971 447 008 530 341 648 466 579 632 023 089 610 701 792 962 435 291 295 119 430 426 670 783 539 241 026 518 700 084 364 761 069 494 415 667 099 510 315 653 780 417 401 231 197 184 989 626 118 787 155 734 151 121 945 714 350 637 287 554 037 488 694 439 848 087 676 197 086 227 855 602 964 484 923 387 415 375 362 325 356 997 873 973 386 552 528 921 589 508 436 338 250 351 134 707 107 220 417 191 306 452 369 399 964 839 386 378 247 081 233 019 661 710 401 346 047 480 797 539 399 245 878 692 290 002 124 201 790 933 773 880 973 251 190 833 368 790 184 510 881 807 437 319 265 694 991 437 689 260 036 974 182 205 455 213 203 948 720 696 079 640 143 331 760 790 240 601 897 724 805 694 722 455 619 621 761 321 653 470 253 442 934 209 731 463 716 940 396 946 966 521 741 956 898 212 698 906 941 052 661 072 835 343 906 074 324 615 341 192 266 243 833 153 208 839 905 003 259 268 159 364 605 180 574 066 560 956 139 920 692 818 832 511 368 645 576 071 840 656 169 219 226 734 468 465 423 892 549 293 990 088 047 247 000 284 340 488 603 096 813 125 259 012 866 231 714 092 752 479 299 201 108 706 283 525 081 702 443 594 406 054 895 200 840 256 336 036 409 729 784 562 500 180 681 768 506 907 974 604 622 945 173 589 915 365 286 333 624 426 057 742 349 831 262 137 784 030 898 988 370 901 107 796 917 077 508 637 007 695 147 715 992 499 783 163 299 210 676 563 221 468 606 931 838 469 693 712 387 091 411 376 388 124 627 051 124 055 115 224 857 667 093 900 033 112 491 079 958 386 254 828 646 620 960 512 973 876 073 752 326 828 811 520 195 950 813 446 967 548 409 277 139 311 173 709 676 799 184 573 920 479 050 161 833 590 641 217 061 565 956 883 310 590 137 858 221 490 922 524 750 893 729 245 684 287 169 306 158 333 040 655 308 685 673 205 069 354 269 115 036 854 329 550 910 687 144 865 947 807 406 276 262 787 620 587 705 512 847 160 415 205 268 684 992 340 053 048 774 858 745 269 697 143 099 949 559 460 679 053 868 469 939 712 780 504 623 330 603 199 366 550 923 588 076 923 074 256 245 388 773 997 263 975 061 561 480 054 863 126 108 469 992 544 470 311 792 372 041 267 423 155 434 189 184 946 121 356 669 597 549 229 959 045 749 366 155 348 637 178 711 006 752 213 290 552 642 908 527 139 630 898 160 003 983 142 150 920 547 369 400 624 501 778 711 301 318 903 957 851 077 095 070 444 988 237 885 843 895 088 004 018 112 296 728 591 218 132 586 516 541 133 162 653 493 134 393 809 446 566 055 034 337 340 176 926 347 308 825 867 176 603 989 668 725 362 719 868 428 051 718 138 635 243 896 082 135 769 416 428 998 463 445 747 307 367 593 089 439 951 889 976 850 021 849 698 221 892 544 955 088 135 513 872 379 791 686 609 526 671 008 808 712 882 551 239 748 323 870 736 404 393 412 535 590 180 618 678 869 221 764 127 236 335 065 555 131 287 984 707 293 424 761 091 838 298 617 899 326 913 596 673 276 161 477 476 555 612 049 827 571 627 406 270 370 650 265 517 130 742 817 178 266 532 422 438 345 102 792 027 639 716 371 665 045 858 971 127 154 563 975 328 842 969 754 489 238 586 287 367 293 164 775 837 063 144 668 961 745 425 846 211 137 068 500 117 325 290 603 934 269 781 528 964 039 725 911 920 382 633 895 962 179 527 889 022 481 342 245 388 713 474 276 796 970 129 390 130 844 691 170 380 864 428 534 573 664 289 447 942 668 848 280 047 099 590 834 247 724 540 247 357 624 372 209 178 571 878 561 288 680 743 560 333 542 464 899 715 188 137 722 660 438 201 605 529 439 878 968 695 113 676 193 626 758 484 243 345 721 914 561 860 313 888 632 196 064 746 636 490 277 451 796 874 036 982 754 508 870 192 137 967 548 071 148 330 513 190 372 837 752 196 500 992 687 189 289 410 606 807 297 146 359 138 560 814 620 475 065 444 339 501 737 971 338 572 405 576 414 301 577 358 059 251 346 387 222 467 479 307 890 976 518 587 473 448 615 094 322 998 301 310 663 352 047 195 055 734 680 745 296 251 329 474 717 265 904 715 576 365 145 762 568 509 312 762 855 973 306 089 962 365 035 419 020 597 841 937 664 458 362 981 702 912 213 569 939 742 899 529 047 355 155 018 191 013 094 112 432 193 657 644 081 168 565 239 891 128 353 515 037 992 777 843 154 570 773 206 501 514 586 750 797 735 495 967 849 572 003 434 738 730 831 918 424 336 532 273 496 109 940 081 195 825 443 586 022 788 490 800 474 616 419 648 321 439 914 673 693 749 127 308 413 262 601 292 119 579 305 564 056 799 185 467 640 706 299 006 434 149 913 653 947 580 013 670 404 088 514 414 221 258 559 833 249 195 583 175 355 211 975 941 887 451 712 860 539 627 076 185 890 837 643 819 875 228 874 690 581 641 643 640 037 907 401 366 331 583 920 508 750 544 113 292 712 700 732 286 705 353 615 063 051 378 880 311 765 195 443 676 087 916 104 760 547 723 695 095 340 841 740 648 938 015 736 072 103 916 616 141 547 538 819 673 952 107 856 197 203 754 438 090 178 756 041 646 132 782 087 068 749 226 579 100 916 808 394 077 691 339 456 269 114 417 686 215 297 353 346 447 656 171 702 775 813 214 978 719 552 287 764 154 598 410 418 503 777 736 461 876 520 226 313 575 164 740 913 589 506 434 942 738 299 612 931 571 985 039 320 093 695 979 325 072 053 426 165 975 967 480 744 552 402 593 091 219 062 927 892 306 105 185 947 484 204 582 833 473 553 167 912 875 057 379 092 587 839 201 885 376 222 761 631 540 356 638 181 235 855 707 979 021 450 535 792 399 485 726 578 805 229 174 736 650 373 754 174 319 063 901 051 971 387 403 372 618 726 786 392 071 677 919 920 237 775 100 827 612 621 033 980 875 716 828 542 132 101 248 224 769 365 708 059 942 196 827 202 374 699 906 522 474 355 061 460 721 213 207 416 481 846 030 371 045 741 679 987 783 082 069 367 833 766 570 856 499 567 381 149 598 826 213 300 216 360 023 726 706 648 465 871 096 924 617 111 281 537 227 210 530 923 520 739 917 385 634 211 565 841 422 233 364 449 906 096 816 656 089 340 046 428 395 676 117 333 631 308 908 766 480 881 104 708 947 772 340 436 201 176 433 660 114 356 966 520 178 612 950 462 834 627 192 463 303 995 116 764 884 648 094 598 603 113 334 909 379 529 241 892 442 589 452 817 202 320 659 048 439 566 414 215 837 509 267 938 259 547 942 789 104 966 946 242 179 278 189 752 500 416 753 930 222 169 356 303 087 430 430 644 413 234 664 133 227 020 969 531 747 389 699 290 447 210 744 927 163 315 458 512 754 647 995 705 774 729 197 996 933 973 060 565 271 541 197 490 793 435 795 858 421 717 670 492 128 099 329 184 932 223 499 757 475 809 647 419 025 295 868 958 439 194 545 490 619 181 151 583 285 358 861 400 721 397 857 609 781 661 120 159 174 269 802 898 248 982 916 066 093 792 805 112 454 756 642 253 117 770 949 814 998 594 916 837 051 325 737 158 844 478 600 345 386 780 814 834 544 456 079 024 603 135 535 385 324 999 551 927 224 149 650 047 091 109 822 775 760 702 237 706 367 846 017 993 587 806 612 336 161 188 118 767 057 803 187 697 019 304 133 618 699 797 536 010 676 746 918 789 294 839 840 231 072 578 807 572 280 671 125 115 775 250 718 711 405 483 602 978 457 937 795 955 878 952 890 689 596 444 518 652 613 497 243 833 276 849 171 976 813 176 254 767 594 423 116 092 789 398 386 313 480 871 932 582 579 321 082 724 268 500 989 515 224 389 985 382 812 251 130 048 926 982 953 512 810 419 744 228 962 293 960 009 942 834 649 988 847 398 867 643 977 979 267 276 148 764 434 485 405 432 267 507 323 966 165 333 891 567 211 787 881 769 953 717 509 193 578 114 943 496 617 259 074 004 194 455 072 510 276 080 348 180 452 193 909 197 742 640 053 999 311 756 932 263 893 392 492 823 657 333 873 162 501 960 954 460 848 158 061 279 241 741 408 138 129 975 173 597 345 219 950 699 927 367 082 825 825 149 313 528 838 920 935 923 872 501 854 265 894 534 942 172 211 409 112 308 965 738 020 359 232 302 232 753 065 748 696 310 619 783 202 485 054 397 560 344 213 940 054 548 216 369 552 143 922 568 521 487 026 724 903 797 221 904 140 678 678 943 529 301 157 205 561 300 085 970 660 114 132 358 008 501 902 795 430 075 774 820 423 344 792 976 766 800 452 138 587 261 476 368 140 116 064 592 194 149 151 284 408 631 747 640 712 662 036 543 359 269 698 849 511 084 362 663 346 255 684 179 016 326 492 872 688 707 962 704 557 986 761 354 428 098 246 799 715 775 875 284 596 917 559 151 440 255 953 532 001 098 277 381 814 625 191 611 708 831 734 742 358 217 207 996 871 845 306 330 247 918 327 368 318 813 427 936 057 214 237 617 515 782 403 960 342 611 376 802 571 546 872 902 210 548 808 259 054 109 844 822 354 523 269 963 900 337 357 805 492 612 600 429 429 777 511 342 829 833 794 131 026 160 746 145 564 829 555 348 847 089 666 304 894 923 264 725 051 477 551 872 805 037 831 902 949 079 497 691 029 705 398 156 685 710 179 759 954 967 275 792 084 879 920 732 303 345 473 610 004 357 026 469 971 565 345 509 859 937 683 525 276 172 329 019 216 005 301 645 494 266 686 286 624 460 398 605 776 342 901 162 610 328 893 341 936 195 459 311 348 053 628 617 329 487 272 772 686 338 654 157 890 325 765 966 815 754 037 257 217 193 460 150 110 780 880 860 271 160 685 741 876 755 049 009 648 604 211 750 470 553 896 700 420 106 034 582 275 308 133 768 962 119 628 907 666 598 103 527 600 161 593 336 275 867 339 758 301 036 311 664 481 266 858 079 352 222 622 672 763 876 417 247 420 737 295 804 793 013 678 065 342 077 564 305 004 663 331 249 576 289 599 506 913 247 543 090 721 243 941 903 580 403 335 615 243 004 536 679 635 404 502 466 414 445 196 647 547 809 928 976 019 511 239 566 788 990 344 392 083 032 077 254 851 333 372 494 398 627 973 789 806 930 155 998 703 982 881 307 563 616 459 534 722 866 175 390 319 254 052 277 732 133 841 864 740 103 876 044 430 614 186 081 603 604 333 803 043 334 544 818 759 279 021 689 499 227 328 374 447 526 002 974 358 812 447 341 487 300 805 512 109 137 248 616 938 495 180 955 462 677 560 481 948 627 877 062 960 791 650 859 717 612 266 605 021 472 175 852 301 788 650 249 270 763 720 641 974 855 960 285 425 011 273 387 448 852 671 693 509 204 131 278 241 638 186 153 094 492 584 343 654 029 602 547 262 598 025 560 678 010 706 503 516 498 042 257 961 067 410 075 742 565 003 144 920 661 310 361 328 225 889 689 905 892 350 237 456 576 650 752 908 490 765 024 735 672 446 312 493 481 349 033 980 446 954 356 327 193 497 904 557 655 597 498 161 779 158 040 446 726 253 444 117 311 555 354 293 890 786 108 889 146 583 818 471 392 798 234 102 623 162 014 271 063 596 202 061 934 001 049 025 486 073 655 487 580 155 835 043 913 125 588 952 668 053 977 569 915 709 133 336 704 316 852 000 605 415 804 995 503 948 825 302 739 638 131 213 905 546 583 968 077 572 325 105 587 862 877 925 844 189 585 762 708 930 542 373 859 255 634 494 312 953 274 912 884 471 112 203 664 584 696 204 550 995 580 546 708 686 853 974 705 827 582 984 659 961 423 511 065 238 996 121 506 959 228 953 104 651 110 050 940 951 173 978 563 846 421 789 811 665 040 347 951 960 561 420 425 487 267 307 134 812 983 740 023 138 496 876 737 139 610 803 422 527 618 437 746 269 988 587 076 473 011 000 492 592 258 588 281 518 206 574 949 385 300 820 854 436 100 168 250 411 055 892 262 389 797 349 442 353 263 134 719 723 073 714 595 372 936 422 638 657 182 204 426 015 522 314 769 381 746 769 883 170 104 285 351 033 279 786 663 412 230 374 345 088 735 839 560 681 195 488 152 172 282 075 807 412 122 647 341 411 185 273 630 430 999 179 143 795 402 840 425 888 480 061 095 278 841 042 320 312 285 117 425 925 313 044 935 126 211 363 512 370 656 707 190 932 151 552 285 367 391 520 785 314 336 314 906 194 906 346 366 988 495 910 705 940 214 835 759 249 648 952 402 018 801 653 878 149 811 604 754 955 539 092 517 964 619 294 381 938 484 931 296 785 346 378 202 536 368 083 267 591 303 835 251 994 488 786 965 367 660 499 309 552 914 129 892 637 217 528 138 253 964 450 391 232 713 726 406 254 714 713 302 803 470 220 911 440 221 706 417 318 036 989 571 778 531 881 037 498 340 121 124 867 099 667 010 220 810 628 304 035 202 684 069 098 281 467 684 263 039 682 949 141 353 447 683 312 776 647 692 888 812 248 971 423 936 325 343 908 586 738 438 413 041 137 088 313 781 583 234 087 255 183 711 851 557 682 083 789 922 546 149 130 452 023 759 854 353 633 073 955 342 533 197 414 812 923 527 879 209 529 021 072 346 938 327 128 749 084 748 864 681 130 127 882 953 119 029 510 969 223 304 406 022 032 631 590 828 682 025 796 314 966 425 641 054 706 194 749 342 606 165 149 276 418 450 077 548 639 650 544 901 624 949 296 638 999 813 197 010 437 936 350 354 478 081 315 869 876 032 248 334 250 737 935 281 316 764 703 511 372 580 556 741 013 250 024 495 480 891 423 265 998 495 382 969 803 611 310 315 262 429 379 170 341 787 610 298 915 845 546 493 853 550 311 474 535 555 699 792 577 555 618 511 784 078 555 175 954 571 143 637 552 247 694 144 786 092 230 810 118 653 937 751 476 256 192 715 572 559 092 607 885 136 851 255 790 104 483 822 142 313 039 428 973 935 498 100 097 753 729 257 901 861 480 125 583 112 712 673 378 616 530 894 740 561 702 730 681 887 573 679 141 062 004 595 553 824 402 927 143 012 540 799 280 343 074 105 906 787 580 845 036 164 759 644 433 148 871 675 662 380 835 725 409 397 422 969 671 180 112 472 609 112 345 641 985 859 229 605 226 445 939 051 194 643 104 904 766 834 965 010 777 554 827 580 636 689 747 433 974 688 526 850 381 505 245 591 039 226 224 164 759 017 021 788 042 813 603 130 431 704 789 031 268 410 074 647 680 447 437 826 461 246 052 400 778 224 875 265 556 136 669 584 648 447 969 333 412 528 797 674 407 233 256 572 304 585 481 066 126 329 067 031 926 542 422 949 976 579 089 907 365 776 824 421 034 605 164 491 027 474 825 966 117 225 811 653 274 160 464 121 852 434 931 963 705 457 406 066 925 319 349 901 467 081 281 018 959 395 771 976 829 328 717 119 440 582 678 118 158 508 127 273 213 864 821 192 590 673 561 593 115 815 882 499 659 933 055 550 374 077 187 839 513 430 731 476 191 434 055 271 154 673 467 394 488 646 192 377 531 540 034 038 143 729 605 282 521 786 715 156 304 869 377 185 914 906 342 022 093 040 150 099 874 284 970 697 851 561 417 029 726 217 894 537 822 184 751 403 479 934 451 174 071 214 565 552 954 016 817 145 568 822 790 530 768 345 583 789 278 794 034 016 116 694 680 449 358 177 937 170 486 792 261 878 297 351 230 127 557 779 692 137 301 030 599 704 545 697 234 541 169 601 111 481 010 809 270 552 388 688 666 053 708 444 715 456 324 218 048 750 388 349 292 342 985 983 436 683 038 860 026 702 884 539 969 492 450 848 427 165 698 026 137 434 822 370 018 345 508 322 640 019 613 713 011 052 319 761 329 000 565 247 588 732 406 445 686 249 630 293 153 957 937 435 326 965 292 989 301 137 982 144 614 215 745 229 245 885 229 602 518 465 689 590 608 464 480 008 065 509 076 447 219 002 258 434 306 755 738 292 747 573 655 495 042 590 509 955 522 065 227 989 687 882 152 773 031 497 602 668 588 921 340 773 281 495 544 167 019 184 913 190 609 797 053 940 617 006 079 382 740 455 826 895 287 085 406 286 617 624 062 529 072 509 065 653 216 571 697 998 461 590 558 690 885 622 226 696 374 920 494 535 348 497 780 036 304 127 723 755 667 016 078 695 061 304 111 815 786 217 691 841 994 986 068 040 174 660 508 592 794 933 636 132 918 688 628 185 177 997 383 413 471 716 033 127 561 358 311 322 901 653 756 186 241 671 196 370 614 873 260 327 442 768 320 334 804 816 153 814 347 543 541 832 642 246 276 918 855 301 349 299 592 719 564 472 345 954 007 435 930 956 978 709 436 193 430 055 365 507 973 874 411 640 003 362 959 613 956 981 566 219 317 009 110 419 743 160 522 258 961 152 857 420 744 265 912 061 727 769 561 408 531 858 027 969 907 561 058 443 246 771 167 792 642 740 681 512 677 704 774 117 738 770 523 027 853 164 434 061 994 062 696 207 070 431 803 521 404 919 150 510 987 963 814 975 934 673 757 608 094 110 736 666 625 987 184 964 303 233 482 561 701 473 602 098 204 617 127 488 469 382 917 484 771 520 707 286 879 585 952 136 061 472 447 977 343 903 051 926 946 696 668 215 077 627 962 498 424 689 514 764 279 208 930 603 982 589 207 880 009 669 655 423 796 193 675 660 257 703 800 411 374 262 532 109 390 676 508 300 614 804 613 106 741 107 838 290 174 232 409 441 892 957 025 297 051 262 270 670 767 027 161 450 678 785 465 405 506 845 465 402 152 648 456 906 177 112 910 998 732 933 379 401 558 105 799 634 959 624 293 274 797 738 345 250 801 507 081 251 253 263 845 118 855 718 147 152 072 330 143 956 039 070 718 855 063 135 531 754 624 679 789 308 746 820 986 762 973 763 578 463 319 987 689 466 895 296 382 752 969 953 890 152 581 995 213 239 232 143 543 926 419 347 993 371 150 294 038 340 626 152 978 488 930 137 094 150 636 043 063 453 581 380 531 786 515 531 488 355 870 428 909 690 846 557 166 780 492 508 936 698 915 185 439 469 139 732 179 018 696 851 761 771 092 558 515 611 768 972 879 833 290 489 000 446 312 079 810 504 840 250 576 937 214 725 478 608 823 110 508 830 709 693 253 147 485 404 887 455 166 114 331 325 587 455 063 028 624 783 732 277 200 318 817 054 488 850 248 146 422 868 725 973 474 862 397 767 171 343 029 720 756 151 354 150 555 662 575 597 068 463 834 766 906 382 587 294 924 895 376 286 199 869 777 971 920 182 902 840 494 695 363 358 808 099 890 051 699 603 632 109 956 366 120 035 108 354 254 082 582 495 312 082 794 706 733 991 521 402 621 451 726 564 069 668 751 852 739 747 371 124 670 100 841 409 082 206 974 122 217 000 620 538 725 781 934 859 970 886 090 179 565 453 679 923 500 092 239 009 661 666 598 092 705 702 821 309 637 955 479 298 111 894 794 917 602 017 555 439 786 198 218 161 267 321 515 064 615 107 907 838 352 114 066 461 714 140 356 733 829 959 501 577 402 994 719 581 695 780 453 090 545 510 599 314 200 833 448 709 900 225 417 877 234 524 618 518 286 747 675 429 607 028 620 987 609 743 108 866 453 528 775 533 534 971 354 588 700 258 351 095 950 422 091 567 435 189 701 096 276 003 285 677 956 946 453 657 632 236 827 735 684 984 182 367 907 670 604 040 167 498 799 024 655 653 998 886 148 804 522 717 515 552 891 156 742 612 904 981 832 116 253 234 208 690 839 773 230 922 117 883 040 015 125 464 844 536 796 775 419 316 676 704 079 845 187 844 085 786 271 811 165 648 087 814 123 284 216 350 967 759 810 037 143 717 588 651 458 782 040 980 126 055 352 784 288 596 215 566 967 468 986 477 577 196 151 132 941 385 810 245 943 121 958 115 016 989 945 977 831 815 004 500 549 634 591 466 165 873 801 024 359 414 877 718 231 789 034 964 123 231 766 310 382 470 331 722 776 911 150 255 247 760 375 694 967 448 997 363 694 969 512 567 940 878 003 924 813 107 855 734 897 352 960 640 409 334 407 488 629 152 457 145 364 661 904 562 136 363 110 593 975 487 047 034 110 776 467 868 978 346 284 406 771 957 852 150 441 694 937 600 326 125 641 621 715 476 965 438 126 079 259 206 244 418 717 190 218 530 313 514 090 586 498 537 212 939 799 906 060 799 189 519 085 111 275 849 032 480 840 480 818 087 418 462 720 484 324 457 311 988 086 115 477 337 122 901 291 347 875 041 586 099 146 985 693 051 332 887 807 877 553 297 414 327 321 703 543 426 159 309 620 291 625 840 948 015 673 238 309 416 840 036 974 184 259 596 945 445 734 922 222 475 543 820 594 878 816 819 337 929 058 450 580 501 774 718 657 088 990 713 560 578 652 739 555 094 767 739 328 095 902 930 028 992 664 174 367 239 601 583 562 359 101 603 779 608 642 266 872 516 031 726 390 823 830 570 292 325 384 893 939 125 762 830 996 484 830 055 487 892 158 748 239 361 111 312 114 030 128 315 103 808 913 416 044 770 665 562 155 855 323 006 103 728 525 042 039 843 327 729 023 858 814 020 040 125 655 648 742 986 755 691 442 569 308 993 253 364 451 724 272 176 465 167 647 846 604 547 202 308 675 676 621 650 344 560 295 866 051 952 145 742 014 815 870 241 913 993 069 242 616 300 954 531 054 498 191 369 811 617 700 798 903 201 553 943 930 272 482 606 462 373 286 320 213 171 249 047 256 578 482 842 691 098 804 215 479 872 613 334 103 277 248 314 179 645 335 869 715 083 108 213 234 758 600 962 254 621 334 281 592 087 327 315 653 716 103 750 093 328 135 764 838 065 485 363 719 055 415 735 923 626 843 029 226 143 757 777 240 684 294 600 693 021 727 883 403 455 833 665 002 408 438 026 486 520 138 438 641 479 503 177 403 039 791 765 999 973 720 238 043 457 980 689 892 896 831 134 816 595 120 945 969 689 928 623 304 269 667 506 417 637 879 776 419 054 801 534 337 240 899 059 685 044 883 662 485 668 009 426 964 361 498 068 990 681 703 569 587 128 823 259 263 218 202 439 025 693 894 483 107 094 098 184 129 604 312 105 880 001 352 296 919 477 630 781 499 419 147 029 938 885 082 829 695 181 940 296 197 534 031 067 972 044 582 894 519 708 734 372 098 122 243 507 485 612 962 269 137 214 396 368 899 299 446 969 557 305 293 663 258 805 375 593 536 298 378 414 584 005 782 216 065 172 427 268 263 716 759 974 169 367 625 431 127 694 204 729 131 406 306 012 766 805 636 415 491 777 932 026 354 028 851 379 789 265 107 769 927 417 102 008 424 031 460 978 787 907 637 937 415 715 944 708 318 648 867 766 412 137 908 943 893 778 390 017 918 046 252 962 908 408 582 984 918 453 293 779 696 819 094 072 834 851 720 781 400 646 780 441 481 133 774 948 193 833 657 164 582 232 504 037 379 653 608 377 830 858 746 247 350 562 299 846 521 126 163 317 679 571 487 172 133 095 450 645 386 981 998 196 163 257 652 802 371 361 637 315 289 201 257 526 474 333 144 145 097 033 424 023 359 469 933 542 975 250 012 484 431 987 821 322 215 342 462 887 849 988 755 184 673 171 123 630 722 997 925 207 007 057 472 100 564 655 465 730 173 266 082 663 409 219 913 578 034 911 143 182 514 035 280 204 587 673 381 275 704 836 290 150 587 721 116 193 712 737 843 864 475 183 622 130 151 599 801 221 834 510 735 220 330 951 670 493 162 813 519 698 699 044 125 887 356 479 231 315 257 856 580 243 256 249 425 109 417 505 404 263 201 726 288 629 121 656 395 648 708 114 552 014 798 865 064 551 817 341 179 640 269 500 060 203 688 587 904 323 451 067 451 784 057 239 071 579 583 954 235 722 661 469 715 177 249 411 441 671 205 788 134 807 683 691 855 056 642 099 662 575 023 240 455 895 929 088 810 480 940 414 524 372 044 059 756 099 948 814 238 272 711 825 272 556 394 721 979 568 092 075 378 999 986 656 198 098 366 389 203 394 217 820 837 238 128 114 180 851 967 852 397 274 002 082 184 415 009 763 458 341 065 041 007 955 422 910 806 180 177 856 429 875 693 208 827 851 803 962 928 526 129 560 695 939 514 868 162 553 401 909 170 429 677 824 850 282 530 081 250 628 727 909 274 292 888 821 494 648 461 521 068 225 086 167 842 134 132 552 786 393 650 350 711 891 683 623 493 014 000 037 116 291 830 540 484 520 939 853 451 914 216 028 618 919 977 418 361 361 056 611 696 475 910 668 812 737 373 933 785 791 849 172 970 916 853 787 317 490 026 752 384 189 228 226 967 390 528 275 392 664 556 216 764 416 327 995 705 306 585 408 236 117 996 880 976 316 250 330 875 869 699 665 984 321 414 782 990 040 837 749 563 565 647 641 081 422 146 304 572 195 984 557 482 269 588 713 548 210 871 892 364 922 211 359 206 098 718 186 098 438 369 326 670 740 678 957 938 191 481 773 859 542 623 942 319 839 698 697 904 335 154 110 924 933 691 772 842 540 827 855 542 604 285 356 137 650 675 380 293 280 587 953 563 173 235 424 467 763 383 746 932 581 458 031 462 414 120 718 770 810 211 375 628 870 909 068 624 520 079 067 443 994 140 407 480 077 739 790 975 810 860 756 751 022 336 836 447 152 117 690 446 753 256 167 829 971 057 337 145 667 630 781 917 753 606 505 216 123 768 536 841 008 785 198 447 908 746 246 849 623 818 384 361 445 509 850 658 629 495 066 346 768 580 169 002 956 445 993 333 197 295 188 950 140 243 819 597 667 657 195 155 894 062 406 086 585 711 638 502 911 074 567 517 559 397 429 742 790 304 543 974 863 582 921 756 912 941 830 037 359 800 436 574 037 048 506 635 415 585 452 359 704 535 256 876 568 182 346 026 545 860 686 011 290 661 361 098 795 165 756 889 030 624 387 282 397 696 099 437 775 379 376 730 972 737 455 485 408 927 237 776 559 870 713 879 079 575 719 763 505 287 702 538 067 066 330 155 648 166 813 560 409 437 116 983 899 239 706 389 826 891 663 389 820 197 981 352 103 910 523 656 077 906 304 269 423 269 150 070 438 969 158 684 981 897 354 298 548 754 374 911 987 201 696 584 968 670 904 586 856 070 632 771 713 566 849 092 735 481 396 046 512 313 249 212 061 390 662 530 115 325 287 251 544 076 446 319 345 890 005 434 368 103 434 570 296 104 263 566 177 052 401 608 741 262 307 385 667 322 846 753 306 049 021 396 318 010 323 562 674 438 548 694 382 650 426 829 122 108 492 757 076 875 185 750 017 960 360 905 697 030 465 183 624 545 033 697 871 337 669 097 015 331 955 115 686 368 707 867 545 679 258 929 075 881 105 145 825 659 842 468 440 213 884 862 228 502 592 920 053 075 105 737 103 400 389 739 118 903 463 932 169 265 363 492 817 581 719 408 150 881 300 173 272 713 784 796 376 567 226 045 111 449 382 835 740 313 355 969 426 717 070 744 043 292 935 976 175 569 784 333 103 872 323 600 000 802 864 942 380 837 630 405 463 530 939 912 633 535 457 341 745 913 382 348 661 292 487 278 918 450 598 697 338 679 154 114 977 244 319 540 722 190 535 808 631 879 978 304 172 037 250 682 032 153 696 700 174 594 409 223 127 498 250 079 478 614 397 042 645 077 429 281 790 488 781 873 460 232 563 048 589 930 041 316 338 866 359 512 817 604 106 330 904 127 964 021 138 980 620 826 574 967 516 348 956 079 031 346 129 851 855 423 910 313 319 546 376 650 754 621 939 127 154 365 968 823 009 388 656 720 445 196 089 214 690 982 733 624 039 025 984 064 781 205 452 528 163 608 673 200 196 310 495 484 475 387 468 726 315 467 434 444 756 855 275 756 548 601 301 484 109 687 875 445 618 324 030 016 912 658 774 314 977 106 673 171 744 331 088 952 961 440 231 630 870 152 466 501 260 587 261 915 942 219 280 865 238 345 795 726 293 538 006 149 072 024 737 390 813 481 552 183 933 819 710 304 089 728 284 917 828 891 400 576 098 460 004 326 993 001 097 076 758 677 619 980 361 941 688 541 492 730 964 153 154 381 381 319 303 443 007 290 693 751 513 731 422 222 503 352 255 805 068 929 531 885 238 233 553 986 170 837 531 197 328 476 347 611 901 238 135 506 642 157 345 674 889 387 123 556 353 704 812 424 230 842 518 146 945 493 955 489 462 252 001 910 119 727 358 643 603 586 475 502 986 612 545 308 336 729 473 540 283 329 009 558 142 861 910 618 109 313 740 938 477 817 648 876 729 826 615 657 291 888 810 803 667 038 521 202 980 385 412 656 452 817 231 190 286 066 551 788 843 874 845 333 924 385 155 521 417 709 265 840 681 569 927 236 862 268 763 876 487 330 006 505 686 382 280 479 433 179 549 090 168 216 950 855 028 048 885 120 543 444 072 780 302 736 336 208 358 192 559 105 853 554 739 654 254 370 756 927 061 879 265 814 891 243 781 971 691 760 791 161 397 438 399 554 382 936 336 444 440 197 327 625 174 142 756 286 414 937 580 844 637 799 496 855 936 567 384 649 462 992 113 953 056 486 690 589 792 568 342 573 772 320 943 975 461 406 453 079 435 580 038 819 452 511 153 455 941 083 776 871 910 571 574 740 568 473 476 536 895 090 036 102 810 554 959 593 733 547 412 033 738 155 355 173 050 684 560 324 233 974 002 969 123 247 192 653 183 047 182 435 241 344 602 404 503 120 940 435 988 241 585 569 683 777 027 078 745 815 728 042 766 300 180 721 946 759 138 875 741 109 728 425 265 902 033 605 614 379 054 591 864 509 528 089 712 891 206 797 017 485 580 301 158 748 229 436 187 302 431 430 093 235 787 937 636 044 544 062 940 328 601 565 433 302 899 876 337 322 030 332 441 309 627 749 463 609 399 156 944 089 595 527 329 237 401 889 322 884 487 110 024 538 573 007 294 601 712 946 855 083 450 147 561 194 735 196 540 338 348 192 309 796 295 243 210 612 023 253 975 996 774 432 565 086 336 501 702 844 698 579 649 281 268 484 484 401 150 676 912 304 764 781 557 149 217 567 318 373 114 124 060 608 055 191 122 989 607 342 116 142 104 510 445 513 375 667 884 058 823 008 380 405 684 637 210 285 444 453 108 237 771 246 161 069 732 754 779 493 702 240 540 845 789 932 511 954 209 322 734 386 632 655 349 422 186 026 337 130 093 298 028 807 053 097 696 367 035 274 232 414 219 882 496 370 058 108 263 034 628 733 541 140 663 398 983 054 855 828 042 945 061 304 966 247 618 623 820 372 537 201 845 751 499 160 664 837 266 745 448 877 692 059 231 783 952 855 536 013 762 362 981 216 406 516 064 152 973 881 403 487 093 213 533 472 485 670 896 782 939 960 381 857 581 802 569 546 321 406 954 407 679 040 235 779 060 540 134 692 976 062 811 959 910 047 579 566 941 550 920 765 839 769 731 294 815 344 472 046 032 332 648 615 052 208 234 751 965 605 824 208 447 890 572 597 705 301 849 890 566 610 922 627 839 856 690 099 537 787 193 316 801 003 710 306 638 992 771 137 218 450 074 537 527 295 552 914 268 947 694 278 871 903 260 189 728 796 280 010 669 699 306 947 514 329 080 119 515 046 291 134 824 976 136 709 700 189 190 525 980 779 779 190 351 629 011 749 806 111 584 198 025 826 064 833 189 017 515 782 290 559 658 731 756 619 059 792 941 734 707 009 776 826 711 572 757 996 637 049 688 903 741 611 770 540 413 366 970 242 072 189 378 972 232 844 663 484 815 105 320 760 378 239 042 717 488 444 630 480 830 643 802 891 639 553 561 458 136 082 457 736 781 314 594 956 222 038 199 187 151 525 389 101 588 002 666 391 677 271 129 668 528 971 401 054 314 284 218 866 471 522 434 221 262 820 690 716 216 242 997 862 119 493 694 879 493 737 290 431 607 453 135 467 243 475 905 573 245 380 010 119 488 072 499 392 894 648 906 977 786 933 681 375 107 926 229 340 216 625 215 390 265 363 013 056 003 416 737 057 486 863 876 354 961 486 673 656 283 345 213 609 169 372 024 652 701 057 155 745 907 547 222 330 920 972 089 090 747 425 382 013 807 244 998 548 563 907 863 690 680 978 433 257 359 242 339 982 323 488 643 816 721 201 143 535 003 784 525 732 596 308 208 912 462 813 263 296 946 672 241 105 897 464 939 702 128 040 557 683 192 613 927 212 413 405 689 769 621 525 044 997 470 863 052 637 231 357 874 345 326 884 489 263 936 673 408 604 945 147 773 892 992 738 370 791 259 054 703 461 513 718 160 496 175 625 820 021 204 379 481 231 051 040 686 074 478 199 181 236 442 637 484 960 317 210 660 252 269 190 262 627 068 973 451 778 211 137 971 561 946 774 429 315 921 531 020 913 804 264 414 350 209 800 782 940 589 315 485 329 220 971 637 591 785 721 309 044 292 431 042 689 208 802 689 064 854 003 484 378 789 595 200 022 120 282 880 590 202 177 191 474 018 456 599 449 190 466 985 162 339 824 993 234 340 705 326 318 445 744 707 858 232 642 006 701 445 012 781 044 842 100 486 393 853 642 063 394 304 235 162 019 371 573 681 093 591 623 308 107 293 754 900 118 561 666 125 788 122 438 297 724 176 043 148 543 735 939 921 945 909 626 409 883 411 050 951 244 291 842 596 958 564 065 559 949 783 455 043 345 569 117 704 328 011 554 812 108 924 142 182 091 674 386 998 292 465 062 595 007 761 607 665 366 395 515 412 586 967 569 590 605 050 881 388 362 769 850 018 807 632 514 013 379 909 386 072 755 443 224 775 308 285 836 674 914 195 904 965 481 070 292 900 592 121 160 713 665 441 211 857 404 953 247 319 646 098 421 793 597 754 960 774 832 435 645 692 960 439 575 197 771 100 633 113 930 195 473 164 485 333 584 273 028 649 165 330 109 618 004 556 403 835 556 950 879 383 425 007 314 016 580 648 869 776 315 521 863 146 520 411 987 492 893 767 592 154 870 237 809 177 957 718 294 837 966 613 757 926 056 917 427 848 168 587 479 951 923 147 778 211 170 672 155 435 867 559 678 922 198 726 238 484 205 284 793 942 816 629 050 803 063 951 797 979 914 787 150 594 169 769 711 226 809 442 112 748 531 461 596 076 989 265 230 210 816 221 979 353 342 248 034 957 976 212 905 264 240 524 797 209 018 348 794 514 686 732 248 812 052 591 134 607 612 693 244 717 813 953 732 055 426 883 454 635 843 498 156 452 395 971 449 648 630 212 523 392 695 020 548 493 249 110 099 269 155 506 385 026 306 233 581 660 237 382 020 409 422 821 804 498 319 799 568 254 463 260 898 180 560 742 884 864 101 004 367 999 133 705 342 951 662 094 790 838 698 523 000 007 194 649 319 282 821 497 063 668 967 566 912 552 853 171 848 891 748 149 044 900 310 610 208 539 952 537 385 073 226 203 395 146 466 419 402 455 959 814 338 433 829 728 245 769 992 948 807 733 354 979 608 448 549 890 766 998 710 275 361 288 091 301 884 858 589 176 725 099 977 732 203 780 947 932 880 496 747 405 379 589 022 648 626 489 949 272 434 542 331 226 758 959 784 410 519 324 067 570 266 195 773 483 730 116 715 193 759 223 335 204 464 112 571 446 376 319 272 076 945 748 976 286 088 907 240 878 055 968 178 982 838 086 525 299 134 113 489 628 804 085 482 315 634 398 824 622 344 184 300 684 163 021 031 759 636 068 734 334 603 942 399 089 497 905 630 117 923 442 633 921 293 093 588 253 325 711 613 388 498 690 531 744 190 858 997 927 361 854 802 536 756 246 720 677 923 923 818 613 628 802 355 745 530 423 184 878 648 370 699 600 296 028 906 409 910 541 398 290 176 581 772 508 104 548 827 817 968 523 624 364 706 705 816 943 077 185 934 991 290 023 033 258 803 281 312 049 326 713 865 203 535 015 085 168 562 787 796 353 231 510 680 105 365 664 227 879 837 128 818 444 156 042 209 525 001 804 260 894 902 508 652 684 514 448 163 469 431 329 423 050 365 173 311 744 182 008 783 787 556 833 904 770 055 875 793 274 477 830 450 602 361 166 442 924 900 035 916 360 953 517 330 013 361 422 194 355 090 781 673 003 890 276 161 309 778 493 789 384 689 303 848 569 272 105 146 920 256 290 270 906 071 727 744 847 548 996 674 647 718 500 492 819 699 546 706 470 068 950 897 565 580 553 489 058 650 583 723 081 310 983 240 422 147 012 916 321 531 615 024 482 592 645 127 285 355 198 138 110 871 656 573 968 651 842 703 477 930 380 567 238 641 466 412 843 406 214 145 955 136 736 562 167 169 326 375 916 855 947 900 820 577 395 614 481 357 837 448 635 219 938 340 639 677 643 180 244 461 534 069 737 060 159 356 031 146 040 759 883 926 910 810 940 743 445 216 439 394 118 646 918 690 715 880 226 613 993 740 822 262 060 691 032 070 852 748 058 777 535 156 603 741 395 740 455 019 288 399 052 721 576 154 840 446 500 669 562 192 182 864 212 628 514 874 632 449 619 838 059 374 911 858 908 549 641 695 706 390 368 112 824 576 822 236 234 841 405 120 623 609 563 366 426 634 931 168 906 556 410 157 565 530 790 190 626 195 377 609 846 508 214 250 072 888 349 281 885 394 632 380 367 223 956 389 760 658 859 245 393 855 326 982 432 604 171 865 027 072 470 807 071 497 051 170 776 216 990 956 290 089 602 109 204 431 687 085 348 038 651 626 558 865 344 868 038 398 708 771 279 751 176 052 913 003 151 170 760 971 041 176 982 058 636 907 633 856 415 465 914 557 048 825 488 308 791 687 618 271 180 557 241 202 981 735 373 439 702 260 386 362 097 004 616 711 761 793 808 339 837 939 266 439 703 624 959 404 938 398 014 274 903 874 561 004 589 007 966 369 823 591 540 181 088 761 433 508 986 812 361 752 639 625 522 933 107 263 153 984 644 293 934 199 933 565 469 976 012 675 723 519 124 781 855 581 456 609 262 641 172 012 320 748 296 825 738 445 297 882 208 140 911 861 679 897 309 976 467 656 463 496 329 822 511 404 207 874 635 745 612 358 147 294 730 163 050 545 958 315 984 725 195 978 104 715 148 156 142 131 836 028 370 397 217 659 998 383 302 196 954 104 640 386 346 500 654 498 891 355 749 230 262 601 852 915 909 656 395 973 769 771 389 132 365 564 969 373 126 439 083 029 777 235 607 179 709 419 785 578 715 308 731 865 369 386 389 405 502 610 570 417 572 796 752 257 330 031 914 242 705 190 360 103 099 642 628 685 405 076 481 858 945 274 522 979 063 501 387 506 391 566 077 132 667 840 060 846 602 271 221 874 421 295 809 931 911 407 746 107 473 221 450 563 463 931 742 488 156 225 874 247 213 023 817 679 151 390 068 368 451 346 684 563 001 874 907 126 548 045 939 211 616 999 233 060 061 558 877 464 138 819 901 262 536 551 583 770 606 676 726 144 210 439 124 035 383 999 876 137 639 801 275 196 592 799 858 030 955 944 559 053 482 756 367 149 646 148 016 684 953 688 669 342 134 824 973 116 474 675 639 844 353 643 287 529 425 356 778 890 116 677 055 553 531 117 056 283 596 275 098 313 010 130 779 692 912 616 493 443 991 225 212 316 133 083 499 666 884 677 246 504 920 146 110 879 348 938 391 518 689 694 217 376 082 776 645 224 661 681 432 176 811 366 485 089 839 528 742 525 488 262 507 205 653 360 838 133 099 965 791 394 118 340 228 540 039 375 866 511 845 148 285 145 300 124 850 028 919 142 376 009 248 186 976 828 954 102 144 940 916 440 770 448 841 975 531 563 319 265 872 951 529 616 499 668 903 088 639 442 999 079 504 339 362 008 314 724 403 430 896 529 374 027 105 572 067 298 712 269 436 492 373 098 828 882 592 784 821 201 670 168 218 736 324 445 251 989 514 280 167 734 096 833 199 074 929 635 790 780 318 124 564 799 479 763 055 042 259 082 137 664 099 244 532 297 784 438 785 372 147 745 117 044 832 966 502 653 077 664 268 067 822 865 586 011 266 262 288 330 151 374 087 039 066 009 884 356 159 912 714 311 640 615 073 555 790 656 276 198 958 394 590 056 877 375 618 192 791 241 205 385 814 704 213 259 082 017 966 321 245 952 356 075 474 531 163 748 798 624 852 530 821 820 445 748 562 494 300 088 508 958 600 342 694 524 461 915 865 160 920 158 077 047 039 830 206 449 409 008 270 059 357 963 354 328 420 331 224 919 835 699 721 115 117 327 197 661 481 006 616 104 651 881 771 194 330 026 510 034 066 826 300 062 054 832 473 030 923 813 984 019 791 709 454 974 999 498 207 613 766 957 455 448 694 161 096 364 637 888 353 497 360 263 309 166 635 197 272 122 631 237 975 724 112 160 879 750 084 097 927 417 087 739 848 574 076 646 509 420 753 774 649 255 880 045 779 204 807 277 023 377 455 454 379 082 113 804 432 411 406 505 965 148 606 362 172 744 650 920 852 622 060 927 479 169 492 673 359 165 221 482 199 469 162 712 002 856 419 472 171 758 273 671 546 110 705 583 025 277 580 988 195 560 161 156 391 585 955 176 902 479 763 736 630 480 169 421 883 369 692 626 047 008 445 092 695 793 556 721 308 014 528 836 379 148 527 469 740 184 098 574 268 433 241 006 021 073 187 952 867 951 874 123 714 967 014 879 862 901 590 356 747 172 841 099 108 621 718 997 738 127 985 702 401 978 526 285 427 525 680 991 029 270 242 073 704 204 887 841 924 512 379 974 253 910 121 813 823 374 040 967 879 426 519 141 131 128 221 560 625 499 124 844 965 585 648 927 161 485 721 600 725 816 473 001 979 495 210 606 760 216 131 383 097 962 567 654 841 452 168 590 320 073 708 524 327 109 900 865 759 761 810 047 228 490 762 726 833 976 236 429 732 163 563 261 997 291 487 646 255 060 724 261 456 384 201 143 482 565 042 958 616 604 231 061 703 199 728 140 971 341 564 134 911 854 119 509 826 316 268 413 022 310 825 721 136 710 141 542 386 830 150 487 542 957 220 078 126 967 488 355 737 504 700 847 637 232 381 971 531 720 393 815 772 489 014 938 239 137 372 557 901 459 894 983 980 863 778 332 134 550 738 105 680 795 639 814 670 269 537 833 191 440 937 879 890 829 219 736 879 154 737 320 716 230 495 008 128 468 078 679 531 329 412 457 819 800 226 080 062 262 510 443 243 847 040 951 697 349 666 216 613 312 933 335 164 400 174 687 553 199 303 409 250 351 105 768 972 679 584 605 419 009 236 101 945 321 694 124 075 190 616 404 182 676 287 282 445 215 049 453 206 112 057 344 255 145 787 482 045 447 377 496 743 308 773 593 917 001 993 288 129 457 120 034 940 408 321 767 224 607 665 388 199 332 315 351 412 456 666 534 582 386 952 365 738 174 769 443 762 601 794 444 786 095 869 848 655 914 006 137 890 187 321 053 139 658 103 477 855 296 197 885 287 334 958 218 837 348 695 664 527 322 738 230 022 169 702 537 746 179 557 070 344 241 191 010 830 684 022 802 215 888 436 033 502 593 236 832 873 383 600 666 499 580 977 845 318 713 572 447 319 142 566 419 569 794 006 890 400 358 383 128 712 051 780 020 593 798 917 858 732 765 370 670 038 525 630 826 764 835 315 697 331 057 875 191 548 637 329 885 928 053 777 229 616 961 834 642 493 747 373 225 323 932 343 079 264 781 990 569 331 330 216 474 142 542 511 446 336 875 668 400 979 922 054 844 362 864 746 546 930 546 773 633 750 680 431 680 226 336 975 867 394 098 895 331 682 399 326 548 541 389 509 082 386 080 217 099 950 912 845 171 696 516 262 948 909 172 091 639 933 926 177 441 587 276 326 892 829 423 874 188 262 398 764 766 000 138 183 920 807 337 007 519 589 884 524 285 075 864 876 316 015 601 348 829 166 680 413 710 546 185 192 957 658 854 764 404 774 894 724 128 839 324 281 797 294 438 184 640 138 561 285 535 844 434 217 549 795 303 451 597 520 879 988 957 233 564 224 569 902 418 878 974 259 749 467 377 900 784 371 473 355 766 594 463 980 782 637 041 511 670 527 320 486 676 111 481 166 256 658 408 683 015 358 755 779 483 222 239 470 973 009 554 138 060 278 771 308 969 280 856 580 862 584 735 726 545 768 138 272 092 915 522 796 971 674 879 919 164 366 646 295 348 088 677 572 299 673 371 566 053 357 434 407 965 597 629 299 568 301 908 443 394 098 558 593 604 477 172 631 531 536 557 813 140 645 413 474 749 284 366 471 945 454 840 779 508 735 807 733 028 155 711 474 090 584 931 545 077 092 116 627 211 255 479 000 930 390 920 598 767 949 834 103 012 783 315 992 203 303 000 507 863 273 845 605 122 152 732 015 635 140 583 786 484 739 050 702 573 372 167 527 262 562 717 641 124 207 422 577 219 997 702 517 258 995 892 850 200 678 338 253 036 539 501 225 771 881 575 559 786 838 624 129 964 661 428 578 493 616 351 361 378 500 045 191 423 521 888 012 941 951 189 289 694 514 757 279 784 798 873 731 023 332 014 274 212 914 677 121 969 648 644 670 425 553 403 324 296 556 493 975 236 782 343 241 426 901 508 745 677 491 770 063 248 469 954 356 298 798 911 209 210 498 206 661 306 514 314 756 524 284 574 618 632 072 218 210 540 595 653 063 238 654 187 138 431 286 285 905 965 466 048 953 924 507 079 957 473 905 794 792 788 069 762 484 631 484 527 094 559 547 897 353 849 434 098 419 457 623 937 495 973 760 186 968 029 983 750 027 923 547 992 187 257 489 369 725 948 970 463 891 217 658 907 973 343 523 373 655 791 857 486 419 298 062 147 998 191 508 464 223 136 883 071 007 239 111 603 876 952 989 100 666 532 814 398 420 222 020 186 709 117 984 600 124 764 224 892 348 199 014 505 635 064 957 011 301 191 454 976 414 705 004 957 627 389 969 583 169 131 566 275 861 192 772 580 276 161 444 423 068 048 737 140 698 291 433 602 712 758 363 488 917 606 207 703 105 150 880 439 988 116 549 327 602 512 064 693 433 016 986 679 581 849 668 147 038 834 190 000 271 920 757 517 814 756 535 176 679 026 699 933 138 275 228 813 200 744 334 150 643 567 458 969 250 993 385 243 867 017 175 284 152 044 150 223 269 858 281 482 591 586 288 170 742 137 044 422 329 570 057 115 207 709 609 521 613 520 137 055 337 323 148 425 595 673 626 270 013 914 808 486 722 722 202 039 610 588 207 602 360 031 524 312 712 741 499 275 715 750 731 829 176 476 918 349 587 633 121 323 408 135 139 904 669 125 032 511 941 635 165 869 854 714 862 381 825 677 897 247 219 997 902 202 478 814 262 819 284 362 803 393 919 063 169 464 996 736 291 353 941 710 803 742 748 242 521 436 896 765 358 783 631 768 855 743 295 671 326 428 484 009 951 164 202 531 839 535 239 180 618 265 275 712 961 806 743 230 543 899 752 691 320 352 871 956 286 073 005 311 803 103 192 509 111 394 022 969 909 822 224 391 845 760 682 627 777 573 302 076 533 925 553 366 696 199 604 973 676 774 128 692 181 721 771 195 416 465 414 418 163 153 409 201 164 173 897 172 836 553 439 804 854 916 206 358 478 197 291 412 917 241 302 534 993 273 746 097 474 511 806 213 190 497 639 474 511 914 143 155 648 135 631 974 440 450 424 826 536 910 133 391 389 769 403 747 985 361 990 299 103 494 280 086 799 045 359 274 657 207 772 788 102 740 389 814 144 473 693 654 948 378 484 389 462 360 818 348 885 336 273 990 510 387 434 350 320 572 145 586 017 039 434 779 606 405 602 572 420 762 562 021 829 916 733 995 269 267 626 349 249 835 096 355 374 842 133 058 724 489 652 909 305 394 131 698 907 238 646 486 701 716 125 208 139 807 210 269 057 879 872 312 516 428 153 206 086 364 755 108 100 176 459 093 257 234 188 556 450 272 067 041 234 537 551 505 444 797 255 763 794 868 097 352 820 907 964 023 547 359 947 418 970 408 656 243 080 059 607 155 457 261 788 219 340 765 405 178 443 352 890 700 516 192 637 084 305 264 265 851 316 567 105 507 864 548 110 167 176 611 802 037 887 242 394 172 353 173 974 205 666 740 860 070 906 694 233 073 531 530 315 429 126 564 090 530 811 334 554 865 681 176 455 992 906 383 776 430 590 879 539 559 304 194 961 498 513 918 704 692 989 217 045 178 905 636 116 082 861 650 388 141 216 870 204 309 444 921 432 886 716 690 809 086 202 468 729 900 034 206 535 819 064 385 444 458 684 724 616 088 007 427 948 713 564 832 901 013 493 481 582 713 750 485 744 168 937 910 249 683 291 617 486 401 850 015 090 742 543 677 505 935 018 188 800 607 477 168 533 070 072 321 424 873 401 251 509 973 246 393 759 855 875 259 168 748 917 090 686 724 715 144 931 181 110 558 918 607 351 423 793 091 942 151 140 723 568 070 349 880 551 019 449 232 249 923 102 412 982 909 269 346 131 228 845 918 954 526 790 685 443 254 651 943 420 629 541 307 218 671 262 507 661 050 824 215 655 683 517 081 320 793 741 900 599 292 460 854 137 548 175 419 033 555 857 226 483 696 105 384 343 097 273 541 048 612 735 332 441 265 655 019 948 956 014 621 323 744 073 402 808 326 326 176 592 114 182 421 708 193 299 464 089 276 821 389 276 086 497 653 058 583 574 566 320 468 366 621 332 632 743 470 057 349 308 343 153 664 143 500 134 948 311 544 529 648 537 622 753 414 719 210 418 588 708 840 049 930 469 826 463 004 252 995 404 106 726 933 300 507 987 343 804 543 644 553 361 543 010 172 046 968 629 921 006 136 034 691 691 649 811 641 523 715 384 591 894 670 123 347 410 015 766 758 049 781 978 974 173 489 205 923 975 405 435 604 083 546 360 438 032 006 678 014 095 394 081 920 501 407 931 980 732 360 218 295 821 954 950 375 568 688 784 401 544 585 075 505 283 627 932 046 905 158 406 889 306 313 513 408 622 974 833 772 385 836 993 317 051 048 904 221 778 260 565 848 152 443 404 176 403 708 199 456 153 447 120 331 644 507 517 043 160 682 970 945 140 511 996 634 238 499 966 678 964 338 355 045 776 104 473 452 692 974 396 167 026 716 305 484 854 726 353 569 148 477 267 774 540 025 056 633 297 466 197 886 539 143 703 958 233 626 501 598 931 624 894 121 793 707 781 683 537 630 058 996 376 020 714 368 400 950 987 262 590 456 764 383 371 011 866 198 701 225 635 447 370 724 381 005 121 151 549 222 810 108 939 514 516 166 468 287 501 487 464 053 786 621 848 788 745 072 806 061 275 093 109 755 860 773 232 967 194 659 675 447 900 989 730 168 805 133 197 703 561 798 346 357 001 651 611 099 910 457 550 556 672 087 444 588 357 344 721 920 126 206 107 686 930 963 364 602 560 695 350 357 016 225 707 693 616 996 404 410 330 591 904 929 466 525 497 678 510 187 017 516 202 092 440 569 609 885 523 428 602 797 509 158 664 659 387 609 537 914 595 110 326 441 875 715 119 412 761 431 242 129 257 291 458 127 042 357 244 344 731 043 054 011 147 113 833 624 526 543 785 925 738 211 345 925 623 864 852 032 397 407 796 599 468 646 081 966 654 019 853 700 871 543 139 624 603 897 081 846 656 304 761 617 425 663 769 693 679 608 355 461 070 888 200 450 425 409 389 255 018 243 857 990 391 566 057 101 247 536 782 314 908 836 627 256 687 792 399 001 473 492 964 693 090 505 636 822 609 563 942 013 706 088 422 664 165 555 159 606 534 808 316 748 181 352 591 410 841 169 473 838 815 583 524 367 234 158 254 736 247 634 712 427 873 917 121 961 783 540 021 773 520 805 177 263 668 679 982 408 982 744 816 696 730 812 664 821 781 260 074 591 674 217 345 968 450 431 605 061 696 294 393 224 355 271 460 609 279 401 756 919 519 015 234 029 208 010 820 035 575 411 723 163 559 286 176 823 192 200 917 201 753 410 104 605 707 537 694 551 635 092 313 480 264 938 026 292 024 465 108 928 672 258 986 210 788 216 521 437 441 537 421 103 307 708 856 400 087 914 897 714 453 577 013 059 958 609 968 063 218 377 525 499 378 812 720 837 056 248 155 098 880 573 903 559 781 031 515 151 715 269 692 671 576 851 823 917 872 724 907 894 669 721 313 159 820 316 058 200 098 976 314 318 913 958 665 759 485 820 565 570 031 263 405 854 012 899 301 504 656 637 590 558 991 824 431 535 524 817 344 494 738 571 741 301 431 795 851 161 754 284 587 248 298 455 329 465 473 013 528 340 314 727 418 160 519 495 295 941 859 700 065 561 459 358 640 101 917 885 722 013 316 964 869 428 240 851 636 914 809 992 104 605 421 492 601 453 033 853 515 751 401 857 952 740 112 170 167 222 523 821 537 882 315 123 151 492 846 709 113 492 102 091 508 913 143 686 373 029 765 787 020 686 588 053 792 619 491 375 211 539 645 230 768 570 770 263 491 292 777 767 774 282 045 776 370 921 874 683 586 823 045 095 011 509 252 560 929 111 174 164 310 326 925 699 008 124 156 908 634 507 531 278 152 350 914 133 766 505 772 754 988 037 274 356 396 574 207 642 600 146 825 359 156 829 266 833 632 157 113 834 209 189 397 568 890 991 206 181 978 831 897 547 435 582 361 991 249 680 001 246 604 741 303 925 004 242 378 108 056 677 909 690 614 813 812 391 623 794 871 950 343 757 452 561 119 431 751 097 570 088 852 386 335 845 404 692 972 617 299 280 108 946 959 519 064 481 929 889 959 081 006 997 561 147 107 113 868 862 937 259 500 306 063 505 431 090 042 656 001 942 478 675 289 020 581 361 422 408 180 860 690 351 616 379 775 992 091 637 445 283 927 086 421 737 767 593 345 327 312 175 073 084 589 621 320 006 741 561 337 735 652 268 949 765 926 593 902 927 094 996 682 751 746 420 831 679 046 611 218 903 669 737 354 634 304 548 659 053 470 549 732 970 888 549 348 294 041 934 639 128 055 737 735 506 189 310 040 738 085 687 884 769 707 314 506 802 085 205 238 818 773 188 781 164 875 559 483 247 402 698 534 742 966 117 963 723 501 865 650 126 184 082 729 589 782 919 584 114 176 366 625 423 623 547 644 270 924 604 448 591 374 047 560 914 529 236 227 409 085 457 373 750 091 240 492 380 019 532 464 718 696 282 322 793 388 610 877 304 213 669 154 450 651 807 715 076 430 017 408 478 616 511 484 801 387 002 008 868 235 787 706 708 087 746 397 214 746 574 039 200 180 127 610 177 653 176 326 911 409 709 094 128 083 286 130 458 614 511 615 671 880 751 076 765 515 221 162 319 137 096 413 600 166 379 812 453 251 524 452 642 150 710 576 728 070 548 190 104 066 922 753 392 603 434 848 975 487 018 863 508 766 210 477 127 143 465 291 527 935 602 351 914 757 291 180 151 321 063 684 381 401 691 930 948 711 677 774 183 565 199 446 551 322 832 557 175 032 608 840 374 254 142 449 461 684 813 249 986 227 823 700 975 939 802 993 259 669 885 279 112 063 657 503 081 550 898 050 802 139 827 610 718 986 359 579 709 540 336 775 867 932 696 518 885 755 114 763 567 870 637 037 645 453 414 332 085 425 481 193 629 411 229 555 356 194 298 587 005 205 372 181 712 898 983 391 770 377 581 410 175 853 159 055 907 970 702 213 486 427 065 322 314 182 787 923 216 660 645 687 195 125 328 714 442 629 258 083 145 731 460 333 202 338 457 295 800 935 121 320 150 087 490 451 697 438 411 262 969 915 818 564 498 850 583 258 312 829 163 971 132 353 464 700 531 963 153 826 602 687 494 068 607 417 525 812 472 680 669 827 997 443 972 200 520 440 977 321 531 252 890 084 461 051 461 485 978 193 614 306 018 362 658 530 075 856 544 448 254 635 908 590 497 391 049 967 465 257 895 180 764 601 850 299 735 770 306 873 818 275 959 695 377 410 992 006 992 839 874 134 766 312 560 647 546 060 246 976 285 844 001 174 193 818 393 250 751 866 927 304 360 057 694 841 374 091 893 749 838 813 451 056 782 663 902 268 312 987 911 609 809 882 526 473 083 619 797 414 854 213 550 663 722 713 398 908 902 785 930 188 659 226 663 837 223 825 869 737 781 222 328 767 597 807 021 677 241 097 250 959 871 456 490 014 186 236 510 852 577 550 881 606 276 287 334 089 325 833 157 809 164 280 572 865 457 448 557 016 640 578 978 776 251 145 067 165 246 626 369 772 450 389 385 646 192 101 043 989 870 845 599 866 706 565 422 070 325 270 828 568 815 028 278 415 155 854 746 159 223 630 356 946 616 177 771 821 834 950 009 091 049 117 276 566 486 291 770 956 790 377 567 695 253 065 046 671 996 846 569 466 908 727 370 967 741 298 317 183 148 972 603 554 349 891 934 905 768 972 778 837 338 007 735 507 669 319 314 913 581 901 155 245 126 305 973 862 900 161 413 638 692 453 254 714 436 483 467 713 573 227 058 079 561 016 854 188 749 632 371 152 461 509 377 869 447 836 560 067 890 244 897 060 517 908 300 902 430 739 082 454 938 082 098 681 104 204 678 524 589 590 075 428 913 406 477 170 135 445 589 861 211 488 938 870 568 001 109 610 880 660 487 540 165 565 003 875 882 895 593 106 135 987 151 719 521 326 954 578 408 849 740 391 345 301 719 142 951 462 320 362 770 338 848 929 682 238 673 185 600 641 140 695 704 349 654 493 746 587 706 773 818 317 707 512 570 945 240 618 772 253 489 973 538 815 615 421 360 477 644 127 759 467 363 305 040 951 433 479 288 191 189 156 439 529 649 129 871 899 661 865 348 265 519 521 366 821 160 882 738 111 216 818 100 978 021 791 844 590 617 666 937 890 837 851 158 466 805 286 698 242 096 425 557 546 513 983 297 239 135 572 425 522 875 894 503 848 592 817 038 504 693 606 473 374 130 018 523 937 991 944 700 420 283 447 208 605 534 363 180 559 277 261 221 107 297 479 140 805 100 177 147 912 357 167 757 062 990 611 475 148 010 323 931 116 688 849 488 084 880 321 273 411 078 987 818 548 810 770 481 763 881 593 631 740 396 170 883 288 622 027 904 562 223 354 869 628 169 957 300 497 580 934 564 577 591 588 534 967 454 139 554 525 075 274 103 531 973 904 929 571 685 057 996 674 513 526 896 270 100 732 770 901 322 671 273 867 978 546 433 152 328 498 039 702 980 138 365 578 238 147 894 306 173 586 347 660 058 119 386 059 805 433 078 588 738 442 794 091 835 735 724 018 130 236 437 053 411 473 024 475 606 026 500 947 388 270 301 461 312 986 929 038 132 934 871 825 395 316 935 368 224 952 782 081 702 435 254 713 783 687 512 137 828 231 190 438 465 424 173 093 721 488 770 157 218 151 912 495 407 643 128 271 826 551 910 753 220 056 910 202 543 049 235 530 923 899 554 859 037 966 052 039 402 711 589 329 356 948 398 320 875 609 496 334 071 645 683 821 317 669 201 199 430 278 748 158 173 839 357 276 444 535 401 978 543 810 088 780 154 140 061 739 864 587 813 052 787 265 924 756 430 094 549 925 847 226 625 665 788 407 639 935 904 285 899 117 117 838 377 640 282 050 399 617 765 366 655 872 829 670 924 486 772 572 590 522 714 031 937 025 995 047 241 089 823 204 424 942 517 431 325 291 651 288 274 097 547 483 062 212 082 723 160 654 121 319 248 949 927 100 326 965 275 272 254 481 810 896 321 519 907 766 851 443 126 257 817 362 601 224 707 224 315 150 314 632 634 158 170 140 251 560 556 984 180 410 812 000 500 406 958 989 651 604 492 760 449 614 128 071 300 934 709 857 128 729 862 510 927 742 217 814 670 148 102 584 780 103 149 570 969 991 632 860 671 464 903 343 941 518 410 669 412 179 667 560 677 805 146 438 310 109 806 511 981 370 923 993 434 440 843 211 643 431 180 586 531 747 741 754 711 514 230 770 440 888 058 042 464 297 691 955 127 204 096 120 612 442 141 800 483 648 746 716 316 473 084 223 220 555 418 669 977 618 533 747 642 720 437 026 570 368 449 497 886 522 928 279 739 449 091 433 753 107 428 556 640 419 699 330 055 437 405 170 181 371 394 331 550 410 951 725 863 482 428 747 548 212 482 197 606 137 102 421 249 295 480 481 980 725 304 801 726 402 746 963 977 024 878 509 307 543 677 190 194 016 565 530 803 790 784 268 893 449 893 163 837 171 940 734 579 099 358 597 834 768 132 809 743 412 394 301 804 490 221 426 285 468 361 792 856 343 282 267 609 325 818 749 708 590 028 975 453 399 310 985 384 397 346 016 784 770 984 608 281 369 609 538 159 184 457 477 686 266 374 777 920 680 684 538 716 847 369 632 062 738 756 383 454 532 143 792 811 914 908 719 063 269 367 849 893 617 741 742 477 782 821 868 096 703 728 398 823 152 785 528 794 112 652 660 468 439 402 652 765 613 980 517 706 140 884 207 431 277 841 087 322 509 450 553 653 277 406 528 897 059 978 395 986 505 220 828 748 083 812 612 871 330 785 525 477 953 294 860 997 881 989 670 291 349 355 131 187 897 186 349 130 784 121 373 372 705 834 849 254 125 304 357 004 516 519 284 053 337 366 938 950 799 756 603 040 245 635 028 048 640 668 378 936 882 742 907 714 081 936 852 803 760 909 298 206 854 473 534 371 140 188 322 168 113 880 091 684 033 265 075 457 825 776 584 958 714 691 298 598 136 519 569 601 512 836 254 388 523 318 183 268 161 485 299 968 254 624 323 834 125 423 964 313 044 182 640 658 551 941 003 509 590 276 616 531 197 480 721 817 404 920 619 488 247 359 785 718 819 100 239 152 578 711 531 689 442 693 706 114 717 857 383 250 975 532 564 838 836 663 751 515 088 336 603 559 041 886 152 458 502 037 964 643 909 679 630 149 306 049 400 667 475 085 069 641 729 392 912 981 732 404 226 873 480 816 565 192 133 521 567 683 354 742 578 992 632 567 336 844 854 733 934 976 608 864 818 987 733 335 895 328 928 841 923 842 015 176 476 139 413 214 240 451 255 474 861 072 737 167 011 012 753 549 736 924 480 134 339 584 652 062 364 366 675 073 961 698 617 557 835 618 245 170 896 053 614 768 546 617 780 469 842 498 153 158 985 333 909 086 923 848 112 092 328 725 881 491 210 592 278 956 141 211 802 879 503 606 717 504 469 121 345 453 518 851 277 868 728 240 526 070 645 720 279 504 001 900 480 357 577 178 575 781 929 554 883 479 674 961 704 862 208 684 759 307 842 961 297 829 055 213 062 919 503 124 493 634 267 536 469 504 508 840 533 966 142 331 839 338 868 286 603 751 913 191 238 829 977 348 064 654 291 091 771 472 751 699 359 349 550 212 336 001 997 532 464 496 699 746 801 130 317 255 247 970 688 543 713 792 227 953 713 615 962 109 537 479 141 848 616 105 988 493 438 547 530 502 752 270 171 369 264 064 917 337 165 986 044 353 775 162 044 209 553 624 368 369 464 361 829 888 005 397 224 357 692 821 838 694 488 428 103 363 969 666 782 679 081 188 728 284 663 805 946 524 101 325 996 878 235 486 855 483 130 967 709 205 250 529 209 848 123 922 799 083 557 138 624 861 372 165 354 714 185 858 128 839 010 925 073 780 690 345 330 019 809 765 372 950 062 696 584 798 625 692 611 399 613 834 330 268 557 773 491 341 822 251 704 182 457 527 241 816 740 356 454 867 703 631 769 648 112 058 805 066 080 599 898 739 435 839 024 496 170 544 261 023 882 089 245 399 901 535 497 264 196 989 127 071 085 794 718 683 074 626 987 005 079 478 092 341 775 746 692 284 257 670 269 506 001 460 147 566 023 145 670 521 506 335 785 833 739 963 583 222 353 686 153 563 798 435 626 928 754 689 611 144 130 481 877 871 962 033 984 187 165 725 870 999 835 062 907 151 150 517 604 798 811 554 395 608 645 102 204 084 610 365 658 092 184 500 023 771 389 391 900 527 229 176 295 715 191 527 116 829 194 891 434 106 061 518 857 145 800 867 511 006 966 277 339 731 259 281 154 748 140 962 104 604 585 681 583 749 920 250 276 520 378 472 685 778 108 980 480 694 398 446 221 472 173 871 706 935 641 086 664 545 483 108 162 093 105 477 190 962 856 396 078 557 111 980 846 267 285 187 894 474 581 710 471 823 361 623 431 516 354 783 553 649 646 872 361 045 589 534 688 042 042 248 951 099 627 337 467 525 449 440 964 975 312 556 710 366 792 967 290 422 079 065 647 204 027 595 392 117 452 963 327 654 742 452 617 287 476 689 739 207 120 622 092 083 544 932 007 492 818 727 779 288 237 260 087 664 787 951 893 114 228 082 872 707 395 817 400 625 339 379 659 853 740 913 098 737 049 464 232 505 742 937 815 411 982 261 026 641 456 761 937 005 196 392 572 009 460 605 290 207 208 098 374 988 860 665 907 105 079 155 644 056 082 239 484 237 831 204 245 556 070 261 193 961 616 575 692 841 595 480 480 274 779 750 059 458 537 942 094 394 397 859 429 617 671 825 980 562 292 231 633 448 725 294 199 636 913 674 956 209 160 039 086 305 855 748 728 480 712 084 658 014 940 965 659 561 509 478 560 750 156 909 419 975 869 384 187 590 666 524 598 571 640 413 650 306 189 557 008 454 469 431 979 015 910 096 357 399 000 409 301 218 682 192 365 829 569 559 286 740 274 021 079 579 289 059 105 313 828 380 472 720 613 249 591 124 697 331 372 857 600 562 861 099 118 271 979 551 001 051 954 582 802 151 022 338 330 320 242 132 051 808 748 504 817 342 642 497 583 590 509 388 265 615 737 896 249 009 680 478 307 305 151 913 450 239 130 315 711 071 914 237 199 111 615 493 591 498 488 193 276 323 587 095 279 524 561 200 702 332 627 346 053 350 227 539 427 255 887 004 195 774 109 792 482 645 996 385 654 698 332 408 184 448 326 681 388 087 534 493 295 444 266 805 078 973 415 724 687 551 875 340 958 983 707 286 372 394 273 793 729 315 004 467 444 797 243 928 616 082 440 079 757 515 896 912 607 570 140 535 062 391 498 352 188 174 235 801 697 846 340 937 371 109 403 064 030 937 251 092 590 812 946 309 385 549 286 451 154 070 464 258 288 729 322 105 312 786 708 609 470 106 258 388 654 832 523 800 382 425 637 158 352 755 573 568 529 095 705 503 660 398 844 823 656 312 602 936 059 980 697 018 924 903 777 198 714 704 938 610 787 635 082 417 863 292 068 013 136 598 116 541 101 653 345 247 297 702 466 017 786 386 398 072 965 101 677 506 305 714 355 664 647 465 448 511 275 077 475 384 089 625 290 642 661 258 861 847 212 067 935 976 101 783 296 506 168 244 174 601 036 783 478 087 274 943 053 214 140 696 574 952 058 787 467 973 064 132 994 717 701 624 055 304 726 871 566 317 280 184 056 044 552 500 832 043 408 928 508 379 455 502 034 416 691 957 426 050 283 533 500 843 466 094 610 698 431 368 674 850 529 814 946 854 476 365 743 648 975 540 118 460 044 272 695 535 498 213 630 853 473 554 096 476 401 237 289 749 679 699 922 419 476 993 455 253 283 732 357 338 345 710 358 499 806 378 708 055 744 842 277 364 673 904 332 770 019 847 556 119 605 847 435 898 381 489 097 667 178 546 486 092 333 633 603 409 913 462 351 233 473 830 829 986 465 510 332 055 864 064 739 412 413 873 983 145 097 178 507 164 142 627 251 414 004 019 274 474 692 793 637 326 055 846 288 713 035 459 186 118 567 891 217 349 740 894 895 050 512 464 222 178 379 147 594 780 565 693 797 553 011 322 646 242 679 254 665 749 556 812 640 670 897 436 543 353 053 689 034 615 749 224 699 434 702 522 858 224 159 775 002 957 370 842 267 768 741 605 434 403 903 647 351 125 960 975 176 115 902 667 730 853 207 669 117 511 657 531 962 826 028 020 534 642 666 507 333 192 960 972 261 507 301 720 735 492 161 493 477 446 808 563 585 322 012 080 768 152 786 711 336 224 843 735 602 253 925 908 278 533 907 701 155 552 776 536 728 136 039 636 756 593 842 879 831 816 808 313 756 237 991 780 681 717 960 413 150 920 335 137 128 451 183 158 949 419 199 129 789 187 955 232 295 413 094 141 481 060 173 516 298 058 599 563 250 553 921 033 815 744 577 374 993 404 908 598 559 802 310 631 583 349 861 877 631 165 555 994 516 501 991 654 033 553 720 906 357 019 845 022 134 181 334 714 861 470 100 613 186 654 649 469 023 445 086 289 801 013 889 434 448 785 893 886 092 360 005 705 429 019 061 911 802 291 967 067 427 495 920 603 970 281 520 283 979 239 079 810 026 656 848 530 827 767 676 015 175 026 460 174 907 962 181 358 783 886 528 533 111 371 294 197 968 904 443 944 787 164 769 446 884 181 637 254 614 059 474 554 970 042 619 194 882 730 723 925 674 566 162 488 135 423 285 771 097 234 662 983 271 568 173 083 729 646 500 728 428 917 507 503 420 926 305 900 680 812 023 125 005 624 262 646 038 994 021 475 971 644 249 682 971 554 327 734 589 729 800 520 152 381 597 366 949 535 529 913 063 883 507 104 930 774 979 299 971 868 068 804 267 975 404 699 382 943 823 898 539 480 855 383 935 156 789 191 698 762 519 868 504 699 661 329 375 361 089 431 186 547 312 266 816 238 209 097 423 879 644 553 831 032 770 147 571 620 169 015 476 117 359 880 701 187 322 429 003 712 258 244 322 930 121 731 948 311 909 529 954 304 564 001 990 619 203 658 854 356 627 141 022 202 499 184 581 569 766 744 377 242 941 087 721 734 124 079 823 037 036 836 787 394 619 473 038 222 712 682 988 918 664 250 404 881 401 192 069 454 966 044 498 523 611 823 578 614 472 707 037 531 310 729 888 614 400 282 060 363 809 626 704 974 122 866 224 472 424 097 236 762 889 582 447 067 763 597 225 521 063 710 353 929 061 449 559 688 765 262 800 217 860 695 050 664 958 543 480 983 786 706 963 187 613 504 694 870 098 811 380 568 359 814 073 372 038 174 364 941 362 969 560 001 643 715 034 733 758 341 857 759 928 984 856 742 881 403 706 888 251 600 688 483 695 334 278 247 767 947 277 173 526 309 588 251 161 675 454 210 176 386 971 617 354 467 875 882 056 104 682 115 749 925 202 754 110 099 581 853 989 057 022 555 156 692 509 995 917 495 860 563 088 368 670 088 951 366 243 064 713 301 420 096 879 815 370 057 069 198 606 897 464 946 826 566 149 737 993 613 005 371 587 356 581 863 579 819 649 459 038 756 649 730 155 295 982 270 903 386 684 051 899 329 829 738 293 571 092 019 215 549 071 705 348 206 615 091 479 202 052 990 673 433 446 615 771 216 918 703 332 059 282 305 142 681 408 403 982 138 974 907 928 068 967 166 494 842 074 099 258 544 837 309 431 146 209 499 693 895 616 902 334 718 749 813 491 722 410 624 791 849 217 836 038 026 029 619 508 381 849 052 002 148 776 280 124 314 540 362 642 589 652 349 617 963 374 167 751 149 148 169 881 643 068 554 511 808 061 733 529 118 820 971 200 646 913 661 444 973 074 784 461 772 089 339 486 163 360 159 583 602 266 854 868 710 050 828 776 501 919 081 830 165 729 187 476 678 638 841 571 836 069 911 039 529 124 092 094 723 382 666 296 415 198 451 673 303 888 244 431 733 705 139 626 607 287 771 113 925 758 718 872 961 008 164 937 021 854 562 225 406 729 760 587 753 480 144 889 475 637 263 920 711 830 081 872 333 333 564 371 416 439 704 386 714 119 724 682 370 793 216 560 662 097 493 325 355 704 575 900 133 044 537 356 988 939 705 449 946 154 640 131 117 325 064 904 895 808 190 335 086 424 425 903 546 213 580 956 238 908 328 174 717 924 582 589 061 515 172 352 084 934 843 888 647 758 056 788 341 339 470 793 482 519 305 951 373 714 097 889 500 640 152 279 823 004 521 778 398 856 583 890 189 186 832 820 185 692 699 013 109 119 082 372 391 475 400 115 530 925 008 876 337 597 643 154 571 636 294 880 716 489 804 764 924 948 550 072 825 948 021 764 105 061 436 928 158 144 097 874 557 610 316 534 280 049 803 355 555 586 957 424 769 975 732 065 010 935 216 639 146 614 427 926 505 114 321 033 358 921 990 202 383 198 679 935 439 473 820 108 754 611 872 142 888 385 672 795 395 915 179 682 851 558 522 010 262 069 877 413 026 031 893 019 401 996 767 287 941 161 702 148 217 188 783 834 598 056 129 544 592 934 170 533 416 963 089 407 218 259 375 357 665 054 819 882 664 231 266 985 797 789 545 488 930 691 971 266 195 761 447 463 439 104 050 574 503 307 058 874 381 469 769 072 729 917 189 399 823 730 757 125 125 624 807 833 861 156 886 480 578 370 377 731 329 479 332 402 236 644 216 090 058 283 655 001 509 810 644 275 755 497 953 511 121 580 489 336 243 181 258 069 665 946 852 106 406 552 152 036 063 888 409 606 995 251 560 608 922 390 089 616 677 072 419 797 060 157 143 207 981 718 504 566 673 806 775 832 263 716 581 305 885 758 422 254 760 856 755 707 996 309 271 082 121 824 028 575 799 156 434 461 965 965 493 777 566 212 362 889 551 297 899 925 903 487 094 656 669 395 620 753 910 379 130 490 183 182 432 140 002 872 424 222 906 946 963 689 859 551 672 625 604 228 465 189 586 524 017 161 843 201 118 328 363 565 514 964 002 381 237 770 770 548 715 711 477 666 415 111 770 174 526 107 641 696 122 932 626 840 740 302 005 374 306 279 903 147 870 684 235 190 680 714 638 329 996 640 070 582 989 737 229 998 657 496 963 469 955 463 751 185 965 456 403 621 238 741 499 914 044 293 424 176 541 937 658 014 284 094 748 699 179 897 782 310 849 903 634 082 842 605 219 734 303 150 314 739 308 571 633 382 503 012 314 239 396 860 583 083 381 495 123 764 627 061 407 511 007 190 220 075 110 844 260 559 017 297 238 391 204 073 886 000 071 361 067 968 826 000 082 010 671 045 237 531 396 860 173 695 114 743 875 313 868 857 694 671 787 484 541 187 345 543 628 853 348 249 675 925 686 455 577 339 754 622 826 221 106 378 077 987 968 593 534 408 467 044 398 950 171 518 631 194 315 527 912 162 448 905 047 176 004 457 766 351 034 453 859 093 507 478 294 193 038 865 939 174 488 912 644 204 981 313 187 708 700 532 849 786 076 962 148 072 897 230 904 949 036 377 073 951 488 807 565 872 243 475 999 949 977 184 962 565 821 369 594 680 063 724 418 482 957 813 795 604 989 799 139 948 361 332 838 527 922 940 688 448 585 173 650 899 625 681 175 026 653 045 985 377 495 226 838 631 889 082 414 809 280 253 509 787 892 609 934 272 822 626 596 190 922 514 245 889 898 949 894 981 153 932 860 725 958 822 659 313 413 047 192 553 780 264 851 835 883 775 057 258 617 793 470 781 174 429 287 951 812 101 585 942 124 418 581 501 409 888 465 064 088 444 949 961 433 346 416 520 585 889 231 636 233 024 468 949 598 777 241 459 746 733 180 875 501 149 140 027 972 058 035 973 948 657 583 354 755 709 103 461 866 766 055 971 746 654 842 895 310 620 544 544 129 478 762 558 358 972 020 406 065 233 511 312 659 948 190 243 564 535 852 682 475 184 656 878 227 520 530 640 116 722 533 409 957 960 934 393 134 231 469 198 495 236 886 478 297 011 489 807 302 718 289 675 311 732 974 943 380 399 136 513 909 480 468 118 995 401 376 473 038 236 229 861 826 651 867 036 749 902 591 130 613 434 674 748 475 147 167 572 352 177 094 339 385 348 762 235 560 609 405 349 828 199 572 109 332 357 379 382 917 985 742 059 029 700 171 914 899 401 447 916 742 708 109 402 172 980 497 291 801 229 877 244 802 652 821 676 686 966 188 781 665 587 980 799 317 667 919 014 032 245 076 820 291 405 646 412 802 414 423 547 103 151 814 779 689 403 104 817 956 495 003 694 226 996 643 292 690 775 514 112 080 208 981 562 492 181 152 783 048 197 216 336 713 208 691 415 678 505 979 728 892 206 129 316 512 902 832 326 962 652 569 489 975 911 827 651 085 934 675 683 937 460 705 398 773 671 557 082 397 393 932 569 959 906 550 921 846 076 176 273 392 421 670 199 281 375 112 091 286 658 731 407 280 447 287 909 766 090 153 979 863 100 889 666 432 249 518 881 894 748 644 993 670 407 208 433 692 064 828 652 688 249 007 977 792 232 436 575 606 498 658 262 747 156 068 398 849 977 103 613 663 245 053 554 049 146 755 267 614 964 794 586 621 096 730 005 263 661 391 969 404 692 389 136 628 608 490 077 612 420 545 719 315 712 226 655 996 807 676 059 775 949 313 348 652 104 427 677 201 936 004 486 687 894 625 648 260 745 066 083 257 460 521 565 282 884 762 522 513 852 455 748 798 065 500 489 082 524 575 145 770 159 479 933 131 550 341 810 049 108 455 864 963 275 498 093 492 876 738 077 505 592 828 639 380 813 355 926 814 721 276 177 349 453 420 895 326 139 144 806 089 964 051 511 889 532 222 613 841 845 701 494 282 246 347 137 687 241 749 585 183 045 579 891 327 255 841 225 834 032 204 825 213 761 839 537 519 629 028 931 121 255 105 087 593 244 107 135 045 789 974 626 194 483 499 756 003 558 494 458 120 018 928 703 803 189 653 925 777 184 993 853 918 575 099 010 180 338 264 432 972 003 876 139 979 417 424 182 787 890 508 979 836 505 028 535 489 599 210 291 560 800 537 577 475 999 254 162 468 044 460 105 055 013 162 252 421 089 575 583 626 552 487 213 544 720 354 813 694 306 629 957 506 257 018 552 057 450 957 173 287 112 970 023 798 660 361 374 464 937 535 346 623 878 307 901 164 460 010 378 609 962 297 831 091 542 664 616 633 837 997 366 950 998 455 342 594 355 088 685 114 112 347 407 475 419 975 895 631 108 208 490 230 130 157 118 008 696 337 762 020 175 111 865 849 332 210 102 000 896 755 296 948 216 761 229 459 527 749 308 895 481 865 469 753 790 151 478 334 774 003 939 736 630 183 347 451 578 646 981 832 874 126 803 760 885 549 964 814 610 094 350 975 908 999 032 515 065 715 541 166 747 357 806 126 915 594 968 184 487 842 021 420 397 780 863 177 584 885 819 741 190 546 875 099 082 467 195 312 133 638 032 221 694 112 126 380 444 834 250 949 920 742 261 282 273 756 407 873 435 395 455 098 859 708 883 444 738 397 602 881 366 390 985 418 311 192 811 169 623 596 191 886 688 938 780 182 282 760 670 634 846 670 863 983 678 634 970 122 735 199 914 504 371 613 071 542 122 739 596 693 859 668 253 799 544 540 836 661 660 651 664 172 741 211 128 461 385 725 770 846 009 561 421 918 507 535 240 070 752 025 685 747 535 330 360 291 627 181 622 940 752 265 946 706 947 969 031 148 840 384 904 062 993 636 253 561 364 493 384 943 641 526 713 629 391 859 461 993 803 507 915 173 889 380 952 548 448 192 221 680 774 979 756 934 928 181 087 210 920 628 804 894 922 578 445 340 957 620 503 416 174 577 313 613 970 870 813 456 786 635 199 291 156 699 234 856 734 433 208 628 627 128 456 184 887 586 859 377 968 759 014 765 021 345 311 328 334 897 414 722 936 404 475 776 200 704 257 360 104 245 696 372 067 369 411 013 007 521 871 785 861 594 972 876 134 083 719 721 432 218 535 054 366 736 964 336 396 184 833 403 958 342 131 548 201 054 696 255 815 502 057 212 221 630 885 649 080 978 874 074 476 155 358 261 819 942 525 956 367 841 377 337 653 791 226 361 582 776 129 604 339 192 177 161 288 483 169 533 267 666 770 234 981 084 604 819 130 093 693 265 751 470 819 060 205 290 275 465 999 650 319 084 565 652 507 464 494 577 974 890 486 643 062 594 717 268 959 092 377 140 320 952 848 269 564 164 405 911 099 640 752 531 578 867 399 465 197 292 807 241 760 554 877 718 603 127 316 520 213 276 618 907 083 101 316 597 571 423 934 429 991 852 951 473 288 258 908 332 864 904 624 355 604 662 709 856 478 031 749 542 013 590 820 756 196 260 096 989 569 729 818 844 827 521 731 401 501 611 981 461 004 554 571 882 599 512 931 864 613 855 853 452 164 508 185 625 675 387 837 941 717 557 427 238 616 978 008 307 220 834 658 475 496 551 581 019 436 424 434 703 514 165 274 819 609 689 239 830 780 597 814 022 676 908 590 840 988 180 055 233 074 824 733 226 909 730 871 732 326 661 150 428 097 124 513 333 430 103 041 910 702 242 716 217 446 057 571 729 941 342 403 101 553 236 910 561 768 163 053 606 224 374 594 199 286 469 926 029 493 523 256 703 570 282 522 658 852 461 235 799 468 490 630 131 101 488 453 032 511 935 296 108 289 641 002 310 706 588 711 406 606 441 926 261 629 032 830 517 052 172 238 981 181 779 111 596 807 098 512 197 838 874 145 164 115 193 190 602 534 819 718 723 438 707 724 129 785 777 602 742 539 494 934 225 204 130 751 789 451 085 505 278 778 361 038 821 016 809 074 888 533 007 671 801 384 282 075 029 313 405 051 896 525 368 492 061 623 769 243 938 786 061 520 266 289 233 298 758 044 981 854 507 220 425 946 475 996 988 454 425 784 111 138 037 962 822 978 026 817 120 688 064 723 761 381 188 346 277 271 426 414 114 827 358 940 766 830 179 584 347 826 182 056 046 770 619 452 590 487 879 591 067 848 341 164 314 376 996 463 818 993 755 626 461 790 898 618 966 561 393 263 607 238 374 995 722 640 386 032 293 343 542 708 675 758 295 075 340 835 540 384 135 054 913 685 234 950 186 874 289 180 445 287 055 058 584 681 181 881 837 354 315 759 243 471 955 917 169 304 903 183 103 666 766 671 983 764 214 229 488 152 200 335 072 822 458 988 919 406 186 868 163 144 541 332 026 410 256 264 268 969 190 313 800 655 105 496 549 185 774 344 102 188 171 022 202 254 141 865 923 016 014 907 372 607 546 274 863 688 276 430 625 026 934 876 961 592 932 613 702 584 628 678 989 495 966 819 388 410 472 629 771 540 215 566 842 314 262 084 638 143 126 309 298 642 521 879 793 365 365 532 271 221 860 520 885 973 821 661 179 559 852 913 403 707 354 077 245 496 783 812 372 179 246 351 811 620 921 769 767 583 824 464 911 139 393 015 152 099 120 901 323 513 906 308 138 496 335 191 172 923 086 328 004 260 037 038 934 383 396 330 966 366 213 296 915 619 156 948 727 225 118 034 528 223 809 464 303 489 529 326 729 633 141 405 619 194 323 225 072 750 280 548 987 997 363 021 956 460 624 208 609 361 749 383 263 662 592 698 360 983 021 452 680 330 449 243 685 667 631 401 996 933 615 044 537 777 536 284 626 234 805 501 682 508 461 150 635 672 774 329 598 089 507 078 012 325 869 931 023 845 196 322 759 665 378 168 280 026 853 464 426 779 645 192 349 306 664 253 757 928 716 903 535 822 131 337 359 867 738 582 958 592 028 825 236 429 374 174 667 071 714 504 488 506 325 316 277 557 804 194 173 961 579 897 518 731 254 284 756 463 788 549 806 749 220 222 090 270 834 061 636 063 515 114 883 690 757 041 546 294 955 608 479 316 122 388 831 563 044 515 573 799 637 835 968 714 451 365 201 710 363 338 778 287 047 426 624 105 400 749 413 504 313 876 989 340 408 150 654 337 495 245 069 864 804 262 659 680 606 853 752 530 383 256 692 238 604 630 692 070 507 176 684 625 169 473 380 839 337 374 074 323 811 452 673 164 269 424 328 317 198 889 399 328 686 564 990 918 623 161 911 888 424 113 307 238 435 073 827 235 439 056 021 914 615 223 067 143 483 678 816 891 814 051 453 809 823 819 685 101 525 404 712 322 003 648 129 375 309 711 474 860 897 862 289 530 201 308 600 745 875 907 383 946 039 504 898 017 088 004 096 757 244 405 504 172 193 459 610 551 230 735 355 104 672 864 281 358 386 089 742 879 921 504 064 380 438 725 114 115 161 650 983 186 342 415 142 872 186 563 864 432 946 130 129 594 704 732 215 075 780 753 868 099 039 901 916 241 900 233 290 836 739 028 115 397 436 194 364 601 406 575 503 348 866 661 106 999 239 129 714 778 900 970 244 028 316 136 238 885 272 678 654 723 648 689 692 648 498 295 637 090 843 407 604 182 956 742 702 737 042 186 493 481 189 866 240 711 237 951 583 406 041 770 529 569 114 277 749 498 576 242 099 069 084 801 233 373 439 900 990 418 707 705 759 664 743 245 452 824 593 507 621 581 846 276 374 081 183 371 981 840 179 767 461 923 795 937 454 175 651 064 415 102 099 475 459 189 823 409 728 719 535 853 946 250 106 921 381 725 774 436 704 527 185 878 812 023 671 372 056 046 335 436 356 453 102 629 524 108 157 990 924 993 527 670 769 064 942 105 851 259 890 814 733 469 589 525 440 958 562 772 220 450 047 913 851 981 913 286 033 873 478 329 647 446 513 326 107 051 382 936 356 405 018 250 408 192 055 443 709 744 048 929 196 771 712 988 774 232 248 037 251 978 145 367 702 520 173 809 219 177 335 313 425 767 775 520 889 737 752 865 329 333 837 275 293 990 117 962 429 235 651 943 000 578 146 330 439 288 341 331 245 778 105 420 076 062 264 318 414 167 255 806 448 276 983 294 049 650 799 117 607 430 122 423 148 244 759 550 723 395 816 541 816 558 463 850 778 135 926 652 840 876 509 867 985 255 975 045 052 248 185 469 578 163 945 150 675 089 805 937 414 420 207 478 955 273 627 377 059 161 913 061 164 002 220 679 521 979 647 561 326 910 356 772 651 587 114 925 887 455 845 584 897 013 500 165 801 206 689 627 148 230 254 607 026 272 305 113 482 817 621 546 278 195 502 115 021 882 294 864 699 269 613 633 807 007 596 336 451 549 655 401 383 970 349 305 458 481 198 978 541 990 894 748 428 639 418 382 456 373 242 089 854 893 114 884 936 753 081 423 399 183 544 624 094 287 939 393 333 436 596 705 696 476 451 354 763 368 321 159 245 588 019 213 646 546 027 037 232 809 719 740 506 968 865 704 369 450 269 825 600 639 925 221 338 289 758 213 771 173 864 591 654 854 826 992 025 334 780 001 670 438 779 179 244 498 843 994 106 704 607 020 532 408 240 886 173 399 026 669 348 841 678 371 963 356 153 470 820 849 884 752 790 257 607 550 858 645 658 216 137 584 656 357 985 882 830 806 525 570 046 743 728 243 698 007 970 565 262 911 812 611 678 105 891 097 279 348 740 883 355 528 029 296 513 060 724 155 180 441 269 457 471 175 329 127 911 125 243 759 023 288 045 429 882 344 101 981 999 721 056 955 991 362 076 307 603 071 164 709 137 236 672 593 657 775 150 989 542 904 009 937 057 254 665 732 837 738 158 420 576 869 784 616 078 361 913 792 510 240 636 971 847 331 105 733 573 687 516 472 237 228 950 291 534 506 172 253 126 200 336 294 056 049 344 877 533 213 945 084 677 290 722 930 637 975 840 100 144 525 558 261 223 358 879 008 290 510 036 816 397 323 616 200 161 052 419 537 119 640 667 586 879 290 334 942 725 074 033 525 073 828 187 571 485 150 335 962 905 089 465 563 946 234 936 293 526 635 510 336 372 730 007 057 667 320 933 688 226 028 133 748 250 628 760 042 276 670 339 073 593 075 195 096 208 499 520 901 729 636 587 492 831 780 054 692 189 199 091 503 147 215 983 925 508 879 527 777 472 206 755 099 035 225 147 678 286 693 709 139 445 024 449 147 110 141 733 151 098 696 995 666 976 211 784 165 092 172 269 895 099 688 888 497 261 140 660 376 862 628 186 294 878 355 538 133 857 866 279 930 062 552 374 991 916 422 278 319 622 958 222 897 924 209 518 543 949 223 503 411 413 671 518 041 647 969 799 859 500 034 848 395 731 902 500 748 622 753 937 167 273 024 798 485 133 473 791 192 536 807 685 705 027 645 252 970 815 029 293 552 305 094 458 285 032 669 944 898 950 650 790 373 989 873 579 055 207 944 041 745 365 469 862 958 431 613 885 150 004 080 364 181 916 207 604 017 409 900 341 977 674 343 714 455 949 637 015 834 179 107 065 533 984 390 034 450 870 877 666 141 265 875 662 009 618 962 881 488 719 043 443 540 550 784 664 256 396 198 136 918 607 608 348 881 551 704 534 347 745 066 223 938 267 296 837 489 713 158 596 630 856 025 859 328 556 274 042 797 182 987 264 012 710 251 386 268 156 108 885 031 754 725 925 744 538 889 418 773 169 056 269 805 464 838 368 154 542 810 204 655 648 811 326 211 581 406 690 429 222 552 683 692 697 018 464 226 892 239 939 529 999 321 524 933 968 057 256 249 492 900 765 106 931 678 808 424 935 806 015 005 413 087 418 137 397 873 168 212 316 973 867 761 301 775 428 348 008 451 856 756 344 361 636 385 064 341 617 899 626 067 226 356 219 474 497 292 575 089 979 545 029 998 833 754 493 634 618 476 829 905 129 430 913 086 145 534 819 848 957 865 838 244 309 982 095 458 552 270 617 184 003 849 521 152 886 654 775 979 357 089 910 161 931 528 932 035 104 503 861 985 944 368 221 165 279 378 546 468 360 286 852 452 100 591 105 973 211 625 645 761 665 369 383 423 995 914 325 475 557 219 215 735 078 840 983 282 476 403 893 678 876 819 048 078 707 094 099 788 964 612 120 187 965 700 441 685 738 463 438 057 687 892 974 376 458 351 790 812 147 308 848 633 626 094 092 299 529 543 655 691 391 927 992 666 639 737 439 333 634 194 101 371 255 954 792 917 305 162 257 154 293 682 996 863 662 638 896 430 072 592 610 396 399 969 824 539 243 243 452 579 276 853 998 948 319 495 095 159 881 556 199 651 923 783 476 492 180 720 129 169 271 794 512 495 492 106 408 228 449 334 228 345 040 993 883 503 284 572 802 301 461 428 439 631 949 592 266 825 066 794 320 844 071 915 309 242 200 177 943 491 544 731 931 697 279 534 552 180 115 245 050 018 001 399 253 629 143 268 193 936 557 203 445 304 835 871 854 533 636 991 629 114 034 296 575 891 323 219 135 412 097 253 449 259 438 686 896 779 241 119 666 406 356 419 343 645 763 781 372 653 287 278 443 100 879 913 911 934 823 689 520 986 842 619 525 907 577 965 424 529 186 687 402 592 780 852 927 607 855 663 478 994 231 382 475 415 690 535 778 451 779 356 857 882 469 704 620 411 261 568 295 373 979 652 412 640 047 477 068 509 802 093 145 651 068 460 693 362 687 347 239 707 064 612 835 631 735 413 133 079 863 578 137 417 725 436 523 941 269 827 343 756 602 005 665 391 518 554 348 982 688 835 039 904 622 763 095 847 863 195 808 580 525 626 584 704 750 111 922 066 626 505 780 693 646 672 464 975 968 666 822 126 395 374 298 390 935 238 619 095 192 464 276 780 310 135 902 203 414 213 414 535 151 253 228 143 276 276 815 258 697 374 173 084 431 151 373 515 971 275 820 079 381 722 096 372 899 738 464 738 402 820 166 308 681 175 834 544 790 421 343 067 822 162 258 375 824 998 399 118 379 619 282 797 220 456 519 844 333 306 455 186 390 319 507 607 382 162 426 118 950 158 312 552 861 059 642 876 374 153 827 520 773 409 662 153 365 517 009 304 068 582 710 164 276 711 931 225 536 771 883 854 610 672 220 850 327 194 630 640 224 953 097 978 175 268 526 283 664 927 577 014 841 696 183 181 796 805 276 225 598 860 844 173 394 277 483 736 098 582 048 469 984 026 975 329 745 293 197 873 828 641 348 065 323 160 099 912 597 390 387 782 389 365 739 681 664 999 103 433 772 438 127 454 568 258 491 750 342 902 663 725 191 749 198 792 435 468 127 567 789 996 847 172 206 786 604 548 102 843 406 784 779 516 103 053 098 858 069 036 310 745 349 120 861 629 306 604 691 529 432 084 239 071 015 214 196 138 121 565 932 530 853 226 830 861 338 699 019 778 889 713 496 861 400 830 680 225 412 929 045 963 250 798 001 756 403 787 269 588 124 165 913 501 700 527 204 716 379 888 787 963 921 807 775 385 451 681 272 019 254 345 837 717 064 038 511 140 711 472 517 537 897 140 207 199 277 802 716 278 940 430 268 138 119 720 101 013 315 340 723 040 420 217 513 526 428 771 514 450 386 146 158 626 827 098 151 375 891 999 508 452 733 360 117 335 101 994 158 075 798 447 423 743 725 190 443 060 483 329 514 711 222 009 443 265 223 933 444 468 659 116 326 492 068 956 845 964 096 960 344 236 198 401 882 174 729 130 010 372 426 626 231 307 378 762 526 177 842 659 590 657 316 244 235 710 244 599 644 510 453 933 802 950 946 012 149 888 351 531 462 393 694 260 505 246 377 923 883 522 825 891 328 491 814 591 895 967 585 266 579 378 616 384 944 603 123 440 816 028 785 165 336 422 065 426 736 439 247 899 482 536 494 989 995 780 610 767 041 243 568 638 541 886 220 433 137 206 280 916 316 433 490 004 697 075 039 019 847 944 113 292 904 389 599 944 929 934 106 378 227 512 516 726 340 211 532 634 716 821 647 970 193 612 077 035 572 442 693 762 850 128 089 021 562 376 588 229 746 921 910 294 039 600 530 158 266 092 312 763 635 443 557 222 554 430 601 372 705 824 218 432 090 544 759 177 694 303 342 871 342 161 357 896 918 616 306 055 239 749 026 175 917 902 268 436 164 011 241 821 769 792 622 139 939 513 353 545 604 496 052 113 313 166 889 776 929 782 222 811 376 377 454 675 427 440 660 975 569 610 983 690 483 081 626 930 721 647 703 449 227 774 616 719 498 678 784 507 288 213 242 590 548 622 120 180 570 954 204 475 863 634 319 920 134 958 757 084 547 287 161 103 722 024 398 459 066 406 238 837 828 121 536 444 108 113 236 262 855 057 513 261 666 753 906 075 357 737 731 357 540 748 259 634 098 285 217 896 134 297 340 996 205 627 640 897 282 738 206 551 768 521 224 835 943 395 773 073 744 931 055 849 742 212 644 718 236 935 747 346 794 230 182 647 300 944 176 904 308 585 685 685 617 798 908 749 956 403 813 824 024 900 863 317 906 485 382 032 303 454 660 840 296 724 130 974 587 688 781 202 626 711 684 901 914 099 321 263 135 186 129 079 958 839 365 742 100 539 131 886 898 160 070 085 275 559 739 655 639 577 855 571 978 925 847 021 249 840 533 531 209 064 547 312 477 093 461 250 744 975 424 932 273 740 053 343 818 173 315 594 061 702 832 349 048 344 005 122 582 573 299 067 242 289 543 546 448 495 584 403 196 028 177 433 229 392 796 867 527 041 511 783 483 378 645 513 574 852 349 691 274 035 856 058 392 432 836 887 468 605 737 044 828 296 974 840 486 728 014 413 222 503 046 961 429 125 509 561 927 572 942 729 963 549 112 622 761 362 895 689 172 081 523 773 309 867 230 716 728 854 882 569 986 911 612 073 466 203 741 874 226 290 380 378 124 379 050 489 913 540 600 853 302 667 818 109 065 951 851 681 158 139 880 050 028 541 247 461 705 849 320 948 076 871 117 848 332 770 514 047 614 761 585 297 357 457 388 782 496 911 490 486 075 458 063 580 318 203 965 626 276 210 587 152 992 736 346 242 800 748 285 948 497 627 468 497 378 114 945 566 984 135 179 258 294 153 727 298 249 724 063 606 824 043 139 285 993 141 165 545 976 802 197 182 408 845 006 121 840 145 837 522 294 333 158 346 139 264 912 077 248 889 168 077 115 906 798 618 825 608 898 136 903 831 110 065 538 369 399 405 200 738 890 583 636 351 937 503 955 663 042 840 582 072 921 533 200 305 472 478 394 131 261 813 900 990 085 695 099 020 189 303 325 642 503 139 607 936 891 057 143 376 789 549 861 663 884 923 061 605 694 690 259 623 416 662 147 622 915 089 609 107 808 896 700 537 213 796 495 844 393 066 334 768 791 283 625 778 097 446 708 927 728 818 968 050 123 980 182 187 549 957 270 991 023 903 304 498 153 274 396 664 408 107 400 820 783 664 908 997 362 167 394 751 599 543 753 490 017 763 748 585 794 225 335 502 901 650 849 322 239 450 553 044 201 538 494 565 331 235 179 626 151 457 843 845 717 387 821 559 079 275 625 590 341 146 088 782 075 301 557 143 234 496 323 204 055 073 694 727 023 097 473 315 057 455 809 076 925 484 824 199 483 939 960 673 440 103 976 484 153 068 224 756 365 492 039 197 650 064 169 393 481 653 199 387 130 355 427 914 940 294 916 626 058 706 753 476 784 722 749 332 051 052 751 810 807 312 912 629 305 947 299 699 503 092 530 517 982 354 781 780 338 386 644 825 839 471 046 141 901 427 535 055 448 987 166 968 289 435 901 579 876 233 639 366 251 026 553 228 721 727 938 118 726 420 436 622 864 539 594 083 369 830 072 902 309 727 060 345 074 153 920 679 764 018 417 397 625 554 907 148 102 095 617 854 923 121 332 665 021 126 609 039 201 778 247 376 794 293 193 181 007 759 961 492 335 472 911 659 586 892 716 799 054 729 640 029 937 062 423 850 958 228 742 077 252 767 135 715 940 898 131 923 469 341 893 547 534 025 810 707 226 946 704 177 489 699 315 567 446 133 271 309 873 968 208 321 699 053 893 942 483 239 861 441 145 689 164 577 829 911 950 516 465 266 336 388 503 861 679 712 410 299 318 005 806 776 903 858 336 582 238 679 126 069 161 117 720 883 779 792 825 009 000 755 808 168 333 669 919 590 324 844 402 169 351 533 743 138 382 510 617 702 831 111 978 465 812 182 495 375 110 633 594 714 817 870 195 204 693 656 304 586 506 659 074 735 078 625 148 057 002 603 318 549 727 533 565 688 519 301 871 370 910 911 147 956 194 753 655 796 382 186 240 208 255 980 354 910 627 382 540 802 471 038 822 141 290 133 906 984 712 555 255 432 136 381 047 940 971 689 220 853 172 665 107 107 853 916 902 141 841 531 600 250 332 281 220 525 651 325 814 353 413 714 925 002 703 394 389 714 427 684 482 318 210 615 408 316 972 815 013 602 154 971 945 033 514 546 088 518 128 668 846 941 294 901 237 803 426 747 486 136 940 322 722 567 401 181 249 982 230 989 089 693 875 626 185 530 386 722 566 029 194 151 937 623 115 300 266 742 714 106 711 778 134 050 206 478 923 568 385 315 178 475 522 564 610 675 467 022 003 285 016 295 896 138 356 803 089 264 481 675 854 981 467 437 130 836 593 041 100 897 469 414 323 625 938 569 198 029 024 923 899 283 335 388 303 737 741 073 441 386 432 622 950 218 541 570 757 319 079 179 256 420 041 947 065 511 227 659 818 745 182 881 495 381 449 602 471 386 620 160 809 240 799 651 700 815 895 151 462 627 760 779 621 802 265 500 608 261 818 336 920 202 040 460 917 694 208 176 343 747 144 427 487 975 764 043 944 983 979 247 217 177 562 642 833 073 538 294 182 009 969 896 238 329 028 583 083 271 736 331 000 577 983 710 703 713 634 209 778 705 458 158 573 704 157 097 596 033 651 763 150 841 395 513 001 020 755 468 042 668 040 648 458 655 021 593 999 271 941 649 783 572 293 759 046 501 337 892 971 555 024 450 354 139 810 612 448 014 523 842 160 594 118 015 239 313 941 610 851 423 337 526 470 897 043 489 448 486 022 068 290 148 091 029 095 701 193 903 810 776 964 027 459 931 921 696 871 106 230 583 151 381 865 213 649 149 139 658 600 992 462 714 376 332 214 828 713 174 489 032 061 912 245 637 844 776 098 324 978 867 072 920 332 833 376 154 053 724 854 024 096 530 243 692 971 252 995 878 815 191 203 312 071 840 403 195 788 590 170 862 107 538 812 467 516 988 755 331 556 697 228 066 718 729 248 624 438 828 386 855 234 767 281 451 868 896 669 194 413 241 584 252 611 485 437 341 292 406 633 122 861 266 781 870 076 955 592 218 699 715 242 752 564 957 950 468 557 945 716 542 532 321 722 915 106 220 267 843 356 087 699 803 177 496 199 628 685 057 477 409 201 293 774 417 169 869 535 761 841 494 595 153 583 551 808 513 505 559 233 733 713 112 610 307 826 284 440 740 323 211 038 555 135 705 994 669 619 608 108 171 064 343 536 745 615 418 105 105 466 532 619 238 857 955 020 989 785 114 166 572 604 632 641 331 560 033 127 478 521 468 985 767 246 480 979 858 482 658 090 831 309 844 614 809 845 445 136 119 642 928 659 558 498 169 227 519 754 706 510 087 925 281 793 357 252 745 611 695 341 332 847 482 389 588 348 730 833 866 682 868 640 557 255 792 192 057 470 528 395 825 273 934 065 686 215 890 626 557 490 654 142 466 863 568 436 812 125 943 238 381 031 981 485 511 007 977 679 451 796 087 178 713 007 168 897 405 682 732 530 216 760 776 012 449 313 707 611 415 032 739 656 623 169 793 765 532 999 206 991 281 864 378 126 021 557 724 887 877 192 356 746 445 591 813 667 091 819 593 901 104 507 500 294 946 970 201 198 269 935 370 096 393 922 218 016 187 135 737 057 265 711 655 976 317 179 506 164 610 819 723 873 382 736 012 098 911 500 857 898 285 509 008 195 605 910 193 777 742 588 560 994 920 484 322 642 618 739 443 287 760 319 781 456 045 656 436 031 828 595 431 180 094 205 956 796 424 834 204 400 348 199 452 764 595 229 185 466 171 432 436 573 012 708 549 448 302 462 976 435 511 136 969 475 139 384 355 151 178 950 477 812 229 017 745 706 918 579 981 842 739 993 670 124 148 534 193 007 822 102 283 913 492 872 407 445 318 427 688 362 602 301 803 407 180 571 620 237 646 256 799 264 271 105 926 927 856 484 308 110 030 030 453 921 176 167 422 477 041 963 934 114 638 859 847 235 452 193 450 495 783 945 540 889 767 709 899 158 870 942 623 558 468 717 142 764 048 183 987 992 334 568 229 381 093 891 968 179 495 405 927 664 232 372 898 073 064 101 903 916 542 487 261 996 569 262 149 333 007 736 975 876 804 025 954 309 129 059 443 098 310 131 049 081 307 966 412 280 019 774 116 064 901 049 247 490 242 644 229 521 133 271 025 050 779 117 662 400 636 421 556 254 244 358 016 122 907 806 455 493 348 098 306 141 132 766 543 153 570 611 064 298 694 939 995 792 663 164 522 659 397 092 210 472 565 646 193 699 783 823 100 839 923 681 983 487 217 911 933 184 940 567 154 487 234 713 971 109 183 921 359 452 625 275 902 042 428 251 841 084 434 404 179 765 110 893 018 118 468 289 567 483 299 702 737 932 119 604 662 943 059 269 607 053 510 051 321 845 107 139 895 317 260 111 249 818 567 090 293 159 574 386 110 335 425 864 724 955 387 910 763 975 630 269 001 064 744 087 611 325 175 541 388 821 802 879 524 965 469 038 063 349 960 860 575 603 787 254 605 068 358 397 749 296 094 772 051 483 086 829 391 310 878 124 039 129 498 634 386 653 668 284 554 286 388 720 575 425 860 717 728 566 064 421 591 019 309 290 238 244 575 581 011 539 606 572 311 111 344 307 508 450 339 581 847 386 572 188 095 826 966 385 857 850 107 608 055 881 023 646 358 683 402 943 357 556 124 613 072 735 493 497 736 919 489 985 799 233 593 466 580 588 466 047 690 617 654 178 629 785 763 621 651 148 329 315 632 453 766 405 461 965 328 654 089 743 959 405 261 793 540 831 191 872 374 386 451 591 834 108 101 236 508 754 975 645 258 363 394 140 317 325 572 774 206 785 299 012 997 052 392 043 115 646 709 412 358 207 728 479 131 705 882 593 851 912 213 914 110 487 395 309 313 779 558 485 169 747 603 642 820 425 463 109 442 027 746 579 133 051 091 124 962 546 213 931 202 941 660 310 498 443 709 865 487 666 504 222 241 997 278 918 330 524 972 379 045 721 479 376 736 251 930 340 390 759 320 501 610 865 181 113 821 264 030 399 127 731 901 159 067 361 318 297 889 207 794 889 935 973 065 688 523 017 544 220 160 675 543 693 473 515 952 480 366 502 581 092 688 280 352 626 451 164 297 019 799 319 407 128 530 930 066 433 706 041 011 187 949 100 817 047 329 859 277 465 332 758 474 329 124 302 974 967 334 320 152 529 506 370 983 847 848 698 175 888 946 013 332 538 569 451 930 141 785 459 485 094 770 252 420 493 399 333 609 867 996 996 730 347 099 372 746 470 475 322 796 738 632 678 343 757 790 830 388 131 772 703 193 318 920 987 308 770 620 300 479 212 881 872 181 253 033 634 447 510 669 482 985 680 901 544 291 250 285 206 146 720 462 007 237 617 550 566 329 830 252 261 895 409 139 942 189 350 653 292 976 616 903 396 150 260 288 383 136 145 159 115 516 302 334 580 759 169 359 291 367 263 148 779 469 254 797 593 129 833 739 108 609 098 162 959 008 746 794 163 977 967 212 628 557 128 930 016 987 565 481 348 919 698 324 519 234 985 726 069 069 164 107 672 898 232 394 444 096 529 887 127 025 997 098 728 358 002 107 717 399 408 154 265 531 472 224 073 315 625 175 634 300 297 848 186 423 190 902 900 715 112 416 777 177 766 288 620 992 519 958 776 390 520 570 619 224 354 655 014 175 389 531 253 593 248 800 945 305 592 267 194 212 424 465 183 003 713 068 354 181 587 462 179 806 542 911 792 583 615 026 831 812 718 833 547 179 527 119 534 841 710 532 567 215 238 418 414 141 863 125 756 176 604 420 306 508 725 153 866 720 614 194 689 891 646 387 164 969 121 754 726 068 705 322 801 905 922 337 974 583 369 454 215 780 522 901 837 937 843 409 267 834 420 576 134 684 390 026 002 842 267 326 505 982 727 825 783 387 831 553 409 163 475 356 094 331 742 010 506 321 010 600 935 393 014 104 421 473 012 713 288 399 253 573 734 009 221 538 027 446 140 158 342 604 666 827 418 401 517 592 323 631 173 245 693 924 247 332 869 848 310 766 874 690 245 155 185 420 006 475 743 459 813 316 212 106 586 510 817 078 847 950 961 984 771 442 789 516 910 802 727 074 368 426 831 885 287 616 906 172 587 872 624 321 552 238 759 101 185 402 021 219 998 937 713 366 907 377 544 341 088 690 904 593 863 795 193 542 472 794 595 148 274 512 946 550 733 332 165 826 446 970 957 432 617 056 998 019 775 870 231 470 716 009 579 752 751 923 022 556 465 329 387 425 099 339 043 686 766 821 100 200 831 330 720 569 837 676 929 988 622 432 673 764 654 037 117 167 818 868 625 878 975 179 418 562 529 516 067 236 683 859 610 812 117 229 902 002 065 788 475 026 347 066 121 422 239 890 731 023 416 405 755 652 709 030 404 851 882 229 346 163 360 190 379 097 953 566 791 607 916 189 243 791 851 445 604 168 904 277 366 146 989 881 082 385 255 621 501 346 329 965 682 292 559 133 496 812 412 407 478 235 466 365 643 643 341 433 530 129 329 020 879 445 778 805 724 347 737 546 577 122 635 995 054 850 872 125 563 890 772 938 939 999 898 863 423 591 579 516 648 848 787 692 445 611 594 112 721 390 598 539 401 146 905 996 493 110 994 900 660 027 206 873 440 276 053 136 619 469 099 715 360 649 701 682 944 062 252 126 876 457 080 081 751 924 624 433 169 073 008 803 016 875 997 699 145 120 410 931 331 431 889 151 851 237 220 569 260 334 327 599 530 201 553 025 106 182 200 537 068 076 473 051 390 703 643 915 974 310 427 117 554 925 806 061 681 577 971 122 308 417 823 899 964 677 731 513 223 745 933 971 180 041 928 718 597 216 394 602 275 800 898 202 272 137 546 333 870 656 456 152 884 439 804 805 622 132 360 287 868 219 889 432 021 473 108 987 719 205 108 826 098 708 968 554 898 010 764 700 551 407 343 242 703 746 807 366 957 903 805 421 158 143 957 196 999 830 786 515 723 318 233 405 770 941 532 982 256 356 501 965 667 820 753 022 418 552 616 109 723 684 804 448 989 709 700 697 119 254 610 104 843 795 478 540 862 931 822 702 942 110 003 381 614 712 044 692 018 554 377 217 094 009 490 093 152 602 674 567 465 243 653 451 754 472 895 605 053 410 564 249 604 569 845 947 062 567 755 198 262 014 079 043 006 620 763 083 876 881 496 228 703 360 722 497 867 433 172 342 480 135 906 148 358 098 928 518 864 730 329 192 304 396 838 421 143 560 979 097 574 683 673 313 718 035 033 260 472 439 319 841 443 330 033 844 629 081 133 013 876 832 674 260 644 964 723 143 849 565 238 600 860 934 958 014 555 303 288 668 208 173 494 410 356 226 381 065 160 056 248 744 795 264 602 673 427 065 488 642 737 464 632 712 730 318 167 703 745 418 207 012 092 104 620 103 972 483 711 917 520 470 616 591 686 729 015 567 653 596 268 728 818 594 189 416 568 488 586 577 921 579 067 717 972 227 678 740 518 690 464 940 593 700 513 207 952 363 312 015 721 989 184 759 228 584 850 260 800 418 817 744 265 356 625 817 567 771 196 550 121 029 326 726 826 897 153 218 063 117 519 612 811 499 580 032 099 912 388 662 050 755 851 087 602 094 601 564 201 124 065 651 486 291 016 607 634 388 752 973 381 158 162 536 517 072 868 795 684 148 882 054 399 602 272 885 573 024 586 201 575 580 351 477 242 334 449 113 696 903 601 066 225 391 777 052 730 628 112 403 994 439 950 481 002 829 586 990 542 686 817 558 570 546 604 011 743 997 920 362 517 653 059 008 349 648 025 686 179 124 284 699 091 851 976 121 654 194 186 236 411 576 693 136 026 327 237 234 094 960 937 873 201 025 086 112 895 072 910 463 986 241 007 067 293 098 411 144 775 934 250 478 268 091 106 284 077 405 852 796 663 457 821 527 438 404 017 170 988 774 360 739 387 630 830 608 542 632 597 434 348 293 674 132 421 687 980 060 734 521 696 974 050 783 953 422 988 717 750 709 251 842 780 646 236 335 831 053 758 369 535 522 459 970 431 469 453 321 290 511 712 546 359 875 687 611 563 934 704 196 133 011 854 124 411 584 000 078 840 181 439 959 741 837 086 750 456 497 108 221 736 471 660 577 452 333 636 526 338 162 582 783 031 188 337 166 748 829 683 865 282 463 464 193 739 733 850 594 650 969 251 942 299 489 747 764 644 759 169 604 443 695 954 396 690 305 913 034 007 506 669 449 038 697 010 483 206 927 444 086 363 559 145 421 573 651 675 061 391 855 894 367 231 256 816 703 599 439 302 294 715 668 868 717 757 222 492 341 558 556 897 608 895 657 891 208 063 000 135 950 975 508 930 500 362 508 683 232 536 781 270 464 929 746 380 352 132 455 567 241 685 596 432 555 748 278 323 936 102 179 769 288 460 490 307 399 767 536 129 263 519 085 215 703 095 328 753 741 946 688 312 652 306 724 850 367 402 738 271 898 906 884 344 241 179 066 759 786 538 199 751 691 667 167 830 324 474 604 869 301 133 263 603 516 780 439 693 950 635 264 028 546 454 540 285 044 165 055 271 860 663 843 880 770 820 816 207 830 905 770 180 563 259 294 471 916 044 926 829 905 200 447 338 755 236 475 993 345 712 435 807 626 876 525 967 664 080 018 830 221 339 542 486 720 852 879 456 977 630 029 690 010 323 797 707 523 175 266 201 170 526 447 174 935 276 270 344 351 603 329 094 883 389 052 611 370 836 627 568 851 088 868 402 108 242 959 599 535 714 158 376 298 941 013 759 222 434 729 512 474 000 228 775 239 232 660 815 877 643 068 531 844 086 292 728 813 754 996 155 017 808 850 751 099 599 141 988 475 314 182 403 291 371 691 239 394 013 764 064 649 938 130 614 645 546 333 232 954 409 035 188 908 239 228 218 403 786 206 048 812 760 353 605 467 657 136 137 379 888 276 457 721 943 853 444 675 495 838 399 536 872 174 609 023 541 408 550 589 626 149 494 142 914 198 914 079 923 281 959 212 194 660 846 390 129 722 169 299 158 707 660 518 799 451 860 939 530 910 380 429 265 336 040 073 151 353 417 280 195 652 216 011 051 106 925 365 375 476 846 894 416 022 359 877 506 180 118 368 566 612 600 772 991 474 211 319 428 804 633 939 810 265 789 523 269 668 386 312 001 728 192 894 615 026 043 899 263 662 975 320 260 556 285 135 734 463 462 749 942 882 161 957 219 634 427 287 834 030 415 372 407 453 513 518 429 491 112 377 025 820 854 908 526 427 935 021 270 422 112 084 293 284 853 107 050 702 677 918 150 425 729 457 377 362 061 594 822 762 949 873 570 310 481 971 026 043 342 828 635 879 682 668 250 950 411 666 524 007 888 075 753 358 109 260 334 171 254 009 560 924 597 546 994 369 756 398 736 063 884 169 989 266 459 537 474 542 370 315 082 695 767 270 466 304 255 126 729 656 383 303 082 087 878 833 703 287 424 115 825 070 950 090 768 000 064 685 144 120 930 013 598 507 300 652 278 206 965 977 318 059 863 464 173 711 092 750 817 249 228 908 823 479 591 326 968 412 801 111 642 385 014 751 552 797 693 839 139 261 432 578 914 238 111 228 348 542 779 923 008 690 099 106 755 990 873 745 596 493 884 457 450 824 041 986 140 368 570 463 414 189 230 986 580 797 371 127 247 843 367 257 860 722 527 798 281 673 960 977 304 137 863 626 585 003 938 850 303 463 187 622 787 231 282 499 747 371 834 492 678 786 202 603 894 741 283 776 340 632 857 165 734 383 720 808 470 143 078 184 748 136 013 686 268 447 671 561 240 956 299 990 602 964 151 227 183 214 742 745 057 973 454 037 856 227 344 653 548 798 449 977 562 828 016 561 092 302 093 889 236 874 937 768 323 370 824 784 760 010 714 026 102 034 305 292 119 832 652 078 669 282 096 243 422 075 781 090 122 610 671 940 498 325 202 593 256 446 214 508 279 699 589 314 487 608 344 529 644 232 680 761 016 633 482 054 771 118 799 826 962 095 486 152 665 197 304 919 388 883 307 661 615 518 792 310 368 116 244 941 577 279 404 215 168 345 290 231 222 797 649 605 183 760 713 044 327 333 475 479 942 824 220 979 516 172 672 969 182 414 249 124 821 520 398 479 659 174 578 201 440 593 539 451 316 710 813 739 580 234 754 020 692 266 433 260 166 326 073 577 915 886 328 363 104 908 355 686 498 056 113 744 010 272 424 598 173 332 826 276 752 093 614 197 422 051 003 641 259 685 722 938 069 761 583 618 068 287 964 954 185 244 824 547 571 257 687 901 003 037 842 880 234 962 724 792 917 760 212 711 350 621 055 947 893 142 610 230 700 090 304 449 023 244 195 454 767 736 475 846 120 309 292 516 119 671 372 401 449 947 188 376 528 831 792 912 829 522 627 796 632 976 285 159 992 118 280 205 088 533 112 668 354 397 461 259 071 554 341 379 153 370 767 134 597 004 473 609 215 156 206 604 771 499 753 272 975 133 391 237 428 572 644 042 472 068 267 329 532 236 218 998 404 561 001 902 241 452 229 671 377 028 973 870 821 472 572 155 392 388 120 477 098 010 295 247 315 297 805 467 707 218 395 634 993 771 466 700 690 955 368 847 697 369 942 893 600 232 693 456 227 772 409 843 890 478 553 789 936 808 999 768 244 741 398 856 697 926 852 029 921 638 451 654 073 853 044 628 366 932 225 846 781 786 577 435 108 471 208 299 418 727 779 680 337 455 900 769 811 240 996 068 243 330 145 025 690 323 418 554 250 983 227 039 713 544 974 702 620 838 492 194 480 228 168 426 509 803 968 552 245 142 349 596 113 690 790 630 379 109 957 839 257 872 069 683 443 957 956 295 902 113 942 466 967 230 732 903 412 696 309 428 555 939 547 828 337 701 205 396 661 042 776 658 573 671 442 059 798 099 939 361 817 924 993 231 889 224 000 757 597 146 947 136 078 714 065 742 630 369 130 231 590 844 485 965 090 426 051 694 245 218 925 897 106 986 288 288 996 152 826 830 276 242 213 975 920 398 096 497 627 220 138 272 238 557 071 239 429 889 971 945 929 149 665 127 241 931 581 999 584 424 126 152 897 898 844 098 315 234 123 855 647 252 764 283 690 967 900 713 205 773 688 673 452 533 066 077 045 189 699 053 622 719 836 670 095 702 310 826 555 733 371 261 197 863 888 583 295 855 096 895 329 029 446 221 876 517 057 913 237 886 015 632 542 969 203 546 336 040 863 064 566 109 437 744 320 371 164 277 173 711 636 221 878 998 771 239 700 026 736 783 540 275 564 567 446 133 340 191 925 316 638 208 210 140 095 497 008 579 279 880 566 696 662 679 156 313 524 804 078 010 702 840 468 060 001 921 584 100 659 796 690 304 337 746 999 261 308 247 183 175 514 594 515 333 604 650 153 632 395 921 141 561 834 772 510 230 118 909 568 653 553 881 599 035 825 688 779 802 368 274 141 595 547 683 464 278 386 330 105 430 280 968 483 753 669 789 044 474 774 902 391 530 614 964 678 723 073 019 203 492 486 824 185 494 900 827 025 082 557 411 633 211 386 310 235 798 448 438 733 325 818 936 528 546 871 365 674 242 671 818 495 394 602 791 819 519 673 425 006 121 973 386 248 628 812 595 388 195 828 476 846 808 069 084 027 647 395 015 065 908 537 681 016 649 548 551 284 143 908 197 179 240 295 900 069 330 303 412 440 060 680 072 743 666 738 271 908 919 660 922 059 462 916 189 397 046 875 964 161 517 664 253 010 816 979 426 025 412 517 206 580 931 399 306 191 463 356 102 198 901 799 762 238 016 675 880 814 429 063 678 348 270 145 345 864 698 622 086 293 145 231 254 323 108 189 654 829 249 304 157 045 412 428 113 810 839 592 631 336 809 473 520 527 122 943 319 541 017 769 852 156 626 386 759 729 415 050 368 262 362 871 436 223 944 862 321 017 645 385 450 831 209 039 954 914 771 574 032 597 804 206 912 016 116 790 451 207 405 478 106 169 672 391 573 973 881 664 141 350 011 832 280 653 937 830 384 832 529 636 718 513 643 104 588 224 882 426 735 261 292 144 520 075 392 907 797 199 814 386 362 398 156 868 255 468 243 239 869 859 794 075 754 711 434 256 612 919 833 176 871 055 075 269 802 195 588 554 020 646 791 999 408 289 136 539 211 201 415 065 143 042 959 824 566 987 736 481 879 094 917 976 961 826 142 382 396 492 140 176 879 252 220 187 408 620 427 881 491 947 103 460 597 706 255 040 515 718 038 376 647 436 461 207 891 383 797 286 001 922 207 079 143 790 338 232 250 669 221 780 524 575 311 449 300 567 876 719 473 446 101 325 763 626 369 185 802 899 987 202 662 515 005 324 345 433 937 373 266 638 714 532 793 754 661 374 286 120 848 942 162 870 349 077 580 777 576 431 311 516 576 172 032 117 074 294 482 928 758 562 690 038 536 900 512 084 457 424 699 421 588 148 287 348 121 168 587 147 164 273 352 633 279 811 269 525 906 242 713 229 435 938 485 415 074 573 804 705 414 220 404 312 126 636 773 697 908 166 121 809 659 846 939 207 075 419 738 975 372 576 949 976 408 458 973 612 615 223 422 223 801 406 785 577 477 154 389 684 147 486 075 777 717 318 618 305 935 147 434 185 855 542 369 231 586 464 958 973 449 955 948 300 205 938 793 048 383 583 395 941 517 098 907 275 732 607 715 698 848 916 274 886 918 772 530 346 958 557 400 216 002 876 131 626 083 559 166 265 409 332 775 080 543 779 004 545 663 337 821 328 804 804 007 631 915 617 977 557 053 658 502 758 369 798 125 697 804 680 710 038 233 699 003 571 730 496 649 156 045 126 689 604 177 962 347 224 449 807 239 351 935 633 005 326 632 337 366 553 107 281 824 253 113 021 518 684 864 369 455 064 785 877 526 523 106 442 868 466 451 351 499 842 543 802 770 016 211 587 722 390 818 045 966 781 412 049 272 596 650 777 555 311 685 644 994 999 543 255 452 948 769 092 336 238 995 437 502 537 528 619 879 469 536 089 671 966 413 593 346 590 018 031 360 686 201 746 385 929 486 024 990 357 464 635 302 833 833 883 037 040 436 108 622 620 869 117 018 903 334 975 287 866 050 205 094 360 847 248 050 093 043 080 289 343 164 168 260 665 748 640 874 203 607 857 684 708 228 269 666 862 595 347 570 340 961 349 302 937 797 746 294 304 769 745 836 804 410 333 389 044 960 988 176 568 760 532 450 012 209 760 830 794 427 688 398 230 609 120 405 436 589 165 240 135 792 817 900 771 152 325 997 781 527 279 748 877 403 725 278 354 100 949 091 018 744 263 476 955 151 208 037 374 540 481 647 912 173 251 194 383 873 862 667 558 963 987 205 760 600 408 473 700 343 642 808 658 090 109 916 290 024 580 671 589 683 304 051 004 987 562 195 985 793 419 134 083 246 906 507 505 430 007 328 601 818 921 788 536 531 817 746 834 401 620 522 251 513 214 310 952 567 254 057 618 404 991 422 894 441 449 457 298 385 534 475 374 263 044 738 832 362 174 535 098 408 090 892 603 946 756 226 099 087 753 457 393 056 016 319 967 708 676 601 140 164 601 467 578 337 932 225 498 281 808 474 493 425 134 246 729 892 955 271 560 579 001 480 838 427 563 704 321 047 003 673 754 721 184 836 778 850 215 066 077 687 428 243 884 048 137 020 189 645 261 513 485 439 043 730 793 623 868 130 761 186 004 913 421 073 296 446 031 697 000 866 785 216 782 260 968 230 738 619 741 982 482 614 397 513 881 671 723 417 660 517 584 241 959 651 011 556 609 303 753 935 027 459 918 787 061 374 197 564 194 474 155 159 026 297 921 089 281 205 893 693 304 341 483 311 533 058 986 937 819 546 104 814 121 828 224 891 372 216 737 490 080 252 206 650 401 644 080 125 984 693 678 196 255 328 918 161 734 585 906 117 222 597 141 459 931 033 135 444 729 280 253 427 948 184 140 724 097 719 883 172 001 758 414 802 775 602 352 561 893 229 502 065 570 180 788 406 978 703 904 899 998 683 832 979 217 227 975 192 983 933 656 467 746 086 708 599 865 416 628 887 215 021 763 881 184 673 356 668 743 755 968 297 144 957 490 958 787 519 800 824 405 289 018 579 568 431 098 858 594 175 953 131 669 075 033 502 610 580 230 845 183 296 737 954 483 455 866 877 676 040 500 548 563 037 107 123 542 193 586 860 490 617 156 240 938 039 854 713 028 533 682 880 261 975 105 602 091 138 604 046 949 473 717 473 347 544 012 179 280 195 991 134 912 800 110 633 034 989 987 743 146 360 987 370 448 051 827 975 278 888 075 203 925 287 856 347 041 991 049 224 001 023 663 146 964 058 641 228 101 009 463 499 139 729 629 054 583 751 865 845 912 182 229 721 743 624 032 029 404 265 674 060 180 919 639 123 653 950 744 039 208 737 834 861 134 437 460 115 002 703 072 145 735 193 998 047 706 348 585 746 328 126 690 194 888 727 671 884 324 157 601 121 926 201 208 608 900 591 542 029 535 413 409 495 683 338 893 997 542 425 138 659 752 203 367 243 635 770 371 889 360 157 462 595 258 725 408 869 856 851 875 112 414 428 070 537 681 098 580 342 843 921 034 171 174 029 018 541 154 184 011 870 653 287 279 575 562 245 719 347 943 753 345 739 873 450 638 352 684 844 126 122 040 874 208 617 250 389 349 542 286 039 342 688 602 049 909 492 428 902 916 372 962 444 649 602 366 406 377 877 815 470 209 959 992 639 991 709 980 409 615 232 660 758 113 832 143 327 849 574 388 555 244 483 955 330 265 018 944 737 896 571 597 281 780 813 824 501 406 088 353 251 203 732 220 414 326 527 267 396 303 772 167 595 494 002 777 215 494 768 353 098 214 187 167 853 129 218 055 755 720 088 044 161 577 250 961 891 010 356 490 818 776 823 148 985 395 361 853 217 032 203 623 192 116 345 162 737 366 325 331 753 822 605 687 087 779 717 388 368 046 245 461 556 423 411 006 615 246 065 900 943 476 456 817 760 629 261 034 539 253 716 813 072 491 292 356 761 496 712 469 943 195 214 382 711 748 201 382 132 469 868 425 494 881 896 007 172 021 461 412 238 112 867 866 146 604 343 883 048 455 730 482 168 745 723 827 294 938 537 286 740 312 238 392 766 242 156 691 805 582 872 535 921 089 655 563 678 131 301 401 048 947 508 847 720 806 460 834 316 799 601 942 377 352 727 425 106 771 459 873 646 778 320 326 580 871 398 439 058 003 025 716 617 242 163 507 847 702 703 306 858 954 749 645 781 250 474 977 668 574 455 124 403 504 061 179 392 768 649 260 018 821 037 158 283 574 119 312 616 318 246 067 041 197 388 191 727 295 700 051 684 971 984 347 479 186 169 797 754 919 564 910 044 859 935 305 404 760 782 437 896 717 163 437 136 273 761 028 327 839 891 566 500 513 969 455 212 825 339 711 629 759 462 057 823 233 134 153 124 192 877 564 516 140 653 649 089 317 701 956 190 379 666 097 888 986 662 349 265 732 850 660 119 988 350 891 474 952 992 811 993 441 796 207 473 601 811 219 727 647 713 135 899 719 936 256 132 420 967 459 878 704 639 239 357 978 526 325 988 925 106 788 205 595 209 036 280 507 371 568 538 443 250 406 223 894 777 159 165 413 816 110 284 471 974 210 482 528 064 376 500 535 577 208 760 485 360 055 581 486 472 552 370 155 136 624 554 380 081 260 282 109 860 916 526 748 074 623 229 817 219 263 465 025 692 318 111 567 033 907 863 214 472 753 543 905 313 248 377 958 604 259 682 373 550 300 584 772 823 563 493 824 661 598 326 819 848 935 802 939 559 524 307 491 405 626 288 844 934 141 666 978 389 037 718 468 706 964 414 633 552 427 596 027 045 719 447 802 719 306 962 530 840 325 770 733 869 591 992 713 607 345 093 665 614 528 624 760 266 606 234 852 120 124 117 231 495 177 895 789 729 839 649 373 236 080 054 315 769 679 410 387 528 188 589 015 924 173 907 599 609 513 328 041 065 442 877 138 648 864 679 671 547 510 924 234 772 714 670 383 949 783 370 201 093 105 429 042 143 784 788 005 120 336 178 226 316 391 177 136 838 163 588 012 670 126 820 505 451 300 945 439 652 063 018 369 893 082 965 227 142 926 047 677 540 051 891 965 271 868 788 793 338 214 394 274 199 410 413 952 327 108 927 081 726 284 582 288 874 737 245 117 834 433 769 973 950 596 736 801 393 852 380 907 228 196 360 202 898 133 498 213 624 392 442 068 067 888 327 076 300 485 321 222 648 267 517 586 388 730 611 696 652 150 846 542 061 544 335 427 442 432 506 898 609 178 788 660 534 916 153 198 224 015 147 070 619 740 607 237 247 135 284 270 110 201 617 024 943 738 110 110 305 484 122 561 433 700 417 047 066 353 003 834 097 136 042 692 869 572 231 900 883 158 562 829 323 363 113 737 337 076 755 534 648 592 205 965 334 428 337 758 489 564 017 782 846 095 434 745 637 261 911 272 709 082 810 445 239 582 510 792 452 798 929 580 379 290 542 122 151 857 460 538 548 457 042 252 451 900 620 796 550 350 201 257 184 537 396 228 050 539 143 456 967 194 422 931 274 248 828 870 519 082 172 410 355 560 796 991 558 332 039 928 115 187 009 131 961 167 229 593 091 812 820 902 226 126 222 778 957 500 879 576 280 704 362 967 060 974 909 434 517 423 746 700 336 763 351 280 699 701 263 185 900 073 492 331 854 328 650 086 224 267 888 401 602 782 577 972 769 653 977 975 895 970 578 849 125 925 755 051 256 076 262 086 960 020 412 787 213 689 649 378 333 661 980 697 482 323 571 608 122 101 383 646 338 145 514 408 206 391 459 262 961 483 119 775 002 792 995 974 257 864 131 921 281 543 939 698 591 435 897 098 765 229 208 591 580 606 599 123 834 215 662 368 688 826 526 721 000 677 127 433 671 291 776 741 694 285 041 792 330 289 346 566 978 314 974 292 028 282 536 160 509 258 914 304 081 010 749 796 103 449 422 628 796 534 523 419 240 304 477 466 792 698 590 712 631 576 137 192 260 665 923 432 718 949 492 795 917 108 917 371 041 836 934 832 432 284 063 365 882 831 454 133 761 618 184 357 597 568 255 620 684 797 813 324 035 474 158 619 475 753 558 019 194 171 986 918 993 286 264 062 656 329 664 327 034 170 713 179 312 494 529 125 894 540 133 289 516 458 918 373 692 048 081 178 782 083 665 359 130 441 585 530 587 648 091 301 684 061 023 158 607 865 188 597 565 759 977 304 500 092 146 382 653 325 095 266 845 221 075 876 992 367 576 184 517 023 769 351 893 294 514 146 156 543 598 956 227 142 416 353 087 988 577 076 733 785 410 567 950 079 210 260 274 876 882 985 027 442 084 482 462 363 723 881 143 977 564 224 831 567 636 016 350 353 778 950 310 757 102 127 465 052 199 856 192 952 636 574 940 217 060 707 778 865 715 414 404 125 137 431 852 443 263 669 582 324 541 939 158 683 513 592 375 471 607 524 864 360 158 987 365 339 386 372 551 694 267 179 383 452 387 133 106 621 736 016 505 433 573 669 345 771 953 954 133 676 959 976 447 844 679 141 713 647 942 947 720 925 338 679 259 638 246 916 947 589 173 011 823 461 744 522 590 291 126 828 763 030 147 753 871 696 467 370 907 258 952 861 228 391 515 359 809 376 247 655 945 074 685 060 238 472 704 737 767 259 515 608 480 685 815 432 384 544 047 510 531 777 897 593 609 155 439 068 640 772 831 191 744 478 710 006 768 561 173 241 219 849 860 413 495 880 063 282 948 783 078 292 413 415 951 594 318 126 327 043 473 614 955 082 522 963 445 012 816 405 921 242 019 473 552 403 377 159 801 079 382 851 666 795 922 260 472 117 102 703 266 549 610 672 585 693 306 569 382 627 968 556 008 850 868 145 119 730 108 092 850 259 442 122 874 967 784 030 882 793 338 592 691 717 969 951 667 142 462 359 620 300 718 827 586 078 840 533 534 418 469 275 785 665 672 076 504 526 805 071 728 626 298 388 387 173 469 258 359 065 847 354 654 969 145 786 217 119 039 435 588 726 293 260 035 101 951 607 173 327 448 773 100 553 184 875 471 285 052 713 586 036 445 836 272 665 989 796 148 926 467 661 945 309 161 719 198 443 842 031 653 412 947 740 382 585 661 551 121 045 006 830 704 039 486 903 096 047 900 224 531 996 100 718 028 695 414 061 331 114 459 218 247 822 661 086 212 587 352 426 087 902 913 620 061 611 522 711 168 285 711 704 971 689 460 380 190 779 463 010 625 978 033 401 402 686 593 569 500 793 462 932 875 432 058 956 204 445 608 506 473 144 539 343 093 425 074 891 668 019 508 868 998 244 832 772 719 361 546 423 099 384 278 843 199 819 428 387 979 349 107 007 321 243 842 950 571 587 456 217 889 199 852 293 940 779 305 739 596 309 924 004 589 406 888 370 951 405 400 057 821 453 038 253 594 880 998 255 677 994 463 084 893 634 811 525 033 417 131 666 500 467 898 551 677 792 462 464 828 570 478 598 812 086 668 432 360 521 759 129 529 903 954 200 814 360 848 653 598 544 544 023 994 860 567 943 706 986 573 960 154 089 016 278 709 899 468 801 559 430 958 928 827 227 649 028 066 942 752 755 295 780 078 814 475 542 330 749 498 610 383 789 975 230 470 143 339 018 494 136 947 368 819 026 147 283 493 636 624 445 356 429 794 150 310 965 535 855 080 402 346 600 190 154 114 944 411 114 426 803 010 094 482 591 257 831 891 131 974 838 359 431 044 085 685 904 885 092 970 169 419 101 456 313 344 283 738 919 168 552 974 839 772 812 906 430 952 726 066 905 440 879 383 264 620 688 403 700 903 104 091 476 150 754 397 106 854 172 043 322 626 350 580 779 304 002 551 424 401 269 764 165 675 583 731 106 565 710 504 278 726 138 895 732 764 657 910 389 382 549 992 736 262 322 416 611 024 906 071 530 273 204 541 222 298 561 911 000 228 839 405 479 088 012 838 668 093 861 810 525 654 541 434 131 474 530 402 673 003 681 272 264 930 728 567 084 069 637 273 710 683 109 910 622 360 548 393 540 280 924 865 523 205 432 162 100 462 171 954 439 363 435 060 531 037 134 055 086 164 705 827 255 293 380 257 827 513 247 846 750 617 579 188 589 698 078 639 190 951 721 288 640 041 340 442 336 390 251 748 401 009 552 708 884 169 336 770 233 974 845 421 403 163 947 990 684 747 245 949 388 793 369 180 977 356 913 064 953 633 756 899 483 364 464 657 392 830 377 220 815 801 005 929 493 080 547 690 671 553 396 062 769 506 792 247 854 176 045 280 270 177 025 138 721 207 228 169 824 433 120 975 832 672 035 312 712 152 748 544 644 566 943 058 966 739 419 506 363 554 974 626 355 268 988 456 614 702 285 999 542 719 868 363 634 818 220 032 740 170 483 824 183 217 963 909 262 449 929 594 037 201 893 655 130 761 667 989 266 527 825 509 255 526 478 038 502 255 948 514 032 724 800 299 008 722 845 044 198 348 658 740 282 671 394 749 215 468 508 880 366 865 068 471 378 792 630 460 433 105 574 134 471 206 087 178 107 275 341 121 526 120 149 157 328 261 309 335 233 601 408 431 137 383 032 856 804 791 561 370 972 951 977 543 536 416 142 151 079 780 147 347 888 654 714 555 187 127 474 222 616 953 251 104 573 547 343 841 220 819 970 294 564 167 178 300 182 224 738 762 351 122 598 968 856 554 659 543 131 889 260 696 879 421 369 797 010 958 611 722 770 142 521 813 294 358 771 350 881 107 266 345 227 969 318 034 822 282 479 202 666 291 268 850 093 989 337 161 759 502 625 388 592 875 928 929 864 605 179 897 085 248 681 598 239 429 926 161 262 376 325 410 472 428 041 458 949 488 208 744 204 139 652 100 348 669 318 174 926 245 449 105 891 748 004 227 056 832 714 376 160 950 828 790 535 226 081 581 234 775 986 697 560 716 128 065 617 415 049 198 906 210 947 926 198 373 566 196 198 866 987 511 415 152 955 695 804 020 838 076 325 128 041 424 484 235 503 761 305 260 007 461 236 542 215 413 535 055 204 581 059 842 412 987 554 298 144 410 180 648 081 248 589 646 866 983 323 415 861 884 341 053 741 650 478 837 139 447 967 124 408 407 574 260 228 822 750 163 401 184 749 987 218 628 550 360 771 930 621 195 546 265 784 744 300 435 355 197 167 842 637 304 747 339 783 747 366 578 838 665 498 812 563 446 209 884 952 610 611 978 902 782 825 968 219 243 557 107 909 765 169 632 135 727 327 812 903 387 762 370 794 929 737 305 076 679 057 342 105 711 904 395 308 854 647 614 661 014 725 590 966 735 904 163 495 379 036 761 721 772 007 858 110 873 613 990 950 902 181 952 435 197 375 103 937 200 062 183 326 498 580 806 532 714 484 701 056 082 148 660 354 297 387 335 534 299 834 032 135 268 636 837 760 956 893 312 105 662 864 539 793 037 202 331 408 649 227 873 012 045 381 185 478 827 881 179 213 673 211 213 706 537 015 814 691 394 847 377 434 575 896 646 250 481 631 322 954 693 359 754 509 979 074 174 544 543 161 939 752 612 016 866 759 541 673 699 549 397 136 785 998 934 798 689 080 724 286 799 072 650 566 064 568 327 520 108 890 148 880 998 837 955 008 285 976 947 933 848 036 226 597 813 525 145 510 443 669 983 496 528 796 686 612 821 575 037 203 408 033 426 269 067 006 304 746 610 345 145 138 284 625 151 842 053 245 473 961 453 108 949 417 456 265 558 573 806 467 250 558 138 451 906 380 117 726 792 175 179 293 798 415 798 379 578 864 874 049 897 534 168 877 577 866 853 782 203 430 111 845 229 789 248 154 583 784 776 810 074 671 082 556 109 963 194 505 309 374 022 182 659 305 979 167 397 375 513 213 733 456 241 650 413 714 115 859 932 208 871 261 371 883 397 670 133 816 306 784 690 406 815 326 196 723 130 051 946 793 827 495 353 080 327 512 045 208 647 696 221 814 610 263 490 753 234 428 030 315 994 032 943 765 293 969 547 577 300 636 568 831 818 250 034 300 175 585 069 505 718 155 735 052 852 574 822 185 916 943 232 527 874 236 832 205 019 970 051 323 631 415 342 521 073 517 261 523 865 814 060 871 756 011 012 000 022 894 072 151 671 763 338 933 338 076 842 535 370 004 130 264 889 364 284 293 708 077 451 112 167 952 732 112 662 414 682 050 107 419 038 294 597 980 633 980 175 462 449 392 516 613 305 064 543 338 946 544 455 123 216 699 637 964 419 976 073 358 904 350 755 528 895 643 277 455 989 723 532 881 299 677 108 629 325 003 323 906 787 099 448 018 970 173 745 903 700 886 941 794 631 446 545 470 425 973 765 142 734 063 247 306 081 873 093 631 775 288 434 475 289 488 852 679 958 718 675 343 224 545 977 798 059 946 617 225 282 660 723 532 071 939 739 065 376 063 491 116 844 430 202 769 930 380 844 978 793 092 252 020 688 653 476 732 244 442 319 640 090 036 202 894 637 533 536 417 516 254 389 958 296 107 402 487 108 595 707 569 780 265 524 189 236 121 555 741 188 004 685 690 828 046 534 174 851 188 378 180 659 809 356 517 278 126 632 008 157 459 906 209 510 561 389 002 685 768 507 800 642 343 096 972 105 348 673 405 098 746 306 087 043 589 256 724 098 467 271 712 818 049 009 091 963 582 373 516 078 526 182 424 635 307 985 755 242 741 125 519 434 402 931 774 211 666 703 836 906 183 337 591 487 399 891 617 356 905 437 660 627 790 858 475 346 441 686 878 362 620 312 994 688 850 828 287 021 069 257 918 865 359 060 019 568 022 888 242 521 750 686 819 677 736 623 295 481 216 055 933 120 555 062 327 200 814 730 738 388 606 139 063 972 814 759 615 417 905 755 748 490 726 064 340 696 906 165 239 087 956 007 227 248 011 088 798 155 200 292 790 956 657 491 798 359 543 721 106 168 757 499 209 680 396 336 312 945 940 055 307 442 868 411 996 688 529 085 085 442 698 710 038 716 534 055 627 485 466 958 617 114 162 934 922 234 350 864 196 880 384 129 340 857 597 582 327 847 449 312 610 373 642 130 786 494 065 965 216 844 071 724 801 508 934 395 903 625 704 630 261 574 387 184 910 643 187 252 519 419 385 358 847 922 493 083 942 575 079 382 594 432 081 834 729 067 498 341 033 699 631 072 439 096 991 131 003 905 179 270 422 072 781 115 493 203 049 288 491 741 960 202 921 649 049 020 116 787 698 094 820 397 414 249 043 587 862 795 533 538 796 753 981 407 854 214 091 610 297 643 269 470 296 397 590 614 380 787 127 213 619 865 741 920 217 493 868 294 826 421 565 275 296 522 203 646 253 572 566 282 337 166 584 772 084 875 910 682 840 287 506 107 635 239 398 212 334 110 667 540 959 501 356 660 798 960 084 091 743 234 587 061 773 725 247 500 743 144 652 223 667 408 009 683 492 687 046 185 531 195 989 889 496 856 610 997 909 930 545 380 863 657 561 815 980 364 651 197 525 087 790 954 673 253 418 707 522 681 419 482 274 089 173 587 116 958 225 431 293 681 633 728 227 610 907 271 015 286 227 710 231 175 502 795 182 677 393 467 916 641 486 153 168 685 359 093 310 139 008 208 891 032 201 845 541 688 334 786 735 035 313 478 745 638 715 187 121 672 372 481 706 800 018 335 676 491 147 071 994 829 507 395 320 328 591 702 780 062 427 820 803 191 133 942 755 502 449 052 896 498 167 392 625 993 008 883 746 461 734 208 214 458 802 005 707 227 112 795 587 705 758 063 982 558 855 692 997 460 412 991 599 794 412 120 087 419 758 698 364 628 560 922 857 503 239 788 072 492 131 798 479 702 126 140 650 129 058 164 159 597 817 516 263 003 867 203 034 913 470 065 174 515 181 937 262 973 685 054 295 531 828 342 064 202 502 769 930 808 185 369 746 198 435 629 340 440 231 342 124 711 053 308 836 226 383 290 432 231 405 934 887 941 623 356 010 724 712 131 322 462 324 869 159 692 851 978 458 630 226 052 885 008 364 408 602 566 951 561 261 221 296 403 508 455 944 455 411 504 854 017 508 870 257 951 991 394 837 383 786 849 207 920 691 956 199 834 445 666 517 377 459 287 243 545 323 576 877 701 230 121 855 076 325 489 337 483 983 613 854 501 935 694 212 032 363 277 838 730 973 751 953 540 557 316 928 505 496 761 350 842 033 955 737 973 219 234 410 615 865 902 770 920 509 576 246 112 479 286 359 643 157 730 307 739 751 923 100 138 814 680 587 446 214 526 660 126 826 044 325 914 903 689 055 110 572 391 784 354 440 340 246 223 914 329 452 816 245 893 807 727 516 779 429 649 565 521 603 274 216 597 173 497 500 144 571 427 166 846 699 459 870 007 070 418 239 120 613 080 884 494 324 829 881 671 004 528 610 392 685 924 629 715 707 274 473 337 337 008 384 348 750 810 331 983 032 339 103 299 760 874 413 912 715 160 759 954 655 350 879 130 638 224 697 562 041 359 424 150 225 020 370 974 553 147 277 003 251 951 580 652 430 771 423 345 588 526 578 815 834 893 110 469 763 633 300 371 912 926 713 972 505 465 846 739 888 911 273 680 921 418 796 995 649 114 889 035 272 683 756 353 587 920 181 533 289 721 769 207 674 391 437 963 069 014 507 654 919 638 187 027 746 869 205 880 027 091 174 682 303 989 405 247 961 980 414 679 594 603 467 366 405 300 375 011 003 705 456 630 458 680 993 863 906 613 558 060 299 555 426 252 383 440 260 464 617 658 619 792 218 740 742 686 947 983 598 973 484 616 256 771 030 983 734 832 214 330 744 841 841 989 450 414 637 792 713 479 872 224 303 813 236 819 386 641 344 039 670 990 419 550 424 181 053 393 950 909 468 216 687 104 357 185 798 060 954 240 110 497 444 060 729 585 709 827 597 090 124 415 892 402 816 100 705 472 159 510 706 285 311 123 866 757 867 156 306 011 508 471 445 770 274 249 298 614 938 105 440 807 969 424 617 230 624 417 765 648 341 801 248 659 628 212 206 735 913 733 923 006 169 125 352 423 937 465 161 099 769 143 977 528 038 303 256 125 618 358 458 513 279 551 728 688 730 541 386 451 680 036 034 336 536 389 356 067 126 354 383 022 319 171 191 270 104 887 248 884 156 269 275 491 922 299 617 235 300 067 220 105 023 227 091 785 884 160 749 133 430 546 097 423 966 286 838 687 782 656 945 391 223 122 282 857 963 369 490 290 185 229 409 986 348 657 366 141 475 024 421 169 813 477 495 176 203 977 814 198 985 031 978 839 037 284 574 496 938 552 657 985 797 225 191 030 510 577 995 688 129 269 965 311 414 485 006 838 369 873 298 144 037 848 667 193 254 539 977 251 853 469 387 541 440 134 687 808 652 181 687 163 700 041 676 313 405 108 905 707 486 532 550 783 203 113 881 836 496 560 182 216 739 083 616 947 509 962 721 890 217 833 981 039 800 223 891 431 273 478 313 963 724 225 343 873 514 079 589 575 188 033 735 149 616 856 965 201 986 717 853 244 857 212 228 891 325 747 233 663 174 262 115 023 759 093 625 336 172 247 396 920 708 344 656 402 725 377 922 257 771 418 293 350 519 957 695 968 415 058 061 040 022 477 380 327 596 152 047 265 095 341 278 341 466 261 757 319 225 692 248 557 050 673 676 889 901 092 886 961 832 272 310 642 389 390 945 310 262 798 990 135 761 890 864 060 004 081 333 743 910 087 040 813 117 580 196 395 574 076 934 370 005 525 903 722 757 175 107 874 967 451 189 559 711 986 083 183 019 841 268 544 718 329 685 408 346 753 659 718 854 662 679 118 611 150 766 427 375 734 384 169 008 256 334 043 859 021 991 046 864 399 984 838 249 351 060 581 573 642 187 579 189 604 835 563 379 760 844 287 507 314 734 565 620 106 595 275 192 362 105 378 487 963 153 944 212 687 845 710 270 203 624 712 264 341 015 044 349 223 387 903 296 696 294 673 751 518 950 258 782 376 174 195 661 272 793 572 695 330 655 927 353 447 549 110 983 030 260 454 868 367 233 368 452 590 409 206 633 190 030 963 713 830 853 746 856 115 413 603 663 266 554 855 029 149 979 913 873 935 185 645 519 611 539 947 625 193 796 617 591 859 325 447 874 160 687 932 449 414 540 767 451 575 909 712 073 357 142 695 530 272 725 935 953 523 954 690 581 060 332 615 690 269 113 665 162 594 685 682 014 595 697 409 925 033 723 811 351 906 448 680 158 975 723 319 358 628 915 298 782 628 883 237 169 509 170 570 281 327 891 926 125 848 282 360 905 748 912 849 156 483 253 886 328 693 708 269 019 825 465 702 744 696 565 973 276 860 834 759 710 790 737 295 672 791 256 993 156 779 983 095 313 600 496 285 383 718 122 511 772 493 932 693 795 580 140 275 238 217 848 943 608 742 465 545 889 532 923 714 719 868 664 888 031 620 988 558 635 664 121 648 407 151 900 657 220 321 947 769 618 304 649 005 994 367 178 661 804 503 946 403 698 059 207 721 275 747 148 742 132 102 088 547 742 596 141 609 570 651 987 023 058 414 100 789 976 726 267 078 492 360 504 131 543 639 148 938 984 093 527 407 278 616 089 844 259 735 506 319 278 070 884 325 372 279 423 807 720 570 999 541 752 734 320 216 011 675 554 954 814 740 132 598 654 925 800 295 073 694 751 780 977 632 503 473 717 471 381 410 632 288 021 935 323 975 621 316 100 535 366 179 875 462 158 551 775 280 304 702 122 698 126 120 319 980 314 059 924 018 590 845 751 241 755 509 575 503 026 468 230 122 739 804 925 267 222 894 388 118 687 138 430 939 506 262 796 412 161 876 078 479 246 093 733 558 385 830 108 361 693 898 159 247 885 524 656 177 412 484 795 704 840 276 854 457 430 736 167 176 074 810 263 946 434 281 227 411 697 665 192 224 877 416 150 932 122 674 397 029 701 982 505 970 570 255 252 042 546 218 528 515 445 140 447 444 050 360 863 883 008 853 326 907 511 332 639 304 097 884 273 202 633 932 054 841 212 809 906 543 443 121 043 672 649 191 920 494 965 118 923 640 312 851 109 472 096 726 572 164 924 548 469 246 174 522 285 444 229 474 910 935 773 501 076 755 463 222 148 877 182 037 762 941 173 052 966 769 691 344 123 362 213 273 960 071 365 149 636 910 180 203 610 698 891 262 104 071 213 792 101 881 827 749 582 806 602 689 890 334 084 397 790 773 981 514 797 119 489 458 050 252 488 066 763 617 612 796 537 571 820 327 777 011 468 898 404 116 190 967 350 675 189 746 585 967 837 706 834 212 981 025 114 455 875 821 538 123 621 309 410 880 871 203 829 137 462 414 294 573 007 010 443 074 496 816 331 462 087 897 736 329 578 323 916 950 491 722 984 453 672 532 184 390 994 987 607 080 696 372 447 992 471 981 629 671 250 294 131 026 475 977 587 523 257 099 311 921 306 867 359 166 888 067 510 115 352 002 795 902 193 880 427 980 445 811 393 481 406 382 071 128 572 250 281 603 142 706 914 614 623 695 015 083 150 618 089 958 663 777 226 990 216 181 598 936 425 037 451 100 553 745 722 962 854 178 900 032 330 714 081 098 651 850 320 419 808 568 827 662 387 551 143 803 736 693 093 953 311 274 086 292 121 532 880 415 034 134 765 100 638 964 121 638 452 112 623 191 969 968 369 588 680 117 546 130 569 490 288 800 418 303 192 864 907 163 797 118 763 251 446 295 751 927 947 334 614 993 389 589 332 599 656 722 913 258 302 403 030 342 905 557 291 892 908 302 050 545 086 307 627 819 004 401 632 140 465 453 729 248 205 259 758 627 254 408 979 562 365 211 041 640 990 683 166 816 534 339 115 815 994 962 322 536 066 036 832 117 143 040 948 526 119 428 642 539 341 746 997 513 515 048 198 767 291 934 025 238 667 948 507 457 835 559 418 253 912 705 282 436 215 932 059 999 584 316 996 161 159 886 952 513 823 004 554 079 246 415 463 881 561 713 819 048 068 734 300 670 379 497 701 495 188 188 559 690 655 654 981 633 716 334 983 613 665 460 939 590 868 538 684 139 818 380 838 178 776 865 267 499 749 293 692 448 573 558 065 192 487 511 867 082 461 224 556 109 701 898 789 067 092 506 239 487 495 353 479 539 097 775 993 616 189 730 193 214 270 069 132 806 713 777 504 123 848 383 478 746 865 235 262 517 886 251 682 616 446 721 366 299 820 081 018 338 551 600 323 381 842 689 950 662 083 018 909 324 067 646 760 854 976 122 808 442 925 830 400 132 543 177 025 713 934 243 012 378 227 725 872 781 824 597 541 685 382 978 656 630 297 096 410 035 426 482 027 552 344 664 184 951 092 183 497 394 295 076 202 334 550 160 353 944 471 344 625 016 231 580 461 518 408 221 577 068 648 556 360 374 737 635 850 980 231 037 326 880 364 632 480 212 572 687 354 653 086 677 078 498 084 819 606 498 439 480 353 993 516 421 953 467 346 279 800 844 355 600 936 584 599 606 220 962 598 544 619 502 574 625 823 291 535 646 595 775 697 042 341 005 955 268 411 866 412 717 290 223 619 632 929 881 250 439 270 046 591 300 561 614 011 554 466 156 952 973 944 545 388 684 992 134 570 717 054 870 628 000 806 283 882 600 578 831 630 191 977 903 449 259 494 466 674 839 144 162 202 576 148 312 813 113 512 919 965 895 461 231 570 234 281 657 007 435 534 449 996 503 150 776 424 605 355 424 881 335 545 338 370 325 542 629 979 632 830 463 775 432 607 942 895 038 928 298 008 692 220 604 883 084 410 627 725 405 653 890 398 476 505 097 172 903 944 627 766 292 426 116 969 638 341 971 779 633 901 587 894 686 167 502 365 845 005 516 953 623 072 214 419 489 698 886 132 093 230 508 548 069 780 857 198 769 886 833 272 821 002 238 921 000 509 848 812 338 831 169 379 992 519 782 628 952 145 774 932 566 612 533 367 371 724 653 234 941 882 090 892 753 904 403 121 287 034 088 703 570 361 751 040 823 228 642 528 091 643 129 311 933 333 742 700 262 354 272 880 242 708 075 679 667 017 309 300 453 994 948 874 222 218 785 091 121 538 088 559 131 818 472 705 548 634 992 209 629 619 473 749 490 550 967 997 634 957 796 135 880 370 652 729 300 343 290 766 604 359 512 347 174 169 064 045 568 549 160 774 046 044 598 578 906 426 866 852 003 505 634 911 038 725 462 026 055 598 569 518 268 423 236 561 076 734 134 983 200 813 367 871 366 791 298 491 790 718 597 400 524 218 951 132 517 938 988 906 423 115 663 705 101 044 144 642 442 119 337 801 327 684 104 235 192 191 741 086 759 778 767 978 674 806 938 696 777 071 053 039 486 662 607 774 906 460 457 720 086 721 608 722 025 213 897 075 399 557 514 881 405 750 419 615 224 354 736 868 504 121 002 513 367 550 563 280 245 312 709 147 483 015 738 361 569 883 271 741 195 267 735 863 239 574 235 308 527 557 206 436 076 143 554 651 888 609 756 726 723 796 640 812 659 538 279 205 978 551 139 649 519 965 210 916 252 281 954 773 240 416 892 747 957 807 158 075 000 432 969 575 262 658 331 846 070 954 358 009 063 027 279 181 043 744 898 194 717 055 057 536 133 771 510 676 311 877 841 500 103 114 501 928 279 773 699 738 507 886 853 679 111 935 645 613 260 362 859 823 430 432 926 718 860 590 128 382 810 035 920 966 508 481 557 487 285 289 815 941 631 888 531 001 150 091 601 727 842 451 403 152 718 322 951 505 279 042 482 108 021 785 167 243 673 608 596 256 026 215 466 094 794 843 278 091 300 098 612 513 832 706 919 083 540 757 354 772 774 470 589 907 108 397 242 586 969 664 024 003 504 765 380 941 833 720 126 752 199 455 417 722 632 311 274 145 172 852 804 011 342 635 170 788 339 924 398 254 039 671 567 249 304 493 013 241 769 047 280 062 888 953 073 095 506 441 111 295 990 531 635 097 034 036 548 841 597 128 819 523 082 221 688 858 745 592 207 419 264 402 084 947 435 042 265 986 462 514 624 218 640 236 031 828 331 522 983 325 110 971 950 542 592 106 809 879 204 817 202 367 661 727 759 106 462 111 892 495 579 898 100 097 016 696 980 233 141 608 516 381 991 421 806 176 352 671 781 059 587 710 700 661 084 659 199 364 244 125 779 930 833 783 632 334 738 629 728 614 607 759 455 398 949 993 944 711 569 496 531 599 239 459 468 028 685 453 532 707 771 240 383 535 659 515 227 773 671 093 102 554 894 840 676 747 093 616 938 150 004 961 339 353 151 775 516 403 914 582 397 111 337 657 611 168 847 067 108 202 284 735 668 586 697 421 692 495 025 050 840 197 821 143 566 685 069 634 514 265 606 111 168 046 223 382 860 178 752 086 175 200 202 545 839 257 637 532 897 085 439 576 885 440 557 381 097 332 154 436 619 632 639 477 273 014 595 381 499 577 256 980 511 865 292 396 315 554 821 774 986 942 732 539 171 940 702 577 879 133 479 836 102 964 656 259 428 726 278 415 817 206 363 255 503 166 475 236 662 509 428 382 181 221 693 017 509 999 456 127 117 137 769 765 746 472 345 783 383 790 174 583 868 041 678 422 230 019 307 156 450 194 452 220 312 042 983 492 257 308 759 676 062 777 117 038 100 730 398 704 682 361 291 353 913 041 154 195 768 535 459 674 626 827 601 470 805 700 804 792 693 912 850 529 559 815 428 611 191 965 860 845 203 540 076 329 283 167 121 667 545 562 328 165 925 737 749 526 253 761 637 979 072 612 014 284 062 448 031 249 882 486 686 350 358 643 123 814 656 780 609 974 645 866 820 305 822 729 326 804 287 803 547 246 085 623 643 861 928 189 325 974 940 214 020 762 548 451 934 451 809 085 462 275 468 182 654 391 666 026 392 698 822 737 549 709 878 949 742 915 083 379 610 260 003 668 292 452 482 182 913 615 804 607 439 206 217 444 471 947 582 741 777 945 322 583 681 323 260 371 499 045 179 508 467 064 188 528 239 915 953 321 355 408 408 129 622 297 425 209 878 119 555 997 930 099 305 404 653 950 634 442 900 349 838 011 888 592 456 886 246 644 469 077 183 492 021 279 166 784 004 985 439 974 040 066 067 117 474 243 490 695 164 083 810 506 229 301 257 446 542 190 130 082 508 935 909 315 385 651 439 099 657 849 245 360 387 630 521 180 452 872 569 005 216 833 241 706 621 473 309 057 660 029 034 240 270 860 686 192 922 533 980 839 576 752 599 741 386 715 669 862 395 938 276 288 202 339 855 376 008 815 082 330 576 891 130 004 764 875 387 920 519 031 604 780 523 240 993 784 542 927 305 207 042 481 938 389 093 635 551 164 480 846 377 973 370 448 450 478 327 124 016 991 833 044 544 040 750 465 164 157 039 835 526 947 839 579 021 044 208 623 849 353 756 320 593 046 696 376 665 190 515 322 562 631 952 059 776 931 789 353 173 883 094 159 694 504 821 934 282 192 585 445 977 429 620 252 607 142 482 130 266 797 034 784 592 296 306 650 701 567 583 312 258 686 423 437 880 496 362 188 405 063 832 779 630 234 382 181 685 720 427 463 422 954 309 398 682 868 057 382 592 872 911 567 276 947 205 377 816 515 935 948 426 761 283 748 833 050 402 639 778 631 950 634 339 537 242 781 385 257 411 550 070 509 153 874 589 489 960 428 716 994 524 441 025 530 448 792 449 681 227 490 483 206 346 437 374 533 419 442 331 963 668 837 356 796 928 644 591 522 740 281 958 354 722 766 867 287 373 814 373 977 252 318 393 534 325 053 377 113 921 626 650 518 913 999 053 912 530 613 949 074 286 037 861 970 382 241 162 078 208 136 713 003 549 132 180 858 609 202 588 611 368 608 153 272 915 154 619 566 568 984 613 671 011 836 795 843 207 660 913 089 268 711 821 061 533 797 664 649 667 432 008 938 310 769 638 548 281 726 993 671 573 422 444 138 044 081 614 562 484 895 789 130 908 473 740 635 522 309 563 645 227 077 699 966 650 999 976 803 238 803 205 421 030 229 934 742 120 086 765 598 793 658 793 483 118 185 991 147 455 342 711 847 582 666 753 289 444 032 315 921 935 427 958 657 771 674 723 668 866 445 671 978 071 366 472 787 846 925 834 327 490 280 858 370 790 050 469 854 352 268 465 143 319 112 573 882 686 779 076 421 780 757 512 594 184 710 531 495 752 309 193 366 044 158 922 112 956 561 156 254 206 592 565 233 589 319 699 868 439 714 629 441 764 017 597 548 158 188 046 815 097 130 027 429 766 884 929 333 974 322 031 002 161 895 629 081 866 884 902 703 010 915 925 147 440 397 101 781 012 630 223 676 975 709 400 910 322 538 126 249 886 909 554 520 108 938 156 414 431 692 989 566 480 104 332 112 217 667 011 708 265 009 195 306 726 765 058 343 019 166 231 254 046 831 754 005 818 005 124 170 045 210 252 676 651 164 151 803 252 326 367 193 508 486 232 880 965 725 069 679 035 371 241 073 727 377 120 777 514 142 125 452 110 757 755 236 620 927 922 569 388 673 529 686 517 170 659 014 521 576 993 467 942 984 551 759 437 073 386 095 851 559 408 915 113 870 660 047 746 180 056 687 132 565 634 921 938 773 390 255 916 144 150 522 339 648 280 336 171 858 392 399 226 043 577 907 313 197 802 791 289 087 262 266 731 552 212 283 053 586 194 237 981 458 675 968 691 231 394 138 546 432 778 670 654 532 922 797 313 964 186 277 998 407 032 941 214 090 123 076 322 011 748 607 909 101 369 519 670 832 989 455 908 665 094 108 873 359 170 027 761 743 816 995 631 996 774 210 660 350 855 656 338 088 988 454 923 559 699 076 646 485 337 337 185 218 421 788 128 577 739 161 620 652 148 247 102 052 696 889 293 485 253 497 284 760 891 453 202 297 947 295 821 755 580 698 794 211 137 641 471 468 963 613 321 313 827 342 978 510 244 944 863 051 426 567 088 652 282 201 664 946 835 667 688 871 336 410 705 986 149 514 384 347 398 845 830 215 204 542 522 142 090 214 100 014 002 726 428 303 233 981 436 539 330 821 525 229 171 955 610 234 288 644 811 749 904 645 001 359 076 641 280 541 384 423 187 925 644 261 087 740 746 291 465 070 069 413 800 613 564 560 241 336 637 840 458 661 340 463 100 958 468 970 191 181 607 198 630 103 349 297 557 963 585 114 877 163 815 406 765 647 979 629 601 267 070 378 129 323 288 545 241 955 734 774 682 173 501 098 388 064 925 422 036 631 543 175 576 903 231 228 328 498 813 931 313 418 694 832 614 469 361 153 023 078 505 306 899 711 649 064 186 146 138 304 735 410 630 087 934 608 873 560 546 516 838 964 628 384 546 478 377 977 350 996 320 293 649 955 238 010 264 951 271 709 073 890 946 381 727 851 147 241 635 300 867 441 120 636 104 858 375 247 711 900 151 720 704 685 958 859 474 938 837 730 922 146 297 073 332 590 773 839 649 805 126 284 091 020 461 179 550 727 431 041 758 052 997 083 274 324 337 270 827 853 068 952 586 045 458 046 455 823 300 649 109 429 225 781 600 975 579 104 728 175 031 995 275 952 907 994 443 552 576 539 317 314 261 231 376 351 601 461 863 533 286 319 503 562 503 961 368 818 452 609 982 652 831 322 577 694 702 800 950 427 493 941 147 018 847 590 236 020 240 072 595 478 636 191 670 480 882 362 076 084 987 648 032 003 175 241 446 777 999 437 255 721 916 494 442 501 610 989 567 461 894 695 836 945 580 375 418 948 664 507 572 583 247 021 763 060 616 875 469 230 846 121 062 154 956 574 107 065 464 079 276 544 374 453 991 805 910 359 669 623 738 444 103 632 458 367 138 999 373 839 100 009 422 720 161 769 171 868 827 421 004 401 194 461 366 991 448 564 861 323 707 811 987 571 842 743 123 147 037 558 407 081 412 164 101 691 034 299 262 733 502 552 223 180 199 060 199 188 019 224 209 969 461 892 315 693 614 587 914 737 542 768 574 319 635 274 911 275 037 129 944 384 568 013 815 308 482 619 923 635 377 125 032 553 285 514 419 920 852 907 354 352 391 124 502 913 124 952 324 348 440 841 887 577 505 639 228 295 080 697 148 298 166 268 695 964 807 632 539 799 477 909 786 559 818 765 432 666 385 310 993 598 395 760 283 946 086 552 036 971 186 875 181 520 140 105 440 858 873 804 526 640 215 075 122 319 926 465 500 301 944 545 857 622 545 646 282 339 477 857 531 543 632 028 941 823 560 285 507 278 775 638 567 429 947 277 460 321 724 990 561 007 145 828 312 158 107 344 600 024 083 306 511 112 785 561 246 764 560 676 342 752 209 227 553 650 476 257 736 201 145 347 573 816 963 542 063 621 082 914 527 883 241 935 909 975 251 497 013 833 396 739 467 532 005 161 499 349 371 678 529 862 466 153 112 431 917 244 013 912 824 966 792 247 950 809 976 359 863 577 880 246 130 320 381 906 828 964 784 427 510 627 180 219 349 771 688 733 661 111 334 805 201 615 696 983 839 347 275 736 192 496 565 889 880 538 866 424 576 698 330 918 474 704 686 620 003 300 960 817 213 559 664 038 492 591 829 372 665 564 186 337 389 896 509 681 806 902 356 154 652 126 417 567 481 603 108 081 187 903 567 024 511 879 669 845 012 190 067 563 877 897 310 340 559 209 664 493 301 529 314 608 147 914 839 795 596 174 549 176 523 796 285 215 583 274 188 629 544 763 573 607 979 891 273 688 997 888 407 214 355 026 405 800 783 466 410 846 921 738 560 064 942 736 670 914 853 446 650 429 486 045 593 867 091 871 585 316 844 141 978 453 713 648 135 802 436 745 261 188 579 687 468 612 629 241 563 371 944 992 647 993 033 166 599 676 986 076 109 645 527 175 371 706 566 405 177 474 868 650 758 815 386 518 470 866 502 115 671 826 215 303 279 785 618 243 885 454 912 359 492 085 586 312 706 529 142 646 251 011 757 245 348 031 257 813 344 960 359 407 036 404 261 911 887 175 579 988 742 151 460 873 022 921 639 713 960 466 695 250 961 445 735 818 958 960 198 795 606 560 039 837 149 346 271 073 959 194 217 540 211 832 526 336 372 535 352 753 727 336 659 823 727 855 934 840 137 965 418 385 072 316 787 069 431 934 119 831 329 426 971 261 319 002 470 140 430 598 541 655 711 039 254 004 275 229 767 480 002 639 856 126 509 831 118 372 783 536 995 628 978 979 474 110 028 310 941 451 667 930 452 120 285 209 964 894 152 624 655 606 990 314 041 291 067 799 992 734 835 696 670 554 291 456 013 314 628 745 650 982 255 334 719 107 131 359 021 971 749 263 126 335 351 776 657 951 952 856 292 672 809 681 988 993 177 973 127 881 316 620 371 912 053 290 333 997 799 336 202 030 955 451 703 340 648 155 448 434 043 940 353 919 118 389 834 768 526 615 927 698 991 353 939 862 072 997 391 100 744 813 112 643 494 962 132 603 024 154 754 296 099 223 426 717 113 163 588 415 607 093 534 216 114 711 114 757 146 154 203 275 031 844 287 284 343 575 419 835 841 542 400 324 308 889 857 855 307 275 644 994 528 984 685 784 328 733 523 110 825 686 787 965 092 748 865 838 780 794 089 176 564 184 256 357 803 320 680 687 737 762 664 246 275 812 536 039 314 081 769 070 001 032 062 272 760 097 298 250 258 106 696 663 617 299 680 948 369 967 261 766 783 474 420 603 055 400 554 249 619 865 728 070 743 106 832 820 690 584 666 084 763 999 104 212 659 658 935 941 358 113 748 636 804 212 453 937 570 009 296 710 804 925 521 221 711 172 580 130 918 421 380 731 434 768 709 089 442 766 406 385 894 095 781 503 372 323 467 118 571 780 872 199 487 756 374 809 768 488 035 467 862 558 878 529 252 009 965 744 556 413 034 902 635 504 144 261 544 442 872 104 897 897 374 004 758 756 006 969 206 326 756 691 326 535 355 248 398 429 298 219 818 143 249 361 697 356 800 937 338 648 903 429 855 526 926 331 512 161 070 563 157 148 371 470 614 624 011 070 834 638 810 485 169 041 879 268 287 592 406 646 704 320 158 694 501 349 172 363 428 835 912 807 571 546 576 339 381 534 687 446 377 706 416 891 175 987 856 692 212 219 558 589 861 810 110 421 569 752 335 332 345 101 547 825 402 057 544 160 839 415 133 239 949 591 247 310 464 755 908 248 565 711 307 043 615 006 823 342 644 941 516 004 171 228 417 341 082 475 130 002 247 596 332 055 823 165 185 270 393 896 116 462 791 366 689 912 097 832 974 397 235 327 323 195 472 560 333 211 249 044 050 803 058 486 935 692 866 751 495 221 160 344 428 045 989 283 448 552 830 349 817 832 488 868 849 462 184 515 310 654 373 505 181 782 195 078 581 160 471 222 408 082 771 459 381 990 474 607 503 873 440 284 728 163 486 743 657 316 506 418 510 176 143 156 377 085 045 195 728 718 934 338 298 977 584 121 817 797 143 919 700 479 973 996 227 755 716 861 689 189 511 467 388 151 637 375 734 388 710 099 852 222 665 592 906 995 969 294 631 287 612 916 631 640 038 688 503 448 194 855 639 351 211 679 888 824 014 837 218 468 926 388 534 594 707 248 518 054 359 124 679 609 938 305 228 923 861 800 637 208 172 685 907 008 527 582 507 730 047 687 990 400 231 819 204 488 838 347 372 630 629 859 855 844 339 778 966 742 782 496 942 869 304 610 493 080 516 064 864 016 295 614 386 579 751 035 517 693 320 200 385 623 608 362 398 289 868 680 960 205 821 767 582 079 588 537 175 997 659 660 645 455 845 781 605 809 316 870 956 167 419 724 723 598 968 014 372 836 536 939 032 026 593 484 183 152 232 994 757 673 775 313 525 124 973 925 151 305 091 981 755 186 347 025 305 164 117 752 357 953 381 361 012 642 738 243 505 511 374 854 931 434 612 725 374 709 555 488 128 692 543 228 055 444 100 542 852 511 702 617 630 422 213 231 266 768 342 152 465 935 989 882 677 159 494 955 074 831 450 445 204 023 224 610 340 179 569 109 059 176 790 044 813 690 081 592 678 746 405 747 385 352 112 381 887 841 491 505 174 840 922 125 618 549 670 658 190 733 115 441 186 316 072 244 703 764 141 943 335 499 138 012 713 292 608 947 055 665 929 106 615 090 628 526 695 573 389 798 214 648 973 038 888 449 185 927 373 602 523 851 363 230 863 695 787 488 100 645 223 769 944 860 854 712 945 734 636 305 176 394 814 878 674 025 915 386 622 660 703 880 228 938 051 613 088 727 165 519 692 473 222 846 518 752 006 336 003 197 692 275 966 578 136 564 058 688 189 587 967 656 764 620 272 891 413 934 872 765 520 358 019 452 839 760 843 911 634 774 957 118 939 848 331 394 412 974 194 552 461 511 307 564 036 401 648 713 071 986 630 121 023 106 745 198 349 375 984 668 137 486 535 906 862 518 427 073 589 923 099 179 827 584 548 372 696 505 412 597 037 615 096 233 073 620 852 572 040 069 932 301 411 570 614 788 714 005 792 977 948 819 314 879 947 963 735 379 210 166 966 469 100 769 969 805 111 204 859 524 262 307 481 797 081 394 935 106 008 232 555 913 240 606 344 175 291 754 876 857 675 005 261 556 274 075 206 907 316 980 201 352 779 736 654 478 950 004 712 239 800 232 342 168 273 450 382 388 501 698 672 920 647 227 531 460 465 515 012 420 109 336 262 044 784 588 883 863 199 071 954 214 977 296 636 417 136 796 796 100 242 903 568 889 733 891 734 928 243 613 388 134 134 384 682 115 140 015 924 838 056 878 478 230 190 191 651 005 678 574 649 578 397 129 477 688 166 724 446 590 655 219 718 129 012 757 521 308 932 107 857 408 882 767 573 953 124 305 843 761 577 456 723 259 757 931 861 050 185 551 855 024 931 745 031 176 598 518 441 474 885 428 351 066 823 729 753 674 781 020 619 518 640 922 818 571 628 322 554 180 890 761 172 001 960 424 209 203 092 686 960 325 844 131 196 636 110 690 242 782 765 705 090 787 013 870 931 957 228 685 761 473 523 728 232 856 336 409 061 003 897 955 506 459 165 210 351 891 596 858 040 315 819 774 891 234 081 984 265 242 430 096 601 867 297 166 714 762 497 782 557 647 000 380 607 204 372 554 468 030 598 594 532 260 906 293 281 884 955 327 890 797 781 492 651 543 667 510 490 953 594 590 465 014 889 591 209 080 304 486 352 702 077 568 348 464 845 413 844 933 820 018 833 259 981 372 699 136 203 007 334 025 366 552 808 155 805 022 442 080 718 171 104 384 482 780 443 776 829 128 638 523 318 893 973 471 892 290 424 997 042 269 590 714 606 572 272 518 123 270 200 592 030 462 086 046 837 854 909 853 415 011 827 225 118 940 071 586 056 568 284 568 993 564 132 286 395 957 975 797 372 094 197 195 046 714 213 224 770 333 319 602 840 769 531 873 533 290 194 852 243 836 509 836 595 981 561 464 773 197 798 944 108 354 684 101 253 323 394 930 627 002 864 025 721 410 738 438 033 794 603 376 649 646 451 674 693 413 815 518 860 552 264 392 071 927 122 686 140 259 663 047 456 727 787 448 551 341 798 876 977 772 631 629 585 564 605 809 914 993 195 490 897 537 341 710 634 209 055 872 652 706 069 618 730 011 530 895 633 568 049 795 229 343 299 326 248 332 916 371 216 000 007 409 418 549 101 829 166 221 106 593 624 870 716 032 169 465 480 815 657 117 403 231 415 575 021 902 316 576 272 069 675 299 473 013 442 924 852 488 193 228 714 720 977 357 675 633 271 633 691 639 617 479 627 401 580 970 150 440 422 919 290 822 062 051 672 248 549 127 087 478 317 943 591 918 366 506 091 866 902 444 605 484 321 949 207 131 867 694 261 767 556 449 601 531 588 992 648 789 713 732 539 102 723 757 421 430 490 838 096 550 799 671 546 522 954 901 928 124 151 515 393 074 217 223 706 534 837 853 043 489 844 085 771 238 653 929 304 074 448 064 110 110 516 755 737 322 668 656 238 878 556 554 756 337 195 606 590 504 380 326 164 918 237 682 369 523 694 193 848 173 432 431 917 694 219 830 126 118 967 264 437 646 256 064 771 028 915 872 042 588 394 737 161 872 319 613 851 944 750 568 860 127 415 036 743 779 282 737 355 771 472 415 967 656 328 036 599 990 501 986 183 242 009 894 766 190 743 788 836 764 165 928 622 413 243 703 330 434 340 767 116 636 665 107 927 936 869 173 132 631 189 904 574 088 243 535 707 440 642 562 261 342 278 465 755 669 220 452 268 963 934 999 974 433 973 847 733 147 194 580 935 759 104 991 378 273 975 351 173 445 852 909 795 927 182 983 676 038 112 553 457 657 548 488 097 778 816 079 452 877 851 972 955 901 807 542 796 569 617 933 956 237 711 664 510 301 477 584 669 547 805 510 405 803 462 263 023 100 987 348 262 988 490 443 866 249 680 080 789 624 013 158 429 110 422 007 818 451 490 738 256 758 632 320 966 901 335 951 637 073 871 171 762 656 061 011 777 375 245 323 516 497 376 363 836 978 060 213 958 799 876 900 422 467 748 937 983 643 002 670 176 104 447 194 898 001 251 130 465 219 559 281 794 565 026 149 125 913 961 656 836 321 312 600 047 890 786 797 267 186 114 802 956 843 182 725 614 457 981 618 464 050 481 453 132 730 775 108 497 977 531 335 848 150 873 488 694 936 333 962 623 796 062 006 079 907 974 617 946 394 457 004 400 634 303 968 383 404 091 422 351 036 409 833 602 041 693 854 131 555 541 113 669 025 843 242 836 184 090 561 540 463 999 724 272 959 897 471 392 544 045 806 512 272 711 929 980 777 727 913 853 709 772 675 869 891 171 351 415 630 126 951 964 718 513 356 775 423 702 978 526 963 401 869 945 368 534 245 352 248 452 547 480 790 458 018 612 352 444 742 644 960 834 559 422 647 246 693 424 556 467 196 486 888 771 349 412 436 601 645 714 860 738 589 964 851 977 161 544 857 901 196 876 951 591 366 612 567 843 353 623 662 749 166 663 143 456 956 277 951 947 796 719 834 128 817 711 206 202 022 567 455 467 317 663 397 123 371 175 797 826 568 971 042 743 838 204 952 697 180 294 794 907 734 315 982 756 480 329 408 846 840 940 210 518 822 001 949 364 497 925 980 826 491 745 844 374 878 573 822 452 230 812 185 724 809 052 345 097 360 558 314 767 320 289 323 297 909 242 458 628 167 553 884 909 964 442 859 680 929 714 054 905 422 728 812 810 903 201 470 967 206 209 299 378 441 499 668 547 551 296 834 600 957 617 158 587 960 095 971 983 410 432 352 221 614 507 386 483 648 699 635 509 652 027 925 007 545 088 355 681 947 287 586 132 517 068 633 193 949 701 396 871 606 253 511 201 955 037 342 038 810 608 972 989 914 136 734 301 834 147 412 578 716 506 176 765 055 330 525 462 843 603 831 856 008 199 263 385 928 694 513 945 040 206 377 836 157 366 777 327 272 405 458 858 031 270 739 494 225 427 992 790 737 931 040 545 780 195 090 095 135 073 553 971 107 523 440 140 981 955 050 658 053 728 639 704 531 519 335 611 285 576 613 260 993 812 851 551 303 115 707 420 934 470 565 954 107 089 901 446 453 765 782 878 603 770 200 664 370 916 881 593 008 218 752 635 030 497 635 261 378 240 345 978 715 669 084 199 095 031 523 615 053 511 815 247 957 042 703 717 228 587 080 564 614 953 290 964 570 918 536 616 803 047 068 723 751 922 371 941 752 850 026 160 869 560 614 925 275 301 366 672 948 633 087 859 703 300 514 327 092 058 095 638 323 368 185 367 895 437 304 195 699 506 553 590 973 787 289 462 565 397 526 563 660 389 683 255 631 074 924 303 445 424 268 775 771 078 410 107 647 266 140 764 470 979 461 509 057 024 840 458 102 041 429 462 673 283 544 130 439 003 067 850 506 281 181 969 847 819 395 555 370 810 952 719 414 652 499 056 170 702 708 118 343 019 947 721 221 722 164 279 685 533 516 753 471 728 228 808 719 420 841 649 821 365 738 215 102 543 315 209 134 194 140 539 503 507 277 104 068 006 508 671 187 313 521 794 614 747 774 317 012 049 403 665 218 677 981 758 582 357 011 209 478 442 916 074 013 143 998 377 020 454 669 018 250 441 362 723 379 881 792 585 241 319 851 712 313 013 808 412 239 702 761 579 638 636 274 123 246 220 896 319 391 683 232 202 074 425 953 667 734 859 797 836 056 050 105 650 040 625 279 257 455 757 655 136 238 255 491 712 217 915 063 235 867 302 112 185 852 376 940 262 720 936 702 330 597 372 066 303 856 518 941 351 130 415 302 209 888 933 575 821 630 353 093 172 598 918 373 930 836 724 611 474 968 029 006 768 556 363 311 114 369 526 304 164 710 734 945 930 234 879 475 648 199 956 312 065 648 238 753 536 247 181 112 789 476 011 884 230 961 010 663 891 744 671 567 086 315 763 477 545 120 492 130 505 153 399 013 361 551 745 010 601 984 600 791 065 287 602 391 520 659 062 941 761 463 292 993 647 828 450 416 025 678 311 416 248 404 188 917 463 545 096 504 530 212 373 619 722 947 733 964 598 456 322 783 216 452 854 397 675 120 344 063 420 782 338 003 041 010 277 942 832 018 454 729 563 756 793 744 295 221 341 401 225 185 425 936 577 324 522 162 908 126 513 860 070 987 934 906 000 909 694 339 141 017 516 165 356 574 671 396 319 291 798 614 375 117 945 995 997 354 984 512 829 551 518 343 861 575 587 720 486 274 153 120 349 933 220 651 697 102 629 774 260 347 537 762 730 423 989 031 761 400 069 560 367 489 526 588 303 430 346 136 823 366 625 439 595 738 565 245 980 384 330 141 371 233 540 563 083 844 849 826 413 202 065 050 702 109 680 097 206 957 429 437 810 565 927 217 458 260 757 326 988 583 930 837 369 164 337 951 484 183 076 168 427 176 481 082 073 871 246 635 785 409 199 293 196 037 101 503 225 194 353 512 856 208 078 599 856 091 686 003 747 176 369 348 356 242 328 228 198 160 319 829 742 241 290 226 315 261 787 819 249 044 028 194 859 733 447 698 320 263 739 680 532 793 799 191 265 092 070 650 343 053 911 906 111 408 195 866 215 482 081 374 948 291 803 467 169 287 761 108 808 231 119 268 818 466 926 518 308 641 449 861 578 531 001 377 714 551 899 611 357 450 244 627 852 566 013 084 465 104 900 170 029 004 546 489 754 161 735 760 548 593 386 866 020 083 645 776 901 168 796 891 490 817 095 525 496 531 377 713 401 260 107 131 712 480 959 525 523 204 614 615 463 745 781 596 221 804 635 440 884 063 146 203 053 449 394 330 834 049 963 747 163 232 278 337 828 496 362 030 387 538 132 832 200 622 625 835 577 056 107 581 934 288 378 109 870 099 635 287 684 212 613 605 877 030 134 675 215 293 097 297 618 084 848 875 887 644 265 004 718 294 449 598 624 977 625 722 393 057 014 464 324 171 362 899 224 045 180 447 364 942 549 751 408 982 880 506 875 944 031 238 207 329 807 142 906 592 619 042 391 531 954 332 887 984 901 074 661 923 874 305 767 278 695 538 372 047 141 902 364 336 699 812 515 975 694 800 327 393 496 443 220 868 398 581 791 712 001 616 477 732 523 528 486 223 571 401 792 107 578 105 504 913 820 968 324 467 343 565 141 163 457 336 356 202 183 043 444 489 665 782 353 511 188 045 810 658 779 166 331 471 762 086 735 925 477 746 710 136 655 465 768 805 558 300 433 151 831 911 997 944 735 628 847 551 636 417 151 331 550 930 959 284 608 616 539 369 590 082 141 174 572 088 801 274 572 564 971 993 119 248 670 748 675 066 743 673 749 426 629 495 179 535 264 846 220 398 008 804 195 622 826 544 763 516 680 426 327 115 579 556 939 051 046 669 665 893 185 265 587 683 456 986 019 212 260 305 353 997 142 466 047 786 172 870 776 689 421 693 527 478 902 690 498 531 399 982 381 159 055 457 601 572 103 491 924 330 355 349 392 549 545 983 721 386 850 408 982 533 385 929 803 470 728 071 060 302 984 189 864 324 015 852 362 988 770 288 535 039 701 021 846 317 652 077 115 776 708 584 049 027 690 975 123 643 509 570 018 288 135 485 901 868 483 632 646 308 618 676 773 059 673 889 529 595 696 104 087 263 564 906 493 914 969 333 029 180 031 658 076 670 183 410 064 754 973 041 993 194 989 212 695 778 345 391 749 925 926 454 794 209 555 955 300 188 751 062 206 125 417 468 510 049 447 510 012 163 945 718 008 223 612 292 559 748 892 561 111 472 676 313 778 715 644 317 679 514 107 572 404 506 215 356 870 290 098 563 572 934 691 469 209 711 191 322 614 570 002 288 240 059 035 079 311 826 614 867 013 381 411 893 871 121 948 505 747 834 727 857 720 649 441 996 694 653 014 467 818 706 489 082 855 904 083 231 858 179 099 396 359 912 739 263 321 461 956 230 036 416 008 621 783 553 290 087 103 745 868 400 293 504 563 045 993 838 341 758 889 890 814 133 162 180 162 315 537 386 376 446 767 625 853 246 029 668 140 421 162 109 859 904 539 033 391 988 736 289 905 292 616 370 969 406 452 906 019 874 792 802 374 239 780 701 735 207 667 212 628 325 731 748 112 721 986 583 685 265 549 427 094 693 233 046 090 529 432 919 049 401 334 973 613 165 262 312 413 490 611 543 019 274 633 225 781 575 294 300 323 220 393 918 727 981 279 367 705 382 776 643 358 252 551 445 541 174 005 709 527 596 956 032 055 993 126 993 740 936 232 135 821 992 286 088 664 880 476 757 023 380 753 048 506 136 493 623 539 269 450 371 000 151 918 932 120 494 965 635 598 163 342 703 161 841 180 941 098 883 684 655 793 465 138 348 780 921 801 315 742 800 848 602 299 535 622 292 210 558 516 206 626 794 305 129 290 647 565 606 290 364 958 533 365 460 975 486 099 999 707 279 135 618 926 101 828 081 418 459 054 557 113 460 525 039 441 062 285 979 357 535 821 526 836 918 570 475 620 092 375 917 682 420 185 426 582 894 441 322 874 725 125 700 768 353 263 863 322 394 800 758 652 771 330 972 551 362 005 281 371 771 606 212 801 443 267 330 317 740 067 869 764 871 390 055 316 186 821 732 986 978 818 990 088 575 113 013 355 868 685 331 779 882 346 436 555 933 837 068 094 710 951 809 108 131 502 892 562 381 208 059 992 833 582 678 148 204 211 090 374 898 420 288 195 317 029 423 830 980 077 866 983 811 048 624 784 752 069 181 738 003 846 889 080 828 534 205 780 982 586 748 512 687 708 413 151 756 591 175 645 242 522 551 384 896 416 059 026 046 579 691 885 946 649 353 865 763 396 064 906 033 255 759 308 646 306 763 242 806 709 360 029 988 839 755 112 221 690 763 467 270 162 989 492 333 004 214 001 519 710 142 784 449 970 343 137 909 181 910 720 888 982 892 001 806 037 779 270 622 742 648 627 767 082 474 102 036 034 848 234 122 385 295 203 758 020 746 924 855 666 723 737 358 639 656 730 230 595 934 371 828 820 427 307 136 080 277 450 296 430 970 024 606 201 037 008 001 760 877 436 629 912 898 061 338 581 702 421 008 783 551 550 193 631 947 352 778 623 038 291 875 514 957 352 504 143 206 546 865 100 444 089 815 455 628 544 700 554 832 064 447 071 978 166 615 473 583 441 790 716 398 020 492 850 084 372 726 673 283 015 707 333 842 489 585 209 103 193 837 052 464 659 351 655 215 700 112 785 868 058 310 663 168 498 790 672 994 206 929 775 697 860 412 959 411 490 315 674 728 296 336 813 838 410 785 762 602 871 328 352 163 895 699 706 422 077 762 148 391 437 083 271 658 872 658 667 776 019 343 617 153 388 610 906 360 570 023 554 253 853 006 854 797 171 408 605 161 738 169 904 540 993 868 808 892 863 215 820 859 747 505 717 700 157 442 287 220 857 789 393 083 098 118 284 521 342 689 501 542 551 159 811 507 101 190 947 274 587 978 787 662 411 676 075 219 764 141 201 978 286 699 453 479 378 480 748 029 161 963 889 593 572 715 200 120 671 768 331 595 309 891 579 579 071 020 529 398 081 448 581 735 386 984 894 796 012 068 285 693 058 819 592 101 066 096 407 959 100 714 333 819 943 257 361 232 393 070 700 682 129 880 623 350 773 597 520 381 056 998 045 598 829 409 704 832 145 776 243 447 525 378 719 834 944 226 700 041 538 053 743 063 991 394 631 147 825 211 935 225 391 471 298 353 054 294 512 722 816 347 054 939 598 252 800 785 026 554 332 582 108 006 787 543 812 098 750 381 587 783 056 956 902 530 527 645 062 004 414 779 994 400 207 141 459 439 881 518 167 358 145 297 662 789 073 655 820 692 808 431 236 842 123 810 667 317 012 450 854 224 403 518 119 185 615 354 574 918 300 886 006 972 957 683 780 716 656 979 740 375 816 959 713 670 140 365 921 308 722 330 784 516 127 759 919 771 321 993 974 171 155 377 495 347 100 706 770 449 361 859 090 842 318 726 622 170 729 041 079 309 675 068 443 135 869 604 950 449 127 267 031 971 808 483 237 562 236 347 678 949 896 765 998 419 498 903 772 539 880 332 650 968 743 103 796 738 025 397 473 906 296 920 749 019 959 161 478 253 140 516 154 167 547 324 073 483 069 248 235 714 725 211 150 320 873 606 885 247 333 173 250 917 744 750 172 070 701 398 564 509 431 515 695 539 370 464 678 632 052 240 006 889 750 027 295 572 769 581 645 124 019 658 674 138 248 120 828 693 891 080 032 950 875 129 531 149 212 239 175 889 744 700 468 601 924 007 471 105 851 944 010 876 389 220 083 654 168 231 370 375 243 575 907 170 592 846 913 518 585 789 482 891 536 073 685 474 446 779 727 794 478 970 645 737 150 413 141 426 524 895 732 239 438 674 400 634 098 397 213 385 566 302 407 985 722 167 555 197 366 185 389 270 004 917 980 494 103 997 664 694 245 399 751 576 528 050 741 155 126 465 960 805 994 057 928 661 754 737 079 109 412 114 710 014 205 187 527 750 964 229 531 600 163 853 279 099 918 450 065 147 468 400 167 385 728 837 404 004 035 357 355 050 510 788 087 032 657 208 923 798 900 842 689 977 123 965 526 349 007 280 947 440 656 519 017 742 264 347 283 211 015 621 058 504 764 399 678 033 827 640 437 334 414 973 182 251 039 629 045 528 639 688 513 764 894 634 670 100 515 464 754 669 134 979 233 939 183 097 694 460 666 090 402 405 790 175 951 819 266 893 197 534 572 856 381 478 077 599 298 862 214 926 776 647 997 080 072 605 239 197 514 634 706 286 857 516 429 151 818 712 016 392 736 471 663 610 479 344 518 438 391 552 990 532 420 556 090 290 153 760 940 914 223 513 906 488 640 863 347 012 079 352 473 153 621 093 919 402 106 571 151 223 468 277 107 460 112 071 783 467 352 537 880 765 647 418 286 679 286 739 330 812 926 711 654 590 669 236 717 216 749 459 736 183 604 630 199 970 870 697 620 842 547 649 643 918 555 768 197 397 023 941 079 844 902 112 265 589 875 370 587 235 328 163 106 431 796 361 697 456 077 554 396 295 550 769 420 233 437 163 509 434 244 880 289 277 324 168 322 516 689 166 785 812 742 198 002 734 116 237 684 484 386 467 448 835 125 791 430 345 035 677 021 288 579 035 812 905 691 205 759 355 178 581 101 466 127 406 227 154 523 088 897 031 275 793 851 662 937 550 025 323 962 821 629 695 877 962 566 908 460 507 744 709 413 350 918 111 368 306 967 457 779 741 200 675 692 157 062 380 029 717 355 468 192 132 387 293 584 605 160 020 445 505 141 844 237 163 715 551 841 933 334 858 200 164 974 191 338 056 922 689 323 412 414 085 823 306 076 804 577 043 626 066 375 460 760 855 421 278 756 797 651 004 351 488 499 750 418 259 923 402 378 522 548 989 156 622 688 210 181 868 351 760 648 395 270 275 523 032 572 827 390 144 566 000 182 325 473 365 363 144 409 327 872 931 825 612 152 848 161 907 905 184 763 042 182 992 154 584 762 990 277 434 977 912 716 378 337 682 787 946 067 862 315 987 885 181 542 788 936 792 567 911 656 268 183 323 464 199 818 627 673 648 120 931 158 428 865 562 532 280 302 823 670 310 559 287 369 024 244 113 337 789 503 666 368 206 150 261 423 701 061 867 604 584 927 862 782 508 210 378 899 692 856 266 080 109 091 493 825 075 332 174 185 541 922 177 804 395 083 161 982 784 479 458 684 341 617 192 899 092 543 888 414 959 152 906 204 328 832 808 667 362 527 308 455 025 198 409 942 404 195 812 328 592 521 458 907 070 958 046 534 788 526 044 204 018 883 430 038 055 271 571 155 224 948 165 839 034 342 663 659 742 753 333 892 328 143 079 800 260 105 232 479 202 019 047 107 305 224 058 385 014 932 043 876 515 891 451 221 570 862 381 136 358 981 698 908 731 699 321 507 245 944 375 548 872 806 387 233 350 472 136 308 861 823 433 931 980 953 516 835 398 044 747 831 575 547 937 301 095 426 150 299 307 925 896 376 287 453 382 564 872 762 084 118 949 314 858 488 792 435 204 000 985 257 896 392 579 186 883 515 488 426 259 108 381 192 520 981 785 975 951 587 057 050 979 496 889 763 656 254 460 099 420 492 629 809 707 797 645 906 278 754 930 528 298 483 569 795 877 383 913 611 150 250 930 767 875 651 644 346 146 303 677 342 027 757 475 086 739 534 525 326 919 652 428 585 156 145 670 725 878 361 644 807 333 643 715 631 440 073 673 897 587 740 178 108 025 872 684 504 526 883 282 153 793 287 646 872 392 882 197 486 008 109 739 688 511 647 805 683 090 638 289 268 079 777 436 038 483 703 254 087 468 418 826 910 962 655 990 407 234 325 913 397 670 254 813 288 756 597 020 407 452 091 650 858 674 913 784 515 256 227 385 320 071 265 530 356 388 912 903 253 822 673 834 334 007 156 549 439 038 071 158 372 532 191 972 256 790 458 980 413 712 956 155 581 382 920 576 399 080 752 750 474 303 866 623 758 195 285 833 104 139 817 395 944 479 337 964 857 351 748 802 344 589 867 662 542 468 293 349 727 306 449 482 731 194 581 562 770 998 675 028 215 304 947 096 993 920 988 065 335 884 886 734 278 763 931 996 469 620 880 504 834 082 762 222 687 992 969 235 419 847 862 945 630 079 276 988 967 773 056 472 993 892 902 965 474 027 841 288 102 841 165 209 950 521 839 591 980 404 972 566 144 219 404 527 102 778 973 693 621 966 871 266 659 771 190 923 943 492 455 264 295 041 797 980 859 746 145 759 663 619 653 368 061 446 949 384 673 589 324 494 022 088 414 574 617 457 560 514 949 890 735 633 078 552 839 550 872 816 107 796 892 873 477 086 304 663 128 678 520 283 419 594 219 836 973 864 936 206 659 070 477 781 941 359 027 620 756 380 241 043 734 257 588 931 118 467 264 064 305 662 056 197 881 931 991 603 310 342 251 770 284 917 865 215 151 552 228 179 193 478 934 578 261 749 403 761 868 928 522 341 364 041 057 331 711 313 523 601 883 315 959 966 689 358 720 429 765 452 619 289 542 088 920 135 910 520 960 421 762 381 272 938 423 411 605 162 124 897 997 130 685 100 008 685 588 180 230 570 991 150 845 183 981 671 340 433 166 283 518 136 805 129 761 645 799 544 506 572 842 300 963 043 196 960 201 464 475 123 658 668 170 296 151 792 861 509 173 731 256 602 481 532 751 878 590 510 935 369 335 662 507 834 651 065 937 931 055 501 815 749 261 652 631 573 294 783 933 590 454 933 605 047 500 126 590 999 958 249 336 253 684 366 962 886 360 659 055 285 422 947 982 229 867 329 839 926 442 295 433 867 294 005 254 032 481 704 912 835 068 284 926 325 645 693 292 284 315 073 544 002 837 290 423 620 957 389 641 503 253 954 513 543 713 987 155 950 051 079 424 635 150 912 021 614 362 308 261 300 844 119 087 575 435 127 797 005 441 883 651 957 325 285 414 996 209 515 399 335 912 073 996 192 368 137 350 646 324 326 615 078 688 496 746 707 136 830 774 517 393 572 526 753 734 988 981 929 453 775 546 502 004 909 568 215 155 950 344 445 915 034 998 399 566 777 132 978 108 788 259 919 185 438 273 241 166 916 515 326 028 875 078 288 370 728 312 225 447 540 599 328 113 606 595 456 396 506 057 233 780 424 537 747 462 168 959 146 253 354 441 013 809 989 704 372 807 238 621 776 002 096 503 757 262 005 475 531 022 129 806 643 989 870 760 850 341 266 369 708 258 459 640 629 005 312 126 456 574 751 209 772 970 135 077 071 863 271 671 063 345 157 320 887 136 626 902 936 011 296 176 207 346 647 644 316 307 532 414 740 676 111 768 081 788 382 583 169 432 341 716 542 792 367 274 195 947 032 753 815 316 673 080 335 672 734 706 907 242 942 651 071 795 161 868 293 579 098 888 134 293 607 998 680 721 109 999 190 245 904 178 078 899 837 908 091 483 604 322 480 513 548 135 843 433 791 653 758 927 813 508 413 361 781 644 122 319 328 373 729 651 462 548 033 483 759 473 609 602 749 681 699 514 567 027 681 479 963 610 149 759 177 349 448 529 307 474 848 629 958 074 013 235 447 578 595 863 245 586 556 149 902 898 104 166 705 073 541 626 737 052 198 758 910 648 943 320 450 456 653 010 760 329 747 497 101 010 632 080 311 718 033 995 869 401 960 641 721 431 739 048 024 495 365 218 035 297 755 066 636 166 352 918 363 463 092 703 045 486 832 019 651 951 795 009 953 206 778 699 954 265 059 804 458 709 875 407 625 248 572 080 619 236 357 540 595 116 638 611 564 218 330 467 125 218 626 114 572 784 034 017 384 533 157 707 429 055 500 181 783 386 077 428 388 728 519 373 118 344 798 823 623 466 114 800 712 556 935 696 386 614 560 209 522 841 854 591 550 342 091 296 524 720 032 513 034 107 669 449 856 878 305 499 703 848 231 085 146 421 027 019 789 573 312 458 418 850 467 325 062 967 551 712 939 165 423 919 282 452 796 418 914 780 200 761 815 001 753 934 204 748 353 173 583 741 481 043 645 280 409 798 925 643 661 070 581 377 298 984 474 351 637 855 657 923 560 114 754 089 511 766 184 538 834 833 183 424 099 153 680 317 324 947 103 890 995 358 186 107 128 249 168 451 504 299 461 725 086 806 528 703 953 049 460 153 082 064 068 333 369 789 622 856 962 299 732 498 440 071 695 432 467 645 536 063 521 540 386 995 038 975 367 613 927 692 258 662 596 682 192 135 162 158 992 218 800 081 775 786 875 195 597 040 702 867 151 525 187 116 244 439 490 616 758 989 622 978 268 339 541 053 180 333 590 160 092 218 662 641 885 563 566 161 237 039 495 276 712 475 659 330 122 874 872 697 438 843 881 223 689 351 292 177 931 831 057 994 712 245 875 124 293 274 120 191 732 672 842 657 685 545 738 081 842 862 549 962 477 099 568 567 675 995 331 826 469 656 727 686 810 088 202 988 335 102 669 620 240 326 329 366 246 935 041 360 209 024 074 720 559 310 753 571 805 508 743 150 088 896 014 817 813 235 321 564 315 760 278 830 068 133 910 730 094 256 931 586 411 714 282 103 051 851 040 278 182 359 736 955 289 252 239 687 915 529 715 917 274 920 830 366 904 261 416 157 759 025 719 786 202 153 012 309 504 680 528 025 333 043 878 164 058 490 564 836 759 108 867 433 649 566 153 515 570 292 006 968 258 545 171 369 499 692 032 298 682 899 374 449 663 321 622 396 357 948 253 652 886 869 066 976 458 273 539 746 207 111 887 736 987 624 150 997 923 711 852 238 015 736 579 162 273 814 802 837 296 892 650 295 256 892 936 241 492 146 652 552 234 563 054 955 302 653 119 804 966 724 755 527 120 121 429 365 493 840 362 727 307 842 047 433 376 920 582 700 503 295 563 043 558 454 443 246 019 068 938 992 846 380 157 721 192 193 006 901 600 882 470 057 830 057 316 086 433 821 049 121 542 137 182 362 241 736 016 200 959 042 454 246 424 603 623 731 271 818 714 857 136 552 647 945 934 215 420 690 035 473 321 640 799 953 624 916 792 577 273 701 100 522 866 241 587 803 218 493 929 785 920 818 643 966 566 213 351 121 033 195 688 583 168 597 065 894 043 165 063 279 509 809 482 354 414 251 282 656 031 247 321 387 555 391 190 369 038 071 363 653 062 842 929 226 494 213 042 558 689 132 297 111 182 969 531 706 255 334 285 436 145 330 850 152 372 848 949 214 746 476 353 747 202 285 664 697 147 803 894 545 882 820 555 496 753 380 476 714 210 622 991 725 363 062 761 637 873 483 356 717 479 058 280 373 441 975 284 415 656 070 998 653 764 975 466 441 207 524 922 850 536 274 863 684 110 305 563 512 148 575 831 858 268 405 317 669 035 114 358 686 278 503 821 624 374 340 924 246 950 325 616 983 352 234 821 350 454 834 749 244 189 482 495 124 106 161 144 129 756 953 017 783 017 669 750 326 985 422 171 172 595 230 150 194 052 796 627 955 546 558 358 940 799 635 460 956 424 927 675 697 959 722 126 033 060 783 800 631 888 219 129 025 554 671 596 446 796 371 071 622 976 794 422 993 259 888 306 780 240 333 211 989 485 955 021 555 726 871 050 648 605 334 553 310 612 936 997 614 081 070 632 597 624 013 877 639 691 119 576 534 407 617 773 251 697 141 819 115 609 101 373 937 008 586 745 235 367 663 236 832 989 767 042 678 358 511 768 931 754 249 381 454 709 299 361 642 946 767 995 820 212 183 196 349 071 434 935 127 147 404 040 234 234 232 676 882 453 706 131 057 749 301 704 640 500 521 125 219 427 676 712 192 779 830 321 573 420 732 778 071 030 682 619 702 212 579 848 238 112 019 324 825 662 773 565 649 145 659 204 839 261 078 147 523 469 200 553 499 897 856 153 631 569 449 469 580 748 978 981 268 207 739 188 225 752 059 301 212 650 537 352 217 040 845 427 716 431 871 063 623 564 215 651 337 493 474 470 239 914 623 005 193 963 732 758 607 166 392 778 845 958 412 586 759 219 570 010 463 615 479 260 628 219 107 147 504 072 953 686 024 959 403 981 916 822 044 125 739 964 936 840 154 645 343 968 538 183 872 892 623 254 729 488 711 674 230 586 261 218 822 882 719 675 904 043 118 626 119 406 920 779 509 749 546 182 270 062 628 894 937 521 396 911 201 132 331 988 968 410 125 088 036 211 244 381 482 512 974 105 864 246 443 122 282 214 804 468 491 726 532 966 348 502 838 247 522 228 604 075 421 006 620 501 883 840 572 948 076 354 298 556 456 838 440 276 942 959 097 461 556 014 224 649 262 212 159 570 246 763 568 866 941 378 955 433 716 281 293 481 470 294 279 256 842 187 634 405 286 051 011 281 027 879 910 278 219 516 012 495 989 907 749 750 292 029 514 246 664 201 655 063 891 247 429 460 548 533 378 637 161 012 959 014 727 744 215 838 385 789 853 713 396 433 569 454 250 825 258 557 742 450 447 113 316 393 304 140 787 604 967 524 744 474 061 368 702 575 608 175 236 212 090 678 269 994 228 331 916 748 034 065 365 748 231 582 780 750 994 929 356 934 978 034 474 349 297 475 029 864 888 788 455 310 817 871 290 346 494 192 013 236 555 672 960 224 239 604 144 216 807 700 261 245 387 230 586 262 664 669 545 466 760 278 350 046 859 601 543 295 992 373 451 192 773 108 705 069 568 349 288 465 195 060 119 123 171 921 661 964 424 389 248 916 468 318 792 986 517 038 269 604 928 466 404 803 486 939 731 223 458 012 022 131 575 616 732 756 157 268 822 313 628 950 782 555 391 707 078 624 218 155 597 333 309 099 789 359 044 180 670 260 319 454 717 819 335 907 333 970 596 392 984 421 531 834 164 022 467 038 860 840 323 756 087 530 731 365 480 220 954 290 278 810 718 065 667 317 058 427 664 448 624 664 587 891 609 153 046 054 791 885 229 018 780 123 151 722 125 848 807 873 141 103 368 053 503 706 570 474 764 844 308 027 954 907 913 331 046 123 871 794 070 395 315 305 508 912 275 050 517 461 654 287 461 287 336 530 263 257 284 742 856 018 543 051 606 197 751 711 034 852 126 754 546 721 483 163 033 853 264 062 828 725 504 879 058 122 868 800 459 376 519 774 813 282 843 041 960 141 912 918 144 184 165 756 759 254 132 653 214 252 248 213 125 094 814 203 878 770 345 114 283 726 236 348 009 640 526 885 026 554 854 418 298 452 387 060 496 005 394 882 796 721 541 675 112 469 761 254 286 506 214 313 596 138 763 218 922 235 762 012 667 111 642 651 951 115 873 489 587 391 354 092 846 935 574 301 070 832 966 109 275 068 032 946 205 746 517 048 068 491 179 744 522 409 417 724 706 629 593 562 900 984 040 141 734 452 182 727 330 534 092 460 078 120 221 322 835 470 431 902 897 225 721 071 228 304 389 369 649 056 825 264 814 873 319 319 875 482 114 987 430 359 183 526 604 349 626 486 968 754 449 358 612 724 108 011 420 785 480 891 623 300 296 953 426 076 150 686 082 928 178 981 669 743 267 981 573 171 797 980 391 629 720 674 933 336 103 895 302 945 021 928 737 064 251 453 137 960 342 325 473 447 965 708 242 631 783 894 797 559 077 678 939 245 932 016 036 995 498 919 568 074 062 519 974 163 096 524 749 493 082 385 869 875 704 692 325 744 594 423 320 104 985 507 405 425 797 751 610 383 287 964 428 715 775 038 123 471 332 638 030 493 674 378 766 348 366 951 851 688 206 876 294 803 585 282 745 017 378 216 144 690 036 108 782 484 548 756 647 381 067 493 369 267 017 495 964 873 346 434 812 742 841 879 071 694 595 425 525 443 412 329 856 738 056 709 349 179 363 977 533 186 538 065 780 900 853 831 927 268 286 768 165 215 568 177 398 226 995 695 865 874 494 280 645 795 815 813 624 591 836 002 727 814 535 959 659 234 486 250 918 934 522 102 866 695 074 399 595 720 155 720 518 198 538 750 916 198 398 793 303 015 561 224 610 735 846 362 680 051 613 885 297 683 188 513 637 578 945 747 120 192 219 330 296 580 607 770 847 062 001 511 507 553 760 369 010 123 211 222 902 259 234 013 509 403 951 035 858 545 656 239 643 721 928 425 827 991 640 000 098 264 607 958 154 350 475 886 418 604 083 488 497 639 316 949 176 909 201 466 406 688 948 321 525 783 376 457 913 212 885 156 253 096 185 518 753 798 274 722 081 215 623 869 714 149 092 702 168 870 520 244 586 624 941 418 621 610 388 681 803 036 612 565 775 470 512 309 235 422 823 551 285 889 862 247 535 366 431 168 819 603 980 232 679 770 747 699 188 646 384 379 788 400 000 899 390 309 127 740 569 499 010 911 895 127 124 661 180 420 030 783 311 437 166 558 936 166 850 008 963 661 952 724 391 389 979 037 835 163 564 295 638 460 141 822 255 590 219 805 177 936 314 668 368 658 104 054 559 914 865 429 399 892 924 098 409 181 077 390 384 116 080 933 722 555 335 909 079 043 950 908 014 844 147 293 260 240 936 246 634 438 271 861 415 159 001 107 369 925 940 751 146 931 932 536 435 548 273 800 248 569 293 629 262 312 902 382 540 295 368 984 809 180 274 425 734 657 309 894 169 576 974 367 432 238 811 735 722 867 678 588 286 019 681 759 324 688 365 825 159 389 826 743 158 186 579 074 776 124 023 408 664 119 343 034 607 517 265 337 219 176 697 846 896 666 150 547 761 386 057 836 251 894 958 948 053 386 145 807 009 352 550 376 445 326 738 798 734 597 974 132 909 161 972 980 282 961 204 279 437 038 960 663 662 349 874 902 260 606 637 702 538 022 987 503 352 855 479 100 567 352 459 567 000 702 483 658 536 197 669 255 330 890 455 767 631 346 350 691 155 948 769 030 286 697 595 455 996 454 206 688 839 674 835 030 740 775 680 852 720 014 405 511 906 993 729 817 340 981 950 495 627 470 096 779 487 012 673 457 311 243 806 724 273 404 650 983 385 974 678 127 335 005 639 843 809 090 948 815 679 540 247 515 275 655 318 620 473 639 612 415 736 069 906 260 808 653 120 388 850 931 249 877 263 507 670 999 323 350 261 585 272 211 235 819 352 129 278 132 720 693 314 789 054 398 954 223 944 527 836 550 720 142 712 622 841 645 059 531 386 424 630 606 758 167 118 384 614 854 366 630 286 178 657 716 472 388 178 323 503 991 973 236 691 533 874 825 228 150 970 655 436 631 874 151 160 689 495 612 866 550 303 980 128 490 701 032 404 886 565 298 770 608 626 538 072 693 210 510 760 122 286 798 974 785 823 694 055 844 662 221 428 076 737 348 841 604 681 075 554 879 907 602 613 678 962 980 539 467 650 852 629 195 791 365 631 914 348 728 545 431 690 946 330 280 928 330 029 599 960 770 904 789 551 704 779 213 544 739 383 510 262 778 960 550 123 641 488 935 063 014 636 720 714 507 520 754 063 283 041 745 036 497 144 474 280 216 267 175 729 778 897 988 168 368 775 745 412 916 161 896 098 131 895 701 305 199 980 600 415 955 917 919 266 402 600 375 891 547 559 661 111 534 137 911 850 170 206 020 182 637 902 079 512 700 814 889 986 567 792 938 069 789 345 079 514 203 627 967 684 477 114 402 467 119 588 204 182 872 331 826 088 126 503 476 949 348 723 987 817 876 011 482 430 229 631 884 181 146 966 369 504 560 276 479 265 474 272 157 070 152 244 836 645 051 364 128 151 139 559 586 120 084 725 545 507 156 678 590 487 017 331 855 893 338 446 955 833 375 516 982 054 168 237 363 093 631 765 987 579 861 152 507 377 889 936 853 041 219 282 780 186 511 445 587 943 153 875 684 994 010 083 153 622 643 945 721 259 728 147 719 424 945 876 299 545 993 599 177 030 449 235 787 526 470 328 162 226 054 454 843 735 072 514 381 124 958 787 915 657 278 653 742 537 810 322 893 138 914 176 017 935 163 094 745 958 678 931 380 600 265 246 152 104 429 170 197 191 611 996 001 386 948 105 635 801 357 605 100 528 340 420 242 273 809 890 012 435 220 289 388 749 207 619 985 496 263 403 119 619 431 539 941 016 265 322 486 121 248 785 478 481 423 538 935 672 767 776 516 140 591 923 284 387 405 671 793 509 015 530 212 014 968 026 512 659 175 971 510 698 581 369 191 269 764 044 572 672 866 506 990 032 302 074 531 561 180 763 962 585 561 314 004 250 283 264 530 008 721 876 253 812 589 027 129 946 123 251 171 758 350 532 492 472 152 131 708 648 854 874 899 183 242 653 598 522 342 375 823 368 975 876 027 642 532 507 238 356 058 317 242 088 209 206 383 924 948 292 504 650 804 117 363 217 143 850 181 539 467 856 807 956 028 729 382 467 461 895 124 003 670 309 714 052 476 174 053 646 742 769 252 515 139 250 284 729 118 584 610 898 894 958 563 297 293 518 629 170 982 434 015 982 473 162 695 992 860 650 389 282 549 217 328 871 178 653 911 771 703 185 315 359 305 702 772 483 094 675 969 733 499 239 372 771 611 858 797 180 694 667 794 634 237 481 955 031 479 445 021 138 373 811 734 193 636 114 289 872 898 560 387 606 243 278 959 134 580 354 540 403 516 178 241 167 172 740 328 730 951 652 802 414 849 581 921 873 514 957 179 286 133 568 921 264 637 006 991 036 829 113 056 114 112 108 005 816 089 064 576 502 706 855 668 507 338 845 025 883 060 966 116 638 892 475 712 654 675 706 323 646 710 382 022 941 852 114 114 324 841 613 330 465 331 818 777 933 860 474 761 419 642 020 090 953 685 726 304 672 549 484 994 727 709 849 565 640 413 718 627 105 400 753 428 019 895 340 153 352 126 580 339 217 026 748 674 439 576 485 658 331 264 286 021 186 133 176 726 684 287 792 871 790 242 334 071 823 111 407 780 968 893 626 131 576 216 999 747 272 325 748 495 882 287 690 420 971 727 178 750 599 821 636 685 548 170 191 714 756 319 960 735 463 690 743 756 096 300 180 938 210 159 017 669 744 600 463 926 066 424 349 795 850 951 134 462 606 804 277 475 013 661 333 489 616 395 893 365 263 771 410 341 123 110 033 458 308 072 080 397 851 536 119 588 517 929 546 181 422 605 279 093 027 338 682 579 656 567 009 470 707 490 575 224 590 097 627 443 384 656 457 800 039 271 552 664 101 086 978 007 602 327 436 126 862 085 386 157 170 809 678 146 326 002 355 482 161 199 146 488 945 997 801 251 581 063 891 719 667 563 355 832 038 234 332 366 542 899 468 156 640 144 296 272 060 073 130 897 115 793 523 059 099 950 099 892 315 364 795 361 877 787 451 256 582 689 879 397 669 352 604 103 333 267 076 614 411 922 679 757 845 631 411 883 155 823 969 746 858 360 579 988 111 492 967 100 632 353 926 865 621 979 089 385 637 262 016 778 311 352 218 635 925 794 206 415 264 665 543 315 079 126 926 347 956 512 611 663 879 513 625 096 933 093 164 107 849 557 059 277 058 389 698 376 561 868 911 400 355 529 444 907 792 242 438 540 061 213 186 540 808 421 075 125 073 769 875 664 614 952 090 856 076 148 876 218 030 415 971 096 371 236 865 637 310 066 216 445 568 314 012 532 004 229 852 152 159 934 151 898 159 991 967 582 328 729 146 504 272 343 129 659 166 789 855 129 036 770 954 433 894 475 918 481 753 590 407 372 726 199 627 843 273 185 696 798 762 347 632 993 961 262 574 043 343 008 507 028 820 991 199 308 304 690 258 595 953 047 687 177 214 310 609 950 908 449 036 019 110 027 445 551 905 320 276 706 490 937 784 882 411 846 483 682 488 374 552 023 835 055 494 635 052 760 072 608 548 386 714 288 614 933 671 241 641 138 725 892 179 964 425 375 166 081 592 980 459 355 981 011 942 703 584 539 405 677 234 990 968 575 959 342 049 353 996 648 878 725 489 446 571 942 490 034 220 325 759 131 407 700 365 070 236 956 171 546 045 063 813 221 601 429 976 641 025 400 510 608 883 849 925 904 958 493 422 223 729 398 854 074 138 752 937 841 640 579 540 626 256 087 282 089 980 510 917 677 504 807 959 352 412 511 439 943 805 943 157 529 610 772 432 571 359 749 428 419 397 103 076 208 525 053 622 347 075 858 109 831 195 610 901 211 241 103 862 697 904 580 164 022 336 847 540 251 360 527 920 502 577 256 087 730 037 973 750 507 863 424 834 173 775 915 872 692 293 710 152 529 951 532 636 807 173 262 328 075 565 199 358 269 208 047 519 628 271 458 481 731 626 522 882 876 387 498 378 072 950 378 510 682 457 076 601 731 005 086 965 234 225 718 314 610 775 402 304 564 877 500 228 435 963 004 509 966 570 724 259 679 213 423 246 750 669 151 689 189 256 085 664 772 060 982 955 964 791 368 882 199 778 699 119 905 709 011 907 495 323 524 268 305 912 745 826 145 576 894 936 525 616 221 540 869 836 640 485 392 174 527 869 526 677 866 189 962 983 648 043 638 262 289 889 548 643 442 470 784 374 416 075 962 721 657 327 359 976 108 745 033 495 313 618 289 803 574 324 936 947 816 300 546 920 623 409 141 795 684 514 842 991 710 179 291 488 695 086 296 961 587 095 909 431 043 725 706 290 824 202 150 167 901 332 221 314 553 366 261 230 456 833 791 466 100 288 241 629 625 924 606 295 047 512 507 487 645 995 752 735 874 990 934 838 682 982 107 373 811 582 403 819 784 974 003 527 751 462 687 056 079 746 633 237 475 087 576 868 001 873 694 952 146 529 174 543 389 143 139 282 248 893 660 193 444 191 962 676 511 976 943 935 935 250 690 707 623 520 491 842 707 671 125 140 763 171 287 976 046 296 129 719 159 166 023 991 177 255 274 153 897 591 734 200 499 082 115 874 855 452 194 760 120 914 737 863 995 157 350 857 223 588 864 815 498 975 526 367 641 664 555 690 378 688 916 977 681 565 152 403 697 413 120 378 924 248 229 586 501 164 147 311 542 791 831 714 516 516 964 232 774 264 434 899 468 345 032 649 313 350 155 994 913 388 625 708 244 736 448 618 658 121 140 411 803 117 514 762 502 370 949 228 622 221 445 016 774 820 271 739 816 564 270 591 286 871 445 640 655 518 951 959 717 473 236 928 487 888 157 516 998 389 460 214 381 366 547 260 496 435 446 096 684 567 755 879 351 626 742 178 104 211 920 420 248 689 646 950 186 306 606 806 898 851 940 452 742 760 290 220 839 925 203 069 869 913 660 412 780 453 986 326 740 331 620 144 019 265 653 766 439 300 713 278 760 496 050 779 942 294 583 852 592 210 173 928 318 296 572 595 936 935 710 550 631 421 594 540 919 151 054 160 267 431 575 779 790 891 840 831 549 165 856 657 819 447 233 511 063 546 609 481 070 661 484 746 827 801 607 597 420 806 508 925 604 913 679 795 242 363 294 029 217 804 589 446 012 151 688 675 254 108 528 065 139 299 783 642 022 187 019 027 051 867 882 485 124 468 888 348 283 576 158 179 081 995 562 487 045 503 675 716 245 785 309 205 664 645 694 399 092 898 096 875 644 451 994 064 156 520 693 271 096 060 892 251 398 592 731 164 153 591 194 391 713 410 582 556 553 709 534 212 330 086 407 799 254 630 932 864 664 654 917 666 298 646 284 476 478 579 117 089 304 605 146 174 696 468 142 244 036 692 777 815 739 096 222 743 510 184 041 858 435 057 771 876 027 139 842 333 233 790 849 396 391 504 901 721 026 441 424 296 682 187 693 251 011 026 411 328 823 410 725 343 529 071 710 063 487 542 835 809 526 767 002 516 988 868 255 324 076 694 867 956 443 773 636 196 694 607 092 399 751 989 730 460 727 853 574 218 256 473 645 884 043 793 615 743 072 093 921 587 981 158 762 638 695 173 718 648 527 470 949 287 006 776 462 839 927 478 374 515 814 733 435 355 960 393 906 832 317 489 099 473 716 344 183 244 107 854 117 770 991 122 637 421 792 426 653 528 686 549 038 010 994 168 134 850 502 271 418 139 460 871 676 778 780 758 423 588 297 527 608 107 635 386 333 441 158 268 206 674 985 472 493 153 156 606 710 397 848 126 338 117 311 744 479 871 912 205 563 609 814 321 678 018 418 316 513 317 489 120 411 157 148 968 053 003 599 924 919 564 863 835 302 679 211 798 773 240 738 983 561 168 669 077 280 416 984 754 868 434 603 544 913 116 596 961 464 686 747 633 411 797 908 734 033 304 830 755 677 081 185 902 323 551 864 051 513 595 009 270 136 536 975 047 766 445 637 961 628 105 309 144 070 539 744 245 050 544 422 681 082 352 888 159 823 682 490 812 543 793 634 291 998 561 766 904 472 342 565 284 751 471 991 301 024 401 764 938 615 488 019 567 485 882 012 302 835 010 084 680 843 917 252 789 502 890 234 179 720 879 708 880 598 520 907 479 620 895 612 677 953 264 965 849 243 360 393 209 318 459 245 324 289 745 529 661 999 987 272 870 995 582 391 236 146 096 903 900 879 133 348 772 074 564 466 878 056 990 023 805 314 938 154 630 938 716 370 577 290 645 931 826 202 859 999 786 717 065 234 003 990 732 554 799 360 928 145 744 709 543 488 352 662 877 108 630 131 378 317 630 029 899 166 925 435 621 897 414 856 547 692 324 624 328 249 492 415 184 668 309 497 605 504 393 852 576 907 811 641 056 589 653 762 194 591 814 444 035 733 652 617 176 348 622 270 375 799 418 745 925 716 290 348 905 440 549 517 901 173 761 490 241 479 256 801 042 571 852 721 354 908 063 441 624 291 434 201 611 447 106 325 258 843 102 861 931 169 399 541 354 649 076 084 605 650 764 228 469 110 567 613 438 830 410 330 662 881 344 811 227 929 383 655 674 865 489 508 728 889 639 001 352 424 004 181 897 168 394 579 048 759 526 746 151 614 565 154 873 623 112 800 186 967 775 009 048 278 392 611 515 125 212 967 273 295 065 837 081 844 323 634 234 904 347 146 984 703 944 362 560 861 283 141 866 075 411 016 012 744 057 930 055 984 604 356 493 786 239 696 997 074 347 081 661 196 490 154 928 424 990 040 446 108 130 456 046 851 611 838 588 018 241 480 345 183 940 866 790 482 298 112 624 715 865 052 240 045 067 412 804 078 902 587 293 678 129 172 828 093 819 850 891 244 024 921 398 860 400 661 334 898 931 938 553 487 964 081 831 106 046 038 359 324 202 349 766 171 659 391 385 658 946 983 709 287 693 480 409 187 308 637 852 625 608 155 546 721 190 853 854 272 392 153 386 798 646 774 044 981 838 705 385 088 661 151 665 085 817 500 108 379 515 153 120 362 538 950 494 590 531 724 065 934 446 563 147 248 144 756 009 300 582 502 977 318 920 256 056 457 386 799 878 247 267 191 544 699 981 263 907 160 120 951 823 903 766 162 230 383 468 978 558 241 886 078 429 922 138 296 995 462 013 836 266 011 831 470 885 203 319 658 021 602 955 430 160 494 985 913 652 239 878 142 483 997 192 158 830 293 290 156 999 192 910 996 625 314 835 917 825 016 598 938 666 427 879 121 457 287 276 769 661 032 384 728 743 648 511 604 466 809 690 225 650 447 240 280 684 363 526 499 451 680 888 244 609 978 847 154 710 081 919 694 075 386 986 198 363 572 065 851 536 943 087 051 267 139 853 823 340 818 264 734 746 599 771 596 602 965 478 500 349 110 271 118 388 737 300 072 985 323 338 683 646 802 567 988 123 566 310 284 219 135 305 091 544 336 471 654 322 703 572 054 357 117 353 668 083 219 506 517 109 043 128 887 432 747 974 359 245 119 902 447 465 320 156 708 905 052 796 746 680 103 748 735 549 709 218 813 477 047 538 652 516 327 518 559 261 806 034 321 922 105 261 402 711 560 750 442 312 240 124 585 783 009 203 541 022 944 083 883 891 921 869 745 784 396 914 552 562 698 434 429 659 835 193 679 102 925 473 589 843 369 831 302 962 503 912 376 887 086 236 011 155 010 811 501 493 743 741 447 916 155 625 842 789 221 901 059 428 965 519 472 228 868 549 024 885 083 826 502 552 424 236 295 090 756 384 923 434 471 191 561 488 887 910 628 680 632 207 241 666 399 991 677 286 440 013 610 019 010 318 470 216 833 316 053 338 551 624 036 303 479 871 871 625 516 530 745 065 460 850 587 541 683 431 773 951 856 998 004 855 415 757 907 556 290 724 855 771 914 455 290 823 378 033 689 251 614 410 834 310 478 309 970 521 061 195 960 698 812 168 849 725 097 219 522 346 330 331 437 303 378 191 872 151 177 257 643 284 914 341 505 430 205 537 098 628 549 631 981 128 559 014 211 851 222 735 509 189 010 879 375 815 375 059 294 423 050 905 329 139 569 443 201 527 243 074 133 414 598 097 176 580 848 881 851 845 185 713 741 633 006 739 356 484 935 610 100 578 698 020 282 761 884 835 384 062 078 874 944 819 005 012 098 523 028 425 709 192 797 609 091 787 800 070 179 012 496 631 631 487 599 635 926 993 021 047 694 469 367 025 048 612 671 952 434 200 689 057 038 344 463 284 160 692 292 858 745 078 684 813 944 892 173 406 292 181 806 672 707 408 176 231 261 813 997 981 500 196 851 569 740 202 616 759 946 321 331 747 903 641 771 439 215 485 414 635 985 178 838 318 603 734 159 631 107 529 048 234 581 377 361 537 147 612 683 123 290 773 607 741 024 756 981 896 962 595 546 290 163 880 356 146 439 809 116 386 397 309 086 149 264 175 329 488 054 559 307 918 400 685 752 074 404 509 503 594 092 339 665 395 675 973 576 175 909 681 721 587 406 976 196 676 606 959 866 744 522 425 256 880 949 622 558 453 536 254 169 397 582 282 944 825 328 486 037 722 415 880 082 056 993 397 453 032 885 822 347 457 501 270 499 180 437 042 576 667 393 197 013 996 021 657 889 106 308 523 848 289 312 221 602 339 027 389 031 425 031 606 533 032 610 068 398 967 177 927 837 715 129 575 169 215 578 628 071 025 055 142 959 567 923 755 933 373 732 802 496 267 664 874 543 009 349 954 178 587 306 675 965 030 971 629 759 770 346 551 494 171 266 374 305 789 151 868 678 092 502 162 482 720 302 067 871 280 371 278 283 061 933 748 232 880 546 060 916 112 231 256 502 550 707 143 858 116 771 105 084 678 383 566 118 517 291 497 062 121 642 386 530 943 119 440 534 818 244 072 359 593 594 594 577 146 785 177 650 518 196 062 397 254 874 143 595 310 350 131 769 988 907 004 035 380 251 878 845 390 236 278 241 334 796 857 327 007 420 776 909 176 098 675 994 906 545 630 850 036 659 772 373 573 931 304 922 048 676 443 745 013 818 620 688 427 638 501 110 312 690 888 485 808 342 444 614 350 353 547 568 886 899 263 106 819 076 903 997 851 525 154 143 987 130 452 900 531 097 031 460 213 271 010 283 276 105 516 220 876 208 226 236 648 777 642 887 419 017 065 896 344 634 055 165 317 246 474 746 893 377 518 791 774 573 624 883 963 695 815 415 827 378 016 993 636 215 202 484 397 404 633 156 471 502 491 141 707 600 433 286 840 753 706 212 527 158 446 839 317 979 588 812 279 763 639 889 992 156 243 954 873 167 803 727 046 802 810 889 169 213 572 148 256 266 426 087 474 682 432 907 780 816 751 415 345 760 700 055 004 126 132 359 789 119 028 183 269 675 537 212 719 276 659 570 814 261 070 171 142 289 483 188 327 382 168 771 425 244 141 104 274 174 536 759 475 508 367 292 957 399 354 158 244 046 747 661 382 851 542 140 263 543 339 644 487 605 133 624 842 230 844 965 586 201 825 331 790 693 910 605 307 493 918 433 448 682 768 103 577 759 784 174 317 048 773 966 576 982 451 876 211 289 318 038 508 286 273 503 283 506 889 443 219 163 277 632 314 251 548 059 135 960 894 543 658 230 693 774 665 526 592 190 858 683 217 071 976 374 659 689 685 208 828 211 146 773 137 659 203 745 504 957 827 775 639 440 254 221 284 137 086 033 253 821 795 054 492 428 109 605 730 464 997 889 797 620 018 914 002 991 266 705 515 627 633 812 013 631 030 107 396 269 120 827 980 989 719 531 610 764 923 145 018 793 480 462 199 098 276 913 195 177 031 972 510 283 316 231 858 582 647 846 698 145 648 333 616 038 466 541 837 318 167 689 443 082 740 396 930 596 759 576 284 102 597 129 500 710 968 900 940 752 192 794 691 341 127 881 928 579 937 298 817 679 046 610 807 708 777 481 029 772 686 131 859 312 936 006 794 981 593 058 180 995 590 319 319 139 464 938 640 374 722 529 328 290 887 447 488 994 285 804 109 811 094 965 926 988 913 503 480 570 588 669 976 851 383 863 687 429 637 516 457 624 083 681 303 842 948 986 107 029 798 306 478 306 952 088 570 989 588 097 288 266 227 131 098 925 290 729 205 867 991 025 867 686 269 603 762 671 237 511 938 602 700 823 568 677 918 457 971 671 302 109 745 263 061 770 321 511 317 163 039 873 865 987 851 031 049 939 614 095 983 969 619 913 870 834 927 461 182 801 141 403 693 600 250 067 173 599 416 369 494 011 174 424 713 698 956 668 231 781 047 618 817 312 483 875 247 786 342 321 523 826 613 546 559 064 678 397 159 080 450 748 321 769 037 868 974 990 621 895 730 910 817 198 944 530 945 274 324 105 713 678 736 075 971 846 044 923 256 286 213 590 256 195 898 302 600 398 491 634 411 579 861 715 258 580 504 353 282 927 319 031 023 755 785 275 209 807 554 266 616 340 457 896 986 950 212 576 662 308 999 626 981 987 939 997 569 401 802 173 354 767 548 579 469 711 440 068 700 921 725 885 587 071 244 708 059 564 392 794 445 354 276 458 244 593 273 921 119 880 183 388 972 319 619 729 606 607 714 139 916 592 298 906 439 600 716 266 243 077 886 325 530 969 917 229 844 170 104 613 908 284 190 327 817 975 559 144 824 791 322 865 918 577 974 659 011 999 240 721 788 788 447 011 659 463 135 304 707 129 674 171 372 409 428 958 457 938 870 497 524 101 271 090 913 429 816 241 083 041 473 529 572 318 954 812 549 481 924 534 938 239 993 628 178 828 528 130 789 486 447 766 894 622 493 410 963 102 433 018 805 717 167 907 749 636 445 549 686 074 372 332 794 118 262 274 057 733 738 197 565 361 355 280 253 460 930 272 026 255 543 595 599 869 016 954 174 890 578 287 555 590 887 892 046 177 093 746 438 208 836 579 490 179 178 851 688 089 684 928 426 018 274 412 980 134 470 169 275 926 699 560 901 831 092 766 639 884 637 376 217 074 574 920 482 267 781 804 688 719 335 082 132 200 007 782 626 027 453 665 362 504 436 198 811 350 051 015 453 670 978 990 386 444 157 141 424 876 264 326 881 482 729 987 648 619 019 927 348 769 634 597 604 890 969 547 949 928 951 562 683 674 178 705 125 163 500 889 569 731 702 579 742 371 284 912 233 242 043 098 421 396 967 498 901 603 503 573 047 004 067 660 749 385 361 745 547 726 570 668 283 317 020 945 852 692 811 428 674 953 476 908 452 305 897 391 956 374 041 291 455 154 134 690 093 237 335 993 301 001 001 375 173 378 181 857 813 122 913 490 159 653 903 090 813 825 097 962 629 758 100 635 934 012 560 920 943 454 666 778 811 550 423 409 050 013 249 429 721 692 245 885 336 689 782 015 338 287 673 045 080 907 304 167 243 177 976 149 845 216 082 565 878 725 544 015 276 609 240 783 011 779 330 246 999 443 585 268 847 963 126 454 975 364 175 144 207 902 620 596 840 790 187 035 751 698 865 012 311 269 962 811 156 605 042 918 935 655 539 678 802 885 022 847 190 165 902 830 012 028 692 068 437 152 666 483 160 978 134 399 703 654 319 719 944 495 585 719 186 925 475 747 489 670 835 880 827 377 640 648 783 759 321 068 152 919 349 696 802 268 820 525 736 820 848 601 990 115 697 966 929 836 623 840 722 290 350 657 944 688 930 725 261 971 499 013 026 127 574 247 612 519 047 601 033 048 681 987 678 904 036 759 349 942 143 732 279 971 557 043 562 078 397 971 166 638 783 344 661 743 736 871 726 890 890 577 289 485 207 781 156 011 624 815 163 936 305 347 800 494 944 388 168 363 524 907 007 225 445 210 195 359 489 096 562 549 585 267 367 368 423 956 080 449 012 795 853 985 708 989 966 750 273 491 760 339 960 296 955 557 700 772 280 782 339 399 150 314 745 094 630 102 496 693 608 837 515 562 855 382 996 257 960 307 099 147 824 334 464 926 360 333 506 685 209 215 465 471 209 546 431 128 511 368 161 288 921 310 651 896 984 807 228 291 605 490 432 058 505 851 210 325 806 869 350 294 994 542 920 032 728 216 114 080 957 733 151 999 604 977 117 042 764 603 706 117 978 739 284 635 058 967 399 841 752 114 762 454 405 621 524 061 655 458 574 488 164 174 743 731 018 849 424 968 886 105 523 675 074 091 996 685 913 227 676 212 986 077 120 690 622 340 907 798 023 604 496 294 880 892 944 648 512 766 766 193 393 934 124 370 907 486 716 607 488 371 883 919 111 224 578 116 724 747 901 168 658 059 489 718 238 290 577 506 352 540 617 727 702 031 824 790 542 060 283 230 002 168 668 137 213 282 521 999 298 121 396 118 342 406 917 247 116 319 708 101 557 521 212 703 115 674 463 093 741 509 553 887 600 725 499 877 522 429 180 814 975 925 749 266 820 664 083 857 072 721 125 324 108 358 260 085 397 204 613 208 623 082 993 317 734 807 874 939 145 682 203 241 425 666 841 191 172 111 343 363 324 706 904 461 904 098 600 324 120 601 835 380 123 728 842 830 652 929 814 375 507 648 875 984 056 222 096 957 516 311 542 250 220 501 533 469 803 018 805 273 799 371 324 523 082 031 225 140 502 487 661 157 834 110 698 280 962 359 125 037 438 192 337 396 331 244 216 395 810 088 410 107 562 459 241 652 821 960 993 624 796 039 279 881 257 241 855 108 072 762 923 800 345 989 589 498 982 976 588 355 232 924 347 716 361 786 886 377 223 860 467 189 701 090 210 350 882 208 091 118 938 222 013 423 203 900 365 390 913 855 469 465 302 586 245 258 676 571 198 535 587 854 738 218 001 129 571 404 406 137 502 681 195 662 794 513 879 390 313 069 051 924 120 621 446 981 461 458 593 459 235 751 239 582 891 209 549 851 732 081 337 442 973 656 195 364 150 778 706 495 059 730 735 795 411 912 768 753 412 874 946 164 686 968 223 680 256 076 400 465 277 704 692 746 829 011 910 096 872 331 988 445 806 441 824 568 031 611 506 528 922 215 461 398 374 053 057 709 498 529 013 135 839 443 131 066 329 402 404 140 355 970 492 774 425 976 909 567 210 871 969 556 627 564 878 490 839 297 247 315 820 343 791 755 002 856 041 338 276 239 361 415 322 027 999 869 182 575 447 982 490 912 556 714 161 466 611 647 564 743 877 110 943 774 999 644 612 290 267 026 762 928 281 863 806 831 060 117 008 922 042 460 156 469 028 114 887 078 207 969 258 803 917 447 608 886 583 585 698 143 827 962 919 579 761 928 472 130 414 524 536 915 370 287 894 090 285 470 467 878 146 047 433 404 473 341 056 225 697 968 266 542 805 491 582 911 376 731 116 375 661 504 882 050 821 615 636 970 238 358 139 266 895 420 579 760 119 333 322 757 921 671 890 922 949 712 015 568 937 533 337 807 958 411 975 721 883 433 463 180 933 149 811 133 461 950 000 735 527 303 167 843 239 483 953 477 082 651 233 283 679 793 240 119 653 229 712 634 099 436 087 796 788 543 161 685 301 428 518 116 699 361 384 267 599 894 421 170 067 294 677 471 807 045 110 282 720 166 237 289 432 375 679 123 220 965 047 316 215 110 446 020 338 972 256 098 018 016 179 543 488 167 521 477 721 251 699 396 234 524 786 735 769 686 123 386 744 656 605 382 718 495 934 947 215 222 283 377 940 234 879 789 724 696 301 839 102 837 895 583 165 148 671 009 287 820 502 750 612 951 691 802 044 844 005 697 160 672 200 350 124 638 890 810 989 686 874 220 724 323 024 463 011 738 294 178 226 849 318 072 460 745 770 077 695 134 322 530 633 581 826 819 893 492 157 841 549 184 092 552 135 668 062 616 824 252 739 551 187 974 721 398 104 785 391 808 397 121 745 395 302 571 136 016 067 575 770 414 305 036 958 136 801 977 336 863 892 187 671 781 541 605 200 398 476 046 774 066 533 628 401 284 205 671 173 574 906 878 370 267 546 021 631 812 781 369 002 792 272 658 545 472 726 555 703 783 709 323 954 810 627 695 398 680 967 713 509 509 158 684 029 146 412 153 637 871 648 200 155 900 479 136 614 609 208 032 388 109 641 562 314 612 099 446 644 719 525 173 624 462 929 450 593 392 812 232 786 954 472 851 826 404 867 212 834 540 145 441 028 457 972 429 657 709 664 929 471 713 988 601 804 327 676 321 739 037 409 245 582 434 109 380 477 949 129 798 829 231 688 426 428 313 901 035 096 331 402 079 434 791 677 903 908 271 935 499 800 440 162 771 099 599 234 454 500 753 420 358 290 646 617 333 495 373 180 466 420 497 968 920 262 138 430 027 232 934 307 964 227 697 924 966 279 574 757 923 674 959 512 737 086 581 225 298 168 061 604 449 273 307 882 948 651 548 862 629 195 892 268 428 341 142 163 966 423 736 003 486 282 058 985 924 483 135 168 145 944 962 795 540 018 399 895 819 928 631 411 000 264 187 553 065 291 130 422 895 805 359 097 204 855 941 483 592 817 678 903 072 562 991 053 253 392 705 984 772 565 096 366 726 258 989 486 944 452 153 073 047 490 217 162 382 448 347 517 379 742 404 994 857 145 350 035 706 269 074 656 528 192 341 435 384 020 759 845 097 443 188 969 893 812 161 732 086 859 265 327 280 980 352 155 271 824 866 235 747 574 218 981 319 919 611 006 586 644 323 186 379 723 545 979 685 748 641 742 770 950 016 212 411 056 347 669 197 468 559 933 940 707 532 388 832 236 307 086 504 474 262 948 175 957 284 694 499 136 864 562 591 415 577 338 206 939 571 753 511 605 472 159 544 809 305 915 933 222 627 899 979 025 707 014 000 302 085 087 463 244 358 063 305 114 923 305 381 896 858 687 803 342 992 734 744 531 302 455 558 884 365 584 869 958 124 807 759 145 206 189 213 607 104 039 624 548 627 573 708 798 455 407 253 697 886 539 138 929 999 200 292 132 552 045 816 552 902 275 088 284 555 320 612 672 731 017 412 195 241 891 447 050 182 467 502 848 660 756 997 500 843 343 805 375 522 079 241 376 321 746 150 061 747 119 881 200 741 760 035 227 791 860 324 354 950 312 507 870 655 079 905 323 833 365 231 339 607 668 070 281 830 683 373 420 967 836 892 956 378 975 503 427 614 181 952 800 636 831 727 266 567 083 795 991 605 262 096 799 329 356 008 253 119 298 806 895 512 630 250 013 781 303 084 739 309 618 055 883 209 607 305 866 459 214 667 853 172 151 634 021 922 227 558 273 526 940 095 572 169 804 269 027 080 833 370 669 843 002 828 325 195 728 219 286 438 296 111 085 187 939 100 098 193 611 479 130 742 554 151 485 910 356 772 829 927 387 248 106 035 036 264 748 696 375 827 660 225 923 353 762 570 147 282 325 332 148 823 087 029 713 090 574 272 160 626 517 585 649 423 447 466 692 162 816 522 965 051 012 284 599 329 606 666 815 019 434 772 000 745 786 659 103 400 763 012 470 287 251 190 775 883 184 589 709 953 355 092 248 128 678 526 352 428 314 045 005 808 477 354 829 229 373 804 326 760 104 394 135 308 433 974 609 233 453 404 093 889 577 629 000 878 061 355 802 153 422 435 140 537 784 772 594 825 988 292 578 088 486 506 352 564 062 290 518 249 908 523 082 632 886 486 889 654 597 241 836 551 365 709 107 022 482 957 915 807 234 582 561 082 932 938 652 397 763 768 736 659 402 794 153 068 822 241 422 203 380 307 086 865 432 438 817 050 715 671 091 762 490 380 089 170 899 408 155 288 121 971 059 916 225 880 187 042 288 156 604 831 933 116 379 933 932 902 277 263 833 241 559 989 387 008 266 934 999 141 758 045 683 890 556 073 094 132 882 102 120 524 520 896 467 143 208 271 742 303 206 348 849 699 724 884 883 811 539 717 049 919 434 627 346 483 195 265 112 895 037 848 499 614 826 231 686 583 142 072 994 692 394 086 663 846 003 246 174 206 021 098 415 936 367 078 186 773 441 461 767 233 728 979 912 328 359 654 185 514 911 917 220 010 523 861 149 383 274 333 496 449 756 364 797 552 002 931 842 770 670 280 063 016 635 039 735 777 380 272 857 264 782 753 003 430 780 791 479 003 498 126 196 243 210 647 645 810 314 007 966 298 542 184 036 518 697 992 985 311 039 186 566 195 773 825 092 664 043 493 918 223 614 672 593 881 248 965 497 228 870 064 594 968 531 853 957 084 924 322 108 326 518 354 316 808 792 870 270 058 316 122 451 273 405 930 070 383 174 248 347 437 167 692 891 309 867 827 507 223 317 660 171 042 262 938 951 375 236 510 445 066 108 067 749 826 713 086 014 259 945 625 370 523 551 583 459 132 828 381 912 956 213 259 635 705 418 366 549 600 429 769 809 482 339 562 287 937 156 765 324 120 675 251 740 668 525 374 567 878 774 574 604 591 020 817 914 965 358 490 177 724 969 187 045 020 641 400 010 757 634 416 157 193 167 831 013 676 596 646 320 864 454 810 287 135 612 361 730 614 358 804 320 514 627 221 478 267 605 540 139 590 587 305 655 829 367 673 583 162 625 841 105 182 428 361 837 090 684 248 353 308 366 347 720 578 544 741 563 312 233 033 963 970 197 346 421 433 236 392 706 417 748 163 794 248 831 121 168 435 334 225 285 433 530 533 625 001 976 786 651 003 924 927 926 039 625 840 886 883 332 012 272 131 983 918 386 945 192 944 870 858 191 506 907 048 528 070 563 287 055 859 916 622 980 457 531 448 383 685 596 328 352 581 703 041 569 069 344 106 707 602 455 372 692 772 788 039 108 315 534 143 754 072 470 494 723 573 152 519 120 828 012 755 112 769 797 178 236 381 867 977 797 969 328 186 382 630 961 603 663 278 718 070 718 577 394 176 192 167 688 999 366 654 821 298 932 105 172 554 008 800 660 669 942 802 204 114 624 588 389 217 303 029 355 451 393 586 812 543 180 036 267 232 477 769 487 292 019 478 581 973 131 908 893 960 665 698 328 300 505 322 302 855 102 076 247 121 823 490 811 982 065 468 702 964 072 308 162 345 702 165 834 804 468 000 183 965 544 891 808 978 303 563 280 194 864 748 292 075 275 064 159 306 539 502 706 241 945 303 273 020 303 010 310 029 791 647 250 337 790 768 138 333 021 986 038 105 623 405 101 796 777 462 255 608 040 837 301 290 355 817 402 171 645 691 555 952 734 330 586 490 947 655 425 081 639 514 427 275 720 606 054 612 160 655 564 263 871 002 453 470 289 166 756 564 931 408 746 341 629 987 728 270 352 556 682 471 186 532 684 609 549 636 907 061 376 857 415 167 882 500 295 121 846 039 135 181 484 625 756 300 002 108 551 666 111 353 261 690 661 850 524 998 922 334 595 570 127 196 450 991 093 906 852 902 807 275 541 912 194 424 276 431 170 674 056 934 204 182 454 259 102 007 258 687 071 274 429 322 337 718 195 668 039 654 812 989 826 318 306 273 558 169 041 248 878 167 959 518 421 803 290 961 614 601 478 383 844 886 758 087 672 050 634 028 837 764 833 312 128 341 882 600 010 413 120 218 538 825 992 695 373 284 340 669 868 968 244 908 021 368 040 311 731 452 922 504 457 305 298 566 991 285 289 487 583 068 303 312 966 230 441 465 003 170 349 181 475 481 534 882 990 656 563 755 296 994 582 981 048 886 563 466 800 289 447 401 530 488 931 886 312 523 926 032 955 851 623 376 820 361 115 566 612 159 100 659 123 513 858 836 241 296 363 253 241 099 456 234 786 383 295 897 257 542 671 169 003 754 329 565 461 875 146 612 859 064 217 977 064 029 313 817 954 964 584 112 009 609 309 838 764 744 208 386 561 415 913 832 383 491 142 730 168 159 142 303 109 048 584 873 281 957 329 655 231 536 297 108 536 257 804 335 656 997 629 948 589 809 176 200 673 228 644 623 808 622 172 668 413 738 650 528 986 850 753 820 648 510 634 514 442 306 482 563 330 623 740 256 713 354 418 030 147 189 465 278 122 207 356 533 937 462 242 113 061 127 462 235 421 308 964 778 485 825 284 059 932 697 121 798 873 998 726 622 725 863 800 895 875 274 108 286 285 768 873 280 363 044 018 385 191 851 606 718 408 986 685 577 530 864 160 456 499 173 754 082 128 718 967 112 863 394 271 748 923 445 024 276 619 256 814 168 000 794 761 637 993 884 668 780 469 746 167 287 798 992 047 810 246 799 244 606 891 870 225 793 894 157 585 899 516 697 232 813 106 549 203 093 211 870 053 282 742 681 579 924 588 557 369 959 366 370 017 465 151 390 603 656 198 864 223 814 334 333 339 527 343 591 705 014 599 928 601 967 510 360 371 630 663 194 539 225 752 444 792 392 537 979 726 357 439 005 537 179 543 757 286 861 521 265 988 390 062 832 021 998 056 428 985 225 710 361 595 783 593 116 877 477 943 300 978 301 254 740 871 655 468 087 732 813 557 843 237 217 591 983 325 074 060 820 419 169 282 088 966 682 768 901 892 895 845 627 183 667 771 050 220 667 510 146 498 630 270 549 596 339 386 500 939 740 129 246 977 846 282 232 868 865 510 990 653 525 407 764 922 104 242 911 894 503 756 562 947 300 177 565 377 609 913 362 734 219 366 833 575 345 286 383 174 899 146 843 608 764 478 234 134 954 794 111 133 626 897 171 552 396 151 763 508 570 363 738 159 899 357 915 451 785 442 473 747 142 535 722 681 422 100 554 688 721 722 501 817 228 311 750 896 364 856 919 968 401 029 001 780 110 666 833 242 069 020 709 966 330 422 585 831 963 424 825 870 029 256 389 897 100 518 050 690 127 751 054 586 579 984 630 051 464 106 465 585 644 979 027 974 179 202 863 419 841 920 575 806 865 261 183 890 230 795 328 383 019 862 276 645 047 302 634 534 341 081 115 726 268 425 528 971 538 906 154 846 437 479 851 439 337 231 169 598 086 612 869 173 099 386 011 071 177 143 044 387 556 082 078 517 550 824 722 756 084 703 838 541 551 428 932 761 292 063 339 381 692 816 138 553 127 656 177 330 346 924 046 401 466 994 719 375 735 018 558 930 909 196 489 170 053 333 941 797 208 148 457 272 000 860 305 966 423 144 216 808 746 900 638 143 069 854 580 689 733 571 835 362 261 971 835 354 537 972 678 789 739 449 508 659 623 493 246 083 654 506 806 751 144 489 523 435 917 393 142 733 323 909 199 544 917 038 986 396 254 163 625 028 931 228 708 713 212 049 464 725 494 994 610 007 295 729 311 602 535 745 041 325 892 269 537 825 295 195 291 418 887 541 257 056 006 255 934 608 500 073 698 575 026 255 140 348 687 622 983 390 104 679 427 454 241 106 650 662 323 894 805 750 164 894 149 913 532 333 456 417 239 436 664 431 420 312 724 353 775 018 775 834 739 200 082 095 435 571 437 777 485 356 015 231 501 965 823 375 312 638 547 284 845 149 491 926 313 290 272 489 384 360 984 821 110 258 460 650 541 145 714 515 722 558 831 443 976 746 366 237 359 280 368 736 490 733 265 902 961 518 139 424 576 123 248 525 129 438 998 843 052 483 456 819 030 856 675 187 317 844 968 639 652 886 693 738 566 317 280 207 403 313 887 286 613 784 559 423 463 045 361 948 122 562 722 135 955 961 292 427 739 175 238 293 144 818 166 986 008 128 972 590 003 893 958 507 394 912 674 637 454 021 869 225 000 321 202 478 320 291 492 193 800 688 738 148 960 497 360 645 520 300 511 798 730 661 778 274 078 018 264 532 707 008 912 736 488 781 706 082 752 835 745 944 456 036 823 327 359 228 458 293 821 338 356 975 274 915 107 638 605 125 487 701 251 843 557 299 297 386 149 523 973 076 337 671 003 849 256 820 506 156 758 847 040 992 998 977 428 790 026 763 077 456 348 970 173 961 504 691 246 285 768 764 310 348 345 637 800 999 362 125 523 456 112 266 988 246 107 781 060 569 230 947 187 269 375 307 022 700 302 187 876 465 436 922 937 966 040 796 328 269 545 959 932 661 721 791 835 404 662 975 451 377 075 937 931 702 121 919 575 025 838 380 020 221 250 049 705 814 252 276 968 590 227 246 994 661 315 083 438 754 411 720 546 446 569 870 599 223 982 996 084 932 735 874 689 564 495 129 501 620 623 053 155 244 026 384 723 777 935 566 818 907 353 300 094 925 117 967 156 725 312 232 617 603 376 727 271 911 748 155 121 138 229 460 750 990 294 049 724 571 410 185 983 880 291 021 875 423 216 906 649 726 362 878 282 089 414 854 075 281 794 048 335 733 930 718 261 751 940 906 312 656 953 806 805 059 972 758 960 200 040 326 822 133 751 265 955 381 360 920 661 781 968 127 081 626 912 273 681 996 268 877 947 739 150 422 326 432 229 687 353 735 078 243 549 441 256 770 467 545 160 964 470 642 092 302 484 260 898 604 314 283 415 162 055 057 433 708 323 211 887 754 444 996 607 780 770 362 193 925 540 082 800 687 508 422 972 022 397 023 977 020 405 150 974 159 034 992 072 108 177 290 343 284 482 294 903 391 096 072 153 883 295 484 436 344 382 156 459 792 476 936 456 922 301 203 659 235 375 564 971 416 567 386 792 628 076 529 523 888 215 675 030 316 110 188 867 651 591 140 809 219 489 352 948 976 735 177 170 885 505 698 363 595 227 772 065 858 458 991 685 530 696 925 241 702 461 825 987 623 422 402 234 469 757 134 938 062 839 142 787 713 840 875 664 045 283 095 067 872 782 492 879 627 855 026 153 919 620 068 289 542 423 808 336 757 074 479 189 005 614 775 987 284 016 850 762 104 687 087 185 788 185 050 879 582 944 410 685 203 620 917 592 535 120 678 105 844 255 420 106 168 464 184 900 959 095 358 235 461 046 660 623 266 042 208 565 893 504 239 546 322 254 987 499 493 549 364 862 235 142 508 401 596 046 947 054 839 763 684 670 798 677 563 076 607 275 595 585 044 426 550 825 276 408 991 698 206 922 459 791 694 282 752 152 909 830 800 618 775 497 420 162 016 536 145 857 512 290 063 973 061 978 699 820 218 250 620 895 941 927 809 795 063 470 879 114 079 044 153 097 444 951 399 981 840 993 294 999 806 339 511 885 870 480 607 884 038 901 084 379 883 035 865 290 956 042 788 516 005 130 046 964 813 538 228 043 735 390 222 542 121 431 365 717 760 743 453 549 728 566 934 498 553 079 290 118 580 426 871 992 880 805 607 835 962 833 975 067 044 830 363 751 126 747 671 554 471 795 761 909 887 252 302 685 249 517 678 464 295 884 137 063 424 117 088 047 034 046 275 385 065 984 521 925 613 102 328 221 947 993 642 929 348 417 404 939 048 031 651 519 537 523 364 919 360 544 851 675 389 733 202 516 682 114 582 832 147 160 308 791 454 508 873 359 379 334 257 648 933 494 295 181 544 111 771 008 989 571 544 409 271 598 531 444 532 944 276 508 556 025 736 423 480 242 571 975 845 511 205 429 739 306 668 448 706 025 175 990 392 913 233 238 226 769 686 641 046 432 511 931 269 996 766 919 376 309 847 040 032 015 737 380 863 667 321 216 520 446 829 855 755 865 412 208 318 640 926 981 336 611 713 678 311 068 383 174 102 556 987 271 994 093 591 561 003 208 583 280 346 113 721 097 170 069 692 199 876 069 447 989 182 292 599 102 629 703 521 785 959 961 238 402 592 186 563 562 019 962 807 142 954 664 898 467 723 837 326 389 144 526 668 504 105 140 527 359 509 866 220 078 060 247 399 041 563 230 494 744 111 888 325 348 739 253 260 760 999 356 352 692 446 949 423 015 857 178 487 883 801 182 052 763 202 282 828 838 723 412 882 075 050 645 067 047 150 979 716 973 025 064 486 513 544 247 236 895 240 922 415 311 199 363 167 118 181 078 619 667 263 230 628 886 632 326 210 712 493 544 379 353 375 696 251 370 669 635 604 673 671 477 996 384 515 836 613 617 692 259 905 245 580 317 699 111 256 312 151 660 887 931 118 711 947 798 669 547 902 867 935 098 925 070 363 230 284 682 114 080 124 850 403 177 075 451 195 701 763 990 845 656 625 445 360 392 711 083 907 013 387 764 377 050 455 016 790 128 528 860 063 739 127 314 560 845 184 790 178 151 640 862 390 966 367 718 711 627 311 838 287 472 055 256 161 380 531 109 153 752 826 850 585 583 843 205 645 109 680 995 818 041 034 435 236 973 361 629 786 440 289 225 692 737 550 974 159 283 145 881 215 303 691 334 503 955 944 197 985 920 557 845 739 177 685 483 026 379 472 365 959 727 364 088 381 645 411 835 950 008 049 967 557 306 062 394 546 697 584 399 947 490 535 321 461 631 664 373 516 614 088 484 077 679 750 496 224 132 675 724 613 548 216 466 332 766 131 591 943 926 267 453 332 855 869 329 609 819 968 575 074 500 036 578 261 774 767 178 471 626 304 416 626 185 299 394 177 505 158 488 337 184 544 178 780 704 578 116 028 370 536 858 237 769 824 954 400 771 449 999 196 150 052 290 072 522 322 701 557 164 726 223 954 751 918 875 441 768 385 468 939 163 272 169 598 223 330 427 120 752 670 794 607 272 595 290 618 083 761 572 034 909 181 742 333 487 903 089 328 855 937 002 042 469 714 147 336 165 936 647 499 232 170 176 020 296 902 473 750 507 012 544 727 382 539 072 112 825 930 546 722 635 083 225 630 301 225 967 854 495 323 038 870 543 660 986 366 122 427 571 493 681 044 031 567 235 709 955 301 536 428 579 792 881 360 228 605 722 086 472 437 364 604 189 705 762 376 155 261 213 362 242 078 584 932 293 131 628 131 542 429 354 036 709 423 844 352 957 872 234 305 181 604 225 783 519 293 564 774 214 020 178 086 779 282 135 538 709 819 472 715 141 388 850 684 210 699 552 689 011 768 711 855 729 005 091 981 971 016 216 537 415 067 041 470 518 934 350 639 544 111 229 402 366 268 226 041 353 517 182 181 726 020 289 945 419 571 671 439 622 606 665 562 643 785 994 001 060 679 506 624 669 913 209 865 366 952 800 044 653 620 464 529 807 038 194 229 386 747 237 993 126 143 664 422 158 941 002 681 977 685 711 654 438 344 193 705 983 798 855 554 454 763 473 365 889 926 949 741 256 666 725 405 583 279 162 229 881 343 919 809 447 159 251 333 609 637 324 575 751 087 881 519 235 095 270 306 430 226 034 246 277 827 066 584 191 840 501 763 552 411 059 737 599 449 057 697 593 037 558 307 904 188 716 416 337 331 015 751 025 502 402 074 190 917 632 450 277 674 762 826 583 377 592 985 380 559 841 495 535 988 184 775 199 778 129 764 033 836 999 742 144 783 885 496 431 263 512 623 375 469 117 331 272 535 809 440 471 825 966 421 358 971 683 046 652 960 757 679 657 012 997 430 237 030 737 939 897 562 355 454 536 832 795 096 936 700 239 674 459 854 796 211 857 403 963 901 085 171 748 754 368 737 606 315 703 637 141 775 566 226 006 568 163 339 224 964 825 687 443 404 369 142 746 287 083 160 300 265 474 949 967 922 637 676 261 079 567 996 089 998 253 172 196 476 500 925 311 431 623 780 305 094 256 240 851 419 150 168 356 375 174 477 470 972 792 960 405 760 896 184 606 787 373 077 379 811 135 779 600 006 495 143 091 523 845 505 200 298 711 778 812 822 737 594 636 122 446 870 059 038 801 134 202 400 734 479 638 494 293 608 995 759 430 142 807 027 374 099 368 674 757 532 483 798 599 913 515 756 447 276 745 594 674 767 460 549 063 269 543 414 568 283 352 903 416 553 688 164 688 797 213 594 431 877 282 586 666 174 737 900 605 384 225 187 201 226 080 954 786 536 872 681 854 967 650 986 314 739 935 878 333 401 535 758 830 652 891 174 776 711 328 265 504 533 544 455 946 299 304 058 032 906 000 176 103 238 888 517 036 911 191 363 988 915 302 522 166 347 079 505 293 997 232 787 114 963 903 483 922 793 893 481 385 780 066 324 775 815 152 983 265 912 152 427 678 933 625 077 537 291 789 330 237 670 185 104 260 611 125 332 508 473 831 724 703 976 673 181 111 218 784 471 647 898 456 896 485 116 177 712 991 368 812 971 067 722 831 929 939 787 762 393 544 564 229 858 656 011 854 805 425 798 771 574 453 811 393 040 981 700 834 637 081 391 276 788 521 795 223 443 824 484 784 375 596 620 274 508 584 952 295 550 721 774 001 166 082 294 677 566 242 592 654 917 963 584 534 534 464 287 160 190 002 344 079 607 232 971 837 240 357 741 556 876 859 637 916 832 637 533 564 040 109 489 341 395 399 386 044 231 582 858 950 955 864 913 996 850 626 552 703 666 994 905 295 718 924 150 722 131 860 695 507 941 952 437 529 813 156 522 736 982 735 480 274 458 518 619 361 096 633 890 984 563 673 963 372 234 305 905 264 272 110 168 742 911 427 757 350 834 099 165 459 892 559 204 623 697 619 475 438 286 185 150 256 773 359 793 963 593 937 419 958 789 525 376 935 506 269 807 281 432 587 696 258 226 887 111 953 992 763 729 141 387 967 049 780 597 934 337 356 833 235 426 172 297 423 868 173 428 827 382 654 023 341 576 127 692 328 388 700 797 388 563 774 247 578 631 040 143 073 947 292 048 810 594 202 149 703 057 751 684 921 439 096 019 186 886 724 251 994 785 044 466 422 046 677 624 802 488 026 368 523 487 446 230 348 263 470 629 742 351 316 933 251 821 276 845 959 857 360 785 790 213 635 640 162 055 266 471 277 770 861 928 735 877 241 064 465 811 528 714 687 679 875 851 885 619 077 271 767 817 639 347 985 897 507 880 706 561 269 967 851 566 134 268 797 347 831 419 448 096 504 327 742 765 445 014 615 040 644 014 161 415 846 005 916 735 820 411 943 393 908 584 842 913 308 328 807 064 283 720 283 754 164 232 607 753 336 038 216 471 989 523 176 050 155 711 865 545 196 526 646 816 750 418 090 783 346 769 064 332 669 810 874 705 462 517 032 925 442 131 235 631 457 782 755 699 014 494 217 152 742 342 397 557 253 098 969 852 485 471 658 639 162 936 434 511 162 432 488 427 186 652 445 717 528 422 551 229 960 908 836 915 539 843 888 717 995 408 230 934 917 004 023 214 948 807 582 572 638 789 209 757 463 269 500 707 028 523 746 882 761 278 037 403 084 093 630 639 846 422 280 329 601 970 644 474 840 468 308 572 060 050 753 098 502 200 160 764 162 152 882 376 365 143 193 683 926 562 167 391 485 957 448 645 062 591 957 762 098 227 947 709 055 430 760 580 754 210 996 903 093 394 181 289 764 521 223 313 639 332 336 126 142 184 980 287 552 451 732 724 543 594 708 670 409 666 178 012 684 529 075 881 993 267 359 832 879 152 626 367 790 255 073 827 879 736 812 914 398 276 130 428 666 292 614 953 810 840 422 083 736 744 480 996 857 593 473 867 566 901 670 629 419 061 871 017 835 316 844 676 241 942 797 623 920 601 748 443 164 941 196 646 139 732 316 006 975 493 698 866 850 077 456 459 515 322 019 522 713 481 940 970 599 377 103 880 456 088 282 158 408 171 044 306 086 145 685 985 733 229 436 574 162 337 321 118 284 516 613 696 913 362 218 728 557 099 224 265 950 013 158 451 354 891 324 717 461 313 593 857 218 206 828 041 204 348 266 715 787 272 578 857 747 425 442 116 651 200 052 705 115 713 672 552 268 837 593 164 585 115 283 026 351 074 563 826 238 264 226 147 082 655 611 478 688 351 987 408 217 530 259 749 460 626 271 832 045 798 389 997 847 302 107 993 477 171 835 455 346 305 600 695 596 075 612 684 989 366 606 613 018 336 337 497 454 748 579 293 267 199 331 869 032 095 787 370 713 316 708 744 385 960 372 190 071 365 714 991 862 797 902 446 138 710 539 211 915 537 389 874 537 330 309 968 090 686 321 812 124 550 113 985 571 707 427 670 377 686 738 251 877 683 081 910 712 801 473 270 317 452 084 919 798 365 521 825 953 837 378 184 123 859 585 489 303 481 360 217 969 172 583 172 721 980 893 855 363 207 559 963 750 776 199 571 981 830 957 898 638 590 271 709 835 114 163 309 790 432 126 814 674 511 626 743 398 341 363 865 322 690 673 940 363 340 473 886 247 743 236 842 452 276 748 621 131 139 224 722 217 290 597 415 906 696 780 615 253 913 414 762 006 121 814 549 749 437 757 901 038 196 689 673 209 291 131 576 344 166 870 905 465 076 518 610 371 848 643 493 311 327 891 037 742 414 377 429 983 956 042 862 130 141 862 497 652 142 336 753 444 882 115 740 225 727 338 570 430 412 750 985 600 776 270 562 905 495 912 028 325 271 032 097 009 040 415 306 028 373 531 436 649 551 351 354 371 208 258 998 932 507 981 365 091 689 974 659 576 898 409 179 686 435 644 811 163 329 978 581 819 641 374 879 663 178 633 687 023 027 333 238 251 196 472 683 941 129 382 271 812 520 590 321 449 614 444 315 219 896 593 699 223 079 957 048 361 083 556 739 878 242 626 433 258 960 610 560 072 900 584 793 995 698 574 944 257 408 810 655 286 026 360 424 243 361 265 247 604 038 505 866 867 934 233 647 501 618 502 871 925 052 831 950 657 019 232 322 554 539 716 776 930 379 981 409 406 846 067 738 479 473 622 446 586 293 028 092 583 379 889 799 648 553 170 418 676 013 070 193 708 679 411 756 167 845 033 613 924 231 432 358 274 450 489 137 099 031 109 092 722 332 201 189 515 625 644 288 930 898 821 558 441 511 854 642 276 108 399 715 452 341 427 559 810 722 626 981 678 552 458 953 297 296 753 497 939 821 942 098 636 895 696 560 185 338 679 162 694 729 545 707 701 343 822 173 961 495 844 762 587 513 849 877 124 331 131 218 134 641 641 578 873 871 182 494 375 567 390 910 779 111 176 364 711 913 607 245 957 612 058 526 290 357 931 689 773 355 621 419 856 847 247 486 136 960 485 544 621 164 397 590 855 175 905 050 529 252 719 297 047 315 700 770 204 527 787 380 557 579 650 141 042 201 724 651 193 754 804 798 457 368 769 983 504 548 950 666 683 252 314 359 804 370 542 345 198 717 145 043 051 082 050 109 535 309 613 104 869 520 056 030 623 536 213 470 894 891 106 713 686 827 924 908 358 077 079 336 605 343 712 796 459 703 372 712 852 882 299 680 622 071 010 636 325 016 518 434 303 656 153 486 029 594 160 904 140 143 858 561 172 761 862 623 856 383 521 365 147 553 890 743 196 478 092 189 060 404 190 699 814 404 089 365 695 060 831 688 788 806 015 689 627 378 685 422 221 775 493 441 361 988 985 650 510 994 103 938 866 312 196 060 065 874 380 332 857 462 712 763 393 936 069 287 284 721 579 583 061 902 699 282 343 988 135 768 041 455 315 446 539 910 709 748 303 843 823 009 684 123 124 811 771 818 423 449 210 625 958 289 791 702 446 946 814 400 760 852 710 409 434 831 942 167 222 676 662 863 304 438 652 006 392 352 860 538 824 336 921 631 322 245 298 142 139 391 143 144 834 366 157 616 376 005 467 021 509 424 218 591 606 939 950 500 793 922 647 959 035 882 678 691 651 311 944 621 562 059 720 097 753 873 688 508 507 340 060 192 044 801 709 346 363 887 436 688 842 724 626 389 442 116 809 826 498 612 908 159 901 521 536 483 560 391 692 216 732 261 325 493 350 452 629 047 771 473 229 355 386 853 374 020 737 900 069 529 815 109 431 890 316 817 547 769 280 722 804 296 517 110 817 378 921 738 667 069 279 797 083 685 508 367 530 363 464 041 748 561 999 526 876 222 240 006 108 580 465 963 824 281 383 082 503 299 755 173 059 782 855 027 279 037 620 638 359 231 044 331 110 613 503 289 252 418 640 231 390 154 201 317 346 315 059 543 034 237 535 463 466 780 570 153 502 914 655 658 958 388 158 205 913 808 585 346 150 051 456 289 866 519 194 043 787 605 045 271 378 920 855 772 715 270 634 983 981 220 638 203 790 844 586 636 243 320 864 125 191 772 058 302 534 148 032 296 482 120 147 499 566 718 270 779 061 689 951 954 205 749 296 917 341 503 978 636 721 726 371 620 594 260 618 584 726 755 836 252 072 961 669 779 136 122 130 400 506 561 255 684 389 710 559 076 291 118 542 875 448 523 362 435 115 572 118 462 655 429 051 049 060 286 599 541 787 842 348 591 219 359 146 178 479 992 583 123 537 786 788 375 998 439 456 616 437 337 396 444 413 098 863 815 130 164 799 826 980 565 242 654 488 503 732 300 860 119 616 774 892 787 508 863 901 729 672 636 019 344 000 576 445 636 751 104 554 494 238 507 934 854 979 150 145 040 097 426 059 083 267 035 713 383 032 619 979 664 394 819 413 404 583 841 156 735 743 329 483 133 531 491 910 018 856 780 081 177 450 123 913 322 497 450 294 744 799 013 913 579 419 590 872 678 254 343 040 387 865 921 837 506 121 056 527 888 452 776 293 015 671 398 840 615 875 950 417 896 931 384 450 162 999 758 574 659 616 119 631 476 420 068 170 179 813 587 649 056 476 076 322 400 259 403 679 633 399 542 170 278 515 759 611 884 947 830 435 231 128 881 460 632 853 814 400 352 582 869 491 615 002 754 361 862 043 944 522 084 025 791 896 449 775 795 153 368 534 078 017 190 469 987 791 041 237 967 784 974 283 808 354 327 022 798 793 384 700 293 675 458 033 286 795 963 288 610 576 095 953 167 402 752 873 470 347 050 619 948 339 552 974 590 880 638 269 001 914 350 145 284 316 745 283 778 846 929 963 246 687 617 107 564 206 863 805 023 625 106 669 546 406 202 818 177 941 890 323 208 269 088 151 786 570 837 974 285 579 930 746 353 966 597 853 696 573 913 795 932 535 969 569 422 665 601 845 929 101 854 128 709 970 897 726 020 351 246 411 198 729 838 940 360 461 650 751 432 315 875 375 445 363 023 908 138 914 683 892 618 036 843 286 512 762 319 125 705 527 297 622 802 339 610 324 332 603 145 484 207 767 172 985 284 797 537 726 501 681 842 858 482 371 116 469 077 610 405 337 807 842 997 053 872 428 006 213 853 464 208 032 683 541 205 199 861 298 191 838 703 206 315 339 241 560 211 242 585 603 780 123 303 103 487 890 505 399 895 924 589 519 441 178 831 672 640 758 395 789 144 407 917 727 093 223 574 526 923 433 210 487 351 565 575 431 643 186 304 905 929 470 639 578 505 947 619 692 156 115 870 513 716 813 936 137 317 619 488 288 475 603 386 820 843 603 833 662 016 220 342 043 498 286 955 608 567 985 283 755 503 831 206 153 028 477 548 885 418 472 199 008 765 100 614 822 482 821 314 035 859 107 012 929 644 345 877 055 194 375 944 251 290 116 083 268 020 439 021 168 040 690 467 523 430 260 790 234 255 065 490 108 559 815 305 284 722 957 697 899 074 055 193 076 223 933 517 862 856 703 538 082 893 167 221 883 438 250 251 963 493 070 317 557 585 855 396 618 258 163 696 314 075 024 694 583 627 778 855 987 520 785 891 169 760 977 140 822 699 361 131 788 247 064 898 447 884 663 434 407 881 677 858 493 600 053 841 860 439 804 400 780 459 132 672 881 222 045 616 355 209 130 257 535 436 199 567 158 768 270 665 196 786 704 730 080 110 775 101 697 599 948 708 055 060 781 442 358 963 088 873 821 163 992 987 890 959 075 666 369 441 566 761 247 876 123 083 046 180 941 308 147 343 270 106 973 550 746 657 537 600 629 301 738 948 091 175 884 399 902 548 450 176 099 894 252 423 210 640 274 390 590 888 754 728 442 800 381 268 172 301 551 752 318 322 390 430 909 903 161 625 073 873 575 090 216 551 364 829 501 754 498 346 648 095 142 157 420 252 290 449 445 951 909 605 712 987 096 555 406 149 712 752 533 211 232 955 322 653 386 637 754 774 123 439 588 382 403 109 360 093 400 159 553 039 902 748 824 859 550 110 145 231 181 237 592 727 989 887 782 200 875 896 556 919 085 140 799 226 009 077 773 914 906 391 374 026 286 036 042 505 294 086 509 662 325 979 768 287 485 377 432 583 732 231 525 642 011 651 594 462 099 610 083 449 082 921 974 524 404 524 167 950 430 523 792 212 111 388 330 153 669 399 113 671 041 055 372 549 561 415 692 522 904 116 053 526 017 314 551 178 627 071 071 632 860 792 988 943 318 723 772 071 290 574 534 468 051 357 447 747 395 835 260 388 820 943 711 698 487 481 866 346 216 419 909 147 854 096 932 513 478 101 293 898 548 100 276 270 579 547 213 958 319 338 990 055 485 460 638 606 755 989 923 829 664 906 173 167 462 837 970 224 847 165 156 757 664 823 612 434 820 767 880 116 878 536 273 011 849 960 720 477 014 159 595 896 224 032 863 973 620 283 768 164 655 115 187 851 128 598 350 315 824 864 766 410 708 328 842 955 178 951 816 434 611 828 630 878 930 960 482 395 902 615 047 310 158 782 773 267 086 268 870 978 527 735 388 467 105 759 712 682 129 161 699 417 995 614 833 627 295 336 889 015 160 057 001 807 114 215 046 249 499 224 664 587 656 371 632 080 611 225 376 293 603 746 962 034 621 678 116 112 630 284 555 414 972 124 598 992 865 650 129 513 356 877 636 204 771 759 430 240 438 805 769 884 932 652 263 318 778 557 705 670 676 658 167 065 360 647 758 200 767 875 067 636 929 602 549 183 118 051 110 604 356 369 388 455 016 912 747 485 208 463 883 935 315 237 781 006 612 559 323 916 764 571 937 529 270 996 076 359 349 959 870 844 118 348 502 671 716 600 663 417 760 273 473 193 583 329 371 641 502 502 332 261 727 071 982 225 235 366 658 040 713 248 410 015 091 441 651 395 189 921 539 355 259 847 741 975 517 740 095 249 627 297 990 160 752 695 266 584 297 290 765 356 015 272 929 462 437 571 454 088 320 186 550 369 851 031 240 040 985 983 277 489 530 253 545 544 028 918 697 096 013 916 765 399 612 847 035 977 673 009 138 904 604 715 639 961 705 160 745 068 946 459 044 260 981 930 073 997 593 709 109 630 481 301 338 061 808 628 918 867 558 662 737 718 327 441 270 911 246 033 741 505 560 710 484 113 945 866 165 361 601 351 826 072 926 385 450 268 870 888 269 141 934 229 553 547 144 856 390 306 611 367 755 742 469 738 145 760 721 096 738 843 153 003 751 549 552 467 454 148 033 614 025 259 087 968 202 210 288 661 524 098 172 307 691 020 722 883 422 855 977 125 627 057 264 638 429 664 060 837 402 791 529 792 650 726 424 883 312 321 458 795 393 967 886 936 763 881 105 832 174 612 211 807 447 285 171 448 800 000 582 777 624 131 961 816 107 643 610 328 961 208 061 333 838 233 533 864 348 254 195 037 427 924 942 581 119 278 199 461 353 277 974 748 828 704 319 862 658 069 505 639 402 741 224 328 434 912 047 627 202 947 044 837 862 381 395 859 751 255 856 656 863 185 403 991 532 516 729 848 487 263 987 936 665 529 668 520 376 122 272 277 880 933 845 080 860 371 953 863 597 815 946 549 057 717 862 534 602 430 179 202 708 081 422 039 510 791 245 925 583 574 160 832 429 690 805 048 516 646 819 161 691 104 748 259 465 788 655 178 326 571 936 639 856 225 185 327 856 093 620 454 633 918 055 154 168 435 368 891 661 412 505 647 818 543 012 808 286 759 946 660 188 925 275 756 238 416 582 546 903 053 310 209 581 095 963 053 249 623 754 374 946 689 829 218 431 770 758 443 281 510 353 809 744 218 620 354 039 646 000 469 548 204 214 963 301 516 221 964 109 597 429 202 162 402 350 551 741 641 327 426 776 599 975 683 781 954 351 983 074 608 791 814 881 625 978 254 496 404 864 069 141 351 506 382 149 528 385 628 778 473 212 178 573 805 953 717 573 473 607 363 297 498 234 967 225 864 323 594 818 782 871 000 653 932 394 339 607 069 349 297 142 457 421 847 545 602 459 585 420 211 313 822 607 894 188 632 207 321 713 449 162 066 763 943 446 201 592 679 226 084 581 217 322 947 541 303 202 883 322 503 883 369 553 737 337 752 029 977 234 682 644 842 200 160 362 063 653 074 575 476 189 798 110 264 243 844 678 983 076 193 598 514 915 546 054 587 824 463 591 580 726 915 889 967 969 625 974 673 381 304 357 386 627 117 521 670 346 066 486 824 845 076 777 120 106 356 312 711 759 681 135 619 345 941 256 763 117 724 147 986 074 422 000 429 991 419 393 019 274 421 223 511 379 634 764 493 314 234 215 241 785 728 425 072 184 672 948 731 264 845 672 403 122 496 683 756 575 738 820 491 467 675 204 652 884 917 708 804 834 172 320 098 573 614 854 531 292 601 795 062 364 932 384 602 977 619 923 892 784 195 588 964 658 550 624 207 731 147 748 111 724 130 604 254 917 358 585 300 285 232 786 527 489 772 542 951 680 173 088 757 573 587 233 700 862 868 465 953 040 669 071 820 500 990 968 798 031 902 798 851 051 160 911 865 136 447 285 100 457 979 723 893 283 017 448 607 961 785 634 091 782 704 918 370 591 383 575 432 621 981 160 560 687 014 534 321 533 522 013 465 262 847 987 484 886 079 775 774 202 123 042 917 810 693 700 391 321 244 909 436 906 207 238 688 484 351 368 078 627 098 998 485 171 281 529 112 954 450 556 802 974 361 255 442 307 495 826 633 704 714 477 809 664 926 305 366 789 860 597 394 754 982 290 595 844 536 993 262 610 014 921 849 679 121 505 103 357 757 052 588 757 759 151 988 269 939 206 962 126 799 955 221 050 529 612 871 882 086 614 311 018 074 302 083 461 582 758 950 416 048 232 737 623 379 305 513 362 996 703 417 400 273 376 914 021 904 974 095 559 404 929 363 595 812 271 507 205 352 883 726 942 439 643 553 983 296 103 340 031 750 950 913 957 199 182 480 416 698 552 258 207 824 395 063 246 407 638 383 623 040 513 811 267 666 423 683 082 978 311 797 993 067 395 063 645 321 675 490 872 434 316 301 984 395 552 836 865 606 505 571 508 693 148 658 954 069 436 716 981 782 286 183 200 204 165 428 708 752 042 867 223 361 705 525 279 877 947 856 149 279 853 995 611 979 315 151 093 428 956 136 580 402 085 001 156 199 926 636 391 316 841 083 434 401 493 571 534 671 435 730 183 544 692 573 736 887 961 478 459 810 550 403 359 778 287 283 921 086 274 633 061 522 400 973 853 740 047 037 378 132 401 656 479 646 617 438 863 833 680 013 336 053 229 222 633 438 726 970 173 691 579 292 547 035 505 676 436 288 524 704 439 455 883 832 829 384 049 029 982 434 307 177 803 381 152 561 384 656 428 806 267 230 681 258 812 820 559 334 586 997 935 713 365 328 546 118 509 234 012 701 682 213 515 351 350 030 486 969 067 608 077 820 153 519 578 467 688 979 433 250 376 527 236 461 696 880 345 350 655 812 519 454 913 503 460 091 010 391 944 512 375 394 161 056 737 531 583 777 015 931 619 862 772 861 249 826 320 118 377 826 511 265 997 583 054 796 361 282 615 155 538 733 045 087 529 765 820 020 397 371 906 858 849 418 805 801 138 672 941 855 168 484 161 165 966 028 434 351 364 298 207 937 251 020 694 446 091 438 383 384 965 691 845 800 710 481 200 175 113 828 510 100 995 197 233 596 231 618 511 020 754 087 654 749 958 783 466 180 258 984 762 101 430 920 910 891 528 888 169 562 399 767 189 890 697 532 144 602 502 504 336 132 133 447 322 523 259 743 581 080 795 032 961 533 029 771 831 015 931 842 461 163 011 049 674 502 927 430 622 434 306 682 976 452 587 366 336 319 333 155 903 945 074 108 541 095 795 258 946 171 833 221 299 325 874 347 262 619 516 223 460 144 734 119 513 217 821 890 592 305 022 239 391 207 637 170 569 162 863 857 705 050 919 410 589 287 431 845 446 086 463 200 980 576 461 527 013 034 891 878 998 863 081 241 224 109 571 967 726 252 387 219 602 464 764 499 476 380 745 390 637 049 215 067 172 669 921 871 154 239 273 041 152 311 546 145 754 793 659 664 643 702 327 530 337 716 443 666 804 172 138 560 556 085 063 568 453 418 021 533 198 430 827 234 004 147 408 397 865 925 870 781 923 368 789 450 834 355 171 541 563 849 801 625 439 095 090 582 291 561 244 746 319 009 432 611 128 089 465 761 006 084 956 509 660 059 883 951 257 791 687 754 587 628 297 142 299 039 210 825 832 048 308 706 789 272 093 299 494 378 547 720 476 263 749 553 191 430 356 598 472 320 726 924 315 437 058 300 617 388 830 151 770 836 224 986 751 684 324 278 963 556 714 323 883 019 276 284 106 533 751 825 142 048 046 373 549 735 414 264 903 197 431 130 453 897 673 894 124 642 348 370 053 535 174 437 705 511 758 104 831 725 008 950 676 256 940 729 200 547 219 303 950 695 830 164 101 283 707 440 359 729 739 787 281 157 427 801 627 967 609 010 187 718 271 575 950 486 270 041 623 075 052 932 633 520 400 470 058 388 222 111 470 144 045 731 917 022 559 523 015 210 360 520 254 643 727 314 824 070 279 881 144 505 318 122 998 990 303 587 155 450 168 646 368 599 442 248 317 608 730 935 724 429 583 529 347 834 062 549 636 541 542 549 575 359 186 061 927 135 354 134 973 813 265 032 728 269 128 927 083 891 858 156 522 468 301 878 804 059 646 832 048 922 642 944 253 099 358 154 386 237 804 060 399 676 178 305 306 746 592 227 497 160 881 674 167 779 563 003 643 303 310 561 825 870 872 620 488 726 957 185 944 252 525 698 145 816 319 395 865 943 392 466 141 257 961 162 353 983 802 290 997 280 079 067 395 192 158 046 782 367 727 979 079 119 348 581 044 859 875 159 237 646 011 175 253 776 143 750 424 006 620 483 810 171 419 443 074 709 029 274 736 730 664 629 153 726 053 131 008 914 375 282 706 589 272 053 500 852 086 976 580 339 464 146 054 319 942 405 425 412 098 887 458 106 106 187 832 911 536 172 308 498 144 223 899 826 069 706 603 229 190 822 871 292 913 509 987 202 202 775 308 546 282 949 448 682 482 636 178 954 082 779 772 223 680 465 796 265 471 682 027 045 430 509 896 028 932 693 556 945 451 636 724 039 194 300 723 102 863 828 811 427 689 923 646 557 581 733 142 531 308 149 629 436 189 270 011 784 954 656 856 379 691 247 555 742 806 028 552 382 081 597 513 846 472 451 225 805 691 097 463 535 403 694 500 037 204 749 015 401 771 065 885 896 149 419 808 838 172 239 805 638 264 419 199 388 893 343 753 997 473 060 381 236 045 979 708 736 237 606 584 627 274 992 461 427 951 506 054 394 977 470 486 075 019 342 963 695 801 580 820 531 228 973 560 902 000 260 350 029 608 293 156 105 037 097 507 898 736 088 575 263 415 051 156 498 109 750 851 152 884 412 401 482 461 827 731 640 011 028 590 801 677 461 427 705 400 823 860 953 146 202 349 669 530 468 674 192 083 610 430 123 252 572 647 298 790 048 125 604 876 403 789 829 692 454 664 524 085 760 374 565 229 021 878 264 437 181 098 244 562 569 042 638 371 176 931 977 697 867 027 297 317 665 360 760 340 491 409 335 663 313 825 480 512 857 657 600 195 486 530 690 352 504 613 078 865 441 709 615 914 117 912 811 028 437 283 377 532 026 641 727 170 622 203 514 902 410 484 526 343 811 483 137 747 275 884 003 012 963 360 674 033 859 648 347 251 563 684 844 865 059 838 659 910 848 101 260 020 461 220 429 290 921 816 208 747 731 276 026 422 640 767 635 171 124 471 131 908 810 042 701 657 016 379 966 793 436 375 899 150 594 327 398 960 202 348 315 824 986 810 774 281 667 461 120 549 856 987 125 295 669 760 804 936 304 326 802 028 142 478 433 148 828 265 250 508 189 003 963 926 291 477 414 309 509 893 271 796 174 882 227 057 013 425 492 480 918 762 462 207 358 270 939 912 635 487 623 516 198 534 136 178 832 329 839 057 866 622 056 794 685 265 828 451 376 485 099 846 516 596 070 119 404 523 334 560 060 507 734 608 856 766 987 224 023 456 669 234 680 306 393 061 497 959 790 917 236 404 575 530 858 830 774 578 532 161 257 484 312 192 199 989 423 285 681 240 787 162 579 097 397 147 885 244 489 299 078 133 434 332 228 632 198 616 768 816 383 907 340 126 928 865 915 453 548 796 565 186 473 101 326 245 409 375 130 109 774 798 253 015 443 526 422 509 641 572 972 269 909 725 374 911 317 724 919 023 293 819 620 012 957 112 436 070 133 452 309 095 098 504 200 546 439 748 852 891 951 388 844 102 468 346 898 201 752 178 396 583 899 572 670 071 825 998 824 072 840 831 053 452 365 581 095 277 054 111 583 740 534 957 155 146 433 525 605 101 439 682 334 234 996 991 705 927 753 069 409 660 792 203 789 589 006 699 115 963 348 387 236 976 440 666 501 522 888 570 374 847 702 222 987 786 239 843 319 965 792 224 288 155 240 088 970 750 199 786 376 544 800 115 333 789 671 673 608 972 803 275 378 098 155 942 678 699 563 269 553 298 088 092 087 559 236 741 662 746 591 651 425 551 635 204 634 686 519 666 309 445 779 924 890 415 745 009 680 715 402 215 959 826 919 961 549 193 110 261 932 479 196 699 349 520 415 446 789 885 589 372 970 664 553 046 631 221 129 720 360 068 056 730 939 053 178 782 716 501 152 946 804 513 895 654 032 305 394 192 086 056 710 509 587 408 083 904 231 421 562 236 682 406 667 482 157 081 976 827 099 223 954 890 034 238 708 873 995 392 165 294 123 526 555 784 631 932 248 113 396 357 803 206 814 479 221 132 969 716 591 628 822 241 415 210 045 231 760 964 299 505 164 886 111 302 561 800 345 155 372 385 539 794 902 309 566 590 359 392 701 513 644 986 739 388 151 880 926 963 109 668 528 441 163 471 770 467 066 786 887 729 042 012 296 785 633 066 291 273 609 050 609 147 129 124 172 158 906 794 419 416 044 389 581 191 396 635 893 480 274 645 611 917 597 544 643 004 604 632 200 725 476 334 131 645 686 944 657 714 566 078 564 895 820 224 277 470 015 691 826 566 789 349 603 368 494 947 351 778 596 953 955 665 074 893 259 734 998 763 957 970 584 811 224 932 088 425 587 254 203 725 397 627 916 228 671 317 438 093 486 441 854 853 101 131 863 674 851 000 432 968 435 251 049 767 742 781 916 842 558 102 786 635 022 428 510 557 835 428 007 850 599 053 415 449 007 465 960 821 183 143 165 745 462 326 033 978 361 234 247 193 982 468 739 319 540 902 817 076 174 106 542 645 317 106 324 744 645 715 617 058 962 065 352 503 427 800 493 349 663 323 249 849 903 575 018 388 238 248 693 116 326 538 434 405 955 654 060 099 336 756 109 040 688 028 662 695 362 163 336 810 559 105 795 022 787 814 783 473 856 180 526 083 502 634 968 872 438 674 228 035 900 333 740 737 405 312 448 887 036 807 995 963 718 947 728 112 152 587 502 462 848 617 181 683 786 310 368 740 551 882 476 106 767 495 521 137 016 669 811 778 540 003 696 900 642 712 409 795 079 870 180 062 497 590 439 497 691 705 066 337 846 942 980 878 844 249 300 534 796 891 208 192 002 520 515 651 546 815 788 789 313 289 324 590 886 222 322 361 602 993 688 863 310 088 977 235 636 617 650 100 310 731 878 883 983 018 995 338 538 421 458 215 845 160 794 939 226 674 894 618 744 977 356 824 432 541 650 740 843 441 577 716 055 277 918 312 241 555 722 855 487 622 762 631 019 262 805 203 409 534 890 153 752 723 086 300 477 432 438 133 225 430 130 731 818 863 501 257 409 346 502 351 023 804 251 410 457 292 175 782 164 514 637 721 503 679 555 579 070 852 262 871 057 832 268 079 555 257 738 523 642 559 393 050 709 179 197 495 802 889 695 311 778 728 419 828 380 318 528 140 208 269 162 708 151 197 295 819 903 389 552 786 830 584 248 783 715 346 930 201 226 607 409 934 681 447 928 156 575 585 352 944 265 891 555 501 807 552 079 157 818 327 894 632 800 555 321 991 692 262 448 568 129 204 918 650 178 911 403 992 006 214 126 950 465 532 961 095 212 844 815 190 509 563 411 813 148 168 253 796 475 451 496 418 939 627 919 995 094 067 153 915 228 032 688 899 721 442 680 174 977 593 712 090 412 108 592 935 327 596 814 665 151 575 236 388 432 365 992 504 273 004 356 425 920 631 629 635 544 820 669 714 474 567 065 855 642 721 592 149 146 824 254 693 792 969 781 638 927 964 165 067 075 196 251 152 476 687 209 810 841 310 035 134 174 445 229 101 256 444 881 536 208 617 523 470 208 205 624 743 478 631 153 252 904 193 131 525 051 654 407 244 995 005 578 181 141 331 798 336 617 812 498 015 474 467 478 912 298 181 263 525 333 400 030 087 842 176 821 004 605 045 318 771 792 816 914 586 181 008 710 437 293 604 697 988 086 087 630 055 279 896 485 788 778 560 863 435 107 724 330 537 923 361 765 541 928 763 115 080 642 816 370 405 029 652 825 526 844 188 111 654 879 820 974 640 972 961 709 730 679 754 796 650 950 752 001 699 549 367 485 848 660 040 285 914 338 897 965 405 633 298 723 410 694 469 828 497 356 242 809 617 089 928 022 708 329 701 102 689 851 588 414 036 654 499 542 159 615 818 477 633 018 247 144 963 555 442 928 632 276 252 192 514 120 526 598 044 221 745 775 706 147 274 416 309 656 848 547 179 739 189 569 157 826 335 096 919 234 523 915 912 562 059 408 725 859 580 994 018 288 082 058 025 272 919 237 944 926 489 562 544 835 415 293 162 239 908 911 476 721 448 965 287 236 688 591 492 212 538 077 193 494 555 849 178 750 945 646 639 963 743 312 329 450 015 899 684 297 943 328 986 294 663 765 743 502 741 470 249 792 825 499 421 281 604 520 711 345 817 277 857 671 590 316 509 122 981 687 269 411 500 916 602 157 841 854 538 424 703 564 896 593 222 864 619 877 290 360 753 580 499 763 892 493 815 239 874 584 206 881 271 305 464 241 952 742 088 944 718 564 979 556 753 485 361 623 520 941 961 910 914 918 164 019 274 439 447 160 246 047 745 916 498 710 010 440 808 536 645 161 784 514 312 867 639 470 890 129 449 890 832 972 698 841 153 222 870 195 501 593 301 445 362 967 790 992 651 161 322 386 549 916 076 567 074 782 999 191 406 045 415 336 085 682 561 309 035 629 168 865 946 356 225 009 170 684 274 492 323 473 325 392 423 880 241 112 549 477 949 145 049 196 030 889 128 543 815 850 053 654 614 464 459 767 263 581 060 548 039 394 598 707 233 190 473 351 920 070 441 520 671 485 300 087 073 471 408 660 285 006 107 205 804 476 411 427 570 298 611 246 964 537 113 513 905 428 812 761 204 492 560 098 192 073 929 541 711 345 128 403 316 883 698 170 654 359 663 743 851 636 920 487 320 586 510 815 648 848 755 713 843 831 021 306 259 415 132 217 943 449 365 210 648 024 000 189 036 622 319 277 440 291 904 804 287 556 539 358 099 319 310 988 171 861 234 095 409 858 167 490 838 197 120 718 981 482 456 619 504 671 817 607 340 436 303 924 752 989 235 552 971 461 530 509 931 145 362 361 058 880 942 060 850 926 506 130 243 127 220 960 164 240 152 542 540 693 215 205 744 436 465 086 739 638 560 638 245 898 551 990 147 533 790 533 167 654 901 392 502 309 878 619 969 570 283 648 334 477 502 069 231 986 655 804 944 229 028 486 442 384 540 135 558 818 712 258 866 278 579 994 773 857 312 545 353 966 525 637 604 196 779 208 670 192 581 767 584 142 072 031 896 311 954 369 061 110 381 684 126 724 896 590 587 417 237 989 491 630 264 445 410 837 306 847 368 469 473 380 385 238 788 437 842 164 624 997 794 283 555 751 495 614 702 525 431 269 691 447 467 023 373 074 908 717 416 384 561 825 338 847 525 140 198 202 664 755 373 703 835 217 572 838 779 918 043 176 558 088 207 326 650 134 701 421 914 823 394 651 567 552 948 129 002 420 494 329 057 840 442 222 020 472 872 393 807 804 067 386 584 477 980 179 159 678 363 270 348 893 440 127 478 386 898 160 424 331 729 607 379 107 712 975 507 889 858 096 985 235 866 517 861 430 306 488 732 602 678 271 953 691 831 310 274 517 457 200 317 547 909 776 818 118 641 248 387 658 707 588 686 026 186 671 932 378 758 878 167 639 093 815 338 259 157 005 055 192 097 585 183 078 524 942 381 445 504 011 649 188 480 863 784 655 767 263 902 903 394 420 868 538 778 439 750 092 769 686 588 223 542 002 154 360 506 957 182 685 197 322 070 303 555 784 711 459 122 643 679 858 764 057 879 179 636 786 228 305 457 059 412 566 706 164 732 755 472 889 737 127 434 697 108 972 850 441 086 324 342 903 553 979 351 227 008 468 620 237 856 639 037 116 231 362 729 511 707 324 337 220 017 938 388 847 012 710 514 748 807 018 545 388 063 150 213 057 907 560 904 456 175 198 270 845 979 303 822 220 385 320 973 667 779 194 949 351 515 260 621 220 886 877 346 314 273 877 319 055 742 919 765 804 180 998 849 787 949 990 006 861 680 269 896 307 237 925 250 249 799 091 334 156 249 985 354 913 365 685 216 267 002 002 257 726 054 650 863 474 261 307 932 925 628 833 616 448 011 742 321 122 620 972 905 311 159 402 036 781 983 320 624 130 406 182 814 418 152 554 758 435 464 315 471 943 543 882 581 211 673 570 314 575 168 079 422 945 946 094 524 796 075 583 147 840 121 149 543 835 074 325 438 174 472 992 813 654 850 160 988 864 363 039 456 898 121 317 532 162 431 043 433 088 672 869 883 266 913 287 707 334 649 779 810 771 641 476 576 020 169 852 589 326 009 992 971 770 912 767 408 103 922 217 030 348 947 382 791 982 234 824 027 801 493 644 299 305 905 789 369 614 854 141 224 828 387 960 655 516 629 925 913 341 401 113 814 708 855 799 243 061 351 795 267 872 079 566 715 043 214 096 090 840 766 926 807 674 628 248 056 936 160 353 937 662 582 154 459 250 431 857 363 751 014 737 624 289 677 256 426 789 644 066 387 063 705 031 801 804 784 633 857 356 457 477 359 127 744 249 236 462 358 397 663 018 016 217 263 030 509 484 844 554 140 800 771 040 553 925 165 755 536 864 016 720 081 531 272 433 261 272 792 549 946 101 376 731 223 907 069 180 400 983 789 768 244 943 215 048 607 114 413 277 397 504 924 386 851 389 999 094 192 169 392 408 333 773 561 845 233 493 715 302 852 703 756 236 162 772 960 193 723 957 695 841 385 229 368 536 627 437 289 704 861 123 999 379 576 752 516 718 099 346 402 415 858 774 286 698 588 143 807 279 996 004 649 586 843 459 527 315 616 341 854 924 118 930 021 114 657 547 023 175 305 411 712 015 701 461 385 159 096 078 694 768 560 463 754 807 725 205 235 433 594 325 269 897 884 318 419 774 154 969 925 440 489 609 738 226 713 589 153 594 979 729 957 187 001 982 695 231 718 119 233 254 047 583 599 264 324 471 395 419 164 419 840 768 255 919 393 045 083 335 526 182 344 173 797 158 614 832 443 135 584 652 336 901 665 685 297 922 780 248 218 625 088 417 173 700 894 547 925 812 462 912 060 481 273 352 583 667 248 436 289 465 384 088 948 468 171 051 500 242 797 453 675 041 730 118 155 930 488 908 929 785 503 718 314 412 051 926 066 383 371 600 916 198 050 676 554 098 892 794 139 632 652 642 667 269 679 641 123 317 587 460 931 011 361 438 432 954 972 296 850 996 694 181 600 193 782 998 003 727 412 382 005 420 577 859 599 628 476 328 934 372 575 256 201 789 615 441 697 318 038 220 454 900 037 628 781 697 835 004 922 799 130 628 162 920 513 042 945 566 335 045 081 734 813 917 691 421 648 855 860 156 612 979 887 741 792 054 920 155 881 880 499 601 938 704 257 542 423 969 703 897 544 791 898 839 447 552 759 952 256 172 768 629 161 989 587 353 775 843 839 492 213 335 903 180 733 823 564 157 030 922 851 842 403 783 390 400 650 621 410 435 679 441 094 852 933 509 902 968 678 859 658 167 508 268 793 192 779 455 527 989 604 305 091 898 523 303 670 183 059 266 205 648 925 826 773 702 883 816 304 396 255 197 588 610 022 306 043 893 810 908 279 260 927 262 270 575 268 689 042 695 085 207 365 851 746 160 812 299 443 860 798 717 159 951 021 991 070 854 900 368 287 122 213 116 771 850 096 023 485 774 524 618 686 537 360 596 252 235 322 648 610 606 830 411 195 916 232 976 382 119 368 944 289 237 272 396 550 638 817 934 393 062 620 017 447 631 911 905 814 119 691 517 645 454 342 160 282 897 275 809 515 903 763 807 642 888 617 722 850 983 106 950 083 083 882 034 537 971 678 944 656 913 198 398 543 567 343 979 814 598 335 305 430 852 396 229 256 449 590 055 020 513 864 692 282 295 698 432 260 603 918 558 213 081 764 156 946 131 855 297 051 410 382 885 392 834 315 477 873 999 618 959 005 628 209 264 275 583 016 917 823 930 981 670 955 392 691 688 077 994 919 881 851 812 229 771 296 527 361 277 952 171 853 447 661 078 397 617 968 016 152 555 013 243 602 085 576 894 277 537 867 264 586 885 777 934 586 404 883 505 050 587 467 806 951 762 912 195 194 660 192 100 026 547 478 021 966 263 554 282 387 220 578 791 620 187 573 013 734 386 690 638 450 651 602 660 353 936 054 283 862 217 878 493 080 157 551 358 696 362 342 527 871 758 261 320 701 153 599 813 636 499 646 472 136 632 306 198 899 196 615 343 741 439 589 733 506 341 508 120 142 850 062 539 689 204 916 446 651 234 533 747 472 400 890 456 644 207 621 016 479 675 583 039 970 987 995 439 865 660 891 638 905 431 365 975 832 181 618 329 333 348 678 115 920 221 118 256 237 680 152 269 595 454 217 084 402 105 325 491 501 201 429 809 947 190 689 043 140 288 932 455 037 987 990 800 831 945 916 414 260 368 630 569 880 138 282 922 183 121 028 013 849 748 722 055 131 066 984 811 484 264 856 494 454 154 271 110 635 082 519 199 364 764 880 925 250 595 009 018 836 869 530 531 606 596 486 936 754 854 796 672 236 106 895 187 245 007 058 954 042 381 921 263 120 607 493 617 026 000 320 942 947 705 412 843 560 285 850 181 925 183 568 006 260 786 519 033 999 210 385 995 865 132 473 391 139 122 453 865 535 090 207 140 524 012 150 061 075 133 732 624 395 373 362 236 273 595 909 341 433 581 691 564 591 044 855 639 746 133 140 248 522 617 544 320 846 047 976 707 866 653 140 323 500 322 573 308 834 729 076 627 377 650 803 250 121 003 671 965 040 987 728 265 362 017 649 536 384 460 519 663 919 432 200 301 386 044 210 552 787 564 300 852 026 452 801 566 748 509 629 966 184 865 991 765 415 938 199 619 648 580 692 014 690 020 462 416 518 445 377 513 782 691 489 303 098 865 096 222 174 072 811 915 885 754 796 428 695 978 325 087 693 229 426 229 709 661 668 498 365 250 024 611 412 332 161 276 342 116 078 030 205 610 563 463 831 539 680 630 736 349 157 709 501 333 657 187 250 086 905 001 472 323 730 995 137 288 705 193 173 726 203 132 602 807 464 874 666 734 594 026 154 704 049 739 289 153 879 525 940 614 067 990 069 207 703 155 997 611 193 812 531 211 900 170 056 704 045 311 431 012 807 763 095 055 326 210 313 596 391 643 834 236 645 313 331 235 775 922 076 598 659 416 600 426 771 508 242 084 880 926 771 788 637 367 258 208 518 559 678 689 742 047 609 143 654 296 825 880 337 076 788 499 546 303 395 229 749 782 797 836 541 719 325 329 408 769 336 825 007 828 562 141 829 419 067 718 986 451 076 231 336 815 116 564 000 888 872 056 446 451 309 853 613 470 836 368 583 245 939 246 682 878 085 148 478 647 694 214 031 737 603 920 066 262 338 794 742 343 522 765 207 402 024 614 935 012 534 807 535 387 304 500 095 365 619 364 275 637 858 200 266 758 480 560 436 758 889 460 072 961 941 773 692 564 472 817 084 946 456 788 089 220 349 362 744 197 665 169 819 182 534 372 092 073 755 581 697 100 219 311 673 949 481 170 537 737 604 239 782 120 875 611 341 970 835 086 511 525 329 368 660 321 496 450 567 964 632 873 664 307 547 065 666 484 164 525 123 535 190 858 493 118 451 924 574 861 295 772 202 481 971 756 154 426 323 181 149 076 679 265 863 233 262 842 743 368 802 694 778 816 645 763 141 093 518 349 461 454 400 984 502 635 987 373 765 820 410 062 235 933 764 974 531 189 907 594 214 303 353 615 781 811 153 558 549 951 754 652 331 311 121 790 803 278 500 107 411 710 221 166 768 125 781 577 120 787 846 303 589 849 673 918 484 060 793 218 555 522 526 148 464 748 255 135 632 548 650 547 163 389 289 337 451 828 678 999 198 906 612 539 072 547 415 284 512 107 114 415 243 038 936 650 846 570 189 654 702 659 632 241 280 125 189 158 168 008 076 629 671 461 548 144 088 791 136 084 707 225 273 044 258 819 177 741 568 208 772 520 854 923 920 545 803 341 456 959 708 876 771 190 863 856 504 960 449 333 067 935 220 722 745 668 519 401 379 635 360 866 628 868 338 513 677 143 924 388 962 015 932 835 679 775 220 144 614 062 567 719 830 890 901 345 560 427 484 992 210 405 791 602 527 297 713 945 888 375 665 859 752 124 510 406 762 950 561 509 320 285 190 086 331 561 867 409 162 377 065 948 790 699 133 723 663 373 809 759 431 169 498 568 791 570 962 968 773 509 225 313 577 317 007 532 689 916 016 039 076 959 632 870 297 432 803 235 846 474 383 784 393 114 560 184 729 222 681 074 260 998 578 794 085 922 083 817 319 109 903 543 266 970 803 469 668 974 475 192 988 854 127 058 342 487 602 897 821 111 817 950 646 531 654 645 552 414 122 003 403 443 946 941 255 479 588 479 444 872 162 158 296 826 256 340 703 364 445 323 677 464 879 600 305 594 384 092 126 267 048 778 654 648 387 074 652 891 161 494 170 074 985 998 611 015 321 827 801 942 166 308 682 844 295 187 347 563 014 540 999 288 876 314 440 531 180 933 320 946 741 429 435 676 023 296 068 773 417 371 119 475 786 529 030 512 400 024 211 016 292 284 371 313 782 860 151 416 422 326 035 396 224 366 708 062 704 596 293 496 659 141 538 703 024 901 300 819 572 403 837 418 894 927 554 094 907 645 070 021 257 306 840 518 332 222 139 195 591 703 080 134 454 582 961 878 847 940 165 237 623 211 084 973 253 716 659 005 431 740 004 646 710 497 094 783 212 547 813 708 005 789 061 773 137 988 707 862 374 174 310 957 153 581 692 164 537 103 325 281 814 446 358 124 344 627 990 137 685 791 053 712 729 636 834 810 971 916 361 504 178 765 596 382 917 343 769 894 065 912 808 965 349 631 654 590 139 505 228 623 312 397 725 899 373 441 770 395 552 970 133 122 584 508 330 486 923 794 400 050 781 797 769 779 752 638 586 745 132 151 575 503 886 616 076 517 562 621 795 143 727 416 427 868 979 493 603 637 348 970 957 144 857 956 197 962 144 035 704 742 280 862 128 223 878 590 258 871 169 667 704 594 450 129 822 545 980 443 540 719 082 580 474 668 532 589 661 701 591 998 219 253 629 947 266 444 632 663 606 745 554 243 772 380 208 372 058 031 874 695 160 800 406 430 370 516 591 397 447 533 527 236 202 231 002 696 290 776 270 642 409 528 452 262 716 777 497 889 540 823 148 242 615 747 142 199 144 332 934 210 755 920 960 454 165 265 685 433 470 512 322 788 494 325 598 235 930 747 432 623 647 007 242 602 949 821 594 663 300 996 155 606 301 264 114 623 512 284 702 330 622 203 743 278 576 476 625 243 486 563 012 135 050 235 216 967 543 499 661 342 381 493 429 665 278 816 814 643 656 254 799 429 837 847 609 031 599 620 034 019 221 029 245 164 236 818 574 948 227 381 836 473 984 549 802 801 030 641 652 963 856 355 429 178 818 093 058 150 880 304 133 899 797 813 232 532 213 743 847 256 944 605 335 953 564 333 261 177 546 681 496 358 801 545 574 675 287 985 072 830 622 086 566 924 335 958 949 531 160 094 935 823 725 878 553 222 589 596 136 162 566 421 425 271 915 975 726 702 533 592 479 004 196 884 434 852 989 748 452 989 392 303 158 931 176 901 035 932 065 216 087 758 583 874 347 855 226 040 517 896 621 479 900 820 471 091 872 309 434 064 989 905 058 809 606 644 393 071 757 513 974 888 468 393 124 634 500 477 242 809 665 536 941 874 173 368 641 427 899 625 172 687 537 381 076 970 901 099 089 492 247 080 885 983 830 580 882 778 970 118 096 594 080 767 966 323 475 694 825 735 606 129 233 913 169 626 530 981 681 539 317 463 270 497 553 989 338 678 685 677 192 463 662 354 377 823 662 627 992 535 584 075 189 318 718 429 614 422 284 168 574 480 192 980 238 304 179 955 319 499 128 075 597 572 661 903 457 961 899 064 972 036 336 603 244 171 379 037 818 189 259 260 945 462 403 464 478 848 725 304 996 269 546 953 208 924 739 312 362 465 288 750 106 448 241 660 182 716 000 485 235 046 579 796 128 145 364 334 542 461 617 607 953 031 753 870 691 968 724 734 294 793 466 607 872 210 567 722 789 507 813 466 702 690 987 424 599 801 659 916 268 429 660 745 422 296 237 382 706 283 134 291 014 646 786 277 064 686 069 579 684 032 756 783 161 190 448 708 857 423 312 689 900 360 225 993 413 861 538 661 815 377 904 351 833 235 201 126 414 358 041 931 029 521 161 301 117 846 551 379 083 810 416 790 594 589 781 398 324 878 441 335 475 518 722 574 186 022 223 021 384 757 254 005 859 043 797 607 337 608 547 381 644 200 791 890 679 684 271 526 992 510 865 950 601 837 287 340 762 099 405 419 077 243 677 853 748 869 384 130 442 541 199 354 657 926 308 465 889 115 167 510 455 872 203 014 378 758 342 515 547 553 847 535 579 638 972 859 844 573 735 278 174 684 452 682 899 970 789 835 908 987 386 897 860 902 331 729 010 997 528 235 035 087 112 797 708 754 321 309 235 649 641 458 448 546 202 641 325 025 116 529 145 343 826 780 698 137 010 715 232 827 563 397 955 177 301 092 036 512 212 709 652 397 330 557 492 552 129 447 411 869 632 662 989 208 666 495 442 357 711 773 977 566 312 805 249 817 883 278 819 946 729 876 844 013 783 351 782 749 069 920 143 344 155 368 367 625 612 491 223 818 404 962 295 912 779 558 490 993 156 692 671 425 246 967 693 304 231 384 385 773 277 986 283 469 810 079 781 594 032 037 751 593 029 354 267 741 095 767 081 143 665 737 347 849 962 423 926 131 022 101 091 671 792 120 706 817 865 007 550 634 607 140 598 439 940 720 065 114 756 277 584 724 354 011 628 612 180 602 577 117 920 088 447 284 785 760 100 413 986 052 461 886 215 528 090 417 485 583 968 753 855 450 299 468 141 301 249 702 016 757 092 334 687 521 643 384 879 075 545 369 924 714 308 550 713 253 445 288 866 223 788 695 405 119 975 537 214 992 242 633 937 270 315 788 296 455 894 443 131 676 675 205 216 799 682 435 550 689 996 496 002 253 059 457 595 257 213 042 679 204 372 267 650 853 901 845 672 104 028 923 598 294 857 536 949 068 286 193 303 315 518 718 439 339 981 816 139 051 432 543 498 242 753 281 030 861 749 881 565 283 654 882 332 000 917 611 123 309 844 311 666 539 011 375 735 302 802 131 884 527 368 794 006 740 457 695 360 475 721 273 835 998 507 145 267 964 203 969 679 281 373 379 964 636 313 410 566 483 081 963 276 057 599 096 219 837 136 057 715 311 511 958 149 593 024 993 820 297 075 241 024 775 361 700 116 599 475 316 519 178 972 871 118 577 073 348 450 982 184 461 590 713 792 141 611 432 169 361 991 266 545 328 806 672 658 394 297 151 043 118 840 035 876 260 035 644 899 603 077 685 339 697 041 481 555 491 097 414 009 427 725 169 939 978 550 293 678 298 669 493 686 618 246 939 625 960 079 040 674 791 105 868 290 723 365 373 685 658 617 310 630 968 590 694 808 722 580 215 247 582 367 735 299 319 378 033 911 188 962 343 028 529 707 366 521 884 490 482 428 568 608 513 134 485 882 842 518 789 824 490 737 313 485 572 431 944 089 163 261 910 461 734 663 504 347 754 866 105 100 326 903 945 455 639 743 346 160 316 585 162 590 894 703 698 620 340 307 139 668 420 198 332 237 436 152 351 635 589 389 692 752 049 789 292 669 722 110 188 723 009 077 349 885 317 177 893 339 938 077 103 623 045 823 831 033 585 103 484 890 523 734 935 628 405 136 305 780 936 414 915 604 979 900 833 937 102 832 614 099 617 492 003 605 184 816 522 309 093 856 799 606 356 658 834 902 137 768 653 539 917 835 272 720 426 011 405 155 494 446 332 904 653 674 149 466 718 016 253 117 916 558 896 782 449 101 338 580 338 060 155 844 906 537 231 027 735 226 553 034 394 409 687 983 139 270 286 437 440 391 738 943 910 949 044 855 021 917 801 008 723 425 223 832 894 238 616 054 465 768 498 019 202 946 287 729 262 455 809 344 625 120 255 070 361 130 061 047 290 694 689 426 404 242 813 461 480 104 427 080 648 411 794 021 599 958 691 443 518 628 321 198 904 228 197 313 421 067 179 559 563 926 697 389 947 254 479 226 121 482 935 128 320 816 994 762 057 284 009 533 789 682 882 057 213 953 631 780 867 173 426 170 944 029 250 417 814 748 328 198 442 954 426 394 526 239 516 426 010 539 893 191 773 850 070 232 709 961 213 487 182 149 136 208 423 456 350 779 170 861 767 890 006 771 013 676 276 827 379 626 545 321 204 147 399 247 798 989 114 163 840 581 716 138 567 260 583 959 609 478 786 022 952 513 015 761 343 739 996 047 713 294 839 316 030 292 063 129 596 908 175 397 636 638 267 222 138 373 118 061 101 697 189 157 727 853 069 671 735 866 013 492 016 888 458 271 801 430 127 286 270 433 351 750 514 832 273 768 551 692 690 129 409 090 122 514 549 894 596 608 474 252 584 917 066 571 836 103 623 496 884 667 353 727 560 066 724 916 885 718 966 255 622 601 079 993 592 476 990 461 759 931 438 953 801 415 765 985 923 608 630 362 089 151 710 235 947 081 238 403 262 902 159 793 249 592 704 579 568 279 861 290 958 371 904 680 614 511 661 643 727 195 748 861 311 933 415 186 155 998 004 202 991 275 020 354 024 027 644 410 899 576 962 277 653 705 108 717 515 670 322 009 682 856 439 131 106 600 803 124 841 739 030 982 341 671 264 062 415 618 690 830 641 357 830 993 094 222 508 543 476 741 954 920 935 720 934 973 738 948 833 775 451 280 748 344 339 545 323 550 714 515 918 450 882 204 901 268 622 480 399 120 126 293 816 053 324 066 634 319 045 058 236 996 277 545 947 430 915 629 682 625 630 130 606 702 294 330 839 662 730 325 546 053 500 861 333 986 040 093 393 344 140 681 702 180 124 103 255 033 551 726 380 579 126 885 579 373 300 433 737 106 490 674 936 203 887 358 658 191 668 184 427 242 206 816 683 989 838 632 174 854 704 366 054 936 594 299 427 687 556 462 515 011 276 741 417 205 502 479 598 320 995 858 791 647 236 592 672 153 031 105 722 230 328 084 731 588 172 092 623 852 028 644 916 817 015 568 820 107 189 039 373 828 300 370 540 967 036 773 275 923 781 457 231 838 332 823 353 250 126 909 216 218 051 203 889 871 793 361 708 462 248 524 940 542 515 212 547 670 159 795 460 493 926 440 827 534 362 348 127 259 710 475 338 115 850 175 291 087 743 250 569 390 754 140 068 571 455 537 529 013 954 839 343 321 513 527 925 511 301 509 623 786 363 989 927 881 347 614 930 093 226 680 458 488 594 354 764 351 884 753 938 012 409 679 462 225 396 358 689 780 721 134 413 281 041 572 609 119 024 684 006 283 463 331 860 521 114 749 139 388 462 673 468 394 588 536 555 400 925 319 856 022 264 710 905 830 696 471 665 088 238 713 285 748 783 368 041 626 773 294 486 543 959 285 382 569 817 407 340 431 414 108 384 401 494 036 799 503 755 292 972 032 998 020 225 086 874 085 890 535 359 542 122 912 793 007 215 723 768 031 508 194 061 180 916 895 197 589 831 335 442 601 173 699 108 967 886 240 003 324 542 818 679 855 430 793 022 301 497 447 932 297 397 305 133 052 702 452 366 862 016 623 994 883 586 870 208 906 969 138 087 247 724 997 507 314 366 606 374 851 694 657 780 758 385 563 268 929 703 192 959 471 046 994 281 970 556 292 968 560 762 483 795 415 977 077 161 131 221 278 083 649 174 096 590 990 546 110 250 818 375 129 907 466 450 812 552 155 851 977 673 168 161 599 532 750 506 138 429 308 890 348 681 789 861 579 915 528 236 682 193 808 296 773 835 030 948 658 992 718 135 151 741 600 089 214 718 427 952 655 701 849 088 891 343 409 714 689 893 454 443 749 446 056 865 447 835 031 911 270 969 195 478 716 221 143 222 675 450 775 500 418 567 804 635 240 831 696 300 549 376 295 418 141 071 780 472 776 784 634 694 741 827 858 976 472 066 772 554 589 162 391 330 557 584 449 125 548 150 451 255 289 312 532 326 241 332 631 025 404 866 526 870 142 929 718 736 803 314 243 924 775 616 225 702 959 890 860 319 301 169 550 960 993 237 850 076 223 069 757 015 761 312 984 296 825 449 051 192 108 026 923 070 120 439 012 230 687 645 183 304 456 417 697 485 510 334 804 676 984 081 411 401 836 599 411 389 678 885 260 626 059 956 154 624 447 803 271 873 240 116 265 980 003 966 923 595 607 850 690 436 809 132 666 623 700 084 620 678 116 523 402 124 968 865 179 327 458 265 354 776 342 081 384 238 245 090 190 254 049 495 692 266 031 872 898 286 097 753 663 497 536 485 571 199 763 496 898 356 201 681 370 292 815 609 591 644 314 902 200 657 841 021 252 388 353 368 942 560 608 686 952 778 499 091 274 277 530 455 349 056 836 620 442 584 656 546 123 473 303 098 953 006 044 615 521 241 946 929 255 611 623 654 953 001 414 407 981 790 119 512 425 709 290 643 798 474 505 295 206 821 999 299 729 186 109 414 797 914 803 465 699 255 523 841 949 402 181 220 808 313 766 103 669 110 314 915 161 114 721 721 545 376 391 853 704 405 365 293 713 475 569 819 172 071 286 069 175 403 603 421 515 977 286 448 891 739 270 044 438 728 457 418 182 058 249 838 903 618 715 743 707 944 883 293 343 149 503 525 178 449 669 561 508 846 709 149 908 829 572 561 389 696 743 264 058 714 058 933 329 620 144 782 214 318 007 753 237 251 583 673 599 580 861 753 835 124 589 964 457 411 498 865 619 452 297 698 029 329 778 774 267 871 154 205 398 865 917 768 118 317 597 345 570 909 894 052 115 509 814 772 787 945 739 568 606 089 073 022 955 597 154 452 449 577 037 474 868 061 949 421 234 062 052 890 173 014 662 672 898 608 416 288 025 352 138 167 230 590 756 423 107 426 112 617 498 948 007 441 919 933 503 135 858 725 569 452 784 019 919 152 278 916 269 733 462 901 747 668 162 818 277 935 542 593 785 714 456 335 073 159 170 555 343 599 524 594 982 635 756 276 122 650 849 237 413 409 490 896 098 044 441 716 002 744 276 136 691 356 746 836 251 338 444 990 888 126 355 488 184 773 388 126 639 094 775 205 873 304 683 095 071 036 228 427 981 459 640 013 438 694 834 115 593 679 026 836 341 765 441 976 265 621 176 762 062 601 505 869 460 584 570 590 328 110 648 287 887 857 183 816 829 412 471 673 586 489 665 504 762 927 494 971 106 234 543 759 303 577 782 208 896 592 327 530 227 534 752 133 746 654 325 464 205 862 516 019 421 278 860 543 090 456 829 550 001 434 554 709 334 241 413 644 217 550 256 455 702 434 811 995 327 781 092 831 500 467 988 705 107 767 303 400 828 068 229 664 688 764 224 044 823 455 916 014 278 351 456 985 596 392 557 070 572 572 685 744 245 179 074 671 569 813 689 480 528 581 782 846 198 623 897 884 359 624 368 710 572 035 450 203 742 273 963 066 322 493 187 868 334 117 033 747 599 491 014 526 786 163 959 664 340 323 232 477 143 298 560 449 776 458 731 338 486 168 061 551 109 546 834 524 260 404 483 253 555 242 183 143 087 772 381 474 742 691 867 933 749 483 296 825 646 462 610 136 699 798 023 613 685 276 180 219 851 544 271 856 088 860 635 966 103 944 090 679 640 702 591 419 119 804 637 068 057 746 322 775 529 741 457 654 090 705 067 403 566 129 560 382 880 722 812 000 807 199 639 677 358 318 605 876 281 068 090 686 342 705 210 877 805 004 084 268 940 878 756 135 711 045 511 817 746 071 022 651 266 861 859 819 616 177 297 041 891 962 952 498 443 152 521 159 184 293 057 024 454 827 906 073 945 670 941 892 072 507 015 915 116 321 898 912 687 187 386 410 783 477 242 544 363 653 329 106 182 341 278 464 644 284 989 992 199 220 167 193 238 159 327 441 178 363 870 350 366 993 142 115 198 567 171 893 119 570 540 208 236 456 624 375 018 587 593 960 297 804 933 146 054 422 065 699 352 145 167 080 236 383 365 945 208 764 614 705 003 179 064 491 515 639 950 936 945 717 440 489 981 060 587 158 259 058 727 290 366 991 670 856 514 900 088 757 816 432 938 673 274 712 726 203 774 304 935 434 096 307 756 907 039 437 430 294 409 069 266 424 972 088 520 484 971 358 888 996 403 439 807 138 504 671 667 203 392 169 009 888 243 338 253 246 019 991 917 013 170 227 982 152 612 963 233 478 043 925 963 526 718 266 074 296 694 494 235 681 059 752 750 951 468 559 672 328 549 392 804 968 438 875 269 260 349 017 127 006 599 360 803 123 971 020 871 215 460 728 462 453 518 279 593 025 162 271 656 301 767 595 214 497 318 373 199 395 845 683 713 241 112 652 482 451 878 032 986 677 977 688 475 081 420 866 125 474 729 737 238 002 658 519 850 993 645 102 947 189 779 562 181 984 813 531 022 586 570 024 391 926 352 047 307 880 655 092 143 200 076 546 970 180 219 400 304 738 176 269 142 336 537 420 539 820 828 678 945 277 856 735 621 975 271 787 777 219 119 179 636 528 179 888 000 358 304 389 933 358 838 169 839 661 969 829 326 474 889 117 468 939 560 108 387 132 110 838 414 879 959 944 923 984 836 641 997 971 935 127 182 946 730 454 115 178 469 077 227 906 223 475 324 493 934 090 782 130 989 900 268 322 611 540 320 626 324 244 958 296 955 909 079 243 868 630 181 004 874 242 573 478 427 809 511 354 704 142 733 678 298 259 572 260 352 612 503 295 611 562 612 745 251 161 345 100 802 452 590 954 842 515 865 082 545 951 734 317 776 870 424 064 887 909 813 578 472 554 376 999 841 013 675 771 247 677 287 233 487 155 748 018 772 544 271 238 114 044 095 425 588 350 504 007 160 537 622 717 277 325 163 877 027 188 858 392 890 154 418 158 360 677 596 331 295 820 939 266 991 710 579 427 597 309 721 055 692 542 100 738 333 866 561 215 192 751 595 131 586 959 165 606 805 674 651 529 426 526 641 136 190 601 001 477 567 441 222 586 231 850 630 457 427 158 780 233 995 546 844 550 073 994 341 030 784 534 211 267 454 401 990 085 470 353 367 140 995 703 149 266 358 294 346 603 834 615 105 166 628 668 873 145 763 138 526 816 514 834 589 842 352 003 313 968 822 201 595 658 557 903 152 921 808 964 957 549 699 985 115 478 912 447 810 682 262 392 794 363 204 136 959 197 252 735 596 335 456 868 774 589 815 985 451 173 282 354 625 354 227 178 150 687 533 240 543 500 975 755 878 175 922 094 124 415 786 426 433 887 405 777 381 829 172 931 654 708 766 967 460 152 115 783 118 508 593 525 015 781 657 474 973 289 468 857 325 164 108 826 398 561 558 366 596 611 061 089 433 195 311 308 534 955 097 061 142 901 847 385 579 052 098 899 590 618 539 472 669 169 192 201 290 789 970 773 497 362 728 037 626 954 852 438 616 063 579 610 840 119 716 934 057 889 604 249 916 013 672 233 006 213 304 851 630 651 802 990 118 852 794 053 970 899 332 072 772 429 869 038 162 161 020 854 906 837 507 369 950 729 367 668 938 849 486 061 332 314 572 078 646 158 421 193 664 840 308 873 526 075 749 967 499 857 832 536 306 477 091 478 989 350 178 203 248 220 922 057 419 828 399 125 414 812 372 637 471 684 586 783 555 900 694 624 811 791 838 186 223 719 834 164 662 070 468 414 200 946 312 146 099 474 731 167 936 963 244 013 310 484 976 333 614 794 608 432 108 257 170 239 033 194 406 244 663 214 506 869 432 998 909 078 754 939 025 976 835 522 319 847 601 988 765 582 713 493 816 051 398 524 341 532 019 564 214 952 337 085 615 144 303 605 011 242 771 046 698 431 542 566 322 725 208 916 233 791 379 408 190 363 104 859 757 908 301 383 393 650 832 284 864 852 684 716 567 246 476 088 282 840 651 999 712 708 018 482 845 223 266 822 452 874 534 207 094 998 985 777 699 069 889 198 177 025 520 197 441 836 635 564 327 307 448 682 951 204 954 122 357 752 942 378 669 312 158 273 753 541 177 019 350 091 238 886 025 319 144 559 840 094 286 656 756 866 272 779 377 235 052 689 781 853 683 639 226 526 308 861 900 642 604 282 830 022 121 690 916 589 869 269 707 921 544 272 609 046 091 964 164 078 215 646 956 731 722 940 777 284 278 948 988 135 224 010 964 586 537 917 803 159 057 905 897 971 092 120 139 645 364 601 653 119 787 109 545 959 398 516 188 418 452 700 281 626 522 692 917 827 195 671 035 325 044 550 698 301 874 971 508 686 695 896 319 985 101 078 349 108 459 308 472 314 561 483 284 750 121 615 147 366 921 144 607 639 349 766 041 684 157 541 982 429 247 943 030 156 014 677 732 657 436 050 792 206 661 985 896 110 167 372 113 129 409 178 949 902 781 919 482 174 296 489 063 819 569 768 441 562 470 822 135 759 266 192 791 214 930 586 555 289 724 266 604 175 407 842 833 407 397 794 609 730 524 665 754 413 523 029 110 607 214 364 302 631 610 362 214 887 557 896 404 303 395 962 748 775 247 334 489 488 804 469 282 219 852 679 810 172 764 074 748 270 730 077 460 556 317 106 371 027 287 755 558 565 990 697 274 711 107 946 211 318 665 187 554 538 731 061 786 323 852 383 540 494 733 539 215 438 320 176 918 877 519 107 187 667 958 240 096 656 550 253 209 845 309 704 522 570 464 576 163 218 897 031 710 677 940 072 133 039 679 756 737 775 068 169 357 645 671 933 711 376 272 009 021 451 335 600 041 605 705 236 923 245 079 051 502 317 004 825 982 548 359 919 076 795 878 371 936 525 225 078 625 179 455 509 939 764 173 716 776 199 408 923 950 618 904 672 480 027 743 651 294 666 022 916 761 259 970 092 638 512 039 405 656 333 436 027 742 045 653 334 934 593 121 811 519 122 704 718 082 771 255 865 245 540 560 461 654 733 071 735 247 272 654 889 385 643 837 470 857 454 813 334 958 540 162 877 432 615 426 994 632 123 836 344 067 133 331 040 148 820 363 672 850 423 814 467 238 029 545 316 431 391 618 670 446 576 225 280 261 060 128 405 228 428 305 665 049 665 221 540 458 767 317 046 506 558 153 379 157 663 924 214 632 060 479 248 852 866 969 187 971 885 373 740 004 599 313 882 433 234 559 992 681 976 729 447 879 210 535 771 836 051 665 218 246 337 925 064 262 646 378 201 807 934 550 466 243 298 036 838 360 040 038 639 281 539 839 901 484 456 778 642 426 640 545 102 612 538 212 603 561 517 830 082 422 820 971 507 574 510 437 592 565 927 171 054 533 772 490 297 727 974 314 879 788 762 440 192 162 947 817 798 674 191 199 247 715 560 111 075 224 294 114 949 595 137 733 545 131 078 612 032 766 209 598 817 000 897 346 608 827 951 670 007 358 670 109 200 403 764 004 773 679 798 577 959 787 581 894 050 273 577 361 698 108 744 601 810 199 631 915 447 801 659 699 544 009 590 664 997 043 217 762 776 718 371 708 917 378 677 351 272 490 503 238 847 534 910 872 463 166 559 093 714 078 438 629 860 504 623 453 080 746 880 912 760 833 008 968 371 328 429 768 386 420 562 990 011 510 047 271 237 942 326 985 482 869 394 407 152 822 967 097 101 369 261 030 949 579 096 434 985 284 870 680 058 659 353 418 182 233 917 112 122 517 440 301 719 415 351 703 340 531 814 383 046 404 268 844 469 733 515 045 307 746 800 602 487 881 427 976 350 341 131 270 566 639 669 225 828 529 514 330 414 902 602 471 579 571 410 422 144 078 416 563 607 889 639 175 203 263 324 012 234 775 977 143 346 710 460 507 759 513 191 731 975 332 318 931 993 404 724 759 478 531 566 154 230 954 838 180 989 028 320 151 422 137 648 618 383 632 371 849 681 054 079 567 776 280 906 728 628 946 932 652 673 847 116 153 392 092 666 050 514 939 087 060 517 951 577 677 940 275 346 261 679 552 551 407 212 809 889 789 862 747 456 613 864 027 440 845 682 640 924 748 938 591 989 894 847 088 026 779 956 784 147 531 831 650 006 534 045 617 794 519 359 015 016 618 607 245 035 219 666 640 613 963 260 203 639 908 219 789 351 803 821 793 802 608 341 876 905 083 882 305 097 888 681 899 610 031 190 878 787 406 456 921 958 488 715 805 460 740 642 314 882 344 614 233 298 305 761 750 926 356 739 821 135 759 306 515 500 654 874 900 080 749 767 976 340 343 040 838 763 411 135 140 626 690 198 554 904 838 429 977 016 355 409 516 243 691 429 162 242 381 823 383 979 332 584 100 768 578 836 093 043 332 511 023 808 043 541 244 736 449 136 550 158 520 126 672 372 197 726 304 765 640 719 545 582 507 670 997 186 350 787 572 333 721 829 022 996 627 852 529 316 314 116 367 131 427 371 763 281 535 461 043 844 034 881 940 233 339 058 773 862 937 403 192 689 117 100 021 270 684 767 303 657 816 562 469 183 048 892 059 171 311 332 051 436 261 050 320 818 112 176 115 942 060 104 551 952 695 525 270 478 856 656 057 897 998 870 414 587 975 217 337 937 745 096 539 223 619 370 157 315 699 985 560 155 541 026 675 436 192 493 462 357 131 760 458 701 551 474 398 147 212 270 434 183 353 032 546 430 152 654 102 648 817 129 100 588 351 582 454 844 639 892 956 194 181 713 853 192 921 210 723 470 979 582 524 898 215 574 847 295 406 608 511 209 882 881 749 807 797 292 639 408 255 685 709 474 162 049 586 409 279 567 129 932 114 831 719 383 590 339 724 982 868 304 751 851 467 321 985 846 446 859 543 834 262 957 951 232 907 832 565 088 107 094 310 069 439 763 005 990 700 472 743 978 364 929 881 952 691 383 958 402 132 988 011 153 212 699 750 857 764 490 803 944 478 469 700 502 189 783 727 131 512 042 616 695 913 269 144 779 236 517 600 767 301 801 090 481 887 812 883 240 039 666 611 838 278 570 978 558 864 508 020 450 132 000 869 081 879 897 187 204 879 297 857 262 694 251 839 072 218 771 080 229 898 238 124 854 041 932 057 064 545 221 647 620 238 129 484 907 276 043 275 903 285 094 882 509 016 323 551 541 528 256 134 286 917 714 386 560 624 623 557 937 627 127 288 218 002 959 162 219 536 724 979 962 868 944 649 186 905 229 214 460 980 216 418 970 715 014 620 092 504 601 366 890 499 751 144 402 806 325 451 032 067 219 551 686 013 566 267 469 443 822 453 976 486 150 639 797 675 562 093 060 163 308 836 334 701 744 401 283 320 419 543 335 626 273 483 366 034 028 529 809 715 243 999 335 247 832 170 271 615 441 328 437 499 695 749 435 018 946 767 683 316 329 067 123 225 736 898 287 766 432 898 183 304 940 230 239 609 020 086 499 043 569 187 755 182 789 701 783 350 059 093 737 416 752 074 457 409 239 273 871 060 596 668 555 614 562 632 764 638 618 051 042 790 743 727 349 389 662 865 127 255 611 392 109 368 394 515 644 781 185 355 372 660 000 180 845 005 714 716 652 207 786 147 394 554 613 112 682 872 590 016 165 466 183 218 488 720 552 174 026 619 882 656 473 942 157 017 524 945 657 276 296 317 631 669 780 521 577 936 926 733 650 840 208 704 143 240 414 213 105 979 117 137 183 055 569 650 847 523 943 364 086 703 859 480 223 613 231 691 389 713 260 847 927 313 346 099 650 941 531 754 956 872 362 992 791 339 552 788 073 983 259 394 009 674 870 485 449 585 545 767 947 155 135 184 099 207 657 419 628 369 028 668 556 248 051 002 081 958 044 680 234 315 068 661 918 696 026 025 089 389 524 983 307 261 668 692 670 857 639 758 952 408 436 706 415 079 742 391 969 823 922 183 405 143 109 264 115 020 313 993 796 565 457 706 633 350 661 806 857 598 768 250 756 762 983 966 988 135 251 893 000 537 778 572 597 477 838 837 935 615 254 081 490 326 727 149 137 025 117 199 933 065 900 955 198 320 607 953 903 606 038 695 815 858 394 152 884 655 833 519 752 589 643 567 206 570 948 607 632 742 316 804 685 823 818 757 753 259 206 975 858 609 364 890 003 708 364 578 054 874 636 903 049 443 764 204 343 541 475 913 614 608 258 236 190 401 122 335 209 304 137 899 383 643 958 201 703 755 596 269 371 595 455 167 374 985 144 956 294 873 864 692 761 467 987 852 415 812 113 466 235 719 452 692 481 777 212 243 302 493 309 169 056 910 419 043 479 868 778 267 346 941 336 655 140 728 264 781 168 950 778 903 596 905 423 991 723 350 102 772 995 355 683 557 053 012 892 895 276 434 870 787 003 253 266 477 863 053 726 201 373 080 882 718 476 154 950 153 754 228 749 612 561 661 226 952 824 996 732 357 630 630 396 106 957 191 999 593 111 949 138 912 207 977 397 042 743 950 609 609 764 112 239 103 529 941 845 990 938 567 175 100 180 783 860 729 533 211 796 658 555 050 066 284 860 836 285 126 297 601 515 810 571 673 879 326 560 003 566 389 516 890 287 550 148 097 058 912 041 622 693 043 495 761 713 120 701 069 283 791 541 159 041 987 625 062 708 848 262 325 512 550 688 080 427 064 642 444 104 979 010 223 920 261 472 946 642 631 092 266 171 170 988 230 424 969 842 916 823 730 538 377 567 350 472 319 619 326 043 384 987 334 844 206 900 043 281 293 529 666 553 190 336 307 601 312 068 754 833 747 688 440 509 552 780 832 991 924 511 609 507 924 186 537 158 474 068 798 873 174 163 006 959 990 748 515 968 218 562 085 016 246 824 918 770 205 436 086 300 104 111 820 347 173 459 171 335 262 589 042 029 627 787 900 391 789 019 193 685 920 594 580 185 870 124 649 718 074 326 791 601 390 481 104 830 876 241 678 111 776 800 392 346 692 935 507 983 290 163 461 756 477 455 864 563 223 267 190 735 351 231 114 625 505 439 735 169 232 245 592 267 480 331 617 154 014 433 245 760 086 186 858 878 565 226 631 384 120 860 519 313 333 879 665 322 260 488 706 906 174 868 291 865 447 108 745 587 163 257 791 015 954 547 831 148 690 057 506 008 148 552 014 238 318 229 004 795 186 462 330 168 445 234 210 923 205 113 941 044 532 710 964 984 441 050 767 967 462 799 143 420 878 576 391 030 442 775 596 571 380 434 808 800 732 112 370 755 343 673 443 360 779 920 332 034 589 169 159 853 787 822 289 196 064 071 219 000 975 758 748 443 442 261 262 588 502 898 065 602 208 106 114 818 628 691 493 518 711 546 583 122 473 129 206 700 961 152 270 648 910 182 009 533 386 473 527 984 477 425 222 540 475 131 492 864 776 231 004 809 455 150 327 629 716 256 004 768 486 270 071 083 984 927 933 916 793 391 616 484 318 377 486 432 184 919 696 683 625 966 691 642 389 162 559 217 317 951 381 225 324 975 322 303 197 740 707 922 547 595 991 263 749 716 236 967 871 929 866 603 679 989 285 756 477 819 596 653 161 434 562 415 341 669 478 641 560 545 621 453 496 902 757 683 529 445 982 046 199 372 457 455 092 165 376 431 927 950 614 947 996 954 800 311 005 183 373 356 970 843 657 816 414 357 188 724 374 507 806 960 699 649 194 695 178 428 888 848 719 398 775 914 431 614 087 139 234 231 596 414 604 228 047 638 596 415 389 385 853 732 934 395 196 322 103 018 457 964 335 883 781 458 255 750 563 946 070 196 888 290 747 756 244 257 269 584 953 986 259 084 021 192 675 478 732 127 851 794 268 984 729 945 755 863 705 914 624 593 932 307 630 403 257 251 859 239 646 681 048 376 381 183 783 608 890 712 780 380 569 525 465 925 661 598 081 192 309 134 501 973 522 234 858 063 453 453 682 615 846 284 160 102 709 242 918 945 866 904 937 868 654 170 517 621 650 680 239 404 570 533 229 882 006 587 827 165 418 787 058 636 855 416 991 899 722 968 437 693 596 933 542 370 945 329 736 275 881 785 734 533 300 655 608 213 267 633 422 471 428 508 113 919 328 934 529 826 400 284 699 374 396 757 713 406 978 909 816 059 188 997 581 770 936 394 579 043 397 184 171 792 094 147 378 254 459 952 693 000 755 294 428 574 645 909 416 548 435 013 512 815 740 544 475 903 407 865 425 092 136 248 626 226 186 403 110 313 279 601 620 632 211 054 371 582 632 034 464 045 795 294 814 860 638 828 012 721 779 593 472 578 209 298 595 736 893 842 073 350 144 862 520 223 803 157 106 748 585 659 402 132 730 851 129 208 572 052 998 387 720 116 693 399 669 924 618 972 092 788 882 539 707 285 684 828 377 502 655 036 495 716 740 702 358 525 375 982 724 384 669 137 996 791 041 935 388 109 742 643 894 315 955 127 025 839 982 585 515 378 968 182 655 311 117 830 442 208 462 121 510 650 605 625 377 630 663 367 137 904 414 243 657 899 908 091 638 023 189 573 602 029 799 460 974 427 880 332 300 567 245 256 073 038 324 032 103 678 655 184 209 746 085 637 906 340 424 642 857 843 619 072 923 160 439 300 635 739 741 433 334 075 075 379 089 568 812 567 399 640 901 878 133 347 139 685 631 407 077 948 101 987 918 498 473 702 594 330 283 163 096 319 313 674 144 017 293 671 989 200 865 696 198 137 930 051 169 100 912 668 050 776 581 009 450 990 780 130 093 815 861 901 249 817 137 547 465 986 820 761 583 354 270 828 757 086 908 218 221 490 416 150 568 088 509 444 531 984 430 442 737 741 985 562 290 887 737 275 406 822 600 010 660 091 978 305 793 517 616 118 465 628 825 476 689 530 477 828 789 507 134 753 250 593 255 038 401 052 328 237 510 158 215 934 286 163 419 333 872 110 451 037 593 069 644 304 455 803 666 714 524 449 257 009 965 991 465 773 721 666 541 113 008 941 650 621 222 645 773 380 872 921 696 303 006 919 670 136 029 459 731 522 804 811 460 515 759 744 289 491 459 083 757 081 867 278 136 661 037 108 609 729 182 357 874 577 294 893 611 557 069 478 950 700 634 995 417 096 418 824 313 727 290 664 387 806 800 924 036 603 584 118 426 837 377 896 468 194 924 466 705 086 311 512 548 082 825 691 767 762 817 755 405 149 540 395 597 409 503 137 618 218 687 757 497 555 218 240 893 928 054 160 766 630 925 491 166 453 990 164 463 431 052 930 844 803 729 944 437 244 964 474 660 120 703 179 184 459 500 588 485 267 196 698 595 639 027 792 311 004 712 568 147 531 583 643 354 079 129 734 779 735 503 042 882 845 450 380 195 074 713 982 107 308 670 779 512 461 387 532 292 139 418 579 642 808 212 887 199 890 585 931 426 948 835 577 719 035 808 159 091 282 682 383 269 512 765 379 754 312 927 404 812 770 033 678 048 880 449 022 012 460 426 242 111 019 448 748 792 850 201 446 517 789 516 937 007 553 379 353 586 198 782 343 575 182 620 311 302 798 400 924 581 265 283 443 848 166 169 658 759 992 456 188 494 541 304 347 877 616 035 621 079 407 919 133 319 329 494 794 258 542 497 315 008 888 680 234 234 713 082 477 915 830 934 098 613 690 245 993 855 826 438 014 702 511 220 252 351 125 029 173 248 048 396 376 832 578 719 327 262 785 416 356 062 309 647 955 013 804 607 958 973 871 957 407 264 034 418 383 053 232 723 617 892 082 629 380 166 444 889 774 191 085 383 173 999 645 803 369 212 829 615 262 194 543 745 459 459 257 203 344 058 274 467 795 194 018 062 085 723 370 780 942 896 433 653 146 673 477 352 593 757 100 938 058 544 140 155 040 713 882 933 540 106 744 566 703 356 765 425 359 904 610 883 692 962 374 188 565 553 146 344 099 092 726 386 985 088 846 985 458 020 958 595 607 050 670 029 606 289 143 684 320 773 997 331 355 883 681 697 884 136 921 683 541 706 085 417 287 399 338 838 404 750 967 662 065 094 271 526 637 902 996 326 444 599 758 041 961 377 682 762 512 815 256 485 095 572 685 002 187 480 295 222 520 901 526 688 602 116 989 687 937 984 983 948 184 901 417 980 398 218 203 197 050 439 721 881 420 618 850 426 133 940 015 058 881 040 238 955 299 774 228 407 610 647 187 115 969 476 377 649 734 237 070 955 502 221 764 198 029 763 171 029 190 345 142 670 402 749 179 640 124 931 010 016 166 942 616 559 421 866 508 280 450 040 521 755 101 392 045 218 244 277 664 154 615 146 768 721 771 237 306 591 947 277 692 686 222 981 952 251 224 431 263 562 095 258 557 514 358 200 712 782 493 392 276 951 753 365 044 981 060 187 159 798 816 640 785 413 860 341 244 336 082 653 212 770 400 326 720 077 404 097 679 888 515 214 631 190 254 633 352 772 277 150 728 878 863 463 121 371 528 412 982 487 344 657 834 914 885 558 011 846 542 135 170 129 987 332 493 683 322 102 079 874 302 455 688 839 278 586 073 431 033 291 773 359 006 614 281 193 890 133 558 991 097 188 894 573 791 078 841 193 143 536 704 386 604 867 523 606 219 466 752 465 500 941 789 045 930 866 069 988 332 072 729 147 079 763 300 963 982 635 250 298 335 659 047 641 034 820 944 693 808 404 718 654 228 366 001 926 600 942 724 624 354 794 647 261 405 649 161 896 124 223 889 068 352 927 754 600 987 220 433 484 481 166 537 949 600 126 674 131 252 319 125 369 982 845 726 134 711 609 537 481 191 543 213 409 021 186 544 584 472 470 157 805 748 794 146 118 448 868 633 061 435 883 789 296 098 064 862 505 932 396 155 131 504 313 270 163 147 201 060 146 067 193 871 523 694 809 915 336 145 110 406 386 868 552 710 275 129 640 546 000 581 432 822 584 939 249 422 144 175 765 628 633 404 718 659 214 502 950 489 687 978 882 754 648 491 688 381 774 139 615 045 395 941 749 058 389 418 013 454 381 774 851 421 894 725 135 959 083 944 434 285 813 617 370 220 488 154 174 692 479 288 890 361 679 516 456 318 320 423 607 233 754 734 728 101 977 681 447 450 444 416 151 032 132 773 037 423 786 319 670 262 412 400 460 714 966 555 223 356 003 697 994 284 188 276 118 662 027 025 605 639 828 773 323 245 963 223 904 849 366 987 658 693 602 690 591 577 367 458 741 352 715 036 091 443 414 932 895 473 675 378 469 725 788 320 637 435 974 985 087 732 245 835 737 811 459 732 181 819 158 296 263 712 826 599 868 471 936 856 410 016 466 733 249 292 201 517 614 032 503 304 067 495 559 893 008 386 577 091 059 845 766 250 608 873 999 836 723 178 173 052 460 453 085 231 975 199 334 941 030 904 744 287 592 330 684 732 850 040 928 396 125 641 393 188 892 248 377 767 975 464 932 644 012 273 423 006 147 469 285 565 502 855 214 644 638 838 674 519 487 797 574 502 045 501 946 548 672 457 391 515 591 509 633 746 000 100 102 936 533 848 204 799 012 975 625 651 867 880 929 824 628 855 486 946 941 962 935 556 944 001 215 480 005 703 336 207 431 830 148 712 339 659 550 858 253 605 776 254 879 548 516 404 446 664 548 867 348 302 070 786 836 455 133 748 577 288 020 122 178 038 340 568 398 120 938 622 613 695 063 631 731 814 518 626 693 880 621 777 295 195 522 834 274 396 537 508 828 337 868 569 403 489 028 181 359 230 281 419 769 881 581 171 515 110 039 110 696 981 143 343 408 324 126 160 191 292 638 152 858 453 999 870 948 783 824 987 463 353 804 123 587 168 551 934 564 382 444 544 405 220 427 952 356 128 151 292 570 792 792 663 284 043 300 419 227 790 548 287 205 917 068 321 722 165 834 592 868 256 137 530 736 820 098 805 023 756 535 907 476 647 369 741 103 447 488 769 112 479 435 386 231 480 802 006 578 801 824 351 747 703 832 150 687 411 642 690 566 346 918 121 545 386 272 684 802 454 712 368 665 137 826 447 293 578 158 167 047 217 037 898 267 827 616 936 496 448 486 543 360 149 272 475 389 916 595 721 981 666 992 982 548 850 735 363 993 731 249 978 203 112 997 029 562 425 103 416 798 585 004 192 631 063 983 649 481 991 412 874 597 881 693 419 328 050 709 534 462 734 820 544 372 564 587 618 961 865 159 518 796 924 802 398 901 595 321 402 172 849 023 999 061 350 142 566 704 819 372 680 498 374 243 808 411 926 289 655 130 860 803 215 745 420 206 179 533 636 876 374 671 518 159 981 459 677 320 430 350 704 519 246 032 850 270 729 483 508 627 485 304 765 582 543 707 220 106 298 048 853 540 002 385 712 099 807 264 811 466 852 623 187 704 581 590 467 068 981 824 038 754 939 689 561 292 100 618 383 231 098 789 870 764 352 340 615 247 185 686 094 084 620 294 048 299 451 976 745 120 222 634 068 810 742 221 831 419 050 594 692 665 354 613 009 345 913 832 947 965 904 946 221 622 549 506 138 250 850 126 524 700 673 266 938 288 949 935 072 676 583 615 802 454 185 517 724 467 480 546 605 818 659 978 590 316 886 078 172 201 351 281 127 951 755 394 235 326 352 463 062 692 895 535 739 725 626 355 399 244 992 630 327 301 462 439 210 212 351 079 488 229 761 851 865 285 478 511 598 773 552 369 679 039 526 304 096 703 597 166 008 258 506 881 525 616 525 399 946 709 480 619 237 734 492 004 539 363 687 962 258 620 129 333 618 225 188 853 895 211 874 880 361 508 928 836 939 313 538 651 637 393 038 477 016 764 635 025 069 021 113 906 354 248 524 937 695 848 223 442 483 164 712 393 192 552 248 450 029 914 995 744 188 242 882 966 967 350 550 533 880 117 657 252 416 220 318 589 988 503 007 272 332 917 616 478 048 245 578 111 846 215 286 760 312 234 885 752 873 273 158 897 951 242 641 884 571 034 889 750 206 632 703 909 622 589 692 036 514 967 304 161 553 284 982 076 241 785 056 449 785 990 903 969 020 344 542 230 458 061 191 167 178 187 968 501 685 858 700 137 588 262 963 060 824 391 634 034 910 570 036 904 761 448 416 494 099 844 227 032 191 308 134 979 919 844 214 730 845 367 309 718 110 286 066 666 837 337 932 847 894 457 694 848 248 774 785 027 569 553 363 195 007 206 277 949 841 636 410 782 298 740 964 575 493 616 718 013 517 651 361 019 561 131 027 908 334 357 080 762 280 570 860 842 576 885 242 470 726 606 015 128 584 034 402 491 072 602 074 273 685 155 150 977 483 014 858 964 378 512 154 539 043 323 095 591 198 511 211 268 532 400 567 146 493 520 304 076 856 097 056 369 198 742 756 704 750 362 092 372 089 430 893 198 567 554 633 123 596 715 909 273 662 268 598 088 461 150 829 036 522 165 776 938 132 234 403 283 433 312 671 810 873 275 887 605 938 921 110 652 817 934 392 716 170 634 625 995 630 970 386 140 111 925 906 279 363 571 455 380 212 125 777 770 153 762 583 201 538 641 582 912 191 509 447 199 328 896 825 345 048 347 951 223 817 253 985 689 176 982 271 268 875 889 402 459 205 033 539 078 569 052 163 813 816 029 373 302 443 010 051 986 735 468 985 349 905 092 136 352 875 686 665 173 762 372 034 280 689 849 471 488 361 070 826 418 530 152 843 721 371 625 781 466 932 011 812 143 586 823 490 425 843 832 267 827 148 836 368 188 063 263 241 598 690 423 393 132 714 785 201 699 951 241 939 568 470 428 744 480 205 204 248 006 284 550 664 421 267 643 869 794 743 797 194 908 597 048 605 595 943 632 271 617 430 469 872 055 882 357 208 838 622 939 653 886 242 850 615 872 146 223 340 732 063 855 854 305 129 244 366 624 174 284 084 995 906 153 510 236 460 992 817 146 665 573 085 329 045 747 035 290 037 704 519 633 099 856 346 780 142 175 886 427 190 733 973 814 081 356 833 273 102 731 880 233 132 088 971 992 343 431 262 501 274 980 613 223 817 794 308 012 842 797 114 183 588 157 849 081 771 238 458 318 661 724 706 261 083 481 370 838 551 424 851 597 991 813 335 296 931 259 137 183 328 487 655 002 524 226 532 614 451 309 662 574 739 378 427 748 624 277 783 105 544 322 866 454 683 872 998 361 465 907 774 956 817 502 003 509 918 750 536 304 993 628 017 890 826 391 365 041 694 779 897 392 352 372 083 827 187 412 273 027 685 887 136 367 005 266 480 182 057 868 321 394 538 469 873 151 150 548 536 301 652 842 299 628 500 321 162 836 060 393 227 548 852 329 814 328 171 218 859 009 744 768 421 206 217 624 053 103 797 873 509 604 592 257 569 281 361 286 593 151 102 791 536 963 273 892 543 694 858 387 914 823 318 098 370 024 141 082 558 428 944 758 633 985 413 607 817 366 656 825 475 106 376 806 899 182 866 699 756 971 394 700 623 697 832 376 321 667 682 927 280 461 746 819 022 956 320 781 397 239 901 288 340 332 577 589 067 759 749 335 254 725 353 450 594 398 475 964 463 888 515 391 068 791 169 452 072 201 972 906 091 485 304 418 753 093 132 010 726 654 711 266 574 480 025 633 538 465 263 616 927 045 362 550 585 486 242 435 092 890 380 055 716 257 635 250 211 356 910 970 298 228 739 022 227 200 802 619 277 631 942 918 956 060 864 216 284 556 911 525 838 957 225 607 989 117 191 637 062 184 652 250 495 134 312 285 693 907 005 712 164 664 089 167 033 199 156 024 761 695 391 039 572 682 440 651 290 143 033 893 904 860 503 608 432 382 516 675 837 305 230 004 356 339 496 905 692 276 590 778 344 678 829 884 986 678 123 468 306 168 962 758 341 551 382 831 229 313 424 130 838 868 632 509 227 163 748 121 533 581 871 651 327 464 326 942 528 352 712 345 006 931 778 763 910 713 016 415 167 866 600 966 860 222 685 703 785 069 967 150 103 554 423 072 810 002 370 180 270 276 064 918 389 663 799 496 644 381 825 553 783 467 313 298 815 546 159 256 027 784 751 533 013 903 777 518 323 561 719 822 333 854 379 599 094 282 180 131 864 302 090 632 398 909 199 773 704 041 432 292 219 536 656 315 555 440 246 456 290 092 136 894 779 387 989 976 697 987 407 080 040 775 901 122 905 587 957 127 459 159 975 635 094 453 941 021 718 143 962 130 923 389 151 241 141 672 582 891 178 885 167 041 997 818 170 529 567 360 851 790 518 236 596 286 562 676 734 707 653 778 152 979 268 958 182 342 762 500 680 222 360 799 930 028 340 423 344 779 718 850 654 967 328 382 804 029 995 676 526 934 592 856 537 904 044 106 806 284 592 007 395 917 145 130 164 377 659 947 515 946 664 796 480 724 630 505 660 171 303 999 261 188 056 214 434 421 229 134 913 077 984 557 066 657 034 697 889 499 350 138 621 883 106 134 962 498 982 116 016 260 171 099 314 006 193 239 555 002 352 001 769 902 783 727 241 908 535 960 026 375 980 732 675 239 432 234 728 357 014 493 109 639 235 798 263 270 379 679 613 624 594 356 391 839 386 520 802 315 498 715 350 536 527 773 621 876 047 353 885 234 604 950 947 419 482 905 571 657 330 775 907 626 501 362 515 203 050 249 723 921 540 042 161 317 927 416 726 660 483 660 316 658 273 616 764 358 070 931 557 958 353 084 145 324 327 491 261 044 679 769 647 358 507 861 642 829 846 953 364 118 850 038 120 285 475 685 395 401 304 613 646 441 409 929 858 935 960 104 873 184 732 295 284 167 969 999 465 620 099 321 115 449 001 678 569 070 873 017 441 633 126 596 270 653 870 948 002 219 937 848 236 578 405 090 932 999 066 917 406 703 831 052 262 432 530 790 011 927 632 348 599 438 639 521 328 664 965 240 058 565 889 557 632 763 126 349 222 914 310 698 347 260 495 395 668 438 403 794 515 885 031 457 573 362 770 675 527 768 263 589 623 845 235 154 755 302 003 689 790 018 330 331 986 238 721 904 002 994 306 471 202 043 496 071 234 848 945 690 157 393 465 949 252 243 516 419 052 037 478 945 715 598 145 611 619 408 343 356 914 481 212 323 105 420 426 800 315 326 878 043 288 301 216 027 427 696 898 103 664 136 308 330 390 090 504 320 251 985 659 351 251 725 464 720 886 582 628 780 031 970 025 291 654 803 688 233 976 031 166 688 261 274 929 141 316 208 814 985 077 461 047 997 836 754 631 317 681 929 871 486 573 281 657 719 156 927 517 413 011 395 554 399 316 671 002 136 034 200 673 947 869 191 844 211 555 688 841 662 854 943 882 129 194 066 441 341 238 274 773 028 470 278 042 512 295 496 456 696 443 900 456 489 580 814 347 572 535 331 157 225 396 860 244 921 557 544 405 358 951 887 957 557 041 368 627 867 914 536 967 606 608 001 219 725 171 461 565 021 844 204 049 561 160 929 346 216 504 533 267 060 632 130 883 076 913 164 466 350 278 500 524 802 028 837 494 531 498 953 970 830 849 919 858 709 638 809 115 215 761 804 010 468 571 510 627 441 042 545 061 073 272 845 115 387 124 103 095 336 025 834 261 053 474 946 109 582 696 112 241 763 041 234 862 306 180 940 641 489 317 344 946 683 234 027 701 121 282 874 799 431 693 275 726 012 546 011 991 209 693 980 977 189 084 594 249 563 368 339 260 453 117 532 810 194 101 730 233 391 151 654 787 290 768 184 217 327 254 697 004 589 179 460 053 833 880 407 018 323 712 377 443 317 384 340 969 417 903 811 405 589 904 192 931 166 424 319 811 026 303 216 605 024 942 422 322 844 213 386 531 402 651 156 876 523 270 962 634 296 362 240 355 633 374 045 120 183 806 036 337 568 475 929 387 349 093 211 059 268 069 645 926 129 882 845 273 712 647 580 077 851 111 441 350 100 662 686 654 870 713 703 842 142 702 830 917 256 262 794 798 678 766 206 098 957 058 197 579 620 853 314 009 679 948 649 285 084 772 534 707 354 126 252 592 934 932 055 263 496 959 725 858 756 503 455 368 015 382 589 013 992 405 156 060 746 381 040 061 303 724 113 172 089 712 704 018 994 325 287 825 855 983 488 090 943 856 297 268 310 014 226 920 299 229 386 235 259 884 326 916 083 063 354 661 310 244 965 862 859 333 690 915 762 032 472 777 404 356 027 905 495 591 141 585 399 154 372 582 600 093 938 579 493 180 694 180 648 314 485 954 157 611 806 190 748 967 575 875 113 304 957 230 916 072 346 354 627 309 703 443 510 604 602 194 766 211 747 922 745 971 224 561 502 913 493 646 816 036 253 486 971 141 541 711 458 669 948 095 400 197 263 540 211 636 538 190 519 200 358 529 636 429 377 996 786 808 009 350 134 531 814 634 943 979 529 805 501 832 609 863 910 206 820 272 442 218 592 214 621 058 446 672 263 567 283 011 169 396 709 117 883 288 897 918 172 034 803 063 085 711 585 190 856 925 273 738 099 336 113 624 550 295 579 698 437 204 666 507 217 451 549 293 403 597 974 838 429 203 305 747 120 720 258 803 380 691 153 794 704 882 650 603 144 003 541 428 177 627 878 707 032 334 380 026 986 409 151 855 096 403 426 167 929 795 595 396 040 196 165 928 397 050 078 787 839 903 999 876 098 331 353 889 507 334 230 010 693 779 062 452 309 443 407 908 336 511 114 485 947 862 214 370 323 902 816 474 070 041 524 312 794 714 065 113 583 977 888 357 139 697 140 596 958 929 245 514 729 740 651 619 580 505 744 843 407 112 742 432 699 584 685 528 799 641 766 723 226 964 485 971 337 664 870 369 758 766 296 006 096 851 272 207 976 248 710 515 437 324 997 406 336 196 079 348 831 208 567 358 288 368 628 245 305 570 759 001 174 807 636 203 586 635 216 255 590 613 429 377 097 217 093 359 946 272 676 946 123 417 696 221 840 465 884 458 275 526 765 348 214 937 125 513 259 972 201 737 828 106 158 629 696 113 342 089 845 314 049 174 132 702 863 588 823 813 582 171 574 060 682 110 587 779 930 101 158 634 050 937 034 325 135 280 799 038 192 398 187 724 268 623 138 231 965 911 947 250 279 829 613 516 854 198 961 439 939 163 740 458 296 989 413 921 309 737 848 339 691 613 786 215 514 755 349 609 422 938 469 651 147 414 966 129 996 861 259 206 271 035 598 779 341 800 725 989 433 710 709 623 691 742 836 365 907 125 588 123 606 146 419 499 322 319 687 352 048 556 683 669 754 155 812 060 285 546 712 744 466 979 273 833 418 908 749 892 821 657 106 804 213 088 706 478 016 431 040 191 065 535 580 628 126 017 478 779 201 035 917 850 020 170 562 775 556 077 852 980 093 702 400 144 850 707 032 470 978 199 699 969 583 607 570 190 251 443 213 018 123 507 019 126 416 575 720 322 062 108 686 647 409 188 792 396 146 420 117 652 245 489 920 542 933 050 030 173 403 707 948 996 405 297 581 712 037 047 208 750 198 635 160 452 025 413 429 947 259 179 643 168 213 249 853 284 623 276 229 202 735 897 083 392 916 330 513 463 441 900 295 083 335 054 076 824 855 082 890 356 553 288 921 174 750 000 344 752 757 486 286 924 996 144 757 570 249 742 433 242 623 336 230 123 342 573 030 786 611 963 605 893 657 438 095 869 386 973 154 128 220 167 369 941 685 663 625 677 199 637 546 906 776 361 805 244 229 608 499 113 104 218 948 512 952 638 461 239 787 538 040 576 448 616 081 172 475 914 711 817 434 429 301 181 435 530 713 538 893 190 373 746 682 833 857 649 863 224 026 813 501 647 529 525 614 033 369 314 283 575 920 537 078 586 885 209 526 352 985 828 340 823 420 932 911 753 289 585 070 240 010 369 302 965 197 196 807 630 986 315 342 625 409 847 689 001 849 384 408 080 673 566 031 999 453 007 210 962 069 365 547 899 000 330 340 224 790 432 299 859 116 241 079 225 457 884 939 694 854 696 824 070 665 132 587 126 919 634 847 617 231 356 092 539 735 211 951 619 353 707 025 072 793 411 122 973 410 266 833 532 215 050 446 044 376 844 506 365 497 273 741 419 131 417 061 481 401 088 257 317 922 171 433 594 669 507 801 119 998 979 581 014 250 107 479 633 738 159 022 088 922 358 706 223 043 129 158 619 376 494 013 558 726 268 812 459 481 651 782 753 135 324 026 133 417 296 681 525 061 204 661 054 396 027 344 955 508 757 979 421 044 714 458 803 539 692 690 958 630 675 282 682 207 456 487 466 834 579 186 456 873 864 195 892 004 039 206 050 575 805 585 139 641 931 924 218 222 610 829 667 811 406 988 280 263 460 980 328 068 111 838 690 802 302 827 614 781 281 794 203 729 040 456 242 831 382 656 090 035 103 295 719 233 453 415 530 455 726 192 263 153 164 521 906 378 917 896 801 096 671 868 566 703 329 878 166 935 918 092 714 085 540 536 206 127 066 098 220 345 089 809 731 971 695 875 967 561 929 379 552 715 529 083 248 786 349 512 212 341 502 232 964 052 577 015 311 573 965 192 639 536 034 826 116 767 987 696 964 386 164 192 858 121 988 921 728 173 553 449 058 878 852 749 480 021 692 658 866 105 767 292 028 243 521 116 822 260 949 707 689 866 644 757 465 083 111 833 855 868 245 538 880 156 526 991 226 222 566 444 538 133 248 622 592 193 124 477 812 333 800 855 350 149 005 979 550 251 334 977 041 158 051 369 216 202 286 263 689 690 341 255 463 510 257 282 087 733 539 103 410 133 789 136 109 303 801 346 914 567 565 194 010 189 708 242 528 335 101 323 482 053 631 472 738 020 782 816 049 481 590 900 511 381 864 295 229 641 747 742 331 632 867 149 357 234 825 258 868 275 237 593 488 100 721 563 739 615 892 123 514 449 599 336 139 492 095 898 708 328 495 772 851 922 178 939 254 238 619 778 973 243 401 823 483 060 928 315 931 550 793 106 791 750 565 042 478 594 105 278 628 495 792 472 504 195 373 831 769 481 108 848 966 546 711 332 948 363 342 163 505 467 654 939 571 363 129 469 080 962 213 899 934 251 140 311 895 860 215 772 120 182 007 867 603 204 228 440 254 637 157 149 953 104 916 970 334 072 448 128 809 842 790 500 519 446 157 472 375 917 785 871 613 130 385 696 893 122 165 810 830 283 527 392 403 647 058 127 260 318 599 289 113 310 346 268 249 427 431 903 388 966 463 996 111 164 206 445 368 241 468 165 774 282 169 002 238 342 624 632 157 971 603 460 294 602 889 183 143 896 803 215 337 271 813 404 974 764 773 843 253 854 138 596 250 819 590 973 087 676 044 217 566 828 019 950 111 038 009 015 849 999 310 170 552 948 006 086 933 163 418 665 918 079 456 117 092 605 664 478 842 853 073 897 694 668 878 895 025 003 912 865 028 199 952 107 675 181 143 218 536 136 718 826 724 419 303 200 318 546 620 596 186 583 921 491 199 143 444 786 554 638 714 371 715 222 779 498 413 100 761 879 994 811 498 818 712 359 255 003 985 261 016 002 774 647 779 159 376 034 999 459 262 480 517 811 296 166 796 028 838 232 066 191 116 504 656 126 620 553 165 598 918 064 747 303 278 948 459 326 351 749 003 553 111 655 610 160 336 054 418 652 243 248 619 840 163 443 658 752 434 724 902 235 671 642 312 561 446 972 100 397 682 941 008 328 978 135 594 236 296 968 283 654 453 795 867 850 174 861 731 035 292 814 104 117 686 898 902 782 031 885 736 518 769 432 299 035 448 220 440 557 582 556 387 253 847 387 738 877 124 712 185 186 077 458 154 803 717 327 160 924 216 862 571 985 678 267 614 820 576 685 954 227 773 089 548 261 275 727 480 654 132 905 038 348 586 160 975 410 459 856 313 723 053 644 399 085 669 813 373 070 895 790 771 665 380 487 850 311 632 687 719 272 091 326 153 933 197 199 916 160 117 103 713 263 147 641 351 866 373 165 551 007 682 984 000 655 205 499 683 456 224 210 135 109 806 292 035 612 085 706 506 009 238 109 738 103 128 639 296 525 972 666 735 102 545 867 298 459 874 475 990 513 357 249 536 649 234 685 392 834 225 987 180 273 939 250 021 074 862 459 631 594 985 334 197 150 195 413 492 525 676 386 059 500 912 620 707 426 315 876 555 055 713 175 759 472 089 983 118 353 089 614 399 139 574 353 196 028 515 835 852 605 506 683 158 491 711 670 998 563 849 068 695 965 524 464 745 399 794 886 008 276 217 913 172 581 167 046 230 908 117 021 754 407 876 034 160 752 693 238 850 247 346 642 272 036 544 363 843 326 237 730 724 644 331 101 296 210 431 569 337 007 109 750 847 662 028 440 925 318 036 631 110 713 611 798 105 507 385 250 997 194 794 481 057 778 129 631 144 617 299 405 395 483 616 078 646 667 146 214 037 797 570 217 024 312 022 012 467 429 662 951 380 129 434 381 485 257 667 409 525 202 732 506 149 310 103 794 979 872 493 526 225 669 777 622 839 301 291 481 911 455 371 992 854 638 838 126 055 249 877 770 961 760 574 884 529 115 366 888 643 289 495 567 336 826 940 844 244 590 221 651 516 130 453 312 810 809 200 603 593 232 111 702 895 092 935 750 069 207 630 510 485 737 925 404 335 569 114 863 601 477 647 699 984 816 919 466 091 271 318 167 340 547 262 469 536 654 191 498 871 935 588 436 135 694 750 534 322 952 313 470 329 163 791 209 019 879 107 827 661 576 434 536 409 910 729 166 302 567 353 571 247 208 969 517 937 961 113 016 786 890 400 658 259 259 921 561 512 005 352 250 040 709 118 331 152 137 118 798 165 600 766 835 408 538 215 047 105 566 252 541 689 325 727 141 214 358 309 342 929 589 425 933 722 870 004 773 067 487 716 559 611 066 253 986 972 883 581 194 271 991 526 497 117 050 579 214 766 409 003 374 507 412 287 183 244 414 190 119 210 740 903 184 125 219 785 829 626 212 760 819 092 875 308 889 064 545 360 318 408 288 259 958 139 311 746 919 120 877 682 543 665 327 376 515 229 501 839 199 240 425 426 538 503 453 213 835 728 740 998 192 032 761 485 517 922 905 080 003 878 333 843 155 202 794 438 253 122 974 581 902 985 207 632 387 377 021 880 969 165 714 318 413 758 524 867 074 705 941 821 619 037 037 435 388 023 227 238 516 138 820 335 258 918 594 999 324 218 649 279 013 660 818 790 087 391 853 562 339 919 148 883 991 855 157 556 001 665 170 194 973 410 364 422 044 233 709 512 261 454 597 864 143 303 786 932 072 899 455 019 179 133 524 654 136 477 328 784 421 269 296 971 700 514 631 057 076 591 085 921 558 856 896 965 895 468 327 328 552 209 411 287 792 679 200 056 321 774 364 068 941 801 099 656 137 446 585 903 104 658 473 588 578 479 434 912 575 962 322 260 173 021 161 974 041 027 613 219 833 342 347 034 390 980 825 512 882 475 973 030 697 396 233 857 015 795 920 365 916 886 843 820 141 685 309 785 420 915 546 712 675 734 917 040 238 625 897 285 138 366 269 984 168 248 315 711 926 678 578 798 978 211 330 086 009 718 126 375 360 253 605 180 982 009 183 911 499 856 272 269 935 391 753 196 165 822 378 657 686 186 390 956 079 777 586 100 166 873 093 952 661 400 861 225 505 070 481 145 977 207 019 296 889 776 750 223 856 237 070 742 424 977 668 072 471 423 874 898 163 621 553 544 712 614 330 876 379 107 278 913 715 113 646 566 228 104 347 264 962 619 951 946 306 849 846 713 538 110 744 096 189 660 572 647 998 230 667 601 048 916 139 807 469 859 894 712 105 050 582 423 807 644 481 033 706 570 681 492 718 373 175 615 249 031 497 567 141 738 887 912 895 043 523 151 502 845 809 659 365 577 484 059 328 123 367 009 876 311 134 371 252 988 308 838 417 294 226 542 990 499 996 159 636 094 192 468 843 760 396 920 610 244 149 057 227 707 759 584 826 620 439 111 293 143 908 107 706 415 991 962 032 647 356 296 403 789 467 673 775 097 417 347 690 864 050 363 515 905 541 250 281 144 683 559 225 350 606 634 816 785 525 944 340 498 000 811 018 163 918 339 977 349 850 500 992 228 398 339 221 502 172 951 971 474 829 679 177 426 215 489 325 967 658 071 949 695 550 759 049 834 619 856 865 066 398 780 081 318 817 845 329 588 599 071 594 996 056 974 282 996 035 788 772 409 222 201 557 533 783 096 069 060 722 560 214 731 282 640 269 958 353 996 691 504 301 072 437 977 733 372 260 933 422 202 236 947 762 461 292 995 977 570 926 640 049 961 498 913 375 023 697 364 326 278 304 166 043 914 409 865 687 133 107 655 482 210 571 140 207 995 209 831 806 244 562 695 029 832 522 306 534 831 692 883 681 910 808 351 865 234 629 679 039 264 784 237 232 154 269 614 250 022 374 981 556 376 262 378 095 596 918 272 685 505 703 187 254 390 674 595 686 559 190 524 520 538 974 976 443 578 542 688 850 097 526 903 660 625 985 726 335 071 154 332 967 005 282 909 785 093 491 341 309 714 084 888 923 387 112 673 139 210 090 960 402 955 711 570 113 882 884 216 485 793 833 162 409 938 314 562 935 822 525 595 874 264 855 094 903 111 121 629 654 392 035 385 464 566 837 865 557 707 945 155 216 512 077 322 879 174 878 021 655 568 351 413 510 031 913 409 363 439 633 935 541 150 203 307 968 403 307 916 305 103 449 438 617 626 687 613 822 888 852 462 787 428 642 000 279 759 543 206 423 575 254 933 507 446 600 057 366 542 695 805 054 982 207 208 366 975 359 659 771 946 684 292 254 370 957 264 206 571 901 389 748 023 191 294 881 781 720 794 938 007 133 654 307 619 225 313 425 141 608 646 057 887 107 151 007 239 612 178 992 331 394 959 407 200 541 447 441 787 843 479 080 492 606 591 936 282 565 318 962 113 290 127 219 128 760 261 676 197 088 016 180 309 874 313 309 570 406 667 252 231 870 140 379 979 581 711 244 580 175 218 186 079 673 907 027 208 204 288 300 618 152 928 551 925 717 535 643 312 614 920 895 504 771 485 656 963 451 896 781 925 227 145 207 380 613 898 795 099 541 979 516 386 619 037 712 691 979 083 175 932 500 048 258 232 261 334 275 579 242 005 900 067 592 399 560 694 064 734 959 209 905 007 134 412 692 949 737 593 324 139 249 579 860 654 909 607 511 947 773 617 811 603 696 299 649 637 499 117 032 227 310 715 818 419 313 739 805 895 600 393 017 078 306 768 223 581 947 454 917 398 699 264 302 266 652 493 551 445 056 292 439 184 157 920 207 906 284 731 778 279 363 014 381 115 996 073 544 923 450 187 063 757 170 734 362 963 343 736 130 204 642 373 798 643 390 490 946 696 603 126 979 921 661 288 816 852 205 561 400 867 004 958 273 874 530 905 823 087 323 206 576 060 888 681 773 545 367 827 422 289 129 029 075 608 931 655 406 157 576 471 655 611 296 143 825 201 861 236 751 312 854 160 561 048 371 055 113 982 046 415 561 607 992 344 975 647 648 104 131 267 111 810 051 131 631 492 086 220 751 061 372 156 717 753 667 658 274 907 037 309 329 430 180 998 119 710 926 481 208 568 802 611 697 285 358 552 499 193 171 662 439 707 356 824 829 031 317 049 514 116 280 706 857 219 375 331 081 753 496 678 691 359 044 146 633 930 775 918 268 240 648 704 136 301 820 200 951 282 686 053 237 213 652 876 688 623 745 363 481 199 352 192 374 399 644 589 052 598 595 497 078 611 376 819 320 131 982 098 145 469 832 728 044 202 863 133 167 363 725 460 190 403 195 270 626 939 985 218 270 108 736 836 961 924 562 057 549 566 674 906 322 065 200 042 749 741 244 584 612 027 841 889 677 994 356 395 214 032 599 159 691 265 122 923 197 633 779 921 350 258 554 134 959 252 251 307 425 769 474 798 356 412 010 364 641 541 821 534 411 342 766 126 341 690 634 990 414 689 966 558 521 756 018 205 541 064 087 118 011 308 787 517 058 169 195 514 453 460 340 125 435 450 829 493 086 336 826 922 986 926 380 250 973 185 903 074 441 127 249 393 429 829 363 111 398 837 920 848 422 445 225 838 625 956 551 676 473 349 790 683 096 982 362 411 147 323 583 464 074 929 247 182 743 579 688 110 226 327 938 764 724 449 522 698 752 234 814 762 090 729 125 045 232 801 171 519 491 288 766 779 294 136 990 400 541 590 075 547 890 386 447 005 381 948 569 515 845 300 495 903 159 229 256 673 190 119 544 383 706 648 582 845 908 701 840 551 799 723 549 633 297 971 041 584 433 661 747 280 611 512 854 900 330 553 901 697 239 554 928 560 400 689 714 573 208 504 224 030 184 194 389 903 449 340 366 631 531 562 430 833 701 603 376 452 510 395 047 412 182 117 860 118 989 202 978 974 598 198 630 557 454 654 887 533 535 102 099 334 601 244 573 889 959 532 104 048 568 170 270 810 871 118 469 207 377 185 726 886 925 300 552 375 687 432 701 311 497 351 085 490 843 205 281 245 914 444 069 870 965 277 653 613 804 702 919 895 292 440 259 439 383 136 022 756 790 339 288 929 346 550 646 105 345 047 419 054 191 374 572 380 245 258 477 266 882 974 478 955 561 906 130 941 982 231 803 332 289 761 779 176 389 577 883 126 107 237 295 385 689 747 017 618 876 365 267 369 542 057 846 050 600 417 491 917 142 038 667 517 666 658 340 485 139 795 586 182 715 277 863 046 250 105 347 032 257 887 834 102 400 977 811 284 129 196 006 927 765 830 778 476 932 045 383 137 941 018 124 865 643 294 136 890 881 832 685 104 774 914 866 067 264 624 810 567 319 061 963 453 446 908 986 221 163 626 016 443 783 463 948 655 547 258 871 603 686 326 266 894 814 583 484 291 366 619 243 485 317 410 886 945 625 688 132 780 999 803 105 622 141 978 920 497 165 691 528 847 769 578 870 484 410 470 392 761 108 782 896 198 578 725 292 389 026 322 745 965 556 285 694 375 355 090 540 455 649 678 647 964 841 954 227 250 690 661 613 162 520 337 483 865 826 712 900 729 809 939 337 688 091 023 475 924 653 582 031 636 316 912 507 940 970 849 514 375 983 350 231 534 573 238 204 202 689 857 430 617 930 053 735 136 420 131 315 036 396 777 522 247 562 931 661 123 231 890 091 044 852 639 296 784 542 444 621 514 000 887 544 911 714 052 876 685 812 726 119 320 443 279 417 804 861 822 870 880 437 144 219 689 593 819 007 568 721 014 299 455 597 280 842 762 994 292 086 047 488 682 322 054 103 328 096 195 697 168 193 754 114 363 023 068 520 287 516 199 892 756 832 020 307 161 692 826 998 743 391 661 460 487 013 416 232 857 706 088 150 579 123 117 533 550 831 235 609 378 826 728 490 165 977 274 649 177 020 113 926 584 588 800 854 462 098 432 193 383 079 605 492 914 290 160 083 670 458 711 392 481 881 151 244 849 531 116 307 556 871 785 299 662 313 811 085 555 439 262 101 771 100 895 964 716 364 053 499 200 606 334 118 415 182 869 398 369 133 267 481 020 626 809 348 939 706 222 541 677 583 978 820 463 826 637 612 098 085 985 089 802 639 855 601 370 526 980 443 296 278 340 056 348 110 508 616 583 170 629 045 237 038 308 814 272 649 242 112 481 598 643 540 623 819 361 689 220 804 618 680 437 527 778 808 637 716 847 550 356 851 995 262 586 433 796 107 957 333 220 496 604 414 332 118 389 178 426 110 547 517 156 010 927 734 778 105 324 177 134 690 782 375 372 865 480 982 515 219 384 153 717 621 576 450 667 706 756 648 972 494 829 946 416 368 309 873 331 137 096 684 405 003 947 261 800 624 602 096 362 866 344 518 034 595 053 127 865 360 045 685 854 769 704 627 234 534 249 446 778 958 192 676 154 246 788 217 685 132 082 153 263 242 167 628 046 067 756 714 122 988 135 607 304 552 615 367 014 284 470 828 421 285 172 600 123 090 239 676 665 440 575 998 013 130 007 328 144 335 611 638 051 131 028 467 641 253 048 668 658 638 273 781 455 063 278 522 603 552 349 078 532 219 584 850 567 748 390 122 220 078 725 635 174 535 315 650 252 614 658 475 308 589 069 609 463 106 713 380 112 776 226 069 893 536 688 542 181 643 253 241 835 299 866 078 903 687 506 779 988 180 419 071 659 705 451 688 082 755 418 712 578 643 095 534 119 384 000 671 080 297 506 554 867 877 156 777 069 263 008 177 915 655 056 848 440 322 649 353 895 247 096 889 966 089 382 252 708 154 221 320 828 150 190 284 916 309 539 067 004 876 068 678 900 939 097 668 447 385 978 179 698 183 146 313 289 762 173 193 764 267 080 262 527 381 766 304 746 244 291 668 042 526 813 758 836 877 673 615 181 114 624 890 674 301 445 217 823 596 038 477 247 472 184 128 137 880 291 651 081 255 774 617 623 858 699 472 444 989 826 194 487 141 963 740 333 578 416 637 112 474 320 454 509 778 730 985 521 624 585 637 414 669 328 239 636 326 601 483 200 445 745 948 132 424 810 556 408 257 445 378 027 835 338 198 676 124 492 931 670 132 514 945 892 611 880 848 805 779 609 952 819 459 566 676 811 773 840 126 103 760 406 685 186 763 100 551 791 321 972 572 697 614 430 581 975 940 204 950 605 332 570 004 489 574 865 523 304 729 078 159 458 377 913 028 818 938 744 166 808 118 392 429 765 142 383 998 655 458 404 342 971 995 678 126 451 311 498 413 075 222 452 929 862 958 389 768 799 552 113 151 917 398 282 397 535 490 477 763 436 474 377 603 987 146 615 336 761 093 016 482 652 162 125 303 035 665 756 662 687 258 710 754 050 649 775 490 000 259 589 553 121 515 091 052 001 113 855 301 482 752 917 927 089 455 035 507 613 574 606 920 890 745 396 423 858 499 396 124 356 776 899 852 770 318 166 997 704 533 586 909 762 177 252 745 451 140 551 811 878 755 106 269 496 818 124 771 934 202 838 184 990 069 339 756 992 038 087 773 375 178 136 540 916 857 658 759 858 819 062 010 399 097 967 564 213 340 217 853 332 600 026 855 011 151 163 479 169 034 857 007 481 276 510 690 166 066 522 060 672 669 207 392 745 549 195 916 622 901 150 175 296 424 007 537 235 716 996 031 851 203 251 963 468 701 524 222 937 598 570 083 858 230 709 917 770 484 525 095 344 336 385 708 950 666 147 897 666 827 114 883 566 087 250 778 777 395 050 470 546 954 826 901 935 518 520 362 554 872 146 446 159 924 333 766 702 379 291 336 769 671 833 925 332 789 293 352 734 943 256 288 482 608 357 279 517 366 545 110 058 709 682 905 119 235 217 687 867 938 316 902 149 344 637 817 647 302 688 609 376 688 823 355 779 916 711 815 847 198 778 085 145 078 247 435 071 238 952 760 061 093 346 427 763 952 374 679 420 678 891 443 767 148 322 201 931 452 565 971 444 182 090 185 345 083 943 278 529 626 847 902 995 928 976 273 357 111 556 769 954 868 608 781 589 778 746 804 648 326 177 294 607 518 374 170 922 632 906 028 663 301 184 239 125 652 482 486 234 192 801 246 939 703 814 258 346 483 380 185 045 437 590 758 483 770 370 843 925 240 999 669 467 431 356 913 502 859 791 087 249 376 949 505 116 488 001 824 390 510 211 295 513 456 229 653 607 056 321 997 509 961 272 264 635 790 414 994 673 332 531 060 077 218 850 174 385 869 375 940 354 576 920 446 098 668 550 734 219 195 484 877 718 705 402 791 291 580 925 208 784 938 065 627 353 325 387 355 170 664 711 370 486 333 795 137 515 757 731 946 094 541 822 804 732 687 938 638 055 284 975 026 235 966 326 419 941 826 574 078 596 899 255 672 349 980 884 249 239 363 359 228 456 540 648 347 454 093 470 327 348 704 760 318 539 645 990 533 007 129 642 461 621 536 652 807 958 872 827 551 495 491 860 731 647 511 138 370 170 847 999 853 695 318 748 901 421 324 118 577 517 567 005 603 361 654 077 399 026 592 984 320 118 475 900 079 757 755 587 346 178 985 105 954 175 508 782 971 615 996 781 387 165 382 882 489 089 755 497 624 614 076 649 282 379 777 524 127 170 571 546 103 145 752 501 549 256 750 214 456 335 686 718 079 472 288 010 631 948 388 041 224 567 284 281 511 400 206 572 210 136 271 335 603 668 064 322 762 134 782 414 994 204 044 441 048 325 951 838 566 588 890 815 336 578 351 937 729 886 214 231 746 159 913 886 941 142 978 105 672 724 462 465 509 712 709 265 907 342 015 429 421 636 107 421 509 303 111 208 170 863 085 632 588 926 605 904 724 914 396 790 014 370 173 035 539 302 462 329 466 653 971 554 709 542 429 007 011 968 906 318 250 534 361 337 464 571 171 456 395 620 887 041 580 045 756 264 946 049 381 813 651 869 755 435 805 437 006 961 338 231 787 835 518 010 614 456 849 055 125 085 478 373 065 615 345 101 381 441 435 199 227 230 595 039 224 672 969 567 891 251 243 637 256 944 009 502 295 362 498 245 775 784 255 703 113 272 776 782 009 002 965 022 555 624 793 297 776 821 479 784 732 797 211 568 739 994 513 173 380 695 077 100 347 086 961 978 694 411 301 494 196 217 923 069 356 044 357 195 584 192 951 172 110 777 297 341 870 847 913 953 261 523 258 985 775 312 129 737 136 917 119 727 916 602 307 242 732 849 501 817 869 131 855 524 344 835 381 096 278 571 399 146 346 933 891 587 719 502 589 640 612 978 963 907 928 193 810 862 647 027 559 402 371 987 128 031 134 530 624 133 434 008 726 537 454 958 141 585 719 233 852 736 514 412 822 594 422 701 833 627 154 346 970 512 842 851 654 908 545 635 559 704 473 005 249 011 294 506 791 138 586 319 457 953 042 118 904 520 775 257 977 269 940 438 047 967 827 650 342 381 517 408 906 609 955 381 762 274 255 065 166 590 655 705 979 151 942 820 884 664 418 427 709 500 963 607 299 603 599 808 186 090 123 120 174 413 829 597 984 769 714 864 505 879 011 185 968 822 994 626 397 780 174 129 206 653 763 499 992 147 383 609 256 223 229 118 104 791 288 084 334 449 199 484 866 041 265 010 287 730 808 823 060 811 312 850 296 493 067 542 060 874 671 531 373 835 928 085 599 010 945 402 310 721 765 522 372 750 865 271 118 639 305 797 163 987 975 796 246 677 267 006 142 511 315 568 889 417 941 665 004 234 935 129 663 602 081 432 712 973 808 585 129 220 495 030 332 458 061 973 916 625 379 837 618 058 813 680 244 698 730 111 190 983 520 166 002 694 360 749 651 344 695 281 334 482 220 782 988 233 426 257 142 953 102 719 199 888 445 405 890 861 445 593 351 368 276 943 228 057 146 457 293 999 898 085 810 306 163 219 375 599 375 505 208 240 146 764 638 178 224 680 295 846 149 514 852 629 089 609 242 988 113 744 357 881 896 356 599 491 055 553 107 394 694 596 275 018 936 560 866 168 614 920 562 740 915 340 880 823 716 382 278 843 759 659 004 416 851 646 679 057 043 151 644 481 106 801 172 360 059 021 118 183 225 080 461 658 624 087 429 407 604 033 744 179 437 623 653 468 614 783 268 827 164 115 323 598 585 769 729 912 596 460 764 881 636 430 360 561 895 241 047 142 522 284 597 076 491 862 886 094 220 904 194 903 885 448 479 701 578 751 399 162 295 453 145 356 379 863 240 970 139 269 098 049 672 983 410 873 250 224 481 610 547 961 714 783 046 072 679 822 394 966 615 899 296 056 793 357 378 571 107 334 536 610 550 337 745 629 001 861 367 873 629 010 488 817 121 214 998 648 229 109 835 092 598 287 078 751 226 301 615 534 085 346 612 456 768 638 884 725 413 970 317 070 830 918 859 429 767 784 569 246 148 675 465 214 781 396 227 701 656 817 502 360 573 219 712 108 472 775 396 086 476 265 887 655 398 616 259 401 402 901 136 311 194 477 272 649 259 650 340 413 405 917 399 713 918 478 748 404 845 414 529 102 785 339 048 094 715 034 899 294 298 991 082 315 039 393 821 153 984 956 954 088 442 411 076 002 335 249 475 473 272 167 148 334 286 239 087 761 699 307 725 098 043 324 519 868 123 344 421 442 802 616 038 052 466 508 638 262 760 143 774 225 622 425 392 551 594 295 329 402 849 711 839 988 383 943 872 100 492 677 170 392 970 321 072 840 432 102 131 372 279 170 766 400 249 598 682 757 740 816 951 115 719 130 457 191 455 265 729 862 577 164 290 329 475 238 942 937 605 596 038 589 656 220 044 298 765 334 381 971 420 697 310 820 711 978 599 957 695 990 955 864 589 588 464 619 668 397 251 661 182 285 070 256 621 541 072 229 923 595 642 033 768 881 683 400 682 524 909 445 641 952 210 498 038 847 466 342 668 103 779 259 621 817 132 567 809 431 698 404 548 289 597 415 353 348 250 804 739 029 636 019 085 089 893 216 797 013 873 021 325 777 635 228 880 095 831 559 834 136 075 883 559 040 205 455 224 714 892 067 965 578 464 925 968 730 228 942 041 308 462 883 496 664 180 771 686 172 812 472 465 432 189 587 347 558 673 440 607 441 124 007 629 082 998 868 399 410 377 950 623 247 814 565 955 805 281 924 255 785 770 898 369 443 876 872 117 504 672 120 856 344 341 489 717 049 049 709 243 370 867 203 775 824 170 257 506 542 129 819 949 039 919 572 041 135 055 626 232 471 487 116 945 632 652 130 572 845 860 875 732 853 777 384 331 016 488 576 818 811 473 531 521 886 638 858 072 018 695 684 650 658 619 112 779 692 554 052 663 622 490 581 931 707 860 792 997 004 524 840 219 976 460 522 178 226 608 292 146 324 350 014 734 710 921 346 769 866 006 735 556 834 281 162 959 156 286 651 925 200 890 699 431 954 257 696 834 640 895 993 445 077 926 227 514 255 156 830 742 447 439 424 693 711 065 098 405 567 863 794 104 253 110 094 690 183 760 774 871 821 244 468 203 886 956 800 404 566 067 415 436 769 077 148 296 084 077 411 504 203 988 499 557 857 965 632 375 193 488 829 146 580 846 252 551 359 887 759 279 761 495 162 474 979 567 355 763 495 318 930 436 797 507 572 324 768 699 399 199 714 682 645 984 475 487 755 170 788 369 974 307 842 721 674 678 607 123 024 296 754 298 925 761 070 407 263 065 555 445 613 401 122 449 956 704 994 328 683 369 078 290 338 691 361 003 865 041 717 828 943 431 018 256 612 832 512 684 702 529 133 139 537 765 209 307 073 025 961 096 955 472 993 778 077 894 076 474 659 991 125 320 773 464 221 894 758 467 915 084 981 015 313 330 134 858 168 458 207 901 352 458 650 026 842 416 859 211 391 265 604 224 873 443 949 940 540 644 877 367 886 875 372 655 749 877 744 928 625 268 860 557 223 173 884 630 425 297 204 713 756 418 159 538 643 536 864 914 953 234 843 746 950 329 496 229 435 819 204 126 629 173 021 362 240 383 911 597 213 326 649 163 946 871 601 396 430 738 741 617 211 420 762 776 138 797 235 201 272 878 475 943 464 645 252 002 513 140 827 712 385 658 189 067 540 613 359 182 805 024 204 169 210 545 758 122 487 738 943 937 973 674 908 781 140 494 426 648 312 769 713 569 173 179 652 793 958 973 726 263 344 931 669 646 907 317 168 688 291 224 518 209 395 987 870 338 424 440 655 845 915 217 090 532 553 925 781 904 063 588 930 448 997 010 042 743 355 818 427 160 024 108 938 496 771 729 319 186 883 726 427 447 842 291 301 753 803 728 218 503 080 124 988 766 563 573 024 171 398 472 784 225 470 402 157 463 369 040 940 256 405 882 053 698 389 214 430 900 483 043 258 330 089 975 773 464 697 151 697 761 661 443 919 391 627 518 474 552 302 996 353 370 644 675 916 895 147 797 332 870 362 929 216 002 113 870 304 695 724 843 063 182 327 322 533 788 924 494 510 574 670 578 704 204 151 090 273 415 743 804 067 891 408 863 235 762 830 870 061 581 731 337 632 126 187 403 567 697 543 614 844 376 155 658 875 475 684 677 187 839 320 237 645 428 600 854 033 109 051 260 804 981 639 850 379 620 055 985 483 751 574 436 341 334 114 916 377 406 696 002 987 272 054 496 175 174 451 862 635 222 730 303 635 272 893 535 907 374 281 624 177 463 284 972 617 491 293 965 008 569 821 350 769 809 353 090 398 588 388 405 188 988 738 173 301 817 893 020 732 782 883 243 222 750 466 991 955 028 102 944 153 015 236 489 121 646 759 297 152 286 243 281 421 162 983 019 536 662 057 392 311 962 954 170 235 088 891 296 276 963 823 031 030 983 425 692 275 367 992 281 580 557 083 181 555 096 696 103 417 498 902 431 962 605 482 270 529 028 220 534 912 429 174 199 684 706 353 452 603 306 865 408 882 815 924 857 940 009 463 043 540 949 097 430 083 266 658 832 761 639 034 062 676 858 872 497 274 165 668 810 772 713 475 288 009 683 694 267 479 369 878 128 188 265 365 250 344 479 837 205 577 361 721 045 417 926 226 009 322 238 196 704 085 175 755 274 177 927 328 035 264 509 075 320 971 847 633 730 943 853 733 470 784 834 482 454 897 899 313 656 938 329 205 496 635 763 107 990 038 618 983 529 147 244 935 252 771 744 338 290 787 889 818 818 186 501 962 764 283 875 417 804 523 106 401 603 956 686 770 820 412 863 489 983 393 576 323 146 867 515 979 895 368 879 852 386 138 313 256 755 634 006 856 674 907 951 583 153 359 030 239 327 886 953 103 257 656 924 518 361 026 619 291 469 331 552 013 476 369 972 541 557 276 161 136 964 441 562 717 940 055 883 831 844 752 965 549 844 261 278 612 472 316 332 122 592 406 355 689 677 528 238 516 160 271 341 333 043 419 931 999 496 029 218 337 562 429 278 982 132 149 987 672 733 369 769 300 252 362 507 771 953 507 017 107 825 359 405 314 511 807 498 158 866 946 970 979 491 258 463 002 021 856 293 902 974 342 179 833 856 241 930 130 923 290 024 489 259 627 690 400 611 496 885 752 642 249 769 613 865 582 160 152 931 966 811 369 581 996 551 032 193 039 685 396 250 314 654 203 580 784 299 372 494 055 803 433 895 105 173 968 584 755 821 249 187 046 980 403 223 528 086 902 152 531 544 817 337 311 709 134 986 702 473 500 009 522 263 653 030 371 547 271 343 136 271 973 542 248 838 149 654 159 106 993 996 528 419 981 872 306 080 177 421 439 304 805 988 625 012 454 927 519 183 736 825 105 557 661 482 972 692 334 158 490 845 558 552 155 438 541 606 037 649 780 226 323 083 530 222 478 647 387 760 651 441 229 198 069 514 287 313 053 866 628 048 921 117 002 852 328 014 320 785 793 203 101 484 703 201 983 853 273 971 508 046 114 377 440 717 713 337 815 869 289 422 537 339 975 477 697 412 864 975 092 126 119 577 118 578 194 936 057 089 895 296 991 838 766 108 470 206 495 326 547 202 880 160 868 138 861 159 825 382 195 660 787 795 355 166 244 997 618 217 060 971 357 850 922 831 700 796 290 057 407 284 102 746 381 852 631 073 081 768 723 837 417 497 323 646 461 952 895 711 736 045 815 912 938 086 442 570 702 905 674 559 199 495 605 209 228 617 160 141 686 344 917 434 720 456 656 054 560 660 871 937 076 340 219 709 612 389 786 494 141 171 854 734 990 837 280 289 078 165 030 422 019 493 357 414 994 753 855 036 299 049 315 256 492 034 682 681 376 876 442 755 652 394 759 783 417 319 260 636 761 948 426 588 445 932 845 122 281 675 359 769 595 617 427 180 401 262 618 235 981 163 699 993 002 080 972 044 055 342 321 643 023 500 911 492 314 439 162 564 082 708 247 807 875 309 839 386 435 069 824 460 856 757 818 932 176 338 315 771 457 767 192 006 566 411 485 186 274 763 821 002 470 927 640 850 605 546 615 050 522 336 703 353 378 688 283 997 459 023 387 840 079 875 738 847 105 357 178 601 772 774 418 628 074 310 583 309 704 464 077 938 818 023 926 859 268 753 180 872 332 991 065 441 841 758 504 471 679 345 013 858 139 898 035 266 597 281 873 547 756 840 551 674 829 968 308 443 132 897 679 704 592 870 838 529 698 292 704 103 839 564 061 262 653 714 248 628 103 550 617 470 806 859 797 944 249 709 261 879 441 498 769 905 879 438 944 376 761 222 020 007 785 500 036 268 769 063 012 148 247 905 569 943 394 297 360 399 527 690 354 144 134 217 723 909 367 999 489 268 897 418 452 613 058 922 044 747 420 251 044 431 327 561 648 197 132 754 364 199 705 031 185 473 217 144 981 284 989 720 239 489 871 136 622 259 743 588 774 369 372 500 583 222 032 137 672 944 785 186 745 914 464 880 948 789 130 309 441 061 438 653 431 677 461 768 687 998 634 832 126 850 803 487 382 075 836 023 633 285 701 534 264 156 646 008 652 130 431 668 577 259 117 511 516 831 548 531 847 156 284 085 549 776 870 418 457 799 977 413 315 182 101 914 526 442 401 809 185 620 733 112 914 712 511 957 438 347 744 242 348 962 438 686 387 624 453 583 823 772 177 748 150 032 117 896 605 624 355 376 448 429 389 774 092 066 232 630 150 769 870 081 620 720 268 811 142 871 258 626 824 300 286 897 837 078 596 118 510 279 077 918 874 583 117 118 078 369 169 300 855 593 913 807 711 007 229 829 158 121 688 216 675 675 842 367 775 418 998 646 456 313 262 670 577 470 295 404 900 085 314 619 441 575 838 213 578 631 929 069 326 955 581 055 322 280 100 577 730 785 243 916 759 659 801 522 184 055 275 370 379 993 712 767 832 546 776 932 158 987 623 649 174 045 662 061 964 196 859 028 810 454 111 501 287 870 776 437 514 074 397 040 121 610 728 905 517 512 484 256 780 003 960 799 077 475 521 592 393 500 795 576 266 663 824 400 132 599 409 591 635 383 671 636 353 122 807 537 758 825 293 503 605 246 889 343 504 538 800 440 713 758 651 048 875 709 992 226 157 860 505 595 389 067 386 559 832 237 554 005 311 475 762 052 861 897 554 582 355 172 849 064 984 484 579 027 114 061 407 832 242 020 994 975 330 891 847 247 343 808 580 610 784 427 196 051 889 083 988 140 268 794 404 744 490 277 475 052 982 556 812 392 711 331 083 234 969 345 436 391 704 771 500 733 423 010 607 151 943 567 779 748 053 266 522 722 643 316 311 788 791 370 468 448 182 001 477 213 891 764 736 925 898 455 135 531 959 980 912 131 201 486 133 061 058 528 201 940 580 602 664 339 292 694 483 089 921 956 188 793 849 061 216 893 705 511 320 756 535 392 928 353 192 909 413 136 260 454 769 678 248 605 270 500 570 838 869 765 664 243 350 133 671 439 542 519 319 062 581 284 154 103 897 751 669 998 429 159 089 130 775 276 782 904 653 612 506 232 867 288 395 232 524 297 784 485 349 410 242 405 677 473 044 576 733 019 126 789 729 281 820 711 980 050 899 299 952 009 247 182 137 051 712 551 074 307 989 392 721 030 608 102 059 290 108 886 791 613 380 959 144 501 113 261 673 776 285 308 279 552 025 812 658 125 887 391 332 109 710 236 873 896 742 234 076 249 892 333 518 784 907 189 934 758 485 864 864 922 471 734 210 200 180 716 474 013 554 864 939 116 436 863 421 032 181 315 096 030 318 516 325 362 274 427 891 597 288 524 391 664 039 595 616 233 848 658 426 128 739 951 739 493 238 497 621 712 999 715 414 971 414 730 262 591 069 753 216 850 437 669 769 059 240 917 802 215 027 760 185 462 972 022 431 653 314 503 632 706 236 479 943 958 907 945 727 580 000 066 902 208 394 026 308 790 598 587 833 221 966 865 811 458 936 646 931 865 613 559 412 400 312 221 675 175 508 245 558 684 285 023 296 979 401 293 438 947 694 476 558 225 746 995 048 230 599 277 670 484 425 888 538 742 506 093 919 937 366 307 181 861 561 762 186 862 675 833 988 255 342 989 340 839 236 180 978 380 205 288 374 714 376 219 590 707 196 170 738 049 266 468 525 705 727 560 322 753 467 795 085 642 634 327 297 167 356 014 162 328 029 026 955 083 215 905 707 647 179 641 258 178 938 003 564 685 362 184 044 465 051 868 065 527 569 128 848 610 844 421 241 355 603 057 074 979 663 756 686 291 340 989 145 420 214 919 347 128 962 461 158 648 093 935 950 050 637 553 150 976 441 940 391 329 282 809 206 750 176 565 004 684 416 958 717 692 871 248 314 145 139 594 868 994 255 017 431 703 818 315 591 811 506 932 940 236 698 922 688 203 507 100 604 972 756 206 724 248 679 858 872 632 156 996 670 650 352 533 109 663 997 431 384 064 911 652 531 235 048 425 115 335 143 334 357 114 123 291 479 167 591 038 215 752 917 203 933 569 650 371 713 810 987 317 028 910 982 252 661 510 531 799 000 708 025 626 922 475 656 760 345 284 565 641 180 031 999 062 085 310 290 034 065 367 749 067 395 514 840 562 703 329 862 464 219 874 049 713 557 809 538 806 671 231 235 053 249 750 623 956 538 072 148 832 017 373 477 914 637 418 804 011 327 470 892 054 962 222 385 019 391 977 183 904 401 953 346 415 934 782 260 005 135 782 130 524 569 478 903 673 841 771 256 489 139 782 599 062 830 323 775 317 723 500 332 491 329 718 727 130 883 141 769 779 791 915 054 537 300 422 937 901 839 234 273 694 904 443 367 499 574 422 937 202 982 586 007 535 015 329 521 330 034 245 110 723 430 369 959 787 766 056 889 292 726 141 250 684 617 390 318 780 620 710 576 532 957 379 999 848 232 032 298 578 560 673 536 283 949 506 885 197 223 457 352 675 651 790 001 050 804 195 702 788 266 762 647 601 875 814 790 526 371 425 001 436 396 739 652 024 960 384 726 372 555 476 904 528 875 308 457 535 580 786 471 263 139 744 069 126 078 018 724 888 596 505 645 286 561 562 113 485 073 869 320 156 609 477 050 818 423 545 007 041 954 096 695 171 805 961 248 462 396 574 053 260 346 710 130 160 613 636 821 015 069 393 206 920 448 585 561 130 705 650 125 057 267 119 113 251 428 215 637 788 942 714 266 984 862 689 163 689 063 450 189 491 018 439 226 111 451 587 020 738 975 792 830 617 443 083 266 293 888 185 994 647 756 542 714 700 218 266 246 828 887 889 387 530 188 000 525 222 141 336 413 543 887 322 960 990 489 091 319 093 888 676 319 899 417 195 227 544 087 635 819 359 369 514 136 725 006 837 951 704 747 723 118 008 132 742 544 931 506 912 131 684 280 324 242 668 031 100 979 355 767 840 316 648 630 929 702 384 468 988 384 981 653 772 795 098 722 983 500 029 905 347 839 481 268 254 176 364 634 365 876 629 664 837 345 864 264 389 122 627 156 554 492 604 732 230 989 536 841 421 376 417 795 684 798 395 612 193 434 544 969 521 166 227 927 060 584 167 321 643 798 702 610 086 006 682 271 486 805 304 469 958 278 651 595 984 627 836 864 896 826 253 550 293 457 168 474 294 253 951 215 150 504 415 488 066 984 025 214 709 180 869 626 408 542 345 945 911 781 111 220 893 216 592 051 949 399 446 375 521 415 289 335 985 878 341 707 574 953 020 850 851 281 866 294 137 310 333 561 284 623 092 790 230 776 677 931 831 294 842 573 167 027 646 753 053 091 850 682 427 994 151 684 159 420 703 083 636 732 097 468 284 070 065 048 980 090 774 042 953 619 942 065 779 220 284 335 943 017 412 713 583 807 979 558 832 993 394 818 701 779 473 807 593 476 922 168 323 984 587 988 661 235 807 073 201 762 918 300 632 753 798 179 280 970 733 035 882 108 262 396 562 361 184 782 799 376 708 024 075 637 059 393 992 870 825 207 419 460 922 509 091 323 860 249 472 019 519 384 648 759 914 960 785 813 356 125 458 612 352 733 436 397 294 595 287 140 420 119 931 826 768 518 767 261 103 544 803 805 738 642 045 410 910 523 865 220 784 877 764 861 097 327 479 385 278 636 857 970 867 104 038 557 829 788 071 799 981 566 227 287 401 530 095 559 923 541 456 566 773 359 383 855 632 234 402 151 555 810 389 227 880 009 932 674 593 726 234 360 252 992 363 137 345 023 194 843 042 437 141 556 872 125 954 755 565 901 863 302 342 381 999 340 078 169 520 038 352 779 111 352 888 614 117 904 970 027 218 049 530 778 156 006 679 670 557 657 406 219 526 623 250 341 531 606 379 340 125 720 365 313 189 894 829 041 503 482 049 372 046 824 540 047 602 422 531 100 152 719 501 465 065 700 793 971 733 579 472 643 253 555 543 714 319 553 572 416 146 674 397 607 927 950 756 600 587 172 681 385 424 078 985 870 523 010 580 885 719 407 579 074 886 247 613 307 279 977 273 234 631 953 912 186 346 907 914 343 155 462 625 736 393 218 421 708 719 343 258 616 877 016 956 648 147 684 869 070 740 355 456 255 484 364 276 918 718 723 266 212 171 868 169 482 792 610 715 664 483 125 178 836 797 325 856 843 563 696 078 966 790 934 328 831 650 869 290 308 448 602 954 437 030 650 038 356 349 676 226 978 530 758 100 126 903 116 809 546 773 251 110 190 804 368 357 777 817 365 860 819 639 746 029 396 217 047 800 978 705 957 719 926 089 247 969 129 636 302 524 326 658 685 701 736 018 488 477 563 669 213 306 566 346 075 796 212 030 975 202 857 951 565 128 636 772 608 018 344 585 638 466 152 855 114 746 211 220 665 461 405 927 136 486 128 196 794 741 384 097 063 071 431 129 888 304 723 690 052 034 006 073 692 933 710 920 282 998 647 130 785 192 416 319 508 206 012 892 349 803 677 859 544 414 778 329 590 313 386 445 820 988 279 731 129 141 745 675 596 107 792 866 695 310 497 836 945 528 446 895 743 825 781 743 426 664 704 228 099 203 920 417 253 559 316 886 294 575 325 662 452 830 175 007 456 776 812 222 609 439 348 741 972 110 987 754 856 594 144 221 880 728 004 600 889 488 492 921 000 180 059 529 233 250 767 044 277 245 868 015 109 291 263 765 851 010 942 771 988 458 592 110 527 300 963 019 192 744 617 458 825 588 945 323 660 124 271 955 403 175 132 350 688 778 944 005 708 507 161 039 503 035 030 706 946 489 527 916 053 522 794 755 847 860 552 769 161 138 705 970 884 758 086 537 994 980 565 940 462 496 551 739 480 634 831 850 544 028 592 468 378 788 895 570 724 084 766 903 194 023 879 980 891 654 639 241 503 434 372 011 269 226 037 989 831 567 541 956 565 981 357 770 869 484 509 373 576 976 276 350 019 439 901 283 072 385 769 556 212 195 719 611 691 566 194 573 315 800 218 270 816 658 152 343 029 337 542 605 967 171 599 739 136 445 915 379 720 273 052 477 235 127 223 302 689 123 957 890 509 346 865 162 279 544 884 467 165 219 698 127 354 508 666 333 972 370 394 057 389 827 740 036 695 350 959 983 421 233 199 839 904 475 803 637 136 840 901 903 458 344 487 281 949 595 303 418 652 434 071 215 123 771 794 793 157 201 552 992 203 822 080 363 516 726 465 794 285 538 152 997 788 040 844 859 124 843 449 859 471 013 961 436 323 889 881 833 124 559 583 524 304 027 456 855 736 434 116 603 502 126 229 107 784 187 022 287 404 272 170 088 733 703 121 058 275 477 383 521 861 037 755 421 488 950 469 358 127 149 387 300 403 286 325 281 513 224 159 662 795 635 925 432 924 020 674 354 819 311 033 841 963 563 176 196 856 032 689 813 809 457 217 709 944 406 450 095 869 259 030 021 008 099 250 349 376 196 617 639 371 778 915 775 013 020 520 737 389 970 969 705 143 207 392 536 990 389 736 966 485 302 959 079 283 149 962 488 918 372 247 676 561 395 990 789 430 060 329 955 715 477 658 512 645 496 657 390 506 800 654 520 480 687 965 923 019 820 948 099 293 154 205 459 269 936 321 590 932 131 994 681 820 193 027 436 669 478 220 357 152 780 454 045 353 330 642 429 453 736 319 577 089 979 578 193 223 408 993 792 640 262 373 762 950 437 577 109 798 890 148 910 762 140 630 260 676 579 386 190 401 209 912 775 075 581 148 132 569 793 026 002 964 348 682 549 482 679 226 119 218 438 376 241 441 114 573 486 109 327 050 079 819 455 922 466 620 101 099 734 947 893 573 150 263 074 662 528 266 120 599 019 770 550 267 852 829 568 450 734 480 970 360 921 075 421 471 912 917 863 822 561 442 081 061 868 619 735 225 558 046 144 481 559 697 736 590 560 745 990 746 148 758 258 549 808 258 217 354 600 960 526 599 999 121 923 626 450 668 040 960 741 995 836 044 430 573 475 151 193 811 966 942 593 793 601 334 700 654 536 515 927 719 456 564 868 093 577 154 348 702 838 947 796 832 936 847 105 500 845 862 942 505 530 075 625 379 138 014 838 581 456 683 963 846 000 779 704 080 618 123 947 854 195 202 392 713 222 563 646 881 467 517 068 992 557 667 120 120 746 018 124 720 589 686 841 576 061 823 933 266 841 082 454 421 207 088 163 475 438 887 521 755 994 937 031 271 847 210 459 594 309 433 763 420 847 464 434 188 602 212 590 799 477 930 629 997 021 497 125 600 836 968 454 160 130 438 958 787 579 340 915 338 905 090 969 872 417 326 456 708 461 104 748 296 618 206 047 006 142 716 279 604 248 283 674 685 617 532 615 696 932 401 786 802 511 937 163 046 347 444 914 831 430 441 858 737 736 739 016 529 619 731 200 784 561 041 178 401 462 134 801 274 289 851 385 102 794 386 830 912 218 955 220 998 731 791 036 079 742 136 454 660 107 609 063 483 198 310 544 588 920 178 241 990 763 268 765 546 015 525 721 272 537 643 018 660 409 387 694 091 874 407 065 877 398 370 220 238 723 027 910 434 061 567 290 255 470 217 562 022 353 400 539 680 724 330 596 701 122 047 443 078 082 268 653 475 712 366 928 019 517 703 024 569 633 837 926 454 518 271 709 089 004 802 378 509 211 253 013 298 270 390 732 636 158 242 041 538 436 539 376 942 711 986 546 397 865 462 997 164 622 161 085 257 972 534 720 130 678 423 012 010 578 373 387 699 098 244 435 336 451 856 909 432 152 677 859 637 142 449 244 054 817 316 686 361 582 174 310 897 461 393 564 502 336 007 455 669 887 546 429 979 206 902 073 026 655 782 419 800 881 289 335 900 476 277 260 746 540 223 452 277 081 162 584 842 949 080 720 639 659 629 786 754 250 199 548 728 544 903 689 759 994 336 415 362 731 113 323 057 774 631 898 458 434 094 158 376 121 127 791 404 129 038 408 878 090 063 001 199 436 713 732 049 275 954 399 582 288 064 109 378 915 252 052 074 648 653 360 597 302 603 783 058 305 489 989 993 372 324 926 075 233 000 428 357 786 060 835 131 513 800 494 249 947 023 533 905 472 617 115 516 706 574 868 873 574 172 977 359 520 666 639 322 057 454 167 850 581 432 507 674 446 849 707 342 395 533 953 237 498 418 036 926 748 883 031 572 993 499 995 787 060 805 057 500 974 341 761 460 457 007 747 397 048 849 733 543 646 353 579 938 450 284 070 606 937 812 301 299 524 487 569 979 526 359 705 241 121 877 332 163 960 274 378 881 074 859 058 453 496 257 284 158 703 526 049 332 470 162 312 160 837 639 955 611 464 766 401 866 382 940 215 129 880 130 887 262 784 193 131 620 437 039 538 471 371 679 522 648 291 520 566 191 989 011 622 915 616 243 758 581 824 221 098 427 078 067 498 722 907 397 003 376 683 184 053 101 875 546 137 699 830 238 216 545 585 884 871 063 376 031 188 740 789 873 897 751 390 945 252 829 449 930 775 980 106 755 699 072 668 088 194 669 824 424 664 186 544 819 092 726 607 522 370 840 358 968 986 322 989 299 465 408 702 149 165 544 798 097 316 182 517 615 299 877 888 847 489 409 335 887 113 284 948 308 018 075 744 490 122 341 960 722 104 156 255 575 864 322 832 852 096 952 144 920 845 370 706 384 399 336 869 081 225 385 188 333 220 877 990 486 636 512 417 069 928 458 788 548 711 575 816 560 462 395 554 947 698 857 203 322 093 376 334 281 002 251 592 826 254 625 357 776 684 761 449 082 917 766 707 289 461 999 826 330 883 935 194 810 253 042 221 839 420 245 060 246 028 891 260 198 155 484 746 751 836 161 596 784 592 626 857 303 984 667 571 492 296 480 559 776 253 683 771 756 538 089 579 229 058 336 637 448 756 031 239 302 652 855 897 099 938 803 662 807 033 755 639 455 311 779 135 291 139 078 832 096 771 991 956 849 560 858 156 375 057 012 175 441 769 687 448 731 316 944 801 588 800 653 863 892 351 224 066 725 793 913 380 576 463 406 566 700 703 781 134 803 019 339 396 713 175 427 738 011 135 003 649 544 326 871 879 010 654 185 658 694 730 004 930 119 589 410 677 841 400 689 574 134 272 362 393 529 919 662 817 790 130 039 984 367 793 185 310 480 427 147 072 691 952 187 790 055 617 099 342 430 974 485 400 945 877 637 948 549 612 998 159 003 442 473 396 981 155 432 267 790 026 078 832 497 801 561 214 810 585 001 245 867 010 243 764 078 833 415 641 732 385 996 435 922 193 018 943 568 809 968 359 842 312 772 464 451 559 287 011 196 992 331 747 620 011 007 205 942 176 106 803 752 302 962 242 173 902 271 716 644 014 109 865 350 142 429 901 415 187 309 811 987 874 354 530 388 564 666 794 105 704 416 875 230 290 831 902 260 885 149 154 379 790 340 079 642 423 597 884 675 606 947 593 189 033 799 888 360 576 008 034 338 887 850 676 106 142 064 523 807 017 159 622 548 601 085 274 087 694 872 615 760 425 847 504 139 445 156 007 555 004 363 864 386 121 210 004 883 744 591 499 217 811 052 171 197 119 848 712 496 947 915 969 762 746 731 672 403 287 303 655 544 916 436 922 615 927 122 336 747 701 921 062 372 485 202 642 633 477 633 448 437 320 791 517 497 775 501 881 950 602 936 531 734 864 291 290 539 755 993 532 827 318 823 218 867 629 382 014 969 094 728 340 728 802 583 204 061 915 983 807 569 446 111 999 488 625 634 585 057 938 343 830 424 740 172 073 175 262 047 046 163 854 595 953 325 428 170 812 977 868 273 668 598 133 771 464 966 258 179 990 060 169 012 897 721 415 942 997 145 426 363 673 459 784 547 132 527 658 204 035 059 437 022 734 553 366 599 575 787 800 471 593 588 176 327 387 778 667 262 595 722 147 547 825 618 661 945 487 090 916 226 598 352 343 538 119 557 331 817 249 014 259 658 159 755 073 299 695 232 698 263 150 528 685 939 713 769 664 749 844 477 992 379 236 895 258 976 859 456 696 536 969 205 948 028 056 144 417 536 283 420 919 116 652 207 563 339 780 281 193 859 293 442 047 467 736 737 650 979 701 304 883 878 336 492 836 424 208 620 025 588 501 193 500 825 987 187 159 162 274 020 621 592 631 388 607 341 962 524 000 136 959 730 926 436 118 541 592 810 588 432 582 508 434 192 948 012 548 624 316 378 486 574 132 954 734 077 073 537 610 640 340 383 300 602 007 740 319 335 249 145 678 383 514 391 009 792 269 314 962 557 691 087 466 713 284 795 333 742 771 009 207 217 368 764 830 176 174 897 096 529 891 394 890 639 301 010 602 834 920 910 346 337 296 151 545 524 475 537 535 588 799 338 654 397 323 553 001 018 073 767 218 006 772 011 029 452 782 288 782 257 037 650 984 273 111 371 371 736 749 012 480 742 084 771 205 769 554 399 415 747 109 971 398 800 208 134 566 163 241 784 394 249 013 334 590 212 323 737 423 992 533 773 766 138 061 889 705 001 906 874 491 629 564 112 499 261 528 893 393 745 066 072 506 994 224 137 765 195 676 295 692 047 254 767 284 344 515 371 067 655 986 712 704 566 969 541 488 240 982 625 186 580 214 884 632 458 115 748 037 391 874 025 849 079 689 857 064 911 472 828 982 578 093 633 337 824 019 418 121 520 565 620 023 540 127 471 817 565 585 905 237 735 459 572 075 463 271 536 561 087 424 027 257 963 613 332 337 382 669 589 079 776 295 144 221 889 905 483 777 286 285 036 115 061 436 579 917 113 716 673 983 148 332 712 021 707 137 252 814 691 461 948 543 701 010 882 833 755 123 252 719 948 748 973 933 418 420 614 744 780 151 319 992 620 454 329 250 028 524 993 068 383 508 750 559 679 075 045 386 360 555 702 129 065 486 947 609 164 478 814 897 979 993 592 687 338 862 432 845 606 893 672 220 452 962 598 299 494 313 198 340 199 527 405 138 980 629 347 524 173 074 753 882 988 192 589 013 811 218 418 652 888 589 405 932 494 403 727 813 449 784 322 572 159 978 592 235 038 278 899 921 125 122 485 397 018 529 820 824 695 956 335 360 728 219 282 457 405 296 206 534 852 685 532 625 924 673 497 000 981 976 972 258 859 224 462 172 541 831 350 606 934 059 026 552 385 395 917 548 022 049 041 356 117 155 895 174 260 826 657 222 222 721 309 811 291 804 121 971 754 729 917 044 199 309 394 996 614 540 887 097 222 539 522 215 558 329 657 216 075 953 732 385 615 398 652 957 890 655 381 745 941 402 924 344 531 600 754 648 281 108 930 551 069 513 835 300 622 642 788 750 926 974 704 305 957 386 639 904 491 804 373 715 622 641 585 417 637 532 401 951 174 553 915 185 660 116 020 249 419 100 866 513 717 071 263 031 500 593 295 100 951 050 303 976 993 502 531 777 423 914 679 428 450 629 514 440 344 791 963 882 799 118 813 618 256 857 301 485 662 627 418 294 755 835 868 529 181 416 554 205 623 923 417 170 066 172 989 131 969 030 596 436 920 191 392 458 112 842 719 142 761 568 791 990 958 795 064 882 627 548 724 033 253 453 693 973 074 213 314 141 766 270 680 593 804 530 996 992 871 576 702 136 313 196 600 358 596 021 132 281 124 468 383 453 975 053 522 341 484 389 807 332 255 444 930 351 268 788 251 100 389 480 562 387 210 852 304 745 030 679 444 576 620 714 391 494 589 100 695 713 105 477 938 407 309 261 871 983 130 897 218 787 561 941 856 724 676 550 592 508 972 569 152 748 626 224 099 642 468 799 409 995 819 340 240 331 687 165 513 370 288 373 219 648 514 630 959 792 065 131 106 703 200 289 653 523 605 087 889 524 286 595 895 778 034 773 453 773 467 660 476 313 933 913 387 521 778 130 876 613 312 565 077 573 565 992 131 236 327 025 144 514 067 626 084 760 201 459 725 639 026 154 616 348 958 984 675 131 794 742 721 724 613 364 728 204 273 784 332 827 581 713 629 799 545 211 462 888 872 379 756 826 014 076 439 401 950 876 428 768 879 472 118 445 253 659 343 392 397 056 213 852 050 387 354 906 730 900 237 612 015 063 076 257 354 238 752 436 496 053 569 274 551 585 620 815 188 098 686 401 234 477 787 868 943 577 175 011 867 637 736 778 927 876 725 636 798 075 716 987 065 026 944 195 914 835 144 392 888 750 354 116 850 075 376 640 326 682 508 477 693 645 435 864 916 436 577 942 983 848 079 983 247 515 232 594 859 569 811 052 445 348 375 943 618 326 543 789 410 983 972 064 045 915 894 749 561 043 309 583 706 950 170 638 662 371 594 868 654 028 295 074 882 199 463 205 090 144 690 220 780 188 537 301 218 583 955 474 987 301 305 806 224 621 711 355 430 411 988 840 837 324 332 137 391 266 780 288 976 729 625 083 395 516 514 935 694 468 167 918 959 938 351 819 459 391 413 954 046 067 858 389 243 288 248 471 769 778 581 748 078 195 715 892 510 243 691 616 933 380 265 341 061 051 287 705 041 216 658 752 325 735 144 823 632 658 701 392 537 237 164 998 452 344 594 442 167 596 301 437 616 167 562 126 028 008 460 077 362 081 592 006 778 552 714 883 474 155 363 744 600 510 314 656 836 428 803 778 180 383 500 206 552 060 570 467 371 111 594 066 315 771 207 010 560 072 917 163 427 881 429 538 669 629 519 086 090 422 922 450 641 199 952 717 348 316 966 959 167 275 876 408 114 920 115 536 534 259 596 292 373 516 674 421 740 149 687 901 101 695 268 127 969 244 250 682 076 716 289 027 898 820 146 024 319 588 677 044 944 224 663 715 822 978 089 380 583 017 637 819 268 414 187 537 167 683 141 374 034 495 430 614 394 703 527 614 869 539 812 159 238 012 938 949 733 290 138 761 781 555 832 652 790 371 928 938 090 899 044 073 472 043 497 208 740 802 237 549 751 982 510 995 389 209 711 856 562 683 306 545 641 264 867 619 274 488 693 699 202 125 235 237 544 385 678 067 766 730 998 737 897 137 213 622 679 416 412 741 992 825 251 929 135 650 447 256 556 654 868 773 798 199 623 991 549 642 660 074 259 428 256 149 658 793 144 023 780 329 316 732 847 641 344 232 008 016 513 263 323 209 692 158 347 478 129 883 356 674 930 913 084 559 981 851 327 528 945 475 270 425 933 619 224 712 239 401 583 751 551 291 327 951 587 294 216 602 271 384 369 855 643 527 629 114 310 481 495 378 950 689 819 096 109 465 314 783 500 204 182 783 248 969 606 793 014 734 423 225 611 819 837 845 083 469 175 769 656 147 761 515 572 954 430 391 722 991 605 725 516 771 146 114 497 259 591 296 145 702 070 889 645 372 059 798 095 962 523 713 092 042 072 103 521 776 596 196 113 453 289 246 617 878 552 295 598 308 933 221 954 662 081 658 309 243 482 618 771 908 108 258 847 363 590 041 705 874 800 408 144 058 710 938 410 973 895 265 825 783 110 899 656 338 451 966 489 001 381 114 111 554 555 065 710 523 483 887 927 000 974 689 062 422 035 302 752 331 939 601 935 416 422 879 655 461 370 632 739 277 221 623 379 708 351 300 551 048 878 420 218 021 305 809 261 658 304 537 066 914 246 603 619 843 724 191 450 338 096 199 752 990 821 166 708 654 965 333 867 529 986 224 744 171 241 590 113 013 647 679 162 793 465 221 319 167 609 717 846 266 324 078 746 757 900 482 694 359 410 649 664 944 765 595 952 818 649 793 640 306 446 931 648 755 566 150 905 305 662 126 572 209 245 055 589 852 089 394 081 606 588 755 445 290 997 423 287 735 846 958 535 908 371 096 550 828 130 485 302 112 930 848 174 875 201 586 011 933 778 594 383 444 192 707 191 694 024 760 064 742 725 492 859 130 543 160 081 688 511 722 526 362 416 868 855 883 793 196 109 594 358 025 774 914 782 761 132 696 466 102 754 584 190 012 135 318 018 349 608 028 272 210 404 807 540 229 330 777 333 844 457 156 382 911 279 283 407 949 135 669 776 297 802 945 664 393 147 929 688 248 738 484 902 851 071 576 311 636 955 942 836 164 427 629 293 835 133 771 733 041 104 420 185 640 230 104 040 446 972 918 278 828 973 996 991 566 454 032 322 664 083 389 940 176 551 530 003 855 595 618 998 817 972 230 498 528 715 217 851 333 940 751 203 709 278 406 930 613 864 397 419 491 117 764 468 455 498 411 281 686 841 902 928 834 797 935 232 937 479 724 462 879 387 105 992 413 061 432 253 917 345 536 482 600 354 308 630 211 748 499 657 036 691 360 191 150 567 898 198 968 186 206 536 699 323 482 064 930 348 343 660 002 226 572 259 429 295 510 398 632 204 390 141 958 179 514 755 190 923 623 212 297 799 553 287 317 793 172 916 395 814 764 877 471 720 774 337 950 804 406 636 811 377 767 202 396 000 049 108 233 787 249 542 641 156 374 606 664 033 655 371 604 979 022 590 267 104 107 577 255 918 795 914 806 243 774 965 085 579 871 092 105 661 087 720 571 787 720 575 496 330 281 254 189 169 884 263 117 854 420 048 572 471 173 032 571 286 222 058 023 122 620 822 112 981 719 799 471 946 863 255 377 247 625 454 824 946 209 412 932 121 474 368 042 884 714 554 041 337 746 035 308 104 251 636 239 739 291 133 257 753 347 646 091 501 594 960 774 031 778 326 664 669 919 991 207 691 967 663 193 875 488 704 175 539 206 492 992 711 312 168 634 335 706 803 200 273 991 963 544 302 747 031 198 288 842 001 731 802 715 643 429 329 593 185 078 143 419 738 381 717 784 991 261 825 911 274 046 486 632 288 187 748 431 630 108 322 042 562 534 214 550 382 958 870 761 696 037 169 801 601 365 459 939 455 836 888 423 238 660 598 613 676 113 938 983 400 584 800 043 422 533 204 489 112 827 323 558 900 580 084 043 630 383 357 899 747 923 101 309 028 145 234 065 153 462 850 154 934 112 323 576 019 581 313 448 673 374 479 526 140 891 369 681 032 421 786 768 789 248 420 867 928 517 425 048 329 800 472 198 559 436 799 755 747 427 500 126 034 673 265 447 981 639 954 473 187 373 104 887 549 368 664 193 309 071 680 971 606 435 025 716 340 721 020 453 161 237 159 197 606 138 986 981 674 385 079 857 849 378 742 833 826 453 593 233 930 269 777 169 960 668 004 668 132 516 612 315 153 617 484 727 865 900 131 801 963 476 209 453 347 400 054 989 359 918 463 125 857 765 666 952 774 699 673 657 485 815 189 039 375 031 106 647 759 664 328 757 853 343 640 499 588 025 286 559 626 326 371 330 761 155 959 484 620 344 045 684 487 146 620 259 991 733 867 479 430 654 900 500 670 382 393 616 150 009 111 696 498 384 977 307 862 974 360 791 845 495 162 375 739 393 862 320 654 962 479 405 588 756 683 276 273 727 008 146 175 997 859 637 973 115 019 004 247 694 205 681 649 842 722 574 225 245 288 969 982 904 174 911 082 137 756 804 380 017 764 114 600 677 855 684 013 813 817 028 520 561 352 332 246 289 411 511 012 394 861 144 411 971 230 746 251 244 571 135 178 077 013 882 128 992 697 322 258 169 182 555 082 823 622 035 083 243 973 665 014 552 228 807 610 168 501 953 989 879 417 611 283 202 580 605 831 672 938 198 586 380 656 715 284 366 117 591 532 732 317 281 375 506 099 246 191 522 350 395 324 304 187 467 785 859 523 205 013 809 816 332 585 481 669 523 826 153 034 486 424 711 338 244 001 016 268 219 299 456 055 553 323 735 146 431 960 455 869 649 867 402 063 737 984 595 614 449 271 764 715 376 436 765 676 284 847 305 474 558 950 438 230 444 185 577 749 933 267 577 231 793 312 189 382 142 265 389 099 543 436 580 020 016 230 029 829 563 356 719 166 159 163 901 719 722 359 040 545 004 455 713 325 757 417 316 770 436 862 237 174 335 778 095 827 304 332 594 568 215 702 241 939 164 761 556 181 210 157 586 332 689 883 850 032 374 042 283 684 064 184 542 417 966 962 986 111 643 353 878 604 346 773 667 840 143 204 185 672 121 382 449 153 505 704 563 135 103 325 790 461 034 782 942 949 090 764 632 571 042 194 577 795 347 504 757 264 136 704 441 814 058 237 795 792 602 438 780 840 297 952 631 332 336 674 121 956 856 594 499 228 485 424 619 081 315 565 856 949 958 865 312 760 420 343 896 921 674 324 936 465 414 034 411 075 197 588 596 445 027 847 557 119 453 344 799 700 668 540 160 005 413 251 197 512 467 436 472 558 693 436 187 613 934 888 546 362 056 083 716 560 425 802 884 815 523 313 793 292 475 766 007 309 440 201 268 092 424 500 034 761 019 804 352 898 511 430 026 662 706 953 100 623 132 151 980 090 759 229 748 979 109 377 423 140 558 776 609 347 127 370 772 999 965 041 869 788 143 960 748 493 502 842 648 867 467 439 044 461 032 336 499 900 909 385 275 718 661 551 586 599 488 793 305 374 185 820 152 748 739 418 973 742 932 914 234 909 302 491 782 760 301 752 023 760 578 091 790 717 757 490 268 778 277 590 791 569 723 494 018 497 107 568 358 592 736 687 252 726 109 183 956 618 830 251 978 090 093 891 807 299 868 690 200 254 694 674 816 097 956 825 177 825 340 066 081 054 325 607 089 159 511 098 989 535 026 204 229 719 401 832 052 847 756 343 392 041 765 732 153 087 227 343 910 632 494 042 605 341 332 439 931 298 258 813 627 235 387 928 971 911 229 298 788 575 338 171 839 346 691 824 460 904 169 622 402 789 498 319 799 007 482 886 266 555 316 895 647 629 103 604 680 785 221 160 218 151 352 753 829 929 929 569 668 953 257 907 570 139 107 844 196 608 330 257 563 780 223 854 248 362 880 517 433 902 659 519 789 706 959 347 924 365 207 710 826 682 276 837 963 168 230 757 173 628 321 077 862 910 777 583 802 653 328 210 551 982 417 527 947 174 188 995 249 805 553 033 608 108 871 710 121 619 279 953 283 555 823 379 251 087 868 553 286 035 949 677 744 448 195 546 731 276 536 024 701 175 697 398 529 570 680 469 507 058 633 078 880 166 170 080 754 876 130 055 137 004 051 408 060 214 501 514 187 295 575 619 549 813 841 696 162 250 597 189 619 204 911 282 899 424 942 049 310 458 961 713 868 881 724 263 351 020 030 728 279 329 184 595 886 045 431 340 201 987 951 575 873 929 546 451 946 198 326 871 488 043 945 529 269 340 721 087 725 120 970 005 706 887 760 571 862 960 870 321 384 446 803 819 821 156 573 946 688 048 463 920 117 815 065 614 349 576 738 499 146 881 341 312 612 885 654 378 722 608 499 730 742 795 107 349 895 339 161 708 569 926 938 985 512 824 089 711 040 135 868 386 872 021 036 813 774 882 522 774 974 960 542 703 149 671 727 848 937 091 021 404 760 402 753 994 281 567 769 084 369 028 983 045 601 861 753 233 239 805 783 009 161 301 341 087 371 143 674 448 427 228 922 274 470 525 923 035 142 832 186 933 020 098 289 308 645 388 724 472 552 381 202 607 544 544 073 713 276 530 506 109 497 300 099 691 603 305 707 171 858 561 410 604 215 246 223 112 306 651 311 977 420 933 441 948 400 025 637 616 001 512 767 453 354 301 157 176 563 693 046 472 906 326 413 021 673 216 732 206 838 644 038 743 520 423 938 196 656 829 796 479 947 551 437 097 892 703 630 317 802 776 873 708 783 335 869 343 015 520 731 501 876 128 239 565 429 492 517 797 765 443 338 614 237 394 772 914 778 743 654 830 769 873 541 573 509 121 289 306 484 852 399 321 568 456 152 465 682 488 872 743 478 382 480 033 831 420 601 979 051 784 712 309 290 348 297 597 500 286 481 176 335 373 617 154 843 519 748 101 601 848 248 467 423 680 443 915 331 275 767 464 857 720 122 509 418 880 996 996 527 314 529 520 447 546 047 995 829 510 765 343 375 151 596 721 084 904 183 506 622 574 567 995 802 922 016 996 701 246 685 770 912 550 957 610 838 733 067 392 011 928 024 114 996 292 552 072 120 579 934 872 977 517 005 606 351 091 734 174 157 215 945 224 413 325 579 098 032 361 384 043 646 615 223 622 928 586 492 020 413 080 654 255 034 636 003 078 976 980 408 117 891 146 920 799 493 315 107 360 978 795 324 474 368 495 351 425 707 437 699 570 757 459 649 772 443 776 879 464 751 694 494 233 982 865 468 790 282 607 391 750 014 366 274 027 547 105 287 195 837 434 111 646 870 060 138 861 926 398 740 093 912 533 755 190 233 097 845 360 008 198 977 482 223 699 970 136 085 676 437 009 012 124 787 022 050 912 185 060 958 547 072 233 475 817 186 922 909 123 732 801 985 892 294 539 214 967 952 532 384 097 046 293 844 692 004 909 205 923 806 603 582 211 230 177 191 682 416 430 239 180 835 720 138 709 772 270 016 027 746 056 666 286 405 057 332 587 645 430 622 406 714 403 436 336 632 259 970 996 516 665 280 629 212 492 436 694 275 660 042 169 733 823 729 870 237 750 637 097 172 629 375 109 135 179 179 537 031 078 387 101 832 870 863 998 700 337 012 695 186 647 464 440 692 957 837 528 267 042 775 797 094 757 466 830 983 649 464 109 316 220 810 066 171 660 408 892 195 934 349 736 971 739 377 571 305 512 430 849 796 235 698 802 688 862 157 732 373 949 108 252 378 525 672 122 286 723 798 102 921 513 897 492 439 432 180 922 426 947 973 492 187 024 156 940 874 742 431 018 311 317 935 664 825 184 717 176 989 961 229 608 282 363 472 739 359 816 329 545 437 587 239 025 601 773 765 556 958 958 155 710 633 147 443 289 897 502 259 448 105 374 890 724 238 188 211 467 136 820 146 865 146 660 071 018 914 705 760 218 806 601 073 198 620 126 897 752 019 965 172 014 027 507 143 457 520 387 170 202 670 066 373 577 769 551 504 767 393 398 673 092 042 280 214 232 657 586 264 807 668 247 758 765 169 116 790 372 036 040 090 254 950 848 181 152 362 731 567 032 266 463 890 282 311 224 986 629 742 033 599 974 801 112 325 390 456 923 747 203 619 681 381 844 618 930 879 877 702 744 955 301 988 596 896 765 932 451 959 774 310 377 886 386 760 750 260 083 158 496 347 209 521 278 802 665 313 942 723 891 155 075 663 325 870 227 882 247 979 986 851 660 185 500 447 250 272 206 932 848 041 990 386 902 073 001 099 445 714 553 823 540 866 999 386 143 984 499 929 563 318 845 520 936 833 904 284 043 112 662 703 667 974 643 178 237 124 123 139 399 731 199 983 740 736 081 339 045 403 607 414 955 132 950 797 557 515 172 106 887 246 797 271 714 591 203 974 240 960 260 833 203 459 792 806 667 160 211 901 112 786 079 065 749 500 106 211 883 913 832 973 740 445 937 186 830 055 361 899 827 310 939 651 199 154 530 116 113 804 444 338 759 439 584 213 298 146 055 783 832 846 151 017 344 952 852 842 504 947 417 449 939 899 608 524 354 741 339 019 994 961 651 914 278 377 023 712 231 938 155 840 387 959 304 433 247 952 316 801 086 587 450 821 318 246 874 851 101 869 500 973 928 609 976 972 871 434 636 923 750 769 840 532 068 390 217 194 044 536 834 386 912 407 795 797 877 944 306 453 686 127 908 449 984 304 849 266 156 901 026 142 467 427 928 815 891 034 321 276 220 618 832 977 124 837 436 675 533 882 278 631 146 062 522 006 410 657 785 461 839 461 091 475 593 959 990 519 509 481 786 457 029 132 444 311 787 829 817 914 331 740 123 838 600 365 104 694 594 314 311 386 340 459 860 811 538 836 564 229 290 280 801 376 407 601 273 884 051 777 427 372 203 709 607 974 786 434 393 450 343 228 438 226 784 603 911 347 493 526 624 398 364 347 404 150 806 376 196 554 526 020 993 664 311 984 832 798 031 524 986 567 799 124 044 479 448 628 999 343 207 895 795 223 979 885 121 644 323 941 050 889 912 723 441 015 073 827 123 376 993 490 433 206 427 645 474 388 334 659 727 046 233 054 901 955 015 640 119 351 136 678 043 155 543 009 148 417 989 652 526 480 858 924 086 504 728 299 182 938 910 582 431 619 298 921 053 462 291 354 617 067 070 244 150 016 612 714 447 113 063 178 259 005 020 430 431 918 268 053 979 337 845 647 056 545 616 044 526 096 405 306 957 382 234 092 229 027 358 295 925 284 666 323 748 719 635 516 930 776 559 829 109 268 595 353 657 005 949 992 709 973 461 671 540 183 231 286 192 404 044 100 506 145 794 969 380 371 859 673 471 331 159 406 882 558 562 629 509 353 389 139 024 959 986 733 900 802 800 058 137 145 083 971 502 305 355 973 356 384 535 901 845 336 697 111 495 627 908 365 839 495 799 166 394 233 197 329 502 364 195 297 351 782 413 813 261 205 521 547 344 803 081 352 472 464 604 877 578 104 650 356 380 994 058 943 941 627 208 812 022 865 581 546 004 622 549 826 275 484 958 305 951 584 621 204 635 235 457 148 804 028 353 293 410 843 293 247 699 921 221 908 878 955 780 775 254 855 326 958 351 139 468 236 156 645 995 347 688 959 099 942 976 987 406 030 491 004 427 047 392 960 148 475 783 626 609 763 118 584 105 329 166 498 967 417 803 853 308 663 297 435 002 556 166 036 792 027 899 693 671 145 751 339 479 388 997 775 820 715 858 905 202 278 656 838 844 770 681 225 523 072 988 388 008 236 400 104 783 536 808 827 160 050 295 236 930 135 061 937 009 333 835 903 248 952 100 439 372 469 558 225 935 684 249 773 728 928 983 076 621 614 073 689 727 641 715 353 680 283 657 916 991 993 179 050 107 997 895 199 215 788 236 492 077 435 143 905 690 921 563 664 833 833 823 633 441 317 983 807 677 779 874 467 309 390 340 779 020 856 322 068 461 499 845 645 585 991 572 345 973 120 223 477 499 931 814 803 714 885 703 540 778 293 999 162 501 227 844 693 340 961 326 593 637 192 895 069 878 572 149 334 781 901 865 716 206 241 500 646 852 354 079 558 610 880 283 253 365 389 980 094 407 158 873 804 184 810 560 466 992 719 027 088 157 091 259 354 731 652 595 273 592 233 732 075 428 680 083 966 652 165 135 797 888 182 560 424 932 709 548 688 474 858 189 160 776 846 193 859 806 587 845 135 760 502 215 621 194 363 108 744 067 170 286 752 110 658 102 811 924 729 797 059 167 956 584 762 933 933 296 405 174 436 550 869 195 721 361 958 531 247 693 293 559 811 573 036 251 237 584 878 008 117 282 872 450 826 123 126 658 280 972 437 781 799 499 206 911 971 409 512 090 957 418 602 987 185 072 415 007 207 088 777 187 057 539 553 370 219 864 313 499 306 151 622 708 879 652 247 786 123 302 472 563 533 390 683 011 238 967 164 128 356 144 358 627 641 170 090 184 438 637 337 560 759 985 150 387 542 987 610 320 475 397 731 787 201 873 059 054 440 254 765 212 259 345 635 971 216 619 287 693 680 849 780 893 354 024 059 613 483 002 235 375 383 018 162 488 834 007 361 973 278 876 886 189 109 898 102 063 435 542 074 658 534 881 825 807 446 317 625 111 674 210 372 460 224 052 143 619 930 320 051 975 536 229 199 418 895 326 813 150 571 655 697 149 992 263 212 550 912 504 344 682 263 319 913 278 731 918 815 105 549 674 390 964 918 354 774 596 119 370 370 041 428 831 071 406 123 722 784 491 224 082 177 743 667 694 878 332 211 147 628 340 914 294 713 670 228 575 736 470 883 407 036 656 786 068 807 430 921 442 692 075 324 347 977 819 646 009 034 688 569 891 132 135 753 355 232 380 830 309 973 631 736 558 846 617 429 582 435 650 955 940 087 468 286 399 982 084 735 560 046 708 707 552 199 518 218 092 028 317 238 781 601 525 849 272 876 001 497 755 120 346 998 431 028 486 655 529 769 204 780 962 040 853 436 646 939 069 770 209 197 514 912 848 358 893 974 730 502 866 196 623 120 880 410 807 363 086 261 566 985 657 047 172 515 021 931 596 155 945 555 769 700 988 039 589 287 358 872 942 396 293 501 401 935 337 927 119 517 229 177 420 459 211 615 453 270 946 623 498 332 829 874 844 231 572 235 709 897 245 240 327 278 624 624 484 253 507 020 606 662 785 860 047 230 424 789 188 858 010 662 374 928 447 568 967 228 190 065 710 932 774 375 798 886 290 829 350 083 087 301 297 900 993 379 141 986 515 215 918 100 277 597 388 531 121 957 346 289 427 627 208 682 798 238 316 471 038 314 597 307 858 131 652 167 490 499 773 677 514 729 579 504 466 561 436 151 673 925 793 720 120 180 327 768 238 117 521 211 692 607 153 527 818 468 484 177 776 529 950 098 045 702 516 286 272 330 181 786 578 849 444 069 542 857 563 755 906 941 501 974 227 263 849 717 956 277 195 304 542 290 930 976 301 205 285 807 608 366 898 842 711 325 259 312 177 469 993 058 290 471 252 501 069 988 572 146 868 150 535 524 773 730 337 076 557 925 179 952 854 104 387 604 727 661 453 864 017 157 211 218 269 308 943 998 549 459 200 488 774 090 709 116 307 172 428 981 084 598 138 183 022 081 713 236 104 753 700 168 747 390 494 757 950 919 033 736 349 771 151 770 271 660 268 728 754 970 173 053 563 006 892 491 508 989 325 407 320 539 559 286 844 990 840 101 227 506 529 503 816 032 069 916 828 600 925 222 058 874 136 332 973 203 146 345 296 705 714 095 209 335 191 336 374 017 044 783 357 368 778 652 270 622 219 400 257 054 975 228 190 947 285 346 386 258 137 608 782 075 774 179 946 108 972 067 879 175 805 096 580 189 726 388 348 068 333 030 733 539 872 123 562 596 503 777 128 548 697 187 953 770 532 833 926 926 269 028 446 140 174 771 360 160 434 693 322 934 075 770 879 554 184 033 532 963 317 743 886 223 136 639 820 765 331 722 074 274 523 877 922 522 439 681 483 789 780 226 184 315 923 502 055 064 285 672 272 399 027 781 559 805 206 600 796 709 686 171 095 719 873 575 886 111 254 690 202 086 621 758 288 967 729 559 340 734 552 632 029 770 095 613 497 621 331 644 248 117 242 942 730 587 370 866 075 792 532 041 817 583 341 861 260 755 015 093 045 781 069 029 296 167 997 634 851 275 622 957 552 391 186 808 315 529 369 131 215 935 793 598 304 611 471 333 827 342 597 269 995 644 848 007 750 788 114 575 988 641 668 860 999 318 210 490 552 610 214 530 657 986 910 382 516 004 070 224 639 130 429 970 494 330 325 580 485 022 082 706 468 819 906 356 564 874 592 788 697 175 739 454 983 252 502 799 650 779 805 914 714 163 922 983 612 276 135 870 483 143 615 877 236 588 051 208 881 732 084 342 494 043 547 551 339 432 980 272 183 308 455 848 011 939 105 551 867 342 998 865 787 126 823 326 840 744 913 082 688 281 976 928 186 094 523 018 216 672 978 518 909 055 384 543 911 292 994 869 060 010 395 456 751 077 308 150 272 479 844 060 870 735 811 949 352 056 316 902 443 373 035 412 601 047 919 556 793 247 429 497 125 978 439 644 135 348 454 481 693 166 988 675 898 260 779 677 281 522 506 972 766 396 924 528 358 662 009 638 771 136 142 939 348 081 070 669 254 050 797 587 309 550 320 730 977 870 725 973 883 335 984 067 726 337 088 217 938 657 269 566 993 289 532 853 538 754 078 323 509 485 862 002 977 531 861 974 130 841 913 863 387 343 258 499 235 419 029 757 099 519 595 588 631 702 121 079 397 477 041 212 042 864 112 418 130 637 209 301 878 709 829 291 480 288 328 999 946 771 192 937 943 743 022 348 426 558 085 581 712 896 790 060 130 388 445 942 313 378 381 742 291 603 858 752 849 735 442 738 717 081 867 033 991 750 542 933 639 912 203 219 235 826 872 817 733 326 631 812 634 740 600 975 517 159 940 689 529 965 369 968 253 935 827 559 257 903 893 960 305 322 703 223 111 074 615 989 093 753 951 935 342 975 949 482 782 486 768 068 682 029 084 313 290 443 179 373 363 207 600 616 153 006 790 890 216 758 588 777 460 807 090 686 386 256 819 648 497 825 244 850 656 928 203 509 455 689 573 125 857 352 072 747 809 504 600 456 231 713 995 467 075 463 056 656 850 915 413 428 125 802 796 734 745 280 257 795 854 441 160 218 903 671 562 229 379 175 204 649 014 343 172 835 500 518 284 568 848 682 666 785 457 912 198 342 195 319 947 752 099 657 382 196 453 318 011 830 615 569 154 444 394 274 722 222 878 986 075 003 008 841 131 119 320 447 128 667 718 349 667 845 805 531 484 714 900 394 985 046 381 270 727 274 587 879 585 992 692 057 901 057 942 754 059 167 755 111 427 416 078 906 211 395 103 351 071 368 040 364 156 109 005 310 870 449 654 873 595 976 452 038 555 387 195 362 690 028 380 408 041 031 922 877 651 854 895 151 010 836 500 574 295 388 673 887 520 463 325 534 615 777 148 412 129 649 729 865 429 717 713 658 505 672 770 831 131 443 442 078 493 673 910 457 815 276 026 107 162 507 879 415 481 173 346 893 455 957 422 989 425 260 447 461 914 543 013 420 215 851 599 323 936 362 552 390 972 722 532 673 690 263 796 101 193 157 790 327 110 893 965 092 910 309 962 100 204 879 795 665 192 579 077 036 284 924 325 646 269 454 698 679 418 464 597 758 656 770 500 176 243 447 651 851 095 206 040 015 665 543 306 868 735 234 631 892 910 371 364 130 889 728 788 794 729 300 044 476 671 706 035 417 613 228 472 600 371 777 384 101 312 116 260 388 412 581 280 038 639 222 081 971 149 142 015 513 498 321 504 822 689 152 592 710 424 290 101 410 381 071 946 926 068 945 510 811 438 443 270 740 823 320 575 628 776 237 959 543 210 523 043 072 601 672 082 152 821 291 610 597 577 418 297 530 348 674 961 750 178 644 970 240 450 008 809 991 008 633 952 442 250 177 370 885 937 329 254 558 245 012 081 896 243 863 074 880 622 047 926 495 844 042 788 990 171 010 212 512 642 735 513 344 988 304 402 536 614 852 881 153 006 065 932 190 129 662 739 411 694 600 606 404 535 887 157 294 962 068 586 526 496 346 723 869 005 751 426 007 561 534 682 038 918 962 312 161 109 796 874 498 653 859 015 720 742 419 475 088 513 370 503 955 037 573 177 582 516 684 859 507 664 177 557 101 728 062 220 019 176 854 954 473 129 510 363 138 072 640 220 248 027 196 189 755 043 640 086 068 914 361 020 173 779 342 236 122 342 238 961 338 377 109 701 971 829 111 976 627 877 873 536 324 027 220 748 083 978 948 238 097 536 137 293 016 560 597 539 686 278 499 444 420 456 545 153 810 265 202 190 914 838 979 517 032 329 447 991 829 999 611 895 684 937 064 481 679 186 512 015 775 751 572 277 586 593 697 808 568 314 503 791 477 615 324 023 816 296 983 000 164 681 233 852 950 032 921 257 561 429 121 363 912 700 493 580 344 015 771 394 675 111 941 947 481 095 304 384 907 642 345 282 562 582 797 965 743 807 654 668 113 048 137 775 023 675 380 186 552 408 067 096 455 842 593 698 317 126 472 143 600 428 384 788 960 867 379 691 976 667 443 405 822 441 512 994 385 201 099 998 096 216 712 994 388 113 366 335 853 227 519 095 559 007 470 602 734 163 067 331 803 195 448 127 419 415 775 637 315 277 835 834 250 391 424 830 150 788 183 601 389 497 821 699 338 553 329 137 849 653 003 819 977 175 151 637 965 260 079 063 375 597 621 666 339 489 392 857 819 103 246 963 178 603 427 719 555 780 896 399 652 683 603 495 663 778 524 956 114 145 128 801 367 896 759 283 676 424 825 593 399 521 670 803 849 433 157 698 412 995 740 900 234 082 267 760 504 482 350 940 925 851 908 131 108 284 078 398 236 771 138 435 094 199 095 244 508 484 890 323 509 684 794 505 709 996 344 378 419 480 733 860 938 174 100 201 603 691 901 054 803 014 898 790 070 895 649 457 786 688 641 975 346 108 723 713 981 752 255 851 785 335 529 973 370 047 033 601 673 593 634 226 316 842 470 431 848 124 607 921 776 806 923 596 530 234 358 242 884 747 938 689 815 134 161 352 086 114 198 651 235 422 963 108 667 046 128 276 137 144 777 553 121 437 464 124 131 714 601 141 989 178 987 793 424 531 477 556 575 880 360 979 113 341 762 159 841 587 963 402 448 089 214 267 979 872 722 181 215 712 134 227 630 546 589 155 342 345 518 016 807 561 866 359 629 746 378 083 701 358 259 157 076 291 752 575 164 314 209 524 258 049 998 313 357 298 754 481 254 690 105 420 875 454 935 045 909 544 897 351 220 386 409 356 858 974 615 148 327 881 918 568 881 011 234 036 517 617 671 862 851 195 259 627 670 307 303 581 291 844 409 599 055 993 332 842 846 222 494 391 011 628 279 174 236 819 597 733 824 253 332 824 288 843 302 247 436 084 186 602 101 412 664 119 055 331 732 688 565 777 793 857 879 648 625 197 737 300 691 926 980 548 371 979 901 156 768 560 082 893 393 574 246 152 342 909 506 317 497 282 908 896 721 725 371 118 394 206 128 047 950 706 082 051 750 552 816 858 123 031 198 863 215 769 722 602 085 065 287 159 569 941 705 034 958 624 201 300 013 209 185 083 005 399 506 633 100 710 195 375 161 311 334 392 272 314 814 931 547 856 933 513 433 190 417 407 398 874 762 757 848 186 215 893 005 289 055 845 585 728 897 503 192 498 652 798 573 557 442 615 616 292 170 440 511 189 492 503 249 952 700 138 226 751 348 785 656 705 893 383 335 463 965 426 446 642 574 651 348 394 146 804 000 853 100 620 490 191 235 236 445 756 052 386 510 728 813 417 408 778 210 963 318 117 471 515 249 889 829 000 343 791 729 755 755 330 036 564 499 661 528 313 993 306 079 496 735 429 253 034 098 553 690 944 899 791 909 824 342 949 583 341 780 170 691 827 652 980 601 829 815 457 144 373 284 310 067 185 728 055 030 880 052 591 551 321 950 888 922 421 429 473 061 176 282 107 015 321 583 616 168 170 454 610 972 916 068 682 443 876 517 508 705 786 086 645 971 113 520 963 053 748 348 030 850 268 588 485 367 530 673 777 051 731 794 371 204 413 028 807 281 833 442 494 389 182 815 444 714 783 783 689 144 636 071 977 412 278 817 859 777 820 473 409 189 477 281 855 499 016 725 459 631 683 055 835 274 885 257 500 715 838 654 751 269 445 982 284 495 031 554 195 879 027 565 346 215 598 669 522 635 195 586 844 100 689 106 980 390 700 153 624 586 171 818 006 539 664 565 148 436 122 815 900 630 010 962 542 710 102 655 191 124 725 671 654 060 874 113 736 327 071 335 706 672 275 148 543 576 191 905 093 870 996 500 085 638 800 933 479 249 150 415 199 010 483 630 928 254 896 563 330 058 248 783 202 823 827 380 367 250 526 367 054 489 847 365 019 981 910 359 151 583 059 794 861 335 301 145 751 244 287 418 964 269 906 182 970 516 803 327 819 358 481 201 569 628 257 343 533 306 462 426 259 790 531 312 874 617 140 808 943 404 213 507 175 864 216 097 832 034 045 271 695 798 923 846 181 876 324 383 404 015 933 623 280 431 489 546 417 779 963 476 219 436 486 594 525 422 188 556 258 198 231 961 185 604 551 761 469 880 230 550 514 864 789 004 595 281 577 000 969 977 728 836 063 551 486 038 336 103 269 628 106 355 335 955 435 775 781 780 384 202 839 639 894 950 568 336 361 738 411 337 886 552 080 712 521 244 374 784 890 199 752 428 687 961 786 864 558 920 989 445 274 617 865 176 872 190 985 632 153 631 339 496 477 087 750 348 395 286 083 835 775 651 777 731 692 702 622 048 966 415 990 598 599 183 733 178 211 317 159 121 934 091 355 960 268 119 266 307 367 876 722 619 717 221 057 763 928 815 829 282 670 075 693 565 059 232 754 720 178 148 849 600 267 538 209 023 025 934 137 727 798 356 455 105 517 966 776 610 512 555 852 160 786 626 232 902 596 807 196 011 700 833 825 471 768 042 697 219 388 520 858 020 819 082 322 076 359 956 754 352 538 752 956 080 525 348 134 911 042 158 612 605 311 759 190 282 860 476 227 525 662 252 484 912 398 901 037 695 238 319 990 543 656 925 752 792 694 448 921 804 415 631 114 351 779 468 311 044 791 126 620 545 636 400 639 969 856 306 893 394 158 822 464 823 878 378 500 166 558 722 037 498 995 691 302 445 563 425 430 389 284 917 900 978 312 002 024 448 932 150 781 984 038 632 856 678 677 660 502 491 925 014 391 167 256 873 117 414 941 836 851 524 646 595 122 289 338 444 119 987 501 223 999 404 279 101 574 612 285 231 869 565 300 478 066 145 924 052 387 024 645 701 491 735 619 770 883 334 697 112 756 639 362 629 522 773 403 146 184 066 858 350 183 542 617 695 238 269 161 631 094 847 669 690 385 665 173 977 369 686 561 181 202 128 247 083 168 746 632 410 783 280 083 567 555 849 229 092 869 180 175 112 128 880 691 224 001 924 300 380 528 262 554 328 233 267 993 829 790 668 071 027 287 006 478 267 457 235 889 190 382 254 694 590 385 699 391 191 395 584 570 407 460 022 167 650 545 735 729 939 616 645 345 406 915 630 145 928 354 958 862 251 359 913 599 350 977 750 828 497 796 803 692 800 267 257 633 373 811 428 869 207 417 065 439 196 720 526 406 686 781 227 000 903 364 418 919 958 028 136 956 052 709 253 134 993 015 121 402 781 757 530 625 740 861 909 222 648 423 523 003 272 413 088 877 368 291 720 815 431 720 296 454 469 372 416 764 696 289 495 019 840 777 888 208 963 531 160 209 054 911 903 622 120 099 665 015 787 031 012 560 945 722 871 227 248 236 296 655 546 006 811 653 393 212 911 750 568 649 958 690 109 955 878 888 301 668 058 645 105 191 287 951 854 627 422 458 780 572 648 232 102 510 445 067 448 977 607 824 987 176 773 530 149 811 348 493 595 513 015 010 953 221 884 277 267 173 388 443 560 025 139 235 706 831 859 318 185 863 082 542 406 604 228 171 021 809 441 861 891 581 867 838 244 446 755 538 834 858 408 967 388 048 894 317 576 443 512 000 997 436 001 184 229 396 894 639 811 380 781 719 554 633 386 151 846 333 878 704 039 188 365 726 989 062 088 133 611 931 028 155 258 143 584 148 471 260 587 299 963 039 038 614 112 519 408 812 966 226 012 011 328 082 402 489 246 115 814 323 055 126 825 936 933 767 409 185 655 163 636 857 805 567 324 550 719 371 208 696 585 051 470 631 508 873 029 016 894 180 203 710 975 642 857 545 601 149 271 263 948 590 282 297 091 570 699 995 420 486 693 656 575 370 247 462 546 143 922 914 630 882 290 267 980 237 202 916 442 368 653 944 832 593 185 762 878 563 834 382 722 582 947 390 273 784 025 320 059 656 978 547 789 128 770 207 412 086 544 757 043 648 493 316 128 997 874 560 680 965 879 400 546 133 506 322 816 046 275 038 248 950 557 395 981 435 221 322 259 288 123 779 143 363 885 846 456 430 710 150 683 256 232 903 701 483 862 459 729 684 250 262 986 699 975 035 108 604 778 224 856 504 267 074 565 644 109 219 850 447 542 165 241 867 083 777 574 696 330 953 378 218 637 114 903 385 427 474 613 260 084 746 696 980 825 989 217 707 585 444 261 213 228 948 124 147 975 872 519 684 782 591 230 401 706 064 642 273 957 613 661 927 378 726 498 811 373 030 846 453 679 694 626 618 067 052 250 111 875 366 766 656 729 521 208 725 028 669 484 017 414 649 359 188 629 226 255 737 322 444 147 399 058 983 331 992 200 167 149 480 189 603 261 776 642 542 171 418 898 002 986 980 815 603 187 482 410 182 419 074 750 541 075 833 229 878 338 753 693 189 215 799 725 658 563 523 518 302 477 964 621 859 104 100 481 900 990 083 983 881 137 682 794 503 737 378 112 714 920 215 814 125 902 157 740 118 855 974 974 332 202 240 577 031 758 664 333 065 248 510 203 462 591 317 906 935 501 424 259 063 869 339 474 818 188 027 500 641 684 085 427 532 407 232 006 778 379 555 657 982 867 659 998 306 231 646 785 474 055 117 854 188 116 341 633 224 288 251 696 367 841 284 540 857 151 195 867 137 883 410 759 254 407 252 685 840 594 765 080 257 999 967 979 852 307 413 893 441 506 348 955 368 450 655 022 703 183 069 981 002 310 949 990 878 084 091 245 792 289 831 437 170 070 785 950 690 361 444 837 743 954 938 552 771 732 225 614 011 322 867 461 963 078 151 981 943 917 757 211 426 023 684 984 128 505 081 648 921 129 972 935 457 991 021 507 395 491 189 821 685 470 465 561 743 966 907 680 743 333 787 929 350 648 450 342 900 537 228 853 885 536 001 358 991 686 291 287 109 308 162 567 632 577 135 191 332 177 800 975 681 187 207 429 762 584 519 399 022 509 957 605 826 283 968 831 344 841 252 916 228 994 873 315 225 833 903 447 888 969 335 469 956 364 328 921 976 081 645 089 552 676 807 474 219 984 404 873 880 908 713 807 510 938 823 378 908 039 314 609 133 333 236 440 445 184 864 533 689 910 864 375 120 369 105 111 163 564 978 969 593 146 891 657 645 179 434 320 912 867 445 122 427 028 494 985 173 567 356 060 239 055 437 097 673 362 089 452 991 034 510 996 925 861 198 013 428 961 062 279 260 730 000 916 297 186 259 887 549 289 454 492 315 246 580 747 100 362 278 784 825 648 792 234 903 123 949 523 518 946 723 952 718 374 856 349 211 579 564 965 886 586 507 439 844 559 906 147 283 142 711 168 845 569 063 097 251 757 209 550 991 122 244 710 927 103 560 588 980 630 052 810 676 011 062 638 999 378 050 514 567 688 878 717 370 734 173 669 301 824 720 025 798 318 419 707 016 268 312 848 894 448 351 079 402 804 938 806 966 830 875 937 868 896 868 195 605 343 908 859 784 877 436 461 531 342 038 657 861 548 879 799 903 420 214 283 853 244 038 776 815 216 473 532 387 965 306 722 778 518 275 071 473 614 996 018 719 751 361 048 409 368 661 964 455 463 271 168 862 390 098 423 268 446 008 501 348 036 988 624 386 522 160 162 136 747 366 598 508 967 982 558 371 733 177 297 443 294 680 759 261 545 915 064 113 162 292 314 817 301 601 008 121 406 610 699 255 035 360 868 389 817 668 914 294 508 431 597 896 165 023 370 175 971 116 191 012 725 960 064 016 298 681 496 453 670 410 830 704 218 388 141 917 057 997 996 837 428 654 701 201 060 515 464 637 426 174 759 114 553 790 985 780 936 896 672 965 101 420 436 391 088 869 751 815 346 892 245 990 662 018 740 218 747 051 724 520 213 656 076 881 170 858 286 329 689 208 042 246 709 952 336 827 459 149 426 929 156 475 800 075 806 389 079 411 238 918 497 272 713 840 978 730 602 719 386 792 216 487 536 312 142 738 496 252 758 941 060 981 655 444 565 938 070 780 556 760 991 373 891 184 316 577 175 714 228 248 818 245 500 661 830 360 016 721 676 773 947 237 548 287 715 351 494 638 005 564 613 207 340 291 710 523 235 714 228 751 095 142 011 069 062 644 318 900 283 712 711 775 112 394 878 315 004 028 101 384 090 003 846 597 327 240 589 374 458 372 239 228 069 263 599 463 282 691 003 380 499 011 135 500 551 731 043 459 075 744 461 123 939 410 807 305 675 840 064 750 451 835 019 211 469 644 183 731 852 237 389 202 577 113 446 674 847 250 252 643 882 468 564 187 466 571 024 885 439 824 121 789 785 783 918 470 749 743 368 561 972 132 587 436 265 778 111 751 247 327 097 099 584 816 009 973 060 348 542 131 322 820 869 867 132 397 580 173 312 262 790 333 080 033 757 188 568 061 356 291 688 418 497 582 954 509 418 850 914 321 325 459 249 098 553 854 469 909 503 276 904 944 518 244 328 750 298 937 523 295 906 709 816 926 661 022 117 245 828 820 747 498 228 655 131 348 990 415 093 274 383 294 969 250 751 273 260 857 389 238 645 851 907 622 894 667 255 974 378 015 828 405 048 465 581 650 261 640 443 871 645 867 220 854 400 601 050 402 841 352 119 352 450 661 460 966 271 603 871 411 027 600 179 581 602 912 276 709 849 479 910 715 925 829 424 468 464 848 400 126 719 778 215 647 370 731 885 428 684 980 810 728 676 871 046 471 269 822 160 407 661 453 701 115 482 921 224 257 931 430 179 526 234 228 663 554 735 338 381 929 018 999 268 349 865 056 167 290 215 083 365 467 916 485 933 453 524 294 507 499 002 239 151 304 652 657 889 173 832 469 758 102 179 896 322 624 924 231 961 576 541 923 260 302 498 958 347 424 230 689 286 780 969 619 552 921 429 964 753 545 485 883 503 477 520 634 592 938 274 130 247 485 906 709 836 647 174 134 906 663 343 117 000 444 708 605 385 872 226 871 274 573 127 154 461 971 177 499 043 899 386 648 848 730 904 817 245 224 404 379 677 284 517 298 160 417 505 237 894 642 157 734 129 527 782 965 832 957 783 061 357 308 553 502 719 650 109 617 378 522 388 997 484 750 697 767 100 484 414 532 654 155 506 013 699 586 419 476 620 971 354 152 090 081 276 255 089 207 747 299 212 361 997 528 633 288 669 855 581 386 789 812 561 070 169 108 989 298 569 930 749 914 523 814 319 323 374 924 760 124 728 967 573 518 775 529 041 064 228 464 204 440 461 024 937 665 900 817 840 312 357 997 709 299 708 939 896 836 666 665 786 251 431 361 008 048 788 000 057 184 269 829 187 057 233 306 710 696 673 955 799 706 758 228 692 132 916 218 827 668 168 049 561 966 247 212 101 504 494 496 829 549 246 441 381 420 360 721 238 423 204 390 004 759 828 839 207 985 336 630 535 342 798 805 318 484 517 457 578 498 386 440 829 332 111 617 801 651 634 389 599 783 966 149 647 824 773 276 244 488 553 471 307 399 690 155 758 179 435 716 213 283 464 756 691 332 975 145 756 563 748 233 090 886 970 819 843 221 958 675 243 981 204 204 120 277 634 029 564 447 145 678 381 880 895 305 250 516 358 697 257 249 550 604 657 472 470 789 902 213 593 305 356 042 097 288 210 386 541 213 778 355 623 747 793 229 486 730 574 035 028 058 859 698 699 951 802 178 740 462 789 460 372 361 485 144 973 182 644 699 178 876 234 318 263 794 638 278 500 738 489 619 456 255 631 543 625 878 235 453 590 232 249 468 557 515 518 502 775 732 540 934 139 240 664 130 807 579 175 397 084 001 735 968 490 468 299 233 358 480 249 162 805 965 270 021 455 252 622 437 763 684 838 721 483 559 838 650 081 046 728 592 759 853 070 522 052 856 501 073 213 025 345 750 689 805 490 344 941 006 614 516 758 242 340 105 324 164 522 988 055 083 309 919 534 601 712 980 291 247 729 964 975 244 687 019 784 944 466 014 811 882 896 199 738 532 622 853 205 758 870 503 952 048 245 413 222 817 090 627 625 948 897 956 257 951 830 346 642 946 889 397 240 440 703 851 152 494 724 551 753 591 889 260 140 388 824 305 666 471 155 458 079 280 918 444 694 440 479 869 307 296 743 160 077 929 269 265 265 018 399 187 931 652 150 592 749 824 050 124 464 506 976 434 686 101 276 042 469 017 197 908 249 560 259 670 593 841 538 274 996 547 352 260 331 420 146 921 722 272 163 565 107 636 606 376 549 391 220 808 292 244 896 125 631 984 741 137 512 443 021 618 179 556 498 829 805 460 301 035 789 757 360 627 573 464 483 634 068 883 769 904 458 144 580 454 671 368 676 343 931 175 958 931 847 440 419 190 597 336 394 694 831 076 886 993 797 091 816 389 274 992 467 154 696 946 819 560 831 525 850 031 104 979 601 109 569 492 903 944 902 779 406 562 884 893 601 879 664 127 301 999 215 386 197 671 398 000 502 953 348 770 133 704 873 009 009 331 455 877 115 323 168 524 876 245 788 553 046 536 408 058 135 837 205 956 511 578 723 529 461 056 088 871 507 298 495 872 805 445 269 754 002 161 030 816 294 397 080 990 957 802 593 749 061 135 646 377 767 845 007 043 009 268 330 102 066 179 144 612 840 843 484 181 911 882 283 517 235 461 044 787 678 408 420 989 978 152 473 284 202 070 052 150 859 149 085 468 152 839 293 485 198 354 635 988 643 327 154 837 412 093 231 912 793 901 171 093 182 629 270 610 638 123 646 843 926 292 110 166 912 818 822 073 523 736 312 560 329 232 878 064 007 734 257 580 490 500 025 518 604 731 286 760 411 861 739 632 027 407 708 435 877 522 956 764 555 003 112 591 876 944 582 464 170 748 431 947 815 348 243 995 504 464 631 232 501 525 209 438 019 362 890 510 159 192 315 279 465 462 144 007 329 788 979 842 630 798 178 267 026 077 632 292 344 199 681 538 024 351 348 047 467 491 231 199 355 777 304 283 485 808 376 898 282 625 274 240 649 818 123 809 494 463 789 107 585 765 606 134 157 550 585 051 889 235 137 718 757 623 883 745 115 598 041 863 539 045 060 237 214 834 279 281 201 439 551 220 733 301 912 009 472 359 143 604 895 935 517 188 479 284 270 740 812 228 779 558 269 713 249 166 027 444 974 731 717 600 051 945 213 413 014 282 715 433 715 998 471 329 096 219 659 355 510 718 712 607 615 956 199 054 972 844 550 364 051 192 391 026 056 114 991 606 454 977 293 886 083 289 480 154 858 467 122 167 900 911 431 898 171 461 896 803 199 545 976 009 926 001 495 450 721 287 895 500 583 731 301 839 624 696 886 855 130 861 855 988 458 776 382 007 368 290 113 568 290 514 354 405 530 783 616 058 974 779 450 686 117 794 382 049 648 254 564 087 752 791 220 489 761 345 400 483 709 035 474 460 197 197 702 342 703 155 171 793 682 351 330 106 279 371 772 565 993 632 351 009 479 587 576 433 097 868 248 313 626 491 068 303 774 428 229 376 522 343 673 611 266 789 844 358 969 767 350 332 830 249 210 898 182 739 235 738 541 289 441 025 585 795 279 957 808 322 257 420 995 016 597 730 546 766 248 654 254 622 040 133 274 459 302 034 244 106 600 765 001 313 513 768 410 807 480 596 883 598 154 708 111 544 489 957 950 091 714 744 539 670 546 884 467 585 367 994 845 620 306 635 455 110 422 910 328 801 617 978 066 468 350 499 057 456 008 058 272 367 851 093 017 702 709 069 871 632 242 578 828 570 661 424 455 937 479 404 362 441 927 792 080 673 240 652 796 001 152 291 061 211 909 290 179 622 992 376 366 065 883 753 619 828 692 553 497 047 577 933 824 094 294 631 277 490 516 919 284 682 531 553 996 985 581 029 914 386 749 262 277 958 238 803 717 602 828 923 328 014 383 769 752 024 871 451 406 049 908 638 150 884 692 251 353 365 246 768 494 914 792 241 822 524 426 569 768 953 472 087 292 508 176 735 520 768 152 200 911 470 689 208 145 245 041 812 980 011 923 002 315 368 630 789 999 256 989 042 436 759 153 133 890 266 771 886 126 013 964 244 044 328 987 783 636 154 675 007 143 663 377 243 703 309 584 694 148 874 064 070 907 367 508 905 498 594 068 210 544 649 917 673 765 718 369 371 615 615 816 904 063 969 108 044 699 943 091 290 551 412 965 484 574 225 590 104 164 411 138 511 663 262 104 120 969 075 537 487 283 865 689 498 906 238 549 401 326 129 339 380 046 442 376 038 432 304 418 300 982 062 479 746 697 375 876 308 945 507 527 291 309 821 177 549 325 565 591 058 731 814 188 535 823 533 976 261 277 285 312 302 361 997 798 762 620 484 179 766 207 425 184 460 983 599 349 126 903 755 946 708 876 504 153 151 420 695 439 499 799 869 257 054 628 795 343 861 623 413 113 307 764 825 889 673 222 829 912 118 820 098 057 871 707 295 651 581 779 481 064 479 562 822 524 780 550 241 766 097 734 803 027 975 726 529 420 427 348 419 196 376 433 908 814 607 564 144 944 648 585 977 072 270 396 846 051 272 629 024 894 444 215 086 208 645 130 090 107 830 310 853 403 060 424 204 017 320 546 193 747 467 310 452 180 883 932 324 336 543 485 103 366 269 457 570 656 778 259 147 048 501 870 178 699 955 306 467 880 085 589 740 482 837 122 024 656 995 375 770 240 057 561 090 620 977 521 382 962 398 821 598 333 140 933 524 859 649 880 273 803 778 806 202 877 362 457 833 563 374 920 682 799 126 399 067 308 703 883 026 353 812 770 914 809 006 659 527 157 219 527 167 070 379 628 528 542 203 941 796 295 274 308 015 410 950 355 770 855 995 866 458 812 326 770 401 724 494 634 450 142 312 990 834 980 344 157 221 140 634 332 600 071 382 814 710 886 024 007 211 568 934 524 536 985 648 902 756 998 644 614 783 706 999 164 998 401 764 274 351 539 427 450 165 900 555 038 793 044 111 986 343 369 551 121 906 714 594 230 135 216 909 278 430 234 080 055 976 815 136 080 742 571 519 751 414 544 395 046 359 779 949 439 064 178 003 196 949 721 917 814 511 421 274 720 931 828 236 339 836 924 327 714 890 093 277 174 329 841 479 792 774 872 776 515 859 104 765 251 795 350 955 662 511 167 717 156 006 385 088 636 959 283 114 575 323 822 825 344 607 094 108 985 094 633 133 606 377 983 086 094 017 344 526 587 973 785 053 174 011 093 397 340 580 222 205 628 635 799 277 920 501 639 829 853 483 664 071 000 271 491 240 341 815 539 215 248 732 836 874 359 821 400 540 195 839 714 684 356 108 211 650 427 228 225 819 455 008 587 053 812 354 542 543 719 859 138 920 046 684 614 176 275 476 409 338 226 843 578 165 239 445 387 124 694 803 385 551 224 981 125 976 801 897 423 576 407 371 826 381 275 680 395 778 745 987 643 453 391 107 792 495 569 089 998 128 838 054 842 967 820 456 140 675 873 116 644 198 144 835 833 945 985 275 921 802 544 032 861 061 988 940 794 280 153 653 046 246 546 307 378 031 200 876 961 953 345 884 456 944 797 543 138 479 918 726 332 978 205 729 688 521 750 196 188 472 895 289 727 844 017 887 986 774 050 966 579 859 864 446 109 584 691 322 923 187 931 884 728 985 839 987 275 875 002 513 362 095 262 360 363 873 568 844 351 610 258 002 329 443 495 827 610 953 793 640 956 683 790 319 176 036 303 325 278 068 640 976 151 253 810 920 525 672 269 900 292 158 585 139 069 690 251 166 339 421 977 524 645 000 275 014 413 639 414 930 066 958 689 060 342 560 882 459 176 942 668 981 937 909 265 091 057 030 410 370 432 173 354 965 520 176 336 802 735 651 851 358 704 922 626 045 585 573 172 145 366 175 938 926 223 030 897 999 297 775 859 362 561 438 482 649 800 839 484 402 750 497 026 826 938 029 852 177 861 639 513 385 854 511 766 980 208 292 475 141 409 314 467 526 897 007 012 080 919 131 473 118 156 597 774 846 517 768 270 251 518 710 994 326 909 046 621 505 812 182 714 114 552 486 766 287 723 265 105 742 055 980 707 257 376 141 737 223 878 010 575 080 024 715 008 156 298 803 798 287 537 277 602 783 236 824 898 686 595 006 939 672 604 997 590 090 127 992 983 637 547 323 866 676 117 978 307 034 295 329 115 539 627 325 892 217 852 620 595 290 810 032 912 059 701 865 367 655 209 459 903 574 325 559 967 790 412 328 357 720 960 328 268 306 396 383 348 919 704 671 936 901 840 468 935 530 924 881 554 144 210 139 171 085 132 389 193 740 381 637 634 574 000 330 846 186 430 395 793 285 504 565 077 466 038 651 983 436 943 140 756 814 420 818 099 984 571 881 913 391 482 393 465 245 283 483 273 656 923 102 350 436 061 778 881 963 194 530 883 854 325 757 393 025 164 285 605 161 142 670 918 873 771 420 860 510 198 449 258 495 729 154 860 632 663 074 492 409 087 901 568 350 749 066 719 807 642 740 480 344 639 530 134 272 748 527 715 208 360 498 513 777 754 507 975 063 203 283 366 268 621 677 022 856 769 348 185 356 421 650 211 157 251 991 728 668 706 252 428 293 257 673 702 724 126 399 717 378 114 406 261 003 683 645 970 123 230 038 776 961 449 378 281 951 049 313 961 433 961 075 785 922 141 121 452 662 943 732 200 253 419 830 225 446 134 507 819 119 715 832 855 128 166 222 985 458 027 140 510 478 896 860 861 380 820 225 908 974 988 715 773 070 322 684 914 585 494 587 587 611 451 583 864 998 700 210 637 930 963 688 635 347 088 002 387 873 222 029 947 471 590 718 035 445 997 666 805 135 333 070 550 567 677 273 862 546 236 971 490 201 692 592 660 654 545 949 662 370 766 081 252 665 036 220 407 861 880 040 764 146 628 221 012 299 635 495 072 332 421 810 193 926 996 658 461 855 741 551 756 600 271 908 089 299 800 268 812 104 041 385 911 030 479 166 734 317 677 127 526 188 660 039 368 773 167 817 225 921 105 338 147 485 495 173 401 092 955 575 178 561 404 067 915 154 267 332 506 974 631 887 961 647 949 620 894 047 133 702 155 956 582 990 531 790 906 671 917 957 912 862 369 770 210 915 687 560 689 306 038 230 571 117 512 078 702 519 354 544 555 419 471 580 709 022 053 246 818 189 295 842 516 522 809 198 546 725 096 237 109 882 378 410 151 426 742 940 608 401 810 105 365 272 376 650 384 516 111 009 359 601 075 822 194 781 005 016 665 140 125 698 605 194 438 669 624 867 908 867 812 923 382 121 217 579 318 892 708 773 610 277 257 530 087 001 681 242 006 059 869 942 067 837 442 591 698 538 806 434 136 029 533 645 848 291 160 138 809 144 510 867 112 627 755 200 118 943 695 369 618 366 336 806 854 789 425 449 262 214 243 264 900 287 906 072 620 700 524 614 455 282 174 706 441 562 702 450 509 239 268 634 891 457 414 656 154 289 095 249 954 814 549 639 746 518 722 433 819 905 120 886 837 094 326 896 348 533 420 222 701 116 786 661 741 903 922 284 090 015 432 896 799 681 550 594 484 582 794 850 666 782 578 886 987 759 966 665 250 680 242 347 182 340 214 846 094 640 965 105 233 247 013 179 886 835 979 712 037 807 909 241 889 306 976 551 269 058 645 665 703 858 978 362 553 920 700 036 156 087 432 826 513 523 534 683 752 914 947 607 672 392 663 870 615 075 744 571 741 213 451 330 617 805 670 660 298 173 147 562 055 194 175 898 073 719 881 076 304 023 178 196 107 511 083 155 691 984 190 009 081 030 742 751 666 992 259 056 917 153 873 995 847 698 104 380 871 017 258 997 230 698 252 077 450 344 541 698 719 600 047 508 733 414 008 333 057 062 150 225 020 822 306 187 672 222 767 323 481 738 234 065 057 102 497 889 518 759 589 073 097 854 041 497 144 545 225 612 389 197 671 257 275 386 489 890 992 294 866 868 519 041 681 865 260 347 960 697 897 553 524 445 330 712 953 250 916 868 548 458 603 082 567 241 542 416 855 240 937 593 980 167 218 521 291 824 572 741 021 601 165 357 408 474 631 104 341 290 147 418 887 780 028 847 164 630 394 281 043 386 539 092 283 644 879 158 020 943 149 674 447 040 804 664 604 736 734 236 605 770 248 183 055 407 638 348 861 086 826 466 620 837 183 997 416 502 921 575 626 291 744 868 790 495 164 101 207 230 184 158 071 383 812 133 503 682 692 651 833 484 330 763 652 377 675 296 058 088 451 899 700 074 003 976 829 479 946 206 596 169 797 906 127 459 498 706 953 492 451 787 451 706 482 391 756 124 945 671 590 806 714 320 579 780 885 474 739 779 625 530 300 262 789 804 720 806 456 628 083 871 739 882 618 884 411 280 728 668 984 090 178 005 117 371 728 965 336 237 170 170 630 861 496 702 595 520 077 866 002 981 103 465 689 846 029 539 212 138 449 706 448 385 096 477 280 028 451 541 551 691 554 604 154 034 798 398 771 093 358 983 295 612 973 252 680 102 805 739 759 464 200 556 004 601 478 948 699 438 047 094 083 365 159 808 123 273 127 406 831 047 783 665 334 471 531 763 759 285 657 738 671 304 617 985 275 799 448 776 472 242 843 929 720 148 074 395 670 194 431 110 291 953 095 140 344 946 345 134 997 467 720 069 303 149 066 998 486 246 550 431 201 896 109 250 441 531 087 336 139 463 142 589 454 206 276 351 445 571 446 053 197 144 622 291 693 051 332 742 828 055 887 113 689 675 629 961 433 189 874 354 477 679 845 773 207 797 936 379 323 188 941 659 783 971 576 541 210 236 381 106 150 874 331 327 128 016 528 799 058 484 480 563 943 557 697 497 115 288 347 597 949 017 472 247 065 876 971 988 061 550 386 394 256 079 651 046 509 687 359 695 995 950 635 285 807 748 141 296 181 290 987 672 933 703 263 594 960 486 204 249 554 514 149 826 881 577 151 247 163 214 441 189 937 592 664 210 606 318 610 838 083 853 778 509 782 483 064 642 253 076 006 667 148 158 249 880 535 664 788 623 636 994 935 382 049 088 487 590 214 733 845 085 823 383 335 171 808 890 090 820 835 420 495 461 012 594 903 296 888 219 545 388 712 591 691 123 728 788 287 189 028 155 481 407 412 195 176 090 020 844 971 353 353 267 111 885 379 161 887 387 681 076 003 933 768 529 508 195 190 297 981 381 164 069 803 646 114 300 647 393 073 278 213 593 056 393 639 431 368 108 695 629 136 746 576 172 129 652 694 389 904 611 789 959 377 078 484 717 763 579 392 180 932 133 695 743 928 583 135 217 192 489 836 616 182 925 425 636 059 263 886 292 298 467 042 958 050 652 357 084 245 321 480 030 184 016 509 512 691 337 531 783 453 865 994 889 133 681 148 197 792 927 418 597 330 088 844 065 064 606 795 620 534 814 635 473 613 162 775 272 343 233 218 210 313 861 530 989 076 093 731 973 028 989 220 195 818 039 867 872 430 195 089 874 970 762 182 632 078 281 633 229 918 477 304 898 539 632 559 853 763 157 979 546 488 700 922 516 061 041 685 178 148 697 845 479 873 606 548 867 594 667 920 442 377 202 585 776 103 859 912 594 355 447 328 845 488 270 958 916 729 133 076 682 831 047 639 212 058 620 309 862 001 074 449 415 560 429 076 956 494 621 661 644 012 955 750 381 157 144 652 146 004 066 954 190 890 893 338 586 833 881 114 477 598 587 296 227 575 629 358 764 250 486 464 688 026 699 593 828 575 129 279 396 185 775 466 538 052 933 218 665 112 505 657 183 343 157 417 322 093 129 290 295 192 528 848 631 368 703 536 577 913 761 202 788 211 799 132 755 097 099 652 309 521 979 020 048 232 974 700 134 471 108 381 337 898 139 416 698 599 118 400 777 929 265 759 384 779 326 163 659 184 694 180 298 504 310 160 937 505 791 833 046 530 378 961 570 291 864 265 626 863 224 539 095 127 813 826 668 318 685 736 406 361 434 360 940 211 783 937 030 509 529 742 862 265 219 305 520 196 693 030 455 086 510 561 316 893 665 659 480 258 466 229 485 171 634 874 776 430 617 853 651 508 278 625 791 663 883 508 925 178 093 891 362 112 626 432 838 191 062 271 666 929 061 145 777 213 111 381 138 169 141 954 968 900 000 870 770 598 176 667 783 313 234 806 674 975 856 899 213 151 279 902 581 601 793 237 477 064 614 918 155 030 703 498 973 974 915 940 131 397 934 414 645 580 310 880 934 777 843 689 665 230 140 324 392 565 150 578 253 899 990 340 109 470 825 645 204 189 863 613 264 963 844 818 249 404 802 214 396 136 579 914 157 691 341 974 502 639 384 111 720 888 023 412 042 063 339 504 789 577 482 120 894 285 142 418 453 389 147 067 008 898 174 395 853 327 085 514 116 244 670 656 401 870 162 177 848 209 919 107 837 524 782 781 493 632 483 161 345 457 322 537 900 758 568 048 129 854 463 493 315 288 074 769 953 712 920 201 466 414 207 206 225 053 720 590 314 846 577 654 582 127 052 588 825 038 436 175 677 318 093 776 770 805 453 799 218 965 005 840 786 352 963 054 636 041 013 632 155 068 120 212 224 375 190 640 068 739 839 656 392 513 771 566 057 265 081 620 431 255 098 200 543 148 500 842 788 841 643 224 712 048 749 063 340 574 201 431 437 345 118 841 736 057 865 927 907 179 365 879 222 276 018 944 135 899 453 676 442 568 787 587 653 004 398 743 453 728 207 796 016 535 273 874 370 379 644 232 080 607 374 314 524 778 122 532 489 468 491 218 033 870 708 009 744 029 637 853 659 185 372 998 070 672 995 607 386 379 636 002 291 927 433 452 236 442 895 949 767 082 151 196 812 133 174 181 724 612 549 205 094 545 138 560 336 130 397 043 704 348 747 263 401 934 347 339 151 352 899 316 192 178 682 517 012 640 421 574 826 951 938 245 758 880 208 062 218 883 103 740 431 642 372 586 757 484 755 344 467 156 624 433 919 885 207 102 592 817 329 274 159 219 903 826 796 449 777 020 838 934 969 038 093 062 123 121 827 159 404 701 652 129 703 609 220 419 972 535 156 911 298 759 449 626 353 990 485 117 437 791 307 318 983 299 905 106 658 507 318 811 377 218 948 517 300 765 955 920 634 234 856 827 583 692 818 401 167 515 786 436 600 632 753 681 021 705 836 145 535 369 880 678 576 534 941 259 380 000 140 158 516 568 017 940 042 879 935 919 670 744 142 337 221 462 082 454 151 704 135 447 665 293 737 693 489 600 196 870 745 761 053 532 594 220 978 780 651 298 305 044 309 991 917 584 204 697 829 149 903 410 547 021 421 655 659 846 488 679 770 314 234 304 329 553 648 650 294 839 040 884 905 482 148 825 064 463 030 756 436 115 167 890 806 237 776 791 970 800 734 931 670 862 330 612 498 875 762 338 495 709 330 241 951 671 557 993 302 083 455 010 082 509 167 200 339 208 292 458 851 790 056 815 568 422 704 811 236 035 361 866 983 541 533 230 198 106 697 996 664 609 708 812 678 138 518 171 948 802 724 424 846 581 649 995 132 821 121 071 747 133 591 409 791 112 061 789 770 887 047 264 611 313 310 872 332 061 949 764 152 570 503 322 068 253 068 214 211 771 321 286 427 929 345 236 429 033 527 767 833 955 564 187 709 029 689 055 490 092 769 166 417 749 985 788 238 678 245 284 624 689 232 971 281 816 418 401 483 101 894 665 659 423 838 395 916 212 186 873 033 605 657 037 549 660 221 559 602 956 115 539 903 543 860 762 690 915 316 465 309 679 251 083 579 110 560 025 457 660 633 805 099 783 762 153 223 006 917 562 660 751 733 575 796 691 663 086 927 335 678 186 800 532 105 469 473 578 920 128 565 870 952 850 437 589 653 403 720 066 329 444 399 132 324 273 085 325 076 706 670 975 230 158 478 186 726 899 790 675 442 727 701 015 062 267 143 976 803 334 095 303 600 932 674 518 555 357 428 887 407 992 799 513 101 236 612 396 577 396 440 891 095 378 978 796 798 334 849 685 671 517 947 061 813 741 687 523 951 878 242 314 665 085 591 868 872 457 478 969 466 353 706 460 204 314 705 533 448 443 423 500 681 128 819 640 179 642 995 685 856 496 774 767 396 730 804 498 933 085 510 781 080 752 826 927 279 307 506 097 384 236 153 667 865 416 677 835 269 344 659 703 015 078 211 463 656 703 404 480 536 102 527 897 581 089 575 123 507 142 621 176 245 880 835 224 158 555 325 907 534 277 575 940 567 130 946 746 870 246 301 102 191 880 879 207 369 520 642 027 274 250 427 762 057 605 624 114 948 660 934 213 380 202 229 163 263 604 297 955 830 715 622 107 367 377 630 387 919 270 861 116 170 753 660 283 047 673 849 295 467 482 011 076 074 911 552 383 508 216 815 225 338 304 757 501 695 271 029 298 809 530 512 750 869 058 997 543 360 140 196 869 853 516 188 891 108 426 939 751 328 568 005 127 949 993 031 831 867 078 989 460 776 536 524 350 286 391 270 816 352 386 212 405 593 034 493 724 758 106 514 796 147 281 723 294 474 051 103 838 493 699 594 262 469 284 974 339 757 941 840 139 262 831 314 889 444 330 215 988 539 153 620 255 079 265 531 698 865 729 397 474 403 934 471 550 582 823 553 391 767 249 704 015 547 508 550 964 985 230 754 025 132 377 156 509 823 198 085 874 281 980 496 716 534 372 402 111 905 593 965 727 594 944 899 440 362 999 328 799 029 986 806 862 642 150 020 195 271 109 938 759 028 147 100 064 194 745 745 790 417 684 433 009 938 176 087 017 556 449 283 388 212 796 906 234 399 755 111 806 412 728 665 565 108 268 504 187 826 940 361 068 101 933 422 254 699 744 291 793 325 156 163 110 036 453 574 695 141 049 867 091 288 214 145 635 253 730 971 812 359 377 543 240 186 008 388 958 637 520 898 998 456 006 592 421 201 895 295 225 792 501 097 857 843 278 468 578 904 679 016 884 118 925 538 840 097 854 548 847 882 572 168 852 748 002 155 915 395 010 244 293 149 592 174 723 767 137 907 237 082 700 883 092 921 719 823 171 375 083 163 389 815 791 204 841 438 489 174 273 866 420 238 416 697 205 932 311 149 285 231 894 764 960 075 047 317 644 058 605 244 166 611 701 066 024 167 627 253 306 988 912 392 105 371 161 314 118 092 054 506 972 564 499 095 559 712 064 208 845 582 090 204 149 992 155 167 466 903 376 554 406 256 196 290 577 961 164 768 064 218 461 239 815 973 116 991 948 696 704 522 875 618 803 570 826 182 224 828 412 985 355 313 341 826 041 116 711 405 743 144 728 954 569 193 689 853 266 354 442 160 035 469 382 128 847 226 968 222 378 764 652 229 307 542 053 789 547 233 182 733 185 154 301 551 928 756 743 661 000 418 153 306 480 062 674 828 304 116 482 608 546 109 939 058 549 354 865 547 219 704 655 647 335 050 413 639 776 224 458 966 523 484 242 152 399 244 046 981 754 272 195 182 283 630 606 161 509 172 848 680 204 834 773 328 294 525 188 745 041 279 581 198 327 293 925 825 579 821 107 454 175 377 715 482 343 128 617 416 004 304 867 592 720 216 970 304 395 750 911 140 481 714 337 838 993 962 455 423 546 554 545 631 909 969 860 922 403 974 189 824 288 678 517 607 101 679 527 532 766 348 482 163 237 495 911 288 497 585 827 632 244 668 585 427 044 535 578 839 416 259 577 645 346 586 891 756 973 475 174 703 223 246 149 322 011 448 771 854 580 597 101 761 636 951 059 783 670 028 259 566 739 308 000 625 567 930 926 854 492 198 972 631 975 287 495 262 400 345 856 459 064 496 082 457 356 909 115 966 978 462 798 019 978 692 260 432 742 793 872 896 176 969 040 489 782 405 085 122 758 885 413 426 593 054 867 328 380 377 137 375 805 237 119 781 143 171 777 520 020 299 012 857 259 939 961 730 346 715 950 193 456 178 720 108 054 014 974 107 743 394 464 387 104 053 839 679 339 794 940 728 960 619 323 339 551 101 343 062 120 819 375 075 756 550 881 831 042 208 476 023 260 229 874 850 839 330 190 541 710 533 840 321 311 925 602 488 710 190 398 901 443 216 694 231 762 581 281 546 989 745 540 858 124 586 041 142 543 151 554 254 030 106 250 261 401 055 525 200 283 783 346 572 227 782 877 309 137 283 934 303 694 978 267 082 955 413 542 627 782 901 727 849 568 120 268 200 390 854 958 042 844 778 490 985 100 720 228 268 199 552 023 414 960 005 791 905 367 327 763 375 227 406 007 620 453 196 122 931 571 731 329 067 253 000 610 627 052 403 214 803 401 995 735 503 538 433 517 848 632 947 961 481 312 271 215 776 951 375 321 878 237 424 009 689 901 356 272 998 089 828 240 146 950 032 680 157 487 403 693 661 543 795 529 616 052 406 915 645 884 129 436 259 989 472 645 221 480 532 121 295 172 150 271 577 644 333 535 093 639 589 105 709 937 331 753 901 200 734 318 845 992 178 856 734 714 411 495 176 236 970 337 357 691 724 879 726 876 140 425 438 614 887 340 918 302 414 758 259 636 971 155 534 044 144 780 221 046 176 085 508 691 527 705 823 637 973 863 470 427 651 087 348 778 498 369 934 371 853 053 653 348 783 401 693 477 108 042 507 771 626 171 916 805 457 838 241 450 801 855 401 586 159 855 430 051 203 971 644 558 620 901 772 165 289 543 831 867 647 590 777 029 902 012 176 272 260 881 948 421 851 973 522 457 220 686 225 937 361 386 455 392 991 628 402 593 106 942 466 340 588 008 248 930 057 341 191 883 888 551 236 726 433 996 697 718 078 716 245 516 695 470 030 268 575 771 937 465 747 045 912 500 025 058 578 603 956 923 641 891 642 567 557 005 618 250 959 053 035 033 356 244 252 387 346 530 586 519 470 649 381 253 724 844 229 393 634 659 292 996 646 319 422 499 268 328 910 354 482 930 653 528 078 950 974 511 787 887 906 355 498 797 528 061 994 131 209 937 775 966 411 247 082 400 170 755 046 409 991 354 079 386 148 219 620 904 012 897 555 632 531 828 458 484 765 989 448 913 536 971 525 612 696 935 097 726 763 529 106 420 977 334 258 496 360 831 018 056 359 826 186 912 951 530 609 578 354 887 724 721 433 451 117 249 331 751 248 970 385 484 069 211 584 059 086 940 750 713 456 232 792 246 817 183 652 595 815 838 561 216 917 091 088 562 483 193 148 566 068 108 557 439 027 958 728 498 113 136 198 036 197 685 305 288 861 874 612 057 836 490 156 179 740 949 515 687 558 171 620 927 281 667 791 574 721 018 034 857 199 850 392 560 548 836 906 565 404 591 817 971 404 604 046 003 735 310 243 811 988 437 200 463 808 687 883 430 646 735 850 092 960 665 040 896 974 010 336 032 733 552 583 764 989 586 265 213 704 493 051 753 784 097 986 041 451 892 376 886 364 645 009 844 602 782 569 211 043 916 998 430 389 044 685 111 097 218 839 650 707 307 898 673 599 497 548 421 118 258 751 680 689 365 262 503 643 513 125 701 832 572 585 881 265 866 050 786 426 525 517 393 577 003 561 013 985 327 109 188 764 456 800 290 254 253 719 200 051 014 832 665 817 596 709 264 743 043 595 648 137 542 563 020 874 356 876 187 686 758 726 553 939 256 447 601 411 875 527 805 167 525 702 583 853 970 528 469 345 048 260 547 957 683 259 220 299 382 324 507 575 972 174 344 452 435 854 169 238 065 676 361 709 511 209 220 259 859 929 603 986 844 077 470 635 986 762 643 201 970 614 055 822 185 653 281 705 481 466 859 064 105 401 017 747 624 495 169 563 010 913 465 179 738 743 103 690 521 615 843 083 952 865 750 186 752 558 994 231 259 724 634 525 951 765 626 164 893 048 430 242 755 289 451 738 480 967 121 577 877 771 081 723 141 222 580 262 717 526 365 345 022 895 837 034 627 448 757 581 748 300 973 485 115 951 157 881 988 738 314 751 461 676 422 124 876 551 843 699 897 021 728 807 349 763 702 290 389 416 933 077 955 786 810 249 186 509 305 340 928 999 486 442 924 911 514 015 488 601 563 816 340 722 785 925 223 057 177 129 463 382 870 856 319 680 557 486 717 610 194 214 270 968 324 208 806 446 319 587 876 252 265 957 558 832 362 312 141 050 273 025 625 758 773 314 355 100 833 196 876 430 520 023 218 092 799 549 899 836 656 457 644 477 579 024 077 863 939 510 139 143 035 982 101 244 710 074 819 420 409 612 404 736 033 078 460 754 259 049 874 134 404 466 800 828 083 289 369 913 176 059 292 161 685 592 435 478 691 370 394 763 852 317 601 636 782 094 743 501 682 817 049 373 714 788 938 465 740 106 338 997 383 849 181 413 475 030 752 207 116 528 277 411 833 893 898 751 571 288 310 143 016 377 324 713 817 485 821 624 732 102 534 295 505 236 013 990 655 613 045 177 945 682 217 034 960 276 146 535 995 782 559 316 541 788 422 566 394 463 962 254 729 341 214 625 270 488 071 458 695 536 818 526 300 494 093 750 467 935 399 558 079 062 903 244 073 501 793 232 163 083 861 525 080 749 883 701 745 992 281 035 344 699 036 970 169 512 400 944 828 848 505 974 922 454 808 220 017 220 510 788 388 998 797 475 035 263 802 856 190 635 343 653 402 102 506 850 502 650 782 996 489 022 093 876 953 942 481 696 466 900 024 177 549 765 812 203 704 344 838 883 674 340 241 073 184 688 634 598 654 381 999 941 527 325 900 901 493 808 902 199 054 169 711 601 171 300 316 965 057 136 529 944 044 201 398 772 463 673 897 230 934 024 223 775 428 595 377 395 836 991 047 113 854 216 124 943 881 485 237 728 918 203 865 852 187 005 953 634 754 340 752 844 015 960 562 075 595 277 271 534 014 421 323 849 326 761 045 672 605 414 563 588 211 904 577 221 885 354 984 187 179 869 286 459 103 789 899 047 793 654 448 293 746 513 658 720 912 447 985 512 483 577 758 026 066 319 467 808 899 816 646 494 998 420 210 310 177 749 968 234 235 502 209 374 465 255 414 619 940 386 325 487 961 218 783 782 606 037 868 130 348 448 071 629 194 132 638 017 477 122 242 715 299 985 466 373 035 995 883 070 705 362 859 081 082 862 086 617 785 813 567 167 698 341 812 480 968 980 111 548 861 271 621 813 052 289 116 233 871 954 098 813 785 852 907 655 854 133 361 769 253 099 797 479 382 589 790 696 577 422 503 419 377 761 086 733 432 601 923 951 966 427 260 047 374 425 572 199 007 126 743 231 115 862 949 215 901 923 121 318 366 682 822 442 863 554 841 493 929 699 970 481 160 075 961 163 273 105 919 909 555 275 327 737 595 217 179 107 675 070 509 913 318 666 568 094 440 513 881 757 762 498 967 234 382 786 323 737 767 413 874 838 978 307 814 472 467 290 219 422 758 553 385 621 400 327 984 995 479 095 081 934 248 352 433 142 759 410 708 531 844 558 690 937 836 069 176 401 996 651 899 502 786 122 499 891 137 905 371 586 243 898 983 443 898 885 072 085 204 451 879 329 004 191 082 456 883 102 014 404 762 326 667 128 421 220 399 311 043 818 199 178 933 291 077 490 821 865 814 121 806 166 675 533 101 030 470 387 388 027 463 544 458 576 903 410 170 476 533 398 088 047 721 935 076 419 849 805 607 774 757 728 837 997 408 437 027 281 057 409 948 114 367 388 932 546 001 578 293 039 627 175 749 037 495 206 294 271 732 793 010 393 591 471 063 870 818 010 017 056 832 259 876 341 773 559 213 125 853 409 860 225 172 926 449 452 121 234 530 575 655 413 347 682 985 200 869 525 896 412 371 638 338 123 876 474 928 209 621 565 145 013 559 593 227 099 584 534 575 221 338 429 212 373 985 983 508 582 993 000 440 570 803 091 817 650 958 203 550 436 261 084 261 505 874 914 129 819 534 928 076 333 942 717 472 495 476 797 744 295 018 675 032 905 098 290 251 180 816 584 896 434 035 842 054 271 140 669 992 431 394 045 249 908 853 275 379 136 435 556 457 180 821 743 060 386 357 883 686 780 968 531 567 719 678 570 633 501 227 118 307 552 019 252 355 428 164 412 684 888 634 668 004 349 488 133 765 585 697 083 135 738 381 119 746 110 322 756 166 879 509 162 630 157 689 899 902 158 188 920 783 787 606 994 056 940 436 253 191 644 826 357 144 185 886 537 089 224 929 498 434 628 303 161 661 809 379 336 346 246 508 231 511 558 672 328 763 073 905 503 839 774 161 093 958 078 989 797 232 368 431 978 644 235 692 547 346 805 691 367 302 218 165 123 125 812 252 679 797 988 802 043 662 353 292 624 396 606 147 377 323 371 658 993 365 905 311 073 052 232 367 308 062 897 413 878 085 814 076 776 733 481 532 714 499 090 201 946 178 316 068 356 105 234 898 118 360 274 212 904 172 378 723 170 781 185 644 698 234 588 650 683 011 175 132 800 207 837 953 707 823 665 404 101 273 603 965 181 087 757 320 127 190 462 131 998 854 538 450 190 962 334 521 981 115 316 001 676 130 646 524 438 159 268 754 732 481 613 498 242 701 726 867 746 515 191 344 379 598 186 786 678 122 415 789 343 949 513 986 718 564 802 821 263 746 656 414 266 340 322 459 578 061 143 053 911 380 180 452 853 537 623 213 279 245 297 532 015 334 049 289 520 506 681 310 523 127 603 854 472 042 498 394 803 756 689 554 085 237 656 279 043 229 309 363 360 591 909 630 920 891 325 045 706 369 113 544 139 672 097 978 190 503 670 047 382 315 764 936 592 351 670 759 573 454 548 529 876 717 416 669 527 016 943 502 060 529 126 605 988 024 223 601 007 527 108 113 576 373 228 077 327 314 701 854 141 989 915 987 840 622 048 494 576 464 652 856 144 318 687 146 393 534 184 994 359 215 260 491 323 312 777 847 367 697 679 548 706 850 901 353 273 164 492 980 041 158 055 762 004 473 830 805 094 784 720 165 607 976 808 660 932 701 571 120 041 326 787 053 981 790 673 324 135 965 785 374 687 513 401 062 288 065 533 087 194 371 093 364 625 318 304 008 175 333 179 781 788 297 935 139 941 520 165 508 613 302 665 549 528 108 661 044 461 111 644 076 560 147 755 784 667 037 257 912 782 671 584 274 383 423 088 593 200 544 837 768 659 034 826 966 075 493 007 642 885 613 800 357 350 011 760 174 232 172 987 579 939 429 084 421 172 328 127 173 087 296 654 955 187 094 566 055 736 810 637 143 098 742 183 313 486 874 094 054 962 973 952 055 370 883 273 586 816 375 704 606 414 034 941 850 092 686 538 886 481 601 781 443 465 053 985 451 849 966 197 326 638 465 762 169 316 338 664 397 844 042 834 344 374 356 338 964 098 425 623 277 843 661 180 658 252 861 897 126 400 638 642 086 211 656 286 763 471 774 121 654 027 216 587 128 346 923 082 854 268 993 939 399 845 220 216 459 197 408 074 265 665 676 004 301 577 865 439 484 243 718 356 251 301 347 984 026 802 681 709 825 105 747 643 705 135 278 470 340 347 986 112 813 108 145 271 852 632 811 094 739 576 308 030 073 358 953 858 991 370 780 623 560 589 039 131 235 116 539 225 030 571 004 110 872 318 315 002 089 307 329 914 376 377 754 107 535 092 623 879 801 638 810 567 198 141 834 337 914 439 658 293 658 852 438 592 476 469 463 915 762 979 709 503 367 051 406 872 740 998 738 236 288 665 073 981 830 713 536 955 154 525 212 874 590 534 340 274 016 501 938 559 230 294 332 702 752 178 915 407 979 579 206 223 378 921 723 553 584 609 760 666 769 467 666 753 012 743 357 025 243 337 949 520 231 247 226 225 702 197 594 941 802 149 699 896 303 115 383 271 038 242 361 072 073 596 559 599 948 624 131 899 945 958 568 132 373 029 308 429 158 258 097 481 610 959 053 121 494 863 420 245 801 737 683 730 117 538 638 716 025 025 497 782 130 497 855 083 833 725 696 199 491 074 378 047 982 538 750 227 773 816 805 378 515 290 353 607 346 529 088 950 081 782 806 480 030 663 777 430 104 333 248 093 556 039 845 926 009 468 775 177 857 305 586 658 304 329 048 848 143 700 230 265 296 438 647 452 015 973 005 205 829 912 436 166 431 305 368 685 723 300 979 882 853 997 855 837 402 337 772 465 695 687 992 228 961 507 623 266 996 466 464 979 239 926 667 306 634 849 251 099 183 270 987 345 659 829 150 360 196 763 495 686 794 946 659 615 978 884 084 593 088 188 752 835 353 463 650 897 551 948 512 267 339 414 322 063 740 523 976 017 636 505 203 781 435 370 660 140 948 268 220 087 405 013 382 540 996 348 572 453 874 718 632 644 843 258 119 165 422 689 682 812 369 839 411 484 253 735 361 749 723 019 434 985 631 619 625 917 358 469 639 673 365 127 002 022 526 005 101 685 828 724 743 278 710 825 728 670 136 728 378 198 503 523 845 478 335 735 023 782 952 096 547 206 424 674 625 587 630 815 152 990 137 759 023 025 830 166 976 539 590 254 689 830 088 184 043 395 220 362 575 386 094 770 025 979 324 579 758 928 364 310 650 991 568 420 254 623 709 031 326 644 193 513 086 058 838 761 987 783 415 244 883 213 219 505 561 362 852 787 948 488 659 531 604 000 373 136 307 655 837 725 577 653 727 573 213 003 176 807 867 802 175 381 300 268 851 945 130 835 443 744 100 249 767 822 033 443 870 884 152 402 533 650 780 216 517 681 984 334 685 342 061 396 870 544 589 852 828 620 211 074 151 985 046 657 940 788 695 034 999 838 732 808 695 332 192 004 346 927 965 730 715 000 253 164 812 461 622 798 118 908 800 761 709 100 969 182 750 228 337 921 846 786 151 141 610 737 233 503 346 271 035 652 681 538 722 613 617 418 934 977 058 320 573 101 747 945 205 782 966 958 863 026 263 279 218 590 709 223 825 947 821 708 492 335 856 244 540 903 612 051 565 973 030 703 160 670 084 062 349 698 036 170 041 944 695 273 819 574 603 555 757 210 418 777 293 374 462 033 816 651 915 071 137 363 957 934 207 756 596 051 290 817 111 037 592 631 615 593 031 341 967 150 942 670 299 909 995 743 964 577 344 025 123 767 207 508 864 595 091 081 755 665 894 538 531 754 661 947 562 296 953 204 965 546 433 578 786 024 865 635 735 638 999 475 661 308 748 482 689 258 692 965 496 496 029 931 500 727 572 085 967 487 248 564 884 697 546 472 134 556 963 853 275 669 440 894 717 879 883 077 228 994 796 609 374 367 004 071 235 249 394 912 534 249 309 099 089 437 703 895 603 778 779 108 383 929 825 640 595 059 742 996 015 151 281 290 199 523 273 989 395 697 173 634 904 236 413 119 563 801 560 297 530 644 635 052 458 091 022 991 799 443 358 599 235 471 150 332 624 689 605 578 944 455 599 374 524 628 275 047 984 122 424 304 359 099 685 572 108 451 948 180 540 006 520 708 421 500 877 550 590 907 605 884 968 561 550 526 867 635 506 481 311 771 983 777 398 060 219 131 046 761 526 543 910 701 331 108 033 909 704 996 303 784 653 823 984 558 801 765 120 907 459 080 903 184 958 610 273 400 574 392 927 408 785 790 758 936 200 318 766 331 847 108 990 132 251 097 303 476 451 566 822 661 792 193 187 586 875 401 868 206 768 809 180 576 063 038 758 843 100 675 837 865 263 264 573 728 894 585 011 452 076 325 759 929 880 971 119 955 157 845 024 384 531 817 654 456 208 060 891 981 051 252 588 097 653 842 731 265 597 785 070 193 502 103 379 642 361 154 697 726 452 519 879 162 432 645 678 395 353 766 245 747 042 074 917 663 605 477 091 747 728 346 289 892 993 781 578 841 015 999 160 901 262 241 738 264 441 087 573 316 702 633 704 241 192 032 656 183 366 260 288 432 144 678 412 499 987 438 546 785 480 147 284 878 714 648 236 234 956 107 724 186 651 738 968 904 140 922 519 642 563 061 284 850 716 125 560 764 703 865 278 136 053 541 654 203 352 466 132 315 332 634 792 216 412 411 930 504 327 732 084 833 851 194 568 706 053 172 551 771 126 584 933 118 520 130 791 304 027 925 596 109 456 128 560 265 561 172 825 572 230 759 866 941 450 984 747 086 845 809 850 888 296 274 684 415 410 353 832 707 852 668 513 325 750 818 141 948 366 219 090 622 577 773 359 288 242 493 103 873 907 136 208 462 657 079 861 147 864 383 553 429 477 397 074 458 611 239 902 281 869 407 588 629 097 654 266 773 636 226 838 490 062 460 914 461 994 584 308 956 577 350 317 306 849 989 198 027 386 072 907 783 589 359 505 121 530 735 473 821 691 619 472 219 492 703 687 424 508 860 318 554 026 928 861 616 019 351 409 562 950 150 507 733 102 501 041 316 205 013 961 590 696 088 408 921 975 524 909 946 501 756 894 277 874 131 816 098 861 258 979 135 628 443 424 999 438 604 315 252 145 194 038 571 688 586 571 211 702 223 829 893 235 339 362 492 431 840 583 267 700 423 253 204 543 075 933 688 915 460 816 830 466 753 289 529 504 245 559 890 628 095 715 019 748 138 318 848 885 927 824 301 529 858 558 097 256 247 800 670 256 132 420 094 302 488 194 379 204 360 584 360 171 339 876 576 034 468 006 220 513 964 119 628 969 447 612 771 724 324 829 164 959 862 887 412 668 614 510 507 699 492 261 467 222 313 008 783 802 943 368 545 789 505 249 561 872 643 610 485 886 789 334 171 357 658 830 502 386 247 665 049 171 238 473 078 342 329 610 897 363 259 729 030 708 691 050 607 724 125 370 882 380 178 072 834 704 476 456 681 100 636 218 340 155 435 453 612 757 297 237 262 243 400 393 343 724 479 500 180 092 780 589 215 638 909 481 217 375 103 367 037 211 212 311 562 342 025 848 409 410 039 851 663 483 520 506 879 591 508 614 849 804 791 125 929 484 860 210 187 499 764 761 279 286 770 612 722 485 851 882 800 331 790 597 206 398 053 887 332 014 672 059 155 760 562 063 915 784 815 122 764 247 755 559 266 835 803 787 121 534 851 770 356 119 401 163 432 421 466 810 325 493 930 525 976 077 258 797 421 975 559 026 881 431 650 732 653 708 603 280 375 477 731 957 364 081 480 629 701 314 707 539 696 209 556 711 699 756 587 723 918 243 979 016 512 443 532 207 914 312 592 083 623 067 530 422 187 480 823 037 027 841 557 445 421 361 186 961 858 558 283 011 651 369 149 819 493 330 569 329 825 824 578 018 357 714 027 801 565 290 918 843 409 929 090 823 371 139 685 417 313 284 541 850 124 262 815 397 316 973 592 924 234 139 586 802 274 921 694 432 596 375 781 926 771 761 765 501 943 514 882 641 244 397 287 525 406 541 904 275 685 336 628 037 016 553 351 477 112 170 902 316 804 430 204 533 896 844 305 764 108 915 046 451 093 307 104 447 367 686 849 474 182 339 991 293 077 089 318 153 010 708 374 763 239 659 993 109 987 361 659 396 297 675 744 579 287 698 834 763 240 381 693 287 208 376 833 522 492 614 795 505 612 352 102 932 134 064 653 196 132 045 909 414 351 424 447 031 498 845 029 181 721 427 603 587 156 047 991 829 187 432 139 829 484 844 435 673 668 877 066 100 758 799 537 956 711 108 151 649 926 240 401 255 312 932 029 576 203 210 891 221 057 096 059 224 880 799 569 956 948 002 774 386 047 603 211 392 495 395 230 540 850 774 696 426 498 722 559 999 868 847 108 434 694 013 854 209 983 464 544 627 275 867 339 556 550 662 742 746 748 672 426 105 991 453 810 118 787 532 007 459 813 536 303 049 661 031 319 032 777 296 250 589 497 340 183 607 180 123 746 751 829 979 832 624 648 318 219 611 307 546 577 496 868 052 167 161 050 843 761 181 581 207 921 485 991 513 075 487 761 368 425 956 385 057 141 416 400 464 853 299 834 067 982 755 251 583 257 122 159 768 443 896 559 507 170 756 534 608 999 576 193 991 701 525 891 628 886 632 531 186 810 444 669 224 306 882 979 592 428 340 052 068 404 707 283 789 567 819 559 453 750 573 866 976 572 246 428 761 515 122 172 678 286 913 901 457 686 818 558 274 702 499 014 242 517 456 676 904 699 732 690 686 217 047 097 569 370 170 274 711 290 383 019 877 516 327 562 789 461 486 121 597 807 844 999 958 148 072 532 483 836 649 702 990 562 826 565 601 921 919 110 248 243 186 032 742 762 392 999 682 764 730 359 182 496 426 718 844 727 829 909 731 396 201 313 871 917 557 655 890 639 771 111 819 108 832 234 866 833 275 811 842 324 454 042 310 831 351 062 203 868 187 655 346 021 443 478 124 241 840 199 229 355 390 383 374 869 759 208 690 994 530 014 623 837 512 709 443 216 816 483 172 116 194 227 730 698 946 281 719 135 154 595 855 098 909 112 220 313 761 184 359 221 624 682 897 322 926 346 656 437 291 548 281 938 584 310 099 969 979 544 817 869 760 664 425 458 271 773 751 754 914 055 985 353 253 722 372 372 254 796 765 201 667 935 532 554 484 230 840 522 939 121 716 259 526 287 516 665 021 035 704 963 347 548 540 251 219 352 245 224 782 312 266 248 995 360 130 126 036 286 947 255 880 990 890 017 991 018 766 965 476 735 900 639 530 612 635 775 460 080 554 949 689 153 926 341 281 252 006 809 300 629 647 733 610 768 237 962 815 807 126 927 323 659 175 860 368 599 880 724 875 299 809 090 966 584 164 422 613 648 351 757 736 869 192 117 532 725 999 737 527 782 433 605 454 944 220 451 007 613 440 322 668 987 699 013 901 920 356 785 430 441 182 426 122 880 291 684 856 334 033 163 163 848 972 790 096 152 600 241 051 295 011 938 017 442 638 806 624 559 441 388 997 255 933 985 544 423 035 933 477 561 226 161 534 913 107 073 830 159 501 900 889 936 176 625 572 789 396 756 050 891 301 279 841 534 364 061 363 639 901 928 599 078 606 489 130 470 727 723 296 340 525 144 096 713 487 202 456 005 860 115 254 688 164 301 347 022 080 735 341 499 288 913 872 555 943 311 875 364 647 665 578 470 058 002 232 245 214 826 596 532 535 204 007 733 316 932 021 357 156 331 860 645 960 320 015 223 627 230 877 827 182 071 672 520 569 781 959 325 921 094 520 854 972 710 061 243 939 367 408 654 491 702 603 588 174 704 452 793 707 759 550 062 853 600 982 554 275 376 199 424 216 241 636 177 210 617 151 841 506 925 124 099 087 178 759 276 079 418 260 131 849 202 401 282 121 615 512 244 103 019 430 350 699 734 865 831 333 242 044 929 261 830 937 148 968 763 771 859 249 621 591 414 829 977 473 409 741 204 495 599 417 997 126 875 804 792 364 477 363 721 616 365 249 691 224 871 509 425 600 906 062 333 118 967 175 279 646 374 429 423 046 473 506 967 626 203 629 656 443 793 643 381 492 595 786 101 739 085 616 618 685 969 289 823 700 088 370 109 882 340 674 544 228 273 178 360 955 357 642 405 608 364 003 193 495 091 268 893 873 752 475 180 768 501 079 700 846 237 886 879 605 812 851 434 360 331 845 471 867 003 765 174 203 130 594 924 059 692 010 230 742 101 601 715 589 216 263 051 057 618 211 561 247 670 359 488 938 950 453 291 388 231 039 718 388 255 678 116 689 158 283 019 911 212 556 078 231 323 702 660 958 394 514 953 407 773 848 744 110 420 396 328 235 832 804 030 709 505 800 463 624 696 830 902 320 056 649 405 776 976 687 459 281 967 315 829 350 463 360 586 043 953 956 402 546 288 071 634 483 235 638 112 813 655 799 731 792 682 994 145 240 470 419 966 228 535 338 874 833 991 307 782 321 668 691 397 239 899 920 687 839 261 104 423 362 111 243 325 496 837 536 325 287 767 066 104 638 990 552 229 692 585 752 930 671 052 610 781 436 527 496 111 686 741 326 325 819 114 232 891 335 141 583 358 880 487 833 600 223 968 131 183 803 025 969 197 581 316 647 747 627 932 336 354 358 778 911 432 379 800 210 892 844 219 567 929 856 319 595 876 425 774 233 947 712 313 649 991 800 406 134 631 596 430 664 097 931 670 877 055 866 923 327 738 900 486 888 955 298 617 519 286 959 372 056 994 769 466 313 231 010 517 870 559 379 023 554 661 624 286 059 835 767 465 448 850 387 563 933 021 780 487 172 570 667 806 030 293 576 733 677 250 711 200 891 507 293 624 445 131 781 791 542 242 722 925 043 451 348 944 640 206 914 931 389 334 068 332 920 758 566 299 742 554 131 979 227 515 132 680 040 319 770 095 836 687 800 536 098 844 580 718 964 194 265 934 174 533 010 450 922 838 842 298 897 182 528 622 806 084 294 108 342 347 300 152 235 906 800 458 664 716 777 421 361 783 414 470 134 181 049 564 428 434 505 154 613 902 072 230 742 945 318 566 147 211 042 487 056 928 136 138 240 816 744 526 434 212 400 437 877 786 566 157 784 308 078 367 023 570 656 189 703 019 103 055 476 466 886 544 443 928 443 313 722 262 769 985 493 282 064 062 365 141 491 244 650 220 121 790 301 226 335 846 851 505 846 885 136 959 015 622 060 782 253 812 971 155 483 770 823 762 570 761 295 307 291 983 279 818 735 321 470 436 318 005 641 452 025 658 433 014 354 323 996 714 274 641 557 257 116 179 477 678 926 351 412 045 982 983 920 967 122 779 622 204 947 699 469 916 882 215 437 891 245 648 327 541 501 484 534 127 206 833 812 574 632 247 030 959 122 623 336 937 437 005 867 536 951 836 032 746 586 877 783 788 349 127 747 437 292 764 663 435 715 999 964 531 936 028 338 365 470 872 695 134 777 546 328 578 498 138 725 744 516 177 905 656 894 017 243 452 132 870 045 728 177 462 652 320 163 089 728 717 922 441 334 517 821 945 942 241 528 167 714 923 554 383 700 149 764 292 413 227 906 797 979 334 706 176 411 066 369 690 077 257 610 874 321 173 737 180 570 786 991 741 329 959 807 510 244 709 224 195 798 538 479 041 770 757 066 036 932 162 299 476 407 911 150 417 429 569 973 193 544 742 924 181 013 735 395 209 730 904 550 728 467 951 131 200 436 308 420 525 618 397 793 669 615 062 210 013 114 401 925 810 344 332 373 942 610 734 412 704 300 122 780 856 797 214 884 344 009 747 774 341 260 682 298 238 500 213 522 638 069 505 341 806 860 895 990 384 622 364 164 153 913 967 034 344 803 201 366 414 579 618 892 507 772 200 169 090 760 940 335 165 695 830 352 467 580 694 637 560 559 125 617 478 058 571 289 436 940 941 122 836 275 189 841 501 064 210 462 043 294 182 805 932 509 861 522 011 451 833 144 401 910 609 978 751 363 565 069 673 150 671 503 857 871 662 469 015 458 142 804 995 471 162 380 175 137 090 927 096 099 280 008 041 036 009 073 722 859 725 262 257 544 753 578 245 575 259 243 737 356 968 081 998 816 717 703 607 239 912 586 376 336 307 054 722 038 596 035 123 771 762 496 268 796 393 783 778 253 960 446 554 761 646 614 859 417 701 387 771 977 662 079 489 733 671 795 997 671 677 545 114 932 277 702 353 920 341 605 197 580 666 576 589 367 095 762 702 601 143 610 727 074 976 196 232 799 717 984 014 475 836 001 992 675 617 568 545 135 319 246 043 974 393 516 263 900 455 542 836 004 523 071 165 891 096 112 222 868 822 762 556 800 347 888 221 625 237 110 848 687 024 983 442 155 753 346 749 942 966 839 203 698 913 896 905 887 959 134 649 235 269 659 709 666 945 792 487 432 491 641 004 851 224 052 531 550 127 737 779 203 895 313 850 091 072 816 227 351 325 662 224 261 977 250 808 651 182 150 601 879 646 816 113 437 859 543 042 506 568 141 710 799 184 146 640 382 510 278 820 849 548 858 013 365 031 515 789 986 987 247 907 990 092 179 149 494 577 500 750 835 704 747 536 716 523 805 626 444 242 324 539 086 865 133 176 268 162 725 418 971 143 006 562 301 695 534 893 069 152 360 787 167 045 856 368 239 554 312 585 713 081 995 766 353 502 831 671 821 534 141 540 346 708 967 521 485 765 766 588 498 703 502 367 769 092 028 111 580 853 504 788 278 526 858 207 142 737 918 516 202 945 787 806 753 546 450 071 199 458 138 470 325 466 004 961 691 266 381 539 635 653 054 741 334 506 867 415 835 135 830 410 221 027 960 216 420 462 788 447 998 427 051 454 063 455 030 884 949 290 436 844 656 340 208 023 922 542 645 685 500 542 352 128 124 028 723 721 567 631 648 802 327 132 810 780 833 970 795 536 705 467 883 981 869 281 834 967 667 768 790 515 788 081 762 769 410 553 171 365 579 220 070 788 350 617 506 257 379 477 570 173 037 433 675 894 317 063 993 084 828 872 823 799 286 411 559 136 973 858 417 990 340 298 876 835 636 698 641 218 211 385 827 938 843 176 543 745 779 862 924 552 768 649 241 186 758 529 760 350 054 574 520 105 086 158 121 369 293 251 358 238 087 308 547 480 016 285 675 308 304 362 768 888 320 112 215 354 639 036 576 705 046 948 963 724 201 086 728 232 644 711 336 866 203 000 780 772 612 768 289 857 032 668 861 522 900 981 188 232 268 526 331 312 588 846 227 403 624 654 714 410 460 959 610 257 350 217 603 524 034 322 408 627 629 332 469 569 832 214 538 919 266 037 112 594 251 071 842 429 378 994 850 064 296 361 789 148 534 195 310 976 306 605 205 371 903 460 724 563 280 279 740 004 115 572 199 438 033 012 396 027 241 183 505 714 510 180 876 138 983 334 821 820 464 556 128 433 922 815 107 649 030 508 504 304 440 533 056 075 072 326 456 475 496 903 456 992 824 912 780 977 584 374 801 061 389 085 446 765 934 113 167 537 962 146 104 981 892 441 390 041 165 409 710 715 907 773 695 627 477 032 257 955 218 017 945 385 002 191 540 735 157 356 070 057 554 523 497 449 903 162 718 218 653 482 171 311 018 375 834 087 364 804 237 728 493 097 088 171 420 368 609 789 998 150 604 428 659 366 870 613 189 647 399 846 775 972 516 105 683 056 223 521 428 949 672 150 624 580 191 133 349 959 542 963 303 905 209 488 885 239 967 004 493 862 574 540 786 005 708 606 777 367 528 581 727 381 727 009 052 967 389 951 334 097 879 735 351 008 370 110 505 395 774 346 174 786 458 333 696 798 218 288 782 043 294 471 271 378 812 413 065 696 876 782 263 275 863 809 400 899 620 022 096 977 517 226 996 642 121 472 531 261 312 816 131 252 709 114 439 479 229 623 980 191 297 512 034 959 512 741 927 537 198 663 024 218 219 300 627 230 943 408 723 819 925 332 734 588 872 880 906 145 328 772 880 806 721 705 256 662 581 780 094 046 257 922 300 518 311 007 244 846 157 225 027 283 835 020 452 848 611 431 414 048 652 321 368 398 858 391 348 589 569 732 051 831 289 614 953 282 759 796 706 437 981 181 319 381 883 815 899 787 088 670 048 423 591 303 959 554 993 529 546 402 474 738 986 484 721 570 251 830 387 621 080 533 211 563 061 897 457 610 073 840 016 843 551 440 517 834 277 365 163 097 794 986 377 142 967 544 632 638 103 656 961 729 113 894 381 205 061 923 815 719 983 457 623 744 829 187 158 707 343 892 225 211 165 827 168 504 837 794 762 987 015 567 763 466 489 312 230 727 343 373 838 550 797 181 247 919 791 257 504 989 655 718 525 421 491 081 911 945 516 778 610 658 409 446 716 863 453 597 356 500 149 212 117 203 194 534 364 038 613 065 224 506 861 310 701 466 702 571 549 513 621 361 157 235 675 097 498 595 946 551 453 520 485 180 873 425 390 257 278 596 971 465 726 609 215 640 220 092 466 142 858 556 671 530 857 272 980 654 323 034 382 106 020 711 001 317 638 010 195 770 783 013 535 810 240 159 699 355 193 410 256 514 773 482 927 317 572 279 016 691 284 517 390 744 158 575 617 885 861 578 516 556 066 683 157 193 553 743 357 771 212 565 145 986 787 015 126 035 371 687 853 260 035 212 824 797 811 759 155 383 560 217 268 173 231 192 847 625 921 693 775 974 588 796 173 296 316 070 850 548 940 634 659 796 516 139 409 581 409 061 099 051 784 353 296 271 604 076 114 966 732 259 008 823 210 239 508 441 911 302 435 338 284 782 602 098 342 238 480 886 843 367 833 559 489 889 953 041 500 650 091 478 109 838 112 157 921 645 711 442 526 760 125 007 562 886 923 078 421 864 391 974 273 220 946 878 698 474 663 503 409 217 009 538 124 858 038 771 606 563 016 498 735 022 774 452 271 645 560 221 587 442 750 375 175 784 394 176 629 179 818 905 264 039 764 873 252 003 378 513 779 540 027 152 420 277 745 285 442 577 405 851 246 683 142 085 363 187 251 097 772 725 261 485 333 476 701 340 921 377 821 496 494 992 325 069 226 680 654 002 178 186 771 019 738 591 384 155 177 633 857 435 868 699 682 243 625 201 556 847 664 659 076 227 646 610 837 090 986 460 453 769 598 909 866 905 071 244 248 740 587 313 025 702 901 882 103 360 823 977 031 766 750 022 482 633 747 975 289 782 003 478 211 113 810 110 314 626 352 659 264 843 321 812 566 201 005 045 444 223 639 878 727 640 545 136 982 898 476 940 014 906 127 706 987 401 054 059 355 700 384 724 828 795 441 540 607 300 535 846 682 940 353 129 299 256 011 114 856 342 328 029 818 142 616 714 077 210 776 596 911 270 398 992 085 153 558 955 793 084 879 038 169 004 244 072 925 193 134 038 400 192 766 154 803 762 109 479 365 310 231 974 622 542 521 972 891 915 120 759 280 153 531 103 422 134 233 249 993 119 923 642 811 779 158 138 001 036 187 931 006 280 489 170 472 446 465 052 102 354 146 411 938 234 641 574 767 716 815 087 417 724 012 994 400 669 328 767 636 330 422 805 910 557 734 826 378 352 817 367 914 069 678 346 805 875 437 864 755 123 190 193 587 688 620 669 403 574 980 976 576 916 187 963 251 400 717 004 866 478 801 638 920 113 797 843 582 549 258 510 803 732 221 504 015 661 400 037 710 416 373 186 269 518 383 712 764 159 381 520 017 743 344 402 262 425 218 419 986 005 052 665 163 513 977 613 612 662 367 425 670 349 125 415 903 880 737 799 725 224 574 795 514 185 408 950 908 607 116 819 221 979 427 993 768 332 727 215 628 518 441 116 493 049 411 311 161 400 749 530 744 998 217 275 799 251 959 326 132 737 167 006 004 797 639 273 221 074 161 891 447 658 409 927 590 693 620 597 364 091 813 953 138 651 887 494 281 477 385 208 663 752 096 708 196 084 385 194 202 223 136 231 242 766 761 430 224 964 722 863 568 213 392 189 255 755 317 838 820 226 997 914 443 731 710 597 425 823 483 247 959 966 718 167 313 002 401 066 015 827 914 566 502 941 839 122 115 636 195 828 104 251 398 383 899 725 777 484 940 257 535 379 245 806 876 530 122 746 327 426 585 010 125 551 103 680 874 805 140 282 465 045 202 068 909 805 024 477 197 238 754 479 267 805 461 744 745 930 650 583 083 018 717 114 430 701 236 178 554 441 685 791 845 041 980 031 944 461 032 736 175 920 245 179 330 803 960 071 835 881 746 922 625 282 321 538 230 394 065 417 392 169 264 865 441 214 394 452 739 383 026 875 002 553 123 205 792 759 930 261 220 189 329 885 694 987 813 438 274 213 308 243 538 148 147 667 735 108 960 197 033 040 688 424 243 402 844 764 300 169 149 848 884 514 296 543 459 626 952 101 190 378 153 684 244 105 951 055 760 433 139 710 268 216 788 318 456 646 641 104 683 679 696 642 137 040 525 170 991 993 488 241 789 953 791 719 567 999 002 312 832 913 007 827 390 921 928 735 731 861 655 186 102 840 684 855 788 440 259 930 956 325 478 423 872 051 786 017 442 190 769 689 036 302 397 822 107 303 443 004 090 508 385 691 136 785 330 284 583 274 266 378 139 727 536 266 141 703 216 969 442 170 689 668 304 406 581 914 666 372 739 801 165 713 322 924 884 448 793 005 032 237 916 014 815 620 829 024 925 208 200 800 914 570 520 949 834 251 725 140 820 498 105 241 357 462 038 377 925 488 910 911 371 711 265 154 395 468 913 472 532 401 121 429 586 797 528 689 312 435 506 738 741 821 924 997 820 361 016 184 632 725 573 945 615 363 917 076 543 431 174 088 374 152 256 042 630 559 399 017 851 186 989 376 257 228 654 108 412 883 794 842 300 095 788 591 145 999 578 544 630 326 085 753 265 960 062 566 015 218 320 503 512 148 818 675 153 519 171 932 709 698 438 515 779 283 695 164 683 531 611 830 269 233 030 832 449 354 936 678 043 058 921 261 775 144 963 049 131 588 244 804 660 312 380 913 644 682 500 393 415 861 865 599 485 069 270 886 818 290 761 366 061 875 587 884 372 530 575 298 432 223 574 482 907 741 389 513 456 228 961 968 483 668 371 053 337 124 263 702 304 372 005 307 708 489 093 106 176 223 892 736 308 741 928 285 927 093 302 717 565 665 054 027 111 530 270 841 067 021 262 300 627 633 499 375 954 048 921 691 481 151 706 645 568 575 595 467 548 317 882 014 969 393 626 743 429 476 770 615 066 014 334 641 930 065 845 102 570 970 425 067 210 110 452 292 722 560 474 665 855 539 273 532 110 640 209 904 581 011 551 861 660 122 639 999 567 781 264 744 008 758 645 115 859 006 908 332 520 444 751 556 555 489 333 572 188 903 806 519 823 797 944 825 001 951 947 930 198 218 170 753 775 347 498 293 261 839 768 646 581 993 290 977 235 939 798 974 260 827 540 297 471 418 849 507 084 068 478 366 369 805 843 716 559 681 132 441 537 879 461 987 340 081 442 295 410 016 752 984 987 494 462 351 422 919 846 444 689 990 750 094 353 539 121 079 691 468 959 303 089 579 358 231 949 012 643 418 628 160 467 229 025 922 619 282 780 452 938 533 507 344 697 987 725 722 863 638 562 295 567 150 040 208 520 264 545 756 767 947 311 028 313 772 126 531 250 567 046 302 771 521 580 239 520 413 806 699 780 481 746 882 895 678 667 587 549 422 781 913 600 221 658 292 352 520 302 768 468 904 921 231 107 549 016 756 797 178 594 616 559 119 129 706 569 500 182 158 956 840 272 054 688 821 086 479 921 739 662 620 968 926 596 312 266 752 871 379 267 125 327 956 015 279 998 928 196 979 731 221 981 335 571 765 718 807 601 181 254 737 862 579 589 994 158 173 261 792 569 794 532 332 118 925 359 000 022 688 997 662 620 040 589 866 823 701 575 356 387 739 978 773 205 852 498 978 035 033 163 546 982 192 427 694 101 414 409 899 905 977 607 118 594 034 872 459 971 068 178 166 471 068 460 566 098 923 323 870 593 085 221 833 548 313 258 704 921 867 967 772 496 003 960 790 115 591 624 032 159 635 081 282 967 037 487 843 761 916 757 297 807 039 855 748 018 916 701 184 590 331 252 340 718 298 963 999 223 476 757 346 968 763 548 510 099 054 483 372 485 369 130 884 903 524 004 101 249 808 606 960 264 792 196 858 165 545 070 190 973 079 576 513 592 978 849 173 738 524 307 327 164 779 339 881 738 930 906 353 773 277 290 230 053 320 632 982 491 697 737 282 389 569 636 670 291 746 157 281 975 550 178 181 128 190 216 831 786 682 222 054 566 909 450 511 510 754 718 752 610 627 156 794 283 953 790 200 603 129 898 798 317 675 375 603 389 879 807 770 840 271 459 433 083 033 056 982 967 935 191 653 018 524 175 277 305 240 529 137 585 601 595 130 120 856 071 200 853 931 265 195 132 203 065 803 535 944 145 162 964 064 284 699 306 685 372 582 655 279 591 022 642 988 596 721 977 026 980 425 514 895 454 201 021 417 376 048 036 759 731 362 731 973 892 913 158 808 085 645 927 736 240 830 792 306 522 389 940 937 119 075 816 536 032 669 701 613 494 894 441 397 108 455 516 023 942 278 079 712 667 537 270 336 581 488 551 975 161 793 553 099 452 894 884 852 363 693 809 348 343 626 516 869 548 569 691 847 578 943 420 101 095 985 523 425 628 700 057 260 197 065 637 022 013 377 180 915 858 718 651 966 868 023 325 905 412 854 936 511 886 057 980 874 153 852 461 100 324 343 412 710 503 863 538 203 258 868 566 001 901 369 350 963 505 821 713 633 996 577 319 239 754 764 110 771 287 031 190 715 164 551 485 977 661 718 148 374 556 512 685 775 855 684 392 085 663 896 310 414 825 338 628 086 970 062 756 840 867 836 642 991 103 126 084 499 892 374 246 233 917 850 188 900 931 216 367 869 917 368 008 295 639 850 290 853 721 591 544 373 197 766 044 012 851 534 861 716 128 123 353 295 882 902 202 535 996 135 836 459 540 874 003 193 692 520 920 335 467 560 529 646 108 306 177 294 412 454 843 535 731 011 592 848 085 754 909 625 315 242 471 429 733 080 381 432 398 941 374 787 512 914 121 234 777 063 329 559 722 982 676 388 434 374 157 855 723 985 480 432 336 193 311 029 449 111 048 992 284 809 073 813 683 681 147 667 240 577 469 667 987 540 558 181 590 613 454 016 696 205 976 247 704 217 006 624 260 198 062 924 101 785 804 344 046 478 184 767 619 850 047 717 017 234 318 637 534 596 975 008 623 852 088 121 979 620 321 855 106 136 199 237 936 504 298 074 979 442 701 283 902 698 927 371 134 144 286 148 877 803 204 672 509 221 158 400 095 254 213 349 512 686 848 447 787 374 942 132 045 889 819 006 712 279 107 754 989 303 254 412 188 711 161 630 120 719 028 149 755 085 417 140 157 094 147 124 145 051 215 162 794 486 868 520 717 306 195 704 271 106 240 039 969 085 424 891 488 603 216 405 614 054 276 910 849 550 803 338 045 034 877 754 078 088 354 781 871 169 874 234 738 805 137 995 887 002 893 884 477 587 893 862 031 855 319 231 554 510 688 095 593 760 090 890 520 313 924 181 243 317 504 361 896 535 536 362 866 384 563 048 062 359 781 761 100 275 789 852 780 082 544 775 906 791 749 049 725 705 147 279 905 339 001 157 953 837 306 157 227 529 116 673 508 360 836 632 098 572 824 652 552 814 002 198 629 343 224 181 523 071 381 681 682 854 426 315 132 968 182 633 161 489 865 314 533 727 826 898 849 825 643 024 696 241 672 444 145 260 984 587 250 203 732 965 999 240 540 656 466 500 106 237 446 898 107 501 428 132 960 282 062 001 255 276 264 540 488 442 754 428 146 476 163 514 725 811 040 045 425 208 302 253 497 337 140 797 014 291 287 312 901 387 608 151 575 195 121 664 990 222 299 737 442 552 224 782 110 279 550 114 376 921 854 713 555 228 287 598 209 217 444 829 698 004 259 451 716 723 084 626 606 538 412 213 268 456 134 421 319 406 106 058 990 467 216 654 782 354 548 487 756 692 707 111 104 293 174 736 728 740 342 936 496 265 611 530 985 723 128 095 435 212 604 179 689 151 529 567 965 682 745 324 039 769 078 908 104 388 936 681 299 653 959 317 051 317 974 360 418 532 834 814 760 478 330 894 062 981 118 649 032 815 239 602 294 624 121 705 130 472 526 331 672 261 763 715 997 673 186 591 722 320 681 285 454 399 339 798 336 645 273 423 962 517 337 973 427 998 134 697 866 282 834 773 196 295 198 052 646 605 732 869 732 675 327 694 129 339 336 098 421 196 894 925 881 712 378 129 926 425 383 658 401 188 634 670 126 555 872 445 738 888 227 230 911 465 490 400 494 349 351 446 690 158 972 346 864 971 117 593 037 834 109 257 603 826 170 507 886 541 155 144 427 384 032 914 855 706 188 785 041 986 120 817 853 017 517 545 421 378 735 719 934 043 741 015 961 429 966 717 504 723 643 182 123 944 870 558 029 004 047 728 642 866 608 481 053 392 134 815 722 018 316 129 403 473 504 959 846 955 877 007 708 540 046 968 138 980 151 438 007 642 802 361 016 510 924 787 351 744 759 458 436 498 041 387 818 565 409 841 687 294 879 163 817 734 031 111 540 414 463 379 382 754 722 616 897 800 149 510 341 431 678 196 274 516 379 252 478 950 022 092 073 110 935 794 954 694 720 031 288 342 518 363 813 249 649 135 248 877 494 131 507 590 206 718 469 136 967 672 190 555 353 491 918 139 721 721 007 000 623 034 263 768 893 569 735 385 878 425 433 556 809 561 488 904 066 771 511 757 324 988 632 095 600 151 480 343 511 678 357 524 514 867 680 125 838 989 937 326 339 585 556 463 786 188 399 414 942 012 245 635 791 580 229 198 022 922 186 685 788 517 543 342 371 661 519 725 721 866 828 851 825 592 318 178 473 815 727 693 624 740 059 471 206 199 724 762 244 658 721 840 629 128 619 606 911 212 822 086 240 446 266 047 932 026 411 191 919 478 431 884 711 195 356 053 014 472 343 297 367 703 452 097 369 634 880 721 507 171 863 116 327 841 903 936 447 124 383 021 962 457 784 913 044 285 150 728 972 406 451 784 524 235 484 962 093 839 497 854 907 843 319 352 373 857 935 309 146 662 159 102 489 851 366 100 543 616 789 664 912 023 290 885 751 920 853 292 513 651 468 351 714 574 539 613 285 037 183 764 203 924 719 947 020 765 048 232 016 723 303 541 689 289 357 427 959 100 395 723 135 753 018 120 515 967 999 810 436 869 554 154 752 063 074 451 284 187 872 925 572 449 489 580 445 553 235 117 178 410 885 833 815 229 328 539 431 380 389 036 949 243 974 837 009 612 800 748 017 801 770 780 484 159 963 238 113 716 265 408 881 323 481 673 720 690 436 290 365 888 272 040 537 146 528 427 464 565 530 784 316 871 216 076 641 366 131 375 585 113 657 904 246 299 715 521 748 886 899 750 489 864 144 154 551 801 160 752 305 612 854 915 241 407 813 903 149 027 364 750 811 785 423 166 068 447 538 550 866 094 610 288 432 957 936 714 761 320 744 657 736 634 221 937 514 113 229 049 641 570 239 137 249 495 868 245 071 501 043 535 230 948 536 546 285 914 248 069 993 431 854 777 101 822 249 511 837 985 635 680 331 754 966 427 414 889 806 903 387 975 423 406 801 846 249 612 492 129 579 429 325 476 067 100 583 616 282 975 246 821 821 187 491 741 894 220 352 086 314 996 496 251 375 625 396 971 970 781 423 470 163 580 502 068 666 615 818 185 637 118 256 125 007 388 124 830 878 417 713 357 291 397 878 291 448 195 125 621 538 446 833 560 372 281 222 551 021 601 307 985 594 336 461 657 320 657 974 904 763 162 209 582 813 671 276 515 550 676 113 152 247 843 343 280 258 767 781 436 763 306 296 471 733 997 005 595 120 404 620 880 436 700 290 581 930 865 120 737 334 160 093 688 449 563 017 075 579 458 509 944 712 678 188 225 066 322 669 395 281 784 909 756 629 294 912 732 160 539 698 708 930 031 207 686 437 210 952 366 824 591 052 081 696 823 844 767 297 762 391 526 858 919 269 426 101 483 479 980 397 965 352 788 484 858 465 602 236 292 886 257 010 935 107 591 865 870 858 972 130 109 816 231 421 101 722 570 918 420 657 767 441 834 283 789 613 925 002 848 620 047 232 246 118 892 138 587 961 582 959 281 720 046 064 793 413 079 373 088 374 334 253 411 101 344 310 642 744 706 675 671 162 660 971 703 667 872 369 379 412 056 079 413 919 555 613 411 342 561 695 932 102 597 321 221 934 110 760 277 589 440 063 932 117 482 587 411 132 335 979 402 031 830 506 598 649 747 658 772 254 773 707 061 080 388 424 495 952 129 593 308 984 153 813 633 180 681 301 042 986 729 746 748 710 139 207 263 823 087 904 412 211 726 982 811 295 783 289 557 644 121 673 790 232 766 330 065 777 133 532 128 552 753 707 109 429 746 835 092 964 638 827 760 360 734 614 738 786 553 847 090 266 916 436 283 869 564 121 181 269 754 047 126 110 201 735 032 566 815 453 701 011 828 555 572 694 332 968 151 584 423 487 268 763 035 813 145 095 941 521 265 641 624 335 936 810 677 787 025 203 537 195 921 559 689 684 657 451 420 666 182 941 528 034 328 136 575 210 032 771 835 683 758 154 711 417 585 158 395 899 573 574 661 140 351 569 288 235 339 425 409 341 809 756 106 804 483 886 283 009 840 802 396 069 811 740 132 343 205 684 833 265 846 092 835 837 367 638 789 943 101 360 856 512 893 751 329 734 975 170 288 680 910 413 435 402 411 484 659 922 431 195 603 603 705 938 321 210 419 377 038 824 567 616 650 386 867 569 983 599 242 320 719 087 866 653 971 430 558 645 203 968 155 823 430 082 649 562 470 422 983 851 071 236 790 913 634 797 721 355 807 287 726 328 609 329 987 583 422 927 536 038 480 049 449 437 050 370 747 179 660 827 854 802 440 284 593 103 360 980 254 899 289 189 843 380 882 758 366 001 448 457 914 886 426 957 718 747 479 687 032 688 262 152 516 942 057 733 502 580 287 714 137 088 310 759 834 906 813 881 213 376 759 272 973 269 258 805 969 785 097 069 560 817 817 255 931 887 511 795 674 798 914 912 965 594 836 060 518 811 117 008 344 157 330 495 437 491 307 554 994 088 496 953 620 786 198 889 535 429 627 263 839 296 687 390 112 536 583 339 548 002 230 132 735 847 854 757 952 605 887 471 542 747 427 507 452 013 025 116 607 111 392 637 713 913 598 539 645 709 999 310 705 346 110 727 295 702 403 830 327 054 933 076 207 506 936 003 282 384 004 099 505 284 283 174 816 434 807 140 806 161 740 209 490 379 889 928 688 542 266 129 439 634 638 914 433 744 408 075 796 657 275 826 890 198 254 364 597 620 670 759 072 714 773 467 326 525 971 942 142 403 439 947 413 570 733 543 045 470 759 404 711 266 647 437 521 099 017 671 660 224 065 120 920 267 263 120 983 882 128 769 899 920 789 946 219 377 795 200 512 263 428 218 506 946 081 960 071 970 102 252 050 578 629 944 236 589 310 767 741 730 604 030 464 686 004 278 235 048 583 180 668 352 632 756 256 001 218 133 842 144 212 321 855 824 359 770 079 409 935 646 775 670 221 195 134 660 010 755 984 414 572 015 483 659 686 392 674 849 537 052 440 574 867 983 037 096 154 290 767 491 286 984 525 061 197 065 234 569 044 235 395 049 248 366 885 248 234 592 615 042 913 401 563 174 465 984 222 350 428 791 420 612 627 794 029 079 265 588 593 000 673 753 428 027 884 611 936 410 398 692 367 491 779 397 393 994 551 583 856 725 239 513 715 459 379 993 271 750 285 389 844 147 200 338 117 165 480 874 932 918 127 562 192 918 395 656 048 249 699 436 239 238 658 869 773 718 225 101 472 650 869 200 640 167 910 534 514 363 651 672 176 564 736 183 593 139 869 012 475 293 701 158 038 985 703 516 418 825 207 215 090 456 565 591 808 761 017 129 386 690 536 482 110 459 820 313 992 180 806 757 990 996 253 143 344 231 446 363 801 405 382 120 706 003 364 626 525 807 125 333 651 787 715 810 841 284 464 893 905 736 022 616 058 656 095 573 888 481 123 757 176 692 017 830 078 802 022 698 878 996 438 297 838 595 884 860 407 041 396 545 643 032 021 439 239 463 501 595 061 888 204 578 095 814 699 889 512 814 255 236 126 238 640 265 942 684 335 760 429 282 911 063 067 313 624 501 555 614 964 945 161 516 592 444 157 507 756 656 788 418 192 295 997 258 265 999 793 180 680 086 978 303 191 120 151 890 544 445 335 644 718 407 364 151 938 238 282 290 210 411 396 330 323 352 030 807 590 167 458 635 364 413 758 879 274 434 991 086 418 450 412 640 130 760 675 662 587 598 068 361 462 737 042 779 743 132 774 242 643 116 069 598 413 077 166 445 483 402 999 542 707 094 791 509 792 966 244 783 051 930 639 653 907 515 387 339 742 800 348 974 634 925 793 175 830 607 595 611 614 752 974 458 586 278 673 789 559 281 527 544 399 792 990 520 865 611 387 452 077 967 635 934 939 237 898 442 623 381 947 677 187 450 153 528 085 156 494 218 305 148 185 865 689 099 220 604 190 569 867 733 605 361 824 788 698 882 347 986 135 442 113 131 302 115 830 678 763 115 902 752 039 119 946 158 342 571 130 957 133 192 504 533 975 793 041 545 452 937 758 977 134 119 357 030 164 091 025 378 673 331 432 047 245 479 566 728 445 087 952 887 047 861 516 985 721 115 528 167 878 173 128 218 227 403 527 874 130 942 740 002 787 555 874 244 384 934 597 301 856 467 451 363 944 587 271 271 958 274 984 592 972 327 414 855 801 637 264 259 851 982 796 640 312 808 480 568 643 404 463 301 303 530 783 367 916 318 859 771 469 607 375 917 652 172 961 733 516 656 727 357 464 140 917 694 299 145 666 993 712 785 837 218 200 237 616 599 714 697 149 988 375 328 043 886 196 341 723 936 671 955 751 954 269 105 316 381 934 372 485 487 257 696 110 940 219 801 864 770 612 067 595 082 333 231 163 028 701 706 220 829 563 488 886 241 916 828 389 168 654 146 575 923 157 755 310 338 727 765 737 222 028 513 019 109 791 648 875 590 094 459 269 018 912 838 291 195 559 574 653 803 567 556 322 269 067 142 920 737 833 440 927 842 119 889 502 348 338 303 221 640 747 518 551 121 377 615 186 222 577 139 995 433 150 839 415 983 147 116 417 606 422 475 504 444 410 874 248 610 813 776 266 698 222 681 617 871 766 694 464 911 420 269 431 388 844 980 295 675 928 201 529 947 209 065 677 392 334 160 590 494 781 493 292 029 370 441 823 673 624 712 248 713 290 451 573 025 280 221 944 386 629 632 433 345 157 391 227 380 884 276 246 714 481 156 785 320 345 754 308 865 650 147 296 152 956 461 295 494 968 443 824 540 442 787 649 913 647 191 574 729 246 478 458 285 953 421 166 284 870 208 533 374 423 434 019 864 688 674 075 896 017 788 195 525 994 231 164 717 120 699 165 670 411 027 602 330 840 877 118 941 192 469 119 037 833 835 605 672 102 555 843 901 506 101 279 565 597 288 760 868 779 162 272 996 813 903 006 793 329 300 455 674 977 277 697 578 334 249 556 950 705 340 316 075 199 910 653 450 494 002 823 853 372 095 454 611 854 652 645 423 818 980 780 815 104 280 703 718 368 898 816 404 364 129 427 790 342 305 422 804 376 818 212 629 080 719 654 278 512 304 846 500 352 982 835 159 783 470 204 510 202 835 744 693 437 572 296 111 381 750 807 495 403 541 069 938 360 971 686 671 374 871 276 860 032 191 252 825 759 073 778 547 375 033 905 908 701 823 109 272 229 757 959 960 603 807 755 803 482 678 304 929 876 857 212 432 184 013 519 286 231 764 442 404 060 502 666 655 423 099 981 247 373 181 477 226 677 785 482 112 538 108 484 674 324 977 955 743 987 101 067 610 913 216 940 051 443 839 822 513 407 486 789 686 776 580 661 620 196 729 671 067 009 321 684 203 294 894 333 162 602 742 280 439 416 980 668 929 003 885 188 971 111 036 425 486 328 802 602 163 743 688 107 626 347 393 061 872 338 087 642 744 673 690 655 803 761 405 462 574 136 141 007 779 887 955 406 275 901 964 651 777 495 368 779 456 248 578 481 445 046 658 791 913 854 962 173 116 691 031 353 198 095 691 928 739 403 722 938 126 953 188 952 459 006 248 651 861 981 283 596 779 517 493 741 187 365 850 857 444 342 015 568 521 480 583 709 862 727 634 614 545 964 457 288 613 812 742 730 485 400 136 533 577 801 908 492 811 747 478 220 996 015 579 947 962 064 510 346 536 291 141 033 685 934 501 386 303 111 671 773 598 471 263 497 245 184 797 657 072 598 379 944 277 490 913 813 273 843 886 279 414 574 112 487 356 127 520 087 850 357 658 205 441 219 233 530 427 210 739 234 334 654 794 192 858 158 824 936 041 598 394 382 428 528 120 847 020 223 263 434 412 424 048 670 431 150 043 256 825 171 332 297 662 858 309 149 520 695 095 019 202 559 128 763 272 926 665 037 947 723 451 281 568 874 307 516 899 053 680 670 471 046 340 208 116 406 154 875 621 791 043 567 867 931 252 913 095 229 745 409 411 367 701 605 481 111 656 196 080 641 965 578 216 899 815 044 751 542 070 592 204 447 429 172 042 058 183 608 171 726 028 712 848 105 654 087 398 666 138 858 132 606 131 149 553 324 815 085 794 977 084 585 059 793 139 694 064 351 118 040 100 224 955 055 453 028 144 918 929 374 442 170 781 313 305 084 682 195 135 783 378 200 001 683 108 081 052 219 444 829 174 628 147 808 590 708 782 672 695 359 508 522 292 103 818 510 306 916 087 814 079 471 398 873 934 697 933 628 379 707 820 856 406 706 569 489 501 102 796 505 716 472 329 799 400 140 099 124 125 301 816 980 270 049 088 572 576 525 463 785 102 013 639 159 571 294 729 089 971 532 096 735 038 228 008 867 120 836 188 306 144 232 406 275 676 415 833 846 555 810 958 616 386 142 928 361 248 156 937 665 630 781 612 837 160 945 242 469 147 622 612 674 604 466 396 653 460 666 579 818 682 343 163 518 587 306 628 903 256 004 497 050 348 154 885 902 951 924 630 831 420 001 162 505 568 883 039 368 801 852 097 631 850 636 289 937 027 585 492 432 714 364 191 613 564 030 310 528 879 239 671 192 161 817 323 447 384 319 367 913 652 632 323 781 884 883 854 378 470 300 237 257 563 854 965 507 223 118 766 498 570 094 845 668 432 237 291 475 408 289 967 501 823 468 683 180 716 377 306 765 413 745 840 742 930 941 792 130 574 870 975 460 629 563 521 478 562 837 314 589 077 556 901 407 147 718 565 006 860 054 974 713 053 513 011 832 545 117 942 914 407 313 196 477 654 117 282 611 421 056 453 159 525 221 181 827 691 628 654 282 551 661 912 421 819 137 899 668 940 902 076 156 494 773 824 695 032 226 699 763 083 522 866 862 269 988 166 726 109 060 752 265 350 614 058 357 954 204 372 558 428 072 631 945 867 111 681 684 161 171 185 508 341 673 532 147 274 120 241 426 431 376 250 981 617 524 760 853 214 182 555 397 918 842 432 546 289 352 203 077 523 351 680 154 758 067 560 299 173 422 091 038 746 164 510 870 387 984 359 324 148 700 999 701 176 837 279 461 392 728 308 371 537 825 278 646 937 430 323 379 200 100 240 923 432 907 291 721 430 716 369 775 554 112 917 331 307 772 610 566 737 957 522 989 604 455 832 127 841 803 706 285 348 500 586 827 179 996 474 751 455 416 343 403 008 941 515 294 814 600 837 488 436 266 262 415 468 236 683 578 296 736 906 113 129 583 500 247 825 135 566 484 186 597 235 546 658 494 503 260 972 371 824 632 486 987 575 338 349 385 405 516 056 383 397 959 674 871 643 169 974 890 363 538 618 823 893 587 192 876 555 021 655 183 522 346 100 808 921 404 204 662 481 614 463 116 482 158 478 024 610 142 734 129 383 523 331 636 775 148 826 758 839 645 106 514 132 598 136 841 039 775 024 476 435 059 945 680 677 875 733 776 669 359 045 692 211 867 292 592 777 312 999 000 561 480 475 278 998 881 458 233 794 209 055 728 209 252 733 621 063 857 766 793 603 259 556 574 321 117 514 149 665 883 819 466 663 036 396 277 364 127 317 758 893 099 082 180 273 229 438 381 791 675 492 426 643 649 504 017 941 008 215 813 227 176 141 837 446 103 183 752 182 195 931 687 628 418 677 982 892 345 325 743 329 708 388 225 921 522 072 302 550 264 970 352 365 081 511 124 072 899 755 125 952 067 085 530 170 845 207 778 609 999 563 759 593 991 647 555 712 067 131 735 179 626 129 852 864 461 783 078 992 366 387 631 107 158 078 026 924 035 678 930 499 483 353 781 830 322 410 530 232 246 132 275 267 228 066 898 631 656 167 950 471 629 684 807 946 260 195 118 443 284 413 495 081 136 078 937 313 216 565 853 471 378 032 310 916 766 976 881 008 965 914 154 803 716 691 748 773 552 188 504 019 634 560 964 874 409 011 531 638 900 894 840 626 306 605 842 394 070 448 840 507 718 260 665 096 258 561 946 871 198 966 117 566 243 951 214 444 657 567 511 977 676 412 230 138 748 864 325 799 049 192 794 021 753 772 596 662 116 346 698 666 249 356 145 923 710 539 397 107 354 772 234 104 045 255 669 367 953 047 250 126 297 422 263 181 246 700 805 842 537 680 404 259 491 698 933 221 757 913 316 179 327 508 205 020 140 061 928 824 596 274 070 978 470 537 782 605 156 733 003 093 012 904 666 886 940 843 696 038 425 570 916 253 916 292 027 976 581 375 026 904 490 589 689 699 410 447 733 497 689 273 130 376 705 780 977 496 737 483 162 097 943 632 839 192 360 628 810 889 965 797 646 548 052 695 535 947 504 425 354 822 628 661 060 757 570 522 896 169 112 798 765 542 785 243 425 324 505 927 505 671 059 994 833 644 626 248 725 282 515 635 190 241 338 144 264 953 743 295 803 421 901 323 498 959 060 459 864 637 004 317 394 266 053 640 825 999 861 601 549 413 413 917 234 177 310 273 020 198 411 088 114 148 358 327 934 439 839 026 574 948 543 456 677 301 874 848 544 755 195 626 230 028 988 875 860 512 992 799 300 283 698 351 083 490 036 170 964 031 332 184 800 291 885 028 657 335 913 211 352 874 074 432 048 680 475 225 716 166 819 409 262 997 146 735 881 218 799 671 656 604 975 470 188 860 360 283 610 985 226 732 438 375 867 274 044 970 502 945 817 633 146 524 441 712 179 238 670 356 461 545 860 556 997 817 827 098 010 963 548 680 677 147 121 413 555 105 273 848 787 053 473 920 110 350 604 501 164 567 881 964 829 976 943 294 113 956 491 162 938 914 545 868 920 499 470 641 762 280 782 705 506 587 893 201 329 179 314 000 235 068 780 133 294 419 747 562 974 518 175 852 718 554 023 391 390 341 177 411 045 938 175 166 538 695 059 941 165 229 934 973 462 546 269 044 385 659 183 366 524 665 943 311 545 161 664 552 688 416 885 506 553 039 030 842 757 287 736 842 160 867 139 888 822 049 477 447 786 548 520 626 730 145 778 471 209 822 546 978 871 609 334 251 729 553 405 674 838 373 812 098 176 122 912 349 994 060 898 797 447 710 674 155 137 735 203 516 914 644 119 688 793 462 120 100 493 300 595 399 055 718 408 759 687 074 596 191 530 369 104 074 475 496 820 957 106 348 500 613 921 639 906 132 690 065 388 247 637 093 586 325 555 585 685 921 419 577 586 172 793 693 819 153 644 709 102 468 623 835 935 414 514 667 410 353 350 821 903 511 392 193 385 657 513 392 179 193 296 431 143 264 761 102 643 225 777 167 094 109 172 916 239 686 045 070 939 582 208 102 444 724 708 705 074 057 564 350 446 315 148 325 868 159 882 186 962 342 403 781 058 818 189 597 677 156 139 714 386 580 678 247 878 615 317 392 050 792 421 863 771 999 578 310 406 285 466 075 479 055 891 549 237 784 248 001 051 844 375 620 634 227 498 389 621 976 609 638 118 301 706 055 544 462 935 377 390 868 571 538 845 399 237 972 515 536 853 359 046 647 523 827 313 496 579 003 042 720 022 344 881 258 441 701 174 449 557 107 446 787 809 097 991 259 509 529 308 374 058 596 384 600 180 942 005 750 197 035 634 554 801 560 010 826 136 142 446 192 540 003 968 000 041 781 725 606 273 989 667 853 042 713 726 518 845 684 069 778 289 232 452 197 974 853 448 135 994 603 687 162 566 622 161 126 635 017 383 155 375 000 179 691 464 612 333 312 198 898 086 732 903 284 853 303 367 243 727 280 087 388 435 104 483 283 772 633 880 529 912 767 997 602 026 044 964 111 725 939 400 851 819 026 302 752 913 324 591 337 956 188 344 909 139 755 009 489 797 139 017 211 668 741 262 072 783 024 924 212 936 618 631 609 622 995 759 342 411 190 191 933 670 931 694 931 211 014 482 912 992 699 904 534 864 478 476 209 627 905 171 253 711 013 940 602 072 965 859 682 717 989 456 389 801 522 742 886 354 487 407 364 371 282 779 824 450 161 711 224 316 155 121 769 567 332 609 767 259 506 675 242 219 896 213 787 881 399 193 085 686 977 951 011 013 018 610 559 983 882 593 483 280 203 219 169 378 485 589 496 065 900 296 685 788 438 072 577 913 967 156 008 031 800 452 733 910 268 778 399 909 989 923 584 589 780 245 996 932 533 624 644 937 464 766 179 688 063 996 136 989 252 202 938 298 120 919 007 923 619 291 937 845 819 389 791 693 300 798 462 434 732 602 058 614 292 764 822 617 885 010 599 613 503 382 187 615 449 836 865 003 720 954 962 655 003 949 276 592 340 184 105 688 205 670 639 290 033 844 355 138 556 975 041 294 031 243 014 043 477 435 664 918 358 388 200 420 256 874 886 390 080 642 734 184 921 110 458 424 154 900 543 154 729 823 644 554 631 223 642 357 846 404 461 662 258 732 494 719 949 332 373 987 687 599 014 803 187 851 739 688 187 893 092 979 077 942 399 360 872 642 150 498 964 087 266 009 428 758 971 190 426 944 139 978 188 988 403 550 201 908 032 014 410 643 529 985 550 283 177 294 539 255 793 693 308 630 561 438 526 753 762 861 554 973 082 879 336 084 075 262 637 046 453 706 191 864 654 699 976 913 510 632 339 548 979 126 412 662 030 834 286 001 490 001 383 785 708 933 180 850 235 937 772 779 696 251 256 436 783 953 843 337 644 979 799 532 727 430 666 195 270 920 168 494 084 710 183 254 388 452 683 984 872 712 811 212 593 753 287 535 994 650 009 615 681 334 775 754 377 828 485 088 426 652 326 430 323 340 181 190 254 220 860 685 157 448 508 199 780 867 577 492 235 773 875 523 149 915 595 529 152 613 679 557 246 111 649 912 348 185 032 472 386 220 954 076 757 966 355 928 855 491 479 952 322 713 115 961 060 288 676 092 196 553 676 862 075 844 271 358 463 640 057 522 349 798 375 771 845 864 133 085 119 345 687 907 807 087 320 726 263 559 320 661 295 119 614 605 253 790 938 502 951 910 018 950 048 988 127 382 095 110 556 104 021 648 651 029 594 530 209 036 759 926 413 401 697 494 103 370 520 568 337 581 449 457 871 062 285 403 808 005 004 519 037 878 175 900 581 662 369 984 670 631 979 712 460 265 638 117 066 242 950 415 441 773 720 128 574 553 292 093 443 522 062 851 172 834 278 830 947 446 047 489 660 548 093 534 445 919 945 170 559 368 046 973 424 988 728 539 162 345 135 503 727 885 824 404 380 844 954 495 190 995 670 466 810 288 512 608 506 017 232 873 909 000 089 980 700 467 404 204 913 488 224 259 558 652 914 331 055 230 077 845 061 509 878 073 768 953 628 810 600 830 904 287 688 573 127 022 059 265 622 906 530 100 133 833 293 857 896 125 992 117 230 712 896 697 859 335 124 716 513 251 543 825 060 705 840 815 217 124 607 167 381 835 490 319 790 423 929 231 060 524 618 830 068 949 626 930 572 024 040 831 638 182 646 190 382 146 824 773 298 861 478 280 956 227 490 071 375 865 533 659 913 307 776 023 692 010 405 491 461 431 839 250 330 153 668 610 222 392 292 633 915 752 912 159 421 446 589 952 735 930 340 857 840 144 371 370 227 839 570 252 291 091 069 736 923 747 898 192 499 516 672 298 990 741 411 007 130 850 462 053 836 818 123 631 104 591 711 065 413 878 897 374 509 538 723 050 646 673 713 502 927 591 477 625 300 874 535 613 099 429 968 657 410 202 493 477 106 058 446 890 010 837 343 699 366 887 590 008 924 923 364 019 922 317 454 384 792 860 822 976 986 230 481 761 217 467 940 259 352 383 962 495 541 458 840 012 902 366 919 608 722 960 702 424 785 802 898 515 147 376 077 293 865 580 968 669 134 254 169 513 702 896 622 035 812 869 840 036 843 304 752 025 598 038 005 968 728 073 031 480 137 001 416 112 597 080 957 394 639 626 743 361 275 801 885 672 388 367 563 660 069 172 307 453 245 372 072 720 198 940 289 073 081 094 937 899 209 976 123 907 746 757 814 595 159 745 389 119 606 584 672 584 458 039 402 573 963 829 493 930 504 800 435 308 095 755 563 248 208 718 898 268 149 647 839 038 104 868 578 232 563 808 484 891 048 614 046 743 474 641 568 890 457 872 835 517 548 056 949 374 747 829 993 377 857 061 498 394 588 305 019 065 044 711 174 235 272 531 458 005 111 730 638 292 265 356 934 411 019 718 258 628 038 174 567 907 034 009 825 876 922 881 154 612 636 128 173 877 812 103 813 258 183 893 490 042 713 939 634 617 200 009 368 931 585 702 053 621 359 608 562 173 167 516 823 710 732 379 458 496 090 504 781 924 176 551 988 264 539 629 923 330 277 136 636 761 003 879 265 425 331 270 144 794 924 031 166 800 963 605 036 071 842 598 266 097 736 180 562 515 795 079 490 321 077 349 546 887 219 751 529 914 970 454 326 078 235 204 142 140 333 079 786 923 345 255 119 598 186 039 216 348 144 332 254 729 318 830 274 135 141 498 622 172 127 006 106 396 557 783 686 146 598 200 097 097 056 205 683 992 328 444 034 709 599 147 450 630 483 495 425 962 311 274 817 524 126 115 513 629 275 963 925 012 449 859 232 801 414 108 075 662 221 070 951 044 232 580 439 441 902 231 355 687 897 608 916 977 740 889 080 128 468 254 513 918 638 602 811 927 341 886 278 791 233 339 089 186 823 120 112 880 776 047 837 760 209 731 282 537 467 773 281 619 693 772 752 961 804 059 691 986 930 615 126 819 468 373 665 002 913 668 905 143 446 977 929 892 499 017 321 337 089 304 864 818 822 124 526 830 328 879 673 325 330 672 617 708 664 247 528 913 787 376 161 847 172 598 639 260 223 596 175 302 523 273 920 374 179 301 985 882 961 712 507 123 393 964 292 946 246 818 478 958 334 563 250 457 120 229 720 687 298 137 893 391 325 435 024 966 023 189 375 638 292 992 825 242 611 657 100 802 323 812 953 758 398 737 461 299 881 588 319 124 079 317 225 635 761 556 697 912 263 439 633 644 195 507 839 254 867 966 993 923 248 897 431 722 344 879 514 128 476 061 116 674 361 425 877 069 538 289 116 230 436 772 863 214 364 669 188 537 754 575 607 098 470 089 104 550 258 588 562 696 646 891 269 717 431 580 375 246 568 606 812 324 886 477 422 999 776 665 711 705 445 296 453 018 427 164 096 575 079 047 698 475 776 383 597 291 692 993 737 946 724 940 995 216 195 564 462 014 119 697 966 830 861 151 965 641 741 293 894 394 170 167 586 950 897 036 312 765 718 597 243 716 416 298 529 143 481 330 126 713 493 236 882 776 336 532 717 549 080 648 102 102 512 524 801 459 779 928 748 202 181 905 873 504 196 377 609 100 591 826 370 996 173 711 001 077 734 195 154 599 434 994 748 316 199 789 122 473 183 810 227 159 177 869 097 116 063 639 490 983 113 922 678 150 768 051 272 608 777 110 856 525 637 397 241 226 398 712 239 111 957 076 791 730 962 616 798 941 791 033 539 288 200 198 469 592 879 423 808 785 739 339 545 271 443 197 536 374 170 646 557 708 364 146 911 569 647 985 481 365 801 178 355 017 056 177 627 546 557 982 882 041 021 703 429 766 621 760 725 850 929 843 425 499 316 475 769 221 247 821 924 888 967 917 839 064 463 838 635 588 990 165 526 215 830 840 834 164 421 910 746 125 895 329 055 988 355 738 857 504 179 976 870 763 709 856 050 485 123 077 587 089 414 850 043 262 739 294 137 575 890 438 839 035 468 081 632 371 511 545 172 003 677 083 467 368 759 986 970 303 250 005 728 616 740 925 355 909 897 649 892 579 553 628 114 216 840 000 921 761 098 120 849 429 708 120 986 097 011 595 423 968 669 126 948 251 624 320 028 393 215 097 026 302 599 182 043 748 407 633 472 420 531 464 411 258 620 285 087 986 343 447 200 201 571 355 895 067 323 177 914 574 595 384 038 205 669 996 954 227 644 286 483 883 318 925 753 492 416 357 064 930 694 014 291 261 587 610 060 426 787 654 608 589 383 656 643 146 824 850 339 786 154 447 565 210 343 832 998 255 059 747 525 645 211 495 564 793 235 205 626 091 743 241 230 840 059 804 511 124 974 898 898 234 209 479 007 122 671 089 393 862 948 746 415 610 785 247 396 059 626 066 175 756 610 982 932 793 932 901 454 021 408 640 746 927 980 897 701 305 282 821 600 828 257 504 849 482 617 526 643 262 050 153 172 838 791 484 474 783 100 871 195 928 554 437 915 534 866 075 963 214 639 512 440 336 418 734 553 061 755 437 777 373 006 005 582 639 489 551 172 346 373 166 581 946 530 038 648 212 311 614 929 568 430 524 592 033 297 614 081 820 770 268 443 557 207 907 071 457 618 909 261 135 053 926 198 779 488 204 716 400 401 439 376 578 392 889 582 668 743 050 458 023 325 404 054 211 766 605 802 899 892 551 671 835 024 312 851 326 324 159 089 765 472 738 378 520 616 884 205 469 402 835 215 612 575 465 310 096 742 420 988 718 095 053 629 799 421 077 900 601 461 355 131 738 041 272 162 661 450 713 371 402 758 315 013 574 927 347 822 968 336 300 614 005 325 861 352 808 626 237 439 898 850 544 124 083 814 449 221 820 190 921 608 600 783 689 675 970 078 511 633 056 238 360 973 089 033 460 932 708 478 662 642 908 436 789 850 437 611 319 176 437 237 122 641 094 176 776 875 756 479 820 287 653 336 035 994 329 943 233 219 651 938 410 030 632 634 196 289 398 802 214 863 913 716 567 517 910 274 389 997 000 465 529 455 077 380 102 520 193 719 691 269 159 701 824 377 298 519 405 498 129 658 607 260 749 648 142 176 015 330 172 402 665 099 440 186 432 381 183 433 388 051 378 509 844 668 926 394 096 526 338 183 495 532 191 440 782 100 728 580 917 220 215 482 121 935 890 317 990 906 154 170 716 081 296 424 308 797 065 708 412 682 650 954 652 108 237 128 233 791 219 694 193 280 901 391 946 646 642 704 909 535 091 874 691 457 904 744 400 242 234 893 992 966 037 989 311 331 554 016 255 934 965 579 672 182 569 798 925 984 469 390 491 069 202 730 434 985 057 215 638 030 063 248 616 870 884 065 570 067 391 878 964 162 097 349 536 003 556 201 746 591 814 304 194 258 836 872 682 605 005 497 010 775 674 536 782 422 027 679 147 759 165 709 500 813 571 254 278 896 356 371 790 092 178 725 343 212 617 547 165 448 654 917 966 696 349 643 615 574 483 719 303 845 367 722 461 607 340 531 759 151 134 182 621 769 128 355 520 684 790 639 322 298 061 263 736 947 089 184 230 619 970 948 558 538 739 907 382 023 493 537 300 116 838 409 609 153 014 217 229 958 516 760 352 900 319 986 880 301 364 458 080 786 036 067 410 608 203 944 551 270 989 329 685 908 545 693 962 092 252 263 021 590 418 179 220 460 629 072 003 713 175 734 379 249 783 311 761 648 910 476 340 974 048 217 162 092 360 464 276 349 815 073 349 078 009 583 894 386 581 409 555 181 555 387 028 252 797 868 647 910 049 175 984 272 591 091 311 705 503 091 053 592 338 835 398 035 557 085 742 989 684 839 209 833 566 396 983 773 593 515 686 488 780 530 059 853 086 738 305 257 423 687 222 206 553 154 953 870 006 391 714 201 037 074 328 066 269 478 406 005 892 865 057 157 795 070 516 017 496 946 624 061 764 509 223 518 652 942 373 046 372 708 366 643 274 012 168 981 493 004 345 236 910 357 370 039 275 543 473 405 954 476 959 148 367 650 398 658 640 719 813 088 450 797 047 313 752 771 205 655 425 304 271 889 199 557 462 447 985 157 077 568 968 696 656 284 670 671 354 759 698 310 510 598 879 742 084 514 572 175 599 128 950 645 684 018 080 809 362 458 271 924 782 277 599 312 690 434 253 491 856 604 908 288 367 150 106 520 766 284 399 004 795 369 524 574 651 469 648 763 986 147 199 449 267 131 801 836 566 652 951 595 982 550 605 949 201 813 867 174 536 785 206 229 699 907 353 429 723 776 398 585 311 764 697 355 326 771 021 043 479 046 998 587 311 663 905 100 830 461 517 716 474 436 555 333 580 761 733 546 553 001 057 364 281 984 645 580 010 123 399 314 173 203 807 605 123 190 064 941 499 258 606 013 534 730 168 929 602 636 782 886 431 044 606 443 609 873 316 854 414 235 296 909 713 486 233 183 901 531 227 745 146 255 367 669 429 972 679 336 708 011 428 017 097 286 178 457 774 120 770 378 733 603 789 880 905 913 791 288 937 465 129 405 722 119 423 549 727 620 344 018 976 450 323 671 871 445 403 541 312 848 635 236 380 750 048 702 404 428 094 822 563 550 746 220 752 538 535 175 127 583 158 147 519 805 183 141 828 341 246 011 704 810 484 764 426 545 969 852 253 136 276 757 805 446 646 612 927 426 092 795 427 429 014 811 983 472 715 998 395 601 323 205 477 117 625 242 980 904 467 172 212 375 118 650 091 624 337 255 535 786 242 349 180 390 900 315 265 833 117 940 894 503 181 527 691 084 659 336 805 394 326 566 547 555 020 203 350 795 368 014 734 629 772 886 372 534 999 473 809 729 401 119 952 059 412 883 720 735 555 070 610 089 256 190 888 734 141 666 653 483 182 723 609 450 279 935 709 076 429 927 012 437 497 969 400 919 381 812 388 838 916 937 070 344 281 734 889 586 791 476 496 454 677 661 933 510 429 780 915 412 337 771 051 802 712 177 090 401 279 808 580 471 144 492 539 132 395 208 836 364 672 644 299 629 900 563 465 364 704 835 897 212 794 834 095 732 984 105 559 041 666 158 532 458 486 629 081 941 917 374 520 883 155 830 499 366 522 170 938 562 234 816 140 865 716 394 395 247 171 871 406 810 303 895 520 565 485 826 312 181 053 051 518 043 491 991 164 129 350 623 417 762 393 755 038 053 125 509 198 293 461 883 277 879 560 206 962 393 938 369 299 463 336 479 742 029 377 370 051 434 133 109 008 119 493 106 198 210 417 945 292 265 653 185 918 601 845 812 018 984 620 449 021 111 595 596 324 708 306 401 994 978 856 504 396 711 250 017 011 981 373 634 352 065 154 161 426 930 237 736 688 378 427 213 396 906 436 792 937 980 108 184 395 394 168 296 484 086 701 694 903 947 457 518 486 389 317 098 439 988 282 423 385 228 809 164 723 190 711 791 531 827 949 912 828 517 332 308 160 848 846 812 520 740 137 768 423 417 590 811 375 924 477 285 789 501 327 806 134 576 580 250 722 686 061 987 186 211 895 228 446 637 793 487 826 419 280 235 220 003 421 916 526 319 195 009 859 238 750 126 809 837 319 651 227 969 605 226 595 050 802 584 300 455 568 993 133 867 860 905 816 535 903 193 106 722 762 629 221 008 117 654 265 970 910 449 737 338 606 378 760 952 040 208 928 470 739 543 432 643 048 920 182 736 340 327 107 550 026 910 392 452 699 498 700 185 052 778 825 540 861 052 572 243 870 417 630 361 812 230 462 387 566 989 605 994 990 966 937 821 931 227 021 160 305 279 325 755 794 117 385 622 103 208 046 922 340 869 319 052 771 147 675 710 110 987 529 640 904 179 296 209 698 770 659 577 572 289 445 126 315 636 355 061 821 995 071 435 261 288 320 423 218 674 554 667 173 159 209 453 642 860 060 709 554 890 599 644 851 985 948 409 245 749 327 516 452 230 114 925 470 293 266 942 601 601 602 108 579 645 202 823 543 677 000 917 595 807 220 558 286 801 980 396 874 428 083 043 787 418 158 177 168 533 592 461 743 685 061 692 212 036 474 179 101 795 553 942 018 670 901 919 774 016 188 653 403 230 792 220 046 490 867 459 717 068 942 655 815 414 503 358 073 990 683 407 835 039 438 622 807 897 001 048 709 464 549 368 072 198 706 181 076 518 271 411 443 980 821 124 827 853 135 756 809 406 816 336 614 729 128 610 743 015 209 701 661 882 345 696 864 895 145 540 157 283 460 997 421 628 677 061 406 299 731 801 195 727 610 015 861 315 569 162 220 495 123 394 536 258 840 862 671 559 674 250 571 231 010 876 363 451 197 880 785 827 567 206 044 584 470 245 238 004 149 829 555 420 229 049 391 205 214 096 189 624 337 544 411 111 071 537 006 836 465 288 178 034 992 897 980 813 830 896 665 477 369 668 069 168 723 837 358 366 635 220 695 389 578 491 908 705 720 147 591 866 919 512 437 589 545 617 388 481 114 887 392 404 039 765 204 380 695 676 111 747 164 840 439 759 404 434 890 059 081 078 698 105 903 297 074 747 352 737 107 338 506 287 213 298 599 105 983 753 557 582 827 162 697 464 654 614 831 109 704 985 753 181 656 145 661 443 960 257 549 936 854 811 785 650 371 184 697 834 974 528 220 678 973 361 609 011 405 949 469 882 353 227 007 528 931 749 286 419 055 117 076 720 182 594 930 817 688 941 256 040 811 683 614 251 305 076 388 045 241 513 307 285 346 358 760 233 125 338 944 238 582 863 938 473 731 763 738 115 015 099 386 346 299 314 265 475 295 224 477 305 568 695 420 194 300 287 578 892 550 145 582 526 222 947 744 714 049 925 547 404 296 626 580 885 883 311 538 652 584 213 945 031 593 236 668 305 788 685 076 845 035 979 612 621 709 211 904 318 660 169 136 229 240 723 913 125 372 459 605 958 351 383 576 162 501 688 996 956 211 842 537 411 170 227 667 311 615 357 872 633 934 458 441 652 376 440 707 505 578 966 031 099 692 332 080 642 511 386 773 623 153 507 935 921 334 346 604 366 427 853 503 118 337 950 250 183 170 596 751 816 680 127 829 824 710 712 105 741 545 036 967 205 548 396 697 663 276 585 693 761 433 396 168 681 785 025 062 514 696 057 503 146 385 358 070 964 603 430 525 835 076 519 554 311 758 501 035 036 386 638 994 506 893 801 957 592 127 560 897 995 085 361 767 100 339 216 530 372 686 473 460 710 615 253 550 177 613 372 644 652 930 353 820 364 866 549 054 421 089 055 857 436 134 006 296 558 279 123 294 078 505 886 869 504 812 649 024 001 850 409 101 548 837 655 191 331 881 590 650 819 500 023 541 909 368 596 603 972 033 843 676 925 442 097 841 831 623 430 051 675 099 942 098 275 959 742 016 863 733 904 632 666 773 430 251 014 369 374 805 363 358 276 448 772 423 725 688 118 622 299 428 444 893 267 186 452 884 997 663 465 560 284 476 163 831 324 602 680 347 613 996 179 236 920 594 664 624 059 739 397 417 435 663 377 226 805 986 353 620 647 053 246 850 722 083 712 674 932 041 242 725 287 174 630 251 585 546 747 363 211 596 792 535 810 181 487 219 429 098 098 620 577 251 448 724 088 019 337 506 608 528 145 396 671 427 625 362 325 888 169 344 318 573 981 996 697 331 677 919 561 649 307 899 768 522 410 973 692 207 495 212 981 195 381 128 557 216 597 847 536 779 766 085 755 437 010 879 465 716 738 058 587 336 427 000 750 190 891 634 793 233 564 805 513 867 507 742 509 734 742 561 511 287 943 748 241 232 513 124 873 053 698 179 051 617 664 433 441 441 709 827 566 592 789 360 697 045 973 315 594 361 693 317 402 967 254 864 571 376 217 814 354 683 506 161 298 603 580 746 892 288 425 325 412 698 233 998 953 015 908 492 725 528 417 022 388 367 738 323 546 871 983 975 867 738 778 047 989 644 669 702 852 172 931 838 711 370 859 069 799 400 825 233 601 500 149 124 622 242 242 962 731 797 641 412 167 662 790 916 963 852 094 728 182 534 453 906 556 986 825 725 585 118 665 516 822 212 790 568 380 490 761 994 629 668 896 083 304 023 946 832 049 815 602 066 731 137 283 756 752 968 566 915 978 118 015 776 799 156 303 118 525 461 629 826 811 457 348 874 336 338 484 179 601 866 846 299 062 702 621 377 883 919 424 467 403 184 194 214 584 336 278 901 059 655 700 540 019 376 669 918 820 266 909 437 182 272 101 054 813 723 599 866 298 499 267 850 765 499 965 592 335 097 730 891 469 811 080 896 760 337 762 204 037 741 009 644 302 538 997 451 303 065 520 500 571 454 569 423 062 178 076 318 439 753 390 226 013 475 298 761 876 173 071 701 323 455 052 445 185 462 272 110 497 925 191 352 089 629 728 409 753 184 810 422 264 974 197 904 584 863 003 972 569 277 479 068 304 418 520 504 745 216 930 787 798 433 725 111 574 192 528 550 365 730 252 956 758 899 541 169 763 986 073 226 808 402 981 473 899 990 164 422 491 401 063 424 046 637 360 159 029 799 830 984 357 570 595 443 818 120 623 479 688 624 274 438 074 837 971 840 448 368 230 928 063 770 951 039 487 168 772 544 952 129 864 654 624 319 634 519 446 681 084 978 309 946 308 920 883 466 323 651 946 040 601 499 718 317 247 565 457 346 135 012 653 997 810 210 158 257 713 342 047 721 494 796 668 594 157 021 173 708 250 972 560 046 608 046 131 989 936 647 839 071 986 271 958 009 852 190 950 405 922 054 752 948 434 729 724 874 046 265 285 970 274 524 231 868 673 939 816 496 579 699 353 283 025 717 829 327 832 952 668 018 948 135 177 864 982 886 986 868 098 286 656 139 723 991 312 315 556 589 567 192 235 715 962 222 436 087 749 875 935 983 063 741 098 236 407 033 957 772 407 501 583 485 854 421 418 288 619 733 485 108 480 196 456 028 550 653 922 380 041 896 176 179 622 226 968 410 676 434 088 702 782 554 529 296 194 891 688 355 127 577 501 376 221 891 001 677 714 369 459 280 926 275 028 740 491 298 911 441 683 430 961 678 611 854 759 370 159 153 081 943 350 239 031 254 069 939 743 329 035 977 864 437 398 560 757 075 930 087 563 308 611 111 670 556 272 040 966 430 031 781 117 786 895 573 293 485 972 140 554 231 718 719 844 421 782 452 864 539 647 390 545 998 322 707 183 407 101 559 091 485 312 832 734 358 534 485 715 398 635 206 569 552 780 506 905 801 664 291 848 140 556 699 164 156 941 673 203 349 726 253 618 046 466 651 013 405 442 199 275 358 963 807 570 254 599 425 310 048 536 076 209 937 602 642 300 851 888 135 168 505 582 509 208 307 493 959 643 940 447 911 297 562 668 427 939 568 321 305 789 873 661 111 553 895 877 871 024 069 561 940 419 704 106 460 825 547 364 587 555 933 187 186 872 840 922 718 952 679 438 182 117 110 104 408 076 156 318 759 095 818 648 438 688 187 666 821 483 907 428 225 373 048 241 807 426 834 605 788 846 353 996 692 657 309 167 744 450 948 082 446 479 479 864 740 998 489 011 277 110 417 011 664 327 818 603 684 086 094 730 332 836 612 506 513 431 877 056 672 940 956 527 964 997 029 601 965 196 220 475 426 969 343 452 799 138 254 279 100 643 045 115 134 531 921 840 134 335 444 137 396 142 076 029 494 510 038 518 443 524 138 236 600 255 208 786 446 461 323 684 559 956 949 302 956 694 882 802 186 904 218 630 614 750 850 177 837 290 027 205 145 059 739 984 719 569 274 005 293 118 404 528 942 675 888 216 326 664 983 387 431 181 161 823 129 314 482 738 298 959 155 053 704 215 364 317 603 178 106 827 783 940 039 315 528 042 006 759 890 007 263 961 356 898 176 500 974 663 956 195 389 855 044 009 493 130 806 384 424 172 614 084 245 469 238 622 537 252 893 772 948 444 387 558 204 231 907 919 671 034 420 700 739 682 940 526 860 280 831 260 768 340 407 698 977 808 047 474 507 835 189 773 286 719 434 061 466 649 314 048 879 275 351 547 391 008 310 183 535 768 893 818 509 404 153 123 750 341 360 740 597 988 396 237 460 167 588 215 057 017 760 424 520 613 619 959 301 459 207 713 593 787 798 072 149 734 853 782 340 957 979 715 369 428 230 727 281 129 776 135 813 997 573 821 553 716 400 136 997 483 377 598 084 042 050 492 536 811 225 949 538 313 154 313 201 077 435 950 228 380 194 444 638 052 609 848 083 417 528 204 008 495 577 775 324 189 728 604 564 895 783 524 293 868 777 250 227 567 428 397 642 634 469 967 945 426 797 805 839 622 013 491 539 788 548 662 166 562 459 742 363 176 707 838 496 595 156 741 299 964 389 252 151 292 842 070 497 082 300 075 654 749 595 237 297 135 217 272 031 279 664 574 021 319 416 772 227 774 625 780 061 219 057 633 846 744 328 105 859 821 580 061 149 144 326 647 258 550 352 323 329 241 008 671 734 511 141 349 085 920 116 145 859 391 700 949 545 445 374 375 041 723 084 882 741 686 325 767 338 824 064 210 142 133 711 275 682 680 111 078 556 246 272 531 837 841 230 377 439 897 490 881 605 944 552 939 194 592 491 079 218 961 711 429 476 936 571 845 947 899 509 894 151 317 434 207 988 765 536 790 719 962 857 602 987 601 003 173 586 904 027 670 285 276 203 102 423 608 401 927 481 874 142 646 410 378 220 837 582 030 846 009 186 543 960 439 247 829 225 591 985 610 524 793 109 683 237 270 398 979 037 594 838 457 045 944 572 968 343 796 586 322 622 469 062 671 155 110 477 737 702 498 907 486 052 240 056 591 817 396 827 358 851 879 172 610 748 777 145 024 453 038 264 229 204 854 322 282 816 071 987 313 646 617 721 524 635 593 881 125 969 975 876 827 665 079 926 897 919 604 759 183 043 242 864 924 193 034 346 726 294 620 165 882 666 738 001 014 337 555 382 662 843 099 078 702 199 798 310 954 134 325 879 508 729 921 413 037 765 505 187 374 677 463 858 942 106 001 200 774 104 688 116 210 361 437 714 929 226 270 684 331 851 815 065 966 590 180 624 795 914 489 453 835 650 823 096 429 875 010 534 719 545 438 376 073 324 088 179 686 141 615 476 180 133 860 140 358 517 512 890 174 947 460 227 151 712 711 877 210 589 933 979 272 179 737 014 559 205 056 885 250 121 350 940 814 133 911 582 407 501 339 694 301 767 411 921 100 767 043 268 827 904 172 620 921 615 056 332 810 927 708 429 448 612 234 729 723 500 118 501 754 002 066 685 820 857 248 081 532 359 216 427 124 374 672 103 672 299 445 847 900 259 877 904 484 741 609 085 328 038 646 939 128 518 086 876 958 388 974 222 392 375 449 568 576 206 837 629 032 709 126 224 786 684 336 272 612 916 282 063 076 714 049 783 864 904 761 352 841 091 359 521 620 539 210 681 676 972 061 356 665 276 694 906 538 402 133 389 324 376 599 747 321 960 863 311 281 067 739 494 404 251 210 804 958 145 284 906 600 925 744 724 296 839 280 600 268 886 764 746 109 195 707 335 688 559 677 707 322 432 146 053 558 830 828 576 945 986 060 129 410 190 019 513 719 766 861 158 809 183 353 016 437 023 087 712 634 613 681 991 578 911 638 466 035 841 302 294 847 202 269 930 404 727 506 043 817 215 090 852 690 601 644 392 212 323 975 162 848 918 001 096 296 642 073 928 682 446 984 030 273 029 949 972 962 383 747 702 063 223 863 454 037 884 688 674 569 817 132 098 600 614 135 644 227 743 300 399 717 070 641 220 393 437 564 109 592 278 715 453 458 206 831 634 169 956 502 901 940 839 966 445 732 430 568 845 974 845 154 877 968 646 638 024 855 816 831 690 640 950 114 799 010 186 129 781 646 472 211 117 429 054 060 594 281 700 605 317 374 167 208 406 436 759 148 111 863 806 230 535 794 208 517 141 589 678 559 012 488 264 430 377 780 172 639 192 127 290 424 446 213 994 124 627 101 424 423 571 534 407 859 036 937 792 005 118 142 991 167 137 716 514 079 424 286 624 811 744 535 305 450 401 855 489 630 579 930 650 600 592 537 910 879 577 574 081 449 946 128 680 636 112 429 447 309 028 188 185 264 144 743 413 397 189 036 804 940 544 446 538 396 603 594 388 298 581 460 568 613 023 988 040 408 345 398 606 014 344 772 491 160 226 188 493 882 824 276 318 763 072 972 646 720 976 512 284 325 564 254 139 539 775 167 450 218 722 563 136 045 977 027 233 339 836 224 041 203 209 895 931 282 165 314 160 297 478 461 234 163 123 142 266 804 951 434 489 122 015 081 851 243 317 099 460 382 580 717 079 675 080 129 112 174 728 970 833 239 157 788 122 715 546 731 033 015 612 358 916 549 463 068 637 050 809 938 609 490 923 902 248 198 171 226 837 626 470 025 511 960 395 331 709 226 969 732 512 700 190 463 502 500 120 605 970 617 460 332 334 146 441 868 459 038 429 015 571 827 260 741 576 897 793 673 160 951 989 441 125 057 539 283 316 350 098 291 939 402 598 671 542 234 355 981 890 526 228 558 143 773 362 103 836 339 533 499 588 205 734 081 826 291 236 628 623 522 367 445 576 920 221 639 802 294 029 369 916 710 785 680 048 313 033 653 108 801 631 745 390 089 317 992 596 398 729 417 458 990 673 326 036 008 888 004 449 479 698 923 154 814 931 047 851 851 797 304 696 894 348 597 600 201 571 959 494 074 031 066 241 977 157 590 031 439 502 214 369 352 433 027 830 378 525 290 306 920 738 554 524 294 796 722 824 349 231 638 967 571 214 445 173 967 735 256 497 427 045 281 470 034 110 156 166 111 136 823 762 662 157 981 968 070 884 180 418 424 994 339 843 111 541 393 043 641 045 982 279 409 965 332 709 914 445 499 968 834 820 132 098 136 276 605 829 930 087 236 795 533 216 942 915 057 701 503 076 222 896 555 165 191 903 911 763 704 456 140 312 617 048 021 231 273 383 349 726 227 081 144 540 522 841 800 250 947 152 551 789 860 269 065 395 632 849 990 130 705 815 334 200 158 729 632 342 780 158 584 932 774 090 770 175 859 597 945 000 598 345 706 161 456 602 481 841 288 336 925 758 844 395 135 639 478 331 361 277 348 698 214 328 701 189 049 188 439 795 529 377 037 970 376 099 936 183 963 259 322 458 201 466 073 116 010 401 095 900 747 059 226 010 394 439 438 663 190 407 247 157 827 931 593 584 971 362 290 735 721 266 779 989 395 581 825 650 997 402 612 049 749 490 804 090 300 539 903 599 038 363 843 318 010 229 031 479 173 499 521 836 243 244 329 203 941 090 208 790 273 863 179 892 913 744 834 849 850 934 906 934 289 291 654 401 835 433 587 206 793 798 849 146 890 777 557 010 776 301 728 672 863 132 628 023 081 264 811 111 564 010 673 543 469 327 082 987 379 028 671 985 352 788 474 999 375 124 778 997 548 496 592 895 782 823 391 170 330 583 410 916 913 552 423 958 242 139 560 993 244 967 172 835 716 687 421 559 245 775 964 710 881 468 214 874 804 396 209 207 018 888 729 498 867 126 097 650 321 347 248 237 517 456 403 017 939 313 849 963 416 692 352 276 750 323 886 737 554 231 865 437 729 059 915 693 111 909 781 542 951 859 451 808 511 331 327 397 448 666 104 090 660 074 092 614 954 052 214 919 140 825 300 309 577 258 555 479 506 842 186 905 075 661 228 909 703 245 560 194 477 879 017 369 310 407 780 286 114 984 972 740 147 836 608 429 943 575 318 654 667 648 019 642 145 725 835 167 549 544 286 952 342 893 892 069 835 999 441 950 610 829 309 861 391 032 089 698 711 748 047 629 470 391 694 647 249 290 928 024 095 374 986 638 355 436 827 141 428 266 418 133 051 017 125 131 139 272 722 282 751 602 598 419 676 810 525 265 824 582 783 200 231 753 541 776 619 543 664 591 538 530 911 770 460 600 563 617 366 471 375 547 700 803 759 091 581 332 643 618 083 305 376 814 804 142 054 070 819 749 574 170 947 799 848 305 137 978 377 108 483 995 029 354 424 006 478 853 833 617 985 265 716 355 630 335 152 406 567 121 831 476 774 191 458 856 061 846 268 533 711 223 531 468 275 957 449 474 563 070 132 371 356 287 083 522 204 422 580 885 239 209 163 792 425 595 824 483 951 666 576 777 834 878 200 015 497 028 986 786 045 446 966 772 973 007 060 836 655 801 162 163 930 901 737 003 730 588 046 048 885 551 044 384 273 695 007 439 290 355 878 404 367 008 153 931 500 950 519 377 356 096 592 483 372 924 933 792 821 611 179 085 120 142 154 644 664 167 147 948 824 525 014 994 312 232 322 047 646 588 988 163 495 039 448 619 256 138 545 682 333 598 078 225 932 080 147 165 033 221 953 671 789 785 435 236 595 931 892 081 177 124 207 519 182 023 673 804 680 576 201 718 483 527 472 769 458 693 483 635 605 386 124 835 286 562 744 278 878 222 992 370 393 627 858 555 430 895 880 411 133 495 459 353 701 323 137 166 701 145 886 281 943 995 848 764 177 858 814 287 463 652 956 285 693 036 941 285 966 817 033 309 230 734 768 604 545 935 886 399 413 371 579 224 877 464 036 378 652 158 688 604 040 851 566 347 798 782 574 001 235 581 177 258 841 524 183 219 572 327 021 257 044 254 844 564 097 531 249 858 115 392 461 038 705 879 872 097 886 926 326 973 845 387 438 057 909 635 201 873 847 613 601 884 599 218 693 805 846 534 746 952 920 006 332 905 931 633 664 911 242 580 095 647 362 844 703 421 098 228 504 510 746 512 148 431 459 164 699 954 059 899 144 741 579 720 970 159 946 217 166 464 899 593 781 122 418 742 905 051 119 301 932 940 756 315 501 248 596 351 107 392 774 819 304 308 296 127 339 773 816 907 422 121 822 920 303 391 244 576 137 175 312 268 943 540 810 530 257 151 147 136 747 269 829 838 150 029 473 801 238 644 713 791 898 217 181 011 799 636 356 971 175 697 588 577 022 734 229 923 142 823 320 933 332 751 191 039 609 097 313 496 928 425 957 245 633 703 350 448 227 442 826 862 209 651 723 234 116 041 357 704 420 489 642 541 559 222 158 435 422 113 401 596 874 474 501 013 826 016 899 593 962 073 655 588 000 399 241 482 273 860 295 485 053 898 979 593 390 418 365 421 895 906 637 153 124 602 159 853 323 745 799 433 351 182 647 171 191 936 100 433 758 062 825 793 630 785 213 956 528 546 737 742 091 787 295 980 923 335 850 728 030 714 483 225 421 398 304 320 994 650 918 403 117 071 235 471 232 990 060 413 117 205 541 340 572 039 220 494 153 961 107 115 884 836 076 026 794 383 314 938 116 523 589 934 461 236 490 107 946 986 006 787 444 304 679 341 946 785 376 089 148 280 420 384 470 674 788 892 891 804 863 252 341 730 700 484 842 137 908 095 089 134 396 189 019 723 130 810 754 739 822 146 572 502 543 257 630 237 235 100 913 980 590 662 974 603 402 983 416 277 690 399 355 802 368 452 031 780 918 527 689 125 936 615 470 812 737 567 928 773 890 903 973 918 160 053 487 552 451 505 906 550 829 635 861 600 237 478 084 493 600 103 542 193 737 154 825 037 647 738 149 915 149 076 938 678 946 295 956 115 767 169 322 817 381 736 166 549 970 382 534 713 734 348 127 641 789 207 302 386 107 770 054 090 276 485 701 530 163 638 628 642 963 462 974 371 160 633 083 427 765 084 909 100 011 647 395 853 279 353 761 651 805 788 183 123 403 859 077 023 832 463 515 790 049 491 789 751 736 412 162 368 856 203 612 468 874 321 132 373 381 549 237 450 629 954 568 198 339 200 761 050 428 272 205 088 148 883 108 704 122 909 117 382 204 257 301 691 273 066 319 632 600 876 518 691 588 922 826 577 439 562 532 953 497 723 718 270 366 584 502 825 267 387 707 386 917 043 929 326 609 533 279 307 760 781 279 372 358 719 680 105 711 370 595 897 865 305 043 607 842 310 905 837 318 738 154 059 198 843 847 670 315 768 111 392 361 622 505 905 224 668 369 162 285 995 073 831 942 067 308 436 070 944 959 943 342 913 052 485 859 743 785 765 473 086 857 975 262 500 957 501 587 589 825 946 960 289 326 755 139 644 428 040 912 649 951 942 296 671 490 695 248 642 306 909 274 701 169 662 498 645 649 213 435 581 284 949 700 596 683 101 041 276 963 682 517 696 980 358 464 389 072 378 876 233 177 002 962 386 190 950 512 588 123 719 177 683 030 460 569 436 382 871 339 373 453 452 446 794 647 442 487 980 251 751 684 319 734 915 571 740 539 173 569 330 191 857 131 786 420 041 505 634 901 244 247 352 558 917 876 652 558 240 004 268 106 906 106 926 917 502 994 437 138 702 457 937 906 258 965 859 781 269 686 828 188 428 296 542 673 025 343 299 917 104 375 640 780 737 565 552 406 289 535 708 679 418 224 315 090 909 422 123 571 036 401 924 565 719 970 424 355 753 262 637 525 119 605 111 675 969 116 577 954 285 110 714 002 664 083 272 531 233 993 509 469 338 045 626 992 648 616 836 001 372 092 813 140 212 573 763 514 477 813 315 640 550 031 924 222 691 309 420 095 831 018 321 775 798 756 450 439 412 773 188 846 928 993 267 936 174 234 924 833 620 180 751 040 143 820 651 401 917 444 861 333 556 785 111 012 046 640 777 995 810 031 955 138 791 349 945 034 767 799 675 527 131 541 839 274 236 581 679 023 178 353 469 970 676 233 352 648 219 939 796 385 741 752 569 635 810 594 847 913 663 353 645 427 670 043 371 422 335 695 618 111 921 967 737 156 592 657 970 872 439 300 743 618 778 931 502 720 753 473 441 409 887 858 381 493 281 635 431 916 678 114 523 446 852 507 126 405 941 803 327 566 967 698 045 761 348 327 607 342 705 219 520 628 770 999 588 523 624 831 882 560 369 225 383 692 528 681 060 389 512 790 246 105 481 739 852 118 551 989 424 161 314 209 437 074 268 932 647 774 321 295 253 521 384 897 253 524 071 826 601 245 706 996 838 772 753 913 140 860 214 534 847 767 722 472 360 661 454 830 578 359 342 247 625 610 595 345 688 114 394 145 274 032 244 998 428 176 959 798 957 963 010 029 543 476 888 253 093 666 851 425 313 517 064 118 043 829 089 033 481 466 825 346 521 674 890 007 170 728 675 173 655 380 262 499 160 771 736 956 629 780 501 300 958 132 198 511 809 513 152 150 274 838 542 289 462 772 521 848 926 669 220 924 071 455 636 618 681 637 623 091 886 012 091 978 351 237 013 213 776 569 900 423 350 602 525 276 233 415 075 669 467 794 895 494 214 840 797 520 260 035 661 237 082 816 934 464 312 910 725 319 840 387 911 911 428 957 450 657 070 630 640 494 685 893 294 291 817 571 491 952 904 439 469 367 988 923 685 911 638 382 840 435 081 866 867 239 176 246 830 197 897 258 333 285 132 829 314 628 503 085 144 431 641 736 806 550 019 356 141 347 503 589 721 748 341 956 698 636 450 336 681 228 510 783 739 955 966 392 570 637 293 447 382 888 805 832 178 595 668 396 617 521 835 650 938 124 143 817 634 370 145 730 754 153 189 485 062 054 093 077 785 579 623 663 788 822 900 434 141 930 998 158 421 365 203 265 585 918 455 280 431 228 132 279 081 826 686 857 649 388 261 131 220 582 432 389 305 356 055 014 102 895 183 911 529 696 112 483 446 989 505 967 780 189 637 971 134 384 359 718 532 160 728 532 670 811 571 023 412 948 233 970 590 719 336 971 728 376 882 178 014 598 807 571 686 066 889 915 778 453 217 375 711 659 148 769 723 587 916 003 749 910 527 768 526 601 789 301 930 282 700 522 629 583 269 857 639 784 172 173 196 799 822 552 085 296 551 137 717 515 166 900 469 127 736 036 120 666 645 824 863 036 457 080 766 487 331 927 169 196 971 461 767 435 883 004 843 401 458 294 080 324 818 863 626 662 761 657 240 358 433 297 544 988 244 394 946 016 008 048 534 637 475 506 682 510 760 474 550 768 465 424 466 942 082 711 948 455 039 672 840 154 949 219 891 670 430 099 020 195 686 538 714 292 805 830 670 572 588 807 388 417 088 645 192 507 380 127 837 597 887 801 922 484 239 039 583 833 596 197 925 554 340 561 749 991 015 065 860 751 014 901 094 173 680 462 314 607 883 729 408 695 254 899 815 392 874 801 223 493 581 595 982 619 107 974 006 400 667 266 785 571 222 747 014 121 973 575 806 807 954 023 501 966 859 879 830 891 064 052 029 025 930 042 121 735 591 214 701 113 643 600 177 664 962 253 408 706 841 371 827 418 005 275 192 513 257 797 005 731 087 519 389 358 698 474 085 617 873 249 505 999 088 411 321 429 243 112 176 772 065 002 502 279 587 415 700 762 181 853 346 991 163 561 890 441 792 989 366 661 521 673 592 384 745 239 999 130 672 914 631 827 283 998 709 864 731 952 428 904 358 142 202 493 864 595 104 810 306 093 824 523 967 125 281 456 761 939 427 310 767 200 284 057 550 563 280 306 682 578 955 124 336 422 971 039 856 343 038 129 438 592 300 333 689 828 048 061 301 044 805 791 490 969 653 994 058 612 554 834 071 164 461 447 663 368 165 254 660 473 398 677 545 147 909 914 978 822 252 101 230 634 729 261 564 058 236 528 742 481 158 359 312 237 005 502 282 724 567 383 861 524 265 344 302 095 676 486 139 303 674 935 341 541 682 161 580 619 061 021 811 205 938 153 268 659 991 160 619 885 879 160 519 996 350 903 525 648 302 183 376 053 456 645 456 440 864 762 335 037 854 446 467 830 407 420 098 884 528 356 449 646 214 477 448 026 673 362 332 345 640 369 524 991 956 665 273 310 826 122 016 394 514 801 283 567 413 287 302 914 088 784 865 505 126 398 272 818 396 528 775 202 224 665 209 035 454 045 160 037 967 584 571 669 143 997 088 400 575 573 834 382 776 599 011 066 654 361 196 002 496 415 560 608 499 803 527 025 134 539 424 288 703 059 395 786 147 917 330 464 064 538 013 091 204 026 074 243 175 594 220 341 342 067 098 049 777 107 424 764 565 382 841 018 076 704 567 571 423 291 741 730 878 341 034 098 443 942 211 288 969 950 228 971 681 562 346 105 444 297 849 222 248 146 191 824 913 189 076 452 976 045 681 254 521 145 357 290 519 089 002 778 665 413 812 385 853 159 406 927 387 600 583 821 942 944 103 551 586 965 556 213 915 777 064 530 999 456 823 391 091 094 114 203 006 754 253 703 348 182 201 781 282 024 330 692 520 972 867 651 370 692 464 673 139 356 759 606 824 912 056 169 077 707 054 895 608 648 856 586 113 722 321 797 865 748 592 134 856 482 586 406 693 074 667 624 530 097 605 489 510 682 200 687 645 748 536 916 258 164 316 163 006 798 227 453 525 819 474 492 169 345 054 185 536 271 314 198 782 669 700 795 947 573 883 906 132 851 485 196 308 941 288 268 889 546 035 561 030 115 725 514 341 497 689 222 289 799 193 927 166 369 539 619 981 645 281 498 840 510 556 220 204 542 415 351 724 002 849 340 522 683 246 313 755 147 239 263 924 778 231 942 181 593 001 152 685 835 925 829 243 020 628 988 323 140 824 944 038 802 718 640 428 991 425 386 287 479 458 630 005 511 746 296 802 961 350 197 372 510 431 139 126 111 817 679 638 266 656 014 717 305 759 689 688 335 293 106 494 759 400 385 672 833 166 999 153 501 187 988 513 773 219 752 113 047 872 662 792 258 562 627 654 051 182 691 528 073 063 582 065 100 020 207 389 462 343 900 343 827 259 912 757 485 595 014 385 223 154 000 507 214 000 021 309 131 461 411 781 010 987 708 303 695 604 194 061 293 015 931 108 059 797 843 342 700 748 027 639 134 512 674 371 510 184 189 230 769 027 893 535 196 404 776 794 911 359 842 810 924 227 635 111 974 442 118 883 005 042 892 108 495 185 269 098 151 662 677 153 025 886 607 080 280 710 115 791 601 037 940 654 330 515 028 076 856 423 570 622 501 346 117 864 202 149 041 847 749 391 843 378 664 926 387 450 698 129 397 369 359 921 061 237 068 388 892 002 449 869 389 287 134 277 337 641 618 904 470 853 429 605 550 311 911 974 190 462 204 099 411 815 407 114 537 777 124 157 273 169 877 399 260 874 351 429 487 858 997 932 973 472 073 671 529 289 485 509 070 105 852 397 254 311 557 997 001 740 369 730 541 827 544 671 981 230 326 465 395 742 528 523 269 562 256 408 655 122 940 327 582 421 321 470 774 788 787 807 421 279 988 064 764 319 279 916 178 946 395 402 778 039 388 207 687 383 149 048 527 824 200 770 881 276 821 602 268 104 809 597 723 462 891 473 732 885 486 169 791 351 671 896 359 337 122 417 103 076 680 057 311 592 256 466 566 445 485 953 629 348 926 791 360 263 737 595 319 363 481 069 224 398 508 930 857 855 332 470 519 157 592 517 570 168 680 945 553 176 695 408 449 125 212 535 238 685 350 896 070 326 501 040 425 674 989 153 776 503 307 451 219 548 623 169 619 895 334 632 063 246 771 627 789 375 345 978 232 159 136 967 448 136 226 900 299 620 985 674 637 234 667 201 782 332 890 147 178 297 162 013 668 232 978 012 964 830 731 897 579 282 802 831 603 671 012 338 693 296 449 623 091 162 557 801 682 235 563 843 696 380 268 188 551 060 389 797 170 975 266 027 428 889 312 599 645 815 550 517 061 173 221 495 194 175 483 494 495 449 655 496 154 220 338 121 331 850 985 043 655 238 116 657 375 600 699 586 477 400 846 391 921 494 682 025 100 359 435 827 659 510 952 406 786 712 511 244 493 337 372 551 151 704 288 364 046 245 295 610 880 693 641 189 288 129 372 634 927 845 529 351 310 021 325 791 916 083 418 991 709 012 241 907 959 373 959 201 693 857 704 890 498 545 038 036 096 138 591 147 317 599 480 197 024 520 791 417 188 679 927 735 214 661 215 031 519 195 288 609 359 022 594 046 983 409 522 489 380 508 071 529 859 736 660 605 600 980 081 633 235 783 590 145 167 126 441 569 639 639 585 766 940 217 733 858 825 900 677 033 033 027 578 577 903 260 109 633 609 009 960 092 791 730 159 048 245 231 317 478 429 191 160 869 416 364 518 694 617 361 153 646 694 777 874 958 913 694 317 350 744 784 688 837 372 231 969 799 990 158 568 120 544 875 947 391 907 139 875 425 360 480 262 200 456 434 935 014 275 938 292 499 263 546 938 171 409 736 756 051 098 537 499 886 898 700 339 923 203 600 212 012 958 073 080 805 804 989 221 275 672 442 253 497 537 268 007 486 608 670 841 776 561 770 219 311 516 581 953 165 093 247 270 638 478 473 402 224 733 225 597 929 955 541 660 894 648 153 334 354 186 048 951 119 997 879 961 672 000 488 732 263 023 521 621 059 666 923 702 793 747 406 030 039 583 440 220 336 428 289 667 865 104 252 760 269 590 597 135 438 074 512 541 345 251 666 127 786 614 567 651 275 960 234 699 017 771 108 609 688 046 252 328 309 554 833 142 074 647 788 929 191 645 964 885 967 025 057 058 714 781 066 645 255 641 124 008 887 555 075 351 160 365 366 418 045 366 214 939 633 016 847 988 818 783 023 289 783 389 396 593 690 215 000 474 209 247 544 880 880 187 120 523 232 829 115 913 643 378 973 398 301 608 129 097 004 584 068 755 118 479 813 119 787 110 772 649 697 624 428 689 076 862 175 502 199 711 523 171 021 989 585 422 225 009 197 525 488 037 233 366 550 473 447 517 530 192 739 887 644 081 210 512 440 471 946 552 592 657 921 473 481 899 378 659 433 397 063 562 804 009 054 672 343 330 800 665 459 325 018 784 103 976 109 286 908 653 081 723 967 637 254 340 397 908 713 723 446 187 071 669 856 094 834 957 938 824 639 239 663 442 015 942 004 108 664 168 972 418 030 797 671 940 900 280 351 265 795 810 741 749 859 587 116 983 291 444 886 467 225 236 966 571 015 895 868 491 386 002 657 761 835 675 838 176 671 628 381 011 291 681 214 933 993 358 017 836 618 715 933 223 801 782 430 321 559 951 596 895 818 981 448 619 805 122 732 130 454 337 723 243 595 300 404 766 050 806 752 988 526 083 616 628 144 015 618 374 458 279 442 313 887 874 332 867 515 595 092 738 842 900 919 009 081 206 660 227 850 830 281 343 491 103 405 709 373 468 733 918 906 494 241 025 416 518 348 747 702 645 661 898 216 551 523 487 345 791 693 266 873 475 639 247 242 523 417 057 016 338 013 471 545 774 639 762 993 216 950 794 884 341 397 614 324 247 564 680 919 589 353 175 076 755 384 823 012 008 433 977 798 408 401 822 500 898 097 876 017 128 457 275 478 162 525 407 904 197 777 426 188 222 608 979 827 204 585 036 197 026 620 359 512 832 402 005 168 855 989 356 394 225 240 725 944 557 176 069 625 292 386 841 258 779 721 519 473 589 297 571 746 529 416 407 746 426 399 039 830 223 495 872 093 717 543 566 396 500 040 357 970 297 907 959 759 215 785 625 760 251 503 297 106 790 944 558 208 080 851 263 054 145 956 737 384 829 881 290 781 291 832 568 666 792 675 327 730 836 982 717 495 364 454 134 315 268 457 209 552 272 526 214 742 787 348 370 833 965 975 374 317 007 784 010 290 710 603 529 473 838 662 410 859 469 714 493 408 157 662 995 907 685 324 451 699 485 804 837 603 906 856 818 376 890 338 003 208 506 016 282 021 750 268 488 086 573 944 425 641 802 606 936 707 849 350 494 895 335 628 627 344 114 978 425 921 736 817 853 317 785 777 341 630 762 297 132 598 400 738 055 006 638 900 101 502 656 154 877 922 344 757 344 352 028 217 227 041 051 600 864 447 713 085 222 955 906 389 059 626 992 022 168 653 217 746 052 618 227 347 970 285 941 836 456 565 273 614 850 639 815 747 910 272 721 088 568 807 346 417 465 818 199 664 451 754 354 536 612 650 046 652 499 067 132 911 639 332 447 444 124 904 747 906 574 590 063 188 252 927 820 154 690 868 560 569 360 037 204 060 398 750 232 721 331 584 216 453 544 216 351 824 079 674 979 972 747 506 355 389 950 359 017 857 930 630 533 590 172 576 971 018 357 527 129 778 206 527 097 745 021 730 226 945 155 942 746 976 574 105 382 835 925 973 092 238 598 135 668 402 096 587 663 799 471 005 598 726 307 021 456 075 313 947 973 030 312 696 638 679 845 189 041 240 827 266 346 807 301 635 147 184 559 400 552 879 450 746 630 536 197 921 032 493 531 663 836 284 118 835 382 575 188 902 643 310 073 225 291 754 304 180 983 572 177 008 863 208 143 052 648 406 682 470 598 202 590 939 821 786 620 460 490 415 866 081 092 524 474 456 275 869 603 793 601 515 529 157 606 994 304 420 304 529 580 280 650 172 388 344 192 982 455 631 845 088 326 980 923 342 014 342 187 825 798 493 599 123 727 222 121 581 234 752 996 013 820 691 620 008 455 953 632 070 118 668 864 113 778 651 535 169 115 254 966 690 855 979 615 587 492 087 853 553 827 216 952 476 789 644 561 395 379 039 760 538 248 386 316 787 957 033 724 128 974 781 932 587 614 298 781 708 658 012 482 344 927 750 889 429 370 297 651 308 150 923 170 438 340 255 602 446 354 060 637 674 821 489 478 417 583 024 819 345 119 905 936 937 423 798 352 524 707 353 253 028 600 254 952 927 772 228 877 363 974 597 540 293 851 842 914 832 989 237 395 464 082 156 622 597 788 496 567 023 770 519 339 592 858 285 407 667 703 746 480 873 160 407 774 791 293 603 408 992 349 782 543 416 660 576 024 447 094 537 565 114 467 587 119 796 298 316 351 176 084 866 948 369 136 947 155 888 090 609 146 793 033 317 517 887 661 567 170 646 805 827 186 557 308 545 954 020 163 414 484 886 833 401 601 058 439 712 157 510 362 513 560 682 127 749 744 683 442 187 900 079 561 797 115 924 824 677 762 653 042 409 390 586 148 322 964 195 633 676 146 130 096 020 242 304 856 059 154 758 078 713 576 910 826 157 891 901 243 794 005 667 080 357 336 960 784 182 967 484 989 332 801 133 709 244 398 643 143 799 351 342 414 342 822 411 414 861 242 425 534 631 786 916 315 201 843 539 393 157 128 027 590 307 036 994 821 640 199 644 037 371 852 782 520 223 383 859 398 991 860 132 993 196 523 166 253 583 990 682 523 103 565 314 542 867 046 709 402 240 186 620 782 880 189 796 059 165 666 902 906 175 776 829 688 353 329 773 546 925 347 872 276 131 573 270 429 619 767 720 184 577 892 676 696 070 601 283 910 253 163 840 116 323 163 426 422 765 938 557 093 027 891 481 699 561 539 582 530 948 119 611 936 294 690 008 131 113 408 984 035 947 776 759 991 544 870 243 208 000 096 067 867 799 082 644 908 174 047 769 655 717 700 881 073 845 280 373 510 403 269 333 173 381 968 860 569 528 205 978 004 779 062 942 233 809 536 335 340 710 120 651 171 089 828 102 855 432 674 392 527 242 495 344 347 792 710 283 254 411 771 533 312 135 366 634 099 832 190 765 685 122 391 156 388 116 376 527 029 871 201 225 671 688 588 940 027 931 775 211 360 553 416 509 312 499 379 523 004 056 337 613 583 955 127 220 188 757 456 573 405 903 404 385 536 273 831 631 543 210 139 922 809 472 523 719 674 878 696 893 204 935 449 879 570 309 505 196 505 397 490 143 738 941 412 445 891 433 190 575 659 349 701 161 035 473 314 856 054 900 196 219 040 817 196 583 628 932 886 631 407 524 527 315 250 831 789 355 311 319 344 471 086 603 146 570 767 534 887 617 206 384 834 568 247 788 649 605 936 766 321 180 145 188 964 787 306 620 673 534 968 908 752 400 515 885 048 643 603 267 766 726 014 531 265 272 350 941 534 145 465 304 833 828 879 412 070 379 085 799 436 585 474 618 191 709 911 796 281 507 836 478 540 417 510 865 859 085 780 727 935 614 077 157 463 895 537 792 997 297 274 158 444 373 556 633 872 924 596 406 694 751 671 527 670 135 930 090 758 791 626 514 704 016 801 193 253 404 808 171 342 755 707 180 016 952 768 202 927 981 723 883 214 213 342 346 754 692 159 239 691 714 195 612 067 704 744 082 071 425 716 230 550 605 905 495 928 348 260 957 792 792 477 293 023 214 278 378 857 154 221 612 404 327 664 629 808 921 362 056 293 014 944 903 882 662 783 202 057 375 108 171 339 407 202 936 471 937 740 469 748 134 259 873 483 962 411 800 478 651 699 865 728 672 471 879 245 763 569 117 081 863 355 190 629 652 255 980 384 997 089 730 509 146 466 797 128 935 538 369 828 147 087 471 004 178 547 936 856 536 881 054 325 939 258 342 939 414 686 438 164 072 308 693 557 885 820 457 635 094 042 143 422 348 026 716 098 879 970 379 232 914 996 912 599 939 918 027 809 161 921 630 113 431 829 114 148 335 480 536 446 544 938 215 029 300 573 544 203 965 072 129 310 028 740 243 422 407 823 349 283 173 757 630 745 550 380 831 266 998 940 999 508 843 220 064 228 228 349 779 688 385 581 489 701 005 741 974 007 715 928 144 242 119 842 395 351 946 435 612 723 415 868 832 666 739 111 273 987 462 328 874 892 034 498 634 148 854 946 069 299 516 465 639 506 021 247 361 228 519 977 314 560 003 564 578 543 416 401 944 900 783 249 907 889 895 119 631 152 241 669 803 458 117 897 559 822 883 030 413 044 941 952 581 089 655 395 199 862 864 296 456 111 016 219 165 745 300 056 991 062 140 607 765 764 272 149 121 190 852 965 906 131 534 271 731 289 626 577 444 304 447 393 074 304 861 729 136 041 759 789 569 550 335 787 102 745 497 761 116 635 117 837 395 391 948 624 153 980 940 076 623 427 706 370 643 327 903 439 041 138 376 106 402 676 740 100 657 262 053 262 213 633 907 361 316 013 917 816 044 614 241 508 851 007 522 307 501 761 270 145 406 111 374 998 825 112 680 501 852 603 068 591 306 637 722 461 824 007 630 992 375 389 186 458 835 066 131 751 449 223 883 649 365 774 208 594 481 963 275 329 853 964 857 807 181 774 090 475 371 973 511 377 898 824 146 075 894 344 622 342 628 655 236 057 296 459 487 015 311 831 046 215 279 356 338 173 747 786 801 762 076 739 256 551 015 151 749 620 518 994 161 862 340 409 769 439 292 187 660 908 003 461 450 072 755 317 733 199 190 615 044 058 883 419 620 331 108 579 789 007 235 241 445 671 937 162 374 508 430 629 319 210 217 750 778 497 559 566 129 518 680 784 417 208 457 904 023 251 589 259 246 613 154 918 482 139 582 153 046 760 723 967 619 290 090 876 130 662 732 116 452 735 446 874 035 269 082 643 937 856 491 550 857 979 638 490 349 679 239 017 200 406 387 893 964 435 821 481 258 951 098 009 897 659 182 311 054 028 546 261 305 513 289 577 317 127 027 689 192 630 980 995 118 140 471 159 147 035 419 916 868 748 385 468 876 510 180 583 686 563 714 226 795 153 847 618 609 094 456 849 025 742 478 931 660 964 894 095 224 318 803 050 370 957 925 838 312 946 185 102 796 129 711 610 536 921 428 731 113 747 660 687 435 752 400 975 563 378 565 025 786 675 519 185 542 511 042 972 424 460 090 384 228 133 774 724 710 446 860 483 295 613 812 723 680 093 182 861 200 295 888 930 153 099 902 957 182 870 822 286 310 814 238 056 350 483 495 263 820 093 743 749 113 191 250 966 238 692 943 484 306 713 137 845 931 083 139 137 982 761 417 777 097 582 305 588 124 214 886 807 109 933 634 322 882 447 157 864 803 612 289 456 507 566 356 470 728 857 166 138 957 328 724 579 800 253 103 525 735 250 175 597 204 141 643 627 487 753 771 915 266 021 010 560 043 447 896 814 664 269 559 773 735 406 665 544 037 713 383 429 054 640 945 874 990 214 253 002 454 042 699 715 604 852 826 797 999 363 455 268 102 729 873 875 770 169 301 018 961 995 760 373 296 841 466 490 157 474 663 196 436 724 116 468 544 094 083 112 234 293 942 738 849 409 656 430 266 462 739 655 733 151 806 254 090 005 122 454 197 146 692 988 534 728 863 010 794 926 960 523 289 993 115 524 676 265 869 452 026 591 045 153 266 531 342 506 708 515 773 850 012 003 736 458 113 722 505 286 746 624 663 894 203 152 155 071 183 254 226 451 219 772 220 603 733 361 329 930 224 824 059 969 880 135 962 692 012 673 610 381 130 244 458 155 999 562 003 001 599 230 382 639 400 193 622 221 499 053 626 326 631 202 096 139 425 923 890 606 927 083 877 434 625 396 113 734 841 493 559 487 362 145 201 673 502 515 334 068 777 959 028 082 945 752 145 102 975 537 920 458 600 730 912 531 470 977 496 425 598 343 225 439 551 908 427 410 382 363 072 902 804 498 733 689 420 657 138 389 280 824 171 184 964 441 850 795 891 806 201 219 766 626 561 253 971 150 448 965 174 556 132 170 847 080 516 704 039 127 248 915 611 768 901 843 969 386 100 167 331 599 514 482 274 581 970 488 459 247 796 258 891 266 309 311 929 065 406 897 734 546 537 373 391 433 351 785 084 456 558 635 048 661 353 605 491 890 330 064 931 515 156 384 757 340 662 023 667 735 498 936 700 332 678 554 155 820 011 817 086 476 720 164 800 377 080 534 250 678 322 288 174 464 578 360 056 121 862 217 385 908 863 200 554 446 264 623 724 728 695 277 330 045 569 650 629 750 678 719 889 328 253 579 948 977 453 657 743 725 847 580 536 249 582 872 628 965 376 196 067 381 751 940 846 176 925 454 747 755 476 996 159 054 443 412 686 703 976 050 431 824 072 750 648 084 432 409 474 221 780 796 906 517 891 524 369 959 470 653 211 252 955 274 077 516 012 783 371 045 158 822 282 338 652 964 991 102 372 458 847 116 618 626 744 827 873 596 838 156 677 776 720 230 190 060 917 452 381 389 531 030 136 728 540 306 728 869 849 815 099 240 330 669 981 444 935 718 576 059 087 526 761 983 842 438 023 172 050 908 536 814 717 715 988 697 375 599 473 793 733 248 297 015 485 659 061 220 406 141 883 303 758 229 574 074 994 635 802 837 544 937 156 501 312 732 534 093 418 043 397 420 132 469 136 163 978 741 997 029 699 652 954 416 759 645 386 939 993 918 207 079 326 939 105 497 900 513 242 597 544 909 985 059 206 310 989 777 683 770 606 454 364 994 178 120 713 278 706 576 854 689 377 561 856 950 629 812 907 909 007 861 779 131 617 109 664 243 052 748 994 164 129 835 950 473 735 703 520 812 874 283 625 150 885 483 728 776 652 615 422 881 283 303 740 099 937 435 965 659 294 946 605 424 243 908 791 039 161 395 999 873 914 149 231 321 292 962 923 042 769 721 575 600 202 581 893 345 224 176 238 162 790 493 675 903 935 618 822 722 622 182 599 608 005 316 878 500 146 824 922 832 285 397 575 272 424 525 990 254 629 439 727 646 372 545 909 451 534 569 623 919 836 663 928 165 217 000 641 491 247 932 211 988 704 848 998 028 967 123 134 413 043 288 297 882 068 707 014 098 699 500 790 628 839 820 456 555 118 680 808 565 599 152 498 788 240 151 371 024 099 501 803 615 488 479 426 565 873 027 001 167 849 413 180 853 435 033 690 400 683 926 577 795 306 420 417 427 222 925 017 940 895 979 286 532 393 821 293 962 570 196 746 189 857 610 792 294 832 003 555 219 628 816 044 458 802 027 786 354 863 982 922 575 356 843 472 478 214 335 877 799 224 723 313 652 514 248 355 569 686 205 530 135 897 505 058 037 601 548 531 086 003 772 276 377 223 383 578 574 445 794 472 335 917 589 450 506 268 466 248 757 857 440 211 413 110 862 030 483 475 303 000 492 958 564 897 880 613 662 932 338 305 958 829 325 314 950 463 910 459 450 750 539 827 939 138 760 602 967 771 016 133 056 001 166 715 365 560 347 353 120 218 442 914 117 175 775 676 275 612 384 269 808 690 547 712 514 389 852 267 348 062 966 112 952 869 258 065 740 127 199 047 122 158 481 552 487 382 395 875 684 771 399 410 771 988 130 430 760 007 081 285 724 309 864 826 752 755 522 709 595 467 520 460 068 646 514 336 916 723 313 741 865 515 867 137 650 003 636 685 179 852 491 392 696 392 514 315 874 536 720 653 752 076 849 758 059 063 629 570 128 915 036 624 128 332 475 018 895 112 165 473 109 793 969 259 472 737 136 512 770 917 604 329 008 164 530 000 636 459 583 517 582 816 435 588 796 820 576 373 360 312 443 482 820 586 212 930 797 188 209 152 220 905 648 845 334 128 306 865 677 911 111 673 817 640 075 899 635 032 589 579 932 921 248 559 904 443 968 427 299 089 685 182 293 243 659 732 902 945 320 900 601 560 083 635 570 850 161 821 513 242 015 642 919 374 242 063 855 828 886 923 425 582 952 064 464 824 500 327 530 959 753 644 704 331 491 736 948 871 829 426 858 805 560 715 881 871 447 358 742 849 581 457 527 739 141 729 416 347 543 033 248 536 841 764 628 493 600 860 159 376 241 707 252 590 467 707 815 996 810 088 443 815 411 372 991 498 724 878 259 581 177 032 207 892 880 575 992 473 292 864 822 946 802 348 740 538 854 718 545 916 933 707 015 980 123 481 129 118 004 835 192 208 335 514 514 450 642 142 428 200 377 921 140 058 193 524 763 734 910 012 329 489 894 106 827 474 690 773 666 019 984 418 931 345 247 988 785 933 420 935 195 433 149 017 384 411 682 775 915 712 297 977 147 936 668 103 679 673 600 743 185 667 358 270 107 674 316 826 868 081 286 991 269 390 487 349 057 585 558 130 605 086 137 286 976 588 055 705 538 520 998 625 480 112 602 327 832 775 303 722 902 173 044 052 962 213 519 214 491 031 942 812 708 899 563 041 300 951 086 226 399 864 384 485 183 405 920 939 565 248 501 886 687 683 715 587 969 075 236 055 746 396 877 724 211 344 089 850 992 174 588 400 025 756 538 179 479 710 798 117 710 927 408 022 218 431 940 890 763 772 905 024 567 275 013 332 489 008 387 690 158 838 971 634 715 534 504 895 960 330 135 007 578 629 778 264 420 848 724 935 489 361 491 361 860 482 246 025 685 839 849 134 755 929 550 472 708 480 408 505 629 515 609 755 212 679 704 549 493 244 710 250 306 227 945 794 596 874 804 873 073 281 700 988 456 673 803 447 685 588 617 137 178 963 632 966 086 464 371 138 239 581 519 881 267 689 212 350 784 552 306 701 466 465 293 194 755 907 392 886 690 532 251 771 386 612 525 196 935 525 685 640 953 699 011 104 244 259 089 277 194 893 220 016 897 944 724 517 293 009 798 683 733 028 136 575 967 234 614 435 313 796 174 391 283 603 413 785 280 372 140 015 339 007 350 102 633 710 857 366 575 866 973 131 208 056 515 582 729 127 849 780 711 222 316 856 997 041 637 809 690 885 731 858 561 844 890 477 006 678 833 747 056 637 311 614 508 814 048 566 213 771 390 265 873 143 379 272 851 012 978 936 595 576 689 772 740 717 581 142 720 698 296 024 509 727 007 194 107 960 168 548 679 003 307 314 557 471 329 797 180 006 963 641 101 576 737 678 512 363 976 766 235 923 544 500 205 053 597 237 615 391 823 387 933 555 078 054 078 760 827 458 401 169 648 438 441 021 791 420 365 952 437 304 228 019 762 726 914 477 030 402 105 801 717 902 988 121 708 540 869 439 946 380 945 701 536 553 182 659 843 663 234 487 177 591 520 038 894 133 146 841 527 141 613 596 602 020 906 959 918 988 015 732 229 900 290 239 383 622 173 111 300 685 136 910 731 019 204 145 556 840 213 901 414 787 488 897 474 573 646 659 298 120 672 890 004 725 584 881 540 190 584 580 411 768 228 274 604 325 468 665 537 959 071 183 804 394 884 489 359 977 479 340 661 745 204 487 505 813 908 110 283 624 796 457 048 566 955 224 751 430 355 503 993 683 612 487 365 759 802 258 899 071 640 646 659 770 980 445 091 971 867 793 431 420 335 305 618 924 365 810 372 762 298 331 213 499 913 332 474 226 993 781 467 669 538 907 665 258 439 292 833 065 941 114 244 958 231 460 158 349 532 928 273 507 189 397 225 555 370 109 619 336 765 325 836 361 792 392 980 701 726 412 171 894 193 779 819 475 459 047 435 184 866 512 322 742 849 331 038 714 509 136 562 236 896 893 963 067 550 819 212 705 089 472 017 665 036 418 795 464 282 574 204 869 548 072 470 263 011 408 907 723 391 596 455 555 467 046 763 489 994 583 516 285 130 411 360 398 818 388 749 267 767 242 560 921 790 639 311 534 705 079 190 163 761 661 952 462 493 156 361 695 256 334 928 796 259 047 994 758 811 389 494 590 009 880 445 371 174 736 644 960 672 705 082 894 351 430 085 754 554 306 962 961 626 668 122 230 977 978 292 611 806 252 990 350 656 300 532 072 889 491 666 479 702 428 681 635 273 550 357 865 768 000 498 000 438 127 482 412 180 545 748 198 903 533 151 271 916 778 367 183 047 483 294 808 169 456 604 345 120 883 631 276 565 003 935 045 421 400 472 572 578 499 666 936 066 568 011 513 713 138 238 781 641 011 189 097 822 777 980 579 010 485 393 513 990 427 967 116 469 109 693 318 162 233 204 684 891 609 502 784 679 036 934 844 690 346 248 354 314 849 102 373 985 894 483 831 409 928 000 454 433 510 599 469 651 764 140 973 193 276 694 566 495 096 490 495 215 692 611 060 682 056 400 312 552 630 576 641 854 728 720 361 271 425 375 455 892 076 302 412 899 866 211 077 429 191 770 091 260 974 671 436 738 657 148 843 696 965 435 840 532 155 962 258 242 436 366 833 032 913 382 726 001 710 671 592 534 684 854 428 326 077 377 227 369 314 592 823 422 418 592 853 028 924 700 839 919 704 990 196 722 056 341 041 873 675 968 079 948 225 699 725 247 273 164 878 632 383 176 437 904 856 967 029 890 139 820 145 348 167 498 775 071 710 650 943 169 984 017 962 501 852 385 218 520 431 357 667 476 436 799 423 150 596 183 786 587 872 689 824 104 488 486 954 758 211 008 742 991 433 713 128 377 616 987 594 482 558 868 768 383 997 417 293 832 363 155 917 223 049 287 804 788 174 055 032 654 124 904 500 241 106 704 271 798 255 064 163 620 558 848 161 571 363 024 040 195 498 056 126 021 790 468 672 873 790 191 349 398 858 803 370 716 686 451 403 025 203 419 882 912 271 411 300 136 207 520 080 078 448 492 367 759 839 755 270 904 925 556 630 995 784 761 105 535 738 193 357 726 877 768 033 501 217 838 487 737 997 107 294 022 262 476 564 495 905 597 409 638 826 448 027 174 908 222 127 011 104 008 141 589 741 411 396 637 141 255 755 608 966 531 424 600 237 569 033 383 746 864 253 161 316 233 666 007 628 629 695 020 097 875 191 243 365 987 598 204 537 581 910 392 762 662 670 997 897 979 612 966 155 747 775 840 412 020 312 908 764 045 636 452 750 954 753 319 394 000 190 433 458 817 858 934 711 408 911 310 445 842 883 969 382 236 589 078 535 829 337 337 942 593 688 497 632 039 149 126 357 302 156 541 805 853 140 206 612 327 856 140 705 052 571 859 291 501 356 956 966 136 452 107 300 543 156 713 591 045 630 268 503 637 977 029 994 230 455 244 556 001 699 028 930 061 443 192 681 641 231 778 516 369 400 019 223 296 170 553 888 370 071 745 439 520 798 253 023 778 986 409 939 006 420 369 404 895 205 507 260 705 660 772 973 137 792 864 703 188 029 818 714 603 258 167 196 088 473 312 468 006 500 244 708 646 734 239 478 175 660 240 662 075 916 560 454 937 121 858 366 048 181 499 238 302 836 448 851 634 875 494 904 648 483 634 795 109 194 685 770 976 891 229 974 552 694 799 711 757 246 955 175 614 992 431 243 522 370 851 026 975 870 430 670 023 526 571 944 001 886 426 569 575 952 296 809 565 176 644 315 401 274 005 919 875 714 559 463 090 613 529 595 503 065 085 873 814 579 255 162 610 171 135 535 384 123 750 860 874 469 754 604 111 567 171 026 222 929 724 790 979 726 542 636 742 130 441 447 383 786 323 799 240 699 431 737 165 722 899 984 238 311 196 009 681 239 751 405 705 253 139 765 029 746 305 583 386 696 678 759 166 420 775 708 450 118 629 204 724 653 499 518 561 682 362 720 220 731 675 979 550 547 647 503 833 854 816 568 863 372 055 972 641 027 662 259 770 751 912 615 654 187 005 432 453 081 368 655 283 602 406 795 953 625 522 025 734 807 990 450 080 362 933 471 461 488 351 440 769 480 369 672 911 619 932 937 809 048 307 886 131 567 385 374 199 620 178 947 914 987 086 645 696 502 324 571 949 064 686 612 020 844 434 873 170 445 471 419 350 803 155 214 303 646 023 021 411 131 520 076 511 091 755 467 680 993 918 478 918 648 822 262 196 857 461 003 591 713 747 538 867 642 499 752 070 927 772 122 836 535 773 494 562 152 834 464 710 773 177 740 504 589 549 367 245 781 939 306 550 463 016 810 906 454 724 419 280 228 045 973 699 329 111 408 022 779 582 825 307 471 366 070 311 970 078 380 597 302 077 013 644 826 472 196 103 240 095 021 045 496 340 014 423 597 620 931 169 038 098 681 452 188 662 342 773 356 080 734 563 587 512 289 594 619 153 564 698 564 831 517 677 782 357 403 519 554 545 739 421 669 519 334 208 313 535 744 591 863 767 675 121 526 798 422 013 704 974 889 172 120 530 062 399 919 265 478 147 797 371 958 028 547 448 437 850 497 075 499 910 678 458 210 269 347 298 940 065 766 917 957 516 193 669 134 814 047 908 362 483 883 582 970 270 928 630 775 157 481 772 308 414 321 178 586 236 468 139 482 396 172 511 137 765 241 190 634 198 786 021 916 626 417 890 333 672 356 515 568 390 590 137 021 738 149 626 863 146 907 707 870 836 017 174 931 913 893 682 182 673 258 041 183 182 470 839 635 501 417 814 060 047 980 266 708 299 350 955 072 605 538 769 205 018 467 934 583 730 509 921 694 851 153 043 893 141 006 202 349 250 818 878 971 216 223 816 872 127 773 176 309 619 322 570 407 546 841 629 833 977 246 020 127 855 935 580 747 971 248 506 379 081 919 206 664 570 421 265 217 599 448 815 311 672 792 326 163 664 094 791 254 670 784 521 139 324 100 316 950 600 037 316 630 885 314 035 022 810 676 063 197 530 199 446 770 514 039 970 057 859 544 167 550 186 188 437 193 534 218 340 644 785 052 917 947 950 496 640 462 263 901 463 502 553 468 089 192 629 421 942 021 894 364 639 918 738 618 001 781 256 657 224 915 471 529 474 054 907 012 950 735 149 917 629 185 346 038 839 726 020 657 616 881 864 040 206 730 693 929 909 798 376 901 027 678 743 803 053 435 080 060 222 960 765 209 016 719 495 465 065 880 817 655 105 587 550 627 371 133 580 007 208 685 503 634 553 734 555 939 535 468 690 132 711 953 093 269 085 560 448 519 824 703 548 816 254 495 542 234 918 747 693 224 057 340 297 973 408 296 573 130 695 625 972 254 940 682 575 216 056 709 121 263 199 490 521 367 169 264 713 422 916 421 017 644 290 436 559 873 936 249 860 264 423 571 159 538 394 918 795 026 627 955 964 532 970 434 700 250 299 028 069 757 500 453 999 535 563 357 008 681 577 786 535 912 697 445 001 143 214 516 343 520 287 616 322 924 564 365 628 394 764 983 771 382 802 920 963 793 584 908 296 776 861 312 578 465 711 021 427 603 257 833 820 453 341 878 019 639 003 521 898 791 872 222 616 627 702 164 965 098 779 359 597 283 020 199 203 367 836 847 092 866 516 690 535 741 369 258 400 633 853 238 389 755 869 387 807 380 683 615 026 239 838 055 604 372 309 542 368 477 078 338 199 835 246 669 636 925 259 801 877 861 640 266 119 912 783 623 071 782 436 656 260 680 576 849 795 658 541 650 053 808 396 210 321 576 065 378 709 711 790 584 589 601 240 449 182 905 257 933 332 395 402 005 308 196 314 657 393 632 538 438 609 535 509 098 353 209 167 854 360 476 505 746 650 266 219 079 667 731 789 271 317 432 472 639 183 801 982 463 227 601 408 613 049 077 115 960 477 601 767 292 598 994 569 889 925 667 429 371 631 384 316 368 780 839 476 237 667 772 616 929 279 637 252 848 955 166 184 191 305 528 091 650 346 381 617 773 254 000 915 243 848 713 071 822 301 751 349 663 917 103 713 366 879 759 210 327 241 286 160 085 616 701 845 372 863 361 485 043 111 311 469 904 852 310 180 153 545 116 098 922 450 983 861 870 190 558 172 679 276 305 703 767 713 165 150 873 698 867 779 239 455 752 050 816 836 290 384 538 674 521 955 119 936 502 355 036 195 420 940 218 180 829 380 621 281 217 772 299 508 056 426 740 443 639 508 422 341 549 451 568 456 350 822 617 276 268 937 676 624 752 697 497 104 899 713 589 926 803 198 579 783 848 231 953 340 881 303 308 305 240 437 975 805 641 716 873 338 148 439 664 826 830 379 516 054 899 354 655 833 361 138 282 114 520 358 241 260 995 915 717 115 266 740 807 312 492 725 532 596 328 848 812 538 140 026 967 585 166 997 885 517 285 805 292 827 994 964 449 482 722 796 003 350 138 081 422 903 565 816 955 034 806 232 277 243 657 983 605 983 904 587 166 699 503 490 299 189 321 499 809 353 861 234 792 911 176 116 632 008 089 702 844 829 909 291 217 342 600 726 809 624 607 751 831 938 670 969 246 954 518 407 416 644 536 237 234 746 483 226 285 674 067 349 642 538 033 901 949 291 813 804 400 651 192 174 426 060 553 126 754 741 038 015 695 883 733 411 365 736 943 991 925 423 726 242 422 760 447 071 361 545 793 824 978 540 541 536 228 025 449 309 595 344 986 005 756 307 727 643 484 201 979 244 019 616 899 709 655 517 281 703 752 231 641 964 313 323 014 079 459 499 729 988 697 089 503 143 578 493 123 944 105 878 328 701 073 752 167 660 355 866 628 007 937 263 002 104 311 412 771 980 713 272 169 063 859 062 174 044 007 059 875 403 706 308 830 143 906 318 340 573 818 183 892 769 811 491 171 615 033 880 792 507 092 886 290 509 073 392 316 145 764 833 130 405 134 936 737 688 572 242 087 926 801 943 075 683 655 397 931 174 885 219 547 373 832 475 728 053 361 055 601 516 459 489 244 153 338 132 129 904 919 816 796 228 542 211 884 847 976 623 290 879 408 308 126 910 762 159 353 820 993 331 056 752 191 535 007 788 063 902 487 347 303 115 505 857 193 451 247 022 473 315 708 512 042 463 885 354 745 600 440 512 807 254 450 116 370 653 467 583 975 807 320 247 214 741 209 762 340 296 029 809 430 742 788 878 357 541 739 268 581 600 993 371 606 805 425 679 876 681 564 576 987 958 095 116 149 352 612 141 691 976 101 596 294 577 462 264 207 987 840 868 650 021 726 917 371 189 557 855 218 060 912 042 317 829 723 285 261 723 645 819 334 311 165 721 167 023 214 782 558 609 019 879 545 944 087 913 154 115 145 890 031 210 833 524 016 333 305 782 628 057 536 024 662 047 120 960 405 301 640 421 474 703 517 579 719 878 331 377 451 794 947 526 658 016 334 589 166 887 222 552 344 566 348 795 930 081 298 513 140 948 418 941 442 298 827 389 880 688 168 446 932 965 178 431 151 246 766 393 286 852 122 314 101 445 602 066 959 131 887 550 664 519 398 176 995 665 627 411 131 955 385 438 170 471 949 990 679 214 203 128 148 890 604 035 571 692 958 659 090 059 301 437 684 556 759 491 235 252 958 500 445 432 691 812 707 811 948 457 104 744 315 987 807 073 487 634 073 058 654 638 898 876 047 884 278 783 961 673 568 846 083 441 365 500 340 508 683 318 648 711 428 830 488 291 943 876 273 096 975 895 233 392 754 544 422 773 261 512 620 828 169 959 395 251 632 703 561 202 890 520 677 093 259 106 501 932 657 628 497 811 811 592 433 840 449 320 910 620 445 759 858 650 321 252 744 610 650 544 965 287 015 909 534 974 842 993 235 666 349 372 519 320 481 148 062 448 218 008 988 348 556 734 598 209 611 912 090 484 177 751 655 604 749 296 319 919 411 983 877 640 812 562 395 794 286 381 146 175 126 977 980 463 823 539 135 861 031 191 763 040 786 295 720 856 792 083 155 799 908 101 123 698 230 525 096 202 006 870 888 858 188 590 203 389 866 536 640 645 077 265 111 371 632 173 105 952 898 730 068 188 613 300 937 203 876 388 959 044 801 586 095 419 208 153 901 738 851 264 602 631 679 829 540 870 209 309 176 482 670 566 912 870 126 922 243 488 636 032 711 302 355 858 358 513 947 662 008 769 940 543 914 959 986 113 809 926 584 785 251 321 050 679 101 206 708 769 502 765 974 335 278 090 420 525 183 019 763 841 799 430 995 243 730 599 446 961 046 232 222 801 953 200 848 906 118 614 351 839 039 150 062 678 812 077 065 391 076 689 029 608 270 799 880 622 072 466 841 684 343 701 763 176 799 251 719 782 454 277 372 688 747 133 325 535 849 723 273 906 986 157 274 800 582 715 364 007 535 953 976 881 203 429 556 169 021 445 561 216 280 770 935 728 913 865 636 405 016 837 567 770 054 100 560 449 294 790 645 216 957 418 148 158 210 413 781 315 758 517 233 880 921 677 219 469 749 608 349 768 036 483 026 561 705 056 487 203 206 000 446 755 552 269 523 126 762 380 773 407 114 294 607 220 555 585 648 751 329 691 260 369 272 769 713 938 885 662 723 535 814 673 246 476 241 366 927 232 260 475 220 431 638 638 401 713 016 595 015 259 452 399 747 492 717 108 705 853 020 185 282 185 307 434 430 402 189 844 292 385 928 399 018 719 722 782 910 417 256 529 166 643 110 486 334 183 808 352 124 233 918 887 922 210 692 261 114 529 833 016 861 086 560 254 593 256 143 553 917 733 998 976 542 919 184 025 210 478 079 805 824 928 121 179 086 636 370 880 386 108 529 514 675 129 254 442 671 474 409 827 514 184 389 855 492 859 446 378 690 485 915 652 471 107 591 030 525 855 434 529 821 593 863 574 853 070 198 687 031 145 429 852 887 288 434 374 551 179 800 354 393 288 270 579 477 450 664 784 362 768 932 566 568 356 112 264 624 824 943 088 612 688 350 468 523 336 265 224 824 312 504 299 769 290 180 621 111 405 642 598 800 938 386 881 932 163 393 431 934 044 768 388 417 788 134 078 162 938 785 545 843 421 547 104 330 565 526 145 645 444 899 634 818 795 466 500 435 421 877 549 820 221 185 538 025 301 544 849 396 564 527 945 700 061 027 509 024 900 040 769 398 113 342 910 372 099 859 236 446 006 258 127 472 372 678 912 149 955 764 698 096 726 006 630 336 581 042 765 690 640 879 182 192 553 426 351 716 242 199 345 617 137 951 192 659 725 632 113 216 082 464 738 512 089 330 868 452 327 626 239 314 281 335 092 536 549 694 004 048 466 653 020 473 353 536 693 700 086 025 039 142 502 822 324 518 788 426 389 626 349 518 967 093 540 187 485 134 999 635 630 287 778 124 077 906 356 710 984 885 669 660 554 790 533 520 830 983 918 029 266 775 886 142 927 520 200 777 166 176 765 299 353 068 477 620 883 506 176 637 959 248 492 542 359 834 730 522 886 668 049 834 918 118 707 523 249 570 565 049 824 878 592 331 644 119 486 359 363 467 105 671 794 739 966 417 277 229 837 373 892 404 869 805 605 826 289 497 266 863 568 089 807 748 209 465 977 007 675 309 803 442 761 152 011 407 516 965 416 811 727 637 078 832 036 966 317 187 785 870 031 821 466 905 034 015 433 505 740 843 689 826 015 839 837 400 581 884 142 543 332 984 880 115 431 364 255 443 310 435 030 411 078 228 423 837 479 499 135 377 730 072 779 322 817 562 843 548 000 694 882 718 382 448 229 225 025 734 631 773 299 276 288 981 222 017 261 159 690 238 387 492 697 317 391 587 055 125 451 109 297 945 626 311 223 058 413 589 740 908 928 361 039 996 942 372 075 264 673 635 853 634 637 053 867 164 435 898 164 030 776 002 684 169 721 420 125 590 024 361 641 060 103 922 102 904 200 999 329 790 010 645 981 021 956 885 539 875 780 975 662 924 049 898 279 298 305 262 352 813 500 829 206 146 700 015 101 830 605 865 523 285 553 650 234 133 164 021 480 914 100 178 429 710 657 115 164 424 587 961 217 436 842 732 365 457 875 272 838 624 211 031 375 001 543 870 671 383 854 651 286 564 247 517 274 871 198 283 114 767 474 463 809 660 935 099 727 511 703 850 039 264 959 188 122 301 691 582 367 173 736 980 991 881 001 001 987 063 836 533 227 561 079 658 489 056 357 750 700 637 674 226 352 790 745 775 379 599 062 035 724 110 397 942 028 921 410 278 190 100 516 717 065 616 999 672 752 267 993 560 241 494 517 073 341 677 196 564 736 534 151 634 810 918 915 354 754 365 936 023 365 657 521 131 058 001 340 226 254 073 441 040 018 362 271 213 691 682 726 400 079 890 470 303 976 119 509 476 104 673 161 082 170 539 536 995 061 624 056 617 205 497 436 651 175 444 096 311 401 688 551 319 934 197 784 611 523 696 868 446 313 056 713 364 773 150 970 246 968 107 578 443 881 670 456 355 542 130 429 165 185 017 758 242 315 715 274 982 871 115 764 186 604 719 677 502 832 545 327 934 611 575 893 753 948 898 394 789 645 169 912 183 324 224 029 616 355 427 884 370 234 129 992 885 007 066 095 881 355 312 744 474 870 076 307 053 773 537 486 635 830 712 424 825 828 974 468 043 652 180 299 994 187 856 781 490 123 409 055 812 621 772 087 937 387 051 708 137 372 702 804 223 342 804 751 809 905 761 585 426 773 894 938 684 447 658 284 040 546 405 465 718 676 006 771 559 424 823 128 330 200 024 235 836 167 480 728 284 404 630 945 999 984 757 822 994 581 567 862 157 919 885 952 912 700 144 239 055 971 096 878 358 974 256 724 550 545 795 136 897 587 630 924 416 823 326 603 229 904 449 982 877 109 016 653 921 476 832 743 972 084 832 697 301 263 108 878 390 333 002 316 397 549 245 992 473 405 441 996 326 893 039 384 604 567 873 807 612 632 312 842 322 040 942 213 624 156 410 494 545 485 120 957 043 959 564 610 727 205 236 776 224 598 016 035 036 560 441 820 922 454 637 545 317 702 061 490 417 050 313 901 171 418 752 133 397 666 582 289 978 508 552 807 076 821 667 822 704 178 558 560 468 053 291 060 035 231 414 534 393 593 424 336 147 334 521 866 811 454 618 406 007 903 974 458 263 121 374 293 497 827 020 138 375 301 529 883 923 826 909 163 584 766 761 017 335 367 048 948 553 285 272 576 700 283 294 062 622 099 662 032 041 233 709 292 865 392 795 555 451 702 399 157 346 835 910 811 084 301 185 908 412 798 689 164 932 292 115 476 132 364 707 258 022 322 076 123 356 582 725 715 202 832 438 760 935 905 236 096 648 360 981 366 589 593 802 546 169 297 014 590 543 770 329 364 708 853 181 666 651 406 697 115 170 451 093 234 544 595 356 710 868 934 742 060 114 591 442 096 945 989 548 380 559 854 021 284 164 963 837 247 965 248 169 161 489 679 133 166 085 959 771 473 750 072 014 589 273 231 220 367 458 077 982 786 852 820 463 654 487 682 666 767 937 732 339 131 888 853 695 441 693 502 328 466 586 257 262 473 757 584 300 983 635 276 696 100 202 975 327 605 858 076 344 491 149 506 042 580 213 119 093 341 926 087 908 112 057 078 254 296 231 450 932 018 893 486 585 335 762 734 586 578 340 556 008 767 366 489 387 345 434 812 564 730 569 145 830 458 795 603 618 560 187 874 591 158 742 385 012 575 834 619 685 439 041 467 037 871 126 583 499 892 434 106 557 630 736 536 857 494 238 775 267 459 636 306 627 370 346 249 535 185 525 778 361 573 170 449 236 516 288 384 790 571 306 958 469 584 789 653 443 596 760 824 380 863 907 955 792 211 475 113 997 598 681 349 705 255 605 067 954 694 876 319 955 384 668 176 800 769 631 165 026 053 047 439 431 678 135 697 683 592 833 358 918 820 218 701 315 144 856 985 439 260 797 522 727 814 982 969 239 956 441 999 725 538 125 177 943 397 213 096 185 762 640 601 584 838 651 446 612 788 140 905 058 995 472 624 268 427 473 833 463 804 056 741 674 534 364 567 457 460 582 062 700 192 614 099 726 668 883 401 933 757 157 997 917 422 804 461 676 904 230 537 703 574 401 114 699 619 958 921 052 416 111 452 412 360 288 476 662 442 415 026 043 972 265 615 001 774 475 196 951 032 245 499 033 714 813 942 710 226 828 239 160 075 648 405 798 336 901 718 802 774 019 353 208 606 914 094 320 082 011 601 356 451 940 271 579 165 615 316 821 756 283 770 563 637 649 938 947 349 179 977 346 334 530 585 277 562 752 327 011 254 228 470 289 888 893 218 536 108 585 921 623 126 616 619 877 410 865 906 604 378 762 739 647 502 834 797 004 220 620 353 587 587 527 236 000 180 722 311 190 782 543 844 155 696 847 933 062 871 120 915 382 329 512 388 798 674 244 532 036 413 996 468 271 413 043 748 265 047 293 773 365 034 773 846 681 584 237 034 702 829 335 473 954 935 034 668 569 929 595 595 515 016 039 350 086 703 262 785 852 942 830 647 943 336 961 116 805 381 488 601 644 313 468 231 496 403 347 014 967 144 155 233 082 381 393 260 070 039 937 613 308 090 881 746 454 952 953 965 569 738 063 042 273 426 416 711 196 180 589 673 202 681 123 231 181 746 344 596 917 105 814 818 415 771 228 239 824 998 181 192 272 441 530 645 168 985 954 358 461 712 452 875 275 400 647 982 765 009 453 390 907 353 574 101 596 002 977 965 433 088 617 770 855 648 353 766 579 633 477 126 457 092 548 187 087 852 288 090 252 857 523 502 873 493 035 044 356 570 695 397 974 556 752 186 968 105 475 784 919 280 374 436 090 954 406 315 185 585 452 401 606 573 309 484 813 635 216 188 148 920 191 847 298 959 495 076 109 521 451 593 864 911 301 661 253 519 666 115 016 861 826 034 853 445 000 375 554 514 529 877 188 645 082 273 780 046 723 732 960 814 626 923 145 344 797 624 144 216 546 817 806 320 979 443 463 280 534 574 181 896 193 329 705 267 225 020 226 844 852 165 335 268 323 270 883 994 882 544 753 042 505 399 144 560 458 510 768 391 418 271 251 517 552 659 182 167 477 153 264 048 600 069 764 362 654 073 214 317 480 690 340 988 836 693 310 546 671 643 421 649 192 085 388 276 488 849 745 085 994 909 675 968 913 245 089 055 068 706 080 036 008 153 692 242 240 123 276 252 308 496 971 072 990 989 199 467 734 851 901 315 211 686 084 244 345 380 745 160 283 077 780 395 698 674 856 513 355 017 298 268 961 092 167 249 379 563 979 929 939 310 361 707 244 281 935 428 006 231 092 672 668 908 977 786 210 410 452 878 656 040 455 577 773 930 891 417 719 045 636 436 596 232 087 283 168 999 804 281 385 788 909 741 192 260 187 309 644 305 035 602 227 130 048 165 616 854 459 363 627 766 228 882 097 673 216 118 655 841 469 607 621 466 006 988 417 649 610 866 102 707 954 734 211 854 990 693 868 882 953 677 182 869 157 230 576 821 038 441 375 382 908 755 699 108 013 519 765 951 371 504 133 566 371 491 349 210 557 166 277 110 123 707 930 577 647 307 773 565 891 063 879 009 382 666 614 786 417 159 186 211 398 093 894 297 567 677 923 653 722 284 518 252 359 710 856 858 820 831 170 651 870 163 930 456 780 420 898 951 196 395 669 631 659 531 107 670 866 981 179 682 296 947 288 913 439 510 758 902 498 572 727 012 272 989 123 118 844 578 422 774 285 680 017 518 040 708 597 063 119 372 771 313 709 023 936 264 835 593 455 632 741 694 946 664 444 937 602 868 051 853 534 485 224 647 093 578 557 327 348 347 365 624 718 444 796 573 785 604 969 010 601 014 095 795 215 664 042 727 340 909 193 423 925 103 004 060 336 182 372 160 999 418 039 405 927 411 575 250 755 994 880 337 718 487 942 025 885 360 379 057 622 138 134 745 165 900 483 273 095 735 351 693 757 948 251 819 149 998 636 331 401 166 768 936 785 212 656 607 511 771 517 573 359 131 171 610 252 116 074 671 358 265 633 251 053 696 638 971 372 278 306 690 385 672 696 879 258 277 526 098 996 693 552 165 384 508 365 580 730 806 664 962 895 135 777 214 644 353 641 969 816 651 292 953 325 260 188 333 510 480 979 221 011 121 516 028 630 393 811 088 975 250 100 115 496 038 451 388 691 756 940 026 316 376 352 471 656 703 108 155 735 884 719 331 805 381 676 927 999 052 699 441 908 598 758 596 836 599 505 906 201 654 593 180 883 428 634 605 136 811 161 319 813 849 726 695 315 400 655 656 842 896 402 827 809 409 254 137 152 259 220 229 465 687 513 216 955 037 810 188 727 851 585 256 913 135 386 053 884 280 849 784 161 447 352 254 553 924 528 695 473 247 579 788 000 399 683 937 810 086 018 009 250 830 262 929 323 964 194 860 582 312 562 807 016 984 895 888 352 650 622 863 279 169 536 553 783 977 436 008 368 967 902 985 849 185 372 501 538 996 059 820 340 648 445 863 983 715 999 663 391 559 704 324 528 432 837 792 010 550 825 862 494 882 976 550 297 328 950 742 824 501 633 628 944 544 083 745 124 387 663 154 882 053 141 213 375 171 044 662 779 796 850 270 150 973 774 622 482 154 039 944 849 246 666 073 416 467 827 778 577 590 845 360 972 382 081 028 714 771 354 107 392 118 334 080 963 708 930 669 007 009 440 340 551 634 738 913 409 903 965 418 052 386 665 588 663 382 557 187 640 839 969 031 138 331 568 059 186 770 900 250 000 583 586 294 495 811 611 242 476 133 685 753 924 285 041 146 815 855 137 368 077 653 213 199 215 910 334 007 996 167 415 239 069 586 109 219 608 015 765 488 081 634 707 279 451 453 960 786 472 603 145 668 193 789 339 345 818 581 516 284 983 302 151 928 776 461 422 877 743 900 559 013 934 191 604 758 785 809 023 748 187 083 702 472 082 199 020 969 411 962 035 418 950 038 320 449 994 325 527 901 657 511 458 530 338 180 170 317 472 712 344 644 137 710 915 104 371 612 852 945 246 278 567 635 030 537 699 772 671 673 934 285 120 860 647 740 039 134 681 814 395 831 471 980 233 313 856 269 224 116 937 608 122 797 328 913 426 259 111 043 171 795 928 924 598 548 305 819 897 487 721 936 215 482 922 204 334 778 301 544 052 721 333 936 050 006 452 532 325 496 727 490 493 490 559 807 039 217 104 082 959 744 240 597 683 504 627 797 152 059 944 596 203 480 214 782 805 171 323 381 680 796 096 867 840 428 901 405 919 831 282 651 538 264 757 649 384 201 266 021 921 395 339 242 926 788 061 521 055 576 011 992 751 064 215 835 520 704 610 782 907 958 568 703 531 849 297 173 377 816 292 336 706 602 583 476 448 460 753 242 233 604 079 340 339 502 298 104 459 485 273 927 200 623 399 326 662 670 610 939 184 987 782 405 929 886 528 809 088 459 002 165 761 599 700 660 573 660 385 121 718 708 953 553 756 309 159 415 696 458 715 619 502 536 121 573 166 661 633 778 519 504 042 161 133 623 482 776 187 812 904 788 293 404 647 449 864 432 489 189 958 928 280 176 688 499 674 742 729 574 004 389 619 179 345 092 362 139 310 398 090 131 565 610 677 504 793 635 348 186 648 964 132 818 790 939 050 800 099 437 397 419 212 075 776 781 221 800 842 504 755 457 752 244 751 994 315 732 172 201 490 048 312 286 124 919 404 725 688 259 103 943 275 260 622 453 102 500 612 950 287 824 485 858 132 994 306 830 217 995 099 316 739 110 137 324 636 481 725 553 625 616 796 531 269 861 293 215 506 556 380 500 866 334 115 788 136 662 527 585 044 218 276 457 771 654 134 692 453 637 561 126 528 702 206 126 441 876 084 416 930 068 940 674 453 528 609 260 835 266 004 867 356 315 201 641 866 621 029 007 192 610 988 099 687 550 210 200 561 082 206 177 348 292 262 166 834 902 258 183 294 668 130 484 605 288 750 752 251 005 135 532 655 917 932 963 086 883 462 980 009 079 196 332 807 526 348 243 547 763 433 236 179 169 197 218 742 813 586 306 141 277 381 303 057 210 055 929 704 173 345 223 382 270 731 177 818 090 756 840 810 077 166 527 191 869 412 642 583 881 553 331 752 029 458 997 135 130 971 916 831 421 089 815 357 260 636 662 167 214 029 660 260 454 567 949 844 579 069 822 341 057 746 981 237 483 988 648 119 992 143 372 307 442 180 156 403 573 404 253 269 657 152 574 339 459 410 424 352 243 179 293 090 317 650 511 061 631 329 551 517 939 391 981 785 281 830 127 932 322 909 627 660 415 075 956 610 563 082 263 840 070 269 265 447 576 160 542 144 945 638 334 055 995 007 437 845 519 683 693 212 006 717 911 739 284 638 436 913 036 658 867 268 960 758 890 217 920 113 705 451 515 765 423 939 386 589 955 041 757 191 796 588 373 954 872 141 574 804 089 638 922 001 102 479 571 355 096 485 960 984 883 338 595 958 571 060 014 021 714 485 217 536 110 562 123 858 973 768 988 528 320 957 982 164 516 142 301 716 963 774 651 289 765 282 183 456 678 761 417 427 338 551 357 928 598 295 140 040 472 510 918 376 429 756 225 769 023 807 168 774 998 107 549 585 050 029 890 205 735 144 029 223 177 616 006 353 876 138 841 776 103 984 264 414 454 535 939 560 065 093 415 315 356 330 086 763 342 400 410 336 747 532 492 860 421 128 551 142 795 648 099 000 804 121 014 461 070 443 764 161 642 830 612 229 914 469 451 768 583 085 918 275 239 761 806 132 650 249 463 179 391 419 380 425 041 743 410 946 918 174 464 668 876 702 779 478 664 954 317 105 575 395 731 214 132 828 120 020 633 143 957 123 899 821 737 604 242 926 094 989 197 190 040 837 821 834 809 776 325 785 623 435 617 638 977 462 197 171 039 244 010 318 233 980 085 671 788 968 523 634 629 677 052 214 384 517 007 282 557 143 167 667 669 564 567 584 989 337 690 913 436 411 982 566 373 874 633 761 784 415 900 000 267 462 337 781 291 993 989 479 255 129 173 777 713 462 096 408 086 764 005 206 116 683 504 670 957 099 485 573 809 672 907 090 331 596 664 424 964 144 812 382 047 267 052 694 774 091 073 357 059 769 694 463 053 015 781 721 245 530 017 265 974 656 469 170 870 389 612 648 920 139 565 262 968 110 894 875 681 482 755 500 431 011 763 401 048 294 472 888 820 391 959 219 441 001 839 821 079 058 401 921 966 342 312 798 585 447 366 456 788 760 844 456 732 148 351 381 524 706 553 665 242 739 538 725 838 749 173 394 334 055 562 413 343 539 542 773 678 125 676 057 979 733 140 468 047 027 524 306 748 776 846 967 927 198 786 739 318 249 930 538 964 790 550 847 803 234 416 409 975 035 733 137 841 978 797 882 520 617 695 637 740 727 263 606 786 298 453 502 713 379 963 846 916 723 129 400 401 457 951 914 111 323 174 914 735 688 101 843 178 332 979 283 396 182 979 704 780 820 671 679 585 345 412 048 442 999 471 681 683 121 912 695 270 966 794 819 693 207 712 602 765 204 401 932 337 485 188 744 848 267 717 791 165 785 658 323 634 017 307 956 412 370 693 655 445 792 237 110 525 867 279 798 085 057 902 935 434 590 908 562 543 533 268 144 981 994 911 741 057 679 022 454 100 438 143 752 416 710 976 776 211 435 856 285 868 733 352 956 872 143 420 654 608 697 526 711 130 027 226 054 963 852 103 950 437 378 828 195 789 478 318 962 206 714 807 852 196 773 081 325 126 174 164 765 276 185 572 122 019 468 709 764 466 892 631 154 072 882 945 797 483 377 597 605 503 151 616 814 939 761 772 109 292 188 227 800 577 180 365 405 640 059 760 005 898 230 607 096 885 384 680 147 626 732 429 361 307 924 936 853 459 154 629 335 712 872 927 047 741 258 604 417 118 607 666 990 803 032 197 955 834 812 804 484 064 393 160 879 339 603 196 569 267 970 245 184 603 846 611 109 732 651 409 526 381 551 478 929 169 396 893 743 978 308 051 436 561 344 464 552 610 804 153 505 702 329 916 614 881 256 764 776 350 576 198 617 872 539 031 067 821 513 964 873 647 643 799 308 403 596 567 718 967 088 884 159 299 882 208 262 144 878 642 465 881 117 826 899 501 978 260 017 703 090 938 554 250 710 719 666 079 411 386 867 256 828 765 972 605 293 724 440 746 983 518 502 050 018 070 789 489 853 037 363 311 710 166 424 411 078 486 039 839 061 651 053 612 763 175 813 842 075 192 540 939 673 082 937 239 487 407 646 459 712 966 442 405 341 988 216 157 125 344 480 616 866 185 602 809 836 856 376 556 522 168 504 184 810 431 566 923 781 046 362 801 298 959 420 846 881 426 871 439 852 000 648 697 960 287 939 444 500 087 661 228 014 302 562 777 993 133 524 294 255 669 490 992 034 636 650 018 463 735 230 399 909 420 888 623 662 367 099 780 765 475 289 171 475 174 614 420 098 110 926 166 493 634 011 145 664 222 724 561 234 647 371 420 482 577 604 550 236 802 769 375 719 237 103 057 776 689 364 765 413 605 009 489 451 823 842 148 296 177 421 828 411 171 531 443 934 238 993 974 928 873 045 253 097 268 166 287 847 913 328 785 388 191 947 578 991 100 489 815 720 158 805 086 359 592 649 830 673 732 501 522 440 978 371 278 965 705 742 965 869 800 447 812 237 640 158 011 362 234 574 992 205 583 837 329 395 739 622 988 931 056 914 319 568 287 603 091 636 428 467 795 124 529 081 235 438 712 755 512 259 493 247 896 034 061 388 084 190 706 511 894 414 202 706 949 858 265 929 188 365 585 895 052 528 406 577 538 850 762 985 606 434 082 532 451 040 546 798 169 592 684 863 000 793 651 540 291 541 324 265 616 800 394 889 790 292 285 137 730 710 744 031 021 925 455 684 689 560 268 824 035 516 196 103 113 008 453 056 912 320 682 806 463 692 258 707 556 930 472 956 225 713 632 236 334 475 068 504 044 305 876 947 571 350 774 340 858 714 150 149 380 312 006 693 281 528 970 487 172 732 533 137 669 946 826 353 734 578 420 977 294 328 474 872 944 519 863 912 171 760 467 217 259 015 596 854 635 613 266 190 472 840 064 910 924 310 786 220 308 813 233 845 964 751 121 388 946 300 236 505 568 254 988 512 223 378 445 950 923 171 743 179 330 913 879 598 898 522 750 202 388 840 394 302 792 136 988 736 340 603 176 081 941 636 008 348 270 023 765 926 754 407 962 357 759 596 028 865 145 239 513 526 987 370 734 108 573 730 351 929 957 712 424 226 428 372 457 034 328 377 087 126 819 488 088 145 749 439 932 749 987 293 309 760 826 272 951 562 947 363 646 560 080 930 813 121 181 592 153 881 861 545 229 077 016 493 124 126 774 359 157 294 864 062 728 917 503 889 958 201 782 800 178 501 277 745 438 956 693 631 930 805 843 862 467 842 805 460 116 027 992 089 518 068 057 017 080 081 475 240 751 940 324 404 045 210 469 722 502 760 671 414 231 251 222 136 515 526 990 112 102 795 684 903 787 072 157 892 276 532 803 893 274 789 849 624 815 494 589 909 250 528 655 992 091 310 738 912 955 072 922 723 125 695 350 649 800 357 661 707 790 291 760 653 476 173 993 211 136 959 750 253 076 833 888 653 758 615 544 845 610 203 938 205 314 467 831 058 190 475 709 526 378 973 748 258 270 276 116 984 374 271 801 454 930 096 697 658 130 673 739 273 307 311 162 177 692 918 582 167 274 206 072 150 143 381 914 329 089 241 110 522 614 137 894 837 724 908 598 051 772 610 787 081 044 537 526 081 171 874 008 348 140 970 623 663 252 368 936 662 974 410 390 270 452 214 110 296 036 783 026 969 328 910 973 019 939 287 336 545 621 878 584 227 034 604 144 927 910 027 304 350 686 002 348 823 376 334 064 301 742 689 162 530 506 594 694 539 760 955 145 054 710 765 995 936 514 122 510 046 181 013 962 698 465 105 456 484 445 550 733 648 859 694 063 146 276 527 624 823 632 359 792 524 028 998 342 890 008 039 195 859 833 713 756 642 413 895 945 024 683 494 223 386 503 903 719 855 586 730 049 278 205 808 121 107 472 959 254 702 932 490 275 411 043 619 234 908 529 169 377 351 658 851 793 268 420 321 351 990 276 819 307 941 043 924 975 934 298 322 663 345 685 706 626 998 401 260 786 009 609 352 607 608 905 316 695 741 020 101 408 936 077 840 394 636 050 670 914 179 713 163 291 533 624 120 995 352 923 387 498 421 399 858 312 125 097 997 822 246 160 842 154 920 766 945 048 867 938 667 334 360 185 877 374 314 281 736 659 872 536 571 203 325 564 686 163 389 552 615 270 567 628 271 709 387 841 411 048 748 540 284 051 381 182 414 286 681 072 561 817 407 478 342 630 713 819 130 727 396 648 467 159 015 881 099 022 930 679 005 456 418 461 630 466 737 361 562 618 933 450 085 051 784 945 997 566 096 509 690 866 458 525 111 353 018 764 944 414 843 843 220 411 220 713 518 387 592 513 000 117 753 606 424 146 987 209 835 437 147 742 978 040 717 777 639 259 381 136 415 789 340 670 096 395 073 728 600 443 548 929 876 750 432 656 456 651 522 517 038 567 400 799 359 093 044 986 025 814 767 891 358 761 204 336 003 883 239 792 086 433 799 198 501 254 482 846 933 243 529 125 440 598 442 062 704 808 479 539 232 086 348 075 809 668 414 659 476 740 874 680 146 618 655 697 977 040 038 979 948 793 815 355 436 188 661 656 178 172 007 431 834 117 831 814 207 718 480 592 366 290 392 736 238 229 514 362 337 942 471 609 505 944 097 874 031 220 590 071 949 706 085 066 881 519 259 245 404 986 933 110 648 452 879 438 032 349 249 960 313 448 119 986 775 990 706 455 677 219 924 430 027 606 409 917 951 785 375 695 729 378 561 458 373 376 327 208 551 386 999 708 295 106 710 404 800 990 206 343 561 964 919 268 844 270 255 424 169 778 554 371 835 415 274 530 775 608 321 585 353 173 724 353 959 752 176 759 445 163 418 926 095 921 265 741 299 201 619 523 971 680 885 209 000 976 835 358 760 774 954 355 502 435 879 600 701 100 936 375 469 394 458 888 291 758 901 871 547 229 773 989 162 042 363 454 823 204 223 628 292 066 871 948 258 925 387 810 120 000 821 583 775 961 804 861 828 900 849 932 676 968 537 293 699 185 058 958 058 464 511 536 301 828 303 573 991 372 412 138 970 357 646 872 017 992 614 459 341 195 251 950 878 698 691 891 961 335 322 020 025 004 179 002 710 170 394 384 827 077 781 448 084 933 598 535 096 889 866 463 490 889 184 758 611 804 103 309 883 976 250 280 402 873 424 792 479 880 012 550 743 297 503 569 511 479 071 947 606 931 645 437 328 171 738 320 921 428 424 165 219 466 165 211 263 809 747 613 539 001 232 404 427 288 679 224 397 924 876 281 375 657 688 549 963 535 704 023 983 436 238 277 583 083 379 729 036 294 428 270 997 886 702 177 961 832 540 484 512 683 702 221 778 396 911 004 982 055 572 694 423 327 531 131 890 945 915 081 613 676 972 230 298 504 222 843 810 592 417 294 403 862 756 998 196 423 076 319 076 909 407 662 060 960 896 823 034 019 531 508 958 820 460 049 312 483 268 757 685 862 928 361 571 766 420 379 040 709 979 996 766 619 223 822 459 520 835 190 318 406 057 714 426 322 173 223 216 949 991 534 148 295 017 547 033 774 819 165 909 186 134 671 434 093 296 193 260 528 848 907 863 576 003 066 290 779 696 970 321 400 320 441 140 499 675 141 900 449 531 975 642 450 223 561 508 983 370 713 271 061 167 314 083 411 321 589 020 535 915 858 878 341 963 213 708 254 464 278 534 270 307 178 645 004 372 482 919 586 567 132 549 019 388 967 573 482 132 285 854 838 945 552 079 729 963 527 921 269 221 454 331 472 301 781 216 776 116 788 518 919 183 966 947 282 470 615 992 691 648 058 124 375 976 652 545 668 518 901 897 764 619 908 999 537 949 815 295 243 172 502 566 769 711 235 262 648 101 947 909 694 664 580 369 886 294 769 808 547 770 275 641 572 788 089 865 840 871 989 656 976 290 354 442 050 108 347 785 766 341 161 167 219 179 183 008 983 459 335 959 299 372 809 546 177 408 658 085 561 017 084 186 546 762 017 127 894 773 320 232 446 355 009 819 321 171 956 052 473 484 279 762 020 831 133 859 372 296 250 779 993 860 658 546 508 996 733 904 038 688 390 112 728 564 750 958 864 987 763 283 340 868 532 354 855 226 388 711 546 783 470 978 360 224 308 251 727 743 012 214 958 586 535 579 456 931 641 881 852 070 021 740 231 052 362 851 606 678 371 958 766 305 917 533 796 668 977 543 312 538 140 653 176 932 300 685 512 333 312 337 801 496 856 702 955 286 537 501 033 639 039 795 167 826 405 168 847 753 019 902 121 770 853 281 743 720 981 180 516 473 417 512 944 176 905 456 658 935 715 332 589 808 231 182 472 167 110 801 908 911 884 677 257 494 669 493 196 673 948 294 329 023 704 075 252 878 150 244 148 374 939 950 931 368 349 412 103 368 863 172 864 679 383 987 390 876 747 724 736 360 685 052 157 760 597 648 697 125 846 153 914 933 447 690 845 590 052 926 513 617 421 961 444 171 967 106 335 236 904 166 768 405 087 414 213 493 391 330 788 276 122 934 844 905 708 410 944 446 857 170 605 645 893 043 015 655 366 231 880 562 294 872 751 290 659 554 993 599 504 138 713 718 068 016 793 813 142 105 754 381 856 542 630 142 686 004 703 643 695 810 515 994 357 050 384 040 775 867 774 316 406 437 599 699 221 732 518 603 847 317 163 205 409 111 348 691 251 937 369 067 760 472 866 476 148 644 675 974 508 735 688 332 473 040 401 071 661 112 809 968 258 610 506 575 861 488 803 543 609 999 300 915 251 103 809 612 820 081 715 809 524 432 012 014 168 317 809 745 840 289 617 374 643 884 805 786 597 264 562 781 463 713 457 585 365 818 141 071 522 013 102 970 124 544 408 076 057 147 584 724 424 444 082 645 911 056 221 395 863 365 659 754 756 861 497 727 927 785 703 954 560 959 065 496 228 815 180 906 644 437 203 212 775 790 943 818 375 241 529 196 120 150 699 590 640 301 321 352 347 889 188 300 652 699 108 025 690 378 025 495 006 253 128 363 123 252 271 710 692 089 511 988 338 748 563 411 136 253 379 374 630 234 688 564 087 151 594 227 554 569 420 376 805 164 365 363 929 745 357 108 508 606 699 839 871 455 703 549 094 447 903 399 672 795 147 012 108 303 296 748 990 906 421 579 645 729 595 198 978 079 665 267 803 457 637 823 494 900 079 959 181 180 618 076 964 294 855 097 228 228 318 721 003 023 668 625 838 157 851 710 956 243 808 253 667 811 117 825 574 270 515 760 525 473 615 521 214 462 379 303 340 572 760 393 631 333 846 266 223 532 187 002 478 802 842 344 781 475 337 801 321 881 583 922 543 622 891 172 329 729 703 038 491 774 743 872 947 165 628 820 052 202 927 645 631 699 275 876 353 226 024 720 017 670 935 124 020 997 348 704 417 537 178 717 634 784 621 252 422 447 509 898 076 394 919 484 797 797 567 985 526 530 777 651 694 204 352 231 638 912 636 784 616 553 166 871 521 025 052 223 483 348 818 235 804 604 996 063 004 490 680 236 506 762 820 905 009 463 781 491 820 731 823 032 271 161 359 402 281 046 075 312 999 074 935 742 704 196 052 988 790 472 087 541 955 023 557 635 409 900 275 771 069 946 413 775 599 173 182 384 454 001 048 706 337 526 113 619 653 136 594 002 014 910 078 582 654 695 029 871 735 741 353 611 793 424 119 006 516 146 135 140 269 858 439 490 763 217 927 342 882 651 073 452 378 049 049 574 908 979 183 091 440 267 758 698 112 808 568 714 297 219 853 419 918 009 510 937 459 665 331 361 995 658 457 952 205 052 591 336 995 435 099 114 173 418 849 140 771 532 665 497 694 051 812 385 274 173 750 349 138 427 285 030 583 419 530 274 197 365 625 424 644 860 347 881 297 468 889 192 433 872 108 771 107 373 771 786 808 431 163 822 943 194 539 822 423 000 743 664 695 391 533 111 315 983 150 325 649 763 356 760 131 130 550 434 373 103 071 309 629 861 895 291 257 547 860 747 298 021 975 059 556 704 124 614 977 599 296 360 527 101 421 775 306 737 005 373 935 782 377 153 624 959 089 855 911 195 571 054 024 094 228 110 823 344 871 083 080 421 049 893 073 694 614 108 163 896 588 221 540 572 565 013 355 214 058 427 242 543 283 209 819 250 395 304 085 058 393 810 767 941 079 935 641 607 941 279 149 670 084 361 102 096 919 826 907 548 604 414 078 711 269 125 069 043 529 300 879 400 742 531 168 971 203 616 522 574 814 647 185 746 487 377 800 940 612 592 830 557 845 571 869 156 597 519 390 298 918 372 542 405 092 690 715 175 191 739 479 598 804 043 435 756 163 319 154 778 179 768 262 345 582 257 668 069 767 738 177 349 215 068 393 297 123 645 301 507 520 607 403 990 850 938 566 955 645 665 658 420 603 093 020 634 088 889 860 449 962 584 045 300 864 291 115 110 345 977 311 064 998 323 872 603 798 431 353 463 967 315 338 055 472 536 053 819 825 766 337 896 821 121 415 809 498 281 703 457 641 361 147 032 806 314 351 883 459 073 738 922 088 636 199 947 696 174 281 918 160 205 672 985 301 320 346 102 873 089 024 205 002 183 280 272 703 739 707 820 832 533 217 018 213 988 427 831 227 002 319 622 160 615 849 628 265 445 052 535 259 929 107 606 577 423 260 732 081 600 301 986 495 017 433 224 363 905 817 242 648 647 695 373 583 998 621 766 167 459 842 891 112 613 790 552 048 757 464 947 728 970 861 425 207 896 401 550 937 991 912 060 609 269 168 009 936 590 341 991 825 167 900 031 746 114 350 390 225 216 478 781 601 285 276 159 983 377 448 186 772 775 857 797 795 851 302 219 414 367 928 491 943 364 312 915 292 133 024 010 394 642 820 292 399 645 122 462 173 141 077 245 839 550 010 633 032 982 283 653 436 990 813 155 604 774 080 656 295 949 853 143 731 145 624 499 699 515 630 715 744 684 663 312 541 338 707 998 236 236 641 637 413 049 883 107 244 756 565 657 679 078 029 137 963 924 307 739 521 688 495 534 573 697 712 032 067 728 985 159 946 075 257 125 548 639 456 346 898 745 553 846 069 834 475 733 693 538 317 644 322 381 372 646 487 029 326 060 730 557 466 608 675 616 689 128 807 888 711 824 902 293 049 571 912 977 127 629 905 071 132 964 804 454 157 396 583 004 407 413 124 585 483 043 830 960 149 327 521 184 845 116 856 695 680 764 611 734 652 213 082 829 887 536 254 413 000 997 019 477 004 035 350 930 105 092 248 611 983 657 531 666 665 828 013 691 846 058 957 186 183 063 269 681 567 365 163 140 247 020 969 304 480 895 809 705 172 965 009 100 531 364 258 676 094 088 628 141 185 123 838 176 461 417 667 806 906 855 686 529 301 965 809 325 546 518 085 699 159 314 576 773 897 931 255 791 761 680 525 382 292 795 546 144 422 680 995 354 758 438 342 599 579 949 012 329 483 032 255 161 904 805 327 596 982 877 136 706 740 494 738 721 294 175 068 890 467 482 233 272 371 369 078 082 946 950 342 901 108 860 373 721 237 945 776 671 860 656 644 284 294 973 144 657 808 267 502 126 259 803 079 362 908 910 021 187 894 289 767 929 123 723 394 559 149 923 888 817 761 235 156 168 317 214 864 472 212 624 026 478 218 701 776 671 427 098 269 524 533 848 049 308 098 785 734 657 023 564 117 329 263 517 949 756 697 648 490 992 149 703 669 987 308 665 609 399 605 306 112 932 247 551 763 943 080 263 111 186 488 663 180 331 199 500 684 627 527 864 597 723 574 748 663 600 155 623 680 520 681 692 109 895 710 672 539 026 356 071 413 969 390 183 067 845 881 164 595 178 321 092 811 765 053 535 855 236 014 764 908 119 569 786 224 954 302 650 200 313 668 178 261 011 736 787 617 525 222 825 916 135 231 948 402 022 494 935 369 913 725 715 634 442 383 803 010 269 861 430 908 176 399 761 716 003 687 346 879 267 774 885 349 747 749 638 736 257 342 541 974 559 700 243 098 044 285 075 429 092 401 047 790 390 175 243 472 310 643 854 771 410 668 421 931 389 352 409 578 840 456 972 724 234 720 121 795 959 362 744 172 541 118 738 595 547 556 683 352 641 993 331 348 760 425 220 522 098 348 150 392 048 038 182 532 266 378 497 698 157 941 322 381 753 351 698 910 855 568 313 941 097 747 977 959 583 570 359 898 048 369 633 972 958 930 870 745 340 191 229 440 152 499 861 632 499 000 220 699 389 577 570 750 990 618 535 141 044 520 720 253 435 962 214 755 124 776 548 537 931 796 698 384 749 274 562 629 413 128 441 790 509 087 832 564 604 145 161 196 575 801 674 968 046 474 625 632 677 992 600 684 160 293 207 438 480 266 723 528 300 661 851 758 489 363 773 247 007 066 302 926 313 133 412 957 556 583 496 592 377 461 147 018 596 569 816 796 055 776 365 109 505 745 934 640 154 176 653 582 655 558 587 472 181 877 453 942 265 860 570 225 467 799 406 519 156 872 265 824 137 335 575 321 217 241 735 072 334 289 342 670 076 964 629 549 741 830 267 936 747 844 564 087 088 637 134 583 305 850 885 030 691 123 570 873 351 588 916 355 092 491 358 824 687 027 642 641 314 509 112 813 988 724 512 965 473 042 338 966 363 405 547 134 508 063 498 717 586 460 107 407 418 076 736 555 922 413 502 146 438 568 354 573 939 283 979 624 368 176 206 889 558 080 388 450 175 975 062 971 260 023 046 650 892 889 843 060 125 877 454 344 532 971 030 246 999 950 856 698 066 513 847 813 575 270 697 183 122 059 439 078 916 914 461 592 216 122 628 865 298 956 713 268 255 213 518 607 609 781 569 021 831 828 447 219 450 529 140 298 771 592 408 260 189 283 620 069 371 586 609 177 935 982 057 367 617 754 302 138 119 872 732 033 742 661 204 146 564 949 002 796 744 926 558 548 411 637 906 751 431 256 822 032 780 842 911 263 082 765 440 240 764 101 512 109 605 468 721 019 974 844 107 928 237 419 997 689 732 363 041 802 917 779 163 392 486 331 561 725 746 882 871 658 237 289 861 306 385 021 337 727 975 392 494 232 404 076 160 784 565 197 697 393 794 789 207 110 879 695 809 906 570 005 731 952 102 166 552 762 997 902 813 268 979 592 789 585 061 321 188 971 665 278 035 993 659 815 626 619 724 647 518 472 574 077 182 413 323 343 664 206 120 111 119 304 895 976 835 330 765 298 434 180 320 030 155 785 398 795 982 657 921 018 926 809 757 996 308 528 123 233 790 442 629 755 831 514 390 977 169 694 167 138 755 179 544 998 901 660 806 045 218 949 054 751 943 864 863 927 840 813 869 642 702 684 735 206 806 498 415 687 824 290 076 250 535 701 047 743 929 679 590 877 634 666 538 145 243 752 721 386 578 395 877 502 001 984 013 459 615 700 044 716 778 816 716 557 903 406 872 573 071 030 389 803 260 553 522 322 940 263 917 990 635 291 434 080 554 081 942 460 661 053 281 525 105 566 551 715 099 111 432 944 217 059 998 595 741 119 649 332 703 034 705 796 909 080 776 104 049 146 567 228 536 924 628 577 381 244 710 708 947 115 989 367 778 740 957 457 263 546 409 232 506 973 238 683 356 200 409 340 782 716 402 439 907 734 226 088 451 517 296 400 168 464 511 656 575 128 566 815 202 306 961 073 906 499 238 772 629 015 816 598 433 366 313 031 158 989 032 723 524 108 602 589 851 059 940 856 226 436 075 871 142 789 045 502 044 677 288 391 841 733 716 119 246 198 246 412 913 453 968 880 820 835 841 521 421 959 056 045 753 366 879 917 468 863 441 862 895 301 318 181 164 265 536 422 127 600 599 840 274 761 991 479 107 530 184 347 774 834 247 129 973 842 827 972 463 450 510 904 249 628 543 370 785 182 090 126 460 434 270 017 152 083 853 040 085 077 556 038 681 025 391 995 091 842 948 075 707 636 788 518 795 214 318 864 118 650 750 147 330 583 760 434 777 439 955 867 517 889 404 440 973 519 016 221 089 833 736 799 361 172 432 724 164 071 042 554 080 200 084 273 538 108 767 837 221 855 302 870 240 924 887 204 538 338 020 660 547 961 641 864 314 020 976 530 087 688 340 135 568 473 678 701 379 240 151 156 620 904 158 765 206 842 706 458 742 019 600 891 563 348 789 893 105 268 935 481 417 900 433 095 806 329 980 132 939 692 778 023 521 687 102 283 172 154 382 526 203 197 338 365 918 455 773 787 279 136 325 206 102 079 631 703 556 187 758 475 510 425 856 897 153 912 141 211 087 680 915 841 580 501 389 091 573 179 433 709 976 972 129 376 081 388 453 079 683 564 339 309 443 125 425 516 559 896 608 411 505 896 548 499 676 092 305 933 467 968 648 807 816 593 412 011 654 128 515 668 611 982 916 967 975 253 249 695 138 286 576 400 249 432 174 916 548 448 311 466 629 820 577 146 487 840 983 420 000 705 655 704 327 738 459 547 657 763 907 781 633 913 216 705 848 382 161 216 532 058 885 425 564 955 131 005 958 802 413 264 675 146 221 077 445 749 027 114 664 594 628 188 194 622 386 483 248 300 083 535 765 803 571 593 602 309 757 024 177 576 747 395 888 724 941 194 245 991 453 695 548 764 091 713 204 548 340 067 102 253 991 969 432 452 089 049 974 338 417 816 422 700 626 719 897 220 985 261 373 000 043 818 579 657 624 468 374 501 996 980 054 317 942 556 883 342 597 072 578 802 000 041 612 654 711 919 414 615 522 252 093 913 395 274 019 381 059 577 430 967 376 496 118 672 988 414 849 051 176 674 658 738 931 494 783 416 815 472 495 035 354 177 109 176 304 707 963 247 534 749 954 799 905 286 993 345 695 564 201 458 020 801 013 230 938 777 020 013 496 495 600 807 317 463 071 473 791 688 979 866 284 765 959 804 739 774 772 262 359 554 500 455 123 709 136 792 399 028 346 899 986 090 191 571 895 023 959 404 554 624 029 972 380 524 055 566 248 063 939 025 589 107 690 003 433 469 531 919 575 441 199 929 213 457 692 624 231 327 585 627 776 693 359 398 405 299 531 003 727 995 657 623 077 572 094 791 524 064 584 824 575 650 683 536 292 791 901 852 987 768 615 365 558 305 405 609 855 104 878 235 208 734 072 904 067 176 346 681 052 956 312 244 780 954 830 905 544 354 530 410 486 845 204 584 154 042 332 452 263 877 728 130 209 272 580 245 274 153 564 288 624 541 117 074 504 116 952 661 168 339 648 866 808 052 254 535 411 259 308 246 653 830 991 825 728 148 142 702 234 495 380 515 181 020 255 861 483 994 386 369 305 205 381 904 320 761 563 106 398 522 672 833 889 612 109 271 820 196 654 786 482 877 331 288 366 871 131 036 674 009 259 709 654 723 586 358 538 706 660 213 172 064 845 254 076 959 747 142 640 737 515 143 801 872 145 889 523 165 921 047 352 668 368 871 977 024 097 896 078 554 119 705 884 705 443 853 896 438 801 558 466 540 605 047 410 462 003 334 620 915 041 927 496 192 596 116 664 781 306 291 444 135 140 158 093 334 180 178 018 610 569 240 198 324 801 348 686 304 003 119 204 391 851 091 841 807 578 646 656 969 921 011 355 554 364 059 089 978 133 214 952 288 505 933 279 071 982 561 091 661 776 622 656 952 481 252 800 347 908 365 885 101 111 773 800 232 786 772 746 828 279 798 141 609 067 429 199 656 985 567 684 964 031 771 647 632 957 051 430 242 276 588 184 836 298 646 976 353 003 959 964 794 736 907 100 034 505 814 512 652 462 274 756 202 003 817 703 491 423 887 272 471 368 262 646 572 708 796 475 554 258 747 960 364 547 783 953 143 947 278 703 414 795 670 346 816 077 566 189 828 263 141 045 598 232 481 319 931 851 105 595 977 696 606 335 439 277 713 972 174 249 847 524 448 170 762 998 609 487 721 370 899 350 212 029 232 484 571 577 043 484 877 852 433 521 257 872 252 395 407 686 573 595 480 584 681 474 835 671 922 178 034 888 600 382 197 642 828 623 707 159 520 137 166 423 361 114 071 846 358 974 152 469 521 726 671 872 056 063 470 710 548 958 073 257 128 748 084 101 210 310 963 736 893 243 091 188 840 718 354 876 982 413 105 066 389 302 517 278 071 356 615 943 451 775 965 941 772 488 537 710 012 864 466 631 109 223 220 334 627 786 187 945 960 565 315 848 839 378 067 814 143 076 443 330 783 466 784 874 657 790 242 587 412 891 168 806 538 460 095 258 119 254 899 497 586 604 817 901 804 472 307 723 744 116 654 279 307 782 075 351 188 058 077 694 700 392 700 330 802 707 846 049 186 347 328 947 006 226 803 919 541 600 057 889 217 914 253 626 368 385 991 699 520 037 720 960 642 481 005 884 812 276 761 837 061 288 313 985 268 464 545 377 546 793 657 803 088 291 621 286 466 237 216 088 136 584 965 383 688 269 954 178 583 676 861 024 299 222 659 644 798 726 382 692 657 701 753 725 524 070 322 667 570 518 209 804 622 373 958 229 423 228 099 368 011 801 905 117 348 069 823 325 154 470 187 115 526 240 722 534 221 428 215 150 795 500 963 485 596 025 853 547 176 489 439 060 149 999 529 984 834 137 472 947 975 965 457 936 501 196 913 294 623 529 581 068 083 774 692 565 881 282 653 173 039 150 674 781 376 412 156 384 030 946 728 177 032 607 888 805 408 139 662 649 263 168 523 006 614 104 300 389 682 227 666 849 449 447 971 418 831 284 199 146 719 309 646 416 045 356 629 375 835 072 931 069 124 188 598 001 534 810 550 465 294 429 510 624 412 964 421 581 310 056 881 228 457 337 133 495 675 495 232 536 972 181 077 207 935 848 337 925 315 132 155 269 794 770 235 209 758 746 458 455 373 704 282 902 738 139 096 841 974 208 043 081 955 372 093 773 203 225 356 329 703 946 664 744 456 829 266 159 779 414 977 381 170 872 872 353 469 440 575 353 901 889 635 996 963 156 647 725 537 429 090 645 590 783 157 908 271 739 774 909 541 807 666 730 646 315 870 456 062 894 439 676 160 645 390 487 736 133 316 331 924 982 604 729 268 579 635 973 504 747 436 275 777 325 147 365 398 259 304 149 154 336 433 369 149 702 288 379 299 239 258 834 981 685 353 968 056 542 483 207 503 152 350 819 967 192 146 545 445 365 501 815 716 908 149 039 951 506 514 028 542 799 384 761 451 352 032 548 012 320 134 162 064 507 343 130 895 220 424 551 117 926 179 950 667 983 383 718 922 831 070 419 663 992 836 915 496 112 098 413 567 468 812 391 996 268 679 873 426 479 419 895 238 617 854 254 637 098 948 508 756 324 616 222 852 450 957 901 336 988 444 365 927 648 757 796 272 557 855 914 888 599 959 708 165 974 700 400 883 951 703 917 170 026 691 510 762 030 575 695 334 062 474 395 877 290 384 324 204 777 809 405 909 338 925 054 769 383 576 134 062 824 307 053 695 876 087 952 156 341 537 728 241 790 307 206 856 369 991 234 700 768 124 734 734 431 089 528 068 785 067 398 432 922 631 192 836 584 284 848 443 975 653 919 220 990 529 569 034 602 926 103 693 546 649 201 645 542 424 969 454 236 818 837 098 259 018 928 096 150 634 906 226 199 556 851 921 782 199 644 968 351 135 156 292 337 605 139 145 920 505 013 013 766 338 280 565 462 075 471 617 661 596 288 349 705 794 969 824 366 939 346 496 978 831 931 817 428 443 616 000 500 858 793 373 599 301 533 334 871 705 027 327 536 481 304 657 825 310 653 631 520 469 078 418 586 004 803 665 249 803 046 264 726 747 106 373 140 651 957 316 795 467 399 113 656 183 688 884 223 506 738 484 743 193 681 627 485 593 403 859 663 737 795 648 218 922 489 013 443 168 771 477 667 548 571 482 494 527 768 695 005 347 055 901 634 025 472 004 586 906 639 292 952 471 888 425 257 215 738 695 106 434 655 073 191 070 722 544 590 776 277 243 081 661 994 882 038 951 427 921 760 939 634 734 478 719 307 179 160 473 908 332 346 320 357 233 262 645 105 408 718 777 105 515 978 392 422 249 987 855 642 988 188 575 154 267 289 839 523 233 715 847 117 250 656 346 190 322 999 454 878 900 300 553 861 664 641 029 417 685 889 163 433 905 165 806 060 388 892 046 156 445 683 937 740 295 276 717 429 510 972 243 157 415 833 803 714 520 429 878 788 306 879 755 087 321 619 820 415 346 698 667 299 358 222 373 515 191 462 993 118 708 617 827 068 930 153 457 748 291 998 865 821 151 239 549 683 902 250 538 254 535 633 014 688 335 672 705 931 382 620 865 652 038 184 292 747 323 592 750 562 558 453 991 403 201 524 032 737 081 025 030 911 142 573 106 048 404 216 009 140 998 221 235 073 650 962 502 075 646 155 554 399 823 972 561 180 348 056 156 758 667 997 654 654 005 850 499 825 066 897 852 261 058 789 644 455 056 356 046 701 497 036 530 664 632 716 618 685 390 843 257 084 445 015 644 724 853 756 345 029 745 394 617 168 759 897 414 263 757 720 657 435 152 758 793 603 500 148 156 808 840 112 648 713 118 308 105 090 746 041 937 089 353 601 712 731 671 823 539 771 878 236 206 548 374 653 249 363 105 189 009 603 991 555 272 627 880 064 735 038 683 472 005 667 296 349 388 664 799 988 206 562 324 648 329 520 581 404 917 861 748 569 248 334 576 559 082 824 243 053 873 986 254 769 658 635 655 081 562 905 773 806 142 843 398 649 430 778 227 331 742 481 068 713 352 544 165 248 584 587 356 367 212 239 299 376 728 342 099 941 778 509 829 229 034 901 697 561 854 274 902 937 024 240 254 536 625 330 868 684 118 828 827 451 322 797 530 472 808 765 131 999 226 598 519 012 255 015 538 594 021 151 198 375 192 388 386 683 230 339 758 895 253 378 764 756 658 115 728 845 852 726 748 622 274 777 920 950 391 320 163 052 756 511 778 820 577 761 920 852 138 518 436 296 548 032 956 317 510 452 386 245 145 943 041 407 651 717 935 443 012 237 194 625 844 865 594 886 172 822 152 034 682 672 952 265 252 271 553 494 007 470 795 669 201 850 383 155 049 251 178 133 641 777 698 512 529 780 819 275 250 947 377 177 887 547 654 388 596 128 305 986 921 214 010 276 233 671 579 713 232 812 197 103 817 933 556 455 842 669 584 910 229 729 903 567 746 512 100 623 992 608 046 742 128 303 617 641 564 315 699 773 833 868 000 250 717 505 681 682 197 288 779 981 101 082 088 976 109 979 010 679 067 616 480 985 771 726 580 436 921 497 463 544 324 598 001 825 098 223 043 868 387 704 007 101 526 858 283 397 382 706 833 183 838 016 866 283 609 399 265 299 526 026 127 806 931 666 482 122 220 974 316 501 872 088 512 170 544 834 590 072 251 285 694 813 318 400 066 364 033 129 683 642 518 809 122 389 504 503 439 712 797 224 494 687 181 404 392 765 232 981 282 803 118 502 207 635 310 110 480 386 713 824 808 668 198 631 100 116 624 434 254 186 924 953 707 924 784 135 801 366 930 915 454 507 172 265 132 682 585 869 769 469 444 087 403 990 349 582 637 935 431 537 777 267 850 676 399 870 092 578 731 355 251 565 503 400 682 048 410 173 517 494 539 004 094 861 744 709 092 949 938 464 847 549 237 648 212 507 233 951 661 679 583 071 564 177 944 055 607 035 195 477 835 126 053 904 717 206 754 308 493 352 646 663 821 290 233 400 668 763 019 180 635 655 204 817 249 072 142 610 608 484 029 506 602 836 824 760 828 356 886 874 811 651 812 919 574 000 294 865 336 645 871 242 140 622 668 753 901 668 097 866 279 839 108 554 019 356 287 540 786 085 401 480 760 496 751 725 230 213 038 539 214 836 567 022 679 612 557 067 501 485 046 537 923 784 465 317 825 023 583 703 902 778 492 004 534 903 053 471 842 900 161 060 201 492 056 945 059 783 131 950 290 493 444 953 976 907 400 095 938 551 761 550 519 026 665 179 496 446 248 230 253 909 671 647 789 768 979 898 216 771 734 921 158 804 278 905 395 804 644 381 626 783 852 583 646 132 314 616 958 589 081 323 073 341 058 560 131 588 825 407 259 626 772 544 239 449 296 714 637 175 948 524 870 114 470 443 831 309 508 819 728 330 684 097 612 059 162 453 669 983 247 488 295 327 706 041 829 829 300 029 156 399 102 804 428 085 272 229 413 568 436 370 409 969 871 027 460 900 359 937 512 331 294 131 305 471 343 540 818 588 184 004 921 207 057 031 093 228 658 742 912 457 859 704 198 319 734 805 085 512 093 200 349 580 369 755 433 579 033 103 193 093 535 346 909 281 219 613 812 375 202 044 723 804 128 237 731 882 586 732 845 436 677 731 808 166 969 640 180 484 597 977 357 560 927 008 610 643 389 930 149 504 842 985 885 448 726 574 460 464 252 079 810 058 735 109 646 931 209 394 610 941 954 446 307 480 715 193 632 668 670 045 751 334 271 926 542 414 108 003 426 365 563 228 793 987 167 840 825 826 677 502 915 938 592 117 801 838 436 790 206 141 785 915 460 237 208 942 871 667 118 203 008 651 633 810 597 992 692 823 302 899 789 289 940 038 444 282 330 565 053 862 983 932 727 610 848 840 331 393 062 033 845 720 347 343 320 492 760 792 410 934 537 119 147 596 861 736 038 606 489 818 606 924 977 677 733 185 602 390 132 105 296 192 902 538 962 178 054 455 158 333 754 166 534 861 247 425 012 158 580 852 330 025 418 990 831 915 029 927 519 124 160 068 216 916 824 659 787 358 382 822 217 418 593 424 149 791 766 444 836 370 123 974 680 441 435 324 928 658 984 076 795 095 060 536 865 243 394 744 422 566 555 414 008 622 379 043 328 318 040 476 828 296 084 154 192 690 878 890 915 139 437 567 835 384 723 019 694 648 734 163 778 378 462 757 018 631 657 339 444 844 872 281 221 513 821 548 693 863 024 912 579 594 170 276 390 870 246 059 499 229 382 530 575 861 660 738 442 916 898 321 758 595 517 976 407 231 979 563 649 580 968 081 634 449 855 838 936 127 172 509 616 372 865 051 235 813 021 427 307 250 874 675 147 077 917 662 566 181 769 569 401 521 294 114 861 755 734 296 496 305 403 331 875 790 849 577 689 736 429 197 811 290 108 366 645 533 984 620 958 616 080 503 744 709 040 471 679 312 027 930 415 726 302 861 800 116 359 985 376 526 080 525 491 211 583 020 406 451 376 772 688 325 047 446 454 092 393 964 049 996 433 591 904 309 203 324 820 950 669 991 667 101 836 545 317 560 010 198 537 380 155 663 474 266 768 173 766 838 124 339 227 649 456 113 183 364 527 442 946 903 577 383 246 320 599 901 455 878 159 458 148 527 897 090 827 692 182 555 094 253 232 587 918 177 014 663 147 414 643 295 206 065 558 796 237 546 552 642 093 390 322 223 440 035 567 353 552 429 597 869 151 711 545 238 198 977 359 606 285 001 071 923 507 539 887 867 047 296 541 824 347 030 731 414 811 707 755 341 285 869 685 031 023 363 722 926 980 860 754 223 403 764 640 187 031 147 293 033 576 494 257 470 757 675 620 775 084 993 876 177 955 226 044 788 164 137 503 746 886 184 818 442 929 726 864 823 152 552 852 122 735 658 005 069 215 026 842 632 581 897 121 663 542 471 861 450 183 301 682 015 941 353 780 888 337 655 526 289 314 913 958 683 277 260 951 977 251 343 620 181 239 198 361 139 637 255 851 261 425 839 316 495 935 444 188 172 523 248 044 650 868 897 953 670 654 418 196 267 534 939 389 471 965 510 641 161 810 489 352 774 188 784 030 463 665 237 173 602 412 237 875 322 588 904 138 287 212 059 441 595 722 839 618 880 948 245 575 768 048 651 661 567 143 432 454 476 604 802 258 197 451 339 839 218 445 334 340 467 841 413 468 134 206 015 541 085 573 523 893 323 121 861 826 983 280 075 896 791 141 759 884 061 441 755 092 159 365 329 307 412 990 158 513 369 107 129 918 508 558 398 096 171 803 132 984 955 040 909 943 253 878 441 175 533 233 041 270 625 173 974 414 936 583 037 249 083 048 177 065 306 925 897 600 888 679 466 884 231 771 819 251 476 755 771 260 665 645 842 412 928 133 131 128 659 516 901 239 539 898 869 488 486 933 466 760 567 706 388 905 650 729 329 879 835 536 714 363 076 305 746 686 625 624 990 898 669 007 963 436 703 409 534 366 640 440 245 188 412 454 028 242 739 141 801 050 954 759 533 083 432 984 571 788 247 699 783 632 629 244 095 783 219 362 493 857 505 213 887 974 134 803 634 067 990 805 398 636 518 519 789 687 782 439 018 022 143 710 706 290 895 181 064 892 457 797 921 788 185 876 105 994 861 072 417 271 940 721 865 711 556 586 163 740 603 733 231 927 055 643 994 204 754 054 184 932 613 379 534 951 833 695 656 221 273 241 616 767 864 227 292 119 970 262 428 473 862 735 994 590 200 448 762 757 249 275 207 208 724 221 550 846 662 141 024 064 960 502 014 436 151 978 174 953 718 251 609 840 859 849 997 592 522 844 438 062 982 018 927 173 702 587 877 213 079 588 352 249 856 923 801 524 032 043 228 037 819 067 003 407 038 942 381 472 824 663 191 500 833 707 340 871 281 162 375 071 639 911 565 130 602 581 642 048 165 747 764 669 426 838 643 593 085 883 512 547 560 297 324 740 448 270 616 490 903 118 928 625 313 011 275 686 418 627 899 455 224 157 428 336 997 651 957 311 377 791 881 623 905 069 061 636 937 248 184 980 968 010 762 169 026 686 440 921 463 529 315 196 586 583 069 146 436 879 008 823 547 334 259 543 063 999 446 612 803 744 438 333 487 857 980 138 888 710 088 207 717 466 608 425 835 359 066 889 789 164 025 249 739 888 909 114 976 214 810 180 801 512 168 359 158 385 872 414 416 296 219 560 057 222 026 672 597 573 534 491 287 020 397 271 423 855 982 068 066 832 004 791 070 105 603 033 723 192 959 154 330 895 232 321 057 480 743 073 540 281 900 243 648 786 569 848 207 509 219 528 595 872 554 876 342 670 818 087 979 690 533 219 679 506 454 839 089 025 329 363 104 879 226 539 927 335 777 345 284 477 274 939 987 510 969 232 509 923 036 172 544 574 298 191 637 396 677 500 258 106 255 617 127 195 323 556 839 732 951 309 311 608 870 147 653 395 431 176 050 208 063 486 073 490 588 532 425 434 121 974 466 025 281 966 761 067 834 247 567 837 646 700 471 303 959 424 369 690 715 826 553 870 686 497 664 368 756 845 848 563 847 547 476 967 232 663 670 849 943 255 281 217 049 283 616 851 003 165 560 075 928 388 372 316 021 407 499 477 262 190 880 166 282 714 958 499 230 586 612 085 032 979 264 570 741 867 616 478 293 579 735 965 220 464 214 879 190 653 955 136 454 366 233 770 328 575 521 175 759 412 845 002 051 225 493 547 095 001 733 055 804 514 056 081 178 865 388 388 601 765 943 128 551 553 992 386 119 750 651 967 254 170 704 739 083 352 654 359 930 181 570 670 081 964 130 577 618 253 902 523 956 823 123 459 469 049 422 347 012 695 501 622 662 991 518 698 326 377 262 121 731 732 854 533 421 945 943 248 133 338 463 961 971 883 222 992 005 438 429 369 217 993 053 310 495 844 206 986 429 509 673 935 068 392 173 449 952 934 577 360 988 940 073 174 683 096 888 386 541 615 131 638 713 761 422 250 842 645 745 212 603 333 756 748 674 649 199 923 166 205 356 509 896 464 542 624 816 057 332 868 114 171 755 483 996 997 738 521 689 964 866 709 181 808 533 036 888 560 880 004 903 043 827 559 434 636 574 888 301 638 220 416 657 014 726 750 128 245 293 421 020 695 331 066 954 576 731 639 180 553 257 302 284 548 175 829 779 148 036 342 105 519 482 879 994 581 450 765 216 464 308 546 836 029 169 752 514 177 345 024 745 629 353 386 618 200 833 342 964 825 482 287 445 770 564 075 598 622 624 140 488 610 025 357 210 735 507 821 465 930 677 434 998 663 977 133 895 708 733 360 621 610 261 741 839 601 253 932 500 949 811 543 965 154 925 873 270 348 504 399 026 181 774 623 551 186 357 259 139 937 513 638 450 853 464 150 661 102 242 379 802 013 875 680 972 256 218 284 623 231 967 040 143 996 901 278 146 363 580 687 235 880 940 079 391 710 192 754 539 649 738 558 651 188 950 839 492 648 669 377 955 953 380 886 552 996 657 062 361 796 768 387 195 309 481 337 058 986 195 578 323 020 234 515 882 579 454 466 299 714 402 781 424 349 784 455 265 269 678 303 188 698 603 893 545 062 904 285 214 448 190 500 117 180 453 024 183 014 897 501 768 611 481 080 450 092 603 994 099 507 528 822 009 304 214 806 487 290 683 578 029 294 949 328 954 887 482 870 909 863 248 301 505 087 530 547 931 807 036 672 240 641 800 190 237 381 417 850 815 656 074 714 267 571 864 096 515 004 591 498 962 819 272 772 643 939 845 609 562 234 984 901 848 795 561 059 587 610 374 062 581 081 332 866 759 598 935 675 116 781 878 396 462 382 035 333 238 062 179 602 040 324 953 644 828 929 068 911 535 297 294 254 686 021 115 793 360 795 359 028 519 722 812 469 647 867 658 304 304 810 068 514 920 109 517 483 842 148 516 645 079 323 678 546 590 860 668 673 631 612 991 676 547 108 036 957 523 816 756 055 916 803 463 066 094 055 086 283 238 096 498 005 570 590 637 361 630 277 257 805 093 257 897 593 741 950 618 514 793 137 646 645 888 871 216 782 081 703 336 563 375 228 987 610 253 309 769 535 627 087 897 676 459 735 825 526 779 816 103 098 457 290 879 077 929 412 450 363 129 557 871 172 695 135 709 389 266 828 899 690 959 096 742 054 351 839 458 415 724 265 757 982 217 323 069 357 709 262 399 086 834 423 110 681 272 367 344 547 264 928 704 177 035 124 661 131 104 059 429 564 341 199 546 541 216 371 179 950 345 842 917 224 714 674 557 812 190 955 496 615 001 618 630 966 845 622 186 947 515 595 752 126 537 293 269 797 030 693 549 297 246 811 125 426 710 550 512 986 071 874 134 807 030 382 876 501 922 875 125 589 085 673 949 377 798 438 275 525 862 325 748 461 430 420 346 585 167 993 300 742 319 404 909 207 219 378 729 754 651 595 200 384 415 140 668 839 980 809 445 010 988 384 747 186 358 533 030 798 896 175 154 269 048 203 582 577 219 031 530 478 889 091 675 142 772 851 217 529 754 244 690 037 702 326 378 297 348 338 391 267 324 769 989 237 602 593 179 732 161 979 129 355 741 831 515 122 029 073 313 590 682 273 280 086 677 617 385 269 835 545 140 008 085 385 030 511 513 462 038 586 976 028 106 823 411 834 948 798 798 200 633 243 461 923 495 616 339 916 785 402 946 234 787 001 679 271 195 555 164 079 521 097 261 899 239 769 385 785 406 290 434 245 315 877 547 079 052 485 107 056 727 620 731 782 263 435 821 585 014 168 894 161 870 493 749 642 559 438 296 888 620 576 549 698 666 801 293 143 521 931 638 541 645 810 025 004 947 353 475 038 398 523 380 462 885 239 039 326 185 142 376 842 294 122 297 740 191 822 393 115 583 831 899 473 831 229 331 911 776 076 895 700 372 900 722 527 367 587 973 242 235 722 315 616 140 086 386 990 014 124 902 909 060 702 385 948 560 016 373 912 556 424 648 872 814 212 972 051 476 217 256 944 984 225 926 609 940 484 694 143 057 515 929 849 135 593 439 526 124 315 212 836 874 068 994 769 470 345 567 399 225 354 133 053 485 122 633 773 284 296 282 742 816 515 555 289 006 320 864 251 905 206 596 661 977 840 879 541 837 839 135 382 939 312 153 771 361 106 995 219 744 545 049 769 301 388 848 944 231 402 405 230 494 386 080 850 180 763 479 997 056 637 473 300 449 796 634 966 896 469 568 003 164 449 856 462 965 910 889 887 067 169 121 992 633 144 744 038 481 580 845 661 345 892 230 122 549 063 048 141 932 923 290 879 941 079 618 889 024 747 996 481 109 900 894 255 399 098 448 420 888 505 227 081 159 545 030 935 845 004 806 347 397 325 390 261 375 102 833 851 953 867 684 331 893 585 378 288 273 635 209 662 286 800 182 994 877 225 800 048 482 765 034 115 460 464 373 977 714 226 790 482 647 980 033 555 247 827 640 180 607 157 142 605 129 213 247 207 716 611 797 788 342 487 734 438 320 651 384 032 371 321 447 286 868 897 583 692 281 508 366 055 321 368 532 576 591 885 260 517 665 707 596 379 392 764 113 425 729 957 188 496 871 762 555 445 574 580 082 494 703 583 581 056 405 795 741 879 468 929 983 340 109 372 898 380 988 932 035 102 029 188 431 895 596 926 252 183 593 659 953 200 249 166 854 732 959 862 305 958 010 578 114 649 034 741 145 209 485 087 062 387 817 387 675 136 626 954 650 004 801 555 340 949 415 317 793 170 011 372 097 163 158 682 771 556 334 361 097 071 452 384 285 200 987 194 514 182 792 740 165 856 704 720 913 236 378 382 005 271 521 561 399 017 642 821 875 730 434 203 481 084 239 205 572 397 499 085 478 900 044 453 489 025 725 342 455 152 811 281 292 461 412 866 353 708 496 113 143 412 198 507 042 355 169 095 086 605 913 395 205 037 829 566 551 896 262 871 855 448 658 998 794 692 023 829 107 778 130 165 700 853 982 672 287 481 872 814 951 110 529 934 586 535 657 711 645 474 657 006 941 427 727 612 232 929 129 700 620 043 900 656 752 066 740 729 270 633 709 000 959 221 414 234 753 299 208 882 685 621 442 964 345 725 968 618 471 434 347 008 280 659 458 134 689 630 069 151 936 753 736 187 220 263 358 228 432 097 186 031 139 242 666 918 416 601 786 384 041 314 272 536 805 174 808 770 511 743 262 411 141 387 557 617 871 133 221 782 566 416 458 337 821 763 938 815 885 544 045 950 046 464 648 032 849 227 899 764 953 780 292 180 419 646 743 747 283 599 138 123 406 610 369 089 244 410 578 230 568 665 947 101 596 114 013 309 558 016 289 062 711 562 777 338 573 339 945 594 990 516 682 056 759 285 146 677 305 489 102 603 328 306 834 024 817 582 305 072 792 104 533 223 526 694 904 528 533 783 059 115 726 941 889 225 210 911 093 151 194 254 315 632 002 227 429 268 585 004 026 688 998 338 944 556 575 395 250 921 224 146 438 366 712 987 051 832 460 292 482 183 413 239 726 259 604 387 739 882 410 421 237 955 888 037 296 689 577 619 244 683 897 463 065 023 675 734 601 111 800 209 970 338 309 981 595 783 359 546 676 642 998 765 128 609 700 463 830 406 219 104 474 498 133 086 630 926 121 954 098 563 458 538 301 361 605 842 498 397 169 815 050 570 934 308 757 503 215 330 407 008 788 410 248 214 973 342 986 410 591 742 158 673 033 623 536 004 600 125 722 524 648 745 845 352 515 408 870 962 093 595 663 805 457 067 714 773 961 720 338 199 934 637 920 305 863 992 083 626 220 476 586 650 432 877 116 789 866 061 982 769 759 101 639 201 098 485 531 018 256 201 880 465 341 823 804 124 896 496 939 693 912 481 131 116 087 351 458 869 153 659 225 257 913 170 253 114 788 756 584 381 617 651 113 379 711 310 762 308 623 604 491 335 304 929 039 735 642 606 476 525 034 850 054 571 705 855 409 037 325 644 668 646 533 426 946 148 017 892 495 872 932 250 693 305 392 149 475 752 974 703 447 704 933 488 208 202 819 735 302 906 280 342 045 020 211 632 341 282 949 897 686 592 473 888 462 962 969 890 165 350 350 492 308 717 855 281 505 775 348 741 269 300 427 123 253 106 895 794 557 749 599 525 560 282 875 999 579 584 363 563 329 003 362 735 891 794 239 489 244 157 520 409 869 566 379 123 433 590 813 922 161 464 516 177 966 813 492 621 380 880 325 029 820 668 687 820 689 792 513 553 247 440 137 805 895 420 975 219 606 255 300 824 207 996 676 868 788 588 138 858 426 385 641 697 003 298 509 051 160 758 824 543 760 024 268 789 216 667 519 906 509 248 289 697 217 453 247 453 944 193 068 824 214 545 084 985 829 241 809 697 092 718 719 920 678 683 382 315 060 088 652 625 672 138 827 379 212 510 178 522 437 050 540 689 453 327 589 791 732 521 470 814 168 088 071 429 707 802 148 091 475 501 875 369 687 241 009 076 991 303 643 705 374 742 188 062 006 513 028 611 527 841 000 252 255 040 283 323 357 062 906 274 906 805 390 076 084 218 902 186 929 816 798 125 716 232 867 613 851 801 515 863 408 081 579 044 445 347 861 202 546 906 573 709 819 064 642 954 104 503 542 549 423 951 416 169 988 270 361 904 919 112 367 681 883 300 854 443 381 961 796 235 525 594 511 184 818 512 263 878 718 505 778 880 684 806 246 330 122 847 975 694 472 900 548 620 373 140 079 672 283 854 964 717 457 220 118 414 476 407 161 385 025 010 764 897 617 467 158 132 088 480 404 546 953 049 464 612 868 368 191 370 069 305 508 639 430 907 511 428 230 719 525 621 910 142 681 031 680 269 554 643 689 288 893 996 928 144 925 436 666 911 657 527 213 749 680 133 682 690 942 107 871 388 691 882 652 711 785 966 658 634 801 264 288 974 383 442 569 978 727 209 914 074 097 494 254 637 505 746 104 773 431 646 444 906 943 490 850 386 198 228 938 179 428 948 252 297 111 244 735 132 570 361 867 351 025 183 500 732 342 229 229 298 706 479 140 849 680 708 384 362 088 509 807 102 711 000 549 599 182 527 644 278 892 610 292 668 727 656 876 685 112 419 436 517 400 138 032 635 927 827 426 455 633 331 097 793 375 328 671 469 037 286 253 646 065 885 310 610 213 803 902 163 034 295 833 577 706 561 873 065 948 249 139 680 979 399 309 711 575 098 168 452 466 691 206 681 952 492 973 025 057 654 840 102 135 325 194 096 506 638 586 373 058 167 130 982 941 960 343 487 132 993 286 403 818 628 493 094 194 848 608 420 480 949 281 504 305 093 449 817 732 506 384 833 128 364 114 554 235 729 002 723 745 367 676 100 932 160 522 660 490 964 009 185 032 704 733 334 801 821 283 676 228 731 224 191 431 967 975 764 753 857 864 775 443 398 000 788 478 570 355 342 393 883 280 942 779 484 817 773 614 726 930 673 443 810 547 237 421 345 406 163 617 610 052 893 220 381 078 042 926 180 918 647 705 435 335 923 305 049 852 288 388 354 186 212 220 709 245 529 474 373 371 971 643 573 204 221 870 279 041 075 191 913 587 460 201 002 547 396 897 821 050 962 140 485 702 919 871 276 633 825 921 994 401 930 539 748 029 584 551 390 442 616 502 546 292 290 994 947 936 711 029 098 876 849 815 852 377 013 852 973 556 797 052 172 842 255 557 994 841 571 850 530 392 496 977 946 036 771 359 596 603 630 917 953 071 390 624 813 805 819 202 215 720 136 996 017 717 351 759 272 763 139 367 386 153 434 802 029 634 553 997 847 103 888 065 011 489 861 985 767 660 114 998 053 063 431 889 025 655 129 607 313 617 824 591 557 780 521 691 644 942 518 975 844 031 576 511 534 215 397 682 331 250 266 679 910 932 036 522 838 686 288 315 388 504 827 682 463 758 681 953 613 917 523 952 682 920 837 796 451 877 163 285 006 701 037 473 412 973 208 981 472 159 387 626 292 811 114 087 303 271 281 545 697 467 866 601 106 582 911 121 704 842 502 211 192 593 842 437 174 702 671 263 353 057 578 159 176 657 157 931 341 519 191 871 473 210 091 441 636 628 435 384 859 497 186 448 202 743 795 211 712 733 305 767 496 143 233 178 795 680 916 735 505 228 452 676 233 224 279 817 905 022 724 238 345 618 274 318 732 824 993 107 261 349 308 715 338 517 844 763 793 522 043 113 741 118 040 119 242 193 649 121 390 314 326 434 459 062 323 711 225 235 793 360 388 422 738 080 689 587 131 356 293 174 436 334 552 128 669 157 903 332 134 103 021 996 281 551 169 978 871 428 505 032 857 515 490 677 330 084 019 954 298 621 580 973 539 334 454 407 280 930 714 892 256 458 713 148 282 449 090 164 469 149 351 348 886 070 493 725 117 587 908 665 864 397 282 502 929 819 121 941 348 610 636 859 310 219 748 841 013 345 437 695 177 608 444 519 274 433 749 729 672 935 611 545 227 905 604 686 810 674 446 703 255 072 691 239 668 666 632 247 283 128 309 950 226 018 966 329 611 552 291 452 388 327 600 544 721 649 761 531 630 987 683 549 730 245 834 249 845 880 674 382 989 444 417 762 269 668 404 019 238 071 078 225 162 473 674 270 535 171 690 503 811 454 106 344 637 047 082 764 814 339 560 477 563 576 448 395 679 930 211 747 167 734 078 533 451 147 122 672 398 922 306 664 727 867 962 454 399 093 742 032 626 020 503 103 507 949 042 600 426 767 091 819 909 132 690 497 212 233 444 146 510 126 881 226 927 193 293 246 732 774 100 721 549 040 494 711 452 548 605 226 470 169 134 207 736 862 731 566 365 998 658 275 092 075 678 739 824 463 962 510 031 778 244 285 063 671 320 003 173 110 836 448 153 654 822 564 316 219 206 547 664 336 352 505 252 381 656 982 274 042 504 079 351 658 299 272 274 398 418 172 063 057 075 415 562 387 420 472 145 232 244 468 427 373 847 480 082 942 729 093 299 875 607 605 881 732 877 204 837 862 281 641 760 829 524 827 225 081 298 219 031 721 778 381 040 285 984 722 008 693 087 991 863 622 140 545 673 190 022 419 852 225 378 310 623 293 627 338 615 971 914 622 263 914 578 704 547 572 341 230 041 156 279 258 485 076 828 488 998 048 594 145 223 594 190 303 061 934 291 476 145 658 275 601 172 546 103 358 367 519 457 316 003 445 453 106 171 497 537 454 296 309 120 972 499 863 048 735 978 509 978 433 834 001 352 892 975 039 525 031 434 042 987 572 774 060 179 807 193 777 352 689 570 857 324 276 298 984 228 096 369 122 094 301 439 843 475 967 225 024 665 888 196 444 156 337 077 571 217 555 168 219 211 642 873 851 810 503 085 936 550 426 824 408 122 415 843 351 209 213 252 143 012 454 367 493 186 867 720 896 829 347 203 937 637 529 367 231 575 261 451 732 659 139 250 169 871 945 562 393 994 661 167 186 167 574 790 045 417 365 343 092 811 763 361 986 398 584 537 521 752 767 165 146 751 795 886 101 798 478 428 123 247 121 163 171 075 474 572 852 310 835 591 511 880 805 102 615 260 234 390 027 953 127 607 333 051 375 446 489 831 355 967 734 750 650 189 001 376 325 732 870 569 124 697 809 737 837 544 701 558 844 713 789 799 627 790 606 310 855 388 079 115 489 788 140 386 080 911 077 993 238 191 167 918 236 715 357 671 803 745 655 234 508 905 756 032 608 247 097 513 155 320 199 918 611 217 587 851 226 452 892 013 936 420 618 798 074 944 343 998 345 852 728 517 082 218 313 415 198 729 212 020 666 884 039 411 046 209 444 918 439 424 009 273 286 870 116 833 228 713 044 167 229 176 967 672 261 220 814 624 392 233 011 012 599 596 455 644 955 864 694 006 817 029 892 431 216 165 918 359 917 530 483 141 533 839 428 311 801 074 372 775 409 723 583 221 778 355 974 347 450 053 937 900 721 690 266 689 141 859 449 135 239 789 327 432 254 540 198 454 268 790 439 848 193 422 731 752 451 122 037 419 096 597 464 467 131 102 645 342 093 461 365 329 226 990 975 972 051 670 093 958 121 945 555 622 289 041 459 714 901 311 220 354 979 874 205 085 657 811 312 522 389 991 404 051 395 947 677 419 645 421 513 497 814 404 324 601 355 115 997 969 350 954 685 939 094 463 353 035 187 616 485 771 498 159 564 318 823 834 402 674 578 697 736 351 364 998 963 462 718 806 549 763 599 599 278 432 573 472 280 568 574 701 065 218 419 943 732 203 296 943 591 472 084 737 089 376 739 479 656 376 704 174 486 696 805 964 302 718 148 109 000 959 925 446 096 711 664 281 331 128 745 904 796 278 704 443 049 057 893 989 892 950 310 190 034 782 575 022 255 229 677 388 910 155 954 106 644 811 758 094 631 080 968 373 288 400 204 669 200 971 672 794 217 735 973 821 550 376 396 915 093 834 201 321 822 099 766 282 379 522 111 607 795 364 389 837 048 388 003 849 319 848 874 524 967 581 811 295 673 599 628 442 423 293 712 460 544 412 828 383 686 371 884 088 234 550 986 101 551 636 269 908 532 437 655 392 608 664 195 262 620 714 849 660 562 296 599 587 587 265 253 683 741 875 449 677 449 171 549 079 727 413 213 611 237 531 930 839 776 200 732 219 958 812 356 490 832 358 151 567 234 307 381 066 894 564 897 717 960 971 576 756 271 989 230 160 375 610 152 383 452 787 880 289 260 559 214 963 521 587 203 812 836 461 380 566 291 089 890 948 999 529 429 627 453 640 025 387 478 605 163 817 168 886 051 662 908 702 269 227 749 365 689 357 173 459 449 108 672 626 628 417 744 161 061 597 270 320 968 706 455 970 556 958 505 029 142 658 028 754 925 543 141 395 608 859 423 376 741 776 926 590 221 580 227 523 103 666 330 377 916 258 061 552 882 368 018 632 275 177 526 194 908 774 288 334 544 239 737 207 434 740 176 951 935 123 971 931 602 633 719 307 025 761 158 863 240 357 635 008 504 360 693 771 443 876 423 686 944 928 286 278 418 314 370 493 280 552 156 337 254 132 883 855 348 908 653 465 146 838 000 733 672 705 094 249 668 797 319 876 817 644 695 943 515 072 003 572 770 391 795 675 340 040 649 428 215 301 609 882 866 245 165 751 836 699 985 225 425 590 340 013 964 717 092 792 188 186 327 373 311 695 879 475 187 245 655 374 867 144 569 860 037 424 408 025 924 768 443 262 370 561 662 985 069 763 268 226 024 917 007 728 366 608 622 183 773 014 707 251 937 586 548 155 102 331 829 388 442 923 841 262 684 248 193 610 645 840 687 251 194 678 302 837 793 933 893 507 366 785 545 799 288 285 854 982 300 250 129 781 695 824 005 143 217 333 594 127 570 353 489 783 739 802 685 316 688 527 875 906 584 721 991 057 638 989 265 702 452 339 052 327 230 427 162 412 170 241 969 875 454 990 984 365 384 376 574 746 725 346 962 189 142 166 625 509 069 356 200 320 506 023 271 617 003 491 454 357 721 413 729 815 434 938 234 863 554 459 065 415 645 109 815 648 400 216 671 761 994 369 251 208 919 180 581 848 049 189 396 300 039 792 704 517 986 579 092 584 515 848 186 732 339 802 204 461 793 578 676 571 016 708 301 554 831 399 931 505 060 269 810 550 255 452 618 703 841 630 416 558 873 793 554 286 810 326 171 401 846 676 646 055 501 783 796 267 469 551 782 606 150 091 997 175 793 051 193 116 400 376 738 734 489 335 043 377 094 134 723 350 685 702 264 559 715 084 245 719 111 483 474 352 042 049 201 920 069 588 497 264 839 900 273 407 827 136 235 987 562 458 925 718 933 409 832 693 197 650 481 734 026 265 134 369 467 301 756 195 730 651 103 616 104 176 770 942 927 329 387 503 720 441 562 676 909 304 006 739 101 259 844 520 422 777 170 266 943 530 483 924 044 920 636 570 733 391 072 284 847 443 565 598 705 719 248 020 722 378 646 842 763 935 762 144 554 375 186 577 425 449 067 223 608 095 689 550 264 680 328 886 983 007 219 768 058 409 522 257 125 606 449 278 058 510 846 909 681 082 536 529 289 687 521 854 189 559 224 645 199 862 123 677 817 795 784 469 213 496 181 755 637 713 827 812 315 398 436 811 373 587 187 911 486 679 950 404 955 921 768 664 319 924 895 145 966 129 973 595 990 019 403 432 688 646 225 653 951 177 330 370 869 928 894 298 595 937 032 599 672 069 098 054 604 553 480 565 728 705 103 729 832 277 341 174 394 940 583 868 036 062 097 245 619 550 347 975 270 553 438 693 277 323 363 858 605 710 835 622 749 318 429 341 870 125 030 694 786 717 031 874 667 479 317 473 466 253 696 397 007 843 261 153 130 577 103 798 107 353 742 242 560 306 571 556 591 700 851 923 443 802 504 653 729 841 561 473 929 663 397 421 854 829 327 709 333 557 295 094 781 757 127 739 278 161 125 270 333 523 320 173 381 440 340 794 667 090 828 453 139 727 053 111 515 930 219 491 461 364 204 165 338 247 645 672 620 181 149 745 616 288 754 014 027 603 041 345 065 032 499 217 186 554 787 752 110 298 232 684 700 830 811 104 467 219 515 759 995 943 364 609 665 737 943 558 882 817 176 153 056 696 362 804 602 400 318 304 886 845 154 418 729 224 582 848 924 962 697 898 230 151 348 559 117 080 546 303 791 483 265 970 434 804 320 948 256 745 359 120 558 477 651 572 583 159 287 464 899 469 518 209 193 736 392 558 143 185 292 130 318 843 127 017 187 857 367 405 314 589 901 661 071 858 959 418 872 933 745 904 978 613 691 377 368 412 187 794 772 037 045 958 755 516 658 381 402 298 888 119 685 864 619 248 810 306 179 188 924 016 758 212 312 207 311 440 171 893 291 661 029 673 443 515 860 919 279 258 746 500 295 792 120 430 642 417 035 723 920 397 931 507 437 501 802 457 981 001 813 701 117 217 574 312 428 837 388 698 383 493 524 806 688 986 906 530 642 909 031 489 470 115 571 809 184 972 104 232 239 784 301 365 202 071 992 676 566 965 369 963 351 394 605 645 013 272 814 883 368 278 747 287 787 014 164 046 284 506 713 021 107 159 892 470 198 927 332 141 138 954 502 239 123 084 620 030 286 970 491 187 519 835 262 171 397 006 081 058 546 286 811 386 445 271 228 577 805 806 655 624 577 289 496 811 575 607 608 856 124 558 185 461 475 802 230 218 324 349 539 842 124 760 582 975 900 994 996 677 685 833 473 546 406 147 617 612 915 463 055 137 145 639 562 882 037 912 181 881 818 404 145 636 982 110 196 527 594 209 932 105 395 742 267 289 981 501 445 477 537 011 641 531 708 843 473 467 716 816 173 660 108 870 620 028 297 762 427 891 355 857 677 950 956 702 691 183 559 812 924 775 483 604 677 222 110 020 504 407 065 321 564 844 010 001 557 493 688 155 117 589 135 859 468 244 135 817 029 676 967 002 046 798 911 339 818 119 518 771 484 269 062 235 290 390 251 730 736 793 599 139 853 747 011 070 741 710 078 821 709 762 293 172 278 816 694 773 652 866 779 115 073 847 274 666 665 728 745 128 172 621 945 826 421 178 677 398 556 664 934 326 314 459 646 972 913 623 524 663 337 837 842 858 415 289 994 992 041 132 046 344 550 106 081 445 356 760 524 281 973 128 704 492 928 337 235 826 907 560 282 864 458 920 512 885 059 959 380 854 722 875 656 655 485 833 168 668 515 055 018 583 672 290 308 793 493 967 944 294 308 657 020 161 214 326 426 518 656 325 166 666 242 167 671 664 954 235 658 919 104 508 854 187 231 886 040 028 202 116 074 081 555 824 237 048 715 278 436 287 217 285 100 648 266 636 281 400 685 942 858 551 079 228 958 749 031 193 332 501 389 259 203 666 599 486 021 865 239 040 455 043 993 066 606 496 654 729 457 173 451 012 046 410 734 821 318 443 376 829 201 135 956 667 665 203 043 894 928 904 927 360 981 303 152 682 360 082 397 845 320 916 398 293 882 277 912 972 119 610 038 977 393 381 270 160 248 618 628 869 626 317 072 133 582 129 370 614 568 735 985 596 476 319 939 538 701 229 055 733 789 928 854 471 456 315 594 002 913 188 629 082 845 450 986 731 250 249 586 003 148 512 624 732 804 692 221 649 468 867 815 008 381 636 950 944 729 446 229 281 541 648 390 203 036 801 669 827 684 653 049 073 203 664 320 319 271 181 911 588 791 055 118 461 311 911 598 335 096 473 929 798 268 025 070 615 858 145 871 068 018 222 709 256 160 899 711 123 919 623 730 062 136 259 805 433 097 645 265 671 308 786 778 605 308 813 277 039 152 491 760 017 626 282 993 970 598 416 816 220 220 398 753 166 370 065 438 281 869 427 041 394 560 369 658 332 039 569 062 755 719 580 385 590 832 015 406 606 220 239 513 546 673 737 676 898 924 018 720 463 662 068 976 693 837 527 988 245 778 559 037 086 401 541 113 314 548 503 418 578 878 776 180 436 865 700 566 293 546 556 682 797 074 438 704 783 589 302 425 924 965 736 057 271 630 927 497 523 198 551 570 752 041 769 298 420 405 567 114 207 609 197 850 461 718 519 781 295 571 440 657 560 605 634 234 415 599 123 092 685 091 740 459 788 050 178 891 434 934 149 759 407 464 824 433 481 459 813 632 582 641 726 104 677 001 992 032 241 762 613 638 878 874 708 452 262 123 147 354 310 450 266 352 473 099 587 459 825 725 328 590 612 016 642 700 194 183 189 373 320 068 297 007 115 401 181 713 562 567 400 832 229 428 854 160 895 412 894 061 355 383 311 402 216 879 096 812 207 827 457 351 601 999 794 109 214 184 581 574 743 668 830 694 628 739 811 719 993 725 947 751 086 869 037 862 826 612 134 702 363 233 347 280 770 435 826 906 639 472 476 032 011 314 858 800 707 315 403 018 682 174 029 044 219 590 755 883 121 164 718 562 965 476 599 357 729 170 591 989 936 778 799 312 371 096 230 556 513 691 790 642 942 768 796 361 637 288 820 451 840 773 028 131 205 290 611 395 251 080 287 971 621 364 635 705 894 446 920 573 482 574 123 666 867 930 608 601 132 913 341 842 189 245 299 813 387 595 986 396 269 938 931 314 874 206 153 043 552 171 948 769 830 469 757 147 718 913 065 465 946 723 997 280 268 375 377 237 090 290 767 161 341 848 007 646 648 881 777 219 839 389 244 276 788 977 907 409 206 415 732 269 121 833 846 064 484 330 293 692 165 381 820 277 602 588 886 796 869 784 571 563 887 696 166 983 011 794 065 666 933 988 314 383 563 662 654 735 586 226 709 727 118 343 668 573 737 501 905 758 973 603 598 147 043 956 158 677 211 037 014 363 638 301 125 085 135 740 930 464 317 929 649 337 959 303 945 247 159 062 747 434 450 838 984 104 496 761 032 740 597 271 259 433 470 220 158 514 394 775 600 565 796 002 678 217 441 132 432 518 931 388 909 292 946 278 146 403 167 402 544 695 983 318 742 641 609 890 413 270 202 431 722 006 925 816 896 555 925 990 091 551 504 732 932 495 297 084 101 351 167 196 743 327 220 823 128 567 609 985 938 942 364 573 795 264 827 093 339 575 420 013 743 013 430 825 273 684 409 000 105 445 747 706 086 917 183 263 675 651 611 850 274 751 746 701 754 889 423 169 866 332 515 668 356 425 838 364 038 908 137 280 153 275 352 978 111 836 175 196 610 377 343 630 669 640 908 470 956 978 848 595 860 269 895 967 160 001 244 333 838 109 700 515 409 438 809 014 308 015 860 544 624 646 783 785 521 123 427 350 114 010 958 952 744 362 445 579 602 747 371 773 664 570 927 491 348 492 572 443 576 471 334 008 191 429 479 458 584 581 057 687 434 726 909 442 384 787 791 204 507 396 136 413 514 164 911 686 873 441 088 372 778 033 884 963 520 334 570 069 936 236 738 369 849 787 447 061 796 492 335 827 929 309 962 066 513 564 808 768 515 154 319 509 726 396 250 993 507 135 633 093 925 089 378 823 358 296 736 986 783 438 483 288 389 156 725 809 086 256 635 922 029 739 907 738 246 013 956 077 111 807 516 537 498 239 256 401 167 238 362 696 807 189 177 663 374 120 155 345 040 791 669 648 162 456 553 150 918 880 482 828 689 866 994 741 393 595 146 677 156 245 726 729 525 426 651 119 675 981 276 142 724 070 436 991 754 615 508 758 401 297 644 317 168 427 419 281 529 463 361 261 241 202 250 673 539 322 285 778 205 644 894 657 013 606 246 589 982 569 612 126 165 269 672 270 055 316 956 911 750 254 623 777 425 458 297 893 594 274 214 181 917 019 850 932 509 709 380 066 535 613 486 621 517 161 936 697 912 003 370 137 289 396 172 503 888 205 076 771 078 357 955 545 575 044 788 117 283 529 350 841 135 039 471 325 297 382 522 374 948 196 623 679 067 629 117 877 078 386 687 208 064 363 698 799 317 616 432 767 342 126 669 826 279 684 875 178 519 356 392 881 104 344 150 787 316 706 010 096 320 219 568 212 968 282 885 789 909 445 020 371 351 560 216 877 877 286 875 870 547 946 609 554 848 758 113 657 860 574 971 865 564 339 543 285 488 435 586 269 465 702 280 105 484 270 373 039 712 130 504 413 896 002 660 517 610 284 467 990 492 792 915 229 015 412 863 847 623 476 267 015 224 241 377 682 677 918 854 144 705 594 721 610 042 175 251 850 578 569 378 601 936 216 093 860 794 171 825 739 102 058 104 118 308 309 390 313 832 555 993 549 744 988 146 163 255 609 212 019 178 049 466 676 902 697 094 649 815 352 965 657 787 553 515 545 055 245 077 099 114 415 620 191 582 060 830 392 627 314 907 362 330 899 665 555 971 330 545 560 974 258 952 322 712 699 558 704 635 508 265 179 118 494 505 606 562 159 823 459 670 966 666 116 125 983 498 007 190 106 717 392 284 243 286 597 671 838 400 085 760 973 975 916 000 601 395 642 067 847 260 769 112 215 378 402 953 772 846 412 714 949 265 025 237 520 686 335 089 106 853 338 284 823 437 015 784 945 169 528 422 484 392 314 127 752 599 252 552 202 520 256 173 061 798 543 797 523 882 154 856 869 346 682 690 868 268 904 437 661 848 114 841 984 878 301 556 599 668 314 107 198 362 105 820 283 357 101 402 383 417 359 683 638 009 681 073 855 778 838 444 154 154 454 722 198 292 117 778 260 248 418 752 641 513 269 877 169 691 215 354 500 785 810 832 059 344 995 179 392 047 898 389 634 929 492 560 863 176 955 762 423 596 928 326 249 594 254 164 623 347 963 268 076 533 806 538 613 621 360 184 446 901 675 461 753 036 655 435 507 662 996 124 449 586 496 600 065 789 430 658 843 173 155 684 976 535 794 923 475 944 461 310 855 760 074 922 922 528 574 679 867 938 477 450 048 056 805 573 060 554 054 255 476 878 930 887 690 282 259 775 423 327 635 285 884 278 246 785 602 770 629 848 995 621 486 036 930 726 732 906 313 494 018 557 810 219 234 014 539 914 947 170 034 087 549 984 648 359 942 703 298 643 420 017 984 150 595 239 080 251 612 684 203 696 864 142 601 082 197 839 108 956 811 815 332 040 474 803 824 585 110 254 460 950 885 047 788 954 042 469 258 052 125 263 397 288 787 079 907 846 076 920 193 532 491 338 530 418 241 058 480 338 768 448 172 627 775 762 569 207 211 852 199 068 352 028 341 990 227 248 102 472 558 990 799 450 824 507 993 942 287 587 126 367 360 421 070 908 072 775 986 559 280 781 201 460 668 968 283 608 458 770 337 636 463 078 538 304 232 893 049 954 704 992 228 909 807 659 133 253 060 171 953 191 427 070 118 409 006 502 322 613 059 892 318 029 890 031 655 947 839 544 039 676 820 156 239 693 726 702 606 389 693 475 546 243 275 939 168 589 159 630 587 948 710 099 806 654 827 266 765 074 064 378 697 570 900 025 416 775 571 139 939 113 341 003 132 438 359 886 251 687 771 736 861 165 702 494 002 146 105 973 647 930 643 713 045 682 260 465 596 606 967 696 226 016 573 011 175 188 220 491 968 582 376 969 073 270 740 265 283 228 553 909 861 261 196 237 244 314 213 137 762 678 631 262 664 075 518 517 163 398 315 506 857 872 703 519 945 050 333 509 526 207 998 156 812 229 872 474 667 591 775 970 409 625 962 519 765 670 321 963 000 679 579 261 544 790 028 941 455 672 460 658 151 975 609 824 469 607 115 615 336 485 510 736 223 476 860 716 841 070 575 790 779 777 946 080 533 953 726 300 626 985 622 528 774 529 816 727 312 824 444 035 154 899 684 603 395 536 244 858 409 675 190 659 074 140 176 439 011 929 373 822 345 843 640 584 470 275 022 935 487 365 546 290 058 017 787 840 071 802 505 418 416 572 114 453 540 427 664 883 263 069 388 416 981 055 915 463 652 001 310 198 203 433 659 364 173 958 786 692 285 762 709 646 133 831 032 429 640 129 264 029 120 912 931 138 810 751 197 352 981 469 887 450 469 458 339 529 609 891 342 058 126 688 903 634 450 636 007 029 904 419 777 941 476 601 444 935 718 801 363 450 123 733 052 402 333 044 140 886 358 546 492 971 579 020 587 981 073 812 153 214 469 295 152 865 282 447 965 185 082 358 836 780 454 345 455 367 079 340 597 024 206 471 757 393 443 473 179 021 802 725 159 771 102 364 076 511 075 475 729 661 070 395 094 329 544 385 064 279 488 685 951 605 727 301 898 639 042 342 526 515 301 536 161 972 939 069 412 341 466 279 783 873 819 153 453 115 550 959 255 823 368 950 630 205 838 978 083 472 439 039 332 076 075 851 140 569 272 707 878 685 704 054 789 212 851 951 419 337 662 727 655 990 323 800 156 560 777 720 950 973 874 711 668 516 035 668 077 114 835 596 612 392 844 148 615 185 566 753 214 017 052 210 356 395 015 149 504 103 557 350 293 760 981 816 509 337 838 759 475 844 450 150 929 323 381 985 165 851 146 683 299 359 004 205 711 012 717 005 169 850 815 730 295 461 968 750 835 297 341 650 015 857 390 238 054 074 023 043 456 368 887 259 556 624 074 268 174 364 228 820 156 266 309 185 883 064 319 467 513 034 249 932 925 275 250 169 526 621 709 206 702 767 447 992 801 133 478 575 863 193 992 369 124 970 556 066 275 915 025 710 186 145 786 090 308 910 115 230 751 738 054 506 472 565 346 147 035 983 433 149 147 853 828 778 433 601 159 326 073 992 924 965 436 715 881 981 000 349 510 293 117 976 375 181 114 373 133 625 344 370 066 302 424 677 669 874 328 374 181 509 428 552 595 616 580 969 241 147 253 373 376 477 077 489 805 728 258 461 624 758 635 044 818 940 680 515 553 550 893 076 401 654 773 169 987 626 383 022 015 035 113 163 075 865 415 090 694 438 572 476 442 452 046 939 710 109 348 539 127 995 844 618 867 616 295 811 178 153 282 397 147 519 576 518 120 031 688 963 691 023 591 660 589 510 577 877 860 277 325 044 549 866 468 399 559 477 692 642 851 378 606 674 431 934 708 602 337 425 331 147 785 590 139 638 117 443 658 644 617 716 588 496 167 741 880 203 496 590 547 320 704 812 537 774 305 036 763 196 753 818 391 303 894 647 399 749 138 478 581 748 122 273 306 220 532 914 908 332 664 227 461 814 741 140 185 633 256 791 235 413 324 143 760 463 239 748 482 483 013 018 496 039 343 085 968 960 805 224 223 596 970 788 655 245 934 340 995 214 951 507 152 796 396 954 295 837 129 098 553 947 994 120 444 420 075 219 447 182 760 535 073 688 357 264 068 153 236 641 580 454 571 314 939 692 581 691 926 460 673 188 612 436 826 669 314 814 298 711 239 140 892 507 229 451 590 494 188 862 462 432 963 574 193 617 512 182 663 573 419 771 938 019 911 962 860 066 173 049 635 323 259 491 370 352 903 933 155 451 740 125 945 977 914 174 025 593 552 869 155 056 217 690 240 176 154 835 413 292 711 845 069 162 943 785 474 733 851 898 291 929 658 063 843 710 276 497 127 666 123 086 426 929 876 601 940 028 595 328 555 951 237 875 757 714 212 658 468 031 307 277 477 261 443 216 820 490 507 684 561 863 107 462 225 866 383 314 638 029 552 061 750 032 644 537 878 502 179 379 135 493 099 003 563 711 916 003 155 110 222 347 346 285 663 663 923 293 912 165 668 431 529 305 920 099 216 183 676 095 373 276 098 818 606 479 724 643 923 734 825 399 581 483 144 643 343 309 794 038 498 322 944 810 829 585 673 969 787 588 751 559 671 283 132 821 225 358 851 476 240 447 543 799 497 967 463 281 748 569 556 712 182 300 188 260 895 001 540 428 007 706 888 800 051 365 098 978 744 103 296 427 558 717 434 569 489 741 467 476 689 057 080 276 864 706 207 046 463 379 205 559 964 160 823 030 141 682 392 804 006 385 967 650 812 614 892 972 897 563 308 266 787 885 530 660 772 929 233 499 767 565 476 543 393 471 165 166 577 134 589 197 664 642 716 645 071 872 438 562 685 327 493 363 378 637 941 980 948 534 486 197 041 968 127 393 140 227 625 596 213 821 912 328 986 484 784 230 786 658 474 589 075 838 635 418 600 435 019 556 830 706 658 760 795 220 595 331 154 211 309 057 918 665 852 206 537 783 674 959 204 048 836 218 639 228 391 426 770 081 093 637 225 278 980 422 990 792 473 557 251 636 585 008 939 273 870 681 702 577 709 053 909 813 924 392 026 189 499 496 857 670 565 432 093 145 763 642 226 420 098 077 012 844 037 585 688 699 467 223 767 778 061 177 296 552 407 096 066 658 740 760 408 351 719 308 926 145 922 881 217 876 873 590 834 860 736 329 012 827 452 946 183 567 433 604 131 181 344 542 706 876 613 243 022 861 652 858 127 123 694 210 599 358 951 864 811 700 666 862 028 303 841 591 162 294 109 817 416 105 922 415 458 630 022 454 673 481 748 553 708 048 045 771 519 113 541 138 962 221 209 640 355 272 691 740 216 924 791 879 278 566 202 319 250 731 388 132 070 773 067 264 935 035 441 128 271 353 234 078 160 034 798 211 264 981 542 640 359 605 098 520 376 292 992 367 770 837 138 616 219 178 106 704 534 684 183 395 306 658 908 319 239 918 840 320 963 382 884 886 967 552 019 359 683 332 299 512 194 568 585 436 050 622 479 617 936 524 655 765 717 511 640 470 316 424 463 882 807 624 170 789 298 339 128 066 820 939 337 164 369 566 679 135 555 142 031 595 197 192 399 437 404 586 896 507 216 406 270 314 889 389 693 973 748 858 971 762 916 131 229 954 808 476 849 920 869 226 228 610 443 352 418 347 020 157 999 239 161 524 722 833 405 026 686 945 428 114 575 926 387 665 440 271 774 316 704 388 037 975 555 955 917 180 852 564 757 860 049 073 068 299 350 692 001 513 750 712 862 463 009 103 055 561 119 830 355 254 179 625 876 329 411 787 674 369 804 028 179 744 498 070 423 522 953 409 866 597 136 221 260 127 985 573 770 519 414 927 118 729 734 342 539 143 742 409 665 106 846 338 716 118 951 705 955 933 250 218 094 423 190 254 489 230 298 111 913 164 772 405 956 873 884 173 349 437 089 728 363 378 945 474 187 214 232 692 826 860 329 722 802 632 622 257 074 368 702 243 340 368 458 685 539 498 690 912 799 663 967 434 434 894 840 054 430 857 369 624 849 989 809 690 097 005 606 387 692 065 467 033 322 433 919 786 377 417 239 495 053 535 895 700 707 028 765 355 444 544 357 970 921 555 406 325 239 986 296 631 348 221 049 335 107 515 015 953 258 966 489 259 995 459 692 946 767 458 453 995 811 483 436 090 123 410 706 253 453 659 410 347 276 796 397 969 947 207 468 616 498 159 803 949 155 784 862 265 765 887 451 039 038 871 876 935 571 658 178 790 177 198 628 548 885 139 262 605 342 896 674 974 862 615 471 006 842 816 399 266 610 898 524 500 035 113 611 781 825 011 444 454 118 055 570 178 494 530 308 044 452 572 958 902 478 184 858 303 513 963 547 891 566 626 656 871 849 817 177 413 269 318 128 724 955 678 362 149 409 898 083 909 845 139 497 754 697 779 628 666 701 371 063 163 098 363 258 224 449 085 190 999 010 851 921 148 385 043 615 895 336 005 525 231 546 355 296 945 598 092 447 114 866 961 206 447 535 871 083 146 052 675 490 783 473 282 580 287 908 087 092 034 895 633 462 998 857 570 336 159 336 342 356 929 116 443 981 383 045 477 648 831 590 583 520 861 126 499 170 962 680 892 200 604 978 086 424 112 156 290 773 000 262 788 146 855 448 707 488 882 575 460 803 567 381 932 880 754 948 981 355 140 619 098 898 789 000 080 100 337 791 347 902 003 672 089 813 274 842 563 438 717 734 005 456 300 248 729 018 180 153 094 063 628 581 178 371 121 022 914 953 755 333 451 045 947 935 177 674 261 220 692 145 472 346 541 700 525 100 021 501 804 113 624 110 905 747 412 193 184 264 473 960 100 687 685 165 441 491 862 377 971 545 852 522 092 472 049 715 062 532 070 779 717 796 719 770 917 938 535 232 151 588 898 674 736 260 740 081 847 653 382 746 135 761 888 551 532 245 573 067 851 803 604 983 587 289 176 276 755 883 356 237 866 191 270 372 412 005 734 694 955 781 879 459 752 172 412 596 144 580 739 399 644 553 141 969 187 858 619 630 611 707 384 910 799 351 300 534 851 754 227 526 938 736 175 131 111 822 301 110 201 152 988 348 395 981 732 465 475 498 129 176 539 092 616 043 452 747 128 119 415 954 086 224 622 426 193 683 035 580 570 285 451 559 844 883 099 842 083 392 483 154 899 863 188 747 941 124 681 639 202 177 659 160 837 513 056 800 874 712 074 662 124 393 541 358 823 731 320 462 916 652 233 520 894 224 857 352 939 207 232 602 502 216 638 038 146 549 939 926 704 780 344 717 789 662 510 905 087 089 516 201 182 031 221 870 669 312 703 739 630 288 031 998 055 753 502 672 012 164 347 839 403 305 049 846 113 412 425 187 619 685 376 557 067 998 305 439 011 620 417 245 680 043 277 219 684 651 535 089 929 560 683 570 087 043 282 880 383 208 174 382 066 776 324 507 053 587 484 919 424 817 970 485 127 633 861 905 612 918 160 708 355 871 149 215 032 591 851 361 471 473 226 576 372 964 319 655 015 475 198 652 842 119 188 565 821 199 506 347 666 326 137 754 757 548 422 125 257 848 567 810 167 508 844 816 506 026 273 304 536 867 871 063 189 449 208 770 623 253 874 474 004 058 538 007 731 179 891 883 201 755 817 245 296 597 527 174 594 814 571 913 852 345 530 888 050 580 997 012 932 799 335 020 296 880 434 537 601 726 734 177 964 781 221 478 210 221 069 186 210 907 806 996 107 400 732 703 234 567 242 165 275 287 941 679 444 442 532 452 387 842 070 838 278 082 521 987 115 346 287 517 376 301 928 007 876 173 962 728 341 530 324 598 768 385 187 000 387 847 228 748 036 815 382 651 965 004 102 825 764 114 038 176 767 466 329 371 573 908 744 815 800 591 654 873 927 209 471 912 334 372 616 380 083 107 206 130 519 154 317 904 293 499 680 942 869 269 632 963 836 324 790 580 557 555 823 516 310 799 223 273 218 317 510 354 178 757 910 093 164 066 231 749 044 506 695 134 711 364 873 649 445 068 949 317 461 273 695 834 314 516 324 479 294 964 958 569 252 403 393 598 414 899 130 546 603 335 981 934 735 946 126 320 266 765 412 827 553 730 819 456 974 145 328 028 186 544 682 946 791 461 682 455 302 015 626 769 515 027 610 584 847 534 894 326 420 840 606 659 279 164 082 426 656 516 766 815 949 524 097 088 212 460 885 326 067 464 233 507 326 391 521 932 875 703 678 788 909 364 746 155 596 721 068 991 261 349 226 172 864 728 805 827 452 198 231 810 485 957 118 058 046 142 469 776 154 572 151 351 531 117 380 963 373 514 639 726 258 572 479 516 858 113 924 949 990 312 372 066 954 894 253 448 713 054 753 623 685 399 041 338 570 128 145 644 236 518 803 639 986 065 618 781 188 214 258 145 244 001 898 615 621 314 921 582 246 167 001 313 267 899 090 699 406 150 126 006 025 978 346 680 207 378 753 939 929 601 513 451 540 087 325 198 740 947 234 601 958 462 692 665 897 843 863 993 563 832 520 837 785 808 972 261 198 298 744 711 249 843 872 994 619 794 509 572 296 114 159 818 503 493 263 378 192 514 290 052 254 924 503 278 243 290 282 312 383 786 202 656 048 587 547 053 598 535 021 004 482 006 464 464 259 867 265 490 032 784 057 577 074 913 435 447 300 124 058 660 673 773 041 801 591 642 403 541 153 081 663 979 288 908 937 718 918 328 856 735 803 057 667 473 976 816 517 733 805 208 968 997 572 343 546 125 597 865 268 613 682 261 648 099 258 488 378 164 531 265 938 841 850 137 542 799 849 993 058 020 852 254 929 531 160 451 981 455 489 377 644 703 006 456 534 262 058 269 261 337 738 997 661 094 466 793 744 897 668 669 848 261 801 307 880 228 085 386 121 975 680 448 341 661 998 411 397 261 730 623 796 179 955 085 559 454 788 601 501 158 155 645 611 635 672 661 189 851 972 998 073 834 909 763 982 089 094 540 956 567 276 773 412 581 671 398 873 141 017 929 419 015 515 176 778 538 191 694 622 355 856 919 224 682 207 678 612 516 615 349 946 693 036 311 387 124 490 214 319 129 672 010 892 088 821 892 858 549 543 207 139 833 370 662 172 964 905 175 450 936 340 896 081 893 952 258 795 970 204 780 055 888 823 422 979 696 205 660 167 658 484 985 872 104 403 588 340 091 701 224 073 289 337 669 807 163 342 487 661 165 148 090 772 886 577 891 200 865 234 035 604 229 018 239 015 585 925 972 610 712 408 386 911 330 789 415 255 585 857 591 419 577 707 679 440 565 791 199 571 909 471 046 241 392 222 660 189 680 550 778 520 572 119 057 124 096 422 445 217 938 980 694 668 237 920 562 770 886 173 278 519 745 287 478 243 762 384 546 386 793 167 065 410 125 814 881 008 365 269 356 447 937 828 261 510 372 373 092 715 157 730 675 456 151 950 259 507 377 444 852 978 207 965 174 788 728 639 257 858 862 362 458 316 445 652 955 564 629 901 670 986 385 925 209 981 142 334 983 218 984 614 323 933 606 250 713 462 730 537 905 317 140 709 699 897 330 481 788 309 581 761 086 062 697 426 884 045 169 609 733 407 363 888 258 201 054 214 703 700 303 512 759 828 406 898 073 534 754 800 199 187 006 395 208 626 262 375 601 208 742 345 353 510 371 000 625 188 828 636 081 079 738 647 730 395 687 637 727 305 352 950 921 570 003 108 668 979 068 450 589 200 926 420 979 879 202 020 014 209 625 676 532 193 576 479 741 513 043 778 964 354 220 834 091 502 578 109 180 699 966 804 330 262 163 977 237 249 715 384 381 875 907 551 141 746 975 120 326 970 717 873 656 034 727 145 891 698 419 762 242 277 815 724 891 307 056 479 595 692 085 474 992 289 097 618 787 105 063 059 964 127 543 762 900 565 307 827 660 428 941 108 633 794 603 435 257 988 693 774 405 610 967 328 914 777 495 301 310 911 818 434 408 001 642 754 970 818 464 538 806 435 631 737 606 102 697 623 796 125 761 204 476 360 375 273 356 133 860 244 746 062 911 697 483 187 773 041 175 157 516 059 879 373 184 320 502 707 356 913 202 020 481 627 599 072 282 152 216 398 685 531 338 550 159 725 919 648 249 079 900 950 353 854 598 576 096 005 335 013 717 470 526 172 093 477 176 127 155 466 214 900 213 254 390 877 356 649 954 690 776 944 761 758 885 557 161 200 311 690 153 274 774 032 978 124 893 712 387 163 690 617 906 473 842 480 886 020 628 739 980 115 359 237 953 544 191 544 687 674 431 405 915 592 270 411 655 120 285 234 498 585 228 856 767 727 172 348 240 574 992 914 805 192 497 117 573 883 348 789 821 983 938 501 310 688 402 646 561 608 064 208 999 592 047 290 038 317 285 426 217 199 540 937 324 665 157 193 298 982 873 659 654 665 811 366 835 661 126 227 243 021 344 728 997 332 798 969 096 092 676 154 529 357 463 731 349 500 701 830 506 479 677 715 400 384 523 638 984 789 666 200 776 100 369 179 604 094 764 466 136 046 947 195 257 031 011 036 267 882 804 223 256 397 455 491 769 901 791 820 304 681 207 453 336 537 390 698 322 915 404 973 703 519 439 181 250 746 463 443 017 695 381 626 154 724 372 095 204 095 873 538 849 771 357 462 359 766 489 864 257 619 850 450 587 158 530 679 501 017 683 182 637 659 227 617 096 123 893 204 356 146 526 788 777 303 622 788 020 984 047 693 184 144 715 805 886 327 141 170 374 293 107 611 778 090 826 999 293 536 280 948 531 681 340 220 206 830 820 267 047 249 672 527 005 228 186 419 193 185 806 587 891 061 185 351 138 040 899 784 819 600 378 719 070 118 553 652 849 040 531 135 300 937 272 851 985 586 611 949 642 199 021 857 573 631 428 083 958 115 055 490 695 562 781 555 002 731 109 115 302 169 315 598 528 393 892 474 085 727 402 729 013 100 135 536 413 485 216 943 582 949 077 341 312 048 183 061 910 149 671 885 104 055 894 853 756 780 277 166 631 812 456 093 963 223 938 616 093 451 328 062 883 565 237 429 386 179 679 983 563 613 898 692 471 234 513 548 743 526 267 785 624 870 173 882 284 945 544 668 012 956 317 441 451 304 538 119 180 085 955 833 572 853 099 252 948 780 600 041 629 598 774 100 085 622 855 022 616 184 999 310 966 495 355 025 638 851 837 997 844 371 353 171 883 455 530 310 585 432 102 374 164 553 414 780 827 710 465 837 878 408 207 324 253 552 176 912 458 424 914 848 532 347 121 142 523 724 267 920 258 447 670 234 725 678 656 929 698 090 595 147 485 512 939 759 783 925 882 976 576 436 015 086 176 064 487 237 056 741 273 106 122 299 631 117 484 656 188 400 695 585 329 993 664 814 294 410 786 815 524 489 773 156 839 322 755 346 999 988 751 817 781 162 421 904 983 439 943 836 172 189 273 578 999 308 639 186 806 430 841 597 890 706 007 770 534 414 362 760 942 967 803 670 133 819 530 969 542 331 960 696 907 458 942 004 029 413 058 080 078 129 766 355 020 029 499 249 672 465 085 086 689 226 910 481 243 027 663 912 984 494 660 905 829 804 172 882 671 029 755 039 309 321 168 112 023 051 529 616 904 974 490 469 170 550 265 615 797 306 184 949 430 865 952 424 206 408 545 541 036 164 188 994 535 621 574 668 945 465 858 648 316 753 387 832 448 494 846 952 471 876 586 037 976 298 825 787 565 861 363 347 112 292 832 644 545 977 785 436 755 525 278 560 418 253 876 557 972 121 215 751 736 025 133 554 143 497 527 188 431 201 868 916 179 192 189 218 844 869 713 217 488 432 947 719 723 178 370 363 021 103 253 256 953 677 844 582 715 177 669 655 111 941 758 052 007 563 187 411 613 226 616 365 768 464 614 561 468 072 474 409 973 206 556 676 197 667 381 579 279 065 471 412 231 636 427 462 456 367 563 247 381 314 485 354 534 736 168 732 118 729 414 684 389 554 680 980 440 003 855 234 460 872 566 591 119 045 006 665 281 821 287 001 334 607 951 492 917 067 732 196 850 329 464 361 106 578 478 172 665 345 646 654 885 695 011 881 737 898 654 635 984 804 525 441 191 282 387 886 448 820 050 371 342 493 867 241 226 831 823 270 024 588 559 037 014 063 316 450 168 715 705 586 971 517 120 209 367 729 199 806 180 458 765 944 315 185 924 567 550 304 091 620 601 867 464 391 982 959 484 758 235 558 583 887 420 108 200 613 881 267 823 951 456 473 810 193 062 929 779 943 210 671 954 762 832 931 560 172 140 194 969 785 827 508 753 668 494 740 639 152 133 622 079 558 263 648 934 164 525 524 462 204 026 392 363 928 014 515 236 963 620 881 156 368 365 503 210 571 055 879 718 177 964 705 274 309 964 739 383 094 841 809 580 156 470 998 966 677 077 643 888 393 886 735 213 952 739 159 518 155 837 434 535 116 907 533 273 118 293 557 696 518 832 587 961 530 350 307 135 553 692 007 028 000 739 221 930 846 523 076 935 062 831 213 227 289 736 150 101 372 339 912 331 354 263 546 335 265 578 345 082 903 644 714 048 322 879 443 065 102 688 051 632 615 738 700 004 601 853 819 272 603 585 213 536 770 103 000 340 870 676 406 580 515 522 552 292 313 692 048 029 637 665 753 380 098 972 883 543 647 699 887 886 599 629 657 229 886 464 965 129 088 356 399 431 756 762 795 969 358 705 589 232 363 389 647 593 943 975 982 175 426 135 211 340 200 480 206 413 741 002 397 611 575 050 082 143 773 596 410 866 872 151 883 509 374 773 284 813 945 077 766 784 647 211 135 536 610 747 521 371 683 816 721 790 358 289 401 991 959 511 555 510 958 821 280 918 858 008 538 104 656 349 155 238 632 994 148 275 730 102 118 356 059 338 136 504 436 758 716 176 318 700 622 050 896 101 823 313 096 744 288 915 392 709 184 158 259 543 981 295 373 902 165 818 893 252 636 179 776 087 611 973 198 185 309 287 057 649 145 757 643 842 370 152 976 447 938 145 963 647 273 432 816 511 744 074 557 406 263 586 055 249 453 502 278 833 780 791 870 325 145 553 308 985 076 902 932 755 219 021 463 467 341 966 981 692 370 993 651 108 542 294 629 588 675 868 181 620 811 960 103 750 187 623 321 200 452 178 353 810 264 520 085 598 592 303 715 801 745 623 112 593 801 140 394 626 135 002 216 399 270 830 749 894 113 418 972 972 790 920 231 290 523 747 401 518 429 500 572 597 001 967 220 464 937 579 827 273 335 926 583 844 428 217 320 990 856 960 415 489 745 538 810 366 086 840 693 289 622 998 202 169 388 769 728 969 403 903 504 770 808 013 019 496 601 387 705 757 211 296 577 936 604 719 842 958 054 714 801 534 706 013 801 314 521 385 798 193 226 012 088 773 217 252 823 998 641 830 548 455 985 400 235 601 537 350 942 187 066 815 465 720 301 208 719 080 397 051 442 242 157 128 849 394 448 132 428 087 979 584 614 305 081 042 078 746 106 423 358 943 118 769 811 314 710 404 282 581 262 637 198 902 365 779 982 999 660 050 185 875 205 906 113 840 652 264 843 758 789 098 193 339 984 360 691 008 898 462 957 644 185 428 814 440 624 941 141 252 295 548 354 992 327 424 503 304 055 089 927 633 708 949 457 798 238 861 352 915 053 825 892 661 208 744 144 074 221 375 816 748 856 762 275 183 098 376 617 320 210 037 773 040 030 886 235 872 979 584 344 464 021 815 492 788 375 849 855 258 101 536 890 652 733 190 558 342 465 614 920 518 225 815 689 418 262 275 927 541 100 161 544 462 078 602 334 931 662 069 591 690 637 839 255 091 016 464 849 589 431 390 770 654 177 401 992 940 180 382 693 839 076 706 026 209 578 287 059 195 225 888 827 468 419 837 383 876 718 213 808 078 027 610 052 554 987 351 807 902 773 657 053 440 984 917 857 124 717 870 044 293 205 452 240 038 843 566 809 933 352 784 891 269 409 862 989 918 111 782 438 494 327 544 812 675 159 453 099 293 885 060 382 146 210 636 430 391 938 229 297 327 153 456 189 784 732 345 362 384 983 464 307 861 829 085 517 166 025 622 094 217 516 198 653 907 134 982 811 400 343 676 447 586 495 587 020 857 400 731 454 826 333 563 931 958 877 366 103 275 501 312 595 760 574 265 212 820 308 058 932 909 793 904 284 661 414 188 480 650 495 265 893 662 736 557 781 685 284 521 342 824 051 050 987 326 347 221 675 806 054 013 167 674 897 658 679 118 992 476 552 371 094 764 255 748 626 440 942 998 392 915 063 775 995 023 174 259 865 614 608 312 608 396 564 099 894 963 693 946 219 281 892 829 013 110 587 880 956 659 420 810 538 241 968 745 117 176 689 657 589 808 572 896 090 884 527 968 782 816 977 558 142 806 066 646 325 850 427 957 405 449 722 094 449 366 774 659 839 603 231 858 141 793 482 572 222 923 125 476 966 793 692 145 574 101 749 452 721 695 760 879 727 877 821 470 610 644 190 326 625 593 406 994 294 201 884 956 376 345 843 055 760 249 015 344 030 243 485 329 420 212 127 166 074 842 841 621 702 831 277 360 959 909 488 723 937 582 863 740 250 379 191 364 644 822 722 268 971 529 538 377 211 902 869 407 470 464 559 391 512 443 597 279 844 929 231 456 581 796 267 973 275 158 819 704 273 289 394 316 103 611 263 187 292 070 728 427 931 579 691 980 241 818 183 478 797 641 714 036 676 768 618 567 343 945 992 670 665 974 955 409 349 620 031 469 909 619 250 481 586 024 623 681 088 376 935 550 754 592 581 472 341 743 681 011 426 572 441 336 097 741 519 584 593 673 176 388 752 522 997 487 869 571 178 211 986 958 138 222 306 813 498 429 529 428 294 220 435 394 335 588 128 921 897 923 976 016 152 621 520 606 388 355 505 592 279 633 288 569 276 108 192 081 538 336 745 958 982 753 485 691 843 434 216 769 665 019 673 936 107 961 765 857 505 049 812 634 868 180 096 179 563 780 431 257 720 422 779 887 070 025 012 452 688 070 679 015 128 713 383 913 109 060 842 230 557 183 177 572 447 562 957 477 978 338 139 379 250 292 289 148 005 881 767 089 672 029 929 950 206 310 616 064 958 078 599 020 220 408 650 145 210 756 519 398 475 878 063 897 264 761 530 885 716 922 040 448 989 548 739 394 517 948 887 529 244 663 573 141 600 668 539 971 846 291 525 418 390 907 663 756 573 199 223 054 721 745 434 627 026 649 452 872 946 982 804 137 562 833 765 122 810 424 101 445 274 917 387 225 566 818 506 412 428 480 252 617 630 298 300 742 984 508 157 974 860 230 841 979 412 178 776 584 632 013 513 444 461 433 187 609 317 742 878 768 467 696 445 494 628 766 206 704 882 763 083 354 692 336 665 761 544 581 227 703 348 521 547 981 276 073 527 971 238 477 914 730 366 605 343 134 016 905 181 096 229 338 147 613 376 260 439 709 325 458 476 774 041 141 610 681 675 455 237 333 432 986 960 844 290 845 400 608 589 372 243 940 423 008 460 616 522 698 997 526 421 624 975 718 495 216 878 530 540 413 584 212 993 398 865 563 082 080 327 052 339 378 381 399 112 458 737 211 903 004 859 610 700 995 146 370 073 682 247 334 819 295 873 720 932 801 467 537 170 506 989 435 827 731 269 684 698 154 955 271 131 139 746 469 618 425 260 449 511 329 641 248 324 540 221 311 195 768 063 342 572 472 223 688 915 117 564 949 543 821 567 121 229 968 880 241 325 688 066 125 418 710 631 190 453 016 727 738 974 363 027 693 701 977 785 231 104 486 144 106 836 461 978 503 256 730 320 194 433 328 555 850 573 455 669 450 594 216 591 096 354 232 748 059 663 660 869 525 762 822 596 066 793 883 969 055 895 626 588 410 561 429 387 702 125 119 562 369 135 917 276 446 192 378 039 704 347 083 392 964 918 483 738 970 097 650 245 028 120 914 994 217 317 062 676 432 221 553 445 267 987 393 126 255 947 463 500 169 358 065 737 701 948 284 026 331 713 782 936 773 199 113 554 375 406 444 703 990 671 433 241 726 742 138 897 117 384 904 579 462 468 832 945 808 680 430 300 905 820 851 563 755 461 751 117 412 701 160 989 115 592 287 635 842 624 218 019 623 769 254 598 036 086 817 841 404 801 346 367 265 673 412 374 657 874 903 157 526 125 309 521 174 845 540 228 939 731 307 054 368 667 169 477 509 136 323 829 263 498 630 154 951 686 134 283 490 859 300 275 118 544 974 112 612 475 759 257 752 229 323 328 426 989 610 948 243 378 936 608 027 083 833 182 274 240 052 646 083 051 151 115 472 082 909 457 894 645 129 731 224 837 092 021 874 592 593 232 358 863 361 432 155 634 233 901 724 618 674 508 531 119 830 952 674 030 945 120 546 579 710 020 730 206 248 669 355 469 833 142 424 682 665 633 739 692 543 182 477 200 864 278 541 104 127 449 869 391 032 850 394 530 242 184 343 854 034 543 188 115 896 730 234 154 769 864 648 188 239 523 646 986 154 134 213 568 684 408 903 350 587 010 645 124 289 505 499 940 844 427 984 945 058 545 698 231 016 309 819 748 186 980 160 275 809 018 905 446 189 439 754 438 263 196 466 277 761 935 711 932 313 939 668 295 961 041 893 948 978 463 634 158 419 996 798 509 143 979 821 062 777 805 037 363 768 735 433 195 743 437 899 231 168 441 654 150 834 732 464 132 544 852 075 227 738 746 045 202 367 277 238 652 110 054 446 326 518 268 918 711 343 017 015 147 803 828 955 017 706 241 157 168 169 183 266 463 097 599 980 660 754 791 151 892 263 389 752 798 403 936 929 051 393 824 501 933 105 271 597 110 153 429 501 554 995 873 179 237 506 062 584 677 941 204 779 155 545 442 348 479 085 415 960 096 313 188 959 980 797 052 647 551 184 672 734 540 309 386 685 624 273 866 864 435 102 450 537 193 484 707 552 013 400 575 793 352 408 807 632 817 643 741 853 917 970 793 016 099 866 335 974 728 478 968 337 439 681 089 297 488 362 519 318 328 804 765 070 025 510 439 492 803 862 137 943 153 945 826 307 629 849 129 580 166 679 010 429 732 275 858 133 187 809 796 787 037 912 134 681 831 401 920 523 052 866 850 417 327 122 901 514 635 516 985 343 840 216 153 543 751 860 305 131 819 980 198 748 989 684 470 481 566 228 475 648 893 753 977 879 278 927 828 288 421 524 795 430 032 085 069 634 272 821 042 425 390 852 509 895 713 631 087 510 529 067 860 022 258 541 085 274 927 300 922 760 440 689 414 794 987 616 354 380 792 846 411 090 784 760 490 042 371 823 249 107 400 001 267 103 158 076 210 744 836 569 320 594 141 177 543 989 348 753 156 563 027 532 658 338 079 097 381 374 218 935 492 953 631 683 702 783 296 783 294 621 661 024 247 330 040 159 026 037 948 253 547 220 520 145 213 039 086 921 060 351 575 255 122 756 134 277 862 151 683 392 308 710 132 802 474 551 694 930 031 833 322 589 812 193 288 417 198 466 941 647 054 244 284 824 449 754 196 075 274 698 415 431 843 839 023 384 970 890 669 299 620 911 405 921 470 637 403 304 189 969 980 999 478 114 909 535 332 996 286 657 387 937 735 000 445 448 298 639 215 966 926 681 109 812 137 313 006 902 929 082 909 224 108 556 041 788 889 808 739 776 418 121 048 930 735 433 043 934 628 502 091 785 403 827 515 063 137 745 497 837 861 829 465 593 934 878 922 280 844 464 883 033 685 639 943 308 154 459 492 439 505 038 419 390 715 682 429 693 341 250 981 242 774 345 588 428 796 523 795 132 548 514 944 680 263 913 927 107 660 529 244 493 570 197 289 406 995 808 822 527 553 845 837 107 944 408 289 009 999 178 395 269 149 509 188 349 367 180 062 654 327 661 178 756 373 977 185 298 481 368 753 838 093 047 530 812 988 689 865 882 343 286 534 151 993 725 313 327 647 199 277 493 660 632 260 266 835 915 275 687 544 475 797 746 129 633 562 631 136 722 717 028 411 949 262 144 756 537 750 590 377 038 115 630 684 065 127 515 143 941 778 205 437 680 591 113 690 894 456 891 480 834 164 840 267 550 360 843 224 632 252 605 029 978 038 369 432 853 341 855 953 287 587 727 166 056 952 149 855 152 706 024 920 685 150 852 310 332 530 809 891 868 014 560 895 787 240 862 444 794 869 612 233 189 018 107 267 056 904 851 618 383 781 375 101 254 690 016 010 511 742 597 509 002 472 678 120 369 398 792 316 991 117 914 156 221 131 188 680 451 161 328 379 270 179 577 296 797 514 127 675 205 522 529 858 271 013 742 102 107 121 383 431 362 264 365 845 580 698 712 615 285 559 972 649 819 534 541 941 242 240 506 301 491 177 743 593 073 822 482 517 557 851 743 966 682 719 933 133 218 163 512 649 815 434 938 088 096 854 514 969 268 458 845 453 730 335 199 340 649 271 478 437 353 850 119 461 182 661 393 550 603 578 127 384 512 189 521 342 742 691 889 170 615 943 779 221 963 713 488 999 764 297 195 504 786 070 576 393 683 477 990 252 719 269 052 977 264 049 143 052 774 387 289 280 023 095 427 926 177 839 686 617 981 469 643 125 682 204 011 656 308 370 154 528 031 914 092 936 798 373 985 540 944 797 938 295 510 093 864 624 206 196 039 701 449 369 583 952 585 757 358 550 136 628 522 844 280 138 289 884 039 214 082 587 424 181 464 628 308 963 254 393 591 055 448 699 038 389 200 525 105 293 948 845 405 533 578 639 859 242 807 491 419 452 969 267 550 138 144 736 733 481 701 385 450 670 083 767 649 469 574 545 210 578 049 161 817 018 769 118 107 219 035 733 700 410 817 027 183 842 483 078 953 825 347 922 216 435 988 570 563 806 219 510 426 291 433 616 362 205 849 355 874 628 476 312 335 437 818 828 374 264 246 930 652 791 186 811 025 384 928 783 683 326 052 746 620 637 150 060 661 320 302 281 846 296 026 423 695 806 934 846 928 211 702 091 815 619 350 043 182 589 197 348 602 964 621 651 894 526 917 501 871 102 650 007 931 876 715 404 802 176 120 668 693 711 514 846 531 302 082 730 423 320 566 602 132 606 024 551 980 569 997 780 250 617 906 220 957 729 943 827 976 390 249 014 921 759 509 091 421 990 592 166 387 320 554 326 369 548 706 253 056 281 434 123 310 569 036 450 028 917 976 056 188 200 596 691 034 655 472 302 858 587 766 478 605 754 219 683 856 750 830 426 889 633 933 432 617 174 755 045 064 716 238 978 344 043 448 104 688 197 224 442 271 993 528 244 148 401 738 816 951 901 161 206 405 429 278 578 132 971 229 677 813 283 077 723 500 946 830 622 336 073 338 971 862 759 375 993 131 379 992 476 517 439 798 726 709 331 595 440 787 885 217 820 552 024 259 594 404 466 832 753 699 005 997 862 187 817 699 384 535 194 657 708 636 192 368 483 906 390 269 792 308 687 940 363 402 337 818 163 471 605 307 029 404 563 855 275 717 605 205 665 829 322 087 941 143 145 930 743 123 366 339 081 070 839 525 094 330 325 441 609 630 984 572 992 604 237 593 012 546 761 755 685 555 336 041 471 892 779 576 486 496 912 882 470 557 501 306 122 505 567 130 236 372 434 991 489 097 757 821 250 278 940 323 994 562 625 486 964 081 678 997 606 463 537 042 363 788 546 168 304 768 486 308 587 352 171 392 170 908 313 273 324 393 073 146 326 295 981 831 979 436 980 544 500 690 660 041 753 716 577 870 377 288 532 004 977 189 800 885 591 794 635 088 846 926 037 754 726 836 864 919 537 114 668 036 908 495 046 753 749 897 732 202 626 107 706 177 079 239 503 042 235 052 820 637 122 040 662 268 523 742 583 461 220 574 462 281 547 915 331 929 108 669 009 795 656 942 154 629 778 575 868 918 992 651 793 845 284 092 491 979 248 006 693 063 664 258 902 110 621 760 817 097 503 078 473 591 652 708 110 138 500 270 546 261 637 322 835 328 795 745 911 978 422 944 866 486 630 651 909 443 059 495 686 590 522 560 191 873 203 303 519 827 189 239 583 001 363 702 288 720 506 649 823 637 218 552 514 788 710 530 765 503 575 544 299 834 411 379 398 931 516 407 604 218 285 437 050 370 551 364 338 491 690 211 279 082 257 442 615 349 017 782 286 546 205 149 552 753 073 595 058 715 111 336 159 249 482 196 919 344 318 055 074 405 706 470 535 304 084 204 724 729 607 784 207 280 117 181 868 893 117 475 017 345 742 246 641 475 841 510 304 984 905 516 186 972 312 970 908 072 128 952 129 145 666 704 669 757 977 724 223 793 886 246 601 495 019 251 980 160 053 297 715 669 787 359 300 030 422 386 847 821 591 111 507 747 227 342 895 717 007 917 524 871 339 093 973 859 011 082 888 371 187 771 519 678 556 718 323 114 918 151 446 226 394 633 621 270 695 168 566 603 985 201 884 203 369 946 397 311 410 223 693 513 085 369 359 271 076 879 508 892 748 010 760 353 388 428 918 744 229 504 445 128 153 019 720 888 895 711 100 525 167 888 185 384 160 792 142 779 092 778 316 677 819 531 173 264 175 174 142 851 183 817 349 018 288 622 171 367 551 001 197 686 568 156 664 811 653 495 358 299 135 910 433 914 335 144 997 146 192 355 979 664 015 875 579 840 718 284 839 685 109 708 262 564 226 609 646 865 136 897 840 608 463 880 520 030 652 100 200 017 234 629 178 279 606 053 585 356 652 229 611 384 351 738 451 409 975 895 150 875 393 324 958 532 194 023 536 543 220 329 952 484 867 860 034 549 560 036 586 659 688 453 365 701 973 379 762 579 499 061 575 098 095 154 031 205 102 443 686 761 992 171 589 911 179 645 768 196 805 281 616 654 553 175 828 558 981 727 642 899 206 323 656 044 752 377 368 495 075 429 929 887 879 822 168 332 480 935 801 051 297 218 834 922 707 934 936 093 436 473 095 938 911 893 527 488 111 619 135 805 596 957 614 458 479 179 385 366 720 212 422 103 592 563 060 378 933 577 537 092 983 731 624 133 790 954 268 503 815 520 717 415 395 271 229 409 861 872 664 363 523 984 272 988 085 730 519 126 684 900 294 920 991 897 042 213 250 770 376 757 330 023 212 509 971 140 575 208 922 831 466 443 359 156 687 873 629 980 601 542 867 433 529 637 337 815 607 833 388 686 298 893 514 488 166 328 584 849 071 031 703 039 262 039 228 395 862 040 851 908 787 085 533 693 981 651 979 030 044 330 170 712 307 723 610 958 739 452 473 339 001 572 198 946 207 166 804 142 028 490 796 281 831 546 919 626 333 410 922 801 368 818 997 901 908 336 188 315 077 205 278 506 775 534 882 047 338 530 244 838 982 576 317 574 463 535 304 033 893 845 514 102 469 511 683 023 800 569 756 415 618 055 753 937 036 755 474 815 630 828 451 642 151 354 381 339 976 917 182 517 547 018 368 397 816 588 107 145 419 148 323 799 188 564 646 980 850 521 730 083 846 293 818 557 090 356 464 520 489 889 808 141 865 348 567 662 998 401 526 016 199 639 581 602 981 583 765 300 345 291 951 124 375 965 388 018 699 851 606 878 671 622 198 614 012 370 071 796 347 933 744 856 708 757 320 325 865 398 895 708 120 412 550 633 558 153 291 261 630 071 024 324 461 170 117 332 150 741 985 894 155 390 145 699 639 204 033 873 445 907 412 366 292 410 533 620 713 862 126 454 296 476 721 836 491 014 457 663 207 698 879 620 397 904 102 856 022 450 533 819 360 728 426 888 823 043 702 747 122 121 504 146 121 382 373 881 324 203 739 012 057 449 937 456 292 340 621 666 729 839 733 355 308 042 104 988 024 513 085 646 831 845 489 708 970 762 626 276 964 448 371 846 918 069 173 404 909 958 385 080 610 213 194 475 738 617 854 038 280 690 613 271 669 728 724 087 093 946 874 356 461 802 303 616 077 994 438 074 416 088 515 205 404 884 192 879 492 477 590 774 363 037 231 230 573 913 996 737 131 004 523 763 448 439 953 120 929 791 352 517 170 129 638 805 262 226 524 579 708 637 049 351 413 973 472 272 594 614 362 537 337 195 191 486 846 895 967 062 828 247 946 430 263 512 173 911 934 608 707 150 149 586 085 135 115 776 586 660 775 829 218 509 550 658 551 886 526 174 759 165 715 812 982 845 070 706 909 159 464 120 417 741 840 096 760 527 442 450 878 218 696 201 875 061 935 362 729 666 447 237 082 314 919 280 679 607 283 567 345 078 537 748 931 381 795 167 405 709 006 033 173 991 329 500 072 003 742 901 477 566 794 560 181 567 084 575 929 767 090 092 599 005 029 799 802 581 890 615 196 890 964 292 486 304 573 366 596 736 785 841 304 833 331 096 786 145 425 509 138 235 313 513 854 820 986 709 312 115 196 092 096 032 518 689 531 667 306 041 311 807 068 170 235 714 264 681 197 440 903 799 378 233 043 307 417 118 603 239 751 286 411 702 590 560 858 366 898 952 022 049 855 685 623 840 065 175 176 628 598 292 172 420 404 736 739 097 835 993 790 400 944 778 700 665 527 017 678 483 898 031 416 094 107 562 364 608 332 634 792 079 218 280 906 724 229 910 804 311 666 503 118 456 199 909 615 415 330 802 694 491 275 301 910 122 997 685 839 633 900 105 167 030 282 941 589 573 076 982 701 870 393 734 074 010 969 820 429 201 650 144 929 855 745 316 773 021 379 950 785 125 307 503 770 387 529 810 639 123 499 445 802 370 246 410 928 953 778 356 087 327 280 533 825 066 746 651 446 786 100 172 475 622 321 568 695 046 051 320 583 483 173 328 468 311 902 539 878 943 053 672 767 019 314 496 619 414 829 249 109 890 934 301 181 773 586 177 672 400 389 128 458 501 826 183 618 620 918 375 558 364 196 501 504 627 403 123 308 413 001 410 737 088 245 652 083 690 776 241 135 384 629 662 521 667 914 835 849 441 345 876 643 496 777 291 049 210 162 415 301 260 127 812 938 905 088 010 858 313 925 758 668 514 671 005 306 436 368 991 485 134 878 556 223 354 275 426 807 388 409 657 181 997 586 845 934 102 761 329 784 286 898 214 756 145 014 673 099 217 650 401 597 942 715 660 291 627 959 573 339 977 845 041 517 074 326 335 888 411 292 194 475 500 994 093 847 024 226 904 796 646 343 845 955 008 907 015 950 849 116 160 349 603 024 089 613 634 848 870 832 921 315 652 536 881 486 098 781 499 949 848 592 734 374 385 614 608 422 578 845 166 054 588 051 927 590 386 067 577 041 509 602 870 943 006 327 490 784 714 416 446 395 395 038 457 837 393 744 139 056 939 529 632 426 775 921 161 075 192 236 022 916 687 432 943 832 117 787 743 143 015 546 852 641 697 112 895 180 241 218 525 900 344 897 089 487 501 906 771 929 644 515 946 987 151 424 153 630 242 987 490 771 872 274 719 107 630 604 429 444 030 606 704 480 310 211 959 624 898 263 679 511 794 702 876 476 755 339 979 055 004 729 837 965 094 985 016 126 358 120 685 597 880 559 786 747 651 775 595 934 283 542 498 965 333 706 315 205 397 839 694 788 001 374 142 134 653 133 403 754 625 744 064 893 823 699 782 842 275 071 817 828 448 462 681 514 210 840 327 552 724 845 296 484 707 443 423 431 618 837 232 807 693 898 517 259 586 071 243 328 424 400 061 049 492 982 354 109 983 796 547 317 145 343 260 537 235 435 122 062 506 509 805 379 946 184 233 304 118 181 204 118 453 226 551 833 386 802 623 672 865 252 216 966 179 703 963 525 343 528 284 856 530 607 635 672 167 415 021 784 293 536 509 009 011 206 670 039 134 569 047 254 155 794 062 211 118 707 746 542 473 010 152 106 711 504 830 792 093 055 446 607 678 024 591 717 002 881 589 515 005 930 681 896 998 097 290 168 344 387 870 232 952 650 247 228 322 001 993 235 001 479 898 338 507 297 566 432 789 318 877 232 496 725 715 824 277 464 680 797 128 457 966 731 362 743 317 446 712 865 949 334 318 873 788 611 589 852 225 875 022 684 366 209 968 562 477 721 881 441 839 927 500 030 839 115 751 672 905 474 372 319 713 356 254 575 709 762 125 519 473 121 458 514 552 095 983 860 338 529 194 314 819 272 530 395 728 473 528 204 011 993 987 030 639 371 456 343 367 227 686 778 353 180 148 626 511 293 063 519 212 548 751 547 090 878 731 539 438 630 810 259 697 029 942 082 643 123 038 292 201 395 312 163 670 810 914 627 170 711 508 553 528 290 763 998 999 808 677 764 115 600 090 726 298 092 382 338 396 286 671 044 731 365 970 162 796 507 742 911 792 712 742 035 066 813 309 352 330 583 448 176 448 481 195 774 610 653 611 756 556 176 620 243 344 108 314 784 551 657 305 046 963 315 509 569 497 461 701 148 215 877 145 153 299 067 952 731 541 011 040 624 680 201 139 419 181 477 242 839 135 841 982 323 177 246 639 541 131 456 778 814 257 528 169 207 073 662 188 409 889 192 155 206 544 439 657 502 461 924 900 507 486 955 553 629 585 943 322 429 363 165 688 555 292 471 703 368 939 721 412 831 613 270 205 074 953 473 523 192 973 679 542 108 876 357 477 988 190 192 130 792 837 931 352 598 837 724 636 615 791 165 393 531 149 635 461 297 152 864 247 830 061 974 207 824 490 701 808 525 554 060 104 910 491 695 023 433 685 252 021 869 685 682 153 523 869 501 137 144 773 963 521 938 179 817 313 674 973 274 103 381 779 954 825 549 666 325 522 005 042 142 690 636 514 735 434 943 400 931 841 708 593 695 402 231 971 550 969 766 536 323 196 934 440 305 893 329 438 243 042 140 005 695 207 299 788 019 374 130 082 033 212 951 716 618 023 926 404 238 810 060 634 694 928 149 336 803 325 880 029 670 643 470 333 925 666 434 768 706 233 918 742 905 240 750 938 203 008 188 380 976 899 704 177 468 046 549 172 665 260 930 411 176 869 645 180 566 341 025 211 177 439 615 570 593 178 838 905 959 523 653 817 776 837 163 082 334 257 962 357 607 873 581 075 301 276 499 777 569 230 009 274 105 810 632 771 082 567 952 560 318 255 592 231 656 615 475 796 289 823 885 396 694 988 957 637 293 360 980 506 399 996 328 137 489 892 899 509 074 681 736 294 843 999 035 247 376 956 759 608 466 547 589 286 999 854 710 548 710 973 889 979 007 136 168 792 704 554 813 471 433 107 368 592 501 233 453 063 094 256 536 759 602 454 717 482 887 557 704 743 605 566 973 612 801 705 321 733 544 662 991 869 269 791 917 466 874 862 421 243 349 416 591 791 235 955 858 419 107 669 080 117 419 761 829 531 736 528 842 243 174 745 714 373 967 347 818 767 174 109 910 012 153 270 201 134 652 892 938 512 728 693 968 550 650 887 301 068 275 144 615 250 031 717 648 790 492 682 140 513 833 631 660 052 890 342 490 709 825 310 357 186 256 116 280 496 176 598 168 996 864 935 378 100 851 390 274 822 483 564 258 500 676 316 698 388 636 418 180 641 608 174 325 030 956 357 018 909 736 221 851 043 068 093 330 578 895 079 853 843 963 386 257 834 205 996 018 590 439 568 569 146 215 753 402 663 120 750 024 680 090 480 095 508 973 114 538 770 710 176 655 567 949 962 868 451 854 481 581 343 230 549 851 735 467 471 826 582 205 331 112 374 962 417 955 125 176 282 794 749 480 508 960 376 206 765 879 569 975 694 037 720 164 756 902 147 209 402 398 300 543 914 222 088 492 474 767 526 553 094 291 177 282 079 933 385 987 414 751 497 746 507 781 959 672 282 030 109 175 803 215 903 354 919 639 168 261 224 333 435 646 598 160 941 305 656 335 784 510 053 802 481 675 269 372 929 722 781 558 620 696 430 363 199 859 734 225 059 672 249 450 250 719 988 642 077 205 523 511 416 635 491 197 964 239 934 151 882 366 552 592 989 165 072 318 056 161 858 763 890 963 634 003 705 016 170 415 470 530 292 301 524 641 220 168 642 450 953 807 455 095 376 191 156 418 941 908 264 881 803 707 394 291 740 628 870 274 411 537 253 954 549 049 086 598 723 822 709 641 040 529 461 963 778 175 853 622 800 530 053 377 844 908 126 171 687 981 157 854 640 696 847 396 343 254 647 800 746 758 518 341 571 363 344 958 421 751 245 998 589 319 748 955 614 556 444 555 033 602 784 147 463 613 993 278 373 519 726 685 690 581 183 859 402 399 252 669 236 090 151 302 065 742 855 451 422 332 396 517 862 457 019 521 253 923 869 157 530 852 368 814 428 435 310 211 458 752 377 792 613 773 673 938 566 379 596 920 964 598 353 398 932 146 736 886 116 498 906 557 373 344 895 089 634 744 383 752 011 011 109 481 055 616 743 572 766 060 289 458 259 954 367 519 738 024 108 166 351 724 447 317 596 731 116 031 699 197 108 707 337 476 007 995 575 872 391 917 720 144 347 294 314 267 949 349 538 450 022 202 561 117 463 177 764 518 976 333 550 322 188 729 993 197 320 585 171 364 438 563 065 638 576 227 757 664 171 498 440 331 773 461 432 506 738 947 148 396 370 155 150 855 154 865 043 996 988 842 710 945 902 250 579 799 314 186 737 215 379 317 430 347 687 838 089 152 012 414 491 752 803 448 332 054 799 365 127 251 223 581 895 712 388 333 294 377 444 479 117 514 462 550 281 602 371 430 780 442 439 805 669 950 641 579 175 818 264 258 144 326 220 122 289 654 526 237 141 304 452 985 147 793 088 378 139 270 248 961 597 934 550 501 867 752 689 385 867 489 472 195 424 072 479 764 085 286 862 506 497 197 479 177 954 752 550 355 250 186 043 935 595 046 740 938 492 587 384 763 663 418 813 900 056 565 335 826 555 236 029 203 457 605 176 294 933 354 388 227 240 432 428 966 513 733 071 127 752 449 701 636 545 738 259 521 300 643 888 735 935 990 223 477 585 437 977 121 488 386 833 653 615 124 588 205 512 259 804 597 830 537 155 163 010 709 716 239 586 192 855 194 044 378 392 841 395 482 767 076 843 988 426 191 744 902 649 349 262 170 360 826 191 695 684 680 048 735 080 189 718 400 750 054 594 658 081 561 379 080 992 555 573 855 821 398 999 467 858 571 567 179 274 633 015 263 801 274 799 773 204 713 451 089 189 752 708 965 665 294 846 224 183 447 201 221 203 178 470 545 382 243 153 386 324 121 807 880 881 364 023 760 894 132 188 283 926 803 218 583 194 494 942 205 917 549 971 003 336 416 246 458 427 997 309 700 033 521 558 455 294 919 563 756 046 947 333 175 594 062 127 318 773 804 463 463 023 590 468 109 866 940 230 555 505 610 541 392 694 659 202 295 971 043 911 280 379 208 026 944 673 325 110 577 228 264 205 636 711 407 454 147 835 308 148 266 441 550 038 199 075 247 459 944 042 066 027 583 166 473 442 796 144 946 734 956 756 965 425 907 003 595 133 201 694 496 418 080 602 136 336 800 705 629 579 938 850 785 802 429 772 755 037 361 075 254 136 903 389 057 262 123 716 729 167 479 288 576 469 104 509 094 244 994 594 405 499 603 539 124 580 068 516 063 230 319 046 676 402 213 097 289 854 296 333 224 647 533 460 404 329 170 703 804 048 471 381 683 919 630 235 373 265 939 869 346 138 203 505 849 387 717 358 236 689 241 341 039 546 792 039 308 468 361 536 862 300 032 753 678 866 728 099 545 785 175 071 761 184 308 537 244 363 119 320 744 095 777 257 987 001 826 990 778 132 097 757 121 754 235 367 537 769 786 477 610 238 003 895 157 574 614 394 959 773 295 615 988 944 119 586 182 656 689 850 753 668 205 096 756 148 460 143 492 754 031 708 466 966 249 988 098 878 633 888 247 826 897 228 793 631 579 536 771 127 771 290 549 460 517 371 890 868 430 379 728 419 925 799 896 455 734 118 454 215 106 491 205 790 395 031 356 055 908 898 100 909 268 407 121 074 029 184 725 459 356 996 999 108 339 961 676 537 271 365 118 183 466 774 582 445 814 549 156 311 492 436 038 464 627 677 966 292 018 480 480 495 632 891 274 526 152 071 467 110 646 301 276 115 176 160 412 721 140 698 849 272 477 129 039 941 738 115 516 819 136 441 799 813 453 516 716 057 162 197 363 303 131 348 141 850 373 283 218 998 914 500 374 714 321 540 748 170 156 247 444 479 630 465 932 027 751 209 279 459 807 238 681 556 075 813 167 641 554 216 056 161 591 235 298 561 125 342 161 048 438 324 357 602 401 058 216 191 563 173 052 190 935 197 615 199 537 413 686 342 747 200 027 992 414 801 298 738 389 782 922 802 445 474 832 299 119 512 275 378 249 441 819 454 006 610 163 291 147 851 308 413 245 580 059 512 953 726 469 507 369 432 191 554 856 554 543 568 803 297 477 351 418 576 973 528 759 527 574 727 863 598 397 975 479 278 908 759 891 613 616 063 524 123 190 549 302 988 674 335 876 169 074 166 846 680 381 936 569 709 530 108 291 227 509 238 836 668 983 455 870 835 979 646 850 932 518 938 114 980 119 608 270 941 605 875 537 645 305 704 664 007 594 374 812 671 934 574 595 538 958 411 474 538 386 226 367 444 790 201 751 549 917 967 249 937 429 798 899 811 565 939 458 121 561 752 799 917 183 645 966 849 920 610 366 781 162 209 002 929 436 305 420 263 198 167 086 141 248 351 237 286 852 736 442 238 123 634 413 269 647 797 229 859 753 589 768 061 929 367 916 333 905 891 292 050 484 945 587 499 152 964 614 291 444 361 298 911 713 150 791 353 500 043 103 606 964 893 415 077 810 037 664 676 430 153 150 390 261 847 964 462 206 722 425 613 977 591 604 900 426 086 466 280 438 702 104 488 257 603 036 026 757 488 311 976 779 983 807 213 929 416 591 619 157 521 305 140 973 764 971 151 880 525 737 256 837 305 939 599 729 837 627 361 794 041 852 538 973 168 278 597 746 478 240 266 472 746 066 229 556 164 316 396 461 201 728 552 719 217 858 495 882 870 474 670 664 871 556 896 270 738 259 174 434 643 269 738 438 913 630 994 355 482 032 025 762 949 859 662 173 785 401 236 062 592 954 467 882 785 820 558 887 285 362 006 884 730 832 727 354 625 690 214 503 330 881 810 830 691 492 952 907 288 027 068 731 448 728 155 247 849 796 489 596 457 417 130 501 980 747 966 911 722 467 549 629 968 482 048 266 497 461 769 359 202 125 146 173 905 948 554 008 530 259 768 656 708 782 380 996 757 979 969 542 268 218 706 502 551 535 711 067 701 837 817 994 357 468 762 332 788 628 034 808 154 389 131 864 263 039 473 592 712 849 655 408 615 960 970 227 965 888 827 356 659 145 398 598 820 441 303 459 062 755 911 005 845 335 050 009 581 130 240 322 500 245 315 700 460 340 219 777 569 867 264 000 705 784 878 194 326 581 379 514 366 936 622 166 468 604 997 769 729 153 900 090 887 659 121 590 713 022 571 598 283 994 425 704 049 124 739 892 066 920 889 616 884 335 451 422 584 716 461 698 317 435 407 335 508 578 740 902 823 985 941 149 095 916 332 396 818 523 909 072 912 153 688 677 583 266 303 376 705 150 976 356 450 751 824 336 592 807 581 927 885 364 034 030 289 457 792 018 379 210 994 557 959 653 999 011 433 199 266 125 333 996 562 110 247 674 877 661 938 611 248 193 078 023 549 002 029 768 973 474 047 820 363 738 227 205 001 859 408 108 112 761 839 741 716 274 494 284 098 473 713 146 034 024 399 851 406 587 917 212 189 006 414 531 177 786 644 325 571 445 857 856 036 076 904 172 238 238 721 390 485 634 936 762 654 524 965 483 103 139 057 002 858 254 212 755 284 742 161 575 261 977 203 272 208 521 555 843 780 555 399 232 960 733 804 206 299 770 360 068 200 207 883 094 104 269 868 350 160 265 515 492 867 355 014 590 684 432 449 564 067 908 445 448 764 028 288 396 176 477 736 288 410 931 609 233 975 410 884 263 599 849 903 066 736 645 696 061 002 856 456 690 743 422 562 004 958 197 195 554 240 524 996 183 192 600 263 244 335 177 481 636 795 858 767 855 557 429 877 072 387 773 357 205 789 616 147 349 897 853 960 466 806 316 295 122 828 456 483 865 539 238 835 683 473 730 413 726 054 401 237 238 449 922 752 260 876 275 520 306 761 907 811 924 150 456 981 737 699 070 736 179 984 273 254 847 383 230 585 392 332 271 776 617 897 780 645 976 264 648 313 727 050 407 669 069 654 983 826 637 199 645 272 482 255 757 013 558 405 263 658 083 555 190 254 656 022 436 552 109 770 572 710 633 846 681 497 218 336 413 114 484 465 375 758 941 054 404 677 288 360 934 860 141 789 443 740 997 665 869 197 010 671 170 226 253 979 912 699 687 351 725 512 995 032 148 670 729 356 373 524 111 119 535 415 563 558 642 694 575 754 199 400 602 848 932 445 325 953 310 268 413 520 692 717 671 351 200 561 693 321 237 538 496 185 743 092 453 057 843 810 156 647 456 230 022 391 896 069 022 294 367 020 556 399 832 215 306 585 173 348 742 124 518 611 837 357 725 652 662 499 500 357 379 722 832 631 273 119 295 078 741 964 257 805 113 515 202 899 984 059 967 715 650 379 308 117 384 128 363 040 892 934 306 749 273 175 477 666 032 962 626 175 649 491 450 904 826 600 138 624 465 646 532 578 361 007 664 642 904 097 324 480 982 959 236 348 226 065 779 703 076 532 968 822 127 338 617 148 206 376 135 168 081 571 159 029 851 712 666 444 903 306 818 439 837 023 214 613 850 314 998 587 531 718 185 177 778 985 570 702 770 316 713 275 823 837 074 374 123 384 868 099 596 982 050 485 977 136 425 363 293 860 923 895 384 896 437 656 696 633 056 538 948 331 522 684 109 604 292 791 213 767 997 395 930 183 390 670 905 817 644 655 033 482 583 752 525 401 826 261 104 977 534 855 354 335 986 158 267 048 753 957 719 142 082 551 164 938 180 254 407 138 035 217 377 587 033 959 817 387 381 770 235 961 236 617 489 907 072 640 551 707 670 052 130 680 836 046 976 870 716 391 966 557 346 632 142 939 729 725 356 185 396 913 247 502 303 249 343 198 186 986 249 918 061 525 534 629 376 306 803 630 355 444 214 442 359 169 590 393 791 359 291 641 960 840 816 661 263 495 306 829 846 601 699 627 970 140 435 656 238 352 864 753 175 795 246 861 841 704 428 316 776 980 746 570 398 263 647 770 086 193 446 110 172 864 651 343 950 521 510 217 897 439 782 101 126 541 877 320 773 761 239 190 671 705 710 253 902 653 416 589 638 461 700 668 785 388 299 166 148 799 071 339 984 614 605 726 614 237 973 119 014 528 799 984 941 131 101 406 111 879 883 920 599 832 402 973 474 049 111 628 717 127 088 683 384 423 532 629 131 219 131 314 203 534 790 989 030 347 179 661 608 132 286 478 332 327 300 485 111 732 807 069 266 422 370 895 748 187 767 139 055 224 305 730 919 572 469 924 028 430 263 938 042 385 075 213 859 504 725 880 890 815 283 677 955 583 131 107 523 589 307 447 522 493 885 934 594 625 032 202 889 774 400 820 119 559 990 629 997 449 454 702 890 698 925 661 494 692 762 927 406 321 070 094 650 656 891 729 996 420 087 546 310 769 346 469 091 349 192 650 226 839 401 609 203 486 424 176 198 978 097 958 944 097 648 190 669 816 201 565 054 971 880 531 611 843 779 872 759 473 033 663 461 002 014 715 430 013 354 282 598 947 050 640 735 487 905 422 025 032 831 126 425 378 887 575 933 568 001 879 830 425 563 433 109 101 244 871 528 377 355 232 650 592 640 356 160 766 540 323 619 510 800 463 442 271 305 096 345 687 199 663 435 030 881 731 628 953 890 961 504 608 196 889 313 963 490 711 822 189 777 816 199 793 261 075 373 170 409 406 207 556 774 736 389 526 828 593 703 946 959 145 270 994 427 436 814 749 892 962 899 685 540 068 694 681 979 024 535 301 942 966 559 882 678 657 492 517 099 732 219 386 508 871 062 828 460 217 489 306 383 792 915 322 585 298 111 082 524 630 474 473 704 488 670 975 925 295 974 885 167 831 069 312 536 656 367 894 159 168 524 199 491 816 988 704 786 311 005 348 295 249 184 055 564 533 390 389 456 670 600 909 494 583 271 173 088 190 309 375 771 274 083 146 423 764 533 349 509 065 036 847 828 793 195 331 628 325 391 755 703 761 629 136 720 159 590 695 771 480 994 810 615 284 118 745 843 762 855 428 380 366 172 281 382 344 957 923 687 249 143 989 455 943 751 514 954 510 817 852 054 576 436 786 020 655 094 201 943 979 325 781 685 177 052 957 048 978 834 031 899 367 361 803 573 901 833 690 550 148 530 594 522 795 289 485 978 335 571 755 247 994 366 167 883 303 181 176 768 571 197 956 129 291 549 900 180 809 993 551 390 207 413 900 723 405 823 499 489 297 245 790 739 603 549 519 193 968 131 694 707 121 735 624 403 743 085 812 536 822 249 907 382 983 598 252 221 172 020 562 823 144 989 680 589 833 391 878 542 621 530 437 238 471 225 002 228 208 897 721 342 047 654 632 021 695 702 114 663 756 032 980 410 682 787 194 207 025 090 603 581 760 205 961 703 347 063 499 780 738 838 147 541 649 833 836 464 879 784 856 893 809 940 896 883 544 994 383 463 047 924 614 742 030 212 223 274 062 385 299 993 226 303 138 038 855 824 411 760 436 049 814 416 953 837 226 003 312 762 156 282 553 893 818 022 054 956 892 920 754 867 824 179 502 790 248 007 337 175 059 207 206 421 213 140 480 763 598 440 778 282 369 933 705 609 497 324 358 752 275 875 369 900 793 776 873 620 921 774 427 902 375 699 372 782 919 810 443 524 390 607 688 139 987 507 386 451 407 227 692 097 140 466 384 359 304 554 118 824 805 257 964 676 433 107 969 574 943 021 350 051 873 020 622 423 138 027 561 777 377 286 442 172 457 398 592 236 400 544 933 680 312 813 425 509 880 721 005 046 584 222 673 812 389 934 965 439 127 439 680 789 333 433 414 659 332 753 487 157 557 293 802 157 098 564 968 647 554 889 337 706 239 673 262 525 505 357 627 321 065 809 534 533 346 089 548 262 868 704 934 154 423 886 910 503 616 294 967 721 443 252 994 157 374 369 561 328 538 999 644 481 100 764 144 922 295 608 231 408 295 754 015 617 274 582 046 744 324 157 753 425 017 611 429 156 704 500 675 207 051 304 212 170 091 342 691 980 622 674 825 593 038 879 358 957 898 682 366 803 276 714 485 030 563 018 416 603 206 822 780 331 276 780 986 535 575 954 663 371 096 477 915 395 569 637 608 311 331 678 827 628 460 026 019 232 021 822 701 091 115 439 971 427 539 321 195 172 958 092 077 231 209 401 815 829 270 900 324 531 043 083 329 173 832 836 738 479 437 559 029 242 748 466 229 790 263 531 671 803 195 504 652 158 467 975 471 000 809 170 811 113 468 935 762 375 164 194 775 935 020 490 305 242 780 380 860 236 424 770 163 905 841 114 862 719 997 038 047 906 501 140 803 678 862 084 700 277 273 134 523 164 395 108 207 534 438 135 109 739 986 858 856 926 583 548 312 210 995 245 289 932 267 667 718 026 686 432 029 247 012 720 321 986 431 321 349 905 407 907 687 651 493 432 929 251 611 099 226 572 134 776 811 757 202 168 895 524 681 418 794 248 402 590 138 712 196 202 626 300 484 677 040 739 447 931 136 469 048 324 698 874 021 673 975 434 038 973 272 956 450 153 951 975 848 520 437 063 736 726 015 081 443 373 712 519 383 631 521 914 369 776 269 090 466 884 220 592 666 463 714 731 677 797 602 133 416 485 338 084 284 925 775 578 496 190 841 251 231 884 789 700 580 480 310 305 095 806 342 048 722 879 448 068 001 299 477 563 383 677 406 000 926 101 478 505 309 100 561 398 591 901 641 004 851 877 899 312 815 097 382 055 683 808 752 050 893 751 955 501 413 217 376 076 967 343 805 976 740 125 215 917 828 223 965 333 135 327 316 902 062 354 751 899 832 625 831 673 528 417 633 635 511 022 979 694 895 588 214 378 755 676 651 041 476 234 432 990 953 600 282 013 602 067 878 266 321 631 016 259 331 579 136 393 726 760 350 448 516 546 003 329 210 477 433 074 862 935 291 475 323 371 537 619 629 603 546 191 656 189 512 986 878 582 376 886 991 525 959 932 478 244 690 075 960 877 693 610 544 908 002 510 392 790 124 304 520 820 637 420 468 150 262 892 983 436 418 576 174 080 629 169 293 005 927 715 735 563 518 992 399 129 877 710 514 432 801 663 516 403 219 243 346 880 628 583 321 448 099 668 917 525 433 355 611 448 809 813 448 234 378 403 304 723 623 734 125 174 188 332 755 975 103 239 307 608 526 552 288 590 192 842 702 517 365 839 651 972 043 658 621 775 425 211 931 861 256 342 689 948 896 226 263 318 529 547 766 877 582 641 796 225 591 615 324 572 292 191 875 352 979 804 592 546 347 523 612 575 682 294 567 971 308 217 423 651 651 028 427 161 874 209 941 740 524 207 106 081 254 337 679 067 786 552 698 047 502 601 457 508 420 091 442 882 081 537 850 958 054 307 960 750 310 033 043 874 446 072 534 158 790 440 360 580 970 778 446 658 300 625 334 046 063 045 400 602 075 996 487 317 270 418 119 379 591 932 081 485 374 201 878 463 936 972 705 238 502 104 887 791 106 211 395 135 076 766 959 925 684 901 666 687 494 097 064 135 270 505 504 185 947 828 201 508 657 639 141 642 520 039 148 671 135 831 282 872 865 474 342 391 399 207 948 059 204 566 860 574 269 891 834 845 592 492 408 976 180 448 166 754 521 658 206 098 675 263 665 278 992 448 412 702 073 483 660 879 225 187 488 583 869 018 977 569 525 545 795 948 035 126 732 121 867 805 222 419 184 578 057 966 670 567 176 553 211 293 455 681 146 522 890 072 056 466 987 461 736 916 748 499 709 283 042 172 243 236 919 397 050 770 584 115 310 118 673 788 324 723 474 415 537 892 010 915 464 015 496 564 381 849 916 528 134 116 398 049 382 821 635 526 993 318 353 293 275 988 563 173 753 268 845 488 425 630 241 462 593 886 392 358 603 489 743 959 027 335 310 505 371 381 983 492 134 386 383 172 077 469 915 371 794 091 034 251 799 696 669 313 875 142 976 618 338 665 585 785 981 585 684 496 290 584 634 829 315 633 921 342 703 777 363 947 149 903 915 691 614 768 687 066 766 044 580 313 838 850 177 601 185 800 020 874 304 479 849 709 438 217 257 121 117 338 599 130 972 938 662 133 583 292 409 866 453 280 527 342 162 055 544 615 770 621 163 483 931 365 308 383 379 392 895 825 438 963 380 493 385 130 757 982 006 956 591 233 413 596 679 064 979 711 458 138 869 251 876 006 179 067 723 174 635 489 634 974 717 018 877 342 928 137 913 185 063 547 392 918 141 653 643 441 402 580 026 005 849 988 245 675 399 702 501 350 209 140 161 157 401 290 326 407 935 119 964 222 584 136 164 178 926 215 178 360 292 806 003 435 422 860 740 447 558 057 655 491 855 868 360 604 400 694 124 713 206 692 455 766 173 806 939 112 170 450 378 966 514 989 901 349 986 357 325 065 294 408 902 171 211 296 231 659 571 364 192 701 698 542 414 962 798 481 226 346 894 263 654 770 275 042 189 137 561 718 903 322 888 738 464 203 411 948 565 867 833 029 520 175 282 057 513 972 494 865 620 221 447 056 470 211 193 976 215 968 585 276 837 922 156 485 843 945 509 603 286 566 118 555 070 965 058 224 780 810 908 443 089 986 668 398 023 300 431 718 257 671 138 094 884 199 091 224 667 675 224 200 521 902 786 424 755 187 005 845 166 401 134 571 723 995 426 865 168 717 028 878 652 376 102 409 394 245 774 394 975 898 681 604 373 204 749 831 453 359 730 230 323 608 136 464 586 834 808 972 564 423 059 019 756 522 455 324 504 665 007 266 933 532 354 213 382 890 132 250 058 016 577 990 749 101 253 618 054 424 757 970 779 321 629 998 684 764 569 386 436 365 729 830 577 439 332 994 071 090 863 293 463 121 520 754 175 878 213 350 825 218 681 987 801 566 451 333 019 777 547 917 205 925 700 122 284 805 344 363 102 533 950 898 963 220 367 475 210 399 557 674 131 227 877 616 621 464 881 995 711 975 541 267 004 522 118 490 315 394 785 819 144 229 789 364 942 251 610 090 089 095 059 107 310 211 744 716 732 541 035 411 208 181 354 439 270 494 300 583 266 970 218 932 722 774 516 918 262 493 444 511 208 899 434 822 074 561 256 904 295 451 268 417 654 164 779 100 765 002 429 633 535 606 998 661 412 441 915 863 041 545 807 808 515 814 693 334 183 492 272 874 451 834 614 821 287 888 590 018 882 415 718 302 581 975 214 245 577 747 934 913 051 774 602 773 648 663 228 081 876 280 648 009 301 600 853 457 885 641 604 870 585 851 460 213 393 745 645 143 411 832 436 687 537 632 442 470 286 325 165 246 014 914 945 161 705 603 710 950 076 730 112 191 407 424 319 620 804 782 703 623 177 915 173 137 344 910 982 185 428 938 720 944 311 481 993 577 823 193 799 998 997 137 282 527 516 058 665 603 089 661 746 423 165 334 024 393 372 201 529 781 642 248 273 269 855 051 073 528 231 785 091 320 719 320 815 374 507 793 783 976 671 068 475 559 698 143 341 725 475 225 833 413 764 982 944 874 997 139 102 203 107 599 212 042 996 416 479 950 042 584 168 585 988 495 543 750 974 478 525 306 923 197 115 555 250 874 283 055 560 473 228 533 462 868 284 652 187 252 345 191 292 165 575 809 649 295 829 982 439 080 615 245 246 727 506 315 650 454 302 216 833 417 377 940 827 011 642 753 361 790 172 943 109 682 249 329 624 888 325 646 475 557 103 624 628 313 662 026 883 718 886 918 768 387 405 746 586 519 096 601 050 780 382 868 419 667 349 113 566 170 792 273 808 756 069 588 219 249 123 668 668 892 193 018 977 937 552 960 389 099 568 733 179 547 061 602 525 832 196 325 935 552 943 038 013 656 646 855 290 748 823 401 640 974 297 958 425 188 521 282 094 172 805 618 468 595 197 146 801 464 250 666 751 605 064 790 883 455 515 140 360 889 112 182 284 217 932 693 534 914 731 762 470 909 192 781 237 829 458 469 707 686 033 635 109 076 453 427 795 908 267 031 935 910 021 600 437 381 857 813 158 235 439 545 767 546 735 311 468 451 568 487 884 988 542 374 070 618 141 550 191 668 060 166 573 121 286 181 589 370 438 546 570 023 741 163 437 366 304 791 546 620 130 214 884 418 784 490 748 363 894 222 098 445 896 082 037 198 710 545 966 371 237 766 482 734 378 727 147 125 105 073 863 207 177 066 054 142 630 167 482 526 185 660 618 236 905 490 637 864 421 706 303 793 026 271 688 047 977 373 427 847 166 942 442 358 676 888 982 438 248 829 458 840 504 862 040 539 203 186 447 202 550 695 787 359 464 436 605 800 107 911 988 492 994 862 601 164 797 824 489 234 267 071 799 025 482 728 652 952 777 234 445 459 699 933 289 897 260 582 065 926 786 643 596 932 222 053 572 253 236 667 084 430 725 236 555 588 848 041 019 511 005 817 317 335 205 858 034 325 088 516 591 925 099 680 624 729 550 713 378 275 034 732 964 907 538 512 894 520 478 295 932 155 197 770 662 029 960 316 128 373 673 253 494 140 395 126 732 723 679 562 575 171 089 939 397 021 663 395 273 738 592 742 266 905 421 132 374 217 163 831 881 119 985 097 100 890 671 007 710 983 915 002 070 279 727 821 050 675 169 057 635 355 410 249 587 071 878 291 582 923 484 730 822 896 470 526 745 009 580 382 694 662 042 561 895 513 502 704 612 944 226 821 739 473 448 908 223 681 553 734 752 463 592 564 663 068 433 035 059 715 615 210 276 560 331 192 130 314 030 523 719 500 456 155 937 444 955 405 969 817 289 873 498 089 466 866 713 652 472 162 541 002 752 011 354 839 335 991 815 924 106 240 180 477 396 039 311 814 539 577 207 064 274 585 381 387 959 929 121 224 726 822 406 775 250 981 770 149 767 440 911 123 597 910 206 270 881 628 408 064 950 319 064 496 961 903 248 766 664 660 845 974 748 204 686 161 083 268 006 898 743 757 997 517 032 472 370 313 677 911 120 601 571 990 444 934 896 640 153 007 098 818 859 385 930 129 074 013 417 687 404 735 739 130 662 088 603 911 089 249 132 669 173 516 836 103 970 296 317 885 822 698 394 463 121 247 081 420 440 229 811 027 910 633 125 888 322 140 289 453 154 133 652 567 316 687 904 397 242 018 380 024 745 970 655 089 560 993 874 863 748 148 858 969 189 458 111 398 186 341 091 061 398 565 611 151 754 214 609 856 514 262 693 033 840 350 124 924 922 847 608 097 098 820 181 546 245 009 200 953 340 223 413 927 563 798 730 232 702 387 899 487 109 338 247 426 637 963 987 995 515 194 186 578 239 156 979 196 984 582 243 921 259 114 689 134 852 224 617 477 748 585 223 880 072 879 918 829 865 908 042 663 224 653 582 443 055 602 786 271 576 982 889 493 947 884 480 384 169 367 399 770 112 689 168 244 821 380 743 964 363 413 675 919 724 269 036 852 395 482 782 658 744 553 159 685 063 379 251 222 316 175 826 390 824 830 410 086 953 488 415 280 820 673 344 653 728 136 997 679 917 136 331 775 131 865 426 919 955 002 955 559 232 115 216 617 034 465 668 058 024 052 647 708 938 146 952 929 147 201 133 491 486 096 805 848 390 586 234 254 972 339 217 435 165 223 033 598 268 467 109 740 300 921 952 878 073 000 972 501 997 345 920 379 694 094 309 619 641 570 238 615 829 124 184 532 669 958 343 374 664 165 627 718 714 268 877 305 486 028 127 326 820 870 800 213 022 486 492 092 730 003 396 556 977 683 559 353 099 542 078 437 046 068 909 575 515 905 481 824 655 507 563 627 722 949 464 218 419 224 337 585 625 001 108 887 684 693 751 962 194 562 775 776 465 782 065 557 789 467 168 052 970 501 368 483 873 750 956 428 850 639 658 061 380 561 024 947 016 816 835 584 641 194 816 226 040 357 203 101 025 668 649 529 700 160 164 766 323 403 890 684 630 518 529 644 783 631 095 707 627 732 126 563 609 307 756 383 719 257 990 160 211 137 391 347 908 750 944 985 263 857 921 929 039 198 384 426 335 985 926 373 173 045 311 181 311 269 183 974 691 173 480 376 790 446 603 443 238 797 073 354 998 906 759 723 063 905 525 704 472 082 532 877 714 158 423 422 290 368 532 155 096 940 408 556 809 144 114 499 224 980 863 640 291 194 201 260 239 533 509 823 469 515 062 852 810 136 009 670 891 476 884 681 792 161 138 525 877 085 128 973 653 496 091 344 890 125 272 940 371 921 767 040 898 128 550 251 334 727 613 466 793 840 871 796 890 804 156 551 575 790 491 407 863 879 637 514 470 615 699 516 210 239 490 585 538 234 869 875 888 606 231 712 404 808 949 097 968 757 270 437 545 124 038 951 851 664 582 880 632 387 081 987 302 684 858 869 845 594 797 346 087 760 187 439 935 511 619 302 040 728 723 851 153 363 386 368 611 177 123 110 944 779 317 573 645 558 049 442 283 906 184 976 608 191 995 402 446 704 841 466 976 472 441 933 425 054 576 588 722 008 876 055 664 466 591 968 846 789 641 732 682 127 517 602 429 485 288 323 624 479 700 785 885 346 349 468 831 140 761 576 707 727 084 880 374 957 147 111 039 167 295 175 544 227 079 797 082 538 965 799 792 713 322 439 369 978 476 317 517 072 190 299 993 300 423 654 420 509 201 653 795 547 524 910 523 960 140 383 451 777 287 719 760 047 521 836 728 972 511 880 187 504 658 701 556 904 041 787 045 267 594 562 190 465 223 109 746 804 052 659 403 827 744 499 538 220 083 739 502 363 517 074 790 191 926 586 238 188 010 519 067 298 420 841 378 530 265 092 530 884 995 596 791 001 165 651 346 688 133 780 421 305 588 386 797 626 890 561 409 065 758 725 546 479 297 087 206 401 437 424 254 152 181 232 609 178 196 247 113 226 416 793 349 540 124 707 889 528 023 335 135 017 875 601 248 478 885 827 975 525 730 977 498 101 741 331 668 506 598 004 970 220 928 697 812 376 784 855 109 299 179 799 069 627 203 983 873 923 862 080 756 813 181 027 567 767 435 777 496 088 160 176 640 531 925 718 719 398 942 412 938 444 595 712 594 846 715 330 515 178 601 744 141 967 693 136 219 653 777 968 956 585 717 762 365 140 571 663 806 979 097 627 531 784 540 159 261 166 172 259 292 166 673 208 041 729 935 024 432 655 084 840 330 146 002 599 387 093 092 804 241 759 926 837 222 666 108 191 904 726 713 295 160 588 118 487 280 423 438 989 981 344 361 870 370 335 619 940 918 831 214 701 763 038 682 015 235 862 187 132 137 551 082 601 626 288 450 518 033 703 535 301 463 939 185 732 616 900 267 254 823 564 337 303 923 370 681 245 638 042 195 764 394 865 363 569 899 448 148 077 323 562 035 990 513 253 442 581 650 141 068 502 882 975 853 609 694 844 571 437 327 709 106 070 646 548 876 439 520 388 245 388 164 829 165 220 594 726 387 527 652 799 504 426 774 387 536 483 138 681 244 272 131 886 433 116 221 043 398 785 099 691 840 815 421 989 329 201 366 734 374 438 430 292 550 904 457 207 647 409 542 798 830 879 550 618 345 657 068 820 964 494 867 350 622 911 606 055 873 447 227 596 143 308 626 718 946 778 490 137 974 212 329 558 024 754 273 008 259 618 661 456 157 130 690 217 310 824 144 396 077 856 676 313 562 510 943 286 459 671 605 111 344 975 855 230 264 511 838 530 506 486 932 635 151 054 219 253 928 202 386 021 275 732 131 867 190 305 337 076 563 239 127 939 340 306 552 173 880 171 646 230 397 843 841 486 491 805 017 469 301 364 281 557 361 587 809 648 324 061 618 280 005 758 885 372 912 630 336 289 298 035 698 941 936 393 533 766 855 373 023 815 137 136 139 886 542 876 169 526 730 684 708 700 562 292 996 606 557 927 181 952 628 941 451 765 356 004 596 823 990 961 210 618 954 816 920 804 706 265 422 611 786 384 417 840 018 475 407 602 304 775 460 326 296 692 312 883 378 762 217 969 993 182 639 161 406 007 405 367 453 167 316 040 481 853 131 179 275 981 415 833 828 668 022 385 642 667 517 661 028 865 234 530 345 389 706 383 342 205 799 293 635 837 579 011 560 998 096 825 959 210 914 291 390 982 254 645 232 436 035 036 470 236 054 516 185 086 597 049 193 326 925 815 704 811 858 988 855 552 984 877 362 054 542 037 795 879 863 328 883 765 833 029 067 155 646 931 904 826 647 688 920 896 449 984 522 648 552 457 170 194 770 193 625 727 684 801 537 992 435 849 211 270 902 831 917 497 031 326 582 961 997 401 076 394 913 176 710 409 606 332 362 198 392 008 155 564 141 472 713 330 383 999 436 458 379 361 084 636 816 711 589 213 764 144 817 269 091 316 678 288 300 859 432 407 335 335 928 736 659 352 557 895 857 318 541 033 318 898 517 616 383 566 848 210 939 424 720 858 132 459 442 283 746 126 823 374 371 881 302 425 982 095 251 532 413 104 102 520 559 630 842 175 228 986 625 871 415 039 101 768 837 410 242 743 041 311 532 093 410 878 897 642 752 726 453 559 030 656 927 407 163 992 007 026 271 112 260 712 150 688 940 859 991 938 999 861 358 745 229 565 964 884 316 531 961 479 087 055 013 250 554 942 928 136 499 146 729 366 902 579 710 148 444 892 423 563 892 353 656 115 094 025 847 225 504 683 761 552 269 970 329 247 882 057 132 875 867 208 623 730 502 086 703 719 006 119 617 294 752 372 869 791 883 157 500 286 603 238 676 391 094 468 047 835 585 919 318 667 893 531 547 953 485 199 551 963 389 433 842 121 478 626 552 259 175 072 385 063 914 107 396 174 320 035 383 029 918 621 434 516 358 507 190 132 916 121 601 452 183 229 714 296 413 310 681 723 353 450 693 014 135 566 767 248 879 433 746 690 150 318 440 936 454 622 331 379 314 340 854 575 848 449 411 906 634 709 359 998 372 072 117 069 308 454 070 951 262 494 213 552 243 224 164 635 931 765 716 075 537 583 225 795 569 608 772 089 559 063 213 091 461 223 711 463 319 270 264 841 373 278 593 676 663 177 324 987 916 980 417 892 287 948 135 829 742 996 233 712 223 141 970 366 022 051 031 426 257 579 001 271 826 726 751 793 649 624 137 401 474 991 298 096 390 527 409 846 211 662 030 158 194 730 598 605 135 530 650 604 449 660 471 125 923 255 272 144 862 707 492 795 356 316 727 068 474 141 236 881 102 592 076 639 035 242 856 750 295 163 576 078 561 846 168 939 715 379 206 299 676 770 132 093 070 786 555 781 579 923 418 884 236 801 860 055 970 894 619 175 276 910 164 173 339 538 955 790 225 213 208 527 781 880 903 829 353 089 475 568 864 366 691 288 985 403 345 437 471 925 890 595 399 718 802 446 135 588 631 049 370 233 168 140 796 365 704 137 592 949 627 575 617 307 113 938 976 819 218 881 125 330 032 845 762 402 629 540 834 043 880 629 659 363 519 398 158 144 681 269 385 148 269 191 867 793 227 848 750 362 178 767 576 558 738 928 136 079 916 827 212 816 831 450 172 161 232 715 956 340 147 015 781 999 873 782 101 835 392 467 199 575 020 161 924 544 540 452 478 792 171 823 094 904 746 392 052 185 349 127 302 639 845 415 696 215 218 531 636 857 982 952 511 932 835 094 254 252 743 694 049 587 697 124 858 585 232 956 514 288 335 756 624 830 579 518 690 918 902 481 900 982 551 500 609 614 774 054 007 527 699 937 091 427 983 328 150 187 753 853 902 629 607 754 040 695 311 618 962 320 249 813 390 341 347 311 034 042 300 894 474 163 013 742 884 841 307 301 547 457 096 918 042 661 102 089 687 689 698 060 681 960 100 422 059 038 839 074 599 494 198 834 397 456 786 158 883 759 352 093 774 458 032 084 956 674 757 465 511 166 859 096 357 042 309 886 801 198 935 412 217 125 788 383 935 607 956 079 227 084 110 769 366 053 485 735 482 487 172 088 939 785 275 032 196 026 584 735 903 583 397 216 519 591 084 874 394 409 753 400 465 889 413 318 530 816 838 344 198 388 291 028 043 022 320 767 081 833 948 123 756 059 188 450 092 330 855 843 951 202 670 388 985 402 934 252 765 692 760 190 068 282 843 212 324 457 070 703 370 886 428 479 431 724 906 653 531 279 353 375 444 493 805 202 802 367 146 317 671 699 068 607 765 731 187 348 425 692 687 751 603 214 118 698 376 729 612 823 181 843 784 517 118 805 630 766 399 048 206 028 526 340 237 609 218 962 433 758 499 167 248 653 558 274 325 046 206 488 047 500 398 480 958 616 486 821 983 209 431 722 972 919 396 840 643 808 244 583 474 181 500 776 519 719 195 557 852 324 632 508 119 416 045 294 460 172 578 107 800 252 002 523 496 649 984 401 118 570 610 366 680 423 102 224 885 577 220 840 429 221 735 809 588 030 567 343 661 116 854 056 877 168 331 948 304 520 474 755 309 261 335 154 620 083 072 411 386 278 361 909 561 420 034 509 606 566 492 261 448 187 963 497 831 213 531 684 258 062 761 106 934 122 530 802 512 995 023 638 754 619 231 289 085 511 614 386 862 001 826 708 778 253 827 611 312 910 900 263 289 828 876 754 086 619 964 767 287 402 386 403 457 528 497 244 337 625 388 823 553 777 076 487 534 469 694 300 073 695 435 253 339 273 959 742 115 839 910 477 983 568 636 118 270 291 833 534 811 324 754 529 346 781 434 489 003 960 517 263 118 519 696 022 335 714 425 296 879 197 123 897 586 777 318 018 949 124 353 585 657 937 657 453 727 691 777 006 538 221 631 462 993 317 598 567 274 338 583 171 271 477 825 468 578 042 356 225 725 819 952 821 230 448 584 497 240 440 349 505 493 558 013 286 875 555 143 145 505 831 818 644 094 159 420 388 408 938 348 460 135 102 371 909 776 840 313 446 003 090 414 692 742 973 284 970 004 427 001 664 396 720 171 423 489 991 974 063 811 998 854 913 362 961 347 312 765 842 555 090 318 469 339 094 530 893 766 873 027 030 996 587 463 919 906 096 438 661 389 008 652 342 939 825 620 960 222 043 366 493 814 845 787 964 492 927 875 448 234 224 266 091 384 810 087 568 476 632 142 650 342 423 045 953 143 886 050 488 556 911 895 223 683 135 682 690 200 050 422 228 360 173 432 536 239 745 691 687 329 783 105 356 556 911 801 573 375 860 429 943 130 131 016 512 214 323 829 614 295 605 820 410 852 939 786 896 161 992 569 896 552 384 264 345 504 026 302 719 388 708 835 028 618 718 605 963 179 804 758 312 941 708 317 607 697 761 790 831 070 304 211 931 918 040 282 270 590 088 181 031 727 039 949 138 845 251 823 304 095 117 164 569 180 488 346 627 591 048 502 135 972 339 554 209 739 808 449 615 000 633 574 229 744 379 478 203 133 830 409 785 202 837 969 822 059 144 218 628 182 451 885 201 401 259 428 588 679 529 123 564 654 308 128 062 886 524 939 483 688 861 815 902 105 118 830 441 260 262 610 080 540 007 208 122 293 890 761 280 924 068 703 163 669 175 917 684 517 759 247 001 949 534 243 278 693 522 663 091 092 008 197 539 703 596 476 386 536 585 839 248 269 579 016 665 935 572 875 328 570 895 288 957 118 835 998 204 115 461 301 209 667 794 818 261 672 443 310 795 002 992 245 534 480 239 355 925 236 886 715 690 560 392 588 423 883 610 764 273 495 856 146 924 391 416 121 621 390 470 380 007 709 171 058 763 738 738 494 216 849 345 771 568 393 768 726 193 837 950 078 357 774 877 485 683 019 463 718 684 290 363 091 128 148 719 574 002 882 326 014 990 192 977 999 905 555 594 676 738 931 935 949 711 735 894 838 564 697 638 646 924 379 559 577 593 960 315 462 308 672 970 134 752 639 782 011 988 093 260 057 270 936 330 075 168 042 895 730 493 365 927 165 854 953 907 619 346 670 983 618 995 771 116 334 262 375 327 698 135 910 731 371 572 671 725 253 211 639 893 188 389 734 633 869 865 629 049 991 406 125 783 567 984 873 956 255 993 429 851 822 324 056 825 136 582 129 885 350 853 477 154 173 808 669 918 872 987 953 621 508 728 719 913 442 620 188 889 375 026 938 011 729 358 256 696 138 247 491 980 180 894 064 388 676 861 997 654 453 280 706 145 109 265 637 703 742 849 944 582 230 345 363 720 810 432 538 541 558 467 829 556 445 954 130 368 809 738 472 211 546 838 045 164 749 611 649 916 412 486 574 316 753 520 827 881 821 123 867 327 347 760 221 797 875 590 225 099 006 345 863 833 782 008 495 934 174 386 796 516 790 204 343 368 320 708 770 521 606 284 579 047 197 695 847 411 642 392 026 720 797 370 155 033 851 715 504 724 593 099 583 459 412 804 168 949 315 015 147 510 713 292 888 647 079 504 125 096 876 819 369 565 314 988 506 793 401 139 919 066 427 863 100 334 727 448 998 086 334 309 663 662 681 062 184 020 852 211 337 892 841 586 629 970 482 377 557 843 875 699 556 002 460 584 375 383 271 246 982 178 121 441 530 988 236 275 132 130 552 835 201 908 313 018 781 505 608 217 522 879 560 565 599 749 418 559 092 915 883 973 455 349 194 513 924 858 874 151 453 345 297 245 672 427 999 426 958 220 113 939 519 009 795 465 651 396 724 037 214 149 080 804 334 550 042 389 453 333 773 427 079 258 753 045 187 498 552 070 975 412 000 699 317 926 530 772 442 890 259 954 527 712 024 530 768 295 415 170 015 320 582 824 164 521 438 681 646 590 556 114 255 065 108 116 834 663 870 517 004 173 692 675 038 993 660 744 014 290 566 959 282 616 036 173 947 289 238 861 614 793 985 654 731 009 810 554 339 604 326 020 760 569 997 679 294 836 068 828 942 586 053 016 340 301 110 826 303 698 942 239 803 614 521 318 188 441 850 064 629 662 989 715 827 274 781 377 285 893 379 252 646 348 510 310 922 766 086 921 709 290 920 751 196 713 057 881 287 966 641 719 084 706 441 168 636 636 513 363 250 324 934 181 136 403 910 710 390 141 823 435 660 027 715 009 424 148 560 859 443 265 504 694 526 800 652 579 109 928 451 910 248 910 677 251 223 294 893 824 784 845 833 206 253 438 987 162 058 004 798 562 231 356 652 384 423 907 122 026 352 567 188 357 498 625 006 208 074 149 104 183 311 515 600 053 926 027 114 440 162 817 056 231 052 302 378 028 059 945 549 006 130 503 856 350 987 521 852 452 589 641 370 751 522 728 001 179 259 597 605 673 284 076 078 205 301 984 666 426 573 132 239 318 106 909 199 685 964 640 822 298 610 652 586 897 484 499 405 299 334 865 865 267 483 315 830 768 607 046 025 834 142 006 653 847 147 695 686 270 441 547 527 124 634 673 794 954 040 018 123 346 237 711 475 031 998 249 944 751 068 310 012 814 175 695 463 471 421 250 525 880 804 269 973 264 436 925 024 390 289 977 403 952 254 885 781 867 704 147 593 897 339 750 937 073 377 562 965 225 699 247 685 011 280 342 320 144 542 504 261 311 119 964 074 454 815 308 847 261 416 985 444 632 858 235 338 726 189 392 391 705 804 552 008 840 962 182 616 723 687 063 928 685 636 639 556 995 893 708 471 179 980 973 826 368 705 229 150 051 147 142 508 159 825 408 868 980 850 292 147 717 866 945 060 179 674 372 634 151 752 441 771 249 746 255 432 789 513 055 387 417 485 876 424 285 602 456 241 949 384 345 310 386 068 873 316 962 946 902 427 023 413 558 022 291 248 269 475 686 468 611 351 835 222 549 310 360 677 740 747 038 212 630 997 899 904 339 406 738 701 006 506 235 280 861 017 270 537 506 371 007 683 542 574 971 945 545 856 230 931 388 135 034 212 890 606 271 811 240 171 352 195 365 290 867 113 025 580 757 960 918 298 480 299 407 252 722 444 707 039 055 488 292 466 909 771 869 717 687 389 233 987 153 437 701 118 847 267 207 065 775 351 430 583 165 034 248 594 570 250 126 374 882 930 625 085 415 803 605 235 826 607 447 130 482 961 048 093 853 405 012 233 448 873 193 399 081 958 784 624 758 796 703 855 811 384 598 085 582 105 746 624 515 586 118 116 165 288 720 220 013 650 152 426 263 034 177 978 289 752 517 253 500 722 102 621 593 202 039 225 047 782 860 606 715 532 250 486 872 867 721 215 873 496 471 510 032 438 462 380 125 711 833 406 226 771 496 329 809 729 882 594 272 898 828 993 877 384 552 284 867 899 277 490 977 828 524 914 497 932 446 403 166 460 955 624 497 565 890 530 371 104 333 829 182 833 681 186 925 011 441 894 343 988 369 226 644 142 551 121 213 958 853 583 530 989 954 073 795 284 336 244 233 742 419 710 099 941 814 652 996 601 393 796 200 242 441 064 778 786 205 011 274 845 429 704 545 192 575 981 567 673 151 153 802 144 452 013 392 508 205 022 868 499 907 044 673 867 112 903 851 064 351 651 830 410 170 182 607 779 936 904 984 017 867 931 101 905 398 184 889 083 298 800 795 694 173 425 413 313 671 001 106 617 363 730 495 557 382 552 848 584 466 164 086 329 946 897 898 502 876 803 689 274 668 129 889 186 765 763 889 303 605 444 770 336 720 569 633 516 694 485 847 744 869 710 082 404 670 606 752 372 810 644 713 785 055 991 645 479 086 305 325 350 840 849 394 200 729 352 623 618 033 872 280 917 441 719 549 930 338 365 810 008 270 653 936 969 060 990 798 153 673 034 548 564 278 005 388 722 037 110 468 113 135 980 431 145 796 237 119 323 885 133 806 382 431 614 260 219 459 574 780 426 877 500 261 166 668 108 741 716 431 268 024 219 496 910 992 653 084 277 020 511 628 852 149 124 613 342 072 912 036 662 332 728 787 475 082 302 631 861 722 276 514 334 792 299 527 375 232 628 754 527 384 078 701 711 990 984 456 546 970 510 774 574 442 587 717 612 622 863 265 216 012 912 844 786 246 892 452 060 734 122 478 560 649 170 866 611 594 573 643 956 342 605 661 155 664 635 340 651 950 024 196 793 848 731 570 598 415 662 216 416 992 777 324 910 813 713 056 457 728 835 193 292 276 273 494 689 718 868 112 785 177 293 591 202 290 059 969 123 326 898 935 408 203 476 856 943 051 183 327 815 640 079 373 486 232 375 912 958 837 946 707 990 582 183 152 694 003 933 711 483 378 169 374 824 644 564 128 192 263 694 427 175 939 912 371 086 618 353 906 242 015 554 281 674 960 239 262 370 586 167 924 863 495 597 909 747 826 273 259 603 967 605 899 404 119 793 825 612 706 629 516 568 930 608 374 096 914 597 757 360 482 359 009 254 112 639 387 522 128 231 343 582 178 114 877 468 918 491 882 158 207 847 048 536 313 585 262 018 430 198 129 242 239 438 224 313 523 445 302 071 091 791 196 249 139 982 532 014 251 141 380 143 039 050 951 309 131 046 521 304 990 030 914 377 639 060 556 949 606 989 322 597 193 836 418 533 867 895 093 125 423 887 723 674 925 239 622 496 316 352 742 316 629 363 851 698 755 621 980 001 180 958 461 711 631 037 431 818 952 695 985 870 251 689 062 101 199 762 503 483 812 257 495 363 529 366 539 419 325 962 020 604 250 745 404 903 322 972 692 563 074 740 692 958 760 763 143 316 475 990 184 728 012 928 776 534 188 247 748 140 289 245 064 333 841 873 952 922 957 611 370 719 812 058 165 238 938 513 424 006 509 705 835 858 627 470 693 571 064 163 515 000 291 481 647 823 883 108 130 012 022 603 954 041 319 837 682 949 455 029 710 010 528 379 535 813 284 913 003 049 984 652 748 061 636 257 755 574 209 560 202 361 217 689 860 020 655 490 238 331 069 959 759 865 474 464 469 100 563 516 610 070 832 756 932 805 251 181 781 201 567 256 866 033 674 065 166 485 798 229 294 992 471 247 980 025 755 301 607 786 278 680 009 688 637 108 226 673 646 182 050 065 159 073 192 060 070 139 478 137 602 455 554 456 572 338 793 921 262 732 797 215 083 962 315 834 276 281 069 079 909 300 078 981 701 802 822 808 048 439 001 428 929 847 887 962 204 558 173 692 298 208 267 520 366 848 998 706 487 703 938 785 509 257 263 591 791 843 497 906 942 332 106 913 115 355 965 990 228 750 622 954 214 862 401 253 726 127 858 531 723 317 310 317 835 985 056 720 935 804 355 027 121 524 671 300 274 476 919 608 471 735 871 617 456 414 828 647 492 855 878 124 172 621 180 085 516 233 757 832 729 956 040 494 174 930 225 827 281 223 395 842 520 030 499 640 401 677 038 141 380 340 023 363 210 104 830 122 589 417 463 809 193 955 472 765 782 914 622 130 802 740 687 787 477 293 257 433 020 227 363 351 245 859 405 436 582 560 484 093 310 194 254 506 755 139 358 548 950 671 349 477 693 006 181 514 709 561 857 243 637 433 557 696 023 817 328 478 569 439 139 169 351 431 330 659 226 631 866 144 449 544 365 619 341 173 123 714 101 856 353 337 749 379 291 525 399 589 136 759 084 951 134 888 281 323 516 411 141 683 194 593 987 222 400 316 570 650 146 715 995 178 328 569 650 899 210 657 863 184 865 222 694 443 133 414 719 590 901 151 778 202 980 051 713 330 694 109 706 767 558 911 483 231 742 160 130 759 011 775 919 552 330 003 302 522 325 109 228 278 614 444 131 130 810 423 082 170 453 632 302 678 109 117 319 439 313 680 998 186 220 856 651 777 747 080 478 577 532 875 590 646 132 251 858 329 919 230 465 560 900 918 061 286 053 931 639 473 318 234 144 353 082 613 407 317 228 148 560 095 032 060 222 065 852 111 082 791 327 753 824 476 904 016 028 367 540 481 958 118 867 336 430 598 925 861 933 385 126 307 028 848 623 051 115 611 071 371 997 280 777 833 285 612 153 253 867 952 282 752 629 341 272 798 392 389 298 782 800 817 376 991 229 065 539 932 258 720 617 408 140 864 895 615 940 720 067 935 830 225 888 356 230 525 831 965 869 008 189 964 522 345 366 918 308 237 086 480 912 984 352 278 746 920 220 227 984 545 652 367 569 564 705 804 859 456 062 746 079 852 508 156 410 665 905 089 805 779 447 440 234 434 675 297 429 313 375 543 502 500 668 272 386 662 374 866 894 477 307 968 393 998 295 910 458 555 552 955 926 660 814 018 334 751 069 844 492 887 917 909 065 412 348 339 262 615 249 263 723 154 999 546 097 339 923 292 919 057 290 311 851 314 405 851 196 792 609 384 200 111 897 204 258 092 558 026 362 171 291 280 284 635 070 624 390 136 205 730 362 854 086 558 067 267 859 116 838 722 698 673 780 891 512 858 615 727 315 533 669 206 702 000 003 652 209 041 356 862 397 738 573 116 523 409 972 911 308 040 710 725 781 961 118 809 761 832 488 174 703 253 033 435 155 906 881 008 198 227 767 595 815 455 064 194 583 990 097 506 038 337 656 191 054 422 234 246 222 515 190 034 269 001 124 796 734 894 803 146 516 721 896 575 939 266 330 208 798 022 842 322 234 555 868 539 395 156 433 050 456 340 165 945 616 801 029 237 532 236 334 536 451 507 711 252 839 095 824 500 256 595 817 333 290 960 777 127 513 965 916 260 989 707 554 304 233 652 028 008 490 767 103 025 535 036 886 572 685 647 634 374 260 641 711 296 119 584 180 127 131 187 738 360 897 525 052 279 350 318 902 208 200 312 022 065 431 020 591 608 114 411 956 228 492 774 149 053 049 949 911 153 252 850 715 400 777 246 781 874 571 843 499 589 952 987 575 694 393 557 603 245 487 094 067 026 035 609 903 868 040 353 957 781 293 058 880 991 233 124 304 381 966 667 429 757 013 320 893 822 169 639 902 495 216 121 865 223 384 476 783 367 100 421 770 752 674 430 099 986 578 684 526 734 826 136 563 358 755 172 767 329 558 391 923 780 191 421 998 797 335 751 076 037 010 082 210 807 725 295 724 853 245 515 755 766 662 861 187 235 906 191 560 761 187 552 534 903 660 327 808 237 435 813 231 016 756 231 003 892 155 321 849 668 037 641 944 739 624 774 962 237 229 746 640 799 426 999 415 794 717 485 251 161 971 281 953 335 459 037 271 906 879 624 680 920 332 104 637 567 015 761 177 352 702 665 628 426 921 872 372 296 760 718 993 105 206 157 740 970 793 610 215 674 509 005 231 054 298 819 594 681 431 329 177 458 224 426 452 920 949 571 246 828 064 938 067 947 887 354 595 482 706 755 218 229 459 663 970 853 096 256 772 550 246 312 426 142 576 066 371 416 145 682 289 411 311 684 921 041 755 075 673 823 645 436 164 742 516 747 146 311 656 216 003 737 915 309 057 870 505 045 449 221 586 158 209 793 188 927 143 351 253 004 718 161 986 428 460 218 581 988 059 702 745 504 741 342 622 815 258 792 915 038 195 482 703 137 731 915 282 429 267 269 005 566 586 117 470 879 911 285 737 879 892 391 600 136 319 980 555 502 279 225 275 397 927 966 666 919 597 749 166 189 204 734 707 774 909 241 658 478 884 933 729 222 280 364 953 720 245 644 654 414 803 014 934 589 894 370 118 722 259 260 546 621 255 888 760 888 509 897 127 590 811 781 858 241 969 367 023 371 016 472 915 123 909 883 667 616 354 954 439 762 365 752 905 432 809 212 255 359 665 331 483 032 039 725 688 146 869 465 532 034 727 956 876 473 826 623 583 848 447 525 401 207 917 230 386 654 378 672 992 799 621 839 838 983 113 678 707 446 020 476 201 121 584 266 077 270 854 721 950 601 015 891 839 936 822 743 085 131 406 470 196 784 202 746 888 335 273 026 244 644 745 423 317 979 446 248 392 643 462 167 076 847 007 190 159 636 380 334 931 735 666 813 674 011 948 636 033 682 752 168 118 058 487 733 557 047 703 423 994 914 894 865 878 928 761 106 895 446 361 902 919 774 931 237 486 975 571 931 100 688 656 731 629 738 254 325 213 860 931 274 931 170 681 120 790 622 168 109 499 654 144 594 106 582 212 195 429 698 193 144 991 299 601 347 246 587 941 139 392 639 322 900 724 549 480 758 773 393 955 757 054 405 693 046 335 236 404 201 131 856 321 917 817 029 034 687 443 248 270 157 347 212 028 137 069 336 109 660 728 512 084 989 034 193 851 115 199 100 089 914 172 100 173 007 921 439 164 927 175 976 728 567 721 540 454 845 494 069 335 313 559 222 046 379 382 769 956 392 344 024 947 693 304 480 307 107 652 588 765 898 420 833 776 765 486 784 550 488 180 086 611 437 721 292 342 511 713 480 503 136 898 917 729 713 591 467 450 630 411 811 798 771 184 425 718 196 210 503 338 690 547 971 360 816 589 340 227 531 628 182 046 173 854 978 324 385 293 085 377 928 320 209 626 888 324 121 814 496 394 793 769 364 081 295 923 268 338 277 490 192 015 131 207 913 463 377 139 366 446 360 612 785 701 527 993 001 907 706 664 951 063 793 714 039 966 614 916 837 718 550 533 153 911 933 449 854 328 681 567 366 024 298 963 857 609 824 769 274 784 862 525 610 166 403 536 894 733 983 243 320 461 655 048 993 594 024 471 860 091 788 027 672 169 258 046 411 714 582 696 214 473 936 984 100 453 605 203 249 844 211 950 334 114 158 705 232 406 464 950 418 864 425 043 648 770 546 370 241 017 797 312 195 293 097 388 474 354 164 170 339 921 561 019 367 640 531 055 499 962 277 822 860 507 853 960 063 137 906 823 969 038 731 026 599 983 612 508 785 482 525 000 300 974 787 032 790 359 860 509 478 994 224 739 126 509 283 217 506 472 273 237 967 772 578 390 212 366 077 525 125 204 310 429 234 745 466 299 940 471 295 808 533 295 336 895 763 124 056 957 759 034 663 722 517 740 184 627 584 763 891 131 692 629 145 806 713 128 772 193 294 662 629 001 314 111 326 777 912 807 928 956 092 237 068 876 711 331 940 476 948 934 910 422 908 539 443 268 986 448 265 439 982 968 931 016 843 697 504 535 568 192 320 906 682 761 293 613 129 087 414 326 149 285 797 505 660 810 225 103 257 386 999 829 626 184 369 316 335 445 155 066 469 201 689 219 456 915 221 633 751 799 988 461 678 480 756 578 070 206 416 077 527 522 083 308 059 501 585 426 648 597 922 783 495 041 811 386 522 754 405 395 909 217 271 086 912 371 256 554 327 096 654 315 161 969 693 804 365 845 827 912 679 499 917 464 838 566 310 262 668 207 690 975 485 709 046 222 179 559 619 846 415 405 427 134 149 132 770 301 698 496 274 961 097 716 741 965 499 039 634 265 995 955 680 499 657 293 668 440 062 328 232 434 644 491 210 287 076 728 197 775 561 664 517 626 052 327 855 010 815 147 290 353 527 807 443 626 593 670 087 156 694 062 808 433 858 521 586 021 249 564 754 595 029 254 842 559 028 089 329 147 089 305 648 917 916 989 466 095 449 090 592 531 078 930 485 859 711 174 435 856 132 237 547 373 117 373 018 122 888 200 283 698 882 753 366 757 708 685 332 559 808 643 252 970 355 543 885 970 614 991 081 901 215 595 990 459 312 005 646 287 180 002 452 355 495 876 242 921 958 840 245 820 209 019 898 434 843 990 571 179 910 414 115 463 660 726 456 880 907 076 776 630 079 523 063 953 436 226 386 854 883 455 237 415 020 366 815 203 092 731 453 753 826 240 570 001 500 077 402 847 582 263 970 761 850 590 773 622 925 594 428 254 314 131 709 279 747 318 458 245 499 881 914 741 247 830 092 720 074 426 858 510 024 768 979 905 572 113 318 367 205 331 360 567 858 423 616 793 768 856 561 119 789 029 272 810 255 506 105 443 078 862 324 053 757 703 512 937 619 644 776 352 952 373 124 553 006 634 749 722 613 433 204 107 185 134 902 799 954 515 553 406 647 849 168 750 372 035 753 217 886 906 049 847 369 800 369 059 772 142 635 093 015 818 198 973 946 599 463 103 756 835 363 868 119 038 934 427 062 854 173 737 303 864 982 873 320 749 873 543 662 338 187 379 866 550 728 668 865 470 616 704 182 303 321 053 047 014 840 112 108 447 577 912 225 334 514 600 394 272 312 721 501 352 348 401 931 905 678 493 763 493 004 153 308 245 306 442 761 037 382 682 569 356 355 580 644 015 084 754 167 678 708 670 300 666 215 834 736 958 162 389 505 807 598 682 242 485 576 659 507 855 370 820 893 076 859 801 470 466 560 616 633 196 216 992 317 589 869 652 468 228 913 375 198 114 176 184 990 113 286 884 193 535 621 740 104 517 734 473 134 588 410 298 567 753 503 331 918 915 979 563 491 275 759 422 369 773 360 544 529 565 452 974 420 759 041 535 357 485 270 097 905 562 131 876 292 752 115 892 237 873 521 227 533 601 737 252 098 329 633 546 791 467 071 144 217 727 179 989 740 389 280 178 309 975 868 057 150 711 469 221 939 848 122 200 680 829 665 374 398 942 361 368 121 623 120 377 044 811 253 908 189 587 560 596 955 631 613 363 030 166 997 856 035 260 016 602 467 439 032 792 417 833 259 506 439 082 217 633 629 155 225 623 710 521 435 528 690 532 106 588 101 789 580 271 674 098 024 500 218 228 808 179 860 746 926 215 849 878 478 998 381 854 517 050 543 336 281 312 539 126 832 538 607 899 742 899 899 089 707 919 204 559 239 196 243 596 090 357 869 665 698 751 536 700 887 641 806 334 676 087 292 764 840 213 511 332 970 828 199 189 228 358 180 724 891 397 000 230 924 589 634 612 078 519 555 686 940 215 952 324 426 426 932 113 525 111 708 171 986 978 317 778 778 144 569 982 058 232 295 230 002 776 589 963 724 946 574 250 342 388 524 786 829 021 200 125 512 109 547 491 543 144 880 339 203 802 171 489 509 798 995 932 014 346 285 392 257 430 416 629 243 713 485 746 251 927 088 247 903 995 014 040 195 859 473 924 110 920 866 364 011 341 191 232 572 157 584 172 949 349 773 441 137 575 890 676 003 087 859 207 933 248 620 410 645 064 655 406 115 038 356 737 187 227 580 153 415 389 668 345 458 836 441 742 362 862 041 244 260 169 582 910 583 906 933 820 531 626 654 500 517 851 593 373 041 697 234 796 092 713 716 576 787 273 172 810 898 190 239 119 255 035 430 173 691 288 193 841 188 036 575 509 441 937 254 433 685 854 067 439 719 674 258 243 602 698 503 739 327 945 272 953 314 809 988 437 876 551 829 925 056 791 960 577 117 724 758 446 289 698 803 185 087 201 449 492 189 001 439 562 319 164 221 520 752 460 075 663 554 078 540 099 929 809 165 053 957 317 784 880 014 480 689 744 936 991 966 845 603 979 244 375 034 044 394 835 202 961 304 889 198 060 932 973 020 823 401 381 759 981 254 251 280 820 767 676 559 334 722 989 112 519 530 866 893 454 183 229 244 097 040 506 710 079 021 404 160 167 022 959 881 683 285 156 654 977 266 868 174 942 761 889 879 323 462 227 415 905 184 524 968 380 179 525 977 254 787 883 187 453 633 437 665 641 977 700 801 350 336 793 765 223 726 106 976 279 636 170 209 239 689 561 380 820 423 353 994 299 088 693 844 071 344 540 202 855 685 861 668 751 467 533 962 046 514 874 165 184 409 326 040 392 948 778 801 196 273 362 392 062 522 582 308 735 749 586 994 057 796 495 069 906 003 024 414 732 119 114 118 665 899 408 640 689 750 336 052 829 212 931 978 581 905 838 379 335 892 197 055 468 423 962 819 740 895 759 077 132 332 892 702 148 824 448 517 945 332 781 303 417 592 370 821 998 074 425 355 692 235 819 482 968 898 606 536 406 624 580 784 765 401 446 065 383 951 105 162 369 792 866 154 413 044 382 232 004 447 777 092 383 175 327 807 687 218 491 803 825 461 107 651 250 401 744 749 853 299 049 754 231 213 614 611 942 656 583 129 192 995 079 743 071 457 296 491 053 041 873 871 126 858 425 809 210 969 534 164 337 290 756 938 165 135 248 691 520 229 770 017 989 226 779 906 407 290 551 744 579 939 754 239 092 659 474 918 665 294 267 028 042 423 770 188 221 378 738 312 987 594 302 854 844 747 407 052 990 011 180 504 256 873 145 872 942 862 111 709 482 023 373 255 905 806 786 078 903 334 855 535 671 491 982 414 229 406 116 887 319 029 861 593 544 806 569 217 091 095 162 440 919 963 595 064 625 643 417 224 802 930 342 728 261 203 893 468 682 290 176 368 467 921 795 078 587 237 308 197 583 880 933 821 187 994 395 546 719 949 523 144 091 578 519 091 773 542 431 966 661 486 379 976 825 803 521 751 163 253 136 817 244 998 444 944 506 218 332 859 896 467 055 642 110 210 896 291 315 038 454 279 851 627 119 064 678 618 309 404 016 878 518 173 626 113 586 340 068 322 948 411 534 767 460 991 544 802 124 675 659 073 718 921 293 151 999 253 057 957 583 868 788 021 122 713 339 201 181 435 531 070 232 186 339 606 432 089 746 872 074 803 601 602 945 294 435 446 495 151 282 983 710 637 948 324 893 832 820 405 181 589 161 381 636 157 658 082 952 190 485 163 277 660 456 841 513 083 842 454 396 026 742 708 096 026 314 824 322 463 668 865 083 747 646 767 687 072 596 029 264 912 919 287 399 555 730 879 879 552 389 505 173 065 311 152 006 753 067 088 632 553 623 791 979 657 700 324 214 608 480 203 859 350 379 726 311 187 298 699 021 219 225 025 094 023 493 090 994 166 166 495 140 067 201 792 383 809 906 350 499 164 255 520 880 384 772 103 063 849 455 627 931 475 684 881 180 242 353 343 859 815 302 694 215 734 543 969 508 264 141 257 540 745 662 942 726 365 614 138 920 929 716 156 085 613 389 813 397 058 432 878 503 072 029 218 361 652 297 704 687 770 090 782 437 702 019 262 050 559 425 175 597 865 773 387 533 259 086 353 245 324 930 527 065 506 445 978 658 411 107 056 378 926 408 131 730 634 391 957 639 550 134 948 343 224 191 936 394 031 088 804 157 479 004 106 647 436 076 592 731 907 492 961 188 931 046 100 171 457 618 413 294 504 365 804 197 582 845 374 244 636 750 140 454 265 814 389 082 892 528 918 500 200 225 301 152 007 946 259 056 648 134 688 230 557 260 451 721 526 289 870 480 297 714 137 586 976 262 714 136 413 910 198 489 574 417 734 604 838 088 900 217 118 623 450 605 802 143 385 837 602 601 052 161 203 992 736 670 159 037 439 161 708 698 522 505 259 754 212 331 828 897 312 981 148 184 352 558 306 189 107 576 699 512 729 087 220 378 550 024 657 798 034 813 547 084 633 330 242 464 498 996 632 716 512 208 690 999 287 703 229 273 307 905 766 269 444 065 333 604 208 052 711 351 912 270 866 542 894 986 446 557 342 861 824 603 922 164 147 722 951 084 709 599 310 020 307 208 861 283 030 715 058 154 660 430 897 473 231 313 514 997 398 894 981 813 586 982 231 833 954 708 462 868 859 819 146 457 420 741 832 238 526 748 332 565 364 636 950 002 590 634 753 546 601 385 318 319 729 699 280 311 033 841 316 073 075 042 495 309 641 523 862 844 735 364 220 595 122 021 819 526 414 518 608 517 410 722 204 825 362 904 227 004 459 110 389 604 022 278 837 239 152 976 293 726 777 727 588 602 201 849 557 720 893 268 741 395 843 569 860 301 245 602 088 185 524 069 109 726 967 667 034 793 680 252 723 562 402 215 192 488 624 136 615 962 081 375 868 999 529 128 958 334 324 210 718 678 057 861 291 132 625 176 042 342 781 111 486 358 295 089 974 532 380 095 666 341 092 953 375 717 729 085 062 230 033 722 056 985 982 835 658 362 609 577 158 363 691 369 637 329 894 162 061 464 456 452 247 888 668 273 057 936 989 242 280 467 160 006 085 144 151 149 998 510 426 670 695 897 279 612 162 577 064 999 978 704 440 288 327 575 252 936 572 747 459 816 014 201 298 293 488 846 200 822 212 163 186 065 145 461 521 104 258 744 265 910 353 068 361 719 079 614 582 844 755 091 337 829 668 911 553 496 090 520 789 098 400 580 749 710 902 306 328 199 140 134 285 722 355 207 675 390 406 472 215 477 012 107 089 297 743 055 956 814 962 772 872 150 815 272 614 201 172 936 857 974 336 716 320 790 670 953 582 401 491 254 142 580 235 485 561 397 145 060 293 496 392 801 014 059 423 024 923 541 429 935 496 804 296 588 159 608 209 500 058 949 575 309 119 716 483 463 970 552 374 107 960 590 770 158 985 096 351 047 335 013 107 173 028 639 707 406 317 750 882 389 658 419 537 601 725 994 996 167 881 063 539 628 871 244 728 443 771 647 525 209 328 524 654 962 226 671 994 976 309 433 265 370 726 900 604 615 605 513 340 493 287 075 966 070 708 383 117 165 942 556 578 402 652 986 688 048 522 685 415 285 680 160 544 696 512 958 226 586 273 325 999 656 352 433 229 114 921 047 478 515 158 688 405 332 193 126 612 206 749 514 137 403 951 063 405 263 643 015 160 856 350 980 585 900 488 060 164 382 980 456 854 393 868 698 841 703 544 626 676 438 996 768 318 293 119 640 403 820 230 580 507 222 320 517 068 211 849 542 713 077 824 108 891 680 372 653 196 635 597 072 575 621 515 874 333 945 406 601 873 932 396 897 868 083 188 282 458 924 191 607 773 111 347 735 845 597 162 128 396 186 578 144 304 012 725 396 026 640 784 890 803 254 006 115 907 657 181 163 633 724 989 898 846 790 115 719 317 944 405 651 704 611 265 497 300 512 990 867 720 916 998 776 919 108 256 012 032 990 160 581 926 009 784 739 954 073 341 295 843 107 025 546 409 008 997 694 537 298 170 771 869 662 398 570 734 945 933 372 248 766 248 464 903 490 418 194 347 795 159 705 334 864 028 748 215 030 400 334 841 237 288 420 351 102 151 095 975 337 593 689 974 494 861 768 556 252 885 780 073 355 378 527 535 328 918 118 909 543 369 213 485 875 518 525 365 165 210 704 967 015 982 422 445 330 961 109 197 614 345 341 747 068 765 709 009 016 044 770 604 451 343 339 774 472 269 293 066 025 056 708 013 606 713 715 948 679 066 065 884 335 693 950 907 582 138 422 418 691 651 369 899 979 539 347 071 430 659 965 106 469 959 261 599 964 686 344 665 867 535 996 587 369 811 023 431 524 699 405 051 628 559 311 685 566 309 448 755 861 040 655 992 117 049 527 582 868 564 963 471 686 541 660 766 465 327 156 628 536 225 214 939 573 171 902 766 081 043 778 673 245 305 247 734 652 485 990 459 393 929 205 395 127 812 512 027 814 275 505 072 805 869 972 729 171 816 127 301 866 900 260 204 296 740 049 295 667 455 215 005 109 117 927 938 560 257 167 586 017 335 936 954 471 869 239 852 636 876 512 456 660 640 256 523 908 036 942 317 438 677 255 314 529 107 131 524 875 226 335 231 864 058 470 118 042 311 446 169 902 845 987 468 834 388 015 859 183 859 031 572 537 978 935 306 607 654 900 647 252 297 118 290 781 727 429 354 772 254 834 236 309 241 580 437 501 048 275 835 125 773 229 313 276 269 481 344 947 370 722 115 509 345 207 529 096 432 973 726 914 817 971 377 276 796 847 066 709 428 083 636 650 449 410 761 578 123 711 024 597 920 391 542 772 643 410 604 849 038 201 397 841 044 419 940 018 265 554 893 986 550 479 282 938 815 724 908 931 674 025 771 183 918 527 149 363 000 532 480 814 298 704 703 498 502 827 253 536 180 300 949 251 609 359 666 307 494 800 398 463 411 519 127 681 868 481 584 554 019 976 749 869 404 238 081 965 774 577 460 682 433 783 204 681 142 643 789 726 722 404 974 274 601 385 088 290 910 882 511 815 084 653 164 957 989 799 513 481 091 148 616 456 553 268 650 198 484 944 881 788 421 769 538 747 847 374 436 584 605 380 355 738 853 516 349 964 490 401 940 312 673 804 305 749 815 011 788 392 948 791 734 776 973 644 349 137 722 630 543 313 466 721 102 024 602 422 906 190 308 500 966 975 981 704 306 106 274 049 044 778 185 159 064 515 555 635 293 384 221 587 554 032 126 000 373 756 950 734 471 498 784 972 189 502 589 395 946 726 444 842 097 853 978 210 199 213 843 706 928 919 664 568 122 903 279 964 502 601 306 832 317 055 836 865 981 572 859 155 235 343 784 945 361 692 962 866 458 992 400 035 186 391 564 086 301 702 231 108 477 698 768 399 506 035 400 725 483 400 761 842 488 640 021 141 900 517 721 073 179 845 646 151 307 928 766 641 402 764 680 150 478 575 493 837 911 088 933 295 827 775 596 133 575 066 137 103 621 170 536 964 043 188 907 345 331 591 943 960 307 984 416 287 468 451 226 176 516 402 420 744 357 611 917 996 789 860 130 530 784 031 781 079 370 980 937 788 660 670 007 831 852 328 617 414 797 492 470 311 834 490 370 251 836 795 823 057 938 996 688 028 109 015 401 649 193 821 680 967 475 403 064 753 478 665 591 479 695 665 652 698 706 349 129 518 578 166 967 509 388 830 900 728 368 477 717 514 092 853 377 973 037 497 072 337 116 732 311 978 224 154 784 288 906 907 901 916 840 175 600 208 428 746 751 291 393 622 013 580 461 139 580 966 381 324 440 936 538 074 255 083 327 884 933 494 949 773 429 168 087 618 587 579 210 824 882 665 210 143 005 461 731 936 433 004 821 793 997 918 698 525 192 550 511 730 783 263 781 955 255 493 712 345 530 598 888 467 054 955 792 007 797 729 913 354 383 812 302 459 168 400 025 442 844 278 795 690 438 007 675 405 524 996 283 325 581 895 029 220 196 119 172 846 674 570 714 533 011 925 810 791 937 180 695 858 487 332 784 730 532 262 584 740 165 950 590 502 065 900 240 437 895 933 066 676 018 494 229 510 885 011 683 498 261 696 385 253 582 730 319 111 849 100 762 336 616 722 716 119 267 443 942 656 965 323 212 077 881 575 014 502 288 385 134 974 105 254 313 761 689 656 210 333 424 656 765 043 980 417 032 164 145 588 408 166 144 137 559 761 168 323 854 545 283 484 283 298 352 702 916 138 312 133 830 211 462 928 734 436 593 425 514 345 197 225 299 592 434 853 432 368 046 080 198 743 624 755 938 220 582 944 660 146 059 460 444 986 044 349 115 184 290 427 040 056 684 011 205 465 952 180 729 820 188 960 476 500 128 924 538 984 044 795 142 904 622 258 507 325 034 767 998 071 778 970 796 759 164 770 157 892 427 842 279 359 247 076 902 897 197 886 715 631 037 418 997 179 108 239 486 903 052 733 657 950 849 771 509 768 263 522 263 113 872 141 883 891 680 870 733 650 871 712 203 898 559 391 583 300 706 578 157 841 291 897 788 068 562 978 376 659 071 598 301 555 422 208 695 470 277 290 187 744 423 988 544 098 598 462 016 816 646 233 692 729 272 138 626 955 705 242 672 224 035 049 593 382 397 323 749 966 057 483 449 421 215 444 212 855 863 278 603 641 671 246 044 746 249 653 579 841 152 429 407 968 938 195 687 251 075 213 714 825 233 287 217 583 392 844 531 971 524 862 383 449 486 767 822 216 387 353 962 609 375 754 903 973 196 360 234 021 648 059 896 541 228 197 210 011 926 870 804 554 974 805 489 964 561 610 280 196 032 929 389 691 656 254 812 713 738 512 785 310 838 351 735 794 214 395 570 586 747 218 338 321 219 149 757 548 064 476 218 637 820 439 175 208 655 595 807 371 879 512 701 932 472 803 973 591 033 809 549 031 013 535 394 298 621 991 216 750 802 391 307 051 461 996 341 863 732 877 609 570 777 596 080 490 334 109 685 889 868 465 948 294 539 290 464 441 203 970 068 928 362 366 117 614 366 853 224 270 235 697 456 861 620 797 654 133 429 332 657 170 978 844 859 721 009 527 034 028 036 430 199 215 829 230 575 724 240 298 552 572 125 573 851 060 603 471 855 828 883 732 093 475 132 550 930 140 006 843 939 047 572 257 023 697 104 794 572 794 894 639 757 812 959 144 219 189 743 402 195 202 707 488 310 822 991 809 654 617 369 578 342 698 476 736 805 328 495 972 580 945 374 368 089 462 346 408 416 216 345 374 029 052 512 718 143 223 846 134 992 522 434 262 720 637 601 183 614 870 758 214 093 351 820 842 281 705 526 973 912 437 992 553 387 745 177 842 962 544 288 858 965 102 630 164 535 816 070 560 825 252 465 344 443 530 077 149 418 440 798 337 742 816 027 274 072 908 985 622 342 961 045 783 714 599 142 385 549 106 013 043 134 937 059 619 863 063 534 714 491 363 193 682 996 577 930 832 597 925 549 551 850 070 722 420 658 306 736 773 873 711 335 649 824 494 180 725 869 112 594 619 461 130 674 139 573 066 739 265 316 837 575 008 555 469 525 579 951 771 341 557 379 151 831 730 394 586 862 841 684 734 024 936 592 364 373 463 318 340 592 479 285 309 615 545 931 946 367 128 811 526 783 303 019 518 489 455 015 569 311 762 896 507 971 507 764 376 671 025 361 121 794 069 163 465 069 663 475 923 095 670 934 904 212 668 131 116 307 657 080 036 565 862 783 047 580 281 880 204 771 154 463 758 140 452 462 068 337 438 956 877 002 574 378 595 111 604 930 644 175 937 439 196 644 750 385 381 652 417 872 324 020 034 430 898 717 605 553 082 884 349 035 765 364 280 340 326 713 412 282 707 576 109 583 202 983 235 186 784 566 164 100 392 705 094 323 667 807 858 193 814 568 309 892 569 701 018 767 999 942 648 203 971 736 530 678 378 247 647 164 974 103 796 648 586 516 381 001 195 601 669 467 440 647 686 033 327 287 540 406 005 383 290 249 982 608 227 922 494 001 700 544 228 501 864 907 350 412 280 774 780 238 347 120 057 382 076 617 487 008 633 683 842 016 879 590 759 245 238 789 347 694 272 018 559 582 048 369 722 161 393 218 401 360 551 976 471 946 512 036 136 406 712 318 913 118 450 857 916 185 957 848 416 129 944 310 981 898 279 287 693 151 648 690 934 405 533 913 177 404 750 342 412 714 593 052 141 709 588 624 893 190 146 140 008 258 638 138 135 317 686 329 834 721 685 656 089 970 052 842 930 714 148 424 741 307 370 195 108 400 156 471 553 483 952 505 932 497 841 755 755 891 540 922 331 644 143 677 246 511 914 997 272 933 816 035 265 359 849 464 445 667 347 675 769 679 063 711 065 116 443 978 092 641 720 198 766 578 009 315 286 221 559 010 904 271 274 876 188 113 229 486 649 419 462 107 478 892 220 124 529 969 816 011 106 380 344 545 375 950 841 097 433 705 655 772 363 230 055 372 863 550 397 122 477 888 971 045 742 197 880 718 939 603 660 767 704 868 423 795 818 672 921 214 955 577 458 860 512 680 895 476 350 729 025 421 959 247 591 524 492 264 547 747 569 859 786 649 927 716 207 193 138 100 604 770 685 100 607 267 133 516 418 653 429 351 924 870 598 026 354 097 336 538 801 692 569 284 916 676 890 240 699 557 096 311 626 915 446 005 802 096 292 780 928 503 382 748 446 821 739 457 726 682 135 875 563 915 269 033 396 294 625 829 925 220 621 382 460 047 489 865 732 114 221 132 834 541 186 676 740 957 462 515 463 175 155 800 402 213 919 598 853 735 166 742 358 134 577 960 258 227 165 626 796 434 363 050 948 710 113 393 132 886 254 397 358 074 600 431 206 146 683 314 069 920 334 964 287 418 149 609 435 176 344 777 622 180 426 169 054 228 397 837 963 473 560 101 341 263 386 239 313 505 346 970 805 733 728 873 742 204 530 026 697 697 379 408 863 006 012 348 993 063 110 136 449 486 551 666 835 925 250 456 081 691 558 655 185 004 753 547 250 775 654 501 628 185 783 330 831 071 886 283 760 351 605 634 792 637 608 702 146 571 378 956 571 637 536 582 386 123 297 988 819 089 511 782 539 266 455 555 323 228 892 237 531 590 787 030 819 204 813 121 210 843 589 343 966 297 515 712 720 385 217 144 463 259 075 049 688 182 608 249 947 252 095 992 326 351 255 022 861 682 580 298 395 707 791 984 766 752 681 863 570 395 630 531 647 697 544 451 516 429 392 262 940 448 806 084 304 593 046 523 488 283 765 370 624 684 252 051 834 260 330 728 120 626 341 603 008 378 890 459 100 696 505 243 823 058 955 438 632 167 448 974 166 873 869 138 802 553 555 773 450 943 820 986 402 902 900 563 505 198 540 780 517 904 045 303 559 780 217 272 522 832 031 569 484 316 830 485 767 533 143 048 757 441 941 970 494 329 293 213 869 701 011 793 402 136 336 015 490 180 518 397 906 171 407 512 405 246 073 177 548 317 335 042 679 817 401 247 816 604 459 951 878 927 230 629 139 814 082 688 951 856 813 553 969 185 820 420 203 513 624 283 247 382 571 397 921 774 466 011 578 452 265 926 151 162 139 558 401 342 872 532 254 411 465 091 762 002 127 713 247 246 289 314 682 630 815 827 824 815 689 736 559 287 721 036 107 612 691 595 694 124 198 095 022 842 400 721 039 135 174 599 878 841 858 909 403 734 638 518 394 089 939 862 887 112 802 164 829 301 083 046 775 468 507 358 045 577 256 083 070 869 551 934 602 886 467 418 926 319 947 685 450 972 386 550 276 075 779 850 927 278 649 923 653 867 778 662 218 957 125 934 398 648 261 577 829 719 472 077 952 922 073 697 918 305 543 326 674 361 113 314 207 603 436 456 332 824 907 908 098 203 483 991 325 621 253 083 528 517 136 970 157 736 685 960 117 428 594 829 131 941 495 699 041 633 220 598 727 807 870 532 242 200 293 407 729 437 503 495 905 125 724 293 236 433 285 172 620 103 953 173 188 085 089 085 278 540 696 095 036 504 580 056 391 661 270 027 380 494 091 328 174 854 388 888 602 372 028 739 087 401 585 595 564 105 399 036 592 154 342 373 080 146 941 332 563 583 953 572 241 542 285 450 441 323 939 034 240 360 584 756 197 428 122 576 586 920 926 138 161 745 511 006 509 968 591 773 305 635 453 160 413 351 552 264 609 312 803 160 165 253 107 169 825 832 372 772 547 956 204 458 926 699 927 145 677 383 225 872 829 557 425 916 182 866 886 199 934 073 775 604 078 637 918 611 961 513 502 395 673 984 750 958 689 741 767 369 426 757 042 811 534 913 790 840 994 388 797 994 656 063 372 318 944 160 346 639 824 261 138 326 609 328 166 547 995 240 051 510 023 162 164 983 617 392 242 262 347 660 041 001 784 928 962 291 851 274 819 957 787 321 489 359 483 961 078 180 525 476 423 333 085 948 486 477 304 848 313 659 756 576 162 248 480 929 011 679 164 995 853 537 207 928 298 216 550 283 027 204 301 065 924 434 777 872 666 128 135 413 515 783 406 494 686 637 980 735 302 849 043 866 008 015 163 104 010 433 186 141 745 274 535 696 486 958 123 004 711 774 775 275 634 395 243 059 883 985 020 086 077 255 685 413 403 897 504 228 877 376 660 184 468 941 127 776 339 747 454 568 832 377 491 655 626 945 385 570 054 956 191 239 350 911 476 582 896 373 440 542 857 923 716 977 688 428 940 011 268 817 853 858 424 715 820 256 907 036 106 552 738 255 926 248 644 626 916 779 799 792 042 825 701 383 976 638 782 710 823 687 960 049 379 444 753 072 663 169 575 506 601 522 275 372 368 994 985 647 356 696 971 044 355 261 801 871 185 401 828 092 014 541 115 364 241 923 286 013 185 268 959 448 023 309 906 033 141 416 974 894 675 434 174 950 735 719 834 117 077 008 907 871 137 348 761 098 777 341 277 825 409 388 264 931 143 109 086 182 954 704 300 374 433 066 892 640 755 170 345 602 410 428 660 835 701 283 336 798 913 849 266 611 810 471 185 844 615 226 429 328 752 159 714 901 462 878 981 345 363 054 931 936 744 394 175 748 423 107 381 548 684 149 249 424 084 108 392 450 487 771 821 816 134 434 998 392 804 210 986 340 290 519 349 242 106 359 013 707 821 613 385 669 394 451 715 611 697 276 483 889 158 347 516 590 843 157 933 877 997 577 559 743 992 621 138 003 252 916 700 746 115 722 565 280 759 074 988 902 574 166 636 311 451 923 243 180 173 216 177 262 616 580 183 478 743 501 783 816 085 671 512 616 593 514 075 939 323 657 346 413 771 640 357 394 312 883 274 999 723 369 345 035 570 491 228 129 823 963 124 669 177 636 578 597 520 009 656 621 400 454 493 470 650 383 249 942 816 551 085 121 785 326 493 711 940 126 769 615 913 524 677 187 243 794 804 694 295 143 509 747 321 931 853 937 297 214 029 655 026 544 742 138 089 020 374 644 611 529 602 074 379 371 540 783 249 353 925 815 654 953 638 931 257 294 394 090 952 859 210 511 666 656 174 635 784 046 003 637 588 179 779 449 293 856 057 928 037 867 346 010 322 846 259 159 900 590 499 771 231 944 976 587 872 331 818 231 007 811 133 492 789 414 261 412 164 243 612 582 444 685 828 337 300 018 459 957 902 735 747 178 637 654 689 549 932 733 283 506 701 097 381 205 752 604 378 497 661 266 996 493 559 521 935 503 359 275 209 960 019 315 093 041 164 580 316 858 715 166 142 907 923 765 377 188 372 429 130 677 358 707 863 227 201 122 726 520 382 717 012 505 059 534 142 453 790 320 380 473 116 799 795 100 012 714 756 124 679 136 586 807 356 161 107 553 318 547 204 659 620 691 608 199 736 461 480 778 732 154 221 810 512 138 223 713 816 520 386 171 534 151 582 182 253 803 195 582 781 800 894 458 852 068 962 040 217 859 050 575 073 221 200 490 581 305 679 862 298 111 478 492 152 793 128 218 275 664 584 827 572 720 616 091 122 448 289 036 713 984 472 663 280 036 775 471 141 686 548 406 302 409 677 046 383 639 871 675 988 564 947 744 458 257 164 678 032 465 663 333 881 169 843 304 891 111 503 753 973 272 600 471 216 182 502 910 803 770 676 076 231 391 901 281 936 963 182 884 248 794 471 133 961 478 964 591 373 165 588 356 304 942 696 778 182 246 316 502 124 165 120 268 180 262 414 452 163 240 467 529 165 401 404 503 069 403 832 258 375 363 711 970 909 293 859 941 547 173 535 996 849 501 047 593 619 459 244 732 014 315 330 214 990 573 418 671 410 312 592 717 729 965 069 243 097 459 228 987 000 007 719 063 244 682 615 289 895 650 500 307 324 689 968 635 759 749 300 861 094 774 068 483 767 058 538 482 789 920 977 494 194 427 235 339 601 627 624 780 449 260 370 540 253 969 817 088 721 680 849 901 260 463 866 278 978 200 383 939 785 030 252 948 288 736 317 500 430 534 416 730 899 235 077 986 074 163 527 724 055 047 850 632 751 636 082 162 743 823 433 659 862 242 296 009 120 865 337 784 419 769 160 265 410 663 484 643 578 687 734 019 563 633 293 360 864 236 955 665 539 493 836 502 422 337 696 171 501 815 952 397 150 777 711 988 510 778 233 621 706 376 746 426 204 980 131 401 476 776 350 314 537 622 198 704 423 689 708 995 665 306 173 256 932 334 767 176 152 369 742 418 683 450 271 849 399 625 220 789 194 247 992 784 844 889 801 958 980 950 488 936 059 462 068 734 041 202 433 056 236 252 922 954 397 636 996 300 529 289 379 947 783 687 926 313 441 646 876 187 999 621 994 711 400 517 291 765 254 609 133 785 643 348 207 089 479 106 188 139 502 950 533 922 930 878 291 238 559 600 055 640 412 447 221 803 984 349 690 616 813 811 564 550 853 465 178 615 030 544 245 413 013 694 725 295 888 542 710 288 290 470 200 082 729 852 265 526 325 124 148 445 396 479 409 693 699 502 867 743 386 262 298 569 344 744 605 198 738 485 195 930 361 994 676 927 286 053 043 803 220 106 861 864 511 714 539 738 522 236 663 378 581 300 020 270 575 402 075 751 801 919 114 128 497 118 352 539 277 026 594 207 832 013 937 727 066 551 434 945 573 938 877 860 507 509 018 659 589 879 480 168 250 820 482 206 326 470 337 999 325 783 450 347 519 280 617 777 435 403 613 125 744 980 173 982 794 365 311 171 366 818 724 090 501 611 109 011 477 023 360 587 009 259 969 851 154 706 407 326 490 095 858 126 210 287 921 691 806 856 763 436 590 048 829 728 278 146 140 195 921 505 503 976 380 190 239 100 326 055 227 715 061 204 068 914 826 549 836 025 694 701 342 035 920 978 797 195 549 522 029 480 801 216 521 300 790 040 122 524 054 769 288 418 496 468 646 751 147 491 808 069 253 073 830 399 480 756 028 670 657 301 822 264 057 484 221 115 777 932 254 088 617 871 217 615 825 335 610 020 395 478 153 110 969 256 335 765 421 971 245 938 191 774 690 304 435 366 991 066 027 068 887 613 669 177 104 341 315 503 043 038 681 974 044 963 386 809 164 621 559 364 044 065 868 355 474 976 199 560 124 447 418 019 150 887 100 156 543 532 340 129 275 214 115 132 954 898 399 688 283 302 431 712 971 819 322 811 740 766 632 223 261 725 167 084 572 935 684 804 531 413 161 541 536 860 377 785 463 845 806 924 565 303 439 071 406 780 987 641 911 367 299 464 632 399 080 769 692 699 929 648 083 694 038 384 516 359 344 866 563 734 180 902 377 799 640 279 081 724 959 840 929 683 863 667 598 899 216 659 244 193 393 072 760 504 824 971 143 859 336 570 165 707 629 951 490 470 755 584 764 010 914 443 943 543 665 623 515 256 833 978 413 484 443 852 526 886 922 519 362 497 632 088 747 860 333 050 142 485 005 625 603 406 901 074 532 004 560 349 772 808 830 511 613 857 145 942 326 773 671 052 462 530 369 994 252 937 673 096 808 363 303 883 028 719 868 312 629 462 859 967 980 464 842 886 942 624 747 480 662 773 549 457 574 306 748 855 123 877 300 232 480 465 688 897 826 694 352 487 200 732 265 740 280 030 703 734 737 147 852 643 983 613 062 447 802 284 163 133 472 861 277 778 469 707 245 854 687 193 022 393 634 382 850 320 881 006 813 163 254 857 735 304 053 967 179 443 857 281 451 463 990 291 991 152 879 958 637 057 058 642 840 980 264 684 497 295 491 170 528 673 854 564 137 588 027 737 354 024 972 934 910 390 174 452 651 974 455 951 408 921 135 186 557 581 011 038 706 906 864 283 337 636 436 491 257 648 634 773 120 096 666 248 362 941 549 591 198 996 261 881 832 439 234 655 223 533 600 991 808 597 468 786 247 907 915 415 808 935 979 115 162 718 343 613 006 377 712 602 815 911 147 458 655 711 350 012 601 420 890 381 787 135 457 252 374 778 836 975 817 126 527 215 166 470 807 316 098 639 507 958 342 816 360 424 139 633 124 396 337 916 734 960 804 833 156 277 225 744 115 404 947 789 475 636 923 721 457 648 616 935 050 724 352 905 672 113 802 540 258 397 951 051 210 017 905 873 346 492 335 796 597 335 379 298 428 048 547 764 035 028 711 863 624 354 133 653 112 096 149 148 159 312 572 430 467 491 099 007 192 078 048 778 462 743 143 508 369 166 204 219 720 455 800 798 330 202 233 856 191 052 426 594 743 667 281 123 630 454 598 365 993 463 319 081 801 835 801 614 118 875 239 564 334 323 087 646 041 319 388 585 456 304 236 013 463 987 061 434 101 438 115 890 075 222 285 739 301 555 482 177 304 326 865 353 529 889 892 277 814 037 646 814 070 593 847 265 797 287 278 050 736 956 525 281 013 761 988 096 946 293 031 925 658 541 195 999 095 442 761 452 575 946 922 918 136 006 385 180 800 028 166 627 761 449 453 360 466 297 784 983 484 616 727 347 068 234 057 419 285 392 876 417 889 280 774 650 317 063 354 245 373 817 167 014 401 385 640 130 657 370 198 426 125 465 768 692 791 129 052 285 270 387 377 667 298 193 564 095 556 682 862 814 739 370 169 370 594 698 495 624 806 628 473 814 504 818 491 527 441 116 036 395 257 816 108 016 528 040 373 831 113 383 322 303 673 373 801 262 821 337 204 630 991 796 722 398 316 533 203 159 033 456 637 384 768 135 077 234 485 634 671 525 896 602 323 127 707 174 044 585 100 110 416 719 584 099 280 545 300 792 604 098 582 158 547 367 685 906 034 305 787 966 145 356 785 110 384 172 996 127 113 207 323 567 551 280 673 450 251 374 640 848 245 044 845 189 624 935 797 578 330 060 220 501 626 119 460 416 663 884 519 420 778 392 136 833 902 475 467 347 482 610 533 954 301 776 963 949 849 079 598 060 216 745 530 833 982 233 862 980 095 108 992 119 986 106 305 138 942 073 326 941 659 387 270 163 717 076 721 591 616 975 894 921 409 708 509 121 804 189 291 718 336 493 309 166 784 415 170 426 686 560 911 266 727 652 815 365 260 550 610 319 333 591 820 132 226 540 780 484 624 730 574 055 262 977 496 139 978 342 561 499 387 555 455 806 846 476 254 850 054 950 026 850 666 736 736 400 909 143 759 989 068 713 572 353 859 570 628 231 847 343 731 455 785 144 799 035 629 785 156 908 301 469 651 032 639 159 243 331 858 693 070 012 907 594 863 459 148 566 434 550 679 841 395 624 890 257 940 679 954 327 912 658 230 320 991 394 619 511 416 398 925 448 393 977 503 743 143 597 928 019 445 098 064 767 185 589 668 974 517 177 033 812 302 084 793 815 049 451 691 445 247 453 542 317 145 360 693 217 728 615 444 504 195 325 736 025 032 493 333 768 429 046 408 591 546 027 091 656 949 277 588 864 017 641 184 234 744 832 817 086 435 982 542 302 778 410 992 164 366 605 520 077 443 482 229 870 557 446 569 070 546 246 862 884 934 582 006 606 226 059 689 668 233 936 371 932 404 106 594 036 485 040 460 979 372 732 104 868 160 334 809 606 381 781 804 612 839 916 877 249 858 933 941 138 750 451 143 946 117 614 647 947 169 641 747 980 868 543 027 652 246 044 049 210 899 992 733 085 343 216 164 829 788 261 564 452 083 093 808 568 517 839 062 435 218 841 351 090 362 043 938 221 560 942 992 336 692 926 449 408 305 623 102 390 670 752 749 470 672 561 478 779 376 046 716 840 029 683 677 335 843 063 101 435 982 888 664 870 741 318 354 307 769 058 744 260 385 741 953 296 482 366 124 346 615 067 138 333 243 543 458 833 615 519 625 219 947 643 060 898 973 490 252 974 631 170 525 750 177 200 594 062 077 552 792 442 646 836 312 456 223 629 772 756 383 149 367 563 460 624 187 733 027 032 374 547 313 478 226 494 949 574 767 081 639 738 842 059 949 561 485 346 226 127 603 479 112 992 906 643 283 425 105 552 754 323 011 706 110 179 712 504 265 420 266 920 353 083 927 020 713 709 443 069 038 763 191 422 489 027 478 708 440 249 268 515 796 065 037 378 537 225 626 180 160 269 836 500 068 387 019 210 722 069 907 474 777 270 179 992 377 913 204 078 026 322 102 045 597 668 417 734 808 422 034 693 784 127 129 130 508 485 748 396 877 196 957 121 830 002 704 664 304 945 485 115 200 550 146 071 108 622 288 608 966 870 613 902 269 121 361 913 251 256 249 848 025 756 606 933 718 987 445 794 718 819 250 559 641 956 528 118 089 594 062 299 596 289 824 754 321 664 331 322 316 425 075 019 400 700 652 924 297 978 312 877 450 227 502 387 095 593 952 029 148 312 030 194 410 474 933 389 537 978 175 419 991 990 925 468 377 862 006 695 572 732 141 847 725 496 361 735 139 918 310 078 271 949 695 088 632 008 358 804 420 553 685 843 914 131 914 199 950 670 058 751 542 045 330 955 091 912 073 963 990 166 103 265 007 974 066 985 701 075 454 374 574 197 371 369 130 847 904 678 000 156 508 041 392 433 020 546 511 139 049 401 761 124 784 708 463 463 536 500 333 050 302 796 437 462 845 895 437 076 397 012 323 649 933 391 057 958 664 818 770 822 512 556 300 219 403 131 850 571 578 242 307 350 992 002 551 203 786 368 328 451 254 253 653 766 203 942 266 672 149 644 100 888 518 735 315 791 989 836 271 646 707 303 257 801 064 860 568 426 009 740 940 282 575 821 575 915 009 319 631 861 969 231 360 363 681 248 505 270 117 816 962 515 186 211 557 766 539 537 381 626 544 165 706 086 180 010 697 065 199 902 852 780 947 186 830 744 163 697 918 658 468 732 098 038 641 993 458 932 132 452 864 237 712 899 918 495 061 097 801 346 258 335 807 641 394 700 093 390 291 200 365 043 221 532 248 439 305 170 181 533 460 451 258 379 593 729 667 354 029 187 218 858 529 916 048 393 249 113 723 053 086 487 778 048 315 016 101 430 125 299 920 438 112 345 102 879 469 434 231 559 577 045 423 114 150 082 374 362 331 284 574 330 190 978 991 259 396 270 992 527 351 846 498 600 144 186 331 869 457 332 158 515 082 586 989 754 609 780 255 210 202 256 010 541 896 860 113 051 351 758 897 189 361 119 847 002 035 137 714 596 485 214 325 146 973 204 642 894 667 940 334 985 448 805 004 202 496 378 904 729 537 505 852 285 988 881 237 371 734 377 264 320 828 450 372 037 443 453 885 792 709 552 146 337 656 690 067 146 209 014 472 602 046 166 123 103 088 048 066 816 092 355 134 495 695 303 998 148 866 859 612 895 296 782 631 733 141 294 096 071 029 066 450 042 690 834 433 395 677 166 000 839 971 534 107 769 443 055 495 593 045 932 435 454 894 683 187 141 886 994 094 189 171 447 059 734 512 320 274 269 153 330 507 789 294 284 888 576 694 604 415 580 756 294 355 139 074 938 197 423 586 348 678 496 958 887 145 842 534 109 153 000 419 961 956 552 928 872 301 425 977 336 722 400 444 068 202 433 464 852 851 546 162 812 183 611 246 498 829 173 072 274 659 995 751 877 174 727 499 130 544 484 213 260 962 912 606 842 697 464 260 810 718 908 574 476 093 849 453 074 951 945 438 123 180 936 713 518 500 576 712 260 115 305 569 808 358 144 335 471 947 192 148 497 582 538 199 185 854 075 769 236 229 395 663 183 594 354 066 169 492 068 311 056 444 723 513 976 607 913 356 373 409 854 058 495 490 381 734 035 252 235 825 381 024 230 664 915 985 168 576 315 376 699 574 813 539 289 169 246 175 064 948 544 460 724 102 719 263 952 906 680 116 687 633 119 525 527 053 287 921 992 891 588 137 206 396 686 356 423 036 201 575 453 195 708 695 630 906 066 476 215 474 684 695 635 615 535 598 587 070 726 188 338 032 768 342 109 840 066 082 808 180 851 265 934 312 802 640 897 930 439 077 916 394 059 845 300 512 060 583 291 415 639 801 870 241 080 231 326 374 509 507 527 537 409 305 686 267 360 698 134 304 756 246 569 667 321 821 432 377 358 046 732 633 414 194 210 977 801 035 044 192 797 410 751 838 156 273 961 072 460 063 206 918 109 761 177 003 216 901 888 174 758 195 878 463 510 718 256 065 975 690 376 360 036 212 698 061 465 846 579 878 672 549 217 249 306 091 521 174 130 083 399 448 425 241 035 794 451 909 127 522 780 121 959 239 313 890 045 962 323 183 957 529 430 991 943 152 688 418 411 308 703 513 374 958 223 222 917 261 464 870 736 437 979 986 797 536 708 360 643 588 281 450 012 164 321 532 048 836 093 943 336 643 005 280 877 545 516 578 037 332 126 904 545 088 905 371 347 153 328 495 443 090 810 699 088 207 749 137 726 727 197 573 011 227 723 962 363 228 067 060 015 753 478 821 343 051 941 802 595 283 527 321 656 235 614 695 430 372 554 316 904 614 087 543 169 552 566 258 648 413 205 186 963 161 895 935 851 539 969 146 141 830 193 094 132 395 011 458 404 342 208 686 110 243 266 298 469 622 699 489 242 733 699 701 858 954 998 593 618 226 586 008 090 590 259 189 744 766 832 229 505 511 833 809 205 937 242 713 688 514 786 996 549 557 970 675 377 102 878 799 879 370 743 258 578 781 982 451 675 987 435 020 366 423 685 092 828 639 583 598 175 445 679 135 544 549 966 924 460 754 988 937 899 814 454 106 236 778 528 319 031 840 545 060 711 729 647 665 690 158 116 614 712 858 163 894 158 971 951 351 519 705 126 112 898 700 331 264 962 011 772 498 911 629 659 880 089 299 909 151 059 825 285 767 629 536 115 934 884 847 806 756 222 802 113 304 995 332 435 118 904 970 797 022 345 433 877 687 584 301 233 598 958 466 975 427 164 476 872 336 319 866 485 981 268 748 756 185 860 886 637 767 762 541 738 743 192 638 882 091 614 326 752 549 986 524 866 092 875 220 408 731 952 353 542 633 264 094 764 951 990 891 680 621 694 670 441 946 492 136 769 445 143 279 833 655 443 032 709 136 073 312 148 443 335 084 907 573 861 621 679 556 708 894 284 450 860 241 498 601 742 381 121 782 020 500 249 047 027 882 361 269 981 198 358 079 525 054 392 031 552 791 615 987 991 016 412 796 125 646 532 075 980 579 534 073 775 079 706 150 888 735 754 636 554 510 957 957 482 480 698 880 971 079 432 958 198 348 323 598 319 783 981 862 210 418 447 320 423 131 969 344 709 814 599 288 385 460 277 447 050 685 491 579 434 611 012 481 657 478 126 025 913 010 163 504 821 937 887 335 775 206 692 545 737 536 018 640 149 768 792 937 364 347 512 791 682 512 872 336 528 466 765 989 308 563 029 681 789 941 285 019 870 752 963 167 836 942 123 853 521 094 448 480 585 294 367 239 252 754 526 683 079 814 583 610 244 743 400 504 452 236 016 288 683 148 119 310 520 132 846 173 148 079 212 401 570 889 821 412 808 468 923 610 876 334 674 419 373 789 639 098 248 758 219 158 270 375 769 417 186 551 190 258 534 139 873 422 295 144 005 441 410 923 872 182 173 818 830 800 651 581 286 734 335 159 145 711 150 247 633 113 665 593 183 337 140 235 235 124 808 415 190 564 707 018 700 455 401 563 246 980 474 519 621 044 258 078 450 537 342 685 700 164 939 542 712 179 919 783 561 883 447 264 582 480 687 496 060 166 951 634 766 860 335 953 562 729 541 792 541 157 419 060 495 195 223 996 847 359 280 960 011 085 316 474 238 802 447 964 889 139 592 339 407 581 074 487 175 663 986 343 593 612 974 862 314 942 779 538 251 031 984 252 493 894 836 827 959 766 654 168 406 553 477 845 888 431 276 245 263 542 104 744 890 587 111 713 405 618 298 215 935 894 280 264 335 635 121 018 489 750 362 446 387 417 347 554 821 026 049 066 738 755 199 249 726 332 555 585 732 013 371 454 689 003 542 248 545 824 263 256 462 908 724 988 037 453 528 044 717 242 352 737 359 292 498 323 981 061 624 783 067 146 105 536 147 619 447 599 317 805 449 191 953 977 526 262 589 604 340 481 581 928 815 834 241 504 674 511 283 824 057 024 995 704 786 999 459 568 841 272 239 587 016 835 161 787 408 877 256 023 370 729 459 572 486 824 423 439 809 865 590 720 443 736 697 676 664 799 834 013 846 415 829 235 590 713 781 323 464 587 705 107 919 677 410 094 868 460 822 842 217 372 209 155 702 214 617 264 682 743 653 788 390 374 348 769 324 827 382 191 793 558 557 370 036 066 619 925 171 662 856 033 463 303 201 705 056 868 604 920 944 152 189 725 670 550 427 315 154 132 030 925 669 196 507 412 954 882 930 327 752 438 305 764 515 806 403 471 533 474 017 862 880 904 491 867 561 255 035 411 991 676 252 713 168 679 417 521 551 941 955 757 796 178 474 524 074 894 786 725 675 237 785 683 864 209 715 245 981 194 219 190 443 425 793 995 714 576 967 665 507 751 605 767 020 129 371 881 820 743 911 281 138 862 035 366 285 200 318 002 666 832 472 460 688 430 905 153 629 779 135 201 502 760 763 061 542 398 698 509 595 262 601 427 901 003 298 086 689 145 959 110 745 979 004 447 171 541 473 878 647 255 159 293 008 805 115 441 383 231 091 469 176 258 603 057 482 528 528 033 954 285 033 432 043 191 585 446 016 905 185 472 108 968 745 401 973 293 886 209 268 955 117 284 573 681 023 964 740 936 963 065 647 849 438 348 651 691 302 944 153 674 756 157 233 181 718 658 931 942 212 999 488 171 018 543 769 342 294 867 041 898 699 149 201 890 076 601 646 429 235 161 755 919 573 479 176 251 170 788 733 946 045 515 905 800 593 021 910 964 786 454 438 885 176 474 974 954 974 221 071 653 420 191 357 250 042 529 379 186 567 451 625 723 624 235 914 674 926 169 752 502 094 179 965 394 726 043 802 802 651 649 575 223 597 980 746 463 512 298 494 489 129 613 385 192 068 909 873 826 147 785 892 324 754 889 575 710 424 748 965 595 632 193 168 007 229 405 798 840 028 517 870 208 436 770 358 419 421 762 756 028 800 960 474 826 064 336 048 501 768 576 935 949 979 592 385 933 114 072 160 236 726 091 555 347 923 838 909 859 331 585 997 981 042 646 173 215 485 669 271 941 169 526 658 515 772 407 018 169 933 840 279 709 571 096 943 066 182 866 995 952 999 571 469 664 007 392 941 936 360 075 385 562 144 330 843 120 358 543 107 202 104 481 807 020 765 186 295 347 277 508 799 958 601 933 852 472 882 796 282 408 352 939 162 574 683 236 932 425 271 838 494 789 397 564 918 797 701 459 988 444 228 420 921 209 270 302 999 723 339 080 879 376 120 479 009 712 896 120 313 288 925 520 220 671 104 697 216 807 475 759 109 931 316 538 665 579 932 183 888 869 470 225 709 004 627 517 884 968 180 059 116 229 839 377 517 375 175 499 342 887 345 594 924 702 073 406 707 291 559 968 810 162 695 372 862 566 793 057 831 287 698 845 216 185 081 560 401 010 990 687 497 963 940 033 951 589 232 539 105 812 694 300 098 766 532 779 950 403 541 348 115 255 020 687 582 967 813 442 323 124 463 991 269 732 282 027 058 290 329 410 697 216 768 357 071 850 158 923 060 766 369 101 759 660 573 092 625 310 045 410 976 607 898 437 278 565 577 460 360 921 018 729 414 004 978 298 215 039 445 713 089 497 932 615 459 944 048 855 329 346 986 723 160 216 382 580 920 352 218 644 139 590 277 520 643 844 823 890 015 796 481 835 923 839 035 407 588 755 506 914 691 333 277 833 968 817 958 420 914 560 320 727 313 006 188 215 965 513 415 598 548 551 613 243 718 375 859 042 145 690 517 945 232 155 922 845 517 832 315 594 650 027 863 307 058 534 067 309 493 817 449 360 121 465 249 910 220 688 855 236 935 568 646 779 685 160 235 874 491 533 159 353 885 894 194 606 677 935 784 636 702 516 020 869 424 230 145 721 690 661 424 598 734 876 425 680 334 353 693 208 005 601 238 841 453 543 821 359 417 737 899 419 550 762 310 128 249 327 755 725 353 377 064 933 920 780 676 888 553 231 217 847 930 231 888 587 107 219 806 677 059 947 544 052 437 904 144 808 730 365 471 852 963 810 579 285 127 563 965 102 787 779 614 521 557 827 243 320 215 724 665 526 513 002 259 665 986 482 957 216 086 156 440 546 951 743 922 114 002 476 848 962 157 658 417 123 638 620 634 481 957 953 133 302 325 287 097 731 483 689 189 563 839 406 232 848 637 491 899 037 416 108 778 119 016 433 217 853 349 953 245 553 515 948 224 110 995 322 517 690 560 247 479 350 736 651 832 942 959 391 897 010 077 557 876 437 033 744 593 795 145 550 437 134 038 872 948 452 553 272 830 189 106 438 490 945 799 488 766 646 523 097 950 522 690 894 238 253 657 004 319 064 531 091 311 783 592 340 567 527 477 129 839 385 924 569 824 405 294 064 304 848 156 223 484 271 786 739 571 457 064 593 054 744 943 367 155 600 448 700 580 350 290 225 412 650 153 564 999 302 551 088 665 981 434 557 408 491 777 478 685 959 318 239 107 238 579 752 745 843 959 309 304 357 280 770 000 619 320 072 030 456 140 085 949 788 329 295 220 623 356 711 261 494 872 288 387 830 199 276 635 732 025 556 695 531 507 868 693 400 703 501 459 030 270 934 052 736 315 566 632 142 294 613 677 268 717 479 095 536 968 684 266 113 082 705 791 797 211 613 279 820 556 407 979 009 102 597 674 729 585 147 787 293 629 493 185 071 411 773 656 606 254 573 715 742 564 989 210 746 426 728 049 921 267 085 247 692 319 893 162 146 498 821 801 125 801 171 214 193 819 175 108 338 011 620 997 976 322 452 954 348 678 207 753 925 479 969 278 634 748 293 213 701 452 388 422 183 906 291 501 714 888 798 393 118 759 405 693 966 885 439 977 129 839 949 633 186 417 007 535 061 439 063 292 962 951 897 582 319 421 238 562 121 453 441 808 207 193 651 445 129 240 681 528 184 393 946 854 943 120 014 290 970 815 516 690 799 939 527 456 628 673 586 643 343 838 141 808 452 935 620 364 115 727 747 115 635 396 165 743 198 642 930 647 612 307 111 115 777 788 856 320 162 123 324 763 390 078 615 768 750 959 768 746 046 392 620 134 852 941 766 184 055 673 502 303 360 662 745 798 475 881 942 298 158 584 129 486 757 366 231 497 395 861 171 330 070 081 243 112 767 857 451 248 290 188 244 298 771 252 447 107 106 792 512 177 046 808 026 663 210 956 524 550 625 582 435 867 587 972 599 723 025 053 844 542 284 600 242 955 094 757 734 656 670 492 443 767 385 533 551 255 009 798 138 809 525 931 600 996 718 830 131 556 077 657 252 095 558 235 920 687 714 504 298 254 653 568 329 497 821 958 786 199 812 917 482 691 030 975 463 093 547 542 130 896 743 025 516 947 230 863 924 631 570 706 709 685 422 376 100 378 428 154 403 173 086 722 415 532 437 146 345 899 927 810 773 987 382 657 786 182 893 630 955 719 709 204 519 577 463 101 228 664 519 274 564 066 119 610 709 838 363 900 818 802 776 819 234 963 769 219 612 134 976 999 013 612 427 439 068 854 612 834 103 539 206 846 090 988 719 813 671 679 744 526 963 474 526 835 781 731 194 361 765 892 528 711 763 763 912 202 214 892 450 833 878 363 294 263 064 505 239 393 393 928 295 644 679 637 093 932 614 882 915 264 123 547 256 184 124 562 393 656 073 783 129 955 139 194 760 620 619 246 624 461 772 619 226 613 641 380 223 060 313 074 610 649 616 964 158 900 111 390 480 759 753 391 107 685 557 608 329 788 376 615 228 305 407 490 847 844 649 014 559 631 510 576 574 451 608 400 753 706 778 673 603 127 236 135 753 589 256 602 087 636 970 061 810 301 585 283 472 248 046 734 927 095 628 560 456 152 837 899 177 566 195 241 905 984 899 097 152 988 801 303 969 149 899 250 909 185 400 850 336 043 719 754 560 095 844 931 608 429 799 404 955 910 710 436 408 012 617 752 581 833 276 393 573 036 073 561 759 332 779 392 701 762 926 512 396 763 521 090 320 118 845 046 882 116 799 245 823 004 485 978 845 060 851 125 899 333 646 672 058 545 449 476 734 885 760 504 025 765 257 403 688 227 446 565 614 873 089 184 745 621 192 312 208 034 506 595 285 133 960 977 393 482 880 409 021 893 758 412 007 397 531 267 854 296 222 810 771 975 834 653 245 793 019 247 623 704 077 089 421 861 122 967 658 792 941 843 509 403 852 408 777 557 778 909 728 947 806 189 266 016 156 194 743 370 109 846 753 112 601 412 733 829 404 993 706 893 720 318 924 988 760 032 713 313 146 464 969 098 279 471 285 915 953 072 606 070 236 760 138 337 533 233 111 907 530 220 290 776 897 536 260 541 866 131 255 940 649 665 073 042 202 683 959 547 446 246 301 546 150 627 692 765 766 805 742 161 122 407 990 799 113 652 626 022 984 526 411 935 206 451 002 332 858 357 670 612 986 583 411 435 893 065 392 804 093 389 108 139 809 693 544 494 826 223 111 295 690 654 199 622 164 335 056 601 998 626 577 589 761 370 852 915 630 295 162 554 799 645 904 839 251 668 863 625 659 667 305 066 323 269 951 591 309 932 041 685 289 069 150 338 385 338 429 823 388 725 821 906 314 357 330 612 307 675 951 698 644 159 834 327 313 863 579 080 170 517 691 905 460 131 168 187 168 524 819 304 717 380 175 389 008 326 399 913 752 899 603 273 478 388 917 292 878 495 515 930 795 142 502 895 365 368 735 194 798 147 716 608 108 662 167 548 778 277 837 382 307 895 452 440 003 519 120 214 734 098 960 291 034 406 340 310 559 718 088 811 974 265 241 948 413 919 979 900 602 725 131 295 962 462 915 831 419 555 826 976 224 206 488 111 800 939 423 723 715 250 138 788 813 110 442 297 202 944 165 394 958 911 226 146 361 944 397 474 409 567 270 961 492 709 302 289 937 056 831 820 262 735 139 415 536 235 853 423 238 041 216 718 204 390 028 814 054 754 072 534 127 649 989 737 340 185 923 905 140 261 790 156 910 860 501 228 428 351 105 862 007 547 362 706 307 829 866 405 338 009 002 406 951 825 344 500 432 890 638 811 636 235 890 221 159 222 383 620 335 293 494 729 143 296 167 972 921 941 867 173 781 965 089 571 327 693 458 306 309 030 943 768 166 536 146 294 027 884 592 121 593 011 216 334 948 155 251 359 717 985 919 445 520 402 709 326 452 271 242 818 308 039 269 548 787 344 643 297 637 656 437 020 964 659 531 518 125 419 704 987 648 712 885 763 798 010 420 097 762 263 179 977 632 202 340 432 595 982 170 924 325 932 522 299 954 357 541 019 881 912 993 438 124 751 849 078 618 245 845 178 157 998 339 378 979 776 815 858 309 517 801 833 244 805 409 805 489 838 702 525 731 062 502 426 264 628 673 718 495 295 900 253 671 370 959 064 045 678 064 397 311 293 665 022 351 048 881 325 424 321 284 262 909 592 993 610 858 020 506 755 701 795 759 825 473 995 829 037 105 064 290 600 268 685 387 205 967 171 751 223 605 548 892 359 853 178 368 561 373 776 316 632 726 983 461 721 664 051 776 477 637 875 544 448 666 300 579 556 457 003 059 416 446 382 309 037 415 049 516 182 612 746 785 145 468 798 451 515 646 303 490 055 413 665 635 749 762 369 798 606 641 729 195 657 796 346 354 462 270 163 906 161 926 559 794 409 680 558 984 200 485 660 229 081 965 649 350 115 910 848 211 095 296 442 588 642 815 440 365 161 874 344 882 231 845 030 878 360 475 620 241 417 099 390 904 473 983 994 758 237 985 104 091 947 313 692 978 363 422 224 136 810 818 500 384 919 849 854 552 043 018 813 477 818 935 799 426 972 454 138 957 101 403 448 497 506 202 212 977 616 140 511 475 502 059 599 012 175 919 093 649 265 070 137 180 832 010 177 301 139 664 142 703 453 628 930 255 543 482 402 563 269 113 639 747 760 041 377 764 354 396 841 314 620 110 564 806 533 613 739 367 738 466 022 697 713 418 311 540 753 945 401 496 349 704 575 586 372 556 808 550 212 189 716 721 258 977 093 379 960 535 755 423 949 714 300 331 063 285 335 609 637 646 465 381 146 725 618 997 480 361 142 294 923 775 982 620 544 401 955 467 962 627 471 449 379 914 356 585 468 780 660 529 630 190 447 863 995 315 023 048 987 498 885 417 327 224 964 825 168 422 613 708 337 434 993 348 196 788 611 272 942 252 767 367 324 885 550 070 343 287 267 096 990 539 266 836 081 447 426 250 214 022 520 639 936 739 312 410 347 873 904 541 904 897 614 345 487 725 736 283 950 462 923 270 254 475 993 090 872 880 880 873 720 574 899 266 419 356 474 057 855 884 031 794 696 573 245 768 820 986 313 325 185 864 601 069 198 843 360 568 170 448 920 048 038 586 931 854 136 748 488 856 427 613 338 343 618 450 113 431 736 923 670 939 911 129 545 457 180 810 041 320 194 073 129 583 480 048 384 022 681 110 292 253 846 710 659 975 883 633 057 816 734 976 509 234 520 157 994 601 294 696 291 876 276 987 228 619 779 921 544 707 425 884 427 032 505 478 258 455 091 183 216 805 031 710 534 397 561 925 596 364 421 972 057 361 328 917 975 950 596 021 632 397 757 359 007 778 175 968 384 508 926 137 608 870 408 423 165 392 660 498 383 442 590 823 223 473 501 294 559 121 137 592 239 092 444 313 056 649 404 604 824 333 759 836 478 917 487 851 927 982 430 719 576 282 696 800 604 352 800 153 168 195 970 662 327 860 457 814 975 131 809 378 830 296 544 114 401 265 420 435 102 847 511 797 525 955 717 779 120 834 507 919 181 954 415 938 592 242 224 960 324 559 923 107 179 968 732 387 906 857 113 624 964 483 005 546 979 998 025 647 174 610 509 582 343 478 748 035 307 897 991 213 685 312 592 538 177 496 172 643 480 478 038 804 456 170 613 933 127 062 155 602 194 005 251 660 729 711 467 778 794 119 513 531 288 715 824 475 527 113 608 155 999 282 101 404 865 711 751 300 937 096 981 206 644 102 708 530 379 809 197 100 652 650 979 639 632 959 852 207 932 146 451 164 652 111 485 048 640 674 352 859 536 828 594 987 784 718 280 434 188 681 284 616 465 680 242 986 436 397 505 263 993 122 365 341 735 692 960 449 018 922 540 846 411 049 829 146 827 822 206 042 929 322 177 421 361 566 819 171 179 753 226 957 998 929 599 247 928 065 590 532 721 734 510 083 851 128 480 542 901 193 144 134 178 755 752 722 266 008 070 542 666 680 654 988 169 929 112 396 153 082 580 454 144 470 670 747 045 118 727 098 820 633 772 191 281 595 094 430 086 053 967 052 567 321 663 750 811 326 972 272 165 030 271 404 885 106 111 985 153 243 186 817 005 212 035 367 641 829 594 864 871 422 114 941 126 631 221 675 708 177 771 201 930 450 989 450 730 819 701 153 707 424 890 859 868 955 716 159 473 250 055 804 616 131 999 414 548 083 978 237 257 215 911 166 007 555 418 690 309 550 471 315 400 498 558 256 092 776 550 452 685 357 723 177 806 808 406 884 681 136 204 320 898 277 983 535 261 897 828 559 306 107 385 056 659 920 691 798 419 977 020 675 526 023 031 114 492 708 583 719 704 018 507 252 994 897 062 001 965 681 164 469 764 218 134 721 271 908 814 475 275 538 486 032 205 502 493 939 547 253 262 596 470 424 907 155 728 130 330 359 428 243 244 452 975 200 022 916 098 112 808 796 923 971 805 458 356 925 181 304 920 849 586 438 448 012 998 111 694 393 704 744 799 935 178 582 785 261 744 533 151 724 134 180 890 557 809 166 711 914 067 134 322 588 328 711 597 396 642 735 676 334 719 877 996 435 027 423 850 502 285 315 630 653 340 592 791 648 553 019 672 110 826 221 703 216 060 389 364 854 142 526 945 114 367 039 642 547 853 478 517 609 720 973 006 402 513 962 106 948 472 390 571 104 156 219 300 919 995 084 597 944 826 473 879 103 404 720 648 766 398 935 318 208 129 079 688 175 797 514 062 170 334 370 674 196 850 900 773 037 243 652 127 344 032 766 402 328 679 980 558 818 653 770 414 121 433 626 402 429 724 425 363 666 642 166 822 504 601 967 444 641 165 232 445 694 484 350 018 241 825 353 865 545 928 646 964 514 764 287 785 118 234 227 024 695 886 067 203 906 713 477 771 853 145 541 081 580 726 094 977 088 568 159 850 544 650 025 963 972 656 257 574 954 818 139 662 097 141 817 281 867 613 863 610 552 769 936 349 274 657 727 964 352 683 497 291 628 013 002 056 983 008 387 340 839 289 802 538 570 424 067 641 983 255 324 538 021 751 106 406 098 136 946 018 435 813 898 434 650 364 647 853 110 012 957 917 783 960 186 652 788 448 838 370 033 568 263 089 114 047 265 335 952 983 690 829 472 069 812 729 982 889 427 096 197 646 401 730 721 750 657 510 115 440 975 198 451 499 469 501 194 859 681 409 455 260 791 447 101 860 302 450 542 720 647 051 177 177 021 910 225 032 069 440 696 419 539 671 189 611 118 706 657 171 684 636 305 498 673 780 609 908 028 749 161 405 178 718 905 748 774 523 232 638 594 675 269 116 230 840 206 931 045 960 852 477 766 459 725 620 307 004 508 290 727 110 652 437 103 566 473 137 655 438 254 472 170 430 463 812 779 968 136 132 849 638 861 467 360 569 148 719 190 476 739 544 657 179 924 011 923 679 148 930 802 516 985 040 881 941 068 686 214 183 600 592 271 035 979 855 959 215 744 867 828 528 397 083 683 814 990 758 640 976 148 279 921 166 868 754 111 256 354 175 933 326 452 801 424 990 037 718 589 428 172 126 505 560 154 448 900 792 255 691 629 723 349 933 251 514 598 836 120 450 578 063 938 318 163 506 417 027 001 560 987 455 987 854 487 360 100 898 455 436 045 075 099 045 702 307 636 839 359 229 010 435 860 555 722 350 767 488 346 465 289 923 237 463 922 866 244 991 898 150 088 248 314 645 093 546 944 422 018 663 443 579 765 485 890 845 288 060 465 806 515 790 616 711 944 910 380 047 277 262 809 280 468 077 941 081 933 476 640 473 145 019 739 508 176 699 869 747 147 843 329 128 283 832 893 749 832 202 524 484 654 789 859 735 953 705 432 289 862 227 850 815 447 957 852 765 298 689 448 954 539 377 421 167 301 257 349 496 122 407 301 169 845 615 402 916 757 607 546 062 459 942 598 283 984 283 089 743 920 409 411 505 914 002 106 553 358 910 310 014 597 407 342 434 026 741 926 511 446 465 863 678 361 239 986 973 832 144 383 361 116 382 441 867 955 494 337 798 511 887 392 653 393 050 131 595 002 243 653 186 179 810 017 712 815 739 864 121 031 786 605 516 055 358 241 977 063 173 682 972 588 963 540 536 803 193 740 963 783 528 303 193 283 355 968 810 935 875 329 015 644 762 476 841 550 443 622 612 656 741 150 585 922 504 082 569 320 439 508 994 187 060 901 695 042 066 164 023 621 893 973 346 630 678 334 694 941 622 906 254 395 152 857 355 763 015 935 173 017 835 160 182 756 321 670 006 660 866 472 330 822 548 625 046 446 807 501 005 040 437 950 242 847 893 086 616 446 467 846 188 003 961 424 613 017 570 038 785 930 289 398 841 205 582 803 447 951 925 038 539 005 170 201 607 659 731 520 374 274 255 212 170 068 583 221 199 185 480 927 928 823 047 058 802 001 469 313 291 572 156 959 603 877 527 336 752 587 653 166 867 806 446 609 027 170 535 118 777 581 258 037 890 853 447 974 010 074 353 542 043 022 505 947 064 303 298 500 778 859 206 256 980 296 657 526 943 076 455 039 389 222 108 734 501 880 712 769 982 081 649 706 836 927 170 240 711 976 023 998 583 759 341 087 977 350 612 101 394 957 534 753 525 509 292 907 232 032 141 336 948 481 674 248 091 381 409 222 631 526 036 727 903 907 119 830 845 509 138 580 194 416 594 831 940 099 365 700 681 197 252 131 865 442 851 522 565 898 110 598 937 342 316 826 200 265 325 530 575 944 900 306 444 576 468 585 483 920 387 632 081 986 240 627 781 587 872 522 290 626 968 814 320 515 782 440 385 364 054 458 141 730 765 416 663 005 154 366 356 290 797 145 598 385 027 561 617 560 310 361 656 476 581 091 415 804 162 074 241 371 254 272 158 817 050 579 357 664 139 369 551 010 038 482 369 328 499 855 811 394 234 228 718 640 150 333 896 054 579 481 518 390 834 818 990 458 855 355 809 876 220 619 782 891 590 524 235 257 437 968 009 840 092 913 893 244 951 880 226 380 901 941 150 149 195 135 375 211 726 723 764 818 530 583 688 688 772 423 285 865 807 304 482 583 768 163 315 158 943 559 339 523 482 815 494 781 048 073 441 706 758 249 585 392 290 208 048 024 638 924 834 936 071 058 086 486 310 178 953 420 677 948 532 986 389 702 956 650 694 927 416 275 011 477 902 151 682 800 903 447 524 801 062 236 199 398 458 674 918 433 288 723 308 619 802 158 611 944 065 125 795 844 546 746 802 166 350 033 495 774 479 999 256 984 090 766 973 754 414 318 765 755 580 634 384 513 565 413 783 518 682 660 717 330 985 258 545 022 880 218 605 965 707 699 265 379 385 372 383 036 268 937 444 788 011 884 568 468 689 908 015 995 239 054 805 008 138 903 653 238 294 891 567 335 862 566 550 468 267 505 684 886 667 050 586 635 464 193 639 769 352 342 416 557 428 879 824 781 202 472 827 118 098 483 329 956 509 672 613 575 748 207 837 212 185 239 299 362 867 721 609 424 243 616 202 398 072 216 261 065 712 807 915 548 061 793 440 468 020 226 395 475 163 848 633 980 069 504 112 302 565 759 503 596 329 908 530 644 810 992 150 990 123 179 876 484 001 061 651 751 683 839 694 913 659 248 632 909 780 073 278 351 722 018 523 527 068 948 142 232 690 682 131 938 738 109 998 885 420 710 922 464 131 119 210 737 022 152 675 089 442 155 550 518 407 768 270 265 356 097 284 075 979 267 496 020 159 941 752 997 988 208 640 184 926 967 531 420 090 957 096 991 805 315 178 623 970 257 919 616 284 162 504 469 453 756 414 187 355 042 313 060 640 409 048 652 333 989 249 778 587 211 184 228 955 065 693 832 433 434 050 030 950 805 002 887 926 513 352 334 737 233 314 462 071 235 947 437 976 505 693 726 366 126 151 055 321 898 132 076 610 962 970 086 635 509 624 737 563 520 152 233 175 129 267 644 338 346 693 049 964 264 101 745 418 052 967 031 161 051 901 443 544 118 211 645 679 688 042 495 762 482 646 158 352 731 034 279 040 437 441 376 680 644 030 601 784 865 866 762 984 419 488 914 723 919 116 525 061 856 402 284 853 745 774 381 193 968 268 828 260 208 181 490 112 813 155 238 078 022 702 506 068 411 397 026 768 183 074 660 778 043 566 437 396 750 239 338 080 001 903 241 078 036 962 237 471 560 028 714 698 625 764 656 204 371 552 308 692 577 114 866 712 005 801 159 076 522 485 866 245 505 087 140 962 481 480 473 944 711 058 903 329 177 917 856 086 518 404 125 091 591 874 075 458 788 019 479 205 053 807 474 919 529 656 745 460 163 531 425 927 822 713 843 623 154 955 361 165 497 339 404 265 661 842 293 509 838 792 834 922 803 685 554 936 452 844 881 722 197 954 061 902 060 198 845 398 123 120 607 376 194 638 903 310 329 597 853 863 397 931 226 558 644 403 865 846 009 512 502 830 389 854 561 548 662 932 922 741 907 469 953 573 468 600 369 581 685 949 171 527 656 825 365 627 484 759 206 395 211 930 800 428 360 986 776 935 434 740 496 697 033 663 493 985 012 612 629 884 551 251 316 425 666 907 781 430 109 132 906 810 522 474 622 941 130 844 304 823 349 443 144 481 685 882 320 407 249 498 897 476 787 169 683 288 644 644 082 776 449 625 232 185 353 833 126 007 683 414 320 084 411 187 819 144 252 669 414 919 102 993 796 174 110 222 212 090 917 112 257 167 708 608 623 620 881 729 774 987 307 200 504 043 031 526 772 753 673 469 630 378 833 892 969 841 126 758 716 498 713 001 804 427 989 246 347 526 054 307 608 637 968 308 480 111 020 537 530 755 083 368 102 585 037 217 380 995 080 483 234 126 796 560 277 445 662 840 258 887 643 841 377 869 608 360 637 496 071 976 695 604 540 740 682 901 613 768 452 353 679 274 864 366 356 836 309 686 283 983 221 286 375 664 962 511 671 195 805 168 586 708 648 883 245 602 881 034 257 742 354 972 195 523 031 894 587 619 732 910 586 834 818 774 673 486 808 694 441 138 389 752 714 262 217 929 494 855 709 196 462 192 863 788 544 327 486 557 574 198 469 453 022 825 258 007 446 926 025 370 824 290 734 120 445 713 151 922 342 521 450 292 339 565 091 203 715 811 561 084 357 464 935 501 699 543 860 139 864 931 327 285 356 316 820 176 996 384 681 714 365 341 500 459 277 753 055 062 158 511 127 632 581 977 005 605 152 619 598 593 892 132 838 520 190 319 297 546 835 039 385 190 617 769 193 706 349 412 862 923 389 236 802 158 907 613 417 092 655 496 536 220 642 138 193 366 375 420 621 461 139 932 743 803 833 022 626 306 725 125 059 749 115 240 980 094 632 163 318 918 643 736 769 939 152 326 991 100 076 780 016 843 086 118 820 831 205 315 427 414 098 005 823 753 852 879 492 476 662 349 235 839 568 700 573 805 826 008 518 808 503 038 193 226 164 174 896 183 997 608 444 715 714 157 944 471 793 156 526 877 712 648 389 271 953 824 164 127 315 035 226 858 225 937 467 849 117 316 998 387 509 795 767 917 017 421 752 173 434 729 324 925 518 446 776 033 332 045 631 284 327 115 657 191 399 587 851 630 318 134 651 125 471 440 769 990 930 460 367 332 411 843 084 298 555 337 354 644 369 315 121 510 723 680 207 858 392 479 366 229 843 438 126 535 757 962 770 548 716 535 287 374 955 350 832 557 562 577 283 951 889 055 997 661 303 416 583 876 137 663 502 999 896 873 323 350 121 586 752 916 707 465 756 985 811 685 295 367 482 303 032 654 346 662 457 937 830 567 201 342 312 447 712 693 779 271 883 906 633 965 808 652 832 931 335 756 286 943 100 076 732 078 778 979 597 623 136 301 402 656 184 925 034 982 251 006 032 431 888 604 789 247 667 332 711 099 180 506 067 925 255 843 027 692 879 971 537 269 351 065 574 352 032 030 382 395 552 466 606 408 166 416 945 237 400 053 280 246 860 187 135 582 662 475 105 980 885 215 195 636 203 135 170 187 448 150 026 681 899 171 007 754 183 344 985 520 712 904 080 366 220 974 523 257 407 896 341 146 731 259 538 447 301 312 066 725 944 113 652 646 787 096 066 220 796 173 184 230 677 159 951 948 198 417 468 027 578 867 022 744 871 657 551 335 758 210 005 682 935 412 483 232 512 763 645 520 298 027 422 780 608 325 385 662 860 011 631 611 009 765 095 186 518 774 845 774 815 653 896 821 601 135 448 517 424 535 238 788 633 433 242 130 515 881 981 056 074 341 474 033 873 053 961 283 582 882 338 612 433 649 604 434 079 832 666 531 615 252 389 119 029 458 137 760 350 874 914 249 026 367 865 317 815 180 260 602 207 179 182 342 346 476 345 569 341 839 510 062 471 169 844 976 835 268 840 517 280 123 918 704 442 754 130 586 727 490 367 536 083 338 538 265 835 366 166 906 934 815 819 060 945 109 208 926 924 836 363 069 626 266 995 408 868 566 066 059 580 293 460 497 579 651 265 518 334 422 673 386 060 301 057 307 974 327 733 614 959 312 015 010 417 329 780 023 050 671 951 638 528 304 352 064 768 517 992 077 175 038 322 567 416 780 420 508 703 743 872 582 354 503 796 081 964 037 010 131 414 305 107 301 040 332 872 103 329 868 848 824 141 739 214 884 116 626 044 867 149 281 368 753 635 107 852 181 192 657 142 249 063 468 265 923 316 987 559 444 173 186 231 560 390 758 600 397 308 997 059 769 531 152 361 023 648 515 974 884 856 448 239 132 366 566 304 285 177 024 443 318 429 476 685 326 116 627 265 207 873 563 669 208 056 642 855 787 166 120 285 187 229 194 983 612 551 013 484 626 867 083 134 748 064 478 474 983 297 261 889 097 266 850 073 128 674 905 720 464 070 541 203 630 626 952 518 073 979 870 504 407 772 592 045 629 018 601 292 058 132 022 408 053 477 083 312 301 599 700 895 641 480 040 353 643 258 395 483 574 556 724 969 480 914 030 615 520 920 707 457 820 590 041 437 392 715 281 194 129 464 571 758 824 864 023 369 088 202 085 929 568 939 384 167 067 651 184 491 579 842 516 336 980 250 662 008 412 153 043 088 472 218 078 719 777 719 560 568 306 167 062 336 258 104 697 956 345 695 845 676 710 391 912 512 893 943 553 745 057 360 876 028 227 721 935 813 941 015 924 873 230 704 752 650 939 949 365 960 276 577 794 848 234 539 432 520 699 014 316 764 478 252 713 551 478 055 481 637 258 371 646 824 003 210 825 026 923 737 400 377 063 903 644 826 718 346 833 330 001 719 578 143 513 154 111 861 765 607 025 805 245 128 051 333 276 377 952 085 171 046 711 927 488 622 692 022 915 675 041 450 444 914 104 833 069 158 987 748 458 581 350 238 660 151 225 323 042 722 930 039 258 089 259 171 664 724 431 529 381 478 425 055 532 288 855 802 114 057 057 563 750 349 431 947 033 675 642 943 564 656 234 660 334 169 754 655 002 605 938 576 475 875 259 266 420 551 655 501 887 301 055 755 020 717 321 504 021 894 386 648 900 973 040 674 919 614 333 080 921 867 940 265 023 410 685 400 716 093 169 532 545 799 623 230 788 588 307 937 392 469 971 325 008 708 087 138 866 232 132 220 524 483 842 073 217 168 271 149 976 744 161 576 071 470 539 867 225 617 985 217 138 432 536 107 013 397 783 375 659 452 304 860 135 372 048 378 576 508 101 196 676 738 957 156 584 293 673 442 292 335 327 340 476 054 919 805 701 704 018 326 339 666 151 604 508 856 748 032 386 610 651 584 839 824 892 434 254 212 856 576 861 556 881 931 088 796 754 713 394 153 863 702 241 425 128 976 776 291 110 184 401 668 358 138 259 448 429 479 193 209 712 750 333 436 948 992 571 758 504 485 087 361 414 337 215 746 377 755 158 774 639 583 724 519 708 520 370 954 504 073 223 060 073 119 879 112 884 264 792 528 841 732 468 277 315 411 677 047 557 637 836 006 301 229 336 742 465 964 011 266 189 316 573 555 685 084 426 644 716 403 400 430 360 715 855 042 201 190 482 809 396 060 437 247 535 989 862 892 347 515 103 954 131 233 727 675 040 120 416 595 609 007 417 475 943 700 974 666 414 448 477 364 307 963 786 005 081 881 102 464 384 382 957 687 260 707 875 937 051 564 360 600 179 315 895 114 846 521 425 751 663 740 432 434 351 665 177 838 547 724 491 051 747 083 584 225 806 802 436 237 574 035 467 373 217 820 491 363 374 435 047 452 981 713 930 900 653 711 347 306 668 980 160 675 056 225 568 495 047 120 734 590 458 326 143 373 624 093 571 931 246 371 949 812 217 800 726 674 878 098 776 796 037 123 320 235 333 641 324 549 569 419 390 526 036 137 866 952 157 120 494 070 613 722 169 222 420 826 132 368 890 446 091 613 776 912 780 689 725 321 137 814 239 390 630 947 804 168 743 844 437 407 975 088 799 250 242 484 898 401 003 206 327 858 009 550 128 614 859 090 589 682 888 464 515 911 691 830 583 926 445 168 196 063 115 218 776 445 924 798 235 023 480 737 424 962 198 064 606 711 794 365 816 494 908 873 579 323 359 071 987 619 185 521 113 060 329 984 472 250 943 192 721 550 646 504 427 179 731 615 722 115 989 405 111 846 582 063 210 522 776 298 427 269 707 215 560 813 825 787 459 032 348 370 022 629 463 267 490 876 100 430 807 269 254 012 349 184 412 589 077 656 890 954 135 753 725 094 486 596 335 841 368 694 315 732 070 632 081 939 624 663 466 947 683 317 732 771 687 761 842 210 065 829 079 025 511 091 448 481 341 329 391 509 435 149 564 256 184 981 221 618 438 772 564 105 244 636 904 853 251 445 870 150 999 573 640 148 070 655 944 383 137 321 979 875 186 576 657 051 932 292 339 133 438 060 006 850 844 216 767 280 028 062 065 805 104 990 057 182 618 634 425 816 971 719 469 197 925 161 749 962 532 238 674 403 181 319 727 309 653 588 996 955 514 326 555 264 694 709 390 473 400 400 422 291 937 758 383 093 486 038 542 921 093 352 733 400 596 895 562 153 733 699 170 660 873 089 607 672 552 296 582 198 734 125 097 667 814 217 354 530 208 196 401 137 822 276 105 561 875 946 547 525 751 727 838 375 001 196 027 748 384 397 303 652 403 836 926 296 155 736 812 761 349 931 160 828 411 229 291 418 968 506 247 711 442 918 449 538 374 671 887 160 853 561 592 433 644 519 332 834 720 809 906 855 252 160 003 387 768 023 088 740 213 450 032 605 760 486 741 117 660 911 280 197 697 648 181 223 492 455 578 153 005 666 128 084 650 908 786 610 833 057 595 592 972 966 680 542 620 887 295 845 054 134 106 372 875 247 026 009 789 159 215 516 339 821 771 400 410 206 459 622 900 691 066 412 379 910 261 127 190 552 402 467 649 860 228 179 319 300 902 198 816 157 207 547 900 266 770 439 752 647 343 980 041 705 835 814 600 911 623 759 518 573 871 007 189 193 363 098 203 142 816 326 736 130 674 236 562 458 314 578 179 965 184 995 712 914 797 683 848 441 477 817 348 021 275 692 911 347 027 481 970 191 072 194 340 830 424 872 429 807 460 087 575 431 697 311 856 418 682 954 170 738 114 065 780 415 081 553 215 666 945 971 039 830 938 301 074 366 495 812 158 344 858 563 172 442 056 858 480 987 612 857 295 098 584 400 219 654 487 963 405 309 787 907 890 458 275 205 724 603 387 858 451 912 112 945 729 810 135 342 858 578 076 593 172 523 125 236 461 401 169 875 273 404 320 182 414 477 335 479 734 594 839 708 567 934 752 056 273 372 424 227 153 581 632 089 850 148 752 952 849 430 688 297 829 588 825 453 261 614 129 312 595 901 001 790 745 912 640 287 514 581 482 411 960 550 926 230 488 340 255 249 842 937 745 371 287 157 965 604 927 429 932 950 351 882 989 981 946 531 558 315 150 703 809 825 532 007 486 170 418 351 201 988 329 753 207 313 520 745 201 833 928 367 107 359 558 133 266 907 416 025 342 257 244 946 286 235 120 862 508 699 201 550 187 704 357 516 899 368 329 235 067 793 822 957 451 621 743 615 979 296 743 913 808 126 632 224 356 892 019 055 242 042 562 888 594 205 643 223 800 353 435 922 709 732 292 662 931 203 080 324 714 774 472 537 623 467 081 686 240 579 667 247 529 987 984 088 599 527 327 121 408 316 857 988 813 233 692 855 171 209 002 223 614 649 105 028 868 657 438 188 508 970 530 547 207 074 519 995 481 271 831 133 139 039 281 723 620 120 126 102 512 215 430 079 316 964 469 184 372 467 086 234 362 704 378 065 705 238 765 534 285 584 935 610 453 516 209 956 022 201 915 240 048 615 769 391 855 769 440 182 768 385 325 310 708 650 902 257 251 228 976 780 022 382 342 218 202 311 464 174 270 362 011 012 580 137 646 679 472 798 424 105 110 678 787 989 492 268 697 458 458 981 563 762 495 604 329 006 777 374 472 386 014 469 638 026 815 473 742 154 380 831 061 215 218 981 056 668 542 535 866 900 912 810 360 647 962 462 883 007 848 261 747 702 626 697 604 575 009 214 562 401 495 459 598 874 914 545 274 488 736 287 357 853 033 166 004 618 215 784 875 381 016 689 767 532 650 333 669 403 697 338 331 378 818 491 906 220 710 748 119 085 526 223 944 116 679 833 112 353 505 006 558 346 599 827 977 115 474 594 817 237 018 198 974 463 742 237 578 642 633 964 520 514 497 907 880 577 074 759 923 795 066 876 472 798 358 207 875 592 836 601 428 775 252 688 943 134 190 487 657 789 692 761 754 696 592 419 427 020 903 632 176 772 936 935 719 659 424 816 122 936 900 589 779 103 502 024 515 316 178 583 459 407 267 131 929 306 751 879 802 910 863 097 992 883 696 997 279 586 937 100 239 865 317 388 135 365 459 292 436 597 375 941 655 781 228 301 215 869 227 646 279 070 297 337 686 798 946 151 475 424 431 536 434 284 211 999 332 925 314 428 045 876 432 041 214 222 285 095 878 797 904 204 972 892 627 271 391 457 633 104 005 108 579 563 178 747 011 713 059 555 036 861 514 237 715 991 370 006 200 445 468 281 930 762 265 926 915 050 236 636 941 071 109 633 205 639 052 656 059 330 302 085 650 305 989 195 584 648 043 494 540 243 085 794 018 407 020 457 350 731 159 749 062 992 299 705 086 178 184 698 681 877 974 366 472 838 933 108 074 592 252 677 508 734 507 989 800 069 696 314 047 613 840 790 550 454 641 530 001 730 623 007 839 609 347 956 904 468 466 581 895 763 259 968 744 045 417 594 197 653 931 213 080 385 566 879 760 146 658 149 876 608 744 310 872 149 962 955 597 446 382 785 436 094 558 826 913 954 469 658 856 269 462 751 211 624 518 804 765 122 129 447 328 304 089 798 470 501 148 310 818 558 894 097 381 761 384 689 398 245 930 581 211 781 615 315 193 639 556 892 313 299 990 224 744 510 370 174 327 927 178 553 599 779 975 601 984 022 819 007 953 210 459 189 828 989 964 365 788 723 990 749 473 000 354 743 116 968 415 219 849 178 360 606 981 061 729 148 530 066 217 062 036 326 678 297 786 341 252 221 354 033 631 293 581 789 692 706 567 407 760 974 090 586 790 333 582 212 860 217 252 793 167 696 506 151 990 615 472 101 590 219 973 215 456 112 404 465 080 401 632 724 506 213 964 943 464 906 171 013 741 873 452 862 519 790 265 949 443 946 794 815 894 506 633 317 962 094 732 856 402 840 633 111 015 049 741 162 343 272 039 925 633 664 110 150 364 591 009 959 148 889 039 477 618 663 796 171 701 971 814 289 124 734 549 062 621 674 221 544 469 314 927 599 779 760 375 044 845 225 062 230 844 023 383 987 133 709 812 628 825 218 385 392 674 227 599 255 455 674 790 592 291 244 344 457 678 264 829 733 593 409 069 075 413 353 978 360 364 188 208 425 823 213 521 145 178 186 966 319 083 437 336 405 995 395 415 330 484 516 686 152 830 569 518 212 495 579 971 790 825 805 519 692 625 403 792 283 855 934 405 372 224 210 064 142 531 971 790 674 242 124 257 943 190 425 339 814 566 551 131 723 380 498 957 723 624 113 071 520 507 792 470 349 345 728 830 926 403 699 759 956 110 470 945 804 214 363 772 012 952 816 802 132 157 510 118 470 830 032 814 598 344 336 346 590 034 428 009 427 865 896 601 649 269 092 069 099 232 215 440 440 688 561 540 784 971 425 985 002 410 427 254 531 476 272 299 913 369 538 732 356 140 618 345 913 222 864 296 426 285 629 413 984 128 051 966 328 866 829 899 836 969 093 317 886 234 716 774 609 361 096 809 041 198 935 574 499 537 626 653 314 682 895 570 755 180 959 644 075 400 636 448 827 399 290 281 375 860 915 546 535 752 754 828 832 720 086 332 352 327 729 901 566 363 136 170 046 600 584 837 106 674 936 095 684 058 766 719 083 015 966 414 682 304 221 254 402 088 141 222 018 550 824 799 948 396 155 828 181 616 141 236 116 285 746 719 858 704 680 378 823 063 423 635 671 198 600 108 910 130 393 938 708 391 885 626 710 521 341 879 546 395 520 248 401 510 599 712 175 780 699 762 815 487 534 179 593 273 918 100 095 994 642 224 815 348 311 762 499 079 973 551 982 233 549 546 070 897 105 402 696 942 012 160 211 881 540 428 364 303 966 662 965 594 063 945 330 682 915 654 341 092 593 152 938 610 725 181 380 027 376 226 521 988 915 221 738 725 790 805 460 635 474 659 721 011 664 676 277 905 702 214 378 782 473 710 810 122 914 839 020 302 756 020 389 628 243 749 230 138 253 588 998 673 153 561 824 985 705 497 977 430 077 820 207 778 812 864 224 871 083 557 907 503 966 175 381 282 354 912 697 368 199 809 626 030 132 822 856 357 192 917 243 418 970 733 224 214 880 465 668 139 938 493 866 060 335 548 001 295 299 651 591 185 449 163 020 152 284 520 227 864 119 642 304 832 125 266 305 238 484 284 943 860 282 326 513 542 784 596 604 988 370 886 234 033 738 552 641 000 967 826 121 826 524 254 614 931 945 772 114 512 802 993 097 573 809 527 283 664 161 880 502 440 726 550 120 223 209 207 216 585 447 397 066 616 000 644 243 956 429 027 076 868 693 250 222 076 298 308 887 874 433 033 620 028 358 119 139 840 655 356 777 133 040 932 226 132 344 914 623 914 694 041 669 284 111 537 871 121 221 717 688 865 451 397 181 755 262 137 385 865 589 437 903 546 573 303 410 021 492 875 893 192 371 818 669 231 209 268 610 590 804 931 472 894 535 652 600 664 425 174 487 901 952 914 853 793 978 659 954 822 811 649 846 414 613 991 933 212 841 945 087 235 776 652 511 481 556 454 347 922 696 753 903 004 957 025 401 516 631 472 344 556 415 903 119 347 254 760 124 248 958 570 833 590 561 010 230 141 777 869 750 670 471 420 551 893 394 363 944 378 664 894 026 849 030 701 005 739 836 976 506 787 481 784 302 930 916 748 010 385 281 809 388 688 358 482 333 178 847 340 274 346 429 219 621 755 830 516 323 373 013 514 736 986 149 763 817 795 978 650 833 572 255 774 473 761 951 961 527 063 754 291 090 572 258 990 493 897 195 165 720 463 042 398 342 784 809 047 705 933 770 540 861 776 687 007 189 899 420 874 197 334 423 146 973 599 050 234 789 180 863 394 087 599 752 522 178 911 191 050 280 678 249 719 839 006 466 591 633 367 589 456 174 939 763 502 585 924 003 698 775 504 792 940 777 856 271 108 620 693 184 242 318 623 331 163 746 446 034 943 044 181 179 866 071 098 424 771 558 276 352 839 760 767 592 679 630 067 726 412 365 136 240 026 843 829 861 814 719 959 375 376 439 155 819 620 516 907 615 454 193 028 853 086 162 994 555 502 584 624 865 729 319 401 167 015 031 312 041 556 060 235 272 823 448 363 749 700 756 910 310 620 872 685 758 120 382 522 609 374 316 552 879 608 155 412 039 918 843 438 618 960 515 121 013 202 250 229 968 886 192 950 380 352 588 540 199 227 204 876 496 490 515 969 885 698 600 859 707 593 454 367 344 551 494 157 304 396 488 855 210 178 910 172 140 988 488 005 891 397 347 261 092 694 635 809 380 521 159 804 680 156 675 620 752 090 560 569 408 375 606 823 266 920 150 303 396 749 960 936 784 371 725 272 787 146 961 324 989 355 451 655 630 723 279 945 182 789 530 294 091 466 045 888 509 264 223 876 707 185 216 784 521 201 142 483 979 339 147 010 285 712 089 823 168 061 415 601 996 137 964 037 626 956 223 832 482 624 369 340 201 477 033 614 246 192 647 351 546 237 115 541 730 084 964 801 196 166 310 668 815 469 627 501 527 313 448 756 923 626 509 695 645 689 586 796 716 862 038 688 801 996 411 724 804 724 995 999 277 721 848 096 259 832 893 908 216 628 325 721 493 140 367 019 618 022 875 063 671 611 754 719 447 638 049 059 344 886 438 881 160 121 859 252 793 671 288 649 782 849 250 518 909 290 897 714 092 043 309 334 230 649 080 633 878 824 635 434 241 313 902 754 238 204 986 707 045 966 468 773 129 351 701 420 011 358 202 352 540 924 603 846 711 138 134 312 542 549 949 957 241 779 406 631 476 042 255 785 983 972 908 702 763 882 450 734 965 381 620 121 560 275 664 273 054 923 363 995 505 432 800 514 883 728 168 153 567 790 327 038 478 334 518 673 224 109 198 103 678 426 474 844 978 539 472 450 498 114 459 358 960 442 458 190 846 722 222 603 499 265 961 507 112 124 876 534 524 809 496 028 109 698 745 313 995 169 775 250 375 948 787 773 991 757 276 853 452 302 919 228 287 160 642 583 208 308 343 032 572 548 432 892 610 200 772 187 736 829 609 028 494 846 511 836 324 010 471 510 934 864 398 004 365 370 780 939 728 112 680 709 616 474 192 110 245 064 378 270 858 472 186 699 274 136 644 366 711 363 278 010 156 963 325 666 721 105 266 919 014 599 385 339 857 258 339 182 744 007 680 959 130 579 207 153 143 695 162 321 165 863 738 108 848 706 176 201 805 655 571 117 092 249 612 592 527 817 286 718 044 440 038 160 659 257 180 041 274 348 433 937 765 741 418 974 007 920 685 510 638 591 723 615 363 841 650 667 401 117 533 347 895 393 361 628 509 398 954 500 948 323 471 690 013 909 566 542 083 463 925 865 222 205 681 214 254 262 006 557 634 905 833 018 536 798 047 901 761 734 073 814 021 754 901 900 169 652 173 911 211 537 198 514 848 513 638 077 100 884 221 467 801 221 529 441 538 452 187 541 484 989 524 450 613 855 422 726 024 011 349 024 417 149 699 816 320 870 304 045 690 332 862 316 312 799 904 829 108 320 923 134 467 202 693 968 120 934 561 184 617 381 498 326 732 836 993 606 357 193 699 974 443 013 832 984 012 235 644 038 724 835 119 739 343 179 297 189 062 762 369 514 136 036 897 069 799 090 831 682 253 982 543 565 611 206 518 989 780 458 970 711 505 221 221 351 999 200 601 005 796 226 799 545 620 496 171 319 822 629 159 912 396 353 147 459 615 113 425 359 951 469 125 952 596 447 644 093 783 275 339 183 068 841 171 221 474 614 002 043 602 426 070 206 595 374 297 944 496 626 385 392 691 179 763 316 012 338 985 504 807 355 002 946 229 703 398 158 645 789 108 811 885 152 206 255 551 629 324 341 638 591 535 556 260 818 147 282 220 802 349 122 839 873 648 634 590 031 600 648 062 487 488 580 961 171 464 753 099 843 292 844 058 788 650 309 997 957 262 168 908 408 453 902 883 949 154 316 550 187 298 777 335 607 709 524 661 330 441 149 327 175 262 884 652 810 154 805 214 687 780 043 718 641 373 168 294 901 468 293 006 983 582 802 868 668 833 125 241 189 835 851 343 469 317 420 416 345 062 979 537 798 151 580 499 971 004 070 548 418 173 156 356 117 358 591 907 568 897 552 124 298 463 123 564 762 540 303 930 834 663 162 354 773 589 674 370 689 605 264 532 528 187 320 197 098 283 023 977 222 587 430 043 470 111 703 186 474 545 907 361 751 875 745 876 212 723 084 655 863 658 556 997 794 131 820 151 525 783 622 259 853 011 420 534 362 458 209 051 412 277 291 536 839 008 963 408 385 109 719 392 969 667 997 698 743 539 990 611 402 527 747 934 342 844 232 129 797 376 890 119 789 439 185 367 597 285 240 306 249 605 284 596 439 241 142 246 777 506 247 808 556 776 007 740 053 559 189 372 377 513 848 722 150 400 947 414 664 447 383 337 672 908 067 634 232 276 495 493 336 398 128 120 619 230 209 288 747 355 064 882 518 536 226 022 319 497 763 402 952 114 017 132 461 709 555 491 590 965 412 821 600 012 342 294 765 707 019 002 040 199 324 356 859 576 174 908 356 563 592 210 010 784 064 140 302 966 787 534 515 950 251 854 359 615 758 440 136 266 478 553 264 962 429 328 288 562 120 543 186 859 604 324 207 302 599 955 327 970 246 405 589 334 252 361 617 071 403 136 907 504 105 856 654 545 874 425 443 153 641 675 312 812 510 784 841 348 892 474 945 325 595 335 572 508 412 556 222 290 753 788 242 239 550 955 562 617 538 688 749 517 161 154 137 422 093 056 626 764 293 721 349 607 275 277 909 542 275 199 785 148 590 862 583 986 030 372 493 531 208 941 835 563 396 193 498 824 590 761 711 572 261 284 344 713 025 808 173 743 319 490 693 352 385 729 504 407 553 822 412 432 425 502 183 301 888 057 984 068 055 704 945 502 617 409 352 553 161 298 852 213 691 341 665 390 331 955 666 558 654 870 071 148 881 461 260 265 043 563 419 266 349 519 006 943 301 495 387 088 200 146 765 471 762 836 394 928 921 252 150 393 906 370 757 410 790 598 587 114 504 641 159 974 236 505 086 993 551 920 919 625 091 532 842 356 672 512 416 649 067 652 862 937 937 359 841 897 945 308 013 348 638 547 089 123 569 698 412 830 037 465 242 728 280 314 193 573 747 707 731 740 043 513 153 002 838 105 493 192 800 881 843 139 765 686 583 895 244 504 739 720 716 452 392 699 868 544 059 613 833 762 480 085 431 247 446 901 632 627 157 153 340 733 691 052 205 543 588 192 992 783 169 050 393 650 301 774 677 809 271 338 815 939 088 509 460 048 931 389 362 204 492 081 278 733 899 210 792 100 835 232 352 322 146 384 761 168 094 971 638 599 594 557 059 536 280 206 993 959 530 235 774 537 566 111 179 993 348 569 932 155 425 313 337 274 234 416 805 199 385 893 912 625 480 867 694 493 108 561 736 155 007 680 639 102 975 523 910 052 856 942 631 389 228 671 277 224 265 169 656 312 927 289 395 535 100 468 348 708 222 967 231 726 886 619 501 107 260 462 456 148 486 740 241 443 636 116 069 924 878 325 664 065 324 798 599 647 279 751 814 547 684 536 808 076 335 920 629 734 636 543 927 780 883 378 951 012 627 286 392 815 063 668 038 292 614 573 470 289 657 758 865 878 825 628 675 218 612 388 211 489 934 911 451 813 291 621 238 144 091 200 292 794 187 756 911 011 198 590 884 744 716 434 658 340 745 858 635 400 265 645 273 418 040 902 010 282 535 855 455 113 422 340 604 865 437 526 327 065 053 007 129 969 240 575 937 522 207 646 746 326 177 492 997 031 381 193 303 057 925 371 941 525 018 368 409 951 489 988 659 533 033 904 031 587 289 674 582 366 844 878 870 208 727 543 217 022 808 018 728 910 489 655 334 660 641 385 979 059 501 044 527 101 181 589 562 480 342 370 071 519 835 443 369 598 890 444 167 790 611 528 757 692 924 132 784 707 151 487 315 538 901 394 135 442 315 478 305 971 750 956 591 031 081 825 777 319 673 273 547 670 576 486 750 228 943 446 363 776 909 649 173 700 056 100 537 666 036 715 221 899 201 642 509 673 893 490 779 508 479 112 876 073 504 973 362 967 326 459 612 599 081 150 041 984 153 623 099 061 136 032 388 014 473 032 682 220 441 267 124 971 651 001 267 498 539 713 243 395 153 343 055 685 903 313 095 893 960 743 040 463 429 920 389 579 620 385 692 512 859 252 845 891 708 708 588 010 511 230 430 454 398 028 730 950 981 045 367 911 704 384 862 373 051 114 270 761 553 844 723 814 654 846 200 529 979 101 404 775 329 492 070 261 158 289 177 219 113 004 342 360 135 387 956 416 502 245 641 785 699 053 329 005 002 200 653 299 369 479 299 780 564 811 726 546 462 992 867 293 061 921 960 886 982 994 686 125 788 698 565 896 571 654 188 480 677 614 637 990 948 834 530 480 158 681 274 837 452 596 492 473 080 724 113 723 165 783 567 549 893 427 870 066 689 640 533 036 580 013 703 392 638 586 305 483 992 407 955 991 161 943 758 859 072 156 050 502 997 676 446 446 391 006 754 841 743 226 318 034 375 915 902 466 408 793 654 302 553 285 617 661 505 784 255 991 247 229 111 292 855 656 581 466 096 068 710 742 515 418 613 675 732 497 840 937 890 513 904 567 827 425 131 685 220 769 441 194 938 197 507 142 040 673 783 144 848 727 246 523 672 152 637 563 715 949 683 507 195 892 515 022 103 983 639 373 052 750 871 410 866 112 237 222 397 897 360 527 072 209 103 865 767 552 262 745 273 854 951 482 858 920 117 816 224 496 945 691 115 988 593 318 213 448 060 706 188 849 398 368 238 642 322 627 139 355 467 813 867 934 702 066 793 681 323 599 294 744 107 838 091 972 246 403 983 561 137 929 623 242 697 704 657 860 016 613 225 605 549 361 837 500 097 791 969 049 411 390 782 618 806 903 537 935 024 070 451 717 775 603 620 407 527 668 360 187 807 802 453 348 402 407 540 906 052 748 256 279 885 184 380 769 436 951 420 413 629 257 641 741 347 707 974 815 462 720 219 895 855 784 539 681 899 425 173 420 826 914 808 946 131 221 818 518 507 549 676 135 876 763 367 127 805 983 282 820 815 774 322 241 127 671 866 942 455 975 649 924 560 632 295 442 184 990 835 483 644 374 863 629 158 045 683 196 903 482 421 881 402 762 548 107 187 855 879 219 929 953 689 622 709 501 435 330 260 227 799 099 008 725 958 967 632 175 441 714 749 479 832 742 411 243 449 018 643 207 471 827 837 768 773 289 507 942 852 246 199 888 720 788 713 910 084 038 011 897 270 217 791 506 804 679 310 836 942 402 427 320 117 280 116 344 895 012 879 299 869 990 701 458 306 701 564 162 824 310 323 751 640 785 965 976 324 158 891 505 345 018 986 772 765 150 011 340 352 854 048 721 870 197 618 027 275 584 106 182 039 105 201 458 482 568 855 786 394 357 833 166 666 069 010 796 800 964 764 067 684 167 906 877 025 433 406 625 197 804 343 960 262 834 291 361 805 887 287 957 230 459 138 983 108 168 128 754 680 834 895 410 284 940 989 417 364 448 432 799 049 785 653 557 329 967 893 647 480 108 428 825 725 368 155 079 014 769 470 526 362 639 852 508 534 595 706 490 282 831 463 979 281 080 853 720 928 041 235 438 237 420 812 733 129 512 679 440 234 309 031 325 388 689 842 269 540 496 590 112 942 314 336 099 552 466 069 301 002 937 910 426 133 205 621 509 825 451 516 866 505 805 063 094 640 720 394 373 101 338 550 331 085 460 594 768 537 787 619 748 259 680 665 014 046 304 481 622 462 997 783 876 818 141 590 039 413 302 585 167 204 345 852 366 434 700 021 419 538 300 326 979 541 064 642 707 329 617 167 847 980 950 290 202 695 220 838 502 452 515 551 764 489 266 379 373 033 862 769 492 293 496 927 388 519 690 605 966 674 299 145 024 977 449 029 574 330 443 516 681 688 502 104 687 549 976 016 251 290 712 245 695 052 661 780 303 712 529 954 623 563 776 626 159 593 988 139 274 797 947 852 868 425 559 084 266 581 208 631 118 714 181 116 187 263 052 650 979 474 112 007 889 759 745 840 557 148 611 991 872 023 806 339 921 542 882 083 906 547 332 933 704 698 033 165 843 496 192 697 714 525 067 008 817 174 801 406 562 801 242 909 109 400 408 001 828 358 704 811 392 262 583 631 569 734 698 020 684 081 262 986 532 416 430 907 569 520 917 430 786 467 513 690 019 834 183 833 182 270 673 142 186 844 120 544 196 871 063 464 293 866 512 578 322 381 138 136 959 567 160 349 647 440 093 290 634 168 213 350 328 950 257 328 661 586 031 286 572 547 520 362 550 925 350 220 668 614 406 829 297 956 264 393 209 096 946 516 594 931 598 676 609 276 796 380 036 503 552 508 517 314 524 486 042 776 890 769 204 353 513 051 159 157 237 538 273 735 568 460 681 779 880 804 138 344 715 924 094 747 573 110 460 845 392 375 687 403 474 867 890 980 740 239 273 236 186 081 705 509 614 474 171 225 729 749 301 146 512 677 514 614 735 432 475 169 355 726 383 527 168 457 493 036 257 313 195 772 076 216 642 339 728 098 810 234 847 352 212 783 148 427 524 785 612 512 731 059 258 630 705 428 854 639 563 286 511 137 501 271 843 230 970 190 528 731 155 871 644 936 553 738 693 222 240 204 186 974 423 734 112 413 354 005 174 532 866 164 990 992 802 203 218 178 338 976 880 491 954 809 724 733 356 167 616 437 452 230 380 566 434 477 426 228 774 028 630 293 552 436 635 252 779 861 301 040 923 830 333 448 487 188 869 639 255 003 221 443 875 876 974 779 956 609 791 705 072 896 426 024 569 248 704 414 795 954 545 942 429 918 462 521 829 388 331 182 195 118 133 536 990 834 680 042 678 046 144 633 081 895 204 579 727 204 752 183 193 583 551 698 159 078 186 369 384 673 420 618 026 794 107 110 737 649 049 552 668 983 695 276 440 993 798 794 915 776 269 781 829 372 450 172 548 406 662 436 909 940 387 914 431 076 638 132 136 671 131 574 859 458 203 875 612 887 433 742 786 208 650 742 907 119 853 054 222 633 252 653 059 157 259 532 738 520 955 638 734 371 057 674 754 800 403 300 476 066 481 763 127 728 597 873 439 768 019 138 006 398 750 378 463 422 681 913 129 900 462 500 933 696 520 562 173 289 286 253 645 726 444 174 619 343 902 117 495 699 270 875 735 407 914 397 422 361 339 846 510 388 692 147 304 247 595 436 019 167 600 942 061 326 572 628 423 972 725 649 610 626 321 753 189 107 300 905 847 410 123 451 614 671 833 469 793 877 677 470 033 162 716 372 706 638 047 679 160 222 857 555 947 428 395 805 927 310 512 959 337 957 131 197 418 318 075 437 893 946 237 942 988 699 295 462 041 431 453 931 701 160 886 071 735 006 551 711 931 188 062 478 742 590 676 349 931 415 484 373 763 308 704 949 146 811 423 362 824 403 492 812 883 858 870 351 148 177 931 677 558 633 245 015 646 407 680 697 557 731 384 650 181 052 879 609 799 184 503 341 391 185 109 161 811 603 726 417 547 934 758 045 891 123 525 617 952 210 558 909 174 661 470 633 794 261 248 316 521 064 584 554 492 877 415 470 708 069 722 061 428 088 685 528 057 667 143 189 539 581 713 586 547 060 030 087 364 080 015 307 702 007 288 987 958 229 954 375 855 320 467 056 612 459 751 214 468 212 230 297 635 675 423 968 701 251 336 116 780 417 279 761 048 680 477 471 070 693 926 168 264 587 805 048 917 810 539 103 286 556 261 309 720 687 722 157 802 808 762 792 477 393 186 618 386 740 457 800 435 304 425 251 747 165 726 624 120 166 755 496 012 862 335 227 054 699 878 057 856 839 300 189 294 639 924 088 297 754 486 918 387 564 247 602 044 374 971 082 341 080 580 844 527 505 820 454 421 707 900 468 066 821 387 767 825 654 220 392 557 563 035 032 598 679 185 491 345 059 452 637 689 713 431 395 642 533 775 571 836 911 969 768 948 842 542 608 470 346 821 431 736 733 511 361 905 742 610 350 227 141 109 657 987 641 986 337 455 356 965 652 555 996 978 377 827 081 202 776 154 182 086 492 791 224 402 186 257 465 355 027 074 514 053 724 347 759 132 807 540 634 342 476 872 563 467 396 357 214 210 243 394 100 268 430 926 345 071 366 726 045 298 780 468 659 889 145 111 773 289 402 667 663 321 324 500 187 903 296 283 662 834 999 319 321 920 464 722 260 074 361 790 098 560 937 984 995 637 881 019 241 254 842 835 958 401 202 516 070 330 731 502 645 007 014 935 001 494 123 218 122 574 133 949 169 191 337 792 869 390 499 456 967 085 662 830 425 413 683 093 328 299 001 016 315 195 370 364 690 528 659 334 004 297 447 751 853 921 057 936 319 598 062 677 837 338 576 493 571 306 560 249 406 824 822 188 649 446 820 830 213 344 772 777 401 700 451 221 579 424 908 742 072 939 468 397 103 094 033 040 766 169 374 636 698 041 609 712 939 526 287 914 128 335 861 395 696 117 829 656 958 712 721 322 669 888 821 977 128 603 258 851 974 409 918 700 210 554 537 369 351 308 740 738 092 237 533 003 663 423 521 744 553 208 544 537 283 235 831 419 354 750 490 647 997 080 480 420 037 310 296 760 259 995 539 771 669 744 263 403 566 370 709 542 436 582 801 427 012 775 748 217 090 573 622 651 043 255 309 266 115 359 156 568 492 990 795 811 606 630 132 464 518 686 897 632 021 768 879 554 540 895 394 574 668 468 840 100 983 849 063 875 619 360 774 464 850 471 684 747 300 349 772 117 172 423 408 476 241 340 703 875 616 375 885 789 238 104 106 378 050 832 401 960 526 823 020 779 732 212 797 943 699 628 850 715 520 672 646 566 312 043 799 472 447 112 678 265 887 433 691 402 920 260 901 278 983 023 943 510 710 303 732 570 006 832 032 906 849 438 208 026 176 091 174 216 113 986 783 469 204 796 908 809 749 020 039 457 177 151 068 559 497 350 345 639 145 282 001 585 046 344 311 852 969 470 572 433 530 466 720 385 959 177 264 932 134 283 931 290 831 011 806 217 427 309 787 471 087 152 935 124 874 021 477 089 902 516 674 766 577 248 204 847 966 982 324 762 228 086 406 494 019 418 329 020 880 966 808 779 563 996 503 263 579 888 061 146 892 698 164 993 431 572 028 495 909 961 524 736 165 349 917 340 482 734 549 794 510 685 211 357 527 118 039 311 363 661 297 853 051 189 255 298 505 284 526 512 640 900 090 113 812 904 763 315 168 787 445 580 983 924 974 952 372 490 277 418 076 915 292 718 784 360 212 603 785 312 022 177 461 457 358 721 977 197 040 098 464 747 782 069 306 876 839 052 104 877 399 135 024 976 427 952 642 354 310 879 170 146 113 084 965 194 243 043 666 345 221 164 849 189 134 742 361 933 043 244 324 693 083 115 460 914 520 274 354 832 204 154 432 623 444 050 889 318 890 289 028 296 801 060 506 859 054 845 894 500 545 579 302 437 384 734 562 154 611 437 840 805 405 511 082 570 467 531 454 368 591 543 004 973 552 554 455 202 596 935 433 046 619 875 266 655 826 691 250 863 349 455 251 639 783 379 525 841 793 883 558 873 483 563 979 867 738 024 997 998 481 330 052 505 066 243 410 034 852 430 057 194 137 573 080 553 934 792 166 063 438 338 409 204 063 980 884 678 848 327 356 508 458 640 433 808 521 538 032 306 431 283 824 195 219 123 334 607 486 490 619 727 199 720 019 793 154 458 801 685 908 151 146 736 849 370 687 214 894 713 367 676 398 626 350 671 099 376 694 136 433 955 341 687 654 801 918 541 594 347 588 314 973 287 654 131 180 886 173 858 467 507 561 560 531 063 739 078 575 244 765 954 446 454 617 565 548 945 582 908 460 816 597 107 051 867 836 305 780 829 534 953 719 115 562 319 151 616 502 551 996 517 794 160 680 975 017 374 985 411 972 199 912 627 253 294 872 836 491 721 191 098 870 998 561 587 336 822 270 837 756 557 326 330 182 032 296 035 962 486 073 149 721 510 296 922 379 879 220 231 405 319 142 687 276 205 195 426 695 562 670 309 828 168 443 413 989 671 168 060 756 118 595 444 807 960 182 933 773 659 038 373 252 320 521 490 569 463 578 492 040 577 424 433 833 501 350 791 484 095 772 244 072 851 055 330 013 164 471 981 707 974 805 281 663 546 782 125 527 795 500 036 987 177 027 636 298 975 757 462 009 015 118 469 460 833 093 980 515 644 542 073 380 283 794 971 007 136 535 712 089 628 025 248 197 109 302 390 380 127 654 701 085 143 880 814 768 661 069 347 371 980 439 678 008 051 207 299 748 349 907 684 294 596 046 297 381 597 129 729 930 550 102 541 883 138 422 758 532 142 206 876 694 996 485 149 121 177 968 648 139 391 793 716 767 421 015 059 758 302 098 812 462 505 390 827 412 946 612 650 739 072 422 371 745 549 867 743 014 077 418 884 207 657 344 163 158 096 458 773 363 783 057 016 535 056 124 770 479 586 556 871 415 953 142 961 564 184 682 218 793 069 619 908 665 081 084 951 499 459 760 242 859 994 586 804 645 793 129 227 157 321 887 175 395 844 496 896 317 837 341 109 172 997 433 263 402 737 821 807 204 369 045 548 653 353 253 647 147 083 245 628 466 781 025 623 787 222 820 198 651 006 764 425 020 735 282 198 551 301 747 662 180 978 897 450 081 068 647 882 285 023 403 107 779 134 491 570 206 217 655 069 091 640 118 217 964 271 893 698 460 512 480 254 375 315 939 212 245 127 461 602 714 286 521 066 739 120 354 341 510 879 098 364 779 989 855 750 911 142 653 176 794 849 158 964 702 768 019 321 072 632 014 367 969 771 862 147 334 354 221 378 484 128 638 194 335 875 663 964 561 314 555 097 295 501 913 118 128 570 212 641 422 099 778 086 457 463 806 497 434 917 809 369 591 023 202 575 241 955 313 820 875 315 662 097 866 195 555 566 668 796 147 700 641 005 814 334 505 608 465 013 637 491 451 716 356 752 706 045 474 513 901 632 004 550 836 413 050 436 344 440 363 782 081 552 932 998 745 611 243 354 316 838 029 417 601 820 332 564 983 050 159 776 187 604 226 133 448 571 417 803 187 366 241 008 133 010 523 592 326 117 777 835 879 318 587 413 849 740 087 214 232 042 783 198 203 267 518 068 174 121 223 601 080 216 683 058 209 804 588 175 231 888 827 006 097 167 157 791 399 674 572 812 613 159 490 179 326 244 160 530 698 191 326 221 500 296 955 537 716 714 277 805 787 227 808 543 013 739 438 149 470 641 807 418 496 050 001 610 764 726 026 869 749 933 058 269 236 110 190 633 615 219 249 733 814 116 891 162 454 538 321 624 422 422 757 685 198 414 107 219 454 391 526 644 365 660 253 838 558 055 245 761 886 809 648 469 757 622 493 413 721 430 575 243 977 477 227 384 200 833 442 060 041 024 484 236 690 331 971 513 693 415 336 326 948 081 720 883 280 199 015 430 381 043 418 872 951 003 438 766 596 485 336 632 288 195 718 847 668 109 359 195 096 068 886 218 740 044 609 986 061 976 201 321 725 966 873 287 250 905 107 933 530 646 579 313 066 661 401 116 060 302 103 528 706 922 068 795 668 504 954 190 018 040 912 490 780 906 545 913 796 899 196 059 106 388 832 085 383 797 299 420 841 093 414 337 906 640 012 330 606 003 831 466 308 739 335 634 152 135 504 028 920 201 124 679 063 048 308 787 976 013 888 883 151 004 325 100 675 474 341 773 727 310 760 635 184 698 299 684 002 108 725 910 451 085 281 268 277 860 545 866 877 271 052 793 038 822 962 106 456 640 694 017 866 580 114 009 652 937 457 942 127 091 424 533 933 892 320 762 776 546 146 082 083 004 828 893 434 760 702 304 061 411 642 325 114 391 167 225 024 855 229 601 120 233 773 277 877 627 801 112 187 012 137 192 547 937 416 700 598 309 649 899 329 561 136 980 479 767 396 617 071 501 372 947 388 260 160 146 854 389 124 607 168 835 379 309 712 286 811 365 332 867 404 333 436 346 179 651 377 239 856 367 504 309 795 280 463 283 936 300 853 154 520 592 154 250 896 555 710 635 529 036 985 381 369 363 354 839 866 219 106 511 645 190 293 783 245 331 009 479 905 584 860 452 633 989 720 463 447 088 602 003 353 124 734 853 024 073 394 010 296 476 649 030 956 762 322 501 161 514 597 018 048 643 995 103 955 374 482 050 307 212 532 592 068 084 857 075 086 292 844 448 226 848 291 989 017 853 687 641 789 476 503 303 463 438 568 719 231 354 409 473 988 952 648 463 485 781 274 203 386 836 727 854 172 910 609 829 650 060 998 095 994 103 665 796 699 866 503 523 548 788 154 639 418 265 056 736 547 090 379 159 288 269 682 037 569 078 135 693 882 995 259 528 601 606 738 207 403 659 003 687 163 392 283 946 988 745 381 442 294 924 557 282 214 609 831 290 690 665 326 387 282 616 446 902 874 528 212 813 026 705 624 770 528 728 654 022 298 844 105 679 334 589 115 824 205 185 453 635 746 672 530 159 324 710 162 586 947 462 958 601 264 892 528 317 778 181 564 551 484 754 488 671 826 153 086 703 077 865 667 048 933 899 241 486 149 517 629 989 695 228 913 525 371 076 015 924 362 427 492 213 053 526 015 353 460 870 914 583 597 255 755 809 237 888 581 508 029 288 294 366 096 300 934 193 372 473 355 337 676 444 909 054 108 050 888 097 615 309 757 009 322 505 515 766 140 481 317 398 077 002 625 164 853 994 369 608 315 710 332 936 305 682 066 575 395 788 473 002 835 702 147 787 637 089 453 930 961 525 988 666 025 406 110 230 995 766 203 989 857 208 943 464 447 644 759 980 511 919 905 511 925 333 420 400 557 408 000 676 571 669 405 401 352 339 735 274 279 187 933 183 918 432 116 766 898 250 271 136 053 680 670 639 313 253 668 792 965 900 264 512 491 858 783 402 797 146 411 676 232 577 433 213 592 788 453 682 590 014 159 181 781 724 514 537 535 629 340 960 786 218 647 463 548 477 091 692 311 330 980 226 614 615 938 280 237 413 083 163 383 959 746 703 969 301 616 220 617 458 514 178 685 169 257 633 680 487 424 371 917 779 826 842 538 941 940 907 659 738 193 739 676 130 157 872 142 546 735 906 552 326 184 291 966 579 530 299 461 377 367 755 614 859 688 679 330 478 877 920 015 068 889 232 773 931 127 954 602 499 576 329 389 149 431 767 141 135 073 522 110 620 003 304 140 628 451 855 090 948 082 942 118 208 054 945 725 604 821 906 653 344 596 468 534 384 430 450 515 952 010 028 272 688 791 894 536 575 346 478 313 936 563 048 474 873 010 330 666 915 222 874 179 644 898 118 140 204 699 688 108 470 101 574 234 637 528 223 705 312 731 976 316 991 452 797 904 726 052 040 336 279 974 890 854 548 889 298 526 928 692 312 650 670 913 699 509 686 862 832 712 422 668 966 581 626 233 107 431 494 746 927 913 612 362 589 331 820 720 323 462 782 210 299 602 045 927 105 526 848 273 820 886 606 112 970 705 103 438 806 557 756 943 915 136 580 324 672 038 609 109 538 362 535 950 423 479 783 275 992 022 984 227 656 035 792 736 772 664 002 475 531 434 648 540 773 746 150 780 432 322 774 496 220 469 534 037 889 201 631 341 983 567 610 257 575 524 654 948 759 168 631 309 607 217 688 201 166 460 466 767 944 454 302 255 187 239 409 592 125 580 872 369 124 330 107 321 327 590 301 242 193 781 503 276 192 949 583 229 655 957 139 195 513 722 466 321 898 422 173 923 474 152 160 094 342 047 755 789 417 742 344 142 518 003 097 498 479 960 390 939 076 509 480 202 940 510 665 683 532 949 047 363 932 420 760 061 736 107 014 783 104 408 575 955 769 283 867 445 688 936 227 169 205 961 563 771 753 896 020 399 426 147 787 057 522 117 312 592 375 985 025 562 684 898 388 656 520 442 110 090 205 971 192 543 155 755 161 549 347 207 773 088 383 399 606 106 188 763 548 745 183 960 650 733 694 431 997 228 008 642 303 972 258 139 273 391 248 217 698 440 358 759 674 332 319 322 732 950 464 286 584 190 421 541 568 890 161 252 168 974 658 522 963 050 010 928 207 350 669 653 153 206 986 962 307 805 234 433 303 390 841 942 445 000 338 129 483 963 210 344 394 569 914 662 634 762 008 872 178 016 512 993 295 411 603 695 641 084 572 767 419 480 251 207 178 446 479 999 937 675 876 284 780 869 090 713 231 860 633 843 979 665 781 143 948 955 845 111 220 924 746 002 130 794 219 432 208 072 372 675 346 460 789 684 474 983 475 157 805 396 241 959 517 280 049 623 742 530 804 341 260 244 275 792 119 703 654 320 310 638 345 313 798 557 792 964 660 040 936 231 149 009 813 851 113 675 367 877 472 792 799 958 198 034 597 014 292 056 886 157 379 264 422 852 521 039 966 759 073 073 295 429 654 574 086 788 850 632 921 285 620 812 431 049 291 431 821 097 713 395 744 695 638 133 154 524 077 058 085 611 190 052 534 032 118 367 345 360 160 277 108 103 323 337 831 546 131 321 505 907 575 523 281 385 306 135 228 700 939 188 451 846 462 492 394 392 166 557 430 615 834 940 199 644 993 274 829 835 031 374 408 139 927 732 267 743 394 886 380 324 331 545 724 842 623 229 027 854 351 709 755 514 162 379 085 121 781 439 380 092 719 542 481 772 834 937 120 318 316 673 794 699 719 122 568 029 722 445 519 160 476 639 841 758 838 598 851 315 639 336 770 566 526 840 858 911 010 997 923 730 132 540 866 452 381 949 908 230 396 060 861 175 152 774 829 038 697 791 769 393 212 289 377 071 817 565 681 958 779 518 946 825 991 606 906 319 196 345 392 191 402 454 897 079 628 304 725 874 312 608 985 283 188 439 804 580 897 283 605 862 218 055 117 914 162 971 209 829 407 783 695 113 975 260 052 410 719 353 471 884 449 947 783 844 772 811 247 216 715 835 606 616 432 758 358 428 374 881 178 369 546 368 803 566 091 425 801 671 307 263 477 964 311 980 543 239 434 376 030 076 330 696 388 057 450 438 960 834 729 170 044 390 842 212 784 564 286 485 419 960 005 280 103 689 609 316 919 261 586 362 550 743 784 695 308 009 416 181 301 682 671 015 444 624 528 084 232 849 946 444 640 775 618 233 105 816 751 664 562 118 361 574 845 185 665 455 376 250 650 453 643 657 750 902 286 482 896 586 181 465 386 083 840 464 515 121 662 889 868 110 869 772 200 968 244 592 713 446 136 844 943 455 901 214 687 104 199 519 726 302 130 369 406 081 107 718 057 034 084 843 819 756 883 799 717 661 340 117 834 466 796 040 757 107 508 822 431 938 174 314 818 775 790 411 729 710 082 736 659 572 720 316 584 613 918 455 318 683 113 106 897 167 948 165 669 248 135 773 039 879 515 098 908 848 558 705 952 660 165 826 901 967 554 870 936 766 314 782 123 309 457 530 900 088 797 187 635 294 841 526 808 675 942 930 249 616 430 648 983 042 304 304 557 408 261 857 944 701 390 214 821 995 947 092 047 413 383 447 391 266 967 471 632 958 314 151 551 903 080 185 470 955 668 333 186 944 427 499 854 886 861 444 323 164 197 565 242 388 110 023 482 973 826 874 065 818 206 295 490 347 887 286 880 890 424 842 353 698 704 852 550 880 630 918 116 203 503 896 803 144 658 876 601 505 689 064 681 855 988 209 999 427 349 500 837 643 839 816 067 513 176 307 664 432 969 423 031 370 670 334 775 041 892 749 831 628 335 392 630 130 464 951 602 897 288 239 415 065 611 994 879 117 835 632 230 588 803 799 891 194 063 533 140 906 197 161 031 195 999 237 854 511 910 388 679 467 313 396 029 150 036 004 608 963 801 467 654 220 873 753 244 985 961 620 724 877 233 948 803 222 770 096 159 850 117 034 879 951 669 765 604 589 553 745 589 000 699 441 002 947 626 446 171 023 202 951 705 505 952 175 340 037 034 216 317 867 018 743 299 781 481 478 863 038 504 013 697 441 937 258 310 484 439 534 860 325 598 741 926 953 199 693 837 192 224 200 181 396 736 196 485 207 460 754 854 681 807 364 739 840 168 231 933 704 998 565 993 569 444 596 162 499 052 006 063 070 738 519 182 653 406 165 519 736 512 862 039 008 233 522 367 218 626 032 231 706 622 869 856 441 297 893 090 252 656 338 687 058 022 708 985 296 803 275 404 309 341 224 012 883 672 773 223 637 415 732 204 990 139 425 920 328 743 508 654 104 369 237 676 760 735 259 870 854 349 241 325 281 980 656 957 067 476 474 715 117 993 522 209 817 835 633 306 416 594 543 305 570 454 623 869 446 088 653 559 326 265 564 345 113 052 679 539 801 082 519 315 661 632 984 029 090 871 096 642 153 550 086 169 244 094 388 275 278 577 466 565 821 903 398 559 259 535 101 439 142 159 327 997 431 218 020 522 445 492 717 113 539 059 339 885 999 678 732 284 121 237 380 836 940 247 027 891 136 606 251 345 412 776 556 036 072 787 467 230 611 169 411 444 574 068 676 037 868 179 988 571 910 442 090 441 139 502 618 624 376 223 870 819 970 463 278 925 529 869 906 142 301 752 266 487 865 479 436 782 926 873 941 992 769 791 748 862 613 547 515 896 331 214 997 223 096 458 934 473 389 046 466 064 456 155 795 368 753 858 323 268 272 649 115 518 526 266 321 718 180 952 630 146 787 470 331 721 155 374 159 108 412 036 160 813 957 456 966 486 292 486 769 164 370 408 976 285 046 428 832 701 514 002 492 862 151 012 051 340 556 728 135 485 736 976 759 556 081 270 687 987 658 948 965 950 846 777 169 230 745 285 759 182 360 263 704 082 909 455 255 046 272 872 187 250 622 798 261 845 026 841 771 151 562 103 417 782 944 143 639 550 414 290 707 500 612 669 993 790 713 749 720 388 175 007 486 069 791 347 676 164 671 104 502 356 994 757 979 832 841 425 004 765 900 750 971 705 517 091 559 891 764 005 901 817 799 175 171 582 746 376 843 714 204 294 414 569 134 233 555 977 288 789 362 601 664 405 901 413 065 717 458 625 601 072 841 735 265 242 162 042 197 984 785 532 798 159 871 695 383 862 662 227 999 761 605 138 655 087 704 446 070 961 627 564 751 255 522 570 483 228 304 878 024 667 858 903 967 511 932 142 537 574 806 416 018 180 837 270 095 258 003 005 738 488 680 525 952 775 983 381 732 411 030 942 982 566 998 016 513 107 865 026 407 874 918 627 620 852 769 059 195 497 581 139 653 213 361 870 839 490 091 289 359 147 866 251 703 151 757 257 687 835 761 892 644 166 328 382 737 318 569 186 297 945 652 982 736 305 690 450 081 085 707 365 425 259 877 904 370 734 362 054 952 728 746 522 467 758 082 008 082 953 979 777 364 834 647 781 003 519 752 737 259 864 962 272 215 176 202 376 779 121 604 242 030 706 632 593 948 786 628 858 232 684 982 529 960 549 982 357 164 256 259 715 002 679 907 745 781 678 756 102 451 140 243 995 249 352 509 091 856 512 149 207 494 773 347 963 618 760 053 313 519 470 215 998 410 224 186 573 403 642 276 976 101 457 536 019 033 085 741 535 904 578 048 465 519 615 683 075 020 395 190 503 773 503 991 900 899 142 315 433 923 565 868 696 652 255 169 255 600 610 488 608 838 263 355 587 853 639 892 201 578 895 679 988 452 215 296 871 595 404 981 524 590 057 190 787 033 158 492 644 806 475 785 098 817 637 642 961 927 474 382 126 824 284 765 530 096 205 317 544 561 665 096 746 507 895 296 690 814 258 886 504 278 362 492 078 710 006 919 197 883 890 520 105 212 298 826 648 859 842 080 800 652 109 859 599 516 759 852 681 219 949 669 176 041 581 555 440 895 683 364 228 262 391 471 042 817 955 242 410 260 458 622 676 671 293 518 527 085 002 140 747 079 118 615 065 494 899 538 730 901 111 013 114 248 328 576 745 159 886 358 940 069 842 673 260 120 889 777 840 241 057 401 902 827 184 816 332 625 818 473 743 794 274 778 373 658 634 929 908 814 621 882 047 349 751 584 855 501 258 138 282 793 694 007 848 379 765 309 691 707 751 433 687 320 549 160 569 458 776 018 172 801 968 441 650 718 629 605 634 594 687 793 803 054 136 756 662 295 959 794 383 607 188 139 416 944 697 673 993 836 285 290 273 729 104 524 191 066 244 551 552 314 878 858 676 884 737 357 535 176 164 291 425 263 226 977 129 281 075 289 689 834 240 035 700 103 569 077 190 004 365 989 300 301 412 442 960 079 572 498 625 834 102 567 100 024 826 670 090 029 121 901 403 255 551 855 896 892 835 175 809 403 048 579 097 080 866 145 877 064 994 657 780 732 112 258 397 905 740 527 212 841 946 455 685 870 472 937 215 070 101 839 618 158 948 379 899 455 822 650 060 389 776 951 730 559 702 377 988 195 709 400 233 246 577 561 988 794 657 405 201 263 146 298 264 245 737 030 339 662 625 644 214 470 283 922 312 066 272 856 175 581 741 755 028 488 856 606 438 368 165 874 267 356 836 345 400 476 315 616 050 717 374 037 696 313 612 401 686 834 705 388 264 567 551 362 301 030 322 918 635 574 499 303 295 077 726 521 079 982 271 947 675 522 382 279 139 740 011 073 265 230 103 409 362 494 579 133 607 599 034 139 792 356 094 649 375 735 755 575 515 162 571 754 698 386 600 866 209 738 192 649 232 900 160 991 837 155 379 887 602 938 913 345 118 846 627 495 370 746 320 913 636 927 585 559 464 905 988 112 499 696 138 314 620 347 449 338 745 644 404 962 248 845 791 436 903 570 619 428 997 925 987 567 437 593 221 235 085 911 769 940 186 112 125 670 936 095 830 577 816 322 458 763 137 568 439 370 326 724 148 800 711 260 908 837 189 444 631 956 005 667 064 805 970 508 112 097 096 483 724 985 819 174 573 971 938 471 505 104 645 425 685 514 217 457 359 549 741 776 068 337 316 112 014 030 803 985 739 651 194 239 244 910 418 935 685 965 121 558 916 623 176 304 922 629 241 017 246 212 978 934 096 552 525 159 357 457 849 855 267 241 551 366 282 791 096 654 376 779 074 638 469 266 574 536 071 177 969 737 370 478 040 941 641 089 225 607 798 707 005 882 124 421 461 930 997 595 943 927 499 071 700 567 416 821 927 383 615 807 049 625 231 653 574 936 131 501 261 716 209 612 899 624 047 736 521 955 722 681 983 763 017 769 388 158 323 553 344 959 921 510 815 948 601 913 046 575 989 140 992 982 888 321 655 587 623 662 507 991 734 682 690 927 541 696 336 679 743 483 428 679 239 531 561 599 120 775 511 041 117 825 882 284 154 107 194 691 795 172 136 388 233 482 498 158 749 354 124 764 599 323 508 829 005 255 718 128 709 572 696 253 131 963 337 901 016 118 690 711 657 939 993 913 250 270 720 505 297 958 845 603 414 579 984 325 095 146 682 157 242 202 770 581 861 278 223 507 009 357 403 343 685 144 150 991 521 412 222 741 389 659 156 765 956 765 833 030 218 478 510 437 134 087 939 443 642 766 257 450 790 239 183 834 135 095 304 444 788 050 921 172 414 853 306 709 052 861 789 325 580 049 348 884 113 043 617 605 761 003 906 713 748 487 475 307 749 103 629 983 460 055 634 894 154 244 856 393 177 551 835 736 383 128 088 930 283 742 320 443 678 124 977 353 991 601 510 684 379 898 224 007 464 843 831 849 220 431 825 067 724 367 017 257 514 809 207 165 979 594 119 377 244 587 997 533 005 962 150 269 787 478 136 830 239 602 117 206 180 023 411 035 019 344 366 591 151 032 915 909 029 835 137 643 670 956 693 693 289 440 626 898 796 741 233 899 703 973 604 917 087 543 409 671 874 781 574 432 086 775 476 495 003 654 969 141 970 030 136 161 120 976 958 844 120 859 455 388 852 951 687 040 926 378 071 029 287 289 269 353 417 594 009 699 735 167 600 781 476 041 665 198 978 880 411 533 149 355 323 004 853 267 892 277 770 903 269 407 486 752 809 869 512 827 147 561 802 949 683 636 174 014 012 741 451 551 991 493 987 823 592 828 160 561 009 687 976 068 734 347 791 339 160 176 039 382 708 813 486 217 037 861 349 417 117 718 737 656 878 160 261 225 029 870 322 947 772 051 824 146 501 759 907 087 314 887 540 239 698 116 411 564 489 984 628 305 755 252 831 506 589 928 889 716 040 026 915 059 951 330 485 422 156 499 684 165 869 468 102 594 420 472 885 304 632 772 014 338 299 921 387 804 940 849 041 658 059 845 271 544 998 683 018 970 918 485 862 384 074 785 330 101 190 226 165 053 539 231 362 362 535 217 013 220 364 538 257 254 051 207 620 417 973 326 494 227 008 985 702 299 689 437 334 226 978 524 060 721 809 544 665 155 062 469 891 260 442 066 429 440 092 261 951 962 566 669 699 994 043 415 581 834 231 439 208 873 253 041 563 659 650 596 340 065 562 134 563 386 256 305 682 706 318 944 692 446 110 138 370 189 709 667 095 997 303 610 095 324 627 650 510 291 571 038 694 497 215 287 106 377 500 942 491 325 598 830 549 563 323 856 773 654 966 880 723 026 780 924 658 103 069 360 448 978 537 961 769 597 296 215 749 508 743 360 751 255 929 739 765 702 218 120 588 620 039 182 278 851 652 344 606 361 071 630 038 240 570 025 571 970 586 663 923 993 507 437 185 391 800 662 370 480 294 379 688 663 343 405 566 590 917 542 491 968 022 584 020 385 382 794 865 444 627 461 447 742 134 563 309 554 578 391 660 754 273 600 690 016 372 945 284 158 600 757 754 711 985 224 072 042 006 309 829 587 286 209 852 455 943 325 648 555 018 277 879 196 031 407 197 150 333 430 528 770 297 085 307 119 730 468 835 749 406 340 933 051 597 622 141 326 734 706 684 151 347 772 024 908 607 285 072 555 003 573 320 791 042 292 580 514 223 040 666 983 023 354 594 908 689 231 585 633 913 645 166 242 428 630 413 551 024 078 871 655 532 326 507 225 467 951 453 634 011 718 312 208 171 823 746 858 630 625 428 659 052 472 151 872 808 059 611 493 557 623 021 670 123 540 395 727 417 134 716 816 335 991 229 629 358 042 167 449 653 521 454 617 339 058 857 417 801 673 987 811 533 793 981 291 542 169 281 393 273 466 549 950 472 643 420 273 316 694 373 042 495 805 864 955 791 860 219 187 328 204 010 653 087 842 614 925 341 663 181 400 764 591 595 014 063 540 610 993 156 971 884 398 423 428 449 602 781 721 641 222 683 486 147 748 090 918 489 855 571 359 643 713 036 703 695 418 919 039 078 543 643 214 959 053 589 079 341 459 760 455 497 556 809 060 266 288 544 990 724 790 184 207 430 384 456 715 050 030 240 657 323 523 570 307 139 370 987 803 890 539 716 908 074 104 328 716 027 423 869 234 956 382 338 086 325 610 849 068 155 933 255 439 749 694 873 311 279 058 773 594 912 147 300 822 495 235 053 600 349 778 377 830 385 464 394 516 929 324 547 155 312 720 292 927 715 735 737 914 316 744 761 611 411 815 727 403 332 276 771 603 424 458 061 650 830 387 270 945 306 166 421 033 257 425 500 609 686 531 957 814 975 123 305 081 247 137 072 761 123 304 607 381 018 306 103 469 545 317 971 637 272 856 359 485 798 074 253 141 676 194 963 702 391 609 452 266 055 671 210 877 644 237 568 021 342 350 914 133 778 816 280 120 575 078 307 937 903 032 870 075 349 519 751 295 271 807 731 619 177 899 756 876 466 927 403 144 398 817 990 838 274 184 420 534 472 024 931 744 905 150 459 816 927 196 528 941 646 745 588 248 234 512 088 384 319 172 494 378 687 218 266 393 647 849 814 030 230 299 421 364 254 618 747 417 860 483 838 276 550 837 763 809 920 158 226 238 801 082 108 730 595 725 482 927 431 344 262 004 260 815 639 781 927 426 312 904 388 967 607 107 344 117 826 753 418 115 184 561 471 823 343 692 496 637 747 617 354 536 041 431 401 462 333 592 420 523 685 231 655 901 436 629 767 224 082 950 535 803 065 804 782 275 491 951 903 910 589 855 054 563 695 958 817 074 780 048 275 886 366 106 818 161 014 008 976 279 129 962 027 711 572 204 329 303 753 721 980 723 158 815 076 123 035 534 440 550 932 655 774 141 225 416 752 488 912 333 956 744 386 465 338 893 494 011 162 208 354 729 244 265 274 810 400 354 075 692 028 502 207 550 240 817 401 057 704 738 294 247 968 975 898 201 263 429 073 022 799 087 322 603 352 995 334 491 486 091 244 437 434 093 644 277 586 638 737 994 860 034 570 087 007 527 541 305 852 210 363 582 989 465 523 416 483 402 132 171 421 873 760 692 213 926 898 252 283 691 003 462 437 173 713 636 780 421 966 620 378 714 997 993 377 189 073 957 594 564 638 228 421 543 805 128 398 090 240 587 040 247 476 775 859 382 262 838 437 321 053 087 228 191 059 125 441 085 090 746 915 788 679 225 853 950 018 391 820 022 757 132 675 484 563 406 286 541 670 757 265 328 759 230 036 580 129 974 505 377 323 729 276 285 641 666 137 011 505 321 019 619 415 726 694 030 386 704 599 441 087 254 035 572 858 499 352 690 143 933 843 482 490 056 101 155 773 254 816 870 684 557 273 801 755 816 970 915 993 975 458 747 617 782 450 681 626 721 510 199 477 139 217 341 915 308 980 949 028 600 448 000 275 328 111 895 854 428 490 321 545 560 935 547 911 770 752 868 406 349 077 986 063 116 138 260 489 255 295 416 853 330 773 598 321 967 360 072 889 183 406 914 142 180 598 622 240 660 688 651 650 290 619 016 966 792 701 248 969 817 077 040 357 890 830 478 376 006 590 420 893 250 432 371 946 671 693 180 226 537 262 919 226 613 210 665 268 657 920 013 574 600 891 835 312 104 782 252 282 219 430 427 983 259 317 355 235 622 255 546 994 940 012 021 763 693 071 279 032 186 095 937 684 471 486 406 094 291 571 348 358 054 883 144 331 476 590 962 126 985 680 427 355 834 200 415 535 190 722 894 249 198 372 841 433 014 245 182 364 849 939 755 134 404 543 243 450 121 666 484 104 682 495 945 732 512 197 287 415 948 148 896 604 906 556 052 767 505 806 498 674 329 801 851 603 832 080 843 473 554 656 172 575 066 960 303 115 536 445 260 862 908 617 523 204 762 682 214 343 314 548 349 196 612 948 708 725 518 769 437 167 939 399 457 474 685 915 009 620 889 699 404 809 481 674 634 975 433 313 948 715 912 738 075 603 011 330 352 414 285 515 037 583 464 924 325 489 993 639 209 377 429 395 785 625 861 262 662 426 122 820 712 373 193 837 519 724 373 871 127 604 785 518 035 408 396 213 290 954 356 176 647 687 197 255 904 291 378 569 605 177 182 455 116 699 706 316 661 605 597 215 493 588 250 437 353 036 254 613 831 744 258 802 303 337 857 371 806 512 087 785 131 211 679 213 070 214 673 047 360 090 249 258 036 194 391 140 631 118 599 434 241 318 017 622 146 467 700 523 200 824 556 780 308 757 166 310 274 573 304 336 983 552 359 727 584 313 351 986 676 386 474 319 161 468 931 553 857 745 260 029 002 241 415 609 925 826 738 629 866 308 811 301 892 684 246 648 821 324 401 532 221 052 270 434 394 094 999 811 817 416 684 024 334 821 859 105 950 295 144 931 450 802 553 014 124 487 210 976 568 392 075 933 686 032 499 973 997 627 406 149 855 520 536 379 350 156 708 588 787 684 880 972 948 169 772 881 336 880 423 845 700 893 220 234 647 511 342 101 597 763 726 669 070 837 344 395 210 498 356 623 412 842 317 604 442 454 116 725 701 593 456 956 433 038 582 562 137 858 638 312 202 193 105 261 416 717 339 965 287 594 672 822 286 500 699 702 334 957 304 852 042 839 968 476 913 002 564 173 444 721 454 009 705 917 927 284 867 034 026 128 109 995 676 507 125 369 186 052 147 754 677 780 532 410 327 516 866 823 728 333 819 738 411 801 261 027 156 395 226 939 438 584 636 420 573 483 825 371 319 774 761 521 942 353 337 246 619 611 302 437 242 820 211 588 359 038 763 462 730 632 164 439 754 114 116 415 785 235 943 407 514 243 892 151 193 042 683 347 294 633 195 684 500 893 501 293 174 062 434 319 418 560 632 824 806 986 041 808 357 378 855 455 990 290 312 543 489 581 751 029 652 472 823 674 280 638 585 154 558 165 295 141 208 958 697 597 042 003 824 940 533 017 576 454 653 181 652 311 868 723 928 837 760 405 670 384 770 591 737 853 954 708 780 419 719 403 616 860 550 042 733 565 633 726 612 656 966 055 336 103 558 929 682 022 185 584 219 398 930 450 948 527 816 232 336 837 620 880 954 168 235 008 238 210 569 496 247 083 140 233 001 931 525 128 394 826 838 900 931 979 348 811 267 863 283 682 852 707 344 550 483 884 152 239 029 060 991 583 756 044 809 029 694 959 431 094 997 679 549 321 334 852 381 977 722 759 305 092 037 656 344 362 794 971 130 466 587 910 771 749 027 507 198 589 151 112 812 161 449 100 884 452 803 527 333 170 077 698 582 580 212 340 874 155 572 517 257 323 022 228 389 240 501 665 800 710 873 111 902 586 295 215 342 304 131 181 823 150 899 367 758 460 708 768 967 415 951 154 619 550 847 734 305 055 127 231 637 334 719 410 603 868 535 354 392 832 691 442 179 903 565 002 969 706 445 906 594 069 748 305 409 311 707 028 873 065 148 863 189 348 140 856 371 722 021 405 572 250 786 037 048 307 369 320 814 012 362 581 966 913 034 693 838 208 688 824 922 832 326 019 893 136 917 148 988 765 940 274 849 891 403 090 246 453 410 601 144 714 707 020 902 092 168 204 267 128 730 852 565 549 252 984 229 287 750 911 532 729 612 525 017 190 764 148 482 392 790 042 879 464 706 315 716 381 051 897 144 479 629 191 098 319 024 506 480 313 965 366 657 324 866 020 493 382 054 695 622 836 860 990 437 385 529 224 466 406 318 201 947 746 484 636 429 235 247 565 780 295 722 329 830 637 453 768 124 466 123 809 315 725 639 545 170 745 266 546 022 288 206 324 106 696 111 054 171 857 621 478 070 082 818 025 699 254 379 936 143 813 611 923 300 496 666 877 648 096 926 237 075 541 255 452 114 183 567 296 792 128 341 011 827 911 345 504 646 780 563 648 566 757 482 976 101 409 075 199 572 421 508 510 224 467 622 854 535 839 639 889 439 255 705 297 431 609 992 137 596 265 096 302 105 033 684 385 961 263 418 522 817 908 212 014 744 809 635 083 185 213 748 466 288 773 259 473 186 713 584 290 774 459 732 463 971 608 333 414 691 107 470 656 908 848 978 255 443 954 884 864 162 022 930 877 862 025 818 251 852 928 452 370 100 032 786 083 264 368 033 271 675 564 583 692 411 590 898 331 712 776 639 288 784 767 088 215 799 357 515 966 437 097 786 687 350 369 589 532 369 806 604 823 673 311 257 170 138 711 852 057 381 098 788 437 059 969 938 368 105 422 478 841 192 697 648 847 302 498 769 746 957 851 084 594 387 482 801 066 923 964 922 252 774 402 299 339 501 202 460 016 912 143 100 410 128 788 377 309 525 581 188 674 815 685 346 608 831 499 068 302 998 072 161 634 933 826 097 265 209 521 238 045 939 038 275 087 371 517 193 364 045 637 832 993 315 015 408 462 085 768 943 655 392 030 459 198 076 979 049 971 933 279 902 582 241 721 926 644 859 737 631 414 844 439 961 597 569 515 566 584 959 853 617 528 592 443 906 430 882 008 066 384 166 646 460 816 811 578 589 220 382 912 785 595 330 304 398 396 730 596 930 876 035 123 446 682 119 897 624 850 596 576 608 189 706 038 324 220 162 611 685 997 254 767 675 399 814 771 893 836 625 603 523 861 736 620 617 010 761 810 982 147 371 052 618 953 758 284 508 178 659 405 417 451 378 900 116 075 532 629 912 447 028 429 155 755 552 963 560 630 350 128 596 868 958 562 169 863 411 411 648 210 373 159 442 165 372 548 637 864 780 867 332 719 681 409 062 681 485 117 373 169 817 954 013 408 507 729 855 312 514 557 651 262 772 012 558 584 330 346 748 228 054 895 110 681 645 537 140 787 023 633 036 840 685 474 586 157 207 755 594 104 071 299 254 761 430 874 287 838 351 229 596 397 839 289 772 801 680 176 994 408 093 298 695 909 340 263 737 963 682 261 139 567 138 247 577 921 742 185 659 723 769 277 801 692 710 524 730 185 356 981 562 733 968 765 796 806 680 997 522 918 669 987 529 804 072 920 428 442 693 212 859 811 499 618 497 801 492 459 793 718 449 209 101 177 461 424 285 872 203 820 796 905 370 992 510 845 735 174 054 013 923 994 755 571 079 873 538 061 110 359 360 749 068 891 271 925 301 963 110 675 619 805 952 945 111 932 196 320 932 020 952 818 922 715 793 061 560 431 946 785 199 381 273 286 259 988 497 251 386 140 453 562 863 281 848 883 342 206 931 984 310 010 162 403 055 408 986 719 677 130 525 171 023 768 767 918 884 171 381 117 063 152 379 789 324 362 795 735 688 237 977 843 985 241 954 636 995 040 117 927 019 239 470 519 973 553 825 565 924 858 552 955 843 775 569 234 948 389 204 219 132 888 915 064 195 156 138 914 674 083 300 969 099 607 581 263 414 540 732 498 153 139 466 499 725 589 952 816 005 633 086 723 767 601 940 785 670 923 623 069 468 148 720 691 198 090 166 626 156 180 904 888 304 375 351 539 205 542 186 409 249 120 414 994 937 360 929 854 303 515 141 027 680 092 648 033 725 874 771 042 231 300 134 561 257 289 646 381 551 582 847 479 379 460 364 270 746 289 270 403 753 725 676 614 293 846 420 244 314 668 171 218 360 552 128 450 073 219 417 686 265 368 490 852 378 663 476 259 208 214 940 808 125 080 518 064 256 019 314 626 280 982 780 160 383 757 689 339 879 285 485 956 877 855 256 380 579 069 266 605 550 422 460 463 404 312 328 717 559 302 387 655 728 871 327 958 965 441 486 310 884 797 472 602 234 136 083 979 890 034 724 800 790 608 996 902 200 995 409 487 290 032 032 441 461 019 946 328 402 516 201 799 758 830 169 707 735 199 261 044 257 688 691 397 190 796 799 220 937 354 504 680 886 465 681 847 714 774 468 049 902 234 200 225 083 201 589 831 318 441 206 844 559 136 208 751 099 047 265 441 171 158 344 955 947 509 844 295 076 315 462 777 069 047 228 422 283 119 229 294 397 749 666 047 272 783 333 446 889 683 228 945 980 815 900 028 965 718 989 797 952 175 173 989 426 245 699 191 601 896 807 126 257 687 962 139 704 800 761 946 980 133 894 011 058 697 942 772 297 508 898 746 809 130 728 385 882 093 866 688 945 968 490 783 558 856 332 112 758 365 562 591 956 151 619 616 302 509 783 561 120 372 383 079 473 578 651 296 035 247 099 099 146 864 580 118 335 717 300 761 961 308 810 999 774 987 702 434 052 252 058 019 789 562 908 023 753 408 726 568 156 916 863 671 476 337 593 371 155 996 864 731 262 589 796 518 525 684 516 535 487 836 410 825 511 119 171 536 012 359 709 643 477 849 317 381 707 198 261 088 842 527 115 430 089 772 884 636 193 994 532 294 262 580 158 631 655 700 208 058 993 240 851 251 796 462 693 739 926 821 037 676 502 232 339 767 831 683 831 962 839 676 242 258 430 155 168 467 559 728 892 493 394 781 428 420 981 839 023 464 259 179 458 277 028 594 640 077 126 984 008 926 076 459 862 330 600 918 533 817 062 950 612 813 299 292 964 335 572 530 799 574 285 461 616 378 820 477 065 580 243 057 746 301 783 463 847 061 256 940 425 233 214 989 805 069 517 889 418 526 926 584 201 608 632 983 592 562 183 933 710 095 884 967 197 753 788 081 143 424 515 085 761 070 071 183 523 591 203 324 810 800 653 485 883 351 059 937 323 176 531 241 245 742 985 620 626 605 117 531 412 950 382 862 929 712 463 599 251 046 286 387 931 063 315 491 061 549 481 616 705 714 308 782 596 782 292 270 577 557 923 621 935 433 806 148 371 160 737 948 672 766 060 784 310 863 272 785 116 163 698 448 942 950 340 075 690 054 444 264 771 653 646 635 322 518 433 921 844 420 261 337 859 997 590 893 310 588 871 153 808 162 956 872 949 962 367 353 693 104 957 143 099 327 186 583 776 122 934 557 510 916 004 459 619 624 803 772 477 995 087 821 752 736 747 339 723 696 612 284 282 104 376 872 633 028 924 593 063 690 579 429 340 662 150 280 477 825 400 512 610 040 663 801 641 241 949 821 498 375 409 900 143 247 479 047 889 835 438 307 413 377 088 630 874 319 302 945 404 258 503 891 393 060 400 841 060 299 674 489 693 125 352 647 207 062 309 462 959 807 819 940 040 503 207 861 810 712 929 401 541 166 683 545 159 159 729 561 020 003 770 734 659 885 115 801 884 626 525 703 594 669 946 514 939 254 651 801 564 227 247 465 321 245 404 541 025 612 090 842 452 091 478 681 586 142 054 202 845 452 061 223 817 014 330 477 080 251 425 120 589 417 378 080 742 090 556 765 096 345 943 442 077 341 053 277 624 880 690 719 370 633 831 250 482 436 764 776 530 462 275 899 436 491 761 450 177 144 421 772 763 800 290 700 491 137 798 303 192 837 808 828 934 342 535 882 199 524 296 489 382 713 518 099 509 090 355 356 299 759 111 100 819 750 363 349 125 346 395 627 261 815 724 573 837 089 837 456 089 241 329 416 789 664 082 576 244 213 353 166 410 228 051 585 245 307 927 997 644 970 729 944 667 022 512 369 367 439 871 071 547 226 761 387 716 439 241 667 219 921 603 914 942 247 482 497 077 164 527 897 626 239 367 346 816 127 337 378 483 038 048 695 886 725 662 606 024 334 437 210 447 931 449 814 838 120 252 469 946 165 192 708 248 560 096 333 766 792 079 996 497 614 386 317 541 489 773 068 892 754 387 261 685 464 189 883 838 056 791 776 000 725 125 727 545 455 238 232 902 389 248 274 571 085 072 600 422 125 188 118 375 329 022 989 164 433 227 922 382 768 269 681 559 772 199 779 923 000 188 299 192 311 209 394 959 372 567 776 847 684 913 300 307 707 068 002 253 908 754 762 721 591 743 934 437 891 043 977 000 417 765 453 610 875 566 536 010 295 870 005 181 147 921 273 593 930 938 119 600 973 524 922 269 917 802 500 526 661 945 097 248 889 339 363 713 461 800 694 551 764 426 013 492 337 004 751 723 670 253 228 827 991 261 204 381 531 326 254 193 112 545 591 349 214 946 774 312 430 565 697 783 353 810 240 546 991 731 827 035 910 636 016 809 249 128 206 133 353 138 797 362 106 890 830 268 682 196 686 891 318 255 860 701 896 283 986 445 010 550 702 284 763 103 304 581 781 280 188 384 183 843 058 793 076 461 329 793 272 070 650 703 806 606 123 036 337 350 844 278 922 857 023 322 890 845 146 226 223 540 499 049 238 773 644 803 504 770 300 090 699 088 726 568 285 717 260 279 207 638 119 183 339 657 641 214 983 062 378 591 525 021 216 222 020 404 118 679 503 702 947 999 349 863 529 290 641 021 551 061 104 922 308 714 364 518 950 558 339 440 035 261 305 254 923 495 076 288 728 337 750 770 551 042 543 675 089 723 446 209 803 881 602 781 914 319 324 618 593 977 574 361 496 409 121 448 260 156 181 422 447 910 993 666 132 635 824 823 153 106 284 045 670 730 923 190 160 383 451 626 158 028 778 886 783 687 640 563 218 653 175 822 921 147 810 690 788 436 521 252 157 118 872 466 343 597 095 996 175 245 594 968 600 994 927 759 200 514 174 786 361 705 935 080 647 675 547 841 853 392 371 638 083 091 638 528 674 562 914 618 241 448 763 818 781 764 382 234 016 179 246 768 344 220 355 428 891 184 051 755 151 473 840 468 224 864 833 399 265 848 201 797 111 413 001 401 336 374 924 653 109 493 410 535 504 709 923 468 566 231 770 208 488 857 224 849 139 654 895 422 430 360 721 493 813 431 851 976 558 037 014 133 628 566 017 303 415 092 704 677 146 836 648 828 535 809 586 502 738 990 214 395 631 275 285 395 302 453 224 882 273 248 383 039 517 084 299 316 600 380 087 290 297 794 422 344 888 596 817 973 576 178 861 751 802 383 667 326 739 152 896 319 850 026 245 221 816 106 134 760 656 127 808 051 712 969 793 714 952 091 105 652 170 520 322 891 780 179 579 561 662 464 852 763 752 042 472 356 462 705 419 740 382 331 165 229 240 942 425 099 432 906 600 857 145 130 641 017 957 942 354 688 031 579 482 545 229 523 005 350 987 148 970 567 839 728 157 175 574 679 553 952 786 426 980 332 372 815 146 976 733 694 651 412 154 744 510 090 742 703 584 864 729 645 274 711 182 007 013 244 005 981 280 731 345 026 259 133 218 066 215 764 880 132 562 443 103 525 712 162 279 584 185 911 217 075 120 120 268 290 799 881 506 430 638 255 066 587 419 911 942 038 797 241 565 565 035 066 844 392 845 915 107 344 629 228 488 958 316 057 335 702 712 245 612 016 005 802 956 858 973 639 069 469 514 063 419 219 481 010 589 613 378 199 565 808 742 359 478 075 946 038 829 602 374 568 660 229 371 535 194 972 909 221 506 895 483 158 312 005 443 177 035 413 377 792 037 387 937 586 992 523 699 709 351 266 866 906 782 633 288 208 572 653 067 338 924 026 769 370 776 208 716 402 512 682 972 058 372 032 860 464 545 233 564 453 379 357 409 308 803 573 757 869 956 663 668 471 144 829 852 548 939 559 654 090 966 286 406 833 182 652 598 086 405 417 052 616 242 630 946 623 199 276 573 305 165 952 599 984 571 481 811 709 275 653 783 558 662 900 275 147 698 602 330 711 304 500 248 976 659 122 047 412 997 491 938 065 409 836 725 389 920 223 185 202 505 617 225 939 823 590 144 601 334 387 871 594 208 661 664 627 183 050 804 650 545 900 795 861 505 884 472 280 209 023 070 067 046 798 692 077 126 809 968 224 855 658 074 868 829 555 718 735 571 827 005 110 790 865 662 133 770 550 142 052 428 663 679 292 196 013 657 250 792 402 191 596 793 631 487 076 114 954 775 123 972 923 696 153 035 635 253 227 035 060 078 661 268 232 237 566 827 076 839 678 211 054 161 575 961 567 492 430 724 719 402 800 776 593 024 199 171 616 648 351 131 521 151 405 211 744 141 798 469 006 947 736 341 578 005 035 231 421 735 987 781 416 081 552 299 356 279 539 153 444 856 013 296 735 931 740 787 242 210 091 727 008 425 181 831 740 685 710 255 337 598 766 249 842 789 338 769 134 610 385 297 604 863 107 173 439 473 570 287 258 501 804 090 237 790 097 202 688 403 375 838 021 500 834 206 366 087 556 015 669 412 603 666 089 524 988 550 263 482 887 884 533 596 665 796 391 080 440 016 060 127 536 025 746 626 901 322 045 159 420 284 892 872 701 827 969 383 207 741 589 802 380 327 580 399 144 525 790 691 358 724 554 754 395 863 307 758 502 623 528 482 822 461 030 127 526 916 358 016 423 233 196 309 120 226 223 971 434 876 231 829 278 425 243 211 649 308 789 074 051 920 262 235 689 140 779 006 297 340 796 207 470 575 881 851 340 247 268 785 573 531 963 362 135 824 512 834 277 625 866 331 410 506 918 070 002 578 775 921 568 463 001 849 165 301 124 082 144 514 188 885 583 410 534 146 957 129 395 550 140 536 872 990 165 081 405 002 215 809 384 912 922 948 330 096 891 729 766 579 659 124 135 656 372 061 290 745 810 707 781 456 327 052 620 747 396 753 739 713 644 633 749 631 656 098 152 369 336 784 951 204 420 163 871 373 855 029 032 159 839 963 250 538 154 058 024 441 610 613 719 552 152 691 644 917 777 822 346 579 843 153 041 586 002 426 271 243 168 098 144 961 192 352 011 092 214 776 032 535 185 977 221 901 266 776 688 965 213 415 817 926 432 066 978 051 041 032 795 779 051 374 952 059 213 806 732 259 820 578 767 205 434 204 757 713 442 430 273 942 756 289 047 731 525 391 650 696 597 814 968 357 970 208 688 270 298 527 863 696 958 845 908 047 930 522 204 864 907 745 118 405 812 891 597 107 804 188 403 234 687 847 226 712 850 755 422 268 524 161 203 277 931 329 742 418 116 389 927 814 514 371 697 615 086 763 563 470 437 072 354 209 270 852 144 286 498 600 521 761 021 478 970 818 202 414 599 530 284 586 228 486 851 846 792 875 015 778 582 849 429 986 049 814 732 273 017 099 320 774 529 516 757 321 768 716 062 566 422 304 345 671 893 870 210 781 093 273 333 629 181 139 606 343 208 297 602 147 185 337 843 365 678 754 591 332 141 792 653 274 125 813 625 532 342 762 453 083 518 175 923 047 542 147 283 625 015 172 494 208 490 987 059 041 192 988 087 406 198 529 909 291 751 428 679 265 531 917 596 319 351 357 296 210 836 859 645 996 453 952 780 207 413 906 039 708 336 145 729 119 045 268 628 693 245 359 582 846 794 588 040 188 021 944 301 800 273 921 608 101 370 817 503 100 715 950 591 432 379 650 655 851 944 665 824 678 744 617 631 724 604 104 775 014 773 701 047 454 170 219 885 968 103 296 317 173 884 861 672 473 688 040 680 777 779 776 819 377 560 408 883 864 106 957 105 754 829 046 107 695 089 652 171 025 859 539 392 903 340 869 799 142 829 424 040 509 565 575 549 721 959 531 684 638 836 372 705 488 788 434 744 075 776 599 521 671 100 761 361 369 746 190 095 228 615 716 433 349 325 311 422 496 019 835 435 051 096 703 855 764 974 049 760 578 037 681 981 130 035 170 819 828 252 639 875 910 607 949 169 308 920 340 997 066 208 923 746 427 977 456 034 081 160 368 313 648 228 065 109 561 410 366 607 459 820 858 874 241 760 689 933 898 947 438 865 205 354 682 000 028 582 295 123 854 999 133 066 274 678 322 873 889 853 096 516 362 995 240 762 682 782 064 840 681 478 753 821 716 627 907 875 595 311 923 392 807 435 027 925 529 038 511 873 985 268 106 602 545 210 261 925 625 886 284 536 555 564 145 007 449 229 185 629 649 848 716 856 974 733 978 061 335 313 639 995 936 071 407 966 937 818 280 834 992 520 659 539 302 319 970 404 022 714 384 771 697 517 793 960 740 147 323 920 204 772 502 731 496 405 584 251 480 653 683 601 390 464 712 697 407 310 833 296 024 236 955 667 983 113 665 093 281 133 940 751 055 407 910 117 335 320 481 863 843 213 880 126 454 181 925 039 086 755 797 723 313 744 417 413 040 401 867 274 761 743 775 640 282 189 060 814 589 301 331 252 139 745 824 242 481 296 970 298 985 871 276 190 099 796 037 256 550 724 133 863 651 504 609 136 832 344 789 795 990 737 898 958 320 738 476 615 075 497 864 728 951 727 177 565 321 656 430 496 740 909 819 687 643 713 493 113 068 812 131 190 846 906 366 292 236 038 426 592 327 274 925 738 858 352 543 825 131 268 135 597 416 577 506 571 060 411 495 937 760 432 482 936 554 594 840 288 681 722 242 841 997 589 498 388 759 817 313 328 928 601 185 267 664 508 873 182 924 019 939 284 834 732 298 449 561 504 779 954 421 619 216 773 825 147 983 688 263 620 631 007 458 259 858 034 501 194 590 736 457 780 093 176 794 288 214 488 943 971 051 496 960 585 616 186 160 799 860 648 868 264 669 416 258 892 094 176 820 959 161 878 006 204 905 003 696 335 680 016 451 047 523 491 056 976 288 770 657 311 402 361 594 055 741 308 413 364 533 116 546 924 199 640 098 565 519 451 576 880 319 752 413 050 007 466 820 943 250 752 097 408 055 606 617 654 969 021 256 815 148 098 749 799 680 057 041 837 574 753 268 241 753 357 064 163 766 466 618 783 675 744 049 743 523 037 913 328 442 832 044 562 928 493 900 567 375 272 480 865 382 457 236 901 003 945 517 482 663 113 844 895 080 303 964 891 144 952 421 972 419 215 925 752 845 106 168 682 473 262 109 193 348 911 336 394 603 418 356 499 711 296 090 887 464 596 931 874 844 927 247 157 536 143 940 428 786 196 815 179 562 222 438 793 766 275 960 694 798 825 353 596 934 598 958 194 870 891 442 611 731 220 151 265 843 759 014 634 179 196 933 726 464 544 369 959 795 610 700 376 934 514 863 291 245 642 301 720 156 013 613 990 988 091 062 273 789 291 589 391 936 128 170 584 947 615 841 932 112 797 623 868 784 428 661 991 936 722 386 339 574 133 376 335 082 731 528 904 456 285 242 541 425 036 527 413 331 860 775 571 433 000 480 034 573 357 711 205 806 974 761 146 127 853 223 511 102 612 545 281 498 244 693 481 492 150 500 779 503 443 732 687 823 530 094 073 743 236 268 606 993 279 126 217 784 725 318 983 523 199 009 903 286 090 577 618 936 805 792 954 461 859 428 501 422 495 423 166 715 427 582 503 036 737 708 621 059 121 999 878 130 029 247 802 720 482 128 485 428 428 562 496 668 322 686 865 210 950 983 530 308 890 011 952 879 966 130 971 942 283 049 374 600 490 917 936 067 569 049 725 156 794 163 617 688 157 588 322 973 591 082 786 287 441 086 170 117 064 652 373 053 098 190 826 464 725 511 315 473 103 377 312 878 638 543 758 536 807 115 163 064 700 550 230 864 748 863 932 170 281 308 493 315 699 233 717 246 474 308 189 190 225 257 587 631 892 182 901 053 319 907 754 938 605 450 212 259 031 674 984 672 778 884 845 230 161 286 653 766 165 474 604 073 575 687 775 332 547 625 082 470 576 540 164 994 317 437 006 454 803 738 163 333 092 626 428 537 280 338 377 525 461 325 459 961 001 264 910 599 000 595 391 384 808 658 632 520 640 867 597 933 091 035 536 127 131 319 077 122 089 714 488 602 388 837 453 058 400 448 265 984 070 122 369 795 594 054 647 930 971 956 424 041 943 124 199 433 986 635 889 438 923 926 403 726 026 336 009 723 976 771 162 058 497 973 027 650 146 766 579 073 114 093 145 127 226 846 335 671 934 737 690 393 779 739 663 779 137 790 028 522 224 701 623 696 001 637 134 014 651 819 480 112 524 869 379 122 094 973 693 232 241 866 631 054 967 298 893 097 461 818 880 293 883 741 707 412 044 008 585 946 139 270 575 660 521 393 739 415 244 599 909 717 539 166 396 389 398 026 255 021 024 269 611 969 880 901 799 601 503 781 338 639 202 192 053 748 898 705 235 613 071 720 928 289 997 941 678 368 528 206 849 360 189 060 409 449 344 935 882 618 720 528 257 545 447 900 435 043 122 649 465 846 751 834 776 376 166 314 476 548 627 366 253 417 821 205 638 186 032 785 117 332 001 676 341 392 812 961 860 451 276 712 649 527 904 948 884 002 386 393 298 429 067 371 519 357 220 577 759 198 800 793 952 649 608 354 953 478 368 960 361 654 288 503 352 445 591 319 209 133 145 505 948 889 610 429 405 539 521 154 858 748 490 976 128 660 635 699 890 371 633 746 051 137 536 880 038 265 471 232 424 270 795 251 231 010 741 991 273 726 703 788 741 024 741 822 115 656 424 361 652 310 059 383 203 326 990 823 582 746 363 413 633 503 608 513 333 775 995 736 793 635 793 421 672 265 923 475 240 718 897 141 295 463 880 979 826 770 514 643 195 619 169 338 413 009 292 054 066 056 860 249 690 862 154 882 699 555 950 080 883 609 955 161 817 572 297 671 258 606 795 044 119 734 269 486 906 677 574 441 011 053 334 348 988 376 238 701 527 870 688 157 002 346 576 050 413 096 682 176 025 344 750 789 501 907 256 253 702 846 874 668 342 920 091 520 678 418 045 705 321 193 216 257 572 292 595 383 389 862 917 848 773 024 162 022 774 339 575 504 334 734 261 383 935 024 373 365 310 345 860 516 242 804 900 784 600 982 091 143 458 638 363 094 357 160 141 267 674 234 266 422 193 652 875 123 254 637 589 532 176 506 635 265 895 731 295 425 772 269 427 019 769 212 022 029 977 300 720 237 408 464 042 109 861 894 441 390 241 847 907 658 673 315 166 690 813 938 519 463 658 692 166 263 624 482 097 007 282 594 908 883 700 386 223 191 159 441 769 292 867 039 791 071 052 845 713 500 511 716 766 390 060 756 472 586 489 011 089 489 732 397 472 250 222 295 239 527 637 075 656 714 034 674 914 597 518 894 717 091 977 256 871 517 479 856 889 342 413 892 566 979 895 755 082 721 069 409 250 143 864 741 692 445 702 809 736 127 660 347 635 061 706 745 294 359 062 986 977 569 220 571 757 870 041 769 458 187 565 461 458 211 646 421 089 785 428 454 983 781 899 324 126 449 604 839 341 925 784 777 768 738 542 052 239 123 483 958 710 603 992 030 861 327 760 986 372 350 053 022 937 543 840 774 619 479 122 030 337 747 858 906 777 546 658 150 650 455 480 246 232 685 947 166 886 479 335 737 798 977 253 457 745 396 547 443 328 865 188 735 021 688 008 115 266 203 184 093 328 348 330 152 605 862 387 713 748 530 604 679 544 868 175 058 434 255 854 013 974 657 330 525 679 219 547 612 406 812 280 295 740 241 924 071 174 686 041 096 263 672 440 264 497 706 037 506 433 727 514 604 582 811 892 496 439 989 441 159 215 698 451 143 939 922 513 355 659 142 714 566 918 074 066 066 021 740 899 054 479 416 651 718 690 776 474 147 736 752 664 783 906 148 670 470 877 503 869 691 858 227 383 912 304 837 313 749 576 135 838 056 536 239 058 808 164 619 341 448 549 467 238 505 336 697 958 515 878 834 148 994 967 194 201 896 239 843 799 911 810 609 491 669 845 093 636 948 033 991 727 946 721 671 992 623 326 054 392 709 566 505 144 321 965 773 152 965 336 209 654 882 115 989 166 954 187 438 661 622 876 352 664 076 738 573 699 653 949 490 218 149 118 623 042 982 913 373 383 907 065 654 029 798 797 762 423 851 040 744 578 647 249 369 193 699 255 421 658 583 646 976 984 464 870 348 304 638 914 352 764 868 087 505 548 432 828 849 172 978 778 153 787 914 284 695 440 902 136 277 652 695 479 401 724 276 900 224 544 638 473 486 473 624 976 284 833 179 261 718 369 908 460 081 276 068 609 715 890 314 776 741 943 157 392 022 948 315 205 002 680 896 306 336 286 919 119 832 079 326 768 201 571 672 684 132 690 462 020 323 421 682 712 161 479 458 052 701 455 957 316 898 287 339 539 230 223 052 381 088 530 241 737 145 225 285 024 190 833 769 842 578 475 827 923 902 543 563 546 611 406 122 965 882 863 108 003 380 653 459 734 961 812 968 417 671 830 596 582 137 679 625 693 995 904 685 458 581 178 053 970 935 034 096 880 331 869 277 206 718 004 900 483 736 875 490 311 067 216 214 333 718 313 403 281 752 293 240 529 887 726 809 445 782 818 807 677 335 537 553 906 811 450 001 356 282 585 679 320 183 162 981 682 867 672 709 894 485 930 768 309 380 623 252 273 013 115 688 223 981 763 505 054 510 495 638 752 781 879 934 894 067 861 310 263 056 320 786 193 976 663 163 077 525 741 443 814 039 983 314 926 095 306 526 922 615 370 657 803 956 486 282 328 723 184 612 912 517 978 093 245 772 733 321 634 815 679 147 557 544 407 939 661 578 876 993 194 390 357 369 623 545 636 242 148 181 145 169 687 300 597 321 484 481 658 889 563 083 746 594 137 260 184 165 979 596 578 800 372 430 534 658 799 255 957 232 310 506 845 156 534 213 851 024 642 362 025 511 201 024 572 812 759 573 520 707 637 017 551 262 593 852 542 488 181 181 898 132 752 030 032 908 832 444 845 845 296 972 077 958 680 350 171 382 029 322 749 478 255 562 784 349 723 325 496 740 201 765 092 991 361 098 094 459 497 595 264 271 881 686 387 922 504 500 773 566 723 249 884 249 823 334 792 727 695 239 887 398 159 393 722 876 437 827 097 438 100 139 342 374 862 497 183 598 720 859 821 533 295 443 640 432 539 701 057 923 405 128 745 308 952 271 001 606 556 476 607 215 210 515 569 715 126 275 825 120 478 018 453 413 488 316 125 707 020 646 737 544 273 987 405 445 130 187 275 948 678 572 799 532 458 686 343 235 635 565 562 762 628 961 430 589 049 249 245 985 477 878 099 185 260 880 616 395 461 178 318 372 235 247 789 774 364 549 928 615 085 213 243 921 459 449 585 661 851 326 773 135 706 951 848 282 073 639 527 714 403 361 796 587 785 087 538 748 908 331 306 862 341 092 181 707 951 240 337 606 386 501 351 745 182 278 224 684 475 536 206 666 045 444 670 009 135 842 635 903 951 629 281 498 130 181 574 749 555 232 951 930 900 801 197 337 479 546 617 477 000 073 310 737 244 071 012 608 063 671 648 725 790 592 169 843 253 535 729 201 456 224 124 082 646 931 397 713 014 719 907 080 410 555 532 151 346 558 323 792 135 278 417 869 952 487 868 276 040 266 570 415 161 611 850 697 017 061 027 533 219 796 924 907 933 154 506 143 772 856 679 560 067 142 671 339 768 030 138 758 908 013 727 262 002 325 924 870 861 758 824 924 255 500 149 677 669 823 826 599 017 481 051 627 217 464 132 830 693 491 825 240 947 996 329 838 970 906 687 467 902 224 840 969 567 108 153 735 251 898 104 309 788 210 486 561 297 572 281 920 087 214 478 929 004 994 952 718 972 514 811 035 912 433 118 491 282 783 712 163 289 607 266 148 531 951 946 057 955 490 938 476 150 355 316 943 579 122 489 884 198 123 571 866 562 118 019 338 013 604 263 836 132 454 850 733 804 074 248 876 946 325 622 896 507 915 218 212 220 222 179 211 246 318 254 337 986 514 705 800 043 203 216 266 231 694 288 586 802 649 019 372 597 736 754 404 007 354 447 795 662 492 076 055 578 262 931 827 582 245 705 676 083 655 713 900 102 916 690 867 910 955 286 994 446 482 753 282 934 707 610 000 268 395 404 264 039 492 109 242 479 088 734 559 183 538 171 948 205 119 577 381 641 691 602 016 840 908 137 706 675 613 581 849 602 423 310 300 903 590 671 931 577 651 087 166 694 702 653 868 978 337 924 189 460 625 211 140 030 146 606 430 607 128 963 544 722 589 970 559 095 638 790 734 664 015 418 749 035 118 721 988 344 905 469 001 019 112 262 009 240 717 784 415 940 101 231 327 907 114 011 979 081 190 157 311 630 957 655 391 579 175 332 703 754 934 008 324 545 609 017 437 602 451 504 412 039 338 496 074 815 609 000 362 853 403 713 849 388 897 792 253 234 820 074 551 943 024 669 923 680 336 485 018 378 120 217 305 553 812 566 357 030 736 798 717 112 060 504 442 978 082 218 217 307 768 140 127 449 639 548 556 150 468 858 682 176 613 185 995 192 225 558 779 308 407 669 090 166 049 176 516 842 253 928 112 070 315 424 086 584 848 671 276 603 019 206 405 239 570 609 494 607 244 177 515 792 385 264 929 855 221 316 935 929 933 054 420 742 103 150 195 665 179 573 508 751 736 767 824 278 494 186 623 643 132 253 905 599 614 027 963 044 583 917 779 803 898 819 825 009 343 338 134 613 516 441 971 648 389 374 077 871 901 267 536 226 159 370 838 806 835 165 387 337 429 251 063 703 022 707 528 661 646 241 393 724 100 768 519 106 323 756 341 647 678 276 839 899 711 971 789 897 789 043 599 343 760 064 981 686 978 244 599 496 133 055 124 273 516 956 661 319 984 804 225 860 605 038 247 279 123 340 176 219 890 388 299 589 824 439 012 273 317 220 823 148 133 903 233 973 111 891 480 889 696 123 531 322 960 147 173 450 959 045 291 824 052 457 682 336 402 386 577 668 279 682 231 085 458 464 981 194 998 191 838 415 410 788 169 877 236 903 052 355 151 753 939 949 517 577 620 672 217 402 583 536 028 903 255 973 851 069 188 321 067 842 907 834 998 100 093 060 367 784 887 753 660 644 586 798 304 828 241 822 085 679 959 324 245 993 463 179 864 823 370 495 672 830 060 547 467 145 024 476 233 036 542 823 972 425 501 448 815 295 492 184 480 812 829 299 763 009 194 363 423 820 134 827 776 535 486 540 859 850 313 507 692 492 562 027 590 145 061 324 427 989 246 633 662 408 347 463 111 633 504 977 000 081 387 623 099 283 705 180 247 346 361 321 859 744 317 281 970 725 138 884 587 708 502 303 228 030 350 816 197 603 819 603 421 572 710 699 646 540 090 979 563 700 889 821 869 541 676 575 474 954 036 177 834 489 261 892 020 629 680 991 052 013 225 785 832 405 766 705 320 787 377 018 739 886 847 062 214 840 597 230 699 963 491 833 267 125 434 450 868 788 007 495 725 784 990 336 179 866 185 534 064 880 840 848 602 681 879 721 296 314 655 294 043 281 414 814 258 020 111 960 425 918 401 611 032 660 220 353 087 760 223 708 534 949 285 339 347 485 435 871 620 660 267 652 686 128 865 982 930 613 058 808 958 101 096 738 990 730 376 339 280 147 282 202 794 534 584 800 438 301 116 422 047 066 974 095 058 887 783 995 899 939 185 892 708 253 542 157 456 720 055 785 772 782 141 669 574 932 160 970 544 078 528 689 103 417 391 456 871 134 495 819 203 617 368 295 160 761 246 394 089 173 826 284 762 635 014 968 823 518 408 403 538 005 905 309 830 988 772 900 057 961 423 375 129 316 661 723 550 420 923 767 383 715 354 102 978 182 268 144 704 299 084 920 169 478 396 835 573 100 175 176 127 449 585 947 963 151 169 567 051 244 602 031 151 902 614 389 277 140 483 232 535 879 043 947 204 442 462 816 219 610 902 814 569 471 507 024 561 890 378 982 210 385 487 682 212 604 505 492 162 541 704 189 757 084 637 528 493 974 075 671 838 694 798 880 965 289 513 788 504 934 295 856 501 425 756 244 938 317 631 492 824 227 769 251 379 422 195 887 125 047 116 509 254 424 728 863 656 579 844 125 458 284 998 703 836 291 348 518 596 847 239 083 720 233 620 168 733 395 248 354 148 445 844 532 604 867 047 399 049 559 626 863 127 326 482 715 677 548 424 816 999 510 108 402 314 366 066 390 007 765 161 997 110 553 408 993 711 770 672 836 205 328 994 721 076 536 292 672 997 756 838 150 443 797 264 308 273 430 929 775 702 921 665 124 270 167 245 969 838 527 787 639 221 627 392 298 313 995 843 650 928 884 193 545 164 516 547 636 010 671 563 674 940 764 924 581 317 036 314 124 734 830 012 539 382 937 884 617 467 583 686 348 184 924 541 604 458 657 580 569 572 052 828 040 779 329 556 331 758 370 740 533 963 086 284 281 016 457 361 553 222 194 458 676 057 044 013 107 805 541 366 441 960 346 218 878 603 194 925 215 215 677 981 543 584 990 992 900 504 116 360 023 356 854 843 506 036 404 773 157 481 798 040 458 266 579 268 972 970 216 477 944 196 864 558 412 428 884 834 431 211 021 233 572 083 266 155 405 458 851 522 580 603 336 512 661 496 049 723 448 830 363 552 788 347 216 206 317 331 873 834 748 454 978 068 231 262 736 492 703 261 882 193 406 374 094 389 633 967 602 552 533 243 635 585 616 004 627 426 545 465 070 173 917 879 929 641 913 905 209 242 369 314 970 472 134 510 612 628 389 331 829 874 380 713 247 139 839 630 156 095 620 716 087 536 490 177 331 228 190 959 569 729 375 321 864 199 507 974 372 087 576 596 808 016 020 449 971 938 648 081 288 604 128 176 250 092 963 462 337 986 981 342 885 075 678 433 876 683 277 321 017 936 141 206 301 272 413 414 215 029 879 741 915 212 833 330 752 673 164 187 250 222 486 626 039 197 634 039 613 873 282 784 681 963 390 175 037 630 080 566 235 535 223 195 932 309 533 513 865 821 283 787 499 937 514 419 180 205 339 876 457 767 867 665 877 925 638 587 875 705 495 657 227 315 971 502 286 618 144 167 999 698 854 868 604 946 408 754 851 879 513 193 107 829 342 951 676 282 089 406 312 354 250 285 215 265 302 313 959 906 591 298 242 052 334 079 531 390 906 491 382 904 734 717 132 165 937 752 803 979 454 652 787 518 764 723 072 527 325 030 384 395 280 566 852 323 911 557 545 953 594 007 828 807 441 387 746 442 709 294 457 149 538 620 512 144 268 195 248 319 110 255 735 497 189 023 022 827 676 828 538 177 303 619 500 375 038 129 293 676 540 392 677 181 720 815 271 779 551 961 288 154 672 423 425 761 116 540 861 096 329 225 412 481 497 968 817 607 575 242 095 077 631 929 655 333 263 255 735 117 323 658 465 444 937 444 806 855 984 176 772 571 133 270 643 920 171 305 100 679 514 266 204 054 092 445 293 928 333 104 670 067 724 857 772 829 766 246 575 666 367 849 526 986 766 328 150 743 946 342 885 647 448 356 891 532 994 678 516 556 472 707 120 472 053 447 741 137 251 827 162 609 484 992 370 753 197 933 494 763 786 666 064 473 669 125 228 146 942 260 371 339 829 765 625 469 805 016 654 678 117 153 371 198 759 426 036 503 365 459 257 757 236 961 033 619 953 237 677 800 965 371 722 182 920 516 342 830 447 441 674 927 370 980 257 454 273 640 339 944 228 670 603 383 251 959 499 358 488 949 442 133 039 992 126 638 132 343 651 135 242 416 451 893 134 714 016 697 582 334 824 617 854 268 588 857 084 415 579 584 423 052 399 662 287 185 070 136 616 614 670 151 508 347 840 827 408 861 703 751 327 564 166 119 717 102 713 125 774 966 381 444 459 116 340 312 910 067 546 089 431 449 552 469 294 262 632 716 391 038 204 272 432 611 180 604 933 742 352 949 097 224 528 157 280 229 065 881 846 899 280 463 066 219 923 826 818 298 893 574 058 426 830 597 714 243 965 708 521 979 922 653 124 069 286 136 417 272 134 019 273 042 540 749 072 903 592 038 418 209 629 107 614 145 448 515 334 883 610 272 505 605 077 620 611 014 696 888 427 521 991 713 275 028 390 985 325 828 565 612 966 619 501 924 880 590 888 019 066 444 890 720 692 001 862 835 058 235 775 683 020 080 903 307 614 710 162 129 853 535 918 114 623 663 783 347 800 042 059 083 159 644 848 925 027 837 683 917 789 539 308 732 347 188 425 499 989 496 487 537 805 437 918 204 995 503 087 757 615 455 908 628 056 804 101 518 900 130 026 592 111 076 365 305 805 665 657 924 370 990 946 814 310 798 850 234 527 940 133 451 333 562 732 561 563 881 208 735 714 597 523 858 828 216 240 673 962 978 088 660 717 260 238 574 903 180 396 052 195 325 051 248 643 279 145 715 143 476 671 011 502 971 572 732 250 646 111 687 679 373 115 188 518 250 149 398 139 706 166 983 583 916 242 788 089 794 015 268 229 953 947 389 298 891 025 043 685 235 945 110 797 515 445 093 530 766 136 968 152 073 453 800 030 835 194 977 165 586 317 926 430 494 803 001 454 640 417 033 387 467 483 856 866 515 541 575 873 600 647 995 732 331 680 719 520 428 222 092 060 095 482 271 536 611 742 486 333 675 441 974 301 722 244 937 191 886 539 071 229 949 359 753 079 385 910 663 513 870 604 627 736 595 280 789 864 441 517 643 992 890 266 039 132 256 821 589 433 812 700 680 444 110 607 645 730 961 040 414 572 301 463 950 232 669 032 996 603 937 861 497 176 943 303 018 185 339 251 406 195 552 649 302 994 521 712 696 559 096 654 316 924 693 899 191 774 290 175 891 617 897 360 227 119 003 333 046 661 670 626 400 085 240 418 885 929 414 927 109 738 634 357 438 984 662 897 210 047 442 064 761 923 916 277 205 258 376 053 816 721 320 502 160 737 569 675 519 222 789 384 473 322 160 205 844 554 034 645 095 965 783 906 723 796 496 190 660 390 685 539 719 841 995 520 442 365 012 729 213 632 441 509 975 047 090 935 753 639 481 806 000 100 091 919 384 006 897 446 248 471 319 678 437 629 111 499 986 442 038 766 075 030 408 326 984 060 771 245 735 330 348 097 465 591 048 728 653 726 655 749 330 017 571 131 313 298 424 209 059 735 939 535 511 017 438 457 532 233 198 836 342 398 201 159 548 878 522 158 701 822 378 498 038 512 611 376 261 975 510 200 863 043 123 778 411 593 383 528 737 745 187 073 472 161 804 995 948 379 984 689 860 271 194 548 686 105 743 902 440 196 215 857 627 150 240 325 386 711 403 918 627 408 818 347 410 793 776 189 792 171 666 819 563 434 173 106 417 985 691 591 094 733 247 858 814 087 113 552 388 636 183 404 456 989 379 646 283 092 388 170 024 256 634 890 535 871 715 957 728 246 411 342 896 370 485 394 482 720 418 909 720 593 701 658 769 236 067 743 482 242 983 952 912 357 265 959 085 634 552 654 034 527 396 723 738 119 715 906 941 180 130 222 723 258 035 661 880 153 617 119 455 219 287 801 565 140 745 927 507 735 865 126 693 160 117 072 879 581 133 605 865 143 141 364 644 303 315 661 362 750 134 431 305 466 532 437 516 387 061 016 038 040 027 405 524 442 136 514 932 015 824 259 036 355 309 674 159 528 159 008 633 028 999 774 273 831 419 540 132 768 538 370 087 718 719 829 402 099 427 814 425 334 715 390 020 031 840 094 819 062 442 775 504 585 898 130 746 459 775 403 008 774 215 559 815 142 795 550 322 307 161 761 708 583 745 230 464 565 471 444 630 144 704 229 397 504 715 854 724 227 750 825 851 413 677 504 664 791 516 617 365 012 004 932 040 622 768 994 775 612 642 199 205 370 924 376 635 541 434 250 093 982 680 834 986 025 808 724 897 829 472 976 634 525 973 265 617 214 278 305 044 143 890 104 128 707 425 561 304 984 779 217 168 192 197 940 455 143 846 192 035 066 085 541 419 755 703 409 926 333 528 455 189 502 345 319 053 696 375 996 391 631 513 344 617 875 259 265 560 233 204 934 869 911 401 375 199 989 269 521 713 707 804 927 893 173 416 629 275 950 288 455 029 967 014 292 255 916 323 397 940 399 301 236 700 163 520 299 193 644 470 420 988 544 853 275 382 818 533 535 281 016 003 690 186 889 181 382 379 555 462 768 151 971 843 555 681 312 153 296 990 431 428 942 288 246 611 663 536 091 109 409 543 541 504 196 137 662 168 694 849 148 446 345 227 109 078 010 876 861 904 803 225 611 267 334 745 915 121 785 531 005 275 738 724 874 900 004 307 321 905 392 745 981 371 796 219 528 257 695 295 110 029 268 289 826 798 526 508 078 887 195 254 567 821 510 515 060 048 210 867 900 780 790 361 218 668 069 753 830 850 302 422 930 222 830 201 800 797 468 633 037 337 710 062 278 498 110 582 361 455 613 326 494 357 097 437 137 441 058 781 574 608 402 095 073 546 175 376 720 823 030 453 322 566 847 358 723 366 388 065 623 506 149 709 765 800 703 887 950 910 039 842 348 938 479 258 144 225 587 784 679 970 290 690 465 756 144 014 889 380 009 566 487 130 559 290 813 179 584 245 819 111 269 668 880 868 599 653 721 777 827 362 865 778 198 647 471 336 227 560 324 249 335 923 715 618 240 838 131 986 022 767 587 363 386 436 194 668 696 503 773 174 865 910 451 932 909 141 434 917 494 732 876 442 973 519 703 340 736 456 985 862 795 926 242 436 656 473 020 002 136 790 287 429 673 740 869 995 204 084 615 564 519 596 854 024 493 440 795 669 208 592 693 412 730 938 113 553 478 184 424 273 384 725 723 275 467 162 562 176 510 425 344 477 131 982 564 107 802 265 198 763 346 525 190 583 546 709 915 761 783 763 932 219 561 211 009 436 311 278 469 543 528 467 779 283 435 759 981 107 593 018 310 706 861 577 060 655 385 869 592 147 361 327 989 620 797 465 722 427 232 702 329 189 069 131 318 041 084 062 858 441 438 601 963 711 307 967 927 021 914 089 999 678 852 280 437 359 295 054 321 209 776 655 568 265 190 184 412 248 713 321 523 959 539 513 963 423 486 325 548 065 540 488 979 935 354 594 868 097 845 609 866 889 212 915 519 641 801 080 572 492 493 297 532 286 654 943 836 547 957 945 029 692 058 320 551 440 436 892 423 159 671 246 570 179 526 751 639 485 156 808 981 070 588 899 017 652 153 746 119 631 849 721 955 693 205 682 282 404 146 001 155 120 586 831 327 412 097 491 201 528 541 682 980 597 280 303 151 614 826 021 123 385 966 951 501 474 571 308 766 901 243 895 306 756 848 336 176 383 480 556 392 702 754 951 306 774 906 709 288 776 401 908 855 087 719 033 230 754 989 613 505 018 807 061 826 507 885 756 154 141 680 258 779 595 875 403 202 425 047 285 982 499 939 325 877 147 443 589 731 707 340 671 580 800 519 307 280 899 800 269 116 583 629 472 608 181 125 939 178 423 088 210 952 130 037 227 187 784 855 883 953 965 578 025 177 670 210 076 946 450 897 206 709 965 740 627 174 498 198 920 399 500 932 827 490 661 708 596 350 891 174 939 189 542 531 746 719 160 547 016 022 462 800 447 941 722 900 074 179 845 374 972 836 766 043 028 789 395 967 649 476 960 339 684 635 664 965 332 827 395 125 636 893 738 139 823 820 388 752 658 169 367 927 454 994 429 381 252 819 144 429 152 774 081 548 489 310 630 761 462 350 271 299 423 698 479 138 497 149 736 515 143 301 783 925 412 880 374 423 725 743 600 511 668 362 324 309 994 054 280 475 107 869 205 659 947 689 143 312 833 203 943 878 126 848 288 095 424 858 521 955 218 901 808 074 531 425 039 053 297 356 762 807 934 894 559 283 314 127 007 186 647 476 845 070 759 525 594 799 406 792 101 165 223 793 993 498 442 573 183 796 049 002 655 177 777 381 329 600 954 986 616 473 664 085 415 045 390 742 831 888 311 691 757 686 460 278 147 584 801 643 927 974 417 456 388 208 463 074 674 193 896 740 094 770 505 663 195 162 799 278 310 779 289 021 359 682 780 290 189 994 919 404 916 222 582 062 760 040 937 293 532 975 508 723 530 993 760 453 294 423 614 698 218 643 736 413 466 889 748 430 419 406 816 554 804 411 219 654 782 553 518 720 351 588 169 954 053 625 506 017 297 291 644 125 826 031 664 168 048 462 551 023 895 291 105 018 725 804 790 056 159 231 640 836 688 441 193 660 449 220 866 256 507 239 219 957 063 780 890 465 815 246 207 299 487 179 844 395 351 708 848 405 964 362 723 232 053 235 545 907 474 235 005 317 066 163 540 256 593 287 016 887 929 372 072 215 467 287 130 553 306 361 336 299 925 466 419 791 120 222 114 998 012 148 995 366 454 449 324 813 561 698 892 159 613 910 317 738 626 548 620 996 858 494 720 981 575 227 755 887 358 982 114 990 709 370 204 886 108 990 732 215 158 591 450 032 414 760 369 096 706 518 897 235 884 377 599 088 733 996 630 812 416 708 365 989 492 126 547 464 327 378 619 701 158 986 894 953 100 454 947 859 785 456 521 015 969 406 251 578 509 471 016 622 740 138 480 978 716 228 590 070 838 592 115 033 041 431 994 661 307 748 607 652 911 919 073 745 828 498 646 007 874 923 845 100 079 355 413 627 180 145 074 490 485 739 789 008 100 128 577 510 017 511 324 636 090 203 123 421 982 835 049 245 354 961 025 916 868 768 386 340 570 718 021 560 122 697 827 651 813 812 346 118 279 457 904 727 139 050 052 622 001 394 835 396 526 659 651 631 446 202 501 192 867 663 565 023 172 071 663 279 482 038 256 398 646 356 304 614 354 295 574 285 036 505 175 326 667 579 602 868 683 535 035 062 383 416 520 522 876 357 148 295 349 637 746 088 135 010 397 960 754 481 453 842 391 758 412 802 702 287 176 948 715 434 225 257 522 982 227 185 725 555 741 197 664 413 496 761 428 861 483 188 240 487 587 153 840 786 932 131 006 608 120 232 811 178 952 559 434 382 260 068 369 024 089 331 847 108 110 791 389 028 607 707 134 753 263 544 360 370 019 460 022 420 507 559 361 795 992 065 972 632 707 089 837 866 711 419 852 313 101 957 836 628 298 026 721 966 535 607 991 397 517 180 678 154 709 019 305 201 800 998 347 793 440 081 467 057 998 208 648 085 752 064 727 490 104 509 619 753 559 784 257 042 226 437 889 718 304 859 511 169 652 342 456 835 859 143 195 504 998 497 573 384 647 791 499 203 392 135 333 441 472 434 195 711 592 997 434 433 376 078 660 445 537 839 222 061 633 830 892 996 166 508 335 159 855 339 614 493 127 487 673 033 548 545 559 347 296 513 666 745 624 398 449 472 874 784 868 247 521 484 837 003 011 117 661 258 628 771 552 471 460 139 328 751 776 893 915 500 065 832 492 037 173 967 934 975 404 611 500 901 356 358 366 176 227 281 814 059 345 005 745 708 938 870 791 363 297 950 026 871 559 416 023 489 407 648 262 296 811 279 581 123 484 830 715 105 306 545 852 397 419 994 946 037 441 551 017 228 829 672 542 898 681 383 045 730 669 911 762 196 998 210 440 742 286 831 282 430 830 337 298 087 851 521 236 497 306 726 442 594 062 601 128 900 001 726 961 063 189 271 049 798 988 700 378 881 096 225 258 325 998 735 273 114 980 823 952 424 878 203 777 188 812 438 043 188 435 784 321 708 563 157 785 683 283 556 344 602 627 043 635 209 814 096 103 341 705 501 718 690 045 178 021 317 831 647 631 283 860 791 315 152 024 611 237 593 254 427 056 598 946 414 555 462 414 443 245 662 829 707 614 601 016 800 814 058 934 236 743 290 931 005 068 985 702 907 449 888 419 484 037 834 900 155 118 536 651 463 490 088 049 445 815 532 472 925 283 138 366 218 379 720 706 329 298 329 154 535 532 291 757 501 966 082 288 893 980 879 095 478 972 145 286 845 774 945 428 807 459 378 624 384 190 513 832 611 475 906 880 209 168 512 230 087 816 026 693 542 340 420 388 486 849 180 400 605 146 291 721 694 884 624 848 394 850 142 207 563 262 482 250 909 692 704 713 637 697 829 004 019 538 583 484 800 196 293 076 174 405 292 608 668 537 047 832 450 979 676 899 902 580 538 110 661 558 510 428 612 257 296 624 632 060 463 708 634 897 526 826 262 690 898 140 256 914 372 824 944 431 233 651 921 459 969 221 422 027 794 883 860 257 045 556 711 863 517 020 036 070 039 230 153 074 773 095 354 322 201 480 727 980 797 224 257 664 054 878 001 936 703 026 922 285 927 300 134 212 428 975 892 671 161 351 546 839 841 215 194 308 014 214 768 768 498 077 037 063 752 708 798 565 939 883 674 469 195 196 027 935 634 506 193 532 512 760 412 374 757 134 593 902 271 152 987 420 850 000 758 370 160 171 642 828 397 560 418 809 317 788 229 733 156 837 996 928 112 776 948 239 845 178 512 955 100 261 203 348 816 792 148 631 405 193 776 315 417 784 850 618 385 932 977 052 238 661 222 347 786 541 611 614 910 881 687 565 973 147 720 863 078 502 925 784 029 311 012 164 030 464 106 465 435 613 635 161 289 808 922 851 181 967 911 540 707 662 507 873 929 945 780 939 305 638 396 934 546 335 681 979 117 587 662 411 044 379 622 407 073 430 672 891 795 773 830 966 856 940 129 584 365 355 831 163 197 495 019 264 947 920 103 736 258 972 545 878 447 201 473 921 900 540 869 765 919 829 166 349 664 106 934 565 357 457 127 632 251 815 442 045 230 948 863 457 016 906 934 543 402 865 363 507 709 186 962 720 107 412 669 781 981 289 805 619 892 635 163 643 398 114 201 058 697 209 447 806 770 963 180 158 614 689 518 927 517 448 482 441 685 251 763 637 103 264 469 917 023 110 921 966 858 871 389 437 158 524 132 876 800 001 801 470 687 332 783 012 949 180 056 936 620 208 272 714 959 867 226 642 242 262 942 165 470 663 556 549 915 693 134 223 795 667 304 128 531 357 396 862 283 277 307 728 742 746 192 523 216 094 456 935 342 728 436 384 917 957 048 665 272 289 361 884 989 739 031 831 249 076 568 423 779 623 188 446 760 557 815 841 036 707 985 383 941 158 896 578 621 518 955 476 301 142 414 626 482 646 958 632 417 384 794 486 594 341 767 172 656 628 337 372 004 792 467 098 666 223 399 795 963 951 033 869 656 519 361 691 042 248 467 824 059 291 259 074 828 854 425 246 138 097 190 868 113 689 859 543 915 337 322 089 961 615 845 844 701 530 172 140 680 254 748 304 128 090 453 252 074 199 830 207 790 501 215 958 092 112 927 408 212 000 562 957 844 783 577 847 043 909 795 912 231 558 635 413 786 697 736 697 128 388 785 120 972 549 825 858 310 779 113 687 583 589 330 691 272 512 362 488 675 365 799 857 977 816 832 079 782 275 916 931 815 255 195 658 133 629 032 089 351 047 286 130 873 965 732 138 205 237 435 179 528 701 091 673 056 718 244 019 645 770 127 469 335 818 185 839 333 702 367 178 813 426 965 057 391 982 688 421 381 940 264 894 407 479 855 197 920 689 282 748 491 869 404 335 001 393 984 078 106 169 186 197 657 162 537 537 892 206 389 515 122 578 580 900 462 277 256 136 106 456 667 947 814 216 200 232 700 891 768 820 448 588 189 054 036 891 175 924 692 791 685 662 783 183 896 724 002 411 633 539 355 560 881 048 544 056 894 231 870 946 768 604 393 233 043 175 968 346 778 442 355 011 580 806 440 700 717 467 333 138 954 121 012 250 255 684 741 413 300 116 299 536 714 886 242 009 204 585 893 760 544 318 211 822 120 897 747 253 616 754 343 652 461 965 588 744 578 518 705 576 118 888 976 158 004 152 912 213 066 720 036 952 616 117 129 786 953 352 395 884 042 274 434 800 228 539 679 417 846 289 815 862 762 579 797 099 722 007 382 402 108 516 475 568 396 068 437 809 626 721 841 843 116 681 741 135 335 874 029 754 521 221 261 360 766 363 902 742 144 193 066 849 411 529 270 796 819 287 724 762 888 415 558 734 228 731 958 108 039 281 397 022 378 256 579 608 760 058 553 362 308 878 063 714 268 600 122 285 069 734 100 383 932 267 720 815 545 661 497 833 116 355 333 872 941 159 940 705 698 324 220 037 844 275 233 433 977 658 298 298 861 130 015 520 636 459 624 446 252 933 933 915 032 905 121 868 229 825 557 017 738 673 436 444 507 560 924 676 389 656 141 853 086 064 532 924 145 397 587 469 369 792 910 561 450 484 265 408 653 720 711 443 403 921 877 155 909 007 106 334 640 131 708 620 768 840 604 487 930 294 577 445 899 440 006 441 648 357 884 790 576 210 673 657 847 474 536 066 227 452 054 498 831 543 996 938 161 884 976 039 436 752 476 471 905 555 708 185 182 726 049 054 805 751 921 155 621 993 382 353 644 373 174 958 956 373 819 310 489 368 156 741 373 745 324 681 001 768 463 158 569 338 777 961 946 721 755 676 391 884 875 273 826 207 998 903 712 315 161 266 607 874 621 157 687 340 956 028 987 120 954 404 330 024 795 115 920 460 186 908 695 788 267 011 217 436 882 622 503 600 280 863 726 051 110 662 229 908 174 161 152 124 526 138 776 951 289 745 758 300 003 290 058 431 204 156 883 281 388 187 287 784 989 538 949 384 350 141 489 062 658 287 693 534 475 479 027 620 850 372 056 834 986 685 373 128 647 946 678 645 244 995 186 248 985 072 099 568 986 567 169 032 868 797 924 142 616 304 001 910 065 217 409 712 951 524 721 239 554 623 920 490 826 414 487 439 738 329 404 401 671 948 577 477 558 681 039 878 118 210 515 084 039 376 371 307 788 822 601 867 402 802 410 361 624 240 593 284 854 262 617 211 355 383 267 650 130 479 640 934 011 965 021 521 282 559 776 955 399 117 626 899 645 679 186 999 337 619 115 329 006 180 642 718 759 698 854 262 343 759 364 972 334 063 219 610 872 716 265 795 507 007 207 609 528 516 977 861 324 457 299 086 787 924 278 197 363 067 236 860 791 778 515 824 391 672 871 859 032 357 062 054 142 329 278 582 446 268 265 682 400 384 365 030 240 979 231 381 116 720 848 479 199 682 808 117 901 042 722 507 636 829 259 165 396 915 619 977 635 868 924 746 666 332 621 354 518 917 883 436 279 007 048 900 617 609 712 665 548 866 045 855 713 250 104 221 317 463 873 757 595 231 719 313 804 293 518 057 378 975 275 583 775 963 679 476 097 954 398 239 225 938 918 473 819 739 763 183 282 776 600 414 083 972 688 462 110 710 804 160 604 394 137 478 333 045 929 047 377 486 646 980 289 098 942 345 206 366 074 650 041 865 546 228 443 268 225 462 983 967 965 303 502 119 867 491 389 858 212 449 527 544 013 449 024 557 742 506 796 296 028 869 712 263 040 434 548 310 447 374 514 149 817 290 552 126 071 099 936 777 562 451 384 109 220 035 031 478 399 259 872 880 912 010 209 171 098 987 531 458 331 381 100 422 107 060 665 381 195 542 597 419 738 594 989 542 891 806 183 777 324 470 944 808 989 984 492 196 027 899 444 146 862 399 546 354 223 817 654 574 508 687 351 531 880 374 691 196 373 678 717 214 740 999 877 504 793 207 406 644 948 411 750 436 019 367 494 268 531 909 120 778 466 808 553 457 020 899 667 099 868 456 401 238 811 963 565 435 101 804 648 328 193 227 992 840 246 827 492 058 316 548 364 061 527 620 528 575 191 532 910 491 276 659 532 993 417 470 472 526 490 027 930 714 340 646 600 475 380 748 821 704 516 524 364 703 202 838 492 357 498 267 032 339 384 412 430 193 480 807 166 315 834 641 293 961 972 209 419 872 396 127 670 533 276 247 833 844 294 140 792 706 746 124 728 503 978 227 803 105 826 245 401 486 923 588 986 620 533 511 150 610 142 901 534 970 127 356 969 825 402 015 639 240 376 297 515 197 684 054 401 222 328 088 721 472 263 125 386 343 859 228 529 267 688 413 486 650 637 241 286 394 526 739 870 842 774 090 204 928 426 958 117 314 392 833 016 377 483 844 352 268 330 480 725 401 850 103 086 752 560 913 862 060 262 980 912 790 256 006 214 283 409 370 530 837 662 062 422 184 806 266 263 086 354 995 472 249 292 992 563 699 132 584 910 731 991 441 325 496 892 044 919 443 709 104 917 036 293 117 930 025 661 115 427 148 790 688 757 319 909 898 012 280 037 181 410 922 182 259 745 782 887 799 914 270 635 234 460 592 732 149 638 578 661 985 326 972 382 987 715 420 620 979 519 167 464 142 821 609 791 639 077 308 304 365 197 733 519 775 930 190 381 759 959 769 895 363 509 471 521 201 118 520 474 469 364 206 967 232 863 192 889 034 588 889 169 071 677 183 795 480 361 707 968 295 786 897 741 276 629 104 329 660 056 369 017 939 288 508 915 217 933 545 761 947 154 214 155 073 729 122 943 127 566 784 888 042 842 614 342 996 596 406 318 662 043 438 054 887 481 017 368 664 388 031 681 207 604 847 810 036 910 650 968 286 131 035 969 345 507 201 577 791 514 463 500 448 628 811 691 961 355 929 813 577 507 254 950 583 028 960 278 764 085 241 316 723 395 026 693 537 687 497 297 808 380 653 510 185 681 254 421 923 891 888 297 970 742 168 165 643 019 087 597 424 480 934 409 481 330 693 851 621 888 523 656 560 378 180 298 388 770 918 161 185 091 022 293 284 957 739 811 026 729 706 403 777 644 281 275 295 638 002 810 054 260 124 478 787 011 557 426 917 461 058 416 643 930 667 566 006 262 936 270 393 952 748 149 918 057 882 907 164 826 156 595 025 220 278 306 126 400 180 018 221 170 772 853 159 958 552 444 720 839 245 952 515 097 985 021 313 437 595 197 366 514 788 774 617 021 218 161 680 144 062 900 588 153 051 023 236 236 088 461 133 081 958 857 232 841 840 023 529 465 958 184 806 255 274 726 580 947 180 731 080 853 738 322 302 736 676 572 162 279 872 272 806 804 959 403 550 485 767 637 332 483 708 588 682 414 604 505 711 674 541 596 331 588 247 963 590 617 762 077 044 747 003 543 334 071 991 796 644 115 120 417 427 728 286 806 866 750 656 519 907 367 166 567 200 321 358 348 717 048 586 485 670 282 896 778 380 090 338 751 203 958 611 606 216 746 951 828 805 491 808 569 687 193 894 613 242 340 050 317 126 111 156 277 929 494 025 319 492 458 592 502 012 838 616 381 132 821 868 135 766 076 722 044 178 155 454 767 261 980 411 547 196 414 632 806 221 750 141 265 116 926 110 997 690 310 934 310 776 790 194 337 372 448 654 894 717 426 233 930 151 782 452 791 614 381 975 194 326 072 363 526 465 463 050 411 926 067 270 154 504 303 336 649 134 619 802 510 498 259 750 955 569 054 058 400 776 032 147 182 781 309 478 339 867 939 923 635 696 777 543 505 820 578 217 900 130 252 623 464 673 579 182 660 693 432 013 274 337 356 705 063 882 054 003 230 104 647 075 437 725 227 889 410 196 888 400 945 325 000 484 318 973 341 239 311 911 019 598 731 569 611 665 459 674 016 359 324 653 974 354 084 087 823 476 659 675 079 592 547 834 711 050 691 243 862 605 251 023 350 474 807 745 796 027 713 960 393 496 940 007 366 209 752 672 036 609 344 246 516 137 734 978 682 573 437 337 175 312 625 465 774 260 681 542 223 204 388 094 505 567 532 079 210 912 518 578 124 824 354 832 433 254 810 054 549 471 819 998 200 198 198 002 903 923 365 387 395 662 341 798 854 858 765 003 781 212 968 231 216 635 689 960 550 841 458 813 414 862 843 584 869 158 200 406 246 515 766 423 551 044 398 053 304 332 272 821 179 852 041 961 016 467 737 814 058 333 528 515 079 521 397 750 150 389 700 935 183 813 742 793 840 363 893 993 490 603 103 125 770 711 746 098 767 722 474 294 788 626 492 884 600 383 008 936 109 207 554 660 388 989 315 285 793 444 450 434 250 767 705 721 177 260 917 134 089 819 817 687 886 068 152 592 202 492 881 881 776 092 153 591 191 609 442 674 226 372 665 830 746 583 286 342 365 252 920 038 339 890 030 601 014 934 586 250 058 361 771 534 845 567 098 606 579 184 861 358 735 476 663 626 219 965 987 694 140 466 811 545 337 209 981 263 398 435 683 068 283 207 987 605 754 505 165 441 691 286 558 750 958 569 252 986 687 014 230 203 627 892 944 405 999 928 138 840 880 212 080 715 873 031 638 010 527 576 326 538 248 177 501 736 642 031 158 527 419 080 026 366 857 731 029 574 030 652 468 864 059 078 930 791 739 629 651 982 782 578 223 981 079 581 085 823 467 643 094 683 062 514 647 279 108 518 140 942 117 611 311 117 315 117 681 067 447 834 870 729 184 145 286 426 613 789 174 638 911 935 961 405 469 116 809 243 313 841 601 680 113 309 328 387 490 114 650 137 411 982 608 964 321 537 815 344 266 730 342 691 819 463 060 190 538 604 819 465 931 922 188 159 570 210 987 426 659 899 612 739 118 107 222 944 379 159 653 826 547 895 274 172 526 768 820 871 362 314 216 504 638 665 771 940 756 520 166 901 715 175 132 743 283 132 604 758 330 957 452 192 685 762 345 995 951 385 045 446 184 052 116 038 924 221 062 365 372 830 650 302 982 382 918 367 915 361 533 073 470 009 394 672 081 101 938 333 791 860 867 107 439 828 534 834 455 737 313 619 940 498 257 336 001 536 395 436 251 929 529 277 513 714 633 010 857 572 586 228 790 392 149 731 978 138 695 497 285 085 445 833 139 681 005 932 445 793 516 276 670 164 107 660 080 161 520 735 126 943 698 858 716 153 981 361 018 808 945 926 407 200 036 344 616 946 150 887 595 980 124 136 072 897 449 842 560 136 343 681 705 116 312 097 664 697 952 706 192 641 082 559 385 332 051 491 019 147 435 251 921 438 368 378 528 095 956 721 479 327 289 013 340 966 590 143 930 369 104 620 501 339 350 359 526 301 938 001 697 798 967 596 470 674 631 023 140 944 839 292 732 286 755 423 324 553 764 623 960 102 062 818 837 447 961 562 735 430 210 384 288 665 309 392 880 204 246 915 091 809 847 829 483 894 601 076 015 380 998 100 897 618 208 369 264 394 040 423 160 511 811 004 285 920 930 343 041 357 276 450 346 233 899 137 421 143 771 215 990 878 476 201 875 839 303 266 714 394 390 501 252 136 882 381 631 708 741 127 224 071 070 578 758 440 236 455 442 825 774 326 878 107 580 896 791 668 560 032 116 714 157 796 716 426 435 649 651 967 018 520 629 446 204 279 469 368 957 798 406 393 723 043 117 845 838 194 963 085 865 985 130 238 405 301 667 932 773 487 818 047 341 199 803 177 639 628 013 451 283 494 522 380 365 933 656 107 391 664 394 065 780 683 407 973 955 903 848 898 086 916 194 780 558 329 161 244 940 636 676 422 829 342 548 047 764 870 094 826 434 462 829 227 330 154 359 806 965 438 519 868 374 407 729 870 903 000 540 433 853 717 825 093 817 463 779 396 064 715 015 674 393 118 329 577 591 809 565 175 745 593 828 723 294 997 006 836 815 998 361 973 232 294 991 701 478 785 015 004 041 761 625 006 515 489 445 390 183 751 837 518 471 015 246 536 255 902 773 408 203 744 263 316 205 908 605 761 059 701 957 535 916 013 723 588 052 573 320 386 601 460 597 752 940 851 901 087 560 337 877 498 652 264 889 643 755 804 824 100 833 629 634 614 514 713 764 396 905 513 690 340 636 328 536 315 981 786 784 392 365 769 867 361 394 563 717 169 950 553 762 910 218 816 340 247 119 884 677 541 425 532 939 058 907 995 004 435 321 255 483 649 862 817 706 624 296 766 341 028 721 939 220 727 730 654 426 831 306 193 790 709 531 751 394 554 576 177 771 138 201 360 392 568 056 726 037 204 215 423 517 989 954 637 543 922 452 340 039 689 808 396 948 500 800 546 370 927 901 091 043 733 797 238 506 324 355 798 256 643 520 680 246 386 331 544 096 907 309 018 697 249 529 578 238 019 016 461 002 371 749 670 131 297 024 297 839 512 911 178 825 813 638 008 163 035 453 470 503 287 747 178 275 789 238 887 285 842 120 445 302 539 601 540 090 263 086 457 457 115 942 023 042 893 886 984 126 882 811 585 626 532 403 324 452 311 249 862 378 308 032 037 127 024 608 992 791 635 817 598 888 521 931 615 822 063 203 633 520 060 906 776 995 731 730 718 779 385 125 351 414 875 819 799 946 987 552 542 782 609 363 182 426 228 564 351 480 194 024 043 674 983 117 751 588 371 156 462 900 706 078 614 684 871 537 059 295 308 454 164 864 131 651 672 570 278 274 664 683 128 827 466 454 031 865 023 083 583 169 094 147 025 537 014 300 526 681 163 781 203 811 673 331 062 486 997 332 525 645 753 900 083 901 822 364 614 264 695 187 068 665 665 651 121 201 791 905 753 327 966 287 761 986 053 573 646 315 668 306 885 147 120 526 341 025 290 351 247 089 884 523 389 888 599 509 429 809 520 009 560 533 118 879 996 649 468 591 234 395 501 649 384 614 222 710 830 791 809 412 555 084 728 845 861 540 279 982 737 141 797 481 101 937 977 195 928 742 138 831 590 135 097 517 234 847 834 139 185 918 979 699 141 171 220 608 862 955 367 389 809 596 970 393 656 673 176 219 254 260 911 142 232 310 434 480 164 546 363 748 280 657 647 186 409 154 146 450 350 483 774 031 663 291 226 257 983 223 579 130 563 998 559 613 810 900 023 270 917 980 436 706 714 134 384 053 525 810 151 430 640 516 076 859 381 738 561 553 079 563 641 153 480 343 005 090 042 756 032 376 758 801 701 356 294 600 141 848 674 412 094 056 082 409 641 221 840 099 387 162 444 394 015 576 209 739 454 000 884 199 322 031 630 814 863 115 473 266 796 247 703 678 205 272 232 987 996 002 020 718 935 820 646 499 645 270 005 838 531 064 338 228 377 617 828 357 351 782 775 013 866 157 570 794 426 413 934 105 376 264 807 429 336 676 889 307 825 563 163 658 867 715 311 434 640 907 335 276 291 539 526 532 789 264 607 921 859 521 794 968 128 732 761 327 538 542 386 196 240 278 329 453 684 898 054 335 057 519 885 738 511 466 925 056 727 592 600 211 510 986 988 067 247 561 738 372 573 473 591 563 739 843 818 340 936 457 835 958 208 921 279 664 841 338 635 671 622 579 634 570 010 165 130 081 026 747 223 391 680 468 303 019 832 824 342 463 783 336 222 719 851 695 363 263 018 378 592 091 867 618 272 693 424 284 449 729 137 074 502 933 194 888 590 213 567 224 644 018 189 561 006 286 891 508 265 497 869 562 129 485 169 587 196 561 995 032 633 041 579 521 038 961 781 612 016 083 012 934 417 992 440 763 500 468 528 161 429 042 448 779 436 638 533 271 450 549 006 496 847 945 027 381 992 772 035 689 807 983 769 005 498 682 911 940 130 539 599 223 624 075 583 017 419 028 296 027 288 113 759 282 906 747 931 805 445 117 033 962 970 328 187 300 690 940 580 904 754 277 472 540 072 647 642 483 124 136 971 708 455 144 918 760 689 974 292 996 603 024 601 905 740 244 761 961 191 867 601 709 575 955 202 631 112 059 347 937 575 333 280 934 732 778 227 064 419 073 270 159 084 268 613 750 875 798 675 505 853 541 654 883 198 009 070 483 500 478 683 192 007 538 667 491 309 291 121 517 152 137 324 456 269 358 456 458 557 016 007 170 501 702 732 817 563 472 279 176 370 171 448 952 765 843 600 408 313 913 603 534 030 444 377 120 420 533 240 520 433 158 246 458 380 455 081 681 379 476 540 063 533 712 542 333 459 490 258 719 637 570 932 155 390 524 746 386 572 593 333 670 135 726 235 063 478 547 110 375 178 120 401 212 694 749 257 878 145 394 806 332 440 634 092 454 103 892 890 383 673 553 221 816 904 720 218 677 218 035 517 166 110 138 457 096 509 772 552 993 664 246 016 386 170 627 414 833 846 747 820 845 645 288 474 187 888 437 157 335 901 702 434 989 369 254 149 983 399 353 486 466 109 738 331 129 759 624 461 564 859 233 523 306 614 604 708 603 736 296 456 354 317 161 938 834 921 572 560 278 818 911 349 937 019 538 703 751 783 931 910 023 250 130 311 972 950 658 861 886 800 920 942 641 243 381 520 927 956 228 915 998 515 399 998 742 059 348 327 914 177 097 177 229 235 393 610 953 725 694 906 840 284 693 312 087 598 233 804 655 014 297 553 597 437 706 180 793 668 262 470 322 083 795 327 350 033 204 430 945 083 209 168 956 630 510 054 516 214 030 288 665 857 503 526 999 252 018 362 948 737 968 645 625 234 143 399 500 903 750 748 255 924 386 927 495 958 708 031 910 648 946 998 114 299 273 139 346 794 375 943 916 762 034 432 689 133 225 145 412 837 015 815 147 518 266 097 711 698 287 863 365 278 881 294 345 350 367 950 360 620 930 784 830 921 238 633 007 693 536 668 420 951 384 647 322 800 428 157 155 549 364 433 821 458 529 510 372 437 488 190 603 517 475 477 087 830 010 386 650 717 566 172 118 554 880 138 427 652 092 509 839 834 413 307 991 647 470 157 572 711 145 443 544 891 809 465 542 518 066 228 804 858 596 117 088 050 232 691 583 241 370 394 567 860 642 800 499 588 249 981 021 740 821 117 700 585 262 682 234 825 335 066 099 634 215 957 873 286 001 280 480 257 100 284 967 597 679 902 808 445 122 563 092 251 654 022 388 336 944 666 547 153 442 295 589 402 516 723 241 466 881 812 064 861 157 493 243 782 265 416 334 488 290 727 450 773 456 714 352 672 757 080 367 134 414 873 734 588 344 399 512 681 786 892 567 229 940 426 401 080 421 185 368 975 776 259 238 419 190 196 734 534 176 349 867 839 472 127 426 080 686 501 175 106 224 885 395 874 195 897 397 025 988 205 379 837 512 333 146 806 847 915 912 892 909 380 026 727 618 250 238 512 750 571 715 102 077 590 078 290 687 852 223 374 049 211 050 336 367 327 944 251 089 299 211 169 159 171 727 034 117 417 533 783 770 858 213 852 060 268 111 997 793 071 957 109 313 453 209 747 903 156 440 755 208 227 194 600 209 561 634 525 062 151 980 946 856 094 891 689 327 562 337 195 202 984 314 602 745 076 045 434 026 796 057 463 732 400 809 109 970 943 053 271 866 567 211 838 087 210 077 615 182 214 385 439 846 744 054 417 170 407 338 075 295 131 660 756 470 377 181 376 866 140 249 644 105 486 115 146 703 129 827 348 011 474 809 001 535 441 477 221 556 953 899 207 166 755 328 422 834 150 721 737 445 788 094 241 503 152 185 772 102 026 886 994 433 245 036 920 680 120 195 261 471 590 619 144 159 191 358 607 682 099 616 088 723 928 502 155 124 691 169 465 685 715 684 486 914 720 613 663 578 675 159 301 412 225 193 613 596 831 951 606 800 348 098 091 653 345 527 438 333 110 994 569 339 761 514 600 819 176 945 262 760 524 655 746 007 884 580 688 557 943 614 144 001 181 792 278 935 923 089 500 029 855 937 579 811 891 597 185 339 172 388 813 752 555 409 849 467 269 008 793 292 104 105 923 332 498 749 646 486 188 279 484 865 357 176 910 925 253 278 150 433 335 904 528 117 935 847 151 159 497 206 535 323 303 129 933 916 119 625 663 614 295 260 310 564 281 252 644 367 652 437 939 490 851 232 376 937 806 040 790 843 505 355 889 548 300 132 828 177 394 941 295 107 686 048 355 676 699 976 210 099 310 855 369 931 452 752 978 521 063 768 342 708 679 730 172 464 806 502 899 808 074 713 141 552 683 564 110 088 115 598 990 833 865 447 123 619 276 336 155 543 818 504 376 555 798 792 843 059 766 531 541 620 158 600 072 532 332 234 292 018 824 144 674 529 149 524 657 038 293 391 599 082 635 255 443 147 853 081 883 264 564 671 999 170 928 321 879 483 263 659 276 454 037 384 901 611 345 853 580 838 897 101 572 143 617 052 977 511 779 468 253 081 718 998 135 412 568 110 171 867 781 891 344 495 917 970 922 522 029 004 701 268 777 462 939 005 421 863 247 389 740 388 717 215 684 283 597 215 852 198 579 941 450 501 542 715 295 227 240 217 178 083 347 820 173 286 327 991 722 540 998 592 437 120 626 304 951 614 930 873 568 416 941 951 589 793 128 328 048 388 098 608 507 780 257 286 671 984 572 019 708 404 953 003 936 234 717 243 678 908 155 707 165 492 476 967 203 095 497 952 067 489 839 583 814 530 694 640 303 002 669 485 016 951 256 100 699 659 459 499 961 512 351 108 378 022 783 224 457 819 925 111 166 639 101 113 904 490 180 542 652 700 671 029 330 965 150 296 932 488 906 616 218 012 864 664 775 041 740 680 573 415 272 498 000 861 270 739 414 700 363 247 562 663 493 026 041 611 367 834 018 216 968 814 390 898 072 920 179 200 394 148 525 004 096 980 609 737 297 538 181 900 764 392 199 644 084 836 937 263 312 231 201 692 626 759 188 064 505 911 659 564 027 783 574 684 264 575 708 091 843 078 709 477 401 349 873 949 959 556 318 049 057 935 940 281 131 979 227 958 583 568 707 196 106 364 678 485 271 049 053 770 921 639 257 277 591 617 116 718 623 963 195 778 015 285 102 121 415 119 784 045 737 543 893 073 086 797 825 672 911 233 943 638 328 098 724 907 852 859 484 945 716 671 079 877 273 354 538 425 130 726 132 203 335 785 685 768 263 878 150 383 805 771 503 727 743 033 552 420 236 033 670 866 812 485 725 449 117 405 010 359 218 936 869 349 303 590 677 612 049 471 849 492 461 060 889 095 352 378 952 674 375 249 563 362 221 549 845 752 212 331 047 416 319 849 656 137 198 829 712 818 475 525 970 190 721 297 002 406 283 433 046 990 087 049 473 500 927 615 163 068 651 082 426 992 969 670 796 757 713 346 224 048 694 759 064 837 053 372 503 797 176 127 002 105 804 895 451 597 195 133 793 352 103 612 763 110 266 172 342 986 940 994 468 257 050 240 232 353 134 617 251 346 152 894 415 575 571 170 988 085 915 867 310 829 509 422 514 504 374 992 521 873 383 509 608 171 970 127 516 066 024 339 697 027 862 824 745 312 794 169 782 581 206 992 644 818 897 589 323 943 567 552 282 538 158 016 967 886 103 941 259 240 673 869 916 637 879 740 056 676 448 008 018 471 956 484 692 567 445 860 559 167 252 339 265 528 417 918 595 979 608 097 470 930 857 037 597 831 841 802 235 022 450 346 759 732 706 928 680 944 184 794 205 983 098 162 467 963 514 506 851 034 684 806 036 307 062 231 234 883 112 772 252 014 108 321 105 864 408 616 832 120 910 672 398 738 817 861 534 681 835 384 328 217 909 038 553 210 614 603 459 890 240 304 620 353 881 172 026 140 544 383 073 720 971 958 341 167 178 501 795 680 848 544 106 433 300 512 426 460 764 901 184 206 539 207 143 001 002 559 077 252 659 686 303 481 697 738 799 825 112 396 992 617 585 724 783 034 971 022 024 742 774 453 868 825 683 563 884 067 887 546 916 678 031 278 525 185 403 718 440 407 535 429 243 201 478 719 292 556 003 592 543 614 116 108 052 147 484 956 201 646 395 151 312 578 940 051 032 561 124 813 726 570 027 730 060 501 276 869 656 974 867 976 049 908 047 906 692 535 027 358 732 361 779 148 325 931 287 665 443 158 874 148 336 633 925 003 318 609 197 786 320 701 196 621 124 905 688 378 263 953 729 126 916 793 350 286 414 548 244 414 426 394 004 324 203 414 317 611 882 823 361 223 936 731 820 788 527 535 818 172 854 195 190 074 005 313 144 101 345 680 668 184 716 462 719 557 324 496 388 884 774 631 567 533 114 659 997 471 956 439 832 068 352 933 791 010 642 343 216 381 920 814 975 875 106 440 242 919 331 154 897 118 914 284 684 918 434 171 455 825 528 767 112 066 509 394 413 600 998 665 265 475 484 824 856 330 602 963 993 547 546 995 905 585 275 698 649 867 190 962 090 553 442 862 774 380 011 552 359 543 265 424 802 999 524 545 091 605 122 050 265 703 134 142 875 678 650 909 409 486 951 045 936 252 837 589 563 244 566 762 890 729 862 242 589 361 495 462 860 342 931 879 739 930 656 550 208 970 028 725 172 223 882 738 322 276 130 777 570 681 892 505 082 730 848 745 299 663 187 975 297 402 315 295 025 987 431 171 815 722 902 092 677 139 124 368 575 189 006 697 150 272 736 900 856 205 521 913 050 027 870 122 941 210 911 736 131 797 309 988 474 289 412 546 749 129 288 174 488 753 955 423 303 369 560 848 304 596 295 963 098 617 774 597 422 388 696 163 845 824 974 594 913 510 704 916 850 971 192 294 909 296 769 104 230 827 076 391 366 434 319 680 282 682 845 684 501 678 936 847 464 108 034 473 369 441 279 987 358 852 613 975 580 522 314 098 616 933 619 893 179 297 762 588 227 291 479 531 883 043 023 831 772 845 495 982 485 023 725 000 982 816 211 819 109 402 654 190 878 071 785 244 153 458 773 203 554 111 893 196 847 521 275 997 935 771 184 516 446 599 699 023 940 292 957 054 734 797 422 915 010 015 313 744 566 036 152 381 330 810 230 391 140 671 607 376 229 091 448 430 675 382 522 915 021 683 688 005 900 805 531 581 865 923 165 675 974 615 563 962 688 859 408 340 572 440 783 777 555 710 297 976 264 510 948 644 190 937 395 672 406 921 571 941 944 698 733 646 839 925 228 220 060 053 540 274 642 369 663 423 980 624 642 076 537 055 745 114 493 770 214 173 905 565 884 266 967 097 254 749 553 898 910 447 644 159 761 322 771 318 308 758 171 999 204 288 598 956 945 387 705 661 741 945 389 066 525 941 652 131 247 805 917 179 767 424 229 997 701 584 735 344 951 116 777 004 313 303 310 933 674 425 518 364 579 851 302 706 678 849 412 058 876 819 344 738 474 814 905 080 256 797 613 233 964 081 935 202 191 269 756 499 960 075 922 564 997 268 520 638 947 430 422 044 667 170 485 546 588 560 064 618 617 341 851 945 968 142 805 842 185 756 828 219 781 889 069 985 187 820 648 170 322 835 518 105 771 505 265 564 191 658 542 237 411 109 191 101 271 601 619 402 866 306 494 248 653 945 246 854 346 260 639 325 985 881 833 571 714 360 510 594 565 227 367 487 294 938 018 484 332 412 100 598 823 502 847 046 961 446 080 904 995 059 584 272 764 176 225 002 385 702 847 860 831 044 747 961 818 043 200 782 835 593 057 991 127 519 227 576 465 758 064 670 005 563 540 903 794 791 467 100 748 085 055 670 477 369 983 344 079 188 005 983 262 561 803 912 537 175 763 601 854 850 682 111 378 340 234 095 025 353 328 662 110 140 419 597 790 506 949 675 654 090 812 443 004 973 739 295 025 029 648 572 578 422 047 901 191 438 152 671 788 831 162 861 610 949 312 910 438 019 620 729 920 039 383 869 589 663 257 518 984 131 457 124 245 044 264 697 265 098 219 416 866 404 231 558 607 094 340 238 420 392 368 093 574 334 967 075 694 324 062 426 503 084 603 764 375 323 400 452 549 149 277 391 188 636 460 562 490 623 159 568 536 587 492 768 685 866 858 535 571 914 439 306 350 439 773 643 078 155 132 615 868 774 057 149 319 464 087 874 253 079 372 991 178 254 188 266 266 657 320 621 392 461 128 785 569 506 094 443 958 621 570 258 973 898 907 290 468 387 205 683 615 070 134 324 671 822 737 563 672 897 581 435 722 399 024 377 240 032 743 949 825 328 414 404 334 117 843 031 702 549 624 055 374 433 489 818 875 479 984 954 453 068 110 251 999 035 116 609 230 773 872 051 050 012 627 254 328 470 386 194 091 306 205 875 038 696 194 738 392 979 503 167 291 573 164 669 654 009 403 893 914 505 785 034 046 887 018 512 916 694 640 744 615 598 018 717 399 975 708 277 758 768 702 704 676 340 496 756 716 270 143 312 683 110 445 771 618 490 942 242 203 709 408 673 711 862 624 001 738 153 738 818 812 212 202 628 496 476 795 695 663 359 514 169 936 803 661 136 545 677 732 987 524 690 344 293 634 966 400 268 393 503 276 511 747 271 918 465 869 102 832 696 112 118 718 023 342 931 293 528 024 499 642 283 285 681 029 711 330 736 904 686 053 861 932 519 461 787 724 931 773 976 579 131 700 946 234 020 458 190 522 753 664 922 023 480 159 012 195 777 395 563 763 165 169 999 366 672 128 353 648 485 096 423 175 295 228 893 911 239 865 582 994 672 402 975 382 814 630 773 096 492 413 604 676 110 324 729 308 510 940 400 001 196 098 012 367 063 707 254 444 715 704 800 884 332 249 838 488 854 821 035 972 395 652 308 751 208 064 512 855 348 746 242 234 654 068 515 565 846 357 614 037 834 717 851 735 351 874 164 089 959 022 105 521 038 755 121 533 758 744 414 212 161 487 418 070 142 359 845 261 431 370 355 803 991 614 284 110 542 254 129 862 973 772 791 430 851 994 479 210 352 598 210 400 234 464 635 624 105 909 869 374 063 188 267 440 483 492 859 239 855 800 577 704 925 512 580 889 717 078 344 405 832 958 433 143 084 155 758 174 498 047 134 366 414 813 152 836 822 762 902 116 107 707 380 159 379 291 942 961 585 046 635 224 523 210 831 352 645 801 685 528 724 762 119 261 244 517 914 182 540 108 464 925 924 892 858 852 071 725 481 391 200 645 908 810 266 122 849 429 892 040 988 650 327 027 498 825 265 382 698 376 126 971 680 236 799 806 553 618 373 404 909 217 492 860 636 608 776 162 854 412 109 470 388 032 940 964 387 649 889 838 235 188 718 206 400 557 047 797 497 931 851 404 844 042 259 585 665 895 560 438 143 762 124 334 926 296 818 984 986 972 274 674 152 898 117 658 497 047 861 175 459 518 083 243 906 734 332 985 407 871 282 145 649 314 663 863 265 045 315 709 167 056 169 083 214 912 660 044 671 931 148 826 481 117 197 449 859 192 223 482 864 386 246 918 538 570 602 257 656 500 602 352 433 374 727 445 707 336 705 599 648 339 434 925 959 456 823 368 157 453 566 672 379 539 584 717 630 490 585 243 052 544 075 962 047 544 479 738 257 357 695 156 608 525 932 131 097 170 371 544 322 921 963 651 957 049 476 561 075 151 434 579 336 144 466 988 865 355 971 911 526 575 792 449 464 616 403 718 275 453 630 616 339 360 333 499 969 827 462 744 316 595 526 762 834 699 380 391 233 040 520 780 874 573 646 555 469 921 322 543 956 096 858 656 948 148 174 885 810 995 087 254 101 415 605 523 933 817 936 299 856 110 198 748 256 086 975 342 527 755 981 207 121 680 119 794 544 930 292 766 185 151 289 361 207 595 321 196 713 168 375 753 395 252 139 025 143 486 536 905 995 817 697 421 744 599 418 920 257 889 464 984 679 908 084 528 699 070 588 740 953 571 647 205 087 312 178 510 234 745 591 848 019 273 469 973 369 709 572 098 443 718 656 902 878 816 036 968 711 009 722 213 449 764 226 768 160 639 066 293 349 435 777 627 742 723 129 775 201 538 198 779 506 954 088 746 681 852 210 843 206 090 515 724 695 749 030 132 321 202 584 451 324 830 758 826 410 425 619 845 081 240 969 088 578 803 536 023 821 583 379 284 320 104 749 866 790 028 019 494 296 809 844 357 670 995 911 273 242 438 951 625 166 494 700 171 099 049 386 697 436 151 298 145 264 010 716 215 584 371 198 336 915 694 161 610 132 113 572 441 005 832 771 022 830 774 889 579 645 210 613 031 108 333 785 346 135 195 963 760 150 648 586 690 193 017 149 658 830 506 531 532 267 033 749 630 018 491 312 509 872 347 434 708 113 753 343 660 740 603 415 002 313 689 843 267 622 881 636 730 920 653 982 282 122 726 594 262 183 219 219 770 344 656 941 654 829 099 017 265 929 040 615 581 277 720 081 121 156 937 455 755 954 740 753 326 219 705 207 455 843 330 841 702 935 019 745 071 965 938 503 941 277 225 202 365 131 416 960 468 881 878 147 175 824 650 159 617 929 820 001 749 315 435 629 811 852 814 070 542 545 297 644 601 035 717 094 866 022 627 700 477 287 353 044 213 102 668 123 977 418 311 639 466 724 997 673 941 901 035 087 749 567 905 994 632 337 638 544 745 173 355 638 393 801 551 923 095 331 596 313 964 116 113 374 311 666 768 984 279 699 988 463 153 460 962 854 861 967 680 681 992 758 350 688 081 921 775 362 018 961 731 768 976 186 250 888 129 289 358 452 169 942 994 695 151 935 976 100 760 386 648 240 467 547 807 205 998 027 190 967 265 212 106 447 686 007 299 354 180 022 029 768 951 932 304 119 702 754 225 767 535 111 529 404 701 215 760 972 448 137 450 263 594 093 890 155 416 481 434 567 292 476 306 688 889 642 975 010 368 715 949 223 213 700 998 768 213 403 370 849 763 172 585 725 368 854 491 477 019 741 456 712 210 591 464 520 491 904 823 562 958 029 162 167 405 133 649 488 764 407 432 859 711 978 393 962 288 611 882 986 941 259 243 863 870 190 175 857 289 861 071 054 918 920 478 029 327 521 973 405 147 048 441 274 652 329 876 414 974 730 164 558 294 661 740 783 571 596 595 545 564 138 181 974 443 687 452 293 935 956 388 414 125 468 234 363 808 656 197 006 928 624 002 740 560 731 053 440 846 340 238 510 993 109 933 119 831 632 408 244 956 775 971 559 961 663 608 854 800 883 545 594 889 417 896 970 587 356 130 992 877 259 329 121 763 720 739 132 240 152 376 077 107 543 452 151 820 786 982 745 515 077 213 168 028 253 296 248 298 661 582 511 985 343 388 382 673 497 671 340 379 482 769 649 170 976 296 674 636 208 299 533 111 838 246 423 419 203 304 355 726 927 988 235 320 267 453 999 106 475 939 167 342 191 111 440 284 054 009 859 218 585 087 068 349 659 870 526 663 425 257 898 600 192 825 025 141 934 273 506 512 813 244 019 888 511 624 328 054 555 386 956 502 347 751 952 919 060 007 340 141 627 133 472 176 772 790 136 860 244 536 087 265 232 838 088 513 012 998 800 612 624 929 941 441 342 096 144 473 022 549 723 923 180 956 960 661 609 244 153 757 155 843 122 028 072 998 794 775 000 823 965 314 991 274 963 359 987 921 007 394 809 882 543 790 715 177 622 273 775 960 557 952 505 228 572 653 110 267 072 040 525 572 846 475 601 288 480 487 274 487 278 825 325 839 332 443 515 969 958 311 971 634 927 008 541 570 250 339 130 409 673 573 840 401 200 384 380 199 129 406 333 404 348 630 720 541 782 409 992 938 659 658 395 922 313 578 439 934 861 768 555 902 758 032 700 949 137 433 271 815 099 829 976 758 560 807 593 786 488 954 727 601 339 065 374 122 394 600 082 288 763 167 660 666 475 802 117 074 546 399 577 708 778 443 425 124 725 146 723 563 615 767 197 675 827 195 501 508 150 423 461 018 819 406 538 166 719 525 940 961 985 362 229 168 735 587 545 217 714 918 542 336 344 435 309 924 038 928 526 126 875 897 254 578 904 660 291 363 761 945 001 043 922 551 612 081 029 569 948 169 792 559 513 438 935 567 508 558 055 321 930 662 473 039 581 216 581 559 636 454 710 239 110 455 902 358 862 359 288 194 851 029 093 577 564 896 832 407 403 579 952 437 486 891 625 619 421 560 162 494 315 297 946 392 169 248 797 331 277 489 062 488 018 412 202 423 134 535 387 201 043 145 129 165 619 723 724 591 380 775 324 307 400 608 106 897 932 929 956 860 642 410 010 434 092 941 983 609 989 857 007 011 513 484 817 596 353 386 223 178 929 371 342 067 452 420 612 307 747 404 783 358 321 261 322 995 492 386 872 337 840 725 310 245 110 001 636 431 939 772 365 860 897 617 383 027 838 363 374 043 459 005 776 367 378 986 363 734 149 580 168 631 981 857 565 718 930 382 559 575 085 829 947 544 333 525 930 668 055 258 762 957 179 282 171 436 157 225 295 155 329 219 513 017 373 955 671 437 712 117 269 641 080 687 505 458 762 360 502 109 477 610 422 392 375 247 642 260 586 791 286 826 801 157 892 657 630 911 062 614 865 983 532 635 176 928 874 363 881 049 332 805 731 093 917 879 797 395 444 677 422 668 763 916 593 337 773 187 317 586 396 488 203 277 392 906 823 736 634 029 541 510 041 173 758 585 450 575 782 915 549 614 752 593 003 972 466 336 305 961 189 299 225 573 200 408 590 892 084 122 100 351 999 565 991 434 890 970 570 852 392 243 821 742 516 317 104 374 228 851 868 318 267 448 104 830 576 962 887 855 554 497 655 910 550 211 105 211 092 382 414 116 352 602 306 373 504 068 962 515 709 200 951 792 425 014 882 385 545 653 743 123 272 773 201 762 138 129 838 613 035 044 834 174 447 537 198 288 577 063 708 975 334 751 347 941 321 557 189 638 211 691 433 541 870 450 718 003 341 013 721 020 890 005 935 682 744 365 792 882 643 785 528 524 309 821 970 564 039 456 463 671 670 436 284 813 848 875 473 643 377 639 518 647 269 853 099 343 392 073 120 818 105 301 282 294 335 357 061 009 829 349 309 374 488 887 726 603 216 871 951 208 337 378 844 998 550 119 335 972 587 654 353 593 319 221 203 607 713 843 728 335 934 583 180 302 850 257 996 253 122 379 893 193 355 844 075 571 541 101 961 139 495 577 648 538 471 799 699 658 810 319 822 200 489 738 049 189 322 907 671 327 523 878 869 892 522 596 285 645 296 291 360 844 833 539 385 534 616 211 733 493 774 149 294 633 673 936 315 231 646 013 695 358 150 893 019 212 449 944 073 900 563 796 152 280 216 946 732 010 190 929 401 472 360 685 809 739 155 959 693 531 474 816 059 716 201 408 333 396 961 460 839 120 655 699 398 945 325 215 448 857 185 868 022 274 234 897 369 738 113 733 045 946 837 961 885 458 085 569 165 792 239 753 023 284 891 103 729 226 592 072 182 564 868 587 406 891 389 121 058 423 416 146 870 800 980 716 902 556 953 329 607 332 735 365 522 017 796 834 722 586 249 786 925 304 179 524 451 491 435 151 002 227 126 402 995 934 782 184 423 221 276 407 104 299 287 045 234 290 761 263 221 392 182 264 262 761 056 243 272 191 354 308 868 650 367 531 885 942 239 452 607 688 584 547 860 274 965 737 333 867 410 425 156 441 385 974 432 440 427 628 504 292 556 770 929 673 900 530 997 142 100 406 027 027 831 655 438 475 380 389 965 889 615 490 605 800 744 531 124 464 350 512 743 673 163 145 481 478 049 350 641 630 187 042 425 701 852 707 420 067 823 019 013 457 649 326 893 682 221 385 430 346 181 104 169 220 053 147 282 827 674 933 550 826 215 344 214 407 859 304 940 647 202 583 067 249 063 014 452 731 553 758 349 978 411 928 507 870 473 724 721 658 614 287 512 874 371 478 092 037 674 388 055 731 867 050 187 846 402 662 125 656 388 313 505 826 762 201 455 014 979 665 225 614 792 451 351 105 615 304 224 180 989 022 409 720 495 092 104 464 562 772 313 967 558 038 317 587 774 663 875 778 441 031 815 131 475 488 814 262 061 074 636 003 900 924 852 881 678 626 741 956 221 080 408 780 873 187 627 022 047 054 081 048 163 872 583 237 931 762 225 081 421 943 674 740 976 106 985 872 367 194 762 225 781 761 604 008 977 400 440 430 562 389 883 070 684 548 723 857 046 704 408 831 135 454 322 346 813 880 933 078 274 570 316 456 356 182 762 758 456 222 107 274 438 670 736 515 307 619 499 824 059 159 125 173 641 153 993 266 776 022 470 644 233 026 867 524 090 568 104 098 286 056 956 382 802 577 748 139 400 517 472 650 572 223 236 266 222 933 222 562 626 482 234 507 925 510 836 024 676 394 956 974 365 900 820 780 628 569 366 990 085 947 837 756 261 123 103 614 832 812 075 373 843 517 148 488 484 462 755 868 290 016 269 819 040 997 729 277 810 897 690 552 782 565 307 307 244 067 857 567 119 193 643 502 705 846 171 325 259 501 091 727 410 985 109 030 311 259 221 154 861 658 926 842 840 555 901 795 446 975 861 295 817 683 225 833 877 792 600 101 828 729 871 635 021 948 135 316 103 889 163 946 639 769 686 365 522 733 881 294 543 708 522 728 710 779 237 687 479 893 663 457 864 421 930 619 741 191 950 116 729 130 228 650 940 593 624 912 680 184 033 001 996 917 037 528 712 385 885 908 663 895 864 735 120 867 099 795 282 652 671 693 648 755 548 311 545 648 395 097 440 841 075 064 962 334 398 450 096 078 877 578 153 666 044 948 604 950 258 966 923 380 430 136 322 682 640 731 439 527 387 735 070 104 772 320 770 065 460 275 780 599 573 660 794 395 354 363 806 453 510 881 908 843 748 200 258 399 796 978 796 031 810 455 839 638 365 978 637 624 772 696 647 136 608 784 955 621 952 150 648 657 478 338 162 103 982 745 353 033 961 182 350 912 810 194 743 514 971 919 183 263 538 236 795 431 303 888 000 472 416 494 199 040 006 782 965 882 380 907 986 295 059 630 914 294 450 708 786 747 835 982 523 973 426 104 423 464 977 161 426 157 349 647 515 695 028 409 938 669 550 137 393 504 888 384 676 025 345 037 632 255 827 241 179 617 409 687 834 375 206 466 652 504 892 254 408 191 214 220 073 353 283 048 352 785 758 659 514 602 982 695 073 114 564 138 619 543 566 677 546 899 191 718 068 626 499 311 148 025 264 863 737 328 526 542 554 704 824 324 134 390 548 629 058 409 094 337 669 202 823 443 022 679 229 366 337 454 778 773 263 427 423 905 472 403 267 234 391 939 271 359 296 279 808 459 906 379 911 007 694 757 278 999 815 701 347 525 538 862 146 823 909 341 989 399 134 876 399 570 961 366 594 038 679 108 405 489 528 859 777 700 463 815 042 586 185 567 674 178 180 959 106 704 132 225 726 511 948 452 571 889 946 122 788 736 276 842 042 084 392 339 849 737 576 012 189 731 474 846 331 386 260 002 775 317 484 252 410 531 882 489 703 672 049 325 058 611 366 892 210 361 127 332 208 464 630 793 978 188 884 705 657 543 186 277 755 111 937 865 682 509 910 137 760 100 449 134 416 587 894 330 351 674 503 192 019 788 505 440 558 258 220 539 757 960 674 909 405 644 609 097 688 627 367 628 968 676 684 270 998 230 436 563 070 071 536 825 156 670 684 356 058 308 548 680 387 396 064 656 190 897 203 591 235 480 224 556 337 840 832 172 105 226 450 926 204 704 544 946 443 806 242 828 218 795 958 363 299 159 559 485 484 434 176 184 342 173 834 189 192 004 918 180 772 324 477 775 608 603 047 065 842 314 974 907 001 957 037 308 209 251 887 053 156 851 744 676 330 486 875 604 635 142 653 941 365 062 082 526 342 342 449 611 784 446 181 540 816 572 115 349 882 821 204 322 202 964 271 822 998 710 577 633 061 173 820 194 944 550 452 275 488 184 942 661 846 163 386 787 343 339 953 903 245 302 069 248 425 123 934 398 255 463 964 858 161 786 979 293 132 229 228 017 580 286 962 149 311 935 483 643 886 457 200 524 191 463 951 330 878 310 642 740 980 891 176 914 500 251 186 925 963 273 121 958 537 395 438 985 752 943 075 827 755 511 917 710 019 262 650 174 146 815 426 697 741 661 517 024 246 664 807 392 030 793 936 097 722 816 688 760 264 696 516 399 061 317 438 358 943 364 289 327 940 530 155 022 554 957 787 316 574 915 385 925 072 549 765 856 329 830 137 385 352 833 444 911 026 427 162 975 506 549 973 908 557 675 910 044 016 005 552 736 731 762 493 895 124 810 204 126 248 435 885 623 729 633 605 673 710 796 473 610 777 571 185 731 255 588 744 668 668 391 655 359 881 904 723 757 954 485 404 150 005 135 342 409 393 468 906 105 537 228 649 776 387 810 018 517 475 313 615 669 729 102 344 963 060 304 723 148 565 588 991 314 681 688 798 377 311 684 257 123 908 581 352 981 768 193 790 123 813 936 573 112 892 420 254 244 719 284 669 470 638 698 273 316 721 623 357 896 550 049 914 708 869 863 715 751 593 979 263 221 868 035 060 511 416 041 683 614 528 880 714 073 131 561 213 942 003 231 301 309 419 236 704 134 322 738 510 359 280 510 886 680 965 252 432 615 777 659 220 297 256 327 046 339 665 594 586 230 684 331 882 097 514 683 735 969 120 763 914 013 653 015 157 864 589 824 663 381 561 332 575 528 304 409 424 664 536 389 219 635 137 781 225 576 166 487 162 710 527 006 820 238 458 818 685 533 638 055 420 208 886 297 535 497 925 514 851 440 331 692 172 376 621 477 965 535 028 726 348 879 587 064 676 505 022 268 633 208 770 114 401 795 250 612 652 104 287 602 909 091 524 423 953 917 427 847 668 487 376 360 266 835 852 334 746 741 230 149 713 029 070 989 662 582 126 083 173 989 087 493 635 146 903 969 121 774 108 665 057 801 872 009 397 537 613 124 525 702 338 116 906 013 514 540 640 041 857 354 982 829 637 777 788 029 522 205 778 381 888 588 326 673 162 631 232 718 307 872 924 955 762 677 975 099 134 775 773 349 275 273 728 565 592 144 889 957 227 028 933 479 875 534 684 853 814 012 572 717 186 769 069 139 403 632 924 760 409 164 149 192 880 542 691 214 172 049 105 639 647 755 305 700 157 399 267 909 882 271 157 886 581 559 124 202 896 893 096 839 396 622 402 462 034 752 844 126 656 143 557 418 491 989 448 154 908 269 578 251 190 957 163 782 973 560 935 834 242 805 244 825 783 470 092 070 506 492 821 246 327 100 262 528 948 570 016 947 075 055 065 292 212 413 744 264 138 074 647 114 930 262 941 447 672 950 685 548 414 536 671 182 672 316 284 513 177 679 016 900 820 618 943 724 673 221 911 096 929 855 160 942 734 438 506 677 266 877 429 540 086 019 921 321 217 390 106 300 774 438 514 998 580 485 519 264 793 537 480 950 493 034 128 701 807 397 927 909 489 809 907 924 857 924 906 862 253 237 324 181 363 001 278 352 833 748 059 367 308 069 311 313 711 120 129 973 891 018 037 232 502 090 479 596 709 026 571 283 227 819 909 756 960 585 825 251 228 192 797 256 914 195 214 027 221 849 996 944 769 731 397 838 452 740 190 810 429 096 876 979 293 168 933 739 960 956 075 423 482 912 378 671 456 535 695 893 005 084 622 071 642 460 478 614 648 304 728 477 678 619 646 302 805 756 939 920 821 785 406 128 185 987 345 152 906 976 709 040 194 531 773 200 577 153 667 297 260 495 241 418 256 746 735 304 595 554 326 313 099 697 231 730 261 718 731 949 133 076 251 393 364 764 405 157 494 856 668 548 957 618 679 205 033 267 100 420 863 604 306 174 371 905 293 924 340 022 973 300 147 171 535 774 752 601 303 123 140 904 837 459 776 252 479 365 392 214 085 709 699 301 982 414 304 877 212 237 557 920 498 755 596 282 123 244 364 229 608 269 703 256 434 796 314 994 261 392 620 471 756 107 535 288 664 226 336 820 894 676 736 888 701 421 452 162 191 199 671 257 084 351 365 915 138 187 569 489 961 207 423 174 877 798 172 496 913 947 087 638 941 591 536 465 842 954 009 396 152 910 276 001 146 683 152 070 114 932 405 570 435 300 826 600 610 460 041 973 380 061 321 884 657 322 089 666 910 952 275 929 736 630 478 596 134 254 167 443 980 190 593 727 753 197 031 014 939 913 727 032 764 904 073 903 655 579 030 573 966 255 762 211 214 574 777 086 442 928 653 789 570 596 136 983 396 542 185 502 578 562 702 126 770 376 519 897 435 655 592 507 553 681 619 856 813 520 217 438 615 141 099 009 812 306 767 115 316 929 242 588 017 780 728 640 447 333 698 346 197 198 799 485 283 738 438 454 428 611 862 419 728 942 354 139 078 499 213 978 451 381 020 634 293 701 945 413 210 253 805 943 148 868 487 821 873 878 218 649 127 594 655 227 076 193 851 118 287 346 159 583 093 174 189 827 625 628 587 356 966 397 343 724 976 715 342 972 103 261 213 620 843 734 569 750 706 186 483 433 802 546 695 161 542 379 150 951 851 516 568 482 280 754 969 274 549 504 383 783 495 736 572 961 100 249 668 130 856 738 225 123 578 685 912 919 620 739 312 097 364 682 813 503 676 267 431 207 914 190 805 381 867 297 691 736 213 705 404 516 453 204 102 986 235 934 330 223 714 940 565 245 115 804 920 428 312 710 363 561 342 973 694 517 917 169 037 344 593 063 366 122 154 849 232 240 806 934 754 024 226 778 061 855 795 522 930 448 229 897 021 465 070 482 921 172 639 573 445 264 452 859 380 469 617 732 377 022 046 203 985 877 217 904 766 300 136 007 716 016 950 861 854 726 534 210 313 377 927 167 109 671 535 528 016 615 159 933 659 009 289 037 009 889 214 385 325 920 379 104 514 420 784 376 375 035 674 497 530 354 841 782 068 525 002 877 826 553 019 023 770 205 686 064 915 262 711 392 642 240 761 301 557 279 661 789 829 973 666 076 759 980 616 165 713 505 667 412 993 379 384 157 410 670 948 367 222 174 942 036 176 837 144 054 618 174 794 132 317 905 246 958 201 058 945 803 537 447 371 444 246 570 123 673 270 544 162 374 853 867 963 351 600 640 357 405 815 436 679 223 229 192 579 280 988 091 683 994 403 677 779 662 398 101 781 986 634 062 432 019 695 398 260 240 616 430 272 831 775 051 214 480 011 319 114 452 065 750 589 903 295 267 715 500 691 612 455 094 767 223 191 842 979 313 513 284 767 854 794 584 443 731 533 122 664 955 849 296 547 330 843 769 917 814 112 915 500 602 545 348 830 907 884 914 844 645 618 195 363 196 659 283 054 461 428 645 946 457 194 250 026 660 691 512 139 255 047 721 617 279 019 842 225 776 324 576 475 171 195 592 448 537 113 738 830 995 403 016 946 071 681 985 962 657 371 902 833 347 245 351 825 545 908 525 431 278 497 335 973 523 382 693 048 904 962 392 310 171 258 896 598 623 196 239 513 387 889 467 878 437 325 287 634 362 457 406 415 513 338 632 263 304 414 536 504 303 404 469 420 328 360 453 232 474 946 986 751 305 558 139 785 622 751 315 386 474 403 185 841 875 587 734 891 183 349 799 466 898 252 795 730 844 818 224 036 269 688 406 935 161 347 127 772 695 398 081 682 256 554 700 019 828 283 590 098 824 561 249 631 011 543 546 136 918 874 959 668 190 019 502 519 828 806 765 033 761 659 828 319 828 537 818 994 712 742 814 313 310 685 934 030 966 339 383 782 859 587 929 553 265 166 911 278 510 387 113 957 678 065 895 914 082 512 122 626 449 005 018 037 502 560 616 648 813 993 490 600 429 600 466 282 899 271 745 226 442 233 112 295 279 876 759 535 105 682 989 079 203 066 221 261 677 204 107 624 167 443 688 927 888 390 727 363 721 238 209 440 149 164 424 880 355 330 869 735 458 014 340 157 222 931 413 279 912 081 131 025 814 858 890 431 246 289 812 885 665 741 343 184 904 537 964 868 037 070 147 696 962 747 655 940 009 944 885 265 714 624 381 360 989 841 682 591 327 507 667 868 908 646 307 228 216 170 247 584 896 715 297 848 978 983 192 033 813 274 800 646 675 087 941 110 407 184 794 861 518 312 863 574 515 425 898 612 703 965 881 777 536 563 076 628 510 195 920 977 946 878 332 931 064 107 854 828 838 787 907 004 590 198 511 284 914 626 041 376 346 065 747 647 204 023 875 937 168 310 027 805 645 867 038 409 975 022 154 411 276 293 292 982 070 977 315 881 439 359 159 009 066 582 081 629 328 525 980 130 088 908 933 423 451 463 510 145 783 739 271 080 276 010 192 282 439 780 603 383 632 194 671 228 606 930 371 416 984 279 991 024 587 700 620 943 928 460 152 071 287 887 285 182 074 399 988 818 524 548 628 802 857 902 042 274 171 724 633 961 447 683 601 381 454 132 861 636 937 849 768 076 528 927 182 413 610 476 049 076 651 265 234 425 244 808 082 612 592 643 708 643 797 643 927 600 432 090 595 558 140 340 663 559 645 622 568 662 283 300 592 334 371 448 508 571 570 037 429 855 661 477 651 494 176 348 884 703 255 584 378 913 138 658 572 548 660 996 887 707 142 897 074 626 917 854 387 864 696 063 449 084 044 885 552 487 184 832 503 799 500 464 407 702 833 252 731 646 991 485 043 431 843 934 458 513 349 282 028 604 172 136 865 723 137 352 209 391 145 450 560 514 393 229 369 850 896 311 415 120 266 215 239 237 441 751 849 992 314 554 517 881 694 291 063 277 401 517 617 152 247 767 090 323 415 949 719 136 940 181 287 623 589 598 973 552 787 386 554 645 295 498 840 460 089 985 413 158 908 899 557 379 878 818 864 901 308 360 869 538 604 069 739 933 304 755 512 756 035 701 191 270 431 592 923 625 425 263 537 256 389 757 354 795 848 136 875 146 896 236 138 400 435 465 917 735 285 648 958 959 291 273 720 428 293 934 643 034 768 984 891 991 729 600 863 477 062 396 794 668 756 210 908 489 413 560 430 215 105 624 245 131 966 432 550 316 516 847 161 092 871 391 941 730 909 713 759 833 708 321 720 573 680 657 415 361 843 801 155 009 607 203 130 681 680 832 127 562 451 768 061 696 606 513 749 553 532 940 003 392 647 982 255 616 331 779 743 385 117 853 240 296 674 587 645 466 712 858 846 742 235 770 263 350 343 920 181 950 288 150 617 006 790 821 959 626 774 409 326 191 726 024 611 590 279 244 469 893 120 496 230 521 110 959 593 837 081 105 687 199 513 259 037 098 721 396 032 300 822 646 908 166 448 010 425 606 171 770 417 757 565 862 458 086 376 158 004 020 572 438 165 176 793 947 407 867 856 019 349 511 021 840 900 389 815 231 258 979 555 909 558 532 605 835 814 437 660 210 838 900 035 644 580 944 298 566 923 949 421 535 624 205 897 956 750 261 235 728 078 173 525 128 135 665 521 698 520 238 433 817 829 783 080 977 886 659 408 209 324 074 408 669 829 367 135 571 900 728 157 996 635 402 260 147 928 252 160 335 504 860 473 346 619 605 468 764 669 536 336 177 481 453 945 353 663 122 541 746 174 910 621 652 838 846 277 299 067 098 043 971 610 400 330 477 592 317 320 438 007 868 367 810 880 979 281 616 891 495 399 791 400 198 550 149 123 742 357 733 488 983 883 717 748 411 113 524 363 297 695 486 463 262 784 422 450 658 542 402 644 879 918 857 549 942 204 874 602 795 077 785 607 720 984 941 507 092 232 716 305 813 359 893 775 295 056 852 378 670 650 054 828 110 853 174 072 284 408 381 164 038 397 567 960 327 224 025 793 963 993 294 564 351 303 190 747 062 900 269 968 829 818 544 391 933 680 385 734 812 787 581 007 916 879 435 246 226 766 599 223 090 639 233 675 071 206 142 194 940 406 986 028 496 439 087 981 789 391 931 434 831 493 123 649 644 669 192 397 983 324 137 587 743 255 739 109 665 584 352 754 932 966 133 236 055 800 538 233 069 543 301 306 677 830 710 373 143 102 849 626 799 025 470 728 356 701 221 120 856 457 738 114 970 659 653 509 787 325 702 742 112 717 835 467 059 573 032 078 878 823 476 118 358 629 712 715 831 154 257 695 950 807 818 380 600 044 132 054 780 571 199 466 493 809 991 218 016 874 302 229 308 908 559 233 425 526 384 771 161 761 706 119 128 772 736 857 329 005 485 822 739 236 782 177 144 342 858 631 755 208 339 687 152 465 986 853 539 151 206 577 047 849 738 290 021 865 108 809 717 673 296 791 229 307 080 325 771 422 914 320 678 878 385 474 033 753 787 381 822 085 597 090 758 412 062 412 481 691 126 815 290 808 063 966 155 146 801 699 297 065 315 173 050 361 459 831 720 106 566 494 733 026 130 192 104 439 546 859 093 319 347 102 646 290 838 997 475 442 164 081 245 611 928 359 528 440 659 280 829 419 202 181 397 413 678 231 746 424 867 417 051 202 405 883 081 503 717 923 204 998 594 038 169 073 777 112 291 244 740 993 724 611 633 055 649 837 127 693 564 982 133 445 023 740 560 523 591 379 074 776 471 917 671 413 081 670 556 026 649 142 259 477 711 802 687 264 872 193 187 234 106 242 952 250 096 194 244 468 812 289 751 467 212 589 422 717 808 482 602 864 988 613 685 341 603 648 424 865 902 348 919 221 305 472 657 746 910 959 621 661 816 320 634 651 416 558 644 128 908 312 982 094 979 861 950 425 123 049 790 370 803 395 835 584 681 185 522 321 809 528 398 252 941 043 200 464 707 374 826 720 743 246 663 828 833 679 906 433 209 673 906 876 779 454 569 012 903 216 608 722 369 840 676 461 083 163 237 291 506 666 044 663 817 672 192 242 898 113 880 069 631 846 272 285 530 945 988 074 145 270 294 163 743 796 425 868 964 557 994 880 970 055 156 646 477 149 668 011 426 236 598 184 206 695 384 240 664 832 548 126 376 866 489 101 790 433 952 501 903 807 129 366 702 418 181 668 011 108 874 322 249 583 352 811 767 037 596 028 338 741 366 045 577 698 660 093 824 038 011 509 138 437 215 270 400 463 752 412 666 412 583 266 535 120 294 528 467 948 789 746 059 926 416 424 070 841 995 453 270 736 361 604 303 919 897 512 135 395 990 014 049 301 875 911 352 017 153 632 038 870 509 637 694 715 249 316 139 538 221 193 935 866 000 468 724 331 068 822 076 780 041 675 902 292 311 971 833 793 702 669 866 501 943 611 658 234 462 174 121 534 458 370 312 650 443 577 148 622 443 669 649 285 895 853 580 926 096 163 223 842 741 854 792 996 106 417 177 639 238 054 293 079 650 594 913 727 736 061 534 727 751 039 451 623 599 746 563 524 425 982 659 432 179 225 084 343 384 035 371 890 965 899 409 721 246 240 069 041 191 082 780 601 512 850 404 554 474 960 252 714 306 441 997 370 664 232 848 177 149 761 141 291 691 717 900 461 997 380 072 150 998 359 086 439 020 680 029 018 628 308 380 613 815 392 853 552 745 078 657 834 662 876 928 991 814 378 116 749 272 258 622 851 629 079 771 572 321 217 099 379 330 701 086 970 202 663 287 366 109 510 387 468 626 317 136 958 967 511 936 282 193 125 477 293 835 998 572 014 701 324 130 750 250 778 161 377 785 163 063 802 673 057 176 607 571 343 342 969 202 829 956 467 645 885 840 271 695 907 971 117 676 597 389 021 640 227 028 460 650 783 581 412 486 538 258 428 916 905 201 531 682 233 927 072 058 039 993 616 270 765 681 405 281 745 685 833 169 251 114 936 594 039 165 364 167 344 313 593 914 027 812 658 032 954 120 202 918 874 147 892 712 538 755 238 016 051 230 198 020 816 157 435 755 615 151 771 028 028 177 601 888 165 860 939 803 897 849 940 054 508 417 209 968 161 310 928 528 107 591 244 663 344 392 072 300 407 911 272 749 829 403 132 663 518 879 488 077 976 551 262 626 768 442 399 196 071 397 399 147 172 109 905 088 823 695 025 214 757 965 349 289 334 404 169 274 194 430 746 855 606 031 876 187 366 868 018 627 757 560 617 364 916 494 102 767 197 340 757 170 896 255 369 131 828 002 811 964 235 195 897 658 839 044 666 334 974 899 065 531 448 831 021 588 314 397 409 089 122 517 475 440 833 747 231 953 378 935 743 425 130 765 609 865 392 617 158 550 769 926 285 143 381 253 072 404 091 684 838 733 050 716 644 538 962 365 165 695 223 967 793 574 920 414 939 185 173 661 472 362 432 821 270 892 662 368 422 226 539 319 587 497 701 460 804 156 935 578 280 524 950 058 139 711 132 709 459 313 193 481 946 913 741 191 767 531 263 576 205 222 174 553 474 921 943 536 284 255 895 410 049 322 269 766 358 963 570 934 779 647 495 439 951 421 307 156 743 094 796 022 628 585 781 466 847 054 408 942 946 034 746 322 377 453 558 939 754 873 883 807 929 728 080 001 637 376 421 269 886 249 691 468 927 120 999 878 371 670 245 853 268 041 297 580 453 363 916 345 241 335 775 647 792 300 733 785 092 041 332 809 111 886 255 512 680 010 837 325 599 822 929 819 279 589 056 732 183 764 812 066 825 659 603 716 661 506 428 679 710 598 052 667 839 867 701 650 039 908 728 880 179 594 243 897 935 961 633 937 189 478 408 313 296 031 275 475 042 253 109 887 529 171 286 559 820 384 046 069 065 588 436 850 972 713 998 471 388 329 190 956 459 085 955 476 774 029 701 453 480 354 471 880 474 604 800 165 479 199 397 892 254 771 378 217 463 025 295 196 987 671 844 491 302 957 458 302 141 313 661 881 424 116 335 365 904 386 114 707 782 798 445 169 157 574 107 536 543 262 412 213 339 541 441 345 103 074 968 005 590 931 823 979 013 528 153 152 652 448 051 870 866 793 071 227 150 295 604 544 244 659 760 527 572 117 287 443 227 327 817 379 126 838 412 250 241 664 618 933 465 243 727 297 625 217 534 420 797 513 978 487 581 168 865 964 186 276 105 420 884 514 825 508 738 463 695 508 109 974 763 437 133 775 919 233 094 344 141 685 252 453 714 951 937 392 437 228 343 158 724 393 059 578 661 406 288 133 746 854 768 339 818 866 170 670 399 374 012 175 014 517 937 120 303 645 397 692 109 105 106 973 278 590 650 110 031 099 611 786 897 951 372 216 573 147 293 469 290 312 287 495 226 180 945 295 252 016 523 116 932 712 280 270 362 850 180 843 183 888 394 655 245 210 237 398 497 928 746 700 317 196 461 194 086 126 840 202 021 398 904 282 087 331 335 785 471 482 588 511 743 390 805 174 254 749 020 473 634 641 520 007 337 981 422 719 398 196 571 769 024 257 929 710 980 454 721 514 603 223 776 304 931 974 416 153 456 495 891 953 382 095 962 165 681 407 820 197 132 550 748 371 275 323 314 111 846 151 507 313 605 294 964 837 705 567 139 935 340 192 475 622 728 569 189 711 341 248 781 069 275 006 388 786 561 446 175 028 380 945 311 476 939 923 018 910 055 338 252 287 998 716 716 664 944 940 005 002 089 841 241 222 703 511 581 995 976 649 135 187 404 571 081 925 026 337 663 623 325 525 592 597 783 676 068 635 732 890 962 577 643 002 877 712 101 361 881 752 833 266 858 351 990 199 754 226 437 133 489 264 193 138 729 703 275 650 489 043 768 973 468 667 491 945 989 727 460 961 791 812 975 827 863 390 938 295 040 276 141 909 617 851 773 307 672 607 221 173 295 044 237 763 718 598 974 154 760 185 215 868 031 714 217 106 697 260 309 185 551 819 908 704 353 731 662 852 262 567 739 107 533 702 288 060 117 775 921 256 918 393 052 615 604 277 323 249 421 603 458 055 596 174 211 703 323 014 166 027 696 135 925 178 544 829 043 562 189 414 814 192 219 478 451 886 386 778 347 836 683 477 860 581 694 850 400 271 548 762 717 093 319 027 317 673 470 527 095 328 814 404 309 888 158 762 806 947 317 632 307 704 364 890 763 472 025 839 581 104 801 405 985 883 276 043 086 244 029 873 512 092 076 997 530 915 546 039 442 736 399 421 074 287 220 625 164 279 447 362 713 983 366 399 432 897 031 525 230 639 404 027 064 579 587 856 021 683 373 486 066 856 813 767 784 334 634 742 942 521 768 975 768 481 996 822 778 736 071 475 830 514 456 659 114 710 689 639 934 045 863 973 771 693 762 033 682 290 213 065 489 842 690 237 193 791 503 217 029 825 339 732 541 652 264 448 114 514 549 554 243 271 859 927 562 162 943 747 399 936 210 950 159 781 756 672 916 390 355 404 406 306 639 461 172 642 083 167 296 482 683 483 316 090 875 466 809 598 928 179 290 144 720 589 310 810 044 866 562 970 291 890 878 166 912 669 042 478 226 933 563 626 770 991 724 630 274 898 846 340 616 563 823 117 940 368 014 622 642 210 904 951 089 482 514 021 736 648 388 090 610 793 816 164 138 284 432 114 381 292 291 762 220 889 320 205 123 447 684 197 579 984 734 342 613 125 675 698 354 747 592 105 417 738 177 108 484 731 635 044 885 287 605 069 939 767 034 394 823 199 214 079 889 834 824 668 199 040 046 289 831 441 609 553 903 545 077 187 042 637 345 771 398 177 806 173 388 346 804 852 982 362 915 142 736 749 397 133 554 812 842 548 588 135 728 411 529 277 085 848 450 304 087 634 875 402 982 597 789 503 964 476 027 684 260 890 232 153 791 275 139 802 131 460 181 061 250 790 760 067 120 792 114 953 101 279 627 085 642 488 827 653 586 970 428 994 147 729 005 557 374 200 225 918 282 444 611 150 093 826 374 457 032 228 503 827 787 757 414 712 006 422 417 272 254 212 760 459 771 358 200 987 368 890 677 607 915 366 779 247 323 201 115 151 945 268 629 224 458 748 020 343 520 123 085 059 902 718 357 197 227 077 707 882 734 292 659 255 585 107 949 218 881 863 507 362 147 332 548 023 037 366 361 095 876 359 923 934 021 383 690 749 193 722 968 817 657 455 965 069 145 265 892 457 748 729 376 300 956 727 345 262 735 425 629 307 418 352 146 013 036 433 255 454 392 225 576 805 554 332 563 575 090 286 904 744 925 174 151 336 840 110 107 957 406 463 017 094 147 626 116 070 468 260 641 739 492 600 274 564 848 118 280 549 609 957 664 644 079 829 939 114 247 114 269 045 463 300 686 265 177 109 744 722 482 220 537 225 807 134 544 624 616 494 640 279 979 831 549 260 319 049 259 392 744 837 384 478 601 709 884 981 530 629 652 917 210 274 213 634 141 898 425 837 303 906 291 582 459 633 966 345 926 714 262 981 394 020 485 534 747 294 176 529 896 938 463 441 303 251 466 034 789 552 721 262 798 564 194 186 801 819 712 121 691 985 231 397 029 957 091 585 000 430 825 362 834 972 688 912 744 577 123 590 002 673 549 941 754 484 439 387 926 275 161 882 350 357 464 211 773 128 008 776 838 689 852 013 561 611 266 811 791 298 752 998 529 230 975 634 555 020 435 156 175 636 807 408 286 445 341 612 987 616 851 832 156 514 229 165 276 895 340 923 430 313 364 055 450 421 887 902 109 989 857 525 124 592 070 737 899 255 785 985 274 891 616 251 639 354 694 551 208 000 995 552 257 698 313 407 587 282 176 993 800 275 468 957 975 276 015 123 107 002 242 646 763 335 587 406 666 729 535 743 880 914 055 395 250 402 324 267 773 986 677 696 143 564 984 826 514 836 713 309 924 925 653 411 763 754 544 768 098 289 813 088 210 207 842 766 542 423 146 167 126 513 755 773 791 430 084 692 879 644 752 726 248 593 662 023 076 316 988 302 150 296 379 667 097 458 307 025 542 689 990 146 359 610 375 402 791 952 231 945 061 031 784 846 936 200 991 963 417 939 939 122 568 340 781 221 701 217 174 332 241 637 907 107 524 448 210 840 192 980 256 861 551 374 316 657 115 537 622 082 214 580 076 986 406 032 823 122 338 389 908 018 412 598 890 132 706 918 321 840 262 891 958 534 331 054 788 209 170 766 836 209 576 427 536 157 678 686 303 890 585 521 487 688 800 443 837 235 058 431 829 966 160 504 555 293 764 806 881 875 039 263 409 283 885 528 878 067 943 072 933 589 397 530 506 572 932 155 462 715 285 247 312 837 800 942 931 306 915 865 569 012 206 411 624 499 245 498 726 244 375 639 122 658 755 075 130 099 326 245 413 110 878 076 654 614 132 145 724 756 175 685 217 091 476 540 938 015 095 110 639 331 267 469 567 729 403 090 769 565 286 716 001 076 097 893 290 786 716 358 229 322 179 230 189 476 012 435 062 696 894 794 862 897 376 782 050 955 590 962 707 567 887 262 667 734 380 485 017 444 555 141 520 106 953 409 375 213 840 030 663 462 877 560 537 174 732 397 945 642 475 605 350 463 574 911 729 403 034 656 991 455 298 632 873 848 266 702 349 938 060 566 895 707 329 718 626 177 048 684 567 654 010 858 186 998 160 715 833 488 623 370 706 215 326 914 345 725 419 760 801 212 088 501 668 912 988 532 695 239 108 817 187 128 036 247 725 436 760 898 277 259 412 558 083 781 899 437 426 663 533 530 492 926 720 962 755 143 059 368 718 513 384 852 711 194 625 939 560 680 307 582 578 722 966 983 172 250 900 301 909 636 549 884 001 805 885 588 793 156 995 758 249 304 410 651 397 314 495 516 855 876 851 750 850 207 153 877 450 701 516 826 813 449 508 795 319 634 748 226 033 808 804 078 875 863 848 885 187 227 401 275 982 046 423 986 157 202 547 581 083 970 779 988 561 080 195 092 888 362 084 678 474 121 514 613 932 469 128 873 731 070 066 081 001 368 865 527 001 128 905 226 895 828 830 252 656 406 453 412 073 492 916 727 337 313 903 081 489 058 610 008 638 461 631 660 835 150 445 680 109 039 632 019 533 064 990 380 468 072 344 270 030 652 812 236 490 257 276 813 459 155 594 483 751 179 121 111 629 718 325 454 996 423 212 111 415 109 868 586 337 836 945 258 747 430 911 496 083 217 156 759 496 011 452 305 408 510 492 631 607 536 557 184 031 964 272 684 546 457 055 736 254 351 867 936 098 922 881 156 348 622 284 118 304 981 341 905 057 886 866 539 733 631 337 176 720 218 178 163 115 251 785 863 622 955 631 581 620 893 753 922 197 884 430 452 983 266 371 882 379 501 748 716 139 013 192 129 859 954 033 163 503 478 427 140 701 860 036 760 294 180 488 962 931 140 406 009 799 695 764 903 194 051 926 379 501 658 595 690 633 457 903 170 554 019 397 279 103 878 750 240 721 539 520 976 895 531 749 898 439 787 869 382 933 996 474 390 020 415 228 242 815 992 166 999 589 236 918 124 636 301 901 080 988 812 971 955 398 284 363 177 694 465 512 109 972 975 030 740 845 620 354 121 237 129 049 633 900 030 725 239 251 890 720 902 204 228 917 937 971 876 054 828 604 448 666 694 675 727 924 736 972 751 247 824 402 536 215 822 227 497 819 037 360 391 104 815 440 909 214 232 061 532 813 388 681 320 386 267 305 700 397 912 557 150 993 460 412 966 197 920 222 878 746 302 847 977 872 497 736 546 325 230 087 476 534 767 756 385 637 729 421 269 643 176 370 647 800 420 467 173 941 978 516 241 894 112 968 872 165 087 816 608 230 213 707 569 562 658 738 647 240 734 946 031 459 151 995 558 451 187 289 055 546 777 766 301 328 084 018 444 032 706 805 703 751 278 636 281 866 818 154 369 557 748 908 725 378 166 632 614 165 494 678 188 521 974 489 924 043 978 318 502 966 291 692 088 782 191 147 440 708 253 102 106 927 485 754 626 118 842 410 114 420 057 786 921 766 946 569 653 412 614 333 616 218 450 533 599 293 927 398 588 970 720 337 425 783 990 554 114 874 522 359 782 917 493 832 565 653 571 699 158 535 996 179 401 283 028 100 014 234 749 046 049 910 609 365 699 637 204 948 398 981 274 915 664 372 289 027 237 616 174 639 243 596 546 733 610 067 203 499 413 592 926 408 272 802 551 980 009 779 587 360 711 993 138 423 790 957 745 378 601 089 373 181 809 229 750 757 628 682 862 729 223 355 124 752 827 545 622 016 819 272 333 193 052 371 770 371 399 360 843 342 441 862 975 760 186 010 593 958 132 631 620 039 945 899 000 853 952 198 911 184 722 970 689 106 303 214 975 985 356 734 144 771 986 637 286 027 731 521 245 624 525 250 975 615 836 204 650 818 317 343 486 563 929 655 744 387 911 379 800 634 770 234 141 806 341 256 498 942 724 451 051 025 023 554 050 630 580 602 122 768 113 428 401 784 090 163 000 188 174 414 136 244 871 776 145 015 417 703 511 803 132 091 606 515 606 508 692 648 907 450 404 527 835 364 398 908 635 651 195 762 176 324 969 426 099 762 714 523 227 371 804 860 765 983 907 351 213 025 729 115 707 280 670 000 162 353 872 115 346 280 375 124 391 687 243 085 987 156 956 087 587 540 511 592 533 953 356 294 347 294 403 019 248 165 836 581 339 069 596 643 556 830 610 651 068 391 318 900 834 000 151 390 696 607 335 588 933 710 221 193 377 076 723 632 525 682 230 021 212 817 750 447 915 271 297 915 572 263 479 971 206 513 062 352 461 522 382 770 576 646 679 175 136 079 570 067 770 453 161 013 912 834 483 368 358 502 354 957 144 430 941 686 762 376 070 922 827 011 195 275 163 654 376 988 190 439 615 331 478 000 650 518 201 565 978 809 358 890 235 899 985 312 520 397 864 814 546 908 424 799 997 602 916 443 437 640 691 686 086 567 456 157 308 736 448 564 661 912 426 749 253 585 119 333 610 485 252 671 770 496 479 914 848 533 618 076 726 961 497 701 397 679 412 511 652 763 639 142 251 399 923 607 268 504 626 624 947 063 644 952 888 823 014 295 999 777 011 722 513 496 940 008 382 387 016 622 336 938 203 921 088 699 109 738 065 496 229 739 210 901 756 912 804 259 650 666 704 667 067 151 527 204 926 011 038 670 054 050 907 862 295 427 843 120 303 575 522 304 261 003 591 372 273 488 150 307 684 908 725 525 588 885 988 179 983 535 044 039 262 938 585 990 025 310 908 821 589 800 425 831 469 223 779 915 066 358 544 020 635 993 010 495 277 918 791 715 550 433 897 588 384 113 408 740 133 213 825 233 090 213 227 543 845 757 989 603 524 256 919 007 636 716 744 814 206 224 647 101 484 444 385 866 932 037 352 271 741 005 543 497 200 659 650 693 743 290 696 644 352 532 353 196 351 358 913 596 001 313 170 878 313 201 057 778 383 154 222 609 017 957 007 173 734 606 853 526 916 002 804 057 908 663 754 482 981 307 398 310 538 483 588 285 802 108 423 747 210 027 002 855 191 449 162 131 875 441 853 556 842 489 770 507 566 321 589 445 893 752 468 205 911 315 998 624 374 346 458 730 286 083 841 315 205 374 100 713 388 793 792 011 308 942 049 684 044 307 561 694 995 773 428 028 016 802 112 373 245 486 069 626 186 816 449 724 059 999 425 279 199 936 170 066 991 673 416 345 784 137 214 405 278 597 782 296 198 803 859 814 834 924 008 139 531 018 289 728 344 111 472 562 039 692 683 993 307 446 576 791 075 618 259 445 517 236 661 982 772 935 772 731 679 191 849 609 829 943 438 811 527 181 705 980 577 384 041 558 553 019 414 299 108 006 992 485 741 899 889 394 790 706 671 993 910 334 404 733 968 340 338 980 072 670 743 478 400 877 213 776 299 155 801 945 642 819 360 497 053 132 944 564 515 637 292 368 370 020 397 424 327 687 964 894 450 494 317 623 221 787 644 200 350 516 972 405 370 038 504 206 481 955 144 134 777 524 720 277 474 443 527 525 652 697 011 504 529 860 674 767 178 300 778 333 909 085 710 003 310 964 211 687 136 375 673 885 646 267 731 004 639 135 416 519 901 283 772 794 338 433 168 069 361 587 849 544 944 569 129 990 614 649 448 818 487 018 017 456 144 244 255 606 496 319 461 964 354 461 116 926 488 489 025 507 970 680 754 529 441 680 711 937 628 105 098 736 850 034 727 762 154 084 544 152 462 011 020 447 079 827 561 214 580 994 446 946 068 688 483 421 817 470 974 309 789 220 081 910 060 028 072 835 896 147 938 081 206 069 108 154 636 476 034 827 406 492 663 423 812 743 062 911 421 358 454 853 950 796 651 464 511 554 183 466 564 608 040 946 000 748 996 932 414 413 508 547 126 836 194 929 736 656 100 783 941 080 406 444 437 543 718 694 901 621 172 724 757 214 241 648 377 326 240 045 586 473 104 082 964 456 625 759 607 320 940 059 856 484 962 285 994 516 701 174 720 636 066 128 227 031 727 232 322 865 578 898 211 057 106 318 805 722 125 813 717 757 753 739 303 968 830 127 217 256 951 877 105 931 930 670 005 588 638 511 883 106 101 036 181 123 546 528 906 692 186 034 777 570 437 952 726 547 162 952 648 814 997 505 021 076 318 082 317 171 272 497 660 000 823 026 343 425 404 299 900 588 078 766 952 887 513 107 921 140 010 364 595 205 894 036 189 320 036 385 823 911 773 565 860 301 905 901 009 678 827 844 505 105 255 911 084 743 168 874 684 430 847 155 265 550 054 868 254 765 689 958 819 695 344 516 489 816 877 399 676 513 476 232 670 443 656 799 452 633 920 571 612 062 453 085 355 504 464 736 819 526 057 315 260 482 432 707 562 594 835 088 083 044 788 571 365 538 123 744 663 160 213 830 825 192 469 036 625 492 833 584 101 787 255 293 422 576 490 661 027 706 981 597 439 753 315 752 269 498 121 219 941 813 013 339 227 127 852 574 426 518 938 052 242 655 871 303 937 784 505 060 461 457 311 608 352 798 139 764 754 982 660 289 937 371 183 824 369 061 037 105 686 841 727 615 489 731 854 251 476 470 005 489 142 567 001 416 143 604 429 751 227 745 367 770 504 731 953 283 312 432 709 483 489 480 859 252 901 286 651 040 478 084 945 008 294 132 319 555 814 613 192 692 866 551 676 084 460 322 483 898 856 126 174 572 900 737 130 326 634 774 011 632 840 450 409 569 681 618 495 722 200 175 821 226 916 057 194 550 313 694 880 549 091 067 328 210 030 431 124 767 029 769 742 437 136 900 763 889 592 429 807 717 695 312 010 237 826 701 936 186 467 369 196 132 993 344 491 226 807 912 864 361 350 298 013 047 794 363 966 512 643 649 558 752 261 016 786 352 543 040 908 231 307 532 592 913 799 489 364 703 913 895 886 932 669 191 465 025 385 379 520 977 576 367 194 972 485 571 233 452 095 040 877 986 279 308 557 582 388 400 599 760 065 254 184 004 552 720 682 794 205 582 249 276 546 147 242 601 103 506 932 144 433 894 656 222 298 261 561 272 521 178 297 713 948 378 948 123 680 912 761 236 668 343 695 959 562 621 501 209 604 478 812 710 271 566 092 185 542 358 324 339 337 717 140 514 081 920 471 322 436 106 805 457 287 350 774 226 645 504 117 912 184 098 316 018 284 747 237 465 595 211 801 351 027 133 163 614 382 406 832 043 092 491 492 279 942 633 640 959 484 285 419 585 640 836 421 704 888 594 578 814 392 221 154 576 467 628 676 651 368 266 523 135 428 718 111 318 923 405 940 723 107 521 785 168 243 768 278 365 404 517 727 344 693 476 627 187 159 649 107 602 821 174 466 396 819 126 915 383 117 123 517 482 365 352 480 120 851 732 419 484 759 789 907 124 228 161 239 510 835 195 478 754 632 736 276 889 231 137 592 624 329 431 147 476 754 323 081 216 766 716 479 700 347 504 841 529 671 531 389 049 205 131 680 735 397 797 532 704 072 954 109 599 826 442 135 837 995 474 441 213 595 639 837 451 440 627 554 487 751 991 237 044 602 959 994 492 540 013 321 108 655 072 183 742 019 328 532 066 277 074 862 430 756 792 687 165 739 191 071 834 003 029 014 666 806 623 593 211 959 456 165 462 300 255 411 169 106 950 340 728 921 352 988 277 958 128 325 016 589 618 103 861 049 981 314 272 128 819 624 276 279 252 910 413 224 532 155 589 451 433 978 279 205 047 504 364 975 263 561 193 363 777 433 473 262 125 583 959 922 162 502 464 645 137 221 394 282 547 914 348 006 066 538 935 487 761 101 759 321 707 562 669 603 267 661 376 470 473 069 738 316 690 384 186 058 741 562 767 686 147 605 716 484 524 406 146 966 824 995 154 930 354 050 191 239 097 320 927 886 571 567 549 826 554 329 195 500 244 185 796 118 230 971 360 810 474 499 433 601 882 375 027 555 810 051 540 375 005 061 008 352 286 863 547 706 566 601 012 560 438 224 928 071 223 401 561 970 426 863 910 691 182 883 540 641 077 489 534 713 113 793 113 860 553 346 549 114 290 939 706 141 096 552 506 440 461 103 832 100 467 616 396 803 897 041 489 170 939 915 150 398 167 340 861 860 621 121 949 401 384 460 480 176 089 951 188 796 486 477 152 318 344 860 820 656 135 819 320 783 160 265 289 909 291 926 901 354 101 564 121 223 813 087 365 578 870 229 836 102 591 807 532 927 453 263 748 927 455 551 009 995 156 405 354 719 272 704 766 753 643 491 162 272 658 038 599 406 532 797 262 722 242 069 801 179 447 906 216 905 034 881 117 253 240 496 065 414 730 759 026 430 119 454 464 406 922 139 734 693 045 890 209 364 394 331 368 653 874 647 758 801 225 409 549 892 862 955 821 700 375 521 460 354 414 323 070 521 928 114 238 335 147 819 180 306 808 790 295 145 119 182 128 901 639 620 193 621 520 634 350 678 497 058 842 666 495 383 775 472 113 826 387 800 765 608 841 263 147 731 429 247 632 865 896 669 616 613 402 932 692 603 939 426 591 083 550 152 251 477 740 670 373 403 431 088 849 093 936 188 755 662 129 544 768 198 819 826 040 871 934 570 795 102 590 361 388 144 261 464 443 011 101 284 196 715 222 154 671 889 048 563 837 732 927 995 184 400 139 946 846 992 773 060 466 017 575 762 781 151 053 039 447 844 110 268 589 896 576 509 103 113 905 255 458 940 332 557 606 359 045 280 056 785 385 691 527 725 536 389 134 977 688 851 809 352 216 280 554 776 376 334 253 062 966 801 153 239 111 389 456 910 545 736 167 691 268 759 688 792 277 911 975 287 532 947 098 095 757 775 514 103 588 321 670 354 361 362 964 133 284 361 268 996 799 379 832 190 333 918 219 168 712 372 661 436 650 196 399 986 158 131 973 978 140 422 022 603 135 136 957 107 797 135 800 890 683 480 326 034 853 284 516 682 121 953 811 486 466 498 083 572 204 512 814 137 057 952 437 247 733 144 802 847 437 156 546 052 202 614 440 260 729 309 375 264 015 710 911 310 527 432 126 072 023 173 063 457 307 989 853 222 902 437 249 090 629 587 841 884 837 174 467 145 909 261 263 320 558 109 571 591 231 839 771 851 228 389 030 967 406 970 706 540 539 803 657 700 950 474 870 590 967 024 941 250 813 982 610 149 929 145 252 142 604 602 872 442 048 960 228 169 768 315 038 592 990 171 301 018 281 223 553 275 811 455 186 568 750 872 595 999 539 803 768 411 002 974 146 424 146 431 243 891 085 805 212 668 406 086 075 291 758 421 446 719 614 052 726 114 674 216 267 731 816 189 729 310 665 393 240 659 349 158 896 325 801 267 463 522 971 380 624 107 470 064 997 478 538 025 030 845 306 800 559 967 338 369 350 238 241 771 914 702 311 584 409 313 046 446 573 293 256 477 506 968 006 558 696 861 192 759 704 532 678 889 579 302 987 854 499 104 843 620 228 929 569 083 547 071 986 438 247 116 477 790 492 185 787 071 213 768 499 234 169 645 135 323 063 907 980 775 512 120 225 129 597 298 792 824 767 764 931 402 250 336 550 677 740 637 829 212 382 957 389 683 649 924 324 704 082 763 168 225 232 404 504 016 595 639 448 123 887 818 950 697 923 619 744 199 067 747 267 939 094 644 164 827 982 099 584 280 534 521 959 798 076 812 811 346 335 748 356 108 012 851 781 026 142 555 782 957 104 309 750 569 440 579 724 115 950 912 058 113 790 411 243 656 582 380 620 289 521 975 436 655 817 439 634 743 072 977 958 248 157 954 198 434 918 473 948 652 156 618 639 834 396 389 813 824 342 767 604 902 382 040 107 445 263 187 766 561 496 878 278 719 168 522 340 219 073 027 171 452 776 178 740 303 086 721 367 541 826 961 968 552 657 233 317 256 186 422 000 868 583 036 848 264 798 549 052 529 382 787 974 781 881 405 353 609 142 648 917 908 021 512 693 071 692 282 649 706 186 448 411 569 882 162 469 081 113 815 103 586 240 885 575 458 958 605 907 461 622 080 008 672 055 956 231 402 919 593 119 367 822 018 009 389 445 783 955 399 378 371 901 406 770 420 452 555 478 723 947 122 857 815 985 985 993 952 305 080 910 684 386 525 187 315 534 371 672 513 996 176 237 060 729 990 954 286 562 015 920 011 965 586 334 807 939 153 262 900 332 239 104 991 823 081 833 881 468 290 642 697 190 752 647 015 807 094 441 873 404 303 175 962 481 274 923 445 874 277 673 438 302 425 655 333 428 151 909 716 750 897 175 976 993 672 773 181 289 509 431 179 852 352 885 494 608 616 585 774 960 474 362 152 360 127 195 199 560 544 924 115 404 080 102 668 617 665 661 144 673 709 881 024 507 686 443 053 986 821 923 263 295 741 560 867 163 659 402 037 611 292 441 561 248 139 382 885 424 318 102 081 336 432 420 606 876 332 482 999 795 143 764 167 644 476 919 203 342 393 243 920 853 739 227 944 304 915 140 228 039 898 982 089 125 733 654 809 477 228 347 791 973 026 335 299 994 268 390 773 238 742 955 407 502 389 139 250 580 119 629 913 984 929 262 871 322 596 373 161 578 610 976 920 578 563 391 344 990 499 719 962 215 805 540 066 203 080 889 564 018 214 437 819 093 419 385 530 599 822 205 743 797 787 511 221 933 826 360 857 534 796 603 015 270 822 563 794 800 815 455 454 093 405 830 116 731 204 579 692 391 855 265 917 826 149 407 920 800 525 147 047 429 470 871 349 865 811 310 150 951 019 120 964 961 393 321 055 690 399 452 252 546 607 316 493 762 653 389 915 789 647 077 262 225 409 381 566 439 156 447 466 334 734 638 501 656 913 014 953 615 614 284 621 967 561 014 789 012 061 147 409 535 121 912 576 572 503 259 224 336 541 805 521 154 604 398 219 990 225 300 733 767 805 439 753 842 315 061 144 310 100 505 952 177 892 325 565 409 344 523 968 682 798 486 245 192 402 353 520 041 782 219 547 096 550 725 577 624 741 477 449 590 993 090 044 798 595 414 946 157 227 630 171 053 248 229 036 849 731 385 959 444 010 218 477 677 370 891 677 451 109 598 515 056 955 397 633 648 631 341 422 491 892 702 294 566 563 397 567 055 244 813 057 060 245 050 189 052 395 681 509 547 774 747 328 629 955 663 355 170 422 484 741 920 898 402 383 645 905 651 414 007 186 541 607 032 058 755 637 954 450 475 204 153 339 347 599 777 931 638 450 090 896 649 182 391 432 706 969 822 351 619 997 945 360 480 408 816 956 476 937 582 022 403 874 646 315 444 525 710 955 602 742 157 985 102 571 352 600 440 394 133 143 605 820 600 447 051 950 129 495 961 643 861 535 549 852 968 137 744 370 770 925 393 101 597 541 099 664 909 324 447 389 085 705 417 888 132 222 344 509 918 000 099 616 936 919 652 664 419 637 927 156 682 502 591 678 206 518 264 727 742 778 173 572 806 578 811 267 511 289 254 796 369 936 926 256 654 909 596 056 168 449 406 617 609 526 877 414 712 792 255 167 417 937 541 146 593 728 070 157 362 620 181 265 491 572 227 539 634 391 614 131 005 964 153 682 768 506 098 256 927 296 195 703 361 968 773 945 346 689 697 665 256 780 449 186 617 562 506 156 009 851 914 985 095 870 613 119 106 006 457 138 515 307 830 434 176 700 591 293 464 112 787 294 997 492 111 008 061 534 786 405 612 441 622 848 217 040 640 311 194 155 944 724 155 063 069 375 040 758 221 257 359 163 578 298 512 945 350 617 906 800 462 555 218 680 704 921 798 572 182 082 049 940 063 964 663 101 693 310 853 066 099 601 762 106 221 533 152 550 427 343 775 798 416 528 814 576 071 134 398 312 478 094 528 314 809 092 917 774 066 130 449 954 702 749 688 839 896 652 088 176 880 344 752 256 276 839 086 973 125 362 810 106 653 566 736 713 247 300 009 748 913 571 758 434 300 925 721 077 722 702 563 355 143 745 956 312 382 681 461 631 927 550 087 754 794 391 501 760 270 218 071 828 623 006 508 177 992 773 828 997 893 662 746 263 393 297 848 398 313 258 935 695 734 332 750 326 366 397 252 872 904 271 016 675 817 500 818 905 951 690 940 065 201 216 174 803 644 014 383 347 865 273 726 119 512 180 016 606 359 976 674 829 858 058 069 440 879 063 121 345 223 638 318 660 293 310 564 450 697 634 883 817 420 176 529 573 170 309 203 644 612 168 952 458 512 257 132 214 760 399 555 217 794 080 487 840 929 900 405 535 314 460 067 236 560 673 310 554 440 485 909 007 462 025 385 555 066 272 023 486 181 935 817 122 526 282 860 670 642 042 068 628 417 751 206 981 523 536 268 345 381 437 471 947 486 113 468 844 369 393 225 561 555 812 953 496 270 179 948 948 594 993 506 188 247 232 631 828 004 421 337 193 613 007 422 987 812 338 074 225 706 601 310 540 098 850 506 756 202 361 139 332 101 679 652 472 958 870 975 774 351 889 720 183 333 238 259 061 587 414 031 560 904 872 731 779 994 909 958 821 321 488 368 977 580 369 407 123 795 424 831 531 487 725 408 980 848 935 076 129 271 000 237 267 683 571 845 991 318 020 183 630 345 558 861 200 366 998 494 019 365 758 560 397 170 636 283 294 958 821 661 387 488 671 778 168 987 467 273 235 027 755 048 898 017 203 077 290 438 633 256 817 771 893 946 070 439 949 216 056 254 545 640 580 702 019 867 283 061 672 219 058 482 295 239 362 159 969 745 260 423 607 097 089 317 088 676 964 137 798 925 416 454 774 245 652 640 612 161 460 466 156 406 691 816 155 346 892 831 004 743 571 211 417 236 788 746 407 864 426 828 655 516 334 683 195 739 163 635 799 138 977 245 930 848 329 272 834 476 778 496 908 673 464 844 369 872 029 439 165 093 680 280 301 727 552 005 210 536 649 455 324 896 562 012 354 483 923 867 504 579 238 421 895 029 533 158 619 243 543 884 694 104 013 240 442 377 112 388 298 763 145 541 641 511 193 010 978 334 316 535 275 347 823 706 699 888 682 373 111 301 620 436 292 991 947 887 532 450 781 431 111 076 241 689 148 270 907 805 342 392 482 758 926 780 590 086 054 339 326 637 550 279 813 241 936 402 209 056 228 816 341 651 504 460 541 683 238 576 636 641 194 396 171 713 213 090 551 486 065 260 547 426 040 809 404 292 915 687 756 658 475 355 413 755 238 972 453 699 638 552 905 294 434 451 205 320 459 004 910 060 365 940 687 244 402 546 398 244 646 376 762 946 436 852 333 220 558 102 423 313 331 733 840 707 961 857 769 799 506 866 675 549 646 751 717 060 459 394 732 806 948 670 635 033 326 724 617 999 635 077 599 592 862 203 799 804 772 119 886 148 612 546 683 625 231 508 277 885 516 345 549 198 852 917 703 344 742 138 239 112 139 815 945 296 754 238 545 401 199 128 403 698 205 203 455 872 179 382 422 235 827 999 871 030 568 072 374 437 078 369 007 039 458 004 889 981 193 802 418 917 515 079 939 149 106 645 366 524 196 297 788 444 743 397 556 357 859 013 778 610 650 690 110 707 622 765 555 536 089 837 268 376 310 481 209 783 142 600 005 425 563 603 774 165 262 278 181 878 961 666 243 866 483 856 592 718 779 972 068 002 386 561 514 888 444 278 637 422 096 814 902 805 396 765 699 342 717 711 237 756 746 501 024 195 145 711 117 243 652 199 616 104 389 625 042 518 428 075 866 410 586 055 512 014 921 417 511 309 521 185 382 043 785 612 898 896 273 617 314 558 868 737 236 594 851 843 693 181 112 850 365 120 882 741 661 961 185 615 963 319 699 837 059 134 927 246 882 664 674 374 957 368 347 262 126 693 525 193 594 504 766 917 087 654 016 012 131 575 224 634 172 897 350 851 858 385 972 483 736 671 777 888 128 297 855 286 529 328 985 628 690 338 836 809 757 188 154 356 060 891 546 584 950 010 028 069 073 554 595 802 267 238 143 353 348 553 861 942 777 475 689 640 877 448 111 235 633 245 430 548 850 512 397 459 498 581 385 786 520 386 034 831 203 610 631 565 966 927 973 490 371 061 018 552 218 291 639 354 635 860 701 035 193 270 053 818 817 004 637 694 470 687 090 204 061 459 444 335 651 820 654 328 749 947 018 569 150 988 949 461 804 928 635 878 607 885 931 044 116 183 364 035 641 556 112 794 724 663 967 409 090 361 019 496 862 351 991 085 178 507 682 206 731 530 909 597 345 649 401 432 276 326 494 975 084 301 379 301 568 257 684 267 099 619 864 836 424 258 392 447 806 846 836 865 764 440 391 168 221 625 268 993 005 177 999 004 628 370 385 133 739 983 163 063 662 340 812 304 725 759 714 447 864 555 146 626 869 595 126 628 382 461 192 905 019 376 454 127 261 009 208 729 359 662 709 117 224 657 555 043 479 524 149 644 925 167 836 702 597 009 942 617 554 756 709 533 521 485 931 137 903 096 440 018 544 486 738 023 363 005 648 488 084 331 096 066 252 849 227 479 603 322 343 172 761 711 287 920 395 042 769 706 903 567 240 300 729 248 543 615 640 465 693 130 538 155 012 235 610 238 448 429 072 384 657 519 288 134 786 966 954 989 642 774 632 533 281 687 803 238 917 067 828 766 278 442 614 594 592 134 671 481 540 885 578 669 212 618 231 063 236 627 588 758 317 577 193 636 221 250 621 430 495 468 488 219 775 093 678 074 652 392 714 922 362 653 456 427 893 464 613 275 328 698 692 193 947 734 831 079 141 512 511 831 010 709 719 478 415 970 623 787 717 826 527 994 188 606 945 203 321 237 532 606 847 545 894 641 514 284 120 173 383 387 422 707 852 083 690 197 872 550 541 066 569 411 501 887 642 716 658 492 387 694 690 884 964 952 279 500 402 290 029 352 625 006 943 611 904 979 098 523 353 789 725 200 174 182 708 380 493 574 581 775 698 393 724 236 161 676 112 107 767 462 924 996 937 339 555 923 578 547 062 798 131 972 261 508 281 735 736 410 530 709 770 852 697 209 710 695 162 392 550 517 447 890 677 855 616 505 088 989 657 931 407 614 629 860 337 514 746 416 271 035 247 438 358 019 362 815 646 639 511 269 218 315 765 047 041 041 855 857 223 263 707 457 520 209 742 404 056 673 899 374 862 472 902 744 562 738 066 885 905 456 641 731 595 579 531 768 846 157 935 367 466 430 372 845 254 399 689 005 832 051 784 753 597 297 241 957 795 184 895 626 811 034 507 192 889 798 053 589 569 591 211 736 369 838 546 516 322 403 269 790 163 644 096 654 560 846 303 375 078 374 337 392 798 594 047 766 527 206 035 482 143 017 193 873 213 379 573 426 142 482 754 734 904 162 818 575 726 232 916 554 223 389 293 902 933 984 104 735 283 567 527 994 291 210 289 933 265 685 860 568 248 379 879 002 348 693 221 531 753 801 067 356 633 761 634 604 688 032 182 891 330 440 434 631 417 953 638 304 608 670 747 931 455 704 934 074 862 468 278 257 464 403 114 688 329 489 614 685 463 031 055 986 348 294 845 405 313 806 643 522 621 493 731 970 156 870 082 069 279 522 326 506 803 900 672 822 545 797 397 270 879 118 993 374 505 600 076 474 381 471 023 480 655 225 171 211 136 994 851 041 264 963 251 179 790 304 962 865 620 520 984 993 527 752 250 945 257 633 060 164 676 147 995 741 622 898 292 868 663 939 375 950 213 183 886 336 292 036 138 586 866 300 725 394 814 016 657 095 097 188 056 150 186 773 998 642 002 549 388 576 145 156 182 249 760 318 926 238 542 674 409 961 239 283 673 835 069 369 269 237 578 929 637 026 664 296 402 268 462 411 493 944 968 905 987 705 497 026 414 146 794 418 020 051 198 316 820 704 534 378 663 931 322 462 945 600 772 439 949 572 332 702 548 553 655 256 286 793 630 185 193 224 615 765 131 843 504 158 565 069 311 786 369 971 046 345 890 158 865 848 921 475 471 152 506 285 604 594 447 927 249 426 932 031 850 786 248 381 975 121 120 239 262 118 823 665 046 286 098 502 641 320 257 710 707 127 591 112 335 566 443 941 508 489 602 737 715 549 765 969 970 064 340 684 051 274 944 935 116 087 132 100 982 643 724 252 558 910 928 984 078 605 910 778 869 912 827 850 178 530 759 813 835 884 199 972 788 403 271 302 151 833 412 725 905 477 715 882 723 789 722 759 670 376 924 678 346 478 275 498 631 368 687 252 851 441 843 628 457 223 721 293 579 995 763 062 675 971 531 489 710 432 431 434 773 383 917 547 927 172 404 165 405 866 604 588 444 486 384 717 867 570 878 627 197 466 394 446 256 549 361 014 940 931 745 976 980 958 656 751 051 954 626 125 108 207 139 072 180 477 372 979 727 831 788 061 017 114 493 782 920 554 617 772 805 600 872 816 106 506 283 113 080 847 962 899 293 620 922 887 524 194 002 146 859 615 967 828 890 347 500 808 440 835 525 022 490 684 623 909 972 858 888 807 749 910 799 839 781 832 432 207 371 811 923 112 847 358 237 310 785 861 914 408 772 780 580 386 057 034 300 142 828 709 784 243 456 898 199 967 264 866 395 626 317 840 538 627 243 144 629 283 971 471 353 160 794 058 814 367 135 297 515 000 429 198 032 733 222 250 359 572 386 245 684 692 117 063 195 718 455 151 553 485 262 239 736 045 653 677 098 226 162 246 778 936 616 874 033 690 670 755 660 361 027 052 518 190 960 847 246 025 731 618 320 707 522 124 488 903 182 470 449 865 771 122 759 728 687 272 330 110 583 259 554 467 368 275 237 738 574 803 839 544 409 583 891 246 493 800 661 702 911 382 262 304 844 493 902 941 347 422 168 740 004 743 640 117 841 230 922 041 702 816 243 544 340 892 879 150 740 910 276 398 745 617 597 109 330 166 470 542 251 196 023 367 415 125 873 152 606 908 733 935 222 201 626 760 099 340 707 413 813 139 211 593 912 557 061 694 911 065 537 481 339 054 905 300 834 185 667 774 205 833 039 369 270 300 323 962 115 779 371 593 370 753 693 045 233 021 543 351 099 516 047 101 790 578 555 596 802 079 160 190 331 095 594 133 168 142 500 097 876 181 576 347 628 671 965 466 939 161 599 871 304 478 385 336 838 702 576 780 189 671 332 225 218 786 931 544 359 884 707 495 610 979 315 254 027 592 336 349 509 997 471 938 418 604 477 462 862 550 479 775 410 853 476 167 417 437 579 906 095 455 563 293 013 703 330 013 899 200 161 432 721 204 917 955 102 959 233 942 149 161 253 073 335 838 824 036 866 323 397 320 412 823 332 055 618 279 082 398 661 421 046 168 467 883 847 903 872 378 143 437 795 333 197 188 872 501 464 614 271 514 711 393 313 874 545 387 073 491 382 177 262 819 832 500 401 035 896 481 222 351 494 572 749 457 515 614 695 505 958 809 094 641 949 373 112 433 113 835 266 099 573 934 902 147 751 702 668 230 651 980 335 062 898 950 052 139 059 845 926 153 763 201 941 467 435 424 797 672 414 502 904 219 072 342 664 738 923 954 561 264 846 037 604 362 881 475 108 541 451 938 599 823 404 717 186 625 262 485 181 672 182 599 852 078 319 203 328 144 574 680 395 352 116 240 337 852 957 658 191 626 905 749 340 490 381 432 721 298 746 403 543 215 743 965 170 788 657 606 233 932 479 594 203 678 881 792 552 053 100 151 432 102 915 946 514 612 072 680 213 239 526 108 030 208 393 129 647 629 595 360 314 708 702 395 123 682 295 209 388 809 740 541 286 147 571 205 702 477 740 814 326 388 129 082 358 725 054 254 539 472 930 869 253 782 824 452 533 605 886 589 777 711 484 119 522 006 177 849 389 284 075 214 061 884 326 987 453 945 911 831 159 061 853 941 951 439 388 837 301 250 486 871 463 217 134 157 150 260 751 222 702 494 052 821 166 470 952 382 584 990 958 754 396 850 147 438 851 893 312 769 361 481 480 803 083 023 722 404 109 637 876 120 772 402 895 425 150 397 835 720 953 466 854 686 267 743 411 998 347 542 765 570 428 873 105 595 194 669 685 931 446 129 312 997 695 521 190 094 013 753 360 836 223 673 311 935 840 735 922 899 008 523 258 770 388 980 609 580 815 150 825 149 128 175 533 299 920 423 092 842 121 707 861 927 567 291 666 244 144 057 756 782 430 670 446 783 085 022 575 684 524 027 715 790 934 183 531 820 004 466 923 893 688 238 556 870 024 803 269 038 781 078 853 397 558 758 330 433 072 134 310 228 748 290 383 825 582 108 273 467 113 636 737 404 507 613 614 748 192 301 364 109 103 818 870 936 620 042 604 234 945 143 026 488 545 588 403 512 641 977 452 731 924 961 323 719 368 465 529 047 492 318 918 345 633 041 928 783 629 592 595 967 625 051 793 994 519 935 063 248 781 185 449 286 180 716 388 021 822 721 974 621 402 143 765 371 279 935 615 896 187 847 520 321 414 701 498 183 811 522 568 334 851 187 420 067 778 731 620 831 471 741 969 934 863 066 190 644 595 013 892 557 542 876 821 989 482 363 964 794 273 834 818 226 777 086 910 196 287 299 932 562 407 780 917 697 392 354 020 864 958 265 509 405 654 425 781 023 730 949 083 804 515 470 870 124 932 949 627 963 361 348 606 122 031 036 565 104 931 807 585 601 779 631 671 618 663 897 877 422 290 146 286 789 030 599 965 323 752 837 545 812 360 312 208 010 211 625 571 338 952 538 482 699 788 225 501 543 598 695 994 969 641 349 797 433 283 259 717 537 409 888 621 794 296 148 012 343 911 956 807 150 672 226 677 280 654 782 530 544 626 725 400 459 660 495 817 886 728 927 128 856 364 912 594 858 460 376 338 121 934 311 027 881 419 245 939 699 169 822 056 224 005 438 504 409 394 389 813 730 799 877 952 374 722 484 166 391 872 784 375 683 246 469 644 145 803 216 371 890 106 758 936 955 732 451 574 765 468 601 095 910 939 568 727 262 446 595 327 211 215 072 354 386 678 369 937 152 128 273 261 647 291 173 498 990 155 803 494 300 776 801 435 344 815 382 015 033 817 231 771 013 865 126 341 480 244 249 175 240 349 327 758 213 400 130 128 800 964 101 135 742 987 232 884 683 496 400 067 226 710 837 109 135 924 884 320 882 919 011 719 937 428 619 002 872 928 523 417 366 241 996 567 456 910 357 981 752 054 642 819 335 395 966 298 697 060 143 733 075 303 970 838 645 743 679 108 110 295 921 316 349 885 090 984 226 295 512 209 573 738 017 977 000 129 410 749 196 534 246 471 824 028 448 112 006 208 259 302 519 149 473 754 214 648 180 838 287 727 005 261 525 517 732 617 325 722 673 656 400 686 107 368 403 099 985 242 633 056 915 967 566 379 989 010 947 682 339 774 776 223 873 994 317 237 763 902 814 025 718 492 356 692 875 176 441 987 951 319 988 126 262 594 700 799 309 242 326 647 581 490 493 812 345 080 644 257 317 145 550 205 302 598 180 804 681 651 160 350 813 427 287 474 887 338 533 918 894 477 572 813 042 142 090 329 769 046 789 823 544 202 438 640 302 621 872 230 403 299 255 951 270 275 826 119 233 033 013 992 114 926 021 396 155 297 258 459 632 286 136 351 010 916 914 450 813 144 104 032 466 632 397 454 033 344 177 917 063 422 923 020 591 039 486 625 958 961 844 043 345 941 930 627 929 112 259 694 052 067 226 968 307 324 945 635 735 159 375 012 507 962 846 559 002 391 562 440 531 337 585 155 258 510 143 648 920 045 026 777 388 706 691 506 401 158 992 168 436 512 179 429 751 288 756 758 318 652 781 169 535 812 588 600 682 025 074 766 309 664 915 492 657 696 535 420 797 372 738 949 968 241 692 248 790 106 420 479 878 131 788 776 540 946 942 041 604 988 621 230 728 907 393 532 426 134 210 432 663 528 441 016 165 687 414 701 197 481 725 242 743 615 985 514 911 005 238 260 811 567 352 589 590 229 146 856 432 752 045 085 608 192 561 430 012 212 946 658 946 518 903 597 001 687 069 171 210 179 165 918 431 726 774 218 989 461 632 273 262 348 171 874 979 168 182 949 589 637 897 286 690 036 596 326 182 117 524 798 461 344 099 721 142 649 695 768 439 622 529 913 321 110 856 837 929 298 949 149 142 672 020 087 631 303 114 602 126 511 731 546 318 167 347 951 213 845 571 268 980 266 269 187 137 803 183 770 423 525 254 944 494 754 143 791 828 542 187 711 233 278 560 485 901 611 234 823 496 043 164 240 404 424 825 602 941 731 064 265 706 785 309 950 974 349 857 891 982 226 515 528 501 047 969 184 133 836 351 673 780 458 919 205 452 362 064 521 712 584 296 065 698 600 570 814 787 050 791 059 728 130 947 244 249 605 593 283 197 653 958 751 558 081 905 035 123 957 442 848 092 679 545 336 525 911 565 301 617 049 459 677 466 323 679 109 010 061 377 799 547 275 781 910 664 903 025 679 009 841 725 015 161 718 259 439 900 803 362 147 299 098 672 223 333 700 261 368 890 295 217 153 839 049 429 973 503 409 252 809 176 509 073 411 701 370 488 320 468 145 429 931 655 466 171 591 529 115 348 238 260 959 119 012 977 417 425 165 740 697 437 891 099 041 863 422 004 865 071 218 753 492 402 442 074 623 836 766 231 536 754 082 066 079 167 248 985 921 865 226 949 206 830 481 001 536 225 750 972 205 987 722 264 027 418 384 934 413 278 779 196 798 535 997 385 095 993 661 100 771 297 353 121 921 142 389 651 467 530 669 312 818 034 899 575 599 787 400 228 370 934 311 724 913 082 733 402 425 198 068 937 722 127 668 072 007 004 994 679 123 598 223 015 717 046 087 204 984 380 974 836 766 500 222 885 409 607 425 062 276 579 086 767 531 737 541 784 902 911 707 907 256 434 845 823 688 925 018 288 832 409 781 715 825 909 193 861 259 317 425 301 675 986 467 006 604 246 653 763 687 774 650 795 899 653 627 177 180 874 533 514 332 403 458 900 297 995 114 341 688 252 176 454 938 397 385 081 984 795 909 962 217 656 005 639 093 141 862 444 201 525 200 182 807 963 894 395 751 447 134 490 233 545 315 882 590 093 469 586 990 017 853 582 106 974 426 195 202 140 039 472 721 942 921 483 570 863 896 291 947 871 404 474 175 905 188 486 990 090 828 380 539 929 278 731 136 607 788 917 579 885 623 717 136 463 628 877 873 394 238 594 278 746 338 609 397 157 398 057 739 457 059 918 775 829 288 013 794 808 796 222 162 769 887 115 178 564 229 213 571 927 526 346 013 796 489 331 287 264 070 207 075 656 984 638 783 170 579 670 521 034 245 691 667 859 384 334 079 608 592 387 048 848 364 629 909 295 729 552 975 778 597 229 769 875 062 489 793 003 094 151 143 653 607 701 169 177 735 610 088 684 825 250 533 060 010 288 540 015 629 935 753 627 415 137 301 501 728 762 829 471 911 363 595 158 683 625 350 347 478 323 686 866 430 786 598 498 190 009 028 844 065 112 026 890 351 567 834 535 843 035 040 662 910 095 162 404 782 973 440 763 835 195 414 751 664 495 485 639 781 192 750 002 907 218 618 029 678 142 599 498 470 455 402 124 148 734 788 983 202 851 331 623 582 148 527 094 055 829 898 162 563 954 063 738 850 106 664 212 694 722 786 235 756 016 587 977 589 621 900 918 137 083 380 462 682 952 440 739 829 234 012 459 616 120 810 269 708 557 035 438 488 025 023 331 117 913 032 198 577 837 321 242 568 817 894 632 275 031 194 287 396 934 837 548 516 322 467 120 056 093 574 811 208 091 306 394 964 141 272 347 612 585 033 569 914 552 032 233 639 882 644 135 553 913 682 728 053 520 032 547 935 325 967 095 371 158 366 741 943 649 280 053 986 517 503 410 056 974 366 830 125 991 746 080 357 327 391 085 516 920 534 159 052 673 352 256 103 799 602 477 675 692 902 985 837 546 906 326 863 946 923 236 872 258 663 504 780 986 112 130 816 000 451 045 753 723 797 986 963 503 370 797 544 599 237 057 270 855 154 839 438 704 538 167 379 724 398 225 732 776 834 258 170 348 047 152 468 404 204 374 944 232 218 440 983 508 999 432 593 077 546 423 940 770 159 178 954 706 403 195 695 748 148 733 136 818 267 997 111 063 866 388 363 582 115 491 871 058 595 755 635 365 649 925 943 528 496 399 630 298 113 156 794 262 006 333 724 072 136 430 322 340 502 561 833 843 346 301 301 566 970 015 957 077 972 500 401 803 613 974 416 516 524 820 559 393 832 135 038 370 036 444 494 206 146 110 785 771 929 096 484 992 022 637 866 299 643 772 512 395 503 335 559 290 610 407 619 234 380 610 179 064 760 289 699 364 007 162 875 919 496 121 683 204 102 168 258 238 676 860 759 445 841 491 655 966 026 588 248 171 246 513 099 864 639 970 880 882 736 866 225 038 270 136 123 338 312 528 120 536 450 164 514 751 996 267 081 374 312 196 824 461 380 682 590 343 024 193 387 932 658 838 818 703 261 961 520 916 842 632 680 442 345 343 094 831 201 081 001 255 464 084 347 535 784 148 619 272 527 954 791 371 433 149 244 503 344 415 381 043 045 077 208 171 751 379 699 800 046 423 594 728 412 415 764 628 138 303 854 003 597 284 407 870 771 256 931 760 280 110 616 518 838 887 621 753 853 132 023 174 518 998 487 064 897 831 902 888 128 370 933 748 318 595 950 122 968 522 005 284 384 194 779 093 509 037 619 131 103 867 561 458 435 735 580 044 389 127 199 145 637 261 028 877 847 290 859 874 098 858 408 739 944 928 649 225 990 286 563 797 365 850 732 990 085 324 673 590 369 465 042 919 094 687 820 484 190 383 778 844 156 715 841 861 640 141 831 422 119 592 519 089 539 517 808 796 344 592 273 012 604 989 194 119 555 942 389 925 506 293 861 181 859 029 286 005 078 540 392 168 606 121 898 923 059 921 814 925 606 791 533 084 240 712 888 839 186 860 176 834 734 102 720 335 375 645 127 951 939 248 095 554 624 610 318 274 851 616 822 896 325 289 598 525 975 422 790 187 992 185 993 470 248 115 382 163 796 932 816 093 041 683 723 308 569 510 954 017 809 113 332 261 086 267 338 347 194 175 681 108 470 864 897 702 469 158 432 805 023 677 703 635 212 275 794 914 852 634 911 410 424 252 224 496 500 393 697 559 524 614 993 045 580 602 454 365 844 778 200 409 930 515 708 718 530 192 965 535 533 716 674 112 736 811 871 749 772 500 155 581 561 513 472 904 561 238 696 108 316 066 460 485 397 179 260 912 782 902 903 310 353 614 524 168 364 169 105 788 307 371 927 108 496 186 246 868 128 749 071 691 395 045 636 358 716 649 322 318 197 902 793 364 086 584 900 434 182 958 178 724 466 358 936 995 560 516 505 553 963 247 897 861 114 130 840 228 736 568 402 369 022 739 034 955 501 748 364 325 617 367 062 609 873 144 088 881 050 523 330 094 383 963 024 698 715 842 323 086 332 449 653 865 973 054 469 873 049 638 005 543 636 301 818 158 961 604 910 841 067 889 146 383 396 817 274 613 456 568 996 828 412 917 414 605 033 947 211 014 535 927 780 475 973 125 967 580 314 127 299 826 575 142 797 202 437 913 366 410 823 680 304 936 423 286 811 124 146 752 521 511 350 832 853 221 584 919 624 161 347 825 086 044 058 150 053 509 053 091 966 119 019 732 219 670 061 358 534 845 092 983 152 160 938 040 606 303 167 628 488 396 320 122 298 238 246 278 440 291 543 181 504 874 400 219 448 682 180 773 076 083 048 843 743 497 701 122 127 451 209 004 567 113 061 220 998 529 017 871 534 874 994 325 422 660 291 250 671 150 874 155 680 348 273 752 873 729 868 040 640 972 651 092 473 781 051 114 554 247 764 435 270 889 102 989 828 191 029 006 294 099 729 101 838 516 553 392 580 450 489 322 239 625 036 843 272 127 641 931 700 296 817 671 416 029 394 719 670 784 208 205 921 282 758 369 568 921 098 449 834 523 774 712 796 641 342 761 111 781 513 545 202 258 493 590 583 705 455 131 764 713 190 337 376 384 524 772 541 269 859 217 663 889 616 056 219 919 102 793 626 336 320 677 477 717 121 552 547 926 903 085 992 817 619 934 657 014 798 076 128 201 459 575 940 231 790 533 538 064 168 593 967 411 831 301 942 085 964 622 682 087 604 793 915 135 066 904 457 621 603 960 186 209 104 100 501 839 138 559 317 864 916 065 736 725 679 982 589 450 073 524 249 452 979 746 547 153 826 403 428 571 107 198 899 450 163 743 591 824 027 593 000 792 463 245 870 942 902 419 919 902 163 471 478 393 649 075 518 976 485 231 001 263 305 252 377 882 138 457 905 425 980 029 237 841 908 475 185 364 241 393 210 947 761 163 495 232 664 482 883 641 206 974 132 403 308 728 605 814 277 836 163 374 641 788 373 731 513 607 607 511 052 841 490 169 737 614 846 184 756 266 356 235 255 016 021 306 550 280 059 884 499 327 052 644 640 511 730 495 472 394 688 774 244 537 230 628 450 942 315 765 773 901 364 494 518 886 820 782 087 829 996 227 573 642 659 085 879 229 464 448 656 904 334 627 127 398 948 416 745 801 832 695 376 004 162 871 318 510 653 832 313 793 668 985 124 310 554 718 243 495 571 778 372 468 281 979 795 656 768 845 781 209 596 668 406 577 497 745 975 303 001 448 911 189 495 465 853 751 796 882 939 658 294 823 175 413 225 220 526 479 636 613 217 064 746 427 376 579 656 401 974 576 902 489 787 120 104 845 425 994 202 408 635 020 792 961 428 690 732 688 271 916 873 629 433 484 833 325 059 933 476 126 695 744 043 468 397 504 562 031 690 805 823 580 259 619 245 211 673 774 473 566 502 982 045 580 093 980 536 651 470 747 120 327 148 517 053 784 939 220 894 506 132 067 890 224 903 335 288 445 965 329 274 211 450 906 892 124 348 087 921 549 741 434 194 582 873 462 217 681 820 455 623 421 298 564 133 047 256 147 887 430 176 530 332 966 709 398 099 585 239 227 670 572 042 600 731 334 579 521 358 806 166 127 420 305 203 145 979 861 877 196 670 106 693 347 417 378 139 435 449 651 996 843 155 644 173 704 581 046 515 517 528 530 410 185 266 091 701 172 624 923 898 531 322 974 663 769 307 280 917 487 589 392 928 833 146 764 574 352 643 706 047 426 143 193 158 791 381 850 404 877 858 688 464 451 108 076 701 679 132 819 294 755 053 172 899 379 873 871 490 706 660 467 686 474 952 213 233 987 373 413 378 952 200 460 895 634 138 287 340 109 993 482 067 950 483 536 890 367 609 055 192 515 161 380 974 332 040 054 390 485 485 796 940 895 234 128 345 643 122 404 506 028 951 532 549 419 214 851 435 672 868 761 823 367 200 254 876 671 617 659 191 248 944 763 221 436 295 575 539 743 394 736 243 139 620 964 615 140 218 794 019 078 496 799 532 273 096 214 452 097 359 858 151 034 055 516 056 518 931 581 454 841 019 216 889 598 817 507 631 018 721 090 803 399 454 078 889 506 429 452 158 024 175 121 570 314 843 781 350 889 824 796 013 526 663 656 233 785 804 993 465 141 402 955 743 233 450 374 815 415 243 574 814 926 426 961 127 358 499 257 336 033 366 457 262 922 275 690 348 498 379 990 902 714 698 048 568 914 605 787 838 166 075 732 660 688 059 728 603 191 220 771 882 057 196 376 579 314 463 111 287 119 335 764 318 270 398 653 001 159 504 349 093 606 135 364 451 039 610 237 024 276 667 100 416 105 081 961 544 004 499 480 281 200 754 525 319 306 711 459 147 196 131 660 374 153 438 844 675 936 882 589 151 052 712 627 114 853 526 301 567 869 368 261 715 156 540 627 590 589 886 061 837 774 568 153 176 426 851 573 511 275 430 036 002 323 153 491 184 441 527 891 056 078 004 988 775 236 907 659 055 603 691 516 711 005 331 261 804 935 201 784 442 694 580 652 598 874 247 831 845 375 203 111 339 621 609 761 648 786 217 432 752 749 354 579 701 517 134 247 511 486 397 146 959 118 224 109 166 602 182 060 566 229 134 934 936 389 943 436 618 579 481 785 402 024 694 345 712 153 992 082 969 838 451 285 094 489 601 047 847 558 427 538 883 931 929 293 034 366 158 553 658 237 348 250 801 819 124 459 244 032 941 964 614 680 608 838 699 615 791 028 445 889 268 695 344 374 272 760 697 476 256 135 564 442 720 488 026 833 732 224 144 446 687 893 655 188 963 285 723 723 696 685 901 021 388 212 761 472 216 468 187 916 618 072 727 408 865 113 186 778 905 753 287 837 032 229 283 508 321 403 762 369 436 449 944 643 743 738 755 992 963 807 990 942 914 253 019 072 771 678 076 612 588 571 025 794 814 163 052 985 316 389 022 991 838 205 506 193 493 832 504 899 062 435 677 690 804 832 071 063 877 849 490 323 398 766 513 971 762 831 738 561 563 625 973 118 198 914 638 325 833 142 123 691 404 162 043 126 951 152 705 494 428 823 848 994 992 044 092 288 552 447 533 692 700 153 581 330 419 438 565 650 753 621 550 247 004 690 474 926 726 702 620 257 668 744 322 191 773 861 090 339 600 844 022 609 579 793 440 931 924 227 442 346 140 000 490 507 857 178 089 299 938 508 074 652 770 260 940 887 878 583 408 665 781 522 010 232 239 799 836 702 280 410 194 088 402 551 897 137 086 289 019 661 183 362 056 139 596 387 391 582 037 106 426 394 112 840 737 323 546 467 552 331 444 577 579 926 346 426 826 277 412 070 832 814 881 314 433 610 293 661 836 162 004 444 956 255 249 301 386 489 027 346 758 481 880 902 520 251 518 053 152 541 587 550 252 967 067 575 632 442 627 142 636 377 101 124 881 756 301 888 560 872 327 517 890 689 770 458 646 802 847 852 513 228 622 481 087 767 386 830 889 877 720 702 944 568 029 852 061 298 394 165 781 088 154 083 519 659 796 429 172 968 712 916 797 875 278 928 302 026 916 598 757 923 914 675 234 907 451 053 242 179 370 666 847 185 841 173 849 182 160 883 686 643 821 118 259 385 470 468 551 486 784 706 815 919 139 733 144 740 924 270 184 774 896 276 023 374 357 616 831 107 321 776 781 226 184 214 436 969 110 478 252 413 227 446 677 408 400 797 522 158 202 963 396 523 092 680 421 203 514 825 183 149 731 597 466 066 034 573 500 019 434 357 611 710 534 380 696 357 241 081 121 410 255 658 222 727 120 858 870 798 313 908 857 665 172 187 779 513 993 744 626 020 354 012 626 136 674 280 183 286 519 467 108 998 792 105 116 027 405 632 631 919 215 227 638 054 454 727 071 824 500 385 866 066 303 186 380 801 537 910 497 910 322 567 284 021 098 019 857 396 116 597 217 762 060 379 971 284 216 950 912 862 069 005 093 788 612 141 291 020 887 388 670 714 135 817 459 884 240 210 201 646 442 380 805 855 567 457 811 394 755 394 847 946 899 398 949 105 232 410 418 823 736 692 637 355 398 809 756 923 352 899 554 385 819 639 932 199 034 920 196 924 579 734 360 372 314 574 204 639 783 462 973 311 812 999 796 865 098 975 061 413 116 868 976 623 478 588 053 268 061 628 717 666 071 475 508 886 561 976 757 862 156 477 041 525 828 024 943 054 701 183 404 323 598 911 890 152 344 399 399 316 247 929 497 231 066 477 026 121 630 080 302 300 084 753 422 703 531 693 018 194 080 561 665 802 045 398 774 304 046 749 084 972 678 889 633 898 951 601 528 484 813 406 288 291 963 178 149 751 503 913 670 118 128 907 699 481 972 942 392 663 209 734 923 549 644 738 959 639 746 775 571 733 601 973 007 765 036 088 000 396 529 762 085 951 394 296 389 553 310 423 309 865 100 923 434 782 412 120 129 167 232 703 718 916 283 204 406 623 137 068 888 097 828 188 687 647 571 916 621 606 020 916 636 332 156 089 720 813 565 714 172 379 314 527 307 369 047 908 421 196 557 749 703 607 685 663 791 418 892 202 648 181 478 634 724 331 226 140 813 297 290 929 697 863 531 967 525 299 097 700 321 789 158 025 900 741 791 779 466 791 981 902 308 901 923 256 124 821 694 356 777 825 249 263 908 618 218 528 480 446 660 758 251 487 708 286 091 998 615 003 829 463 750 222 826 122 174 508 281 935 114 580 288 843 782 306 582 416 517 065 827 117 390 172 693 167 054 137 485 497 401 142 600 631 668 205 647 386 385 790 365 316 046 542 911 768 232 163 095 347 765 949 411 047 428 595 545 738 072 300 976 750 740 717 041 128 582 074 646 490 620 842 749 499 463 556 086 933 626 446 210 466 364 313 588 421 217 919 468 514 300 598 520 075 369 157 638 829 491 111 709 619 760 436 251 986 348 599 344 708 817 257 847 865 389 022 644 045 409 711 880 653 380 165 483 174 713 123 802 858 997 925 364 448 999 192 017 359 853 481 170 863 984 072 942 201 831 969 881 544 151 868 186 748 589 624 388 516 065 034 363 025 053 768 165 569 499 564 992 766 286 945 901 924 692 645 425 785 347 106 129 539 324 757 098 105 903 197 301 312 890 639 844 032 440 664 210 559 386 356 361 573 146 820 984 652 035 893 104 143 584 927 718 383 059 200 043 734 691 439 127 026 565 560 775 475 511 878 150 304 084 395 384 724 369 065 361 819 067 706 410 265 126 328 624 536 387 286 647 215 368 727 484 334 723 532 025 846 435 974 117 511 721 755 715 483 964 894 309 073 581 616 710 591 044 459 976 294 179 958 610 022 671 742 998 430 541 725 195 520 303 660 765 482 142 894 905 687 107 517 629 828 606 965 814 181 614 306 615 651 307 522 800 890 855 807 794 081 429 388 212 715 177 363 637 312 409 122 229 826 664 696 853 500 611 921 635 983 033 569 409 551 438 161 453 540 488 393 312 547 413 002 340 185 937 241 682 684 798 507 692 931 105 150 089 906 813 475 086 690 808 141 294 645 662 553 877 903 342 734 820 954 633 061 186 452 552 735 836 595 290 361 872 213 238 708 444 251 975 283 450 376 758 187 158 171 771 511 231 552 480 345 320 384 718 330 041 886 661 408 920 772 699 571 174 771 818 514 787 169 294 129 410 661 463 046 421 459 594 268 127 753 891 427 643 730 370 313 258 686 081 198 453 842 903 891 979 748 334 280 936 133 894 341 068 951 803 153 570 794 717 617 504 451 634 062 961 440 010 183 399 902 311 807 967 155 608 735 417 141 993 552 331 358 567 444 432 668 745 905 389 160 013 415 026 436 802 573 078 039 828 571 320 521 589 554 907 561 907 509 428 897 260 579 543 629 793 676 269 734 855 624 820 085 918 443 756 999 288 535 018 078 270 593 602 011 052 085 885 891 872 261 926 968 234 430 621 831 988 832 891 152 009 167 242 525 646 660 022 873 533 806 020 756 369 550 705 802 478 616 267 009 912 389 706 956 425 629 462 698 468 037 926 083 673 183 750 870 214 870 497 225 006 287 742 182 549 740 703 032 604 641 620 417 189 271 368 095 838 185 433 376 568 938 628 334 257 813 265 557 265 774 170 702 461 688 280 498 660 217 092 851 361 814 099 599 524 703 533 073 823 374 564 332 064 586 093 788 846 293 595 124 538 163 225 934 587 022 570 369 302 600 091 307 198 311 613 769 335 394 514 734 611 002 487 603 224 089 647 551 561 603 045 716 351 899 869 673 495 354 997 863 454 927 648 862 241 587 476 884 101 611 126 854 212 607 594 731 866 145 343 047 323 730 476 005 616 986 782 357 247 981 142 401 677 279 498 116 467 045 127 212 060 038 140 600 697 982 981 478 218 351 587 138 759 254 121 842 827 528 031 640 085 359 407 236 889 459 739 043 759 288 924 619 547 484 286 308 644 567 253 722 398 523 731 840 634 227 541 330 919 038 652 198 904 701 001 072 063 115 767 425 757 547 724 206 762 300 436 019 047 100 379 630 206 152 117 051 783 869 564 853 740 559 688 879 441 703 879 393 520 862 595 440 577 359 381 678 077 015 056 979 361 888 168 747 399 466 853 803 325 061 139 431 157 961 487 553 368 890 812 348 050 685 884 450 088 604 220 383 176 692 540 821 030 285 637 469 437 228 105 807 125 932 316 210 751 822 333 704 596 369 065 074 209 413 691 478 428 322 304 452 765 619 678 748 186 484 921 108 064 539 261 645 880 523 113 238 915 433 657 080 563 568 779 773 070 323 305 008 770 086 043 041 953 086 006 403 237 284 504 442 740 625 699 355 670 422 691 998 045 336 956 344 086 163 468 265 172 607 027 870 148 982 257 394 291 337 280 339 601 436 637 266 768 490 911 093 274 339 177 026 813 226 565 113 282 176 094 059 083 684 847 521 808 640 417 198 325 179 923 216 802 332 487 923 142 771 064 183 671 623 041 835 774 801 701 767 970 261 204 005 034 480 857 513 135 904 303 031 227 886 882 172 400 612 283 812 036 173 094 637 391 693 049 015 106 538 878 123 772 982 685 123 296 743 926 649 675 914 513 193 578 915 786 672 346 834 761 277 741 701 216 691 897 777 985 097 863 542 686 459 728 646 783 411 109 862 011 248 758 050 095 820 919 151 787 304 219 738 507 350 008 485 577 727 378 138 122 494 715 923 585 196 303 441 821 200 166 082 555 670 080 519 470 891 611 957 989 234 108 938 718 813 461 953 602 111 761 573 877 863 160 773 426 770 362 185 188 391 818 407 722 648 980 551 468 613 308 307 182 133 551 810 091 295 441 340 171 637 592 609 471 352 393 147 460 651 533 923 491 232 581 471 953 543 077 773 472 737 629 709 018 508 005 514 804 327 239 834 745 207 302 351 238 581 226 813 269 837 198 871 052 602 004 089 302 317 871 241 595 209 189 225 817 697 787 099 918 087 523 135 330 478 812 781 033 337 393 917 762 386 159 316 538 149 364 502 890 165 449 176 088 248 686 808 295 524 488 639 862 514 841 067 259 336 843 034 784 674 352 545 695 502 948 576 840 155 747 365 066 177 149 250 209 178 695 216 263 533 016 904 790 084 951 851 774 904 895 036 488 239 945 830 013 384 716 616 577 043 424 249 990 489 990 884 863 467 056 193 604 533 738 440 201 243 918 855 103 572 388 402 478 649 965 248 655 202 859 485 619 018 071 826 081 910 816 975 913 867 928 204 092 053 539 609 878 975 072 968 181 294 174 994 351 660 158 463 301 455 997 340 966 268 002 267 947 557 315 394 008 088 858 824 502 072 813 381 431 209 465 692 595 524 685 576 090 740 941 782 137 898 337 543 986 858 691 277 694 746 268 317 244 037 847 068 369 643 289 906 227 409 224 064 326 180 685 084 880 657 646 262 635 221 142 350 705 613 232 949 616 971 917 575 390 300 191 182 339 780 950 744 496 456 659 108 985 863 135 233 337 615 586 581 508 720 097 763 229 320 824 546 254 736 695 063 981 632 191 166 740 541 522 045 866 594 718 334 451 626 439 634 472 380 362 754 230 686 096 916 055 754 140 191 038 263 303 310 177 369 845 057 690 957 824 097 157 325 391 842 204 947 065 492 553 257 038 101 407 122 091 626 416 448 704 000 830 933 654 079 426 702 360 002 145 792 657 181 839 894 946 090 809 933 301 350 844 082 807 846 499 323 300 956 044 435 338 226 828 363 982 195 395 396 656 278 357 224 551 692 628 642 523 749 498 427 803 117 015 455 570 796 634 348 866 597 668 196 943 347 106 114 845 061 984 360 025 001 167 716 889 486 127 707 415 750 017 799 308 009 539 825 881 541 930 009 124 651 866 702 481 233 899 668 146 971 983 411 340 498 395 741 130 723 595 464 418 277 126 065 607 697 013 918 236 501 009 123 880 556 039 008 844 010 436 045 222 930 781 988 385 705 625 381 924 866 399 783 446 069 633 696 203 036 810 162 458 642 649 347 091 631 828 789 391 576 688 020 382 987 831 975 687 221 233 400 410 054 777 671 960 948 165 564 010 446 195 631 060 857 023 549 448 917 349 883 330 739 964 404 764 968 122 674 797 453 546 780 694 920 832 704 062 278 112 955 431 015 431 283 273 373 123 032 355 363 738 286 148 570 648 366 163 761 676 510 671 015 977 015 681 656 775 319 178 546 625 092 983 481 135 006 192 274 447 076 904 382 170 599 662 821 243 183 288 228 441 374 663 714 307 233 454 776 485 793 106 198 310 721 160 677 217 947 745 066 654 641 154 010 651 573 935 627 952 615 011 542 361 728 718 568 144 730 036 763 194 535 076 627 777 515 021 337 762 217 110 860 721 435 985 831 583 053 709 277 608 000 315 245 336 050 648 657 555 462 122 152 630 316 113 405 003 677 276 892 220 316 131 781 031 321 372 246 509 161 958 422 701 690 896 544 144 386 577 072 386 954 055 631 893 167 079 550 876 167 525 575 505 326 810 077 504 226 294 523 420 794 792 887 604 149 092 943 408 156 653 081 243 648 964 387 540 065 522 375 167 669 016 184 131 553 117 405 192 108 687 452 598 079 117 463 678 894 968 039 744 699 653 771 498 542 506 224 995 982 113 096 846 343 530 717 420 371 064 104 632 521 881 499 338 810 388 693 566 695 568 404 196 722 437 168 702 383 995 613 667 621 678 243 536 892 134 877 884 181 549 585 812 159 282 218 033 676 086 884 510 398 451 838 949 255 818 996 306 835 902 707 929 143 902 006 626 809 699 772 362 927 702 937 767 908 246 469 994 078 617 331 573 665 600 096 849 948 597 567 955 091 149 442 134 488 595 068 482 405 958 724 781 609 109 555 052 882 316 017 512 917 683 962 977 406 804 553 485 314 705 024 299 064 473 328 539 263 555 011 188 598 230 434 315 834 796 979 115 445 109 272 747 968 268 641 218 548 252 984 410 795 622 238 152 542 100 602 674 894 187 674 925 919 608 653 203 913 551 383 283 782 875 378 990 194 771 487 862 829 392 544 780 602 762 323 295 488 349 131 099 820 221 332 611 329 719 111 124 648 319 700 094 256 715 733 626 562 903 558 861 055 449 295 431 897 667 027 972 346 125 341 830 438 355 234 759 542 840 020 665 167 339 391 220 411 638 342 867 102 343 823 813 219 686 671 207 462 949 631 609 190 167 420 807 411 654 279 560 578 994 309 503 501 907 609 267 030 506 110 240 307 927 718 655 459 666 982 138 236 407 852 546 021 460 034 524 298 583 420 505 558 750 250 769 586 215 244 433 596 859 913 228 054 180 886 122 501 156 896 584 639 781 600 021 951 861 078 246 599 517 262 940 974 311 237 432 572 479 771 153 633 560 108 547 606 783 074 454 516 715 236 485 605 286 689 656 202 383 445 804 306 023 599 314 430 655 786 640 725 311 409 556 979 133 528 482 829 773 998 658 544 807 474 190 652 335 593 618 985 251 088 505 127 318 990 585 955 658 464 376 962 114 499 394 758 266 821 669 947 082 431 999 623 464 409 851 082 320 637 063 027 775 225 357 346 244 025 928 427 528 539 293 404 426 951 119 563 573 643 100 873 584 778 198 239 982 507 926 656 369 253 832 975 822 286 221 495 949 848 161 788 562 743 440 446 656 873 832 214 457 189 870 239 544 902 783 162 561 500 115 563 609 754 412 966 289 820 545 848 192 530 441 008 249 923 947 729 010 368 799 773 673 985 755 639 028 377 330 816 425 067 236 648 122 244 708 816 516 293 256 251 275 881 974 700 768 817 618 551 604 025 242 671 717 885 921 650 594 573 119 112 836 461 227 079 229 134 846 081 882 536 402 694 539 885 831 190 266 431 842 378 961 021 619 448 216 191 938 333 084 755 503 091 644 966 608 857 695 406 920 352 189 741 881 092 000 211 201 489 879 131 897 421 579 211 617 238 549 636 568 055 802 995 456 021 369 662 545 072 543 393 891 648 665 298 682 103 607 346 772 444 204 668 894 118 102 395 034 634 125 864 867 753 360 150 473 328 599 401 904 862 445 628 442 118 712 101 989 228 321 990 199 666 708 694 999 442 922 211 473 636 482 648 417 210 352 507 479 811 401 717 027 078 805 129 645 492 962 278 978 140 033 434 205 904 332 332 259 545 383 392 162 055 344 100 082 958 894 210 211 192 819 697 242 042 135 422 288 472 399 686 447 650 543 963 098 314 995 169 521 624 967 041 424 973 680 273 168 105 778 961 051 514 198 530 466 824 075 818 922 161 283 848 184 850 143 525 268 700 584 241 090 612 659 446 440 274 989 266 886 984 712 944 564 696 387 144 175 047 419 731 894 872 764 753 763 440 544 351 457 859 783 726 626 510 919 737 437 510 663 281 123 444 825 256 650 235 630 934 798 192 841 704 543 638 848 515 163 141 388 364 907 744 745 186 767 862 285 429 147 255 598 274 477 574 003 393 441 741 330 363 193 688 452 864 128 317 494 598 851 318 355 907 653 307 161 560 625 731 032 205 406 249 843 886 602 768 243 837 823 559 826 561 704 444 793 905 418 201 805 116 705 058 392 361 629 670 963 959 558 732 805 518 373 291 962 710 209 114 580 422 335 402 115 273 673 957 161 837 446 634 037 600 586 570 872 904 074 282 742 515 736 681 074 686 561 992 276 322 738 329 532 299 879 778 891 493 915 402 931 943 650 448 429 535 203 083 420 744 297 057 648 467 744 225 857 982 923 471 557 291 935 724 029 111 924 583 721 356 409 905 775 507 477 372 265 262 742 245 613 342 768 585 132 959 906 520 004 731 236 251 171 164 722 835 238 226 243 667 495 256 499 919 132 641 529 840 100 744 279 979 680 043 083 554 978 394 195 774 051 128 935 391 183 144 992 848 054 555 595 067 404 793 926 023 009 180 766 051 698 691 004 528 603 909 757 288 155 387 139 386 795 603 811 948 395 732 252 795 291 658 379 348 018 223 376 412 179 365 797 417 917 637 719 449 843 468 081 625 261 518 188 598 100 716 779 983 627 859 926 501 827 541 678 248 590 212 601 783 313 615 703 634 511 133 667 971 993 648 696 021 968 109 658 516 634 684 938 997 761 569 513 655 417 178 291 321 563 337 031 335 517 853 200 204 527 599 057 939 950 772 316 933 206 053 811 981 519 011 989 357 508 388 815 672 444 049 213 577 246 050 748 809 671 475 263 329 323 959 457 090 083 859 744 304 567 924 626 857 566 748 877 869 017 722 960 930 358 634 895 549 054 955 877 820 273 286 925 488 361 086 291 285 463 534 578 117 695 384 243 654 144 866 152 159 911 190 848 864 780 196 962 419 935 192 121 357 181 177 970 601 590 733 568 870 509 295 942 467 495 906 572 161 463 517 508 782 260 241 647 811 218 340 367 709 877 241 227 436 673 108 311 102 512 037 809 174 066 338 186 289 167 774 634 737 126 870 508 831 179 735 597 379 581 263 090 015 781 385 574 246 959 003 444 081 910 362 890 400 055 742 751 885 619 347 403 660 644 594 042 078 430 159 203 995 630 734 781 898 435 191 822 587 030 956 801 463 839 910 313 062 401 545 259 160 085 839 188 870 194 802 439 828 523 584 213 384 727 207 356 430 073 848 823 471 534 274 511 105 555 129 568 136 684 010 452 182 309 729 041 090 175 800 296 735 571 415 169 880 582 976 091 461 255 495 248 119 564 430 968 658 872 771 473 332 233 910 994 299 045 643 179 354 862 015 325 202 683 518 674 619 511 854 437 849 736 981 849 649 512 745 360 800 918 851 937 592 847 457 179 922 660 810 462 982 972 322 343 412 909 595 798 507 408 311 148 152 600 796 032 559 863 127 188 308 881 226 391 534 712 208 193 266 328 233 452 038 887 326 175 061 087 245 214 236 364 957 028 788 246 306 709 968 045 855 536 646 148 601 832 950 060 090 558 657 012 110 337 464 767 756 187 975 592 398 256 381 940 569 094 595 638 203 165 259 743 092 000 352 877 403 307 762 979 268 028 058 433 890 565 284 214 287 348 910 171 738 033 761 155 712 965 684 180 936 148 295 125 292 445 206 541 838 857 787 480 310 094 466 495 584 612 930 432 018 471 225 687 619 083 779 113 515 631 447 022 066 390 677 038 275 400 869 855 421 979 216 362 837 213 028 492 807 888 766 512 750 525 589 590 294 735 300 574 945 560 083 202 153 463 792 865 457 524 998 886 795 937 674 512 650 778 558 075 766 457 750 833 743 791 995 997 015 566 236 429 014 494 436 447 996 772 324 480 979 376 428 730 940 120 140 144 540 520 738 477 942 436 481 623 134 646 477 621 411 683 436 722 343 477 766 603 269 890 245 224 603 882 664 164 731 996 917 207 294 525 102 881 796 730 528 205 375 515 845 853 462 983 952 945 660 112 650 046 082 671 692 157 740 207 937 740 833 747 228 008 565 637 292 462 577 901 981 171 413 686 650 463 862 880 089 847 799 630 267 117 104 364 104 661 305 853 996 777 906 218 865 526 593 033 672 795 826 150 882 548 548 143 705 143 902 186 581 449 982 970 418 870 317 064 080 311 414 122 342 819 472 587 445 346 541 215 597 877 615 704 186 988 961 167 908 606 760 742 097 285 141 580 609 025 469 289 480 557 362 047 025 937 344 417 779 786 587 304 952 482 954 711 206 662 316 130 140 111 740 498 166 852 211 505 894 735 345 265 233 836 647 363 864 399 748 756 066 095 475 435 743 994 040 354 207 359 504 181 699 379 933 692 848 166 213 523 463 002 260 939 430 407 554 309 207 923 575 468 254 137 883 116 556 933 869 765 103 175 427 010 740 185 128 271 343 972 704 500 968 493 090 680 853 002 384 290 961 181 029 756 937 703 379 646 478 700 208 918 394 371 347 320 129 271 223 175 067 500 443 359 939 212 215 495 828 759 179 850 792 997 076 510 914 995 760 490 072 853 707 602 857 113 862 226 715 591 808 372 557 884 738 105 114 852 734 651 895 091 719 685 266 545 769 292 888 388 241 599 801 893 227 693 720 089 954 319 789 696 341 519 445 100 393 274 559 007 149 124 069 950 755 874 847 355 780 924 685 320 212 598 862 936 087 993 533 306 235 771 327 732 059 677 273 018 268 332 594 329 165 920 555 948 407 497 187 868 745 565 060 101 325 498 437 438 152 432 741 124 536 333 451 225 947 274 042 595 142 876 183 741 972 953 782 003 269 463 182 857 885 827 565 370 100 172 376 554 860 434 767 880 353 951 758 812 189 508 359 294 462 378 022 919 452 978 041 421 257 769 841 886 441 962 878 218 467 718 445 191 074 657 347 426 891 703 713 492 894 855 897 603 495 530 025 661 167 630 372 010 637 156 598 339 652 654 099 139 721 118 913 729 402 240 661 475 557 805 908 035 117 816 113 202 959 299 537 271 780 479 414 026 158 631 184 259 834 409 164 138 523 324 755 995 182 767 669 687 284 075 572 984 852 537 325 662 023 251 368 120 785 682 298 213 834 781 071 827 344 560 998 358 240 053 805 389 445 323 314 257 655 663 205 686 730 678 822 230 811 853 313 365 796 155 981 832 324 699 280 073 485 688 176 845 210 850 452 919 540 490 103 724 020 463 409 350 431 652 956 275 411 396 996 381 560 352 188 865 913 972 359 024 638 334 257 417 025 889 199 128 071 796 400 747 414 625 917 515 227 724 778 622 562 222 465 877 864 195 804 163 154 894 580 921 368 261 001 484 966 308 014 653 015 234 068 920 231 601 958 333 568 168 539 329 359 272 002 154 828 530 244 188 567 383 031 683 107 804 939 789 264 666 003 178 119 466 313 644 849 872 300 782 867 349 108 244 227 567 455 763 782 272 555 298 420 982 827 430 642 852 298 509 422 337 820 773 529 931 846 489 720 632 986 976 055 313 080 705 897 127 420 280 285 631 482 594 674 764 667 488 810 485 962 444 504 580 420 185 428 903 261 061 810 749 625 044 197 880 398 236 139 258 881 715 593 100 368 782 720 550 927 800 516 981 551 064 349 586 883 827 877 798 379 611 828 748 913 213 977 115 155 587 526 750 260 071 091 256 209 309 098 121 850 908 849 518 940 079 383 305 580 000 684 609 925 782 598 509 768 107 940 472 115 770 383 699 962 166 240 751 020 672 878 447 061 839 609 615 341 772 900 287 937 058 840 860 105 732 190 329 481 568 304 728 211 913 315 068 474 592 977 332 415 667 827 786 768 130 697 043 587 611 473 476 690 576 530 831 706 419 676 753 703 201 296 104 491 198 153 130 342 000 163 347 287 279 519 653 293 210 024 394 203 984 701 375 592 457 858 263 133 443 774 108 537 853 496 723 888 539 883 415 228 428 082 729 591 811 834 301 425 740 899 974 210 411 737 932 259 372 344 419 974 648 659 275 624 893 294 476 734 320 550 954 305 961 859 466 765 200 255 957 556 047 817 536 539 286 053 913 599 453 291 510 294 175 151 816 052 197 494 804 132 354 300 274 431 202 043 181 177 928 647 374 550 868 322 708 294 530 990 372 518 566 356 176 464 106 632 340 673 436 026 283 339 402 840 131 681 328 111 598 814 663 293 321 765 927 381 367 805 055 484 973 526 910 337 222 430 691 424 396 240 867 663 144 439 307 595 668 532 805 406 131 292 242 701 081 744 409 727 150 494 885 790 748 283 060 394 228 232 739 284 556 153 116 966 011 528 978 800 599 052 645 650 657 594 509 420 675 848 260 942 256 793 971 287 049 097 143 050 335 914 966 864 187 535 176 082 959 363 194 073 689 252 430 609 352 067 721 820 781 923 887 827 293 501 513 134 827 435 444 019 600 126 502 815 822 165 398 027 737 649 973 082 761 766 905 769 714 017 003 120 830 368 310 528 049 964 944 300 771 388 608 267 349 928 224 440 191 492 293 863 021 056 968 961 584 064 784 854 166 732 338 661 098 145 935 956 694 940 632 158 679 898 953 683 025 697 852 816 641 045 984 559 838 292 359 995 729 602 720 866 394 766 951 958 079 483 660 000 879 432 120 062 586 011 864 756 183 537 636 084 647 796 532 835 490 960 048 448 877 777 806 836 236 582 891 912 224 331 182 605 972 406 147 172 264 087 632 399 626 486 688 367 159 789 839 019 051 952 998 455 966 232 374 177 840 157 142 973 643 099 328 850 076 397 658 885 647 097 415 698 406 454 069 818 451 564 881 453 665 269 458 020 604 646 195 850 887 303 811 707 676 583 265 648 145 689 524 878 315 856 710 685 871 072 530 510 609 828 352 996 790 016 362 725 158 171 148 598 679 169 327 575 531 198 807 142 111 812 138 506 464 616 845 760 047 473 561 732 219 614 716 341 239 675 296 637 706 275 756 937 886 818 245 019 309 992 060 783 458 943 190 568 454 453 788 640 782 756 484 697 262 480 016 793 405 711 697 121 246 300 676 888 446 297 313 340 060 168 823 024 734 645 835 198 182 081 362 262 665 457 945 935 632 054 234 134 397 614 134 057 151 867 238 169 809 185 603 422 907 391 607 959 609 500 764 650 685 641 010 092 600 486 205 557 830 009 325 891 993 629 349 442 433 144 501 533 878 892 093 715 607 080 250 068 757 530 200 766 432 424 776 888 072 286 880 163 458 722 087 766 761 999 437 333 485 678 229 039 614 048 521 783 615 997 861 109 013 606 489 608 019 652 370 368 217 530 570 792 228 879 742 050 918 937 147 054 539 434 185 762 841 874 725 266 337 905 239 342 770 162 567 242 767 624 951 423 999 224 058 938 780 945 426 959 739 639 507 907 265 231 613 724 637 450 647 279 456 722 714 099 066 974 388 305 759 053 985 369 103 868 932 624 768 102 251 555 654 680 708 459 269 661 166 958 213 099 476 598 153 955 036 103 991 385 637 274 745 031 597 598 187 570 609 544 391 412 777 188 811 694 467 586 761 087 193 790 459 632 956 351 959 948 636 014 100 128 627 058 468 925 643 788 113 805 720 564 120 668 631 946 087 233 737 836 203 474 788 194 019 259 435 531 871 517 468 763 044 204 673 140 553 240 342 441 362 108 420 227 002 053 552 085 698 041 637 404 352 131 026 853 360 873 693 442 642 183 178 107 817 426 004 657 785 595 802 542 342 941 077 394 251 464 510 137 717 124 155 803 044 187 204 158 872 268 880 303 678 888 209 303 968 061 250 175 495 069 213 397 771 326 091 491 909 282 607 966 167 461 027 537 999 160 512 652 287 909 733 450 097 371 522 163 195 360 302 411 979 330 676 139 125 223 513 408 809 810 109 945 274 929 193 654 929 760 045 773 276 871 598 286 276 524 178 716 077 493 579 398 181 239 721 448 123 401 080 500 249 647 445 420 939 864 560 702 298 544 265 346 892 680 870 160 133 811 160 003 154 830 197 990 922 319 072 159 131 842 731 053 659 577 721 227 550 788 385 179 652 502 366 686 598 858 557 706 911 095 568 306 827 993 294 077 855 750 388 179 040 934 113 309 402 381 529 764 518 245 169 871 271 105 486 298 331 441 901 566 268 579 525 673 119 312 921 416 820 404 881 158 434 331 149 159 015 010 197 091 536 721 585 269 085 139 712 107 266 202 610 587 601 219 033 644 604 791 013 874 101 785 781 292 042 637 724 557 034 016 801 098 190 320 180 211 437 591 931 842 428 289 463 347 990 529 624 653 499 032 493 442 737 994 629 435 164 258 796 615 987 477 384 152 993 896 341 526 351 117 797 977 812 519 209 000 573 657 430 594 320 672 350 527 762 744 974 840 336 926 690 730 796 876 323 254 269 796 958 469 769 597 514 935 518 245 751 742 599 558 370 952 458 838 535 469 142 701 965 405 200 066 376 708 209 754 494 888 459 452 361 291 244 232 402 097 711 049 973 782 137 743 127 648 682 083 305 235 884 299 353 006 351 249 061 751 414 358 607 410 212 997 999 304 536 808 083 745 664 010 014 993 273 622 394 155 405 824 039 161 810 493 698 739 290 569 656 811 881 448 112 789 493 794 454 544 387 378 239 689 085 749 426 847 194 191 155 845 585 080 549 400 300 244 126 527 692 658 891 529 969 610 779 460 471 961 056 434 409 638 319 753 267 221 782 863 744 400 731 445 079 376 456 365 613 585 954 705 557 246 023 389 967 190 431 698 144 720 671 780 961 247 309 408 132 556 000 011 319 769 247 015 695 143 442 061 081 906 548 809 009 754 826 670 029 896 426 395 611 332 639 006 257 615 000 870 889 158 401 133 330 247 319 285 533 150 814 158 023 389 895 911 610 060 398 892 699 113 953 091 424 745 951 407 704 285 712 183 862 873 882 610 077 964 330 014 407 857 987 156 113 397 318 477 062 147 337 245 829 581 431 772 595 293 069 938 546 927 744 899 342 761 570 062 243 979 736 199 566 679 595 646 757 956 679 166 823 117 227 483 184 867 157 865 003 679 717 592 429 559 230 644 196 040 866 184 239 277 201 346 698 188 667 146 804 390 818 149 782 883 010 724 439 194 971 397 477 012 927 126 874 332 588 512 815 708 648 507 274 139 730 877 842 681 075 261 562 471 284 925 655 883 381 133 927 760 698 064 171 317 880 126 650 574 510 790 734 756 567 195 377 225 467 593 493 816 067 781 419 282 202 218 832 824 288 037 639 562 875 274 291 879 859 914 892 005 504 647 096 972 337 992 672 369 007 379 015 000 626 657 752 036 307 571 544 623 780 272 768 447 893 965 098 188 036 843 843 238 875 600 342 589 655 477 775 560 322 530 170 861 296 560 548 572 785 453 138 487 287 844 584 381 475 481 997 491 122 897 432 803 841 389 786 127 577 526 283 028 598 826 418 667 563 189 051 741 076 458 765 858 566 325 919 416 986 654 460 037 663 738 421 763 967 741 746 209 773 624 330 467 576 247 079 967 713 920 535 803 624 712 552 266 481 473 261 978 151 475 662 787 342 964 385 119 443 427 087 722 666 095 099 935 690 934 287 083 370 414 964 567 120 160 501 953 653 021 205 028 357 049 500 357 232 558 667 057 316 478 404 931 636 592 673 365 063 622 869 668 709 034 584 588 705 604 924 855 259 543 433 162 168 620 226 243 928 591 749 888 504 174 277 739 247 187 692 518 447 860 431 795 815 333 752 726 429 500 438 156 269 837 654 508 178 052 875 278 355 384 054 532 229 400 226 526 329 359 282 455 381 415 830 758 172 324 109 426 273 902 891 606 442 003 035 541 989 050 644 352 632 376 027 024 104 677 190 065 405 846 434 344 061 554 186 254 851 466 217 468 168 507 897 976 006 423 551 759 959 680 442 810 374 242 183 255 885 685 017 831 117 209 394 586 385 994 021 591 179 185 767 311 532 594 251 003 735 344 519 098 034 174 878 176 208 608 137 190 989 232 334 035 345 087 778 592 042 660 180 326 765 964 002 089 983 085 064 017 760 133 938 080 995 636 662 797 541 331 058 854 956 602 917 349 524 326 202 312 337 820 245 159 739 897 387 284 752 877 999 342 004 619 118 975 943 079 052 314 922 089 743 001 663 899 421 746 571 364 790 252 572 538 762 075 991 401 086 042 646 825 605 214 771 218 843 839 235 212 180 074 797 947 392 774 558 299 624 216 154 686 338 118 560 952 339 264 329 472 436 857 526 819 030 447 724 551 677 302 094 495 341 593 377 179 658 554 197 175 511 509 232 516 181 469 764 578 014 362 355 075 667 611 419 383 566 903 390 372 347 543 995 353 372 556 010 210 129 778 046 172 400 145 986 216 768 070 632 890 662 415 406 999 443 826 359 490 890 236 678 134 035 654 041 921 273 611 912 105 829 838 819 122 321 428 673 130 237 871 763 003 072 039 393 938 540 260 430 334 122 950 978 844 233 252 059 962 968 215 992 536 311 287 242 260 022 141 370 059 639 859 422 733 828 917 391 212 617 304 538 487 729 713 407 080 148 819 255 515 390 613 691 133 898 338 417 023 057 095 078 239 078 354 012 079 866 657 339 934 278 316 246 418 916 668 921 793 684 095 128 045 096 477 309 327 235 565 414 033 191 077 532 439 900 978 447 157 211 826 228 473 699 735 675 761 118 669 553 378 892 660 868 050 096 425 968 842 069 331 726 652 666 075 538 272 170 757 413 803 236 775 827 749 386 004 171 844 329 851 101 769 270 277 570 589 241 005 594 374 558 542 245 874 917 706 337 134 933 361 606 728 530 489 195 491 733 766 360 179 570 057 478 650 822 878 994 856 995 823 533 438 492 562 780 831 205 883 605 563 929 652 663 273 519 950 676 051 459 113 711 602 510 886 194 420 933 086 495 156 857 485 054 969 210 570 884 563 709 144 872 064 270 894 827 999 546 617 619 834 617 203 545 476 804 685 559 134 396 904 331 565 235 500 162 972 015 930 168 680 035 873 664 650 008 998 062 148 672 495 910 924 329 517 621 990 293 525 617 017 585 167 868 445 669 371 731 658 222 975 616 151 224 748 701 714 263 756 733 660 744 805 088 592 422 981 582 894 856 835 080 977 254 970 606 610 629 073 664 357 536 103 316 615 292 496 719 438 035 014 684 353 285 652 334 330 825 473 890 726 929 878 043 074 506 586 228 132 859 914 138 825 319 727 398 138 537 886 914 664 001 109 092 153 776 496 655 562 492 779 832 189 072 602 986 457 476 068 596 024 206 040 011 151 731 186 244 495 611 664 994 963 719 178 722 103 411 566 640 641 485 690 798 871 108 521 079 633 222 146 434 687 415 264 216 757 246 762 845 718 136 037 519 779 546 825 102 667 002 551 330 828 513 542 838 125 145 990 460 696 585 708 019 843 456 247 978 542 332 400 909 222 652 326 387 675 597 680 164 527 303 016 249 372 883 664 596 775 965 973 406 324 561 428 216 297 752 392 440 109 663 126 004 270 890 032 811 076 539 713 088 782 696 624 520 072 174 669 009 049 218 854 673 292 259 692 639 236 609 381 225 647 815 517 305 115 449 120 335 589 938 803 895 923 919 569 396 186 000 561 662 366 105 505 646 616 794 934 581 291 348 856 441 674 370 807 584 228 530 097 048 517 133 857 669 922 584 282 162 345 432 021 698 877 052 403 010 079 305 570 653 775 119 006 909 449 946 615 347 199 124 363 503 509 156 345 632 767 098 859 446 669 018 282 236 347 113 158 959 056 198 032 829 872 697 748 372 418 247 622 606 990 614 965 208 166 080 248 636 041 593 629 600 500 195 541 701 907 504 683 053 926 961 042 088 660 383 590 622 622 044 994 711 219 411 801 379 846 894 947 160 154 612 986 928 051 247 761 774 943 502 350 441 833 506 574 363 314 538 031 299 487 477 270 718 271 142 629 291 429 583 604 288 229 596 037 464 073 423 707 541 696 863 299 857 654 064 677 953 404 704 316 150 836 303 738 738 437 705 774 663 453 428 847 404 321 652 713 329 123 097 375 903 450 137 432 104 123 071 961 176 143 831 808 561 702 036 704 048 423 338 031 816 132 703 177 304 116 251 963 458 823 307 203 338 076 109 211 100 110 154 998 562 490 952 205 021 845 076 368 022 498 076 805 262 331 503 541 304 562 002 589 594 699 392 719 580 889 078 273 983 956 032 170 968 829 167 295 743 190 231 750 845 935 851 121 274 884 815 967 038 022 504 424 563 130 989 251 602 194 289 406 118 922 906 231 470 718 324 830 230 578 804 123 425 449 870 409 792 171 124 683 737 588 953 480 991 909 245 925 844 690 954 222 544 993 446 582 565 913 918 737 964 574 148 543 080 097 469 263 526 404 906 882 365 813 831 723 347 994 208 167 391 655 209 515 530 492 657 080 050 231 123 457 324 371 105 509 029 018 218 535 448 392 194 912 300 289 908 298 404 576 320 990 861 324 602 320 795 723 707 859 514 260 680 215 417 147 042 023 836 698 243 962 786 967 594 407 187 723 482 256 155 221 277 229 102 485 367 221 356 756 151 050 220 061 011 577 974 698 076 678 780 126 256 457 740 850 087 109 407 693 053 312 134 481 875 457 613 748 803 184 307 470 670 679 958 103 741 855 717 092 908 869 644 825 333 394 829 155 766 549 023 254 968 988 857 085 653 316 740 286 385 317 180 154 287 636 665 171 882 750 991 025 430 685 464 986 061 248 032 973 825 131 444 041 709 678 262 465 510 486 361 573 253 296 114 833 438 983 543 129 292 211 249 818 117 091 611 384 827 847 636 328 727 895 116 920 924 603 756 284 032 979 248 385 017 678 684 908 875 329 437 629 762 710 321 718 021 915 823 510 096 845 551 090 455 075 397 892 884 343 695 288 047 004 707 229 264 162 581 027 850 289 846 470 233 997 109 008 639 533 414 498 998 515 426 025 214 383 323 009 694 817 866 358 139 705 359 219 863 348 702 368 371 948 931 779 843 413 775 689 360 561 536 943 748 595 910 603 474 840 031 132 870 549 346 254 483 201 789 291 766 228 520 202 980 450 510 432 983 937 270 354 099 511 517 507 014 055 695 378 107 691 866 586 897 178 791 105 679 666 642 443 178 575 229 869 639 042 416 373 968 111 294 954 222 670 810 853 893 276 832 017 197 979 909 938 106 077 229 615 399 338 260 454 915 142 253 383 666 752 589 808 395 039 963 684 304 604 800 849 048 301 655 975 571 992 515 453 427 026 680 628 286 326 804 424 750 328 676 432 404 858 294 691 128 236 707 102 510 828 266 048 191 392 566 498 346 470 842 889 904 067 428 946 102 515 519 162 238 624 811 983 733 239 269 012 683 736 795 587 896 762 356 031 802 305 322 599 847 863 149 190 375 066 873 849 301 305 934 371 618 812 384 420 099 633 581 069 762 677 329 851 897 163 150 266 570 647 692 971 219 862 805 586 213 539 468 668 821 900 906 246 465 546 768 260 725 113 211 918 974 223 306 395 084 246 984 394 889 779 802 648 374 694 881 100 134 081 732 714 556 177 954 097 832 330 274 439 302 481 802 159 338 703 533 420 773 686 278 316 308 729 061 268 501 563 922 028 134 401 311 581 899 870 523 383 735 158 239 109 198 599 038 819 245 159 094 102 956 029 249 857 149 438 586 587 744 300 497 173 972 727 115 333 875 528 140 588 646 803 195 187 759 107 104 019 522 671 376 376 611 258 738 304 566 316 290 721 430 161 774 663 586 037 532 349 141 395 641 737 658 698 051 142 213 264 088 340 953 912 801 621 795 679 665 266 977 124 010 890 130 768 754 415 254 981 607 783 043 975 094 483 078 612 351 733 120 164 256 710 432 668 676 344 919 949 446 328 492 847 475 232 042 172 488 620 220 240 513 944 783 049 183 559 092 726 419 705 164 709 491 056 096 336 833 463 408 361 592 764 511 428 672 943 274 846 958 237 109 826 204 586 295 473 950 459 865 147 190 688 348 169 830 614 860 066 082 565 263 748 764 882 687 538 697 245 662 199 028 518 076 579 331 292 855 026 688 234 480 317 727 776 269 287 766 548 488 505 831 275 031 979 549 765 501 534 946 729 704 421 384 896 986 384 828 845 687 534 352 936 101 635 620 863 218 448 192 157 913 688 621 483 918 080 827 140 324 921 752 163 566 454 449 892 731 540 705 193 205 327 082 727 526 863 107 020 953 099 965 677 507 064 283 244 287 782 716 285 553 957 395 046 548 393 926 014 005 144 375 824 916 588 349 571 954 025 303 898 807 507 659 817 282 813 284 915 331 978 479 595 563 599 395 317 857 719 717 210 183 402 404 812 518 021 431 216 831 632 340 972 109 969 109 416 050 961 902 990 736 929 322 180 973 881 917 946 346 977 396 489 294 138 063 798 459 365 188 771 398 868 024 537 380 879 472 176 059 328 427 877 245 424 140 367 572 231 797 588 912 910 753 462 664 131 713 066 084 883 958 698 696 460 793 974 496 776 474 865 091 469 414 987 761 598 385 035 661 317 481 543 511 628 292 172 933 247 241 454 626 492 822 952 408 239 135 133 755 713 933 998 096 742 966 172 938 861 230 769 882 351 246 677 876 452 106 430 519 655 204 644 372 428 510 075 173 870 333 555 297 991 569 931 131 645 167 353 966 119 362 564 337 003 224 099 465 798 896 903 394 693 073 018 204 030 276 464 204 912 690 491 382 455 720 371 891 091 690 343 654 569 003 728 275 669 697 473 339 003 168 791 006 614 790 462 175 548 450 734 479 938 180 415 746 153 698 620 822 353 952 977 073 465 861 087 314 838 160 594 157 994 608 666 910 101 139 730 675 852 672 746 031 437 785 833 950 729 542 632 829 759 231 456 216 725 613 393 650 319 055 318 888 769 212 142 086 201 294 884 027 484 020 058 961 713 178 435 663 497 648 022 411 163 733 481 085 652 319 420 184 485 943 869 432 650 661 532 110 250 233 742 472 640 035 947 438 552 706 925 023 250 458 610 416 329 849 142 994 134 854 697 448 591 826 599 740 674 730 875 513 756 494 514 054 156 651 413 648 974 589 234 897 347 551 396 839 528 849 570 772 259 197 484 922 227 553 479 382 542 251 134 845 014 066 446 782 311 466 065 750 191 092 273 449 015 107 834 871 984 659 012 509 626 047 641 424 022 619 531 850 996 833 762 489 852 622 767 986 064 786 053 893 635 923 116 723 174 792 694 328 008 839 470 456 833 504 665 504 063 821 654 637 696 688 036 721 737 094 535 318 603 405 191 371 166 415 507 831 726 723 145 618 061 388 091 098 185 464 004 972 689 787 297 555 530 201 507 115 619 946 088 720 961 738 329 696 469 296 557 868 758 570 359 826 165 462 812 044 489 405 425 336 821 183 927 483 085 171 914 608 891 019 903 628 408 856 875 349 299 097 063 350 281 472 642 085 364 363 731 741 239 231 275 325 669 108 931 888 286 429 969 385 763 108 482 609 429 356 126 704 583 625 252 115 835 963 599 983 424 831 493 472 643 051 375 674 277 300 809 979 270 697 175 428 841 310 603 941 684 077 562 781 821 401 410 311 979 325 393 603 619 617 803 477 543 415 644 769 927 034 967 195 219 260 403 408 025 785 199 577 898 578 181 676 369 938 489 575 093 936 834 515 146 534 242 039 914 762 303 309 551 436 998 653 605 486 042 631 539 598 837 968 441 109 877 448 032 996 768 523 899 919 781 976 270 174 963 519 117 233 375 018 400 260 096 138 607 337 441 471 320 816 258 446 385 490 277 973 782 956 022 786 785 527 610 347 341 565 407 837 686 788 474 015 567 621 070 681 821 273 683 849 942 581 789 507 244 129 001 908 217 100 152 935 424 559 844 042 791 730 475 594 677 265 362 617 652 815 494 535 966 083 397 896 517 860 029 141 356 518 081 256 906 670 278 380 014 113 481 077 158 977 288 476 525 717 533 962 458 509 927 384 802 953 142 775 092 547 111 355 550 396 997 500 542 667 853 271 670 550 636 714 409 555 938 245 662 088 566 942 156 129 111 141 811 767 469 057 773 544 725 033 790 898 969 438 515 858 679 259 248 681 714 141 526 672 326 429 190 751 582 713 842 354 102 054 006 588 035 834 422 361 601 316 565 488 662 253 222 056 938 093 683 322 351 030 446 133 545 411 799 177 389 522 438 108 748 356 288 230 204 224 317 051 700 537 375 351 800 185 523 154 233 919 250 207 516 731 990 057 428 142 479 009 749 565 687 972 726 034 829 769 918 926 748 652 415 985 216 611 402 456 702 180 635 652 469 914 950 128 754 865 148 659 212 751 829 072 838 664 799 900 384 671 377 049 181 338 174 948 029 555 659 007 516 737 328 549 676 100 781 669 986 208 832 487 609 145 060 566 961 849 373 084 903 921 951 918 242 684 405 994 207 499 724 990 077 495 781 745 499 300 616 145 660 705 850 624 228 763 784 354 200 368 544 809 909 213 194 064 121 572 766 830 892 630 101 640 894 195 222 321 475 151 594 662 788 306 213 300 734 046 900 378 354 180 470 479 836 228 940 142 756 147 342 320 357 542 538 068 453 147 335 190 788 269 533 542 348 844 881 047 567 736 259 724 944 763 195 072 552 177 731 275 501 811 157 623 231 919 227 770 533 380 209 825 922 866 516 949 072 773 911 556 236 247 226 062 202 458 811 381 956 923 308 729 303 695 614 342 296 450 551 599 041 486 449 899 977 572 049 108 584 841 636 756 070 362 979 632 810 551 974 818 424 356 273 331 130 590 548 109 877 971 427 188 772 214 345 666 952 896 080 447 403 226 269 270 719 411 144 757 132 086 800 255 325 106 979 120 580 003 826 484 586 971 501 042 482 026 902 283 988 322 527 622 570 713 635 016 944 544 820 995 593 241 786 889 184 898 030 493 805 334 060 597 715 976 542 741 746 713 672 162 383 268 520 954 749 834 552 617 130 752 318 737 714 009 405 837 931 254 481 682 544 012 600 576 457 645 915 881 572 602 040 851 804 680 571 066 007 471 666 170 641 393 282 665 717 126 242 181 945 853 389 048 903 155 498 001 822 887 994 179 169 675 617 715 892 026 150 348 752 278 216 775 121 611 742 485 975 617 773 567 064 233 208 948 240 652 329 476 057 545 597 450 785 313 629 650 061 401 693 460 436 741 048 843 154 227 423 746 311 484 586 530 532 647 730 822 899 484 327 510 892 805 868 037 150 625 293 418 741 315 057 226 343 484 891 296 221 016 314 392 260 735 148 213 053 716 357 763 448 160 996 907 769 758 151 551 474 940 883 503 936 104 327 070 460 464 894 528 741 067 054 347 078 891 002 909 438 492 473 066 076 387 538 092 519 781 670 797 726 397 781 117 679 399 002 990 190 503 676 419 088 374 349 713 571 061 960 717 216 620 722 037 246 744 729 883 263 108 984 565 339 618 322 148 076 260 147 787 050 862 892 524 627 609 119 465 083 030 315 943 165 515 635 845 625 239 687 690 567 123 333 679 665 074 977 299 726 126 588 114 063 123 666 612 511 847 844 647 844 767 971 988 617 820 408 665 217 752 419 901 709 416 699 335 648 430 674 670 100 568 794 084 515 748 612 186 163 309 367 403 066 798 034 687 493 945 942 728 056 517 129 083 336 607 582 915 881 654 802 388 588 580 548 349 305 768 624 381 235 524 112 154 568 608 005 931 477 089 635 499 463 304 486 536 764 146 128 485 703 847 277 688 257 714 968 671 477 458 084 904 050 186 777 691 489 944 844 170 914 287 826 533 603 347 002 442 002 816 957 883 793 315 552 728 733 409 521 103 230 506 546 732 000 729 475 927 938 482 635 211 025 541 342 840 388 602 405 705 639 768 828 001 803 811 056 701 804 764 508 875 775 738 935 088 539 582 913 460 166 144 397 440 544 310 432 224 644 146 026 057 136 349 184 088 561 502 225 707 155 959 278 847 814 259 690 089 657 800 937 536 773 928 495 607 055 338 558 054 112 104 681 198 747 685 857 005 219 015 852 539 230 262 458 088 720 793 674 006 528 458 466 468 580 059 307 132 544 280 987 105 020 968 423 809 122 219 732 369 380 628 002 329 976 976 338 741 368 374 612 401 195 381 689 069 351 075 202 660 914 576 074 066 743 457 988 413 954 469 334 682 436 660 469 482 363 062 012 010 923 102 758 217 996 855 900 455 400 797 643 858 060 378 281 363 868 412 199 070 405 586 909 279 105 145 901 379 266 047 169 333 588 736 511 361 967 489 588 829 083 464 446 728 419 649 838 432 885 846 333 634 751 011 859 260 043 784 565 080 436 957 585 495 643 203 120 131 770 018 133 066 806 310 275 302 415 302 851 339 812 776 739 144 339 784 779 323 323 548 822 612 315 346 302 500 730 922 694 150 054 904 466 009 060 814 110 846 858 418 610 417 809 402 864 135 272 295 019 126 017 121 406 890 042 111 499 491 515 907 733 175 094 064 734 916 403 218 379 800 739 172 943 452 437 851 240 538 758 713 158 543 874 797 402 736 791 970 256 115 636 509 484 765 635 157 385 435 149 432 166 432 529 891 602 334 966 756 863 222 140 369 479 933 502 125 086 368 002 232 815 929 999 658 968 026 756 041 989 251 952 906 680 862 313 832 830 431 550 158 554 607 758 030 758 939 901 474 654 250 228 620 935 631 532 571 921 520 651 815 293 680 223 695 829 759 569 177 919 543 529 234 008 110 577 132 430 098 969 654 366 435 508 824 517 317 533 637 668 955 409 051 185 557 346 716 798 983 192 072 295 070 629 549 382 321 339 425 479 937 930 462 074 107 185 058 341 455 291 324 567 791 316 098 215 019 281 299 479 206 255 374 973 789 644 073 078 905 376 668 728 321 019 843 959 929 183 985 737 233 095 574 046 856 216 033 885 506 729 653 469 139 012 089 138 953 774 733 570 080 415 872 801 658 897 426 358 515 698 682 277 559 253 706 498 159 327 888 900 580 735 128 433 020 286 249 828 001 928 255 145 141 666 202 817 860 032 793 245 469 100 160 688 451 940 564 329 091 286 075 101 754 066 137 814 902 825 273 755 170 908 142 724 152 431 608 722 045 426 758 172 575 070 900 552 659 046 814 676 810 975 320 555 593 554 811 050 092 431 493 558 724 094 212 073 742 179 732 657 380 858 087 312 690 329 260 584 307 510 671 443 355 847 710 540 326 732 861 549 342 226 871 524 681 496 611 188 971 117 620 281 449 491 433 577 277 093 512 667 721 502 329 492 992 331 451 155 521 935 194 004 214 517 569 479 938 265 175 756 458 626 832 429 610 868 264 326 301 440 064 197 402 949 630 708 634 167 876 589 385 660 277 324 106 060 602 241 527 356 912 753 254 796 697 827 783 406 576 304 933 809 386 579 884 447 075 239 106 779 066 567 320 364 980 397 892 646 605 848 688 995 060 111 587 519 923 121 435 731 793 005 027 681 600 827 774 374 046 648 437 270 656 515 565 267 194 450 582 905 439 658 612 362 019 722 921 849 245 426 424 459 396 999 311 925 148 196 009 345 860 674 577 910 112 421 680 704 017 160 271 487 950 951 112 492 993 225 935 946 566 418 484 195 193 525 704 012 479 593 871 839 345 085 694 789 347 944 185 943 631 801 793 309 020 844 753 518 349 998 766 661 022 296 139 894 097 772 553 977 308 178 617 064 249 554 113 867 486 825 763 557 640 086 731 222 581 638 031 377 681 425 439 632 752 557 480 938 231 745 809 493 274 581 987 995 913 714 402 393 131 494 338 292 698 865 402 861 934 821 844 832 860 081 306 244 228 610 922 405 065 289 689 448 218 256 469 145 895 539 891 510 015 630 086 770 008 392 407 647 451 934 716 304 911 855 936 964 501 369 067 682 819 039 556 867 668 374 789 289 474 427 707 436 644 812 140 394 972 147 954 617 610 743 968 664 962 806 509 100 181 388 691 542 169 662 855 669 733 845 966 847 846 024 211 579 004 048 784 475 687 059 950 545 848 885 604 746 745 821 973 707 309 048 781 174 081 153 498 457 714 206 861 914 742 105 344 234 149 141 614 172 883 618 562 202 269 570 842 058 937 479 391 680 561 567 075 399 710 929 225 920 895 731 953 627 893 441 669 184 073 764 809 878 078 688 800 162 439 966 609 693 966 676 081 734 344 133 650 700 249 432 290 988 331 247 118 447 600 492 914 979 647 809 519 536 817 941 398 615 290 044 269 050 459 212 168 977 806 975 561 593 617 449 267 809 672 509 504 440 533 093 652 747 665 590 388 905 208 727 115 243 287 387 700 576 822 521 486 715 006 664 205 015 916 819 342 991 214 621 203 515 939 972 498 490 442 150 666 524 970 045 424 392 235 705 057 706 008 677 057 882 157 672 781 528 938 597 930 540 898 866 443 083 084 861 452 869 761 283 714 499 903 880 764 135 459 301 736 945 206 022 920 717 158 726 574 071 661 772 467 905 858 131 814 746 017 319 093 398 224 924 964 322 516 492 709 333 806 194 665 602 600 406 484 447 457 609 550 379 047 013 003 087 483 823 297 434 749 187 624 382 821 983 621 247 181 880 742 956 465 261 334 201 805 392 330 264 522 941 535 364 529 512 046 539 193 452 822 812 394 660 333 826 176 490 012 603 239 542 789 930 320 577 027 688 726 033 494 249 886 828 561 935 838 940 812 513 753 854 956 851 370 658 323 209 004 197 799 532 299 478 543 463 537 317 436 713 516 621 537 722 788 766 278 523 193 316 557 021 638 258 759 855 997 781 160 629 953 191 848 240 142 052 044 262 329 329 288 893 497 806 105 774 528 799 499 941 082 074 083 091 872 793 985 143 602 480 824 617 719 952 368 119 826 755 515 727 789 286 568 071 342 239 749 060 545 972 958 776 525 478 089 847 408 391 556 346 125 647 196 316 729 236 603 551 367 476 197 728 495 374 311 248 441 369 472 616 233 592 216 855 399 311 310 815 714 727 620 898 311 254 612 839 598 352 214 139 593 317 048 984 309 890 631 935 941 058 477 751 115 030 056 458 962 145 637 119 652 006 959 576 414 293 900 226 906 003 997 978 113 343 911 078 493 339 508 800 875 617 086 057 935 471 674 842 729 870 222 738 058 478 184 183 660 931 271 923 812 808 776 988 634 207 898 874 132 929 300 117 980 820 764 852 205 790 043 529 310 313 010 707 036 300 964 636 602 808 763 588 608 690 856 685 341 569 985 664 465 793 079 066 420 173 966 710 407 163 895 367 143 697 457 595 233 692 758 893 300 897 367 014 303 010 496 221 972 552 148 902 004 409 225 074 191 690 702 717 539 203 193 184 508 051 285 470 513 418 123 037 014 342 746 673 890 031 686 012 548 201 713 538 994 862 424 496 222 615 925 354 313 343 330 577 571 401 912 061 678 649 270 089 729 220 710 259 018 770 304 024 215 186 896 890 907 193 995 926 161 220 294 586 643 429 712 463 581 846 521 187 728 735 345 558 911 076 812 308 616 796 390 424 183 580 228 297 083 412 967 869 379 936 592 133 099 253 537 435 301 790 242 779 883 919 613 268 788 746 330 539 677 868 523 719 255 725 892 543 173 471 658 675 888 187 272 297 012 243 945 655 562 481 534 654 460 098 327 348 618 938 038 306 097 959 532 113 772 693 973 812 410 046 979 402 039 815 410 699 669 609 630 526 713 575 136 822 042 736 649 307 171 311 266 107 370 363 043 212 812 081 859 003 899 810 171 111 672 963 460 098 731 423 892 435 959 657 215 675 347 881 958 821 716 627 290 239 636 465 124 587 028 821 879 925 850 977 687 880 859 294 525 410 911 804 178 561 648 258 358 390 120 510 351 450 076 831 342 939 562 777 966 814 847 959 937 279 048 093 451 578 718 044 265 728 889 337 895 889 383 756 028 889 624 627 761 587 255 946 724 998 163 582 287 724 479 043 307 814 827 961 253 316 194 871 370 771 398 128 613 208 066 128 335 374 666 170 762 113 467 822 968 339 890 907 610 870 068 907 375 160 410 273 057 428 270 379 393 570 687 361 552 876 964 541 808 338 605 448 319 127 028 899 959 973 564 306 700 025 016 442 498 276 733 897 000 689 527 405 139 551 519 402 505 590 850 477 574 793 893 046 808 267 907 407 147 028 384 880 500 517 167 624 340 344 487 595 484 773 371 438 775 171 663 014 116 883 172 949 703 685 997 486 922 473 152 118 392 521 288 002 989 524 704 081 543 496 849 685 874 635 157 963 144 166 463 783 098 559 842 618 557 023 594 023 600 690 458 131 713 548 748 158 538 353 790 473 489 606 038 127 683 831 561 552 895 148 695 265 626 813 460 317 141 375 988 590 622 904 137 566 220 983 482 195 207 946 115 397 755 002 506 564 678 963 087 834 899 269 924 892 646 981 232 021 366 662 392 056 151 281 257 411 110 770 349 576 641 915 357 619 281 564 548 673 884 897 960 028 495 024 502 718 828 677 750 471 049 825 665 955 297 204 825 208 824 552 560 013 694 215 948 720 076 104 737 326 639 851 991 378 511 977 239 824 090 359 889 141 146 764 274 681 011 654 450 940 116 861 532 040 356 799 403 854 637 761 707 480 040 153 087 888 021 169 573 165 075 793 416 903 899 237 750 649 273 775 940 250 603 885 344 805 220 153 132 228 885 835 887 973 418 333 634 008 388 919 096 044 559 256 670 446 198 236 540 626 560 908 098 098 932 465 485 276 321 250 533 625 075 950 025 553 142 200 660 476 266 496 119 038 724 161 621 737 468 820 190 122 905 482 456 146 456 231 855 727 153 448 499 537 191 691 187 346 749 159 713 205 882 727 399 346 949 618 427 836 654 373 483 862 236 351 879 103 429 213 446 397 493 049 891 993 990 002 650 874 078 006 330 500 203 940 730 919 010 170 638 313 397 442 625 577 483 429 863 487 321 535 426 216 562 907 340 216 557 659 531 518 790 604 103 938 091 496 808 238 744 680 434 461 618 455 971 848 370 637 707 416 241 822 651 781 183 273 608 955 219 005 498 557 048 939 428 460 496 001 683 237 498 577 646 369 529 647 811 862 151 490 478 726 419 385 035 167 574 261 799 076 734 965 980 902 754 130 001 810 064 788 464 611 981 642 382 280 339 752 779 216 433 978 027 312 840 246 505 036 155 270 827 327 252 568 833 164 439 781 369 527 459 605 363 429 851 361 472 821 373 070 467 570 053 119 869 665 814 196 488 890 621 497 420 977 861 062 860 975 803 667 444 023 611 693 787 987 864 056 114 479 900 702 662 855 879 553 045 097 762 595 741 077 854 502 005 825 630 642 791 633 083 315 875 557 796 619 548 235 379 881 664 759 601 975 129 634 188 129 332 072 185 712 616 900 031 406 254 160 796 013 253 224 004 700 715 892 727 153 018 345 139 365 341 609 811 732 041 238 807 911 070 568 828 799 335 555 959 184 410 329 482 433 931 640 259 849 391 414 062 815 631 079 988 880 021 155 027 630 021 900 580 904 341 517 561 549 503 964 045 907 708 605 469 562 926 333 877 771 172 768 703 784 133 532 306 664 534 268 799 008 313 668 703 560 876 810 254 138 017 655 535 855 219 204 835 741 018 368 931 446 631 657 093 328 455 609 982 710 551 501 541 245 154 690 581 866 881 005 791 963 969 615 534 065 939 024 651 754 378 650 543 571 109 963 930 093 228 503 692 675 978 320 131 744 847 004 019 634 455 740 434 051 309 523 432 358 922 297 925 299 324 502 984 583 766 271 872 684 202 160 745 020 528 752 701 865 293 805 615 201 402 914 811 257 234 488 701 113 050 002 428 779 578 371 120 027 789 968 135 648 975 459 739 495 895 738 544 450 596 713 326 441 575 122 804 968 382 249 903 108 828 054 958 335 844 228 413 880 399 245 005 454 607 950 433 881 632 386 043 433 758 639 394 724 109 836 180 820 923 796 068 094 583 913 352 911 314 830 351 366 008 407 615 575 722 796 448 613 379 805 409 838 697 368 618 245 524 455 760 497 252 315 239 186 975 306 768 195 689 654 058 497 124 220 224 485 004 259 471 246 681 537 417 675 590 239 739 403 051 959 987 219 950 823 347 993 220 588 501 110 887 018 624 936 314 771 706 324 470 171 271 410 347 709 277 598 042 828 504 590 196 511 717 969 550 411 603 281 872 802 581 556 105 509 741 387 662 352 881 992 061 409 953 072 472 357 131 519 242 233 663 246 485 815 279 244 554 688 194 050 911 765 867 155 132 878 495 458 634 782 952 968 413 268 042 379 367 819 539 475 272 863 257 699 321 915 523 118 601 792 412 009 759 996 665 992 772 376 984 037 475 807 736 754 134 372 549 568 799 552 818 978 267 668 119 831 610 605 511 267 754 589 979 100 304 887 099 014 675 572 721 821 624 379 582 195 919 405 681 921 744 139 178 523 315 491 810 417 512 196 766 840 213 821 000 523 326 329 870 995 427 852 706 258 750 658 983 518 825 363 184 097 494 920 651 825 819 794 150 658 169 915 341 674 651 793 489 695 002 255 801 878 303 657 397 729 755 242 105 972 406 693 119 469 716 202 917 616 957 001 036 348 796 278 309 051 460 978 481 730 406 411 831 022 083 793 234 145 930 717 579 376 227 934 477 520 713 124 396 452 895 760 386 175 966 305 990 968 822 347 630 619 235 653 222 582 002 304 568 759 125 234 725 739 295 216 107 382 948 545 267 251 557 488 368 071 668 974 949 910 431 385 540 488 776 028 902 735 233 690 374 997 782 283 175 438 100 189 225 514 424 272 432 186 315 243 511 577 872 524 036 343 035 363 201 567 320 768 400 029 524 456 318 349 899 734 128 540 513 362 936 586 874 207 185 983 914 336 423 421 645 253 822 837 878 241 997 628 267 872 138 673 560 411 672 127 008 455 572 173 900 239 585 110 395 592 359 106 663 407 164 203 282 937 706 103 116 823 692 651 211 043 012 326 189 163 425 289 179 497 399 470 711 760 428 761 888 324 592 717 615 080 405 777 555 824 417 594 133 863 233 750 045 889 892 171 218 259 136 999 242 005 477 220 921 542 444 467 535 146 954 514 963 107 144 711 837 485 074 036 233 517 018 978 691 620 202 056 635 469 114 939 855 180 061 553 325 536 887 704 144 980 986 580 822 428 794 863 056 794 472 862 495 894 478 604 065 721 290 384 710 844 269 802 507 643 818 171 763 197 506 521 293 266 541 645 037 208 660 613 040 864 544 584 112 053 868 579 024 298 731 973 661 049 483 811 512 233 720 376 055 424 213 777 852 914 447 970 720 497 599 009 106 840 131 152 935 035 523 199 236 250 851 883 462 097 387 242 229 590 029 999 716 491 043 883 213 359 354 536 548 275 864 212 943 850 436 907 035 624 466 804 397 775 130 343 239 986 977 170 911 875 528 088 630 349 596 075 453 670 905 647 232 439 188 370 570 849 993 074 640 943 263 044 980 238 914 449 677 035 602 968 304 971 390 124 477 567 666 130 233 002 289 368 682 737 843 115 582 685 453 899 767 894 790 164 620 485 857 035 958 697 414 111 759 127 612 059 909 317 967 559 570 049 968 325 122 894 401 658 099 964 065 782 724 702 376 242 452 485 983 410 831 016 874 734 462 767 276 799 325 377 913 733 832 892 143 769 804 528 623 559 502 051 428 452 759 312 415 141 771 676 623 107 402 857 932 924 578 558 890 190 739 497 999 623 874 904 950 658 828 758 948 148 473 268 692 394 876 100 374 333 982 742 653 268 716 816 094 862 119 654 601 410 191 630 693 485 906 688 409 536 733 837 459 650 835 470 221 093 526 339 445 411 936 447 737 003 339 562 534 621 561 529 188 439 152 478 812 702 507 128 073 509 097 978 746 775 850 955 670 587 791 954 000 104 574 696 920 721 589 838 894 488 022 318 875 754 151 085 063 625 659 791 342 040 117 277 290 764 299 104 602 942 072 106 148 635 601 273 621 898 452 940 143 944 840 130 014 490 298 786 240 110 443 438 294 785 452 562 409 799 345 074 378 637 344 861 953 432 330 074 532 697 479 953 886 554 793 279 220 154 635 227 104 508 710 117 438 583 056 713 632 532 021 229 662 396 702 280 315 525 676 783 127 086 860 642 402 914 565 393 009 848 689 015 941 307 745 214 975 801 799 829 103 194 164 478 013 417 834 780 374 291 874 399 633 058 226 626 645 404 817 844 494 101 485 839 862 110 561 693 919 763 815 448 526 381 945 579 891 050 157 659 788 396 544 727 838 936 324 757 445 606 056 897 721 382 474 106 362 356 050 459 858 696 070 126 950 186 247 846 631 295 195 207 920 328 574 116 881 176 694 551 470 410 805 932 751 470 864 375 480 637 491 679 852 615 808 883 624 923 053 233 103 562 771 680 657 025 436 150 263 048 492 658 764 957 193 757 957 370 794 058 999 591 238 598 042 940 362 875 287 912 330 141 419 905 788 246 498 473 009 012 053 281 570 188 104 701 140 697 166 803 350 608 369 369 011 162 819 174 257 316 179 003 764 938 868 883 014 017 389 943 593 125 733 494 796 691 771 743 809 356 618 714 763 033 804 055 871 542 493 723 092 779 936 825 976 237 687 045 410 819 490 314 366 156 039 354 777 743 843 362 032 986 527 203 182 779 839 091 951 769 742 632 915 825 417 453 073 828 541 113 887 562 821 659 845 046 008 846 971 665 277 577 008 161 204 999 427 458 803 161 540 138 199 225 610 928 510 933 777 015 480 627 249 088 106 398 921 071 872 361 247 111 847 187 646 410 657 289 231 651 238 351 868 191 933 420 871 304 075 881 155 027 677 246 747 220 604 760 003 074 370 524 057 777 307 359 936 494 224 262 806 279 738 578 863 857 243 116 373 136 319 862 304 932 442 895 377 238 068 735 729 493 320 396 336 634 515 925 261 636 223 685 862 233 937 871 089 656 331 390 694 980 293 836 009 969 063 225 326 298 622 780 779 178 514 048 489 924 105 708 262 355 906 832 811 893 935 331 421 491 413 030 587 612 325 620 065 408 290 790 479 619 320 522 519 134 105 912 633 037 769 375 041 011 410 604 355 580 499 193 423 384 548 516 337 590 107 817 508 028 830 375 695 177 312 192 662 966 337 728 710 587 485 502 607 890 832 960 860 024 956 547 472 268 451 771 485 242 590 971 423 845 155 506 204 569 991 769 318 524 761 864 404 750 047 353 075 895 783 982 850 800 225 216 311 611 848 145 832 831 311 421 240 966 305 469 351 408 863 465 116 534 790 460 905 969 091 994 321 347 972 453 179 503 058 753 876 537 464 810 771 710 900 632 260 202 634 360 697 196 779 216 417 862 093 730 622 682 920 169 523 577 086 355 412 582 009 159 478 629 988 296 765 749 362 956 256 552 708 204 034 622 957 387 315 806 459 173 019 219 002 644 191 612 738 449 053 844 668 360 496 388 914 772 314 240 948 407 287 323 343 579 119 096 172 451 077 195 457 323 977 532 064 704 257 281 893 358 692 844 162 912 710 362 257 912 877 711 194 984 871 210 630 150 699 181 358 469 688 013 608 317 470 683 936 868 164 284 018 188 786 328 792 832 500 618 441 664 103 117 758 948 061 162 417 764 040 107 048 498 903 103 644 053 735 323 656 426 961 238 514 325 866 121 998 273 887 283 311 368 961 807 131 012 478 933 555 303 208 749 360 731 314 522 255 179 400 368 066 434 982 557 020 384 912 321 091 309 775 980 743 968 548 897 312 687 285 745 927 079 698 418 718 357 751 434 168 817 294 015 801 012 160 112 908 097 859 367 441 180 040 821 326 389 166 205 384 335 937 642 718 930 434 244 570 973 888 867 089 330 269 182 011 571 063 938 279 643 087 890 213 479 129 940 782 778 221 558 383 687 356 683 707 425 176 454 659 465 059 052 326 434 655 650 363 317 875 755 165 785 543 943 244 659 708 335 290 726 578 236 491 092 669 197 212 101 326 089 059 359 454 659 978 129 884 131 392 679 370 861 314 722 464 396 642 349 768 018 615 641 705 054 670 557 293 775 833 984 845 450 799 647 114 637 201 847 512 973 065 171 131 383 895 942 826 075 824 593 235 787 704 922 987 948 409 451 318 960 558 600 620 439 637 628 474 919 859 832 760 479 391 075 962 728 401 224 173 056 603 248 483 495 937 269 549 235 186 405 377 889 349 466 138 965 551 935 687 778 315 517 677 096 833 653 084 774 397 284 051 190 830 441 195 518 375 495 529 187 723 504 618 484 952 860 802 026 071 808 093 272 448 963 152 472 831 179 363 428 838 459 527 630 700 853 689 654 912 236 295 318 197 682 665 926 497 371 206 609 780 839 963 046 173 648 864 663 130 613 337 403 934 375 584 993 719 429 343 570 047 637 800 072 865 791 873 323 684 632 938 756 198 900 555 342 438 614 198 044 674 050 297 697 155 712 003 847 175 687 408 926 396 909 054 679 481 187 243 622 518 398 053 525 863 301 489 820 566 884 157 585 477 218 796 947 697 929 252 114 831 880 701 418 382 305 335 775 578 323 680 459 903 233 323 974 065 069 897 982 547 319 687 750 841 070 263 710 697 148 743 754 829 617 830 060 236 921 565 229 826 234 109 706 185 809 282 044 714 305 954 031 237 264 234 534 792 002 810 316 238 066 562 846 277 311 767 710 670 288 105 445 776 397 891 820 293 660 475 925 748 693 867 604 311 584 687 467 759 500 480 426 446 123 546 678 992 393 503 219 364 504 664 305 800 057 551 036 586 946 434 374 064 509 238 321 204 163 857 993 730 090 203 978 303 484 756 137 502 965 266 154 067 689 042 963 060 243 958 862 929 542 715 508 548 620 065 611 080 387 765 805 583 611 457 481 035 464 501 925 797 891 043 944 689 546 397 226 418 286 216 642 969 459 187 731 690 410 349 613 060 165 813 810 572 473 716 821 937 570 218 051 453 751 953 910 364 659 415 397 236 738 470 402 801 900 258 304 528 385 660 413 507 895 938 882 767 690 140 973 548 874 171 354 271 894 807 010 810 912 131 174 421 304 404 816 280 544 633 734 474 514 617 687 084 434 605 844 405 402 867 480 125 432 870 335 260 960 530 972 516 072 499 766 154 067 899 593 988 696 865 649 061 549 002 784 289 162 126 585 748 960 391 545 399 960 641 964 322 284 961 232 345 019 680 874 690 504 787 734 410 207 818 539 079 458 563 869 552 192 992 693 159 314 381 232 096 867 096 392 191 009 392 141 376 300 557 371 508 103 267 311 677 521 952 048 788 100 164 621 448 586 720 177 722 965 074 172 577 296 706 374 897 696 531 455 214 106 919 858 686 507 653 290 199 955 632 084 539 291 537 651 125 544 860 128 963 389 447 208 407 596 037 658 751 397 114 641 025 909 775 510 555 081 591 113 471 000 092 801 384 904 591 299 816 869 341 759 784 199 813 993 377 901 955 206 193 552 268 921 236 013 263 962 824 117 685 851 368 913 494 183 385 773 274 782 982 518 718 823 524 266 828 495 930 578 719 172 982 213 039 734 843 625 691 408 028 575 411 167 897 106 240 681 720 127 497 772 966 851 752 575 170 241 481 481 335 264 649 110 516 140 234 339 452 096 423 221 703 163 693 192 969 600 104 831 006 818 769 719 392 980 810 471 539 809 512 639 833 146 129 785 875 977 008 720 046 471 490 155 006 018 032 509 639 933 276 950 588 351 507 060 692 284 784 243 566 173 509 480 492 096 919 654 465 768 371 225 601 064 600 208 454 417 655 209 855 301 085 955 051 573 941 191 681 890 123 906 845 443 174 529 920 822 200 281 428 523 340 758 886 283 536 158 000 598 444 214 125 481 860 144 145 305 510 715 339 580 288 367 671 045 572 050 779 687 842 734 086 322 520 457 161 483 280 499 195 874 879 399 981 572 281 997 190 786 493 490 512 493 449 395 898 154 277 984 412 500 225 038 178 309 795 000 808 445 558 989 311 821 018 702 551 224 249 996 969 858 233 285 629 832 364 681 207 243 606 851 993 036 667 124 181 785 040 776 442 112 279 702 385 502 569 415 167 802 789 532 525 884 254 087 145 630 289 555 019 954 537 984 369 032 382 814 490 500 170 355 510 302 326 018 867 308 281 995 745 563 699 102 108 912 300 656 654 472 818 488 907 570 403 847 487 878 795 056 134 906 242 416 771 468 261 899 396 434 992 567 525 676 883 270 767 691 458 661 315 272 447 005 457 077 731 480 802 528 475 344 551 568 290 217 270 558 950 920 923 806 378 008 412 489 374 645 085 297 998 981 212 302 566 676 130 482 054 395 414 169 338 778 618 298 919 389 437 706 757 429 732 285 918 316 082 743 875 041 815 061 911 188 679 891 353 547 942 379 788 070 681 613 444 815 567 124 081 113 160 421 438 889 467 527 979 229 260 489 061 646 204 016 695 089 072 593 115 640 693 515 603 589 089 979 757 190 522 226 805 995 386 726 738 103 045 489 691 010 127 758 693 087 153 775 859 471 570 150 240 456 427 292 678 200 487 721 852 351 395 904 797 887 108 241 270 457 595 518 540 655 053 150 596 108 995 991 804 036 210 694 280 062 739 157 224 739 805 671 532 192 834 612 982 189 767 877 004 322 657 927 212 195 314 265 497 626 220 576 228 696 772 640 384 418 521 895 566 668 789 650 857 568 405 312 240 381 392 055 502 761 388 783 268 241 313 714 465 150 140 124 033 938 138 933 506 574 155 102 966 371 492 717 718 671 442 988 336 126 796 247 553 911 610 636 435 349 704 640 971 662 266 268 622 113 017 618 974 220 011 389 088 612 927 374 456 883 288 214 886 214 891 553 779 834 175 745 190 609 389 440 336 930 489 275 243 917 919 508 993 023 422 388 503 571 290 030 555 221 272 228 075 773 077 040 450 638 491 498 650 571 081 709 288 927 306 662 656 253 502 235 474 175 230 841 772 637 174 494 062 390 864 048 001 741 047 777 626 836 492 713 685 568 469 179 331 031 146 057 368 326 681 461 335 918 228 662 394 743 986 443 254 882 380 884 017 118 548 693 591 439 634 822 096 062 537 997 079 780 135 824 709 757 262 300 340 367 371 707 712 553 204 890 680 740 079 312 463 097 933 954 728 392 445 853 339 677 771 078 555 601 523 813 753 635 881 392 731 917 204 029 583 154 744 231 981 146 217 531 879 065 750 055 654 769 294 332 118 844 044 191 382 031 367 415 672 722 992 901 238 146 463 738 654 612 406 893 316 227 509 159 993 398 685 643 505 919 914 617 643 872 379 238 623 091 954 422 505 803 356 249 188 310 536 683 356 758 034 508 987 288 960 956 929 281 244 464 722 402 510 084 622 065 068 445 055 292 576 308 821 140 249 544 774 716 355 213 250 355 991 120 016 852 856 090 177 672 031 843 256 753 279 648 317 048 288 323 874 173 273 571 212 079 412 795 223 942 255 799 146 033 003 980 484 514 240 579 851 021 347 217 271 191 280 748 725 428 220 229 083 242 533 986 151 702 510 620 740 596 520 244 284 440 864 369 864 645 583 904 561 957 921 428 246 132 676 674 739 840 981 343 719 707 431 410 820 883 862 518 295 901 840 123 100 595 919 030 959 947 869 279 309 393 021 924 754 685 108 692 273 625 775 456 905 364 762 490 636 761 795 045 821 350 615 867 756 958 092 943 568 421 947 177 080 306 078 336 621 281 122 985 888 184 799 721 617 798 371 141 020 766 069 782 554 462 144 000 158 290 940 380 624 942 759 870 335 836 042 232 522 799 259 332 668 219 817 517 177 654 861 076 363 707 180 503 373 653 680 775 271 541 928 354 386 054 308 913 808 413 308 826 176 879 037 889 173 418 602 897 158 569 070 798 309 009 619 484 052 682 047 068 114 496 879 477 146 152 048 540 602 841 028 234 693 125 398 336 082 084 642 164 631 033 633 759 359 024 556 991 069 215 174 465 827 245 861 033 824 006 096 020 707 112 973 145 267 097 655 418 219 435 134 661 788 296 185 082 997 093 795 340 737 966 358 499 871 523 904 944 129 679 754 029 052 045 412 937 150 961 453 333 620 323 113 942 264 962 214 904 833 525 080 804 701 162 193 299 069 749 892 571 212 468 722 988 310 357 873 610 742 577 172 152 688 158 850 729 585 376 808 006 138 238 201 619 904 483 878 886 548 318 931 547 240 506 892 458 405 693 068 172 789 404 405 017 768 572 312 366 341 213 562 906 487 419 304 870 126 879 270 764 761 189 029 838 807 816 059 648 721 220 276 682 049 692 492 958 898 273 813 464 664 181 481 953 238 239 948 632 347 032 169 188 454 533 596 577 940 523 783 233 774 299 390 547 164 970 936 263 462 090 317 756 039 506 558 191 477 522 770 444 585 598 254 361 713 062 626 234 117 621 562 996 314 564 600 489 531 865 306 934 317 599 966 532 116 765 776 112 460 654 569 802 871 879 494 778 256 616 397 965 686 966 198 311 363 013 331 391 239 446 326 199 181 202 741 372 086 036 360 538 727 570 018 984 090 027 510 789 594 066 731 105 022 515 127 787 634 472 281 049 895 313 250 708 624 070 220 386 078 081 598 195 041 101 063 202 001 556 759 227 735 904 391 177 514 470 414 763 890 692 953 891 680 636 093 227 978 527 014 979 130 162 700 779 698 417 603 865 235 274 625 704 535 031 376 890 550 820 675 821 356 168 795 235 005 156 266 202 052 988 026 586 734 660 526 257 517 652 647 132 750 040 930 917 735 002 147 758 404 736 933 513 412 612 249 793 639 837 445 789 781 939 656 355 201 153 048 564 283 366 283 157 771 353 844 144 340 113 402 863 165 121 563 973 685 317 704 227 705 015 640 281 083 008 169 530 399 153 311 012 403 065 483 288 315 873 865 658 721 144 035 141 815 313 968 789 316 809 608 505 738 157 983 255 955 281 540 364 590 087 788 937 456 491 343 528 992 509 122 707 065 891 486 007 648 220 364 345 432 192 940 750 239 678 452 771 725 857 599 759 549 895 965 733 177 039 178 302 560 941 368 279 206 562 408 131 111 960 096 797 064 585 776 893 572 445 683 815 510 356 552 237 904 155 164 826 011 167 983 932 108 640 773 592 958 056 829 609 007 165 253 797 829 616 416 779 288 493 675 425 844 576 838 707 426 951 608 367 079 955 046 601 707 196 959 055 184 070 457 203 907 540 639 531 266 005 834 063 207 602 429 539 101 356 180 859 120 493 560 172 386 840 978 097 242 089 641 664 240 284 511 390 773 913 156 947 792 566 347 634 895 996 350 395 991 172 854 881 784 782 864 358 117 063 557 405 148 118 866 078 608 064 993 927 744 819 176 702 970 681 063 670 607 323 153 607 689 727 105 439 881 158 802 609 684 764 248 173 393 503 106 164 452 606 748 427 432 695 423 316 605 325 332 655 888 159 402 431 896 793 300 282 834 521 532 734 592 578 863 730 594 658 940 315 786 557 814 519 828 389 090 345 720 605 073 451 850 661 833 955 409 484 244 055 401 812 071 865 585 036 507 991 050 104 732 599 854 210 010 915 099 655 658 159 186 423 660 151 022 539 852 577 095 383 883 561 281 081 903 409 725 134 215 900 759 407 639 906 365 613 247 939 713 519 297 001 775 670 230 663 248 712 589 028 787 557 223 211 257 663 863 342 250 785 676 849 186 619 864 405 231 768 552 312 676 404 779 212 060 508 733 796 882 978 484 345 748 530 038 578 864 014 302 769 086 919 799 541 856 299 076 601 107 028 892 636 461 546 239 378 565 107 349 598 270 607 875 383 815 761 867 424 766 569 221 731 321 143 648 783 911 992 238 251 218 719 214 580 302 495 230 717 004 514 806 033 215 074 691 817 959 445 898 422 499 019 449 221 302 890 411 011 503 701 618 503 716 176 131 585 414 037 953 695 784 525 734 973 018 976 310 702 692 346 437 778 281 717 051 793 845 973 173 030 998 313 653 043 841 768 415 709 858 180 990 958 836 791 935 753 007 280 142 670 361 977 723 168 137 668 306 825 662 459 508 009 555 568 578 027 538 132 399 266 514 005 816 492 004 171 662 051 186 270 733 247 794 197 585 984 286 805 164 583 165 822 481 518 524 944 075 354 477 695 085 529 304 803 748 152 955 485 598 981 127 639 928 147 196 071 917 932 218 395 404 760 794 999 364 776 894 943 377 545 180 433 934 391 995 133 403 728 078 730 844 601 090 506 935 506 436 316 016 379 394 714 180 738 502 538 217 723 940 426 658 324 179 311 878 340 988 640 976 307 896 416 522 425 153 345 138 319 025 843 044 195 870 560 911 585 872 188 042 629 554 976 859 713 346 907 399 649 694 685 636 666 403 060 572 016 242 745 477 125 111 441 150 507 402 537 325 139 017 912 696 062 489 759 451 589 460 538 939 196 021 095 469 546 319 022 989 984 010 041 504 475 098 165 305 395 520 845 077 376 664 129 732 566 170 893 600 393 439 810 480 854 582 840 023 844 036 043 985 415 901 832 766 215 641 343 407 967 768 265 873 694 293 012 295 370 856 909 127 155 207 653 271 361 075 025 040 321 509 648 756 839 856 736 314 515 258 178 416 892 404 666 017 006 156 608 803 805 954 185 848 771 100 751 122 460 851 053 968 207 059 966 944 348 753 112 235 650 296 861 754 879 909 981 751 539 858 234 106 439 564 910 424 371 894 280 958 685 691 151 603 757 529 715 986 926 136 809 881 064 091 912 962 926 648 192 728 363 526 314 111 189 893 378 315 653 478 169 397 738 070 308 942 633 196 308 831 542 088 176 141 506 453 309 482 124 997 019 573 531 594 807 417 005 120 743 937 880 535 076 372 999 834 959 170 188 591 873 351 454 472 620 633 666 691 878 795 478 136 428 588 232 787 941 663 412 852 411 571 551 218 662 627 842 630 260 012 650 661 965 486 092 667 154 690 469 990 993 194 905 123 449 536 865 962 583 074 829 515 089 414 009 123 830 782 481 067 088 556 677 885 469 645 602 523 261 911 299 105 566 617 194 830 960 657 846 892 194 693 995 207 564 178 771 081 420 729 475 629 263 986 777 588 331 655 314 310 288 023 414 524 787 602 294 648 840 742 666 151 137 256 728 987 046 934 544 673 543 987 362 424 217 745 620 625 589 572 403 903 867 928 867 845 218 728 178 567 442 978 426 778 569 620 825 583 016 901 011 092 717 459 866 552 216 905 981 394 422 156 001 931 960 320 948 000 833 898 222 329 389 879 186 967 363 819 496 025 392 597 305 599 977 640 095 774 354 560 947 383 922 994 766 753 315 835 495 745 892 145 480 817 476 905 081 494 506 661 183 705 503 686 340 813 925 959 503 249 925 382 048 789 544 415 440 817 276 859 492 891 428 172 401 347 410 475 771 552 363 702 356 171 155 117 758 190 136 720 207 583 120 278 747 997 248 655 438 499 233 949 859 586 359 872 180 795 595 920 161 851 184 509 909 344 198 909 676 821 087 772 503 133 692 451 938 942 847 277 069 625 134 686 559 440 265 015 606 899 825 463 723 684 197 191 691 439 880 481 137 068 691 965 418 282 031 246 861 764 867 684 735 919 677 227 448 451 510 379 586 143 959 968 463 699 984 683 785 334 892 484 835 220 077 724 808 796 843 153 195 342 834 898 860 193 922 997 304 382 652 193 673 252 594 742 906 793 955 350 312 218 032 792 504 077 702 912 990 110 113 213 766 041 427 249 890 341 969 162 849 194 450 314 080 890 190 161 102 801 312 465 308 104 038 175 275 734 319 253 196 268 962 270 411 273 745 978 012 544 466 538 695 034 841 178 482 805 380 639 245 976 344 997 574 491 866 014 385 355 085 411 394 312 248 569 243 017 793 371 859 947 001 095 040 439 804 650 106 423 409 439 058 313 567 460 427 396 422 872 125 376 227 544 838 982 484 119 480 334 694 763 989 349 847 524 536 475 026 894 017 555 420 239 816 809 518 176 776 095 165 169 885 450 706 196 056 326 901 263 212 199 708 536 123 018 110 880 660 675 719 908 774 497 138 316 439 857 533 111 775 924 180 053 002 661 353 856 864 198 436 476 132 253 562 595 667 421 317 973 080 991 128 105 475 726 328 469 492 403 172 683 541 330 773 009 251 734 925 442 921 955 571 345 245 659 314 886 754 734 946 414 783 633 054 465 662 253 964 373 954 320 154 594 469 108 479 163 897 190 755 592 110 972 394 022 102 766 094 586 878 086 982 289 482 789 261 299 236 834 760 351 742 739 286 748 383 996 370 648 096 757 627 126 524 469 326 968 493 905 640 127 551 206 686 589 202 192 899 199 437 206 666 403 718 092 388 405 867 814 892 008 258 935 979 438 211 679 103 355 061 752 133 171 719 739 042 042 632 653 027 577 195 242 828 146 660 743 170 740 047 038 950 549 818 647 053 811 718 563 226 813 529 766 703 692 959 641 887 277 891 735 655 648 272 495 681 388 248 362 237 271 860 257 598 360 490 852 263 824 095 915 252 005 202 242 034 617 495 666 898 317 235 436 186 223 067 777 910 776 279 984 191 555 722 428 346 869 860 032 787 348 336 532 440 146 295 765 778 492 525 389 467 240 224 585 404 053 681 975 101 315 413 385 137 494 544 879 513 188 016 606 010 832 990 879 825 790 408 304 518 025 374 697 419 778 764 019 912 852 077 431 747 145 429 391 023 172 957 588 427 152 109 737 697 577 347 197 903 919 451 309 941 109 057 843 418 007 485 895 161 502 110 117 594 353 899 920 522 747 936 031 542 444 182 724 658 529 277 315 500 523 240 163 165 246 391 227 169 116 363 196 262 510 838 601 176 284 869 718 038 777 164 912 662 960 090 602 486 346 336 065 107 335 682 763 173 909 028 881 414 000 357 212 115 506 315 038 295 821 315 299 660 867 647 956 100 395 471 404 685 658 215 595 878 435 275 852 894 500 725 480 254 401 840 393 546 530 296 192 870 998 073 659 322 511 341 538 430 606 889 653 393 593 720 890 894 373 035 108 509 532 352 465 349 189 071 007 521 626 518 040 400 683 178 860 792 156 182 051 655 558 607 931 358 775 374 089 796 378 147 054 240 560 175 340 545 431 350 340 097 884 913 460 177 744 139 542 995 117 769 760 643 864 770 944 834 734 449 484 546 088 650 831 355 388 308 058 137 983 014 367 653 960 603 266 395 370 970 327 769 931 256 409 266 937 964 987 949 139 564 033 944 076 288 721 997 863 469 596 448 032 863 591 591 087 339 688 519 859 471 562 276 840 694 528 517 150 411 854 842 827 659 313 006 115 511 232 726 532 317 643 909 548 735 743 236 630 292 639 435 235 801 045 272 456 974 323 988 784 917 352 742 457 421 746 261 535 394 582 898 141 045 136 436 589 312 646 587 181 449 513 277 878 777 863 242 930 076 958 216 299 224 790 119 757 280 188 879 976 710 183 748 617 619 446 980 640 629 889 407 681 035 001 680 504 033 894 925 820 055 021 872 135 546 801 814 105 530 908 740 055 599 309 385 618 793 325 373 235 453 513 351 834 263 814 474 349 863 306 512 241 968 188 987 715 494 164 127 243 847 863 269 584 399 117 843 117 620 078 927 380 068 772 451 522 243 548 098 671 168 314 630 094 000 248 513 577 826 783 399 415 522 050 960 185 236 920 101 261 399 932 206 956 218 566 869 654 360 339 335 146 219 753 012 560 204 947 570 959 054 683 587 918 307 729 101 957 351 626 957 371 402 293 362 188 837 522 083 529 633 458 959 893 235 826 190 781 293 165 845 362 742 958 121 253 214 373 856 374 389 769 645 635 447 129 231 560 514 231 827 171 443 199 667 987 102 038 083 553 308 210 203 651 592 148 964 583 923 476 446 417 495 366 409 624 646 498 928 787 233 287 932 633 671 941 457 688 276 568 756 124 696 998 536 907 070 874 575 696 048 767 701 437 629 300 196 047 582 799 121 232 298 867 123 731 492 306 685 987 901 369 716 521 899 841 835 031 143 774 303 408 268 495 493 476 150 668 138 725 448 426 360 898 265 274 706 079 601 349 219 416 834 636 572 907 834 203 932 425 661 991 314 379 491 682 523 037 542 811 743 970 579 941 485 196 190 165 873 887 968 056 345 583 022 633 980 089 422 281 501 828 250 410 437 636 902 019 197 657 103 473 808 633 956 056 854 491 078 866 712 329 263 995 936 341 302 905 523 973 652 968 019 480 721 991 538 455 958 729 005 014 889 978 560 514 624 530 026 653 003 973 497 928 458 996 785 267 708 240 396 952 460 807 225 573 252 639 861 746 086 036 401 446 900 781 863 510 519 012 992 005 959 129 033 219 284 418 112 478 361 363 794 334 036 635 182 560 068 229 530 235 535 308 361 426 678 918 397 042 524 739 367 834 948 946 774 166 092 988 921 520 987 481 007 378 103 632 996 155 879 106 556 117 595 544 267 712 344 661 576 681 755 966 505 652 230 139 233 958 929 432 736 427 580 995 263 462 523 236 050 486 896 354 999 589 377 869 136 655 313 777 602 360 377 002 974 809 791 047 956 249 196 177 569 270 925 011 447 151 506 643 633 694 076 726 368 395 069 767 019 706 569 089 433 922 551 944 812 683 223 751 723 593 547 497 144 555 469 515 649 338 685 453 012 740 442 395 238 825 676 082 944 778 310 234 191 640 055 578 773 729 185 896 392 442 984 009 437 408 134 086 953 535 237 431 070 336 052 574 464 455 187 096 498 673 749 477 369 586 611 487 522 908 403 114 950 097 246 226 090 207 636 696 660 718 038 087 011 155 168 142 363 311 462 107 466 226 444 389 243 864 551 508 106 795 975 598 166 061 202 370 225 603 333 538 372 029 324 816 323 744 313 095 287 956 121 455 056 691 560 468 395 429 135 266 521 583 594 575 948 036 932 939 637 081 864 903 846 153 351 555 777 080 059 200 095 267 178 495 983 461 995 543 689 195 813 069 164 593 916 604 604 383 360 323 721 077 586 249 191 745 338 597 631 678 653 925 841 397 498 145 440 781 469 251 422 331 716 637 842 772 575 192 137 112 546 446 389 708 867 178 460 327 628 872 400 877 363 397 223 591 234 166 463 798 849 452 957 703 668 287 414 957 628 895 863 819 180 990 975 953 134 539 546 035 550 250 779 669 084 358 621 774 800 268 762 744 605 673 700 366 553 057 612 503 536 871 920 280 053 034 437 017 457 135 401 778 894 097 833 041 951 172 956 340 200 295 305 757 840 355 714 261 663 274 316 064 514 079 086 775 267 637 345 060 673 384 053 274 054 338 471 824 021 836 661 700 957 921 472 686 820 413 257 355 148 148 774 954 076 141 026 767 697 654 399 102 465 305 570 383 958 865 084 006 216 172 118 019 802 567 149 700 519 420 384 725 806 750 044 122 579 858 656 698 540 101 125 229 772 238 815 819 428 432 485 153 412 882 717 961 252 067 004 699 310 585 435 980 606 460 794 913 378 459 763 028 147 478 331 391 191 499 199 688 491 788 802 765 805 033 928 928 498 101 410 008 676 144 273 497 222 553 205 822 415 529 373 701 380 590 102 248 637 301 197 639 582 599 492 600 115 895 905 740 144 423 778 337 975 417 035 932 334 420 816 700 952 399 383 463 490 000 652 551 077 907 065 274 077 568 861 980 109 778 351 901 718 447 753 686 443 007 524 602 415 514 129 114 568 737 207 789 701 924 925 506 811 587 742 309 331 090 897 777 364 662 009 604 798 658 992 760 295 346 624 197 497 986 752 127 589 449 599 565 062 586 371 744 297 975 078 447 569 125 754 389 228 653 436 211 591 886 564 933 838 057 466 962 087 388 606 503 519 641 454 320 611 999 311 025 765 409 557 307 408 338 383 595 236 282 449 795 907 194 277 018 778 360 806 062 804 313 927 022 774 511 371 243 227 161 041 497 501 540 654 762 521 738 753 248 114 652 370 588 451 294 207 466 109 900 404 460 244 282 864 951 068 387 674 427 926 472 320 640 724 685 701 933 608 022 496 166 956 875 533 790 545 001 415 184 137 955 588 924 647 203 718 453 333 037 736 934 333 610 470 130 991 931 393 915 033 844 872 112 853 942 797 707 434 226 807 508 584 808 817 828 419 885 031 539 489 266 413 622 916 722 638 213 933 274 045 898 309 535 946 655 113 609 632 563 728 233 040 088 525 294 545 080 808 552 546 778 005 063 929 679 454 333 573 249 270 294 125 052 935 867 926 919 194 867 288 214 232 755 946 033 191 012 644 817 225 499 151 123 650 263 935 104 775 531 646 814 467 291 127 906 033 052 418 819 494 414 067 019 862 034 493 046 069 399 541 625 139 339 141 470 835 540 600 646 947 571 050 345 463 153 694 077 366 572 122 419 972 447 578 540 775 514 122 015 450 156 280 440 912 294 232 920 625 506 175 840 273 719 883 302 254 419 410 122 500 622 969 039 550 557 079 809 230 918 265 073 478 081 578 013 929 046 057 033 474 941 339 711 975 496 746 506 333 955 336 001 634 095 311 427 704 259 719 658 995 480 123 457 243 249 127 432 357 212 485 221 060 006 366 735 003 835 078 070 512 590 006 258 129 271 781 761 157 186 439 373 261 902 157 544 895 416 711 690 785 783 941 414 478 766 156 407 198 134 869 442 016 792 035 649 044 900 662 433 275 509 544 505 718 856 784 863 056 673 721 717 741 179 364 845 062 501 187 176 174 010 163 445 938 912 842 857 562 942 072 051 187 366 789 573 432 748 079 910 406 468 306 327 770 146 395 485 687 779 825 130 450 142 842 479 336 317 327 820 088 893 827 678 456 420 442 936 056 887 093 403 520 770 476 994 843 378 140 753 647 347 194 151 688 811 211 432 752 283 552 039 669 521 560 815 090 368 080 688 761 497 357 788 930 935 588 550 426 208 311 484 677 307 918 302 096 245 662 175 488 882 650 354 897 769 855 299 676 218 160 399 581 034 406 730 416 971 293 471 810 955 426 230 580 513 308 864 773 861 089 141 788 173 129 357 213 785 489 106 090 705 114 052 251 222 879 854 012 828 626 126 819 739 627 650 126 014 166 897 431 536 506 578 047 906 960 714 655 488 929 564 300 814 664 628 505 292 027 328 192 928 973 430 942 027 670 094 950 616 255 930 183 564 687 804 212 273 658 392 540 125 786 214 073 520 153 037 772 668 659 037 581 234 716 140 706 014 770 303 156 771 730 910 516 295 475 033 307 445 603 730 684 815 582 212 728 520 757 964 016 388 271 016 890 127 357 914 355 340 891 131 635 029 084 148 857 007 101 796 440 951 214 703 226 537 776 176 816 358 752 054 219 151 064 458 155 611 520 236 396 637 940 688 270 261 792 494 413 695 900 173 207 483 171 393 890 907 708 793 625 697 645 481 327 750 052 440 582 336 644 747 138 636 021 351 388 015 635 175 688 729 305 566 050 682 004 803 579 687 115 281 875 638 587 119 894 635 963 569 820 867 418 589 373 595 764 398 381 713 349 981 010 175 027 205 153 568 606 379 263 009 783 577 147 537 847 759 809 655 190 041 748 865 632 179 314 456 976 673 245 739 615 379 071 731 693 374 443 105 209 843 094 640 197 283 444 266 677 456 738 650 613 431 339 373 421 513 645 626 323 180 403 811 710 261 374 823 378 773 815 096 502 225 337 233 324 021 320 483 173 448 077 456 875 862 629 555 029 455 805 408 795 090 390 925 946 179 070 204 413 333 894 544 884 109 880 743 069 482 203 805 204 677 284 241 617 354 278 033 983 739 980 579 309 009 075 047 566 267 411 554 859 286 966 273 440 559 407 402 496 390 075 051 015 225 174 339 506 215 339 841 580 765 907 535 194 568 978 190 778 572 475 754 192 628 231 220 355 986 938 535 715 598 679 591 421 567 362 370 048 708 588 346 304 202 468 141 511 840 619 771 192 066 716 488 071 053 040 007 344 202 372 801 025 197 414 460 061 801 905 461 679 701 173 082 123 623 088 165 321 883 350 721 973 384 612 611 307 139 756 908 157 266 844 656 604 577 165 281 970 287 249 619 452 776 989 569 788 503 477 743 732 636 470 319 592 826 820 632 411 741 406 226 686 558 082 308 374 053 518 759 196 755 210 057 140 159 756 737 072 351 819 198 789 749 464 791 832 414 908 585 632 703 952 739 944 954 292 025 694 157 213 909 020 079 001 160 380 079 187 046 602 508 291 074 749 300 174 156 412 777 664 545 264 826 617 737 868 604 291 708 347 440 224 411 626 105 210 057 555 000 132 831 981 734 986 973 734 488 893 115 199 002 056 217 040 123 379 564 712 384 612 798 417 512 380 343 369 120 132 830 959 877 956 650 489 232 864 492 023 796 080 781 941 476 857 140 940 216 587 136 161 437 424 773 046 992 171 188 902 937 036 592 762 634 826 180 135 254 702 892 636 845 725 348 047 698 214 923 693 588 502 760 041 823 089 368 301 244 076 121 361 220 872 751 173 193 085 016 300 630 732 560 149 783 276 534 571 234 130 356 581 565 514 890 652 643 530 570 266 305 210 162 107 825 514 274 807 714 624 422 401 121 239 520 741 936 570 102 838 176 936 719 463 232 703 747 997 397 211 859 267 403 890 392 462 175 666 607 310 126 472 027 301 575 666 488 942 733 798 380 817 033 487 274 623 779 311 145 696 549 799 785 098 725 550 111 584 101 461 182 799 302 202 627 000 788 279 530 829 707 920 218 008 878 118 636 869 318 968 160 923 523 887 189 730 454 390 072 244 611 439 998 533 360 335 386 099 393 998 254 807 911 920 851 846 899 514 412 108 767 027 021 440 433 530 175 062 223 963 003 502 886 838 722 764 684 711 485 240 105 990 168 223 710 538 069 905 159 644 209 463 818 738 982 439 600 472 353 043 699 821 077 187 284 827 771 696 285 588 399 601 072 910 754 902 789 928 523 349 575 625 980 308 376 225 316 883 781 469 251 568 610 657 746 565 221 572 160 300 802 034 899 546 276 167 434 112 496 782 845 754 695 674 463 201 301 663 153 361 721 469 573 376 627 780 704 195 677 109 970 071 857 735 470 122 460 613 353 343 999 587 795 723 264 614 638 106 199 721 130 644 043 531 649 314 931 869 839 018 848 507 724 085 881 760 595 642 548 764 894 950 195 630 488 050 752 312 825 423 248 656 589 421 904 651 620 980 945 755 013 150 830 539 578 168 729 374 957 729 143 046 350 386 439 276 105 879 387 745 961 189 299 868 264 606 491 862 549 317 516 358 647 576 782 557 756 270 430 817 405 663 806 358 967 744 724 205 971 251 795 438 373 028 413 531 573 384 735 490 402 718 561 792 778 309 647 160 615 239 373 031 960 852 932 639 219 185 788 562 530 866 978 247 030 767 736 945 329 702 126 048 359 264 043 213 217 547 984 288 987 376 866 101 971 360 410 594 608 141 928 200 567 184 799 036 987 249 181 242 081 294 780 118 741 122 863 164 914 233 677 573 840 135 364 078 769 148 880 713 251 709 207 888 901 834 948 166 686 326 155 080 129 585 729 140 689 382 299 387 423 185 610 602 051 849 424 936 844 624 093 788 170 212 065 655 002 935 602 554 956 234 137 700 873 613 750 512 508 133 042 130 276 587 536 325 448 915 222 344 329 635 746 681 250 449 782 893 683 617 464 932 220 918 557 718 819 600 854 726 267 250 845 485 739 537 073 752 201 655 994 057 130 298 642 449 515 036 377 659 956 682 178 454 087 726 740 455 970 265 465 770 775 550 618 526 023 589 617 998 458 127 614 989 125 062 202 933 140 660 100 048 260 422 541 958 237 779 573 305 724 324 686 190 930 611 075 314 945 508 366 689 823 970 525 638 150 103 594 477 901 631 858 802 734 344 068 926 234 063 515 137 218 933 612 304 757 783 978 905 375 204 876 236 770 969 353 724 190 198 707 953 390 903 278 639 429 235 120 061 064 083 785 227 453 086 302 473 117 197 250 536 955 623 785 687 709 269 388 930 197 804 341 030 150 710 303 434 632 335 080 609 591 529 463 524 507 913 525 602 458 521 301 247 307 391 563 839 635 342 082 572 873 898 554 412 859 458 204 974 797 983 554 770 243 493 802 408 698 810 061 437 852 959 312 879 483 334 846 876 022 304 384 835 639 739 776 872 445 259 230 005 835 296 036 458 468 990 682 553 892 256 884 892 516 126 692 428 012 438 989 815 961 649 378 549 461 980 452 471 102 324 680 473 365 981 353 996 225 977 851 644 301 824 328 337 183 656 284 756 773 271 864 022 414 856 060 704 235 409 806 482 707 436 413 630 000 793 063 360 368 092 284 338 502 059 783 136 259 298 212 125 554 173 891 783 137 360 074 779 204 229 485 406 593 670 772 666 270 923 290 408 296 424 116 998 370 982 029 858 763 682 768 607 307 118 352 200 652 900 530 173 489 035 456 571 353 926 241 968 942 223 211 851 434 241 488 585 135 732 202 234 740 794 487 253 558 735 253 240 872 332 994 728 092 340 648 077 114 793 701 450 835 454 440 551 945 205 244 799 734 708 975 976 730 897 693 505 237 918 640 605 063 046 113 844 474 912 986 539 362 069 482 359 277 465 915 369 634 497 512 571 654 452 851 397 594 680 060 783 043 059 043 115 419 469 216 219 686 404 185 236 078 547 391 897 544 164 037 550 554 309 858 642 161 124 671 416 661 909 540 092 926 612 595 903 496 225 678 793 541 320 288 012 550 621 197 573 712 702 221 640 165 132 509 342 270 778 137 668 076 119 513 311 560 924 503 656 402 487 622 744 282 771 623 865 844 794 085 753 490 994 871 558 507 249 513 978 246 854 529 200 737 666 079 774 186 000 926 364 181 431 008 362 027 226 080 746 782 520 189 589 027 298 205 834 980 069 789 702 309 622 079 071 436 938 419 661 273 988 717 755 974 303 942 663 336 001 075 088 715 718 347 543 835 389 302 197 491 313 149 086 403 675 775 984 579 889 154 534 279 489 639 061 216 185 591 388 885 763 108 641 686 179 724 036 457 189 817 734 137 538 416 174 072 447 883 299 427 731 178 775 718 616 459 879 942 251 705 410 159 764 056 477 184 167 826 803 233 866 285 082 773 973 642 109 102 499 830 081 406 334 001 505 876 248 129 346 860 067 752 830 279 131 944 555 451 768 501 303 465 605 520 363 762 522 432 743 201 084 240 230 171 259 278 745 199 518 428 480 226 205 944 954 529 669 805 318 344 091 330 064 654 200 910 640 251 073 142 001 991 156 916 586 802 691 126 961 700 715 306 818 330 864 584 477 781 415 546 227 773 737 033 159 254 718 926 545 097 363 973 235 441 724 609 725 678 217 307 243 563 323 646 962 016 488 925 581 086 344 615 223 506 675 950 686 017 551 510 340 084 010 587 784 444 288 441 471 693 293 869 855 480 175 133 274 186 268 558 027 317 381 951 561 180 616 046 036 201 298 176 518 082 187 865 551 121 198 783 959 386 069 082 930 459 951 823 438 874 188 893 617 935 815 247 588 930 180 206 144 649 318 022 354 826 939 903 357 430 971 155 326 360 914 301 110 056 373 998 023 686 989 435 541 053 003 329 379 840 659 159 782 942 215 503 787 023 674 160 620 886 762 082 818 335 619 836 578 345 135 804 585 866 617 298 932 874 215 932 885 991 379 723 081 634 750 666 039 793 096 001 849 687 658 301 481 115 991 873 752 978 640 889 288 458 515 179 867 710 699 711 951 754 175 479 067 322 433 433 073 964 231 776 141 776 799 094 197 723 312 936 529 782 446 812 375 336 793 009 372 564 889 220 740 234 348 665 588 350 891 339 592 456 990 395 359 991 792 105 331 112 002 531 566 548 732 586 106 542 641 379 518 395 441 450 771 176 801 698 444 881 600 198 974 262 950 362 395 981 807 261 539 170 097 854 444 694 617 386 204 158 045 891 515 321 012 525 570 105 322 200 345 386 483 272 045 335 543 646 186 769 687 887 974 825 002 901 739 178 903 100 226 330 647 613 383 659 781 517 867 193 779 223 844 627 315 548 650 032 547 264 651 240 994 066 925 318 216 840 135 445 679 002 397 013 297 296 398 194 663 821 860 218 911 481 487 354 482 239 840 481 976 235 159 930 964 668 614 292 360 594 926 734 840 283 653 984 505 339 871 638 513 422 999 126 228 678 325 073 446 518 676 920 113 260 032 850 677 997 163 030 700 122 820 399 128 473 898 112 175 989 256 214 975 553 904 542 335 858 861 841 671 397 893 021 102 473 837 357 377 175 714 654 186 616 189 020 278 309 586 707 752 810 896 057 659 672 790 501 406 503 516 068 096 158 310 367 432 653 170 087 559 647 844 070 447 526 285 580 699 233 280 585 991 896 211 875 409 351 375 499 805 855 697 354 460 650 495 094 087 016 176 100 784 235 124 057 464 722 563 628 537 755 796 854 521 169 718 469 725 889 664 720 469 056 471 740 943 948 103 834 641 217 437 841 761 966 880 416 240 143 528 014 925 059 296 151 472 782 705 307 167 449 586 426 698 810 833 190 127 179 536 003 830 059 556 422 729 802 238 940 136 189 495 513 015 815 031 489 688 719 045 622 572 333 032 648 487 249 008 147 134 866 863 354 910 165 500 798 297 795 583 898 435 842 145 854 141 646 528 909 508 974 801 940 798 700 410 521 496 449 090 441 193 351 944 770 199 795 178 553 737 551 315 721 373 058 610 667 826 138 424 340 402 163 081 032 080 819 482 889 252 791 985 227 143 981 892 234 257 846 351 692 311 390 603 406 084 653 240 303 172 986 582 037 188 451 668 289 298 626 980 720 558 212 165 722 901 502 786 492 989 261 364 499 978 551 603 673 906 850 107 848 747 305 408 488 902 432 287 763 951 815 177 284 008 093 778 389 300 465 788 608 102 021 326 908 388 954 606 373 685 017 058 885 395 238 411 582 945 026 003 952 835 611 516 949 025 333 607 775 845 507 930 243 503 966 704 662 607 039 195 345 816 046 393 970 195 562 342 712 741 811 445 189 820 582 225 364 139 760 973 716 704 102 472 404 924 684 028 851 020 206 215 394 961 244 982 807 929 527 631 012 665 876 674 905 876 114 494 459 371 675 039 248 555 192 505 443 231 317 105 414 482 771 537 321 672 259 005 440 470 459 420 149 754 251 426 700 756 993 624 997 800 284 034 221 746 495 994 946 201 405 740 310 852 787 457 617 293 592 845 975 144 742 286 918 644 602 634 316 602 389 795 399 929 381 888 763 140 843 301 168 339 793 280 762 594 219 564 308 623 471 414 828 542 842 304 694 368 061 413 858 568 410 867 532 841 823 743 241 760 295 625 594 242 018 679 720 379 897 012 225 241 657 436 926 532 359 490 494 135 013 658 880 968 995 573 374 354 487 367 588 832 191 242 165 454 889 011 441 116 816 984 083 775 101 431 476 214 376 571 453 599 632 285 006 064 219 251 023 003 133 118 789 000 478 452 996 824 127 360 522 573 757 418 336 384 091 263 738 312 888 973 253 365 985 996 426 395 518 862 554 795 719 003 316 868 746 262 168 464 615 425 088 379 187 918 972 120 096 509 787 880 132 803 127 280 270 829 075 222 084 965 101 459 804 889 253 703 295 495 841 618 589 724 292 279 944 284 879 656 283 698 611 542 562 029 447 349 414 736 618 463 243 450 812 649 709 523 466 335 394 506 970 788 670 609 356 482 002 293 024 591 894 209 444 835 342 269 377 584 224 724 059 313 668 230 914 889 282 556 044 320 686 255 593 752 578 689 218 670 623 001 883 628 758 469 239 819 963 598 892 892 541 442 532 585 902 467 337 464 434 449 642 861 972 231 920 085 931 107 553 916 270 894 797 763 734 408 053 280 233 526 404 394 179 981 645 260 234 234 418 435 273 869 759 326 044 819 849 169 192 702 455 272 724 902 502 122 879 093 660 515 317 347 978 938 916 533 748 560 135 658 540 856 936 451 827 383 152 633 003 883 391 347 220 052 021 820 602 607 752 144 666 822 496 800 210 567 463 584 379 960 786 462 027 331 208 620 839 342 447 092 407 011 629 325 831 700 117 600 737 730 471 945 461 509 011 399 089 238 502 578 741 394 302 321 763 100 120 314 677 146 219 522 064 856 722 805 561 144 580 485 185 413 128 961 203 055 132 532 644 434 651 579 480 850 787 473 051 668 874 060 535 865 102 836 521 989 751 590 051 735 293 701 123 727 601 507 121 694 141 676 568 590 471 235 387 299 517 201 951 265 830 037 321 143 208 878 141 051 660 153 413 637 555 188 388 989 487 925 401 434 902 965 053 825 089 318 062 182 748 353 793 380 189 716 680 573 538 952 979 114 445 159 624 892 150 617 103 049 924 319 906 567 360 339 314 163 234 907 960 106 861 073 584 751 417 150 079 679 951 786 595 920 808 538 971 932 908 321 105 396 178 672 671 990 219 805 175 648 504 389 706 080 649 448 162 030 420 118 566 180 378 895 797 457 142 985 505 647 143 517 680 646 050 543 262 699 496 995 920 947 292 042 709 084 606 942 351 290 323 078 243 421 548 848 227 148 078 740 477 130 652 915 599 637 429 638 207 413 307 448 613 137 602 863 484 834 468 647 154 921 187 431 428 983 929 164 713 220 667 800 173 543 776 893 712 775 367 343 667 070 869 908 199 591 910 255 659 047 780 778 438 630 917 366 817 407 746 105 986 982 970 695 165 182 258 214 679 633 241 201 078 809 624 482 622 937 749 032 789 712 987 688 845 999 827 667 617 823 919 721 219 709 431 838 933 272 712 621 563 012 665 907 564 946 405 630 369 546 886 085 054 203 537 733 186 812 414 092 495 292 356 878 226 743 721 445 934 711 329 600 722 475 986 734 115 531 263 228 183 354 598 968 128 525 644 407 766 707 157 501 978 500 434 338 257 498 373 704 032 016 360 326 932 352 405 780 117 854 310 486 796 855 137 533 261 071 017 651 252 352 560 260 055 125 904 612 462 916 463 573 806 235 295 510 235 675 250 730 845 780 710 810 487 212 807 863 462 987 171 302 558 833 041 996 953 664 198 131 171 763 939 541 706 101 863 801 743 331 009 903 648 906 211 077 960 498 601 016 364 807 611 368 613 843 973 173 726 753 493 813 731 091 593 556 753 569 581 598 887 792 665 855 994 883 173 804 178 565 515 467 336 734 217 416 004 918 745 463 994 210 180 536 138 893 710 599 625 838 157 840 681 856 056 354 716 635 100 907 002 844 765 736 548 075 633 166 343 150 314 050 014 946 333 591 915 965 554 091 928 623 805 731 891 104 343 492 964 614 442 716 033 443 571 266 020 632 309 260 504 160 477 471 975 900 013 819 374 320 427 684 683 643 316 652 085 093 266 210 367 018 710 185 714 964 372 770 049 575 769 766 090 631 625 637 112 933 496 663 933 164 454 021 099 763 438 058 462 037 612 401 708 181 323 761 264 777 368 635 610 467 847 584 543 063 241 942 619 329 338 726 266 145 518 581 372 954 941 281 692 045 989 330 284 906 496 591 662 059 090 334 807 072 800 617 639 399 705 139 822 738 528 025 338 571 168 852 702 554 650 657 823 050 737 955 208 086 892 696 524 533 941 650 850 619 171 558 202 516 897 503 370 860 404 620 513 070 841 590 076 932 109 560 006 055 724 258 225 213 246 770 203 834 295 883 927 192 148 040 137 156 235 118 602 501 358 195 659 619 618 469 872 362 395 718 921 924 780 737 493 242 262 707 747 821 419 098 153 222 983 968 381 538 783 520 072 187 197 749 307 248 286 009 957 915 562 242 398 606 301 121 573 253 576 594 812 594 630 759 467 819 787 293 695 468 086 160 960 929 578 958 079 032 977 273 723 442 340 872 308 374 820 875 380 759 535 986 675 009 270 855 206 983 853 779 747 038 306 172 542 070 204 715 962 590 813 447 419 886 355 686 239 026 455 159 602 066 319 356 897 416 788 348 920 312 977 189 124 144 276 123 294 614 492 912 860 603 981 871 174 105 564 157 474 800 237 299 392 461 301 379 875 599 259 968 670 198 132 493 508 265 937 196 732 286 507 686 411 545 107 685 476 458 580 278 564 849 764 706 597 008 669 987 143 085 540 723 083 537 201 292 830 381 109 455 678 453 137 844 506 228 215 432 116 289 742 216 296 583 605 341 638 961 544 748 345 079 213 470 979 039 711 989 454 385 407 726 786 795 964 973 425 344 017 058 624 410 652 230 643 594 738 568 172 191 745 746 749 350 712 478 336 163 331 928 220 481 506 621 143 690 301 380 116 316 963 174 498 681 726 987 857 108 230 640 672 348 996 342 093 548 760 028 464 597 637 680 782 944 715 901 077 497 659 615 399 117 536 125 248 737 001 071 597 173 751 514 816 947 687 918 661 356 805 732 410 885 339 292 284 911 927 271 887 680 424 779 286 446 474 238 665 834 635 153 882 727 663 091 712 358 797 329 010 222 715 776 205 037 187 383 529 916 713 745 737 434 304 377 341 946 068 862 885 711 925 282 386 963 625 266 193 244 925 429 657 563 184 705 537 726 715 114 614 454 626 802 996 978 095 431 069 980 425 490 222 377 460 536 123 245 613 378 803 609 981 785 858 439 722 605 424 007 269 172 968 258 178 049 797 319 403 777 850 550 903 266 048 819 399 486 908 917 466 087 150 004 293 836 932 205 043 666 029 103 223 496 829 648 304 213 726 529 757 397 365 461 930 223 955 210 840 932 787 595 738 530 255 778 262 423 948 079 429 615 004 983 186 209 244 133 595 517 103 201 674 818 973 222 629 549 196 046 675 367 346 834 197 320 320 475 560 777 381 436 933 334 830 308 786 485 941 044 022 964 453 451 558 005 549 185 369 085 560 888 646 007 117 873 996 329 141 046 715 413 991 651 998 954 896 891 411 240 555 228 961 446 987 720 654 092 415 623 062 385 016 327 338 121 782 775 849 657 179 668 635 743 724 139 598 999 080 065 404 680 059 745 331 445 660 844 246 809 826 413 680 883 373 292 306 398 466 782 042 142 811 934 135 856 891 275 642 578 735 271 972 373 488 713 721 275 731 258 326 242 790 652 230 493 808 017 532 625 840 899 689 985 500 002 210 685 992 211 092 514 515 844 821 171 026 078 132 692 647 767 910 313 048 329 038 045 363 928 452 252 790 299 711 005 944 641 940 189 923 436 976 454 877 932 888 841 156 386 874 757 114 672 285 439 081 831 139 037 724 617 669 210 250 819 930 354 244 157 997 766 935 152 319 610 991 792 768 409 532 194 462 281 671 740 060 302 967 158 848 302 660 730 979 128 165 513 026 871 535 513 681 213 001 415 817 153 546 204 335 154 453 996 102 374 761 236 592 016 725 417 394 903 306 359 502 526 252 626 773 060 968 300 042 118 424 428 422 214 924 029 824 909 315 306 719 304 577 159 605 833 685 851 141 272 862 834 521 391 035 013 593 099 713 278 810 478 140 497 496 670 774 073 898 751 449 077 405 594 905 143 685 752 261 061 229 791 567 069 305 406 823 456 804 251 923 269 783 127 272 294 582 927 613 906 279 148 281 325 816 631 888 511 869 396 983 388 439 411 508 970 142 669 220 609 910 948 178 903 669 816 852 361 541 967 430 094 628 031 175 522 434 511 045 122 708 137 005 965 017 987 031 925 872 021 853 306 906 781 680 843 297 029 445 009 211 004 629 962 034 660 568 963 221 420 188 194 861 525 257 797 708 648 945 187 465 582 795 156 473 081 324 394 008 855 926 965 345 787 031 244 661 867 025 868 256 962 758 744 057 517 725 784 213 607 734 016 407 712 424 316 728 408 706 881 792 038 977 480 019 488 134 686 587 566 079 608 407 873 982 807 344 468 568 251 096 478 268 410 601 994 565 983 970 793 545 694 258 175 394 548 095 591 709 775 558 747 411 903 778 375 076 563 309 691 821 418 011 859 138 433 818 131 808 421 159 223 132 864 895 411 195 006 261 152 684 509 091 616 431 809 657 376 685 081 186 781 746 106 309 162 819 344 803 608 247 218 881 856 994 192 478 879 750 477 780 559 456 507 285 685 613 782 428 021 127 944 593 651 165 713 115 584 131 313 597 229 044 889 251 650 854 308 723 282 177 390 147 726 300 921 649 838 768 326 790 650 592 680 410 224 816 451 314 250 494 095 649 843 787 474 346 412 377 697 095 955 115 350 702 605 478 299 588 104 703 693 958 135 416 435 936 422 121 674 004 048 242 598 285 067 401 271 626 974 015 887 529 951 179 370 547 917 425 354 648 088 055 426 460 904 409 231 749 782 112 885 321 807 131 495 976 018 781 372 155 391 395 460 283 442 762 882 385 477 972 046 455 918 229 064 156 529 292 636 232 178 725 910 591 295 448 040 573 818 251 229 591 745 914 987 942 281 046 638 846 236 852 921 552 648 758 223 689 346 498 163 646 511 498 547 825 544 536 969 134 938 180 952 576 574 562 626 216 946 075 960 296 323 322 928 774 128 376 976 033 667 760 097 896 244 241 231 902 769 552 936 047 918 333 931 400 103 823 710 471 574 955 551 591 515 485 924 241 108 876 430 335 421 051 267 792 082 311 600 249 286 052 925 194 695 944 862 685 972 907 791 001 873 102 692 178 148 546 324 948 570 601 244 006 119 183 865 708 402 436 158 583 248 298 143 490 218 937 612 172 326 179 896 577 468 252 383 024 558 581 803 491 244 627 424 539 011 792 778 734 859 843 984 955 399 644 936 730 028 540 159 341 398 980 991 163 949 450 400 179 211 728 777 500 367 884 466 825 093 089 788 596 019 448 422 866 391 707 944 202 192 312 512 855 328 500 602 709 813 607 792 835 751 734 458 923 198 312 010 250 547 334 736 127 639 725 878 382 829 918 877 769 661 391 936 630 174 120 404 874 478 473 010 224 154 667 703 366 174 895 020 451 838 038 869 795 658 567 882 653 674 596 595 586 734 762 459 369 259 889 487 309 968 958 494 406 347 331 278 531 012 824 527 685 983 824 193 584 860 429 973 944 726 478 826 645 740 451 452 558 835 849 828 176 866 841 922 973 856 230 771 232 434 949 013 726 391 162 941 316 439 764 525 703 676 140 999 186 030 882 953 320 115 867 658 822 118 732 595 455 190 693 226 355 048 800 398 030 247 918 302 672 277 199 299 710 027 611 784 638 905 081 596 833 077 692 685 161 460 981 537 625 648 096 288 281 363 147 634 061 744 640 436 410 253 251 429 656 401 910 751 466 731 366 820 708 303 549 480 742 378 360 209 552 174 853 500 699 543 601 932 508 970 714 574 378 957 525 727 549 305 883 473 404 943 024 687 884 265 926 781 419 512 235 544 941 267 442 899 547 363 127 194 545 465 774 777 857 073 245 903 275 531 471 875 556 167 066 242 857 363 745 169 201 688 419 216 086 044 885 276 137 878 411 028 761 595 582 018 705 121 777 857 952 557 250 539 974 634 402 078 852 804 864 794 510 996 806 743 836 982 464 037 539 798 708 183 136 825 698 924 325 065 364 152 716 061 605 636 072 476 226 717 546 687 179 138 670 200 290 460 337 435 269 649 956 336 755 709 326 556 727 381 619 722 635 690 161 810 783 943 378 940 796 178 417 829 879 347 045 687 074 951 344 388 714 834 767 439 551 484 031 132 914 877 555 842 341 430 539 237 246 896 823 308 512 572 662 317 885 293 608 537 778 946 842 803 284 217 725 180 868 813 702 607 051 104 434 434 855 566 070 278 598 528 340 154 628 554 785 825 429 889 375 705 507 324 489 611 032 409 342 347 737 878 421 620 641 137 976 113 776 426 895 724 616 412 422 112 851 392 273 273 254 840 983 221 461 702 010 942 575 490 677 589 511 717 651 313 890 177 559 342 028 496 681 718 076 024 456 904 504 348 056 311 805 346 599 890 997 832 746 667 566 918 596 189 836 198 341 354 122 164 347 946 257 362 215 047 474 249 250 689 855 626 527 172 342 475 176 161 252 504 225 893 823 733 506 107 718 799 147 480 796 244 687 102 916 224 866 370 160 762 501 890 141 461 999 914 691 222 979 753 137 811 762 991 250 745 250 559 772 348 442 770 493 920 537 619 543 248 766 936 881 672 278 342 178 180 132 711 663 972 259 998 490 030 934 648 191 260 974 770 191 530 221 703 114 995 622 689 057 936 621 627 276 557 955 767 161 148 074 584 474 440 424 026 238 599 114 805 971 195 593 995 931 563 900 654 785 383 783 102 377 791 955 197 960 546 684 862 754 794 768 456 359 662 616 359 345 718 817 784 568 826 215 174 692 501 466 121 052 485 863 386 699 921 473 052 552 350 404 332 922 778 696 618 017 922 790 145 281 315 870 286 931 713 321 137 992 759 888 335 261 364 300 523 919 030 999 009 745 456 907 114 162 728 652 782 173 027 729 123 267 797 480 170 980 646 163 893 979 587 243 649 158 498 918 499 862 253 063 748 309 134 620 831 633 705 434 161 896 370 733 284 568 086 968 348 917 699 144 004 587 399 493 637 681 814 371 475 770 967 545 067 920 096 608 013 501 424 463 873 448 602 375 296 829 663 471 959 144 798 395 885 889 933 645 625 867 889 958 640 284 003 247 140 430 436 709 259 959 218 378 608 953 577 795 137 805 656 334 729 352 753 143 091 040 560 082 720 885 750 651 915 217 927 392 598 291 554 523 617 391 115 383 772 242 592 236 978 405 352 052 447 316 965 089 817 491 117 594 090 395 405 894 965 703 718 979 007 794 906 028 232 797 451 281 263 452 967 279 650 646 947 604 280 208 154 385 525 060 944 427 325 625 005 151 093 175 832 351 318 352 146 130 008 535 943 313 299 992 918 369 506 141 858 232 804 605 312 459 448 445 305 058 741 571 958 038 778 747 772 131 799 111 105 262 190 196 674 547 514 257 879 460 193 884 636 528 771 505 252 010 999 839 843 012 298 479 484 701 917 043 772 115 592 839 117 949 092 644 185 161 805 852 413 693 515 407 273 417 410 448 826 328 929 890 487 410 476 891 109 746 100 045 200 881 641 893 559 075 994 520 723 430 023 263 580 068 661 833 558 550 235 548 029 233 457 668 226 888 837 231 867 106 102 909 225 071 192 820 293 453 173 821 710 833 569 151 982 229 515 106 567 655 034 222 246 542 386 915 887 077 971 103 147 834 779 442 014 856 431 707 810 471 436 266 420 005 072 955 587 237 887 835 605 413 579 691 439 260 118 075 540 307 821 206 436 795 952 048 950 629 191 964 939 786 375 306 298 741 474 140 820 900 856 968 218 144 461 155 210 773 108 975 026 856 026 895 580 735 304 694 764 265 766 595 168 186 776 100 083 816 526 988 903 757 051 018 229 934 879 266 953 601 082 681 148 717 476 591 332 288 027 340 831 742 404 717 262 467 609 199 796 283 751 019 031 565 253 486 094 214 042 185 671 998 873 054 409 777 404 823 989 350 137 162 862 842 224 470 213 329 748 046 842 434 030 639 537 368 753 960 567 843 437 931 997 568 513 929 659 820 976 494 569 697 970 064 366 999 737 611 597 983 623 544 488 691 173 498 900 208 211 878 905 466 988 854 450 151 044 014 680 573 517 591 964 072 139 966 599 683 320 617 587 170 914 273 403 704 256 160 354 657 500 080 223 920 503 754 231 362 213 815 859 161 600 077 664 411 599 616 448 532 392 027 307 703 325 835 796 270 892 768 112 334 240 104 293 938 854 674 280 617 500 820 600 793 816 331 787 353 350 203 144 950 725 845 158 175 815 908 482 802 139 392 369 878 853 628 116 881 728 114 912 496 532 084 390 362 791 502 185 956 941 909 336 909 308 891 426 433 090 348 250 166 934 777 733 457 199 123 818 921 420 292 402 656 790 459 894 905 762 624 990 355 744 110 730 021 052 108 835 221 024 023 023 155 623 705 673 983 429 730 589 530 707 362 086 100 087 928 844 026 363 811 363 094 393 478 137 456 537 904 938 239 148 662 833 466 876 897 660 618 098 352 923 485 010 464 098 923 698 200 644 891 625 424 139 108 466 553 195 104 248 082 181 987 189 244 598 252 398 000 311 897 894 252 990 783 505 600 880 548 536 742 505 744 530 227 734 859 137 545 657 362 907 387 349 583 631 174 941 142 899 518 077 038 482 865 357 003 557 292 672 550 315 109 417 761 832 404 155 711 487 451 266 899 079 229 870 220 672 240 232 947 934 779 891 758 845 378 718 398 760 627 491 598 345 456 167 391 800 497 875 568 471 058 971 865 939 730 444 212 143 699 881 514 244 329 512 505 161 617 871 304 646 125 653 154 476 938 621 740 009 571 899 018 893 492 981 950 044 936 712 963 573 665 759 915 334 012 447 011 628 204 473 794 678 180 386 863 029 046 640 556 641 198 814 255 397 751 002 922 085 889 645 758 020 605 788 690 977 798 827 330 598 113 228 867 730 073 367 459 295 321 207 289 658 745 394 485 970 040 088 801 041 139 968 143 491 067 099 142 829 582 112 294 427 594 772 775 929 762 645 979 453 958 825 054 136 678 545 882 210 170 339 277 087 089 818 424 611 640 130 391 857 851 465 064 679 730 153 102 140 080 118 305 884 082 126 896 461 360 913 662 090 401 148 778 543 457 115 462 080 580 548 799 141 896 281 361 455 548 232 132 255 566 436 374 369 040 993 064 068 481 646 162 301 918 843 362 448 787 124 715 845 450 212 285 494 160 050 439 971 983 693 098 174 154 236 351 095 739 980 944 933 530 739 351 679 772 898 301 987 638 016 955 290 835 652 945 591 221 583 310 635 715 931 397 579 680 160 575 102 380 762 806 909 390 055 347 325 632 445 489 092 984 965 461 846 807 722 546 099 306 996 126 699 606 919 299 703 539 825 261 682 672 430 705 782 041 337 851 375 960 938 898 598 266 677 793 873 697 178 818 326 041 837 524 117 549 039 620 941 551 661 518 477 572 652 074 584 009 371 446 147 628 298 201 653 228 019 566 641 874 820 724 555 754 468 540 660 467 019 755 470 965 599 672 823 478 238 974 531 563 690 246 684 375 984 485 067 135 487 289 677 618 544 825 369 349 515 261 351 689 636 307 914 353 675 011 968 840 586 829 679 368 159 063 051 384 037 393 522 019 735 893 182 872 872 219 805 916 294 008 404 567 681 648 432 100 937 086 311 755 438 816 866 645 661 892 325 007 376 321 537 111 066 732 443 569 551 097 527 902 040 656 887 088 636 843 581 380 063 148 893 955 810 599 377 047 552 599 973 349 973 682 400 149 149 856 689 639 099 213 133 754 355 762 171 060 521 556 001 322 978 351 817 718 326 085 902 178 010 490 065 234 864 213 756 745 943 711 229 353 284 435 691 661 695 354 151 322 157 934 383 615 542 455 503 509 630 352 871 245 014 708 294 487 204 193 233 156 544 655 194 414 793 389 168 125 890 996 209 262 715 548 356 937 592 415 049 354 714 143 157 029 346 154 627 526 489 648 255 522 022 902 683 172 350 923 604 250 109 108 995 291 483 626 553 306 422 922 383 223 536 403 513 130 972 098 139 344 948 579 433 386 153 623 431 555 365 516 876 673 780 749 244 903 958 551 388 271 705 842 580 939 180 911 067 108 872 092 104 754 697 863 049 948 983 342 456 266 989 064 802 855 429 533 289 717 740 145 257 100 331 199 685 821 076 509 456 773 801 550 712 943 279 162 146 043 693 468 663 324 846 260 820 588 092 030 061 414 514 383 325 567 211 246 990 409 065 491 414 690 119 017 165 216 362 683 558 905 905 947 571 950 570 553 883 769 096 284 990 508 223 187 924 984 797 451 572 558 859 539 381 517 755 081 212 333 608 681 632 895 975 057 290 798 050 074 486 725 616 801 351 215 297 211 357 479 391 411 997 322 495 690 188 019 271 980 595 895 151 709 513 292 659 063 130 536 008 724 358 009 359 973 078 026 089 996 696 865 932 032 205 804 404 272 807 563 221 379 073 771 190 737 791 799 025 642 077 420 067 313 820 978 779 733 560 069 819 428 139 724 165 421 115 528 406 065 686 718 546 061 678 231 133 820 205 917 784 501 475 537 611 730 088 589 899 812 575 278 980 720 413 409 572 822 951 704 334 877 754 759 899 512 295 608 835 438 785 571 222 123 663 396 323 951 106 519 456 195 714 223 637 301 949 864 966 575 012 493 994 929 312 691 728 157 839 914 611 509 619 462 051 866 577 451 007 599 456 709 541 762 309 807 241 823 171 255 326 018 761 664 540 108 356 258 544 044 356 336 451 214 883 615 788 140 590 726 178 909 128 026 205 090 727 582 919 064 964 284 477 332 464 285 577 153 509 948 222 043 219 019 019 033 314 322 500 287 337 168 824 774 579 110 829 428 267 522 081 731 899 409 844 455 406 953 126 533 450 916 199 896 422 294 854 232 140 945 285 390 774 100 216 505 869 426 907 852 082 995 544 229 480 655 034 443 142 486 680 385 217 931 527 475 552 086 080 658 439 966 701 191 407 131 819 047 005 621 146 353 365 654 401 520 888 695 946 048 620 724 008 201 126 171 917 808 773 621 810 318 473 242 351 733 987 019 977 922 420 574 482 771 555 277 333 577 103 536 325 060 109 105 721 949 157 840 531 248 113 411 093 124 898 683 371 083 128 587 701 856 397 432 000 190 314 458 134 699 296 141 724 961 958 900 429 213 728 622 797 609 299 856 413 461 074 193 540 032 548 370 600 939 270 562 819 940 902 405 469 905 175 959 395 991 614 992 144 749 672 491 930 191 369 018 608 349 357 801 210 484 032 145 381 688 444 550 428 474 078 627 345 320 685 819 110 614 542 520 114 392 870 279 857 809 217 185 232 092 357 506 208 016 422 561 347 573 394 318 410 575 793 199 925 244 259 256 869 540 199 072 945 386 471 547 909 946 462 605 171 116 680 608 816 867 874 892 339 786 317 736 297 964 580 806 943 890 776 866 579 333 444 984 222 576 677 602 319 578 444 955 015 872 998 054 966 012 915 424 730 635 023 657 586 439 608 363 593 350 434 704 265 764 183 910 317 783 712 770 135 187 011 317 270 332 064 755 619 160 413 538 197 913 395 790 591 585 069 192 545 447 378 007 254 597 302 465 885 915 079 975 221 144 588 552 980 130 353 600 625 373 913 787 815 281 152 526 490 404 016 765 016 955 021 879 486 024 426 836 777 345 583 817 951 085 076 037 260 086 159 797 102 832 307 332 474 850 813 999 270 871 521 270 672 216 604 123 249 082 554 250 256 923 382 521 602 000 416 038 477 605 107 471 920 837 709 074 266 020 404 618 451 297 440 009 029 817 381 731 565 523 402 541 944 642 947 333 760 731 592 726 502 827 453 287 602 180 832 238 859 343 683 180 548 870 926 858 996 589 748 683 346 859 354 706 719 903 353 135 965 508 601 517 454 201 411 114 497 267 631 903 203 222 700 896 868 592 291 395 632 385 939 990 285 519 748 995 233 816 343 703 457 431 829 219 074 869 651 291 720 961 502 349 489 132 581 523 720 599 121 157 418 955 259 167 056 373 330 293 283 961 698 479 067 051 419 214 936 690 778 676 954 491 076 628 697 550 021 687 835 856 850 629 136 739 702 065 488 669 841 151 713 721 648 640 907 890 909 638 618 224 923 682 310 150 237 685 969 442 144 759 177 211 397 558 954 687 683 480 799 436 414 571 496 907 364 874 377 926 856 228 357 115 796 968 184 290 256 370 568 188 647 982 608 884 894 811 846 203 428 964 718 819 907 627 816 417 418 220 014 101 559 012 932 201 654 437 016 960 458 802 757 774 536 930 178 544 397 844 939 070 642 605 273 420 133 359 878 889 830 046 456 546 614 588 963 316 529 664 349 283 287 225 752 087 293 306 635 837 987 608 028 823 692 341 052 524 015 328 719 635 302 163 143 161 465 210 986 031 307 499 145 767 812 118 874 434 386 871 667 058 289 102 183 118 699 783 577 839 721 749 871 550 903 841 509 180 199 050 360 307 680 917 561 916 903 469 975 249 759 707 360 936 972 959 863 185 493 973 500 651 349 769 608 313 200 406 826 198 501 728 347 444 248 890 702 649 413 547 737 295 102 890 133 223 419 906 384 449 546 101 972 324 269 963 649 637 816 493 011 796 883 261 818 480 844 641 330 675 743 602 217 569 153 700 559 516 772 630 761 586 395 342 445 258 320 398 794 413 371 396 120 545 158 833 545 957 822 198 496 870 809 021 407 123 943 391 449 245 621 324 026 756 045 184 891 782 493 266 276 624 286 807 591 516 059 716 043 031 714 863 602 797 539 222 302 279 249 290 767 940 678 796 020 454 652 628 726 605 186 528 485 077 088 905 535 528 186 689 229 578 384 435 966 496 360 511 005 868 782 270 146 816 552 969 835 417 691 505 614 934 206 956 444 423 249 617 658 059 452 023 174 118 991 279 814 026 925 558 544 210 920 976 600 290 929 043 649 004 831 536 811 501 639 134 864 096 953 675 638 745 274 582 254 423 321 897 420 167 120 664 796 368 997 353 349 816 523 919 668 311 243 371 120 202 072 062 616 223 616 515 085 094 547 643 497 281 578 850 445 788 274 793 571 807 683 309 371 648 593 153 393 296 968 564 463 107 801 862 777 717 835 204 000 596 353 057 736 378 816 247 880 055 266 979 959 071 392 987 581 250 398 867 889 687 451 062 142 160 950 763 742 100 215 497 338 521 171 859 363 057 256 489 774 326 758 173 692 975 666 837 334 832 519 147 634 086 043 954 640 902 489 343 708 686 269 021 735 803 700 395 997 238 488 217 816 204 985 263 036 887 111 883 300 895 815 058 286 624 200 119 351 341 520 221 836 252 997 269 798 071 019 962 525 591 741 757 409 115 368 222 516 442 994 317 463 523 313 399 866 285 701 067 768 028 494 854 331 667 983 005 249 987 692 991 099 503 602 313 873 026 320 389 963 445 412 004 394 005 779 264 479 750 392 992 493 481 292 726 761 309 019 263 208 608 958 027 736 638 984 901 283 188 370 327 975 008 911 723 012 814 595 324 604 253 769 955 029 031 803 850 165 655 636 018 909 330 671 031 802 005 699 927 066 873 090 129 106 160 685 598 542 837 320 795 721 608 781 519 972 449 167 730 053 668 106 149 922 430 005 791 775 843 573 492 886 436 891 182 296 991 770 400 895 163 015 177 400 870 553 213 489 209 241 114 772 780 375 965 007 667 244 984 977 947 837 260 991 576 205 783 341 797 956 867 751 136 590 986 992 064 618 442 917 036 925 184 871 789 257 545 580 850 079 476 843 215 840 619 165 423 523 349 794 073 750 393 033 743 205 730 850 383 520 663 348 320 175 473 575 732 154 640 924 473 901 033 001 813 858 368 284 363 440 968 930 540 495 020 724 655 844 756 820 979 913 233 357 845 649 952 763 942 466 417 994 188 526 781 275 384 782 731 804 736 849 467 977 440 363 290 554 694 883 564 834 180 416 132 710 148 396 392 752 374 126 583 633 833 052 251 025 043 447 500 810 197 031 569 693 013 095 443 681 725 356 857 943 518 291 738 897 220 340 933 940 729 163 119 438 751 046 255 296 705 830 363 219 809 621 771 240 575 491 485 012 464 127 681 435 688 982 768 477 969 132 953 312 077 140 749 402 112 325 982 390 603 715 563 151 107 135 150 817 381 153 955 209 018 280 466 264 328 107 245 419 231 392 547 806 822 032 837 722 742 956 596 073 853 927 907 657 500 948 994 533 641 707 779 164 051 813 938 580 094 575 531 442 221 871 925 381 894 902 096 140 548 671 287 516 358 054 600 399 467 619 767 453 919 234 699 789 896 183 718 454 725 602 774 178 234 992 621 627 837 346 962 653 080 145 921 247 146 480 409 099 466 862 002 690 922 564 580 089 124 606 011 438 128 168 251 300 704 489 709 080 605 968 070 513 995 590 556 860 822 571 202 731 413 474 302 256 297 161 507 849 865 375 079 174 067 909 978 472 067 003 407 225 420 778 873 225 049 767 659 529 573 046 535 488 792 262 735 551 594 073 135 658 838 726 636 480 602 988 954 491 104 885 499 161 505 228 818 641 883 841 965 064 772 690 310 511 523 826 566 763 100 156 746 648 173 410 114 759 240 630 505 529 940 120 695 891 880 892 235 715 006 553 167 621 047 378 443 480 797 979 257 445 059 475 717 650 587 179 551 038 559 982 380 883 827 926 787 443 086 561 303 407 196 443 098 909 684 630 453 194 174 602 950 945 906 829 336 263 633 145 110 005 458 684 127 954 984 134 842 148 276 099 655 752 678 279 523 055 603 776 065 364 765 270 621 999 856 503 758 835 990 994 770 050 185 605 857 409 841 821 015 423 783 864 287 862 914 189 463 611 425 976 390 377 944 928 076 764 744 244 916 897 764 109 437 701 176 793 957 942 215 532 868 467 566 708 353 926 284 666 051 349 161 656 208 854 068 960 616 676 063 129 149 644 471 842 113 278 609 395 972 754 979 033 431 334 197 590 560 010 372 468 684 191 186 696 798 590 618 757 288 813 846 832 868 268 089 219 736 780 318 896 215 295 784 423 202 473 693 736 622 727 845 603 860 766 608 532 985 059 845 332 612 833 832 255 485 799 754 137 777 718 207 261 364 131 188 695 928 974 099 530 454 659 470 829 366 998 743 166 396 836 507 060 661 638 517 022 530 398 405 059 521 096 259 199 616 859 059 958 079 873 018 887 882 272 414 533 314 008 419 637 781 538 488 971 667 683 203 809 820 169 433 950 371 217 883 574 052 424 829 263 068 466 993 281 901 918 742 656 653 598 208 183 958 781 629 092 882 963 402 582 950 963 638 132 846 794 308 187 666 412 654 763 530 063 610 360 290 546 629 428 702 990 030 065 030 672 366 854 724 421 698 975 333 191 319 261 716 023 349 642 574 208 710 021 509 072 602 665 161 288 291 872 278 074 478 339 245 900 428 891 491 249 736 690 386 225 202 543 466 194 144 661 391 711 043 342 505 069 857 514 587 478 873 874 872 091 850 522 899 940 798 859 667 219 827 218 052 233 832 581 671 886 315 346 425 513 244 759 105 152 224 696 330 312 717 273 737 718 084 385 223 609 309 966 298 909 331 801 921 813 601 801 088 877 311 286 677 525 784 383 624 350 596 547 659 300 907 152 974 645 365 048 598 112 100 205 215 237 042 661 667 860 347 812 454 899 080 661 004 379 267 189 215 231 904 145 533 683 070 852 433 740 726 089 963 634 774 872 297 434 161 141 193 959 930 808 281 347 799 398 600 486 233 005 376 367 437 212 274 254 055 579 100 237 225 772 965 977 332 265 516 507 695 255 553 481 811 170 647 961 302 355 065 624 374 296 546 363 598 154 124 502 744 328 574 354 344 364 423 136 256 236 034 885 325 487 223 392 889 772 918 499 202 979 829 160 417 837 630 492 008 358 967 098 426 974 561 589 870 597 122 917 340 575 452 689 710 936 879 054 851 525 734 275 901 356 407 119 871 996 782 584 020 573 478 867 893 437 499 567 283 302 985 977 078 352 677 214 594 923 902 064 404 559 369 278 115 595 762 428 321 000 973 618 040 365 536 338 203 080 638 783 364 051 478 081 894 645 858 803 177 531 595 354 909 822 245 958 332 294 738 283 932 489 014 689 580 684 853 891 872 555 540 128 444 253 198 870 588 478 400 323 038 118 341 220 944 502 790 635 881 131 523 690 193 746 924 933 234 130 565 755 515 565 975 490 005 086 873 808 417 192 582 101 871 372 257 131 081 416 102 528 040 885 163 493 942 081 694 287 909 778 918 388 491 047 213 157 397 285 388 804 836 471 638 376 340 506 208 702 495 362 960 334 068 532 533 002 725 537 268 353 916 275 239 139 446 866 108 305 479 856 108 347 982 579 434 827 654 593 038 670 956 538 807 848 459 711 945 379 260 194 487 691 098 109 386 780 307 278 340 564 915 174 874 971 011 973 570 251 693 770 085 366 910 052 067 241 073 414 733 239 549 864 728 569 358 395 977 000 804 187 559 545 678 931 880 775 336 499 045 774 207 841 354 978 364 651 129 944 086 010 608 076 478 999 777 874 799 360 339 887 603 880 366 530 213 058 052 990 451 115 522 967 699 430 959 644 332 257 682 846 184 954 296 429 430 499 575 991 313 837 866 524 658 542 462 636 837 448 602 849 201 903 612 232 263 806 411 793 001 610 477 075 458 418 002 400 275 358 201 319 549 579 643 790 381 003 879 957 968 276 448 977 564 599 952 106 722 329 989 594 600 044 735 196 796 932 731 584 185 628 708 250 055 284 000 783 935 615 365 106 606 812 459 110 408 890 690 167 472 645 483 655 750 955 311 729 307 892 038 308 543 696 546 825 479 408 597 503 386 180 141 612 843 090 243 630 263 843 478 913 547 536 445 048 121 161 486 877 798 535 529 437 494 264 833 544 979 787 097 223 364 019 985 643 659 779 430 953 872 146 395 365 216 497 829 176 267 870 733 181 446 295 061 698 455 736 993 002 381 848 901 265 831 448 703 429 778 373 380 359 633 154 360 626 686 047 856 430 091 687 142 619 021 378 201 529 346 007 465 174 169 730 336 162 522 809 887 050 575 849 703 203 193 188 539 380 073 811 055 633 657 539 740 862 678 190 875 803 171 924 628 786 828 010 439 737 868 161 806 861 801 464 825 996 181 303 273 106 153 219 855 094 797 458 738 666 643 854 175 785 149 690 184 891 159 739 770 898 721 850 294 390 460 739 011 689 253 940 462 458 876 454 905 113 175 173 852 061 698 639 081 436 542 784 577 157 688 821 307 385 307 534 405 973 171 562 168 297 681 885 514 515 499 149 447 346 009 233 671 596 711 873 332 859 546 879 894 257 288 723 772 793 617 476 351 177 269 372 916 475 485 921 877 825 443 485 137 736 809 962 564 847 495 226 750 238 709 323 055 513 576 332 335 573 688 315 934 511 636 159 988 898 309 008 346 718 696 898 614 171 086 404 732 725 277 600 977 351 272 987 261 719 417 694 665 559 063 636 703 728 285 783 468 626 412 654 117 837 945 178 031 638 831 992 376 497 572 380 200 324 831 304 132 369 456 877 065 649 981 688 075 564 246 108 715 606 385 603 064 560 348 793 973 006 231 079 780 062 827 140 016 375 099 400 887 713 664 037 293 492 144 087 009 122 384 048 385 642 318 972 802 941 363 008 100 352 865 370 574 580 902 437 604 659 302 794 960 360 254 136 106 095 372 821 135 096 209 912 959 296 276 006 329 787 143 765 294 070 403 700 626 826 167 755 442 880 777 551 307 309 015 223 240 782 923 754 739 631 025 812 908 697 597 896 802 663 377 702 949 133 298 964 037 520 139 539 519 953 722 543 641 589 732 043 524 702 010 166 916 084 415 647 052 758 235 590 285 090 707 806 571 646 016 650 733 514 184 452 116 170 955 134 026 285 588 541 597 906 160 896 764 578 693 027 955 532 503 439 203 771 871 773 096 143 811 334 494 222 952 993 865 477 043 860 039 294 164 518 423 962 820 989 396 011 743 823 788 936 175 008 576 964 414 034 826 016 246 276 782 846 017 607 617 567 743 593 724 628 688 936 699 145 713 361 276 506 889 784 676 611 114 828 622 534 783 350 623 118 805 682 375 574 365 986 083 355 205 839 212 168 754 448 361 411 535 206 423 361 266 186 854 829 221 190 214 530 076 780 162 407 840 657 810 627 025 829 992 670 081 159 965 563 508 766 911 617 516 896 643 368 604 366 935 811 891 687 514 053 305 112 513 012 240 116 481 241 846 361 769 295 762 887 578 038 268 001 569 925 471 340 839 952 332 515 667 547 759 211 825 071 326 282 698 670 588 954 618 224 238 060 694 876 719 311 207 170 100 959 559 166 603 734 250 040 559 639 719 332 578 563 170 816 740 650 011 091 990 805 813 274 523 562 463 193 816 914 326 914 066 168 511 897 322 712 491 486 574 361 707 764 571 544 586 884 307 963 871 107 530 679 728 010 840 097 285 859 413 686 571 853 879 515 675 976 766 543 981 551 607 445 553 138 988 493 695 870 099 316 643 927 365 872 675 530 950 827 324 852 865 257 653 656 264 343 727 641 309 162 811 943 156 255 638 685 687 901 171 717 476 114 770 998 043 818 245 232 772 263 026 121 063 145 243 340 761 867 600 129 410 486 293 307 901 427 954 924 442 259 680 535 132 914 216 206 786 807 264 598 148 989 697 979 497 191 811 799 131 204 812 608 290 515 566 472 392 254 739 229 803 661 996 701 211 541 341 477 192 307 685 790 119 854 046 427 576 143 366 640 594 804 198 956 715 240 468 469 180 908 160 209 751 904 554 068 839 711 008 481 622 836 088 923 441 988 800 112 567 526 665 706 719 848 903 706 145 440 488 141 651 020 177 720 558 429 798 566 400 008 341 710 189 872 087 648 492 210 132 127 974 181 955 847 140 959 038 925 319 332 467 499 307 418 340 388 982 080 020 940 436 097 368 692 930 027 810 384 280 945 740 415 195 206 455 848 528 535 965 522 538 639 872 424 570 188 585 885 268 355 483 606 175 588 779 102 928 847 551 614 516 744 376 128 588 909 496 195 405 324 379 395 944 311 674 580 051 330 011 627 145 304 973 056 496 144 914 128 207 350 338 990 644 591 531 998 703 697 916 899 940 430 923 144 386 810 927 408 509 262 884 736 181 171 213 611 675 194 057 617 812 003 402 640 797 409 135 417 546 920 537 439 601 921 012 690 647 132 964 117 561 742 919 681 659 597 766 108 566 370 588 492 069 780 752 903 220 777 752 165 085 043 016 372 676 258 473 388 395 800 663 225 399 685 348 141 217 221 871 425 667 173 277 309 972 302 810 448 780 212 711 616 056 008 410 402 329 007 446 162 830 643 807 096 755 502 438 231 119 223 554 681 678 788 086 749 866 587 099 334 788 909 074 481 492 870 772 884 640 001 234 883 497 039 680 697 637 956 102 709 100 408 580 210 696 706 124 084 158 624 726 798 119 174 121 667 134 365 353 681 636 586 355 617 370 594 112 224 889 576 741 091 524 298 679 364 954 740 414 365 347 516 073 782 870 614 103 251 345 101 353 327 750 222 680 493 381 867 323 380 204 212 067 294 440 534 352 692 936 069 440 895 619 414 153 028 739 613 958 573 791 629 541 002 896 207 666 590 955 748 120 550 910 829 547 479 247 142 778 820 160 072 274 255 231 408 294 247 297 712 671 434 843 613 159 497 137 515 857 339 790 785 636 777 016 134 386 646 632 772 093 061 949 936 866 263 103 311 998 291 433 511 516 565 249 758 243 748 588 105 863 861 589 263 785 133 558 255 999 653 699 339 537 089 660 679 367 641 859 161 191 307 980 798 372 672 926 217 681 076 728 229 958 262 055 053 158 421 844 325 483 925 448 101 578 363 025 481 494 274 358 634 734 563 927 403 330 427 103 647 489 982 650 824 471 403 806 735 788 423 343 828 032 354 502 903 795 842 987 953 226 770 323 367 867 269 181 868 613 945 677 777 835 601 236 267 512 104 572 561 823 535 536 422 052 578 600 332 320 829 093 527 742 788 343 497 007 306 980 744 877 979 895 187 280 243 819 037 711 787 378 909 881 283 745 630 975 265 878 523 222 861 777 674 605 630 408 315 289 201 827 686 660 879 033 124 503 496 995 186 612 023 051 120 500 128 271 032 966 221 075 164 853 733 058 522 778 401 718 521 534 887 685 720 145 460 344 137 661 129 818 761 012 888 420 152 763 937 922 595 657 883 803 192 882 065 113 322 780 346 813 716 898 016 909 744 511 350 477 603 497 998 574 365 183 213 430 673 619 093 059 856 332 547 648 255 642 517 695 116 719 606 182 587 339 369 114 185 263 954 259 603 827 340 487 906 533 194 464 806 219 315 474 915 950 427 276 963 466 975 911 585 237 466 593 800 649 071 364 839 962 221 411 782 550 731 798 755 146 260 058 974 997 697 943 274 510 211 555 379 587 625 866 781 407 878 578 110 649 082 720 621 858 732 718 475 177 728 992 799 391 248 956 800 049 911 673 949 262 235 245 748 687 350 443 215 471 988 229 211 482 159 097 393 003 074 831 714 917 123 068 147 667 033 662 892 956 601 793 343 545 712 441 351 511 196 492 976 057 212 832 787 661 175 156 828 777 328 947 485 373 156 473 193 309 774 066 644 623 033 979 480 061 210 150 996 852 468 672 733 972 615 604 463 973 080 717 248 765 389 050 424 466 839 395 614 822 646 045 153 237 860 938 613 979 735 494 880 033 686 740 040 295 524 664 368 278 214 393 769 777 273 802 703 559 996 621 003 088 067 799 257 604 784 791 318 203 544 896 330 036 655 716 643 996 000 670 627 216 884 711 464 943 702 879 424 138 616 608 866 359 211 053 301 143 296 515 812 293 246 437 870 770 119 106 364 479 658 675 434 398 186 103 178 497 511 849 695 363 294 705 231 381 323 981 259 754 040 488 449 975 202 998 909 552 855 986 018 733 241 886 535 468 253 491 162 091 866 018 447 141 442 648 290 628 441 652 511 613 108 932 674 117 877 072 756 854 199 735 387 560 642 641 512 179 787 078 349 811 696 961 682 011 034 672 563 477 790 843 451 713 387 234 687 798 052 130 966 671 754 250 760 438 865 996 760 367 576 485 676 841 048 052 751 188 444 278 238 678 947 463 535 449 199 896 365 366 552 962 364 231 097 428 010 268 001 595 998 348 036 567 208 133 094 466 728 185 258 639 693 370 335 479 214 246 294 837 975 939 662 962 325 701 441 812 676 761 439 622 120 268 549 749 223 614 424 542 863 673 409 760 621 503 367 223 507 601 244 706 965 880 001 266 994 460 828 351 685 639 540 686 937 205 942 602 134 695 000 595 539 200 822 466 019 112 727 582 046 646 541 305 840 245 866 223 379 515 341 204 481 764 257 648 802 696 336 682 579 030 309 515 019 215 529 040 498 976 962 209 955 398 877 516 878 889 328 985 316 543 549 752 783 617 874 666 862 896 614 015 677 826 631 678 879 219 518 027 302 836 540 734 249 726 851 296 430 050 486 854 302 392 853 135 998 967 386 812 431 835 601 890 549 826 438 560 801 073 293 620 005 211 586 081 496 188 159 291 299 498 140 724 011 085 974 818 937 288 963 772 512 893 081 791 471 557 517 086 362 139 599 709 311 680 378 553 480 842 088 666 210 073 228 561 596 010 317 836 270 524 063 632 022 917 103 814 259 233 217 300 351 083 152 235 242 207 756 620 373 065 614 574 415 320 545 498 929 057 923 314 122 736 590 379 414 321 570 288 070 131 494 350 688 737 964 922 331 848 832 706 523 735 608 795 483 062 230 424 024 976 724 047 071 018 092 943 107 398 883 244 441 242 618 722 225 941 776 278 760 536 667 477 921 538 954 289 931 141 052 341 177 301 390 084 798 580 636 574 408 922 110 719 558 394 654 129 985 272 629 427 767 231 038 430 405 547 543 479 759 904 118 482 387 944 504 861 263 148 306 904 502 602 779 916 969 438 196 413 152 684 728 540 152 554 989 290 401 147 246 259 125 109 575 548 419 875 377 924 641 882 631 668 556 441 997 303 773 714 743 460 872 601 253 366 841 362 997 443 433 081 411 828 188 401 446 785 051 592 537 653 035 473 924 691 324 488 413 807 785 944 596 426 974 090 072 940 144 735 525 029 246 539 296 532 815 163 894 168 272 131 822 354 330 955 845 353 207 347 241 163 535 763 317 706 501 572 781 267 872 435 323 091 404 864 303 120 891 371 917 289 942 482 294 447 540 615 137 923 988 456 153 091 141 784 678 205 717 580 885 721 525 483 759 311 253 631 882 457 958 611 948 175 726 266 926 264 180 412 388 641 429 587 202 855 939 910 243 732 426 381 833 310 352 487 404 953 094 268 376 529 600 641 380 910 689 156 553 863 931 067 827 555 090 695 396 473 778 247 664 820 127 579 638 374 426 101 477 371 738 917 862 435 423 770 766 976 709 520 404 354 801 650 972 058 637 068 046 384 205 392 448 695 169 027 053 807 317 279 673 353 980 214 503 134 017 644 146 026 151 770 282 554 705 609 409 817 945 193 134 631 720 639 958 529 002 249 999 160 336 001 778 417 186 168 636 169 236 312 348 005 995 212 089 991 910 048 123 324 030 129 465 802 476 011 708 315 268 082 052 625 027 291 600 320 237 834 902 804 826 399 806 742 325 799 517 848 087 634 903 234 691 392 435 190 730 382 562 663 831 002 948 819 688 387 856 977 108 511 710 714 080 415 564 067 659 192 093 600 273 949 938 033 953 423 523 470 765 220 157 021 881 058 248 533 450 840 916 684 246 766 422 824 163 510 724 394 350 324 234 698 320 043 560 288 444 475 955 518 647 371 852 402 874 085 296 998 576 319 058 621 104 132 947 430 433 986 427 073 894 633 978 611 087 009 331 223 957 164 361 949 023 703 271 132 597 877 747 085 057 349 629 845 841 119 881 751 800 432 104 014 217 527 881 259 211 932 497 423 425 725 713 855 691 244 091 810 506 832 570 249 137 622 031 857 226 738 503 375 017 753 217 968 379 725 735 912 936 116 668 464 547 957 345 705 230 340 060 241 390 948 041 527 439 950 006 465 034 950 992 880 554 905 499 243 742 927 062 508 479 606 338 679 470 485 214 447 262 792 424 435 611 375 891 309 823 662 006 193 177 873 763 549 812 338 915 502 378 482 472 221 090 754 706 631 381 552 521 374 327 447 482 116 471 838 873 556 127 697 176 337 991 263 352 441 848 446 146 795 334 174 529 569 659 596 715 925 182 535 751 607 199 088 394 107 839 310 829 144 097 845 418 677 959 391 431 179 177 728 958 993 737 162 690 094 389 735 766 890 912 126 152 304 665 805 767 752 403 316 518 076 150 475 207 263 296 938 810 437 977 610 177 766 708 606 296 804 455 513 154 856 576 516 590 605 201 561 278 371 460 817 623 347 786 261 867 137 884 283 443 685 528 949 078 594 389 484 993 374 863 351 034 475 860 394 399 499 316 108 001 853 729 446 095 014 156 192 448 851 657 135 711 539 363 228 355 994 320 822 303 597 191 019 659 167 377 218 231 447 491 345 815 837 791 685 015 194 321 938 881 266 073 623 168 241 149 894 206 367 262 904 319 317 225 632 421 771 428 863 022 418 320 378 214 443 852 606 781 823 455 724 382 115 254 965 994 939 134 486 949 911 067 752 345 034 460 468 124 960 526 635 814 254 747 013 630 107 836 271 321 748 874 237 654 899 727 782 246 097 677 410 711 273 228 359 353 550 115 392 006 937 415 197 402 809 689 911 323 163 740 466 625 886 698 580 561 370 822 386 382 983 632 752 655 937 655 275 764 775 015 855 728 563 078 604 413 110 388 517 482 323 981 907 548 985 177 342 267 357 840 124 975 541 183 896 722 847 547 131 461 372 057 012 263 670 113 508 055 128 534 135 664 402 533 936 606 001 754 744 345 693 949 386 188 121 744 787 411 278 837 515 782 109 272 594 463 465 472 694 522 970 750 574 678 149 479 388 456 128 347 111 720 746 350 503 331 897 711 264 116 673 445 263 508 216 151 205 303 163 436 123 775 024 509 840 559 637 041 739 431 094 151 762 071 701 293 976 836 624 460 372 488 796 127 828 608 557 210 434 128 215 739 626 756 066 672 587 294 888 987 250 593 598 299 582 389 401 798 795 466 905 601 391 795 156 128 239 976 856 429 186 898 916 397 012 817 456 933 084 573 190 271 285 052 260 010 538 844 169 559 708 052 027 827 048 114 768 355 111 726 676 055 661 407 502 283 919 696 136 195 231 724 534 670 836 619 860 176 979 305 260 725 090 930 640 017 334 262 435 983 880 737 218 638 941 858 076 092 352 158 908 222 185 784 608 683 913 548 962 486 649 966 666 391 494 319 500 466 098 068 536 823 332 725 606 895 837 641 483 077 526 219 097 551 123 564 844 700 569 123 514 373 278 210 620 312 735 567 273 540 093 594 495 369 927 464 039 576 971 802 639 385 120 235 735 321 254 956 034 203 020 265 667 086 554 467 324 726 139 396 989 421 561 130 967 090 587 046 945 114 176 437 679 888 425 903 824 593 521 625 489 777 597 668 837 157 160 923 454 924 475 416 464 317 624 304 664 798 986 340 350 752 051 100 245 783 266 327 607 124 535 084 393 982 979 519 920 877 254 256 447 538 449 543 603 439 298 986 642 245 817 498 959 783 050 933 298 354 945 194 963 503 717 744 989 640 726 954 118 383 539 449 745 589 537 543 886 969 677 351 091 665 821 126 889 333 842 014 562 432 812 477 877 137 188 571 819 161 596 912 127 154 428 340 762 504 114 702 587 502 054 844 529 432 288 779 036 459 865 203 416 145 886 857 794 760 376 493 082 535 172 487 819 672 312 498 020 103 026 279 253 645 483 885 590 898 322 428 276 521 276 475 790 176 457 719 977 086 055 845 272 048 212 333 140 230 635 682 229 044 889 322 124 471 155 960 844 838 563 614 831 150 076 585 526 788 264 728 938 331 860 726 439 660 895 300 545 688 402 074 694 161 667 895 547 910 768 844 258 717 636 672 280 658 566 044 519 772 089 932 998 109 174 965 102 228 119 731 982 170 855 642 560 523 171 246 711 036 738 042 424 671 736 325 161 125 679 951 446 527 383 015 580 301 152 448 182 188 857 967 358 500 842 990 659 254 566 761 061 438 186 077 006 455 248 182 593 673 743 232 989 556 032 115 265 344 338 200 162 375 799 831 225 793 614 743 687 413 722 157 354 319 544 010 362 866 140 377 853 369 055 006 994 633 815 357 539 051 298 167 215 799 714 158 955 938 995 796 682 079 020 886 172 144 160 082 201 776 720 317 697 294 875 980 202 393 584 831 673 483 439 521 630 580 982 887 474 757 574 780 624 059 166 183 342 546 041 678 102 599 983 145 222 958 674 027 069 371 383 727 311 958 483 421 234 787 185 576 006 312 692 127 189 732 619 602 107 094 619 570 695 165 443 954 789 394 015 856 345 437 817 263 632 201 607 007 927 000 829 938 291 484 270 518 064 478 220 349 465 058 492 698 344 895 845 595 982 656 722 095 534 777 773 953 953 342 527 678 720 261 063 172 900 189 434 292 759 947 702 882 334 170 757 532 653 795 131 403 083 795 388 493 310 126 231 238 953 261 018 479 471 896 167 347 512 319 373 803 924 102 110 364 447 174 692 037 762 028 563 659 614 398 912 621 107 868 805 137 343 186 900 778 525 761 721 624 675 123 873 194 966 084 157 256 239 577 815 904 570 245 971 908 724 094 240 225 858 769 033 069 026 874 527 029 860 847 626 618 924 363 945 305 193 610 530 356 994 398 212 862 355 590 296 597 491 571 233 620 694 143 460 679 779 706 684 570 683 557 313 804 967 081 940 707 072 172 103 938 082 177 492 827 095 905 492 991 972 036 929 371 164 909 124 815 375 234 306 624 760 163 093 294 396 562 523 748 639 827 294 505 193 913 525 564 207 001 290 906 523 316 212 985 011 903 217 301 659 474 439 965 166 275 869 110 655 232 142 899 612 162 841 546 896 776 740 455 151 609 343 658 895 653 343 941 596 237 390 660 078 797 119 168 890 590 693 468 616 935 725 651 820 533 670 251 840 694 993 966 990 936 410 961 479 400 477 771 544 649 319 291 488 091 538 926 016 721 058 325 237 031 029 445 387 111 963 412 298 339 966 783 397 797 954 438 813 892 742 371 152 112 661 467 690 073 557 722 417 361 576 096 438 842 571 196 861 959 951 514 538 044 800 768 462 110 029 562 383 908 942 720 306 913 407 328 994 366 465 007 102 798 863 588 302 742 241 821 581 071 169 852 781 183 942 176 009 250 252 144 762 941 411 970 331 467 742 873 452 902 960 155 710 295 212 623 616 978 901 230 667 580 040 920 496 200 640 242 812 763 679 594 424 558 339 348 719 105 984 128 934 551 856 977 880 818 723 809 048 339 419 185 854 186 332 058 468 966 846 488 432 258 236 716 425 900 686 561 659 314 211 940 588 466 931 926 988 255 641 253 484 265 551 942 412 558 679 934 170 820 536 114 518 415 892 291 911 091 204 615 778 932 881 686 777 196 196 078 193 442 270 121 572 154 014 406 938 233 663 177 067 927 714 747 428 709 129 617 594 631 754 384 652 185 354 001 255 433 989 174 147 139 375 073 861 169 788 065 434 894 022 986 037 670 162 989 541 062 339 685 339 297 909 096 428 482 679 350 092 580 977 041 736 677 181 803 864 122 774 605 405 694 667 398 074 978 085 987 160 343 950 536 051 338 128 261 644 241 694 215 877 122 483 865 947 666 806 416 760 729 485 554 473 060 260 611 195 749 239 497 796 792 590 077 438 268 272 443 855 738 459 630 360 052 022 308 000 139 768 132 890 073 776 765 965 846 970 005 779 619 960 716 200 077 988 088 710 714 180 444 065 567 110 699 299 026 324 793 007 749 013 737 657 904 583 210 757 686 399 815 502 418 706 446 918 307 885 560 047 414 165 232 933 969 072 509 770 862 388 146 764 361 071 786 589 086 542 219 628 146 819 366 904 627 000 415 100 852 637 211 569 149 531 055 701 760 990 001 899 130 771 115 870 304 722 978 472 562 401 022 822 611 150 688 974 661 043 252 934 421 078 557 830 930 867 788 010 133 829 484 138 756 103 690 415 247 554 706 453 056 488 647 786 865 073 369 456 730 933 378 371 368 361 892 563 438 311 128 825 164 109 436 676 246 436 787 138 544 065 489 990 779 209 764 969 734 749 352 607 576 927 920 209 144 354 406 168 407 482 782 520 766 930 711 067 781 435 938 170 589 716 674 046 955 320 855 332 882 367 206 600 911 177 684 689 905 603 293 658 789 331 457 307 738 144 760 078 399 135 924 518 372 854 584 366 175 390 566 076 487 438 945 571 617 548 148 416 500 568 582 307 712 724 164 405 469 471 393 007 460 554 895 454 020 721 185 538 353 753 172 063 012 569 136 263 921 471 922 582 130 780 198 146 283 042 471 342 166 074 284 841 092 477 180 615 126 155 239 463 138 931 793 942 185 152 236 336 464 183 049 938 081 876 284 355 730 656 520 852 098 685 146 812 632 483 498 169 721 714 268 307 596 527 975 549 146 664 909 026 210 159 567 764 985 772 029 369 805 547 860 065 011 149 685 984 308 372 470 624 602 996 819 346 506 439 380 740 892 711 036 076 789 378 392 622 542 708 886 864 101 571 217 129 644 423 744 165 890 159 893 894 076 774 286 476 863 192 955 962 460 356 249 830 971 226 836 925 463 150 898 655 844 850 342 806 352 802 014 872 460 074 369 370 305 632 667 730 417 653 592 482 006 033 939 403 508 839 100 311 987 846 585 780 150 599 728 103 687 265 600 716 420 891 863 833 899 921 516 746 324 514 308 374 439 700 017 287 136 481 927 776 554 190 017 564 049 318 738 808 930 879 285 406 092 591 404 752 881 005 815 308 808 092 948 433 931 283 219 573 109 812 820 862 939 060 612 667 538 832 603 761 038 519 600 359 304 365 917 398 374 788 874 035 547 443 568 346 605 549 501 949 521 994 312 570 928 910 044 486 601 128 383 011 876 860 639 996 576 792 243 278 307 247 907 365 649 770 488 249 028 536 578 214 107 710 483 950 369 263 881 270 956 787 065 599 259 415 413 059 575 277 460 393 759 752 855 416 169 822 697 109 006 533 733 117 170 215 804 219 422 128 965 602 411 381 808 985 609 407 631 110 491 645 692 789 106 267 650 846 322 044 657 808 163 638 498 585 125 847 294 327 206 864 291 467 927 089 425 001 063 870 643 012 142 180 157 043 579 487 962 218 273 704 100 930 290 528 776 067 340 983 849 556 332 865 347 410 357 070 444 453 323 923 632 488 510 475 799 661 625 400 540 227 314 803 583 286 731 497 728 667 744 037 969 803 367 074 247 302 334 767 953 541 059 142 325 949 146 077 275 294 861 831 736 633 391 639 438 116 555 017 098 273 649 178 519 683 661 488 195 162 393 786 378 540 265 531 979 114 465 529 162 011 281 490 761 425 232 257 291 187 057 779 435 899 119 837 624 819 996 752 537 549 195 510 110 727 938 361 046 220 447 552 836 635 197 410 032 355 441 837 896 662 160 765 105 026 570 471 574 733 762 550 451 723 351 119 797 100 966 320 345 040 241 820 494 635 647 824 694 917 418 514 134 326 157 558 205 700 272 083 091 257 543 902 034 133 268 244 190 468 546 483 830 215 505 162 111 696 954 124 968 766 926 428 693 925 037 394 919 340 788 014 879 983 562 912 051 092 846 048 570 150 653 988 241 407 487 952 144 646 802 882 226 692 622 280 557 551 391 046 563 974 725 634 844 451 716 450 416 539 145 451 842 500 909 023 433 227 890 084 756 908 640 036 459 736 237 542 324 797 233 509 043 264 282 495 254 169 158 090 929 767 743 536 675 309 366 636 920 827 634 823 640 681 386 190 056 405 098 833 868 634 645 393 096 621 451 351 713 305 793 429 118 661 755 304 617 122 997 552 512 729 705 441 719 583 550 559 346 781 691 557 771 521 548 892 628 865 692 661 385 553 395 232 875 398 945 155 600 530 643 893 658 155 291 492 601 002 593 714 815 629 844 309 114 918 530 899 860 582 344 818 938 915 756 174 928 743 903 480 110 551 764 377 016 445 888 949 652 188 952 359 341 125 615 172 159 518 482 029 756 904 574 480 199 092 733 663 774 505 245 051 233 583 203 874 396 046 833 172 588 560 860 285 427 157 409 430 865 081 644 512 965 205 768 834 511 956 356 988 767 361 757 684 506 307 114 790 930 000 388 528 512 220 093 787 258 721 113 635 616 408 495 335 422 591 280 898 533 412 799 404 521 864 774 430 717 912 451 430 849 875 586 819 282 806 392 123 788 042 416 194 907 832 491 239 419 825 808 025 108 646 078 205 752 445 793 691 129 208 392 494 390 831 937 090 987 404 005 060 825 671 160 107 358 238 506 471 285 400 922 224 950 342 427 531 319 895 808 360 282 576 551 158 230 745 490 365 424 700 768 495 702 997 111 518 726 142 391 539 117 587 296 812 745 314 812 066 130 982 836 392 991 856 680 370 922 904 006 671 096 593 108 765 883 103 429 855 547 804 112 328 598 482 518 647 070 754 158 816 403 518 026 205 819 311 077 189 974 913 187 220 871 621 617 866 057 280 356 459 153 298 932 740 330 498 450 038 846 689 838 235 368 494 087 572 707 529 033 020 537 718 929 205 068 193 060 722 387 225 187 088 121 457 514 920 472 452 556 612 083 096 772 019 560 139 488 068 233 345 774 960 846 214 079 859 854 660 435 911 241 398 429 264 647 909 571 300 468 947 367 670 333 226 264 274 056 020 454 005 373 571 526 148 269 909 785 805 296 059 743 392 491 927 883 666 907 037 941 993 109 881 101 200 096 698 913 014 712 232 514 938 211 505 112 312 469 020 347 385 300 702 809 845 956 214 471 655 345 268 831 777 362 501 188 917 963 739 916 708 574 365 681 509 489 097 797 490 980 871 617 650 210 232 875 103 674 309 657 527 875 229 507 790 082 226 800 555 881 875 258 095 674 303 380 304 158 025 525 561 997 879 083 535 771 920 561 897 727 047 228 396 677 767 098 222 792 233 720 335 570 560 247 842 301 363 012 891 195 110 862 328 864 718 076 484 067 576 182 222 930 577 862 160 501 332 210 054 695 281 192 333 049 747 321 767 658 104 562 000 169 472 167 782 353 839 181 981 312 213 396 306 657 958 845 949 083 565 787 398 755 525 249 293 648 880 977 826 435 252 423 052 421 761 401 212 111 754 249 884 044 787 401 015 313 055 766 802 819 167 072 379 795 058 307 168 155 503 622 513 849 710 489 938 350 135 647 115 092 374 632 273 110 003 485 094 305 878 613 957 368 470 603 667 489 797 426 195 216 682 710 639 530 944 777 216 015 643 395 779 531 605 539 131 856 559 511 953 415 701 842 882 410 529 366 410 942 158 448 619 874 443 346 733 825 717 737 469 053 394 445 312 447 048 917 342 039 304 192 851 448 058 788 753 210 141 664 195 421 701 936 438 607 094 795 110 081 699 250 762 074 008 263 258 072 764 535 329 968 219 871 368 672 913 448 500 121 796 491 952 952 481 923 632 981 011 456 949 615 539 053 413 369 170 141 990 895 459 811 317 181 565 108 444 079 831 550 399 629 926 993 924 173 494 150 231 854 492 403 004 107 959 057 839 085 904 307 669 951 261 285 161 685 738 906 591 647 320 887 437 265 066 133 921 725 646 959 211 045 058 671 944 599 958 422 973 927 334 180 374 352 126 951 399 065 528 046 786 864 992 160 439 887 893 447 518 342 422 446 880 955 335 830 192 675 228 423 635 623 228 590 787 102 330 603 753 630 109 606 544 824 799 328 706 221 627 211 480 566 455 682 777 259 084 324 809 973 370 625 696 152 356 722 318 094 130 092 083 454 730 746 301 393 242 188 496 869 078 025 898 732 755 168 240 552 263 639 764 892 990 079 935 726 678 748 333 913 458 575 808 243 845 886 713 447 651 203 927 596 276 204 942 153 937 748 660 729 240 346 352 933 201 419 800 714 289 410 508 068 896 017 243 723 854 807 689 934 643 763 984 867 450 215 020 727 843 687 266 137 354 947 060 636 718 925 880 503 792 486 954 298 604 530 510 923 918 875 570 834 799 304 955 382 859 019 161 309 749 880 083 975 736 640 826 677 137 781 137 958 413 744 052 488 313 686 880 858 265 842 031 253 632 302 811 155 917 148 550 046 086 609 615 220 680 116 440 237 301 795 455 434 872 482 542 808 418 232 074 904 163 060 361 338 290 136 354 758 588 704 529 450 782 673 992 046 403 419 483 400 176 121 609 671 919 281 872 907 704 355 195 697 672 637 255 940 616 916 356 145 353 414 441 621 439 711 156 518 471 881 462 378 276 195 725 936 441 001 806 593 037 570 127 788 897 539 361 135 362 343 864 074 964 900 626 777 642 284 815 948 844 734 339 339 885 460 349 687 399 816 896 430 341 418 155 580 498 605 485 238 161 204 142 663 220 884 336 276 480 212 926 955 015 605 808 520 045 152 779 085 317 854 741 299 680 968 984 113 813 246 600 262 109 400 935 710 404 432 982 669 594 553 338 245 113 811 958 038 502 564 555 434 179 523 785 307 430 184 000 867 114 463 615 023 643 674 994 518 579 665 530 586 837 349 832 158 302 763 388 380 878 500 266 559 071 696 517 339 415 118 391 914 451 892 827 497 688 352 608 658 908 213 761 922 261 575 723 324 797 784 989 387 132 075 331 726 762 291 981 121 904 600 606 391 895 318 036 119 421 655 638 453 620 949 551 190 450 954 185 590 176 564 096 848 817 048 897 516 634 846 239 209 086 236 753 593 492 002 743 083 513 939 775 277 719 195 102 247 388 617 814 633 881 083 999 087 503 829 118 925 269 826 265 256 356 938 892 615 638 811 351 550 965 893 778 642 173 270 956 365 464 551 259 988 242 297 002 678 644 767 662 979 940 615 372 280 516 301 132 940 386 786 977 844 913 161 299 423 879 204 154 281 887 071 598 053 006 746 448 033 802 054 846 107 827 881 315 082 176 726 141 379 485 683 970 643 591 160 683 236 045 695 341 283 033 749 305 907 471 909 673 355 222 496 278 369 585 740 106 626 759 920 862 938 975 883 282 076 192 755 291 318 832 854 530 885 607 911 503 568 026 310 362 375 225 671 899 144 234 167 088 696 170 829 349 397 639 685 849 798 643 986 273 123 320 461 897 259 570 667 746 297 387 076 548 205 160 725 411 112 399 582 500 761 364 578 035 370 516 622 493 689 391 143 881 604 610 034 361 213 931 697 266 008 779 897 888 264 758 225 236 815 599 418 768 604 058 095 292 639 373 553 590 515 100 775 158 201 821 144 053 370 729 678 373 881 697 925 591 002 335 315 079 821 813 401 123 845 700 814 577 473 080 631 665 004 776 322 591 306 555 745 788 271 231 875 468 624 993 180 616 665 974 577 295 040 213 425 824 855 917 275 608 418 810 348 035 471 436 614 722 202 055 961 946 628 948 302 555 429 952 701 126 559 074 156 507 772 715 275 247 725 277 535 698 818 656 019 077 646 274 401 636 532 729 675 292 582 894 626 127 510 242 601 597 758 523 408 288 681 249 227 660 215 530 571 303 222 463 291 358 539 753 278 764 105 494 497 931 526 686 394 980 062 954 580 539 009 849 858 957 552 854 705 310 067 190 110 212 107 873 193 907 969 389 839 826 482 109 039 001 295 341 222 407 450 789 394 719 967 292 694 578 637 956 211 198 935 578 227 587 682 034 626 215 553 808 076 775 750 467 495 809 872 545 824 352 882 333 334 101 636 677 850 060 856 817 475 350 779 138 458 116 291 008 408 709 471 419 847 597 786 289 505 270 042 413 452 217 984 911 069 648 166 855 485 954 920 341 256 222 193 271 551 440 742 560 132 894 955 520 104 349 472 961 582 097 238 708 554 168 481 893 358 018 557 952 044 199 259 960 533 180 655 460 213 147 784 128 273 128 664 777 532 480 274 646 009 394 627 987 323 586 434 338 062 798 651 231 604 989 215 276 336 931 335 078 522 908 734 019 668 456 463 238 319 253 796 772 905 832 189 541 624 077 500 722 129 423 961 518 430 871 498 156 943 523 719 774 655 630 676 150 606 648 525 646 443 971 493 651 695 822 477 938 334 832 507 334 286 338 749 972 687 928 814 694 261 130 738 973 014 628 636 793 204 875 157 405 695 019 274 176 253 071 397 938 114 942 224 596 089 844 658 360 590 183 712 814 379 251 763 517 690 203 411 153 322 887 708 443 506 908 188 196 779 679 361 635 776 357 732 246 617 419 413 331 515 709 123 806 245 006 236 689 156 568 368 438 097 229 148 105 020 597 594 148 297 862 873 271 770 487 754 060 289 677 288 240 127 152 287 732 624 204 001 697 452 521 524 978 865 885 784 008 869 549 011 525 503 805 295 391 479 597 646 896 551 833 773 333 512 334 793 644 860 790 335 647 334 093 320 726 506 351 095 193 949 854 111 264 628 158 331 534 910 103 458 538 007 193 524 461 220 771 073 598 102 866 304 514 889 521 926 927 802 615 263 096 169 511 116 747 189 146 096 384 291 655 158 264 575 665 593 609 350 835 622 132 569 670 264 844 459 567 688 923 545 050 180 310 749 712 689 055 493 627 920 211 112 989 784 762 207 399 956 427 192 457 886 587 892 431 361 668 777 127 773 016 579 700 499 907 108 323 247 905 791 186 985 388 394 724 529 791 966 127 980 623 620 645 814 698 729 352 698 843 153 362 930 517 121 272 238 395 092 928 479 131 218 273 770 296 588 443 253 319 293 036 486 136 875 683 713 757 162 195 925 491 714 778 880 297 029 068 125 767 643 499 537 018 999 467 863 166 688 443 161 087 984 692 864 705 137 989 585 874 352 775 200 002 149 703 443 339 255 473 413 380 223 878 278 527 608 200 968 752 456 098 485 254 833 795 447 952 215 180 241 692 035 326 719 696 572 923 722 654 684 733 114 041 202 193 941 483 142 087 557 609 361 280 767 900 406 369 451 603 196 412 584 898 212 971 298 725 983 050 493 479 391 697 656 992 396 286 094 139 727 697 411 478 361 270 787 857 641 784 106 892 489 926 839 891 807 639 909 516 924 204 822 414 405 369 088 545 605 714 338 025 004 355 145 230 166 193 395 496 617 523 721 562 627 735 609 831 022 968 703 251 834 543 451 163 077 787 642 766 539 267 037 621 376 694 708 589 539 529 754 773 930 169 795 999 546 137 220 180 133 411 574 461 272 399 895 436 705 961 992 745 521 808 986 578 803 378 635 592 991 863 438 705 355 685 316 763 972 247 888 815 416 068 835 741 997 522 355 678 584 204 020 801 329 299 305 082 643 563 203 047 003 221 060 023 418 878 220 104 618 309 565 593 969 329 526 286 041 924 077 371 083 228 756 380 111 299 416 529 103 552 902 469 141 642 070 259 241 507 637 641 415 169 202 237 686 681 242 113 315 299 632 679 933 256 724 529 507 142 466 968 451 360 196 248 929 875 369 524 969 926 479 538 434 692 192 591 508 574 198 508 003 070 240 289 563 738 580 229 830 327 964 514 251 194 733 995 788 971 911 780 340 874 630 753 004 102 935 963 258 334 158 644 152 027 865 734 158 345 726 599 941 421 761 753 821 367 077 675 370 422 523 657 878 877 106 151 928 657 179 906 537 490 833 075 527 565 667 533 740 242 474 935 683 334 914 315 084 119 964 051 405 503 096 158 919 523 838 249 607 378 392 713 122 842 285 474 956 185 346 340 796 309 311 808 531 307 004 869 540 171 273 169 455 975 243 169 190 069 333 314 594 291 410 652 898 659 594 064 159 345 643 839 661 884 857 890 444 411 250 152 544 780 856 820 417 139 360 519 500 528 659 547 751 648 095 431 009 950 727 028 755 477 518 028 644 557 482 037 175 015 483 401 526 083 152 786 866 944 651 138 852 801 107 119 704 087 229 502 694 495 374 022 831 490 086 445 203 618 705 288 691 650 979 646 345 636 824 382 962 336 399 615 650 743 534 937 258 960 567 360 131 086 818 985 388 370 132 484 096 872 682 193 393 879 247 635 557 299 775 205 078 580 934 906 777 078 675 389 410 209 957 030 001 249 631 554 070 211 084 967 970 906 281 275 023 036 016 316 375 005 669 306 394 966 467 103 083 817 739 942 238 458 615 382 707 587 447 095 581 422 131 792 254 564 535 284 577 588 109 616 039 976 978 613 470 190 093 867 029 574 652 009 671 714 301 147 215 789 215 453 085 648 590 122 036 964 091 275 208 508 175 184 160 349 407 113 854 364 611 981 414 380 404 755 962 820 267 294 336 364 134 181 358 456 997 976 006 888 467 102 985 550 747 170 935 195 062 141 984 110 183 014 358 124 691 615 587 926 153 846 517 676 900 332 160 812 014 547 624 345 958 510 688 311 852 249 594 672 672 800 889 938 446 398 376 316 790 545 824 618 861 342 546 398 892 006 056 405 107 142 249 924 807 024 219 782 576 809 499 060 433 006 205 609 477 583 581 018 519 360 548 112 165 643 764 368 008 014 773 233 005 867 505 362 210 427 048 562 628 591 371 547 533 466 764 914 304 846 995 578 714 875 226 124 334 500 938 861 710 261 513 197 415 741 409 689 651 086 367 018 576 894 321 622 466 217 351 226 249 683 196 118 115 622 971 057 984 951 324 423 741 164 537 732 663 975 573 005 335 984 179 213 552 225 174 863 308 240 089 296 980 621 681 649 521 138 186 026 200 366 339 613 470 778 216 583 359 377 481 754 669 567 878 513 290 562 481 281 081 446 896 727 815 544 870 637 416 352 206 904 472 188 065 661 867 896 548 693 751 889 457 291 010 462 087 405 003 738 121 360 513 557 309 836 258 034 915 562 394 412 946 703 555 407 027 430 281 271 574 732 505 318 534 123 469 582 030 990 201 109 313 288 596 740 511 758 052 097 635 998 806 920 845 461 551 588 509 874 490 421 304 130 237 095 458 514 531 506 343 553 583 436 943 216 364 344 300 494 727 885 228 893 896 805 916 372 685 804 337 789 477 455 563 516 853 300 047 789 435 292 243 669 476 689 790 013 555 755 905 458 763 449 244 384 946 624 042 519 548 610 434 091 983 471 719 374 422 406 560 185 569 910 709 787 144 705 954 976 392 434 506 508 248 299 744 973 990 441 878 664 481 583 836 358 394 256 638 614 921 783 813 873 220 135 489 355 942 654 684 647 005 096 381 275 837 986 873 858 572 920 173 645 917 415 308 412 924 710 778 682 969 882 569 842 999 939 758 264 847 370 358 994 975 953 179 216 074 752 840 530 049 829 477 175 644 567 122 508 266 845 871 975 056 928 707 083 826 813 556 400 947 212 834 665 005 814 127 957 120 311 118 775 477 135 645 465 908 305 139 918 831 190 200 472 151 575 685 184 524 928 552 780 579 071 810 653 836 568 963 101 361 003 092 840 150 809 277 937 209 065 251 380 616 226 219 429 582 824 570 394 282 914 914 066 783 577 337 757 218 897 547 722 675 961 487 909 202 440 442 567 972 528 215 153 670 118 577 122 807 312 863 437 466 816 105 748 027 211 695 408 152 054 539 923 783 037 357 543 414 906 552 825 376 612 508 706 443 913 122 925 627 832 358 401 247 521 696 738 487 724 090 943 246 272 194 493 843 273 732 504 989 842 482 293 941 853 489 212 761 783 822 388 589 648 997 258 837 984 825 763 632 415 704 036 306 726 325 939 079 867 710 750 507 234 566 444 678 454 578 071 647 226 047 940 954 617 603 351 236 861 450 445 925 917 225 642 380 433 734 572 669 249 691 325 658 475 961 784 967 797 197 018 212 476 398 721 069 328 350 564 743 362 497 896 432 467 394 064 436 520 618 572 154 448 572 636 081 794 118 434 972 805 008 043 280 681 110 198 318 326 256 439 765 996 425 438 806 837 945 257 877 625 703 176 958 768 773 078 373 005 393 214 776 349 917 862 441 435 614 791 429 946 922 038 546 258 630 004 316 961 586 723 574 625 904 022 009 863 014 090 348 394 952 962 626 089 895 981 511 364 718 277 685 817 570 426 592 730 813 191 231 746 897 950 179 026 417 809 614 170 456 005 449 198 924 976 750 098 996 943 232 862 741 726 144 517 116 911 630 837 262 687 750 381 213 572 969 800 965 066 922 072 684 479 728 205 333 704 703 228 228 248 610 584 471 821 271 452 164 109 669 675 868 199 914 453 343 192 866 948 238 168 928 793 206 924 931 723 391 755 609 001 921 364 685 354 457 339 903 756 707 601 596 876 217 315 303 122 271 245 468 904 929 154 281 013 352 483 199 916 201 224 127 636 695 024 982 540 207 175 651 072 303 994 335 481 874 929 496 161 339 928 758 768 382 292 345 635 753 921 097 409 469 584 937 378 410 580 942 146 250 693 420 381 545 406 301 406 710 562 008 332 188 940 439 104 167 622 548 170 670 609 056 917 567 120 066 371 615 213 106 208 456 216 304 043 624 922 138 013 271 974 945 085 052 447 987 433 877 073 567 167 370 943 142 217 654 589 515 315 288 709 080 911 811 571 190 040 916 574 398 947 216 809 892 309 954 754 952 632 334 734 788 325 630 575 459 352 464 964 383 516 027 325 743 925 692 535 744 353 291 478 873 519 620 435 270 860 699 314 117 363 037 793 650 926 621 850 120 514 537 074 164 459 166 565 113 334 628 800 251 368 881 220 553 435 006 222 745 348 505 365 505 583 406 024 059 372 149 990 501 945 790 105 460 692 887 999 972 272 218 116 144 741 283 279 537 447 404 225 267 491 352 905 967 601 495 548 744 737 138 577 901 378 699 107 896 635 824 795 901 482 601 906 735 710 448 262 781 829 378 304 729 756 747 342 154 928 726 849 719 537 957 527 658 618 204 417 412 690 591 250 503 692 563 658 714 012 012 049 584 834 170 771 127 132 150 927 364 522 522 303 064 764 822 052 726 479 034 292 609 054 718 561 851 194 242 293 202 563 908 947 202 734 095 991 689 920 610 756 112 967 882 781 321 851 549 769 649 771 974 938 693 233 420 495 508 599 572 787 484 106 056 013 979 578 993 538 025 434 810 168 534 226 169 804 512 688 894 385 216 529 403 676 334 253 881 560 923 383 866 566 836 571 685 349 894 894 451 667 661 750 191 288 283 858 296 255 287 416 142 367 657 713 452 614 234 134 798 172 743 924 334 167 020 915 562 352 135 944 674 018 156 885 523 564 088 388 989 366 632 287 556 847 418 562 325 505 050 021 937 841 789 579 379 187 759 848 639 511 648 702 236 190 979 441 795 603 017 722 959 947 850 991 237 315 702 538 375 986 975 092 698 112 491 005 063 487 586 457 140 334 949 126 615 956 924 142 368 990 927 506 501 532 848 048 191 124 519 731 474 947 179 362 506 695 198 595 767 769 495 452 910 103 529 625 254 526 289 301 439 661 845 550 725 417 978 307 963 243 136 787 127 961 833 757 567 050 608 909 121 733 035 475 841 260 415 228 860 400 677 765 317 936 089 264 171 764 535 932 589 583 841 486 125 377 922 057 446 006 392 743 345 027 353 485 403 693 145 357 123 740 526 481 943 733 008 659 201 081 019 117 551 678 954 083 727 691 354 404 570 141 519 385 417 391 040 162 860 679 447 396 287 845 005 640 758 910 746 645 297 337 073 863 133 512 211 989 999 723 344 777 648 888 503 657 575 125 725 552 775 916 969 002 982 574 652 861 589 818 668 730 902 312 466 648 047 422 617 951 047 101 036 416 640 379 962 717 041 593 118 155 807 072 973 712 639 120 844 455 095 924 804 249 967 900 174 570 971 461 667 291 275 714 356 667 450 436 686 726 424 347 533 911 630 570 267 149 690 346 827 507 017 107 720 363 443 494 774 192 841 443 058 957 181 480 439 814 774 833 215 687 743 996 857 207 125 973 115 496 537 427 644 878 886 596 840 907 357 793 108 874 332 184 806 212 934 095 187 995 612 003 375 372 002 393 077 878 124 393 278 846 159 114 938 822 058 955 832 356 641 781 628 045 085 291 715 429 300 619 082 612 001 561 568 608 352 043 868 004 235 285 778 999 300 941 689 772 969 668 662 808 814 090 470 639 889 757 705 362 120 790 578 598 090 996 647 107 857 998 974 097 726 851 339 207 284 005 798 210 358 730 200 787 254 509 702 383 374 082 898 740 686 141 040 796 880 012 024 028 397 783 811 190 912 464 262 016 696 893 044 596 614 013 363 593 839 837 742 619 167 106 120 858 061 052 331 943 644 184 355 492 868 649 307 404 447 056 219 687 429 201 533 906 308 132 345 118 826 215 135 460 752 563 041 135 395 797 925 263 368 028 570 001 524 356 627 974 336 710 734 229 742 336 202 144 861 243 208 031 371 386 797 532 304 701 498 777 668 822 945 074 092 956 441 300 973 136 506 227 821 767 427 321 784 498 982 842 116 455 904 400 288 523 122 762 449 323 638 228 125 811 948 565 803 399 494 822 471 013 482 398 615 596 034 196 144 887 222 259 939 683 215 375 660 243 313 283 552 871 312 484 672 651 747 755 823 703 292 868 086 857 742 612 127 426 166 679 713 915 005 006 034 937 589 728 852 729 067 093 331 853 621 758 092 235 962 473 027 624 137 066 218 506 389 237 407 390 993 775 354 576 360 684 822 934 666 414 604 401 752 714 397 963 514 756 410 758 465 187 255 773 058 673 232 861 315 070 106 239 702 388 206 218 663 148 874 224 889 745 433 945 919 051 224 114 767 537 053 551 718 197 878 700 528 934 661 047 603 063 954 272 253 892 205 190 595 348 352 192 203 274 766 506 049 058 948 920 586 185 335 456 978 633 077 065 007 638 469 147 036 807 963 009 009 849 580 337 774 265 255 568 724 571 688 237 241 209 059 350 684 798 187 936 384 317 329 191 662 647 563 636 673 966 307 865 112 877 691 634 160 805 817 581 130 562 806 097 525 841 742 360 081 741 215 452 129 912 483 135 192 901 883 101 092 955 919 037 449 134 721 304 617 258 900 230 581 100 949 807 574 117 933 706 558 161 338 477 834 666 529 070 662 475 831 409 088 963 629 129 484 652 794 344 163 869 745 738 365 435 990 933 393 085 191 708 850 603 445 594 472 530 855 225 306 515 700 861 974 146 791 528 832 252 869 613 368 407 825 602 245 210 816 938 106 695 939 981 655 684 866 221 346 637 727 711 848 045 250 303 693 860 372 752 868 068 818 320 568 331 960 214 517 794 391 072 007 508 549 756 266 932 587 191 225 894 094 371 722 201 548 357 747 860 474 067 898 334 752 281 416 156 040 321 882 650 984 546 203 936 155 033 802 307 608 276 478 043 367 733 781 232 332 632 047 394 251 876 276 160 946 462 732 703 174 192 320 204 459 808 405 793 888 444 082 304 814 580 406 763 313 121 453 752 241 653 693 971 455 566 219 209 734 602 328 643 449 860 630 850 295 328 789 755 020 667 611 209 246 569 084 325 966 219 806 512 907 636 502 522 599 792 290 552 018 018 524 113 459 089 181 427 585 581 612 391 545 904 032 087 327 495 209 941 931 108 740 719 938 859 560 838 529 476 358 052 974 839 517 732 330 923 287 329 597 434 139 715 212 574 688 037 512 998 941 360 514 944 410 496 722 551 000 307 940 187 432 443 082 878 684 392 924 440 523 313 237 447 348 781 562 685 294 095 271 028 112 862 748 094 363 790 911 263 802 366 033 317 027 516 538 194 884 473 538 587 033 096 209 027 016 213 093 576 599 637 621 160 755 477 750 964 890 710 656 946 827 548 762 894 854 768 030 534 975 809 054 363 598 093 442 699 913 417 302 935 262 142 813 536 156 510 435 025 634 173 750 484 894 377 028 711 141 261 546 146 538 818 517 064 186 217 480 543 318 387 747 892 487 835 264 993 587 606 694 330 858 559 188 068 341 374 774 074 227 444 145 420 569 628 472 296 082 391 847 870 192 046 090 742 275 792 752 888 065 727 279 285 927 431 048 721 957 090 915 782 097 904 179 444 117 814 650 963 219 508 720 438 364 379 162 775 122 331 315 334 832 554 754 427 703 838 655 328 541 457 502 298 656 726 579 284 757 075 653 721 012 176 422 779 045 344 851 627 217 135 554 394 719 573 188 968 961 120 225 447 925 585 555 161 456 808 914 350 661 293 830 663 513 866 229 822 407 303 216 117 955 046 988 145 546 573 961 824 533 493 642 473 238 884 213 857 046 577 804 588 024 398 036 188 738 889 336 561 678 215 351 606 270 021 213 528 505 474 356 063 879 020 522 993 052 406 827 625 707 835 820 541 918 112 871 105 332 504 858 176 985 619 316 950 253 683 081 243 690 596 825 235 552 376 626 902 728 484 788 341 375 530 591 064 940 103 939 275 790 025 352 269 337 159 610 737 990 138 437 899 067 618 538 772 727 572 575 593 830 751 278 645 735 408 946 515 893 184 489 787 514 191 092 439 448 252 569 439 191 877 329 903 061 159 510 488 089 725 093 468 494 507 902 994 627 117 234 879 494 202 477 462 982 453 232 427 206 041 694 614 773 927 330 455 260 096 124 764 834 975 718 003 791 993 905 213 769 289 437 577 303 211 556 360 174 719 022 262 837 806 642 739 996 541 485 109 028 241 394 369 122 844 480 084 621 548 929 885 887 320 645 045 773 963 454 348 878 622 941 553 732 076 254 696 754 354 651 338 977 363 679 395 942 967 088 426 497 962 436 047 432 754 819 251 247 382 759 154 711 929 112 151 242 532 275 350 501 561 618 229 963 273 748 769 981 037 773 614 609 424 436 073 600 800 536 124 217 657 051 878 111 102 999 708 007 936 660 492 133 960 293 901 717 543 773 099 322 221 964 636 552 215 105 996 924 769 994 584 674 362 107 955 537 900 384 064 352 685 682 210 816 664 226 398 035 672 404 834 369 912 599 749 690 195 584 541 426 355 189 071 424 655 610 724 548 966 369 525 654 489 705 495 555 942 858 224 025 535 580 132 445 902 015 732 369 920 913 615 648 402 753 944 488 740 694 906 490 691 993 306 087 279 637 119 760 107 320 139 407 449 376 232 683 648 193 731 719 309 444 062 214 215 393 060 679 116 277 057 913 093 246 351 327 357 090 059 668 691 268 523 091 776 609 904 348 370 887 267 786 028 226 146 937 529 760 410 322 103 973 719 992 163 340 064 471 560 007 107 749 477 042 934 708 864 600 867 564 968 329 472 563 448 453 166 961 161 040 346 905 836 748 048 192 975 852 038 154 175 375 861 654 809 913 471 833 481 609 170 319 937 283 221 699 308 391 463 083 187 542 993 646 710 908 262 759 446 361 088 254 603 461 965 676 819 644 356 841 016 903 794 487 656 130 640 951 503 224 903 841 912 488 931 603 115 631 647 680 761 671 860 629 431 613 236 218 255 963 260 065 294 957 064 405 175 395 866 019 467 985 157 236 447 167 593 425 992 187 310 547 451 569 827 787 758 564 755 780 841 424 432 089 569 389 175 295 409 737 876 662 538 525 841 022 076 379 126 827 909 104 534 756 457 820 557 642 702 637 214 076 477 527 209 416 899 337 799 894 110 219 915 070 213 470 278 298 331 626 333 959 826 455 360 246 036 837 932 949 129 473 265 521 693 425 093 040 966 766 588 176 533 292 058 976 091 381 707 247 824 767 617 353 737 906 051 652 429 874 818 719 555 885 332 184 001 058 907 984 001 254 140 872 689 015 132 276 485 630 437 895 170 162 381 074 683 111 487 157 130 010 035 729 686 174 072 940 307 633 937 203 687 254 945 055 650 650 115 535 688 062 698 043 967 927 121 006 639 884 316 133 942 788 052 805 653 152 717 974 037 534 976 624 101 453 293 053 913 572 407 569 318 497 511 550 167 039 031 108 110 216 125 601 395 414 715 637 408 189 348 533 709 048 133 758 675 127 975 032 275 906 583 110 385 886 797 042 613 938 166 420 611 743 152 172 977 604 415 758 183 461 373 996 738 544 642 388 875 231 324 526 454 227 311 422 221 631 138 391 264 924 380 890 447 327 288 024 664 648 478 296 617 344 683 292 325 171 381 282 764 382 271 443 962 271 474 699 280 775 312 011 085 156 081 113 587 849 862 374 779 409 530 484 987 412 223 391 904 614 064 373 907 699 600 621 128 125 766 887 489 016 139 375 101 676 138 981 010 453 875 567 900 880 038 586 616 738 389 526 680 388 114 514 092 948 866 729 491 407 779 736 623 333 629 711 035 859 238 304 255 810 995 184 742 900 030 882 893 287 167 624 935 781 059 373 732 649 130 729 526 856 310 789 831 400 664 568 468 973 590 673 582 621 099 413 749 944 126 123 220 291 110 964 808 169 215 017 512 959 614 856 811 723 926 711 080 663 157 342 329 778 599 885 080 371 796 042 182 310 256 692 420 945 655 037 157 209 140 139 845 960 403 167 290 336 832 750 525 446 470 021 547 391 421 634 953 681 177 302 244 753 517 820 067 012 253 854 250 726 327 762 175 202 815 452 743 492 908 403 412 080 652 765 324 621 213 501 598 298 182 624 060 572 803 634 833 517 215 695 191 604 364 602 443 421 830 435 328 524 704 749 404 291 325 339 428 197 253 832 575 122 509 887 326 780 191 198 860 983 588 040 746 153 961 434 450 662 658 500 874 197 386 055 904 773 309 954 511 298 089 557 595 910 485 869 407 586 837 646 350 336 812 252 548 216 917 737 153 254 677 932 965 117 471 774 816 671 386 135 450 410 129 343 519 560 295 860 186 993 980 352 511 467 689 979 619 762 637 948 979 190 530 515 010 397 163 023 278 682 949 698 593 511 302 876 154 968 136 977 997 381 544 898 512 488 901 890 874 526 574 734 142 450 793 112 612 341 677 369 041 583 490 549 389 989 260 965 099 379 278 161 894 367 290 610 062 900 473 573 387 903 060 234 131 695 202 487 866 705 218 445 660 811 878 678 651 839 159 477 835 107 353 969 584 818 814 878 155 748 524 319 346 053 843 128 839 078 260 710 890 936 411 005 762 019 392 045 805 310 307 098 896 763 335 859 455 627 334 043 198 041 077 615 669 726 492 546 445 694 275 674 623 732 449 578 908 128 891 833 755 999 414 320 179 555 243 241 398 481 620 187 921 066 343 319 345 975 937 505 774 378 022 349 959 257 608 087 345 124 020 291 297 579 187 210 757 020 998 253 481 950 996 425 437 477 116 949 842 739 124 753 885 616 078 084 422 236 190 266 051 641 786 681 755 697 566 118 610 225 190 237 895 042 787 967 149 055 060 676 436 327 984 228 617 558 933 821 346 726 982 526 510 915 095 078 805 576 838 577 009 309 488 378 543 216 266 558 961 212 802 500 144 985 265 984 940 751 128 523 890 543 008 446 098 833 465 061 924 954 178 216 866 824 711 427 607 885 549 399 918 993 782 622 570 944 854 823 739 721 655 309 927 275 431 055 907 710 150 048 607 163 175 098 497 987 101 477 626 845 810 939 107 184 565 912 660 081 465 357 711 409 267 322 637 477 175 757 900 715 017 339 446 290 240 798 434 918 798 165 280 152 231 587 691 705 375 810 225 033 763 085 263 620 700 720 675 658 819 636 589 927 550 775 120 780 386 167 253 734 973 770 008 306 061 805 034 728 533 708 567 348 356 720 989 604 046 265 632 991 440 579 540 734 780 857 262 025 996 865 782 936 392 712 043 374 547 036 234 724 932 123 076 241 118 446 486 705 192 172 061 265 538 003 909 272 248 786 909 410 068 625 308 840 324 157 255 999 079 807 021 161 589 676 226 678 003 024 886 637 655 400 839 082 041 376 258 884 560 427 971 047 091 350 800 341 348 783 642 869 018 319 817 661 456 348 134 959 522 154 480 961 634 683 999 675 411 757 169 902 478 072 605 322 283 076 177 720 779 213 422 005 925 670 574 737 848 302 874 233 767 231 111 279 006 958 833 928 272 147 426 744 357 432 692 872 730 190 488 675 791 208 103 676 800 036 099 556 362 471 986 483 194 076 411 783 727 878 214 704 531 084 167 708 012 941 692 413 393 008 103 375 576 367 724 476 182 538 469 781 525 322 233 191 602 584 719 235 808 133 704 548 940 978 769 249 283 352 768 160 459 149 377 551 877 021 674 113 014 505 438 181 684 452 141 339 324 685 788 464 923 109 518 779 952 099 306 161 910 809 329 721 702 143 588 224 466 284 527 523 802 365 511 759 187 715 554 193 405 934 353 540 004 798 910 134 123 682 430 677 123 596 190 922 415 541 504 066 850 652 635 632 869 210 517 675 766 026 114 463 291 522 578 469 342 283 746 505 840 921 508 829 921 881 487 740 498 256 619 224 706 933 892 666 675 493 454 775 582 396 369 293 870 876 845 416 132 712 369 013 808 137 277 740 921 007 030 324 815 748 561 641 244 157 232 521 630 438 404 880 745 215 757 887 485 979 009 690 468 013 621 525 170 182 979 555 837 658 812 638 068 534 172 580 062 317 503 898 761 704 626 762 852 650 253 768 533 816 839 526 032 001 460 020 849 036 310 459 319 935 324 443 882 689 434 056 152 313 666 400 038 434 248 823 396 986 254 869 542 581 261 633 568 315 260 053 622 582 976 345 611 997 229 228 261 364 969 338 554 248 878 347 599 590 844 042 817 140 328 688 175 779 395 492 038 027 644 916 244 003 487 229 141 668 159 945 479 665 682 984 371 461 169 046 436 262 637 666 415 349 820 025 608 727 787 201 135 898 649 326 689 745 237 799 926 996 930 163 773 232 571 432 196 236 220 054 052 515 604 263 672 910 375 153 769 102 349 081 433 836 543 832 196 073 083 571 295 157 931 209 191 010 161 824 517 649 809 324 210 245 767 698 069 755 923 302 405 962 039 176 338 474 933 234 224 730 940 552 139 433 928 277 433 635 408 088 991 372 827 657 690 276 478 940 167 923 183 456 929 467 862 259 572 146 293 008 065 548 780 514 623 539 541 947 158 902 031 624 376 746 041 153 066 661 492 040 192 226 579 002 545 175 044 716 254 998 306 459 723 197 978 308 203 423 135 060 031 300 264 616 167 215 250 974 989 053 068 010 660 857 632 196 864 951 859 174 349 686 086 672 817 776 639 578 222 113 181 209 155 192 978 329 750 035 063 559 182 336 897 363 735 948 410 115 528 538 056 531 119 997 255 244 209 316 017 659 432 185 519 690 390 735 714 741 658 181 218 864 401 693 770 629 356 969 517 884 585 784 848 168 270 905 499 113 111 909 170 393 962 316 092 349 258 136 642 760 595 337 316 165 793 280 604 275 977 092 337 794 751 576 554 537 317 144 044 916 492 525 591 033 538 894 812 319 570 622 183 490 738 185 178 778 579 462 588 108 194 185 060 852 434 390 690 162 612 913 099 938 845 430 124 072 251 057 692 401 764 516 297 791 039 239 980 495 884 596 193 528 380 453 961 950 098 146 158 352 502 653 183 399 291 279 169 533 626 220 377 561 629 327 501 279 118 131 873 125 233 549 671 558 814 424 212 098 663 990 402 690 198 945 571 165 939 342 633 776 471 066 681 866 954 728 850 798 566 434 912 227 098 314 945 662 259 631 466 391 722 380 381 236 766 842 920 242 538 976 199 149 626 081 402 961 978 073 780 565 831 307 418 827 997 511 924 107 993 642 642 224 753 677 179 578 037 393 816 702 869 978 756 590 286 509 754 898 486 598 925 461 462 917 501 028 028 714 370 663 007 442 349 741 366 144 306 405 723 203 246 217 593 170 103 612 184 331 101 555 370 109 822 019 019 483 191 821 757 963 322 838 146 972 349 455 709 592 050 006 797 534 942 333 559 540 232 470 920 063 426 567 047 835 188 843 402 803 743 756 613 898 662 778 541 557 239 767 315 673 542 053 655 644 421 404 481 617 094 190 888 266 027 716 524 631 778 071 565 458 404 918 618 009 761 651 438 518 701 626 080 527 731 747 089 865 847 317 911 956 743 080 484 265 687 775 976 264 231 598 713 951 008 764 995 582 079 081 269 319 309 643 488 938 871 987 526 219 584 813 351 881 987 550 032 152 442 831 587 417 201 457 474 052 219 755 608 818 663 376 965 747 893 434 507 294 617 102 821 308 113 952 456 617 612 362 871 861 607 087 240 924 855 166 353 205 838 385 795 640 388 635 480 692 939 583 435 121 755 687 868 210 372 134 609 468 575 585 446 772 760 819 758 695 868 735 695 267 464 896 516 672 096 408 930 010 276 053 515 776 743 561 440 488 944 569 448 513 966 670 137 891 177 054 819 739 500 731 347 522 017 164 174 685 854 276 751 876 631 693 445 791 057 632 148 653 283 714 890 015 621 251 295 722 108 599 738 357 907 743 931 425 350 889 521 104 978 670 722 735 723 931 614 463 285 890 313 499 053 705 528 463 459 111 031 621 838 228 155 924 848 249 728 008 263 137 474 504 397 676 520 460 476 685 571 265 172 472 103 464 509 219 509 523 418 215 226 972 065 190 683 951 267 226 647 311 178 587 276 049 757 530 933 978 289 044 552 209 968 681 059 541 887 499 153 826 006 789 120 227 254 370 162 696 909 929 083 044 264 625 137 678 303 255 919 083 435 962 729 808 957 242 688 491 219 168 579 158 938 292 122 979 703 473 628 100 408 559 213 948 496 773 482 316 185 796 618 775 220 203 448 821 274 374 476 142 987 542 976 489 410 249 821 452 532 295 062 713 640 874 791 631 992 216 828 687 320 657 358 874 076 335 397 635 188 064 080 438 342 423 119 642 260 159 723 742 117 635 681 997 849 818 366 851 529 999 806 797 366 094 525 992 795 740 193 246 899 029 316 591 037 514 090 811 039 717 221 391 156 997 571 333 646 292 399 365 290 160 332 018 382 499 896 444 318 859 137 777 715 086 548 546 945 487 002 874 281 417 111 985 729 255 323 282 531 527 489 264 556 058 027 470 061 785 900 588 045 133 100 810 687 631 887 473 210 416 178 426 823 448 901 410 919 935 951 323 856 637 182 656 334 244 071 327 346 860 484 107 883 488 627 636 270 474 161 310 981 718 111 328 525 964 405 095 164 366 216 940 893 757 505 580 338 379 722 294 157 082 258 243 077 973 355 478 488 084 533 436 090 562 625 454 001 909 405 807 094 686 036 067 073 813 049 770 002 186 172 924 310 980 269 989 442 693 781 011 629 951 353 590 691 732 405 668 574 301 055 168 612 044 053 935 869 060 533 662 047 197 645 276 801 026 312 481 396 663 937 639 200 623 299 010 032 398 077 316 250 866 337 577 775 401 089 729 922 569 031 516 246 587 533 519 871 901 075 959 367 481 824 458 625 970 174 499 856 725 863 924 697 240 408 815 345 709 499 545 590 104 623 958 225 358 756 702 006 695 460 265 115 530 193 865 372 629 444 558 561 740 506 046 463 217 773 816 767 334 288 707 972 349 496 304 768 750 437 822 251 741 974 606 140 586 281 105 214 299 029 969 148 272 960 910 026 013 268 580 253 287 746 060 657 197 706 776 580 502 497 171 586 433 579 147 583 928 241 787 892 612 492 701 580 799 502 046 041 357 506 849 210 290 470 767 440 315 227 593 101 753 721 526 656 780 531 972 241 117 728 188 763 552 706 259 658 539 309 146 532 453 809 836 966 177 498 913 276 018 210 094 046 651 431 061 913 925 368 153 983 436 407 223 617 129 653 203 560 036 373 682 646 978 527 235 667 234 056 493 203 235 693 836 539 009 952 141 978 517 133 636 385 399 918 943 990 423 138 614 933 284 529 021 115 155 361 599 916 040 552 045 971 381 706 217 460 922 197 959 738 323 498 233 385 050 690 557 437 979 171 797 358 495 330 076 427 144 989 114 696 398 456 602 202 536 108 502 546 569 213 566 302 331 661 003 429 241 178 372 321 736 993 290 136 906 605 947 281 637 447 867 310 741 415 205 548 305 515 106 983 988 046 418 845 338 887 474 187 587 836 954 850 181 468 453 000 800 490 534 431 838 822 518 910 206 691 034 893 443 183 395 518 908 954 413 970 240 515 685 341 405 890 956 973 330 557 948 362 761 782 126 448 492 663 898 566 896 843 497 913 704 217 026 956 222 816 010 165 132 874 084 488 593 316 373 500 493 443 853 829 701 422 618 984 337 618 043 066 535 855 748 531 237 237 324 336 501 227 826 318 349 703 948 197 281 818 973 015 577 260 536 849 055 105 549 906 693 501 730 061 582 946 264 861 872 889 811 456 411 007 258 690 688 915 446 213 652 182 238 211 216 901 730 456 769 449 754 106 171 779 811 097 247 893 916 256 788 992 711 142 876 338 373 281 883 937 847 499 839 323 098 580 733 796 588 447 828 149 407 296 895 561 715 227 739 067 739 068 066 744 110 122 735 269 580 778 691 993 725 360 539 376 926 371 031 938 621 817 087 885 679 442 483 545 477 877 076 659 984 420 714 507 524 237 993 756 050 113 905 349 682 891 529 064 102 246 337 829 699 594 712 261 673 825 399 631 041 299 020 886 868 001 903 214 591 333 837 067 808 592 136 272 438 661 680 899 693 048 537 271 849 622 925 943 909 075 579 399 611 459 535 614 866 520 639 078 416 917 044 460 624 877 713 923 839 129 448 777 657 529 233 353 486 291 044 201 741 060 720 434 106 258 638 289 258 632 125 432 598 842 151 076 272 126 334 726 750 943 876 491 183 912 268 992 376 803 948 827 669 139 982 651 564 092 426 214 926 725 571 726 657 765 289 516 037 997 171 456 402 783 118 741 974 498 453 874 108 989 488 792 892 763 124 281 331 887 206 686 587 743 922 244 767 105 218 379 119 058 025 595 541 301 935 461 758 816 328 701 257 722 956 282 818 686 093 145 881 602 690 284 470 875 813 228 773 133 354 620 453 130 178 117 653 958 420 313 818 803 562 073 137 593 792 511 268 584 868 981 660 341 021 864 852 622 347 323 890 725 584 176 480 305 739 457 109 168 453 301 220 418 296 453 491 892 870 834 748 097 113 390 962 550 933 225 072 453 927 280 651 367 243 641 088 297 189 175 489 528 649 450 567 219 326 995 130 695 378 675 426 582 317 255 858 069 493 574 466 976 590 443 422 071 232 415 902 286 109 108 548 719 221 047 251 365 436 489 452 583 888 435 510 313 231 423 804 322 543 156 595 618 291 483 864 772 041 170 361 950 553 922 035 773 229 887 047 340 103 996 674 286 767 563 639 484 013 312 516 044 365 934 950 908 404 141 837 880 056 453 901 154 617 170 776 335 238 670 653 893 349 336 502 282 915 956 776 568 304 611 005 644 701 240 256 513 020 659 108 866 050 368 166 636 054 340 812 402 786 777 083 166 021 919 411 083 901 236 568 882 720 692 538 639 661 056 251 064 947 862 408 999 755 469 737 515 986 422 612 779 202 379 750 778 090 393 760 091 962 943 290 037 231 811 070 491 748 124 701 657 538 085 022 321 346 025 123 481 721 377 997 449 434 959 746 194 048 388 398 418 846 111 594 511 405 466 182 256 258 891 803 995 758 102 688 915 366 346 038 085 153 701 363 593 111 117 126 941 863 858 538 021 925 477 461 466 392 402 802 693 979 654 405 186 360 615 721 901 517 008 809 475 626 539 085 797 070 722 547 676 182 646 046 404 152 336 747 891 490 571 118 928 833 143 426 593 066 831 216 240 462 324 388 408 576 579 411 019 045 301 811 093 986 248 433 841 762 769 212 662 059 637 727 202 045 530 165 762 233 732 726 495 493 528 515 490 710 581 004 280 774 138 380 013 891 208 864 052 690 672 584 388 302 987 747 294 578 839 335 618 574 310 755 837 018 151 080 014 669 951 738 881 580 518 401 145 185 198 202 886 487 260 031 049 245 995 353 940 816 229 205 341 305 793 254 451 828 974 750 185 090 163 090 061 376 675 551 920 689 809 723 084 304 034 879 817 012 187 833 770 486 816 867 870 289 410 792 944 508 283 116 784 312 323 654 253 471 998 919 592 191 731 581 400 822 355 151 642 887 686 770 191 100 557 145 319 826 821 407 605 771 213 040 024 985 509 902 913 215 409 312 661 768 806 747 199 919 959 262 387 583 822 446 345 590 838 059 509 971 143 034 922 348 853 215 844 600 109 496 791 060 428 653 246 853 704 366 682 753 517 108 343 458 654 106 539 169 134 752 091 134 636 540 984 631 676 920 574 053 177 307 898 463 004 566 979 755 560 413 669 609 024 425 468 664 739 750 477 319 975 148 986 566 630 809 177 358 296 759 299 018 410 844 571 295 800 694 629 044 727 388 935 098 832 287 196 203 518 375 140 499 776 284 401 655 338 813 942 351 587 534 798 695 557 826 907 822 943 888 483 331 875 445 857 496 996 716 105 714 520 981 960 205 099 887 010 931 819 910 635 524 389 987 858 421 865 611 107 432 467 615 176 999 893 400 960 207 692 178 306 377 985 935 058 056 758 505 817 144 877 307 196 874 574 833 292 825 708 323 498 448 033 548 412 399 816 315 640 565 359 155 876 844 453 935 345 192 185 341 525 440 693 698 591 858 158 074 650 287 011 167 233 820 012 960 320 565 394 746 075 459 965 575 839 677 214 548 218 087 049 619 628 550 388 773 019 164 748 364 475 754 225 452 048 660 367 319 223 023 217 816 913 474 014 650 519 177 228 673 896 292 811 369 968 282 526 671 153 824 054 280 969 031 998 951 012 437 422 975 168 542 299 763 759 043 110 597 425 351 317 682 467 632 817 749 132 775 564 846 547 681 149 352 065 117 408 057 124 641 044 506 689 887 874 901 481 338 461 133 076 413 901 781 851 328 214 199 854 591 311 452 287 098 385 966 614 635 545 437 844 824 883 996 880 241 635 925 688 075 677 483 156 543 625 394 258 200 146 667 235 122 518 134 002 160 088 974 776 557 238 125 344 717 710 918 875 221 501 359 947 776 608 593 748 734 284 813 324 584 145 965 672 291 765 700 395 698 839 270 441 247 774 443 950 210 193 414 051 522 964 315 635 798 999 443 006 554 070 063 945 988 710 184 837 471 275 594 111 935 441 633 436 939 793 556 623 932 514 087 800 233 508 058 316 019 831 658 116 849 964 533 292 194 698 752 549 497 727 569 181 803 614 014 154 371 967 090 989 532 690 185 746 951 162 100 410 333 588 539 314 237 488 945 564 874 079 243 315 626 335 682 083 011 608 441 766 400 402 389 776 126 088 533 920 966 471 621 580 748 793 928 549 877 226 890 875 698 602 571 134 999 887 775 327 258 471 017 987 743 276 300 717 557 951 264 520 856 447 577 059 280 212 692 283 276 737 117 578 040 582 239 909 005 236 755 613 040 064 342 944 534 080 343 596 685 728 920 138 074 494 367 802 821 158 040 054 057 290 479 056 429 020 552 630 176 302 843 191 199 439 211 498 698 647 409 080 006 973 153 628 225 462 519 718 440 726 513 472 698 111 756 954 806 153 869 004 967 865 603 202 291 177 999 409 717 894 233 824 616 697 452 825 424 737 215 641 950 370 499 005 696 118 253 728 082 154 448 590 942 518 915 693 461 436 243 051 521 941 236 918 175 869 286 453 655 283 380 647 391 848 751 927 901 193 425 670 092 128 495 673 204 777 638 728 568 637 661 540 213 723 647 583 394 612 136 855 287 383 382 338 640 966 751 547 868 285 493 062 144 917 098 223 990 177 512 637 441 672 809 526 702 732 834 528 614 408 688 869 240 198 114 241 750 583 624 507 540 255 148 226 132 440 910 645 767 483 836 711 814 833 815 051 256 365 999 240 008 672 104 313 322 795 395 493 931 694 946 426 388 342 059 389 172 276 635 112 475 283 413 519 313 775 330 829 346 774 049 827 518 800 445 910 153 508 218 310 305 894 683 641 115 544 654 629 626 504 047 457 228 584 804 670 430 587 686 421 927 112 345 872 543 862 158 065 279 869 569 563 577 119 914 233 077 830 499 890 407 776 173 345 701 298 125 409 730 037 837 361 117 568 588 055 908 651 760 692 495 496 992 385 673 281 564 398 932 785 361 441 845 607 147 833 520 497 551 788 424 924 110 776 578 833 922 447 035 684 456 871 651 157 971 645 882 875 803 661 022 274 287 345 680 429 566 719 045 764 912 024 149 134 184 090 596 496 242 912 492 320 945 053 350 014 508 633 924 398 955 018 442 662 643 633 140 487 831 969 774 764 207 000 653 703 722 207 781 764 313 437 491 203 224 825 089 192 261 629 026 909 764 858 252 286 882 748 705 978 496 786 190 084 130 563 693 521 072 521 605 997 151 967 567 157 217 035 806 392 802 748 941 387 885 834 124 608 256 781 264 078 808 482 620 911 630 175 370 333 076 386 019 846 227 332 859 148 098 773 483 462 383 397 153 178 889 199 492 548 221 980 782 582 022 237 852 552 773 494 905 400 149 499 590 017 096 070 312 478 056 608 893 496 215 253 432 425 212 135 940 349 038 605 355 870 225 691 155 351 203 896 350 489 392 419 559 926 147 273 010 518 642 354 059 401 461 029 810 306 503 784 869 958 500 604 225 736 880 215 154 201 334 646 926 157 696 536 841 688 158 005 793 718 264 638 528 265 156 690 688 163 846 696 461 263 230 710 403 005 621 029 732 082 105 833 144 391 340 776 179 324 565 141 569 873 934 331 301 470 106 753 573 524 696 094 104 217 283 272 753 668 899 346 516 288 295 849 477 760 738 742 509 969 780 474 647 950 422 615 296 826 285 503 169 689 969 173 180 620 616 072 783 967 927 316 539 955 524 258 847 282 020 182 089 132 489 324 406 178 167 569 865 885 387 443 895 812 605 515 566 138 052 435 483 841 959 205 292 884 203 691 919 406 514 405 169 870 124 337 376 759 523 594 778 841 560 047 305 795 811 705 390 109 688 355 607 039 368 524 985 590 547 402 091 807 034 197 423 152 864 953 436 034 647 063 039 357 530 683 574 129 933 043 428 683 456 676 564 736 897 295 589 962 367 017 764 100 311 844 832 292 188 300 669 704 354 370 377 545 256 448 132 060 930 961 570 962 614 632 722 016 055 118 830 416 972 222 147 962 831 976 035 751 143 760 858 935 493 461 681 014 625 775 696 546 390 531 457 623 130 360 861 450 667 715 652 872 357 540 235 630 225 593 952 923 296 077 086 977 724 398 568 930 699 759 034 726 363 337 894 039 855 254 486 870 882 295 537 430 003 709 728 436 925 160 136 447 360 241 973 937 791 134 832 465 405 032 425 353 830 464 392 763 697 546 680 958 723 650 665 921 867 957 544 565 172 663 891 152 874 732 127 971 355 561 418 294 571 518 951 013 427 769 069 800 550 002 101 315 306 490 029 508 869 963 952 876 653 369 134 701 460 088 620 706 911 151 518 088 952 280 688 259 636 270 418 901 006 463 343 241 326 120 550 837 619 209 762 160 192 940 327 640 143 936 334 487 182 518 896 767 305 989 175 424 332 716 333 002 308 434 948 407 730 368 135 746 542 599 275 748 083 299 599 609 284 883 131 038 260 908 982 999 739 288 044 648 444 020 082 174 473 572 831 541 530 881 020 754 477 052 524 778 744 879 139 974 242 705 083 470 324 052 467 789 945 879 092 193 952 938 485 267 317 728 550 458 649 704 008 652 568 680 156 458 476 365 042 369 368 630 933 933 042 546 102 548 657 429 181 008 183 997 703 096 123 538 508 867 795 394 154 385 211 427 472 603 523 993 047 027 372 176 826 295 054 862 729 033 937 066 586 078 304 833 810 209 416 250 337 868 713 547 040 467 630 997 921 291 859 032 627 332 252 635 570 838 320 305 530 193 711 629 191 369 328 466 131 658 201 926 254 154 826 101 033 207 466 229 327 651 555 989 854 746 339 834 825 061 831 091 728 550 293 220 470 320 701 489 943 774 148 597 538 051 845 934 362 034 191 042 624 253 089 452 810 354 098 164 384 575 890 937 347 922 219 925 664 558 148 636 061 870 243 253 495 430 555 918 849 556 987 147 737 518 684 675 624 769 823 538 471 066 647 785 665 865 558 287 774 463 253 395 265 923 519 646 578 499 841 607 880 278 226 291 741 301 896 728 390 942 329 812 033 546 618 985 198 467 829 491 449 982 229 612 931 241 972 150 746 157 561 894 334 728 409 707 335 401 717 032 630 321 129 751 769 713 774 474 320 312 241 376 366 976 850 579 442 317 364 646 954 288 850 365 163 028 403 647 029 588 577 240 422 880 451 379 322 316 065 371 958 745 934 536 798 423 911 555 546 621 607 148 722 639 237 392 590 239 157 270 121 147 919 410 576 902 724 640 451 715 050 538 951 220 898 210 960 896 453 116 200 891 131 997 592 794 705 193 234 047 628 097 134 082 147 631 070 427 902 916 964 732 731 687 184 729 578 761 473 896 904 312 178 329 834 750 324 080 943 457 796 486 457 480 138 191 406 563 969 902 052 460 369 146 222 194 046 643 481 666 034 677 752 307 672 270 889 843 854 284 946 682 897 122 750 885 568 553 275 685 383 031 300 680 444 200 526 298 946 802 376 807 958 854 000 479 186 908 332 112 300 108 856 888 666 417 322 767 544 033 852 064 592 127 715 567 199 969 305 602 522 812 106 999 381 497 163 432 914 540 682 509 631 847 678 340 019 621 378 584 450 847 913 856 308 269 242 208 484 493 938 110 368 643 745 280 118 040 124 963 302 157 284 360 459 224 206 114 862 264 658 710 150 308 330 831 457 002 946 280 439 617 826 121 742 179 901 303 699 104 409 485 690 201 470 785 039 008 001 725 542 337 398 001 178 885 266 539 617 409 741 287 118 948 112 062 886 393 693 315 792 649 178 170 767 221 673 621 201 134 636 750 304 727 491 477 690 431 991 474 501 724 245 897 224 916 201 877 235 300 467 117 196 561 203 797 229 863 586 390 643 938 708 133 637 432 564 858 685 238 250 670 117 171 472 636 194 849 083 354 232 534 814 683 430 023 120 974 891 796 751 116 229 317 751 116 542 105 865 392 324 489 307 001 023 950 880 255 826 321 875 864 019 997 292 802 694 452 734 208 797 289 017 335 319 046 849 134 938 076 116 458 388 797 317 849 321 546 224 665 279 393 074 627 383 721 256 492 704 076 914 510 630 307 680 937 485 220 782 129 937 023 019 567 909 409 588 611 285 701 548 700 375 543 832 427 472 337 793 161 334 846 426 241 768 513 681 412 934 452 509 627 112 955 456 350 599 778 051 415 648 471 755 919 137 485 264 551 184 879 796 834 415 221 869 401 159 408 081 679 715 485 438 396 793 143 068 660 925 891 695 878 553 980 024 883 222 331 349 505 946 352 421 449 529 341 572 872 806 175 154 246 137 447 616 439 863 963 577 485 825 220 730 563 326 279 897 536 004 961 649 935 792 287 541 716 183 827 213 145 899 573 350 051 131 706 188 091 763 431 396 569 359 231 934 561 695 741 072 443 702 932 052 193 024 749 853 513 249 486 503 230 157 398 015 054 942 297 017 972 362 264 611 786 508 762 825 362 560 888 008 758 304 234 366 016 489 017 310 069 858 298 160 835 753 869 835 521 251 398 228 397 660 315 367 326 982 847 030 754 249 024 767 829 269 650 525 254 755 973 424 394 700 874 688 938 436 241 690 656 385 261 609 414 292 948 111 461 186 611 472 371 710 507 656 896 710 461 277 613 002 645 801 597 707 720 253 990 463 949 305 304 725 952 467 893 357 609 189 495 668 851 237 614 639 710 644 402 664 820 844 017 743 639 748 361 682 093 251 021 332 020 867 601 899 172 488 772 321 592 236 649 914 926 367 538 718 390 014 100 162 829 781 220 045 906 086 220 255 133 841 505 696 617 861 027 808 614 251 926 391 315 359 035 476 891 403 213 265 270 774 153 404 075 327 371 932 519 026 751 043 741 235 607 917 838 581 130 708 925 714 757 217 830 625 057 123 961 097 337 159 664 956 721 182 068 755 773 650 307 444 195 811 386 868 193 638 366 683 362 969 219 481 981 072 550 899 507 197 767 869 615 084 152 288 224 327 817 761 981 297 664 852 048 701 455 433 047 673 742 898 394 773 106 020 804 979 913 523 742 048 447 965 731 603 074 013 850 848 488 669 773 991 404 063 257 150 881 942 835 692 443 572 906 083 756 932 242 886 743 169 310 707 203 592 765 933 757 233 727 302 538 595 008 920 226 705 973 968 860 160 223 679 485 137 415 976 937 756 453 529 847 312 973 299 355 676 451 499 855 882 887 591 141 678 851 565 404 858 714 407 566 350 408 261 728 132 350 292 757 785 374 709 232 304 197 132 931 183 550 757 840 108 868 262 780 396 567 835 555 061 556 733 110 136 234 911 091 313 231 781 843 599 837 767 322 413 506 222 525 108 217 922 491 181 381 664 657 242 241 983 904 511 915 133 444 689 042 058 522 383 849 563 405 407 341 265 576 674 493 437 017 727 757 350 674 931 858 968 065 426 058 070 686 626 426 260 609 421 910 923 465 469 965 772 947 587 451 906 134 538 453 446 771 854 315 053 283 157 796 789 991 535 900 565 340 624 299 200 460 826 573 174 945 588 109 975 125 775 200 321 498 244 601 057 166 544 379 713 464 464 436 896 034 522 139 934 334 480 704 682 612 069 978 701 731 841 744 732 574 536 447 919 913 667 589 738 229 425 675 796 726 123 701 655 113 395 234 809 243 143 714 309 072 123 985 509 278 018 586 658 202 121 528 382 040 795 060 020 410 841 422 433 805 784 313 168 227 138 576 407 387 051 541 627 104 310 097 322 946 363 966 838 313 866 572 479 442 657 885 759 530 659 832 525 511 545 789 437 972 875 617 159 899 720 400 660 097 644 786 590 214 839 765 232 340 241 082 312 502 455 576 354 248 478 117 197 899 114 733 891 735 057 926 386 781 707 891 858 106 929 061 399 031 075 771 934 220 140 132 106 611 692 529 164 031 948 723 325 539 627 231 355 549 078 424 891 687 489 400 240 059 930 267 018 357 677 945 728 712 401 951 554 446 612 874 655 727 908 370 614 957 161 523 838 708 598 089 557 827 163 914 517 520 336 891 486 209 872 495 256 399 607 822 473 966 878 124 830 955 529 791 736 674 625 012 668 451 699 802 338 821 775 358 477 407 965 464 818 254 534 642 047 719 613 962 013 424 846 900 702 082 129 360 485 184 964 630 931 304 681 509 343 131 994 111 533 943 373 435 127 567 940 488 875 229 290 996 375 760 897 171 800 114 020 342 906 489 106 406 851 380 284 853 042 825 534 993 831 830 797 704 562 926 541 959 237 557 364 036 731 297 929 489 887 110 042 501 446 392 464 936 305 618 704 609 529 840 232 790 206 698 696 153 394 895 811 630 387 136 035 191 994 588 520 131 962 858 668 104 102 440 161 375 045 001 063 451 599 581 961 203 727 224 949 757 862 370 653 876 195 685 227 118 057 550 896 681 782 396 827 196 246 302 501 389 342 213 857 977 490 115 297 331 261 098 609 793 600 495 618 414 381 008 530 032 001 600 443 943 893 802 250 915 156 919 300 839 795 427 013 380 844 901 396 177 789 334 745 427 388 170 728 037 299 427 190 085 591 961 768 788 327 728 220 041 425 334 088 860 712 336 300 264 010 635 590 656 928 471 861 712 320 882 618 116 672 185 275 899 170 384 385 402 018 869 989 176 759 604 157 926 175 097 894 951 382 366 471 073 554 433 786 055 580 481 268 889 820 475 623 261 289 384 015 189 994 495 902 958 409 931 212 112 740 743 911 066 348 515 964 121 375 442 264 504 310 843 384 724 951 183 028 168 986 810 127 865 695 786 977 440 312 168 831 595 588 486 367 374 321 582 589 654 934 634 562 323 215 303 532 951 881 342 383 921 036 224 724 865 570 555 784 800 724 414 284 857 298 902 896 768 805 491 203 593 177 145 808 541 749 928 563 875 935 051 789 491 533 693 033 485 792 584 670 236 333 805 000 217 550 409 639 073 335 925 228 276 143 029 057 512 205 489 018 419 516 630 125 775 524 964 062 748 898 708 657 936 333 881 199 963 714 438 101 284 965 614 668 353 133 100 782 613 997 466 051 931 146 953 737 957 147 680 479 590 459 329 244 163 496 437 476 257 108 331 837 767 172 229 202 019 925 142 161 640 625 966 794 636 634 766 118 980 192 155 690 349 800 036 860 185 321 851 776 664 632 756 426 169 803 668 186 335 507 605 914 294 620 936 308 443 043 307 033 462 249 540 087 278 541 956 823 233 089 639 453 481 180 264 672 048 529 958 703 500 546 482 853 386 502 022 647 493 703 790 814 482 670 852 136 152 704 532 456 769 860 374 250 484 064 985 614 640 622 296 922 668 012 299 309 407 624 883 598 619 003 660 504 608 577 367 503 849 113 952 241 077 512 495 356 024 339 903 570 021 675 009 135 678 843 630 544 387 305 369 320 896 463 083 670 496 082 908 690 853 172 076 874 347 008 098 825 009 440 884 733 006 368 864 390 419 572 669 394 338 087 150 362 115 795 207 657 183 313 341 475 080 858 609 427 851 221 888 641 668 675 155 390 249 145 464 663 289 847 550 385 878 318 266 994 345 836 711 515 416 719 264 699 167 171 803 555 730 501 303 211 799 077 445 381 079 519 001 453 413 173 320 120 813 333 332 378 930 838 062 510 893 882 713 104 803 986 677 814 702 009 392 577 376 922 729 246 299 981 146 517 925 600 223 069 108 760 655 802 300 793 174 634 791 857 245 299 365 233 814 763 862 238 598 870 779 705 921 831 942 624 494 769 430 793 805 468 860 504 329 371 256 636 888 900 097 020 832 024 732 635 945 159 788 647 187 822 206 649 951 637 805 830 371 818 771 880 598 161 706 486 537 935 531 263 569 919 036 239 702 196 641 731 902 413 301 197 801 395 429 514 318 937 359 294 601 042 957 760 003 349 629 989 629 943 187 673 234 396 084 056 380 646 749 826 684 868 488 755 106 541 182 130 800 123 989 027 338 724 868 531 123 404 525 610 923 303 967 446 773 995 642 156 362 619 378 289 490 728 546 958 840 894 592 241 918 126 486 071 079 500 724 456 684 237 080 533 280 848 923 924 524 903 947 036 083 723 044 803 452 914 825 479 352 555 545 408 073 292 390 068 616 824 382 360 402 066 196 933 680 775 272 781 304 141 255 387 786 347 501 160 646 560 597 506 368 787 327 347 894 072 601 433 423 584 332 018 099 647 184 249 237 784 613 212 793 919 487 887 714 514 435 420 148 898 185 213 640 633 064 516 354 056 687 267 344 124 051 508 090 826 417 444 155 091 912 519 183 868 245 952 164 534 242 027 600 265 031 036 138 482 120 269 197 520 177 721 143 549 799 169 776 657 757 751 029 549 381 637 957 402 229 941 243 824 291 192 172 997 845 797 371 128 788 724 755 237 280 547 437 077 670 404 558 360 475 498 206 471 116 161 307 600 485 801 774 431 434 571 182 227 083 357 573 707 532 946 742 964 855 512 443 099 612 381 350 002 551 009 959 205 436 027 347 581 817 374 935 307 085 928 531 232 794 167 783 023 045 714 517 039 837 307 417 637 781 334 424 042 768 971 858 232 169 892 927 526 284 856 101 438 066 103 416 799 878 515 391 626 442 619 189 762 391 702 373 781 529 465 618 361 999 373 446 536 203 230 949 682 835 557 751 190 430 614 880 606 818 452 522 267 392 998 520 705 042 490 362 100 869 375 610 101 925 193 059 896 442 817 294 860 288 758 268 576 935 572 758 921 601 339 579 533 867 189 507 623 738 063 063 436 484 180 791 100 867 244 858 932 563 303 456 922 080 126 095 184 666 332 497 922 921 427 389 738 465 081 804 292 967 790 329 658 986 988 194 964 825 546 017 726 732 921 066 425 221 972 509 611 967 230 425 912 020 463 309 896 055 752 413 307 844 779 559 020 890 615 291 210 489 518 116 883 727 578 730 574 825 648 913 079 734 996 788 873 157 995 351 069 132 238 144 248 121 603 617 553 071 087 271 585 060 843 764 883 704 708 732 727 136 120 032 234 203 602 335 119 366 159 085 843 068 577 665 355 495 857 221 644 110 683 427 937 094 492 857 374 269 485 349 120 812 803 896 819 441 681 633 020 243 750 316 157 084 584 036 163 042 007 068 550 059 895 150 680 101 715 883 656 753 282 259 333 359 564 446 553 343 389 196 651 580 945 689 667 476 514 335 372 240 939 243 215 456 396 516 705 540 720 564 640 308 382 906 305 954 949 751 514 654 612 825 718 047 697 212 226 156 735 175 192 166 599 060 359 636 850 254 900 063 484 207 860 215 136 095 816 195 786 963 052 079 014 343 050 464 052 755 642 629 874 536 201 358 607 334 808 820 507 499 301 271 245 628 663 187 767 134 880 945 124 457 601 228 135 246 503 083 733 203 988 988 297 321 859 307 839 412 525 135 118 137 850 142 789 678 687 181 828 792 746 463 698 615 999 388 551 267 387 505 200 581 306 026 116 094 388 008 168 620 769 683 436 893 625 888 355 084 813 320 021 392 913 824 435 989 105 576 349 109 832 329 169 057 569 389 166 825 861 057 517 171 761 498 453 651 128 350 061 364 956 807 756 365 706 113 077 141 653 316 793 603 000 405 292 310 067 668 312 938 498 381 594 711 604 627 958 592 226 075 561 509 315 835 456 657 773 910 545 498 141 875 514 994 505 327 419 721 798 466 763 815 957 327 778 678 680 549 772 971 425 989 092 538 560 406 974 487 717 390 875 103 925 031 260 402 655 705 688 417 328 293 083 965 909 777 640 069 816 463 309 748 810 261 765 051 898 668 668 367 721 478 917 757 044 564 699 531 622 835 065 001 893 728 698 276 788 892 062 556 012 130 797 470 694 710 558 709 828 337 198 286 233 329 583 281 646 915 092 892 398 157 234 802 221 684 599 929 728 721 627 419 915 059 359 603 333 462 510 184 715 632 929 240 501 109 495 954 764 646 211 326 294 830 817 657 138 498 230 037 831 529 458 144 206 798 423 392 026 113 014 297 900 746 773 357 171 335 306 497 613 330 084 078 428 364 605 781 127 718 730 661 693 205 933 628 036 505 008 031 516 205 936 431 592 010 523 794 934 538 489 072 141 970 304 483 335 137 475 753 117 963 184 459 647 128 936 575 615 017 510 552 695 938 163 784 335 706 643 800 838 948 073 496 282 192 363 278 145 153 819 333 049 400 074 950 754 278 937 161 895 866 617 288 935 930 397 326 004 304 706 871 089 427 502 775 434 251 169 133 613 937 956 684 328 790 381 712 429 573 247 082 773 314 649 219 375 388 598 803 976 649 717 654 139 057 656 724 692 332 458 489 638 496 940 896 402 216 144 723 767 499 410 054 079 675 695 264 144 620 246 352 089 865 968 009 988 204 985 903 451 577 428 810 686 815 650 452 433 581 507 661 073 815 243 119 177 435 166 449 067 417 352 537 117 788 957 196 661 989 098 591 819 035 454 793 971 944 710 182 780 710 785 044 559 804 519 060 111 231 834 099 692 884 003 348 670 781 118 338 840 557 350 063 956 205 169 344 804 154 692 856 422 151 842 631 393 553 039 149 675 853 702 280 027 966 633 014 498 801 647 649 711 417 459 332 883 530 910 076 435 265 154 053 038 676 736 905 668 827 515 861 976 859 297 777 995 282 806 950 534 903 890 504 610 363 297 258 678 897 236 094 987 582 829 289 472 321 553 689 556 565 957 236 401 670 189 052 915 113 322 180 231 461 141 684 059 677 676 857 921 168 721 260 056 816 598 523 238 614 047 296 142 157 558 252 873 303 637 369 016 053 737 893 360 812 606 185 937 885 692 324 784 229 712 031 933 520 220 694 022 345 007 218 280 915 313 619 746 992 520 547 098 797 658 928 613 576 049 083 712 966 843 849 611 897 678 371 778 318 295 458 768 357 453 266 073 558 443 082 665 082 810 899 690 164 047 105 777 284 575 736 352 523 426 133 140 318 381 552 856 396 178 905 019 796 630 081 276 015 336 999 843 864 237 864 040 301 469 640 289 954 643 555 174 979 488 552 344 793 188 563 639 660 315 861 927 991 050 676 067 048 870 787 573 529 770 964 708 132 053 427 407 662 763 756 193 646 553 919 930 731 887 425 456 948 713 988 116 577 880 274 148 323 733 702 309 293 357 584 415 892 182 180 349 672 625 715 746 134 656 245 283 547 239 848 275 609 376 353 182 608 776 304 835 684 695 117 577 858 836 949 848 378 438 529 118 794 273 436 703 134 669 900 464 614 175 848 627 653 838 502 094 609 072 117 461 995 770 291 321 045 939 903 496 949 666 463 544 158 755 569 769 740 328 716 862 995 222 039 170 111 465 818 568 075 825 284 404 255 486 729 724 475 514 288 689 851 695 811 780 022 894 775 859 333 699 810 555 015 135 128 602 889 825 547 417 941 749 335 213 264 287 491 504 311 884 538 924 006 446 394 664 001 744 253 650 457 696 998 172 353 981 294 501 512 465 531 034 790 545 528 745 846 337 085 303 619 661 285 295 460 018 642 685 820 251 770 270 123 412 535 696 126 224 940 792 750 442 943 548 382 163 961 298 239 185 489 397 377 656 267 539 059 621 515 356 067 044 610 836 133 618 059 541 046 550 162 011 125 767 083 513 770 954 634 296 344 051 873 998 489 340 841 272 385 627 967 170 132 744 344 864 112 595 428 929 138 627 718 130 630 022 787 778 061 488 722 072 739 553 869 444 031 424 962 096 249 575 971 126 814 235 664 784 909 200 608 837 084 232 543 098 565 158 189 535 119 659 616 216 916 356 715 177 646 123 536 185 145 266 796 668 286 716 978 305 189 793 567 559 348 714 307 177 351 817 867 939 576 146 931 163 820 923 829 433 126 971 333 903 901 381 411 909 510 467 749 763 591 292 921 262 033 155 654 564 615 285 444 476 050 276 476 039 888 771 887 359 429 411 917 469 576 083 435 853 035 006 533 030 029 609 986 894 305 226 735 126 996 729 633 958 360 915 964 587 071 310 697 477 667 347 183 057 988 498 472 788 207 543 625 804 254 084 939 810 294 200 211 139 170 891 647 443 421 022 970 340 520 966 484 021 515 760 341 866 590 073 398 327 152 622 030 661 949 573 772 113 634 217 863 528 880 973 696 289 054 568 362 315 055 689 767 017 859 575 084 471 005 058 981 210 009 903 825 361 649 761 283 286 301 464 395 961 247 453 113 464 708 481 788 443 255 055 596 126 435 858 704 113 854 874 440 172 072 657 819 774 035 995 879 136 065 191 041 410 993 782 461 821 545 098 803 341 112 471 817 560 224 073 268 015 210 293 915 291 364 312 360 913 192 700 931 161 292 579 788 234 044 053 283 411 681 027 376 659 088 758 648 725 876 978 196 671 270 829 449 851 190 350 069 234 891 501 552 330 199 227 857 196 225 883 556 467 060 615 661 890 610 341 232 358 071 154 047 880 880 579 326 366 455 636 142 101 227 791 455 221 841 048 069 781 666 557 689 207 362 464 266 966 724 960 331 142 986 444 528 415 819 805 443 093 113 703 770 340 536 325 583 843 609 442 703 269 595 742 838 625 629 914 588 719 122 927 211 929 227 948 915 826 218 145 092 426 938 836 790 412 905 851 248 966 347 858 621 946 480 668 906 104 488 913 364 534 905 826 814 357 009 642 452 847 692 306 404 804 093 625 618 492 804 733 639 977 521 710 376 581 661 442 270 728 668 009 327 117 351 829 406 583 115 022 129 164 124 472 211 995 829 068 196 217 083 715 104 841 224 260 935 993 083 130 453 696 434 073 750 683 328 363 713 020 032 409 506 284 706 395 219 569 859 084 808 861 994 508 866 953 752 448 135 026 815 852 155 588 207 957 790 008 775 458 691 908 472 235 664 417 861 403 740 489 937 161 238 760 724 441 302 355 082 051 218 035 306 587 784 698 318 370 936 752 813 056 402 427 623 552 404 826 271 019 543 630 379 622 416 492 187 122 735 856 530 682 530 843 805 093 792 653 515 072 623 981 971 012 736 707 057 768 474 187 241 373 910 413 343 227 364 754 241 920 457 070 362 004 762 943 833 370 937 848 868 877 355 665 964 140 605 054 813 050 989 194 537 981 301 389 437 392 605 429 653 592 331 273 137 677 897 398 974 483 668 800 614 389 246 906 058 055 013 207 543 472 411 438 929 292 376 751 704 340 561 209 068 964 396 983 681 830 469 574 339 904 118 038 025 119 280 797 961 678 079 060 544 087 748 645 993 745 662 858 832 545 698 522 339 127 307 673 742 248 042 339 819 334 579 906 977 617 764 319 631 951 111 341 510 064 374 645 816 183 842 235 600 382 976 177 481 198 052 806 820 555 658 581 183 193 848 896 254 925 043 102 453 366 997 361 428 965 959 103 153 601 074 140 686 753 733 371 608 694 328 815 374 376 475 846 839 108 078 454 318 718 063 179 194 216 510 696 430 395 451 457 974 727 603 420 994 180 436 619 428 302 566 837 810 033 957 887 532 778 406 258 928 367 769 045 069 055 506 103 040 454 178 712 874 202 999 117 556 721 140 150 011 927 977 458 459 724 586 300 417 079 663 068 467 340 488 014 881 714 892 579 360 225 050 533 931 424 215 957 474 626 074 149 587 213 760 251 886 042 902 127 487 328 050 512 169 448 105 342 628 323 384 748 168 227 455 086 344 002 814 077 069 716 632 705 777 115 163 242 944 417 850 869 014 391 582 373 661 506 136 083 685 321 343 247 170 303 154 864 489 228 343 096 188 609 548 072 521 362 022 939 258 445 051 963 724 258 645 787 348 736 604 701 525 674 591 125 598 232 744 778 388 825 814 513 281 803 607 066 148 442 370 827 168 054 878 310 080 367 113 960 479 090 891 234 218 013 657 892 704 227 775 550 364 915 146 008 979 765 159 327 785 082 891 286 782 075 871 171 427 646 821 823 854 974 456 215 343 800 983 031 984 125 065 783 840 120 953 227 863 027 503 346 732 230 823 486 529 398 513 388 506 569 262 805 897 739 288 767 204 267 198 989 660 472 942 394 968 703 166 188 011 476 269 739 278 967 350 062 602 406 550 109 541 501 047 593 849 997 920 545 407 951 787 616 914 992 388 173 506 681 481 467 329 007 171 250 130 012 730 967 048 407 850 526 884 998 668 692 301 623 878 461 639 497 387 464 053 915 610 701 337 829 122 950 999 897 246 434 958 336 828 799 860 123 539 838 241 987 636 710 334 206 336 926 816 378 164 857 567 757 540 859 814 957 705 933 836 069 432 492 273 923 763 677 667 462 426 262 455 664 156 437 855 478 140 886 685 387 420 042 681 643 864 850 952 529 282 305 840 019 751 874 809 714 716 100 907 792 170 214 314 104 989 574 892 318 052 449 935 299 241 810 178 813 083 346 527 594 705 055 500 677 214 672 266 271 229 793 472 989 724 982 720 587 983 332 123 228 828 230 681 321 894 882 165 194 371 689 098 689 160 211 822 657 166 093 623 582 070 189 730 382 079 520 309 390 295 006 875 808 286 847 012 632 632 575 255 490 587 080 903 274 388 969 848 385 874 791 425 292 488 459 225 603 402 015 913 150 345 308 604 961 498 251 621 277 589 781 415 759 966 137 723 387 202 969 446 050 714 781 558 211 156 950 516 416 671 793 348 456 519 810 545 812 644 580 676 655 805 956 081 387 239 323 880 861 312 747 092 791 349 861 646 438 294 644 048 923 479 408 529 573 289 344 038 398 294 544 905 361 623 037 693 173 864 013 463 284 128 454 624 412 979 914 995 833 330 096 245 315 400 153 890 035 967 183 743 297 276 133 512 238 392 480 662 406 611 941 077 579 612 347 620 945 931 774 023 993 219 455 286 237 523 203 075 556 852 217 223 464 753 510 621 727 103 234 608 614 097 134 438 867 154 926 555 904 052 631 294 619 503 981 987 407 813 812 483 372 563 805 593 255 931 637 599 086 890 870 175 368 618 265 215 880 290 741 457 498 263 573 625 612 053 922 805 445 839 937 843 469 873 384 952 704 940 797 172 683 798 327 989 961 202 238 027 923 144 611 731 541 670 185 322 202 852 717 265 255 378 291 971 355 542 397 222 970 365 861 990 319 092 543 988 233 934 194 781 836 020 588 892 270 297 923 732 683 779 337 464 657 004 866 618 804 660 181 735 404 340 132 641 487 187 023 896 553 725 591 888 338 859 763 607 733 237 643 924 712 157 205 228 951 835 170 719 963 236 276 393 299 701 762 115 617 795 528 031 481 222 695 529 132 506 293 555 169 023 948 061 217 414 422 122 825 627 014 704 246 893 957 096 371 682 518 991 714 359 549 066 170 268 327 093 865 619 027 693 611 098 067 821 140 200 451 888 758 155 891 649 536 707 611 587 940 151 210 237 374 192 706 509 406 743 166 874 062 432 110 417 680 667 150 035 213 484 455 145 636 150 395 966 865 586 406 322 019 517 387 906 457 809 700 363 155 518 257 052 981 214 541 172 986 286 272 788 267 618 041 141 791 610 420 914 473 494 604 969 187 479 679 822 252 800 440 418 927 061 518 330 520 353 327 849 613 531 213 919 384 556 701 984 101 311 335 030 100 112 499 599 647 546 075 382 220 453 456 068 755 226 338 761 905 368 738 277 918 213 260 699 402 258 514 651 284 625 535 501 153 137 433 103 900 114 980 840 698 752 406 831 144 755 471 100 637 494 557 925 871 774 786 033 185 563 482 068 511 359 153 416 901 805 507 796 186 053 617 071 303 564 942 151 325 302 544 714 853 345 914 875 913 810 272 116 867 757 171 568 013 873 627 864 638 750 355 910 129 433 023 360 857 565 440 034 220 548 727 956 183 170 854 522 318 268 386 079 717 807 366 772 076 361 366 367 175 325 677 702 129 269 563 530 625 344 222 749 235 903 265 070 917 859 643 981 748 996 598 722 446 189 264 590 013 721 448 626 366 350 809 488 055 290 275 865 198 744 068 335 082 604 254 749 944 711 078 116 276 926 152 516 721 318 818 119 464 327 784 710 406 591 897 299 842 249 694 292 946 240 445 323 385 894 244 395 677 568 214 564 675 685 500 884 151 098 679 723 121 471 923 216 729 251 459 194 573 180 784 727 289 591 125 630 580 005 092 043 818 892 748 912 158 097 608 997 672 255 007 133 062 801 339 898 214 171 982 770 141 261 469 671 745 475 388 131 679 817 325 139 306 005 045 501 703 858 857 550 624 678 443 894 047 714 240 716 595 187 065 766 630 225 488 045 440 798 439 502 402 656 701 891 449 711 636 952 041 717 833 455 936 356 440 480 460 846 329 793 043 991 548 986 104 327 371 233 900 489 748 432 631 147 504 729 552 427 113 843 391 678 415 315 752 114 376 056 385 385 640 745 248 152 845 182 875 309 269 120 345 120 419 881 010 676 445 544 035 635 567 003 747 357 680 796 581 921 260 324 556 687 196 502 507 413 689 012 676 094 413 727 019 424 152 511 905 770 893 864 237 260 446 318 975 731 288 550 871 141 902 481 657 830 307 062 254 921 193 261 782 136 231 123 664 361 128 472 227 763 428 114 775 745 077 819 844 778 565 538 843 089 882 182 265 080 913 344 635 570 010 079 545 215 162 365 698 811 688 566 150 654 198 827 202 470 962 852 080 467 368 224 498 866 440 055 579 053 237 752 973 427 749 306 907 138 382 788 868 687 674 734 507 454 454 902 498 225 965 740 568 719 596 312 351 128 928 308 493 357 862 798 509 033 724 114 986 600 069 248 067 710 449 450 308 341 055 009 720 607 966 179 593 856 118 272 475 057 441 866 028 519 108 754 462 065 145 154 041 108 597 633 478 921 647 839 118 427 955 712 159 759 586 343 107 983 102 805 027 408 294 214 138 914 735 239 377 338 737 057 034 382 721 142 704 196 897 281 269 125 252 641 393 904 466 842 936 690 308 169 154 457 412 277 897 523 938 014 644 982 755 191 064 686 187 156 012 377 361 251 758 409 206 612 014 112 862 943 256 049 065 284 457 824 923 774 627 986 949 114 660 215 797 417 936 904 635 494 210 892 287 101 358 138 168 932 506 426 961 809 258 666 322 459 203 659 896 709 366 785 916 285 181 604 496 014 922 227 008 745 421 507 899 989 240 063 479 466 351 020 797 249 249 823 649 125 457 629 505 080 868 180 756 020 625 616 762 423 649 048 276 311 320 201 327 703 803 822 573 546 547 773 289 561 028 291 332 837 806 890 936 559 178 817 334 079 471 662 371 520 723 983 008 631 792 310 822 712 815 270 482 277 650 568 127 530 237 289 093 779 027 212 767 948 789 925 625 878 204 188 948 650 378 742 979 208 542 122 506 895 361 129 309 752 405 145 365 864 433 643 321 963 529 699 929 946 838 085 525 781 100 073 934 576 535 148 940 024 043 885 276 595 522 057 408 087 497 746 506 047 652 367 451 136 882 651 608 643 628 895 843 944 373 147 346 310 604 248 225 201 127 469 940 902 111 854 505 065 723 229 481 001 248 793 618 114 572 136 046 055 451 810 021 361 539 585 679 096 272 844 714 486 970 265 179 056 815 836 692 276 856 278 578 632 051 731 482 637 175 481 952 027 647 287 023 429 541 958 734 289 626 421 800 564 542 442 205 975 708 854 681 728 629 330 998 744 747 249 396 432 841 281 475 840 233 496 477 337 475 976 548 762 780 257 861 338 664 262 232 691 377 950 605 600 509 724 975 346 781 352 437 802 081 656 163 507 167 930 982 628 936 288 996 112 574 030 684 447 780 419 999 128 794 907 730 630 697 776 091 768 853 710 420 949 693 689 336 185 809 524 829 386 414 125 213 942 813 959 878 629 236 649 221 227 375 711 702 332 311 250 689 988 393 880 117 825 975 898 424 759 698 235 039 804 144 581 654 932 965 099 837 057 696 490 484 117 625 501 439 856 068 263 732 406 025 875 238 568 095 000 163 695 023 967 049 479 023 886 617 248 154 830 840 602 404 844 483 526 384 449 963 647 986 225 911 248 450 817 059 498 042 696 767 221 271 310 377 835 833 252 179 192 441 044 658 738 504 970 455 048 346 564 962 206 933 623 394 194 143 182 295 282 553 571 303 624 226 196 243 028 335 372 992 803 602 313 202 160 055 611 800 892 358 897 314 782 040 137 196 015 296 318 573 413 933 656 284 917 055 835 941 845 735 782 749 378 658 111 217 977 583 777 429 467 206 865 666 047 252 827 387 954 738 569 928 523 951 243 913 342 683 944 263 119 870 229 082 751 034 347 521 229 366 926 000 732 619 855 656 982 255 599 390 073 579 095 421 896 636 182 450 000 205 590 687 947 071 327 814 159 468 345 973 913 240 322 768 219 124 780 476 565 302 580 103 443 805 088 048 601 440 340 438 809 643 832 089 945 675 282 774 249 111 934 926 047 567 679 754 648 295 952 493 219 343 696 692 320 458 698 257 775 015 040 455 359 566 844 909 872 533 254 591 296 326 355 824 453 106 714 276 672 440 021 768 094 658 849 997 885 319 246 846 707 886 875 518 610 741 186 725 402 420 365 624 311 631 469 370 604 717 156 116 056 930 399 389 983 370 212 077 182 849 836 146 411 903 483 236 781 012 706 536 182 808 216 563 947 530 149 010 062 657 205 595 469 918 728 614 541 359 401 354 874 494 335 650 549 181 972 103 622 337 003 910 914 279 598 558 556 648 957 165 046 820 201 113 604 009 286 170 135 355 299 550 633 464 857 470 312 748 034 983 293 842 417 730 882 132 889 548 337 213 995 813 947 012 430 146 125 833 905 390 970 300 716 128 642 275 283 345 054 470 574 046 106 149 354 350 573 464 652 829 084 021 440 980 657 281 152 126 249 038 106 312 363 979 473 957 196 216 209 988 037 636 484 142 626 336 320 546 047 314 859 811 457 742 791 213 080 859 514 361 106 040 615 224 905 719 303 097 057 020 707 865 573 589 857 790 585 456 321 183 591 329 591 577 031 042 284 994 904 635 013 598 179 523 800 620 558 457 691 798 261 740 693 931 272 704 411 228 297 059 025 527 231 709 421 756 999 880 827 406 207 334 955 739 791 038 799 120 762 235 140 054 339 087 504 810 219 506 486 023 961 754 257 441 096 192 870 987 951 819 901 027 460 165 687 867 363 237 282 873 692 869 708 007 737 473 859 685 555 183 684 521 448 946 465 346 182 467 220 639 663 042 931 418 206 200 477 471 178 898 966 370 406 852 198 667 051 562 290 868 972 739 651 619 358 746 306 657 732 967 998 320 086 691 409 449 022 068 194 794 642 250 005 713 202 080 021 182 419 790 777 617 466 426 882 196 304 019 077 398 934 147 130 459 837 506 271 700 703 186 996 082 203 296 072 113 799 866 174 266 117 104 793 445 641 337 000 443 078 659 462 737 697 474 515 277 113 964 098 022 412 992 186 592 418 013 337 660 865 083 313 497 981 828 762 368 167 920 716 785 165 448 521 848 818 700 348 645 711 853 058 047 414 625 752 190 238 090 537 283 861 139 942 357 533 898 137 256 373 138 044 741 628 925 224 170 593 228 255 782 957 070 447 110 517 879 814 304 116 325 914 287 403 900 638 808 490 730 956 285 981 696 998 385 869 766 104 424 842 790 683 374 739 621 895 028 190 609 422 112 026 207 661 961 239 149 449 687 413 792 781 947 123 294 226 586 629 150 727 617 998 301 017 714 491 123 183 203 567 973 199 984 603 315 933 930 988 185 596 215 146 202 243 672 160 273 953 674 238 734 833 881 859 556 658 829 290 421 865 372 247 945 261 896 000 013 013 248 532 955 604 053 885 917 897 545 566 248 467 536 752 251 555 908 979 840 694 164 485 342 080 975 240 646 793 808 037 473 764 989 492 529 362 125 349 902 765 789 093 571 121 017 564 792 651 022 188 805 028 604 830 658 795 248 678 020 412 470 374 082 913 271 450 056 544 036 321 259 027 542 430 110 580 516 636 558 221 767 440 080 254 005 031 643 411 303 988 998 408 894 412 891 183 230 259 210 736 220 327 104 850 804 414 088 389 364 450 882 252 447 658 021 052 939 102 672 820 392 079 776 107 853 604 535 117 455 619 824 194 164 420 225 276 119 331 948 577 300 176 291 494 321 991 235 538 778 413 844 170 646 903 998 052 300 645 907 726 936 618 828 340 392 972 396 081 049 788 829 787 303 626 141 379 728 093 150 640 160 564 717 134 172 144 174 274 512 538 626 244 222 727 100 171 124 056 241 503 676 350 079 115 007 142 073 360 681 143 588 475 871 048 444 902 213 302 336 059 764 264 876 343 767 825 308 854 529 659 695 235 405 727 603 675 392 189 516 647 938 652 456 074 678 731 254 141 690 117 656 327 378 359 867 610 281 873 581 528 780 732 367 052 561 800 974 403 210 369 841 388 091 111 419 241 051 548 548 932 758 578 283 176 192 725 601 560 067 275 291 296 766 558 802 593 899 265 649 589 879 265 897 019 436 331 943 241 657 636 393 309 255 695 331 534 464 729 966 852 970 117 241 134 461 351 725 176 484 872 585 570 708 072 803 172 240 441 929 725 916 677 579 049 744 502 020 530 579 660 801 706 280 161 442 040 413 028 851 360 851 967 518 623 087 721 794 089 186 007 715 610 770 997 999 928 881 420 623 328 041 924 399 526 123 139 566 073 531 763 520 722 032 268 216 490 255 462 538 217 287 821 542 325 037 215 716 241 570 784 903 674 538 541 900 115 803 612 824 660 869 088 016 408 912 676 044 762 601 789 636 406 221 333 714 706 372 706 899 728 657 660 257 487 568 916 890 410 132 102 650 798 271 528 748 865 032 271 156 669 572 045 434 965 531 621 200 258 556 603 115 966 579 877 616 773 535 452 371 636 102 264 082 152 406 075 755 519 798 927 066 054 034 788 661 390 034 331 146 666 716 009 039 841 917 980 962 494 743 680 259 584 269 017 927 441 247 151 758 507 873 906 982 661 312 794 895 730 790 603 936 479 731 090 347 794 535 598 986 679 905 628 802 827 147 267 774 899 061 358 889 618 104 738 329 092 551 124 140 971 799 693 709 674 925 114 339 473 495 476 384 442 281 872 420 080 334 656 101 863 901 108 153 465 955 471 646 428 831 670 356 632 025 559 687 140 475 529 433 088 578 576 479 253 616 224 057 787 713 802 389 959 541 200 852 712 254 002 721 060 228 299 123 818 374 166 760 636 813 381 350 031 102 235 204 669 975 560 274 528 814 673 262 317 376 218 829 662 156 761 775 576 507 378 495 837 187 699 543 152 398 244 290 879 252 031 864 179 272 429 167 250 472 314 721 341 489 583 657 301 352 263 736 118 183 527 068 373 117 409 467 093 007 885 551 622 243 030 972 474 733 281 920 433 998 036 278 519 725 452 228 083 815 273 126 457 926 710 195 873 376 551 996 531 206 916 977 370 761 343 546 386 908 657 257 436 979 638 452 962 869 225 700 303 833 531 776 918 046 042 841 558 694 110 875 032 577 249 414 363 060 830 991 505 376 083 866 875 306 791 557 399 290 362 609 535 699 758 183 590 766 210 647 991 789 765 721 556 600 132 969 856 179 833 283 096 138 323 202 176 710 721 050 251 366 808 664 402 884 960 437 656 435 575 812 065 866 557 595 656 927 099 899 848 602 330 996 230 161 421 456 416 045 479 196 279 373 402 554 818 587 267 979 068 875 815 352 436 052 916 748 213 253 272 815 316 724 446 461 462 623 595 891 043 353 592 229 858 592 520 185 696 991 599 251 064 079 208 795 436 053 581 406 496 723 836 249 440 573 752 368 417 817 546 273 676 289 629 758 914 838 824 931 036 924 491 461 675 754 531 712 755 833 073 711 779 506 802 392 298 511 330 840 195 530 664 541 223 499 033 228 482 999 674 141 608 787 888 685 478 559 835 579 557 658 499 034 903 222 861 243 684 438 248 278 463 198 306 848 114 845 447 136 445 191 431 628 692 465 683 658 716 608 519 673 959 357 292 925 916 505 330 926 567 443 636 566 801 336 197 138 558 983 759 657 952 585 832 931 585 662 577 188 909 121 212 500 575 944 964 768 465 128 857 018 248 143 556 231 858 477 983 298 404 501 756 901 345 661 983 155 715 545 179 404 184 241 707 175 407 940 020 499 333 366 471 551 240 772 339 379 216 983 378 863 938 109 131 489 463 135 102 795 630 432 617 634 576 876 114 603 167 037 667 022 532 680 272 364 637 343 261 611 430 771 623 617 588 336 441 981 287 361 071 333 192 766 859 150 519 739 774 240 654 749 064 678 415 582 346 089 480 375 638 162 544 261 095 814 201 779 316 169 561 254 669 790 247 738 199 435 190 123 245 278 161 400 554 646 603 547 073 170 124 474 396 228 044 252 949 959 877 749 948 007 508 382 593 113 107 623 254 704 588 407 625 336 571 947 065 832 822 830 580 899 486 644 227 457 491 996 615 021 023 678 466 949 546 162 726 276 612 283 455 066 235 911 795 274 766 273 283 630 599 799 884 153 309 558 643 288 853 793 629 001 476 209 449 604 637 627 445 491 213 024 003 749 020 005 678 296 208 502 024 421 884 650 371 323 542 166 216 512 400 124 205 581 107 434 006 883 418 197 933 931 595 831 642 225 800 309 559 744 587 624 411 378 585 582 782 840 068 605 148 216 503 467 571 536 912 224 909 356 571 719 018 994 370 053 097 774 204 848 200 144 509 354 099 372 400 821 972 469 499 947 620 181 651 609 495 804 244 215 634 282 685 951 668 390 541 223 172 514 791 043 770 454 265 066 440 034 018 364 426 254 701 823 083 922 597 008 018 721 694 720 499 219 008 784 577 386 662 435 894 541 483 211 951 817 214 843 701 902 440 548 454 577 849 940 022 380 630 465 531 925 864 995 882 591 267 975 441 447 181 966 103 795 689 905 581 844 422 557 007 182 668 026 067 890 391 962 505 675 548 678 473 731 267 444 637 512 972 476 696 809 439 366 503 338 513 199 334 080 517 147 472 672 955 196 947 295 036 536 310 159 514 691 291 135 696 352 845 665 821 422 226 134 587 048 696 414 379 739 136 973 780 612 401 614 895 162 766 413 723 692 180 637 175 192 728 844 776 520 444 138 636 540 459 724 286 884 261 953 636 066 689 165 706 255 916 128 440 424 239 686 776 753 874 530 444 267 995 246 634 606 734 498 555 408 430 340 320 310 931 584 203 708 545 233 632 621 684 021 117 502 103 600 598 763 156 597 895 224 677 913 068 603 479 558 712 539 108 739 292 227 300 334 594 230 396 960 075 703 514 907 582 154 827 369 457 282 219 438 863 045 727 268 472 639 601 541 717 549 501 708 659 819 571 108 372 014 748 028 052 307 989 979 774 465 712 374 958 287 998 559 332 402 236 642 577 704 089 076 038 510 309 137 326 803 984 475 172 110 372 151 176 922 989 469 469 722 734 169 235 060 159 941 046 008 794 213 981 081 339 066 289 671 259 092 163 896 083 159 787 550 158 518 747 110 755 589 903 719 279 026 955 378 814 893 394 655 591 204 890 520 339 510 306 564 555 903 258 778 294 182 494 506 706 969 601 711 429 122 440 542 036 772 204 108 503 512 629 043 043 673 071 620 237 561 540 688 421 474 788 357 593 158 815 433 190 562 829 647 631 521 738 533 023 977 930 785 758 727 720 923 957 607 338 640 965 355 333 179 453 465 045 613 535 649 432 023 644 879 900 268 139 211 547 590 350 398 113 314 688 307 327 928 625 779 648 723 980 727 099 684 626 031 314 804 666 634 351 427 605 756 682 959 860 593 354 748 036 307 839 076 150 484 263 781 407 076 421 571 239 598 641 671 264 108 263 596 976 197 331 470 121 927 093 096 790 531 498 446 836 013 530 502 976 885 270 519 177 426 350 945 723 718 628 516 435 568 157 516 184 986 413 527 547 875 308 712 214 075 533 478 855 369 609 223 008 130 638 032 606 151 626 976 459 416 746 980 904 548 238 274 463 467 942 066 495 057 474 982 863 791 841 214 074 724 054 103 158 988 195 056 318 084 916 140 652 038 393 078 625 375 823 696 706 385 728 126 719 164 811 689 251 549 383 618 354 994 909 442 152 112 904 487 339 573 949 467 017 206 147 102 111 118 461 672 638 571 790 102 889 076 392 625 068 778 183 853 933 601 366 144 993 007 993 545 376 695 790 277 736 874 900 027 083 764 470 499 481 207 634 389 847 663 364 088 464 640 449 499 124 313 168 465 383 808 076 551 662 661 557 763 806 154 850 209 211 564 846 576 750 561 537 388 490 747 824 709 327 703 569 334 969 772 668 268 255 070 034 194 473 765 863 793 386 884 952 202 000 705 793 179 121 696 926 640 571 184 963 818 614 482 402 922 016 238 915 193 223 586 689 680 589 079 594 342 553 004 751 610 638 417 928 523 227 450 719 688 196 125 179 337 352 765 079 071 835 564 175 987 846 484 451 890 304 445 864 144 811 248 063 660 547 012 525 044 997 561 928 008 797 496 021 980 346 241 313 342 716 708 498 615 959 492 456 736 193 258 227 547 805 215 269 164 867 391 868 594 538 975 683 274 428 545 261 459 914 069 398 234 808 007 412 556 205 238 974 476 708 579 701 819 586 562 516 532 402 633 408 568 542 099 384 815 545 677 792 715 101 510 901 832 604 908 569 426 037 974 485 997 756 550 261 108 147 950 485 399 050 256 642 083 621 950 308 381 238 512 551 050 076 797 236 736 313 222 112 744 500 413 799 026 458 552 868 474 697 432 435 521 492 111 077 677 901 092 387 465 673 658 453 371 882 128 026 019 984 505 416 468 614 402 459 060 327 643 396 495 279 998 228 010 588 825 519 123 637 874 678 409 117 171 189 604 853 972 158 823 310 092 928 572 825 762 155 686 154 476 954 027 627 076 964 525 180 646 813 050 512 046 344 747 840 474 589 164 510 712 717 452 330 068 813 631 146 885 576 163 771 284 884 882 318 478 305 814 467 563 176 659 729 655 919 551 994 936 699 046 778 868 987 748 036 207 353 265 099 165 027 656 055 495 642 298 919 728 434 140 017 206 730 158 658 881 278 766 005 531 059 617 878 730 309 908 413 726 778 818 168 730 381 179 836 182 275 880 621 167 943 376 553 713 949 381 773 969 517 691 482 699 567 341 856 973 042 159 545 415 342 922 471 096 470 842 696 215 804 036 346 413 195 369 878 830 319 330 915 946 106 611 233 102 249 283 482 357 965 365 136 553 366 741 440 131 549 438 751 219 057 154 443 339 775 393 626 738 244 670 936 992 103 825 214 543 341 944 911 543 200 063 707 878 971 360 052 548 477 084 654 336 795 942 586 640 733 863 700 479 843 206 860 010 879 720 689 745 007 267 839 186 943 452 754 661 005 231 717 830 238 852 069 760 254 759 095 043 802 531 177 343 426 547 680 141 507 400 995 573 458 124 032 911 341 236 207 429 358 088 254 962 820 125 972 404 630 382 868 791 275 129 122 340 294 412 490 644 652 168 268 948 632 613 874 392 386 150 467 595 494 090 893 713 957 760 466 153 268 184 320 127 708 570 020 484 818 143 876 866 819 371 082 934 871 485 665 410 591 853 875 455 572 237 465 350 875 580 602 119 426 048 359 183 669 667 623 673 065 205 121 972 176 601 200 253 873 034 817 964 154 576 488 504 608 987 460 514 475 229 511 491 035 188 406 918 196 610 458 952 907 201 700 645 072 852 863 604 082 523 052 417 197 692 092 119 201 898 469 772 310 566 186 476 846 651 993 809 154 245 392 545 060 757 189 897 365 832 111 845 331 314 242 453 026 883 809 727 147 542 097 552 730 209 521 964 317 997 609 762 515 123 127 341 084 556 959 234 906 998 512 284 140 586 184 288 879 460 956 275 363 674 164 977 765 560 631 854 036 462 052 897 044 849 003 032 817 113 354 064 998 366 135 503 812 439 205 169 178 140 917 836 083 684 492 571 971 058 742 880 509 584 817 760 258 731 853 611 918 986 953 513 271 169 158 694 041 493 524 621 213 579 832 215 279 601 985 405 375 841 097 856 716 473 176 659 693 378 376 260 998 181 139 330 898 470 817 953 714 604 217 156 819 269 906 799 116 893 808 236 147 266 763 862 966 071 667 780 480 574 300 759 224 657 114 906 387 357 279 450 568 573 445 932 973 664 833 056 441 695 238 910 658 315 052 276 224 790 630 110 681 111 188 341 037 538 993 062 897 217 872 987 233 523 034 918 599 555 598 156 152 518 870 500 493 499 364 860 230 637 451 216 463 432 767 902 395 986 220 090 564 304 386 086 184 377 094 420 468 240 471 415 965 013 874 262 257 409 334 939 658 547 282 635 872 056 916 716 834 703 794 135 174 271 076 767 298 829 218 895 759 069 024 525 996 906 848 565 432 732 413 314 944 127 293 246 561 886 228 352 182 900 261 229 171 967 917 724 055 569 060 075 141 173 615 114 634 210 001 308 411 164 468 939 816 438 695 471 580 421 846 164 380 467 400 601 318 446 432 244 142 313 559 435 493 091 231 053 866 033 807 407 608 552 754 996 456 801 695 371 103 511 909 620 618 895 027 078 999 306 137 907 684 406 406 296 237 243 454 994 500 708 894 796 945 803 362 857 213 424 127 648 768 843 701 931 352 742 001 532 051 916 797 261 749 937 608 989 000 584 060 701 261 399 165 338 798 748 503 453 468 453 296 429 454 657 829 506 480 906 235 587 889 138 897 172 056 358 627 925 618 656 563 201 055 954 891 816 365 697 127 748 495 355 437 313 955 943 386 707 473 443 532 076 734 535 616 743 884 342 813 203 060 363 671 606 619 457 563 468 457 543 434 859 493 918 700 891 373 391 511 163 797 132 285 904 112 761 260 382 268 722 284 576 247 725 686 494 988 545 398 485 739 040 112 206 247 780 282 075 038 421 371 824 759 577 010 746 068 556 393 829 670 159 924 424 946 375 450 478 939 128 390 452 916 333 226 622 166 478 636 677 714 163 046 842 643 753 315 018 334 664 800 318 489 764 941 675 059 676 876 713 771 302 196 923 441 222 557 894 672 813 292 254 734 735 092 068 991 522 998 589 731 627 082 098 817 081 019 455 008 254 481 307 013 359 036 746 920 101 189 333 877 837 673 472 647 760 906 172 410 170 587 948 262 146 287 804 153 353 094 083 075 285 575 600 724 424 882 219 608 582 357 930 848 352 539 778 743 536 959 150 337 320 925 039 160 835 217 688 381 615 127 136 238 951 219 774 099 793 118 828 661 081 531 611 351 871 628 168 487 786 964 492 486 096 462 613 954 826 974 815 034 663 041 714 134 129 009 188 946 039 961 271 603 949 814 059 132 624 178 950 896 202 019 618 972 045 981 458 620 142 559 048 555 185 641 620 879 347 349 450 822 423 994 379 249 756 301 483 353 340 944 025 449 765 147 653 198 640 774 368 804 270 748 472 471 114 961 374 268 971 910 791 506 898 491 699 598 531 826 400 493 860 323 855 012 157 468 607 495 510 142 918 465 953 288 842 487 052 923 719 124 220 048 426 964 264 305 734 490 548 257 924 388 332 146 469 371 881 255 401 149 165 281 226 908 660 718 642 579 906 423 680 294 827 575 453 642 652 632 045 861 286 776 885 412 945 782 880 052 631 144 636 001 287 812 000 754 355 377 182 308 443 327 745 873 704 348 530 832 790 142 607 143 893 726 888 235 272 344 012 041 332 575 173 920 746 799 772 309 885 254 544 193 596 880 642 257 088 698 528 559 998 307 862 491 375 411 162 597 149 465 175 021 671 577 845 448 568 620 254 977 793 540 716 901 874 022 508 797 776 463 827 335 483 611 041 041 165 798 014 765 099 470 797 061 659 981 974 057 191 315 588 954 312 536 326 900 128 350 387 280 899 310 625 398 152 030 306 517 385 686 931 302 862 935 843 033 140 768 971 806 321 616 876 475 864 618 866 975 972 438 028 428 728 571 121 024 709 790 771 994 586 409 289 854 450 820 890 259 014 500 796 775 753 904 209 911 786 872 760 939 433 235 353 431 078 670 589 936 759 356 861 359 779 766 906 006 455 070 122 395 402 478 905 774 726 030 020 751 631 694 194 611 853 051 336 714 768 900 112 371 219 122 555 910 754 815 541 849 069 262 111 434 860 354 586 982 383 319 150 425 496 601 075 811 593 828 558 529 208 036 766 549 448 399 450 099 796 341 602 023 101 355 543 211 667 143 218 021 896 814 535 136 490 878 593 463 510 818 797 035 977 919 180 332 080 662 403 079 980 424 550 934 850 789 441 462 847 623 726 317 621 989 096 496 918 393 575 333 150 870 359 222 197 412 981 976 506 187 502 956 103 518 550 491 923 475 101 594 097 229 449 204 897 223 069 921 098 261 301 860 991 237 783 868 773 470 900 126 855 068 073 626 535 189 172 986 928 759 812 889 275 456 646 489 704 662 502 863 501 088 396 409 312 965 261 690 301 523 037 214 022 534 189 726 424 982 070 596 125 726 508 741 760 370 558 108 382 867 935 137 853 997 075 313 830 585 362 477 108 726 237 044 589 869 149 135 747 311 242 951 925 780 307 868 272 340 788 699 591 073 672 644 192 826 082 226 370 761 049 846 320 738 985 325 609 541 527 835 310 320 323 242 202 651 897 384 538 658 876 283 632 534 601 074 614 228 283 978 763 881 755 030 686 163 280 469 717 603 606 079 033 254 353 172 300 407 716 270 476 024 530 702 911 201 801 170 737 091 571 032 548 998 609 626 913 381 255 109 170 257 011 834 105 218 466 394 292 236 781 517 086 839 557 246 345 074 642 756 758 676 477 282 203 673 728 377 789 041 965 773 412 596 355 005 160 039 677 754 186 325 490 318 765 196 835 006 489 448 777 651 338 393 474 429 863 501 787 889 941 046 054 983 658 860 341 115 957 272 356 042 459 980 342 699 502 420 178 587 661 125 385 385 528 789 004 823 720 798 266 432 593 958 645 799 955 827 897 679 110 947 648 382 509 889 108 439 679 514 009 329 358 665 150 918 297 433 291 093 155 298 571 717 636 564 048 523 151 604 308 691 454 478 312 916 723 787 410 067 827 548 357 749 174 705 071 665 450 119 439 662 872 004 576 200 404 861 867 743 392 331 388 701 644 136 931 220 472 661 005 642 303 077 790 383 760 879 552 125 739 381 118 127 847 839 322 519 399 953 817 784 574 555 882 170 599 994 628 194 760 657 869 706 635 204 144 072 401 794 185 761 239 696 474 238 760 828 958 570 411 705 736 935 079 119 791 769 195 525 657 573 288 575 253 769 585 499 076 789 288 902 835 498 336 379 657 108 126 811 085 629 766 936 569 743 066 037 173 438 844 322 227 631 386 864 788 385 721 633 742 520 741 041 015 186 431 943 400 760 996 236 787 813 974 824 985 589 420 134 876 106 203 754 046 908 401 308 139 147 507 072 036 502 316 707 433 928 709 131 761 255 655 782 250 733 887 647 153 280 908 358 572 103 121 592 703 919 781 697 145 533 533 750 740 479 744 600 647 041 127 275 368 997 968 088 470 518 663 258 167 849 746 683 691 189 264 725 284 998 779 692 577 612 863 370 386 077 199 983 877 754 819 862 624 405 218 078 729 041 502 268 757 516 200 299 701 455 406 765 601 275 707 129 343 245 546 608 886 174 832 864 150 675 849 079 575 452 993 040 752 278 290 453 110 959 644 542 233 739 022 601 190 728 473 108 998 437 747 687 313 045 790 304 476 547 989 014 728 498 102 520 316 117 514 222 568 881 131 630 134 371 858 352 722 252 745 050 504 094 975 540 736 898 042 262 947 872 393 627 860 972 639 668 129 651 074 892 704 310 856 855 898 094 336 748 925 141 374 518 279 236 141 137 406 123 219 431 565 919 114 474 327 318 412 369 839 703 657 000 667 716 118 225 492 089 106 959 434 441 563 882 841 954 943 244 237 261 891 837 795 046 464 808 272 782 322 710 298 158 244 235 412 986 539 038 941 154 664 729 461 863 744 504 414 151 630 390 495 597 631 938 353 470 066 155 288 549 230 027 143 428 531 389 013 668 780 619 259 353 668 030 490 702 498 675 731 883 370 695 989 329 170 113 238 252 060 994 687 212 981 437 010 656 337 443 822 919 556 955 224 386 804 050 880 530 885 158 020 093 306 099 380 556 640 610 433 469 699 475 143 623 444 455 141 262 094 984 868 885 551 288 082 539 220 756 464 166 383 372 910 159 444 431 613 135 188 094 107 909 190 598 071 286 230 321 405 694 137 637 989 045 289 401 659 215 910 386 690 438 616 266 122 841 741 365 253 691 590 973 036 572 832 788 081 933 448 601 690 298 105 128 309 464 559 973 760 795 470 160 169 913 681 641 911 030 746 717 033 794 216 308 078 876 263 474 342 058 101 020 415 239 207 697 154 562 558 385 250 514 904 969 439 292 763 208 936 819 407 620 663 512 464 704 166 808 381 327 924 154 321 787 629 986 443 374 203 881 097 908 808 047 125 004 123 041 066 053 982 745 665 485 795 391 494 138 686 141 203 203 979 115 280 454 207 478 089 119 816 713 512 617 515 824 501 133 287 447 077 129 883 995 598 380 681 045 406 475 471 598 928 012 880 333 483 835 948 607 076 992 255 022 323 215 250 706 382 352 184 635 337 208 761 011 207 747 059 147 718 210 787 922 675 983 936 278 851 087 471 092 137 084 947 491 421 769 166 818 253 779 424 099 607 487 893 452 544 303 958 695 733 939 450 771 399 856 585 214 834 523 642 483 639 715 017 041 418 582 971 984 477 599 559 607 945 086 804 589 540 855 348 904 111 612 217 572 873 745 444 679 889 365 321 356 115 001 443 229 426 876 018 552 232 105 611 117 802 803 181 047 261 748 763 240 008 942 882 901 798 731 060 836 521 401 903 845 522 482 283 396 711 465 710 647 507 799 364 296 040 110 696 261 919 936 455 091 859 068 890 955 245 551 424 239 835 646 786 680 851 141 156 985 517 477 423 353 337 267 456 428 315 240 967 172 694 784 848 579 171 861 558 403 559 852 234 878 929 767 368 520 565 385 061 085 620 359 712 382 550 870 971 951 563 927 733 740 544 076 718 933 505 855 762 507 820 849 526 861 549 214 353 187 315 588 098 397 080 941 729 045 575 297 378 820 096 413 522 530 324 404 537 520 768 871 392 375 292 117 709 582 145 206 805 686 428 321 507 067 910 479 209 118 024 993 324 601 012 225 655 205 607 333 202 679 954 412 956 258 426 346 545 248 088 148 481 788 124 230 527 217 196 622 587 576 389 165 727 237 002 527 679 789 924 960 801 646 631 639 475 091 529 488 405 705 314 055 673 542 469 852 011 745 036 705 532 071 290 875 210 360 820 743 468 014 770 219 372 823 123 030 115 244 943 472 961 349 590 045 479 393 585 544 636 328 532 591 346 433 302 725 772 891 999 321 441 597 040 397 389 797 464 578 964 176 820 882 440 940 474 024 580 876 705 666 878 371 093 749 028 567 343 623 546 394 482 833 849 675 090 414 639 076 261 190 060 370 810 349 994 789 098 099 290 668 857 360 844 262 082 398 235 235 404 095 533 935 376 726 436 320 718 508 276 727 417 707 493 518 225 425 138 450 581 293 645 682 733 996 210 458 003 260 489 802 947 034 817 287 640 160 400 256 671 203 270 934 593 284 417 099 869 909 274 778 363 407 339 716 745 202 238 803 158 339 785 085 044 408 457 250 715 158 650 158 759 797 968 371 414 292 981 000 909 046 771 581 326 542 334 462 003 225 259 219 359 440 898 718 133 282 048 980 157 896 282 565 924 056 510 848 141 545 609 919 053 985 442 284 632 606 924 808 593 005 059 493 133 482 558 004 349 903 520 148 911 059 366 170 198 940 631 947 991 768 892 408 489 097 350 330 120 397 519 627 456 216 710 527 045 985 389 629 039 290 608 802 020 881 355 404 905 636 797 297 543 944 480 249 843 628 668 919 604 033 504 268 163 770 276 163 948 460 924 827 986 203 226 762 976 163 565 901 059 397 414 228 396 085 412 287 474 542 694 729 268 103 035 929 308 246 350 912 159 258 338 648 807 434 694 546 928 761 577 804 269 599 236 656 990 439 536 799 255 429 902 881 761 062 882 785 571 734 402 263 739 063 587 764 111 827 133 932 149 889 506 256 135 773 040 230 150 469 434 967 036 794 206 518 166 291 703 238 384 150 697 972 870 030 527 194 646 772 872 995 179 915 936 276 881 535 101 971 497 208 825 633 858 595 717 281 804 653 862 908 113 830 846 858 562 537 428 971 570 301 987 869 986 308 600 889 624 570 444 458 936 861 952 180 314 710 570 588 710 083 465 696 037 723 133 421 128 486 486 701 483 174 510 058 698 146 613 437 410 743 350 107 134 520 661 554 189 594 819 647 073 659 134 362 949 046 877 601 566 946 269 587 966 260 729 582 404 849 325 429 313 629 850 877 911 483 039 300 487 270 872 409 767 592 116 151 791 027 484 310 862 880 106 348 092 699 463 472 691 407 613 962 531 594 559 943 972 196 659 478 393 701 097 678 847 861 545 851 770 107 925 622 434 194 904 215 740 543 306 021 411 663 265 630 529 708 296 246 490 643 387 934 265 526 281 356 439 066 787 542 787 052 008 183 419 857 114 730 329 763 487 011 686 249 159 090 903 118 237 651 270 356 647 037 531 428 965 533 826 553 556 552 852 630 347 366 641 968 226 082 545 570 665 565 969 313 048 294 439 642 561 225 765 860 122 629 194 122 049 565 384 608 651 312 976 473 603 136 491 111 340 015 573 846 971 598 562 782 173 896 999 867 286 953 259 142 652 138 761 102 579 481 215 329 465 424 365 030 088 056 463 593 534 294 202 165 479 158 575 815 549 877 444 487 055 481 007 066 224 387 005 209 980 507 648 451 585 355 825 127 105 774 653 288 059 338 897 786 343 457 138 675 415 160 585 621 528 775 082 600 134 975 032 561 419 323 165 804 446 255 331 966 523 875 587 656 077 520 411 074 974 839 931 554 501 478 140 174 646 827 289 326 780 802 581 973 162 682 499 066 607 679 528 729 336 404 420 577 267 104 787 516 270 987 979 510 658 523 355 519 311 497 338 096 050 435 459 837 228 758 391 443 014 071 734 826 210 649 343 216 531 141 426 267 347 822 980 493 944 058 881 864 775 997 498 759 704 947 479 030 137 401 139 034 958 456 804 175 777 104 949 575 114 052 081 106 586 517 330 180 526 565 042 160 681 676 478 971 475 687 735 760 047 659 756 677 982 127 044 682 978 735 665 949 602 810 502 892 157 595 974 361 077 009 134 558 806 181 639 807 423 761 960 277 287 211 662 046 470 301 700 154 890 833 492 315 468 003 564 126 198 619 023 944 343 401 624 162 786 686 452 314 060 167 236 785 647 271 143 444 577 700 002 547 919 103 435 762 267 847 027 490 034 334 626 729 477 112 493 952 223 972 808 899 451 703 267 903 059 706 061 636 533 824 528 726 503 728 518 878 354 424 558 936 802 644 213 038 776 910 844 402 262 883 238 794 214 901 009 266 151 674 617 413 844 353 386 606 263 927 423 573 692 183 810 736 997 387 020 439 496 387 522 576 739 815 173 054 331 090 288 537 729 739 598 608 547 489 139 723 640 123 862 615 922 126 655 071 733 352 589 639 014 054 179 261 727 101 010 766 857 601 628 238 030 933 989 611 828 358 667 439 228 571 073 294 192 594 385 626 232 369 723 749 711 575 593 117 839 915 382 469 897 634 758 583 831 085 293 960 097 933 824 119 752 296 498 921 370 363 486 594 449 636 709 031 328 009 961 175 279 157 610 982 586 619 736 712 366 224 069 050 344 966 415 296 533 565 012 244 495 474 432 996 435 076 743 220 122 011 239 001 571 892 266 497 678 462 890 668 525 642 703 742 153 018 045 301 806 983 289 162 674 854 175 517 423 295 754 388 607 946 864 320 537 395 874 462 317 481 222 989 389 067 772 984 941 189 941 785 954 230 585 138 461 125 368 324 809 545 719 290 995 315 430 275 979 774 374 791 191 697 590 149 148 123 258 334 130 401 221 031 591 917 307 539 240 450 800 201 922 511 996 782 436 035 305 464 095 960 733 999 439 113 880 616 080 990 626 372 697 901 713 033 160 351 789 681 741 637 279 252 874 016 266 651 940 034 035 775 540 123 123 010 685 401 989 455 494 312 919 970 354 731 708 032 480 336 123 483 004 527 637 243 495 131 439 471 741 788 660 766 339 011 616 936 160 439 913 143 104 265 956 810 716 332 859 002 528 071 551 727 777 232 391 702 129 916 583 860 145 730 130 035 628 380 578 029 808 162 311 464 743 974 956 173 376 837 658 962 356 989 900 908 366 643 195 224 228 292 995 223 941 339 779 084 445 252 210 101 430 124 820 035 839 502 268 381 291 660 059 251 329 287 119 866 279 559 396 098 934 795 570 832 011 733 006 301 988 316 089 406 310 159 515 137 284 007 752 856 869 086 449 061 142 427 692 021 875 887 957 627 789 713 530 991 228 304 663 424 515 917 864 963 260 582 909 546 532 055 860 977 066 056 586 978 618 198 903 052 639 749 806 614 619 146 110 556 042 387 650 086 789 247 548 812 930 242 057 425 574 202 408 055 991 355 255 965 479 065 729 995 200 250 052 328 647 201 297 988 342 400 652 329 421 907 550 289 482 778 269 472 766 878 785 191 783 139 073 649 103 627 274 446 696 410 432 093 691 296 853 089 399 467 568 243 287 823 392 507 484 878 510 369 789 334 875 593 712 864 426 720 958 970 215 079 370 917 651 091 642 281 684 184 499 495 624 046 546 872 607 171 232 892 846 599 901 387 876 000 663 527 531 670 777 723 927 014 973 924 754 588 409 995 926 571 104 361 532 512 714 771 292 312 607 584 189 059 083 022 264 828 800 657 714 221 767 706 863 267 724 909 575 095 386 090 366 998 978 562 796 441 168 667 560 925 608 307 665 060 098 295 895 685 751 002 947 560 135 030 761 911 632 577 005 902 616 082 543 950 677 536 035 453 740 560 091 532 249 946 005 156 101 386 618 164 290 675 644 857 788 820 834 619 940 193 514 455 548 252 435 741 034 765 924 466 061 239 792 722 666 227 746 483 293 283 761 818 700 767 701 527 148 416 223 188 529 548 493 430 785 329 265 485 339 419 859 864 111 323 719 566 528 773 559 325 268 957 971 002 289 382 216 380 483 118 832 646 238 695 011 649 781 057 880 270 136 628 039 409 991 877 927 414 170 462 577 715 618 162 630 417 684 395 798 235 651 153 480 199 812 859 929 685 263 510 318 709 466 362 229 510 744 106 183 851 966 356 712 491 202 509 713 018 509 000 961 329 970 812 627 196 825 000 874 822 678 172 251 590 100 726 163 910 827 907 592 033 244 594 144 853 234 048 007 302 982 522 422 678 864 070 856 246 474 731 261 387 759 553 720 604 860 775 783 096 826 192 269 937 384 265 586 933 028 086 959 637 767 414 325 860 193 383 815 157 114 691 201 798 660 299 574 916 810 485 703 943 584 265 087 842 058 276 446 411 243 271 617 410 815 407 390 312 054 255 050 966 463 815 313 598 697 510 798 955 429 715 116 426 619 917 731 679 487 677 523 478 043 248 429 903 561 056 028 004 746 704 139 644 875 018 703 966 260 686 678 768 897 283 005 943 894 092 386 896 865 407 946 278 807 568 369 746 270 221 084 309 572 467 901 576 600 490 461 497 725 558 928 424 416 430 873 929 191 433 965 615 625 247 872 728 401 597 302 321 469 602 377 333 810 595 777 189 156 450 520 495 262 018 500 798 770 578 175 837 791 817 247 412 187 212 179 457 531 432 919 197 035 587 768 014 906 942 094 101 174 436 755 375 153 206 667 753 017 599 964 722 509 926 298 724 663 021 948 921 686 953 113 343 078 534 647 284 568 796 343 591 912 553 766 967 215 423 590 101 596 196 870 827 634 650 078 920 882 339 422 583 316 944 145 773 652 691 018 643 313 578 587 296 557 579 496 118 871 242 525 542 344 373 087 755 509 449 449 002 605 617 508 105 911 225 587 233 960 211 867 304 204 393 385 516 175 021 328 083 151 799 775 099 789 716 983 426 430 563 894 187 466 233 326 453 129 586 592 263 270 946 750 575 467 072 008 631 362 377 807 789 222 312 807 930 107 538 851 848 720 219 627 314 586 480 831 224 106 375 211 028 953 456 551 356 095 462 988 210 875 974 446 186 995 358 534 052 639 594 440 145 138 127 369 896 818 114 138 300 646 942 400 298 853 211 332 398 627 734 563 527 290 058 024 160 333 805 840 658 823 002 560 442 267 299 099 992 848 500 376 210 015 512 855 133 690 721 302 076 856 755 524 316 972 696 615 519 444 676 354 566 319 484 521 138 507 771 778 431 638 242 147 384 047 909 212 215 109 259 179 647 360 863 281 380 929 647 183 313 460 347 146 626 167 867 269 574 728 293 538 797 123 845 383 549 858 598 077 335 884 503 191 699 175 621 412 612 996 044 235 672 661 884 103 130 112 534 902 074 115 506 636 587 885 384 200 037 474 302 128 714 532 495 665 715 289 877 638 668 807 300 602 658 942 102 446 387 501 629 449 589 945 372 229 001 525 947 345 475 761 157 345 473 616 651 136 709 567 660 137 668 524 433 321 248 760 734 888 702 555 383 916 848 357 567 408 504 866 412 197 996 764 603 248 798 422 889 941 616 169 026 360 882 012 966 316 454 045 598 194 058 843 894 144 379 330 896 302 279 053 837 584 386 530 797 689 690 702 266 970 574 795 070 082 736 858 084 086 355 473 435 344 973 054 301 921 420 953 666 341 181 275 538 233 955 697 578 355 925 716 553 971 905 426 312 397 486 661 081 417 743 588 547 481 204 820 835 022 833 961 945 368 673 972 961 077 819 157 674 271 573 220 477 878 213 084 167 953 823 864 657 149 815 496 197 380 046 623 152 861 990 255 791 003 533 016 475 329 415 530 739 630 777 076 104 764 791 038 510 521 595 091 381 573 260 942 044 954 466 278 427 671 155 867 915 564 166 362 743 197 916 426 535 115 184 739 084 126 467 217 788 101 019 267 510 678 163 631 334 969 592 567 423 508 618 030 426 768 063 947 524 401 541 390 671 341 543 729 606 896 138 903 346 167 470 985 578 114 854 979 934 586 409 989 153 383 193 948 396 947 620 444 410 927 539 983 543 321 199 739 538 652 244 245 706 107 162 372 080 157 033 252 535 624 845 283 469 914 358 290 539 247 544 698 689 469 609 190 814 063 369 449 831 778 409 668 166 639 829 610 489 276 826 067 820 223 976 195 277 317 591 490 256 499 481 035 892 068 756 411 879 288 881 982 171 073 489 447 995 135 745 475 506 423 948 234 993 462 859 525 713 406 302 000 887 730 906 180 140 395 584 060 312 413 682 783 970 464 803 018 468 361 143 073 222 480 083 624 599 305 667 667 246 560 727 808 243 469 267 492 171 205 264 079 290 527 874 925 785 606 211 813 886 448 615 812 660 940 914 138 145 458 616 548 256 908 314 560 772 894 161 831 966 399 366 321 432 710 345 904 442 942 459 938 131 706 003 796 144 766 917 963 967 473 781 185 800 410 280 979 626 415 009 520 111 923 647 075 319 413 844 427 488 785 266 581 992 673 943 418 737 408 470 403 953 739 322 914 939 141 841 943 608 063 872 584 709 695 967 785 484 744 966 727 022 784 339 616 435 622 532 841 315 952 890 470 456 672 542 597 924 544 148 620 028 054 623 372 048 716 348 729 133 018 679 324 348 745 389 396 613 933 239 162 909 667 958 188 514 220 682 868 326 839 544 392 490 200 638 925 453 884 111 817 761 092 048 084 132 172 734 070 939 227 080 602 097 315 395 187 730 157 414 328 342 052 360 746 220 699 644 282 664 215 482 738 907 656 848 663 606 532 270 289 760 034 656 440 077 377 603 132 345 016 352 961 600 697 927 382 295 684 528 308 318 289 566 026 937 880 841 809 992 343 384 459 140 894 316 811 757 194 806 716 523 338 058 101 989 918 484 179 186 228 596 882 270 678 391 176 233 033 928 400 464 654 838 846 439 497 244 020 892 734 673 519 978 108 738 095 880 919 501 836 053 034 068 668 681 913 998 230 503 612 386 308 973 413 000 785 812 687 370 647 608 382 795 418 316 628 233 793 937 314 468 857 399 988 775 189 479 718 955 834 160 323 742 173 241 985 927 907 478 122 781 475 075 680 271 861 401 533 487 864 397 678 153 307 132 783 251 990 527 871 144 705 980 531 199 537 584 700 887 351 568 778 781 186 038 526 569 704 125 915 503 586 578 078 590 568 587 684 214 696 186 304 749 984 916 708 041 923 461 925 553 432 618 799 086 020 524 082 219 070 665 791 125 783 318 017 090 472 062 413 260 297 577 145 930 281 227 229 626 001 545 306 426 337 618 899 198 165 344 954 370 629 264 438 898 354 355 364 380 906 314 924 847 324 030 136 067 720 526 781 426 137 169 521 032 812 595 877 556 024 832 004 914 321 345 827 873 391 133 064 203 561 578 729 273 436 556 980 697 484 696 129 295 527 205 354 399 029 893 172 298 398 638 126 301 301 392 290 961 956 330 077 846 414 405 889 145 513 904 400 201 106 447 242 704 403 438 038 029 645 489 713 983 375 882 713 740 984 991 134 497 743 324 653 677 228 061 317 541 134 022 231 013 403 918 315 812 419 048 961 567 564 880 007 806 686 496 034 238 124 788 914 748 364 923 374 270 309 056 323 498 250 612 454 429 710 719 814 255 847 862 381 179 524 791 334 047 719 386 116 184 079 265 653 485 387 272 119 141 339 823 887 930 709 881 304 877 909 177 209 026 761 673 159 317 728 667 224 693 851 726 593 768 639 463 717 003 084 665 070 826 616 623 675 637 246 724 963 150 980 644 723 014 853 284 127 807 704 063 238 734 938 822 542 693 531 739 658 422 477 164 030 766 916 543 973 604 035 988 258 185 455 848 639 481 970 000 051 113 263 640 816 615 768 410 029 764 419 790 648 458 757 659 568 889 141 681 544 180 791 700 145 982 678 736 973 753 338 131 335 401 094 071 810 818 480 744 565 675 907 808 326 268 668 602 766 355 803 556 931 352 724 930 544 609 593 844 643 088 795 043 213 484 873 084 832 896 243 095 830 408 551 228 851 168 926 363 516 545 207 751 907 724 099 763 234 502 451 816 370 159 019 055 030 801 777 088 758 790 497 220 787 819 948 756 092 971 515 705 860 070 886 118 789 669 639 764 825 050 262 516 709 349 258 307 192 632 994 497 629 457 080 012 177 912 211 530 482 511 145 430 688 020 112 188 782 030 845 670 040 183 152 108 400 744 475 080 314 252 971 972 212 841 216 437 822 674 092 714 880 905 751 588 797 067 642 770 193 038 624 507 577 022 843 382 771 255 410 947 073 772 620 217 407 894 208 552 970 023 132 181 020 548 330 548 270 186 447 871 032 313 115 142 691 940 336 904 255 737 871 806 390 236 683 702 368 495 519 595 857 983 520 618 014 229 719 729 725 090 900 155 081 168 397 587 487 570 822 106 193 267 160 607 706 497 887 736 217 865 243 478 962 026 396 409 299 373 816 686 124 888 410 173 442 048 570 116 956 211 753 696 385 479 279 076 869 204 238 267 191 012 277 211 553 486 704 301 452 295 653 402 697 761 014 321 972 564 287 430 842 077 025 571 950 067 866 368 142 771 664 017 990 446 514 430 542 045 191 548 909 484 687 045 414 868 456 332 646 359 299 377 033 046 785 602 158 812 545 558 580 604 744 143 123 876 114 457 526 890 185 753 454 667 065 515 174 119 336 620 360 765 932 565 339 071 588 353 042 742 174 485 493 407 447 068 090 831 470 466 684 821 248 557 867 219 403 605 234 266 717 799 059 094 880 199 675 452 989 294 225 067 785 670 248 292 876 984 679 437 276 447 409 939 323 773 054 449 361 192 953 554 443 371 126 346 719 634 386 622 300 562 931 720 233 185 727 698 160 811 492 370 976 274 232 414 354 797 995 119 652 340 751 640 137 221 707 248 485 377 199 577 891 001 525 289 779 363 283 605 628 384 749 238 186 605 500 641 657 255 488 885 766 389 641 919 005 740 019 692 530 372 301 513 772 343 765 782 199 035 226 288 348 215 011 293 898 841 996 436 199 344 546 476 764 838 466 385 177 783 279 980 620 774 990 304 272 345 933 035 975 413 213 302 939 101 596 806 824 375 822 616 542 431 352 002 855 170 774 378 195 145 478 833 838 122 439 488 319 766 753 215 576 870 129 401 855 117 896 053 288 068 527 942 600 787 382 713 624 965 611 289 708 691 255 099 542 114 895 191 576 563 456 747 424 636 924 366 986 969 795 594 490 221 227 592 594 794 323 265 512 304 217 692 660 279 601 185 823 656 279 714 774 861 607 123 156 612 120 068 116 181 099 688 240 206 586 243 627 966 259 400 441 291 999 626 461 799 440 514 835 668 514 377 051 162 619 616 761 836 021 935 862 636 992 395 916 276 951 624 697 116 625 178 422 446 420 878 030 487 473 209 563 128 555 836 661 482 334 114 425 465 481 820 826 661 932 628 659 912 651 855 994 474 354 598 167 138 781 343 159 624 961 743 752 664 474 919 470 217 249 398 398 387 298 128 538 686 655 945 957 628 537 721 168 840 148 857 335 389 340 923 219 253 264 464 358 272 739 720 989 614 166 212 697 230 027 932 718 630 377 455 095 257 136 073 641 729 422 258 391 776 094 113 915 589 151 522 313 499 960 091 082 517 726 168 348 801 751 593 853 172 535 953 146 672 057 619 103 886 115 988 608 450 410 773 997 527 920 395 451 775 987 009 958 632 772 026 557 866 791 308 896 726 762 727 773 261 231 587 588 460 279 731 965 385 052 773 416 304 811 491 883 911 389 228 344 471 501 194 380 086 466 636 894 766 454 774 195 409 055 836 050 694 170 210 680 191 327 175 741 823 380 465 238 350 029 092 730 493 015 326 008 395 788 898 443 837 777 712 125 010 248 327 658 150 400 168 705 442 898 435 132 983 241 881 776 884 743 970 971 612 792 981 908 858 901 755 400 912 305 076 437 585 921 351 720 107 879 992 199 791 648 033 113 683 559 743 250 130 436 439 284 681 312 782 295 579 360 723 851 877 954 225 629 358 973 395 129 077 034 603 824 029 388 616 135 749 655 243 013 850 824 397 052 426 321 948 182 403 100 181 006 911 010 108 092 671 859 257 704 683 974 488 849 088 333 287 856 688 880 377 327 013 994 117 508 065 816 594 217 275 038 195 267 272 559 641 103 425 220 460 887 049 806 552 764 839 941 846 601 860 076 380 237 136 991 647 380 125 867 408 604 502 247 222 628 305 458 782 061 578 124 005 176 951 256 924 715 001 555 516 849 815 353 321 639 291 467 893 855 142 086 385 481 720 648 088 129 947 846 098 473 937 135 540 298 891 347 344 300 539 645 833 341 111 340 658 348 211 803 050 467 616 411 645 862 023 211 276 308 893 878 552 820 320 947 682 989 271 103 718 103 476 247 227 013 121 936 432 146 237 728 517 578 420 022 459 290 332 041 714 021 219 403 806 947 968 624 666 427 818 521 648 253 898 069 941 989 234 462 243 736 137 946 026 031 328 754 531 814 720 140 440 156 529 043 269 612 153 294 013 427 293 136 896 336 871 768 267 980 856 820 663 457 224 638 811 985 491 921 256 099 973 656 919 561 461 065 622 913 036 733 317 850 344 168 273 636 855 179 131 606 907 156 889 571 295 117 477 109 418 068 379 409 617 274 167 162 349 210 211 796 199 581 958 246 967 694 488 063 202 292 993 146 163 580 704 527 084 555 601 570 234 390 981 160 195 735 536 947 011 050 241 670 911 752 811 157 480 641 700 338 635 784 495 734 661 891 382 394 248 414 186 306 905 233 785 663 132 895 458 653 841 282 478 860 943 661 800 072 628 095 999 262 926 498 352 778 236 359 557 423 129 084 955 326 811 800 727 696 255 649 760 866 227 371 298 905 287 553 667 463 967 862 104 743 308 859 425 488 879 324 686 432 552 990 459 749 844 859 268 889 257 800 350 002 810 334 410 195 324 026 042 009 506 021 464 468 074 816 121 887 799 817 359 278 988 864 536 770 313 832 103 775 613 252 188 162 283 677 729 171 385 239 260 421 272 068 015 307 815 683 988 473 537 681 954 083 852 952 107 257 132 766 651 501 064 724 474 998 298 403 360 434 604 660 410 658 046 713 000 185 433 340 498 285 368 074 512 659 968 418 954 649 206 093 100 052 916 364 350 030 758 789 559 821 661 522 068 230 151 929 336 030 019 492 195 233 892 781 440 106 821 347 572 261 748 619 861 000 912 221 588 500 624 096 401 294 407 984 891 075 730 310 313 469 082 659 606 074 744 822 138 752 844 738 671 821 771 275 241 076 760 519 487 130 561 283 324 953 846 710 349 064 305 729 431 403 776 483 929 704 175 688 966 094 820 522 211 462 405 043 862 470 275 721 646 986 745 164 660 552 926 081 810 564 276 284 465 994 602 157 908 152 769 704 208 443 818 211 815 860 088 243 708 180 691 930 916 077 344 824 385 087 724 938 560 535 309 407 499 649 528 220 454 368 023 022 176 204 097 304 843 198 026 038 144 208 851 784 512 165 776 655 839 150 646 256 427 856 452 948 369 690 331 776 199 901 231 627 841 482 899 005 805 941 039 380 760 439 604 419 618 376 825 265 258 882 699 092 492 806 293 304 193 443 801 466 997 739 938 683 998 387 936 140 597 442 868 336 435 366 022 557 411 015 588 248 170 949 934 024 977 627 936 281 174 213 418 028 261 602 941 002 687 898 633 929 740 229 558 750 908 931 937 322 910 077 965 002 150 408 732 067 226 968 041 521 992 509 946 611 463 742 189 699 275 021 878 175 073 302 378 963 853 389 723 250 904 610 039 575 760 833 359 681 249 821 423 081 519 332 884 039 263 827 562 515 087 516 411 761 584 563 237 979 263 053 862 570 724 688 318 541 802 477 799 833 219 676 112 345 244 667 461 407 366 345 280 510 447 577 240 406 650 017 504 899 754 181 732 596 743 517 190 837 651 340 231 356 034 341 058 783 682 452 561 087 355 837 725 398 995 399 088 983 789 842 155 034 735 579 392 905 345 995 791 736 931 109 893 683 350 959 340 719 475 251 857 615 304 753 817 021 828 116 495 406 479 249 306 149 675 231 005 792 639 507 433 707 832 525 049 723 410 909 255 951 843 163 540 638 109 194 828 429 288 544 038 576 220 473 263 366 727 800 178 145 556 322 705 200 609 481 933 477 418 304 620 875 551 257 068 527 493 938 354 526 500 632 513 265 865 485 492 586 446 525 156 023 352 754 680 263 534 934 779 224 564 500 603 386 771 783 601 155 967 419 513 948 835 661 105 945 038 360 234 507 824 190 558 672 290 172 608 509 093 914 626 876 824 659 104 624 641 971 578 324 215 734 449 371 298 791 658 761 860 407 581 526 885 892 612 337 544 658 076 736 488 084 345 688 877 416 333 790 527 245 262 058 890 892 298 823 066 889 681 075 777 613 805 028 252 953 183 137 659 874 696 440 431 796 066 062 440 746 350 390 202 309 449 329 201 169 641 569 714 824 422 325 644 778 030 395 554 662 605 817 722 940 377 114 925 171 935 382 048 848 505 282 918 958 024 872 255 197 793 626 200 992 574 671 083 687 614 373 473 814 711 331 979 963 650 681 185 939 392 107 114 450 387 657 683 209 753 092 972 670 665 916 198 385 358 465 942 868 014 772 598 897 659 467 823 738 713 692 513 835 302 856 594 196 394 585 828 974 953 589 402 272 592 924 936 289 522 990 993 147 035 332 041 315 340 278 710 828 407 672 327 022 081 325 771 819 426 168 454 170 446 027 418 986 466 507 437 446 805 478 815 266 084 336 354 087 165 713 132 953 980 048 909 936 160 402 824 907 925 655 477 295 308 635 487 716 877 489 045 073 724 667 154 941 078 222 419 358 536 382 620 634 234 706 475 264 685 114 006 361 659 506 981 689 125 839 813 904 704 727 332 875 664 365 100 565 898 545 701 757 792 152 775 527 038 634 018 974 325 403 415 178 889 451 967 921 812 125 681 989 660 439 871 172 432 168 298 293 553 643 165 345 381 183 271 471 964 220 326 958 074 495 102 314 670 064 010 985 303 793 503 723 868 883 361 442 933 161 662 000 121 076 186 468 361 761 156 722 867 931 684 950 162 816 960 059 414 304 382 736 871 513 069 119 885 755 476 630 242 976 088 784 384 242 357 797 896 913 386 223 761 907 502 307 105 774 073 791 934 062 723 710 170 101 833 051 587 117 856 417 452 112 822 468 214 538 621 366 135 287 496 999 429 050 262 756 840 862 150 425 068 946 269 334 372 686 612 687 265 038 310 948 403 413 143 249 199 938 422 106 384 351 353 280 186 227 705 311 753 497 096 332 967 287 441 037 752 974 134 802 987 391 846 479 556 240 839 955 419 228 763 730 301 232 441 059 404 780 678 029 695 767 677 669 745 791 274 383 502 914 054 977 022 732 332 649 619 061 474 834 287 956 120 602 571 061 572 758 424 557 969 129 961 392 255 955 020 311 135 409 608 730 090 109 842 906 283 941 976 180 552 057 863 305 598 076 870 634 915 161 157 896 636 154 993 765 154 247 752 279 065 262 104 463 336 550 694 425 300 195 448 881 432 370 200 909 394 464 796 222 806 178 587 198 711 635 695 056 299 092 928 390 098 312 178 100 825 673 061 975 398 576 375 144 379 408 864 980 744 327 842 818 021 551 039 628 859 705 048 404 849 652 626 579 334 728 047 716 657 371 941 612 171 720 750 865 499 003 578 443 278 794 241 183 757 622 136 589 354 907 674 677 377 434 753 977 910 272 513 243 822 652 126 088 584 186 408 789 879 341 551 352 300 685 996 429 988 760 323 068 673 213 910 669 814 814 229 463 512 106 738 526 456 937 888 214 397 862 073 193 500 602 092 626 241 497 079 600 464 508 479 738 153 924 346 692 776 843 276 893 302 459 362 319 269 344 906 287 520 939 626 031 137 282 515 910 211 836 778 450 063 398 747 754 396 157 067 375 343 020 281 778 872 007 486 652 921 680 286 902 172 745 962 499 727 719 019 451 880 326 725 516 968 085 744 472 230 990 740 932 255 366 054 671 637 417 888 617 520 041 888 238 226 169 632 692 492 456 684 207 236 319 493 816 257 273 738 285 213 155 768 653 241 434 351 922 752 156 927 539 986 106 207 134 949 735 708 898 293 449 510 221 968 030 050 620 487 157 028 920 473 332 163 849 848 463 241 293 777 493 922 956 556 577 217 730 217 306 888 940 071 792 600 038 934 034 338 438 381 266 201 982 945 630 646 629 735 872 089 993 823 804 947 026 338 046 636 895 660 317 418 175 094 645 512 480 231 435 665 681 798 073 391 844 624 716 770 606 288 998 064 217 022 297 275 388 592 964 858 368 240 540 587 734 632 011 747 926 789 862 737 750 797 677 468 174 481 209 768 335 840 314 498 350 673 244 862 502 436 807 621 344 381 769 822 347 082 642 724 136 543 607 239 303 429 462 481 414 736 479 083 154 737 705 170 034 876 902 224 348 299 810 877 430 437 449 529 624 315 512 947 663 301 615 248 540 840 553 582 907 697 134 511 238 189 106 315 786 182 726 709 803 390 049 540 134 324 819 200 975 063 424 137 823 888 443 441 547 066 379 022 344 124 494 520 305 390 620 946 867 986 713 573 271 656 264 893 800 533 643 385 303 425 521 505 781 433 002 011 908 353 360 760 133 856 932 024 203 706 493 091 032 638 287 664 350 359 064 356 381 717 787 985 800 756 638 806 423 500 763 309 896 909 730 374 734 848 617 940 140 490 335 317 767 531 441 928 053 578 911 199 633 120 254 072 997 244 982 494 417 629 305 423 982 962 685 338 132 273 711 361 431 044 398 488 579 070 016 321 384 589 078 399 162 090 410 639 202 567 692 398 049 471 350 427 943 170 350 990 322 378 324 107 799 531 672 419 158 070 637 887 093 910 608 952 572 937 532 188 538 454 862 048 403 508 388 928 220 552 981 018 588 441 263 226 368 467 732 156 519 464 322 316 691 935 654 630 778 281 252 144 797 406 971 473 325 771 446 615 230 313 130 783 662 240 658 058 423 765 548 864 771 809 186 567 917 907 390 219 022 235 905 032 574 380 896 444 207 003 781 223 600 633 110 408 009 956 223 199 559 627 396 536 535 249 000 693 182 274 566 492 360 444 367 606 705 353 344 176 121 918 305 435 427 142 304 630 647 849 090 931 347 115 506 976 553 174 786 941 605 519 104 732 692 287 174 833 187 732 356 794 825 171 673 669 023 579 937 062 270 934 606 814 839 584 239 124 251 010 863 136 417 570 360 381 244 242 550 045 884 435 073 809 786 645 837 220 678 358 018 127 784 105 497 118 584 603 169 278 175 588 724 945 168 864 065 582 235 183 453 498 498 964 635 699 410 794 263 981 056 149 899 689 454 974 466 717 464 017 750 025 384 657 187 806 678 177 611 718 400 485 270 161 926 195 210 171 362 452 568 624 699 207 389 021 683 270 339 572 744 888 957 495 148 090 139 816 218 484 848 124 629 755 077 886 536 435 430 803 780 914 104 325 383 862 375 437 017 179 970 715 088 745 353 936 266 993 463 329 713 789 504 012 832 437 654 595 730 311 021 773 782 295 289 887 702 965 317 637 828 934 989 833 733 755 451 077 705 347 621 908 393 659 974 963 257 063 551 514 306 721 333 237 141 248 068 285 222 283 218 599 812 244 215 333 757 538 255 674 376 585 157 920 235 337 749 300 553 280 135 326 280 981 515 052 130 442 449 583 986 425 329 008 401 701 695 066 585 603 047 655 832 595 722 266 921 602 111 102 031 602 825 187 749 414 000 102 867 291 296 601 102 840 709 566 606 626 676 846 988 404 506 485 341 640 941 829 231 883 574 092 434 783 289 381 865 366 399 896 606 866 589 503 205 847 878 423 444 162 519 293 389 879 274 069 824 890 750 988 614 273 383 080 776 751 978 073 770 888 451 743 820 942 052 900 972 706 786 896 911 243 497 626 516 503 416 378 614 080 063 997 554 189 134 848 582 699 528 110 977 003 637 780 512 461 494 712 226 586 584 536 121 520 291 006 510 835 859 438 410 345 002 180 609 036 011 431 990 349 338 200 228 715 386 643 172 571 120 068 874 229 718 773 577 828 317 484 438 291 365 627 611 961 019 189 389 637 471 704 965 541 136 021 157 133 269 765 983 991 557 413 040 810 616 055 642 585 549 473 804 266 339 566 362 807 801 421 187 407 821 325 958 556 646 942 197 114 378 637 146 209 880 616 484 823 084 240 594 720 900 966 751 633 811 192 620 320 810 802 800 151 613 299 777 195 173 583 412 784 833 129 105 435 591 590 721 008 960 670 136 337 952 441 692 412 826 489 348 258 868 968 909 056 750 446 731 235 795 326 044 277 239 832 218 711 804 761 375 586 014 171 199 135 157 674 849 595 901 386 821 342 529 059 414 705 440 597 494 504 256 753 575 013 646 773 458 706 529 208 307 250 392 856 499 025 738 418 255 589 765 668 808 713 655 526 287 365 820 508 602 758 468 692 361 873 771 305 609 687 054 668 170 010 259 587 125 008 971 050 515 559 269 397 435 320 161 687 534 272 034 897 180 423 919 825 989 358 483 709 211 949 943 493 567 863 805 226 118 317 696 197 771 252 875 056 862 797 579 440 452 906 561 266 626 114 402 189 479 343 841 817 541 361 683 815 953 354 394 068 763 471 373 829 411 228 934 323 246 169 387 556 298 426 217 658 897 929 890 134 672 915 037 307 421 722 824 531 710 986 950 356 276 336 378 484 332 724 635 510 903 954 297 286 198 986 272 926 013 034 749 244 735 019 137 521 302 435 694 732 676 921 824 250 194 596 036 316 912 708 178 872 039 026 627 869 468 163 166 113 247 601 820 847 587 334 223 227 593 111 906 356 268 719 969 456 949 323 685 212 466 282 464 461 768 873 087 930 933 531 509 388 074 723 127 601 392 935 407 777 670 375 814 703 297 838 351 544 247 512 927 735 912 222 097 280 245 830 474 662 508 360 348 528 895 691 487 210 329 945 156 436 543 987 614 957 427 861 359 151 019 511 033 620 588 475 021 919 613 455 395 302 928 971 409 100 602 193 170 684 506 298 347 081 269 900 136 977 287 432 025 351 409 379 332 818 194 231 165 676 997 325 520 372 752 881 812 866 565 340 308 267 480 079 266 950 816 104 231 234 901 015 862 801 019 764 122 084 042 899 617 378 996 547 014 529 573 174 612 715 229 706 062 863 417 724 444 673 984 942 662 407 968 890 920 186 783 146 890 106 328 922 454 946 396 849 155 471 968 897 932 434 080 657 580 588 877 846 997 986 801 062 526 602 166 550 263 173 786 829 596 302 471 907 474 811 378 969 131 301 878 711 295 154 650 379 860 236 462 668 680 585 003 819 864 700 006 479 996 639 420 890 787 721 592 151 610 623 466 001 908 574 060 233 208 826 633 118 805 161 800 210 589 313 296 735 496 591 147 339 480 043 443 130 632 468 657 779 384 686 634 830 349 276 816 756 897 106 861 118 645 993 236 572 783 658 899 843 097 271 542 008 734 235 455 956 125 555 150 990 767 904 662 089 932 867 795 248 323 181 211 405 608 949 623 517 144 378 540 468 152 446 254 710 222 588 852 472 706 019 815 639 265 933 986 357 591 216 128 779 352 589 146 316 954 298 305 908 103 787 300 135 704 932 136 505 590 484 366 919 990 855 939 824 578 123 124 189 486 330 725 935 903 060 311 861 027 401 359 756 875 158 602 722 330 419 533 308 189 724 203 957 591 456 509 414 993 869 294 407 546 402 535 921 610 591 895 023 411 920 734 058 660 313 703 970 517 206 320 839 991 829 485 756 235 970 592 646 828 992 158 174 592 971 435 513 454 230 104 110 193 734 265 459 997 091 652 183 585 829 384 921 724 675 745 517 906 218 109 626 459 850 629 748 723 928 924 270 268 833 186 887 425 884 305 238 030 103 406 977 284 042 428 770 249 408 410 495 728 235 242 789 152 423 170 626 961 612 623 250 733 255 337 190 353 567 942 829 247 953 600 406 417 822 811 402 581 712 478 420 906 622 690 221 645 684 182 686 708 652 813 392 117 865 274 588 949 410 256 934 936 719 699 545 649 072 731 866 196 006 758 410 917 336 258 780 309 824 343 917 451 046 712 612 540 242 358 232 400 155 788 917 710 512 616 955 909 076 604 367 827 729 017 872 401 778 034 196 849 077 237 387 181 264 293 266 871 028 879 434 087 582 867 314 460 968 781 802 968 718 136 586 485 729 754 185 625 732 856 832 373 122 233 395 233 004 824 517 040 828 713 555 700 645 730 234 031 949 489 422 894 920 101 293 267 812 677 751 900 382 594 104 772 188 301 227 596 373 611 780 980 503 049 207 587 697 089 055 186 205 420 984 118 610 773 392 079 221 534 682 174 971 238 186 393 524 904 223 115 234 761 559 732 312 482 411 803 994 509 447 211 389 814 294 822 357 269 558 859 377 346 103 126 482 967 772 592 788 308 942 850 838 301 517 469 910 807 547 342 941 913 145 645 346 005 609 444 108 758 889 986 135 982 697 267 540 941 018 218 011 593 121 410 425 936 632 081 638 589 082 866 423 689 131 664 697 391 540 286 755 406 668 057 644 134 208 736 845 355 898 300 758 992 359 475 350 789 441 064 780 786 890 129 987 132 991 828 922 815 978 406 237 538 662 671 915 526 711 136 834 070 812 607 064 917 199 631 079 468 529 463 010 550 885 413 472 705 918 795 352 468 686 140 244 370 639 842 005 739 730 997 247 053 112 431 937 603 501 477 122 924 161 389 633 986 613 900 265 822 736 080 857 504 221 817 833 629 664 839 143 705 577 276 664 850 431 716 465 317 313 891 027 702 049 195 073 026 418 178 148 576 065 369 391 173 518 714 733 928 764 456 075 811 035 849 181 312 488 884 256 882 653 027 923 938 332 508 274 298 217 736 160 904 180 810 397 281 186 223 825 112 026 474 372 204 334 089 368 396 838 972 215 637 353 509 547 052 179 944 208 799 435 301 897 325 928 507 803 261 783 825 057 448 952 739 324 794 560 743 467 463 321 929 022 909 810 036 392 541 523 550 057 450 041 124 659 620 737 687 685 537 929 719 272 967 036 249 173 497 432 106 896 272 357 280 635 319 468 774 831 713 290 754 908 161 474 195 584 896 852 466 841 597 973 117 585 018 470 739 406 068 311 415 066 906 941 141 449 670 625 272 569 449 411 933 974 257 167 911 810 549 584 980 006 192 820 126 076 706 681 818 626 297 614 231 370 387 279 168 230 281 521 609 439 097 101 248 919 627 279 156 894 752 500 386 764 435 010 138 430 408 344 117 523 026 288 008 411 101 550 882 755 900 785 850 958 366 375 210 243 881 396 664 237 131 415 416 886 435 347 454 410 780 574 403 219 887 877 827 897 327 611 600 201 675 803 547 762 981 586 294 055 195 002 885 370 941 725 114 014 535 445 576 431 484 803 353 404 968 433 737 837 791 128 559 475 250 497 102 591 724 870 270 780 827 001 351 812 767 018 987 375 982 767 603 267 008 920 840 914 830 511 122 719 581 162 476 954 437 494 080 739 147 294 025 939 542 053 027 777 893 497 802 476 543 511 521 513 297 043 038 848 620 469 031 001 353 042 530 349 038 927 126 100 766 094 390 599 684 663 575 206 654 414 988 684 852 541 848 351 790 743 023 048 638 674 691 468 007 993 406 903 685 630 911 038 045 478 782 644 431 755 296 254 922 251 620 013 261 939 208 572 041 155 038 939 398 693 173 524 888 343 371 796 470 469 501 792 210 255 109 244 602 557 277 696 394 233 887 835 740 060 048 794 347 378 017 140 773 161 852 532 878 569 486 181 901 028 903 549 716 472 832 787 870 706 435 519 257 323 625 098 050 009 824 255 879 825 535 958 139 963 549 048 902 478 054 761 004 441 882 120 626 108 377 611 012 027 947 630 731 656 006 948 604 142 725 396 825 505 806 645 304 773 774 460 853 934 237 217 395 140 405 533 522 365 566 223 029 683 602 365 047 902 528 277 395 943 128 834 172 010 935 926 058 600 432 518 855 676 481 783 449 509 692 490 208 732 143 477 386 516 059 102 851 479 428 243 877 248 390 087 823 613 562 156 454 783 992 675 119 314 054 009 957 434 849 736 827 373 589 031 790 128 196 847 303 012 233 772 377 633 103 325 294 373 376 155 454 936 802 315 786 255 768 188 572 525 494 541 809 058 629 396 593 924 897 079 204 206 344 063 869 568 536 980 222 737 531 068 845 615 286 643 303 977 246 700 611 836 366 308 441 907 680 227 186 412 097 665 162 670 573 185 151 149 945 391 043 753 671 393 734 362 263 155 080 819 458 912 466 196 857 395 127 956 586 934 212 949 081 673 788 319 637 496 805 919 123 094 985 700 559 773 178 519 892 561 745 956 942 520 098 135 529 622 486 434 014 134 094 105 423 844 281 507 417 712 544 741 342 877 789 252 705 328 519 301 422 623 217 159 124 253 571 924 548 792 233 832 073 414 617 076 488 475 924 866 112 797 656 324 698 154 934 501 131 390 277 008 709 541 230 310 781 992 200 100 227 617 185 010 901 505 756 313 623 997 961 793 172 043 712 123 804 778 900 839 382 950 455 472 258 870 596 318 922 333 582 196 481 150 384 756 617 252 439 739 590 844 486 121 735 784 625 098 566 925 307 246 583 259 443 818 653 361 394 534 155 133 111 110 679 332 659 212 919 412 725 155 385 861 866 958 333 043 938 262 423 805 097 711 512 148 282 046 543 467 322 963 855 551 587 075 328 426 520 707 476 727 278 425 966 885 210 526 872 555 047 917 378 235 470 045 160 224 178 021 208 269 527 979 461 607 002 963 571 288 603 683 749 804 384 907 766 266 091 698 182 132 546 834 495 777 524 071 656 788 796 875 379 922 024 560 972 601 636 039 777 148 897 260 563 295 677 620 872 720 291 009 130 866 715 562 249 016 432 119 930 880 473 173 656 487 153 553 513 262 464 822 075 367 038 370 006 694 964 595 141 435 770 373 863 435 850 528 589 426 992 672 016 508 648 994 252 143 895 417 507 296 767 656 421 410 695 697 174 777 393 902 845 367 737 443 197 301 818 139 435 870 367 897 810 936 932 914 399 863 022 892 296 601 550 270 481 500 581 629 964 437 495 204 434 884 031 922 100 035 690 780 817 745 420 165 442 291 527 456 851 730 954 840 767 642 709 306 257 883 932 057 527 030 310 072 996 575 223 256 452 376 786 929 489 564 746 316 073 669 700 637 550 889 029 030 023 990 215 245 111 878 983 742 733 636 071 368 308 139 215 721 440 538 557 403 005 152 528 450 255 120 948 603 131 493 007 190 782 855 293 795 525 487 656 391 499 285 324 252 804 723 964 753 519 568 633 075 085 003 810 099 506 854 465 405 147 106 362 720 853 891 621 534 799 330 737 489 621 851 294 827 368 916 858 761 204 926 185 203 260 470 417 540 449 674 268 940 625 996 629 126 092 785 367 925 656 372 504 555 703 241 526 970 818 744 268 260 697 579 453 093 996 993 777 008 031 391 944 621 934 228 949 611 016 377 232 218 388 064 870 700 167 325 384 583 723 540 724 662 071 696 685 174 476 421 432 602 372 516 800 994 911 686 115 299 954 377 742 794 468 664 041 160 693 783 703 399 668 203 527 297 260 055 290 364 859 627 011 196 005 194 340 323 915 657 526 960 086 759 117 763 586 489 238 017 050 966 476 419 895 125 949 671 639 705 266 116 452 165 016 825 288 209 563 426 974 178 483 889 264 411 988 201 828 968 666 705 003 919 170 549 395 402 862 972 846 385 532 026 113 121 759 900 104 739 403 401 417 277 693 178 626 073 821 028 297 787 493 579 807 951 969 083 174 856 870 887 326 293 355 610 658 446 296 718 751 445 312 863 535 181 992 448 943 497 323 473 306 843 525 697 675 601 966 625 019 987 226 923 945 877 258 617 451 387 425 205 714 166 958 631 955 968 998 815 333 591 429 068 942 006 079 575 120 139 952 481 192 755 096 946 343 577 769 942 018 306 590 660 541 560 123 259 209 236 601 088 838 030 027 182 915 268 580 155 328 948 728 720 390 418 736 022 433 070 034 392 053 266 349 868 298 003 358 001 359 558 643 147 299 972 117 436 900 708 357 074 497 411 502 035 648 952 732 068 580 688 942 021 785 652 680 521 830 684 709 650 140 160 658 407 950 190 654 348 751 101 604 128 533 304 957 168 358 200 498 959 457 755 562 537 067 974 033 993 000 452 873 907 867 941 336 017 920 881 630 564 294 069 061 233 667 641 441 005 607 165 814 445 274 976 063 077 560 976 081 468 319 841 133 556 642 440 438 433 915 447 875 898 046 755 711 147 429 608 477 138 094 146 078 525 255 858 286 155 104 690 392 316 845 467 086 580 825 927 720 673 447 436 440 945 758 098 291 175 177 457 367 749 311 245 805 402 637 662 904 032 629 674 402 503 898 068 157 439 364 291 065 536 974 553 135 005 493 911 346 537 166 165 030 227 864 459 920 042 418 744 412 598 643 265 417 033 981 065 459 930 019 791 814 319 003 212 594 310 611 004 030 213 756 301 445 559 337 958 119 365 259 892 470 580 731 803 508 502 881 892 278 346 765 889 102 661 769 966 830 003 588 597 941 566 956 177 138 182 471 546 125 182 818 883 091 079 700 238 056 069 209 847 666 463 107 043 081 576 064 327 515 230 637 079 627 484 850 368 198 201 722 247 040 896 118 162 404 745 314 205 997 282 912 974 445 147 998 266 746 869 401 240 246 960 881 832 746 045 854 281 842 801 604 176 114 481 112 878 739 649 081 708 166 787 980 292 170 444 640 505 875 054 065 452 358 962 011 109 238 482 746 452 722 043 544 376 201 516 647 629 003 646 481 392 287 051 572 410 793 901 778 669 882 392 411 808 827 313 504 579 471 844 419 422 333 330 823 831 824 890 807 808 635 150 277 379 723 916 932 186 508 936 082 059 272 689 786 687 289 965 715 536 436 778 386 702 603 107 202 392 404 035 110 805 988 299 526 116 936 160 013 387 911 155 633 329 550 857 141 789 050 272 465 374 011 047 453 161 192 227 329 784 274 733 181 372 525 071 453 773 718 870 140 636 885 913 655 894 556 786 806 038 756 979 656 171 310 938 917 686 865 319 715 789 452 244 045 511 359 971 725 070 640 047 370 403 332 556 317 053 629 670 634 187 340 608 009 183 722 467 268 613 267 373 609 507 018 940 331 035 023 552 538 626 599 434 603 863 111 132 402 172 720 799 647 177 877 692 426 092 325 361 095 881 929 665 926 755 049 204 283 707 428 199 734 524 769 537 215 622 469 695 202 152 525 846 047 104 321 498 711 728 882 370 943 473 377 007 622 238 256 584 942 354 205 821 672 690 331 000 011 755 404 857 055 502 620 451 599 354 510 113 914 097 352 658 953 802 757 049 019 952 960 822 236 306 323 983 772 801 269 843 046 937 279 823 356 486 879 364 212 625 631 224 936 139 715 688 822 773 422 871 425 453 263 928 972 841 670 012 823 679 512 803 421 126 595 031 344 857 311 876 634 318 586 554 307 839 081 819 974 000 250 303 776 266 464 933 321 883 495 654 987 261 094 555 789 151 083 648 400 812 660 398 576 053 320 493 407 946 123 871 603 067 744 067 467 057 160 114 253 243 706 675 070 113 383 875 759 856 669 108 281 124 442 998 335 004 953 413 354 180 490 626 664 642 087 398 631 805 940 736 732 983 053 182 240 571 401 743 754 051 294 484 829 164 230 274 671 888 460 912 405 385 319 325 519 637 499 692 278 753 237 594 212 315 189 032 783 978 338 729 423 134 790 762 398 327 131 151 162 424 952 468 341 040 072 313 772 340 314 398 501 625 250 428 898 169 235 443 739 599 329 222 936 170 519 175 893 629 052 837 537 314 553 769 724 260 438 311 136 608 923 500 314 040 132 157 386 515 461 024 765 712 311 887 006 701 648 639 682 917 040 749 234 089 837 342 791 140 349 513 201 776 753 229 824 666 842 640 318 463 680 205 912 188 729 643 236 122 240 432 781 843 961 018 769 012 224 959 492 366 168 596 515 393 796 407 015 874 870 013 234 840 044 787 611 664 074 001 500 258 291 929 261 008 879 028 372 172 958 946 332 477 443 537 969 081 117 469 031 315 208 742 724 563 747 137 259 799 951 877 138 833 465 848 527 604 615 240 610 748 700 424 269 940 942 053 040 930 927 365 616 795 027 251 342 865 060 269 239 109 408 730 613 324 050 886 576 877 646 738 476 079 889 211 065 760 546 500 626 922 176 369 981 453 397 389 517 728 200 053 945 416 489 375 777 201 897 436 502 320 434 139 395 838 084 498 421 691 433 273 127 075 461 810 143 101 009 815 954 925 254 894 412 090 527 197 941 933 128 365 239 508 843 458 865 396 817 740 214 436 140 061 893 840 551 597 604 389 117 752 779 065 601 364 336 425 294 498 307 419 847 287 090 548 795 130 944 336 095 537 228 339 948 817 112 860 919 003 229 418 238 830 347 032 068 171 085 548 577 784 615 414 822 454 570 767 625 611 020 674 829 327 101 422 295 219 324 688 679 928 680 208 940 104 075 673 870 886 908 391 495 998 973 877 021 821 367 406 270 224 449 355 129 305 967 598 916 664 002 579 767 126 427 454 416 904 282 152 986 433 771 648 734 452 163 044 295 534 548 276 279 621 666 840 655 952 088 565 148 338 956 233 634 200 634 550 025 554 999 178 258 268 514 024 429 815 665 260 970 479 389 863 931 488 490 008 727 929 189 097 151 528 997 812 597 934 615 450 723 094 836 525 682 755 860 975 641 763 765 949 557 507 240 769 064 558 892 884 697 371 631 191 251 470 504 200 397 528 155 753 731 291 158 908 013 724 552 606 314 481 704 576 037 245 385 013 997 334 662 422 529 389 139 120 100 996 983 974 881 515 130 603 793 400 672 762 292 704 500 247 872 450 017 493 060 477 320 416 241 578 698 403 305 692 122 002 820 692 228 915 231 354 193 819 916 110 366 231 282 142 860 437 104 558 906 166 444 031 800 684 975 031 209 403 364 946 854 438 781 032 638 730 099 249 393 336 969 098 704 765 019 146 700 717 748 836 563 545 895 925 172 890 810 820 612 345 803 500 932 926 685 545 345 366 245 337 924 358 626 818 876 110 415 826 169 578 902 505 317 126 586 376 658 882 120 637 668 233 367 361 627 222 893 470 685 024 095 231 059 355 993 282 553 038 038 591 651 614 840 289 824 106 196 172 350 613 293 538 092 115 599 897 440 376 305 530 636 284 598 871 548 637 640 387 269 751 706 914 882 230 728 740 366 798 646 215 712 733 821 677 313 159 540 753 762 378 648 489 827 252 974 856 820 593 941 742 410 717 496 379 932 423 907 869 901 096 592 992 065 213 974 682 291 775 989 084 280 448 340 459 236 600 456 725 995 702 645 778 465 487 429 260 871 045 568 247 311 643 270 937 404 439 175 185 144 876 469 780 174 203 145 462 743 854 095 908 154 695 951 343 403 703 503 718 933 107 273 312 275 406 241 813 457 379 124 221 164 873 074 194 580 788 003 017 070 044 066 694 717 547 396 823 475 273 318 219 898 156 046 312 194 255 995 197 618 046 340 571 836 302 737 333 522 389 621 014 537 662 343 203 308 087 758 026 031 806 793 629 615 402 478 384 757 587 381 108 426 212 012 009 416 641 400 465 165 360 947 997 427 978 775 560 392 741 893 700 138 995 896 231 831 682 228 569 360 253 198 210 379 373 846 204 317 860 732 644 018 252 075 988 924 270 986 108 276 681 305 890 722 741 780 010 882 545 121 868 502 189 714 687 288 775 906 227 833 125 662 325 368 991 878 404 102 139 660 960 686 485 111 342 245 522 379 689 645 060 907 155 350 508 585 639 860 394 863 071 750 038 603 669 654 167 718 951 325 236 468 942 568 694 288 866 505 797 822 296 758 696 408 861 469 824 237 044 799 853 975 766 905 687 530 479 715 272 086 044 348 234 972 923 225 166 341 944 234 391 755 473 658 057 924 168 903 490 958 903 409 689 312 132 936 281 691 456 336 076 577 811 695 983 113 009 615 868 133 835 159 088 954 164 920 479 532 141 373 229 532 231 767 150 091 254 137 394 366 147 148 146 312 589 954 976 908 018 278 730 918 834 802 616 109 920 795 281 222 058 066 809 077 342 345 946 993 573 476 076 795 765 946 154 772 272 670 722 532 775 155 807 366 486 172 006 813 273 105 923 862 529 771 943 004 259 846 231 427 200 057 987 015 012 968 117 305 254 669 519 371 153 637 978 208 115 067 519 051 117 555 446 314 048 907 715 312 604 254 631 191 192 971 777 634 529 194 580 902 962 984 263 868 892 483 624 897 551 079 184 407 776 654 198 131 341 249 466 832 339 364 602 796 642 136 005 699 173 296 140 396 227 948 875 225 007 964 784 393 739 168 181 170 814 708 639 527 556 806 662 387 054 775 400 031 415 542 240 861 650 081 887 160 178 617 680 366 644 980 073 744 243 728 690 988 478 693 566 704 503 597 624 694 258 951 828 084 937 816 553 694 272 679 083 154 005 008 886 398 313 918 946 980 902 530 268 855 659 001 636 585 841 197 333 279 370 045 595 370 934 333 246 252 860 872 664 094 930 421 148 409 546 893 437 019 026 124 586 813 712 999 774 562 979 729 674 311 755 701 230 253 679 241 853 606 018 853 254 452 884 627 115 596 430 540 186 800 682 387 193 819 089 727 064 740 176 218 974 012 957 496 139 298 978 432 180 263 760 166 578 985 905 198 773 568 958 783 899 260 900 395 672 992 816 362 712 242 174 659 786 560 767 661 346 348 260 282 000 678 726 711 098 632 998 654 678 156 947 630 273 139 687 165 985 551 076 857 211 081 692 169 936 642 660 627 164 927 604 473 395 460 744 236 309 634 499 336 225 761 540 467 487 979 238 018 564 604 747 780 917 659 425 661 776 096 844 991 973 219 375 023 218 427 888 688 788 614 259 293 233 692 448 770 506 420 243 476 198 291 120 883 957 930 474 482 303 767 257 380 924 348 187 272 417 917 246 533 490 903 121 922 277 632 134 143 172 774 460 285 356 224 027 506 259 946 653 418 466 052 118 432 716 537 973 442 510 159 239 612 330 045 003 730 448 717 614 891 808 196 963 789 949 378 887 672 876 784 502 402 838 250 083 875 501 412 686 588 866 376 277 193 373 383 876 959 543 477 698 781 421 395 636 045 574 091 267 007 676 718 115 039 709 112 356 083 150 827 315 519 006 534 866 997 203 544 421 812 385 600 108 968 897 350 993 794 608 889 630 145 569 381 783 385 888 330 421 449 783 751 010 966 969 217 738 517 666 844 792 282 104 203 608 512 747 803 110 657 520 002 635 601 368 620 897 693 377 772 820 918 792 341 676 663 983 804 229 583 838 294 253 077 186 895 956 885 166 210 959 779 756 544 924 426 131 763 305 253 300 841 616 902 822 159 322 773 481 116 843 194 437 411 791 902 810 985 987 369 535 110 348 526 126 212 839 613 187 596 492 209 636 433 008 230 018 001 219 013 251 249 538 423 824 158 222 321 839 457 830 159 231 896 953 412 131 278 785 287 466 755 266 939 133 973 320 846 136 549 263 487 006 189 580 415 838 110 027 000 657 519 249 874 425 521 583 341 727 793 547 476 020 037 381 095 882 452 046 588 528 272 480 008 096 881 056 833 500 122 500 416 644 178 188 390 113 090 376 664 158 612 062 151 760 371 628 989 571 573 467 095 333 680 741 969 684 743 102 168 853 255 953 275 633 830 594 930 706 794 039 370 995 024 569 494 709 182 800 584 191 553 723 771 041 312 866 457 572 025 823 157 456 139 787 636 435 407 431 342 043 099 505 257 950 514 184 979 982 194 896 395 553 348 010 281 351 560 835 879 016 238 554 157 024 316 547 550 232 084 142 883 849 993 271 548 722 492 227 517 878 176 299 599 583 283 150 018 378 011 420 323 594 623 958 259 806 603 581 034 138 117 420 483 053 240 499 588 882 646 204 234 720 282 004 662 478 600 088 980 888 295 171 387 904 049 910 804 989 001 256 537 292 027 940 049 648 629 276 598 878 904 826 957 236 828 886 862 551 884 026 883 190 301 047 527 959 478 287 540 502 874 512 665 388 312 818 345 657 463 373 319 403 319 907 351 394 757 924 339 579 911 753 192 606 850 234 464 098 224 982 442 327 702 572 600 342 158 269 322 239 606 842 406 852 296 193 684 981 931 437 234 279 433 451 863 397 893 644 675 777 409 299 804 256 892 589 718 883 587 832 876 727 210 152 311 578 505 200 210 708 528 290 389 918 204 090 652 477 769 025 223 765 809 504 486 525 033 075 929 967 754 695 099 373 695 064 679 902 771 575 368 014 353 158 357 257 967 156 258 264 664 114 249 374 462 091 470 411 646 848 613 892 508 220 617 253 952 032 334 476 602 175 275 079 472 842 160 865 050 321 899 472 699 729 388 505 919 329 646 294 675 468 859 019 768 772 547 185 872 718 321 839 350 071 998 743 102 977 824 892 858 689 598 329 602 043 727 982 588 281 086 289 748 118 333 472 236 584 896 609 392 081 517 270 354 925 547 765 494 137 844 405 511 859 160 814 449 107 377 368 340 773 204 482 342 153 125 394 944 204 891 551 745 120 493 971 248 162 492 751 008 757 563 366 370 563 110 786 366 707 417 886 339 075 478 043 425 545 162 490 523 296 387 723 363 706 042 211 123 428 956 126 938 576 064 342 229 585 941 049 785 878 674 048 666 242 300 464 901 235 012 736 905 395 529 969 847 767 272 689 681 329 627 793 522 495 246 524 435 387 173 226 296 097 876 210 963 236 362 743 948 403 678 486 987 739 419 257 092 415 204 315 135 832 258 137 358 659 118 250 220 324 894 260 757 492 791 785 950 600 085 247 335 515 661 539 324 786 934 609 989 017 125 742 476 540 506 738 147 917 271 718 334 121 652 519 749 002 334 221 336 480 596 869 885 237 597 353 349 350 726 057 212 697 366 675 901 791 886 625 815 027 792 964 697 854 335 271 282 184 986 431 843 799 891 164 294 430 902 184 892 452 586 165 445 288 662 733 003 585 192 165 322 139 857 559 444 477 532 825 161 412 061 648 306 755 383 161 093 229 855 837 233 256 877 089 402 716 590 610 201 737 546 578 353 969 071 896 816 275 010 986 124 056 495 445 967 235 384 340 823 460 692 614 719 102 579 849 899 225 578 809 359 429 177 752 326 485 988 596 023 333 884 603 390 812 506 403 979 318 171 724 609 169 531 106 957 290 869 813 996 165 758 560 310 706 645 963 844 677 580 216 531 473 008 880 563 102 073 993 262 488 292 286 823 871 089 752 069 605 123 504 858 267 930 827 286 084 716 980 823 998 569 233 576 858 808 919 926 401 675 922 527 845 248 370 929 111 806 985 075 085 053 556 606 799 748 629 050 192 950 571 795 822 114 267 168 526 520 980 806 457 823 489 755 782 751 009 726 269 838 933 240 214 691 092 856 040 508 264 840 929 339 128 138 699 384 823 380 391 460 804 218 460 395 184 359 666 655 662 922 975 488 320 841 761 023 331 837 041 898 527 332 073 618 140 297 915 222 619 440 478 837 816 023 430 250 457 661 012 531 690 521 498 635 852 988 536 253 161 332 052 695 380 532 098 813 067 815 774 316 492 866 475 086 876 474 281 445 701 475 461 536 488 024 852 585 081 694 007 377 752 508 028 055 472 657 999 439 602 416 344 939 771 843 558 973 228 626 531 326 672 328 509 060 576 837 677 861 697 467 057 985 324 568 541 546 516 178 552 407 071 303 483 443 785 346 989 750 900 339 414 398 740 065 895 937 075 316 615 899 942 811 008 109 898 739 460 363 308 788 006 606 405 074 581 773 465 948 181 426 848 588 238 769 544 602 103 724 631 759 901 640 238 570 287 418 899 116 718 770 641 927 078 365 331 642 226 347 793 371 681 772 522 981 898 320 720 160 330 399 925 628 746 083 247 779 638 067 033 101 348 606 681 353 512 995 427 942 314 795 541 254 493 517 363 186 862 551 067 450 901 365 826 599 079 453 828 772 606 891 379 315 591 887 250 262 936 213 498 444 941 961 656 102 627 425 880 695 917 868 135 546 883 465 687 416 002 933 641 691 467 267 909 955 190 687 049 885 897 403 514 220 707 181 346 298 692 996 085 153 611 886 866 803 334 605 175 734 417 246 394 514 096 542 666 426 084 252 067 650 516 728 067 402 310 563 477 378 569 987 924 346 860 817 729 268 455 565 086 615 025 750 552 026 477 369 881 720 887 020 073 664 454 028 386 591 122 327 993 845 687 657 074 621 147 348 298 037 227 781 505 730 787 194 766 299 893 148 445 972 204 333 171 275 435 914 122 454 130 482 856 719 693 872 331 752 594 842 365 808 204 321 526 267 369 388 012 910 475 643 175 245 422 492 263 990 232 428 350 322 982 296 780 993 680 820 014 550 524 100 460 905 211 927 232 221 670 373 054 471 216 001 454 123 790 888 886 729 356 618 745 477 378 879 251 320 501 723 078 904 519 404 752 128 842 009 161 772 401 496 095 809 576 854 145 435 184 071 160 560 663 798 387 253 356 764 990 441 016 553 248 019 346 811 284 199 862 470 562 509 736 848 465 524 359 790 686 532 278 403 767 837 067 238 556 073 748 125 101 475 249 764 346 891 684 491 542 086 804 067 307 702 391 256 404 894 857 538 771 322 679 953 602 938 497 497 290 133 192 632 378 175 068 220 222 375 519 973 076 534 451 521 501 226 389 926 406 130 477 533 051 687 871 751 190 548 760 914 671 520 593 227 239 170 551 349 621 265 852 935 618 315 862 050 924 240 653 691 368 466 041 545 068 647 766 714 221 463 866 831 847 037 214 646 339 984 309 487 178 582 334 678 539 617 879 094 683 675 380 511 677 837 602 563 723 154 741 542 878 848 470 860 244 485 755 578 007 191 747 102 564 618 476 066 584 180 927 046 239 768 015 147 606 310 495 835 371 282 452 399 830 761 943 320 239 390 120 205 425 525 052 569 498 936 976 233 215 457 757 565 335 674 741 948 870 057 391 844 991 715 655 071 901 621 919 216 519 347 671 647 718 112 109 149 146 420 887 273 977 203 344 538 269 966 156 983 376 636 424 269 594 203 842 390 775 543 056 549 834 680 153 493 532 794 780 476 695 804 359 677 125 448 243 951 565 483 622 293 425 034 882 214 226 786 612 097 484 090 535 555 361 208 535 044 600 326 529 906 277 834 039 620 140 513 790 310 763 574 298 801 677 331 143 274 654 013 144 213 327 847 351 321 203 276 480 725 987 386 429 321 631 478 500 660 924 639 470 099 579 105 800 463 924 459 546 201 099 570 873 532 395 402 472 223 197 040 303 413 442 291 605 497 031 622 282 627 140 719 220 382 065 346 408 428 327 060 428 975 044 411 591 388 062 921 001 624 233 508 568 180 241 370 977 785 500 110 457 676 803 011 179 965 736 461 425 941 418 558 013 300 193 322 210 122 406 115 406 814 630 744 867 194 725 039 120 738 279 687 517 296 756 321 800 794 511 749 275 584 191 611 901 139 918 324 374 405 636 409 428 333 125 864 886 173 239 230 730 969 002 871 672 614 241 964 191 236 627 929 981 616 339 936 260 102 720 812 336 419 217 759 216 205 881 650 121 128 882 225 696 476 361 801 958 515 490 869 316 958 235 299 782 939 299 470 414 351 749 964 709 659 074 952 750 875 034 273 388 367 689 842 210 299 066 380 205 039 103 030 789 439 127 755 530 703 433 180 482 100 585 893 614 194 638 063 867 752 402 204 976 906 109 652 173 763 798 749 753 929 569 765 644 418 493 997 802 343 682 314 376 498 320 583 241 733 293 317 624 032 759 712 222 029 867 669 985 868 085 834 789 537 688 139 864 743 577 095 915 939 378 547 541 182 754 370 590 180 003 640 111 010 459 212 716 046 194 729 111 855 471 806 656 138 289 186 049 852 452 950 482 536 720 064 631 146 292 970 676 668 053 033 540 184 920 614 772 584 536 959 539 889 586 778 294 220 298 246 939 335 972 582 310 755 762 146 688 027 306 725 671 889 246 085 345 965 355 467 624 728 131 408 731 901 131 534 223 684 378 371 322 716 736 300 986 672 747 410 729 289 254 031 079 150 602 754 296 975 435 469 533 733 503 743 593 694 050 480 858 659 876 378 007 529 824 928 986 421 293 076 671 104 249 227 966 663 200 396 897 505 239 745 898 987 968 515 794 018 947 056 705 922 537 459 288 779 512 528 112 560 076 660 890 473 638 285 972 450 703 958 562 256 675 526 016 315 613 449 653 028 798 673 233 285 514 060 480 146 662 995 679 174 841 843 561 884 569 513 324 301 733 758 188 389 592 878 275 603 295 793 218 110 185 042 801 345 918 330 999 120 187 443 600 342 839 571 770 076 703 937 763 687 522 058 306 740 405 965 498 539 988 377 441 537 318 763 837 735 054 473 329 212 712 363 202 144 871 666 090 188 965 696 515 447 497 378 200 912 028 504 324 550 598 074 529 895 651 084 636 963 053 808 800 151 949 010 093 982 457 046 846 992 482 664 660 730 716 798 216 107 682 682 112 921 569 409 447 820 518 065 665 240 105 258 079 251 566 484 025 217 803 267 124 618 350 279 935 646 938 395 705 638 784 576 630 438 205 466 363 530 887 734 958 122 883 135 935 414 745 013 466 769 979 015 672 530 982 524 752 436 719 748 646 860 316 745 190 953 003 817 665 910 037 454 609 794 718 575 306 732 959 182 337 482 729 096 320 213 800 674 984 299 673 817 485 191 567 164 222 433 325 740 587 935 952 802 757 423 306 163 182 122 526 600 991 440 041 140 943 752 056 092 795 939 239 896 297 934 938 211 654 241 130 672 729 561 478 013 317 358 455 031 507 866 117 789 145 236 503 713 529 509 482 859 227 891 808 091 530 883 632 170 286 402 172 613 461 176 077 091 920 154 280 615 932 180 428 310 673 035 881 828 297 714 407 693 971 403 518 424 195 127 253 653 956 598 144 460 652 392 246 846 021 485 103 659 420 877 978 557 002 490 426 310 950 138 505 982 057 744 307 795 802 961 694 461 714 290 336 622 461 518 929 731 111 397 685 829 830 810 695 521 399 237 941 310 629 941 267 943 688 422 869 974 947 690 622 271 636 222 199 506 083 481 011 579 036 181 207 782 869 733 200 148 172 332 107 981 234 863 873 338 207 993 422 730 696 792 480 099 528 064 695 957 557 180 483 732 281 157 530 808 118 851 366 637 464 902 050 519 870 470 179 022 485 457 421 380 911 391 172 806 861 492 374 700 227 451 397 437 631 763 977 518 596 933 986 155 479 898 304 649 513 886 737 582 933 366 086 342 492 630 496 269 135 861 105 252 389 538 270 069 511 243 353 114 439 417 869 454 460 932 071 783 508 406 509 314 322 698 073 706 298 560 638 430 759 711 907 602 824 671 466 251 733 711 719 719 368 861 295 043 214 721 880 988 115 325 965 375 904 327 393 496 391 447 206 661 394 159 161 955 539 463 613 878 281 435 529 660 968 040 881 882 493 162 739 115 467 568 673 230 553 759 170 693 521 620 630 469 599 284 054 245 791 723 384 083 891 767 118 073 077 193 066 337 832 438 706 086 400 162 888 573 677 428 683 599 400 050 122 023 354 647 731 489 477 437 445 641 129 472 695 553 713 646 109 585 320 135 102 350 543 465 842 180 639 218 784 218 461 981 317 619 551 208 405 140 768 187 795 504 879 477 713 282 863 756 079 710 880 923 460 315 579 658 733 684 336 457 681 105 066 679 243 580 785 074 874 460 760 136 251 336 225 994 782 160 920 197 226 971 012 204 347 334 532 252 212 701 262 668 344 023 380 139 657 513 654 366 380 405 276 325 091 522 170 715 281 233 683 492 474 292 113 779 459 022 639 727 642 656 645 213 151 994 732 472 071 810 335 803 536 219 961 121 698 563 663 880 650 287 614 827 454 026 387 690 615 815 157 140 427 583 573 142 371 437 920 297 940 899 632 865 881 903 135 005 712 035 455 980 503 890 790 565 842 102 013 080 614 096 426 556 298 356 921 670 177 961 510 765 132 347 745 436 391 574 442 393 306 075 275 933 960 977 139 137 116 525 147 083 890 219 112 327 161 621 789 372 274 737 198 537 783 469 700 364 818 619 981 818 203 763 589 041 452 277 656 254 347 457 683 473 387 244 543 352 472 931 263 488 628 725 687 804 880 943 538 128 255 640 411 987 547 060 738 514 231 741 834 184 527 327 001 945 828 235 581 917 470 046 537 816 401 924 636 272 411 122 110 145 527 521 008 725 490 187 117 861 424 282 130 220 197 219 020 995 156 855 343 995 220 172 240 557 100 949 987 592 118 707 352 935 191 305 977 364 322 393 419 377 084 927 542 082 821 247 974 430 573 478 759 065 188 229 315 666 893 479 698 709 573 560 786 782 614 980 526 039 014 850 184 383 542 423 915 550 065 324 904 180 262 391 176 036 735 203 095 197 197 429 291 414 594 860 955 620 563 745 453 790 586 985 675 490 295 840 721 226 928 451 461 108 116 880 171 134 524 622 591 062 041 079 628 218 392 506 698 599 159 327 219 234 176 701 902 785 042 044 398 456 317 767 590 465 724 005 108 354 082 683 225 543 520 144 877 248 020 040 747 352 669 830 426 048 727 762 389 805 887 388 265 809 014 630 383 026 375 729 800 813 173 950 879 251 500 877 179 453 427 203 513 715 111 740 219 859 226 713 705 959 041 066 105 786 134 187 494 503 858 964 771 272 572 148 061 754 177 092 058 813 923 018 226 280 529 890 052 442 811 726 402 652 719 239 038 994 525 433 082 188 147 771 518 813 108 095 344 607 000 851 479 287 132 632 085 750 795 509 992 810 150 147 692 288 639 249 752 715 574 502 542 317 215 321 470 528 310 358 589 329 633 473 949 113 497 241 342 022 303 507 548 622 533 062 465 824 403 267 203 764 378 239 237 012 792 784 028 305 891 889 683 577 737 884 564 537 820 000 571 168 992 034 939 890 050 057 515 691 820 343 355 292 042 175 029 890 410 548 205 386 934 723 193 586 043 068 534 371 723 328 746 622 710 829 229 379 343 687 428 943 784 358 592 491 100 261 855 586 046 380 916 908 566 362 515 169 660 598 325 908 913 405 680 084 590 300 200 829 326 512 323 921 126 298 081 442 145 724 191 986 115 119 876 915 114 516 604 495 097 470 059 979 859 045 949 439 553 929 606 556 676 893 204 511 343 443 275 336 187 484 102 226 460 158 427 460 418 550 006 332 634 981 085 565 414 196 670 748 174 564 814 683 656 504 915 352 239 379 025 827 409 914 289 064 944 012 026 432 724 540 386 914 634 866 112 665 472 293 283 238 095 242 276 211 995 963 695 847 563 246 336 966 373 075 902 940 464 534 480 522 989 290 249 649 860 954 369 655 600 653 711 031 168 227 691 996 496 391 471 108 534 224 573 997 983 151 590 082 306 871 906 107 390 380 742 008 967 838 642 011 815 412 630 837 425 843 263 732 454 852 893 608 343 472 456 681 013 826 102 430 298 771 582 640 574 982 922 554 768 389 830 827 993 413 777 124 131 267 817 538 890 894 587 267 064 213 472 370 906 547 534 699 510 745 851 054 586 914 512 078 095 618 099 792 039 668 282 538 290 880 959 028 457 864 416 180 984 137 048 508 571 393 443 294 781 090 996 847 685 969 542 646 862 294 628 296 178 221 855 808 050 141 360 775 286 277 600 698 034 452 916 982 207 691 674 534 714 668 151 153 272 845 161 054 934 303 468 275 094 400 389 734 384 956 684 056 776 626 842 455 816 615 791 606 868 201 456 196 976 275 273 480 320 706 858 903 178 301 072 851 328 930 934 027 675 408 588 324 428 194 706 540 348 125 079 860 015 719 613 157 164 449 548 541 284 397 568 822 205 936 908 597 761 897 499 531 308 963 574 014 260 271 428 228 382 978 532 136 776 695 365 572 247 141 650 465 180 052 206 497 227 921 889 367 955 062 438 147 313 257 392 114 196 227 998 808 286 890 999 347 917 734 170 684 028 863 246 700 165 984 323 174 077 521 566 349 830 951 300 842 270 770 515 583 500 508 377 031 952 158 384 883 355 342 524 486 029 459 657 474 151 158 635 447 077 979 311 306 418 142 829 391 601 315 993 900 686 569 113 584 784 719 524 445 160 388 439 612 067 544 858 371 558 466 548 279 908 805 599 810 786 291 041 295 872 815 772 808 956 544 247 787 489 926 772 144 045 345 690 385 733 098 315 315 986 092 189 577 857 460 749 068 145 649 343 684 311 378 273 663 205 833 204 560 738 230 520 230 869 879 364 224 004 112 516 245 707 419 561 611 000 868 690 407 614 588 999 848 592 783 900 042 987 195 015 698 245 927 461 307 880 685 368 617 256 444 643 711 778 845 397 788 926 710 530 115 155 969 584 904 856 538 567 880 477 104 425 496 829 919 851 011 285 141 919 741 392 876 876 569 134 097 857 811 139 831 651 535 146 927 195 722 730 536 344 835 595 421 802 423 560 595 930 602 979 723 504 284 615 098 809 781 267 626 171 247 850 375 613 405 287 572 480 363 083 163 276 920 525 720 276 126 213 629 503 069 117 777 072 969 919 314 137 633 053 214 841 910 796 933 658 210 821 514 908 457 468 706 672 856 837 696 135 729 608 361 096 156 352 995 769 067 817 698 115 448 340 186 502 343 006 009 503 679 960 997 102 245 871 151 067 580 688 355 834 688 715 905 323 308 773 388 512 385 643 956 020 673 947 878 204 538 248 159 004 899 274 238 006 928 997 231 933 013 108 814 722 283 545 982 240 277 948 779 826 203 105 694 142 770 679 905 518 101 874 303 906 570 481 806 613 841 579 122 725 112 536 595 162 265 200 978 090 451 926 135 005 490 276 677 736 262 627 423 047 791 541 958 997 370 414 286 682 188 718 619 739 920 592 989 863 730 609 925 135 090 480 014 717 979 599 338 723 081 072 372 070 631 312 885 907 871 864 248 022 458 615 571 397 782 775 021 856 201 965 133 096 859 428 059 545 144 277 968 425 122 433 759 160 776 722 046 855 542 275 741 916 748 791 377 565 798 215 916 603 538 757 425 034 672 793 980 611 944 359 160 953 870 009 531 073 979 380 070 617 759 992 375 437 930 221 382 760 115 909 718 693 530 963 200 000 112 399 481 064 064 215 146 058 315 590 554 610 875 583 962 326 146 052 567 924 162 787 498 673 424 974 420 992 916 159 415 430 130 861 192 412 377 373 234 184 933 184 152 842 811 114 420 505 116 149 665 963 026 771 497 618 134 432 928 940 597 609 211 128 656 476 398 922 267 958 479 067 243 274 406 883 398 561 055 422 814 032 303 124 164 598 624 058 598 827 126 224 650 670 363 254 269 782 931 712 421 369 484 266 521 248 686 037 965 961 873 958 355 819 245 002 971 986 669 865 302 923 248 915 236 026 811 897 271 469 216 287 103 259 231 414 513 939 353 877 120 405 101 437 240 154 012 671 395 477 279 680 237 505 646 657 938 163 005 134 507 298 947 833 786 404 658 157 317 257 164 758 400 554 088 336 570 512 667 917 666 795 002 231 435 845 545 798 673 388 432 580 380 976 663 797 716 932 017 250 913 938 446 896 385 447 863 321 598 832 628 108 039 760 988 410 615 284 023 536 019 911 639 868 385 012 020 845 238 500 551 775 211 476 110 555 588 920 397 092 831 783 469 477 656 397 705 141 658 867 850 385 622 752 125 252 438 133 488 997 946 194 005 890 636 100 058 783 521 946 478 828 212 246 790 222 574 868 821 827 744 356 843 081 874 136 787 190 702 593 295 527 497 065 887 569 894 511 039 670 963 086 676 860 629 415 436 161 230 654 297 475 314 681 091 893 472 936 163 880 043 312 173 435 040 599 353 553 227 303 642 173 641 232 241 718 231 428 639 696 482 306 837 229 348 962 876 369 331 828 324 784 504 221 654 686 336 751 829 931 795 805 431 727 906 079 732 592 515 023 823 225 532 170 977 424 774 346 588 993 263 132 504 089 498 198 893 009 395 443 575 383 642 309 613 188 569 314 010 591 246 546 683 609 645 399 675 884 527 057 940 490 165 049 866 898 125 908 008 894 137 276 623 724 819 441 077 568 161 686 499 275 271 027 750 370 086 679 318 954 909 963 814 254 477 886 639 531 283 989 309 811 334 656 120 335 275 083 503 071 378 336 948 712 141 305 440 112 229 356 553 707 947 219 959 155 096 334 942 456 863 078 096 123 382 891 332 435 437 085 027 150 805 118 937 080 343 219 661 147 682 722 904 895 981 159 627 010 672 590 914 942 243 807 596 455 557 968 352 738 904 733 913 022 250 392 632 237 583 338 937 775 735 984 171 364 125 996 775 247 586 311 867 718 505 228 427 204 663 732 491 872 148 114 734 263 325 161 334 378 149 363 265 556 557 153 086 120 014 781 267 409 372 798 086 399 383 736 203 988 315 264 170 349 897 805 709 080 521 417 836 933 812 517 530 211 359 779 445 755 598 470 195 765 076 754 191 011 521 563 118 502 248 214 452 527 673 109 552 558 580 476 991 178 252 337 763 361 947 509 148 698 590 548 717 790 162 800 928 549 858 364 263 561 486 003 897 084 293 237 287 579 844 238 661 065 689 047 441 966 276 481 726 257 376 046 010 644 484 024 440 778 564 318 938 295 055 810 541 209 141 956 624 758 061 921 924 132 427 238 074 923 363 581 177 215 642 606 125 212 732 338 502 604 480 522 209 344 349 825 307 849 772 742 749 329 925 219 105 382 121 093 679 960 620 835 448 211 446 674 820 952 390 556 014 987 412 221 557 987 262 592 237 720 126 448 164 644 969 111 597 363 263 653 680 836 391 541 823 411 303 494 821 995 980 936 002 274 524 800 180 915 794 154 838 747 674 971 860 999 521 543 860 120 188 758 523 654 158 018 052 969 393 290 828 541 285 590 118 599 306 006 348 113 648 722 913 813 636 814 733 698 177 452 411 921 300 059 472 102 721 122 759 964 276 775 482 664 340 649 441 179 922 537 758 101 018 816 781 306 055 284 421 527 515 932 864 154 274 651 951 456 243 194 104 928 677 338 535 699 252 564 907 535 652 141 151 242 770 542 819 035 257 149 251 364 125 472 209 252 647 161 777 618 006 274 966 867 655 299 078 173 578 750 501 553 261 788 879 261 480 605 028 083 171 821 362 958 875 253 560 822 864 740 484 755 714 332 015 728 361 119 106 541 608 674 630 289 891 655 472 733 863 665 391 511 398 176 334 897 258 467 373 463 928 425 695 524 200 922 147 759 438 097 124 024 922 922 055 629 695 172 951 708 740 489 955 385 357 283 280 531 621 811 868 264 562 232 933 040 107 085 670 993 434 862 581 807 481 279 807 402 245 373 695 074 190 056 952 789 250 417 704 945 913 146 991 674 279 060 583 010 463 299 462 151 262 660 612 851 063 020 135 935 986 965 894 821 888 978 842 023 038 453 091 666 890 214 946 373 529 392 118 754 807 588 168 298 131 254 725 111 401 467 947 590 887 098 838 552 322 496 129 952 628 156 031 374 625 966 066 831 734 614 248 002 832 371 577 054 199 079 233 665 039 936 998 840 128 533 757 086 109 221 748 122 872 977 738 147 011 491 549 711 934 193 343 098 871 234 720 451 590 775 850 462 969 966 666 452 687 015 589 969 182 790 167 748 200 067 313 108 884 563 181 348 757 360 600 670 202 110 172 978 894 887 277 636 444 379 645 859 077 896 217 044 335 335 787 327 695 521 565 455 857 453 091 672 522 469 617 331 461 695 811 145 435 809 812 271 824 731 841 875 635 764 064 030 006 702 791 781 240 390 164 779 222 623 064 780 163 007 471 008 067 914 825 209 248 266 897 082 233 690 755 379 023 881 561 680 046 870 455 521 866 585 916 653 181 867 636 268 425 280 912 108 308 237 760 424 299 136 128 297 246 367 309 247 944 065 299 972 872 611 716 642 523 356 970 449 897 732 616 796 572 304 159 322 725 028 019 379 616 394 695 304 751 145 855 801 932 505 541 423 551 532 410 922 652 537 716 132 220 854 714 660 894 676 613 680 250 539 353 557 911 500 924 366 731 252 139 868 102 548 232 269 449 390 580 338 908 953 535 525 586 367 284 813 356 238 629 789 092 888 408 607 946 124 942 790 003 927 998 039 727 407 266 023 873 864 152 626 398 973 506 038 786 105 315 652 160 923 894 383 108 094 175 971 541 978 942 383 467 304 347 613 644 146 821 498 745 238 549 586 991 479 091 975 361 197 142 200 698 641 356 979 048 689 521 519 282 744 180 736 722 548 688 071 054 728 709 141 062 738 105 957 683 195 556 093 377 315 489 663 368 848 638 515 607 330 572 417 287 899 064 475 515 693 489 281 951 552 545 749 163 340 105 253 949 038 405 975 308 468 534 169 782 954 094 565 134 073 085 431 811 448 624 656 931 572 986 546 583 197 363 124 702 687 094 420 487 072 299 371 655 781 780 257 387 092 572 035 727 337 265 311 646 825 888 053 595 430 320 396 191 583 354 966 462 731 173 615 614 397 694 250 432 069 837 168 445 884 791 009 151 536 629 115 296 847 129 093 565 795 819 240 573 837 214 425 733 032 566 330 704 334 900 036 425 969 120 520 493 298 947 797 676 416 917 639 017 715 981 465 183 554 560 195 644 793 577 854 283 790 875 786 708 784 902 199 373 374 057 869 588 053 391 748 783 586 715 069 349 435 786 257 288 883 533 722 249 066 122 128 342 529 432 914 189 187 730 664 120 029 799 723 604 070 062 260 174 038 173 711 452 330 041 797 693 337 648 840 450 655 317 813 244 867 218 899 002 483 146 219 627 814 634 893 234 202 679 447 294 516 704 901 809 861 182 014 730 389 212 481 236 788 954 303 164 679 797 612 087 859 898 299 068 167 831 212 832 718 126 595 346 618 161 944 223 052 251 995 989 366 096 433 587 489 299 353 269 555 891 883 421 215 700 646 135 515 564 933 891 795 938 543 966 874 104 854 592 854 925 228 078 282 925 720 657 345 459 929 218 179 364 206 833 359 588 197 248 493 112 895 866 943 729 639 892 058 848 414 798 673 006 519 290 790 942 536 338 942 001 908 439 216 614 225 489 541 272 812 899 591 385 803 011 912 671 529 212 745 999 964 596 861 844 052 135 754 815 073 828 864 285 279 270 577 986 078 408 723 962 903 572 885 428 817 174 921 688 764 511 596 153 549 231 140 616 800 573 387 458 789 789 090 440 939 876 397 509 686 870 276 169 274 644 460 075 148 538 029 758 680 140 530 079 549 303 480 268 434 056 518 073 093 297 211 603 552 770 783 094 660 098 171 499 092 550 981 199 991 174 413 630 599 134 690 696 052 944 915 360 054 904 854 561 572 953 530 708 959 994 736 285 974 386 539 512 312 044 432 280 134 062 797 499 246 610 217 354 762 101 889 874 235 009 256 270 329 847 139 093 780 100 609 082 191 412 092 965 971 399 421 349 559 842 669 380 965 545 066 675 710 756 734 928 480 231 231 570 940 235 126 929 407 125 463 689 173 413 473 084 279 352 259 923 478 269 193 410 427 939 234 172 345 823 001 493 530 598 812 135 402 821 147 950 307 559 240 144 411 229 790 128 750 955 448 606 806 826 375 960 341 679 435 412 229 465 257 009 970 489 288 631 585 022 378 203 438 392 323 339 490 075 208 302 515 851 510 316 099 926 770 415 747 754 062 318 970 817 398 498 914 384 290 947 702 986 200 463 061 334 992 795 820 667 447 149 337 754 651 418 160 570 916 501 112 913 255 342 593 490 512 747 980 023 317 529 538 736 948 809 936 905 771 647 493 507 376 331 732 954 746 370 627 215 585 992 743 573 897 119 387 114 327 394 867 171 184 444 104 177 961 241 821 778 187 237 482 100 843 621 851 993 498 665 904 744 572 998 153 733 032 150 311 814 756 326 523 054 832 957 363 321 887 439 642 247 961 611 770 900 502 684 876 763 170 894 728 619 700 055 800 656 985 249 766 647 053 819 818 142 695 106 183 149 747 913 145 069 431 234 472 465 403 000 077 728 920 762 081 778 655 018 931 207 058 170 852 076 800 230 294 830 568 006 082 940 564 406 997 697 731 924 092 196 296 775 484 194 135 907 488 427 550 506 427 306 902 458 191 771 565 805 368 776 276 424 600 901 257 646 444 122 359 237 810 397 485 415 418 816 863 121 558 235 126 277 113 400 192 701 997 957 255 525 539 929 212 872 384 387 067 013 077 761 946 539 640 689 516 481 847 726 340 303 562 336 592 908 485 916 779 405 951 537 382 065 913 534 409 217 427 662 315 891 505 082 626 996 414 718 739 083 562 474 563 752 259 989 849 509 123 392 966 843 885 544 768 052 905 719 290 231 588 289 049 842 936 749 541 839 875 598 492 105 232 908 188 687 178 208 694 418 274 589 737 970 005 624 873 570 108 788 845 585 972 733 053 800 690 036 721 532 755 366 636 799 128 646 260 473 806 916 621 475 116 719 587 904 972 882 036 285 888 409 844 879 323 818 513 149 223 572 011 043 538 835 973 318 017 780 680 812 921 950 098 557 487 061 333 722 244 603 990 977 208 639 602 297 182 803 882 847 358 849 687 146 607 362 667 309 894 910 005 898 149 072 126 162 705 477 947 582 148 680 973 912 566 639 054 545 535 056 907 163 639 855 593 306 204 957 254 562 850 146 808 043 275 780 334 948 172 601 736 834 161 118 962 239 804 834 411 098 845 341 602 126 954 485 446 723 649 669 955 127 452 369 106 915 173 322 470 144 702 080 197 404 589 210 665 224 459 317 251 481 205 789 418 800 282 873 635 896 311 951 681 347 424 223 608 795 528 688 559 054 337 815 489 749 925 783 744 796 338 982 283 765 559 024 459 495 885 565 485 096 514 179 135 471 806 202 890 419 362 075 719 784 474 543 973 530 946 772 448 994 571 891 920 670 744 746 867 341 528 566 223 938 970 753 025 331 687 756 055 305 069 572 543 868 589 890 179 460 553 390 874 480 374 389 351 910 309 424 984 901 610 369 265 471 822 663 607 106 672 891 502 930 081 251 840 699 559 671 302 084 630 591 310 770 098 018 669 611 853 562 821 585 796 509 506 343 959 372 250 999 282 980 248 779 433 278 403 549 684 979 905 252 032 784 909 381 259 630 209 691 361 815 320 423 294 277 412 088 861 806 090 816 371 341 067 598 038 633 121 511 742 832 228 117 955 147 185 358 044 717 562 974 171 176 899 597 434 247 012 387 852 123 896 715 171 553 533 659 054 913 817 382 825 360 963 401 590 844 783 762 152 201 326 715 003 906 654 539 163 460 680 774 371 167 272 071 250 493 665 818 461 901 599 400 531 786 179 863 588 692 731 344 480 071 365 240 552 573 617 239 297 714 420 015 030 818 354 970 663 593 440 025 178 225 176 024 795 934 097 459 879 471 461 146 250 879 380 088 244 103 005 186 475 008 276 480 672 699 480 916 553 917 239 581 274 065 425 665 037 165 428 378 303 095 489 597 945 942 761 432 683 679 594 019 319 120 091 581 322 650 087 484 234 905 380 113 014 708 400 347 125 516 436 841 498 511 257 182 592 471 306 704 060 992 372 877 583 988 991 223 650 862 879 590 088 515 636 868 188 437 416 257 435 916 373 160 716 767 917 808 197 988 167 478 126 586 791 937 958 977 151 967 808 990 646 628 897 152 100 411 442 396 733 254 535 255 469 023 340 864 543 773 438 479 399 455 167 948 723 651 641 990 577 541 440 851 435 035 855 023 105 481 803 643 333 942 820 781 317 725 546 594 984 137 794 746 112 791 804 792 364 348 254 682 341 429 956 762 278 319 162 853 679 514 606 131 129 596 417 787 998 410 866 374 701 861 408 667 063 567 384 008 592 725 793 209 718 184 017 705 204 393 166 971 278 266 722 541 662 896 960 719 726 147 342 278 241 299 158 778 976 728 506 094 259 421 085 454 445 719 440 359 098 906 340 055 141 362 261 670 296 219 827 513 431 713 185 370 533 980 341 067 001 786 104 379 938 853 975 495 828 365 091 558 353 127 373 606 351 010 325 850 373 432 553 659 654 706 313 796 732 592 142 549 468 689 424 632 275 234 907 306 412 235 853 473 349 037 537 672 217 201 435 957 685 292 871 357 528 071 920 052 322 977 267 806 341 083 945 672 601 047 954 609 967 869 570 984 591 440 653 601 208 831 444 204 858 242 329 413 514 436 365 108 316 832 057 944 306 087 976 417 368 129 513 841 465 773 322 845 224 841 172 569 084 773 565 419 122 901 957 335 279 140 043 015 358 000 834 200 905 105 635 506 751 258 908 089 146 232 076 574 709 931 287 301 733 066 607 932 426 714 575 517 357 426 572 071 196 913 919 937 591 867 175 436 338 824 338 347 755 976 918 202 362 928 432 882 292 452 437 850 455 745 744 200 809 893 147 166 534 412 193 611 866 490 056 969 452 225 753 101 038 579 268 126 832 410 961 541 364 487 282 197 126 929 856 668 688 682 349 986 195 395 559 581 153 794 058 938 062 236 126 760 751 903 530 055 028 691 254 446 514 504 764 400 402 585 600 055 961 279 469 046 378 803 608 159 804 050 705 911 482 720 580 803 884 035 668 131 071 007 292 809 404 078 928 320 344 129 155 800 219 685 646 601 147 613 745 521 889 821 366 062 392 063 720 810 500 879 020 744 896 299 099 732 765 326 781 727 479 735 832 265 618 022 087 234 396 371 778 452 277 168 933 371 641 432 921 393 041 997 961 154 843 148 808 479 560 624 034 771 019 200 467 877 671 336 655 835 278 476 753 071 834 236 885 639 984 968 005 026 770 142 558 314 965 471 862 275 815 834 375 963 069 248 178 350 317 762 036 010 737 283 170 608 731 482 282 678 764 045 310 202 031 324 598 618 500 268 115 061 824 355 966 607 621 835 812 849 173 359 505 872 851 292 308 097 222 418 495 175 707 109 176 521 320 362 109 081 829 076 622 467 040 277 565 809 989 665 922 517 153 362 227 978 037 786 663 458 403 003 105 507 268 692 382 249 076 431 365 341 075 389 380 721 227 769 111 909 975 072 830 981 106 229 434 682 830 377 947 454 317 737 398 642 372 881 462 643 581 655 935 531 475 921 347 518 638 154 927 609 272 236 629 242 775 903 723 705 357 717 371 188 924 817 425 325 467 936 738 545 786 196 774 407 486 036 565 518 558 918 184 972 181 989 600 413 027 401 468 658 948 028 153 156 207 027 534 570 904 729 206 874 182 936 179 359 683 012 468 834 376 900 057 747 350 414 792 109 883 733 759 988 558 776 044 839 687 937 841 694 694 662 284 059 240 434 943 286 065 193 393 195 627 771 296 201 861 769 331 652 189 113 624 211 062 801 975 684 667 402 140 672 428 569 448 889 769 921 194 283 835 607 915 636 363 258 567 886 579 470 836 146 761 479 368 655 697 076 348 791 351 439 445 016 966 042 257 466 114 896 951 108 394 315 658 977 666 556 003 153 029 500 366 939 842 227 507 366 374 747 954 644 423 668 497 219 604 633 999 300 636 150 363 666 786 681 678 601 188 527 680 273 048 410 377 842 355 966 266 246 759 925 072 806 324 586 080 664 635 794 573 642 836 741 427 965 259 232 980 307 789 518 315 860 164 119 211 415 668 302 643 600 396 290 962 044 884 776 582 004 989 200 189 891 719 303 705 222 360 153 454 110 115 662 646 755 845 988 419 386 074 315 803 747 997 582 118 572 031 889 256 342 349 128 650 498 662 113 410 002 702 655 885 891 433 396 010 780 628 387 491 580 787 751 070 523 829 200 211 804 852 076 000 273 358 849 565 409 570 222 985 287 186 487 463 603 840 898 332 905 407 249 096 620 885 367 100 921 476 126 647 886 036 357 560 606 256 035 791 234 260 906 329 822 044 888 149 016 234 376 410 208 092 441 268 731 568 667 849 902 399 936 458 858 647 762 040 659 178 347 588 882 903 602 325 859 314 883 139 005 255 695 461 153 245 870 341 282 402 339 339 876 666 708 199 673 017 350 258 495 519 600 490 856 238 476 486 392 388 442 981 559 392 367 227 613 841 102 667 693 728 207 119 768 581 580 190 242 580 087 942 424 539 510 082 425 231 944 036 500 046 099 686 212 989 405 270 436 122 777 473 570 386 795 446 451 218 834 961 291 359 923 691 583 012 465 598 968 407 833 279 325 055 656 713 363 219 107 172 723 372 522 947 246 508 141 165 714 104 568 700 706 658 879 341 018 422 157 129 032 961 659 286 166 204 699 755 891 376 599 447 362 533 962 067 664 399 562 383 745 338 155 497 820 160 388 698 746 350 263 313 790 623 905 566 362 347 049 808 169 422 960 203 802 772 478 238 296 774 538 344 111 500 724 140 795 462 831 578 010 505 304 315 289 190 971 037 867 966 315 519 936 822 883 552 149 482 549 982 212 098 073 211 436 308 623 169 639 065 189 855 403 599 355 143 590 362 559 724 217 705 958 335 594 286 544 260 252 252 837 580 609 280 041 157 933 157 451 889 234 783 865 422 005 107 493 287 368 982 943 570 651 131 979 132 814 937 802 942 451 435 964 922 469 897 229 626 601 533 747 608 594 017 532 945 302 763 127 986 426 293 082 557 761 093 103 310 177 214 803 543 663 634 155 990 029 210 532 810 577 438 818 502 555 516 737 386 642 968 877 516 353 549 162 857 807 205 884 095 809 167 578 859 238 385 218 498 165 630 103 640 384 911 835 416 158 606 888 778 564 469 665 697 668 171 493 170 947 457 414 870 990 096 221 628 975 744 176 073 273 550 023 285 805 194 141 646 503 626 890 969 548 591 774 301 989 383 321 562 235 073 473 171 058 092 627 267 705 378 218 907 960 339 100 609 183 272 385 170 371 918 325 068 588 730 489 293 246 595 374 283 984 969 001 993 344 379 234 050 684 361 166 686 205 076 567 395 191 905 970 892 467 170 822 960 046 590 099 668 211 075 282 194 852 156 636 437 996 627 868 566 620 146 881 322 932 640 541 344 994 923 333 023 747 071 002 230 077 264 545 070 483 724 842 049 306 429 022 504 691 132 404 763 788 636 217 390 606 633 314 532 594 347 391 476 858 889 184 987 181 238 807 580 947 186 033 684 057 281 213 034 517 635 239 605 461 689 414 726 738 918 249 599 347 687 035 000 545 282 727 970 306 606 112 634 322 026 918 647 705 597 550 095 769 111 542 088 176 190 114 170 276 626 699 683 931 383 578 264 485 772 703 437 272 622 796 486 223 621 599 682 207 889 304 649 483 610 359 095 708 561 738 905 751 987 678 280 722 097 728 096 016 901 252 497 227 935 144 929 734 655 833 404 621 876 439 366 678 485 118 116 175 974 845 997 409 123 422 147 025 979 269 036 827 117 425 254 515 105 314 675 857 531 650 666 931 558 997 991 672 926 927 977 994 812 543 133 865 687 742 992 960 873 687 235 578 887 931 089 306 961 189 075 803 564 238 447 752 698 931 868 338 832 419 144 651 495 649 644 234 902 836 209 669 090 688 760 325 398 988 874 584 514 997 397 490 006 698 347 171 873 159 957 742 163 466 907 496 415 565 659 966 458 362 247 427 147 063 237 113 786 305 395 288 893 024 161 609 037 609 862 961 203 019 125 801 322 341 378 647 508 934 529 500 530 179 587 379 673 633 488 092 038 540 269 466 805 429 851 252 640 577 442 343 070 955 527 742 593 609 379 405 621 326 712 484 352 252 109 963 222 863 553 535 544 837 971 319 664 047 765 266 416 344 487 549 902 455 070 762 337 818 299 128 912 038 238 015 961 742 789 216 996 337 857 554 628 667 139 646 594 738 938 598 584 182 881 971 148 386 726 624 271 697 831 355 726 270 471 852 400 751 916 310 027 623 883 811 296 570 398 863 770 648 724 554 827 676 972 372 357 763 698 625 518 378 366 458 909 998 084 077 121 537 505 303 648 777 852 222 044 132 623 632 691 839 539 798 505 838 215 564 840 062 594 221 881 520 043 756 299 714 765 667 246 366 426 135 296 533 304 748 599 193 938 043 526 001 060 867 064 675 837 552 830 843 049 073 130 778 941 417 326 404 738 846 172 461 207 875 509 565 539 082 967 124 845 374 764 878 741 051 783 112 439 840 062 437 285 654 539 704 431 513 875 243 395 331 811 473 897 012 540 350 170 024 968 380 423 752 887 892 164 896 959 603 364 159 004 364 257 864 031 294 050 555 986 770 032 393 761 538 046 616 250 518 572 596 165 544 334 670 095 870 151 784 805 307 692 877 903 398 777 158 236 632 529 031 694 227 433 017 873 252 272 183 361 618 832 723 885 307 901 377 840 653 028 950 279 907 000 747 180 115 806 287 047 912 772 830 076 061 748 023 382 854 157 241 170 122 408 592 764 090 187 410 428 803 777 835 920 971 325 077 597 161 229 591 553 403 055 709 207 407 547 302 629 969 563 988 743 369 427 146 695 960 611 358 104 588 325 504 354 781 715 425 596 164 286 095 128 080 089 854 314 494 832 730 166 027 863 660 172 200 874 791 335 310 469 226 447 800 423 022 554 117 776 789 801 052 937 918 512 975 605 990 485 215 107 239 840 645 240 601 210 408 813 735 357 107 231 579 896 689 103 932 930 710 704 693 005 583 122 323 477 104 365 231 225 220 480 437 745 544 881 893 915 205 843 469 459 268 010 994 398 025 554 079 679 454 481 281 118 364 855 064 762 433 688 776 974 693 376 435 468 918 310 236 368 610 731 436 679 946 859 987 227 643 147 527 337 276 999 614 447 063 400 605 530 380 883 601 035 284 639 825 997 923 905 099 199 160 329 543 470 657 948 040 974 525 737 668 901 250 484 545 977 515 584 370 444 221 885 183 851 839 448 709 244 182 992 272 353 227 664 023 560 863 794 488 733 404 425 315 318 078 168 277 569 645 592 820 132 034 336 773 316 954 550 239 629 304 239 611 081 343 298 116 318 437 744 527 411 693 722 164 637 663 697 708 973 735 969 993 058 561 837 862 461 278 958 538 767 015 576 653 639 302 487 070 005 200 734 410 270 663 926 748 202 601 071 931 301 389 261 112 484 239 700 366 859 016 859 387 665 106 273 582 962 249 671 457 769 169 966 893 409 768 221 572 718 761 655 219 507 182 658 596 797 980 432 865 704 593 566 637 576 077 152 483 617 808 381 620 835 207 509 571 630 370 460 561 683 578 351 349 544 985 999 416 858 824 210 298 966 453 995 671 573 461 781 166 749 890 877 881 544 140 889 423 712 460 505 057 003 999 846 465 719 526 668 935 234 853 857 648 413 984 618 894 658 305 743 777 675 431 486 880 241 188 012 840 483 180 372 327 641 471 857 455 966 523 475 819 857 564 226 429 404 994 006 887 314 913 751 315 355 411 343 682 336 003 346 094 464 733 879 648 845 558 462 933 139 639 727 037 827 162 316 526 097 492 502 307 694 057 246 234 954 978 086 249 636 305 868 525 885 906 222 006 859 831 841 257 752 266 167 545 158 111 467 842 185 935 739 400 309 698 011 115 133 171 943 473 479 117 736 299 589 946 713 511 537 036 146 378 681 712 153 823 614 128 284 343 637 278 096 884 788 010 563 459 925 138 061 158 733 192 461 014 603 074 320 905 527 806 646 237 895 927 695 857 055 410 335 653 883 547 835 934 272 573 327 941 342 179 089 336 061 482 412 326 926 451 414 966 136 123 231 420 111 755 062 404 432 427 078 093 516 073 826 237 766 089 903 432 551 243 272 421 337 276 590 843 003 049 764 659 157 912 212 188 620 754 487 395 712 030 510 849 410 608 460 156 742 228 690 718 099 750 914 021 028 749 884 399 788 506 921 843 313 123 096 114 537 631 758 203 248 723 046 615 511 529 478 448 856 763 812 566 067 667 212 884 252 903 253 987 042 213 221 692 677 772 452 738 710 588 784 076 657 832 134 712 797 067 869 632 107 655 133 352 384 656 815 036 198 554 767 218 270 889 914 866 443 278 023 031 900 928 095 460 175 274 725 442 813 122 637 853 284 695 022 022 986 752 100 823 947 134 665 433 760 856 102 239 289 030 396 754 694 145 068 159 634 087 340 371 178 919 486 795 784 005 485 093 825 967 892 361 039 858 931 460 016 441 935 011 363 669 653 808 796 614 616 966 147 562 424 295 526 512 125 047 826 470 818 128 974 101 132 976 470 894 636 689 593 782 214 867 264 634 998 689 104 735 154 205 592 348 523 089 299 577 481 644 880 385 283 666 702 041 858 985 498 192 427 817 120 293 152 282 947 508 838 138 581 443 097 792 905 950 816 216 117 576 693 098 755 657 444 199 080 451 899 195 496 325 758 033 165 292 018 159 014 691 491 232 615 586 322 718 351 967 910 185 206 163 516 726 534 958 583 067 119 090 020 604 583 421 094 775 504 237 446 327 569 808 309 078 499 691 228 515 015 029 555 352 714 912 741 799 872 775 402 265 932 232 288 146 528 563 302 705 539 587 652 540 676 601 827 884 218 042 078 381 303 635 593 246 205 473 485 985 610 390 122 615 717 979 699 798 358 567 306 410 516 730 730 257 537 284 999 688 028 596 812 262 864 093 752 885 490 376 471 666 358 578 646 366 619 400 432 506 729 583 154 618 976 105 380 898 960 987 567 753 056 948 678 484 938 096 471 088 597 424 577 376 226 126 197 482 600 849 877 633 057 250 588 235 854 394 640 601 604 840 917 769 151 900 524 956 394 461 786 387 367 939 686 448 891 382 979 703 291 138 527 742 998 509 049 209 515 304 240 866 781 876 890 726 193 848 877 575 550 330 924 185 184 237 554 067 281 113 405 892 424 713 809 456 786 939 268 498 262 397 988 544 437 613 215 779 125 755 225 794 192 560 877 234 233 715 024 706 703 773 194 353 489 600 514 301 424 842 585 394 982 383 587 500 907 650 705 987 553 412 288 405 596 852 974 505 732 500 751 188 924 205 519 927 836 063 893 061 639 450 723 667 693 113 096 120 884 698 334 819 092 033 115 411 394 265 059 348 577 883 005 102 563 612 898 460 323 061 237 391 385 736 937 317 509 878 849 341 385 378 134 149 021 460 833 219 464 106 294 622 554 954 503 583 641 663 276 810 620 329 111 870 963 494 575 196 845 996 985 800 752 872 283 312 034 119 844 397 702 794 366 669 411 241 284 660 430 255 844 386 570 182 620 736 102 408 536 237 259 908 375 885 644 071 613 478 332 905 127 878 507 239 953 811 763 221 743 418 742 292 256 951 586 334 435 661 958 165 124 620 682 878 241 899 451 909 979 373 420 891 908 687 061 414 110 044 212 068 250 094 864 588 728 434 753 497 919 008 281 222 553 275 090 482 821 990 064 317 566 922 474 367 799 746 834 582 660 853 282 781 527 762 259 135 697 657 228 062 989 597 565 792 996 887 478 714 441 322 195 683 212 020 227 821 658 612 099 493 985 467 834 264 760 591 685 005 335 604 192 784 264 379 352 614 346 025 783 862 868 651 528 778 671 964 017 710 254 693 260 300 019 102 744 320 971 510 524 037 350 875 562 598 844 842 212 011 509 504 542 135 584 564 399 096 029 528 251 156 820 543 050 464 590 777 069 647 997 920 784 574 214 302 479 948 104 471 206 107 077 579 128 577 639 249 566 846 059 566 900 054 051 207 908 677 112 461 093 118 807 056 602 995 966 990 403 672 527 008 281 926 034 748 481 471 113 259 520 545 212 297 528 864 704 288 538 054 773 642 483 291 274 664 007 171 757 270 063 035 995 318 800 463 505 035 013 800 901 312 532 575 040 473 526 661 533 185 170 590 662 424 284 813 494 982 810 897 895 606 777 982 675 331 864 435 395 726 807 316 503 163 751 008 040 599 861 311 962 549 729 401 843 075 809 163 313 929 539 579 104 548 013 113 202 269 223 323 021 301 977 680 290 996 948 468 387 703 009 097 473 915 963 354 338 418 797 511 422 194 449 748 171 743 852 562 989 779 512 968 249 588 876 505 806 327 315 051 163 752 079 776 707 709 434 530 071 797 857 287 440 873 833 129 755 041 196 151 593 260 960 528 700 493 903 153 403 767 824 725 712 329 437 939 112 815 960 473 199 641 591 486 676 545 683 344 130 725 539 265 505 873 955 815 516 473 195 999 623 308 834 926 205 887 989 833 570 399 669 223 055 548 585 807 168 077 709 920 395 860 296 021 284 340 314 594 258 978 999 195 565 382 774 694 379 818 308 064 280 069 647 308 257 584 394 392 928 507 879 356 736 130 172 999 143 652 873 358 680 360 947 293 851 738 051 557 869 079 076 527 825 122 975 172 512 030 414 515 479 236 453 497 722 089 177 594 316 138 003 125 282 715 458 870 071 871 724 371 387 128 003 394 923 894 034 458 368 745 099 118 469 606 898 898 624 117 004 309 199 447 959 491 316 650 453 553 959 730 227 827 535 861 752 132 043 443 132 865 747 998 119 760 138 548 165 847 014 034 954 349 344 100 479 570 155 782 510 694 972 102 056 253 422 469 302 631 789 938 827 415 212 723 492 076 260 110 078 922 510 957 907 060 122 935 178 511 154 447 908 850 335 538 200 744 570 137 741 095 740 673 312 144 613 368 634 188 373 232 832 420 860 116 016 474 114 423 544 341 636 475 281 167 879 199 441 602 595 714 234 772 791 847 204 930 192 033 128 360 876 615 013 711 583 948 669 064 321 185 554 418 123 321 664 857 331 729 653 262 413 976 243 694 889 612 109 310 363 634 669 491 532 051 096 538 316 917 300 168 877 038 303 683 095 399 265 863 404 566 447 207 814 003 093 645 258 503 925 979 459 166 080 733 464 015 079 493 697 314 383 251 729 632 248 901 431 786 127 855 161 779 108 000 261 995 490 514 185 254 449 430 280 342 982 840 070 249 045 948 284 432 490 470 536 759 842 842 873 568 053 734 260 657 584 840 632 546 625 473 397 012 905 338 220 383 816 221 420 817 364 693 800 823 203 869 788 463 047 243 809 335 919 655 769 427 857 295 153 725 155 340 627 969 498 038 507 272 531 825 942 333 439 958 762 005 255 144 255 595 542 319 542 653 452 224 858 645 130 868 042 783 593 305 987 938 248 500 175 387 422 719 482 997 018 937 147 953 728 541 276 117 355 959 904 124 929 391 215 060 201 114 713 245 919 569 656 180 633 853 736 988 413 310 916 636 092 568 493 552 742 340 068 652 013 029 026 620 351 740 223 038 274 546 368 408 355 010 264 892 658 279 646 365 375 641 521 206 079 444 013 385 184 475 791 476 369 833 659 049 202 078 221 400 342 703 176 333 501 943 586 944 697 031 542 125 358 464 592 236 384 974 501 323 884 348 272 701 153 981 327 311 782 901 822 396 991 607 130 205 299 683 405 671 506 810 342 913 110 056 366 773 904 646 563 354 572 268 107 422 216 460 216 647 104 356 069 304 704 094 041 437 145 220 217 767 395 576 410 320 272 716 508 709 621 110 156 668 423 271 525 808 576 837 708 937 866 199 197 267 037 255 853 676 187 508 374 642 410 575 632 371 006 273 652 512 078 286 099 243 037 080 903 369 555 179 787 337 069 138 768 122 926 399 533 957 115 373 799 048 194 087 162 881 398 805 656 822 958 132 870 710 212 716 583 360 582 563 919 871 143 267 472 790 396 362 400 709 437 667 938 252 454 289 307 040 755 737 769 974 628 754 782 028 376 623 124 271 591 273 009 913 865 593 856 609 940 570 715 995 860 267 185 779 540 813 221 230 579 679 395 818 539 468 092 575 963 432 690 770 481 132 055 686 240 801 333 841 617 467 995 389 514 730 062 439 237 390 055 915 219 923 661 410 034 616 598 135 060 658 276 173 493 559 294 930 779 062 327 676 687 052 429 156 126 203 992 523 318 446 628 729 757 903 761 268 066 054 405 445 847 425 377 298 411 025 673 578 398 585 426 767 738 755 423 108 446 145 181 805 774 651 329 710 450 052 583 371 888 358 331 601 799 368 997 443 623 761 775 432 199 422 744 825 756 581 108 033 205 218 834 007 413 777 912 647 098 683 937 081 377 430 327 043 675 871 626 783 793 247 962 448 692 755 698 504 893 005 740 312 404 644 347 963 719 667 782 739 171 335 321 681 844 636 287 008 040 835 055 507 843 629 759 784 316 894 562 400 803 892 145 626 130 726 791 322 092 153 702 211 376 645 734 011 817 085 905 208 129 847 343 733 378 170 402 291 827 339 464 218 171 256 595 108 572 038 414 687 291 707 346 790 707 059 555 360 493 296 294 396 876 863 737 717 556 627 624 514 266 531 439 719 406 263 819 946 498 680 844 480 647 693 866 196 121 866 075 752 277 079 806 617 561 655 251 821 360 219 155 658 231 039 847 694 881 125 293 165 038 578 552 548 006 921 296 753 497 782 902 164 473 962 609 282 364 771 310 011 603 636 418 635 113 680 114 437 545 737 251 907 298 751 200 703 265 364 616 360 834 241 476 409 571 552 359 577 038 219 704 180 544 947 554 293 760 453 166 303 878 688 487 381 792 515 575 634 829 785 748 582 947 485 220 862 416 657 586 114 889 284 050 891 489 467 477 082 269 674 651 223 996 064 719 799 543 754 003 764 932 315 981 037 183 355 717 004 208 410 615 797 046 374 415 167 895 951 108 702 795 659 845 401 589 287 328 826 537 065 914 398 243 573 526 908 600 849 914 554 407 911 976 775 767 773 672 002 134 317 947 589 371 769 412 743 979 136 788 150 965 281 972 581 677 905 290 092 697 608 452 523 083 990 368 470 776 526 278 806 152 609 515 321 879 132 035 983 993 519 261 596 881 125 194 505 326 923 635 421 595 557 574 942 949 910 471 630 985 332 593 963 309 835 638 386 145 730 481 470 899 985 628 285 815 642 828 842 891 069 684 109 589 319 921 324 465 671 145 747 575 911 259 675 287 679 369 657 058 197 966 165 535 159 787 212 442 676 293 818 593 153 047 897 075 039 949 581 729 613 213 538 143 486 864 175 373 432 764 413 721 902 379 883 797 369 961 802 188 292 692 832 713 374 300 406 338 401 267 673 803 116 753 875 358 465 509 192 498 457 055 291 694 580 713 462 811 746 937 902 767 110 578 012 531 964 483 764 925 031 747 004 234 686 487 636 586 447 879 296 551 081 414 227 167 886 131 643 947 834 255 546 067 986 978 521 119 048 394 955 081 071 424 297 436 573 231 127 858 784 992 612 350 955 769 210 441 554 827 903 199 856 444 327 845 621 083 883 224 552 802 163 723 595 966 004 936 317 729 496 666 037 996 893 396 782 999 044 723 574 098 366 159 109 910 664 898 444 652 806 073 545 302 386 087 230 538 262 374 105 656 241 700 168 821 277 608 789 327 275 405 190 793 491 648 270 902 322 377 089 734 285 263 988 327 150 941 544 357 481 894 672 658 762 589 286 356 336 558 896 532 893 531 449 585 952 473 780 380 116 212 177 378 820 811 080 583 039 466 281 951 529 430 614 742 697 543 178 485 230 778 424 540 946 856 813 996 657 449 493 212 691 744 273 928 110 905 467 934 552 866 276 828 734 330 697 636 739 969 970 574 013 609 374 761 240 970 672 074 138 534 009 895 221 612 599 398 928 940 622 712 323 163 122 992 087 803 096 386 969 411 143 314 247 249 890 912 664 903 609 886 518 110 030 425 164 451 616 825 309 346 697 139 230 967 345 213 695 537 759 211 153 573 202 557 287 010 275 926 442 994 573 893 092 078 970 715 687 051 419 444 313 706 103 545 363 666 247 989 176 030 684 816 385 989 077 879 802 779 004 715 269 374 732 671 155 853 218 920 218 020 755 227 373 104 193 976 051 290 477 366 256 617 272 440 864 305 388 111 449 195 315 915 766 016 405 902 854 296 938 423 139 863 841 565 295 511 335 170 385 606 912 960 944 037 513 842 605 305 496 039 003 440 106 758 006 002 491 180 551 984 031 831 266 601 191 680 246 184 058 513 237 535 729 832 445 267 971 435 769 710 872 099 536 960 994 685 195 337 959 944 524 721 749 925 492 090 174 799 971 079 483 005 588 083 325 968 080 061 714 228 864 897 442 899 094 568 785 285 315 059 515 421 901 090 820 467 092 639 338 814 895 991 524 690 196 577 413 092 800 561 440 079 947 888 636 169 438 013 746 603 517 288 556 749 043 333 538 927 293 622 432 308 491 029 771 942 138 848 272 955 054 670 677 799 574 821 778 169 735 913 731 918 395 132 905 221 317 616 921 793 965 279 419 424 602 584 233 559 035 110 028 184 762 454 903 499 417 710 502 876 289 147 817 090 189 830 818 187 482 478 485 885 840 428 913 521 433 937 515 538 306 469 024 259 022 775 996 517 701 117 627 524 820 550 791 021 978 280 740 220 461 674 474 099 953 039 859 336 750 354 820 370 018 458 179 644 121 317 839 874 385 626 579 826 336 489 619 335 194 378 789 366 709 334 335 801 225 535 681 989 741 154 919 395 566 972 801 692 516 816 049 493 227 393 148 388 015 824 000 448 541 920 149 867 158 553 935 227 537 641 868 430 282 541 815 038 280 974 710 253 036 338 781 316 044 241 662 383 671 024 701 704 658 109 331 866 802 859 255 624 226 766 178 426 125 663 729 083 938 015 341 129 052 892 449 242 157 137 154 358 713 816 277 163 551 609 472 408 380 497 561 818 499 938 439 800 353 718 169 444 323 602 892 912 239 949 904 851 397 566 238 240 458 208 667 944 148 728 876 716 854 432 399 797 320 121 439 689 014 530 707 857 868 132 135 276 310 334 228 495 106 776 152 644 010 793 270 230 374 266 298 748 614 702 618 330 901 465 406 147 435 956 044 786 070 696 222 539 954 131 300 857 084 670 376 568 814 431 078 039 851 815 001 199 965 250 751 476 787 061 546 100 263 071 983 425 988 142 345 805 821 236 762 009 529 094 039 791 454 083 888 929 764 367 323 464 196 685 649 396 733 371 431 425 000 812 274 869 758 030 337 372 634 226 058 820 724 687 934 609 924 298 973 523 875 161 351 587 988 592 434 252 392 913 212 475 012 143 486 268 826 738 888 791 545 892 159 801 376 570 376 671 433 184 225 416 311 136 215 902 822 098 059 809 753 140 935 864 019 369 948 626 220 755 268 740 427 890 283 307 164 132 764 696 675 620 452 775 420 643 020 815 263 227 302 932 704 532 887 930 349 095 313 365 592 728 034 289 032 891 433 182 896 149 129 501 807 586 136 321 951 553 377 994 589 513 235 324 056 624 292 367 117 718 978 425 508 094 389 918 707 692 489 157 240 571 485 531 092 478 462 809 004 366 622 424 169 213 721 388 113 343 228 828 548 641 218 205 153 782 402 203 517 902 887 540 381 810 306 011 554 307 074 205 306 450 995 115 680 939 993 441 359 403 881 259 901 411 211 737 904 860 821 025 976 241 152 824 954 914 562 946 186 911 126 187 073 951 412 213 466 854 825 361 777 735 724 474 772 388 623 863 831 873 118 743 125 139 329 924 990 399 116 748 679 442 382 636 139 945 335 041 229 562 775 095 671 111 142 600 257 437 659 959 805 090 382 922 111 775 633 257 384 069 288 276 144 623 626 613 454 095 433 241 082 826 462 756 461 830 756 044 565 967 121 259 025 545 136 320 969 057 577 007 704 751 455 742 583 488 920 160 524 492 206 663 198 544 289 265 477 283 203 327 146 513 756 009 760 923 204 356 096 908 909 929 993 214 752 670 085 149 608 713 113 919 293 134 462 997 639 028 757 203 375 470 816 312 032 857 246 413 834 896 428 287 477 681 127 424 079 250 189 622 227 997 809 262 044 822 025 694 545 786 746 632 079 627 070 014 351 210 019 462 950 921 795 653 896 303 901 889 464 703 901 589 413 977 675 201 453 427 078 629 499 627 987 276 932 336 328 467 012 628 686 590 283 821 089 607 780 729 697 901 022 086 031 760 677 199 384 812 634 794 850 309 402 341 916 381 910 234 057 828 153 760 801 929 746 948 799 759 653 237 075 168 562 947 284 767 091 603 479 317 172 884 487 932 925 472 420 203 759 735 409 320 322 184 797 823 718 902 656 763 763 581 752 456 515 587 128 852 089 100 561 493 396 529 398 394 160 572 586 223 838 356 219 460 081 842 746 716 473 487 688 079 280 979 149 848 744 713 687 379 495 789 204 458 320 504 980 770 215 478 266 338 923 212 526 551 189 947 020 777 024 541 364 348 851 867 868 933 443 812 620 817 625 884 250 976 639 278 797 275 632 901 780 804 960 115 356 081 639 087 920 734 214 831 937 659 715 569 335 473 876 121 983 933 339 552 307 117 786 818 526 094 090 245 911 820 352 338 544 671 851 563 975 745 725 204 909 958 408 046 755 543 600 901 565 118 898 668 326 956 522 110 353 435 529 548 673 171 852 176 199 068 892 799 035 792 433 664 309 863 175 942 559 484 155 252 774 835 904 479 046 153 380 721 578 831 034 652 246 918 920 567 691 293 510 438 278 113 757 384 443 317 791 444 168 007 613 237 690 407 640 058 593 151 961 361 923 651 336 359 264 591 282 707 689 316 988 369 975 525 095 421 074 359 973 500 228 666 468 162 031 565 663 213 375 600 158 346 933 431 958 429 280 574 477 930 710 151 041 316 047 753 634 456 089 585 532 432 194 992 737 322 403 294 738 549 786 550 661 634 861 289 854 312 133 590 363 449 175 085 824 556 529 981 191 662 623 274 285 767 149 053 141 107 404 271 500 321 977 845 514 927 492 157 072 778 551 214 151 083 028 993 644 240 790 683 488 581 312 630 542 765 576 941 848 535 501 032 395 959 580 966 692 175 664 642 418 452 562 756 640 458 705 801 184 995 577 226 579 857 285 378 193 864 331 389 244 163 655 344 869 979 577 942 290 326 402 515 630 641 840 845 115 955 108 550 483 028 544 611 101 343 907 060 284 134 591 514 628 531 994 740 842 551 851 242 132 984 083 430 397 950 587 517 373 097 877 487 812 870 600 960 091 291 169 906 057 057 475 353 745 463 882 548 282 009 371 838 356 992 263 429 820 397 375 473 835 532 938 082 687 813 447 419 327 783 165 927 489 414 319 474 444 279 790 740 310 148 829 144 452 342 232 860 985 833 037 854 187 890 996 495 944 459 308 023 314 540 922 556 955 137 222 188 709 250 904 982 792 966 273 406 480 436 312 571 078 046 508 553 986 163 774 243 519 577 561 436 783 882 613 376 195 381 905 257 460 385 752 232 691 980 832 916 528 541 365 451 134 351 000 942 837 540 461 445 279 623 057 449 803 780 251 265 289 275 245 732 813 043 971 429 822 039 061 454 608 489 538 628 855 562 091 503 967 514 602 554 727 135 774 538 279 228 377 055 004 077 840 375 897 109 645 487 219 784 377 245 710 146 245 351 969 974 341 471 698 319 469 108 618 125 538 861 462 353 722 839 382 874 682 661 727 661 889 033 164 470 973 116 816 668 046 852 329 815 066 817 834 683 179 051 273 510 695 836 127 506 304 973 507 854 375 812 950 746 782 481 678 129 944 947 394 896 673 053 507 119 028 882 712 170 296 300 993 743 437 856 987 844 640 491 906 346 839 829 170 110 418 462 402 951 988 179 103 228 793 754 876 081 886 508 240 691 169 173 568 168 959 136 933 296 051 236 698 394 198 016
Click +1/64 if you want to see the first 1/32nd part.
Click +1/32 if you want to see the first 1/16th part.
Click +1/16 if you want to see the first 1/8th part.
Click +1/8 if you want to see the first one quarter.
based on a binary iterative partition.
The outcome of the Online Big Number Calculator consists of 1,683,483 characters (figures and spaces) from '20 650 635' (the beginning) to '394 198 016 ' (the end with space after '6'). First add one '0' in front, so that the notation starts with '020 650 '. Now the full number notation contains nothing but 4-character segments starting with three figures and ending in one space. Hence, there are (1683483+1)/4=420871 segments and the same number of spaces. Substract 420871 (spaces) from 1683484 and the next-to-final result is 1683484-420871=1262613. Finally delete the '0' before '20 ' at the beginning again, and the total number of digits turns out to be 1262613-1=1262612, which is also the number of decimal digits according to WolframAlpha.
| * | The first-person singular pronoun is spelled with a small i, as i do not consider myself a Supreme Being or anything else of that Ilk (nor the eternal start of a new sentence) | [<] |
| ** | Where there is some existing orthographical variation preference will be given to the (more) phonematic variant | [<] |